















Preview text:
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 1. Bài 1: Trong không gian 3 R cho dạng toàn phương: Q = 5x2 + x2 + λx2 + 4x 1 2 3 1x2 − 2x1x3 − 2x2x3.
a. Với λ = 1, hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đổi tọa độ.
b. Tìm λ để dạng toàn phương trên là xác định dương. Bài 2: Cho ánh xạ f : 3 3
R → R được xác định bởi
f (x; y; z) = (x − y + z; x + 2y − z; 2x + y).
a. Chứng minh f là ánh xạ tuyến tính; b. Tìm Ker(f ). x +2y +z = 2
Bài 3: Giải hệ phương trình sau bằng phương pháp khử Gauss: x −y −2z = −5 . 2x +y −z = 3
Bài 4: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 2.
Bài 1: Tìm giá trị riêng và không gian riêng ứng với giá trị riêng tìm được của ma trận A, biết: 1 2 1 A = 2 4 2 . 1 2 1 Bài 2: Trong không gian 3
R cho các dạng toàn phương:
Q = 2x2 − 10x2 − 8x2 − 4x 1 2 3 1x2 + 8x1x3 + 16x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. √ 1 + 3i
Bài 3: Tìm căn bậc ba của các số phức: z = . 1 + i
Bài 4: Một hãng sử dụng 4 loại vật liệu khác nhau để sản xuất 3 loại sản phẩm. Cho biết, định
mức về số đơn vị vật liệu cho một đơn vị sản phẩm mỗi loại tương ứng và giá của một đơn vị vật
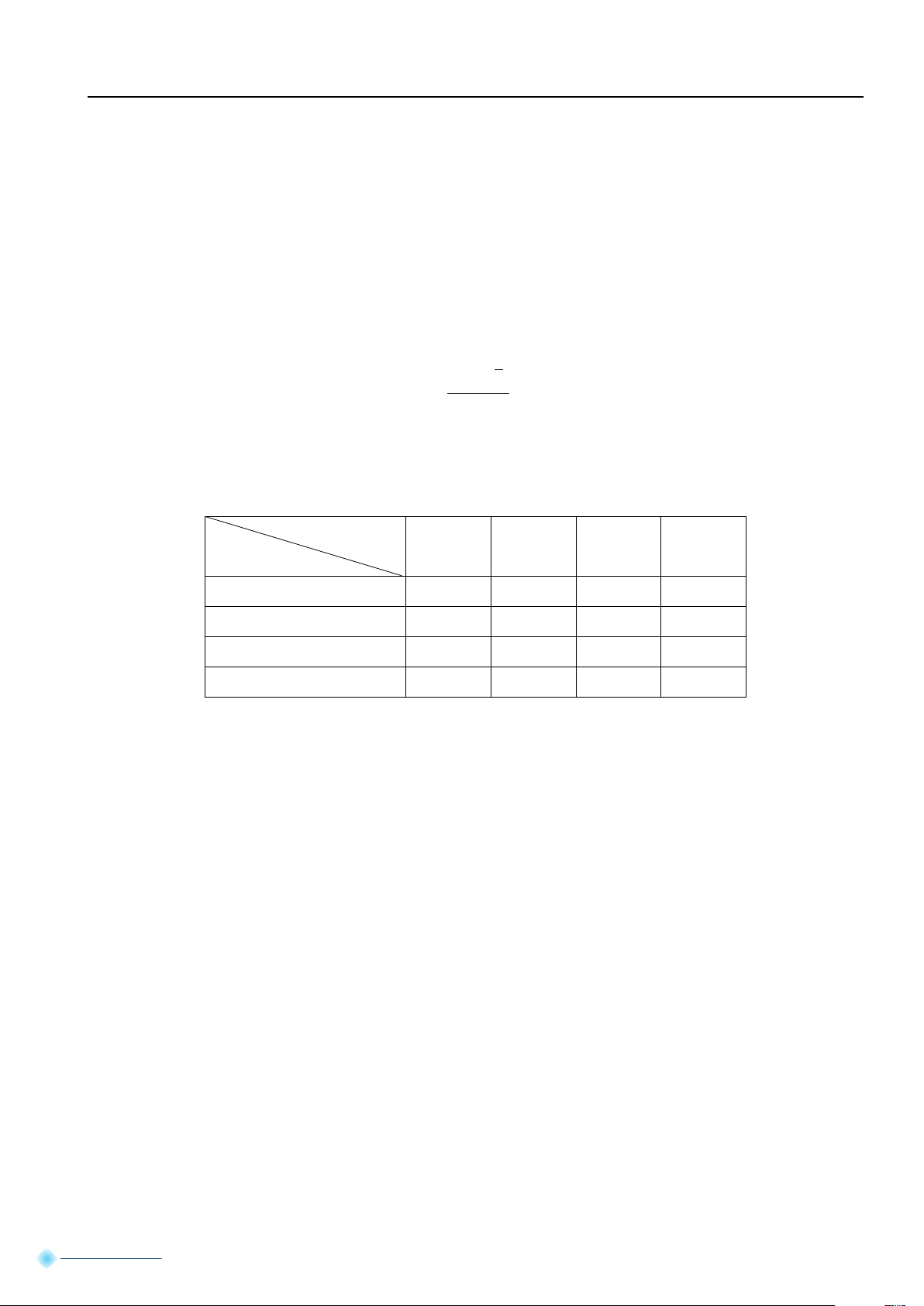
liệu (tính bằng nghìn đồng) mỗi loại ở bảng sau Vật liệu 1 2 3 4 Sản phẩm I 2 4 0 1 II 3 0 1 2 III 1 2 3 4 Giá vật liệu 15 8 12 9
a. Viết ma trận A là ma trận định mức số đơn vị vật liệu trên mỗi đơn vị sản phẩm và ma trận
B là ma trận giá của đơn vị vật liệu mỗi loại.
b. Từ đó hãy tính chi phí vật liệu cho một đơn vị sản phẩm mỗi loại.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 3.
Bài 1: Tìm giá trị riêng và không gian riêng ứng với giá trị riêng tìm được của ma trận A, biết: 5 −3 1 A = −3 5 1 . 0 0 8 2x +4y +3z = 2
Bài 2: Giải hệ phương trình sau bằng phương pháp khử Gauss: 3x +y −2z = −2 . 4x +11y +7z = 5 Bài 3: Trong không gian 3 R cho dạng toàn phương: ϕ = 5x2 + x2 + λx2 + 4x 1 2 3 1x2 − 2x1x3 − 2x2x3.
a. Với λ = 3, hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đổi tọa độ;
b. Tìm λ dể dạng toàn phương trên là xác định dương.
Bài 4: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 4.
Bài 1: Một nhà máy cùng sản xuất 2 loại thiết bị với số lượng lần lượt là Q1, Q2 và giá thị trường
là p1 = 110, p2 = 200. Chi phí sản suất của nhà máy đạt được khi sản xuất 2 loại thiết bị này là C = 2Q2 + Q + 64 1 1Q2 + 3Q2 2
Hãy xác định cơ cấu sản xuất (Q1, Q2) để nhà máy đạt lợi nhuận lớn nhất. Bài 2: Trong không gian 3
R cho các dạng toàn phương: Q = x2 − x2 + x2 + 2x 1 2 3 1x2 − 3x2x3 − x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. 1 1 6 Bài 3: Cho ma trận A = 1 −1 3 . −3 −1 −5
Chứng minh rằng A khả nghịch. Tìm ma trận nghịch đảo A−1?
Bài 4: Trong không gian véctơ 3
R cho họ véctơ S = {u1, u2, u3}. Trong đó
u1 = (1; 7; −4), u2 = (−3; 1; 0), u3 = (10; 4; −4).
a. Hỏi rằng họ véctơ S là độc lập tuyến tính hay phụ thuộc tuyến tính.
b. Tìm biểu diễn tuyến tính của véctơ u3 đối với họ {u1, u2}.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 5. √3 − i
Bài 1: Chuyển các số phức sau về dạng lượng giác: z = . 1 − i Bài 2: Trong không gian 3
R cho các dạng toàn phương:
Q = 2x2 − 10x2 − 8x2 − 4x 1 2 3 1x2 + 8x1x3 + 16x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
Bài 3: Kết quả bỏ phiếu của cuộc bầu cử thứ k tại nước M được đại diện bởi một véctơ Xk = (x 3
1(k), x2(k), x3(k)) trong không gian R , trong đó x1(k), x2(k) và x3(k) lần lượt là tỷ lệ người dân
bầu cho đảng dân chủ (D), đảng tự do (R) và đảng cầm quyền (L) ở cuộc bầu cử thứ k. Giả sử
rằng kết quả của cuộc bầu cử lần sau chỉ phụ thuộc vào kết quả của cuộc bầu cử trước đó thông qua mô hình sau: 0.7 0.1 0.3 X
k+1 = P Xk , P = 0.2 0.8 0.3 . 0.1 0.1 0.4
Biết kết quả bầu cử lần thứ nhất là X1 = (0.55, 0.4, 0.05)t và có 10 triệu người đi bầu ở cuộc bầu
cử thứ 3. Hãy xác định số người bầu cho đảng dân chủ, đảng tự do và đảng cầm quyền trong cuộc bầu cử thứ 3.
Bài 4: Tìm giá trị riêng và không gian riêng ứng với giá trị riêng tìm được của ma trận A, biết: 2 −2 2 A = −2 5 1 . 2 1 5
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 6. x 1 +x2 +ax3 = 2022
Bài 1: Giải và biện luận hệ phương trình sau theo tham số a: x . 1 +ax2 +x3 = 2022 ax1 +x2 +x3 = 2022 Bài 2: Trong không gian 3
R cho các dạng toàn phương: Q = 4x2 + 2x2 + 2x2 + 4x 1 2 3 1x2 − x2x3 − 4x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. Bài 3: Cho ánh xạ f : 3 3 R → R , xác định bởi:
f (x, y, z) = (x + 8y + z, x − y + 6z, 9x + y + 3z).
a. Chứng minh rằng f là ánh xạ tuyến tính.
b. Tìm ma trận A của f đối với cơ sở B = {v1 = (1, 0, 1); v2 = (1, 3, 0); v3 = (0, −2, 1)} trong 3 R . Bài 4:
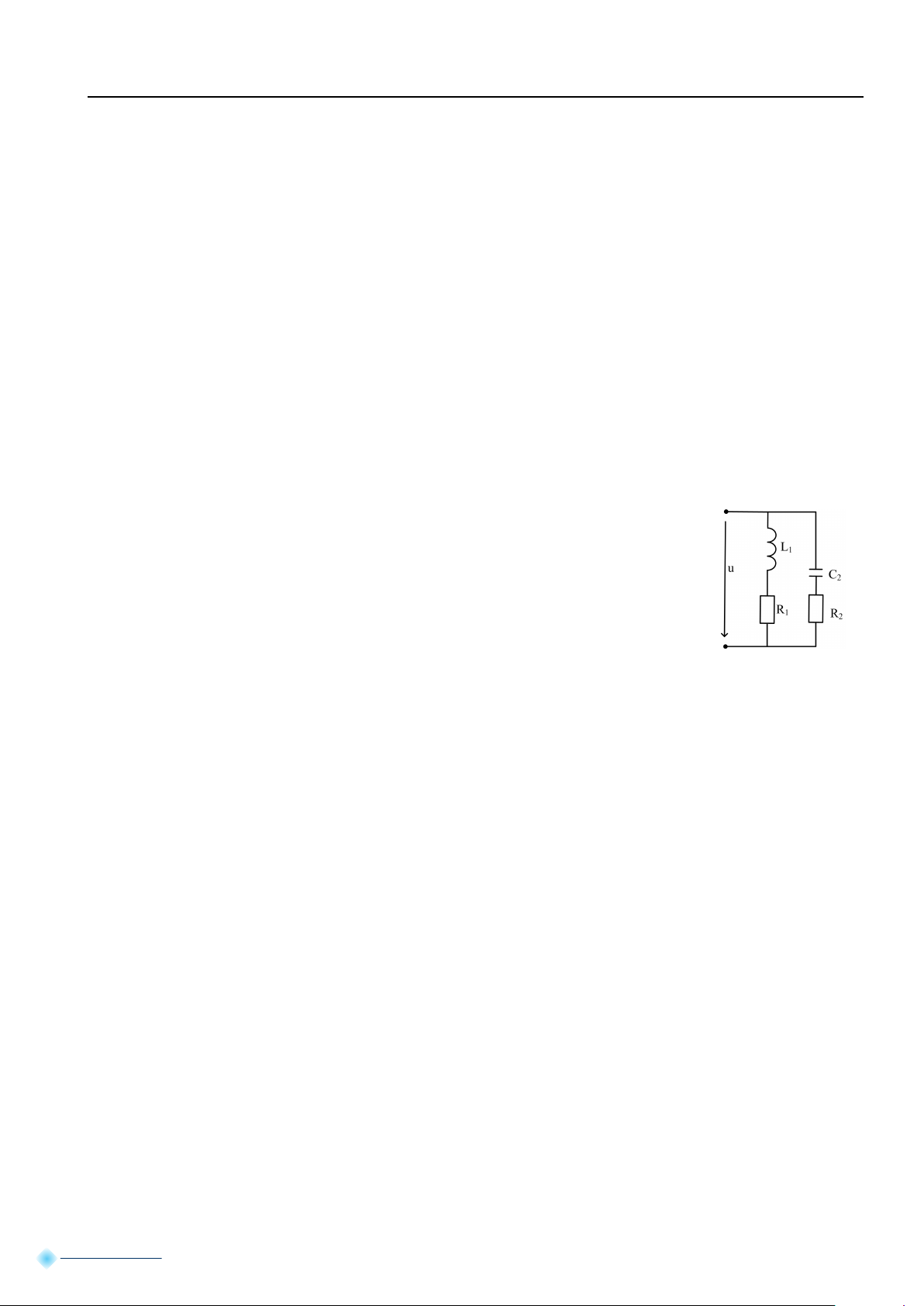
Một mạch điện gồm hai nhánh mắc song song. Nhánh 1 gồm có điện trở 15Ω
mắc nối tiếp với cuộn cảm với độ tự cảm L = 150mH. Nhánh 2 có điện trở
10Ω mắc nối tiếp với tụ điện có điện dung C = 100µF . Với tần số làm việc của
mạch là f = 50 Hz. Xác định tổng trở phức tương đương của mạch?
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 7.
Bài 1: Mô hình cân bằng cung cầu 3 thị trường của 3 loại hàng hóa 1, 2, 3 có các phương trình
quan hệ giữa lượng cung và lượng cầu của mỗi loại hàng hóa theo giá của chúng được cho bởi các phương trình sau: qs = −10 + p = 2p = −5 + 3p 1 1, qs 2 2, qs 3 3, qd = 20 − p = 40 − 2p = 10 − p 1 1 − p3, qd 2 2 − p3, qd 3 1 + p2 − p3,
trong đó qs và qd lần lượt là lượng cung và lượng cầu của loại hàng hóa i, i = 1, 2, 3; p i i i là giá của
loại hàng hóa i, i = 1, 2, 3. Hãy xác định các mức giá cân bằng thị trường của 3 loại hàng hóa trên. Bài 2: Cho f : 3 3 R → R xác định bởi:
f (x1, x2, x3) = (x1 − x2, x2 − x1, x1 − 9x3) .
a. Tìm ma trận của f đối với cơ sở B = {v1 = (1, 0, 1); v2 = (0, 1, 1); v3 = (1, 1, 0)};
b. Dùng ma trận thu được ở câu a) tính f (3, 0, 2). 2x +4y +3z = 10
Bài 3: Giải các hệ phương trình sau bằng phương pháp Cramer: 3x +y −2z = −6 . 4x +11y +7z = 10 Bài 4: Trong không gian 3
R cho các dạng toàn phương: Q = x2 + x2 + 2x2 + 2x 1 2 3 1x2 + 2x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 8. √ 1 − i 3 Bài 1: Cho z = √ , tính z60. 3 + i
Bài 2: Kết quả bỏ phiếu của cuộc bầu cử thứ k tại nước M được đại diện bởi một véctơ Xk = (x 3
1(k), x2(k), x3(k)) trong không gian R , trong đó x1(k), x2(k) và x3(k) lần lượt là tỷ lệ người dân
bầu cho đảng dân chủ (D), đảng tự do (R) và đảng cầm quyền (L) ở cuộc bầu cử thứ k. Giả sử
rằng kết quả của cuộc bầu cử lần sau chỉ phụ thuộc vào kết quả của cuộc bầu cử trước đó thông qua mô hình sau: 0.7 0.1 0.3 X
k+1 = P Xk , P = 0.2 0.8 0.3 . 0.1 0.1 0.4
Biết kết quả bầu cử lần thứ nhất là X1 = (0.55, 0.4, 0.05)t và có 10 triệu người đi bầu ở cuộc bầu
cử thứ 3. Hãy xác định số người bầu cho đảng dân chủ, đảng tự do và đảng cầm quyền trong cuộc bầu cử thứ 3. Bài 3: Cho ánh xạ f : 3 3 R → R , xác định bởi:
f (x, y, z) = (x − 8y − z, 10x + y − z, 6x − y − 7z).
a. Chứng minh rằng f là ánh xạ tuyến tính;
b. Tìm ma trận A của f đối với cơ sở B = {e1 = (1, 1, 1); e2 = (−2, −2, 0); e3 = (3, 0, 0)} trong 3 R . Bài 4: Trong không gian 3
R cho các dạng toàn phương: Q = x2 − x2 + x2 + 2x 1 2 3 1x2 − 3x2x3 − x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 9. 7i
Bài 1: Tìm mô đun và argument của các số phức: z = √ . 3 − i Bài 2:
Một mạch điện gồm hai nhánh mắc song song. Nhánh 1 gồm có điện trở 15Ω
mắc nối tiếp với cuộn cảm với độ tự cảm L = 150mH. Nhánh 2 có điện trở
10Ω mắc nối tiếp với tụ điện có điện dung C = 100µF . Với tần số làm việc của
mạch là f = 50 Hz. Xác định tổng trở phức tương đương của mạch? Bài 3: Trong không gian 3
R cho các dạng toàn phương: Q = x2 − x2 + x2 + 2x 1 2 3 1x2 − 3x2x3 − x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
Bài 4: Trong không gian véctơ 3
R cho họ véctơ S = {u1, u2, u3}. Trong dó
u1 = (3; 0; 4), u2 = (−1; 4; −2), u3 = (7; −4; 10).
a. Hỏi rằng họ véctơ S là độc lập tuyến tính hay phụ thuộc tuyến tính.
b. Tìm biểu diễn tuyến tính của véctơ u3 đối với họ {u1, u2}.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 10. √ 2 − 2i 3 Bài 1: Cho z = , tính z70. −1 − i Bài 2: Cho ánh xạ: T : 3 3 R → R với
T (x; y; z) = (2x − y + 3z; 9x + 2y − 6z; 8x + y + 5z).
a. Chứng minh T là ánh xạ tuyến; b. Tìm Im(T ). Bài 3: Trong không gian 3 R cho dạng toàn phương: ϕ = 5x2 + x2 + λx2 + 4x 1 2 3 1x2 − 2x1x3 − 2x2x3.
a. Với λ = 3, hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đổi tọa độ;
b. Tìm λ dể dạng toàn phương trên là xác định dương.
Bài 4: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 11.
Bài 1: Một hãng sử dụng 4 loại vật liệu khác nhau để sản xuất 3 loại sản phẩm. Cho biết, định
mức về số đơn vị vật liệu cho một đơn vị sản phẩm mỗi loại tương ứng và giá của một đơn vị vật
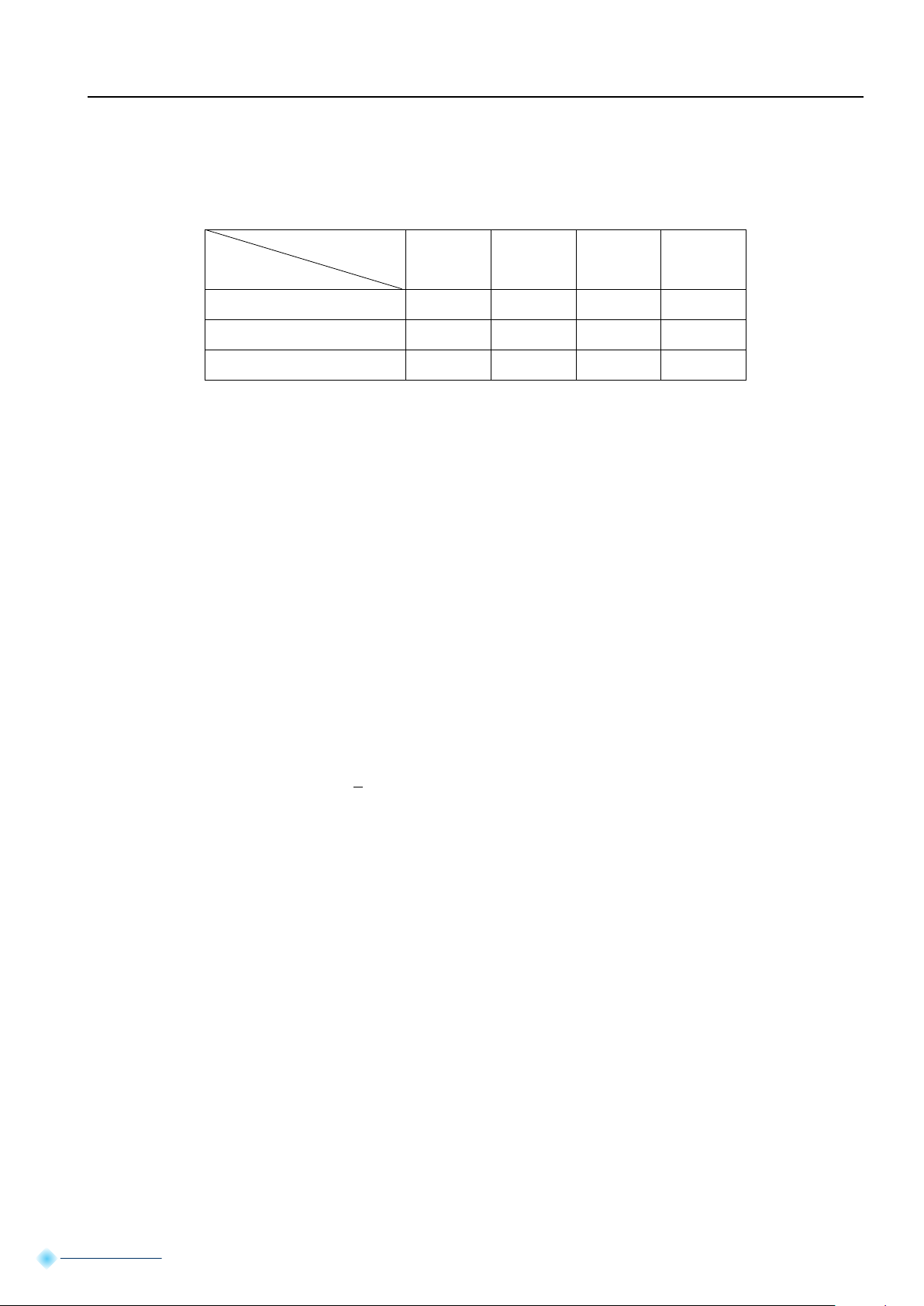
liệu mỗi loại ở bảng sau Vật liệu 1 2 3 4 Sản phẩm I 2 4 0 1 II 3 0 1 2 III 1 2 3 4
Biết chi phí sản xuất của các sản phẩm I, II, III tương ứng là 68, 66, 104 nghìn đồng và giá
của mỗi đơn vị vật liệu 1 là 11 nghìn.
a. Viết ma trận A là ma trận định mức số đơn vị vật liệu trên mỗi đơn vị sản phẩm và ma trận
P là ma trận chi phí về vật liệu của một đơn vị sản phẩm mỗi loại.
b. Từ đó hãy tính giá của mỗi đơn vị vật liệu mỗi loại 2, 3, 4 (đơn vị: nghìn đồng). Bài 2: Trong không gian 3 R cho 2 cơ sở
B = {v1 = (0, 1, −1); v2 = (2, 1, 0); v3 = (2, −3, −1)} ; và
B0 = {e1 = (1, 0, 0); e2 = (0, 1, 0); e3 = (0, 0, 1)}.
a. Tìm ma trận chuyển cơ sở từ B sang B0.
b. Tìm (v)B nếu biết (v)B0 = (8, 0, −10). 1
Bài 3: Tìm mô đun và argument của các số phức: z = √ . 3 − i Bài 4: Trong không gian 3
R cho các dạng toàn phương:
Q = 2x2 − 10x2 − 8x2 − 4x 1 2 3 1x2 + 8x1x3 + 16x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 12.
Bài 1: Một hãng sử dụng 4 loại vật liệu khác nhau để sản xuất 3 loại sản phẩm. Cho biết, định
mức về số đơn vị vật liệu cho một đơn vị sản phẩm mỗi loại tương ứng và giá của một đơn vị vật
liệu mỗi loại ở bảng sau Vật liệu 1 2 3 4 Sản phẩm I 2 4 0 1 II 3 0 1 2 III 1 2 3 4
Biết chi phí sản xuất của các sản phẩm I, II, III tương ứng là 68, 66, 104 nghìn đồng và giá
của mỗi đơn vị vật liệu 1 là 10 nghìn.
a. Viết ma trận A là ma trận định mức số đơn vị vật liệu trên mỗi đơn vị sản phẩm và ma trận
P là ma trận chi phí về vật liệu của một đơn vị sản phẩm mỗi loại.
b. Từ đó hãy tính giá của mỗi đơn vị vật liệu mỗi loại 2, 3, 4 (đơn vị: nghìn đồng).
Bài 2: Trong không gian véctơ 3
R cho họ véctơ B = {u1, u2, u3}. Trong đó
u1 = (1; 2; 3), u2 = (4; −5; −6), u3 = (7; −8; 9).
a. Hỏi B có là một cơ sở của 3 R hay không? Tại sao?
b. Nếu B là một cơ sở của 3 3
R , hãy tìm ma trận chuyển cơ sở từ B sang cơ sở chính tắc của R . Bài 3: Trong không gian 3
R cho các dạng toàn phương: Q = x2 + x2 + x2 + 4x 1 2 3 1x2 + 4x2x3 + 4x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. √
Bài 4: Giải phương trình: z3 + 3 + i = 0.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 13.
Bài 1: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3. Bài 2: Cho ánh xạ f : 3 3 R → R , xác định bởi:
f (x, y, z) = (x − 10y − z, 7x + y − z, 10x − y − 7z).
a. Chứng minh rằng f là ánh xạ tuyến tính;
b. Tìm ma trận A của f đối với cơ sở B = {e1 = (1, 1, 1); e2 = (−2, −2, 0); e3 = (3, 0, 0)} trong 3 R . (a − 1)x 1 +x2 +x3 = 8
Bài 3: Xác định a để hệ sau có nghiệm duy nhất: 3x . 1 −x2 +2x3 = 9 2x1 +x2 +3ax3 = a Bài 4: Trong không gian 3
R cho các dạng toàn phương: Q = x2 + 3x2 − x2 + 4x 1 2 3 1x2 + 2x1x3 + 2x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 14.
Bài 1: Tìm giá trị riêng và không gian riêng ứng với giá trị riêng tìm được của ma trận A, biết: 1 0 1 A = 0 0 0 . 1 0 1 Bài 2: Trong không gian 3 R cho dạng toàn phương: ϕ = 5x2 + x2 + λx2 + 4x 1 2 3 1x2 − 2x1x3 − 2x2x3.
a. Với λ = 3, hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đổi tọa độ;
b. Tìm λ dể dạng toàn phương trên là xác định dương.
Bài 3: Một nhà máy cùng sản xuất 2 loại thiết bị với số lượng lần lượt là Q1, Q2 và giá thị trường
là p1 = 110, p2 = 200. Chi phí sản suất của nhà máy đạt được khi sản xuất 2 loại thiết bị này là C = 2Q2 + Q + 64 1 1Q2 + 3Q2 2
Hãy xác định cơ cấu sản xuất (Q1, Q2) để nhà máy đạt lợi nhuận lớn nhất. √ (2 − 2i)8(− 3 + i)7
Bài 4: Chuyển các số phức sau về dạng lượng giác: I = . (1 + i)7
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 15. Bài 1: Trong không gian 3
R cho các dạng toàn phương: Q = 2x2 + 2x2 + 2x2 − 2x 1 2 3 1x2 + x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. Bài 2: Cho ánh xạ f : 3 3 R → R xác định bởi:
f (x, y, z) = (x + 9y − z; −x + y + z; 7x + z).
a. Tìm ma trận của f đối với cơ sở B = {v1 = (−1, 1, 2); v2 = (−2, 2, 0); v3 = (1, 0, 4)};
b. Dùng ma trận thu được ở câu a) tính f (0, 3, 4).
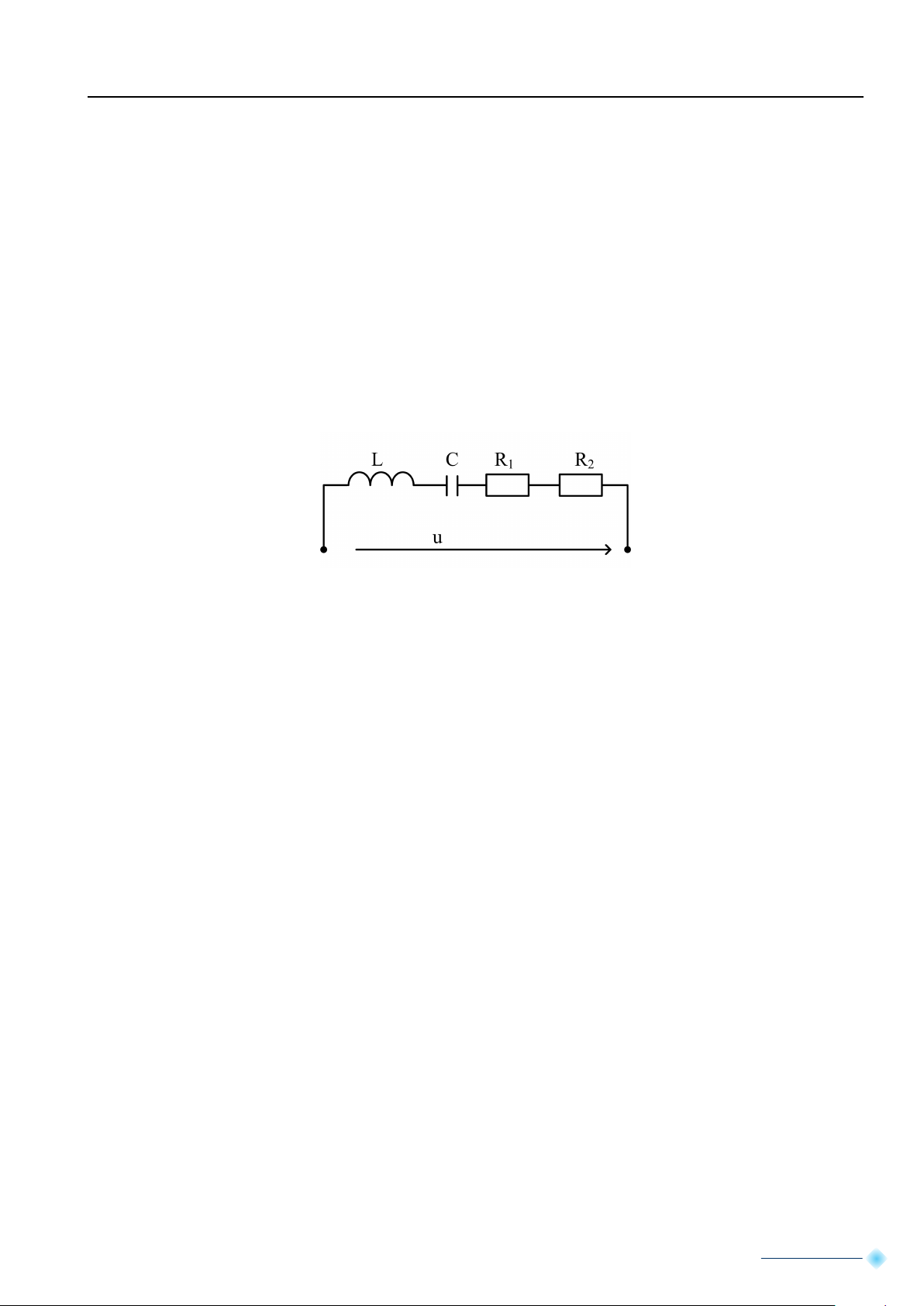
Bài 3: Mạch điện gồm điện trở 5Ω mắc nối tiếp điện trở 7Ω nối tiếp với cuộn cảm với độ tự cảm
L = 50mH nối tiếp tụ điện có điện dung C = 100µF với tần số f = 100 Hz. Xác định tổng trở phức của mạch? x 1 +2x2 +ax3 = 7
Bài 4: Xác định a để hệ sau có nghiệm duy nhất: 3x . 1 −x2 −ax3 = −8 2x1 +x2 +3x3 = 9
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 16. √ −1 − i 3 Bài 1: Cho z = √ , tính z800. 3 − i
Bài 2: Một hãng sử dụng 4 loại vật liệu khác nhau để sản xuất 3 loại sản phẩm. Cho biết, định
mức về số đơn vị vật liệu cho một đơn vị sản phẩm mỗi loại tương ứng và giá của một đơn vị vật
liệu (tính bằng nghìn đồng) mỗi loại ở bảng sau Vật liệu 1 2 3 4 Sản phẩm I 2 4 0 1 II 3 0 1 2 III 1 2 3 4 Giá vật liệu 15 8 12 9
a. Viết ma trận A là ma trận định mức số đơn vị vật liệu trên mỗi đơn vị sản phẩm và ma trận
B là ma trận giá của đơn vị vật liệu mỗi loại.
b. Từ đó hãy tính chi phí vật liệu cho một đơn vị sản phẩm mỗi loại.
Bài 3: Tìm giá trị riêng và không gian riêng ứng với giá trị riêng tìm được của ma trận A, biết: 2 −2 2 A = −2 5 1 . 2 1 5 Bài 4: Trong không gian 3
R cho các dạng toàn phương: Q = x2 + 3x2 − x2 + 4x 1 2 3 1x2 + 2x1x3 + 2x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 17. Bài 1: Cho ánh xạ f : 3 3
R → R được xác định bởi
f (x; y; z) = (x + y − z; 2x + 3y − z; 3x + 5y − z).
a. Chứng minh f là ánh xạ tuyến tính; b. Tìm Ker(f ).
Bài 2: Giải phương trình ma trận AX = B với 1 2 3 9 2 6 A =
2 5 3 ; B = 3 −3 −1 . 1 0 8 0 −9 2 1 2 1 Bài 3: Cho ma trận A =
2 2 −1 và một sự tương ứng giữa các kí tự và các số như sau: 1 0 1 1 2 3 4 5 6 7 8 9 10 H N E D A O I M T K
Một người muốn gửi một dòng mật khẩu cho đồng nghiệp. Để đảm bảo bí mật anh ta dùng
bảng tương ứng trên chuyển dòng mật khẩu này thành một dãy số và viết dãy số này thành ma
trận B theo nguyên tắc: lần lượt từ trái sang phải mỗi số là một vị trí trên dòng của B. Sau khi
tính C = BA và chuyển ma trận C về dãy số thì được dãy: 16 20 13 6 6 3 15 20 6.
Hãy giải mã dòng thông tin trên? Bài 4: Trong không gian 3
R cho các dạng toàn phương: Q = x2 − x2 + x2 + 2x 1 2 3 1x2 − 3x2x3 − x1x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 18.
Bài 1: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3. Bài 2: Cho ánh xạ f : 3 3
R → R được xác định bởi
f (x; y; z) = (x + y − z; 2x + 3y − z; 3x + 5y − z).
a. Chứng minh f là ánh xạ tuyến tính; b. Tìm Ker(f ). Bài 3: Trong không gian 3
R cho các dạng toàn phương: Q = 3x2 + 2x2 + x2 − 3x 1 2 3 1x2 + x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ. √
Bài 4: Tìm căn bậc ba của các số phức: z = 2 − 2i 3.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 19. 1 1 9 Bài 1: Cho ma trận A = 1 −1 3 . −3 −1 −5
Chứng minh rằng A khả nghịch. Tìm ma trận nghịch đảo A−1? Bài 2: Cho ánh xạ f : 3 3 R → R , xác định bởi:
f (x, y, z) = (x − 8y − z, 9x + y − z, 10x − y − 7z).
a. Chứng minh rằng f là ánh xạ tuyến tính;
b. Tìm ma trận A của f đối với cơ sở B = {e1 = (1, 1, 1); e2 = (−2, −2, 0); e3 = (3, 0, 0)} trong 3 R . Bài 3: Trong không gian 3
R cho các dạng toàn phương: Q = x2 + 3x2 − x2 + 4x 1 2 3 1x2 + 2x1x3 + 2x2x3.
Hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đồi tọa độ.
Bài 4: Nhà máy sử dụng 3 loại vật liệu thô để sản xuất 4 loại sản phẩm. Lượng vật liệu thô cần
thiết để sản xuất mỗi loại sản phẩm được cho bởi 1 1 0 5 u
1 = 2 , u2 = 0 , u3 = 5 , u4 = 31 , 1 2 2 17
a. Biểu diễn tuyến tính u4 qua các véctơ còn lại, nêu ý nghĩa kinh tế của nó;
b. Xác định số lượng các loại vật liệu thô cần thiết để sản xuất 4 sản phẩm loại 1, 3 sản phẩm
loại 2 và 1 sản phẩm loại 3.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................
BỘ MÔN TOÁN - KHOA KHTN- TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
Kiểm tra điều kiện môn: Toán cao cấp 1- Thời gian: 60 phút - Đề số: 20.
Bài 1: Trong không gian véctơ 3
R cho họ véctơ S = {u1, u2, u3}. Trong đó
u1 = (−1; 2; −1), u2 = (−2; 0; −1), u3 = (3; −10; 4)
a. Hỏi rằng họ véctơ S có là cơ sở của R3 không? Tai sao?
b. Hãy biểu diễn véctơ u3 thành một tổ hợp tuyến tính của {u1, u2}.
Bài 2: Kết quả bỏ phiếu của cuộc bầu cử thứ k tại nước M được đại diện bởi một véctơ Xk = (x 3
1(k), x2(k), x3(k)) trong không gian R , trong đó x1(k), x2(k) và x3(k) lần lượt là tỷ lệ người dân
bầu cho đảng dân chủ (D), đảng tự do (R) và đảng cầm quyền (L) ở cuộc bầu cử thứ k. Giả sử
rằng kết quả của cuộc bầu cử lần sau chỉ phụ thuộc vào kết quả của cuộc bầu cử trước đó thông qua mô hình sau: 0.7 0.1 0.3 X
k+1 = P Xk , P = 0.2 0.8 0.3 . 0.1 0.1 0.4
Biết kết quả bầu cử lần thứ nhất là X1 = (0.55, 0.4, 0.05)t và có 10 triệu người đi bầu ở cuộc bầu
cử thứ 3. Hãy xác định số người bầu cho đảng dân chủ, đảng tự do và đảng cầm quyền trong cuộc bầu cử thứ 3. √
Bài 3: Giải phương trình: z5 − (1 − 3i)11 = 0. Bài 4: Trong không gian 3 R cho dạng toàn phương: Q = 5x2 + x2 + λx2 + 4x 1 2 3 1x2 − 2x1x3 − 2x2x3.
a. Với λ = 1, hãy đưa dạng toàn phương trên về dạng chính tắc và chỉ ra phép biến đổi tọa độ.
b. Tìm λ để dạng toàn phương trên là xác định dương.
∠ Họ tên sinh viên:......................................................... Mã sinh viên:...............................................



