Btvn2 Môn Kinh tế lượng |Trường Đại học Kinh Tế - Luật, Đại học Quốc gia Thành phố Hồ Chí Minh

Bài 2.11:
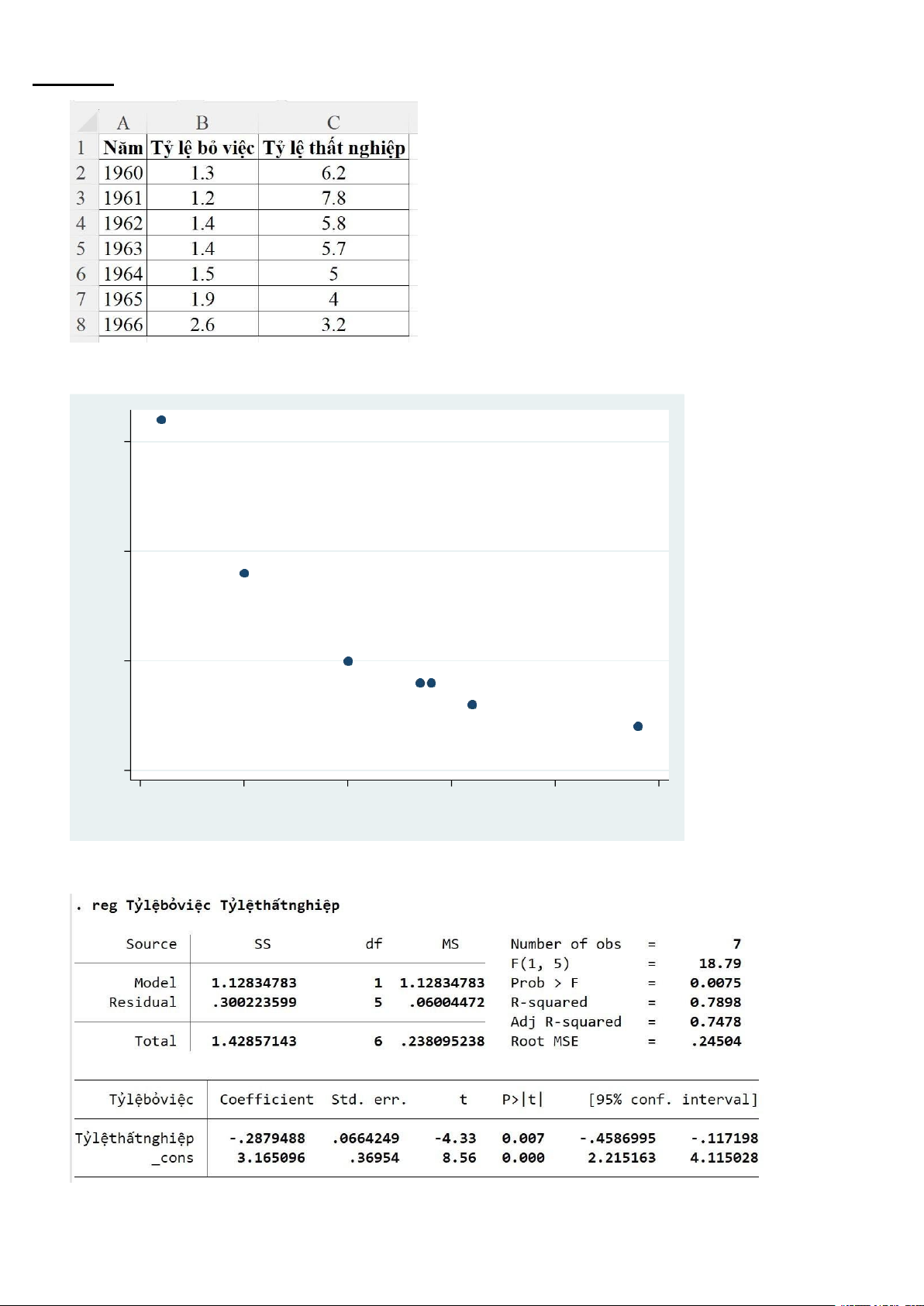
a. Vẽ đồ thị phân tán (Scatter diagram) của hai tỷ lệ: 3 4 5 6 7 8 Tỷ lệ thất nghiệp
b. Ước lượng mô hình tuyến tính:
Từ hình ảnh trên ta có phương trình hồi quy tuyến tính: y = 3,165096 – 0,2879488.x Ước lượng khoả g
n tin cậy 95% cho α và β ta có: α ϵ (2,215163; 4,115028) β ϵ (2,215163; 4,115028)
c. Giải thích các kết quả:
Hệ số góc β= −0.2879488: Khi tỷ lệ thất nghiệp tăng thêm 1%, thì tỷ lệ bỏ việc giảm trung
bình 0.288%, cho thấy mối quan hệ ngược chiều giữa thất nghiệp và bỏ việc.
Hệ số chặn α= 3.165096: Khi tỷ lệ thất nghiệp bằng 0, tỷ lệ bỏ việc ước tính trung bình là khoảng 3.165%.
d. Tính R2. Giải thích ý nghĩa của hệ số này:
Từ hình ở câu b ta có R2 = 0,7898.
Nghĩa là khoảng 78,98% sự biến động của tỷ lệ bỏ việc được giải thích bởi mô hình tuyến
tính theo tỷ lệ thất nghiệp. Đây là một mô hình phù hợp khá tốt với dữ liệu. Bài 2.12:
a. Xây dựng các mô hình kinh tế cho lý thuyết trên.
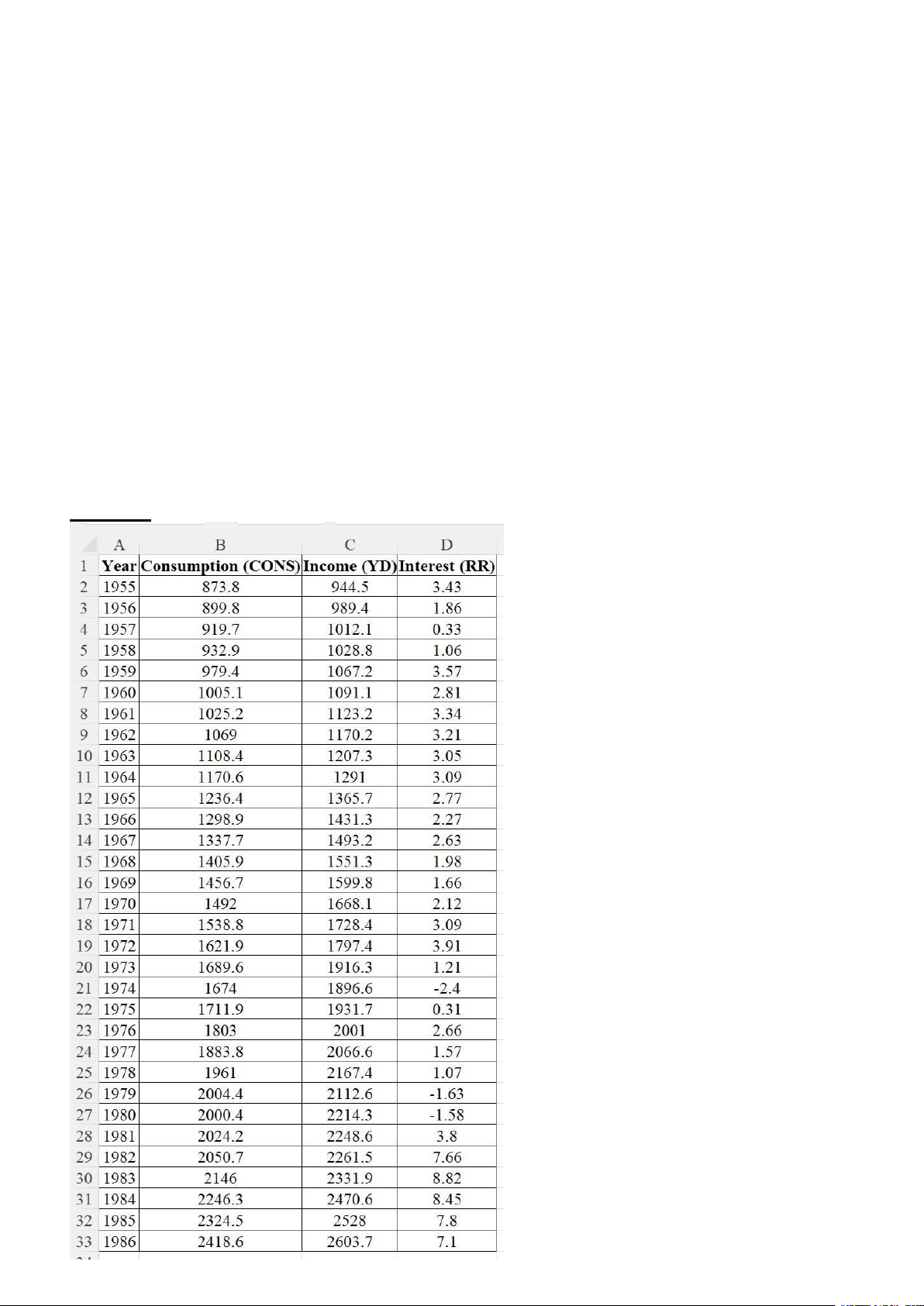
Mô hình lý thuyết kinh tế của Keynes: CONS = β1 + β2.YD + ε
Mô hình lý thuyết kinh tế của các nhà kinh tế học cổ điển: CONS = β1 + β2.RR + ε ( Với β2<0)
b. Ước lượng các thông số cho mỗi mô hình:
*Mô hình lý thuyết kinh tế của Keynes:
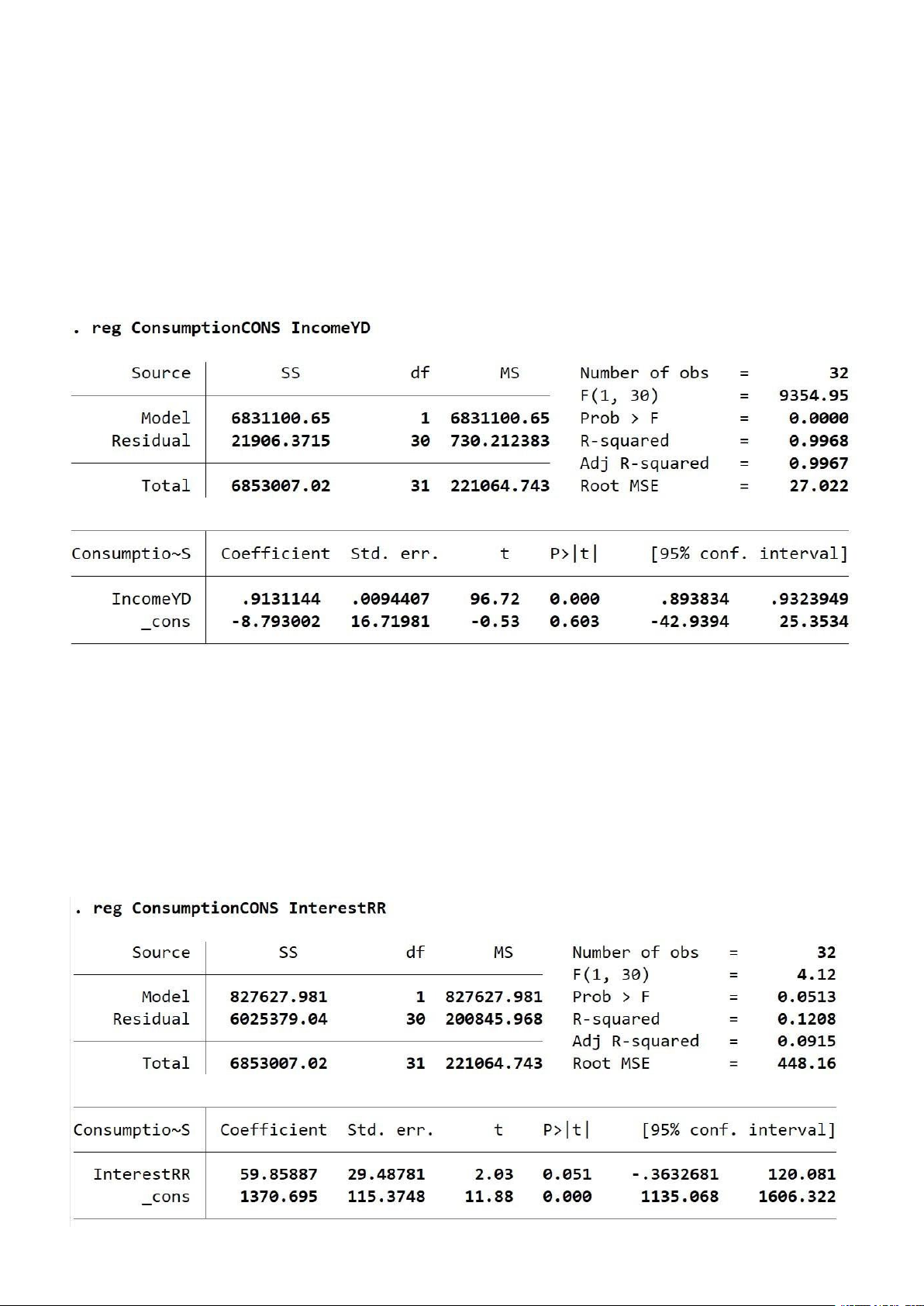
Ta có phương trình hồi quy tuyến tính: CONS= - 8,793002 + 0,9131144.YD
Ước lượng khoảng tin cậy 95% cho β1 và β2 ta có: Β1 ϵ (-42,9394; 25,3534) Β2 ϵ (0,893834; 0,9323949)
*Mô hình lý thuyết kinh tế của các nhà kinh tế học cổ điển:
Ta có phương trình hồi quy tuyến tính: CONS= 1370,695 + 59,85887.RR
Vậy ta có: β^2= 59,85887; β^1= 1370,695
Ước lượng khoảng tin cậy 95% cho β1 và β2 ta có:
β 1 ϵ (1135,068; 1606,322)
β2 ϵ (-0,3632681; 120,081)
c. Nhận xét về giá trị của hai giả thiết trên:
Ở mô hình lý thuyết kinh tế của Keynes:
Ta có R2 = 0,9968 => Thu nhập khả dụng giải thích được 99,68% cho sự biến động của tổng tiêu dùng.
Kiểm định sự phù hợp với mức ý nghĩa 5%:
H0: β2 = 0 (thu nhập khả dụng không tác động đến tổng tiêu dùng)
H0: β2 # 0 (thu nhập khả dụng tác động đến tổng tiêu dùng)
Kết quả thống kê: p-value = 0,0000 < 0.05 Kết luận: bác bỏ H0
Vậy với mức ý nghĩa 5%, thu nhập khả dụng tác động đến tổng tiêu dùng.
Ở mô hình lý thuyết kinh tế của các nhà kinh tế học cổ điển:
Ta có R2 = 0,1208 => Lãi suất giải thích được 12.08% cho sự biến động của tổng tiêu dùng.
Kiểm định sự phù hợp với mức ý nghĩa 5%:
H0: β2 = 0 (Lãi suất không tác động đến tổng tiêu dùng)
H0: β2 # 0 (Lãi suất tác động đến tổng tiêu dùng)
Kết quả thống kê: p-value = 0,0513 > 0.05 Kết luận: chấp nhận H0
Vậy với mức ý nghĩa 5%, lãi suất không tác động đến tổng tiêu dùng.
⇨ Nhận xét: Cả hai lý thuyết đều có ý nghĩa thống kê và giải thích được phần biến động
đáng kể của tổng tiêu dùng. Lý thuyết Keynes có khả năng giải thích cao hơn vì R2 cao hơn. Bài 2.14: a.
Có thể thấy, các điểm gần như tạo thành đường ngang, giá trị Y gần như không thay đổi
nên không có mối quan hệ tuyến tính giữa X và Y. Do đó, hệ số xác định (R2) của đường
hồi quy của X theo Y dự kiến sẽ rất thấp, gần 0. Nên X không giải thích được biến động
của Y, đường hồi quy không giải thích được phương sai của Y. b.
Trong Kinh tế lượng, việc đánh giá kết quả hồi quy luôn cần kết hợp cả thống kê và phân
tích trực quan dữ liệu. Một R2 cao không được tin tưởng nếu nó không được hỗ trợ bởi biểu đồ phân tán.
Cần kiểm tra trực quan dữ liệu để đảm bảo: Không có outlier, không có phi tuyến tính, dữ
liệu không bị ảnh hưởng bởi các giả định bị vi phạm (ví dụ phương sai thay đổi, sai số tự tương quan. .).
Document Outline

• a.Vẽ đồ thị phân tán (Scatter diagram) của hai tỷ lệ
• c.Giải thích các kết quả:
• d.Tính R2. Giải thích ý nghĩa của hệ số này:
• a.Xây dựng các mô hình kinh tế cho lý thuyết trên.
• b.Ước lượng các thông số cho mỗi mô hình:
• c.Nhận xét về giá trị của hai giả thiết trên:
• a.
• b.