Buổi 02 - Cấu Trúc Rời Rạc. Môn Cấu trúc rời rạc | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

lOMoAR cPSD| 58968691
Buổi 02 – Ngày 20-09-2023 – môn Cấu trúc rời rạc – lớp MA004.O12.CNVN
Ví du ̣mẫu: Dùng các luât logic đ ̣ ể chứng minh rằng biểu thức sau là hằng đúng [(p q) q] (p r) Giải: Biểu thức Quy luât logịc [(p q) q] (p r) tiền đề [( p q) q] ( p r) luât ḳ éo theo [ q ( p q)] ( p r) luât giao họ án [( qp) ( q q)] ( p r) luât phân ḅ ố [( q p) 0] ( p r) luât ṿ ề phần tử bù ( q p) ( p r) luât tṛ ung hòa ( q p) ( p r) luât ḳ éo theo (q p) ( p r) luât DeMorgan, lụ
ât pḥủ đi ̣nh của pđ q(p p) r luât ḳ ết hơp ̣ [q(p p)] r luât ḳ ết hơp ̣ [q 1] r
luật về phần tử bù 1 r luât tḥ ống tri ̣ 1 luât tḥ ống tri ̣.
Như vây, bịểu thức đa ̃ cho là hằng đúng (đpcm). Lưu ý:
Khi chứng minh hằng đúng hoăc ḥ ằng sai, ta có thể găp c ̣ác trường hơp sau:̣
1 1 1 luât ḷ ũy đẳng/ luât trung ḥòa
1 1 1 luât ḷ ũy đẳng/ luât tḥống tri ̣ [(p q) r]
[(p q)r] đăt ̣ A [(p q) r]
Biểu thức đa ̃ cho tương đương A
A A A luât ḳ éo theo
1 luât ṿ ề phần tử bù lOMoAR cPSD| 58968691
Hoăc ḷà trường hơp bị ểu thức A A (A A)
(A A) luât tương đương ̣
A A luât ḷ ũy đẳng
A A luât ḳ éo theo
1 luât ṿ ề phần tử bù
Bài tập tương tư:̣
1/ Làm bài 12 trang 2 (file bài tâp CTRṚ -UIT.pdf).
2/ Dùng các luât logic đ ̣ ể chứng minh rằng biểu thức sau là hằng đúng
a/ [(p q) (q r)] (p r) b/ [(p
q) (p r)] ( q s) c/ [(p
r) (q r)] [ r (p q)] d/ [(p
q) ( q r) p] ( r s) e/ [(p
r) ( q p) (q s)] ( r s) f/ [(p
r) (r s) (t s) ( t u) u] (p m) g/ [[(
p q) (r s)] [h (r k)] h (k s) (r t) t] ( p u) h/ [(p
r) ( q p) r] ( q k) i/ [(p q) r] [p (q r)] j/ [p (p q)
(s r) (r q)] (s t) k/ [(p q) ( r s) (p r)] ( q s) l/ [[( p q) r] [r (s t)] ( s u)( u t)] ( p m)
* QUY TẮ C SUY DIỄN
Trong quá trình chứng minh môt bị ểu thức, hay chứng tỏ môt ṃ ênh đ ̣ ề là hằng đúng hoăc ̣
hằng sai, ta có thể dùng nhiều cách lâp lụ ân kḥ ác nhau. Ở đây ta xét những lâp lụ ân c ̣ ó dang:̣
Nếu có p1, có p2, có p3, và có … pn Thì có q
Ta goi đây ḷ à dang ḷ âp lụ ân đ ̣ úng (hay là dang cḥ ứng minh hơp l ̣ê)̣, nếu ta chứng tỏ đươc ̣ rằng
biểu thức sau là hằng đúng (p1 p2 ... pn) q
Khi đó, ta goi đây ḷ à môt ̣ quy tắc suy diễn. Như vây, ̣ quy tắc suy diễn là môt ḥ ằng đúng, dưới dang pḥ ép kéo theo.
Các cách biểu diễn của quy tắc suy diễn:
Cách 1: Dùng biểu thức hằng đúng (p1 p2 ...pn) q ... ... ... 1 lOMoAR cPSD| 58968691
Cách 2: Dùng dòng suy diễn (p1 p2 ...pn) h ... k ... m n ... q
Cách 3: Dùng mô hình suy diễn (phổ biến nhất) p1 p2
đoc ḷ à “có q ” p n q
hay là “tồn tai ̣ q ”
a/ Phương pháp khẳng đi ̣nh (luật Modus Ponens)
đươc tḥ ể hiên ḅởi hằng đúng
[(p q) p] q Hay dưới dang mô ḥ ình p q p q
b/ Phương pháp tam đoạn luận (Syllogism) (pp bắc cầu)
đươc tḥ ể hiên ḅ ởi hằng đúng
[(p q) (q r)] (p r)
Hay dưới dang mô ḥ ình p q q r (p r)
c/ Phương pháp phủ định (luật Modus Tollens)
đươc tḥ ể hiên ḅ ởi hằng đúng [(p q) q] p lOMoAR cPSD| 58968691
Hay dưới dang mô ḥ ình p q q p
d/ Phương pháp tam đoạn luận rời:
đươc tḥ ể hiên ḅ ởi hằng đúng [(p q) q] p (TH1) hay [(p q) p] q (TH2)
Hay dưới dang mô ḥ ình p q p q q hay p p q (TH1) (TH2)
e/ Quy tắc mâu thuẩn (phương pháp chứ ng minh bằng phản chứ ng) * đươc tḥ ể hiên ḅ ởi hằng đúng [(p1 p2 ... pn) q] 0
Hay dưới dang mô ḥ ình p1 p2 pn q 0
f/ Phép chứ ng minh theo trường hợp: đươc tḥ ể hiên ḅ ởi hằng đúng
[(p r) (q r)] (p q) r
Hay dưới dang mô ḥ ình p r q r
(p q) r g/ Phép đơn giản nối liền:
đươc tḥ ể hiên ḅ ởi 1 trong các hằng đúng sau: lOMoAR cPSD| 58968691
(p q) p (TH1) hay (p q)
q (TH2) hay p (p q) (TH3)
hay q (p q) (TH4)
Hay dưới dang mô ḥ ình p q p q p q hay hay hay p q (p q) (p q) (TH1) (TH2) (TH3) (TH4)
Ví du ̣mẫu 2: Dùng các luât logic, c ̣ ác quy tắc suy diễn để kiểm tra tính đúng đắn của mô hình suy diễn sau: (p q) (r s) h m h r m s (p t) Giải: Biểu thức Quy tắc suy diễn Ta có h m (1) tiền đề Nên h
phép đơn giản nối liền Mà h r tiền đề Nên r (2) pp khẳng đi ̣nh Từ (1) m
phép đơn giản nối liền Ngoài ra m s tiền đề Nên s
phép tam đoan lụân ṛ ời Hay ( s) (3)
phủ đi ̣nh của phủ đi ̣nh Từ (2),(3): r( s) Hay (r s) luât DeMorgaṇ Ngoài ra (p q) (r s) tiền đề Nên (p q)
phương pháp phủ đi ̣nh Hay p q
luât DeMorgan, lụ ât pđ c ̣ủa pđi ̣nh lOMoAR cPSD| 58968691 Hay p
phép đơn giản nối liền Hay p t
phép đơn giản nối liền Hay (p t) luât ḳ éo theo
Vây mô ḥ ình suy diễn là đúng.
Bài tập tương tư:̣
1/ Làm bài 19 trang 4-5 (file Bài tâp CTRṚ -UIT.pdf).
2/ Dùng các luât logic, lụ ât suy dị ễn để kiểm tra tính đúng đắn của suy luân sau:̣
( p q) r s t ( p q) s (h k) (r s) a/ h t t p r h r h k (p q) r s h p q d/ t s r
b/ s k k r c/ q s (r s) u u k ( p u) (q u) ( r s) ( p n) (p q) r h s e/ h p s q ( r t)
* VI ̣ TỪ VÀ LƯƠNG ṬỪ :
Vi ̣ từ là phát biểu dưới dang kḥ ẳng đi ̣nh chứa biến số. Bản thân phát biểu này không phải là
mênh đ ̣ ề. Tuy nhiên, khi thay biến số bằng những giá tri ̣ cu ̣ thể thì ta thu đươc ṃ ênh đ ̣ ề đúng hoăc sai.̣
Để khảo sát vi ̣ từ ở dang ṭổng quát, ta xét p x( ) là vi ̣ từ theo môt bịến x X .
Ta có các trường hơp ̣ sau:
TH1: Khi thay x a X , với a tùy ý, ta có p a( ) là mênh đ ̣ ề đúng, thì khi đó ta viết lOMoAR cPSD| 58968691
x X p x, ( ) → là mênh đ ̣ ề
đoc ḷ à “với moị”
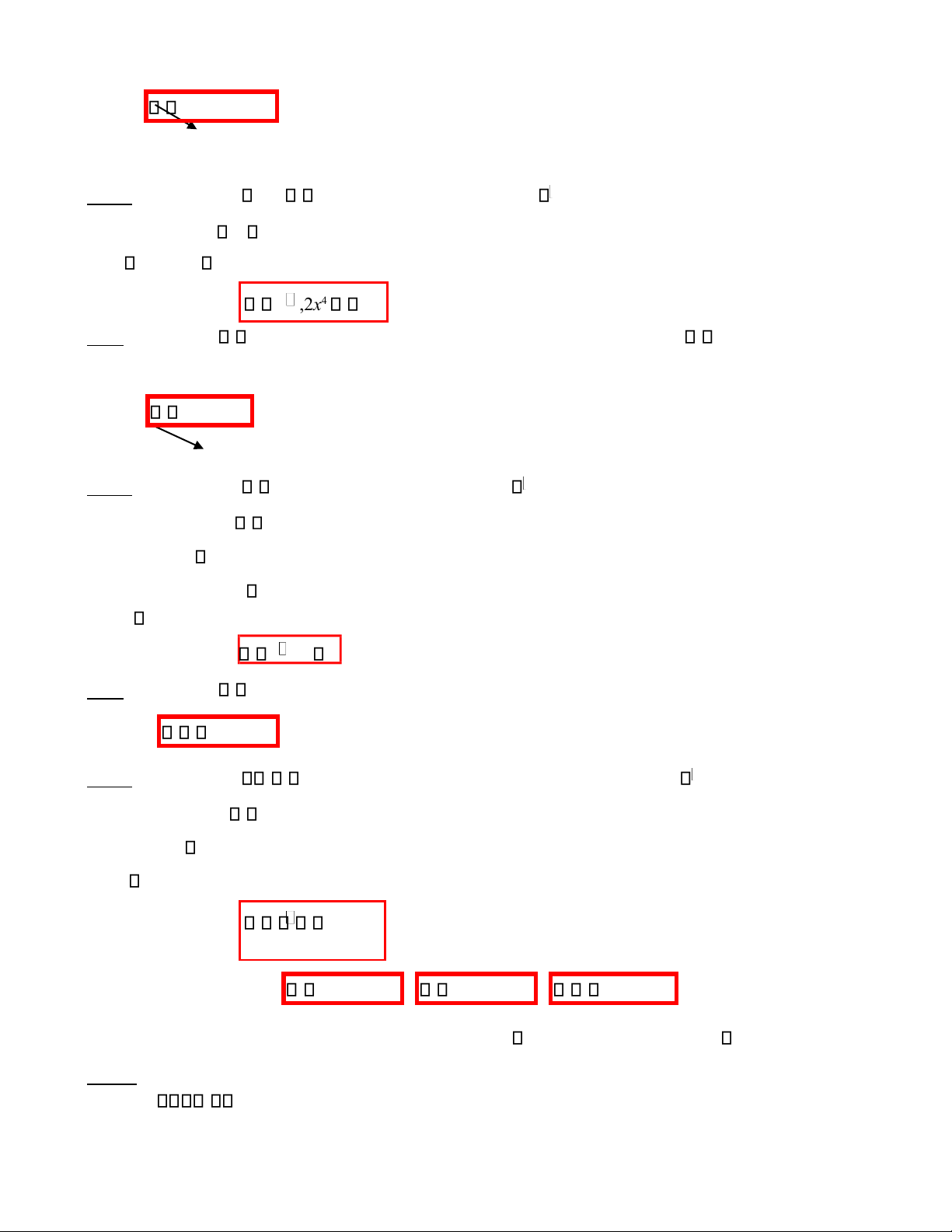
Ví du:̣ Ta xét p x( ) 2x4 3 0 là vi ̣ từ theo môt bị ến x Ta có p( 2) 1 p(0) 1 p(3) 1
x ,2x4 3 0 Nên ta viết → mênh đ ̣ ề
TH2: Khi thay x a X , ta có p a( ) là mênh đ ̣ ề đúng, nhưng khi thay x b X ta có p b( ) là
mênh đ ̣ ề sai; khi đó ta viết
x X p x,( ) → là mênh đ ̣ ề
đoc ḷ à “tồn taị”
Ví du:̣ Ta xét p x( ) "x 5" là vị từ theo môt bị ến x Ta có: p( 3) 0 p(1) 0 p(8) 1 p(20) 1
Nên ta viết x ,x 5 → mênh đ ̣ ề
TH3: Khi thay x a X , với a tùy ý, ta có p a( ) là mênh đ ̣ ề sai, thì khi đó ta viết
xX, p x( ) → là mênh đ ̣ ề
Ví du:̣ Ta xét p x( ) x2 1
0 là vi ̣ từ theo môt bị ến x . Ta có p( 3) 0 p(0) 0 p(5) 0 x , x2
Nên ta viết → mênh đ ̣ ề. 1 0
Ta goi c ̣ ác mênh đ ̣ ề x X p x, ( ) , x X p x, ( ) , x X, p x( ) là dang lự ơng t ̣ừ hóa
của vi ̣ từ p x( ) thông qua các lương ṭ ừ phổ dung ̣ ( ) hay lương ṭ ừ tồn tai ̣ ( ) . Lưu ý: 1/ Ta có ( ) lOMoAR cPSD| 58968691 ( )
2/ Ta có dang lự ơng ṭ ừ hóa của vi ̣ từ theo 2 biến x X y, Y là: x X y Y p x y, , ( , ) x X y Y p x y, , ( , ) x X y Y p x y, , ( , ) x X y Y p x y, , ( , )
Ví du ̣mẫu 1: Viết dang pḥ ủ đi ̣nh cho biểu thức 0, 0 sao cho x thỏa
(| x x0 | )(| f x( ) L | )
Ví du ̣mẫu 2: Cho biết chân tri ̣ của mênh đ ̣ề sau và viết dang pḥủ đi ̣nh cho mênh đ ̣ ề x , y ,xy 4 Giải:
Ví du ̣mẫu 1: Ta có dang pḥ ủ đi ̣nh của biểu thức là:
0, 0, sao cho x thỏa (| x x0 | )(| f x( ) L | ) (ta dùng tính chất (p q) ( p q) p q )
(nếu xét phủ đi ̣nh của luât tương đương, ta x ̣ ét: (p q) [(p q) (q p)] [( p q)( qp)] (p q) (q p)]) Ví du ̣mẫu 2:
Ta chứng tỏ đây là mênh đ ̣ ề đúng, như sau:
Cách 1: x 0, ta chon ̣ y 2 thì xy 0.2 0 4 (đây là mênh đ ̣ ề đúng) 8 8
x 0, ta chon ̣ y thì xy x. 8 4 (đây là mênh đ ̣ ề đúng) x x
Vây bịểu thức đa ̃ cho là đúng.
Cách 2: x , ta chon ̣ y 0 thì xy x.0 0 4 nên mênh đ ̣ ề luôn đúng.
Vây bịểu thức đa ̃ cho là đúng.
Ta có dang pḥ ủ đi ̣nh của biểu thức là: x , y ,xy 4