Buổi 08 - Cấu trúc rời rạc. Môn Cấu trúc rời rạc | Đại học Trường Đại học Công nghệ thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh.

lOMoAR cPSD| 58968691
Buổi 08 – Ngày 08-11-2023 – môn Cấu trúc rời rạc – lớp MA004.O12.CNVN
CHƯƠNG 4: ĐAI ṢỐ BOOL VÀ HÀ M BOOL
1/ MÔT ṢỐ KHÁ I NIỆM
Cho tâp ḥơp ̣ S {0,1}. (S = Set)
Trên S ta có 2 phép toán 2 ngôi: phép công ̣ (+), phép nhân (.), cùng với 1 phép toán 1 ngôi:
phép lấy phần bù (), thỏa: 0 0 0.0 0.1 1.0 0 1 0 0 1 1.1 1 1 1 1 0 0 1
Ta goi c ̣ ấu trúc đai ṣ ố (S, , , ,0, 1) là môt đ ̣ ai ṣ ố
Bool. Môt ̣ hàm bool n biến là môt ̣ ánh xa ̣ f B: n B
(x x1, 2,...,xn)
f x x( 1, 2,...,xn) Vi ́ du:̣
Ta có hàm bool 3 biến f B: 3 B, với
f x y z( , , ) (xy yz xy)(xz y yz) xyz
Ta có hàm bool 4 biến f B: 4 B, với f x y z t( , , , ) xyz xy yz z yzt
(xyz yt ) ztxyz yzt
Từ công thức ban đầu của hàm bool f ta có thể viết lai ̣ f dưới dang ṭ ổng các tích cơ bản của
các biến, mà ta thường goi ḷ à daṇ g chính tắc tuyển (dang cḥ ính tắc nối rời) (disjunctive normal
form – d.n.f) của f .
Vi ́ du:̣ ta có dang cḥính tắc tuyển (chính tắc nối rời – d.n.f) của hàm bool 3 biến là:
f x y z( , , ) xyz xyz xyz xyz xyz xyz
Vi ́ dụ: ta có dang cḥ ính tắc tuyển (chính tắc nối rời – d.n.f) của hàm bool 4 biến là:
f x y z t( , , , ) xyzt xyzt xyzt xyzt xuýt xyzt xuýt xyzt xyzt lOMoAR cPSD| 58968691
2/ CÁ CH TÌM DẠNG CHÍNH TẮ C NỐ I RỜ I (CHÍNH TẮ C TUYỂ N – D.N.F) CHO HÀ M BOOL
a/ Cách 1: dùng bảng chân trị
+ Ta lâp ḅ ảng chân tri ̣ cho f .
+ Ta xét các dòng làm cho chân tri ̣ của f bằng 1.
+ Ta viết công thức cho dang d.n.f theo quy ṭ ắc:
• Các biến có chân tri ̣ bằng 0 thì ta ghi biến đó “có gac ̣ h đầu”
• Các biến có chân tri ̣ bằng 1 thì ta ghi biến đó “không có gach đ ̣ ầu”
Lưu ý: ta có xy x.y do xy x y
Ví du ̣mẫu: Tìm dang cḥ ính tắc nối rời cho hàm bool
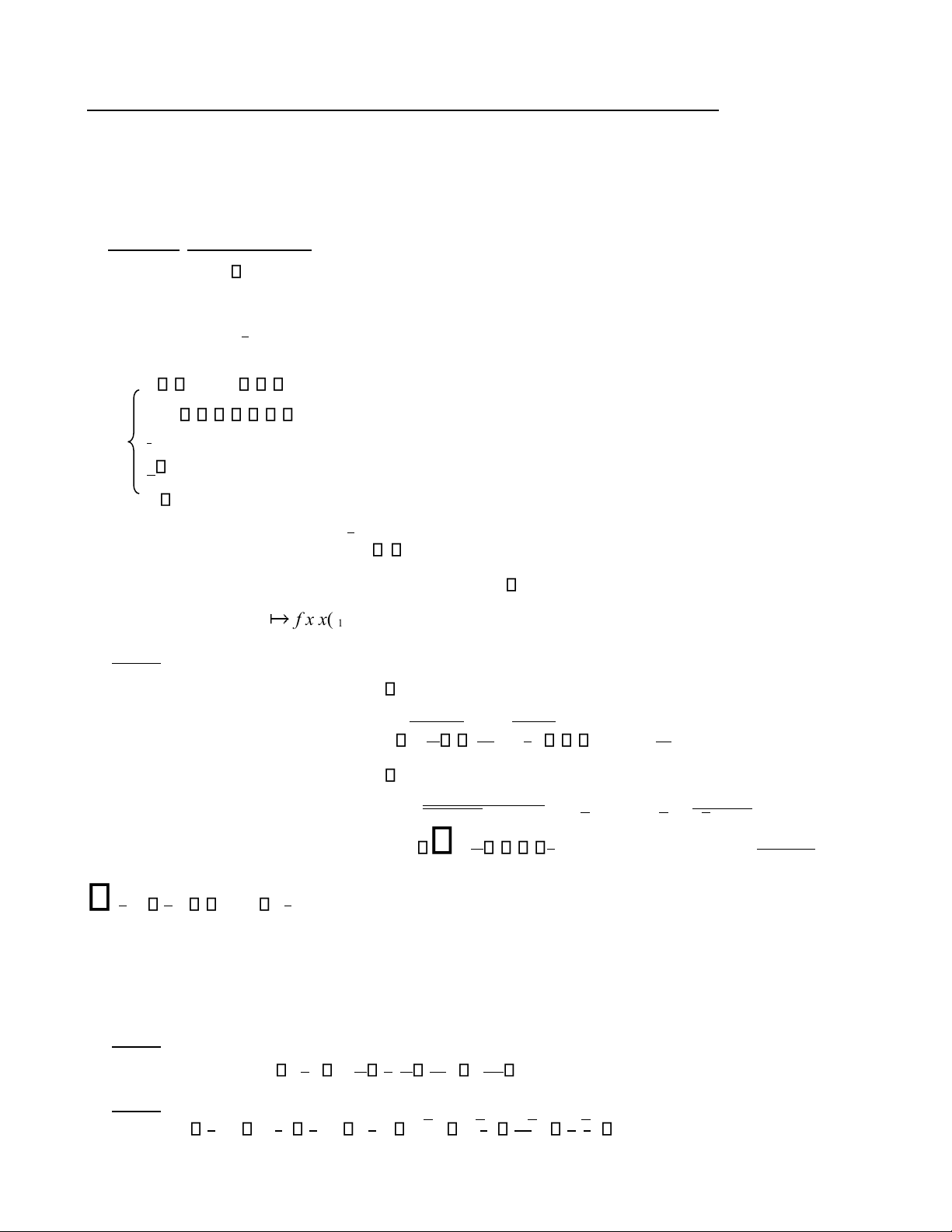
f B: 3 B, với f x y z( , , ) xy yz xz (xyz yz xz) x.y A C B D Giải:
Ta có bảng chân tri ̣ của f là:
x y z x
y z xy yz xz A B xyz yz C xz D x.y BD f 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
Từ bảng chân tri ̣ của f ta có dang d.n.f ḷ à:
f x y z( , , ) x.y z. x.yz xy z. xyz xyz
Bài tập tương tư:̣ tìm dang cḥ ính tắc tuyển (chính tắc nối rời) cho hàm bool sau:
1/ f x y z( , , ) (xy zxz xy)(z y yz) xy 2/ f x y z( , , ) xy yz xá x
(xy ý) xy lOMoAR cPSD| 58968691 3/ f x y z( , , ) xyz yzxy xy z xz 4/ f x y z( , , ) xy yz xz (xyz xz y) xy 5/ f x y z( , , ) xy yzx (xy z yz) xz 6/ f x y z t( , , , ) xyt yz zt xzt (xyz zt xy) zt yz
7/ f x y z t( , , , ) (xyt ztxy yt)( xyz) xzt yzzt
8/ f x y z t( , , , ) (xyz yt yzxz xt)( xy zt) xyt zt
9/ f x y z t( , , , ) (zt yz xyz yz)(xyt zt ) xy zt yz
10/ f x y z t( , , , ) (xyt zt yz yt)( xzzt) xyt zt xyz
b/ Cách 2: biến đổi trực tiếp từ công thứ c
Ví du ̣mẫu: Tìm công thức dang cḥ ính tắc nối rời cho hàm bool:
f x y z t( , , , ) (xyt xz y)( z xt) yzt ztyzt Giải:
f x y z t( , , , ) (xyt xz y)( z xt) yzt zt yzt xyzt (y z
t )(z t )
yzt xyzt yz yt zt zt t yzt t yz yzt
(x x)(y y)(z z)t (x
x)yz t( t ) (x x)yzt
xyzt xyzt xyzt xy z. t xyzt xyzt x.yzt x.y z. t xyzt x.yzt xyzt xyzt
Đây là dang d.n.f c ̣ ần tìm của hàm bool f .
Bài tâp tương tư:̣ tìm dang cḥ ính tắc nối rời cho hàm bool sau
11/ f x y z t( , , , ) (xyt zt xzyz xt)( zt yz) xzt zt
12/ f x y z t( , , , ) (xy zt yt )(xz yt xy) xzt yzt
13/ f x y z t( , , , ) (zt
xzyzt )(xy yz) xyt xz zt y
14/ f x y z t( , , , ) (xz yt
xyz yt zt)( xy) xyz zt xz
15/ f x y z t( , , , ) (xz
ytxyz y)( zt xz) xyt yz zt xy zt
c/ Cách 3: dùng phương pháp biểu đồ Karnaugh (bia Karnaugh) c̀ ủa hàm bool lOMoAR cPSD| 58968691
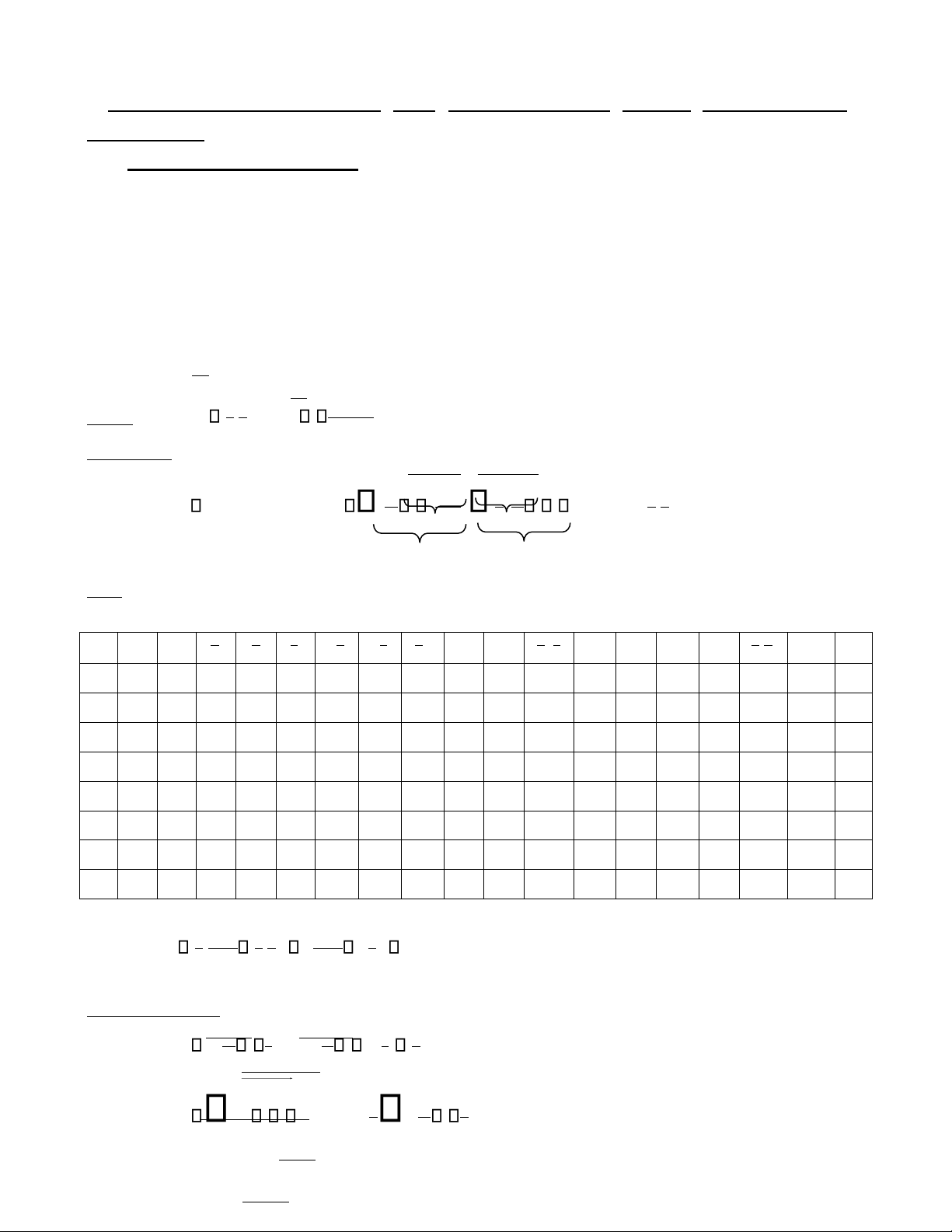
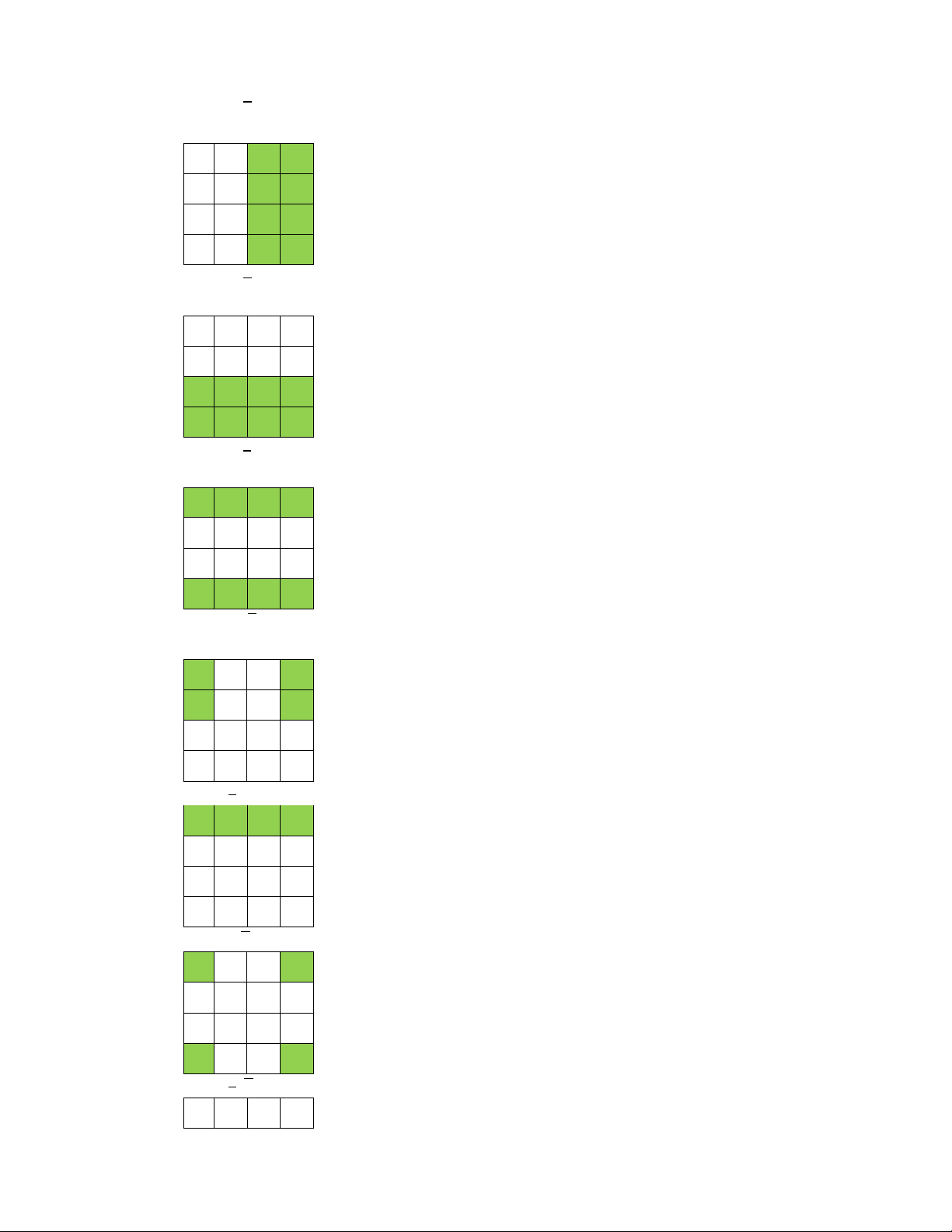
Ta có biểu đồ Karnaugh (bìa Kar(f)) của hàm bool 3 biến là biểu đồ có cấu trúc như sau: x x z z y y y
Ta có biểu đồ Karnaugh (bìa Kar(f)) của hàm bool 4 biến là biểu đồ có cấu trúc như sau: x x t z t zt y y y
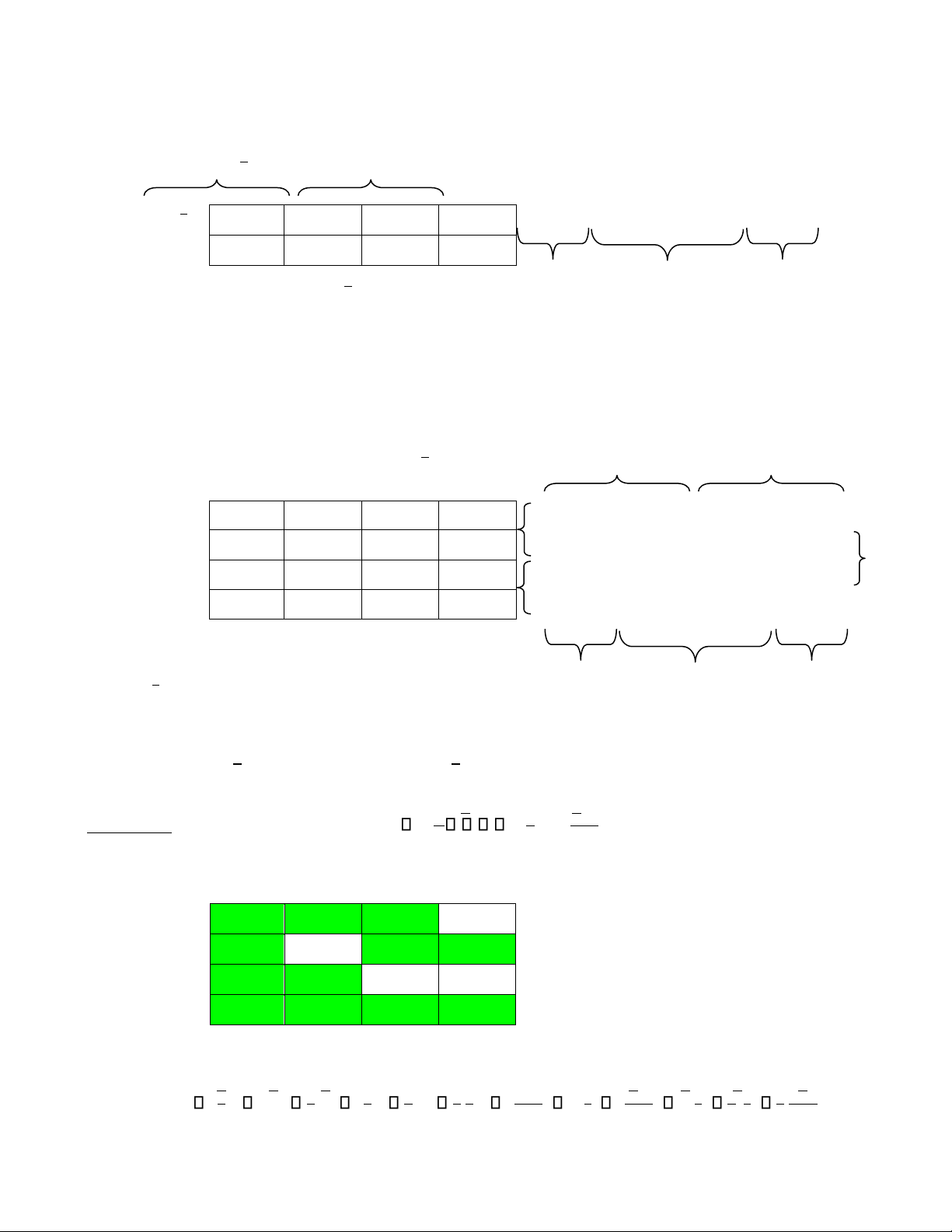
Ví du ̣mẫu: Cho hàm bool f x y z t( , , , ) xyz yt xzt xy zt
Ta có biểu đồ Kar(f) của hàm f là
Từ biểu đồ Karnaugh của f ta có dang d.n.f c ̣ ần tìm là:
f x y z t( , , , ) xyzt xyzt xyzt xyzt xyzt x.yzt xy z. t xyzt xy z. t xyzt xyzt x.y z. t lOMoAR cPSD| 58968691 Ngoài ra, ta có:
f 1(1) {1010,1110,0110,1011,0111,0011,1001,1101,1000,1100,0100,0000} f 1(0) =
ảnh ngược của hàm bool f = những ô đươc tô trong ̣ bìa Kar(f) của f.
f 1(0) {0010,1111,0101,0001} f 1(1)
= ảnh ngươc c ̣ ủa hàm bool f = những ô bi ̣ bỏ trống (không đươc tô) trong ḅ ìa Kar(f) của f.
Bài tập tương tư:̣
+ Vẽ biểu đồ Karnaugh cho f.
+ Tìm dang d.n.f cho ̣ f.
+ Viết dang ̣ f 1(1) f 1(0) ? và dang ̣ f 1(0) f 1(1) ?
+ Phân tích các tế bào lớn có trong biểu đồ Kar(f) của f.
16/ f x y z t( , , , ) xzt xz yzt yt xyz
17/ f x y z t( , , , ) xy zt yzt xz xyt
18/ f x y z t( , , , ) xyz yzt xt yzt yt
19/ f x y z t( , , , ) xyz zt xy
y z. t xz
20/ f x y z t( , , , ) xyt yzt xyz zt yt
21/ f x y z t( , , , ) xy yzt xzt zt xzt
22/ f x y z t( , , , ) xy yzt xz yt zt
* Phân tích các tế bào lớn có trong bia Kar(f) c̀ ủa hàm bool:
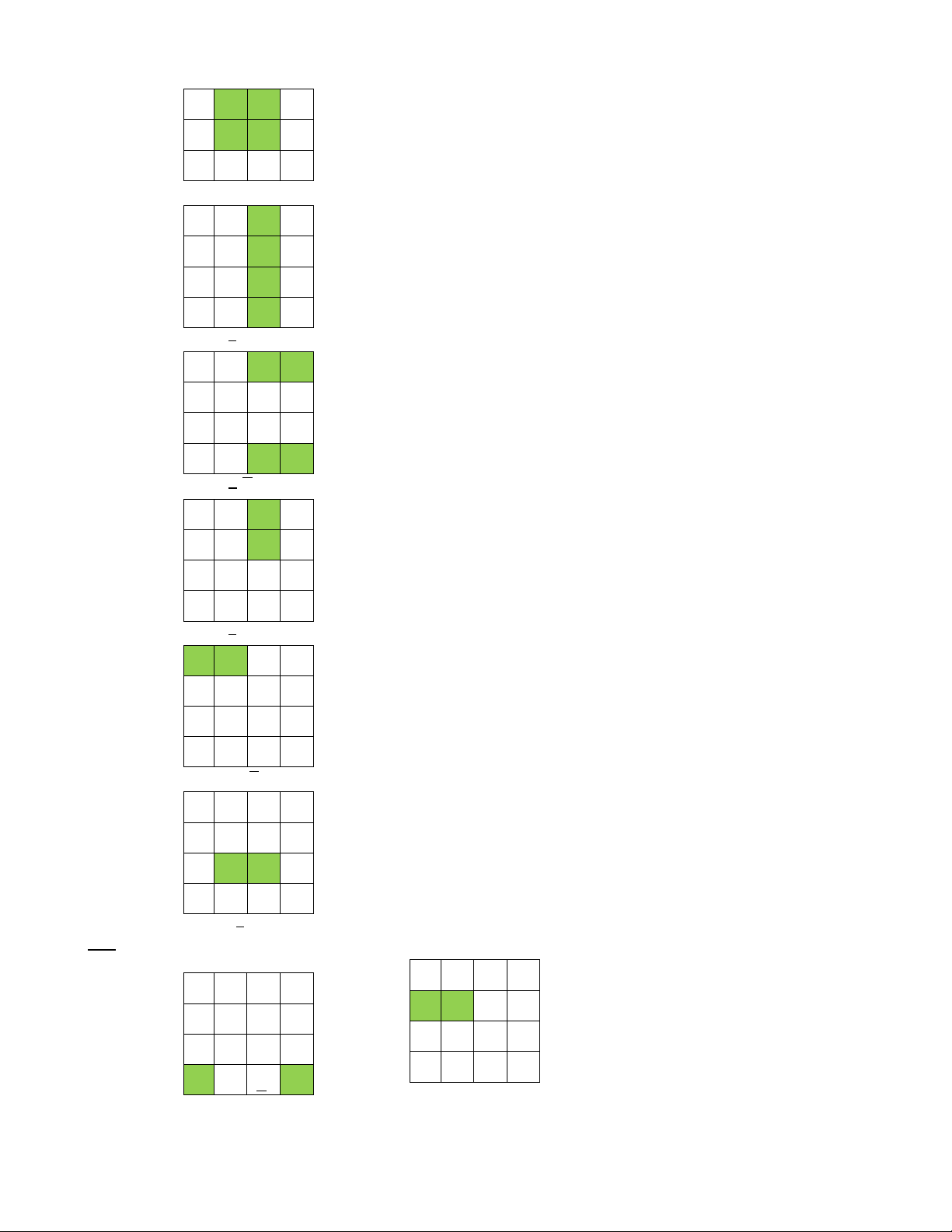
Từ biểu đồ Kar(f) của f, ta phân tích thành các tế bào lớn như sau: + Tế bào 8 ô: z lOMoAR cPSD| 58968691 y x z t + Tế bào 4 ô: yz zt yt lOMoAR cPSD| 58968691 yt xy
xt + Tế bào 2 ô: xyz xzt yzt y z. t
xzt + Tế bào 1 ô: lOMoAR cPSD| 58968691 x.yzt xyzt xyzt xy z. t
Á p dung ̣: phân tích tế bào có trong bìa Kar(f) của hàm bool f.
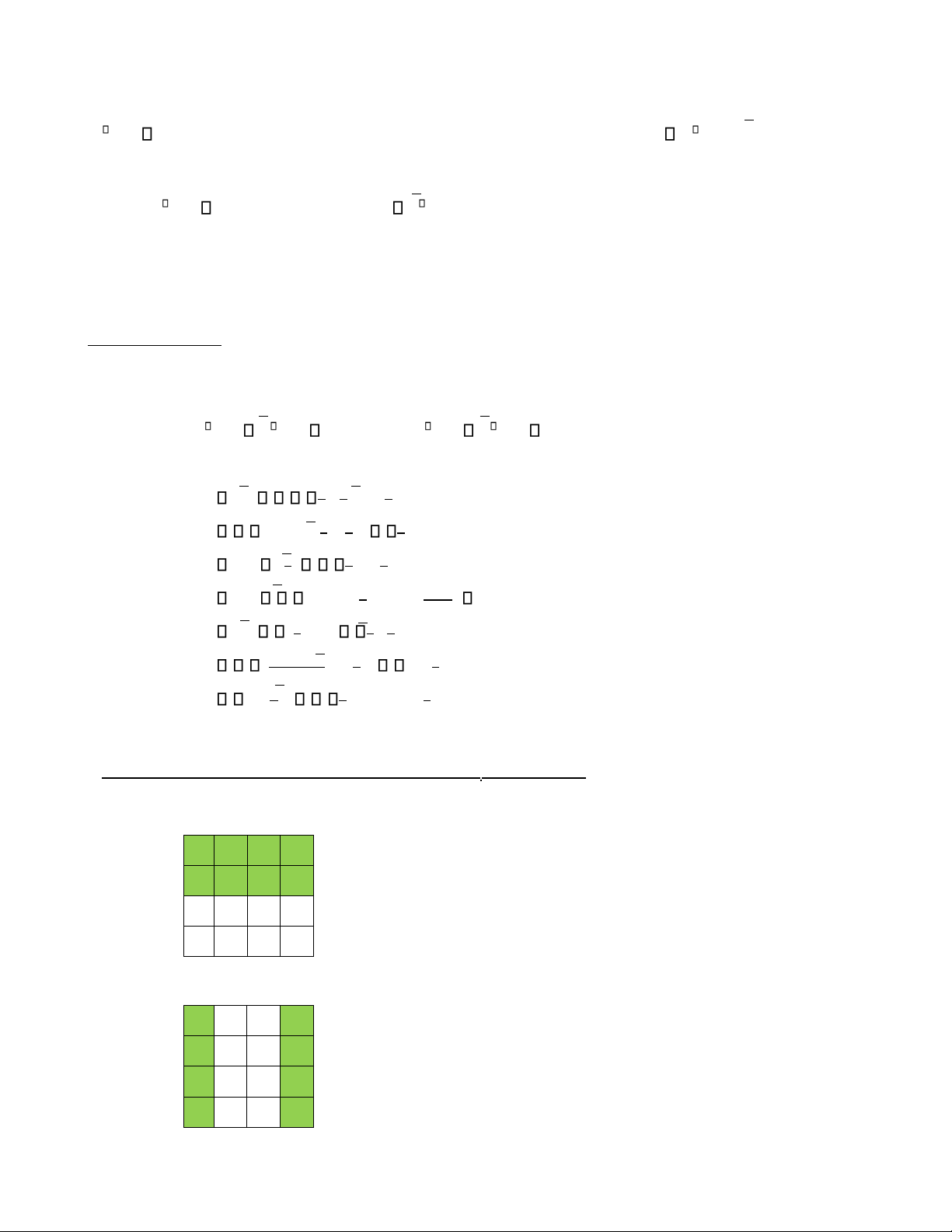
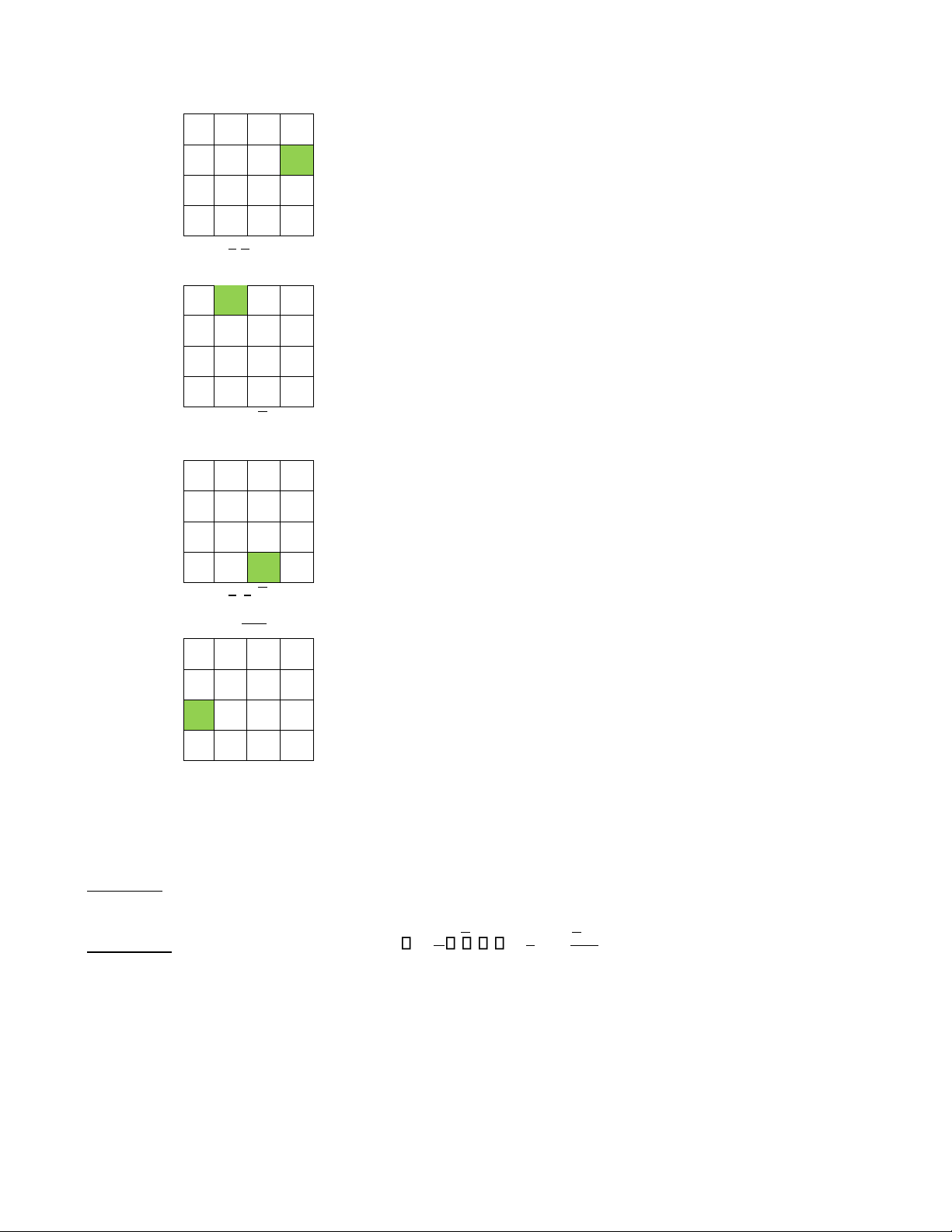
Ví du ̣mẫu: Cho hàm bool f x y z t( , , , ) xyz yt xzt xy zt lOMoAR cPSD| 58968691
Ta c o bi ê u đ ồ Kar( f ) c u a h a m f l a
Ta có các tế bào lớn trong bìa Kar(f) của f là:
+ Tế bào 8 ô: không có;
+ Tế bào 4 ô: T1 : xy ; T2 : zt ; T3 : xz ; T4 : xt ; T5 : yt
+ Tế bào 2 ô: T6: : xyz; T7: : xzt ; T8: : yzt
+ Tế bào 1 ô: không có.