-
Thông tin
-
Hỏi đáp
Buổi 3 Ước lượng cho hệ số hồi quy - Tài liệu tham khảo | Đại học Hoa Sen
Buổi 3 Ước lượng cho hệ số hồi quy - Tài liệu tham khảo | Đại học Hoa Sen và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả
Môn: Thống kê trong kinh doanh (DC 119DV02) 90 tài liệu
Trường: Đại học Hoa Sen 4.8 K tài liệu
Thông tin:
Tác giả:
Preview text:
Bu B ổi i3 3 : :N g N à g y à y 0 6 0 / 6 1 / 0 1 /2 / 0 2 2 0 1 2 ƯỚ Ư C Ớ C LƯỢNG C N H G C O H O H Ệ S Ố S H Ồ H I IQ U Q Y U – Y ƯỚ Ư C Ớ C LƯỢNG C N H G C O H O PH P Ư H Ơ Ư N Ơ G S N A G S I A IS AI S AI S Ố Ố NG N ẪU U N H N I H Ê I N Ê
X =... → X =.... i S = X −n X = XX = ( i ( )2 2 ... 2 ) X ... i S XY B = =
Y = ...→ Y = ... → S = Y − n Y = → S i YY ( i ( )2) 2 2 ... XX 2 ...
B = Y − B X Y = = i S
= X Y −nXY = XY ( i i ) 1 2 ... X Y =... i i - Ph P ươ h n ươ g n gsa s i a hệ ệs ố ố h ồi ồ iq uy u : y 2
Var(β1) = ∑Xi σ2 → Độ lệch chuẩn hệ số β = √Var(β n.S 1: Se 1) XX β1
Var(β2) = 1 σ2 → Độ lệch chuẩn hệ số β = √Var(β S 2: Se 2) XX β2 ƯỚ Ư C Ớ C LƯỢ LƯ NG C G H C O H O K H K O H ẢNG N H G Ệ S Ố H ỒI IQ U Q Y U M Y ẪU U 1. 1 Ướ Ư c ớ lượn ượ g n gđi đ ểm m : β1 ≈ β1 2. 2 Độ Đ ti n ti c
ậy 1 − 𝛼 → 𝑡𝑛−2 𝛼/2 3. 3 Độ Đ c h c í h nh n h x á x c á c : 𝜀 = 𝑡𝑛−2 𝛼/2 . √Var(β𝑖) 4. 4 Ướ Ư c ớ lượng n g : :
+ Ước lượng β1 ∶ β1 ∈ (β1 − 𝜀; β1 + 𝜀)
+ Ước lượng β2 ∶ β2 ∈ (β2 − 𝜀; β2 + 𝜀) ƯỚ Ư C Ớ C LƯỢ LƯ NG C G H C O H O K H K O H ẢNG N S G AI S AI SỐ NG N ẪU U N H N I H Ê I N Ê n − n −
+ Sử dụng bảng tra Phân phối Chi bình phương : 2 2 ; /2 1− / 2 (𝑛 − 2)𝜎2 𝜎2 (𝑛 − 2)𝜎2 ∈ [ ; ] n 2 − n 2 − /2 1 − /2
(𝑛−2)𝜎2 (𝑛−2)𝜎2 → √ ; √ n 2 − n 2 − [ /2 1 − /2 ] Bài Bà it ập ậ p v í v íd ụ ụ : :
Cho bảng số liệu về chi tiêu và thu nhập của n = 1
0 hộ gia đình tại một khu vực, trong đó X
là thu nhập của một hộ gia đình trong tuần và Y là mức chi tiêu của một hộ gia đình trong
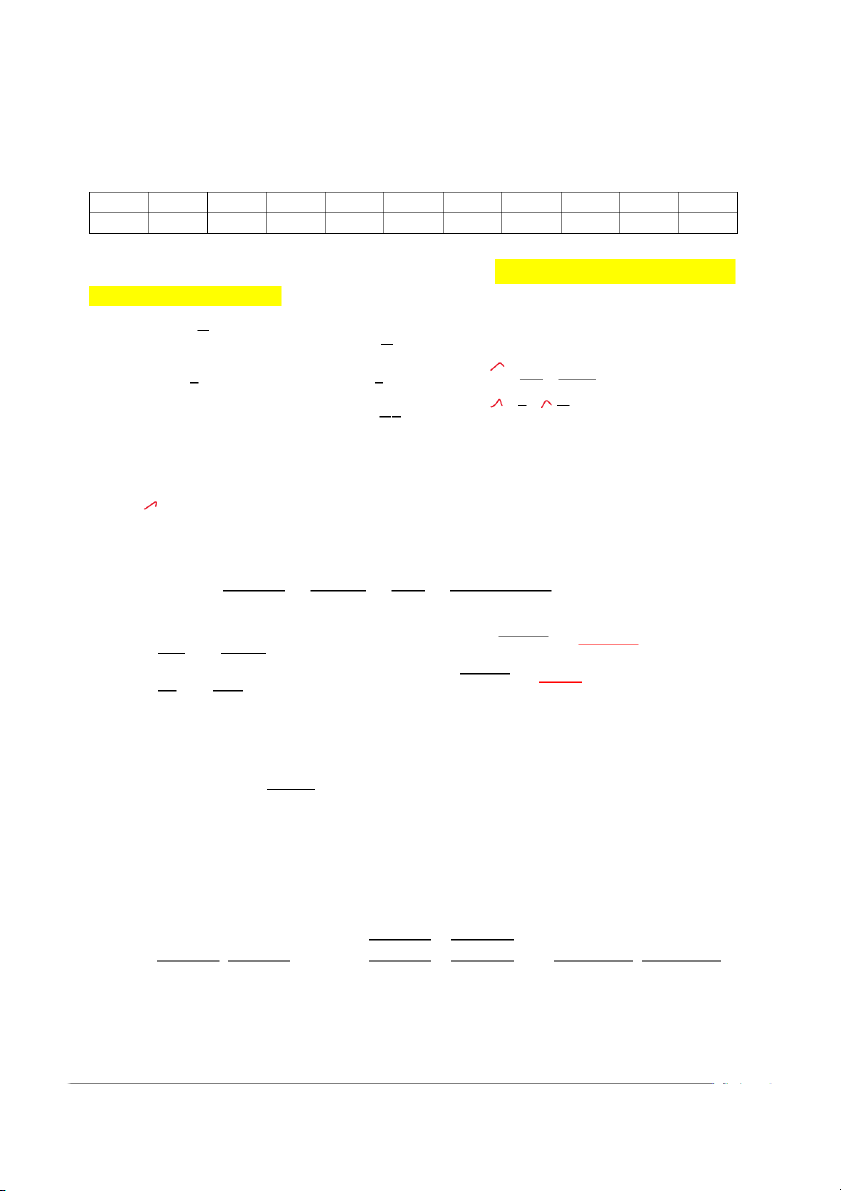
tuần. Xây dựng mô hình hồi quy dạng tuyến tính ước lượng trung bình chi tiêu của một hộ gia đình theo thu nhập X X 11 1 0 1 13 1 0 3 15 1 0 5 17 1 0 7 19 1 0 9 21 2 0 1 23 2 0 3 25 2 0 5 27 2 0 7 29 2 0 9 Y 71 7 95 9 71 7 85 8 12 1 0 2 10 1 8 0 13 1 0 3 13 1 0 3 15 1 0 5 16 1 0 6
Dạng hồi quy tổng thể (PRF) : E(Y | X ) = + X 1 2
Ước lượng khoảng cho hệ số hồi quy tổng thể β1, β2 và phương sai của sai số ngẫu nhiên
với độ tin cậy 1 – 𝛼 = 95% X = 2000 → X = 200 i S = X − n X = XX X = ( i ( )2 2 33000 2 ) 433000 i S XY = = =
Y = 1120 → Y = 112 → S = ( 16040 Y − n (Y)2) 0.4861 2 2 = 8856 → S 33000 XX i YY i 2 Y = = Y − X = − = i S = X Y − n X Y = XY ( i i ) . 112 0, 4861.200 14,7878 134296 1 2 16040 X Y =240040 i i - Các i l đạ ượng sai s ượ ố ố : : T + SS = S = 8856 yy 2 2
+ESS = .S = 0.4861 33000 = 7797,67593 2 xx
+RSS = TSS − ESS = 8856 − 7797.67593 = 1058.32407 + Phương sai phần d ương sai phầ ư : ư : 𝑅𝑆𝑆 𝑅𝑆𝑆 𝑅𝑆𝑆 1058.32407
𝜎2 = (𝑛 − 2) = 10 − 2 = 8 = 8 = 132.29051 + Phươ ư ng sai h ơ ư ệ s ệ ố h ố ồi quy ồ mẫu : 2
Var(β1) = ∑Xi σ2 = 433000 . 132,29051 = 173,5812 → 𝑆𝑒 = √Var(β , = 13.7502 n.S 1) = √173 5812 XX 10.33000 β1
Var(β2) = 1 σ2 = 1 . 132,29051 = 0.0040 → 𝑆𝑒 = √Var(β S 2) = √0.0040 = 0.0633 XX 33000 β2 - Ước l Ướ ượng cho kho ượ ảng h ả ệ s ệ ố h ố ồi qu ồ y tổng th ổ ể ể: :
1. Ước lượng điểm : β1 ≈ β1 = 14,7878 2. Độ tin c Độ ậy 1 - ậ
𝜶 = 95% → 𝛼 = 1 − 95% = 5% = 0.05 → 𝛼/2 = 0,025 → 𝑡𝑛−2 8 𝛼/2 = 𝑡0.025 = 2.306 3. Độ Độ ch c ính xác : h c 𝜀 = 𝑡𝑛−2
𝛼/2 . √Var(β𝑖) = 2.306 x 13.7502 = 31.7080
+ Ước lượng β1 ∶ β1 ∈ (β1 − 𝜀;β1 + 𝜀) = (14,7878 − 31.7080;14,7878 + 31.7080)
+ Ước lượng β2 ∶ β2 ∈ (β2 − 𝜀;β2 + 𝜀) = ⋯ - Ước l Ướ ượng cho ph ượ ương sai của sai s sai củ ố ố ng n ẫu nhiên : ẫ n −2 8 = =17.5345 /2 0.025 n −2 8 = = 2.1797 1 − /2 0.475 (𝑛 − 2)𝜎2 (𝑛 − 2)𝜎2 (𝑛 − 2)𝜎2 8.132,29051 8.132,29051 𝜎2 (𝑛 − 2)𝜎2 ∈ [ ; ] → 𝜎 = [ √ ; √ ] = [ n 2 − n 2 − n 2 − n 2 − 17.5345 ; 2.1797 ] /2 1 − /2 /2 1 − /2 Bài tập 2 : ậ
Số vi khuẩn Y (triệu con) sinh sản sau X giờ được ghi lại trong bảng sau qua một thí nghiệm X 0 1 2 3 4 5 6 7 8 Y 30 32 35 40 48 52 58 62 69
Dạng hồi quy tổng thể (PRF) : E(Y | X ) = + X 1 2
Ước lượng khoảng cho hệ số hồi quy tổng thể β1, β2 và phương sai của sai số ngẫu nhiên
với độ tin cậy 1 – 𝛼 = 95%
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .