C2 - B5 - Phép nhân các số nguyên - T1 | Bài giảng PowerPoint Toán 6 | Cánh diều
Bài giảng điện tử môn Toán 6 sách Cánh diều bao gồm đầy đủ các bài giảng trong cả năm học 2022 - 2023, được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng đẹp mắt.
Preview text:
PHÉP NHÂN CÁC SỐ NGUYÊN (Tiết 1)
Hoạt động 1: Khởi động
Trò chơi “Ai nhanh hơn”
Luật chơi: Mỗi nhóm là một đội chơi. Nhiệm vụ của
mỗi đội là:Điền số thích hợp hợp vào ô trống.
Trong vòng 2 phút, đội nào đúng nhiều nhất và nhanh
nhất sẽ giành chiến thắng và nhận được một món quà.
Hoạt động 1: Khởi động
Điền số thích hợp vào ô trống. a) A = 17+17+17+17 = 1 . ?7 ?4
b) B = (-3).4 = (-3)+(-3)+(-3)+(-3) = ?-12 c) C = -(3.4) = ?-12
d) D = (-3).(-2) = ??
Để biết cách tính kết quả chính xác của phép tính
(-3) .(-2), tích của hai số nguyên âm là số thế
nào? Chúng ta sẽ tìm hiểu trong bài mới ngày hôm nay?
PHÉP NHÂN HAI SỐ NGUYÊN KHÁC DẤU PHÉP NHÂN
PHÉP NHÂN HAI SỐ NGUYÊN CÙNG DẤU CÁC SỐ NGUYÊN
TÍNH CHẤT CỦA PHÉP NHÂN CÁC SỐ NGUYÊN
PHÉP NHÂN CÁC SỐ NGUYÊN
Hoạt động : Hình thành kiến thức
I. PHÉP NHÂN HAI SỐ NGUYÊN KHÁC DẤU
a) Hoàn thành phép tính:
(- 3).4 = (-3) + (-3) + (-3) + (-3) = ? ?
a) So sánh (- 3) . 4 và - (3 . 4) Giải: a) (- 3) . 4
= (- 3) + (- 3) + (- 3) + (- 3) = - 12 b) - (3 . 4) = - (12) (- 3) . 4 = – (3 . 4)
Vậy để tìm tích (- 3) . 4 ta làm như thế nào? – 3 . ( 4 ) = -12
PHÉP NHÂN CÁC SỐ NGUYÊN
I. PHÉP NHÂN HAI SỐ NGUYÊN KHÁC DẤU
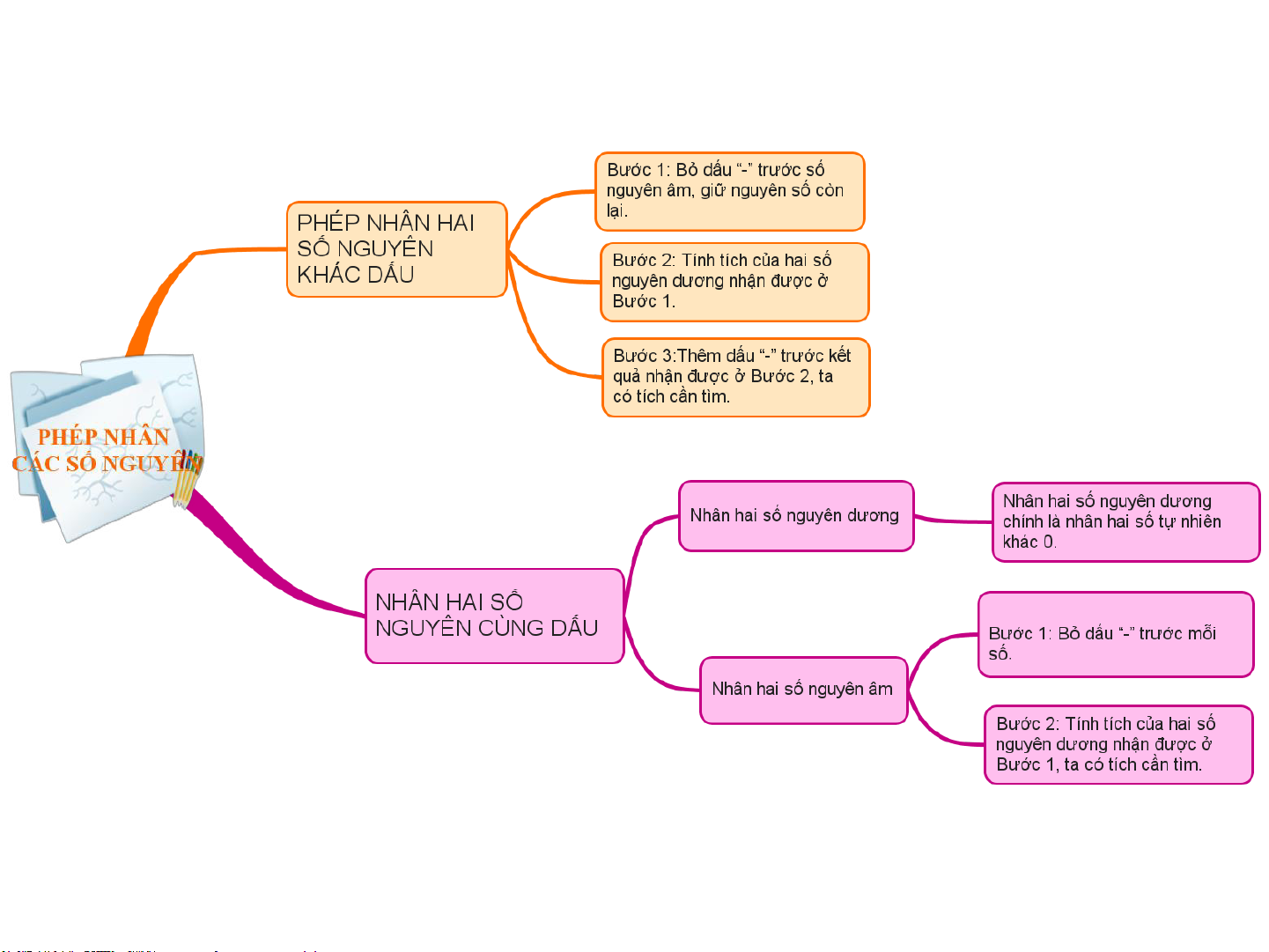
Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại.
Bước 2: Tính tích của hai số nguyên dương nhận được ở Bước 1.
Bước 3:Thêm dấu “-” trước kết quả nhận được ở Bước 2, ta có tích cần tìm.
PHÉP NHÂN CÁC SỐ NGUYÊN
I. PHÉP NHÂN HAI SỐ NGUYÊN KHÁC DẤU Ví dụ 1: Tính a) (-5) . 6
Nhận xét về kết quả của tích b) 5 . (-2) hai số nguyên khác dấu ? Giải:
a) (-5) . 6 = - (5 . 6) = -30
b) 5 . (-2) = - (5 . 2) = -10 * Lưu ý:
Tích của hai số nguyên khác dấu là số nguyên âm.
PHÉP NHÂN CÁC SỐ NGUYÊN
II. PHÉP NHÂN HAI SỐ NGUYÊN CÙNG DẤU
1. Nhân hai số nguyên dương.
Tích của hai số nguyên dương là tích của
hai số tự nhiên khác 0. 5.13 = 65 (+5).(+13) = 65
PHÉP NHÂN CÁC SỐ NGUYÊN
1. Nhân hai số nguyên dương.
2. Nhân hai số nguyên âm.
a) Hãy quan sát kết quả ba tích đầu, ở đó mỗi lần ta giảm đi 1 đơn
vị thừa số thứ hai. Tìm kết quả hai tích cuối? (-3) . 2 = - 6 Tăng 3 đơn vị (-3) . 1 = - 3 Tăng 3 đơn vị (-3) . 0 = 0 Tăng 3 đơn vị (-3) . (-1) = 3? Tăng 3 đơn vị (-3) . (-2) = ?6
PHÉP NHÂN CÁC SỐ NGUYÊN
II. PHÉP NHÂN HAI SỐ NGUYÊN CÙNG DẤU
2. Nhân hai số nguyên âm.
b) So sánh (-3) . (-2) và 3 . 2 (-3) . (-2) = 6
Để tìm tích (-3) . (-2), ta 3 . 2 = 6 làm như thế nào? (-3) . (-2) = 3 . 2 = 6
Để nhân hai số nguyên âm ta làm như sau:
Bước 1: Bỏ dấu “-” trước mỗi số.
Bước 2: Tính tích của hai số nguyên dương
nhận được ở Bước 1, ta có tích cần tìm.
PHÉP NHÂN CÁC SỐ NGUYÊN
II. PHÉP NHÂN HAI SỐ NGUYÊN CÙNG DẤU Ví dụ 2: Tính a) (-5) . (-2) b) -3x với x = -12
Nhận xét về kết quả của tích hai số nguyên cùng dấu ? Giải: a) (-5) . (-2) = 5 . 2 = 10
b) Với x = -12 thì -3x = (-3) . (-12) = 3 . 12 = 36 * Lưu ý:
Tích của hai số nguyên cùng dấu là số nguyên dương.
Hoạt động 3: Luyện tập HOẠT ĐỘNG NHÓM
1.Tính giá trị của mỗi biểu thức trong mỗi trường hợp sau:
a) -6x – 12 với x = -2 b) -4y +20 với y = - 8 Giải: a) Thay x = - 2
=> - 6 . (- 2) – 12 = 12 – 12 = 0 b) Thay y = - 8
=> - 4 . (- 8) + 20 = 32 + 20 = 52
Hoạt động 3: Luyện tập Bài 2: Tính: 8. 25
Từ đó suy ra kết quả của các tích sau: (-8). 25 8.(-25) (-8).(-25)
Giải: Ta có: 8.25 = 200 Suy ra: (-8). 25 = -200 8.(-25) = -200 (-8).(-25) = 200
Hoạt động 3: Luyện tập
3. Điền dấu (+) hay (-) vào ô trống để được khẳng định đúng
Dấu của thừa số Dấu của tích (+) . (+) (+) (–) . (–) (+) (+) . (–) (–) (–) . (+) (–)
Hoạt động 3: Luyện tập Bài 4:
a) Tích hai số nguyên trái dấu luôn là một số nguyên dương S
b) Tích hai số nguyên trái dấu luôn bằng 0 S
c) Tích hai số nguyên dương luôn là một số nguyên dương. Đ
TRÒ CHƠI: “Ô CHỮ” 01s 02s 03s 04s 05s 06s 07s 08s 09s 10s 11s 12s 13s 14s 15s 16s HẾT 17s 18s 19s 20s 21s 22s 23s 24s 25s 26s 27s 28s 29s 30s 31s 32s 33s 34s 35s 36s 37s 38s 39s 40s BẮT ĐẦU GIỜ
Đố: Giáo sư toán học nổi tiếng người Việt Nam? H 21.(-3) = -63 U (-5).2= -10 N (-25).4= -100 G (-16).5 = -80 O (-21).(-6)=126 C (-3) + 5= 2 B -10-50 = -60 A 12 . 20 = 240 -100 -80 126 -60 240 126 2 -63 240 -10 N G O Ô B A Ả O C H A Â U
Ngô Bảo Châu sinh năm 1972 tại Hà Nội, là con
duy nhất của Giáo sư tiến sĩ khoa học Ngô Huy Cẩn
của Viện Cơ học và Phó giáo sư tiến sĩ Trần Lưu
Vân Hiền, công tác tại Bệnh viện Y học cổ truyền
trung ương. Giáo sư Ngô Bảo Châu đoạt giải
toán học Fields ngày 19/8/2010.
Giáo sư Bảo Châu là nhà toán học đầu tiên của
Việt Nam giành được giải thưởng danh giá này. Việt
Nam trở thành quốc gia châu Á thứ hai sau Nhật có
nhà toán học đoạt giải Fields.
Thành tựu của giáo sư Ngô Bảo Châu đã được tạp chí uy tín Time của Mỹ
đánh giá là một trong 10 phát kiến khoa học quan trọng nhất của năm 2009.
Huy chương Fields là một giải thưởng được trao cho tối đa bốn nhà toán học
không quá 40 tuổi tại mỗi kỳ Đại hội Toán học Thế giới của Hiệp hội toán học quốc tế (IMU).
Từ một học sinh chuyên toán ở Hà Nội những năm đầy khó khăn, giáo sư
Ngô Bảo Châu đã trở thành nhà toán học tầm cỡ trong ngành toán thế giới. Hoạt động 4: Vận dụng
Bài 9 : Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong
quý I là – 30 triệu đồng. Quý II lợi nhuận mỗi tháng của
công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của
côn ty Ánh Dương là bao nhiêu? Giải:
+ Lợi nhuận Quý I : (- 30) . 3 = - 90 triệu đồng.
+ Lợi nhuận Quý II: 70 . 3 = 210 triệu đồng.
Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là:
(- 90) + 210 = 120 triệu đồng.