Các dạng bài tập lũy thừa, mũ và lôgarit

Tài liệu gồm 49 trang, được biên soạn bởi quý thầy, cô giáo giảng dạy bộ môn Toán học tại trường THPT Marie Curie, quận 3, thành phố Hồ Chí Minh, phân dạng và tuyển chọn các bài toán trắc nghiệm + tự luận 

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

49 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
THPT Marie Curie
1
Chuyeân ñeà: 3
DẠNG 1.
1. Lũy thừa với số mũ nguyên
Với mỗi số nguyên dương
n
, lũy thừa bậc
n
của số
a
là số
n
a
xác định bởi:
thöøa soá
. ...
n
n
a a a a
với
1n
và
1
aa
Tên gọi:
gọi là cơ số,
n
gọi là số mũ của
n
a
Với mỗi số nguyên
0n
và
0a
, lũy thừa bậc
n
của số
a
là số
n
a
xác định bởi:
1
n
n
a
a
với
0n
và
0
1a
Chú ý:
0
0
và
0
n
(với
n
nguyên âm) không có nghĩa.
1
aa
đúng với mọi
a
.
0
1a
đúng với mọi
0a
.
2. Căn bậc n
Với
n
nguyên dương, căn bậc
n
của một số thực
a
là số thực
b
sao cho
n
ba
.
Khi
n
là số lẻ, mỗi số thực
a
chỉ có một căn bậc
n
được kí hiệu là
n
a
.
Khi
n
là số chẵn, mỗi số thực dương
a
có đúng hai căn bậc
n
là hai số đối nhau được kí
hiệu là
n
a
và
n
a
. Ta gọi
n
a
là căn số học bậc
n
của
a
.
Chú ý:
Căn bậc 1 của số thực
a
chính là
.a
Căn bậc 2 của số thực dương
a
kí hiệu là
a
.
00
n
Số âm không có căn bậc chẵn.
CÔNG THỨC LŨY THỪA
MŨ VÀ LOGRRIT
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
Với
n
nguyên dương lẻ, ta có:
0
n
a
khi
0a
và
0
n
a
khi
0a
.
khi leû
khi chaün
n
n
an
a
an
3. Lũy thừa với số mũ hữu tỉ
Cho
a
là một số thực dương và
m
r
n
, trong đó
m
là một số nguyên còn
n
là một số nguyên
dương. Khi đó, lũy thừa của
a
với số mũ
r
là số
r
a
xác định bởi
m
n
rm
n
a a a
.
Nếu
'
'
mm
nn
thì
'
'
mm
nn
aa
. Do đó trong biểu thức
r
a
, với
r
là một số hữu tỉ, ta thường viết
r
dưới dạng phân số tối giản có mẫu số dương.
1
n
n
aa
(
a
dương,
n
nguyên dương)
4. Lũy thừa với số mũ thực
Mọi số vô tỉ
, bao giờ cũng tồn tại một dãy số hữu tỉ
n
r
để
lim
n
r
.
Cho
là một số thực dương và
là một số vô tỉ. Xét dãy số hữu tỉ
n
r
mà
lim
n
r
. Khi
đó:
alim
n
r
a
.
5. Ghi nhớ
a
với số mũ
nguyên dương thì cơ số
a
có điều kiện
a
.
a
với số mũ
0
hoặc
nguyên âm thì cơ số
a
có điều kiện
0a
.
a
với số mũ
không nguyên thì cơ số
a
có điều kiện
0a
.
6. Công thức
1.
.
m n m n
a a a
2.
m
mn
n
a
a
a
3.

.
nm
m n m n
a a a
4.
..
n
nn
a b a b
5.



n
n
n
aa
b
b
6.
..
n n n
a b a b
7.
n
n
n
aa
b
b
8.
.
n
m n m
aa
9.

m
m
n
m
n
n
a a a
THPT Marie Curie
3
Ví dụ 1. Cho
a
và
b
là các số thực dương, rút gọn biểu thức
1 1 1 1 1 1
4 4 2 2 4 4
P a b a b a b
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Cho
a
là số thực dương, rút gọn biểu thức

31
31
5 3 1 5
.
a
P
aa
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho
a
là số thực dương, rút gọn biểu thức
5
2
3
aa
P
aa
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
B. VÍ DỤ
Tài liệu học tập Toán 12
4
Ví dụ 4. Cho
a
là số thực dương, rút gọn biểu thức


2
3 8 5 4
. : .P a a a a
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Câu 1. Cho
a
là số thực thì căn bậc 1 của
a
bằng
A.
. B.
a
.
C.
0
. D.
a
.
Câu 2. Cho
a
là số thực dương và
n
là số nguyên dương
thì
1
n
a
bằng
A.
na
. B.
a
.
C.
n
a
. D.
n
a
.
Câu 3. Cho
a
là số thực khác 0 thì
0
a
bằng
A.
0
. B.
a
.
C.
1
. D.
1
.
Câu 4. Cho
a
là số thực khác 0 thì
1
n
a
bằng
A.
1
n
a
. B.
n
a
.
C.
n
a
. D.
n
a
.
Câu 5. Cho
a
là số thực dương thì
n
m
a
bằng
A.
.nm
a
. B.
m
n
a
.
C.
n
m
a
. D.
nm
a
.
Câu 6. Cho
a
là số thực dương thì
n
m
a
bằng
A.
n
m
a
. B.
m
n
a
.
C.
m
n
a
. D.
.nm
a
.
Câu 7. Cho
a
là số thực dương thì
n
m
a
bằng
A.
n
m
a
. B.
m
n
a
.
C.
nm
a
. D.
.nm
a
.
C. CÂU HỎI TRẮC NGHIỆM
THPT Marie Curie
5
Câu 8. Cho
a
và
b
là các số thực dương thì
.
n
ab
bằng
A.
.
nn
ab
. B.
nn
ab
.
C.
.
n
ab
. D.
.
n
ab
.
Câu 9. Cho
a
là số thực dương thì
n
m
a
bằng
A.
mn
a
. B.
mn
a
.
C.
m
n
a
. D.
.mn
a
.
Câu 10. Cho
,a
b
là hai số thực dương và
,x
y
là hai số
thực tùy ý. Mệnh đề nào sau đây sai?
A.
xy
y
x
a b ab
. B.
y x y
x
a a a
.
C.
.
x
xx
ab a b
. D.
y
xy
x
aa
.
Câu 11. Cho các số thực
a
,
b
,
m
với
a
và
b
dương. Mệnh
đề nào sau đây là mệnh đề sai?
A.
2
aa
. B.
1
m
m
a
.
C.
.
m
mm
a
ab
b



. D.
.
m
mm
ab a b
.
Câu 12. Cho các số thực
,a
,b
với
0ab
và
1
.
Mệnh đề nào sau đây là mệnh đúng?
A.
.a b a b

B.
a b a b

.
C.
..ab a b
D.
.
aa
b
b



Câu 13. Cho
a
là một số thực dương, biểu thức
3
1
a
bằng
A.
3
a
. B.
1
3
a
.
C.
1
3
a
. D.
1
2
a
.
Câu 14. Rút gọn biểu thức
1
6
3
.P x x
với
0x
ta được
A.
1
8
Px
. B.
2
Px
.
C.
Px
. D.
2
9
Px
.
Câu 15. Rút gọn biểu thức
5
3
3
:Q b b
với
0b
ta được
A.
2
Qb
. B.
5
9
Qb
.
C.
4
3
Qb
. D.
4
3
Qb
.
Câu 16. Cho
a
là một số thực dương, biểu thức
1
3
.aa
bằng
A.
2
5
a
. B.
1
3
a
.
C.
5
6
a
. D.
1
6
a
.
Tài liệu học tập Toán 12
6
Câu 17. Rút gọn biểu thức
3
3
2
.P a a
với
0a
ta được
A.
1
2
Pa
. B.
9
2
Pa
.
C.
11
6
Pa
. D.
3
Pa
.
Câu 18. Cho
a
là một số thực dương, biểu thức
2
3
.aa
bằng
A.
7
6
a
. B.
7
3
a
.
C.
5
3
a
. D.
1
3
a
.
Câu 19. Cho
a
là một số thực dương, biểu thức
2 3 2 3 2 2
.aa

được kết quả bằng
A.
. B.
62
a
.
C.
4
a
. D.
1
.
Câu 20. Cho
a
là một số thực dương, biểu thức
2
1 2 2 1 2
.aa

bằng
A.
. B.
3
a
.
C.
5
a
. D.
1
.
Câu 21. Giá trị của biểu thức
2017 2016
7 4 3 4 3 7
bằng
A.
. B.
7 4 3
.
C.
7 4 3
. D.
2016
7 4 3
.
Câu 22. Với
x
là số thực không âm thì biểu thức
3
23
xx
bằng
A.
7
6
x
. B.
5
3
x
.
C.
21
2
x
. D.
8
9
x
.
Câu 23. Cho biểu thức
6
5
3
..P x x x
(
0x
). Mệnh đề nào
dưới đây đúng?
A.
5
2
.Px
B.
2
3
.Px
C.
5
3
.Px
D.
7
3
.Px
Câu 24. Cho hai số thực dương a và b. Biểu thức
5
3
aba
bab
được viết dưới dạng lũy thừa với số mũ hữu tỉ là
A. . B. .
C. . D.
7
30
.
a
b



31
30
.
a
b



30
31
.
a
b



1
6
.
a
b



THPT Marie Curie
1
DẠNG 2.
1. Định nghĩa
Cho hai số dương
,a
b
với
1a
. Số
thỏa
ab
gọi là logarit cơ số
a
của
b
và ghi
log
a
b
.
Như vậy:
log
a
a b b
với
,a
0b
và
1a
.
2. Định nghĩa
Lôgarit thập phân:
10
log logaa
Lôgarit Néper:
ln log
e
aa
(với
1
lim 1 2,7183
x
x
e
x




)
3. Công thức
1.
log 1 0
a
2.
log 1
a
a
3.
log
n
a
an
4.
log
a
n
an
5.
log . log log
a a a
b c b c
6.




log log log
a a a
b
bc
c
7.
log log
n
aa
b n b
8.
1
log log
n
a
a
bb
n
9.
1
log
log
a
b
b
a
10.
log log .log
a a c
b c b
11.
log
log
ln
log
log log ln
c
a
c
b
b
b
b
a a a
12.
log log
bb
ca
ac
CÔNG THỨC LOGARIT
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
Ví dụ 1. Tính
1 3 2
4
log log 4.log 3P
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tính

25
4
1
log 3 log 5
1 log 5
2
16 4P
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Cho
2
log 4a
và
9
1
log
2
b
. Tính







2
2 2 2 1
2
3
1
log log log logPa
b
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Cho
2
log 2x
. Tính
2
2 4 1
2
log 3log 5log 2 7P x x x
.
B. VÍ DỤ
THPT Marie Curie
3
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Câu 1. Với
a
là số thực dương bất kì, mệnh đề nào sau đây
đúng?
A.
log 3 3logaa
. B.
3
1
log log
3
aa
.
C.
3
log 3logaa
. D.
1
log 3 log
3
aa
.
Câu 2. Với
a
và
b
là hai số thực dương tùy ý,
2
log ab
bằng
A.
2log logab
. B.
log 2logab
.
C.
2 log logab
. D.
1
log log
2
ab
.
Câu 3. Với các số thực dương
a
,
b
bất kì. Mệnh đề nào
dưới đây đúng?
A.
ln ln lnab a b
. B.
ln ln .lnab a b
.
C.
ln
ln
ln
aa
bb
. D.
ln ln ln
a
ba
b

.
Câu 4. Cho
1, 0, 0, 1a a b b
. Đng thc nào sau đây
sai?
A.
2
1
log log
2
aa
bb
. B.
1
log
log
a
b
b
a
.
C.
2
log b log
a
a
b
. D.
2
log .log 2
ab
ba
.
Câu 5. Cho
,a
b
là hai số thực dương và khác 1. Khng
định nào sau đây sai?
A.
log .log
n
aa
b n b
. B.
1
log
log
a
b
b
a
.
C.
log 1 log
aa
a
b
b

. D.
log log 1
aa
b
b
a

.
Câu 6. Cho
,a
,b
c
là các số thực dương,
a
và
c
khác 1.
Mệnh đề nào dưới đây sai?
C. CÂU HỎI TRẮC NGHIỆM
Tài liệu học tập Toán 12
4
A.
log log log
a c c
b a b
. B.
log log
c
a
a
b c b
.
C.
log log log
a a a
b
bc
c




. D.
log log log
a a a
bc b c
.
Câu 7. Cho
a
là số thực dương và khác 1. Mệnh đề nào sau
đây đúng?
A.
2
ln
log
ln2
a
a
. B.
2
lna
log
log 2
a
.
C.
2
log 2
log
loga
a
. D.
2
loga
log
ln2
a
.
Câu 8. Cho hai số thực dương
a
và
b
. Mệnh đề đề nào sau
đây sai?
A.
2
22
log 2logab ab
. B.
2 2 2
log log loga b ab
.
C.
2 2 2
log log log
a
ab
b

. D.
2 2 2
log log loga b a b
.
Câu 9. Cho
,a
,b
c
là các số dương và
1a
. Mệnh đề nào
sau đây sai?
A.
log .log log ( )
a a a
b c b c
. B.
log log log ( . )
a a a
b c b c
.
C.
log log log
a a a
b
bc
c




. D.
1
log log
aa
b
b




.
Câu 10. Cho hai số dương
a
,
b
và
1a
. Mệnh đề nào dưới
đây sai?
A.
log
a
a
. B.
1
log
a
a
.
C.
1
log
log
a
a
a
bb



. D.
log 1 log
aa
ab b
.
Câu 11. Giá trị của
3
log 5
9
bằng
A.
2
5
. B.
10
.
C.
25
. D.
5
.
Câu 12. Cho
a
là số thực dương khác 1. Với mọi số thực
dương
x
và
y
, biểu thc
log
a
x
y
bằng
A.
log log
aa
xy
. B.
log log
aa
xy
.
C.
log
a
xy
. D.
log
log
a
a
x
y
.
Câu 13. Cho
a
là số thực dương tùy ý khác 1. Biểu thc
2
log a
bằng
A.
log 2
a
. B.
2
1
log a
.
C.
1
log 2
a
. D.
log 2
a
.
THPT Marie Curie
5
Câu 14. Với
a
là số thực dương tùy ý,
ln 5 ln 3aa
bằng
A.
ln 5
ln 3
a
a
. B.
ln 2a
.
C.
5
ln
3
. D.
ln 5
ln 3
.
Câu 15. Với
a
là số thực dương tùy ý,
3
log 3a
bằng
A.
3
3log a
. B.
3
3 log a
.
C.
3
1 log a
. D.
3
1 log a
.
Câu 16. Với
a
là số thực dương tùy ý,
3
3
log
a



bằng
A.
3
1
log a
. B.
3
1 log a
.
C.
3
1 log a
. D.
3
3 log a
.
Câu 17. Với
a
là số thực dương tùy ý,
3
log 9a
bằng
A.
3
2 log .a
B.
3
2log .a
C.
3
2 log .a
D.
3
9log .a
Câu 18. Cho
a
là số thực dương khác 2. Giá trị của
2
2
log
4
a
a



bằng
A.
1
2
. B.
2
.
C.
1
2
. D.
2
.
Câu 19. Cho
a
là số thực dương khác
4
, khi đó
3
4
log
64
a
a



bằng
A.
3
. B.
1
3
.
C.
3
. D.
1
3
.
Câu 20. Giá trị của
3
log
a
a
(
0a
và
1a
) bằng
A. 3. B.
1
3
.
C.
1
3
. D.
3
.
Câu 21. Cho
a
là số thực dương và khác 1, khi đó
log
a
a
bằng
A.
1
2
. B.
0
.
C.
2
. D.
2
.
Câu 22. Cho
a
là số thực dương,
1a
, khi đó
3
3
log
a
a
bằng
A.
3
. B.
1
.
Tài liệu học tập Toán 12
6
C.
9
. D.
1
3
.
Câu 23. Với
01a
, giá trị của
log
a
aa
bằng
A.
3
4
. B.
4
3
.
C.
3
2
. D.
3
4
.
Câu 24. Xét
a
là số thực bất kì và
0a
, khi đó
2
2
log a
bằng
A.
2
4log a
. B.
2
1
log
2
a
.
C.
2
1
log
2
a
. D.
2
1
log
4
a
.
Câu 25. Cho các số thực dương
,a
b
với
1a
. Biểu thc
2
log ( )
a
ab
bằng
A.
1
log
2
a
b
. B.
2 2log
a
b
.
C.
1
log
4
a
b
. D.
11
log
22
a
b
.
Câu 26. Cho
a
và
b
là hai số thực dương tùy ý,
ln ab
bằng
A.
1
ln ln
2
ab
. B.
1
ln ln
2
ab
.
C.
2ln ab
. D.
1
ln ln
2
ab
.
Câu 27. Cho
log 2
a
b
, khi đó
4
82
log
a
ba
bằng
A.
9
2
. B.
9
.
C.
2
. D.
8
.
Câu 28. Cho
log 2
a
b
và
log 3
a
c
, khi đó
23
log
a
bc
bằng
A.
31
. B.
13
.
C.
30
. D.
108
.
Câu 29. Với
,a
b
là các số thực dương tùy ý và
a
khác 1, khi
đó biểu thc
2
36
log log
a
a
bb
bằng
A.
9log
a
b
. B.
27log
a
b
.
C.
15log
a
b
. D.
6log
a
b
.
Câu 30. Cho
2
log xa
, khi đó
2
2
log 4x
bằng
A.
2.a
B.
4 2 .a
C.
4.a
D.
2 2 .a
Câu 31. Với các số thực dương
,a
b
bất kì, khi đó
3
2
2
log
a
b



bằng
THPT Marie Curie
7
A.
22
1 3log logab
. B.
22
1
1 log log
3
ab
.
C.
22
1 3log logab
. D.
22
1
1 log log
3
ab
.
Câu 32. Với
a
và
b
là hai số thực dương tùy ý,
23
ln ab
bằng
A.
6 ln lnab
. B.
2ln 3lnab
.
C.
6ln lnab
. D.
11
ln ln
23
ab
.
Câu 33. Với
a
,
b
là hai số thực dương tùy ý, khi đó
2
ln
1
ab
a



bằng
A.
ln 2ln ln 1a b a
. B.
ln ln ln 1a b a
.
C.
ln 2ln ln 1a b a
. D.
2lnb
.
Câu 34. Cho
3
log 2a
và
2
1
log
2
b
. Giá trị của biểu thc
2
3 3 1
4
2log log (3 ) logab

bằng
A.
5
4
. B.
4
.
C.
0
. D.
3
2
.
Câu 35. Cho
,0ab
và
,1ab
, biểu thc
34
log .log
b
a
ba
có
giá trị bằng
A.
18
. B.
24
.
C.
12
. D.
6
.
Câu 36. Cho
1n
là một số nguyên. Giá trị của biểu thc
23
1 1 1
..
log ! log ! log !
n
n n n
bằng
A.
.n
B. 0.
C. 1. D.
!.n
Câu 37. Cho
log 3,
a
x
log 4
b
x
với
,a
b
là các số thực lớn
hơn 1, khi đó
log
ab
x
bằng
A.
7
12
. B.
1
12
.
C.
12
. D.
12
7
.
Câu 38. Với các số thực dương
,x
y
tùy ý, đặt
3
log xa
và
3
log yb
, khi đó
3
27
log
x
y




bằng
A.
9
2
a
b



. B.
2
a
b
.
Tài liệu học tập Toán 12
8
C.
9
2
a
b



. D.
2
a
b
.
Câu 39. Cho
,a
b
là các số thực dương thỏa mãn
1,a
ab
và
log 3
a
b
, khi đó
log
b
a
b
a
bằng
A.
5 3 3
. B.
13
.
C.
13
. D.
5 3 3
.
Câu 40. Cho
a
và
b
là các số thực dương và
1a
thỏa
mãn
log 2
a
b
, khi đó
2
2
log
ab
b
a
bằng
A.
2 3 2
2
. B.
2
2 2 1
.
C.
21
21
. D.
6 5 2
2

.
Câu 41. Với
,ab
là hai số thực dương và
3
1,log
aa
a a b
bằng
A.
33
log
22
a
b
. B.
3
log
2
a
b
.
C.
24
log
39
a
b
. D.
2
log
3
a
b
Câu 42. Đặt . Hãy biểu diễn
theo và .
A. . B. .
C. . D. .
Câu 43. Cho là các số thực dương khác 1 và thỏa mãn
. Tính giá trị của biểu thức
A. . B. .
C. . D. .
Câu 44. Đặt
35
log 4, log 4.ab
Hãy biểu diễn
12
log 80
theo
a
và
.b
.
A
2
12
22
log 80
a ab
ab b
.. B.
2
12
22
log 80
a ab
ab
.
C.
12
2
log 80
a ab
ab b
. D.
12
2
log 80
a ab
ab
.
12 12
log 6 ;log 7ab
2
log 7
a
b
2
log 7
1
b
a
2
log 7
1
b
a
2
log 7
1
a
b
2
log 7
1
a
b
,ab
log 3
a
b
3
T log .
b
a
b
a
1T
3
4
T 
4T 
4T
THPT Marie Curie
1
DẠNG 3.
1.
log
fx
a
a b f x b
2.
f x g x
a a f x g x
3.

01
log
a
b
a
f x b f x a
4.



hoaëc
01
00
log log
a
aa
f x g x
f x g x
f x g x
Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 1. Giải phương trình
2
5
6
2
2 16 2
xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Giải phương trình
2
4 5 1
39
x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
PHƯƠNG TRÌNH MŨ VÀ LOGARIT
B. VÍ DỤ
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
Ví dụ 3. Giải phương trình
11
3 6.3 2.3 3
x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Giải phương trình
12
2 .3 .5 200
x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Giải phương trình
4 2 6 0
xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Giải phương trình
2
2
log ( 1) 2x 
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 7. Giải phương trình
2
log (9 2 ) 3
x
x
.
Lời giải
THPT Marie Curie
3
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 8. Giải phương trình
22
log ( 2) log 2 2xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 9. Giải phương trình
5 5 5
log log 6 log 2x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 10. Giải phương trình
2
31
3
log ( 1) log (2 1) 2xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Tài liệu học tập Toán 12
4
Câu 1. Nghiệm của phương trình
1
3 27
x
là
A.
9x
. B.
3x
.
C.
4x
. D.
10x
.
Câu 2. Phương trình
21
5 125
x
có nghiệm là
A.
5
2
x
. B.
3
2
x
.
C.
3x
. D.
1x
.
Câu 3. Phương trình
21
2 32
x
có nghiệm là
A.
5
2
x
. B.
2x
.
C.
3
2
x
. D.
3x
.
Câu 4. Phương trình
2
2 4 5
2 32
xx
có bao nhiêu nghiệm?
A. 3. B. 0.
C. 1. D. 2.
Câu 5. Tổng các nghiệm của phương trình
42
3
3 81
xx
bằng
A.
0.
B.
1.
C.
3.
D.
4.
Câu 6. Tập nghiệm của phương trình
31
4 7 16
0
7 4 49
xx

là
A.
1
2



. B.
2
.
C.
11
;
22



. D.
1
;2
2



.
Câu 7. Số nghiệm thực của phương trình
31
39
xx
là
A. 2. B. 0.
C. 1. D. 3.
Câu 8. Tổng bình phương các nghiệm của phương trình
2
32
1
5
5
x
x



bằng
A. 0. B. 5.
C. 2. D. 3.
Câu 9. Phương trình
2 3 4
48
xx
có nghiệm là
A.
6
7
. B.
2
3
.
C.
4
5
. D. 2.
C. CÂU HỎI TRẮC NGHIỆM
THPT Marie Curie
5
Câu 10. Phương trình
1
2
1
125
25
x
x



có nghiệm là
A.
1
4
x 
. B.
1
8
x 
.
C.
1
4
x
. D.
4x
.
Câu 11. Tập hợp nghiệm của phương trình
2
24
56
65
x x x
là
A.
1; 4
. B. .
C.
1
. D.
0; 4
.
Câu 12. Phương trình
21
16 8
x
x
có nghiệm là
A.
3x 
. B.
2x
.
C.
3x
. D.
2x 
.
Câu 13. Tổng các nghiệm của phương trình
x
2
8 2 3
(0,4) (6,25)
x
bằng
A. 3. B. 5.
C.
5
. D.
3
.
Câu 14. Cho
1
2
4
b
a



. Đẳng thức nào sau đây đúng?
A.
2ab
. B.
2ab
.
C.
2ab 
. D.
4ab
.
Câu 15. Cho phương trình
1
4 2 3 0
xx
. Khi đặt
2
x
t
, ta
được phương trình nào dưới đây?
A.
2
2 3 0t 
. B.
2
30tt
.
C.
4 3 0t 
. D.
2
2 3 0tt
.
Câu 16. Số nghiệm của phương trình
9 4.3 3 0
xx
là
A. 3. B. 1.
C. 2. D. 0.
Câu 17. Số nghiệm nguyên của phương trình
12
4 2 1 0
xx
là
A. 0. B. 1.
C. 4. D. 2.
Câu 18. Nghiệm của phương trình
2
log 3x
là
A. 9. B. 6.
C. 8. D. 5.
Câu 19. Nghiệm của phương trình
2
log 1 2x
là
A.
4x 
. B.
3x 
.
C.
3x
. D.
5x
.
Câu 20. Nghiệm của phương trình
25
1
log 1
2
x 
là
A.
6x 
. B.
6x
.
Tài liệu học tập Toán 12
6
C.
4x
. D.
23
2
x
.
Câu 21. Nghiệm của phương trình
2
log 5 4x 
là
A.
21x
. B.
3x
.
C.
11x
. D.
13x
.
Câu 22. Nghiệm của phương trình
4
log ( 1) 3x 
là
A.
63x
. B.
65x
.
C.
80x
. D.
82x
.
Câu 23. Phương trình
log 9 1x 
có nghiệm là
A.
1x
. B.
8x
.
C.
9x 
. D.
0x
.
Câu 24. Tập nghiệm của phương trình
2
2
log 1 3x 
là
A.
3;3
. B.
3
.
C.
3
. D.
10; 10
.
Câu 25. Phương trình
2
3
log 1 1x 
có nghiệm là
A.
2x 
. B.
4x 
.
C.
2x 
. D.
6x 
.
Câu 26. Tập nghiệm của phương trình
2
3
log 2 1xx
là
A.
;13
. B.
;13
.
C.
0
. D.
3
.
Câu 27. Nghiệm của phương trình
25
1
log 1
2
x 
là
A.
6x 
. B.
6x
.
C.
4x
. D.
23
2
x
.
Câu 28. Nghiệm của phương trình
3
log 2 2x 
là
A.
9x
. B.
8x
.
C.
11x
. D.
10x
.
Câu 29. Tập nghiệm của phương trình
2
3
log 2 3 1xx
là
A.
1
0;
2



. B.
0
.
C.
1
2



. D.
1
0;
2



.
Câu 30. Số nghiệm của phương trình là
A.
B.
C. D.
Câu 31. Tập nghiệm của phương trình
2
2
log 2 1xx
là
A.
0
. B.
0;1
.
2
2
log 3 2xx
2.
1.
0.
3.
THPT Marie Curie
7
C.
1;0
. D.
1
.
Câu 32. Phương trình
33
log 2 1 log 1 1xx
có tập
nghiệm là
A.
4
. B.
3
.
C.
2
. D.
1
.
Câu 33. Phương trình
22
log 1 log 1 3xx
có tập
nghiệm là
A.
3;3
. B.
4
.
C.
3
. D.
10; 10
.
Câu 34. Phương trình
3 3 3
log 2 log 2 log 5xx
có tất
cả bao nhiêu nghiệm?
A. 2. B. 0.
C. 1. D. 3.
Câu 35. Tích giá trị tất cả các nghiệm của phương trình
2
1 log log 2 8xx
bằng
A.
3
. B.
4
.
C.
2
. D.
3
.
Câu 36. Tập nghiệm của phương trình
2
33
log 2 3 log 1 1x x x
là
A.
0;5
. B.
0
.
C.
1; 5
. D.
5
.
Câu 37. Phương trình
24
log 3 log ( 8) 2 0xx

có tất
cả bao nhiêu nghiệm?
A. 1. B. 2.
C. 3. D. 4.
Câu 38. Giá trị của
a
sao cho phương trình
2
log 3xa
có nghiệm
2x
là
A. 10. B. 5.
C. 6. D. 1.
Câu 39. Tổng giá trị tất cả các nghiệm của phương trình
3 9 27 81
2
log .log .log .log
3
x x x x
bằng
A.
82
9
. B.
80
9
.
C.
9
. D.
0
.
Câu 40. Với mọi
,a
,b
x
là các số thực dương thỏa mãn
2 2 2
log 5log 3logx a b
, mệnh đề nào dưới đây đúng?
A.
35x a b
. B.
53x a b
.
C.
53
x a b
. D.
53
x a b
.
Tài liệu học tập Toán 12
8
Câu 41. Số nghiệm của phương trình
7
log 6 7 1
x
x
là
A. 3. B. 0.
C. 1. D. 2.
Câu 42. Tổng tất cả các nghiệm của phương trình
2
log 6 2 1
x
x
bằng
A.
. B.
1
.
C.
0
. D.
3
.
Câu 43. Tổng tất cả các nghiệm của phương trình
3
log 7 3 2
x
x
bằng
A. 2. B. 1.
C. 7. D. 3.
THPT Marie Curie
1
DẠNG 4.
Nếu
1a
thì
( ) ( )f x g x
a a f x g x
()
log
fx
a
a b f x b

log
0
b
a
f x a
f x b
fx

log log
0
aa
f x g x
f x g x
fx
Nếu
1a
thì
( ) ( )f x g x
a a f x g x
()
log
fx
a
a b f x b

log
0
b
a
f x a
f x b
fx

log log
0
aa
f x g x
f x g x
gx
Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 1. Giải bất phương trình
2
6
31
xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Giải bất phương trình
2
54
1
4
2
xx



.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT
B. VÍ DỤ
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Giải bất phương trình



3
1
1
2
16
x
x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Giải bất phương trình
1
9 3 4
xx

.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Giải bất phương trình

3
log 4 3 2x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Giải bất phương trình
1
2
3 log 6 1 0x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
THPT Marie Curie
3
.......................................................................................................................................................................
Ví dụ 7. Giải bất phương trình
2
0,8 0,8
log ( 1) log (2 5)x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 8. Giải bất phương trình
22
log 3 1 log 1xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 9. Giải bất phương trình
2
22
log log 0xx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 10. Giải bất phương trình
2
log( 2) 2log(3 )x x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Tài liệu học tập Toán 12
4
Câu 1. Tập nghiệm của bất phương trình
31
x
là
A.
;0
. B. .
C.
1; 
. D.
0; 
.
Câu 2. Nghiệm của bất phương trình
2
3 243
x
là
A.
7x
. B.
7x
.
C.
7x
. D.
27x
.
Câu 3. Tập nghiệm của bất phương trình:
2
1
3
9
x
là
A.
4; 
. B.
;0
.
C.
0; 
. D.
;4
.
Câu 4. Tập nghiệm của bất phương trình
1
1
50
5
x

là
A.
1; 
. B.
1; 
.
C.
2; 
. D.
;2
.
Câu 5. Tập nghiệm của bất phương trình
13
2 25
54
x



là
A.
;1
. B.
1
;
3



.
C.
1
;
3




. D.
1; 
.
Câu 6. Tập nghiệm của bất phương trình
4
1
8
2
x



là
A.
1; 
. B.
1; 
.
C.
;1
. D.
;1
.
Câu 7. Tập nghiệm của bất phương trình
34
1
9
3
x



là
A.
5
;.
4




B.
5
;.
4




C.
5
;
4



D.
5
;.
4



Câu 8. Tập nghiệm của bất phương trình
1
3 1 4 2 3
x
là
A.
1; 
. B.
1; 
.
C.
;1
. D.
;1
.
Câu 9. Bất phương trình
6 5 6 5
x
có tập
THPT Marie Curie
5
nghiệm là
A.
;1
. B.
;1
.
C.
1; 
. D.
1; 
.
Câu 10. Tập nghiệm của bất phương trình
2
2
3 27
xx
là
A.
;1
. B.
3; 
.
C.
1;3
. D.
; 1 3; 
.
Câu 11. Tập nghiệm của bất phương trình
2
2
28
xx
là
A.
;1
. B.
1;3
.
C.
3;
. D.
; 1 3;
.
Câu 12. Tập nghiệm của bất phương trình
2
2
11
3 27
xx



là
A.
3;1
. B.
1;3
.
C.
1;3
. D.
; 3 1; 
.
Câu 13. Bất phương trình
2
2
1
5
5
xx



có tập nghiệm là
A.
( 1; ) 
. B.
( ;1)
.
C. . D.
.
Câu 14. Tập nghiệm của bất phương trình
26
22
xx
là
A.
0;6
. B.
;6
.
C.
0;64
. D.
6;
.
Câu 15. Tập nghiệm của bất phương trình
13
33
44
xx
là
A.
2;
. B.
;2
.
C.
2; 
. D.
;2
.
Câu 16. Tập nghiệm của bất phương trình
1
3
3
55
x
x
là
A.
5;
. B.
0;
.
C.
18
. D.
;0
.
Câu 17. Tập nghiệm của bất phương trình
2
6
22
xx
là
A.
2;
. B.
;3
.
C.
3;2
. D.
2;3
.
Câu 18. Tập hợp nghiệm của bất phương trình
2
6
22
xx
là
A.
2;
. B.
;3
.
C.
3;2
. D.
2;3
.
Câu 19. Tập nghiệm của bất phương trình
Tài liệu học tập Toán 12
6
2
56
1
0,125
8
x
x



là
A.
3; .
B.
;2 3; .
C.
;2 .
D.
2;3 .
Câu 20. Tập nghiệm của bất phương trình
32.4 18.2 1 0
xx
là
A.
4; 1
. B.
1; 4
.
C.
2; 4
. D.
11
;
16 2



.
Câu 21. Tập nghiệm của bất phương trình
3
log 2 3 1x 
là
A.
1; 
. B.
1
;
6




.
C.
2;
. D.
3; 
.
Câu 22. Bất phương trình
1
2
log 2 1x
có tập nghiệm là
A.
0; 
. B.
( 2; 0]
.
C.
;0
. D.
1
2;
2


.
Câu 23. Tập nghiệm của bất phương trình
2
log (3 1) 3x 
là
A.
3; 
. B.
1
;3
3



.
C.
;3
. D.
10
;
3




.
Câu 24. Bất phương trình
2
log 1 3x 
có tập nghiệm là
tập con của tập
X
nào sau đây?
A.
0;10X
. B.
1;7X 
.
C.
9;X 
. D.
10;X
.
Câu 25. Bất phương trình
3
log 2 1 3x
có nghiệm là
A.
4x
. B.
14x
.
C.
2x
. D.
2 14x
.
Câu 26. Tập nghiệm của bất phương trình

1
2
log (1 ) 2x
là
A.
3
;1
4


. B.
3
;
4



.
C.
3
;
4



. D.
3
;1
4



.
Câu 27. Tập nghiệm của bất phương trình
2
2
log 1x
là
THPT Marie Curie
7
A.
2; 2 \ 0
. B.
; 2 \ 0
.
C.
2; 2
. D.
0; 2
.
Câu 28. Tập nghiệm của bất phương trình
2
1
2
log 3 2 1xx
là
A.
;1
. B.
[0; 2)
.
C.
[0;1) (2; 3]
. D.
[0; 2) (3;7]
.
Câu 29. Tập nghiệm của bất phương trình
2
1
2
log ( 5 7) 0xx
là
A.
( ; 2) (3; ) 
. B.
3; 
.
C.
2; 3
. D.
;2
.
Câu 30. Số nghiệm nguyên của bất phương trình
2
0,5
log ( 3 2) 1xx
là
A. 2. B. 3.
C. 4. D. Vô số.
Câu 31. Tập nghiệm
S
của bất phương trình
11
22
log ( 3) log 4x 
là
A.
3;7](.S
B.
[3;7].S
C.
]( ;7 .S
D.
[7; ).S 
Câu 32. Bất phương trình
0,5 0,5
log 2 3 log 3 1xx
có
tập nghiệm là
A.
3
;
2




. B.
2;
.
C.
;2
. D.
1
;
3




.
Câu 33. Bất phương trình
11
22
log 1 log 2 1xx
có tập
nghiệm là
A.
2;
. B.
;2
.
C.
1
;2
2



. D.
1;2
.
Câu 34. Tập nghiệm của bất phương trình
log ( 1) log (3 1)
ee
xx

là
A.
;1
. B.
1; 
.
C.
1
;1
3



. D.
1;3
.
Câu 35. Tập nghiệm của bất phương trình
22
2log 1 log 5 1xx
là
Tài liệu học tập Toán 12
8
A.
3;5

. B.
1;5
.
C.
1; 3
. D.
3;3

.
Câu 36. Tập nghiệm
của bất phương trình
2
log log(4 4)xx
là
A.
(2; ).
B.
(1; ).
C.
\ 2 .
D.
(1; )\ 2 .
Câu 37. Bất phương trình
2
22
log 5log 4 0xx
có tập
nghiệm là
A.
;2 16; 

. B.
2;16

.
C.
0;2 16;

. D.
;1 4; 

.
THPT Marie Curie
1
DẠNG 5.
1. Hàm số
log
a
y f x
xác định khi:
0
0
1
fx
a
a
.
2. Hàm số
fx
ya
xác định khi:
toàn taïi
0
1
fx
a
a
.
3. Hàm số
yx
:
Với
nguyên dương thì hàm số xác định với mọi
x
.
Với
0
hoặc
nguyên âm thì hàm số xác định với mọi
0x
.
Với
không nguyên thì hàm số xác định với mọi
0x
.
Chú ý
Theo định nghĩa, đẳng thức
1
n
n
xx
chỉ xảy ra nếu
0x
. Do đó, hàm số
1
n
yx
không đồng
nhất với hàm số
n
yx
.
Chẳng hạn, hàm số
3
yx
xác định với mọi
x
; còn hàm số
1
3
yx
chỉ xác định với mọi
0x
.
Ví dụ 1. Tìm tập xác định của hàm số
2
log 1 2log 3y x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tìm tập xác định của hàm số
25
3
x
y
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
TẬP XÁC ĐỊNH
B. VÍ DỤ
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
Ví dụ 3. Tìm tập xác định của hàm số
4
2
y x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Tìm tập xác định của hàm số
4
2
y x x

.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Tìm tập xác định của hàm số
1
2
3
y x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Câu 1. Tập xác định của hàm số
13
2yx

là
A.
; 
. B.
;2
.
C.
;2
. D.
2;
.
Câu 2. Tập xác định hàm số
1
3
1yx
là
A.
;1
. B.
1; 
.
C. . D.
\1
.
Câu 3. Tập xác định của hàm số
6
5yx

là
A.
5;
. B.
;5
.
C.
\5
. D. .
Câu 4. Tập xác định hàm số
2
2
1yx
là
C. CÂU HỎI TRẮC NGHIỆM
THPT Marie Curie
3
A.
; 1 1; 
. B.
1;1
.
C. . D.
\ 1;1
.
Câu 5. Tập xác định của hàm số
2
3
3yx
là
A.
;3
. B.
;3
.
C.
3;
. D.
; 
.
Câu 6. Tập xác định của hàm số
4
5
4yx
là
A.
;4
. B.
4;
.
C. . D.
\4
.
Câu 7. Tập xác định của hàm số
3
2
y x x

là
A.
;0 1;
. B.
1; 
.
C. . D.
\ 0;1
.
Câu 8. Hàm số
6
2
7
16 4yx
có tập xác định là
A.
; 2 2; 

. B.
; 
.
C.
2;2
. D.
\ 2;2
.
Câu 9. Tập xác định của hàm số
2
2y x x

là
A.
0;2

. B.
1
0;
2



.
C.
;0 2; 
. D.
0;2
.
Câu 10. Tập xác định của hàm số
3
2
2y x x
là
A. . B.
0;
.
C.
; 1 2;
. D.
\ 1;2
.
Câu 11. Tập xác định của hàm số
5
2
2y x x
là
A. . B.
0;
.
C.
; 1 2;
. D.
\ 1;2
.
Câu 12. Tập xác định của hàm số
2
4
x
y
là
A. . B.

1;
.
C.
4;
. D.
0;
.
Câu 13. Tập xác định của hàm số



2
1
2
x
y
là
A. . B.
\0
.
C.



1
\
2
. D.
\2
.
Tài liệu học tập Toán 12
4
Câu 14. Tập xác định của hàm số
1
3
x
y
là
A. . B.
\3
.
C.
0;
. D.
\0
.
Câu 15. Tập xác định của hàm số

2
12
x
y
là
A. . B.
\0
.
C.
. D.
0;
.
Câu 16. Tập xác định của hàm số
2
2
log (4 )y x x
là
A.
0;4

. B.
4;
.
C.
0;4
. D.
0;
.
Câu 17. Hàm số
2
7
log 2y x x
có tập xác định là
A.
;1
. B.
2;0
.
C.
1; 
. D.
; 2 0;
.
Câu 18. Tập xác định của hàm số
2
3
log 4 3y x x
là
A.
2 2;1 3; 2 2
. B.
1;3
.
C.
;1 3;
. D.
;2 2 2 2; 
.
Câu 19. Tập xác định của hàm số
2
2
log 2 3y x x
là
A.
; 1 3;

. B.
1;3

.
C.
; 1 3; 
. D.
1;3
.
THPT Marie Curie
1
DẠNG 6.
1.
ln
xx
a a a
2.
. ln
uu
a u a a
3.
xx
ee
4.
.
uu
e u e
5.
1
log
ln
a
x
xa
6.
log
ln
a
u
u
ua
7.
1
ln x
x
8.
ln
u
u
u
9.
1
log
ln10
x
x
10.
log
ln10
u
u
u
Ví dụ 1. Tính đạo hàm của hàm số
2
xx
ye
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tính đạo hàm của hàm số
27
3
yx
x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Tính đạo hàm của hàm số
2
ln 3 y x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
ĐẠO HÀM
B. VÍ DỤ
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
Ví dụ 4. Tính đạo hàm của hàm số
2
log 2 3 7 y x x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Tính đạo hàm của hàm số
3
2
2
37 yx x
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Câu 1. Đạo hàm của hàm số
logyx
là
A.
1
'y
x
. B.
ln10
'y
x
.
C.
1
'
ln10
y
x
. D.
1
'
10ln
y
x
.
Câu 2. Đạo hàm của hàm số
4
logyx
là
A.
1
2 ln2
y
x
. B.
1
log4
y
x
.
C.
ln4
y
x
. D.
2
ln2
y
x
.
Câu 3. Đạo hàm của hàm số
2
log 2 1yx
là
A.
1
2 1 ln2
y
x
. B.
2
2 1 ln2
y
x
.
C.
2
21
y
x
. D.
1
21
y
x
.
Câu 4. Hàm số
2
2
log 2f x x x
có đạo hàm
A.
2
ln2
2
fx
xx
. B.
2
1
2 ln 2
fx
xx
.
C.
2
2 2 ln 2
2
x
fx
xx
. D.
2
22
2 ln 2
x
fx
xx
.
Câu 5. Đạo hàm của hàm số
22
ln 2y x e
là
C. CÂU HỎI TRẮC NGHIỆM
THPT Marie Curie
3
A.
2
22
2
x
y
xe
. B.
22
4
2
x
y
xe
.
C.
2
22
42
2
xe
y
xe
. D.
2
22
4
2
x
y
xe
.
Câu 6. Đạo hàm của hàm số
13
x
y
là
A.
1
.13
x
yx
. B.
13 .ln13
x
y
.
C.
13
x
y
. D.
13
ln13
x
y
.
Câu 7. Đạo hàm của hàm số
5
x
y
là
A.
1
' .5
x
yx
. B.
'5
x
y
.
C.
5
'
ln5
x
y
. D.
' 5 .ln5
x
y
.
Câu 8. Đạo hàm của hàm số
21x
ye
là
A.
2
4
x
ye
. B.
21
2
x
ye
.
C.
21
ln 2
x
e
y
. D.
21
2
ln10
x
e
y
.
Câu 9. Đạo hàm của hàm số
3
x
y
là
A.
3
ln 3
x
y
. B.
1
3 ln 3
2
x
y

.
C.
3 ln 3
x
y

. D.
3 ln 3
x
y
.
Câu 10. Mệnh đề nào sau đây đúng?
A.
log
xx
e
e e e
. B.
2
2 2 log 2
xx
.
C.
10
10 10 log 10
xx
. D.
3
3 3 log 3
xx
.
Câu 11. Đạo hàm của hàm số
2
x
yx
là
A.
' 2 1 ln2
x
yx
. B.
' 2 1 ln2
x
y 
.
C.
' 2 ln2
x
y
. D.
' 2 1
x
yx
.
Câu 12. Đạo hàm của hàm số
lny x x
là
A.
1
'y
x
. B.
' lnyx
.
C.
'1y
. D.
' ln 1yx
.
Câu 13. Đạo hàm của hàm số
2
( 1)
x
y x e
là
A.
2
' ( 1)
x
y e x
. B.
2
' ( 2 )
x
y e x x
.
C.
2
' ( 1)
x
y e x
. D.
2
' ( 1)
x
y e x
.
Câu 14. Đạo hàm của hàm số
1
4
x
x
y
là
A.
2
1 2( 1)ln2
2
x
x
y

. B.
2
1 2( 1)ln2
2
x
x
y

.
Tài liệu học tập Toán 12
4
C.
2
1 2( 1)ln 2
2
x
x
y

. D.
2
1 2( 1)ln 2
2
x
x
y

.
Câu 15. Cho hàm số
2
ln 3y x x
. Phương trình
'0fx
có tập nghiệm là
A.
.
B.
3
2



.
C.
0;3
. D.
2
3



.
Câu 16. Cho
2
.
x
f x x e
. Phương trình
'0fx
có tất cả
bao nhiêu nghiệm?
A. 2. B. 3.
C. 1. D. 0.
Câu 17. Cho hàm số
2
5
( ) log ( 1)f x x
. Giá trị của
'(1)f
bằng
A.
2
ln 5
. B.
1
ln 5
.
C.
1
2ln5
. D.
3
2ln5
.
Câu 18. Cho hàm số
xx
y e e

. Giá trị của
1y

bằng:
A.
1
e
e

. B.
1
e
e
.
C.
1
e
e
. D.
1
e
e

.
THPT Marie Curie
1
DẠNG 7.
1. Hàm số y=a
x
Có tập xác định là và tập giá trị là
0;
Đồng biến trên khi
1a
, nghịch biến trên khi
01a
Đồ thị:
Đi qua điểm
0;1
Nằm ở phía trên trục hoành
Nhận trục hoành làm tiệm cận ngang
2. Hàm số y=logax
Có tập xác định là
0;
và tập giá trị là
Đồng biến trên
0;
khi
1a
, nghịch biến trên
0;
khi
01a
Đồ thị:
Đi qua điểm
1;0
Nằm ở bên phải trục tung
Nhận trục tung làm tiệm cận đứng
3. Hàm số y=x
(Chỉ xét
0
và
0x
)
Có tập xác định là
0;
và tập giá trị là
0;
Đồng biến trên
0;
khi
0
, nghịch biến trên
0;
khi
0
Có đồ thị đi qua điểm
1;1
TÍNH CHẤT ĐƠN ĐIỆU VÀ ĐỒ THỊ
A. PHƯƠNG PHÁP
y
1
O
x
0 < a < 1
y
1
O
x
a > 1
y
1
O
x
a > 1
y
1
O
x
0 < a <1
y
O
x
1
1
Tài liệu học tập Toán 12
2
Chú ý
Đồ thị hai hàm số
x
ya
và
log
a
yx
đối xứng với nhau qua đường phân giác góc phần tư
thứ nhất
yx
.
Đồ thị hai hàm số
x
ya
và
1
x
y
a



đối xứng với nhau qua trục tung
Đồ thị hai hàm số
log
a
yx
và
1
log
a
yx
đối xứng với nhau qua trục hoành
Ví dụ 1. Xét tính đơn điệu của các hàm số sau:
a.
2
x
y
b.
21
x
y 
c.
1
2
logyx
d.
7
2
logyx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
B. VÍ DỤ
1
O
x
y = a
x
y = x
y = log
a
x
1
a > 1
y
0 < a < 1
O
x
y = x
y = log
a
x
y
y = a
x
1
1
1
O
x
y
y = a
x
O
x
y = log
a
x
y
1
THPT Marie Curie
3
Ví dụ 2. Vẽ đồ thị của hai hàm số
2
x
y
và
1
2
x
y



.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Vẽ đồ thị của hai hàm số
2
logyx
và
1
2
logyx
.
Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Câu 1. Trong các hàm số sau, hàm số nào nghịch biến trên
tập xác định của nó?
A.
2
3
x
y




. B.
3
2
x
y



.
C.
x
y
. D.
x
ye
.
Câu 2. Hàm số nào dưới đây đồng biến trên ?
A.
1
3
x
fx



. B.
3
x
fx
.
C.
3
x
fx
. D.
3
3
x
fx
.
C. CÂU HỎI TRẮC NGHIỆM
Tài liệu học tập Toán 12
4
Câu 3. Hàm số nào dưới đây nghịch biến trên tập xác định
của nó?
A.
lnyx
. B.
3
logyx
.
C.
log
e
yx
. D.
logyx
.
Câu 4. Trong các hàm số sau, hàm số nào đồng biến trên
tập xác định của nó?
A.
1
2
logyx
. B.
3
2
logyx
.
C.
2
2
logyx
. D.
logyx
.
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số
2
1 logyx
?
A.
1;1M
. B.
1;0N
.
C.
1;3P
. D.
1;2Q
.
Câu 6. Hàm số nào trong các hàm số sau có đồ thị là hình
vẽ bên?
A.
2
x
y
. B.
2
logyx
.
C.
1
2
x
y



. D.
1
2
logyx
.
Câu 7. Hàm số nào trong các hàm số sau có đồ thị là hình
vẽ bên?
A.
1
2
logyx
. B.
2
logyx
.
C.
1
2
x
y



. D.
2
x
y
.
Câu 8. Hàm số nào trong các hàm số sau có đồ thị là hình
vẽ bên?
A.
2
x
y
. B.
1
2
logyx
.
C.
1
2
x
y



. D.
2
logyx
.
Câu 9. Hàm số nào trong các hàm số sau có đồ thị là hình
vẽ bên?
A.
2
logyx
. B.
1
2
x
y



.
C.
1
2
logyx
. D.
2
x
y
.
y
1
O
x
y
1
O
x
y
1
O
x
y
1
O
x
THPT Marie Curie
5
Câu 10. Cho hai hàm số
,
x
ya
x
yb
với
,a
b
là hai số thực
dương khác 1, lần lượt có đồ thị là
1
C
và
2
C
như hình
bên. Mệnh đề nào dưới đây đúng?
A.
01ab
.
B.
01ba
.
C.
01ab
.
D.
01ba
.
Câu 11. Cho ba số thực dương
,a
,b
c
khác 1. Đồ thị các
hàm số
,
x
ya
,
x
yb
x
yc
được cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
a b c
.
B.
a c b
.
C.
b c a
.
D.
c a b
.
Câu 12. Cho
a
,
b
,
c
là các số thực dương và khác 1. Đồ thị
các hàm số
x
ya
,
x
yb
và
x
yc
được cho trong hình bên.
Khẳng định nào sau đây là đúng?
A.
1a c b
.
B.
1b c a
.
C.
1c b a
.
D.
1a b c
.
Câu 13. Cho hai hàm số
log ,
a
yx
log
b
yx
lần lượt có đồ
thị
1
()C
và
2
()C
được vẽ trên cùng mặt phẳng tọa độ. Mệnh
đề nào sau đây đúng?
A.
01ba
.
B.
01ba
.
C.
01ab
.
D.
01ab
.
Câu 14. Cho ba số thực dương
,a
,b
c
khác 1. Đồ thị các
hàm số
log ,
a
yx
log ,
b
yx
log
c
yx
được cho trong hình
bên. Mệnh đề nào dưới đây đúng?
A.
c a b
.
B.
b c a
.
C.
a b c
.
D.
a c b
.
Câu 15. Cho ba số thực dương
,a
,b
c
khác 1. Đồ thị các
hàm số
log ,
a
yx
log ,
b
yx
log
c
yx
được cho trong hình
bên. Mệnh đề nào dưới đây đúng?
A.
a b c
.
B.
b c a
.
C.
c a b
.
D.
a c b
.
(C1)
(C2)
O
x
y
1
O
x
y
y
1
x
O
1
y
O
x
1
y
O
x
1
y
O
x
Tài liệu học tập Toán 12
6
Câu 16. Cho
a
,
b
,
c
là các số thực dương. Đồ thị các hàm
số
a
yx
,
b
yx
và
c
yx
trên khoảng
+0;
được cho
trong hình bên. Khẳng định nào sau đây là đúng?
A.
b c a
.
B.
c b a
.
C.
b a c
.
D.
a b c
.
Câu 17. Cho hàm số
1x
f x a
có đồ thị như hình bên.
Khi đó
'1f
bằng
A.
ln 2
4
. B.
4ln 2
.
C.
ln 2
4
. D.
4ln2
.
Câu 18. Đồ thị hàm số
lnyx
đi qua 3 điểm
;'M a a
,
;'N b b
,
;'P c c
với
' ' 2 'a c b
như hình bên. Khẳng định
nào sau đây là đúng?
A.
2
ac b
.
B.
ac b
.
C.
2
2ac b
.
D.
2a c b
.
Câu 19. Cho hàm số
log
a
yx
và
log
b
yx
có đồ thị như
hình bên. Đường thẳng
1y
cắt hai đồ thị tại các điểm có
hoành độ là
1
x
,
2
x
. Biết
12
23xx
, giá trị
a
b
bằng
A.
3
3
.
B.
3
2
.
C.
3
2
.
D.
2
3
.
y
O
x
y
O
x
1
y
O
c
x
a
b
c’
a’
b’
M
N
P
1
y
O
x
1
THPT Marie Curie
1
DẠNG 8.
1. Gửi vào ngân hàng một số tiền
0
P
đồng với lãi suất
%r
mỗi năm (hoặc mỗi quý, hoặc
mỗi tháng) theo hình thức lãi đơn thì sau
n
năm (hoặc
n
quý, hoặc
n
tháng) số tiền cả gốc
lẫn lãi là
0
1
n
P P nr
2. Gửi vào ngân hàng một số tiền
0
P
đồng với lãi suất
%r
mỗi năm (hoặc mỗi quý, hoặc
mỗi tháng) theo thể thức lãi kép thì sau
n
năm (hoặc
n
quý, hoặc
n
tháng) số tiền cả gốc
lẫn lãi là
0
.1
n
n
P P r
3. Gửi vào ngân hàng một số tiền
0
P
đồng với lãi suất
%r
mỗi năm theo hình thức lãi kép
và có kì hạn
m
tháng thì sau
n
kì hạn số tiền cả gốc lẫn lãi là
0
.1
n
n
P P mr
4. Với số vốn ban đầu là
A
, theo thể thức lãi kép liên tục, lãi suất mỗi năm là
r
thì sau
N
năm số tiền thu được cả vốn lẫn lãi sẽ là
Nr
S Ae
Nhiều hiện tượng tăng trưởng (hoặc suy giảm) của tự nhiên và xã hội, chẳng hạn sự tăng dân số,
cũng được ước tính theo công thức
Nr
S Ae
.
5. Một người mỗi tháng đều gửi vào ngân hàng số tiền
a
đồng vào đầu mỗi tháng theo
hình thức lãi kép với lãi suất là
%r
/tháng thì sau
n
tháng, người ấy có số tiền cả gốc lẫn lãi
là
1 1 1
n
n
a
P r r
r



6. Một người gửi vào ngân hàng số tiền
0
P
đồng theo hình thức lãi kép với lãi suất là
%r
/tháng và mỗi tháng đều rút ra
a
đồng vào ngày tính lãi thì sau
n
tháng, người ấy còn lại
số tiền trong ngân hàng là
0
11
1
n
n
n
ar
P P r
r




LÃI SUẤT
A. PHƯƠNG PHÁP
Tài liệu học tập Toán 12
2
7. Vay
0
P
(đồng) từ ngân hàng với lãi suất
%r
/tháng. Biết rằng số hoàn nợ hàng tháng ở
mỗi lần là như nhau và lãi suất ngân hàng không thay đổi trong thời gian hoàn nợ. Sau
n
tháng thì hết nợ. Khi đó, mỗi tháng phải hoàn nợ số tiền là
0
.1
11
n
n
P r r
a
r

Câu 1. Một người gửi 50 triệu đồng vào một ngân hàng với
lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân
hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để
tính lãi cho năm tiếp theo. Sau 5 năm người đó rút tiền bao
gồm cả gốc và lãi. Hỏi người đó rút được số tiền bao nhiêu?
A. 101 triệu đồng. B. 90 triệu đồng.
C. 81 triệu đồng. D. 70 triệu đồng.
Câu 2. Một người gửi 50 triệu đồng vào một ngân hàng với lãi
suất 6%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng
thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi
cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó
nhận được số tiền nhiều hơn 100 triệu đồng bao gồm gốc và
lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra.
A. 13 năm. B. 14 năm.
C. 12 năm. D. 11 năm.
Câu 3. Một người gửi 15 triệu đồng vào ngân hàng theo
thể thức lãi kép kỳ hạn một quý với lãi suất 1,65% một quý.
Hỏi sau bao nhiêu quý thì người đó có được ít nhất 20 triệu?
A. 15 quý. B. 16 quý.
C. 17 quý. D.18 quý.
Câu 4. Một người gửi tiết kiệm vào một ngân hàng với lãi
suất 7,5% / năm. Biết rằng nếu không rút tiền ra khỏi ngân
hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn
để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm
người đó thu được (cả số tiền gửi ban đầu và lãi) gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi
suất không thay đổi và người đó không rút tiền ra?
A. 11 năm. B. 9 năm.
C. 10 năm. D. 12 năm.
Câu 5. Bạn A gửi tiết kiệm số tiền 58.000.000 đồng tại một
ngân hàng theo thể thức lãi kép. Sau 8 tháng bạn đó nhận
B. CÂU HỎI TRẮC NGHIỆM
THPT Marie Curie
3
được 61.329.000 đồng cả gốc lẫn lãi. Hỏi lãi suất hàng tháng
của ngân hàng đó là bao nhiêu?
A. 0,6%. B. 6%.
C. 0,7%. D. 7%.
Câu 6. Ông A gửi vào ngân hàng 100 triệu đồng theo hình
thức lãi kép. Lãi suất ngân hàng là 8% trên năm và không
thay đổi qua các năm ông gửi tiền. Sau 5 năm ông cần tiền
để sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa
số tiền đó vào công việc, số còn lại ông tiếp tục gửi ngân
hàng với hình thức như trên. Hỏi sau 10 năm ông A đã thu
được số tiền lãi gần nhất với số nào dưới đây (đơn vị tính là
triệu đồng)?
A.
79,412
. B.
80,412
.
C.
81,412
. D.
100,412
.
Câu 7. Đầu năm 2016, ông A thành lập một công ty. Tổng số
tiền ông A dùng để trả lương cho nhân viên trong năm 2016 là
1 tỷ đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả
lương cho nhân viên trong cả năm đó tăng thêm 15% so với
năm trước. Hỏi năm nào dưới đây là năm đầu tiên mà tổng số
tiền ông A dùng để trả lương cho nhân viên trong cả năm lớn
hơn 2 tỷ đồng?
A. Năm 2023. B. Năm 2022.
C. Năm 2021. D. Năm 2020.
Câu 8. Một người gửi mỗi tháng 10 triệu đồng vào một ngân
hàng với lãi suất 0,5%/ tháng. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập
vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau hai tháng, số
tiền cả gốc và lãi mà người đó có được là bao nhiêu? Giả
định trong suốt thời gian gửi, lãi suất không đổi.
A. 20.150.250 đồng. B. 20.100.000 đồng.
C. 20.150.000 đồng. D. 20.100.250 đồng.
Câu 9. Một người gửi vào ngân hàng 100 triệu đồng với kì
hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi kép (sau
3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng,
người đó gửi thêm 50 triệu đồng với kì hạn và lãi suất như
trước đó. Tổng số tiền người đó nhận được sau 1 năm (Tính
từ lần gửi tiền đầu tiên) là
A. 179,676 triệu đồng. B. 177,676 triệu đồng.
C. 178,676 triệu đồng. D. 176,676 triệu đồng.
Câu 10. Một người gửi mỗi tháng 5 triệu đồng vào một ngân
hàng với lãi suất 0,7%/ tháng. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập
vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau 10 tháng, số
tiền cả gốc và lãi mà người đó có được gần nhất với số nào
trong các số tiền sau, giả định trong suốt thời gian gửi, lãi suất
không đổi?
Tài liệu học tập Toán 12
4
A. 54 triệu đồng. B. 53 triệu đồng.
C. 51 triệu đồng. D. 52 triệu đồng.
Câu 11. Bạn A muốn có 100 triệu đồng sau 10 tháng thì bạn
A phải gửi tiết kiệm mỗi tháng gần nhất với số nào trong
các số tiền sau, biết lãi suất gửi là
0,6%
/tháng và theo thể
thức lãi kép?
A. 9,5 triệu đồng. B. 9,9 triệu đồng.
C. 9,7 triệu đồng. D. 9,4 triệu đồng.
Câu 12. Một người gửi số tiền là 11000 USD trong ngân
hàng theo hình thức lãi kép với lãi suất 0,73% một tháng.
Mỗi tháng người đó đến rút 60USD để chi phí cho sinh hoạt
gia đình. Hỏi sau một năm số tiền còn lại là bao nhiêu? ( Kết
quả làm tròn đến hàng đơn vị)
A. 11254USD. B. 1259USD.
C. 1257USD. D. 1256USD.
Câu 13. Ông A gửi vào ngân hàng 20 triệu đồng theo thể
thức lãi kép với lãi suất
0.75%
mỗi tháng. Hằng tháng ông
A rút ra 300 nghìn đồng vào ngày tính lãi. Hỏi sau hai năm
ông A còn lại bao nhiêu tiền (làm tròn đến 1000 đồng)?
A.
1.607.000
đồng. B.
16.071.000
đồng.
C.
16.072.000
đồng. D.
16.073.000
đồng.
Câu 14. Ông A gửi vào ngân hàng 11 triệu đồng theo thể
thức lãi kép với lãi suất
0.73%
mỗi tháng. Hằng tháng ông
A rút ra 200 nghìn đồng vào ngày tính lãi. Hỏi sau bao lâu
thì ông A hết tiền?
A. 71 tháng. B. 72 tháng.
C. 70 tháng. D. 73 tháng.
Câu 15. Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với
lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo
cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn
nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số
tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau
đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền
m
mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ
là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay đổi
trong thời gian ông A hoàn nợ.
A.
3
100.(1,01)
3
m
(triệu đồng).
B.
3
3
(1,01)
(1,01) 1
m
(triệu đồng).
C.
100 1,03
3
m
(triệu đồng).
D.
3
3
120.(1,12)
(1,12) 1
m
(triệu đồng).
THPT Marie Curie
5
Câu 16. Ông A vay ngân hàng
100
triệu đồng với lãi suất
1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách:
Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ;
hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền
hoàn nợ ở mỗi tháng là như nhau và ông A trả hết nợ sau
đúng 5 năm kể từ ngày vay. Biết rằng mỗi tháng ngân hàng
chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền
mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền
nào dưới đây?
A.
2,22
triệu đồng. B.
3,03
triệu đồng.
C.
2,25
triệu đồng. D. 2,20 triệu đồng.
Câu 17. Ông A vay ngân hàng 300 triệu đồng. Nếu cuối mỗi
tháng bắt đầu từ tháng thứ nhất ông A trả hằng tháng
5.500.000 đồng và chịu lãi số tiền chưa trả là 0,5%/tháng thì
sau ít nhất là bao lâu, ông A trả hết số tiền trên?
A. 65 tháng. B. 64 tháng.
C. 63 tháng. D. 66 tháng.
| 1/49
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THPT Marie Curie Chuyeân ñeà: 3 MŨ VÀ LOGRRIT DẠNG 1.
CÔNG THỨC LŨY THỪA A. PHƯƠNG PHÁP
1. Lũy thừa với số mũ nguyên
 Với mỗi số nguyên dương n , lũy thừa bậc n của số a là số n a xác định bởi: n a  . a .
a ..a với n  1 và 1 a a n thöøa soá
Tên gọi: a gọi là cơ số, n gọi là số mũ của n a
 Với mỗi số nguyên n  0 và a  0, lũy thừa bậc n của số a là số n a xác định bởi: n 1 a  với n  0 và 0 a  1 n a Chú ý:  0
0 và 0n (với n nguyên âm) không có nghĩa.  1
a a đúng với mọi a .  0
a  1 đúng với mọi a  0.
2. Căn bậc n
Với n nguyên dương, căn bậc n của một số thực a là số thực b sao cho n b a .
 Khi n là số lẻ, mỗi số thực a chỉ có một căn bậc n được kí hiệu là n a .
 Khi n là số chẵn, mỗi số thực dương a có đúng hai căn bậc n là hai số đối nhau được kí
hiệu là n a và n
a . Ta gọi n a là căn số học bậc n của a . Chú ý:
Căn bậc 1 của số thực a chính là . a
Căn bậc 2 của số thực dương a kí hiệu là a .  n 0  0
Số âm không có căn bậc chẵn. 1
Tài liệu học tập Toán 12
Với n nguyên dương lẻ, ta có: n a  0 khi a  0 và n a  0 khi a  0 .
a khi n leû  n n a  
a khi n chaün 
3. Lũy thừa với số mũ hữu tỉ m
Cho a là một số thực dương và r
, trong đó m là một số nguyên còn n là một số nguyên n m
dương. Khi đó, lũy thừa của a với số mũ r là số r
a xác định bởi r n m n
a a a . m m' m m'  Nếu  thì n n'
a a . Do đó trong biểu thức r
a , với r là một số hữu tỉ, ta thường viết r n n'
dưới dạng phân số tối giản có mẫu số dương. 1  n n
a a ( a dương, n nguyên dương)
4. Lũy thừa với số mũ thực
 Mọi số vô tỉ  , bao giờ cũng tồn tại một dãy số hữu tỉ r để lim r   . n n
 Cho a là một số thực dương và  là một số vô tỉ. Xét dãy số hữu tỉ r mà lim r   . Khi n n đó: lim arn a  . 5. Ghi nhớ
a với số mũ  nguyên dương thì cơ số a có điều kiện a .
a với số mũ   0 hoặc  nguyên âm thì cơ số a có điều kiện a  0 .
a với số mũ  không nguyên thì cơ số a có điều kiện a  0 . 6. Công thức m a n m 1. m n m .  n a a a 2. m  n a
3. m    n   m.n a a a n a n n na a
4.  .   n. n a b a b 5.   
6. n .  n .n a b a b b n b n a a m m 7. n 8. n mn.m a
a 9. n m   n   n a a a n b b 2 THPT Marie Curie B. VÍ DỤ  1 1  1 1  1 1 
Ví dụ 1. Cho a và b là các số thực dương, rút gọn biểu thức   4  4  2  2  4  4 P a b a b a b  .     Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................  1 a  31 3 
Ví dụ 2. Cho a là số thực dương, rút gọn biểu thức P  . 5 3  1 5 a .a Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 5 2 Ví dụ 3. a a
Cho a là số thực dương, rút gọn biểu thức P  . 3 a a Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 3
Tài liệu học tập Toán 12 Ví dụ 4. 2
Cho a là số thực dương, rút gọn biểu thức P   3 8 5 4
a .a  : a .a  . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho a là số thực thì căn bậc 1 của a bằng A. 1 . B. a . C. 0 . D. a .
Câu 2. Cho a là số thực dương và n là số nguyên dương 1 thì n a bằng A.na . B.a . C. n a . D. n a .
Câu 3. Cho a là số thực khác 0 thì 0 a bằng A. 0 . B. a . C. 1  . D. 1 . Câu 4. 1
Cho a là số thực khác 0 thì bằng n a 1 A.  . B. na . n a C. n a . D. n a .
Câu 5. Cho a là số thực dương thì n m a bằng
A. n.m a . B. m n a . C. n m a .
D. nm a .
Câu 6. Cho a là số thực dương thì n m a bằng A.  n m a . B. m n a . n m C.  m n a .
D. a  . .
Câu 7. Cho a là số thực dương thì n m a bằng n m A. m a . B. n a . C. n m a  . D. .nm a .  4 THPT Marie Curie
Câu 8. Cho a và b là các số thực dương thì n .ab bằng A. n .n a b . B. n n a b .
C. n a. b . D. .n a b .
Câu 9. Cho a là số thực dương thì  n m a bằng A. m n a  . B. m n a  . m C. n a . D. . m n a .
Câu 10. Cho a, b là hai số thực dương và x, y là hai số
thực tùy ý. Mệnh đề nào sau đây sai?  A. x
a b  abx y y . B. x y x y a a a   . x C.   x  . x ab a b . D. x a y xya .
Câu 11. Cho các số thực a , b , m với a và b dương. Mệnh
đề nào sau đây là mệnh đề sai? m A. 2 a a . B. m a   1. ma m C. m    a . m b . D.   m  . m ab a b .  b
Câu 12. Cho các số thực a, b,  với a b  0 và   1.
Mệnh đề nào sau đây là mệnh đúng?   A. a bab    . B. a bab    .     a a C. ab . a b  . D.    . b b Câu 13. 1
Cho a là một số thực dương, biểu thức 3 bằng a 1  A. 3 a . B. 3 a . 1 1 C. 3 a . D. 2 a . 1 Câu 14.
Rút gọn biểu thức 6 3
P x . x với x  0 ta được 1 A. 8 P x . B. 2 P x . 2
C. P x . D. 9 P x . 5 Câu 15.
Rút gọn biểu thức 3 3
Q b : b với b  0 ta được 5 A. 2 Q b . B. 9 Q b . 4  4 C. 3 Q b . D. 3 Q b . 1 Câu 16.
Cho a là một số thực dương, biểu thức 3
a . a bằng 2 1 A. 5 a . B. 3 a . 5 1 C. 6 a . D. 6 a . 5
Tài liệu học tập Toán 12 3 Câu 17.
Rút gọn biểu thức 3 2
P a . a với a  0 ta được 1 9 A. 2 P a . B. 2 P a . 11 C. 6 P a . D. 3 P a . 2 Câu 18.
Cho a là một số thực dương, biểu thức 3 a . a bằng 7 7 A. 6 a . B. 3 a . 5 1 C. 3 a . D. 3 a .
Câu 19. Cho a là một số thực dương, biểu thức 23 2 3 22 a .a được kết quả bằng A. a . B. 6 2 a . C. 4 a . D. 1 .
Câu 20. Cho a là một số thực dương, biểu thức   2 1 2 21 2  a .a bằng A. a . B. 3 a . C. 5 a . D. 1 . Câu 21. 2017 2016
Giá trị của biểu thức 7  4 3  4 3 7 bằng A. 1 . B. 7  4 3 . C. 7  4 3 . D.   2016 7 4 3 . Câu 22.
Với x là số thực không âm thì biểu thức 3 2 3 x x bằng 7 5 A. 6 x . B. 3 x . 21 8 C. 2 x . D. 9 x .
Câu 23. Cho biểu thức 3 6 5
P x. x. x ( x  0 ). Mệnh đề nào dưới đây đúng? 5 2 A. 2 P x . B. 3 P x . 5 7 C. 3 P x . D. 3
P x . Câu 24. a b a
Cho hai số thực dương a và b. Biểu thức 5 3 b a b
được viết dưới dạng lũy thừa với số mũ hữu tỉ là 7 31 30  a  30  a A. .   . B. .   .  b   b  30 1 31  a  6  a C. .   . D. .    b   b   6 THPT Marie Curie DẠNG 2. CÔNG THỨC LOGARIT A. PHƯƠNG PHÁP 1. Định nghĩa
 Cho hai số dương a, b với a  1. Số  thỏa a  b gọi là logarit cơ số a của b và ghi log b . a
 Như vậy: a  b    log b với a, b  0 và a  1. a 2. Định nghĩa
 Lôgarit thập phân: log a  log a 10 x  1 
 Lôgarit Néper: ln a  log a (với e  lim 1     2,7183 ) e x  x 3. Công thức
1. log 1  0 2. log a  1 a a 3. log n
a n 4. log n a an ab 5. log  .
b c  log b  log c 6. log
 log b  log c a a a a    c a a 7. log n
b nlog b 8. b b n  1 log log a a a a n 9. b  1 log
10. log b  log . c log b a log a a a c b log b log b ln b 11. log b c   12. log c a  log a b b c a log a log a ln a c 1
Tài liệu học tập Toán 12 B. VÍ DỤ
Ví dụ 1. Tính P  log log 4.log 3 1  3 2  4 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1 Ví dụ 2. log 3log 5 Tính  P  1 log 5  2 5 4 2 16 4 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 3. 1 1
Cho log a  4 và log b  . Tính P  2 log log a log log 2  2        2  1  2 9 2   2   b 3  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Cho log x  2 . Tính 2
P  log x  3 log x  5 log 2x  7 . 2 4 1   2 2  2 THPT Marie Curie Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Với a là số thực dương bất kì, mệnh đề nào sau đây đúng?
A. log 3a  3log a . B. 3 1
log a  log a . 3 C. 3
log a  3log a . D. a 1 log 3  log a . 3
Câu 2. Với a và b là hai số thực dương tùy ý,  2 log ab bằng
A. 2log a  log b .
B. log a  2log b . 1
C. 2log a  log b.
D. log a  log b . 2
Câu 3. Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng?
A. lnab  ln a  lnb .
B. lnab  ln . a ln b . a ln a a C. ln  .
D. ln  ln b  ln a . b ln b b
Câu 4. Cho a  1,a  0,b  0,b 1. Đẳng thức nào sau đây sai? 1 A. 2 1
log b  log b . B. log b  . a 2 a a log a b C. log b  log b . D. 2 log . b log a  2 . 2 a a a b
Câu 5. Cho a, b là hai số thực dương và khác 1. Khẳng
định nào sau đây sai? 1 A. log n b  .
n log b . B. log b  . a a a log a b a b C. log  1 log b . D. log  log b 1 . a a b a a a
Câu 6. Cho a, b, c là các số thực dương, a và c khác 1.
Mệnh đề nào dưới đây sai? 3
Tài liệu học tập Toán 12
A. log blog a  log b .
B. log b c b . c log a c c a ab C. log  log b   
log c . D. log bc b c . a   log log a a ac a a
Câu 7. Cho a là số thực dương và khác 1. Mệnh đề nào sau đây đúng? ln a lna A. log a  . B. log a  . 2 ln 2 2 log 2 log 2 loga C. log a  . D. log a  . 2 loga 2 ln 2
Câu 8. Cho hai số thực dương a và b . Mệnh đề đề nào sau đây sai? 2 A. log ab
 2log ab . B. log a  log b  log ab . 2 2 2   2   2   a
C. log a  log b  log
. D. log a  log b  log a b . 2 2 2   2 2 2 b
Câu 9. Cho a, b, c là các số dương và a  1. Mệnh đề nào sau đây sai? A. log .
b log c  log (b  )
c . B. log b  log c  log ( . b c). a a a a a ab   1 
C. log b  log c  log
. D.  log b  log . a a a      c a a b
Câu 10. Cho hai số dương a , b và a  1. Mệnh đề nào dưới đây sai? 1
A. log a   . B. log   a . a a   a  1 C. log  .
D. log ab   b . a   1 log a    b  log b a a
Câu 11. Giá trị của log 53 9 bằng 2 A. . B. 10 . 5 C. 25 . D. 5 .
Câu 12. Cho a là số thực dương khác 1. Với mọi số thực x
dương x và y , biểu thức log bằng a y
A. log x  log y .
B. log x  log y . a a a a log x
C. log x y . D. a . a   log y a
Câu 13. Cho a là số thực dương tùy ý khác 1. Biểu thức log a bằng 2 1 A. log 2 . B. . a log a 2 1 C. . D.  log 2 . log 2 a a 4 THPT Marie Curie
Câu 14. Với a là số thực dương tùy ý, ln5aln3a bằng ln 5a A. .
B. ln 2a . ln 3a 5 ln 5 C. ln . D. . 3 ln 3
Câu 15. Với a là số thực dương tùy ý, log 3a bằng 3   A. 3log a .
B. 3  log a . 3 3
C. 1  log a .
D. 1  log a . 3 3 Câu 16.  3 
Với a là số thực dương tùy ý, log bằng 3    a  1 A. .
B. 1  log a . log a 3 3
C. 1  log a .
D. 3  log a . 3 3
Câu 17. Với a là số thực dương tùy ý, log 9a bằng 3  
A. 2  log a.
B. 2 log a. 3 3
C. 2  log a.
D. 9 log a. 3 3
Câu 18. Cho a là số thực dương khác 2. Giá trị của 2  a  log   bằng a  4  2 1 A. . B. 2 . 2 1 C.  . D. 2  . 2 3   Câu 19. a
Cho a là số thực dương khác 4 , khi đó log   a  64  4 bằng 1 A. 3 . B. . 3 1 C. 3  . D.  . 3
Câu 20. Giá trị của log a ( a  0 và a  1) bằng 3 a 1 A. 3. B. . 3 1 C.  . D. 3  . 3
Câu 21. Cho a là số thực dương và khác 1, khi đó log a a bằng 1 A. . B. 0 . 2 C. 2  . D. 2 .
Câu 22. Cho a là số thực dương, a  1, khi đó 3 log a bằng 3 a A. 3 . B. 1 . 5
Tài liệu học tập Toán 12 1 C. 9 . D. . 3
Câu 23. Với 0  a  1, giá trị của log a a bằng a 3 4 A.  . B. . 4 3 3 3 C. . D. . 2 4
Câu 24. Xét a là số thực bất kì và a  0, khi đó 2 log a bằng 2 1 A. 4 log a . B. log a . 2 2 2 1 1 C. log a . D. log a . 2 2 2 4
Câu 25. Cho các số thực dương a, b với a  1. Biểu thức log (ab) bằng 2 a 1 A. log b .
B. 2  2 log b . 2 a a 1 1 1 C. log b . D.  log b . 4 a 2 2 a
Câu 26. Cho a và b là hai số thực dương tùy ý, ln ab bằng 1 1 A.
lnalnb.
B. ln a  ln b . 2 2 1
C. 2 ln ab .
D. ln a  ln b . 2
Câu 27. Cho log b  2 , khi đó 8 2 log b a bằng 4 a   a 9 A. . B. 9 . 2 C. 2 . D. 8 .
Câu 28. Cho log b  2 và log c  3 , khi đó  2 3
log b c bằng aa a A. 31. B. 13 . C. 30 . D. 108 .
Câu 29. Với a, b là các số thực dương tùy ý và a khác 1, khi đó biểu thức 3 6
log b  log b bằng 2 a a A. 9log b . B. 27 log b . a a
C. 15 log b . D. 6log b . a a
Câu 30. Cho log x a , khi đó 2 log 4x bằng 2 2 A. 2  . a B. 4  2 . a C. 4  . a D. 2  2 . a
Câu 31. Với các số thực dương a, b bất kì, khi đó 3  2a  log   bằng 2  b   6 THPT Marie Curie 1
A. 1  3 log a  log b .
B. 1 log a  log b . 2 2 2 2 3 1
C. 1  3 log a  log b .
D. 1 log a  log b . 2 2 2 2 3
Câu 32. Với a và b là hai số thực dương tùy ý,  2 3 ln a b bằng
A. 6ln a  lnb .
B. 2lna  3lnb . 1 1
C. 6ln a  lnb.
D. ln a  ln b . 2 3
Câu 33. Với a , b là hai số thực dương tùy ý, khi đó 2  ab  ln   bằng a   1 
A. ln a  2ln b  lna   1 .
B. ln a  ln b  lna   1 .
C. ln a  2ln b  lna   1 . D. 2ln b . Câu 34. 1
Cho log a  2 và log b
. Giá trị của biểu thức 3 2 2 2 2 log log (3 ) a   log b 3  3  bằng 1 4 5 A. . B. 4 . 4 3 C. 0 . D. . 2
Câu 35. Cho a,b  0 và a,b  1, biểu thức 3 4
log b .log a có b a giá trị bằng A. 18 . B. 24 . C. 12 . D. 6 .
Câu 36. Cho n  1là một số nguyên. Giá trị của biểu thức 1 1 1   .. bằng log n! log n! log n! 2 3 n A. . n B. 0. C. 1. D. n!.
Câu 37. Cho log x  3, log x  4 với a, b là các số thực lớn a b
hơn 1, khi đó log x bằng ab 7 1 A. . B. . 12 12 12 C. 12 . D. . 7
Câu 38. Với các số thực dương x, y tùy ý, đặt log x a và 3 3  x
log y b , khi đó log   bằng 3 27  y     aa A. 9   b  . B.b .  2  2 7
Tài liệu học tập Toán 12  aa C. 9   b  . D.b .  2  2
Câu 39. Cho a, b là các số thực dương thỏa mãn a  1, b
a b và log b  3 , khi đó log bằng a b a a A. 5  3 3 . B. 1  3 . C. 1  3 . D. 5  3 3 . Câu 40.
Cho a và b là các số thực dương và a  1 thỏa 2 b
mãn log b  2 , khi đó log bằng a 2 a b a 2  3 2 2 A. . B. . 2 2 2  1 2  1 6   5 2 C. . D. . 2  1 2 Câu 41. Với a, b
là hai số thực dương và a   3 1, log a b bằng a a  3 3 3 A.  log b . B.  log b . 2 2 a 2 a 2 4 2 C.  log b . D.  log b 3 9 a 3 a Câu 42. Đặt log 6  ;
a log 7  b . Hãy biểu diễn log 7 12 12 2 theo a và b . b b A. log 7  . B. log 7  . 2 1 2 a 1 a a a C. log 7  . D. log 7  . 2 1 2 b 1 b Câu 43.
Cho a, b là các số thực dương khác 1 và thỏa mãn 3 b
log b  3 . Tính giá trị của biểu thức T  log . a b a a A. T  3 1 . B. T   . 4 C. T  4  . D. T  4 . Câu 44.
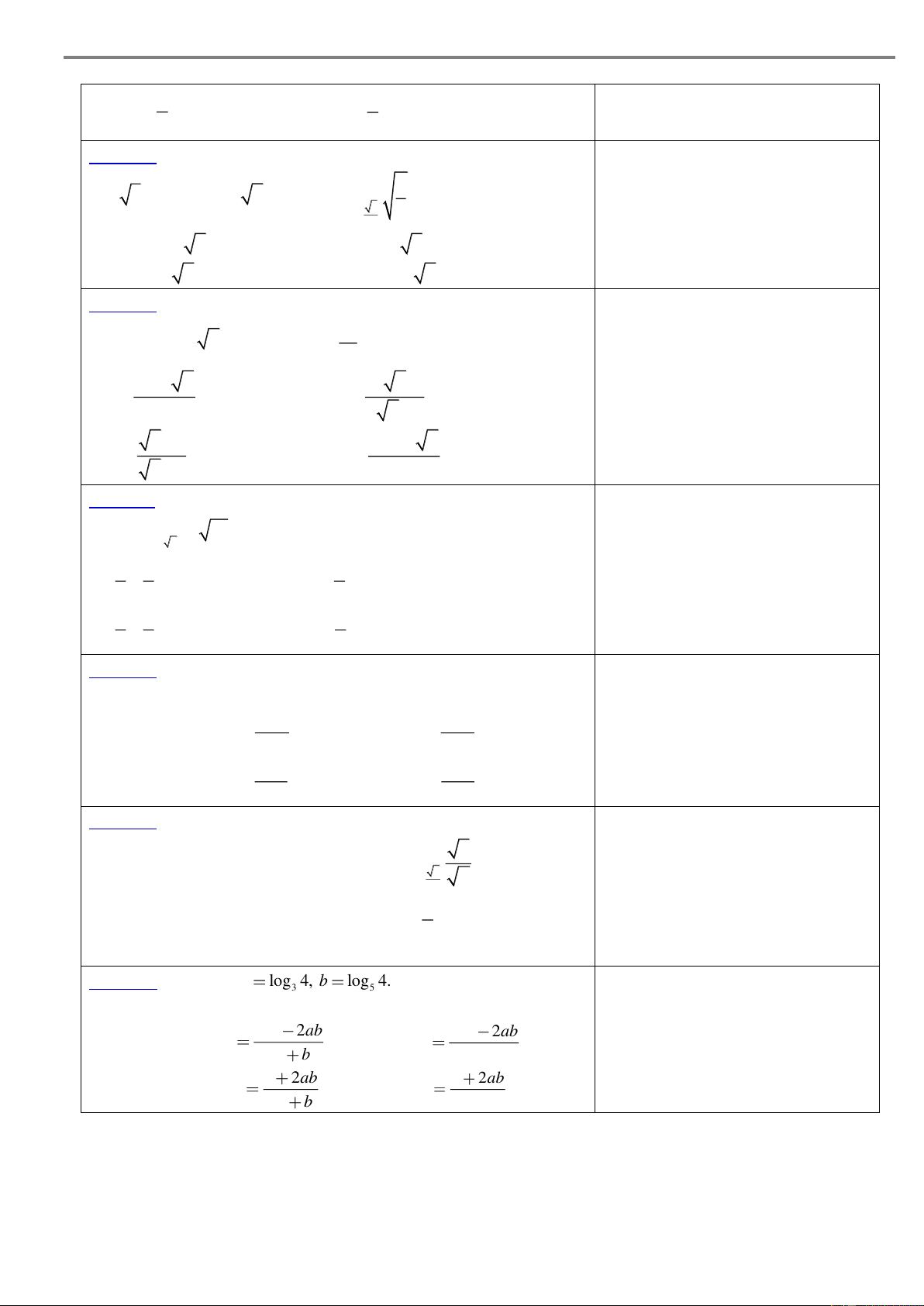
Đặt a log 4, b log 4. Hãy biểu diễn log 80 3 5 12 theo a và . b . 2 2a 2ab 2 2a 2ab A log 80 .. B. log 80 . 12 ab b 12 ab a 2ab a 2ab C. log 80 . D. log 80 . 12 ab b 12 ab 8 THPT Marie Curie DẠNG 3.
PHƯƠNG TRÌNH MŨ VÀ LOGARIT A. PHƯƠNG PHÁP f x 1. a
b f x  log b a f xgx 2. aa
f x  gx 0a1
3. log f x  b f x  b a a
0a1  f x  0 hoaëc g x   0 4. log f x g x a
   loga      
 f xgx Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ 2 5 Ví dụ 1. x 6x
Giải phương trình 2 2  16 2 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 2. 2
Giải phương trình x 4x5 x1 3  9 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
Ví dụ 3. Giải phương trình x x 1  x 1 3 6.3 2.3     3 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Giải phương trình x1 x2 2 .3 .5x  200 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Giải phương trình 4x 2x   6  0 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Giải phương trình 2 log (x  1)  2 . 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 7. Giải phương trình log (9  2x)  3  x . 2 Lời giải 2 THPT Marie Curie
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 8. Giải phương trình log (x  2) log x  2  2 . 2 2   Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 9. Giải phương trình log x  log x  6 log x  2 . 5 5   5   Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 10. Giải phương trình 2
log (x  1)  log (2x  1)  2 . 3 1 3 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 3
Tài liệu học tập Toán 12
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Nghiệm của phương trình x 1 3   27 là A. x  9 . B. x  3 . C. x  4 . D. x  10 .
Câu 2. Phương trình 2x 1
5   125 có nghiệm là 5 3 A. x  . B. x  . 2 2 C. x  3 . D. x  1.
Câu 3. Phương trình 2x 1 2   32 có nghiệm là 5 A. x  . B. x  2 . 2 3 C. x  . D. x  3 . 2 Câu 4. 2
Phương trình 2x 4x5 2
 32 có bao nhiêu nghiệm? A. 3. B. 0. C. 1. D. 2. Câu 5. 4 2
Tổng các nghiệm của phương trình x 3 3 x  81 bằng A. 0. B. 1. C. 3. D. 4. Câu 6. Tập nghiệm của phương trình x 3x1  4   7  16       0 là  7   4  49  1 A.   . B.   2 .  2  1 1   1  C.  ;   . D.  ; 2 . 2 2   2 
Câu 7. Số nghiệm thực của phương trình 3x 1 3   9 x là A. 2. B. 0. C. 1. D. 3.
Câu 8. Tổng bình phương các nghiệm của phương trình 2  xx  1 3 2 5    bằng  5  A. 0. B. 5. C. 2. D. 3.
Câu 9. Phương trình 2x3 4 4
 8 x có nghiệm là 6 2 A. . B. . 7 3 4 C. . D. 2. 5  4 THPT Marie Curie x1 Câu 10.  1  Phương trình 2   
125 x có nghiệm là  25  1 1
A. x   .
B. x   . 4 8 1 C. x  . D. x  4 . 4 2 x 2 x x4 Câu 11.  5   6 
Tập hợp nghiệm của phương trình       6   5  là A. 1;  4  . B. . C.   1 . D. 0;  4  . Câu 12.x 21  Phương trình 16
 8 x có nghiệm là A. x  3  . B. x  2 . C. x  3 . D. x  2  . Câu 13. Tổng các nghiệm của phương trình 2 82x 3x (0,4)  (6,25) bằng A. 3. B. 5. C. 5  . D. 3  . b Câu 14.   a 1
Cho 2    . Đẳng thức nào sau đây đúng?  4  A. a  2  b .
B. a  2b . C. ab  2  . D. ab  4 .
Câu 15. Cho phương trình x x1 4  2  3  0. Khi đặt 2x t  , ta
được phương trình nào dưới đây? A. 2 2t  3  0 . B. 2
t t  3  0 .
C. 4t  3  0 . D. 2
t  2t  3  0 .
Câu 16. Số nghiệm của phương trình 9x 4.3x   3  0 là A. 3. B. 1. C. 2. D. 0. Câu 17. Số nghiệm nguyên của phương trình x 1  x2 4  2 1  0 là A. 0. B. 1. C. 4. D. 2.
Câu 18. Nghiệm của phương trình log x  3 là 2 A. 9. B. 6. C. 8. D. 5.
Câu 19. Nghiệm của phương trình log 1 x  2 là 2   A. x  4  . B. x  3  . C. x  3 . D. x  5 . Câu 20. 1
Nghiệm của phương trình log x  1  là 25   2 A. x  6  . B. x  6 . 5
Tài liệu học tập Toán 12 23
C. x  4 . D. x  . 2
Câu 21. Nghiệm của phương trình log x  5  4 là 2   A. x  21. B. x  3 .
C. x  11. D. x  13 .
Câu 22. Nghiệm của phương trình log (x 1)  3 là 4 A. x  63 . B. x  65 . C. x  80 . D. x  82 .
Câu 23. Phương trình logx9  1 có nghiệm là A. x  1. B. x  8 . C. x  9  . D. x  0 .
Câu 24. Tập nghiệm của phương trình log  2 x  1  3 là 2  A.  3  ;  3 . B.   3  . C.   3 . D.  10; 10 .
Câu 25. Phương trình log  2
x  1  1 có nghiệm là 3  A. x  2  . B. x  4  .
C. x   2 .
D. x   6 .
Câu 26. Tập nghiệm của phương trình log  2
x  2x  1 là 3  A.  ; 1  3  . B.  ; 1  3 . C.   0 . D.   3  . Câu 27. 1
Nghiệm của phương trình log x  1  là 25   2 A. x  6  . B. x  6 . 23
C. x  4 . D. x  . 2
Câu 28. Nghiệm của phương trình log x  2  2 là 3   A. x  9 . B. x  8 . C. x  11. D. x  10 .
Câu 29. Tập nghiệm của phương trình log  2
2x x  3  1 là 3   1 
A. 0;  . B.   0 .  2   1   1  C.   . D. 0;  .  2   2 
Câu 30. Số nghiệm của phương trình log  2
x x  3  2 2  là A. 2. B. 1. C. 0. D. 3.
Câu 31. Tập nghiệm của phương trình log  2
x x  2  1 là 2  A.   0 . B. 0;  1 .  6 THPT Marie Curie C.  1  ;  0 . D.   1 .
Câu 32. Phương trình log 2x 1 log x 1  1 có tập 3   3   nghiệm là A.   4 . B.   3 . C.   2  . D.   1 .
Câu 33. Phương trình log x 1  log x 1  3 có tập 2   2   nghiệm là A.  3  ;  3 . B.   4 . C.   3 . D.  10; 10 .
Câu 34. Phương trình log x  2  log x  2  log 5 có tất 3   3   3 cả bao nhiêu nghiệm? A. 2. B. 0. C. 1. D. 3.
Câu 35. Tích giá trị tất cả các nghiệm của phương trình x   2 1 log log 2x  8 bằng A. 3  . B. 4 . C. 2 . D. 3 . Câu 36. Tập nghiệm của phương trình log  2
x  2x  3  log x  1  1 là 3  3   A. 0;  5 . B.   0 . C. 1;  5 . D.   5 .
Câu 37. Phương trình log x 3 log (x8)2  0 2  4  có tất cả bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Câu 38. Giá trị của a sao cho phương trình log x a  3 2  
có nghiệm x  2 là A. 10. B. 5. C. 6. D. 1.
Câu 39. Tổng giá trị tất cả các nghiệm của phương trình 2 log . x log . x log . x log x  bằng 3 9 27 81 3 82 80 A. . B. . 9 9 C. 9 . D. 0 .
Câu 40. Với mọi a, b, x là các số thực dương thỏa mãn
log x  5log a  3log b , mệnh đề nào dưới đây đúng? 2 2 2
A. x  3a  5b .
B. x  5a  3b . C. 5 3
x a b . D. 5 3 x a b . 7
Tài liệu học tập Toán 12
Câu 41. Số nghiệm của phương trình log 6  7x  1 x là 7   A. 3. B. 0. C. 1. D. 2.
Câu 42. Tổng tất cả các nghiệm của phương trình
log 6  2x  1  x bằng 2   A. 1 . B. 1 . C. 0 . D. 3 .
Câu 43. Tổng tất cả các nghiệm của phương trình
log 7  3x  2  x bằng 3   A. 2. B. 1. C. 7. D. 3.  8 THPT Marie Curie DẠNG 4.
BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT A. PHƯƠNG PHÁP
 Nếu a  1 thì  f (x) ag(x) a
f x  gx  f(x) a
b f x  log b af x   b af x   g x  log f x b  log f x g x a
   loga         a    
   f x  0 f x   0  Nếu a  1 thì  f (x) ag(x) a
f x  gx  f(x) a
b f x  log b af x   b af x   g x  log f x b  log f x g x a
   loga         a    
   f x  0 g x   0 Chú ý
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... B. VÍ DỤ Ví dụ 1. 2
Giải bất phương trình x x6 3  1 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 2 x 5x4 Ví dụ 2.  1 
Giải bất phương trình    4 .  2  Lời giải
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... x3 Ví dụ 3. x 1
Giải bất phương trình    1 2    .  16  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 4. Giải bất phương trình x x 1 9 3    4 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Giải bất phương trình log 4x  3  2 . 3 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 6. Giải bất phương trình 3  log 6x   1  0 . 1 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................  2 THPT Marie Curie
.......................................................................................................................................................................
Ví dụ 7. Giải bất phương trình 2
log (x x  1)  log (2x  5) . 0,8 0,8 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 8. Giải bất phương trình log x  3  1 log x 1 . 2   2   Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 9. Giải bất phương trình 2
log x  log x  0 . 2 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 10. Giải bất phương trình 2
log(x x  2)  2 log(3  ) x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM 3
Tài liệu học tập Toán 12
Câu 1. Tập nghiệm của bất phương trình 3x  1 là A.  ;  0 . B. . C. 1;    . D. 0;   .
Câu 2. Nghiệm của bất phương trình x2 3  243 là A. x  7 . B. x  7 . C. x  7 .
D. 2  x  7 . Câu 3.
Tập nghiệm của bất phương trình: x2 1 3  là 9 A.  4;    . B.  ;  0 . C. 0;   . D. ; 4   . Câu 4.
Tập nghiệm của bất phương trình x1 1 5   0 là 5 A. 1;  . B.  1;   . C.  2;   . D.  ;  2   . 13x Câu 5.  2  25
Tập nghiệm của bất phương trình    là  5  4  1  A. ;1 . B. ;    .  3   1  C.   ;  . D. 1;    .  3  x4 Câu 6.  1 
Tập nghiệm của bất phương trình    8 là  2 
A. 1;  . B.  1;   . C.   ;1  . D.  ;    1 . 34 x Câu 7.  1 
Tập nghiệm của bất phương trình    9 là  3   5   5  A. ;   . B.   ; .  4   4   5   5  C. ;    D.   ; .   4   4  Câu 8. Tập nghiệm của bất phương trình   x1 3 1  4  2 3 là A. 1;    . B. 1;  . C. ;1 . D.   ;1  . Câu 9. x
Bất phương trình  6  5   6  5 có tập  4 THPT Marie Curie nghiệm là A.  ;    1 . B.   ;1  . C.  1;   . D. 1;  . Câu 10. 2
Tập nghiệm của bất phương trình x 2 3 x  27 là A.  ;    1 . B. 3;  . C.  1  ;3 . D.  ;    1 3;  . Câu 11. 2
Tập nghiệm của bất phương trình x 2 2 x  8 là A. ;   1 . B.  1  ; 3 . C. 3;  . D. ;   1 3;   . 2 x 2x Câu 12.  1  1
Tập nghiệm của bất phương trình    là  3  27 A.  3  ;  1 . B. 1; 3 . C.  1  ;3 . D.  ;  3  1;. 2 x 2 x Câu 13.  1  Bất phương trình    5 có tập nghiệm là  5  A. (1; ) .
B. (;1) . C. . D. .
Câu 14. Tập nghiệm của bất phương trình 2x x6 2  2 là A. 0; 6 . B. ; 6 . C. 0;64 . D. 6;  . x1 x3 Câu 15.  3   3 
Tập nghiệm của bất phương trình       4   4  là A. 2;  . B. ; 2 . C. 2;   . D.  ;  2 .  Câu 16. x
Tập nghiệm của bất phương trình  3 5 1 x3  5 là A.  5;   . B. 0;  . C. 18 . D. ; 0 . Câu 17. 2
Tập nghiệm của bất phương trình x 6 2  2 x là A. 2;  . B.  ;  3   . C.  3  ;2. D.  2  ;3. Câu 18. 2
Tập hợp nghiệm của bất phương trình x 6 2  2 x là A. 2;  . B.  ;  3   . C.  3  ;2. D.  2  ;3. Câu 19. Tập nghiệm của bất phương trình 5
Tài liệu học tập Toán 12 5x6   2x  1  0,125    là  8 
A. 3; . B.  ;
 23;. C.  ;  2. D. 2; 3. Câu 20. Tập nghiệm của bất phương trình 32.4x 18.2x  1 0 là A.  4;    1 . B. 1; 4 .  1 1  C. 2; 4 . D.  ;  .  16 2 
Câu 21. Tập nghiệm của bất phương trình log 2x  3  1 3   là  1  A. 1;  . B. ;    .  6  C. 2; . D. 3;  .
Câu 22. Bất phương trình log x  2  1
 có tập nghiệm là 1   2 A. 0;   . B. (2; 0].  1  C.  ;  0 . D. 2;    .  2 
Câu 23. Tập nghiệm của bất phương trình log (3x 1)  3 là 2  1  A. 3;  . B.  ; 3 .  3   10  C. ; 3 . D. ;    .  3 
Câu 24. Bất phương trình log x 1  3 có tập nghiệm là 2  
tập con của tập X nào sau đây?
A. X  0;10 . B. X   1  ;7.
C. X  9;  .
D. X  10;  .
Câu 25. Bất phương trình log 2x 1  3 có nghiệm là 3   A. x  4 . B. x 14 . C. x  2 .
D. 2  x 14.
Câu 26. Tập nghiệm của bất phương trình log (1 x)  2 là 1 2  3   3  A. ; 1   . B. ;    .  4   4   3   3  C.   ;  . D.  ;1.  4   4 
Câu 27. Tập nghiệm của bất phương trình 2 log x  1 là 2  6 THPT Marie Curie A.  2; 2   \  0 . B. ; 2   \  0 . C.  2; 2  . D. 0; 2  . Câu 28. Tập nghiệm của bất phương trình log  2
x  3x  2  1  là 1  2 A.   ;1  . B. [0; 2) . C. [0;1)  (2; 3] . D. [0; 2) (3; 7] . Câu 29. Tập nghiệm của bất phương trình 2
log (x  5x  7)  0 là 1 2
A. (; 2) (3; ) . B. 3;  . C. 2; 3 . D. ; 2 .
Câu 30. Số nghiệm nguyên của bất phương trình 2
log (x  3x  2)  1  là 0,5 A. 2. B. 3. C. 4. D. Vô số.
Câu 31. Tập nghiệm S của bất phương trình
log (x  3)  log 4 là 1 1 2 2 A. S  3 ( ;7].
B. S  [3;7].
C. S  ( ;7].
D. S  [7 ;  )  .
Câu 32. Bất phương trình log 2x  3  log 3x  1 có 0,5   0,5   tập nghiệm là  3  A.  ;    . B. 2;  .  2   1  C. ; 2. D.  ;    .  3 
Câu 33. Bất phương trình log x 1  log 2x 1 có tập 1   1   2 2 nghiệm là A. 2;  . B. ; 2 .  1  C.  ; 2 . D.  1  ;2 .  2  Câu 34. Tập nghiệm của bất phương trình
log (x  1)  log (3x  1) là e e   A.   ;1  . B. 1;  .  1  C.  ;1 . D.  1  ;3 .  3  Câu 35. Tập nghiệm của bất phương trình
2 log x 1  log 5  x  1 là 2   2   7
Tài liệu học tập Toán 12 A. 3; 5   . B. 1; 5 . C. 1; 3 . D.  3  ; 3   . Câu 36. Tập nghiệm của bất phương trình 2
log x  log(4x  4) là A. (2; ). B. (1; ). C.  \  2 . D. (1; )   \  2 .
Câu 37. Bất phương trình 2
log x  5log x  4  0 có tập 2 2 nghiệm là A.  ;  2  1  6;   . B. 2;16   . C. 0; 2  1  6;   . D.  ;  1  4;    .  8 THPT Marie Curie DẠNG 5. TẬP XÁC ĐỊNH A. PHƯƠNG PHÁP
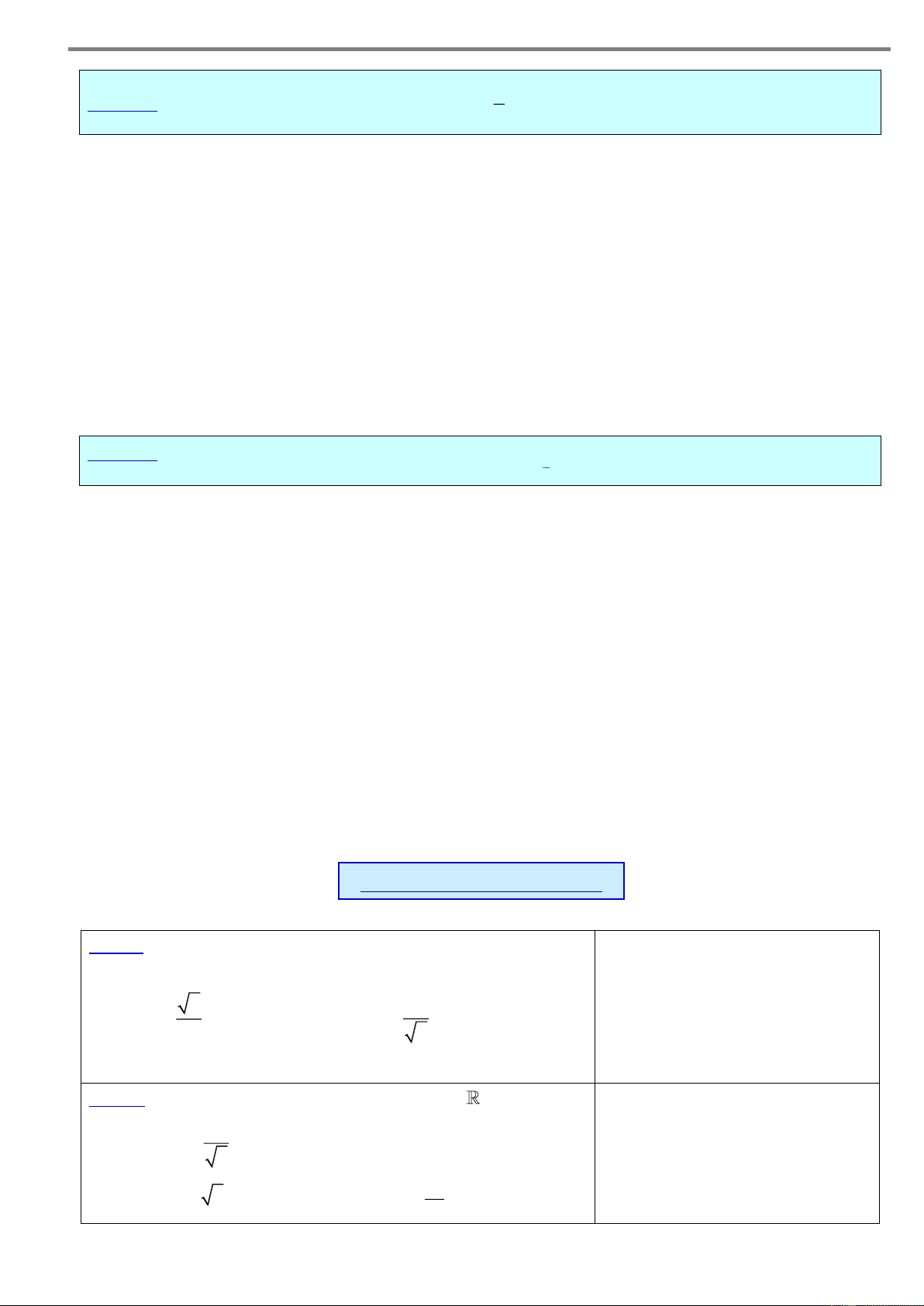
f x  0 
1. Hàm số y  log f x xác định khi: a  0 . a   a  1 
f x toàn taïi  f x
2. Hàm số y a
xác định khi: a  0 . a  1  3. Hàm số y x  :
Với  nguyên dương thì hàm số xác định với mọi x .
Với   0 hoặc  nguyên âm thì hàm số xác định với mọi x  0.
Với  không nguyên thì hàm số xác định với mọi x  0 . Chú ý 1 1
Theo định nghĩa, đẳng thức n n
x x chỉ xảy ra nếu x  0 . Do đó, hàm số n
y x không đồng nhất với hàm số n y x . 1 Chẳng hạn, hàm số 3
y x xác định với mọi x ; còn hàm số 3
y x chỉ xác định với mọi x  0 . B. VÍ DỤ
Ví dụ 1. Tìm tập xác định của hàm số y  log x  
1  2 log 3  x . 2  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tìm tập xác định của hàm số   2 5 3 x y . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
Ví dụ 3. Tìm tập xác định của hàm số    4 2 y x x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... Ví dụ 4.
Tìm tập xác định của hàm số     4 2 y x x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Tìm tập xác định của hàm số    1 2 3 y x x . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM Câu 1.
Tập xác định của hàm số y    x1 3 2 là A.  ;  . B.  ;  2 . C. ; 2. D. 2;  . Câu 2.
Tập xác định hàm số y  x  13 1 là A.   ;1  . B. 1;  . C. . D.  \  1 . Câu 3.
Tập xác định của hàm số y    x 6 5 là A. 5;  . B. ; 5 . C.  \  5 . D. .
Câu 4. Tập xác định hàm số y  x  2 2 1 là 2 THPT Marie Curie A.  ;   
1 1;  . B.  1  ;1. C. . D.  \ 1  ;  1 . Câu 5.
Tập xác định của hàm số y    x23 3 là A. ; 3 . B.  ;  3   . C. 3;  . D.  ;  . Câu 6.
Tập xác định của hàm số y  x  45 4 là
A. ; 4 . B. 4;  . C. . D.  \  4 . Câu 7.
Tập xác định của hàm số     3 2 y x x là A.  ;
 01; . B. 1;  . C. . D.  \ 0;  1 . Câu 8.
Hàm số y    x 6 2 7 16 4 có tập xác định là A.  ;  2    2;    . B.  ;  . C.  2  ; 2 . D.  \ 2;   2 . Câu 9. 
Tập xác định của hàm số y   2
2x x  là  1  A. 0; 2   . B.  0;  .  2  C.  ;  02;. D. 0; 2 . Câu 10.
Tập xác định của hàm số y  x x   3 2 2 là A. .
B. 0;  . C.  ;   
1 2;  . D.  \ 1  ;  2 .
Câu 11. Tập xác định của hàm số y  x x 5 2 2 là A. .
B. 0;  . C.  ;   
1 2;  . D.  \ 1  ;  2 .
Câu 12. Tập xác định của hàm số  2 4x y là A. . B.   1; . C.   4; . D. 0;  . 2x Câu 13.  1 
Tập xác định của hàm số y    là  2  A. . B.  \  0 .  1  C. \  . D.  \  2 . 2  3
Tài liệu học tập Toán 12 1
Câu 14. Tập xác định của hàm số   3x y là A. . B. \ 3. C. 0;  . D.  \  0 . Câu 15. 2 x
Tập xác định của hàm số y 1 2    là A. . B.  \  0 . C. . D. 0;  .
Câu 16. Tập xác định của hàm số 2
y  log (4x x ) là 2 A. 0; 4   . B. 4;  . C. 0; 4 . D. 0;  .
Câu 17. Hàm số y  log  2
x  2x có tập xác định là 7  A.  ;    1 . B.  2  ;0. C.  1;   . D.  ;  2  0; .
Câu 18. Tập xác định của hàm số y  log  2
x  4x  3 là 3 
A. 2  2;1 3; 2  2  . B. 1;3. C.  ;   1 3;  .
D. ; 2  2  2  2;  .
Câu 19. Tập xác định của hàm số y  log  2
x  2x  3 là 2  A.  ;  1    3;    . B.  1  ; 3   . C.  ;    1 3;  . D.  1  ;3 .  4 THPT Marie Curie DẠNG 6. ĐẠO HÀM A. PHƯƠNG PHÁP u
1. x   x a a ln a
2.    . u a
u a ln a
3. x   x e
e 4. u   . u e u e u 5. x 6. log u a     a   1 log x ln a uln a u 7.    1 ln x 8. lnu    x u u 9. x  1 log 10. log u    x ln 10 uln 10 B. VÍ DỤ Ví dụ 1. 2
Tính đạo hàm của hàm số   x x y e . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 2. Tính đạo hàm của hàm số 2 x 7 y x 3    . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Tính đạo hàm của hàm số y   2
ln x x  3 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
....................................................................................................................................................................... 1
Tài liệu học tập Toán 12
Ví dụ 4. Tính đạo hàm của hàm số y   2
log 2x  3x  7 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 5. Tính đạo hàm của hàm số y  x x  3 2 2 3 7 . Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Đạo hàm của hàm số y  log x là 1 ln10 A. y '  . B. y'  . x x 1 1 C. y '  . D. y '  . x ln10 10 ln x
Câu 2. Đạo hàm của hàm số y log x là 4 1 1 A. y  . B. y  . 2x ln 2 x log 4 ln 4 2 C. y  . D. y  . x x ln 2
Câu 3. Đạo hàm của hàm số y  log 2x 1 là 2   1 2 A. y   . B. y  . 2x   1 ln 2 2x 1ln2 2 1 C. y  . D. y  . 2x  1 2x  1
Câu 4. Hàm số f x  log  2
x  2x có đạo hàm 2  ln 2 1
A. f x  .
B. f x  . 2 x  2x
 2x 2xln2 2x  2 ln 2 2x  2
C. f x    .
D. f x  . 2 x  2x
 2x 2xln2
Câu 5. Đạo hàm của hàm số y   2 2
ln 2x e  là 2 THPT Marie Curie x 4x A. y     . B. y . 2 2  x e 2 2 2 2 2x e 4x  2e 4x C. y    . D. y  . 2x e 2 2 2 2x e 2 2 2
Câu 6. Đạo hàm của hàm số 13x y  là A. 1 .13x y x    . B. 13x y  .ln13 . 13x C. 13x y  . D. y  . ln13
Câu 7. Đạo hàm của hàm số 5x y  là A. 1 ' .5x y x   . B. ' 5x y  . 5x C. y '  . D. ' 5x y  .ln 5 . ln 5
Câu 8. Đạo hàm của hàm số 2x 1 y e   là A. 2   4 x y e . B. 2 1 2 x y e    . 2 x1 e 2 x1 2e C. y  . D. y  . ln 2 ln 10  Câu 9. x
Đạo hàm của hàm số y   3  là  x 3  1 x A. y  .
B. y    3 ln3 . ln 3 2 xx
C. y    3  ln 3 .
D. y   3 ln 3 .
Câu 10. Mệnh đề nào sau đây đúng?   A. x e xe log e .
B. 2x   2x log 2 . e 2  
C. 10x   10x log 10 .
D. 3x   3x log 3 . 10 3
Câu 11. Đạo hàm của hàm số  2x y x là A. '  2x y 1xln2. B. ' 2x y  1ln2. C. ' 2x y  ln 2 . D. '  2x y 1 x.
Câu 12. Đạo hàm của hàm số y xln x là 1 A. y '  .
B. y'  ln x. x C. y'  1 .
D. y'  ln x  1.
Câu 13. Đạo hàm của hàm số 2  ( 1) x y x e là A. x 2
y'  e (x  1) . B. x 2
y'  e (x  2x) . C. x 2
y'  e (x  1) . D. x 2
y'  e (x  1) . Câu 14. x  1
Đạo hàm của hàm số y  là 4x 1 2(x  1)ln 2 1 2(x  1)ln 2 A. y  . B. y  . 2 2 x 2 2 x 3
Tài liệu học tập Toán 12 1  2(x  1) ln 2 1  2(x  1) ln 2 C. y  . D. y  . 2 2 2x 2x
Câu 15. Cho hàm số y   2
ln x  3x . Phương trình f 'x  0 có tập nghiệm là  3  A. .  B.   .  2   2  C. 0;  3 . D.   .  3  Câu 16. Cho   2  . x f x
x e . Phương trình f 'x  0 có tất cả bao nhiêu nghiệm? A. 2. B. 3. C. 1. D. 0. Câu 17. Cho hàm số 2 f ( )
x  log (x  1) . Giá trị của f '(1) 5 bằng 2 1 A. . B. . ln 5 ln 5 1 3 C. . D. . 2 ln 5 2 ln 5 Câu 18. Cho hàm số x x y e e  
. Giá trị của y  1 bằng: 1 1 A. e  . B. e  . e e 1 1 C. e  . D. e  . e e 4 THPT Marie Curie DẠNG 7.
TÍNH CHẤT ĐƠN ĐIỆU VÀ ĐỒ THỊ A. PHƯƠNG PHÁP
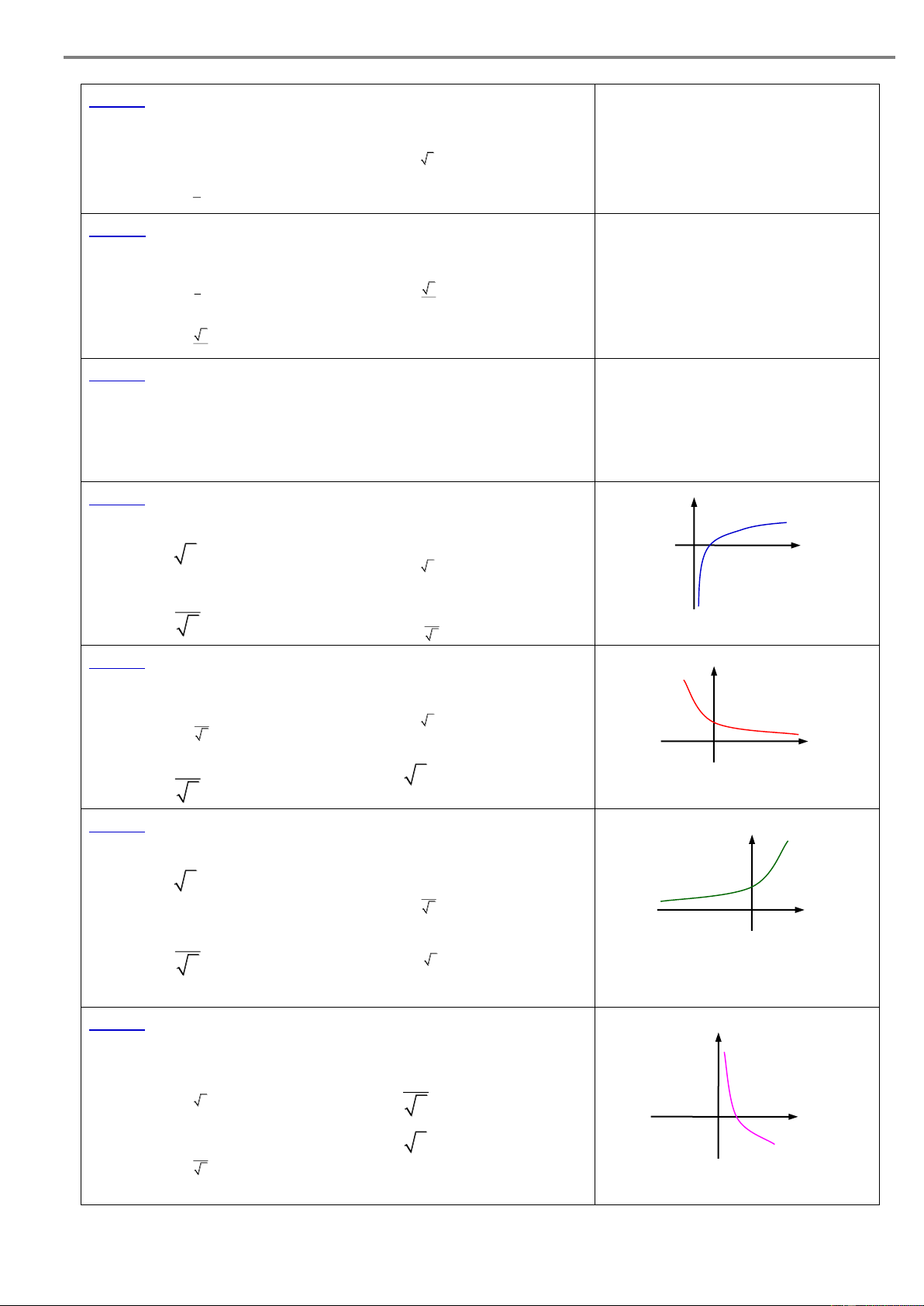
1. Hàm số y=ax Có tập xác định là
và tập giá trị là 0;  Đồng biến trên
khi a  1, nghịch biến trên khi 0  a  1 Đồ thị: y y Đi qua điểm 0;  1
Nằm ở phía trên trục hoành 1 1
Nhận trục hoành làm tiệm cận ngang O x O x a > 1 0 < a < 1
2. Hàm số y=logax
Có tập xác định là 0;  và tập giá trị là
Đồng biến trên 0;  khi a  1, nghịch biến trên 0;  khi 0  a  1 Đồ thị: y y Đi qua điểm 1;0
Nằm ở bên phải trục tung O 1 x 1
Nhận trục tung làm tiệm cận đứng O x a > 1 0 < a <1
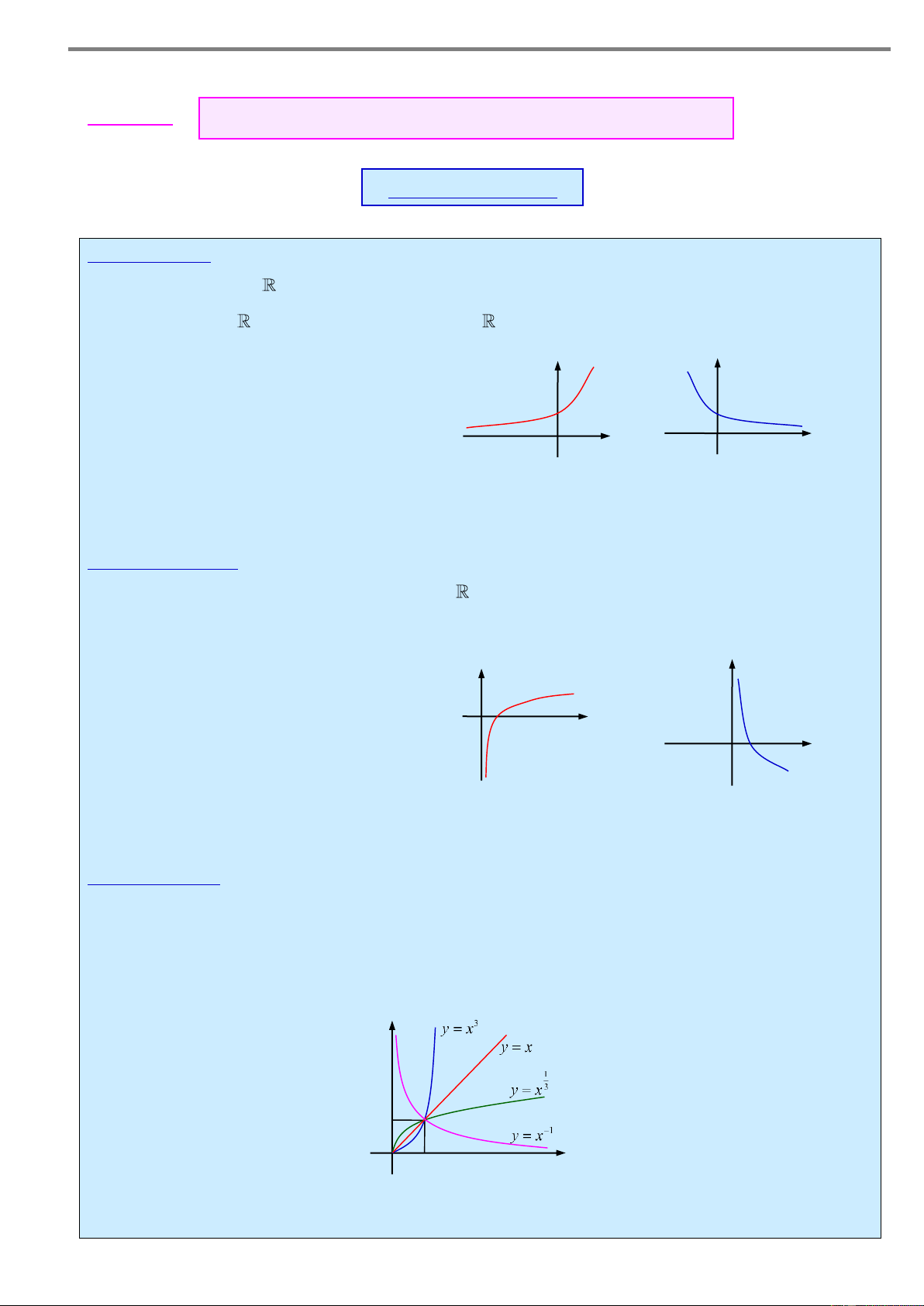
3. Hàm số y=x (Chỉ xét   0 và x  0 )
Có tập xác định là 0;  và tập giá trị là 0; 
Đồng biến trên 0;  khi   0 , nghịch biến trên 0;  khi   0
Có đồ thị đi qua điểm 1;  1 y 1 O 1 x 1
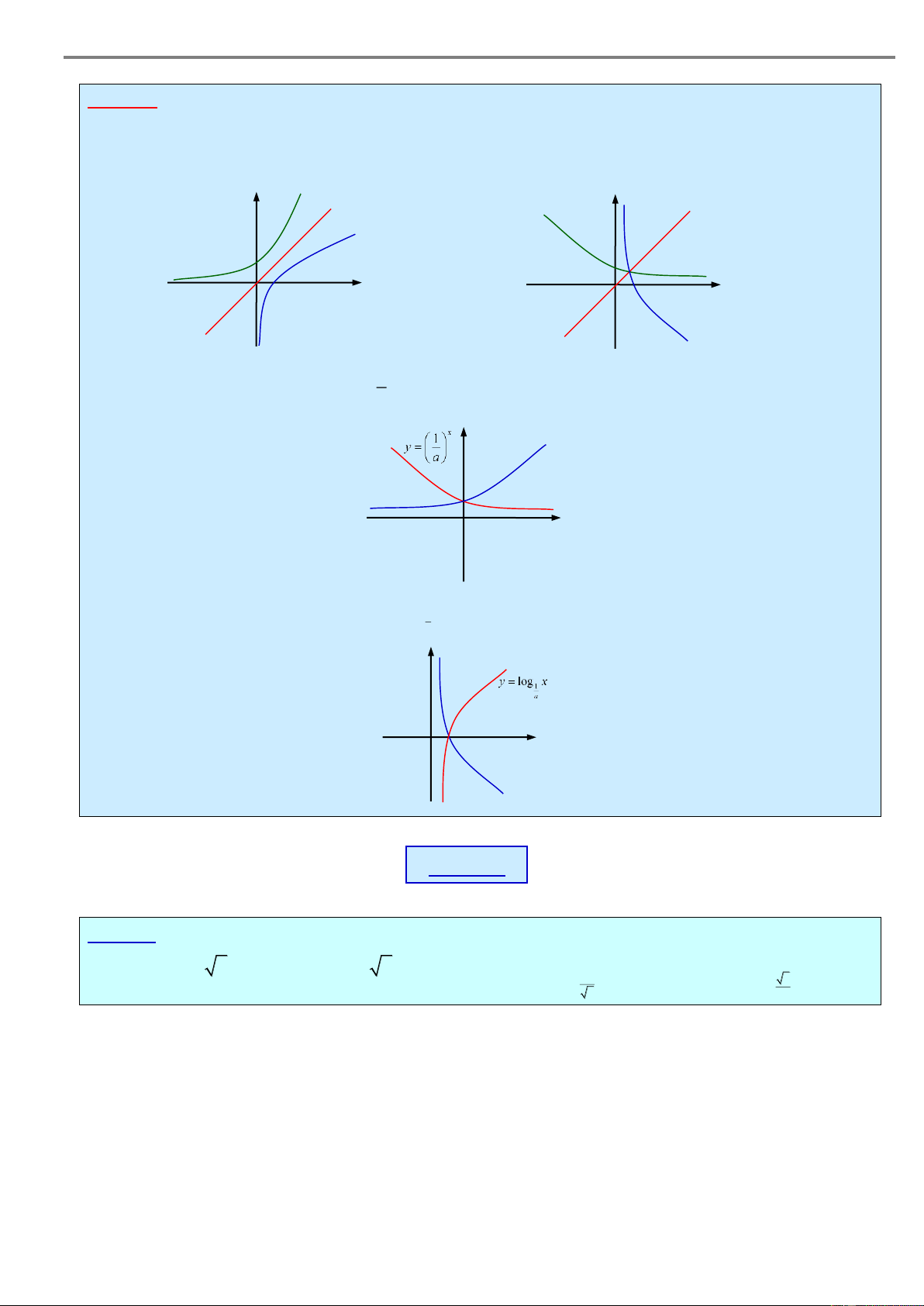
Tài liệu học tập Toán 12 Chú ý Đồ thị hai hàm số x
y a và y  log x đối xứng với nhau qua đường phân giác góc phần tư a
thứ nhất y x . y y = ax y y = x y = ax y = x y = log ax 1 1 O 1 x O 1 x y = logax a > 1 0 < a < 1 x  1  Đồ thị hai hàm số x
y a và y    đối xứng với nhau qua trục tung  a y y = ax 1 O x
Đồ thị hai hàm số y  log x và y  log x đối xứng với nhau qua trục hoành a 1 a y O 1 x y = logax B. VÍ DỤ
Ví dụ 1. Xét tính đơn điệu của các hàm số sau: x x
a. y   2  b. y   2 1 c. y  log x d. y  log x . 1 7 2 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................  2 THPT Marie Curie x Ví dụ 2.  1 
Vẽ đồ thị của hai hàm số 2x y  và y    .  2  Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
Ví dụ 3. Vẽ đồ thị của hai hàm số y  log x và y  log x . 2 1 2 Lời giải
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
.......................................................................................................................................................................
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Trong các hàm số sau, hàm số nào nghịch biến trên
tập xác định của nó? xx 2   3  A. y     . B. y    . 3     2  C. x y   . D. x y e .
Câu 2. Hàm số nào dưới đây đồng biến trên ? x  
A. f x 1    . B.   3 x f x   . 3  x
C. f x   3  .
D. f x 3  . 3x 3
Tài liệu học tập Toán 12
Câu 3. Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A. y  ln x . B. y  log x . 3
C. y  log x .
D. y  log x . e
Câu 4. Trong các hàm số sau, hàm số nào đồng biến trên
tập xác định của nó?
A. y  log x . B. y  log x . 1 3 2 2 C. y  log x .
D. y  log x . 2  2
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số y  1 log x 2 ? A. M 1;  1 .
B. N 1;0 .
C. P1; 3 .
D. Q1; 2 .
Câu 6. Hàm số nào trong các hàm số sau có đồ thị là hình y vẽ bên? x
A. y   2  . B. y  log x . O 1 x 2 x  1  C. y    . D. y  log x .  1 2  2
Câu 7. Hàm số nào trong các hàm số sau có đồ thị là hình y vẽ bên? A. y  log x . B. y  log x . 1 2 1 2 xO x 1  x C. y    .
D. y   2  .  2 
Câu 8. Hàm số nào trong các hàm số sau có đồ thị là hình y vẽ bên? x
A. y   2  . B. y  log x . 1 1 2 O x x  1  C. y    . D. y  log x .  2  2
Câu 9. Hàm số nào trong các hàm số sau có đồ thị là hình y vẽ bên? x  1  A. y  log x . B. y    . 2  2  1 x O x C. y  log x .
D. y   2  . 1 2  4 THPT Marie Curie
Câu 10. Cho hai hàm số x y a , x
y b với a, b là hai số thực y
dương khác 1, lần lượt có đồ thị là C và C như hình (C2) (C1) 2  1 
bên. Mệnh đề nào dưới đây đúng?
A. 0  a b  1.
B. 0  b  1  a . O x
C. 0  a  1  b .
D. 0  b a  1.
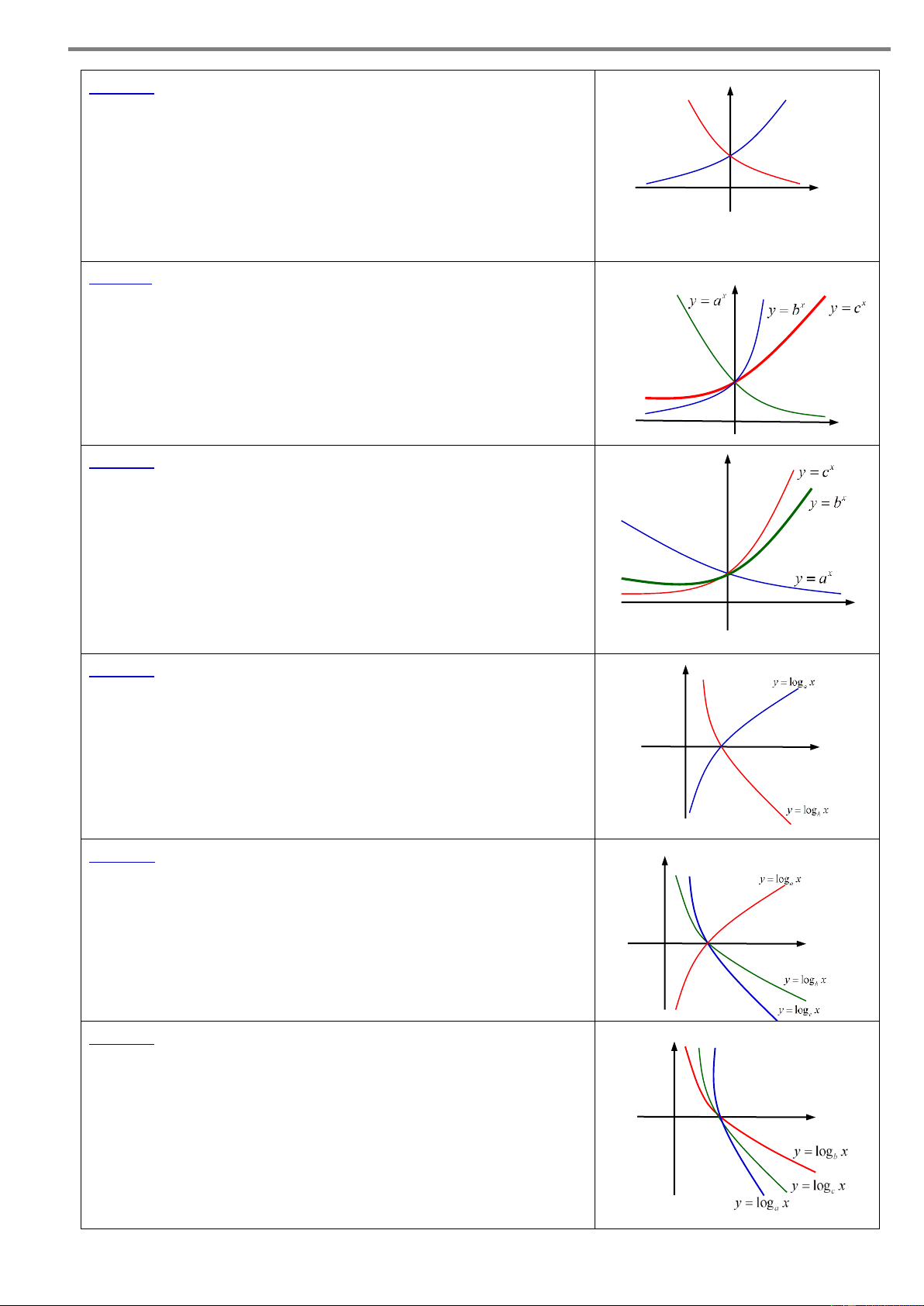
Câu 11. Cho ba số thực dương a, b, c khác 1. Đồ thị các y hàm số x y a , x y b , x
y c được cho trong hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a b c .
B. a c b . 1
C. b c a .
D. c a b . O x
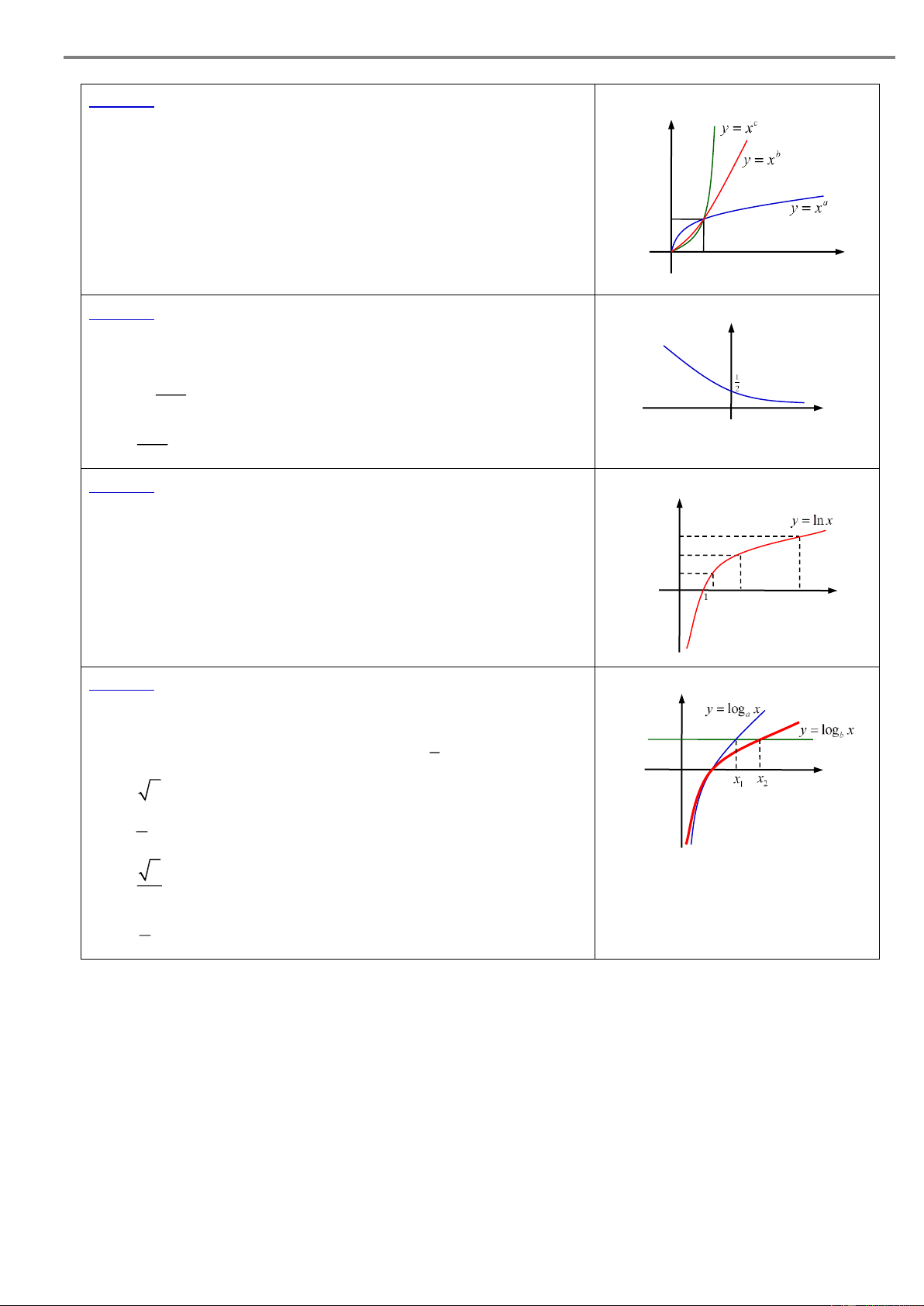
Câu 12. Cho a , b , c là các số thực dương và khác 1. Đồ thị y các hàm số x y a , x y b và x
y c được cho trong hình bên.
Khẳng định nào sau đây là đúng?
A. a  1  c b .
B. b c  1  a .
C. c b  1  a . 1
D. a  1  b c . x O
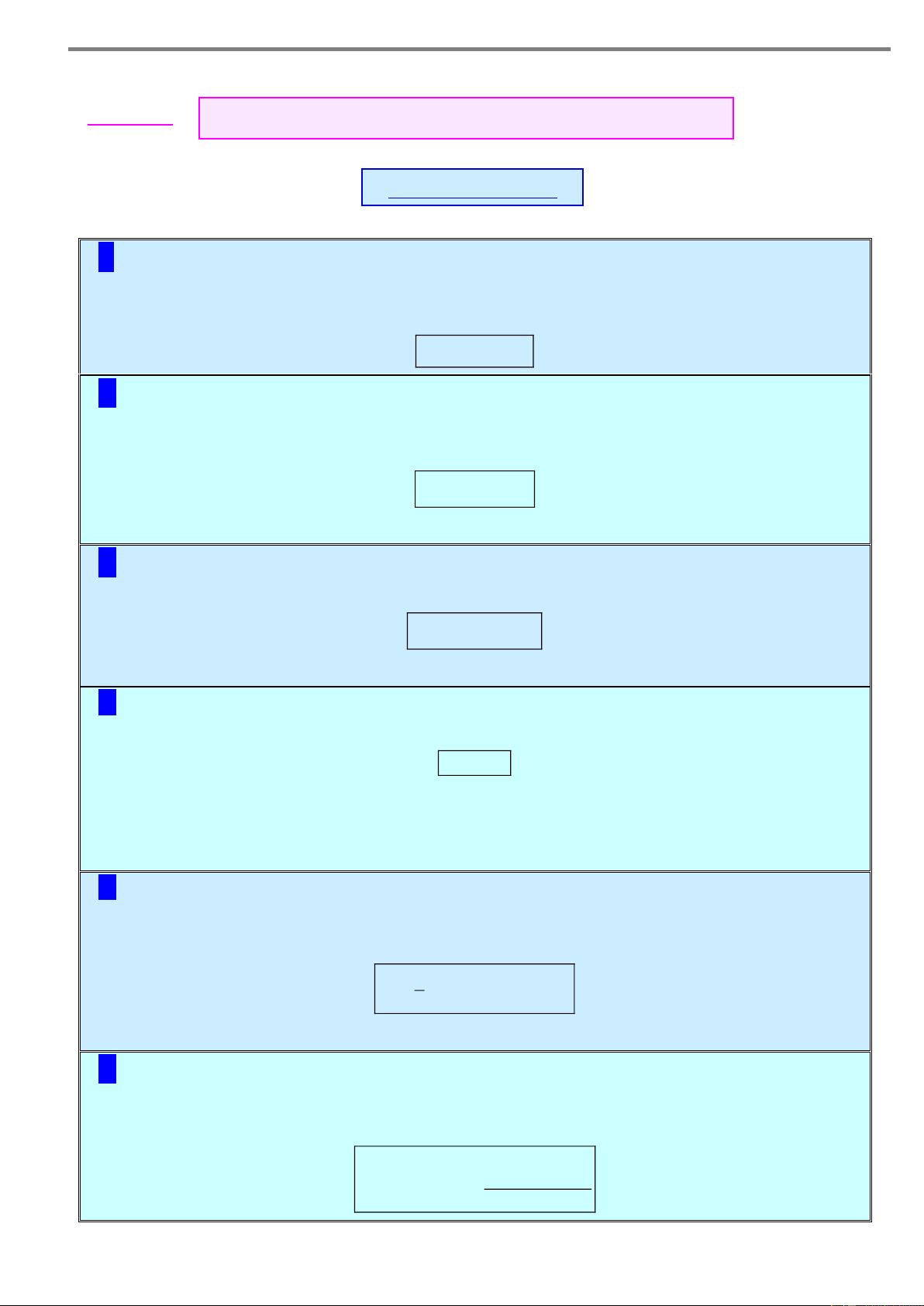
Câu 13. Cho hai hàm số y  log x, y  log x lần lượt có đồ y a b
thị (C ) và (C ) được vẽ trên cùng mặt phẳng tọa độ. Mệnh 1 2 đề nào sau đây đúng?
A. 0  b a  1. O 1 x
B. 0  b  1  a .
C. 0  a b  1.
D. 0  a  1  b .
Câu 14. Cho ba số thực dương a, b, c khác 1. Đồ thị các y
hàm số y  log x, y  log x, y  log x được cho trong hình a b c
bên. Mệnh đề nào dưới đây đúng?
A. c a b .
B. b c a . O 1 x
C. a b c .
D. a c b .
Câu 15. Cho ba số thực dương a, b, c khác 1. Đồ thị các y
hàm số y  log x, y  log x, y  log x được cho trong hình a b c
bên. Mệnh đề nào dưới đây đúng?
A. a b c . O 1 x
B. b c a .
C. c a b .
D. a c b . 5
Tài liệu học tập Toán 12
Câu 16. Cho a , b , c là các số thực dương. Đồ thị các hàm số a y x , b y x và c
y x trên khoảng 0; + được cho y
trong hình bên. Khẳng định nào sau đây là đúng?
A. b c a .
B. c b a .
C. b a c .
D. a b c . O x
Câu 17. Cho hàm số f xx 1 a  
có đồ thị như hình bên. y Khi đó f '  1 bằng ln 2 A.  . B. 4 ln 2 . 4 O x ln 2 C. . D. 4  ln 2 . 4
Câu 18. Đồ thị hàm số y  lnx đi qua 3 điểm M ;aa' , y N  ;
b b' , Pc;c' với a' c'  2b' như hình bên. Khẳng định c’ nào sau đây là đúng? b’ P N A. 2 ac b . a’ M
B. ac b . 1 O a b c x C. 2 ac  2b .
D. a c  2b .
Câu 19. Cho hàm số y  log x và y  log x có đồ thị như a b y
hình bên. Đường thẳng y  1 cắt hai đồ thị tại các điểm có a 1
hoành độ là x , x . Biết 2x  3x , giá trị bằng 1 2 1 2 b O 1 x A. 3 3 . 3 B. . 2 3 C. . 2 2 D. . 3  6 THPT Marie Curie DẠNG 8. LÃI SUẤT A. PHƯƠNG PHÁP
1. Gửi vào ngân hàng một số tiền P đồng với lãi suất r% mỗi năm (hoặc mỗi quý, hoặc 0
mỗi tháng) theo hình thức lãi đơn thì sau n năm (hoặc n quý, hoặc n tháng) số tiền cả gốc lẫn lãi là
P P 1  nr n 0  
2. Gửi vào ngân hàng một số tiền P đồng với lãi suất r% mỗi năm (hoặc mỗi quý, hoặc 0
mỗi tháng) theo thể thức lãi kép thì sau n năm (hoặc n quý, hoặc n tháng) số tiền cả gốc lẫn lãi là n
P P . 1  r n 0  
3. Gửi vào ngân hàng một số tiền P đồng với lãi suất r% mỗi năm theo hình thức lãi kép 0
và có kì hạn m tháng thì sau n kì hạn số tiền cả gốc lẫn lãi là n
P P . 1  mr n 0  
4. Với số vốn ban đầu là A , theo thể thức lãi kép liên tục, lãi suất mỗi năm là r thì sau N
năm số tiền thu được cả vốn lẫn lãi sẽ là Nr S Ae
Nhiều hiện tượng tăng trưởng (hoặc suy giảm) của tự nhiên và xã hội, chẳng hạn sự tăng dân số,
cũng được ước tính theo công thức Nr S Ae .
5. Một người mỗi tháng đều gửi vào ngân hàng số tiền a đồng vào đầu mỗi tháng theo
hình thức lãi kép với lãi suất là r% /tháng thì sau n tháng, người ấy có số tiền cả gốc lẫn lãi là a Pr      r nn 1  1 1  r  
6. Một người gửi vào ngân hàng số tiền P đồng theo hình thức lãi kép với lãi suất là r% 0
/tháng và mỗi tháng đều rút ra a đồng vào ngày tính lãi thì sau n tháng, người ấy còn lại
số tiền trong ngân hàng là a  n 1 r 1   n  
P P 1  r n 0   r 1
Tài liệu học tập Toán 12
7. Vay P (đồng) từ ngân hàng với lãi suất r% /tháng. Biết rằng số hoàn nợ hàng tháng ở 0
mỗi lần là như nhau và lãi suất ngân hàng không thay đổi trong thời gian hoàn nợ. Sau n
tháng thì hết nợ. Khi đó, mỗi tháng phải hoàn nợ số tiền là n
P .r 1 r 0   a   n 1 r 1
B. CÂU HỎI TRẮC NGHIỆM
Câu 1. Một người gửi 50 triệu đồng vào một ngân hàng với
lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân
hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để
tính lãi cho năm tiếp theo. Sau 5 năm người đó rút tiền bao
gồm cả gốc và lãi. Hỏi người đó rút được số tiền bao nhiêu?
A. 101 triệu đồng. B. 90 triệu đồng. C. 81 triệu đồng. D. 70 triệu đồng.
Câu 2. Một người gửi 50 triệu đồng vào một ngân hàng với lãi
suất 6%/ năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng
thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi
cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó
nhận được số tiền nhiều hơn 100 triệu đồng bao gồm gốc và
lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra. A. 13 năm. B. 14 năm. C. 12 năm. D. 11 năm.
Câu 3. Một người gửi 15 triệu đồng vào ngân hàng theo
thể thức lãi kép kỳ hạn một quý với lãi suất 1,65% một quý.
Hỏi sau bao nhiêu quý thì người đó có được ít nhất 20 triệu? A. 15 quý. B. 16 quý. C. 17 quý. D.18 quý.
Câu 4. Một người gửi tiết kiệm vào một ngân hàng với lãi
suất 7,5% / năm. Biết rằng nếu không rút tiền ra khỏi ngân
hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn
để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm
người đó thu được (cả số tiền gửi ban đầu và lãi) gấp đôi số
tiền gửi ban đầu, giả định trong khoảng thời gian này lãi
suất không thay đổi và người đó không rút tiền ra? A. 11 năm. B. 9 năm. C. 10 năm. D. 12 năm.
Câu 5. Bạn A gửi tiết kiệm số tiền 58.000.000 đồng tại một
ngân hàng theo thể thức lãi kép. Sau 8 tháng bạn đó nhận  2 THPT Marie Curie
được 61.329.000 đồng cả gốc lẫn lãi. Hỏi lãi suất hàng tháng
của ngân hàng đó là bao nhiêu? A. 0,6%. B. 6%. C. 0,7%. D. 7%.
Câu 6. Ông A gửi vào ngân hàng 100 triệu đồng theo hình
thức lãi kép. Lãi suất ngân hàng là 8% trên năm và không
thay đổi qua các năm ông gửi tiền. Sau 5 năm ông cần tiền
để sửa nhà, ông đã rút toàn bộ số tiền và sử dụng một nửa
số tiền đó vào công việc, số còn lại ông tiếp tục gửi ngân
hàng với hình thức như trên. Hỏi sau 10 năm ông A đã thu
được số tiền lãi gần nhất với số nào dưới đây (đơn vị tính là triệu đồng)? A. 79,412 . B. 80, 412 . C. 81,412 . D. 100, 412 .
Câu 7. Đầu năm 2016, ông A thành lập một công ty. Tổng số
tiền ông A dùng để trả lương cho nhân viên trong năm 2016 là
1 tỷ đồng. Biết rằng cứ sau mỗi năm thì tổng số tiền dùng để trả
lương cho nhân viên trong cả năm đó tăng thêm 15% so với
năm trước. Hỏi năm nào dưới đây là năm đầu tiên mà tổng số
tiền ông A dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng? A. Năm 2023. B. Năm 2022. C. Năm 2021. D. Năm 2020.
Câu 8. Một người gửi mỗi tháng 10 triệu đồng vào một ngân
hàng với lãi suất 0,5%/ tháng. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập
vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau hai tháng, số
tiền cả gốc và lãi mà người đó có được là bao nhiêu? Giả
định trong suốt thời gian gửi, lãi suất không đổi. A. 20.150.250 đồng. B. 20.100.000 đồng. C. 20.150.000 đồng. D. 20.100.250 đồng.
Câu 9. Một người gửi vào ngân hàng 100 triệu đồng với kì
hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi kép (sau
3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng,
người đó gửi thêm 50 triệu đồng với kì hạn và lãi suất như
trước đó. Tổng số tiền người đó nhận được sau 1 năm (Tính
từ lần gửi tiền đầu tiên) là
A. 179,676 triệu đồng.
B. 177,676 triệu đồng.
C. 178,676 triệu đồng.
D. 176,676 triệu đồng.
Câu 10. Một người gửi mỗi tháng 5 triệu đồng vào một ngân
hàng với lãi suất 0,7%/ tháng. Biết rằng nếu không rút tiền ra
khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập
vào gốc để tính lãi cho tháng tiếp theo. Hỏi sau 10 tháng, số
tiền cả gốc và lãi mà người đó có được gần nhất với số nào
trong các số tiền sau, giả định trong suốt thời gian gửi, lãi suất không đổi? 3
Tài liệu học tập Toán 12 A. 54 triệu đồng. B. 53 triệu đồng. C. 51 triệu đồng. D. 52 triệu đồng.
Câu 11. Bạn A muốn có 100 triệu đồng sau 10 tháng thì bạn
A phải gửi tiết kiệm mỗi tháng gần nhất với số nào trong
các số tiền sau, biết lãi suất gửi là 0,6% /tháng và theo thể thức lãi kép?
A. 9,5 triệu đồng.
B. 9,9 triệu đồng.
C. 9,7 triệu đồng.
D. 9,4 triệu đồng.
Câu 12. Một người gửi số tiền là 11000 USD trong ngân
hàng theo hình thức lãi kép với lãi suất 0,73% một tháng.
Mỗi tháng người đó đến rút 60USD để chi phí cho sinh hoạt
gia đình. Hỏi sau một năm số tiền còn lại là bao nhiêu? ( Kết
quả làm tròn đến hàng đơn vị) A. 11254USD. B. 1259USD. C. 1257USD. D. 1256USD.
Câu 13. Ông A gửi vào ngân hàng 20 triệu đồng theo thể
thức lãi kép với lãi suất 0.75% mỗi tháng. Hằng tháng ông
A rút ra 300 nghìn đồng vào ngày tính lãi. Hỏi sau hai năm
ông A còn lại bao nhiêu tiền (làm tròn đến 1000 đồng)? A. 1.607.000 đồng. B. 16.071.000 đồng. C. 16.072.000 đồng. D. 16.073.000 đồng.
Câu 14. Ông A gửi vào ngân hàng 11 triệu đồng theo thể
thức lãi kép với lãi suất 0.73% mỗi tháng. Hằng tháng ông
A rút ra 200 nghìn đồng vào ngày tính lãi. Hỏi sau bao lâu thì ông A hết tiền? A. 71 tháng. B. 72 tháng. C. 70 tháng. D. 73 tháng.
Câu 15. Ông A vay ngắn hạn ngân hàng 100 triệu đồng, với
lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo
cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn
nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số
tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau
đúng 3 tháng kể từ ngày vay. Hỏi, theo cách đó, số tiền m
mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ
là bao nhiêu? Biết rằng, lãi suất ngân hàng không thay đổi
trong thời gian ông A hoàn nợ. 3 100.(1,01) A. m  (triệu đồng). 3 3 (1,01) B. m  (triệu đồng). 3 (1,01)  1 1001,03 C. m  (triệu đồng). 3 3 120.(1,12) D. m  (triệu đồng). 3 (1,12)  1  4 THPT Marie Curie
Câu 16. Ông A vay ngân hàng 100 triệu đồng với lãi suất
1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng theo cách:
Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ;
hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền
hoàn nợ ở mỗi tháng là như nhau và ông A trả hết nợ sau
đúng 5 năm kể từ ngày vay. Biết rằng mỗi tháng ngân hàng
chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền
mỗi tháng ông ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
A. 2, 22 triệu đồng.
B. 3,03 triệu đồng.
C. 2, 25 triệu đồng.
D. 2,20 triệu đồng.
Câu 17. Ông A vay ngân hàng 300 triệu đồng. Nếu cuối mỗi
tháng bắt đầu từ tháng thứ nhất ông A trả hằng tháng
5.500.000 đồng và chịu lãi số tiền chưa trả là 0,5%/tháng thì
sau ít nhất là bao lâu, ông A trả hết số tiền trên? A. 65 tháng. B. 64 tháng. C. 63 tháng. D. 66 tháng. 5
Document Outline

  • dang-1-cong-thuc-luy-thua_3112021131059
  • dang-2-cong-thuc-logarit_3112021131059
  • dang-3-phuong-trinh-mu-va-logarit_3112021131059
  • dang-4-bat-phuong-trinh-mu-va-logarit_3112021131059
  • dang-5-tap-xac-dinh_3112021131059
  • dang-6-dao-ham_3112021131059
  • dang-7-tinh-chat-don-dieu-va-do-thi_3112021131059
    • Word Bookmarks
      • MTBlankEqn
  • dang-8-lai-suat_3112021131059