Các dạng bài tập VDC hàm số mũ và hàm số lôgarit

Tài liệu gồm 37 trang, tóm tắt lý thuyết cơ bản cần nắm và hướng dẫn phương pháp giải các dạng bài tập trắc nghiệm vận dụng cao (VDC / nâng cao / khó) hàm số mũ và hàm số lôgarit, phù hợp với đối tượng học sinh khá – giỏi khi học chương trình Giải tích 12

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

19 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
BÀI 3. LÔGA
RIT
A.
K
IẾN THƯC CƠ BẢN CẦN NẮ
M
1.
Khá
i
niệm lôgarit
Cho hai số dương
,ab với 1a . Số
thỏa mãn
đẳng thức
ab
được gọi là lôgarit cơ số
a
của
b , và ký hiệu là log
a
b .
2. Tính chất
Cho , 0, 1ab a. Ta có:

log
log 0; log 1
;log


a
aa
b
a
a
ab a
Nhận xét:
log , 0, 1

a
bababa
Bài tập:
3
2
log 8 3 2 8

Chú ý:
Không có lôgarit của số âm và số 0.
3. Quy tắ
c tính lôgarit
a.
Lôgarit c
ủa một tích
Cho
12
,, 0ab b với 1a
, ta có:
12 1 2
log ( ) 
aaa
b b log b log b
Chú ý: Định lý trên có thể mở rộng cho tích của n
số dương:
11
log ... log ... log
an a an
bb b b
trong đó
12
, , ,..., 0, 1.
n
ab b b a
Bài tập:
11
log log 2 log .2 log 1 0;
22





333 33
123 78
log log log ... log log
234 89

3
123 78
log . . ..... .
234 89



3
1
log 2.
9

b. Lôgarit của một t
hươ
ng
Cho
12
,, 0ab b với 1,a
ta có:
1
12
2
log log log
aaa
b
bb
b

Đặc b
iệt:
1
log log
aa
b
b

0, 0 .ab
Bài tập:
•
555
125
log log 125 log 25 3 2 1;
25

•
77
1
log log 49 2.
49

c. Lôgarit của một lũy thừa Bài tập:
Cho ha
i số dương
,,ab 1.a
Với mọi
, ta có:
log log
aa
bb
Đặc biệt:
1
log log
n
aa
bb
n
•
3
22
log 8 3log 8 3.3 9;

•
4
22
113
log 8 log 8 .3 .
444

4. Đổi cơ số
Cho
,, 0; 1; 1,abc a c
ta có:
log
log
log
c
a
c
b
b
a
Đặc biệt:

1
log 1 ;
log
a
b
bb
a


1
log log 0 .
a
a
bb

Bài tập:
•
2
8
2
log 16
4
log 16 ;
log 8 3
•
3
27
1
log 27 3;
log 3
•
7
128 2
2
11
log 2 log 2 log 2 .
77

5. Lôg
arit thập phâ
n – lôgarit tự
nhiên
a.
Lôg
arit thập phân
Lôgarit thập phân là lôgarit cơ số 10. Với
10
0, logbb thường được viết là logb hoặc
lgb .
b. Lôgarit tự nhiên
Lôgarit tự nhiên là lôgarit cơ số e . Với
0, log
e
bb
được viết là ln b .
SƠ ĐỒ HỆ THỐNG HÓA
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TÂP
Dạng 1. Tính giá trị của biểu thức không có điều kiện. Rút gọn biểu thức.
1. Phương pháp giải
Để tính
log
a
b
ta có thể biến đổi theo một trong các cách
sau:
•
,ba
từ đó suy ra log log ;
aa
ba

•
,ab
từ đó suy ra
1
log b log ;
a
b
b

•
,ac
,bc
từ đó ta suy ra
log log .
a
c
bc

Để tính
log
a
c
b , ta biến đổi ba
, từ đó suy ra
log log
aa
cc
ba c

Bài tập:
•
5
7
32
2
7
log 128 log 2 ;
5
•
22
log 9 5log 9
5
32 2 9 .
2. Bài tập
Bài tậ
p 1:
Cho ,b,c,d 0a . Rút gọn biểu thức Sln ln ln ln
abcd
bcda

ta được
A.
1.S
B.
S0.
C.
ln .
abcd
S
bcda




D.
ln .S abcd
Hướng dẫn giải
Chọn B.
Ta có: ln ln ln ln ln . . . ln1 0.
abcd abcd
S
bcda bcda




Bài tập 2: Cho ,0ab và ,1ab , biểu thức
34
log .log
b
a
P
ba bằng
A. 6 B. 24 C. 12. D. 18.
Hướng dẫn giải
Chọn B.
Ta có :
1
2
34 34
31
log .log log .log .4.log . 24.
1
log
2
bba
a
a
a
Pba ba b
b

Bài tập 3: Cho ,ab là các số thực dương thỏa mãn 1,a
ab và
log 3.
a
b
Biến đổi biểu
thức
Plog
b
a
b
a
ta được
A.
533.P 
B.
13.P 
C.
13.P  D. 533.P 
Hướng dẫn giải
Chọn C.
Ta có:


11
log
log 1 3 1
31
22
13.
1
log 1 3 2
log 1
log
2
a
a
a
a
a
b
b
a
P
bb
b
a



Bài tập 4 : Biến đổi biểu thức

2
3
10 2 2
log log log
a
ab
a
Pab b
b




(với
01, 01ab 
)
ta được
A. 2.P B. 1.P C. 3.P D.
2.P
Hướng dẫn giải
Chọn B.
Sử dụng các quy tắc biến đổi lôgarit ta có:

2
3
10 2 2
log log log
a
ab
a
Pab b
b





10 2
1
log log 2 log log 3. 2 log
2
aa aa b
ab ab b





11
10 2log 2 1 log 6 1.
22
aa
bb






Bài tập 5. Rút gọn biểu thức
32
log 2 log log log log log
bbbaabb
Pa aabba
với
0,1ab.
A.
1
P
. B.
2
P
. C.
0P
. D.
3P
.
Hướng dẫn giải
Chọn A.
Ta có:
32
log 2 log log log log log
bbbaabb
Pa aabba

2
1
log log 2 log 1 log log
log
bb b a b
b
aa a b a
ab





2
1
log log 1 log log
log 1
bb a b
b
aa b a
a





2
log log 1 1
log log 1 log
log 1
ab
bb b
b
ba
aa a
a






log log 1 log log log 1 log
bb ab a b
aa ba b a

log log 1 log log
bb a b
aa b a
log 1 log 1
bb
aa
.
Bài tập 6. Cho 0a , 0b thỏa mãn
22
221 4 1
log 4 1 log 2 2 1 2
ab ab
ab ab


. Giá trị của
2ab
bằng:
A.
15
4
. B. 5. C.
4
. D.
3
2
.
Hướng dẫn giải
Chọn
A.
Ta có
22
44ab ab , với mọi ,0ab . Dấu ‘
’ xảy ra khi 2ba

1
.
Khi đó

22
221 4 1
2log 4 1 log 2 2 1
ab ab
ab ab



221 4 1
log 4 1 log 2 2 1
ab ab
ab a b


.
Mặt khác, theo bất đẳng thức Cauchy ta có

221 4 1
log 4 1 log 2 2 1 2
ab ab
ab a b


.
Dấu ‘
’ xảy ra khi
221
log 4 1 1
ab
ab

41221ab a b

2
.
Từ
1
và
2
ta có
2
860aa
3
4
a
. Suy ra
3
2
b
. Vậy
15
2
4
ab
.
Bài tập 7. Cho
3
log 7
27a
,
7
log 11
49b
,
11
log 25
11c
. Tính


22
2
37
11
log 7 log 11
log 25
Sa b c
.
A. 33S . B. 469S
. C. 489S
. D. 3141S .
Hướng dẫn giải
Chọn B
Ta có:
3
log 7
27a
3
log 7 log 27
a
33 3
log 7.log 7 log 27.log 7
a

2
33
log 7 3log 3.log 7
a


2
3
3
log 7 log 7
a


2
3
3
log 7
log 7
a
aa
3
7
.
Tương tự ta có

2
7
7
log 11
log 11
2
49 11bb
;

2
11
11
log 25
log 25
11 5bc

.
Vậy


22
2
37
11
log 7 log 11
log 25
Sa b c
32
7115

469
.
Bài tập 8. Đặt
7
log 2 a
,
7
log 3 b
,
77 7 7
1 2 2014 2015
log log ... log log
2 3 2015 2016
Q 
. Tính Q
theo
a ,
b
.
A.
521ab
. B.
521ab
. C.
521ab
. D.
521ab
.
Hướng dẫn giải
Chọn D
Ta có
77 7 7
1 2 2014 2015
log log ... log log
2 3 2015 2016
Q 
77 7 7 7 7 7 7
log 1 log 2 log 2 log 3 ... log 2014 log 2015 log 2015 log 2016
77 7
log 1 log 2016 log 2016
7
log 32.9.7
777
log 32 log 9 log 7
52
77
log 2 log 3 1
77
5log 2 2log 3 1

521ab
 .
Bài tập 9. Cho hai số thực dương ,ab (1a
) thỏa mãn các điều kiện
log
4
a
b
b
và
2
16
log
a
b
.
Tính tổng
Sab.
A.
12S
. B.
10S
. C.
16S
. D.
18S
.
Hướng dẫn giải
Chọn D
Ta có
2
log
4
16
log
a
b
b
a
b
4
16
2
b
b
ba
a
16
4
16
2
2
b
b
b
b
a




16
.
4
16
2
2
b
b
b
b
a
16
2
b
a
.
Vậy ta có 16 2 18S .
Bài tập 10. Gọi
12
,
x
x
là các nghiệm của phương trình
2
20 2 0xx

. Tính giá trị của biểu thức
12 1 2
log( ) log logPxx xx
.
A.
1
2
. B.
1
. C.
0
.
D.
10
.
Hướng dẫn giải
Chọn B
Ta có
12 1 2
log( ) log logPxx xx
12 12
log log .
x
xxx
12
12
log
.
x
x
x
x
.
Vì
1
x
,
2
x
là hai nghiệm của phương trình
2
20 2 0xx

nên ta có
12
20xx
;
12
.2xx
.
Vậy ta có
20
log 1
2
P
.
Bài tập 11. Cho
=+ ++
216
11 1
...
log log log
a
aa
M
xx x
. Tính
M
.
A.
=
272
log
a
M
x
. B.
=
136
log
a
M
x
. C.
=
1088
log
a
M
x
. D.
=
272
3log
a
M
x
.
Hướng dẫn giải
Chọn B
Ta có
216
11 1
...
log log log
a
aa
M
x
xx

216
log log ... log
xx x
aa a
216
log log ... log
xx x
aa a log 2 log ... 16 log
x
xx
aa a

12...16log
x
a
16 1 16
log
2
x
a
136
log
a
x
.
Bài tập12. Với
,,
x
yz
là các số nguyên dương thỏa mãn
1512 1512 1512
log 2 log 3 log 7 1xyz

.
Tính giá trị của biểu thức
3Qxy z .
A. 1512 . B.
12
. C. 9. D. 7.
Hướng dẫn giải
Chọn C
Ta có
1512 1512 1512
log 2 log 3 log 7 1xyz
1512 1512 1512 1512
log 2 log 3 log 7 log 1512
xyz

1512 1512
log 2 .3 .7 log 1512
xyz

2.3.7 1512
xyz

33
2 .3 .7 2 .3 .7
xyz

3
3
1
x
y
z

.
Vậy
331.39Q  .
Bài tập 13. Giá trị biểu thức
2 3 2017
11 1
...
log 2017! log 2017! log 2017!
P 
là
A.
0. B. 2. C. 1. D. 4.
Hướng dẫn giải
Chọn C
Ta có
2 3 2017
11 1
...
log 2017! log 2017! log 2017!
P 
2017! 2017! 2017!
log 2 log 3 ... log 2017


2017!
log 2.3...2017
2017!
log 2017! 1
.
Bài tập 14. Giả sử
3
0;cos
2
10
xx

. Giá trị của biểu thức
log sin log cos log tan
x
xx là
A.
3
.
10
B.
1
.
10
C.
3
.
10
D.
1
.
Hướng dẫn giải
Chọn D
Ta có
22
sin 1 cos
x
x
91
1
10 10

.
Khi đó
log sin log cos log tan
x
xx
2
log sin .cos .tan log sin
x
xx x
1
log 1
10

.
Bài tập 15. Cho
7
log 12
x
,
12
log 24
y
và
54
1
log 168
axy
bxy cx
, trong đó ,,abc là các số
nguyên. Tính giá trị biểu thức 2 3 .Sa b c
A. 4S . B. 19.S
C. 10.S
D. 15.S
Hướng dẫn giải
Chọn D.
Ta có:
7
54
7
log 24.7
log 168
log 54
7
7
log 24 1
log 54
712
7
log 12log 24 1
log 54
712
712
log 12log 24 1
log 12log 54
12
1
.log 54
xy
x
Tính

12 12
log 54 log 27.2
12 12
3log 3 log 2
12 12
3.2.12.24 24
3log log
2.12.24 12

.
3
12 12
2
12 24
3log log
24 12

12 12
3 3 2 log 24 log 24 1
12
85log24
85y .
Do đó:

54
1
log 168
85
xy
x
y
1
58
xy
x
yx
.
Vậy
1
5
8
a
b
c

2315Sa b c .
Bài tập 16. Với
,ab
thỏa mãn để hàm số

2
1
1
xkhix
fx
ax b khi x
có đạo hàm tại
0
1x
. Khi đó
giá trị biểu thức
2
log 3 2Sab
bằng?
A.
1S
.
B.
2S
. C.
3S
. D.
4S
.
Hướng dẫn giải
Chọn B.
Hàm số

f
x
có đạo hàm tại
0
1x
suy ra:.
+ Hàm số liên tục tại
0
1x
:
11
lim lim 1 1 1
xx
fx fx f ab



.
+ Tồn tại giới hạn
1
1
lim
1
x
f
x
f
x
.

11
11
lim lim
11
xx
f
x
ff
x
f
xx





.
2
11
11
lim lim
11
xx
x
ax b
xx





.
1
2lim
1
x
ax b a b
x


.

22a
.
Từ
1
và
2
suy ra
2
1
a
b

.

22
log 3 2 log 4 2Sab
.
Dạng 2. Đẳng thức chứa logarit
1. Phươngpháp
2. Bàitập
Bài tập 1: Cho ,0
x
y và
22
412.
x
yxy Khẳng đinh nào sau đây đúng?
A.
222
log 2 log log 1.xy x y
B.
222
2
log log log .
4
xy
x
y




C.
 
222
1
log 2 2 log log .
2
x
yxy
D.

222
4log 2 log log .
x
yxy
Hướng dẫn giải
Chọn C.
Với ,0
x
y , ta có:
2
22
412 2 16
x
yxyxy xy
2
22
log 2 log 16
x
yxy
222
2log 2 4 log log
x
yxy
 

222
1
log 2 2 log log .
2
x
yxy
Bài tập 2: Cho
,
x
y
là các số thực lớn hơn 1 thỏa mãn
22
96
x
yxy
. Tính
12 12
12
1log log
2log ( 3 )
xy
M
xy

.
A.
1
4
M
. B.
1
M
. C.
1
2
M
. D.
1
3
M
.
Hướng dẫn giải
Chọn B
Ta có
22
96
x
yxy

2
30xy
3
x
y
.
Vậy ta có

12 12
12
1log log
2log 3
x
y
M
x
y

12 12
12
1 log 3 log
2log 6
yy
y

12 12 12 12
12 12
log 12 log 3 log log
2 log 6 log
yy
y

12 12
12 12
log 36 2 log
1
log 36 2 log
y
y

.
Bài tập 3: Cho biểu thức
3
log
2
5
3 log .log 25
a
a
Ba
với a là số dương, khác 1. Khẳng định nào
sau đây là đúng?
A.
25Ba. B.
2
4
log 1
a
B
. C. 4Ba
. D. 3B .
Hướng dẫn giải
Chọn C
Ta có
3
log
2
5
3 log .log 25
a
a
Ba
5
2log .log 25
a
aa
2
5
2log .log 5
a
aa
5
4log .log 5
a
aa
4a.
Vậy 4Ba
.
Bài tập 4: Gọi
c
là cạnh huyền,
a
và
b
là hai cạnh góc vuông của một tam giác vuông. Trong các
khẳng định sau khẳng định nào đúng?
A.
log log 2 log .log
bc cb bc cb
aa aa


.
B.
log log 2 log .log
bc bc bc bc
aa aa


.
C.
log log log .log
bc cb bc cb
aa aa


.
D.
log log 4 log .log
bc bc bc bc
aa aa


.
Hướng dẫn giải
Chọn A
Ta có:
222
cab
22 2
cb a
2
.cb cb a

log . 2
a
cb cb

log log 2
aa
bc cb
 
11
2
log log
aa
bc cb


log log 2 log .log
bc cb bc cb
aa aa


(đpcm).
Bài tập 5: Cho
27
log 5 a
,
8
log 7 b
,
2
log 3 c
. Khẳng định nào sau đây đúng?
A.
12
32
log 35
2
bac
c
. B.
12
33
log 35
2
bac
c
.
C.
12
32
log 35
3
bac
c
. D.
12
33
log 35
1
bac
c
.
Hướng dẫn giải
Chọn B
Ta có :
 
27 3 8 2 2
log 5 lo g 5 3 ; log 7 lo g 7 3 ; log 3aabbc


2
333
2
12
333 3
log 7
3
log 5 log 5 log 7
log 3
log 35
log 12 log 3 l og 4 1 2log 2
a

3
3
33
1
2
12.
b
a
ac b
c
c
c
.
Bài tập 6: Cho

14
4
1
log log 1yx
y

, với 0,yyx. Chọn khẳng định đúng trong các khẳng
định sau?
A. 34
x
y . B. 3
x
y
. C.
3
4
x
y
. D.
3
4
yx
.
Hướng dẫn giải
Chọn C
Ta có

14
4
1
log log 1yx
y

44
log log 1yx y
44
log 1 logyyx

44
log log 4.yyx
4yyx

3
4
x
y
.
Bài tập 7: Số thực dương ,ab thỏa mãn
41216
log log log ( )ab ab

. Mệnh đề nào dưới đây
đúng?
A.
2
;1
3
a
b



. B.
2
0;
3



a
b
C.

9;12
a
b
. D.
(9;16)
a
b
.
Hướng dẫn giải.
Chọn B.
Giả sử
41216
log log log ( ) tab ab
. Khi đó, ta có:
4; 12; 16
tt t
ab ab
. Từ đây,
ta có phương trình:
13
412 16 1
44
tt
tt t
 

 
 
*
.
Vế trái của phương trình
*
nghịch biến nên
*
có 1 nghiệm duy nhất là
1t
. Suy ra
4; 12ab suy ra
12
0;
33
a
b




.
Bài tập8: Có tất cả bao nhiêu số dương
a
thỏa mãn đẳng thức
235 235
log log log log .log .logaaa aaa
.
A. 3. B. 1. C. 2. D. 0.
Hướng dẫn giải
Chọn A
Ta có
235 235
log log log log .log .logaaa aaa
23252 2355
log log 2.log log 2.log log .log 5.log .logaaaaaa
2
235235
log . 1 log 2 log 2 log .log 5.logaaa
2
23535
log . 1 log 2 log 2 log 5.log 0aa
2
2
3535
log 0
1 log 2 log 2 log 5.log 0
a
a

35
5
3
1
1 log 2 log 2
log
log 5
a
a


35
3
1log2log2
log 5
1
5
a
a

.
Bài tập 9: Cho
n
là một số nguyên dương, tìm
n
sao cho
3
22 2 22
log 2019 2 log 2019 3 log 2019 ... log 2019 1008 .2017 .log 2019
n
a a
aa a
n
A. 2017 . B. 2019 . C. 2016 . D. 2018 .
Hướng dẫn giải
Chọn C
Đặt
3
22 2 22
log 2019 2 log 2019 3 log 2019 ... log 2019 1008 .2017 .log 2019
n
a a
aa a
n
.
Ta có
23
log 2019 log 2019
n
a
a
nn
.
Vậy VT


2
333 3
1
1 2 3 ... log 2019 .log 2019
2
aa
nn
n




.
Hay từ
ta có

2
22
1
.log 2019 1008 .2017 .log 2019
2
aa
nn



2
2222
1 2 .1008 .2017nn

2
222
1 2016 .2017nn
2
4066272 0nn

2016
2017
n
n

2016n
(vì
n
).
Bài tập 10: Cho

22
22
log 1 log
x
yxy
, với 0xy . Chọn khẳng định đúng trong các khẳng
định sau?
A.
x
y
. B.
x
y
. C.
x
y
. D.
2
x
y
.
Hướng dẫn giải
Chọn C
Ta có

22
22
log 1 log
x
yxy
22
22
log log 2
x
yxy
22
2
x
yxy

2
0xy
x
y
.
Dạng 3. Biểu thị biểu thức theo một biểu thức đã cho và từ đó tìm GTLN, GTNN
1. Phương pháp giải
2. Bài t
ập
Bài tậ
p 1.
Cho hai số thực
x
,
y
thỏa mãn
22
log 2 4 1
xy
xy
. Tính
x
P
y
khi biểu thức
435Sxy đạt giá trị lớn nhất.
A.
8
5
P
. B.
9
5
P
. C.
13
4
P
. D.
17
44
P
.
Hướng dẫn giải
Chọn C
Ta có

22
log 2 4 1
xy
xy

22
21xyx y

22
124xy

.
Khi đó ta có
435Sxy



22
22
413 27 43 1 2 73xy xy .
Dấu
""
xảy ra khi và chỉ khi
12
43
4353
xy
xy


13
5
4
5
x
y
.
Vậy ta có
x
P
y
13
13
5
4
4
5

.
Bài tập 2. Xét các số thực
a
, b thỏa mãn 1ab . Tìm giá trị nhỏ nhất
min
P
của biểu thức

22
log 3log




ba
b
a
Pa
b
.
A.
min
19P
. B.
min
13
P
. C.
min
14
P
. D.
min
15P
.
Hướng dẫn giải
Chọn D
Với điều kiện đề bài, ta có

2
2
2
2
log 3log 2 log 3log 4 log . 3log


  

  


  

aaa
bb
b
b
bb
aaaa
Pa a b
bbbb
2
4 1 log 3log .







ba
b
a
b
b
Đặt
log 0
a
b
tb
(vì 1
ab ), ta có
 
2
2
33
41 4 48 Pt t
t
t
f
t
t
.
Ta có
2
32
22 2
214 3
38 3
() 8
6
8
8


t
t
tt
t
ft t
tt t
Vậy

1
0
2
ft t
. Khảo sát hàm số, ta có
min
1
15
2



Pf
.
Bài tập 3. Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 2 4
2
xy
xy
x
y
xy

. Tìm giá trị nhỏ
nhất
min
P
của
P
xy
.
A.
min
911 19
9
P
. B.
min
911 19
9
P
.
C.
min
18 11 29
9
P
. D.
min
211 3
3
P
.
Hướng dẫn giải
Chọn D.
3
1
log 3 2 4
2
xy
xy x y
xy

33
log 1 log 2 3 1 2 1xy xy xy xy
33
log 3 1 log 2 3 1 2
x
yxyxyxy
33
log 3 1 3 1 log 2 2
x
yxy xyxy
Xét
3
log
f
ttt
,
0t

1
10, 0
ln 3
ft t
t

Suy ra
:
31 2
f
xy f x y
33 2
x
yx y

32
13
y
x
y

Điều kiện
2
1522
00
25
63
xy y
y
xy
y


32
13
y
Pxyy
y


2
111
11
3
10
13
111
3
y
P
y
y



Lập bảng biến th
iên ta có
min
211 3
3
P
.
Bài tập 4. Cho các số thực ,, 1;2abc


thỏa mãn điều kiện
333
222
log log log 1abc

Khi biểu thức
333
222
3 log log log
abc
Pa b c a b c
đạt giá trị lớn nhất thì giá trị của
abc bằng
A. 3. B.
3
1
33
3.2 . C. 4. D. 6.
Hướng dẫn giải
Chọn C.
Ta xét hàm số
33
22
3log logfx x x x c
với
1; 2 .x
Ta có
đạo hàm

2
2
2
2
3log
3
f33log ;
ln2 ln2
x
xx x
x


2
22
22 2
63log
3
f6 .
ln2
ln 2 ln2
log x x
xx
x
xx


Vì

22
33 2 32
6log 3 log
13
61 0 1;2
ln 2 ln2 ln 2
xx
fx x
xx x





nên
11,670.fx f
 

Như vậy hà
m số
fx
đồng biến và có nghiệm duy nhất trên 1; 2
vì
10; 20ff

và có đồ
thị lõm trên
1; 2


. Do đó ta có bảng biến thiên
Từ bảng b
iến thiên ta nhận thấy rằng
1fx
cho nên
333
222
3 log log log 4Pabc
Đẳng thức xảy ra khi và chỉ khi
1, 2ab c và các hoán vị.
Bài tập 5. Trong tất cả các cặp
;
x
y thỏa mãn
22
2
log 4 4 4 1.
xy
xy


Với giá trị nào của m
thì tồn tại duy nhất cặp

;
x
y sao cho
22
222 0?xy xy m

A.
2
10 2 . B.
2
10 2 và
2
10 2 .
C.
10 2
và
10 2.
D.
10 2.
Hướng dẫn giải
Chọn B.
Điều kiện: 4440.
x
y
Ta có
22
2
log 4 4 4 1
xy
xy


22
22
1
444 2 2 2 2 .
x
yxy x y C
Miền nghiệm của bất phương trình là hình tròn (cả bờ)
1
C có tâm
1
2;2I bán kính
1
2.R
Mặt khác:
22
22
222 0 1 1 *.xy xy m x y m
Với
0m thì 1; 1
x
y (không thỏa mãn
22
222xy
 ).
Với
0m
thì
* là đường tròn

2
C có tâm
2
1; 1I bán kính
2
.
R
m
Để tồn tại duy nhất cặp

;
x
y thì
1
C và
2
C tiếp xúc với nhau.
Trường hợp 1:
1
C
và
2
C
tiếp xúc ngoài.
Khi
đó:
2
1212
210 102.RR II m m
Trường hợp 2:
1
C nằm trong

2
C và hai đường tròn tiếp xúc trong.
Khi
đó:
2
2112
210 102.RRII m m
Vậy
2
10 2m  và
2
10 2m  thỏa mãn yêu cầu bài toán.
Bài tập 6. Xét các số thực a, b thỏa mãn 1.ab Giá trị nhỏ nhất
min
P
của biểu thức

22
log 3log
ab
b
a
Pa
b




bằng
A.
min
19.P B.
min
13.P C.
min
14.P D.
min
15.P
Hướng dẫn giải
Chọn D.
Ta có:


2
22
2
log 3log 3 log 1
log
ab b
b
a
a
Pa a
a
b
b











2
2
3log 1.
1log
b
a
a
b





Đặt
log 0 1 .
a
bt t Khi đó


2
43
3
1
Pft
t
t

với
01.t
Ta có



32
83 1
0.
3
1
ft ft t
t
t


Bảng bi
ến thiên:
Từ bảng b
iến thiên, ta có
min
15.P
Bài tập 7. Cho hai số thực x, y thỏa mãn:
22
3xy
và
22
222
log 4 3 4 3 2
xy
xx x y y



Gọi
M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức .
P
xy
Khi đó biểu thức
21TMm có giá trị gần nhất số nào sau đây?
A. 7. B. 8. C. 9. D. 10.
Hướng dẫn giải
Chọn D
Ta có
22 22
222 22
log 4 3 4 3 2 log 4 3 2
xy xy
xx x y y x y x






2
2
22 22 2
43 2 1.xy x xy x y 
Tập hợp các số thực
x, y thỏa mãn:

22
2
2
3
21
xy
xy


những điểm thuộc miền trong hình tròn
1
C
có tâ
m
2;0 ,I bán kính
1
1R
và nằm ngoài hình tròn
2
C có tâm
0;0O và bán kính
2
3.R
Biểu thức: 0Pxy xyP là họ đường thẳng
song song với đường .
y
x
Các giao điểm của hai hình tròn là
33 3 3
;,;
22 2 2
AB




P đạt giá trị nhỏ nhất khi đường thẳng
đi qua A.
Khi đường thẳng
qua điểm A, ta có:
min min
33 33
0.
22 2
PP

P đạt giá trị lớn nhất khi đường thẳng
tiếp xúc với đường tròn
1
C ta có:

1max
2
; 1 22 22.
11
P
dI R P P

Do đó

33
2 1 2 2 2 10.
2
TMm





| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI 3. LÔGARIT
A. KIẾN THƯC CƠ BẢN CẦN NẮM
1. Khái niệm lôgarit Nhận xét: log 
b    a b  , a b  0, a a  1
Cho hai số dương a,b với a  1 . Số  thỏa mãn Bài tập: 3
log 8  3  2  8 2
đẳng thức a  b được gọi là lôgarit cơ số a của
Chú ý: Không có lôgarit của số âm và số 0.
b , và ký hiệu là log  b . a 2. Tính chất Cho ,
a b  0,a  1. Ta có: log  0; log a  1 a a loga b a  ; b log a a     
3. Quy tắc tính lôgarit Bài tập:
a. Lôgarit của một tích  1  1  log  log 2  log .2  log 1  0;    2    2  
Cho a,b ,b  0 với a  1 , ta có: 1 2 1 2 3 7 8
log (b b )  log b log b  log  log  log  ...  log  log 3 3 3 3 3 a 1 2 a 1 a 2 2 3 4 8 9
Chú ý: Định lý trên có thể mở rộng cho tích của n  1 2 3 7 8   log . . ..... . 3   số dương:  2 3 4 8 9 
log b ...b  log b ... log b 1 a 1 n a 1 a n  log  2  . 3 9 trong đó ,
a b ,b ,...,b  0,a  1. 1 2 n
b. Lôgarit của một thương Bài tập: Cho ,
a b ,b  0 với a  1, ta có: 125 1 2 • log
 log 125  log 25  3  2  1; 5 5 5 25 b1 log 
 log b  log b a a 1 a 2 b 1 2 • log   log 49  2.  7 7 49 1 Đặc biệt: log
  log b a  0,b  0. a a b
c. Lôgarit của một lũy thừa Bài tập:
Cho hai số dương a,b, a  1. Với mọi  , ta có: • 3
log 8  3log 8  3.3  9; 2 2
log b   log b 1 1 3 a a • 4 log 8  log 8  .3  . 2 2 4 4 4 Đặc biệt: n 1 log b  log b a a n 4. Đổi cơ số Bài tập: Cho a, ,
b c  0;a  1;c  1, ta có: log 16 4 • 2 log 16   ; 8 log 8 3 log b 2 log c b a log a c 1 • log 27   3; 3 log 3 27 1 Đặc biệt: log b b a   1 ; log a 1 1 b
• log 2  log 2  log 2  . 7 128 2 2 7 7 1 log     b log b a  0. a
5. Lôgarit thập phân – lôgarit tự nhiên
a. Lôgarit thập phân
Lôgarit thập phân là lôgarit cơ số 10. Với
b  0, log b thường được viết là log b hoặc 10 lg b . b. Lôgarit tự nhiên
Lôgarit tự nhiên là lôgarit cơ số e . Với
b  0, log b được viết là ln b . e
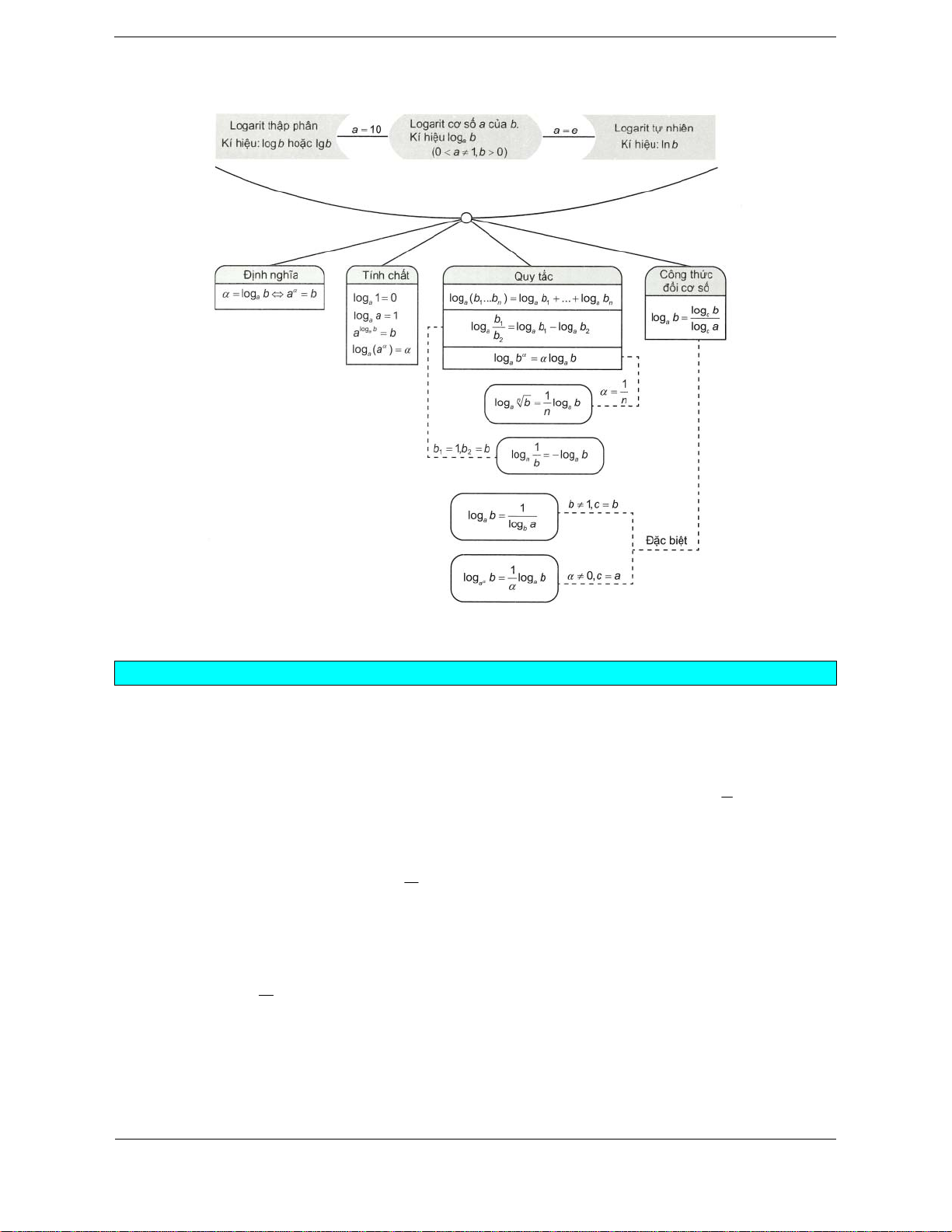
SƠ ĐỒ HỆ THỐNG HÓA
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TÂP
Dạng 1. Tính giá trị của biểu thức không có điều kiện. Rút gọn biểu thức.
1. Phương pháp giải
Để tính log b ta có thể biến đổi theo một trong các cách Bài tập: a sau: 7 • 7 log 128  log 2  ; 5 32 2 5 • b a 
, từ đó suy ra log b  log a  ; a a • log2 9 5log2 9 5 32  2  9 . 1 • a b 
, từ đó suy ra log b  log   b ; a b  • a c  , b c  , từ đó ta suy ra log b  log     c . a c   Để tính loga c b
, ta biến đổi b a  , từ đó suy ra log c  log a a c b a c   2. Bài tập a b c d Bài tập 1: Cho ,b
a ,c,d  0 . Rút gọn biểu thức S  ln  ln  ln  ln ta được b c d a A. S  1. B. S  0.  a b c d C. S  ln     .
D. S  ln abcd.  b c d a Hướng dẫn giải Chọn B. a b c da b c d
Ta có: S  ln  ln  ln  ln  ln . . .  ln1    0. b c d ab c d a Bài tập 2: Cho , a b  0 và ,
a b  1, biểu thức 3 4
P  log b .log a bằng a b A. 6 B. 24 C. 12. D. 18. Hướng dẫn giải Chọn B. Ta có : 3 4 3 4 3 1
P  log b .log a  log b .log a  .4.log . b  24. 1 a b b a 1 a 2 log b a 2 Bài tập 3: Cho ,
a b là các số thực dương thỏa mãn a  1, a b và log b  3. Biến đổi biểu a b thức P  log ta được b a a A. P  5   3 3. B. P  1   3. C. P  1   3. D. P  5   3 3. Hướng dẫn giải Chọn C. Ta có: b 1 b   aa  1 log log 1 a  3 1 2 2 3 1 P      1   3. b log b 1 1 3  2 log a log b 1 a 2 a aa
Bài tập 4 : Biến đổi biểu thức 10 2 2
P  log a b  log 
  log b (với 0  a  1, 0  b  1) 2 a   3 a bb  ta được A. P  2. B. P  1. C. P  3. D. P  2. Hướng dẫn giải Chọn B.
Sử dụng các quy tắc biến đổi lôgarit ta có:   10 2 a 2
P  log a b  log    log b 2 a   3 a bb  1 10 2
 log a  log b   2 log a  log b   3. 2    log b 2 a a a a b   1  1  10  2log  
b  2 1 log b  6  1. 2  a    2 a  
Bài tập 5. Rút gọn biểu thức P   3 2
log a  2 log a  log alog b  log b  log a với b b b a ab b
0  a,b  1. A. P  1 . B. P  2 . C. P  0 . D. P  3 . Hướng dẫn giải Chọn A. Ta có: P   3 2
log a  2 log a  log alog b  log b  log a b b b a ab b    log a a a   b    a b  1 2 log 2log b b 1 log log a log b abb     a a   b    a bb 2 1 log log 1 log log a log a 1 bb   b a     a a     a bb
2 loga logb 1 1 log log 1 log log a 1 bb
 log a log a  
1 log b log a  log b   1  log a b b a b a b
 log a log a  
1 log b  log a b b a b
 log a 1 log a  1. b b
Bài tập 6. Cho a  0 , 0 b  thỏa mãn log a b   a b   . Giá trị của ab  2 2 4 1 log 2 2 1 2 2 2 1  4ab 1   
a  2b bằng: 15 3 A. . B. 5 . C. 4 . D. . 4 2 Hướng dẫn giải Chọn A. Ta có 2 2
4a b  4ab , với mọi a,b  0 . Dấu ‘  ’ xảy ra khi b  2a 1 . Khi đó 2  log a b   a b ab  2 2 4 1 log 2 2 1 2 2 1  4ab 1     log 4ab 1  log
2a  2b 1 . 2a2b 1    4ab 1   
Mặt khác, theo bất đẳng thức Cauchy ta có log 4ab 1  log
2a  2b 1  2 . 2a2b 1    4ab 1   
Dấu ‘  ’ xảy ra khi log
4ab 1  1  4ab 1  2a  2b 1 2 . 2a2b 1    3 15
Từ 1 và 2 ta có 2 8a  6a  3
0  a  . Suy ra b  . Vậy a  2b  . 4 2 4
Bài tập 7. Cho log3 7 a  27 , log7 11 b  49 , lo 11 g 25 c  11 . Tính log 72 log 1 2 1 log 252 3 7 11 S abc . A. 33 S  . B. 46 S  9 . C. 48 S  9 . D. 3141 S  . Hướng dẫn giải Chọn B Ta có: log3 7 a  27  log3 7  log 27 a
 log3 7.log3 7  log 27.log3 7 a  log 72 log3 7 log 7 3 3  3log 3.log3 7 a  log 72 3 3   2 3 log 7 a aaa  7 . log 11 log 25 lo 11 g 252 7 11 log71 2 Tương tự ta có 1 2 b  49  b 11 ; b  11  c  5 . 2 2 2 Vậy log3 7 log71 1 lo 11 g 25 S abc 3 2  7 11  5  469 . 1 2 2014 2015
Bài tập 8. Đặt log 2  a , log 3  b , Q  log  log  ... log  log . Tính Q 7 7 7 7 7 7 2 3 2015 2016 theo a , b .
A. 5a  2b 1.
B. 5a  2b 1.
C. 5a  2b 1. D. 5
a  2b 1. Hướng dẫn giải Chọn D 1 2 2014 2015
Ta có Q  log7  log7 ... log7  log7 2 3 2015 2016
 log71 log7 2  log7 2  log7 3 ... log7 2014  log7 2015  log7 2015  log7 2016
 log71 log7 2016  log7 2016  log7 32.9.7  log7 32  log7 9  log7 7   5 2 log7 2  log7 3  
1  5log7 2  2log7 31  5
a  2b 1. b 16
Bài tập 9. Cho hai số thực dương a ,b ( a  1) thỏa mãn các điều kiện log b  và log a  . a 4 2 b
Tính tổng S a b . A. S 12 . B. S 10 . C. S 16 . D. S 18 . Hướng dẫn giải Chọn D b   b 16    log b b  4 16 b   . a  4 b   a
b   2 b   b 4 b  2 b  16 Ta có 4            . 16    16 16 a  2 log a     2  b 16 b ba  2  a  2 a  2 b
Vậy ta có S  16  2  18 .
Bài tập 10. Gọi x , x là các nghiệm của phương trình 2
x  20x  2  0 . Tính giá trị của biểu thức 1 2
P  log(x x )  log x  log x . 1 2 1 2 1 A. . B. 1. C. 0 . D. 10 . 2 Hướng dẫn giải Chọn B x x
Ta có P  log(x x )  log x  log x  log  x x  log x .x 1 2  log . 1 2   1 2  1 2 1 2 x .x 1 2
Vì x , x là hai nghiệm của phương trình 2
x  20x  2  0 nên ta có x x  20 ; 1 2 1 2 x .x  2 . 1 2 20 Vậy ta có P  log 1. 2
Bài tập 11. Cho M = 1 + 1 + + 1 ... . Tính M . log x log x log x 2 16 a a a
A. M = 272 . B. M = 136 . C. M = 1088 . D. M = 272 . log x log x log x 3 log x a a a a Hướng dẫn giải Chọn B 1 1 1 Ta có M   ... 2 16
 log a  log a  ... log a log x log x log x x x x a 2 16 a a 2 16
 log a  log a  ... log a  log a  2log a  ...16log a x x x x x x 16116
 1 2 ...16log a  136 log a  . x 2 x log x a
Bài tập12. Với x, y, z là các số nguyên dương thỏa mãn x log 2  y log 3  z log 7  1. 1512 1512 1512
Tính giá trị của biểu thức Q x y  3z . A. 1512 . B. 12 . C. 9. D. 7 . Hướng dẫn giải Chọn C Ta có x log 2  y log 3  z log 7  1 log 2x log 3y log 7z     log 1512 1512 1512 1512 1512 1512 1512 1512 x  3  log 2x.3y.7z   log 1512 2x.3y.7z   1512 x y z 3 3
 2 .3 .7  2 .3 .7  y  3. 1512 1512 z 1 
Vậy Q  3  3 1.3  9 . 1 1 1
Bài tập 13. Giá trị biểu thức P   ... là log 2017! log 2017! log 2017! 2 3 2017 A. 0. B. 2. C. 1. D. 4. Hướng dẫn giải Chọn C Ta có 1 1 1 P    ...  log 2  log 3  ... log 2017 log 2017! 2017! 2017! 2 2017! log3 2017! log2017 2017!  log 2.3...2017  log 2017!  1. 2017!   2017!  3
Bài tập 14. Giả sử 0  x  ; cos x
. Giá trị của biểu thức 2 10 log sin x  log cos x  log tan x là 3 1 3 A.  . B. . C. . D. 1 . 10 10 10 Hướng dẫn giải Chọn D Ta có 2 2 sin x 1 9 1 cos x  1  . 10 10
Khi đó log sin x  log cos x  log tan x   x x x 2 log sin .cos .tan  1 log sin x log  1. 10 axy 1
Bài tập 15. Cho log 12  x , log 24  y và log 168  , trong đó a, , b c là các số 7 12 54 bxy cx
nguyên. Tính giá trị biểu thức 2
S a b  3 . c A. S  4 . B. S  19. C. S  10. D. S  15. Hướng dẫn giải Chọn D. log 24.7   7   log 24 1 log 12log 24 1 Ta có: log 168  7  7 12  54 log 54 log 54 log 54 7 7 7 log 12 log 24 1 xy 1 7 12   log 12 log 54 . x log 54 7 12 12 3.2.12.24 24 Tính log 54  log
27.2  3log 3  log 2  3log  log . 12 12   12 12 12 12 2.12.24 12 3 12 24  3log  log
 33  2log 24  log 24 1  8  5log 24  8  5y . 12   12  12 2 12 24 12 12 xy 1 xy 1 Do đó: log 168   . 54 x 8  5y 5  xy  8xa 1  Vậy b   5
  S a  2b  3c 15. c   8  2 x khi x 1
Bài tập 16. Với a,b thỏa mãn để hàm số f x  
có đạo hàm tại x  1. Khi đó
ax b khi x 1 0
giá trị biểu thức S  log 3a  2b bằng? 2   A. S  1. B. S  2 . C. S  3. D. S  4 . Hướng dẫn giải Chọn B.
Hàm số f x có đạo hàm tại x  1 suy ra:. 0
+ Hàm số liên tục tại x  1: lim f x  lim f x  f  
1  a b 1  1 . 0 x 1 x 1  
f x  f   1 + Tồn tại giới hạn lim . x 1  x 1
f x  f   1
f x  f   1  lim  lim . x 1  x 1 x 1    x 1 2 x 1 ax b 1  lim  lim . x 1  x 1 x 1    x 1
ax b  a b  2  lim . x 1  x 1  a  2 2 . a  2
Từ 1 và 2 suy ra  . b   1 
S  log 3a  2b  log 4  2 . 2   2
Dạng 2. Đẳng thức chứa logarit 1. Phương pháp 2. Bài tập
Bài tập 1: Cho x, y  0 và 2 2
x  4y  12xy. Khẳng đinh nào sau đây đúng?
A. log x  2y  log x  log y 1. 2   2 2  x  2y B. log  log x    log y. 2 2 2  4  1
C. log x  2y  2 
log x  log y . 2    2 2  2
D. 4 log x  2y  log x  log y. 2   2 2 Hướng dẫn giải Chọn C.
Với x, y  0 , ta có: x y
xy  x y2 2 2 4 12 2  16xy
 log x  2y2  log 16xy 2 2
 2 log x  2y  4  log x  log y 2   2 2 1
 log x  2y  2  log x  log y . 2 2 2  2
Bài tập 2: Cho x, y là các số thực lớn hơn 1 thỏa mãn 2 2
x  9 y  6xy . Tính
1 log x  log y 12 12 M  . 2 log (x  3y) 12 1 1 1 A. M  . B. M  1 . C. M  . D. M  . 4 2 3 Hướng dẫn giải Chọn B Ta có 2 2
x  9 y  6xy   x y2 3
 0  x  3y . Vậy ta có
1 log x  log y
1 log 3y  log y
log 12  log 3  log y  log y 12 12 M  12 12  12 12 12 12  2 log x  3y 2 log 6 y 2log 6  log y 12 12  12   12 log 36  2 log 12 12 y   1. log 36  2 log y 12 12
Bài tập 3: Cho biểu thức log3 a 2 B  3  log5 a .log 25 a
với a là số dương, khác 1. Khẳng định nào sau đây là đúng?
A. B  2a  5 . B. log B  1.
C. B a  4 . D. B  3 . 2 a 4 Hướng dẫn giải Chọn C Ta có log a 2 2 3 B  3
 log a .log 25  a  2log .
a log 25  a  2 log .
a log 5  a  4 log . a log 5 5 a 5 a 5 a 5 aa  4 . Vậy 4 B a  .
Bài tập 4: Gọi c là cạnh huyền, a và b là hai cạnh góc vuông của một tam giác vuông. Trong các
khẳng định sau khẳng định nào đúng? A. log a  log a  2 log . a log a . bc cb bc cb B. log a  log a  2 log . a log a . bc bc bc bc C. log a  log a  log . a log a . bc cb bc cb D. log a  log a  4 log . a log a . bc bc bc bc Hướng dẫn giải Chọn A Ta có: 2 2 2
c a b 2 2 2
c b a  c b c b 2 .
a  log c b.c b  2 a  1 1
log b c  log c b  2    a ab c c b 2 log log a a  log a  log a  2 log . a log a (đpcm). bc cb bc cb
Bài tập 5: Cho log 5  a , log 7  b , log 3  c . Khẳng định nào sau đây đúng? 27 8 2 3b  2ac 3b  3ac A. log 35  . B. log 35  . 12 c  2 12 c  2 3b  2ac 3b  3ac C. log 35  . D. log 35  . 12 c  3 12 c 1 Hướng dẫn giải Chọn B
Ta có : log 5  a  log 5  3a ; log 7  b  log 7  3b ; log 3  c 27 3 8 2 2 3a  log 7 2 b 3a  3 log 5 log 5  3ac  3b log 35  log 7 log 3 3  3 3  2  c  . 12 log 12 log 3  log 4 1  2 log 2 1 c  2 3 3 3 3 1  2. c 1 Bài tập 6: Cho log y x  log 1   1   4
, với y 0, y x . Chọn khẳng định đúng trong các khẳng y 4 định sau? 3 3
A. 3x  4 y .
B. x  3y . C. x y .
D. y x . 4 4 Hướng dẫn giải Chọn C Ta có 1 log y x  log
1   log y x  log y  1  log y  1 log y x 4 4   4   1   4 y 4 4
 log y  log 4. y x y  4 y  3
x  x y . 4 4   4
Bài tập 7: Số thực dương a,b thỏa mãn log a  log b  log (a b) . Mệnh đề nào dưới đây 4 12 16 đúng? a  2  a  2  a a A.  ;1   . B.  0;   C.  9;12 . D. (9;16) . b  3  b  3  b b Hướng dẫn giải. Chọn B.
Giả sử log a  log b  log (a b)  t . Khi đó, ta có:  4t ;  12t ;   16t a b a b . Từ đây, 4 12 16 t t t
 1 t  3 t
ta có phương trình: 4 12  16    1      * .  4   4 
Vế trái của phương trình   * nghịch biến nên  
* có 1 nghiệm duy nhất là t  1. Suy ra a 1  2 
a  4;b  12 suy ra   0;   . b 3  3 
Bài tập8: Có tất cả bao nhiêu số dương a thỏa mãn đẳng thức
log a  log a  log a  log . a log . a log a . 2 3 5 2 3 5 A. 3. B. 1. C. 2. D. 0. Hướng dẫn giải Chọn A Ta có
log a  log a  log a  log . a log . a log a 2 3 5 2 3 5
 log a  log 2.log a  log 2.log a  log . a log 5.log . a log a 2 3 2 5 2 2 3 5 5  log .
a 1 log 2  log 2 2  log . a log 5.log a 2 3 5 2 3 5  log a. 2
1 log 2  log 2  log 5.log a  0 2 3 5 3 5  a 1 log a  0 2     1 log 2  log 2 2
1 log 2  log 2  log 5.log a  0   3 5 log a   3 5 3 5 5  log 5  3 a 1   1log  . 3 2 log5 2   log3 5 a  5
Bài tập 9: Cho n là một số nguyên dương, tìm n sao cho 2 2 2 2 2 log 2019  2 log 2019  3 log 2019  ...  n log  n 2019 1008 .2017 .log 2019 3 a a a a a A. 2017 . B. 2019 . C. 2016 . D. 2018 . Hướng dẫn giải Chọn C Đặt 2 2 2 2 2 log 2019  2 log 2019  3 log 2019  ...  n log  n 2019 1008 .2017 .log 2019 3 a a a a a  . Ta có 2 3 n log  n . n 2019 log 2019 a an n 1 
Vậy VT   1  2  3 ... n    2 3 3 3 3 log 2019    .log 2019 a . 2 a   Hay từ  ta có
nn   2 1  2 2 
 .log 2019 1008 .2017 .log 2019 2
n n  2 2 2 2 1  2 .1008 .2017 2 a a   n  2016 2
n n  2 2 2 1  2016 .2017 2
n n  4066272  0    n  2016 (vì n  2017  n    ).
Bài tập 10: Cho log  2 2 x y
 1 log xy , với xy  0 . Chọn khẳng định đúng trong các khẳng 2  2 định sau?
A. x y .
B. x y .
C. x y . D. 2 x y . Hướng dẫn giải Chọn C Ta có log  2 2 x y
 1 log xy  log  2 2 x y  log 2xy 2 2
x y  2xy  x y2  0 2  2  2 2  x y .
Dạng 3. Biểu thị biểu thức theo một biểu thức đã cho và từ đó tìm GTLN, GTNN 1. Phương pháp giải 2. Bài tập x
Bài tập 1. Cho hai số thực x , y thỏa mãn log
2x  4 y  1. Tính P  khi biểu thức 2 2 x y   y
S  4x  3y  5 đạt giá trị lớn nhất. 8 9 13 17 A. P  . B. P  . C. P   . D. P  . 5 5 4 44 Hướng dẫn giải Chọn C Ta có log 2x  4 y  1 2 2
 2x y x y 1  x  2   y  2 1 2  4 . 2 2 x y   Khi đó ta có
S  4x  3y  5   x     y      2 2 4 1 3 2 7
4  3 x  2
1   y  22  7  3.  13
x 1 y  2 x    
Dấu "  " xảy ra khi và chỉ khi 5  4 3   .  4
4x  3y  5  3  y    5 13 x 13 Vậy ta có P  5    . y 4 4  5
Bài tập 2. Xét các số thực a , b thỏa mãn a b  1 . Tìm giá trị nhỏ nhất P của biểu thức min a 2 P a . a  2    log 3logb    b b A. P 19 . B. P  13. C. P 14 . D. P  15. min min min min Hướng dẫn giải Chọn D
Với điều kiện đề bài, ta có 2 2  a     a    a  a 2   P  log a a b
a  2   3 logb
  2loga   3logb    4 log  a  .   3log  b    b   b   b   b bb   b  2    a   4 1   log b a   3logb  .  b   b  3 3
Đặt t  log b  0 (vì a b  1 ), ta có P  41 t2 2
  4t  8t   4  f t . a t t b 3
8t  8t  3 2t   1  2 3 2
4t  6t  3 Ta có f (
t)  8t  8    2 2 2 t t t  1 
Vậy f t 1
 0  t  . Khảo sát hàm số, ta có P f   15 . 2 min  2  1 xy
Bài tập 3. Xét các số thực dương x , y thỏa mãn log
 3xy x  2y  4. Tìm giá trị nhỏ 3 x  2y
nhất P của P x y . min 9 11 19 9 11 19 A. P  . B. P  . min 9 min 9 18 11  29 2 11  3 C. P  . D. P  . min 9 min 3 Hướng dẫn giải Chọn D. 1 xy log
 3xy x  2y  4 3 x  2y
 log 1 xy  log x  2y  3 xy 1  x  2y 1 3   3      
 log 3 1 xy  log x  2y  3 xy 1  x  2y 3   3      
 log 3 1 xy  3 1 xy  log x  2y x  2y 3     3    
Xét f t  log t t , t  0 3 f t 1  1  0, t   0 t ln 3 3  2y
Suy ra : f 31 xy  f x  2y  3  3xy x  2y x  13y 1 xy 5y  2 2 Điều kiện  0   0  y  2 x  2y 6y  3 5 3  2y
P x y y  13y  1   11  y  11  3 P 1  0   13y2  1   11  y   3 2 11  3
Lập bảng biến thiên ta có P  . min 3
Bài tập 4. Cho các số thực a, , b c  1  ;2 
 thỏa mãn điều kiện 3 3 3
log a  log b  log c  1 2 2 2 Khi biểu thức 3 3 3  
  3log a  log b  log c P a b c a b
c đạt giá trị lớn nhất thì giá trị của 2 2 2 
a b c bằng 1 A. 3. B. 3 3 3 3.2 . C. 4. D. 6. Hướng dẫn giải Chọn C.
Ta xét hàm số f x 3 3
x  3x log x  log c với x  1;  2. 2 2   3 3log x
Ta có đạo hàm fx 2 2 2
 3x  3log x   ; 2 ln 2 x ln2 log x x fx 2 3 6 3log 2 2  6x    . 2 2 2
x ln 2 x ln 2 x ln2  1  3
6log x 3  log x
Vì f x 2  2   6 1    0 x     1  ;2 nên 3 3 2 3 2 x ln 2 x ln 2 x ln 2    
f x  f    1  1,67  0.
Như vậy hàm số f x đồng biến và có nghiệm duy nhất trên 1;  2   vì f  
1  0; f 2  0 và có đồ thị lõm trên 1;  2 
 . Do đó ta có bảng biến thiên
Từ bảng biến thiên ta nhận thấy rằng f x  1 cho nên 3 3 3
P  3  log a  log b  log c  4 2 2 2
Đẳng thức xảy ra khi và chỉ khi a b  1,c  2 và các hoán vị.
Bài tập 5. Trong tất cả các cặp x; y thỏa mãn log
4x  4y  4  1. Với giá trị nào của m 2 2 x y 2  
thì tồn tại duy nhất cặp x; y sao cho 2 2
x y  2x  2y  2  m  0? A.   2 10 2 . B.   2 10 2 và   2 10 2 .
C. 10  2 và 10  2. D. 10  2. Hướng dẫn giải Chọn B.
Điều kiện: 4x  4y  4  0. Ta có log
4x  4y  4  1 2 2 x y 2  
 4x  4y  4  x y  2  x  22  y  22 2 2  2  C . 1 
Miền nghiệm của bất phương trình là hình tròn (cả bờ) C có tâm I 2;2 bán kính R  2. 1   1  1 2 2 Mặt khác: 2 2
x y  2x  2y  2  m  0  x   1  y   1  m *. 2 2
Với m  0 thì x  1;
y  1 (không thỏa mãn x  2  y  2  2).
Với m  0 thì * là đường tròn C có tâm I 1;
 1 bán kính R m. 2   2  2
Để tồn tại duy nhất cặp x; y thì C và C tiếp xúc với nhau. 2  1 
Trường hợp 1: C và C tiếp xúc ngoài. 2  1 
Khi đó: R R I I m  2  10  m   10  22 . 1 2 1 2
Trường hợp 2: C nằm trong C và hai đường tròn tiếp xúc trong. 2  1 
Khi đó: R R I I m  2  10  m   10  22 . 2 1 1 2 Vậy m    2 10 2 và m    2 10
2 thỏa mãn yêu cầu bài toán.
Bài tập 6. Xét các số thực a, b thỏa mãn a b  1. Giá trị nhỏ nhất P của biểu thức min 2  2    log 3log a P a bằng a b   b bA. P  19. B. P  13. C. P  14. D. P  15. min min min min Hướng dẫn giải Chọn D. Ta có: 2       2 a P a        a a  2  2 log 3log 3 b logb 1  b a b   log   a b    2  2      3   log a 1. 1 log b ba  4 3
Đặt log b t  0  t   1 . Khi đó P
  3  f t với 0  t  1. 2   a 1  t t 8 3 1
Ta có f t  
f t  0  t  . 3 2    tt 3 1 Bảng biến thiên:
Từ bảng biến thiên, ta có P  15. min
Bài tập 7. Cho hai số thực x, y thỏa mãn: 2 2
x y  3 và 2 2 2 log
x 4x 3x  4y 3y   2 2 2 x y    
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P x y.
Khi đó biểu thức T  2M m  
1 có giá trị gần nhất số nào sau đây? A. 7. B. 8. C. 9. D. 10. Hướng dẫn giải Chọn D Ta có 2 2 2 2 2 log
x 4x 3x  4y 3y   2  log
x y 4x 3   2 2 2 x y    2 2  x y   
 x y  x    x y 2  x  2 2 2 2 2 2 4 3 2  y  1. 2 2 x y  3 
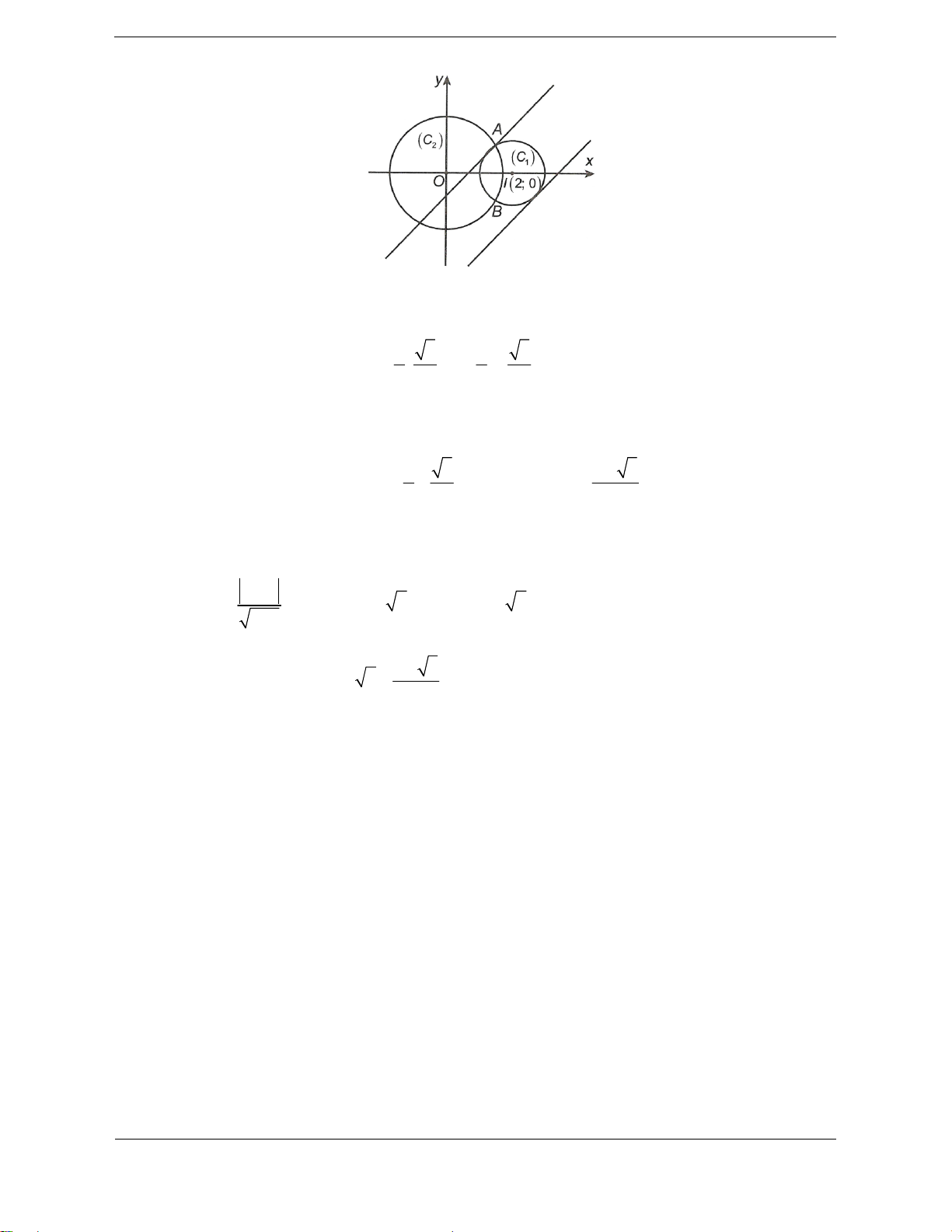
Tập hợp các số thực x, y thỏa mãn: 
những điểm thuộc miền trong hình tròn C1 x  22 2  y  1
có tâm I 2;0, bán kính R  1 và nằm ngoài hình tròn C có tâm O0;0 và bán kính 2  1 R  3. 2
Biểu thức: P x y x y P  0 là họ đường thẳng  song song với đường y x.  3 3   3 3 
Các giao điểm của hai hình tròn là A ; ,B ;   2 2   2 2     
P đạt giá trị nhỏ nhất khi đường thẳng  đi qua A. 3 3 3 3
Khi đường thẳng  qua điểm A, ta có: P 0 P       . min min 2 2 2
P đạt giá trị lớn nhất khi đường thẳng  tiếp xúc với đường tròn C ta có: 1    2  P d I;  R
 1  P  2  2  P  2  2. 1 max 11   
Do đó T  M m   3 3 2 1  22  2    10.  2   