Các dạng bài tập VDC phương trình mũ và phương trình lôgarit

Tài liệu gồm 41 trang, tóm tắt lý thuyết cơ bản cần nắm và hướng dẫn phương pháp giải các dạng bài tập trắc nghiệm vận dụng cao (VDC / nâng cao / khó) phương trình mũ và phương trình lôgarit

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

41 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
BÀI 5. PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LOGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. PHƯƠNG TRÌNH MŨ
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản là phương trình có dạng
0; 1
x
aba a

- Nếu
0b
thì phương trình có duy nhất một nghiệm
log
a
x
b
;
- Nếu
0b
hoặc
0b
thì phương trình vô nghiệm.
2. Cách giải một số phương trình mũ cơ bản
a) Đưa về cùng cơ số
 
 
,0,1
Ax Bx
aa AxBxaa
b) Phương pháp đặt ẩn phụ
2
.0
xx
aa


. Đặt
,0
x
tat
c) Logarit hóa
Nếu phương trình cho ở dạng
()
01
0
() log
fx
a
a
abb
f
xb
ì
<¹
ï
ï
ï
ï
= >
í
ï
ï
ï=
ï
î
.
II. PHƯƠNG TRÌNH LOGARIT
1. Phương trình logarit cơ bản: là phương trình có dạng
log
a
x
b
với
01a<¹
log
b
a
bxa
2. Cách giải một số phương trình mũ cơ bản
a) Đưa về cùng cơ số
 
 
0, 1
() 0( () 0)
log log
aa
aa
f x hoac g x
fx gx
fx gx



b) Phương pháp đặt ẩn phụ
2
log .log 0
aa
xx


. Đặt
log , 0
a
txx
c) Mũ hóa


() 0
log
a
b
fx
fx b
f
xa

HỆ THỐNG HÓA BẰNG SƠ ĐỒ
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Phương pháp đưa về cùng cơ số
1. Phương pháp
Phương pháp đưa phương trình mũ về cùng cơ số
- Biến đổi các hàm số có mặt trong phương trình về cùng cơ số, sau đó rút gọn, đưa về dạng cơ bản
hoặc về dạng:
() ()
() (). (
fx gx
aa fxgx
 Vôùi 0 a 1).
(Thường gặp)
- Nếu cơ số a thay đổi thì:

0)()()1(
0
)()(
xgxfa
a
aa
xgxf
(Ít gặp).
Phương pháp đưa phương trình loga về cùng cơ số
Biến đổi phương trình để đưa về dạng cơ bản đã nêu hoặc là dạng:
log log .
aa
M
NMN

2. Bài tập
Bài tập 1. Tìm tích số của tất cả các nghiệm thực của phương trình
2
3
2
7497
xx
A.
1
. B.
1
. C.
1
2
. D.
1
2
.
Lời giải
Chọn A
22
335
22
222
15
35
2
749777 10
22
15
2
xx xx
x
xx xx
x
 
 
Khi đó tích các nghiệm là
:
1515
.1
22

.
Bài tập 2. Cho phương trình

2
12
743 2 3


x
xx
. Mệnh đề nào sau đây đúng?
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt.
Lời giải
Chọn A
Do
2
743 2 3
nên phương trình ban đầu tương đương với


2
21 2
23 23


xx x
2
222 2xx x
2
20
xx
0
1
2

x
x
.
Vậy phương trình đã cho có hai nghiệm không dương.
Bài tập 3. Phương trình có bao nhiêu nghiệm?
A. Vô nghiệm. B. Một nghiệm. C. Hai nghiệm. D. Ba nghiệm.
Lời giải
Chọn C
Điều kiện: và
.
Ta có
.
Đối chi
ếu điều kiện, phương trình đã cho có hai nghiệm
và .
Bài tập 4.
Tập nghiệm
S
của phương trình
31
47 16
0
74 49



xx
là
A.
1
2




S
. B.
2S
. C.
11
;
22

. D.
1
;2
2




S
.
Lời giải
Chọn A
Ta có
31
47 16
0
74 49




xx
21 2
44
77

 

 
 
x
212
x
1
2
x .
Cách trắc nghiệm: Nhập VT phương trình vào máy tính, dùng nút Calc thử các nghiệm.
Bài tập 5. Phương trình

21
7
1
8 0,25. 2
x
x
x
có tích các nghiệm bằng?
A.
4
7
.
B.
2
3
.
C.
2
7
.
D.
1
2
.
 
23
48
2
log 1 2 log 4 log 4
x
xx
44x 1x 
 
23
48
2
log 1 2 log 4 log 4
x
xx

22
log 4 1 log 4 4
x
xx


2
4116
x
x


2
2
4116
41 16
x
x
xx


2
2
4120
4200
xx
xx


2
6
226
226
x
x
x
x



2x
226x 
Lời giải
Chọn C
Ta có

21 21
7
7
3.
2
11
2
8 0,25. 2 2 2 .2
xx
x
x
xx



21 21
774
3. 3.
2
11
22
22.222
xx
xx
xx


 
2
1
2174
3. 7 9 2 0
2
12
7
x
xx
xx
x
x


.
Vậy tích các nghiệm bằng
22
1.
77
.
Bài tập 6. Tìm số nghiệm của phương trình
7
2
1
3
27
243
x
x
x
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn A
Điều kiện
1
x
.
Ta có:
7
2
2
1
5
3
27
3
x
x
x
36
710
1
2
33
x
x
x

36710
12
xx
x

612710 1xxx
2
723220xx (PT vô nghiệm)
Bài tập 7. Cho phương trình . Tổng các nghiệm của phương trình
là
A. . B. . C. . D. .
Lời giải
Chọn B
Điều kiện:
Ta có:

 
2
3
33
3
2log 1 log 2 1 log 1xxx
2
3
41

3
2
10
1
21 0
1
2
10
x
x
x
x
x








 
2
3
33
3
2log 1 log 2 1 log 1xxx

3
333
2log 1 2log 2 1 2log 1xxx

3
33
log 1 log 2 1 1xxx


3
12 1 1xxx
Trường hợp 1: . Ta có:
. So sánh điều kiện nên .
Trường hợp 2: . Ta có:
. So sánh điều kiện nên .
Kết luận: Tổng các nghiệm của phương trình là .
Bài tập 8. Cho là số nguyên dương và , . Tìm sao cho
.
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có
.
Do là số nguyên dương nên .
Bài tập 9. Tổng tất cả các nghiệm thực của phương trình là:
A. . B. . C. . D. .
Hướng dẫn giải
Chọn B
ĐKXĐ: .
1
2
x
3
12 1 1xxx


3
121 1xxx

32
220xxx
121
x
xx 21
x
x
1
2
x
3
12 1 1xxx


3
112 1xxx

32
20xxx
0
1
x
x

0x
012 3

n 0a 1a
n
3
log 2019 log 2019 log 2019 ... log 2019 2033136.log 2019
n
a a
aa a

2017n 2016n 2018n
2019n
3
log 2019 log 2019 log 2019 ... log 2019 2033136.log 2019
n
a a
aa a

log 2019 2.log 2019 3.log 2019 ... .log 2019 2033136.log 2019
aaa a a
n

1 2 3 ... .log 2019 2033136.log 2019
aa
n

1
2033136 .log 2019 0
2
a
nn




0, 1aa

2
1
2033136 4066272 0
2
nn
nn

2016
2017
n
n

n 2016n

2
44
2log 3 log 5 0xx

8 82 82 42
30
50
x
x


3
5
x
x
.
.
Vậy tổng tất cả các ngh
iệ
m của phương trình là .
Bài tập 10. Giải phương trình có nghiệm là
A. . B. . C. . D. .
Lời giải
Chọn B
Điều kiện: .
Ta có
.
Bài tập 11. Số nghiệm của phương trình:
42 24
log log log log 2xx
là
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Điều kiện:
2
0
1
log 0
x
x
x

.
Ta có:
  
42 24 22 2 2
11
log log log log 2 log log log log 2
22
xx x x





3
2
22
1
log 4 log 4 16
2
xxx thỏa điều kiện.
Bài tập 12. Phương trình
8
349
.
4316
x
x
 
 
 
có hai nghiệm
1
x
và
2
x
. Tổng
12
Sxx
là

2
44
2log 3 log 5 0xx
4
2log 3 5 0xx





351xx


3 5 1 khi 5
3 5 1 khi 3 5
xx x
xx x


2
2
8 15 1 khi 5
8 15 1 khi 3 5
xx x
xx x


42
4
x
x

82
2 3 2018
11 1
... 2018
log log logxx x

2018.2018!x
2018
2018!x
2017!x

2018
2018!x
01
x

2 3 2018
11 1
... 2018
log log logxx x

log 2 log 3 ... log 2018 2018
xx x


log 2.3...2018 2018
x

log 2018! 2018
x

2018
2018!x
2018
2018!x
A.
1
. B.
4
. C.
2
. D.
3
Lời giải
Chọn C
Đk:
0x
Xét phương trình
84
349349
..
4 3 16 4 3 16
xx
xx
  

  
  

44
2
2
33 9 3 3 4
.22401
44 16 4 4
xx
xx
xxx
x

  

  
  
Vì
0x
không phải là nghiệm của phương trình
1
và
1. 4 0
nên
Phương trình

1
có hai nghiệm
1
x
,
2
x
và
12
2xx
. Vậy
2S
.
Dạng 2: Phương pháp đặt ẩn phụ
1. Phương pháp
Loại 1: Phương trình có dạng
kf(x) (k-1)f(x) f(x)
kk-1 10
b a +b a + ...+ b a + b = 0
Khi đó ta đặt: t = a
f(x)
điều kiện: t > 0 . Ta được một phương trình đại số ẩn t, giải pt đại số này ta biết
được nghiệm của phương trình ẩn t.
Nếu có nghiệm t thì cần xét xem có thỏa điều kiện t > 0 hay không. Nếu thỏa điều kiện thì giải phương trình
()
f
x
ta để tìm nghiệm của phương trình đã cho.
Ví dụ:
11 121
4 6.2 8 0 (2 ) 6.2 8 0
xx x x
 
Đặt t =
1
2
x
. Điều kiện t > 0. Ta có
2
2
680
4
t
tt
t

Với t = 2 ta có
1
2
x
=2
0x
Với t = 4 ta có
1
2
x
= 4
1
x

.
Vậ
y phương trình đã cho có hai nghiệm:
0x
và
1.x
Loại 2: Phương trình đưa được về dạng:
f(x)
2
13
f(x)
α
α a+ +α =0
a
Hướng giải: Đặt
()
f
x
ta .
Ví dụ 1: Giải phương trình
13
5125
55 26 260
55
x
xx
x


Đặt
5; 0
x
tt
Ta được phương trình:
2
125 ( )
125
26 0 26 125 0
5( )
55
t
tt
t
t
t

nhaän
nhaän
Với t =125 ta có 5125 3
x
x.
Với t = 5 ta có 55 1.
x
x
Vậy phương trình đã cho có hai nghiệm:
x = 1 và x = 3.
Lưu ý: Một số những cặp số là nghịch đảo của nhau. Ví dụ:
,... 83 ; 32 ; 12
Loại 3: Phương trình có dạng:
2f(x) f(x) 2f(x)
12 3
α a+α (ab) + α b=0
Hướng giải: Chia cả hai vế cho
2()
f
x
b
ta được phương trình
1
)(2 xf
b
a
+
2
)(xf
b
a
+
3
= 0
Ta đặt: t =
)(xf
b
a
điều kiện: t > 0, giải phương trình ẩn t, sau đó tìm nghiệm x.
Chú ý: Cũng có thể chia hai vế phương trình cho:
()
()
f
x
ab
hoặc:
2()
f
x
a .
Ví dụ: Giải phương trình 962.4
x
xx
 .
2
3
1
2
96 3 3
962.4 () 20 () 20 0
44 2 2
3
2( )
2
x
xx
xx x x x
x
x



 
 
 
 




Voâ nghieäm
Một số dạng phương trình logarit sử dụng phương pháp đặt ẩn phụ thường gặp:
Ví dụ1: Giải phương trình
12
1
5lg 1lg
xx


.
Phân tích: Ta nhận thấy trong phương trình chỉ có một hàm số lôgarit duy nhất, đó là lg
x
. Vì vậy ta giải pt
bằng cách đặt lg .tx
Đặt
lgtx
đk
5t
và
1t 
.Ta được phương trình:
12
1
51
tt



2
11
11154
51
t
ttt
tt





2
2
560
3
t
tt
t

thoûa ñieàu kieän
thoûa ñieàu kieän
Với t = 2 ta có
lg 2 100xx
Với t = 3 ta có
lg 3 1000xx
Vậy phương trình đã cho có hai nghiệm
x = 100; x = 1000.
Ví dụ 2: Giải phương trình
22 3
22
log ( 1) log ( 1) 7.xx
Điều kiện:
1
x
22 3
22
log ( 1) log ( 1) 7xx 
2
22
4log 1 3log 1 7 0xx
Đặt

2
log 1tx
, ta được phương trinh:
2
1
4370
7
4
t
tt
t

Với t =1 ta có

2
log 1 1 1 2 3xxx
Với
7
4
t
ta có

77
44
2
7
log 1 1 2 1 2
4
xxx

. Kết luận:....
2. Bài tập
Bài tập 1.
Phương trình

21 21 22 0
xx

có tích các nghiệm là:
A.
1
. B.
2
. C.
1
. D.
0
.
Hướng dẫn giải
Chọn
A

21 21 22 0
xx
 

1
21 22 0
21
x
x

.
 
2
21 22 21 10
xx


21 21
1
1
21 21
x
x
x
x



.
Vậy tích các nghiệm của phương trình là
1
.
Bài tập 2. Phương trình
11
9 13.6 4 0
xxx
 có 2 nghiệm
1
x
,
2
x
. Phát biểu nào sau đây đúng?
A. Phương trình có
2
nghiệm nguyên. B. Phương trình có
2
nghiệm vô tỉ.
C. Phương trình có
1
nghiệm dương. D. Phương trình có
2
nghiệm dương.
Lời giải
Chọn A
Ta có:
11
9 13.6 4 0
xxx
 9.9 13.6 4.4 0
xxx

96
9. 13. 4 0
44
xx
xx

2
33
9. 13. 4 0
22
xx
 

 
 
3
1
2
34
29
x
x






0
2
x
x
.
Vậy phương trình có
2
nghiệm nguyên.
Bài tập 3. Tính tổng của tất cả các nghiệm thực của phương trình

33 3
39 93 9312
xxxx

.
A.
3
. B.
7
2
.
C.
4
. D.
9
2
.
Lời giải
Chọn B
Đặt
39
93
x
x
a
b


.
Phương trình đã cho

3
33
ab ab
30ab a b

0
0
0
a
b
ab

.
0a 2x
.
0b
1
2
x.
0ab
93120
xx


33
34
x
x
VN

1
x
.
Vậy tổng tất cả các nghiệm thực của phương trình là
7
2
.
Bài tập 4. Tích các nghiệm của phương trình
2
25
log 125 log 1
x
x
x
bằng
A.
7
25
.
B.
630
625
.
C.
1
125
.
D.
630
.
Lời giải
Chọn C
Điều kiện:
01
x

, ta có:

2
25
log 125 log 1
x
x
x
22
25 25
log log .log 125 1
x
xx
2
25 25
3
log log 1 0
2
xx

25
25
1
log
2
log 2
x
x

2
5
1
25
x
x
.
Vậy tích các nghiệm của phương trình là:
1
125
.
Bài tập 5. Phương trình
2
5
log 2 log
2
x
x
A. Có hai nghiệm dương. B. Vô nghiệm.
C. Có một nghiệm âm. D. Có một nghiệm âm và một nghiệm dương.
Lời giải
Chọn A
Điều kiện:
01
x

.
2
5
log 2 log
2
x
x
2
2
15
log 0
log 2
x
x

2
2
log 2
4
1
log
2
2
x
x
x
x

.
Vậy phương trình đã cho có hai nghiệm dương.
Bài tập 6. Gọi
S
là tập nghiệm của phương trình
22 2
21
22 4 1
xx xx xx
. Số phần tử của tập
S
là
A.
1
. B.
2
. C.
3
. D.
4
Lời giải
Chọn
D
TXĐ:
D
Xét phương trình:
2
22 2 2 2
21 1
2
22 4 12 4 1
4
xx
xx xx xx xx xx


2
22 2 2
2
1
4.2 2 4.4 4 5.2 2 4
xx
xx xx xx xx


2
2
2
25.240
xx
xx
. Đặt
2
2, 0
xx
tt
Phương trình trở thành:
2
1
540
4
t
tt
t

Với
2
2
0
12 1 0
1
xx
x
txx
x

Với
2
22
2
42 2 20
1
xx
x
txx
x
 
Vậy tập nghiệm của phương trình
1; 0; 1; 2S 
có
4
phần tử.
Bài tập 7.
Gọi
a
là một nghiệm của phương trình
2log log 2log
4.2 6 18.3 0

xx x
. Khẳng định nào sau đây là
đúng khi đánh giá về
a
.
A.

2
10 1a
. B.
2
12aa .
C. a cũng là nghiệm của phương trình
log
29
34



x
. D.
2
10a .
Lời giải
Chọn
C
Điều kiện:
0x
. Chia hai vế cho
2log
3
x
ta được phương trình:
2log log
22
4. 18 0
33
 

 
 
xx

log
log
29
34
2
2
3







x
x
VN
log
29
34



x
.
Bài tập 8. Biết phương trình
2
2log 3log 2 7
x
x
có hai nghiệm thực
12
x
x
. Tính giá trị của biểu thức

2
1
x
Tx
A.
64T
. B.
32T
. C.
8
T
. D.
16T
.
Lời giải
Chọn D
Điều kiện:
0
1
x
x
.
Ta có:
2
2log 3log 2 7
x
x
2
2
3
2log 7
log
x
x
2
22
2log 7log 3 0xx
2
2
log 3
1
log
2
x
x
8
2
x
x
(thỏa mãn).
1
2x
;
2
8x

2
1

x
Tx
8
2
16
.
Bài tập 9. Tổng tất cả các nghiệm thực của phương trình
22
21 3 61
25.220
xxxx

bằng
A.
4
.
B.
10.
C.
6.
D.
8 .
Lời giải
Chọn C
Ta có
22 22
21 3 61 2 3 6
2 5.2 2 0 2.2 5.2 2.2 0
xxxx xxxx

.
Vì
6
20
x
, chia cả 2 vế của phương trình cho
6
2
x
, ta được
22
26 3
2.2 5.2 2 0
xx xx

.
Đặt
2
3
2
xx
t
, điều kiện
0t
.
Ta có phương trình:

2
2
2520
1
2
tN
tt
tN

.
+ Với
2
32
313
22 2 310
2
xx
txxx
  
.
+ Với
2
32
11 35
231
22 2
xx
txxx
 
.
Vậy tổng các nghiệm bằng
6
.
Bài tập 10. Cho phương trình . Khi đặt , ta được phương trình
nào dưới đây?
A. . B. . C. . D. .
Lời giải
Chọn
B
TXĐ: .
Ta có .
Đặt .
Phương trình trở thành .

1
525
log 5 1 .log 5 5 1
xx

5
log 5 1
x
t
2
10t 
2
20tt
2
20t
2
2210tt

1
525
log 5 1 .log 5 5 1

xx

1

0;D 
 
2
1
25 5
5
1
log 5 5 log 5.5 5 log 5 1 1
2
xxx
 

5
log 5 1
x
t 

0t

1

1
.11
2
tt
2
20tt

Bài tập 11. Gọi a là một nghiệm của phương trình . Khẳng định nào sau đây đúng
khi đánh giá về ?
A. .
B. cũng là nghiệm của phương trình .
C. .
D. .
Lời giải
Chọn D
Điều kiện .
Chia cả hai vế của phương trình cho ta được .
Đặt , .
Ta có .
Vớ
i
.
Vậ
y .
Bài tập 12. Tích tất cả các nghiệm của phương trình
2
22
log log 1 1xx

A.
15
2
2

. B.
1
. C.
15
2
2
. D.
1
2
.
Lời giải
Chọn A
Điều kiện
2
0
log 1 0
x
x

0
1
2
x
x
1
2
x
.
Đặt
2
log 1
x
t
,

0t
2
2
log 1xt
ta có phương trình
2log log 2log
4.2 6 18.3 0
xx x

a

2
10 1a 
a
log
29
34
x



2
12aa
2
10a
0x
2log
3
x
2log log
33
4180
22
xx
 

 
 
log
3
2
x
t



0t
2
4180tt

9
4
2
t
tL

9
4
t
log
39
24
x




log 2x
100x
2
100 10a 

2
2
11tt
42
20ttt
3
21 0tt t

2
1210tt t t




0 /
1 /
15
/
2
15
2
ttm
ttm
ttm
tloai


.
Với
0t
thì
1
2
log 1 2xx

.
Với
1t
thì
0
2
log 0 2xx
.
Với
15
2
t

thì
15
2
2
15
log 2
2
xx

.
Vậy tích các nghiệm của phương trình là
15
2
2

.
Bài tập 13. Phương trình
22
sin 1 cos
22
xx
m

có nghiệm khi và chỉ khi
A.
432m
. B.
32 5m
. C.
05m
. D.
45m
.
Lời giải
Chọn D
Ta có
22 22 2
2
sin 1 cos sin 2 sin sin
sin
4
22 22 2
2
xx xx x
x
mmm


*
.
Đặt
2
sin
2
x
t
,
1; 2t
,
*
trở thành
4
tm
t
.
Xét hàm số

4
ft t
t
 với
1; 2t
. Ta có



2
22
21;2
44
10
21;2
t
t
ft
tt
t



.
Khi đó

15f
;

24f
. Do đó

1; 2
min 4ft
và

1;2
max 5ft
.
Phương trình đã cho có nghiệm khi và chỉ khi phương trình
*
có nghiệm
1; 2t




1;2
1;2
min max 4 5ft m ft m
.
Vậy:
45m
.
Bài tập 14. Cho phương trình

22
11
42.2210
xx
mm


. Có bao nhiêu giá trị nguyên của m thuộc
đoạn
10;20
để phương trình có nghiệm?
A.
6
. B.
7
. C.
8
. D.
9
.
Lời giải
Chọn B
Điều kiện:

1; 1x
.
Với
1; 1x
thì
2
01 1x
, do đó,
2
01 1
22 2
x
hay
2
1
12 2
x
.
Đặt
2
1
2
x
t
1; 2t
. Phương trình trở thành:
2
2210tmtm

2
21 2tt mt
2
21
2
tt
m
t


(do
2t
không là nghiệm của phương trình).
Xét hàm số

2
21
2
tt
ft
t

trên
1; 2
.
Có


2
2
45
2
tt
fx
t

,

0fx
11;2
51;2
x
x


.
Lập bảng biến thiên
Do đó, để phương trình đã cho có nghiệm thì
4m
.
Suy ra, giá trị nguyên của
m thuộc đoạn
10;20
để phương trình có nghiệm là
10;9;8;7;6;5;4m
.
Vậy có
7
giá trị cần tìm của m .
Bài tập 15.
Có bao nhiêu số nguyên m để phương trình
1
4.220

xx
mm có hai nghiệm
1
x
,
2
x
thỏa mãn
12
3xx
?
A.
2
.
B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C
Phương trình
42.22 0 1
xx
mm
Đặt
2
x
t ,
0t
phương trình trở thành
2
2. 2 0 2tmtm
.
Để phương trình

1
có hai nghiệm
1
x
,
2
x
thỏa mãn
12
3
xx
điều kiện là phương trình
2
có
hai nghiệm
12
, 0tt
thỏa mãn
12 12
12
.2.22 8

xx xx
tt
. Vậy điều kiện là
2
20
20 4
28




mm
b
mm
a
c
m
a
.
Bài tập 16. Cho phương trình . Tìm để phương trình có hai nghiệm phân
biệt , thỏa mãn .
A. . B. . C. . D. .
Lời giải
Chọn
B
.
Điều kiện .
Đặt . Ta được phương trình .
Ta có: .
Phương trình có hai nghiệm phân biệt , thỏa mãn khi và chỉ khi có hai
nghiệm phân biệt , thỏa mãn .
Vậy suy ra .
Thử lại thấy thỏa mãn.
Bài tập 17. Giá trị của để phương trình có nghiệm là:
A.
. B. . C. . D. .
Lời giải
Chọn B
Đặt với . Khi đó phương trình đã cho trở thành: (*).
Phương trình đề cho có nghiệm khi và chỉ khi phương trình (*) có ít nhất một nghiệm dương.
Xét hàm số có . Xét .

22
22
log 3 log 3 0xm m x
m
1
x
2
x
12
16xx
1
4
m
m
1
4
m
m

1
1
m
m
1
4
m
m


22
22
log 3 log 3 0 1xm m x
0x
2
log
x
t
22
3302tmmt
12
16xx

212
log 4xx
21 22
log log 4xx


1
1
x
2
x
12
16xx
2
1
t
2
t
12
4tt
2
34mm
4
1
m
m

m
93 0
xx
m

0m 0m 1m 01m
3
x
t
0t
2
0ttm


2
f
ttt

21
f
tt

1
0
2
ft t

Bảng biến thiên:
Dựa vào bảng biến thiên, phương trình có ít nhất một nghiệm dương khi và chỉ khi
.
Bài tập 18. Với giá trị nào của tham số thì phương trình có hai nghiệm , thoả
mãn ?
A.
. B. . C. . D. .
Hướng dẫn giải
Chọn
A
Đặt , .
Phương trình đã cho có 2 nghiệm , thoả mãn khi phương trình
có 2 nghiệm thoả mãn .
Bài tập 19. Với điều kiện nào sau đây của thì phương trình có hai nghiệm phân biệt?
A. . B. . C. . D. .
Lời giải
Chọn D
Đặt thì phương trình trở thành .
Phương trình đã cho có 2 nghiệm phân biệt khi có nghiệm dương phân biệt
2
tt m

00mm
m
1
4.220
xx
mm

1
x
2
x
12
3xx
4m 3m 2m
1m
2
x
t
0t
1
x
2
x
12
3xx
2
2. 2 0tmtm
0t
12 12
12
.2.22 8
xx xx
tt

2
12
0
20
4
.8
28
mm
m
tt
m




m
9.360
xx
m

26m 6m 6m 26m

30
x
tt
2
60 1tmt
1
2
0 0

x

1
2
0

y
y

1
4
0
.
Bài tập 20. Tìm tất cả các giá trị tham số m để phương trình

22 2
221242
9.9 2 1 15 4 2 5 0
xx xx xx
mm


có
2
nghiệm thực phân biệt.
A.
1m
hoặc
1
2
m .
B.
36 36
22
m


.
C.
1
1
2
m.
D.
36
2
m
hoặc
36
2
m
.
Lời giải
Chọn C

22 2
221242
9.9 2 1 15 4 2 5 0
xx xx xx
mm







22 2
11 1
9211542250
xx x
mm





22
21 1
33
21 420
55
xx
mm

 

 
 
.
Đặt

2
1
3
5
x
t



. Do

2
10x 
nên
01t
.
Phương trình có dạng:

2
21420tmtm
2
21
t
tm
. Do
01t
nên
21tm
.
Để phương trình có 2 nghiệm thực phân biệt thì
02 11m

1
1
2
m
.
Bài tập 21. Tìm tất cả các giá trị của tham số m để phương trình

22 2
221242
4.4 2 2 6 6 3 3 0
xx xx xx
mm


có hai nghiệm thực phân biệt.
A.
1
1
2
m

.
B.
432m 
hoặc
432m 
.
C.
432 432m
. D.
1m 
hoặc
1
2
m
.
Lời giải
Chọn A
Viết lại phương trình ta được:
 
22
21 21
42
22 630
93
xx xx
mm
 
 

 
 
.
0
0
0
S
P


2
24 0
0
60
m
m


26
0
m
m
26m
Do

2
2
21 1 0xx x
nên
2
21
2
1
3
xx



Đặt
2
21
2
3
x
x
t




,
01t
. Phương trình trở thành:

2
22 630tmtm
3
21
t
tm

.
Để phương trình đã cho có hai nghiệm thực phân biệt thì
0211m

1
1
2
m  .
Vậy giá trị cần tìm của
m là
1
1
2
m .
Bài tập 22. Cho phương trình
32ln3ln9
e2.e e 0
xx x
m

, với m là tham số thực. Tất cả các giá trị của tham
số
m để phương trình có nghiệm duy nhất là
A.
0m
hoặc
4m
. B.
0m
hoặc
4m
.
C.
40m
. D.
0m
hoặc
4m
.
Hướng dẫn giải
Chọn
B
32ln3ln9
e2.e e 0
xx x
m


32ln3ln9
e2.e.e e.e 0
xx x
m
32
e6.e9.e 0
xxx
m
.
Đặt
e
x
t

0t
, phương trình tương đương với
32
69mt t t
 .
Xét

32
69
f
t ttt
trên

0;
.

2
3129
f
ttt

,

0ft
1
3
t
t
.
Ta có bảng biến thiên
Dựa vào bảng biến thiên: với
0m
hoặc
4m
thì phương trình có nghiệm duy nhất.
Chú ý:
Ta không lấy giá trị
0x
nên tại
0m
đường thẳng
y
m
vẫn cắt đồ thị tại duy nhất một điểm
(điểm tiếp xúc tại
3x
).
Bài tập 23. Tập hợp tất cả các giá trị của tham số m để phương trình
22
2
42 6
xx
m

có đúng
3
nghiệm
thực phân biệt là
A.
3
. B.
2
. C.
3;
. D.

2;3
.
Lời giải
Chọn A
Đặt
2
2
x
t
. Do
2
01
x
t.
Ta có phương trình
2
46 01tt m
.
Do với mỗi
1t
thì có hai nghiệm
2
log
x
t
, còn với
1t
chỉ có một nghiệm
0x
. Nên để
phương trình ban đầu có đúng 3 nghiệm thì phương trình
1
có một nghiệm
1
1t
và một nghiệm
2
1t
.
Phương trình

1
có nghiệm
1t
khi
146 0m
 3m
.
Thay
3m
vào

1
, ta có:
2
430tt
1
3
t
t
. Vậy
3m
thỏa mãn.
Bài tập 24. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn
10
để phương trình
ee
x
x
mm
có
nghiệm thực?
A.
9
. B.
8
. C.
10
. D.
7
.
Lời giải
Chọn C
Điều kiện:
e0
e0
x
x
m
mm


.
Đặt
e
x
tm

0t
ta suy ra:
2
2
e
e
x
x
mt
tm



22
e 0 1
eeee10
e102
x
xxxx
x
t
tt t t
t



.
Phương trình

2
vô nghiệm vì
e10
x
t

.
Phương trình

1
tương đương với
2
ee e ee
x
xx xx
tmm


3
Phương trình
ee
x
x
mm
*
có nghiệm thực khi phương trình

3
có nghiệm thực.
Xét hàm số
2
ee
x
x
fx
với
x
, ta có:

2
1
2e e 0 e ln 2
2
xx x
fx x
.
Bảng biến thiên của hàm số

2
ee
x
x
fx

là
Lập bảng biến thiên
Số nghiệm của
3
bằng số giao điểm của đồ thị hàm số
2
ee
x
x
fx
và đường thẳng
y
m
.
Dựa vào bẳng biến thiên suy ra phương trình
3
có nghiệm khi
1
4
m 
.
Kết hợp với giả thiết
m là số nguyên nhỏ hơn
10
ta suy ra
0,1, 2,3, 4,5,6,7,8,9m
.
Vậy có
10
giá trị thỏa mãn.
Dạng 3: Phương pháp logarit hóa, mũ hóa
1. Phương pháp
2. Bài
tập
Bài tập 1.
Phương trình
1
27 .2 72
x
x
x
có một nghiệm viết dưới dạng
log
a
x
b
, với a,
b
là các số nguyên
dương. Tính tổng
Sab
.
A.
4S
. B.
5S
. C.
6S
. D.
8S
.
3.
Lời
giải
Chọn
B
Điều kiện
0x
.
Phương trình
1
27 .2 72
x
x
x
1
3
23
3.23.2
x
x
x




33
3
2
32
32
x
x
x

33
2
3
32
x
x
x

3
3
32
x
x
x

3
3
3
log 2
x
x
x


3
3
3log2
x
x
x


3
1
3log20x
x




3
3
1
log 2
x
x



2
3
log 3
xN
x
N

.
Suy ra
2
3
a
b
. Vậy tổng
5Sab
.
Bài tập 2. Phương trình
2
log 5 2 2
x
x

có hai ngiệm
1
x
,
2
x
. Tính
1212
Pxx xx

.
A.
11
. B.
9
. C.
3
. D.
2
.
Lời giải
Chọn D
Điều kiện:
25
x
2
log 5 2 2
x
x

2
52 2
x
x

4
52
2
x
x

21
24
x
x
0
2
x
x
1212
2Px x xx
.
Bài tập 3. Gọi S là tổng tất cả các nghiệm thực của phương trình
2
7.3 1
xx
. Tìm S.
A.
7
log 3.S
B.
3
log 7.S
C.
2
S log 3.
D.
3
log 2.S
Hướng dẫn giải
Chọn A.
Ta có:

22 2
3333
7 .3 1 log 7 .3 log 1 log 7 log 3 0
xx xx x x


2
33
7
3
0
.log 7 0 log 7 1 0 .
1
log 3
log 7
x
xxxx
x


Vậy tổng các nghiệm là
7
log 3.S
Lấy logarit cơ số 3
hoặc cơ số 7 hai
vế.
Bài tập 4. Phương trình
21
3.5 15
x
x
x
có một nghiệm dạng
log
a
x
b
, với a,
b là các số nguyên dương lớn hơn 1 và nhỏ hơn 8. Giá trị của
2Pa b
bằng
bao nhiêu?
A.
8.P
B.
5.P
C.
13.P
D.
3.P
Hướng dẫn giải
Chọn C
Ta có:
21
21 1 1
11
3
3.5
3.5 15 1 3 .5 1 log 3 .5 0
3.5
x
xxx
x
x
xxx
xxx






1
1
33 3
1
log 3 log 5 0 1 .log 5 0
x
x
x
x
x
x


3
3
1
1
1.1 .log 5 0 .
log 5
x
x
x
x





Vậy
3, 5ab suy ra
213.ab
Dạng 4: Phương biến đổi thành tích
1. Phương pháp
(thường sử dụng trong trường hợp hai vế không cùng cơ số).
Hướng giải: Biến đổi phương trình về dạng:
).10 ,1,0.(log).(log).(
)()(
cbabxgaxfba
cc
xgxf
Lưu ý: Ta thường lôgarit hóa hai vế với cơ số a hoặc b.
2. Bài tập
Bài tập 1.
Giải phương trình
23 3
log .log .log 3
x
xx x
23
log 3log
x
xx

. Ta có tổng tất cả các nghiệm
bằng
A.
35
. B.
5
. C.
10
. D.
9
.
Lời giải
Chọn B
Điều kiện
0x
.
23 3
log .log .log 3
x
xx x
23
log 3log
x
xx
23
log 3 log 1 0xx x

2
3
log 3 0
x
xx

.
Ta có hàm số

2
log
f
xxx
liên tục và đồng biến trên
0;
và

23f
nên phương trình
2
log 3 0xx
có một nghiệm
2x
.
Vậy tổng tất cả các nghiệm bằng
5
.
Bài tập 2. Số nghiệm của phương trình
2
2
1
4. 25.2 100 100
5
x
x
x




là
A.
3
. B.
1
. C.
2
. D. vô nghiệm.
Lời giải
Chọn B
Ta có
2
2
1
4. 25.2 100 100
5
x
x
x




4.5 25.2 100 10
x
xx

42.5 25 0
xx

2x
.
Vậy ph
ương trình đã cho có
1
nghiệm.
Bài tập 3. Số nghiệm của phương trình
23 2
log .log 2 1 2log
x
xx
.
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn
A
ĐK:
1
2
x .

23 2
log .log 2 1 2log
x
xx

23
log . log 2 1 2 0xx

2
3
log 0
log 2 1 2 0
x
x

1
219
x
x


1
5
x
n
x
n
.
Vậy phương trình đã cho có hai nghiệm.
Bài tập 3. Biết n là số rự nhiên thỏa mãn phương trình 33 2cos
xx
nx
 có
2018
nghiệm. Tìm số nghiệm
của phương trình
99 42cos2
xx
nx
 .
A.
4036
. B.
2018
. C.
4035
. D.
2019
.
Lời giải
Chọn A
99 42cos2
xx
nx
 9 9 2.3 .3 2 2cos 2
xx xx
nx



2
2
33 4cos
xx
nx


33 2cos 1
33 2cos 2
xx
xx
nx
nx


Khi đó n
ếu

1
và
2
có nghiệm chung thì 33 3 3
x
xxx
 33
x
x

0x
Thay
0x
vào

1
ta được
00
33 2cos0
02
, tức là
1
và
2
không có nghiệm chung.
Mặt khác ta thấy n
ếu
0
x
là nghiệm của
1
thì
0
x
sẽ là nghiệm của
2
Mà
1
có
2018
nghiệm nên

2
cũng có
2018
nghiệm.
Vậy phương trình đã cho có
4036
nghiệm.
Bài tập 4. Cho phương trình
22 2
23 6
log 1 .log 1 log 1xx xx xx  
. Biết phương trình có
một nghiệm là
1
và một nghiệm còn lại có dạng

log log
1
2
bb
cc
xa a
 (với a, c là các số nguyên
tố và
ac ). Khi đó giá trị của
2
23abc
bằng:
A.
0
. B.
3
. C.
6
. D.
4
.
Lời giải
Chọn B
Điều kiện
2
11
10
x
xx


*
22 2
23 6
log 1 .log 1 log 1xx xx xx  
22
23 6
2
1
log 1 .log log 1
1
xx xx
xx


222
236 6
log 1 .log 6.log 1 log 1xx xx xx   
22
632
log 1 log 6.log 1 1 0xx xx






2
6
2
32
log 1 0 1
log 6.log 1 1 0 2
xx
xx



2
111xx
2
11
x
x

2
2
1
11
x
xx

1
x
.

2
23
2log 1.log61xx
2
26
log 1 log 3xx
6
log 3
2
12xx

6
6
log 3
2
log 3
2
2
12
x
x
x


66
log 3 log 3
1
22
2
x

.

66
log 2 log 2
1
33
2
x

. (thỏa mãn
*
)
Như v
ậy phương trình đã cho có các nghiệm là
1
x
,

66
log 2 log 2
1
33
2
x
.
Khi đó
3a
,
6b
,
2c
. Vậy
2
233abc
.
Bài tập 5. Gọi
S
là tập hợp tất cả các giá trị thực của tham số m để phương trình
22
712 2 105
.3 3 9.3
xx xx x
mm


có ba nghiệm thực phân biệt. Tìm số phần tử của
S
.
A.
3
. B. Vô số. C.
1
. D.
2
.
Lời giải
Chọn
A
Ta có:
22
712 2 105
.3 3 9.3
xx xx x
mm


222
712 2 712
313310
xx xx xx
m
 


22
712 2
3130
xx xx
m


2
2
712
2
310
30
xx
xx
m


2
3
3
4
2log0*
x
x
xx m

.
Phương trình đã cho có ba nghiệm thực phân biệt, ta có các trường hợp sau:
Trường hợp 1:
*
có một nghiệm
3x
và nghiệm còn lại khác
3
và
4
.
Thay
3x
vào
*
ta được
3
1
log 3
27
mm . Khi đó
*
trở thành
2
1
230
3
x
xx
x


(Thỏa yêu cầu).
Trường hợp 2:
*
có một nghiệm
4x
và nghiệm còn lại khác
3
và
4
.
Thay
4x
vào
*
ta được
8
3
log 8 3mm

.
Khi đó
*
trở thành
2
4
280
2
x
xx
x

(Thỏa yêu cầu).
Trường hợp 3:
*
có nghiệm kép khác
3
và
4
3
3
3
1log 0
log 3
log 8
m
m
m



3m
.
Bài tập 6. Phương trình
1111
ln .ln .ln .ln 0
2248
xxxx




có bao nhiêu nghiệm?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn A
Điều kiện:
1
0
2
1
0
2
1
0
4
1
0
8
x
x
x
x




1
2
1
2
1
4
1
8
x
x
x
x



1
2
x
.
Khi đó:
1111
ln .ln .ln .ln 0
2248
xxxx




1
ln 0
2
1
ln 0
2
1
ln 0
4
1
ln 0
8
x
x
x
x












1
1
2
1
1
2
1
1
4
1
1
8
x
x
x
x




3
2
1
2
3
4
7
8
x
x
x
x
.
So với điều kiện, ta được tập nghiệm của phương trình là
337
;;
248
S

.
Vậy phương trình đã cho có
3
nghiệm.
Bài tập 7. Gọi a là một nghiệm của phương trình

26 15 3 2 7 4 3 2 2 3 1
xxx
 
. Khi đó giá
trị của biểu thức nào sau đây là đúng?
A.
2
2aa. B.
2
sin cos 1aa
. C.
2cos 2a
. D. 32a5
a
.
Lời giải.
Chọn B
Ta có

26 15 3 2 7 4 3 2 2 3 1
xxx

.

32
23 223 223 1
xxx

43
23 223 23 20
xxx

 
3
23 123 20
xx





23 1
x

0x
.
0a
2
sin cos 1aa.
Bài tập 8. Gọi
A
là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình
.2 1 2 1
xx
xxxm m
có hai phần tử. Tìm số phần tử của
A
.
A.
1
. B. Vô số. C.
3
. D.
2
.
Lời giải
Chọn
D
Xét phương trình

.2 1 2 1
xx
xxxm m


210
x
xm x
21
x
xm
x
.
Mà phương trình
21
x
x
 có hai nghiệm là
0x
;
1
x
.
Thật vậy: dựa vào hình vẽ
Với
0x
hoặc
1
x
thì 21
x
x
, đẳng thức xảy ra khi
0x
hoặc
1
x
.
Với
01
x

thì 21
x
x

phương trình 21
x
x
vô nghiệm.
Do đó tập
A
có hai phần tử khi
0m
hoặc
1m
.
Dạng 5: Phương pháp sử dụng tính đơn điệu
1. Phương pháp
* Ta thường sử dụng các tính chất sau:
Tính chấ
t 1: Nế
u hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có
không quá một nghiệm trong khoảng (a;b). ( do đó nếu tồn tại x
0
(a;b) sao cho
f(x
0
) = C thì đó là nghiệm duy nhất của phương trình f(x) = C)
Tính chấ
t 2 : Nếu hàm
f tăng trong khoảng (a;b) và hàm g là hàm một hàm giảm trong khoảng
(a;b) thì phương trình f(x) = g(x) có nhiều nhất một nghiệm trong khoảng (a;b) .
( do đó n
ếu tồn tại x
0
(a;b) sao cho f(x
0
) = g(x
0
) thì đó là nghiệm duy nhất của phương trình
f(x) = g(x))
2. Bài tập
Bài tập 1.
Số nghiệm của phương trình
2
3
5
2018 2016 2017 2018
x
x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn
B
O
1
x
y
1
2
Đặt

2
3
5
2018 2016 2017 2018
x
fx x
,
D
.
Suy ra

2018 .ln 2018 2
x
f
xx

,,
M
AB liên tục trên
.

2018 .ln 2018 2
x
f
xx


2
2018 .ln 2018 2 0,
x
f
xx


Từ đó
f
x
đồng biến trên
D
mà
1. 0 0ff

nên
0fx
có nghiệm duy nhất trong
khoảng

1; 0
suy ra phương trình
0fx
có nhiều nhất hai nghiệm, mặt khác nhập hàm số vào
TABLE của casio (START
10
END
10
STEP
1
), ta được:
Dựa vào TABLE ta được


7. 6 0
0. 1 0
ff
ff

Vậy phương trình đã cho chỉ có hai nghiệ
m trên hai khoảng
7; 6
và
0;1
.
Chú ý: Máy tính hiể
n thị “Insuff
icient MEM” thì tiến hành cài đặt để không xuất hiện
gx
bằng
cách bấ
m SHIFT MODE mũi tên xuống,
5
,
1
.
Bài tập 2.
Tập nghiệm của phương trình
2
log 6 log 2 4xx x x

là:
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải.
Chọn B
Điều kiện:
2
60
3.
20
xx
x
x



Phương trình đã cho tương đương với
 
log 2 ( 3) log 2 4xx x x
log( 3) 4 * .xx
Vế trái của phương trình cuối là hà
m tăng, còn vế phải là hàm giảm nên nghiệm của phương
trình(nếu có) là duy nhất.
Bằng cách nhẩm nghiệm ta chọn kết quả
4.x
Bài tập 3. Cho
x
,
y
là các số thực thỏa
26
log 3log 3log
x
yxy

. Tìm giá trị Txy.
A.
28T
. B.
22T
. C.
34T
. D.
30T
.
Lời giải
Chọn
A
Đặt
26
log 3log 3log 3
x
yxyt
8
6
10
t
t
t
x
y
xy


8610
tt t

43
1
55
tt




1
.
Nhận xét:
2t
là nghiệm của phương trình
1
.
Vớ
i
2t
:
22
4343
1
5555
tt
 

 
 
.
Vậy
2t
không là nghiệm của phương trình

1
.
Vớ
i
2t
:
22
4343
1
5555
tt
 

 
 
.
Vậy
2t
không là nghiệm của phương trình

1
.
Vậ
y
2t
là nghiệm duy nhất của

1
.
Khi đó, ta có
2
2
864
636
x
y


28Txy .
Bài tập 4. Phương trình
22 2
sin cos sin
23 4.3
x
xx

có bao nhiêu nghiệm thuộc
2017; 2017
.
A.
1284
. B.
4034
. C.
1285
. D.
4035
.
Lời giải
Chọn
C.
Ta có
22 2 2 2 2
sin os sin sin 1 sin sin
234.3 23 4.3
x
cx x x x x

Đặt
2
sin
x
t với
0;1t
, ta có phương trình
321
24.3 3.4
339
tt
tt
t
 

 
 
. Vì hàm số

21
3.
39
tt
ft




nghịch biến với
0;1t
nên phương trình có nghiệm duy nh
ất
0t
. Do đó
sin 0
x
xk

,
k
.
Vì
2017; 2017x
nên ta có
2017 2017
2017 2017kk
 nên có
1285
giá trị
nguyên của
k
thỏa mãn. Vậy có
1285
nghiệm.
Bài tập 5. Tìm số nghiệm của phương trình 2 3 4 ... 2017 2018 2017
xxx x x
x
 .
A.
1
. B.
2016
. C.
2017
. D.
0
.
Lời giải
Chọn A
Xét hàm số
2 3 4 ... 2017 2018
x
xx x x
fx
Ta có

2 ln 2 3 ln 3 ... 2018 ln 2018 0
xx x
fx

,
x
.
Suy ra hàm số
2 3 4 ... 2017 2018
xxx x x
y 
đồng biến trên
.
Hàm số

2017gx x
nghịch biến trên
.
Mặ
t khác
 
0 0 2017fg
.
Do đó, ph
ương trình
 
f
xgx
có nghiệm duy nhất
0x
.
Bài tập 6. Tìm tất cả các giá trị của tham số a để phương trình 33
33
x
x
xx
a

có nghiệm duy nhất.
A.
a
. B.
10a
. C.
0a
. D. không tồn tại a.
Lời giải
Chọn A
Ta có:
33
33
x
x
xx
a

33 33
x
xx x
a


22
33
x
x
a

1
.
Xét
hàm số

22
33
x
x
fx

.
Có

22
2.3 2.3 0
xx
fx

,
x
.
Do đó, hà
m số
yfx
luôn đồng biến trên
.
Suy ra vớ
i mọi giá trị của
a thì
1
luôn có nghiệm duy nhất.
Bài tập 7. Số nghiệm của phương trình

2
2
ln 2 2018
2
x
xx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn C
Xét hàm số


2
2
ln 2
2
x
fx x x
với
;2 2;x
 
.
Ta có

2
2
1
2
x
fx x
x

;



2
2
2
24
10,;22;
2
x
fx x
x

 
.
Nên suy ra hàm số

2
2
1
2
x
fx x
x

đồng biến trên mỗi khoảng
;2
và
2;
.
Mặ
khác

 
2. 3 1.1 3 0ff


và

8
3. 2 .1 0
7
ff

 nên
f
x
có đúng một
nghiệ
m

;2a
và đúng một nghiệm
2;b

.
Ta có bả
ng biến thiên
Ta có


3
3 3 2018
2
fa f và

3
3 3 2018
2
fb f
Bài tập 8. Tìm số thực a để phương trình:
99 3cos
xx
ax

, chỉ có duy nhất một nghiệm thực
A.
6a 
. B.
6a
. C.
3a
. D.
3a
.
Hướng dẫn giải
Chọn
A
Giả sử
0
x
là nghiệm của phương trình. Ta có
00
0
99.3cos()
xx
ax

.
Khi đó
0
2
x
cũng là nghiệm của phương trình.
Thật vậy
00
22
0
993cos2
xx
ax





00
0
81 9
9cos
93
xx
ax

00
0
99.3cos
xx
ax

.
Vậy phương trình có nghiệm duy nhất khi và chỉ khi
00
2
x
x
0
1x
.
Với
0
1x
6a
.
Ngược lại, với
6a 
, phương trình
99 6.3cos
xx
x


9
36cos
3
x
x
x
 .
+
9
36
3
x
x

+

6cos 6x

Khi đó d
ấu
""
xảy ra khi và chỉ khi
9
36
3
cos 1
x
x
x
1
x
.
Vậy
00
0
99.3cos()
xx
ax

có nghiệm duy nhất khi và chỉ khi
6a
.
Bài tập 9. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số

;
x
y
thỏa mãn
2132
ee 1
xy x y
xy


, đồng thời thỏa mãn
22
22
log 2 1 4 log 4 0xy m xm

.
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn A
Ta có:
2132
ee 1
xy x y
xy


21 32
e21e32
xy x y
x
yxy


.
Xét
hàm số

e
t
f
tt
trên
. Ta có
e10
t
ft

nên hàm số đồng biến trên
.
Do đó ph
ương trình có dạng:

2132
f
xy f x y
2132
x
yxy
 1yx.
Thế
vào phương trình còn lại ta được:
22
22
log 4 log 4 0xm xm

.
Đặt
2
logtx
, phương trình có dạng:
22
440tmtm

.
Để ph
ương trình có nghiệm
thì
0
2
380mm

8
0
3
m
.
Do đó có
3
số nguyên m thỏa mãn.
Bài tập 10. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số

;
x
y
thỏa mãn
35 31
ee 122
xy xy
x
y


, đồng thời thỏa mãn
22
33
log 3 2 1 6 log 9 0xy m xm

.
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn B
Ta có:
35 31
ee 122
xy xy
xy


35 31
e35e 31
xy xy
xy xy


.
Xét
hàm số

e
t
f
tt
trên
. Ta có
e10
t
ft

nên hàm số đồng biến trên
.
Do đó ph
ương trình có dạng:

35 31fx y fx y

35 31
x
yx y
 212yx.
Thế
vào phương trình còn lại ta được:
22
33
log 6 log 9 0xm xm

.
Đặt
3
logtx
, phương trình có dạng:
22
690tmtm

.
Để ph
ương trình có nghiệm thì
0
2
3120mm

04m

.
Do đó có
5
số nguyên m thỏa mãn.
Bài tập 11. Gọi
0
3ab
x
c
là một nghiệm lớn hơn
1
của phương trình

1
1
2
1
23 121
3
x
x
xx








.
Giá trị của
Pabc
là
A.
6P
. B.
0P
. C.
2P
. D.
4P
.
Lời giải
Chọn D
Điều kiện xác định:
0x
.

1
1
1
23 1
3
x
x
x








2
21x
1
1
2
1
331
2
x
x
x
x

1
1
2
1
331
2
x
x
x
x

1
. Xét hàm số
3
t
f
tt
0t
,
3.ln3 1 0
t
ft

 
1
11
2
ffx
x




1
1
2
x
x

13
2
x

1a
,
1b
,
2c
. Vậy
4P
.
Bài tập 12. Tìm tất cả các giá trị của tham số m để phương trình
ln lnmmxx

có nhiều nghiệm
nhất.
A.
0m
. B.
1m
. C. em
. D.
1m 
.
Lời giải
Chọn B
Ta có



ln ln 1mmxx
.
Điề
u kiện
e
m
x
m
.
Đặt

ln mx y
ta được e
y
mx. Thay vào
1
ta được
ln my x
e
x
m
y

.
Ta có hệ
e
ee e e
e
x
xy x y
y
my
yx x y
mx



. Do hàm số
e
t
f
tt
đồng biến trên
nên suy ra
x
y

ln
x
xm
e
x
x
m
 .
Xét
hàm số

e
x
gx x
;

e1
x
gx
;
00gx x

.
BBT
Suy ra phương trình có nhiều nhất là hai nghiệm
1m
. (chú ý nghiệm luôn thỏa điều kiện).
Bài tập 13. Có bao nhiêu số nguyên m để phương trình
2
2
2
2
33 1
log 5 2
21
xxm
x
xm
x
x


Có hai nghiệm phân biệt lớn hơn
1
.
A.
3
. B. Vô số. C.
2
. D.
4
.
Lời giải
Chọn C
Điều kiện:
2
33 10xxm.
Ta có:
2
2
2
2
33 1
log 5 2
21
xxm
x
xm
x
x



2
2
2
2
33 1
log 1 5 1
21
xxm
x
xm
xx






2
2
2
2
33 1
log 5 1
422
xxm
x
xm
x
x




2222
22
log 3 3 1 log 4 2 2 4 2 2 3 3 1xxm xx xx xxm  

22 22
22
log 3 3 1 3 3 1 log 4 2 2 4 2 2xxm xxm xx xx
1
Xét hàm
số:
2
log
f
tt t
trên
0;
, ta có

1
10
.ln2
ft
t

,
0;t
.
Do đó hà
m số
f
t
đồng biến trên
0;
.
Suy ra:


22
1422331fx x fx xm
22
42233 1xx xxm
2
51xxm

2
. Điều này đúng với mọi
x
.
Xét
hàm số:
2
5gx x x
trên
, ta có

5
250
2
gx x x
 .
Bả
ng biến thiên:
- Theo bảng biến thiên ta thấy: phương trình

2
có hai nghiệm phân biệt lớn hơn
1
khi và chỉ khi
25
14
4
m
21
3
4
m
.
Do
m
nên

5; 4m
.
Vậy có
2
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Bài tập 14. Cho phương trình
22 2
25
log 1 .log 1 log 1 .
m
xx xx xx 
Có bao nhiêu giá trị
nguyên dương khác
1
của
m
sao cho phương trình đã cho có nghiệm
x
lớn hơn
2
?
A. Vô số. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Điều kiện xác định:
2
1xx
1x
.
Đặt
2
2
log 1txx
thì
2
2
1
1
1
.
ln 2
1
x
x
t
xx

2
22
11
.
ln 2
11
xx
xx x


2
1
0
1ln2x

BBT:
Do
2x

2
log 2 3t
.
Phương trình trở thành
5
1
.log 2 log
2
t
m
t
t
5
.log 2 log 2
m
t
5
1
log m
t

Ycbt

5
2
1
log
log 2 3
m 

2
1
log 2 3
5m

. Do
*
m
và
1m
nên
2m
.
Bài tập 15. Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
3
3 27 3 27.2 2
xx
mm
có
nghiệm thực?
A. 6. B. 4.
C. Vô số. D. Không tồn tại m.
Hướng dẫn giải
Chọn C.
Ta có

3
333
3 27 3 27.2 2 27 3 27.2 2 3 . 1
xx x x
mm m m
Đặt
2,
x
u
điều kiện:
0u
và

3
3
3 27.2 3 27. . 2
x
mvvmu
(1) trở thành
3
27 3 . 3uvm
Từ (3) và (2) suy ra
33 22
27 27 . 27 0uvvuuvuuvv
.uv
Do
2
2
22
13
4270,,,
24
v
uuvv u v uv




nên
3
3
27
327 ,
3
uu
muum

với
0.u
Xét hàm số

3
27
3
uu
fu
với
0.u
Ta có



3
1
327; 0 3
3
fu u fu u

 do
0.u
Suy ra

0;
min 54.fu


Do đó có vô số giá trị nguyên của m để phương trình có nghiệm thực.
Bài tập 16. Có bao nhiêu giá trị nguyên của tham số m để phương trình 4.2250
xx
mm
 có hai
nghiệm trái dấu?
A. Vô số. B. 0. C. 1. D. 4.
Hướng dẫn giải
Chọn C.
Ta có

2
4 .22 50 2 .22 50
xx x x
mm mm 
Đặt
2, 0,
x
tt
phương trình thành
2
2502.tmtm
Đặt

2
25ft t mt m
Nhận xét rằng với một giá trị
0t
ta tìm được một nghiệm x nên để phương trình có hai nghiệm
12
0
x
x
thì phương trình (2) có hai nghiệm phân biệ
t
21
0tt
đồng thời
12
1tt
(vì
12
0
222
x
x
 ). Từ đó, ta có:



2
2
8200
0
42 5 0
5
0
250
5
4.
2
0
0
2
0
1. 0
1. 1 2 5 0
4
mm
mm
P
m
m
m
S
m
m
ft
mm
m











Vậy chỉ có một giá trị nguyên của tham số m thỏa đề.
Bài tập 17. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình

23 41*
xx
m
có
nghiệm duy nhất?
A. 3. B. Vô số. C. 1. D. 2.
Hướng dẫn giải
Chọn D.
Đặt
2, 0,
x
tt
phương trình
 
2
2
3
*3 1 1.
1
t
tmt m
t

Xét hàm số

2
3
1
t
ft
t
xác định trên tập
0; .D

Ta có


22
13
.
11
t
ft
tt

Cho

1
0130 .
3
ft t t
 
Bảng biến thiên
x

0
1
3

y
+ 0
y
10
3
1
Dựa vào bảng biến thiên ta thấ
y với
13m
hoặc
10m
phương trình có nghiệm duy nhất nên có hai
giá trị nguyên của tham số m.
Bài tập 18. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình

11
2.4 5.2 0, *
xx
m


có nghiệm?
A. 3. B. 0. C. 1. D. 4.
Hướng dẫn giải
Chọn A.
Đặt
1
2,
x
t
điều kiện
1
2
t vì
11.x 
Khi đó
2
*25 .ttm
Xét hàm số
2
25
y
tt
trên
1
;.
2



Ta có
45.
yt

Cho
5
0450 .
4
yt t
 
x

1
2
5
4

y
+ 0
y
25
8
2

Do đó phương trình có nghiệm khi
25
.
8
m
| 1/41
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI 5. PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LOGARIT
A. KIẾN THỨC CƠ BẢN CẦN NẮM I. PHƯƠNG TRÌNH MŨ
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản là phương trình có dạng x a b
a  0;a  1 -
Nếu b  0 thì phương trình có duy nhất một nghiệm x  log b ; a -
Nếu b  0 hoặc b  0 thì phương trình vô nghiệm.
2. Cách giải một số phương trình mũ cơ bản
a) Đưa về cùng cơ sốA xBxaa
Ax  Bx, a  0,a   1
b) Phương pháp đặt ẩn phụ 2x   . x a
a    0 . Đặt x
t a , t  0 c) Logarit hóa 0 ìï < a ¹1 ï
Nếu phương trình cho ở dạng ï f ( x ) a = b b í > 0 .
ïïïf (x) = log b ïî a
II. PHƯƠNG TRÌNH LOGARIT
1. Phương trình logarit cơ bản: là phương trình có dạng log x b với 0 < a ¹ 1 a log b x b x a a
2. Cách giải một số phương trình mũ cơ bản
a) Đưa về cùng cơ số    f x hoac g x   f x g x   a   a
 a 0,a 1 ( ) 0 ( ( ) 0) log log  f
  x  g x
b) Phương pháp đặt ẩn phụ 2
 log x  .log x    0 . Đặt t  log x,x  0 aa a c) Mũ hóa    f xf (x) 0 log  b   af   xba
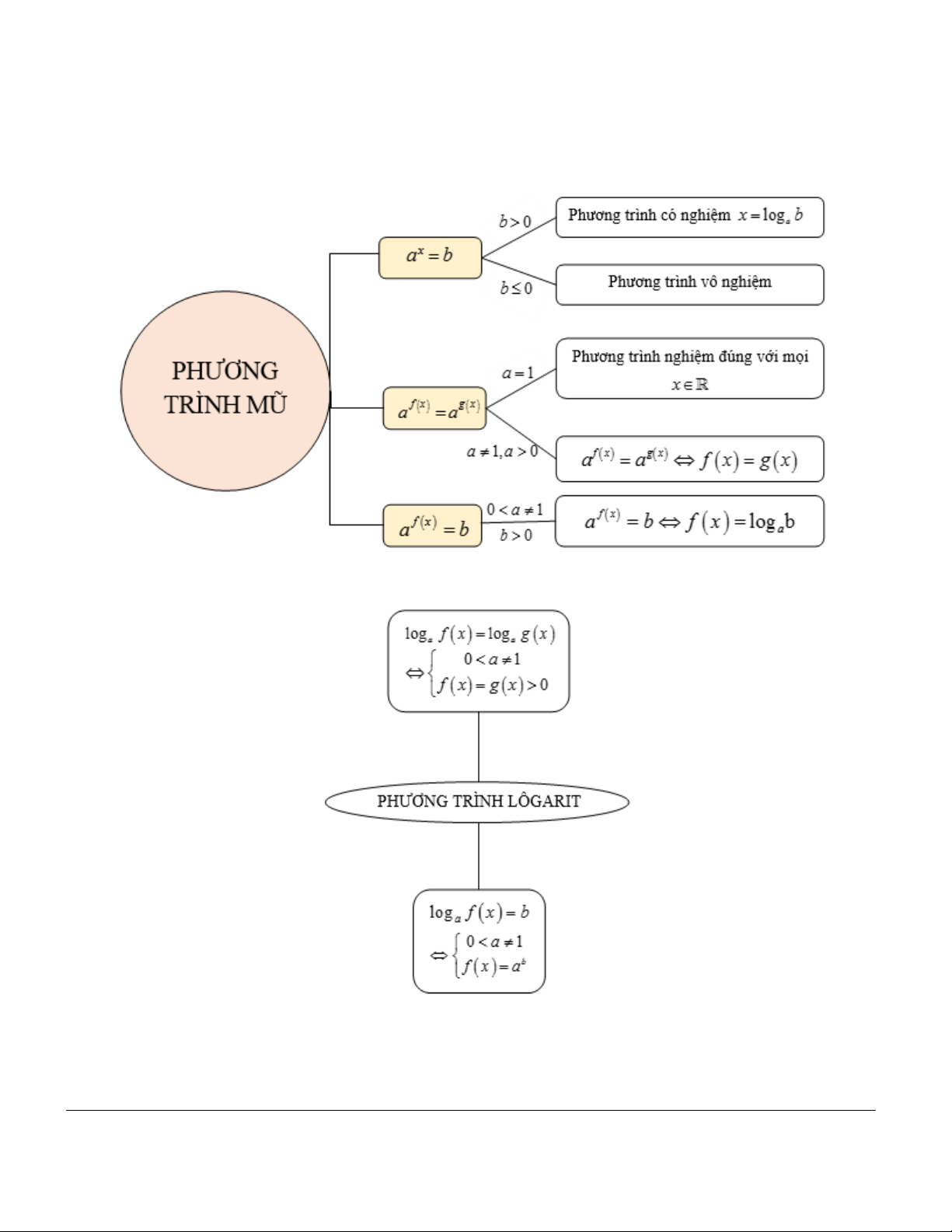
HỆ THỐNG HÓA BẰNG SƠ ĐỒ
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Phương pháp đưa về cùng cơ số 1. Phương pháp
Phương pháp đưa phương trình mũ về cùng cơ số
- Biến đổi các hàm số có mặt trong phương trình về cùng cơ số, sau đó rút gọn, đưa về dạng cơ bản
hoặc về dạng: f (x) g ( x) aa
f (x)  g(x) . (Vôùi 0  a  1).(Thường gặp) a f ( x) g ( x)   0
- Nếu cơ số a thay đổi thì: aa   (Ít gặp). (a   )
1 f (x)  g(x)  0
Phương pháp đưa phương trình loga về cùng cơ số
Biến đổi phương trình để đưa về dạng cơ bản đã nêu hoặc là dạng: log M  log N M N. a a 2. Bài tập 2 3  
Bài tập 1. Tìm tích số của tất cả các nghiệm thực của phương trình x x 2 7  49 7 1 1 A. 1  . B. 1. C.  . D. . 2 2 Lời giải Chọn A  1 5 x  2 3 2 3 5 x xx x 3 5 2 2 2 2 2 2 7  49 7  7
 7  x x    x x 1  0   2 2  1 5 x   2 1 5 1 5
Khi đó tích các nghiệm là: .  1. 2 2 2 x x 1  x2
Bài tập 2. Cho phương trình 7  4 3
 2 3 . Mệnh đề nào sau đây đúng?
A. Phương trình có hai nghiệm không dương.
B. Phương trình có hai nghiệm dương phân biệt.
C. Phương trình có hai nghiệm trái dấu.
D. Phương trình có hai nghiệm âm phân biệt. Lời giải Chọn A Do     2 7 4 3 2
3 nên phương trình ban đầu tương đương với x  0
    22xx 1   x2 2 3 2 3 2  2 
x  2x  2  x  2 2
 2x x  0  1  . x    2
Vậy phương trình đã cho có hai nghiệm không dương.
Bài tập 3. Phương trình log  x  2 1  2  log
4  x  log 4  x3 4 2 8 có bao nhiêu nghiệm? A. Vô nghiệm. B. Một nghiệm. C. Hai nghiệm. D. Ba nghiệm. Lời giải Chọn C Điều kiện: 4   x  4 và x  1  .
Ta có log  x  2 1  2  log
4  x  log 4  x3  log 4 x 1  log  4  x 4   2   2   x 4 2 8  x  2   4 x   2 1  16  x 2
x  4x 12  0 x  6 2  4 
x 1  16  x      . 4 2    x   2 1  x 16
x  4x  20  0 x  2  2 6  x  2  2 6
Đối chiếu điều kiện, phương trình đã cho có hai nghiệm x  2 và x  2  2 6 . x 3x 1 
Bài tập 4. Tập nghiệm  4   7  16
S của phương trình   0     là  7   4  49  1  1 1   1 
A. S    . B. S    2 . C.  ;   .
D. S   ; 2.  2 2 2   2  Lời giải Chọn A x 3x 1 4 7      16 2  x 1  2  4   4  1 Ta có   0            2
x 1  2  x   .  7   4  49  7   7  2
Cách trắc nghiệm: Nhập VT phương trình vào máy tính, dùng nút Calc thử các nghiệm. 2 x 1  7 x
Bài tập 5. Phương trình x 1
8   0, 25. 2 có tích các nghiệm bằng? 4 2 2 1 A. . B. . C. . D. . 7 3 7 2 Lời giải Chọn C 2x 1  2x 1  7    7 2x 1 7 x 2x 1 7 x 4 3. x x 3. 3. Ta có x     2 1 x 1  2 8 0, 25. 2  2  2 .2  2 x 1  2 x 1  2  2  2 .2  2  2 x  1 2x 1 7x  4 2 3. 7   
x  9x  2  0  2 . x 1 2 x   7 2 2
Vậy tích các nghiệm bằng 1.  . 7 7 7 2 3 x x
Bài tập 6. Tìm số nghiệm của phương trình x 1 27   . 243 A. 0 . B. 1. C. 2. D. Vô số. Lời giải Chọn A
Điều kiện x  1. 7 x x2 2 3 3x6 7 x 1  0   Ta có: x x x 1 27   x 1  2  3  3 6 7 10 3   5 3 x 1 2
 6x 12  7x 10x   1 2
 7x  23x  22  0 (PT vô nghiệm)
Bài tập 7. Cho phương trình 2log  x  
1  log 2x  2 3 1  log x 1 3 3 
 . Tổng các nghiệm của phương trình 3 là A. 2 . B. 3 . C. 4 . D. 1. Lời giải Chọn B 3 x 1  0 x  1   Điều kiện:   2x  2 1  0   1 x    x 1  0  2 
Ta có: 2log x  
1  log 2x  2 3 1  log x 1 3 3   3  2log  3
x 1  2 log 2x 1  2 log x 1  log  3
x 1  log 2x 1 x 1 3  3   3  3 3   3
x 1  2x 1 x   1 1
Trường hợp 1: x  . Ta có: 3
x 1  2x 1  x   1 3
x 1  2x   1 x   1 2 3 2
x  2x x  2  0  x  1
  x  2  x 1 . So sánh điều kiện nên x  2 x 1. 1
Trường hợp 2: x  . Ta có: 3
x 1  2x 1  x   1 3
x 1  1 2xx   1 2  x  0 3 2
x  2x x  0  
. So sánh điều kiện nên x  0 . x  1 
Kết luận: Tổng các nghiệm của phương trình là 0 1 2  3 .
Bài tập 8. Cho n là số nguyên dương và a  0 , a  1 . Tìm n sao cho
log 2019  log 2019  log 2019  ... log  n 2019 2033136.log 2019 3 a a . a a a A. n  2017 . B. n  2016 . C. n  2018 . D. n  2019 . Lời giải Chọn B
Ta có log 2019  log 2019  log 2019  ... log  n 2019 2033136.log 2019 3 a a a a a
 log 2019  2.log 2019  3.log 2019 ... .
n log 2019  2033136.log 2019 a a a a a
 1 2  3... n.log 2019  2033136.log 2019 a a
nn   1   
 2033136.log 2019  0 a  0,a   1 2 a   n n   1 n  2016 2 
 2033136  n n  4066272  0  . 2  n  2017 
Do n là số nguyên dương nên n  2016 .
Bài tập 9. Tổng tất cả các nghiệm thực của phương trình 2 log  x  3  log  x  52  0 4 4 là: A. 8 . B. 8  2 . C. 8  2 . D. 4  2 .
Hướng dẫn giải Chọn B x  3  0 x  3 ĐKXĐ:    . x  5  0 x  5
2 log  x  3  log  x  52  0  2log  x  3 x  5   0 4      4 4 
x 3x 5 1 khi x  5
 x  3 x  5  1   .
x 35 x 1 khi 3  x  5 2
x  8x 15 1 khi x  5     x 4 2    . 2
x  8x 15  1 khi 3  x  5 x  4
Vậy tổng tất cả các nghiệm của phương trình là 8  2 . 1 1 1
Bài tập 10. Giải phương trình   ...  2018 có nghiệm là log x log x log 2 3 2018 x
A. x  2018.2018! . B. 2018 x  2018!. C. x  2017!. D. x   2018 2018! . Lời giải Chọn B Điều kiện: . 0  x  1 1 1 1 Ta có   ...
 2018  log 2  log 3 ... log 2018  2018 log x log x log x x x 2 3 2018 x  log   log  2018  x  2018! 2018  x  2018! x  2018  ! 2018 x  2.3...2018 2018 .
Bài tập 11. Số nghiệm của phương trình: log log x  log log x  2 là 4  2  2  4  A. 0 . B. 2. C. 3 . D. 1. Lời giải Chọn D x  0 Điều kiện:   x 1. log x  0  2 1  1 
Ta có: log log x  log log x  2  log log x  log log x  2 4  2  2  4  2  2  2  2  2  2  1
 log x32  4  log x  4  x 16 thỏa điều kiện. 2 2 2 8 3 x 4 x     9
Bài tập 12. Phương trình .      có hai nghiệm
x . Tổng S x x là  4   3  16 1 x và 2 1 2 A. 1. B. 4. C. 2. D. 3 Lời giải Chọn C Đk: x  0 8 4 3 x 4 9 3 x x 4 x         9 Xét phương trình .   .           4   3  16  4   3  16 4 4 xx 2  3   3 x  9  3 x   3  4 2  .   
x   2  x  2x  4  0           1  4   4  16  4   4  x
Vì x  0 không phải là nghiệm của phương trình   1 và 1. 4    0 nên Phương trình   1 có hai nghiệm
x x  2 . Vậy S  2 . 1 x , x và 2 1 2
Dạng 2: Phương pháp đặt ẩn phụ 1. Phương pháp
Loại 1: Phương trình có dạng kf(x) (k-1)f(x) f(x) b a + b a + ... + b a + b = 0 k k-1 1 0
Khi đó ta đặt: t = af(x) điều kiện: t > 0 . Ta được một phương trình đại số ẩn t, giải pt đại số này ta biết
được nghiệm của phương trình ẩn t.
Nếu có nghiệm t thì cần xét xem có thỏa điều kiện t > 0 hay không. Nếu thỏa điều kiện thì giải phương trình f ( x) t a
để tìm nghiệm của phương trình đã cho.
Ví dụ: x 1  x 1  x 1  2 x 1 4 6.2 8 0 (2 ) 6.2       8  0 t  2 Đặt t = 1
2x . Điều kiện t > 0. Ta có 2
t  6t  8  0  t  4  Với t = 2 ta có 1
2x =2  x  0  Với t = 4 ta có 1
2x = 4  x  1.
Vậy phương trình đã cho có hai nghiệm: x  0 và x  1. α
Loại 2: Phương trình đưa được về dạng: f(x) 2 α a + + α = 0 1 f(x) 3 a Hướng giải: Đặt f ( x) t a .   5x x x 125
Ví dụ 1: Giải phương trình 1 3 5  5  26    26  0 5 5x 2 t 125 tt 125 (nhaän) Đặt  5x t
;t  0 Ta được phương trình:   26  0 
 26t 125  0  5  t 5 t  5 (nhaän)
 Với t =125 ta có 5x  125  x  3.
 Với t = 5 ta có 5x  5  x  1.
Vậy phương trình đã cho có hai nghiệm: x = 1 và x = 3.
Lưu ý: Một số những cặp số là nghịch đảo của nhau. Ví dụ: 2  2 ; 1  3 ; 3  8 ,...
Loại 3: Phương trình có dạng: 2f(x) f(x) 2f(x) α a + α (ab) + α b = 0 1 2 3 2 f ( x)   f ( x)  
Hướng giải: Chia cả hai vế cho 2 a a f ( x ) b
ta được phương trình    +    +  = 0 1  2 3 b   b f ( x)   Ta đặt: t = a  
điều kiện: t > 0, giải phương trình ẩn t, sau đó tìm nghiệm x. b
Chú ý: Cũng có thể chia hai vế phương trình cho: ( ) ( ) f x ab hoặc: 2 f (x) a .
Ví dụ: Giải phương trình 9x 6x 2.4x   .  3 x  1         x x x 9 x 6 x 3 x 3 x 2 2 9  6  2.4  ( )   2  0  ( )   2  0   x  0     4 4 2 2       3 x    2(  Voâ nghieäm)    2 
Một số dạng phương trình logarit sử dụng phương pháp đặt ẩn phụ thường gặp: 1 2
Ví dụ1: Giải phương trình   1.
5  lg x 1 lg x
Phân tích: Ta nhận thấy trong phương trình chỉ có một hàm số lôgarit duy nhất, đó là lg x . Vì vậy ta giải pt
bằng cách đặt t  lg . x
Đặt t  lg x đk t  5và t  1
 .Ta được phương trình: 1 2  
t  2 thoûa ñieàu kieän   t 11 1 2   1 t
 11  5  4t t 2
t  5t  6  0   5  t 1 t
5t1t t  3  thoûa ñieàu kieän
 Với t = 2 ta có lg x  2  x 100
 Với t = 3 ta có lg x  3  x 1000
Vậy phương trình đã cho có hai nghiệm x = 100; x = 1000.
Ví dụ 2: Giải phương trình 2 2 3
log (x 1)  log (x 1)  7. 2 2 Điều kiện: x 1 2 2 3
log (x 1)  log (x 1)  7 2
 4 log x 1  3log x 1  7  0 2   2   2 2 t  1
Đặt t  log x 1 , ta được phương trinh: 2 4 
t  3t  7  0  2   7 t   4
 Với t =1 ta có log x 1 1  x 1  2  x  3 2   7  7 7 7  Với t  ta có log x 1 
x 1  2  x  1 2 . Kết luận:.... 2   4 4 4 4 2. Bài tập x x
Bài tập 1. Phương trình  2   1   2  
1  2 2  0 có tích các nghiệm là: A. 1  . B. 2. C. 1. D. 0 .
Hướng dẫn giải Chọn A x x 1 x 2   1   2   1  2 2  0      . x  2     1 2 2 0 2 1 x    2   1  2 1 x  1   2x x  2 1  2 2  2   1 1  0    .     xx  1 2 1  2 1
Vậy tích các nghiệm của phương trình là 1  .
Bài tập 2. Phương trình x 1  x x 1 9 13.6 4   
 0 có 2 nghiệm 1x , x . Phát biểu nào sau đây đúng? 2
A. Phương trình có 2 nghiệm nguyên.
B. Phương trình có 2 nghiệm vô tỉ.
C. Phương trình có 1 nghiệm dương.
D. Phương trình có 2 nghiệm dương. Lời giải Chọn A 9x 6x Ta có: x 1  x x 1 9 13.6 4     0
9.9x 13.6x 4.4x     0  9. 13.  4  0 4x 4x  3 x   1 2   3 x 3 x      2 x  0   9. 13.  4  0        .  2   2   3 x 4 x  2       2  9
Vậy phương trình có 2 nghiệm nguyên. 3 3 3
Bài tập 3. Tính tổng của tất cả các nghiệm thực của phương trình 3x 9 9x 3 9x 3x      12 . 7 9 A. 3 . B. . C. 4. D. . 2 2 Lời giải Chọn B
a  3x 9 Đặt  . b   9x 3 a  0 Phương trình đã cho      3 3 3  a b a b
 3aba b  0  b  0  . a b  0 
a  0  x  2.  1
b  0  x  . 2 3x  3
a b  0 9x 3x   12  0    x 1. 3x  4   VN  7
Vậy tổng tất cả các nghiệm thực của phương trình là . 2
Bài tập 4. Tích các nghiệm của phương trình log 125x 2 log x 1 bằng x 25 7 630 1 A. . B. . C. . D. 630 . 25 625 125 Lời giải Chọn C
Điều kiện: 0  x  1, ta có: 3 log 125x 2 log x 1 2 2  log x  log . x log 125  1 2
 log x  log x 1  0 x 25 25 25 x 25 25 2  1 x  5 log   25 x  2   .  1   log x x  2  2 25  25 1
Vậy tích các nghiệm của phương trình là: . 125 5
Bài tập 5. Phương trình log 2  log x x 2 2
A. Có hai nghiệm dương. B. Vô nghiệm.
C. Có một nghiệm âm. D. Có một nghiệm âm và một nghiệm dương. Lời giải Chọn A
Điều kiện: 0  x  1. log x  2 5 1 5 2 x  4 log 2  log x    log x   0     . x 2 2 2 1 log x 2 log    2 x x 2 2  2
Vậy phương trình đã cho có hai nghiệm dương.
Bài tập 6. Gọi S là tập nghiệm của phương trình 2 2 2 x x x x2 x x 1 2 2 4   
1. Số phần tử của tập S là A. 1. B. 2. C. 3 . D. 4 Lời giải Chọn D TXĐ: D   2  x x x xx xx x 2x x Xét phương trình: 2 2 2 2 2 2 1 x x 1 2 2 4 1 2 4        1 4       2 2 2 2 2 2 1 x x x x x x x x x x   4.2  2  4.4  4  5.2  2  4 2 2 x x 2  2 2
 5.2x x  4  0 . Đặt  2x x t , t  0 t 1
Phương trình trở thành: 2
t  5t  4  0  t  4   2 x 0 Với x x 2 t  1  2
1  x x  0  x 1   2 x 2 Với x x 2 2 t  4  2
 2  x x  2  0  x  1
Vậy tập nghiệm của phương trình S   1  ;0;1;  2 có 4 phần tử.
Bài tập 7. Gọi a là một nghiệm của phương trình 2log x log x 2log 4.2  6
18.3 x  0 . Khẳng định nào sau đây là
đúng khi đánh giá về a . A. a  2 10  1. B. 2
a a 1  2 . log  2  x 9
C. a cũng là nghiệm của phương trình    . D. 2 a  10 .  3  4 Lời giải Chọn C
Điều kiện: x  0 . Chia hai vế cho 2log 3
x ta được phương trình: log  2  x 9   2log   x log  2   2  x  3  4 log  2  x 9 4.  18  0          .  3   3   log  2  x   3  4  2    VN   3 
Bài tập 8. Biết phương trình 2 log x  3log 2  7 có hai nghiệm thực x  2
x . Tính giá trị của biểu thức x 1 2  x  2x T 1 A. T  64 . B. T  32 . C. T  8. D. T 16 . Lời giải Chọn Dx  0 Điều kiện:  . x 1 3
Ta có: 2 log x  3log 2  7  2 log x   7 2 x 2 log2 x log x  3 2 x  8 2  2 log 
x  7 log x  3  0   (thỏa mãn). 2 2 1   log x  x  2 2  2  x  2 ; x
x  8  T     8 2  16 . 1 x  2 1 2
Bài tập 9. Tổng tất cả các nghiệm thực của phương trình 2 2 2 x 1  x 3 x 6 x 1 2 5.2 2     0 bằng A. 4. B. 10 . C. 6 . D. 8 . Lời giải Chọn C Ta có 2 2 2 2 2 x 1  x 3 x 6 x 1  2 x x 3 x 6 2  5.2  2  0  2.2  5.2  2.2 x  0 . Vì 6
2 x  0 , chia cả 2 vế của phương trình cho 6 2 x , ta được 2 2 2 x 6 x x 3 2.2  5.2 x  2  0 . Đặt 2 3 2x x t  
, điều kiện t  0.
t  2N  Ta có phương trình: 2 2 
t  5t  2  0  1  . t  N   2 x   x 3 13 + Với 2 3 2 t  2  2
 2  x  3x 1  0  x  . 2 1 x   x 1 3 5 + Với 2 3 2 t   2
  x  3x  1  x  . 2 2 2
Vậy tổng các nghiệm bằng 6 .
Bài tập 10. Cho phương trình log 5x 1.log  x 1 5    5 1 log 5x t  1 5   5 25  . Khi đặt , ta được phương trình nào dưới đây? A. 2 t 1  0 . B. 2
t t  2  0 . C. 2 t  2  0 . D. 2
2t  2t 1  0. Lời giải Chọn B log 5x  1 .log  x 1 5   5 1   1 5 25  TXĐ: . D   0;  xx 1 Ta có log  1 5  5  log 5.5  5  log 5x 1 1 25  2    5 5    . 2 Đặt log 5x t  1 t  0 5   . 1 Phương trình  
1 trở thành t. t   1  1 2
t t  2  0 . 2 Bài tập 11. Gọi 2log x log x 2log
a là một nghiệm của phương trình 4.2 6 18.3 x  
 0 . Khẳng định nào sau đây đúng khi đánh giá về ? a A. a  2 10  1 . log 2 x   9
B. a cũng là nghiệm của phương trình    .  3  4 C. 2
a a 1  2 . D. 2 a  10 . Lời giải Chọn D Điều kiện . x  0 2log x log 3 3 x    
Chia cả hai vế của phương trình cho 2log 3 x ta được . 4  18  0      2   2  log  3 x  Đặt , t    t  0 .  2   9 t  Ta có . 2 4 
t t 18  0  4  t  2   L 9 log 3 x   9 Với t       log x  2  x 100 . 4  2  4 Vậy . 2 a  100  10
Bài tập 12. Tích tất cả các nghiệm của phương trình 2
log x  log x 1  1 2 2 1 5 1 5 1 A. 2 2 . B. 1. C. 2 2 . D. . 2 Lời giải Chọn A    x 0 x  0  1 Điều kiện    1  x  . log x 1  0   2 2 x  2
Đặt log x 1  , t  0 2
 log x t 1 ta có phương trình 2 t 2 t  2 2 1  t  1 4 2
t  2t t  0  t  3t  2t  
1  0  t t   2
1 t  2t   1  0 t   0 / t m  t   1 / t m   1   5  . t  t / m  2  1   5 t  loai  2 Với t  0 thì 1
log x  1  x  2 . 2 Với t  1 thì 0
log x  0  x  2 . 2 1 5 1 5 1 5 Với t  thì 2 log x   x  2 . 2 2 2 1 5
Vậy tích các nghiệm của phương trình là 2 2 .
Bài tập 13. Phương trình 2 2 sin x 1cos 2  2
x m có nghiệm khi và chỉ khi
A. 4  m  3 2 .
B. 3 2  m  5 .
C. 0  m  5.
D. 4  m  5 . Lời giải Chọn D xx xx x 4 Ta có 2 2 2 2 2 sin 1 cos sin 2 sin sin 2  2  m  2  2  m  2   m * . 2 sin 2 x 4 Đặt 2 sin 2 x t  , t 1; 
2 , * trở thành t   m . t 2 4 t  4 t  21;2 Xét hàm số   4 f t t  với t 1; 
2 . Ta có f t 1   0   . t 2 2 t tt  2  1;2 Khi đó f  
1  5 ; f 2  4 . Do đó min f t  4 và max f t  5 . 1;2 1;2
Phương trình đã cho có nghiệm khi và chỉ khi phương trình  
* có nghiệm t 1;  2
 min f t  m  max f t  4  m  5 . 1;2 1;2 Vậy: 4  m  5 .
Bài tập 14. Cho phương trình 2 x     2 1 1 4 2 .2 x m
 2m 1  0 . Có bao nhiêu giá trị nguyên của m thuộc đoạn  10  ; 
20 để phương trình có nghiệm? A. 6 . B. 7 . C. 8 . D. 9 . Lời giải Chọn B
Điều kiện: x  1  ;  1 . Với x   1  ;  1 thì 2
0  1 x 1, do đó, 2 0 1x 1 2  2  2 hay 2 1 1  2 x  2 . Đặt 2 1 2 x 2 t    t 1; 
2 . Phương trình trở thành: t m  2t  2m 1 0 2 2  t  2t 1
t  2t 1  mt  2 
m (do t  2 không là nghiệm của phương trình). t  2 2 t  2t 1
Xét hàm số f t  trên 1;2 . t  2 2 t  4t  5
x  11;2
Có f  x      , f x 0  . t  22 x  5  1;2 Lập bảng biến thiên
Do đó, để phương trình đã cho có nghiệm thì m  4  .
Suy ra, giá trị nguyên của m thuộc đoạn  10  ;2 
0 để phương trình có nghiệm là m 1
 0;9;8;7; 6;5;  4 .
Vậy có 7 giá trị cần tìm của m .
Bài tập 15. Có bao nhiêu số nguyên m để phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm 1x , x thỏa mãn 2 x x  3 ? 1 2 A. 2 . B. 0 . C. 1. D. 3 . Lời giải Chọn C
Phương trình  4x  2 .2x m  2m  0   1 Đặt  2x 2 t
, t  0 phương trình trở thành t  2 .
m t  2m  0 2 . Để phương trình   1 có hai nghiệm
x x  3 điều kiện là phương trình 2 1
x , x thỏa mãn 2 1 2   có hai nghiệm t , t  0 thỏa mãn x x x  1 2 1 x2 t .t  2 .2  2
 8 . Vậy điều kiện là 1 2 1 2  2
  m  2m  0   b   2m  0  m  4 .  a
c  2m  8 a
Bài tập 16. Cho phương trình 2 log x   2
m  3m log x  3  0 2  2
. Tìm m để phương trình có hai nghiệm phân biệt ,
thỏa mãn x x  16 . 1 x 2 x 1 2 m  1 m  1  m  1  m  1 A. . B. . C. . D. .     m  4 m  4 m  1 m  4  Lời giải Chọn B 2 log x   2
m  3m log x  3  0 1 2  2   . Điều kiện . x  0 Đặt . log 2 2 x t Ta
được phương trình t  m  3mt  3  0 2 . 2
Ta có: x x  16  log x x  4  log x  log x  4 2  1 2  . 1 2 2 1 2 2 Phương trình  
1 có hai nghiệm phân biệt ,
thỏa mãn x x  16 khi và chỉ khi 2 có hai 1 x 2 x 1 2 nghiệm phân biệt , t
thỏa mãn t t  4 . 1 t 2 1 2 m  4 Vậy suy ra 2
m  3m  4  .  m  1 
Thử lại thấy thỏa mãn.
Bài tập 17. Giá trị của
m để phương trình 9x  3x m  0 có nghiệm là: A. m  0 . B. m  0 . C. m 1.
D. 0  m 1 . Lời giải Chọn B Đặt 3x t  với . t  0 Khi
đó phương trình đã cho trở thành: 2
t t m  0 (*).
Phương trình đề cho có nghiệm khi và chỉ khi phương trình (*) có ít nhất một nghiệm dương. Xét hàm số   2
f t t t có f t   2t 1 . Xét f t  1  0  t   . 2 Bảng biến thiên:  1 x  0  2 y  0  0    y 0 1  4
Dựa vào bảng biến thiên, phương trình 2
t t  m có ít nhất một nghiệm dương khi và chỉ khi
m  0  m  0 .
Bài tập 18. Với giá trị nào của tham số m thì phương trình x x 1 4 . m 2  
 2m  0 có hai nghiệm , thoả 1 x 2 x mãn ?
x x  3 1 2 A. m  4 . B. m  3 . C. m  2 . D. m 1.
Hướng dẫn giải Chọn A Đặt , 2x t t  0 .
Phương trình đã cho có 2 nghiệm , thoả mãn 2
x x  3 khi phương trình t  2 .
m t  2m  0 1 x 2 x 1 2 có 2 nghiệm t  0 thoả mãn  1 x 2 x 1 x 2 .  2 .2  2 x t t  8 1 2 . 2   0
m  2m  0      m  4 t .t  8  2  m  8 1 2
Bài tập 19. Với điều kiện nào sau đây của m thì phương trình 9x  .3x m
 6  0 có hai nghiệm phân biệt? A. m  2 6 . B. m  6 . C. m  6 . D. m  2 6 . Lời giải Chọn D Đặt  3x t
t  0 thì phương trình trở thành 2t mt  6  0  1 .
Phương trình đã cho có 2 nghiệm phân biệt khi  
1 có 2 nghiệm dương phân biệt   0 2 m  24  0      m 2 6
S  0  m  0    m  2 6 .   m  0 P  0  6  0 
Bài tập 20. Tìm tất cả các giá trị tham số 2 2 2
m để phương trình
x 2 x   m   x 2x 1   m   2x 4x2 9.9 2 1 15 4 2 5  0
có 2 nghiệm thực phân biệt. 1 3  6 3  6
A. m  1 hoặc m  . B. m  . 2 2 2 1 3  6 3  6 C.m 1. D. m  hoặc m  . 2 2 2 Lời giải Chọn C 2 2 2 2 x x   x 1 x 1  x 1  m   2
x x   m   2 2 2 1 2 x 4 x2 9.9 2 1 15 4 2 5  0  9
 2m     1 15
 4m  2   25  0 x 2 x 2 2 1 1  3         m   3 2 1  4m  2  0   .  5   5  x 2 1  3  Đặt t    . Do  x  2
1  0 nên 0  t 1.  5  t  2 Phương trình có dạng: 2
t  2m  
1 t  4m  2  0  
. Do 0  t 1 nên t  2m 1. t  2m 1
Để phương trình có 2 nghiệm thực phân biệt thì 0  2m 1  1 1   m  1. 2
Bài tập 21. Tìm tất cả các giá trị của tham số m để phương trình 2
x x   m   2xx   m   2 2 2 1 2 x 4x2 4.4 2 2 6 6 3 3
 0 có hai nghiệm thực phân biệt. 1  A. 1   m  .
B. m  4  3 2 hoặc m  4  3 2 . 2 1
C. 4  3 2  m  4  3 2 . D. m  1  hoặc m  . 2 Lời giải Chọn A 2 2 x 2 x 1  x 2 x 1 4 2     
Viết lại phương trình ta được:    2m 2    6m3  0.  9   3  2 x 2 x 1 2   
Do x x    x  2 2 2 1 1  0 nên 1    3  2 x 2 x 1 2    Đặt t   
, 0  t 1. Phương trình trở thành:  3  t  3 2
t  2m  2t  6m  3  0   . t  2  m 1
Để phương trình đã cho có hai nghiệm thực phân biệt thì 0  2  m 1 1 1  1   m   . 2 1
Vậy giá trị cần tìm của m là 1   m   . 2
Bài tập 22. Cho phương trình 3x 2 xln 3 xln 9 e  2.e  e
m  0 , với m là tham số thực. Tất cả các giá trị của tham
số m để phương trình có nghiệm duy nhất là
A. m  0 hoặc m  4 . B. m  0 hoặc m  4  . C. 4   m  0 .
D. m  0 hoặc m  4  .
Hướng dẫn giải Chọn B 3x 2 xln 3 xln 9 e  2.e  e  m  0 3x 2 x ln 3 x ln 9
 e  2.e .e  e .e  m  0 3x 2
 e  6.e x  9.ex m  0 . Đặt ex t
t  0, phương trình tương đương với 3 2
m  t  6t  9t . Xét f t 3 2  t
  6t 9t trên 0;. t 1 f t  2  3
t 12t 9 , f t  0   . t  3 Ta có bảng biến thiên
Dựa vào bảng biến thiên: với m  0 hoặc m  4
 thì phương trình có nghiệm duy nhất. Chú ý:
Ta không lấy giá trị x  0 nên tại m  0 đường thẳng y m vẫn cắt đồ thị tại duy nhất một điểm
(điểm tiếp xúc tại x  3).
Bài tập 23. Tập hợp tất cả các giá trị của tham số m để phương trình 2 2 x x  2 4  2
 6  m có đúng 3 nghiệm thực phân biệt là A.   3 . B.   2 . C. 3; . D. 2;3. Lời giải Chọn A Đặt 2 2x t  . Do 2
x  0  t  1 . Ta có phương trình 2
t  4t  6  m  0   1 .
Do với mỗi t  1 thì có hai nghiệm x   log
, còn với t  1 chỉ có một nghiệm x  0 . Nên để 2 t
phương trình ban đầu có đúng 3 nghiệm thì phương trình  
1 có một nghiệm t  1 và một nghiệm 1 t  1. 2 Phương trình  
1 có nghiệm t  1 khi 1 4  6  m  0  m  3. t 1
Thay m  3 vào   1 , ta có: 2
t  4t  3  0  
. Vậy m  3 thỏa mãn. t  3
Bài tập 24. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình   ex  ex m m có nghiệm thực? A. 9 . B. 8 . C. 10 . D. 7 . Lời giải Chọn C
m  ex  0  Điều kiện:  .
m m  ex  0 2
m t  e x Đặt   ex t m
t  0 ta suy ra:  2t
  m  ex
ex t  0 1 2 x 2
 e  t t  ex  ex tex t     1  0   .
ex t 1  0  2
Phương trình 2 vô nghiệm vì ex t 1  0 . Phương trình  
1 tương đương với x x x 2 e   e 
 e   e x  ex t m m   3 Phương trình   ex  ex m m  
* có nghiệm thực khi phương trình   3 có nghiệm thực. x x x 1 Xét hàm số   2 e x ex f x
 với x , ta có: f x 2
 2e  e  0  e   x   ln 2 . 2
Bảng biến thiên của hàm số   2 e x ex f x   là Lập bảng biến thiên Số nghiệm của  
3 bằng số giao điểm của đồ thị hàm số   2 e x ex f x
 và đường thẳng y m. 1
Dựa vào bẳng biến thiên suy ra phương trình  
3 có nghiệm khi m   . 4
Kết hợp với giả thiết m là số nguyên nhỏ hơn 10 ta suy ra m0,1,2,3,4,5,6,7,8,  9 .
Vậy có 10 giá trị thỏa mãn.
Dạng 3: Phương pháp logarit hóa, mũ hóa 1. Phương pháp 2. Bài tập x 1 
Bài tập 1. Phương trình 27 .2x x
 72 có một nghiệm viết dưới dạng x  log b , với a, b là các số nguyên a
dương. Tính tổng S a b . A. S  4 . B. S  5. C. S  6 . D. S  8 . 3. Lời giải Chọn B
Điều kiện x  0 . 3x3 x 1   x 1   3 3x3   3 3 x 2 2 Phương trình 27 .2x x  72  x x 2 3  3 .2  3 .2   3  3  2 x x 2 3 2 x x3   3  x 3 x 3  1  3  2 x x 3   log 2 x
 x 3log 2  x  3  log 2  0 3 3  3  x xx  x  3
x  3N    1  .    log 2  x   log 3  2 N  3  xa  2 Suy ra 
. Vậy tổng S a b  5 . b   3
Bài tập 2. Phương trình log 5  2x  2  có hai ngiệm    . 2   x 1 x , x . Tính 2 P 1 x x2 1 x 2 x A. 11. B. 9 . C. 3 . D. 2. Lời giải Chọn D
Điều kiện: 2x  5 2x  1 x  0
log 5  2x  2   x 2 5  2  2 x x 4 5  2    2   x   2x 2x  4 x  2
P x x x x  2 1 2 1 2 .
Bài tập 3. Gọi S là tổng tất cả các nghiệm thực của phương trình 2
7x .3x 1. Tìm S.
A. S  log 3. B. S  log 7. C. S  log 3. D. S  log 2. 7 3 2 3 Hướng dẫn giải Chọn A. Lấy logarit cơ số 3 Ta có: hoặc cơ số 7 hai vế. 2
7x .3x  1  log  2 7x .3x  2
 log 1  log 7x  log 3x  0 3 3 3 3 x  0 2 
x .log 7  x  0  x x log 7 1  0  1 . 3  3  x   log 3 7  log 7  3
Vậy tổng các nghiệm là S  log 3. 7 2x 1 
Bài tập 4. Phương trình 3x.5 x  15 có một nghiệm dạng x  log b , với a, a
b là các số nguyên dương lớn hơn 1 và nhỏ hơn 8. Giá trị của P a  2b bằng bao nhiêu? A. P  8. B. P  5. C. P 13. D. P  3. Hướng dẫn giải Chọn C 2 x 1  2 x 1  x x 1  x 1    x 3 .5 x Ta có: x 1  x 1 3 .5 x  15 
1  3 .5 x 1  log 3  .5 x   0 3 3.5   x 1   x x 1 1
 log 3  log 5 x  0  x 1 .log 5  0 3 3 3 x       x   1 x 1 1 . 1 .log 5  0  .  3    xx   log 5  3
Vậy a  3,b  5 suy ra a  2b 13.
Dạng 4: Phương biến đổi thành tích 1. Phương pháp
(thường sử dụng trong trường hợp hai vế không cùng cơ số).
Hướng giải: Biến đổi phương trình về dạng: f ( x) g ( x) ab
f (x).log a g(x).log .(
b 0  a, b  0 , 1  c  ). 1 c c
Lưu ý: Ta thường lôgarit hóa hai vế với cơ số a hoặc b. 2. Bài tập
Bài tập 1. Giải phương trình log . x log x  .
x log x  3  log x  3log
 . Ta có tổng tất cả các nghiệm 2 3 3 2 3 x x bằng A. 35 . B. 5 . C. 10 . D. 9 . Lời giải Chọn B
Điều kiện x  0 . log . x log x  .
x log x  3  log x  3 log
  log x x 3 log x 1  0 2  3  2 3 3 2 3 x xx  3   .
log x x  3  0  2
Ta có hàm số f x  log  liên tục và đồng biến trên 0; và f 2  3 nên phương trình 2 x x
log x x  3  0 có một nghiệm x  2 . 2
Vậy tổng tất cả các nghiệm bằng 5 . 2  1  x x
Bài tập 2. Số nghiệm của phương trình x 2 4.  25.2 100 100   là  5  A. 3 . B. 1. C. 2 . D. vô nghiệm. Lời giải Chọn B 2  1  x x  Ta có x 2 4.  25.2 100 100    5 
4.5x 25.2x 100 10x     4 2x.5x  
 25  0  x  2.
Vậy phương trình đã cho có 1 nghiệm.
Bài tập 3. Số nghiệm của phương trình log .
x log 2x 1  2log . 2 3   2 x A. 2. B. 1. C. 0 . D. 3 . Lời giải Chọn A 1 ĐK: x  . 2 log .
x log 2x 1  2log 2 3   2 x log x  0 x 1
x  1 n  log . 2
x log 2x 1  2  0    . 2  3     log 2  x 1  2  0  2x 1  9 x  5  n 3  
Vậy phương trình đã cho có hai nghiệm.
Bài tập 3. Biết n là số rự nhiên thỏa mãn phương trình 3x  3x  2cos nx có 2018 nghiệm. Tìm số nghiệm
của phương trình 9x  9x  4  2 cos 2nx . A. 4036 . B. 2018 . C. 4035 . D. 2019 . Lời giải Chọn A
9x  9x  4  2 cos 2nx  9x  9x  2.3x.3x  2  2 cos 2nx
3x  3x  2cos nx   1   x x  2 2 3 3
 4cos nx  3x 3x  2cosnx  2 Khi đó nếu  
1 và 2 có nghiệm chung thì 3x  3x  3x  3x  3x  3x x  0
Thay x  0 vào   1 ta được 0 0
3  3  2 cos 0  0  2 , tức là  
1 và 2 không có nghiệm chung.
Mặt khác ta thấy nếu x là nghiệm của  
1 thì  sẽ là nghiệm của 2 0 x0 Mà  
1 có 2018 nghiệm nên 2 cũng có 2018 nghiệm.
Vậy phương trình đã cho có 4036 nghiệm.
Bài tập 4. Cho phương trình log  2
x x 1.log  2 x x 1 2
 log x x 1 . Biết phương trình có 2 3 6 1
một nghiệm là 1 và một nghiệm còn lại có dạng   log c log b b c x aa
 (với a, c là các số nguyên 2
tố và a c ). Khi đó giá trị của 2
a  2b  3c bằng: A. 0 . B. 3 . C. 6 . D. 4 . Lời giải Chọn B  1   x 1  Điều kiện   * 2
x x 1  0 log  2
x x 1.log  2 x x 1 2
 log x x 1 2 3 6  log  1 2 x x 1.log   x x x x 1 log  2 1 2 3 6 2   log  2
x x 1.log 6.log  2
x x 1  log  2 x x 1 2 3 6 6  log  2   
x x 1 log 6.log   2
x x 1 1  0 6 3 2   log   2
x x 1  0 1 6     log 6.log   2
x x 1 1  0 2 3 2        x 1 2 
1  x x 1 1 2
x 1  x 1    x  1. x 1   x  2 2 1 2  log  2
x x 1 .log 6  1   log  2
x x 1  log 3 2  2  3 6 log6 3 x  2 2 log  1 6 3
x x 1  2     x   log63 log6 3 2  2 . 2 x 1    2 log6 3 2  x 2 1   x   log62 log6 2 3  3 . (thỏa mãn  *) 2 1
Như vậy phương trình đã cho có các nghiệm là x 1,  x   log62 log62 3  3 . 2
Khi đó a  3, b  6 , c  2 . Vậy 2
a  2b  3c  3 .
Bài tập 5. Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình 2 2 x 7 x 1  2 2xx 105 .3  3  9.3 x m
m có ba nghiệm thực phân biệt. Tìm số phần tử của S . A. 3 . B. Vô số. C. 1. D. 2 . Lời giải Chọn A Ta có: 2 2 x 7 x 1  2 2xx 105 .3  3  9.3 x 2 2 2 m
m m x 7x 12   2xx
x 7x 12 3 1 3 3   1  0 x  3 2 x 7 x 1  2 3 1  0 
  2xx   2 7 12 2 3 1  3 xx m   0    x  4  . 2 2
  3 xx m  0  2
2x x  log m  0 *  3  
Phương trình đã cho có ba nghiệm thực phân biệt, ta có các trường hợp sau:
Trường hợp 1:  
* có một nghiệm x  3 và nghiệm còn lại khác 3 và 4 . 1
Thay x  3 vào  
* ta được log m  3   . Khi đó   * trở thành 3 m 27 x  1  2
x  2x  3  0   (Thỏa yêu cầu). x  3
Trường hợp 2:  
* có một nghiệm x  4 và nghiệm còn lại khác 3 và 4.
Thay x  4 vào   * ta được 8
log m  8  m  3 . 3 x  4 Khi đó   * trở thành 2
x  2x 8  0   (Thỏa yêu cầu). x  2 
  1 log m  0 3 
Trường hợp 3:  
* có nghiệm kép khác 3 và 4  log m  3  m  3 . 3 log m  8  3  1   1   1   1 
Bài tập 6. Phương trình ln x  .ln x  .ln x  .ln x   0         có bao nhiêu nghiệm?  2   2   4   8  A. 3 . B. 4. C. 1. D. 2. Lời giải Chọn A  1  1 x   0  x  2   2  1  1  x   0  x    1 Điều kiện: 2 2     x  . 1  1 2 x   0     x 4  4  1   1 x   0 x    8  8 Khi đó:   1  ln x   0     1  3  2  x   1 x    2  2   1    ln 1 1 x   0      x   1   x 1   1   1   1   2    ln  2 2 x  .ln x  .ln x  .ln x   0              .  2   2   4   8    1  1 3 ln x   0   x  1 x   4    4  4     1  1 7 ln x   1   x   0   x   8   8  8 3 3 7 
So với điều kiện, ta được tập nghiệm của phương trình là S   ; ; . 2 4 8 
Vậy phương trình đã cho có 3 nghiệm. x x x
Bài tập 7. Gọi a là một nghiệm của phương trình 26 15 3  27  4 3  22  3 1. Khi đó giá
trị của biểu thức nào sau đây là đúng? A. 2 a a  2 . B. 2
sin a  cos a  1. C. 2  cos a  2 .
D. 3a  2a  5 . Lời giải. Chọn B x x x
Ta có 26 15 3  27  4 3  22  3 1.
   3x    2xx 2 3 2 2 3  22 3 1
  4x    3x x  2 3 2 2 3  2  3  2  0  3x x  2 3 1    2 3 2       0    x
 2  3 1  x  0. a  0 2
 sin a  cos a  1.
Bài tập 8. Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình .2x      1  2x x x x m m  
1 có hai phần tử. Tìm số phần tử của A . A. 1. B. Vô số. C. 3 . D. 2. Lời giải Chọn D
Xét phương trình .2x      1  2x x x x m m   1 x m    2x x mx   1  0   . 2x x 1
Mà phương trình 2x x 1 có hai nghiệm là x  0 ; x 1.
Thật vậy: dựa vào hình vẽ
 Với x  0 hoặc x 1 thì 2x x 1, đẳng thức xảy ra khi x  0 hoặc x 1.
 Với 0  x 1 thì 2x x 1  phương trình 2x x 1 vô nghiệm. y 21 O 1 x
Do đó tập A có hai phần tử khi m  0 hoặc m  1.
Dạng 5: Phương pháp sử dụng tính đơn điệu 1. Phương pháp
* Ta thường sử dụng các tính chất sau:
 Tính chất 1: Nếu hàm số f tăng ( hoặc giảm ) trong khỏang (a;b) thì phương trình f(x) = C có
không quá một nghiệm trong khoảng (a;b). ( do đó nếu tồn tại x0 (a;b) sao cho
f(x0) = C thì đó là nghiệm duy nhất của phương trình f(x) = C)
 Tính chất 2 : Nếu hàm f tăng trong khoảng (a;b) và hàm g là hàm một hàm giảm trong khoảng
(a;b) thì phương trình f(x) = g(x) có nhiều nhất một nghiệm trong khoảng (a;b) .
( do đó nếu tồn tại x0  (a;b) sao cho f(x0) = g(x0) thì đó là nghiệm duy nhất của phương trình f(x) = g(x)) 2. Bài tập
Bài tập 1. Số nghiệm của phương trình x 2 3 5
2018  x  2016  2017  2018 là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B
Đặt f xx 2 3 5
 2018  x  2016  2017  2018 , D   .
Suy ra    2018 .x f x ln 2018  2x M , ,
A B liên tục trên  .    2018 .x f x ln 2018  2x f  xx 2
 2018 .ln 2018 2  0, x
Từ đó f  x đồng biến trên D mà f  
1 . f 0  0 nên f x  0 có nghiệm duy nhất trong khoảng  1
 ;0 suy ra phương trình f x  0 có nhiều nhất hai nghiệm, mặt khác nhập hàm số vào TABLE của casio (START 10
 END 10 STEP 1), ta được:  f
 7. f 6  0
Dựa vào TABLE ta được  f 0.f  10
Vậy phương trình đã cho chỉ có hai nghiệm trên hai khoảng  7;  6   và 0;  1 .
Chú ý: Máy tính hiển thị “Insufficient MEM” thì tiến hành cài đặt để không xuất hiện g x bằng
cách bấm SHIFT MODE mũi tên xuống, 5 , 1.
Bài tập 2. Tập nghiệm của phương trình  2
log x x  6  x  logx  2  4 là: A.   1 . B.   4 . C.   3 . D.   2 . Lời giải. Chọn B 2
x x  6  0 Điều kiện:   x  3. x  2  0
Phương trình đã cho tương đương với
log x  2(x 3)  x  log x  2  4  log(x 3)  4  x  * .
Vế trái của phương trình cuối là hàm tăng, còn vế phải là hàm giảm nên nghiệm của phương
trình(nếu có) là duy nhất.
Bằng cách nhẩm nghiệm ta chọn kết quả x  4.
Bài tập 3. Cho x , y là các số thực thỏa log x  3log y  3log
 . Tìm giá trị   . 2 6 x yT x y A. T  28 . B. T  22 . C. T  34 . D. T  30 . Lời giải Chọn Ax  8tt t    
Đặt log x  3log y  3log x y  3  y  6t 8t 6t 10t    4 3    1   1 . 2 6   t       5   5 
x y  10t
Nhận xét: t  2 là nghiệm của phương trình   1 . t t 2 2  4   3   4   3  Với t  2:    1        
Vậy t  2 không là nghiệm của phương trình   1 .  5   5   5   5  . t t 2 2  4   3   4   3  Với t  2:    1        
Vậy t  2 không là nghiệm của phương trình   1 .  5   5   5   5  .
Vậy t  2 là nghiệm duy nhất của   1 . 2 x  8  64 Khi đó, ta có 
T x y  28 . 2 y  6  36
Bài tập 4. Phương trình 2 2 2 sin x cos x sin 2 3 4.3 x  
có bao nhiêu nghiệm thuộc  2017  ; 2017 . A. 1284 . B. 4034 . C. 1285 . D. 4035 . Lời giải Chọn C. Ta có 2 2 2 2 2 2 sin x cos x sin x sin x 1sin x sin 2  3  4.3  2  3  4.3 x Đặt 2
sin x t với t 0;  1 , ta có phương trình     t t     t 3 t 2 t 1 t 2   4.3   3.  4    
. Vì hàm số f t 2 1   3.  
  nghịch biến với t 0;  1 3t  3   9   3   9 
nên phương trình có nghiệm duy nhất t  0. Do đó sin x  0  x k , k  . 2017  2017 Vì x  2017  ; 2017 nên ta có 2017   k  2017   k  nên có 1285 giá trị  
nguyên của k thỏa mãn. Vậy có 1285 nghiệm.
Bài tập 5. Tìm số nghiệm của phương trình 2x  3x  4x  ... 2017x  2018x  2017  x . A. 1. B. 2016 . C. 2017 . D. 0 . Lời giải Chọn A
Xét hàm số   2x 3x 4x ... 2017x 2018x f x      
Ta có    2x ln 2  3x ln3... 2018x f x ln 2018  0 , x    . Suy ra hàm số
2x 3x 4x ... 2017x 2018x y       đồng biến trên  .
Hàm số g x  2017  x nghịch biến trên  .
Mặt khác f 0  g 0  2017 .
Do đó, phương trình f x  g x có nghiệm duy nhất x  0 .
Bài tập 6. Tìm tất cả các giá trị của tham số a
a để phương trình
 3x  3x có nghiệm duy nhất. 3x  3x A. a   . B. 1   a  0 . C. a  0 .
D. không tồn tại a . Lời giải Chọn A Ta có: a  3x  3x
3x 3 x3x 3 x a        2 x 2 3 3 x a       1 . 3x  3x Xét hàm số   2x 2 3 3 x f x    . Có   2x 2 2.3 2.3 x f x      0, x    .
Do đó, hàm số y f x luôn đồng biến trên  .
Suy ra với mọi giá trị của a thì  
1 luôn có nghiệm duy nhất. 2
Bài tập 7. Số nghiệm của phương trình x x   2
ln x  2  2018 là 2 A. 3 . B. 1. C. 4 . D. 2 . Lời giải Chọn C 2
Xét hàm số   x f x   x   2
ln x  2 với x ;
  2 2; . 2 2 2 2x  4 Ta có    1 x f x x
; f  x 1  0, x   ;   2  2; . 2     2 x  2  2x 2 2
Nên suy ra hàm số    1 x f x x
đồng biến trên mỗi khoảng  ;
  2 và  2; . 2 x  2
Mặ khác f 2. f  3 1.1 3  0 và f   f   8 3 .
2   .1  0 nên f  x có đúng một 7 nghiệm a  ;
  2 và đúng một nghiệm b 2; . Ta có bảng biến thiên
Ta có f a  f   3
3   3  2018 và f b  f   3 3   3  2018 2 2
Bài tập 8. Tìm số thực a để phương trình: 9x  9  3x a
cos x , chỉ có duy nhất một nghiệm thực A. a  6  . B. a  6 . C. a  3  . D. a  3.
Hướng dẫn giải Chọn A
Giả sử x là nghiệm của phương trình. Ta có 0x 0 9  9  .3x a cos( x ) . 0 0 Khi đó 2 
cũng là nghiệm của phương trình. 0 x 81 9 Thật vậy 2  0 x 2 0 9  9  3 x a cos   2      9  a cos  0 x  x x x  0 0 0 9 3 0 x 0  9  9  .3x a cos . 0 x
Vậy phương trình có nghiệm duy nhất khi và chỉ khi x  2   x  1 . 0 0 x 0
Với x  1  a  6  . 0 x 9
Ngược lại, với a  6
 , phương trình 9x  9  6
 .3x cos x  3   6  cos  x . x   3 x 9 + 3   6 3x + 6c  os x  6  x 9 3   6
Khi đó dấu "  " xảy ra khi và chỉ khi  3xx 1. cos x  1 Vậy 0x 0 9  9  .3x a
cos( x ) có nghiệm duy nhất khi và chỉ khi a  6  . 0
Bài tập 9. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa mãn 2 xy 1  3x2 e  e y  2 2
x y 1 , đồng thời thỏa mãn log
2x y 1  m  4 log x m  4  0 . 2     2 A. 3 . B. 4. C. 5 . D. 6 . Lời giải Chọn A Ta có: 2xy 1  3x2 e  e y  2xy 1  3x2
x y 1  e  2    1  e y x y
3x  2y.
Xét hàm số    et f t
t trên  . Ta có    et f t
1 0 nên hàm số đồng biến trên  .
Do đó phương trình có dạng: f 2x y  
1  f 3x  2y  2x y 1  3x  2y y 1 x .
Thế vào phương trình còn lại ta được: 2
log x m 4 2
log x m  4  0 . 2 2 Đặt 2 2 t  log
, phương trình có dạng: t  m  4t m  4  0 . 2 x
Để phương trình có nghiệm thì   0 2
 3m  8m  8 0  0  m  . 3
Do đó có 3 số nguyên m thỏa mãn.
Bài tập 10. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa mãn 3x5 y x3 y 1 e e    1 2 2 2
x  2 y , đồng thời thỏa mãn log
3x  2y 1  m  6 log x m  9  0 . 3     3 A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn B Ta có: 3x5y x3 y 1 e e    1 2 3x5 y x3 y 1  x  2 y  e
 3x 5y  e
 x 3y   1 .
Xét hàm số    et f t
t trên  . Ta có    et f t
1 0 nên hàm số đồng biến trên  .
Do đó phương trình có dạng: f 3x  5y  f x  3y  
1  3x  5y x  3y 1  2y  1 2x .
Thế vào phương trình còn lại ta được: 2
log x m 6 2
log x m  9  0 . 3 3 Đặt 2 2 t  log
, phương trình có dạng: t  m  6t m  9  0 . 3 x
Để phương trình có nghiệm thì   0  2 3
m 12m  0  0  m  4 .
Do đó có 5 số nguyên m thỏa mãn. 1 x a b 3  1    Bài tập 11. Gọi 
là một nghiệm lớn hơn 1 của phương trình 2x  3 1 x 2  1     2x 1. 0 x c   3   
Giá trị của P a b c là A. P  6 . B. P  0 . C. P  2 . D. P  4 . Lời giải Chọn D
Điều kiện xác định: x  0 .  1 x 1  1 1 1 x    2 3 x x  1    2  2x 1 1 2
 3 x  3 1  x    3    2x 1 1 x 1 2 3 x 3      x 1  
1 . Xét hàm số    3t f t
t t  0 ,    3t f t .ln 31  0 2x    1  1  1  ff x     1   x  1 3 1  x
a 1, b 1, c  2 . Vậy P  4 .  2x  2x 2
Bài tập 12. Tìm tất cả các giá trị của tham số m để phương trình ln m  lnm x  x có nhiều nghiệm nhất. A. m  0 . B. m  1. C. m  e . D. m  1. Lời giải Chọn B
Ta có ln m  lnm x  x   1 .
Điều kiện  em xm .
Đặt ln m x  y ta được ey m x . Thay vào  
1 ta được ln m y  x  ex m y .
ex m y Ta có hệ 
 ex  ey y x  ex x  ey y . Do hàm số    et f t
t đồng biến trên
ey m x
 nên suy ra x y x  ln x m  ex x m .
Xét hàm số    ex g x
x ;    ex g x
1; gx  0  x  0 . BBT
Suy ra phương trình có nhiều nhất là hai nghiệm  m 1. (chú ý nghiệm luôn thỏa điều kiện).
Bài tập 13. Có bao nhiêu số nguyên m để phương trình 2
3x  3x m 1 2 log
x  5x  2  2 m 2 2x x 1
Có hai nghiệm phân biệt lớn hơn 1. A. 3 . B. Vô số. C. 2 . D. 4 . Lời giải Chọn C Điều kiện: 2
3x  3x m 1  0 . Ta có: 2 3 2
x  3x m 1
 3x  3x m 1 2 log  2
x  5x  2   log 
 1  x  5x 1 m 2 m 2 2 2 x x 1 2
 2x x 1  2
3x  3x m 1 2  log
x  5x 1 2 m 2 4x  2x  2  log  2
3x  3x m   1  log  2
4x  2x  2   2
4x  2x  2   2
3x  3x m 1 2 2   log  2
3x  3x m   1   2
3x  3x m   1  log  2
4x  2x  2   2 4x  2x  2  1 2 2 
Xét hàm số: f t  t  log trên 0; , ta có f t 1  1  0 , t  0; . 2 t t.ln 2
Do đó hàm số f t đồng biến trên 0; .
Suy ra:    f  2
x x    f  2 1 4 2 2
3x  3x m   1 2 2
 4x  2x  2  3x  3x m 1 2
x  5x m 1 2 . Điều này đúng với mọi x .
Xét hàm số: g x 2
x 5x trên  , ta có gx 5
 2x  5  0  x  . 2 Bảng biến thiên:
- Theo bảng biến thiên ta thấy: phương trình 2 có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi 25   m 1  4  21    m  3  . 4 4
Do m nên m 5;    4 .
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Bài tập 14. Cho phương trình log  2
x x 1.log  2
x x 1  log x x  Có bao nhiêu giá trị m  2 1 . 2 5 
nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2 ? A. Vô số. B. 3 . C. 2 . D. 1. Lời giải Chọn D Điều kiện xác định: 2
x x 1  x  1. 1 x  2 2 x 1 1 x 1  x 1 Đặt t  log  2
x x 1 thì t  .  . 2  2
x x 1 ln 2  2
x x   2 ln 2 1 x 1 1   0 2 x 1 ln 2 BBT:
Do x  2  t  log 2  3 . 2   1 t 1
Phương trình trở thành t.log 2  log
t.log 2   log 2  log   5 m m 2t 5 m 5 t 1 1 log  2 2 3 Ycbt log  m  5 . Do * nên m  2 . 5 m  
m   và m  1 log 2  3 2  
Bài tập 15. Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
3  27 3  27.2x  2x m m có nghiệm thực? A. 6. B. 4. C. Vô số.
D. Không tồn tại m. Hướng dẫn giải Chọn C. Ta có 3 3 x x 3 x 3
3  27 3  27.2  2  27 3  27.2  2 x m m m  3 . m   1
Đặt 2x u, điều kiện: u  0 và 3 x 3
3m  27.2  v v  3m  27.u. 2 (1) trở thành 3
u  27v  3 . m 3 Từ (3) và (2) suy ra 3 3 u v v
u  u v  2 2 27 27
. u uv v  27  0  u  . v 2 2  1  3 Do 2 2    4 v u uv vu v   27  0, u  ,v  ,   nên  2  4 3 u  27 3 3  27 u m
u u m  , với u  0. 3 3 u  27 Xét hàm số   u f u  với u  0. 3 1
Ta có f u   3
3u  27; f u  0  u  3 do u  0. 3
Suy ra min f u  5
 4. Do đó có vô số giá trị nguyên của m để phương trình có nghiệm thực. 0;
Bài tập 16. Có bao nhiêu giá trị nguyên của tham số m để phương trình 4x  .2x m
 2m  5  0 có hai nghiệm trái dấu? A. Vô số. B. 0. C. 1. D. 4. Hướng dẫn giải Chọn C. Ta có x x       x 2 4 .2 2 5 0 2  .2x m m m  2m  5  0 Đặt  2x t
,t  0, phương trình thành 2
t mt  2m  5  0 2. Đặt f t 2
t mt  2m  5
Nhận xét rằng với một giá trị t  0 ta tìm được một nghiệm x nên để phương trình có hai nghiệm x  0  1 2 x
thì phương trình (2) có hai nghiệm phân biệt t t  0 đồng thời t  1  (vì 1x 0 2 2 2 2x   ). Từ đó, ta có: 2 1 1 t2          m    m   2 2 m 8m 20 0 0 4 2 5  0   5  P  0  2m  5  0  m  5      2   m  4. S  0 m  0 2    
f t 
   m m   m 0 1. 0 1. 1 2 5  0       m  4
Vậy chỉ có một giá trị nguyên của tham số m thỏa đề.
Bài tập 17. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2x  3  4x m 1* có nghiệm duy nhất? A. 3. B. Vô số. C. 1. D. 2. Hướng dẫn giải Chọn D. t  3 Đặt  2x t
,t  0, phương trình * 2
t  3  m t 1  m   1. 2 t 1 t  3
Xét hàm số f t 
xác định trên tập D  0;. 2 t 1 1 3 Ta có   t f t  
. Cho f t 1
 0  1 3t  0  t  . 2 t   2 1 t 1 3 Bảng biến thiên 1 x  0  3 y + 0  10 y 3 1
Dựa vào bảng biến thiên ta thấy với 1  m  3 hoặc m  10 phương trình có nghiệm duy nhất nên có hai
giá trị nguyên của tham số m.
Bài tập 18. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình x 1  x 1 2.4 5.2    m  0,* có nghiệm? A. 3. B. 0. C. 1. D. 4. Hướng dẫn giải Chọn A. 1 Đặt x 1 t 2  
, điều kiện t  vì x 1  1  . 2 Khi đó   2
*  2t  5t   . m 1  Xét hàm số 2 y  2
t  5t trên ; .   2  5
Ta có y  4t  5. Cho y  0  4t  5  0  t  . 4 5 x  1  2 4 y + 0  25 8 y 2  25
Do đó phương trình có nghiệm khi m  . 8