52 trang 2 lượt tải

Các Dạng Toán 9 Kết Nối Tri Thức Bài 9 Biến Đổi Đơn Giản Và Rút Gọn Biểu Thức Chứa Căn Thức Bậc Hai

3

Khi tính toán với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (tức là biến đổi căn thức bậc hai đó thành  một biểu thức mà trong căn thức không còn mẫu). Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Chương 3: Căn bậc hai và căn bậc ba (KNTT) 5 tài liệu

Môn: Toán 9 2.7 K tài liệu

Sách: Kết nối tri thức

Tác giả:

Profile

Mỹ Châu

2 ngày trước
Danh sách Quiz
/52
Trang 1
BIẾN ĐỔI ĐƠN GIẢN VÀ RÚT GỌN BIỂU THỨC
CHỨA CĂN THỨC BẬC HAI
A. TRỌNG TÂM KIẾN THỨC
1. Đưa thừa số ra ngoài dấu căn
Nếu
a
là một số và
b
là một số không âm thì
2
=a b a b
.
* Khi tính toán với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử
mẫu của biểu thức lấy căn (tức là biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn
thức không còn mẫu).
Ví dụ:
a)
22
3 2 3 2 3 2 3 2 = = =
b)
( ) ( )
22
5 7 5 7 5 7 5 7− = − = − =
c)
2
xy
(với
0, 0xy
)
d)
32
xy
(với
0, 0xy
)
( ) ( )
22
= = xy x xy x
= = −xy x xy x
2. Đưa thừa số vào trong dấu căn
+ Nếu
a
và
b
là hia số không âm thì
2
=a b a b
+ Nếu
a
là số âm và
b
là số không âm thì
2
=−a b a b
.
Ví dụ:
a)
2
1 1 1
8 8 8 2
2 2 4

= = =


b)
2
3 5 3 5 45− = − = −
c)
1
x
x
(với
0x
)
2
1
= =xx
x
d)
2
3
y
y
(với
0y
)
2
22
33
= − = −yy
y
3. Trục căn thức ở mẫu
+ Với các biểu thức
A
,
B
và
0B
, ta có
=
A A B
B
B
+ Với các biểu thức
A
,
B
,
C
mà
0A
,
2
AB
, ta có:
( )
2
−
=
−
+
C A B
C
AB
AB
;
( )
2
+
=
−
−
C A B
C
AB
AB
+ Với các biểu thức
A
,
B
,
C
mà
0A
,
0B
,
2
AB
, ta có:
Trang 2
( )
−
=
−
+
C A B
C
AB
AB
;
( )
+
=
−
−
C A B
C
AB
AB
4. Rút gọn biểu thức chứa căn thức bậc hai
Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân,
chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẫu của
biểu thức lấy căn; trục căn thức ở mẫu).
B. Bài tập
Dạng 1: Đưa thừa số ra ngoài dấu căn
I. Cách giải:
Để đưa thừa số ra ngoài dấu căn, ta có 2 bước:
Bước 1: Chia các số trong căn thành các số chính phương 4, 9, 16, 25, 36,...
Bước 2: Dùng công thức: Với
0B
, ta có:
22
0
0
= = =
−
A B khi A
A B A B A B
A B khi A
II. Bài toán
Bài 1: Đưa thừa số ra ngoài dấu căn
a)
45
b)
2400
c)
147
d)
1,25
e)
12
f)
3 27
g)
5 48
h)
45
Lời giải
a)
45 9.5 3 5==
b)
2400 400 6 200 6= =
c)
147 49 4 7 4= =
d)
1,25 0,25 5 0,5 5= =
e)
2
12 2 3 2 3= =
f)
2
3 27 3 3 3 9 3= =
g)
2
5 48 5 4 3 20 3= =
h)
2
45 3 5 3 5= =
.
Bài 2: Đưa thừa số ra ngoài dấu căn
a.
8
b.
24
c.
52
d.
18
e.
45
f.
99
g.
72
h.
108
i.
180
k.
540
Bài 3: Đưa thừa số ra ngoài dấu căn
a.
75
b.
125
c.
175
d.
48
e.
80
f.
176
g.
98
h.
147
i.
245
k.
343
Bài 4: Đưa thừa số ra ngoài dấu căn
a)
50 6
b)
14 21
Trang 3
c)
32 45
d)
125 27
Lời giải
a)
50 6 100 3 10 3 = =
b)
14 21 7 7 2 3 7 6 = =
c)
32 45 16 2 9 5 16 9 10 4 3 10 12 10 = = = =
d)
125 27 25 5 9 3 25 9 5 5 3 5 15 15 = = = =
.
Bài 5: Viết gọn các biểu thức sau
a.
25.90
b.
96.125
c.
75.54
d.
245.35
Lời giải
a) Ta có:
25.90 15 10=
b) Ta có:
96.125 16.6.5.25 20 30==
c) Ta có:
75.54 45 2=
d) Ta có:
245.35 49.5.5.7 35 7==
Bài 6: Đưa thừa số ra ngoài dấu căn
a)
18x
b)
2
75xy
c)
32
605xy
d)
( )
2
128 −xy
e)
( )
2
150 4 4 1−+xx
f)
32
6 12 8− + −x x x
Lời giải
a)
18 9 2 3 2= =x x x
với
0x
b)
22
75 25 3 5 3= =x y x y x y
với
0y
( )
( )
5 3 0
5 3 0
=
−
x y x
x y x
c)
3 2 2 2
605 121 5 11 5= =x y x y x x y x
với
0x
( )
( )
11 5 0
11 5 0
=
−
xy x y
xy x y
d)
( ) ( )
22
128 64 2 8 2− = − = −x y x y x y
( ) ( )
( ) ( )
82
82
−
=
−
x y x y
y x x y
e)
( )
( )
2
2
150 4 4 1 25 6 2 1 5 2 1 6− + = − = −x x x x
( )
( )
1
5 2 1 6
2
1
5 1 2 6
2

−

=

−


xx
xx
Trang 4
f)
( ) ( ) ( )
32
32
6 12 8 2 2 2− + − = − = − −x x x x x x
( )
22= − −xx
với
2x
.
Bài 7: Đưa thừa số ra ngoài dấu căn
a.
( )
2
27 0xx
b.
( )
2
8 0; 0xy x y
c.
( )
3
25 0xx
d.
( )
4
48 0;xy x y R
Lời giải
a) Ta có:
( ) ( )
2
2
27 3 .3 3 3 3 3 0= = = x x x x x
b) Ta có:
( ) ( )
2
2
8 2 .2 2 2 2 2 0; 0= = = − xy y x y x y x x y
c) Ta có:
( )
3
25 5 0=x x x x
d) Ta có:
( )
( )
4 2 2
48 0; 4 3 0 = xy x y R y x y
Bài 8: Đưa thừa số ra ngoài dấu căn
a.
32a
với
0a
b.
75a
với
0a
c.
2
80a
với
0a
d.
2
15 12 a
với
0a
e.
24
28xy
với
0x
f.
42
54xy
với
0y
g.
( )
3
125 1−x
h.
( )
5
192 3+x
Lời giải
g) Điều kiện xác định
1x
Ta có:
( ) ( ) ( )
32
125 1 25 5 1 1− = − −x x x
( ) ( )
5 1 5 1= − −xx
h) Điều kiện xác định
3−x
Ta có:
( )
( )
( )
5
2
192 3 8 3 3 3+ = + +x x x
( )
( )
2
8 3 3 3= + +xx
.
Bài 9: Đưa thừa số ra ngoài dấu căn
a.
( )
2
27 0xx
b.
( )
2
8 0; 0xy x y
c.
( )
3
25 0xx
d.
( )
4
48 0;xy x y R
Lời giải
a) Ta có:
( ) ( )
2
2
27 3 .3 3 3 3 3 0= = = x x x x x
b) Ta có:
( ) ( )
2
2
8 2 .2 2 2 2 2 0; 0= = = − xy y x y x y x x y
c) Ta có:
( )
3
25 5 0=x x x x
d) Ta có:
( )
( )
4 2 2
48 0; 4 3 0 = xy x y R y x y
Bài 10: Đưa thừa số ra ngoài dấu căn
a.
32a
với
0a
b.
75a
với
0a
c.
2
80a
với
0a
d.
2
15 12 a
với
0a
Trang 5
e.
24
28xy
với
0x
f.
42
54xy
với
0y
g.
( )
3
125 1−x
h.
( )
5
192 3+x
Lời giải
g) Điều kiện xác định
1x
Ta có:
( ) ( ) ( )
32
125 1 25 5 1 1− = − −x x x
( ) ( )
5 1 5 1= − −xx
h) Điều kiện xác định
3−x
Ta có:
( )
( )
( )
5
2
192 3 8 3 3 3+ = + +x x x
( )
( )
2
8 3 3 3+ +xx
Dạng 2: Đưa thừa số vào trong dấu căn
I. Cách giải:
Để đưa thừa số vào trong dấu căn, ta có 2 bước:
Bước 1: Viết biểu thức thành
2
A
(với
0A
)
Bước 2: Dùng quy tắc nhân các căn bậc hai:
+
22
= = A B A B A B
(với
0A
,
0B
)
+ Nếu
0A
thì đặt dấu trừ ở ngoài căn
22
= − = − A B A B A B
(với
0A
,
0B
)
II. Bài toán
Bài 1: Đưa thừa số vào trong dấu căn
a)
35
b)
56
c)
2
35
7
d)
53
e)
52−
f)
27−
Trang 6
g)
1
4
8
−
h)
0,06 250−
Lời giải
a)
2
3 5 3 5 45= =
b)
2
5 6 5 6 150= =
c)
2
2 2 20
35 35
7 7 7

= =


d)
2
5 3 5 3 75= =
e)
2
5 2 5 2 50− = − = −
f)
2
2 7 2 7 28− = − = −
g)
2
11
4 4 2
88
− = − = −
h)
( )
2
0,06 250 0,06 250 0,9− = − = −
.
Bài 2: Đưa thừa số vào trong dấu căn
a)
( )
20−aa
b)
3
2
10
a
a
(với
0a
)
c)
3
−x
x
(với
0x
) d)
1−
−x
x
(với
0x
)
Lời giải
a)
2
2 2 4− = − = −a a a
b)
2
3 3 6
24
10 10 5
= =
a
aa
aa
(vì
0a
)
c)
2
33
3− = = −x x x
xx
với
0x
d)
( )
2
11−

− = − − = −


x x x
xx
với
0x
Bài 3: Chỉ ra chỗ sai trong các biến đổi sau
a)
2
33
77
=
x
x
b)
2
= =
yy
xy y x y xy
xx
Lời giải
a) Biến đổi
2
33
77
=
x
x
chỉ đúng khi
0x
Nếu
0x
thì
2
33
77
=−
x
x
b) Biến đổi
2
= =
yy
xy y x y xy
xx
chỉ đúng khi
0x
Nếu
0x
thì
2
= − = −
yy
xy y x y xy
xx
.
Bài 4: Đưa thừa số vào trong dấu căn
a)
xx
b)
x
y
y
Trang 7
c)
xy
yx
Lời giải
a)
23
= =x x x x x
(với
0x
)
b) Điều kiện:
0x
,
0y
;
0y
Xét trường hợp
0x
;
0y
, ta có
2
= =
xx
y y xy
yy
Xét trường hợp
0x
;
0y
, ta có
2
= − = −
xx
y y xy
yy
c) Điều kiện:
0xy
Ta có
2
2
= =
x y x y x
y x y x y
.
Bài 5: Đưa thừa số vào trong dấu căn
a.
( )
13 0aa
b.
( )
15
0
−
aa
a
c.
( )
12
0
2
a
a
a
d.
( )
20aa
Lời giải
a) Ta có:
( )
2
13 13 0=a a a
b) Ta có:
( ) ( )
2
15 15 15
15 0
− − −
= − − = − = − −
a
a a a a
a a a
c) Ta có:
( )
12
30
2
=
a
aa
a
d) Ta có:
( )
2
2 2 0= − a a a
Trang 8
Dạng 3: Khử mẫu của biểu thức lấy căn
I. Cách giải:
- Khử mẫu của biểu thức lấy căn
Bước 1: Nhân cả tử và mẫu của phân thức với ở trong căn với mẫu
Bước 2: Khai phương một thương
Bước 3: Đưa thừa số ra ngoài dấu căn rồi giản ước cho nhân tử chung
Với
0AB
,
0B
ta có:
2
2
===
A AB AB AB
B B B
B
- Rút gọn biểu thức chứa căn bậc hai của phân thức
Bước 1: Khử mẫu của biểu thức lấy căn
Bước 2: Thu gọn đơn thức đồng dạng
II. Bài toán
Bài 1: Khử căn thức ở mẫu số các phân số
a.
7
108
b.
5
6
c.
10
13
d.
4
75
e.
3 2 2
2
+
f.
5 2 6
3
−
Lời giải
a) Ta có:
7 7 7 7. 3 21
108 8
36.3 6 3 6 3.3
= = = =
b) Ta có:
5 5 5. 6 30
6 6 6
6
= = =
c) Ta có:
10 10 10. 13 130
13 13 13
13
= = =
d) Ta có:
4 4 2 2 3 2 3
75 15
25.3 5 3 5 3. 3
= = = =
e) Ta có:
( )
2
21
3 2 2 3 2 2
2
22
+
++
==
( )
2 1 . 2
2 1 2 2
22
2
+
++
= = =
f) Ta có:
( )
2
32
5 2 6 5 2 6
3
33
−
−−
==
3 2 2 2. 3 6
1 1 1
3
3 3 3. 3
−
= = − = − = −
Bài 2: Khử mẫu của biểu thức lấy căn
Trang 9
a)
2
3
a
b
với
0ab
b)
2
5a
với
0a
c)
3
4
4
x
xy
với
0x
,
0y
Lời giải
a)
( )
2
2 2 3 6 6
3 3 3
3
= = =
a a b ab ab
b b b b
b
b)
( )
2
2 2 5 10
5 5 5
5
==
aa
aa
a a a
a
10 10 10
5 5 5
===
a a a
aa
aa
c)
( )
2
12 12
3 3 4
4 4 4
4 4 4
4
= = =
xy xy
xy
x a x
xy xy xy y
xy
.
Bài 3: Khử mẫu của biểu thức lấy căn
a)
4
7
b)
3
5
c)
11
2
d)
11
6
Lời giải
a)
2
2
4 4 7 2 2 7
7
7 7 7 7

= = =


b)
2
3 3 5 15
5 5 5
==
c)
2
11 11 2 22 22
2 2 2 2
2
= = =
.
d)
11 11 6 66
6 6 6 6
==
Bài 4: Khử mẫu của biểu thức lấy căn
5
72
Lời giải
Ta có
5 5 2 10 1
10
72 72 2 144 12
= = =
* Chú ý: Nếu nhân cả tử và mẫu của phân số
5
72
với
72
thì vẫn ra kết quả nhưng biến đổi
phức tạp hơn:
22
5 5 72 360 6 1
10 10
72 72 72 72 12
= = = =
Vậy tìm thừa số phụ như thế nào cho hợp lí?
Trước hết, phân tích mẫu số ra thừa số nguyên tố:
32
72 2 3=
. Ta thấy ngay thừa số phụ là
2, lúc đó số mũ của các thừa số nguyên tố đều chẵn.
Trang 10
Bài 5: Khử mẫu của các biểu thức lấy căn
a)
11
27x
b)
3
3
5
x
y
c)
32
1
3 3 1+ + +x x x
d)
23
11
−
xx
Lời giải
a)
2
11 11 3 33 1
27 27 3 81 9
= = =
xx
x x x x x
(điều kiện
0x
)
b)
3 3 4 2
3 3 5 15 1
15
5 5 5 24 5
= = =
x x y xy
xy
y y y y y
(điều kiện
0; 0xy y
)
c)
( ) ( )
34
32
1 1 1
3 3 1
11
+
==
+ + +
++
x
x x x
xx
( )
2
1
1
1
=+
+
x
x
(điều kiện
1−x
)
d)
( )
( )
2 3 3 4 2
1
1 1 1 1
1
−
−
− = = = −
xx
x
xx
x x x x x
(điều kiện
1x
hoặc
0x
).
Bài 6: Khử mẫu của mỗi biểu thức dưới dấu căn bậc hai sau
a.
( )
3
5
0; 0
49

x
xy
y
b.
( )
3
7 0; 0
−
xy x y
xy
Lời giải
a) Ta có:
( )
3
2
5 5 5
0; 0
49 7 7
= =
x x x x xy
xy
y y y
( )
5 5 0; 0
77
= =
xx
xy xy x y
yy
b) Ta có:
( )
22
33
7 0; 0 7
−−
=
xy
xy x y xy
xy x y
( )
7
3 7 3 0; 0= − = − −
xy
xy xy x y
xy
Bài 7: Khử mẫu của mỗi biểu thức dưới dấu căn bậc hai sau
a.
( )
3
5
0, 0
49

b
ab
a
b.
( )
1 16
0, 0
4
−
ab a b
ab
Lời giải
a)
( )
32
5 1 5 1 5
0, 0
49 7 7
= =
b b ab
ab
a a a a a
( )
2
1
5 0, 0
7
= ab a b
a
b)
( )
1 16 1
0, 0
4
−
= −ab a b ab
ab ab
22
= − = −
ab
ab ab
ab
Trang 11
Bài 8: Thu gọn biểu thức
3 3 4 3 4
2 3 1 5 2 3
−+
=−
+−
A
Lời giải
Ta có:
3 3 4 3 4
2 3 1 5 2 3
−+
=−
+−
A
( )( )
( )( )
( )( )
( )( )
3 3 4 2 3 1 3 4 5 2 3
2 3 1 2 3 1 5 2 3 5 2 3
− − + +
=−
+ − − +
18 3 3 8 3 4 5 3 6 20 8 3
12 1 25 12
− − + + + +
=−
−−
22 11 3 26 13 3
11 13
−+
=−
( ) ( )
11 2 3 13 2 3
2 3 2 3
11 13
−+
= − = − − +
Suy ra
(
)
2 2 2 3 2 3 4 2 3 4 2 3= − − + = − − +A
( ) ( )
22
3 1 3 1 3 1 3 1= − − + = − − +
( )
3 1 3 1 2= − − + = −
Do đó
2=−A
Bài 9: Thu gọn biểu thức
1 3 2 2 3
2 3 3 2 2 3
−
=
−+
A
Lời giải
Ta có:
1 3 2 2 3
2 3 3 2 2 3
−
=
−+
A
( )
( )
6 3 2
1 1 3 2
2 3 2 3 3 2
6 3 2
−
−
= =
− − +
+
( )
2
32
1
32
23
−
=
−
−
1 3 2
3 2 1
2 3 2 3
−
= − = = −
−−
.
Trang 12
Dạng 4: Trục căn thức ở mẫu
I. Cách giải:
- Khử mẫu của biểu thức lấy căn
+ Bước 1: Xác định biểu thức liên hợp
+ Bước 2: Nhân liên hợp để làm mất căn
+ Bước 3: Giản ước, thu gọn (nếu được)
- Rút gọn biểu thức chứa căn bậc hai của phân thức
+ Bước 1: Trục căn thức ở mẫu
+ Bước 2: Thu gọn căn thức đồng dạng.
II. Bài toán
Bài 1: Trục căn thức ở mẫu các biểu thức sau:
a)
2
5
b)
3
26
c)
43
2
−
d)
9
23
e)
2
35
f)
3
7
g)
33
53
+
h)
7
3
i)
10
35
−
j)
22
40
Lời giải
a)
( )
2
2 2 5 2 5 2 5
3 5 15
5
35
= = =
b)
3 3 6 3 6 6
2 6 4
2 6 2 6 6
= = =
c)
4 3 4 3 2 4 6
26
2
2 2 2
− = − = − = −
d)
9 9 3 9 3 3 3
62
2 3 2 3 3
= = =
e)
( )
2
2 2 5 2 5 2 5
3 5 15
35
35
= = =
f)
3 3 7 3 7
7
7 7 7

==
Trang 13
g)
( )
3 3 1
3 3 3 1
5
5 3 5 3
+
++
==
h)
7 7 3 21
3
3 3 3
==
i)
10 10 5 10 5 2 5
3 5 3
3 5 3 5 5
− = − = − = −
j)
2 2 2 2 40 8 5 5
40 5
40 40 40
= = =
Bài 2: Trục căn thức ở mẫu các biểu thức sau:
a)
2
31−
b)
3
15 4+
c)
4
31−
d)
2
53+
e)
5
23+
f)
2
52−
g)
7
32−
h)
32
32
−
+
Lời giải
a)
( )
( )( )
( )
2 3 1 2 3 1
2
31
31
31
3 1 3 1
++
= = = +
−
−
−+
b)
( )
( )( )
( )
( )
3 15 4 3 15 4
3
3 4 15
15 4
15 4
15 4 15 4
−−
= = = −
−
+
+−
c)
( )
( )
( )
2
4 3 1 4 3 1
4
2 3 2
2
31
31
++
= = = +
−
−
d)
( )
( )( )
( )
2 5 3 2 5 3
2
53
53
53
5 3 5 3
−−
= = = −
−
+
+−
e)
( )
( )( )
5 2 3
5 10 5 3
10 5 3
43
23
2 3 2 3
−
−
= = = −
−
+
+−
f)
( )
( )( )
2 5 2
2 10 2 10 2
5 2 3
52
5 2 5 2
+
++
= = =
−
−
−+
g)
( )
( )( )
( )
7 3 2 7 3 2
7
32
7
32
3 2 3 2
++
= = = +
−
−+
h)
( )
( )( )
2
32
3 2 5 2 6
5 2 6
1
32
3 2 3 2
−
−−
= = = −
+
+−
Bài 3: Trục căn thức ở mẫu và rút gọn
Trang 14
a.
1
2 2 3 3−
b.
35
35
−
+
Lời giải
a) Ta có:
( )
8 27
1 1 8 27 8 27
8 27 19 19
2 2 3 3 8 27
−+
++
= = = =
−−
−−
b) Ta có:
( )( )
( )( )
( )
2
3 5 3 5 3 5
3 5 3 5
42
35
3 5 3 5
− − −
−−
= = =
+
+−
Bài 4: Trục căn thức ở mẫu rồi rút gọn
a.
8
53−
b.
23
23
−
+
Lời giải
a) Ta có:
( )
2 2 5 3
8
10 6
53
53
+
= = +
−
−
b) Ta có:
( )
( )
2
2
2
23
23
23
23
23
−
−
= = −
+
−
Bài 5: Trục căn thức ở mẫu:
a)
3 2 2−
a
b)
5 3 3 5
5 3 3 5
−
+
c)
2
1 2 3−+
Lời giải
a)
( )
( )( )
( )
( )
2
2
3 2 2 3 2 2
3 2 2
3 2 2 3 2 2
3 2 2
++
==
−
−+
−
aa
a
( )
( )
3 2 2
3 2 2
98
+
= = +
−
a
a
b)
( )
( )( )
2
5 3 3 5
5 3 3 5 75 45 30 15
75 45
5 3 3 5
5 3 3 5 5 3 3 5
−
− + −
==
−
+
+−
( )
30 4 15
4 15
30
−
= = −
c)
( )
( )( )
2 1 2 3
2
1 2 3
1 2 3 1 2 3
−−
=
−+
− + − −
( )
( )
( )
2
2 1 2 3 2 1 2 3
1 2 2 2 3
1 2 3
− − − −
==
− + −
−−
Trang 15
( )
2 1 2 3
3 2 1
2
22
−−
+−
==
−
.
Bài 6: Trục căn thức và thực hiện phép tính
a.
( )
3 2 3 2 2
23
3 2 1
++
= + − +
+
A
b.
5 2 5 5 3 5
22
2 5 3 5
−+
= − −
−+
B
Lời giải
a) Ta có:
( )
3 2 3 2 2
2 3 2
3 2 1
++
= + − + =
+
AA
b) Ta có:
5 2 5 5 3 5
2 2 1
2 5 3 5
−+
= − − = −
−+
BB
Bài 7: Rút gọn các biểu thức sau
a.
14 7
22
−
=
−
A
b.
11
7 24 1 7 24 1
=−
− + + −
B
c.
15 4 12
( )( 6 11)
6 1 6 2 3 6
= + − +
+ − −
C
d.
33
3 1 1 3 1 1
=−
+ − + +
D
Lời giải
a) Ta có:
14 7 7( 2 1) 7 7. 2 14
2
2 2 2( 2 1) 2 2. 2
−−
= = = = =
−−
A
b) Ta có:
11
7 24 1 7 24 1
=−
− + + −
B
22
1 1 1 1
7 2 6 1 7 2 6 1 ( 6 1) 1 ( 6 1) 1
= − = −
− + + − − + + −
11
0
6 1 1 6 1 1
=−=
− + + −
c) Ta có:
( )
15 4 12
6 11
6 1 6 2 3 6

= + − +

+ − −

C
( ) ( ) ( )
( )
15 6 1 4 6 2 12 3 6
6 11 115
6 1 6 2 9 6

− + +

= + + + = −

− − −

d) Ta có:
33
3 1 1 3 1 1
=−
+ − + +
D
Trang 16
(
)
(
)
(
)
(
)
3 1 1 3 1 1
3
3 1 1 3 1 1

+ + − + −

=

+ − + +


2
3. 2
3 1 1
==
+−
Bài 8: Trục căn thức ở mẫu
a.
6 14
2 3 7
+
=
−
A
b.
3 4 3
6 2 5
+
=
+−
B
c.
1
2 5 2 2 10
=
+ + +
C
d.
31
2 2 5
=
+−
D
e.
1
10 15 14 21
=
+ + +
E
f.
3 2 3 2 2
( 2 3)
3 2 1
++
= + − +
+
F
Lời giải
a.
6 14 2( 3 7)(2 3 7)
2 3 7 (2 3 7)(2 3 7)
+ + +
==
− − +
A
2(6 2 21 21 7) 2(13 3 21)
12 5 5
+ + + +
==
−
b.
3 4 3 (3 4 3)( 6 2 5)
6 2 5 ( 6 2 5)( 6 2 5)
+ + + +
==
+ − + − + +
B
(3 4 3)( 6 2 5)
6 2 5
3 4 3
+ + +
= = + +
+
c.
11
2 5 2 2 10 ( 2 1)( 5 2)
==
+ + + + +
C
( 2 1)( 5 2)
( 2 1)( 5 2)
(2 1)(5 4)
−−
= = − −
−−
d.
2
31 31(2 2 5) 31(2 2 5)
2 2 5 (2 2) 5 1 4 2
+ + + +
= = =
+ − + − +
D
2
31(2 2 5)(4 2 1)
(2 2 5)(4 2 1)
(4 2) 1
+ + −
= = + + −
−
e.
11
10 15 14 21 ( 2 3)( 5 7)
==
+ + + + +
E
( 3 2)( 7 5)
2
−−
=
f.
3 2 3 2 2
( 2 3) 2
3 2 1
++
= + − + =
+
F
Bài 9: Trục căn thức ở mẫu:
a)
2
a
với
0a
b)
5
3+x
với
0x
;
9x
c)
1
3−x
với
0x
;
3x
d)
1
1
−
+
a
a
với
0x
;
1x
Trang 17
e)
1
1+x
với
1−a
f)
1
3−x
với
0x
;
9x
Lời giải
a)
2 2 2
==
aa
a
a a a
b)
( )
( )( )
( )
5 3 5 3
5
9
3
33
−−
==
−
+
+−
xx
x
x
xx
c)
( )( )
1 3 3
3
3
33
++
==
−
−
−+
xx
x
x
xx
d)
( )
( )( )
2
1
1 1 2
1
1
11
−
− − +
==
−
+
−+
a
a a a
a
a
aa
e)
( )
2
1 1 1 1
1
1 1 1
1
+ + +
= = =
+
+ + +
+
x x x
x
x x x
x
f)
( )( )
1 3 3
9
3
33
++
==
−
−
+−
xx
x
x
xx
.
Bài 10: Trục căn thức và thực hiện phép tính
a.
( )
15 4 12
6 11
6 1 6 2 3 6

= + − +

+ − −

A
b.
5 5 5 5
11
1 5 1 5
+−
= − −
+−
B
Lời giải
a) Ta có:
( )
( ) ( )
15 6 1
15 4
3 6 1 ; 2 6 2
61
6 1 6 2
−
= = − = +
−
+−
( )
12
4 3 6 115
36
= + = −
−
A
b) Ta có:
5 5 5 5
5; 5 4
1 5 1 5
+−
= = − → =
+−
B
Bài 11: Trục căn thức ở mẫu của các biểu thức
a)
2
51
23
−+x
b)
2
2
2
−
+
aa
a
( )
0, 2aa
c)
1
1
−
−
x
x
với
0, 1xx
d)
2 +
x
xy
với
0x
,
0y
,
4 xy
Lời giải
a)
( )
2
22
5 3 1
5 1 5 1 3
6
2 3 2 3 3
−+
− + − +
==
x
xx
b)
( )
( )
( )( )
2
2
22
2
2
22
−−
−
=
+
+−
a a a
aa
a
aa
Trang 18
( )
( )
( )
22
2
2
−−
= = −
−
a a a
aa
a
( )
0, 2aa
c)
( )
( )
( )( )
( )
( )
1 1 1 1
1
1
1
1
11
− + − +
−
= = = +
−
−
−+
x x x x
x
x
x
x
xx
với
0, 1xx
d)
( )
( )( )
( )
22
4
2
22
−−
==
−
+
+−
x x y x x y
x
xy
xy
x y x y
với
0x
,
0y
,
4 xy
Bài 12: Trục căn thức ở mẫu
a)
2
1
1
−
−
x
x
với
1x
b)
1
2 3 2
+
+ − +
a
aa
với
1−a
c)
1
1+−xx
với
0x
d)
1
1+−ab
với
0, 0ab
,
1
4
=ab
.
Lời giải
a)
( ) ( )
( )
22
2
2
1 1 1 1
1
1 1 1
1
− − − −
−
==
− − −
−
x x x x
x
x x x
x
( )( )
( )
1 1 1
11
1
− + −
= = + −
−
x x x
xx
x
b)
( )
( )
( )( )
1 2 3 2
1
2 3 2
2 3 2 2 3 2
+ + − +
+
=
+ − +
+ − + + + +
a a a
a
aa
a a a a
( )
( )
( ) ( )
22
1 2 3 2
2 3 2
+ + − +
=
+ − +
a a a
aa
( )
( )
( ) ( )
1 2 3 2
2 3 2
+ + − +
=
+ − +
a a a
aa
( )
( )
1 2 3 2
1
+ + − +
=
+
a a a
a
2 3 2= + − +aa
c)
( )( )
11
1
11
++
=
+−
+ − + +
xx
xx
x x x x
( ) ( )
( )
22
11
1
1
+ + + +
==
+−
+−
x x x x
xx
xx
1
1
++
=
xx
1= + +xx
d)
( )
( )( )
11
1
1
11
+−
=
+−
+ − + +
ab
ab
a b a b
Trang 19
11
1 2 1
+−
=
+ − + + −
ab
a b a b ab
11
1
21
4
+ − + −
==
+
+ + −
a b a b
ab
ab
Bài 13: Trục căn thức và thực hiện phép tính
a.
( )
15 4 12
6 11
6 1 6 2 3 6

= + − +

+ − −

A
b.
5 5 5 5
11
1 5 1 5
+−
= − −
+−
B
Lời giải
a) Ta có:
( )
( ) ( )
15 6 1
15 4
3 6 1 ; 2 6 2
61
6 1 6 2
−
= = − = +
−
+−
( )
12
4 3 6 115
36
= + = −
−
A
b) Ta có:
5 5 5 5
5; 5 4
1 5 1 5
+−
= = − → =
+−
B
Bài 14: Trục căn thức và thực hiện phép tính
a.
( )
3 2 3 2 2
23
3 2 1
++
= + − +
+
A
b.
5 2 5 5 3 5
22
2 5 3 5
−+
= − −
−+
B
Lời giải
a) Ta có:
( )
3 2 3 2 2
2 3 2
3 2 1
++
= + − + =
+
AA
b) Ta có:
5 2 5 5 3 5
2 2 1
2 5 3 5
−+
= − − = −
−+
BB
Bài 15: Trục căn thức ở mẫu
a.
6 14
2 3 7
+
=
−
A
b.
3 4 3
6 2 5
+
=
+−
B
c.
1
2 5 2 2 10
=
+ + +
C
d.
31
2 2 5
=
+−
D
e.
1
10 15 14 21
=
+ + +
E
f.
3 2 3 2 2
( 2 3)
3 2 1
++
= + − +
+
F
Lời giải
a.
6 14 2( 3 7)(2 3 7)
2 3 7 (2 3 7)(2 3 7)
+ + +
==
− − +
A
Trang 20
2(6 2 21 21 7) 2(13 3 21)
12 5 5
+ + + +
==
−
b.
3 4 3 (3 4 3)( 6 2 5)
6 2 5 ( 6 2 5)( 6 2 5)
+ + + +
==
+ − + − + +
B
(3 4 3)( 6 2 5)
6 2 5
3 4 3
+ + +
= = + +
+
c.
11
2 5 2 2 10 ( 2 1)( 5 2)
==
+ + + + +
C
( 2 1)( 5 2)
( 2 1)( 5 2)
(2 1)(5 4)
−−
= = − −
−−
d.
2
31 31(2 2 5)
2 2 5 (2 2) 5
++
==
+ − + −
D
2
31(2 2 5) 31(2 2 5)(4 2 1)
1 4 2 (4 2) 1
+ + + + −
==
+−
(2 2 5)(4 2 1)= + + −
e.
11
10 15 14 21 ( 2 3)( 5 7)
==
+ + + + +
E
( 3 2)( 7 5)
2
−−
=
f.
3 2 3 2 2
( 2 3) 2
3 2 1
++
= + − + =
+
F
.
Dạng 5: So sánh hai số chứa căn
I. Cách giải:
Để so sánh các căn bậc hai, ta cần chú ý:
- Với
,ab
không âm thì
a b a b
- Đưa thừa số vào trong dấu căn để đưa về so sánh
a
và
b
.
II. Bài toán
Bài 1: Không dùng MTCT hãy so sánh
a)
32=a
và
23=b
b)
56=a
và
73=b
c)
2
32
3
=a
và
1
51
5
=b
Lời giải
a) Ta có
2
3 2 3 2 18= =
;
2
2 3 2 3 12= =
Vì
12 18
nên
2 3 3 2
Vậy
ab
.
b) Ta có
5 6 25 6 150= = =a
;
7 3 49 3 147= = =b
Vì
150 147
nên
5 6 7 3
.

Tài liệu khác của Toán 9

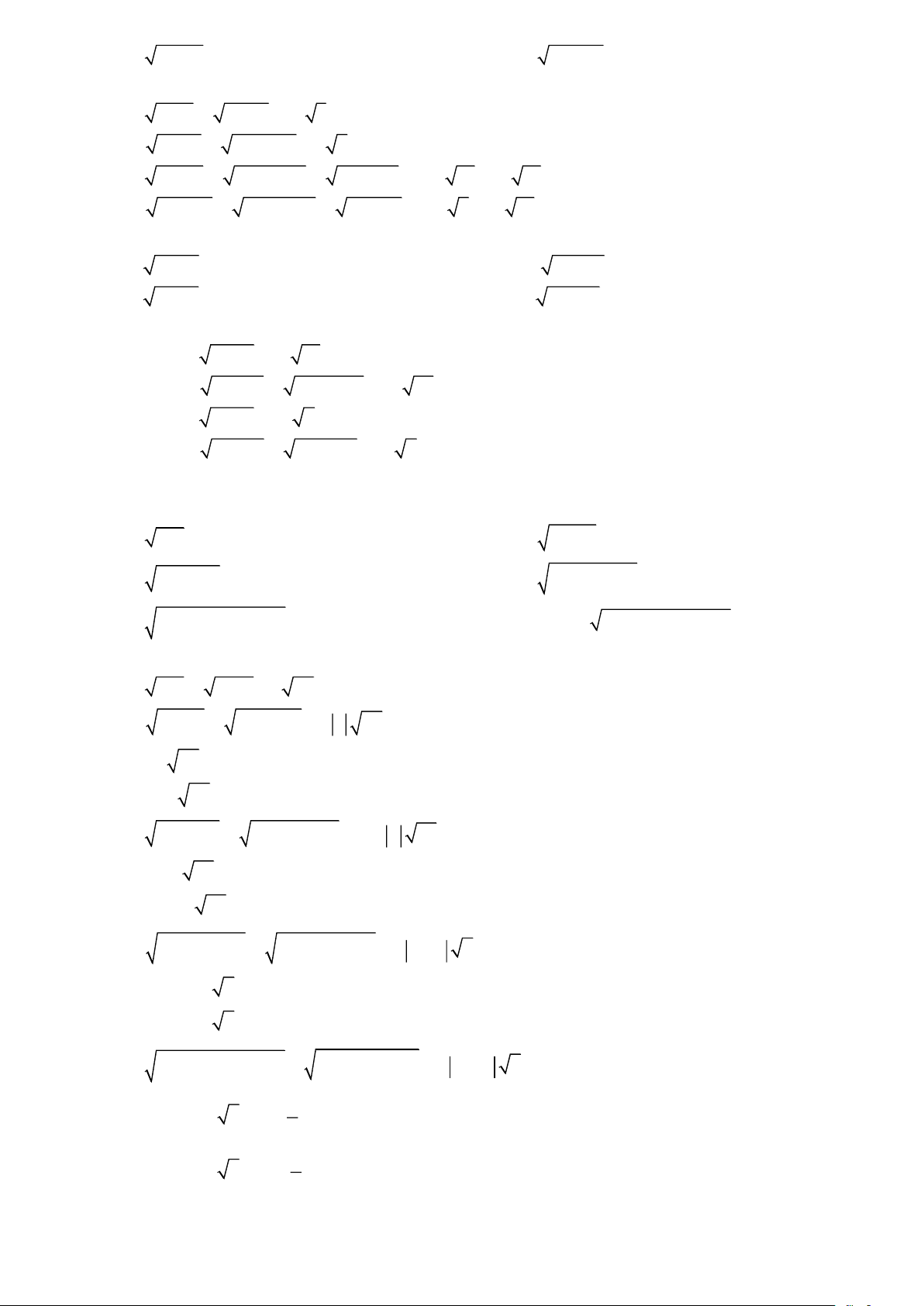
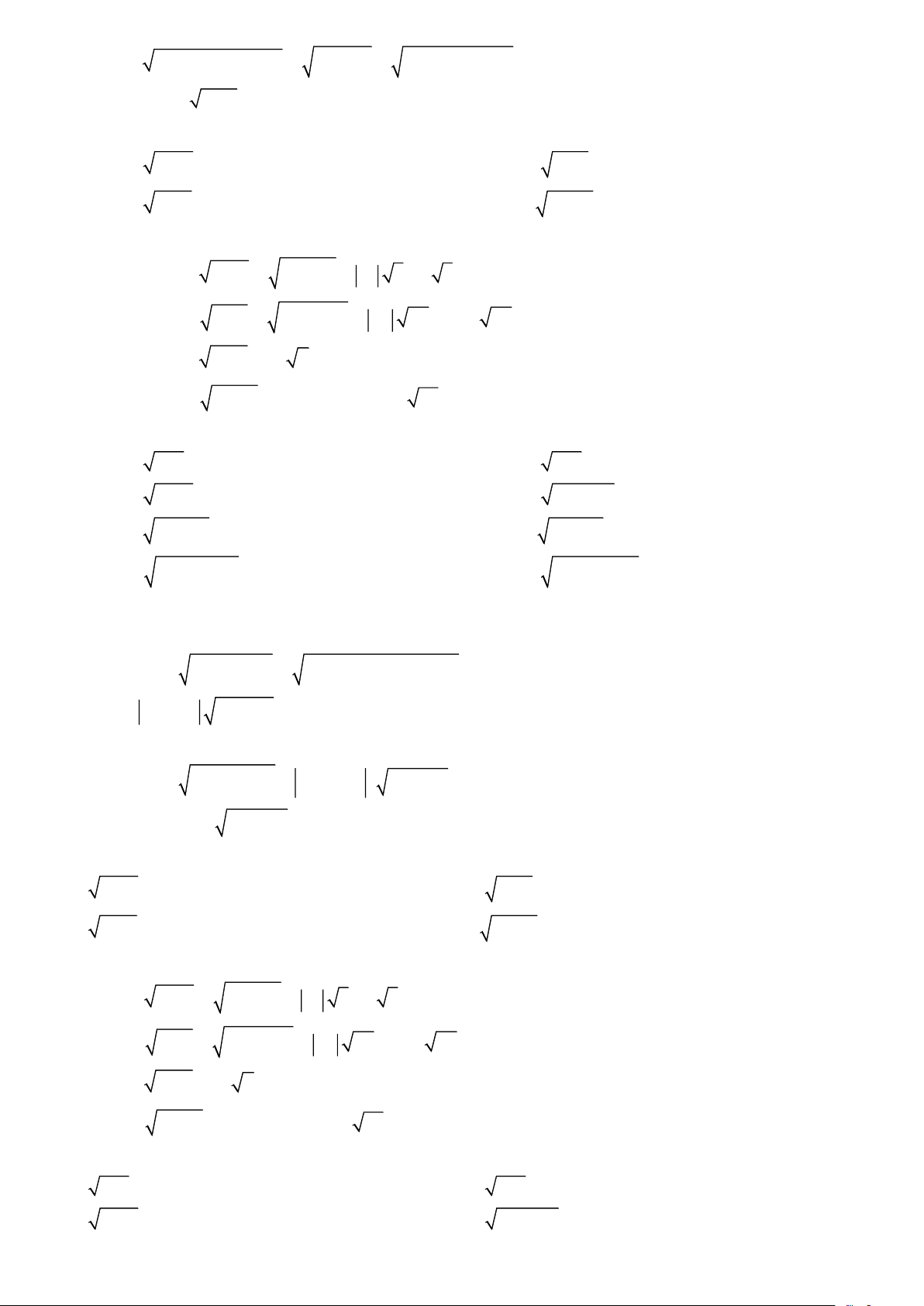
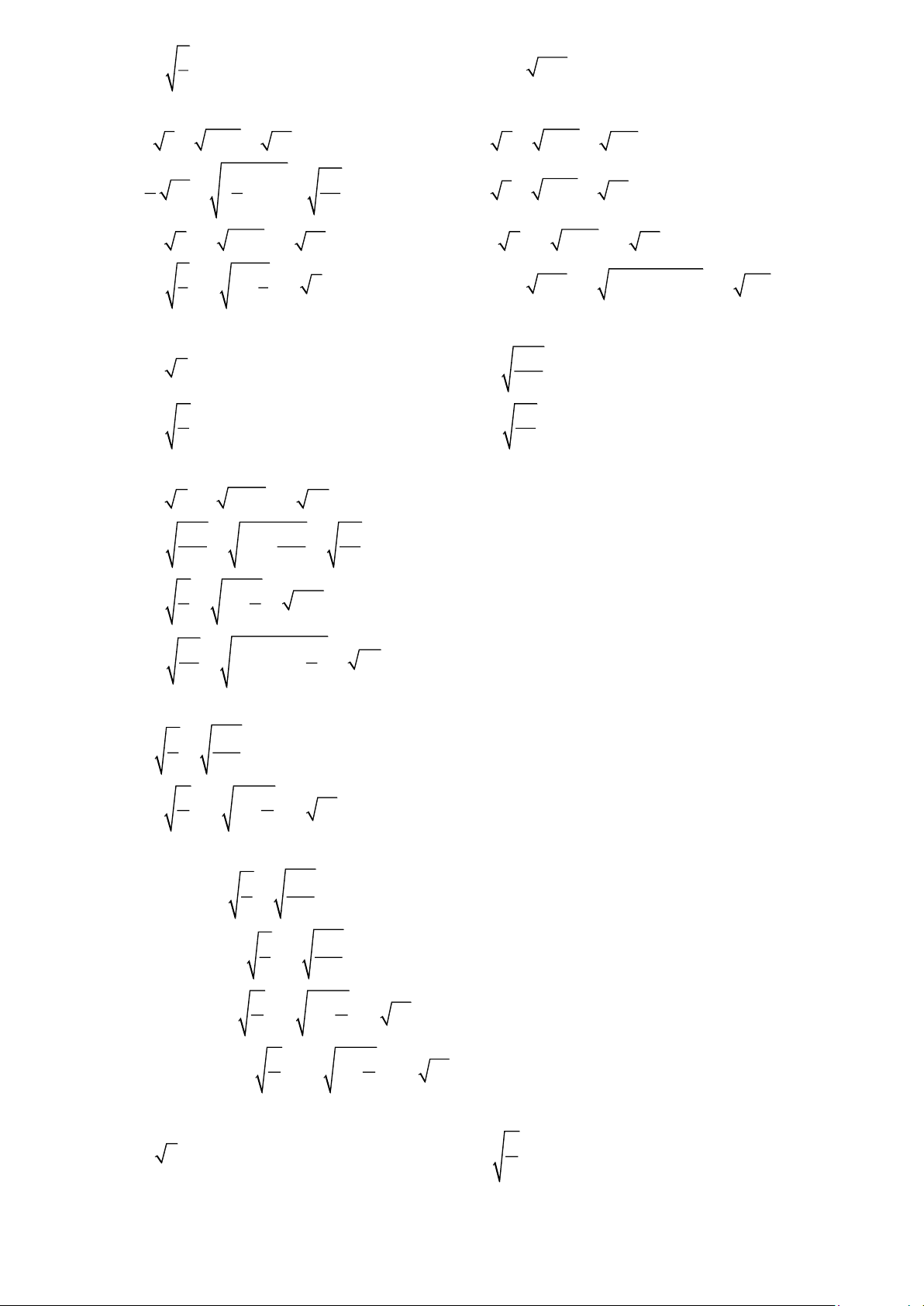
Preview text:

BIẾN ĐỔI ĐƠN GIẢN VÀ RÚT GỌN BIỂU THỨC
CHỨA CĂN THỨC BẬC HAI
A. TRỌNG TÂM KIẾN THỨC
1. Đưa thừa số ra ngoài dấu căn
Nếu a là một số và b là một số không âm thì 2 a b = a b .
* Khi tính toán với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử
mẫu của biểu thức lấy căn (tức là biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu). Ví dụ: a) 2 2 3  2 = 3  2 = 3 2 = 3 2 b) (− )2  = (− )2 5 7 5  7 = 5 −  7 = 5 7 c) 2
x y (với x  0, y  0 ) 2
= x y = x y = x y d) 3 2
x y (với x  0, y  0 ) (xy)2 x (xy)2 = =  x
= xy x = −xy x
2. Đưa thừa số vào trong dấu căn
+ Nếu a và b là hia số không âm thì 2 a b = a b
+ Nếu a là số âm và b là số không âm thì 2 a b = − a b . Ví dụ: 2 1  1  1 a) 8 = 8 = 8 = 2   2  2  4 b) 2 3 − 5 = − 3 5 = − 45 c) 1 x (với x  0 ) x 1 2 = x  = x x 2 d) y (với y  0 ) 3y 2 2 2 = − y  = − y 3y 3
3. Trục căn thức ở mẫu A A B
+ Với các biểu thức A , B và B  0 , ta có = B B
+ Với các biểu thức A , B , C mà A  0 , 2
A B , ta có:
C ( A − B C ) C ( A + B C ) = ; = 2 A + B A − B 2 A − B A − B
+ Với các biểu thức A , B , C mà A  0 , B  0 , 2
A B , ta có: Trang 1
C ( A − B C ) C ( A + B C ) = ; = A + B A − B A − B A − B
4. Rút gọn biểu thức chứa căn thức bậc hai
Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân,
chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẫu của
biểu thức lấy căn; trục căn thức ở mẫu). B. Bài tập
Dạng 1: Đưa thừa số ra ngoài dấu căn I. Cách giải:
Để đưa thừa số ra ngoài dấu căn, ta có 2 bước:
Bước 1: Chia các số trong căn thành các số chính phương 4, 9, 16, 25, 36,...
Bước 2: Dùng công thức: Với B  0 , ta có: A B khi A  0 2 2
A B = A B = A B = 
−A B khi A  0 II. Bài toán
Bài 1: Đưa thừa số ra ngoài dấu căn a) 45 b) 2400 c) 147 d) 1, 25 e) 12 f) 3 27 g) 5 48 h) 45 Lời giải a) 45 = 9.5 = 3 5 b) 2400 = 4006 = 200 6 c) 147 = 49 4 = 7 4 d) 1, 25 = 0, 255 = 0,5 5 e) 2 12 = 2 3 = 2 3 f) 2 3 27 = 3 3 3 = 9 3 g) 2 5 48 = 5 4 3 = 20 3 h) 2 45 = 3 5 = 3 5 .
Bài 2: Đưa thừa số ra ngoài dấu căn a. 8 b. 24 c. 52 d. 18 e. 45 f. 99 g. 72 h. 108 i. 180 k. 540
Bài 3: Đưa thừa số ra ngoài dấu căn a. 75 b. 125 c. 175 d. 48 e. 80 f. 176 g. 98 h. 147 i. 245 k. 343
Bài 4: Đưa thừa số ra ngoài dấu căn a) 506 b) 14 21 Trang 2 c) 32 45 d) 125 27 Lời giải a) 506 = 1003 =10 3
b) 14 21 = 7 7  23 = 7 6
c) 32 45 = 16 295 = 16910 = 43 10 =12 10
d) 125 27 = 25593 = 2595 = 53 5 = 15 15 .
Bài 5: Viết gọn các biểu thức sau a. 25.90 b. 96.125 c. 75.54 d. 245.35 Lời giải a) Ta có: 25.90 =15 10
b) Ta có: 96.125 = 16.6.5.25 = 20 30 c) Ta có: 75.54 = 45 2
d) Ta có: 245.35 = 49.5.5.7 = 35 7
Bài 6: Đưa thừa số ra ngoài dấu căn a) 18x b) 2 75x y c) 3 2 605x y d) (x y)2 128 − e) ( 2
150 4x − 4x + ) 1 f) 3 2
x − 6x +12x − 8 Lời giải
a) 18x = 9 2x = 3 2x với x  0 b) 2 2
75x y = 25x 3y = 5 x 3y với y  0 5  x 3  y ( x  0) =  −5x 3  y ( x  0) c) 3 2 2 2
605x y = 121x y 5x = 11x y 5x với x  0 1  1xy 5  x ( y  0) =  −11xy 5  x ( y  0) d) (x − y)2 = (x − y)2 128 64
2 = 8 x − y 2 8
 (x − y) 2 (x   y) =  8
 ( y − x) 2 (x y) e) ( x − x+ ) =  ( x − )2 2 150 4 4 1 25 6 2 1 = 5 2x −1 6   ( x − )  1  5 2 1 6 x      2  =   ( − x)  1  5 1 2 6 x      2  Trang 3
f) x − x + x − = (x − )3 = (x − )2 3 2 6 12 8 2 2 (x − 2)
= (x − 2) x − 2 với x  2 .
Bài 7: Đưa thừa số ra ngoài dấu căn a. 2 27x ( x  0) b. 2
8xy ( x  0; y  0) c. 3 25x ( x  0) d. 4
48xy ( x  0; y R) Lời giải a) Ta có: x = ( x)2 2 27 3
.3 = 3x 3 = 3 3x (x  0) b) Ta có: xy = ( y)2 2 8 2
.2x = 2y 2x = 2
− y 2x (x  0; y  0) c) Ta có: 3
25x = 5x x ( x  0) d) Ta có: 4
xy ( x y R) 2 = y x ( 2 48 0; 4 3 y  0)
Bài 8: Đưa thừa số ra ngoài dấu căn
a. 32a với a  0
b. 75a với a  0 c. 2
80a với a  0 d. 2
1512a với a  0 e. 2 4
28x y với x  0 f. 4 2
54x y với y  0 g. (x − )3 125 1 h. (x + )5 192 3 Lời giải
g) Điều kiện xác định x  1 Ta có: (x − )3 =  (x − )2 125 1 25 5 1 (x − ) 1 = 5(x − ) 1 5( x − ) 1
h) Điều kiện xác định x  −3 Ta có: (x + )5 = ( 2 192 3
8 x + 3 )  3(x + 3) = ( 2
8 x + 3 ) 3(x + 3) .
Bài 9: Đưa thừa số ra ngoài dấu căn a. 2 27x ( x  0) b. 2
8xy ( x  0; y  0) c. 3 25x ( x  0) d. 4
48xy ( x  0; y R) Lời giải a) Ta có: x = ( x)2 2 27 3
.3 = 3x 3 = 3 3x (x  0) b) Ta có: xy = ( y)2 2 8 2
.2x = 2y 2x = 2
− y 2x (x  0; y  0) c) Ta có: 3
25x = 5x x ( x  0) d) Ta có: 4
xy ( x y R) 2 = y x ( 2 48 0; 4 3 y  0)
Bài 10: Đưa thừa số ra ngoài dấu căn
a. 32a với a  0
b. 75a với a  0 c. 2
80a với a  0 d. 2
1512a với a  0 Trang 4 e. 2 4
28x y với x  0 f. 4 2
54x y với y  0 g. (x − )3 125 1 h. (x + )5 192 3 Lời giải
g) Điều kiện xác định x  1 Ta có: (x − )3 =  (x − )2 125 1 25 5 1 (x − ) 1 = 5(x − ) 1 5( x − ) 1
h) Điều kiện xác định x  −3 Ta có: (x + )5 = ( 2 192 3
8 x + 3 )  3(x + 3) ( 2
8 x + 3 ) 3(x + 3)
Dạng 2: Đưa thừa số vào trong dấu căn I. Cách giải:
Để đưa thừa số vào trong dấu căn, ta có 2 bước:
Bước 1: Viết biểu thức thành 2
A (với A  0 )
Bước 2: Dùng quy tắc nhân các căn bậc hai: + 2 2
A B = A B = A B (với A  0 , B  0 )
+ Nếu A  0 thì đặt dấu trừ ở ngoài căn 2 2
A B = − A B = − A B (với A  0 , B  0 ) II. Bài toán
Bài 1: Đưa thừa số vào trong dấu căn a) 3 5 b) 5 6 c) 2 35 d) 5 3 7 e) −5 2 f) −2 7 Trang 5 g) 1 4 − h) 0 − ,06 250 8 Lời giải a) 2 3 5 = 3 5 = 45 b) 2 5 6 = 5  6 = 150 2 2  2  20 c) 35 = 35 =   d) 2 5 3 = 5 3 = 75 7  7  7 e) 2 5 − 2 = − 5  2 = − 50 f) 2 2 − 7 = − 2 7 = − 28 g) 1 1 2 4 − = − 4  = − 2 h) − = − ( )2 0,06 250 0,06  250 = − 0,9 . 8 8
Bài 2: Đưa thừa số vào trong dấu căn a) 2 − a (a  0) b) 3 2a (với a  0 ) 10a c) 3 −x (với x  0 ) d) 1 − −x (với x  0 ) x x Lời giải a) 2 2 −
a = − 2  a = − 4a b) 3 3 6 2 2 = 4  = a a a (vì a  0 ) 10a 10a 5 c) 3 3 2 −x = x  = 3
− x với x  0 x x 1 −  1 d) x ( x)2  − = −  − = −  
x với x  0 xx
Bài 3: Chỉ ra chỗ sai trong các biến đổi sau 2 3 3 a) = x x 7 7 b) y y 2 xy
= y x  = y xy x x Lời giải 2 3 3 a) Biến đổi = x x
chỉ đúng khi x  0 7 7 2 3 3 Nếu x  0 thì = − x x 7 7 b) Biến đổi y y 2 xy
= y x  = y xy chỉ đúng khi x  0 x x Nếu y y x  0 thì 2 xy
= −y x  = −y xy . x x
Bài 4: Đưa thừa số vào trong dấu căn x a) x x b) y y Trang 6 x y c) y x Lời giải a) 2 3
x x = x x = x (với x  0 )
b) Điều kiện: x  0 , y  0 ; y  0 x x
Xét trường hợp x  0 ; y  0 , ta có 2 y = y  = xy y y x x
Xét trường hợp x  0 ; y  0 , ta có 2 y
= − y  = − xy y y
c) Điều kiện: xy  0 2 x y x y x Ta có =  = . 2 y x y x y
Bài 5: Đưa thừa số vào trong dấu căn − a. 15 a 13 (a  0) b. a (a  0) a
c. a 12 (a  0)
d. a 2 (a  0) 2 a Lời giải a) Ta có: 2
a 13 = 13a (a  0) 2 1 − 5 1 − 5 1 − 5a b) Ta có: a = −(−a) = − = − 1
− 5a (a  0) a a a
c) Ta có: a 12 = 3a (a  0) 2 a d) Ta có: 2
a 2 = − 2a (a  0) Trang 7
Dạng 3: Khử mẫu của biểu thức lấy căn I. Cách giải:
- Khử mẫu của biểu thức lấy căn
Bước 1: Nhân cả tử và mẫu của phân thức với ở trong căn với mẫu
Bước 2: Khai phương một thương
Bước 3: Đưa thừa số ra ngoài dấu căn rồi giản ước cho nhân tử chung A AB AB AB
Với AB  0 , B  0 ta có: = = = 2 2 B B B B
- Rút gọn biểu thức chứa căn bậc hai của phân thức
Bước 1: Khử mẫu của biểu thức lấy căn
Bước 2: Thu gọn đơn thức đồng dạng II. Bài toán
Bài 1: Khử căn thức ở mẫu số các phân số a. 7 b. 5 108 6 c. 10 d. 4 13 75 3 + 2 2 5 − 2 6 e. f. 2 3 Lời giải 7 7 7 7. 3 21 a) Ta có: = = = = 108 36.3 6 3 6 3.3 8 5 5 5. 6 30 b) Ta có: = = = 6 6 6 6 10 10 10. 13 130 c) Ta có: = = = 13 13 13 13 4 4 2 2 3 2 3 d) Ta có: = = = = 75 25.3 5 3 5 3. 3 15 3 2 2 3 2 2 ( + + + )2 2 1 e) Ta có: = = 2 2 2 ( 2 + + )1. 2 2 1 2 + 2 = = = 2 2 2 5 2 6 5 2 6 ( − − − )2 3 2 f) Ta có: = = 3 3 3 3 − 2 2 2. 3 6 = =1− =1− =1− 3 3 3. 3 3
Bài 2: Khử mẫu của biểu thức lấy căn Trang 8
a) 2a với ab  0 b) 2 với a  0 3b 5a 3 c) 4x
với x  0 , y  0 4xy Lời giải a a  a) 2 2 3b 6ab 6 = = = ab 3b 3b b ( )2 3 3 b b  b) 2 2 5a 10 = = a a a 5a 5a 5a (5a)2 10a 10a 10 = = = a a a 5 a 5a 5 3 3 4xy 12xy 12xy c) 4x = 4a = 4x = . 4xy 4xy  4xy (4 )2 y xy
Bài 3: Khử mẫu của biểu thức lấy căn a) 4 b) 3 7 5 c) 11 d) 11 2 6 Lời giải 2 4 47  2  2 7 a) = = 7 = 2   7 7  7  7  b) 3 3 5 15 = = 2 5 5 5 11 11 2 22 22 c) = = = . 2 2 2 2 2 2  d) 11 11 6 66 = = 6 66 6
Bài 4: Khử mẫu của biểu thức lấy căn 5 72 Lời giải  Ta có 5 5 2 10 1 = = = 10 72 72 2 144 12
* Chú ý: Nếu nhân cả tử và mẫu của phân số 5 với 72 thì vẫn ra kết quả nhưng biến đổi 72 phức tạp hơn: 5 572 360 6 1 = = = 10 = 10 2 2 72 72 72 72 12
Vậy tìm thừa số phụ như thế nào cho hợp lí?
Trước hết, phân tích mẫu số ra thừa số nguyên tố: 3 2
72 = 2 3 . Ta thấy ngay thừa số phụ là
2, lúc đó số mũ của các thừa số nguyên tố đều chẵn. Trang 9
Bài 5: Khử mẫu của các biểu thức lấy căn 3x a) 11 b) 27x 3 5y c) 1 d) 1 1 − 3 2
x + 3x + 3x +1 2 3 x x Lời giải  a) 11 11 3x 33x 1 = = =
(điều kiện x  0 ) 2 27x 27x 3x 81x 9x 3x 3x 5y 15xy 1 b) = = =
15xy (điều kiện xy  0; y  0 ) 3 3 4 2 5y 5y 5y 24y 5y 1 1 x +1 c) = = 3 2
x + 3x + 3x +1 (x + )3 1 (x + )4 1 1 =
x +1 (điều kiện x  −1 ) (x + )2 1 1 1 x −1 x( x − ) 1 1 d) − = = =
x x −1 (điều kiện x  1 hoặc x  0 ). 2 3 3 4 2 ( ) x x x x x
Bài 6: Khử mẫu của mỗi biểu thức dưới dấu căn bậc hai sau 3 5x 3 − a.
(x  0; y  0) b. 7xy
(x  0; y  0) 49y xy Lời giải 3 5x x 5x x 5xy a) Ta có:
(x  0; y  0) = = 2 49y 7 y 7 y = x x 5xy =
5xy ( x  0; y  0) 7 y 7 y 3 − 3 − b) Ta có: 7 (  0;  0) = xy xy x y 7xy 2 2 xy x y 7 = xy 3 − xy = 7 − 3
− xy (x  0; y  0) xy
Bài 7: Khử mẫu của mỗi biểu thức dưới dấu căn bậc hai sau − a. 5b 1 16 a  0,b  0 b. ab
(a  0,b  0) 3 ( ) 49a 4 ab Lời giải a) 5b 1 5b 1 5  ab a 0,b  0 = = 3 ( ) 2 49a 7a a 7a a 1 =
5ab a  0,b  0 2 ( ) 7a − b) 1 16 ab (a b  ) 1 0, 0 = −ab 4 ab ab = − ab ab = − ab 2 2 a b Trang 10 − +
Bài 8: Thu gọn biểu thức 3 3 4 3 4 A = − 2 3 +1 5 − 2 3 Lời giải − + Ta có: 3 3 4 3 4 A = − 2 3 +1 5 − 2 3
(3 3−4)(2 3− )1 ( 3+4)(5+2 3) = ( − 2 3 + ) 1 (2 3 − ) 1 (5−2 3)(5+2 3) 18 − 3 3 − 8 3 + 4 5 3 + 6 + 20 + 8 3 = − 12 −1 25 −12 22 −11 3 26 +13 3 = − 11 13 11(2 − 3) 13(2 + 3) = − = 2 − 3 − 2 + 3 11 13
Suy ra 2A = 2 ( 2− 3 − 2+ 3) = 4−2 3 − 4+2 3 = ( − )2 − ( + )2 3 1 3 1 = 3 −1 − 3 +1 = 3 −1− ( 3 + ) 1 = 2 − Do đó A = − 2 1 3 2 − 2 3
Bài 9: Thu gọn biểu thức A =  2 − 3 3 2 + 2 3 Lời giải 1 3 2 − 2 3 Ta có: A =  2 − 3 3 2 + 2 3 6 ( 3 − 2 1 ) 1 3 − 2 =  = 2 − 3 6 ( 3 + 2) 2 − 3 3 + 2 ( − )2 3 2 1 =  2 − 3 3 − 2 1 3 − 2 =  3 − 2 = = 1 − . 2 − 3 2 − 3 Trang 11
Dạng 4: Trục căn thức ở mẫu I. Cách giải:
- Khử mẫu của biểu thức lấy căn
+ Bước 1: Xác định biểu thức liên hợp
+ Bước 2: Nhân liên hợp để làm mất căn
+ Bước 3: Giản ước, thu gọn (nếu được)
- Rút gọn biểu thức chứa căn bậc hai của phân thức
+ Bước 1: Trục căn thức ở mẫu
+ Bước 2: Thu gọn căn thức đồng dạng. II. Bài toán
Bài 1: Trục căn thức ở mẫu các biểu thức sau: 2 a) b) 3 5 2 6 4 3 c) − d) 9 2 2 3 e) 2 f) 3 3 5 7 3 + 3 7 g) h) 5 3 3 10 2 2 i) − j) 3 5 40 Lời giải 2 2 5 2 5 2 5 a) = = = 5 3( 5)2 35 15 3 3 6 3 6 6 b) = = = 2 6 2 6  6 26 4 4 3 4 3  2 4 6 c) − = − = − = 2 − 6 2 2  2 2 9 9  3 9 3 3 3 d) = = = 2 3 2 3  3 6 2 2 2 5 2 5 2 5 e) = = = 3 5 3( 5)2 35 15 3 3 7 3 7 f) = = 7 7  7 7 Trang 12 3 ( 3 + + )1 3 3 3 +1 g) = = 5 3 5 3 5 7 7  3 21 h) = = 3 3  3 3 10 10 5 10 5 2 5 i) − = − = − = − 3 5 3 5  5 35 3 2 2 2 2  40 8 5 5 j) = = = 40 40  40 40 5
Bài 2: Trục căn thức ở mẫu các biểu thức sau: a) 2 b) 3 3 −1 15 + 4 c) 4 d) 2 3 −1 5 + 3 2 e) 5 f) 2 + 3 5 − 2 3 − 2 g) 7 h) 3 − 2 3 + 2 Lời giải 2( 3 + ) 1 2( 3 + ) 1 2 a) = = = + 3 −1 ( 3 − ) 1 ( 3 + ) 3 1 1 3 −1 3( 15 − 4) 3( 15 − 4 3 ) b) = = = − 15 + 4 ( 15+4)( 15 −4) 3(4 15) 15 − 4 4 4 ( 3+ )1 4( 3+ )1 c) = = = + 3 −1 ( 3) 2 3 2 2 2 −1 2( 5 − 3) 2( 5 − 3 2 ) d) = = = − 5 + 3 ( 5+ 3)( 5 − 3) 5 3 5 − 3 5(2 − 3 5 ) 10 − 5 3 e) = = = − 2 + 3 (2+ 3)(2− 3) 10 5 3 4 − 3 2 ( 5 + 2 2 ) 10 + 2 10 + 2 f) = = = 5 − 2 ( 5 − 2)( 5 + 2) 5−2 3 7(3+ 2) 7 (3+ 2 7 ) g) = = = + 3 − 2 (3− 2)(3+ 2) 3 2 7 3 2 ( − − )2 3 2 − h) 5 2 6 = = = − 3 + 2 ( 3+ 2)( 3− 2) 5 2 6 1
Bài 3: Trục căn thức ở mẫu và rút gọn Trang 13 − a. 1 b. 3 5 2 2 − 3 3 3 + 5 Lời giải − + + ( 8 + 27 1 1 8 27 8 27 ) a) Ta có: = = = = 2 2 − 3 3 8 − 27 8 − 27 19 − 19 ( − )( − ) ( − − )2 3 5 3 5 3 5 3 5 3 − 5 b) Ta có: = = = 3 + 5 (3+ 5)(3− 5) 4 2
Bài 4: Trục căn thức ở mẫu rồi rút gọn 8 − a. b. 2 3 5 − 3 2 + 3 Lời giải 2 2 ( 5 + 3 8 ) a) Ta có: = = 10 + 6 5 − 3 5 − 3 − (2− 3 2 3 )2 b) Ta có: = = − 2 + 3 2 − ( 3) 2 3 2 2
Bài 5: Trục căn thức ở mẫu: 5 3 − 3 5 a) a b) 3 − 2 2 5 3 + 3 5 2 c) 1− 2 + 3 Lời giải a (3+ 2 2) a a (3+2 2) a) = = 3 − 2 2 (3−2 2)(3+2 2) 3 −(2 2)2 2 a (3+ 2 2) = = a(3+ 2 2) 9 − 8 5 3 3 5 ( − − )2 5 3 3 5 + − b) 75 45 30 15 = = 5 3 + 3 5 (5 3+3 5)(5 3−3 5) 75 − 45 30(4 − 15) = = 4 − 15 30 2 (1− 2 − 3 2 ) c) = 1− 2 + 3 (1− 2 + 3)(1− 2 − 3) 2 (1− 2 − 3) 2 (1− 2 − 3) = ( − ) = 2 1− 2 2 + 2 − 3 1 2 − 3 Trang 14 2 (1− 2 − 3) 3 + 2 −1 = = . −2 2 2
Bài 6: Trục căn thức và thực hiện phép tính 3 + 2 3 2 + 2 a. A = + − ( 2 + 3) 3 2 +1  5− 2 5  5+ 3 5  b. B =  − 2 − 2  2 5  3 5  − +    Lời giải 3 + 2 3 2 + 2 a) Ta có: A = + − ( 2 + 3)  A = 2 3 2 +1  5− 2 5  5+ 3 5  b) Ta có: B =  − 2 − 2  B = 1 −  2 5  3 5  − +   
Bài 7: Rút gọn các biểu thức sau 14 − 7 a. A = 2 − 2 1 1 b. B = − 7 − 24 +1 7 + 24 −1 c. 15 4 12 C = ( + − )( 6 +11) 6 +1 6 − 2 3 − 6 d. 3 3 D = − 3 +1 −1 3 +1 +1 Lời giải 14 − 7 7( 2 −1) 7 7. 2 14 a) Ta có: A = = = = = 2 − 2 2( 2 −1) 2 2. 2 2 1 1 b) Ta có: B = − 7 − 24 +1 7 + 24 −1 1 1 1 1 = − = − 2 2 7 − 2 6 +1 7 + 2 6 −1 ( 6 −1) +1 ( 6 +1) −1 1 1 = − = 0 6 −1+1 6 +1−1  15 4 12  c) Ta có: C = + −  ( 6 +1 ) 1  6 +1 6 − 2 3 − 6 
15( 6 − )1 4( 6 + 2) 12(3+ 6) =  + +  ( 6 + ) 11 = 11 − 5  6 −1 6 − 2 9 − 6    3 3 d) Ta có: D = − 3 +1 −1 3 +1 +1 Trang 15 ( 3 1 )1 ( 3 1 )1 + + − + −   = 3   (  3 +1 − )1( 3 +1+ )1    2 = 3. = 2 3 +1−1
Bài 8: Trục căn thức ở mẫu 6 + 14 3 + 4 3 a. A = b. B = 2 3 − 7 6 + 2 − 5 c. 1 C = d. 31 D = 2 + 5 + 2 2 + 10 2 + 2 − 5 3 + 2 3 2 + 2 e. 1 E = f. F = + − ( 2 + 3) 10 + 15 + 14 + 21 3 2 +1 Lời giải 6 + 14 2( 3 + 7)(2 3 + 7) a. A = = 2 3 − 7 (2 3 − 7)(2 3 + 7) 2(6 + 2 21 + 21 + 7) 2(13 + 3 21) = = 12 − 5 5 3 + 4 3 (3 + 4 3)( 6 + 2 + 5) b. B = = 6 + 2 − 5 ( 6 + 2 − 5)( 6 + 2 + 5) (3 + 4 3)( 6 + 2 + 5) = = 6 + 2 + 5 3 + 4 3 c. 1 1 C = = 2 + 5 + 2 2 + 10 ( 2 +1)( 5 + 2) ( 2 −1)( 5 − 2) = = ( 2 −1)( 5 − 2) (2 −1)(5 − 4) 31 31(2 + 2 + 5) 31(2 + 2 + 5) d. D = = = 2 2 + 2 − 5 (2 + 2) − 5 1+ 4 2 31(2 + 2 + 5)(4 2 −1) = = (2 + 2 + 5)(4 2 −1) 2 (4 2) −1 e. 1 1 E = = 10 + 15 + 14 + 21 ( 2 + 3)( 5 + 7) ( 3 − 2)( 7 − 5) = 2 3 + 2 3 2 + 2 f. F = + − ( 2 + 3) = 2 3 2 +1
Bài 9: Trục căn thức ở mẫu: 2 5 a) với a  0 b)
với x  0 ; x  9 a x + 3 1 1− a c)
với x  0 ; x  3 d)
với x  0 ; x  1 x − 3 1+ a Trang 16 e) 1 với a  −1 f) 1
với x  0 ; x  9 x +1 x − 3 Lời giải 2 2 a 2 a a) = = a a a a 5( x −3) 5( x −3 5 ) b) = =
x + 3 ( x + 3)( x −3) x − 9 x + x + c) 1 3 3 = = x − 3
( x − 3)( x + 3) x−3 1 ( − − a a )2 1 − a + d) 1 2 = = a 1+ a (1− a)(1+ a) 1− a 1 x +1 x +1 x +1 e) = = = x +1 x +1 x +1 ( x+1)2 x+1 x + x + f) 1 3 3 = = . x − 3
( x +3)( x −3) x−9
Bài 10: Trục căn thức và thực hiện phép tính  15 4 12  a. A = + −  ( 6 +1 ) 1  6 +1 6 − 2 3 − 6   5 + 5  5 − 5  b. B = 1−  −1  1 5  1 5  + −    Lời giải 15( 6 − ) 1 15 4 a) Ta có: = = 3( 6 − ) 1 ; = 2( 6 + 2) 6 +1 6 −1 6 − 2 12 = 4(3+ 6)  A = 1 − 15 3 − 6 5 + 5 5 − 5 b) Ta có: = 5; = − 5 → B = 4 1+ 5 1− 5
Bài 11: Trục căn thức ở mẫu của các biểu thức 2 5 − x +1 2 a − a) b)
2a (a  0,a  2) 2 3 a + 2 x −1 x c)
với x  0, x  1 d)
với x  0 , y  0 , 4x y x −1 2 x + y Lời giải − x x ( 2 2 2 5 3 x + − + − +  )1 5 1 5 1 3 a) = = 2 3 2 3  3 6 a − a ( 2 2
a − 2a)( a − 2 2 ) b) = a + 2
( a + 2)( a − 2) Trang 17
a (a − 2)( a − 2) =
= a( a − 2) (a  0,a  2) a − 2 x (x − ) 1 ( x + ) 1 (x − ) 1 ( x + − )1 1 c) = =
= x + với x  0, x  1 x −1 ( x − ) 1 ( x + ) 1 1 x −1
x (2 x − y )
x (2 x − y x ) d) = =
với x  0 , y  0 , 4x y 2 x + y
(2 x + y)(2 x − y) 4x − y
Bài 12: Trục căn thức ở mẫu 2 x − a + a) 1 với x 1 b) 1 với a  −1 x −1 2a + 3 − a + 2 c) 1 với x  0 d) 1
với a  0,b  0 , 1 ab = . x +1 − x a + b −1 4 Lời giải x −1
( 2x − )1 x−1 ( 2 2 x − ) 1  x −1 a) = = x −1 x −1 x −1 (x − )2 1 (x − ) 1 ( x + ) 1 x −1 = = (x + ) 1 x −1 x −1 a + (a + )
1 ( 2a + 3 − a + 2 1 ) b) = 2a + 3 − a + 2
( 2a+3− a+2)( 2a+3+ a+2) (a + )
1 ( 2a + 3 − a + 2) = (
2a + 3)2 −( a + 2)2 (a + )
1 ( 2a + 3 − a + 2) = (
2a + 3) − (a + 2) (a + )
1 ( 2a + 3 − a + 2) = a +1
= 2a + 3 − a + 2 x + + c) 1 1 = x x +1 − x
( x+1− x)( x+1+ x) x +1 + x x +1 + = x ( ) = 2 ( )2 (x+ )1 1 − + − x x x +1 + = x x 1 = x +1 + x 1( a + b − ) 1 1 d) =
a + b −1 ( a + b − ) 1 ( a + b + ) 1 Trang 18 1 a + b −1 =
a + b −1 a + b + 2 ab −1 a + b −1 a + b −1 = = 1 a + b a + b + 2 −1 4
Bài 13: Trục căn thức và thực hiện phép tính  15 4 12  a. A = + −  ( 6 +1 ) 1  6 +1 6 − 2 3 − 6   5 + 5  5 − 5  b. B = 1−  −1  1 5  1 5  + −    Lời giải 15( 6 − ) 1 15 4 a) Ta có: = = 3( 6 − ) 1 ; = 2( 6 + 2) 6 +1 6 −1 6 − 2 12 = 4(3+ 6)  A = 1 − 15 3 − 6 5 + 5 5 − 5 b) Ta có: = 5; = − 5 → B = 4 1+ 5 1− 5
Bài 14: Trục căn thức và thực hiện phép tính 3 + 2 3 2 + 2 a. A = + − ( 2 + 3) 3 2 +1  5− 2 5  5+ 3 5  b. B =  − 2 − 2  2 5  3 5  − +    Lời giải 3 + 2 3 2 + 2 a) Ta có: A = + − ( 2 + 3)  A = 2 3 2 +1  5− 2 5  5+ 3 5  b) Ta có: B =  − 2 − 2  B = 1 −  2 5  3 5  − +   
Bài 15: Trục căn thức ở mẫu 6 + 14 3 + 4 3 a. A = b. B = 2 3 − 7 6 + 2 − 5 1 31 c. C = d. D = 2 + 5 + 2 2 + 10 2 + 2 − 5 1 e. E = 10 + 15 + 14 + 21 3 + 2 3 2 + 2 f. F = + − ( 2 + 3) 3 2 +1 Lời giải 6 + 14 2( 3 + 7)(2 3 + 7) a. A = = 2 3 − 7 (2 3 − 7)(2 3 + 7) Trang 19 2(6 + 2 21 + 21 + 7) 2(13 + 3 21) = = 12 − 5 5 3 + 4 3 (3 + 4 3)( 6 + 2 + 5) b. B = = 6 + 2 − 5 ( 6 + 2 − 5)( 6 + 2 + 5) (3 + 4 3)( 6 + 2 + 5) = = 6 + 2 + 5 3 + 4 3 c. 1 1 C = = 2 + 5 + 2 2 + 10 ( 2 +1)( 5 + 2) ( 2 −1)( 5 − 2) = = ( 2 −1)( 5 − 2) (2 −1)(5 − 4) 31 31(2 + 2 + 5) d. D = = 2 2 + 2 − 5 (2 + 2) − 5 31(2 + 2 + 5) 31(2 + 2 + 5)(4 2 −1) = = 2 1+ 4 2 (4 2) −1 = (2 + 2 + 5)(4 2 −1) e. 1 1 E = = 10 + 15 + 14 + 21 ( 2 + 3)( 5 + 7) ( 3 − 2)( 7 − 5) = 2 3 + 2 3 2 + 2 f. F = + − ( 2 + 3) = 2 . 3 2 +1
Dạng 5: So sánh hai số chứa căn I. Cách giải:
Để so sánh các căn bậc hai, ta cần chú ý:
- Với a,b không âm thì a b a b
- Đưa thừa số vào trong dấu căn để đưa về so sánh a và b . II. Bài toán
Bài 1: Không dùng MTCT hãy so sánh
a) a = 3 2 và b = 2 3
b) a = 5 6 và b = 7 3 c) 2 a = 3 2 và 1 b = 5 1 3 5 Lời giải a) Ta có 2 3 2 = 3  2 = 18 ; 2 2 3 = 2 3 = 12
Vì 12  18 nên 2 3  3 2 Vậy a b .
b) Ta có a = 5 6 = 256 = 150 ; b = 7 3 = 493 = 147
Vì 150  147 nên 5 6  7 3 . Trang 20

Tài liệu liên quan: