43 trang 2 lượt tải

Các Dạng Toán Bài Công Thức Lượng Giác Toán 11 Giải Chi Tiết

4

Các Dạng Toán Bài Công Thức Lượng Giác Toán 11 Giải Chi Tiết. Tài liệu gồm 43 trang. Mời các bạn tham khảo

Chủ đề: Tài liệu chung Toán 11 84 tài liệu

Môn: Toán 11 3.5 K tài liệu

Tác giả:

Profile

jang linh

1 ngày trước
Danh sách Quiz
/43
Trang 1
CÁC DẠNG TOÁN BÀI CÔNG THỨC LƯỢNG GIÁC
Dạng 1: Tính giá trị biểu thức chứa các giá trị lượng giác
Phương pháp: Sử dụng các công thức lượng giác để giải quyết bài toán
A. BÀI TẬP TỰ LUẬN
Bài tập 1: Tính:
a)
cos
6
a

+


biết
1
sin
3
a =
và
2
a

b)
tan
4
a

−


biết
cos
1
3
a =−
và
3
2
a

Lời giải
a) Vì
2
a

nên
.
Mặt khác, từ
22
sin a cos a 1+=
suy ra
2
2
16
cos 1 sin 1 .
3
3
aa

= − − = − − = −


Ta có:
6 3 1 1 6 1 3 3 2
cos cos cos sin sin .
6 6 6 3 2 2 6
3 2 3
a a a

− − +

+ = − = − − = = −





b) Vì
3
2
a

nên
sin 0a
, do đó
sin
tan 0
cos
a
a
a
=
.
Mặt khác:
2
2
1
1 tan
cos
a
a
+=
suy ra
2
2
11
tan 1 1 2 2
cos
1
3
a
a
= − = − =

−


.
Ta có:
tan tan
2 2 1 9 4 2
4
tan
47
1 2 2.1
1 tan tan
4
a
a
a
−
−−

− = = =

+

+
.
Bài tập 2: Tính sin
sin 2 ; cos2 ; tan2a a a
, biết:
a)
1
sin
3
a =
và
2
a

b)
2
1
sin cosaa+=
và
3
24
a


Lời giải
a) Vì
2
a

nên
.
Mặt khác:
22
sin cos 1aa+=
suy ra
2
2
1 2 2
cos 1 sin 1
33
aa

= − − = − − = −


1 2 2 4 2
sin2 2sin cos 2
3 3 9
a a a

= = − = −



;
2
2
17
cos2 1 2sin 1 2. .
39
aa

= − = − =


Trang 2
Suy ra
42
sin2 4 2
9
tan2 .
7
cos2 7
9
a
a
a
−
= = = −
b) Ta có:
( )
2
2
22
11
sin cos sin cos 2sin cos
24
a a a a a a

+ = + + =


13
1 sin2 sin2 .
44
aa + = = −
Vì
3
24
a


nên
3
2
2
a

. Do đó
cos2 0a
.
Mặt khác:
( ) ( )
22
sin 2 cos 2 1aa+=
suy ra
( )
2
2
37
cos2 1 sin 2 1
44
aa

= − − = − − − = −


.
Do đó:
3
sin2 3 3 7
4
tan2
cos2 7
77
4
a
a
a
−
= = = =
−
.
Bài tập 3: Tính giá trị của các biểu thức sau:
a)
1
sin
3
a =
và
2
a

b)
2
1
sin cosaa+=
và
3
24
a


Lời giải
a) Ta có:
sin cos sin cos sin cos cos sin
15 10 10 15 15 10 15 10
2 2 2 2
cos cos sin sin cos cos sin sin
15 5 15 5 15 5 15 5
A
++
==
−−
1
sin
sin
15 10
6
2
1
1
2
cos
cos
32
15 5



+


= = = =

+


b) Ta có:
1
sin cos cos cos 2sin cos cos cos
32 32 16 8 2 32 32 16 8
B

= =


11
sin 2 cos cos sin cos cos
2 32 16 8 2 16 16 8

= =


1 1 1 1 1 2 2
2sin cos cos sin cos 2sin cos sin
4 16 16 8 4 8 8 8 8 8 8 4 8 2 16
= = = = = =
Bài tập 4: Rút gọn các biểu thức sau:
a)
( ) ( ) ( ) ( )
sin 14 sin 74 sin 76 sin 16A x x x x= + + + − −
Trang 3
b)
( ) ( ) ( )
sin sin sin
cos .cos cos .cos cos .cos
a b b c c a
B
a b b c c a
− − −
= + +
Lời giải
a) Ta có
( ) ( ) ( ) ( )
sin 14 cos 16 sin 76 sin 16A x x x x= + − + − −
( ) ( ) ( ) ( )
sin 14 cos 16 cos 14 sin 16x x x x= + − + + −
( )
1
sin 14 16 sin30
2
xx= + + − = =
.
b)
( ) ( ) ( )
sin sin sin
cos .cos cos .cos cos .cos
a b b c c a
A
a b b c c a
− − −
= + +
Ta có:
sin .cos sin .cos sin .cos sin .cos sin .cos sin .cos
cos .cos cos .cos cos .cos
a b b a b c c b c a a c
A
a b b c c a
− − −
= + +
sin .cos sin .cos sin .cos sin .cos sin .cos sin .cos
cos .cos cos .cos cos .cos cos .cos cos .cos cos .cos
a b b a b c c b c a a c
a b a b b c b c c a c a
= − + − + −
tan tan tan tan tan tan 0a b b c c a= − + − + − =
.
Bài tập 5: Không dùng máy tính cầm tay. Hãy tính các giá trị lượng giác sau:
a)
0
cos795
b)
7
tan
12
Lời giải
a) Tính
0
cos795
Vì
0 0 0 0 0 0
795 75 2.360 30 45 2.360= + = + +
nên
0 0 0 0 0 0
3 2 1 2 6 2
cos795 cos75 cos30 cos45 sin 30 sin 45 . .
2 2 2 2 4
−
= = − = − =
b) Tính
7
tan
12
tan tan
7 3 1
34
tan tan 2 3
12 3 4
13
1 tan tan
34


+
+

= + = = = − −

−

−
Bài tập 6: Tính
44
cos sin
12 12
A

=−
Lời giải
Ta có:
2 2 2 2 2 2
3
cos sin cos sin cos sin cos
12 12 12 12 12 12 6 2
A
= − + = − = =
.
Bài tập 7: Cho
4
cos2
5
x =−
, với
42
x


. Tính
sin ,cos ,sin ,cos 2
34
x x x x

+−
.
Lời giải
Trang 4
Vì
42
x


nên
sin 0, cos 0xx
.
Áp dụng công thức hạ bậc, ta có :
2
1 cos2 9 3
sin sin
2 10
10
x
xx
−
= = =
;
2
1 cos2 1 1
cos cos
2 10
10
x
xx
+
= = =
Theo công thức cộng, ta có
3 1 1 3 3 3 30 3 10
sin sin cos cos sin . .
3 3 3 2 2 20
10 10 2 10
x x x
++

+ = + = + = =


4 2 2 3 1 2
cos 2 cos2 sin cos sin 2 . .2. .
4 4 4 5 2 2 10
10 10
x x x

− = + = − + = −


.
Bài tập 8: Rút gọn các biểu thức sau:
a)
2
sin sin
5 15
2
cos cos
5 15
A


−
=
−
b)
57
sin sin sin
9 9 9
B
= − +
Lời giải
a)
1 2 1 2
2
2cos sin
sin sin cos
2 5 15 2 5 15
5 15 6
cot 3
2
1 2 1 2
6
cos cos sin
2sin sin
5 15 6
2 5 15 2 5 15
C
+−
−
= = = − = − = −
−
− + −
b)
7 5 4 5 4 5
sin sin sin 2sin .cos sin sin sin 0
9 9 9 9 3 9 9 9
D

= + − = − = − =


.
Bài tập 9: Đơn giản biểu thức sau:
a)
cos 2cos2 cos3
sin sin 2 sin3
a a a
A
a a a
++
=
++
b)
cos cos
33
cot cot
2
aa
B
a
a

+ + −
=
−
c)
( ) ( ) ( ) ( )
cos cos cos 2 ... cos nC a a b a b a nb= + + + + + + +
Lời giải
a)
( )
( )
( )
( )
cos cos3 2cos2 2cos2 cos 1
2cos2 cos 2cos2
cot 2
sin sin3 2sin 2 2sin 2 cos 2sin 2 2sin 2 cos 1
a a a a a
a a a
Aa
a a a a a a a a
+ + +
+
= = = =
+ + + +
b) Ta có
cos cos 2cos cos cos
3 3 3
a a a a
+ + − = =
và
sin
cos sin cos cos sin sin
cos 1
2
2 2 2 2
cot cot
2 sin sin
sin sin sin sin sin sin sin
2 2 2 2
a
a a a a
a
aa
aa
a
a a a a
aa
a a a

−
−−


− = − = = = = −
Trang 5
Suy ra
cos sin 2
sin cos
1
2
sin
aa
B a a
a
= = − = −
−
.
c) Ta có
( ) ( ) ( )
.2sin 2sin cos 2sin cos 2sin cos 2 ... 2sin cos
2 2 2 2 2
b b b b b
C a a b a b a nb= + + + + + + +
( ) ( )
3 5 3
sin sin sin sin sin sin
2 2 2 2 2 2
2 1 2 1
... sin sin
22
b b b b b b
a a a a a a
n b n b
aa
= + + − + + + − − + + + − −
+−
+ + + + − −
( )
( )
21
sin sin 2sin 1 cos
2 2 2
nb
b nb
a a n b a
+

− + + = + −


Suy ra
( )
sin 1 cos
2
sin
2
nb
n b a
C
b

+−


=
B. BÀI TẬP TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Tính
0
sin105
ta được:
A.
62
4
−
. B.
62
4
−
−
. C.
62
4
+
. D.
62
4
+
−
.
Lời giải
Có:
( )
0 0 0
sin105 sin 60 45=+
=
0 0 0 0
sin60 .cos45 cos60 .sin 45+
.
0
3 2 1 2
sin105 . .
2 2 2 2
=+
=
62
4
+
.
Câu 2: Tính
0
tan105
ta được:
A.
( )
23−+
. B.
23+
. C.
23−
. D.
( )
23−−
.
Lời giải
0
tan105
=
=
62
4
62
4
+
−
−
=
62
62
+
−
−
=
(2 3)−+
.
Câu 3: Rút gọn biểu thức:
0 0 0 0
cos54 cos4 cos36 cos86−
, ta được:
A.
0
cos50
. B.
0
cos58
. C.
0
sin 50
. D.
0
sin 58
.
Lời giải
Ta có:
( )
0 0 0 0 0 0 0 0000
cos54 cos4 cos36 cos86 cos54 cos4 sin54 sin 4 cos 4 cos5854− − +===
Trang 6
Câu 4: Rút gọn biểu thức
c
4
cos o
4
sxx

−
+
−
ta được
A.
2sin x
. B.
n2si x−
. C.
2cosx
. D.
s2 co x−
.
Lời giải
Ta có:
2
4 4 4 4
sin .sin
4 4 2 2
cos cos
x x x x
xx

+ + − + − +
+ − −
=−


2sin . n2 si sin
4
xx
=− =−
Câu 5: Giá trị của biểu thức
cos
37
12
bằng
A.
62
4
+
. B.
62
4
−
. C. –
62
4
+
. D.
26
4
−
.
Lời giải
Ta có:
37 7 7
cos cos 2 cos
12 2 12 2 12
= + + = +
7 7 6 2
cos cos sin sin
2 12 2 12 4
+
= − = −
Câu 6: Rút gọn biểu thức
4 o 4 o
cos 15 sin 15 .M =−
A.
1.M =
B.
3
.
2
M =
C.
1
.
4
M =
D.
0.M =
Lời giải
Ta có
( ) ( )
22
4 o 4 o 2 o 2 o
cos 15 sin 15 cos 15 sin 15M = − = −
( )( )
2 o 2 o 2 o 2 o
cos 15 sin 15 cos 15 sin 15= − +
( )
2 o 2 o o o
3
cos 15 sin 15 cos 2.15 cos30 .
2
= − = = =
Câu 7: Tính giá trị của biểu thức
0 0 0 0
cos10 cos20 cos40 cos80 .M =
A.
0
1
cos10
16
M =
. B.
0
1
cos10
2
M =
. C.
0
1
cos10
4
M =
. D.
0
1
cos10
8
M =
.
Lời giải
Vì
0
sin10 0
nên suy ra
M
=
0 0 0 0 0
0
16sin10 cos10 cos20 cos40 cos80
16sin10
=
0 0 0 0
0
8sin20 cos20 cos40 cos80
16sin10
M
=
0 0 0
0
4sin40 cos40 cos80
16sin10
=
00
0
2sin80 cos80
16sin10
=
0
0
sin160
16sin10
.
M
=
0
0
sin20
16sin10
=
00
0
2sin10 cos10
16sin10
=
0
1
cos10
8
.
Trang 7
Câu 8: Công thức nào sau đây sai?
A.
( )
cos sin sin cos cos .a b a b a b− = +
B.
( )
cos sin sin cos cos .a b a b a b+ = −
C.
( )
sin sin cos cos sin .a b a b a b− = −
D.
( )
sin sin cos cos sin .a b a b a b+ = +
Lời giải
Ta có
( )
cos cos cos sin sina b a b a b+ = −
.
Câu 9: Khẳng định nào sai trong các khẳng định sau?
A.
22
cos6 cos 3 sin 3 .a a a=−
B.
2
cos6 1 2sin 3 .aa=−
C.
2
cos6 1 6sin .aa=−
D.
2
cos6 2cos 3 1.aa=−
Lời giải
Áp dụng công thức
2 2 2 2
cos2 cos sin 2cos 1 1 2sin
= − = − = −
, ta được
2 2 2 2
cos6 cos 3 sin 3 2cos 3 1 1 2sin 3a a a a a= − = − = −
.
Câu 10: Khẳng định nào sai trong các khẳng định sau?
A.
2
1 cos2
sin .
2
x
x
−
=
B.
2
1 cos2
cos .
2
x
x
+
=
C.
sin 2sin cos .
22
xx
x =
D.
33
cos3 cos sin .x x x=−
Lời giải
Ta có
3
cos3 4cos 3cosx x x=−
.
Câu 11: Khẳng định nào đúng trong các khẳng định sau?
A.
sin cos 2 sin .
4
a a a

+ = −


B.
sin cos 2 sin .
4
a a a

+ = +


C.
sin cos 2 sin .
4
a a a

+ = − −


D.
sin cos 2sin .
4
a a a

+ = − +


Lời giải
Ta có:
sin cos 2 sin .
4
a a a

+ = +


Câu 12: Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?
1)
cos sin 2 sin .
4
x x x

− = +


2)
cos sin 2 cos .
4
x x x

− = +


3)
cos sin 2 sin .
4
x x x

− = −


4)
cos sin 2 sin .
4
x x x

− = −


A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Ta có
cos sin 2 cos 2 cos 2sin
4 2 4 4
x x x x x

− = + = − − = −


.
Câu 13: Nếu
( )
cos 0ab+=
thì khẳng định nào sau đây đúng?
Trang 8
A.
( )
sin 2 sin .a b a+=
B.
( )
sin 2 sin .a b b+=
C.
( )
sin 2 cos .a b a+=
D.
( )
sin 2 cos .a b b+=
Lời giải
Ta có :
( )
cos 0
22
a b a b k a b k


+ = + = + → = − + +
.
( ) ( )
sin 2 sin 2 cos cos
2
a b b b k b k b


+ = − + + + = + =


.
Câu 14: Nếu
( )
sin 0ab+=
thì khẳng định nào sau đây đúng?
A.
( )
cos 2 sin .a b a+=
B.
( )
cos 2 sin .a b b+=
C.
( )
cos 2 cos .a b a+=
D.
( )
cos 2 cos .a b b+=
Lời giải
Ta có
( )
sin 0a b a b k a b k

+ = + = → = − +
.
( ) ( ) ( )
cos 2 cos 2 cos cosa b b b k b k b

+ = − + + = + =
.
Câu 15: Rút gọn
( ) ( )
sin cos cos sin .M x y y x y y= − + −
A.
cos .Mx=
B.
sin .Mx=
C.
sin cos 2 .M x y=
D.
cos cos 2 .M x y=
Lời giải
Áp dụng công thức
( )
sin sin cos sin cosa b a b b a+ = +
, ta được
( ) ( ) ( )
sin cos cos sin sin sin .M x y y x y y x y y x= − + − = − + =


Câu 16: Rút gọn
( ) ( ) ( ) ( )
cos cos sin sin .M a b a b a b a b= + − − + −
A.
2
1 2cos .Ma=−
B.
2
1 2sin .Ma=−
C.
cos4 .Ma=
D.
sin4 .Ma=
Lời giải
Áp dụng công thức
( )
cos cos sin sin cosx y x y x y− = +
, ta được
( ) ( ) ( ) ( ) ( )
2
cos cos sin sin cos cos2 1 2sin .M a b a b a b a b a b a b a a= + − − + − = + + − = = −
Câu 17: Rút gọn
( ) ( ) ( ) ( )
cos cos sin .M a b a b a b sin a b= + − + + −
A.
2
1 2sin .Mb=−
B.
2
1 2sin .Mb=+
C.
cos4 .Mb=
D.
sin4 .Mb=
Lời giải
Áp dụng công thức
( )
cos cos sin sin cosx y x y x y+ = −
, ta được
( ) ( ) ( ) ( )
cos cos sin sinM a b a b a b a b= + − + + −
( )
2
cos ( ) cos2 1 2sin .a b a b b b= + − − = = −
Câu 17: Giá trị nào sau đây của
x
thỏa mãn
sin2 .sin3 cos2 .cos3x x x x=
?
A.
18 .
B.
30 .
C.
36 .
D.
45 .
Trang 9
Lời giải
Áp dụng công thức
( )
cos .cos sin .sin cosa b a b a b− = +
, ta được
sin2 .sin3 cos2 .cos3 cos2 .cos3 sin2 .sin3 0x x x x x x x x= − =
cos5 0 5 .
2 10 5
x x k x k
= = + = +
Câu 18: Rút gọn
cos cos .
44
M x x

= + − −
A.
n.2siM x=
B.
sin .2M x=−
C.
s.2coM x=
D.
cos .2M x=−
Lời giải
Áp dụng công thức
cos cos 2sin .sin
22
a b a b
ab
+−
− = −
, ta được
4 4 4 4
sin .sin
4 4 2
2s
2
co cos
x x x x
M x x

+ + − + − +
= + − −
−
=
sin .sin sin .2
4
2xx
= − = −
Câu 19: Rút gọn biểu thức
tan tanM x y=−
.
A.
( )
tan .M x y=−
B.
( )
sin
.
cos .cos
xy
M
xy
+
=
C.
( )
sin
.
cos .cos
xy
M
xy
−
=
D.
tan tan
.
1 tan .tan
xy
M
xy
−
=
+
Lời giải
Ta có
( )
sin
sin sin sin cos cos sin
tan tan .
cos cos cos cos cos cos
xy
x y x y x y
M x y
x y x y x y
−
−
= − = − = =
Câu 20: Rút gọn biểu thức
22
cos cos .
44
M


= + − −
A.
sin2 .M
=
B.
cos2 .M
=
C.
cos2 .M
=−
D.
sin2 .M
=−
Lời giải
Vì hai góc
và
4

+


phụ nhau nên
cos sin .
44


− = +
Suy ra
2 2 2 2
cos cos cos sin
4 4 4 4
M
= + − − = + − +
cos 2 sin 2 .
2


= + = −


Câu 21: Chọn đẳng thức đúng.
A.
2
1 sin
cos .
4 2 2
aa
−

+=


B.
2
1 sin
cos .
4 2 2
aa
+

+=


Trang 10
C.
2
1 cos
cos .
4 2 2
aa
−

+=


D.
2
1 cos
cos .
4 2 2
aa
+

+=


Lời giải
( )
2
1
1
1
2
cos
4 2 2 2 2
cos
sin
sin
a
a a
a

++

+−
−


+ = = =


.
Câu 22: Gọi
( )
sin
sin .sin
yx
M
xy
−
=
thì
A.
tan tan .M xy= −
B.
cot cotxyM −=
C.
cot cot .M yx= −
D.
.
sin
1
sin
1
M
xy
=−
Lời giải
Ta có :
sin .cos cos .sin sin .cos cos .sin cos cos
cot cot
sin .sin sin .sin sin .sin sin sin
y x y x y x y x x y
xy
x y x y
M
x y x y
= = − −=
−
−=
.
Câu 23: Gọi
cos cos2 cos3M x x x= + +
thì
A.
( )
2cos2 cos 1 .M x x=+
B.
1
4cos2 . cos .
2
M x x

=+


C.
( )
cos2 2cos 1 .M x x=−
D.
( )
cos2 2cos 1 .M x x=+
Lời giải
Ta có:
( )
cos cos2 cos3 cos cos3 cos2M x x x x x x= + + = + +
( )
2cos2 .cos cos2 cos2 2cos 1x x x x x= + = +
.
Câu 24: Rút gọn biểu thức
2
sin3 sin
2cos 1
xx
M
x
−
=
−
.
A.
tan2x
B.
sin .x
C.
2tan .x
D.
2sin .x
Lời giải
Ta có:
2
sin3 sin 2cos2 sin
2sin
2cos 1 cos2
x x x x
x
xx
−
==
−
.
Câu 25: Rút gọn biểu thức
2
1 cos cos2 cos3
2cos cos 1
x x x
A
xx
+ + +
=
+−
.
A.
cos .x
B.
2cos 1.x −
C.
2cos .x
D.
cos 1.x −
Lời giải
Ta có:
( ) ( )
( )
2
2
1 cos2 cos cos3
2cos 2cos2 cos
cos cos2
2cos 1 cos
x x x
x x x
A
xx
xx
+ + +
+
==
+
−+
( )
2cos cos cos2
2cos .
cos cos2
x x x
x
xx
+
==
+
Câu 26: Rút gọn biểu thức
tan cot
cos2
tan cot
A


−
=+
+
.
A.
0.
B.
2
2cos .x
C.
2.
D.
cos2 .x
Trang 11
Lời giải
Ta có :
22
22
22
22
22
sin cos sin cos
sin cos
cos sin sin .cos
sin cos cos2
sin cos
sin cos
sin cos
cos sin
sin .cos






−
−
−
= = = − = −
+
+
+
.
Do đó
cos2 cos2 0.A

− == +
Câu 27: Rút gọn biểu thức
1 sin 4 cos4
1 sin 4 cos4
A


+−
=
++
.
A.
sin2
. B.
cos2
. C.
tan2
. D.
cot2
.
Lời giải
Ta có :
( )
( )
2
2
1
2sin 2 2sin 2 cos2 2sin 2 (sin2 cos2 )
tan2
1 2cos 2 2sin 2 cos2 2cos2 (sin 2
cos4 sin 4
o2cos4 s s)in 4 c
A

−+
++
= = = =
+ + + +
.
Câu 28: Biểu thức
3 4cos2 cos4
3 4cos2 cos4
A


−+
=
++
có kết quả rút gọn bằng:
A.
4
tan .
−
B.
4
tan .
C.
4
cot .
−
D.
4
cot .
Lời giải
Ta có
( )
2
2 2 2
1cos2 1 2sin ;cos4 2cos 1 2 22 1 sin
= − = − = −−
.
Do đó:
( ) ( )
( ) ( )
2
22
2 2 4
4
2
2 2 4
22
3 4 1 2sin 2 1 2sin 1
8sin 8sin 8sin
tan
8cos 8cos 8cos
3 4 2cos 1 2 2cos 1 1
a
A
a




− − + − −
−+
= = =
−+
+ − + − −
.
Câu 29: Rút gọn biểu thức
sin sin
co co
2
12ss
A


+
=
++
.
A.
tan .
B.
2tan .
C.
tan2 tan .

+
D.
tan2 .
Lời giải
Ta có
( ) ( )
( )
2
sin 2 os 1 sin 2 os 1
sin 2 sin
= tan
1 os2 os 2 os os os 2 os 1
cc
A
c c c c c c

++
+
= = =
+ + + +
.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho biết
1
sin
3
=
và
2


. Xét tính đúng sai của các mệnh đề sau:
a)
22
cos
3
=−
b)
42
sin 2
9
=−
c)
7
cos2
9
=
d)
72
cot 2
8
=
Trang 12
Lời giải
a) Đúng:
nên cos 0.
2
Ta có:
22
1 8 2 2
cos 1 sin 1 cos
9 9 3
= − = − = = −
b) Sai:
1 2 2 4 2
sin 2 2sin cos 2
3 3 9

= = − = −



c) Đúng:
2
2
17
cos2 1 2sin 1 2
39


= − = − =


d) Sai:
sin 2 4 2 1 7 2
tan 2 cot 2
cos2 7 tan 2 8


= = − = = −
Câu 2: Cho biết
1
cos2
4
=−
và
3
2


. Xét tính đúng sai của các mệnh đề sau:
a)
sin 0,cos 0


b)
10
sin
4
=
c)
6
cos
4
=
d)
15
cot
5
=
Lời giải
a) Đúng: Vì
3
2


nên
sin 0,cos 0


.
b) Sai: Ta có:
22
1 1 5 10
cos2 1 2sin sin sin
4 4 8 4
= − − = − = = −
;
c) Sai:
2
10 6
cos 1 sin 1 ;
16 4

= − − = − − = −
d) Đúng:
sin 15 1 15
tan cot
cos 3 tan 5


= = = =
Câu 3: Cho biết
3
sin ,
52
=
. Xét tính đúng sai của các mệnh đề sau:
a)
cos 0
b)
4
cos
5
=−
c)
3
tan
4
=
Trang 13
d)
48 3
tan
3 11
−

+=


Lời giải
a) Đúng:
Vì cos 0.
2
b) Đúng: Ta có:
2
4
cos 1 sin
5

= − − = −
c) Sai:
sin 3
tan .
cos 4
= = −
d) Sai: Ta có:
tan tan
tan 3
3
tan
3
1 3 tan
1 tan tan
3

+
+

+ = =

−

−
.
Suy ra:
3
3
3 4 3 48 25 3
4
tan
3
3 11
4 3 3
13
4
−+
− + −

+ = = =


+

−−


.
Câu 4: Cho biết
12 3
sin , 2
13 2
= −
. Xét tính đúng sai của các mệnh đề sau:
a)
cos 0
b)
5
cos
13
=
c)
5
tn
1
a
2
=−
d)
53
cos
3 26
−

−=


Lời giải
a) Đúng: Ta có:
cos cos cos sin sin
3 3 3

− = +


1 3 12 1 6 3
cos cos .
2 2 13 2 13


= + − = −


Do
3
2 cos 0
2
.
b) Đúng: Ta có
2
5
cos 1 sin
13

= − =
.
c) Đúng:
12
cos 5
sin
tan
= = −
d) Sai:
1 5 6 3 5 12 3
cos
3 2 13 13 26
−

− = − =


.
Trang 14
Câu 5: Cho biết
1
sin
3
x =
và
0
2
x

. Xét tính đúng sai của các mệnh đề sau:
a)
cos 0x
b)
6
cos
3
x =
c)
3
tan
3
x =
d)
63
cos .
38
x
−

+=


Lời giải
a) Đúng: Vì
0
2
x

nên
cos 0x
.
b) Đúng: Ta có:
2
1 1 6
sin cos 1 sin 1
33
3
x x x= = − = − =
.
c) Sai:
sin 2
tan
2cos
x
==
d) Sai:
6 1 1 3 6 3
cos cos cos sin sin .
3 3 3 3 2 2 6
3
x x x
−

+ = − = − =


Câu 6: Cho biết
12
cos
13
x =−
và
3
2
x

. Xét tính đúng sai của các mệnh đề sau:
a)
sin 0x
b)
5
sin
13
x =−
c)
5
cot
12
x =
d)
5 12 3
sin
3 26
x
−

−=


Lời giải
a) Sai: Vì
3
2
x

nên
sin 0x
.
b) Đúng: Ta có:
2
2
12 12 5
cos sin 1 cos 1
13 13 13
x x x

= − = − − = − − − = −


.
c) Sai:
cosx 12
cot
sinx 5
x ==
d) Đúng:
3 12 1 5 5 12 3
sin sin cos cos sin
3 3 3 2 13 2 13 26
x x x
−
− = − = − − − =
Câu 7: Cho biết
tan 2x =
và
0 90x
. Xét tính đúng sai của các mệnh đề sau:
Trang 15
a)
cos 0x
b)
3
cos
3
x =
c)
6
sin
3
x =
d)
( )
36
cos 30
6
x
−
− =
Lời giải
a) Đúng: Vì
0 90x

nên
cos 0x
.
b) Đúng: Ta có:
22
2
1 1 3
1 tan 1 2 3 cos cos
cos 3 3
x x x
x
= + = + = = =
.
c) Đúng: Mặt khác:
sin 6
tan sin tan cos
cos 3
x
x x x x
x
= = =
.
d) Sai:
( )
3 3 6 1 3 6
cos 30 cos cos30 sin sin30
3 2 3 2 6
x x x
+
− = + + =
Câu 8: Biết
85
sin ,tan
17 12
ab==
và
a
,
b
là các góc nhọn. Xét tính đúng sai của các mệnh đề sau:
a)
8
tan
15
a =
b)
( )
21
sin
221
ab−=
c)
( )
14
cos
22
ab+=
d)
( )
17
tan .
14
ab+=
Lời giải
a) Đúng: Vì
,ab
là các góc nhọn nên
cos 0,cos 0ab
.
Ta có:
2
15 sin 8
cos 1 sin tan
17 cos 15
a
a a a
a
= − = = =
;
b) Đúng:
2
1 12 5
cos sin cos tan .
1 tan 13 13
b b b b
b
= = = =
+
Khi đó:
( )
8 12 15 5 21
sin sin cos cos sin
17 13 17 13 221
a b a b a b− = − = − =
.
c) Sai:
( )
15 12 8 5 140
cos cos cos sin sin
17 13 17 13 221
a b a b a b+ = − = − =
Trang 16
d) Sai:
( )
85
tan tan 171
15 12
tan .
85
1 tan tan 140
1
15 12
ab
ab
ab
+
+
+ = = =
−
−
Câu 9: Biết
0 , ,
24
a b a b

+ =
và
tan tan 3 2 2ab=−
. Xét tính đúng sai của các mệnh đề sau:
a)
tan tan 2 2 2. ab+ = − +
b)
tan 1 2a = − +
c)
tan 1 2b = − −
d)
tan tan 2 2 2. ab− = − −
Lời giải
a) Đúng:
( ) ( )( )
tan tan
tan tan tan tan 1 tan tan
1 tan tan
ab
a b a b a b a b
ab
+
+ = + = + −
−
mà
4
ab
+=
và
tan tan 3 2 2ab=−
tan tan tan [1 (3 2 2)] 2 2 2.
4
ab
+ = − − = − +
b) Đúng: Đặt
tan tan ; tan tanS a b P a b= + =
.
Khi đó
tan ,tanab
là nghiệm của phương trình
( )
22
0 2 2 2 3 2 2 0X SX P X X− + = − − + − =
1 2. X = − +
Suy ra
tan tan 1 2ab= = − +
.
c) Sai:
tan 1 2b = − +
d) Sai:
tan tan 0ab−=
Câu 10: Cho
2
sin ,
32
=
. Xét tính đúng sai của các mệnh đề sau:
a)
5
cos
3
=−
b)
25
tan
5
=−
c)
5 2 3
cos
36
−

+=


d)
10 2 2
cos
46
−

−=


Lời giải
a) Đúng:
2
sin ,
32
=
. Ta có:
2
22
2 5 5
cos 1 sin 1 cos
3 9 3

= − = − = =


Vì
2


nên
5
cos
3
=−
Trang 17
b) Đúng:
sin 2 5
tan
cos 5
= = −
.
c) Sai:
1 5 3 2 5 2 3
cos cos cos sin sin
3 3 3 2 3 2 3 6

− − −

+ = − = − =





d) Sai:
2 5 2 2 10 2 2
cos cos cos sin sin
4 4 4 2 3 2 3 6

− − +

− = + = + =





.
Câu 11: Cho góc
thỏa mãn
0
2
−

và
cot 3
=−
. Xét tính đúng sai của các phát biểu sau:
a)
sin 0
b)
10
sin
10
=−
c)
33
sin 10
3sin 2 21
cos
cos osc

−
=
++
d)
( )
2
2
17 7 13
t 0an tan cot cot 7
4 2 4
2

+ − + + −





=

Lời giải
a) Sai: Do
0
2
−

nên
sin 0
.
b) Đúng:
10
sin
10
=−
. Do
0
2
−

nên
sin 0
Từ hệ thức
2
2
1
1 cot
sin
+=
, suy ra
2
1 10
sin
1 cot 10
= − = −
+
.
c) Đúng:
33
sin 10
3sin 2 21
cos
cos osc

−
=
++
Xét biểu thức
33
sin
s
cos
co s2so3 in
P
c

−
=
++
Chia cả tử và mẫu cho
3
sin
ta được
( ) ( )
( )
3
3
3
22
2
32
3
1
cot 1 cot 1 cot
sin
cot 3
cos
sin
cos o
2cot 1
s
sin n
cot
32
si
P
c


−
+ − +
==
+ + +
++
Thay
cot 3
=−
vào P ta được
10
21
P =
.
d) Đúng :
( )
2
2
17 7 13
t 0an tan cot cot 7
4 2 4
2

+ − + + −





=

Trang 18
Ta có
17
tan tan 4 tan 1
4 4 4

= + = =


và
7
tan cot .
2


−=


Và
13
cot cot 3 cot 1
4 4 4

= + = =


;
( )
cot 7 cot
− = −
Suy ra
( )
2
2
17 7 13
tan tan cot cot 7
4 2 4

+ − + + −




( ) ( )
22
22
1 cot 1 cot 2 2cot 2 2.( 3) 20x x x= + + − = + = + − =
.
Câu 12: Cho
3
cos
4
a =
;
;
3
sin
5
b =
;
cos 0b
. Xét tính đúng – sai của các phát biểu sau:
a) Giá trị của
7
tan
3
a =
.
b) Giá trị của
2
cot
3
b =−
.
c) Giá trị của
cos2 cos2ab+
thuộc khoảng
1
;1
2



.
d) Giá trị của
( )
cos ab+
thuộc khoảng
11
;
23

−−


.
Lời giải
a) Đúng : Ta có
2
22
1 1 16 7
tan 1 tan 1 1
cos cos 9 3
aa
aa
+ = = − = − =
b) Sai: Ta có
2
22
1 1 25 4
cot 1 cot 1 1
sin sin 9 3
bb
ba
+ = = − − = − − = −
c) Sai :Ta có
22
9 9 81 1
cos2 cos2 2cos 1 1 2sin 2. 2. 0,405 ;1
16 25 200 2
a b a b

+ = − + − = − = =


d) Sai :
2
3
cos
7
sin 1 cos
4
4
sin 0
a
aa
a
=
= − =
và
2
3
sin
4
cos 1 sin .
5
5
cos 0
b
bb
b
=
= − − = −
Suy ra
( )
3 4 7 3 3 7 1 1
cos cos cos sin sin . . 1 ;
4 5 4 5 5 4 2 3
a b a b a b

+ = − = − − = − + − −



Câu 13: Xét tính đúng sai của các mệnh đề sau:
a)
2
1 sin 2
sin
2
x
x
+
=
b) Nếu
1
cos
3
=
thì
7
cos2
9
=−
c) Nếu
3
sin
4
x =
với
0;
2
x



thì
37
sin 2
8
x =
Trang 19
d) Cho
2
cos
3
=
với
;0
2

−


biết
tan
4
a b c

+ = +


.
( )
, , , 0a b c c
Khi đó
0abc+ + =
.
Lời giải
a) Sai:
2
1 cos2
sin
2
x
x
−
=
b) Đúng:
2
2
17
cos2 2cos 1 2 1
39

−

= − = − =


c) Đúng : Ta có
2
22
37
cos 1 sin 1
4 16
xx

= − = − =


.
Vì
0;
2
x



nên
7
cos 0 cos
4
xx =
suy ra
7 3 3 7
sin 2 2sin .cos 2
4 4 8
x x x= = =
d) Đúng: Ta có
2
2
2
1 1 5
tan 1 1
cos 4
2
3
= − = − =



Vì
;0
2

−


nên
5
tan 0 tan
2

−
=
5
tan tan 1
42
tan 9 4 5
4
5
1 tan tan
1 .1
4
2
−
++

+ = = = − +



−
−
−


Vậy
9, 4, 5a b c= − = =
nên mệnh đề đúng.
Câu 14: Xét tính đúng sai của các phát biểu sau:
a)
( )
sin sin cos cos sina b a b a b+ = +
.
b)
0 0 0 0 0
sin31 .cos12 cos12 .sin31 sin19 .+=
c)
Cho
4
cos , ;0
52
xx

= −


. Giá trị của
sin2x
là
24
25
−
.
d) Cho
1
sin
3
=
và
2


. Biết giá trị của
16
cos
6
a
b
−

−=


với
,ab
thì
4ab+=
.
Lời giải
a) Đúng: Theo công thức cộng
( )
sin sin cos cos sina b a b a b+ = +
b) Sai: Áp dụng công thức cộng:
( )
0 0 0 0 0 0 0
sin31 .cos12 cos12 .sin31 sin 31 12 sin 43+ = + =
Trang 20
c)
Đúng : Ta có
22
16 9
sin 1 cos 1
25 25
xx= − = − =
3
sin
5
x = −
.
Mặt khác, vì
;0 sin 0
2
xx

−


.
Vậy
4 3 24
sin 2 2sin .cos 2. .
5 5 25
x x x

= = − = −


.
d) Vì
1
sin ,
32
=
nên
22
cos
3
=−
.
Do đó
2 2 3 1 1 1 2 6
cos cos .cos sin .sin . .
6 6 6 3 2 3 2 6
−

− = + = − + =


.
với
2, 6ab==
. Tính
8ab+=
. Nên
4ab+=
là sai.
Câu 15: Xét tính đúng sai của các đẳng thức sau:
a)
31
sin sin cos
6 2 2
x x x

− = +


.
b)
4sin .sin2 .sin3 sin4 sin2 sin6x x x x x x= + −
.
c)
1 sin 2 cos2 2 2 sin .cos .
4
x x x x

+ + = −


.
d)
( ) ( )
2 2 2
sin 2sin .sin .cos sin cosx a x x a a x a+ − + − =
.
Lời giải
a) Sai: Theo công thức cộng ta có
31
sin sin .cos cos .sin sin cos .
6 6 6 2 2
x x x x x

− = − = −


b) Đúng: Áp dụng quy tắc từ tích sang tổng, ta được:
( )
4sin .sin2 .sin3 2 cos cos3 sin3 sin4 sin2 sin6x x x x x x x x x= − = + −
.
Do đó
4sin .sin2 .sin3 sin4 sin2 sin6x x x x x x= + −
c) Sai: Ta có
2
1 sin2 cos2 2sin cos 2cos 2cos (sin cos )x x x x x x x x+ + = + = +
.
Mà
11
sin cos 2 cos sin 2 cos .
4
22
x x x x x


+ = + = −




d) Ta có:
( ) ( )
22
sin 2sin .sin .cos sinx a x x a a x+ − + −
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
22
2
2
sin sin . sin sin sin
sin sin . sin sin sin
sin sin . sin sin sin
x a x x a x a a x
x a x x a x a a x
x a x x a x a x a
= + − + + − + −


= + − + + − + −


= + − + + − − −



Tài liệu khác của Toán 11

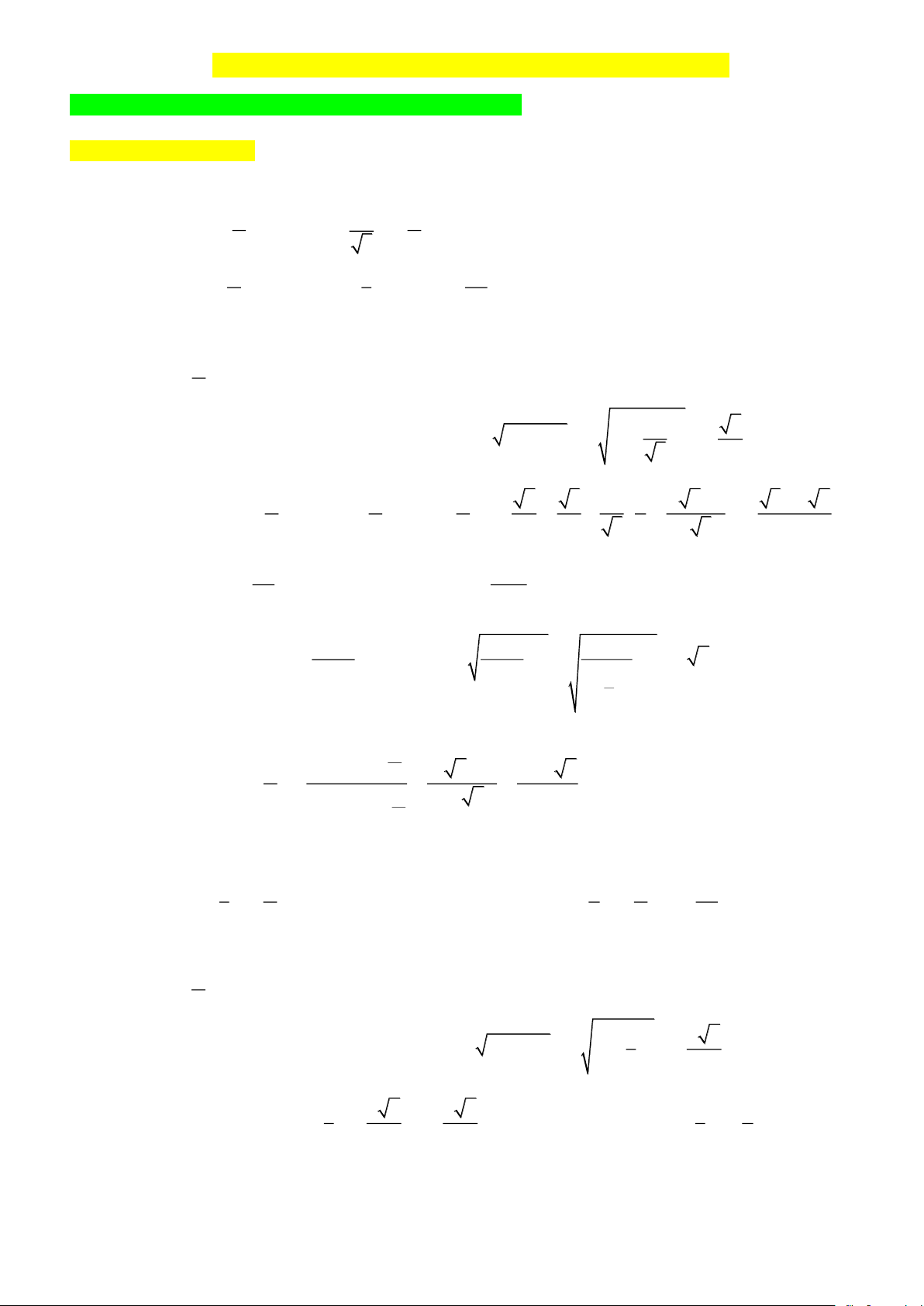
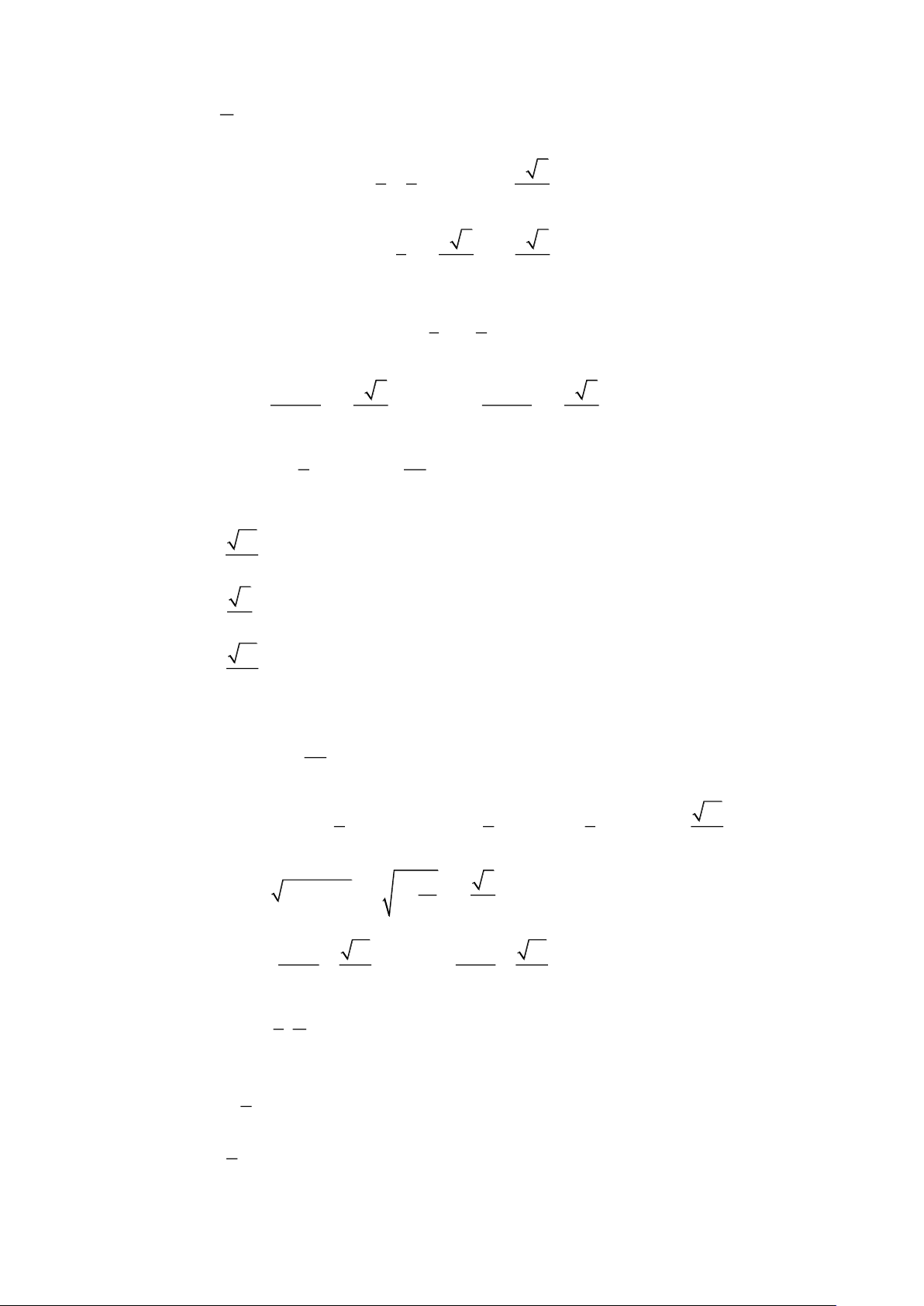
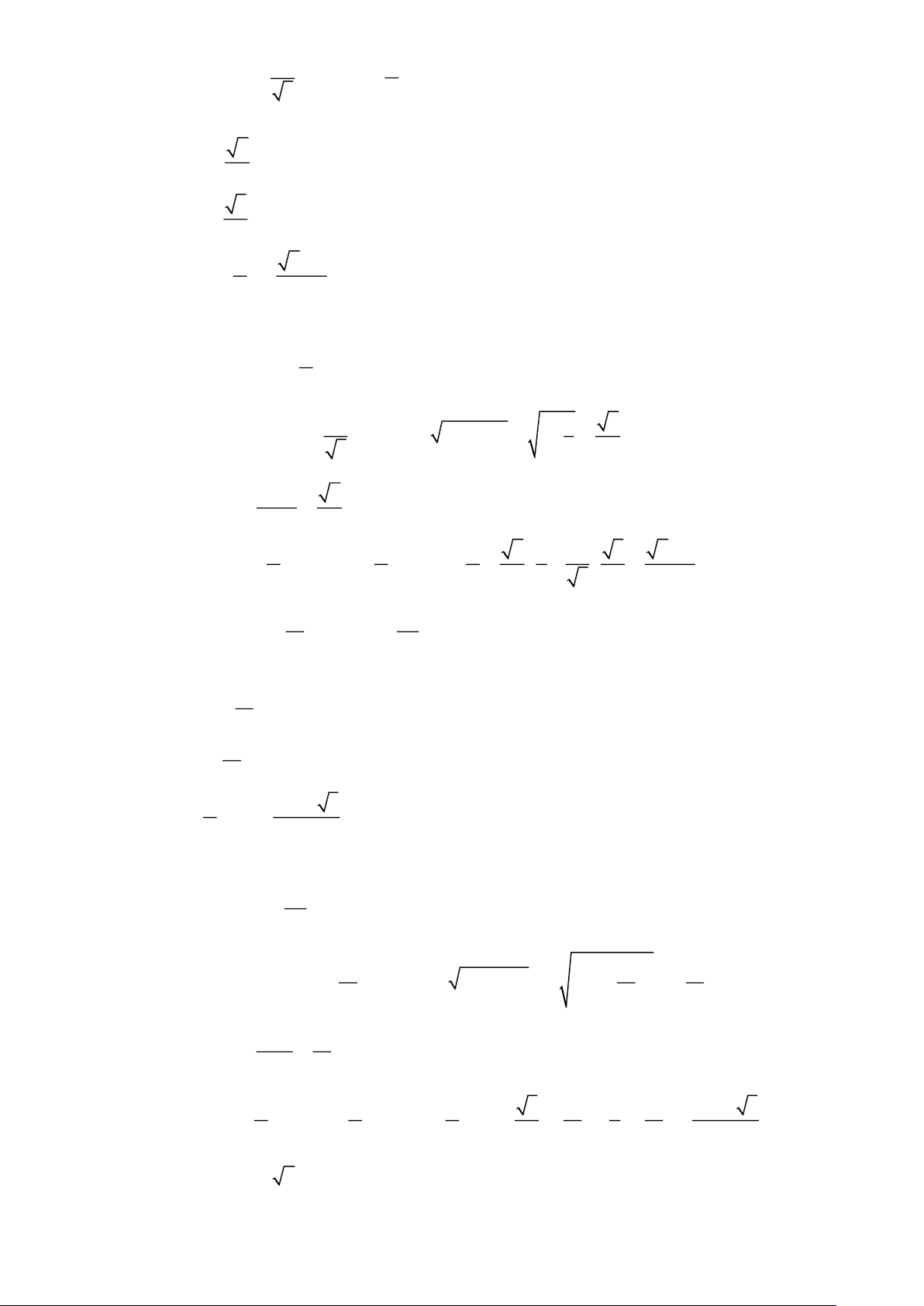
Preview text:


CÁC DẠNG TOÁN BÀI CÔNG THỨC LƯỢNG GIÁC
Dạng 1: Tính giá trị biểu thức chứa các giá trị lượng giác
Phương pháp: Sử dụng các công thức lượng giác để giải quyết bài toán A. BÀI TẬP TỰ LUẬN Bài tập 1: Tính:    1  a) cos a +   biết sina = và  a    6  3 2    1 3 b) tan a − 
 biết cosa = − và   a  4  3 2 Lời giải  a) Vì
a   nên cosa  0 . 2 2  1  6 Mặt khác, từ 2 2 sin a + cos a = 1 suy ra 2
cosa = − 1− sin a = − 1− = − .    3  3       6  3 1 1 − 6 −1 3 + 3 2 Ta có: cos a + = cos c a os − sin sin a =    −   −  = = − . 6 6 6  3    2 3 2 2 3 6   3 sina b) Vì   a
nên sina  0 , do đó tana =  0 . 2 cosa 1 1 1 Mặt khác: 2 1 + tan a = suy ra tana = −1 = −1 = 2 2 . 2 cos a 2 2 cos a  1  −    3   tana − tan    2 2 −1 9 − 4 2 Ta có: 4 tan a − = = =   .  4   1+ 2 2.1 7 1+ tana tan 4
Bài tập 2: Tính sin sin 2a; cos2a; tan2a , biết: 1  1  3 a) sina = và  a  
b) sina + cos a = và  a  3 2 2 2 4 Lời giải  a) Vì
a   nên cosa  0 . 2 2  1  2 2 Mặt khác: 2 2
sin a + cos a = 1 suy ra 2
cosa = − 1− sin a = − 1− = −    3  3 1  2 2  4 2 2  1  7 sin2a = 2sin c
a osa = 2    −  = − ; 2
cos2a = 1− 2sin a = 1− 2. = .   3  3  9    3  9 Trang 1 4 2 − sin2a 4 2 Suy ra 9 tan2a = = = − . cos2a 7 7 9 2  1  1
b) Ta có: (sina + cosa)2 2 2 =
 sin a + cos a + 2sin c a osa =    2  4 1 3
 1+ sin2a =  sin2a = − . 4 4  3 3 Vì  a  nên   2a  . Do đó cos2a  0. 2 4 2 2  3  7 Mặt khác: 2 ( a) 2
sin 2 + cos (2a) =1 suy ra 2
cos2a = − 1− sin (2a) = − 1− − = −   .  4  4 3 − sin2a 3 3 7 Do đó: 4 tan2a = = = = . cos2a 7 7 7 − 4
Bài tập 3: Tính giá trị của các biểu thức sau: 1  1  3 a) sina = và
a   b) sina + cosa = và  a  3 2 2 2 4 Lời giải         sin cos + sin cos sin cos + cos sin a) Ta có: 15 10 10 15 15 10 15 10 A = = 2  2  2  2  cos cos − sin sin cos cos − sin sin 15 5 15 5 15 5 15 5      1 sin +   sin 15 10  6 2 = = = = 1  2    1 cos + cos    15 5  3 2      1      b) Ta có: B = sin cos cos cos =  2sin cos cos cos   32 32 16 8  2 32 32  16 8 1      1    = sin 2  cos cos = sin cos cos   2  32  16 8 2 16 16 8 1    1   1   1  1 2 2 =  2sin cos cos
= sin cos =  2sin cos = sin =  = 4 16 16 8 4 8 8 8 8 8 8 4 8 2 16
Bài tập 4: Rút gọn các biểu thức sau:
a) A = sin(x +14)sin(x + 74) + sin(x − 76)sin(x −16) Trang 2
sin(a − b) sin(b − c) sin(c − a) b) B = + + cos . a cosb cos . b cosc cos . c cos a Lời giải
a) Ta có A = sin(14 + x)cos(16 − x) + sin(76 − x)sin(16 − x)
= sin(14 + x)cos(16 − x) + cos(14 + x)sin(16 − x) =
(  +  + x − x) 1 sin 14 16 = sin30 = . 2
sin(a − b) sin(b − c) sin(c − a) b) A = + + cos . a cosb cos . b cosc cos . c cos a sin . a cosb − sin . b cos a sin . b cosc − sin . c cosb sin . c cosa − sin . a cosc Ta có: A = + + cos . a cosb cos . b cosc cos . c cosa sin . a cosb sin . b cos a sin . b cosc sin . c cosb sin . c cos a sin . a cosc = − + − + − cos . a cosb cos . a cosb cos . b cosc cos . b cosc cos . c cos a cos . c cosa
= tana − tanb + tanb − tanc + tanc − tana = 0 .
Bài tập 5: Không dùng máy tính cầm tay. Hãy tính các giá trị lượng giác sau: 7 a) 0 cos795 b) tan 12 Lời giải a) Tính 0 cos795 Vì 0 0 0 0 0 0
795 = 75 + 2.360 = 30 + 45 + 2.360 nên 3 2 1 2 6 − 2 0 0 0 0 0 0
cos795 = cos75 = cos30 cos 45 − sin 30 sin 45 = . − . = 2 2 2 2 4 7 b) Tính tan 12   tan + tan 7     3 +1 3 4 tan = tan + = = = 2 − − 3   12  3 4    1− 3 1− tan tan 3 4   Bài tập 6: Tính 4 4 A = cos − sin 12 12 Lời giải           3 Ta có: 2 2 2 2 2 2 A = cos − sin cos + sin = cos − sin = cos =    .  12 12  12 12  12 12 6 2 4        
Bài tập 7: Cho cos 2x = − , với
x  . Tính sin x,cos x,sin x + ,cos 2x −     . 5 4 2  3   4  Lời giải Trang 3   Vì
x  nên sin x  0, cos x  0 . 4 2
Áp dụng công thức hạ bậc, ta có : 1− cos 2x 9 3 1+ cos 2x 1 1 2 sin x = =  sin x = ; 2 cos x = =  cos x = 2 10 10 2 10 10
Theo công thức cộng, ta có      3 1 1 3 3 + 3 30 + 3 10 sin x +
= sin xcos + cos xsin = . + . = =    3  3 3 10 2 10 2 2 10 20      4 2 2 3 1 2 cos 2x −
= cos2xsin + cos sin 2x = − . + .2. . = −   .  4  4 4 5 2 2 10 10 10
Bài tập 8: Rút gọn các biểu thức sau:  2 sin − sin  5 7 a) 5 15 A = = − +  b) B sin sin sin 2 cos − cos 9 9 9 5 15 Lời giải  2 1   2  1   2   sin − sin 2cos + sin −     cos 5 15 2  5 15  2  5 15   a) 6 C = = = − = −cot = − 3  2 1   2  1   2   6 cos − cos 2 − sin + sin − sin 5 15     2  5 15  2  5 15  6   7  5 4  5 4 5 b) D = sin + sin − sin = 2sin .cos − sin = sin − sin = 0   .  9 9  9 9 3 9 9 9
Bài tập 9: Đơn giản biểu thức sau:
cos a + 2cos 2a + cos3a a) A =
sin a + sin 2a + sin 3a       cos a + + cos a −      3   3 b) B  = a cot a − cot 2
c) C = cosa + cos(a + b) + cos(a + 2b) +...+ cos(a + nb) (n  ) Lời giải
(cosa + cos3a) + 2cos2a 2cos2acosa + 2cos2a 2cos2a(cosa + ) 1 a) A = ( = = = a + a) + a a a + a a( a + ) cot 2a sin sin 3 2sin 2 2sin 2 cos 2sin 2 2sin 2 cos 1        b) Ta có cos a + + cos a −
= 2cosacos = cosa     và  3   3  3 a a aaa cos
sin cos a − cos sin a sin − a   −sin a cos a 2 2 2  2  1 2 cot a − cot = − = = = = − 2 sin a a a a a sin sin sin sin sin sin sin sin a a a a 2 2 2 2 Trang 4 cos a sin 2a Suy ra B =
= −sin acosa = − . 1 2 − sina b b b b b
c) Ta có C.2sin = 2sin cos a + 2sin cos(a + b) + 2sin cos(a + 2b) + ... + 2sin cos(a + nb) 2 2 2 2 2  b   b   3b   b   5b   3b  = sin + a + sin − a + sin
+ a + sin − − a + sin + a + sin − − a              2   2   2   2   2   2   (2n + ) 1 b   (2n − ) 1 b  . + .. + sin + a  + sin− − a 2 2      b   (2n + ) 1 b   nb  sin − a + sin   
+ a = 2sin(n + ) 1 bcos − a    2  2    2   nb  sin (n + ) 1 bcos − a    2 Suy ra C  = b sin 2
B. BÀI TẬP TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. 0
Câu 1: Tính sin105 ta được: 6 − 2 6 − 2 6 + 2 6 + 2 A. . B. − . C. . D. − . 4 4 4 4 Lời giải Có: 0 = ( 0 0 sin105 sin 60 + 45 ) = 0 0 0 0
sin 60 .cos 45 + cos60 .sin 45 . 3 2 1 2 6 + 2  0 sin105 = . + . = . 2 2 2 2 4 0
Câu 2: Tính tan105 ta được: A. −(2 + 3) . B. 2 + 3 . C. 2 − 3 .
D. −(2 − 3). Lời giải 6 + 2 0 + 0 sin105 tan105 = = 4 = 6 2 − = −(2 + 3) . 0 cos105 6 − 2 − 6 − 2 4
Câu 3: Rút gọn biểu thức: 0 0 0 0
cos54 cos 4 − cos36 cos86 , ta được: A. 0 cos50 . B. 0 cos58 . C. 0 sin 50 . D. 0 sin 58 . Lời giải Ta có: 0 0 0 0 0 0 0 0 − = − = ( 0 0 cos54 cos 4 cos36 cos86 cos54 cos 4 sin 54 sin 4 cos 54 + 4 ) 0 = cos58 Trang 5      
Câu 4: Rút gọn biểu thức cos x + − cos x  
 −  ta được  4   4 
A. 2 sin x . B. − 2 n si x .
C. 2 cos x . D. − 2 s co x . Lời giải         x + + x − x + − x      +      Ta có: cos x + − cos x − =−2 4 4 4 4 sin      .sin   4   4  2 2          =−2sin . x sin =− 2 sin x 4 37
Câu 5: Giá trị của biểu thức cos bằng 12 6 + 2 6 − 2 6 + 2 2 − 6 A. . B. . C. – . D. . 4 4 4 4 Lời giải 37   7    7  Ta có: cos = cos + + 2 = cos +     12  2 12   2 12   7  7 6 + 2 = cos cos − sin sin = − 2 12 2 12 4 4 o 4 o
Câu 6: Rút gọn biểu thức M = cos 15 − sin 15 . 3 1 A. M =1. B. M = . C. M = . D. M = 0. 2 4 Lời giải 2 2 Ta có 4 o 4 o M = − = ( 2 o ) − ( 2 o cos 15 sin 15 cos 15 sin 15 ) = ( 3 2 o 2 o − )( 2 o 2 o cos 15 sin 15 cos 15 + sin 15 ) 2 o 2 o = cos 15 − sin 15 = cos( o 2.15 ) o = cos30 = . 2
Câu 7: Tính giá trị của biểu thức 0 0 0 0
M = cos10 cos 20 cos 40 cos80 . 1 1 1 1 A. 0 M = cos10 . B. 0 M = cos10 . C. 0 M = cos10 . D. 0 M = cos10 . 16 2 4 8 Lời giải Vì 0 sin10  0 nên suy ra 0 0 0 0 0
16sin10 cos10 cos 20 cos 40 cos80 0 0 0 0 8sin 20 cos 20 cos 40 cos80 M = = 0 16sin10 0 16sin10 0 0 0 0 0 0  4sin 40 cos 40 cos80 2sin80 cos80 sin160 M = = = . 0 16sin10 0 16sin10 0 16sin10 0 0 0 1  sin 20 2sin10 cos10 M = = = 0 cos10 . 0 16sin10 0 16sin10 8 Trang 6
Câu 8: Công thức nào sau đây sai?
A. cos(a − b) = sinasinb + cosacos . b
B. cos(a + b) = sinasinb − cosacos . b
C. sin(a − b) = sinacosb − cosasin . b
D. sin(a + b) = sinacosb + cosasin . b Lời giải
Ta có cos(a + b) = cosacosb − sinasinb.
Câu 9: Khẳng định nào sai trong các khẳng định sau? A. 2 2
cos6a = cos 3a − sin 3 . a B. 2 cos6a = 1− 2sin 3 . a C. 2 cos6a = 1− 6sin . a D. 2
cos6a = 2cos 3a −1. Lời giải Áp dụng công thức 2 2 2 2
cos 2 = cos  − sin  = 2cos  −1 = 1− 2sin  , ta được 2 2 2 2
cos6a = cos 3a − sin 3a = 2cos 3a −1 = 1− 2sin 3a .
Câu 10: Khẳng định nào sai trong các khẳng định sau? 1− cos 2x 1+ cos 2x A. 2 sin x = . B. 2 cos x = . 2 2 x x
C. sin x = 2sin cos . D. 3 3
cos3x = cos x − sin . x 2 2 Lời giải Ta có 3
cos3x = 4cos x − 3cos x .
Câu 11: Khẳng định nào đúng trong các khẳng định sau?      
A. sin a + cos a = 2 sin a − .  
B. sin a + cos a = 2 sin a + .    4   4       
C. sin a + cos a = − 2 sin a − .  
D. sin a + cos a = − 2 sin a + .    4   4  Lời giải   
Ta có: sin a + cos a = 2 sin a + .    4 
Câu 12: Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?      
1) cos x − sin x = 2 sin x + .  
2) cos x − sin x = 2 cos x + .    4   4       
3) cos x − sin x = 2 sin x − .  
4) cos x − sin x = 2 sin − x .    4   4  A. 1. B. 2. C. 3. D. 4. Lời giải          
Ta có cos x − sin x = 2 cos x + = 2 cos − − x = 2 sin − x        .  4   2  4   4 
Câu 13: Nếu cos(a + b) = 0 thì khẳng định nào sau đây đúng? Trang 7
A. sin (a + 2b) = sin a .
B. sin (a + 2b) = sinb .
C. sin (a + 2b) = cosa .
D. sin (a + 2b) = cosb . Lời giải  
Ta có : cos(a + b) = 0  a + b = + k → a = b − + + k . 2 2   
 sin(a + 2b) = sin b
− + 2b + + k = cos  
(b + k ) = cosb .  2 
Câu 14: Nếu sin(a + b) = 0 thì khẳng định nào sau đây đúng?
A. cos(a + 2b) = sin a .
B. cos(a + 2b) = sinb .
C. cos(a + 2b) = cosa .
D. cos(a + 2b) = cosb . Lời giải
Ta có sin(a + b) = 0  a + b = k → a = b − + k .
 cos(a + 2b) = cos( b
− + 2b + k ) = cos(b + k ) = cosb .
M = sin(x − y)cos y + cos(x − y) Câu 15: Rút gọn sin . y A. M = cos . x B. M = sin . x
C. M = sin x cos 2 . y
D. M = cos xcos 2 . y Lời giải
Áp dụng công thức sin(a + b) = sinacosb + sinbcosa , ta được
M = sin ( x − y)cos y + cos( x − y)sin y = sin (x − y) + y = sin .x
M = cos(a + b)cos(a − b) − sin(a + b)sin(a − b). Câu 16: Rút gọn A. 2 M = 1− 2cos . a B. 2 M = 1− 2sin . a C. M = cos4 . a D. M = sin4 . a Lời giải
Áp dụng công thức cos xcos y − sin xsin y = cos(x + y) , ta được M =
(a +b) (a −b) − (a +b) (a −b) =
(a +b + a −b) 2 cos cos sin sin cos = cos2a =1− 2sin . a
M = cos(a + b)cos(a − b) + sin(a + b)sin(a − b). Câu 17: Rút gọn A. 2 M = 1− 2sin . b B. 2 M = 1+ 2sin . b C. M = cos4 . b D. M = sin4 . b Lời giải
Áp dụng công thức cos xcos y + sin xsin y = cos(x − y) , ta được
M = cos(a + b)cos(a − b) + sin(a + b)sin(a − b) =
(a +b − a −b ) 2 cos ( ) = cos2b =1− 2sin . b
Câu 17: Giá trị nào sau đây của x thỏa mãn sin2 . x sin3x = cos2 .
x cos3x ? A. 18 .  B. 30 .  C. 36 .  D. 45 .  Trang 8 Lời giải Áp dụng công thức cos . a cosb − sin .
a sinb = cos(a + b), ta được sin2 . x sin3x = cos2 .
x cos3x  cos2 .
x cos3x − sin2 . x sin3x = 0   
 cos5x = 0  5x = + k  x = + k . 2 10 5       M = cos x + − cos x − .     Câu 18: Rút gọn  4   4  A. M = 2 n si . x
B. M = − 2 sin . x C. M = 2 s co . x
D. M = − 2 cos . x Lời giải a + b a − b
Áp dụng công thức cos a − cosb = 2 − sin .sin , ta được 2 2         x + + x − x + − x      +   4 4   4 4  M = c s o x + − cos x − = 2 − sin      .sin   4   4   2   2   = 2 − sin . x sin = − 2 sin . x 4
Câu 19: Rút gọn biểu thức M = tan x − tan y . sin ( x + y)
A. M = tan(x − y). B. M = . cos . x cos y sin ( x − y) tan x − tan y C. M = . D. M = . cos . x cos y 1 + tan . x tan y Lời giải sin x sin y
sin xcos y − cos xsin y sin( x − y)
Ta có M = tan x − tan y = − = = . cos x cos y cos xcos y cos xcos y      2 2  M = cos +  − cos −  .    
Câu 20: Rút gọn biểu thức  4   4 
A. M = sin2.
B. M = cos2.
C. M = −cos2.
D. M = −sin 2. Lời giải             Vì hai góc −    và +    phụ nhau nên cos − = sin +  .      4   4   4   4              Suy ra 2 2 2 2 M = cos +  − cos − = cos +  − sin +           4   4   4   4     = cos + 2 = −sin 2.    2 
Câu 21: Chọn đẳng thức đúng.   a  1− sin a   a  1+ sin a A. 2 cos + = .   B. 2 cos + = .    4 2  2  4 2  2 Trang 9   a  1− cos a   a  1+ cos a C. 2 cos + = .   D. 2 cos + = .    4 2  2  4 2  2 Lời giải    1+ cos + a   a     2 1+ sin −a  1− sin a 2 ( ) cos + = = =   .  4 2  2 2 2 sin( y − x) M = Câu 22: Gọi sin . x sin y thì 1 1
A. M = tan x − tan . y
B. M = cot x − cot y C. M = cot y − cot . x D. M = − . sin x sin y Lời giải sin .
y cos x − cos . y sin x sin . y cos x cos . y sin x cos x cos y Ta có : M = = − = −
= cot x − cot y . sin . x sin y sin . x sin y sin . x sin y sin x sin y
Câu 23: Gọi M = cos x + cos2x + cos3x thì  1 
A. M = 2cos2x(cos x + ) 1 . B. M = 4cos 2 . x + cos x .    2 
C. M = cos2x(2cos x − ) 1 .
D. M = cos2x(2cos x + ) 1 . Lời giải
Ta có: M = cos x + cos2x + cos3x = (cos x + cos3x) + cos2x = 2cos2 .
x cos x + cos2x = cos2x(2cos x + ) 1 . sin 3x − sin x M =
Câu 24: Rút gọn biểu thức 2 2cos x −1 .
A. tan 2x B. sin . x C. 2tan . x D. 2sin . x Lời giải sin 3x − sin x 2cos 2xsin x Ta có: = = 2sin x . 2 2cos x −1 cos 2x
1+ cos x + cos 2x + cos3x A =
Câu 25: Rút gọn biểu thức 2
2cos x + cos x −1 . A. cos . x B. 2cos x −1. C. 2cos . x D. cos x −1. Lời giải
(1+ cos2x) + (cos x + cos3x) 2
2cos x + 2cos 2xcos x Ta có: A = ( = 2 2cos x − ) 1 + cos x cos x + cos 2x
2cos x(cos x + cos2x) = = 2cos . x cos x + cos 2x tan − cot A = + cos2
Câu 26: Rút gọn biểu thức tan + cot . A. 0. B. 2 2cos . x C. 2. D. cos2 . x Trang 10 Lời giải 2 2 sin cos sin  − cos  − 2 2 sin      − cos  Ta có : cos sin sin .cos 2 2 = =
= sin  − cos  = −cos2 . 2 2 2 2 sin cos sin  + cos  sin  + cos  + cos sin sin.cos
Do đó A = −cos2 + cos2 = 0. 1+ sin 4 − cos 4 A =
Câu 27: Rút gọn biểu thức 1+ sin 4 + cos 4 . A. sin 2 . B. cos2 . C. tan 2 . D. cot 2 . Lời giải Ta có : (1− cos4 ) 2 + sin 4 2sin 2 + 2sin 2 cos 2 2sin 2(sin 2 + cos 2) A = ( = = =  . 1+ cos 4 ) tan 2 2 + sin 4 2cos 2 + 2sin 2 cos 2 2cos 2(sin 2 + o c s 2 ) 3 − 4cos 2 + cos 4
Câu 28: Biểu thức A =
có kết quả rút gọn bằng: 3 + 4cos 2 + cos 4 A. 4 − tan . B. 4 tan . C. 4 −cot . D. 4 cot . Lời giải
Ta có cos2 =1− 2sin ;cos4 = 2cos 2 −1 = 2(1− 2sin  )2 2 2 2 −1.
3 − 4(1− 2sin  ) + 2(1− 2sin  )2 2 2 2 2 4 −1
8sin a − 8sin  + 8sin  Do đó: 4 A = . + ( = =  − ) + (  − ) tan  2 2 2 4 2 2 8cos a − 8cos −  + 8cos 3 4 2cos 1 2 2cos 1 1  sin 2 + sin A =
Câu 29: Rút gọn biểu thức 1+ cos 2 + cos . A. tan. B. 2tan.
C. tan2 + tan. D. tan 2. Lời giải sin 2 + sin sin (2 os c  + ) 1 sin (2 os c  + ) 1 Ta có A = = = = tan . 2 1+ os c 2 + os c  2 os c  + os c  os c  (2 os c  + ) 1
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. 1 
Câu 1: Cho biết sin = và
    . Xét tính đúng sai của các mệnh đề sau: 3 2 2 2 a) cos = − 3 4 2 b) sin 2 = − 9 7 c) cos 2 = 9 7 2 d) cot 2 = 8 Trang 11 Lời giải  a) Đúng:
    nên cos  0. 2 1 8 2 2 Ta có: 2 2
cos  = 1− sin  = 1− =  cos = − 9 9 3 1  2 2  4 2
b) Sai: sin 2 = 2sin cos = 2    −  = − 3  3  9   2 1 7 c) Đúng: 2 cos 2 1 2sin    = − = 1− 2 =    3  9 sin 2 4 2 1 7 2 d) Sai: tan 2 = = −  cot 2 = = − cos 2 7 tan 2 8 1 3
Câu 2: Cho biết cos 2 = − và    
. Xét tính đúng sai của các mệnh đề sau: 4 2 a) sin  0,cos  0 10 b) sin = 4 6 c) cos = 4 15 d) cot = 5 Lời giải 3 a) Đúng: Vì    
nên sin  0,cos  0. 2 1 1 5 10 b) Sai: Ta có: 2 2
cos 2 = −  1− 2sin  = −  sin  =  sin = − ; 4 4 8 4 10 6 c) Sai: 2
cos = − 1− sin  = − 1− = − ; 16 4 sin 15 1 15 d) Đúng: tan = =  cot = = cos 3 tan 5 3 
Câu 3: Cho biết sin = ,
    . Xét tính đúng sai của các mệnh đề sau: 5 2 a) cos  0 4 b) cos = − 5 3 c) tan = 4 Trang 12    48 3 d) tan  − + =    3  11 Lời giải  a) Đúng: Vì
     cos  0. 2 4 b) Đúng: Ta có: 2
cos = − 1− sin  = − 5 sin 3 c) Sai: tan = = − . cos 4  tan + tan    tan + 3 d) Sai: Ta có: 3 tan  + = =   .  3   1− 3 tan 1− tan tan   3 3 − + 3    3 − + 4 3 48 − 25 3 Suy ra: 4 tan  + = = =   .  3   3  4 + 3 3 11 1− 3 −    4  12 3
Câu 4: Cho biết sin = − ,
   2 . Xét tính đúng sai của các mệnh đề sau: 13 2 a) cos  0 5 b) cos = 13 12 c) t n a  = − 5    5 3 d) cos − − =    3  26 Lời giải      1 3  12  1 6 3 a) Đúng: Ta có: cos
−  = cos cos + sin sin   = cos +  − = cos − .  3  3 3   2 2  13  2 13 3 Do
   2  cos  0. 2 5 b) Đúng: Ta có 2 cos = 1− sin  = . 13 sin 12 c) Đúng: tan = = − cos 5    1 5 6 3 5 12 3 d) Sai: cos − − =  − =   .  3  2 13 13 26 Trang 13 1 
Câu 5: Cho biết sin x = và 0  x
. Xét tính đúng sai của các mệnh đề sau: 3 2 a) cos x  0 6 b) cos x = 3 3 c) tan x = 3    6 − 3 d) cos x + = .    3  8 Lời giải
a) Đúng: Vì 0  x  nên cos x  0. 2 1 1 6 b) Đúng: Ta có: 2 sin x =
 cos x = 1− sin x = 1− = . 3 3 3 sin 2 c) Sai: tan x = = cos 2      6 1 1 3 6 − 3 d) Sai: cos x +
= cos xcos − sin xsin =  −  = .    3  3 3 3 2 3 2 6 12 3
Câu 6: Cho biết cos x = − và   x
. Xét tính đúng sai của các mệnh đề sau: 13 2 a) sin x  0 5 b) sin x = − 13 5 c) cot x = 12    5 −12 3 d) sin − x =    3  26 Lời giải 3
a) Sai: Vì   x  nên sin x  0. 2 2 12  12  5 b) Đúng: Ta có: 2 cos x = −
 sin x = − 1− cos x = − 1− − = −   . 13  13  13 cosx 12 c) Sai: cot x = = sinx 5     
3  12  1  5  5 −12 3 d) Đúng: sin
− x = sin cos x − cos sin x = − − − =        3  3 3 2  13  2  13  26
Câu 7: Cho biết tan x = 2 và 0  x  90. Xét tính đúng sai của các mệnh đề sau: Trang 14 a) cos x  0 3 b) cos x = 3 6 c) sin x = 3 − d) (x − ) 3 6 cos 30 = 6 Lời giải
a) Đúng: Vì 0 x 90   nên cos x  0. 1 1 3 b) Đúng: Ta có: 2 2
= 1+ tan x = 1+ 2 = 3  cos x =  cos x = . 2 cos x 3 3 sin x 6
c) Đúng: Mặt khác: tan x =
 sin x = tan xcos x = . cos x 3 + d) Sai: (x  − )   3 3 6 1 3 6 cos
30 = cos x cos30 + sin xsin 30  +  = 3 2 3 2 6 8 5
Câu 8: Biết sin a = , tan b =
và a , b là các góc nhọn. Xét tính đúng sai của các mệnh đề sau: 17 12 8 a) tan a = 15 b) (a − b) 21 sin = 221 c) (a + b) 14 cos = 22 d) (a + b) 17 tan = . 14 Lời giải
a) Đúng: Vì a,b là các góc nhọn nên cos a  0,cosb  0 . 15 sin a 8 Ta có: 2
cos a = 1− sin a =  tan a = = ; 17 cos a 15 1 12 5 b) Đúng: cosb = =
 sinb = cosbtanb = . 2 1+ tan b 13 13 Khi đó: (a − b) 8 12 15 5 21 sin
= sin acosb − cosasinb =  −  = . 17 13 17 13 221 c) Sai: (a + b) 15 12 8 5 140 cos
= cosacosb − sin asinb =  −  = 17 13 17 13 221 Trang 15 8 5 + tan a + tan b 171 d) Sai: (a + b) 15 12 tan = = = . 1− tan a tan b 8 5 140 1−  15 12  
Câu 9: Biết 0  a,b  ,a + b =
và tan a tanb = 3 − 2 2 . Xét tính đúng sai của các mệnh đề sau: 2 4
a) tan a + tanb = 2 − + 2 2. b) tan a = 1 − + 2 c) tanb = 1 − − 2
d) tan a − tanb = 2 − − 2 2. Lời giải tan a + tan b
a) Đúng: tan (a + b) =
 tan a + tanb = tan(a + b)(1− tan a tanb) mà a + b = và 1− tan a tan b 4 
tan a tanb = 3 − 2 2  tan a + tan b = tan [1− (3 − 2 2)] = 2 − + 2 2. 4
b) Đúng: Đặt S = tan a + tan ;
b P = tan a tanb .
Khi đó tan a, tan b là nghiệm của phương trình 2 2
X − SX + P = 0  X − (2 2 − 2) X + 3− 2 2 = 0  X = 1 − + 2.
Suy ra tan a = tanb = 1 − + 2 . c) Sai: tanb = 1 − + 2
d) Sai: tana − tanb = 0 2  Câu 10: Cho sin = ,
    . Xét tính đúng sai của các mệnh đề sau: 3 2 5 a) cos = − 3 2 5 b) tan = − 5    5 2 3 c) cos +  − =    3  6    10 2 2 d) cos − − =    4  6 Lời giải 2  2  2  5 5 a) Đúng: sin = ,     . Ta có: 2 2 cos  = 1− sin  = 1− =  cos =    3 2  3  9 3  5 Vì
    nên cos = − 2 3 Trang 16 sin 2 5 b) Đúng: tan = = − . cos 5      1  − 5  3 2 − 5 − 2 3 c) Sai: cos
+  = cos cos − sin sin =      −  = 3 3 3 2  3    2 3 6        2  − 5  2 2 − 10 + 2 2 d) Sai: cos
− = cos cos + sin sin =      +  = . 4 4 4 2  3    2 3 6    −
Câu 11: Cho góc  thỏa mãn    0 và cot = 3
− . Xét tính đúng sai của các phát biểu sau: 2 a) sin  0 10 b) sin = − 10 cos − sin 10 c) = 3 3 cos  + 3sin  + 2 os c  21 2 2  17  7   13  d) tan + tan − + cot + cot    (7 − ) = 0 2  4 2    4    Lời giải  − a) Sai: Do
   0 nên sin  0. 2 10  − b) Đúng: sin = − . Do
   0 nên sin  0 10 2 1 1 10 Từ hệ thức 2 1+ cot  = , suy ra sin = − = − . 2 sin  2 1+ cot  10 cos − sin 10 c) Đúng: = 3 3 cos  + 3sin  + 2 os c  21 cos − sin Xét biểu thức P = 3 3
cos  + 3sin  + 2c s o  cos 1 − 2 2 3 2 cot sin   (1+cot )−(1+cot sin   ) Chia cả tử và mẫu cho 3 sin  ta được P = = 3 3 cos  o c s cot  + 3 + 2cot ( 2 1+ cot  ) + 3 + 2 3 3 sin  n si  10 Thay cot = 3
− vào P ta được P = . 21 2 2  17  7   13  d) Đúng : tan + tan − + cot + cot    (7 − ) = 0 2  4 2    4    Trang 17 17      7  Ta có tan = tan + 4 = tan = 1   và tan − = cot.   4  4  4  2  13     Và cot = cot + 3 = cot = 1  
; cot(7 − ) = −cot 4  4  4 2 2  17  7   13  Suy ra tan + tan − + cot + cot    (7 − )  4 2   4      = ( + x)2 + ( − x)2 2 2 1 cot 1 cot
= 2 + 2cot x = 2 + 2.( 3 − ) = 20 . 3 3
Câu 12: Cho cos a = ; sin a  0 ; sin b = ; cosb  0 . Xét tính đúng – sai của các phát biểu sau: 4 5 7
a) Giá trị của tan a = . 3 2
b) Giá trị của cot b = − . 3  1 
c) Giá trị của cos2a + cos2b thuộc khoảng ;1 .    2   1 1 
d) Giá trị của cos(a + b) thuộc khoảng − ;−   .  2 3  Lời giải 1 1 16 7 a) Đúng : Ta có 2 tan a +1 =  tan a = −1 = −1 = 2 2 cos a cos a 9 3 1 1 25 4 b) Sai: Ta có 2 cot b +1 =  cotb = − −1 = − −1 = − 2 2 sin b sin a 9 3 9 9 81  1  c) Sai :Ta có 2 2
cos 2a + cos 2b = 2cos a −1+1− 2sin b = 2. − 2. = = 0,405 ;1   16 25 200  2   3  3 cosa = 7 sin  b = 4 d) Sai : 2 
4  sin a = 1− cos a = và 2 
5  cosb = − 1− sin b = − . 4 5 si  na  0 cosb  0       Suy ra (a + b) 3 4 7 3 3 7 1 1 cos
= cosacosb − sin asinb = . − − . = −   1+  − ;−     4  5  4 5 5 4    2 3 
Câu 13: Xét tính đúng sai của các mệnh đề sau: 1+ sin 2x a) 2 sin x = 2 1 7
b) Nếu cos = thì cos 2 = − 3 9 3    3 7 c) Nếu sin x = với x  0;   thì sin 2x = 4  2  8 Trang 18 2     d) Cho cos = với     − ;0   biết tan  + = a + b c   . ( , a ,
b c  , c  0) Khi đó 3  2   4 
a + b + c = 0. Lời giải 1 − cos 2x a) Sai: 2 sin x = 2 2  1  7 b) Đúng: 2 cos 2 = 2cos  − −1 = 2 −1 =    3  9 2  3  7 c) Đúng : Ta có 2 2
cos x = 1− sin x = 1− =   .  4  16    7 7 3 3 7 Vì x  0; 
 nên cos x  0  cos x = suy ra sin 2x = 2sin . x cos x = 2   =  2  4 4 4 8 1 1 5 d) Đúng: Ta có 2 tan  = −1 = −1 = 2 2 cos   2  4    3   5 Vì     − ;0   nên tan 0 tan −   =  2  2  − 5 tan + tan +1    4 2 tan  + = = = −9 + 4 5    4    − 5 1− tan  tan  1−  .1 4 2   Vậy a = 9
− , b = 4, c = 5 nên mệnh đề đúng.
Câu 14: Xét tính đúng sai của các phát biểu sau:
a) sin(a + b) = sinacosb + cosasinb . b) 0 0 0 0 0
sin 31 .cos12 + cos12 .sin 31 = sin19 . 4    24
c) Cho cos x = , x  − ;0 
 . Giá trị của sin 2x là − . 5  2  25 1     1 a 6 d) Cho sin = và
    . Biết giá trị của cos  − − =
với a,b   thì 3 2    6  b a + b = 4 . Lời giải
a) Đúng: Theo công thức cộng sin(a + b) = sinacosb + cosasinb
b) Sai: Áp dụng công thức cộng: 0 0 0 0 + = ( 0 0 + ) 0 sin 31 .cos12 cos12 .sin 31 sin 31 12 = sin 43 Trang 19 16 9 c) Đúng : Ta có 2 2
sin x = 1− cos x = 1− = 3  sin x = − . 25 25 5   
Mặt khác, vì x  − ;0  sin x  0   .  2  4  3  24 Vậy sin 2x = 2sin .
x cos x = 2. . − = −   . 5  5  25 1  2 2 d) Vì sin = ,
    nên cos = − . 3 2 3      2 2 3 1 1 1 2 6 Do đó cos  − = cos.cos + sin − .sin = − . + . =   .  6  6 6 3 2 3 2 6
với a = 2, b = 6 . Tính a + b = 8 . Nên a + b = 4 là sai.
Câu 15: Xét tính đúng sai của các đẳng thức sau:    3 1 a) sin x − = sin x + cos x   .  6  2 2 b) 4sin . x sin2 .
x sin3x = sin4x + sin2x −sin6x .   
c) 1+ sin 2x + cos 2x = 2 2 sin . x cos x − .   .  4  d) 2 x + (a − x) 2 x a + (a − x) 2 sin 2sin .sin .cos sin = cos a . Lời giải      3 1
a) Sai: Theo công thức cộng ta có sin x − = sin . x cos − cos . x sin = sin x − cos . x    6  6 6 2 2
b) Đúng: Áp dụng quy tắc từ tích sang tổng, ta được: 4sin . x sin 2 .
x sin3x = 2(cos x − cos3x)sin3x = sin4x + sin2x − sin6x . Do đó 4sin . x sin2 .
x sin3x = sin4x + sin2x −sin6x c) Sai: Ta có 2
1+ sin 2x + cos2x = 2sin xcos x + 2cos x = 2cos ( x sin x + cos ) x .  1 1    
Mà sin x + cos x = 2 cos x + sin x = 2 cos x − .      2 2   4  d) Ta có: 2 x + (a − x) 2 sin 2sin .sin .
x cosa + sin (a − x) 2
= sin x + sin(a − x).sin 
(x + a) + sin(x − a) 2  + sin  (a − x) 2
= sin x + sin(a − x).sin(x + a) + sin(x − a) + sin(a − x)   2
= sin x + sin(a − x).sin(x + a) + sin(x − a) − sin(x − a)   Trang 20

Tài liệu liên quan: