Các dạng toán tính đơn điệu của hàm số – Nguyễn Bảo Vương Toán 12

Các dạng toán tính đơn điệu của hàm số – Nguyễn Bảo Vương Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

12 6 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ÑÔN ÑIEÄU HAØM SOÁ

NGUYEÃN BAÛO VÖÔNG

Naêm hoïc: 2017 -2018

SÑT: 0946798489

Soá 17 Hoaøng Vaên Thuï – TT. Chö Seâ – Gia Lai.

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Bµi 1. tÝnh ®¬n ®iÖu cña hµm sè. ........................................................................................................... 3

A. KiÕn thøc cÇn nhí. ............................................................................................................................. 3

1. Định nghĩa ....................................................................................................................................... 3

2. Điều kiện cần và đủ để hàm số đơn điệu .................................................................................... 3

Điều kiện cần để hàm số đơn điệu.

...........................................................

Điều kiện đủ để hàm số đơn điệu.

...........................................................

phÇn 1. D¹ng kh«ng chøa tham sè. ...................................................................................................... 3

B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i. ......................................................................... 3

D¹ng to¸n 1: §¬n ®iÖu cña mét hµm têng minh, râ rµng vÒ sè liÖu. ........................................................ 3

D¹ng to¸n 2: D¹ng b¶ng biÕn thiªn. ........................................................................................................ 6

D¹ng to¸n 3: D¹ng cho ®å thÞ hµm sè

 

'y f x

. ................................................................................. 7

D¹ng to¸n 4: D¹ng lý thuyÕt, kiÓm tra tÝnh ®óng sai. .............................................................................. 8

phÇn 2. D¹ng chøa tham sè. ................................................................................................................ 10

B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i. ....................................................................... 10



Bµi to¸n 1: T×m

®Ó hµm sè

 

,y f x m

®ång biÕn (nghÞch biÕn) trªn miÒn x¸c

®Þnh, c¸c kho¶ng x¸c ®Þnh cña hµm sè. ..................................................................................... 10

D¹ng to¸n 1:T×m

®Ó hµm sè

 

,y f x m

®ång biÕn(nghÞch biÕn) trªn

.

D¹ng to¸n 2:T×m

®Ó hµm sè

 

,y f x m

®ång biÕn(nghÞch biÕn) trªn tõng

kho¶ng x¸c ®Þnh cña hµm sè. ...............................................................



Bµi to¸n 2: T×m

®Ó hµm sè

 

,y f x m

®ång biÕn (nghÞch biÕn) trªn kho¶ng

trong ®ã

     

; , ; , ; ...D a a a b  

. ........................................................................................ 13

D¹ng to¸n 1: Hµm sè

 

,y f x m

lµ hµm d¹ng

 

ax b

y f x

cx d



 



. ............

D¹ng to¸n 2: Hµm sè

 

,y f x m

lµ hµm d¹ng ®a thøc. .........................

D¹ng to¸n 3*: Hµm sè

 

,y f x m

lµ hµm d¹ng lîng gi¸c, c¨n... ..........



Bµi to¸n 3. T×m tham sè m ®Ó hµm sè bËc 3 ®¬n ®iÖu trªn ®é dµi l. ............................. 17

C. c©u hái tr¾c nghiÖm. ........................................................................................................................ 18

PhÇn 1. Bµi tËp kh«ng chøa tham sè. ............................................................................................. 18

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

PhÇn 2. Bµi tËp chøa tham sè. .......................................................................................................... 23

ĐÁP ÁN ............................................................................................................................................... 27

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Bµi 1. tÝnh ®¬n ®iÖu cña hµm sè.

A. KiÕn thøc cÇn nhí.

1. Định nghĩa

Cho hàm số

( )y f x

xác định trên

với

là khoảng hoặc đoạn hoặc nửa khoảng.

—

Hàm số

( )y f x

đồng biến (tăng) trên

nếu

1 2 1 2 1 2

, , ( ) ( ).x x K x x f x f x    

—

Hàm số

( )y f x

nghịch biến (giảm) trên

nếu

1 2 1 2 1 2

, , ( ) ( ).x x K x x f x f x    

Hàm số đồng biến hoặc nghịch biến trên

được gọi chung là đơn điệu trên

2. Điều kiện cần và đủ để hàm số đơn điệu

a) Điều kiện cần để hàm số đơn điệu.

Giả sử hàm số

( )y f x

có đạo hàm trên khoảng

—

Nếu hàm số đồng biến trên khoảng

thì

( ) 0, f x x K



  

và

( ) 0f x





xảy ra tại một

số hữu hạn điểm.

—

Nếu hàm số nghịch biến trên khoảng

thì

( ) 0, f x x K



  

và

( ) 0f x





xảy ra tại một

số hữu hạn điểm.

b) Điều kiện đủ để hàm số đơn điệu.

Giả sử hàm số

( )y f x

có đạo hàm trên khoảng

—

Nếu

( ) 0, f x x K



  

thì hàm số đồng biến trên khoảng

—

Nếu

( ) 0, f x x K



  

thì hàm số nghịch biến trên khoảng

—

Nếu

( ) 0, f x x K



  

thì hàm số không đổi trên khoảng

phÇn 1. D¹ng kh«ng chøa tham sè.

B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.

D¹ng to¸n 1: §¬n ®iÖu cña mét hµm têng minh, râ rµng vÒ sè liÖu.



Phương pháp chung: ........................................................................................................................

..................................................................................................................................................................

Ví dụ 1. Cho hàm số

3 2

3 1.

y x x x   

Trong các phát biểu sau, phát biểu nào đúng?

A. Hàm số đồng biến trên khoảng

 

1;3 .

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

B. Hàm số nghịch biến trên khoảng

 

3; .

C. Hàm số đồng biến trên khoảng

   

; 1 3; .   

D. Hàm số đồng biến trên khoảng

 

; 1 

và

 



......................................................................................................................................................

Cần nhớ: Cách xét dấu ...........................................................................................................

......................................................................................................................................................

Ví dụ 2. Hỏi hàm số

4 2

2 2y x x   

nghịch biến trên khoảng nào trong các khoảng sau

đây ?

( 3; 2). 

( 2; 1). 

(0;1).

(1;2).

......................................................................................................................................................

Cần nhớ: Cách xét dấu ...........................................................................................................

......................................................................................................................................................

Ví dụ 3. Xét tính đơn điệu của hàm số

2 1



 



A. Hàm số đồng biến trên các khoảng

( ;1) (1; ).  

B. Hàm số nghịch biến trên các khoảng

( ;1)

và

(1; ).

C. Hàm số nghịch biến trên tập xác định

\ {1}. D

D. Hàm số nghịch biến trên khoảng

( ; ). 

......................................................................................................................................................

Cần nhớ: Công thức đạo hàm .................................................................................................

......................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Ví dụ 4. (Đề THPTQG – 2017 – 101) Hàm số





nghịch biến trên khoảng nào dưới

đây ?

(0; ).

( 1;1).

( ; ). 

( ; 0).

.....................................................................................................................................................

Cần nhớ: Công thức đạo hàm ................................................................................................

.....................................................................................................................................................

Ví dụ 5. Trên khoảng nào sau đây, hàm số

2y x x  

đồng biến ?

(1; ).

(1;2).

(0;1).

( ;1).

.....................................................................................................................................................

Cần nhớ: Công thức đạo hàm ................................................................................................

.....................................................................................................................................................

Ví dụ 6. Cho hàm số

sin 2, [0;2 ].y x x x     

Tìm tất cả các khoảng đồng biến của

hàm số.

(0;2 ).

(0; ).

;



 



















 



 



















 

.....................................................................................................................................................

Cần nhớ: Công thức đạo hàm lượng giác ..............................................................................

.....................................................................................................................................................

Nhắc lại phương pháp:

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

......................................................................................................................................................

D¹ng to¸n 2: D¹ng b¶ng biÕn thiªn.



Phương pháp: Cách nhìn bảng ...........................................................................................

......................................................................................................................................................

Ví dụ 7. Cho hàm số

 

y f x

, xác định và liên tục trên



có bảng biến thiên như hình sau,

xác định mệnh đề đúng ?



2















A. Hàm số đồng biến trên

 

2; 0

B. Hàm số đồng biến trên

   

; 2 0; .   

C. Hàm số nghịch biến trên

 

2; 0

D. Hàm số đồng biến trên

   

;5 , 1; 

......................................................................................................................................................

Ví dụ 8. Cho hàm số

 

y f x

, xác định và liên tục trên



có bảng biến thiên như hình sau,

xác định mệnh đề đúng ?



1















A. Hàm số nghịch biến trên

 

1;

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

B. Hàm số đồng biến trên

   

1; 0 1; .  

C. Hàm số nghịch biến trên

 

1;0

D. Hàm số đồng biến trên

 

1; , 2;

 







  











 

.....................................................................................................................................................

Ví dụ 9. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ?







 







 



2 1



 



2 5



 





 



.....................................................................................................................................................

Ví dụ 10. Cho hàm số

( )y f x

có bảng xét dấu đạo hàm như sau:



1











Mệnh đề nào dưới đây đúng ?

A. Hàm số đồng biến trên khoảng

( 2;0).

B. Hàm số đồng biến trên khoảng

( ; 0).

C. Hàm số nghịch biến trên khoảng

(0;2).

D. Hàm số đồng biến trên khoảng

( ; 2). 

.....................................................................................................................................................

D¹ng to¸n 3: D¹ng cho ®å thÞ hµm sè

 

'y f x



Phương pháp:

Đồ thị trên trục

ở đâu thì .................................................................................................

.....................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Đồ thị dưới trục

ở đâu thì: ................................................................................................

......................................................................................................................................................

Ví dụ 11. Cho hàm số

 

y f x

, xác định và liên tục trên



có đồ

thị hàm số

 

'y f x

như hình sau, xác định mệnh đề

đúng?

A. Hàm số

 

y f x

đồng biến trên khoảng

 

4;2 .

B. Hàm số

 

y f x

đồng biến trên khoảng

 

; 1 

C. Hàm số

 

y f x

đồng biến trên khoảng

 

0;2 .

D. Hàm số

 

y f x

nghịch biến trên khoảng

 

; 4 

và

 

2;

......................................................................................................................................................

Ví dụ 12. (THPT Chuyên Thái Bình lần 3 năm 2016 – 2017) Cho hàm số

( )f x

xác định, liên

tục trên



và có đồ thị hàm số



 ( )y f x

là đường cong trong hình bên dưới. Hỏi

mệnh đề nào dưới đây đúng ?

A. Hàm số

( )f x

đồng biến trên khoảng

(1;2).

B. Hàm số

( )f x

nghịch biến trên khoảng

(0;2).

C. Hàm số

( )f x

đồng biến trên khoảng

( 2;1).

D. Hàm số

( )f x

nghịch biến trên khoảng

( 1;1).

......................................................................................................................................................

D¹ng to¸n 4: D¹ng lý thuyÕt, kiÓm tra tÝnh ®óng sai.



Ví dụ 13.

Cho các mệnh đề sau.

a) Hàm số

 

y f x

được gọi là đồng biến trên

1 2

,D x x D 

và

1 2

x x

thì

   

1 2

.f x f x

b) Hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

2; 3

thì hàm số

 

3y f x 

đồng biến trên khoảng

 

1; 6 .

c) Hàm số

   

' 0, ;f x x a b  

thì

 

y f x

đồng biến trên

 

;a b

d) Hàm số

 

y f x

đồng biến trên khoảng

     

; ' 0, ;a b f x x a b   

4

1

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Có bao nhiêu mệnh đề đúng?

.....................................................................................................................................................

 Ghi nhớ: ...............................................................................................................................

Ví dụ 14. Nếu hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

2;0

và nghịch biến trên

khoảng

 

1; 4

thì hàm số

 

3 2

y f x

   

nghịch biến trên khoảng nào?

 

2;0 .

 

2;1 .

 

1; 3 .

 

5; 3 . 

.....................................................................................................................................................

 Ghi nhớ: ...............................................................................................................................

Đồ thị Đồ thị Phép biến đổi

 

y f x

 

, 0

y f x a a

  

 

y f x

 

, 0

y f x a a

  

 

y f x

 

y f x 

 

y f x

 

, 0

y f x a a

  

 

y f x

 

, 0

y f x a a

  

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

phÇn 2. D¹ng chøa tham sè.

B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.

 Bµi to¸n 1: T×m

®Ó hµm sè

 

,y f x m

®ång biÕn (nghÞch biÕn) trªn miÒn x¸c

®Þnh, c¸c kho¶ng x¸c ®Þnh cña hµm sè.

D¹ng to¸n 1:T×m

®Ó hµm sè

 

,y f x m

®ång biÕn(nghÞch biÕn) trªn

.



• Phương pháp cách giải trực tiếp: ...................................................................................................

..................................................................................................................................................................

• Phương pháp cách giải gián tiếp: ..................................................................................................

..................................................................................................................................................................

Ví dụ 1. Tìm tất cả các giá trị của tham số

để hàm số

   

3 2

1 1 1

y x m x m x     

đồng biến trên tập xác đinh của nó.

1m  

hoặc

2m  

. B.

2 1.m   

2 1.m   

1m  

hoặc

2.m  

.................................................................................................................................................

Ví dụ 2. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 101) Có bao nhiêu giá trị nguyên của

để hàm số

3 2

(4 9) 5y x mx m x     

nghịch biến trên

( ; ). 

.................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Ví dụ 3. Gọi S là tập các giá trị

của

để hàm số

1y x mx  

nghịch biến trên



và

là giá trị nhỏ nhất thuộc tập S. Giá trị gần

nhất là:

3.

1.

.................................................................................................................................................

Ví dụ 4. Có bao nhiêu giá trị nguyên của

để hàm số

   

2 3 2 2

y m m x m m x mx

     

đồng biến trên

.

D.Vô số .

.................................................................................................................................................

Cần nhớ, nếu

chứa tham số thì xét 2 trường hợp.

TH1:

0a 

xét trực tiếp trên hàm số

 

,y f x m

........................................................

.................................................................................................................................................

TH2:

0a 

...........................................................................................................................

.................................................................................................................................................

Ví dụ 5. (Đề thi minh họa lần 3 – Bộ GD & ĐT năm 2017) Hỏi có bao nhiêu số nguyên

để

hàm số

2 3 2

( 1) ( 1) 4y m x m x x     

nghịch biến trên khoảng

( ; ). 

.................................................................................................................................................

Ví dụ 6. Tìm tất cả các giá trị thực

để hàm số

sin cosy x x mx  

đồng biến trên

.

2 2.m  

2.m  

2.m 

2 2.m  

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

.................................................................................................................................................

D¹ng to¸n 2:T×m

®Ó hµm sè

 

,y f x m

®ång biÕn(nghÞch biÕn) trªn tõng

kho¶ng x¸c ®Þnh cña hµm sè.



Phương pháp: Thường hàm số

 

ax b

y f x m

cx d



 



...................................................

.................................................................................................................................................

Ví dụ 7. Tất cả các giá trị của

để hàm số

x m







nghịch biến trên từng khoảng xác

định của hàm số là:

3.m  

hoặc

3.m 

3 3.m  

3.m  

hoặc

3.m 

3 3.m  

.................................................................................................................................................

Ví dụ 8. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 104) Cho hàm số

4mx m

x m







với

là tham số. Gọi

là tập hợp tất cả các giá trị nguyên của

để hàm số nghịch biến

trên các khoảng xác định. Tìm số phần tử của

C. Vố số. D.

.................................................................................................................................................

Ví dụ 9. Tìm tất cả các giá trị thực của tham số

sao cho hàm số

x m







đồng biến

trên từng khoảng xác định của nó.

1.m 

1 1.m  

3 3.m  

1 1.m  

......................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

.....................................................................................................................................................

 Bµi to¸n 2: T×m

®Ó hµm sè

 

,y f x m

®ång biÕn (nghÞch biÕn) trªn kho¶ng

trong ®ã

     

; , ; , ; ...D a a a b  

D¹ng to¸n 1: Hµm sè

 

,y f x m

lµ hµm d¹ng

 

ax b

y f x

cx d



 





Phương pháp: ........................................................................................................................

.................................................................................................................................................

Ví dụ 10. Giá trị của

để hàm số

16mx

x m







nghịch biến trên khoảng

 

1; 5

là:



 











 











 









4 5.m 

.................................................................................................................................................

Cần nhớ: .................................................................................................................................

.................................................................................................................................................

Ví dụ 11. Tìm tập hợp tất cả các giá trị của tham số

để hàm số

2 1x

x m







nghịch biến

trên

(2; ).

 







 











 







 











 

;

 





 











;

 







 











 

.....................................................................................................................................................

Ví dụ 12. Tìm tất cả các giá trị thực của tham số

để hàm số





x m

nghịch biến trên

[1; ).

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

 0 1.m

B.  0 1.m C.  0 1.m D.

 1.m

......................................................................................................................................................

.................................................................................................................................................

D¹ng to¸n 2: Hµm sè

 

,y f x m

lµ hµm d¹ng ®a thøc.



Phương pháp cô lập .............................................................................................................

.................................................................................................................................................

Ví dụ 13. Trong tât cả các giá trị của

để hàm số

   

3 2

1 3 10

y x m x m x      

đồng biến trên khoảng

 

0; 3

thì

m m

là giá trị nhỏ nhất. Giá trị gần

là

1, 5.

1, 6.

1, 7.

1, 8.

.................................................................................................................................................

Cần nhớ: .................................................................................................................................

.................................................................................................................................................

Ví dụ 14. Cho hàm số

4 2

(2 3) .y x m x m    

Nếu hàm số luôn nghịch biến trên khoảng

(1;2)

thì sẽ tồn tại các giá trị của tham số

; ;

 





 











trong đó phân số

tối giản

và

0.q 

Hỏi tổng

p q

bằng bao nhiêu ?

3.p q 

5.p q 

7.p q 

9.p q 

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

.................................................................................................................................................

Ví dụ 15. (THPT Chuyên Đại Học Vinh lần 2 năm 2017) Tìm tất cả các giá trị của tham số

để hàm số

2 4 2

1)( 2y m x mx 

đồng biến trên

(1; ).

1m  

hoặc

1 5



 

1m  

hoặc

1 5



 

1m  

hoặc

1.m 

1.m  

.................................................................................................................................................

D¹ng to¸n 3*: Hµm sè

 

,y f x m

lµ hµm d¹ng lîng gi¸c, c¨n...



Phương pháp .........................................................................................................................

.................................................................................................................................................

Ví dụ 16. Cho hàm số

 

1 1 2

m x

x m

  



 

. Tìm tập tất cả các giá trị tham số

để hàm

số đồng biến trên

 

17;37 .



4; 1 .m



  





   

; 6 4; 1 2; .m

 

       

 

 

  

; 4 2; .m



    





 

1;2 .m  

Phương pháp đặt ẩn phụ .....................................................................................................

.................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

.................................................................................................................................................

Cần nhớ: .................................................................................................................................

.................................................................................................................................................

Ví dụ 17. Tất cả các giá trị thực của tham số

để hàm số

sin

x m







nghịch biến trên

khoảng

; .



 

















 

0.m 

0m 

hoặc

1.m 

0 1.m 

1.m  

Phương pháp đặt ẩn phụ .....................................................................................................

.................................................................................................................................................

Cần nhớ: .................................................................................................................................

.................................................................................................................................................

Ví dụ 18. (Đề thi minh họa – Bộ GD & ĐT năm 2017) Tìm tất cả các giá trị thực của tham số

sao cho hàm số

tan 2

tan

x m







đồng biến trên khoảng



 



















 

 0m

hoặc

1 2.m 

 0.m

  1 2.x

 2.m

.................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

.................................................................................................................................................

 Bµi to¸n 3. T×m tham sè m ®Ó hµm sè bËc 3 ®¬n ®iÖu trªn ®é dµi l.



Tìm

để hàm số

3 2

y ax bx cx d   

đơn điệu trên khoảng có độ dài đúng bằng l

Phương pháp:

Ví dụ 1. Tìm tất cả các giá trị thực của tham số

sao cho hàm số

3 2

( 1) 3

y x mx m x m      

đồng biến trên đoạn có độ dài đúng bằng

1m  

hoặc

2.m 

1.m  

C. Không tồn tại

2.m 

.....................................................................................................................................................

Ví dụ 2. Tìm các giá trị của tham số

sao cho hàm số

3 2

( 1) 4 7y x m x x    

có độ

dài khoảng nghịch biến đúng bằng

2 5.

2m  

hoặc

4.m 

1m 

hoặc

3.m 

0m 

hoặc

1.m  

2m 

hoặc

4.m  

.....................................................................................................................................................

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

......................................................................................................................................................

Ví dụ 3. Tìm tất cả các giá trị thực

để hàm số

3 2

( ) 3 ( 1) 2 3f x x x m x m      

đồng biến trên một khoảng có độ dài lớn hơn

0.m 

0.m 

  

  

......................................................................................................................................................

C. c©u hái tr¾c nghiÖm.

PhÇn 1. Bµi tËp kh«ng chøa tham sè.

Câu 1. (THPTQG – 2017 – 101) Cho hàm số

3 2y x x  

. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

;0

và nghịch biến trên khoảng

 

0; .

B. Hàm số nghịch biến trên khoảng

 

;

 

C.Hàm số đồng biến trên khoảng

 

; . 

D. Hàm số nghịch biến trên khoảng

 

;0

và đồng biến trên khoảng

 

0; .

Câu 2. (THPTQG – 2017 – 101) Hàm số





nghịch biến trên khoảng nào dưới đây?

 

0; .

 

1;1 .

 

; . 

 

;0 .

Câu 3. Trong các phát biểu sau về hàm số

2 1







, phát biểu nào sau đây là đúng?

A. Hàm số luôn đồng biến với

3.x 

B. Hàm số đồng biến trên

   

; 3 3; .    

C. Hàm số đồng biến trên

 

; 3 

và

 

3; . 

D. Hàm số đồng biến trên tập

 

\ 3 .



Câu 4. Cho hàm số

4 2

2 4.y x x  

Trong các phát biểu sau, phát biểu nào không đúng?

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

A. Hàm số đồng biến trên khoảng

 

1; 0

và

 

1; .

B. Hàm số nghịch biến trên

 

; 1 

và

0;1 .

 

 

 

C. Hàm số đồng biến trên

1; 0

 



 

 

và



1; .









D. Hàm số nghịch biến trên

   

; 1 0;1 .  

Câu 5. (THPTQG – 2017 – 103) Cho hàm số

4 2

2y x x 

. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

; 2 . 

B. Hàm số nghịch biến trên khoảng

 

; 2 . 

C. Hàm số đồng biến trên khoảng

 

1;1 .

D. Hàm số nghịch biến trên khoảng

 

1;1 .

Câu 6. (THPTQG – 2017 – 102) Cho hàm số

3 2

3 .y x x 

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng

 

0;2 .

B. Hàm số nghịch biến trên khoảng

 



C. Hàm số đồng biến trên khoảng

 

0;2 .

D. Hám số nghịch biến trên khoảng

 

;0 .

Câu 7. (THPTQG – 2017 – 103) Cho hàm số

 

y f x

có đạo hàm

 

' 1

f x x

 

với

.x  

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng

 

;0 .

B. Hàm số nghịch biến trên khoảng

 

1; .

C. Hàm số nghịch biến trên khoảng

 

1;1 .

D. Hàm số đồng biến trên khoảng

 

; . 

Câu 8. (THPTQG – 2017 – 103) Hàm số nào dưới đây đồng biến trên khoảng

 

; . 







.y x x 







3 .y x x  

Câu 9. Có nhiều nhất bao nhiêu số nguyên thuộc khoảng nghịch biến của hàm số

3 2

3 1?

y x x x   

A. Vô số. B.

Câu 10. Hàm số

3 2

3 9 2y x x x   

đồng biến trên khoảng nào?

 

; 3 

và

 

1; .

 

3;1 .

 

; 1 

và

 

3; .

 

1; 3 .

Câu 11. (Đề minh họa THPTQG – 2017) Hàm số

2 1y x 

đồng biến trên khoảng nào?

; .

 







 











 

 

0; .

; .

 







 











 

 

;0 .

Câu 12. Khi nói về tính đơn điệu của hàm số

4 2

4 10y x x   

ta có những phát biểu sau:

1) Hàm số đồng biến trên khoảng

 

;3 .

2) Hàm số nghịch biến trên



3; .









3) Hàm số nghịch biến trên khoảng

 

;0

và

 

3; .

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

4) Hàm số đồng biến trên khoảng



;3 .









Trên những phát biểu trên, có bao nhiêu phát biểu đúng?

Câu 13. Trong các phát biểu sau về hàm số

 

, phát biểu nào sau đây là đúng?

A. Hàm số luôn nghịch biến với

0.x 

B. Hàm số nghịch biến trên

 

;0

và

 

0; .

C. Hàm số đồng biến trên

 

;0

và

 

0; .

D. Hàm số đồng biến trên tập

 

\ 0 .



Câu 14. Khi nói về tính đơn điệu của hám số

2 1

x x

 





, ta có những phát biểu sau:

1) Hàm số nghịch biến trên khoảng

 

1; 3 .

2) Đồng biến trên khoảng

   

; 1 3; .   

3) Hàm số nghịch biến trên khoảng

   

1; 3 \ 2 .

4) Hàm số đồng biến trên khoảng

 

;1

và

 

3; .

Trong những phát biểu trên có bao nhiêu phát biểu đúng?

Câu 15. Cho hàm số

2 1







Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng

 

; . 

B. Hàm số nghịch biến trên khoảng

 

; . 

C. Hàm số nghịch biến trên từng khoảng xác định.

D. Hàm số đồng biến trên từng khoảng xác định.

Câu 16. Hàm số nào trong các hàm số sau đồng biến trên

.

3 2

3 2.y x x  

3 2

3 3 .y x x x  

.y x 

3 2

6 .y x x  

Câu 17. Trong các hàm số sau, hàm số nào đồng biến trên

.

4 2

2 3.y x x  

4 5.y x x  

2 3.







1.y x x  

Câu 18. Hàm số

3 2

2 9 12 4y x x x   

nghịch biến trên khoảng.

 

1;2 .

 

2; .

 

2; 3 .

 

;1 .

Câu 19. Nếu hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

2;3

thì hàm số

 

y f x

 

đồng biến trên khoảng nào?

 

1;6 .

 

5;0 .

 

2;6 .

 

2;3 .

Câu 20. Nếu hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

1;2

thì hàm số

 

y f x

 

đồng biến trên khoảng nào?

 

1;2 .

 

0;3 .

 

2;6 .

 

2;3 .

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Câu 21. Nếu hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

3;1

và nghịch biến trên

khoảng

 

2; 3

thì hàm số

 

y f x 

đồng biến trên khoảng nào?

 

3;1 .

 

2; 3 .

 

3;1 .

 

2; 3 . 

Câu 22. Nếu hàm số

 

y f x

liên tục và đồng biến trên khoảng

 

2;0

và nghịch biến trên

khoảng

 

1; 4

thì hàm số

 

3 3y f x   

đồng biến trên khoảng nào?

 

2; 0 .

 

2;1 .

 

1; 3 .

 

5; 3 . 

Câu 23. Cho hàm số

3 1







. Ta có các phát biểu sau:

I. Hàm số đồng biến trên

   

; 1 1; .    

II. Hàm số đồng biến trên tập

 

\ 3 .

III. Hàm số nghịch biến trên

 

; 1 

và

 

1; . 

IV. Hàm số đồng biến trên

   

; 1 , 0; .  

Hỏi trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

Câu 24. Cho hàm số

 

y f x

có đồ thị như hình vẽ bên. Mệnh đề nào sau đây sai?

A. Hàm số đồng biến trên khoảng

   

;0 ; 2; . 

B. Hàm số nghịch biến trên khoảng

 

0;2 .

C. Hàm số đồng biến trên khoảng

   

1;1 ; 3; . 

D. Hàm số nghịch biến trên khoảng

 

1;2 .

Câu 25. Cho hàm số

 

y f x

có bảng biến thiên như hình vẽ sau:

Mệnh đề nào sau đây sai?

A. Hàm số đã cho đồng biến trên khoảng

 

2; .

B. Hàm số đã cho đồng biến trên khoảng

 

;1 .

C. Hàm số đã cho đồng biến trên khoảng

 

3; .

D. Hàm số đã cho nghịch biến trên khoảng

 

0; 3 .

Câu 26. Cho hàm số

 

y f x

xác định trên



và có đồ thị

 

'y f x

là đường cong trong

hình bên. Mệnh đề nào dưới đây đúng?

A. Hàm số

 

y f x

đồng biến trên khoảng

   

; 2 , 0; .  

B. Hàm số

 

y f x

nghịch biến trên khoảng

 

2; 0 .

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

C. Hàm số

 

y f x

đồng biến trên khoảng

 

3; . 

D. Hàm số

 

y f x

nghịch biến trên khoảng

 

;0 .

Câu 27. Cho hàm số

 

y f x

xác định trên khoảng

 

; .a b

Phát biểu nào sau đây đúng?.

 

f x

đồng biến trên

 

;a b

khi và chỉ khi

     

1 2 1 2 1 2

, ; : .x x a b x x f x f x    

 

f x

nghịch biến trên

 

;a b

khi và chỉ khi

     

1 2 1 2 1 2

, ; : .x x a b x x f x f x    

 

f x

đồng biến trên

 

;a b

khi và chỉ khi

     

1 2 1 2 1 2

, ; : .x x a b x x f x f x    

 

f x

nghịch biến trên

 

;a b

khi và chỉ khi

     

1 2 1 2 1 2

, ; : .x x a b x x f x f x    

Câu 28. Cho các phát biểu sau:

I. Hàm số

 

y f x

được gọi là đồng biến trên miền

khi và chỉ khi

1 2

,x D x x  

thì

   

1 2

.f x f x

II. Hàm số

 

y f x

được gọi là nghịch biến trên miền

khi và chỉ khi

1 2

,x D x x  

thì

   

1 2

.f x f x

III. Nếu

   

' 0, ;f x x a b  

thì hàm số

 

y f x

đồng biến trên khoảng

 

; .a b

IV. Hàm số

 

y f x

đồng biến trên khoảng

 

;a b

khi và chỉ khi

   

' 0, ; .f x x a b  

Có bao nhiêu phát biểu đúng?

Câu 29. Cho hàm số

 

y f x

có đạo hàm trên

 

;a b

. Phát biểu nào sau đây là đúng?

A. Hàm số

 

y f x

đồng biến trên

 

;a b

khi và chỉ khi

   

' 0, ;f x x a b  

 

, ' 0

f x



xảy ra tại hữu hạn điểm thuộc

 

; .a b

B. Hàm số

 

y f x

đồng biến trên

 

;a b

khi và chỉ khi

   

' 0, ; .f x x a b  

C. Hàm số

 

y f x

nghịch biến trên

 

;a b

khi và chỉ khi

   

' 0, ;f x x a b  

 

, ' 0

f x



xảy ra tại hữu hạn điểm thuộc

 

; .a b

D. Hàm số

 

y f x

nghịch biến trên

 

;a b

khi và chỉ khi

   

' 0, ; .f x x a b  

Câu 30. Cho hàm số

 

y f x

đơn điệu trên khoảng

 

; .a b

Trong các khẳng định sau, khẳng

định nào đúng?

   

' 0, ; .f x x a b  

   

' 0, ; .f x x a b  

   

' 0, ;f x x a b  

 

'f x

không đổi dấu trên

 

;a b

Câu 31. Cho hàm số

 

y f x

và

 

y g x

đều nghịch biến trên



. Cho các khẳng định sau:

I) Hàm số

   

y f x g x 

nghịch biến trên

.

II) Hàm số

   

y f x g x

nghịch biến trên

.

III) Hàm số

   

y f x g x 

nghịch biến trên

.

IV) Hàm số

  

y kf x k

 

nghịch biến trên

.

Có bao nhiêu khẳng định đúng?

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Câu 32. Cho

là một khoảng. Ta có 3 phát biểu sau:

1) Hàm số

 

y f x

đồng biến trên

khi và chỉ khi

 

' 0, .f x x D  

2) Hàm số

 

y f x

đạt cực đại tại điểm

x x

khi và chỉ khi

 

' 0

f x



và

 

'' 0

f x



3) Hàm số

 

y f x

có

 

' 0

f x



với

1 2

,x D D  

khi đó

 

f x

đồng biến trên

1 2

.D D

Số các phát biểu đúng là:

PhÇn 2. Bµi tËp chøa tham sè.

Câu 33. Tìm

để hàm số

   

3 2

1 1 1

y x m x m x

     

đồng biến trên tập xác định.

1m  

hoặc

2.m  

2 1.m   

2 1.m   

1m  

hoặc

2.m  

Câu 34. Trong tất cả các giá trị của

làm cho hàm số

3 2

y x mx mx m   

đồng biến

trên

.

Có giá trị nhỏ nhất của

là:

4.

1.

Câu 35. (THPTQG – 2017 - 101) Cho hàm số

 

3 2

4 9 5

y x mx m x

     

với

là tham

số. Có bao nhiêu giá trị nguyên của

để hàm số nghịch biến trên khoảng

 

; . 

Câu 36. Cho hàm số

   

3 2

7 7 2 1.

y m x m x mx

     

Có bao nhiêu giá trị nguyên của

để hàm số nghịch biến trên

.

Câu 37. Cho hàm số

   

2 3 2 2

2 2 3.

y m m x m m x mx

     

Tất cả các giá trị thực của

tham số

để hàm số nghịch biến trên





2; 1 .



  





  

2; 1 0 .



   





 

2; 1 0 .

 

   

 

 

2; 1 .

 

  

 

 

Câu 38. Hàm số

3 2

3 4 1y mx mx x   

đồng biến trên



khi và chỉ khi.

0 .

m 

0 .

m 

0m 

hoặc

m 

0 .

m 

Câu 39. Tất cả các giá trị của

để hàm số

sin 3y ax x  

đồng biến trên

.

1.a 

1.a  

1.a 

1.a  

Câu 40. Hàm số

x m







đồng biến trên



khi giá trị của

là:

1.m 

1.m 

1.m 

.m  

Câu 41. Hàm số

3 2

y ax bx cx d   

nghịch biến trên



khi và chỉ khi:

3 0.b ac 

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

0a 

và

3 0.b ac 

0a 

và

3 0b ac 

hoặc

0, 0a b c  

0a 

và

3 0b ac 

hoặc

0, 0.a b c  

Câu 42. (THPTQG – 2017 – 101) Đường cong ở hình bên là đồ thị của hàm số

ax b

cx d







với

, , ,a b c d

là các số thực.

Mệnh đề nào dưới đây đúng?

' 0, .y x   

' 0, .y x   

' 0, 1.y x  

' 0, 1.y x  

Câu 43. Điều kiện cần và đủ để hàm số







đồng biến trên từng khoảng xác định là:

5.m  

5.m  

5.m 

5.m 

Câu 44. Tất cả các giá trị của

để hàm số

x m

mx m





 

đồng biến trên từng khoảng xác

định là:

1 2.m  



 









m 

hoặc

m 

1 2.m  

Câu 45. Tất cả các giá trị thực của tham số

để hàm số

3 2mx m

x m

 





nghịch biến trên

từng khoảng xác định là:

1 2.m 

1 2.m 

1m 

hoặc

2.m 

1m 

hoặc

2.m 

Câu 46. Hàm số







nghịch biến trên các khoảng xác định khi và chỉ khi

nhận giá

trị nào?

2.m 

2.m 

2.m 

2.m 

Câu 47. Có bao nhiêu giá trị nguyên của

để hàm số

x m





 

nghịch biến trên từng

khoảng xác định của nó?

Câu 48. Tất cả các giá trị thực của

để hàm số

3 4mx m

x m

 





đồng biến trên khoảng

 

1;2

là:

4 1.m   

4 1.m  

1m  

hoặc

2.m 

4m  

hoặc

2.m 

Câu 49. Giá trị của

để hàm số

16mx

x m







nghịch biến trên khoảng

 

1; 5

là:

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang



 











 











 









4 5.m 

Câu 50. Cho hàm số

4mx

x m







với

là tham số thực. Tất cả các giá trị của

để hàm số

đồng biến trên khoảng

 

2; .



 











 









2.m 

2.m 

Câu 51. Cho hàm số

4mx

x m







. Điều kiện đầy đủ của

để hàm số nghịch biến trên











là:

2 1.m  

2 1.m  

2 2.m  

2 1.m  

Câu 52. Giá trị của

để hàm số

9mx

x m







nghịch biến trên khoảng

 

;2

là:

3 3.m  

2 3.m  

3 2.m   

3 3.m  

Câu 53. Tìm tất cả các giá trị của tham số

để hàm số

 

4 2

2 4 2y x m x m    

nghịch

biến trên khoảng

 

1; 0

2.m 

2.m 

4.m 

4.m 

Câu 54. Tìm tất cả các giá trị tham số

để hàm số

   

3 2

1 3 10

y x m x m x      

đồng biến trên khoảng

 

0;3 .

m 

m 

m 

.m  

Câu 55. Có bao nhiêu giá trị nguyên của

để hàm số

 

3 2 2

2 3 2 3 1

y x m x m m x

     

nghịch biến trên khoảng

 

1; 3 .

Câu 56. Trong tất cả các giá trị của

để hàm số

 

3 2

2 3 1 6 1

y x m x mx

     

đồng

biến trên khoảng

 

2;0

thì

m m

là giá trị lớn nhất. Hỏi trong các số sau, đâu là

số gần

nhất?

1.

4.

Câu 57. Cho hàm số

 

3 2

3 3 1, 1

y x x mx

    

với

là tham số thực. Tìm

để hàm số

 

nghịch biến trên khoảng

 

0; .

2.m  

0.m 

1 1.m  

1.m  

Câu 58. Cho hàm số

 

3 2 2

1 2 3 2 1

y x m x m m x

       

với

là tham số thực.

Trong các điều kiện sau của

, đâu là điều kiện đầy đủ nhất để hàm số nghịch biến

trên

 

2; .

  

.m  

2.m 

 

hoặc

2.m 

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

Câu 59. Hàm số

2 cos

4 cos

m x m

x m







đồng biến trên khoảng

;



 

















 

thì điều kiện đầy đủ của

tham số

là:

2m  

hoặc

0.m 

2m  

hoặc

4.m 

2 4.m  

2 0.m  

Câu 60. Tất cả các giá trị thực của tham số

để hàm số

sin

x m







nghịch biến trên

khoảng

;



 

















 

là:

0.m 













0 1.m 

1.m  

Câu 61. (Đề minh họa THPTQG – 2017) Tìm tất cả các giá trị thực của tham số

sao cho

hàm số

tan 2

tan

x m







đồng biến trên khoảng

0; .



 

















 

0m 

hoặc

1 2.m 

0.m 

1 2.m 

2.m 

Câu 62. Tìm tất cả các giá trị thực của tham số

để hàm số

sin

cos

m x





nghịch biến trên

0; .



 

















 

1.m 

m 

2.m 

Câu 63. Cho hàm số

 

1 1 2

m x

x m

  



 

. Tìm tập tất cả các giá trị của tham số

để hàm

số đồng biến trên khoảng

 

17;37 .



4; 1 .



  





   

; 6 4; 1 2; .

 

       

 

 

  

; 4 2; .



    





 

1;2 .

 

Câu 64. Cho hàm số

   

2 2 2

1 2 2 1 1 1.

y x x m x x x

x x



        

 

Có bao

nhiêu giá trị nguyên dương của tham số

để hàm số nghịch biến trên

.

B. Vô số. C.

Câu 65. Cho hai hàm số

 

sinf x x m x 

và

     

3 2 1 cos .g x m x m x   

Tất cả các

giá trị của

làm cho hàm số

 

f x

đồng biến trên



và

 

g x

nghịch biến trên



là:

1.m  

0.m 

1 0.m  

1 .

m  

Câu 66. Cho hàm số

sin cosy a x b x x  

với

,a b

là các tham số thực. Điều kiện của

,a b

để hàm số đồng biến trên



là:

, .a b  

2 2

1.a b 

a b 

2 2

1.a b 

Tt GIA SÖ CHö seâ- 094.6798.489

giaûi tích LÔÙP 12

Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai https://www.facebook.com/phong.baovuong

Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489

Trang

ĐÁP ÁN

1C 2A 3C 4D 5B 6A 7D 8B 9C 10C 11B

12B 13B 14A 15D 16B 17A 18A 19D 20B 21B 22D

23B 24C 25D 26C 27C 28B 29C 30D 31A 32 33C

34B 35A 36C 37D 38B 39B 40D 41D 42D 43D 44D

45B 46D 47B 48A 49A 50C 51D 52C 53B 54A 55C

56B 57D 58A 59A 60A 61A 62C 63B 64D 65D 66B

Lớp học duy nhất tại Số 17 Hoàng Văn Thụ. TT Chư Sê. Gia Lai

Theo dõi facebook: https://www.facebook.com/phong.baovuong

Để nhận được các bài học tiếp nhé.

Bấm Tải xuống để xem toàn bộ.

| 1/28

| | Tải xuống

Preview text:

ÑÔN ÑIEÄU HAØM SOÁ NGUYEÃN BAÛO VÖÔNG Naêm hoïc: 2017 -2018 SÑT: 0946798489
Soá 17 Hoaøng Vaên Thuï – TT. Chö Seâ – Gia Lai.
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Bµi 1. tÝnh ®¬n ®iÖu cña hµm sè. ........................................................................................................... 3
A. KiÕn thøc cÇn nhí. ............................................................................................................................. 3
1. Định nghĩa ....................................................................................................................................... 3
2. Điều kiện cần và đủ để hàm số đơn điệu .................................................................................... 3
a) Điều kiện cần để hàm số đơn điệu. ........................................................... 3
b) Điều kiện đủ để hàm số đơn điệu. ........................................................... 3
phÇn 1. D¹ng kh«ng chøa tham sè. ...................................................................................................... 3
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i. ......................................................................... 3
D¹ng to¸n 1: §¬n ®iÖu cña mét hµm têng minh, râ rµng vÒ sè liÖu. ........................................................ 3
D¹ng to¸n 2: D¹ng b¶ng biÕn thiªn. ........................................................................................................ 6
D¹ng to¸n 3: D¹ng cho ®å thÞ hµm sè y  f ' x  . ................................................................................. 7
D¹ng to¸n 4: D¹ng lý thuyÕt, kiÓm tra tÝnh ®óng sai. .............................................................................. 8
phÇn 2. D¹ng chøa tham sè. ................................................................................................................ 10
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i. ....................................................................... 10
 Bµi to¸n 1: T×m m ®Ó hµm sè y  f  ,
x m ®ång biÕn (nghÞch biÕn) trªn miÒn x¸c
®Þnh, c¸c kho¶ng x¸c ®Þnh cña hµm sè. ..................................................................................... 10
D¹ng to¸n 1:T×m m ®Ó hµm sè y  f x,m ®ång biÕn(nghÞch biÕn) trªn .  10
D¹ng to¸n 2:T×m m ®Ó hµm sè y  f x,m ®ång biÕn(nghÞch biÕn) trªn tõng
kho¶ng x¸c ®Þnh cña hµm sè. ............................................................... 12
 Bµi to¸n 2: T×m m ®Ó hµm sè y  f  ,
x m ®ång biÕn (nghÞch biÕn) trªn kho¶ngD
trong ®ã D   ;
 a,a;,a;b.... ........................................................................................ 13 
D¹ng to¸n 1: Hµm sè y  f x,m lµ hµm d¹ng    ax b y f x  . ............ 13 cx  d
D¹ng to¸n 2: Hµm sè y  f x,m lµ hµm d¹ng ®a thøc. ......................... 14
D¹ng to¸n 3*: Hµm sè y  f x,m lµ hµm d¹ng lîng gi¸c, c¨n... .......... 15
 Bµi to¸n 3. T×m tham sè m ®Ó hµm sè bËc 3 ®¬n ®iÖu trªn ®é dµi l. ............................. 17
C. c©u hái tr¾c nghiÖm. ........................................................................................................................ 18
PhÇn 1. Bµi tËp kh«ng chøa tham sè. ............................................................................................. 18
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 1
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
PhÇn 2. Bµi tËp chøa tham sè. .......................................................................................................... 23
ĐÁP ÁN ............................................................................................................................................... 27
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 2
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Bµi 1. tÝnh ®¬n ®iÖu cña hµm sè. A. KiÕn thøc cÇn nhí. 1. Định nghĩa
Cho hàm số y  f (x) xác định trên K với K là khoảng hoặc đoạn hoặc nửa khoảng.
— Hàm số y  f (x) đồng biến (tăng) trên K nếu x
 , x  K, x  x  f (x )  f (x ). 1 2 1 2 1 2
— Hàm số y  f (x) nghịch biến (giảm) trên K nếu x
 , x  K, x  x  f (x )  f (x ). 1 2 1 2 1 2
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
2. Điều kiện cần và đủ để hàm số đơn điệu
a) Điều kiện cần để hàm số đơn điệu.
Giả sử hàm số y  f (x) có đạo hàm trên khoảng K.
— Nếu hàm số đồng biến trên khoảng K thì f (  x)  0, x
  K và f (x)  0 xảy ra tại một số hữu hạn điểm.
— Nếu hàm số nghịch biến trên khoảng K thì f (  x)  0, x
  K và f (x)  0 xảy ra tại một số hữu hạn điểm.
b) Điều kiện đủ để hàm số đơn điệu.
Giả sử hàm số y  f (x) có đạo hàm trên khoảng K. — Nếu f (  x)  0, x
  K thì hàm số đồng biến trên khoảng K. — Nếu f (  x)  0, x
  K thì hàm số nghịch biến trên khoảng K. — Nếu f (  x)  0, x
  K thì hàm số không đổi trên khoảng K.
phÇn 1. D¹ng kh«ng chøa tham sè.
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
D¹ng to¸n 1: §¬n ®iÖu cña mét hµm têng minh, râ rµng vÒ sè liÖu. 
Phương pháp chung: ........................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1 Ví dụ 1. Cho hàm số 3 2
y  x  x  3x  1. Trong các phát biểu sau, phát biểu nào đúng? 3
A. Hàm số đồng biến trên khoảng 1; 3.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 3
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
B. Hàm số nghịch biến trên khoảng 3;.
C. Hàm số đồng biến trên khoảng  ;    1  3;.
D. Hàm số đồng biến trên khoảng  ;    1 và 4;.
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
Cần nhớ: Cách xét dấu ...........................................................................................................
......................................................................................................................................................
...................................................................................................................................................... Ví dụ 2. Hỏi hàm số 4 2 y  x 
 2x  2 nghịch biến trên khoảng nào trong các khoảng sau đây ? A. (3;2). B. (2;1). C. (0;1). D. (1;2).
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
Cần nhớ: Cách xét dấu ...........................................................................................................
......................................................................................................................................................
...................................................................................................................................................... 2x  1
Ví dụ 3. Xét tính đơn điệu của hàm số y   x  1
A. Hàm số đồng biến trên các khoảng ( ;  1)  (1; )  .
B. Hàm số nghịch biến trên các khoảng ( ;  1) và (1; )  .
C. Hàm số nghịch biến trên tập xác định D   \ {1}.
D. Hàm số nghịch biến trên khoảng ( ;   )  .
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
Cần nhớ: Công thức đạo hàm .................................................................................................
......................................................................................................................................................
......................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 4
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2
Ví dụ 4. (Đề THPTQG – 2017 – 101) Hàm số y 
nghịch biến trên khoảng nào dưới 2 x  1 đây ? A. (0; )  . B. (1;1). C. ( ;   )  . D. ( ;  0).
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Cần nhớ: Công thức đạo hàm ................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Ví dụ 5. Trên khoảng nào sau đây, hàm số 2 y  x 
 2x đồng biến ? A. (1;  )  . B. (1;2). C. (0;1). D. ( ;  1).
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Cần nhớ: Công thức đạo hàm ................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Ví dụ 6. Cho hàm số y  x  sin x  2, x  [0;2]. Tìm tất cả các khoảng đồng biến của hàm số.         A. (0;2). B. (0; ). C.  ;        D. ;2  2  2 
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Cần nhớ: Công thức đạo hàm lượng giác ..............................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Nhắc lại phương pháp:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 5
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
D¹ng to¸n 2: D¹ng b¶ng biÕn thiªn. 
Phương pháp: Cách nhìn bảng ...........................................................................................
......................................................................................................................................................
......................................................................................................................................................
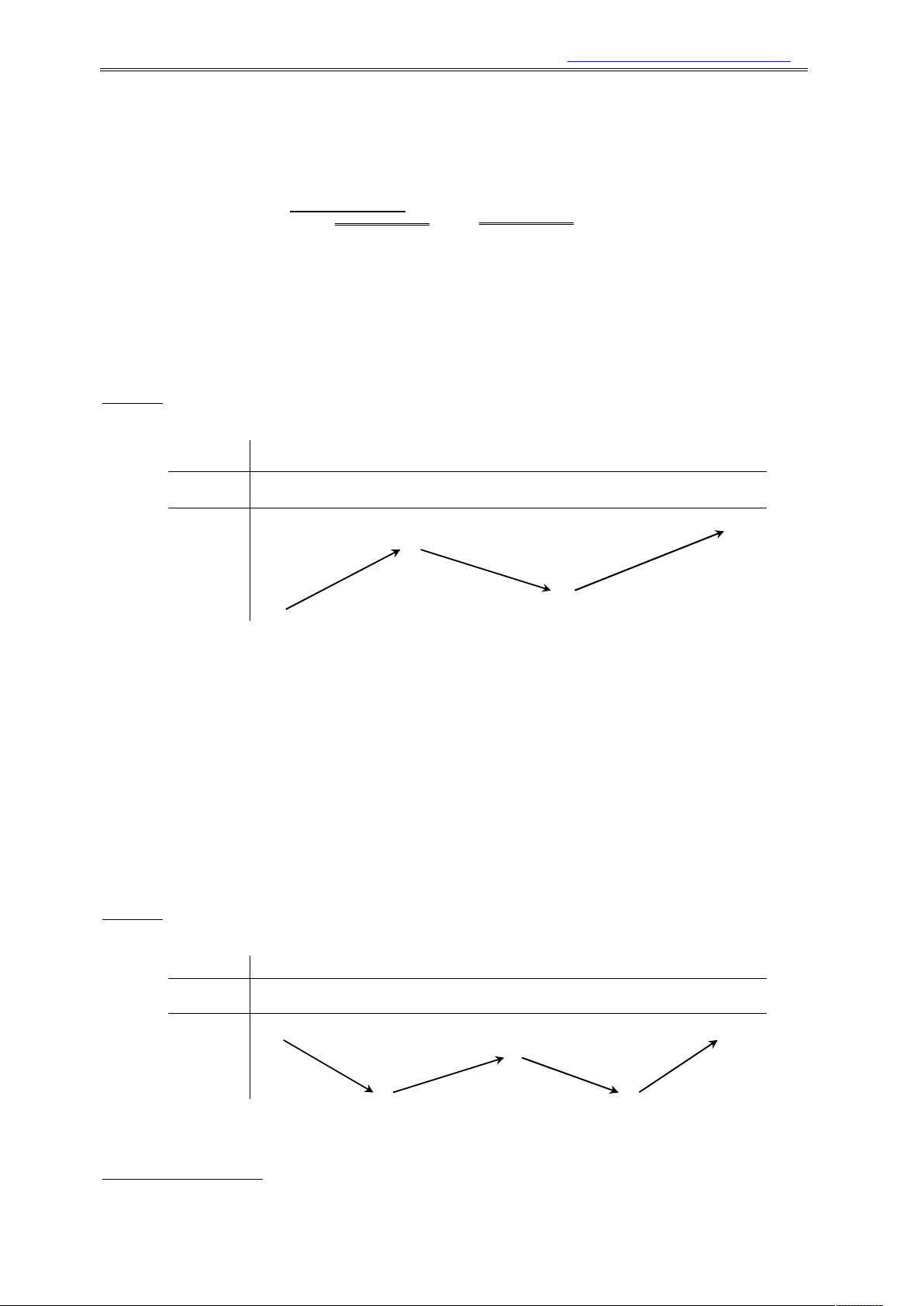
Ví dụ 7. Cho hàm số y  f x , xác định và liên tục trên  có bảng biến thiên như hình sau,
xác định mệnh đề đúng ? x  2 0  y  0  0   y 5 1 
A. Hàm số đồng biến trên 2; 0.
B. Hàm số đồng biến trên  ;
 2  0;.
C. Hàm số nghịch biến trên 2; 0 .
D. Hàm số đồng biến trên  ;  5,1; .
......................................................................................................................................................
......................................................................................................................................................
Ví dụ 8. Cho hàm số y  f x , xác định và liên tục trên  có bảng biến thiên như hình sau,
xác định mệnh đề đúng ? x  1 0 1  y  0  0  0    y 2 1 1
A. Hàm số nghịch biến trên 1;.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 6
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
B. Hàm số đồng biến trên 1; 0  1;.
C. Hàm số nghịch biến trên 1; 0 .  1  
D. Hàm số đồng biến trên  1  ; ,   2;  .  2
.....................................................................................................................................................
.....................................................................................................................................................
Ví dụ 9. Hàm số nào sau đây có bảng biến thiên như hình bên dưới ? x  2  y   1  y  1 x  1 2x  1 2x  5 x  3 A. y   B. y   C. y   D. y   x  2 x  2 x  2 x  2
.....................................................................................................................................................
.....................................................................................................................................................
Ví dụ 10. Cho hàm số y  f (x) có bảng xét dấu đạo hàm như sau: x  1 0 2  y  0   0 
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng (2; 0).
B. Hàm số đồng biến trên khoảng ( ;  0).
C. Hàm số nghịch biến trên khoảng (0;2).
D. Hàm số đồng biến trên khoảng ( ;  2).
.....................................................................................................................................................
.....................................................................................................................................................
D¹ng to¸n 3: D¹ng cho ®å thÞ hµm sè y  f 'x  .  Phương pháp:
Đồ thị trên trục Ox ở đâu thì .................................................................................................
.....................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 7
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Đồ thị dưới trục Ox ở đâu thì: ................................................................................................
......................................................................................................................................................
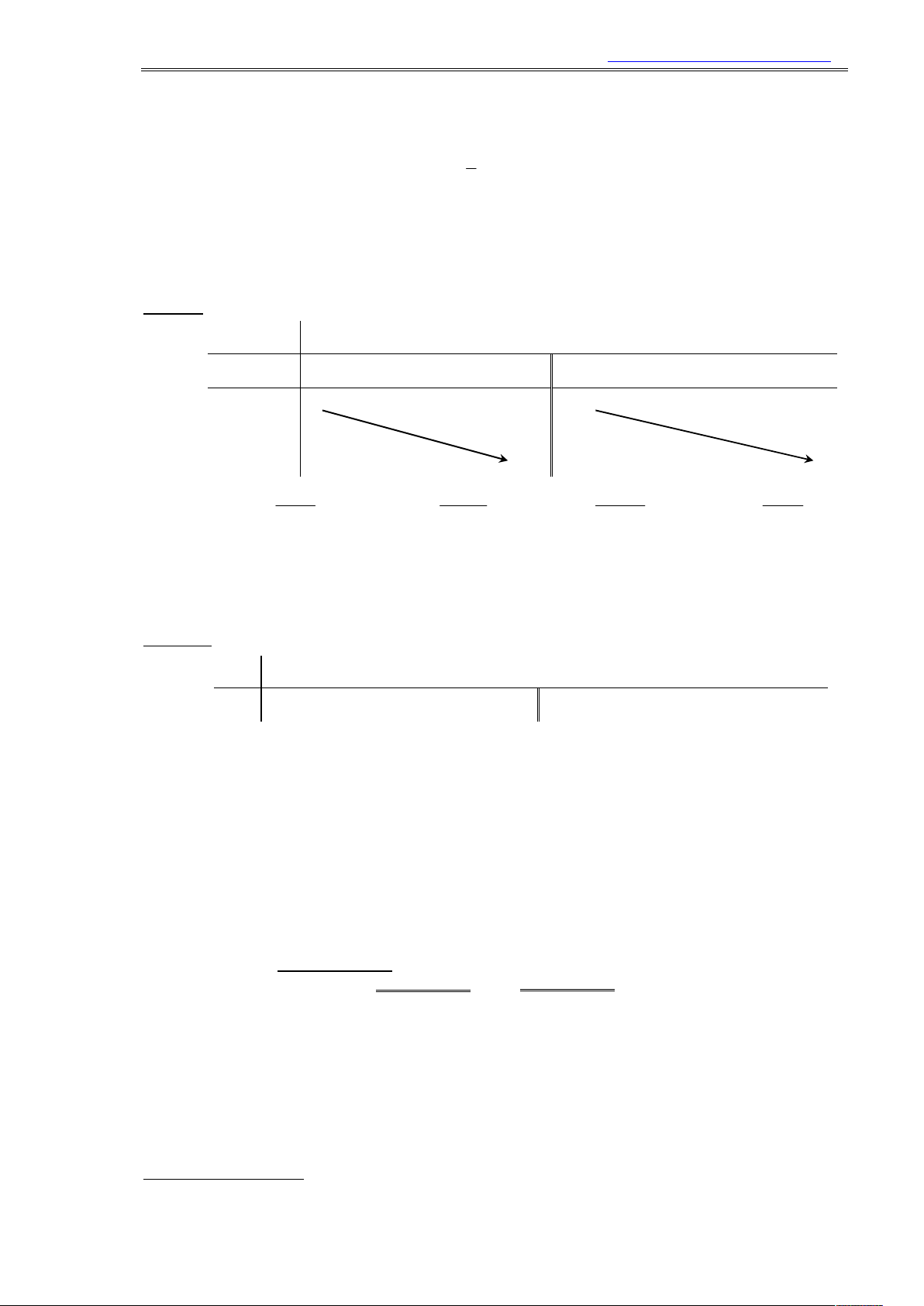
Ví dụ 11. Cho hàm số y  f x , xác định và liên tục trên  có đồ y
thị hàm số y  f 'x  như hình sau, xác định mệnh đề 2 đúng? 1 O x
A. Hàm số y  f x  đồng biến trên khoảng 4;2.
B. Hàm số y  f x  đồng biến trên khoảng  ;    1
C. Hàm số y  f x  đồng biến trên khoảng 0;2. 4
D. Hàm số y  f x  nghịch biến trên khoảng  ;
 4 và 2;.
......................................................................................................................................................
......................................................................................................................................................
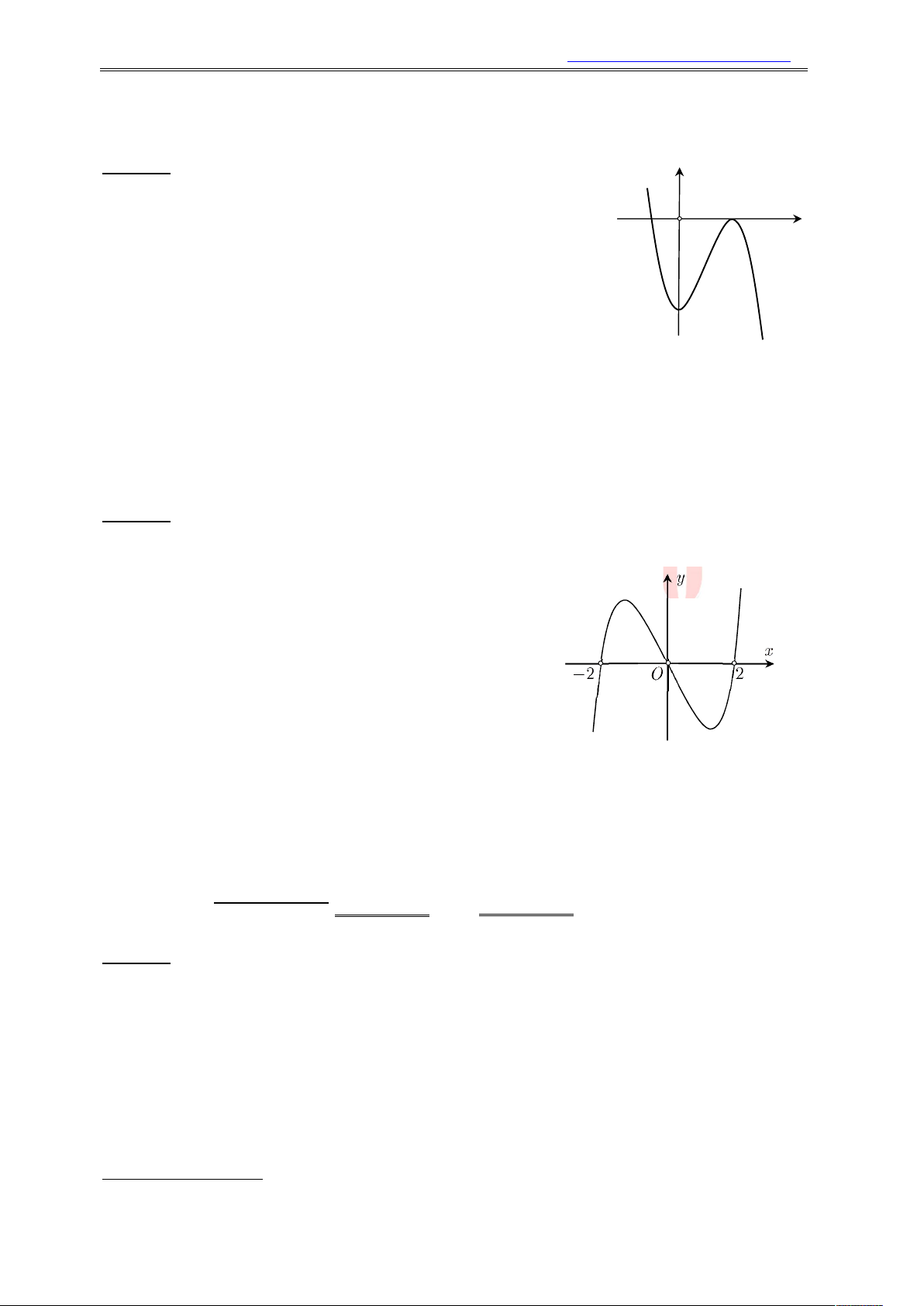
Ví dụ 12. (THPT Chuyên Thái Bình lần 3 năm 2016 – 2017) Cho hàm số f (x) xác định, liên
tục trên  và có đồ thị hàm số y  f (x) là đường cong trong hình bên dưới. Hỏi
mệnh đề nào dưới đây đúng ?
A. Hàm số f (x) đồng biến trên khoảng (1;2).
B. Hàm số f (x) nghịch biến trên khoảng (0;2).
C. Hàm số f (x) đồng biến trên khoảng  ( 2;1).
D. Hàm số f (x) nghịch biến trên khoảng  ( 1;1).
......................................................................................................................................................
......................................................................................................................................................
D¹ng to¸n 4: D¹ng lý thuyÕt, kiÓm tra tÝnh ®óng sai. 
Ví dụ 13. Cho các mệnh đề sau.
a) Hàm số y  f x  được gọi là đồng biến trên D  x ,x  D và x  x thì 1 2 1 2
f x  f x . 1   2
b) Hàm số y  f x  liên tục và đồng biến trên khoảng 2; 3 thì hàm số
y  f x  3 đồng biến trên khoảng 1;6.
c) Hàm số f 'x   0, x  a;b thì y  f x  đồng biến trên a;b .
d) Hàm số y  f x  đồng biến trên khoảng a;b  f 'x   0, x  a;b.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 8
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Có bao nhiêu mệnh đề đúng? A. 1. B. 2. C. 3. D. 4.
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
 Ghi nhớ: ...............................................................................................................................
Ví dụ 14. Nếu hàm số y  f x  liên tục và đồng biến trên khoảng 2; 0 và nghịch biến trên
khoảng 1; 4 thì hàm số y  f x  3  2 nghịch biến trên khoảng nào? A.2;0. B.2;  1 . C.1; 3. D.5;3.
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
 Ghi nhớ: ............................................................................................................................... Đồ thị Đồ thị Phép biến đổi
y  f x
y  f x  a,a  0
y  f x
y  f x a,a  0
y  f x
y  f x
y  f x
y  f x  a,a  0
y  f x
y  f x a,a  0
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 9
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
phÇn 2. D¹ng chøa tham sè.
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
 Bµi to¸n 1: T×m m ®Ó hµm sè y  f  ,
x m ®ång biÕn (nghÞch biÕn) trªn miÒn x¸c
®Þnh, c¸c kho¶ng x¸c ®Þnh cña hµm sè.
D¹ng to¸n 1:T×m m ®Ó hµm sè y  f x,m ®ång biÕn(nghÞch biÕn) trªn .  
• Phương pháp cách giải trực tiếp: ...................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
• Phương pháp cách giải gián tiếp: ..................................................................................................
..................................................................................................................................................................
..................................................................................................................................................................
.................................................................................................................................................................. 1
Ví dụ 1. Tìm tất cả các giá trị của tham số m để hàm số 3
y  x  m   2
1 x  m   1 x  1 3
đồng biến trên tập xác đinh của nó. A. m  1  hoặc m  2 . B. 2   m  1.  C. 2   m  1. D.m  1  hoặc m  2  .
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ví dụ 2. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 101) Có bao nhiêu giá trị nguyên của m để hàm số 3 2 y  x
  mx  (4m  9)x  5 nghịch biến trên ( ;   )  . A. 7. B. 4. C. 6. D. 5.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 10
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Ví dụ 3. Gọi S là tập các giá trị của m để hàm số 2
y  x  1  mx nghịch biến trên  và
m là giá trị nhỏ nhất thuộc tập S. Giá trị gần m nhất là: 0 0 A. 3  . B. 2. C. 1  . D. 3.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ví dụ 4. Có bao nhiêu giá trị nguyên của m để hàm số 1 y   2 m  m 3 x   2 m  m 2
x  mx  1 đồng biến trên .  3 A. 1. B. 2. C. 3. D.Vô số .
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Cần nhớ, nếu a chứa tham số thì xét 2 trường hợp.
TH1: a  0 xét trực tiếp trên hàm số y  f x,m ........................................................
.................................................................................................................................................
TH2: a  0 ...........................................................................................................................
.................................................................................................................................................
Ví dụ 5. (Đề thi minh họa lần 3 – Bộ GD & ĐT năm 2017) Hỏi có bao nhiêu số nguyên m để hàm số 2 3 2
y  (m 1)x  (m 1)x  x  4 nghịch biến trên khoảng ( ;   )  . A. 2. B. 1. C. 0. D. 3.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ví dụ 6. Tìm tất cả các giá trị thực m để hàm số y  sin x  cos x  mx đồng biến trên . 
A.  2  m  2. B. m   2. C. m  2. D.  2  m  2.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 11
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
D¹ng to¸n 2:T×m m ®Ó hµm sè y  f x,m ®ång biÕn(nghÞch biÕn) trªn tõng
kho¶ng x¸c ®Þnh cña hµm sè.  ax  b
Phương pháp: Thường hàm số y  f x,m 
................................................... cx  d
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. mx  3
Ví dụ 7. Tất cả các giá trị của m để hàm số y 
nghịch biến trên từng khoảng xác 3x  m
định của hàm số là: A. m  3  . hoặc m  3. B. 3   m  3.
C.m  3. hoặc m  3. D. 3   m  3.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. mx  4m
Ví dụ 8. (Đề thi THPT Quốc Gia năm 2017 – Mã đề 104) Cho hàm số y  với m x  m
là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến
trên các khoảng xác định. Tìm số phần tử của S. A. 5. B. 4. C. Vố số. D. 3.
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. 2 x  m
Ví dụ 9. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y  đồng biến x  1
trên từng khoảng xác định của nó. A. m  1. B. 1   m  1. C. 3   m  3. D. 1  m  1.
......................................................................................................................................................
......................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 12
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
.....................................................................................................................................................
 Bµi to¸n 2: T×m m ®Ó hµm sè y  f  ,
x m ®ång biÕn (nghÞch biÕn) trªn kho¶ngD
trong ®ã D   ;
 a,a;,a;b.... 
D¹ng to¸n 1: Hµm sè y  f x,m lµ hµm d¹ng    ax b y f x  . cx  d 
Phương pháp: ........................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. mx  16
Ví dụ 10. Giá trị của m để hàm số y 
nghịch biến trên khoảng 1;5 là: x  m m   4     m  4  m  1  A. . B. . C. . D. 4  m  5. m   5       m 4  m 4 
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Cần nhớ: .................................................................................................................................
................................................................................................................................................. 2x  1
Ví dụ 11. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y  nghịch biến x  m trên (2;  ).   1  1    1   1   A.  2  ;              B. 2;  C. ;  D. ;  2         2  2  2
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
..................................................................................................................................................... x
Ví dụ 12. Tìm tất cả các giá trị thực của tham số m để hàm số y  nghịch biến trên x  m [1; ). 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 13
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong A. 0  m  1. B. 0  m  1. C. 0  m  1. D. m  1.
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
.................................................................................................................................................
D¹ng to¸n 2: Hµm sè y  f x,m lµ hµm d¹ng ®a thøc. 
Phương pháp cô lập .............................................................................................................
.................................................................................................................................................
................................................................................................................................................. 1
Ví dụ 13. Trong tât cả các giá trị của m để hàm số 3
y   x  m   2
1 x  m  3x 10 3
đồng biến trên khoảng 0; 3 thì m  m là giá trị nhỏ nhất. Giá trị gần m là 0 0 A. 1, 5. B.1, 6. C.1, 7. D.1, 8.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Cần nhớ: .................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. 4 2
Ví dụ 14. Cho hàm số y  x
 (2m  3)x  .
m Nếu hàm số luôn nghịch biến trên khoảng  p  p
(1;2) thì sẽ tồn tại các giá trị của tham số m     ;   ;  trong đó phân số tối giản  q  q
và q  0. Hỏi tổng p  q bằng bao nhiêu ?
A. p  q  3.
B. p  q  5.
C. p  q  7.
D. p  q  9.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 14
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ví dụ 15. (THPT Chuyên Đại Học Vinh lần 2 năm 2017) Tìm tất cả các giá trị của tham số m để hàm số 2 4 2
y  (m 1)x  2mx đồng biến trên (1; ).  1  5 1  5 A. m  1  hoặc m   B. m  1  hoặc m   2 2 C. m  1  hoặc m  1. D. m  1.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
D¹ng to¸n 3*: Hµm sè y  f x,m lµ hµm d¹ng lîng gi¸c, c¨n... 
Phương pháp .........................................................................................................................
................................................................................................................................................. m   1 x  1  2
Ví dụ 16. Cho hàm số y 
. Tìm tập tất cả các giá trị tham số m để hàm x  1  m
số đồng biến trên 17;37. A.m   4;  1.    B.m   ;  6  4;  1  2;   .  C.m  ; 4     2;  .  D.m  1;2.
Phương pháp đặt ẩn phụ .....................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 15
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
.................................................................................................................................................
.................................................................................................................................................
Cần nhớ: .................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
................................................................................................................................................. sin x  m
Ví dụ 17. Tất cả các giá trị thực của tham số m để hàm số y  nghịch biến trên sin x  m     khoảng  ; .   2  A. m  0.
B.m  0 hoặc m  1. C. 0  m  1. D.m  1  .
Phương pháp đặt ẩn phụ .....................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Cần nhớ: .................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Ví dụ 18. (Đề thi minh họa – Bộ GD & ĐT năm 2017) Tìm tất cả các giá trị thực của tham số tan x  2   m  
sao cho hàm số y 
đồng biến trên khoảng 0;   tan x  m    4  
A. m  0 hoặc 1  m  2. B. m  0. C. 1  x  2. D. m  2.
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 16
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
.................................................................................................................................................
.................................................................................................................................................
.................................................................................................................................................
 Bµi to¸n 3. T×m tham sè m ®Ó hµm sè bËc 3 ®¬n ®iÖu trªn ®é dµi l.  3 2
Tìm m để hàm số y  ax bx cx d đơn điệu trên khoảng có độ dài đúng bằng l Phương pháp:
Ví dụ 1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 1 3 2
y   x  mx  (m  1)x  m  3 đồng biến trên đoạn có độ dài đúng bằng 2. 3 A. m  1  hoặc m  2. B. m  1  . C. Không tồn tại . m D. m  2.
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Ví dụ 2. Tìm các giá trị của tham số m sao cho hàm số 3 2
y  x  (m  1)x  4x  7 có độ
dài khoảng nghịch biến đúng bằng 2 5. A. m  2  hoặc m  4.
B. m  1 hoặc m  3.
C. m  0 hoặc m  1  .
D. m  2 hoặc m  4  .
.....................................................................................................................................................
.....................................................................................................................................................
.....................................................................................................................................................
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 17
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
Ví dụ 3. Tìm tất cả các giá trị thực m để hàm số 3 2
f (x)  x
  3x  (m 1)x  2m  3
đồng biến trên một khoảng có độ dài lớn hơn 1. 5 5 A. m  0. B. m  0. C. 
 m  0. D. m    4 4
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
......................................................................................................................................................
...................................................................................................................................................... C. c©u hái tr¾c nghiÖm.
PhÇn 1. Bµi tËp kh«ng chøa tham sè.
Câu 1. (THPTQG – 2017 – 101) Cho hàm số 3
y  x  3x  2 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;
 0 và nghịch biến trên khoảng 0;.
B. Hàm số nghịch biến trên khoảng  ;  .
C.Hàm số đồng biến trên khoảng  ;  .
D. Hàm số nghịch biến trên khoảng  ;
 0 và đồng biến trên khoảng 0;. 2
Câu 2. (THPTQG – 2017 – 101) Hàm số y 
nghịch biến trên khoảng nào dưới đây? 2 x  1 A. 0;. B.1;  1 . C. ;  . D. ;  0. 2x  1
Câu 3. Trong các phát biểu sau về hàm số y 
, phát biểu nào sau đây là đúng? x  3
A. Hàm số luôn đồng biến với x   3.
B. Hàm số đồng biến trên  ;
 3  3;.
C. Hàm số đồng biến trên  ;
 3 và 3;.
D. Hàm số đồng biến trên tập  \   3 . Câu 4. Cho hàm số 4 2
y  x  2x  4. Trong các phát biểu sau, phát biểu nào không đúng?
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 18
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
A. Hàm số đồng biến trên khoảng 1; 0 và 1;.
B. Hàm số nghịch biến trên  ;    1 và 0;1 .  
C. Hàm số đồng biến trên  1; 0      và 1;  . 
D. Hàm số nghịch biến trên  ;    1  0;  1 .
Câu 5. (THPTQG – 2017 – 103) Cho hàm số 4 2
y  x  2x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;  2.
B. Hàm số nghịch biến trên khoảng  ;  2.
C. Hàm số đồng biến trên khoảng 1;  1 .
D. Hàm số nghịch biến trên khoảng 1;  1 .
Câu 6. (THPTQG – 2017 – 102) Cho hàm số 3 2
y  x  3x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 0;2.
B. Hàm số nghịch biến trên khoảng 2;.
C. Hàm số đồng biến trên khoảng 0;2.
D. Hám số nghịch biến trên khoảng  ;  0.
Câu 7. (THPTQG – 2017 – 103) Cho hàm số y  f x  có đạo hàm f x  2 '  x  1 với x   .
 Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  ;  0.
B. Hàm số nghịch biến trên khoảng 1;.
C. Hàm số nghịch biến trên khoảng 1;  1 .
D. Hàm số đồng biến trên khoảng  ;  .
Câu 8. (THPTQG – 2017 – 103) Hàm số nào dưới đây đồng biến trên khoảng  ;  . x  1 x  1 A. y  . B. 3
y  x  x. C.y  . D. 3 y  x   3x. x  3 x  2
Câu 9. Có nhiều nhất bao nhiêu số nguyên thuộc khoảng nghịch biến của hàm số 1 3 2
y  x  x  3x  1? 3 A. Vô số. B. 2. C. 3. D. 5. Câu 10. Hàm số 3 2
y  x  3x  9x  2 đồng biến trên khoảng nào? A.  ;
 3 và 1;. B. 3;  1 . C.  ;    1 và 3;. D. 1; 3.
Câu 11. (Đề minh họa THPTQG – 2017) Hàm số 4
y  2x  1 đồng biến trên khoảng nào?  1    1    A.   ;   .  0; .   ;   .  ;  0 .  B.   C. D.    2  2 
Câu 12. Khi nói về tính đơn điệu của hàm số 4 2 y  x 
 4x  10 ta có những phát biểu sau:
1) Hàm số đồng biến trên khoảng  ;  3.
2) Hàm số nghịch biến trên 3;  . 
3) Hàm số nghịch biến trên khoảng  ;  0 và 3;.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 19
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
4) Hàm số đồng biến trên khoảng  ; 3  . 
Trên những phát biểu trên, có bao nhiêu phát biểu đúng? A. 1. B. 2. C. 3. D. 4. 1
Câu 13. Trong các phát biểu sau về hàm số y  1 
, phát biểu nào sau đây là đúng? x
A. Hàm số luôn nghịch biến với x   0.
B. Hàm số nghịch biến trên  ;  0 và 0;.
C. Hàm số đồng biến trên  ;  0 và 0;.
D. Hàm số đồng biến trên tập  \   0 . 2 x  2x  1
Câu 14. Khi nói về tính đơn điệu của hám số y 
, ta có những phát biểu sau: x  2
1) Hàm số nghịch biến trên khoảng 1; 3.
2) Đồng biến trên khoảng  ;    1  3;.
3) Hàm số nghịch biến trên khoảng 1; 3 \   2 .
4) Hàm số đồng biến trên khoảng  ;   1 và 3;.
Trong những phát biểu trên có bao nhiêu phát biểu đúng? A. 1. B. 2. C. 3. D. 4. 2x  1
Câu 15. Cho hàm số y 
. Khẳng định nào sau đây đúng? x  1
A. Hàm số đồng biến trên khoảng  ;  .
B. Hàm số nghịch biến trên khoảng  ;  .
C. Hàm số nghịch biến trên từng khoảng xác định.
D. Hàm số đồng biến trên từng khoảng xác định.
Câu 16. Hàm số nào trong các hàm số sau đồng biến trên .  A. 3 2
y  x  3x  2. B. 3 2
y  x  3x  3x. C. 3 y  x  . D. 3 2 y  x   6x .
Câu 17. Trong các hàm số sau, hàm số nào đồng biến trên .  A. 4 2
y  x  2x  3. B. 3
y  x  4x  5. x  1 C. y  D. 2
y  x  x  1. 2x  3. Câu 18. Hàm số 3 2
y  2x  9x  12x  4 nghịch biến trên khoảng. A. 1;2. B. 2;. C. 2;3. D.  ;   1 .
Câu 19. Nếu hàm số y  f x  liên tục và đồng biến trên khoảng 2; 3 thì hàm số
y  f x  3 đồng biến trên khoảng nào? A. 1;6. B. 5;0. C. 2;6. D. 2; 3.
Câu 20. Nếu hàm số y  f x  liên tục và đồng biến trên khoảng 1;2 thì hàm số
y  f x  
1 đồng biến trên khoảng nào? A. 1;2. B. 0;3. C. 2;6. D. 2; 3.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 20
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 21. Nếu hàm số y  f x  liên tục và đồng biến trên khoảng 3;  1 và nghịch biến trên
khoảng 2; 3 thì hàm số y  f x  đồng biến trên khoảng nào? A. 3;  1 . B. 2;3. C. 3;  1 . D. 2;3.
Câu 22. Nếu hàm số y  f x  liên tục và đồng biến trên khoảng 2;0 và nghịch biến trên
khoảng 1; 4 thì hàm số y  f x  3  3 đồng biến trên khoảng nào? A. 2; 0. B. 2;  1 . C. 1; 3. D. 5;3. 3x  1
Câu 23. Cho hàm số y 
. Ta có các phát biểu sau: x  1
I. Hàm số đồng biến trên  ;    1  1;.
II. Hàm số đồng biến trên tập  \ 3.
III. Hàm số nghịch biến trên  ;    1 và 1;.
IV. Hàm số đồng biến trên  ;    1 ,0;.
Hỏi trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A. 0. B. 1. C. 2. D. 3.
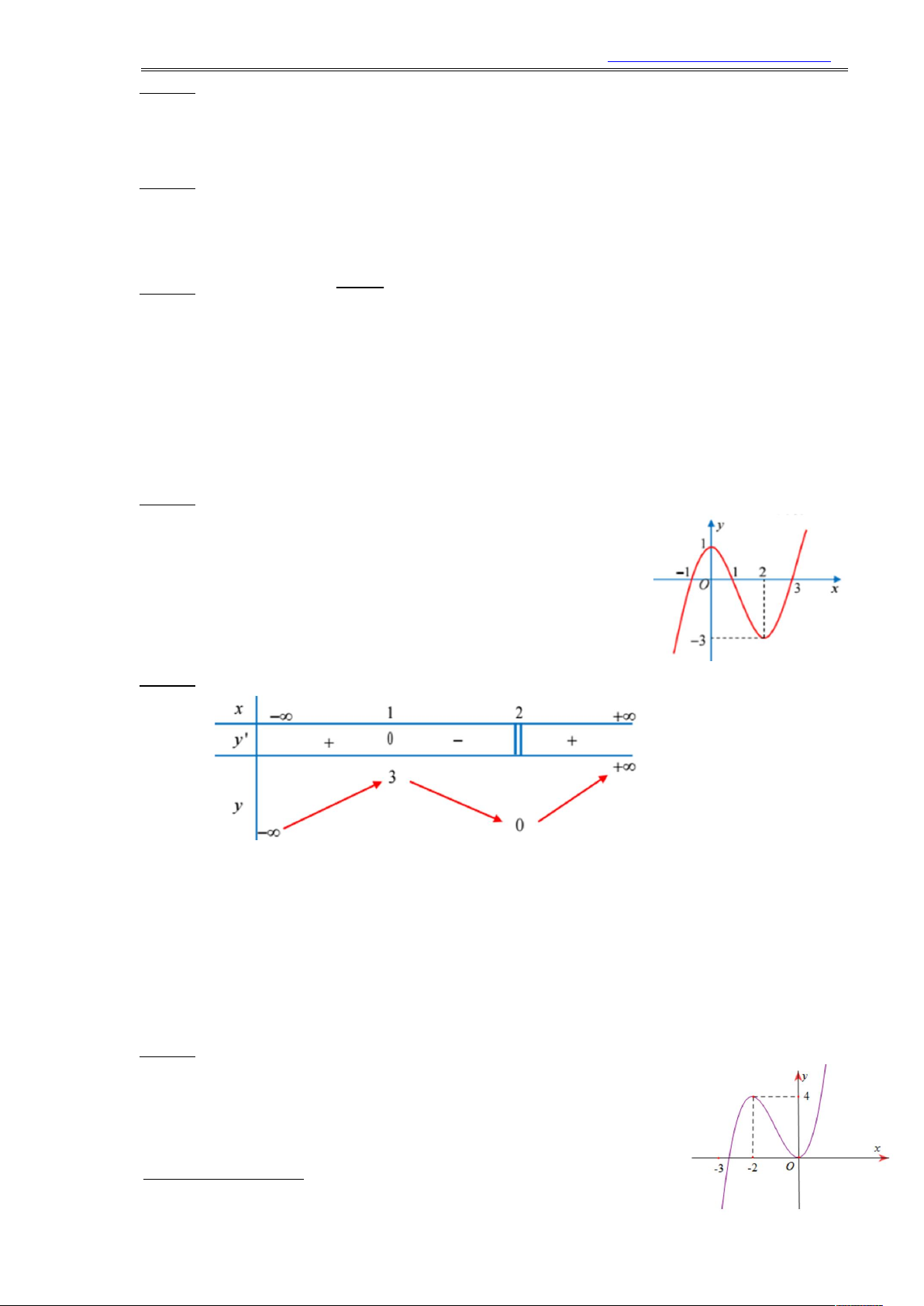
Câu 24. Cho hàm số y  f x  có đồ thị như hình vẽ bên. Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng  ;  0;2;.
B. Hàm số nghịch biến trên khoảng 0;2.
C. Hàm số đồng biến trên khoảng 1;  1 ;3;.
D. Hàm số nghịch biến trên khoảng 1;2.
Câu 25. Cho hàm số y  f x  có bảng biến thiên như hình vẽ sau:
Mệnh đề nào sau đây sai?
A. Hàm số đã cho đồng biến trên khoảng 2;.
B. Hàm số đã cho đồng biến trên khoảng  ;   1 .
C. Hàm số đã cho đồng biến trên khoảng 3;.
D. Hàm số đã cho nghịch biến trên khoảng 0;3.
Câu 26. Cho hàm số y  f x  xác định trên  và có đồ thị y  f 'x  là đường cong trong
hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số y  f x  đồng biến trên khoảng  ;  2,0;.
B. Hàm số y  f x  nghịch biến trên khoảng 2; 0.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 21
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
C. Hàm số y  f x  đồng biến trên khoảng 3;.
D. Hàm số y  f x  nghịch biến trên khoảng  ;  0.
Câu 27. Cho hàm số y  f x  xác định trên khoảng a;b. Phát biểu nào sau đây đúng?.
A. f x  đồng biến trên a;b khi và chỉ khi x ,x  a;b : x  x  f x  f x . 1 2   1 2  1  2
B. f x  nghịch biến trên a;b khi và chỉ khi x ,x  a;b : x  x  f x  f x . 1 2   1 2  1  2
C. f x  đồng biến trên a;b khi và chỉ khi x ,x  a;b : x  x  f x  f x . 1 2   1 2  1  2
D. f x  nghịch biến trên a;b khi và chỉ khi x ,x  a;b : x  x  f x  f x . 1 2   1 2  1  2
Câu 28. Cho các phát biểu sau:
I. Hàm số y  f x  được gọi là đồng biến trên miền D khi và chỉ khi x  D,x  x 1 2
thì f x  f x . 1   2
II. Hàm số y  f x  được gọi là nghịch biến trên miền D khi và chỉ khi
x  D,x  x thì f x  f x . 1   2 1 2
III. Nếu f 'x   0, x
  a;b thì hàm số y  f x đồng biến trên khoảng a;b.
IV. Hàm số y  f x  đồng biến trên khoảng a;b khi và chỉ khi
f 'x  0, x  a;b.
Có bao nhiêu phát biểu đúng? A. 1. B. 2. C. 3. D. 4.
Câu 29. Cho hàm số y  f x  có đạo hàm trên a;b . Phát biểu nào sau đây là đúng?
A. Hàm số y  f x  đồng biến trên a;b khi và chỉ khi f 'x   0, x  a;b
, f 'x  0 xảy ra tại hữu hạn điểm thuộc a;b.
B. Hàm số y  f x  đồng biến trên a;b khi và chỉ khi f 'x   0, x
  a;b.
C. Hàm số y  f x  nghịch biến trên a;b khi và chỉ khi f 'x   0, x  a;b
, f 'x  0 xảy ra tại hữu hạn điểm thuộc a;b.
D. Hàm số y  f x  nghịch biến trên a;b khi và chỉ khi f 'x   0, x
  a;b.
Câu 30. Cho hàm số y  f x  đơn điệu trên khoảng a;b. Trong các khẳng định sau, khẳng định nào đúng?
A. f 'x   0, x  a;b.
B. f 'x   0, x  a;b.
C. f 'x   0, x  a;b
D. f 'x  không đổi dấu trên a;b .
Câu 31. Cho hàm số y  f x  và y  g x  đều nghịch biến trên  . Cho các khẳng định sau:
I) Hàm số y  f x   g x  nghịch biến trên . 
II) Hàm số y  f x .g x  nghịch biến trên .
III) Hàm số y  f x   g x  nghịch biến trên . 
IV) Hàm số y  kf x k  0 nghịch biến trên . 
Có bao nhiêu khẳng định đúng? A. 1. B. 2. C. 3. D. 4.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 22
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 32. Cho D là một khoảng. Ta có 3 phát biểu sau:
1) Hàm số y  f x  đồng biến trên D khi và chỉ khi f 'x   0, x   . D
2) Hàm số y  f x  đạt cực đại tại điểm x  x khi và chỉ khi f 'x  0 và 0  0
f ' x  0 . 0 
3) Hàm số y  f x  có f 'x   0 với x
  D  D , khi đó f x đồng biến trên 1 2 D  D . 1 2
Số các phát biểu đúng là: A. 1. B. 2. C. 3. D. 0.
PhÇn 2. Bµi tËp chøa tham sè. 1
Câu 33. Tìm m để hàm số 3
y  x  m   2
1 x  m  
1 x  1 đồng biến trên tập xác định. 3 A. m  1  hoặc m  2. B. 2   m  1.  C. 2  m  1. D. m  1  hoặc m  2  . 1
Câu 34. Trong tất cả các giá trị của m làm cho hàm số 3 2
y  x  mx  mx  m đồng biến 3 trên .
 Có giá trị nhỏ nhất của m là: A. 4. B. 1. C. 0. D. 1.
Câu 35. (THPTQG – 2017 - 101) Cho hàm số 3 2 y  x
  mx  4m  9x  5 với m là tham
số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng  ;  . A. 7. B. 4. C. 6. D. 5.
Câu 36. Cho hàm số y  m   3
x  m   2 7
7 x  2mx  1. Có bao nhiêu giá trị nguyên của
m để hàm số nghịch biến trên .  A. 4. B. 6. C. 7. D. 9. 1
Câu 37. Cho hàm số y   2 m  2m 3 x   2 m  2m 2
x  mx  3. Tất cả các giá trị thực của 3
tham số m để hàm số nghịch biến trên  . A. m  2; 1    .   
B. m  2;1     0 .  C. m  2; 1           0 .  D. m   2;1 .   Câu 38. Hàm số 3 2
y  mx  3mx  4x  1 đồng biến trên  khi và chỉ khi. 4 4 A. 0  m  . B. 0  m  . 3 3 4 4
C. m  0 hoặc m  . D. 0  m  . 3 3
Câu 39. Tất cả các giá trị của a để hàm số y  ax  sin x  3 đồng biến trên .  A. a  1. B. a  1. C. a  1. D. a  1  . 2 x  m
Câu 40. Hàm số y 
đồng biến trên  khi giá trị của m là: 2 x  1 A. m  1. B. m  1. C. m  1. D. m  .  Câu 41. Hàm số 3 2
y  ax  bx  cx  d nghịch biến trên  khi và chỉ khi: A. 2 b  3ac  0.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 23
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong B. a  0 và 2 b  3ac  0. C. a  0 và 2
b  3ac  0 hoặc a  b  0,c  0 . D. a  0 và 2
b  3ac  0 hoặc a  b  0,c  0. ax  b
Câu 42. (THPTQG – 2017 – 101) Đường cong ở hình bên là đồ thị của hàm số y  với cx  d a, , b ,
c d là các số thực.
Mệnh đề nào dưới đây đúng?
A. y '  0, x  . 
B. y '  0, x  .  C. y '  0, x   1. D. y '  0, x   1. mx  5
Câu 43. Điều kiện cần và đủ để hàm số y 
đồng biến trên từng khoảng xác định là: x  1 A. m  5. B. m  5  . C. m  5. D. m  5. x  m
Câu 44. Tất cả các giá trị của m để hàm số y 
đồng biến trên từng khoảng xác mx  m  2 định là: m   1  A. 1   m  2. B. . m   2  1 3 C. m  hoặc m  . D. 1   m  2. 2 2 mx  3m  2
Câu 45. Tất cả các giá trị thực của tham số m để hàm số y  nghịch biến trên x  m
từng khoảng xác định là: A. 1  m  2. B. 1  m  2.
C. m  1 hoặc m  2.
D. m  1 hoặc m  2. mx  8
Câu 46. Hàm số y 
nghịch biến trên các khoảng xác định khi và chỉ khi m nhận giá x  4 trị nào? A. m  2. B. m  2. C. m  2. D. m  2. mx  3
Câu 47. Có bao nhiêu giá trị nguyên của m để hàm số y  nghịch biến trên từng x  m  2
khoảng xác định của nó? A. 2. B. 3. C. 4. D. 5. mx  3m  4
Câu 48. Tất cả các giá trị thực của m để hàm số y 
đồng biến trên khoảng x  m 1;2 là: A. 4  m  1  . B. 4  m  1.
C. m  1 hoặc m  2.
D. m  4 hoặc m  2. mx  16
Câu 49. Giá trị của m để hàm số y 
nghịch biến trên khoảng 1;5 là: x  m
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 24
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong m   4     m  4   m  1  A. . B. . C. . D. 4  m  5. m   5       m 4  m 4  mx  4
Câu 50. Cho hàm số y 
với m là tham số thực. Tất cả các giá trị của m để hàm số x  m
đồng biến trên khoảng 2;. m   2   m  2  A. . B. . C. m  2. D. m  2. m   2     m 2  mx  4
Câu 51. Cho hàm số y 
. Điều kiện đầy đủ của m để hàm số nghịch biến trên x  m  ;1   là:
A. 2  m  1. B. 2  m  1. C. 2   m  2. D. 2   m  1. mx  9
Câu 52. Giá trị của m để hàm số y 
nghịch biến trên khoảng  ;  2 là: x  m
A. 3  m  3. B. 2  m  3.
C. 3  m  2. D. 3   m  3.
Câu 53. Tìm tất cả các giá trị của tham số m để hàm số 4
y  x    m 2 2
x  4  2m nghịch
biến trên khoảng 1; 0 . A. m  2. B. m  2. C. m  4. D. m  4. 1
Câu 54. Tìm tất cả các giá trị tham số m để hàm số 3
y   x  m   2
1 x  m  3x 10 3
đồng biến trên khoảng 0;3. 12 12 12 A. m  . B. m  . C. m  . D. m  .  7 7 7
Câu 55. Có bao nhiêu giá trị nguyên của m để hàm số 2 3
y  x  2m  3 2 x  2 2
m  3mx  1 nghịch biến trên khoảng 1;3. 3 A. 4. B. 1. C. 2. D. 3.
Câu 56. Trong tất cả các giá trị của m để hàm số 3
y   x  m   2 2 3
1 x  6mx  1 đồng
biến trên khoảng 2; 0 thì m  m là giá trị lớn nhất. Hỏi trong các số sau, đâu là 0 số gần m nhất? 0 A. 2. B. 1. C. 4. D. 4. Câu 57. Cho hàm số 3 2 y  x
  3x  3mx  1,  
1 với m là tham số thực. Tìm m để hàm số
 1 nghịch biến trên khoảng 0;. A. m  2. B. m  0. C. 1  m  1. D. m  1. Câu 58. Cho hàm số 3 y  x   m   2 x   2 1
2m  3m  
2 x  1 với m là tham số thực.
Trong các điều kiện sau của m , đâu là điều kiện đầy đủ nhất để hàm số nghịch biến trên 2;. 3 A.   m  2. B. m  .  2 3 C. m  2.
D. m   hoặc m  2. 2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 25
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
2m cos x  m  3  
Câu 59. Hàm số y 
đồng biến trên khoảng  ; 
 thì điều kiện đầy đủ của 4 cos x  m  2  tham số m là: A. m  2  hoặc m  0. B. m  2  hoặc m  4. C. 2  m  4. D. 2   m  0. sin x  m
Câu 60. Tất cả các giá trị thực của tham số m để hàm số y  nghịch biến trên sin x  m     khoảng  ;   là:  2  m   0  A. m  0. B. . C. 0  m  1. D. m  1  . m   1 
Câu 61. (Đề minh họa THPTQG – 2017) Tìm tất cả các giá trị thực của tham số m sao cho tan x  2     hàm số y 
đồng biến trên khoảng 0; . tan x  m  4
A. m  0 hoặc 1  m  2. B. m  0. C. 1  m  2. D. m  2. m  sin x
Câu 62. Tìm tất cả các giá trị thực của tham số m để hàm số y  nghịch biến trên 2 cos x   0; .   6 5 5 A. m  1. B. m  . C. m  . D. m  2. 2 4
m  1 x 1  2
Câu 63. Cho hàm số y 
. Tìm tập tất cả các giá trị của tham số m để hàm x  1  m
số đồng biến trên khoảng 17;37. A. m   4;  1.    B. m   ;  6  4;  1  2;   .  C. m  ; 4     2;  .  D. m  1;2. 3 m  6
Câu 64. Cho hàm số y   2
x  1  x m 2 2
2x  2x x  1   1   1. Có bao 2 x  1  x
nhiêu giá trị nguyên dương của tham số m để hàm số nghịch biến trên .  A. 5. B. Vô số. C. 2. D. 3.
Câu 65. Cho hai hàm số f x   x  m sin x và g x   m  3x  2m  
1 cos x. Tất cả các
giá trị của m làm cho hàm số f x  đồng biến trên  và g x  nghịch biến trên  là: 2 A. m  1. B. m  0. C. 1  m  0. D. 1   m  . 3
Câu 66. Cho hàm số y  a sin x  b cos x  x với a,b là các tham số thực. Điều kiện của a,b
để hàm số đồng biến trên  là: 2 A. a,b  .  B. 2 2 a  b  1. C. a  b  . D. 2 2 a  b  1. 2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 26
Tt GIA SÖ CHö seâ- 094.6798.489 giaûi tích LÔÙP 12
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong ĐÁP ÁN 1C 2A 3C 4D 5B 6A 7D 8B 9C 10C 11B 12B 13B 14A 15D 16B 17A 18A 19D 20B 21B 22D 23B 24C 25D 26C 27C 28B 29C 30D 31A 32 33C 34B 35A 36C 37D 38B 39B 40D 41D 42D 43D 44D 45B 46D 47B 48A 49A 50C 51D 52C 53B 54A 55C 56B 57D 58A 59A 60A 61A 62C 63B 64D 65D 66B
Lớp học duy nhất tại Số 17 Hoàng Văn Thụ. TT Chư Sê. Gia Lai
Theo dõi facebook: https://www.facebook.com/phong.baovuong
Để nhận được các bài học tiếp nhé.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489 Trang 27
Document Outline

Bµi 1. tÝnh ®¬n ®iÖu cña hµm sè.
A. KiÕn thøc cÇn nhí.
- 1. Định nghĩa
- 2. Điều kiện cần và đủ để hàm số đơn điệu
  - a) Điều kiện cần để hàm số đơn điệu.
  - Giả sử hàm số có đạo hàm trên khoảng
  - b) Điều kiện đủ để hàm số đơn điệu.
phÇn 1. D¹ng kh«ng chøa tham sè.
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
- D¹ng to¸n 1: §¬n ®iÖu cña mét hµm têng minh, râ rµng vÒ sè liÖu.
- D¹ng to¸n 2: D¹ng b¶ng biÕn thiªn.
- D¹ng to¸n 3: D¹ng cho ®å thÞ hµm sè .
- D¹ng to¸n 4: D¹ng lý thuyÕt, kiÓm tra tÝnh ®óng sai.
phÇn 2. D¹ng chøa tham sè.
B. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
- ( Bµi to¸n 1: T×m ®Ó hµm sè ®ång biÕn (nghÞch biÕn) trªn miÒn x¸c ®Þnh, c¸c kho¶ng x¸c ®Þnh cña hµm sè.
  - D¹ng to¸n 1:T×m ®Ó hµm sè ®ång biÕn(nghÞch biÕn) trªn
  - D¹ng to¸n 2:T×m ®Ó hµm sè ®ång biÕn(nghÞch biÕn) trªn tõng kho¶ng x¸c ®Þnh cña hµm sè.
- ( Bµi to¸n 2: T×m ®Ó hµm sè ®ång biÕn (nghÞch biÕn) trªn kho¶ng trong ®ã .
  - D¹ng to¸n 1: Hµm sè lµ hµm d¹ng .
  - D¹ng to¸n 2: Hµm sè lµ hµm d¹ng ®a thøc.
  - D¹ng to¸n 3*: Hµm sè lµ hµm d¹ng lîng gi¸c, c¨n...
- ( Bµi to¸n 3. T×m tham sè m ®Ó hµm sè bËc 3 ®¬n ®iÖu trªn ®é dµi l.

Các dạng toán tính đơn điệu của hàm số – Nguyễn Bảo Vương Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số