Các dạng toán trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án)

Các dạng toán trắc nghiệm Đại cương về đường thẳng và mặt phẳng có lời giải chi tiết và đáp án được soạn dưới dạng file PDF gồm 80 trang. Các bạn xem và tải về ở dưới.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

80 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
CÁC DẠNG TOÁN TRẮC NGHIỆM
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. Khái niệm mở đầu
1. Mặt phẳng
+ Mặt bàn, mặt bảng, mặt hồ nước yên lặng . . . Cho ta hình ảnh của một phần của mặt phẳng.
+ Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng
vào một góc của hình biểu diễn.
+ Để kí hiệu mặt phẳng, ta thường dùng chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ( ).
+ mặt phẳng (P ), mặt phẳng ( Q ), mặt phẳng (a), mặt phẳng (b) hoặc viết tắt là mp( P ), mp( Q ),
mp (a) , mp ( b) , hoặc ( P ) , ( Q ) , (a) , ( b),
2. Điểm thuộc mặt phẳng
Cho điểm A và mặt phẳng (P).
+ Điểm A thuộc mặt phẳng (P) ta nói A nằm trên (P) hay (P) chứa A, hay (P) đi qua A và kí hiệu A Î
( P) .
+ Điểm A không thuộc mặt phẳng (P) ta nói điểm A nằm ngoài (P) hay (P) không chứa A và kí hiệu
A Ï ( P) .
3. Hình biểu diễn của một hình không gian
P
A
P
P
A
Trang 2
Để vẽ hình biểu diễn của một hình trong không gian, ta dựa vào những qui tắc sau :
+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
+ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai đường thẳng
cắt nhau là hai đường thẳng cắt nhau.
+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
+ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che
khuất.
II. CÁC TÍNH CHẤT THỪA NHẬN
1. Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
2. Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
3. Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó.
* Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P ) thì ta nói đường thẳng d nằm trong mặt
phẳng (P) . Hay (P) chứa d và kí hiệu d Ì (P) hay (P) É d
4. Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng
Nếu có nhiều điểm cùng thuộc một mp thì ta nói những điểm đó đồng phẳng .
5. Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung
khác nữa.
* Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua
điểm chung ấy.
* Đường thẳng chung d của hai mặt phẳng phân biệt ( P ) và ( Q ) được gọi là giao tuyến của ( P)
và (Q)
kí hiệu d = ( p) Ç ( Q )
6. Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
III. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG
Có 3 cách xác định mặt phẳng
+ Qua 3 điểm không thẳng hàng xác định duy nhất một mặt phẳng.
A
C
Trang 3
+ Qua một điểm và một đường thẳng không chứa điểm đó ta xác định duy nhất một mặt phẳng.
Kí hiệu mp(A,d) hay (A,d)
+ Hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng.
Kí hiệu mp (a, b) hay (a, b)
IV. HÌNH CHÓP VÀ HÌNH TỨ DIỆN
1. Hình chóp:
+ Hình gồm miền đa giác A
1
A
2
A
3
. . .An. Lấy điểm S nằm ngoài (a) . lần lượt nối S với các đỉnh
A
1
, A
2
, … A
n
ta được n tam gíác SA
1
A
2
, SA
2
A
3
. . . SA
n
A
1
. Hình gồm đa giác A
1
A
2
A
3
. . .An và n tam
giác SA
1
A
2
, SA
2
A
3
. . . SA
n
A gọi là hình chóp, kí hiệu là S. A
1
A
2
A
3
. . .An. ta gọi S là đỉnh và đa giác
A
1
A
2
A
3
. . .An là mặt đáy. Các tam giác SA
1
A
2
, SA
2
A
3
. . . SA
n
A gọi là các mặt bên. Các đoạn SA
1
, SA
2
. . SA
n
là các cạnh bên., các cạnh của đa giác đáy gọi là cạnh đáy của hình chóp.
2. Hình tứ diện
+ Một hình chóp có đáy là tam giác gọi là tứ diện.
+ Tứ diện có các mặt là tam giác đều gọi là tứ diện đều.
V. HÌNH LĂNG TRỤ
1. Hình lăng trụ: Hình hợp bởi các hình bình hành A
1
A
2
A'
2
A'
1
, A
2
A
3
A'
3
A'
2
,...,A
n
A
1
A'
1
A'
2
và hai đa
giác A
1
A
2
...A
n
, A'
1
A'
2
...A'
n
gọi là hình lăng trụ hoặc lăng trụ, và ký hiệu là A
1
A
2
...A
n
.A'
1
A'
2
...A'
n
.
Trong một hình lăng trụ thì
A
C
A
d
a
Trang 4
• 2 mặt đáy là đa giác song song và bằng nhau.
• các cạnh bên song song và bằng nhau
• các mặt bên là hình bình hành
2. Hình hộp: là hình lăng trụ có đáy là hình bình hành.
Trong một hình hộp thì
• Các mặt bên là các hình bình hành
• Các đường chéo của hình hộp cắt nhau
tại trung điểm mỗi đường.
PHẦN 1
ĐỀ BÀI
DẠNG 1
LÝ THUYẾT
Câu 1. Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Câu 2. Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân
biệt từ bốn điểm đã cho ?
A. B. C. D.
,,MNP
2.
3.
4.
6.
hình hộp
Trang 5
Câu 3. Trong mp , cho bốn điểm , , , trong đó không có ba điểm nào thẳng hàng. Điểm
. Có mấy mặt phẳng tạo bởi và hai trong số bốn điểm nói trên?
A. . B. . C. . D. .
Câu 4. Cho 2 đường thẳng cắt nhau và không đi qua điểm . Xác định được nhiều nhất bao nhiêu
mặt phẳng bởi a, b và A ?
A. 1 B. 2 C. 3 D. 4.
Câu 5. Cho tứ giác lồi và điểm S không thuộc mp (ABCD). Có nhiều nhất bao nhiêu mặt
phẳng xác định bởi các điểm A, B, C, D, S ?
A. 5 B. 6 C. 7 D. 8
Câu 6. Trong mặt phẳng cho tứ giác , điểm . Hỏi có bao nhiêu mặt phẳng tạo bởi
ba trong năm điểm ?
A. . B. . C. . D. .
Câu 7. Cho năm điểm , , , , trong đó không có bốn điểm nào ở trên cùng một mặt phẳng.
Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?
A. . B. . C. . D. .
Câu 8. Trong các hình sau :
Hình (I) Hình (II) Hình (III) Hình (IV)
Hình nào có thể là hình biểu diễn của một hình tứ diện ? (Chọn Câu đúng nhất)
A. (I). B. (I), (II). C. (I), (II), (III). D. (I), (II), (III), (IV).
Câu 9. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :
A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh.
Câu 10. Một hình chóp cụt có đáy là một n giác, có số mặt và số cạnh là :
A. mặt, cạnh. B. mặt, cạnh.
C. mặt, cạnh. D. mặt, cạnh.
Câu 11. Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
A. . B. . C. . D. .
DẠNG 2
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG
Phương pháp :
( )
a
A
B
C
D
( )
ÏSmp
a
S
4
5
6
8
,ab
A
ABCD
( )
a
ABCD
( )
ÏE
a
,,,,ABCDE
6
7
8
9
A
B
C
D
E
10
12
8
14
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
2+n
2n
2+n
3n
2+n
n
n
3n
3
4
5
6
Trang 6
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng và cần thực hiện:
• Bước 1: Tìm hai điểm chung và của và .
• Bước 2: Đường thẳng là giao tuyến cần tìm .
Chú ý :
• Để tìm điểm chung của và
ta thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai
mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng.
• Khi điểm
Câu 12. Cho hình chóp có và Giao tuyến của mặt phẳng
và mặt phẳng là đường thẳng
A. B. C. D.
Câu 13. Cho hình chóp có và Giao tuyến của mặt phẳng
và mặt phẳng là đường thẳng
A. B. C. D.
Câu 14. Cho hình chóp có đáy là hình thang . Khẳng định nào sau đây
sai?
A. Hình chóp có mặt bên.
B. Giao tuyến của hai mặt phẳng và là ( là giao điểm của và ).
C. Giao tuyến của hai mặt phẳng và là ( là giao điểm của và ).
D. Giao tuyến của hai mặt phẳng và là đường trung bình của .
Câu 15. Cho tứ diện . Gọi là một điểm bên trong tam giác và là một điểm trên đoạn
. Gọi là hai điểm trên cạnh , . Giả sử cắt tại , cắt tại và cắt tại
, cắt tại . Giao tuyến của hai mặt phẳng và là đường thẳng:
()a
()b
A
B
()a
()b
AB
( )
() ()AB ab=«
()a
()b
( )
( )
Md
M
d
a
a
Ï
Ô
Œ
Ô
Ô
fiŒ
Ì
Ô
Ã
Ô
Ô
Ó
.S ABCD
Ç=AC BD M
.Ç=AB CD N
( )
SAC
( )
SBD
.SN
.SC
.SB
.SM
.S ABCD
Ç=AC BD M
.Ç=AB CD N
( )
SAB
( )
SCD
.SN
.SA
.MN
.SM
.S ABCD
ABCD
( )
//AB CD
.S ABCD
4
( )
SAC
( )
SBD
SO
O
AC
BD
( )
SAD
( )
SBC
SI
I
AD
BC
( )
SAB
( )
SAD
ABCD
ABCD
O
BCD
M
AO
,IJ
BC
BD
IJ
CD
K
BO
IJ
E
CD
H
ME
AH
F
( )
MIJ
( )
ACD
a
A
b
b
a
Trang 7
A. . B. . C. . D. .
Câu 16. Cho tứ diện . là trọng tâm tam giác . Giao tuyến của hai mặt phẳng và
là:
A. , là trung điểm . B. , là trung điểm .
C. , là hình chiếu của trên . D. , là hình chiếu của trên .
Câu 17. Cho hình chóp . Gọi là trung điểm của , là điểm trên và không trùng
trung điểm . Giao tuyến của hai mặt phẳng và là:
A. , là giao điểm và . B. , là giao điểm và .
C. , là giao điểm và . D. , là giao điểm và .
Câu 18. Cho tứ diện . Gọi ,
lần lượt là trung điểm và . Giao tuyến của hai mặt
phẳng và là:
A. . B. .
C. , với là trọng tâm tam giác . D. , với là trực tâm tam giác .
Câu 19. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm
và .Giao tuyến của hai mặt phẳng và là:
A. . B. , là tâm hình bình hành .
C. , là trung điểm . D. , là trung điểm .
Câu 20. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm
và .Khẳng định nào sau đây là sai?
A. là hình thang.
B. .
C. .
D. , là tâm hình bình hành .
Câu 21. Cho hình chóp có đáy là hình thang . Gọi là trung điểm .
Giao tuyến của hai mặt phẳng và là:
A. , là giao điểm và . B. , là giao điểm và .
C. , là giao điểm và . D. , là giao điểm và .
Câu 22. Cho tứ diện . là trọng tâm tam giác , là trung điểm , là điểm trên đoạn
thẳng , cắt mặt phẳng tại . Khẳng định nào sau đây sai?
A. . B. , , thẳng hàng.
C. là trung điểm . D . .
KM
AK
MF
KF
ABCD
G
BCD
( )
ACD
( )
GAB
AM
M
AB
AN
N
CD
AH
H
B
CD
AK
K
C
BD
.S ABCD
I
SD
J
SC
SC
( )
ABCD
( )
AIJ
AK
K
IJ
BC
AH
H
IJ
AB
AG
G
IJ
AD
AF
F
IJ
CD
ABCD
M
N
AC
CD
( )
MBD
( )
ABN
MN
AM
BG
G
ACD
AH
H
ACD
.S ABCD
ABCD
M
N
AD
BC
( )
SMN
( )
SAC
SD
SO
O
ABCD
SG
G
AB
SF
F
CD
.S ABCD
ABCD
I
J
SA
SB
IJCD
( ) ( )
Ç=SAB IBC IB
( ) ( )
Ç=SBD JCD JD
( ) ( )
Ç=IAC JBD AO
O
ABCD
.S ABCD
ABCD
( )
AD BCÄ
M
CD
( )
MSB
( )
SAC
SI
I
AC
BM
SJ
J
AM
BD
SO
O
AC
BD
SP
P
AB
CD
ABCD
G
BCD
M
CD
I
AG
BI
( )
ACD
J
( ) ( )
=ÇAM ACD ABG
A
J
M
J
AM
( ) ( )
=ÇDJ ACD BDJ
Trang 8
Câu 23. Cho hình chóp có đáy là hình thang . Gọi là giao điểm của
và , là trung điểm . cắt mặt phẳng tại . Khẳng định nào sau đây sai?
A. , , thẳng hàng. B. .
C. . D. .
Câu 24. Cho hình chóp , đáy là tứ giác có các cặp cạnh đối không song song, điểm
thuộc cạnh .
a) Tìm giao tuyến của các cặp mặt phẳng: và
A. SC B. SB
C. SO trong đó D.
b) Tìm giao tuyến của các cặp mặt phẳng: và
A. SM B. MB
C. OM trong đó D. SD
c) Tìm giao tuyến của các cặp mặt phẳng: và
A. SM B. FM trong đó
C. SO trong D. SD
d) Tìm giao tuyến của các cặp mặt phẳng và
A. SE trong đó B. FM trong đó
C. SO trong D. SD
Câu 25. Cho tứ diện , là một điểm thuộc miền trong tam giác , là điểm trên đoạn
a) Tìm giao tuyến của mặt phẳng với các mặt phẳng .
A. PC trong đó ,
B. PC trong đó ,
C. PC trong đó ,
D. PC trong đó ,
b) Tìm giao tuyến của mặt phẳng với các mặt phẳng .
A. DR trong đó ,
B. DR trong đó ,
C. DR trong đó ,
D. DR trong đó ,
c) Gọi là các điểm tương ứng trên các cạnh và sao cho không song song với . Tìm
giao tuyến của hai mặt phẳng và .
.S ABCD
ABCD
//AD BC
I
AB
DC
M
SC
DM
( )
SAB
J
S
I
J
( )
ÌDM mp SCI
( )
ÌJM mp SAB
( ) ( )
=ÇSI SAB SCD
.S ABCD
ABCD
M
SA
( )
SAC
( )
SBD
=ÇO AC BD
{ }
S
( )
SAC
( )
MBD
=ÇO AC BD
( )
MBC
( )
SAD
=ÇF BC AD
=ÇO AC BD
( )
SAB
( )
SCD
=ÇE AB CD
=ÇF BC AD
=ÇO AC BD
ABCD
O
BCD
M
AO
( )
MCD
( )
ABC
=ÇP DC AN
=ÇN DO BC
=ÇP DM AN
=ÇN DA BC
=ÇP DM AB
=ÇN DO BC
=ÇP DM AN
=ÇN DO BC
( )
MCD
( )
ABD
=ÇRCM AQ
=ÇQCABD
=ÇRCB AQ
=ÇQCO BD
=ÇRCM AQ
=ÇQCO BA
=ÇRCM AQ
=ÇQCO BD
,IJ
BC
BD
IJ
CD
( )
IJM
( )
ACD
Trang 9
A. FG trong đó , , ,
B. FG trong đó , , ,
C. FG trong đó , , ,
D. FG trong đó , , ,
Câu 26. Cho tứ diện có là các đường phân giác trong của
tam giác . Giao tuyến của hai mặt phẳng và là:
A. trong đó thuộc sao cho
B. trong đó thuộc sao cho
C. trong đó thuộc sao cho
D. trong đó thuộc sao cho
DẠNG 3
TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Phương pháp
Cơ sở của phương pháp tìm giao điểm của đường thẳng và mặt phẳng là xét hai trường hợp:
•
Trường hợp 1: chứa đường thẳng và cắt .
=ÇFIJCD
=ÇG KM AE
=ÇK BE IA
=ÇE BO CD
=ÇFIACD
=ÇG KM AE
=ÇK BA IJ
=ÇE BO CD
=ÇFIJCD
=ÇG KM AE
=ÇK BA IJ
=ÇE BO CD
=ÇFIJCD
=ÇG KM AE
=ÇK BE IJ
=ÇE BO CD
SABC
,,.,,AB c BC a AC b AD BE CF== =
ABC
( )
SBE
( )
SCF
SI
I
AD
bc
AI ID
a
+
=
!! " !!"
SI
I
AD
bc
AI I D
a
+
=-
!! " !!"
SI
I
AD
a
AI ID
bc
=
+
!! " !!"
SI
I
AD
a
AI ID
bc
-
=
+
!! " !!"
d
()a
()mp a
D
D
d
{ }
{ }
()
()
mp
Idmp
dI
a
a
Ï
Ô
DÃ
Ô
Ô
fi=«
Ì
Ô
D« =
Ô
Ô
Ó
Trang 10
•
Trường hợp 2: không chứa đường thẳng nào cắt .
+ Bước 1: Tìm sao cho
+ Bước 2: Tìm .
Câu 27. Cho bốn điểm không cùng nằm trong một mặt phẳng. Trên lần lượt lấy các
điểm và sao cho cắt tại . Điểm không thuộc mặt phẳng nào sao đây:
A. . B. . C. . D. .
Câu 28. Cho hình chóp tứ giác với đáy có các cạnh đối diện không song song với
nhau và là một điểm trên cạnh .
a) Tìm giao điểm của đường thẳng với mặt phẳng .
A. Điểm H, trong đó ,
B. Điểm N, trong đó ,
C. Điểm F, trong đó ,
D. Điểm T, trong đó ,
b) Tìm giao điểm của đường thẳng và mặt phẳng .
A. Điểm H, trong đó ,
B. Điểm F, trong đó ,
C. Điểm K, trong đó ,
D. Điểm V, trong đó ,
Câu 29. Cho hình chóp tứ giác , là một điểm trên cạnh , là trên cạnh . Tìm giao
điểm của đường thẳng với mặt phẳng .
A. Điểm K, trong đó , ,
B. Điểm H, trong đó , ,
d
a
I
()mp a
d
()mp db …
() ()ab«=D
{ }
Id=«D
()Idafi=«
d
b
a
I
,,,ABCD
,AB AD
M
N
MN
BD
I
I
( )
BCD
( )
ABD
( )
CMN
( )
ACD
.S ABCD
ABCD
M
SA
SB
( )
MCD
=ÇE AB CD
=ÇH SA EM
=ÇE AB CD
=ÇN SB EM
=ÇE AB CD
=ÇF SC EM
=ÇE AB CD
=ÇT SD EM
MC
( )
SBD
=ÇI AC BD
=ÇH MA SI
=ÇI AC BD
=ÇF MD SI
=ÇI AC BD
=ÇK MC SI
=ÇI AC BD
=ÇV MB SI
.S ABCD
M
SC
N
BC
SD
( )
AMN
=ÇK IJ SD
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
=ÇH IJ SA
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
Trang 11
C. Điểm V, trong đó , ,
D. Điểm P, trong đó , ,
Câu 30. Cho hình chóp có đáy là một tứ giác ( không song song ). Gọi M là
trung điểm của là điểm nằm trên cạnh sao cho là giao điểm của và .
Giả sử đường thẳng là giao tuyến của và . Nhận xét nào sau đây là sai:
A. cắt . B. cắt . C. cắt . D. cắt .
Câu 31. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của cạnh .
Gọi là giao điểm của đường thẳng vơí mặt phẳng . Khi đó tỉ số bằng bao nhiêu:
A. . B. . C. . D. .
Câu 32. Cho hình chóp , đáy là hình thang với là đáy lớn , là trọng
tâm tam giác . Mặt phẳng cắt cạnh tại . Khi đó, tỷ số bằng:
A. B. C. D.
Câu 33. Cho tứ diện có lần lượt là trung điểm của và . là điểm thuộc cạnh
sao cho Gọi là giao điểm của với . Tỉ số bằng:
A. B. C. D.
Câu 34. Cho hình chóp , đáy là hình thang , là điểm thuộc
cạnh sao cho . Mặt phẳng cắt cạnh tại . Khi đó, tỷ số bằng:
A. B. C. D.
Câu 35. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là
trung điểm của và . Gọi là giao điểm của với . Tính
A. . B. . C. . D. .
Câu 36. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của và . Trên đường thẳng lấy điểm sao cho là trung điểm . Gọi là giao điểm
của với mặt phẳng . Tính
A. . B. . C. . D. .
=ÇV IJ SB
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
=ÇP IJ SC
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
.S ABCD
ABCD
AB
CD
,SD N
SB
2,SN NB O=
AC
BD
d
( )
SAB
( )
SCD
d
CD
d
MN
d
AB
d
SO
.S ABCD
ABCD
M
SC
I
AM
( )
SBD
MA
IA
2
3
3
2
4
3
S.ABCD
ABCD
AD
AD = 2BC
G
SCD
( )
SAC
BG
K
KB
KG
2
3
2
1
1
2
ABCD
P,Q
AB
CD
M
AD
MA = 2MD.
N
BC
( )
MPQ
NB
NC
1
2
2
3
2
1
S.ABCD
ABCD
( )
AD // BC, AD > BC
E
SA
SE = 2EA
( )
EBC
SD
F
SF
SD
2
3
1
3
1
2
1
4
.S ABCD
ABCD
O
,,MNP
,AB AD
SO
H
SC
( )
MNP
?
SH
SC
1
3
1
4
3
4
2
3
.S ABCD
ABCD
,MN
AD
CD
DS
P
D
SP
R
SB
()MNP
?
SR
SB
1
3
1
4
3
4
2
5
Trang 12
Câu 37. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là các
điểm nằm trên cạnh sao cho . Gọi là điểm trên cạnh sao cho .
là giao điểm của với . Tính
A. . B. . C. . D. .
Câu 38. Cho hình chóp Gọi M, N lần lượt là trung điểm của SA và P là điểm nằm trên cạnh
AB sao cho . Gọi Q là giao điểm của SC với mặt phẳng .Tính
A. . B. . C. . D. .
Câu 39. Cho tứ diện lần lượt thuộc đoạn Gọi là giao điểm của và . Gọi
là giao điểm của với . Mệnh đề nào sau đây đúng?
A. . B. .
C. . D. .
Câu 40. Cho hình chóp lần lượt là trung điểm của . Gọi là giao điểm của
với là giao điểm của với . Tính ?
A. . B. . C. D. .
DẠNG 3
CHỨNG MINH BA ĐIỂM THẲNG HÀNG VÀ BA ĐƯỜNG THẲNG ĐỒNG QUY
1. Chứng minh ba điểm A; B; C thẳng hàng:
Phương pháp
+ Bước 1: Chứng minh 3 điểm .
.S ABCD
ABCD
O
,MN
,AB AD
21
,
32
BM NC
MA BN
==
P
SD
1
5
PD
PS
=
J
SO
( )
MNP
?
SJ
SO
10
11
1
11
3
4
5
2
..SABC
.BC
1
3
AP
AB
=
( )
MNP
SQ
SC
1
3
1
6
1
2
2
3
,,SABC E F
,.AC AB
K
BE
CF
D
( )
SAK
BC
6
AK BK CK
KD KE KF
++³
6
AK BK CK
KD KE KF
++£
6
AK BK CK
KD KE KF
++>
6
AK BK CK
KD KE KF
++<
.,,SABCD DM
,BC AD
E
( )
SBM
,AC F
( )
SCM
AB
MF ME
CM ME BM ME
+
--
1
2
1
2
1
3
,, ()ABC mpaŒ
Trang 13
+ Bước 2: Chứng minh 3 điểm .
+ Bước 3: Kết luận 3 điểm thuộc giao tuyến chung của 2 mặt phẳng và
thẳng hàng.
2. Chứng minh 3 đường thẳng
đồng quy:
Phương pháp
+ Bước 1: Tìm .
+ Bước 2: Chứng minh đi qua .
đồng quy tại .
3. Chứng minh đường thẳng trong không gian qua một điểm cố định
Phương pháp 1
Cơ sở của phương pháp là:
Ta cần tìm trên hai điểm tùy ý , và chứng minh hai điểm
đó thẳng hàng với điểm cố định có sẵn trong không gian
đi qua điểm cố định.
Phương pháp 2
Cơ sở của phương pháp là:
- Bước 1: Tìm đường thẳng cố định ở ngoài
mặt phẳng cố định chứa di động.
- Bước 2: Tìm giao điểm của và
là điểm cố định mà đi qua.
Câu 41. Cho tứ diện . Gọi , lần lượt là trung điểm và . Mặt phẳng qua cắt
và lần lượt tại , . Biết cắt tại . Ba điểm nào sau đây thẳng hàng?
A. , , . B. , , . C. , , . D. , , .
Câu 42. Cho tứ diện . Trên và lấy các điểm và sao cho cắt tại ,
cắt tại , cắt tại .Khẳng định nào sau đây đúng?
A. Ba điểm thẳng hàng
,, ()ABC mpbŒ
,,ABC
()mp a
()mp b
,,ABCfi
d
b
a
A
B
C
123
,,ddd
12
Idd=«
3
d
I
123
,,dddfi
I
d
A
B
I
dfi
I
D
()a
d
I
D
d
Ifi
d
ABCD
M
N
AB
CD
( )
a
MN
AD
BC
P
Q
MP
NQ
I
I
A
C
I
B
D
I
A
B
I
C
D
SABC
,SA SB
SC
,DE
F
DE
AB
I
EF
BC
J
FD
CA
K
B, ,JK
d
(cố định)
a
A
B
I
d
(cố định)
a
I
d
1
d
2
d
3
a
I
Trang 14
B. Ba điểm thẳng hàng
C. Ba điểm không thẳng hàng
D. Ba điểm thẳng hàng
Câu 43. Cho tứ diện có lần lượt là trung điểm của và
là trọng tâm của tam
giác . Mặt phẳng đi qua cắt lần lượt tại . Một mặt phẳng đi qua cắt
tương ứng tại và .
a) Gọi . Khẳng định nào sau đây là đúng?
A. Bốn điểm thẳng hàng. B. Bốn điểm không thẳng hàng.
C. Ba điểm thẳng hàng. D. Bốn điểm thẳng hàng.
b) Giả sử . Khằng định nào sau đây là đúng?
A. Ba điểm thẳng hàng. B. Ba điểm không thẳng hàng
C. Ba điểm thẳng hàng D. Ba điểm thẳng hàng
Câu 44. Cho hình chóp tứ giác , gọi là giao điểm của hai đường chéo và . Một mặt
phẳng cắt các cạnh bên tưng ứng tại các điểm . Khẳng định nào đúng?
A. Các đường thẳng đồng qui. B. Các đường thẳng chéo nhau.
C. Các đường thẳng song song. D. Các đường thẳng trùng nhau.
Câu 45. Cho hai mặt phẳng và cắt nhau theo giao tuyến là đường thẳng . Trong lấy hai
điểm nhưng không thuộc và là một điểm không thuộc . Các đường thẳng cắt
tương ứng tại các điểm . Gọi là giao điểm của và .Khẳng định nào đúng?
A. và đồng qui. B. và chéo nhau.
C. và song song nhau. D. và trùng nhau
Câu 46. Cho hình bình hành , S là điểm không thuộc ,M và N lần lượt là trung điểm
của đoạn AB và Xác định các giao điểm I, J của AN và MN với , từ đó tìm khẳng định đúng
trong các khẳng định sau:
A. Ba điểmJ, I, M thẳng hàng. B. Ba điểmJ, I, N thẳng hàng.
C. Ba điểmJ, I, D thẳng hàng. D. Ba điểmJ, I, B thẳng hàng.
Câu 47. Cho tứ giác và . Gọi I, J là hai điểm trên AD và SB, AD cắt BC tại O và
OJ cắt SCtại M. Xác định các giao điểm K, L của IJ và DJ với , từ đó tìm khẳng định đúng trong
các khẳng định sau:
A. Ba điểm thẳng hàng. B. Ba điểm thẳng hàng.
C. Bốn điểm thẳng hàng. D. Bốn điểm thẳng hàng.
,,IJK
,,IJK
,,CIJ
SABC
,DE
,AC BC
G
ABC
( )
a
AC
,SE SB
,MN
( )
b
BC
,SD SA
P
Q
,=Ç =ÇIAMDNJBPEQ
,, ,SIJG
,, ,SIJG
,,PI J
,,QIJ
,=Ç =ÇKANDMLBQEP
,,SKL
,,SKL
B, ,KL
C, ,KL
.S ABCD
O
AC
BD
( )
a
,,,SA SB SC SD
,,,MNPQ
,,MP NQ SO
,,MP NQ SO
,,MP NQ SO
,,MP NQ SO
( )
P
( )
Q
a
( )
P
,AB
a
S
( )
P
,SA SB
( )
Q
,CD
E
AB
a
,AB CD
a
,AB CD
a
,AB CD
a
,AB CD
a
ABCD
( )
ABCD
.SC
( )
SBD
ABCD
( )
SABCDÎ
( )
SAC
,,AK L
,,ALM
,,,AK LM
,,,AK LJ
Trang 15
Câu 48. Cho tứ diện .Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho
LMkhông song song với AB, LN không song song với Gọi LK giao tuyến của mp và
. Xác định I, J lần lượt là giao điểm của BC và SC với . Khẳng định nào sau đây đúng:
A. Ba điểm L, I, J thẳng hàng. B. Ba điểm L, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng. D. Ba điểm M, I,K thẳng hàng.
Câu 49. Cho tứ giác và S không thuộc mặt phẳng . Gọi M, N là hai điểm trên BC và
Xác định I, J lần lượt là giao điểm của BN và MN với . Từ đó tìm bộ 3 điểm thẳng hàng trong
những điểm sau:
A. Ba điểm A, I, Jthẳng hàng. B. Ba điểm K, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng. D. Ba điểm C, I,Jthẳng hàng.
Câu 50. Cho tứ diện . là điểm thuộc đoạn sao cho là các điểm thuộc
đường thẳng sao cho là các điểm thuộc đường thẳng sao cho
thuộc tia đối của tia sao cho là trung điểm của . Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Bốn điểm đồng phẳng B. Bốn điểm đồng phẳng.
C. Bốn điểm đồng phẳng. D. Bốn điểm đồng phẳng.
Câu 51. Cho hình chóp có đáy là hình bình hành .Mặt phẳng di động
chứa đường thẳng và cắt các đoạn lần lượt tại . Mặt phẳng di động chứa đường
thẳng và cắt lần lượt tại là giao điểm của là giao điểm của . Xét
các mệnh đề sau:
Đường thẳng luôn đi qua một điểm cố định.
Đường thẳng luôn đi qua một điểm cố định.
Đường thẳng luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng?
A. . B. . C. . D. .
Câu 52. Cho tứ diện và các điểm lần lượt thuộc các cạnh sao cho
không song song với . đồng phẳng khi :
A. B.
C. D. .
SABC
.SC
( )
LM N
( )
ABC
( )
LM N
ABCD
( )
ABCD
.SD
( )
SAC
ABCD
E
AB
2.,EA EB F G=
BC
5, 5.,FC FB GC GB H I==-
!!!" !!!" !!!" !!!"
CD
5, 5,HC HD ID IC J=- =-
!!!" !!! " !!" !!"
DA
D
AJ
,, ,EFH J
,,,EFI J
,, ,EGH I
,,,EGI J
.S ABCD
ABCD
( )
//BC AD
( )
P
AB
,SC SD
( )
Q
CD
,SA SB
,.GHI
,;AE BF J
,CG DH
( )
1
EF
( )
2
GH
( )
3
IJ
0
1
2
3
ABCD
,,,MNPQ
,,,AB BC CD DA
MN
AC
,,,MNPQ
... 1
AM BN CP DQ
BM CN DP AQ
=
... 1
BM CN CP DQ
AM BN DP AQ
=
... 1
BM CN DP DQ
AM BN CP AQ
=
... 1
AM BN DP AQ
BM CN CP DQ
=
Trang 16
Câu 53. Cho hình chóp Giả sử AD và BC cắt nhau tại H. Gọi O là giao điểm của AC và BD, E
và F lần lượt là trung điểm của SA và Điểm M di động trên cạnh Gọi N là giao điểm của SD và
mp(EFM). Tìm tập hợp giao điểm J của EN và FM.
A. Tập hợp J là đoạn thẳng SJ
1
với J
1
= CF Ç SH.
B. Tập hợp J là đoạn thẳng SJ
1
với J
1
= DE Ç SH.
C. Tập hợp J là đoạn thẳng SH.
D. Tập hợp J là đường thẳng SH.
Câu 54. Cho hình chóp S.ABCD, trong đó AD không song song với Gọi O là giao điểm của AC và
BD, E là giao điểm của AD và Điểm M di động trên cạnh SB, EM cắt SC tại N. Tập hợp giao điểm I
của AN và DM.
A. Tập hợp giao điểm I là đoạn thẳng SO.
B. Tập hợp giao điểm I là đường thẳng SO.
C. Tập hợp giao điểm I là đoạn thẳng SO trừ 2 điểm S và O.
D. Tập hợp giao điểm I là đoạn thẳng SE.
Câu 55. Cho tứ diện Một mặt phẳng di động luôn song song với và cắt các cạnh
AC, tại . Tìm tập hợp tâm I của hình bình hành
A. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và CD (trừ 2 điểm P và
Q).
B. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và
C. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC (trừ 2 điểm P và
Q).
D. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và
DẠNG 4
XÁC ĐỊNH THIẾT DIỆN CỦA MỘT MẶT PHẲNG VỚI HÌNH CHÓP
..S ABCD
.SB
.SC
.BC
.BC
.ABCD
( )
P
AB
CD
,,AD BD BC
,,,MNEF
.MNEF
.CD
.BC
Trang 17
Để xác định thiết diện của hình chóp cắt bởi mặt phẳng , ta tìm giao điểm của mặt phẳng
với các đường thẳng chứa các cạnh của hình chóp. Thiết diện là đa giác có đỉnh là các giao điểm
của với hình chóp ( và mỗi cạnh của thiết diện phải là một đoạn giao tuyến với một mặt của hình
chóp)
Câu 56. Cho là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp
?
A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác.
Câu 57. Cho hình chóp với đáy là tứ giác lồi. Thiết diện của mặt phẳng tuỳ ý với
hình chóp không thể là:
A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác.
Câu 58. Cho hình chóp có đáy là hình bình hành và điểm ở trên cạnh . Mặt
phẳng cắt hình chóp theo thiết diện là
A. tam giác. B. hình thang. C. hình bình hành. D. hình chữ nhật.
Câu 59. Cho hình chóp tứ giác , có đáy là hình thang với là đáy lớn và là một điểm
trên cạnh .
a) Thiết diện của hình chóp cắt bởi mặt phẳng là hình gì?
A. Tam giác B. Tứ giác C. Hình thang D. Hình bình hành
b) Gọi lần lượt là trung điểm của các cạnh . Thiết diện của hình chóp cắt bởi là
hình gì?
A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
Câu 60. Cho hình chóp . Điểm nằm trên cạnh . Thiết diện của hình chóp với mp
là một đa giác có bao nhiêu cạnh?
A. . B. . C. . D. .
Câu 61. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm . Thiết diện
của hình chóp cắt bởi mặt phẳng là:
A. Tam giác B. Hình thang ( là trung điểm ).
C. Hình thang ( là trung điểm ). D. Tứ giác .
Câu 62. Cho hình chóp có đáy là một hình bình hành tâm . Gọi là ba điểm
trên các cạnh . Thiết diện của hình chóp với mặt phẳng là hình gì?
A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
12
....
n
SAA A
( )
a
( )
a
( )
a
ABCD
.S ABCD
.S ABCD
ABCD
( )
a
.S ABCD
ABCD
M
SB
( )
ADM
.S ABCD
AD
P
SD
()PAB
,MN
,AB BC
( )
MNP
.S ABCD
¢
C
SC
( )
¢
ABC
3
4
5
6
.S ABCD
ABCD
I
SA
.S ABCD
( )
IBC
.IBC
IJCB
J
SD
IGBC
G
SB
IBCD
.S ABCD
ABCD
O
,,MNP
,,AD CD SO
()MNP
Trang 18
Câu 63. Cho tứ diện , và lần lượt là trung điểm và . Mặt phẳng qua cắt
tứ diện theo thiết diện là đa giác Khẳng định nào sau đây đúng?
A. là hình chữ nhật. B. là tam giác.
C. là hình thoi. D. là tam giác hoặc hình thang hoặc hình bình hành.
Câu 64. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của các cạnh Thiết diện của hình chóp với mặt phẳng là đa giác có bao nhiêu
cạnh ?
A. B. C. D.
Câu 65. Cho hình chóp có đáy là hình bình hành, gọi lần lượt là 2 điểm thuộc
cạnh sao cho . Mặt phẳng cắt tại thỏa mãn . Số k
bằng?
A. B. C. D.
Câu 66. Cho tứ diện đều có các cạnh bằng . Gọi là trung điểm , là điểm thuộc cạnh
sao cho là điểm thuộc cạnh sao cho . Tính độ dài đoạn giao tuyến của
mặt phẳng với mặt phẳng của hình chóp theo .
A. . B. . C. . D. .
Câu 67. Cho hình chóp có đáy là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho . F là trọng tâm tam giác là điểm thay đổi trên cạnh Thiết diện cắt bởi mặt
phẳng là:
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 68. Cho hình chóp có đáy là hình thang với đáy lớn AD, E là một điểm thuộc mặt
bên . F, G lần lượt là các điểm thuộc cạnh AB và Thiết diện của hình chóp cắt bởi
mặt phẳng có thể là:
A. Tam giác, tứ giác. B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 69. Cho hình chóp là trung điểm của thuộc SC sao cho là một
điểm thuộc miền trong tam giác . Thiết diện của hình chóp cắt bởi mặt phẳng là:
A. Tam giác, tứ giác. B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 70. Cho tứ diện có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho . Gọi M là trung điểm của đoạn
Diện tích S thiết diện của tứ diện cắt
bởi mặt phẳng là:
ABCD
M
N
AB
AC
()
a
MN
ABCD
( )
.T
( )
T
( )
T
( )
T
( )
T
.S ABCD
ABCD
,,MNQ
, , .AB AD SC
( )
MNQ
3.
4.
5.
6.
S.ABCD
ABCD
M, N
SB,SD
SM = MB,SN = 2ND
( )
AMN
SC
P
SP = kSC
2
5
3
5
3
2
2
3
ABCD
a
E
AB
F
BC
2,BF FC G=
CD
2CG GD=
( )
EFG
( )
ACD
ABCD
a
19
15
a
141
30
a
34 15 3
15
a +
34 15 3
15
a -
.S ABCD
ABCD
3SD SE=
,SAB G
.BC
( )
EFG
.S ABCD
ABCD
( )
SCD
.SB
.S ABCD
( )
EFG
.,S ABCD E
,SB F
32,SF SC G=
!! !" !! !"
SAD
( )
EFG
ABCD
,CE a DF a==
.AB
ABCD
( )
MEF
Trang 19
A. . B. . C. . D. .
Câu 71. Cho hình chóp có đáy là hình bình hành. Một mặt phẳng cắt các cạnh
bên tương ứng tại các điểm . Gọi . Mệnh đề nào
sau đây đúng?
A. . B. .
C. . D. .
Câu 72. Cho tứ diện có lần lượt là trung điểm của và là điểm thuộc cạnh
( không là trung điểm ). Gọi là giao điểm của với là giao điểm của
với . Mệnh đề nào sau đây đúng?
A. . B. . C. D. .
Câu 73. *Cho hình chóp với đáy là đa giác lồi Trên tia đối của tia
lấy điểm là các điểm nằm trên cạnh . Thiết diện của hình chóp cắt bởi mặt
phẳng là:
A. Đa giác cạnh. B. Đa giác cạnh. C. Đa giác cạnh. D. Đa giác cạnh.
2
33
18
a
S =
2
3
a
S =
2
6
a
S =
2
33
9
a
S =
.S ABCD
ABCD
( )
a
,,,SA SB SC SD
,,,EFGH
,IACBDJEGSI=Ç =Ç
SA SC SB SD
SE SG SF SH
+=+
2
SA SC SI
SE SG SJ
+³
SA SC SB SD
SE SG SF SH
+>+
2
SB SD SI
SF SH SJ
+³
ABCD
,MN
,AB CD
P
BC
P
BC
Q
( )
MNP
,AD I
MN
PQ
2
MNPQ MPN
SS=
2
MNPQ MPQ
SS=
4
MNPQ MPI
SS=
4
MNPQ PIN
SS=
12
...
n
SA A A
( )
12
... 3, .
n
AA A n n³Î•
1
AS
12
,,...
n
BB B
2
,
n
SA SA
( )
12n
BB B
2n -
1n -
n
1n +
Trang 20
PHẦN 2
HƯỚNG DẪN GIẢI
CHỦ ĐỀ 1
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. Khái niệm mở đầu
1. Mặt phẳng
+ Mặt bàn, mặt bảng, mặt hồ nước yên lặng . . . Cho ta hình ảnh của một phần của mặt phẳng.
+ Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng
vào một góc của hình biểu diễn.
+ Để kí hiệu mặt phẳng, ta thường dùng chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ( ).
+ mặt phẳng (P ), mặt phẳng ( Q ), mặt phẳng (a), mặt phẳng (b) hoặc viết tắt là mp( P ), mp( Q ),
mp (a) , mp ( b) , hoặc ( P ) , ( Q ) , (a) , ( b),
2. Điểm thuộc mặt phẳng
Cho điểm A và mặt phẳng (P).
+ Điểm A thuộc mặt phẳng (P) ta nói A nằm trên (P) hay (P) chứa A, hay (P) đi qua A và kí hiệu A Î
( P) .
+ Điểm A không thuộc mặt phẳng (P) ta nói điểm A nằm ngoài (P) hay (P) không chứa A và kí hiệu
A Ï ( P) .
P
A
P
P
A
Trang 21
3. Hình biểu diễn của một hình không gian
Để vẽ hình biểu diễn của một hình trong không gian, ta dựa vào những qui tắc sau :
+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
+ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai đường thẳng
cắt nhau là hai đường thẳng cắt nhau.
+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
+ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che
khuất.
II. CÁC TÍNH CHẤT THỪA NHẬN
1. Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
2. Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
3. Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó.
* Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P ) thì ta nói đường thẳng d nằm trong mặt
phẳng (P) . Hay (P) chứa d và kí hiệu d Ì (P) hay (P) É d
4. Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng
Nếu có nhiều điểm cùng thuộc một mp thì ta nói những điểm đó đồng phẳng .
5. Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung
khác nữa.
* Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua
điểm chung ấy.
* Đường thẳng chung d của hai mặt phẳng phân biệt ( P ) và ( Q ) được gọi là giao tuyến của ( P)
và (Q)
kí hiệu d = ( p) Ç ( Q )
6. Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
A
C
Trang 22
III. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG
Có 3 cách xác định mặt phẳng
+ Qua 3 điểm không thẳng hàng xác định duy nhất một mặt phẳng.
+ Qua một điểm và một đường thẳng không chứa điểm đó ta xác định duy nhất một mặt phẳng.
Kí hiệu mp(A,d) hay (A,d)
+ Hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng.
Kí hiệu mp (a, b) hay (a, b)
IV. HÌNH CHÓP VÀ HÌNH TỨ DIỆN
1. Hình chóp:
+ Hình gồm miền đa giác A
1
A
2
A
3
. . .An. Lấy điểm S nằm ngoài (a) . lần lượt nối S với các đỉnh
A
1
, A
2
, … A
n
ta được n tam gíác SA
1
A
2
, SA
2
A
3
. . . SA
n
A
1
. Hình gồm đa giác A
1
A
2
A
3
. . .An và n tam
giác SA
1
A
2
, SA
2
A
3
. . . SA
n
A gọi là hình chóp, kí hiệu là S. A
1
A
2
A
3
. . .An. ta gọi S là đỉnh và đa giác
A
1
A
2
A
3
. . .An là mặt đáy. Các tam giác SA
1
A
2
, SA
2
A
3
. . . SA
n
A gọi là các mặt bên. Các đoạn SA
1
, SA
2
. . SA
n
là các cạnh bên., các cạnh của đa giác đáy gọi là cạnh đáy của hình chóp.
2. Hình tứ diện
+ Một hình chóp có đáy là tam giác gọi là tứ diện.
+ Tứ diện có các mặt là tam giác đều gọi là tứ diện đều.
A
C
A
d
a
Trang 23
V. HÌNH LĂNG TRỤ
1. Hình lăng trụ: Hình hợp bởi các hình bình hành A
1
A
2
A'
2
A'
1
, A
2
A
3
A'
3
A'
2
,...,A
n
A
1
A'
1
A'
2
và hai đa
giác A
1
A
2
...A
n
, A'
1
A'
2
...A'
n
gọi là hình lăng trụ hoặc lăng trụ, và ký hiệu là A
1
A
2
...A
n
.A'
1
A'
2
...A'
n
.
Trong một hình lăng trụ thì
• 2 mặt đáy là đa giác song song và bằng nhau.
• các cạnh bên song song và bằng nhau
• các mặt bên là hình bình hành
2. Hình hộp: là hình lăng trụ có đáy là hình bình hành.
Trong một hình hộp thì
• Các mặt bên là các hình bình hành
• Các đường chéo của hình hộp cắt nhau
tại trung điểm mỗi đường.
hình lăng trụ tam giác
hình hộp
Trang 24
DẠNG 1
LÝ THUYẾT
Câu 1. Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Lời giải
Chọn B.
Hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó, chúng có vô số đường thẳng
chung B sai.
Câu 2. Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân
biệt từ bốn điểm đã cho ?
A. B. C. D.
Lời giải
Chọn C.
Do bốn điểm không đồng phẳng nên không tồn tại bộ ba điểm thẳng hàng trong số bốn điểm đó. Cứ ba
điểm không thẳng hàng xác định một mặt phẳng nên số mặt phẳng phân biệt có thể lập được từ bốn điểm
đã cho là
Câu 3. Trong mp , cho bốn điểm , , , trong đó không có ba điểm nào thẳng hàng. Điểm
. Có mấy mặt phẳng tạo bởi và hai trong số bốn điểm nói trên?
A. . B. . C. . D. .
Lời giải
Chọn C.
Điểm cùng với hai trong số bốn điểm , , , tạo thành một mặt phẳng, từ bốn điểm ta có
cách chọn ra hai điểm, nên có tất cả mặt phẳng tạo bởi và hai trong số bốn điểm nói trên.
Câu 4. Cho 2 đường thẳng cắt nhau và không đi qua điểm . Xác định được nhiều nhất bao nhiêu
mặt phẳng bởi a, b và A ?
A. 1 B. 2 C. 3 D. 4.
Lời giải
Chọn B.
Có 3 mặt phẳng gồm .
,,MNP
Þ
2.
3.
4.
6.
3
4
4.=C
( )
a
A
B
C
D
( )
ÏSmp
a
S
4
5
6
8
S
A
B
C
D
6
6
S
,ab
A
( ) ( ) ( )
,,,,,ab Aa Bb
Trang 25
Câu 5. Cho tứ giác lồi và điểm S không thuộc mp (ABCD). Có nhiều nhất bao nhiêu mặt
phẳng xác định bởi các điểm A, B, C, D, S ?
A. 5 B. 6 C. 7 D. 8
Lời giải
Chọn A.
Có mặt phẳng.
Câu 6. Trong mặt phẳng cho tứ giác , điểm . Hỏi có bao nhiêu mặt phẳng tạo bởi
ba trong năm điểm ?
A. . B. . C. . D. .
Lời giải
Chọn B.
Điểm và 2 điểm bất kì trong 4 điểm tạo thành 6 mặt phẳng, bốn điểm tạo thành
1 mặt phẳng.
Vậy có tất cả 7 mặt phẳng.
Câu 7. Cho năm điểm , , , , trong đó không có bốn điểm nào ở trên cùng một mặt phẳng.
Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?
A. . B. . C. . D. .
Lời giải
Chọn A.
Cứ chọn ra ba điểm trong số năm điểm , , , , ta sẽ có một mặt phẳng. Từ năm điểm ta có
cách chọn ra ba điểm bất kỳ trong số năm điểm đã cho, nên có phẳng tạo bởi ba trong số năm điểm đã
cho.
Câu 8. Trong các hình sau :
Hình (I) Hình (II) Hình (III) Hình (IV)
Hình nào có thể là hình biểu diễn của một hình tứ diện ? (Chọn Câu đúng nhất)
A. (I). B. (I), (II). C. (I), (II), (III). D. (I), (II), (III), (IV).
Lời giải
Chọn B.
Hình (III) sai vì đó là hình phẳng.
Câu 9. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :
A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh.
Lời giải
ABCD
2
4
17+=C
( )
a
ABCD
( )
ÏE
a
,,,,ABCDE
6
7
8
9
E
,,,ABCD
,,,ABCD
A
B
C
D
E
10
12
8
14
A
B
C
D
E
10
10
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
Trang 26
Chọn C.
Hình chóp ngũ giác có 5 mặt bên + 1 mặt đáy. 5 cạnh bên và 5 cạnh đáy.
Câu 10. Một hình chóp cụt có đáy là một n giác, có số mặt và số cạnh là :
A. mặt, cạnh. B. mặt, cạnh.
C. mặt, cạnh. D. mặt, cạnh.
Lời giải
Chọn A.
Lấy ví dụ hình chóp cụt tam giác ( ) có 5 mặt và 9 cạnh Þ đáp ánB.
Câu 11. Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
A. . B. . C. . D. .
Lời giải
Chọn D.
Hình tứ diện là hình chóp có số cạnh ít nhất.
2+n
2n
2+n
3n
2+n
n
n
3n
3=n
3
4
5
6
Trang 27
DẠNG 2
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG
Phương pháp :
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng và cần thực hiện:
• Bước 1: Tìm hai điểm chung và của và .
• Bước 2: Đường thẳng là giao tuyến cần tìm .
Chú ý :
• Để tìm điểm chung của và
ta thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai
mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng.
• Khi điểm
Câu 12. Cho hình chóp có và Giao tuyến của mặt phẳng
và mặt phẳng là đường thẳng
A. B. C. D.
Lời giải
Chọn D.
Giao tuyến của mặt phẳng và mặt phẳng là đường thẳng
()a
()b
A
B
()a
()b
AB
( )
() ()AB ab=«
()a
()b
( )
( )
Md
M
d
a
a
Ï
Ô
Œ
Ô
Ô
fiŒ
Ì
Ô
Ã
Ô
Ô
Ó
.S ABCD
Ç=AC BD M
.Ç=AB CD N
( )
SAC
( )
SBD
.SN
.SC
.SB
.SM
( )
SAC
( )
SBD
.SM
a
A
b
b
a
Trang 28
Câu 13. Cho hình chóp có và Giao tuyến của mặt phẳng
và mặt phẳng là đường thẳng
A. B. C. D.
Lời giải
Chọn A.
Câu 14. Cho hình chóp có đáy là hình thang . Khẳng định nào sau đây
sai?
A. Hình chóp có mặt bên.
B. Giao tuyến của hai mặt phẳng và là ( là giao điểm của và ).
C. Giao tuyến của hai mặt phẳng và là ( là giao điểm của và ).
D. Giao tuyến của hai mặt phẳng và là đường trung bình của .
Lời giải
Chọn D.
Hình chóp có mặt bên , , , nên A đúng.
, là hai điểm chung của và nên B đúng.
.S ABCD
Ç=AC BD M
.Ç=AB CD N
( )
SAB
( )
SCD
.SN
.SA
.MN
.SM
.S ABCD
ABCD
( )
//AB CD
.S ABCD
4
( )
SAC
( )
SBD
SO
O
AC
BD
( )
SAD
( )
SBC
SI
I
AD
BC
( )
SAB
( )
SAD
ABCD
.S ABCD
4
( )
SAB
( )
SBC
( )
SCD
( )
SAD
S
O
( )
SAC
( )
SBD
Trang 29
, là hai điểm chung của và nên C đúng.
Giao tuyến của và là , rõ ràng không thể là đường trung bình của hình thang
.
Câu 15. Cho tứ diện . Gọi là một điểm bên trong tam giác và là một điểm trên đoạn
. Gọi là hai điểm trên cạnh , . Giả sử cắt tại , cắt tại và cắt tại
, cắt tại . Giao tuyến của hai mặt phẳng và là đường thẳng:
A. . B. . C. . D. .
Lời giải
Chọn D.
Do là giao điểm của và nên (1)
Ta có là giao điểm của và
Mà , nên
(2)
Từ (1) và (2) có
Câu 16. Cho tứ diện . là trọng tâm tam giác . Giao tuyến của hai mặt phẳng và
là:
A. , là trung điểm . B. , là trung điểm .
C. , là hình chiếu của trên . D. , là hình chiếu của trên .
Lời giải
Chọn B.
S
I
( )
SAD
( )
SBC
( )
SAB
( )
SAD
SA
SA
ABCD
ABCD
O
BCD
M
AO
,IJ
BC
BD
IJ
CD
K
BO
IJ
E
CD
H
ME
AH
F
( )
MIJ
( )
ACD
KM
AK
MF
KF
K
IJ
CD
( ) ( )
Î !KMIJ ACD
F
ME
AH
( )
ÌAH ACD
( )
ÌME MIJ
( ) ( )
Î !FMIJ ACD
( ) ( )
=!MIJ ACD KF
ABCD
G
BCD
( )
ACD
( )
GAB
AM
M
AB
AN
N
CD
AH
H
B
CD
AK
K
C
BD
Trang 30
là điểm chung thứ nhất của và
là trọng tâm tam giác , là trung điểm nên nên là điểm chung thứ hai của
và . Vậy giao tuyến của hai mặt phẳng và là .
Câu 17. Cho hình chóp . Gọi là trung điểm của , là điểm trên và không trùng
trung điểm . Giao tuyến của hai mặt phẳng và là:
A. , là giao điểm và . B. , là giao điểm và .
C. , là giao điểm và . D. , là giao điểm và .
Lời giải
Chọn D.
là điểm chung thứ nhất của và
và cắt nhau tại , còn không cắt , , nên là điểm chung thứ hai của
và . Vậy giao tuyến của và là .
A
( )
ACD
( )
GAB
G
BCD
N
CD
ÎN BG
N
( )
ACD
( )
GAB
( )
ACD
( )
GAB
AN
.S ABCD
I
SD
J
SC
SC
( )
ABCD
( )
AIJ
AK
K
IJ
BC
AH
H
IJ
AB
AG
G
IJ
AD
AF
F
IJ
CD
A
( )
ABCD
( )
AIJ
IJ
CD
F
IJ
BC
AD
AB
F
( )
ABCD
( )
AIJ
( )
ABCD
( )
AIJ
AF
Trang 31
Câu 18. Cho tứ diện . Gọi ,
lần lượt là trung điểm và . Giao tuyến của hai mặt
phẳng và là:
A. . B. .
C. , với là trọng tâm tam giác . D. , với là trực tâm tam giác .
Lời giải
Chọn C.
là điểm chung thứ nhất của và .
là trọng tâm tam giác nên do đó là điểm chung thứ hai của và
. Vậy giao tuyến của hai mặt phẳng và là .
Câu 19. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm
và .Giao tuyến của hai mặt phẳng và là:
A. . B. , là tâm hình bình hành .
C. , là trung điểm . D. , là trung điểm .
Lời giải
Chọn B.
là điểm chung thứ nhất của và .
ABCD
M
N
AC
CD
( )
MBD
( )
ABN
MN
AM
BG
G
ACD
AH
H
ACD
B
( )
MBD
( )
ABN
G
ACD
,ÎÎGANGDM
G
( )
MBD
( )
ABN
( )
MBD
( )
ABN
BG
.S ABCD
ABCD
M
N
AD
BC
( )
SMN
( )
SAC
SD
SO
O
ABCD
SG
G
AB
SF
F
CD
S
( )
SMN
( )
SAC
Trang 32
là giao điểm của và nên do đó là điểm chung thứ hai của và
. Vậy giao tuyến của hai mặt phẳng và là .
Câu 20. Cho hình chóp có đáy là hình bình hành. Gọi , lần lượt là trung điểm
và .Khẳng định nào sau đây là sai?
A. là hình thang.
B. .
C. .
D. , là tâm hình bình hành .
Lời giải
Chọn D.
Ta có và . Mà trong đó là tâm hình bình hành
.
Câu 21. Cho hình chóp có đáy là hình thang . Gọi là trung điểm .
Giao tuyến của hai mặt phẳng và là:
A. , là giao điểm và . B. , là giao điểm và .
C. , là giao điểm và . D. , là giao điểm và .
Lời giải
Chọn A.
O
AC
MN
,ÎÎOACOMN
O
( )
SMN
( )
SAC
( )
SMN
( )
SAC
SO
.S ABCD
ABCD
I
J
SA
SB
IJCD
( ) ( )
Ç=SAB IBC IB
( ) ( )
Ç=SBD JCD JD
( ) ( )
Ç=IAC JBD AO
O
ABCD
( ) ( )
ºIAC SAC
( ) ( )
ºJBD SBD
( ) ( )
Ç=SAC SBD SO
O
ABCD
.S ABCD
ABCD
( )
AD BCÄ
M
CD
( )
MSB
( )
SAC
SI
I
AC
BM
SJ
J
AM
BD
SO
O
AC
BD
SP
P
AB
CD
Trang 33
là điểm chung thứ nhất của và .
là giao điểm của và nên , do đó là điểm chung thứ hai của và
. Vậy giao tuyến của hai mặt phẳng và là .
Câu 22. Cho tứ diện . là trọng tâm tam giác , là trung điểm , là điểm trên đoạn
thẳng , cắt mặt phẳng tại . Khẳng định nào sau đây sai?
A. . B. , , thẳng hàng.
C. là trung điểm . D . .
Lời giải
Chọn C.
Ta có , nên .
Nên vậy A đúng.
, , cùng thuộc hai mặt phẳng phân biệt nên , , thẳng hàng, vậy B đúng.
Vì là điểm tùy ý trên nên không phải lúc nào cũng là trung điểm của .
Câu 23. Cho hình chóp có đáy là hình thang . Gọi là giao điểm của
và , là trung điểm . cắt mặt phẳng tại . Khẳng định nào sau đây sai?
A. , , thẳng hàng. B. .
C. . D. .
Lời giải
Chọn C.
S
( )
MSB
( )
SAC
I
AC
BM
ÎI AC
ÎI BM
I
( )
MSB
( )
SAC
( )
MSB
( )
SAC
SI
ABCD
G
BCD
M
CD
I
AG
BI
( )
ACD
J
( ) ( )
=ÇAM ACD ABG
A
J
M
J
AM
( ) ( )
=ÇDJ ACD BDJ
( ) ( )
ÎÇAACD ABG
( ) ( )
Î
ì
ÞÎ Ç
í
Î
î
MBG
MACD ABG
MCD
( ) ( )
=ÇAM ACD ABG
( ) ( )
=ÇAM ACD ABG
A
J
M
( ) ( )
,ACD ABG
A
J
M
I
AG
J
AM
.S ABCD
ABCD
//AD BC
I
AB
DC
M
SC
DM
( )
SAB
J
S
I
J
( )
ÌDM mp SCI
( )
ÌJM mp SAB
( ) ( )
=ÇSI SAB SCD
Trang 34
, , thẳng hàng vì ba điểm cùng thuộc hai mp và nên A đúng.
nên vậy B đúng.
nên vậy C sai.
Hiển nhiên D đúng theo giải thích A.
Câu 24. Cho hình chóp , đáy là tứ giác có các cặp cạnh đối không song song, điểm
thuộc cạnh .
a) Tìm giao tuyến của các cặp mặt phẳng: và
A. SC B. SB
C. SO trong đó D.
b) Tìm giao tuyến của các cặp mặt phẳng: và
A. SM B. MB
C. OM trong đó D. SD
c) Tìm giao tuyến của các cặp mặt phẳng: và
A. SM B. FM trong đó
C. SO trong D. SD
d) Tìm giao tuyến của các cặp mặt phẳng và
A. SE trong đó B. FM trong đó
C. SO trong D. SD
Lời giải
S
I
J
( )
SAB
( )
SCD
( )
ÎÞÎMSC M SCI
( )
ÌDM mp SCI
( )
ÏMSAB
( )
ËJM mp SAB
.S ABCD
ABCD
M
SA
( )
SAC
( )
SBD
=ÇO AC BD
{ }
S
( )
SAC
( )
MBD
=ÇO AC BD
( )
MBC
( )
SAD
=ÇF BC AD
=ÇO AC BD
( )
SAB
( )
SCD
=ÇE AB CD
=ÇF BC AD
=ÇO AC BD
Trang 35
a) Chọn C.
Gọi
Lại có .
b) Chọn C.
.
Và .
c) Chọn B.
Trong gọi
Và
d) Chọn A.
Trong gọi , ta có .
Các bạn muốn tải đầy đủ 38 chuyên đề ôn thi 12 file word (hơn 5500 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 12 file word thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 11 file word ( 3042 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 9 file word ( 1062 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
O
A
E
D
S
F
B
C
M
=ÇO AC BD
( )
( )
( ) ( )
O AC SAC
O SAC SBD
O BD SBD
ÎÌ
ì
ï
ÞÞÎÇ
í
ÎÌ
ï
î
( ) ( )
ÎÇSSAC SBD
( ) ( )
Þ= ÇSO SAC SBD
=ÇO AC BD
( )
( )
ÎÌ
ì
ï
Þ
í
ÎÌ
ï
î
O AC SAC
O BD MBD
( ) ( )
ÞÎ ÇOSAC MBD
( ) ( ) ( ) ( )
ÎÇ Þ=ÇMSAC MBD OMSAC MBD
( )
ABCD
( )
( )
( ) ( )
ÎÌ
ì
ï
=ÇÞ ÞÎ Ç
í
ÎÌ
ï
î
FBC MBC
F BC AD F MBC SAD
F AD SAD
( ) ( ) ( ) ( )
ÎÇÞ= ÇMMBC SAD FMMBC SAD
( )
ABCD
=ÇE AB CD
( ) ( )
=ÇSE SAB SCD
Trang 36
Câu 25. Cho tứ diện , là một điểm thuộc miền trong tam giác , là điểm trên đoạn
a) Tìm giao tuyến của mặt phẳng với các mặt phẳng .
A. PC trong đó ,
B. PC trong đó ,
C. PC trong đó ,
D. PC trong đó ,
b) Tìm giao tuyến của mặt phẳng với các mặt phẳng .
A. DR trong đó ,
B. DR trong đó ,
C. DR trong đó ,
D. DR trong đó ,
c) Gọi là các điểm tương ứng trên các cạnh và sao cho không song song với . Tìm
giao tuyến của hai mặt phẳng và .
A. FG trong đó , , ,
B. FG trong đó , , ,
C. FG trong đó , , ,
D. FG trong đó , , ,
Lời giải
a) Chọn D.
ABCD
O
BCD
M
AO
( )
MCD
( )
ABC
=ÇP DC AN
=ÇN DO BC
=ÇP DM AN
=ÇN DA BC
=ÇP DM AB
=ÇN DO BC
=ÇP DM AN
=ÇN DO BC
( )
MCD
( )
ABD
=ÇRCM AQ
=ÇQCABD
=ÇRCB AQ
=ÇQCO BD
=ÇRCM AQ
=ÇQCO BA
=ÇRCM AQ
=ÇQCO BD
,IJ
BC
BD
IJ
CD
( )
IJM
( )
ACD
=ÇFIJCD
=ÇG KM AE
=ÇK BE IA
=ÇE BO CD
=ÇFIACD
=ÇG KM AE
=ÇK BA IJ
=ÇE BO CD
=ÇFIJCD
=ÇG KM AE
=ÇK BA IJ
=ÇE BO CD
=ÇFIJCD
=ÇG KM AE
=ÇK BE IJ
=ÇE BO CD
M
I
A
B
D
C
O
F
N
Q
P
E
K
G
J
R
Trang 37
Trong gọi , trong gọi
Lại có .
b) Chọn D.
Tương tự, trong gọi , trong gọi
là điểm chung thứ hai của và nên .
c) Chọn D.
Trong gọi , ; trong gọi .
Có ,
Mà
Câu 26. Cho tứ diện có là các đường phân giác trong của
tam giác . Giao tuyến của hai mặt phẳng và là:
A. trong đó thuộc sao cho
B. trong đó thuộc sao cho
C. trong đó thuộc sao cho
D. trong đó thuộc sao cho
Lời giải
Chọn A.
( )
BCD
=ÇN DO BC
( )
ADN
=ÇP DM AN
( )
( )
ÎÌ
ì
ï
Þ
í
ÎÌ
ï
î
PDM CDM
P AN ABC
( ) ( )
ÞÎ ÇPCDM ABC
( ) ( ) ( ) ( )
ÎÇÞ=ÇCCDM ABC PCCDM ABC
( )
BCD
=ÇQCO BD
( )
ACQ
=ÇRCM AQ
( )
( )
( ) ( )
ÎÌ
ì
ï
ÞÞÎÇ
í
ÎÌ
ï
î
R CM CDM
R CDM ABD
RAQ ABD
D
( )
MCD
( )
ABD
( ) ( )
=ÇDR CDM ABD
( )
BCD
,=Ç =ÇEBOCDFIJCD
=ÇK BE IJ
( )
ABE
=ÇG KM AE
( )
( )
( ) ( )
ÎÌ
ì
ï
ÞÎ Ç
í
ÎÌ
ï
î
FIJ IJM
FIJM ACD
FCD ACD
( )
( )
ÎÌ
ì
ï
í
ÎÌ
ï
î
GKM IJM
G AE AC D
( ) ( )
FG IJM ACDÞ= Ç
SABC
,,.,,AB c BC a AC b AD BE CF== =
ABC
( )
SBE
( )
SCF
SI
I
AD
bc
AI ID
a
+
=
!! " !!"
SI
I
AD
bc
AI I D
a
+
=-
!! " !!"
SI
I
AD
a
AI ID
bc
=
+
!! " !!"
SI
I
AD
a
AI ID
bc
-
=
+
!! " !!"
Trang 38
Do thuộc đoạn nên cùng hướng. Do đó B, D bị loại.
là phân giác trong của tam giác nên theo tính chất đường phân giác ta có:
Ta có: là phân giác trong của tam giác nên theo tính chất đường phân giác ta có:
. Do đó:
DẠNG 3
TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Phương pháp
Cơ sở của phương pháp tìm giao điểm của đường thẳng và mặt phẳng là xét hai trường hợp:
•
Trường hợp 1: chứa đường thẳng và cắt .
•
Trường hợp 2: không chứa đường thẳng nào cắt .
+ Bước 1: Tìm sao cho
+ Bước 2: Tìm .
I
E
D
F
B
A
C
S
I
AD
,AI ID
!!" !!"
AD
ABC
BD AB c ac
BD
DC AC b b c
==Þ=
+
BI
ABD
IA BA b c b c
IA ID
ID BD a a
++
== Þ=
bc
AI ID
a
+
=
!! " !!"
d
()a
()mp a
D
D
d
{ }
{ }
()
()
mp
Idmp
dI
a
a
Ï
Ô
DÃ
Ô
Ô
fi=«
Ì
Ô
D« =
Ô
Ô
Ó
d
a
I
()mp a
d
()mp db …
() ()ab«=D
{ }
Id=«D
()Idafi=«
Trang 39
Câu 27. Cho bốn điểm không cùng nằm trong một mặt phẳng. Trên lần lượt lấy các
điểm và sao cho cắt tại . Điểm không thuộc mặt phẳng nào sao đây:
A. . B. . C. . D. .
Lời giải
Chọn D.
Câu 28. Cho hình chóp tứ giác với đáy có các cạnh đối diện không song song với
nhau và là một điểm trên cạnh .
a) Tìm giao điểm của đường thẳng với mặt phẳng .
A. Điểm H, trong đó ,
B. Điểm N, trong đó ,
C. Điểm F, trong đó ,
D. Điểm T, trong đó ,
b) Tìm giao điểm của đường thẳng và mặt phẳng .
A. Điểm H, trong đó ,
B. Điểm F, trong đó ,
C. Điểm K, trong đó ,
D. Điểm V, trong đó ,
Lời giải
Chọn B.
d
b
a
I
,,,ABCD
,AB AD
M
N
MN
BD
I
I
( )
BCD
( )
ABD
( )
CMN
( )
ACD
(),()ÎÞÎIBD I BCDABD
()ÎÞÎIMN I CMN
.S ABCD
ABCD
M
SA
SB
( )
MCD
=ÇE AB CD
=ÇH SA EM
=ÇE AB CD
=ÇN SB EM
=ÇE AB CD
=ÇF SC EM
=ÇE AB CD
=ÇT SD EM
MC
( )
SBD
=ÇI AC BD
=ÇH MA SI
=ÇI AC BD
=ÇF MD SI
=ÇI AC BD
=ÇK MC SI
=ÇI AC BD
=ÇV MB SI
Trang 40
a) Chọn B.
Trong mặt phẳng , gọi .
Trong gọi.
Ta có và nên .
b) Chọn C.
Trong gọi .
Trong gọi .
Ta có và nên .
Câu 29. Cho hình chóp tứ giác , là một điểm trên cạnh , là trên cạnh . Tìm giao
điểm của đường thẳng với mặt phẳng .
A. Điểm K, trong đó , ,
B. Điểm H, trong đó , ,
C. Điểm V, trong đó , ,
D. Điểm P, trong đó , ,
Lời giải
Chọn A.
D
A
C
N
K
I
E
S
M
B
( )
ABCD
=ÇE AB CD
( )
SAB
( ) ( )
ÎÌ ÞÎNEM MCD N MCD
ÎN SB
( )
=ÇNSB MCD
( )
ABCD
=ÇI AC BD
( )
SAC
=ÇK MC SI
( )
ÎÌKSI SBD
ÎKMC
( )
=ÇKMC SBD
.S ABCD
M
SC
N
BC
SD
( )
AMN
=ÇK IJ SD
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
=ÇH IJ SA
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
=ÇV IJ SB
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
=ÇP IJ SC
=ÇI SO AM
,=Ç =ÇOACBDJ AN BD
Trang 41
Trong mặt phẳng gọi .
Trong gọi và .
Ta có .
Do đó .
Vậy
Câu 30. Cho hình chóp có đáy là một tứ giác ( không song song ). Gọi M là
trung điểm của là điểm nằm trên cạnh sao cho là giao điểm của và .
Giả sử đường thẳng là giao tuyến của và . Nhận xét nào sau đây là sai:
A. cắt . B. cắt . C. cắt . D. cắt .
Lời giải
Chọn B.
Gọi .
Ta có:
J
I
O
S
A
B
D
C
M
N
K
( )
ABCD
,=Ç =ÇOACBDJ AN BD
( )
SAC
=ÇI SO AM
=ÇK IJ SD
( ) ( )
,ÎÌ ÎÌIAM AMNJAN AMN
( )
ÞÌIJ AMN
( ) ( )
ÎÌ ÞÎKIJ AMN K AMN
( )
=ÇKSD AMN
.S ABCD
ABCD
AB
CD
,SD N
SB
2,SN NB O=
AC
BD
d
( )
SAB
( )
SCD
d
CD
d
MN
d
AB
d
SO
I
O
A
D
B
C
S
M
N
I AB CD=Ç
Trang 42
Lại có
Do đó
Vậy cắt .
Giả sử cắt . Khi đó thuộc mp . Suy ra thuộc (vô lý). Vậy không cắt
.Đáp án B sai.
Câu 31. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm của cạnh .
Gọi là giao điểm của đường thẳng vơí mặt phẳng . Khi đó tỉ số bằng bao nhiêu:
A. . B. . C. . D. .
Lời giải
Chọn C.
Gọi . Ta có: ; .
Suy ra .
Xét tam giác có hai đường trung tuyến và cắt nhau tại điểm . Vậy là trọng tâm tam
giác . Vậy ta có .
Câu 32. Cho hình chóp , đáy là hình thang với là đáy lớn , là trọng
tâm tam giác . Mặt phẳng cắt cạnh tại . Khi đó, tỷ số bằng:
A. B. C. D.
Lời giải
( ) ( )
( ) ( )
( ) ( )
,
,
I AB AB SAB I SAB
I SAB SCD
I CD CD SCD I SCD
ÎÌÞÎ
ì
ï
ÞÎ Ç
í
ÎÌÞÎ
ï
î
( ) ( )
.SSAB SCDÎÇ
( ) ( )
.SI SAB SCD=Ç
.d SI޺
d
,,AB CD SO
d
MN
M
( )
SAB
D
( )
SAB
d
MN
.S ABCD
ABCD
M
SC
I
AM
( )
SBD
MA
IA
2
3
3
2
4
3
I
M
O
D
B
A
C
S
O AC BD=Ç
( ) ( )
SO mp SAC SBD=Ç
I AM SO=Ç
( )
IAM SBD=Ç
SAC
SO
MA
I
I
SAC
3
2
MA
IA
=
S.ABCD
ABCD
AD
AD = 2BC
G
SCD
( )
SAC
BG
K
KB
KG
2
3
2
1
1
2
Trang 43
Chọn B.
Gọi là trung điểm của
Ta có:
Suy ra, I là trung điểm của BM
Xét
Câu 33. Cho tứ diện có lần lượt là trung điểm của và . là điểm thuộc cạnh
sao cho Gọi là giao điểm của với . Tỉ số bằng:
A. B. C. D.
Lời giải
Chọn C.
M
BC
( ) ( ) ( )
ABCD : BM AC = I; SBM : SI BG K BG SAC NÇÇ=ÞÇ=
( )
ABCD : BM AD = NÇ
BI BC 1 MC MC 1
AD // BC 1 ; 1 BM = BN
IN AD 2 MN 2MD
Þ= = = =Þ
KB SG IM KB 3
BGM: . . = 1
KG SM IB KG 2
DÞ=
ABCD
P,Q
AB
CD
M
AD
MA = 2MD.
N
BC
( )
MPQ
NB
NC
1
2
2
3
2
1
( ) ( )
ACD : MG AC = I; ABC : PI BC = NÇÇ
Trang 44
Suy ra:
Xét
Xét
Câu 34. Cho hình chóp , đáy là hình thang , là điểm thuộc
cạnh sao cho . Mặt phẳng cắt cạnh tại . Khi đó, tỷ số bằng:
A. B. C. D.
Lời giải
Chọn A.
Ta có:
Suy ra:
Câu 35. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là
trung điểm của và . Gọi là giao điểm của với . Tính
A. . B. . C. . D. .
Lời giải
Chọn B.
Trong mp , gọi . Dễ thấy .
( )
BC MNP NÇ=
IC MG QD IC 1
ACD: . . = 1
IA MD QC IA 2
DÞ=
NB IC PA NB
ABC: . . = 1 1
NC IA PB NC
DÞ=
S.ABCD
ABCD
( )
AD // BC, AD > BC
E
SA
SE = 2EA
( )
EBC
SD
F
SF
SD
2
3
1
3
1
2
1
4
( ) ( )
( ) ( )
EBC SAD , E d
BC EBD , AD SAD // BC // AD
BC//AD
d
d
Ç=Î
ì
ï
ÌÌÞ
í
ï
î
( )
SA D : SD = F EF // A D // B Cd ÇÞ
SF SE 2
SD SA 3
==
.S ABCD
ABCD
O
,,MNP
,AB AD
SO
H
SC
( )
MNP
?
SH
SC
1
3
1
4
3
4
2
3
( )
ABCD
I MN AO=Ç
H PO SC=Ç
Trang 45
Do là đường trung bình của tam giác nên là trung điểm AO.
Suy ra và là đường trung bình của tam giác . Do đó .
Áp dụng định lý Thales ta có:
Câu 36. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của và . Trên đường thẳng lấy điểm sao cho là trung điểm . Gọi là giao điểm
của với mặt phẳng . Tính
A. . B. . C. . D. .
Lời giải
Chọn D.
Trong mp , gọi .
Dễ thấy .
Do là đường trung bình của tam giác nên là trung điểm DO. Suy ra .
Áp dụng định lý Menelaus vào taam giác ta có:
Câu 37. Cho hình chóp có đáy là hình bình hành tâm . Gọi lần lượt là các
điểm nằm trên cạnh sao cho . Gọi là điểm trên cạnh sao cho .
là giao điểm của với . Tính
A. . B. . C. . D. .
Lời giải
Chọn A.
MN
ABD
I
1
4
AI
AC
=
PI
//IH SA
1
.
4
SH AI
SD AC
==
.S ABCD
ABCD
,MN
AD
CD
DS
P
D
SP
R
SB
()MNP
?
SR
SB
1
3
1
4
3
4
2
5
()ABCD
,IBDMNOACBD=Ç =Ç
R IP SB=Ç
MN
ABD
I
1
3
DI
IB
=
SBD
12
.. 1 .2.1
33
BR PS BI BR SR
RS PD ID RS SB
=Þ =Þ =
.S ABCD
ABCD
O
,MN
,AB AD
21
,
32
BM NC
MA BN
==
P
SD
1
5
PD
PS
=
J
SO
( )
MNP
?
SJ
SO
10
11
1
11
3
4
5
2
Trang 46
Theo chú ý câu 30 ta có:
Áp dụng định lý Menelaus trong tam giác ta có:
Câu 38. Cho hình chóp Gọi M, N lần lượt là trung điểm của SA và P là điểm nằm trên cạnh
AB sao cho . Gọi Q là giao điểm của SC với mặt phẳng .Tính
A. . B. . C. . D. .
Lời giải
Chọn A.
Trong mặt phẳng , gọi
Khi đó Q chính là giao điểm của SC với EM.
Áp dụng địnhlý Menelaus vào tam giác ABC ta có:
Áp dụng địnhlý Menelaus vào tam giác SAC ta có:
Câu 39. Cho tứ diện lần lượt thuộc đoạn Gọi là giao điểm của và . Gọi
là giao điểm của với . Mệnh đề nào sau đây đúng?
53 2 1 1
442
22 2 2
BA BC BO BO OI OI
BM BN BI BI BO OD
+=+=Þ =Þ=Þ=Þ=
SOD
10
.. 1 10
11
IO PD JS JS SJ
ID PS JO JO SO
=Þ = Þ =
..SABC
.BC
1
3
AP
AB
=
( )
MNP
SQ
SC
1
3
1
6
1
2
2
3
( )
ABC
E NP AC=Ç
.. 1 2
AP BN CE CE
PB NC EA EA
=Þ =
11
.. 1
23
AM SQ CE SQ SQ
MS QC EA QC SC
=Þ = Þ =
,,SABC E F
,.AC AB
K
BE
CF
D
( )
SAK
BC
Trang 47
A. . B. .
C. . D. .
Lời giải
Chọn A.
Nếu K trùng với trọng tâm G thì .Do đó C, D bị loại.
Ta có
Áp dụng định lý bất đẳng thức Cauchy ta có:
Câu 40. Cho hình chóp lần lượt là trung điểm của . Gọi là giao điểm của
với là giao điểm của với . Tính ?
A. . B. . C. D. .
Lời giải
Chọn A.
6
AK BK CK
KD KE KF
++³
6
AK BK CK
KD KE KF
++£
6
AK BK CK
KD KE KF
++>
6
AK BK CK
KD KE KF
++<
6
AK BK CK
KD KE KF
++=
1
KBC KAC
KAB
ABC ABC ABC
SS
S
DK EK FK
DA EB FC S S S
++= + + =
9
96
DK EK FK DA EB FC
DA EB FC DK EK FK
DA EB FC AK BK CK
DK EK FK KD KE KF
æöæö
++ ++ ³
ç÷ç÷
èøèø
Þ++³Þ++³
.,,SABCD DM
,BC AD
E
( )
SBM
,AC F
( )
SCM
AB
MF ME
CM ME BM ME
+
--
1
2
1
2
1
3
Trang 48
Ta có: .
Tương tự ta cũng chứng minh được:
Và
Từ (1), (2), (3) suy ra
DẠNG 3
CHỨNG MINH BA ĐIỂM THẲNG HÀNG VÀ BA ĐƯỜNG THẲNG ĐỒNG QUY
1. Chứng minh ba điểm A; B; C thẳng hàng:
Phương pháp
+ Bước 1: Chứng minh 3 điểm .
+ Bước 2: Chứng minh 3 điểm .
+ Bước 3: Kết luận 3 điểm thuộc giao tuyến chung của 2 mặt phẳng và
thẳng hàng.
2. Chứng minh 3 đường thẳng
đồng quy:
Phương pháp
CBM ABM CBM ABM CBM
ABM
AME CME AME CME AME
SSSSS
S
BM BD BF
ME S S S S S CD FA
++
=== = =+
+
( )
11
BF BM BM ME
AF ME ME
-
Þ= -=
( )
12
CM CE CD CE CM CM MF
MF AE BD AE MF MF
-
=+Þ= -=
( )
13
AM AE AF
MD CE BF
==+
1
MF ME
CM MF B M ME
+=
--
,, ()ABC mpaŒ
,, ()ABC mpbŒ
,,ABC
()mp a
()mp b
,,ABCfi
d
b
a
A
B
C
123
,,ddd
d
1
d
2
d
3
a
I
Trang 49
+ Bước 1: Tìm .
+ Bước 2: Chứng minh đi qua .
đồng quy tại .
3. Chứng minh đường thẳng trong không gian qua một điểm cố định
Phương pháp 1
Cơ sở của phương pháp là:
Ta cần tìm trên hai điểm tùy ý , và chứng minh hai điểm
đó thẳng hàng với điểm cố định có sẵn trong không gian
đi qua điểm cố định.
Phương pháp 2
Cơ sở của phương pháp là:
- Bước 1: Tìm đường thẳng cố định ở ngoài
mặt phẳng cố định chứa di động.
- Bước 2: Tìm giao điểm của và
là điểm cố định mà đi qua.
Câu 41. Cho tứ diện . Gọi , lần lượt là trung điểm và . Mặt phẳng qua cắt
và lần lượt tại , . Biết cắt tại . Ba điểm nào sau đây thẳng hàng?
A. , , . B. , , . C. , , . D. , , .
Lời giải
Chọn B.
Ta có cắt tại .
.
.
Vậy , , thẳng hàng.
12
Idd=«
3
d
I
123
,,dddfi
I
d
A
B
I
dfi
I
D
()a
d
I
D
d
Ifi
d
ABCD
M
N
AB
CD
( )
a
MN
AD
BC
P
Q
MP
NQ
I
I
A
C
I
B
D
I
A
B
I
C
D
MP
NQ
I
( )
( )
Î
ì
Î
ì
ï
ÞÞ
íí
Î
Î
î
ï
î
I ABD
I MP
INQ
I CBD
( ) ( )
ÞÎ ÇIABD CBD
ÞÎI BD
I
B
D
d
(cố định)
a
A
B
I
d
(cố định)
a
I
Trang 50
Câu 42. Cho tứ diện . Trên và lấy các điểm và sao cho cắt tại ,
cắt tại , cắt tại .Khẳng định nào sau đây đúng?
A. Ba điểm thẳng hàng
B. Ba điểm thẳng hàng
C. Ba điểm không thẳng hàng
D. Ba điểm thẳng hàng
Lời giải
Chọn B.
Ta có .
Tương tự
Từ (1),(2) và (3) ta có là điểm chung của hai mặt phẳng và nên chúng thẳng
hàng.
Câu 43. Cho tứ diện có lần lượt là trung điểm của và
là trọng tâm của tam
giác . Mặt phẳng đi qua cắt lần lượt tại . Một mặt phẳng đi qua cắt
tương ứng tại và .
a) Gọi . Khẳng định nào sau đây là đúng?
A. Bốn điểm thẳng hàng. B. Bốn điểm không thẳng hàng.
C. Ba điểm thẳng hàng. D. Bốn điểm thẳng hàng.
b) Giả sử . Khằng định nào sau đây là đúng?
A. Ba điểm thẳng hàng. B. Ba điểm không thẳng hàng
C. Ba điểm thẳng hàng D. Ba điểm thẳng hàng
Lời giải
SABC
,SA SB
SC
,DE
F
DE
AB
I
EF
BC
J
FD
CA
K
B, ,JK
,,IJK
,,IJK
,,CIJ
K
I
J
S
A
B
C
D
E
F
( ) ( )
,;=Ç Ì ÞÎIDEABDE DEF I DEF
( ) ( ) ( )
1ÌÞÎAB ABC I ABC
=ÇJ EF BC
( )
( )
( )
2
ÎÎ
ì
ï
Þ
í
ÎÌ
ï
î
JEF DEF
JBC ABC
=ÇK DF AC
( )
( )
( )
3
ÎÌ
ì
ï
Þ
í
ÎÌ
ï
î
K DF DEF
K AC ABC
,,IJK
( )
ABC
( )
DEF
SABC
,DE
,AC BC
G
ABC
( )
a
AC
,SE SB
,MN
( )
b
BC
,SD SA
P
Q
,=Ç =ÇIAMDNJBPEQ
,, ,SIJG
,, ,SIJG
,,PI J
,,QIJ
,=Ç =ÇKANDMLBQEP
,,SKL
,,SKL
B, ,KL
C, ,KL
Trang 51
a) Chọn A.
Ta có , (1)
Từ (1),(2),(3) và (4) ta có là điểm chung của hai mặt phẳng và nên chúng thẳng
hàng.
b) Chọn A.
Câu 44. Cho hình chóp tứ giác , gọi là giao điểm của hai đường chéo và . Một mặt
phẳng cắt các cạnh bên tưng ứng tại các điểm . Khẳng định nào đúng?
A. Các đường thẳng đồng qui. B. Các đường thẳng chéo nhau.
C. Các đường thẳng song song. D. Các đường thẳng trùng nhau.
Lời giải
Chọn A.
K
L
J
I
P
M
G
E
D
S
A
C
B
N
Q
( ) ( )
ÎÇSSAE SBD
( )
( )
ÎÌ
ì
ï
=ÇÞ
í
ÎÌ
ï
î
G AE SAE
GAEBD
G BD SBD
( )
( )
( )
2
Î
ì
ï
Þ
í
Î
ï
î
G SAE
G SBD
( )
( )
ÎÌ
ì
ï
=ÇÞ
í
ÎÌ
ï
î
I DN SBD
IAMDN
I AM SAE
( )
( )
( )
3
Î
ì
ï
Þ
í
Î
ï
î
I SBD
I SAE
( )
( )
( )
( )
( )
4
ÎÌ Î
ìì
ïï
=ÇÞ Þ
íí
ÎÌ Î
ïï
îî
J BP SBD J SBD
JBPEQ
J EQ SAE J SAE
,, ,SIJG
( )
SBD
( )
SAE
.S ABCD
O
AC
BD
( )
a
,,,SA SB SC SD
,,,MNPQ
,,MP NQ SO
,,MP NQ SO
,,MP NQ SO
,,MP NQ SO
Trang 52
Trong mặt phẳng gọi .
Ta sẽ chứng minh .
Dễ thấy .
Vậy đồng qui tại .
Câu 45. Cho hai mặt phẳng và cắt nhau theo giao tuyến là đường thẳng . Trong lấy hai
điểm nhưng không thuộc và là một điểm không thuộc . Các đường thẳng cắt
tương ứng tại các điểm . Gọi là giao điểm của và .Khẳng định nào đúng?
A. và đồng qui. B. và chéo nhau.
C. và song song nhau. D. và trùng nhau
Lời giải
Chọn A.
I
O
A
D
B
C
S
M
N
P
Q
( )
MNPQ
=ÇIMPNQ
ÎI SO
( ) ( )
=ÇSO SAC SBD
( )
( )
ÎÌ
ì
ï
í
ÎÌ
ï
î
I MP SAC
I NQ SBD
( )
( )
Î
ì
ï
ÞÞÎ
í
Î
ï
î
I SAC
I SO
I SBD
,,MP NQ SO
I
( )
P
( )
Q
a
( )
P
,AB
a
S
( )
P
,SA SB
( )
Q
,CD
E
AB
a
,AB CD
a
,AB CD
a
,AB CD
a
,AB CD
a
Trang 53
Trước tiên ta có vì ngược lại thì
(mâu thuẫn giả thiết) do đó không thẳng hàng, vì vậy ta có mặt phẳng .
Do
Tương tự
Từ (1) và (2) suy ra .
Mà .
Vậy và đồng qui đồng qui tại .
Câu 46. Cho hình bình hành , S là điểm không thuộc ,M và N lần lượt là trung điểm
của đoạn AB và Xác định các giao điểm I, J của AN và MN với , từ đó tìm khẳng định đúng
trong các khẳng định sau:
A. Ba điểmJ, I, M thẳng hàng. B. Ba điểmJ, I, N thẳng hàng.
C. Ba điểmJ, I, D thẳng hàng. D. Ba điểmJ, I, B thẳng hàng.
Lời giải
Chọn D.
P
Q
a
S
A
C
E
D
B
ÏS AB
( ) ( )
ÎÌ ÞÎSAB P S P
,,SAB
( )
SAB
( )
( )
( )
ÎÌ
ì
ï
=Ç Þ
í
Î
ï
î
C SA SAB
C SA Q
CQ
( )
( )
( )
1
Î
ì
ï
Þ
í
Î
ï
î
C SAB
CQ
( )
( )
( )
ÎÌ
ì
ï
=Ç Þ
í
Î
ï
î
D SB SAB
D SB Q
DQ
( )
( )
( )
2
Î
ì
ï
Þ
í
Î
ï
î
D SAB
DQ
( ) ( )
=ÇCD SAB Q
( )
( )
( )
( )
ÎÌ Î
ìì
ïï
=ÇÞ Þ
íí
ÎÌ Î
ïï
îî
E AB SAB E SAB
E AB a
Ea Q E Q
ÞÎECD
,AB CD
a
E
ABCD
( )
ABCD
.SC
( )
SBD
Trang 54
*Xác định giao điểm
Chọn mặt phẳng phụ
Tìmgiao tuyến của và :
Trong (SAC), gọi , , mà
Vậy:
* Xác địnhgiao điểm
Chọn mp phụ
Tìmgiao tuyến của và , S là điểm chung của và
Trong , gọi
Trong , gọi , mà
Vậy
* Chứng minh I, J, B thẳng hàng
Ta có: B là điểm chung của và
• mà
• mà
Ilà điểm chung của và
• mà
• mà
Jlà điểm chung của và . Vậy: B, I, Jthẳng hàng.
Câu 47. Cho tứ giác và . Gọi I, J là hai điểm trên AD và SB, AD cắt BC tại O và
OJ cắt SCtại M. Xác định các giao điểm K, L của IJ và DJ với , từ đó tìm khẳng định đúng trong
các khẳng định sau:
A. Ba điểm thẳng hàng. B. Ba điểm thẳng hàng.
( )
IAN SBD=Ç
( )
SAC ANÉ
( )
SAC
( )
SBD
( ) ( )
SAC SBD SOÇ=
I AN SO=Ç
I ANÎ
I SOÎ
( ) ( )
SO SBD I SBDÌÞÎ
( )
IAN SBD=Ç
( )
JMN SBD=Ç
( )
SMC MNÌ
( )
SMC
( )
SBD
( )
SMC
( )
SBD
( )
ABCD
E MC BD=Ç
( ) ( )
SAC SBD SEÞÇ=
( )
SMC
J MN SE=Ç
H SEÎ
( ) ( )
SE SBD J SBDÌÞÎ
( )
JMN SBD=Ç
( )
ANB
( )
SBD
I SOÎ
( ) ( )
SO SBD I SBDÌÞÎ
I ANÎ
( ) ( )
AN ANB I ANBÌÞÎ
Þ
( )
ANB
( )
SBD
J SEÎ
( )
SE SBDÌ
( )
JSBDÞÎ
JMNÎ
( )
NM ANBÌ
( )
JANBÞÎ
Þ
( )
ANB
( )
SBD
ABCD
( )
SABCDÎ
( )
SAC
,,AK L
,,ALM
Trang 55
C. Bốn điểm thẳng hàng. D. Bốn điểm thẳng hàng.
Lời giải
Chọn C.
* Tìmgiao điểm
• Chọn mp phụ
•Tìmgiao tuyến của và , S là điểm chung của và . Trong , gọi
•Trong , gọi mà
Vậy:
* Xác địnhgiao điểm
• Chọn mp phụ
•Tìmgiao tuyến của và , S là điểm chung của và
Trong , gọi
Trong , gọi mà
Vậy:
* Chứng minh A,K,L,Mthẳng hàng
Ta có:A là điểm chung của và
• mà
• mà
Þ Klà điểm chung của và
mà
,,,AK LM
,,,AK LJ
M
K
F
E
L
A
D
C
B
O
J
I
S
( )
KIJ SAC=Ç
( )
SIB IJÉ
( )
SIB
( )
SAC
( )
SIB
( )
SAC
( )
ABCD
E AC BI=Ç
( ) ( )
SIB SAC SEÞÇ =
( )
SIB
.,KIJSEKIJKSE=Ç Î Î
( ) ( )
SE SAC K SACÌÞÎ
( )
KIJ SAC=Ç
( )
LDJ SAC=Ç
( )
SBD DJÉ
( )
SBD
( )
SAC
( )
SBD
( )
SAC
( )
ABCD
( ) ( )
FACBD SE SBD SAC=ÇÞ= Ç
( )
SBD
,,LDJ SELDJLSF=Ç Î Î
( ) ( )
SF SAC L SACÌÞÎ
( )
LDJ SAC=Ç
( )
SAC
( )
AJO
KIJÎ
( ) ( )
IJ AJO K AJOÌÞÎ
K SEÎ
( ) ( )
SE SAC K SACÌÞÎ
( )
SAC
( )
AJO
LDJÎ
( ) ( )
DJ AJO L AJOÌÞÎ
Trang 56
mà
Þ Llà điểm chung của và
mà
mà
Þ M là điểm chung của và
Vậy: Bốn điểm A,K,L,M thẳng hàng
Câu 48. Cho tứ diện .Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho
LMkhông song song với AB, LN không song song với Gọi LK giao tuyến của mp và
. Xác định I, J lần lượt là giao điểm của BC và SC với . Khẳng định nào sau đây đúng:
A. Ba điểm L, I, J thẳng hàng. B. Ba điểm L, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng. D. Ba điểm M, I,K thẳng hàng.
Lời giải
Chọn C.
* Tìm giao tuyến của mp và
Ta có: N là điểm chung của và
Trong (SAB), LM không song song với AB
Gọi
mà
mà
* Tìm giao điểm
• Chọn mp phụ
•Tìmgiao tuyến của và . Trong ,
gọi , mà
L SFÎ
( ) ( )
SF SAC L SACÌÞÎ
( )
SAC
( )
AJO
MJOÎ
( ) ( )
JO AJO M AJOÌÞÎ
M SCÎ
( ) ( )
SC SAC M SACÌÞÎ
( )
SAC
( )
AJO
SABC
.SC
( )
LM N
( )
ABC
( )
LM N
K
J
I
S
C
M
L
N
B
A
( )
LM N
( )
ABC
( )
LM N
( )
ABC
K AB LM=Ç
KLMÎ
( ) ( )
LM LMN K LM NÌÞÎ
K ABÎ
( ) ( )
AB ABC K ABCÌÞÎ
( )
IBC LMN=Ç
( )
ABC BCÉ
( )
ABC
( ) ( ) ( )
LM N ABC LMN NKÞÇ =
( )
ABC
I NK BC=Ç
,IBCINKÎÎ
( ) ( )
NK LM N I LM NÌÞÎ
Trang 57
Vậy:
*Tìm giao điểm
•Trong , LN không song song với Gọi mà
Vậy:
* Chứng minh M, I, Jthẳng hàng
Ta có: M, I, Jlà điểm chung của và
Vậy: M, I, Jthẳng hàng
Câu 49. Cho tứ giác và S không thuộc mặt phẳng . Gọi M, N là hai điểm trên BC và
Xác định I, J lần lượt là giao điểm của BN và MN với . Từ đó tìm bộ 3 điểm thẳng hàng trong
những điểm sau:
A. Ba điểm A, I, Jthẳng hàng. B. Ba điểm K, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng. D. Ba điểm C, I,Jthẳng hàng.
Lời giải
Chọn D.
* Tìm giao điểm
Chọn mp phụ
•Tìmgiao tuyến của và
Trong ,
•Trong , gọi mà
Vậy:
* Tìm giao điểm :
• Chọn mp phụ
( )
IBC LMN=Ç
( )
JSC LMN=Ç
( )
SAC
.SC
,,JLNSCJSCJLN=Ç Î Î
( ) ( )
LN LMN J LMNÌÞÎ
( )
JSC LMN=Ç
( )
LM N
( )
SBC
ABCD
( )
ABCD
.SD
( )
SAC
O
J
K
I
M
N
A
D
C
B
S
( )
IBN SAC=Ç
( )
SBD BNÉ
( )
SBD
( )
SAC
( )
ABCD
( ) ( )
OACBD SBD SAC SO=ÇÞ Ç =
( )
SBD
,,IBNSOIBNISO=Ç Î Î
( ) ( )
SO SAC I SACÌÞÎ
( )
IBN SAC=Ç
( )
JMN SAC=Ç
( )
SMD MNÉ
Trang 58
•Tìmgiao tuyến của và
Trong , gọi
•Trong , gọi mà
Vậy:
* Chứng minh C, I, Jthẳng hàng:
Ta có: C, I, Jlà điểm chung của và
Vậy: C, I, Jthẳng hàng
Câu 50. Cho tứ diện . là điểm thuộc đoạn sao cho là các điểm thuộc
đường thẳng sao cho là các điểm thuộc đường thẳng sao cho
thuộc tia đối của tia sao cho là trung điểm của . Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Bốn điểm đồng phẳng B. Bốn điểm đồng phẳng.
C. Bốn điểm đồng phẳng. D. Bốn điểm đồng phẳng.
Lời giải
Chọn A.
Dựa vào nhận xét ví dụ 2, ta có:
nên đồng phẳng.
nên không đồng phẳng.
nên không đồng phẳng.
nên không đồng phẳng.
Câu 51. Cho hình chóp có đáy là hình bình hành .Mặt phẳng di động
chứa đường thẳng và cắt các đoạn lần lượt tại . Mặt phẳng di động chứa đường
( )
SMD
( )
SAC
( )
ABCD
( ) ( )
KACDM SMD SAC SK=Ç Þ Ç =
( )
SMD
,,JMNSKJMNJSK=Ç Î Î
( ) ( )
SK SAC J SACÌÞÎ
( )
JMN SAC=Ç
( )
BCN
( )
SAC
ABCD
E
AB
2.,EA EB F G=
BC
5, 5.,FC FB GC GB H I==-
!!!" !!!" !!!" !!!"
CD
5, 5,HC HD ID IC J=- =-
!!!" !!! " !!" !!"
DA
D
AJ
,, ,EFH J
,,,EFI J
,, ,EGH I
,,,EGI J
B
A
J
C
F
I
D
E
H
( )
11
.. . 2..5.1
52
AE BF CH DJ
BE CF DH AJ
=- - =
,, ,EFH J
111 1
... 2...
552 25
AE BF CI DJ
BE CF DI AJ
æö
=- =
ç÷
èø
,,,EFI J
( )
11
.. . 2. .5. 1
52
AE BG CH DJ
BE CG DH AJ
æö
=- - - =-
ç÷
èø
,, ,EGH J
1111
... 2. ..
55225
AE BG CI DJ
BE CG DI AJ
æöæö
=- - =
ç÷ç÷
èøèø
,,,EGI J
.S ABCD
ABCD
( )
//BC AD
( )
P
AB
,SC SD
( )
Q
Trang 59
thẳng và cắt lần lượt tại là giao điểm của là giao điểm của . Xét
các mệnh đề sau:
Đường thẳng luôn đi qua một điểm cố định.
Đường thẳng luôn đi qua một điểm cố định.
Đường thẳng luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng?
A. . B. . C. . D. .
Lời giải
Chọn D.
Trong mp , gọi . Khi đó cố định.
Như vậy: cùng nằm trên hai mp và , do đó ba điểm thẳng hàng. Vậy
đường thẳng luôn đi qua một điểm cố định .
Tương tự, ta có cùng nằm trên hai mp và ,do đó thẳng hàng. Vậy các
đường thẳng luôn đi qua một điểm cố định .
Do .
Tương tự ta cũng có
Do đó ba điểm thẳng hàng. Vậy luôn đi qua điểm cố định .
Câu 52. Cho tứ diện và các điểm lần lượt thuộc các cạnh sao cho
không song song với . đồng phẳng khi :
A. B.
CD
,SA SB
,.GHI
,;AE BF J
,CG DH
( )
1
EF
( )
2
GH
( )
3
IJ
0
1
2
3
( )
ABCD
;MABCDOACBD=Ç = Ç
,MO
,,EFM
( )
P
( )
SCD
,,EFM
EF
M
,,GH M
( )
Q
( )
SAB
,,GH M
GH
M
( )
( )
( ) ( )
I AE SAC
I SAC SBD
I BF SBD
ÎÌ
ì
ï
ÞÎ Ç
í
ÎÌ
ï
î
( ) ( ) ( ) ( )
;JSAC SBDOSAC SBDÎÇ ÎÇ
,,IJO
IJ
O
ABCD
,,,MNPQ
,,,AB BC CD DA
MN
AC
,,,MNPQ
... 1
AM BN CP DQ
BM CN DP AQ
=
... 1
BM CN CP DQ
AM BN DP AQ
=
Trang 60
C. D. .
Lời giải
Chọn A.
+ Giả sử cùng thuộc mặt phẳng .
Nếu cắt tại thì là điểm chung của các mặt phẳng , nên cũng đi
qua
Áp dụng định lí cho các tam giác ta được :
;
Nhận xét :
Trường hợp song song với thì ví dụ trên vẫn đúng.
+ Liệu trường hợp ngược lại, có thì có đồng phẳng hay không ?
Câu trả lời là trường hợp ngược là ví dụ vẫn đúng. Ta sẽ cùng chứng minh nhé :
Trong mặt phẳng , cắt tại thì các điểm đồng phẳng.
Theo ví dụ 2 ta có: . Ví dụ được chứng minh.
+ Ví dụ này có thể được mở rộng đối với các điểm bất kì trên các đường thẳng
như sau :
đồng phẳng khi và chỉ khi ( khẳng định này dôi khi còn được gọi là
định lí Menelaus mở rộng trong không gian)
Câu 53. Cho hình chóp Giả sử AD và BC cắt nhau tại H. Gọi O là giao điểm của AC và BD, E
và F lần lượt là trung điểm của SA và Điểm M di động trên cạnh Gọi N là giao điểm của SD và
mp(EFM). Tìm tập hợp giao điểm J của EN và FM.
A. Tập hợp J là đoạn thẳng SJ
1
với J
1
= CF Ç SH.
B. Tập hợp J là đoạn thẳng SJ
1
với J
1
= DE Ç SH.
C. Tập hợp J là đoạn thẳng SH.
D. Tập hợp J là đường thẳng SH.
Lời giải
Chọn A.
... 1
BM CN DP DQ
AM BN CP AQ
=
... 1
AM BN DP AQ
BM CN CP DQ
=
,,,MNPQ
( )
a
MN
AC
K
K
( ) ( )
, ABC
a
( )
ADC
PQ
.K
Menelaus
,ABC ADC
.. 1
AM BN CK
BM CN AK
=
.. 1
AK CP DQ
CK DP AQ
=
... 1
AM BN CP DQ
BM CN DP AQ
Þ=
MN
AC
... 1
AM BN CP DQ
BM CN DP AQ
=
,,,MNPQ
( )
ACD
KO
AD
Q
¢
,,,MNPQ
¢
... 1
AM BN CP AQ
BM CN DP DQ
¢
=
¢
DQ DQ
QQ
AQ AQ
¢
¢
Þ=Þº
¢
,,,MNPQ
,,,AB BC CD DA
,,,MNPQ
¢
... 1
AM BN CP DQ
BM
CN DP AQ
=
..S ABCD
.SB
.SC
Trang 61
Gọi O là giao điểm của AC và Suy ra (SAC) cắt (SBD) theo giao tuyến là SO. Gọi I là giao của EM
và SO. Khi đó FI cắt SD tại N. Do FM thuộc mp (SBC) cố định và EN thuộc mp (SAD) cố định nên giao
điểm J của FM và EN thuộc giao tuyến của mp (SBC) và mp (SAD). Gọi H =AD Ç BC, suy ra (SBC)
Ç(SAD) =SH. Do đó I thuộc đường thẳng SH.
Giới hạn: Nếu thì ; Nếu thì với J
1
= CF Ç SH.
Vậy tập hợp J là đoạn thẳng SJ
1
.
Câu 54. Cho hình chóp S.ABCD, trong đó AD không song song với Gọi O là giao điểm của AC và
BD, E là giao điểm của AD và Điểm M di động trên cạnh SB, EM cắt SC tại N. Tập hợp giao điểm I
của AN và DM.
A. Tập hợp giao điểm I là đoạn thẳng SO.
B. Tập hợp giao điểm I là đường thẳng SO.
C. Tập hợp giao điểm I là đoạn thẳng SO trừ 2 điểm S và O.
D. Tập hợp giao điểm I là đoạn thẳng SE.
Lời giải
Chọn C.
.BD
MSº
JSº
MCº
1
JJº
.BC
.BC
Trang 62
Do AN thuộc mp (SAC) cố định và DM thuộc mp (SBD) cố định nên giao điểm I của AN và DM thuộc
giao tuyến của (SAC) và (SBD) là SO. Khi M trùng S thì I trùng S; Khi M trùng B thì I trùng O. Vậy tập
hợp I là đoạn thẳng SO.
Câu 55. Cho tứ diện Một mặt phẳng di động luôn song song với và cắt các cạnh
AC, tại . Tìm tập hợp tâm I của hình bình hành
A. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và CD (trừ 2 điểm P và
Q).
B. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và
C. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC (trừ 2 điểm P và
Q).
D. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và
Lời giải
Chọn B.
Gọi P, Q lần lượt là trung điểm của AB và Khi đó AQ cắt MN tại K; BQ cắt FE tại H. Dễ thấy H, K
lần lượt là trung điểm của MN và FE nên I thuộc KH, đồng thời là trung điểm KH. Do đó I thuộc đường
trung tuyến QP của tam giác
.ABCD
( )
P
AB
CD
,,AD BD BC
,,,MNEF
.MNEF
.CD
.BC
.CD
.QAB
Trang 63
DẠNG 4
XÁC ĐỊNH THIẾT DIỆN CỦA MỘT MẶT PHẲNG VỚI HÌNH CHÓP
Để xác định thiết diện của hình chóp cắt bởi mặt phẳng , ta tìm giao điểm của mặt phẳng
với các đường thẳng chứa các cạnh của hình chóp. Thiết diện là đa giác có đỉnh là các giao điểm
của với hình chóp ( và mỗi cạnh của thiết diện phải là một đoạn giao tuyến với một mặt của hình
chóp)
Câu 56. Cho là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp
?
A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác.
Lời giải
Chọn D.
Hình chóp có mặt nên thiết diện của hình chóp có tối đa 5 cạnh. Vậy thiết diện không thể
là lục giác.
Câu 57. Cho hình chóp với đáy là tứ giác lồi. Thiết diện của mặt phẳng tuỳ ý với
hình chóp không thể là:
A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác.
Lời giải
Chọn A.
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi
mặt của hình chóp.
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến.
12
....
n
SAA A
( )
a
( )
a
( )
a
ABCD
.S ABCD
.S ABCD
5
.S ABCD
ABCD
( )
a
Trang 64
Hình chóp tứ giác có 5 mặt nên thiết diện của với có không qua 5 cạnh, không
thể là hình lục giác 6 cạnh.
Câu 58. Cho hình chóp có đáy là hình bình hành và điểm ở trên cạnh . Mặt
phẳng cắt hình chóp theo thiết diện là
A. tam giác. B. hình thang. C. hình bình hành. D. hình chữ nhật.
Lời giải
Chọn B.
Câu 59. Cho hình chóp tứ giác , có đáy là hình thang với là đáy lớn và là một điểm
trên cạnh .
a) Thiết diện của hình chóp cắt bởi mặt phẳng là hình gì?
A. Tam giác B. Tứ giác C. Hình thang D. Hình bình hành
b) Gọi lần lượt là trung điểm của các cạnh . Thiết diện của hình chóp cắt bởi là
hình gì?
A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
Lời giải
a) Chọn B.
Trong mặt phẳng , gọi .
Trong mặt phẳng gọi .
Ta có nên , do đó .
Thiết diện là tứ giác .
b) Chọn A.
.S ABCD
( )
a
.S ABCD
.S ABCD
ABCD
M
SB
( )
ADM
.S ABCD
AD
P
SD
()PAB
,MN
,AB BC
( )
MNP
Q
E
S
A
D
B
C
P
( )
ABCD
=ÇE AB CD
( )
SCD
=ÇQSC EP
ÎE AB
( ) ( )
ÌÞÎEP ABP Q ABP
( )
=ÇQSC ABP
ABQP
Trang 65
Trong mặt phẳng gọi lần lượt là các giao điểm của với và
Trong mặt phẳng gọi
Trong mặt phẳng gọi .
Ta có ,
Vậy
Tương tự .
Thiết diện là ngũ giác .
Câu 60. Cho hình chóp . Điểm nằm trên cạnh . Thiết diện của hình chóp với mp
là một đa giác có bao nhiêu cạnh?
A. . B. . C. . D. .
Lời giải
Chọn B.
K
H
F
G
N
M
S
B
C
D
A
P
( )
ABCD
,FG
MN
AD
CD
( )
SAD
=ÇH SA FP
( )
SCD
=ÇK SC PG
( )
ÎÞÎFMN F MNP
( ) ( )
ÞÌ ÞÎFP MNP H MNP
( )
( )
Î
ì
ï
Þ= Ç
í
Î
ï
î
HSA
HSA MNP
HMNP
( )
=ÇKSC MNP
MNKPH
.S ABCD
¢
C
SC
( )
¢
ABC
3
4
5
6
Trang 66
Xét và có là điểm chung 1.
Gọi
Có là điểm chung 2.
Gọi .
Ta có:
Thiết diện là tứ giác .
Câu 61. Cho hình chóp có đáy là hình bình hành. Gọi là trung điểm . Thiết diện
của hình chóp cắt bởi mặt phẳng là:
A. Tam giác B. Hình thang ( là trung điểm ).
C. Hình thang ( là trung điểm ). D. Tứ giác .
Lời giải
Chọn B.
M
I
A
D
B
C
S
A'
( )
¢
ABA
( )
SCD
( )
( )
,
¢
ÎÌ
ì
ï
í
¢¢
Î
ï
î
A SC SC SCD
A ABA
¢
Þ A
=ÇI AB CD
( )
( )
,
,
¢
ÎÌ
ì
ï
í
ÎÌ
ï
î
I AB AB ABA
ICDCD SCD
Þ I
( ) ( )
¢¢
ÞÇ=ABA SCD IA
¢
=ÇM IA SD
( ) ( )
¢¢
Ç=ABA SCD A M
( ) ( )
¢
Ç=ABA SAD AM
( ) ( )
¢
Ç=ABA ABCD AB
( ) ( )
¢¢
Ç=ABA SBC BA
¢
ABA M
.S ABCD
ABCD
I
SA
.S ABCD
( )
IBC
.IBC
IJCB
J
SD
IGBC
G
SB
IBCD
Trang 67
Gọi là giao điểm của và , là giao điểm của và .
Khi đó là trọng tâm tam giác . Suy ra là trọng tâm tam giác .
Gọi . Khi đó là trung điểm .
Do đó thiết điện của hình chóp cắt bởi là hình thang ( là trung điểm ).
Câu 62. Cho hình chóp có đáy là một hình bình hành tâm . Gọi là ba điểm
trên các cạnh . Thiết diện của hình chóp với mặt phẳng là hình gì?
A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
Lời giải
Chọn A.
Trong mặt phẳng gọi lần lượt là giao điểm của với .
Trong mặt phẳng gọi
Trong mặt phẳng gọi
C
S
B
A
D
I
J
G
O
O
AC
BD
G
CI
SO
G
SAC
G
SBD
=ÇJ BG SD
J
SD
( )
IBC
IJCB
J
SD
.S ABCD
ABCD
O
,,MNP
,,AD CD SO
()MNP
R
T
H
F
E
K
O
C
A
B
D
S
M
N
P
()ABCD
,,EKF
MN
,,DA DB DC
( )
SDB
=ÇH KP SB
( )
SAB
=ÇT EH SA
Trang 68
Trong mặt phẳng gọi .
Ta có
.
Lí luận tương tự ta có .
Thiết diện là ngũ giác .
Câu 63. Cho tứ diện , và lần lượt là trung điểm và . Mặt phẳng qua cắt
tứ diện theo thiết diện là đa giác Khẳng định nào sau đây đúng?
A. là hình chữ nhật. B. là tam giác.
C. là hình thoi. D. là tam giác hoặc hình thang hoặc hình bình hành.
Lời giải
Chọn D.
qua cắt ta được thiết diện là một tam giác.
qua cắt hai cạnh và ta được thiết diện là một hình thang.
Đặc biệt khi mặt phẳng này đi qua trung điểm của và , ta được thiết diện là một hình bình hành.
Câu 64. Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
của các cạnh Thiết diện của hình chóp với mặt phẳng là đa giác có bao nhiêu
cạnh ?
A. B. C. D.
Lời giải
Chọn C.
( )
SBC
=ÇR FH SC
( )
Î
ì
ÞÌ
í
Î
î
EMN
EH MNP
HKP
( )
( )
Î
ì
ï
Þ= Ç
í
ÎÌ
ï
î
TSA
TSA MNP
TEH MNP
( )
=ÇRSC MNP
MNRHT
ABCD
M
N
AB
AC
()
a
MN
ABCD
( )
.T
( )
T
( )
T
( )
T
( )
T
A
B
C
D
M
N
( )
a
MN
AD
( )
a
MN
BD
CD
BD
CD
.S ABCD
ABCD
,,MNQ
, , .AB AD SC
( )
MNQ
3.
4.
5.
6.
Trang 69
Thiết diện của hình chóp với mặt phẳng là ngũ giác Đa giác này có cạnh.
Câu 65. Cho hình chóp có đáy là hình bình hành, gọi lần lượt là 2 điểm thuộc
cạnh sao cho . Mặt phẳng cắt tại thỏa mãn . Số k
bằng?
A. B. C. D.
Lời giải
Chọn A.
Xét
( )
MNQ
.MNPQR
5
S.ABCD
ABCD
M, N
SB,SD
SM = MB,SN = 2ND
( )
AMN
SC
P
SP = kSC
2
5
3
5
3
2
2
3
( )
ABCD : AC BD = ;OÇ
( )
SBD : MN BD = TÇ
( ) ( )
ABCD : AT CD = K, SCD : KN SC = PÇÇ
TD NS MB TD 1
ABD: . . = 1
TB ND MS TB 2
DÞ=
Trang 70
Ta có:
Xét
Câu 66. Cho tứ diện đều có các cạnh bằng . Gọi là trung điểm , là điểm thuộc cạnh
sao cho là điểm thuộc cạnh sao cho . Tính độ dài đoạn giao tuyến của
mặt phẳng với mặt phẳng của hình chóp theo .
A. . B. . C. . D. .
Lời giải
Chọn A.
Trong mp , gọi .
Trong mp , gọi .
Khi đó .
Áp dụng định lý Menelaus cho tam giác với ba điểm thẳng hàng ta có:
Áp dụng định lý Menelaus cho tam giác với ba điểm thẳng hàng ta có:
Áp dụng định lý cosin vào tam giác ta có:
Câu 67. Cho hình chóp có đáy là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho . F là trọng tâm tam giác là điểm thay đổi trên cạnh Thiết diện cắt bởi mặt
phẳng là:
TD KD KD 1 KC
3
TB AB DC 2 KD
===Þ=
PS ND KC PS 2 2
SCD: . . = 1 SP= SC
PC NS KD PD 3 5
DÞ=Þ
ABCD
a
E
AB
F
BC
2,BF FC G=
CD
2CG GD=
( )
EFG
( )
ACD
ABCD
a
19
15
a
141
30
a
34 15 3
15
a +
34 15 3
15
a -
( )
BCD
I FG BD=Ç
( )
ADB
H IE AD=Ç
( ) ( )
HG EFG ACD=Ç
BCD
,,IGF
1
.. 1
4
ID FB GC ID
IB FC GD IB
=Þ =
ABD
,H,EI
1
.. 1
45
HD EA IB HD a
HD
HA EB ID HA
=Þ = Þ =
HDG
222 0
222 2
2..cos60
19 19
25 9 15 225 15
HG HD DG DH DG
aaa a
HG a
=+-
=+-= Þ =
.S ABCD
ABCD
3SD SE=
,SAB G
.BC
( )
EFG
Trang 71
A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Lời giải
Chọn C.
Cách 1:
Gọi là trung điểm của , khi đó , , thẳng hàng.
Trong mặt phẳng , gọi là giao điểm của với . Khi đó .
Trong mặt phẳng , gọi là giao điểm của với . Ta thấy thuộc nên thuộc
. Trong , gọi là giao điểm của với . Trong mặt phẳng , gọi là giao
điểm của với .
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng , gọi là
giao điểm của với .
Ta có: .
Vậy ngũ giác là thiết diện của hình chóp cắt bởi .
Chú ý:Mấu chốt của ví dụ trên là việc dựng được điểm là giao điểm của với (thông qua
việc dựng giao tuyến của mặt phẳng với mặt phẳng ). Có thể dựng thiết diện trên bằng
nhiều cách với việc dựng giao điểm (khác ) của một trong các đường thẳng ; hoặc
với một mặt của hình chóp. Sau đây, tôi xin trình bày cách hai, điểm mấu chốt là xác định giao điểm của
với mặt phẳng .
Cách 2:
M
AB
S
F
M
( )
ABCD
I
MG
AD
( ) ( )
SI SMG SAD=Ç
( )
SMG
J
FG
SI
J
FG
J
( )
EFG
( )
SAD
K
JE
SA
( )
SAB
L
KF
AB
( )
ABCD
H
LG
CD
( )
SCD
N
EH
SC
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD LG EFG SBC GN
EFG SCD NE EFG SAD EK
EFG SAB K L
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
LGNEK
( )
EFG
J
FG
( )
SAD
SI
( )
SFG
( )
SAD
,,EFG
,EF FG
GE
EF
( )
ABCD
Trang 72
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với , .
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với .
Ta có: .
Vậy ngũ giác là thiết diện của hình chóp cắt bởi .
Câu 68. Cho hình chóp có đáy là hình thang với đáy lớn AD, E là một điểm thuộc mặt
bên . F, G lần lượt là các điểm thuộc cạnh AB và Thiết diện của hình chóp cắt bởi
mặt phẳng có thể là:
A. Tam giác, tứ giác. B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Lời giải
Chọn B.
Trong mặt phẳng , gọi là giao điểm của và . Trong mặt phẳng , gọi là giao
điểm của và .
Xét các trường hợp sau:
( )
SM D
P
EF
( )
ABCD
,HL
CD
AB
( )
SAB
K
LF
SA
( )
SCD
N
EH
SC
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD LG EFG SBC GN
EFG SCD NE EFG SAD EK
EFG SAB K L
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
LGNEK
( )
EFG
.S ABCD
ABCD
( )
SCD
.SB
.S ABCD
( )
EFG
( )
ABCD
H
AB
CD
( )
SAB
I
FG
SH
Trang 73
Trường hợp 1:
Trong mặt phẳng , cắt tại và cắt đoạn tại .
Ta có nên là giao điểm của với ,
nên là giao điểm của với .
Ta có
Suy ra tứ giác là thiết diện của hình chóp cắt bởi .
Trường hợp 2:
( )
SCD
IE
SC
J
CD
K
( )
JIE EFGÎÌ
J
( )
EFG
SC
( )
KIE EFGÎÌ
K
( )
EFG
CD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
;
;
EFG ABCD FK EFG SAB FG
EFG SBC GJ EFG SCD JK
Ç= Ç=
ì
ï
í
Ç= Ç=
ï
î
KFGJ
( )
EFG
Trang 74
Trong mặt phẳng , cắt tại và cắt đoạn tại (cắt tại một điểm nằm ngoài đoạn
).
Trong mặt phẳng :
Nếu song song với thì ta có: . Gọi là giao điểm của với .
Áp dụng định lí Menelaus vào các tam giác và ta có
. Điều này chỉ xảy ra khi thuộc đoạn (vô lí)
Do vây cắt , giả sử tại .
Trong mặt phẳng , gọi là giao điểm của với .
Ta có
Suy ra ngũ giác là thiết diện của hình chóp cắt bởi .
Vậy thiết diện của hình chóp cắt bởi mặt phẳng hoặc là tứ giác hoặc là ngũ giác.
Câu 69. Cho hình chóp là trung điểm của thuộc SC sao cho là một
điểm thuộc miền trong tam giác . Thiết diện của hình chóp cắt bởi mặt phẳng là:
A. Tam giác, tứ giác. B. Tứ giác, ngũ giác. C. Tam giác, ngũ giác. D. Ngũ giác.
Lời giải
Chọn B.
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng , gọi là giao
điểm của với . Trong mặt phẳng , gọi là giao điểm của với . Trong mặt
phẳng , gọi là giáo điểm của với .
Trong mặt phẳng , có hai khả năng xảy ra như sau:
Trường hợp 1: cắt đoạn tại .
( )
SCD
IE
SC
J
SD
K
CD
CD
( )
SBC
GJ
BC
SS
BG CJ
GJ
=
T
IE
CD
SBH
SCH
SS
.. 1 ..
FB IH G TC IH J FB TC
FH IS GB TH IS JC FH TH
== Þ =
T
CD
GJ
BC
L
( )
ABCD
M
LF
AD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD FM EFG SAB FG
EFG SBC GJ EFG SCD JK
EFG SAD KM
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
KJGFM
( )
EFG
.S ABCD
( )
EFG
.,S ABCD E
,SB F
32,SF SC G=
!! !" !! !"
SAD
( )
EFG
( )
SBC
J
EF
BC
( )
SAD
I
SG
AD
( )
ABCD
N
IJ
CD
( )
SIJ
K
JG
SN
( )
SCD
FK
CD
P
Trang 75
Trong mặt phẳng , gọi là giao điểm của với . Trong mặt phẳng , gọi là
giao điểm của với .
Ta có
Trường hợp này, ngũ giác là thiết diện của hình chóp cắt bởi .
Trường hợp 2: cắt tại ( không cắt đoạn ).
Trong mặt phẳng , gọi là giao điểm của với ( không thể cắt đoạn vì giả sử
ngược lại cắt cạnh tại , khi đó sẽ cắt cạnh (vô lí vì đã cắt cạnh )).
Khi đó
Trường hợp này, tứ giác là thiết diện của hình chóp cắt bởi .
G
R
J
I
Q
P
K
N
F
E
D
C
B
A
S
( )
ABCD
Q
JP
AD
( )
SAD
R
QG
SA
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
;
;
EFG ABCD PQ EFG SAD QR
EFG SAB RE EFG SBC EF
EFG SCD FP
Ç= Ç=
ì
ï
Ç= Ç=
í
ï
Ç=
î
REFPQ
.S ABCD
( )
EFG
FK
SD
H
FK
CD
G
M
J
I
H
P
K
N
F
E
D
C
B
A
S
( )
SAD
M
HG
SA
HG
AD
HG
AD
O
JO
CD
( )
EFG
,SC SD
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
;
;
EFG SCD FH EFG SAD MH
EFG SAB ME EFG SBC EF
Ç= Ç=
ì
ï
í
Ç= Ç=
ï
î
MEFH
( )
EFG
Trang 76
Câu 70. Cho tứ diện có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho . Gọi M là trung điểm của đoạn
Diện tích S thiết diện của tứ diện cắt
bởi mặt phẳng là:
A. . B. . C. . D. .
Lời giải
Chọn C.
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của và .
Ta có: .
Do đó tam giác là thiết diện của tứ diện cắt bởi .
Dễ thấy lần lượt là trọng tâm của các tam giác và .
Ta có: .
Xét hai tam giác và có chung, nên hai tam giác
này bằng nhau. Suy ra . Vậy tam giác cân tại .
Áp dụng định lí cosin trong tam giác :
.
Gọi là trung điểm của đoạn . Ta có .
ABCD
,CE a DF a==
.AB
ABCD
( )
MEF
2
33
18
a
S =
2
3
a
S =
2
6
a
S =
2
33
9
a
S =
K
H
D
C
B
F
E
A
M
( )
ABC
H
ME
AC
( )
ABD
K
MF
AD
( ) ( )
( ) ( )
( ) ( )
MEF ABC MH
MEF ABD MK
MEF ACD HK
Ç=
ì
ï
Ç=
í
ï
Ç=
î
MHK
( )
MEF
,HK
ABE
ABF
2
3
a
AH AK HK===
AMH
AMK
AM
∑
∑
0
2
60 ,
3
a
MAH MAK AH AK== ==
MH MK=
MHK
M
AMH
22
22
222 0
2 13 13
2 .cos 60
2 3 3 36 6
aaaa a
MH AM AH AMAH MH
æö æ ö
=+- =+ -=Þ=
ç÷ ç ÷
èø è ø
I
HK
MI HK^
Trang 77
Suy ra: .
Diện tích thiết diện là: .
Câu 71. Cho hình chóp có đáy là hình bình hành. Một mặt phẳng cắt các cạnh
bên tương ứng tại các điểm . Gọi . Mệnh đề nào
sau đây đúng?
A. . B. .
C. . D. .
Lời giải
Chọn C.
Xét trường hợp đặc biệt lần lượt là trung điểm của Khi đó ta dễ dàng loại được
đáp ánD.
Dựng
Theo định lý Thales, ta có:
Suy ra:
Như vậy, ý B bị loại.
Tương tự, ta chứng minh được
Từ đây ta thấy ngay ý C bị loại và A là đáp án A là đáp án lựa chọn.
22 2
222
13
36 9 4 2
aa a a
MI MH HI MI=-=-=Þ=
MHK
2
112
...
22326
aa a
SMIHK===
.S ABCD
ABCD
( )
a
,,,SA SB SC SD
,,,EFGH
,IACBDJEGSI=Ç =Ç
SA SC SB SD
SE SG SF SH
+=+
2
SA SC SI
SE SG SJ
+³
SA SC SB SD
SE SG SF SH
+>+
2
SB SD SI
SF SH SJ
+³
S
C
K
E
G
T
,,,EFGH
,,,.SA SB SC SD
( ) ( )
// , //AT EG T SI CK EG KESIÎ
,; 1
SA ST SC SK IT IA
SE SJ SG SJ IK IC
====
2
SA SC ST SK SI IT SI IK SI
SE SG SJ SJ SJ
+-++
+= = =
2.
SB SD SI
SF SH SJ
+=
Trang 78
Chú ý: Cho tam giác Gọi O là trung điểm AC, M, N là hai điểm nằm trên cạnh MN cắt BO
tại I. Khi đó: .
Câu 72. Cho tứ diện có lần lượt là trung điểm của và là điểm thuộc cạnh
( không là trung điểm ). Gọi là giao điểm của với là giao điểm của
với . Mệnh đề nào sau đây đúng?
A. . B. . C. D. .
Lời giải
Chọn A.
Do tứ diện ABCD có 4 mặt nên thiết diện không thể là ngũ giác hay lục giác. Nó chỉ có thể là tam giác
hoặc tứ giác.
Trong mp , gọi (P không phải là trung điểm đoạn BC nên MP cắt AC)
Trong mp , gọi
Do nên
Ta có:
Suy ra thiết diện cần tìm là tứ giác
Ta chọn đáp án B.
do đồng phẳng nên
(Do M, N lần lượt là trung điểm của AB, CD).Từ đây suy ra
.ABC
,.AB AC
2BA BC BO
BM BN BI
+=
ABCD
,MN
,AB CD
P
BC
P
BC
Q
( )
MNP
,AD I
MN
PQ
2
MNPQ MPN
SS=
2
MNPQ MPQ
SS=
4
MNPQ MPI
SS=
4
MNPQ PIN
SS=
j
I
B
D
C
A
M
Q
N
P
( )
ABC
K MP AC=Ç
( )
ACD
QKN AD=Ç
( )
QKN MNPÎÌ
( )
QMNP AD=Ç
( ) ( )
( ) ( )
( ) ( )
( ) ( )
MNP ABD MQ
MNP ABC MP
MNP BCD PN
MNP ACD NQ
Ç=
ì
ï
Ç=
ï
í
Ç=
ï
ï
Ç=
î
.MPNQ
,,,MNPQ
.. . 1 . 1
AM BP CN DQ BP DQ
BM CP DN AQ CP AQ
=Þ =
.
BP AQ
CP DQ
=
Trang 79
Giả sử . Khi đó ta suy ra
Suy ra
Do J là trung điểm của PQ.
Ta có:
Chứng minh tương tự ta cũng có:
Từ (1,2,3) suy ra . Điều này dẫn đến M, N, J thẳng hàng. Như vậy I trùng J.
Điều này suy ra .
Câu 73. *Cho hình chóp với đáy là đa giác lồi Trên tia đối của tia
lấy điểm là các điểm nằm trên cạnh . Thiết diện của hình chóp cắt bởi mặt
phẳng là:
A. Đa giác cạnh. B. Đa giác cạnh. C. Đa giác cạnh. D. Đa giác cạnh.
Lời giải
Chọn D.
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với .
Trong mặt phẳng , gọi là giao điểm của với .
Do nên là giao điểm của với mặt phẳng .
BP
k
PC
=
,BP k PC AQ kQD==
!!!" !!!" !!!" !!!"
( )
( )
1BP AQ k CP QD+=- +
!!!" !!!" !!!" !!!"
( )
22
MJ MB BP PJ
MJ AQ BP
MJ MA AQ QJ
ì
=++
ï
Þ=+
í
=++
ï
î
!!!" !!!" !!!" !!!"
!!!" !!!" !!!"
!!!" !!!" !!!" !!!"
( )
23NJ CP DQ=+
!!!" !!!" !!! "
MJ k NJ=-
!!!" !!!"
2
MNPQ MPN
SS=
12
...
n
SA A A
( )
12
... 3, .
n
AA A n n³Î•
1
AS
12
,,...
n
BB B
2
,
n
SA SA
( )
12n
BB B
2n -
1n -
n
1n +
C
1
C
2
O
k
I
k
B
1
B
2
B
k
B
n
A
n
A
k
A
2
A
1
S
( )
12
SA A
2
C
( )
1 n
SA A
n
C
( )
12
...
n
AA A
k
O
( )
3, 4, ..., 1kn=-
2 n
AA
( )
2 n
SA A
k
I
( )
3, 4, ..., 1kn=-
k
SO
2 n
BB
( )
1 k
SA A
k
B
( )
3, 4, ..., 1kn=-
k
SA
1 k
BI
( )
112kk n
BBI BBBÎÌ
k
B
k
SA
( )
3, 4, ..., 1kn=-
( )
12n
BB B
Trang 80
Vậy thiết diện của hình chóp cắt bởi là đa giác .
( )
12n
BB B
22
...
nn
CB BC
| 1/80
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC DẠNG TOÁN TRẮC NGHIỆM
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. Khái niệm mở đầu 1. Mặt phẳng
+ Mặt bàn, mặt bảng, mặt hồ nước yên lặng . . . Cho ta hình ảnh của một phần của mặt phẳng.
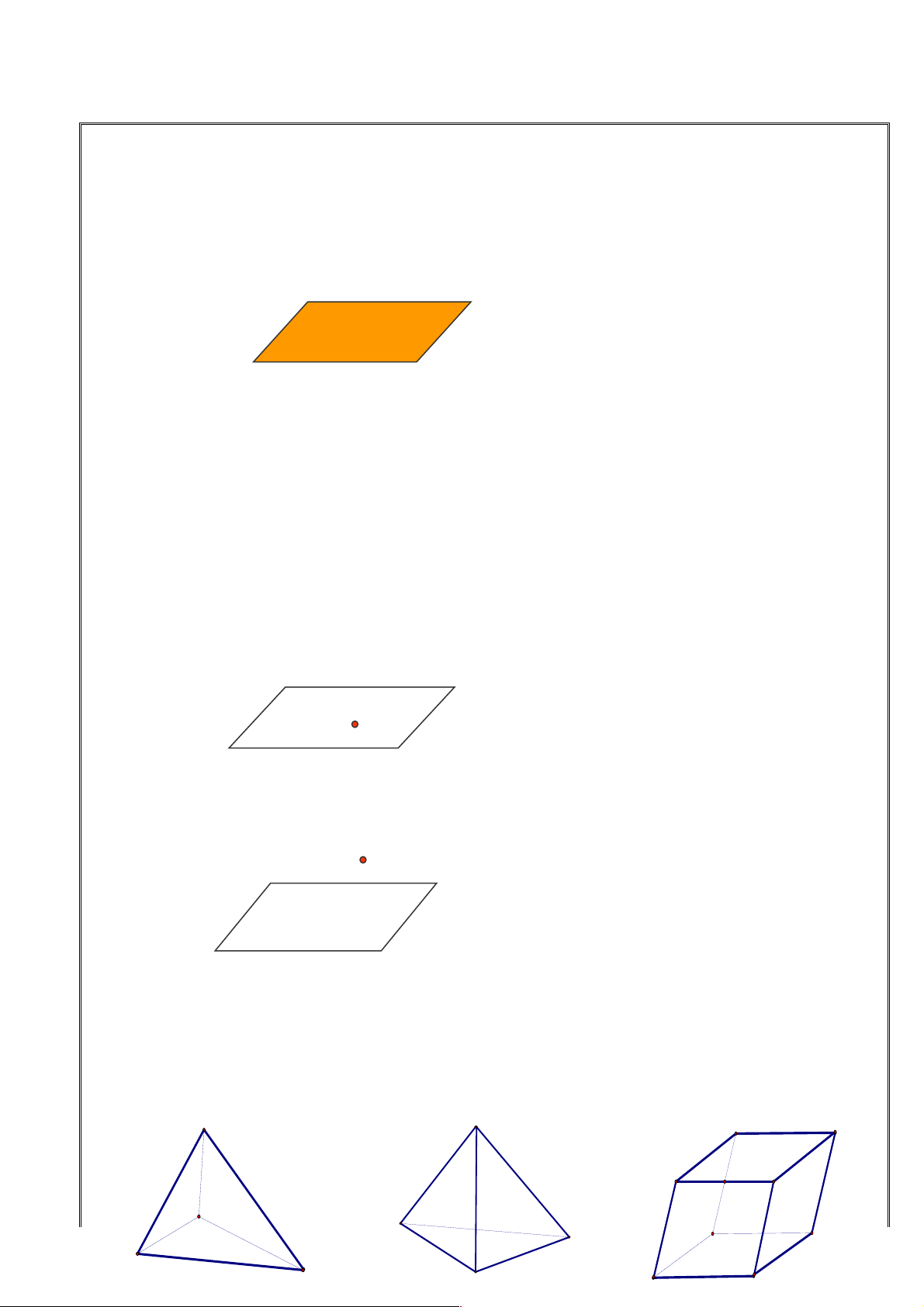
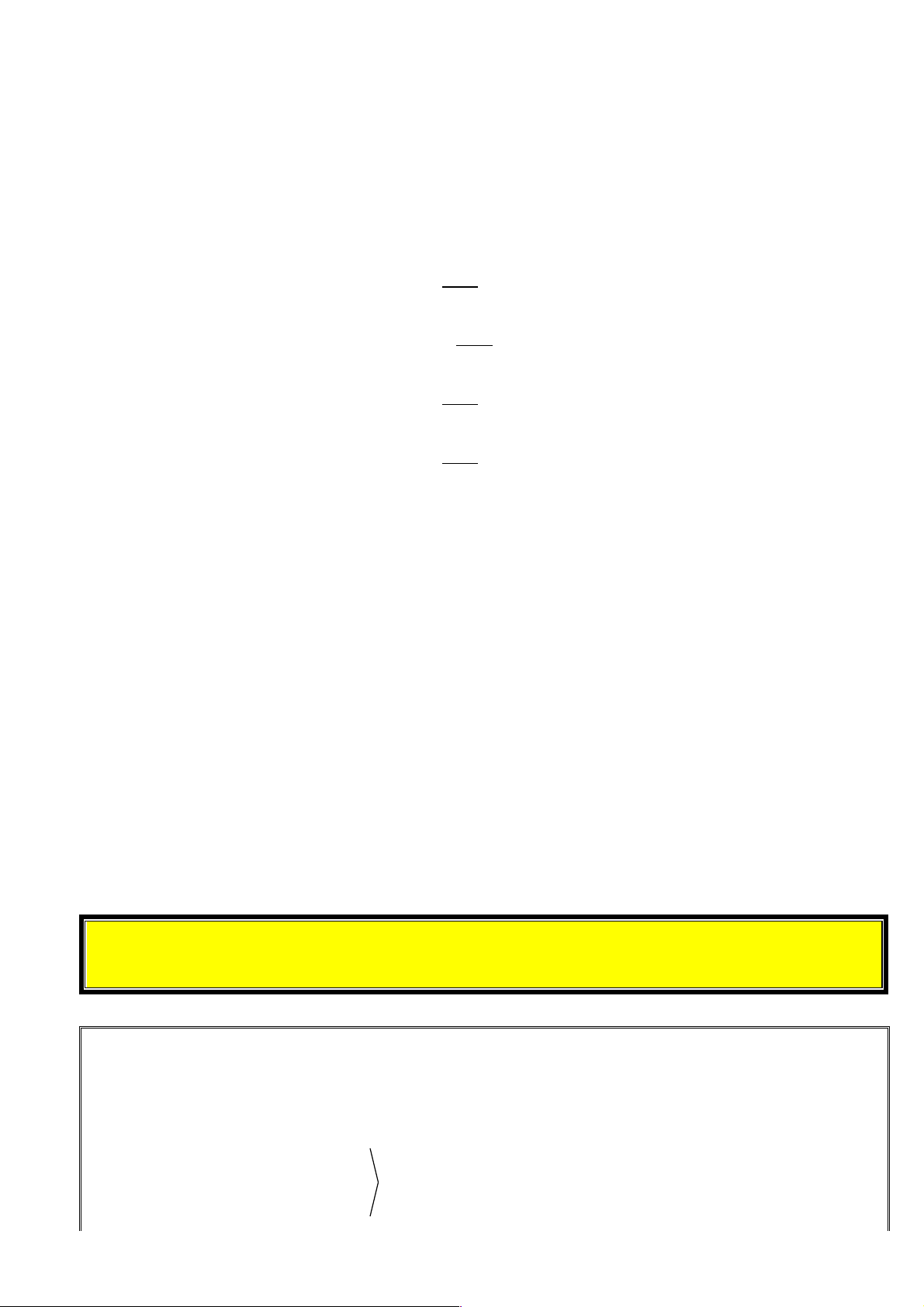
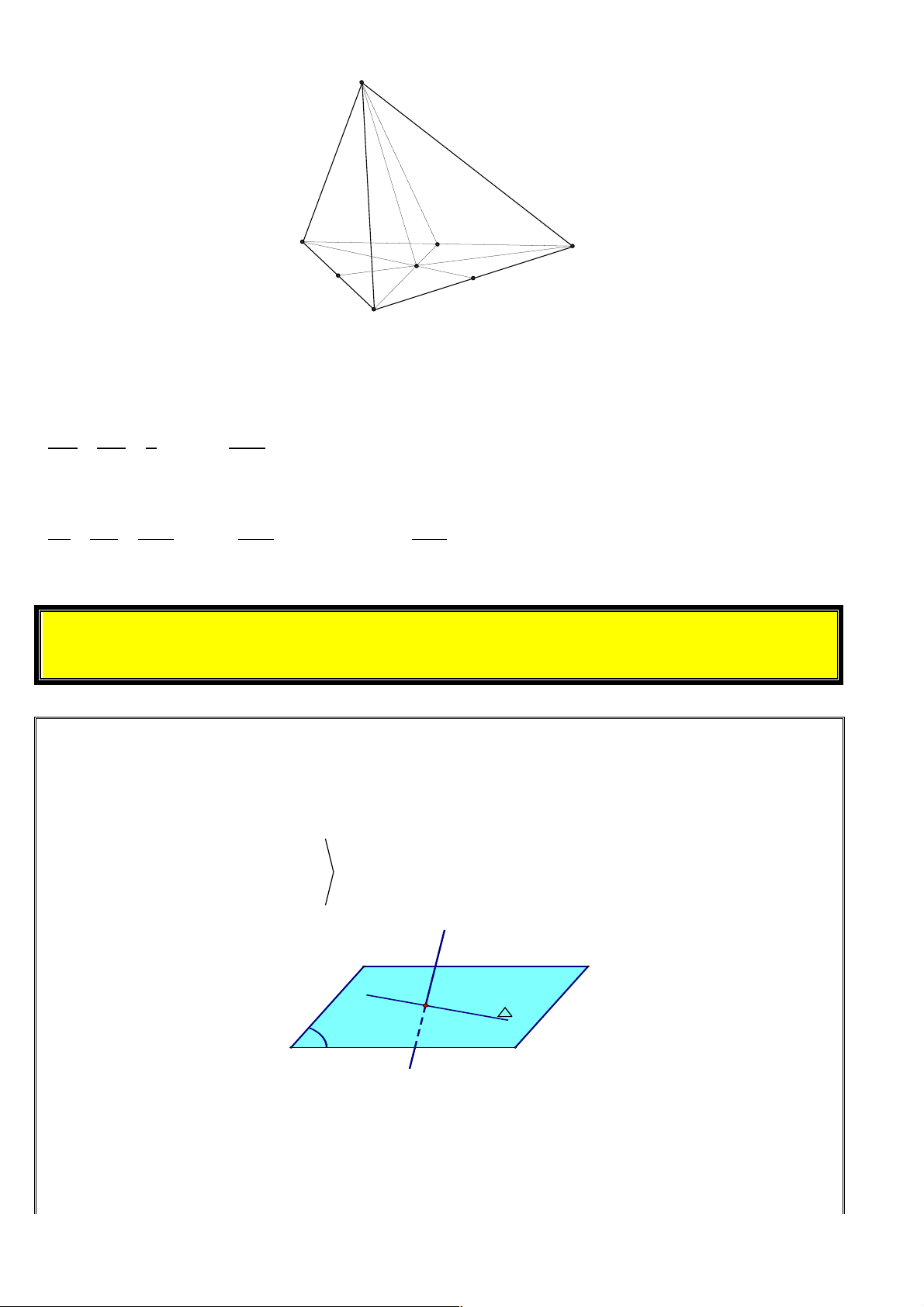
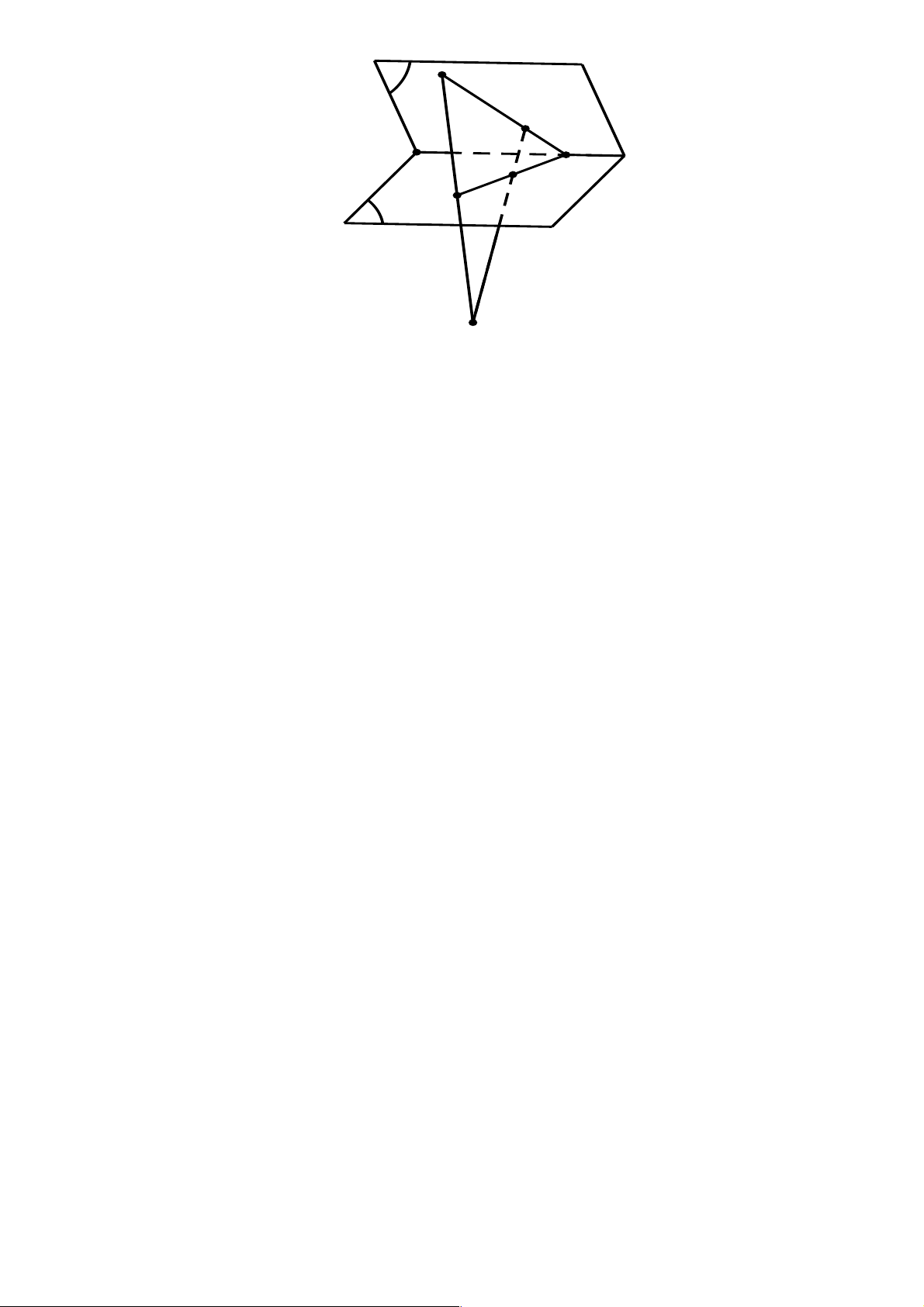
+ Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng
vào một góc của hình biểu diễn. P
+ Để kí hiệu mặt phẳng, ta thường dùng chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ( ).
+ mặt phẳng (P ), mặt phẳng ( Q ), mặt phẳng (a), mặt phẳng (b) hoặc viết tắt là mp( P ), mp( Q ),
mp (a) , mp ( b) , hoặc ( P ) , ( Q ) , (a) , ( b),
2. Điểm thuộc mặt phẳng
Cho điểm A và mặt phẳng (P).
+ Điểm A thuộc mặt phẳng (P) ta nói A nằm trên (P) hay (P) chứa A, hay (P) đi qua A và kí hiệu A Î ( P) . A P
+ Điểm A không thuộc mặt phẳng (P) ta nói điểm A nằm ngoài (P) hay (P) không chứa A và kí hiệu A Ï ( P) . A P
3. Hình biểu diễn của một hình không gian Trang 1
Để vẽ hình biểu diễn của một hình trong không gian, ta dựa vào những qui tắc sau :
+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
+ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai đường thẳng
cắt nhau là hai đường thẳng cắt nhau.
+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
+ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.
II. CÁC TÍNH CHẤT THỪA NHẬN
1. Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
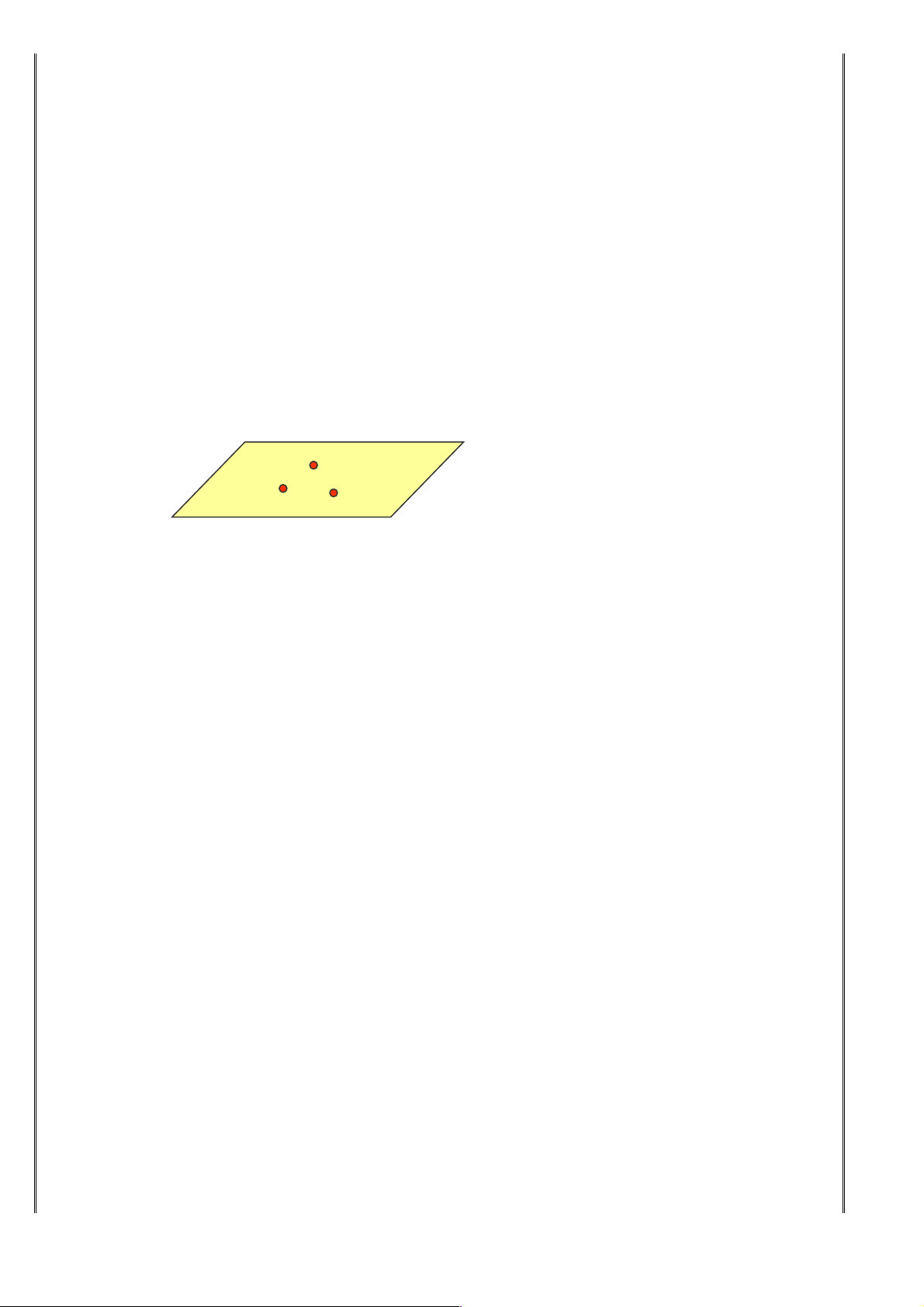
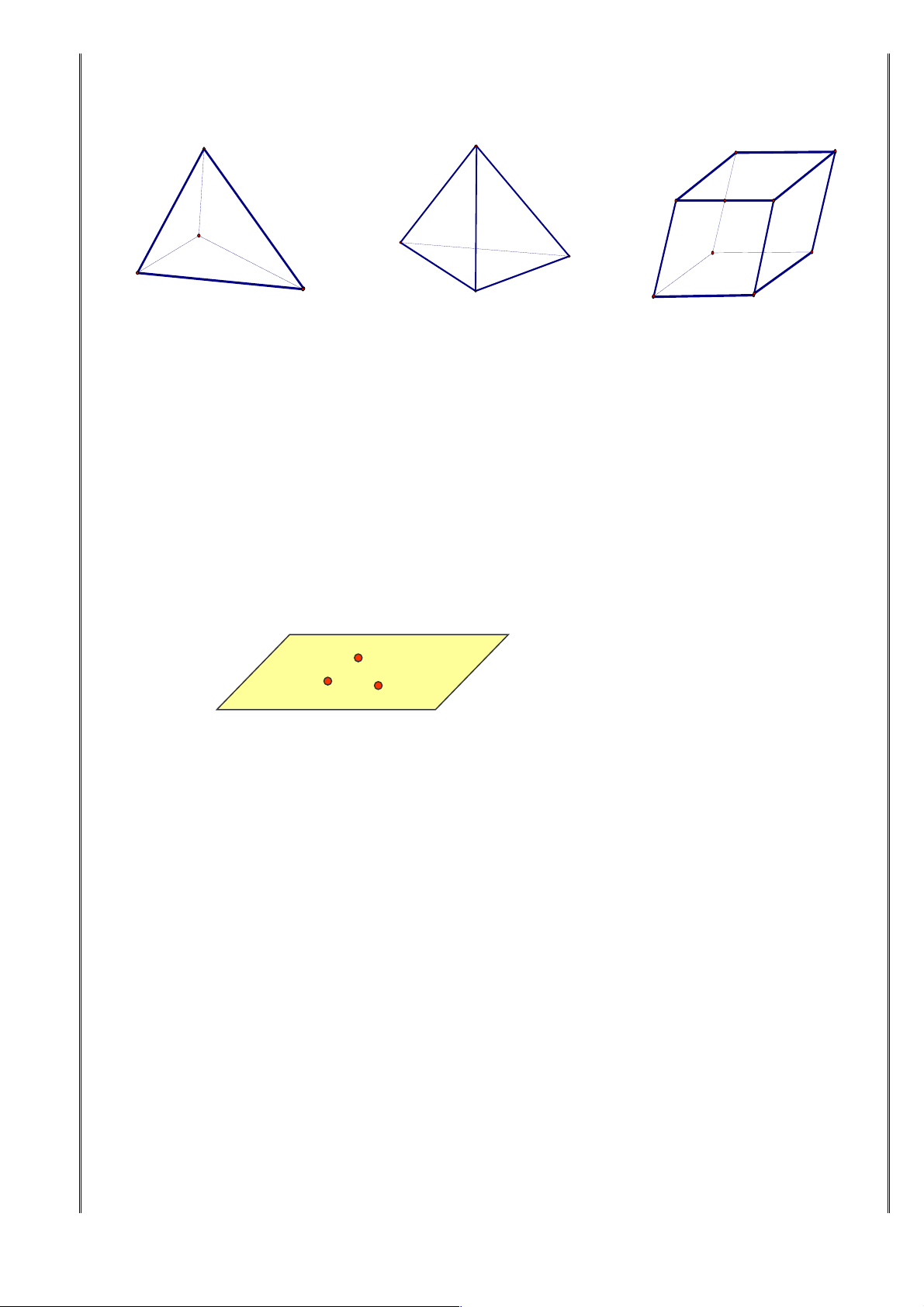
2. Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. A B C
3. Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó.
* Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P ) thì ta nói đường thẳng d nằm trong mặt
phẳng (P) . Hay (P) chứa d và kí hiệu d Ì (P) hay (P) É d
4. Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng
Nếu có nhiều điểm cùng thuộc một mp thì ta nói những điểm đó đồng phẳng .
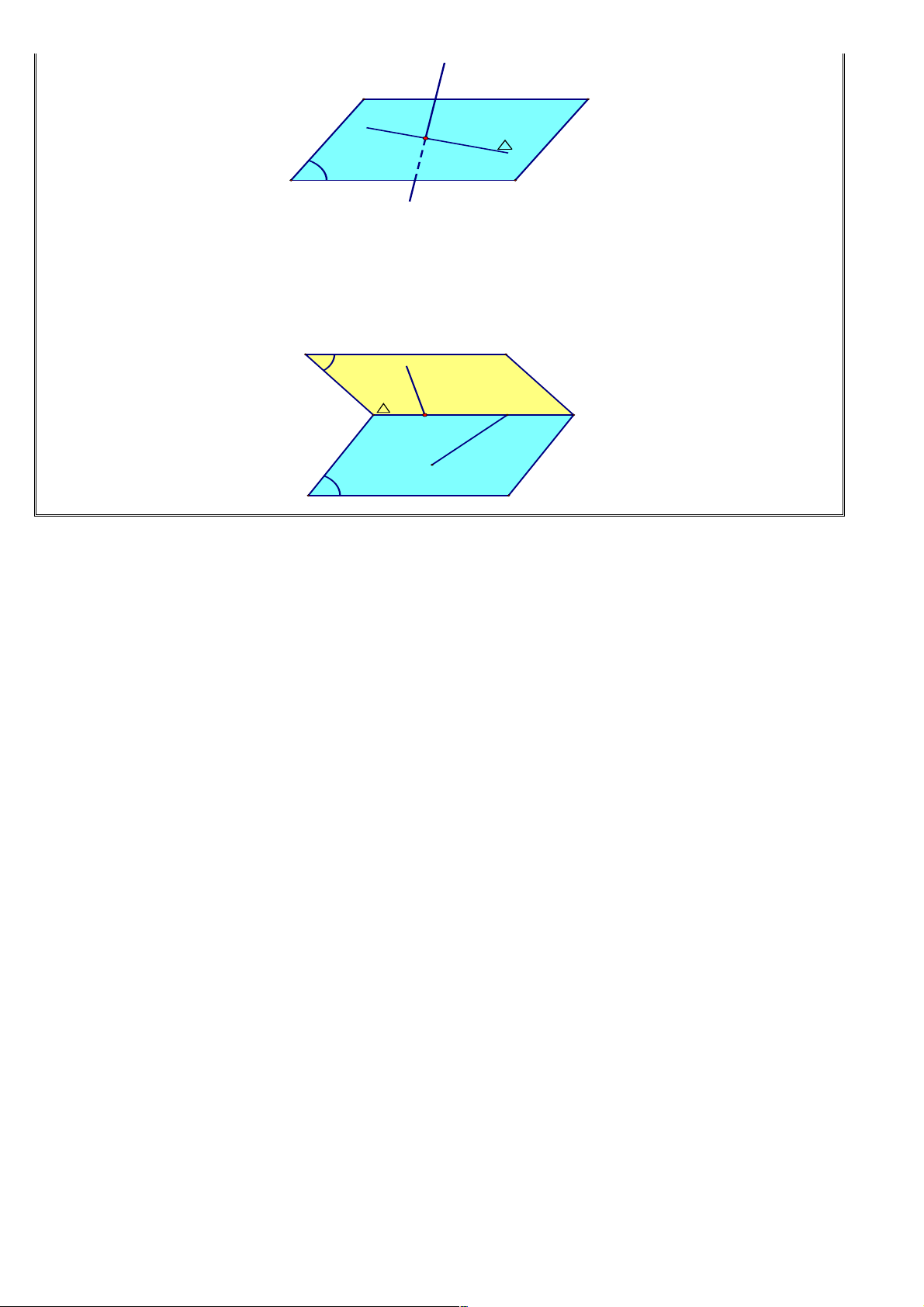
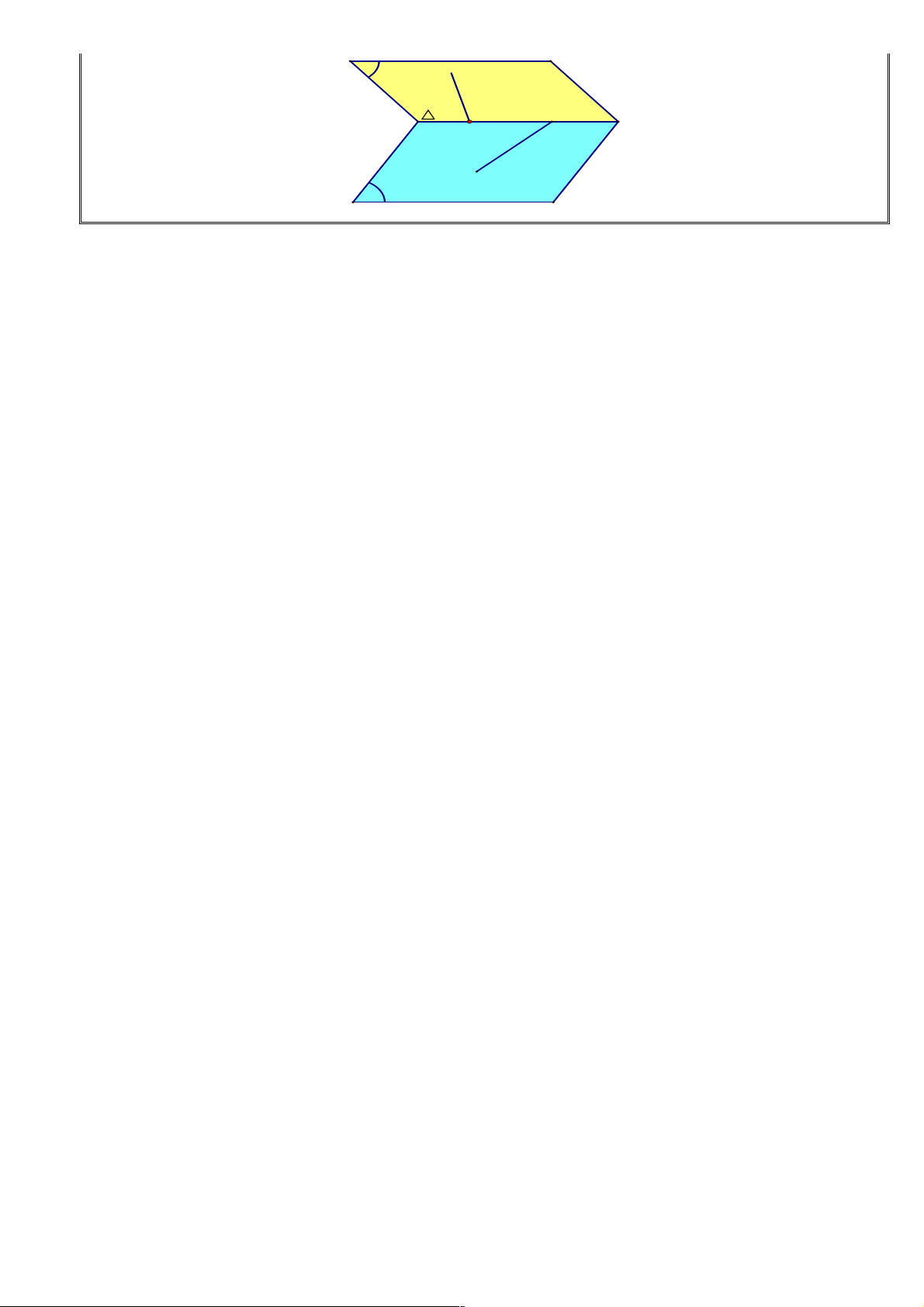
5. Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
* Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua điểm chung ấy.
* Đường thẳng chung d của hai mặt phẳng phân biệt ( P ) và ( Q ) được gọi là giao tuyến của ( P) và (Q) kí hiệu d = ( p) Ç ( Q )
6. Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
III. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG
Có 3 cách xác định mặt phẳng
+ Qua 3 điểm không thẳng hàng xác định duy nhất một mặt phẳng. Trang 2 A B C
+ Qua một điểm và một đường thẳng không chứa điểm đó ta xác định duy nhất một mặt phẳng. A d Kí hiệu mp(A,d) hay (A,d)
+ Hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng. a
Kí hiệu mp (a, b) hay (a, b) b
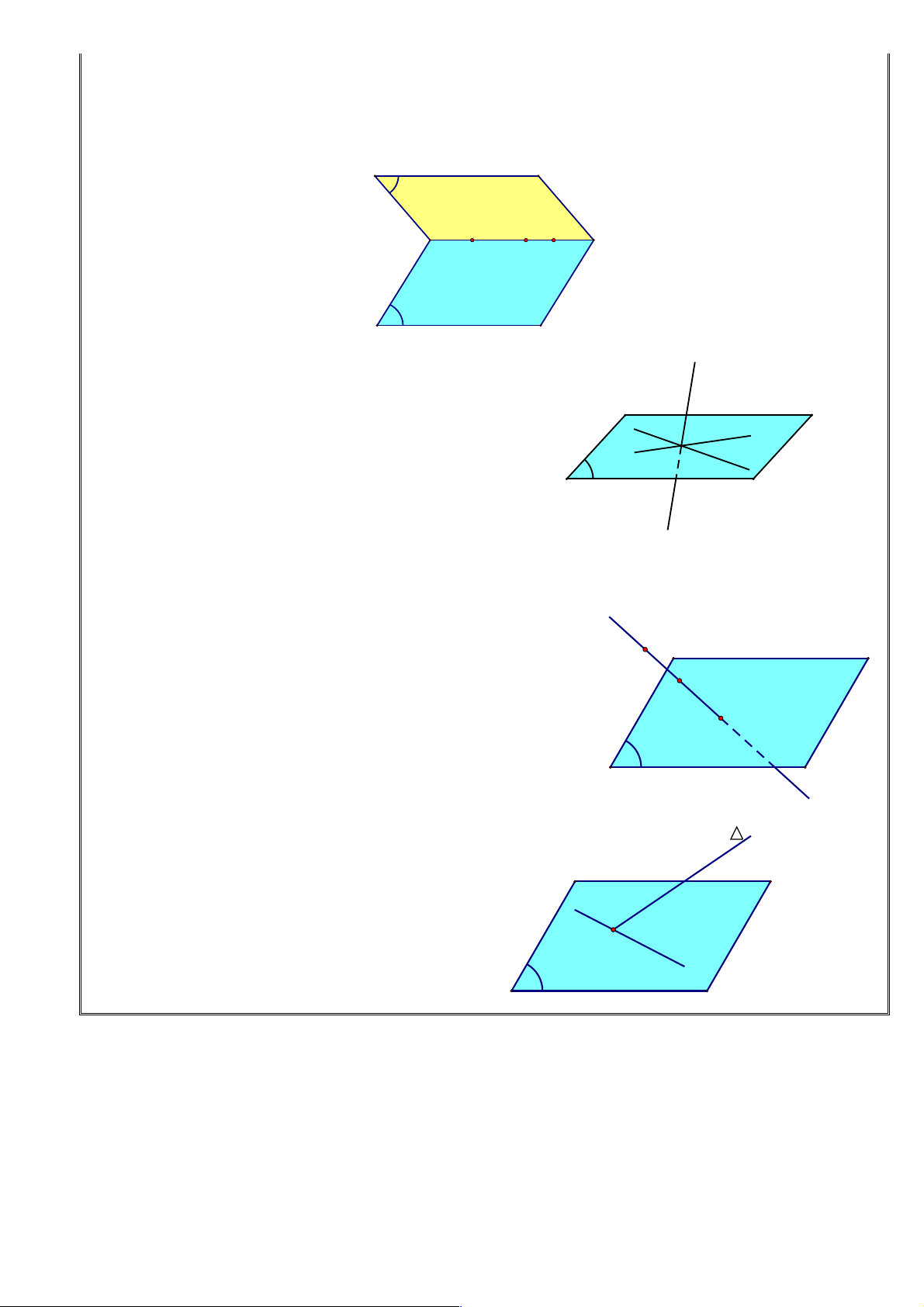
IV. HÌNH CHÓP VÀ HÌNH TỨ DIỆN 1. Hình chóp:
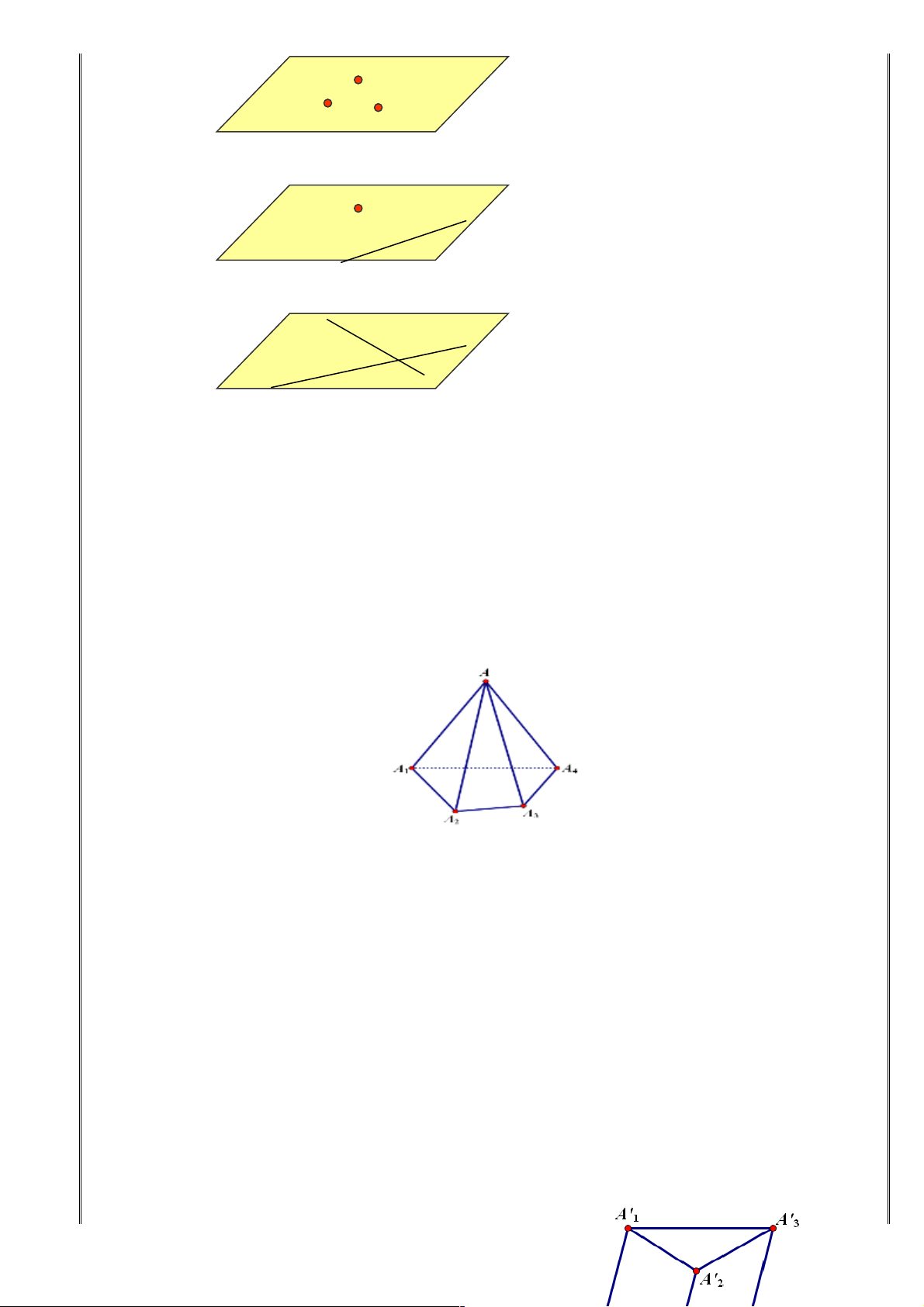
+ Hình gồm miền đa giác A1A2A3. . .An. Lấy điểm S nằm ngoài (a) . lần lượt nối S với các đỉnh
A1, A2, … An ta được n tam gíác SA1A2 , SA2A3 . . . SAnA1. Hình gồm đa giác A1A2A3. . .An và n tam
giác SA1A2 , SA2A3 . . . SAnA gọi là hình chóp, kí hiệu là S. A1A2A3. . .An. ta gọi S là đỉnh và đa giác
A1A2A3. . .An là mặt đáy. Các tam giác SA1A2 , SA2A3 . . . SAnA gọi là các mặt bên. Các đoạn SA1, SA2
. . SAn là các cạnh bên., các cạnh của đa giác đáy gọi là cạnh đáy của hình chóp. 2. Hình tứ diện
+ Một hình chóp có đáy là tam giác gọi là tứ diện.
+ Tứ diện có các mặt là tam giác đều gọi là tứ diện đều. V. HÌNH LĂNG TRỤ
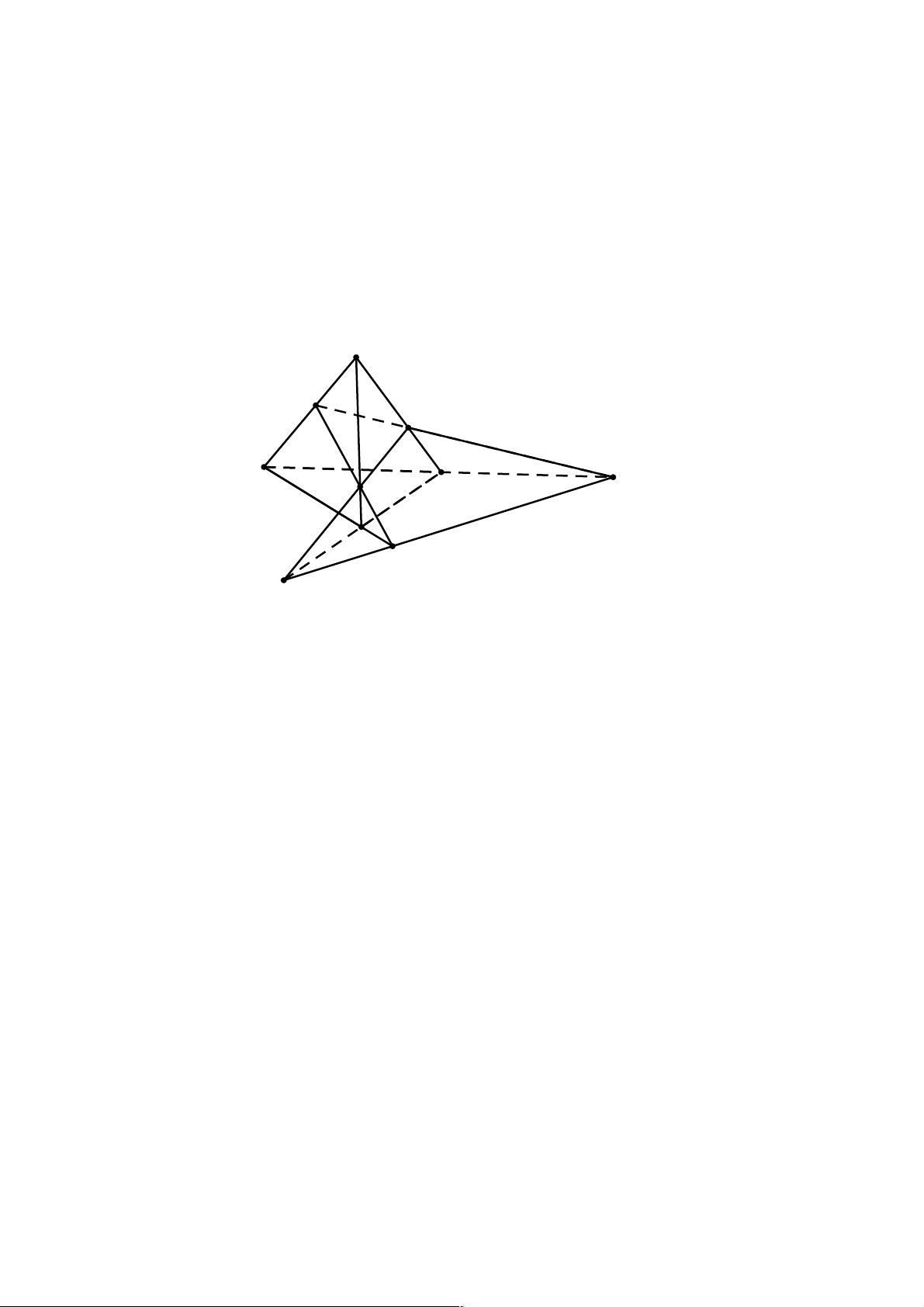
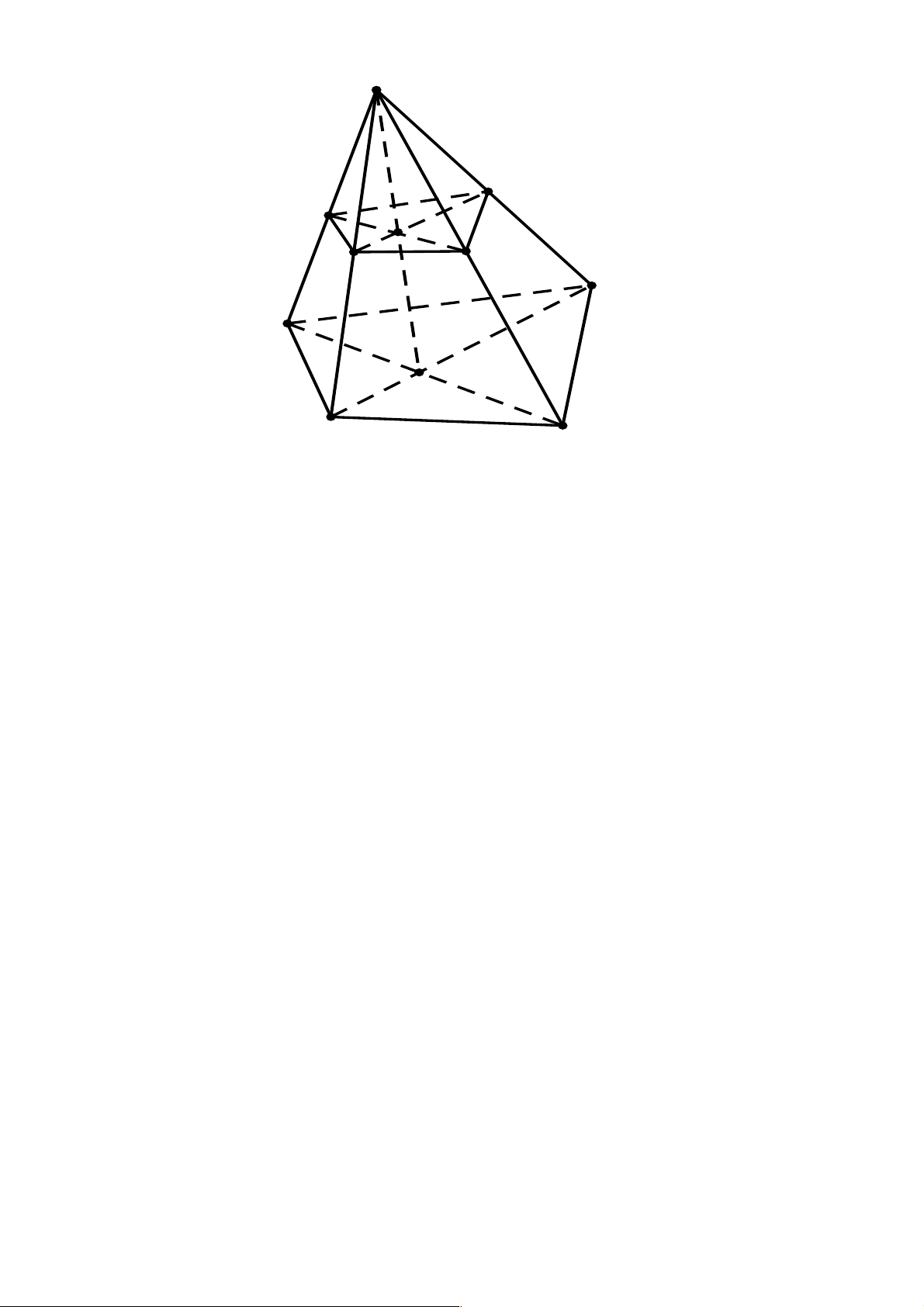
1. Hình lăng trụ: Hình hợp bởi các hình bình hành A1A2A'2A'1, A2A3A'3A'2,...,AnA1A'1A'2 và hai đa
giác A1A2...An, A'1A'2...A'n gọi là hình lăng trụ hoặc lăng trụ, và ký hiệu là A1A2...An.A'1A'2...A'n.
Trong một hình lăng trụ thì Trang 3
• 2 mặt đáy là đa giác song song và bằng nhau.
• các cạnh bên song song và bằng nhau
• các mặt bên là hình bình hành
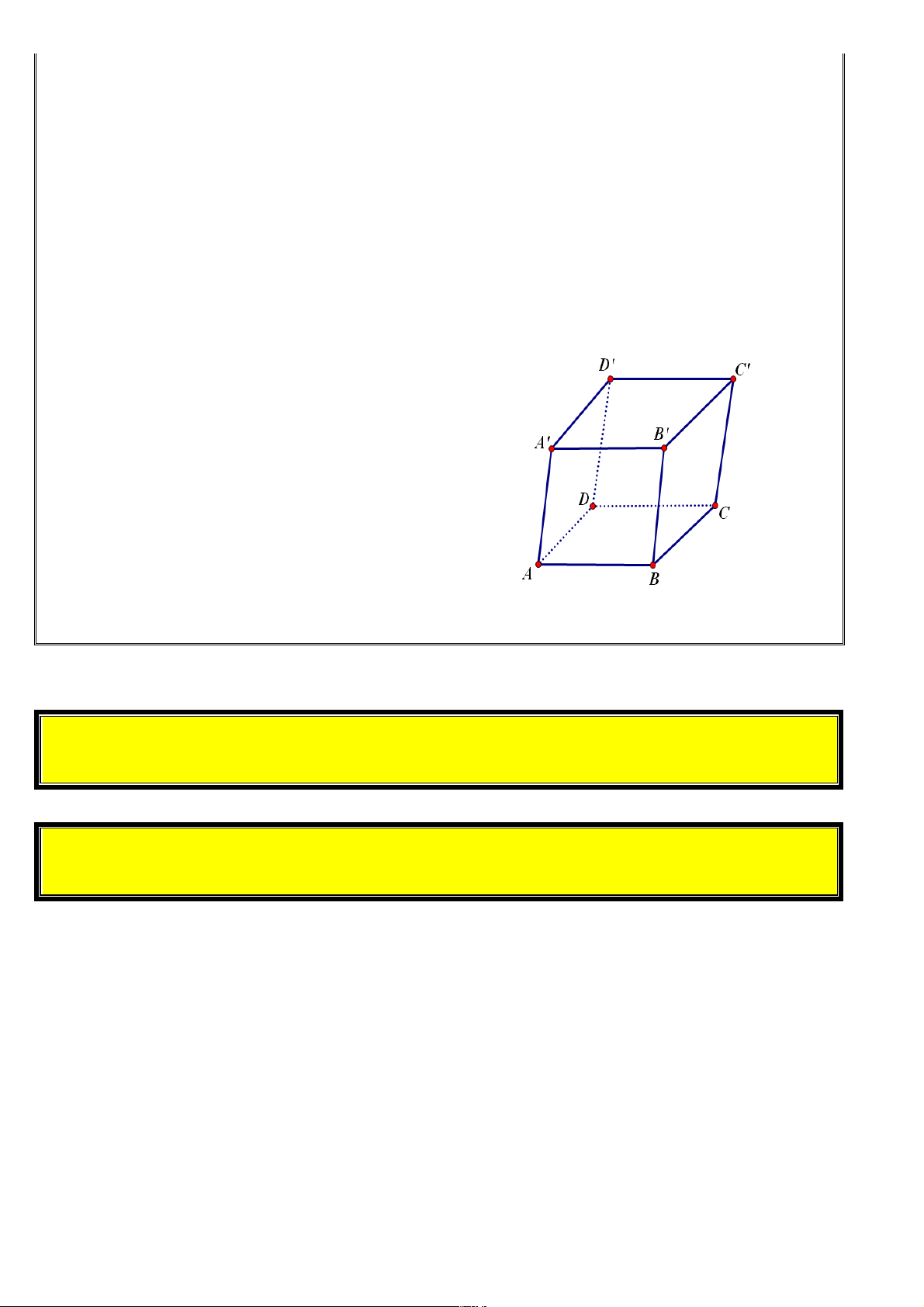
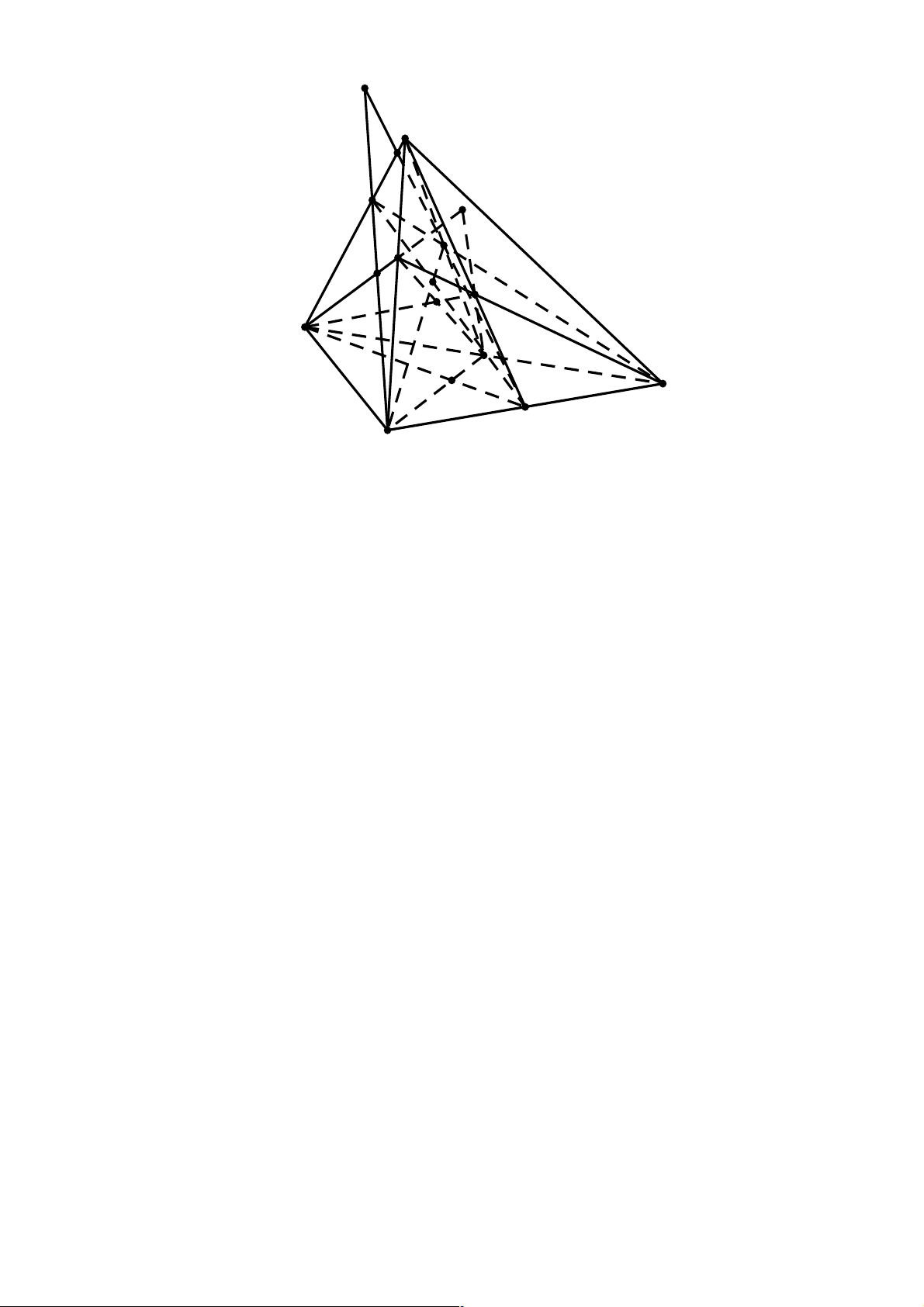
2. Hình hộp: là hình lăng trụ có đáy là hình bình hành. Trong một hình hộp thì
• Các mặt bên là các hình bình hành
• Các đường chéo của hình hộp cắt nhau
tại trung điểm mỗi đường. hình hộp PHẦN 1 ĐỀ BÀI DẠNG 1 LÝ THUYẾT
Câu 1. Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt M, N, P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Câu 2. Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân
biệt từ bốn điểm đã cho ? A. 2. B. 3. C. 4. D. 6. Trang 4
Câu 3. Trong mp (a ), cho bốn điểm A , B , C , D trong đó không có ba điểm nào thẳng hàng. Điểm
S Ïmp(a ). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên? A. 4 . B. 5 . C. 6 . D. 8 .
Câu 4. Cho 2 đường thẳng a,b cắt nhau và không đi qua điểm A . Xác định được nhiều nhất bao nhiêu
mặt phẳng bởi a, b và A ? A. 1 B. 2 C. 3 D. 4.
Câu 5. Cho tứ giác lồi ABCD và điểm S không thuộc mp (ABCD). Có nhiều nhất bao nhiêu mặt
phẳng xác định bởi các điểm A, B, C, D, S ? A. 5 B. 6 C. 7 D. 8
Câu 6. Trong mặt phẳng (a ) cho tứ giác ABCD , điểm E Ï(a ). Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm , A , B C, , D E ? A. 6 . B. 7 . C. 8 . D. 9 .
Câu 7. Cho năm điểm A , B , C , D , E trong đó không có bốn điểm nào ở trên cùng một mặt phẳng.
Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho? A. 10 . B. 12 . C. 8 . D. 14 .
Câu 8. Trong các hình sau : A A A A B D C C B D C B B D C D Hình (I) Hình (II) Hình (III) Hình (IV)
Hình nào có thể là hình biểu diễn của một hình tứ diện ? (Chọn Câu đúng nhất) A. (I). B. (I), (II). C. (I), (II), (III).
D. (I), (II), (III), (IV).
Câu 9. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là : A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh.
Câu 10. Một hình chóp cụt có đáy là một n giác, có số mặt và số cạnh là :
A. n + 2 mặt, 2n cạnh.
B. n + 2 mặt, 3n cạnh.
C. n + 2 mặt, n cạnh.
D. n mặt, 3n cạnh.
Câu 11. Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu? A. 3 . B. 4 . C. 5 . D. 6 . DẠNG 2
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG
Phương pháp : Trang 5
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng (a ) và (b ) cần thực hiện:
• Bước 1: Tìm hai điểm chung A và B của (a ) và (b).
• Bước 2: Đường thẳng A B là giao tuyến cần tìm (AB = (a) « (b) .) Chú ý :
• Để tìm điểm chung của (a )và (b) ta thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai
mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng. b b a a A ÏM Ô d Œ Ô • Khi điểm Ì
fi M Œ a d Ô Ã Ô (a) ( ) Ô Ó
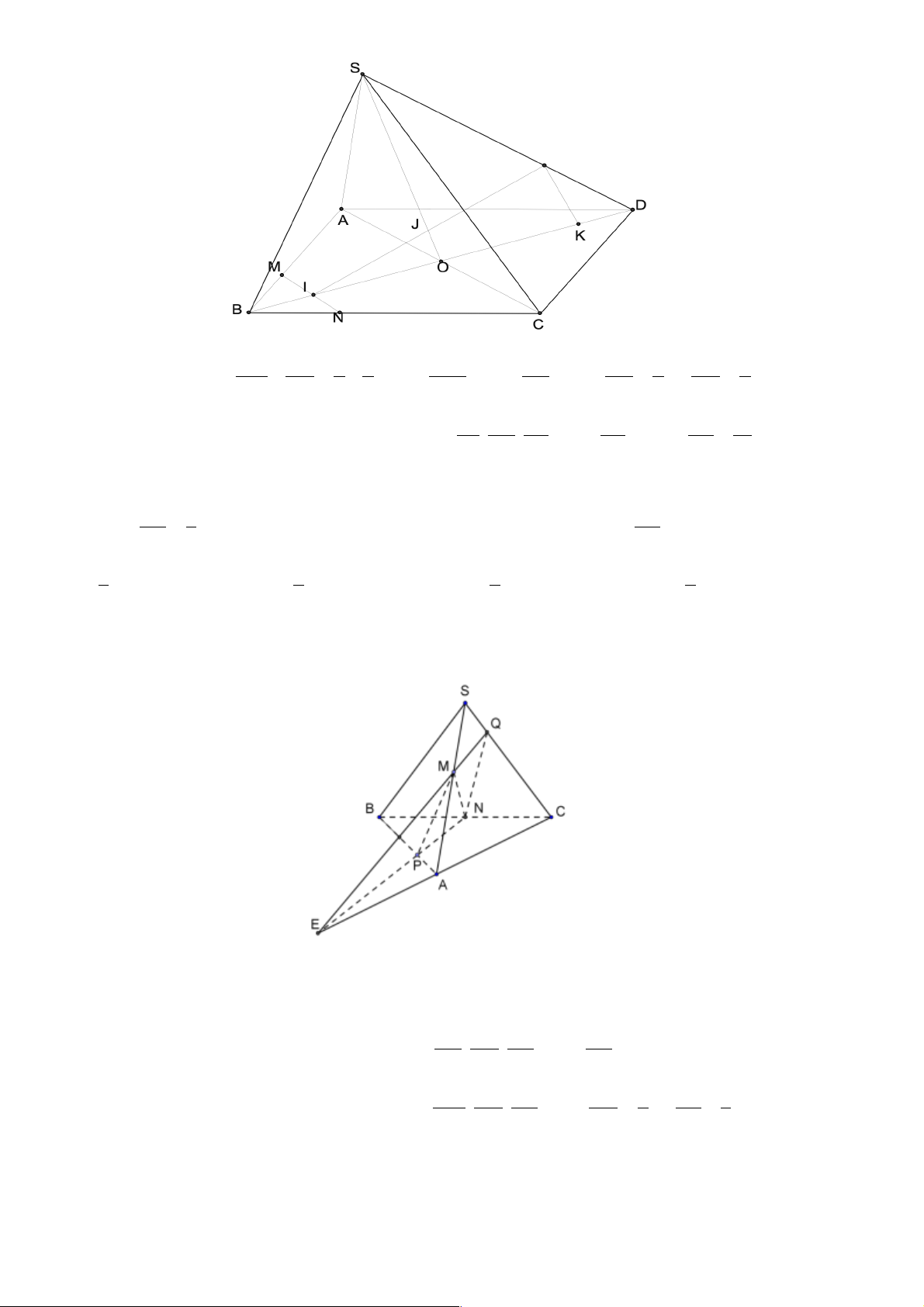
Câu 12. Cho hình chóp S.ABCD có AC Ç BD = M và AB Ç CD = N. Giao tuyến của mặt phẳng
(SAC) và mặt phẳng (SBD) là đường thẳng A. SN. B. SC. C. . SB D. SM .
Câu 13. Cho hình chóp S.ABCD có AC Ç BD = M và AB Ç CD = N. Giao tuyến của mặt phẳng
(SAB) và mặt phẳng (SCD) là đường thẳng A. SN. B. . SA C. MN. D. SM .
Câu 14. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB / /CD). Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO ( Olà giao điểm của AC và BD).
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI ( I là giao điểm của AD và BC ).
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD.
Câu 15. Cho tứ diện ABCD . Gọi O là một điểm bên trong tam giác BCD và M là một điểm trên đoạn
AO . Gọi I, J là hai điểm trên cạnh BC , BD . Giả sử IJ cắt CD tại K , BO cắt IJ tại E và cắt CD tại
H , ME cắt AH tại F . Giao tuyến của hai mặt phẳng (MIJ ) và ( ACD) là đường thẳng: Trang 6 A. KM . B. AK . C. MF . D. KF .
Câu 16. Cho tứ diện ABCD . G là trọng tâm tam giác BCD . Giao tuyến của hai mặt phẳng ( ACD) và (GAB) là:
A. AM , M là trung điểm AB .
B. AN , N là trung điểm CD .
C. AH , H là hình chiếu của B trên CD .
D. AK , K là hình chiếu của C trên BD .
Câu 17. Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng
trung điểm SC . Giao tuyến của hai mặt phẳng ( ABCD) và ( AIJ ) là:
A. AK , K là giao điểm IJ và BC .
B. AH , H là giao điểm IJ và AB .
C. AG , G là giao điểm IJ và AD .
D. AF , F là giao điểm IJ và CD .
Câu 18. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AC và CD . Giao tuyến của hai mặt
phẳng (MBD) và ( ABN ) là: A. MN . B. AM .
C. BG , với G là trọng tâm tam giác ACD .
D. AH , với H là trực tâm tam giác ACD .
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
AD và BC .Giao tuyến của hai mặt phẳng (SMN ) và (SAC) là: A. SD .
B. SO , O là tâm hình bình hành ABCD .
C. SG , G là trung điểm AB .
D. SF , F là trung điểm CD .
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung điểm SA
và SB .Khẳng định nào sau đây là sai?
A. IJCD là hình thang.
B. (SAB)Ç(IBC) = IB.
C. (SBD)Ç(JCD) = JD.
D. (IAC)Ç(JBD) = AO, O là tâm hình bình hành ABCD .
Câu 21. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AD BC Ä
). Gọi M là trung điểm CD.
Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:
A. SI , I là giao điểm AC và BM .
B. SJ , J là giao điểm AM và BD.
C. SO , O là giao điểm AC và BD .
D. SP , P là giao điểm AB và CD .
Câu 22. Cho tứ diện ABCD . G là trọng tâm tam giác BCD , M là trung điểm CD , I là điểm trên đoạn
thẳng AG , BI cắt mặt phẳng ( ACD)tại J . Khẳng định nào sau đây sai?
A. AM = ( ACD)Ç( ABG).
B. A , J , M thẳng hàng.
C. J là trung điểm AM . D
. DJ = ( ACD)Ç(BDJ ). Trang 7
Câu 23. Cho hình chóp S.ABCD có đáy là hình thang ABCD AD / /BC . Gọi I là giao điểm của AB
và DC , M là trung điểm SC . DM cắt mặt phẳng (SAB) tại J . Khẳng định nào sau đây sai?
A. S , I , J thẳng hàng.
B. DM Ì mp(SCI ).
C. JM Ì mp(SAB).
D. SI = (SAB)Ç(SCD).
Câu 24. Cho hình chóp S.ABCD , đáy ABCD là tứ giác có các cặp cạnh đối không song song, điểm M thuộc cạnh SA .
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD) A. SC B. SB
C. SO trong đó O = AC Ç BD D. {S}
b) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (MBD) A. SM B. MB
C. OM trong đó O = AC Ç BD D. SD
c) Tìm giao tuyến của các cặp mặt phẳng: (MBC) và (SAD) A. SM
B. FM trong đó F = BC Ç AD
C. SO trong O = AC Ç BD D. SD
d) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD)
A. SE trong đó E = AB Ç CD
B. FM trong đó F = BC Ç AD
C. SO trong O = AC Ç BD D. SD
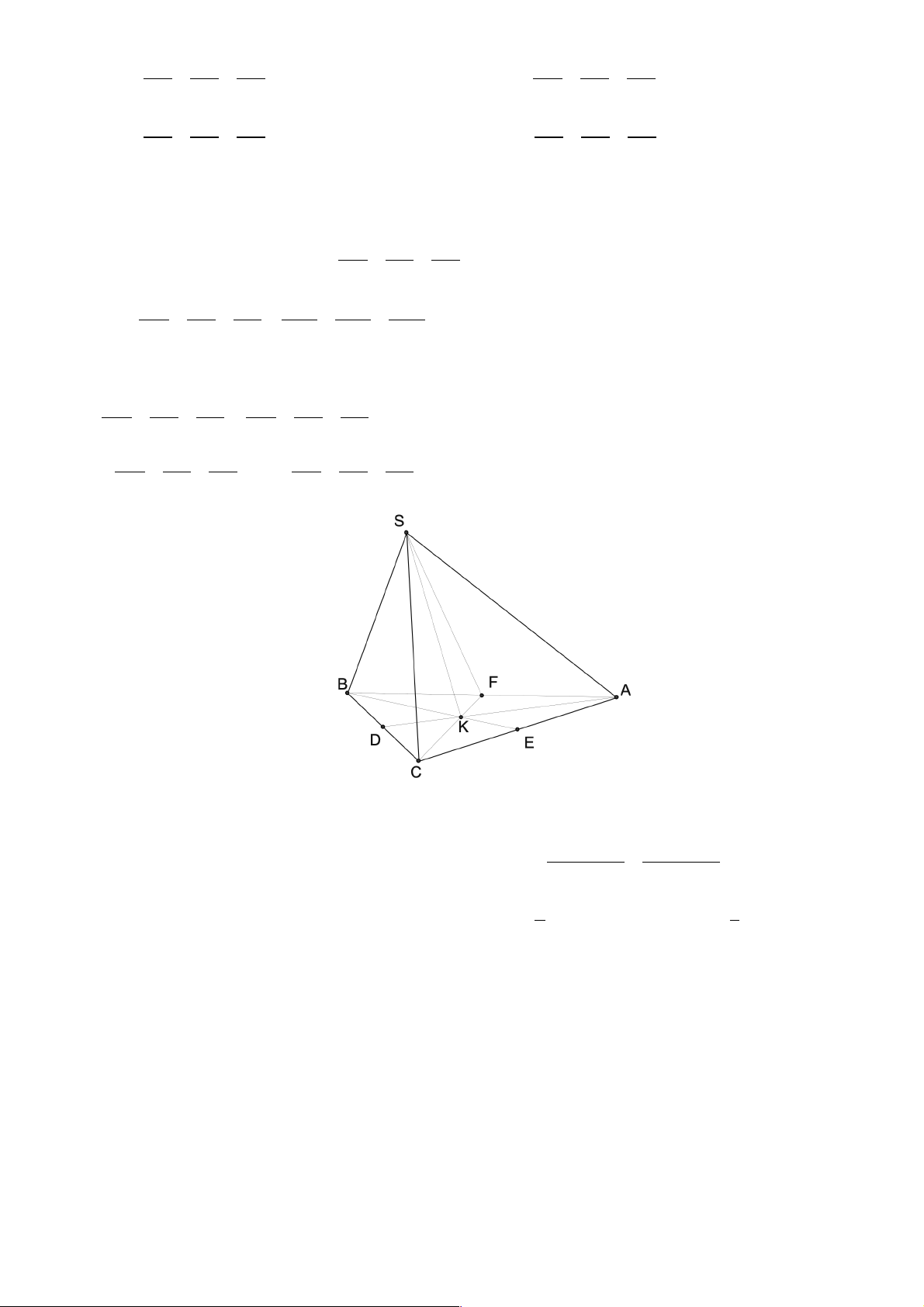
Câu 25. Cho tứ diện ABCD , O là một điểm thuộc miền trong tam giác BCD , M là điểm trên đoạn AO
a) Tìm giao tuyến của mặt phẳng (MCD) với các mặt phẳng ( ABC).
A. PC trong đó P = DC Ç AN , N = DO Ç BC
B. PC trong đó P = DM Ç AN , N = DA Ç BC
C. PC trong đó P = DM Ç AB , N = DO Ç BC
D. PC trong đó P = DM Ç AN , N = DO Ç BC
b) Tìm giao tuyến của mặt phẳng (MCD) với các mặt phẳng ( ABD).
A. DR trong đó R = CM Ç AQ, Q = CA Ç BD
B. DR trong đó R = CB Ç AQ, Q = CO Ç BD
C. DR trong đó R = CM Ç AQ, Q = CO Ç BA
D. DR trong đó R = CM Ç AQ, Q = CO Ç BD
c) Gọi I, J là các điểm tương ứng trên các cạnh BC và BD sao cho IJ không song song với CD . Tìm
giao tuyến của hai mặt phẳng (IJM ) và ( ACD). Trang 8
A. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BE Ç IA, E = BO Ç CD
B. FG trong đó F = IA Ç CD , G = KM Ç AE , K = BA Ç IJ , E = BO Ç CD
C. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BA Ç IJ , E = BO Ç CD
D. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BE Ç IJ , E = BO Ç CD
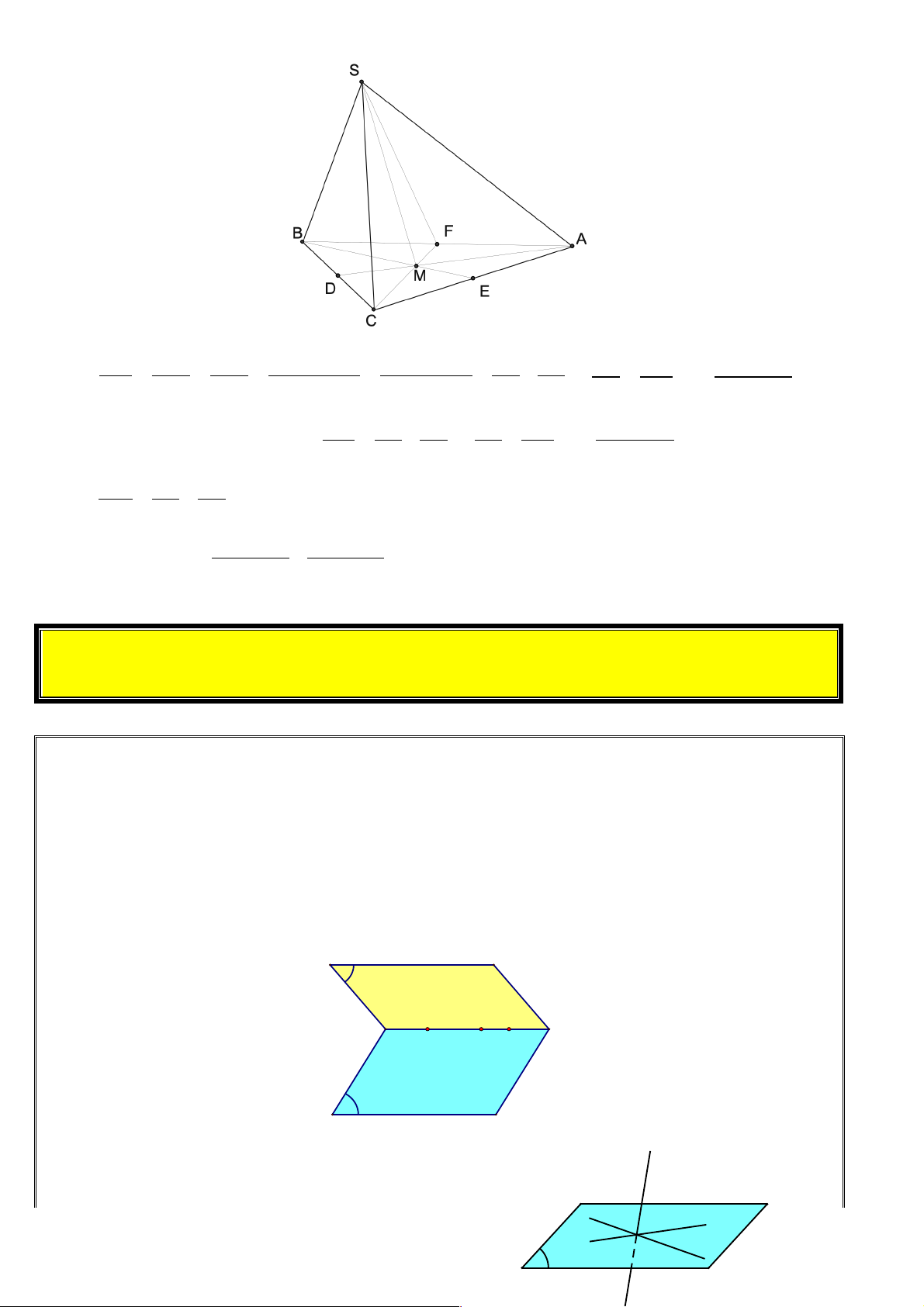
Câu 26. Cho tứ diện SABC có AB = ,
c BC = a, AC = . b ,
AD BE,CF là các đường phân giác trong của
tam giác ABC . Giao tuyến của hai mặt phẳng (SBE) và (SCF ) là: !!" b + c !!"
A. SI trong đó I thuộc AD sao cho AI = ID a !!" b + c !!"
B. SI trong đó I thuộc AD sao cho AI = - ID a !!" a !!"
C. SI trong đó I thuộc AD sao cho AI = ID b + c !!" -a !!"
D. SI trong đó I thuộc AD sao cho AI = ID b + c DẠNG 3
TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG Phương pháp
Cơ sở của phương pháp tìm giao điểm của đường thẳng d và mặt phẳng (a ) là xét hai trường hợp: • Trường hợp 1: (
mp a ) chứa đường thẳng D và D cắt d . ÏÔD Ã ( mp a ) Ô Ì
fi I = d « m ( p a ) ÔD « d = Ô {I } { } Ô Ó Trang 9 d I a • Trường hợp 2: (
mp a ) không chứa đường thẳng nào cắt d .
+ Bước 1: Tìm ( mp b) d
… sao cho (a ) « (b) = D
+ Bước 2: Tìm {I }= d « D fi I = d « (a ). b d I a
Câu 27. Cho bốn điểm ,
A B,C, D không cùng nằm trong một mặt phẳng. Trên AB, ADlần lượt lấy các
điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây: A. (BCD).
B. ( ABD).
C. (CMN ). D. ( ACD).
Câu 28. Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song song với
nhau và M là một điểm trên cạnh SA.
a) Tìm giao điểm của đường thẳng SB với mặt phẳng (MCD).
A. Điểm H, trong đó E = AB Ç CD , H = SA Ç EM
B. Điểm N, trong đó E = AB Ç CD , N = SB Ç EM
C. Điểm F, trong đó E = AB Ç CD , F = SC Ç EM
D. Điểm T, trong đó E = AB Ç CD ,T = SD Ç EM
b) Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD).
A. Điểm H, trong đó I = AC Ç BD , H = MA Ç SI
B. Điểm F, trong đó I = AC Ç BD , F = MD Ç SI
C. Điểm K, trong đó I = AC Ç BD , K = MC Ç SI
D. Điểm V, trong đó I = AC Ç BD , V = MB Ç SI
Câu 29. Cho hình chóp tứ giác S.ABCD , M là một điểm trên cạnh SC , N là trên cạnh BC . Tìm giao
điểm của đường thẳng SD với mặt phẳng ( AMN ).
A. Điểm K, trong đó K = IJ Ç SD , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
B. Điểm H, trong đó H = IJ Ç SA , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD Trang 10
C. Điểm V, trong đó V = IJ Ç SB , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
D. Điểm P, trong đó P = IJ Ç SC , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác ( AB không song song CD ). Gọi M là
trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB,O là giao điểm của AC và BD .
Giả sử đường thẳng d là giao tuyến của (SAB) và (SCD). Nhận xét nào sau đây là sai:
A. d cắt CD .
B. d cắt MN .
C. d cắt AB .
D. d cắt SO .
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC . MA
Gọi I là giao điểm của đường thẳng AM vơí mặt phẳng (SBD). Khi đó tỉ số bằng bao nhiêu: IA 3 4 A. 2 . B. 3 . C. . D. . 2 3
Câu 32. Cho hình chóp S.ABCD , đáy ABCD là hình thang với AD là đáy lớn AD = 2BC , G là trọng KB
tâm tam giác SCD . Mặt phẳng (SAC)cắt cạnh BG tại K . Khi đó, tỷ số bằng: KG 3 1 A. 2 B. C. 1 D. 2 2
Câu 33. Cho tứ diện ABCD có P,Q lần lượt là trung điểm của AB và CD . M là điểm thuộc cạnh AD NB
sao cho MA = 2MD.Gọi N là giao điểm của BC với (MPQ). Tỉ số bằng: NC 1 2 A. B. C. 2 D. 1 2 3
Câu 34. Cho hình chóp S.ABCD , đáy ABCD là hình thang (AD// BC,AD > BC), E là điểm thuộc SF
cạnh SA sao cho SE = 2EA. Mặt phẳng (EBC)cắt cạnh SD tại F. Khi đó, tỷ số bằng: SD 2 1 1 1 A. B. C. D. 3 3 2 4
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N, P lần lượt là SH
trung điểm của AB, AD và SO . Gọi H là giao điểm của SC với (MNP). Tính ? SC 1 1 3 2 A. . B. . C. . D. . 3 4 4 3
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
của AD và CD . Trên đường thẳng DS lấy điểm P sao cho D là trung điểm SP . Gọi R là giao điểm SR
của SB với mặt phẳng (MNP). Tính ? SB 1 1 3 2 A. . B. . C. . D. . 3 4 4 5 Trang 11
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N lần lượt là các BM 2 NC 1 PD 1
điểm nằm trên cạnh AB, AD sao cho = ,
= . Gọi P là điểm trên cạnh SD sao cho = . MA 3 BN 2 PS 5 SJ
J là giao điểm của SO với (MNP). Tính ? SO 10 1 3 5 A. . B. . C. . D. . 11 11 4 2
Câu 38. Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AP 1 SQ AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP).Tính AB 3 SC 1 1 1 2 A. . B. . C. . D. . 3 6 2 3
Câu 39. Cho tứ diện SABC, E, F lần lượt thuộc đoạn AC, .
AB Gọi K là giao điểm của BE và CF . Gọi
D là giao điểm của (SAK ) với BC . Mệnh đề nào sau đây đúng? AK BK CK AK BK CK A. + + ³ 6. B. + + £ 6. KD KE KF KD KE KF AK BK CK AK BK CK C. + + > 6. D. + + < 6. KD KE KF KD KE KF
Câu 40. Cho hình chóp S.ABC , D ,
D M lần lượt là trung điểm của BC, AD . Gọi E là giao điểm của ( MF ME
SBM ) với AC, F là giao điểm của (SCM ) với AB . Tính + ? CM - ME BM - ME 1 1 A. 1. B. 2 . C. D. . 2 3 DẠNG 3
CHỨNG MINH BA ĐIỂM THẲNG HÀNG VÀ BA ĐƯỜNG THẲNG ĐỒNG QUY
1. Chứng minh ba điểm A; B; C thẳng hàng: Phương pháp
+ Bước 1: Chứng minh 3 điểm A, B,C m Œ ( p a ). Trang 12
+ Bước 2: Chứng minh 3 điểm A, B,C m Œ ( p b).
+ Bước 3: Kết luận 3 điểm ,
A B,C thuộc giao tuyến chung của 2 mặt phẳng ( mp a ) và ( mp b) fi ,
A B,C thẳng hàng. b d A B C a
2. Chứng minh 3 đường thẳng d ,d ,d đồng quy: 1 2 3 d3 Phương pháp d
+ Bước 1: Tìm I = d « d . 1 I 1 2 d2
+ Bước 2: Chứng minh d đi qua I . a 3
fi d ,d ,d đồng quy tại I . 1 2 3
3. Chứng minh đường thẳng trong không gian qua một điểm cố định
Phương pháp 1
Cơ sở của phương pháp là: A
Ta cần tìm trên d hai điểm tùy ý A , B và chứng minh hai điểm B I (cố định)
đó thẳng hàng với điểm I cố định có sẵn trong không gian
fi d đi qua điểm I cố định. a d
Phương pháp 2
Cơ sở của phương pháp là:
- Bước 1: Tìm đường thẳng D cố định ở ngoài
mặt phẳng cố định (a ) chứa d di động. I (cố định)
- Bước 2: Tìm giao điểm I của D và d d a
fi I là điểm cố định mà d đi qua.
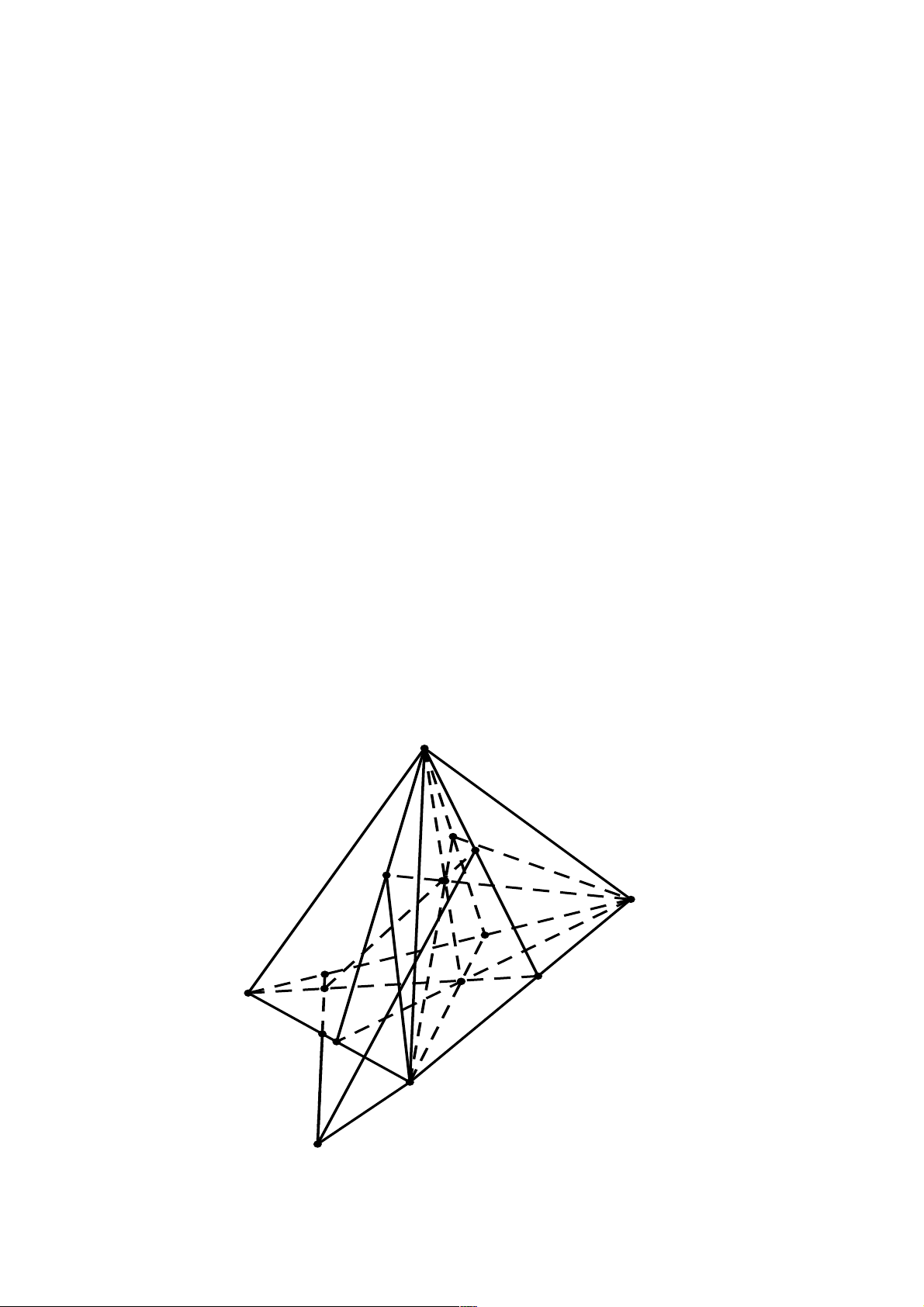
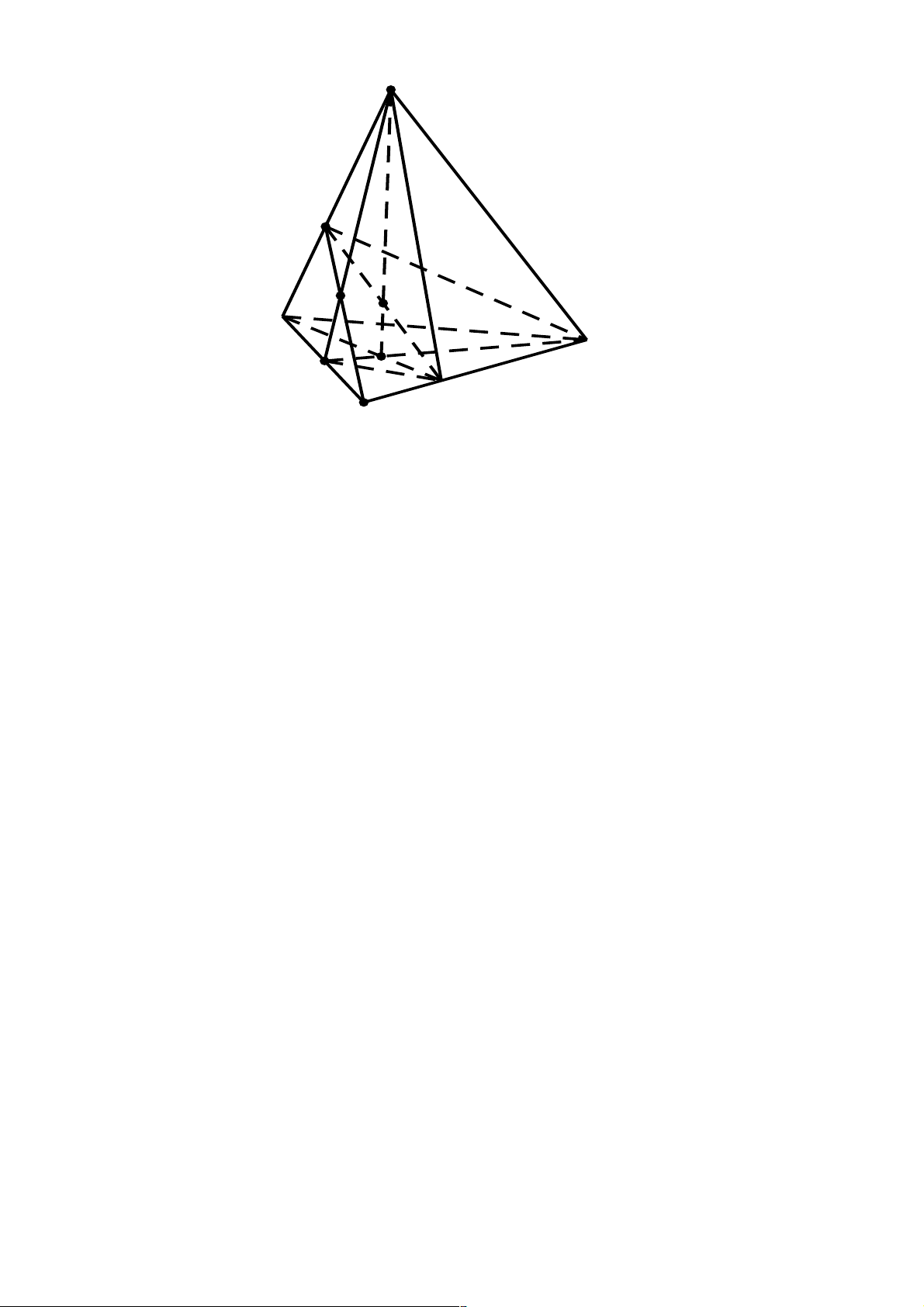
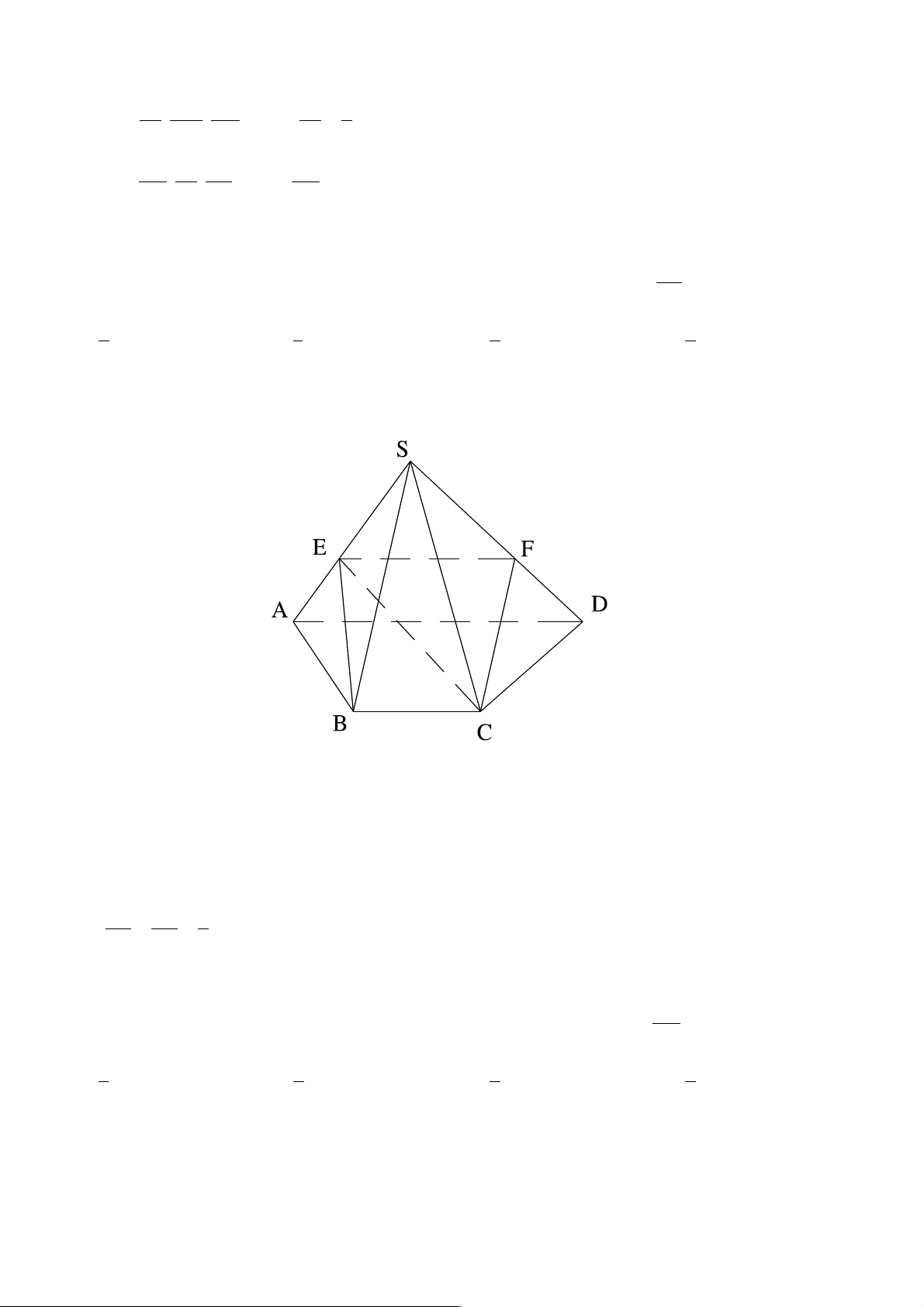
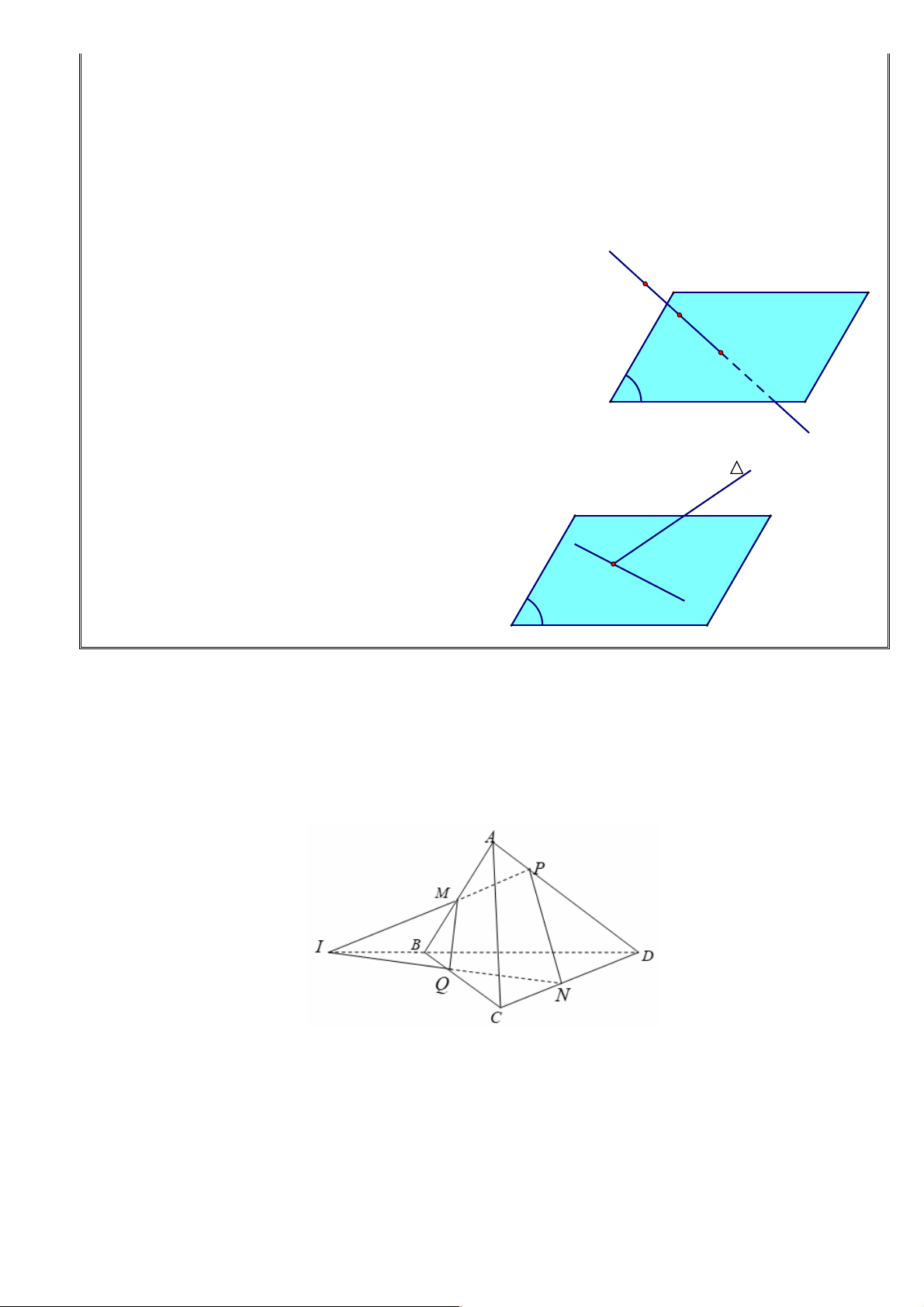
Câu 41. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AB và CD . Mặt phẳng (a ) qua MN cắt
AD và BC lần lượt tại P , Q . Biết MP cắt NQ tại I . Ba điểm nào sau đây thẳng hàng?
A. I , A , C .
B. I , B , D .
C. I , A , B .
D. I , C , D .
Câu 42. Cho tứ diện SABC . Trên ,
SA SB và SC lấy các điểm D, E và F sao cho DE cắt AB tại I ,
EF cắt BC tại J , FD cắt CA tại K .Khẳng định nào sau đây đúng?
A. Ba điểm B, J , K thẳng hàng Trang 13
B. Ba điểm I, J , K thẳng hàng
C. Ba điểm I, J , K không thẳng hàng
D. Ba điểm I, J,C thẳng hàng
Câu 43. Cho tứ diện SABC có D, E lần lượt là trung điểm của AC, BC và G là trọng tâm của tam
giác ABC . Mặt phẳng (a ) đi qua AC cắt SE, SB lần lượt tại M , N . Một mặt phẳng (b ) đi qua BC cắt ,
SD SA tương ứng tại P và Q .
a) Gọi I = AM Ç DN, J = BP Ç EQ . Khẳng định nào sau đây là đúng?
A. Bốn điểm S, I, J ,G thẳng hàng.
B. Bốn điểm S, I, J ,G không thẳng hàng.
C. Ba điểm P, I, J thẳng hàng.
D. Bốn điểm I, J,Q thẳng hàng.
b) Giả sử K = AN Ç DM , L = BQ Ç EP. Khằng định nào sau đây là đúng?
A. Ba điểm S, K, L thẳng hàng.
B. Ba điểm S, K, L không thẳng hàng
C. Ba điểm B, K, L thẳng hàng
D. Ba điểm C, K, L thẳng hàng
Câu 44. Cho hình chóp tứ giác S.ABCD , gọi O là giao điểm của hai đường chéo AC và BD . Một mặt
phẳng (a ) cắt các cạnh bên ,
SA SB, SC, SD tưng ứng tại các điểm M , N, ,
P Q. Khẳng định nào đúng?
A. Các đường thẳng , MP N ,
Q SO đồng qui.
B. Các đường thẳng , MP N ,
Q SO chéo nhau.
C. Các đường thẳng , MP N ,
Q SO song song.
D. Các đường thẳng , MP N , Q SO trùng nhau.
Câu 45. Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến là đường thẳng a . Trong (P) lấy hai điểm ,
A B nhưng không thuộc a và S là một điểm không thuộc (P). Các đường thẳng , SA SB cắt (Q)
tương ứng tại các điểm C, D . Gọi E là giao điểm của AB và a .Khẳng định nào đúng?
A. AB,CD và a đồng qui.
B. AB,CD và a chéo nhau.
C. AB,CD và a song song nhau.
D. AB,CD và a trùng nhau
Câu 46. Cho hình bình hành ABCD , S là điểm không thuộc ( ABCD),M và N lần lượt là trung điểm
của đoạn AB và SC. Xác định các giao điểm I, J của AN và MN với (SBD), từ đó tìm khẳng định đúng
trong các khẳng định sau:
A. Ba điểmJ, I, M thẳng hàng.
B. Ba điểmJ, I, N thẳng hàng.
C. Ba điểmJ, I, D thẳng hàng.
D. Ba điểmJ, I, B thẳng hàng.
Câu 47. Cho tứ giác ABCD và S Î( ABCD). Gọi I, J là hai điểm trên AD và SB, AD cắt BC tại O và
OJ cắt SCtại M. Xác định các giao điểm K, L của IJ và DJ với (SAC), từ đó tìm khẳng định đúng trong các khẳng định sau: A. Ba điểm ,
A K, Lthẳng hàng. B. Ba điểm ,
A L, M thẳng hàng. C. Bốn điểm , A K, ,
L M thẳng hàng. D. Bốn điểm ,
A K, L, J thẳng hàng. Trang 14
Câu 48. Cho tứ diện SABC .Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho
LMkhông song song với AB, LN không song song với SC. Gọi LK giao tuyến của mp (LMN )và
(ABC). Xác định I, J lần lượt là giao điểm của BC và SC với (LMN). Khẳng định nào sau đây đúng:
A. Ba điểm L, I, J thẳng hàng.
B. Ba điểm L, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng.
D. Ba điểm M, I,K thẳng hàng.
Câu 49. Cho tứ giác ABCD và S không thuộc mặt phẳng ( ABCD). Gọi M, N là hai điểm trên BC và .
SD Xác định I, J lần lượt là giao điểm của BN và MN với (SAC). Từ đó tìm bộ 3 điểm thẳng hàng trong những điểm sau:
A. Ba điểm A, I, Jthẳng hàng.
B. Ba điểm K, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng.
D. Ba điểm C, I,Jthẳng hàng.
Câu 50. Cho tứ diện ABCD . E là điểm thuộc đoạn AB sao cho EA = 2 .
EB F,G là các điểm thuộc !!!" !!!" !!!" !!!"
đường thẳng BC sao cho FC = 5FB,GC = 5 - G .
B H , I là các điểm thuộc đường thẳng CD sao cho !!!" !!!" !!" !!" HC = 5 - HD, ID = 5
- IC, J thuộc tia đối của tia DA sao cho D là trung điểm của AJ . Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Bốn điểm E, F, H, J đồng phẳng
B. Bốn điểm E, F, I, J đồng phẳng.
C. Bốn điểm E,G, H, I đồng phẳng.
D. Bốn điểm E,G, I, J đồng phẳng.
Câu 51. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (BC / /AD).Mặt phẳng (P) di động
chứa đường thẳng AB và cắt các đoạn SC, SD lần lượt tại E, F . Mặt phẳng (Q) di động chứa đường thẳng CD và cắt ,
SA SB lần lượt tại G, H.I là giao điểm của AE, BF; J là giao điểm của CG, DH . Xét các mệnh đề sau: ( )
1 Đường thẳng EF luôn đi qua một điểm cố định.
(2)Đường thẳng GH luôn đi qua một điểm cố định.
(3)Đường thẳng IJ luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng? A. 0 . B. 1. C. 2 . D. 3 .
Câu 52. Cho tứ diện ABCD và các điểm M , N, ,
P Q lần lượt thuộc các cạnh AB, BC,CD, DA sao cho
MN không song song với AC . M , N, ,
P Qđồng phẳng khi : AM BN CP DQ BM CN CP DQ A. . . . = 1 B. . . . = 1 BM CN DP AQ AM BN DP AQ BM CN DP DQ AM BN DP AQ C. . . . = 1 D. . . . = . 1 AM BN CP AQ BM CN CP DQ Trang 15
Câu 53. Cho hình chóp S.AB .
CD Giả sử AD và BC cắt nhau tại H. Gọi O là giao điểm của AC và BD, E
và F lần lượt là trung điểm của SA và .
SB Điểm M di động trên cạnh SC. Gọi N là giao điểm của SD và
mp(EFM). Tìm tập hợp giao điểm J của EN và FM.
A. Tập hợp J là đoạn thẳng SJ1 với J1 = CF Ç SH.
B. Tập hợp J là đoạn thẳng SJ1 với J1 = DE Ç SH.
C. Tập hợp J là đoạn thẳng SH.
D. Tập hợp J là đường thẳng SH.
Câu 54. Cho hình chóp S.ABCD, trong đó AD không song song với BC. Gọi O là giao điểm của AC và
BD, E là giao điểm của AD và BC. Điểm M di động trên cạnh SB, EM cắt SC tại N. Tập hợp giao điểm I của AN và DM.
A. Tập hợp giao điểm I là đoạn thẳng SO.
B. Tập hợp giao điểm I là đường thẳng SO.
C. Tập hợp giao điểm I là đoạn thẳng SO trừ 2 điểm S và O.
D. Tập hợp giao điểm I là đoạn thẳng SE.
Câu 55. Cho tứ diện ABC .
D Một mặt phẳng (P) di động luôn song song với AB và CD cắt các cạnh AC, , AD ,
BD BC tại M , N, E, F . Tìm tập hợp tâm I của hình bình hành MNEF.
A. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và CD (trừ 2 điểm P và Q).
B. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và . CD
C. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC (trừ 2 điểm P và Q).
D. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC. DẠNG 4
XÁC ĐỊNH THIẾT DIỆN CỦA MỘT MẶT PHẲNG VỚI HÌNH CHÓP Trang 16
Để xác định thiết diện của hình chóp S.A A ...A cắt bởi mặt phẳng (a ), ta tìm giao điểm của mặt phẳng 1 2 n
(a) với các đường thẳng chứa các cạnh của hình chóp. Thiết diện là đa giác có đỉnh là các giao điểm
của (a ) với hình chóp ( và mỗi cạnh của thiết diện phải là một đoạn giao tuyến với một mặt của hình chóp)
Câu 56. Cho ABCD là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp S.ABCD ? A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác.
Câu 57. Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng (a ) tuỳ ý với hình chóp không thể là: A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác.
Câu 58. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và điểm M ở trên cạnh SB . Mặt
phẳng ( ADM ) cắt hình chóp theo thiết diện là A. tam giác. B. hình thang. C. hình bình hành. D. hình chữ nhật.
Câu 59. Cho hình chóp tứ giác S.ABCD , có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD .
a) Thiết diện của hình chóp cắt bởi mặt phẳng (PAB)là hình gì? A. Tam giác B. Tứ giác C. Hình thang
D. Hình bình hành
b) Gọi M , N lần lượt là trung điểm của các cạnh AB, BC. Thiết diện của hình chóp cắt bởi (MNP)là hình gì? A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành
Câu 60. Cho hình chóp S.ABCD . Điểm C¢ nằm trên cạnh SC . Thiết diện của hình chóp với mp
(ABC¢) là một đa giác có bao nhiêu cạnh? A. 3 . B. 4 . C. 5 . D. 6 .
Câu 61. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA . Thiết diện
của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là:
A. Tam giác IBC.
B. Hình thang IJCB ( J là trung điểm SD ).
C. Hình thang IGBC ( G là trung điểm SB ).
D. Tứ giác IBCD .
Câu 62. Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành tâm O . Gọi M , N, P là ba điểm
trên các cạnh AD,CD, SO. Thiết diện của hình chóp với mặt phẳng (MNP)là hình gì? A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành Trang 17
Câu 63. Cho tứ diện ABCD , M và N lần lượt là trung điểm AB và AC . Mặt phẳng (a ) qua MN cắt
tứ diện ABCD theo thiết diện là đa giác (T ). Khẳng định nào sau đây đúng?
A. (T ) là hình chữ nhật. B. (T ) là tam giác.
C. (T ) là hình thoi.
D. (T ) là tam giác hoặc hình thang hoặc hình bình hành.
Câu 64. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N,Q lần lượt là trung điểm của các cạnh , AB ,
AD SC. Thiết diện của hình chóp với mặt phẳng (MNQ) là đa giác có bao nhiêu cạnh ? A. 3. B. 4. C. 5. D. 6.
Câu 65. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M, Nlần lượt là 2 điểm thuộc
cạnh SB,SD sao cho SM = MB,SN = 2ND . Mặt phẳng (AMN)cắt SC tại P thỏa mãn SP = kSC . Số k bằng? 2 3 3 2 A. B. C. D. 5 5 2 3
Câu 66. Cho tứ diện đều ABCD có các cạnh bằng a . Gọi E là trung điểm AB , F là điểm thuộc cạnh
BC sao cho BF = 2FC,G là điểm thuộc cạnh CD sao cho CG = 2GD . Tính độ dài đoạn giao tuyến của
mặt phẳng (EFG) với mặt phẳng ( ACD) của hình chóp ABCD theo a . 19 a 141 a 34 +15 3 a 34 -15 3 A. a. B. . C. . D. . 15 30 15 15
Câu 67. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho SD = 3SE . F là trọng tâm tam giác SAB,G là điểm thay đổi trên cạnh BC. Thiết diện cắt bởi mặt phẳng (EFG) là: A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác.
Câu 68. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là một điểm thuộc mặt
bên (SCD). F, G lần lượt là các điểm thuộc cạnh AB và .
SB Thiết diện của hình chóp S.ABCD cắt bởi
mặt phẳng (EFG) có thể là:
A. Tam giác, tứ giác.
B. Tứ giác, ngũ giác.
C. Tam giác, ngũ giác. D. Ngũ giác. !!!" !!!"
Câu 69. Cho hình chóp S.ABCD, E là trung điểm của SB, F thuộc SC sao cho 3SF = 2SC, G là một
điểm thuộc miền trong tam giác SAD . Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:
A. Tam giác, tứ giác.
B. Tứ giác, ngũ giác.
C. Tam giác, ngũ giác. D. Ngũ giác.
Câu 70. Cho tứ diện ABCD có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho CE = a, DF = a . Gọi M là trung điểm của đoạn .
AB Diện tích S thiết diện của tứ diện ABCD cắt
bởi mặt phẳng (MEF ) là: Trang 18 2 a 33 2 a 2 a 2 a 33 A. S = . B. S = . C. S = . D. S = . 18 3 6 9
Câu 71. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (a ) cắt các cạnh bên ,
SA SB, SC, SD tương ứng tại các điểm E, F, G, H . Gọi I = AC Ç BD, J = EG Ç SI . Mệnh đề nào sau đây đúng? SA SC SB SD SA SC SI A. + = + . B. + ³ 2 . SE SG SF SH SE SG SJ SA SC SB SD SB SD SI C. + > + . D. + ³ 2 . SE SG SF SH SF SH SJ
Câu 72. Cho tứ diện ABCD có M , N lần lượt là trung điểm của AB,CD và P là điểm thuộc cạnh
BC ( P không là trung điểm BC ). Gọi Q là giao điểm của (MNP) với AD, I là giao điểm của MN
với PQ. Mệnh đề nào sau đây đúng? A. S = 2S . B. S = 2S . C. S = 4S D. S = 4S . MNPQ MPN MNPQ MPQ MNPQ MPI MNPQ PIN
Câu 73. *Cho hình chóp SA A ...A với đáy là đa giác lồi A A ...A n ³ 3,nΕ . 1 2 n ( ) Trên tia đối của tia 1 2 n
A S lấy điểm B , B ,...B là các điểm nằm trên cạnh SA , SA . Thiết diện của hình chóp cắt bởi mặt 1 1 2 n 2 n phẳng (B B B 1 2 n ) là:
A. Đa giác n - 2 cạnh.
B. Đa giác n -1 cạnh.
C. Đa giác n cạnh.
D. Đa giác n +1 cạnh. Trang 19 PHẦN 2 HƯỚNG DẪN GIẢI CHỦ ĐỀ 1
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
I. Khái niệm mở đầu 1. Mặt phẳng
+ Mặt bàn, mặt bảng, mặt hồ nước yên lặng . . . Cho ta hình ảnh của một phần của mặt phẳng.
+ Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng
vào một góc của hình biểu diễn. P
+ Để kí hiệu mặt phẳng, ta thường dùng chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ( ).
+ mặt phẳng (P ), mặt phẳng ( Q ), mặt phẳng (a), mặt phẳng (b) hoặc viết tắt là mp( P ), mp( Q ),
mp (a) , mp ( b) , hoặc ( P ) , ( Q ) , (a) , ( b),
2. Điểm thuộc mặt phẳng
Cho điểm A và mặt phẳng (P).
+ Điểm A thuộc mặt phẳng (P) ta nói A nằm trên (P) hay (P) chứa A, hay (P) đi qua A và kí hiệu A Î ( P) . A P
+ Điểm A không thuộc mặt phẳng (P) ta nói điểm A nằm ngoài (P) hay (P) không chứa A và kí hiệu A Ï ( P) . A P Trang 20
3. Hình biểu diễn của một hình không gian
Để vẽ hình biểu diễn của một hình trong không gian, ta dựa vào những qui tắc sau :
+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
+ Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, hai đường thẳng
cắt nhau là hai đường thẳng cắt nhau.
+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
+ Dùng nét vẽ liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.
II. CÁC TÍNH CHẤT THỪA NHẬN
1. Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
2. Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. A B C
3. Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó.
* Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P ) thì ta nói đường thẳng d nằm trong mặt
phẳng (P) . Hay (P) chứa d và kí hiệu d Ì (P) hay (P) É d
4. Tính chất 4: Tồn tại bốn điểm không cùng thuộc một mặt phẳng
Nếu có nhiều điểm cùng thuộc một mp thì ta nói những điểm đó đồng phẳng .
5. Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
* Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua điểm chung ấy.
* Đường thẳng chung d của hai mặt phẳng phân biệt ( P ) và ( Q ) được gọi là giao tuyến của ( P) và (Q) kí hiệu d = ( p) Ç ( Q )
6. Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng. Trang 21
III. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG
Có 3 cách xác định mặt phẳng
+ Qua 3 điểm không thẳng hàng xác định duy nhất một mặt phẳng. A B C
+ Qua một điểm và một đường thẳng không chứa điểm đó ta xác định duy nhất một mặt phẳng. A d Kí hiệu mp(A,d) hay (A,d)
+ Hai đường thẳng cắt nhau xác định duy nhất một mặt phẳng. a
Kí hiệu mp (a, b) hay (a, b) b
IV. HÌNH CHÓP VÀ HÌNH TỨ DIỆN 1. Hình chóp:
+ Hình gồm miền đa giác A1A2A3. . .An. Lấy điểm S nằm ngoài (a) . lần lượt nối S với các đỉnh
A1, A2, … An ta được n tam gíác SA1A2 , SA2A3 . . . SAnA1. Hình gồm đa giác A1A2A3. . .An và n tam
giác SA1A2 , SA2A3 . . . SAnA gọi là hình chóp, kí hiệu là S. A1A2A3. . .An. ta gọi S là đỉnh và đa giác
A1A2A3. . .An là mặt đáy. Các tam giác SA1A2 , SA2A3 . . . SAnA gọi là các mặt bên. Các đoạn SA1, SA2
. . SAn là các cạnh bên., các cạnh của đa giác đáy gọi là cạnh đáy của hình chóp. 2. Hình tứ diện
+ Một hình chóp có đáy là tam giác gọi là tứ diện.
+ Tứ diện có các mặt là tam giác đều gọi là tứ diện đều. Trang 22 V. HÌNH LĂNG TRỤ
1. Hình lăng trụ: Hình hợp bởi các hình bình hành A1A2A'2A'1, A2A3A'3A'2,...,AnA1A'1A'2 và hai đa
giác A1A2...An, A'1A'2...A'n gọi là hình lăng trụ hoặc lăng trụ, và ký hiệu là A1A2...An.A'1A'2...A'n.
Trong một hình lăng trụ thì
• 2 mặt đáy là đa giác song song và bằng nhau.
• các cạnh bên song song và bằng nhau
• các mặt bên là hình bình hành
hình lăng trụ tam giác
2. Hình hộp: là hình lăng trụ có đáy là hình bình hành. Trong một hình hộp thì
• Các mặt bên là các hình bình hành
• Các đường chéo của hình hộp cắt nhau
tại trung điểm mỗi đường. hình hộp Trang 23 DẠNG 1 LÝ THUYẾT
Câu 1. Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt M, N, P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng. Lời giải Chọn B.
Hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó, chúng có vô số đường thẳng chung Þ B sai.
Câu 2. Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân
biệt từ bốn điểm đã cho ? A. 2. B. 3. C. 4. D. 6. Lời giải Chọn C.
Do bốn điểm không đồng phẳng nên không tồn tại bộ ba điểm thẳng hàng trong số bốn điểm đó. Cứ ba
điểm không thẳng hàng xác định một mặt phẳng nên số mặt phẳng phân biệt có thể lập được từ bốn điểm đã cho là 3 C = 4. 4
Câu 3. Trong mp (a ), cho bốn điểm A , B , C , D trong đó không có ba điểm nào thẳng hàng. Điểm
S Ïmp(a ). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên? A. 4 . B. 5 . C. 6 . D. 8 . Lời giải Chọn C.
Điểm S cùng với hai trong số bốn điểm A , B , C , D tạo thành một mặt phẳng, từ bốn điểm ta có 6
cách chọn ra hai điểm, nên có tất cả 6 mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên.
Câu 4. Cho 2 đường thẳng a,b cắt nhau và không đi qua điểm A . Xác định được nhiều nhất bao nhiêu
mặt phẳng bởi a, b và A ? A. 1 B. 2 C. 3 D. 4. Lời giải Chọn B. Có 3 mặt phẳng gồm ( , a b),( , A a),( , B b). Trang 24
Câu 5. Cho tứ giác lồi ABCD và điểm S không thuộc mp (ABCD). Có nhiều nhất bao nhiêu mặt
phẳng xác định bởi các điểm A, B, C, D, S ? A. 5 B. 6 C. 7 D. 8 Lời giải Chọn A. Có 2
C +1 = 7 mặt phẳng. 4
Câu 6. Trong mặt phẳng (a ) cho tứ giác ABCD , điểm E Ï(a ). Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm , A , B C, , D E ? A. 6 . B. 7 . C. 8 . D. 9 . Lời giải Chọn B.
Điểm E và 2 điểm bất kì trong 4 điểm ,
A B,C, D tạo thành 6 mặt phẳng, bốn điểm ,
A B,C, D tạo thành 1 mặt phẳng.
Vậy có tất cả 7 mặt phẳng.
Câu 7. Cho năm điểm A , B , C , D , E trong đó không có bốn điểm nào ở trên cùng một mặt phẳng.
Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho? A. 10 . B. 12 . C. 8 . D. 14 . Lời giải Chọn A.
Cứ chọn ra ba điểm trong số năm điểm A , B , C , D , E ta sẽ có một mặt phẳng. Từ năm điểm ta có 10
cách chọn ra ba điểm bất kỳ trong số năm điểm đã cho, nên có 10 phẳng tạo bởi ba trong số năm điểm đã cho.
Câu 8. Trong các hình sau : A A A A B D C C B D C B B D C D Hình (I) Hình (II) Hình (III) Hình (IV)
Hình nào có thể là hình biểu diễn của một hình tứ diện ? (Chọn Câu đúng nhất) A. (I). B. (I), (II). C. (I), (II), (III).
D. (I), (II), (III), (IV). Lời giải Chọn B.
Hình (III) sai vì đó là hình phẳng.
Câu 9. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là : A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh. Lời giải Trang 25 Chọn C.
Hình chóp ngũ giác có 5 mặt bên + 1 mặt đáy. 5 cạnh bên và 5 cạnh đáy.
Câu 10. Một hình chóp cụt có đáy là một n giác, có số mặt và số cạnh là :
A. n + 2 mặt, 2n cạnh.
B. n + 2 mặt, 3n cạnh.
C. n + 2 mặt, n cạnh.
D. n mặt, 3n cạnh. Lời giải Chọn A.
Lấy ví dụ hình chóp cụt tam giác ( n = 3) có 5 mặt và 9 cạnh Þ đáp ánB.
Câu 11. Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn D.
Hình tứ diện là hình chóp có số cạnh ít nhất. Trang 26 DẠNG 2
TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG
Phương pháp :
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng (a ) và (b ) cần thực hiện:
• Bước 1: Tìm hai điểm chung A và B của (a ) và (b ).
• Bước 2: Đường thẳng A B là giao tuyến cần tìm (AB = (a) « (b) .) Chú ý :
• Để tìm điểm chung của (a )và (b ) ta thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai
mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng. b b a a A ÏM Ô d Œ Ô • Khi điểm Ì
fi M Œ a d Ô Ã Ô (a) ( ) Ô Ó
Câu 12. Cho hình chóp S.ABCD có AC Ç BD = M và AB Ç CD = N. Giao tuyến của mặt phẳng
(SAC) và mặt phẳng (SBD) là đường thẳng A. SN. B. SC. C. . SB D. SM . Lời giải Chọn D.
Giao tuyến của mặt phẳng (SAC) và mặt phẳng (SBD) là đường thẳng SM. Trang 27
Câu 13. Cho hình chóp S.ABCD có AC Ç BD = M và AB Ç CD = N. Giao tuyến của mặt phẳng
(SAB) và mặt phẳng (SCD) là đường thẳng A. SN. B. . SA C. MN. D. SM . Lời giải Chọn A.
Câu 14. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB / /CD). Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO ( Olà giao điểm của AC và BD).
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI ( I là giao điểm của AD và BC ).
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD. Lời giải Chọn D.
Hình chóp S.ABCD có 4 mặt bên (SAB), (SBC), (SCD), (SAD )nên A đúng.
S , O là hai điểm chung của (SAC) và (SBD )nên B đúng. Trang 28
S , I là hai điểm chung của (SAD )và (SBC )nên C đúng.
Giao tuyến của (SAB) và (SAD) là SA, rõ ràng SA không thể là đường trung bình của hình thang ABCD .
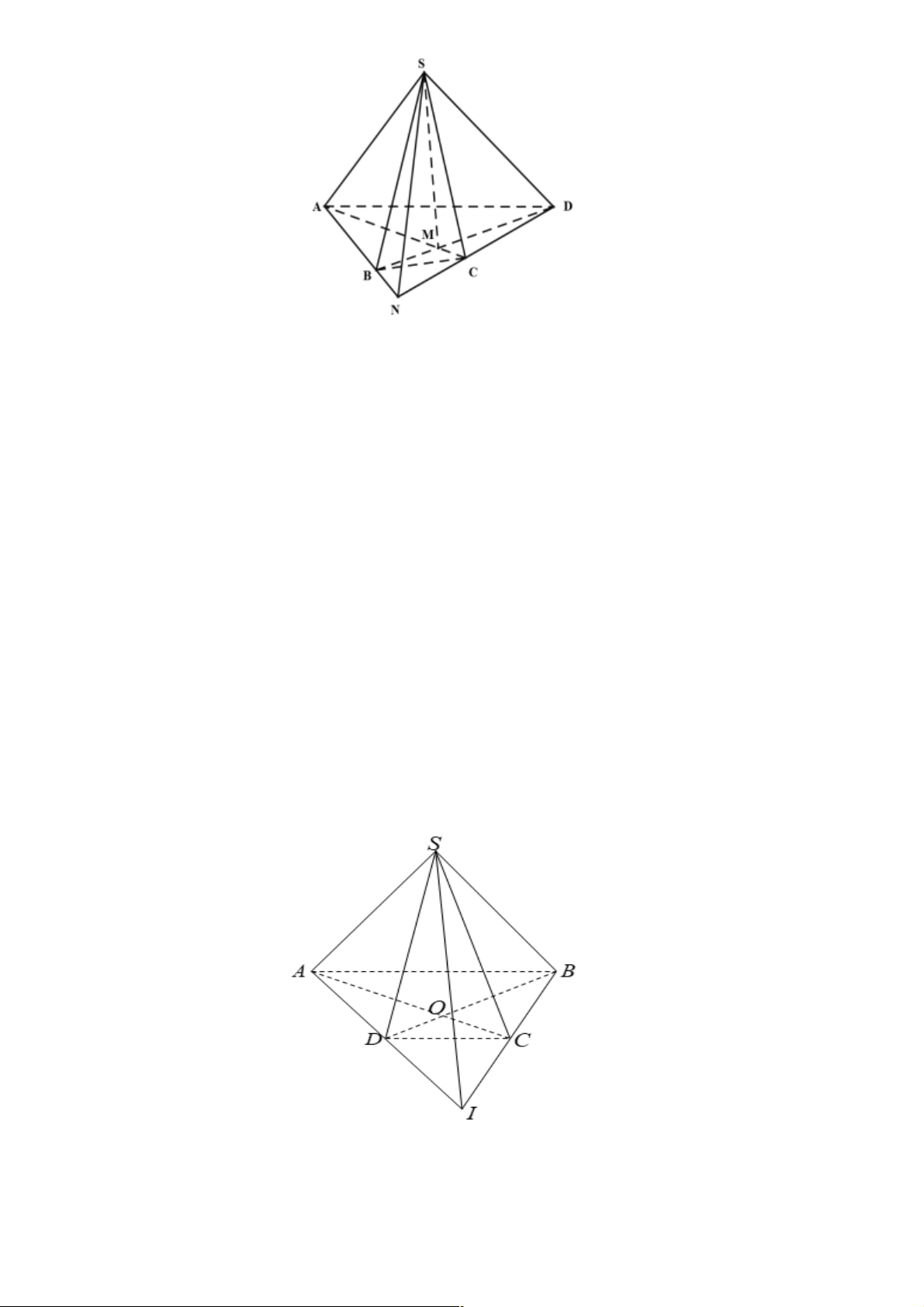
Câu 15. Cho tứ diện ABCD . Gọi O là một điểm bên trong tam giác BCD và M là một điểm trên đoạn
AO . Gọi I, J là hai điểm trên cạnh BC , BD . Giả sử IJ cắt CD tại K , BO cắt IJ tại E và cắt CD tại
H , ME cắt AH tại F . Giao tuyến của hai mặt phẳng (MIJ ) và ( ACD) là đường thẳng: A. KM . B. AK . C. MF . D. KF . Lời giải Chọn D.
Do K là giao điểm của IJ và CD nên K Î(MIJ )!( ACD) (1)
Ta có F là giao điểm của ME và AH
Mà AH Ì ( ACD), ME Ì (MIJ ) nên
F Î(MIJ )!( ACD) (2)
Từ (1) và (2) có (MIJ )!( ACD) = KF
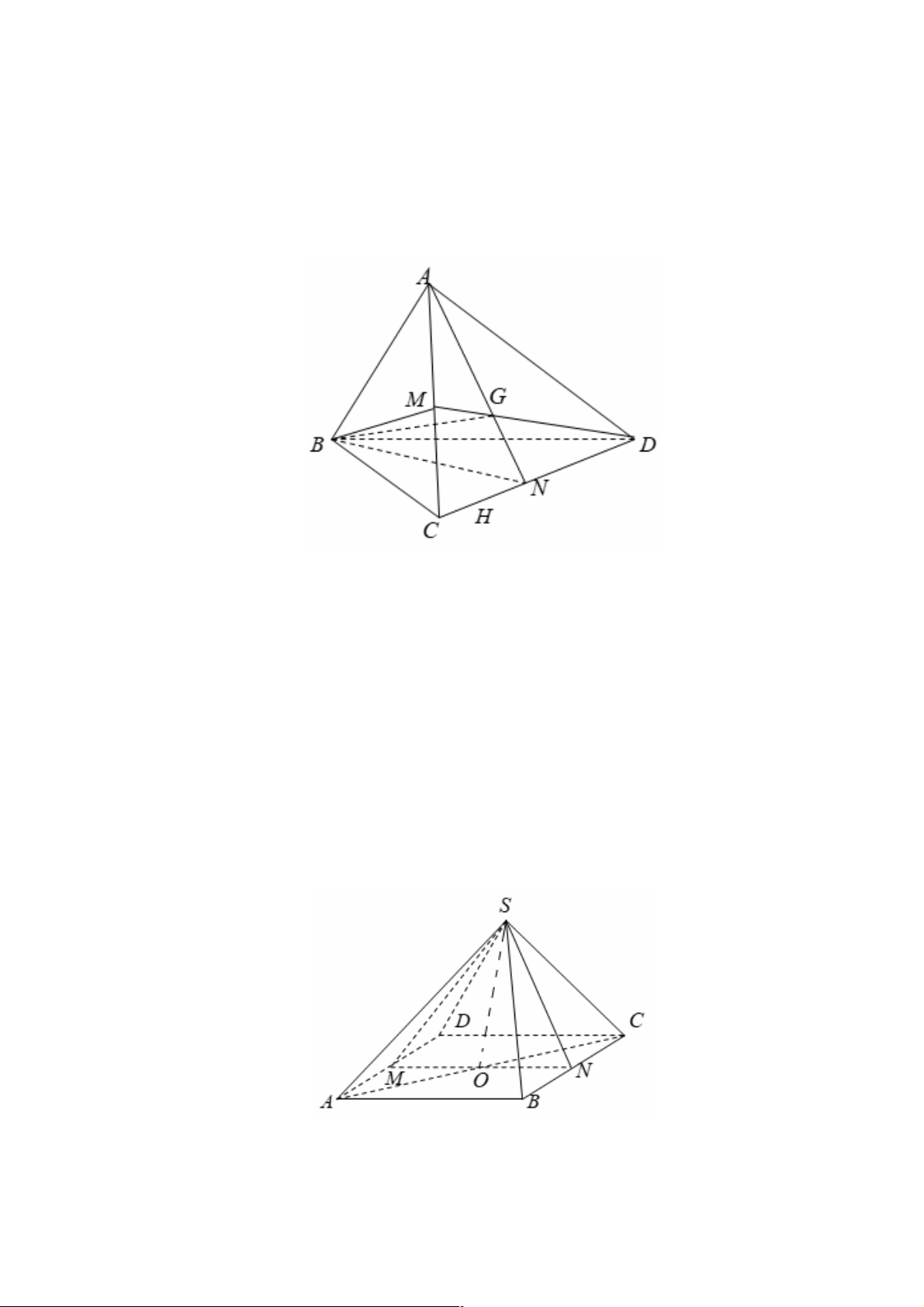
Câu 16. Cho tứ diện ABCD . G là trọng tâm tam giác BCD . Giao tuyến của hai mặt phẳng ( ACD) và (GAB) là:
A. AM , M là trung điểm AB .
B. AN , N là trung điểm CD .
C. AH , H là hình chiếu của B trên CD .
D. AK , K là hình chiếu của C trên BD . Lời giải Chọn B. Trang 29
A là điểm chung thứ nhất của ( ACD) và (GAB)
G là trọng tâm tam giác BCD , N là trung điểm CD nên N Î BG nên N là điểm chung thứ hai của
(ACD) và (GAB). Vậy giao tuyến của hai mặt phẳng (ACD) và (GAB) là AN .
Câu 17. Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng
trung điểm SC . Giao tuyến của hai mặt phẳng ( ABCD) và ( AIJ ) là:
A. AK , K là giao điểm IJ và BC .
B. AH , H là giao điểm IJ và AB .
C. AG , G là giao điểm IJ và AD .
D. AF , F là giao điểm IJ và CD . Lời giải Chọn D.
A là điểm chung thứ nhất của ( ABCD) và ( AIJ )
IJ và CD cắt nhau tại F , còn IJ không cắt BC , AD , AB nên F là điểm chung thứ hai của ( ABCD)
và ( AIJ ). Vậy giao tuyến của ( ABCD) và ( AIJ )là AF . Trang 30
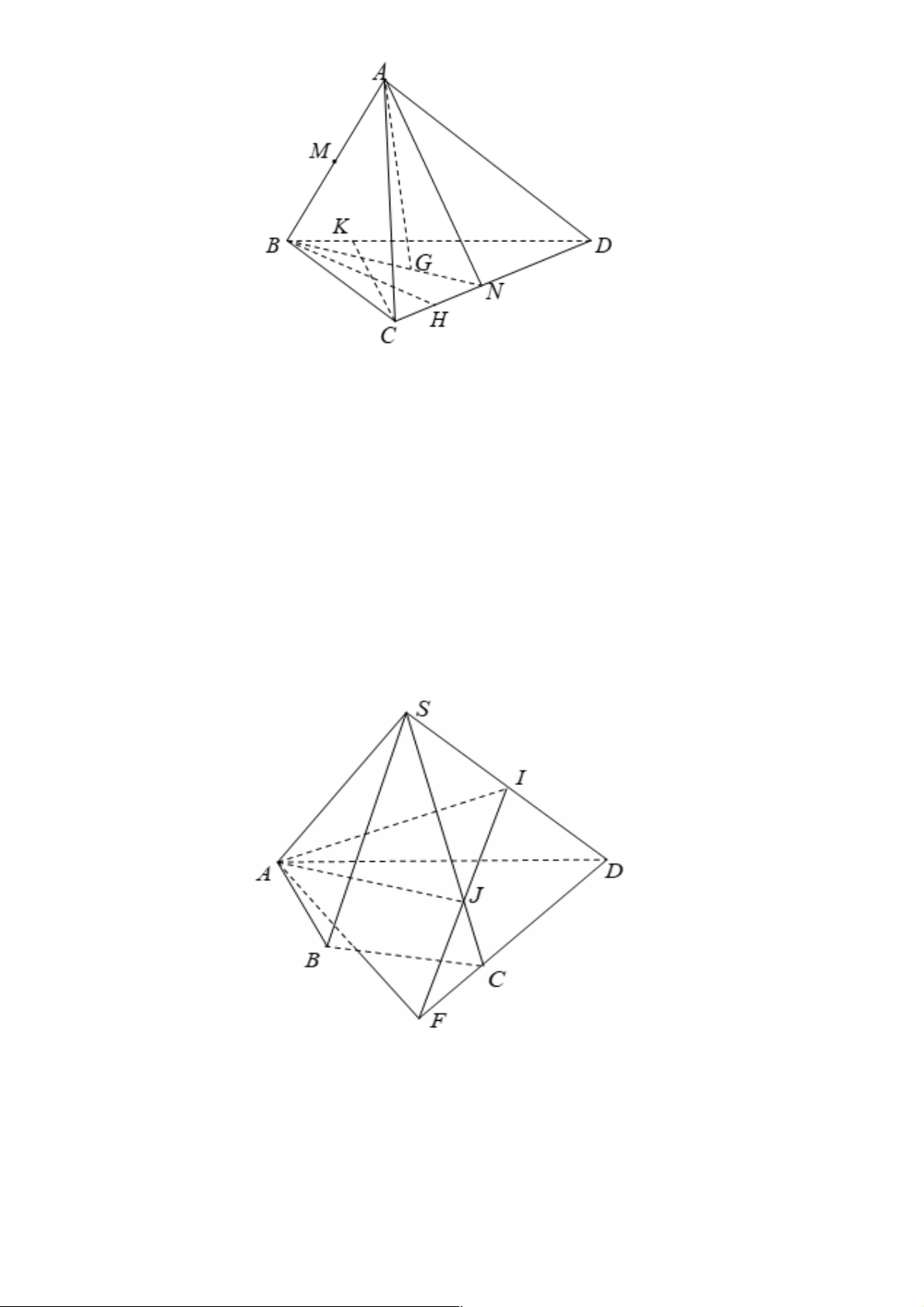
Câu 18. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AC và CD . Giao tuyến của hai mặt
phẳng (MBD) và ( ABN ) là: A. MN . B. AM .
C. BG , với G là trọng tâm tam giác ACD .
D. AH , với H là trực tâm tam giác ACD . Lời giải Chọn C.
B là điểm chung thứ nhất của (MBD) và ( ABN ).
G là trọng tâm tam giác ACD nên G Î AN,G Î DM do đó G là điểm chung thứ hai của (MBD) và
(ABN). Vậy giao tuyến của hai mặt phẳng (MBD) và (ABN) là BG .
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
AD và BC .Giao tuyến của hai mặt phẳng (SMN ) và (SAC) là: A. SD .
B. SO , O là tâm hình bình hành ABCD .
C. SG , G là trung điểm AB .
D. SF , F là trung điểm CD . Lời giải Chọn B.
S là điểm chung thứ nhất của (SMN ) và (SAC). Trang 31
O là giao điểm của AC và MN nên O Î AC,O Î MN do đó O là điểm chung thứ hai của (SMN ) và
(SAC). Vậy giao tuyến của hai mặt phẳng (SMN) và (SAC) là SO.
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung điểm SA
và SB .Khẳng định nào sau đây là sai?
A. IJCD là hình thang.
B. (SAB)Ç(IBC) = IB.
C. (SBD) Ç(JCD) = JD.
D. (IAC) Ç(JBD) = AO, O là tâm hình bình hành ABCD . Lời giải Chọn D.
Ta có (IAC) º (SAC) và (JBD) º (SBD). Mà (SAC) Ç(SBD) = SO trong đó O là tâm hình bình hành ABCD .
Câu 21. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AD BC Ä
). Gọi M là trung điểm CD.
Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:
A. SI , I là giao điểm AC và BM .
B. SJ , J là giao điểm AM và BD.
C. SO , O là giao điểm AC và BD .
D. SP , P là giao điểm AB và CD . Lời giải Chọn A. Trang 32
S là điểm chung thứ nhất của (MSB) và (SAC).
I là giao điểm của AC và BM nên I Î AC , I Î BM do đó I là điểm chung thứ hai của (MSB) và
(SAC). Vậy giao tuyến của hai mặt phẳng (MSB) và (SAC) là SI .
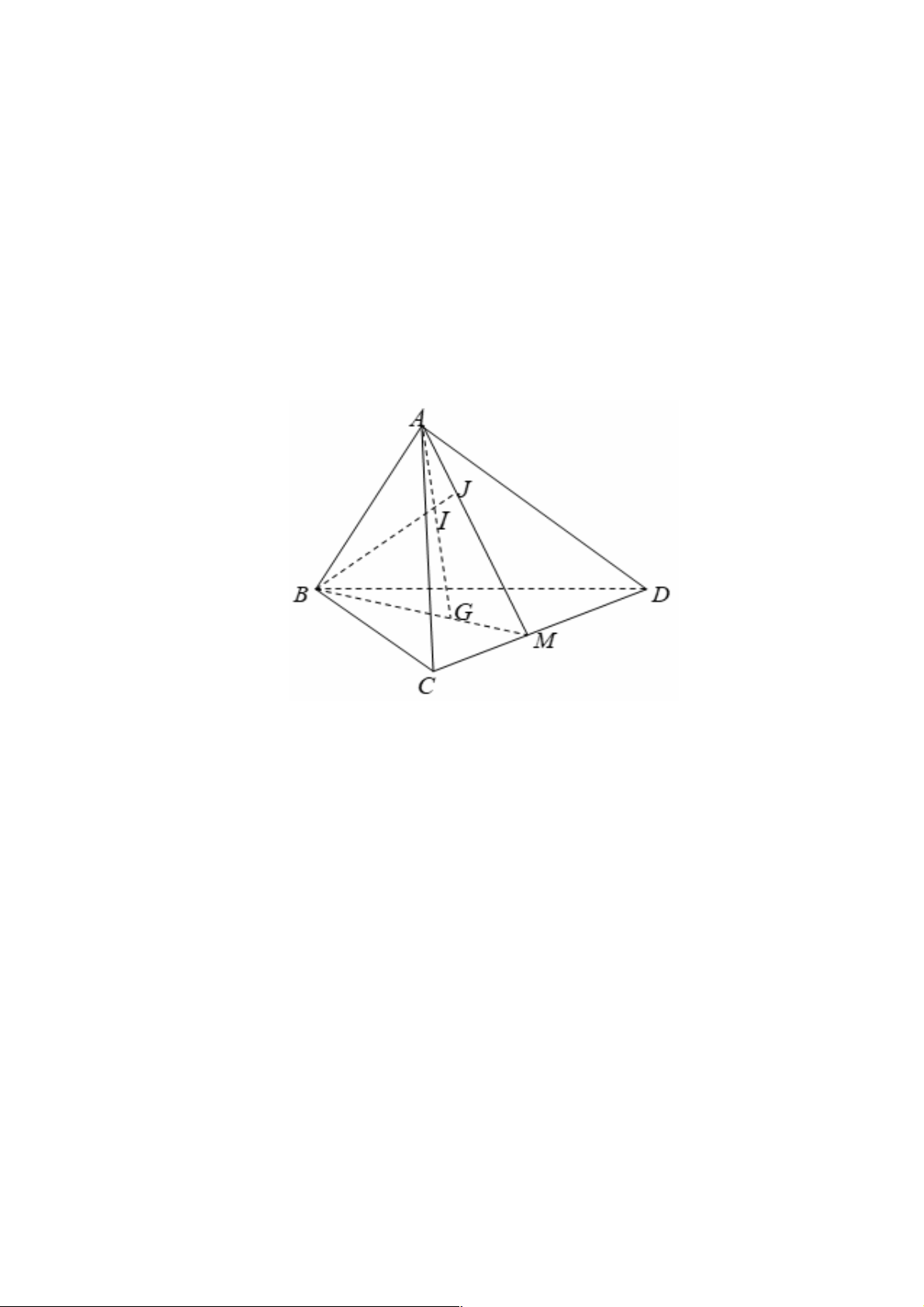
Câu 22. Cho tứ diện ABCD . G là trọng tâm tam giác BCD , M là trung điểm CD , I là điểm trên đoạn
thẳng AG , BI cắt mặt phẳng ( ACD)tại J . Khẳng định nào sau đây sai?
A. AM = ( ACD)Ç( ABG).
B. A , J , M thẳng hàng.
C. J là trung điểm AM . D
. DJ = ( ACD)Ç(BDJ ). Lời giải Chọn C. ìM Î BG
Ta có AÎ( ACD)Ç( ABG), í
Þ M Î( ACD)Ç( ABG) nên AM = ( ACD)Ç( ABG). îM ÎCD
Nên AM = ( ACD)Ç( ABG) vậy A đúng.
A , J , M cùng thuộc hai mặt phẳng phân biệt ( ACD),( ABG) nên A, J , M thẳng hàng, vậy B đúng.
Vì I là điểm tùy ý trên AG nên J không phải lúc nào cũng là trung điểm của AM .
Câu 23. Cho hình chóp S.ABCD có đáy là hình thang ABCD AD / /BC . Gọi I là giao điểm của AB
và DC , M là trung điểm SC . DM cắt mặt phẳng (SAB) tại J . Khẳng định nào sau đây sai?
A. S , I , J thẳng hàng. B. DM Ì mp(SCI ).
C. JM Ì mp(SAB).
D. SI = (SAB)Ç(SCD). Lời giải Chọn C. Trang 33
S , I , J thẳng hàng vì ba điểm cùng thuộc hai mp (SAB) và (SCD) nên A đúng.
M Î SC Þ M Î(SCI ) nên DM Ì mp(SCI )vậy B đúng.
M Ï(SAB)nên JM Ë mp(SAB) vậy C sai.
Hiển nhiên D đúng theo giải thích A.
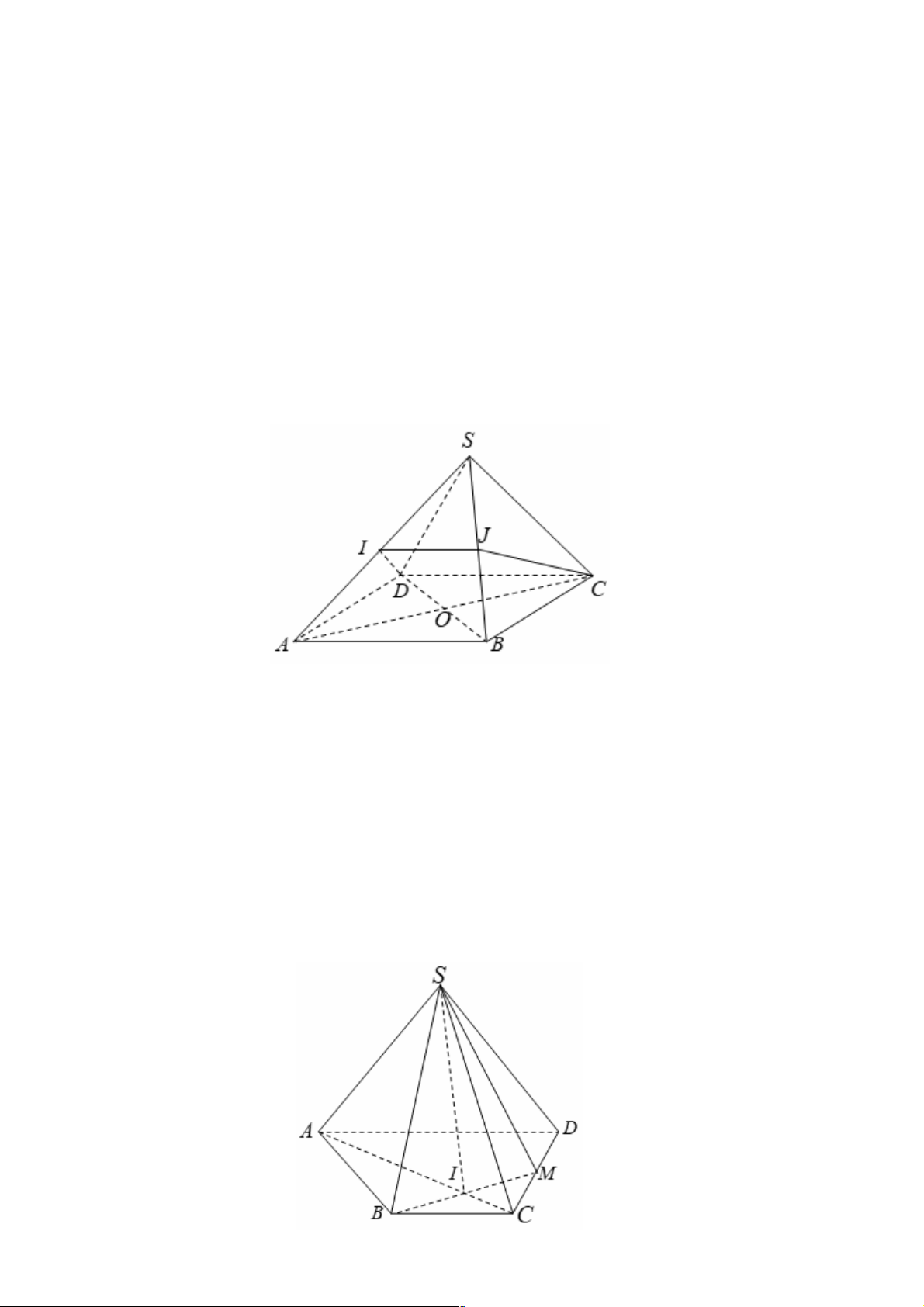
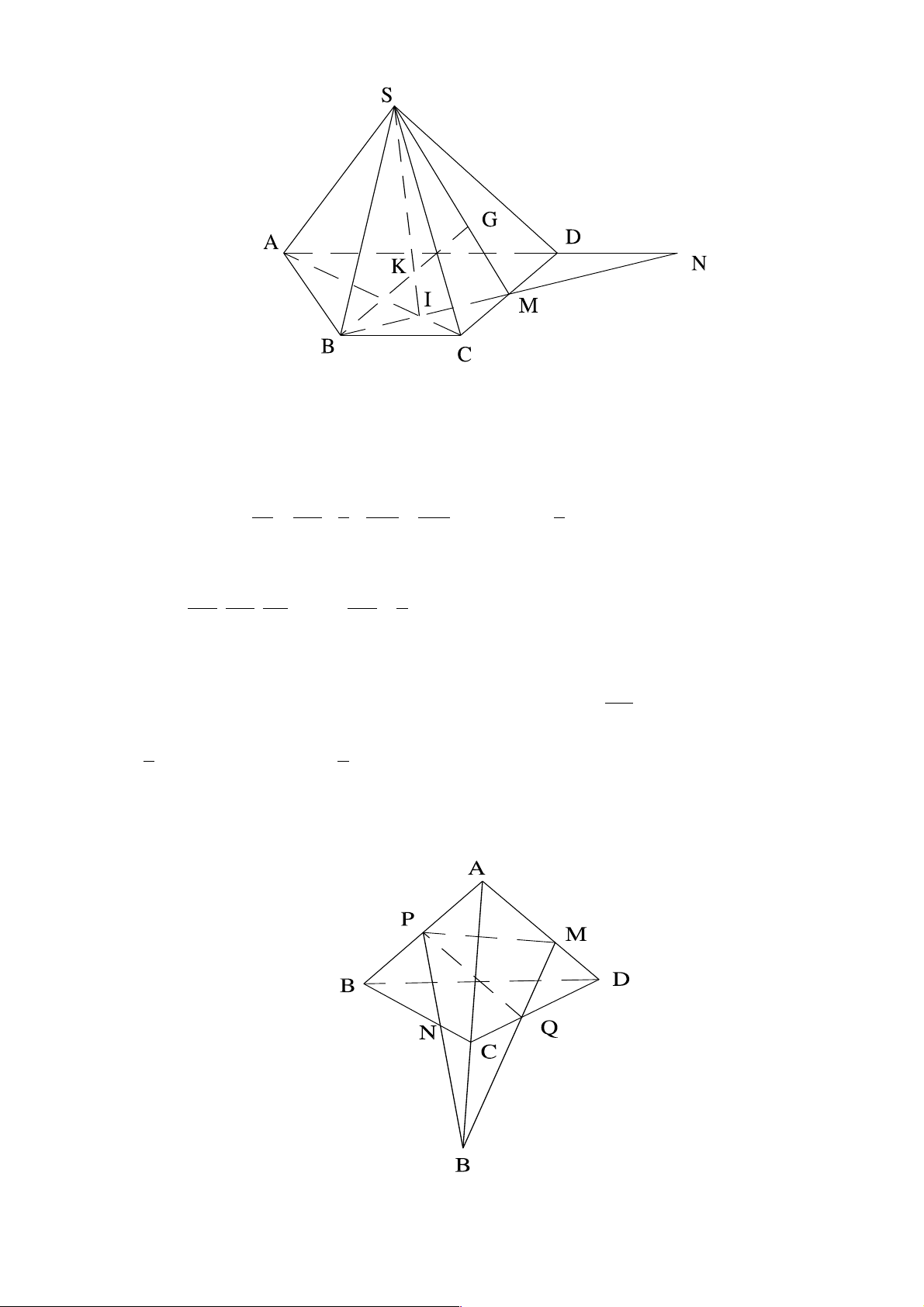
Câu 24. Cho hình chóp S.ABCD , đáy ABCD là tứ giác có các cặp cạnh đối không song song, điểm M thuộc cạnh SA .
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD) A. SC B. SB
C. SO trong đó O = AC Ç BD D. {S}
b) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (MBD) A. SM B. MB
C. OM trong đó O = AC Ç BD D. SD
c) Tìm giao tuyến của các cặp mặt phẳng: (MBC) và (SAD) A. SM
B. FM trong đó F = BC Ç AD
C. SO trong O = AC Ç BD D. SD
d) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD)
A. SE trong đó E = AB Ç CD
B. FM trong đó F = BC Ç AD
C. SO trong O = AC Ç BD D. SD Lời giải Trang 34 S M A D F O C B E a) Chọn C. O ì Î AC Ì ï (SAC)
Gọi O = AC Ç BD Þ í
Þ O Î(SAC) Ç(SBD) O ï Î BD Ì î (SBD)
Lại có S Î(SAC)Ç(SBD) Þ SO = (SAC)Ç(SBD). b) Chọn C. ìO Î AC Ì ï (SAC)
O = AC Ç BD Þ í
Þ OÎ(SAC)Ç(MBD). ïO Î BD Ì î (MBD)
Và M Î(SAC)Ç(MBD) Þ OM = (SAC)Ç(MBD). c) Chọn B. ìF Î BC Ì ï (MBC)
Trong ( ABCD) gọi F = BC Ç AD Þ í
Þ F Î(MBC) Ç(SAD) ïF Î AD Ì î (SAD)
Và M Î(MBC)Ç(SAD) Þ FM = (MBC)Ç(SAD) d) Chọn A.
Trong ( ABCD) gọi E = AB ÇCD , ta có SE = (SAB)Ç(SCD).
Các bạn muốn tải đầy đủ 38 chuyên đề ôn thi 12 file word (hơn 5500 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 12 file word thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 11 file word ( 3042 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/
Các bạn muốn tải đầy đủ bộ tài liệu lớp 9 file word ( 1062 trang) thì liên hệ
https://www.facebook.com/truong.ngocvy.509/ Trang 35
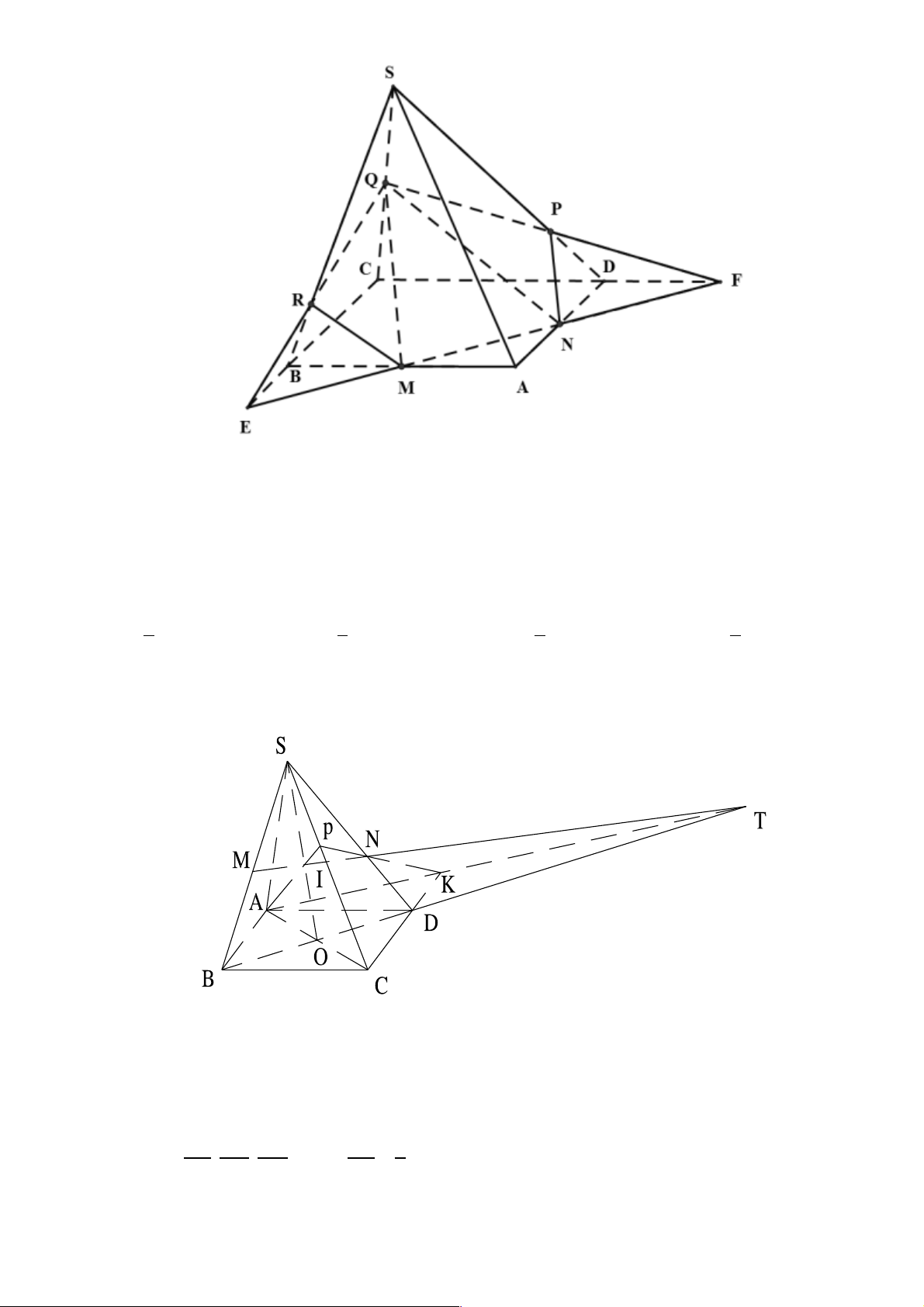
Câu 25. Cho tứ diện ABCD , O là một điểm thuộc miền trong tam giác BCD , M là điểm trên đoạn AO
a) Tìm giao tuyến của mặt phẳng (MCD) với các mặt phẳng ( ABC).
A. PC trong đó P = DC Ç AN , N = DO Ç BC
B. PC trong đó P = DM Ç AN , N = DA Ç BC
C. PC trong đó P = DM Ç AB , N = DO Ç BC
D. PC trong đó P = DM Ç AN , N = DO Ç BC
b) Tìm giao tuyến của mặt phẳng (MCD) với các mặt phẳng ( ABD).
A. DR trong đó R = CM Ç AQ, Q = CA Ç BD
B. DR trong đó R = CB Ç AQ, Q = CO Ç BD
C. DR trong đó R = CM Ç AQ, Q = CO Ç BA
D. DR trong đó R = CM Ç AQ, Q = CO Ç BD
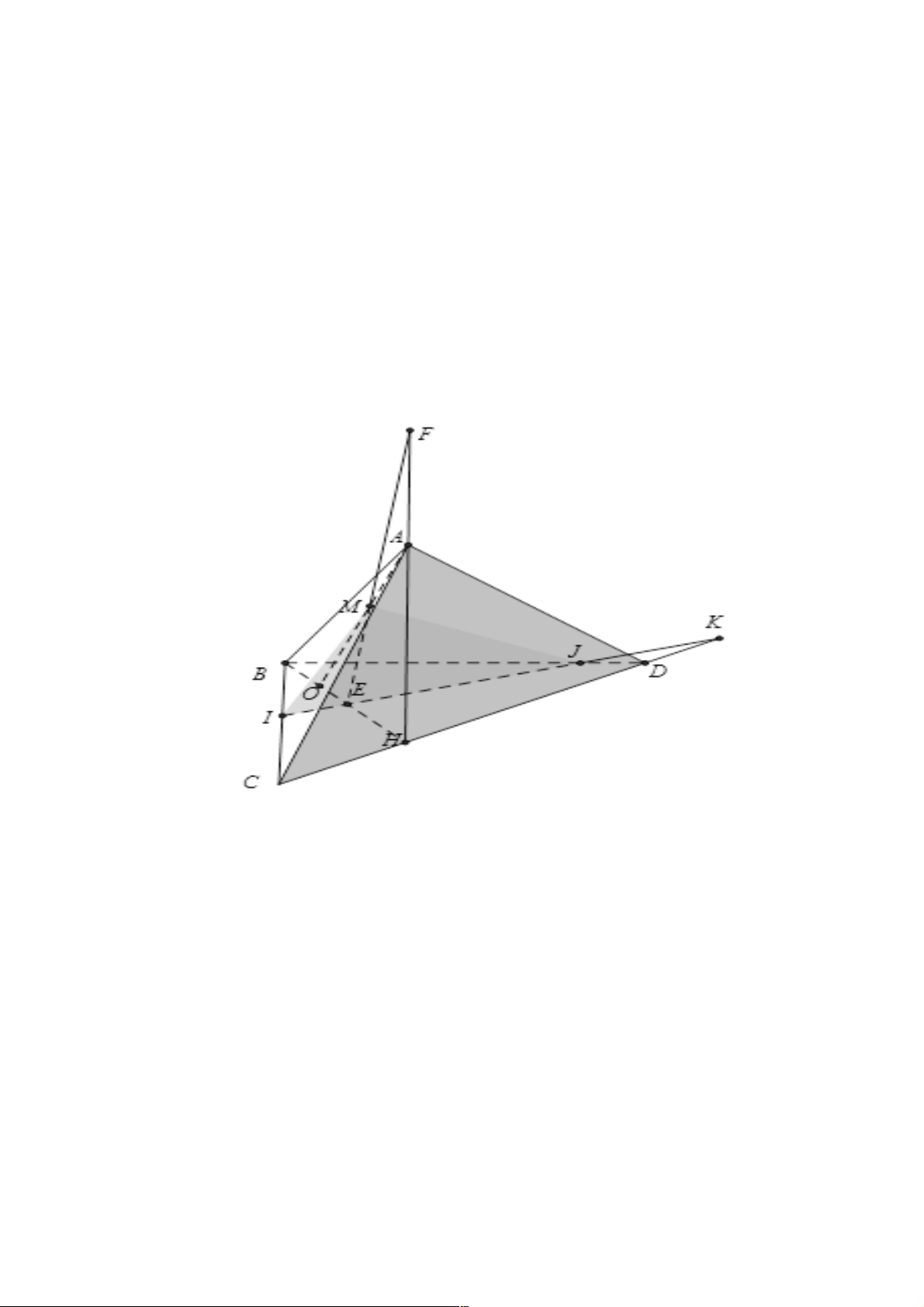
c) Gọi I, J là các điểm tương ứng trên các cạnh BC và BD sao cho IJ không song song với CD . Tìm
giao tuyến của hai mặt phẳng (IJM ) và ( ACD).
A. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BE Ç IA, E = BO Ç CD
B. FG trong đó F = IA Ç CD , G = KM Ç AE , K = BA Ç IJ , E = BO Ç CD
C. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BA Ç IJ , E = BO Ç CD
D. FG trong đó F = IJ Ç CD , G = KM Ç AE , K = BE Ç IJ , E = BO Ç CD Lời giải A R G P M D Q J B O E K I N C F a) Chọn D. Trang 36 ìP Î DM Ì ï (CDM )
Trong (BCD) gọi N = DO Ç BC , trong ( ADN ) gọi P = DM Ç AN Þ í ïP Î AN Ì î ( ABC)
Þ PÎ(CDM )Ç( ABC)
Lại có C Î(CDM )Ç( ABC) Þ PC = (CDM )Ç( ABC). b) Chọn D.
Tương tự, trong (BCD) gọi Q = CO Ç BD, trong ( ACQ)gọi R = CM Ç AQ ìR ÎCM Ì ï (CDM ) Þ í
Þ R Î(CDM ) Ç( ABD) ïR Î AQ Ì î ( ABD)
D là điểm chung thứ hai của (MCD) và ( ABD) nên DR = (CDM )Ç( ABD). c) Chọn D.
Trong (BCD) gọi E = BO ÇC ,
D F = IJ ÇCD, K = BE Ç IJ ; trong ( ABE) gọi G = KM Ç AE . ìF Î IJ Ì ï (IJM ) Có í
Þ F Î(IJM )Ç( ACD), ïF ÎCD Ì î (ACD) ìG Î KM Ì ï (IJM ) Mà íïGÎAE Ì î ( ACD)
Þ FG = (IJM )Ç( ACD)
Câu 26. Cho tứ diện SABC có AB = ,
c BC = a, AC = . b ,
AD BE,CF là các đường phân giác trong của
tam giác ABC . Giao tuyến của hai mặt phẳng (SBE) và (SCF ) là: !!" b + c !!"
A. SI trong đó I thuộc AD sao cho AI = ID a !!" b + c !!"
B. SI trong đó I thuộc AD sao cho AI = - ID a !!" a !!"
C. SI trong đó I thuộc AD sao cho AI = ID b + c !!" -a !!"
D. SI trong đó I thuộc AD sao cho AI = ID b + c Lời giải Chọn A. Trang 37 S B F A I D E C !!" !!"
Do I thuộc đoạn AD nên AI , ID cùng hướng. Do đó B, D bị loại.
AD là phân giác trong của tam giác ABC nên theo tính chất đường phân giác ta có: BD AB c ac = = Þ BD = DC AC b b + c
Ta có: BI là phân giác trong của tam giác ABD nên theo tính chất đường phân giác ta có: IA BA b + c b + c !!" + !!" = = Þ IA = b c
ID. Do đó: AI = ID ID BD a a a DẠNG 3
TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG Phương pháp
Cơ sở của phương pháp tìm giao điểm của đường thẳng d và mặt phẳng (a ) là xét hai trường hợp: • Trường hợp 1: (
mp a ) chứa đường thẳng D và D cắt d . ÏÔD Ã ( mp a ) Ô Ì
fi I = d « m ( p a ) ÔD « d = Ô {I } { } Ô Ó d I a • Trường hợp 2: (
mp a ) không chứa đường thẳng nào cắt d .
+ Bước 1: Tìm ( mp b) d
… sao cho (a ) « (b) = D
+ Bước 2: Tìm {I }= d « D fi I = d « (a ). Trang 38 b d I a
Câu 27. Cho bốn điểm ,
A B,C, D không cùng nằm trong một mặt phẳng. Trên AB, ADlần lượt lấy các
điểm M và N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sao đây: A. (BCD).
B. ( ABD).
C. (CMN ). D. ( ACD). Lời giải Chọn D.
I Î BD Þ I Î(BCD),(ABD)
I Î MN Þ I Î(CMN)
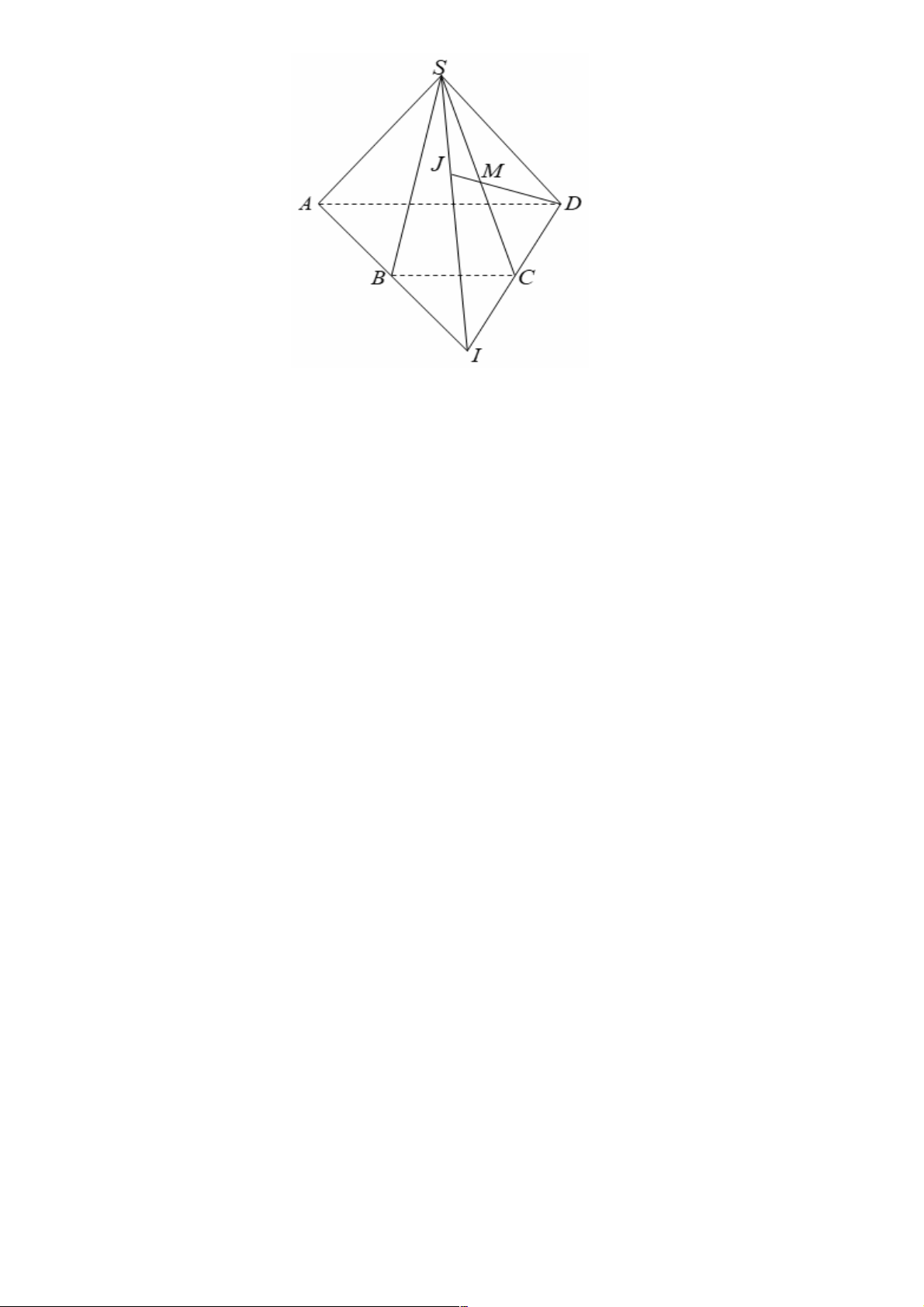
Câu 28. Cho hình chóp tứ giác S.ABCD với đáy ABCD có các cạnh đối diện không song song với
nhau và M là một điểm trên cạnh SA.
a) Tìm giao điểm của đường thẳng SB với mặt phẳng (MCD).
A. Điểm H, trong đó E = AB Ç CD , H = SA Ç EM
B. Điểm N, trong đó E = AB Ç CD , N = SB Ç EM
C. Điểm F, trong đó E = AB Ç CD , F = SC Ç EM
D. Điểm T, trong đó E = AB Ç CD ,T = SD Ç EM
b) Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD).
A. Điểm H, trong đó I = AC Ç BD , H = MA Ç SI
B. Điểm F, trong đó I = AC Ç BD , F = MD Ç SI
C. Điểm K, trong đó I = AC Ç BD , K = MC Ç SI
D. Điểm V, trong đó I = AC Ç BD , V = MB Ç SI Lời giải Chọn B. Trang 39 S M N K A I D B C E a) Chọn B.
Trong mặt phẳng ( ABCD), gọi E = AB ÇCD . Trong (SAB) gọi.
Ta có N Î EM Ì (MCD) Þ N Î(MCD) và N Î SB nên N = SB Ç(MCD). b) Chọn C.
Trong ( ABCD) gọi I = AC Ç BD .
Trong (SAC) gọi K = MC Ç SI .
Ta có K ÎSI Ì (SBD) và K Î MC nên K = MC Ç(SBD).
Câu 29. Cho hình chóp tứ giác S.ABCD , M là một điểm trên cạnh SC , N là trên cạnh BC . Tìm giao
điểm của đường thẳng SD với mặt phẳng ( AMN ).
A. Điểm K, trong đó K = IJ Ç SD , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
B. Điểm H, trong đó H = IJ Ç SA , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
C. Điểm V, trong đó V = IJ Ç SB , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD
D. Điểm P, trong đó P = IJ Ç SC , I = SO Ç AM , O = AC Ç B ,
D J = AN Ç BD Lời giải Chọn A. Trang 40 S K I A M B J N O D C
Trong mặt phẳng ( ABCD) gọi O = AC Ç B ,
D J = AN Ç BD .
Trong (SAC) gọi I = SO Ç AM và K = IJ Ç SD .
Ta có I Î AM Ì ( AMN ), J Î AN Ì ( AMN ) Þ IJ Ì ( AMN ).
Do đó K Î IJ Ì ( AMN ) Þ K Î( AMN ).
Vậy K = SD Ç( AMN )
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác ( AB không song song CD ). Gọi M là
trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB,O là giao điểm của AC và BD .
Giả sử đường thẳng d là giao tuyến của (SAB) và (SCD). Nhận xét nào sau đây là sai:
A. d cắt CD .
B. d cắt MN .
C. d cắt AB .
D. d cắt SO . Lời giải Chọn B. S N A D M O C B I
Gọi I = AB Ç CD . Ta có: Trang 41
ìI Î AB, AB Ì ï
(SAB) Þ I Î(SAB) í
Þ I Î(SAB) Ç(SCD)
ïI ÎCD,CD Ì î
(SCD) Þ I Î(SCD)
Lại có S Î(SAB)Ç(SCD).
Do đó SI = (SAB)Ç(SCD). Þ d º SI.
Vậy d cắt AB,CD, SO.
Giả sử d cắt MN . Khi đó M thuộc mp (SAB). Suy ra D thuộc (SAB) (vô lý). Vậy d không cắt MN .Đáp án B sai.
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC . MA
Gọi I là giao điểm của đường thẳng AM vơí mặt phẳng (SBD). Khi đó tỉ số bằng bao nhiêu: IA 3 4 A. 2 . B. 3 . C. . D. . 2 3 Lời giải Chọn C. S M I B A O C D
Gọi O = AC Ç BD . Ta có: SO = mp(SAC)Ç(SBD); I = AM Ç SO .
Suy ra I = AM Ç(SBD).
Xét tam giác SAC có hai đường trung tuyến SO và MA cắt nhau tại điểm I . Vậy I là trọng tâm tam MA 3
giác SAC . Vậy ta có = . IA 2
Câu 32. Cho hình chóp S.ABCD , đáy ABCD là hình thang với AD là đáy lớn AD = 2BC , G là trọng KB
tâm tam giác SCD . Mặt phẳng (SAC)cắt cạnh BG tại K . Khi đó, tỷ số bằng: KG 3 1 A. 2 B. C. 1 D. 2 2 Lời giải Trang 42 Chọn B.
Gọi M là trung điểm của BC
(ABCD): BMÇAC = I; (SBM): SIÇBG = K Þ BGÇ(SAC) = N (ABCD): BMÇAD = N BI BC 1 MC MC 1 Ta có: AD // BC 1Þ = = ; = =1 Þ BM = BN IN AD 2 MN MD 2
Suy ra, I là trung điểm của BM KB SG IM KB 3 Xét BG D M: . . = 1 Þ = KG SM IB KG 2
Câu 33. Cho tứ diện ABCD có P,Q lần lượt là trung điểm của AB và CD . M là điểm thuộc cạnh AD NB
sao cho MA = 2MD.Gọi N là giao điểm của BC với (MPQ). Tỉ số bằng: NC 1 2 A. B. C. 2 D. 1 2 3 Lời giải Chọn C.
(ACD): MGÇAC = I; (ABC): PIÇBC = N Trang 43 Suy ra: BC Ç(MNP) = N IC MG QD IC 1 Xét AC D D: . . = 1 Þ = IA MD QC IA 2 NB IC PA NB Xét AB D C: . . = 1 Þ =1 NC IA PB NC
Câu 34. Cho hình chóp S.ABCD , đáy ABCD là hình thang (AD// BC,AD > BC), E là điểm thuộc SF
cạnh SA sao cho SE = 2EA. Mặt phẳng (EBC)cắt cạnh SD tại F. Khi đó, tỷ số bằng: SD 2 1 1 1 A. B. C. D. 3 3 2 4 Lời giải Chọn A. (
ì EBC) Ç(SAD) = d, EÎd ï
Ta có: íBC Ì (EBD), AD Ì (SAD) Þ d // BC // AD ïBC//AD î
(SAD): d ÇSD =F ÞEF//AD//BC SF SE 2 Suy ra: = = SD SA 3
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N, P lần lượt là SH
trung điểm của AB, AD và SO . Gọi H là giao điểm của SC với (MNP). Tính ? SC 1 1 3 2 A. . B. . C. . D. . 3 4 4 3 Lời giải Chọn B.
Trong mp ( ABCD), gọi I = MN Ç AO . Dễ thấy H = PO Ç SC . Trang 44
Do MN là đường trung bình của tam giác ABD nên I là trung điểm AO. AI 1 Suy ra
= và PI là đường trung bình của tam giác OSA. Do đó IH / /SA. AC 4 SH AI 1
Áp dụng định lý Thales ta có: = = . SD AC 4
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm
của AD và CD . Trên đường thẳng DS lấy điểm P sao cho D là trung điểm SP . Gọi R là giao điểm SR
của SB với mặt phẳng (MNP). Tính ? SB 1 1 3 2 A. . B. . C. . D. . 3 4 4 5 Lời giải Chọn D.
Trong mp (ABCD) , gọi I = BD Ç MN,O = AC Ç BD .
Dễ thấy R = IP Ç SB . DI 1
Do MN là đường trung bình của tam giác ABD nên I là trung điểm DO. Suy ra = . IB 3
Áp dụng định lý Menelaus vào taam giác SBD ta có: BR PS BI BR 1 SR 2 . . =1Þ .2. =1Þ = RS PD ID RS 3 SB 3
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M , N lần lượt là các BM 2 NC 1 PD 1
điểm nằm trên cạnh AB, AD sao cho = ,
= . Gọi P là điểm trên cạnh SD sao cho = . MA 3 BN 2 PS 5 SJ
J là giao điểm của SO với (MNP). Tính ? SO 10 1 3 5 A. . B. . C. . D. . 11 11 4 2 Lời giải Chọn A. Trang 45 BA BC 5 3 2BO BO OI 1 OI 1 Theo chú ý câu 30 ta có: + = + = 4 Þ = 4 Þ = 2 Þ = Þ = BM BN 2 2 BI BI BO 2 OD 2 IO PD JS JS SJ 10
Áp dụng định lý Menelaus trong tam giác SOD ta có: . . =1Þ =10 Þ = ID PS JO JO SO 11
Câu 38. Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AP 1 SQ AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP).Tính AB 3 SC 1 1 1 2 A. . B. . C. . D. . 3 6 2 3 Lời giải Chọn A.
Trong mặt phẳng ( ABC), gọi E = NP Ç AC
Khi đó Q chính là giao điểm của SC với EM. AP BN CE CE
Áp dụng địnhlý Menelaus vào tam giác ABC ta có: . . =1Þ = 2 PB NC EA EA AM SQ CE SQ 1 SQ 1
Áp dụng địnhlý Menelaus vào tam giác SAC ta có: . . =1Þ = Þ = MS QC EA QC 2 SC 3
Câu 39. Cho tứ diện SABC, E, F lần lượt thuộc đoạn AC, .
AB Gọi K là giao điểm của BE và CF . Gọi
D là giao điểm của (SAK ) với BC . Mệnh đề nào sau đây đúng? Trang 46 AK BK CK AK BK CK A. + + ³ 6. B. + + £ 6. KD KE KF KD KE KF AK BK CK AK BK CK C. + + > 6. D. + + < 6. KD KE KF KD KE KF Lời giải Chọn A. AK BK CK
Nếu K trùng với trọng tâm G thì + + = 6.Do đó C, D bị loại. KD KE KF DK EK FK S S S Ta có KBC KAC KAB + + = + + =1 DA EB FC S S S ABC ABC ABC
Áp dụng định lý bất đẳng thức Cauchy ta có:
æ DK EK FK öæ DA EB FC ö + + + + ³ 9 ç ÷ç ÷
è DA EB FC øè DK EK FK ø DA EB FC AK BK CK Þ + + ³ 9 Þ + + ³ 6 DK EK FK KD KE KF
Câu 40. Cho hình chóp S.ABC , D ,
D M lần lượt là trung điểm của BC, AD . Gọi E là giao điểm của ( MF ME
SBM ) với AC, F là giao điểm của (SCM ) với AB . Tính + ? CM - ME BM - ME 1 1 A. 1. B. 2 . C. D. . 2 3 Lời giải Chọn A. Trang 47 BM S S S + S S + S BD BF BF BM BM - ME Ta có: ABM CBM ABM CBM ABM CBM = = = = = + Þ = -1 = ( )1. ME S S S + S S CD FA AF ME ME AME CME AME CME AME CM CE CD CE CM CM - MF
Tương tự ta cũng chứng minh được: = + Þ = -1 = (2) MF AE BD AE MF MF AM AE AF Và 1 = = + (3) MD CE BF MF ME Từ (1), (2), (3) suy ra + = 1 CM - MF BM - ME DẠNG 3
CHỨNG MINH BA ĐIỂM THẲNG HÀNG VÀ BA ĐƯỜNG THẲNG ĐỒNG QUY
1. Chứng minh ba điểm A; B; C thẳng hàng: Phương pháp
+ Bước 1: Chứng minh 3 điểm A, B,C m Œ ( p a ).
+ Bước 2: Chứng minh 3 điểm A, B,C m Œ ( p b).
+ Bước 3: Kết luận 3 điểm ,
A B,C thuộc giao tuyến chung của 2 mặt phẳng ( mp a ) và ( mp b) fi ,
A B,C thẳng hàng. b d A B C a
2. Chứng minh 3 đường thẳng d ,d ,d đồng quy: 1 2 3 d3 Phương pháp d1 I Trang 48 d2 a
+ Bước 1: Tìm I = d « d . 1 2
+ Bước 2: Chứng minh d đi qua I . 3
fi d ,d ,d đồng quy tại I . 1 2 3
3. Chứng minh đường thẳng trong không gian qua một điểm cố định
Phương pháp 1
Cơ sở của phương pháp là: A
Ta cần tìm trên d hai điểm tùy ý A , B và chứng minh hai điểm B I (cố định)
đó thẳng hàng với điểm I cố định có sẵn trong không gian
fi d đi qua điểm I cố định. a d
Phương pháp 2
Cơ sở của phương pháp là:
- Bước 1: Tìm đường thẳng D cố định ở ngoài
mặt phẳng cố định (a ) chứa d di động. I (cố định)
- Bước 2: Tìm giao điểm I của D và d d a
fi I là điểm cố định mà d đi qua.
Câu 41. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AB và CD . Mặt phẳng (a ) qua MN cắt
AD và BC lần lượt tại P , Q . Biết MP cắt NQ tại I . Ba điểm nào sau đây thẳng hàng?
A. I , A , C .
B. I , B , D .
C. I , A , B .
D. I , C , D . Lời giải Chọn B. ìI Î MP ìI Î ï ( ABD)
Ta có MP cắt NQ tại I Þ í Þ í . îI Î NQ ïI Î î (CBD)
Þ I Î( ABD)Ç(CBD). Þ I Î BD .
Vậy I , B , D thẳng hàng. Trang 49
Câu 42. Cho tứ diện SABC . Trên ,
SA SB và SC lấy các điểm D, E và F sao cho DE cắt AB tại I ,
EF cắt BC tại J , FD cắt CA tại K .Khẳng định nào sau đây đúng?
A. Ba điểm B, J , K thẳng hàng
B. Ba điểm I, J , K thẳng hàng
C. Ba điểm I, J , K không thẳng hàng
D. Ba điểm I, J,C thẳng hàng Lời giải Chọn B. S D F A K C E B I J
Ta có I = DE Ç A ,
B DE Ì (DEF ) Þ I Î(DEF ); AB Ì ( ABC) Þ I Î( ABC) ( ) 1 . ìJ Î EF Î ï (DEF )
Tương tự J = EF Ç BC Þ í (2) ïJ Î BC Ì î (ABC) ìK Î DF Ì ï (DEF )
K = DF Ç AC Þ í (3) ïK Î AC Ì î ( ABC)
Từ (1),(2) và (3) ta có I, J , K là điểm chung của hai mặt phẳng ( ABC) và (DEF ) nên chúng thẳng hàng.
Câu 43. Cho tứ diện SABC có D, E lần lượt là trung điểm của AC, BC và G là trọng tâm của tam
giác ABC . Mặt phẳng (a ) đi qua AC cắt SE, SB lần lượt tại M , N . Một mặt phẳng (b ) đi qua BC cắt ,
SD SA tương ứng tại P và Q .
a) Gọi I = AM Ç DN, J = BP Ç EQ . Khẳng định nào sau đây là đúng?
A. Bốn điểm S, I, J ,G thẳng hàng.
B. Bốn điểm S, I, J ,G không thẳng hàng.
C. Ba điểm P, I, J thẳng hàng.
D. Bốn điểm I, J,Q thẳng hàng.
b) Giả sử K = AN Ç DM , L = BQ Ç EP. Khằng định nào sau đây là đúng?
A. Ba điểm S, K, L thẳng hàng.
B. Ba điểm S, K, L không thẳng hàng
C. Ba điểm B, K, L thẳng hàng
D. Ba điểm C, K, L thẳng hàng Lời giải Trang 50 L S Q K N P J M I A D C G E B a) Chọn A.
Ta có S Î(SAE)Ç(SBD), (1) ìG Î AE Ì ï (SAE) ìGÎ ï (SAE)
G = AE Ç BD Þ í Þ í (2) ïG Î BD Ì î (SBD) ïGÎ î (SBD) ìI Î DN Ì ï (SBD) ìI Î ï (SBD)
I = AM Ç DN Þ í Þ í (3) ïI Î AM Ì î (SAE) ïI Î î (SAE) ìJ Î BP Ì ï (SBD) ìJ Î ï (SBD)
J = BP Ç EQ Þ í Þ í (4) ïJ Î EQ Ì î (SAE) ïJ Î î (SAE)
Từ (1),(2),(3) và (4) ta có S, I, J ,G là điểm chung của hai mặt phẳng (SBD) và (SAE) nên chúng thẳng hàng. b) Chọn A.
Câu 44. Cho hình chóp tứ giác S.ABCD , gọi O là giao điểm của hai đường chéo AC và BD . Một mặt
phẳng (a ) cắt các cạnh bên ,
SA SB, SC, SD tưng ứng tại các điểm M , N, ,
P Q. Khẳng định nào đúng?
A. Các đường thẳng , MP N ,
Q SO đồng qui.
B. Các đường thẳng , MP N ,
Q SO chéo nhau.
C. Các đường thẳng , MP N ,
Q SO song song.
D. Các đường thẳng , MP N , Q SO trùng nhau. Lời giải Chọn A. Trang 51 S Q M I N P D A O B C
Trong mặt phẳng (MNPQ) gọi I = MP Ç NQ .
Ta sẽ chứng minh I Î SO .
Dễ thấy SO = (SAC)Ç(SBD). ìI Î MP Ì ï (SAC) í ïI Î NQ Ì î (SBD) ìI Î ï (SAC) Þ í Þ I Î SO ïI Î î (SBD) Vậy , MP N ,
Q SO đồng qui tại I .
Câu 45. Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến là đường thẳng a . Trong (P) lấy hai điểm ,
A B nhưng không thuộc a và S là một điểm không thuộc (P). Các đường thẳng , SA SB cắt (Q)
tương ứng tại các điểm C, D . Gọi E là giao điểm của AB và a .Khẳng định nào đúng?
A. AB,CD và a đồng qui.
B. AB,CD và a chéo nhau.
C. AB,CD và a song song nhau.
D. AB,CD và a trùng nhau Lời giải Chọn A. Trang 52 Q C D a E B A P S
Trước tiên ta có S Ï AB vì ngược lại thì S Î AB Ì (P) Þ S Î(P)
(mâu thuẫn giả thiết) do đó S, ,
A B không thẳng hàng, vì vậy ta có mặt phẳng (SAB). ìC Î SA Ì ï (SAB) ìC Î ï (SAB)
Do C = SA Ç (Q) Þ í Þ í ( ) 1 ïC Î î (Q) ïC Î î (Q) ìD Î SB Ì ï (SAB) ìDÎ ï (SAB)
Tương tự D = SB Ç (Q) Þ í Þ í (2) ïD Î î (Q) ïD Î î (Q)
Từ (1) và (2) suy ra CD = (SAB)Ç(Q). ìE Î AB Ì ï (SAB) ìE Î ï (SAB)
Mà E = AB Ç a Þ í Þ í Þ E ÎCD . ïE Î a Ì î (Q) ïE Î î (Q)
Vậy AB,CD và a đồng qui đồng qui tại E .
Câu 46. Cho hình bình hành ABCD , S là điểm không thuộc ( ABCD),M và N lần lượt là trung điểm
của đoạn AB và SC. Xác định các giao điểm I, J của AN và MN với (SBD), từ đó tìm khẳng định đúng
trong các khẳng định sau:
A. Ba điểmJ, I, M thẳng hàng.
B. Ba điểmJ, I, N thẳng hàng.
C. Ba điểmJ, I, D thẳng hàng.
D. Ba điểmJ, I, B thẳng hàng. Lời giải Chọn D. Trang 53
*Xác định giao điểm I = AN Ç(SBD)
Chọn mặt phẳng phụ (SAC) É AN
Tìmgiao tuyến của (SAC)và (SBD): (SAC) Ç(SBD) = SO
Trong (SAC), gọi I = AN Ç SO , I Î AN , I Î SO mà SO Ì (SBD) Þ I Î(SBD)
Vậy: I = AN Ç(SBD)
* Xác địnhgiao điểm J = MN Ç(SBD)
Chọn mp phụ (SMC) Ì MN
Tìmgiao tuyến của (SMC) và (SBD), S là điểm chung của (SMC)và (SBD )
Trong ( ABCD), gọi E = MC Ç BD Þ (SAC)Ç(SBD) = SE
Trong (SMC), gọi J = MN Ç SE , H Î SE mà SE Ì (SBD) Þ J Î(SBD)
Vậy J = MN Ç(SBD)
* Chứng minh I, J, B thẳng hàng
Ta có: B là điểm chung của ( ANB) và (SBD)
• I Î SO mà SO Ì (SBD) Þ I Î(SBD)
• I Î AN mà AN Ì ( ANB) Þ I Î( ANB)
Þ Ilà điểm chung của ( ANB) và (SBD)
• J Î SE mà SE Ì (SBD) Þ J Î(SBD)
• J Î MN mà NM Ì ( ANB) Þ J Î( ANB)
Þ Jlà điểm chung của ( ANB)và (SBD). Vậy: B, I, Jthẳng hàng.
Câu 47. Cho tứ giác ABCD và S Î( ABCD). Gọi I, J là hai điểm trên AD và SB, AD cắt BC tại O và
OJ cắt SCtại M. Xác định các giao điểm K, L của IJ và DJ với (SAC), từ đó tìm khẳng định đúng trong các khẳng định sau: A. Ba điểm ,
A K, Lthẳng hàng. B. Ba điểm ,
A L, M thẳng hàng. Trang 54 C. Bốn điểm , A K, ,
L M thẳng hàng. D. Bốn điểm ,
A K, L, J thẳng hàng. Lời giải Chọn C. S J M K L B A I E F C D O
* Tìmgiao điểm K = IJ Ç(SAC)
• Chọn mp phụ (SIB) É IJ
•Tìmgiao tuyến của (SIB) và (SAC), S là điểm chung của (SIB) và (SAC). Trong ( ABCD), gọi
E = AC Ç BI Þ (SIB)Ç(SAC) = SE
•Trong (SIB), gọi K = IJ Ç SE. K Î IJ, K ÎSE mà SE Ì (SAC) Þ K Î(SAC)
Vậy: K = IJ Ç(SAC)
* Xác địnhgiao điểm L = DJ Ç(SAC)
• Chọn mp phụ (SBD) É DJ
•Tìmgiao tuyến của (SBD)và (SAC), S là điểm chung của (SBD )và (SAC )
Trong ( ABCD), gọi F = AC Ç BD Þ SE = (SBD)Ç(SAC)
Trong (SBD), gọi L = DJ Ç SE, LÎ DJ, LÎ SF mà SF Ì (SAC) Þ LÎ(SAC)
Vậy: L = DJ Ç(SAC)
* Chứng minh A,K,L,Mthẳng hàng
Ta có:A là điểm chung của (SAC)và ( AJO)
• K Î IJ mà IJ Ì ( AJO) Þ K Î( AJO)
• K Î SE mà SE Ì (SAC) Þ K Î(SAC)
Þ Klà điểm chung của (SAC)và ( AJO)
L Î DJ mà DJ Ì ( AJO) Þ LÎ( AJO) Trang 55
L Î SF mà SF Ì (SAC) Þ LÎ(SAC)
Þ Llà điểm chung của (SAC)và ( AJO)
M Î JO mà JO Ì ( AJO) Þ M Î( AJO)
M Î SC mà SC Ì (SAC) Þ M Î(SAC)
Þ M là điểm chung của (SAC)và ( AJO)
Vậy: Bốn điểm A,K,L,M thẳng hàng
Câu 48. Cho tứ diện SABC .Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho
LMkhông song song với AB, LN không song song với SC. Gọi LK giao tuyến của mp (LMN )và
(ABC). Xác định I, J lần lượt là giao điểm của BC và SC với (LMN). Khẳng định nào sau đây đúng:
A. Ba điểm L, I, J thẳng hàng.
B. Ba điểm L, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng.
D. Ba điểm M, I,K thẳng hàng. Lời giải Chọn C. S L C N A M I J B K
* Tìm giao tuyến của mp (LMN )và ( ABC)
Ta có: N là điểm chung của (LMN )và ( ABC)
Trong (SAB), LM không song song với AB
Gọi K = AB Ç LM
K Î LM mà LM Ì (LMN ) Þ K Î(LMN )
K Î AB mà AB Ì ( ABC) Þ K Î( ABC)
* Tìm giao điểm I = BC Ç(LMN )
• Chọn mp phụ ( ABC) É BC
•Tìmgiao tuyến của ( ABC)và (LMN) Þ ( ABC)Ç(LMN) = NK . Trong ( ABC),
gọi I = NK Ç BC , I Î BC, I Î NK mà NK Ì (LMN ) Þ I Î(LMN ) Trang 56
Vậy: I = BC Ç(LMN )
*Tìm giao điểm J = SC Ç(LMN )
•Trong (SAC), LN không song song với SC.Gọi J = LN Ç SC, J ÎSC, J Î LN mà
LN Ì (LMN ) Þ J Î(LMN )
Vậy: J = SC Ç(LMN )
* Chứng minh M, I, Jthẳng hàng
Ta có: M, I, Jlà điểm chung của (LMN )và (SBC) Vậy: M, I, Jthẳng hàng
Câu 49. Cho tứ giác ABCD và S không thuộc mặt phẳng ( ABCD). Gọi M, N là hai điểm trên BC và .
SD Xác định I, J lần lượt là giao điểm của BN và MN với (SAC). Từ đó tìm bộ 3 điểm thẳng hàng trong những điểm sau:
A. Ba điểm A, I, Jthẳng hàng.
B. Ba điểm K, I,K thẳng hàng.
C. Ba điểm M, I, Jthẳng hàng.
D. Ba điểm C, I,Jthẳng hàng. Lời giải Chọn D. S N I J D A O K C B M
* Tìm giao điểm I = BN Ç(SAC)
Chọn mp phụ (SBD) É BN
•Tìmgiao tuyến của (SBD)và (SAC)
Trong ( ABCD), O = AC Ç BD Þ (SBD)Ç(SAC) = SO
•Trong (SBD), gọi I = BN Ç S ,
O I Î BN, I Î SOmà SO Ì (SAC) Þ I Î(SAC)
Vậy: I = BN Ç(SAC)
* Tìm giao điểm J = MN Ç(SAC):
• Chọn mp phụ (SMD) É MN Trang 57
•Tìmgiao tuyến của (SMD)và (SAC)
Trong ( ABCD), gọi K = AC Ç DM Þ (SMD)Ç(SAC) = SK
•Trong (SMD), gọi J = MN Ç SK, J ÎMN, J ÎSK mà SK Ì (SAC) Þ J Î(SAC)
Vậy: J = MN Ç(SAC)
* Chứng minh C, I, Jthẳng hàng:
Ta có: C, I, Jlà điểm chung của (BCN )và (SAC) Vậy: C, I, Jthẳng hàng
Câu 50. Cho tứ diện ABCD . E là điểm thuộc đoạn AB sao cho EA = 2 .
EB F,G là các điểm thuộc !!!" !!!" !!!" !!!"
đường thẳng BC sao cho FC = 5FB,GC = 5 - G .
B H , I là các điểm thuộc đường thẳng CD sao cho !!!" !!!" !!" !!" HC = 5 - HD, ID = 5
- IC, J thuộc tia đối của tia DA sao cho D là trung điểm của AJ . Trong các mệnh
đề sau, mệnh đề nào đúng?
A. Bốn điểm E, F, H, J đồng phẳng
B. Bốn điểm E, F, I, J đồng phẳng.
C. Bốn điểm E,G, H, I đồng phẳng.
D. Bốn điểm E,G, I, J đồng phẳng. Lời giải Chọn A. A E D F B H J C I
Dựa vào nhận xét ví dụ 2, ta có: AE BF CH DJ 1 = - (- ) 1 . . .
2. . 5 . = 1 nên E, F, H, J đồng phẳng. BE CF DH AJ 5 2 AE BF CI DJ 1 æ 1 ö 1 1 . . . = 2 - . . . =
nên E, F, I, J không đồng phẳng. ç ÷ BE CF DI AJ 5 è 5 ø 2 25 AE BG CH DJ æ 1 ö = - - ç ÷ (- ) 1 . . . 2. . 5 . = 1
- nên E,G, H, J không đồng phẳng. BE CG DH AJ è 5 ø 2 AE BG CI DJ æ 1 ö æ 1 ö 1 1 . . . = 2 - . - . . =
nên E,G, I, J không đồng phẳng. ç ÷ ç ÷ BE CG DI AJ è 5 ø è 5 ø 2 25
Câu 51. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (BC / / AD).Mặt phẳng (P) di động
chứa đường thẳng AB và cắt các đoạn SC, SD lần lượt tại E, F . Mặt phẳng (Q) di động chứa đường Trang 58 thẳng CD và cắt ,
SA SB lần lượt tại G, H.I là giao điểm của AE, BF; J là giao điểm của CG, DH . Xét các mệnh đề sau: ( )
1 Đường thẳng EF luôn đi qua một điểm cố định.
(2)Đường thẳng GH luôn đi qua một điểm cố định.
(3)Đường thẳng IJ luôn đi qua một điểm cố dịnh.
Có bao nhiêu mệnh đề đúng? A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn D.
Trong mp ( ABCD), gọi M = AB ÇC ;
D O = AC Ç BD . Khi đó M ,O cố định.
Như vậy: E, F, M cùng nằm trên hai mp (P) và (SCD), do đó ba điểm E, F, M thẳng hàng. Vậy
đường thẳng EF luôn đi qua một điểm cố định M .
Tương tự, ta có G, H, M cùng nằm trên hai mp (Q) và (SAB),do đó G, H, M thẳng hàng. Vậy các
đường thẳng GH luôn đi qua một điểm cố định M . ìI Î AE Ì ï (SAC) Do í
Þ I Î(SAC) Ç(SBD). ïI Î BF Ì î (SBD)
Tương tự ta cũng có J Î(SAC)Ç(SBD);OÎ(SAC)Ç(SBD)
Do đó ba điểm I, J ,O thẳng hàng. Vậy IJ luôn đi qua điểm cố định O .
Câu 52. Cho tứ diện ABCD và các điểm M , N, ,
P Q lần lượt thuộc các cạnh AB, BC,CD, DA sao cho
MN không song song với AC . M , N, ,
P Qđồng phẳng khi : AM BN CP DQ BM CN CP DQ A. . . . = 1 B. . . . = 1 BM CN DP AQ AM BN DP AQ Trang 59 BM CN DP DQ AM BN DP AQ C. . . . = 1 D. . . . = . 1 AM BN CP AQ BM CN CP DQ Lời giải Chọn A.
+ Giả sử M , N, ,
P Q cùng thuộc mặt phẳng (a ).
Nếu MN cắt AC tại K thì K là điểm chung của các mặt phẳng (a ),( ABC),( ADC) nên PQ cũng đi qua K.
Áp dụng định lí Menelaus cho các tam giác ABC, ADC ta được : AM BN CK AK CP DQ AM BN CP DQ . . = 1 ; . . =1 Þ . . . = 1 BM CN AK CK DP AQ BM CN DP AQ Nhận xét :
Trường hợp MN song song với AC thì ví dụ trên vẫn đúng. AM BN CP DQ
+ Liệu trường hợp ngược lại, có . . . = 1 thì M , N, ,
P Q có đồng phẳng hay không ? BM CN DP AQ
Câu trả lời là trường hợp ngược là ví dụ vẫn đúng. Ta sẽ cùng chứng minh nhé :
Trong mặt phẳng ( ACD), KO cắt AD tại Q¢ thì các điểm M , N, P,Q¢ đồng phẳng. AM BN CP AQ¢ DQ¢ DQ Theo ví dụ 2 ta có: . . . =1 Þ =
Þ Q º Q¢. Ví dụ được chứng minh. BM CN DP DQ¢ AQ¢ AQ
+ Ví dụ này có thể được mở rộng đối với các điểm M , N, ,
P Q bất kì trên các đường thẳng
AB, BC,CD, DA như sau : AM BN CP DQ
M , N, P,Q¢ đồng phẳng khi và chỉ khi . . . =
1 ( khẳng định này dôi khi còn được gọi là BM CN DP AQ
định lí Menelaus mở rộng trong không gian)
Câu 53. Cho hình chóp S.AB .
CD Giả sử AD và BC cắt nhau tại H. Gọi O là giao điểm của AC và BD, E
và F lần lượt là trung điểm của SA và .
SB Điểm M di động trên cạnh SC. Gọi N là giao điểm của SD và
mp(EFM). Tìm tập hợp giao điểm J của EN và FM.
A. Tập hợp J là đoạn thẳng SJ1 với J1 = CF Ç SH.
B. Tập hợp J là đoạn thẳng SJ1 với J1 = DE Ç SH.
C. Tập hợp J là đoạn thẳng SH.
D. Tập hợp J là đường thẳng SH. Lời giải Chọn A. Trang 60
Gọi O là giao điểm của AC và .
BD Suy ra (SAC) cắt (SBD) theo giao tuyến là SO. Gọi I là giao của EM
và SO. Khi đó FI cắt SD tại N. Do FM thuộc mp (SBC) cố định và EN thuộc mp (SAD) cố định nên giao
điểm J của FM và EN thuộc giao tuyến của mp (SBC) và mp (SAD). Gọi H =AD Ç BC, suy ra (SBC)
Ç(SAD) =SH. Do đó I thuộc đường thẳng SH.
Giới hạn: Nếu M º S thì J º S ; Nếu M º C thì J º J với J1= CF Ç SH. 1
Vậy tập hợp J là đoạn thẳng SJ1.
Câu 54. Cho hình chóp S.ABCD, trong đó AD không song song với BC. Gọi O là giao điểm của AC và
BD, E là giao điểm của AD và BC. Điểm M di động trên cạnh SB, EM cắt SC tại N. Tập hợp giao điểm I của AN và DM.
A. Tập hợp giao điểm I là đoạn thẳng SO.
B. Tập hợp giao điểm I là đường thẳng SO.
C. Tập hợp giao điểm I là đoạn thẳng SO trừ 2 điểm S và O.
D. Tập hợp giao điểm I là đoạn thẳng SE. Lời giải Chọn C. Trang 61
Do AN thuộc mp (SAC) cố định và DM thuộc mp (SBD) cố định nên giao điểm I của AN và DM thuộc
giao tuyến của (SAC) và (SBD) là SO. Khi M trùng S thì I trùng S; Khi M trùng B thì I trùng O. Vậy tập
hợp I là đoạn thẳng SO.
Câu 55. Cho tứ diện ABC .
D Một mặt phẳng (P) di động luôn song song với AB và CD cắt các cạnh AC, , AD ,
BD BC tại M , N, E, F . Tìm tập hợp tâm I của hình bình hành MNEF.
A. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và CD (trừ 2 điểm P và Q).
B. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AB và . CD
C. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC (trừ 2 điểm P và Q).
D. Tập hợp tâm I là đoạn thẳng PQ với P, Q lần lượt là trung điểm của AD và BC. Lời giải Chọn B.
Gọi P, Q lần lượt là trung điểm của AB và .
CD Khi đó AQ cắt MN tại K; BQ cắt FE tại H. Dễ thấy H, K
lần lượt là trung điểm của MN và FE nên I thuộc KH, đồng thời là trung điểm KH. Do đó I thuộc đường
trung tuyến QP của tam giác QA . B Trang 62 DẠNG 4
XÁC ĐỊNH THIẾT DIỆN CỦA MỘT MẶT PHẲNG VỚI HÌNH CHÓP
Để xác định thiết diện của hình chóp S.A A ...A cắt bởi mặt phẳng (a ), ta tìm giao điểm của mặt phẳng 1 2 n
(a) với các đường thẳng chứa các cạnh của hình chóp. Thiết diện là đa giác có đỉnh là các giao điểm
của (a ) với hình chóp ( và mỗi cạnh của thiết diện phải là một đoạn giao tuyến với một mặt của hình chóp)
Câu 56. Cho ABCD là một tứ giác lồi. Hình nào sau đây không thể là thiết diện của hình chóp S.ABCD ? A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác. Lời giải Chọn D.
Hình chóp S.ABCD có 5 mặt nên thiết diện của hình chóp có tối đa 5 cạnh. Vậy thiết diện không thể là lục giác.
Câu 57. Cho hình chóp S.ABCD với đáy ABCD là tứ giác lồi. Thiết diện của mặt phẳng (a ) tuỳ ý với hình chóp không thể là: A. Lục giác. B. Ngũ giác. C. Tứ giác. D. Tam giác. Lời giải Chọn A.
Thiết diện của mặt phẳng với hình chóp là đa giác được tạo bởi các giao tuyến của mặt phẳng đó với mỗi mặt của hình chóp.
Hai mặt phẳng bất kì có nhiều nhất một giao tuyến. Trang 63
Hình chóp tứ giác S.ABCD có 5 mặt nên thiết diện của (a ) với S.ABCD có không qua 5 cạnh, không
thể là hình lục giác 6 cạnh.
Câu 58. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và điểm M ở trên cạnh SB . Mặt
phẳng ( ADM ) cắt hình chóp theo thiết diện là A. tam giác. B. hình thang. C. hình bình hành. D. hình chữ nhật. Lời giải Chọn B.
Câu 59. Cho hình chóp tứ giác S.ABCD , có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD .
a) Thiết diện của hình chóp cắt bởi mặt phẳng (PAB)là hình gì? A. Tam giác B. Tứ giác C. Hình thang
D. Hình bình hành
b) Gọi M , N lần lượt là trung điểm của các cạnh AB, BC. Thiết diện của hình chóp cắt bởi (MNP)là hình gì? A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành Lời giải a) Chọn B. S P Q A B D C E
Trong mặt phẳng ( ABCD), gọi
E = ABÇCD .
Trong mặt phẳng (SCD) gọi Q = SC Ç EP.
Ta có E Î AB nên EP Ì ( ABP) Þ QÎ( ABP), do đó Q = SC Ç( ABP).
Thiết diện là tứ giác ABQP . b) Chọn A. Trang 64 S P H F A D K M B N C G
Trong mặt phẳng ( ABC
D) gọi F,G lần lượt là các giao điểm của MN với AD và CD
Trong mặt phẳng (SAD) gọi H = SAÇ FP
Trong mặt phẳng (SCD) gọi K = SC Ç PG .
Ta có F ÎMN Þ F Î(MNP), Þ FP Ì (MNP) Þ H Î(MNP) ìH Î ï SA Vậy í H SA MNP ïH Î î (MNP) Þ = Ç( )
Tương tự K = SC Ç(MNP).
Thiết diện là ngũ giác MNKPH .
Câu 60. Cho hình chóp S.ABCD . Điểm C¢ nằm trên cạnh SC . Thiết diện của hình chóp với mp
(ABC¢) là một đa giác có bao nhiêu cạnh? A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B. Trang 65 S M A' A D C B I ì ¢
A Î SC, SC Ì ï (SCD) Xét ( ¢
ABA ) và (SCD) có í Þ ¢
A là điểm chung 1. ¢ ïA Î î ( ¢ ABA )
Gọi I = AB Ç CD
ìI Î AB, AB Ì ï ( AB ¢ A ) Có í
Þ I là điểm chung 2.
ïI ÎCD,CD Ì î (SCD) Þ ( ¢
ABA )Ç(SCD) = I ¢ A Gọi M = I ¢ A Ç SD . Ta có: ( ¢
ABA )Ç(SCD) = ¢ A M ( ¢
ABA )Ç(SAD) = AM ( ¢
ABA )Ç( ABCD) = AB ( ¢ ABA ) Ç(SBC) = ¢ BA
Thiết diện là tứ giác AB ¢ A M .
Câu 61. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm SA . Thiết diện
của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là:
A. Tam giác IBC.
B. Hình thang IJCB ( J là trung điểm SD ).
C. Hình thang IGBC ( G là trung điểm SB ).
D. Tứ giác IBCD . Lời giải Chọn B. Trang 66 S I J B C G O A D
Gọi O là giao điểm của AC và
BD, G là giao điểm của CI và SO.
Khi đó G là trọng tâm tam giác SAC . Suy ra G là trọng tâm tam giác SBD .
Gọi J = BG Ç SD . Khi đó J là trung điểm SD .
Do đó thiết điện của hình chóp cắt bởi (IBC) là hình thang IJCB ( J là trung điểm SD ).
Câu 62. Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành tâm O . Gọi M , N, P là ba điểm
trên các cạnh AD,CD, SO. Thiết diện của hình chóp với mặt phẳng (MNP)là hình gì? A. Ngũ giác B. Tứ giác C. Hình thang D. Hình bình hành Lời giải Chọn A. S H R T P F N D C K M O E A B
Trong mặt phẳng (ABCD) gọi E, K, F lần lượt là giao điểm của MN với , DA , DB DC .
Trong mặt phẳng (SDB) gọi H = KP Ç SB
Trong mặt phẳng (SAB) gọi T = EH Ç SA Trang 67
Trong mặt phẳng (SBC) gọi R = FH Ç SC . ìE Î MN Ta có í Þ EH Ì (MNP) îH Î KP ìT Î ï SA í
Þ T = SAÇ MNP . ïT Î EH Ì î (MNP) ( )
Lí luận tương tự ta có R = SC Ç(MNP).
Thiết diện là ngũ giác MNRHT .
Câu 63. Cho tứ diện ABCD , M và N lần lượt là trung điểm AB và AC . Mặt phẳng (a ) qua MN cắt
tứ diện ABCD theo thiết diện là đa giác (T ). Khẳng định nào sau đây đúng?
A. (T ) là hình chữ nhật. B. (T ) là tam giác.
C. (T ) là hình thoi.
D. (T ) là tam giác hoặc hình thang hoặc hình bình hành. Lời giải Chọn D. A M N D B C
(a) qua MN cắt AD ta được thiết diện là một tam giác.
(a) qua MN cắt hai cạnh BD và CD ta được thiết diện là một hình thang.
Đặc biệt khi mặt phẳng này đi qua trung điểm của BD và CD , ta được thiết diện là một hình bình hành.
Câu 64. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N,Q lần lượt là trung điểm của các cạnh , AB ,
AD SC. Thiết diện của hình chóp với mặt phẳng (MNQ) là đa giác có bao nhiêu cạnh ? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn C. Trang 68
Thiết diện của hình chóp với mặt phẳng (MNQ) là ngũ giác MNPQ .
R Đa giác này có 5 cạnh.
Câu 65. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M, Nlần lượt là 2 điểm thuộc
cạnh SB,SD sao cho SM = MB,SN = 2ND. Mặt phẳng (AMN)cắt SC tại P thỏa mãn SP = kSC . Số k bằng? 2 3 3 2 A. B. C. D. 5 5 2 3 Lời giải Chọn A. (ABCD): ACÇBD= ; O (SBD): MNÇBD = T
(ABCD): ATÇCD = K, (SCD): KNÇSC = P TD NS MB TD 1 Xét AB D D: . . = 1 Þ = TB ND MS TB 2 Trang 69 TD KD KD 1 KC Ta có: = = = Þ = 3 TB AB DC 2 KD PS ND KC PS 2 2 Xét SC D D: . . = 1 Þ = Þ SP= SC PC NS KD PD 3 5
Câu 66. Cho tứ diện đều ABCD có các cạnh bằng a . Gọi E là trung điểm AB , F là điểm thuộc cạnh
BC sao cho BF = 2FC,G là điểm thuộc cạnh CD sao cho CG = 2GD . Tính độ dài đoạn giao tuyến của
mặt phẳng (EFG) với mặt phẳng ( ACD) của hình chóp ABCD theo a . 19 a 141 a 34 +15 3 a 34 -15 3 A. a. B. . C. . D. . 15 30 15 15 Lời giải Chọn A.
Trong mp (BCD), gọi I = FG Ç BD .
Trong mp ( ADB), gọi H = IE Ç AD .
Khi đó HG = (EFG)Ç( ACD).
Áp dụng định lý Menelaus cho tam giác BCD với ba điểm I,G, F thẳng hàng ta có: ID FB GC ID 1 . . =1Þ = IB FC GD IB 4
Áp dụng định lý Menelaus cho tam giác ABD với ba điểm I, H, E thẳng hàng ta có: HD EA IB HD 1 a . . =1Þ = Þ HD = HA EB ID HA 4 5
Áp dụng định lý cosin vào tam giác HDG ta có: 2 2 2 0
HG = HD + DG - 2DH. . DG cos 60 2 2 2 2 a a a 19a 19 = + - = Þ HG = a 25 9 15 225 15
Câu 67. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E là điểm thuộc cạnh bên SD sao
cho SD = 3SE . F là trọng tâm tam giác SAB,G là điểm thay đổi trên cạnh BC. Thiết diện cắt bởi mặt phẳng (EFG) là: Trang 70 A. Tam giác B. Tứ giác C. Ngũ giác. D. Lục giác. Lời giải Chọn C. Cách 1:
Gọi M là trung điểm của AB , khi đó S , F , M thẳng hàng.
Trong mặt phẳng ( ABCD), gọi I là giao điểm của MG với AD . Khi đó SI = (SMG)Ç(SAD).
Trong mặt phẳng (SMG), gọi J là giao điểm của FG với SI . Ta thấy J thuộc FG nên J thuộc
(EFG). Trong (SAD), gọi K là giao điểm của JE với SA. Trong mặt phẳng (SAB), gọi L là giao
điểm của KF với AB .
Trong mặt phẳng ( ABCD), gọi H là giao điểm của LG với CD . Trong mặt phẳng (SCD) , gọi N là
giao điểm của EH với SC . (
ì EFG) Ç( ABCD) = LG;(EFG) Ç(SBC) = GN ï Ta có: (
í EFG) Ç(SCD) = NE;(EFG) Ç(SAD) = EK . ( ï EFG î )Ç(SAB) = KL
Vậy ngũ giác LGNEK là thiết diện của hình chóp cắt bởi (EFG).
Chú ý:Mấu chốt của ví dụ trên là việc dựng được điểm J là giao điểm của FG với (SAD) (thông qua
việc dựng giao tuyến SI của mặt phẳng (SFG) với mặt phẳng (SAD)). Có thể dựng thiết diện trên bằng
nhiều cách với việc dựng giao điểm (khác E, F,G ) của một trong các đường thẳng EF, FG ; hoặc GE
với một mặt của hình chóp. Sau đây, tôi xin trình bày cách hai, điểm mấu chốt là xác định giao điểm của
EF với mặt phẳng ( ABCD). Cách 2: Trang 71
Trong mặt phẳng (SMD), gọi P là giao điểm của EF với M D .
Trong mặt phẳng ( ABCD), gọi H, L là giao điểm của P,G với CD, AB .
Trong mặt phẳng (SAB), gọi K là giao điểm của LF với SA.
Trong mặt phẳng (SCD), gọi N là giao điểm của EH với SC . (
ì EFG) Ç( ABCD) = LG;(EFG) Ç(SBC) = GN ï Ta có: (
í EFG) Ç(SCD) = NE;(EFG) Ç(SAD) = EK . ( ï EFG î )Ç(SAB) = KL
Vậy ngũ giác LGNEK là thiết diện của hình chóp cắt bởi (EFG).
Câu 68. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD, E là một điểm thuộc mặt
bên (SCD). F, G lần lượt là các điểm thuộc cạnh AB và .
SB Thiết diện của hình chóp S.ABCD cắt bởi
mặt phẳng (EFG) có thể là:
A. Tam giác, tứ giác.
B. Tứ giác, ngũ giác.
C. Tam giác, ngũ giác. D. Ngũ giác. Lời giải Chọn B.
Trong mặt phẳng ( ABCD), gọi H là giao điểm của AB và CD . Trong mặt phẳng (SAB), gọi I là giao
điểm của FG và SH .
Xét các trường hợp sau: Trang 72 Trường hợp 1:
Trong mặt phẳng (SCD), IE cắt SC tại J và cắt đoạn CD tại K .
Ta có J Î IE Ì (EFG) nên J là giao điểm của (EFG) với SC ,
K Î IE Ì (EFG) nên K là giao điểm của (EFG) với CD . ( ì EFG ï
)Ç( ABCD) = FK; (EFG)Ç(SAB) = FG Ta có í ( ï EFG î
)Ç(SBC) = GJ; (EFG)Ç(SCD) = JK
Suy ra tứ giác KFGJ là thiết diện của hình chóp cắt bởi (EFG). Trường hợp 2: Trang 73
Trong mặt phẳng (SCD), IE cắt SC tại J và cắt đoạn SD tại K (cắt CD tại một điểm nằm ngoài đoạn CD ).
Trong mặt phẳng (SBC): BG CJ
Nếu GJ song song với BC thì ta có: =
. Gọi T là giao điểm của IE với CD. S G S J
Áp dụng định lí Menelaus vào các tam giác SBH và SCH ta có FB IH S G TC IH S J FB TC . . =1 = . . Þ =
. Điều này chỉ xảy ra khi T thuộc đoạn CD (vô lí) FH IS GB TH IS JC FH TH
Do vây GJ cắt BC , giả sử tại L .
Trong mặt phẳng ( ABCD), gọi M là giao điểm của LF với AD . (
ì EFG) Ç( ABCD) = FM; (EFG) Ç(SAB) = FG ï Ta có (
í EFG) Ç(SBC) = GJ; (EFG) Ç(SCD) = JK ( ï EFG î )Ç(SAD) = KM
Suy ra ngũ giác KJGFM là thiết diện của hình chóp cắt bởi (EFG).
Vậy thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (EFG) hoặc là tứ giác hoặc là ngũ giác. !!!" !!!"
Câu 69. Cho hình chóp S.ABCD, E là trung điểm của SB, F thuộc SC sao cho 3SF = 2SC, G là một
điểm thuộc miền trong tam giác SAD . Thiết diện của hình chóp cắt bởi mặt phẳng (EFG) là:
A. Tam giác, tứ giác.
B. Tứ giác, ngũ giác.
C. Tam giác, ngũ giác. D. Ngũ giác. Lời giải Chọn B.
Trong mặt phẳng (SBC), gọi J là giao điểm của EF với BC . Trong mặt phẳng (SAD , gọi ) I là giao
điểm của SG với AD . Trong mặt phẳng ( ABCD), gọi N là giao điểm của IJ với CD. Trong mặt
phẳng (SIJ ), gọi K là giáo điểm của JG với SN .
Trong mặt phẳng (SCD), có hai khả năng xảy ra như sau:
Trường hợp 1: FK cắt đoạn CD tại P . Trang 74 S R G E Q D A I K F P B N C J
Trong mặt phẳng ( ABCD), gọi Q là giao điểm của JP với AD . Trong mặt phẳng (SAD , gọi ) R là
giao điểm của QG với SA. (
ì EFG) Ç( ABCD) = P ;
Q (EFG) Ç(SAD) = QR ï Ta có (
í EFG) Ç(SAB) = RE; (EFG) Ç(SBC ) = EF ( ï EFG î )Ç(SCD) = FP
Trường hợp này, ngũ giác REFPQ là thiết diện của hình chóp S.ABCD cắt bởi (EFG).
Trường hợp 2: FK cắt SD tại H ( FK không cắt đoạn CD ). S M G H E K I D A F P B N C J
Trong mặt phẳng (SAD), gọi M là giao điểm của HG với SA ( HG không thể cắt đoạn AD vì giả sử
ngược lại HG cắt cạnh AD tại O , khi đó JO sẽ cắt cạnh CD (vô lí vì (EFG) đã cắt cạnh SC, SD )). ( ì EFG ï
)Ç(SCD) = FH; (EFG)Ç(SAD) = MH Khi đó í ( ï EFG î
)Ç(SAB) = ME; (EFG)Ç(SBC) = EF
Trường hợp này, tứ giác MEFH là thiết diện của hình chóp cắt bởi (EFG). Trang 75
Câu 70. Cho tứ diện ABCD có cạnh bằng a. Trên tia đối của các tia CB, DA lần lượt lấy các điểm E, F
sao cho CE = a, DF = a . Gọi M là trung điểm của đoạn .
AB Diện tích S thiết diện của tứ diện ABCD cắt
bởi mặt phẳng (MEF ) là: 2 a 33 2 a 2 a 2 a 33 A. S = . B. S = . C. S = . D. S = . 18 3 6 9 Lời giải Chọn C. A M K H B F D C E
Trong mặt phẳng ( ABC), gọi H là giao điểm của ME với AC .
Trong mặt phẳng ( ABD), gọi K là giao điểm của MF và AD . (
ì MEF ) Ç( ABC) = MH ï Ta có: (
í MEF ) Ç( ABD) = MK . ( ï MEF î )Ç( ACD) = HK
Do đó tam giác MHK là thiết diện của tứ diện cắt bởi (MEF ).
Dễ thấy H , K lần lượt là trọng tâm của các tam giác ABE và ABF . 2a
Ta có: AH = AK = HK = . 3 2a
Xét hai tam giác AMH và AMK có AM chung, ∑ ∑ 0
MAH = MAK = 60 , AH = AK = nên hai tam giác 3
này bằng nhau. Suy ra MH = MK . Vậy tam giác MHK cân tại M .
Áp dụng định lí cosin trong tam giác AMH : 2 2 2 2 æ a ö æ 2a ö a 13a a 13 2 2 2 0
MH = AM + AH - 2AMAH.cos 60 = + - = Þ MH = . ç ÷ ç ÷ è 2 ø è 3 ø 3 36 6
Gọi I là trung điểm của đoạn HK . Ta có MI ^ HK . Trang 76 2 2 2 13a a a a Suy ra: 2 2 2
MI = MH - HI = - = Þ MI = . 36 9 4 2 2 1 1 2a a a
Diện tích thiết diện MHK là: S = MI.HK = . . = . 2 2 3 2 6
Câu 71. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (a ) cắt các cạnh bên ,
SA SB, SC, SD tương ứng tại các điểm E, F, G, H . Gọi I = AC Ç BD, J = EG Ç SI . Mệnh đề nào sau đây đúng? SA SC SB SD SA SC SI A. + = + . B. + ³ 2 . SE SG SF SH SE SG SJ SA SC SB SD SB SD SI C. + > + . D. + ³ 2 . SE SG SF SH SF SH SJ Lời giải Chọn C. S G E T C K
Xét trường hợp đặc biệt E, F,G, H lần lượt là trung điểm của , SA SB, SC, .
SD Khi đó ta dễ dàng loại được đáp ánD.
Dựng AT / /EG(T ÎSI ),CK / /EG(KESI ) SA ST SC SK IT IA
Theo định lý Thales, ta có: = , = ; = = 1 SE SJ SG SJ IK IC SA SC ST + SK
SI - IT + SI + IK SI Suy ra: + = = = 2 SE SG SJ SJ SJ Như vậy, ý B bị loại. SB SD SI
Tương tự, ta chứng minh được + = 2 . SF SH SJ
Từ đây ta thấy ngay ý C bị loại và A là đáp án A là đáp án lựa chọn. Trang 77
Chú ý: Cho tam giác ABC. Gọi O là trung điểm AC, M, N là hai điểm nằm trên cạnh AB, AC. MN cắt BO BA BC 2BO tại I. Khi đó: + = . BM BN BI
Câu 72. Cho tứ diện ABCD có M , N lần lượt là trung điểm của AB,CD và P là điểm thuộc cạnh
BC ( P không là trung điểm BC ). Gọi Q là giao điểm của (MNP) với AD, I là giao điểm của MN
với PQ. Mệnh đề nào sau đây đúng? A. S = 2S . B. S = 2S . C. S = 4S D. S = 4S . MNPQ MPN MNPQ MPQ MNPQ MPI MNPQ PIN Lời giải Chọn A. A M Q B D j I P N C
Do tứ diện ABCD có 4 mặt nên thiết diện không thể là ngũ giác hay lục giác. Nó chỉ có thể là tam giác hoặc tứ giác.
Trong mp ( ABC), gọi K = MP Ç AC (P không phải là trung điểm đoạn BC nên MP cắt AC)
Trong mp ( ACD), gọi Q = KN Ç AD
Do QÎ KN Ì (MNP) nên Q = (MNP)Ç AD (
ì MNP) Ç( ABD) = MQ ( ï
ï MNP) Ç( ABC) = MP Ta có: í (MNP ï )Ç(BCD) = PN ( ï MNP î )Ç(ACD) = NQ
Suy ra thiết diện cần tìm là tứ giác MPN . Q Ta chọn đáp án B. AM BP CN DQ BP DQ do M , N, ,
P Q đồng phẳng nên . . . =1Þ . = 1 BM CP DN AQ CP AQ BP AQ
(Do M, N lần lượt là trung điểm của AB, CD).Từ đây suy ra = . CP DQ Trang 78 BP !!!" !!!" !!!" !!!" Giả sử
= k. Khi đó ta suy ra BP = k PC, AQ = kQD PC !!!" !!!" !!!" !!!"
Suy ra BP + AQ = -k (CP + QD)( ) 1
Do J là trung điểm của PQ. !!!" !!!" !!!" !!!"
ìïMJ = MB + BP + PJ !!!" !!!" !!!"
Ta có: í!!!" !!!" !!!" !!!" Þ 2MJ = AQ + BP(2)
ïîMJ = MA+ AQ + QJ !!!" !!!" !!!"
Chứng minh tương tự ta cũng có: 2NJ = CP + DQ(3) !!!" !!!"
Từ (1,2,3) suy ra MJ = k
- NJ . Điều này dẫn đến M, N, J thẳng hàng. Như vậy I trùng J. Điều này suy ra S = 2S . MNPQ MPN
Câu 73. *Cho hình chóp SA A ...A với đáy là đa giác lồi A A ...A n ³ 3,nΕ . 1 2 n ( ) Trên tia đối của tia 1 2 n
A S lấy điểm B , B ,...B là các điểm nằm trên cạnh SA , SA . Thiết diện của hình chóp cắt bởi mặt 1 1 2 n 2 n phẳng (B B B 1 2 n ) là:
A. Đa giác n - 2 cạnh.
B. Đa giác n -1 cạnh.
C. Đa giác n cạnh.
D. Đa giác n +1 cạnh. Lời giải Chọn D. S Bn Bk Ik An C1 A1 A O k k B2 C2 B1 A2
Trong mặt phẳng (SA A C B B A A 1 2 ) gọi là giao điểm của với . 2 1 2 1 2
Trong mặt phẳng (SA A C B B A A 1 n ) gọi là giao điểm của với . n 1 n 1 n
Trong mặt phẳng ( A A ...A
O (k = 3,4,...,n - ) 1 A A A A 1 2 n ) gọi là giao điểm của với . k 1 k 2 n
Trong mặt phẳng (SA A
I (k = 3,4,...,n - ) 1 SO B B 2 n ) , gọi là giao điểm của với . k k 2 n
Trong mặt phẳng (SA A
B (k = 3,4,...,n - ) 1 SA B I 1 k ) , gọi là giao điểm của với . k k 1 k
Do B Î B I Ì B B B B
SA (k = 3,4,...,n - ) 1 (B B B 1 2 n ) k 1 k
( 1 2 n) nên là giao điểm của với mặt phẳng . k k Trang 79
Vậy thiết diện của hình chóp cắt bởi (B B B C B ...B C 1 2 n ) là đa giác . 2 2 n n Trang 80