









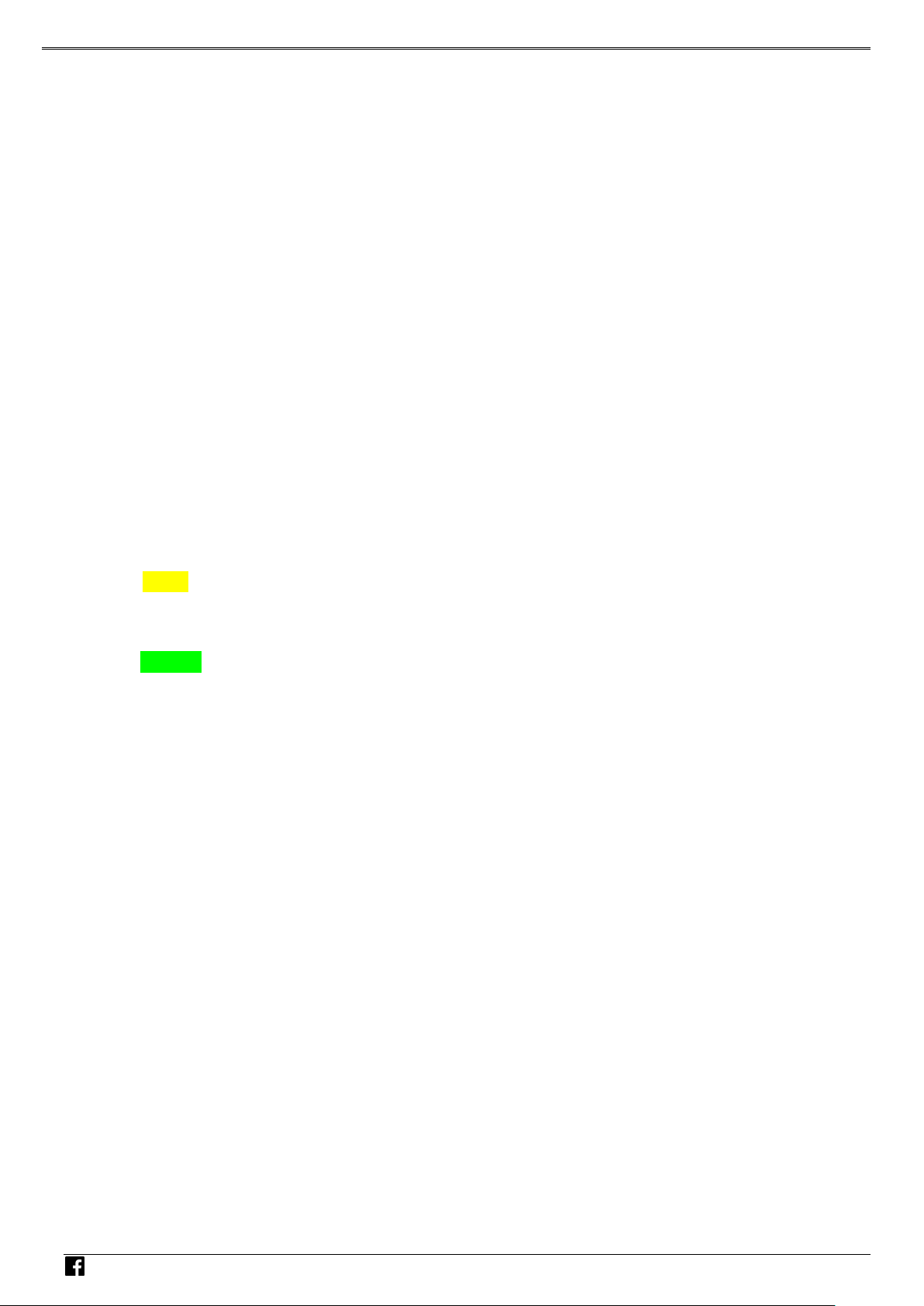


















Preview text:
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chuyên đề:
CÁC DẠNG TOÁN VỀ HÀM ẨN
LIÊN QUAN ĐẾN CỰC TRỊ NHÓ CỦA HÀM SỐ M TOÁN
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ V D
PHẦN 1: BIẾT ĐẶC ĐIỂM CỦA HÀM SỐ y = f (x) – VD Dạng toán 1.
Các bài toán về cực trị của hàm ẩn bậc 2 (dành cho khối 10). C Dạng toán 2.
Dạng toán có thể tìm được biểu thức cụ thể của hàm số y = f (x) trong bài toán
không chứa tham số. Dạng toán 3.
Dạng toán có thể tìm được biểu thức cụ thể của hàm số y = f (x) trong bài toán chứa tham số. Dạng toán 4.
Biết đặc điểm của hàm số hoặc đồ thị, hoặc BBT hoặc đạo hàm của hàm f (x) , tìm
cực trị của hàm y = f (ϕ (x)); y = f ( f (x)),...y = f ( f ( f ...(x))) trong bài toán không chứa tham số Dạng toán 5.
Biết đặc điểm của hàm số hoặc BBT, hoặc BBT hoặc đạo hàm của hàm f (x) , tìm
cực trị của hàm y = f ( f (x)),...y = f ( f ( f ...(x))) trong bài toán chứa tham số. Dạng toán 6.
Biết đặc điểm của hàm số hoặc BBT, hoặc đồ thị, hoặc đạo hàm của hàm f (x) , NHÓ
tìm cực trị của hàm y = ln ( f (x)) f (x)
, y = e ,sin f (x), os
c f (x)... trong bài toán không chứa tham số M T Dạng toán 7.
Biết đặc điểm của hàm số hoặc BBT, hoặc đồ thị, hoặc đạo hàm của hàm f (x) , OÁN
tìm cực trị của hàm y = ln ( f (x)) f (x)
, y = e ,sin f (x), os
c f (x)... trong bài toán chứa tham số. Dạng toán 8.
Các dạng khác với các dạng đã đưa ra… VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
DẠNG 1. Các bài toán về cực trị của hàm ẩn bậc 2 (dành cho khối 10).
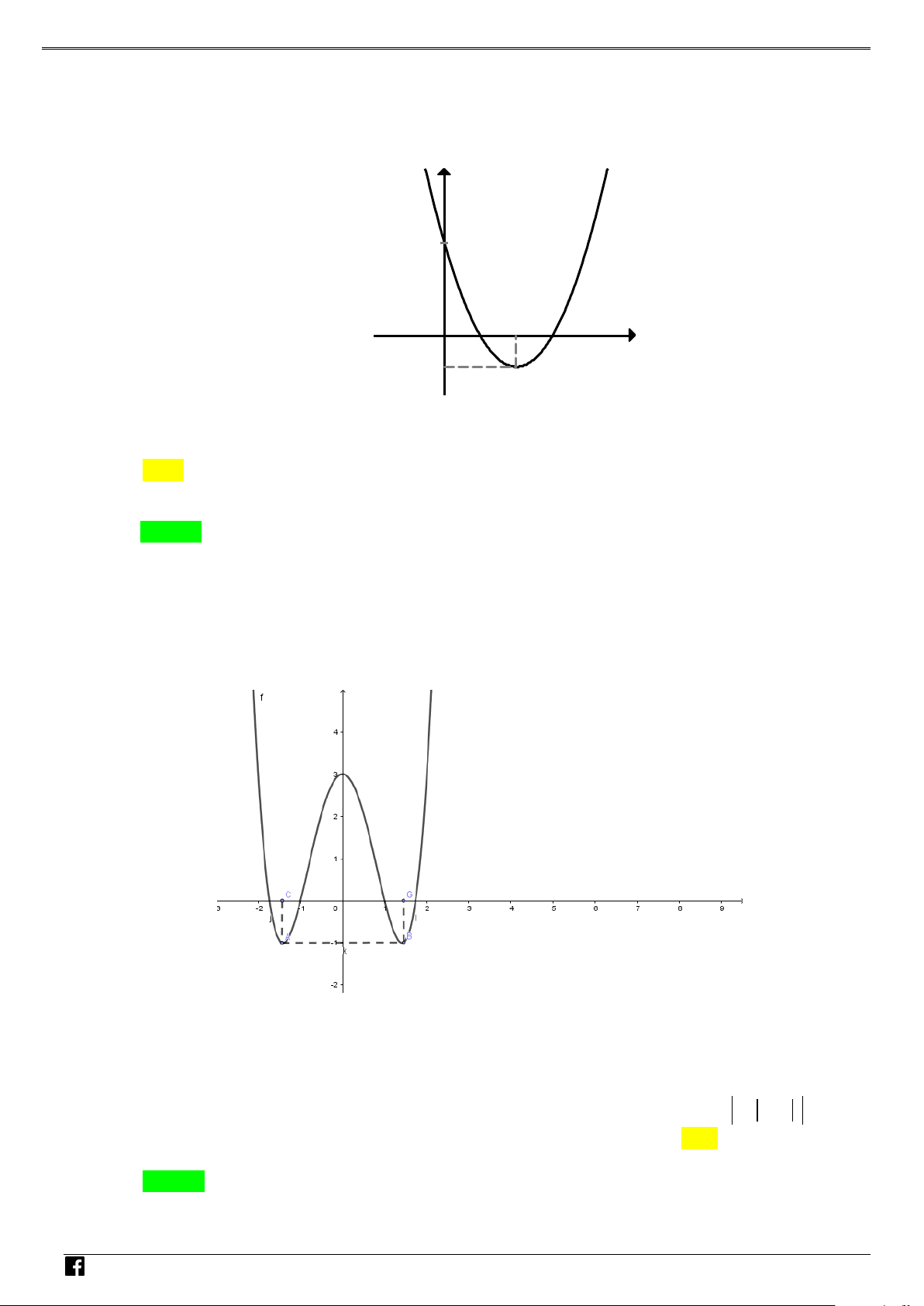
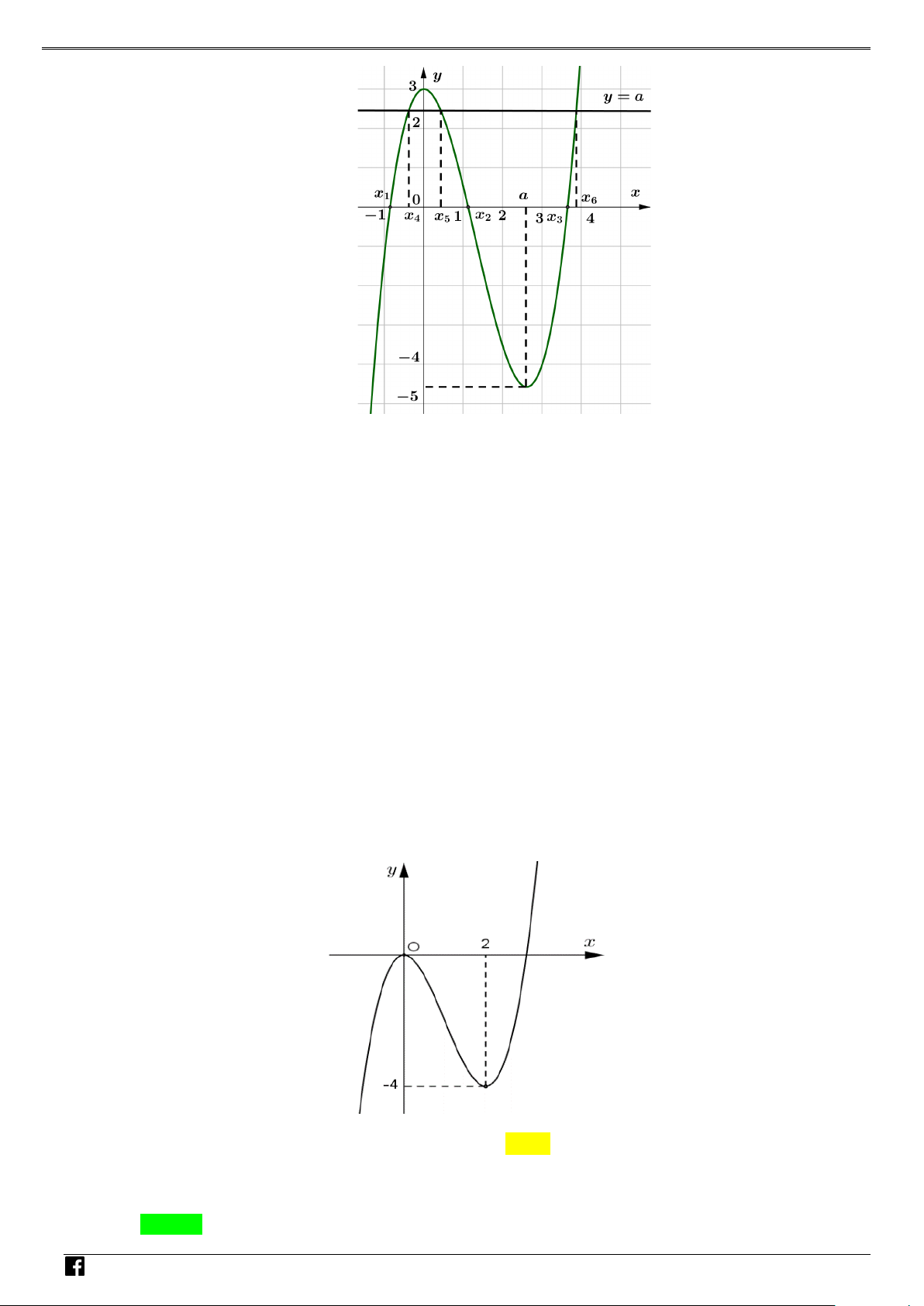
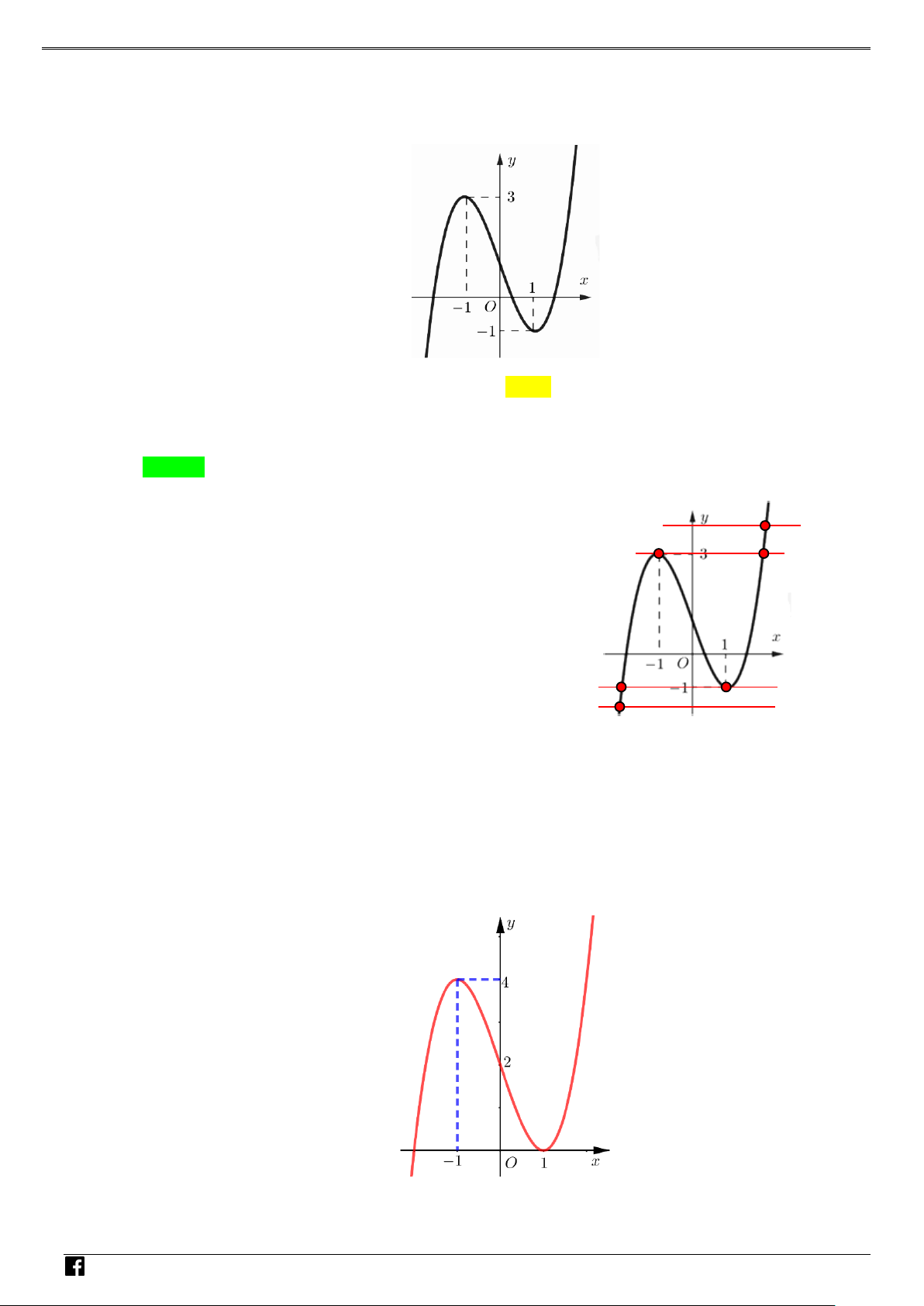
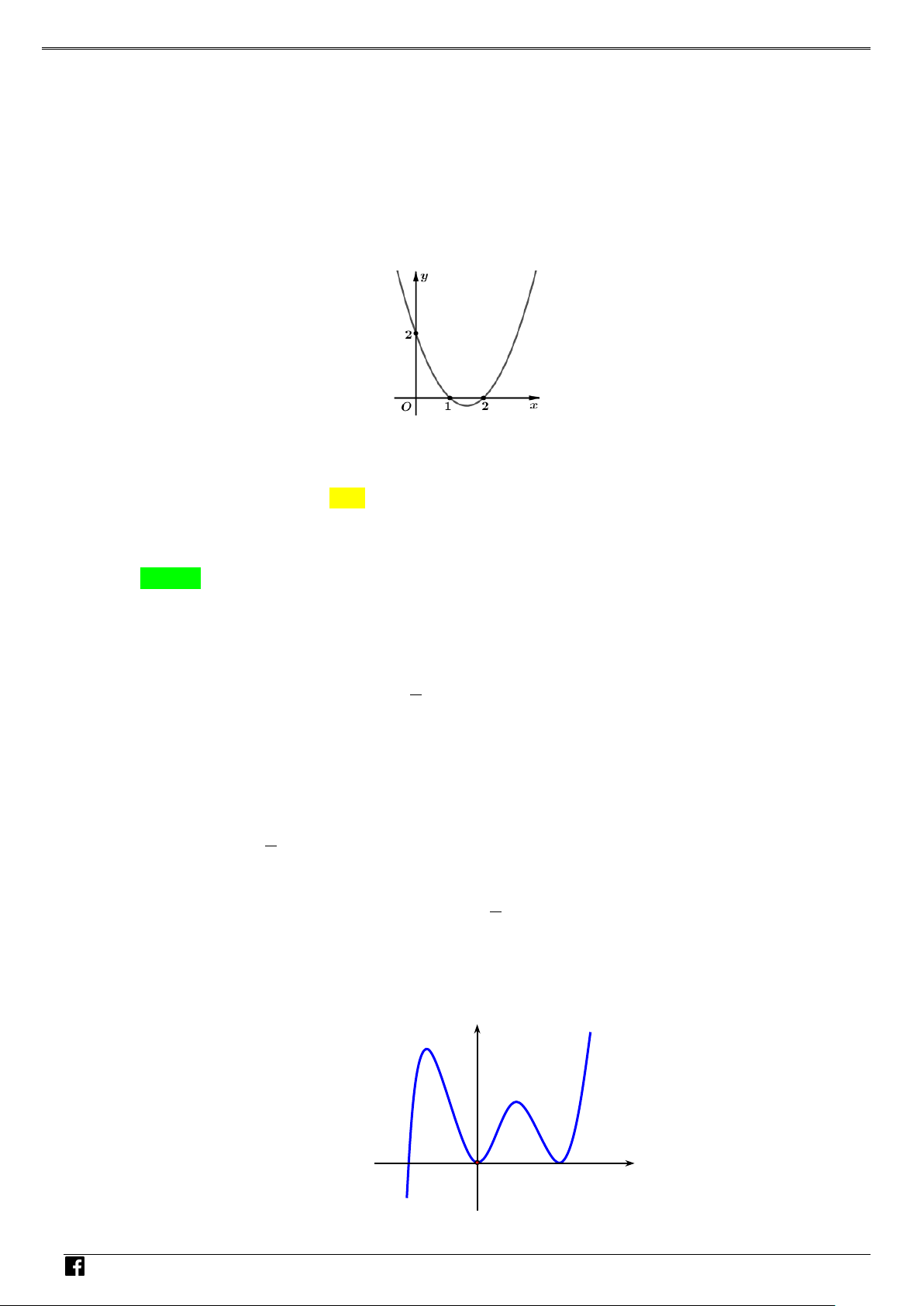
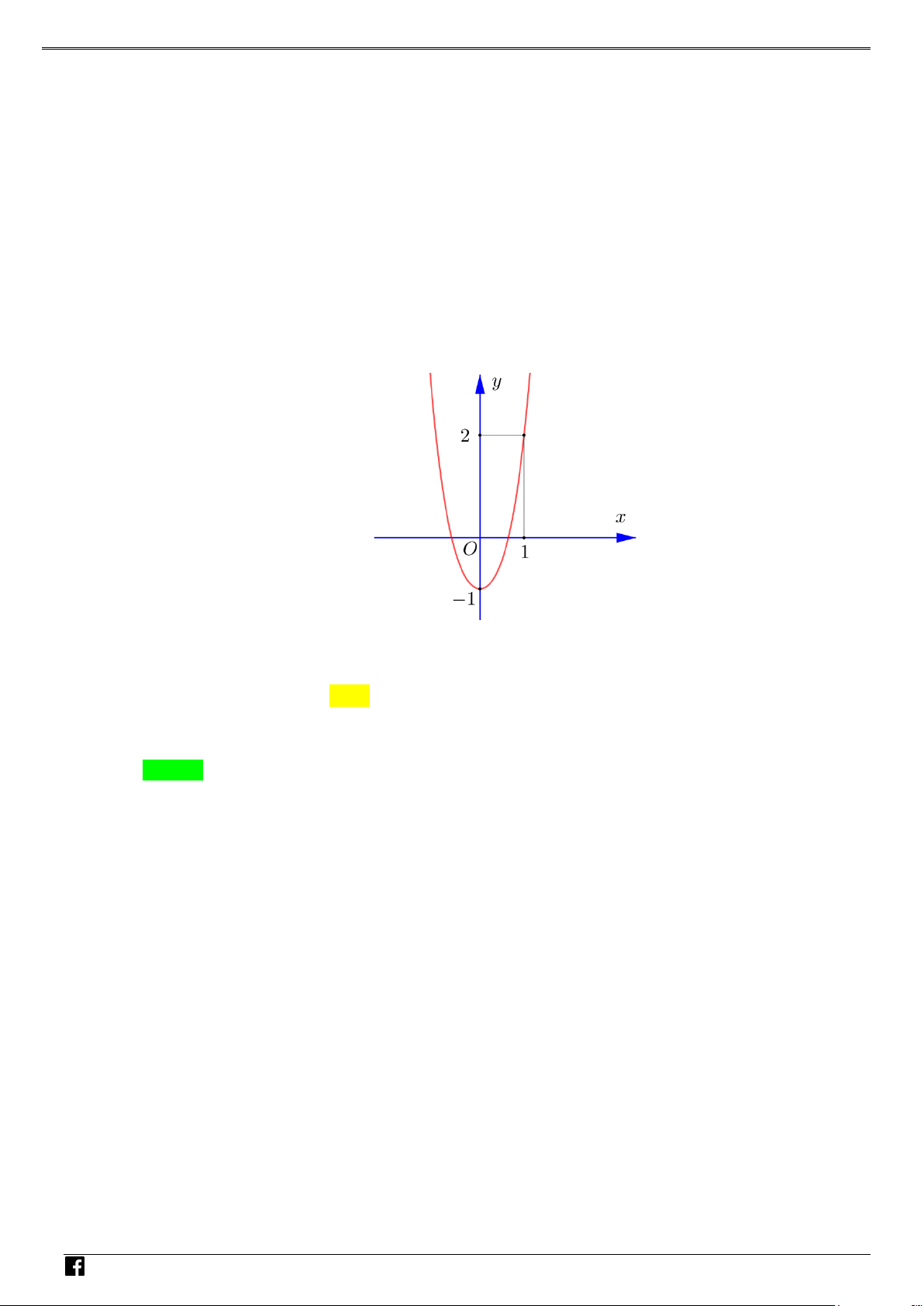
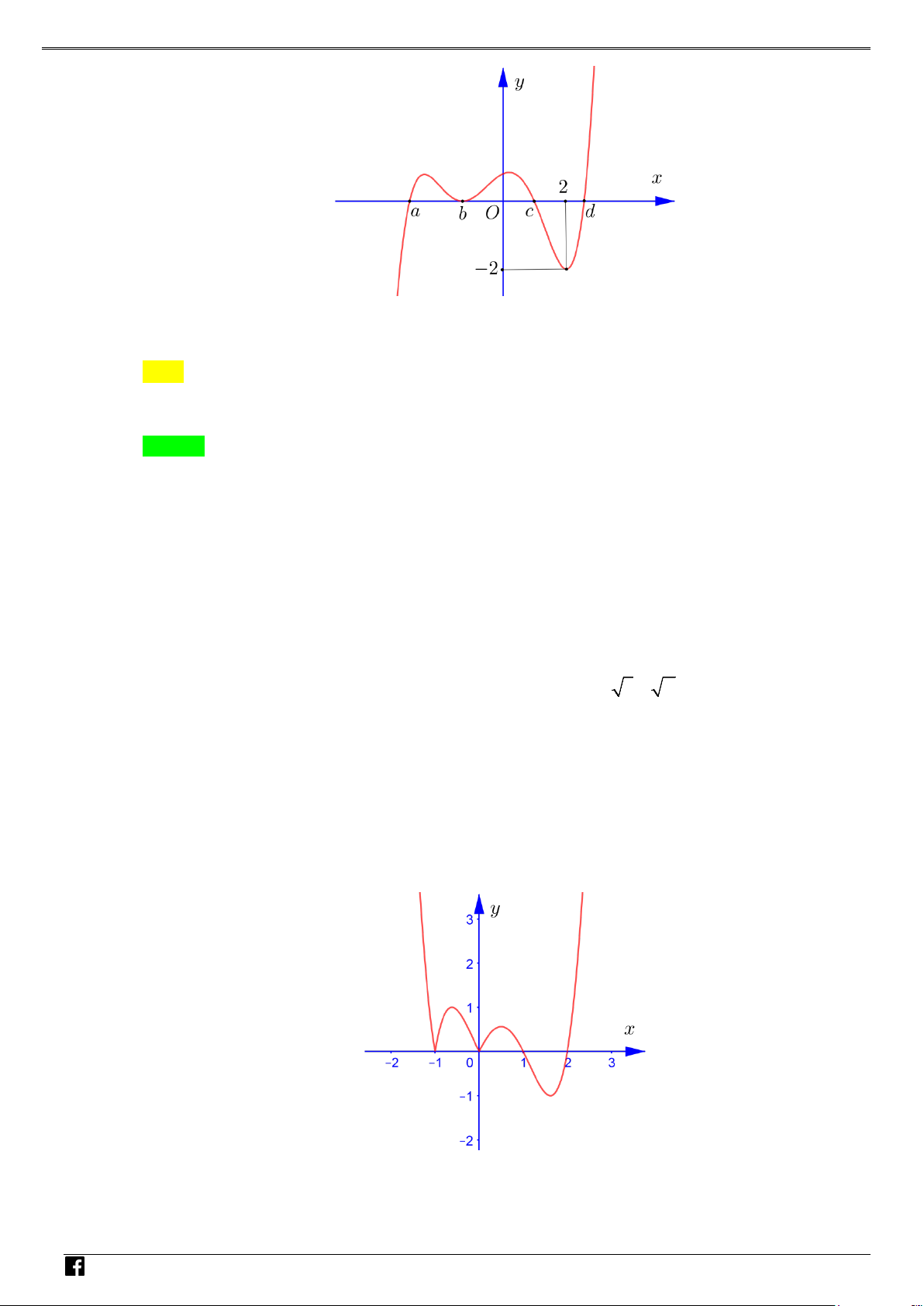
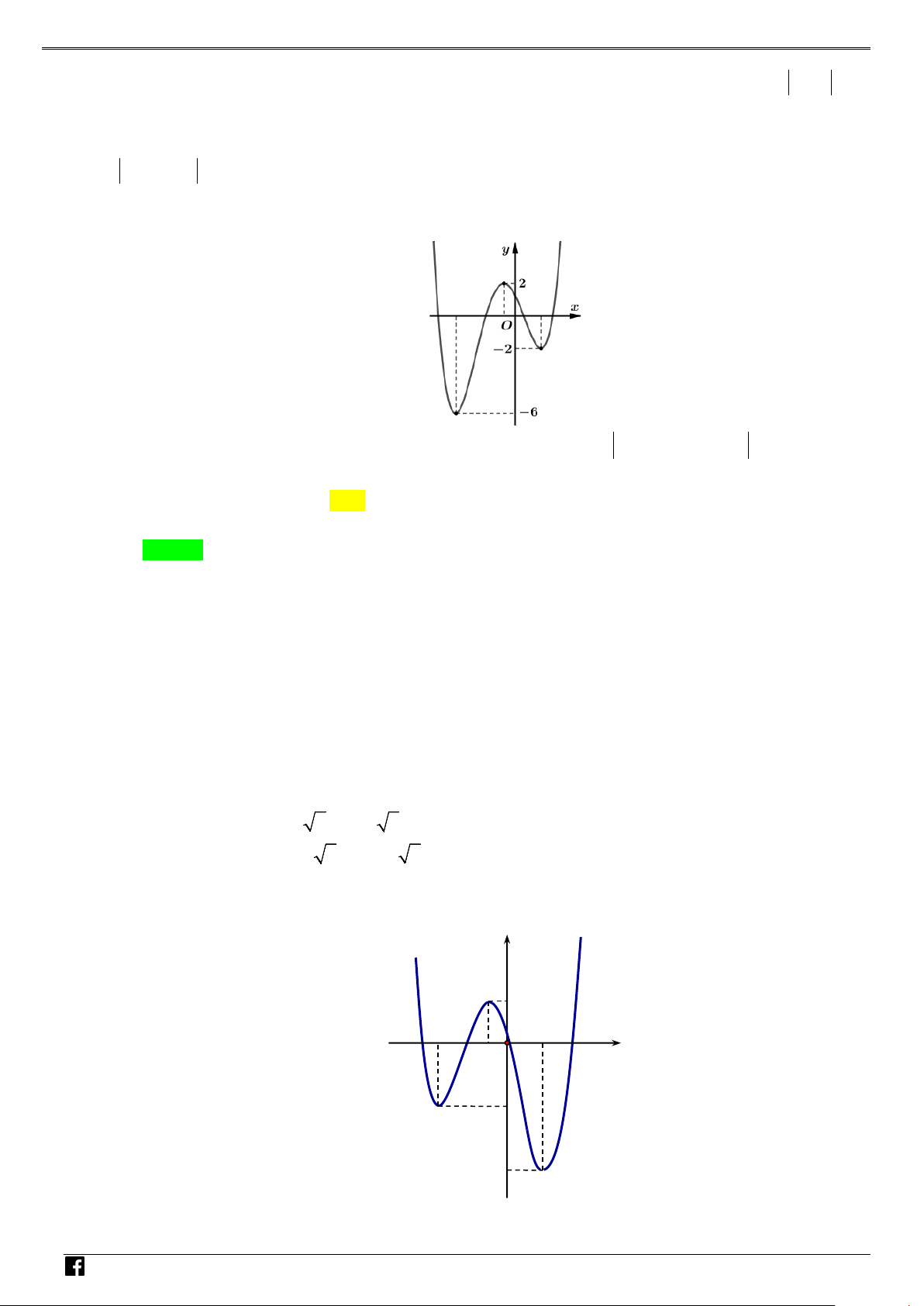
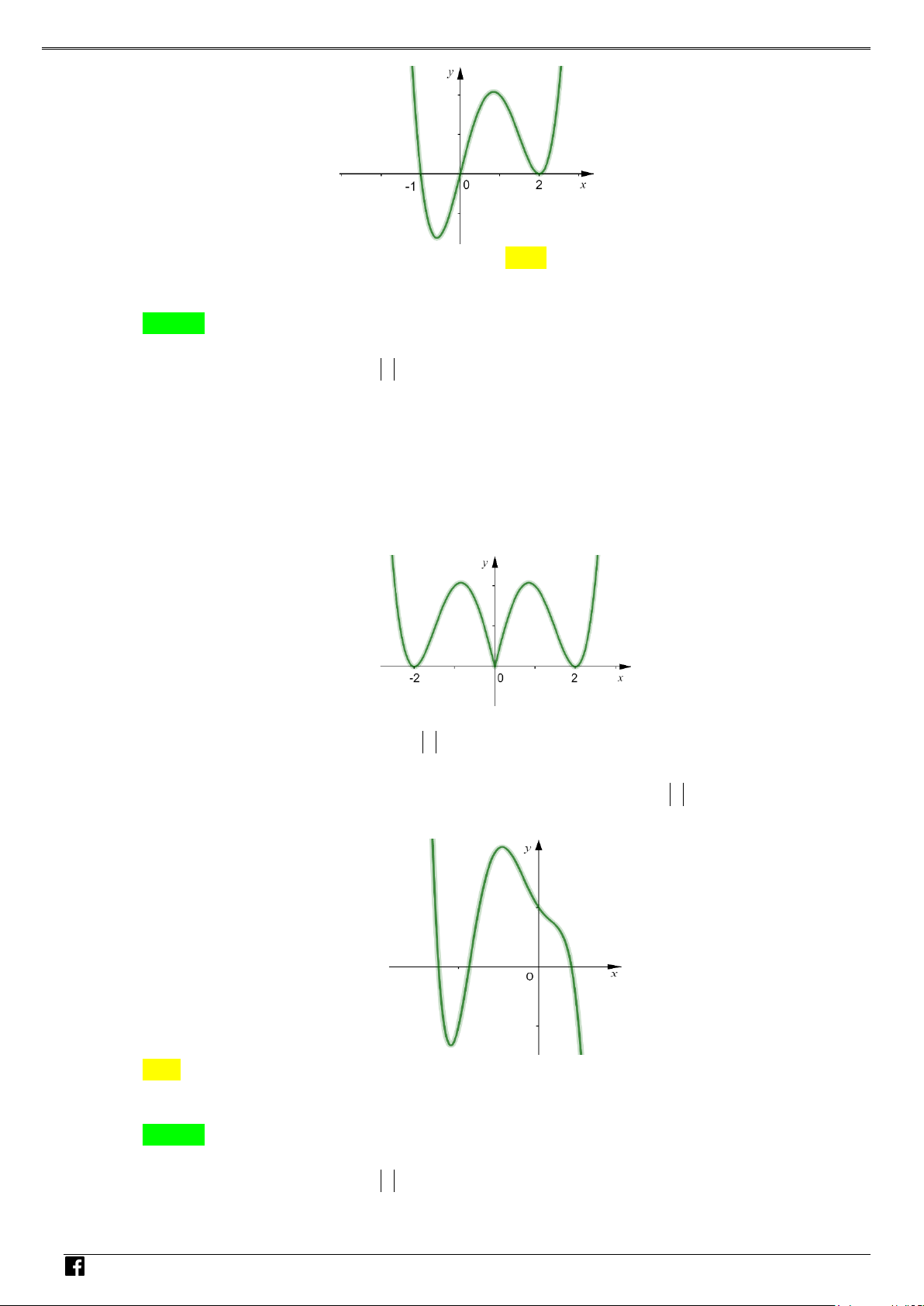
Câu 1: Cho hàm số 2
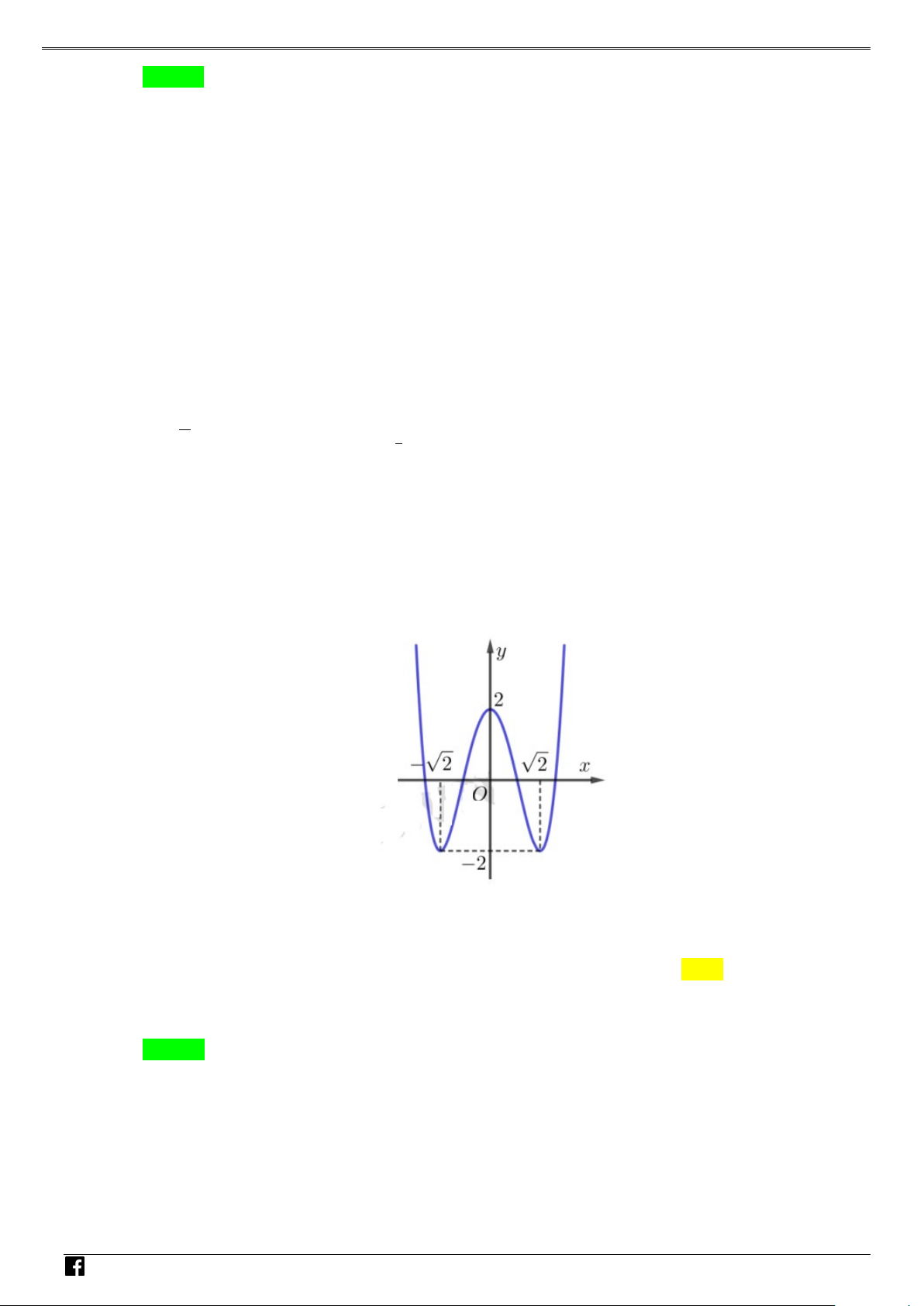
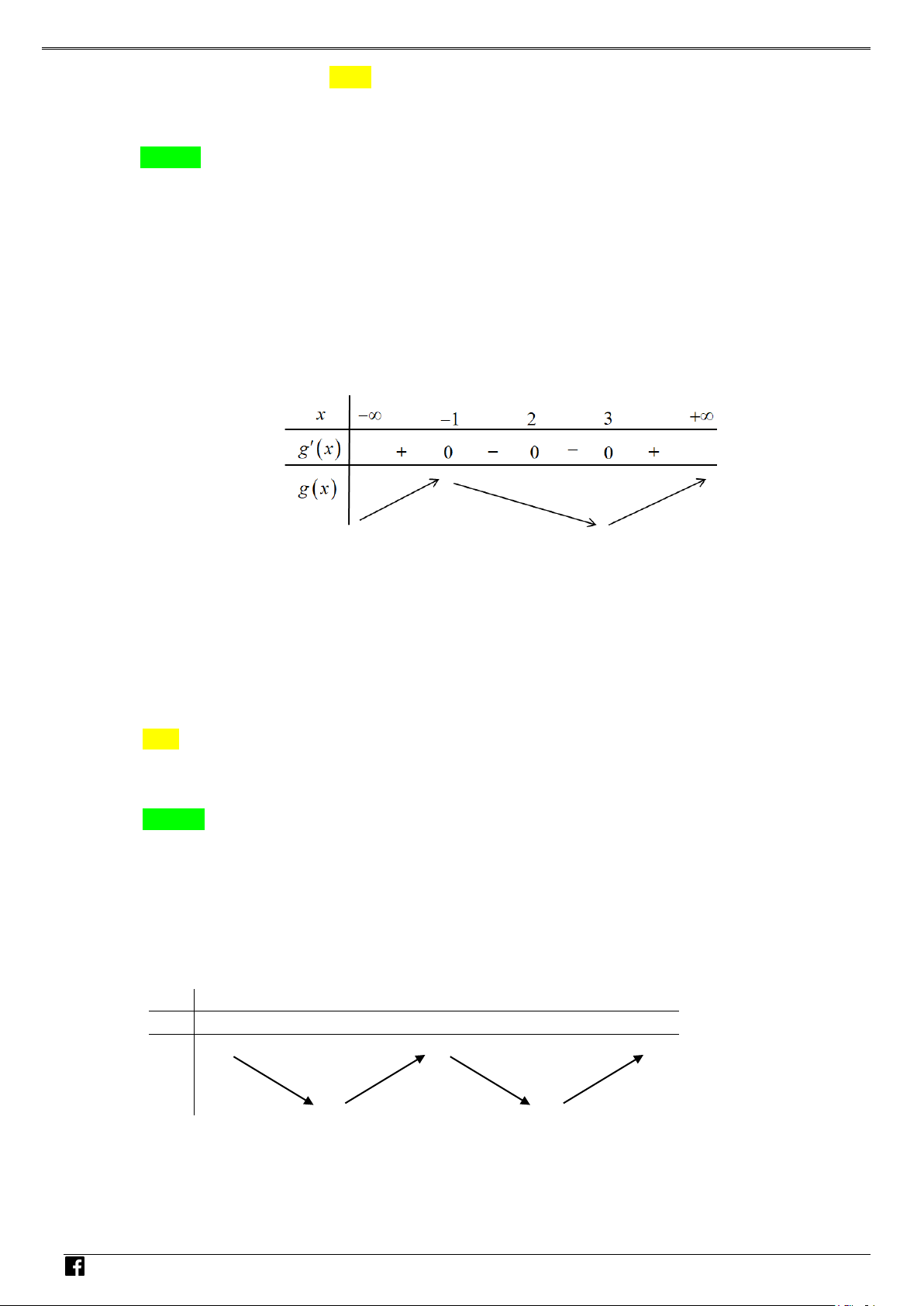
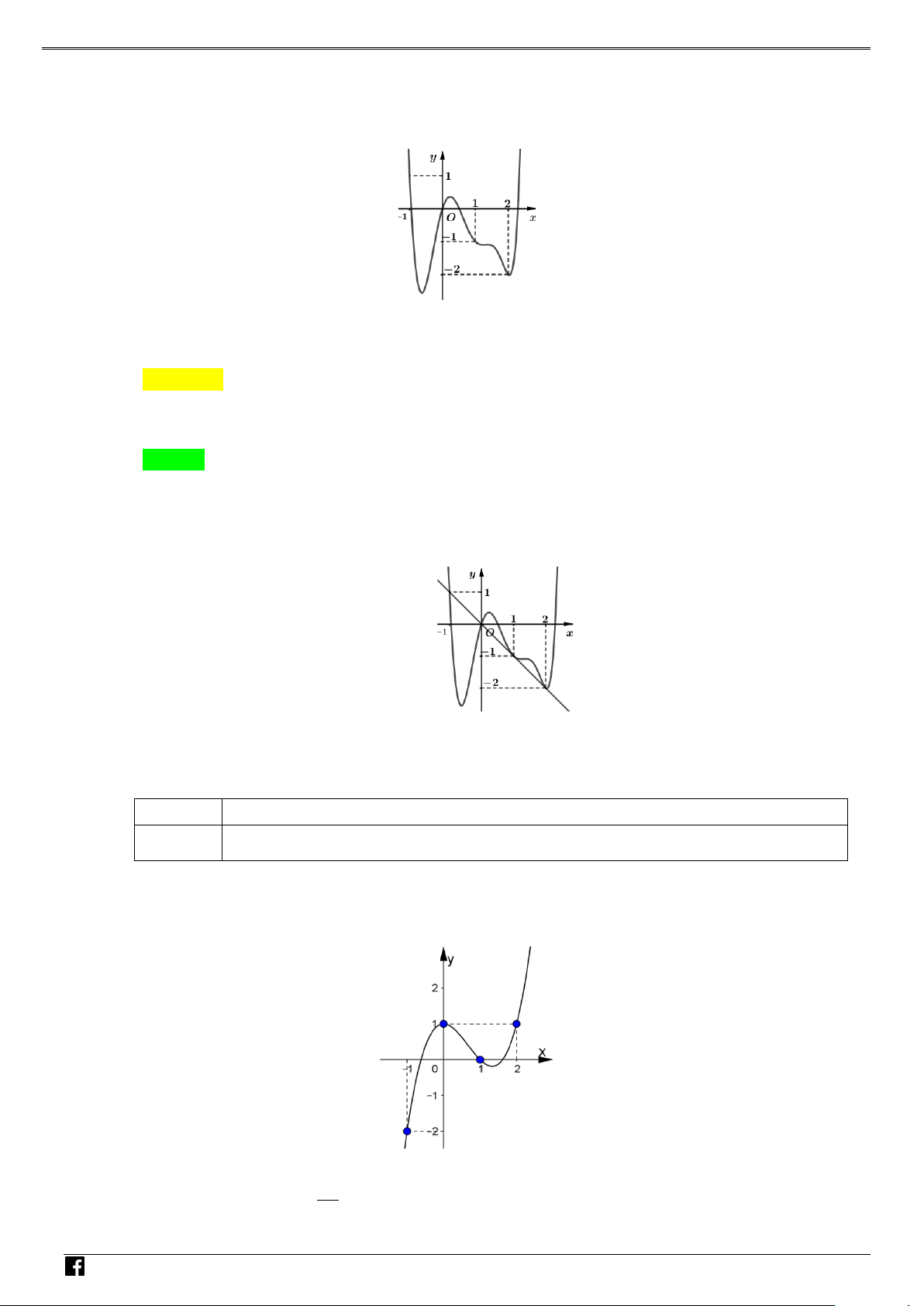
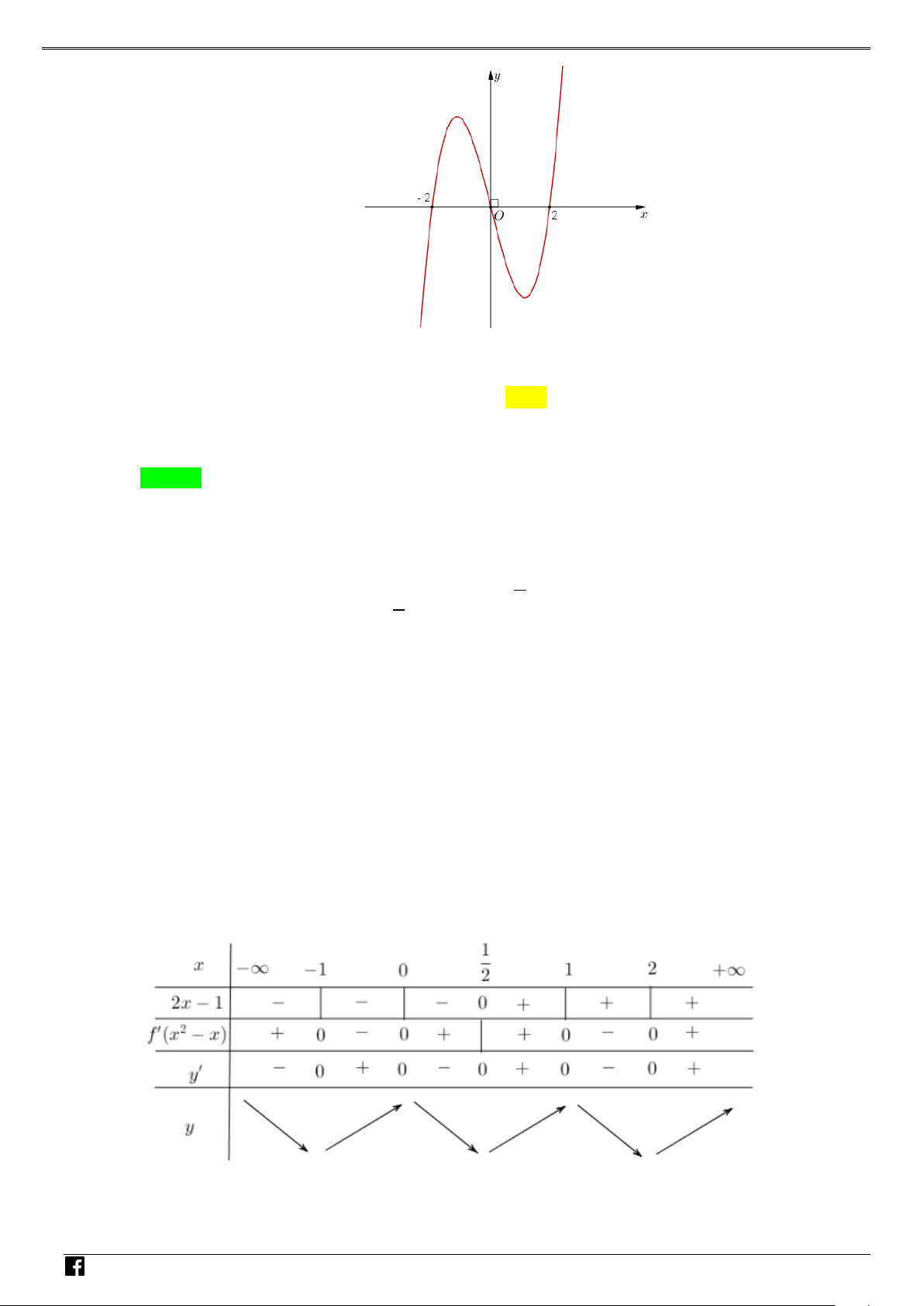
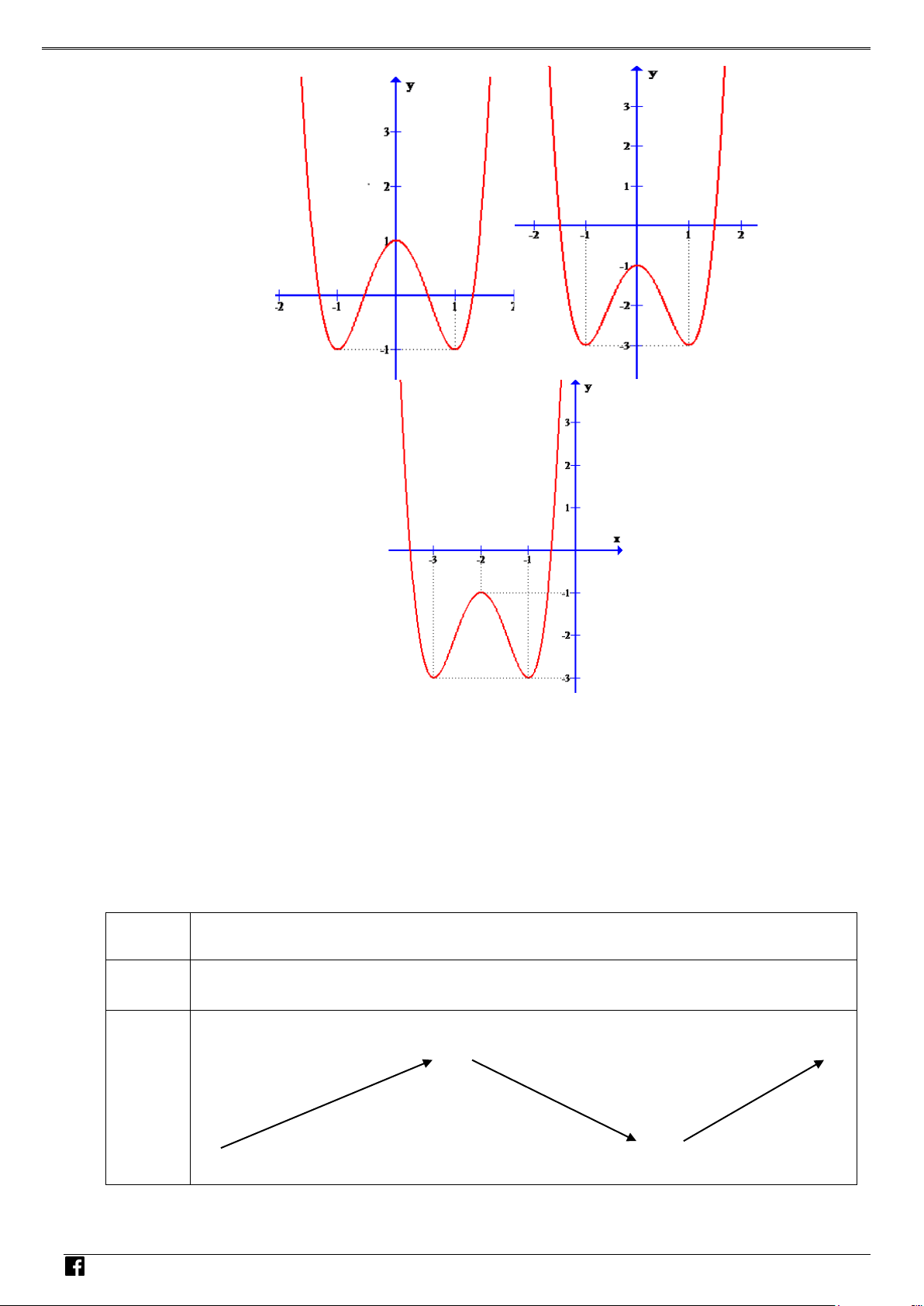
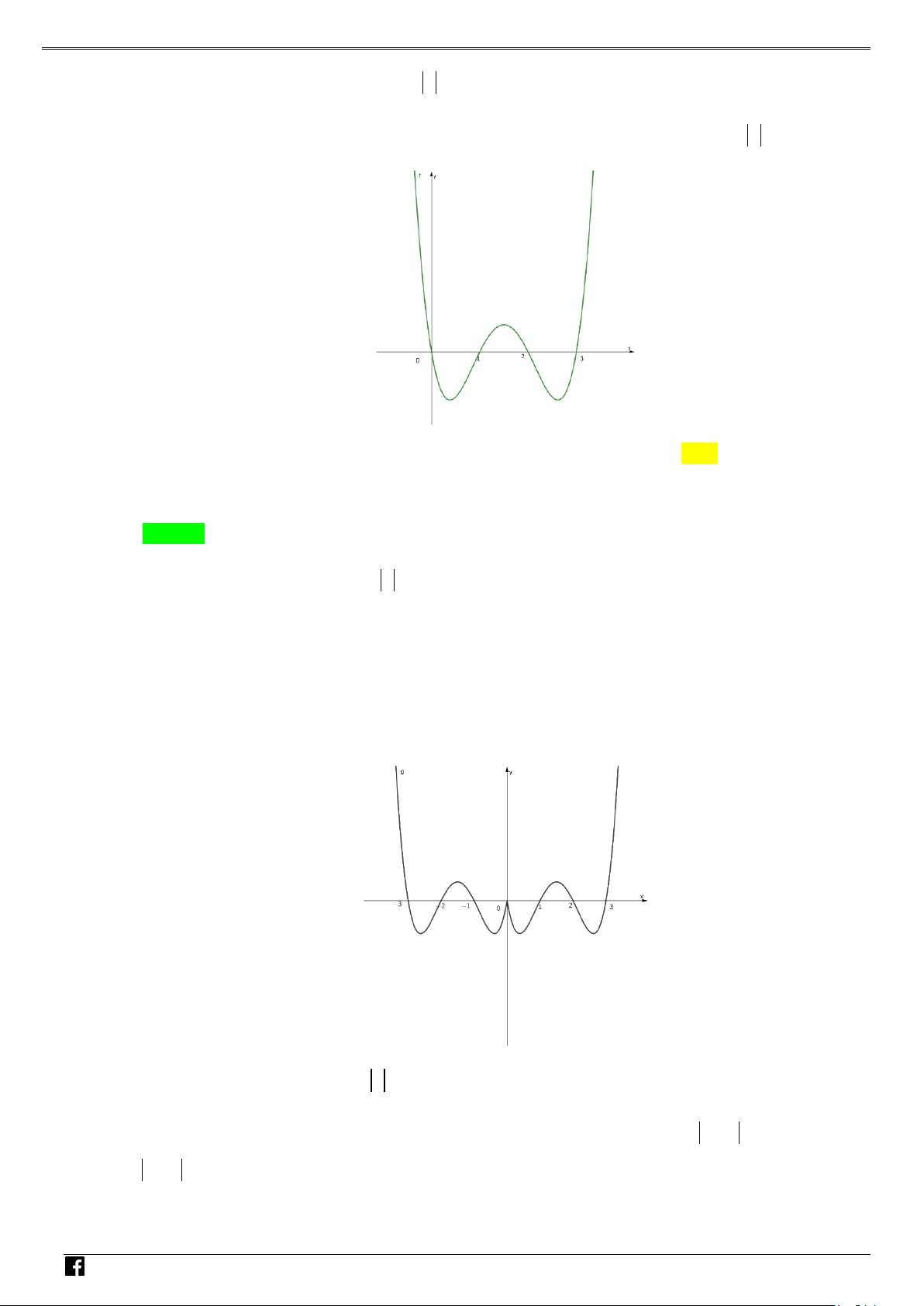
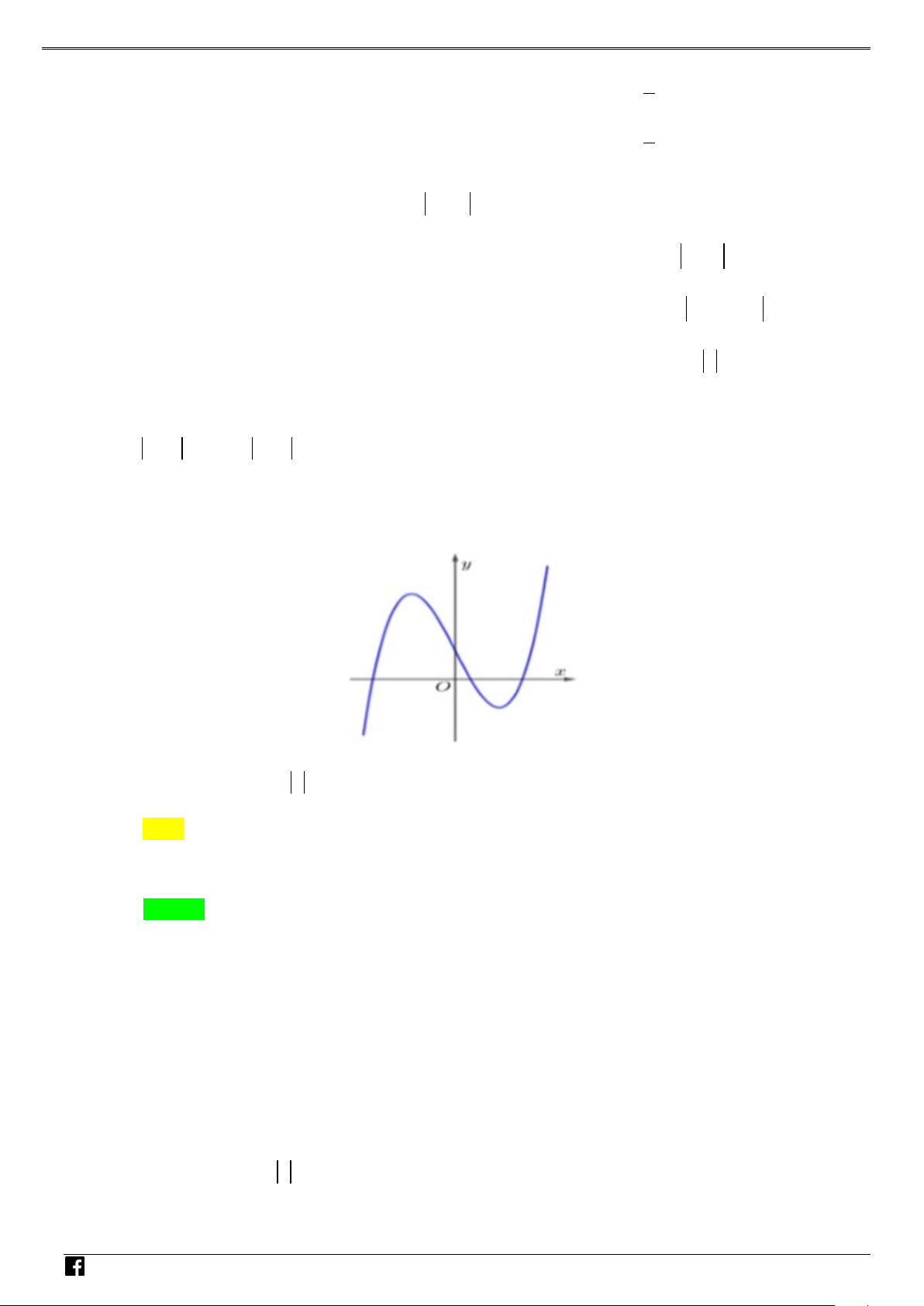
f x ax bx c đồ thị như hình bên. Hỏi hàm số 2 g
f x có mấy điểm cực trị? NHÓ y M T 3 OÁN V x D O 2 – VD 1 C A. 1 . B. 2 . C. 3. D. 4 . Lời giải Chọn C Xét hàm số = ( 2 g f x ) . Đặt 2
t = x . Khi đó với t ≥ 0 , hàm g = f (t) có đồ thị là dạng của đồ thị hàm số f (x) bên phải
trục Oy . Hàm số = ( 2
g f x ) là hàm chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng.
Từ đó ta có đồ thị hàm g (t) như sau: NHÓ M T OÁN VD – VD C
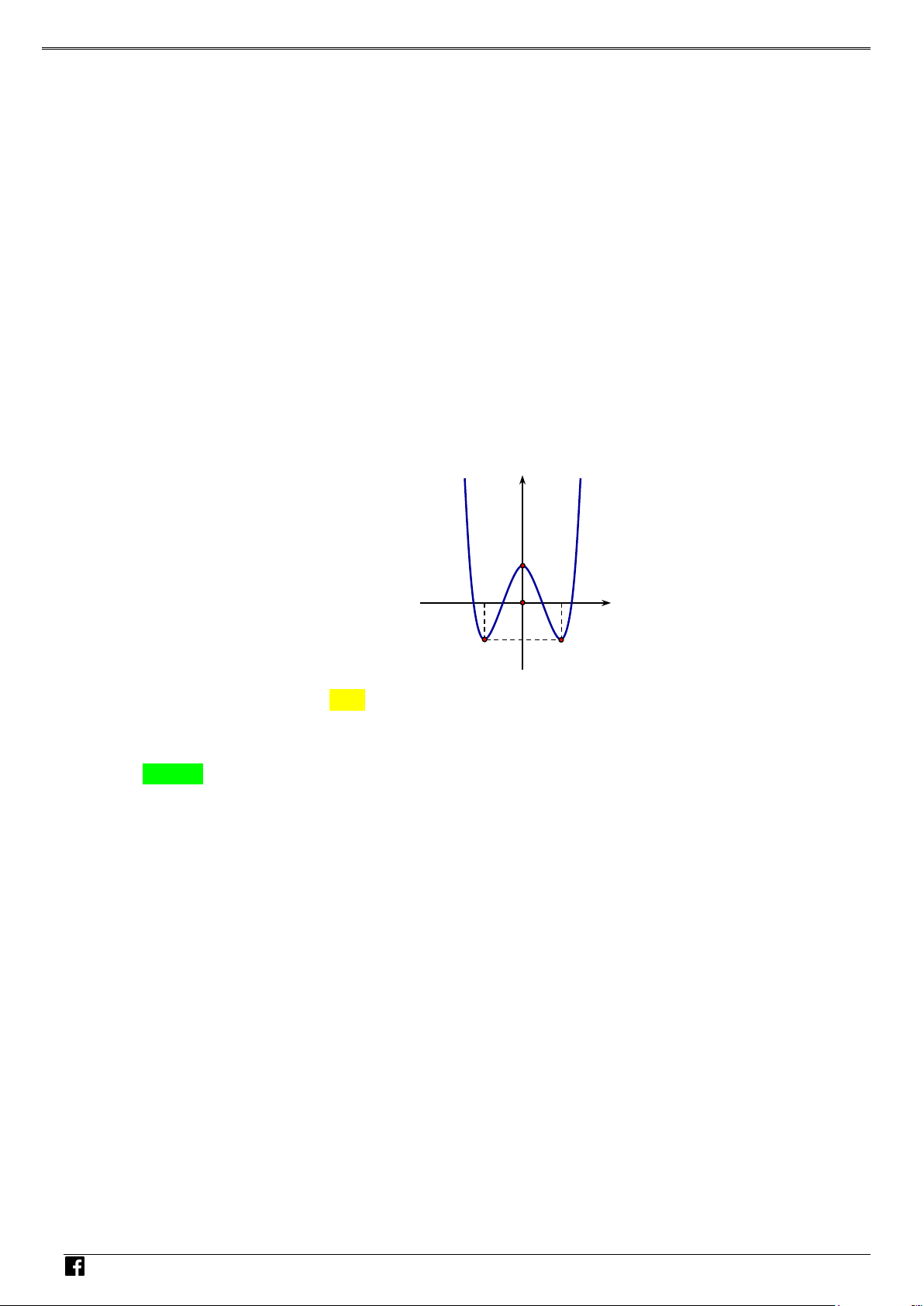
Dựa vào đồ thị hàm số ta thấy hàm số có 3 điểm cực trị. Câu 2: Cho parabol 2
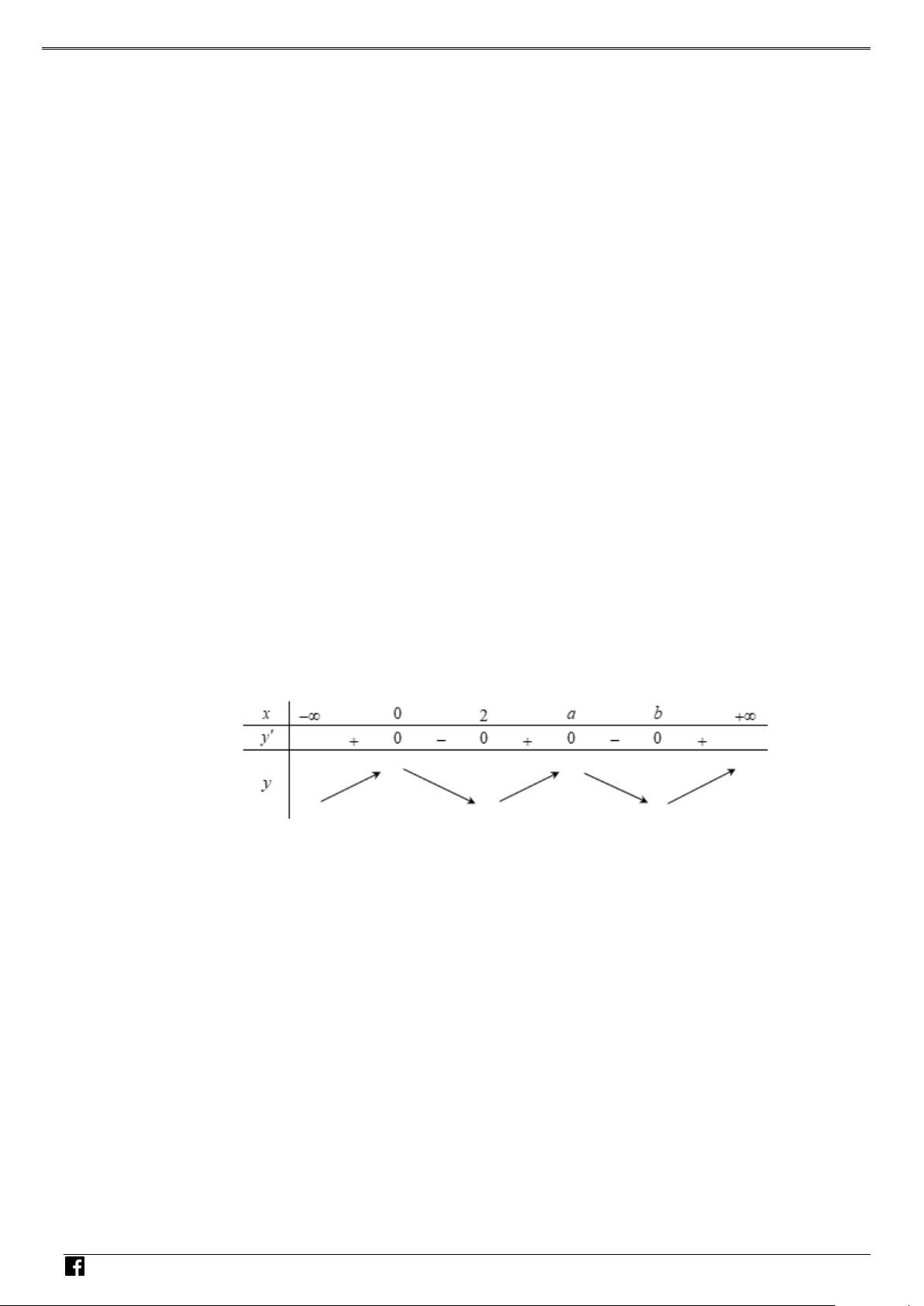
y = f (x) = ax + bx + c (a ≠ 0) cắt trục hoành tại hai điểm có hoành độ bằng 1 và 2,
biết rằng hàm số y = f (x) nghịch biến trên khoảng (x ;+∞) 0
và khoảng cách từ giao điểm của
parabol với trục tung đến điểm O bằng 4. Tìm số điểm cực trị của hàm số y = f ( x +1) . A. 2 . B. 3. C. 5. D. 7. Lời giải Chọn D
Do hàm số y = f (x) nghịch biến trên khoảng (x ;+ ∞ 0 ) nên a < 0 .
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Biết 2
y = f (x) = ax + bx + c (a ≠ 0) cắt trục hoành tại hai điểm có hoành độ bằng 1 và 2 nên 2 2
f (x) = a(x −1)(x − 2) = a(x −3x + 2) = ax −3ax + 2a . a = 2
Parabol cắt trục tung tại điểm có tung độ bằng 2a , ta có 2a = 4 ⇔ . NHÓ a = 2 −
Do hàm số y = f (x) nghịch biến trên khoảng (x ;+∞) − 0 nên a = 2 . M Vậy parabol là 2
y = f (x) = 2
− x + 6x − 4 TOÁN
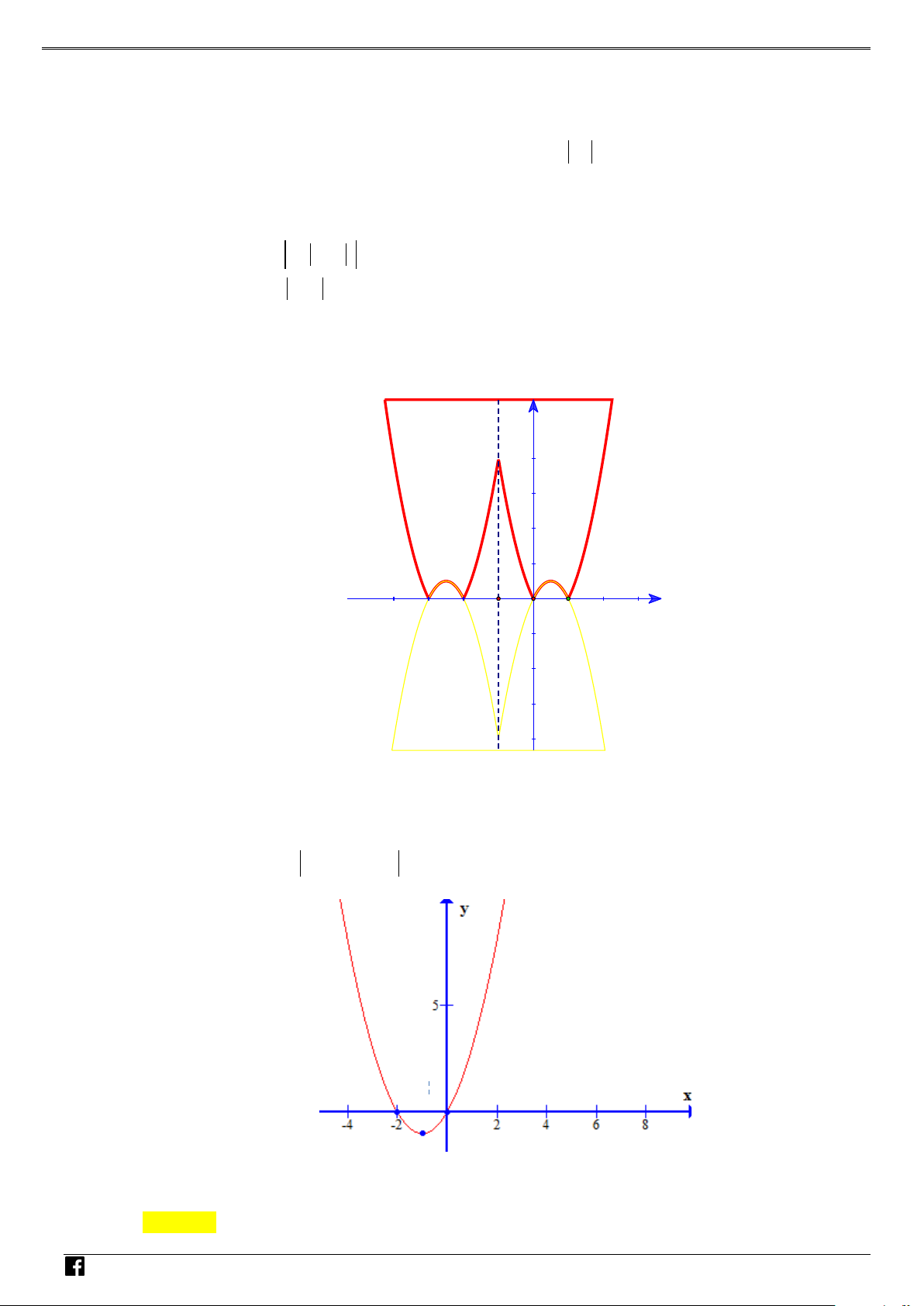
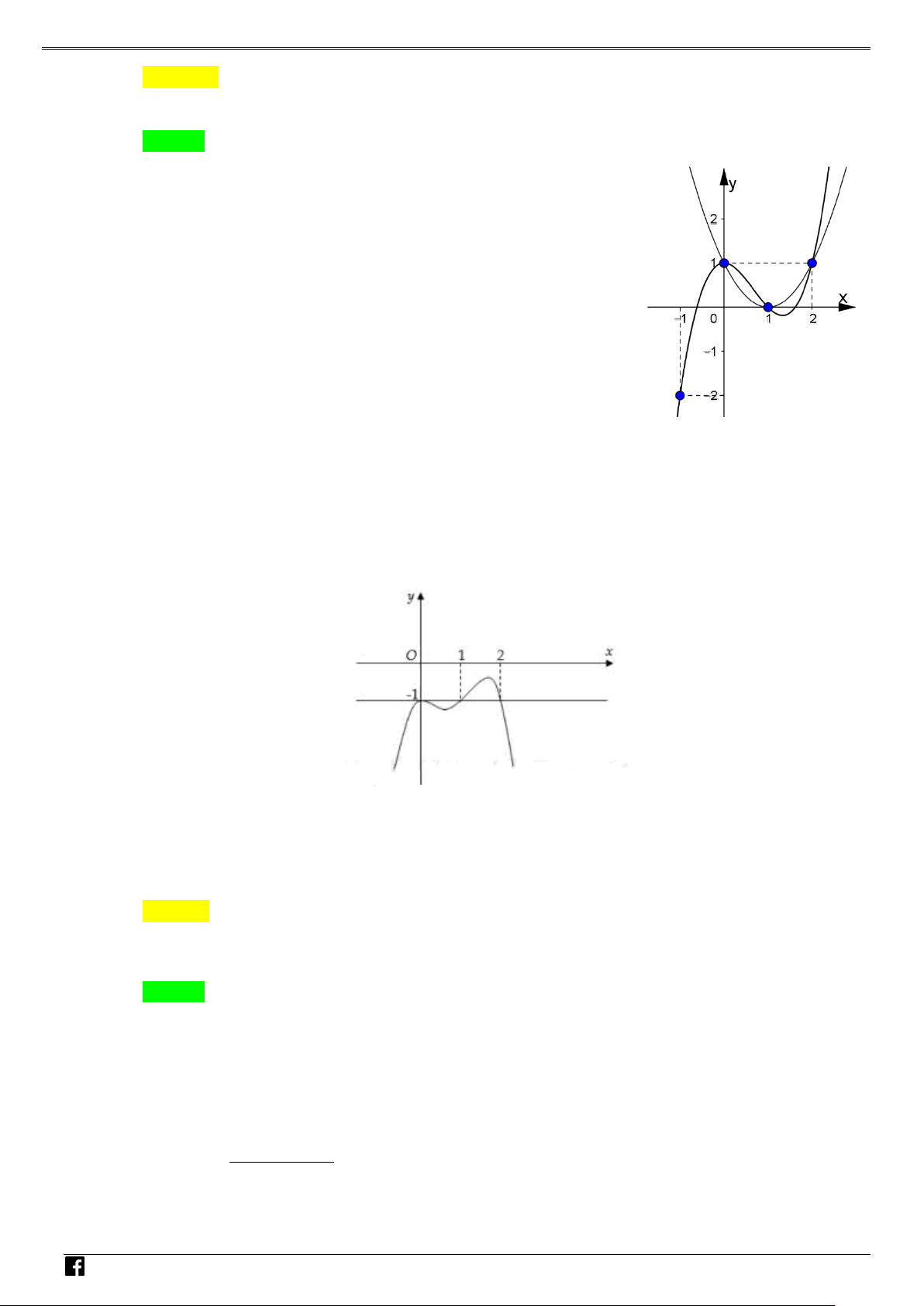
Đồ thị hàm số y = f ( x +1) (hình vẽ phần tô đậm) có được bằng cách
+ Vẽ đồ thị y = f ( x +1) (C 1 ) V D
+ Giữ nguyên phần đồ thị (C trên trục hoành và lấy đối xứng phần (C dưới trục hoành. 1 ) 1 ) –
y = f x = − x + x − VD
Để vẽ (C lấy đối xứng phần đồ thị 2 ( ) 2 6
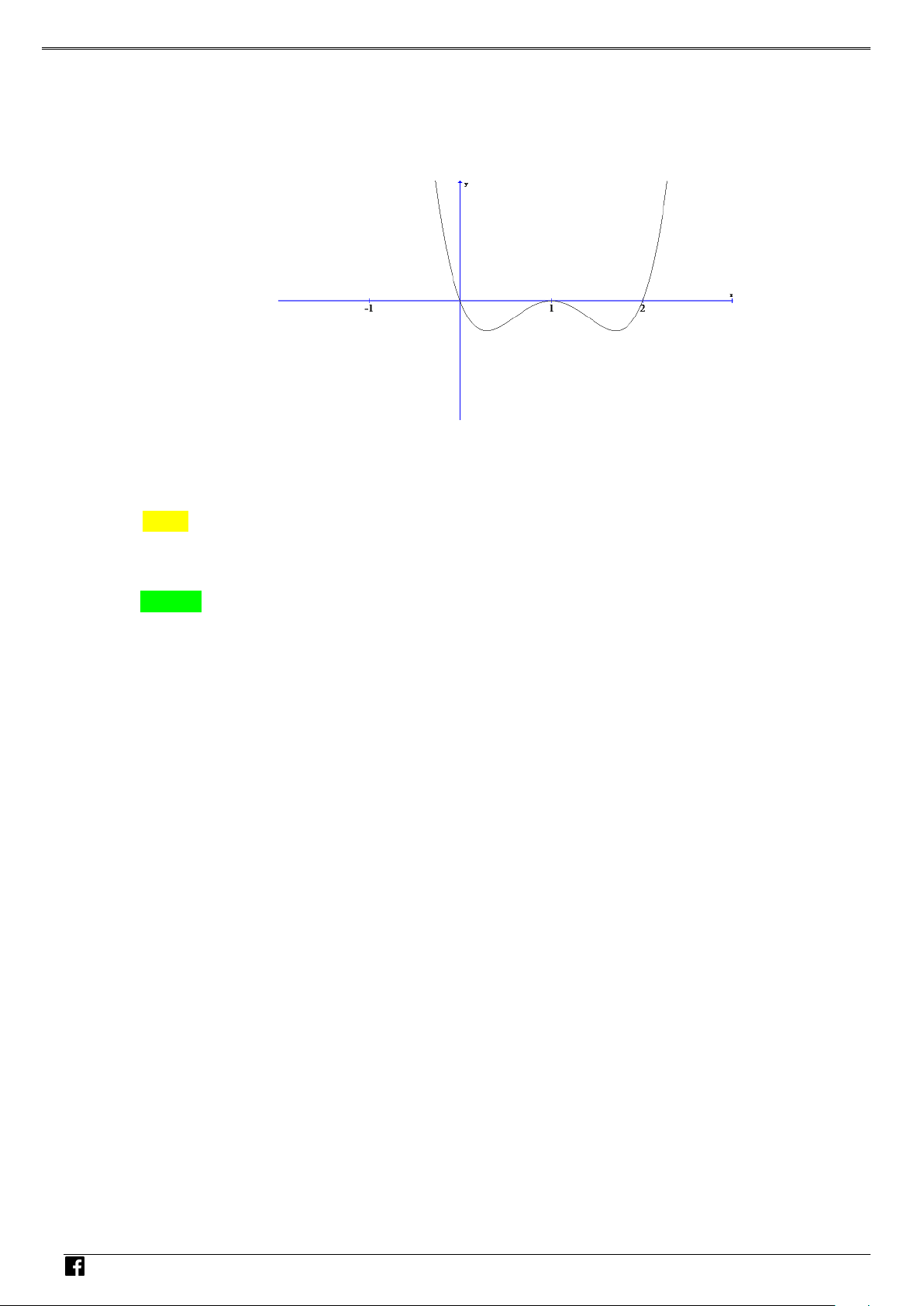
4 qua trục tung sau đó tịnh tiến 1 ) sáng trái 1 đơn vị. C y x -1 O 1 NHÓ M T OÁN
Từ đồ thị suy ra hàm số có 7 điểm cực trị.
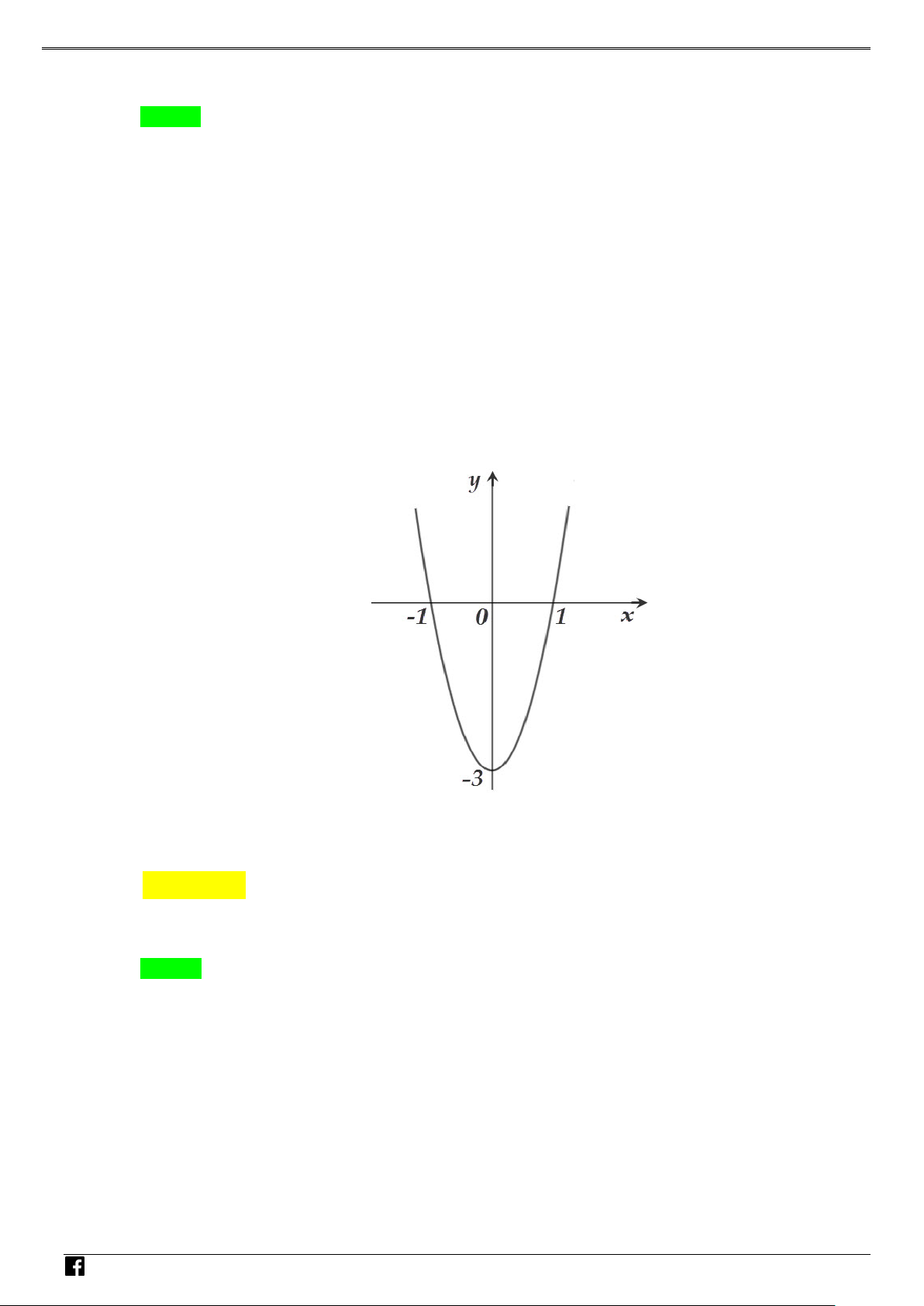
Câu 3: Cho hàm số f (x) 2
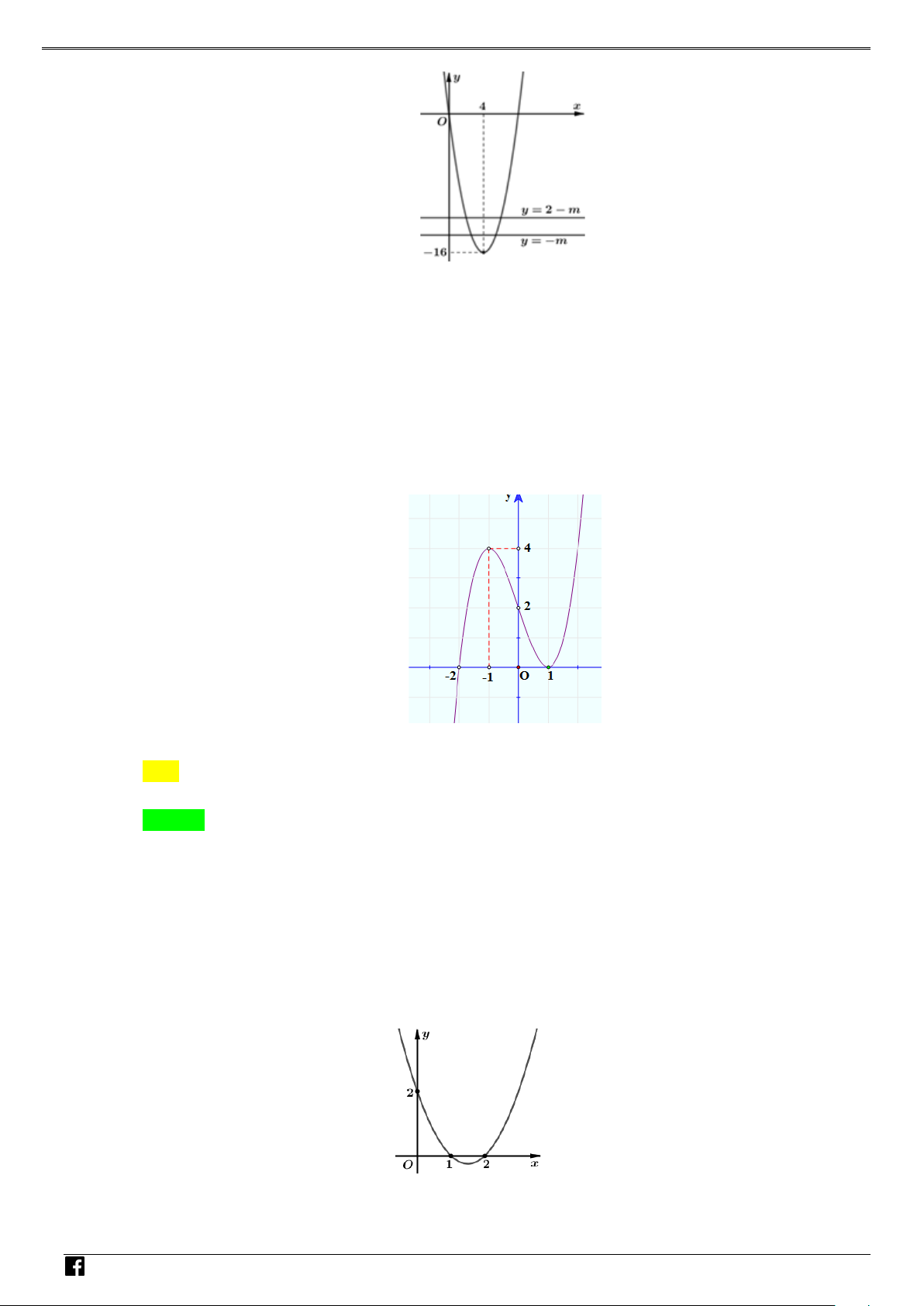
= ax + bx + c(a ≠ 0) có đồ thị là parabol như hình vẽ. Tìm m để giá trị lớ VDn
nhất của hàm số y = f (x) + m − 4 trên [ 2; − ]
1 đạt giá trị nhỏ nhất. – VD C A. m = 5 . B. m = 4 . C. m = 3 . D. m =1.
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn C NHÓ
Từ giả thiết suy ra y = (x + )2
1 + m − 5 . Đặt g (x) = (x + )2 1 + m − 5. M Với x ∀ ∈[ 2; − ]
1 ta có g (x)∈[m −5;m − ] 1 . TOÁN
Giá trị lớn nhất của hàm số y = max m − 5 , m −1 . max { } V 2 2 D
+ Trường hợp 1: m − 5 ≥ m −1 ⇔ (m −5) ≥ (m − ) 1 ⇔ m ≤ 3 . – VD Khi đó y
= m − 5 = 5 − m ≥ 2 ⇒ GTLN của hàm số đạt GTNN bằng 2, khi m = 3 . max C
+ Trường hợp 2: m −1 ≥ m − 5 ⇔ m ≥ 3. Khi đó y
= m −1 = m −1≥ 2 ⇒ GTLN của hàm số đạt GTNN bằng 2, khi m = 3 . max Vậy m = 3 .
DẠNG 2. Dạng toán có thể tìm được biểu thức cụ thể của hàm số y = f (x) trong
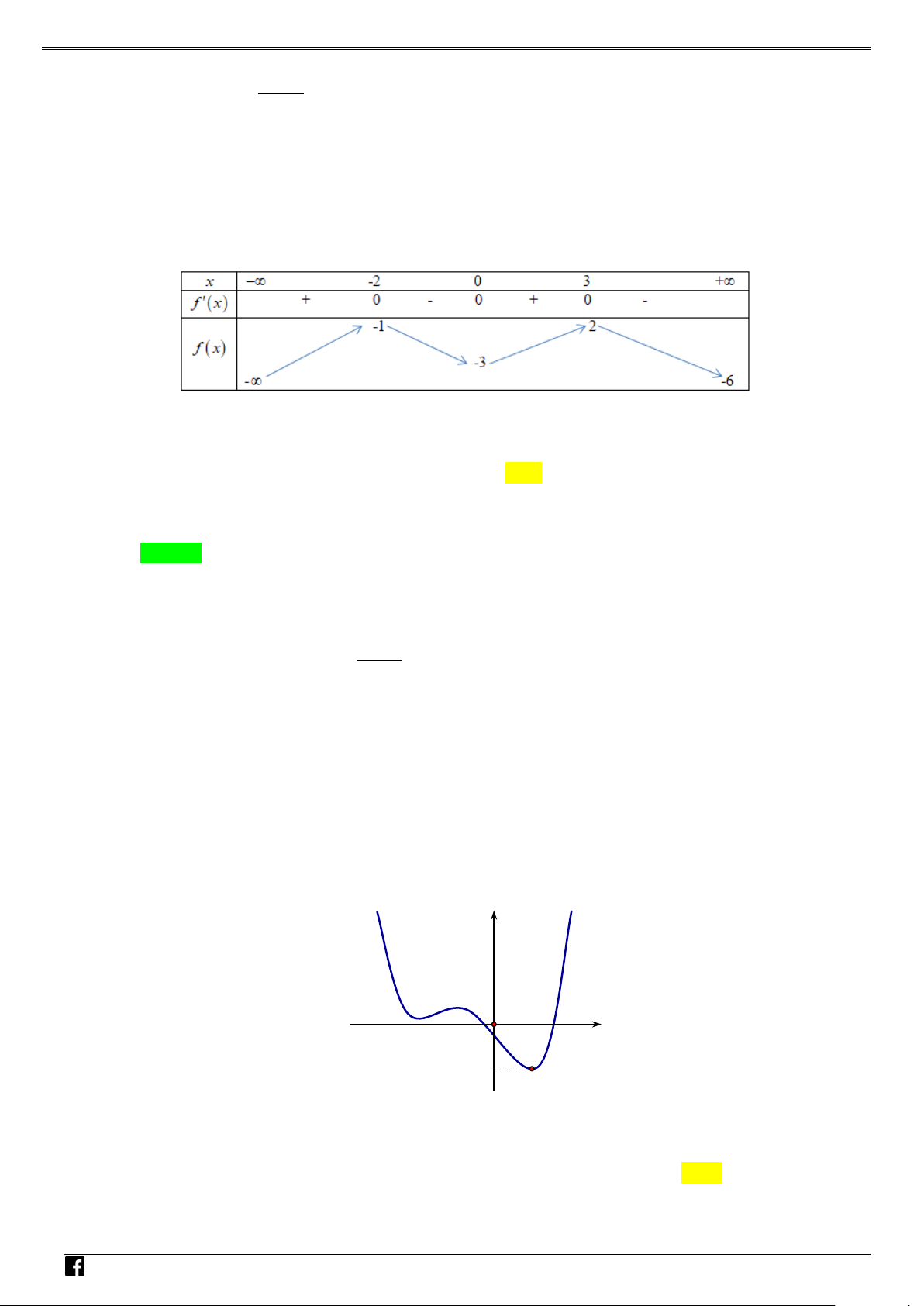
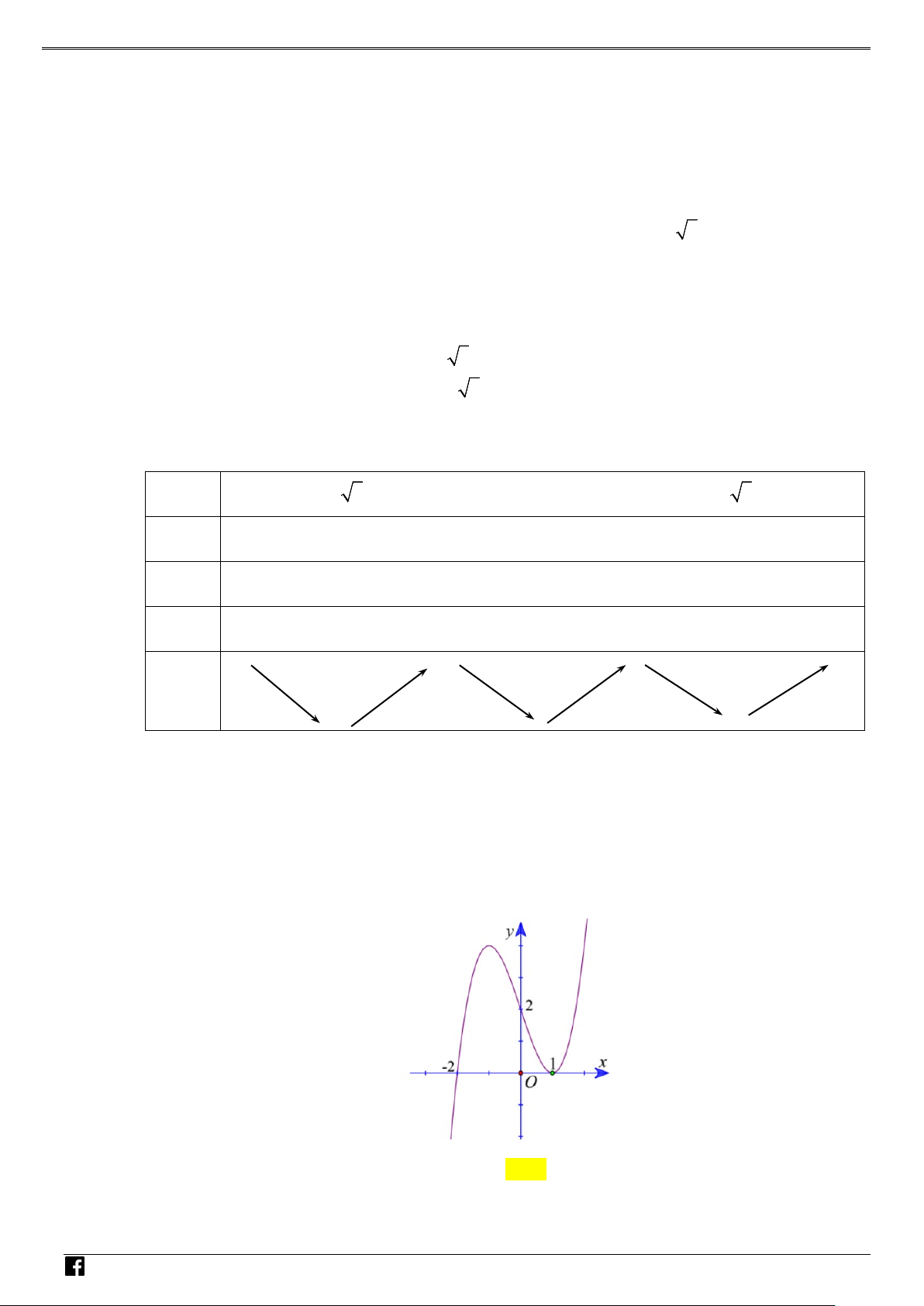
bài toán không chứa tham số. Câu 1: Cho hàm số 3 2
y = ax + bx + cx + d . Biết rằng đồ thị hàm số có một điểm cực trị là M (1;− ) 1 và nhận I (0; )
1 làm tâm đối xứng. Giá trị y(2) là NHÓ
A. y(2) = 2. B. y(2) = 2 − . C. y(2) = 6 . D. y(2) = 3 . M T Lời giải OÁN Chọn D VD Ta có: 2
y′ = 3ax + 2bx + c, y '' = 6ax + 2b . – M − VD
Do đồ thị hàm số có một điểm cực trị là (1; ) 1 và nhận I (0; )
1 làm tâm đối xứng nên: C y ( ) 1 = 1 −
a + b + c + d = 1 − a =1 y ( ) 1 0 3 a 2b c 0 ′ = + + = b = 0 ⇔ ⇔ . y ' (0) = 0 2b = 0 c = 3 − y (0) = 1 d =1 d =1 Vậy: 3
y = x − 3x +1. Suy ra y ( ) 3 2 = 2 − 3.2 +1 = 3 .
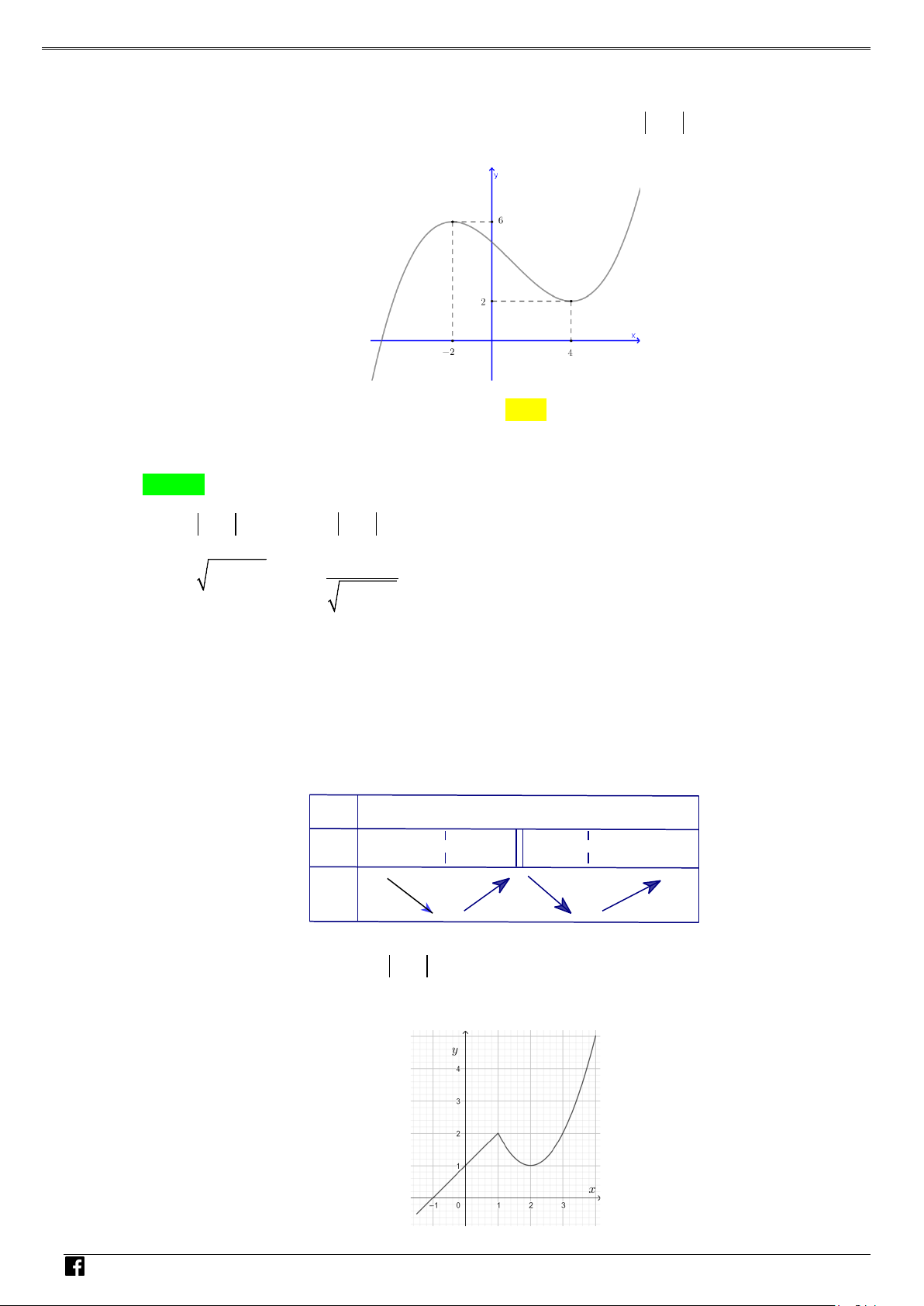
Câu 2: Đồ thị của hàm số 3 2
y = ax + bx + cx + d có hai điểm cực trị là A(1;2) và B( 1; − 6) . Giá trị của 2 2 2 2
P = a + b + c + d bằng bao nhiêu?
A. P =18. B. P = 26 .
C. P =15.
D. P = 23.
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn B
Tập xác định D = . NHÓ Ta có 2
y ' = 3ax + 2bx + c và y '' = 6ax + 2b . M
Vì A(1;2) và B( 1;
− 6) là điểm cực trị nên TOÁN y '( ) 1 = 0 3
a + 2b + c = 0 6a + 2c = 0 a =1 y ( ) 1 2 a b c d 2 b d 4 b = + + + = + = = 0 V ⇔ ⇔ ⇔ . y '(− ) 1 = 0
3a − 2b + c = 0 2a + 2c = 4 − c = 3 − D – y (− ) 1 = 6
−a +b −c + d = 6 4b = 0 d = 4 VD Vậy 2 2 2 2
P = a + b + c + d = 26 . C Câu 3: Cho hàm số 3 2
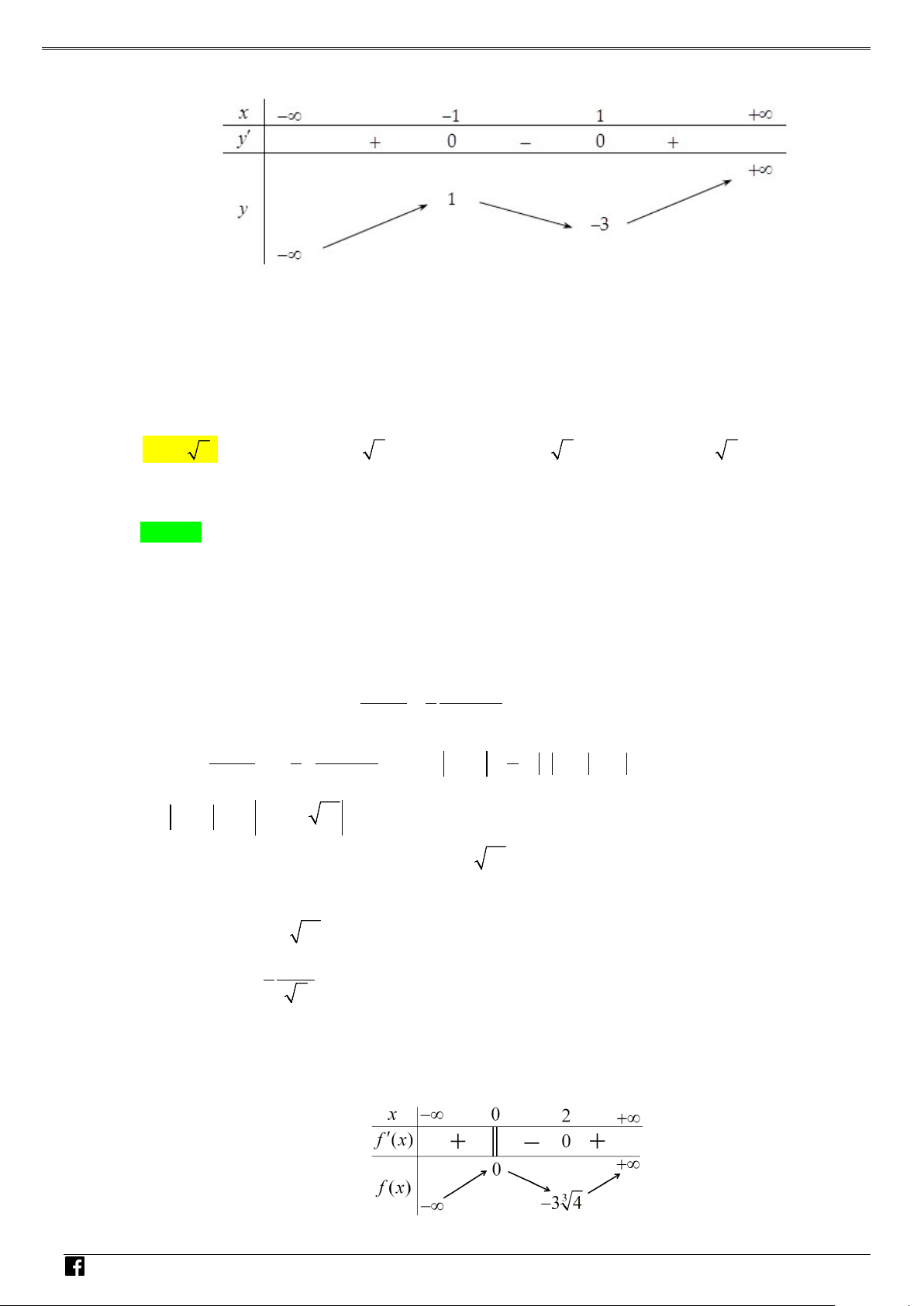
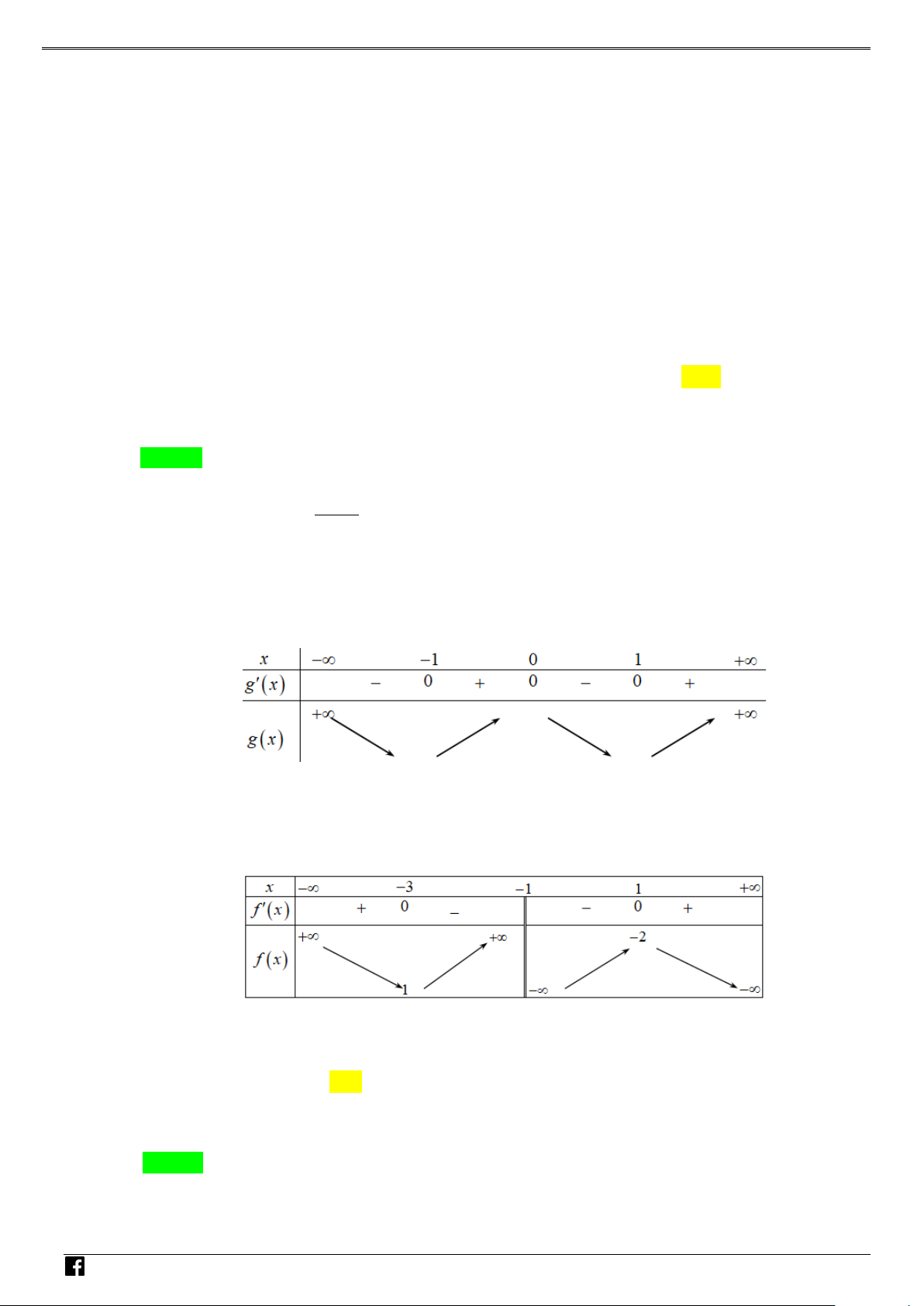
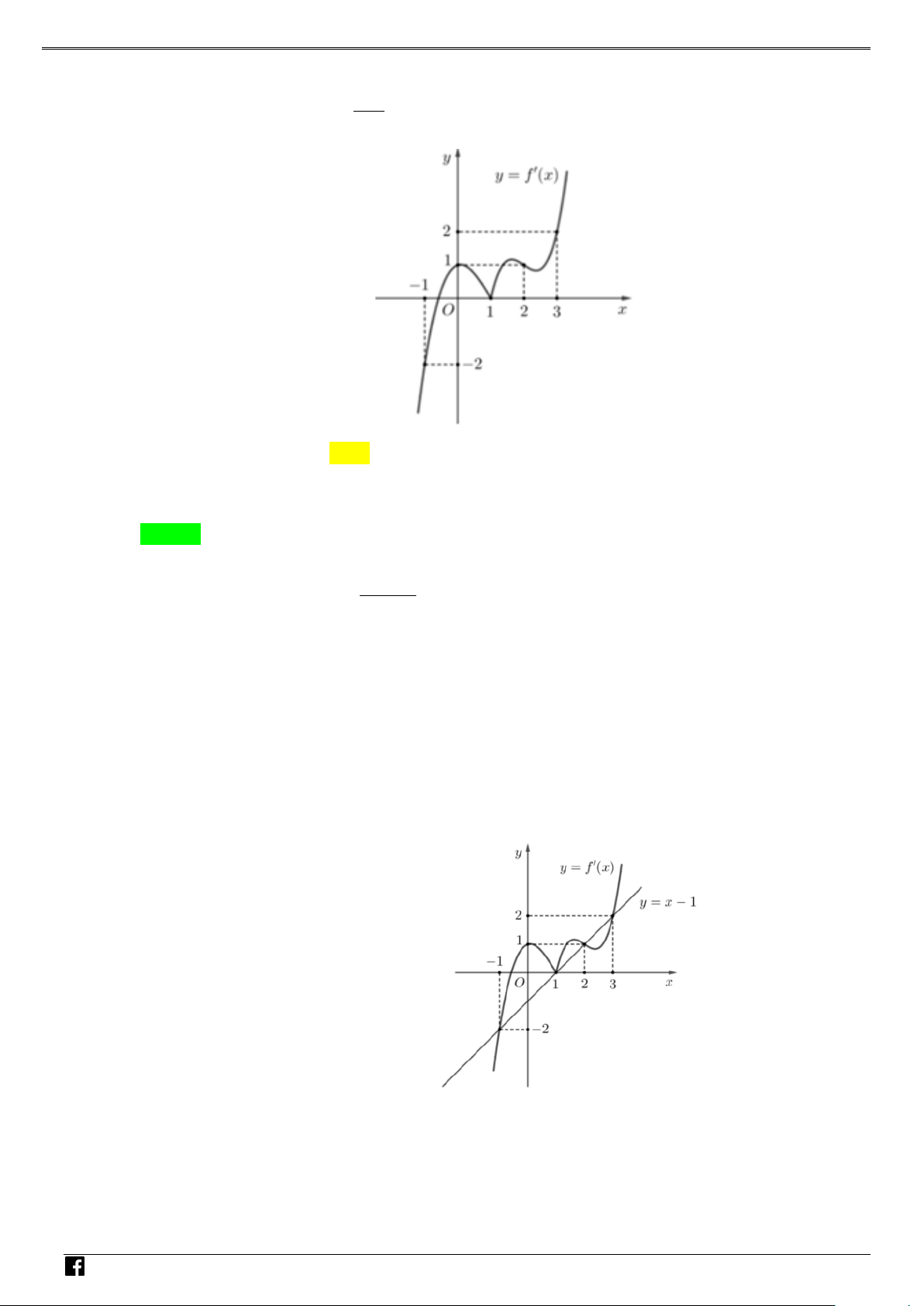
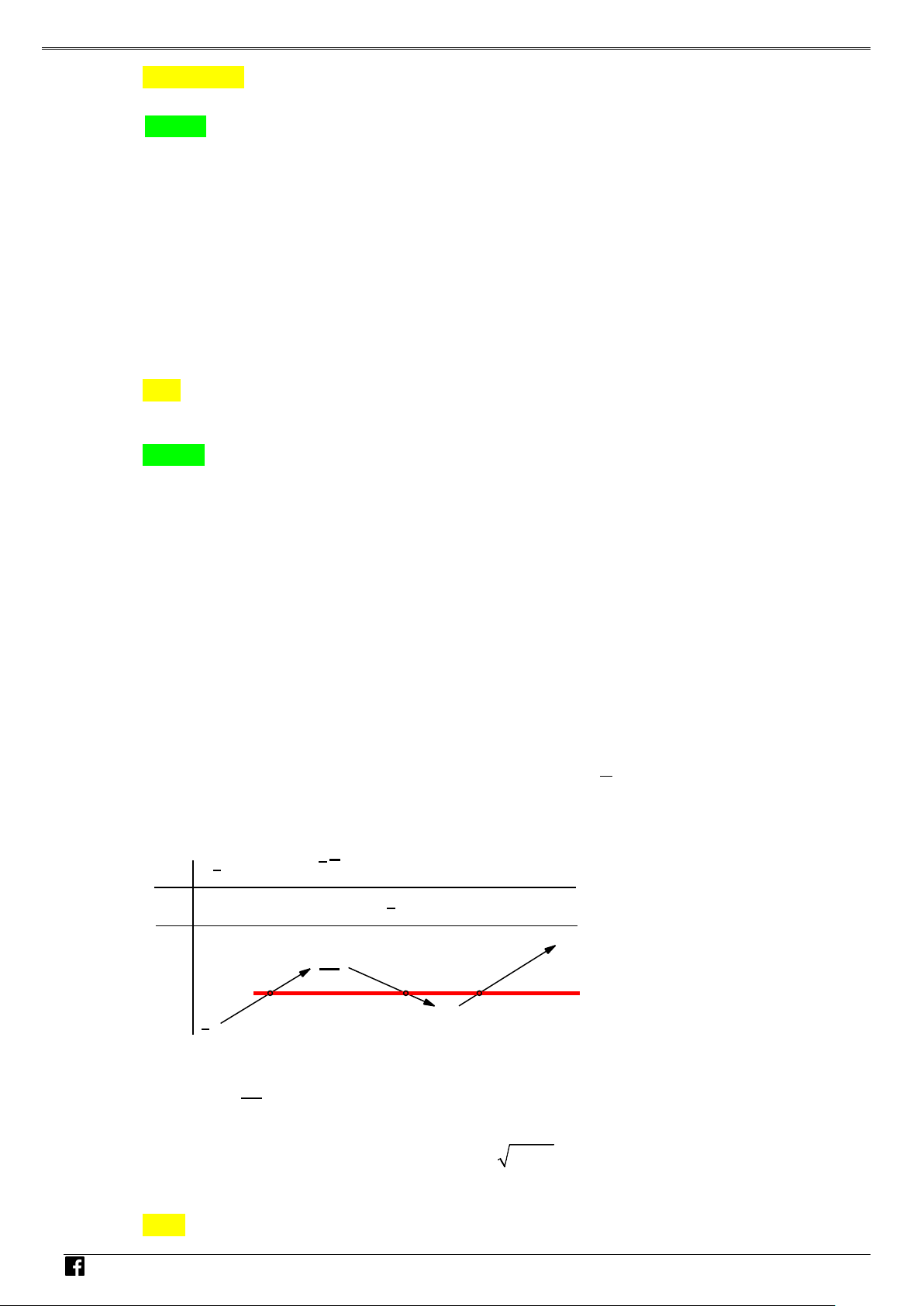
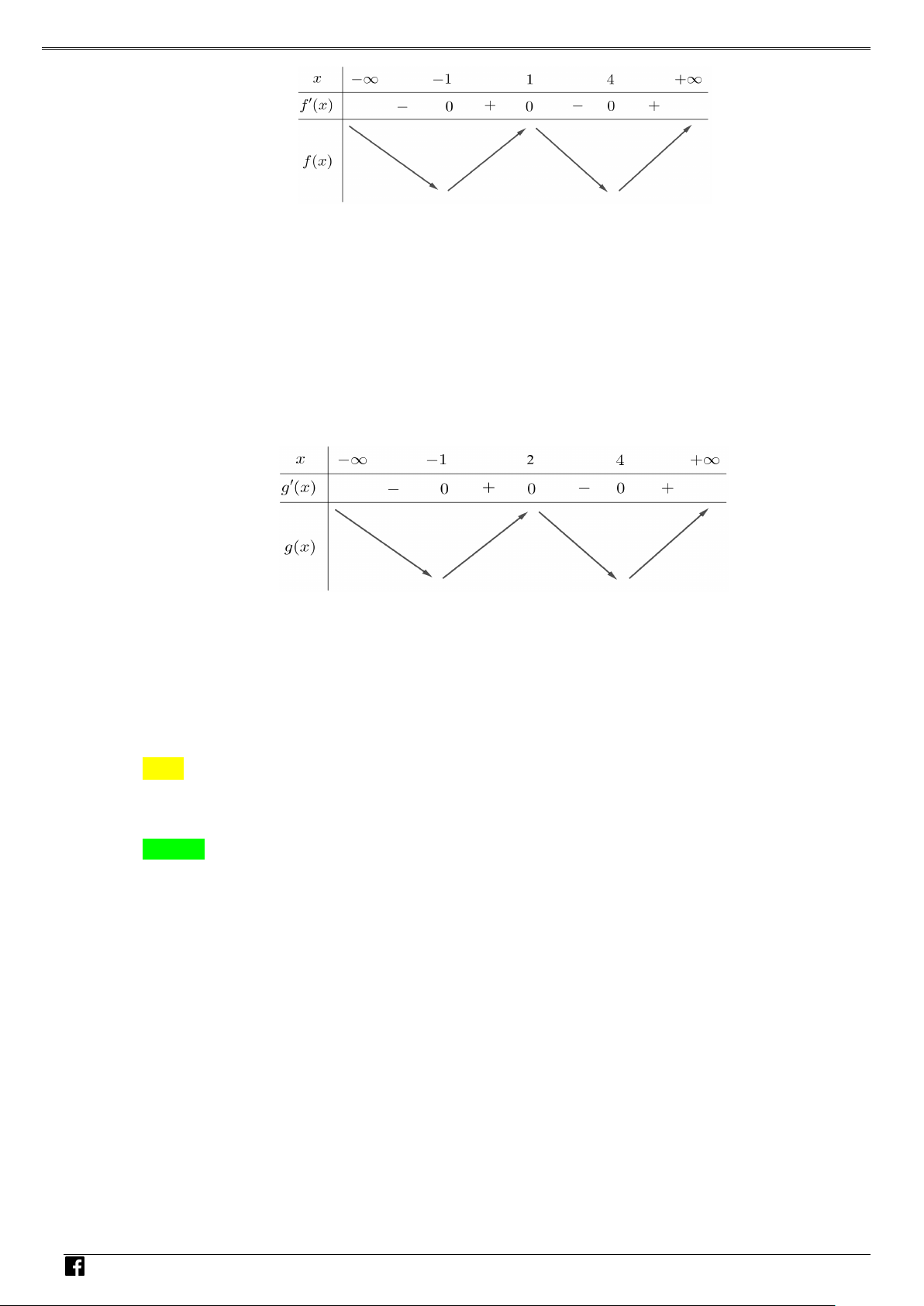
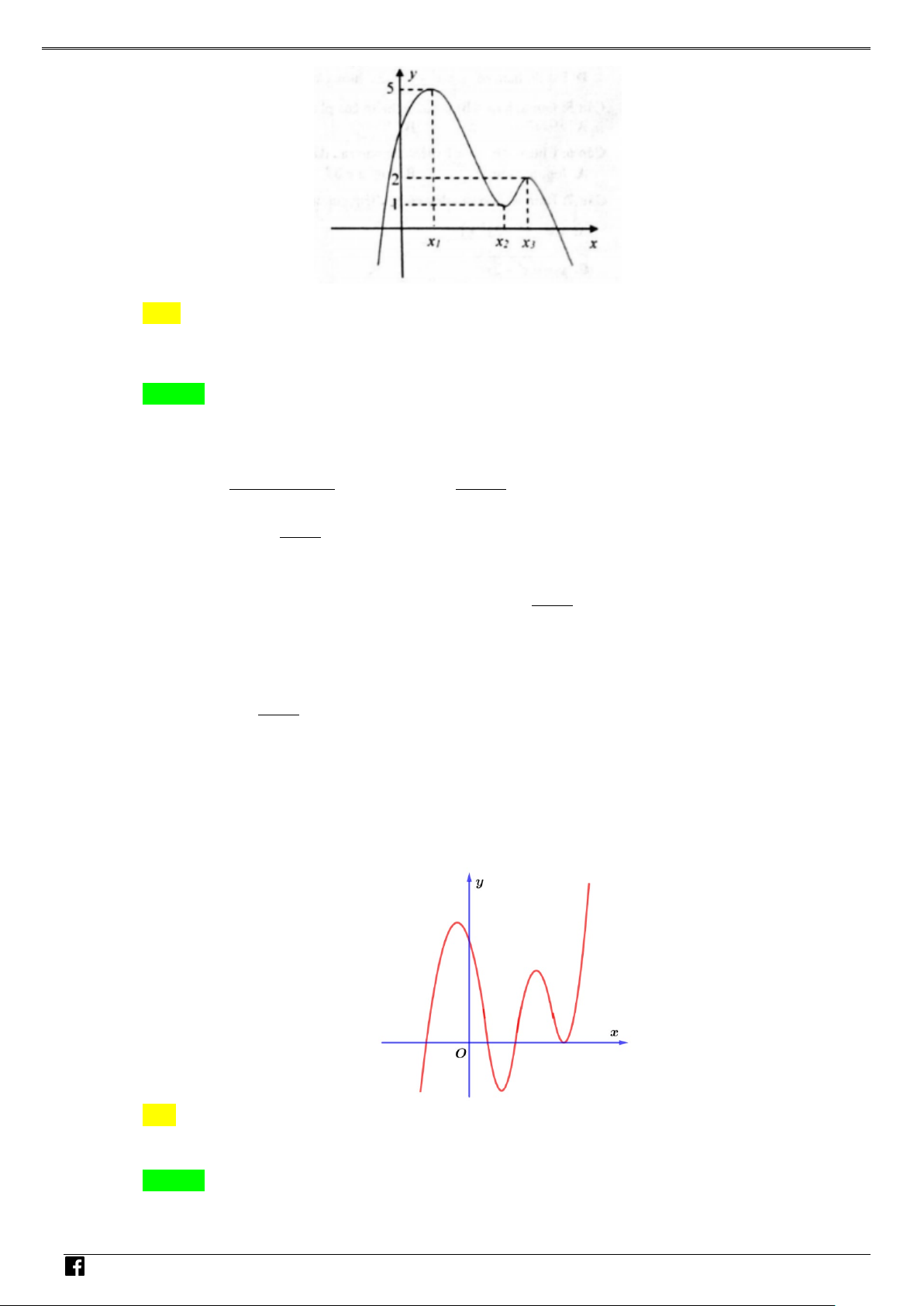
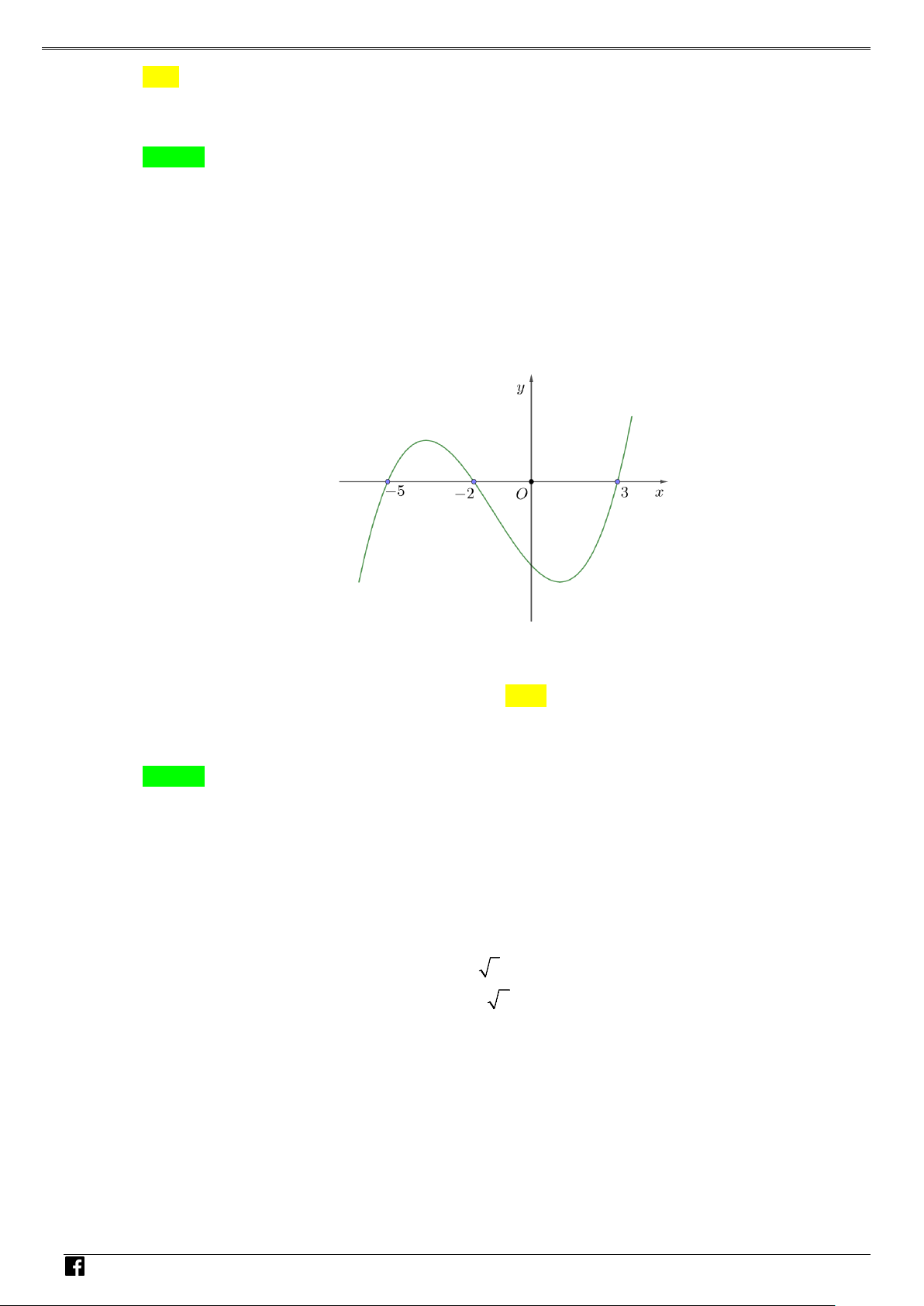
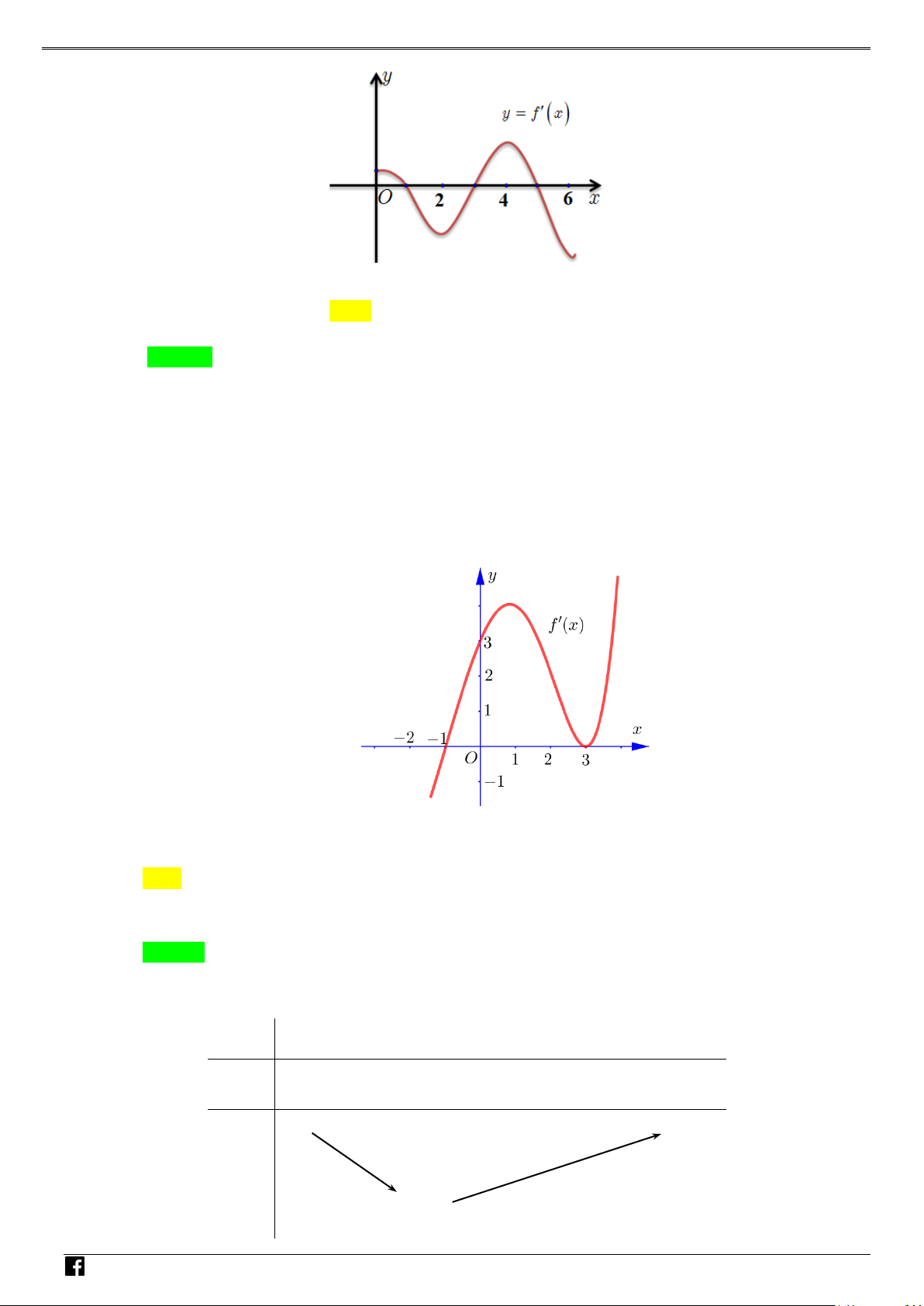
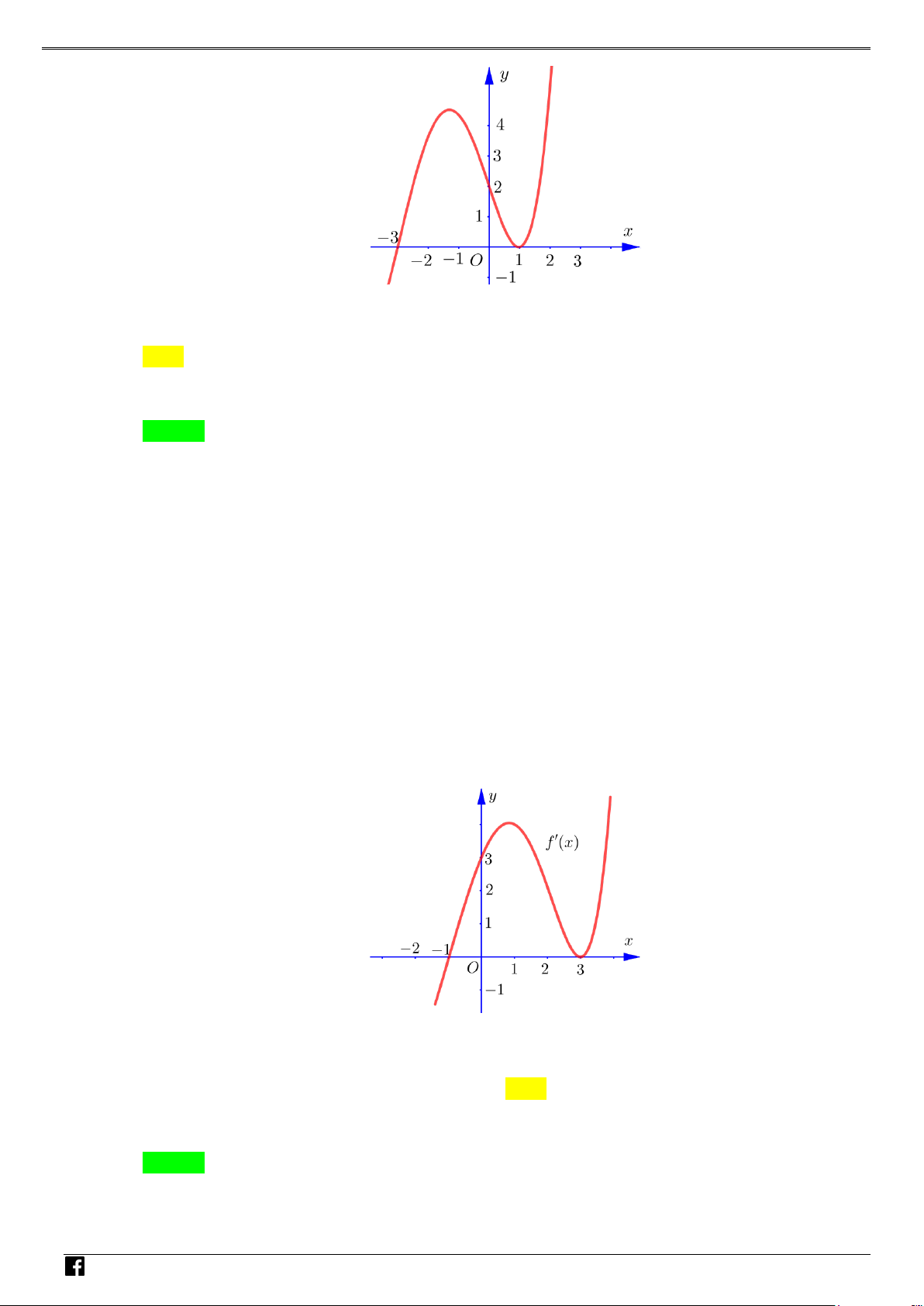
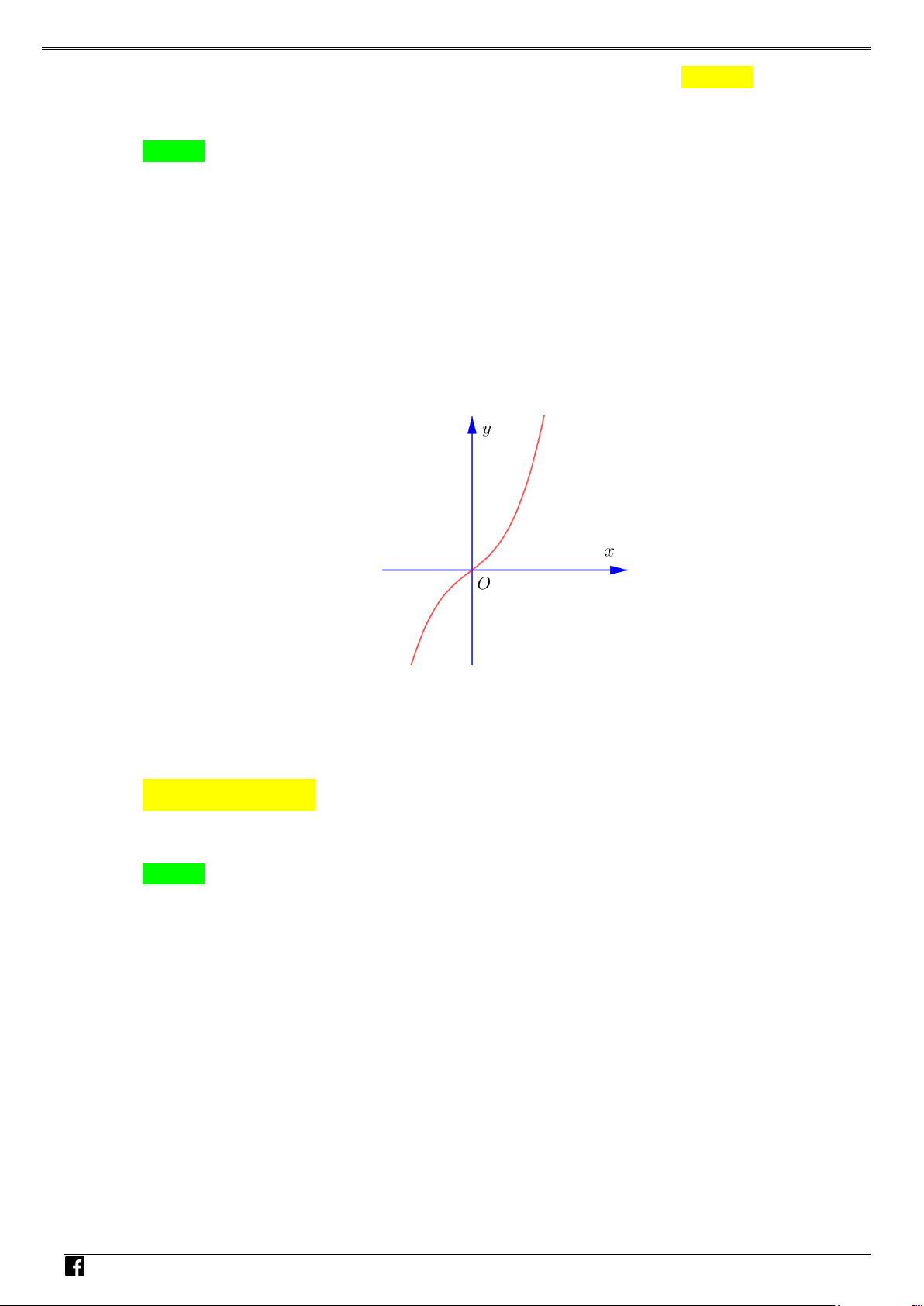
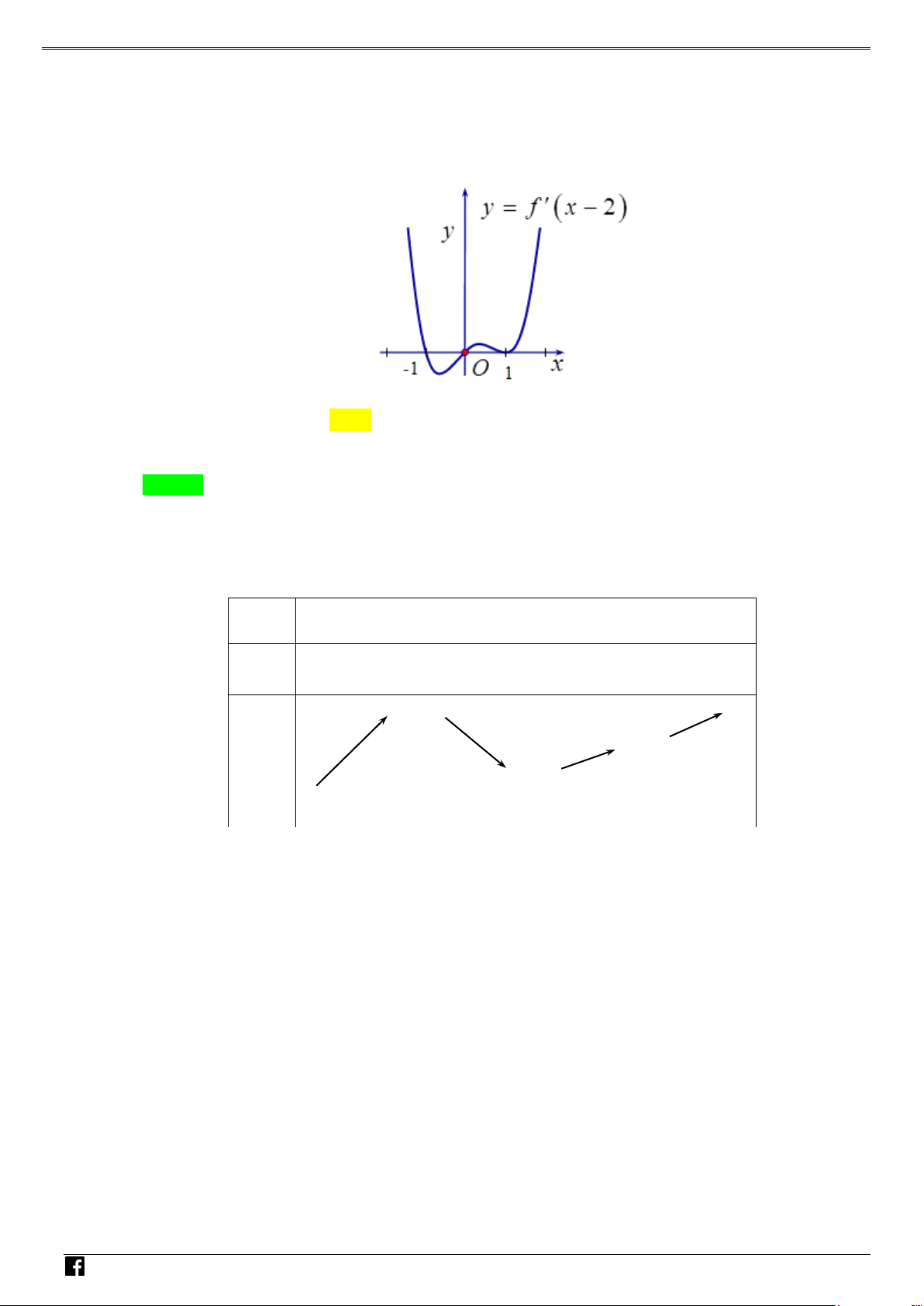
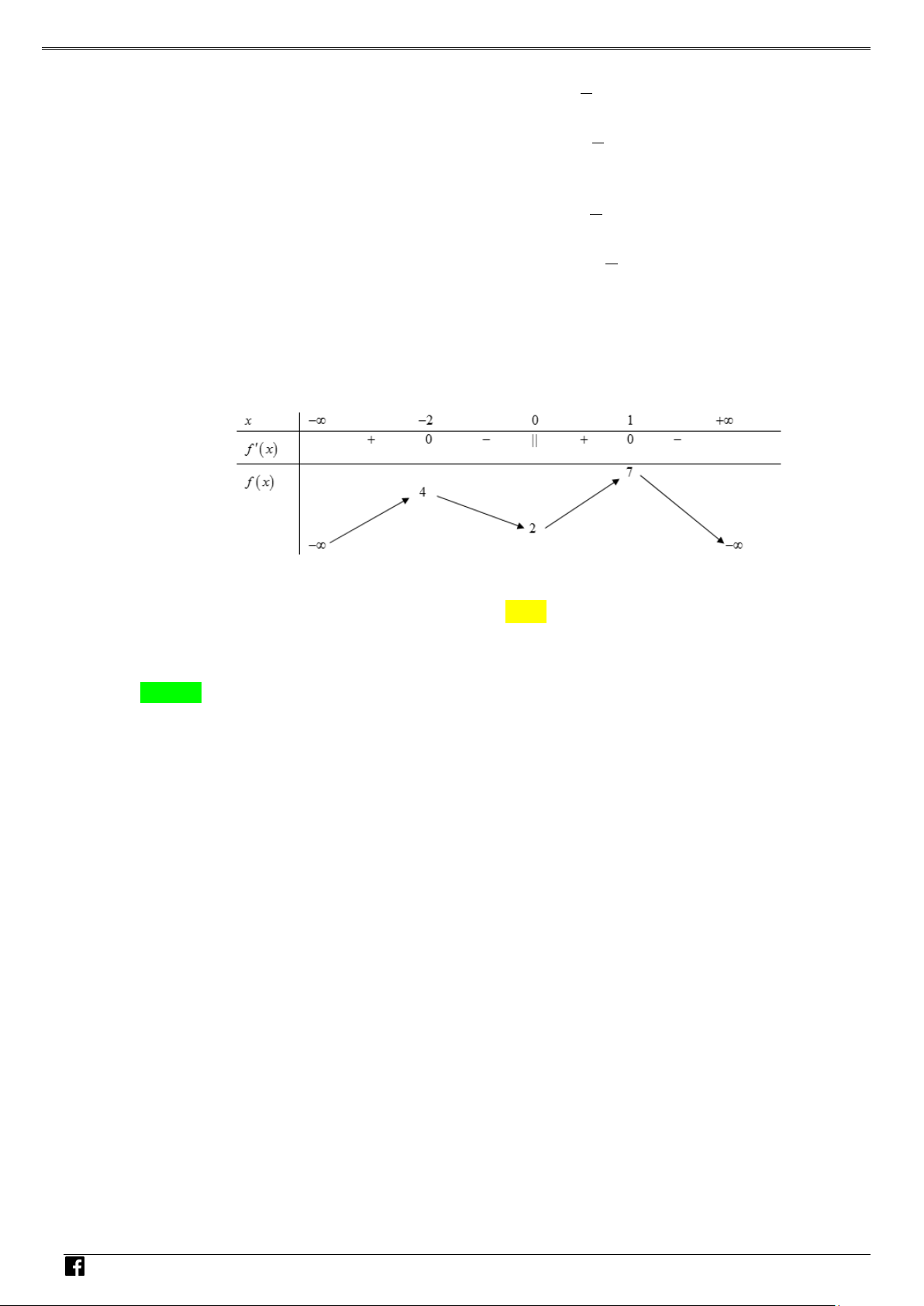
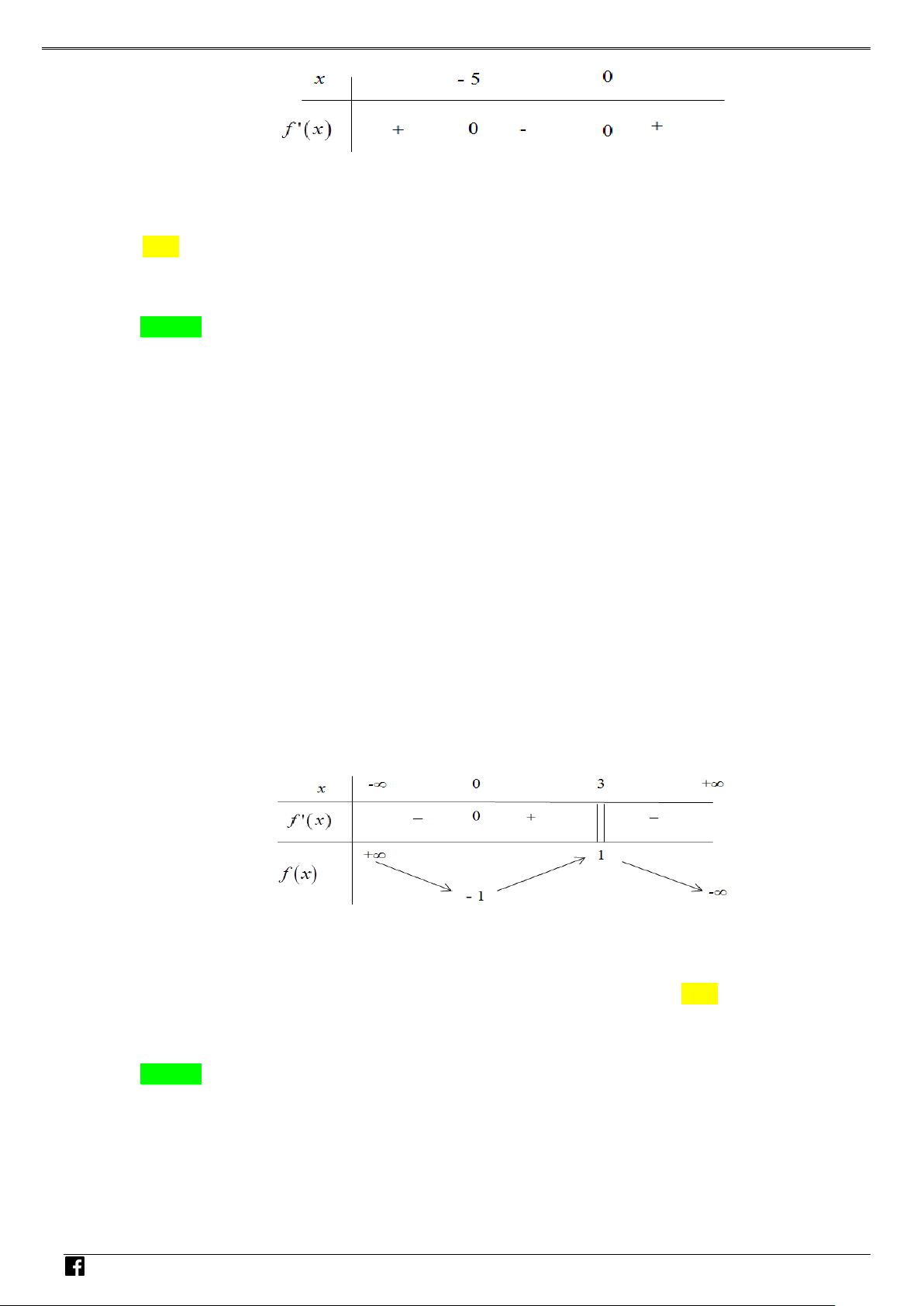
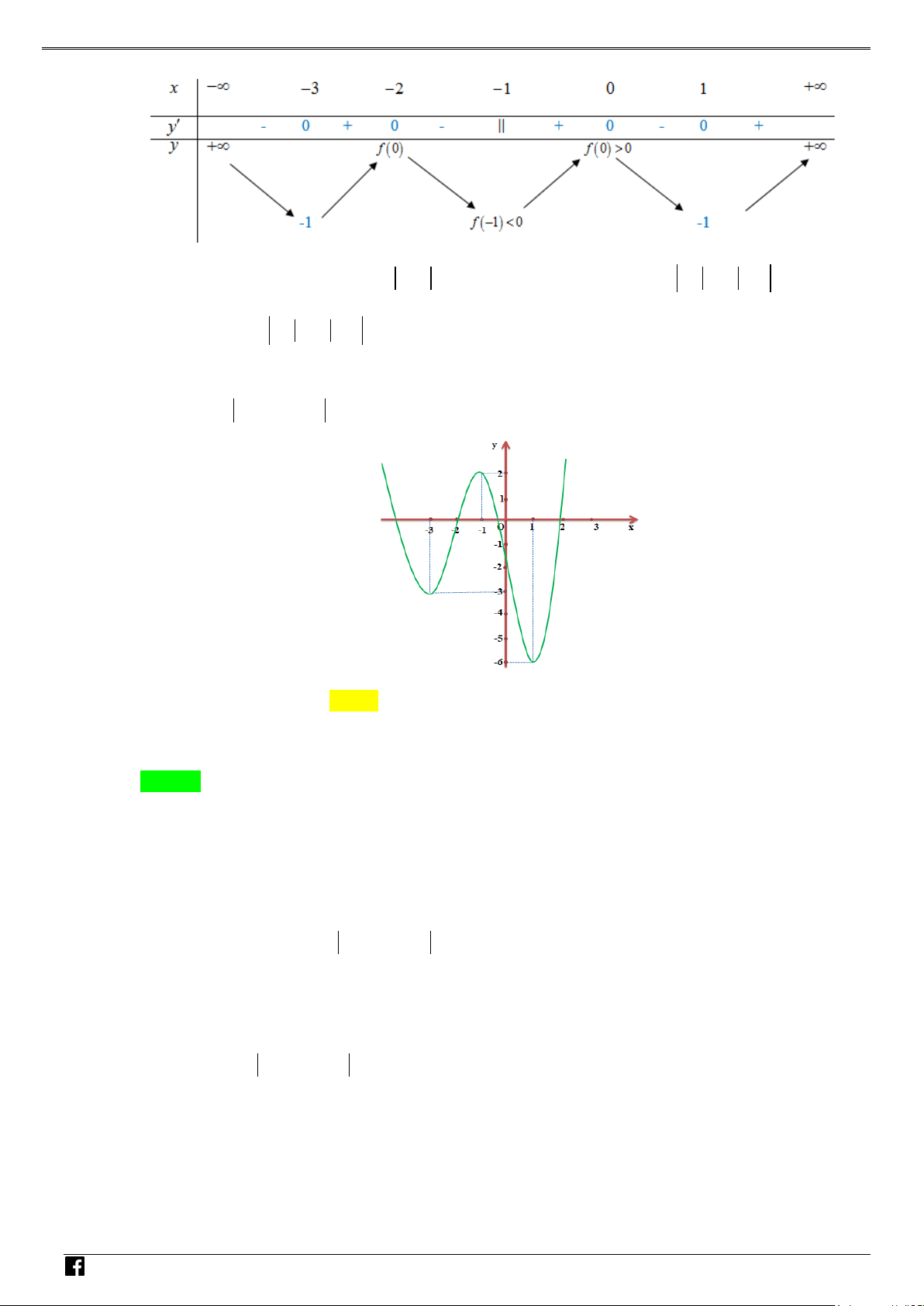
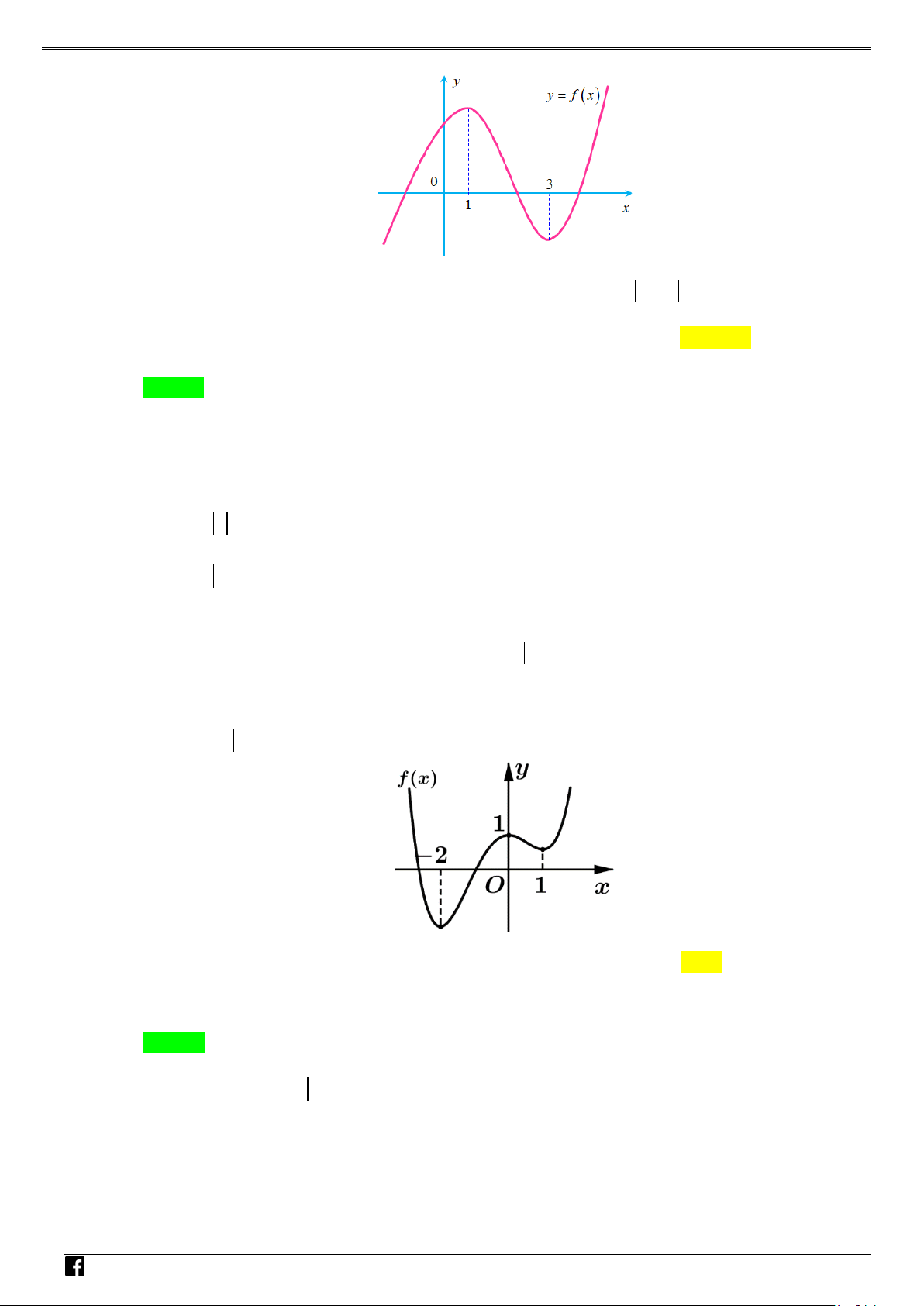
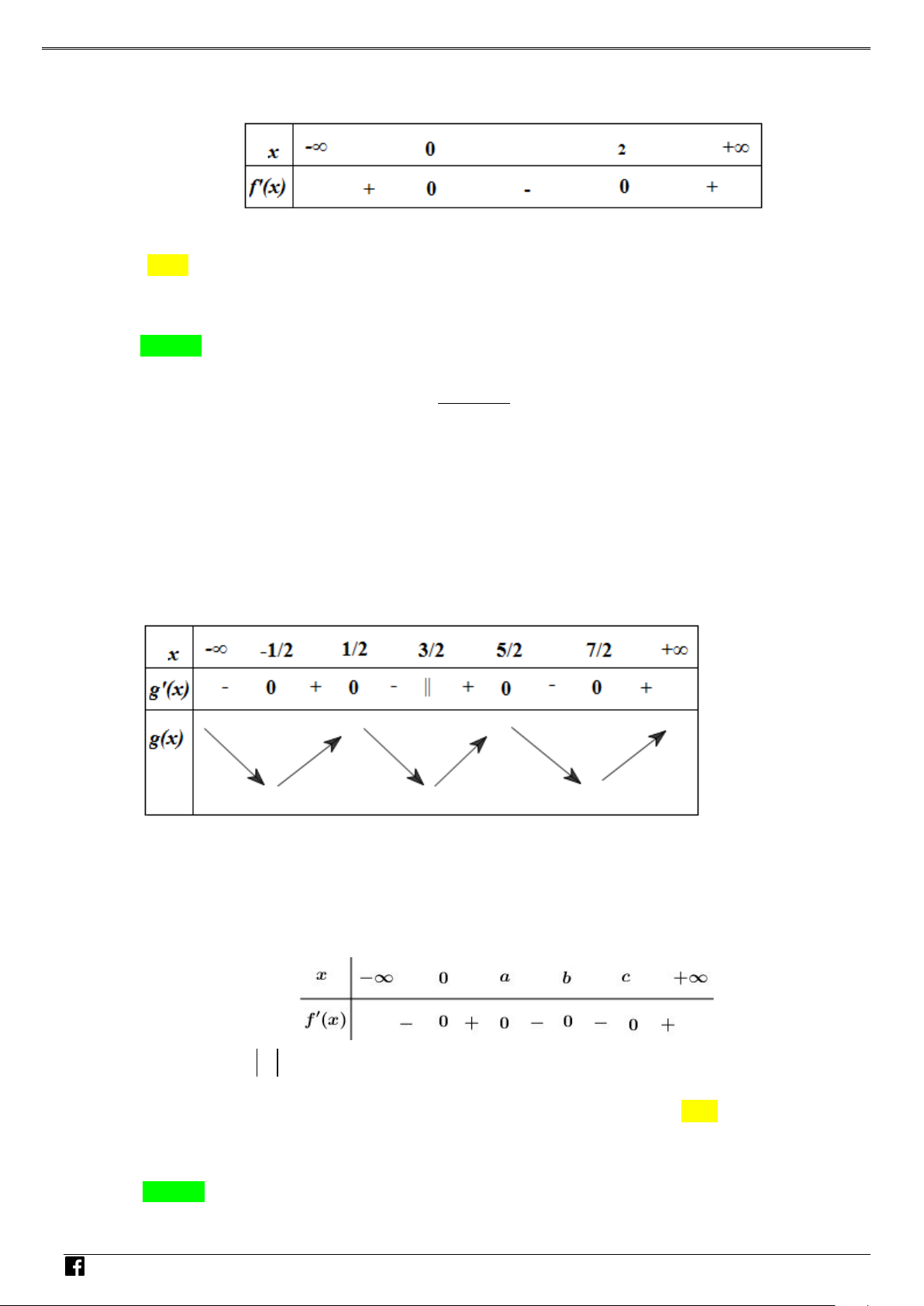
y f (x) ax bx cx d (a 0) xác định trên và thỏa mãn f (2) 1. Đồ
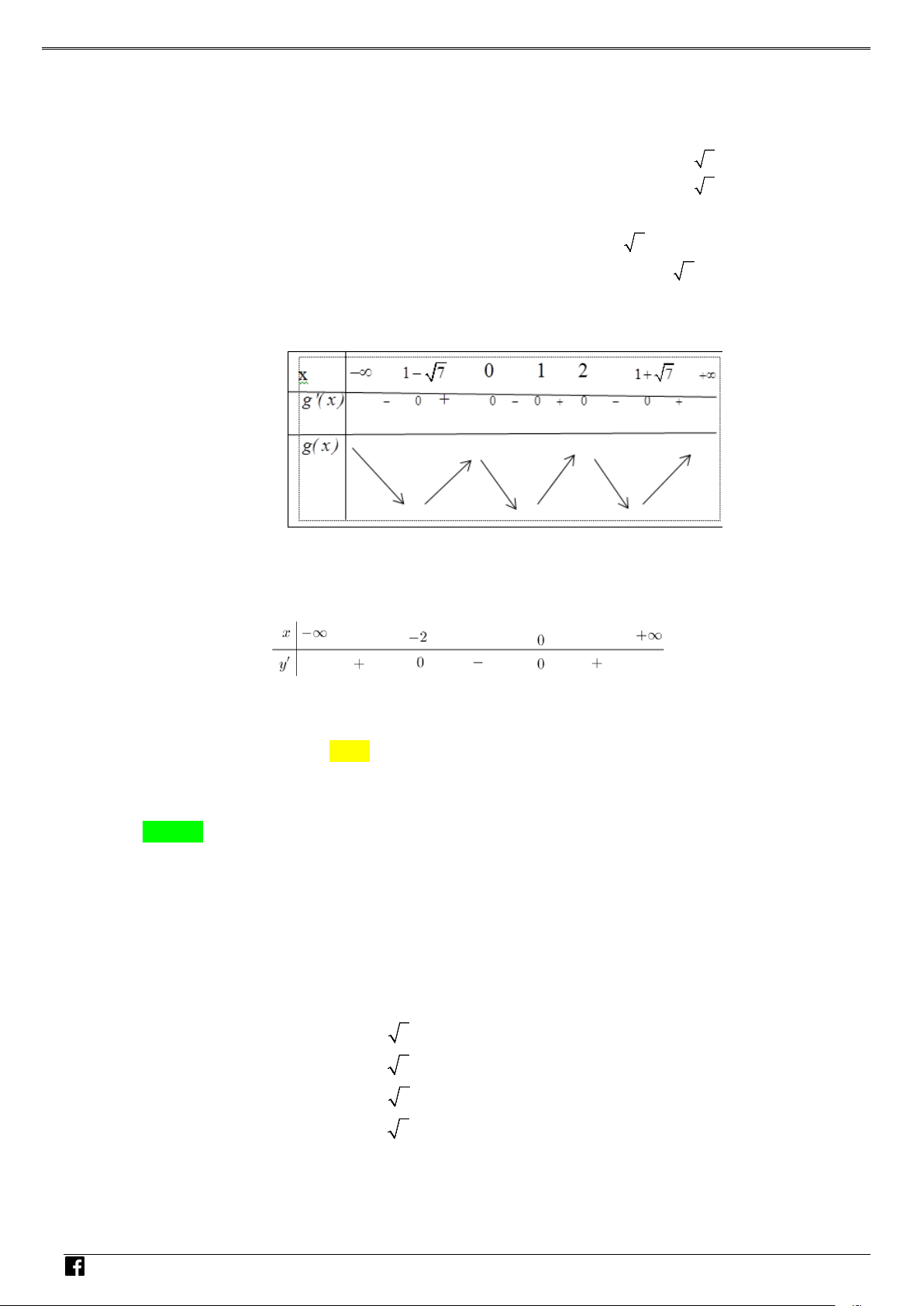
thị hàm số f '(x) được cho bởi hình bên dưới. NHÓ M T OÁN
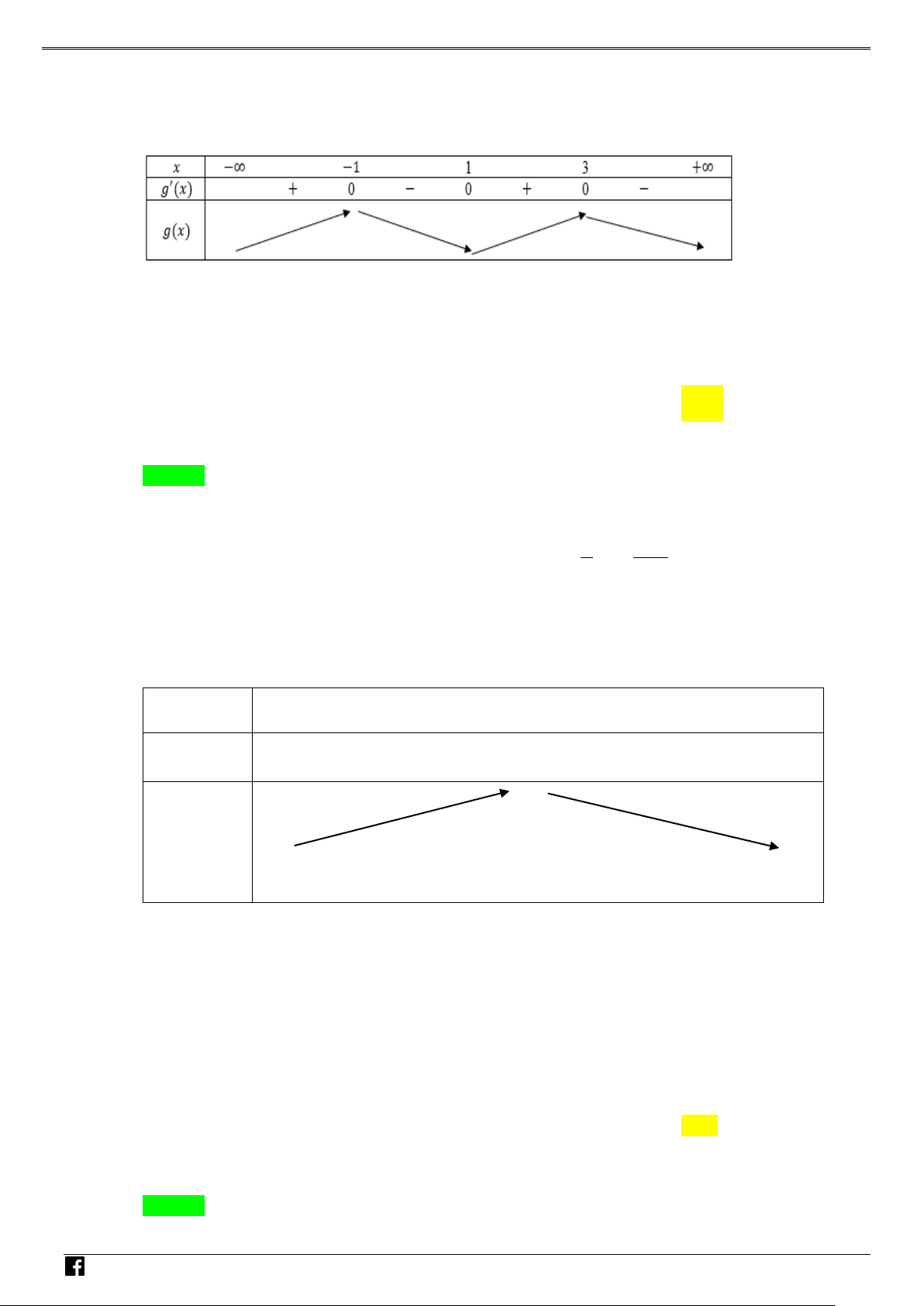
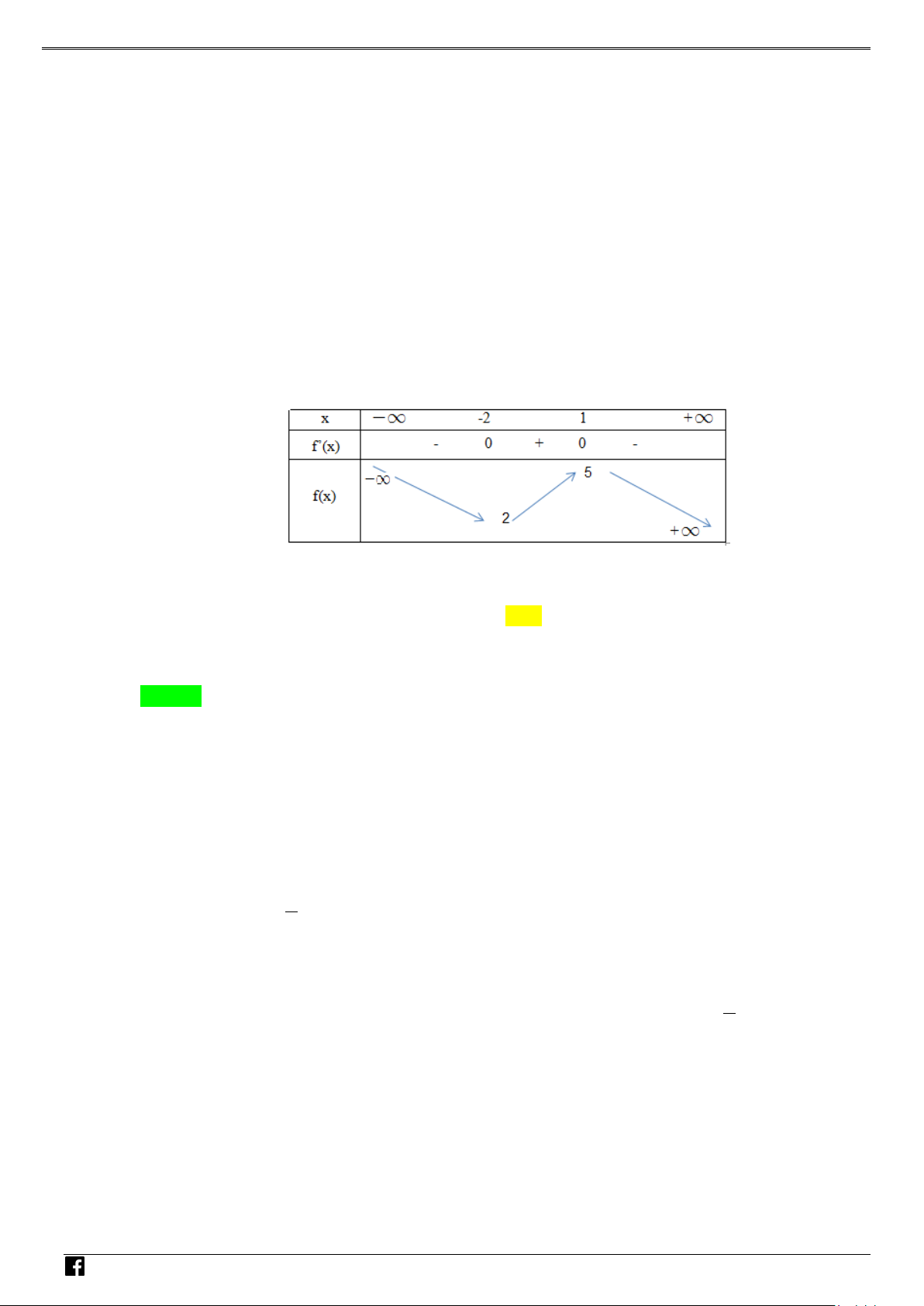
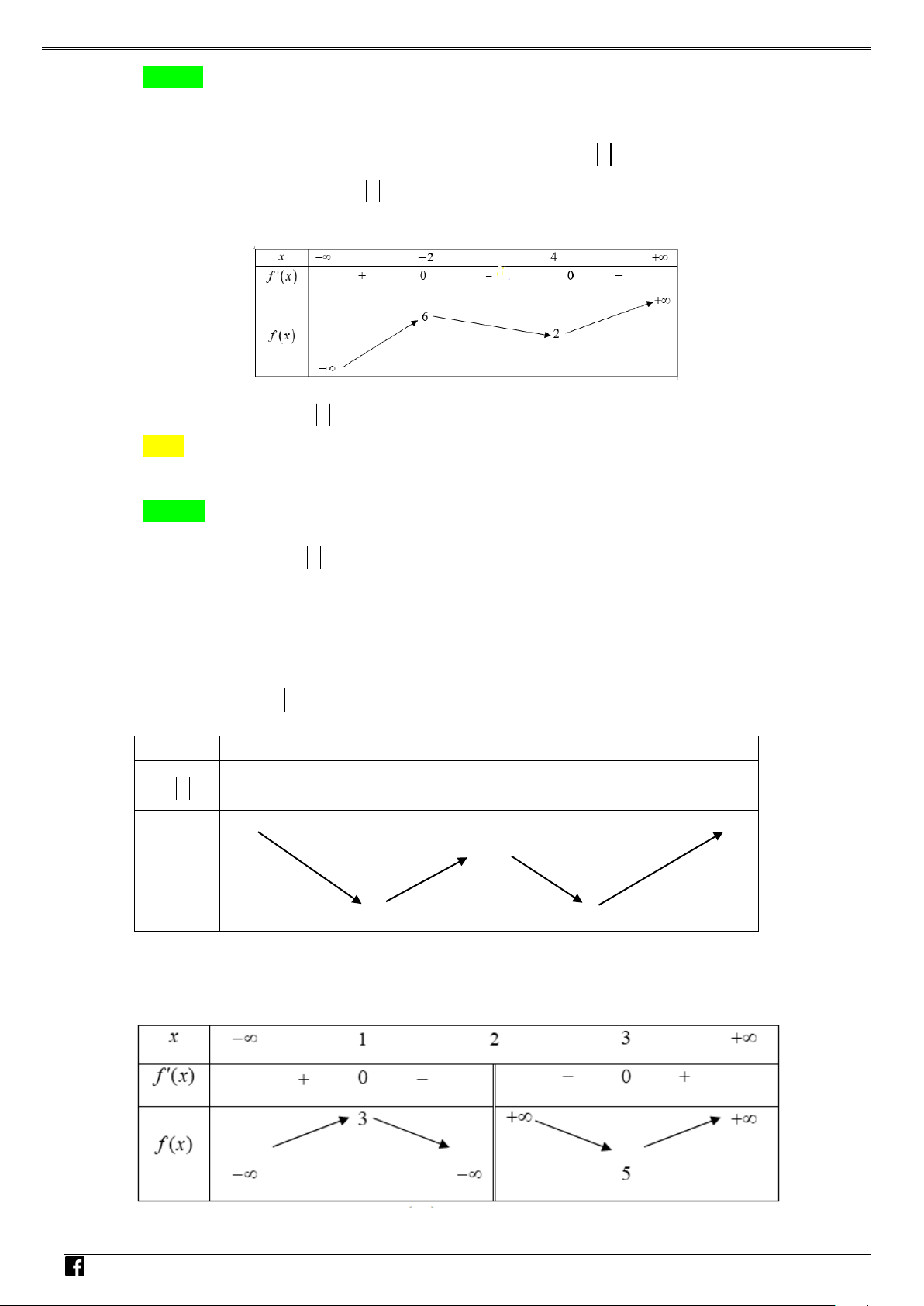
Tìm giá trị cực tiểu y của hàm số f (x). VD CT – A. y . B. y . C. y . D. y . CT 2 CT 1 CT 1 CT 3 VD C Lời giải Chọn A
Vì đồ thị hàm f '(x) cắt Ox tại hai điểm phân biệt có hoành độ x 1 và x 1 nên
f '(x) k(x1)(x 1) với k là số thực khác 0.
Vì đồ thị hàm f '(x) đi qua điểm (0;3) nên ta có 3 k k 3. Suy ra 2
f '(x) 3x 3. Mà 2
f '(x) 3ax 2bx c nên ta có được a 1,b 0,c 3. Từ đó 3
f (x) x 3x d. Mặt khác f (2) 1 nên d 1. Suy ra 3
f (x) x 3x1. x 1
Ta có f '(x) 0 . x 1
https://www.facebook.com/groups/toanvd.vdc Trang 5
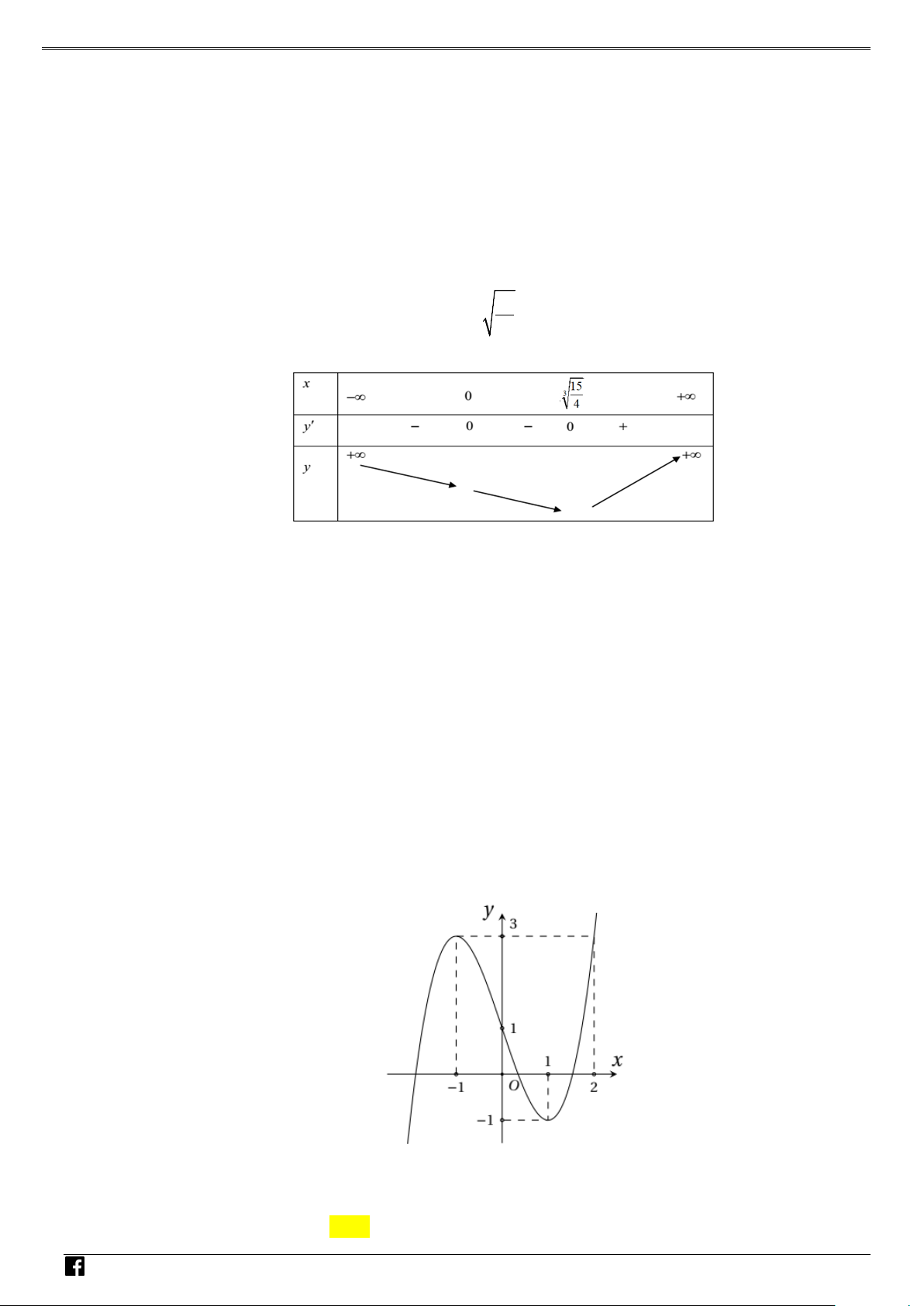
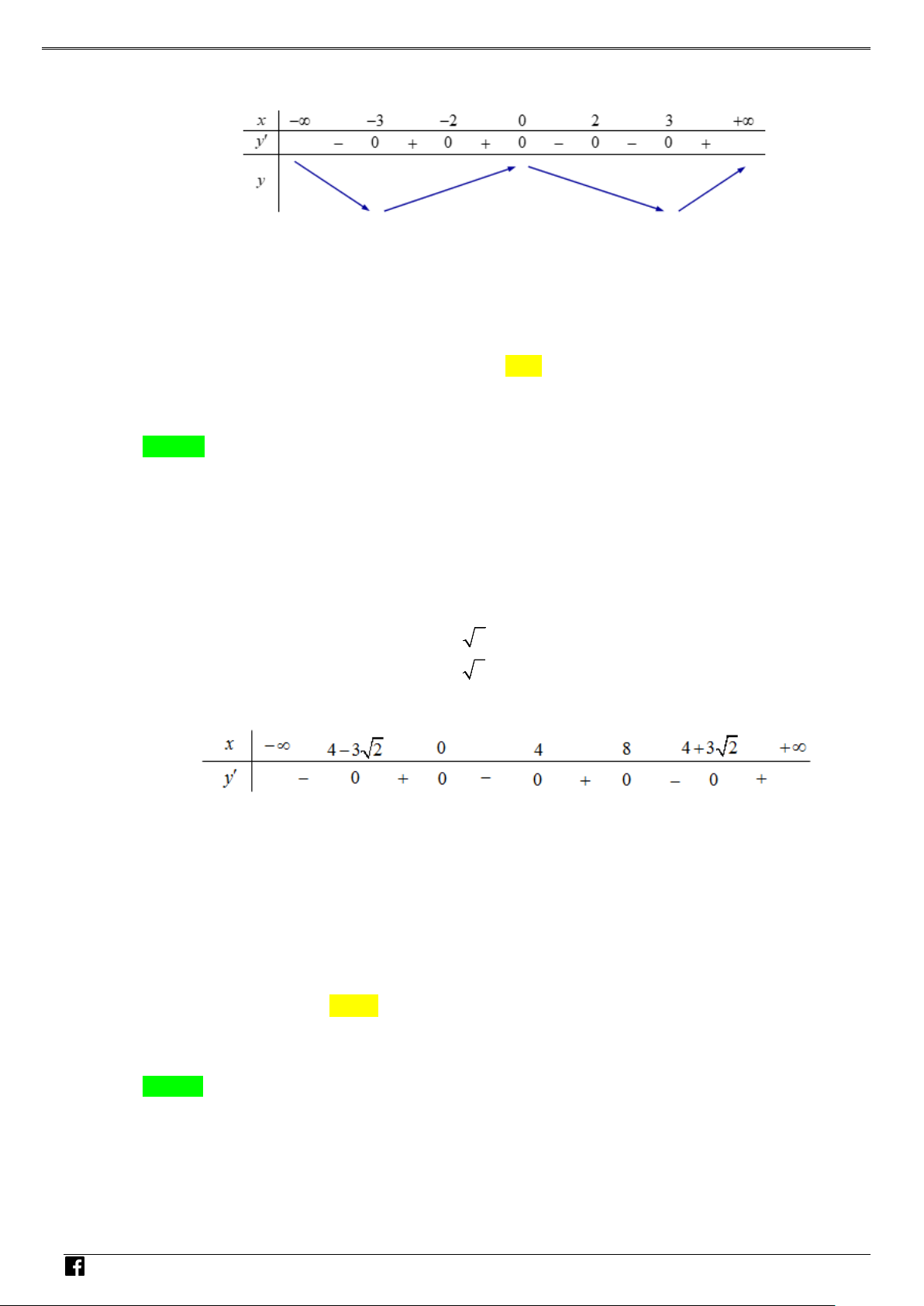
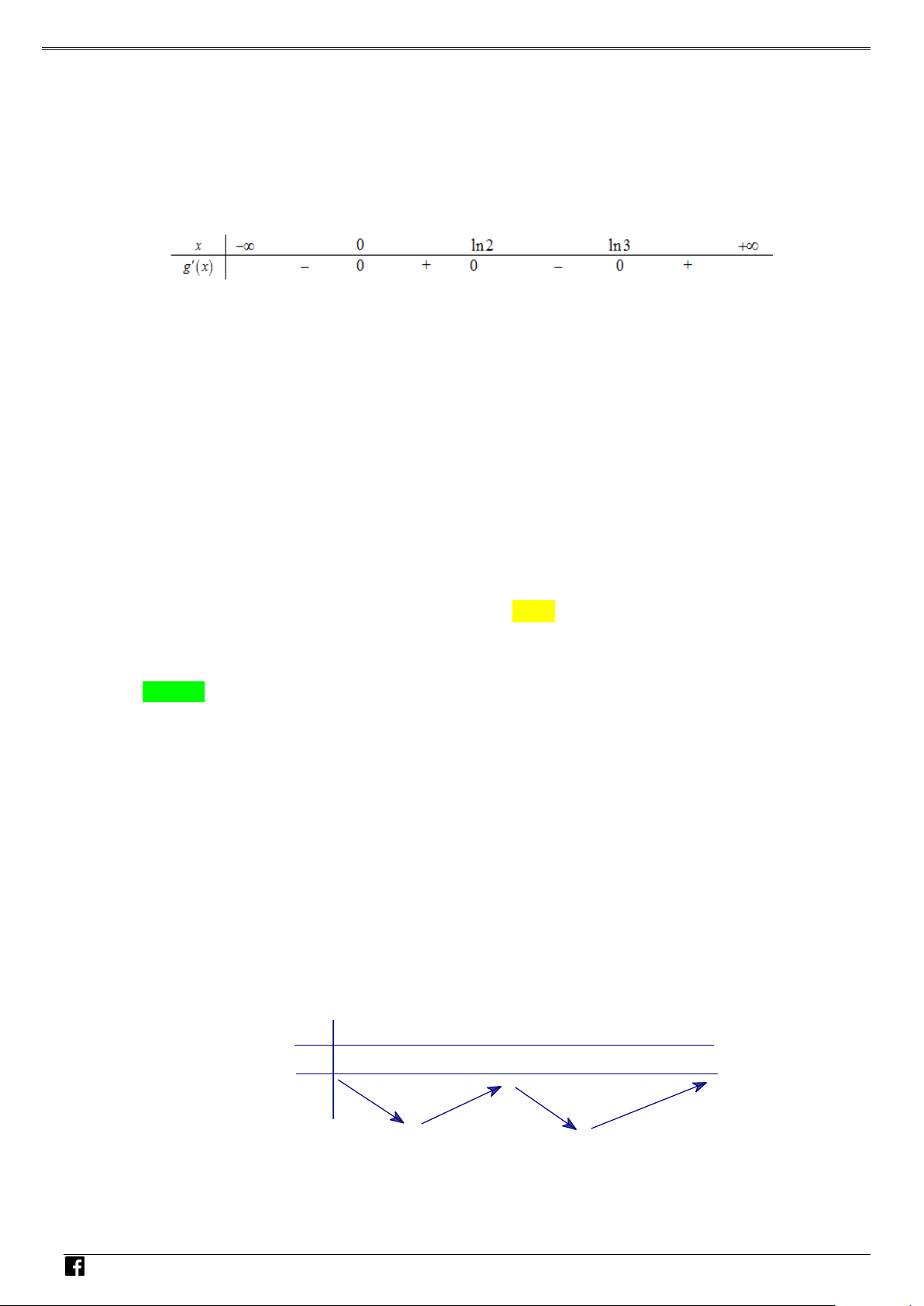
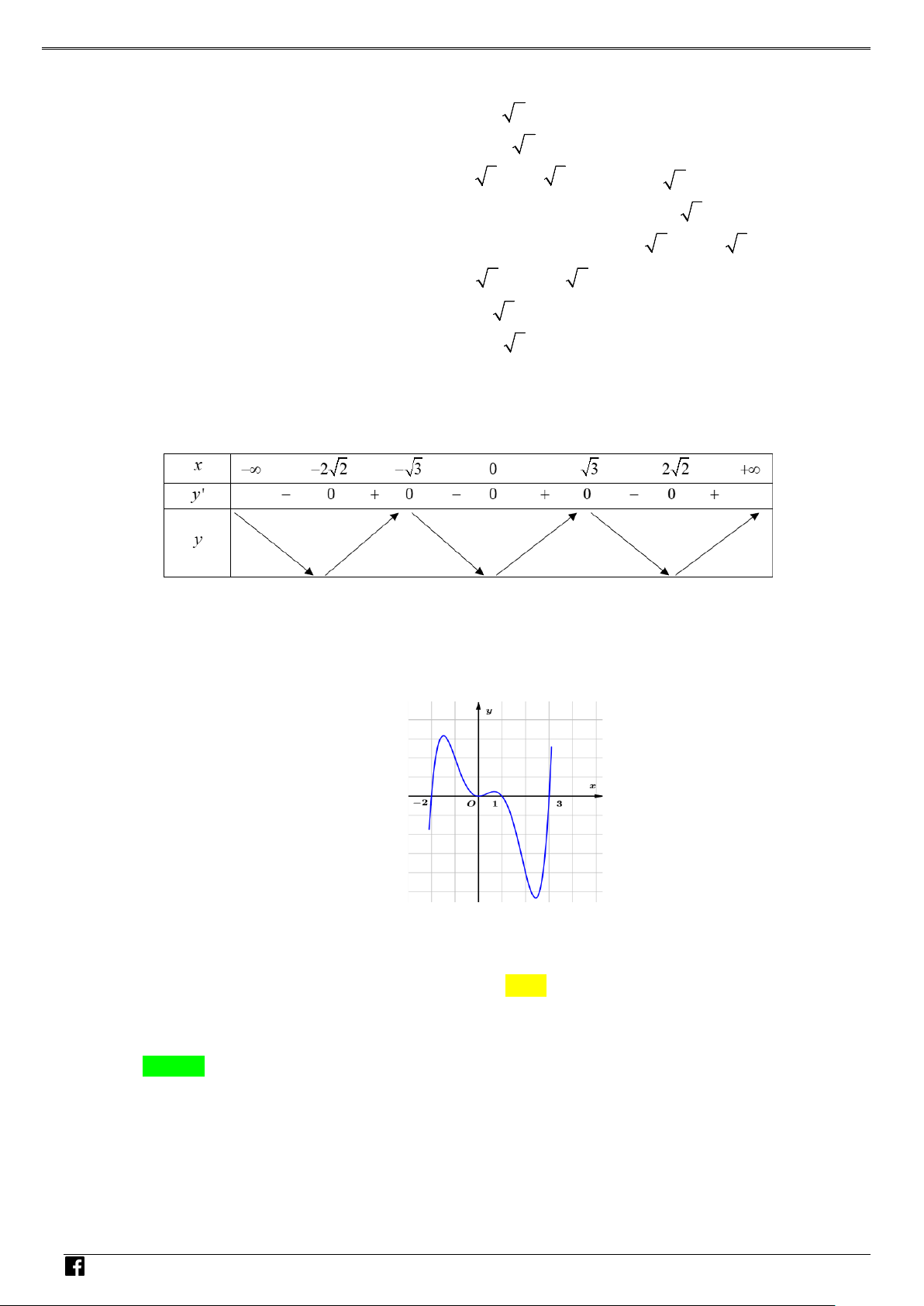
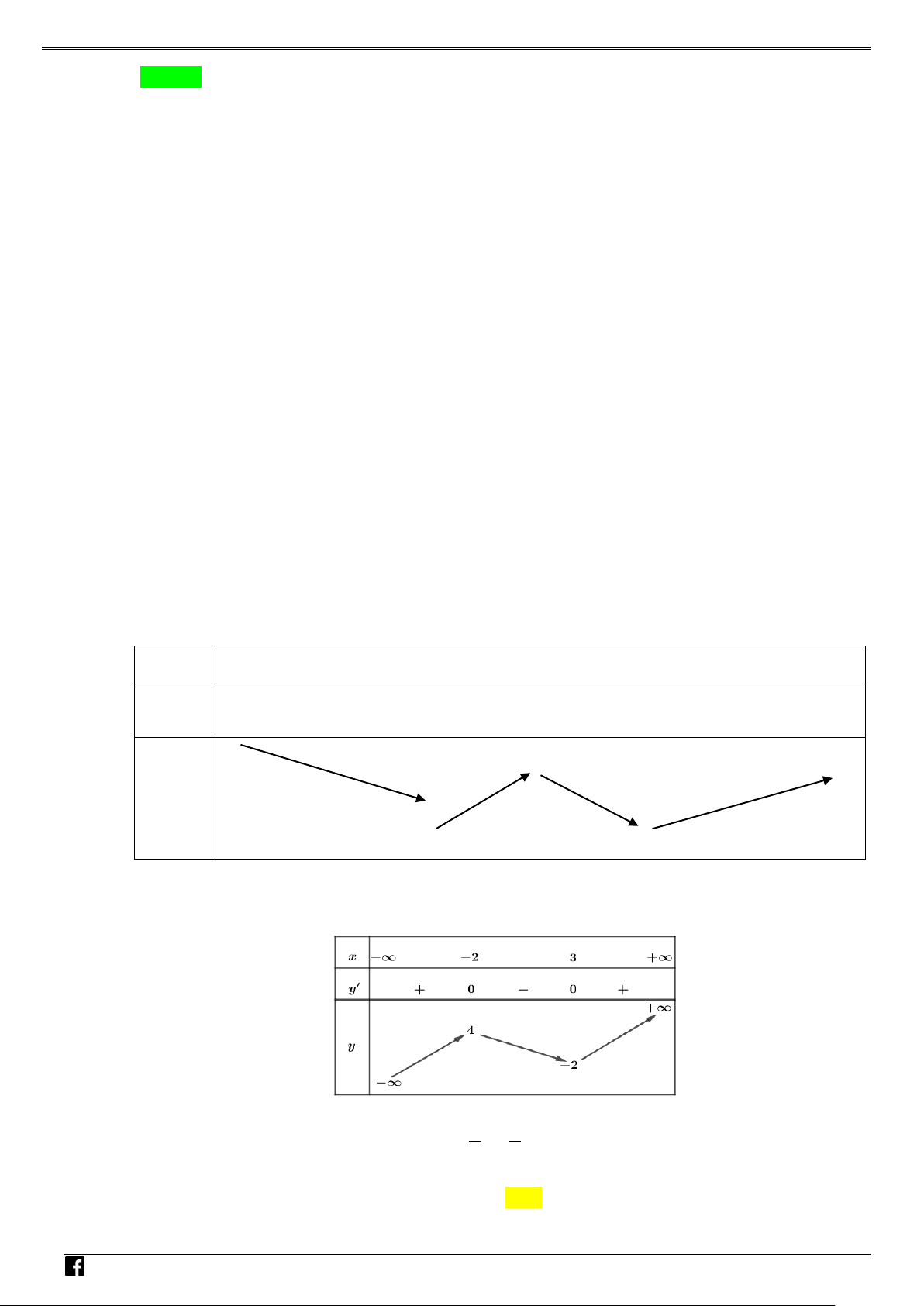
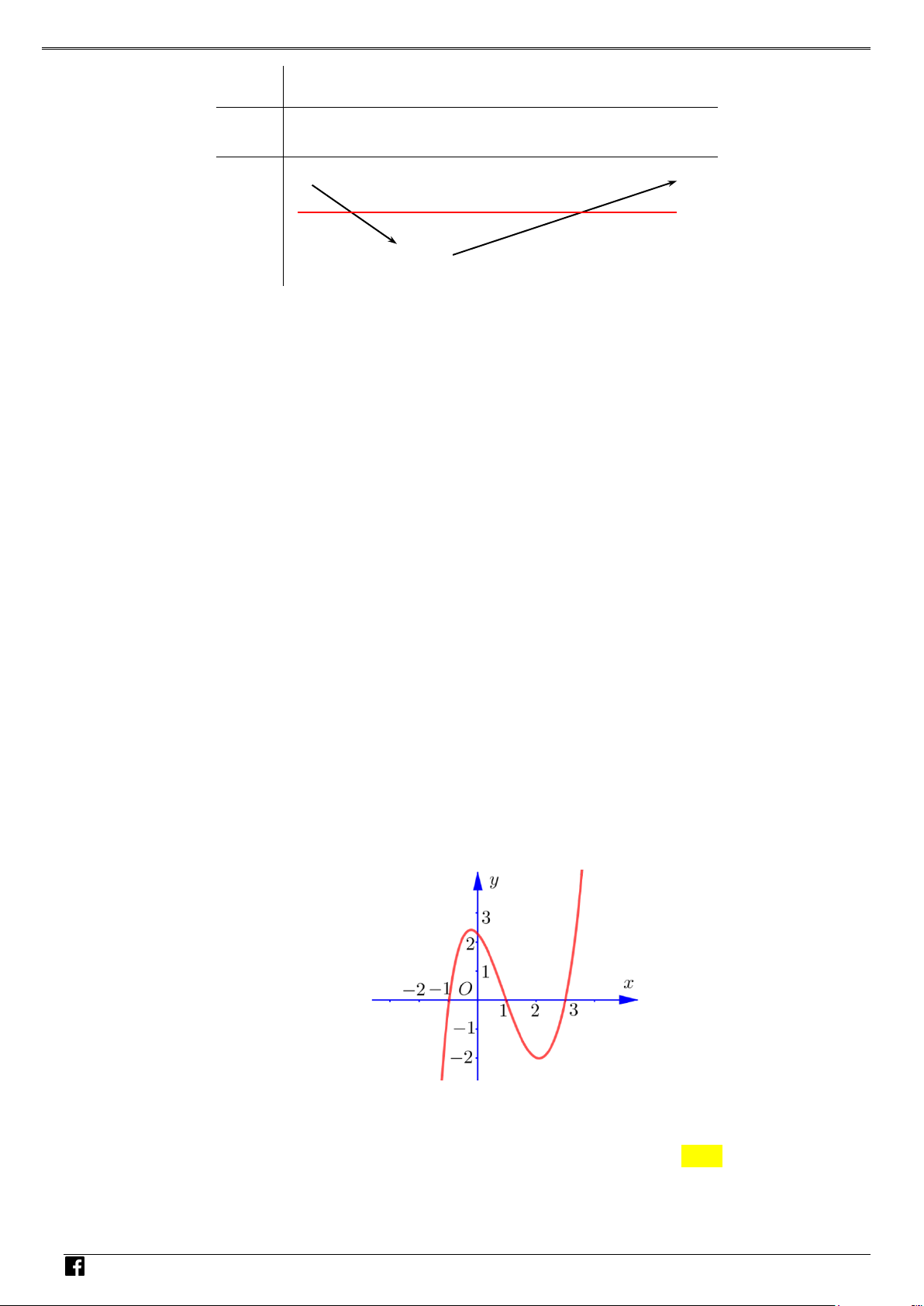
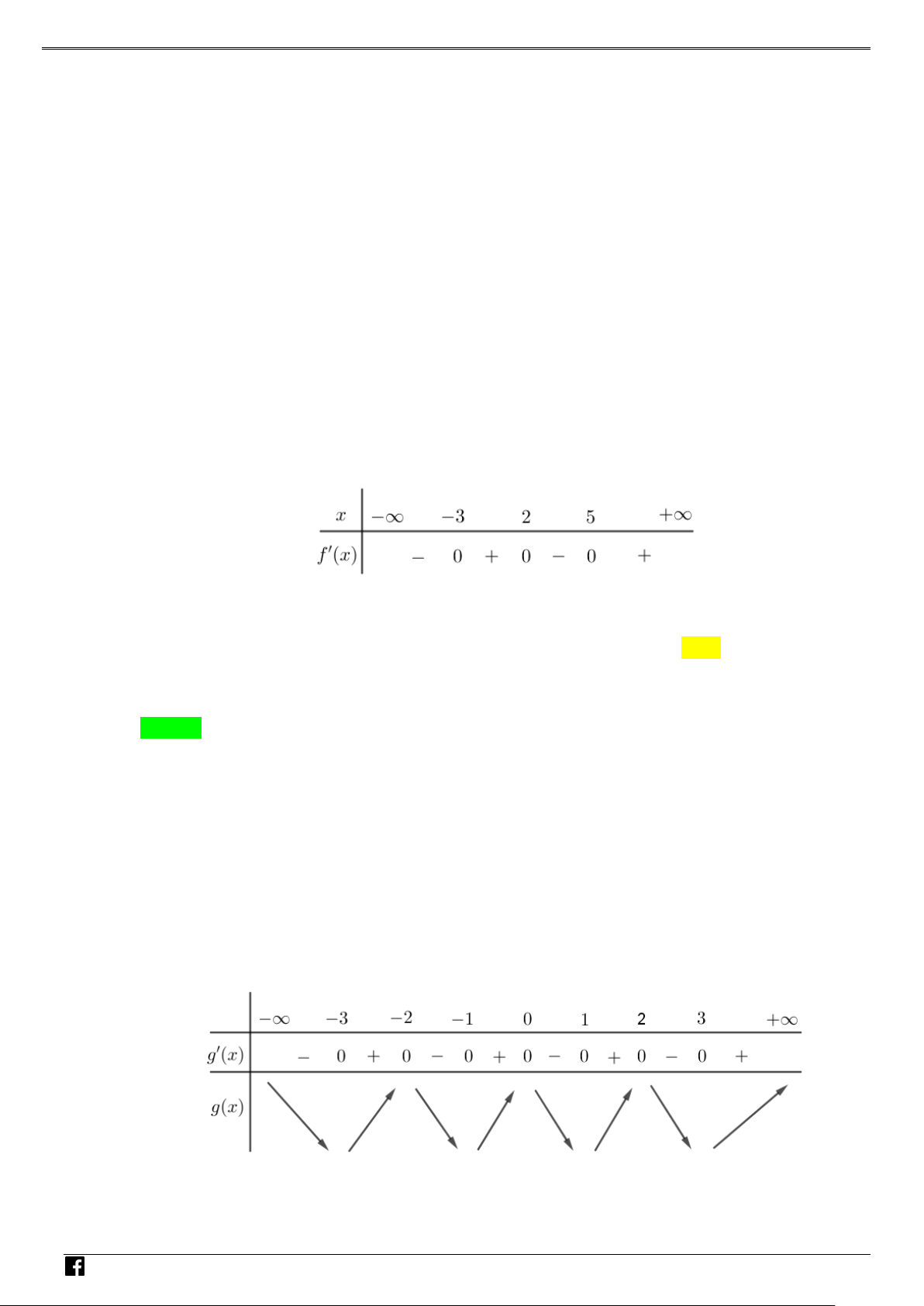
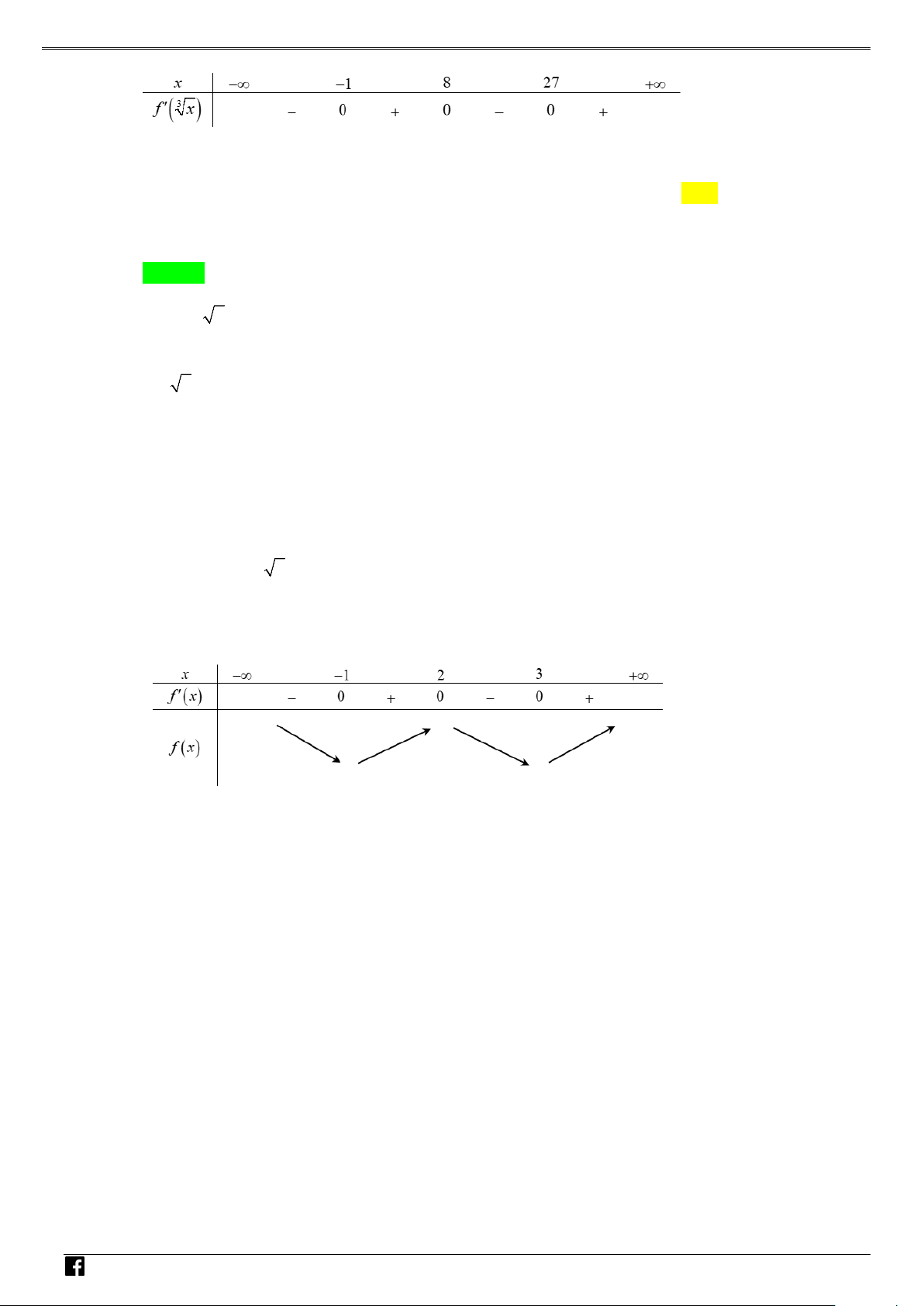
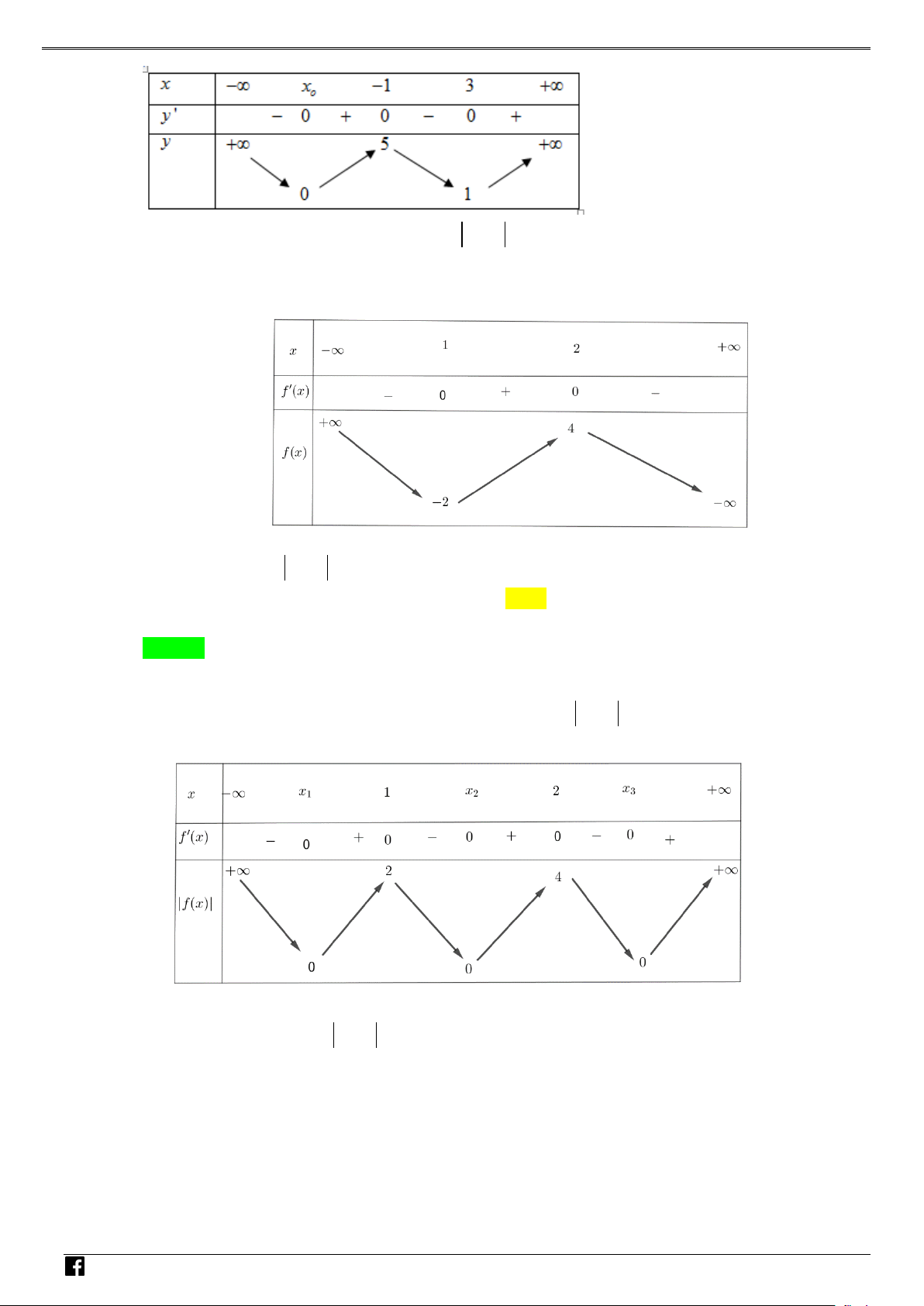
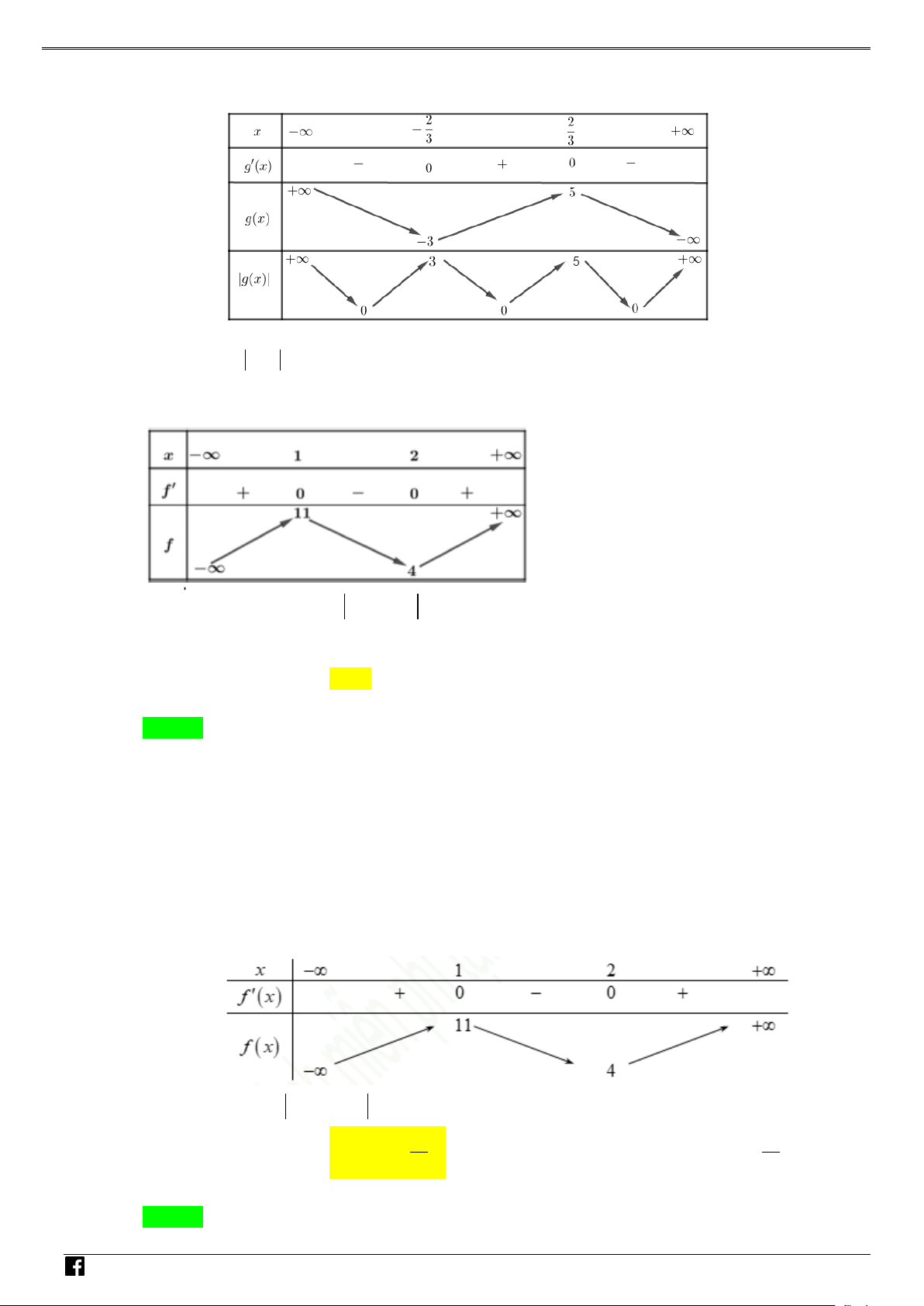
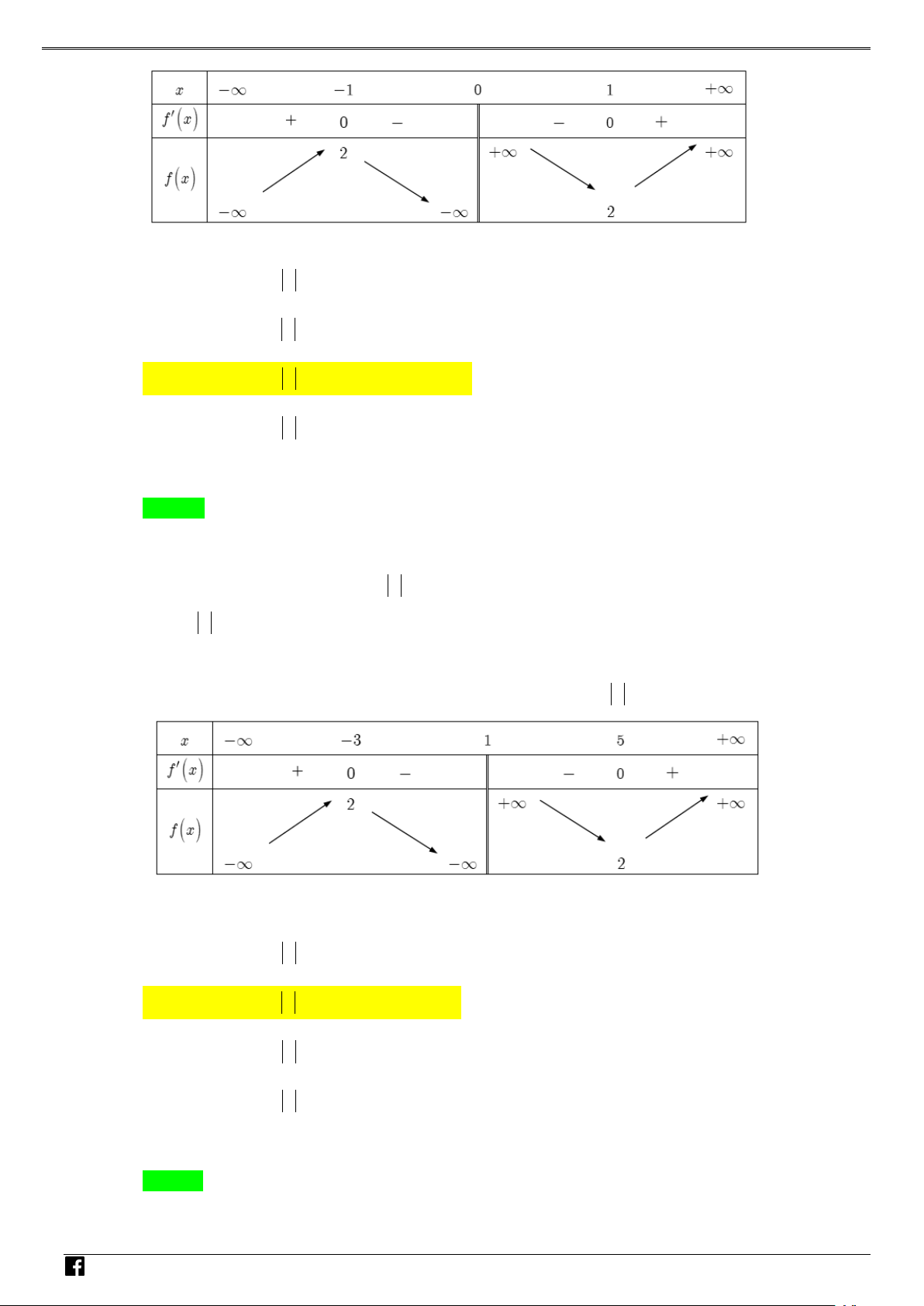
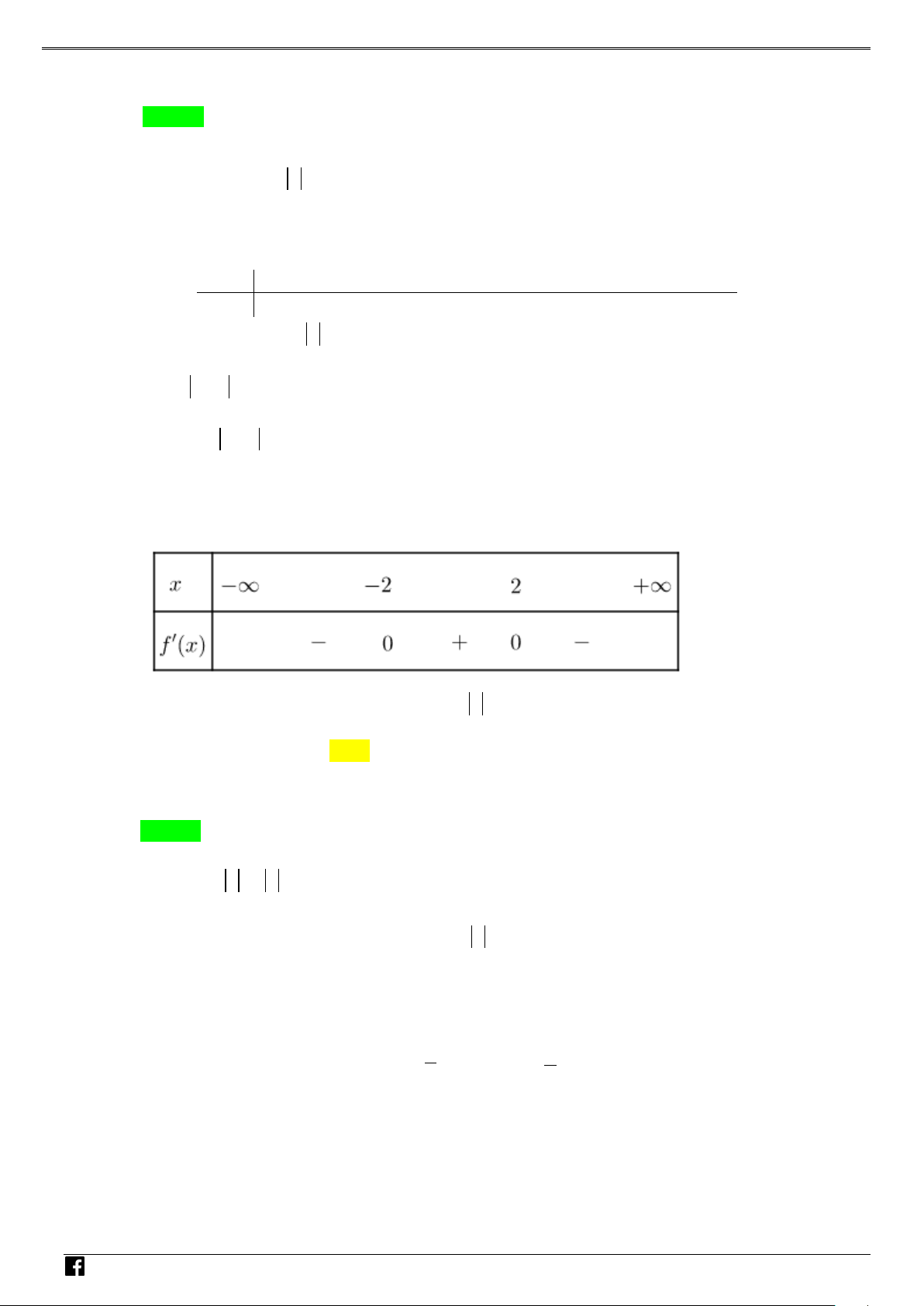
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Bảng biến thiên NHÓ M TOÁN V Vậy y CT 3. D 2 – (3x −15x
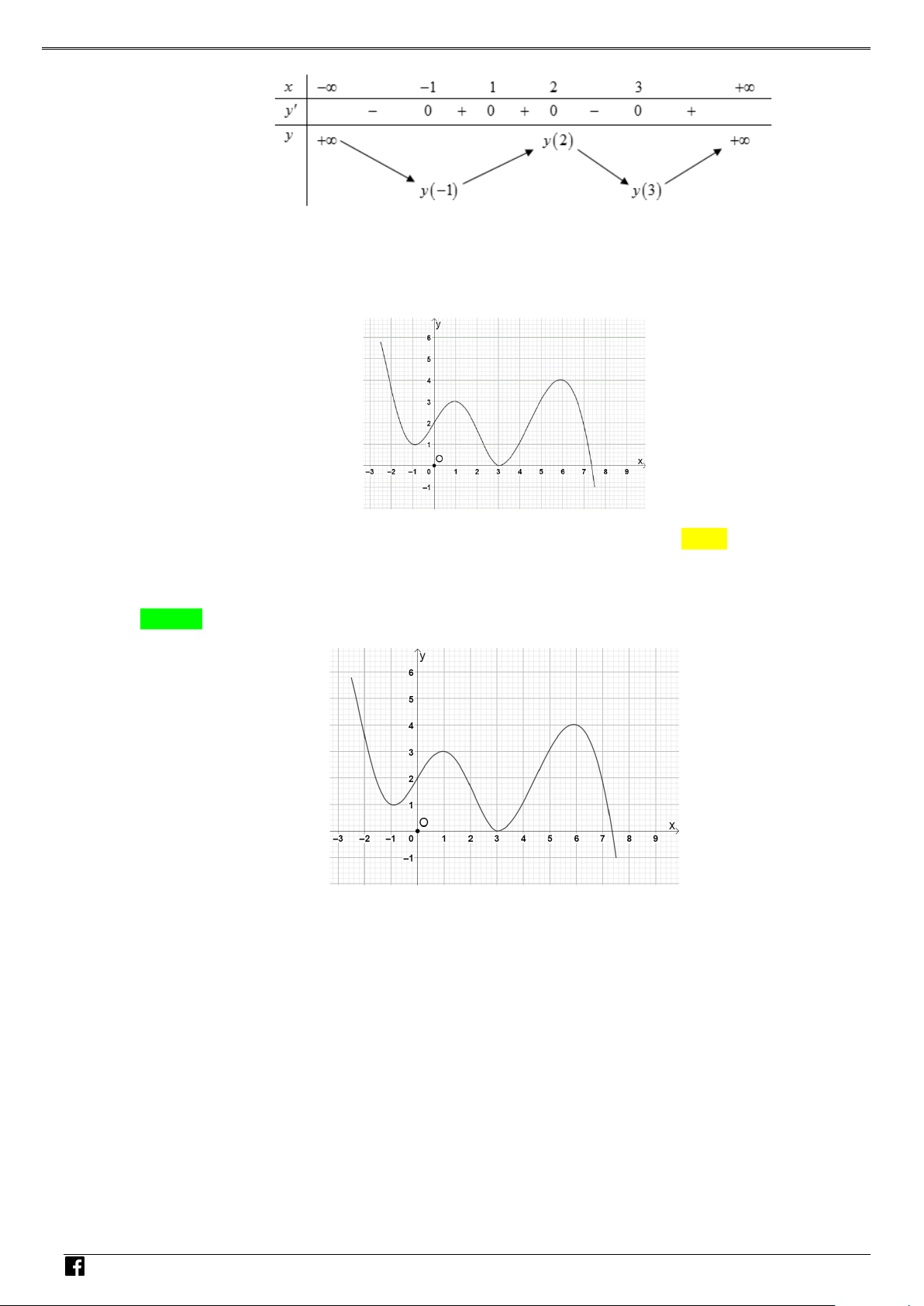
) f ′(x)+(10−5x) f (x) = 0 VD
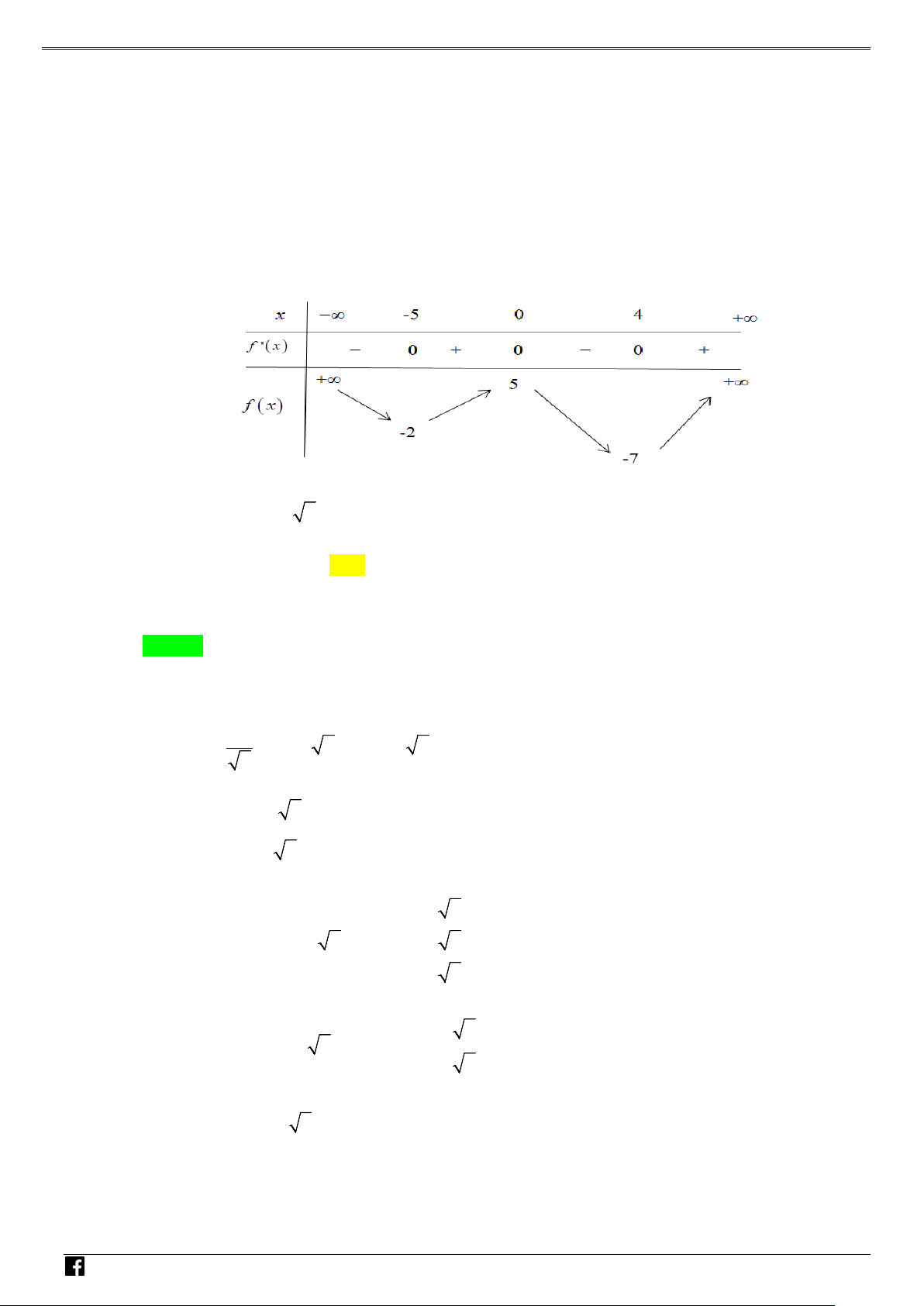
Câu 4: Cho hàm số y = f (x) liên tục trên , thỏa mãn với f ′ ( x) 2 + f ( x) 2 > 0 C x ∀ ≠ 0 và f ( ) 1 = 4
− . Tổng cực đại và cực tiểu của hàm số y = f (x) bằng A. 3 3 − 4 . B. 3 3 4 . C. 3 2 − 4 . D. 4 3 2 . Lời giải Chọn A Từ f ′ ( x) 2 + f ( x) 2 > 0 với x
∀ ≠ 0 ta suy ra: Với x ≠ 0 ta có f (x) = 0 ⇒ f '(x) ≠ 0. Do đó từ ( 2
3x −15x) f ′(x) + (10 −5x) f (x) = 0 với x ∀ ≠ 0, ta suy ra:
Với x ≠ 0 ta có f (x) = ⇔ ( 2 0
3x −15x) f ′(x) = 0 ⇔ x = 5. f ′(x)
Với các kết quả trên ta được 5 x − 2 = x ∀ ∉ 0;5 NHÓ
f (x) 3 x(x − 5) { } f ′(x) 5 x − 2 M T Suy ra ∫ ( )dx = dx ⇔ f (x) 2 ln
= ln x + ln x − 5 + C f x 3 ∫ x(x − 5) 3 OÁN ⇔ ( ) C
f x = e (x − ) 3 2 5 x VD Do f ( ) 1 = 4
− nên C = 0 và f (x) = (x − ) 3 2 5 x với x ∀ ∉{0; } 5 – VD
Vì f (x) liên tục trên nên f (x) liên tục tại x = 0, x = 5 suy ra f (0) = f (5) = 0 C
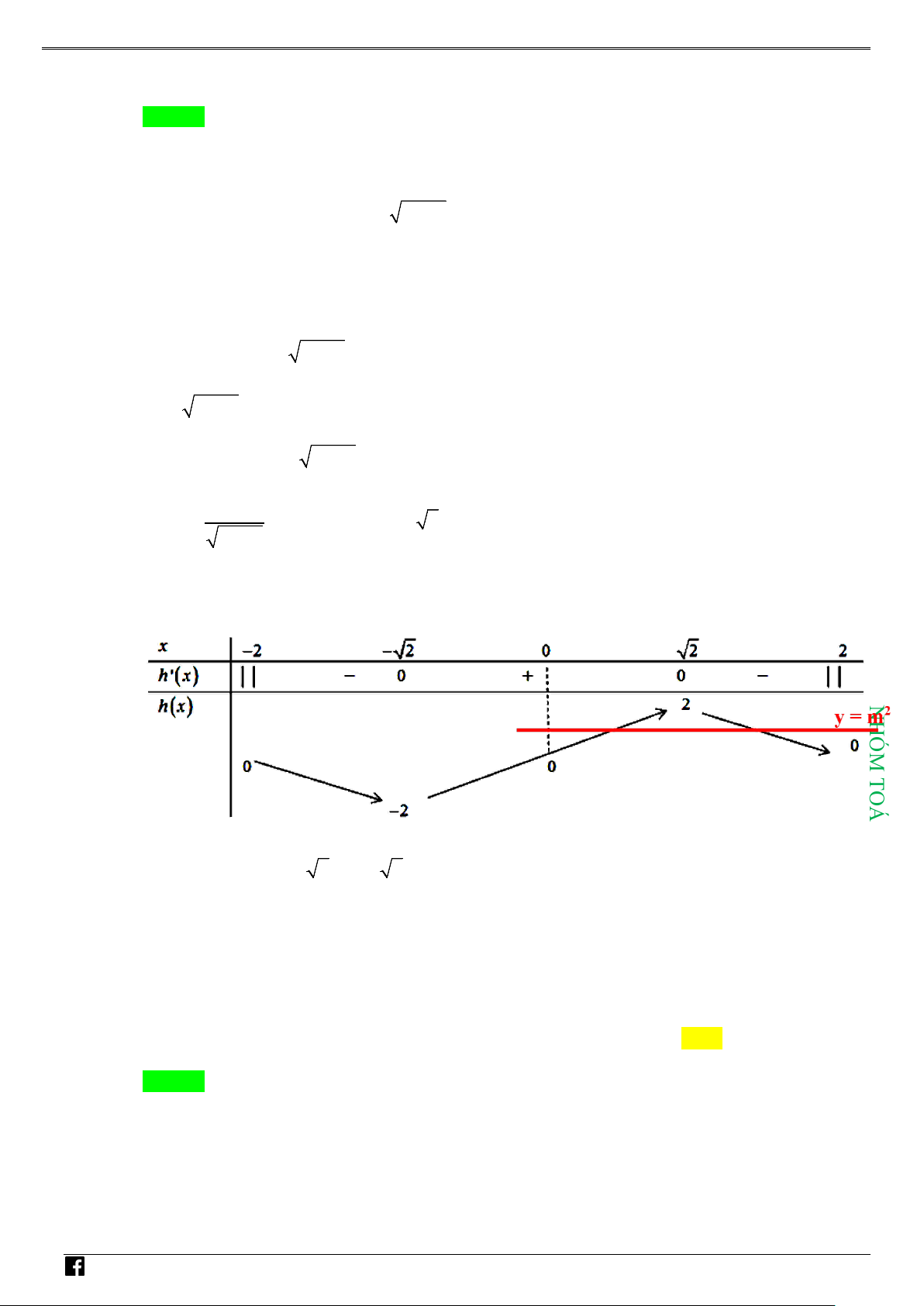
Hay f (x) = (x − ) 3 2 5 x với x ∀ ∈ . Khi đó −
f ′(x) 5 x 2 = . 3 3 x
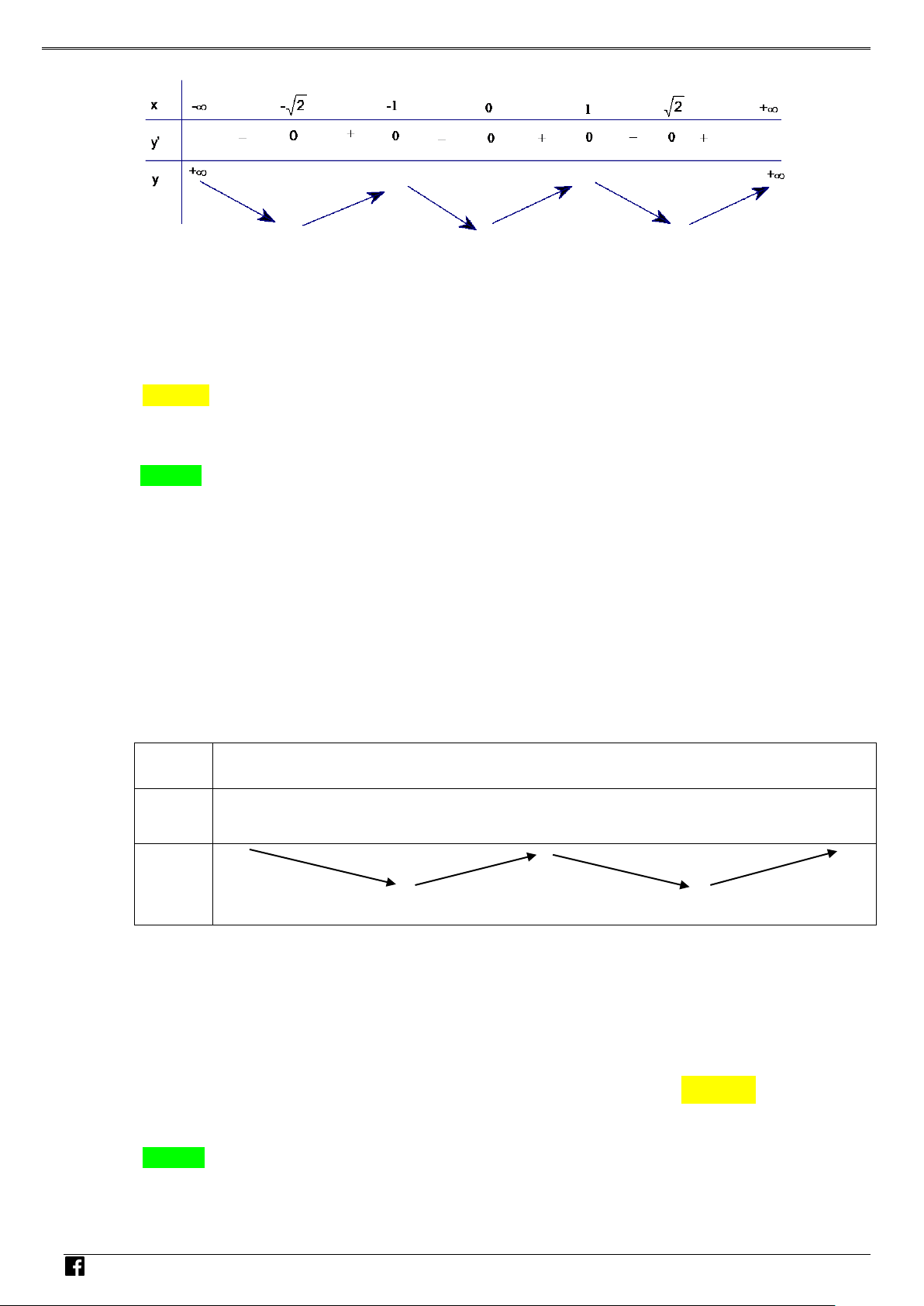
Ta có f ′(x) = 0 ⇔ x = 2 , f ′(x) không xác định khi x = 0 .
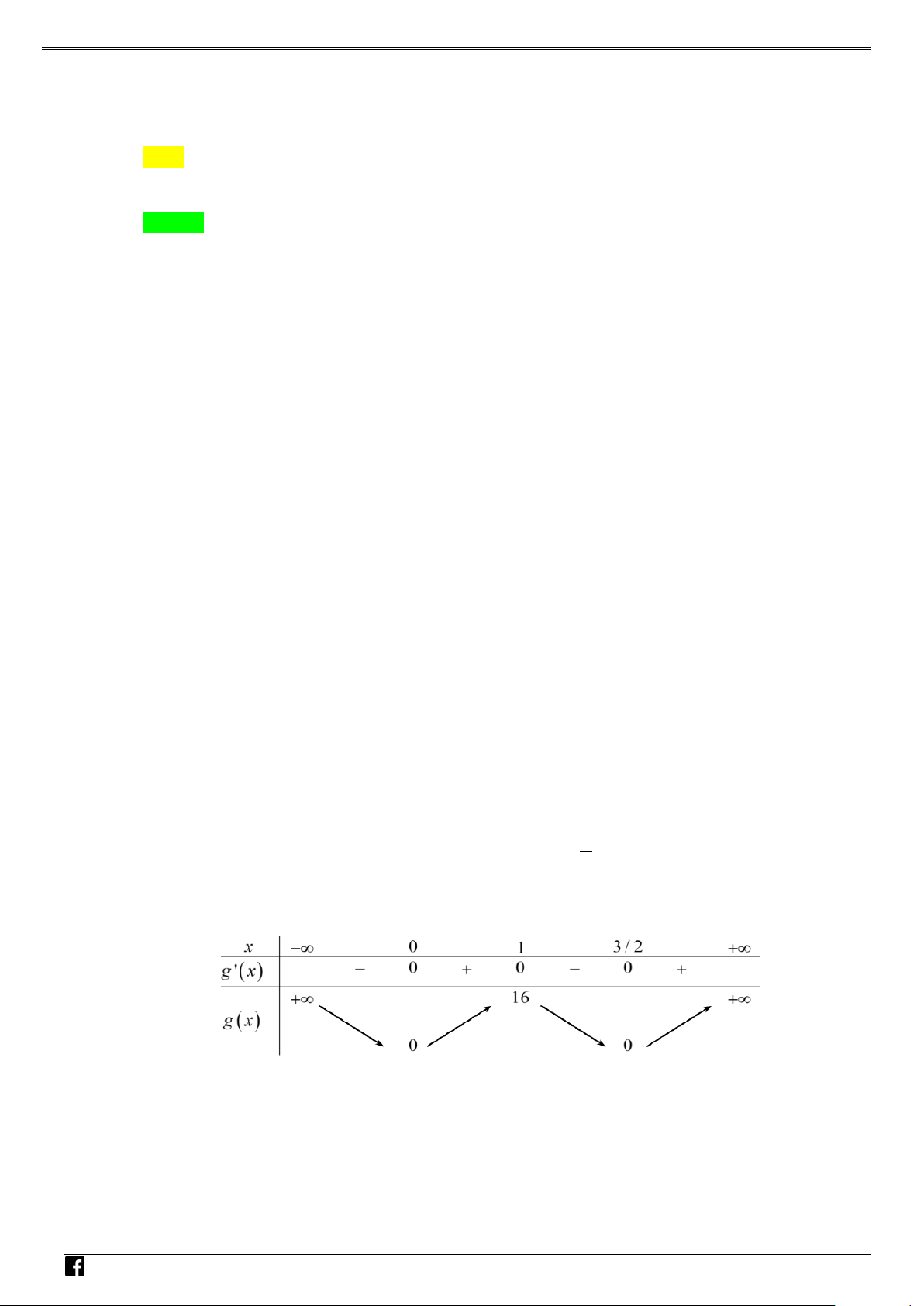
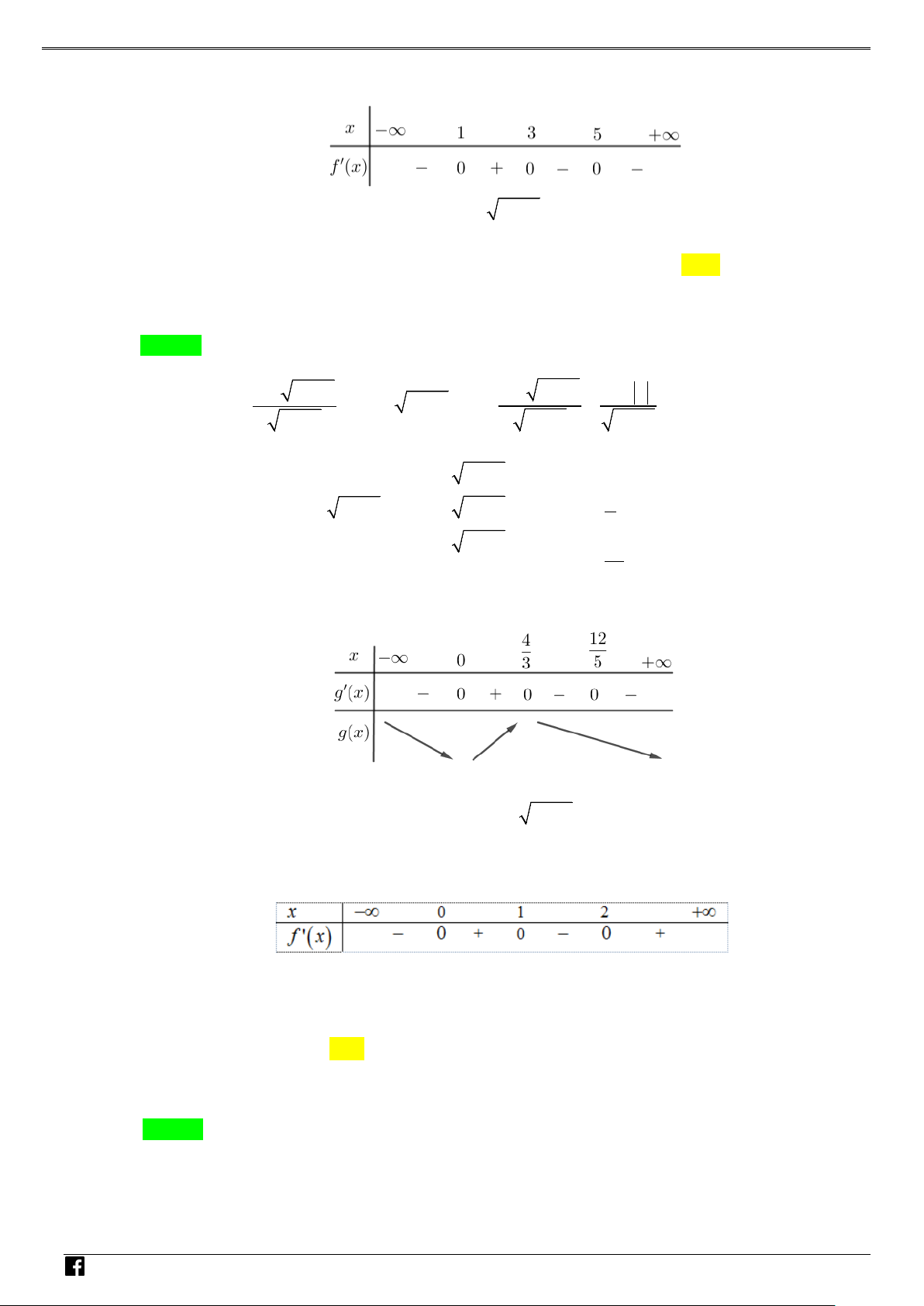
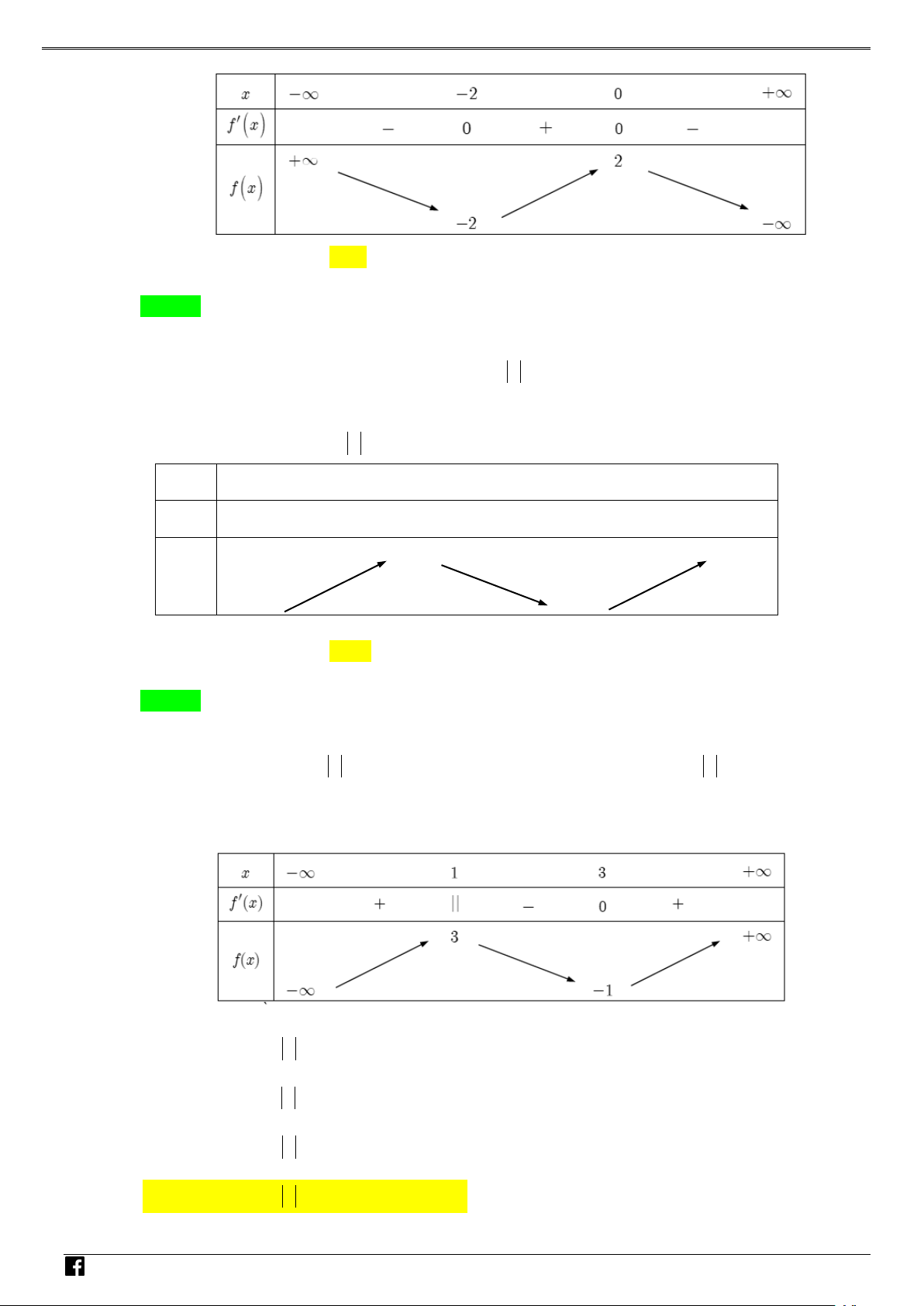
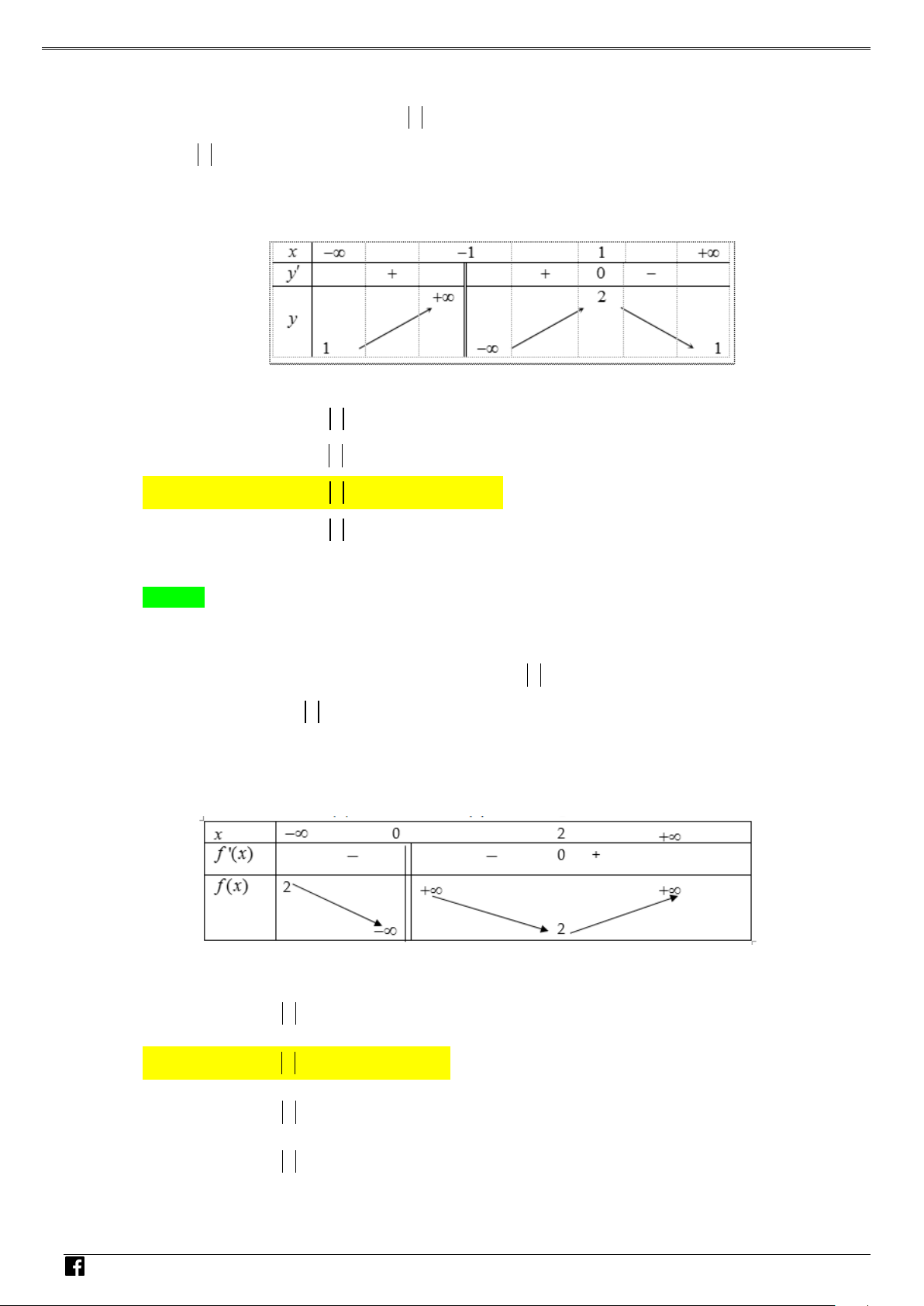
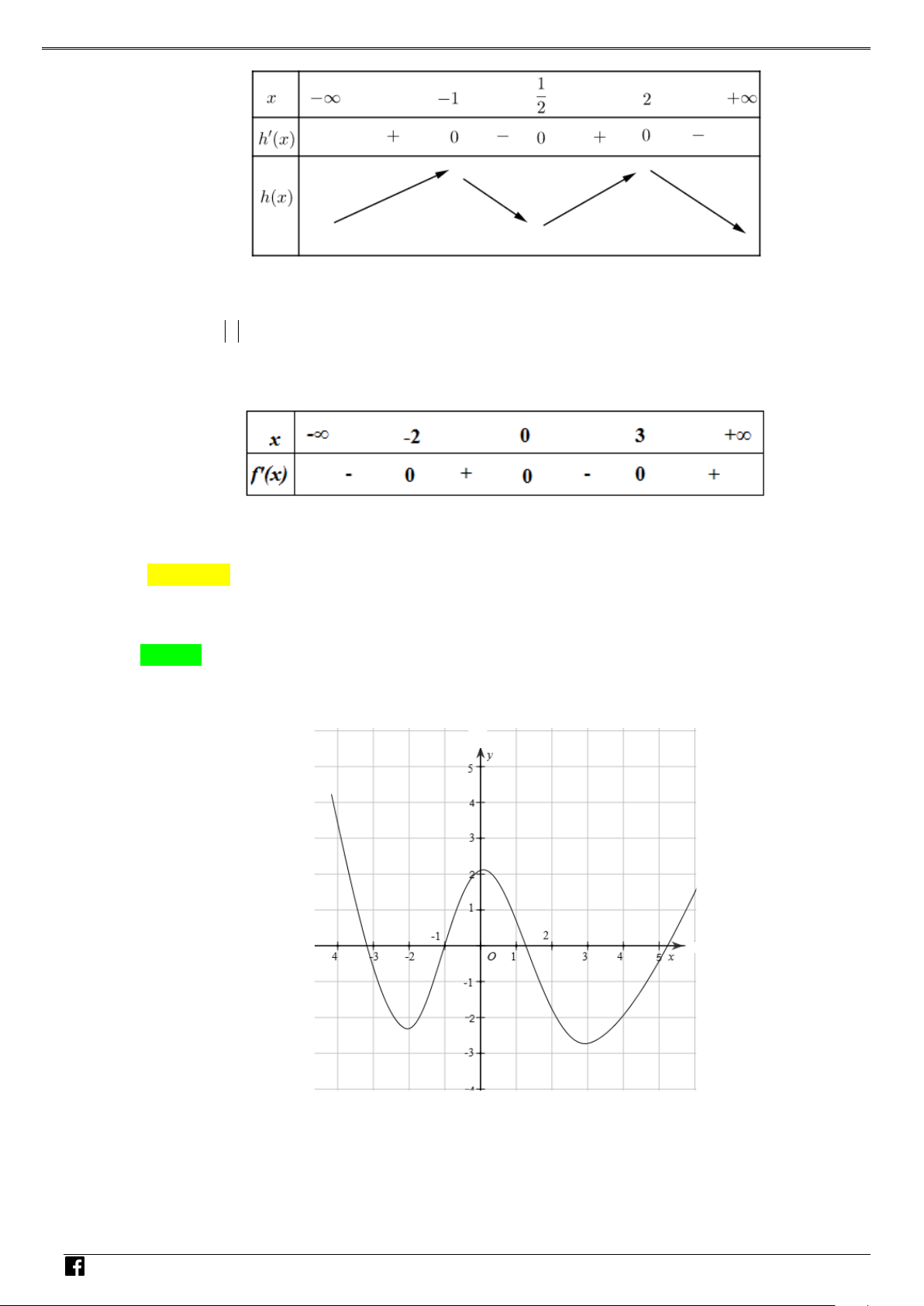
Bảng biến thiên của f (x) :
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ đó suy ra y = f = y = f = − . Vậy 3 y + y = − . CD CT 3 4 CD ( ) CT ( ) 3 0 0; 2 3 4
DẠNG 3. Dạng toán có thể tìm được biểu thức cụ thể của hàm số y = f (x) NHÓ
trong bài toán chứa tham số.
Câu 1. Tổng tất cả các giá trị của tham số thực m sao cho đồ thị hàm số 3 2 3
y = x − 3mx + 4m có điểm M
cực đại và cực tiểu đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất là TOÁN A. 2 . B. 1 . C. 0 . D. 1 . 2 2 4 V Lời giải D Chọn C – VD x = 0 Ta có: 2
y′ = 3x − 6mx , y′ = 0 ⇔ . x = 2m C
Để hàm số có cực đại cực tiểu thì m ≠ 0 .
Khi đó các điểm cực trị của đồ thị hàm số là: A( 3
0;4m ) , B(2m;0) . Ta có I ( 3
m;2m ) là trung điểm của đoạn thẳng AB .
Đường phân giác của góc phần tư thứ nhất là d : x − y = 0.
Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua d thì: 3
2m − 4m = 0 2 2
⇔ 1− 2m = 0 ⇔ m = ± . 3
m − 2m = 0 2
Vậy tổng tất cả các giá trị của tham số thực m là 0 . Câu 2. Cho hàm số 4 2 2 2
y = x − 2m x + m có đồ thị (C). Để đồ thị (C) có ba điểm cực trị A , B , C sao
cho bốn điểm A , B , C , O là bốn đỉnh của hình thoi (O là gốc tọa độ) thì giá trị tham số m là NHÓ A. m = − 2 . B. 2 m = ± . C. m = ± 2 . D. 2 m = . 2 2 M T Lời giải OÁN Chọn B x = 0 Ta có 3 2
y′ = 4x − 4m x ; y′ = 0 ⇔ . VD 2 x = m –
Điều kiện để hàm số có ba cực trị là y′ = 0 có ba nghiệm phân biệt ⇔ m ≠ 0 . VD x = 0 C
Khi đó: y′ = 0 ⇔ . x = ±m
Tọa độ các điểm cực trị là A( 2 0;m ), B( 4 2 ;
m −m + m ) , C ( 4 2 ;
m −m + m ).
Ta có OA ⊥ BC , nên bốn điểm A , B , C , O là bốn đỉnh của hình thoi điều kiện cần và đủ là
OA và BC cắt nhau tại trung điểm mỗi đoạn
x + x = x + x 0 = 0 A O B C ⇔ ⇔
y + y = y + y 2 m + 0 = ( 4 2 −m + m ) + ( 4 2 −m + m ) A O B C 4 2 ⇔ 2m − m = 0 2 1 ⇔ m = 2 ⇔ m = ± . 2 2 Vậy 2 m = ± . 2
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 3. Tìm tất cả các giá trị thực của tham số m để điểm M ( 3
2m ;m) cùng với hai điểm cực trị của đồ thị hàm số 3
y = x − ( m + ) 2 2 3 2
1 x + 6m(m + )
1 x +1 tạo thành một tam giác có diện tích nhỏ nhất. A. m = 1 − . B. m = 2 . C. m =1. D. m = 0. NHÓ Lời giải Chọn D M
Tập xác định: D = . T 2 OÁN
y′ = 6x − 6(2m + )
1 x + 6m(m + ) 1 3 2 x = m
⇒ y = 2m + 3m +1 2 V
y′ = 0 ⇔ 6x − 6(2m + )
1 x + 6m(m + ) 1 = 0 ⇔ . 3 2 D
x = m +1 ⇒ y = 2m + 3m – 2 ∆′ > ⇔ + − + > ⇔ > ∀ ∈ VD Hàm số có 2 cực trị: 0 9(2m ) 1 36m(m ) 1 0 9 0, x . C Gọi ,
A B là hai điểm cực trị của đồ thị hàm số ⇒ A( 3 2
m m + m + ) B( 3 2 ;2 3
1 , m +1;2m + 3m ) ⇒ AB = (1;− ) 1 ⇒ AB = 2
Phương trình đường thẳng ∆ đi qua 2 điểm cực trị: 3 2
x + y − 2m − 3m − m −1 = 0 3 3 2 2 + − − − −
d (M ∆) 2m m 2m 3m m 1 3m +1 , = = 2 2 2 2 1 m + m S + = ∆ = = . ∆ d M AB MAB ( ) 1 3 1 3 1 , . . . 2 2 2 2 2 1 S = ⇔ m = 0. min 2 Câu 4. Cho hàm số 4 2
y = x − 2mx + m (C) . Tìm m để đồ thị hàm số có 3 điểm cực trị đồng thời ba
điểm cực trị của đồ thị hàm số tạo thành tam giác có bán kính đường tròn nội tiếp bằng 1. NHÓ A. m =1. B. m = 0. C. m = 2 − . D. m = 2 . Lời giải M T Chọn D OÁN Ta có 3
y′ = 4x − 4mx . x = 0 VD y′ = 0 ⇔ . 2 x = m –
Hàm số có 3 điểm cực trị ⇔ y′ = 0 có 3 nghiệm phân biệt ⇔ m > 0. VD 2 2 C
Các điểm cực trị của đồ thị là A(0;m), B( m;− m + m) , C(− m;− m + m) Ta có: 4
AB = AC = m + m , BC = 2 m .
Gọi I là trung điểm BC . Suy ra I ( 2
0;−m + m) và 2 AI = m . 1 .
AB + BC + CA S AI BC = = .r 2 ⇔ m m = ( 4 .2
2 m + m + 2 m ).1 2 2 m = 0(loai) ⇔ m ( 2 3 2
m − m +1 − )1 = 0 ⇔ 3 2
m +1 = m −1
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số m ≥1 2 m −1≥ 0
m = 0(loai) ⇔ ⇔ ⇔ m = 2 . 3 4 2
m +1 = m − 2m +1 m = 1 − (nhan) NHÓ m = 2 (nhan) M 1 T
Câu 5. Cho (P) là đường Parabol qua ba điểm cực trị của đồ thị hàm số 4 2 2
y = x − mx + m . Gọi m là a OÁN 4
giá trị để (P) đi qua B( 2; 2) . Hỏi m thuộc khoảng nào dưới đây? a V D A. ( 10; 15). B. ( −2; 5). C. ( −5; 2). D. ( −8; 2) . – VD Lời giải Chọn B C 3
y′ = x − 2mx = x( 2 x − 2m) .
Để hàm số có ba cực trị thì ab < 0 m ⇔ − < 0 ⇔ m > 0 . 4 2
x = 0, y = m
y′ = 0 ⇔ x = 2m, y = 0 . x = − 2m, y = 0
Gọi parabol đi qua điểm A( 2
0; m ), B( 2m; 0), C (− 2m; 0) có dạng: 2
y = ax + bx + c m
2ma + 2mb + c = 0 a = − 2 Ta có: m
2ma − 2mb + c = 0 ⇔ b = 0 hay 2 2
y = − x + m . 2 NHÓ 2 c = m 2 c = m M T
Theo yêu cầu bài toán parabol đi qua m B( 2; 2) nên: a = − ( )2 2 2 2 + m 2
⇔ m − m − = a a 2 0 a OÁN 2 m = − a 1 ⇔ . VD m = a 2 – VD Vậy m = . a 2 C
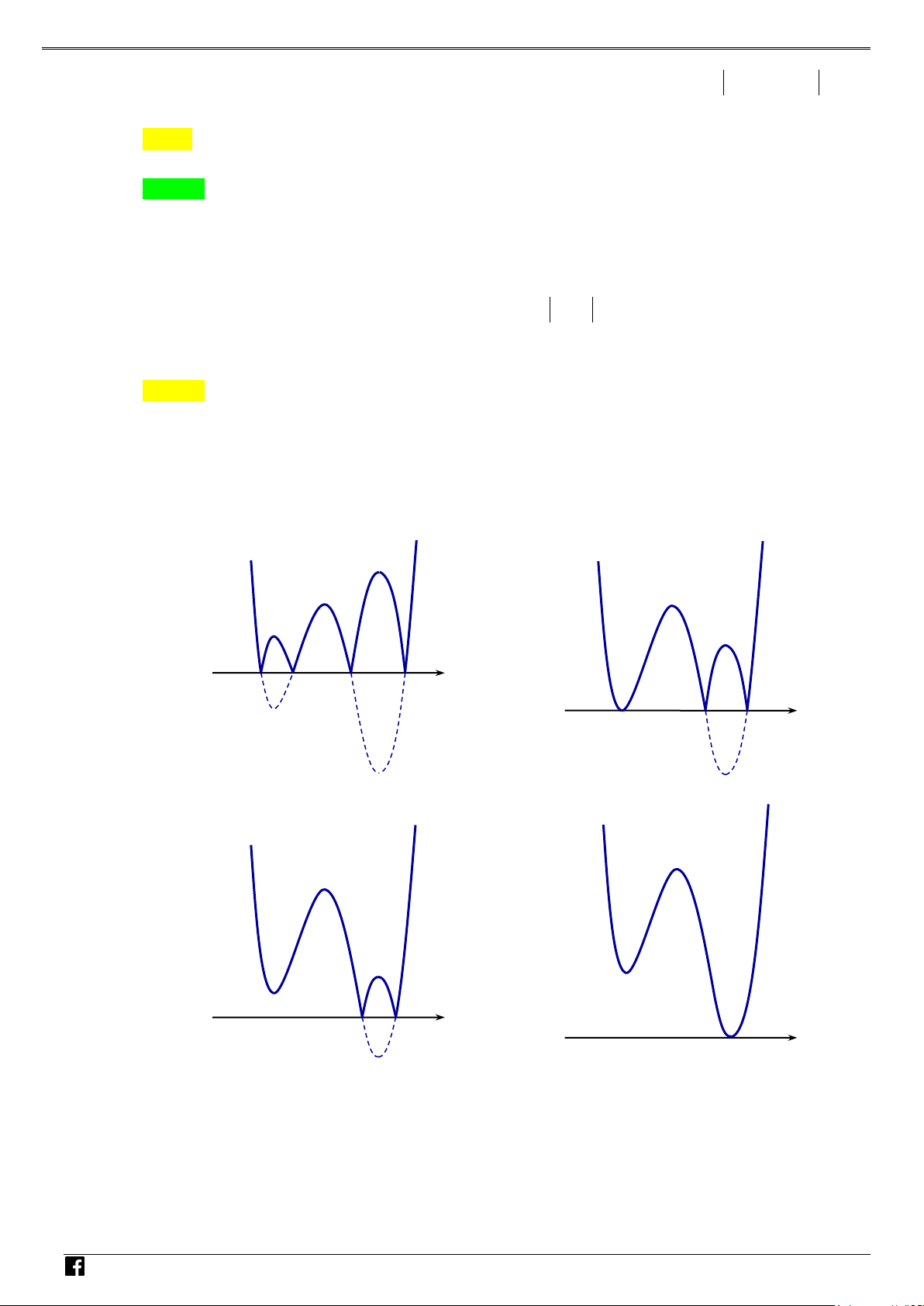
Câu 6. Có bao nhiêu giá trị nguyên của tham số m để hàm số 8
y = x + (m − ) 5 x − ( 2 m − ) 4 3 9 x +1 đạt
cực tiểu tại x = 0 ? A. 4 . B. 7 . C. 6 . D. Vô số. Lời giải Chọn C Ta có 8
y = x + (m − ) 5 x − ( 2 m − ) 4 3 9 x +1 7
⇒ y′ = x + (m − ) 4 x − ( 2 m − ) 3 8 5 3 4 9 x . y′ = 0 3
⇔ x ( 4x + (m − ) x − ( 2 8 5 3 4 m − 9) = 0 x = 0 ⇔ . g (x) 4
= 8x + 5(m − 3) x − 4 ( 2 m − 9) = 0
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Xét hàm số g (x) 4
= x + (m − ) x − ( 2 8 5 3
4 m − 9) có g′(x) 3
= 32x + 5(m −3) .
Ta thấy g′(x) = 0 có một nghiệm nên g (x) = 0 có tối đa hai nghiệm.
+) TH1: Nếu g (x) = 0 có nghiệm x = 0 ⇒ m = 3 hoặc m = 3 − . NHÓ
Với m = 3 thì x = 0 là nghiệm bội 4 của g (x) . Khi đó x = 0 là nghiệm bội 7 của y′ và y′ đổi M
dấu từ âm sang dương khi đi qua điểm x = 0 nên x = 0 là điểm cực tiểu của hàm số. T
Vậy m = 3 thỏa ycbt. OÁN x = 0 V Với m = 3 − thì g ( x) 4
= 8x − 30x = 0 ⇔ 15 . = 3 x D 4 – VD Bảng biến thiên C
Dựa vào BBT x = 0 không là điểm cực tiểu của hàm số. Vậy m = 3 − không thỏa ycbt.
+) TH2: g (0) ≠ 0 ⇔ m ≠ 3 ± .
Để hàm số đạt cực tiểu tại x = 0 ⇔ g (0) > 0 2
⇔ m − 9 < 0 ⇔ 3 − < m < 3.
Do m∈ nên m∈{ 2 − ; 1; − 0;1; } 2 .
Vậy cả hai trường hợp ta được 6 giá trị nguyên của m thỏa ycbt. NHÓ
DẠNG 4. Biết đặc điểm của hàm số hoặc đồ thị, hoặc BBT, hoặc đạo hàm của = ϕ = = M T
hàm f (x), tìm cực trị của hàm y f ( (x)); y f ( f (x)),...y f ( f ( f ...(x))) trong OÁN
bài toán không chứa tham số. VD
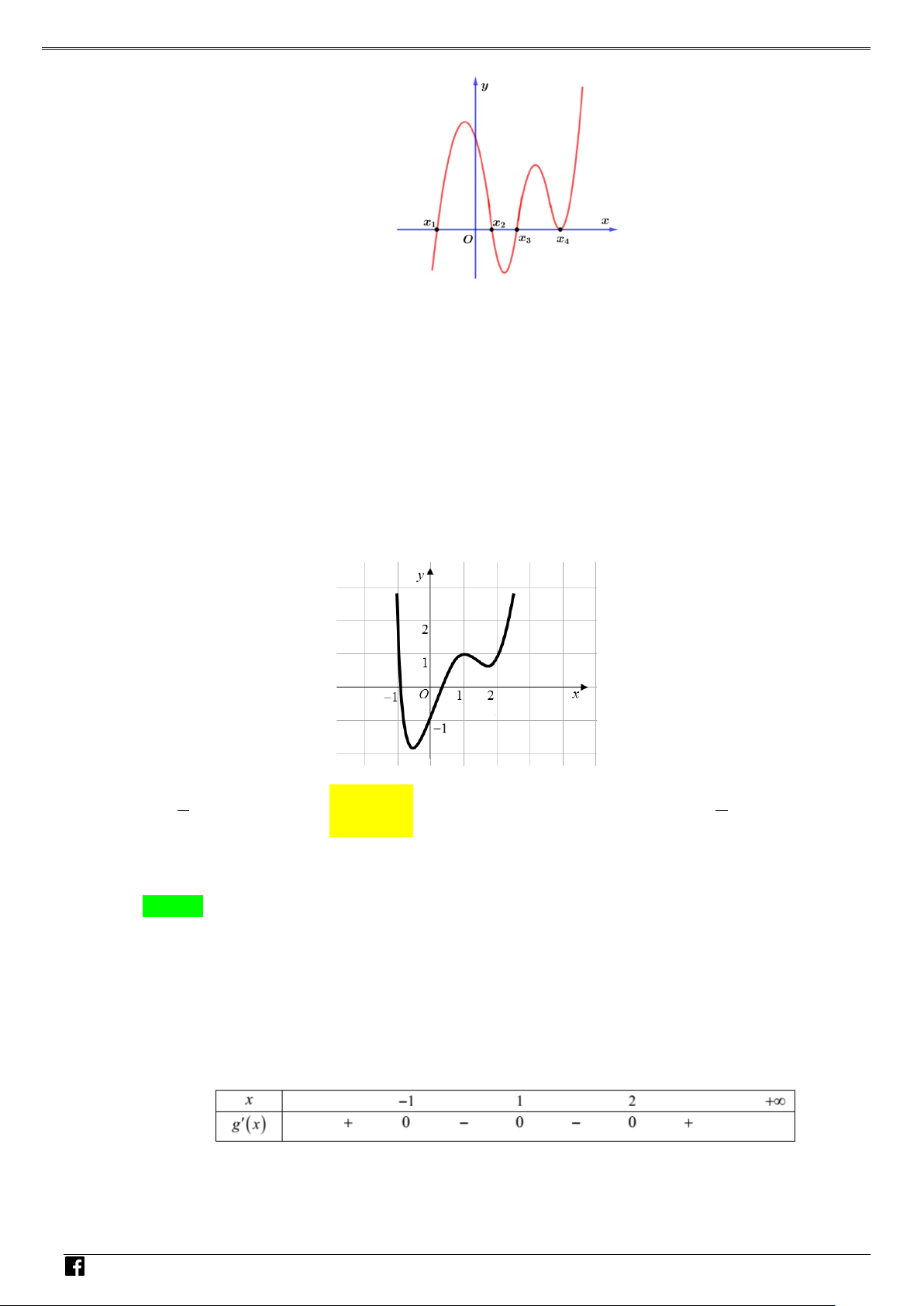
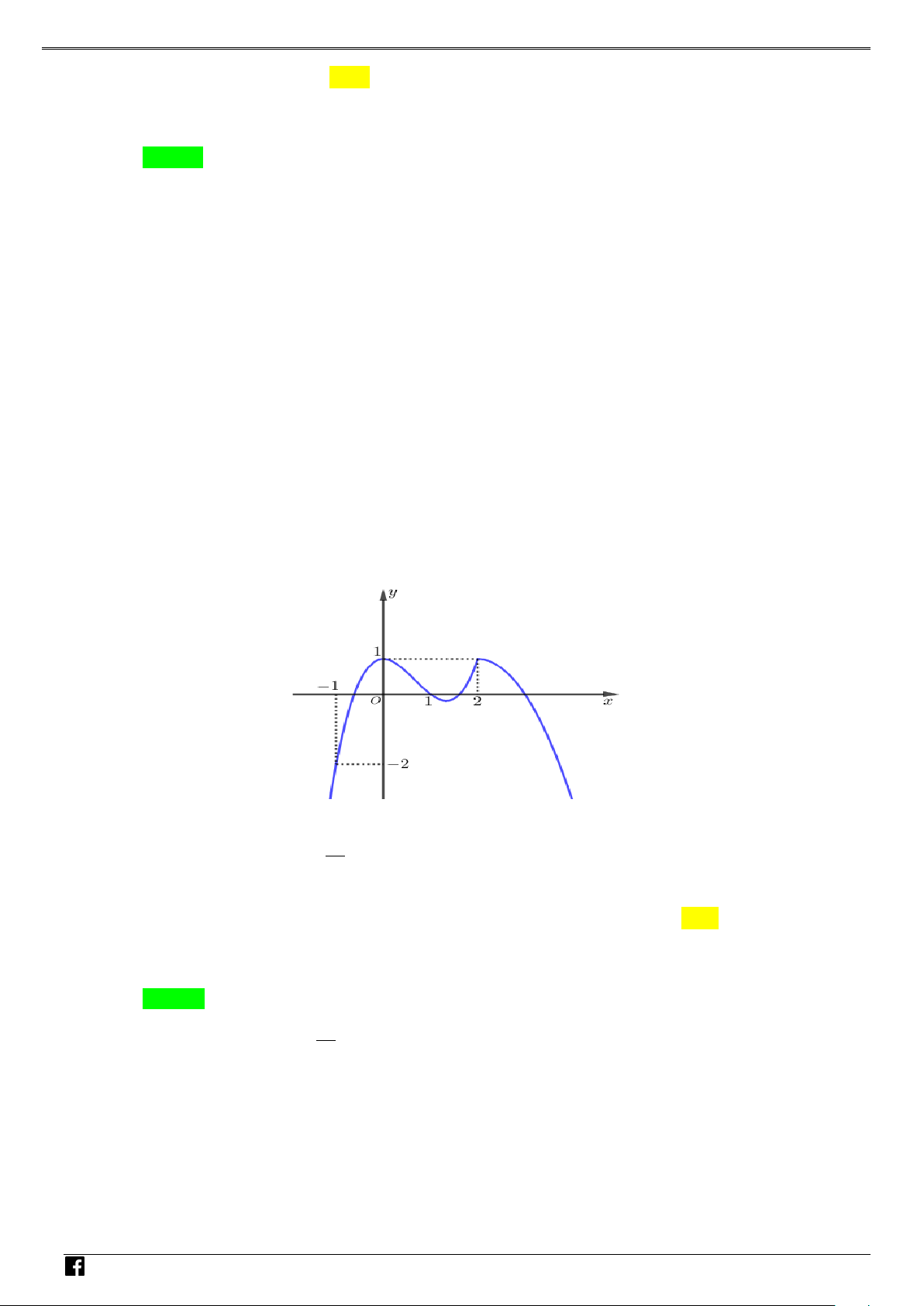
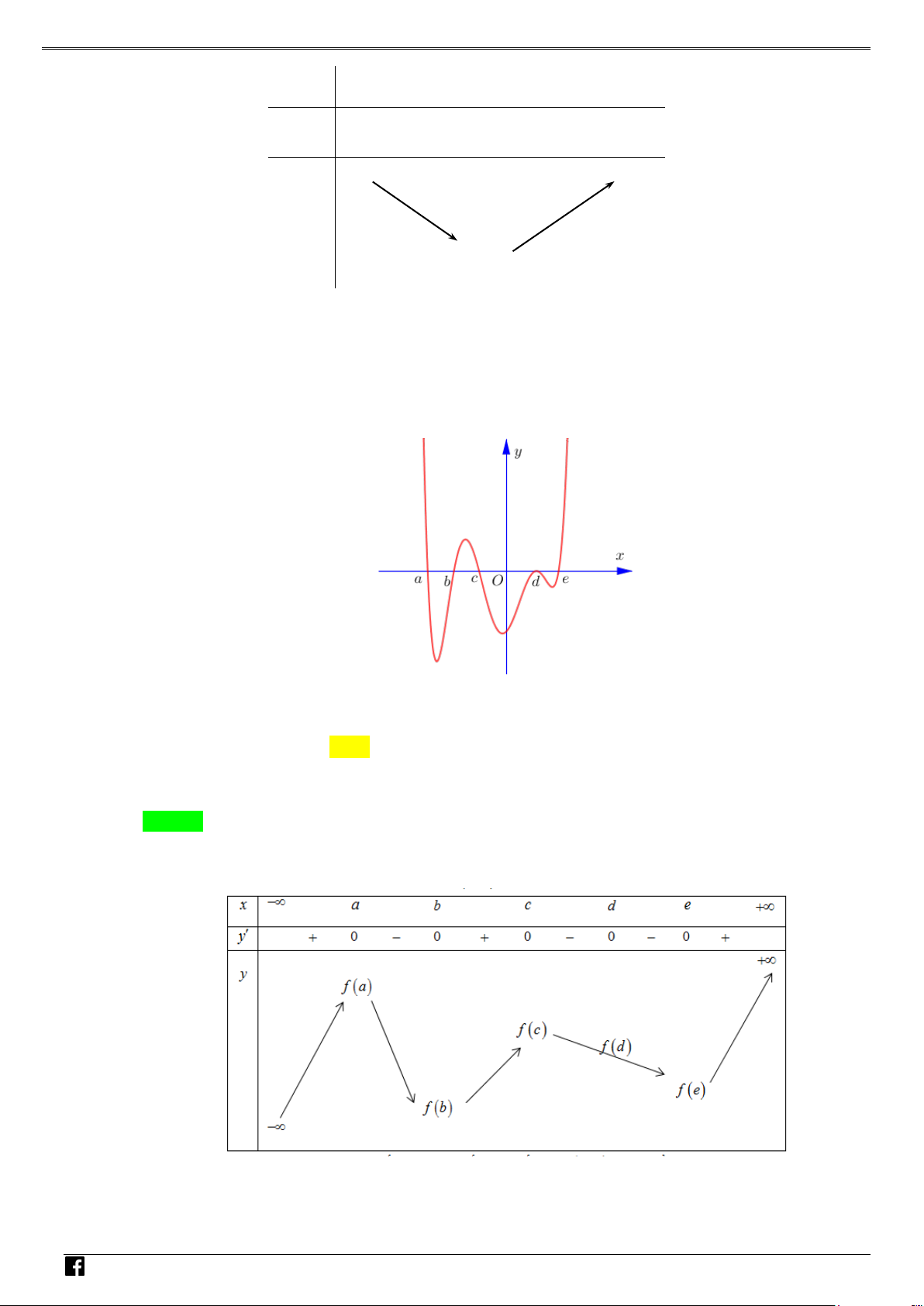
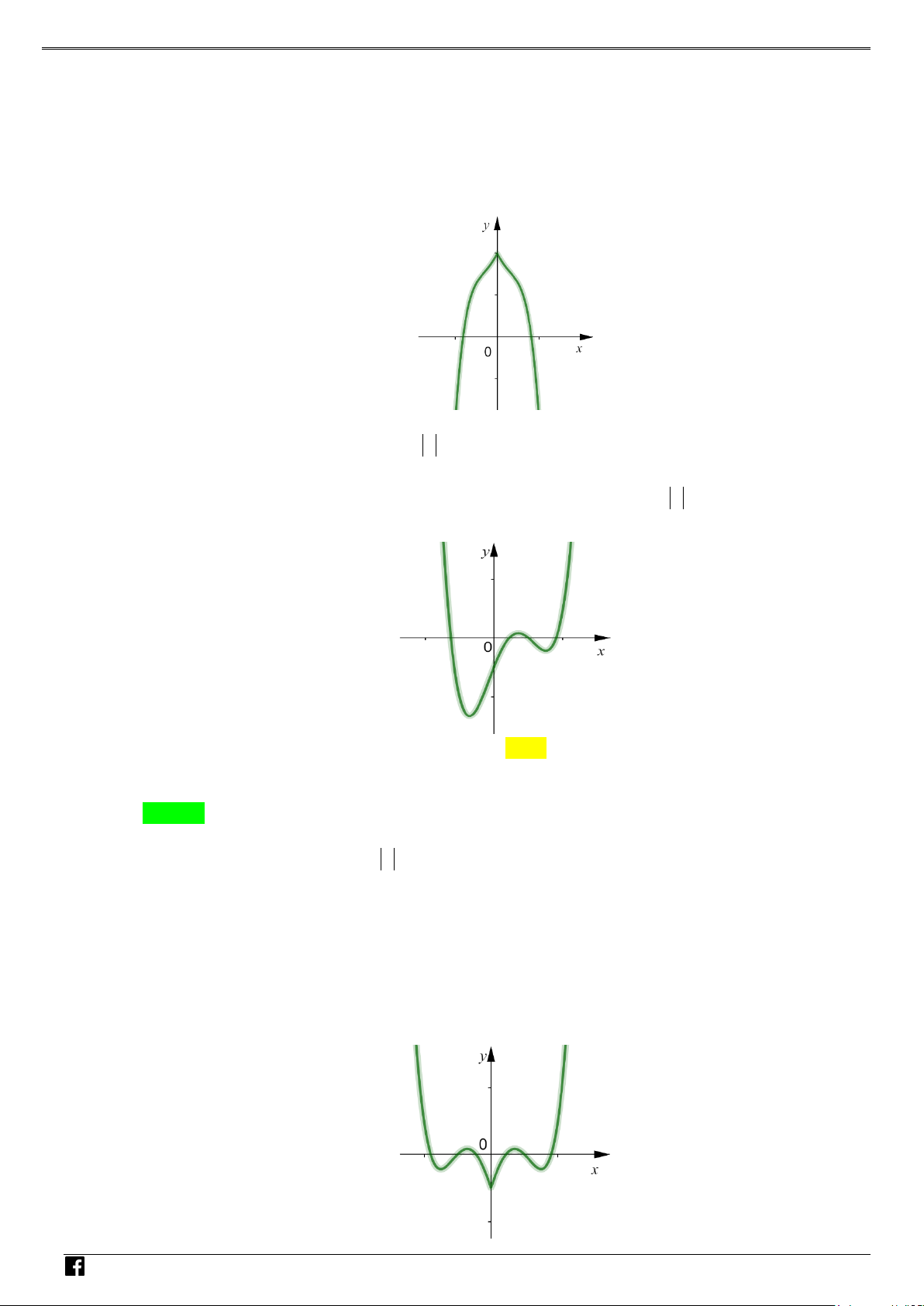
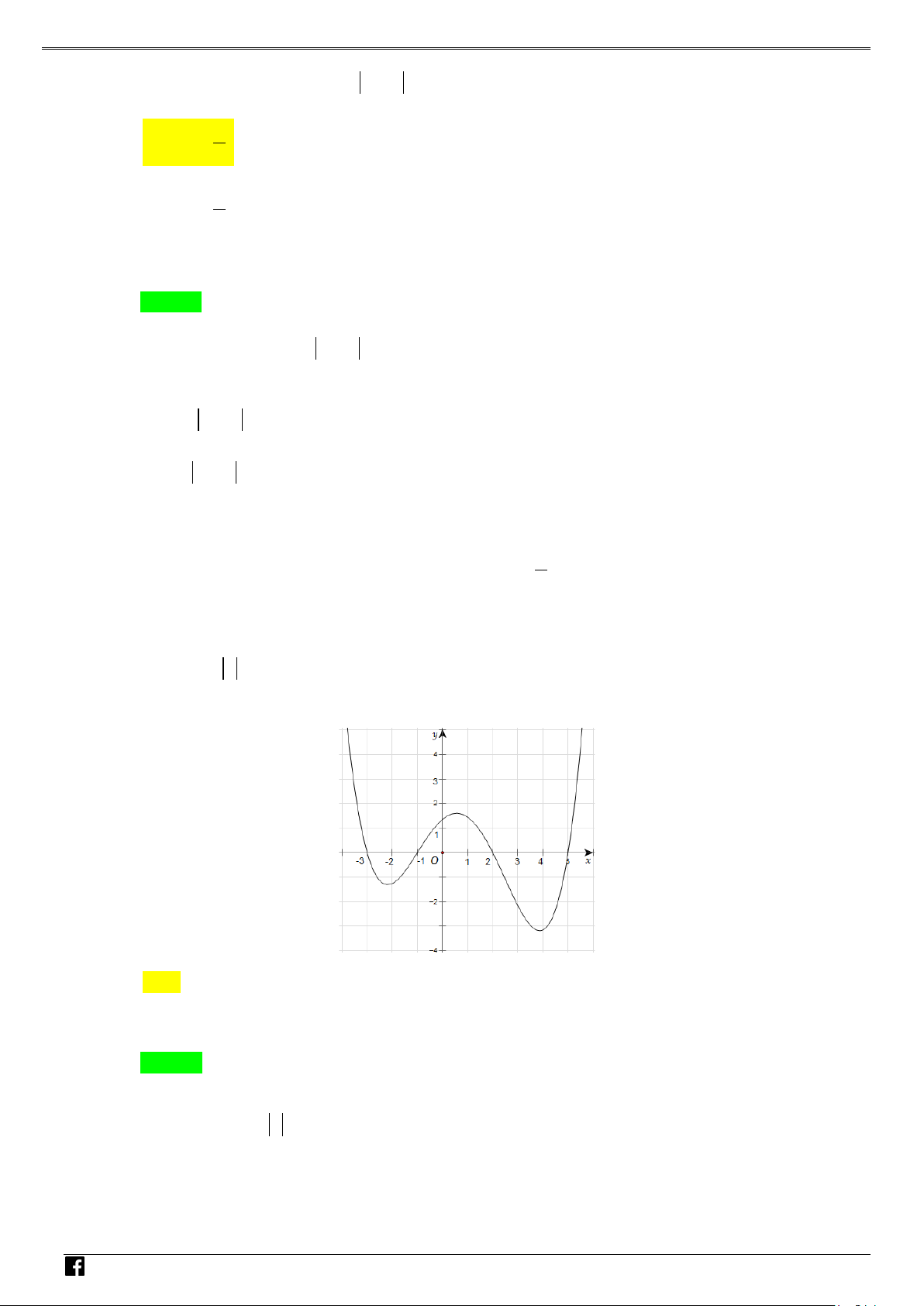
Câu 1: Cho hàm số y = f (x) xác định, liên tục trên và có đúng hai điểm cực trị x = −1, x = 1, có đồ – thị như hình vẽ sau: VD C
Hỏi hàm số y = f ( 2 x − 2x + )
1 + 2019 có bao nhiêu điểm cực trị? A. 4 . B. 3. C. 1. D. 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn B
Do hàm số y = f (x) có đúng hai điểm cực trị x = 1,
− x =1nên phương trình f ′(x) = 0 có hai NHÓ
nghiệm bội lẻ phân biệt x = 1, − x =1. M 2 T
Ta có y′ = (2x − 2) f ′(x − 2x + ) 1 . OÁN 2x − 2 = 0 x =1 V 2 D
y′ = 0 ⇔ x − 2x +1 = 1 − ⇔ x = 0 . – 2 − + = x 2x 1 1 x = 2 VD C Ta có x > 1 x > 1 2x − 2 > 0 2 x 2x 1 1 − + > x > 2 2
f '(x − 2x +1) > 0 > ⇔ ⇔ − + < − ⇔ x > 2 2 y ' 0 x 2x 1 1 x < 0 ⇔ 2x − 2 < 0 0 < x < 1 x < 1 x < 1 2
f '(x − 2x +1) < 0 2
−1< x − 2x +1< 1 0 < x < 2
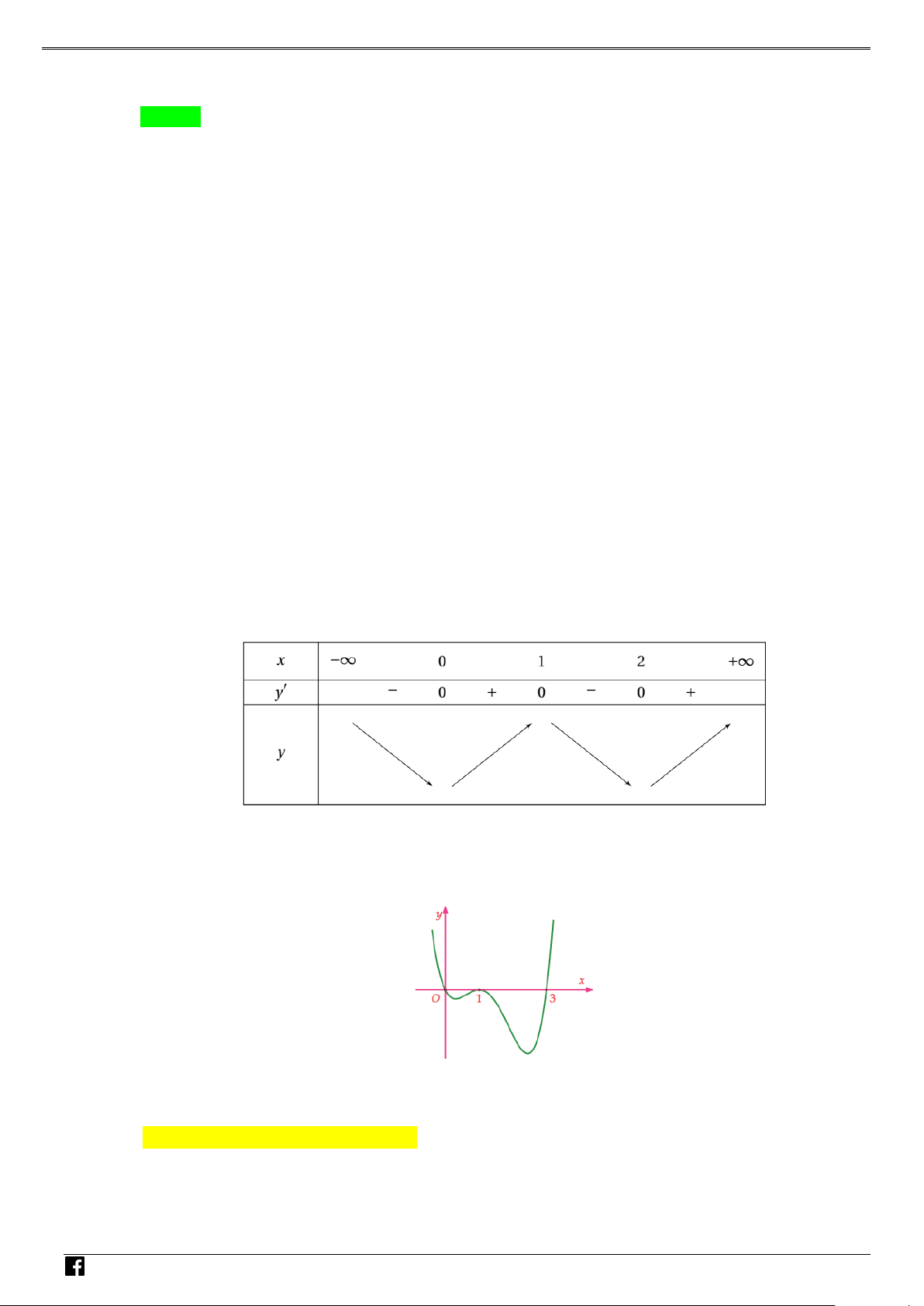
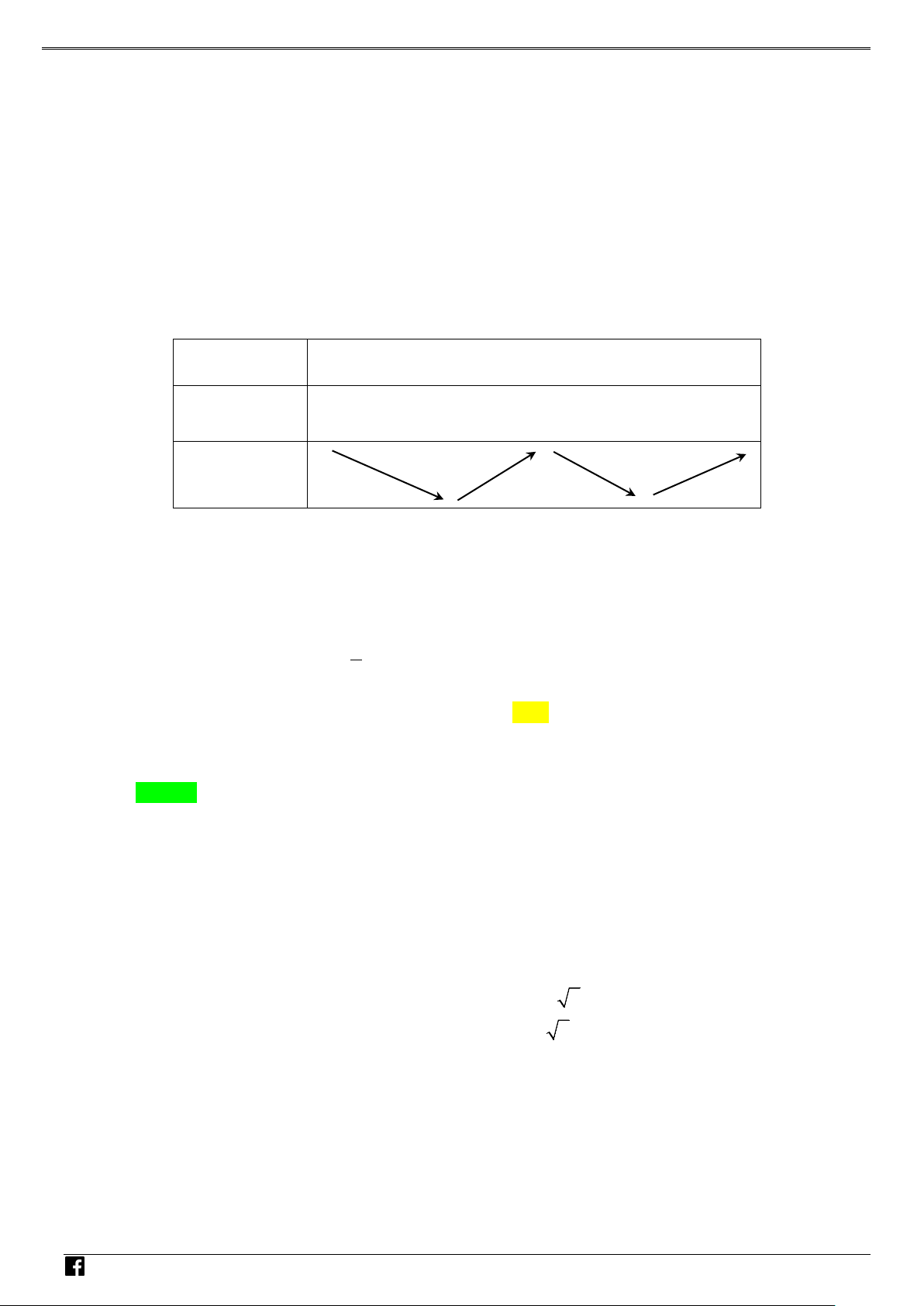
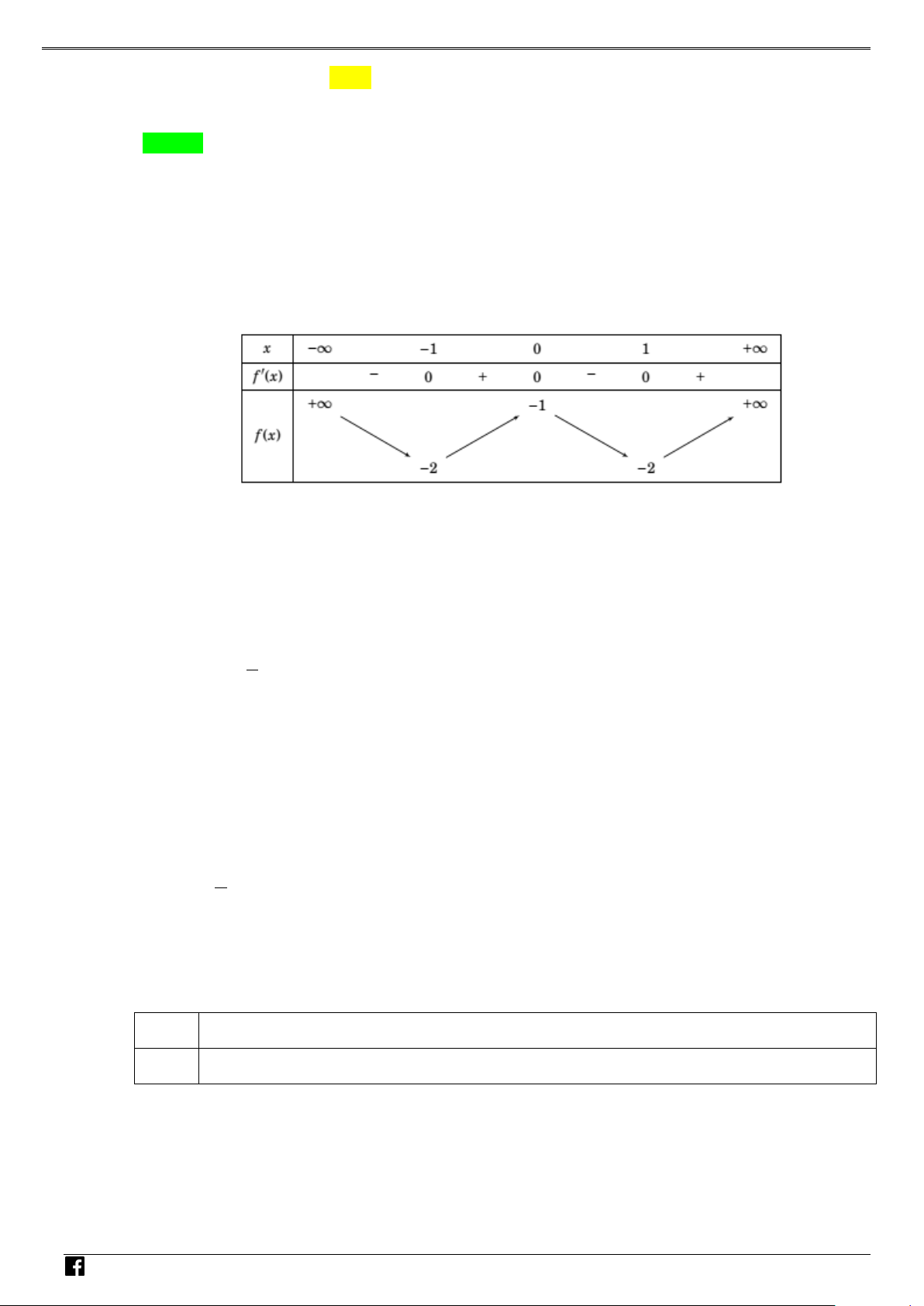
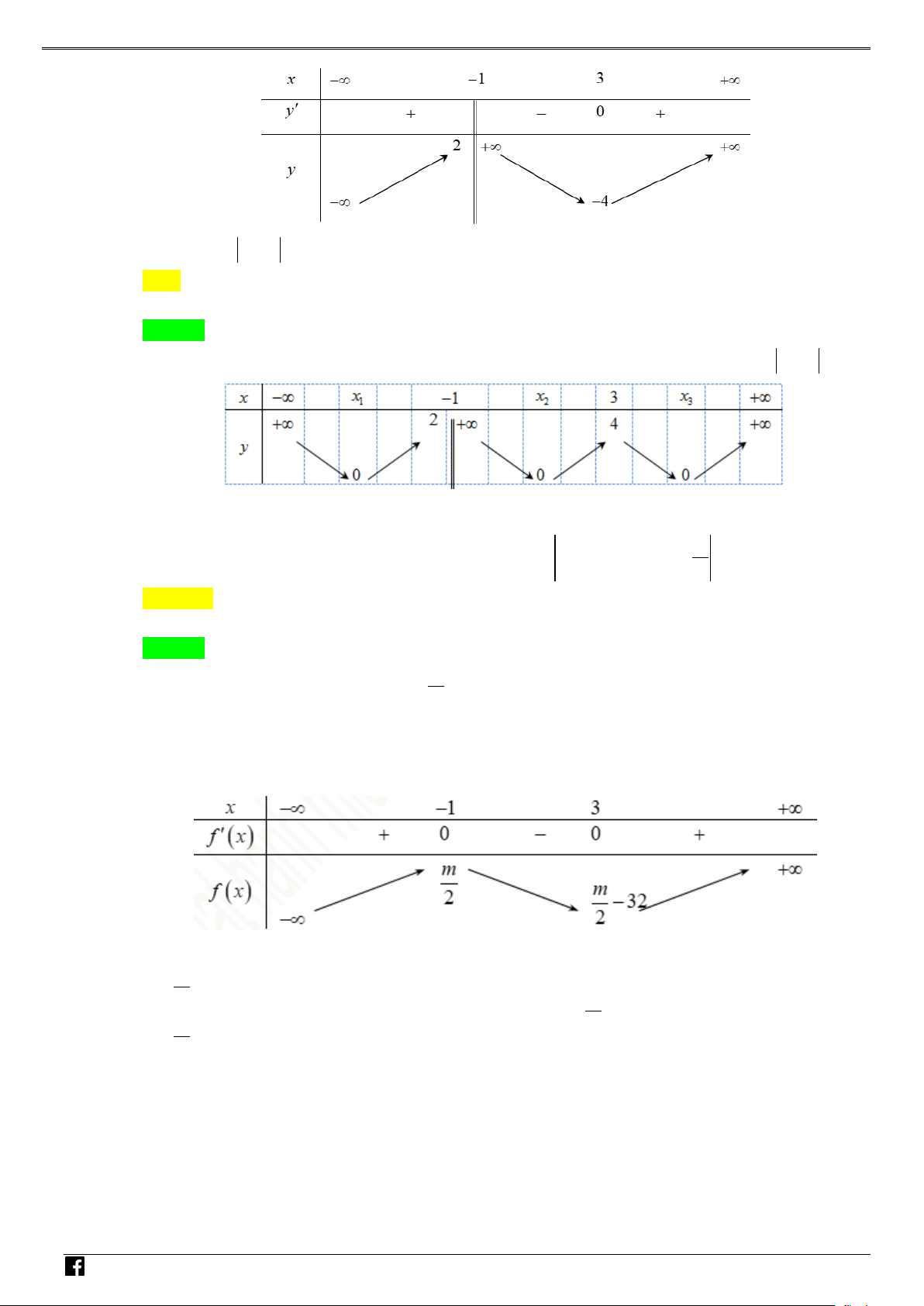
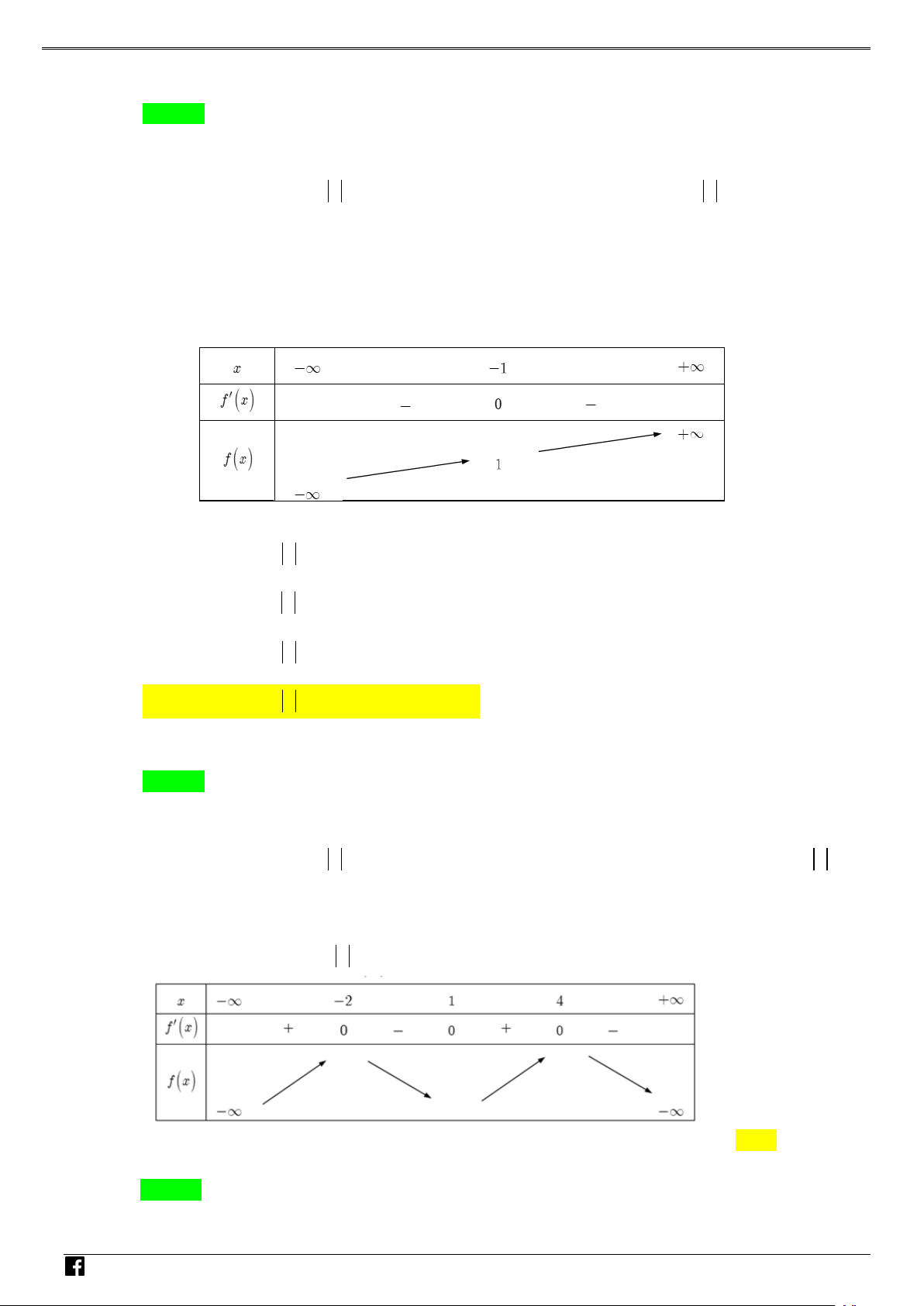
Do đó ta có bảng biến thiên: NHÓ M T OÁN 2 VD
Từ bảng biến thiên ta suy ra hàm số y = f (x − 2x + )
1 + 2019 có 3 cực trị. Chọn phương án B. –
Câu 2: Cho hàm số y = f (x) có đạo hàm f (′x) trên . Đồ thị của hàm số y = f (x) như hình vẽ VD C
Đồ thị hàm số y = ( f x )2
( ) có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 2 điểm cực tiểu, 3 điểm cực đại.
C. 2 điểm cực đại, 2 điểm cực tiểu.
D. 1 điểm cực đại, 3 điểm cực tiểu. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn A
Từ đồ thị ta có: f (x) = 0 có nghiệm đơn là x = 0;x = 3 và nghiệm kép x =1.
Và f '(x) = 0 có 3 nghiệm đơn x = ; = ∈ và . 1 x ∈(0;1) x 2 x (1;3) x =1 NHÓ
Ta có: y = ( f x )2
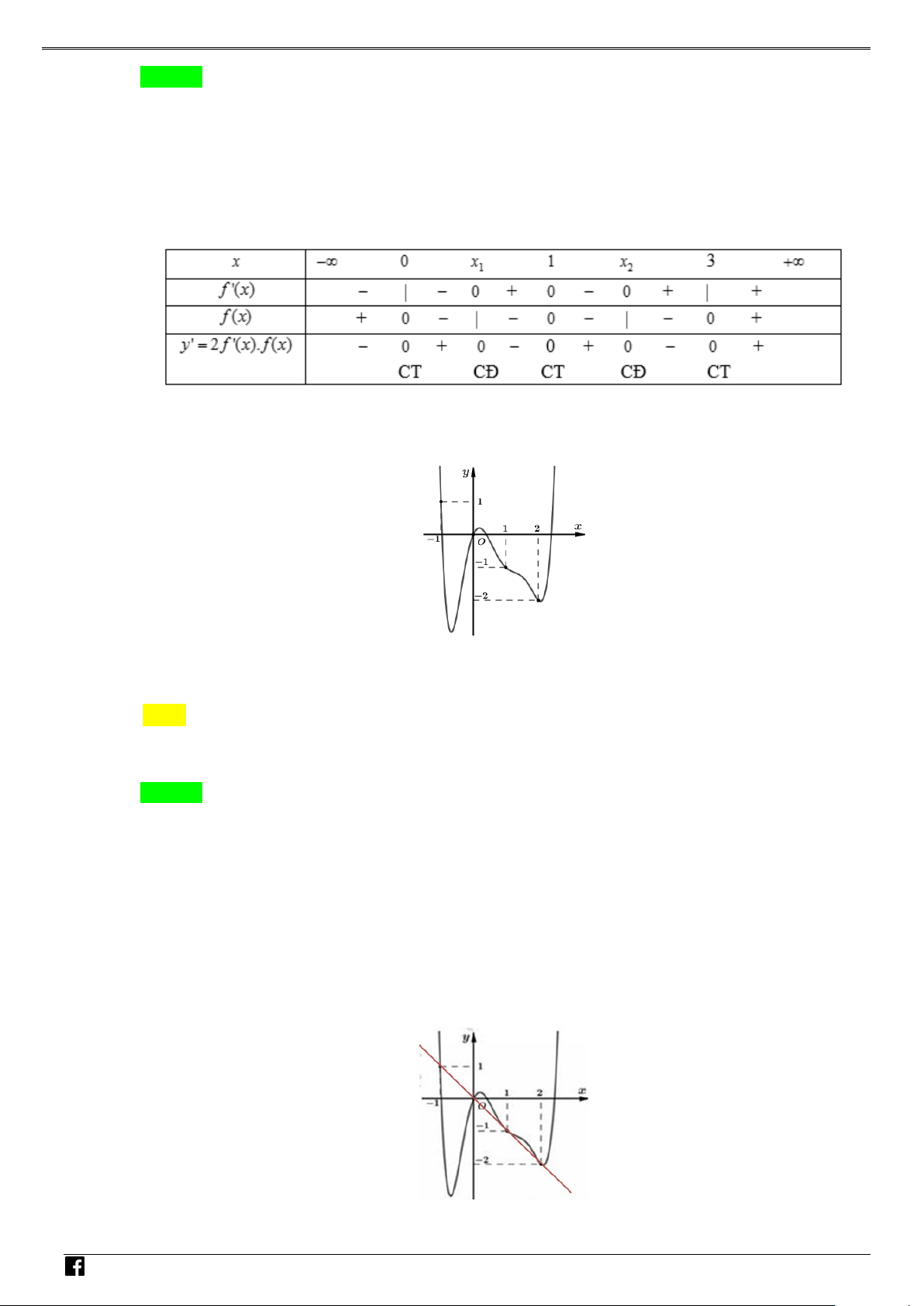
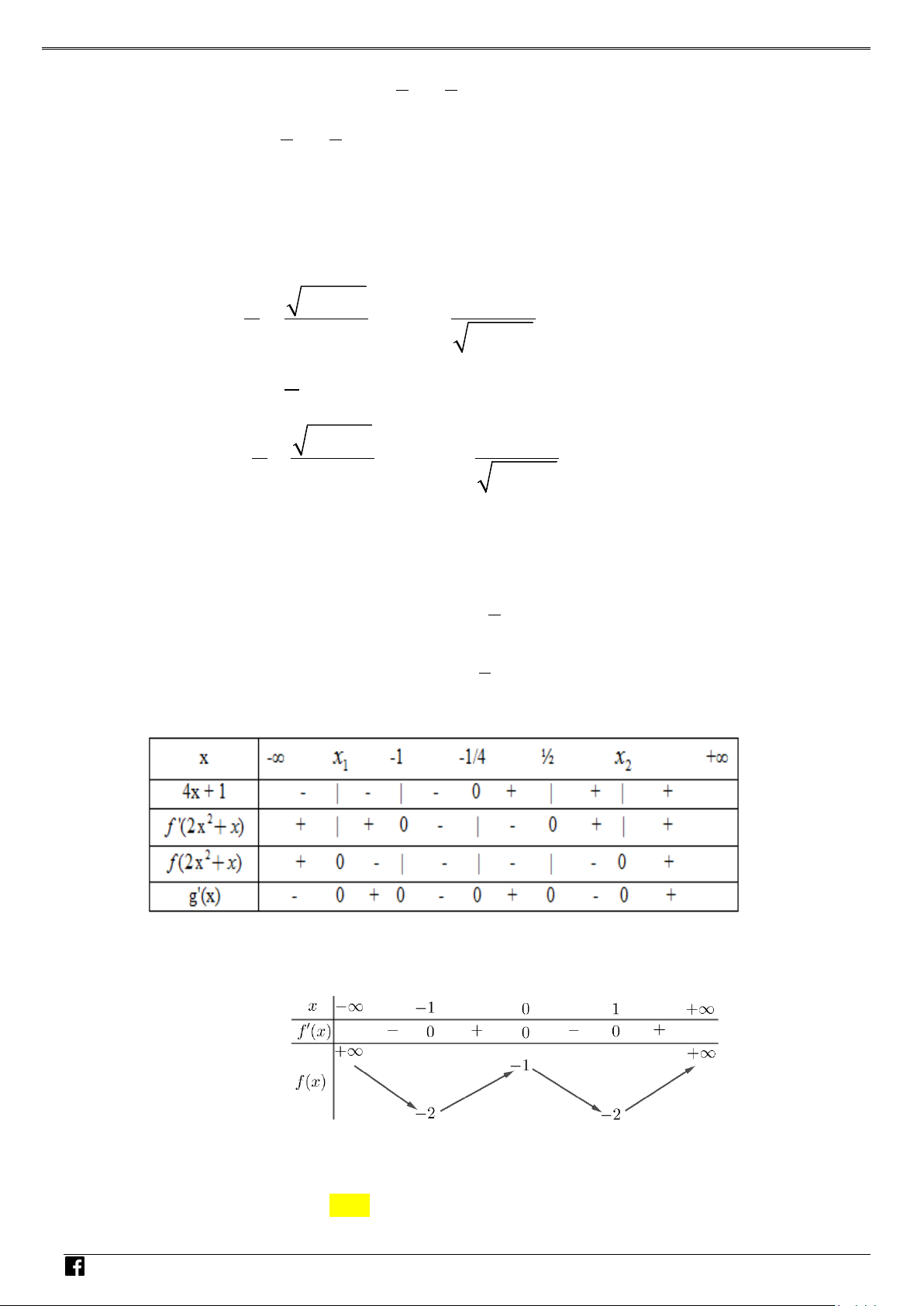
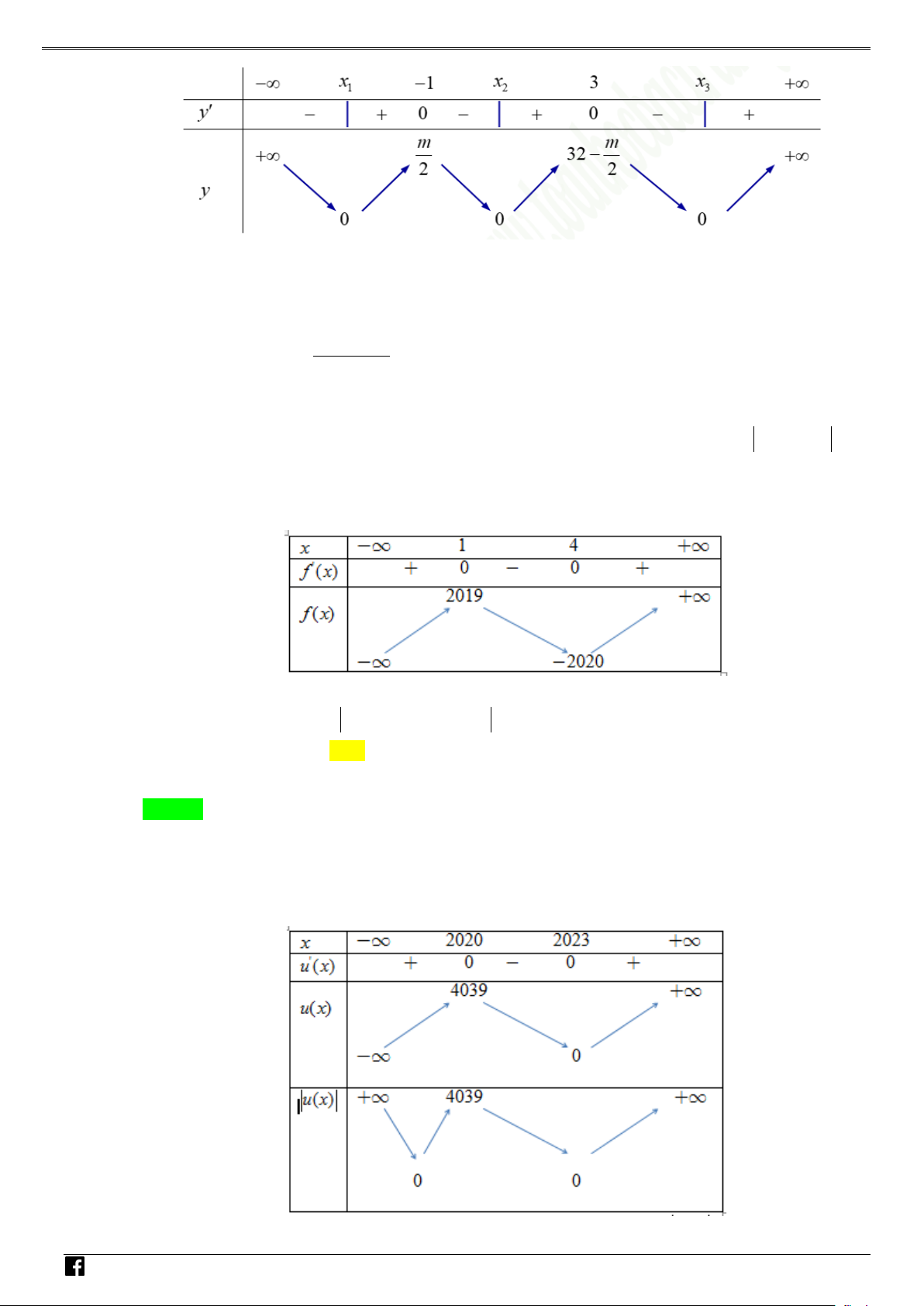
( ) ⇒ y ' = 2 f '(x). f (x) có các nghiệm đơn là x = 0; x = 3; và nghiệm bội 3 là 1 x ; 2 x x =1. M Ta có bảng xét dấu sau: TOÁN V D – VD C
Vậy đồ thị hàm số có 2 điểm cực đại, 3 điểm cực tiểu.
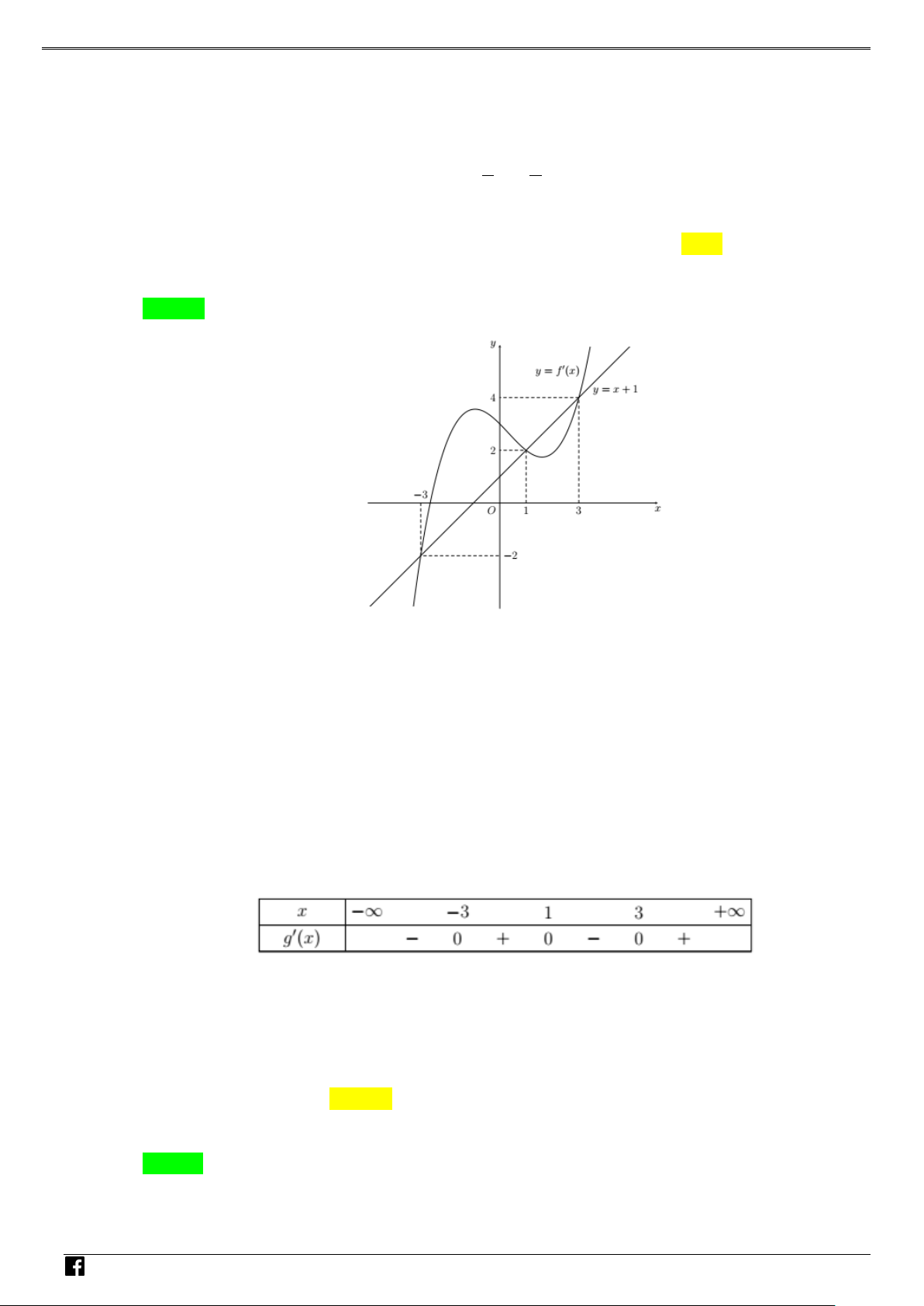
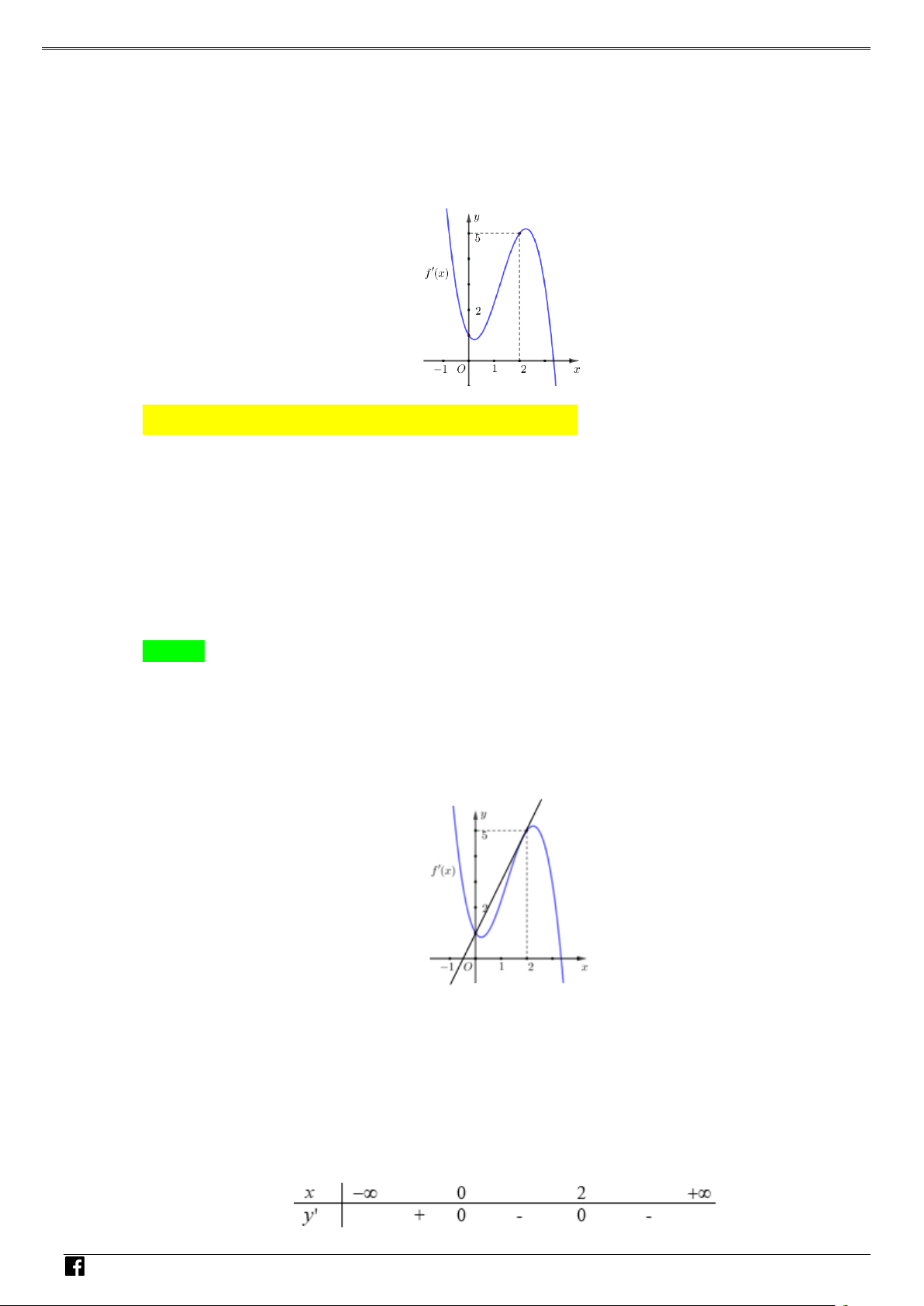
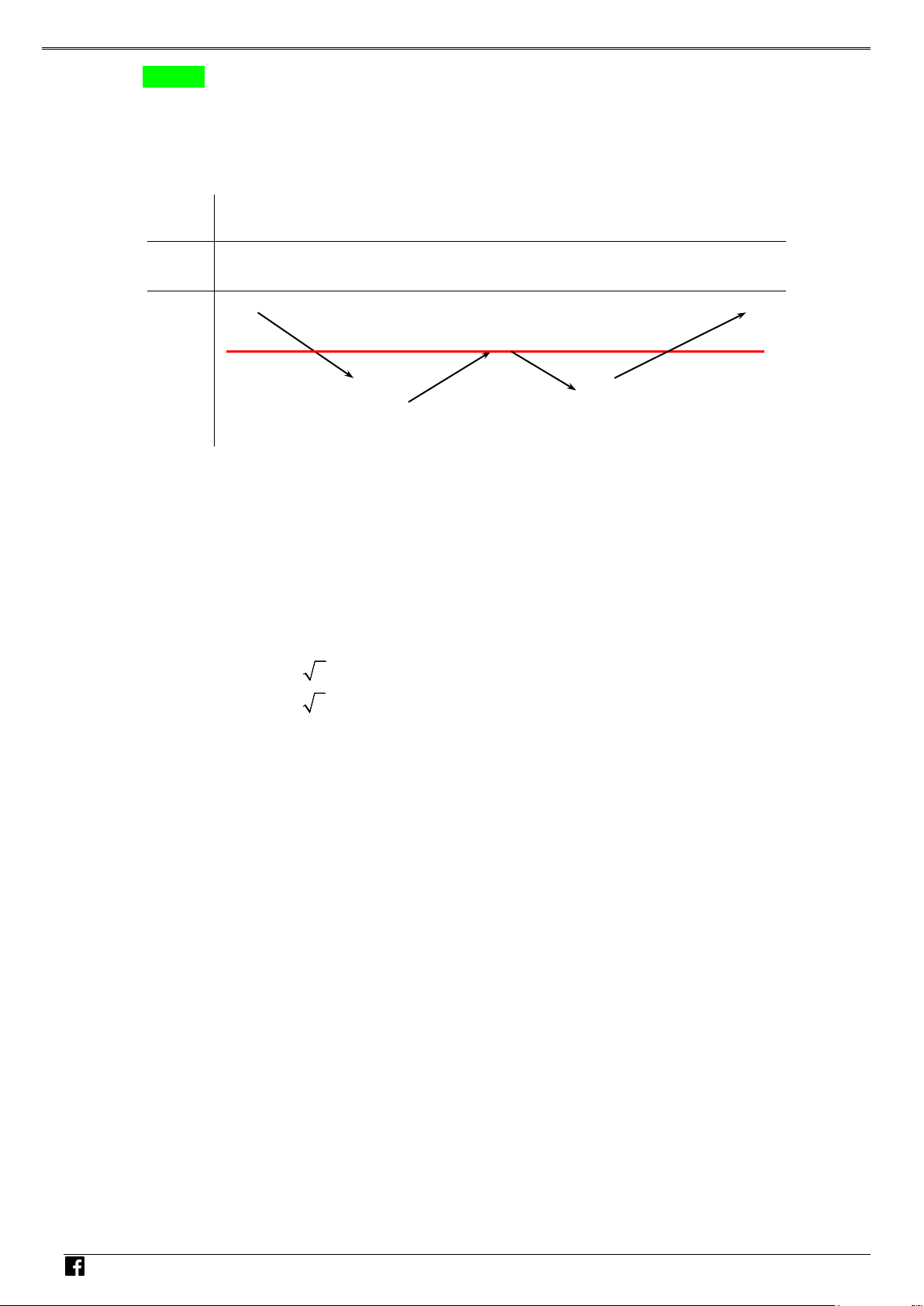
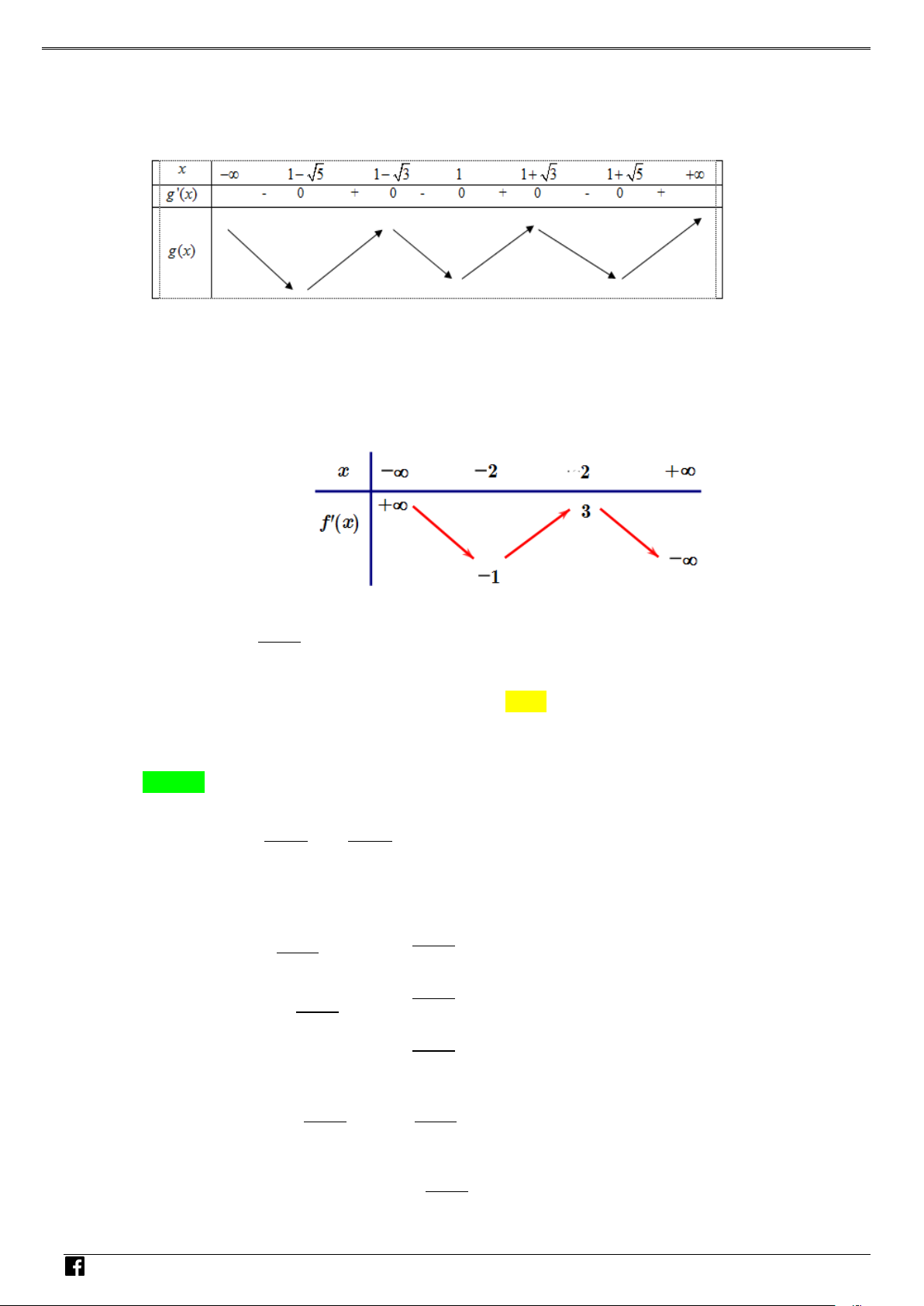
Câu 3: Cho hàm số y = f (x) có đạo hàm trên . Đồ thị hàm số như hình vẽ bên dưới.
Số điểm cực tiểu của hàm số g (x) = 2 f (x + 2) + (x + ) 1 (x + 3) là NHÓ A. 2 . B. 1. C. 3. D. 4 . M T Lời giải OÁN Chọn A
Ta có g′(x) = 2 f ′(x + 2) + 2x + 4 . VD –
g′(x) = 0 ⇔ f ′(x + 2) = −(x + 2). VD C
Đặt t = x + 2 ta được f ′(t) = t − . ( ) 1
( )1 là phương trình hoành độ giao điểm của đồ thị f ′(t) và đường thẳng d : y = t − (hình vẽ)
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Dựa vào đồ thị của f ′(t) và đường thẳng y = t − ta có t = 1 − x = 3 − t = 0 x = 2 − NHÓ
ta có f ′(t) = t − ⇔ hay . t =1 x = 1 − M t = 2 x = 0 TOÁN
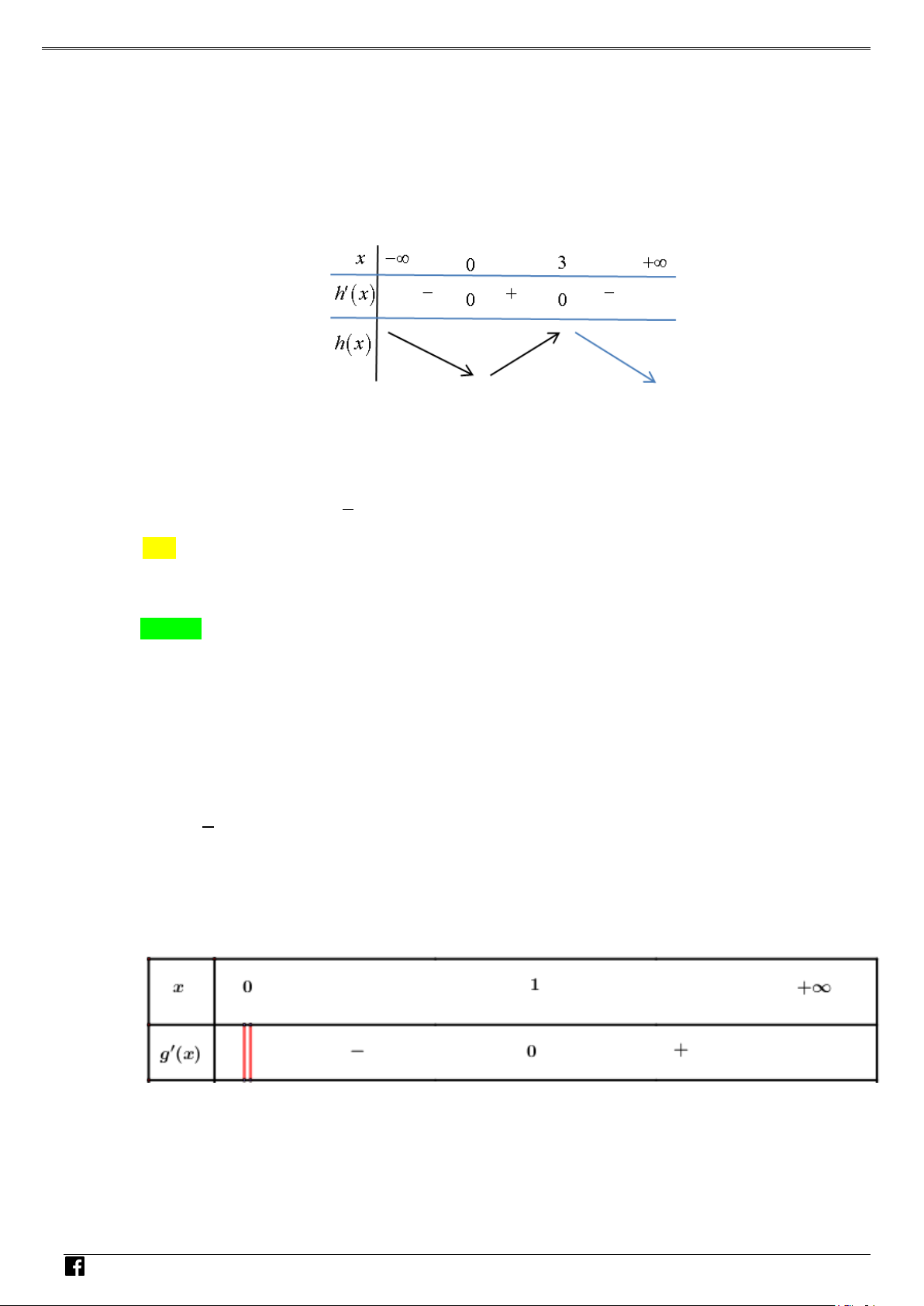
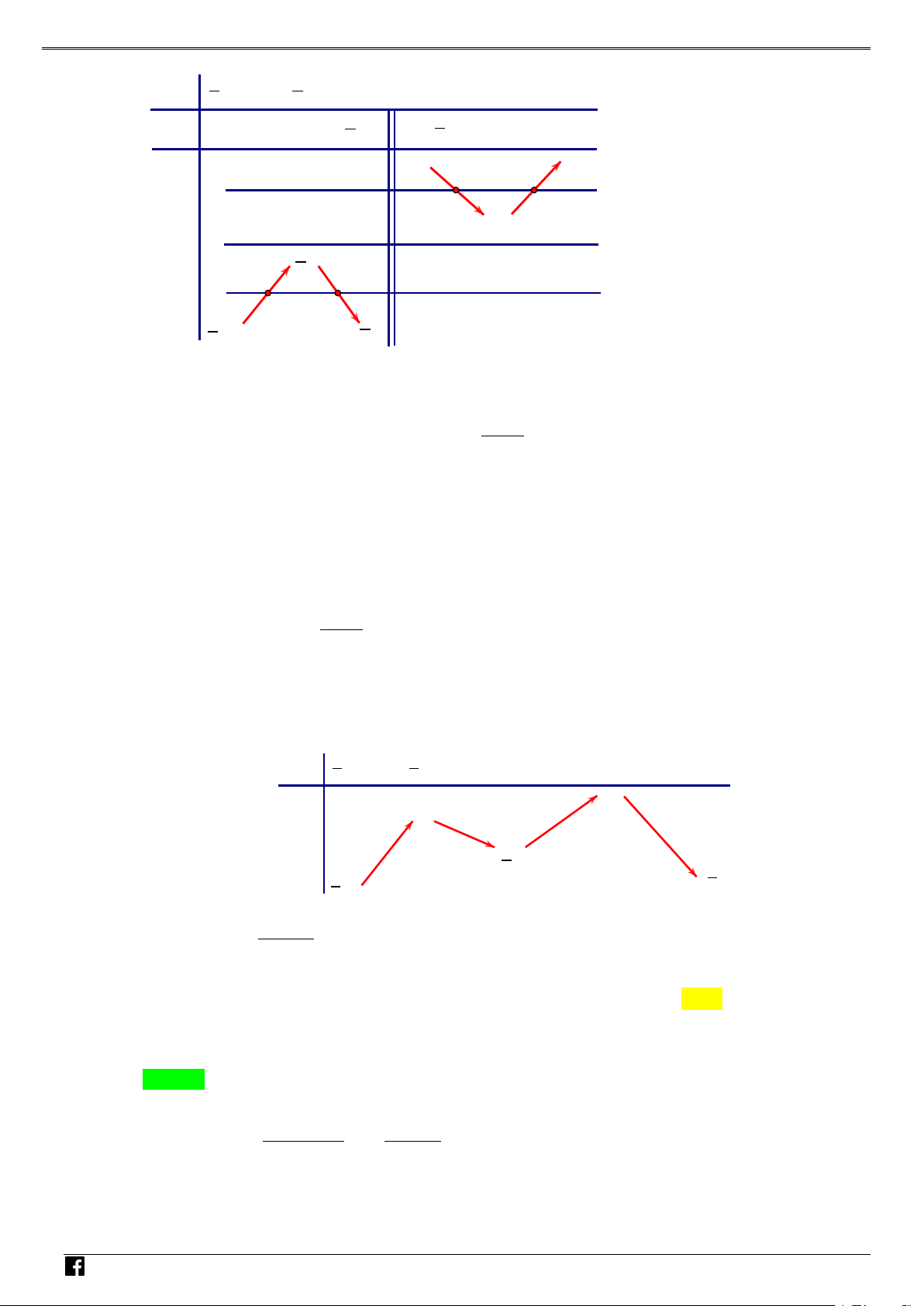
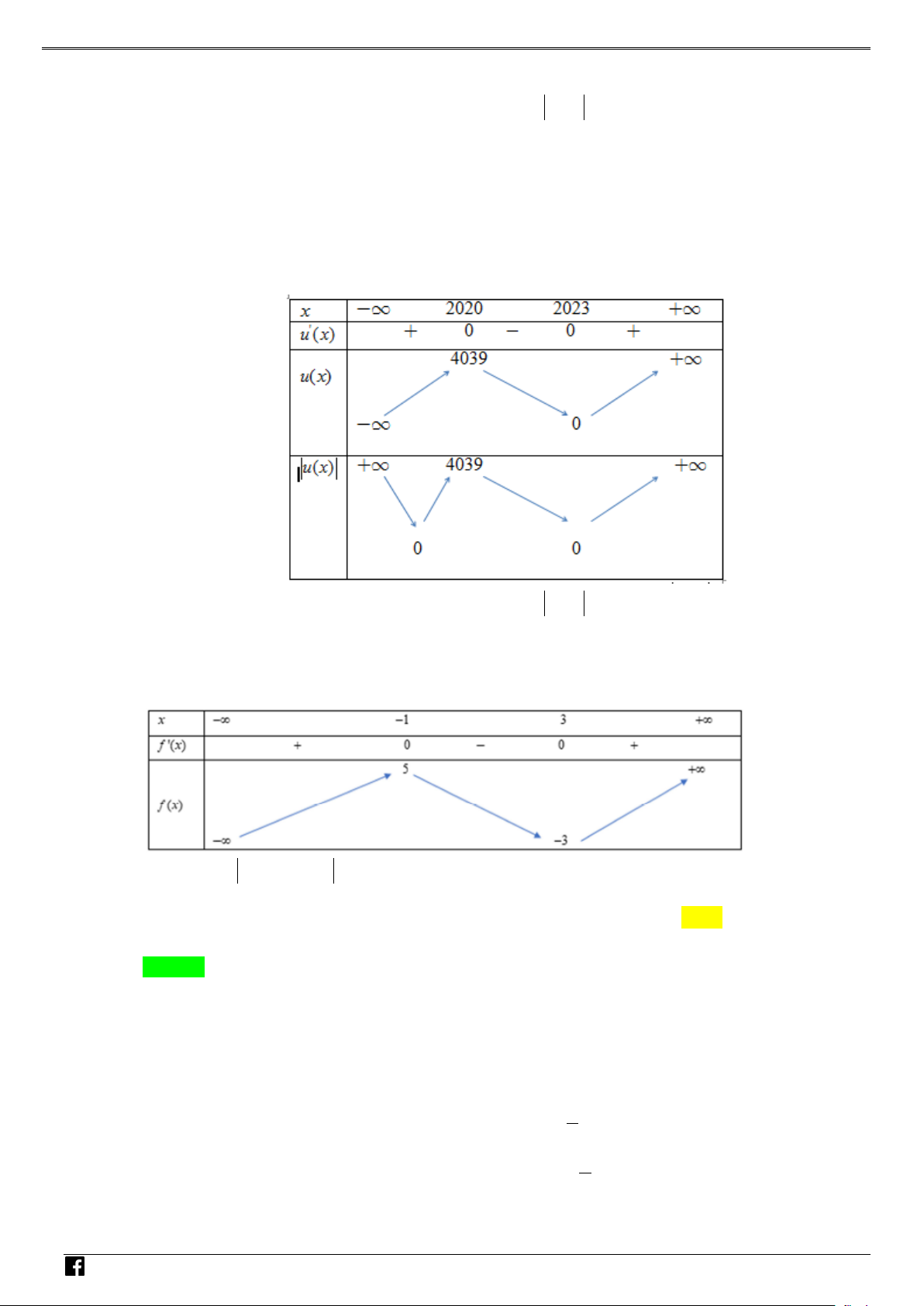
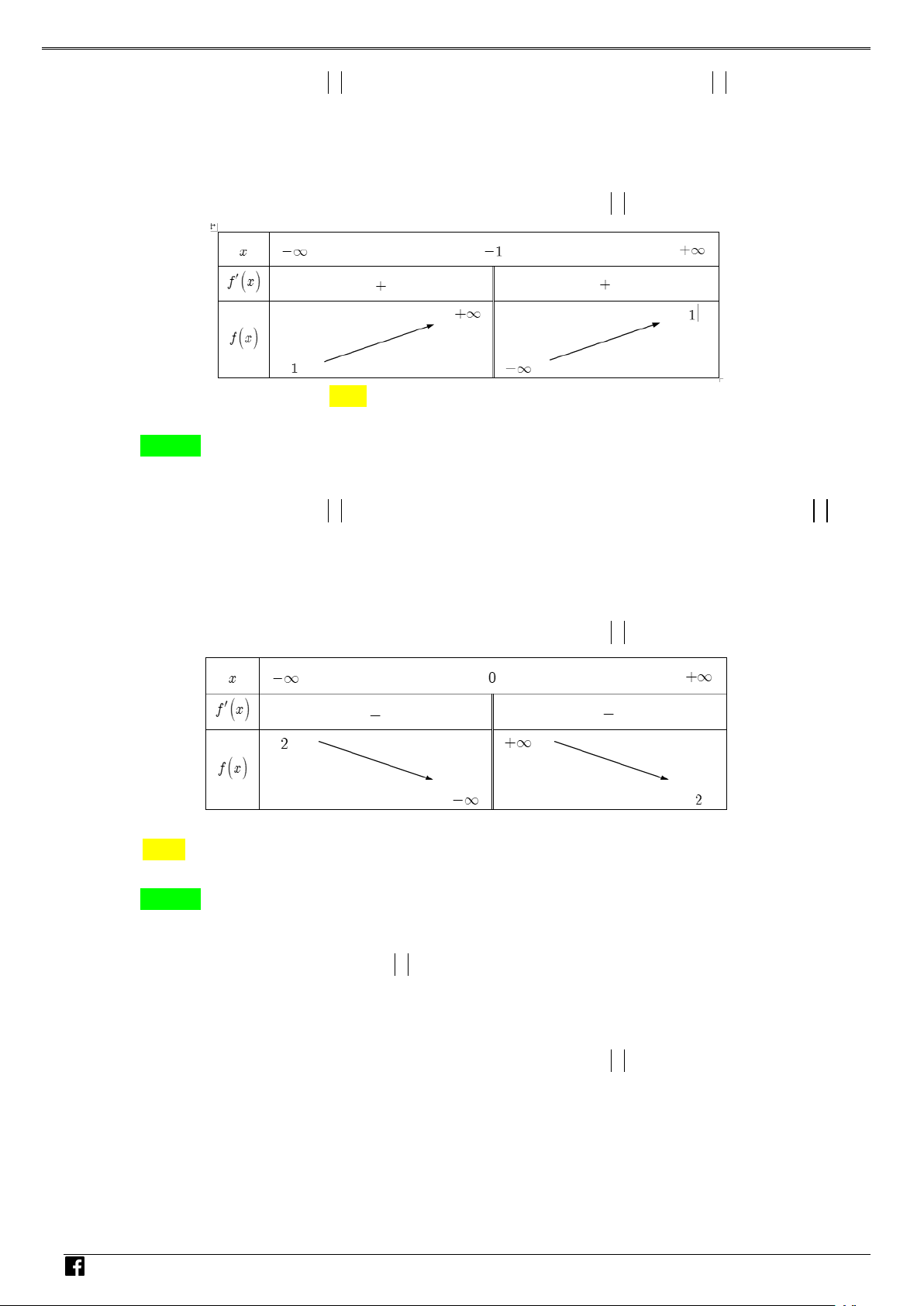
Bảng biến thiên của hàm số g (x) . V D – VD C
Vậy đồ thị hàm số có một điểm cực tiểu.
Câu 4: Cho hàm số y = f (x) có đạo hàm trên và có đồ thị là đường cong như hình vẽ. Đặt
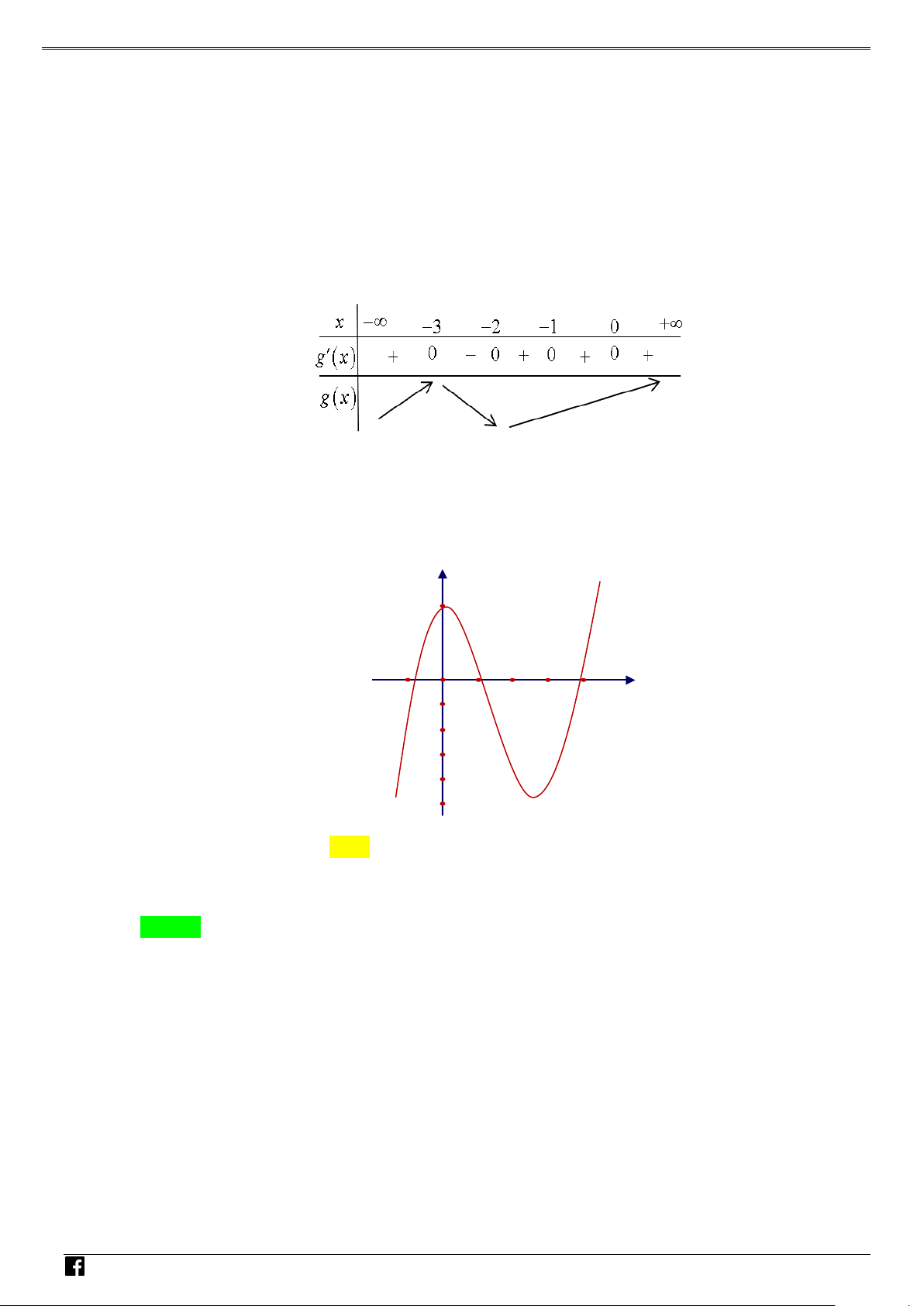
g (x) = 3 f ( f (x)) + 4 . Tìm số điểm cực trị của hàm số g (x)? y 3 1 − 1 2 3 4 O x NHÓ M T OÁN VD A. 2 . B. 8 . C. 10. D. 6 . – Lời giải VD C Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 13
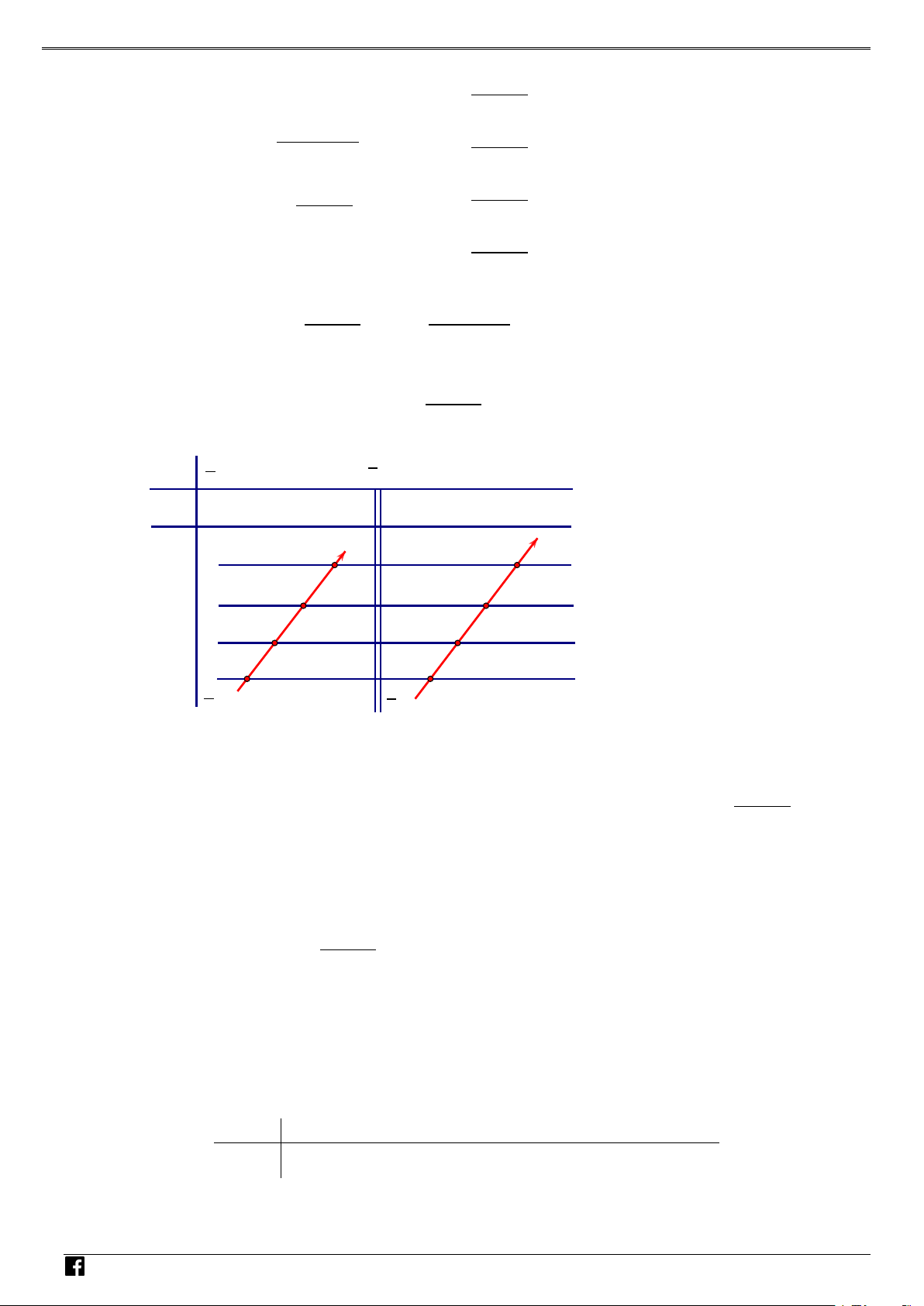
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D – VD C
g′(x) = 3 f ′( f (x)). f ′(x) . f (x) = 0
f ′( f (x)) = 0
f ( x) = a
g′(x) = 0 ⇔ 3 f ′( f (x)). f ′(x) = 0 ⇔ ⇔ , (2 < a < 3) . f ′ ( x) = 0 x = 0 x = a
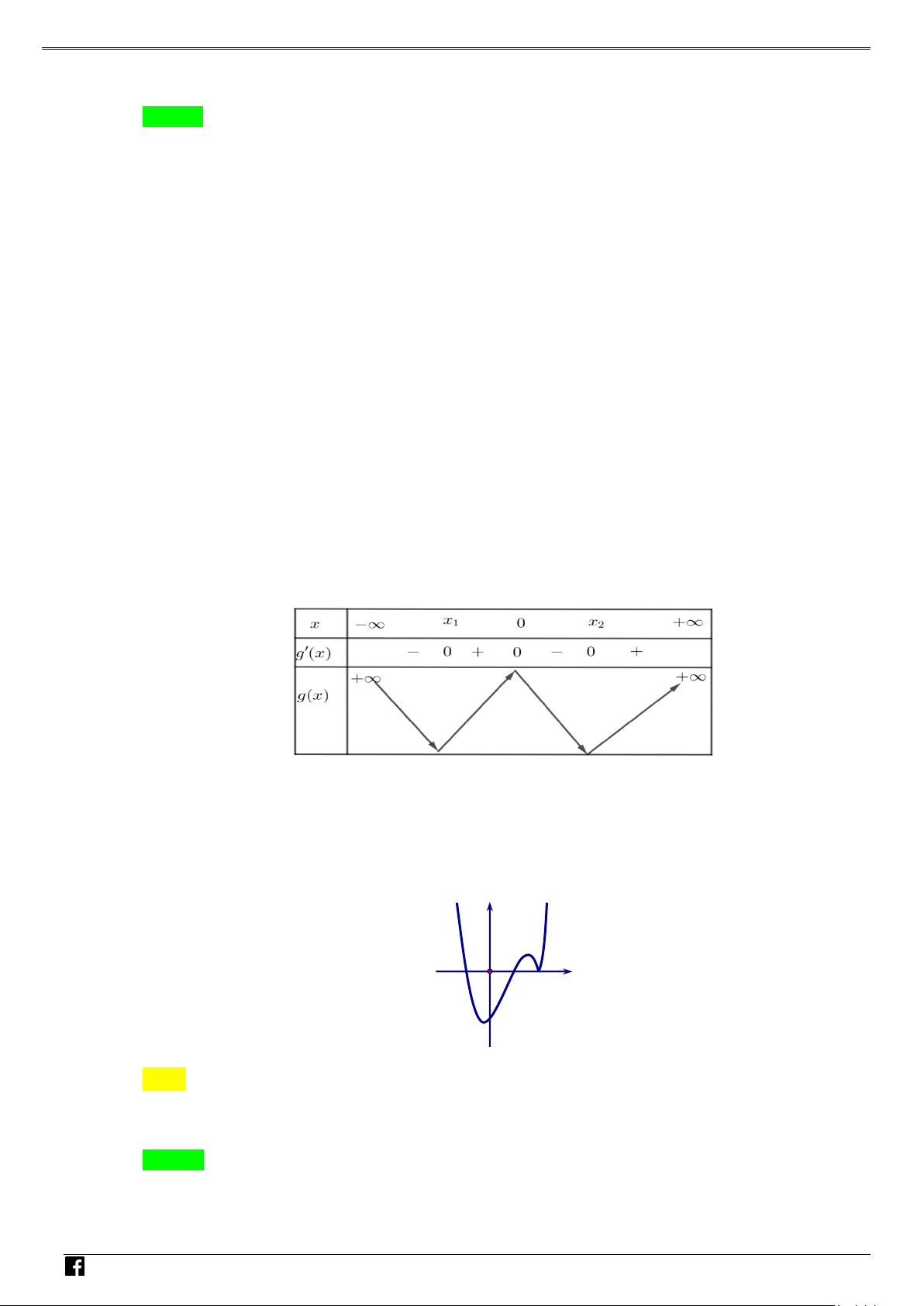
f (x) = 0 có 3 nghiệm đơn phân biệt x , x , x khác 0 và 1 2 3 a .
Vì 2 < a < 3 nên f (x) = a có 3 nghiệm đơn phân biệt x , x , x khác x , x , x , 0 , 4 5 6 1 2 3 a . NHÓ
Suy ra g′(x) = 0 có 8 nghiệm đơn phân biệt. Do đó hàm số g (x) = 3 f ( f (x)) + 4 có 8 điểm cực M T trị. OÁN
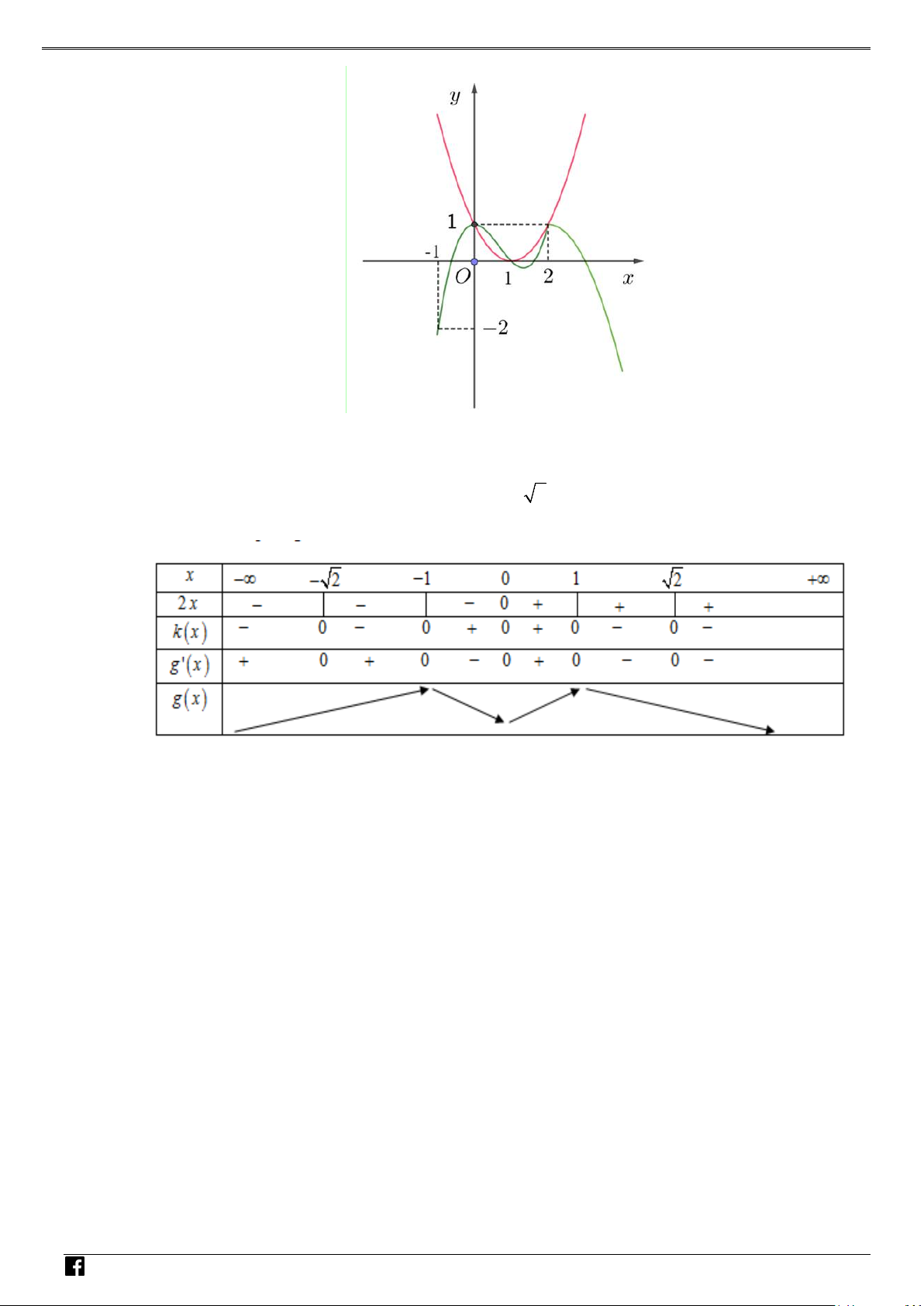
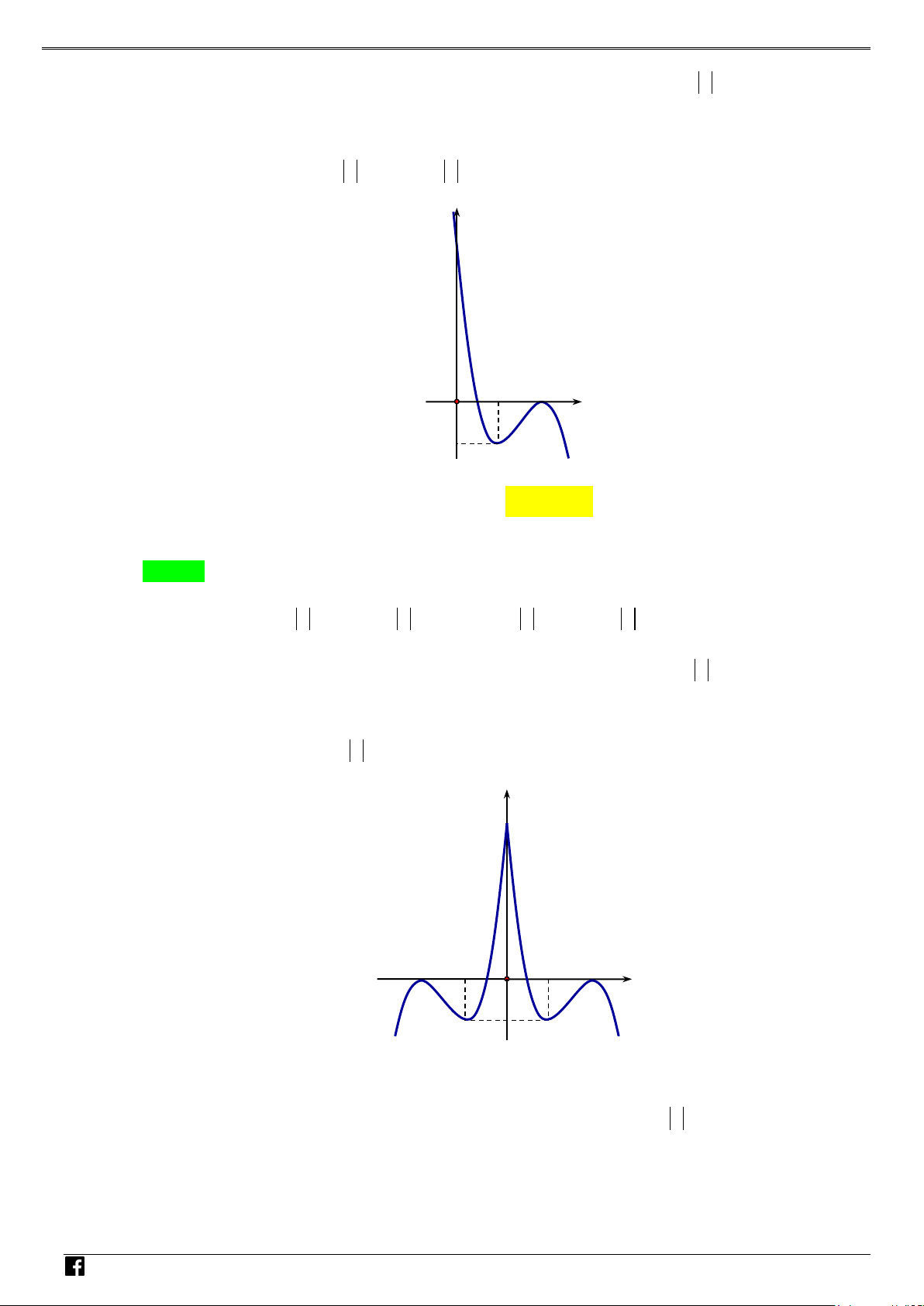
Câu 5: Biết rằng hàm số f (x) xác định, liên tục trên có đồ thị được cho như hình vẽ bên. Tìm số VD
điểm cực trị của hàm số y = f f (x) . – VD C A. 5. B. 3. C. 4 . D. 6 . Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Xét hàm số y = f f (x)
, y′ = f ′( x). f ′ f ( x) ; x = 0 x = 0 f (x) 0 x = 2 ′ = x = 2 NHÓ y 0 ′ = ⇔ ⇔ ⇔ . f ′ f ( x) = 0 f (x) = 0
x = a∈(2;+∞) M f ( x) = 2 x = b ∈ ( ;a+∞) TOÁN
f ′(x) > 0
Với x ∈(−∞;0) ⇒ ⇒ y′ > 0. V
f ( x) < 0 ⇒ f ′ f ( x) > 0 D – ′ VD
f ( x) < 0 Với x∈(0;2) ⇒ ⇒ y′ < 0 .
f ( x) < 0 ⇒ f ′ f ( x) > 0 C
f ′(x) > 0
Với x∈(2;a) ⇒ ⇒ y′ > 0.
f ( x) < 0 ⇒ f ′ f ( x) > 0
f ′(x) > 0
Với x∈(a;b) ⇒ ⇒ y′ < 0 .
0 < f ( x) < 2 ⇒ f ′ f ( x) < 0
f ′(x) > 0
Với x∈(b;∞) ⇒ ⇒ y′ > 0.
f ( x) > 2 ⇒ f ′ f ( x) > 0 Ta có bảng biến thiên NHÓ M T OÁN VD
Dựa vào BBT suy ra hàm số y = f f (x)
có bốn điểm cực trị. – VD
DẠNG 5. Biết đặc điểm của hàm số hoặc đồ thị, hoặc BBT, hoặc đạo hàm củ Ca
hàm f (x), tìm cực trị của hàm y = f (ϕ (x)); y = f ( f (x)),...y = f ( f ( f ...(x))) trong bài toán chứa tham số.
DẠNG 6. Biết đặc điểm của hàm số hoặc BBT, hoặc đồ thị, hoặc đạo hàm của
hàm f (x), tìm cực trị của hàm y = ln( f (x)) f (x)
, y = e ,sin f (x),cosf (x)... trong bài
toán không chứa tham số.
Câu 1: Cho hàm số f (x) có đồ thị như hình dưới đây
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D
Hàm số g (x) = ln ( f (x)) có bao nhiêu điểm cực trị ? – VD A. 0 . B. 1. C. 2 . D. 3. C Lời giải Chọn D f ′(x) g′(x) = ln
( f ( x)) ′ = . f (x)
Từ đồ thị hàm số y = f (x) ta thấy f (x) > 0 với mọi x∈ . Vì vậy dấu của g′(x) là dấu của
f ′(x) . Ta có bảng biến thiên của hàm số g (x) NHÓ M T OÁN
Vậy hàm số g (x) = ln ( f (x)) có 3 điểm cực trị. VD
Câu 2: Cho hàm số y = f (x) có bảng biến thiên sau – VD C
Tìm số cực trị của hàm số y = g (x) = ln ( f (x)) . A. 0 . B. 1. C. 2 . D. 4 Lời giải Chọn B
Điều kiện: f (x) > 0 ⇔ x < 1 −
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số f ′ x Ta có g '(x) ( ) =
; giải phương trình y′ = 0 ⇔ f ′(x) = 0 ⇔ x = 3
− và y′ đổi dấu khi qua f (x) x = 3 − . NHÓ
Do đó hàm số y = g (x) = ln ( f (x)) có một cực trị. M
Câu 3: Cho hàm số f (x) liên tục trên và có bảng biến thiên như sau TOÁN V D – VD C
Hàm số y = ln ( f (x)) có tất cả bao nhiêu điểm cực đại? A. 0. B. 2 . C. 1. D. 3. Lời giải Chọn C
Điều kiện : f (x) > 0 ⇔ x∈( ;
a b) :0 < a < 3 < b . f ′ x
Ta có: y = ln ( f (x)) ( ) ⇒ y′ = . f (x) NHÓ
Dấu của y′ là dấu của f ′(x) . M T Dễ thấy trên ( ;
a b) hàm số f (x) đạt cực đại tại duy nhất 1 điểm x = 3 . OÁN
Do đó hàm số y = ln ( f (x))có đúng 1 điểm cực đại. VD
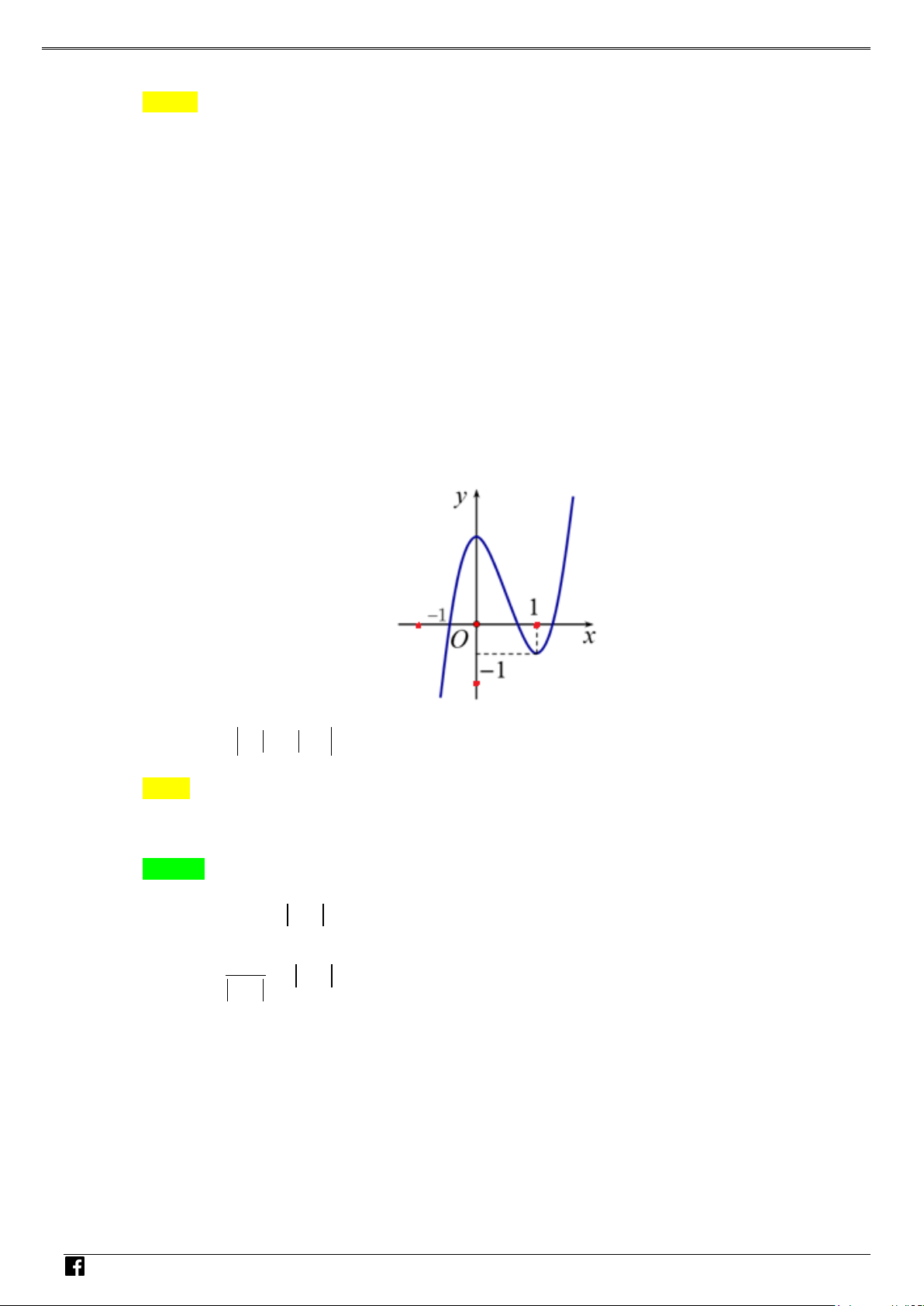
Câu 4: Cho hàm số y = f (x) có đồ thị như hình vẽ bên: – VD y C O x 1 − .
Tìm số điểm cực trị của hàm số f (x) f (x) y = 2 − 3 . A. 6 . B. 5. C. 4 . D. 3. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn D
Dựa vào đồ thị hàm số f (x) ta thấy f (x) ≥ 1, − ∀x ∈ . NHÓ
Khi đó xét hàm số g (x) f (x) f (x) = 2 − 3 M
Ta có g′(x) = f ′(x ) f (x) f (x) . 2 .ln 2 − 3 .ln 3 TOÁN f ′(x) = 0 g′ x = ⇔ V ( ) 0 f (x) f (x) 2 .ln 2 −3 .ln 3 = 0 D – VD
Xét phương trình f (x) f (x)
2 .ln 2 − 3 .ln 3 = 0 trên khoảng ( ; −∞ + ∞). C f (x) 2 ⇔
= log 3 ⇔ f x = log log 3 ≈ 1 − ,4 (loại). 2 ( ) 2 ( 2 ) 3 3
Do đó số điểm cực trị của hàm g (x) cũng bằng số điểm cực trị của hàm f (x) .
Tức là hàm g (x) có 3 điểm cực trị.
Câu 5: Cho hàm số y = f ′(x) có đồ thị như hình vẽ bên: NHÓ M T OÁN VD – VD f x f x C
Tìm số điểm cực trị của hàm số ( ) ( ) y = 3 + 2 . A. 2 . B. 3. C. 5. D. 4 . Lời giải Chọn D
Ta thấy f ′(x) xác định trên nên f (x) xác định trên .
Ta có: y′ = f ′(x) f (x) + f ′(x) f (x) = f ′(x) f (x) f (x) .3 .2 3 + 2 .
Xét y′ = 0 ⇔ f ′(x) = 0 (do f (x) f (x) 3 + 2 > 0 , x ∀ ∈ ).
Dựa vào đồ thị hàm số ta thấy f ′(x) = 0 có 4 nghiệm phân biệt. Vậy y′ = 0 có 4 điểm cực trị.
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 6: Cho hàm số y = f (x) có đạo hàm liên tục trên và có đồ thị f ′(x) như hình vẽ bên. Số điểm x− cực trị của hàm số f (x) ( )2 1 − 2 y = e là NHÓ M TOÁN V D – VD C A. 4 . B. 3. C. 2 . D. 5. Lời giải Chọn B x − Xét ( ) eg x y =
, g (x) = f (x) ( )2 1 − 2
Hàm số xác định trên , có y′ = g′(x) g(x) = f ′ g x
( x) − ( x − ) g(x) e 1 .e , trong đó ( ) e > 0, x ∀ ∈ x = 1 − x =1 NHÓ
nên y′ = 0 ⇔ g′(x) = 0 ⇔ f ′(x) −(x − )
1 = 0 ⇔ f ′(x) = x −1 ⇔ x = 2 = M T x 3
(Vì đường thẳng y = x −1 cắt đồ thị f ′(x) tại 4 điểm có hoành độ x = 1;
− x =1; x = 2; x = 3) vàOÁN
dấu của y′ là dấu của g′(x) . VD – VD C Bảng biến thiên:
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T Suy ra hàm số ( ) eg x y =
có ba điểm cực trị là x = 1;
− x = 2; x = 3. OÁN
Câu 7: Cho hàm số y = f (x) có đạo hàm liên tục trên và đồ thị hàm số y = f (x) như hình vẽ bên. Tìm ( )1 V
số điểm cực trị của hàm số ( ) 2019f f x y − = . D – VD C A. 13. B. 11. C. 10. D. 12. Lời giải Chọn D NHÓ M T OÁN VD – VD
Ta có y = f (x) f ( f (x) − )
f ( f (x)− ) 1 ' ' ' 1 2019 ln 2019. C f '(x) = 0 (1) y ' = 0 ⇔ . f '
( f ( x) − ) 1 = 0 (2) x = 1 − 1 x =1
Giải (1) : f '(x) 2 0 = ⇔ . x = 3 3 x = 6 4
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
f (x) −1 = 1 − f (x) = 0 f (x)−1=1 f (x) = 2
Giải (2) : f '( f (x) − ) 1 = 0 ⇔ ⇔ .
f (x) −1 = 3 f (x) = 4 − = = NHÓ f (x) 1 6 f (x) 7
Dựa vào đồ thị ta có: M TOÁN
+) f (x) = 0 có 1 nghiệm x > 6 5 là nghiệm bội l, V
+) f (x) = 2 có 5 nghiệm x < 1; − 1
− < x <1;1< x < 3;3 < x < 6;6 < x < x 6 7 8 9 10
5 là các nghiệm bội 1, D –
+) f (x) = 4 có 1 nghiệm x < x 11 6 là nghiệm bội 1. VD C
+) f (x) = 7 có 1 nghiệm x < x 12 11 là nghiệm bội 1.
Suy ra y ' = 0 có 12 nghiệm phân biệt mà qua đó y ' đổi dấu. Vậy hàm số ( ( ) )1 2019f f x y − = có 12 điểm cực trị.
DẠNG 7. Biết đặc điểm của hàm số hoặc BBT, hoặc đồ thị của hàm f (x), hoặc
đạo hàm của hàm f (x), tìm cực trị của hàm y = ln( f (x)) f (x)
, y = e ,sin f (x), os
c f (x)...
trong bài toán chứa tham số.
DẠNG 8. Các dạng khác với các dạng đã đưa ra…
Câu 1. Cho hàm số y = f (x) có đạo hàm cấp ba liên tục trên thỏa mãnNHÓ
f (x) f ′′′(x) = x(x − )2 (x + )3 . 1 4 , x
∀ ∈ . Hàm số g (x) = ( f ′(x))2 − 2 f (x). f ′′(x) có bao nhiêuM T điểm cực trị? OÁN A. 3. B. 1. C. 2 . D. 6 . VD Lời giải – VD Chọn C C .
g′(x) = f ′(x) f ′′(x) − f ′
( x) f ′′( x) + f ( x) f ′′′( x) = − f
(x) f ′′′(x) = − x(x − )2 (x + )3 2 2 2 2 1 4 .
Suy ra g′(x) đổi dấu khi qua hai điểm x = 0, x = 4 − .
Câu 2. Cho hàm số f (x) có đạo hàm cấp hai liên tục trên thỏa mãn
( f ′(x))2 + f (x) f ′′(x) 4 .
=15x +12x, x
∀ ∈ . Hàm số g (x) = f (x). f ′(x) có bao nhiêu điểm cực trị? A. 3. B. 1. C. 2 . D. 4 .
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn C 2 4 NHÓ
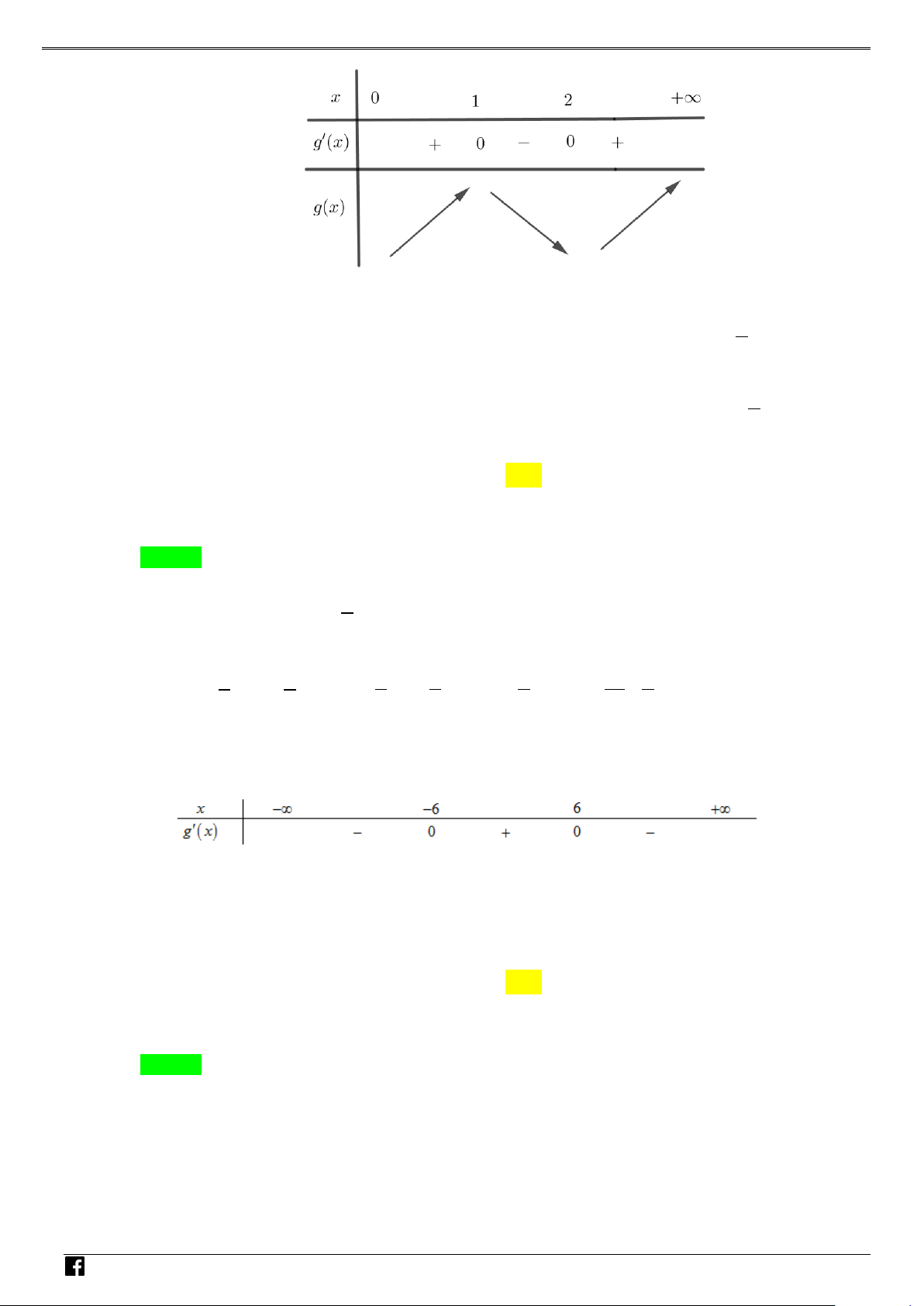
g′(x) = ( f ′(x)) + f ′(x) f ′′(x) =15x +12x M g′(x) 4 = ⇔ = = 3 0 x 0; x . T 5 OÁN
Suy ra hàm số g (x) = f (x). f ′(x) có hai điểm cực trị. V D – VD C NHÓ M T OÁN VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chuyên đề:
CÁC DẠNG TOÁN VỀ HÀM ẨN
LIÊN QUAN ĐẾN CỰC TRỊ NHÓ CỦA HÀM SỐ M TOÁN
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ V D
PHẦN 2: BIẾT BIỂU THỨC CỦA HÀM SỐ y = f '(x) . – VD Dạng toán 1.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (x) + h(x) C
trong bài toán không chứa tham số. Dạng toán 2.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (x) + h(x)
trong bài toán chứa tham số. Dạng toán 3.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) trong
bài toán không chứa tham số . Dạng toán 4.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) trong
bài toán chứa tham số . Dạng toán 5.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) + h(x)
trong bài toán không chứa tham số. Dạng toán 6.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) + h(x) NHÓ
trong bài toán chứa tham số. Dạng toán 7.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x M T
trong bài toán không chứa tham số. OÁN Dạng toán 8.
Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x VD
trong bài toán chứa tham số . Dạng toán 9.
y = f ′(u x ) xét cực trị của hàm số y = f (x) trong bài
Biết biểu thức hàm số ( ) – VD
toán không chứa tham số. C Dạng toán 10.
Biết biểu thức hàm số y = f ′(u(x)) xét cực trị của hàm số y = f (x) trong bài
toán chứa tham số.
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
DẠNG 1. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán không chứa tham số. NHÓ
Câu 1: Cho hàm số y = f (x) có đạo hàm f ′(x) 2 3 2 2
= x − x − x + 3 . Khi đó số điểm cực trị của hàm 9 9 M
số y = g (x) = f (x) −(x + )2 2 1 là T A. 1. B. 2 . C. 4 . D. 3. OÁN Lời giải V Chọn D D – VD C
Ta có y = g (x) = f (x) −(x + )2 2
1 ⇒ g′(x) = 2 f ′(x) − 2(x + )
1 = 2 f ′(x) −(x + ) 1 .
Vẽ hai hàm số y = f ′(x) và y = x +1 trên cùng một hệ trục tọa độ, ta có NHÓ = − M T x 3 g (x) 0 ′ = ⇔ x =1 . OÁN x = 3 VD
Bảng xét dấu của hàm g′(x) : – VD C
Từ bảng xét dấu ta có đáp án đúng là hàm số y = g (x) có 3 điểm cực trị.
Câu 2: Cho hàm số y = f (x) có đạo hàm f (x) = ( − x)( 2 ' 3 x − ) 1 + 2x, x ∀ ∈ . Hỏi hàm số
g (x) = f (x) 2
− x −1 đạt cực tiểu tại điểm nào dưới đây? A. x = 1 − . B. x =1. C. x = 3.
D. x = 0 . Lời giải Chọn B
Ta có g (x) = f (x) − x = ( − x)( 2
x − ) + x − x = ( − x)( 2 ' ' 2 3 1 2 2 3 x − ) 1 .
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x =
g '(x) = 0 ⇔ (3− x)( 3 2 x − ) 1 = 0 ⇔ . x = 1 ± Ta có bảng biến thiên NHÓ M TOÁN
Dựa vào bảng biến thiên suy ra hàm số g (x) đạt cực tiểu tại x =1 . V D –
Câu 3: Cho hàm số f (x) liên tục và có đạo hàm trên (0;+∞) và f '(x) = ln x − x . Hỏi hàm số VD
g(x) = f (x) + x + 2019 có bao nhiêu điểm cực trị trên khoảng (0;+∞)? C A. . B. . C. . D. 0 . 3 2 1 Lời giải Chọn D
Ta có: g '(x) = f '(x) +1 = ln x − x +1. Xét hàm số −
h(x) = ln x − x +1trên (0;+∞). Ta có: 1 1 '( ) = −1 x h x = . x x
Có h'(x) = 0 ⇔ x =1.
Bảng biến thiên của hàm h(x) như sau: x 0 1 +∞ NHÓ h'(x) + - M T OÁN 0 h(x) VD −∞ −∞ – VD C
Vậy h(x) ≤ 0, x
∀ ∈(0;+∞) ⇔ g '(x) ≤ 0, x ∀ ∈(0;+∞)
Do đó g '(x) không đổi dấu trên (0;+∞) nên hàm số g(x) không có cực trị trên khoảng đó.
Câu 4: Cho hàm số y = f (x) liên tục trên và có f (x) = (x + )( 2 '
1 2x − 3x − 9). Hỏi hàm số
g (x) = f (x) 3 2
+ x − 3x − 9x + 6 có bao nhiêu điểm cực trị? A. 2. B. 1. C. 0. D. 3. Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Vì hàm số y = f (x) liên tục trên nên hàm số g (x) = f (x) 3 2
+ x − 3x − 9x + 6 cũng liên tục trên .
Có g (x) = f (x) 2
+ x − x − = (x + )( 2 ' ' 3 6 9
1 2x − 3x − 9) + 3(x + )
1 (x −3) = (x + )
1 (x −3)(2x + 6) NHÓ x = 1 − M T
g '(x) = 0 ⇔ x = 3 OÁN x = 3 − V Ta có bảng biến thiên D – VD x −∞ 3 − 1 − 3 +∞ C g '(x) − 0 + 0 − 0 + g (x)
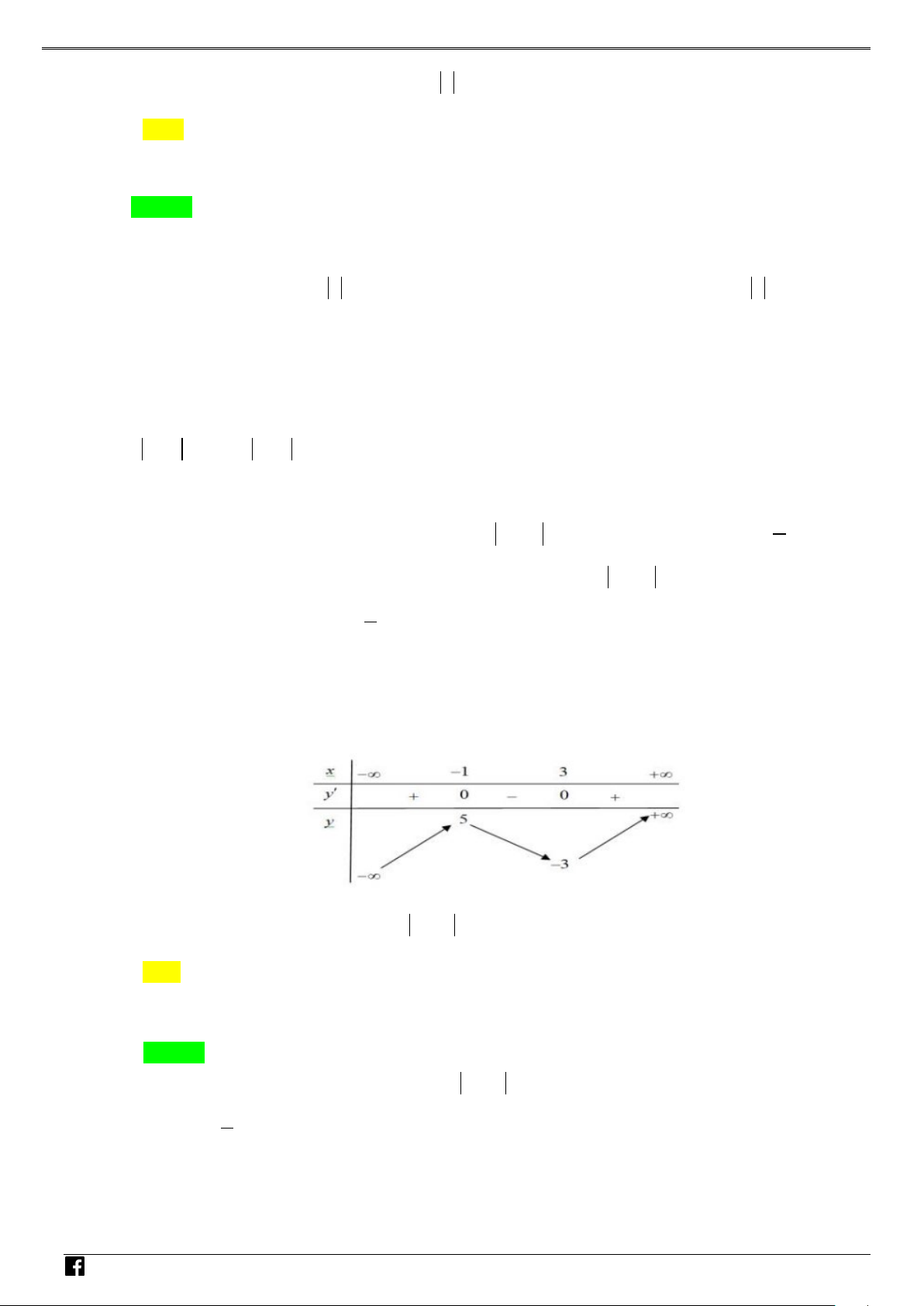
Từ bảng biến thiên suy ra hàm số g (x) có 3 điểm cực trị.
Câu 5: Cho hàm số y = f (x) liên tục trên và có đạo hàm f (x) 2 ' = x (x + )2 1 (x − 2).
Hỏi hàm số g (x) = f (x) 2 3 2
+ x + x − 9 có bao nhiêu điểm cực tiểu? 3 NHÓ A. 5. B. 4. C. 3. D. 2. M T Lời giải OÁN Chọn C Ta có: VD 3 2 –
g '(x) = f '(x) + 2x(x + ) 1 = x(x + )
1 (x − x − 2x + 2) VD x = 0 C x = 1 −
g '(x) = 0 ⇔ x(x + ) 1 (x − ) 1 ( 2 x − 2) = 0 ⇔ x = 1 x = − 2 x = 2
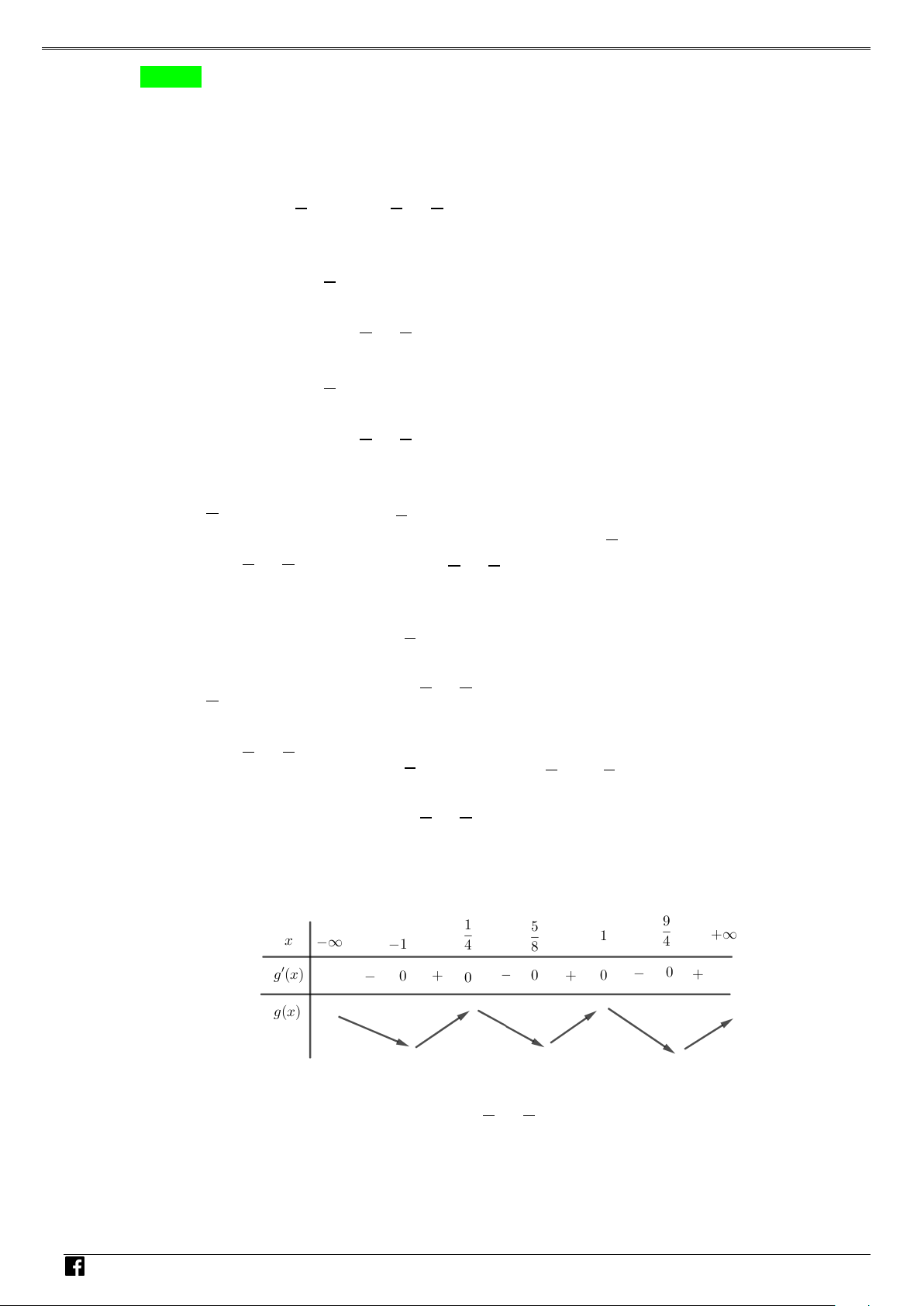
Lập bảng biến thiên của hàm số y = g (x)
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN
Dựa vào bảng biến thiên ta thấy hàm số y = g (x) có 3 điểm cực tiểu. V D
Câu 6: Cho hàm số y = f (x) có đạo hàm f ′(x) = ( 2 3. x − )
1 (x − 2) . Khi đó hàm số – VD
g (x) = f (x) 3
− x + 3x đạt cực đại tại C A. x =1. B. x = 2 . C. x = 1 − . D. x = 3. Lời giải Chọn A Ta có:
g (x) = f ′(x) 2 − x + = ( 2
x − ) (x − ) − ( 2 x − ) = ( 2 3 3 3. 1 . 2 3 1 3 x − ) 1 .(x − 3) x =1 2 − = g (x) x 1 0 0 ′ = ⇔ ⇔ x = 1 − x 3 0 − = x = 3 NHÓ Bảng biến thiên: M T x −∞ 1 − 1 3 +∞ OÁN g′(x) − 0 + 0 − 0 + VD g (x) – VD C
Dựa vào bảng biến thiên, ta thấy hàm số y = g (x) đạt cực đại tại x = 1.
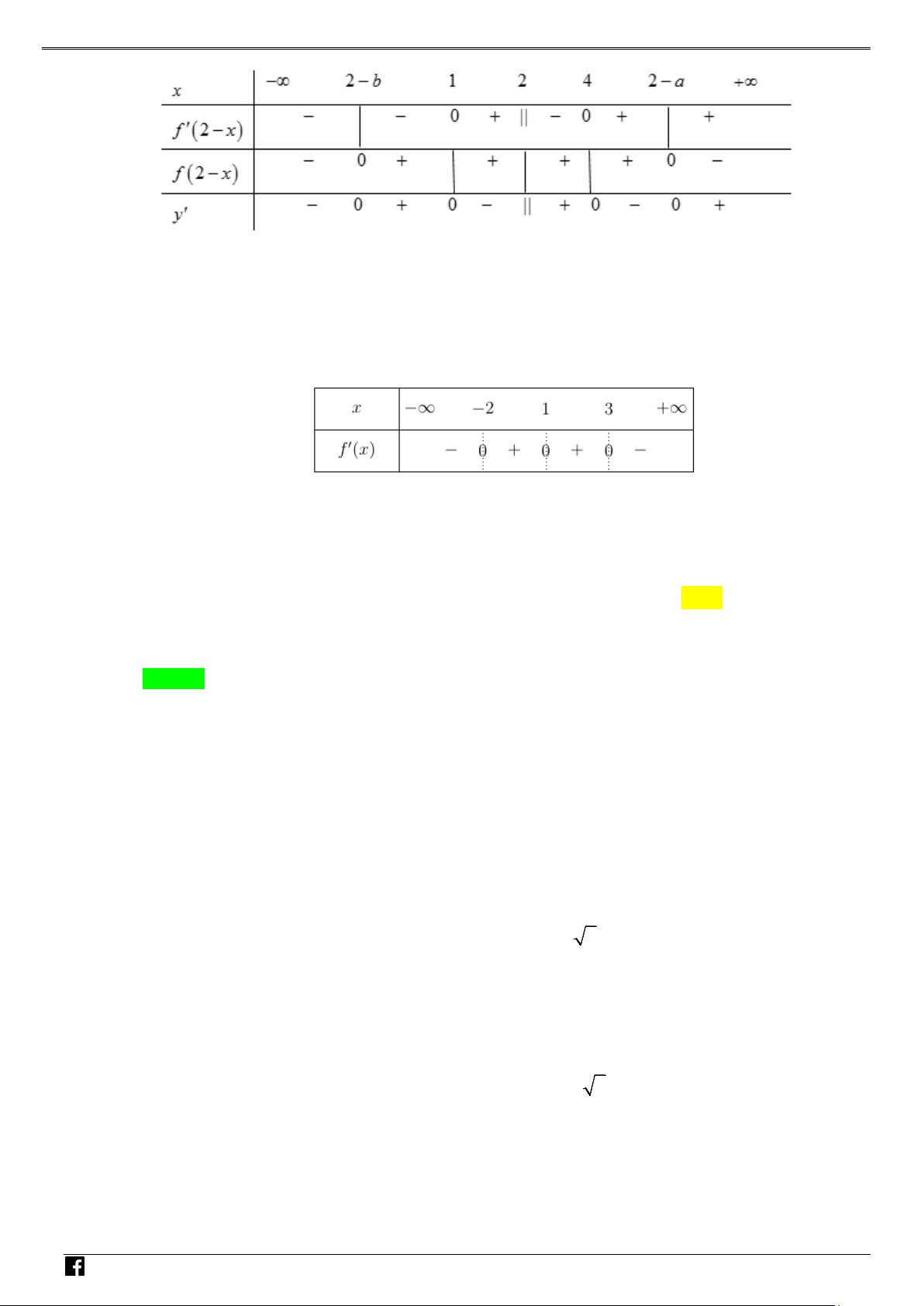
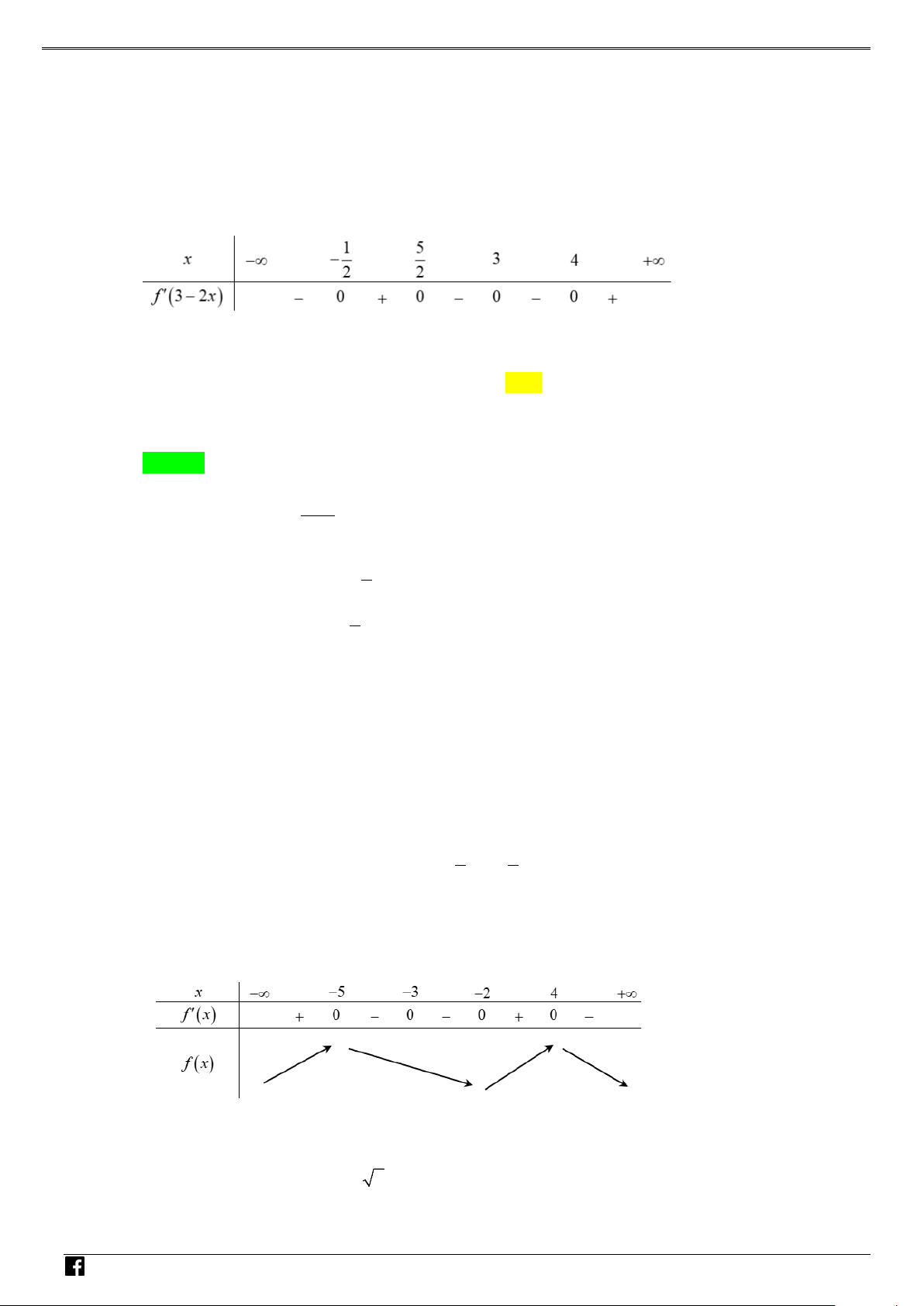
Câu 7: Cho hàm số y = f (x) xác định trên và có đạo hàm f '(x) thỏa mãn
f ′(x) = (1− x)(x + 2) g (x) + 2019 với g (x) < 0 với x ∀ ∈ .
Hàm số y = f (1− x) + 2019x + 2020 đạt cực đại tại
A. x =1 . B. x = 2. C. x = 0 . D. x = 3. 0 0 0 0 Lời giải Chọn D
Đặt h(x) = f (1− x) + 2019x + 2020
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Ta có: h′(x) = − f ′(1− x) + 2019 = − 1 − (1− x)
(1− x) + 2 g
(1− x) − 2019 + 2019 x =
= −x(3− x) g (1− x) ; h′(x) 0 = 0 ⇔ . x = 3 NHÓ
Bảng biến thiên của hàm số h(x) . M TOÁN V D – VD C
Vậy hàm số đạt cực đại x = 3. 0
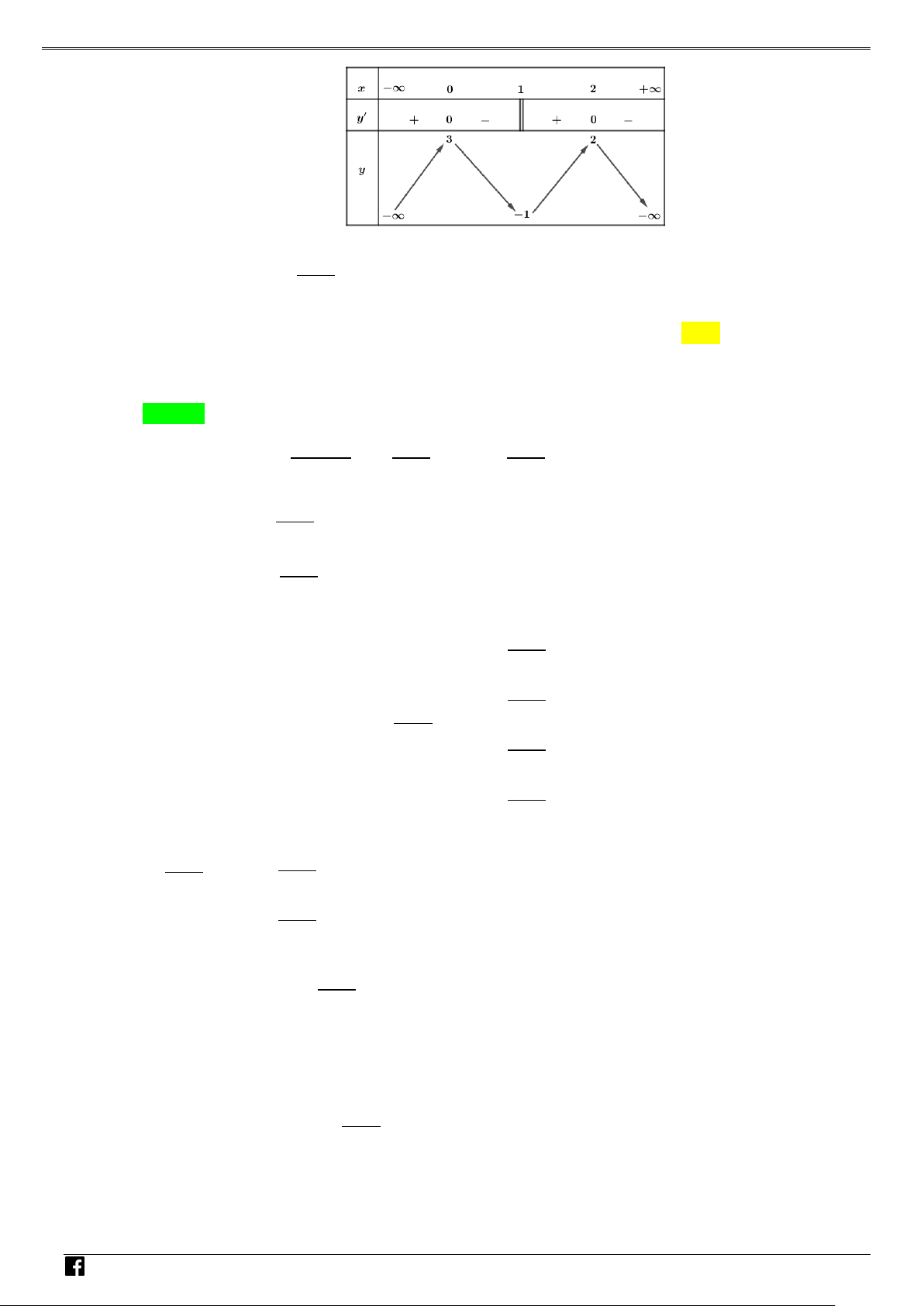
Câu 8: Cho hàm số y = f (x) có tập xác định D = (0;+∞) và có đạo hàm f '(x) = 2xln x + x , x 0 . Hàm số 1 3 2
y = g(x) = f (x) + x − x có bao nhiêu điểm cực trị? 3 A. 1 B. 0 . C. 2 . D. 3. Lời giải Chọn A Ta có: 2 2
g '(x) = f '(x) + x − 2x = 2xln x + x − x = x(2ln x + x − ) 1 , x ∀ > 0 NHÓ
g '(x) = 0 ⇔ 2ln x + x −1 = 0 (*) M T
Xét hàm số h(x) = 2ln x + x −1, x ∀ > 0 OÁN h (x) 2 ' = +1 > 0, x
∀ > 0 ⇒ Hàm số y = h(x) đồng biến trên khoảng (0;+∞) VD x –
Mặt khác: h(1) = 0 ⇒ Phương trình (*) có nghiệm duy nhất x =1 VD C Bảng xét dấu:
Dựa vào bảng biến thiên suy ra hàm số y = g (x) có một điểm cực trị.
Câu 9: Cho hàm số f (x) có đạo hàm f ′(x) = x(x − )3
2 . Số điểm cực trị của hàm số
g (x) = f (x) + ( − x)3 2 là
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B NHÓ
Ta có g′(x) = f ′(x) − ( − x)2 = f ′(x) − (x − )2 = (x − )2 ( 2 3 2 3 2
2 x − 2x − 3) M TOÁN x = 2 g (x) 0 ′ = ⇔ x = 1 − . V x = 3 D – VD
Bảng biến thiên của hàm số g (x) C
Từ BBT suy ra hàm số có 2 điểm cực trị.
DẠNG 2. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (x)+ h(x)
trong bài toán chứa tham số.
Câu 1: Cho hàm số y = f (x) có đạo hàm f ′(x) = ( 2 x − )( 2 3 x + )
1 với x∈ . Có bao nhiêu giá trị NHÓ
nguyên dương của tham số m để hàm số y = f (x) − mx có 4 điểm cực trị? A. 0. B. 1. C. 2. D. 3. M T Lời giải OÁN Chọn A VD
Xét đạo hàm y′ = f ′(x) − m = ( 2 x − )( 2 3 x + )
1 − m ; y′ = ⇔ ( 2 x − )( 2 0 3 x + ) 1 = m – VD
YCBT ⇔ y′ = 0 có 4 nghiệm phân biệt C
Đặt g (x) = ( 2 x − )( 2 x + ) 4 2 3
1 = x − 2x − 3 ; g′(x) 3
= x − x = x( 2 4 4 4 x − ) 1 ; BBT x –∞ 1 − 0 1 +∞ y′ – 0 + 0 – 0 + +∞ 3 − +∞ y 4 − 4 − Vậy 4 − < m < 3
− , mà m nguyên nên không có m nào.
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 2: Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m thuộc khoảng ( 12 −
; 12) sao cho hàm số y = f (x) + mx +12 có đúng một điểm cực trị? NHÓ M TOÁN V D – VD C A. 5. B. 18. C. 20. D. 12. Lời giải Chọn C
Đạo hàm y′ = f ′(x) + m ; y′ = 0 ⇔ f ′(x) = −m
YCBT ⇔ Phương trình y′ = 0 (có 1 nghiệm đơn) y= -m
hoặc (có 1 nghiện đơn và nghiệm kép)
⇔ đường thẳng y = −m cắt đồ thị đạo hàm y = f ′(x)
tại 1 điểm có có hoành độ là nghiệm đơn (bội lẻ)
hoặc tại hai điểm trong đó có điểm có hoành độ bội y= -m NHÓ −m ≥ 3 m ≥1 chẵn ⇔ ⇔ M T −m ≤ 1 − m ≤ 3 − OÁN
Kết hợp với m∈( 12 −
; 12) ta được m∈( 12 − ; − ]
3 ∪[1 ; 12) và m là số nguyên nên VD
có tất cả 9 +11 = 20 giá trị nguyên. – VD
Câu 3: Cho hàm số y = f (x) có đạo hàm liên tục trên . Đồ thị hàm số y = f ′(x) như hình vẽ sau: C
Tìm m để hàm số y = f (x) − mx có 3 điểm cực trị
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
A. 0 < m < 4 .
B. 0 ≤ m ≤ 4 . C. m > 4 . D. m < 0 . Lời giải Chọn A
Ta có: y′ = f ′(x) − m ; y′ = 0 ⇔ f ′(x) = m . NHÓ
Dựa vào đồ thị y = f ′(x) , suy ra phương trình f ′(x) = m có 3 nghiệm phân biệt và các đó là M
nghiệm đơn ⇔ đường thẳng y = m cắt đồ thị đạo hàm y = f ′(x) tại 3 điểm phân biệt TOÁN ⇔ 0 < m < 4 .
Vậy để hàm số y = f (x) − mx có 3 điểm cực trị thì 0 < m < 4 . V D
Câu 4: Cho hàm số y = f (x) có đạo hàm f (x) 3 2 '
= −x − 2x , x
∀ ∈ . Có tất cả bao nhiêu giá trị nguyên – VD
dương của tham số m để hàm số g (x) = f (x) + mx + 3 có 3 điểm cực trị. C A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Hàm số g (x) = f (x) + mx + 3 xác định trên .
g (x) = f (x) 3 2 ' '
+ m = −x − 2x + m
Hàm số g (x) = f (x) + mx + 3 có 3 điểm cực trị ⇔ g '(x) = 0 có 3 nghiệm phân biệt ⇔ 3 2
−x − 2x + m = 0 có 3 nghiệm phân biệt ⇔ 3 2
x + 2x = m có 3 nghiệm phân biệt NHÓ x = 0 M T Đặt g (x) 3 2
= x + 2x ; g′(x) 2
= 3x + 4x ; g′(x) = 0 ⇔ 4 ; BBT: x = − 3 OÁN VD 4 x ∞ 3 0 +∞ – VD y' + 0 0 + C +∞ y 32 27 y = m 0 ∞ Vậy 32 0 < m <
, mà m nguyên dương nên m =1. 27
Câu 5: Cho hàm số y = f (x) có đạo hàm f (x) 2 '
= x 4 − x , x ∀ ∈[ 2;
− 2]. Có tất cả bao nhiêu giá trị
nguyên dương của tham số m để hàm số g (x) = f (x) 2
− m x + 3m có 2 điểm cực trị. A. 2 . B. 1. C. 3. D. 4 .
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn A
Hàm số g (x) = f (x) 2
− m x + 3m xác định trên [ 2; − 2]. NHÓ M
Đạo hàm g (x) = f (x) 2 2 2 ' '
− m = x 4 − x − m TOÁN
YCBT: Hàm số g (x) = f (x) 2
− m x + 3m có 2 điểm cực trị ⇔ g '(x) = 0 có 2 nghiệm phân V
biệt và g '(x) đổi dấu qua các nghiệm đó D – 2 2 VD
Xét phương trình x 4 − x − m = 0 (*) C ⇔ 2 2
x 4 − x = m
Xét hàm số h(x) 2
= x 4 − x , x ∈[ 2; − 2] 2 ( ) 4− 2 ' x h x =
, h'(x) = 0 ⇔ x = ± 2 2 4 − x
Bảng biến thiên của hàm h(x) NHÓ M T OÁN VD − < m < – Vậy 2 2 2 0 < m < 2 ⇔
, m nguyên dương nên m∈{ 1; − } 1 . VD m ≠ 0 C
Câu 6: Cho hàm số y = f (x) có biểu thức đạo hàm f ′(x) = (x + 3)(x − )
1 (x − 2) và hàm số
y = g (x) = f (x) 3 + x + (m + ) 2 6 2 3
1 x − 6(m + 2) x + 2019 . Gọi S = ( ; −∞ a) ∪( ;
b c) là tập tất cả
các giá trị thực của tham số m để hàm số y = g (x) có ba cực trị. Giá trị của a + 2b + 3c bằng A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn D
Từ yêu cầu bài toán ta có: g′(x) = f ′(x) 2 6 + 6x + 6(m + )
1 x − 6(m + 2)
⇔ g′(x) = (x + )(x − )(x − ) 2 6 3 1 2 + 6x + 6(m + )
1 x − 6(m + 2)
⇔ g′(x) = (x − )( 2 6
1 x + 2x + m − 4) .
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x =1
Suy ra g′(x) = 0 ⇔ . 2
x + 2x + m − 4 = 0
Để hàm số y = g (x) có ba cực trị thì g′(x) = 0 có ba nghiệm phân biệt NHÓ ⇔ phương trình 2
x + 2x + m − 4 = 0 có hai nghiệm phân biệt khác 1.
∆′ = 5 − m > 0 m < 5 Hay ⇔ . Suy ra S = ( ; −∞ ) 1 ∪(1;5) . M m −1 ≠ 0 m ≠ 1 TOÁN
Như vậy a =1, b =1, c = 5 và a + 2b + 3c = 8 .
Câu 7: Cho hàm số y = f (x) ′
có biểu thức đạo hàm f (x) 3 2
= x + 3x −1 và hàm số V
y = g (x) = f (x) − mx + 2020 . Gọi S = ( ;
a b) là tập tất cả các giá trị thực của tham số m để hàm D = a + –
số y g (x) có ba cực trị. Giá trị của 2 3b bằng VD A. 1. B. 3 . C. 5. D. 7 . C Lời giải Chọn D
Từ yêu cầu bài toán ta có: g′(x) = f ′(x) − m ⇔ g′(x) 3 2
= x + 3x −1− m .
Suy ra g′(x) = 0 3 2
⇔ x + 3x −1− m = 0 3 2
⇔ x + 3x −1 = m .
Để hàm số y = g (x) có ba cực trị thì g′(x) = 0 có ba nghiệm phân biệt. Hay phương trình 3 2
x + 3x −1 = m có ba nghiệm phân biệt. x = 2 −
Xét hàm số y = h(x) 3 2
= x + 3x −1 có ′ h (x) 2
= 3x + 6x và ′
h (x) = 0 ⇔ . x = 0
Do đó ta có bảng biến thiên của hàm số y = h(x) như sau: x −∞ 2 − 0 +∞ y′ + 0 − 0 + NHÓ 3 +∞ y M T −∞ 1 − OÁN Để phương trình 3 2
x + 3x −1 = m có ba nghiệm phân biệt thì đường thẳng y = m cắt đồ thị hàm
số y = h(x) tại ba điểm phân biệt. Nghĩa là 1
− < m < 3. Hay S = ( 1;
− 3). Do đó 2a + 3b = 7 VD
DẠNG 3. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x) )– VD
trong bài toán không chứa tham số . C
Câu 1: Cho hàm số y = f (x) có đạo hàm f ′(x) =( 2 x − )
1 (x − 4) với mọi x∈ . Hàm số
g (x)= f (3− x) có bao nhiêu điểm cực đại? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B
Từ giả thiết, ta có bảng biến thiên của hàm số f (x)
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T
Ta có g (x)= f (3− x) ⇒ g′(x)=− f ′(3− x) . OÁN
Từ bảng biến thiên của hàm số f (x) ta có V D 3− x ≤ 1 − x ≥ 4 –
g′(x)≥ 0 ⇔ f ′(3− x) ≤ 0 ⇔ ⇔ . VD 1 3 x 4 ≤ − ≤ 1 − ≤ x ≤ 2 C
Như thế ta có bảng biến thiên của hàm số g (x)
Từ bảng biến thiên, ta nhận thấy hàm số g (x) có một điểm cực đại.
Câu 2: Cho hàm số y = f (x) xác định, liên tục, có đạo hàm trên và 2 2 NHÓ
f ′(x) = x (x − 2028)(x − 2023)2 . Khi đó hàm số y = g(x) = f (x + 2019) có tất cả bao nhiêu điểm cực trị? M T A. 3. B. 4 . C. 5. D. 6 . OÁN Lời giải VD Chọn A – VD
Ta có y = g x = f ( 2 ( )
x + 2019) ⇒ y′ = g x = ( 2 x + )′ ′ f ′( 2 x + ) = x f ′( 2 ( ) 2019 2019 2 . x + 2019). C
Mặt khác f ′(x) 2
= x (x − 2028)(x − 2023)2 . Nên suy ra:
y′ = g′(x) = 2 .
x f ′(x + 2019) = 2 .x(x + 2019)2 (x + 2019 − 2028)(x + 2019 − 2023)2 2 2 2 2 . = 2 . x ( 2 x + 2019)2 ( 2 x − 9)( 2
x − 4)2 = 2 .x( 2
x + 2019)2 (x − ) 3 (x + )
3 (x − 2)2 (x + 2)2
x = 0 (nghiem don)
x = 3 (nghiem don) y′ = 2 . x ( 2
x + 2019)2 (x −3)(x + 3)(x − 2)2 (x + 2)2 = 0 ⇔ x = 3 ( − nghiem don)
x = 2 (nghiem boi 2) x = 2 − (nghiem boi 2)
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Ta có bảng biến thiên sau: NHÓ M TOÁN
Từ bảng biến thiên suy ra hàm số y = g x = f ( 2 ( )
x + 2019) có tất cả 3 điểm cực trị. V
Câu 3: Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x − 2x , x
∀ ∈ . Hàm số y = f ( 2
x −8x) có bao D – nhiêu điểm cực trị? VD A. 6 . B. 3. C. 5. D. 2 . C Lời giải Chọn C
Ta có: f ′(x) 2
= x − 2x = x(x − 2)
và y′ = ( x − ) f ′( 2
x − x) = (x − )( 2 x − x)( 2 2 8 . 8 2 4 8 x −8x − 2) x = 4 x − 4 = 0 x = 0 ⇒ y′ = 0 2 ⇔ x −8x = 0 ⇔ x = 8 . 2 x −8x − 2 = 0 x = 4 +3 2 x = 4 −3 2
Bảng xét dấu y′ như sau: NHÓ M T OÁN
Vậy hàm số y = f ( 2
x −8x) có 5 điểm cực trị. VD
DẠNG 4. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) – VD
trong bài toán chứa tham số. C Câu 1:
y f x có đạo hàm 2 2 2
f x x x 3x 2 x x , với mọi x Cho hàm số . Có bao
nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( 2
x −16x + 2m) có 5 điểm cực trị? A. 30. B. 31. C. 32. D. 33. Lời giải Chọn B
Ta có: y f 2
x 16x 2m2x16.
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x 8 2 x 8
x 16x 2m 1 (1) Cho y 0 . f 2
x 16x 2m 2 0
x 16x 2m 0 (2) NHÓ 2
x 16x 2m 2 (3) M
Do các nghiệm của (1) đều là nghiệm bội bậc chẵn còn (2) và (3) không thể có nghiệm trùng T
nhau nên hàm số đã cho có 5 điểm cực trị khi (2) và (3) có 2 nghiệm phân biệt khác 8 . OÁN ' 0 2 64 2m 0 V ' D 0 64 2m 2 0 3
m 32 mà m nguyên dương nên m có 31 giá trị. – 2 64 m 0 8 16.8 m 0 VD 2 8 16.8 m 2 64 m 2 C
Câu 2: Cho hàm số y f (x) có đạo hàm 2
f x x x 2 '( )
1 x 2mx 4 . Có bao nhiêu giá trị
nguyên của m không vượt quá 2019 để hàm số 2 y
f x có đúng 1 điểm cực trị? A. 2021. B. 2022 . C. 5. D. 4 . Lời giải Chọn B Ta có: y 2 f x 2 4 2 4 2 5 2 4 2 ' ( ) 2 .
x f '(x ) 2 .
x x (x 1)(x 2mx 4) 2x (x 1)(x 2mx 4) ; x 0 Khi đó: y ' 0 2 . 4 2 tx 2
x 2mx 4 0 t 2mt 4 0 1 NHÓ
Ta thấy nghiệm của
1 nếu có sẽ khác 0 . Nên x 0 là 1 cực trị của hàm số.
Do đó để hàm số có 1 điểm cực trị thì
1 hoặc vô nghiệm hoặc có nghiệm kép, hoặc có 2 M T nghiệm âm OÁN 2
' m 4 0 2 m 2 2
' m 4 0 m 2 2 m 2 VD m 2 .
S 2m 0 m2 m 2 – P 4 0 VD m 0 C m Kết hợp với
m 2;1;0;1;2;...;2018;
2019 : có 2022 giá trị nguyên của m . m 2019
Câu 3: Cho hàm số f x có f x xx 2
1 x 2mx
1 . Hỏi có tất cả bao nhiêu số nguyên m
không vượt quá 2018 sao cho hàm số 2 g x
f x có 7 điểm cực trị? A. 2019. B. 2016. C. 2017. D. 2018. Lời giải Chọn C
Ta có: gx x f 2 x 2 x x 2 x 4 2 x mx 3 x 2 x 4 2 2 . 2 . 1 2 1 2
1 x 2mx 1 .
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x 0 g x 0 x 1 4 2
x 2mx 1 0 NHÓ
Do x 0 là nghiệm bội lẻ và x 1 là các nghiệm đơn nên để gx có 7 điểm cực trị thì M phương trình
phải có 4 nghiệm phân biệt khác 0 và khác 1, hay phương trình TOÁN 2
t 2mt 1 0 phải có 2 nghiệm dương phân biệt khác 1. V m 1 2 D
m 1 0 m 1 – S 2m 0 VD m 0 m 1. P 1 0 C m 1 2 1 2 .1 m 1 0
Kết hợp với điều kiện m nguyên, không vượt quá 2018 suy ra có 2017 giá trị của m .
Câu 4: Cho hàm số y f x có đạo hàm f xx 2 2
1 x 2x với mọi x . Có bao nhiêu giá
trị nguyên dương của tham số m để hàm số gx f 2
x 8x m có 5 điểm cực trị ? A. 15. B. 16. C. 17. D. 18. Lời giải Chọn A NHÓ
x 1 nghiem boi 2
Xét f x 0 x 2 1 2 x 2x 0 x 0 . M T x 2 OÁN
Ta có gx x f 2 2 4
x 8x m; VD x 4 – VD 2
x 8x m 1 nghiem boi 2
g x 0 2x4 f 2
x 8x m 0 . C 2
x 8x m 0 1 2
x 8x m 2 2
Yêu cầu bài toán gx 0 có 5 nghiệm bội lẻ mỗi phương trình 1 , 2 đều có hai
nghiệm phân biệt khác 4. *
Xét đồ thị C của hàm số 2
y x 8x và hai đường thẳng d : y , m
d : y m 2 (như 1 2 hình vẽ).
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V Khi đó
* d , d cắt C tại bốn điểm phân biệt m
16 m 16. 1 2 D –
Vậy có 15 giá trị m nguyên dương thỏa. VD 2 2 C
Câu 5: Cho hàm số y f x có đạo hàm f 'xx xx 4x 3 , x .
Tính tổng tất cả các
giá trị nguyên của tham số m để hàm số 2 g x
f x m có 3 điểm cực trị. A. 0 . B. 6 . C. 3. D. 2 . Lời giải Chọn C x 0
Ta có f 'x xx 2 1 x
3 ; f 'x 0 x 1
( x 0, x 3 là nghiệm đơn; x 1 là x 3 nghiệm bội chẵn). NHÓ x 0 x 0 2 2 x 0 x m 0 x m 1 M T
Lại có g 'x 2 .x f ' 2
x m; g 'x 0 f ' 2 x m 2 2 0 x m 1
x 1m 2 OÁN 2 2 x m 3 x 3 m 3 VD
Do 2 có nghiệm luôn là nghiệm bội chẵn; các phương trình 1 ,
3 có nghiệm không chung – VD nhau và m 3 . m C m 0
Hàm số gx có 3 điểm cực trị g 'x 0 có ba nghiệm bội lẻ 0 m 3. 3 m 0
Vì m m 0;1; 2 .
Vậy tổng các giá trị nguyên của tham số m bằng 3.
Câu 6: Cho hàm số y = f (x) có f xx 2 2
2 x 4x 3 với mọi x .
. Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số y f 2
x 10x m
9 có 5 điểm cực trị? A. 18. B. 17. C. 16. D. 15. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn C
Theo đề bài f xx 2 2
2 x 4x 3 x 2 2 x 1 x 3 NHÓ
Ta có y x f 2 2 10
x 10x m 9 . M 2x10 0 T y 0 OÁN f 2
x 10x m 9 0 x 5 V 2 D 2
x 10x m 7 2
x 10x m 8 2
x 10x m 6 0 – VD x 5 C
x 10xm72 2 0 . 2
x 10x m 8 0 1 2
x 10x m 6 0 2
Giả sử x là một nghiệm của (1) 2
x 10x m 8 0 . 0 0 0 Do đó 2
x 10x m 6 2 0, m , suy ra
1 và 2 không có nghiệm chung. 0 0
Hàm số y f 2
x 10x m
9 có năm điểm cực trị khi mỗi phương trình 1 ,2có hai nghiệm phân biệt khác 5 NHÓ 25m8 0 m 17 25m6 0 m 19 m 17 m
m 1;2;3;...;15; 16 . M T m17 0 m 17 m19 0 m 19 OÁN 2 VD
Vậy có 16 giá trị nguyên của m để hàm số y f x 10xm 9 có 5 điểm cực trị. – = ′ VD
DẠNG 5. Biết biểu thức hàm số y f (x) xét cực trị của hàm số C
y = g (x) = f (u(x)) + h(x) trong bài toán không chứa tham số.
Câu 1. Cho hàm số y = f (x) có đạo hàm f ′(x) = ( − x)(x − )2019 2 2 8 , x ∀ ∈ . Hàm số y = f ( 2 x − 2) 1 4 2
+ x − 4x + 2020 có bao nhiêu điểm cực trị ? 2 A. 4 . B. 2019 . C. 5. D. 2020 . Lời giải Chọn C
Xét hàm số g (x) = f ( 2 x − 2) 1 4 2
+ x − 4x + 2020 . 2
+ g′(x) = x f ′( 2 x − ) 3 2 . 2 + 2x −8x .
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
+ g′(x) = ⇔ x f ′( 2 x − ) 3
+ x − x = ⇔ x f ′ ( 2 x − ) 2 0 2 . 2 2 8 0 2 2 + x − 4 = 0 x = 0 ⇔ . f ′ ( 2 x − 2) 2 + x − 4 = 0 (∗ ) NHÓ
Giải phương trình (∗) : Đặt 2 t = x − 2 . M
(∗) ⇔ f ′(t)+t − 2 = 0 ( t)(t )2019 (t ) ( t)(t )2019 2 2 2 8 2 0 2 8 1 ⇔ − − + − = ⇔ − − − = 0 T OÁN 2 − t = 0 t = 2 t = 2 ⇔ ⇔ ⇔ . 2 V (t −8)2019 2 −1 = 0 t −8 =1 t = 3 ± D 2 2 – x − 2 = 2 x = 4 VD x = 2 ± Suy ra 2 2
x − 2 = 3 ⇔ x = 5 ⇔ . C x = ± 5 2 2 x − 2 = 3 − x = 1 −
⇒ g′(x) = 0 có 5 nghiệm (không có nghiệm bội chẵn).
Vậy hàm số có 5 cực trị.
Câu 2. Cho hàm số y = f (x) có đạo hàm ′( ) = ( x − 2)( x f x e
e + x) , x
∀ ∈ . Biết hàm số
y = g (x) = f (ln x) − x + 2ln x đạt cực tiểu tại x = x . Chọn khẳng định đúng? 0 A. 3 x 3 0; ∈ . x ∈ ;3 . 0 B. 2 0 2 C. x ∈( 2 3 e ;e . x ∈ ln 2;ln 3 . 0 ) D. 0 ( ) Lời giải NHÓ Chọn B M T
Xét hàm số y = g (x) = f (ln x) − x + 2ln x , x > 0 . OÁN 1 2 1 lnx ln x x − 2 1 x − 2 VD
Ta có y′ = g′(x) = f ′(ln x) −1+ = (e − 2)(e + ln x) −
= (x − 2)(x + ln x) − x x x x x x – x − 2 VD = (x + ln x − ) 1 . x C x > 0 x > 0 g (x) 0 ′ = ⇔ x − 2 = 0 ⇔ x = 2 .
x + ln x −1 = 0
x + ln x −1 = 0 (1)
Hàm số y = x + ln x −1 đồng biến trên (0;+∞) nên phương trình (1) nếu có nghiệm thì nghiệm là
duy nhất. Dễ thấy x =1 là nghiệm duy nhất của (1). Bảng biến thiên
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D 3 = = = x ;3 ∈ –
Từ bảng biến thiên suy ra hàm số y g (x) đạt cực tiểu tại x x 2. Vậy . 0 0 2 VD C x
Câu 3. Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x − 2x , x
∀ ∈ . Hàm số y = f 1− + 4x có mấy 2 điểm cực trị? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Xét hàm số ( ) 1 x g x f = − + 4x . 2 2 2 ( ) 1 1 x x x 9 = − 1 x g x f ′ ′ − + 4 = = − 1− −
21− + 4 = − + = 0 ⇔ x = 6 ± . 2 2 2 2 2 8 2 NHÓ ′ M T
Bảng xét dấu g (x) OÁN VD –
Dựa vào bảng biến thiên ta thấy hàm số có 2 điểm cực trị. VD = ′ = − + C
Câu 4. Cho hàm số y f (x) có đạo hàm f (x) 2
x 6x 11, x
∀ ∈ . Hàm số = (ex y f )−6x c ó mấy điểm cực tiểu? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C
Xét hàm số ( ) = (ex g x f )−6x.
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số ex =1 x = 0
′( ) = ex ′(ex ) 3x 2
− 6 = e − 6e x +11ex g x f − 6 = 0 ex 2 ⇔ = ⇔ x = ln 2 .
ex = 3 x = ln3 NHÓ
Bảng xét dấu g′(x) M TOÁN V D
Dựa vào bảng biến thiên ta thấy hàm số có 2 điểm cực tiểu. – VD
DẠNG 6. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số C
y = g (x) = f (u(x)) + h(x) trong bài toán chứa tham số.
DẠNG 7. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x
trong bài toán không chứa tham số.
Câu 1: Cho hàm số y = f (x) có đạo hàm 3
f '(x) = 4x + 2x và f (0) =1. Số điểm cực tiểu của hàm số 3 g x = f ( 2 ( )
x − 2x − 3) là A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C NHÓ
Ta có f x = ∫( 3x + x) 4 2 ( ) 4
2 dx = x + x + C và f (0) =1⇒ C =1. M T Do đó ta có 4 2
f (x) = x + x +1 > 0, x ∀ . OÁN
Ta có: g x = ( x − ) 2 f ( 2
x − x − ) f ( 2 '( ) 3 2 2 . 2
3 . ' x − 2x − 3) VD – x =1 VD 2x − 2 = 0 g '(x) = 0 ⇔ 3 ⇔ x = 1 − C 4 ( 2 x 2x 3) 2( 2 x 2x 3) 0 − − + − − = x = 3 Bảng biến thiên x -∞ -1 1 3 +∞ g'(x) - 0 + 0 - 0 + g(x)
Từ bảng biến thiên ta suy ra hàm số y = g(x) có 2 cực tiểu.
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 2: Cho hàm số y = f (x) có đạo hàm f (x) 2 '
= 3x − 3 và f (2) = 4 . Hàm số g (x) = f ( − x) 2 1 2
có bao nhiêu điểm cực trị? A. 3. B. 4 . C. 5. D. 6 . NHÓ Lời giải M Chọn A TOÁN
+ Hàm số y = f (x) có đạo hàm f (x) 2 ' = 3x − 3 . 2 3 V
⇒ y = f (x) = f '
∫ (x)dx = ∫(3x −3)dx = x −3x+C . D – Mà f ( ) 3
2 = 4 ⇒ 2 − 3.2 + C = 4 ⇔ C = 2 . VD C ⇒ f (x) 3
= x − 3x + 2 .
+ g (x) = f ( − x) 2 1 2
⇒ g '(x) = 2 f (1− 2x). f
(1− 2x) ' = −4 f
(1− 2x).f '(1− 2x). 3 1
− 2x =1 nghiem kep ( − x − − x + = f 1− 2x) (1 2 ) 3(1 2 ) ( ) 2 0 = − = − g (x) 0 1 2x 2 ' = 0 ⇔ ⇔ − = ⇔ f ( − x) 1 2x 1 ' 1 2 = 0 1 − 2x =1 1− 2x = 1 − 1 − 2x = 1 − NHÓ
x = 0 (nghiem boi ba) ⇔ x = 1 . M T 3 x = OÁN 2 VD
⇒ phương trình g′(x) = 0 có 2 nghiệm đơn là 3
x =1, x = và một nghiệm bội ba x = 0 . 2 – VD Bảng biến thiên: C
Vậy hàm số g (x) = f ( − x) 2 1 2
có 3 điểm cực trị.
Câu 3: Cho hàm số bậc bốn trùng phương y = f (x) có đạo hàm f (x) 3 '
= 4x − 4x và f (0) = 1, − f (− ) 1 = 2
− . Hàm số g ( x) 3 = f (x) 2 2
+ 4 f (x) +1 có nhiều nhất bao nhiêu điểm cực tiểu?
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 4 . B. 5 . C. 7 . D. 9 . Lời giải Chọn B NHÓ x = 1 − M + f '(x) 3
= 0 ⇔ 4x − 4x = 0 ⇔ x = 0 . T x = 1 OÁN
Bảng biến thiên của hàm số bậc bốn trùng phương y = f (x) V D – VD C + g′(x) 2
= 6 f (x). f ′(x) +8 f (x). f ′(x) = 0 f (x) = 0
⇔ f ′(x) = 0 . f (x) 4 = − 3 NHÓ
Dựa vào bảng biến thiên trên ta có: M T = x = x f ′(x) x 0 = 0 ⇔ , f (x) 1 = 0 ⇔ , OÁN x = 1 ± x = x2 VD x = a x = b – = − ⇔
< < − < < < < < < f (x) 4 thỏa mãn: x a
1 b 0 c 1 d x . VD 3 x = c 1 2 C x = d
Khi đó để có nhiều điểm cực tiếu nhất thì bảng xét dấu của g′(x) có dạng: x −∞ x a x 1 1 −
b 0 c 1 d 2 +∞ g′(x) − 0 + 0 − 0 − 0 − 0 + 0 + 0 + 0 − 0 +
Vậy hàm số g (x) 3 = f (x) 2 2
+ 4 f (x) +1 có nhiều nhất 5 điểm cực tiểu.
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
DẠNG 8. Biết biểu thức hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x
trong bài toán chứa tham số . NHÓ
DẠNG 9. Biết biểu thức hàm số y = f ′(u(x)) xét cực trị của hàm số y = f (x) trong
bài toán không chứa tham số. M T = ′ = OÁN
DẠNG 10. Biết biểu thức hàm số y f (u(x)) xét cực trị của hàm số y f (x) trong
bài toán chứa tham số. V D – VD C NHÓ M T OÁN VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D – VD C NHÓ M T OÁN VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chuyên đề:
CÁC DẠNG TOÁN VỀ HÀM ẨN NHÓ
LIÊN QUAN ĐẾN CỰC TRỊ CỦA HÀM SỐ M T OÁN V D
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ – VD
PHẦN 3: BIẾT ĐỒ THỊ CỦA HÀM SỐ y = f '(x) C Dạng toán 1.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (x) + h(x)
trong bài toán không chứa tham số. Dạng toán 2.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (x) + h(x)
trong bài toán chứa tham số. Dạng toán 3.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) trong
bài toán không chứa tham số . Dạng toán 4.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) trong
bài toán chứa tham số . Dạng toán 5.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) + h(x)
trong bài toán không chứa tham số. NHÓ Dạng toán 6.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x)) + h(x)
trong bài toán chứa tham số. M T Dạng toán 7.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x OÁN
trong bài toán không chứa tham số. VD Dạng toán 8.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x f u x –
trong bài toán chứa tham số . VD Dạng toán 9.
Biết ĐỒ THỊ hàm số y = f ′(u(x)) xét cực trị của hàm số y = f (x) trong bài toán C
không chứa tham số. Dạng toán 10.
Biết ĐỒ THỊ hàm số y = f ′(u(x)) xét cực trị của hàm số y = f (x) trong bài toán chứa tham số.
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 1.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán không chứa tham số. NHÓ
Câu 1: Cho hàm số y = f (x) có đạo hàm trên và đồ thị hàm số y = f '(x) như hình bên. Khẳng
định nào sau đây là đúng? M TOÁN V D – VD C
A. Hàm số y = f (x) 2
− x − x + 2019 đạt cực đại tại x = 0 .
B. Hàm số y = f (x) 2
− x − x + 2019 đạt cực tiểu tại x = 0 .
C. Hàm số y = f (x) 2
− x − x + 2019 không có cực trị.
D. Hàm số y = f (x) 2
− x − x + 2019 không đạt cực trị tại x = 0 . Lời giải Chọn A Ta có:
y ' = f '(x) − 2x −1 NHÓ
y ' = 0 ⇔ f '(x) = 2x +1 (1) M T
Nghiệm của phương trình (1) là hoành độ giao điểm của 2 đồ thị y = f ′(x) và y = 2x +1 OÁN VD – VD C
Dựa vào đồ thị hàm số y = f ′(x) và đường thẳng y = 2x +1có x∈{0, } 2 là các nghiệm của phương trình (1) y '(− ) 1 = f '(− ) 1 + 2 −1 > 0 y '( ) 1 = f '( ) 1 − 2 −1< 0
y '(3) = f '(3) − 6 −1< 0 Bảng xét dấu:
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
⇒ Hàm số y = f (x) 2
− x − x + 2019 đạt cực đại tại x = 0 .
Câu 2: Cho hàm số y = f (x) có đạo hàm trên và có đồ thị hàm số y = f ′(x) như hình vẽ. NHÓ M TOÁN V D
Hàm số g (x) = f (x) 2 2
+ x đạt cực đại tại điểm nào dưới đây? – VD A. x = 1 − . B. x = 0 . C. x =1. D. x = 2 . C Lời giải Chọn A
Có g′(x) = 2 f ′(x) + 2x
g′(x) = 0 ⇔ f ′(x) = −x (1)
Nghiệm của phương trình (1) là hoành độ giao điểm của 2 đồ thị y = f ′(x) và y = −x NHÓ
Dựa vào đồ thị hàm số y = f ′(x) và đường thẳng y = −x có x∈{ 1, − 0,1, } 2 là các nghiệm của M T
phương trình (1) (trong đó x =1,
x = 2 là các nghiệm bội chẵn). Có bảng xét dấu OÁN x −∞ 1 − 0 1 2 +∞ ′ VD
g (x) + 0 − 0 + 0 + 0 + – VD
Từ đó suy ra hàm số g (x) đạt cực đại tại điểm x = 1 − . C
Câu 3: Cho hàm số y f x liên tục trên và có đồ thị hàm số y f x như hình bên dưới. 3 Hàm số x 2
g(x) f (x)
x x 2 đạt cực đại tại điểm nào? 3
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. x 1. B. x 1. C. x 0 .
D. x 2 . Lời giải Chọn A NHÓ
Ta có g(x) xác định trên và 2 g (
x) f (x) (x 1) do đó số M
nghiệm của phương trình g (x) 0 bằng số giao điểm của hai đồ TOÁN
thị y f (x) và parabol 2
y (x 1) ; g (x) 0 khi đồ thị y f (
x) nằm trên parabol 2
y (x 1) và ngược lại. V D – x 0 VD
Từ đồ thị suy ra g (x) 0 x 2
nhưng g (x) chỉ đổi dấu từ C x 1
dương sang âm khi qua x 1 . Do đó hàm số đạt cực đại tại x 1.
Câu 4 : Cho hàm số y = f (x) xác định và liên tục trên , có đạo hàm f ′(x) . Biết đồ thị của hàm số
f ′(x) như hình vẽ. NHÓ M T OÁN
Xác định điểm cực tiểu của hàm số g (x) = f (x) + x . VD
A. Không có cực tiểu. B. x = 0 . – VD C. x =1. D. x = 2 . C Lời giải Chọn C
g′(x) = f ′(x) +1. Dựa vào đồ thị thấy g′(x) đổi dấu từ “-” sang “+” qua điểm x =1 nên hàm
số g (x) đạt cực tiểu tại x =1.
Câu 5 : Cho hàm số y = f (x) liên tục trên , hàm số y = f '(x) có đồ thị như hình vẽ. Hàm số ( ) 2017 2018x y f x − = +
có số điểm cực trị là 2017
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V A. 4 . B. 3 . C. 2 . D. 1 . D – VD Lời giải C Chọn A Ta có: ( ) 2017 −2018x y f x y f (x) 2018 ' ' − = + ⇒ = + 2017 2017
y = ⇔ f (x) 2018 ' 0 ' = 2017
Dựa vào hình vẽ ta nhận thấy phương trình f (x) 2018 ' = có 4 nghiệm phân biệt. 2017
Vậy hàm số có 4 điểm cực trị. NHÓ Lưu ý: Do 2018 1 <
< 2 nên dựa vào đồ thị nhìn thấy đường thẳng nằm trong vùng từ 1 đến 2 2017 M T
từ đó quan sát thấy có 4 nghiệm. OÁN
Câu 6 : Cho hàm số y = f (x) xác định, liên tục trên và có đồ thị của đạo hàm y = f ′(x) như hình vẽ
bên dưới. Tìm số điểm cực đại của đồ thị hàm số y = f (x) . VD – VD C A. 1 B. 2 C. 3 D. 4 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V
Đồ thị hàm số y = f ′(x) giao với trục hoành tại 4 điểm. x , x , x , x 1 2 3 4 . D ′ –
Nhận thấy f (x) đổi dấu từ âm sang dương khi đi qua x và x nên hàm số y = f (x) đạt cực 1 3 VD
tiểu tại x và x . 1 3 C
Và f ′(x) đổi dấu từ dương sang âm khi đi qua x nên hàm số y = f (x) đạt cực đại tại x . 2 2
f ′(x) không đổi dấu khi đi qua x nên x không là điểm cực trị của hàm số. 4 4
Vậy hàm số y = f (x) có một điểm cực đại.
Câu 7 : Cho hàm số f (x) xác định trên và có đồ thị f ′(x) như hình vẽ bên. Đặt g (x) = f (x) − x .
Hàm số g (x) đạt cực đại tại điểm thuộc khoảng nào dưới đây? NHÓ M T OÁN A. 3 ;3 . B. ( 2; − 0) . C. (0; ) 1 . D. 1 ;2 . 2 2 VD Lời giải – VD Chọn B C
Ta có g′(x) = f ′(x) −1.
g′(x) = 0 ⇔ f ′(x) =1. Từ đồ thị, ta được x = 1
− , x =1, x = 2 .
Từ đồ thị, ta cũng có bảng xét dấu của g′(x) :
Ta được hàm số g (x) đạt cực đại tại x = 1 − .
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 2.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán chứa tham số. NHÓ DẠNG TOÁN 3.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) trong bài toán không chứa tham số . M TOÁN
Câu 1: Cho hàm số y f x có đồ thị hàm 2
f x ax bx c như hình bên. V D – VD C Hỏi hàm số 2 g x
f x x có bao nhiêu cực trị ? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Xét 2 g x
f x x gx x f 2 1 2 x x . 1 x NHÓ 12x 0 2 g x 0 2
x x 1 (*) f 2 x x 0 M T 2
x x 2 (**) OÁN VD 1
x (vì phương trình (*)(**) vô nghiệm). 2 – VD
Ta có: gx đổi dấu 1 lần khi qua nghiệm 1 x . C 2
Câu 2: Cho hàm số f (x) có đồ thị f ′(x) của nó trên khoảng K như hình vẽ. Khi đó trên K, hàm số
y = f (x − 2020) có bao nhiêu điểm cực trị? y O x
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 1. B. 4. C. 3. D. 2. Lời giải Chọn A NHÓ
Đồ thị hàm số f 'x2020 là phép tịnh tiến của đồ thị hàm số f ′(x) M theo phương song song T
trục hoành nên đồ thị hàm số f 'x2020vẫn cắt trục hoành tại 3 điểm và đổi dấu 1 lần do đó OÁN
hàm số y = f (x − 2020) có một cực trị. Ta chọn đáp án A. V D
Câu 3: Cho hàm số y = f (x) xác định và liên tục trên . Biết rằng hàm số y = f ′(x) có đồ thị như – hình vẽ bên dưới: VD C
Hàm số y = g x = f ( 2 ( )
x − 5) có tất cả bao nhiêu điểm cực trị? A. 3. B. 4 . C. 5. D. 6 . NHÓ Lời giải M T Chọn C OÁN
Xét hàm số y = g x = f ( 2 ( ) x − 5) VD 2
Ta có y′ = g '(x) = 2 .x f ′ x − 5 – ( ) VD C x = 0 x = 0 =
x 0 (nghiem boi 3) 2 2 x − 5 = −5 x = 0 + y = 0 ′ ⇔ ⇔ ⇔ x = ±
3 (nghiem don) . 2 2
x − 5 = −2 x = 3 x = ± 2 2 (nghiem don) 2 2 x − 5 = 3 x = 8
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x > 0 x > 2 2 x > 0 x < −2 2 2 NHÓ x − 5 > 3 − 3 < x < 3 x > 2 2 2
−5 < x − 5 < −2 M
+ g '(x) > 0 ⇔ . ⇔ ⇔ 0 < x < 3 x < 0 T x < 0 −
2 2 < x < − 3 OÁN 2 2 x 5 3 − < − < 2
−2 2 < x < −2 2
x − 5 < 5 − V x > 3 D –
x < − 3 VD C
Từ đó ta có bảng biến thiên của hàm số 2
y = g(x) = f x − 5 như sau: ( )
Từ bảng biến thiên suy ra hàm số y = f ( 2
x − 5) có tất cả 5 điểm cực trị.
Câu 4: Cho hàm số y = f (x) . Đồ thị của hàm số f ′(x) như hình bên. NHÓ M T OÁN VD – VD C 2 =
Hàm số g (x) f (x ) có bao nhiêu điểm cực trị? A. 4 . B. 3. C. 5. D. 2 . Lời giải Chọn C x = 2 − x = 0
Từ đồ thị y = f ′(x) ta có f ′(x) = 0 ⇔ ; x =1 x = 3
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số > x < − f ′(x) x 3 > 0 ⇔ ; f ′(x) 2 < 0 ⇔ . 2 − < x <1 1 < x < 3 x = 0 NHÓ x = 0 2 x = 0 x =1
Ta có g′(x) = xf ′( 2 2 x );
g′(x) = 0 ⇔ ⇔ ⇔ . ′ = x = 1 ± 2 2 M f ( x ) 0 x = 3 x = ± 3 T 2 x = 0 OÁN V 1 − < x <1 D < < x ≠ 0 0 x 1 – Ta có f ′(x ) 2 2 > 0 ⇔ ⇔ . 2 VD x > 3 x > 3 C x < − 3 Ta có bảng biến thiên x −∞ − 3 1 − 0 1 3 +∞ 2x − − − 0 + + + ′( 2 f x ) + 0 − 0 + 0 + 0 − 0 + g′(x) − 0 + 0 − 0 + 0 − 0 + g (x) NHÓ M T OÁN
Từ bảng biến thiên ta có hàm số ( ) = ( 2 g x
f x ) có 5 điểm cực trị. VD
Câu 5: Cho hàm số y = f (x) có đạo hàm liên tục trên và có đồ thị hàm số y = f '(x) như hình vẽ . – 2
Tìm số điểm cực trị của hàm số y = g (x) = f (x −3). VD C A. 2 . B. 4 . C. 3. D. 5. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn C x = 2 − (nghiem don)
- Dựa vào đồ thị ta thấy: f '(x) = 0 ⇔ . x =1 (nghiem kep) NHÓ
- Ta có g (x) = x f ( 2 ' 2 . ' x −3) . M TOÁN x = 0
x = 0(nghiem don) g '(x) 2 = 0 ⇔ x − 3 = 2 − ⇔ x = 1 ± (nghiem don) . V 2 D x − 3 = 1 x = 2 ± (nghiem kep) – VD
(Đến đây có thể kết luận hàm số có 3 điểm cực trị. Nếu muốn tìm điểm cực đại, cực tiểu của hàm C
số thì ta cần lập bảng biến thiên) x > 0 x > 0 f ( x − ) 2 2 x − 3 > 2 − x >1 ' 3 > 0 g '(x) 2 > ⇔ ⇔ − ≠ ⇔ 0 x 3 1 x ≠ 2 . x < 0 x < − < x < f ' ( 0 1 0 2 x − 3) < 0 2 x −3 < 2 −
Ta có bảng biến thiên của hàm số y = g (x) . x −∞ -2 -1 0 1 2 +∞ g '(x) - 0 - 0 + 0 - 0 + 0 + NHÓ M T g (x) OÁN VD
Suy ra hàm số có 3 điểm cực trị – VD
Câu 6: Cho hàm số y = f (x) có bảng biên thiên như hình vẽ C
Số điểm cực trị của hàm số g (x) 2 5 3 f 2x x = − − là 2 2 A. 3. B.4. C. 5. D.6. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn C x < −
Dựa vào bảng biến thiên, suy ra f ′(x) 2 > 0 ⇔
và f ′(x) < 0 ⇔ 2 − < x < 3. x > 3 NHÓ Ta có g (x) 5 2 5 3 = 4x −
f 2x − x ′ ′ − . M 2 2 2 TOÁN 5 4x − > 0 V 2 D 2 5 3
f ′ 2x − x − < 0 – 2 2 VD
Xét g′(x) < 0 ⇔ . 5 C 4x − < 0 2 2 5 3
f ′ 2x − x − > 0 2 2 5 5 4x − > 0 > 2 x 8 9 ⇔ ⇔ 1< x < . 2 5 3 ′ − − < 2 5 3 4 f 2x x 0 2
− < 2x − x − < 3 2 2 2 2 5 x < 8 5 3 x < 1 − 2 5
2x − x − > 3 4x − < 0 2 2 NHÓ 2 ⇔ ⇔ . 2 5 3
f ′ 2x − x − > 0 M T 5 1 5 2 2 x < < x < 8 4 8 OÁN 2 5 3
2x − x − < 2 − 2 2 VD – Bảng biến thiên VD C
Từ bảng xét dấu của hàm số g (x) 2 5 3 f 2x x = − −
ta được hàm số có 5 cực trị. 2 2
Câu 7: Cho hàm số y f x có đạo hàm trên tập . Hàm số y f x có đồ thị như hình sau:
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D – 2
Hàm số y f x x có bao nhiêu điểm cực tiểu? VD C A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn C Xét hàm số 2 y
f x x. Ta có y x f 2 2 1 x x. 1 1 x 2 x 2 x 0 2x1 0 2 y 0
x x 2 . f 2 x x x 1 0 2 x x 0 x 1 2 NHÓ x x 2 x 2 M T 0 x 1 2 OÁN f 2 x x 2 x x 0 0 x 2 . 2 x x 2 x 1 VD – 2
Ta có bảng biến thiên của hàm số y f x x là: VD C Vậy hàm số 2 y
f x x có 3 điểm cực tiểu.
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 4.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) trong bài toán chứa tham số . NHÓ
Câu 4: Cho hàm số y f x có đạo hàm y = f x với mọi x .
và có đồ thị như hình vẽ. M TOÁN V D O – VD C
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số gx f 2x 8x m có 5 điểm cực trị? A. 15. B. 16. C. 17. D. 18. Lời giải Chọn A
Ta có gx x f 2 2 4 x 8x m x 4 NHÓ 2
x 8x m 1 nghiem boi 2
g x 0 2x 4 f 2 x 8x m 0 . 2 x 8x m 0 1 M T 2 x 8x m 2 2 OÁN
Yêu cầu bài toán gx 0 có 5 nghiệm bội lẻ mỗi phương trình 1 , 2 đều có hai VD
nghiệm phân biệt khác 4. * – VD 16 m 0 C 16 m 2 0 Cách 1: * m 16 . m 16 m 18
Vậy có 15 giá trị m nguyên dương thỏa mãn điều kiện.
Cách 2: Xét đồ thị C của hàm số 2
y x 8x và hai đường thẳng d : y , m d : y m 2 1 2 (hình vẽ).
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V Khi đó
* d , d cắt C tại bốn điểm phân biệt 1 2 m 16 m 16. D –
Vậy có 15 giá trị m nguyên dương thỏa mãn điều kiện. VD C DẠNG TOÁN 5.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) + h(x) trong bài toán không chứa tham số.
Câu 1: Cho hàm số y = f (x) có đạo hàm và liên tục trên R, có đồ thị hàm y = f ′(x) như hình vẽ sau: NHÓ
Tìm số điểm cực trị của hàm số y = g (x) = f (x − 2019) + 2017x − 2018. M T A. 1. B. 2. C. 3. D. 4. OÁN Lời giải Chọn A VD
Ta có: y′ = g '(x) = f ′(x − 2019) + 2017 – VD
Tịnh tiến sang phải 2019 đơn vị rồi tịnh tiến lên trên 2017 đơn vị ta thấy đồ thị hàm số ′ = = ′ C
y g '(x) f (x − 2019) + 2017 cắt trục Ox tại 1 điểm.
Do đó hàm số có 1 cực trị.
Câu 2: Cho hàm số y f x liên tục trên và có đồ thị hàm số y f x như hình bên dưới.
Hàm số g (x) = f ( 4 2 −x + x ) 6 2 15 2
−10x + 30x − 20 có bao nhiêu điểm cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 0 . B. 3. C. 2 . D. 5. Lời giải Chọn B NHÓ
g (x) = f ( 4 2 −x + x ) 6 2 15 2
−10x + 30x − 20 liên tục trên . M TOÁN
Có g′(x) = ( 3
−x + x) f ′( 4 2 −x + x ) 5 − x + x = ( 3
−x + x) f ′ ( 4 2 −x + x ) 2 60 2 60 60 60 2 + x +1 x = 0, x = 1 ± V
g′(x) = 0 ⇔ D f ′ ( 4 2 −x + 2x ) 2 + x +1 = 0(*) – VD
Ta thấy −x + x = −(x − )2 4 2 2 2 1 +1≤1 x
∀ , kết hợp với đồ thị hàm số y f x , C suy ra f ′( 4 2
−x + 2x ) ≥ 0 x ∀ . Hơn nữa, 2 x +1 > 0 x
∀ nên phương trình (*) vô nghiệm. mà x = 0, x = 1
± là các nghiệm đơn của phương trình g′( x) = 0 nên hàm số y = g ( x) có 3 điểm cực trị.
Câu 3: Cho hàm số f '(x) như hình vẽ. NHÓ M T OÁN VD
Hàm số g (x) = f (x ) 6 2 x 4 2 −
+ x − x đạt cực tiểu tại bao nhiêu điểm? 3 – VD A. 3. B. 2 . C. 0 . D. 1. C Lời giải Chọn D 6
Ta có: g (x) = f ( 2 x ) x 4 2 −
+ x − x ⇒ g (x) = x f ( 2 x ) −( 4 2 ' 2 ' x − 2x + )1 3 x = 0 x = 0 g '(x) = 0
⇔ f '( 2x)−( 4 2 x − 2x + ) 1 = 0 ⇔ f '
( x ) = ( x )2 2 2 2 − 2x + ( 1 ∗) k(x) Đặt 2
t = x (t ≥ 0),phương trình (∗) trở thành f (t) 2 2 '
= t − 2t +1(∗∗).
Vẽ thêm đồ thị hàm số 2
x − 2x +1 (màu đỏ) trên đồ thị f '(x) đề cho.
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D – VD C 2 t = 0 x = 0 x = 0(boäi chaün).
Dựa vào đồ thị, (∗∗) 2
⇔ t =1 ⇒ x =1 ⇔ x = 1. ± 2 t = 2 x = 2 x = ± 2.
Theo đó ta lập bảng biến thiên như sau: NHÓ M T
Vậy g (x) đạt cực tiểu tại 1 điểm x = 0 . OÁN VD DẠNG TOÁN 6.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số –
y = g (x) = f (u(x)) + h(x) trong bài toán chứa tham số. VD C DẠNG TOÁN 7.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x
f u x trong bài toán không chứa tham số.
Câu 1. Cho hàm số f (x) liên tục và có đạo hàm trên [0;6]. Đồ thị của hàm số f ′(x) trên đoạn [0;6]
được cho bởi hình bên dưới.
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN Hỏi hàm số = ( ) 2 y f x
có tối đa bao nhiêu cực trị? V A. 3. B. 7 . C. 6 . D. 4 D – Lời giải VD Chọn B f (x) = 0 C
Ta có: y′ = 2 f (x). f ′(x) nên y′ = 0 ⇔ f ′ ( x) = 0
Từ đồ thị ta suy ra f (x) = 0 có tối đa 4 nghiệm, f ′(x) = 0 có tối đa 3 nghiệm. Do đó, hàm số = ( ) 2 y f x
có tối đa 7 điểm cực trị nên có tối đa 7 cực trị.
Câu 2: Cho hàm số y = f (x) là hàm đa thức bậc bốn có f (− )
1 = 0, đồ thị hàm số y = f ′(x) như hình vẽ NHÓ M T OÁN
Số điểm cực trị của hàm số ( ) = ( ) 2 g x f x VD là – A. 1. B. 2. C. 3. D. 4. VD Lời giải C Chọn A
Từ hình vẽ ta có bảng biến thiên hàm số y = f (x) x −∞ 1 − 3 +∞ f ′(x) − 0 + 0 + +∞ +∞ f (x) f ( ) 1 −
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Ta có g′(x) = 2 f ′(x) f (x). f ′(x) = 0
Xét g′(x) = 0 ⇔ f (x) . = 0 NHÓ Do f (− )
1 = 0 nên f (x) ≥ 0,∀x∈ M T x = − OÁN
Dựa vào đồ thị, ta có f ′(x) 1 = 0 ⇔ .
x = 3 (nghiÖm kÐp) V
Do vậy hàm số g (x) chỉ có 1 điểm cực trị. D – = ′ VD
Câu 3: Cho hàm số = ( ) 5 3
y f x = mx + nx + px có đồ thị hàm số y f (x) như hình vẽ: C
Số điểm cực trị của hàm số g (x) = f (x + ) 5 2 là A. 1. B. 2. C. 3. D. 4. NHÓ Lời giải M T Chọn B OÁN
Ta có g (x) = f (x + ) 5 2
⇒ g′( x) = f ′( x + ) f ( x + ) 4 5 2 2 . VD Do f ( x + ) 4 2 ≥ 0
nên dấu g′(x) chỉ phụ thuộc dấu của 5 f ′(x + 2). – VD
Dựa vào đồ thị ta thấy hàm số y = f ′(x) cắt trục hoành tại hai điểm phân biệt nên C
f ′(x) = a(x − x x − x , a > 0 f ′(x) = a(x + 2 − x x + 2 − x , 1 ) ( 2 ) 1 ) ( 2 )
Suy ra g′(x) đổi dấu từ + sang - khi qua x = x − 2 , từ - sang + khi qua x = x − 2 . 1 2
Hàm số g (x) có 2 điểm cực trị.
Câu 4: Cho hàm số y = f (x) là hàm đa thức bậc bốn có đồ thị hàm số y = f ′(x) như hình vẽ
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V = − D
Số điểm cực đại của hàm số g (x) f ( x) 3 1 2 là – VD A. 0. B. 1. C. 2. D. 3. C Lời giải Chọn A
Ta có g (x) = f ( − x) 3 1 2
⇒ g′( x) = − f ′( − x) f ( − x) 2 6 1 2 1 2 . Do f ( − x) 2 1 2 ≥ 0
nên dấu g′(x) chỉ phụ thuộc dấu của 6
− f ′(1− 2x).
Dựa vào đồ thị ta có f ′(x) = a(x + )(x − )2 3 1 , a > 0
⇒ f ′( − x) = a( − x)(− x)2 1 2 4 2 2
Suy ra g′(x) đổi dấu từ - sang + khi qua x = 2 nên x = 2 là điểm cực tiểu của hàm số g(x) .
Hàm số g (x) không có điểm cực đại. NHÓ
Câu 5: Cho hàm số y = f (x) là hàm đa thức bậc bốn có f (3) < 0, đồ thị hàm số y = f ′(x) như hìnhM T vẽ OÁN VD – VD C
Số điểm cực trị của hàm số g (x) = f (x − ) 2020 1 là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Từ hình vẽ ta có bảng biến thiên hàm số y = f (x)
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x −∞ 1 − 3 +∞ f ′(x) − 0 + 0 + NHÓ +∞ +∞ M f (x) f ( ) 1 − y = 0 TOÁN V D Ta có g′(x) =
f ′(x − ) 2019 2020 1 f (x − ) 1 . – VD
f ′(x − ) 1 = 0 ( ) 1 C
Xét g′(x) = 0 ⇔ .
f (x − ) 1 = 0 (2) x = − Xét ( )
1 . Dựa vào đồ thị, ta có f ′(x) 1 = 0 ⇔ .
x = 3 (nghiÖm kÐp) − = − =
⇒ f ′(x − ) x 1 1 x 0 1 = 0 ⇒ ⇒ x 1 3 − =
x = 4(nghiÖm kÐp)
Xét (2) . Do f (3) < 0 nên f (x) = 0 có hai nghiệm phân biệt thuộc ( ; −∞ 2 − ) và (3;+∞)
Suy ra f (x − )
1 = 0 có hai nghiệm phân biệt x ∈ ; −∞ 1
− và x ∈ 4;+∞ 2 ( ) 1 ( ) x = 0
x = 4 (nghiÖm kÐp) NHÓ Ta có g (x) 0 ′ = ⇔ . x = x ∈ ; −∞ 1 − 1 ( ) M T
x = x ∈ 4;+∞ 2 ( ) OÁN
Do vậy hàm số g (x) có 3 điểm cực trị. VD
Câu 6: Cho hàm số y = f (x) là hàm đa thức bậc bốn có f ( )
1 = 0 đồ thị hàm số y = f ′(x) như hình vẽ – VD C
Số điểm cực trị của hàm số g (x) = f ( x − x) 4 2 2 là A. 1. B. 2. C. 3. D. 4. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn D
Ta có g (x) = f ( x − x) 4 2
2 ⇒ g′(x) = − f ′(x − x) f ( x − x) 3 2 2 8 2 2 . NHÓ
Từ hình vẽ ta có bảng biến thiên hàm số y = f (x) x −∞ x 1 − 1 3 x M 1 2 +∞ TOÁN f ′(x) − − 0 + 0 − + + V +∞ +∞ D y = 0 – f (x) 0 VD C f (− ) 1 f (3)
f ′( 2x − 2x) = 0 ( ) 1
Ta có g′(x) = 0 ⇔ f ( . 2
x − 2x) = 0 (2) Xét ( )
1 . Dựa vào đồ thị ta có f ′(x) = a(x − ) 1 (x + )
1 (x + 3), a > 0 f ′( 2
x − x) = ⇒ a( 2 x − x − )( 2 x − x + )( 2 2 0 2 1
2 1 x − 2x + 3) = 0 x =1+ 2
f ′(x) = 0 ⇔ x =1− 2 . NHÓ
x =1 (nghiÖm kÐp) M T Xét (2) : Do f ( )
1 = 0 nên f (x) = 0 có hai nghiệm phân biệt nghiệm phân biệt x ∈ ; −∞ 1 − và 1 ( ) OÁN x ∈ 3;+∞ 2 ( ) VD Với nghiệm x ∈ ; −∞ 1 − thì f ( 2 x − 2x) 2
= 0 ⇒ x − 2x = x 2 x − 2x ≥ 1 − 1 ( ) 1 vô nghiệm do – VD
Với nghiệm x ∈ 3;+∞ thì f ( 2 x − 2x) 2
= 0 ⇒ x − 2x = x 2 ( )
2 có 2 nghiệm phân biệt. C Ta có ′( ) 0
g x = có 4 nghiệm đơn phân biệt nên hàm số g (x) có 4 điểm cực trị.
Câu 7: Cho hàm số y = f (x) là hàm đa thức có đồ thị hàm số y = f ′(x) như hình vẽ
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D
Số điểm cực trị của hàm số ( ) = ( ) 2021 2 g x f x – là VD A. 5. B. 6. C. 3. D. 4. C Lời giải Chọn A Ta có ( ) = ( ) 2021 2 g x
f x ⇒ g′(x) =
x f ′(x ) f ( x ) 2020 2 2 4042 . .
Dựa vào đồ thị ta có ′( ) = ( − )( − )2m f x k x a x b
(x −c)(x − d ), k > 0 ′( ) = ⇒ ( − )( − )2 2 2 2 ( 2 − )( 2 0 m f x k x a x b x c x − d ) ⇒ ′( ) = ( − )( − )2 2 2 m g x k x x a x b
( 2x −c)( 2x −d) f ( 2 4042 . . . x ) 2020 Do ( ) 2020 ≥ ( − )2 2 2 0; m f x x b
≥ 0 ⇒ g′(x) = 0 có 5 nghiệm ± c;± d ;0 NHÓ
Vậy hàm số g (x) có 5 điểm cực trị. M T DẠNG TOÁN 8.
Biết ĐỒ THỊ hàm số y = f ′(x) xét cực trị của hàm số OÁN = ( ) = ( ( )) k y g x
f u x trong bài toán chứa tham số . VD
Câu 1: Cho hàm số y = f (x) là hàm đa thức bậc 6 có đồ thị hàm số y = f ′(x) như hình vẽ: – VD C
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + ) 7 3 1 + m có 2 điểm cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 2. B. 0. C. 1. D. Vô số. Lời giải Chọn D NHÓ 6
Ta có g (x) = f (x + ) 7 3 1 + m 3 2 ⇒ ′ = + +
g (x) 21. f (x ) 1
m . f (x + ) 1 . f ′(x + ) 1 M 6 3 2 T
Ta có f (x + )
1 + m . f (x + ) 1
g′ x phụ thuộc vào dấu f ′(x + ) 1 . OÁN nên dấu của ( )
Hàm số f ′(x)cắt trục hoành tại 2 điểm phân biệt nên có 2 điểm cực trị, số điểm cực trị hàm V D f (x + )
1 bằng số điểm cực trị hàm f (x) nên g (x) có 2 điểm cực trị với mọi m . –
Vậy với mọi m hàm số g (x) đều có 2 điểm cực trị. VD C
Câu 2: Cho hàm số y = f (x) là hàm đa thức bậc 3 có đồ thị hàm số y = f ′(x) như hình vẽ: Biết f ( 2
x − 4) = m để hàm số g (x) = f (x − ) 2 2
4 có 5 điểm cực trị. Khẳng định nào đúng? NHÓ
A. m ≠ { f ( 2
− ); f (0); f (2)}.
B. m ≠ { f ( 4 − ); f ( 2 − ); f (2)}. M T OÁN
C. m ≠ { f ( 4 − ); f (0)}.
D. m ≠ { f (0); f (2)}. VD Lời giải – Chọn C VD
Ta có g (x) = f (x − 2 2 ) 2 2
4 ⇒ g′ x = 2 .
x f x − 4 . f ′ x − 4 C ( ) ( ) ( ) x = 0
⇒ g′(x) = ⇒ x f ( 2 x − ) f ′( 2 0 2 . 4 .
x − 4) = 0 ⇔ f ′( 2 x − 4) = 0 ( ) 1 . f ( 2 x − 4) = 0 (2) Xét ( )
1 . Do đồ thị y = f ′(x) đổi dấu 1 lần khi qua x = 0 nên f ′(x) = 0 ⇒ x = 0 Do đó f ′( 2 x − ) 2
4 = 0 ⇒ x − 4 = 0 ⇒ x = 2. ±
Để hàm số g (x) có 5 điểm cực trị thì (2) phải có 3 nghiệm phân biệt khác 2; − 0;2.
Từ hình vẽ ta có bảng biến thiên hàm số y = f (x)
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x −∞ 0 +∞ f ′(x) − 0 + NHÓ +∞ +∞ M f (x) TOÁN f (0) V D 2 –
Để f (x − 4) = m có 2 nghiệm thì 2
x − 4 ≠ 0 ⇒ x ≠ 2. ± VD
Vậy m ≠ { f ( 4 − ); f (0)}. C
Câu 3: Cho hàm số y = f ( ;
x m) có đồ thị hàm số y = f ′( ; x m) như hình vẽ:
Biết f (a) > f (c) > 0; f (b) < 0 < f (e) . Số điểm cực trị của hàm số ( ) = ( + ) 2 g x f x m NHÓ là A. 4. B. 7. C. 5. D. 9. M T Lời giải OÁN Chọn B VD
Từ đồ thị của hàm số y = f ′( ; x m) ta có bảng biến thiên: – VD C
Dựa vào bảng biến thiên ta thấy hàm số y = f ( ;
x m) có 4 điểm cực trị.
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Khi f (a) > f (c) > 0; f (b) < 0 < f (e) thì đồ thị hàm số y = f ( ;
x m) cắt trục hoành tại 3 điểm
phân biệt f (x + m) = 0 có 4 nghiệm phân biệt ⇒ ′ = ′ NHÓ Ta có ( ) = ( + ) 2 g x f x m
g (x) 2 f (x + m). f (x + m). ′ + = → M f (x m) nghiÖm
⇒ g′(x) = ⇔ = f (x + m) 0 3 0 2 . ⇒ T f
( x + m) = 0 → 4 nghiÖm OÁN
Các nghiệm không trùng nhau nên hàm số g (x) có 7 điểm cực trị. V D DẠNG TOÁN 9.
Biết ĐỒ THỊ hàm số y = f ′(u(x)) xét cực trị của hàm số – VD
y = f (x) trong bài toán không chứa tham số. C
Câu 1: Cho hàm số y = f (x) liên tục trên R, biết rằng hàm số y = f '(x − 2) + 2 có đồ thị như hình vẽ
sau. Hỏi hàm số y = f (x) có bao nhiêu cực trị? y 1 1 − 1 O x 1 − A. 1. B. 2. C. 3. D. 4. NHÓ Lời giải M T Chọn B OÁN VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V D – VD C NHÓ
Đồ thị các hàm số lần lượt theo thứ tự: M T
y = f '(x − 2) + 2 , y = f '(x − 2) , y = f '(x) OÁN
Từ đồ thị của hàm số y = f '(x) ta có bảng biến thiên sau: (với x , x là hoành độ giao điểm của 1 2 VD
đồ thị của hàm số y = f '(x) với Ox ) – BBT: VD C x −∞ x x +∞ 1 2 f '(x) + 0 - 0 + +∞ f (x) y cd −∞ yct
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ bảng biến thiên ta có hàm số y = f (x) có 2 cực trị. Chọn đáp án B.
Câu 2: Cho hàm số y = f (x) có đạo hàm liên tục trên , hàm số y = f ′(x − 2) có đồ thị như hình NHÓ
dưới. Số điểm cực trị của hàm số y = f (x) là: M TOÁN V D – VD C A. 0 . B. 2 . C. 1. D. 3. Lời giải Chọn B
Ta có: đồ thị hàm số y = f ′(x − 2) là phép tịnh tiến của đồ thị hàm số y = f ′(x) sang phải 2 đơn vị.
Khi đó hàm số y = f (x) có bảng biến thiên: x −∞ 3 − 2 − 1 − +∞ f ′(x) + 0 − 0 + 0 + NHÓ f ( 3 − ) − M T f (x) f ( ) 1 OÁN f ( 2 − ) VD Dựa vào bảng bi
ến thiên ta có số điểm cực trị của hàm số y = f (x) là 2 . – VD C DẠNG TOÁN 10.
Biết ĐỒ THỊ hàm số y = f ′(u(x)) xét cực trị của hàm số
y = f (x) trong bài toán chứa tham số.
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chuyên đề:
CÁC DẠNG TOÁN VỀ HÀM ẨN
LIÊN QUAN ĐẾN CỰC TRỊ NHÓ CỦA HÀM SỐ M T OÁN
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ V D
PHẦN 4: BIẾT BẢNG XÉT DẤU CỦA HÀM SỐ y = f '(x) – VD = ′ C Dạng toán 1.
Biết BẢNG XÉT DẤU hàm số y f (x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán không chứa tham số. Dạng toán 2.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán chứa tham số. Dạng toán 3.
Biết BẢNG XÉT DẤU y = f ′(x) xét cực trị của hàm số y = g (x) = f (u(x))
trong bài toán không chứa tham số . Dạng toán 4.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) trong bài toán chứa tham số . Dạng toán 5.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) + h(x) trong bài toán không chứa tham số. NHÓ Dạng toán 6.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) + h(x) trong bài toán chứa tham số. M T Dạng toán 7.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số OÁN = ( ) = ( ( )) k y g x
f u x trong bài toán không chứa tham số. VD Dạng toán 8.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số – VD = ( ) = ( ( )) k y g x
f u x trong bài toán chứa tham số . C = ′ = Dạng toán 9.
Biết BẢNG XÉT DẤU hàm số y f (u(x)) xét cực trị của hàm số y f (x)
trong bài toán không chứa tham số. Dạng toán 10.
Biết BẢNG XÉT DẤU hàm số y = f ′(u(x)) xét cực trị của hàm số y = f (x)
trong bài toán chứa tham số.
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 1.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (x) + h(x) trong bài toán không chứa tham số. NHÓ
Câu 1: Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau: M TOÁN V
Hỏi hàm số g (x) = f (x) 3 2
+ x + 3x − 9x − 5 có bao nhiêu điểm cực trị? D – A. 2. B. 1. C. 0. D. 3. VD C Lời giải Chọn A
Từ bảng xét dấu của f ′(x) ta nhận thấy f (x) A(x)(x )2n 1+ (x )2m 1 3 1 + ′ = + − với , m n∈ và
A(x) > 0, x ∀ ∈ . .
Ta có: g (x) = f (x) 2
+ 3x + 6x − 9 = A(x)(x + 3)2n 1+ (x − )2m 1 1 + ′ ′
+ 3(x + 3)(x − ) 1
′( ) = ( + )( − ) ( )( + )2n ( − )2 3 1 3 1 m g x x x A x x x + 3
Do A(x) > 0, x
∀ ∈ nên ( )( + )2n ( − )2 3 1 m A x x x + 3 > 0, x ∀ ∈ . x = −
Từ đó ta có g′(x) 3 = 0 ⇔ . x = 1 NHÓ
Do g′(x) = 0 tại x = 3
− và x =1, đồng thời g′(x) đổi dấu khi đi qua hai điểm đó nên hàm số
y = g (x) có hai điểm cực trị. M T
Câu 2: Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau: OÁN x −∞ 1 − 2 +∞ VD f ′(x) − 0 + 0 − – VD
Hỏi hàm số g (x) = f (x) 3 3 2
− x + x + 6x + 2020 có bao nhiêu điểm cực trị? C 2 A. 3. B. 2. C. 1. D. 4. Lời giải Chọn B
Từ bảng xét dấu của f ′(x) ta thấy f (x) a(x )2m 1+ (x )2n 1 1 2 + ′ = + − với ,
m n∈ và a < 0 .
Ta có: g (x) = f (x) 2
− 3x + 3x + 6 = a(x + )2m 1
1 + (x − 2)2n 1+ ′ ′
− 3(x − 2)(x + ) 1
′( ) = ( − )( + ) ( + )2m ( − )2 2 1 1 1 n g x x x a x x − 3
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Do a < 0 nên ( + )2m ( − )2 1 2 n a x x − 3 < 0, x ∀ ∈ x = −
Từ đó ta có g′(x) 1 = 0 ⇔ x = 2. NHÓ
Do g′(x) = 0 tại x = 1
− và x = 2 ; đồng thời g′(x) đổi dấu khi qua hai điểm này nên hàm số M T
g (x) có hai điểm cực trị. OÁN DẠNG TOÁN 2.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số VD
y = g (x) = f (x) + h(x) trong bài toán chứa tham số. – VD DẠNG TOÁN 3.
Biết BẢNG XÉT DẤU y = f ′(x) xét cực trị của hàm số C
y = g (x) = f (u(x)) trong bài toán không chứa tham số .
Câu 1: Cho hàm số y = f (x) liên tục trên .
Biết hàm số y = f '(x) có bảng xét dấu sau
Số điểm cực tiểu của hàm số y = g (x) = f ( 2 6 − x ) là A. 5. B. 7. C. 3. D. 4. Lời giải NHÓ Chọn D M T
Ta có g′(x) = − x f ′( 2 2 . 6 − x ) . OÁN x = 0 x = 0 x = 0 2 − = − = ± VD 6 x 3 x 3
g′(x) = 0 ⇔ ⇔ ⇔ . f ′ 2 ( 2 6 − x ) = 0 6 − x = 2 x = 2 ± – 2 VD 6 − x = 5 x = 1 ± C Ta có g′(4) = 8. − f ′( 10
− ) > 0 và bảng xét dấu f '(x) không có nghiệm bội chẵn.
Bảng biến thiên y = g (x) .
Vậy số điểm cực tiểu của hàm số y = g (x) = f ( 2 6 − x ) là 4.
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 2: Cho hàm số y = f (x) liên tục trên .
Biết hàm số y = f '(x) có bảng xét dấu sau NHÓ 2 M
Số điểm cực trị của hàm số y = g (x) = f (x + x +1) là TOÁN A. 0. B. 1. C. 3. D. 2. V Lời giải D – Chọn D VD C 2 x + x +1 2 x + x + x + x 2 1 Ta có g′(x) =
. f ′ x + x +1 . Do > ≥ 0 2 ( ) x +1 2 2 x +1 x +1 2 x + x +1 =1 x = 0 nên g′(x) 4 = ⇔ f ′( 2 0 x + x +1) 2
⇔ x + x +1 = 3 ⇔ x = . 3 2 x + x +1 = 5 12 x = 5
Bảng biến thiên y = g (x) . NHÓ M T OÁN
Vậy số điểm cực trị của hàm số y = g (x) = f ( 2
x + x +1) là 2. VD
Câu 3: Cho hàm số f ( x) xác đinh, liên tục trên
f ' x như sau: –
và có bảng xét dấu ( ) VD C Hàm số (2x f
) đạt cực tiểu tại x bằng A. 0 B. 1 C. 2 D. 0 và 2 Lời giải Chọn B
Xét hàm số ( ) = (2x g x f )
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
'( ) = 2x ln 2. '(2x g x f ) x = = g (x) 2 1 x 0 ' = 0 ⇔ ⇔ NHÓ 2x = 2 x =1 M Nếu x∈( ;0
−∞ ) thì 2x ∈(0; ) 1 ; TOÁN Suy '(2x f ) > 0, x ∀ ∈( ;
−∞ 0) , hay '( ) = 2x ln 2. '(2x g x f ) > 0, x ∀ ∈( ;0 −∞ ) V D x – Nếu x∈(0; ) 1 thì 2 ∈(1;2); VD C x < ∀ ∈ x x = <
Suy f '(2 ) 0, x (0; )
1 , hay g '(x) 2 ln 2. f '(2 ) 0, x ∀ ∈(0; ) 1
Nếu x ∈(1;+∞) thì 2x ∈(2;+∞) ; Suy '(2x f ) > 0, x
∀ ∈(1;+∞), hay '( ) = 2x ln 2. '(2x g x f ) > 0, x ∀ ∈(1;+∞)
Bảng xét dấu g '( x)
Từ bảng xét dấu ta có g '( x) đổi dấu từ âm sang dương khi x qua 1. NHÓ
Kết luận: Hàm số ( ) = (2x g x f
) đạt cực tiểu tại x =1 M T OÁN
Câu 4: Cho hàm số f ( x) xác đinh, liên tục trên và f '( x) có bảng xét dấu như sau x −∞ 2 − 0 1 +∞ VD –
f '(x) − 0 + 0 − 0 + VD 2 C
Số điểm cực trị của hàm số x x 2 f e − − là ( ) A. 2 B. 3 C. 4 D. 5 Lời giải Chọn D 2
Đặt g ( x) f ( x x 2 e − − = )
f (x) xác định trên suy ra g (x) xác định trên
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số 2 2
Hơn nữa g (−x) (−x) = f ( − − x −2 e
)= f ( x −x−2 e )= g(x)
Suy ra g ( x) là hàm số chẵn, đồ thị hàm số g ( x) đối xứng qua trục Oy . NHÓ Xét x ≥ 0 M T 2 x x 2 OÁN
g (x) f (e − − = ) V 2 2 x −x−2 x −x−2 = − D
g '(x) (2x ) 1 .e . f '(e ) – VD 2x −1 = 0 2x −1 = 0 C = ⇔ ⇔ g '(x) 0 f ' ( 2x−x e − ) 2 = 0 x −x e − = ( 2 2 2 x −x−2 1 vì e > 0, x ∀ ) 1 2x −1 = 0 x = ⇔ ⇔ 2 2
x − x − 2 = 0 x = 2 (vì x ≥ 0) Nếu x > 2 thì 2
x − x − 2 > 0, suy ra 2x x 2 e − − >1
suy ra f ( 2x x 2 ' e − − ) > 0 NHÓ
Nếu 0 ≤ x < 2 thì 2
x − x − 2 < 0 , M T x x OÁN suy ra 2 2 0 e − − < <1 2 VD suy ra f ( x x 2 ' e − − ) < 0 – VD
Từ đó ta có bảng xét dấu g ( x) trên 0;+∞ ) C x 0 1 2 +∞ 2 g'(x) + 0 − 0 +
Suy ra g ( x) có hai điểm cực trị dương.
Do g ( x) là hàm số chẵn, liên tục trên suy ra g ( x) có 5 điểm cực trị trên
Câu 5: Cho hàm số y = f (x) xác định và có đạo hàm liên tục trên . Có bảng xét dấu của y f x như hình vẽ.
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ
Số điểm cực trị của hàm số g (x) = f (log x . 2 ) Chọn đáp án đúng M A. 1. B. 3.. C. 2 . D. 5. TOÁN Lời giải V Chọn A D – x > Đk: 0 VD C 1 1 log x = 2 − x =
Ta có g′( x) = f ′(log x ; 2 2 ) g'(x) = 0 ⇔ ⇔ xln2 4 log x = 1 2 x = 2 Bảng biến thiên
Dựa vào bảng biến thiên và đối chiếu với các đáp án ta chọn A. NHÓ
Câu 6: Cho hàm số y f x. Xác định và có đạo hàm liên tục trên R. Bảng xét dấu hàm số y f x M T như hình bên dưới OÁN VD 2 = = − + –
Tìm số điểm cực trị của hàm số y g(x) f log x 2x 3 3 (
). Chọn đáp án đúng: VD C A. 5. B. 3. C. 4. D. 7. Lời giải Chọn A Đk: x∈ 2x - 2 2 Ta có: y' g'( x ) f ' log = = 3 + 2
( x - 2x 3)
( x - 2x 3)ln3 + ;
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x =1 x 1 = x = 0 2x − 2 = 0 2 = ⇔ ⇔ − + = ⇔ = Khi đó g'( x ) 0 2
log3( x 2x 3) 1 x 2 f '(log
3( x − 2x + 3 )) = 0 2
log ( x − 2x + 3) = 2 x =1+ 7 NHÓ 3 x =1− 7 M T 2 l
og ( x − 2x + 3) >1 1
− 7 < x < 0 OÁN 2 3
Mặt khác: f ' log3( x − 2x + 3) < 0 ⇔ ⇔ 2 l
og3( x − 2x + 3) < 2 2 < x <1+ 7 V D Ta có bảng biến thiên. – VD C
Vậy hàm số có 5 điểm cực trị. Chọn đáp án A
Câu 7: Cho hàm số y = f (x) xác định và liên tục trên và có bảng xét dấu của đạo hàm như sau:
Hàm số y = g x = f ( 2 ( )
x − 2x − 4) có bao nhiêu điểm cực tiểu? NHÓ A. 1. B. 3. C. 2 . D. 4 . M T OÁN Lời giải Chọn B VD
Ta có : g x = x − f x − x − . – ( ) 2 '( ) 2 1 '( 2 4) VD C x = 1
g '(x) = 0 ⇔ (x − ) 2
1 f '(x − 2x − 4) = 0 ⇔ 2
f '(x − 2x − 4) = 0 x = 1 x = 1 x = 1+ 3 2 x 2x 4 2 ⇔ −
− = − ⇔ x = 1− 3
(Tất cả đều là nghiệm bội lẻ). 2 x − 2x − 4 = 0 x =1+ 5 x = 1− 5 Ta chọn x = 2
− để xét dấu của g '(x) : g '( 2) − = 2.( 3
− ). f '(4) . Vì hàm số y = f (x) đồng biến
trên khoảng (0;+∞) do đó: f '(4) > 0 .
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Suy ra: g '( 2 − ) < 0 .
Theo tính chất qua nghiệm bội lẻ g '(x) đổi dấu, ta có bảng biên thiên của g(x) như sau: NHÓ M TOÁN V D y = –
Từ bảng biến thiên suy ra, hàm số
g(x) có 3 điểm cực tiểu. VD
y = f x có đạo hàm liên tục trên C Câu 8: Cho hàm số ( )
và có bảng biến thiên của đạo hàm như hình vẽ. 2 + Đặt g (x) x 1 = f
. Tìm số điểm cực trị của hàm số y = g (x). x A. 4. B. 5. C. 6. D. 8. NHÓ Lời giải M T Chọn C OÁN 2 2
x −1 x +1 VD
+ Đặt g '(x) = f ′ 2 x x – VD x = 1 ± C 2 2 − x +1 x 1 = a (a < 2 − = ) 0 2 x x + g '(x) 2 = 0 ⇔ ⇔ x + 1 2 x +1 = b ( 2 − < b < 2) f ′ = 0 x x 2 x +1 = c (c > 2) x 2 2
+ Xét hàm số h(x) x +1 =
h (x) x −1 , ' =
,h' x = 0 ⇔ x = 1 ± 2 ( ) x x 2
+ Bảng biến thiên của hàm số h(x) x +1 = x
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số x ∞ 1 0 1 +∞
h'(x) + 0 0 + +∞ NHÓ
h(x) +∞
y=c (c>2) x3 x4 M 2
y=b (-2<b<2) TOÁN 2 x y=a 1 x2 (a<-2) V D ∞ ∞ – VD C
+ Dựa vào bảng biến thiến trên ta thấy phương trình h(x) = a,h(x) = c , mỗi phương trình có hai 2 + nghiệm phân biệt khác x 1 1
± , mà a ≠ c ⇒ f ′
= 0 có 4 nghiệm đơn phân biệt x , x , x , x x 1 2 3 4 khác 1
± và phương trình h( x) = b vô nghiệm.
Do đó phương trình g '(x) = 0 có 6 nghiệm đơn phân biệt lần lượt theo thứ tự từ nhỏ đến lớn là x , 1,
− x , x ,1, x . 1 2 3 4 2 +
Vậy hàm số g (x) x 1 = f có 6 cực trị. x
Câu 9: Cho hàm số y = f (x) có đạo hàm liên tục trên và có bảng biến thiên của đạo hàm như hìnhNHÓ vẽ. M T x ∞ 1 0 3 +∞ OÁN 2
f'(x) 1 VD 1 – ∞ ∞ VD 2 C x + 2x
Đặt g (x) = f
. Tìm số điểm cực trị của hàm số y = g (x). x 1 + A. 4. B. 10. C. 6. D. 8. Lời giải Chọn D 2 2 + + + + Đặt ( ) x 2x 2 x 2 ' x g x = f ′ ( x + )2 1 x +1
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số 2
x + 2x = a (a < − )1 x +1 2 + + 2 x 2x 2 = x + 2 0( ) x VN 2 = b (−1< b < 0) x +1 x +1 NHÓ + g '(x) ( ) = 0 ⇔ ⇔ 2 2 + x + 2 2 x x x = c f (0 < c < ′ = 3 0 ) M x + + 1 x 1 2 T x + 2x OÁN = d (d > 3) x +1 V 2 2 x + 2x x + 2x + 2 D
+ Xét hàm số h(x) = ,h'(x) =
,h' x = 0 (VN) 2 ( ) – x +1 (x + )1 VD 2 C x + 2x
+ Bảng biến thiên của hàm số h(x) = x +1 x ∞ 1 +∞
h'(x) + +
h(x) +∞ x +∞ 7 x8
y=d (d>3) x5 x6
y=c (0<3) x3 x4
y=b (-1<b<0) x1 x2
y=a (a<-1) ∞ ∞ NHÓ M T
+ Dựa vào bảng biến thiến trên ta thấy phương trình h(x) = a,h(x) = b,h(x) = c,h(x) = d , mỗi 2 OÁN +
phương trình có hai nghiệm phân biệt mà x 2x
a,b,c,d đôi một khác nhau ⇒ f ′ = 0 có 8 x +1 VD
nghiệm đơn phân biệt x , x , x , x , x , x , x , x . Do đó phương trình g '(x) = 0 có 8 nghiệm đơn 1 2 3 4 5 6 7 8 –
phân biệt lần lượt theo thứ tự từ nhỏ đến lớn là x , x , x , x , x , x , x , x . VD 1 3 5 7 2 4 6 8 C 2 + Vậy hàm số ( ) x 2x g x = f có 8 cực trị. x 1 + DẠNG TOÁN 4.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số
y = g (x) = f (u(x)) trong bài toán chứa tham số .
Câu 1: Cho hàm số y = f (x) có bảng xét dấu f '(x) như sau x −∞ 1 − 1 4 +∞
f '(x) − 0 + 0 + 0 −
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Có bao nhiêu giá trị nguyên của tham số m thuộc [ 10
− ;10] để g (x) = f ( 2
x − 2x − m) có 5 điểm cực trị? A. 10. B. 15. C. 20. D. 21. NHÓ Lời giải M T Chọn A OÁN
Ta có g (x) = (x − ) f ( 2 ' 2
1 ' x − 2x − m) V D x =1 x =1 – 2 VD 2
x − 2x − m = 1 −
x − 2x − m +1 = 0 ( )1 g '(x) = 0 ⇔ ⇒ C 2 2
x − 2x − m =1
x − 2x − m −1 = 0 (2) 2 2
x − 2x − m = 4
x − 2x − m − 4 = 0 (3)
Nhận xét: Phương trình (2) nếu có nghiệm là nghiệm bội chẵn; phương trình (1) và (3) nếu có
nghiệm thì nghiệm không chung nhau.
Hàm số g (x) có 5 điểm cực trị ⇔ phương trình g '(x) = 0 có 5 nghiệm bội lẻ
⇔ Phương trình (1) và (3) có hai nghiệm phân biệt, khác 1. ∆′( ) > 0 1 m > 0 ∆′ > ( 0 3) m + 5 > 0 ⇔ ⇔ ⇔ m > 0 V ( T ) ≠ 0 −m ≠ 0 1 NHÓ V
T ≠ 0 −m−5 ≠ 0 (3) M T m∈ OÁN Vì ⇒ ∈ m ∈ [−
] m {1;2;3;4;5;6;7;8;9;1 } 0 10;10 VD
Vậy có 10 giá trị của tham số m. – VD DẠNG TOÁN 5.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số C
y = g (x) = f (u(x)) + h(x) trong bài toán không chứa tham số.
Câu 1: Cho hàm số y = f (x) có đạo hàm liên tục trên và bảng xét dấu đạo hàm Hàm số 4 2 6 4 2
y = 3 f (−x + 4x − 6) + 2x − 3x −12x có tất cả bao nhiêu điểm cực tiểu? A. 3. B. 0. C. 1. D. 2. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn D Có 3 4 2 5 3
y′ = −(12x − 24x). f (′−x + 4x − 6) +12x −12x − 24x 2 4 2 4 2 NHÓ
= −12x(x − 2). f (′−x + 4x − 6) +12x (x − x − 2) 2 4 2 2 M
= −12x(x − 2).( f (′−x + 4x − 6) − (x + ) 1 . TOÁN x = 0 x = 0 V Khi đó 4 2 2
y ' = 0 ⇔ f (′−x + 4x − 6) − (x +1) = 0 ⇔ x = ± 2 . D 2 x − 2 = 0 4 2 2
f (′−x + 4x − 6) = x +1 – VD Ta có 4 2 2 2
−x + 4x − 6 = −(x − 2) − 2 ≤ −2, ∀x ∈ . C Do đó 4 2
f (′−x + 4x − 6) ≤ f ′(−2) = 0, x ∀ ∈ . Mà 2
x +1 ≥ 1, ∀x ∈ . Do đó phương trình 4 2 2
f '(−x + 4x − 6) = x +1 vô nghiệm. Hàm số 4 2 6 4 2
y = 3 f (−x + 4x − 6) + 2x − 3x −12x có bảng xét dấu đạo hàm như sau Vậy hàm số 4 2 6 4 2
y = 3 f (−x + 4x − 6) + 2x − 3x −12x có 2 điểm cực tiểu. NHÓ DẠNG TOÁN 6.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số M T
y = g (x) = f (u(x)) + h(x) trong bài toán chứa tham số. OÁN DẠNG TOÁN 7.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số VD = ( ) = ( ( )) k y g x f u x –
trong bài toán không chứa tham số. VD C Lý thuyết:
Bước 1: Tính y g x k u x f u x k 1 ' '( ) . '( ). ( ( )) . f '(u(x)) u '(x) 0
+ Nếu: k chẵn: y' g '(x) 0 f (u(x)) 0 . f '(u(x)) 0 + Nếu k lẻ: u '(x) 0
y ' g '(x) 0 f '(u(x)) 0
Bước 2: Giải tìm nghiệm:
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
u '(x) 0 ta giải bình thường.
f '(u(x)) 0 thì ta cho u(x) bằng các điểm cực trị của hàm số y f (x) NHÓ
f (u(x)) 0 thì ta cho u(x) bằng các các nghiệm x của phương trình hoặc điều 0 f (x) 0
kiện của x để chứng minh được phương trình có bao nhiêu nghiệm cụ thể. M 0 TOÁN
Kiểm chứng các nghiệm trên có nghiệm nào bội chẵn không V
Bước 3: Kết luận D – 2. Bài tập: VD
Câu 1: Cho hàm số y = f (x) có bảng biến thiên như sau: C
Số cực trị của hàm số 2 2
g(x) = f (2x + x) là A. 3. B. 4. C. 5. D. 6. Lời giải Chọn C NHÓ 2 2 2 2 2
g '(x) = 2(2 x + x)'. f '(2x + x). f (2x + x) = 2(4 x+1). f '(2x + x). f (2x + x) = 0 . M T Ta có: OÁN 4x +1 = 0 2
⇔ f '(2x + x) = 0 . VD 2
f (2x + x) = 0 – VD 1
4x 1 0 x C 4 x 1
Dựa vào bảng biến thiên ta có 2 2
2x x 2(VN)
f '(2x x) 0 2 1 2x x 1 x 2
Dựa vào bảng biến thiên phương trình f (x) = 0 chỉ có 1 nghiệm x 1 0
(vì đồ thị y = f (x) cắt
trục Ox tại một điểm có hoành độ lớp hơn 1). Khi đó 2 2 2
f (2x x) 0 2x x x 2x x x 0 a c 0 0
(*) phương trình có hai nghiệm vì , trái dấu.
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Mặt khác, thay các nghiệm 1 1
x ;1; vào (*) ta được x 1 không thỏa mãn điều kiện 4 2 0 của x0 nên 1 1
x ;1; không là nghiệm của (*). 4 2 NHÓ
Vậy phương trình g '(x) 0 có 5 nghiệm đơn. Suy ra hàm số y g(x) có 5 cực trị M
LỜI BÌNH: Yêu cầu đề bài có thể thay đổi số cực đại hoặc số cực tiểu của hàm số, khi đó ta cần T
phải xét dấu g’(x). Cụ thể: OÁN
Ta có 2 nghiệm của phương trình 2 2 2
f (2x x) 0 2x x x 2x x x 0 0 0 là V 1 18x0 1 D x x ' 0;x 1 1 1 0 – 4 4 18x0 VD 1 C
x x (1) 1 1 2 1 18x0 1 x x ' 0;x 1 1 1 0 4 4 18x 0
x x (1) 1 1 1 Mặt khác: 2 x < 1 − + < − 2 2x x 2(VN) f '(2x x) 0 + < ⇔ ⇔ 2 1 2x + x >1 x > 2 2 + > − 2 2x x 2 1
f '(2x + x) > 0 ⇔ ⇔ 1 − < x < 2 2x + x <1 2 NHÓ Bảng xét dấu: M T OÁN VD – VD C
Dựa vào bảng biến thiên ta được: 2 cực đại và 3 cực tiểu.
Câu 2: Cho hàm số y = f (x) có bảng biến thiên như sau
Số điểm cực tiểu của hàm số g (x) 3 = f ( 3 x + 3x) là A. 5. B. 2. C. 3. D. 4.
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn B 2 3 2 3 ′ = + ′ + + NHÓ
Ta có: g (x) 3(3x 3) f (x 3x). f (x 3x). 2 2 3 M
Ta thấy g′(x) = 3(3x + 3) > 0, x ∀ ∈ + ≥ ∀ ∈
và f (x 3x) 0, x nên dấu của g '(x) chính là T 3 OÁN
dấu của f ′(x +3x) V 3 x + 3x = 1 − x = x ≈ 0, − 32 1 D f ′( 3
x + 3x) = 0 ⇔ 3 x 3x 0 + = ⇔ x = 0 – VD 3 x + 3x =1
x = x ≈ 0,32 2 C − < x <
Từ bảng biến thiên của hàm f (x) ta có f ′(x) 1 0 > 0 ⇔ x > 1 1
− < x + 3x < 0
x < x < 0
Do đó f ′( 3x +3x) 3 1 > 0 ⇔ ⇔ 3
x + 3x >1 x > x2
Ta có bảng biến thiên của hàm số g (x) NHÓ M T OÁN
Vậy hàm số g (x) có 2 điểm cực tiểu. VD
Câu 3: Cho hàm số f (x) có đạo hàm trên tập và đồ thị hàm số y = f ′(x) được cho như hình vẽ 2019 3 –
bên. Số điểm cực trị của hàm số y = f (x − )1 là VD y C 1 − O 1 2 x 4 − A. 2 . B. 4 . C. 3. D. 5. Lời giải Chọn A Ta có 2018 y′ = f
( 3x − ) f ′( 3x − ) 2 2019. 1 . 1 .3x ,
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Ta có 2018 y′ = f
( 3x − )1 ≥ 0 ∀x∈ và 2 3x ≥ 0 x
∀ ∈ nên dấu của y′ cũng chính là dấu của biểu thức f ′( 3 x −1). NHÓ 3 x −1 = 1 − x = 0 Ta có f ′( 3 x −1) = 0 3 ⇔ x −1 = 1 3 ⇔ x = 2 . M 3 x − = 3 T 1 2 x = 3 OÁN 3 x −1 < 1 − x < 0 V 3 3 3 D
Dựa vào đồ thị của hàm số y = f ′(x) ta thấy f ′(x −1) > 0 ⇔ x −1 > 1 ⇔ x > 2 . – 3 3 x − 1 ≠ 2 x ≠ 3 VD C 3 3 3
Tương tự f ′(x −1) < 0 ⇔ 1
− < x −1 < 1 ⇔ 0 < x < 2 . Vì vậy suy ra hàm số 2019 y = f
( 3x − )1 có hai điểm cực trị.
Câu 4: Cho hàm số y = f (x) có đạo hàm trên thỏa f (2) = f ( 2
− ) = 0 và đồ thị hàm số y = f ′( x)
có dạng như hình vẽ bên dưới. y 1 2 − 1 − 2 O 3 x 2 NHÓ
Số điểm cực trị của hàm số y = ( f ( x − ))2018 2 1 là M T A. 3. B. 4 . C. 2 . D. 5. OÁN Lời giải VD Chọn A –
Dựa vào đồ thị hàm số y = f ′(x) ta lập được bảng biến thiên của y = f (x) như sau: VD C
Xét hàm số y = ( f ( x − ))2018 2 1 , ta có 2017 y′ = 2018. f (2x − )
1 .2. f ′(2x − ) 1 .
Dựa vào bảng biến thiên ta thấy f ( x − ) 2017
2 1 ≤ 0, ∀x ∈ ⇒ f (2x − ) 1 ≤ 0, ∀x ∈ .
Nên dấu của y′ cũng chính là dấu của biểu thức: − f ′(2x −1) .
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số 1 2x −1 ≤ 2 x ≤ − −
Ta có y′ ≤ 0 ⇔ f ′(2x − ) 1 ≥ 0 2 ⇔ ⇔ . 1 ≤ 2x −1 ≤ 2 3 1≤ x ≤ 2 NHÓ 1 M − < x <1 2 − < 2x −1<1 2 T
Tương tự y′ > 0 ⇔ f ′(2x − ) 1 < 0 ⇔ ⇔ OÁN 2x −1 > 2 3 x > 2 V D
Từ đó suy ra hàm số y = ( f ( x − ))2018 2 1 có 3 điểm cực trị. – VD
Câu 5: Cho hàm số y = f (x) có bảng biến thiên C
Hỏi hàm số y = f ( − x) 2 2
có bao nhiêu điểm cực trị? A. 4 . B. 3. C. 5. D. 7 . Lời giải Chọn C NHÓ y′ = 2.
− f (2 − x). f ′(2 − x) . M T
2 − x = a < 2 −
x = 2 − a > 4 OÁN f (2 x) − = − = > = − <
y′ = ⇔ − f ( − x) f ′( − x) 0 2 x b 1 x 2 b 1 0 2. 2 . 2 = 0 ⇔ ⇔ ⇔ VD f ′ (2 − x) = 0 2 − x = 2 − x = 4 2 x 1 − = x = 1 – VD
y′ không xác định ⇔ f ′( 2 − x) không xác định ⇔ 2 − x = 0 ⇔ x = 2 C
Dựa vào đồ thị f (x) ta thấy f (2 − x) > 0 ⇔ a < 2 − x < b ⇔ 2 − b < x < 2 − a − < − > f ′( − x) 2 x 2 x 4 2 > 0 ⇔ ⇔ 0 2 x 1 1 < − < < x < 2
Ta có bảng xét dấu y′
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN
Vậy hàm số y = f ( − x) 2 2
có 5 điểm cực trị. V D
Câu 6: Cho hàm số y = f (x) có đạo hàm trên và có bảng xét dấu f ′(x) như sau – VD C
Biết rằng hàm số y = f (x) là hàm đa thức có đồ thị cắt trục hoành tại một điểm duy nhất. Hỏi hàm số 2 y = f ( 2
x − 2x) có nhiều nhất bao nhiêu điểm cực tiểu? A. 4 . B. 2 . C. 5. D. 3. Lời giải Chọn D = NHÓ
+) Ta có y f (x) là hàm đa thức có đồ thị cắt trục hoành tại một điểm duy nhất nên = < − f (x) x a 2 = 0 ⇒ M T x = b > 3 OÁN Đặt g (x) 2 = f ( 2
x − 2x). Ta có g′(x) = ( x − ) f ′( 2
x − x) f ( 2 2 2 2 x − 2x) . Để hàm số 2 2
y = f x − 2x có nhiều điểm cực tiểu nhất thì phương trình 2
f x − 2x = 0 có VD ( ) ( ) nhiều nghiệm nhất 2
⇒ x − 2x = b > 3(vì 2 x − 2x ≥ 1, − x ∀ ) – VD x =1 x =1 x =1 C 2 x 2x 2 0 − + = 2 x = 1± 2 x − 2x = 2 − 2 − − = = − g′(x) x 2x 1 0 2 x 1
= 0 ⇔ x − 2x =1 ⇔ ⇔ . 2
x − 2x − 3 = 0 x = 3 2 x − 2x = 3 x = x < 1 − x = x < 1 − 2 1 1 x 2x b − =
x = x > 3
x = x > 3 2 2 Trong đó các nghiệm 1, − 1, 3 x ; x ± 1
2 là nghiệm bội lẻ và 1
2 là nghiệm bội chẵn. Vì vậy hàm
số g′(x) chỉ đổi dấu khi đi qua các nghiệm 1, − 1, 3; x ; x 1 2 . Ta có g′(0) = 2
− f ′(0) < 0 (do f ′(0) > 0 ).
Bảng xét dấu g′(x)
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ Vậy hàm số 2 y = f ( 2
x − 2x) có đúng 3 điểm cực tiểu. M
Câu 7: Cho hàm y = f (x) xác định và liên tục trên thỏa mãn f (1) f (2) < 0 và bảng xét dấu của TOÁN f '(x) V D – VD Hỏi hàm số 2
g(x) = f (x − 2019) có bao nhiêu cực trị? C A. 4. B. 6. C. 5. D. 7. Lời giải Chọn C
g (′x) = 2 f (x − 2019) f (′x − 2019)
f (x − 2019) = 0(1)
g (′x) = 0 ⇔
f (′x − 2019) = 0(2)
+) Vì f (1) f (2) < 0 và từ BBT suy ra đồ thị y = f (x) cắt Ox tại 3 điểm phân biệt có hoành độ
x <1,1< x < 2, x > 2 f x − 1 2 3 . Mà đồ thị hàm số (
2019) có được bằng cách tịnh tiến theoNHÓ
phương trục hoành sang phải 2019 đơn vị, nên nó sẽ cắt trục hoành tại 3 điểm phân biêt có hoành M T
độ x < 2020,2020 < x < 2021, x > 2021 1 2 3 OÁN x − 2019 = 1 x = 2020 (2) ⇔ ⇔ x 2019 2 − = x = 2021 VD – ′
Do vậy pt g (x) = 0 có 5 nghiêm đơn phân biệt +) KL hàm g(x) có 5 cực trị VD C
LỜI BÌNH: Chúng ta có thể tổng quát: Cho hàm y = f (x) xác định và liên tục trên thỏa
mãn f (a ) f (a ) < 0 f (a ) f (a ) < 0 f (a < − f a n ) ( n ) 0 1 2 , 2 3 …., 1
và bảng xét dấu của f '(x)
( f (′x) đổi dấu đan xen khi qua 𝑎𝑎1,…𝑎𝑎𝑛𝑛)
Số cực trị của hàm số 2 ( ) k
g x = f (x ± c) là 2n +1
Câu 8: Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như sau?
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN 2018
Hàm số g (x) x −1 = f
có bao nhiêu điểm cực trị? x 2 + V D A. 7 B. 3 C. 5 D. 6 – VD Lời giải C Chọn D 2017 Ta có g (x) 3 x −1 x −1 = 2018. . f . f ′ ′ (
x + 2)2 x + 2 x + 2 x −1 f = 0 ( )1 + g′(x) x 2 = 0 ⇔ x −1 f ′ = 0 (2) x + 2
x −1 = a; (a < 0) x + 2 x−
1 = ;b(0 < b <1) NHÓ −
Dựa vào bảng biến thiên ta có: x 1 f = x + 2 0 ⇔ x + 2 x −1 = ;
c (1< c < 2) M T x + 2 x −1 OÁN = d; (d > 2) x + 2 VD x −1 x −1 = f ′ = 0 0 – + x + 2 x 2 VD ⇔ x − 1 = 2 C x + 2 − Nhận xét: hàm số x 1 y =
là hàm số đơn điệu trên tập xác định nên phương trình ( ) 1 có 4 x + 2
nghiệm đơn, phương trình (2) có 2 nghiệm đơn và nghiệm của phương trình ( ) 1 và phương
trình (2) không trùng nhau.
x −1 =1 (VN)
g′(x) không xác định ⇔ x + 2 x = 2 − Nhận xét: x = 2
− không thuộc tập xác định của y = g (x)
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Vậy g′(x) = 0 có 6 nghiệm đơn khác 2
− nên hàm số y = g (x) có 6 điểm cực trị.
Câu 9: Cho hàm số y = f (x) xác định và liên tục trên và có bảng biến thiên như sau: NHÓ x −∞ 3 − 1 +∞ M y ' − 0 + 0 − TOÁN +∞ 3 y 2 − −∞ V D – VD Hỏi hàm số ( ) 2 = (ex g x f − 3) C
có bao nhiêu điểm cực trị? A. 4. B. 3. C. 2. D. 5. Lời giải Chọn B
'( ) = 2. x. (ex − 3). '( x g x e f f e − 3)
g '(x) = 0 ⇔ ( x f e − 3) = 0 Hoặc '( x f e − 3) = 0 Dựa vào BBT ta được: Giải ( x f e − 3) = 0 x
e − 3 = a(a < 3) − x
⇔ e = a + 3 < 0 (vô nghiệm) NHÓ x e − 3 = b( 3 − < b <1) M T
⇔ x = b + 3 (*) OÁN
⇔ x = ln(b + 3) ( 1 nghiệm) x
e − 3 = c(c >1) VD x
⇔ e = c + 3 (**) –
⇔ x = ln(c + 3) ( 1 nghiệm) VD Giải '( x f e − 3) = 0 C x x ⇔ e − 3 = 3
− ⇔ e = 0 (vô nghiệm) Hoặc x − 3 =1 x e
⇔ e = 4 ⇔ x = ln 4 (1 nghiệm)
Lấy x = ln 4 thay vào (*) và (**) không thỏa mãn đều kiện của b và c nên 3 nghiệm trên không
trùng nhau ⇒ g '(x) = 0 có 3 nghiệm đơn
Vậy g(x) có 3 cực trị
Câu 10: Cho hàm số y = f (x) liên tục trên , có bảng xét dấu của f '(x) như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ Biết rằng f ( 5
− ) < 0 và f (5) > 0 . Số điểm cực trị của hàm số y = f ( x − x) 2 2 6 là M TOÁN A. 7. B. 8. C. 9. D. 6. Lời giải V D Chọn A – VD
2x −6 = 0 ⇔ x = 3 C
Ta có: y ' = 2(2x − 6). f '( 2
x − 6x). f ( 2
x − 6x) = 0 ⇔ f '( 2
x − 6x) = 0 ( ) 1 f ( 2
x − 6x) = 0 (2) x − 6x = 5
− ⇔ x = 5, x =1
+) Từ (1) kết hợp với bảng dấu f '(x) ta có f '(x − 6x) 2 2 = 0 ⇔ 2
x − 6x = 0 ⇔ x = 0.x = 6
+) Từ (2) kết hợp bảng dấu f '(x) và đk f ( 5
− ) < 0 và f (5) > 0 ta có f ( 2 x − 6x) 2
= 0 ⇔ x − 6x = x ∈ 0;5 − − = 0
( ) nên pt 2x 6x x 0 có 2 nghiệm phân biệt khác các 0 nghiệm trên.
+) Các nghiệm đó là nghiệm bội lẻ (nghiệm đơn) => hàm số y = f ( x − x) 2 2 6 có 7 cực trị NHÓ
Câu 11: Cho hàm số liên tục trên , có bảng xét dấu của f ′(x) như sau: M T OÁN VD – VD C
Hàm số y = f ( − x ) 3 2 4
có bao nhiêu cực trị? A. 2. B. 3. C. 4. D. 5. Lời giải Chọn D x = 0
TH1. Ta có y ' = 6 − . x f (4 − x ) 2 . f '
(4− x ) = 0 ⇔ f (4− x ) 2 2 2 2 = 0 ( ) 1 f ' ( 2 4 − x ) = 0 (2)
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
+) Dựa vào bảng xét dấu y’ ta có pt(1) có nghiệm nhưng đều là nghiệm bội chẵn nên tại đó
không phải là điểm cực trị. +) Từ (2) ta có 2
4 − x = 0 ⇒ x = 2, x = 2 − NHÓ
TH2. Điểm làm cho y’ không xác định: 2
4 − x = 3 ⇒ x =1, x = 1 − M T
Vậy ta có 5 điểm cực trị OÁN
Câu 12: Cho hàm số y = f (x) liên tục trên , có bảng xét dấu của f '(x) như sau: V D – VD C
Hàm số y = f ( − x ) 4 4
+ 3 có bao nhiêu cực trị? A. 1. B. 3. C. 5. D. 7. Lời giải Chọn B TXĐ D = [0;+∞) NHÓ 3 Ta có 2 y ' − =
. f '(4− x). f
(4 − x ) + 3 ,( x > 0) M T x OÁN
f '(4− x) = 0 ( )1 y ' 0 = ⇔ VD
f (4− x)+3=0 (2) – VD 4 − x = 5 − ⇔ x = 81 C
+) Từ (1) ta có: f '(4− x) = 0 ⇔ 4− x = 0 ⇔ x =16
4− x = 4 ⇔ x = 0∉(0;+∞ )
4 − x = a∈ 0;4 ⇔ x = x
+) Từ (2) ta có f (4− x) ( ) 1 + 3 = 0 ⇔
4 − x = b∈(4;+∞) ⇔ x∈∅
Vậy có y = f ( − x ) 4 4
+ 3 có 3 cực trị.
Câu 13: Cho hàm bậc ba y = f (x) có đạo hàm trên và có bảng xét dấu y′ như sau.
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Gọi m và n lần lượt là số điểm cực trị nhiều nhất và ít nhất của hàm số NHÓ
y = g(x) = f (2x + 2
1) , biết f (3) < 0 . Khi đó 2m− 3n bằng M T A. 4 . B. 1 . C. −3. D. 2 . OÁN Lời giải V D Chọn A – VD
f (2x +1) = 0
f (2x +1) = 0 f 2x + 1 = 0 C
Ta có g′(x) = 4 f (2x +1). f ′(2x +1) ( ) = 0 ⇔ ⇔ 2x +1 = 1 ⇔ x = 0 . f ′ (2x + 1) = 0 2x + 1 = 3 x = 1
Suy ra số điểm cực trị của hàm số g(x) phụ thuộc số nghiệm của phương trình f (2x +1) = 0 .
Trường hợp 1: f (1) > 0 . Suy ra phương trình a −1 x = < 0
2x + 1 = a < 1 2 f ( x 1) 0
2x 1 b,b (1,3) b − 1 2 + = ⇔ + = ∈ ⇔ x = ∈ (0;1) . 2
2x + 1 = c > 3 c − 1 x = > 1 2 NHÓ
Vậy trường hợp này g′(x) có 5 nghiệm đơn phân biệt nên hàm số y = g(x) có năm điểm cực M T trị. OÁN x = x + = 0 2 1 1 VD
Trường hợp 2: f (1) = 0 . Suy ra phương trình f (2x + 1) = 0 ⇔ ⇔ a − .
2x + 1 = a > 3 1 x = > 1 2 – VD
Vậy trường hợp này g′(x) có 2 nghiệm đơn phân biệt nên hàm số y = g(x) có hai điểm cực C trị. a 1
Trường hợp 3: f (1) < 0 . Suy ra phương trình f (2x 1) −
+ = 0 ⇔ 2x + 1 = a > 3 ⇔ x = > 1. 2
Vậy trường hợp này g′(x) có 3 nghiệm đơn phân biệt nên hàm số y = g(x) có ba điểm cực trị. DẠNG TOÁN 8.
Biết BẢNG XÉT DẤU hàm số y = f ′(x) xét cực trị của hàm số = ( ) = ( ( )) k y g x
f u x trong bài toán chứa tham số .
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 9.
Biết BẢNG XÉT DẤU hàm số y = f ′(u(x)) xét cực trị của hàm
số y = f (x) trong bài toán không chứa tham số. NHÓ
Câu 1: Cho y = f (x) là hàm số xác định và có đạo hàm trên . M
Biết bảng xác dấu của y = f ′(3− 2x) như sau: TOÁN V D = –
Hỏi hàm số y f (x) có bao nhiêu điểm cực đại VD C A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Đặt − u u = 3 − 2x 3 ⇒ x = 2 1 x = − 2 Ta có 5
f ′(3 − 2x) = 0 ⇔ x = 2 x = 3 x = 4 NHÓ u = 4 M T u = 2 −
⇒ f ′(u) = 0 ⇒ u = 3 − OÁN u = 5 − VD 1 5 − < x < − < u < ′ ⇔ ′ ⇔ –
Hơn nữa f (u) > 0
f (3 − 2x) > 0 2 2 2 4 ⇔ u < 5 − VD x > 4 C Bảng biến thiên
Câu 2: Cho y = f (x) xác định và có đạo hàm trên .
Biết bảng xét dấu của = ′(3 y f x ) như sau
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Tìm số điểm cực trị của hàm số y = f (x) NHÓ A. 0. B. 1. C. 2. D. 3. M T Lời giải OÁN Chọn D V D Đặt 3 u = x 3 ⇒ x = u – VD x = 1 − 3 ′ ⇔ = C f ( x ) = 0 x 8 x = 27 u = 1 −
Suy ra f ′(u) = 0 ⇒ u = 2 u = 3 − < x < 3 < < − < u < f ′(u) 1 u 8
> 0 ⇒ f ′(3 x) > 0 1 8 ⇒ ⇔ 1 2 ⇔ 27 < x 3 27 < u 3 < u Bảng biến thiên NHÓ M T OÁN DẠNG TOÁN 10.
Biết BẢNG XÉT DẤU hàm số y = f ′(u(x)) xét cực trị của hàm VD
số y = f (x) trong bài toán chứa tham số. – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Bbbbbbh Chuyên đề:
CÁC DẠNG TOÁN VỀ HÀM ẨN
LIÊN QUAN ĐẾN CỰC TRỊ NHÓ CỦA HÀM SỐ M TOÁN V
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ D – VD
PHẦN 5: CỰC TRỊ CỦA HÀM CHỨA GIÁ TRỊ TUYỆT ĐỐI C Dạng toán 1.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f (x) Dạng toán 2.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f (ax + b) Dạng toán 3.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f ( x ) Dạng toán 4.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số
y = f ( x + a ), y = f ( x + a + b) … Dạng toán 5.
Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f (x) Dạng toán 6.
Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f (ax + b) Dạng toán 7.
Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f ( x ) Dạng toán 8.
Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số NHÓ
y = f ( x + a ), y = f ( x + a + b) … M T Dạng toán 9.
Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f (x) OÁN Dạng toán 10.
Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f (ax + b) VD Dạng toán 11.
Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f ( x ) – Dạng toán 12.
Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số VD
y = f ( x + a ), y = f ( x + a + b) … C Dạng toán 13.
Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f (x) Dạng toán 14.
Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f (ax + b) Dạng toán 15.
Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f ( x ) Dạng toán 16.
Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số
y = f ( x + a ), y = f ( x + a + b) …
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số DẠNG TOÁN 1.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f (x) . DẠNG TOÁN 2.
Biết đồ thị hàm số y = f (x) xét cực trị của hàm số NHÓ
y = f (ax + b) . M
Câu 1: Cho hàm số y = f (x) có đồ thị như hình vẽ bên. TOÁN V D – VD C
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + ) 2
2019 + m có 5 điểm cực trị ? A. 1 . B. 2. C. 3. D. 5. Lời giải Chọn B
Vì hàm f (x) đã cho có 3 điểm cực trị nên f (x + ) 2
2019 + m cũng luôn có 3 điểm cực trị (do
phép tịnh tiến không làm ảnh hưởng đến số cực trị).
Do đó yêu cầu bài toán ⇔ số giao điểm của đồ thị f (x + ) 2
2019 + m với trục hoành là 2.
Để số giao điểm của đồ thị f (x + ) 2
2019 + m với trục hoành là 2 , ta cần NHÓ
+Tịnh tiến đồ thị f (x) xuống dưới tối thiểu 2 đơn vị 2 → m ≤ 2 − : vô lý M T
+ Hoặc tịnh tiến đồ thị f (x) lên trên tối thiểu 2 đơn vị nhưng phải nhỏ hơn 6 đơn vị OÁN 2 ≤ m < 6 2 → 2 ≤ m < 6 m∈ ⇔ →m∈ 2; − 2 . VD { }
− 6 < m ≤ − 2 – VD
Câu 2: Hình vẽ bên là đồ thị của hàm số y = f (x) . C y 2 O x 3 − 6 −
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f (x − ) 1 + m có 5
điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 12. B. 15. C. 18. D. 9. NHÓ Lời giải Chọn A M Phương pháp: TOÁN
+ Xác định đồ thị hàm số y = f (x − ) 1 V
+ Áp dụng tính chất: Số cực trị của đồ thị hàm số y = f (x) bằng tổng số cực trị của đồ thị hàm D –
số y = f (x) và số giao điểm (không phải là cực trị) của đồ thị hàm số y = f (x) với Ox. VD C Cách 1:
Nhận xét: Số giao điểm của (C) : y = f (x) với Ox bằng số giao điểm của (C′) : y = f (x − ) 1 với Ox .
Vì m > 0 nên (C′′) : y = f (x − )
1 + m có được bằng cách tịnh tiến (C′) : y = f (x − ) 1 lên trên m đơn vị. x NHÓ x M T TH1: 0 < m < 3 TH2 : m = 3 OÁN VD – VD C x x TH3:3 < m < 6 TH4 : m ≥ 6
TH1: 0 < m < 3. Đồ thị hàm số có 7 điểm cực trị. Loại.
TH2: m = 3 . Đồ thị hàm số có 5 điểm cực trị. Nhận.
TH3: 3 < m < 6 . Đồ thị hàm số có 5 điểm cực trị. Nhận.
TH4: m ≥ 6 . Đồ thị hàm số có 3 điểm cực trị. Loại.
Vậy 3 ≤ m < 6 . Do *
m∈ nên m∈{3;4; } 5 .
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Vậy tổng giá trị tất cả các phần tử của S bằng 12. Cách 2
Tịnh tiến đồ thị hàm số y = f (x) sang phải 1 đơn vị, ta được đồ thị hàm số y = f (x − ) 1 . NHÓ
Do đó đồ thị hàm số y = f (x − )
1 có 3 cực trị và có 4 giao điểm với Ox. M T
Để được đồ thị hàm số y = f (x) + m với m nguyên dương ta phải tịnh tiến đồ thị hàm số OÁN
y = f (x − ) 1 lên trên m đơn vị V D
Để thỏa mãn điều kiện đề bài thì đồ thị hàm số y = f (x − )
1 + m cắt Ox tại đúng 2 điểm (không – VD
phải là điểm cực trị của chính nó), do đó 3 ≤ m < 6 ⇒ S = {3;4; } 5 . C
Tổng giá trị các phần tử của S là 12.
Câu 3: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ. NHÓ
Hàm số y = f ( x +1 − )
1 có bao nhiêu cực trị? M T A. 11. B. 7 . C. 5. D. 6 . OÁN Lời giải VD Chọn A – VD
Xét hàm số y = f ( x +1 − ) 1 C Ta có x +1 y′ =
f ′( x +1 − ) 1 x +1 x =1 | x 1| 1 0 + − = x = 0 y′ = 0 ⇔ ⇔ | x +1| 1 − =1 x = 2 − x = 3 −
y′ không xác định tại x = 1 − . Bảng biến thiên
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN
Dựa vào BBT của hàm số y = f ( x +1 − )
1 suy ra BBT của hàm số y = f ( x +1 − ) 1 . V D
Vậy hàm số y = f ( x +1 − ) 1 có 11 cực trị. – VD
Câu 4: Hình vẽ là đồ thị hàm số y = f (x) . Gọi S là tập hợp các giá trị nguyên dương của tham số m để C
hàm số y = f (x −1) + m có 5điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 9. B. 12. C. 18. D. 15. NHÓ Lời giải M T Chọn B OÁN
Dựa vào đồ thị hàm số y = f (x) ta thấy hàm số có 3cực trị. VD
Số cực trị của hàm số y = f (x −1) + m bằng với số cực trị của hàm số y = f (x −1) và bằng số – VD
cực trị của hàm số y = f (x) . C
Số cực trị của hàm số y = f (x −1) + m bằng số cực trị của hàm số y = f (x) cộng với số nghiệm
đơn của phương trình f (x −1) + m = 0 (*) .
Ta có f (x −1) + m = 0 ⇔ f (x −1) = −m ⇔ f (t) = −m với t = x −1.
Để hàm số y = f (x −1) + m có có 5điểm cực trị thì phương trinh (*) phải có 2 nghiệm đơn phân biệt. Do đó 6
− < −m ≤ 3 hoặc 2 ≤ −m ⇒ m∈{3,4, }
5 ⇒ S = 3+ 4 + 5 =12 .
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
DẠNG TOÁN 3. Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f ( x )
Câu 1: Đồ thị hàm số y = f (x) 3 2 = 2
− x + 9x −12x + 4 như hình vẽ. Tìm tất cả các giá trị của tham số NHÓ
thực m để phương trình 3 2
2 x − 9x +12 x + m = 0 có 6 nghiệm phân biệt M y T 4 OÁN V D – VD C 1 2 O x 1 − A. ( 1; − 0) . B. ( 3 − ; 2 − ) . C. ( 5; − 4 − ) . D. ( 4; − 3 − ) . Lời giải Chọn C Xét phương trình: 3 2 3 2
2 x − 9x +12 x + m = 0 ⇔ 2
− x + 9x −12 x + 4 = m + 4(*)
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f ( x ) và đường thẳng y = m + 4 . NHÓ
Ta có đồ thị hàm số y = f ( x ) như sau: M T OÁN y 4 VD – VD C 2 − 1 − 1 2 O x 1 −
Dựa vào đồ thị hàm số ta thấy để (*) có 6 nghiệm phân biệt thì 1
− < m + 4 < 0 ⇔ 5 − < m < 4 − .
Câu 2: Cho hàm số y = f (x) có đồ thị (C) như hình vẽ bên. Hàm số y = f ( x ) có bao nhiêu điểm cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN A. 3. B. 4 . C. 5. D. 6 . Lời giải V D Chọn C – VD
Đồ thị (C ') của hàm số y = f ( x ) được vẽ như sau: C
+ Giữ nguyên phần đồ thị của (C) nằm bên phải trục tung ta được (C 1 )
+ Lấy đối xứng qua trục tung phần đồ thị của (C ta được (C 2 ) 1 )
+ Khi đó (C ') = (C ∪ C có đồ thị như hình vẽ dưới 1 ) ( 2) NHÓ
Từ đồ thị (C ') ta thấy hàm số y = f ( x ) có 5 điểm cực trị M T OÁN
Câu 3: Cho hàm số y = f (x) có đồ thị (C) như hình vẽ bên. Hàm số y = f ( x ) có bao nhiêu điểm cực trị? VD – VD C A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Đồ thị (C ') của hàm số y = f ( x ) được vẽ như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
+ Giữ nguyên phần đồ thị của (C) nằm bên phải trục tung ta được (C . 1 )
+ Lấy đối xứng qua trục tung phần đồ thị của (C ta được (C . 2 ) 1 ) NHÓ
+ Khi đó (C ') = (C ∪ C có đồ thị như hình vẽ dưới 1 ) ( 2) M TOÁN V D – VD C
Từ đồ thị (C ') ta thấy hàm số y = f ( x ) có 1 điểm cực trị.
Câu 4: Cho hàm số y = f (x) có đồ thị (C) như hình vẽ bên. Hàm số y = f ( x ) có bao nhiêu điểm cực trị? NHÓ A. 3. B. 4 . C. 5. D. 6 . M T Lời giải OÁN Chọn C VD
Đồ thị (C ') của hàm số y = f ( x ) được vẽ như sau: – VD
+ Giữ nguyên phần đồ thị của (C) nằm bên phải trục tung ta được (C . 1 ) C
+ Lấy đối xứng qua trục tung phần đồ thị của (C ta được (C . 2 ) 1 )
+ Khi đó (C ') = (C ∪ C có đồ thị như hình vẽ dưới 1 ) ( 2)
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ đồ thị (C ') ta thấy hàm số y = f ( x ) có 5 điểm cực trị.
Câu 5: Cho hàm số f (x) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số y = f ( x ) là NHÓ M TOÁN V D – VD C A. 3. B. 4. C. 5. D. 7. Lời giải Chọn D
Đồ thị (C ') của hàm số y = f ( x ) được vẽ như sau:
+ Giữ nguyên phần đồ thị của (C) nằm bên phải trục tung ta được (C . 1 )
+ Lấy đối xứng qua trục tung phần đồ thị của (C ta được (C . 2 ) 1 ) NHÓ
+ Khi đó (C ') = (C ∪ C có đồ thị như hình vẽ dưới 1 ) ( 2) M T OÁN VD – VD C
Dựa vào đồ thị hàm số y = f ( x ) có 7 cực trị.
DẠNG TOÁN 4. Biết đồ thị hàm số y = f (x) xét cực trị của hàm số y = f ( x + a ),
y = f ( x + a + b) …
Câu 1: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên dưới
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f ( x + m ) có 5 điểm cực trị ? V D – A. 3. B. 4. C. 5. D. Vô số. VD Lời giải C Chọn D
Từ đồ thị hàm số ta thấy:
Hàm số f (x) có 2 điểm cực trị dương.
→ f ( x ) có 5 điểm cực trị.
→ f ( x + m ) có 5 điểm cực trị với mọi m (vì tịnh tiến sang trái hay sang phải không ảnh
hưởng đến số điểm cực trị của hàm số) .
Vậy có vô số giá trị m để hàm số g (x) = f ( x + m ) có 5 điểm cực trị.
Câu 2: Cho hàm số = ( ) 4 3 2
y f x = ax + bx + cx + dx + e có đồ thị như hình vẽ bên. Hỏi hàm sốNHÓ
y = f ( x +1 −3) có bao nhiêu điểm cực trị? M T OÁN VD – VD C A. 3. B. 5. C. 6. D. 7. Lời giải Chọn D
Đồ thị hàm số y = f ( x +1 −3) được suy từ đồ thị hàm số y = f (x) bằng cách
• Tịnh tiến sang phải 3 đơn vị;
• Xóa bỏ phần đồ thị phía bên trái trục tung, phần đồ thị phía bên phải trục tung thì lấy đối xứng qua trục tung;
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
• Cuối cùng tịnh tiến đồ thị sang trái 1 đơn vị.
Câu 3: Cho hàm số y = f ( x) có đồ thị như hình vẽ sau. Hàm số y = f ( x −3 ) có bao nhiêu điểm cực trị? NHÓ M TOÁN V D – VD C A. 5. B. 6 . C. 3. D. 1. Lời giải Chọn C
y = f ( x −3 )( )
1 , Đặt t = x − 3 , t ≥ 0 . Thì ( )
1 trở thành: y = f (t) (t ≥ 0).
Có t = (x − )2 3 / x − 3 ⇒ t = x (x −3)2 Có / / / y = t f t x x ( ) / t = t = 2 − (L) x 0(VN) x = 7 / y = / / ⇔ t f t = ⇔ ⇔ ⇔ x ( ) 0 x 0 NHÓ / f (t) = 0 t = 4 x = 1 − M T Ta có bảng biến thiên: OÁN x - ∞ -1 3 7 +∞ VD _ y / 0 + _ 0 + – +∞ +∞ CĐ VD y CT CT C
Dựa vào BBT thì hàm số y = f ( x −3 ) có 3 cực trị.
Câu 4: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên dưới.
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Tìm m để hàm số g (x) = f ( x + m ) + 2019m có 5 điểm cực trị A. 1 m > − . B. m >1. 2 NHÓ C. 1 m ≥ − . D. m ≥1. M 2 TOÁN Lời giải V Chọn A D – = +
Tịnh tiến đồ thị y f ( x m )lên trên hoặc xuống dưới không làm ảnh hưởng đến số điểm cực VD
trị của hàm số đã cho. Do đó số cực trị của hàm số y = g (x) bằng số cực trị của hàm số C
y = f ( x + m ).
Để f ( x + m ) có 5 điểm cực trị thì f (x + m) phải có 2 điểm cực trị dương với x+m > 0.
Dựa vào đồ thị ta thấy f (x) đạt cực trị tại x =1, x = 2 nên f (x + m) đạt cực trị tại
2 + m + m > 0 x 1 = 2 + ;
m x =1+ m . Do đó ⇔ m > − . 1
+ m + m > 0 2
Câu 5: Cho hàm số y = f (x) xác định trên và hàm số y = f ′(x) có đồ thị như hình bên. Đặt
g (x) = f ( x + m) . Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) có đúng 7 điểm cực trị? NHÓ M T OÁN VD – VD C A. 2 . B.3. C.1. D.Vô số. Lời giải Chọn A
f x + m , khi x ≥ 0
Ta có g (x) = f ( x + m) ( ) = f
(−x + m), khi x < 0
Do hàm số y = f (x) xác định trên ⇒Hàm số g (x) xác định trên
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Và ta lại có g (−x) = f ( x + m) = g (x) ⇒Hàm số g (x) là hàm số chẵn⇒Đồ thị hàm số
y = g (x) đối xứng qua trục Oy . NHÓ
Hàm số y = g (x) có 7 điểm cực trị ⇔ Hàm số y = g (x) có 3 điểm cực trị dương, 3 điểm cực
trị âm và một điểm cực trị bằng 0 (*) M T x = 3 − OÁN x = 1 −
Dựa vào đồ thị hàm số y = f ′(x) , ta có: f ′(x) = 0 ⇔ V x = 2 D x = 5 – VD
Xét trên khoảng (0;+∞), ta được g (x) = f (x + m) C
+ Ta có g′(x) = f ′(x + m) x + m = 3 −
x = −m − 3 x m 1 + = − x = −m −1
+ g′(x) = 0 ⇔ ⇔ x + m = 2 x = −m + 2 x m 5 + = x = −m + 5
+ Nhận thấy −m − 3 < −m −1< −m + 2 < −m + 5 −m −1 > 0 m∈
Theo yêu cầu (*) bài toán ⇔ ⇔ 3 − ≤ m < 1 − ⇔ −m − 3 ≤ 0 m∈ { 3 − ;− } 2 NHÓ
DẠNG TOÁN 5. Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f (x) M T
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như sau. Đồ thị hàm số y = f (x) có bao nhiêu điể OÁNm cực trị VD – VD C A. 5. B. 6 . C. 3. D. 7 . Lời giải Chọn D
Đồ thị hàm y = f (x) gồm 2 phần: + Phần đồ thị y = f (
x) nằm trên Ox (Kể cả giao điểm trên trục Ox )
+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f (
x) nằm dưới Ox
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ đó ta có bảng biến thiên của y = f (x) . NHÓ M T OÁN
Từ bảng biến thiên này hàm số y = f (x) có 7 cực trị. V D
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như sau. Đồ thị hàm số y = f (x) có bao nhiêu điểm – cực trị VD C A. 5. B. 6 . C. 3. D. 7 . Lời giải Chọn C
Đồ thị hàm y = f (x) gồm 2 phần: + Phần đồ thị y = f (
x) nằm trên Ox (Kể cả giao điểm trên trục Ox ) NHÓ
+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f (
x) nằm dưới Ox M T
Từ đó ta có bảng biến thiên của y = f (x) . OÁN VD – VD C
Từ bảng biến thiên này hàm số y = f (x) có 3 cực trị.
Câu 3. Cho hàm số y = f (x) có bảng biến thiên như sau. Đồ thị hàm số y = f (x) có bao nhiêu điểm cực trị
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số A. 5. B. 6 . C. 3. D. 7 . Lời giải Chọn D
Đồ thị hàm y = f (x) gồm 2 phần: NHÓ + Phần đồ thị y = f (
x) nằm trên Ox (Kể cả giao điểm trên trục Ox ) M
+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f (
x) nằm dưới Ox TOÁN
Từ đó ta có bảng biến thiên của y = f (x) . V D – VD C
Từ bảng biến thiên này hàm số y = f (x) có 7 cực trị.
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như sau. Đồ thị hàm số y = f (x) có bao nhiêu điểm cực trị NHÓ M T A. 5. B. 6 . C. 3. D. 7 . Lời giải OÁN Chọn A VD
Đồ thị hàm y = f (x) gồm 2 phần: – + Phần đồ thị y = f (
x) nằm trên Ox (Kể cả giao điểm trên trục Ox ) VD
+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f (
x) nằm dưới Ox C
Từ đó ta có bảng biến thiên của y = f (x) .
Từ bảng biến thiên này hàm số y = f (x) có 5 cực trị.
Câu 5. Cho hàm số y f x có bảng biến thiên sau:
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN
Hàm số y = f (x) có bao nhiêu điểm cực trị ? V A.5 . B. 4. C. 3. D. 2. D Lời giải – VD Chọn C
Đồ thị hàm y = f (x) gồm 2 phần: C + Phần đồ thị y = f (
x) nằm trên Ox (Kể cả giao điểm trên trục Ox )
+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f (
x) nằm dưới Ox
Từ đó ta có bảng biến thiên của y = f (x) .
Dựa vào bảng biến thiên, suy ra đồ thị hàm số y f x có 3 điểm cực trị. NHÓ
Câu 6. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ: M T OÁN VD – VD
Đồ thị hàm số y = f (x) có bao nhiêu điểm cực trị? C A. 2 B. 4 . C. 3. D. 5. Lời giải Chọn C
Vì đồ thị hàm số y = f (x) gồm hai phần:
+) Phần đồ thị của hàm số y = f (x) nằm trên Ox .
+) Phần đồ thị đối xứng qua Ox với phần đồ thị hàm số y = f (x) nằm dưới Ox
Nên từ bảng biến thiên của hàm số y = f (x) suy ra bảng biến của hàm số y = f (x) như sau:
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M = T
Từ bảng biến thiên trên suy ra hàm số y
f (x) có 3 điểm cực trị. OÁN
Câu 7. Cho hàm số y = f (x) có bảng biến thiên như sau: V D – VD C
Đồ thị hàm số y = f (x) có bao nhiêu điểm cực trị? A. 4 . B. 2 . C. 5. D.3. Lời giải Chọn C
Từ bảng biến thiên của hàm số y = f (x) suy ra phương trình f (x) = 0 có ba nghiệm phân biệt NHÓ
là x , x , x y = f (x) 1 2
3 . Khi đó ta có bảng biến thiên của hàm số : M T OÁN VD – VD C
Suy ra đồ thị hàm số y = f (x) có 5 điểm cực trị.
Câu 8: Cho hàm số y = f (x) xác định trên \{ }
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN
Hàm số y = f (x) có bao nhiêu điểm cực trị? A. 4 . B. 3. C. 2 . D. 5. V Lời giải D Chọn A – VD
Từ bảng biến thiên của hàm số y = f (x) , suy ra bảng biến thiên của hàm số y = f (x) là C
Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.
Câu 9: Tổng các giá trị nguyên của tham số m để hàm số 3 2 = − 3 − 9 − 5 m y x x x +
có 5 điểm cực trị là 2 A. 2016 . B. 1952. C. 2016 − . D. 496 − . Lời giải Chọn A Xét hàm số ( ) 3 2 = − 3 − 9 − 5 m f x x x x + . 2 NHÓ x = 1 − Ta có f ′(x) 2
= 3x − 6x − 9 = 0 ⇔ . = M T x 3 Ta có bảng biến thiên OÁN VD – VD C
Để thỏa yêu cầu thì trục Ox phải cắt ngang đồ thị tại 3 điểm phân biệt, tức là: m > 0 2 m
⇔ 0 < m < 64 thì f (x) 3 2
= x − 3x − 9x − 5 + = 0 có ba nghiệm x ; x ; x với m 1 2 3 −32 < 0 2 2 x < 1
− < x < 3 < x , ta có bảng biến thiên của hàm số đã cho là 1 2 3
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN
Trường hợp này hàm số đã cho có 5 điểm cực trị.
Như vậy, các giá trị nguyên của m để hàm số đã cho có 5 điểm cực trị là m∈{1;2;3;...; } 63 . V D
Tổng các giá trị nguyên này là: – 63(1+ 63) VD S =1+ 2 + 3+...+ 63 = = 2016 . 2 C
DẠNG TOÁN 6. Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f (ax + b)
Câu 1: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ NHÓ
Hỏi đồ thị hàm số g (x) = f (x − 2019) + 2020 có bao nhiêu điểm cực trị? A. 2 . B. 3. C. 4. D. 3. M T Lời giải OÁN Chọn B
u x = f x − 2019 + 2020 có được từ đồ thị f (x) bằng cách tịnh tiế VD
Cách 1: Đồ thị hàm số ( ) ( ) n
đồ thị f (x) sang phải 2019 đơn vị và lên trên 2020 đơn vị. – VD
Suy ra bảng biến thiên của u (x) C
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Dựa vào bảng biến thiên suy ra đồ thị hàm số g (x) = u(x) có 3điểm cực trị. Chọn B. NHÓ Cách 2:
Đặt u (x) = f (x − 2019) + 2020 M x = 2020 ' ' ' T
⇒ u (x) = f (x − 2019) ⇒ u (x) = 0 ⇔ OÁN x = 2023 Bảng biến thiên V D – VD C
Dựa vào bảng biến thiên suy ra đồ thị hàm số g (x) = u(x) có 3điểm cực trị. Chọn B.
Câu 2: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ NHÓ M T OÁN VD = − + Hàm số y
f (1 3x) 1 có bao nhiêu điểm cực trị? – VD A. 2 . B. 3. C. 4 . D. 5. C Lời giải Chọn D
Đặt g (x) = f (1−3x) +1 . ⇒ g′(x) = 3.
− f (1−3x) . 2 1 − 3 = 1 x x = −
⇒ g′(x) = 0 ⇔ f (1− 3x) = 0 3 ⇔ ⇔⇔ 1 − 3x = 3 2 x = − 3
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Suy ra bảng biến thiên: NHÓ M TOÁN V D – VD
Vậy hàm số y = g(x) có 5 điểm cực trị. C
Câu 3: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ.
Biết đồ thị hàm số g (x) = f (x) − m có 5 điểm cực trị. Khi đó số các giá trị nguyên của tham số của m là A. 6 . B. 7 . C. 8 . D. 9. Lời giải NHÓ Chọn B M T
Do hàm y = f (x) có hai điểm cực trị nên y = f (x) − m có hai điểm cực trị. = − OÁN
Để thoả mãn yêu cầu bài thì số giao điểm của đồ thị y f (x) m với trục hoành phải là 3 hay
số giao điểm của y = f (x) và y = m phải là 3. g(x) = f (1−3x) ⇒ g (′x) = 3 − . f (1 ′ − 3x) VD
Suy ra 4 < m <11 . – ∈ ⇒ ∈ Do m m {4,5,6,7,8,9,1 } 0 nên chọn đáp án B. VD C
Câu 4: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ
Đồ thị hàm số y = f (x) − 2m có 5 điểm cực trị khi và chỉ khi A. m∈(4;1 ) 1 . B. 11 m 2; ∈ . C. m = 3 . D. 11 m ∈ 2; . 2 2 Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ bảng biến thiên ta có đồ thị hàm số y = f (x) có hai điểm cực trị.
y = f (x) − Để đồ thị hàm số
2m có 5 điểm cực trị thì đồ thị y = f (x) cắt đường thẳng NHÓ
y = 2m tại 5 − 2 = 3 điểm phân biệt ⇔ 4 < 2m <11 11 ⇔ 2 < m < . 2 M
DẠNG TOÁN 7. Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số y = f ( x ) TOÁN Lý thuyết: V f x khi x ≥ 0
Ta có y = f ( x ) ( ) = . D f
(−x) khi x < 0 – VD
Do đó, đồ thị (C′) của hàm số y = f ( x ) có thể được suy từ đồ thị (C) của hàm số y = f (x) C như sau:
+ Giữ nguyên phần đồ thị (C) ở bên phải trục tung ( kể cả giao điểm của (C) với
trục tung – nếu có), bỏ phần bên trái trục tung.
+ Lấy đối xứng phần bên phải trục tung qua trục tung.
+ Đồ thị (C′) là hợp của hai phần trên.
Từ bảng biến thiên của hàm số y = f ( x) ta suy ra số điểm cực trị, dấu của các điểm cực trị
của hàm số và sự tồn tại giao điểm với trục tung (nếu có).
Phương pháp chung giải quyết Bài toán: Biết bảng biến thiên của hàm số y = f ( x) . Tìm
số điểm cực trị của hàm số y = f ( x ) :
- Bước 1: Từ bảng biến thiên của hàm số y = f (x) , suy ra số điểm cực trị dương của hàm số NHÓ
y = f (x) . Giải sử có n điểm.
- Bước 2: Xét sự tồn tại giao điểm của đồ thị (C) của hàm số y = f (x) với trục tung. M T
- Bước 3: Xác định số điểm cực trị của hàm số y = f ( x ) OÁN
Trường hợp 1: Đồ thị (C) của hàm số y = f ( x) cắt trục tung. Khi đó số điểm cực VD
trị của hàm số y = f ( x ) bằng 2n +1 – =
Trường hợp 2: Đồ thị (C) của hàm số y f (x) không cắt trục tung. Khi đó số VD
điểm cực trị của hàm số y = f x bằng 2n . C ( ) 2. Bài tập:
Câu 1: Cho hàm số y = f (x) xác định và liên tục trên , có bảng biến thiên như hình vẽ. Tìm số điểm
cực trị của hàm số y = f ( x ) .
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M T OÁN A. 0 . B. 1. C. 2 . D. 3. Lời giải V Chọn B D
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy tại điểm cực đại và hàm số – VD
không có điểm cực trị dương nên hàm số y = f ( x ) có đúng 1 điểm cực trị x = 0 . C
Câu 2: Cho hàm số y = f (x) xác định và liên tục trên , có bảng biến thiên như hình vẽ. Tìm số điểm
cực tiểu của hàm số y = f ( x ) . x 2 1 f ( x) + || 0 + 3 f (x) 1 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B NHÓ
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và có 1 điểm cực tiểu dương, M T
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên hàm số y = f ( x ) có 2 điểm cực OÁN tiểu là x = 1 ± .
Câu 3: Cho hàm số y = f (x) xác định và liên tục trên , có bảng biến thiên như hình vẽ. VD – VD C
Mệnh đề nào sau đây đúng?
A. Hàm số y = f ( x ) có 3 điểm cực trị.
B. Hàm số y = f ( x ) có một điểm cực đại.
C. Hàm số y = f ( x ) có hai điểm cực tiểu.
D. Hàm số y = f ( x ) có ba điểm cực tiểu.
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn D
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và có 2 điểm cực trị dương, NHÓ
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên hàm số y = f ( x ) có 2.2 +1= 5 M
điểm cực trị trong đó có 3 điểm cực tiểu là các diểm x = 0, x = 3 ± . TOÁN
Câu 4: Cho hàm số y = f (x) xác định và liên tục trên , có bảng biến thiên như hình vẽ. V D – VD C
Mệnh đề nào sau đây sai?
A. Hàm số y = f ( x ) không có điểm cực đại.
B. Hàm số y = f ( x ) có một điểm cực trị.
C. Hàm số y = f ( x ) có một cực trị dương.
D. Hàm số y = f ( x ) không có điểm cực trị. NHÓ Lời giải M T Chọn D OÁN
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và không có cực trị, VD
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên từ BBT suy ra hàm số y = f ( x ) có –
đúng 1 điểm cực trị là điểm cực tiểu x = 0 . VD
Câu 5: Cho hàm số y = f (x) xác định và liên tục trên , có bảng biến thiên như hình vẽ. Tìm số điể C m
cực trị của hàm số y = f ( x ) . A. 2 . B. 4 . C. 3. D. 5. Lời giải Chọn D
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và có 2 điểm cực trị dương,
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên hàm số y = f ( x ) có 2.2 +1= 5 điểm cực trị. NHÓ
Câu 6: Cho hàm số y = f (x) xác định trên \{ } 1
− và liên tục trên các khoảng xác định của nó, có bảng
biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số y = f ( x ) . M TOÁN V D – VD C A. 2 . B. 1. C. 3. D. 0 . Lời giải Chọn B
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và không có cực trị,
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên từ BBT suy ra hàm số y = f ( x ) có
đúng 1 điểm cực trị là điểm cực tiểu x = 0 .
Câu 7: Cho hàm số y = f (x) xác định trên \{ }
0 và liên tục trên các khoảng xác định của nó, có bảng
biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số y = f ( x ) . NHÓ M T OÁN VD A. 0 . B. 1. C. 2 . D. 3. – Lời giải VD Chọn B C
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) không cắt trục Oy và không có cực trị,
nên từ BBT suy ra hàm số y = f ( x ) không có điểm cực trị.
Câu 8: Cho hàm số y = f (x) xác định trên \{ }
0 và liên tục trên các khoảng xác định của nó, có bảng
biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số y = f ( x ) .
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN
Mệnh đề nào sau đây đúng?
A. Hàm số y = f ( x ) có một điểm cực đại, một điểm cực tiểu. V D
B. Hàm số y = f ( x ) có hai điểm cực đại. – VD
C. Hàm số y = f ( x ) có hai điểm cực tiểu. C
D. Hàm số y = f ( x ) có ba điểm cực trị. Lời giải Chọn C
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) không cắt trục Oy và có 1 điểm cực trị
dương, mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên từ BBT suy ra hàm số
y = f ( x ) có đúng 2 điểm cực trị là 2 điểm cực tiểu x = 1 ± .
Câu 9: Cho hàm số y = f (x) xác định trên \{ }
1 và liên tục trên các khoảng xác định của nó, có bảng
biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số y = f ( x ) . NHÓ M T OÁN VD – VD C
Mệnh đề nào sau đây sai?
A. Hàm số y = f ( x ) hai điểm cực trị không âm.
B. Hàm số y = f ( x ) có hai điểm cực đại.
C. Hàm số y = f ( x ) có hai điểm cực tiểu.
D. Hàm số y = f ( x ) có ba điểm cực trị. Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và hàm số y = f (x) có một cực
trị dương, mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên từ BBT suy ra hàm số
y = f ( x ) có 3 điểm cực trị, trong đó có 2 điểm cực tiểu x = 5
± và một điểm cực đại x = 0 . NHÓ
Câu 10: Cho hàm số y = f (x) xác định trên \{ } 1
− , liên tục trên các khoảng xác định của nó và có M
bảng biến thiên như hình vẽ: TOÁN V D – VD C
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số y = f ( x ) có 1 điểm cực trị.
B. Đồ thị hàm số y = f ( x ) có 1 điểm cực đại.
C. Đồ thị hàm số y = f ( x ) có 1 điểm cực tiểu.
D. Đồ thị hàm số y = f ( x ) không có điểm cực tiểu . Lời giải Chọn C
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và hàm số y = f (x) có một cực
trị dương là điểm cực đại, mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên từ BBT NHÓ
suy ra hàm số y = f ( x ) có 3 điểm cực trị, trong đó có 2 điểm cực đại x = 1 ± và một điểm cực tiểu x = 0 . M T
Câu 11: Cho hàm số y = f (x) xác định trên \{ }
0 và liên tục trên từng khoảng xác định, có bảng biế OÁNn thiên như hình dưới. VD – VD C
Khẳng định nào sau đây đúng?
A. Hàm số y = f ( x ) có một điểm cực trị.
B. Hàm số y = f ( x ) có hai điểm cực trị.
C. Hàm số y = f ( x ) có ba điểm cực trị.
D. Hàm số y = f ( x ) có một điểm cực tiểu. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Chọn B
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) không cắt trục Oy và hàm số y = f (x) có
một cực trị dương là điểm cực tiểu, mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên NHÓ
từ BBT suy ra hàm số y = f ( x ) có 2 điểm cực trị là 2 điểm cực tiểu x = 2 ± . M
Câu 12: Cho hàm số y = f (
x) liên tục trên và có bảng biến thiên như sau TOÁN V D – VD C
Đồ thị hàm số y = f ( x ) có bao nhiêu điểm cực trị? A. 3. B. 2 . C. 4 . D. 1 Lời giải Chọn A
Đồ thị hàm số y = f ( x ) gồm 2 phần:
+ Phần bên phải trục Oy của đồ thị y = f (x) ( Kể cả giao điểm với trục Oy)
+ Đối xứng phần đồ thị trên qua trục Oy
• Hàm số y = f ( x ) có bảng biến thiên sau: NHÓ x −∞ - 4 0 4 +∞ M T ( - 0 + 0 - 0 + f ( x ))′ OÁN +∞ +∞ VD f (0) – f ( x ) VD 2 2 C
Từ BBT ta thấy đồ thị hàm số y = f ( x ) có 3 điểm cực trị.
Câu 13: Cho hàm số y = f (x) xác định và liên tục trên \{ }
2 có bảng biến thiên như sau
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Số điểm cực trị của đồ thị hàm số y = f ( x ) là A. 5. B. 4 . C. 7 . D. 3. NHÓ Lời giải Chọn A M TOÁN
Từ bảng biến thiên ta thấy đồ thị hàm số y = f (x) cắt trục Oy và có 2 điểm cực trị dương,
mà đồ thị hàm số y = f ( x ) nhận Oy làm trục đối xứng nên đồ thị hàm số y = f ( x ) có V D
2.2 +1 = 5 điểm cực trị. – VD C
DẠNG TOÁN 8. Biết bảng biến thiên hàm số y = f (x) xét cực trị của hàm số
y = f ( x + a ), y = f ( x + a + b) … 1. Lý thuyết:
Nhận xét: đồ thị của hàm số y = g (x) = f ( ax + b + m) nhận đường thẳng b x = − là trục a
đối xứng, do đó số điểm cực trị của hàm số y = g (x) = f ( ax + b + m) bằng 2t +1 , với t là
số điểm cực trị lớn hơn b
− của hàm y = f (ax + b + m). a 2. Bài tập: NHÓ
Câu 1: Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. M T OÁN VD – VD C
Số điểm cực trị của hàm số y = f ( 2x +1 + 3) là A. 1. B. 5. C. 0 . D. 3. Lời giải Chọn A
+/ Ta có : Số điểm cực trị của hàm y = f ( 2x +1 + 3) bằng 2α +1 , với α bằng số điểm cực trị lớn hơn 1
− của hàm y = f (2x +1+ 3) = f (2x + 4) . 2
https://www.facebook.com/groups/toanvd.vdc Trang 29
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số 5 2 + 4 = 1 x x = − −
+/ Hàm y = f (2x + 4) có 2 điểm cực trị là: 2 ⇔ 2x + 4 = 3 1 x = − 2 NHÓ
Vậy: Số điểm cực trị của hàm y = f ( 2x +1 + 3) bằng 2.0 +1=1 ⇒ Chọn A. M TOÁN
DẠNG TOÁN 9. Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f (x) V
DẠNG TOÁN 10. Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f (ax + b) D – VD
DẠNG TOÁN 11. Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số y = f ( x ) C
DẠNG TOÁN 12. Biết đồ thị hàm số y = f '(x) xét cực trị của hàm số
y = f ( x + a ), y = f ( x + a + b) …
Câu 1: Hàm số f (x) có đạo hàm f '(x) trên .
Hình vẽ bên là đồ thị của hàm số f '(x) trên . NHÓ M T
Hỏi hàm số y = f ( x ) + 2018 có bao nhiêu điểm cực trị? OÁN A. 5. B. 3. C. 2 . D. 4 . VD Lời giải – VD Chọn A C Phương pháp:
Tính đạo hàm của hàm hợp, giải phương trình đạo hàm để tìm số điểm cực trị Cách giải:
x = x < 0
Dựa vào hình vẽ, ta thấy f '(x) = 0 có 3 nghiệm phân biệt 1 x = { . x ; x > 0 2 3}
f x + 2018 khi x ≥ 0
Ta có: g (x) = f ( x ) ( ) + 2018 = f (−x) . + 2018 khi x < 0
https://www.facebook.com/groups/toanvd.vdc Trang 30
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số f '(x) ≥ ⇒ g (x) khi x 0 ' = − f '
(−x)khi x < 0 NHÓ x = x2 f '(x) khi x = ≥ x = x g '(x) 0 0 3 0 = ⇔ ⇔ M − f '
(−x) = 0 khi x < 0 x = −x2 T OÁN x = − x3 V
Do đó g '(x) = 0 bị tiệt tiêu tại 4 điểm x ,−x , x ,−x và không có đạo hàm tại x = 0. 2 2 3 3 D –
Vậy hàm số đã cho có 5 điểm cực trị. VD C
DẠNG TOÁN 13. Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f (x)
DẠNG TOÁN 14. Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f (ax + b)
DẠNG TOÁN 15. Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số y = f ( x )
Câu 1: Cho hàm số y = f (x) có đạo hàm f (x) = (x + )2 ( 2 2 '
1 x + m − 3m − 4)3 (x + 3)5 với mọi x∈ .
Có bao nhiêu số nguyên m để hàm số g (x) = f ( x ) có đúng 3 điểm cực trị? A. 3. B. 5. C. 6 . D. 4 . Lời giải Chọn D NHÓ
Để g (x) = f ( x )có đúng 3 điểm cực trị ⇒ y = f (x) có đúng 1 cực trị có hoành độ dương. M T OÁN x = 1 − Mặt khác, y ' 0 = ⇔ x = 3 − (trong đó x = 1 − là nghiệm kép). VD 2 2
x = −m + 3m + 4 – VD 2
ycbt ⇔ −m + 3m + 4 > 0 ⇔ 1 − < m < 4 . C
Do m∈ ⇒ m∈{0;1;2; } 3 .
DẠNG TOÁN 16. Biết bảng xét dấu hàm số y = f '(x) xét cực trị của hàm số
y = f ( x + a ), y = f ( x + a + b) …
Câu 1: Cho hàm số y = f (x) xác định và liên tục trên có bảng xét dấu của hàm y = f ′(x) như sau
Hàm số y = f ( x − 2 ) + 2020 có bao nhiêu điểm cực trị? A. 5. B. 4 . C. 3. D. 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 31
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số Lời giải Chọn A ≥ NHÓ f x khi x 0
Xét hàm số y = f ( x ) ( ) = f
(−x) khi x < 0 M T
Khi đó ta có bảng biến thiên OÁN x −∞ 2 − 1 − 0 1 2 +∞ V
y′ − || + 0 − || + 0 − || + D
Do đó hàm số y = f ( x ) có 5 cực trị. – VD C
⇒ f ( x − 2 ) có năm cực trị (tịnh tiến đồ thị sang phải hai đơn vị thì số cực trị không thay đổi)
⇒ y = f ( x − 2 ) + 2020 có 5 cực trị (tịnh tiến đồ thị lên 2020 đơn vị không làm thay đổi số cực trị).
Câu 2: Cho hàm số y = f (x) có đạo hàm trên và f ′(x) có bảng xét dấu như sau:
Số điểm cực trị của hàm số ( ) = ( 2 g x f x − x ) là NHÓ A. 7. B. 5. C. 3. D. 9. M T OÁN Lời giải Chọn B VD 2 –
g (x) = f ( x − x ) VD C Xét hàm số ( ) = ( 2 h x
f x − x) ⇒ g (x) = h( x )
Ta có h (x) = ( f ( 2x − x) ′ ′
= ( x − ) f ′( 2 2 1 . x − x) 1 x = 1 x = 2x −1 = 0 2 2
h′(x) = 0 ⇔ 2
⇔ x − x = 2 − ⇔ x = 1 − f ′ ( 2 x − x) = 0 2 x − x = 2 x = 2
Ta có bảng biến thiên của hàm số ( ) = ( 2 h x f x − x) :
https://www.facebook.com/groups/toanvd.vdc Trang 32
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số NHÓ M TOÁN V
Dựa vào bảng biến thiên ta thấy hàm số h(x) có 2 điểm cực trị dương nên hàm số D
g ( x) = h( x ) có 5 điểm cực trị. – VD
Câu 3: Cho hàm số f (x) liên tục trên và có bảng xét dấu như sau: C
Tìm tất cả các giá trị của m để đồ thị hàm số f (| x | +m) có 7 điểm cực trị. A. m < 2. − B. m ≥ 2. − C. m < 3. D. 2 − ≤ m ≤ 3. Lời giải Chọn A
Từ bảng xét dấu của f (x) ta có dạng đồ thị của f (x) : NHÓ M T OÁN VD – VD C
Đồ thị hàm số f (| x | +m) có được bằng cách tịnh tiến đồ thị hàm số f (x) theo vectơ v = (− ; m 0)
, sau đó lấy đối xứng phần đồ thị của f (x + m) với x ≥ 0 qua trục Oy .
Vậy để đồ thị hàm số f (| x | +m) có đúng 7 điểm cực trị thì m < 2 − .
https://www.facebook.com/groups/toanvd.vdc Trang 33
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số
Câu 4: Cho hàm số f (x) liên tục trên và có bảng xét dấu như sau: NHÓ M T
Số điểm cực trị của đồ thị hàm số g(x) = f (| 2x − 3| 2 − ) là OÁN A. 5. B. 4. C. 3. D. 7. V Lời giải D – Chọn A VD C 2(2x −3)
g '(x) = (| 2x − 3| 2
− )'. f '(| 2x − 3| 2 − ) =
. f '(| 2x − 3| 2 − ) | 2x − 3| x = 5 / 2 | 2x − 3| 2 − = 0 x =1/ 2 g '(x) = 0 ⇔ ⇔ | 2x −3| 2 − = 2 x = 7 / 2 x = 1/ − 2 BBT: NHÓ M T OÁN VD
Vậy đồ thị hàm số đã cho có 5 điểm cực trị . – VD
Câu 5: Xét các số thực c > b > a > 0 . Cho hàm số y = f (x) có đạo hàm liên tục trên và có bảng xét C
dấu của đạo hàm như sau: Đặt ( ) = ( 3 g x
f x ) . Số điểm cực trị của hàm số y = g (x) là A. 3 B. 7 C. 4 D. 5 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc Trang 34
NHÓM TOÁN VD–VDC Các dạng toán về hàm ẩn liên quan đến cực trị của hàm số 2 x = 0 Đặt ( ) = ( 3 h x
f x ) , h′(x) 2 = x f ′( 3 3
x ) , h′(x) 2 = ⇔ x f ′( 3 0 3 x ) = 0 ⇔ f ′ ( 3 x ) = 0 NHÓ x = 0 x = 0 3 x = 0 3 M x = a 3 ⇔ x = a ⇔ . Ta có ( ) = ( 3 g x f x ) = ( 3
f x ) = h( x ) . T 3 x = b OÁN 3 x = b 3 3 = x x c = c V D –
BBT của hàm số g′(x) VD C
Số điểm cực trị của hàm số y = g (x) là 5. NHÓ M T OÁN VD – VD C
https://www.facebook.com/groups/toanvd.vdc Trang 35
Document Outline
- SP-CỰC TRỊ hàm ẩn phần 1
- SP-CỰC TRỊ hàm ẩn phần 2
- SP-CỰC TRỊ hàm ẩn phần 3
- SP-CỰC TRỊ hàm ẩn phần 4
- SP-CỰC TRỊ hàm ẩn phần 5




