
MỤC LỤC
Trang
Chương I. MỘT SỐ PHƯƠNG PHÁP GIẢI TOÁN
Chủ đề 1 Kỹ thuật biến đổi tương đương 3
Chủ đề 2
Sử dụng các tính chất của tỉ số, tính chất giá trị tuyệt đối và tính
chất của tam thức bậc hai trong chứng minh bất đẳng thức
44
1. Sử dụng tính chất của tỉ số 45
2. Sử dụng tính chất giá trị tuyệt đối 54
3. Sử dụng tính chất tam thức bậc hai. 59
Chủ đề 3 Chứng minh bất đẳng thức bằng phương pháp phản chứng 68
Chủ đề 4
Chứng minh các bất đẳng thức về tổng, tích của dãy số - Phương
pháp quy nạp
86
Chủ đề 5 Kỹ thuật sử dụng bất đẳng thức CAUCHY 117
1. Kỹ thuật chọn điểm rơi trong đánh giá từ trung bình cộng sang
trung bình nhân
118
2. Kỹ thuật chọn điểm rơi trong đánh giá từ trung bình nhân sang
trung bình cộng.
141
3. Kỹ thuật ghép cặp trong bất đẳng thức Cauchy 161
4. Kỹ thuật thêm bớt 175
5. Kỹ thuật Cauchy ngược dấu 191
6. Kỹ thuật đổi biến số 199
Chủ đề 6 Kỹ thuật sử dụng bất đẳng thức BUNHIACOPXKI 220
1. Kỹ thuật chọn điểm rơi 221
2. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng cơ bản 236
3. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng phân thức 252
4. Kỹ thuật thêm bớt 275
5. Kỹ thuật đổi biến trong bất đẳng thức Bunhiacopxki 289
Chương II. MỘT SỐ KỸ THUẬT GIẢI TOÁN ĐẶC SẮC
Chủ đề 7 Ứng dụng nguyên lý DIRICHLET trong chứng minh bất đẳng thức 307
Chủ đề 8 Phương pháp hệ số bất định trong chứng minh bất đẳng thức 319
Chủ đề 9 Ứng dụng một hệ quả của bất đẳng thức SCHUR 333
Chủ đề 10 Ứng dụng của đạo hàm trong chứng minh bất đẳng thức và bài toán 344

tìm cực trị.
1. Dồn biến nhờ vận dụng kỹ thuật sử dụng các bất đẳng thức kinh
điển
344
2. Dồn biến nhờ kết hợp với kỹ thuật đổi biến số. 367
3. Dồn biến nhờ kết hợp với kỹ thuật sắp thứ tự các biến 382
4. Phương pháp tiếp tuyến 389
5. Khảo sát hàm nhiều biến số 393
6. Kết hợp với việc sử dụng Bổ đề 398
7. Vận dụng kỹ thuật dồn biến cổ điển 405
Chương III. TUYỂN CHỌN MỘT SỐ BÀI TOÁN BẤT ĐẲNG THỨC
Chủ đề 11 Một số bất đẳng thức hay và khó 409
Chủ đề 12
Một số bất đẳng thức trong các đề thi học sinh giỏi, thi TSĐH và
tuyển sinh lớp 10 chuyên toán.
649

MỘT SỐ KIẾN THỨC CƠ BẢN VỀ BẤT ĐẲNG THỨC
I. Định nghĩa
Giả sử A và B là hai biểu thức bằng số hoặc bằng chữ. Khi đó
+
AB;AB;AB;AB
được gọi là các bất đẳng thức.
+ Các bất đẳng thức trên được viết lại như sau
A B 0; A B 0; A B 0; A B 0
+ Một bất đẳng thức bất kì có thể đúng, cũng có thể sai.
Quy ước: Khi nói về một bất đẳng thức mà không nói gì thêm thì ta hiểu đó là một bất đẳng thức
đúng.
II. Tính chất cơ bản của bất đẳng thức
+ Tính chất giao hoán
Với các số thực A và B bất kì, ta luôn có
AB BA
+ Tính chất bắc cầu
Với các số thực A, B, C bất kì, ta luôn có
AB,BC AC
+ Tính chất liên hệ với phép cộng
- Với các số thực A, B và M bất kì, ta luôn có
AB AMBM
- Với các số thực A, B, C, D bất kì , ta luôn có
AB;CD ACBD
AB;CD ADBC
+ Tính chất liên hệ với phép nhân
- Với các số thực A, B bất kì, ta luôn có
AB;M0 A.MB.M
AB;M0 A.MB.M
- Với các số thực A, B, C, D bất kì , ta luôn có
0AB
0A.CB.D
0CD
+ Tính chất liên hệ với lũy thừa
- Với các số thực A, B bất kì, ta luôn có
nn
AB0 A B 0 , với n là số thực dương.
nn
AB A B , với n là số tự nhiên lẻ.
nn
AB A B 0, với n là số tự nhiên chẵn.
mn
mn0;A1 A A
mn
mn0;0A1 A A
+ Tính chất liên hệ với tính nghịch đảo
- Với các số thực dương A, B bất kì, ta luôn có
11
AB
AB
III. Một số bất đẳng thức cơ bản cần nhớ
+
2
A0
với A

+
2k
A0 với A và k là số tự nhiên
+
A0 với A
+
AB A B
+
AB A B

Chương I – MỘT SỐ PHƯƠNG PHÁP CHỨNG MINH BẤT ĐẲNG THỨC
Nội dung cơ bản của chương I gồm:
Giới thiệu các phương pháp chứng minh bất đẳng thức.
Nêu một số tính chất liên quan, một số lưu ý của các phương pháp chứng minh bất đẳng thức trên.
Giới thiệu các bài tập mẫu cùng quá trình phân tích, suy luận để tìm ra các lời giải và các lời giải được
trình bày cụ thể.
Giới thiệu một số bài tập tự luyện.
Chủ đề 1
MỘT SỐ KỸ THUẬT BIẾN ĐỔI TƯƠNG ĐƯƠNG
1. Kiến thức cần nhớ
Giả sử ta cần chứng minh bất đẳng thức AB . Tư tưởng của phương pháp là biến đổi tương
đương bất đẳng thức trên thành một bất đẳng thức đúng mà phổ biến là các dạng sau:
+ Sử dụng định nghĩa bất đẳng thức:
AB AB0
+ Dạng tổng bình phương:
222
AB mX nY kZ 0 , với các số m, n, k dương.
+ Dạng tích hai thừa số cùng dấu:
AB X.Y0 hoặc
2n
AB X.Y0
+ Xây dựng các bất đẳng thức từ các điều kiện ban đầu: Nếu
x, y, z [a, b]
thì ta nghĩ ngay tới
một trong các bất đẳng thức đúng sau đây
xaxb 0;xayaza 0;xbybzb 0
Một số đẳng thức cần nhớ
+
22
2
2222
ab ab
ab a 2abb;a b
22
+
2
222
abc a b c 2ab2bc2ca
+
222222
a b b c c a a b ab b c bc c a ca 2abc
+
222222
abcabbcca abab bcbc caca 3abc
+
a b b c c a abc a b c ab bc ca
+
a1b1c1 abcabbccaabc1
+
a1b1c1 abc abbcca abc1
+
333 222
abc3abcabcabcabbcca
+
3
333
abc a b c 3abbcca
+
222 3332 22 22 2
abcabc abcababbcbccaca
Một số bất đẳng thức cơ bản
+
2
22 22
a b 2ab; 2 a b a b 4ab

+
2
22
3a b
abab
4
+
222
abcabbcca
+
2
222
3a b c a b c 3ab bc ca
+
2
444
3 a b c ab bc ca 3abc a b c
+ Bất đẳng thức tam giác
bc a bc
abc0
ca b ca bca 0
cab 0
ab cab
Với a, b, c là ba cạnh của một tam giác.
Một số kỹ thuật cơ bản trong phép biến đổi tương đương
+ Kỹ thuật xét hiệu hai biểu thức.
+ Kỹ thuật sử dụng các hằng đẳng thức.
+ Kỹ thuật thêm bớt một hằng số, một biểu thức.
+ Kỹ thuật đặt biến phụ.
+ Kỹ thuật sắp thứ tự các biến.
+ Kỹ thuật khai thác tính bị chặn của các biến.
2. Một số ví dụ minh họa
Ví dụ 1. Cho a, b, c là các số thực bất kì. Chứng minh rẳng:
222
222
a) a b c ab bc ca
b) a b c 3 2 a b c
Phân tích: Các bất đẳng thức trên khá quen thuộc, ta có thể giải bằng cách xét hiệu vế trái và vế phải rồi
phân tích thành tổng các bình phương.
Lời giải
a) Xét hiệu hai vế của bất đẳng thức
222222
222
222
a 2ab b b 2bc c c 2ca a
abc abbcca
2
ab bc ca
0
2
Suy ra
222
abcabbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
b) Xét hiệu hai vế của bất đẳng thức
222 2 2 2
222
abc32abca2a1b2b1c2c1
a1 b1 c1 0
Suy ra
222
abc32abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 2. Cho a, b, c là các số thực bất kì. Chứng minh rẳng:

2
222
abc abc
33
Phân tích: Đây là một bất đẳng thức khá quen thuộc, ta có thể giải bằng cách xét hiệu vế trái và vế phải
rồi phân tích thành tổng các bình phương.
Lời giải
Xét hiệu hai vế của bất đẳng thức
2
222
2
222
222
3a b c a b c
abc abc
a
33 9
ab bc ca
9
Suy ra
2
222
abc abc
33
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Nhận xét: Qua hai ví dụ trên ta nhận thấy khi biến đổi tương đương bất đẳng thức bậc hai thường xuất
hiện các đại lượng
22 2
;;ab bc ca với điều kiện dấu đẳng thức xẩy ra tại abc. Do đó
trước khi biến đổi bất đẳng thức ta nên dự đoán dấu đẳng thức xẩy ra để từ đó có hướng đi hợp lí.
Ví dụ 3.
Cho a, b, c là các số thực bất kì. Chứng minh rẳng:
22222
abcdeabcde
Phân tích: Bất đẳng thức cần chứng minh có hình thức tương tự như các bất đẳng thức trên, ta có thể giải
bằng cách xét hiệu vế trái và vế phải rồi phân tích thành tổng các bình phương. Để được các tích
ab, ac, ad, ae
vào trong bình phương ta cần ghép a với b, c, d, e, và vì vai trò của b, c, d, e như nhau nên
ta có thể nghĩ đến việc biến đổi như sau
22222
22 22
a b c d e abcde
akb akc akd ake 0
Trong trường hợp trên ta có thể chọn
k2 , tức là ta phải nhân hai vế với 4.
Lời giải
Xét hiệu hai vế của bất đẳng thức
22222
a b c d e abcde
22222
22222222
22 22
4abcde 4abacadae
4
a 4ab 4b a 4ac 4c a 4ad 4d a 4ae 4e
4
a2b a2c a2d a2e
0
4
Suy ra
22222
a b c d e abcde
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
a2b2c2d2e.

Nhận xét: Với bất đẳng thức trên, ngoài phép biến đổi tương đương ta còn có thể dùng tính chất của tam
thức bậc hai để chứng minh.
Ví dụ 4.
Cho a, b, c là các số thực thỏa mãn điều kiện
a, b, c 1
. Chứng minh rẳng:
22 333
11 2 111 3
a) b)
1ab 1abc
1a 1b 1a 1b 1c
Phân tích: Để ý ta thấy, mẫu của các biểu thức xuất hiệt các bình phương, ý tưởng chứng minh bất đẳng
thức trên là xét hiệu và phân tích làm xuất hiện các bình phương. Chú ý đến giả thiết
a, b 1 ab 1 0 .
Lời giải
a) Xét hiệu hai vế của bất đẳng thức
22 2 2
2
22
112 1111
1ab 1ab 1ab
1a 1b 1a 1b
ab ab1
0
a1b1ab1
Suy ra
22
11 2
1ab
1a 1b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab1.
b) Bất đẳng thức cần chứng minh tương đương với.
333 333
111 3 111 1 4
1 abc 1 abc 1 abc
1a 1b 1c 1a 1b 1c
Áp dụng bất đẳng thức ở câu a ta được
333
33 4
33 4
111 1 2 2
1abc
1a 1b 1c
1ab1abc
44
1abc
1ababc
Suy ra
333
111 3
1abc
1a 1b 1c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 5. Cho a, b, c là các số thực dương thỏa mãn
33
abab. Chứng minh rẳng:
22
abab1
Phân tích: Quan sát bất đẳng thức cần chứng minh ta thấy có biểu thức
22
abab. Trong khi đó giả
thiết lại xuất hiện biểu thức
ab . Vậy mối liên hệ của hai biểu thức này như thế nào? Dễ thấy được
hằng đẳng thức
22 33
aba b ab a b. Do đó một cách rất tự nhiên ta nhân hai vế của giả thiết
với biểu thức
22
abab để làm xuất hiện
33
ab và
22
abab, khi đó ta được
33
22
33
ab
aabb
ab
. Tới đây chỉ cần chứng minh
33
33
ab
1
ab
là xong.
Lời giải
Biến đổi giả thiết ta được

33 332 2 2 2
33
332 2 33 2 2
33
abab abaabb abaabb
ab
abaabb ab aabb
ab
Ta cần chứng minh được
33
33 33 3
33
ab
1abab 02b 0b
ab
Do
b0 hiển nhiên đúng. Nên bất đẳng thức được chứng minh.
Ví dụ 6. Cho a, b là các số thực dương thỏa mãn điều kiện ab . Chứng minh rằng:
22 2
ab 2abb a
Phân tích: Bất đẳng thức có chứa căn bậc hai và các biểu thức trong căn có chứa các bình phương, lại có
thêm điều kiện
ab0
, nên ta bình phương hai vế để biến đổi bất đẳng thức.
Lời giải
Bất đẳng thức cần chứng minh tương đương với:
2
22 2 2
22 22 2 2 2
22 2
ab 2abb a
a b 2 a b . 2ab b 2ab b a
2b a b 2 a b . 2ab b 0
Vì
ab0 nên
ba b 0. Vậy bất đẳng thức được chứng minh
Ví dụ 7. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
444
abcabcabc
Phân tích: Bất đẳng thức trên là một bất đẳng thức cơ bản có vế trái là các lũy thừa bậc chẵn. Để ý ta
thấy
abc a b c ab.bc bc.ca ca.ab
, do đó rất tự nhiên ta nghĩ đến việc biến đổi bất đẳng thức
thành tổng của các bình phương.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
4442 2 2 4 4 4 2 2 2
222
2 2 2 2 2 2 22 2 2 22 2 2 2
222
222
22 22 22
a b c abcbaccab 0 2a 2b 2c 2abc2bac2cab 0
a b 2a b b c 2b c c a 2a c 2a bc 2b ac 2c ab 0
a b b c c a ab bc bc ac ab ac 0
Suy ra
444
abcabcabc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 8. Cho a, b là các số thực dương tùy ý. Chứng minh rẳng:
101022 8844
a bab abab
Phân tích: Để ý ta thấy
10 2 8 4 10 2 8 4
a.a a.a,b.b b.b, do đó ta biến đổi tương đương để thu gọn và
chứng minh bất đẳng thức.
Lời giải
Biến đổi tương đương bất đẳng thức

10 10 2 2 8 8 4 4
12 10 2 2 10 12 12 8 4 4 8 12
a bab abab
aababbaababb
8222 2822 222266
2
22 2 2 4 22 4
ab a b ab b a 0 ab a b a b 0
ab a b a ab b 0
Bất đẳng thức cuối đúng. Vậy ta có điều phải chứng minh.
Ví dụ 9. Cho các số thực a, b, c thỏa mãn điều kiện
abc0
. Chứng minh rằng:
ab 2bc 3ca 0
Phân tích: Từ giả thiết abc0 ta có thể rút một biến theo các biến còn lại, chẳng hạn cab ,
thay vào biểu thức của bất đẳng thức ta được
22
3a 4ab 2b là biểu thức chỉ chứa hai biến và xuất hiện
các bình phương. Đến đây ta tìm cách phân tích thành tổng các bình phương để chứng minh bất đẳng
thức.
Lời giải
Theo giả thiết thì
cab , nên bất đẳng thức đã cho tương ứng với
2
22 2 2 2
ab c 2a 3a 0 ab a b 2b 3a 0
ab 2ab 3a 2b 3ab 0 3a 4ab 2b 0 a 2 a b 0
Từ đó ta có điều phải chứng minh . Dấu đẳng thức xảy ra khi và chỉ khi
abc0.
Ví dụ 10. Chứng minh với các số thực a dương, ta có:
2
2
5a 1
a11
2a 2
a1
Phân tích: Bất đẳng thức cần chứng minh chỉ chứa một biến a, nên thông thường ta sử dụng phương
pháp biến đổi tương đương để chứng minh. Để ý thêm nữa ta thấy, bất đẳng thức chứa các đại lượng
2
a1 và 2a làm ta liên tưởng đến hằng đẳng thức
2
a1 , lại thấy đẳng thức xẩy ra khi a1 nên suy
nghĩ rất tự nhiên là biến đổi tương đương bất đẳng thức làm xuất hiện đại lượng
2
a1 xem có thể
chứng minh bài toán được không. Với
a1 khi đó ta có
2
2
5a 1
a1
;5
22a
a1
và
11 1
5
22
nên
ta chuyển vế để biến đổi bất đẳng thức.
Lời giải
Biến đổi tương đương bất đẳng thức
22
22
22 2
2
2
2
22
2
2
22
5a 1 5a 1
a11a1
50
2a 2 2 2a
a1 a1
a1 5a1 a1
51
00
2a 2 a
a1
2a 1
a1 9a 1
a1 a1
5a a 5
.0. 0
22
aa 1 2a 1
Bất đẳng thức cuối đúng nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
a1 .

Ví dụ 11. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
33 3333
ab bc ca
2a b c
ab bc ca
Phân tích: Quan sát bất đẳng thức cần chứng minh ta nhận thấy những đặc điểm sau:
+ Hai vế của bất đẳng thức cùng có bậc một.
+ Bất đẳng thức cần chứng minh làm ta liên tưởng đến một bất bất đẳng thức khá hay dùng
33
xyxyxy
.
Lời giải
Trước hết ta chứng minh bất đẳng thức
33
xyxyxy
với x, y là các số dương
Thật vậy
2
33 22
x y xy x y x y x y xy xy x y x y 0
Áp dụng bất đẳng thức trên ta được
33 33 33
ab a b bc b c ca c a
abbcca
2a b c
ab bc ca ab bc ca
Suy ra
33 33 33
ab bc ca
2a b c
ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 12. Chứng minh rằng với mọi số thực x ta luôn có
22
2x 1 . x x 1 2x 1 . x x 1
Phân tích: Bất đẳng thức chỉ chứa một biến và có chứa căn bậc hai. Trước hết ta kiểm tra điều kiện xác
định của các căn thức
2
2
13
xx1x 0
24
và
2
2
13
xx1 x 0
24
Nên bất đẳng thức được xác định với mọi x.
Quan sát bất đẳng thức ta thấy nếu thay x bằng
x thì vế trái của bất đẳng thức trở là
2
2x 1 . x x 1 và vế phải của bất đẳng thức là
2
2x 1 . x x 1, khi đó nếu nhân hai vế với
1
thì được
22
2x1.x x1 2x1.x x1
, tức là bất đẳng thức không thay đổi gì cả.
Như vậy ta chỉ cần xét trường hợp x không âm là được.
Với
1
0x
2
, ta thấy vế trái luôn dương và vế phải nhỏ hơn hoặc bằng không nên ta có thể
chia nhỏ các trường hợp
1
0x
2
và
1
x
2
để chứng minh bất đẳng thức.
Lời giải
Vì
2
2
13
xx1x 0
24
và
2
2
13
xx1 x 0
24
Nên bất đẳng thức được xác định với mọi x.
Nếu
x0 , ta đặt
xt,t0
khi đó bất đẳng thức trở thành.

22
22
2t 1 t t 1 2t 1 t t 1
2t 1 t t 1 2t 1 t t 1
Bất đẳng thức cuối này có dạng như bất đẳng thức ở đề bài và quan trọng hơn lúc này ta lại có
t0 . Như vậy, với lập luận này ta thấy rằng chỉ cần xét bài toán trong trường hợp x0 là đủ. Lúc này
có hai khả năng xảy ra :
+ Nếu
1
0x
2
thì
22
2x 1 . x x 1 0; 2x 1 . x x 1 0
suy ra
22
2x1x x1 2x1x x1. Nên bất đẳng thức đúng.
+ Nếu
1
x
2
thì hai vế cùng dương, nên bình phương hai vế ta được
22
22
42 42
2x 1 x x 1 2x 1 x x 1
4x x 3x 1 4x x 3x 1 x 0
Mà
1
x
2
nên bất đẳng thức cuối cùng đúng.
Vậy bất đẳng thức được chứng minh.
Ví dụ 13. Cho các số thực
a, b, c [0, 1]
. Chứng minh rằng:
432
abcabbcac1
Phân tích: Từ giả thiết
a, b, c [0, 1]
ta được
0a,b,c1
, khi đó theo tính chất của lũy thừa ta được
432
aa;bb;cc. Biểu thức ở vế trái của bất đẳng thức được thay bằng đại lượng
abcabbcca
. Cũng từ giả thiết
a, b, c [0, 1]
và biểu thức bên làm ta liên tưởng đến tích
1a1b1c 0
. Do đó ta sử dụng phép biến đổi tương đương để chứng minh bất đẳng thức
trên.
Lời giải
Theo giả thiết
a, b, c [0, 1]
ta có
1a1b1c 0
1 a b c ab bc ac abc 0
1 a b c ab bc ac abc
Cũng từ giả thiết
a, b, c [0, 1] nên abc 0 và
432
aa;bb;cc.
Do đó ta suy ra
432
1 a b c ab bc ac a b c ab bc ac
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1 hoặc
a1;bc0
và các hoán vị.
Ví dụ 14. Chứng minh rằng với mọi số thực khác không a, b ta có:
22
22
abab
ba
ba

Phân tích: Để ý ta thấy
2
22
22
ab ab
2
ba
ba
, do đó ta có thể biến đổi bất đẳng thức thành
2
ab ab
20
ba ba
. Đến đây ta có thể phân tích thành tích rồi quy đồng hoặc đặt biến phụ
ab
t
ba
, chú ý điều kiện t2 .
Lời giải
Bất đẳng thức đã cho tương đương với
2
22
22
a b ab ab ab ab ab
20120
ba ba ba ba ba
ba
Đến đây ta có hai hướng xử lý bất đẳng thức trên.
+ Hướng 1: Biến đổi tương đương tiếp ta được bất đẳng thức
2
22
22
ababab
0
ab
Mà
2
22
22
ab a b
abab 0
2
Do đó bất đẳng thức được chứng minh.
+ Hướng 2: Đặt
ab
t
ba
, khi đó ta được
2
2
ab
t4t2
ba
Khi đó bất đẳng thức cần chứng minh được viết lại thành
t1t2 0.
-
Nếu
t2
, suy ra
t2 0
nên
t1t2 0
.
-
Nếu
t2
, suy ra
t10;t2 0
nên
t1t2 0
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab
Ví dụ 15. Chứng minh rằng với mọi số thực a, b ta có:
22
ab a 2 b 6 12a 24a 3b 18b 36 0
Phân tích: Quan sát bất đẳng thức ta nhận thấy vế trái của có sự xuất hiện các đại lượng
aa 2;bb 6 và chú ý thêm các đại lượng bên ta nhận thấy
2
aa 2 1 a 1 và
2
bb 6 9 b 3 . Đến đây ta thấy có hai ý tưởng chứng minh bất đẳng thức trên.
+ Thứ nhất là ta biến đổi tương đương làm xuất hiện các bình phương
22
a1,b3
.
+ Thứ hai là đặt biến phụ
xaa2;ybb6 và sử dụng điều kiện của biến phụ để chứng
minh.
Lời giải
Cách 1:
Gọi P là vế trái của bất đẳng thức đã cho, ta có
22
22
Paba2b6 12a 24a3b 18b36
a a 2 b b 6 12 3 b b 6 12
bb 6 12 aa 2 3 b 3 3 a 1 2 0

Vậy bất đẳng thức được chứng minh.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
22
ab a 2 b 6 12 a 1 3 b 3 3 0
Đặt
2
2
xaa2 x1 a1 0
ybb6
y9 b3 0
Khi đó bất đẳng thức được viết lại thành
xy 12 x 1 3 y 9 3 0 x 3 y 12 0
Bất đẳng thức cuối cùng luôn đúng vì
x10;y3 0 .
Vậy bất đẳng thức được chứng minh.
Ví dụ 16. Cho a, b, c là các số thực bất kì. Chứng minh rằng:
24 2 22
1019a 18b 1007c 30ab 6b c 2008ca
Phân tích: Quan sát bất đẳng thức cần chứng minh ta thấy vế trái xuất hiện các lũy thừa bậc chẵn và vế
phải xuất hiện tích của hai trong ba biến nên ta nghĩ đến việc biến đổi bất đẳng thức thành tổng các bình
phương. Tuy nhiên vì hệ số khác nhau nên ta cần phải tinh ý khi phân tích.
Sau khi chuyển vế ta phân tích thành
22
2
22
ma b nb c kc a và cần tìm m, n, k sao
cho
m k 1019; n k 18; k m 1007
. Giải hệ điều kiện trên ta tìm được
m 15; n 3; k 1004. Đến đây ta chứng minh được bất đẳng thức.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 422 2 2
22
2
22
15 a 2ab b 3 b 2b c c 1004 c 2ca a 0
15 a b 3 b c 1004 c a 0
Vật bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
2
ab c
.
Ví dụ 17. Cho a, b là các số thực thỏa mãn
a1;b1
. Chứng minh rằng:
ab 1 ba 1 ab
Phân tích: Bất đẳng thức có chứa căn bậc hai và đẳng thức xẩy ra tại
ab2
, do đó ta có các ý tưởng
chứng minh bất đẳng thức sau đây:
+ Thứ nhất là đặt biến phụ
xa1;yb1 để làm mất căn bậc hai và phân tích thành các bình
phương.
+ Thứ hai là khử căn bậc hai bằng một đánh giá quen thuộc
22
xy2xy . Để ý đến chiều bất đẳng thức
và điều kiện dấu bằng xẩy ra tại
ab2 ta đánh giá được
a11 a b11 b
a1 a1.1 ;b1 b1.1
22 22
Lời giải
Cách 1:
Đặt xa1;yb1 , khi đó x0;y0. Bất đẳng thức cần chứng minh được viết lại
thành
22 22
x1yy1y x1y1

22 22
22 2 22 2
22
22
x1yy1y x1y1
x1y12x1yx1y12y1x0
x1y1 y1x1 0
Bất đẳng thức cuối cùng đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
xy1 hay ab2.
Cách 2: Áp dụng một bất đẳng thức quen thuộc ta được
a11 a
a1 a1.1
22
b11 b
b1 b1.1
22
Do đó ta được
ab ab
ab 1 ba 1 ab
22
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
ab2.
Ví dụ 18. Chứng minh rằng với mọi số thực a, b ta có:
44 33 22
2a b ab ab 2ab
Phân tích: Để ý ta thấy, với ab thì dấu đẳng thức xẩy ra nên ta tách các hạng tử để tạo ra nhân tử
chung
2
ab
.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
42244343 22 33
22 2 2
22 22
a2abbaabbab0 ab abab0
ab ab a abb 0 ab 3ab a b 0
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
ab .
Ví dụ 19. Cho a, b là hai số thực khác không. Chứng minh rằng:
22 2 2
222
22
4a b a b
3
ba
ab
Phân tích: Quan sát bất đẳng thức ta nhận thấy khi
22
ab
thì bất đẳng thức xẩy ra dấu bằng và
2
22
22
22 22
ab
ab
2
ba ab
. Nên ta có các ý tưởng biến đổi tương đương bất đẳng thức như sau:
+ Thứ nhất là quy đồng hai về và phân tích làm xuất hiện nhân tử chung
2
22
ab
+ Thứ hai là đặt biến phụ
2
22
2ab
t
ab
, chú ý điều kiện 0t1.
Lời giải
Cách 1:
Bất đẳng thức đã cho tương đương với.

2
22 2 2
22 2 2 4 22 4
222 2 22
22 22
22
22 22
2
22
222 22 2
22 22
22
2
22 22 22
22 4422
22
22 2 2 22 2 2
4a b a b
4a b a b a 2a b b
120 0
ba ab
ab ab
ab ab
11
0ab 0
ab ab
ab ab
ab ab ab
ab abab
00
ab a b ab a b
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi và chỉ khi
ab .
Cách 2: Bất đẳng thức được viết lại thành
2
22
22
222
22
ab
4a b
5
ab
ab
.
Đặt
2
22
2ab
t
ab
, khi đó ta được
0t1
. Suy ra
2
2
22
22
22
ab
ab 4
4
2ab t
ab
Bất đẳng thức cần chứng minh trở thành
2
4
t5t5t40t1t40
t
Bất đẳng thức cuối cùng luôn đúng vì
0t1
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
ab .
Ví dụ 20. Cho các số thực dương
a, b, m, n m n . Chứng minh rằng:
ab2
na mb mb na m n
Phân tích: Nhận thấy bất đẳng thức xẩy ra dấu bằng tại
ab,
do đó một cách tự nhiên ta nghĩ đến biến
đổi bất đẳng thức làm xuất hiện
2
ab , chú ý đến điều kiện mn
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
ma b ma b
a1b1
00
na mb n m nb ma n m
na mb n m nb ma n m
ma b ma b
11 mn
0. 0
n m na mb nb ma n m
na mb nb ma
Vì
a, b 0 và mn nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xảy ra khi
ab
hoặc
mn
.
Ví dụ 21. Cho a, b là các số thực dương tùy ý. Chứng minh rằng:
22
33 22
ab 2 a 2ab
3
2a b 2a b
Phân tích: Quan sát bất đẳng thức ta nhận thấy dấu đẳng thức xảy ra với ab , khi đó rất tự nhiên ta
nghĩ đến biến đổi bất đẳng thức làm xuất hiện đại lượng
2
ab . Mặt khác với ab ta lại có

22
33 22
ab 1 a 2ab
;1
3
2a b 2a b
. Để ý là
21
1
33
, nên ta ta biến đổi bất đẳng thức thành
22
33 22
ab 1 a 2ab
1
3
2a b 2a b
. Tới đây ta quy đồng hai vế và phân tích thành các bình phương.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
22 22
33 22 33 22
22
2
22 22
33 33
2
33 22
2 4
332 2
ab 2 a 2ab ab 1 a 2ab
1
33
2a b 2a b 2a b 2a b
ab 2ab ab
12ab
ab 0
2a b 2a b
32ab 32ab
ab 32a b 2a b 2ab 0
a b 2a 2b 2a b 2ab 0 a b a b 0
Bất đẳng thức cuối cùng luôn đúng.
Vật bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab .
Ví dụ 22. Cho các số thực a , b không đồng thời bằng 0. Chứng minh rằng:
2
22 22
2ab b 3
5
a4b 3a2b
Phân tích: Dấu đẳng thức xảy ra với ab , khi đó
2
22 22
2ab 2 b 1
;
55
a4b 3a2b
. Nên ta ta biến đổi
bất đẳng thức thành
2
22 22
22ab1 b
0
55
a4b 3a2b
. Tới đây ta quy đồng hai vế và phân tích thành
các bình phương.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
22
22 22 22 22
2ab b 3 2 2ab 1 b
0
55 5
a4b 3a2b a4b 3a2b
2222
22 22 22 22
22 22
22
32 23
2a ba 4b 3a ba b
2a 10ab 8b 3a 3b
00
a4b 3a2b a4b 3a2b
a b 2 a 4b 3a 2b 3 a b a 4b 0
a b 9a 21a b 16ab 4b 0 a b 3a 2b 0
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
ab hoặc 3a 2b
Ví dụ 23. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
666 5 5 5
a) a a b a c b b c b a c c a c b 0
b) a b c a b b c c a
Phân tích:

a) Quan sát bất đẳng thức thứ nhất ta nhận thấy
ac ab bc do đó bất đẳng thức lúc này
tương đương với
2
aa b ca c b c 0
. Đến đây chỉ cần sắp thứ tự các biến sao cho
ca c b c 0 là xong.
b) Tương tự như trên ta có
ac ab bc , biến đổi tương đương bất đẳng thức ta được bất
đẳng thức
55 55
aba b acb c 0
. Đến đây ta chỉ cần sắp thứ tự các biến sao cho
55
acb c 0 là xong.
Lời giải
a) Vì vai trò của a, b, c trong bất đẳng thức như nhau nên không mất tính tổng quát ta giả sử
abc0
. Khi đó ta có
2
2
aa b a c ab c b a cc a c b 0
aa b a b b c bb c b a cc a c b 0
aab aabbc abcab cacbc 0
ab abc cacbc 0
Vì abc0 nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
b) Vì vai trò của a, b, c trong bất đẳng thức như nhau nên không mất tính tổng quát ta giả sử
ac0;bc0 . Khi đó ta có
65 65 65 5 5 5
55 5
55 55
aabbbccca0 aabbbccca0
aa b b a b ca cca 0
aba b acb c 0
Vì
ac0;bc0 nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 24. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
bc ca ab
abc
abc
Phân tích: Quan sát bất đẳng thức ta có các nhận xét như sau:
+ Quy đồng hai vế của bất đẳng thức thì vế trái xuất hiện
222
bc ca ab và vế phải xuất hiện
abc a b c ab.bc bc.ca ca.ab . Như vậy chỉ cần chuyển vế trái ta viết được thành tổng các bình
phương
+ Để ý ta thấy
2
ca b
bc ca
2c
ab ab
. Như vậy ta cần nhân hai vế với 2 và ghép tương tự.
Lời giải
Cách 1:
Biến đổi tương đương bất đẳng thức trên như sau

222
222
222
bc ca ab
abc bc ca ab abcabc
abc
2bc 2ca 2ab 2abca b c 0
ab bc bc ca ca ab 0
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Biến đổi tương đương bất đẳng thức trên như sau
22 22 22
222
bc ca ab bc ca ab
abc 2 2abc
abc abc
bc ca ca ab ab bc
2c 2a 2b 0
ab bc ca
cba2ab acb2bc bca2ca
0
ab bc ca
ca b ab c bc a
0
ab bc ca
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 25. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
abc
abc
bca
Phân tích: Nhận thấy
2
2
ab
a
2a b
bb
. Áp dụng tương tự ta được bất đẳng thức cần chứng minh.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222222
222
abc
2a b 2b c 2c a 0
bca
a 2ab b b 2bc c c 2ca a
0
bca
ab bc ca
0
bca
Vì a, b, c là các số thực dương nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 26. Cho a, b là các số thực dương, tìm hằng số k lớn nhất thỏa mãn bất đẳng thức.
22 2 2 2
k1182k
aba b
ab
Phân tích: Vì vai trò của a, b như nhau nên ta dự đoán dấu đẳng thức xẩy ra tại ab , do đó khi biến đổi
bất đẳng thức ta cần làm xuất hiện nhân tử
2
ab
. Khi đó bất đẳng thức trở thành
2
222222
a b a 4ab b a b ka b 0
. Để tìm k lớn nhất ta cho ab , khi đó ta được
44
12a ka 0 k 12. Đến đây ta chỉ cần chứng minh
k12
bất đẳng thức đúng là được.
Lời giải

Bất đẳng thức cần chứng minh tương đương với
22 2 2 2
22 2 2 2 2 2
2
22 2
22 2 2
2
2
22
22
22 2 2
2
222222
k1182k
aba b
ab
k2k1414
0
ab a b
ab ab ab
k a b b a b 3a a b 3a b
0
a b ab aab bab
a b a 4ab b
ka b
0
ab a b a b a b
ab a 4abb a b kab 0
Vì
2
ab 0 nên bất đẳng thức đúng khi và chỉ khi
222222
a 4ab b a b ka b 0
Cho
ab
thì bất đẳng thức trên trở thành
44
12a ka 0 k 12
. Ta chứng minh
k12
là hằng số lớn nhất thỏa mãn bất đẳng thức đã cho
Thật vậy, ta xét các trường hợp sau
+ Với k12 thì ta được
222222
a 4ab b a b ka b 0
.
+ Với
k12 thì bất đẳng thức
222222
a 4ab b a b ka b 0 trở thành
222222
2 2
2
22 22 22 22
a 4ab b a b 12a b 0
a b 4a b 4ab a b 2ab 0 a b 4ab a b 0
Bất đẳng thức cuối cùng hiển nhiên đúng. Vậy hằng số k lớn nhất là 12.
Ví dụ 27. Cho a, b là các số thực dương, tìm hằng số k lớn nhất thỏa mãn bất đẳng thức
33 3 3 3
k11164k
aba b
ab
Lời giải
Biến đổi tương đương bất đẳng thức cần chứng minh ta được
33 3 3 3
k11164k
aba b
ab
33 3 3 3 3 3
2
2222
33 3 3
33
2
2
43 22 34
33 2 2
2
43 22 342 2 33
k4k1818
0
ab a b
ab ab ab
3k a b a b
a b 7b 4ab a 7a 4ab b
0
ba
ab a b ab
ab a 5ab12ab 5ab b
3k a b
0
ab a ab b
a b a 5a b 12a b 5ab b a ab b 3ka b 0
Vì
2
ab 0 nên bất đẳng thức đúng khi và chỉ khi

43 22 342 2 33
a 5a b 12a b 5ab b a ab b 3ka b 0
Cho
ab
thì bất đẳng thức trên trở thành
66
24a 3ka 0 k 8. Ta chứng minh
k8
là
hằng số lớn nhất thỏa mãn bất đẳng thức đã cho. Thật vậy, ta xét các trường hợp sau
+ Với
k8 thì
43 22 342 2 33
a 5a b 12a b 5ab b a ab b 3ka b 0
.
+ Với
k8
thì bất đẳng thức trên được viết lại thành
43 22 342 2 33
a 5a b 12a b 5ab b a ab b 24a b 0
Ta có
44 2222
a b 2a b ; a b 2ab nên
4 3 22 3 4 4 4 2 2 22 22
a 5a b 12a b 5ab b a b 5ab a b 12a b 24a b
Và
22
aabbab
Do đó ta có
43 22 342 2 33
a 5a b 12a b 5ab b a ab b 24a b
Suy ra bất đẳng thức được chứng minh. Vậy hằng số k lớn nhất là 8.
Ví dụ 28. Cho a, b là các số thực dương tùy ý. Chứng minh rằng:
22
22
3a 2ab 3b
22a b
ab
Phân tích: Đẳng thức xẩy ra khi ab , do đó ta cố biến đổi bất đẳng thức làm xuất hiện đại lượng
2
ab . Bất đẳng thức cần chứng minh có chứa căn, nên để xuất hiện nhân tử chung có dạng
2
ab ta
cần chú ý đến phép biến đổi
22
22
2a b a b a b
Khi đó ta có
2
22
22
ab
2a b a b
2a b a b
Lời giải
Ta biến đổi bất đẳng thức cần chứng minh như sau
22
22
22
22
3a 2ab 3b
22a b
ab
3a 2ab 3b
2a b 2 2a b 2a b
ab
22
22
2
22
4
2
22
22
ab 2ab
0
ab
2a b a b
ab 2a b ab 2ab 0
ab
ab 2a b ab 0 0
2a b a b
Bất đẳng cuối cùng đúng do a , b dương. Vậy bất đẳng thức được chứng minh.
Ví dụ 29. Cho a, b là các số thực dương tùy ý. Chứng minh rằng:
22
2ab a b a b
ab
22
ab

Phân tích: Để ý ta thấy
22
ab 4ab ab
ab 2ab
2ab
2a b 2a b
Lại có
22
2
22
22
22
ab
ab
ab
ab
2
ab
2
ab
ab
ab
2ab
2
2
Do đó ta biến đổi tương đương để chứng minh bất đẳng thức
Lời giải
Bất đẳng thức cần chứng minh được biến đổi như sau
2
22
22
2
22
ab
ab ab2ab 1 1
ab 0
22ab2 ab
ab
ab
2
a b 2a 2b 2 a b 2 ab 0
Vì
2
ab 0 nên ta cần chứng minh
22
2a 2b 2 a b 2 ab 0
Thật vậy, ta có
2
22
22
2
2
2
ab
ab 2a b
2a b a b
ab
ab2ab a b
ab
Do vậy bất đẳng thức trên tương đương với
2
2
22
2
2
22
22
22
22
22
4
22
11
ab 0
2a b a b
ab
ab 2a b ab a b 0
2a b 4ab
ab 2a b 2ab 0 ab 0
2a b 2 ab
2a b
0
2a b 2 ab
Bất đẳng thức cuối này hiển nhiên đúng, Vậy bất đẳng thức được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
ab
.
Ví dụ 30. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
222
a) a b c 2 ab bc ca
b) abc a b c b c a c a b
Lời giải
a) Vì a, b, c là độ dài ba cạnh của một tam giác nên ta có

2
2
2
aa(bc)
0abc
0bac b b(ac)
0cab
cc(ab)
Cộng theo vế ba bất đẳng thức trên ta được
222
abc2abbcca
b) Vì a, b, c là độ dài ba cạnh của một tam giác nên ta có
2
22
a a bc abcabc 0
Chứng minh tương tự ta được
22 2 22 2
bb(ca)0;cc(ab)0
Nhân vế các bất đẳng thức ta được
222
222 2 2 2
222
222
abc a b c b c a c a b
abc a b c b c a c a b
Mà ta lại có
abc0;bca 0;cab0
Nên từ bất đẳng thức trên ta được
abc a b c.b c a.c a b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Nhận xét: Bất đẳng thức
abc a b c b c a c a b không chỉ đúng với a, b, c là các cạnh
của một tam giác, mà nó còn đúng cho a, b, c là các số thực dương bất kì. Bât đẳng này là một trường
hợp của bất đẳng thức Schur. Trong phần Phụ lục 3, ta sẽ bàn nhiều về bất đẳng thức này hơn.
Bài 31.
Cho a, b, c là độ dài ba cạnh của tam giác chứng minh rằng:
222
333
ab c bc a ca b a b c
Lời giải
Biến đổi tương đương bất đẳng thức trên ta được
222
333
222
333
222
222
ab c bc a ca b a b c
ab c bc a ca b a b c 0
abc a bca b cab c 0
abcabca bcabcab cabcabc 0
abccabcab 0
Do a, b, c là độ dài ba cạnh trong một tam giác nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh.
Ví dụ 32. Cho a, b, c là các số thực dương thỏa mãn abc1. Chứng minh rằng:
a bc b ca c ab 1 ab bc ca
Phân tích: Quan sát bất đẳng thức ta có các nhận xét như sau:
+ Dự đoán đẳng thức xẩy ra khi
1
abc
3
.

+ Khi thay 1 bằng
abc
vào bất đẳng thức và chuyến vế thì ta được các nhóm
abca bc;bcab ca;cabc ab
. Vì vai trò a, b, c như nhau nên ta dự đoán
mỗi nhóm trên không âm. Để chứng minh dự doán trên ta có thể bình phương làm mất căn bậc hai rồi
biến đổi tương đương thành tổng các bình phương.
+ Để ý giả thiết
abc1
, khi đó ta có
abc abac
. Dễ dàng nhận ra
abac a bc. Như vậy chỉ cần áp dụng tương tự cho hai trường hợp còn lại thì bất đẳng
thức được chứng minh.
Lời giải
Cách 1:
Bất đẳng thức cần chứng minh tương đương với
a bc b ca c ab a b c ab bc ca
abca bc bcab ca cabc ab 0
Ta cần chứng minh
a bc a bc 0; b ca b ca 0; c ab c ab 0
Thật vậy, ta có
2
2
a bc a bc 0 a bc a bc a bc a 2a bc bc
1a2bc abca2bc b c 0
Chứng minh tương tự ta được
bca b ca 0; cabc ab 0
.
Đến đây bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Cách 2: Kết hợp với giả thiết
abc1
ta có
abc abac;bca abbc;cab cabc
Khi đó bất đẳng thức được viết lại thành
abac abbc cabc 1 ab bc ca
Mặt khác ta có
22
2
abac a bc a abbccaa 2abcbc
bc2bc b c 0
Chứng minh tương tự ta được
bcab b ca; cabc c ab
Cộng theo vế các bất đẳng thức trên ta được
abac abbc cabc abc ab bc ca
Hay
abac abbc cabc 1 ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ví dụ 33. Cho a, b, c là các số thực không âm. Chứng minh rằng:

222
abca bca b ca bc 3abc
Phân tích: Quan sát bất đẳng thức ta có những nhận xét sau:
+ Dễ thấy đẳng thức xẩy ra khi
abc và vai trò các biến là như nhau.
+ Để ý ta thấy
2
abcabca aabac
, như vậy bất đẳng thức được viết lại thành
aa b a c bb c b a ca c b c 0
, là bất đẳng thức được chứng minh ở Ví dụ
23.
+ Để đơn giản hóa bất đẳng thức ta có thể sử dụng cách đặt biến phụ:
xbca;ycab;zabc
Khi đó bất đẳng thức được viết lại thành
222
xyz yzx zxy 3xyyzzx
444 8
Chú ý đến đẳng thức
222222
x y y z z x x y xy y z yz z x zx 2xyz ta có thể
biến đổi tương đương để chứng minh bất đẳng thức trên.
Lời giải
Cách 1:
Vai trò của a, b ,c là như nhau nên có thể giả thiết
abc0
.
Bất đẳng thức đã cho tương đương với
222
2
abc a b c a abc b c a b abc c a b c 0
aa b a c bb c b a ca c b c 0
abaac bbc cacbc 0
ab abc cacbc 0
Vì
abc0 nên
abc0;acbc 0 , suy ra bất đẳng thức cuối cùng luôn đúng. Do
đó bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc hoặc
ab;c0
và các hoán vị.
Cách 2: Đặt xbca;ycab;zabc . Khi đó ta được
yz zx xy
a;b;c
222
Bất đẳng thức cần chứng minh được viết lại thành
222
xyz yzx zxy 3xyyzzx
444 8
Biến đổi tương đương bất đẳng thức trên như sau
222
222222
xyz yzx zxy 3xyyzzx
444 8
2xyxy yzyz zxzx 6xyz 3xyyzzx
2x yy zz x 8xyz 3x yy zz x
8xyz x y y z z x
Ta cần chứng minh
8xyz x y y z z x
Thật vậy, áp dụng một bất đẳng thức quen thuộc ta được

xy2xy;yz2yz;zx2zx
Nhân theo vế các bất đẳng thức trên ta được
8xyz x y y z z x
.
Do đó bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc hoặc
ab;c0
và các hoán vị.
Ví dụ 34. Cho các số thực
a, b, c [-1, 2]
và abc0. Chứng minh rằng:
222
222
222
a) a b c 6
b) 2abc a b c 2abc 2
c) a b c 8 abc
Phân tích:
a) Từ điều kiện
a, b, c [-1, 2]
, để tạo ra
2
a ta có thể sử dụng các bất đẳng thức
a1a2 0, áp dụng tương tự và để ý đến giả thiết abc0
b) Để chứng minh được bất đẳng thức ta cần làm như thế nào để vừa có thể tạo ra
222
abc
vừa
làm xuất hiện tích
abc . Để ý giả thiết abc0 có thể biến đổi tương đương thành
222
abc
ab bc ca
2
. Như vậy trong bất đẳng thức có thêm sự xuất hiện của ab bc ca. Từ
điều kiện
a, b, c [-1, 2]
ta cũng nên để ý đến bất đẳng thức
a1b1c1 0.
c) Cũng tương tự như câu b nhưng trong bất đẳng thức ở câu c có sự xuất hiện của biểu thức
8abc nên ta lại chú ý đến
a2b2c2 0.
Lời giải
a) Do a, b, c [-1, 2] nên ta có
a1a2 0 hay
2
aa2.
Chứng minh tương tự ta được
22
bb2;cc2 .
Cộng theo vế các bất đẳng thức trên và kết hợp với giả thiết
abc0 ta được
222
abcabc66
Vậy bất đẳng thức được chứng minh.
b) Trước hết ta chứng minh
222
abc2abc2
Do
a, b, c [-1, 2] nên ta có
a1b1c1 0
Hay
abc ab bc ca a b c 1 0 abc ab bc ca 1 0
Mặt khác, vì
abc0
nên
2
abc 0
Hay
222
abc
ab bc ca
2
Khi đó ta được
222
222
abc
abc 1 0 a b c 2abc 2
2
Ta cần chứng minh
222
abc2abc .
Thật vậy, vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta có thể giả sử
abc. Từ đó
suy ra
abc
1c 0 c 1
3

Khi đó ta được
2abc 2a.b.c 2a.b
Suy ra
2
222 222 2
a b c 2abc a b c 2a.b a b c 0
Do đó ta có
222
abc2abc
Kết hợp hai kết quả trên ta được bất đẳng thức cần chứng minh chứng minh.
c) Do
a, b, c [-1, 2]
nên ta có
a2b2c2 0
Hay
abc 2 ab bc ca 4 a b c 8 0 abc 2 ab bc ca 8 0
Mà ta có
222
abc
ab bc ca
2
Nên
222
abc a b c 8 0 hay
222
abc8abc .
Vậy bất đẳng thức được chứng minh.
Ví dụ 35. Cho các số thực a, b, c [0, 2] và abc3. Chứng minh rằng:
222
3a b c 5
Lời giải
Đặt x a 1; y b 1; z c 1 , khi đó ta được x, y, z [ 1, 1] và xyz0
Ta có
222
222
222 222
abc x1 y1 z1
xyz2xyz3xyz33
Dấu đẳng thức có khi
xyz0 hay
abc1
.
Mặt khác do
x, y, z [ 1, 1] nên ta có
2
222
222
1x1y1z 1x1y1z 0
2 2 xy yx zx 0 2 x y z x y x 0
xyz2
Suy ra
222
abc5. Đẳng thức xẩy ra khi a2;b1;c0 và các hoán vị.
Kết hợp hai bất đẳng thức trên ta được
222
3a b c 5.
Vậy bài toán được chứng minh.
Ví dụ 36. Cho các số thực a, b, c [0, 2] và abc 3. Chứng minh rằng:
333
3 a b c 3a1b1c1 9
Lời giải
Đặt
x a 1; y b 1; z c 1
, khi đó ta được x, y, z [ 1, 1] và
xyz 0
Đặt
333
P a b c 3a 1b1c1
, khi đó P được viết lại thành
333
333 222
P x 1 y 1 z 1 3xyz
x y z 3xyz 3x y z 3x y z 3
Mà
xyz 0 nên ta có
333 222
xyz3xyz xyzxyzxyyzxz 0
Do đó
222
P3x y z 3

Mà ta chứng minh được
222
0x y z 2 nên 3P9.
Vậy bất đẳng thức được chứng minh.
Ví dụ 37. Cho các số thực
a, b, c [0, 1]
. Chứng minh rằng:
abc
2
1bc 1ca 1ab
Phân tích: Quan sát bất đẳng thức ta nhận thấy
+ Với
abc0 thì abc0, bất đẳng thức hiển nhiên đúng. Như vậy ta cần tìm cách
chứng minh cho trường hợp
abc0
+ Từ giả thiết
a, b, c [0, 1] và trường hợp abc0 dẫn đến 0a,b,c1.
Khi đó để tạo ta
1bc
ta nghĩ đến bất đẳng thức
1b1c 0 1bc bc
. Để ý vế phải của
bất đẳng thức có thể được viết thành
2a b c
abc
, do đó rất tự nhiên ta nghĩ đến chứng minh bất đẳng
thức
a2a
1bc abc
.
Lời giải
Vì
a, b, c [0, 1]
nên ta có
0a,b,c1
.
+ Xét trường hợp
abc0 suy ra abc0, khi này bất đẳng thức cần chứng minh hiển nhiên
đúng.
+ Xét trường hợp
abc0, khi đó ta có
a1
a1
b1c1 0 bc1bc 0 abc 2bc2
bc 0 0 bc
Khi đó ta có
12 a2a
1bc abc 1bc abc
Chứng minh tương tự ta được
b2bc 2c
;
1ca abcab1 abc
Cộng theo vế các bất đẳng thức trên ta được
abc 2a 2b 2c
2
1bc1ca 1ab abc abc abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab1;c0 và các hoán vị
Ví dụ 38. Cho a, b, c là các số thực dương thỏa mãn điều kiện abc1. Chứng minh rằng:
abc bca cab 3
abcbca cab 2
Phân tích: Để ý từ giả thiết abc1 ta có
abc abac , khi đó bất đẳng thức có thể viết
lại thành
aabc bc babc ca cabc ab
3
2
abac bcba cacb
Đến đây ta quy đồng hai vế và biến đổi tương đương bất đẳng thức, chú ý đến đẳng thức
22 2 222
a b b c c a ab ac bc ba ca cb 2abc
Lời giải
Áp dụng giả thiết abc1 ta được

abcaabc bc abac
Áp dụng tương tự ta được
bca bcab;cab cabc
Khi đó bất đẳng thức cần chứng minh tương đương với
22
2
22 2 222
222
aabc bc babc ca cabc ab
3
2
abac bcba cacb
aabacbcbc bbabccaca
3
ccbcaabab abbcca
2
ab ac bc ba ca cb 6abc
ab c bc a ca b 0
Vậy bất đẳng thứ được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Nhận xét: Trong bất đẳng thức trên, có một kinh nghiệm nên nhớ khi tìm lời giải đó là tìm cách đổi chiều
bất đẳng thức. Cách đơn giản nhất là nhân hai vế với
1 khi đó ta được:
3
2
bc a ca b ab c
abc bca cab
Bây giờ ta chưa biến đổi ngay mà tìm cách triệt tiêu các đại lượng âm trong các biểu thức trước
và đổi dấu vế phải. Để ý ta thấy
2abcbca bc, do vậy chỉ cần cộng 1 vào mỗi phân số rồi quy
đồng là ta triệt tiêu được các đại lượng âm, không những vậy ta còn đổi được dấu bên vế phải, cụ thể là
32 2 2 3
111 3
22
bc a ca b ab c bc ca ab
abc bca cab abc bca cab
Đến đây ta sẽ tìm thấy các hướng khác để xử lí bài toán.
Ví dụ 39.
Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abc3
bc ca ab 2
Phân tích: Bất đẳng thức cần chứng minh là bất đẳng thức Neibizt nổi tiếng, hiện nay có rất nhiều cách
chứng minh cho bất đẳng thức này. Để chứng minh bằng phương pháp biến đổi tương đương ta có các ý
tưởng như sau
+ Thứ nhất ta xét hiệu hai vế và chú ý
a 1 ab ac
bc2
2b c 2b c
, khi đó ta có 6 phân thức.
Dự đoán dấu đẳng thức xẩy ra khi
abc, nên ta ghép hai phân thức làm một nhóm sao cho có thể
phân tích được thành bình phương của hiệu hai trong ba số a, b, c. Để ý là
2
ab
abab
bc ca
bcca
.
+ Thứ hai ta để ý đến biến đổi
aabc
1
bc bc
. Do đó ta cộng vào hai vế của bất đẳng thức với
3, thực hiện biến đổi như trên ta đươc được bất đẳng thức về dạng như sau
111
2a 2b 2c 9
bc ca ab
, đến đây ta có thể đơn giản hóa bất đẳng thức bằng việc đặt
biến phụ
xbc;yca;zab
.

+ Thứ ba là ta tiến hành đặt biến phụ
xbc;yca;zab
ngay từ đầu, khi đó ta được
yzx zxy xyz
a;b;c
222
và bất đẳng thức cần chứng minh thu được ở đây là
yzx zxy xyz
3
xyz
sẽ chứng minh dễ dàng hơn.
Lời giải
Cách 1:
Bất đẳng thức cần chứng minh tương đương với
22 2
a1b1c1
0
bc2 ca 2 ab 2
ab ac bc ba ca cb
0
bc bc ca ca ab ab
abab bc bc ca ca
0
bc ca ca ab ab bc
ab bc cb
0
bcca caab abbc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Bất đẳng thứ cần chứng minh tương đương với
a1b1c19 1 1 1
2a 2b 2c 9
bc 2 ca 2 ab 2 2 bc ca ab
Đặt
xbc;yca;zab
, khi đó bất đẳng thức cần chứng minh trở thành
222
111 xyyzzx
xyz 9 6
xyz yxzxxz
xy yz zx
xy yz xz
2220 0
yx zy zx 2xy 2yz 2zx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 3: Đặt xbc;yca;zab , khi đó ta được
yzx zxy xyz
a;b;c
222
Bất đẳng thức cần chứng minh trở thành
222
yzx zxy xyz
3
xyz
xy yz zx
xy yz xz
2220 0
yx zy zx 2xy 2yz 2zx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 40. Cho a, b, c là các số thực dương thỏa mãn 6a 2b 3c 11. Chứng minh rằng:
2b 3c 16 6a 3c 16 6a 2b 16
15
6a 1 2b 1 3c 1
Phân tích: Quan sát giả thiết và bất đẳng thức cần chứng minh ta nghĩ ngay đến việc đổi biến
x6a1;y2b1;z3c1
, chính việc đổi biến này ta thu được kết quả không thể hợp lý hơn là
xyz14
và bất đẳng thức cần chứng minh trở thành

xy yz zx 111
14 15
yx zy xz xyz
Đến đấy việc chứng minh bất đẳng thức hết sức đơn giản.
Lời giải
Đặt
x6a1;y2b1;z3c1
, suy ra
xyz14
.
Bất đẳng thức cần chứng minh được viết lại thành
y z 14 z x 14 x y 14
15
xyz
xy yz zx 111
14 15
yx zy xz xyz
xy yz zx 111
xyz 15
yx zy xz xyz
xy yz zx
222315
yx zy xz
xy
2
yx
222
xy yz zx
yz xz
220 0
zy zx 2xy 2yz 2zx
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
14
xyx
3
hay
11 11 11
a;b;c
18 6 9
.
Ví dụ 41. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
ab a b 2c bc b c 2a ca c a 2b 0
Phân tích: Với bất đẳng thức trên ta có các ý tưởng chứng minh sau:
+ Thứ nhất là ta khai triển các tích và nhóm các hạng tử với nhau một cách hợp lý, chú ý là
2
22 22
ab ac 2abc a b c 2bc a b c
.
+ Thứ hai là vì a là số thực dương nên ta có
ab a b 2c
ab
2
abc c c
, áp dụng tương tự ta biến
đổi được bất đẳng thức về dạng đơn giản.
Lời giải
Cách 1:
Bất đẳng thức cần chứng minh tương đương với
22 22 22
22 2 2 2 2
222
a b ab 2abc b c bc 2abc c a ca 2abc 0
ab c 2bc bc a 2ca ca b 2ab 0
ab c bc a ca b 0
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
ab a b 2c bc b c 2a ca c a 2b
0
abc abc abc
a b 2c b c 2a c a 2b a b b c c a
06
cab bacbac
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 42. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

2
333
222
2a b c
9a b c
33
abc
abc
Phân tích: Dự đoán dấu đẳng thức xẩy ra tại abc. Khi đó ta có được kết quả đẹp là
2
333
222
2a b c
9a b c
6; 27
abc
abc
, do đó ta rất tự nhiên ta nghĩ đến xét hiệu hai vế của bất đẳng
thức. Hơn nữa ta lại có hai kết quả sau
333 222
2
222 222
2a b c 6abc 2a b c a b c ab bc ca
27 a b c 9 a b c 18 a b c ab bc ca
Đến đây càng thấy yên tâm là đã đi đúng hướng.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
333
222
2a b c
9a b c
6270
abc
abc
222 222
222
222
222
222
222
2a b c a b c ab bc ca 18a b c ab bc ca
0
abc
abc
abc 9
2a b c ab bc ca 0
abc
abc
ab bc ca abca b c 9abc 0
Do
222
ab bc ca 0 nên ta chỉ cần chứng minh
222
333 22 22 22
abca b c 9abc0
abc3abcabc bca cab 6abc0
Bất đẳng thức này đúng vì ta có
222
333
abc ab bc ca
abc3abc 0
2
Và
222
22 2 2 2 2
ab c bc a ca b 6abc ab c bc a ca b 0
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Ví dụ 43. Cho a, b, c là các số thực tùy ý. Chứng minh rằng:
4444
444
abc bca cab abc 28a b c
Phân tích: Bài toán gợi cho ta hằng đẳng thức:
44
4224
xy xy 2x 6xy y
Khi đó ta có
4442
24
4442
24
44
4224
a bc bca 2bc 6abc a
ca b a bc 2bc 6abc a
bc bc 2b 6bc c
Để ý đến bất đẳng thức
222
xyzxyyzzx
Lời giải

Dễ dàng chứng minh được
44
4224
xy xy 2x 6xy y
Áp dụng hằng đẳng thức trên ta được
4442
24
4442
24
44
4224
a bc bca 2bc 6abc a
ca b a bc 2bc 6abc a
bc bc 2b 6bc c
Do đó ta được
4444
22
444 22 2
444 222222
abc bca cab abc
4 a b c 24b c 12a b c b c
4a b c 24ab bc ca
Như vậy ta cần chứng minh
444 222222 444
22 22 22 4 4 4
4 a b c 24 a b b c c a 28 a b c
ab bc ca a b c
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Ví dụ 44. Cho a, b, c là các số thực khác 1 thỏa mãn abc 1 . Chứng minh rằng:
222
222
abc
1
a1 b1 c1
Phân tích: Từ giả thiết abc 1 ta nghĩ đến cách đặt biến phụ
111
a;b;c
xyz
. Khi đó bất đẳng
thức cần chứng minh trở thành
222
111
1
1x 1y 1z
.
Sử dụng các biến đổi cơ bản và giả thiết
xyz 1 ta có các kết quả sau
3xyz
111
1
1x 1y 1z
xy yz zx x y z
3xyz
111
1x1y 1y1z 1z1x xyyzzx xyz
Đến đây ta viết lại bất đẳng thức cần chứng minh thành
2
111 1 1 1
21
1x 1y 1z
1x1y 1y1z 1z1x
Và sử dụng các kết quả trên.
Lời giải
Vì abc 1 nên a, b, c 0 . Đặt
111
a;b;c
xyz
, khi đó xyz 1 và x, y, z 1
Bất đẳng thức cần chứng minh trở thành
222
111
1
1x 1y 1z
Bất đẳng thức trên tương đương với

2
2
2
111 1 1 1
21
1x 1y 1z
1x1y 1y1z 1z1x
32xyz xyyzzx 3 xyz
21
xy yz zx x y z xy yz zx x y z
3xyz 3xyz
12110
xy yz zx x y z xy yz zx x y z
2
3xyz
10
xy yz zx x y z
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Ví dụ 45. Cho a, b, c là các số thực đôi một khác nhau. Chứng minh rằng:
222
222
ab bc ca
2
ab bc ca
Phân tích: Quan sát kĩ bất đẳng thức cần chứng minh ta có các nhận xét như sau
+ Để ý ta thấy
ab 2a ab 2b
1, 1
ab abab ab
, do đó ta có kết quả sau
ab bc ca ab bc ca
111 111
ab bc ca ab bc ca
Để đơn giản hóa bất đẳng thức ta có thể đặt
ab bc ca
x;y;z
ab bc ca
, khi đó ta được
x1y1z1 x1y1z1 hay xy yz zx 1 và bất đẳng thức cần chứng minh
được viết lại là
222
xyz2. Đến đây ta có thể chứng minh được bất đẳng thức
+ Với cách đặt
ab bc
x;y
ab bc
như trên ta có được một kết quả khác như sau
xy 1 a b b c a b b c a c
.1:
xy abbc ab bc ac
Khi đó bất đẳng thức cần chứng minh trở thành
22
2
22
xy 1 xy 1
xy 2 xy 2xy2
xy xy
Đến đây ta cũng có thể chứng minh được bất đẳng thức.
Lời giải
Cách 1:
Đặt
ab bc ca
x;y;z
ab bc ca
.
Khi đó ta có
8abc
x1y1z1
abbcca
Và
8abc
x1y1z1
abbcca
Suy ra
x1y1z1 x1y1z1
2 xy yz zx 2 xy yz zx 1
Bất đẳng thức cần chứng minh trở thành

2
222 222
xyz2 xyz2xyyzzx0 xyz 0
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh
Đẳng thức xẩy ra khi và chỉ khi
xyz0 hay một trong ba số a, b, c bằng 0.
Cách 2: Đặt
ab bc
x;y
ab bc
. Khi đó ta được
xy 1 a b b c a b b c
.1:
xy abbc ab bc
abbc abbc abbc abbc
:
abbc abbc
2ab 2bc a c
2ab 2bc a c
Khi đó bất đẳng thức cần chứng minh trở thành
22
2
22
xy 1 xy 1
xy 2 xy 2xy2
xy xy
Dễ thấy
2
2
xy 1
xy 2xy1
xy
Do đó ta được
2
2
xy 1
x y 2xy 2 xy 1 2xy 2
xy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi một trong ba số a, b, c bằng 0.
Ví dụ 46. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abc3
2abc a2bc ab2c 4
Phân tích: Quan sát bất đẳng thức cần chứng minh ta có thể đưa ra các ý tưởng sau
+ Thứ nhất ta để ý đến biến đổi sau
aabc
1
2a b c 2a b c
. Áp dụng tương tự ta có thể đổi
chiều bất đẳng thức. Đến đây để đơn giản hóa bất đẳng thức ta có thể đặt biến phụ
x 2a b c; y a 2b c; z a b 2c .
+ Đặt biến phụ
x 2a b c; y a 2b c; z a b 2c ngay từ đầu và khi đó ta được bất
đẳng thức
3x y z 3y x z 3z x y 3
4x 4y 4z 4
.
+ Đặt biến phụ
x b c; y a c; z a b và viết lại bất đẳng thức cần chứng minh như sau
yzx zxy xyz 3
4
2y z 2z x 2x y
.
Với các bất đẳng thức ở cả ba ý tưởng trên ta có thể chứng minh tiếp bằng biến đổi tương đương.
Lời giải
Cách 1:
Biến đổi tương đương bất đẳng thức cần chứng minh
abc9
111
2abc a2bc ab2c 4
abc abc abc 9
2abc a2bc ab2c 4
111
4a b c 9
2a b c a 2b c a b 2c

Đặt
x2abc;ya2bc;zab2c xyz4abc
Khi đó bất đẳng thức trên trở thành
222
111 xy yz xz
xyz 9 2 2 2 0
xyz yx zy zx
xy yz zx
0
2xy 2yz 2zx
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Đặt
x2abc;ya2bc;zab2c
Suy ra
3x y z 3y x z 3z x y
a;b;c
444
Bất đẳng thức cần chứng minh được viết lại thành
222
3x y z 3y x z 3z x y 3
4x 4y 4z 4
1x y y z z z 3 x y y z z z
6
4y x z y x x 2 y x z y x x
xy yz zx
xy yz xz
2220 0
yx zy zx 2xy 2yz 2zx
Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 3: Đặt x b c; y a c; z a b
Suy ra
yzx xzy xyz
a;b;c
222
Bất đẳng thức cần chứng minh được viết lại thành
yzx zxy xyz 3 x y z 3
4yzzxxy2
2y z 2z x 2x y
Bất đẳng thức cuối cùng là bất đẳng thức Neibizt.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 47. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
111 bc ca ab
abc
abcbcacab
Phân tích: Bất đẳng thức cần chứng minh thực sự đã gây ra rất nhiều khó khăn khi giải nó. Khi thực hiện
biến đổi tương đương thì ý nghĩ đầu tiên là chuyển vế và xét các hiệu theo nhóm, nhưng ta cần ghép các
nhóm như thế nào cho phù hợp. Để ý một công cụ rất hiệu quả trong lúc bế tắc đó là vai trò các biến như
nhau nên có thể sắp thứ tự các biến. Cho nên ta ghép đại các nhóm như sau
22 2
2
3
22
1ab 1bc 1 ca
acb
cab abc bca
ca cabcabab bcba
babc
ca a bc c ab

Đến đây thì hay rồi, chỉ cần chọn b là số lớn nhất trong ba số a, b, c là bài toán coi như xong. Nói
thật nếu khi ghép theo cách khác và được kết quả khác thì ta có thể sắp thứ tự các biến theo kiểu khác
cũng không sao cả.
Lời giải
Biến đổi tương đương bất đẳng thức như sau
222
22 2
22
3
22
2
3
22
111 bc ca ab
abc
abcbcacab
1ab 1bc 1ca
0
acb
cab abc bca
bcba
11
ca 0
babc
ac ab ca bc
c a c a bc ab ab b c b a
0
babc
ca a bc c ab
Không mất tính tổng quát ta giả sử b là số lớn nhất trong ba số a, b, c khi đó ta được
3
bcba
bc ab ca 0; 0
babc
Do vậy bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 48. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
22 22 2 2
abcabc
bc ca ab
bc ac ab
Phân tích: Bất đẳng thức cần chứng minh có hình thức cồng kềnh và phức tạp, ở đây ta cũng có dấu bằng
xẩy ra tại
abc
nên khi biến đổi tương đương ta thường nghĩ đến các đại lượng
222
ab;bc;ca
. Ta để ý đến việc xét các hiệu
22 2
22 22 2 2
aabbc c
;;
bc ca ab
bc ac ab
Kết quả thu được là
2
22
22 22
2
22
22 22
ab a b ac c a
aa
bc
bc
bcbc bcbc
bc b c ab a b
bb
ca
ac
caca caca
2
22
22 22
ca c a bc b c
cc
ab
ab
abab abab
Khi đó có 6 phân thức rất phức tạp. Đến đây ta chọn các biểu thức cùng tử để ghép cặp vì ghép
các phân thức cùng mẫu lại không cho ta kết quả tốt. Chẳng hạn
22 22
abab abab
bcbc caca
Với các biểu thức như trên ta có thể biến đổi tiếp hoặc tìm cách sắp thứ tự biến.
Lời giải
Xét hiệu hai vế ta được bất đẳng thức

222
22 22 2 2
aabbc c
0
bc ca ab
bc ac ab
Đặt
22 2
22 22 2 2
aa bb c c
A;B;C
bc ca ab
bc ac ab
Ta có
222
2
22
22 22 22
abc ab c
ab a b ac c a
aa
A
bc
bc
b c bc b c bc b c bc
Chứng minh tương tự ta được
22 22 22 22
bc b c ab a b ca c a bc b c
B;C
caca caca abab abab
Khi bất đẳng thức cần chứng minh trở thành
22 22 22 2 2
22 22
ab a b ac c a bc b c ab a b
bcbc bcbc caca caca
ca c a bc b c
0
a b ab a b ab
Đến đây ta có hai hướng chứng minh bất đẳng thức trên
+ Hướng 1: Xét các hiệu sau
2
222
22 2 2 22 22
ab a b a b c ab bc ca
ab a b ab a b
0
b c bc c a ca b c bcc a ca
2
222
22 22 22 22
2
222
22 22 22 22
bc b c a b c ab bc ca
bc b c bc b c
0
caca abab cacaabab
ca c a a b c ab bc ca
caca acca
0
abab bcbc ababbcbc
Cộng theo vế các bất đảng thức trên ta được bất đẳng thức cần chứng minh.
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
+ Hướng 2: Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta có thể giả sử
abc0.
Khi đó ta có
22 2 2 22 2 2
22 22 22 22
22 22 22 22
abab abab
ab ab
ab 0
b c bc c a ca b c bc c a ca
bc b c bc b c
bc bc
bc 0
caca abab caca abab
ca c a ac c a
ca ca
ac 0
a b ab b c bc b c bc a b ab
Cộng theo vế các bất đảng thức trên ta được bất đẳng thức cần chứng minh.
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Một số bài toán khác
Ví dụ 49.
Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222 22 22 22
abcabbcca
bca 2 2 2
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 222222
222
22 22 22
222 2
22
22
22 2 2
222
abc abbccaabc
2a b 2b c 2c a
bca 2222
ab bc ca
ab ab bc bc ca ca
bcc 222222
ab bc ca ab
bcc
22a b 2a b
bc ca
22b c 2b c 22c a 2c a
Aa b Bb c Cc a 0
Với
22
22
22
11
A
b
22a b 2a b
11
B
c
22b c 2b c
11
C
c
22c a 2c a
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
A, B, C 0 . Thật vậy
22
22 22
22a b 2a b
11
A0
b
22a b 2a b 22a b 2a b
Hoàn toàn tương tự ta có
B, C 0 . Vậy bài toán được chứng minh xong.
Ví dụ 50. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
22 22 22
abc
abab bcbc caca
bca
Lời giải
Nhận thấy
2
2
ab
a
2a b
bb
và
2
22
22
3a b
ab
aabb
2
4a ab b 2a 2b
Áp dụng tương tự ta được bất đẳng thức tương đương với

222 2
22
22
22 2 2
222
ab bc ca 3ab
bcc
4a b 2ab 2a b
3b c 3c a
4b c bc 2b c 4c a ca 2c a
Aa b Bb c Cc a 0
Với
22
22
22
13
A
b
4a b ab 2a b
13
B
c
4b c bc 2b c
13
C
c
4c a ca 2c a
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
A, B, C 0 . Thật vậy
22
22 22
13 4abab2ab
A0
b
4a b ab 2a b 4a b ab 2a b
Hoàn toàn tương tự ta có
B, C 0
. Vậy bài toán được chứng minh xong.
Nhận xét: Hai bất đẳng thức trên ngoài phép biến đổi tương đương ta còn có thể chứng minh bằng nhiều
cách khác nhau. Lời giải các cách khác được trình bày trong chủ đề “Tuyển chọn các bất đẳng thức hay
và khó”.
Ví dụ 51.
Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222 222
abc abc
bc ca ab ab bc ca
Lời giải
Ta có
22 22 22
ab bc ca
abbcca 0
ab bc ca
Do đó
222 222
abcbca
ab bc ca ab bc ca
Khi đó ta cần chứng minh
222222222
2a 2b 2c a b b c c a
bc ca ab ab bc ca
Bất đẳng thức trên tương đương với
222 222 222
222
2a b c 2b c a 2c a b
0
bc ca ab
ab ab bc bc ca ca
0
acbc abac abbc
Như vậy bất đẳng thức được chứng minh.
Ví dụ 52. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
22 22 22
222222
ab bc ca 5
2
a 2ab b b 2bc c c 2ca a
Lời giải

Bất đẳng thức cần chứng minh tương đương với
22 22 22
222
222
222
ab ab bc bc ca ca
5
ab bc ca
ab bc ca
2
ab bc ca
Đặt
ab bc ca
x;y;z
ab bc ca
, khi đó bất đẳng thức cần chứng minh trở thành
222
xyz2
Ta có
abbc bcca caab
xy yz zx
abbc bcca caab
abbcca bccaab caabbc
abbcca
abbcca
1
abbcca
Mà
2
xyz 0 , do vậy
222
x y z 2 xy yz zx 2 .
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Ví dụ 53. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
22 22 22
3a b c
ab bc ca
ab bc ca abc
Lời giải
Biến đổi tương đương bất đẳng thức như sau
222
22 2222
22 22 22
222 222
222
222
222
3a b c
ab bc ca
ab bc ca abc
ca b ab c bc a
2a b c 3a b c
ab bc ca
ca b 2ab abc 2bc bca 2ca
abc
ab bc ca
111
2ab bc ca a b c abc
ab bcca
Theo bất đẳng thức dạng
111 9
xyzxyz
ta được
222 222
111 9abc
abc2abc abc
ab bc ca abc
Ta cần chỉ ra được
222
9abc
abc 2abbcca
abc
, bất đẳng thức này tương đương với
333
abc3abcabcbcacab .
Không mất tính tổng quát ta giả sử a là số lớn nhất trong ba số a, b, c. Khi đó ta có

2
333
ab abc cacbc 0
abc3abcabcbcacab
Như vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Ví dụ 54. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
33 33 33
232
5b a 5c b 5a c
abc
ab 3b bc 3c ca 3a
Lời giải
Cách 1:
Ta sẽ chứng minh
33
2
5b a
2b a
ab 3b
với a, b là các số thực dương.
Thật vậy, biến đổi tương đương bất đẳng thức trên ta được
33 2 33 2 32 2
2
332 2
5b a 2b a ab 3b 5b a 2ab 6b a b 3ab
ababab abab 0
Bất đẳng thức cuối cùng luôn đúng, do đó bất đẳng thức trên được chứng minh.
Chứng minh tương tự ta được
33 33
32
5c b 5a c
2c b; 2a c
bc 3c ca 3a
Cộng theo vế các bất đẳng thức trên ta được
33 33 33
232
5b a 5c b 5a c
abc
ab 3b bc 3c ca 3a
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Ta có
33 233 2
32 32 22 2
22222 2
a5b2bab3b ab2ab
aab bab2ab abab
2a b 2ab 2ab a b ab a ab 3b
Do đó ta có
33
2
a5b
2b a
ab 3b
hay ta được
33
2
5b a
2b a
ab 3b
Áp dụng tương tự ta được
33 33
32
5c b 5a c
2c b; 2a c
bc 3c ca 3a
Cộng theo vế các bất đẳng thức trên ta được
33 33 33
232
5b a 5c b 5a c
abc
ab 3b bc 3c ca 3a
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi abc.
Nhận xét: Trong hai cách chứng minh trên, mục đích chung đều là đi chứng minh bất đẳng thức
33
2
5
2
3
ba
ba
ab b
, nhưng vấn đề đặt ra là làm thế nào để tìm ra được đại lượng 2 ba. Câu trả lời sẽ
được trình bày trong phụ lục “Phương pháp hệ số bất định trong chứng minh bất đẳng thức”.
Ví dụ 55.
Cho a, b, c là các số thực thỏa mãn
0a,b,c2
và abc3. Chứng minh rằng:
333
abc9
Lời giải
Cách 1:
Đặt
333
Aa b c
và kết hợp với giả thiết của bài toán ta được

3
333
Aa b c abc 3abbcca
27 3 3 c 3 a 3 b 27 9 ab bc ca 3abc
Mặt khác, do
0a,b,c2 nên
2a2b2c 0 hay
8 4 a b c 2 ab bc ca abc 0
2ab bc ca abc 4a b c 8 4
2ab bc ca abc 4
Khi đó ta được
2A 54 9.2 ab bc ca 6abc 54 9. abc 4 3abc 18 6abc 18
Suy ra
A9
, do đó ta được bất đẳng thức
333
abc9.
Dấu đẳng thức xẩy ra khi và chỉ khi
abc 0
2ab bc ca 4
abc3
Giải hệ trên ta được
a2;b1;c0
và các hoán vị của nó.
Cách 2: Không mất tính tổng quát, ta giả sử a là số lớn nhất. Khi đó ta được
3abc3a , suy ra 1a2. Do đó ta được
a1a2 0
Ta có
33
333333 3 3
Aa b c a b c 3bcbc a bc a 3a 9 a1a2 9
Hay ta được bất đẳng thức
333
abc9
.
Dấu đẳng thức xẩy ra khi và chỉ khi
a2;b1;c0
và các hoán vị của nó.

Chủ đề 2
SỬ DỤNG CÁC TÍNH CHẤT CỦA TỈ SỐ, TÍNH CHẤT GIÁ TRỊ TUYỆT ĐỐI VÀ TÍNH CHẤT
CỦA TAM THỨC BẬC HAI TRONG CHỨNG MINH BẤT ĐẲNG THỨC
A. Kiến thức cần nhớ
1. Một số tính chất của tỉ số
+ Với các số thực dương a, b bất kì, ta luôn có
11
ab
ab
+ Với các số thực dương a, b, c, d bất kì, ta có:
- Nếu
a
1
b
thì
aac
bbc
- Nếu
a
1
b
thì
aac
bbc
- Nếu
ac
bd
thì
aacc
bbdd
2. Một số tính chất của giá trị tuyệt đối trong bất đẳng thức
+
aa;a0
+
ab bab
+
ab
ab0
ab
+
ab a b. Đẳng thức xẩy ra khi và chỉ khi a, b cùng dấu.
+
ab ab. Đẳng thức xẩy ra khi và chỉ khi a, b cùng dấu.
+
abab. Đẳng thức xẩy ra khi và chỉ khi ab0 hoặc ab0.
+ Cho các số thực
12 n
a ,a ,...,a
, thế thì hiển nhiên ta có
12 n 1 2 n
a a ... a a a ... a
+ Cho các số thực khác không bất kì a; b, thế thì hiển nhiên ta có
ab
2
ba
. Đẳng thức xẩy ra khi và chỉ khi ab .
3. Một số tính chất của tam thức bậc hai thường dùng trong bất đẳng thức.
Cho tam thức bậc hai
2
f(x) ax bx c với a0 . Khi đó ta viết được
2
2
2
b
f(x) ax bx c a ax
2a
4a
với
2
b 4ac
Từ đó ta có một số tính chất sau:
Tính chất 1: Đa thức có nghiệm khi và chỉ khi
2
b 4ac 0
Tính chất 2: Nếu
2
b 4ac 0
thì af(x) 0 .
Tính chất 3: Nếu
2
b 4ac 0 và đa thức có hai nghiệm
12 1 2
x;x x x thì
+
af(x) 0 với mọi giá trị
12
xxx .

+
af(x)>0 với mọi giá trị
1
xx hoặc
2
xx .
B. Một số ví dụ minh họa.
1. Sử dụng tính chất của tỉ số.
Ví dụ 1. Cho a, b là các số thực dương bất kì. Chứng minh rằng:
ab
1
2a b a 2b
Phân tích: Để ý ta thấy
ab
1
abab
, như vậy để chứng minh bất đẳng thức ta cần đánh giá được
aabb
;
2a b a b 2b a a b
.
Lời giải
Do a, b là các số dương nên ta có
2abab;a2bab
Từ đó suy ra
aabb
;
2a b a b 2b a a b
Cộng theo vế các bất đẳng thức trên ta được
ababab
1
2ab2ba abab ab
Vậy bài toán được chứng minh.
Ví dụ 2. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
abc
12
abbcca
Phân tích: Quan sát bất đẳng thức kép trên ta nhận thấy khó có thể biến đổi tương đương để chứng minh
bài toán, ở đây ta cũng không cần phải dự đoán dấu đẳng thức xẩy ra. Để ý một chút ta có
abc
1
abc abcabc
, như vậy cần đánh giá được
aa
abc ab
. Dễ nhận thấy
đánh giá đó hiển nhiên đúng, do đó chỉ cần áp dụng tương tự thì bất đẳng thức bên trái được chứng minh.
Để chứng minh được bất đẳng thức bên phải thì ta cần phải đánh giá được
a
ac
abc
ab
, việc này
hoàn toàn có thể thực hiện được nhờ tính chất của tỉ số.
Lời giải
Do a, b, c là các số dương nên ta có
a
1
ab
. Vì vậy theo tính chất của tỉ số ta được
aa
ac
abc
abc ab
Áp dụng tương tự ta có
bb cc
ab bc
abc abc
abc bc abc ca
,
Cộng vế theo vế của ba bất đẳng thức kép trên ta được
abc
12
abbcca
Vậy bài toán được chứng minh.
Ví dụ 3. Cho a, b, c, d là các số thực dương bất kì. Chứng minh rằng:

abcd
12
abc bcd cda dab
Lời giải
Theo tính chất của tỉ số ta có
aaad
1
abc abc abcd
Mặt khác ta lại có
aa
abc abcd
Kết hợp hai bất đẳng thức trên ta được
aaad
abcd abc abcd
Tương tự ta có
bbba
abcd bcd abcd
ccbc
abcd cda abcd
dddc
abcd dab abcd
Cộng theo vế các bất đẳng thức trên ta được.
abcd
12
abc bcd cda dab
Nhận xét: Để chứng minh các bất đẳng thức ta cần tinh ý sử dụng các tính chất của tỉ số. Ngoài ra các
bất đẳng thức trong ở hai ví dụ trên có thể được phát biểu lại như sau: Cho các biểu thức với a, b, c là
các số thực dương.
abc
A
ab bc ca
abcd
B
abc bcd cda dab
Chứng minh A, B không thể nhận các giá trị nguyên.
Ví dụ 4. Cho a, b, c, d là các số thực dương thỏa mãn
ac
bd
. Chứng minh rằng:
22
aabcdc
bd
bd
Phân tích: Để ý ta nhận thấy
22
ac abcd
bd
bd
, đến đây ta áp dụng tính chất của tỉ số để chứng minh
bất đẳng thức.
Lời giải
Từ
ac
bd
suy ra
22
ab cd
bd
, theo tính chất tỉ số ta được
2222
ab ab cd cd c
d
bbdd
Do đó ta có
22
aabcdc
bd
bd
Vậy bất đẳng thức được chứng minh.
Ví dụ 5. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:

abc
1
bc ca ab
Phân tích: Bất đẳng thức cần chứng minh có chứa căn, nhìn chiều bất đẳng thức ta nghĩ đến sử dụng bất
đẳng thức Cauchy. Tuy nhiên để đánh giá được bất đẳng thức theo Cauchy không hề đơn giản tí nào với
những ai mới học bất đẳng thức.
Chú ý đến giả thiết a, b, c là ba cạnh của một tam giác, nó có mối liên hệ như thế nào với
a
bc
,
do
bca nên ta thấy được
a
01
bc
, với kết quả đó ta có thể khử căn bằng đánh giá
aa
bc bc
. Đến đây thì bài toán đươc giải quyết triệt để tương tự như ví dụ thứ nhất.
Lời giải
Vì a, b, c là độ dài ba cạnh của một tam giác nên ta có
aaa
01
bc bc bc
Vì a là số dương nên theo tính chất của tỉ số ta được
aa
bc abc
Do đó ta có
aa
bc abc
Chứng minh tương tự ta được
bb c c
;
ca abc ab abc
Cộng theo vế ba bất đẳng thức trên ta được
abc
1
bc ca ab
Vậy bài toán được chứng minh.
Ví dụ 6. Cho a, b là các số thực dương tùy ý. Chứng minh rằng:
1a b ab a b
2a1 b1 ab1 a1 b1
Phân tích: Để ý ta thấy
a
1
a1
nên có
aa
ab1 a1
và
aab
a1 ab1
, áp dụng tương tự ta
chứng minh được bất đẳng thức.
Lời giải
+ Trước hết ta chứng minh
1a b ab
2a 1 b 1 a b 1
Do a là số thực dương nên ta có
a
1
a1
suy ra
aab
a1 ab1
Chứng minh tương tự ta có
bab
b1 ab1
Cộng vế với vế của hai bất đẳng thức cuối ta được
1a b ab
2a 1 b 1 a b 1
+ Ta chứng minh
ab a b
ab1 a1b1
Do a, b dương ta có
aa
a1 ab1
và
bb
b1 ab1

Cộng vế với vế của hai bất đẳng thức này ta được
ab a b
ab1 a1b1
Kết hợp hai bất đẳng thức trên ta được bài toán cần chứng minh.
Ví dụ 7. Cho
12 n12 n
a ; a ;...; a ; b ; b ;...; b
là các số thực dương. Kí hiệu
12 n 12 n
12 n 12 n
aa a aa a
M Max ; ; ...; ; m Min ; ; ...;
bb b bb b
Chứng minh rằng:
12 n
12 n
a a ..... a
mM
bb....b
Phân tích: Nhận thấy
12 n 12 n
12 n 12 n
aa a aa a
M Max ; ; ...; ; m Min ; ; ...;
bb b bb b
nên ta có
i
i
a
mM
b
với mọi
i1,2, ,n
. Do đó ta được
ii i
mb a Mb , đến đây ta áp dụng cho
i1,2, ,n
thì ta
được bất đẳng thức cần chứng minh.
Lời giải
Vì
12 n 12 n
12 n 12 n
aa a aa a
M Max ; ; ...; ; m Min ; ; ...;
bb b bb b
nên ta được
i
i
a
mM
b
với mọi
i1,2, ,n
.
Suy ra
ii i
mb a Mb với mọi
i1,2, ,n
.
Lần lượt cho i bằng các giá trị
1, 2, , n rồi cộng các theo vế lại với nhau ta được
12 n 12 n 12 n
b b .... b m a a ..... a M b b .... b
Hay
12 n
12 n
a a ..... a
mM
b b .... b
. Vậy bài toán được chứng minh.
Ví dụ 8. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
33 33 33
1111
abc
ababcbcabccaabc
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc. Quan sát bất đẳng thức ta nhận thấy cần
phải thay đại lượng ở các mẫu bên vế trái bởi các đại lượng nhỏ hơn sao cho khi biểu thức thu được vẫn
nhỏ hơn hoặc bằng vế phải. Điều đó có nghĩa là cần tìm vế phải cho bất đẳng thức
33
ababc?
, để
ý trong vế trái của bất đẳng thức ta không đánh giá được gì từ tích abc, cho nên ta tập trung đánh giá
33
ab . Trong vế phải của bất đẳng thức cần chứng minh có chứa tích abc ở mẫu nên khi đánh giá mẫu
vế trái ta cũng cần làm xuất hiện tích abc ở các phân thức, như vậy khi đánh giá
33
ab
cần làm xuất
hiện tích ab, điều này gợi ý cho ta đánh giá rất đẹp
33
ababab . Nếu chứng minh được bất đẳng
thức đó thì ta thu được kết quả là
33
ababab khi đó ta suy ra được đánh giá
33
ababc ababc . Đến đây ta có các đánh giá tiếp theo
33
11 c
ababc
ababc abcabc

Như vậy ta cần tập trung chứng minh
33
ababab , bất đẳng thức này được biến đổi tương
đương thành
2
abab 0
là một đánh giá đúng.
Lời giải
Ta có
33 2 2
22 2 2
2
a b abab aba abb abab
a b a ab b ab a b a 2ab b
abab 0
Suy ra
33 33
33
ababab a b abc ab a b abc
ababc ababc
Từ đó ta được
33
11 c
ababc
ababc abcabc
Chứng minh tương tự ta có
33
33
11 a
bcabc
bc a b c abc a b c
11 b
caabc
acabc abcabc
Cộng theo vế các bất đẳngthức trên ta được
33 33 33
1111
abc
ababcbcabccaabc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Nhận xét: Bất đẳng thức trên là một bất đẳng thức hay. Để chứng minh được nó ta cần chứng minh
33
ab abab
. Nhưng vấn đề là làm sao tìm ra được bất đẳng thức phụ đó. Đầu tiên là do yêu cầu
làm xuất hiện tích ab, kế đến là cần phải làm cho hai vế đồng bậc 3 và cuối cùng là chú ý khi
ab thì
hai vế của bất đẳng thức đó bằng nhau. Khi phân tích bài toán ta cần chú ý đến các yếu tố như đẳng thức
xẩy ra ở đâu, tính đồng bậc của bất đẳng thức, chọn chiều đánh giá như thế nào cho hợp lí,... Tuy nhiên
khi tiến hành các bước phân tích mà giả thiết càng gần với kết luận thì cơ hội càng lớn.
Ví dụ 9. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
22 22 22
1111
2
a2b3b2c3c2a3
Phân tích: Ý tưởng tương tự như ví dụ trên, ở đây ta chú ý đến dấu đẳng thức xẩy ra khi abc1,
như vậy ta cần có các đánh giá sao cho đảm bảo có đẳng thức xẩy ra. Nhận thấy
22 2
ab2ab;b12b nên
22
a2b32abb1 .
Khi đó ta có đánh giá
22
111
2ab b 1
a2b3
. Áp dụng tương tự ta được bất đẳng thức
22 22 22
1111111
2ab b 1 bc c 1 ac a 1
a2b3b2c3c2a3
Vấn đề còn lại là chứng minh được
111
1
ab b 1 bc c 1 ca a 1
. Đây là một đẳng
thức quen thuộc và nhiều hướng để xử lí nó.
Lời giải

Ta có
22 2 2 2
ab2ab;b12ba2b32abb1
Do đó ta được
22
111
2ab b 1
a2b3
Chứng minh tương tự ta có
22 2 2
111 111
;
2bc c 1 2ac a 1
b2c3 c2a3
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
1111111
2ab b 1 bc c 1 ac a 1
a2b3b2c3c2a3
Ta cần chứng minh
111
1
ab b 1 bc c 1 ca a 1
Đến đây ta có hai cách chứng minh đẳng thức trên như sau
Cách 1: Do
abc 1 , nên tồn tại các số dương x, y, z để
xyz
a;b;c
yzx
Khi đó ta có
111 111
ab b 1 bc c 1 ca a 1 x y y z x z
111
zz xx yy
zxy
1
xyz xyzxyz
Cách 2: Do
abc 1 , nên ta được
111 abc a 1
ab b 1 bc c 1 ca a 1 ab b abc abc ac a ca a 1
ac a 1
1
a1ac 1aca caa1
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 10. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
22 2
222
1
a1 b 1 b1 c 1 a1 b 1
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
2
222
a 1 b 1 a b 2a 2 2ab 2a 2
Áp dụng tương tự ta được
222
22 2
222
a1 b 1 b1 c 1 a1 b 1
111
ab a 1 bc b 1 ca c 1
Ta cần chứng minh
111
1
ab a 1 bc b 1 ca c 1
Đến đây ta có hai cách chứng minh đẳng thức trên như sau
Cách 1: Do abc 1 , nên tồn tại các số dương x, y, z để
xyz
a;b;c
yzx
Khi đó ta có

111111
ab a 1 bc b 1 ca c 1 x x y y z z
111
zy xz yx
yz xz yy
1
xy yz zx xy yz zx xy yz zx
Cách 2: Do
abc 1 , nên ta được
111abc1 b
ab a 1 bc b 1 ca c 1 ab a abc bc b 1 cab bc b
bc 1 b
1
bc b 1 bc b 1 1 bc b
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Nhận xét: Các bất đẳng thức trong ví dụ 8, 9 và 10 cho thấy kỹ thuật đánh giá ở mẫu được sử dụng như
thế nào trong chứng minh bất đẳng thức, thực chất của việc đánh giá này là thay thế các mẫu bởi các đại
lượng khác sao cho các đánh giá cùng chiều và đảm bảo dấu đẳng thức xẩy ra. Điều quan trọng là biết
cách chọn các đánh giá phù hợp sao cho càng chặt càng tốt.
Ví dụ 11.
Cho a, b, c là các số thực dương thỏa mãn điều kiện abc 1 . Chứng minh rằng:
ab bc ca
1
ababbcbc caca
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức ta có nhận
xét là tử của các phân thức là các đại lượng ab, bc, ca. Chú ý đến giả thiết
abc 1 ta có thể viết lại phân
thức bên vế trái theo các ý tưởng như
ab 1
a b ab ac bc 1
hoặc là
ab 1
abab 1 1
1
ab
.
Đến đây ta viết được vế trái của bất đẳng thức cần chứng minh thành các biểu thức
111
ac bc 1 ab bc 1 bc ca 1
hoặc
111
11 11 11
111
ab bc ca
và để đơn giản ta có
thể đặt
333
xab;ybc;zca hoặc
333
111
x;y;z
abc
và chú ý đến giả thiết abc 1 dẫn đến
được
xyz 1 , lúc này ta được bất đẳng thức như ví dụ 9.
Lời giải
Để ý với điều kiện
abc 1 , khi đó bất đẳng thức cần chứng minh tương đương với
111
1
11 11 11
111
ab bc ca
Đặt
333
111
x;y;z
abc
, khi đó ta được xyz 1 .
Bất đẳng thức cần chứng minh trở thành
33 33 33
111
1
xy1yz1zx1
Ta chứng minh được
33
x y 1 xy x y xyz xy x y z và áp dụng tương tự ta được
33 33 33
1111111
1
xyzxy yzzx
xy1yz1zx1

Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1
.
Nhận xét: Bất đẳng thức trên là một bất đẳng thức khó, khi tôi phân tích để tìm lời giải thì các câu hỏi
được đặt ra như biến đổi các biểu thức như thế nào để bài toán đơn giản hơn, sử dụng giả thiết như thế
nào đây, thay vì đánh giá cả tử và mẫu ta có quy vế đánh giá mẫu được không. Sau các bước biến đổi
như trên thì bài toán nhìn có vẻ dễ hơn đôi chút và n
ếu tận dụng tốt các lợi thế này thì công việc còn lại
sẽ không gây được khó khăn nữa.
Ví dụ 12. Cho các số thực
a; b; c [0; 1] . Chứng minh rằng:
abc
1
ac b 1 ab c 1 bc a 1
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức ta nhận thấy
không thể trực tiếp đánh giá tử của các phân thức, do vậy ta tìm cách đánh giá mẫu của mỗi phân thức.
Chú ý đến chiều của bất đẳng thức trên, ta cần một đánh giá kiểu
ab c 1 ?
. Giả thiết có gợi cho ta
điều gì? Nên nhớ là khi
a; b; c [0; 1] ta thường thu được các bất đẳng thức dạng
1a1b 0 hay
1ab ab, đến đây ta cộng vào hai vế với c thì được ab c 1 a b c. Lúc này ta có đánh giá
tốt cho việc chứng minh bất đẳng thức là
aa
ab c 1 a b c
. Chỉ cần áp dụng tương tự cho các
trường hợp còn lại là ta hoàn thành chứng minh bài toán.
Lời giải
Vì
a; b [0; 1]
nên ta có
1a1b 0
suy ta 1ab ab
Do đó ta được
ab c 1 a b c
suy ra
aa
ab c 1 a b c
.
Chứng minh tương tự ta được
bbc c
;
ab c 1 a b c bc a 1 a b c
Cộng theo vế các bất đẳng thức trên ta được
abc
1
ac b 1 ab c 1 bc a 1
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 13. Cho a, b, c là các số thực không âm thỏa mãn
abc1. Chứng minh rằng:
222
22 2
1a 1b 1c 7
2
1b 1c 1a
Phân tích: Quan sát bất đẳng thức ta nhận thấy đẳng thức không xẩy ra tại abc mà xẩy ra tại
a1;bc0 và các hoán vị. Trong trường hợp này để dễ có những đánh giá hợp lí ta có thể sắp thứ
tự các biến. Vì đẳng thức xẩy ra tại
a1;bc0
nên không mất tính tổng quát ta sắp thứ tự các biến
bằng cách chọn a là số lớn nhất. Khi đó ta mạnh dạn có các đánh giá kiểu như
22
1b 1;1c 1 mà
vẫn bảo toàn được dấu đẳng thức xẩy ra, các đánh giá này dẫn tới
22
22
22
1a 1b
1a; 1b
1b 1c
. Còn
lại
2
2
1c
1a
cần phải đánh giá như thế nào để cùng chiều với hai đánh giá trước đó. Để ý là sau khi đánh giá
hai phân thức đầu ta thu được
22
ab như vậy ta cần làm xuất hiện
2
c trong đánh giá
2
2
1c
1a
. Để ý đến a

là số lớn nhất nên ta có
2
2
22
1c 1
c
1a 1a
. Kết quả là sau một số bước đánh giá như trên ta thu được
đại lượng
222
2
1
2a b c
1a
, bây giờ nếu biến đổi được thành biểu thức chỉ chứa biến a thì càng
dễ chứng minh hơn. Từ giả thiết
abc1
và chú ý đến
bc0
ta có một đánh giá rất tự nhiên là
22
22
bc bc 1a
. Bây giờ việc chứng minh bất đẳng thức hoàn toàn đơn giản.
Lời giải
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta giả sử a là số lớn nhất trong ba số a, b, c.
Khi đó ta có
22
1b 1;1c 1 .
Do đó
222
222
2222
1a 1b 1c 1
1a; 1b; c
1b 1c 1a 1a
Từ đó ta được bất đẳng thức
222
222
22 2 2
22
22
22
1a 1b 1c 1
2a b c
1b 1c 1a 1a
11
2a bc 2a 1a
1a 1a
Ta cần chứng minh
2
23
2
17
2a 1a a14a 3a1 0
2
1a
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
a1;bc0
và các hoán vị.
Nhận xét: Điểm mấu chốt để tìm ra cách chứng minh bất đẳng thức trên chính là các đánh giá
222
222
2222
1111
1; 1;
1111
abc
abc
bcaa
, việc phát hiện ra các đánh giá đó đòi hỏi phải có
sự suy luận một cách lôgic.
Ví dụ 14. Cho a, b, c là các số thực không âm thỏa mãn
abc
3
1bc 1ca 1ab
.
Chứng minh rằng:
abc3
1abc 1bca 1cab 4
Lời giải
Đặt
abc
x;y;z
1bc 1ca 1ab
, suy ra ta có xyz3
Bất đẳng thức cần chứng minh được viết lại thành
xyz3
1x 1y 1z 4
Mà ta có
xxyyzz
;;
1x 1xyz1y 1xyz1z 1xyz
Cộng theo vế các bất đẳng thức trên ta được
xyz3
1x 1y 1z 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi
a3;bc0 và các hoán vị.
2. Sử dụng tính chất giá trị tuyệt đối.
Ví dụ 15. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
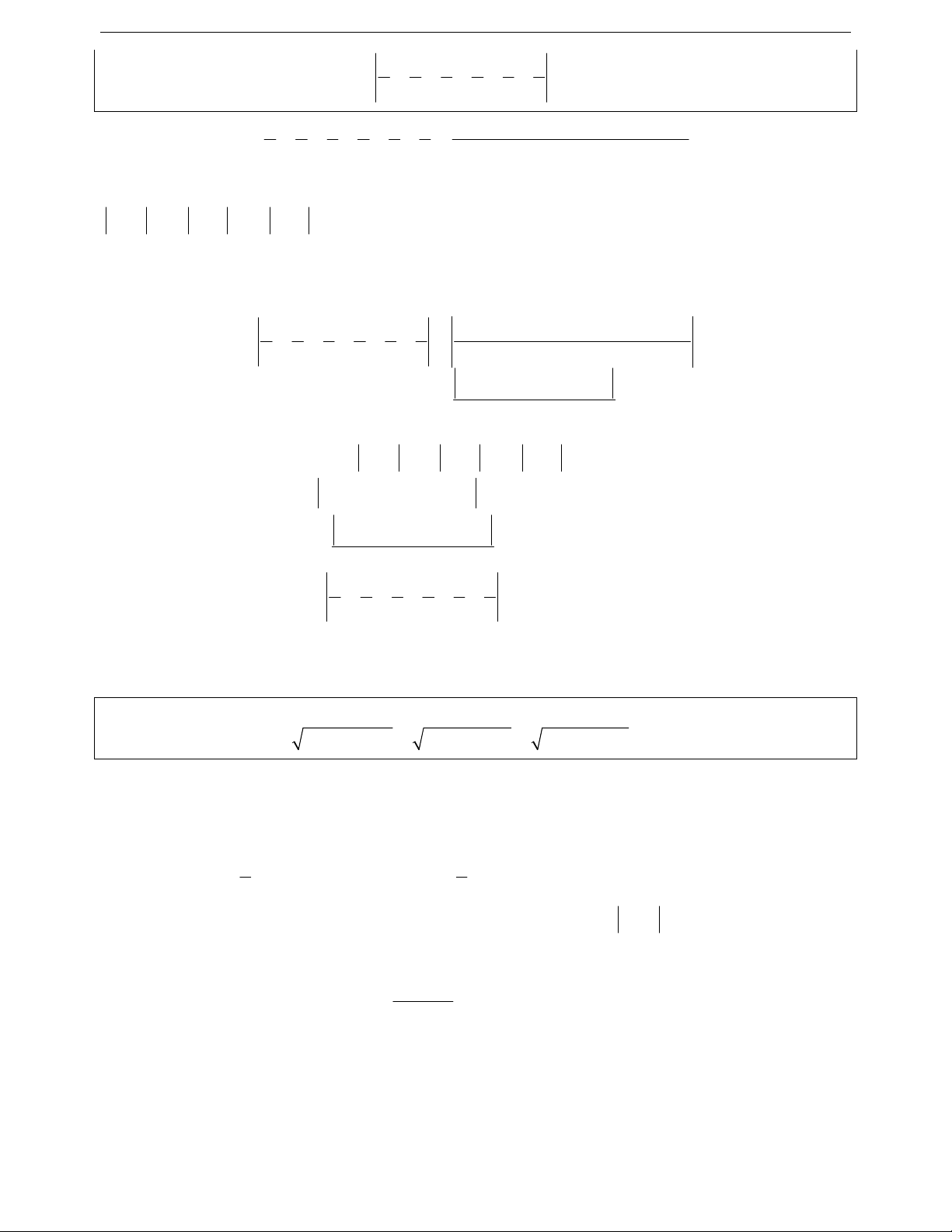
abcbca
1
bcacac
Phân tích: Để ý ta có
222222
abcbcaacbacbabcabc
bcacac abc
, phân tích thành nhân
tử
222222
ac ba cb ab ca bc a b b c c a , mà a, b, c là ba cạnh của một tam giác nên
ab c;bc a;ca b
. Đến đây ta chứng minh được bất đẳng thức.
Lời giải
Ta có
222 222
a b c b c a ac ba cb ab ca bc
bcacac abc
abbcca
abc
Vì a, b, c là ba cạnh của một tam giác nên ta có
ab c;bc a;ca b
Do đó ta suy ra
abbcca abc
Hay
abbcca
1
abc
Suy ra
abcbca
1
bcacac
Vậy bất đẳng thức được chứng minh.
Ví dụ 16. Cho a, b, c là các số thực thỏa mãn abc3. Chứng minh rằng:
222222
aabb bbcc ccaa 3
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát kĩ bất đẳng thức ta có
nhận định là cần phải có một đánh giá kiểu
2
22
aabbkab để khi khử căn ta thu được ab .
Vấn đề là cần xác định giá trị của k để đánh giá trên là đúng, nhớ là đẳng thức xảy ra tại
abc
nên ta
xác định được
1
k
4
, tức là ta có
2
22
1
aabb ab
4
. Một điều nữa cần chú ý là các biến a, b, c là
các số thực bất kì nên khi khử căn ta cần lấy giá trị tuyệt đối và để ý đến
ab ab.
Lời giải
Trước hết ta chứng minh
2
22
ab
aabb
4
.
Thật vậy, bất đẳng thức trên tương đương với
2
22 22 2 2
4ababab2ab 3a2abb 0 3ab 0
Bất đẳng thức cuối cùng đúng nên bất đẳng thức trên được chứng minh.
Từ bất đẳng thức trên ta có
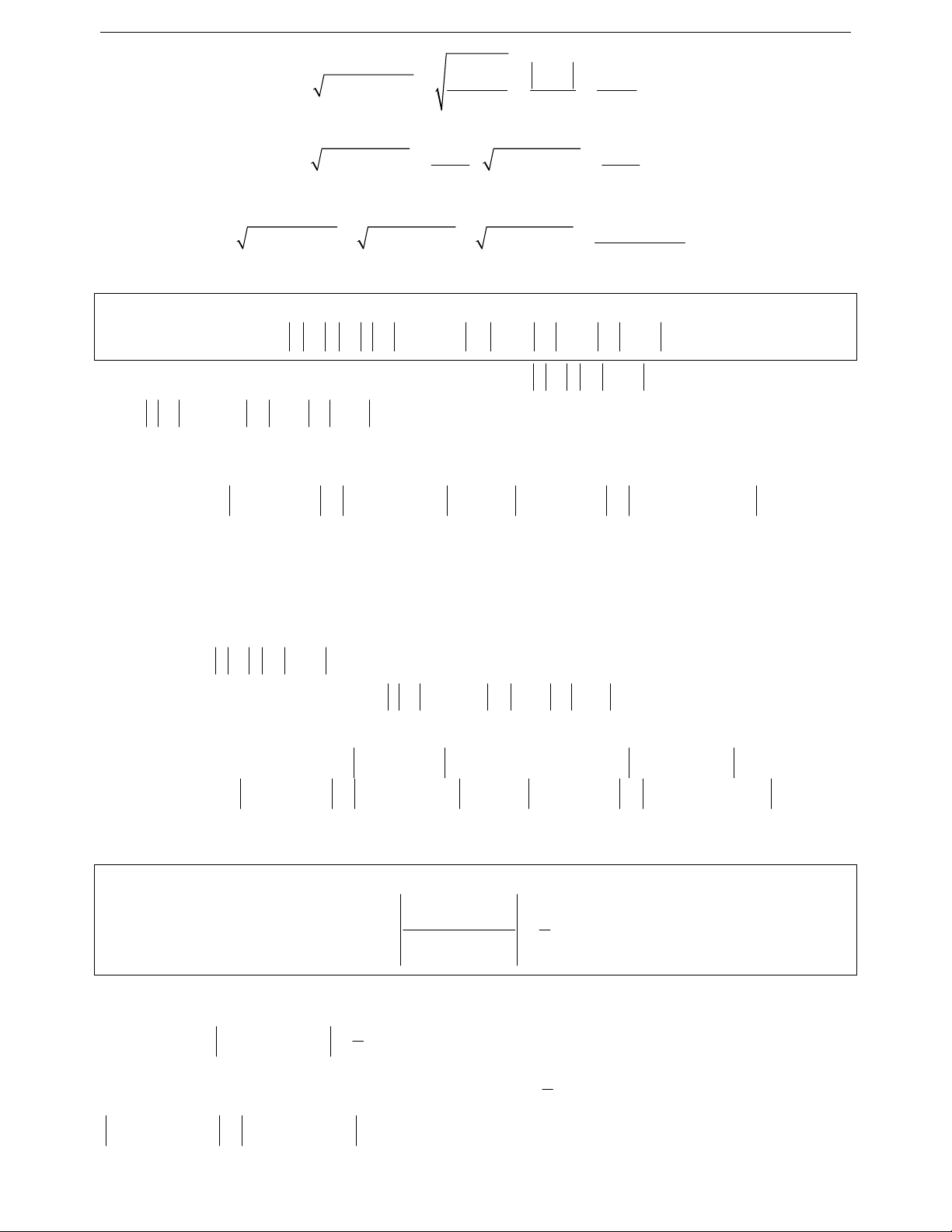
2
22
ab
ab
ab
aabb
422
Chứng minh tương tự ta được
22 22
bc ca
bbcc ;ccaa
22
Cộng theo vế các bất đẳng thức trên ta được
222222
2a b c
aabb bbcc ccaa 3
2
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 17. Cho a, b, c là các số thực bất kì. Chứng minh rằng:
abcabcabbcca
Phân tích: Theo bất đẳng thức giá trị tuyệt đối ta luôn có abab, bây giờ ta tìm cách chứng
minh
c abc bc ca
. Để là mất các giá trị tuyệt đối ta thường sử dùng cách xét dấu các
số hoặc là bình phương hai vế, trong trường hợp này ta chọn cách bình phương hai vế vì việc xét dấu rất
khó khăn. Khi bình phương hai vế ta thu được kết quả là:
ab ca b c a c b c ab ca b c ab ca b c
Bất đẳng thức sẽ được giải quyết nếu như ta khẳng định được ab 0 . Chú ý đến vai trò của a, b, c
trong bất đẳng thức thì việc giả sử
ab 0 là hoàn toàn thực hiện được. Bây giờ ta cần trình bày lại lời
giải nữa là xong.
Lời giải
Trong ba số a, b, c có ít nhất hai số cùng dấu, không mất tính tổng quát ta giả sử hai số đó là a, b.
Khi đó ta được
abab
Như vậy ta chỉ cần chứng minh
c abc bc ca
Bất đẳng thức cần chứng minh tương đương với
222
2
c abc 2cabc ac bc 2acbc
ab cabc acbc ab cabc abcabc
Bất đẳng thức cuối cùng đúng theo bất đẳng thức giá trị tuyệt đối.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi a, b, c cùng dấu.
Ví dụ 18. Cho a, b là các số thực không âm. Chứng minh rằng:
2
ab1ab
1
4
1a1b
Phân tích: Ta có một đẳng thức quen thuộc là
22 2
1a 1b 1abab
và như vậy nếu ta
đánh giá được
2
1
ab1ab 1abab
4
thì bài toán xem như được giải quyết. Để ý đến
đánh giá theo bất đẳng thức Cauchylaf
2
1
ab1ab 1abab
4
và ta cần chỉ ra được
ab1ab ab1ab
, đánh giá này là hoàn toàn đúng đắn theo bất đẳng thức giá trị tuyệt
đối.
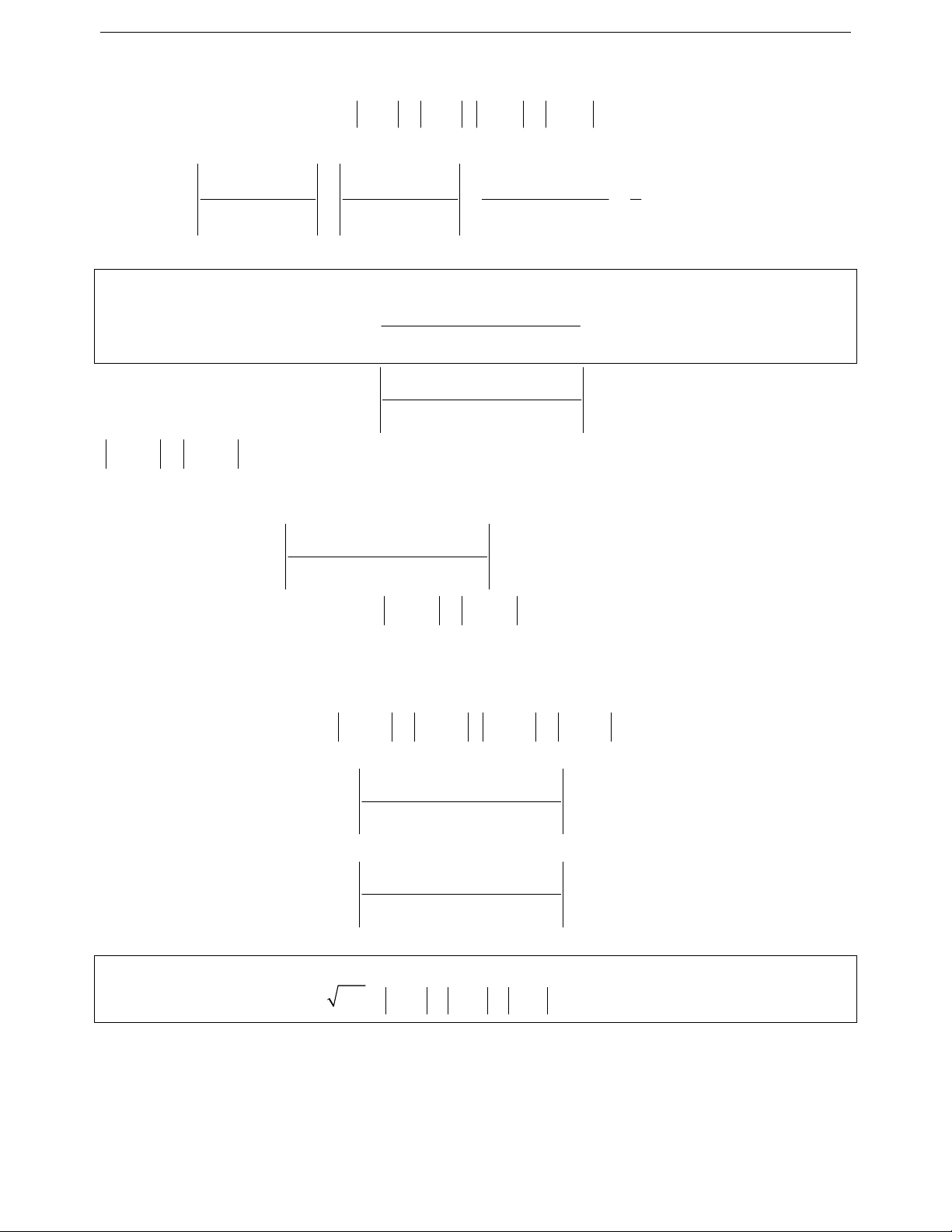
Lời giải
Theo bất đẳng thức giá trị tuyệt đối ta được
ab ab;1ab 1ab
Do đó ta được
2
22 22 22
a b 1 ab a b 1 ab ab a b 1
1
4
1a 1b 1a 1b 41a 1b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi
a0;b1
hoặc
a1;b0
.
Ví dụ 19. Cho a, b, c là các số thực đôi một không đồng thời bằng 0. Chứng minh rằng:
222222
222222
abbcca
11
abbcca
Phân tích: Ta viết lại bất đẳng thức là
222222
222222
abbcca
1
abbcca
, như vậy nếu đánh giá được
22 22
ab ab thì bài toán được chứng minh.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222222
222222
abbcca
1
abbcca
Trước hết ta chứng minh bất đẳng thức
22 22
ab ab
.
Thật vậy, bất đẳng thức trên tương đương với
22
22 22 22
ab ab 4ab0 , Đúng với mọi a, b.
Chứng minh tương tự như trên ta được
22 222 2 2 2
bc bc;ca ca
Nhân theo vế các kết quả trên ta được
222222
222222
abbcca
1
abbcca
Vì đẳng thức không xẩy ra nên ta được
222222
222222
abbcca
1
abbcca
Vậy bất đẳng thức được chứng minh.
Ví dụ 20. Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:
3
3abc a b b c c a a b c
Phân tích: Nhận định đầu tiên khi tìm hiểu bất đẳng thức trên là tìm cách phá giá trị tuyệt đối. Quan sát
kĩ ta thấy không thể bình phương cũng không thể xét dấu các đại lượng để phá giá trị tuyệt đối được.
Trong trường hợp này ta thử nghĩ đến cách sắp thứ tự các biến để phá giá trị tuyệt đối xem có thể chứng
minh được hay không. Chẳng hạn ta chọn
abc, khi đó ta phá được các giá trị tuyệt đối và bất đẳng
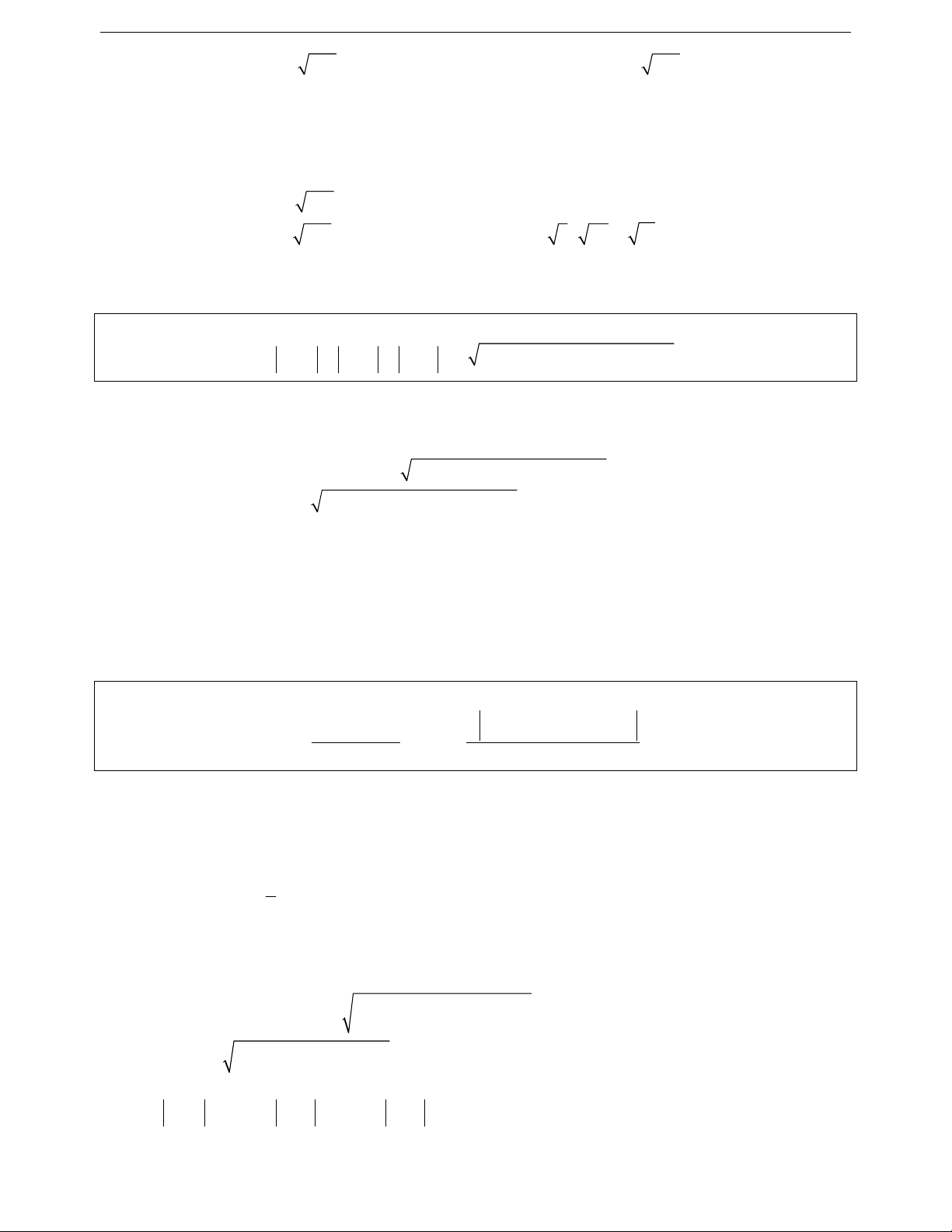
thức được viết lại thành
3
3abc a b 3c 0 , nhận thấy
3
ab0;3abc3c0 nên bất đẳng
thức thu được hoàn toàn đúng.
Lời giải
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta giả sử
abc
.
Khi đó bất đẳng thức cần chứng minh trở thành
3
3
333
2
3abc ab bc ac abc
3abc a b 3c 0 a b 3c ab c 0
Bất đẳng thức cuối cùng luôn đúng vì
abc.
Vậy bất đẳng thức được chứng minh.
Ví dụ 21. Cho a, b, c là các số thực bất kì. Chứng minh rằng:
222
ab bc ca 2a b c abbcca
Lời giải
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta giả sử abc.
Khi đó bất đẳng thức cần chứng minh trở thành
222
222
2222
2
222 22
abbcac2a b c abbcca
2a c 2 a b c ab bc ca
4a c 2 a b b c c a
ac bc ca ab bc bc ca
2a b b c 0
Bất đẳng thức cuối cùng luôn đúng do
abc.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 22.
Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:
333
3a b b c c a
abc
abc
34
Phân tích: Trước hết ta dự đoán được đẳng thức xẩy ra tại abc. Quan sát bất đẳng thức ta nhận
thấy vế phải xuất hiện các đại lượng
ab;bc;ca nên suy nghĩ đầu tiên khi biến đổi bất đẳng thức
là cần phải làm thế nào để xuất hiện ở vế trái các đại lượng
ab;bc;ca, chính yêu cầu này làm ta
liên tưởng đến một hằng đẳng thức bậc ba hết sức quen thuộc đó là
222
333
1
abc3abc abcab bc ca
2
. Như vậy sau khi áp dụng thì vế trái
của bất đẳng chứa đại lượng
222
ab bc ca mà bên vế phải lại là tích các đại lượng
ab;bc;ca, từ chiều của bất đẳng thức cần chứng minh ta nghĩ đến đánh giá
2
222
3
ab bc ca 3 abbcca
. Bây giờ ta cần một đánh giá kiểu
3
2a b c 3 a b b c c a là hoàn thành chứng minh bất đẳng thức. Chú ý đến dấu giá trị
tuyệt đối và các biến không âm ta có được các đánh giá đúng là
ab ab;bc bc;ca ca , đến đây thì các yêu cầu để chứng minh bài toán đã được
xử lí, việc trình bày lời giải hoàn toàn đơn giản.
Lời giải
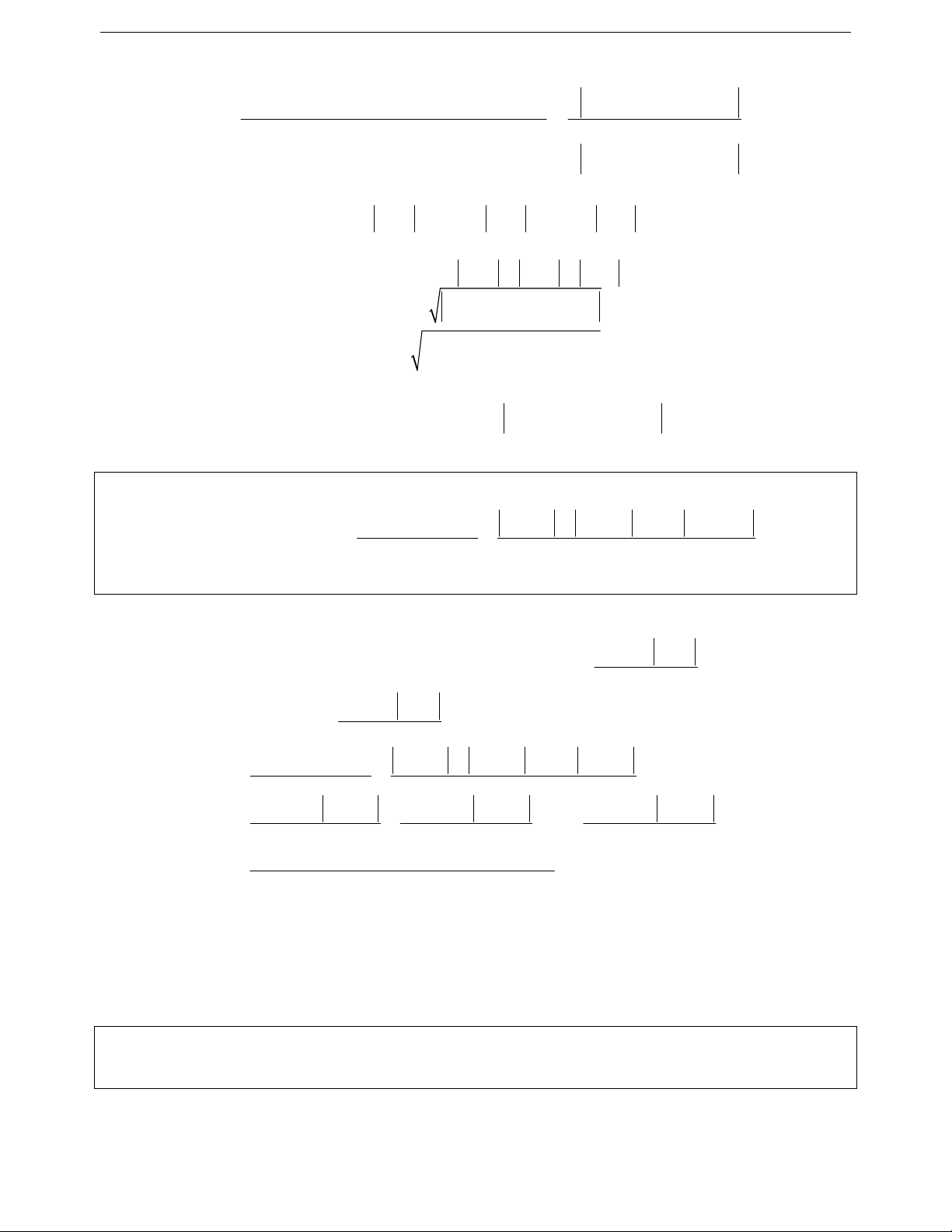
Bất đẳng thức cần chứng minh tương đương với
222
222
abc ab bc ca
3a b b c c a
64
2a b c a b b c c a 9 a b b c c a
Theo tính chất của bất đẳng thức giá trị tuyệt đối ta có
ab ab;bc bc;ca ca
Do đó áp dụng bất đẳng thức Cauchy ta được
3
2a b c a b b c c a a b b c c a
3abbcca
Và
2
222
3
ab bc ca 3 abbcca
Nhân theo vế hai bất đẳng thức trên ta được
222
2a b c a b b c c a 9 a b b c c a
Vậy Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 23. Cho n số thực
12 n
x ; x ;...; x
(với n3 ). Chứng minh rằng:
12 n
12 23 nx1
12 n
x x ... x
xx xx ...x x
Max{x ; x ;...; x }
n2n
Trong đó
12 n
Max{x ; x ;...; x }
là số lớn nhất trong các số thực
12 n
x ; x ;...; x
Lời giải
Để ý là trong hai số thực x, y bất kì ta luôn có
Min{x, y} x, y Max{x, y} và
xy xy
Max{x, y}
2
Sử dụng đẳng thức
xy xy
Max{x, y}
2
, ta có:
12 n
12 23 n1
12 12 22 23 n1 n1
12 2 n1
12 n
x x ... x
x x x x ... x x
n2n
xx xx xx xx xx xx
...
2n 2n 2n
Max{x , x } Max{x , x} Max{x , x }
Max{x ; x ;...; x }
n
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
12 n
x x ... x
.
3. Sử dụng tính chất của tam thức bậc hai.
Ví dụ 24.
Cho a, b là các số thực thỏa mãn
22
a a 2b 4b 4ab 0
Chứng minh rằng:
0a2b1

Phân tích: Để ý rằng bất phương trình bậc hai
2
12
At Bt C 0 t t t với
A0
, trong đó
12
t;t
là các nghiệm của tam thức
2
At Bt C
. Phân tích bất đẳng thức giả thiết ta thu được
2
a2b a2b 0, ta xem vế trái là đa thức biến a2b , khi đó ta có lời giải sau.
Lời giải
Bât đẳng thức giả thiết tương đương với
2
22
a 4ab4b a2b 0 a2b a2b 0
Đặt
2
t a 2b t t 0 0 t 1 0 a 2b 1
Vậy bài toán được chứng minh.
Ví dụ 25. Cho a, b là các số thực bất kì. Chứng minh rằng:
24 2 2 2 3
a b 2 a 2 b 4ab a 4ab
Phân tích: Bất đẳng thức có hai biến và biến a có bậc cao nhất là 2, do đó ta biến đổi bất đẳng thức theo
hướng xuất hiện một tam thức bậc hai có biến là a như sau
2
22 2 2
b1a4b1ba4b 0
Ta xem vế trái của bất đẳng thức là tam thức bậc hai, để ý đến
2
2
b1 0
, ta cần chứng minh
được biệt thức
của tam thức có giá trị âm.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
22 2 2
b1a4b1ba4b 0
Xét đa thức
2
22 2 2
f(a) b 1 a 4b 1 b a 4b
Khi đó ta có
2
2
2222
4b 1 b 4 b 1 .4b 16b 0
Do đó ta có
2
2
b1f(a)0
mà
2
2
b1 0
nên ta được
2
22 2 2
f(a) b 1 a 4b 1 b a 4b 0
Vậy bất đẳng thức được chứng minh.
Ví dụ 26. Cho a, b, c, d là các số thực thỏa mãn
bcd
. Chứng minh rằng:
2
abcd 8acbd
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
2
a 2b3cda bcd 8bd0
Xét tam thức
2
2
f(a)a 2b3cda bcd 8bd
Khi đó ta có
22
'b3cd bcd 8bd cbcd8
Do
bcd nên ta được '0 suy ra f(a) 0
Hay
2
2
a 2b3cda bcd 8bd0
.
Vậy bất đẳng thức được chứng minh.

Ví dụ 27. Cho a, b, c, d, e là các số thực bất kì. Chứng minh rằng:
22222
abcde abcde
Phân tích: Bất đẳng thức này đã được chứng minh bằng kĩ thuật biến đổi tương đương. Ở đây ta sử dụng
tư tưởng của tam thức bậc hai để chứng minh. Để ý ta viết lại được bất đẳng thức như sau
22222
f(a) a b c d e ab c d e
, đến đây ta cần phải chứng minh được
22222
bcde 4b c d e 0 . Việc này hoàn toàn thực hiện được nhờ phép biến đổi
tương đương hoặc bất đẳng thức Bunhiacpoxki.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
22222
a b c d e abcde 0
Xét
22222
f(a) a b c d e ab c d e
Khi đó ta có
22222
bcde 4b c d e
Theo bất đẳng thức Bunhiacopxki ta có
22 22 22 22
2
4b c d e 1111b c d e
bcce
Suy ra
22222
bcde 4b c d e 0
Do đó ta được
22222
f(a) a b c d e ab c d e 0
Hay bất đẳng thức được chứng minh.
Ví dụ 28. Cho a, b, c là các số thực thỏa mãn 1 a,b,c 2 và abc0.
Chứng minh rằng:
222
abc 6
Phân tích: Từ giả thiết
1a2
, ta có thể thiết lập được bất đẳng thức bậc hai dạng
a2a1 0, áp dụng tương tự và chú ý đến giả thiết abc0.
Giải
Theo tính chất về dấu của tam thức bậc hai ta có
1a2 a2a1 0
1b2 b2b1 0
1c2 c2c1 0
Cộng từng vế ba bất đẳng thức trên ta được
222 222
aa2 bb2 cc2 0 a b c a b c 6
Vì
abc0 nên
222
abc 6. Vậy bất đẳng thức được chứng minh.
Ví dụ 29. Chứng minh bất đẳng thức Bunhiacopxki.
a) Cho các số thực bất kỳ
123123
a,a,a,b,b,b
khác 0. Chứng minh rằng:
2
222222
11 22 33 1 2 3 1 2 3
ababab aaabbb

Đẳng thức xẩy ra khi và chỉ khi
123
123
aaa
bbb
b) Cho các số thực bất kỳ
12 n 12 n
a , a , ..., a , b , b ,..., b
khác 0. Chứng minh rằng:
2
22 222 2
11 22 n n 1 2 n 1 2 n
a b a b ... a b a a ... a b b ... b
Đẳng thức xẩy ra khi và chỉ khi
12 n
12 n
aa a
...
bb b
Lời giải
a) Xét đa thức
2222 222
123 112233 123
22 2 22 2 22 2
111122223333
222
11 22 33
f(x) a a a x 2 a b a b a b b b b
a x 2a b x b a x 2a b x b a x 2a b x b
ax b ax b ax b 0
Vì
f(x) 0, x R
nên ta có
2
222222
112233 123123
'ababab aaabbb 0
Hay
2
222222
11 22 33 1 2 3 1 2 3
ababab aaabbb
Đẳng thức xẩy ra khi và chỉ khi
123
112233
123
aaa
ax b ax b ax b
bbb
Vậy bất đẳng thức được chứng minh.
b) Xét da thức
22 22 22 2
12 n 1122 nn 12 n
22 2 22 2 22 2
11112222 nnnn
22 2
11 22 n n
f(x) a a ... a x 2 a b a b ... a b b b ... b
a x 2a b x b a x 2a b x b ... a x 2a b x b
a x b a x b ... a x b 0
Vì
f(x) 0, x R nên ta có
2
22 222 2
11 22 n n 1 2 n 1 2 n
' a b a b ... a b a a ... a b b ... b 0
Hay
2
22 222 2
11 22 n n 1 2 n 1 2 n
a b a b ... a b a a ... a b b ... b
Đẳng thức xẩy ra khi và chỉ khi
12 n
1122 n n
12 n
aa a
a x b a x b ... a x b ...
bb b
Vậy bất đẳng thức được chứng minh.
Ví dụ 30. Cho a, b, c, d là các số thực thỏa mãn adbc. Chứng minh rằng: Nếu tồn tại số thực m
sao cho 2m ad bc thì với mọi xR ta luôn có:
2
xaxbxcxd m 0
Phân tích: Quan sát biểu thức bên vế trái ta nhận thấy ngay đây là đa thức bậc 4, với phép đặt biến phụ
22
y x a d x x b c x
, khi đó vế trái trở thành đa thức bậc hai, bây giờ ta cần chứng minh được

biệt thức
âm, cần chú ý đến giả thiết
2m ad bc
vì chắc chắn phải cần đến nó mới có thể chứng
minh được.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
22 2
xadxadxbcxbcm0
Do
adbc nên ta đặt
22
y x a d x x b c x
, khi đó ta được bất đẳng thức
22 2
yadybcm0 y adbcyabcdm0
Xét
22
f(y) y ad bc y abcd m
Ta có
22
22
y
ad bc 4.1. abcd m ad bc 4m
Vì
2m ad bc nên
2
2
y
4m ad bc 0 do đó ta có f(y) 0
Hay
2
xaxbxcxd m 0
Vậy bài toán được chứng minh.
Ví dụ 31. Cho a, b, c là các số thực thỏa mãn abc1. Chứng minh rằng:
2
3a 4b 5c 44 ab bc ca
Phân tích: Bất đẳng thức có bậc hai đối với mỗi biến, nên ta nghĩ đến việc đưa về tam thức bậc hai. Bất
đẳng thức có ba biến nhưng có thêm điều kiện
abc1 cho nên ta có thể chuyển bất đẳng thức
thành bất đẳng thức chỉ có hai biến. Đến đây ta chọn một biến làm biến chính, còn lại ta xem như là tham
số và sử dụng tính chất tam thức bậc hai là một ý tưởng không tồi chút nào.
Lời giải
Từ giả thiết abc1 suy ra c1ab, thay vào bất đẳng thức ta được
2
22
3a 4b 5 5a 5b 44ab 44 a b 1 a b
48a 16 3b 4 a 45b 54b 25 0
Xét
22
f(a) 48a 16 3b 4 a 45b 54b 25 , khi đó ta được
22
2
' 64 3b 4 48 45b 54b 25 176 3b 1 0
Do đó suy ra
f(a) 0 hay
22
48a 16 3b 4 a 45b 54b 25 0
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
111
a;b;c
236
.
Ví dụ 32. Cho a, b là các số thực bất kì. Chứng minh rằng:
22 22
31 a a 1 b b 21 ab ab
Phân tích: Quan sát bất đẳng thức ta nhận thấy, bất đẳng thức có tính đối xứng với hai biến a, b và là có
bậc hai đối với mỗi biến do đó một cách tự nhiên ta nghĩ đến sử dụng tính chất tam thức bậc hai để chứng
minh. Trước hết ta viết lại bất đẳng thức
222 2
b3b3a 3b5b3a3b3b10
Xem vế trái là một tam thức bậc hai biến a khi đó, để ý đến
2
b3b30 ta cần chứng minh
được biệt thức
0
.

Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 2
b3b3a 3b5b3a3b3b10
Xét tam thức bậc hai
222 2
f(a) b 3b3a 3b 5b3a3b 3b1
Khi đó ta được
2
2222
3b 5b 3 4 b 3b 3 3b 3b 1 a 3a 1 0
Để ý ta thấy
2
2
33
b3b3 b 0
24
, do đó ta được f(a) 0
Hay
222 2
b3b3a 3b5b3a3b3b10
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra ki và chỉ khi
2
2
2
b3b10
35
3b 5b 3
ab
a
2
2b 3b 3
Ví dụ 33. Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:
222 222
31 a a 1 b b 1 c c 1 abc abc
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức ta nhận thấy
bất đẳng thức có tính đối xứng và có bậc hai đối với mỗi biến, do đó một cách tự nhiên ta nghĩ đến tam
thức bậc hai. Như vậy ta cần chọn một biến chính, là c chẳng hạn, khi đó các biến a, b đóng vai trò tham
số. Để ý thấy vế trái của bất đẳng thức có đại lượng
22
1aa 1bb rất cồng kềnh khi biến đổi,
do đó ta cần thay đại lượng đó bằng một đại lượng bé hơn, chú ý đến dấu đẳng thức xẩy ra ta có hai ý
tưởng là
22
1aa 1bb 2aa2bb ab
Hoặc
222
22
22
22
1ab ab 1a 1b
1ab
1aa 1bb
22
Nhận thấy ngay ý tưởng đầu không thực hiện được vì chẳng hạn
ab 0 thì bất đẳng thức
2222
3ab 1 c c 1 abc a b c không đúng. Do đó ta chỉ có thể theo ý tưởng thứ hai. Lúc ta được
bất đẳng thức
222222
21aa1bb1cc 1ab1cc
Bây giờ ta cần chứng minh
22 2 222
31 ab 1 c c 21 abc abc, viết thành
22 2 22 22
f(c) 3abc 32ab 3abc13ab 0 . Công việc cuối cùng là chứng minh
2
22 22 22
3 2ab 3a b 4 3 a b 1 3a b 0
thì bài toán xem như được chứng minh. Ở đây nếu
như ta không chứng minh được biệt thức
0 thì ý tưởng trên hoàn toàn phá sản. Cũng may trong bài
toán này ta thu được
4
31 ab 0 . Đến đây chỉ cần trình bày lại lời giải nữa là xong.
Lời giải

Ta có
222
2 2 22 22
21aa 1bb 1ab ab 1a 1b 1ab
Do đó ta được bất đẳng thức
222222
21aa1bb1cc 1ab1cc
Ta cần chứng minh
22 2 222
22 2 22 22
31ab 1cc 21abcabc
3abc 32ab 3abc13ab 0
Xét tam thức bậc hai
22 2 22 22
f(c) 3 a b c 3 2ab 3a b c 1 3a b
Khi đó ta được
2
4
22 22 22
3 2ab 3a b 4 3 a b 1 3a b 3 1 ab 0
Dễ thấy
22
3ab 0 nên ta được f(c) 0
Hay
22 2 22 22
3abc 32ab 3abc13ab 0
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Nhận xét: Đây là một bài toán khó, ban đầu nếu xem c là biến và a, b là tham số mà chứng minh biệt
thức
0 thực sự rất khó khăn, cho nên ý tưởng làm đơn giản hóa vế trái là hoàn toàn tự nhiên. Nhưng
để có một đánh giá hợp lí cần phải xem xét bài toán một cách tổng thể và luôn để ý đến các tình huống có
thể xẩy ra.
Ví dụ 34.
Cho a, b, c là các số thực không âm thỏa mãn
abc ab bc ca 4
. Chứng minh r
ằ
ng:
abcabbcca
Phân tích: Dự đoán dấu đẳng thức xẩy ra tại abc1 hoặc ab2;c0 . Quá trình đánh giá
bất đẳng thức cần chú ý đến đẳng thức xẩy ra. Quan sát bất đẳng thức ta nhận thấy bất đẳng thức có tính
đối xứng đối với ba biến và có điều kiện nên ta có thể đưa về dạng tam thức bậc hai. Chẳng hạn từ giả
thiết ta rút được
4bc
a
bcbc
. Khi đó bất đẳng thức được viết lại thành:
4bc 4bc
bc bc bc
bcbc bcbc
Và nếu xem b là biến và c là tham số thì ta thu được bất đẳng thức có bậc hai đối với một biến
22 2 2
f(b) 1 c c b c c 4 b c 4c 4 0
.
Lúc này ta có
2
222
cc441ccc4c4cc15c8 . Bây giờ ta cần
phải chỉ ra được
0 và
2
1cc 0
. Chú ý trong trường hợp này đẳng thức xẩy ra tại c1 hoặc
c0
, ta nhận thấy khi c1 thì hai yêu cầu trên được đáp ứng ngay. Nhận thấy từ giả thiết
abc a b c 4 nếu chọn c nhỏ nhất thì ta có ngay c1 , do đó ta có thể giả sử c là số bé nhất trong
ba số a, b, c. Việc giả sử này là hoàn toàn có thể vì vai trò của các biến như nhau. Đến đây ta trình bày lại
lời giải như sau.
Lời giải
Không mất tính tổng quát ta giả sử c là số bé nhất trong ba số a, b, c. Khi đó ta có
32
4 abc ab bc ca c 3c c 1
Từ abc ab bc ca 4 suy ra
4bc
a
bcbc
. Như vậy ta cần chứng minh
4bc 4bc
bc bc bc
bcbc bcbc

Hay
22 2 2
1ccb c c4bc 4c4 0
Xét
22 2 2
f(b) 1 c c b c c 4 b c 4c 4
Khi đó ta có
2
222
cc441ccc4c4cc15c8
Vì
c1
nên ta có
22 2
cc 1 5c 8 cc 1 5 8 3cc 1 0
Lại thấy khi
c1
thì
2
1cc 0 nên f(b) 0
Hay
22 2 2
1ccb c c4bc 4c4 0 .
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi
abc1 hoặc ab2;c0 và các hoán vị.
Nhận xét: Sử dụng nguyên lí Dirichlet cũng có thể chứng minh được bất đẳng thức trên, tuy nhiên để sử
dụng được nguyên lí Dirichlet không hề đơn giản. Qua đó ta nhận thấy với các bất đẳng thức bậc hai thì
nghĩ đến sử dụng các tính chất của tam thức bậc hai là điều hết sức tự nhiên và thực tế các tính chất của
tam thức bậc hai cũng đã cho thấy hiệu qu
ả trong chứng minh bất đẳng thức.
Ví dụ 35.
Cho a, b, c là các số thực bất kì thỏa mãn điều kiện:
abc2
và
333
abc3abc2
.
Gọi M là số lớn nhất và m là s
ố
nhỏ nh
ấ
t trong ba s
ố
a, b, c. Chứng minh r
ằ
ng:
2
Mm
3
Phân tích: Quan sát bất đẳng thức ta thấy được vai trò như nhau của ba biến a, b, c nên để đơn giản ta có
thể sắp thứ tự các biến để quy định M và m cho bất đẳng thức. Chẳng hạn ta chọn
Ma;mc, khi đó
ta cần chứng minh
2
ac
3
.
Chú ý đẳng thức
222
333
1
abc3abc abcab bc ca
2
, kết hợp với
abc2, ta viết lại được
222
ab bc ca 2, vì ta cần phải chứng minh
2
ac
3
nên ta có thể xem đẳng thức bên là phương trình bậc hai ẩn
Xac
và viết lại ta được
2
2
XbcXbc10 . Đến đây ta thấy được hai ý tưởng để chứng minh
2
X
3
. Một là ta
cần giải ra các nghiệm X theo
bc sau đó chứng minh
2
X
3
. Hai là đổi vai trò trong phương trình
và xem X là tham số, khi đó từ điều kiện có nghiệm của phương trình ta suy ra được
2
X
3
.
Lời giải
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta có thể giả sử a là số lớn nhất và c là
số nhỏ nhất trong ba số a, b, c.
Khi đó ta cần chứng minh
2
ac
3
Ta có
333 222
2 a b c 3abc a b c a b c ab bc ca
Hay
222
ab bc ca 2. Đặt Xac, khi đó ta được
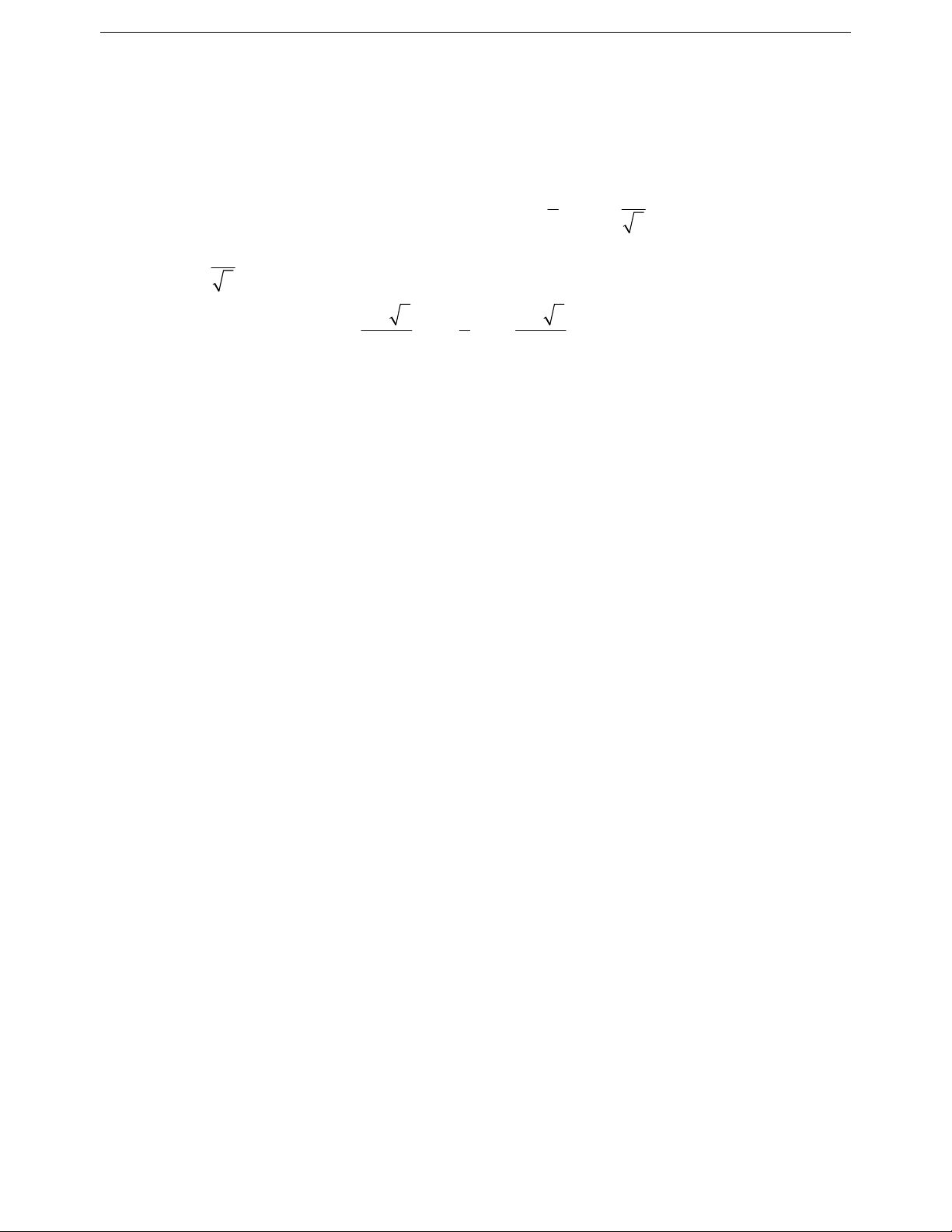
22 22
22
22
2
22
22
Xab bc2Xacbc bc2
Xac2bc2acbc2
2X 2 b c X 2 b c 2 X b c X b c 1 0
Xem phương trình trên có ẩn là
bc , khi đó để phương trình có nghiệm thì
22 2
42
X4X10 X X
2
3
Suy ra
2
ac
3
. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
23 2 23
a;b;c
333
và các hoán vị.

Chủ đề 3
CHỨNG MINH BẤT ĐẲNG THỨC BẰNG PHƯƠNG PHÁP PHẢN CHỨNG
1. Kiến thức cần nhớ
a. Nội dung phương pháp
Giả sử ta cần chứng minh bất đẳng thức
AB
. Tư tưởng của phương pháp là ta hãy giả sử bất
đẳng thức đó sai, sau đó vận dụng các kiến thức đã biết và giả thiết của đề bài để suy ra điều vô lý. Điều
vô lý có thể là trái với giả thiết, hoặc là những mệnh đề mâu thuẫn nhau, từ đó suy ra đẳng thức cần
chứng minh là đúng.
Các bước suy luận phản chứng
Bước 1: Giả sử điều cần chứng minh là sai (phủ định lại mệnh đề cần chứng minh).
Bước 2: Từ điều giả sử ta suy ra một số tính chất hoặc quan hệ mới, mà những tính chất này mâu thuẫn
với điều đã cho hoặc trái với tính chất ta đã biết.
Bước 3: Ta kết luận điều giả sử ban đầu là sai. Vậy bài toán được chứng minh.
Chú ý: Trong các bước suy luận phản chứng nêu trên, bước 1 rất quan trọng vì cần tạo ra mệnh đề
phủ định điều cần chứng minh thực sự chính xác.
b. Một số hình thức chứng minh bất đẳng thức
+ Dùng mệnh đề đảo.
+ Phủ định rồi suy ra điều trái với giả thiết.
+ Phủ định rồi suy ra trái với điều đúng.
+ Phủ định rồi suy ra hai mệnh đề trái ngược nhau.
+ Phủ định rồi suy ra kết luận.
c. Một số đẳng thức và bất đẳng thức cần nhớ.
+
222
222
ab bc ca
abc abbcca 0
2
+
222
a1 b1 c1 0
+
222
ab bc ca 0
2. Một số ví dụ minh họa
Ví dụ 1. Cho a, b, c là các số thực bất kì. Chứng minh rằng có ít nhất một trong các bất đẳng thức sau đây
là đúng:
22 22 22
ab2bcbc2ca ca2ab
Phân tích: Vì bài toán yêu cầu ta phải chứng minh có ít nhất một bất đẳng thức đúng, điều này có nghĩa
là không thể có trường hợp cả ba bất đẳng thức trên cùng sai. Như vậy ta chỉ cần chứng minh cả ba bất
đẳng thức trên cùng sai không thể xẩy ra là được.
Lời giải
Giả sử cả ba bất đẳng thức trên cùng sai, tức là ta có ba bất đẳng thức sau
22 22 22
ab2bcbc2ca ca2ab
Cộng theo vế ba bất đẳng thức trên ta được

22 22 22
ab2ab bc2bc ca2ca0
Hay
222
ab bc ca 0.
Điều này mâu thuẫn với bất đẳng thức
222
ab bc ca 0.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 2. Cho các số thực
a, b , c (0 , 2) . Chứng minh rằng có ít nhất một trong ba bất đẳng thức sau đây
là sai:
a2 b 1 b2 c 1 c2 a 1
Phân tích: Vì bài toán yêu cầu ta phải chứng minh có ít nhất một bất đẳng thức sai, điều này có nghĩa là
không thể có trường hợp cả ba bất đẳng thức trên cùng đúng. Như vậy ta chỉ cần chứng minh cả ba bất
đẳng thức trên cùng đúng không thể xẩy ra là được. Chú ý ở đây ta có giả thiết
a, b , c (0 , 2) nên có thể
sử dụng đến các hiệu
2a,2b,2c là các số dương.
Lời giải
Giả sử cả ba bất đẳng thức đã cho đều đúng, nhân chúng với nhau theo vế với vế ta có
a2 b.b2 c.c2 a 1 a2 a.b2 b.c2 c 1
Mặt khác do
a(0,2)
nên ta có 2a 0. Do đó ta được
2
22
0a2a 2aa 1 12aa 1 a1 1
Chứng minh hoàn toàn tương tự ta có
0b2b 1;0c2c 1
Nhân theo vế các bất đẳng thức trên ta được
a2 a.b2 c.c2 c 1
Bất đẳng thức này mâu thuẫn với bất đẳng thức
a2 a.b2 b.c2 c 1.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 3. Cho a, b, c là các số thực thỏa mãn thỏa mãn các điều kiện sau
abc0;abbcac0;abc0
Chứng minh rằng cả ba số a, b, c đều là số dương.
Phân tích: Vì bài toán yêu cầu ta phải chứng minh cả ba số a, b, c đều là số dương, điều này có nghĩa là
không thể có trường hợp một số nào đó không dương. Như vậy ta chỉ cần chứng minh một số bất kì
không dương không thể xẩy ra là được.
Lời giải
Giả sử rằng trong ba số a, b, c có một số không dương, không mất đi tính tổng quát ta chọn số đó là
a, tức là ta có
a0 .
Vì
abc 0 nên a0 , do đó suy ra a0 .
Lại có
abc0 nên bc 0, từ đây suy ra
ab c 0

Theo giả thiết thứ hai
ab bc ca 0 hay
ab c bc 0 dẫn đến
bc 0
Như vậy ta được
a0;bc0
vì thế ta có
abc 0
. Bất đẳng thức này mâu thuẫn với giả thiết thứ ba
của bài toán.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 4. Chứng minh rằng không có 3 số dương a, b, c nào thoả mãn cả 3 bất đẳng thức:
111
a2b2c2
bca
Phân tích: Vì bài toán yêu cầu ta phải chứng minh không tồn tại ba số dương a, b, c để cả ba bất đẳng
thức trên đều đúng, điều này có nghĩa là không thể có trường hợp cả ba bất đẳng thức trên cùng đúng.
Như vậy ta chỉ cần chứng minh trường hợp cả ba bất đẳng thức trên cùng đúng không thể xẩy ra là được.
Chú ý các bất đẳng thức trên làm ta liên tưởng đến bất đẳng thức Cauchy dạng
1
x2
x
.
Lời giải
Giả sử tồn tại ba số dương a, b, c thoả mãn cả 3 bất đẳng thức:
111
a2;b2;c2
bca
Cộng theo từng vế ba bất đẳng thức trên, ta được:
111 1 1 1
abc6a b c 6(1)
bca a b c
Vì a, b, c là các số dương nên theo bất đẳng thức Cauchy ta được
111
a2;b2;c2
abc
Cộng theo vế ba bất đẳng thức trên ta được
111
abc62
abc
Ta thấy hai bất đẳng thức (1) và (2) mâu thuẫn với nhau.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 5: Cho ba số thực a, b, c đôi một khác nhau. Chứng minh rằng tồn tại ít nhất một trong các số 9ab ,
9bc , 9ac nhỏ hơn
2
abc .
Phân tích: Vì bài toán yêu cầu ta phải chứng minh tồn tại ít nhất một trong ba số 9ab, 9bc, 9ca nhỏ hơn
2
abc , điều này có nghĩa là không thể có trường hợp cả ba số 9ab, 9bc, 9ca cùng lớn hơn
2
abc . Như vậy ta chỉ cần chứng minh ba số 9ab, 9bc, 9ca cùng lớn hơn
2
abc không xẩy
ra là được. Chú ý các đại lượng 9ab, 9bc, 9ca,
2
abc
làm ta liên tưởng đến bất đẳng thức
222
abcabbcca .

Lời giải
Giả sử điều cần chứng minh là sai, tức là ta có các bất đẳng thức sau
222
9ab abc;9bc abc;9ca abc
Cộng vế với vế ba bất đẳng thức ta được
22
222
222
3a b c 9ab bc ca a b c 3ab bc ca
abcabbcca ab bc ca 0 1
Theo bài ra a, b, c đôi một khác nhau nên ta lại có
222
ab bc ca 0 2
Ta thấy hai bất đẳng thức (1) và (2) mâu thuẫn với nhau.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 6: Cho a, b, c, d là bốn số thực dương bất kì. Chứng minh rằng ba bất đẳng thức sau không thể
cùng xảy ra:
abcd 1
abcd abcd 2
abcd cdab 3
Phân tích: Vì bài toán yêu cầu ta phải chứng minh cả ba bất đẳng thức trên không cùng xẩy ra tức là có ít
nhất một bất đẳng thức sai, điều này có nghĩa là không thể có trường hợp cả ba bất đẳng thức trên cùng
đúng. Như vậy ta chỉ cần chứng minh cả ba bất đẳng thức trên cùng đúng không thể xẩy ra là được.
Lời giải
Giả sử tồn tại bốn số dương a, b, c, d thỏa mãn cả ba bất đẳng thức.
Từ bất đẳng thức (1) và bất đẳng thức (2) ta có
2
22
ab abcd abcd
cd a b ab a b 3ab 3ab
cd 3ab 4
Mặt khác ta lại có
2
2
abcd cdab
a b cd c d a b ab ab cd ab
ab ab cd a b cd 4ab.cd
ab ab cd 4ab.cd
ab 3cd 5
Ta thấy hai bất đẳng thức (4) và (5) mâu thuẫn với nhau.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 7: Cho a, b, c là các số thực thỏa mãn điều kiện
22
ababbcca0.
Chứng minh rằng:
222
abc
Phân tích: Đại lượng
22
ababbcca làm ta liên tưởng đến hằng đẳng thức
2
222
abc a b c 2abbcca . Như vậy từ giả thiết của bài toán đã cho ta suy ra được
giả thiết mới
22
2a b ab bc ca 0 . Vậy nếu
222
abc, thì ta được bất đẳng thức mới
2
222
abc2abbcca 0 abc 0 . Rõ ràng bất đẳng thức thu được là sai, do đó
ta nghĩ đến sử dụng phương pháp phản chứng để chứng minh bài toán.
Ngoài ra, để ý bất đẳng thức
22
2a b ab bc ca 0 và
2
abc 0 ta được bất
đẳng thức
2
22
abc 2a b abbcca . Khai triển và thu gọn ta cũng được
222
abc.
Lời giải
Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có bất đẳng thức
222
abc
, khi đó ta được
2222 222
2
22
abab2abbcca abc2abbcca
2a b abbcca abc
Kết hợp với giả thiết ta có
22
22
02a b abbcca abc abc 0
Bất đẳng thức cuối cùng là sai. Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Bất đẳng thức trên cũng có thể chứng minh theo cách sau đây:
Giả thiết của bài toán tương đương với
22
2a b ab bc ca 0
Mà ta luôn có
2
abc 0
, do đó ta được bất đẳng thức
2
22
222 22
222
abc 2a b abbcca
a b c 2 ab bc ca 2 a b 2 ab bc ca
cab
.
Vậy bất đẳng thức được chứng minh.
Ví dụ 8. Cho hai số dương a, b thỏa mãn điều kiện
33
abab. Chứng minh rằng:
22
ab1
Phân tích: Quan sát giả thiết ta nhận thấy ab0 và hai đại lượng
33
ab;ab không đồng bậc.
Do đó ta có thể đồng bậc hai vế bằng cách nhân thêm
22
ab . Vì yêu cầu chứng minh
22
ab1 nên
kết hợp với giả thiết ta quy bài toán về chứng minh bất đẳng thức
33 22
ab abab
. Đến đây
ta có thể sử dụng phương pháp phản chứng hoặc biến đổi tương đương để chứng minh bài toán.
Lời giải

Từ giả thiết ta có
ab0
. Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có bất đẳng thức
22
ab1
. Khi đó kết hợp với giả thiết ta được
33 22 333223
22 3 2 2
ab abab abaababb
ab a b 2b 0 b ab a 2b 0
Vì
ab0 nên ta có
3
ab a 0 ab a 2b 0
. Do đó bất đẳng thức trên không thể xẩy
ra.
Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng minh.
Bất đẳng thức trên cũng có thể chứng minh theo cách sau đây:
Từ giả thiết ta có
ab0. Bất đẳng thức cần chứng minh tương đương với
33 22 33 3 22 3
223 2 2
ab abab abaababb
a b ab 2b 0 a ab 2b 0
Mà ta có
ab0
nên
2
aab0
nên ta được
22
aab2b 0
.
Vậy bất đẳng thức được chứng minh.
Ví dụ 9. Cho a, b, c là các số thực thỏa mãn
a4,b5,c6 và
222
abc90
Chứng minh rằng:
abc16
Phân tích: Từ điều kiện của biến a4,b5,c6, để quy về một điều kiện ta có thể sử dụng cách
đặt biến phụ
ax4;by5;zc6
, khi đó điều kiện của biến mới là
x, y, z 0
.
Giả thiết lúc này được viết lại là
222
x y z 12 x y z 4x 2z 13 và bất đẳng thức
cần chứng minh trở thành
xyz1. Từ những kết quả thu được ở trên ta nếu ta giả sử
xyz1
thì ta thu được điều kiện
0x,y,z1
. Khi đó ta có
222
xyz xyz
suy ra
222
x y z 12 x y z 4x 2z 13
. Đến đây
xem như bài toán được giả quyết xong.
Lời giải
Đặt
ax4;by5;zc6 , khi đó ta có x, y, z 0 .
Giả thiết lúc này được viết lại là
222
222
x 4 y 5 z 6 90 x y z 12 x y z 4x 2z 13
Bất đẳng thức cần chứng minh trở thành
xyz1
Giả sử tồn tại
x, y, z 0 , thỏa mãn điều kiện
222
x y z 12 x y z 4x 2z 13
Nhưng bất đẳng thức
xyz1
không đúng. Tức là ta có
xyz1
.
Khi đó hiển nhiên có
0x,y,z1
nên
222
xx;yy;zz
.
Suy ra
222
xyz xyz. Từ đó ta có

222
13 x y z 12 x y z 4x 2z 13 x y z 4x 2z
13 x y z 13
Hay
13 13 , đây là một mâu thuẫn. Vậy điều giả sử trên không thể xẩy ra, tức là bài toán được chứng
minh.
Ví dụ 10. Cho a, b, c là ba số thực bất kì thỏa mãn các điều kiện sau:
3
abc 2015
và
ab bc ca 2015 a b c
Chứng minh rằng trong ba số a, b, c đó có đúng một số lớn hơn 2015.
Phân tích: Từ bài toán ta nhận thấy không thể có trường hợp cả ba số a, b, c cùng lớn hơn 2015. Bài toán
yêu cầu chứng minh rằng trong ba số a, b, c đó có đúng một số lớn hơn 2015. Điều này có nghĩa là không
thể có hai số lớn hơn 2015 cũng không thể có cả ba số cùng không lớn hơn 2015. Như vậy để chứng minh
bài toán ta chỉ cần chứng minh hai trường hợp này không xẩy ra là được. Để ý là khi so sánh các số a, b, c
với 2015 ta thường so sánh
a 2015; b 2015; c 2015
với 0.
Lại thấy từ giả thiết ta được
2015 a b c ab bc ca 0
nên ta được
P a 2015 b 2015 c 2015 2015 2015 a b c ab bc ca 0
.
Lời giải
Xét biểu thức
23
P a 2015 b 2015 c 2015
abc 2015 ab bc ca 2015 a b c 2015
2015 2015 a b c ab bc ca 0
Giả sử khẳng định của bài toán là sai, khi đó sẽ có hai trường hợp
+ Trường hợp thứ nhất cả ba số a, b,c đều không lớn hơn 2015, khi đó ta có
a 2015 0; b 2015 0; c 2015 0
Suy ra
P0
, điều này mâu thuẫn với bất đẳng thức trên.
+ Trường hợp thứ hai là có ít nhất hai số lớn hơn 2015, chẳng hạn là a, b. Khi đó ta được
a 2015; b 2015 suy ra a 2015 0; b 2015 0.
Do đó ta có
P
a 2015 b 2015 0 c 2015 0
a 2015 b 2015
Suy ra
c 2015 , dẫn đến
3
abc 2015 , điều này mâu thuẫn với giả thiết
3
abc 2015 .
Vậy điều giả sử không thể xẩy ra. Do đó bài toán được chứng minh.
Ví dụ 11. Cho a, b, c là các số thực thỏa mãn
222222222
a 2b 2ac bc 3abc 9
Chứng minh rằng: abc 1
Phân tích: Trước hết ta nhận thấy, nếu một trong ba số a, b, c bằng 0 thì bài toán được chứng minh. Như
vậy ta cần phải chứng minh cho trường hợp cả ba số a, b, c khác 0. Để ý từ giả thiết ta thu được

222 222
2 2 22 22 2 22 2 2 2 22
22
abc abc
a 2b 2ac bc 3abc a 2 b 3abc
ab
Mà ta lại có
222 222
22222 222
22
abc abc
a 2 b 3a b c 2 abc 4 abc 3a b c
ab
Đến đây ta có thể sử dụng phép phản chứng hoặc phân tích thành nhân tử để chứng minh bài toán.
Lời giải
Nếu một trong ba số a, b, c bằng 0 thì bài toán được chứng minh.
Như vậy ta cần phải chứng minh cho trường hợp cả ba số a, b, c khác 0. Từ giả thiết ta thu được
222 222
2 2 22 22 2 22 2 2 2 22
22
abc abc
a 2b 2ac bc 3abc a 2 b 3abc
ab
Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có bất đẳng thức
abc 1
Đặt
2
xabc1 x 1. Khi theo bất đẳng thức Cauchy ta có
22
2 2 22 22 2 22 2 2 2
22
22
22
xx
9a2b2acbc3abc a 2b 3x
ab
11
a2b 39
ab
Hay
99
, điều này là vô lý. Vậy điều ta giả sử là không xẩy ra hay bài toán được chứng minh.
Ngoài ra ta cũng có thể trình bày như sau: Biến đổi tương tự như trên ta được
222 222
22222 222
22
abc abc
9 a 2 b 3a b c 2 abc 4 abc 3a b c
ab
Đặt
xabc0 khi đó ta được
22
96x3x x 2x30 x1x3 0 x1
.
Ví dụ 12. Cho a, b là các số thức dương thỏa mãn
ab2
. Chứng minh rằng:
33
ab2
Phân tích: Để bài toán đơn giản hơn ta có thể thực hiện làm mất căn bậc ba bằng cách đặt
33
xa;yb, khi đó giả thiết của bài toán trở thành
33
xy2
và ta cần chứng minh xy2.
Để ý ta thấy
xy2 tương đương với
3
xy 8, khai triển ta và sử dụng giả thiết ta được được
33
xyxy x y
. Như vậy bất đẳng thức cuối cùng luôn đúng nên ta có được bất đẳng thức cần
chứng minh. Tuy nhiên nếu
xy2, với cách biến đổi như trên ta thu được
33
xyxy x y là
một bất đẳng thức sai. Do đó ta có thể sử dụng phép biến đổi tương đương hoặc phép phản chứng để giải
quyết bài toán.
Lời giải

Đặt
33
xa;yb, khi đó giả thiết của bài toán trở thành
33
xy2 và ta cần chứng minh
xy2
.
Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có bất đẳng thức
xy2.
Biến đổi tương đương bất đẳng thức ta được
3
33
33
xy 8 x y 3xy 8 23xyxy 8
xy x y 2 xy x y x y
Chia 2 vế cho số dương
xy khi đó ta được bất đẳng thức
2
22
xy x xy y 0 x y
Bất đẳng thức cuối cùng là một bất đẳng thức sai. Vậy điều ta giả sử là không xẩy ra hay bài toán được
chứng minh.
Ví dụ 13. Cho 25 số tự nhiên
12 25
aa a...,,, khác 0 thoả mãn điều kiện:
12 25
11 1
9
aa a
Chứng minh rằng trong 25 số tự nhiên đó luôn tồn tại hai số bằng nhau.
Phân tích: Để chứng minh trong hai 25 số tự nhiên trên luôn tồn tại hai số bằng nhau ta có thể giả sử 25
số đó khác nhau từng đôi một, để dễ biến đổi ta nên sắp thứ tự cho 25 số đó, chẳng hạn
12 25
aa a... . Với cách sắp thứ tự như vậy ta sẽ nhận được kết quả là
12 25
a1a2 a 25,,..., . Khi đó ta có
12 25
11 111 1
aa a 12 25
Đến đây ta chỉ cần chỉ ra
11 1
9
12 25
là bài toán được giải quyết
Lời giải
Giả sử trong 25 số tự nhiên
12 25
aa a...,,, không có hai số nào bằng nhau. Không mất tính tổng
quát ta có thể chọn
12 25
aa a... . Khi đó ta có
12 25
a1a2 a 25,,...,
Suy ra ta được
12 25
11 111 1
aa a 12 25
Mặt khác ta chứng minh được

11 1 2 2 2
1...
1 2 25 22 23 225
11 1
12 ...
2 1 3 2 25 24
1 2 2 1 3 2 ...... 25 24
12 251 9
Điều này dẫn tới
12 25
11 1
9
aa a
Bất đẳng thức thu được mâu thuẫn với giả thiết của bài toán.
Vậy điều ta giả sử là không xẩy ra hay bài toán được chứng minh.
Ví dụ 14. Cho 25 số tự nhiên
1 2 2015
aa a...,,, khác 0 thoả mãn điều kiện:
1 2 3 2015
111 1
... 89
aaa a
Chứng minh rằng trong 2015 số tự nhiên đó luôn tồn tại hai số bằng nhau.
Lời giải
Giả sử trong 2015 số tự nhiên
12 2015
aa a...,,, không có hai số nào bằng nhau. Không mất tính tổng quát
ta có thể chọn
1 2 2015
aa a... . Khi đó ta có
1 2 3 2015
a 1,a 2,a 3,...,a 2015
Suy ra ta được
1 2 3 2015
111 1 111 1
... ...
aaa a 123 2015
Mặt khác ta chứng minh được
11 1 2 2 2
1...
1 2 2015 2 2 2 3 2 2015
11 1
1 2 ...
2 1 3 2 2015 2014
1 2 2 1 3 2 ... 2015 2014
1 2 2015 1 89
Điều này dẫn tới
1 2 2015
11 1
89
aa a
Bất đẳng thức thu được mâu thuẫn với giả thiết của bài toán.
Vậy điều ta giả sử là không xẩy ra hay bài toán được chứng minh.
Ví dụ 15. Cho a, b là các số thực dương thỏa mãn
44 33
abab. Chứng minh rằng:
ab2
Lời giải
Giả sử bất đẳng thức cần chứng minh sai, khi đó ta có bất đẳng thức
ab2.
Đặt
ax1;by1
khi đó ta được
xy0
Xét hiệu hai vế của giả thiết ta được
4433
4433
22 33
22 2 2
a b a b 1x 1y 1x 1y
xy 3x y 3x y
xy 3x y 3xyx xyy 0
Hay
4433
abab0
Mà ta lại có
ab2
do đó suy ra
44 33
abab. Bất đẳng thức thu được trái với giả thiết của bài
toán.
Vậy điều ta giả sử là không xẩy ra hay bài toán được chứng minh.
Ví dụ 16. Cho a, b, c là các số nguyên dương thỏa mãn
222
abc1ab .
Chứng minh rằng:
ac
và
bc
Phân tích: Quan sát bài toán ta nhận thấy vai trò của a, b là như nhau, do đó ta chỉ cần chứng minh
ac
, trường hợp còn lại hoàn toàn tương tự. Để tìm mối liên hệ của a và c ta viết lại giả thiết là
22 2
ac bacb . Do đó nếu như ac thì ta được bất đẳng thức
22 2 2
ac bacb 0 bac . Mặt khác ta lại thấy
22
bb ac b ac. Như vậy ta được
22 2
caac 0 , nhưng do a, c là các số nguyên dương nên ta lại thu được
22 2 2 2
caac c1aa 0
, hai bất đẳng thức này mâu thuẫn với nhau, bài toán được giải quyết
xong.
Lời giải
+ Trước hết ta chứng minh
ac . T viết lại giả thiết là
22 2
ac bacb .
Giả sử
ac khi đó ta được
22 2 2
acbacb 0 bac
.
Mà ta lại thấy
22
bb ac b ac.
Như vậy ta được
22 2
caac 0 .
Mà do a, c là các số nguyên dương nên ta được
22 2 2 2
caac c1aa 0 .
Hai bất đẳng thức này mâu thuẫn với nhau. Do đó không thể xẩy ra
ac , tức là ta có bất đẳng thức
ac .
Hoàn toàn tương tự ta chứng minh được
bc
.
Vậy bài toán được chứng minh xong.
Ví dụ 17. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abcabc . Chứng minh rằng 2
trong 3 bất đẳng thức sau là bất đẳng thức đúng

236 236 236
6; 6; 6
abc bca cab
Phân tích: Từ cách phát biểu bài toán ta ưu tiên lựa chọn phương pháp phản chứng để chứng minh. Vì
bài toán yêu cầu ta phải chứng minh có ít nhất hai trong ba bất đẳng thức là đúng, điều này có nghĩa là
không thể có trường hợp có ít nhất hai bất đẳng thức trên cùng sai. Như vậy ta chỉ cần chứng minh trường
hợp có ít nhất hai bất đẳng thức trên cùng sai không thể xẩy ra là được. Chú ý giả thiết và các bất đẳng
thức ta có thể đặt
111
x;y;z
abc
. Khi đó giả thiết trở thành
xy yz zx 1
và các bất đẳng
thức là
2x 3y 6z 6; 2y 3z 6x 6; 2z 3x 6y 6
.
Lời giải
Đặt
111
x;y;z
abc
. Khi đó giả thiết trở thành xy yz zx 1 và các bất đẳng thức là
2x 3y 6z 6; 2y 3z 6x 6; 2z 3x 6y 6
.
Ta cần chứng minh có ít nhất hai trong ba bất đẳng thức trên là đúng.
Giả sử điều cần phải chứng minh là sai. tức là có ít nhất hai bất đẳng thức trên không đúng. Không
mất tính tổng quát ta chọn
2x 3y 6z 6; 2y 3z 6x 6 là hai bất đẳng thức bị sai, khi đó ta
được
2x 3y 6z 6; 2y 3z 6x 6
Cộng theo vế hai bất đẳng thức trên ta được
8x 5 y 9z 12
Từ
xy yz zx 1 ta được
1yz
x
yz
, khi đó ta có bất đẳng thức
22
22
81 yz
5y 9z 12 8 1 yz y z 5y 9z 12 y z
yz
5y 9z 6yz 12y 12z 8 0
y3z2 4y1 0
Bất đẳng thức cuối cùng là một bất đẳng thức sai.
Vậy điều giả sử không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 18. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc 1 . Chứng minh rằng:
111
1
18a 18b 18c
Phân tích: Để ý ta thấy
2
2
11x
xa
8x
18a
và vì a là số thực dương nên ta có điều kiện
0x1. Như vậy để đơn giản hóa bất đẳng thức cần chứng minh ta có thể đổ biến
111
x;y;z
18a 18b 18c
, khi đó ta được
0x;y;z1
.

Giả thiết được viết lại là
32 22 2 2 2
8x.y.z 1 x 1 y 1 z và bất đẳng thức cần chứng
minh là
xyz1
. Nhìn giả thiết ta liên tưởng đến một bất đẳng thức quen thuộc
8xyz x y y z z x
, như vậy ta cần cách tìm biến đổi làm xuất hiện các đại lượng
xy,yz,zx . Nhận thấy theo bất đẳng thức Cauchy ta có
2
2
xyz x yz xy xz 2yz xyxz
Như vậy nếu
xyz1
thì
2
22
1x xyz x , lúc này ta được các bất đẳng thức
ngược chiều nhau. Đến đây một cách tự nhiên ta nghĩ đến phép phản chứng.
Lời giải
Đặt
111
x;y;z
18a 18b 18c
.
Suy ra
222
222
1x 1y 1z
a;b;c
8x 8y 8z
, khi đó ta được 0x;y;z1.
Vì
abc 1 nên giả thiết được viết lại là
32 22 2 2 2
8x.y.z 1x 1y 1z và bất đẳng thức cần
chứng minh là
xyz1.
Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có bất đẳng thức
xyz1
.
Khi đó áp dụng bất đẳng thức Cauchy ta được
2
22
1x xyz x yz xy xz
2y z x y x z 0
Áp dụng tương tự ta có
22
1y 2xz xyyz 0;1z 2xy xzyz 0
Nhân theo vế các bất đẳng thức trên ta được
222
32 22 2 2 2
8x.y.z 1x 1y 1z xy yz zz
Hay
8xyz x y y z z x
, rõ ràng bất đẳng thức cuối cùng là một bất đẳng thức sai. Vậy điều
giả sử không thể xẩy ra, tức là bài toán được chứng minh.
Một số ví dụ khác
Ví dụ 19. Cho a, b, c là các số thực dương thỏa mãn
111
3
abc
. Chưng minh rằng:
ab bc ca 32
Lời giải
Đặt
xab;ybc;zca , khi đó ta được
222 222 222
2a x z y ; 2b x y z ; 2c z y x

Giả thiết được viết lại thành
22 2 2 22 2 2 2
1113
2
xzy xyz zyx
Bất đẳng thức cần chứng minh là
xyz32
Giả sử bất đẳng thức cần chứng minh là sai, tức là ta có
xyz32
.
Áp dụng bất đẳng thức Cauchy ta được
222 222222
22 22 222 2 2
3
3111
2
xzy xyzzyx
3
xzyxyzzyx
Mặt khác theo một bất đẳng thức quen thuộc ta lại có
6
22 22 222 2 2 222
xyz
xzyxyzzyx xyz 8
3
Do đó ta được
3
222222222
3
333
2
8
xzyxyzzyx
Hay ta được
33
22
, bất đẳng thức thu được là một bất đẳng thức sai.
Vậy điều giả sử không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 20. Cho a, b là các số thực thỏa mãn các điều kiện sau:
1ab1; 1abab1
Chứng minh rằng: 2a,b2
Lời giải
Vì vai trò của a, b như nhau nên ta chỉ cần chứng minh
2a2 . Việc chứng minh
2b2
hoàn toàn tương tự.
Giả sử bất đẳng thức
2a2 là sai, khi đó ta có a2 hoặc a2 .
+ Xét trường hợp
a2 , khi đó từ 1ab1 suy ra b1a12 1, do đó ta được
ab 2 mà ab1 nên a b ab 1 điều này mâu thuẫn với giả thiết thứ hai của bài toán. Như
vậy trường hợp này không xẩy ra.
+ Xét tường hợp
a2
, khi đó từ
1ab1
suy ra
b1a121
, do đó ta được
ab 2 mà ab1 nên a b ab 1 điều này mâu thuẫn với giả thiết thứ hai của bài toán. Như
vậy trường hợp này cũng không xẩy ra.
Các kết quả trên chứng tỏ điều giả sử không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 21. Cho a, b, c là các số thức không âm thỏa mãn
abcabc . Chứng minh rằng:
222
abcabc
Lời giải
Nếu
abc 0 , thì bất đẳng thức được chứng minh.
Xét
abc 0 , khi đó ta được a, b , c 0 . Giả sử bất đẳng thức cần chứng minh là sai, tức là
222
abcabc
. Khi đó ta có
222 2
abc a b c a
nên
bc a
.

Chứng minh tương tự ta được
bac,cab
Từ đó suy ra
abcabbcca .
Mặt khác ta lại có
222
abc a b c ab bc ca abc ab bc ca
Kết hợp hai bất đẳng thức ta được
abc a b c, bất đẳng thức này mâu thuẫn với giả thiết của bài
toán.
Vậy điều giả sử không thể xẩy ra, tức là bài toán được chứng minh.
Ví dụ 22. Cho a, b, c là các số thực dương thỏa mãn
111
abc
abc
.
Chứng minh rằng:
abcbcacab 1
Lời giải
Bất đẳng thức có tính đối xứng giữa các biến, do đó không mất tính tổng quát ta giả sử
abc, Khi
đó
abc0 và acb0 .
+ Nếu
bca 0 , bất đẳng thức hiển nhiên đúng.
+ Nếu
bca 0 . Khi này ta đặt
xbca;ycab;zabc
.
Khi đó ta viết lại giả thiết là
x; y; z 0
và
222
xyz
xy yzzx
.
Bất đẳng thức cần chứng minh trở thành
xyz 1 .
Ta chứng minh bất đẳng thức trên bằng phương pháp phản chứng
Thật vậy, giả sử
xyz 1 . Khi đó theo bất đẳng thức Cauchy ta được
222111
xyz
xy yzzx
xy yz zx
Hay
xyz xyzxyz , vì xyz 1 nên
xyzxyz
Tuy nhiên cũng theo bất đẳng thức Cauchy ta được
x1
x
2
, thiết lập các đánh giá tương tự ta có
xyz3
xyzxyzxyz3
2
Mặt khác
222 9
xyz xyz3
xy yzzx xyz
Mâu thuẫn này chứng tỏ điều giả sử trên là sai, do vậy
xyz 1 . Như vậy bất đẳng thức trên được chứng
minh, dấu đẳng thức xẩy ra khi
abc1.
Nhận xét: Ta có thể sử dụng phương pháp phản chứng theo hướng như sau
Giả sử
1xyz , khi đó từ giả thiết của bài toán suy ra
2
22 x y z xy yz zx x y z xy yz zx xyz x y z
Theo bất đẳng thức Cauchy và kết hợp với giả sử ta lại có

222
3
33; 3 xy yz zx x y z x y z
Do đó
2
2
2
2
2
2
3
2
2
9
2
9
xyz xyyzzx
xyz
xyz xyyzzx
xy yz zx
xyz xyyzzx
xyz x y z
Cộng theo vế a bất đẳng thức trên ta được
2
22 x y z xy yz zx x y z xy yz zx xyz x y z
Điều này mâu thuẫn với đẳng thức trên, do đó điều giả sử là sai. Như vậy bất đẳng thức trên được chứng
minh.
Ví dụ 23. Cho a, b, c là các số thực thỏa mãn đồng thời các điều kiện sau:
abc;abc6;abbcca9
Chứng minh rằng:
0a1;1b3;3c4
Lời giải
Từ giả thiết của bài toán, ta suy ra
2
222
a b c abc 2abbcca 18
Mặt khác, vì a, b, c là các số dương cho nên
22
bc 6a
9 abbcca abc a6a
42
Hay
3
3a
3a 0
4
, từ đó suy ra 0a4, do vậy 0abc
Khi đó
222 2
18 a b c acbcc cabc 6c
. Suy ra c3 .
Bây giờ ta chứng minh
c4 . Thật vậy, giả sử c4 khi đó ta được
2
c4c , từ đây ta suy ra
22
222 2
ab 6c
18 a b c c 4c
22
Hay
2
c
2c 0 0 c 4
2
. Mâu thuẫn với c4 , do vậy c4
Từ đó ta có
3c4
Cũng từ đây ta suy ra
abc4. Ta chứng minh
a1
. Thật vậy, giả sử
a1
Khi đó ta được
1abc4
, suy ra
a1a4 0;b1b4 0;c1c4 0
Hay
222
a5a4;b5b4;c5c4
Cộng theo vế ba bất đẳng thức trên ta được
222
abc5abc1218
Điều này mâu thuẫn với điều kiện
222
abc18. Do đó a1 . Vậy 0a1.
Cuối cùng ta chứng minh
1b3
Thật vậy, vì
a1 và c4 , do đó b6ac6141 hay b1
Ta cần chứng minh
b3 .

Giả sử
b3 , khi đó ta có
b3c3 0
Hay
bc 3 b c 9 3 6 a 9 9 3a
Từ đó suy ra
9 abbcca abc bc abc 93a
Hay
ab c 3 0
Đánh giá cuối cùng là một đánh giá sai do
3c4. Vì vậy giả sử b3 là sai.
Do đó
b3
. Vậy ta được
1b3
.
Như vậy bài toán được chứng minh xong.

Chủ đề 4
CHỨNG MINH CÁC BẤT ĐẲNG THỨC VỀ TỒNG, TÍCH CỦA DÃY SỐ - PHƯƠNG PHÁP
QUY NẠP TOÁN HỌC
1. Một số kiến thức cần nhớ
a) Phương pháp làm trội, làm giảm
Giả sử cần chứng minh
AB
, khi đó ta cần làm trội biểu thức A thành
AM
rồi chứng minh
MB . Cũng có thể làm giảm B thành MB rồi chứng minh AM .
Phương pháp làm trội, làm giảm thường được áp dụng cho bất đẳng thức về tổng hoặc tích của một
dãy số. Khi đó dùng các tính chất bất đẳng thức để đưa một vế của bất đẳng thức về dạng tính được tổng
hữu hạn hoặc tích hữu hạn.
+ Ý tưởng chung cho bất đẳng thức dạng tổng của dãy số là:
Giả sử ta cần chứng minh
123 n
Ax Ax Ax ... Ax M, khi đó ta thực hiện làm
trội
ii1i
Ax By By
để thu được
123 n n1
Ax Ax Ax ... Ax By By
Sau đó ta chỉ cần chứng minh bất đẳng thức
n1
By By M.
+ Ý tưởng chung cho bất đẳng thức dạng tích của dãy số là:
Giả sử ta cần chứng minh
123 n
Ax .Ax .Ax ...Ax M , khi đó ta thực hiện làm trội
i1
i
i
By
Ax
By
để thu được
n
123 n
1
By
Ax .Ax .Ax ...Ax
By
Sau đó ta chỉ cần chứng minh bất đẳng thức
n
1
By
M
By
.
+ Một số tổng sai phân hay dùng
111 a11
;
nn1 nna
nn 1 nn a
2a 1 1
nn a n 2a nn a n a n 2a
11 1 1
1
1.2 2.3 n
nn 1
11 1 k
...
nn a n a n 2a xn ka
nk1anka
11 1 11 1
1.2.3 2.3.4 2 1.2.3
nn 1 n 2 nn 1 n 2
Chú ý:
- Ta cần áp dụng làm trội, làm giảm sao cho bất đẳng thức cuối cùng cần chứng minh phải càng
đơn giản càng tốt.

- Thông thường ta tìm quy luật viết các số hạng của dãy rồi đưa ra cách viết tổng quát, từ đó ta
mới làm trội cho số hạng tổng quát và áp dụng cho các số hạng cụ thể.
b) Phương pháp quy nạp toán học
+ Nội dung của phương pháp quy nạp
Một bất đẳng thức phụ thuộc vào số nguyên dương n được xem là đúng nếu thỏa mãn hai điều kiện
sau:
- Bất đẳng thức đúng với giá trị đầu tiên của n
- Từ giả thiết bất đẳng thức đúng với n = k
kN
suy ra được bất đẳng thức đúng với
nk1
+ Các bước chứng minh bất đẳng thức bằng phương pháp quy nạp
Giả sử ta cần chứng minh bất đẳng thức
An Bn
với
0
nn,nN
, ta tiến hành các
bước như sau:
- Bước 1: Kiểm tra bất đẳng thức đúng với
0
nn
- Bước 2: Giả sử bất đẳng thức đúng với
0
nkkn,kN
- Bước 3: Chứng minh bất đẳng thức đúng với
nk1 và kết luận bất đẳng thức đúng với
0
nn .
Chú ý:
- Thông thường khi chứng minh bất đẳng thức có sự phụ thuộc vào số nguyên dương n, thì ta nên
chú ý sử dụng phương pháp quy nạp toán học.
- Trong phương pháp quy nạp toán học thì bất đẳng thức có được từ bước thứ hai chính là một
giả thiết mới được dùng để chứng minh bất đẳng thức trong bước thứ ba. Do đó cần phải khai thác thật
hiệu quả giả thiết quy nạp.
2. Một số ví dụ minh họa
Ví dụ 1. Với mọi số tự nhiên n >1. Chứng minh rằng:
11 1 1
...
2n1n2 nn
Phân tích và lời giải
Nhận thấy tổng trên có n số hạng, do đó ta làm trội bằng cách thay mẫu
nk
với
k 1, 2, 3, ..., n 1 bằng nn . Tức là ta có:
111
nk nn 2n
, với k 1, 2, 3, ..., n 1
Khi đó ta được:
11 11 1n1
... ...
n 1 n 2 2n 2n 2n 2n 2
Vậy bất đẳng thức được chứng minh.
Ví dụ 2. Với mọi số tự nhiên
n1 . Chứng minh rằng:
111 1
1 ... 2
n1 n2 n3 3n1
Phân tích và lời giải

+ Trước hết ta chứng minh:
111 1
... 2
n1 n2 n3 3n1
Tổng trên có
2n 1 số hạng và lại thấy
2n 1 2n 2
2
n1 n1
, do đó áp dụng tư tưởng như ví
dụ trên ta làm trội bằng cách thay mỗi số hạng bằng số hạng lớn nhất. Tức là ta được
111 1 111 12n1
... ... 2
n1n2n3 3n1 n1n1n1 n1 n1
+ Bây giờ ta chứng minh:
111 1
1...
n1 n2 n3 3n1
Tổng trên có
2n 1
số hạng và số hạng chính giữa là
1
2n 1
, ta chuyển bất đẳng thức cần
chứng minh thành
2n 1 1 1 1 1
...
2n 1 n 1 n 2 n 3 3n 1
Ở đây ta lại nhận thấy
2n 1 2 1
n.
2n 1 2n 1 2n 1
có chứa số hạng chính giữa, do đó ý tưởng ở
đây là ghép các cặp dạng
111111
; ; ...;
n1 3n1n2 3n 2n 2n2
thì được n tổng, rồi chứng
minh mỗi tổng đó đều lớn hơn
2
2n 1
. Để chứng minh các tổng trên đều lớn hơn
2
2n 1
ta chỉ cần
chứng minh được
11
2n 1 k 2n 1 k
, trong đó k nhận các giá trị từ 1; 2; ...; n . Thật vậy:
22
2
114n24n22
2n 1 k 2n 1 k 2n 1
2n 1 k 2n 1
Đến đây ta có lời giải như sau:
Ta có
11 1 11
... ...
n1 n2 2n1 3n 3n1
11 11 1
...
n1 3n1 n2 3n 2n1
4n 2 4n 2 1 2 1
... .n 1
2n 1 2n 1 2n 1
n13n1 n13n
Vậy ta được
111 1
1...
n1 n2 n3 3n1
Vậy bài toán được chứng minh
Nhận xét: Bất đẳng thức bên trái là một bất đẳng thức khó, sử dụng cách làm như bất đẳng thức bên
phải không đem lại hiệu quả, cho nên ta phải tìm một phương án khác. Điểm quan trọng để tìm ra lời giải
cho bài toán này chính là phát hiện các tổng bằng nhau
131 23...2 22221 nnnnnn n và ý tưởng ghép các cặp

111111
; ; ...;
13 1 23 2 2 2
nnnnnn
sao cho khi quy đồng có cùng một tử số là
22 1n
và bước tiếp theo chính là đánh giá mẫu về cùng
21n .
Ví dụ 3. Chứng minh rằng với mọi số nguyên dương
n2 ta có:
2n 1 1 1 1 1 3n 2
...
3n 2 2n 2 2n 3 2n 4 4n 2
4n 1
Phân tích và lời giải
Đặt
111 1
P...
2n 2 2n 3 2n 4 4n 2
+ Chứng minh
2n 1
P
3n 2
. Tổng P có 2n 1 số hạng, ta ghép thành n cặp cách đều hai đầu, còn lại
một số hạng đứng giữa là
1
3n 2
, mỗi cặp có dạng:
22
2
23n 2 23n 2
11 2
3n 2 k 3n 2 k 3n 2
3n 2 k 3n 2
k1,2,...,n-1, n
Do đó ta được:
2n 1 2n 1
P
3n 2 3n 2 3n 2
+ Chứng minh
3n 2
P
4n 1
.
Để chứng minh bất đẳng thức này, chúng ta cần có bổ đề sau:
Bổ đề: Với mọi
0km2k,mZ , ta có:
1111
*
mk2m2k m 2m2
Chứng minh: Từ giả thiết
0km2k,mZ
, ta thấy các mẫu số đều dương và 3m 2 0.
Quy đồng mẫu số hai vế ta có
22 22
3m 2 3m 2
*m2m2mk2m2k
mk2m2k m2m2
2m 2m 2m 2m km 2km 2k k k km 2k k m 2
Bất đẳng thức cuối cùng đúng theo giả thiết, nên bổ đề được chứng minh
Viết lại biểu thức P và áp dụng bổ đề ta có
11 11 11
2P ...
2n 2 4n 2 2n 3 4n 1 4n 2 2n 2
11
2n 1
2n 2 4n 2
Hay
13n2 3n2
P2n1
2
2n 1 2n 1 4n 1
Vậy bất đẳng thức được chứng minh.

Nhận xét: Ý tưởng của bài toán trên cũng là ghép theo cặp, với bất đẳng thức bên trái ta thấy không có
vấn đề gì lớn cả. Tuy nhiên với bất đẳng thức bên phía phải, sẽ thực sự gây ra nhiều khó khăn nếu không
phát hiện ra bổ đề: Với
02, km kmZ, ta có:
1111
22 22
mk m k m m
Ví dụ 4. Chứng minh rằng với mọi số nguuyên dương
n2 ta có
n
n1 1 1 1 1
1 ... n
2234
21
Phân tích và lời giải
Bất đẳng thức cần chứng minh là một bất đẳng thức kép nên ta chia thành hai bất đẳng thức để
chứng minh. Nhận thấy tổng trên có
n
21
phân số nên nếu chia theo nhóm tương tự như ví dụ trên
không đem lại hiệu quả vì khi quy đồng theo nhóm thì các tử số không bằng nhau. Để tiện cho việc tìm
lời giải ta đặt:
n
111 1
P1 ...
234
21
Tức là ta cần chứng minh
n1
Pn
2
Quan sát yêu cầu bài toán, ta thấy có thể làm trội bằng cách chia biểu thức thành nhiều nhóm, rồi
làm trội từng nhóm.
+ Trước hết ta chứng minh
Pn .
Để ý ta thấy
n11...1 (có n số 1), nên ta có thể chia P thành n nhóm sao cho mỗi nhóm
đều có thể bé hơn hoặc bằng 1. Ta có thể làm như sau:
n1
n1 n n1
11 1 1 1 1 1 1 1
1 1; 2. 1; ... 4. 1; ...; ... 2 . 1
23 2 4 7 4
2212
Như vậy P được chia thành các nhóm có số phân số lần lượt là:
n1
1; 2; 4; 8; ...; 2
, ta cần kiểm tra xem
tổng các phân số có phải là
n
21 không?
Ta có
n1 n
1 2 4 8 ... 2 2 1
, điều này có nghĩa là ta nhóm vừa đủ, và có tất cả n nhóm như
vậy, khi này ta có thể giải được như sau:
Ta có:
2334 n1n
11 1 1 1 1 1 1 1
P 1 ... ... ... ...
23 5
221221221
Làm trội biểu thức bằng cách thay các phân số trong mỗi ngoặc bằng phân số lớn nhất trong mỗi
nhóm ta được
n1
23 n1
11 1 1
P 1 .2 .4 .8 ... .2 1 1 ... 1 n
2
22 2
+ Để chứng minh
n1
P
2
ta cũng làm tương tự.
Ta có
23n1nn
111 11 1 1 11
P 1 ... ... ...
2214 6
21 2 2 1 2 2
Làm trội biểu thức bằng cách thay phân số trong mỗi ngoặc bằng phân số nhỏ nhất trong mỗi
nhóm ta được.

n1
23 n n n
n1
nn
11 1 1 1 n1
P 1 .2 .4 ... .2 1
22
22 2 2 2
n 1 n12 1 n1
P1
22 2
22
Kết hợp hai bất đẳng thức ta được bất đẳng thức cần chứng minh.
Ví dụ 5. Chứng minh rằng với n là số nguyên dương, ta luôn có:
22 2
11 1
1 .... 2
23 n
Phân tích và lời giải
Để chứng minh bất đẳng thức trên ta cần làm trội mỗi phân số bằng các thay mẫu số bằng một số
nhỏ hơn. Để ý đến đánh giá
2
kkk1
, khi đó ta thu được các đánh giá có dạng
2
11 11
k1 k
k
kk 1
, cho k 2,3, ...,n ta thì ta được một bất đẳng thức
22 2
11 1 1111 1 1
1 .... 1 ...
1223 n1n
23 n
. Bây giờ ta cần kiểm tra xem
1111 1 1
1...2
1223 n1n
có đúng không. Dễ thấy bất đẳng thức trên đúng, do đó ta trình
bày lại lời giải như sau:
Ta có:
2
11 11
,k
k1 k
k
kk 1
là số nguyên dương.
Cho
k 2,3, ...,n
ta có:
2
2
2
11
1
2
2
111
23
3
...
111
n1 n
n
Cộng từng vế các bất đẳng thức trên ta được:
22 2
11 1
.... 1
23 n
Suy ra
22 2
11 1
1 .... 2
23 n
. Vậy bất đẳng thức được chứng minh.
Ví dụ 6. Chứng minh rằng với mọi số tự nhiên n, ta luôn có:
222 2
111 1 1
...
4
468
2n
Lời giải
Ta có

222 2222 2
222 2
111 1111 1
... ...
4.2 4.3 4.4 4.n
2.2 2.3 2.4 2.n
11 1 1 1 1 1
... 1
444
234 n
Vậy bất đẳng thức được chứng minh.
Nhận xét: Bất đẳng thức tổng quát của ví dụ trên là:
222 22
111 11
...
.2 .3 .4 .
k
kkk kn
,
*
kN
Ta thay k bởi một số tự nhiên khác 0 tuỳ ý sẽ được các bài toán mới, chẳng hạn với
k5
ta
có
222 2
111 1 1
...
25
10 15 20
5n
Ví dụ 6. Chứng minh rằng:
22 2
1 1 1 2014
....
2015
2 3 2015
Lời giải
Ta có với mọi
k1 thì
2
kkk10 nên
2
11 11
k1 k
k
kk 1
Cho
k 2, 3, 4, ..., 2015 , ta có:
2
2
2
11 1
1
1.2 2
2
1111
2.3 2 3
3
...
1111
2014.2015 2014 2015
2015
Cộng vế với vế các bất đẳng thức cùng chiều, ta được
22 2
1 1 1 1 2014
..... 1
2015 2015
2 3 2015
Vậy bất đẳng thức được chứng minh.
Ví dụ 7. Chứng minh rằng với mọi số nguyên dương n ta có:
222 2
111 15
1...
3
123 n
Phân tích và lời giải
Dễ thấy vì n là số nguyên dương nên ta có:
222 2 2
111 1 1
... 1 1
123 n 1
Bây giờ ta chứng minh
222 2
111 15
...
3
123 n
.
Thực hiện ý tưởng làm trội như các ví dụ trên với đánh giá
2
111
k1 k
k
. Tức là ta sẽ thu được
một bất đẳng thức
222 2
111 1 1 1
... 1 1 2
nn
123 n
, tuy nhiên ở đây ta không thể khẳng

định được
15
2
n3
là đúng. Do đó trong bất đẳng thức trên ta không thể làm trội theo các đánh giá
như trên được. Tất nhiên là với bài toán này ta vẫn thực hiên ý tưởng làm trội nhưng với một đánh giá tốt
hơn, khi đó ta cần một đánh giá theo kiểu
222
222
2
1a a a 1 1
2b ak b ak b
k
ak ak b
. Để ý ta
viết lại được bất đẳng thức cần chứng minh là
22 2
11 12
...
3
23 n
nên với
k2
khi đó ta chọn các
giá trị a, b nguyên dương sao cho
2
a2
3
2b 2a b
, thử một vài trường hợp ta chọn được a2,b1.
Tức là ta được
222
14 4 1 1
2
2k 1 2k 1
k4k4k1
. Vấn đề bây giờ ta cần kiểm tra xem đánh
giá được chọn có đủ tốt hay không:
22 2
11 12222 2 2 2 2 2
... ...
3 5 5 7 2n12n1 3 2n1 3
23 n
Như vậy đánh giá ta chọn là một đánh giá đủ tốt nên ta chỉ cần trình bày lại lời giải cho bài toán
như sau:
Ta có, với mọi
k1 , ta có:
222
14 4 1 1
2
2k 1 2k 1
k4k4k1
Cho
k2, 3, 4, ,n ta có:
222
222
222
14 4 2 2 22
2.2 1 2.2 1 3 5
24.24.21
14 4 2 2 22
2.3 1 2.3 1 3 7
34.34.31
...
14 4 2 2 2 2
2n 1 2n 1 2n 1 2n 1
n4n4n1
Cộng vế với vế các đánh giá trên ta được:
222 2
111 1 2 2 25
... 1 1 2
32n1 3 3
123 n
Từ (1) và (2) được bất đẳng thức cần chứng minh.
Ví dụ 8. Chứng minh rằng với mọi số tự nhiên n, ta luôn có:
33 3
11 11
....
4
23 n
Phân tích: Để ý ta thấy với mọi kN* ta luôn có
3
kk kkk1k1 , khi đó ta có đánh
giá
33
11 1
kkk
k1.k.k1
, bây giờ ta làm trội theo đánh giá đó bằng cách cho
k2, 3, 4, ,n.
Lời giải

Ta có:
33
2
11 1 1
,k2
kkk
k1.k.k1
kk 1
Cho
k2, 3, 4, ,n ta có:
3
3
3
11
1.2.3
2
11
2.3.4
3
...
11
n
n1.n.n1
Cộng theo vế các bất đẳng thức trên ta được:
33 3
11 1 1 1 1
... ...
1.2.3 2.3.4
23 n
n1.n.n1
Mặt khác ta lại có
11 1 111 1 1
...
2.3.4 3.4.5 2 1.2 2.3
n1.n.n1 n1n nn1
11 1 1 1 1
21.2 4 4
nn 1 2nn 1
Như vậy bất đẳng thức được chứng minh.
Nhận xét: Bài toán tổng quát là với mọi số nguyên dương n ta luôn có:
33 3
11 11 1
....
4
23 n
2n n 1
Ta có thể đặc biệt hóa bằng cách
- Chọn n là một số tự nhiên bất kì, chẳng hạn với
n100
ta có bài toán:
Chứng minh rằng:
33 3
11 1 1 1
...
4 101.200
2 3 100
- Chọn giá trị n là năm thi, chẳng hạn với
2015n
ta có bất đẳng thức:
33 3
11 1 1
...
4
2 3 2015
Ví dụ 9. Chứng minh rằng:
33 3
111 1 1
65 40
5 6 2014
Phân tích: Bất đẳng thức cần chứng minh là bất đẳng thức kép nên ta cần một đánh giá kép là
3
111
k
kk 1 k 2 k 1kk 1
, bây giờ ta làm trội và làm giảm theo đánh giá đó bằng cách
cho
k 5, 6, 7, , 2014.
Lời giải

Ta có:
33
2
11 1 1
kkk
k1kk1
kk 1
33 2
2
11 1 1
k k 3k 2k
kk 1 k 2
kk 3k 2
Kết hợp hai bất đẳng thức trên ta được:
3
111
k
kk 1 k 2 k 1kk 1
Cho
k 5, 6, 7, , 2014 ta có:
3
3
3
111
5.6.7 4.5.6
5
111
6.7.8 5.6.7
6
...
111
2014.2015.2016 2013.2014.2015
2014
Đặt
33 3
11 1
A
5 6 2014
, cộng theo vế các bất đẳng thức trên ta được:
11 1 11 1
A
5.6.7 6.7.8 2014.2015.2016 4.5.6 5.6.7 2013.2014.2015
Ta cần chứng minh:
11 1 1
65 5.6.7 6.7.8 2014.2015.2016
Và
11 1 1
4.5.6 5.6.7 2013.2014.2015 40
+ Chứng minh:
11 1 1
65 5.6.7 6.7.8 2014.2015.2016
Ta có:
11 1 11 1 1111
5.6.7 6.7.8 2014.2015.2016 2 5.6 2015.2016 2 30 390 65
+ Chứng minh:
11 1 1
4.5.6 5.6.7 2013.2014.2015 40
Ta có:
11 1 11 1 1
4.5.6 5.6.7 2013.2014.2015 2 4.5 2014.2015 40
Vậy bất đẳng thức được chứng minh.
Ví dụ 10. Chứng minh rằng với mọi số tự nhiên
n1 , ta luôn có:
2
2
11 1 1 9
...
51325 20
nn1
Phân tích và lời giải

Để ý ta thấy các mẫu số được viết dưới dạng
2
2
kk1, ta cần một đánh giá kiểu
2
2
kk1?
. Trước hết ta thử với bất đẳng thức Cauchy, khi đó ta được
2
2
kk12kk1 . Do đó ta có
2
2
11111
2k k 1
2k k 1
kk1
.
Bây giờ ta cho
k1,2, 3, 4, ,n thì ta thu được
222 2
2
11 1 1111
... 1
2n12
12 2 3
2n 1
nn1
Bất đẳng thức được chứng minh nếu ta chỉ ra được
11 9
220
2n 1
, tuy nhiên đánh giá đó
không đúng với giá trị n lớn. Có phải ta đang làm trội với một đánh giá sai.
Đến đây hoặc ta vẫn sử dụng các đánh giá đó nhưng với k nhận giá trị lớn hơn 1 hoặc ta tìm một
đánh giá khác. Chú ý một tí ta nhận thấy
911
20 5 4
, do đó ta cần làm trội từ k2, 3, 4, ,n và
khi đó ta thu được kết quả là
22 22 2
2
11 1 111111
....
22 n 1 4 4
23 34
2n 1
nn1
Đến đây, chỉ cần trình bày lại lời giải mà không cần phải tìm đánh giá khác nữa.
Lời giải
Ta có:
2
2
11111
2k k 1
2k k 1
kk1
Cho
k2, 3, 4, ,n
ta có:
22
22
22
1111
22 3
23
1111
23 4
34
...
1111
2n n 1
n(n1)
Cộng theo vế các bất đẳng thức trên ta được:
22 22 2
2
11 1 111111
....
22 n 1 4 4
23 34
2n 1
nn1
Hay
22 22 2
2
11 1 1 119
....
55420
23 34
nn1
Ví dụ 11. Chứng minh rằng với mọi số nguyên dương
n3
, ta có:

333 3
111 165
...
54
123 n
Lời giải
Đặt
333 3
111 1
P...
123 n
, thực hiện làm trội mỗi phân số ở vế trái bằng cách làm giảm mẫu, ta
có
33
221 2 1 1
,k 1
k
kkk
k1k1 k1k k1k
Cho
k4, 5, ...,n
, ta có:
333
111 1 1 1 1 1 1
2P 2 ...
3.4 4.5 4.5 5.6
123
n1n nn1
251 1 1 251 1 65
108 3.4 108 3.4 27
nn 1
Do đó ta được
65
P
54
hay bất đẳng thức được chứng minh.
Ví dụ 12. Chứng minh rằng với mọi số nguyên dương
n
, ta có:
1 4 7 10 3n 2 3n 1 1
36912 3n 3n 3
3n 1
Phân tích và lời giải
Gọi vế trái của bất đẳng thức là P, ta cần làm trội P thành Q với điều kiện là Q phải dễ thu gọn
hơn, điều này có nghĩa là Q phải có các tử và mẫu giống nhau. Để ý rằng các phân số có tử, mẫu hơn kém
nhau hai đơn vị, nên ta nghĩ đến bất đẳng thức
22
nn1
nnn2 n2
n2 n
.
Đặt
14710 3n 23n 1
P
36912 3n 3n 3
, lúc này ta có
1 4 7 10 3n 2 3n 1 1 3 6 9 3n 3 3n
PQ
3 6 9 12 3n 3n 3 3 6 7 10 3n 2 3n 1
Nhận thấy Q không thể thu gọn được hết nên rất khó để có đánh giá tiếp theo. Để ý tiếp ta thấy
các tử của biểu thức Q và các mẫu của biểu thức P là
3, 6, 9, ... và các mẫu của biểu thức Q và các tử
của biểu thức P là
4, 7, 10, ... do đó thì tích PQ có thể thu gọn được. Chú ý là
2
PPQ , do đó ta có thể
trình bày lời giải như sau:
2
1 4 7 10 3n 2 3n 1 1 4 7 10 3n 2 3n 1
P
36912 3n 3n 3 36912 3n 3n 3
1 3 6 9 3n 3 3n 1 4 7 10 3n 2 3n 1
3 6 7 10 3n 2 3n 1 3 6 9 12 3n 3n 3
113467 3n 33n 2 3n 3n 1
334679 3n 2 3n 3n 13
11
n3
33n 3 9n 1

Từ đây suy ra
1
P
3n 1
. Vậy bất đẳng thức được chứng minh.
Ví dụ 13. Chứng minh rằng với mọi số nguuyên dương
n2
ta có
2
1511 nn1
... 2
2! 3! 4!
n1!
Phân tích: Để ý ta biến đổi được số hạng tổng quát của các số hạng trên như sau:
2
kk 1
kk1 1 1
,k2,kN
k1! k1! k1! k1!
Bây giờ ta làm trội bất đẳng thức trên bằng cách cho
k2, 3,..., n .
Lời giải
Ta có:
2
kk 1
kk1 1 1
,k2,kN
k1! k1! k1! k1!
Cho k nhận được giá trị 2, 3 ,…, n rồi cộng lại ta được:
2
15 nn111111 1 1
... ...
2! 3! 2! 1! 3! 2! 4!
n1! n1! n1!
1111 1 1 1
22
2! 1! 2! n! n!
n1! n1!
Vậy bất đẳng thức được chứng minh.
Ví dụ 14. Chứng minh bất đẳng thức sau với mọi
n2,nN
22 2
11 1 1
...
8
2.3 3.4
nn 1
Phân tích và lời giải
Dễ nhận ra các phân số có dạng tổng quát là
2
1
kk 1
, cho nên trước khi đánh giá ta cần biến
đổi
22 2
1k1k1 1
kk 1
kk1 kk1 k1
Quan sát chiều bất đẳng thức ta nhận thấy để đánh
giá làm trội thì ta có hai cách
- Thay phân số
2
1
k1
bởi số nhỏ hơn.
- Thay phân số
1
kk 1
bởi số lớn hơn.
Trong hai cách trên dù thực hiện theo cách nào thì kết quả thu được càng đơn giản càng tốt và có thể
liên tiếp được.

Theo bất đẳng thức Cauchy ta có:
22
1111
2
k
kk 1
k1
, với cách đánh giá này ta thu
được kết quả
22 2 22 2
1111 1111
22
kk
kk 1 k 1 k 1 k 1
.
Rõ ràng với kết quả đó ta có thể khử được liên tiếp. Bây giờ kiểm tra xem với đánh giá như vậy ta
có chứng minh được bài toán không?
Cho
k 2, 3, ..., n
rồi cộng lại ta được:
22 2 2222 2 2
22
11 1 11111 1 1
... ...
2
2.33.4 2334 n
nn 1 n 1
11 1 1
28
2
n1
Đây là kết quả đúng, ta có thể trình bày lại lời giải như sau:
Sử dụng bất đẳng thức
22
xy
xy , x; y R
2
, ta có k2 thì:
22 2
22 222
1k1k1 1
kk 1
kk1 kk1 k1
11 1 1 11 1
22
kk
k1 k1 k1
Cho
k 2, 3, ..., n rồi cộng lại ta được:
22 2 2222 2 2
11 1 11111 1 1
... ...
2
2.33.4 2334 n
nn 1 n 1
22
11 1 1
28
2
n1
Vậy bất đẳng thức được chứng minh.
Ví dụ 15. Chứng minh rằng với n là số nguyên dương, ta luôn có:
11 1
1....2n11
23 n
Phân tích và lời giải
Để chứng minh bất đẳng thức có chứa căn thức ở mẫu thì điều đầu tiên là tìm cách trục căn thức
mẫu, trong bài toán này khi trục căn thức ở mẫu trực tiếp thì ta thu được kết quả
1k
k
k
, để ý thấy
trong căn là các số tự nhiên liên tiếp nên ta cần viết được
k về dạng k1 k hoặc kk1,
tuy nhiên các phân số còn phụ thuộc vào k ở mẫu nên không thể khử liên tiếp được, do đó cách làm này
không đem lại kết quả. Cũng thực hiện theo ý tương này, nhưng ta cần tìm cách cố định mẫu số, do đó ta
cần biến đổi chút ít trước khi trục căn thức.

Để ý ta thấy 2k k 1 k, do đó ta làm trội được
12
kkk1
, đến đây ta mới
trục căn thức thì thu được kết quả
2
2k1 k
kk1
. Lúc này chỉ cần cho
k 1, 2, 3, ..., n là có thể khử được các căn thức ở giữa và kết quả thu được là
2n11 chính
là vế phải của bất đẳng thức. Bây giờ ta trình bày lại lời giải như sau:
Ta có:
12 2
2k1 k,k
k2k k k1
là số nguyên dương.
Cho
k 1, 2, 3, ..., n ta có:
1221
1
23 2
2
...
1
2n1 n
n
Cộng từng vế các bất đẳng thức trên ta được
11 1
1....2n11
23 n
Vậy bất đẳng thức được chứng minh.
Ví dụ 16. Chứng minh rằng với mọi số nguyên dương n ta có:
11 1 1
... 2
2
32 43 n 1 n
Phân tích và lời giải
Để ý cách viết các số hạng của tổng trên có dạng
1
k1 k
, ta cần làm trội sao cho có thể khử
được liên tiếp. Nhận nhấy ở mẫu có chứa k và
k1 nên ta cần viết 1 thành
1k1k k1 k k1 k
, quan sát chiều của bất đẳng thức ta làm trội được
k1 k k1 k 2k1 k1 k , đến đây ta có kết quả là:
2k1k1k2k1k
122
k1 k k1 k k1.k k k1
Bây giờ ta có thể trình bày lời giải như sau:
Ta có:
k1 k k1 k
1k1k
k1 k k1 k k1 k
2k 1 k 1 k 2 k 1 k
22
k1 k k1.k k k1

Cho
k 1, 2, 3, ..., n
rồi cộng vế với vế ta có:
11 1 22 2 2 2 2
... ...
2
32 n1 n 1 2 2 3 n n1
2
22
n1
Vậy bất đẳng thức được chứng minh.
Nhận xét: Bài toán tổng quát là với mọi số nguyên dương n ta luôn có:
11 1 2
... 2
2
32 n 1 n n 1
Ta có thể đặc biệt hóa bằng cách
- Chọn n để
n1 là một số chính phương, chẳng hạn với n99 ta có bài toán:
Chứng minh rằng:
11 1 9
...
25
32 10099
- Chọn giá trị n là năm thi, chẳng hạn với
n 2009 ta có bất đẳng thức:
11 1 1 2 88
... 2
245
3 2 4 3 2010 2009 2010
Đây là đề thi tuyển sinh lớp 10 chuyên Thái Bình năm 2009 – 2010
Ví dụ 17. Với số tự nhiên
n3
.
Đặt
n
11 1
S ...
31 2 5 2 3 2n 1 n n 1
Chứng minh rằng:
n
1
S
2
Phân tích: Để ý ta biến đổi được số hạng tổng quát của các số hạng trên như sau:
1k1kk1k11
2k 1
2k 2k 1
2k 1 k 1 k
2kk 1
Bây giờ ta làm trội bất đẳng thức trên bằng cách cho
k1, 2, 3,..., n .
Lời giải
Vì
2
22
2k 1 4k 4k 1 4k 4k nên
2k 1 2 k k 1 .
Do đó ta được:
1k1kk1k11
2k 1
2k 2k 1
2k 1 k 1 k
2kk 1
Cho
k 1, 2, 3, ..., n rồi cộng vế với vế ta có
n
111111 1 1
S...
21 22 22 23 23 24 2n 2n 1
11 1
22
2n 1
Vậy bất đẳng thức được chứng minh.
Nhận xét: Bài toán tổng quát là với mọi số nguyên dương n ta luôn có:

11 1 11
...
2
21
31252 3 21 1
n
nnn
Ta có thể đặc biệt hóa bằng cách
- Chọn n để
n1 là một số chính phương, chẳng hạn với n99 ta có bài toán:
Chứng minh rằng:
11 1119
...
22.10 20
3 1 2 5 2 3 199 99 100
- Chọn giá trị n là năm thi, chẳng hạn với
n 2001 ta có bất đẳng thức:
1 1 1 1 1 2001
...
22003
2 2002
3 1 2 5 2 3 4003 2001 2002
Đây là đề thi tuyển sinh lớp 10 chuyên Lam Sơn Thanh Hóa năm 2001 – 2002
Hoặc
n 2007
ta có bất đẳng thức:
1 1 1 1 1 2007
...
2 2009
2 2008
3 1 2 5 2 3 4015 2007 2008
Đây là đề thi tuyển sinh lớp 10 chuyên Ninh Bình năm 2007 – 2008
Ví dụ 18. Chứng minh rằng:
43 1 1 1 44
...
44 45
2 1 1 2 3 2 2 3 2016 2015 2015 2016
Phân tích: Để ý ta biến đổi được số hạng tổng quát của các số hạng trên như sau:
2
2
k1 kkk1 k1 k kk1
111
kk 1
k1 k kk1 k k1
k1kkk1
Bây giờ ta làm trội bất đẳng thức trên bằng cách cho
k1, 2, 3,..., n .
Lời giải
Đặt
n
11 1
S ...
2112 3223 n1 n nn1
Để ý rằng với
k1 , ta có:
2
2
k1 k kk1 k1 k kk1
111
kk 1
k1 k kk1 k k1
k1kkk1
Cho
k 1, 2, 3, ..., n rồi cộng vế với vế ta có:
n
1111 1 1 1
S...1
1223 nn1 n1
Do đó ta được
2015
1
S1
2016
. Như vậy, ta phải chứng minh:

43 1 44
1 44 2016 45 1936 2016 2025
44 45
2016
.
Bất đẳng thức cuối cùng đúng nên có điều phải chứng minh.
Nhận xét: Thực chất đây là bài toán tính tổng:
11 1 1
... 1
21 12 32 23 1 1 1
n
S
nnnn n
Đến đây ta có thể chọn n là một giá trị nào đó rồi có thể làm trội, làm giảm để tự sáng tạo ra các
bất đẳng thức tương ứng.
Ví dụ 19. Chứng minh rằng với mọi số nguyên dương n ta có:
11 1 1
... 1
2211 3322 n1 n1nn n1
Phân tích và lời giải
Nhận thấy số hạng tổng quát được viết dước dạng
1
k1 k1kk
. Quan sát chiều bất
đẳng thức cần chứng minh ta thấy cần phải chứng minh được bất đẳng thức kiểu
k1 k1kk A với điều kiện biểu thức A phải chứa k và k1 đồng thời phải phân tích
được thành tích, do đó biểu thức A có thể là
kk 1 k 1 k . Bây giờ ta cần chứng minh
k1 k1kk kk1 k1 k. Để đơn giản hơn ta có thể đặt xk;yk1 rồi
chứng minh
xy yx xx yy, bất đẳng thức này được chứng minh bằng phép biến đổi tương
đương. Đến đây ta thu được bất đẳng thức:
1111
... ...
2211 n1 n1nn 2112 n1 n nn1
.
Bây giờ ta cần chứng minh được :
11 1 1
... 1
2112 3223 n1 n nn1 n1
Rõ ràng đây là kết quả của bài toán trong ví dụ trên. Ta có thể trình bày lời giải như sau:
Bổ đề: Với mọi số thực dương x, y ta có:
xy yx xx yy
Chứng minh: Sử dụng phương pháp biến đổi tương đương, ta được:
2
xy yx xx yy xx yy xy yx 0
xx yyy x0 xyx y0
xyxy 0
Vậy bổ đề được chứng minh.
Áp dụng bổ đề ta có:
n 1 n 1 nn nn 1 n 1 n
11
n 1 n 1 nn nn 1 n 1 n

Vì thế ta được:
11 1
...
22 11 33 22 n 1 n 1 nn
11 1
...
21 12 32 23 n 1 n nn 1
Mà theo kết quả của ví dụ trên thì
11 1 1
... 1
2112 3223 n1 n nn1 n1
Vậy bài toán đươực chứng minh.
Nhận xét: Quan sát kĩ hai ví dụ 14 và 15 ta nhận thấy, để chứng minh được bất đẳng thức trong ví dụ 15
thì ta chỉ cần chứng minh được:
1111
... ...
22 11 1 1 21 12 1 1
nnnn nnnn
Điều này tương đương với chứng minh
11 1 1nnnnnn nn.
Tuy nhiên trong tình huống không có ví dụ 14 thì bất đẳng thức trong ví dụ 15 thực sự là khó, để
tìm ra được đánh giá
11 1 1nnnnnn nn cần phải phân tích thật kĩ mối
quan hệ giữa các con số trong bài toán.
Ví dụ 20. Chứng minh bất đẳng thức sau đúng mọi
nN :
11 1
1...22
22 33 nn
Lời giải
Bổ đề: Với mọi x, y > 0, ta có
22 22
xy xy 2xyxy
Chứng minh: sử dụng phương pháp biến đổi tương đương ta được
22 22
22 22 22
2
22
2
22
22
2
2
22
22
xy xy 2xyxy
xy2xyxyxy2xy 2xy 0
4x y 2x y
xy x y xy 0
2x y 2x y
2x y
xy x y xy 0
2x y 2x y
Do x, y > 0 nên bất đẳng thức cuối cùng đúng, bổ đề được chứng minh.
Áp dụng bổ đề với
11
xk;yk
22
, ta được:

11 11 1 1 1 1
kk kk 2kk k k
22 22 22 2 2
11 1 1
2k k k k k k
22 2 2
Từ đây suy ra:
12 22
,k 1
kk 1 1
11 1 1
kk
kk k k
22
22 2 2
Cho
k 1, 2, ..., n rồi cộng vế với vế ta được:
11 12222 2 2
1 ... ...
22 33 nn 1 3 3 5 1 1
nn
2222 2 2
22 2
22
111
n
222
Vậy bất đẳng thức được chứng minh.
Ví dụ 21. Cho n là một số nguyên dương. Chứng minh rằng:
22
nn 1 1 2 3 ... n n 1 n
33
Lời giải
Ta sẽ chứng minh:
22
kk1 k1k k k1kkk1,k1*
33
Thật vậy, bất đẳng thức bên trái tương đương với
2
2
2k k 1 2 k 1 k 3 k 2k k 1 2k 1 k
2kk 1 2k 1 4k 4k 2k 1 0 1
Bất đẳng thức bên phải tương đương với
2
2
3 k 2 k 1 k 2k k 1 2k k 1 2k 1 k
2kk1 2k1 4k 4k 2k1 0 1
Cả hai đánh giá cuối cùng đề đúng, do đó bất đẳng thức (*) được chứng minh.
Bây giờ ta áp dụng bất đẳng thức trên cho
k 1, 2, ..., n , khi đó ta được:

22
20 1 21 0
33
22
23 2 2 32 21
33
22
34 23 3 43 32
33
...
22
nn1 n1n n n1nnn1
33
Cộng các bất đẳng thức này lại vế theo vế, ta thu ngay được kết quả cần chứng minh.
Ví dụ 22. Chứng minh rằng với mọi số nguyên
n5 , ta có:
n2
2n
Phân tích: Với bất đẳng thức dạng như bài toán này ta thường dùng phương pháp quy nạp toán học để
chứng minh. Do đó ta thực hiện theo trình tự các bước quy nạp, vấn đề là khi thực hiện quy nạp ta sử
dụng giả thiết quy nạp như thế nào mà thôi. Trong bài toán này ta có giả thiết quy nạp là
k2
2k và cần
phải chứng minh
2
k1
2k1
. Để ý là k5 nên ta được
22
2
2k k1 kk5 3k1 k1 . Do đó để hoàn tất chứng minh ta cần chỉ ra được
k1 2
22k
, đây là kết quả đúng theo giả thiết quy nạp. Đến đây ta trình bày lời giải như sau:
Lời giải
+ Với
n5 , bất đẳng thức trở thành:
52
25 3225 (đúng)
Suy ra bất đẳng thức đúng với
n5
+ Giả sử bất đẳng thức đúng đến
nkkN,k5 , tức là ta được
k2
2k
+ Ta cần chứng minh bất đẳng thức đúng với
nk1
, hay
2
k1
2k1
Thật vậy, theo giả thiết quy nạp, ta có:
k1 k 2
22.22k 1
Vì
k5 nên
22
22 2
2k k 2k1k 2k1 k1 kk5 3k1 k1
Suy ra ta được
2
2
2k k 1 2
Từ (1) và (2) ta có bất đẳng thức đúng với
nk1, nên theo nguyên lý quy nạp thì bất đẳng thức được
chứng minh.
Ví dụ 23. Cho
x1 là một số thực cho trước. Chứng minh rằng với mọi số nguyên dương n, ta luôn có:
n
1x 1nx
Phân tích: Ta sử dụng phưng pháp quy nạp để chứng minh bài toán này. Ở đây giả thiết quy nạp là
k
1x 1kx và ta cần chứng minh
k1
1x 1 k1x
. Nhận thấy từ giả thiết quy nạp ta
có
k1 k
1x 1x 1x 1x1kx
, ta cần chỉ ra được
1x1kx 1 k1x,
nhưng đây rõ ràng là một kết quả đúng. Do đó ta trình bày lại lời giải như sau:
Lời giải
+ Với
n1
, bất đẳng thức trở thành
1x1x
(đúng).

Suy ra bất đẳng thức đúng với
n1
.
+ Giả sử bất đẳng thức đúng đến
nkkN,k1 , tức là ta được
k
1x 1kx
+ Ta cần chứng minh bất đẳng thức đúng với
nk1, hay
k1
1x 1 k1x
Thật vậy, vì
x1x10
nên theo giả thiết quy nạp, ta có
k1 k
1x 1x 1x 1x1kx
Mà
2
1x1kx 1 k1xkx 1 k1x nên
k1
1x 1x1kx 1 k1x
Hay bất đẳng thức đúng với
nk1
, nên theo nguyên lý quy nạp suy ra bất đẳng thức được chứng
minh.
Ví dụ 24. Chứng minh với mọi số thực a, b thỏa mãn
ab0
, ta có:
n
nn
ab ab
22
Phân tích: Ta chứng minh bất đẳng thức trên bằng phương pháp quy nạp, tuy nhiên để chứng minh được
k1
k1 k1
ab ab
22
, ta cần chứng minh được bất đẳng thức
kk k1k1
ababa b
22 2
.
Lời giải
+ Với
n1 , bất đẳng thức hiển nhiên đúng.
+ Giả sử bất đẳng thức đúng đến
nkkN,k1 , tức là ta có:
k
kk
ab ab
22
+ Ta chứng minh bất đẳng thức đúng với
nk1, hay
k1
k1 k1
ab ab
22
Thật vậy, vì
ab0, nên theo giả thiết quy nạp ta có:
k1 k
kk
ab ab ab a bab
22222
Bất đẳng thức đúng với
nk1nếu ta chứng minh được
k k k1 k1
ababa b
*
22 2
Mà (*) tương đương với
k k k1 k1 k1 k1 k k
kk
abab2a b a b abba0
aba b 0 **
Vì vai trò của a, b như nhau nên ta có thể giả sử
ab , khi đó
ab0 1
Mặt khác, từ
ab0 a b nên
k
kkkk
ab0 a b b ab 0 2
Từ (1) và (2) suy ra bất đẳng thức (**) luôn đúng.
Vậy theo nguyên lý quy nạp suy ra bất đẳng thức được chứng minh.
Ví dụ 25. Chứng minh rằng với mọi số nguyên dương n ta có:

135 2n 1 1
246 2n
3n 1
Phân tích: Bất đẳng thức trên có thể chứng minh được theo cách làm trội như ví dụ 12. Tuy nhiên ở đây
ta chứng minh bằng phương pháp quy nạp.
Theo bài toán ta có giả thiết quy nạp là
135 2k 1 1
246 2k
3k 1
và cần chứng minh được
135 2k 12k 1 1
2 4 6 2k 2k 2
3k 4
, như vậy để hoàn thành bài toán ta cần chỉ ra được
12k1 1
2k 2
3k 1 3k 4
. Đây là bất đẳng thức đúng có thể chứng minh bẳng phép biến đổi tương
đương.
Lời giải
+ Kí hiệu bất đẳng thức đã cho là (*) , với
n1 , bất đẳng thức trở thành
11 11
222
3.1 1
(đúng)
Bất đẳng thức đúng với
n1 .
+ Giả sử (*) đúng đến
nkkN,k1 , tức là ta được
135 2k 1 1
246 2k
3k 1
+ Ta cần chứng minh (*) đúng với
nk1, hay
135 2k 12k 1 1
246 2k 2k 2
3k 4
Theo giả thiết quy nạp, ta có
1 3 5 2k 1 2k 1 1 2k 1
246 2k 2k 2 2k 2
3k 1
Bất đẳng thức (*) đúng với
nk1khi
12k1 1
2k 1 3k 4 2k 2 3k 1
2k 2
3k 1 3k 4
22
2k 1 3k 4 2k 2 3k 1 k 0
(đúng)
Do đó (*) đúng với
nk1, nên theo nguyên lý quy nạp bất đẳng thức đúng với mọi số nguyên dương
n.
Ví dụ 26. Chứng minh rằng với mọi số nguyên dương n, ta có
111 1
... 1
n1 n2 n3 n2n1
Lời giải
+ Với
n1 bất đẳng thức có dạng:
111 13
11
11 12 13 12
(đúng)
Nên bất đẳng thức đúng với
n1
+ Giả sử bất đẳng thức đúng đến
nkkN,k1
, tức là
k
111 1
S ... 1
k1 k2 k3 3k1
+ Ta phải chứng minh bất đẳng thức đúng với
nk1, hay

k1
111 1
S ... 1
k2 k3 k4 3k4
Thật vậy, theo giả thiết quy nạp ta có
k1 k k
1111 2
SS S
3k 2 3k 3 3k 4 k 1
3k 1 3k 2 3k 4
Hay
k1 k
SS1
. Do đó bất đẳng thức đúng với nk1, nên theo nguyên lý quy nạp ta có bất đẳng
thức đúng với mọi số nguyên dương n.
Ví dụ 27. Tìm tất cả các số nguyên dương n thỏa mãn bất đẳng thức:
nn
327n
Lời giải
Thử trực tiếp với
n1, 2, 3,4
ta thấy
n4
thì bất đẳng thức đúng.
Ta sẽ chứng minh mọi giá trị cần tìm của n là
n4,nN
. Tức là chứng minh bất đẳng thức
sau đúng với mọi
n4,nN
:
nn
327n
+ Với
n4 thì bất đẳng thức trở thành có dạng
44
327.4 8144 (đúng)
Nên bất đẳng thức đúng với n = 4
+ Giả sử bất đẳng thức đúng đến
nkkN,k4
tức là:
kk
327k
+ Ta phải chứng minh bất đẳng thức đúng với
nk1, hay
k1 k1
327k1
Thật vậy, theo giả thiết quy nạp, ta có
k1 k k
33.3327
Nhưng với mọi
k4 thì
kk1kk1 k k1
32 7k 2 2 21k 2 7k 1 2 72k 1 2 7k 1
Suy ra bất đẳng thức đúng với
nk1, nên theo nguyên lý quy nạp ta có bất đẳng thức đúng. Vậy bài
toán được hoàn thành.
Ví dụ 28. Cho n số thực dương
12 n
x , x , ..., x có tích bằng 1. Chứng minh rằng:
12 n
x x ... x n
Lời giải
+ Với
n1 , thì
1
x11 (đúng) nên bất đẳng thức đúng với n1 .
+ Giả sử bất đẳng thức đúng đến
nkkN,k1, tức là với mọi
12 k
x , x , ..., x 0 thỏa mãn
12 k
x.x...x 1 thì
12 k
x x ... x k
+ Ta phải chứng minh bất đẳng thức đúng với
nk1
, nghĩa là với mọi
12 kk1
x , x , ..., x , x 0
thỏa mãn
12 k k1
x .x ... x . x 1
thì
12 kk1
xx...xx k1
Do
12 k k1
x.x...x.x 1
và vai trò các biến số như nhau nên có thể coi
kk1 kk1
x1x 1x1x 0
hay
kk1 kk1
xx 1xx 1
Đặt
'
kkk1
xxx
thế thì
'
12 k
x , x , ..., x là k số dương thỏa mãn
'
12 k
x.x...x 1 , do vậy theo giả thiết
quy nạp ta có:
'
12 k
x x ... x k 2

Từ (1) và (2), ta suy ra
'
12 kk1 12 k
xx...xx xx...x 1k1
'
12 kk1 12 k
x x ... x x x x x 1 k 1
Điều này chứng tỏ bất đẳng thức cũng đúng với nk1, theo nguyên lý quy nạp ta có bất đẳng
thức đúng với mọi số nguyên dương n .
Ví dụ 29. Chứng minh rằng với mọi số tự nhiên n2 ta có:
n1
n
nn1
Lời giải
+ Với n2 , thì bất đẳng thức có dạng:
21
2
221 43
(đúng),
Nên bất đẳng thức đúng với n = 2
+Giả sử bất đẳng thức đúng đến
nkkN,k2, tức là
k1
2
kk1
+ Ta phải chứng minh bất đẳng thức đúng với
nk1
, hay
k1 k
k1 k2
Sử dụng giả thiết quy nạp ta được:
k1 k1 k1
k
kk1 k1 k1
Vì
2
22
k1 k 2k1 k 2k
nên
k
k1 k1 2k
2
k1 k1 k1 k 2k
Do đó ta được
k
k1 k1 k k1 k
k2kk
kk1 k 2k kk1 kk2 k1 k2
Vậy bất đẳng thức đúng với
nk1
nên theo nguyên lý quy nạp ta có bất đẳng thức đúng với mọi số
nguyên dương
n2 .
Ví dụ 30. Chứng minh rằng với mọi
n1,nN
, ta có
11 17
...
n 1 n 2 2n 10
Phân tích tìm lời giải
Khác với bài toán trước, ở bài này các bạn sẽ gặp “một chút rắc rối” ở bước chuyển quy nạp, tức là
ở đây ta gặp trường hợp “giả sử bất đẳng thức đúng với k nhưng không chứng minh được sẽ đúng cho k +
1”, thật vậy nếu bất đẳng thức đúng cho n = k, tức ta có :
k
11 17
S ...
k 1 k 2 2k 10
Khi đó nếu sử dụng giả thiết quy nạp này cho
nk1, ta sẽ có :
k1 k
k
11 1 1 1 1
S ... S
k 2 k 3 2k 2 2k 1 2k 2 k 1
171
S
10
2k 1 2k 1 2k 1 2k 1
Nhưng
71 7
10 10
2k 1 2k 1
nên ta chẳng thu được điều gì ở đây!
Như vậy, ta nên làm gì để vượt qua chướng ngại này?

Nếu để nguyên dạng như ban đầu thì khó mà giải quyết thành công bài toán bằng quy nạp, do đó
ta cần biến đổi bất đẳng thức đã cho một chút, ở đây ta chọn một biểu thức trung gian kiểu
7m
,m 0
10 n
thích hợp sao cho bất đẳng thức sau đúng:
11 17m
...
n 1 n 2 2n 10 n
Số m này phải thỏa mãn hai điều kiện sau:
+ Bước chuyển quy nạp từ k sang k + 1 có thể thực hiện được.
+ Bất đẳng thức trên đúng với một “giá trị đầu” của n (lưu ý “giá trị đầu” ở đây có thể khác với
giá trị đầu của bất đẳng thức cho ở đề bài ). Đây sẽ là khởi điểm phép quy nạp của ta .
Xét điều kiện đầu tiên ta có:
k1 k
17m1
SS
10 n
2k 12k 1 2k12k 1
Do đó m phải thỏa mãn
m1 m 1 11
m
nk1 kk1
2k 1 2k 1 2k 1 2k 1
1m
2m 2k 1 k 4m 1 k 2m 0
2k 1 2k 1 kk 1
Bất đẳng thức cuối cùng này đúng với mọi k khi và chỉ khi
1
4m 1 0 m
4
Xét điều kiện thứ hai:
+ Với n = 1 bất đẳng thức trở thành:
17 1
mm
210 5
(không được vì m
1
4
)
+ Với n = 2 bất đẳng thức trở thành:
117m 7
m
21 22 10 2 30
(không được vì m
1
4
)
+ Với n = 3 bất đẳng thức trở thành:
1117m 1
m
31 32 33 10 3 4
(không được vì m
1
4
)
+ Với n = 4 bất đẳng thức trở thành:
11117m 11
m
4142 43 44 10 4 42
Bất đẳng thức này đúng với m
1
4
. Như vậy ta sẽ chọn m =
1
4
và điểm xuất phát quy nạp là n = 4, ta đi
đến lời giải cho cả bài toán như sau
Lời giải
Kiểm tra trực tiếp ta thấy bất đẳng thức đã cho đúng với n = 1, 2, 3
Xét trường hợp
n4 . khi đó ta sẽ chứng minh bất đẳng thức mạnh hơn
11 171
...
n 1 n 2 2n 10 4n
+ Với
n4 bất đẳng thức trở thành

1 1 1 1 7 1 533 51
1066 1071
4 1 4 2 4 3 4 4 10 4.4 840 80
(đúng)
Nên bất đẳng thức đúng với
n4 .
+ Giả sử bất đẳng thức đúng với
nkkN,k4, tức là
k
11 171
S ...
k1 k2 2k 10 4k
+ Ta phải chứng minh bất đẳng thức đúng với
nk1
, hay
k1
11 17 1
S...
k2 k3 2k2 10
4k 1
Sử dụng giả thiết quy nạp ta được
k1 k
k
11 1 1 1 1
S...S
k2 k3 2k2 k12k2 2k2
1711
S
10 4k
2k 1 2k 1 2k 1 2k 1
Do vậy chỉ cần chứng minh
11 1 211
4k k k 1
2k12k1 4k1 k12k1
21
2k 1 2k 1 0
k12k1 kk1
Đánh giá cuối cùng hiển nhiên đúng. Vậy bất đẳng thức đúng với
nk1, nên theo nguyên lý quy nạp
ta có bất đẳng thức đúng với mọi
n4
.
Bài toán được chứng minh xong.
Ví dụ 31: Chứng minh bất đẳng thức sau đúng với mọi nN
22 2
11 179
1...
48
23 n
Lời giải
Kiểm tra trực tiếp, ta dễ thấy bất đẳng thức đúng với
n 1, 2, 3, 4
.
Xét trường hợp
n5 , khi đó ta sẽ chứng minh bất đẳng thức mạnh hơn
22 2
11 179 2
1 ... , n 5, n N
48 2n 1
23 n
+ Với
n5 bất đẳng thức trở thành
2222
1 1 1 1 79 2 205 1 79 2
1 99 100
48 2.5 1 144 25 48 11
2345
(đúng)
Nên bất đẳng thức đúng với
n5
+ Giả sử bất đẳng thức đúng với
nkk5,kN, tức là
22
11792
1 ...
48 2k 1
2k
+ Ta sẽ chứng minh bất đẳng thức đúng với
nk1, hay
22 2
111792
1 ...
48 2k 3
2k
k1

Sử dụng giả thiết quy nạp ta được
22 2 2
111792 1
1...
48 2k 1
2k
k1 k1
Do đó ta chỉ cần chứng minh
22
2
2
22
21 2 1 22
2k 1 2k 3 2k 1 2k 3
k1 k1
14
2k 1 2k 3 4 k 1
2k 1 2k 3
k1
4k 8k 3 4k 8k 4 0 1
Đánh giá cuối cùng hiển nhiên đúng.
Vậy bất đẳng thức đúng với
nk1, nên theo nguyên lý quy nạp ta có bất đẳng thức đúng với mọi
n5 .
Vậy bài toán được chứng minh xong.
Ví dụ 32: Cho các số thực dương
12 n
a ; a ; ...; a thỏa mãn điều kiện
12 n
a .a ...a x . Chứng minh rằng:
333 3 3
123 n
aaa...a xn1
Lời giải
+ Với n1 ta có
33
1
ak là một đẳng thức đúng.
+ Giả sử bất đẳng thức đúng với
nkkN*, tức là ta có
333 3 3 3333
123 k 123k
a a a ... a x k 1 a.a.a...a k 1
+ Ta cần chứng minh bất đẳng thức đúng với nk1, tức là
3 3 3 3 3 333 33
1 2 3 k1 1 2 3 k k1
a a a ... a x k a .a .a ...a .a k
Thật vậy theo giả thiết quy nạp ta được
3 3 3 3 333 3 3
123 k1 123k k1
a a a ... a a .a .a ...a a k 1
Ta cần chứng minh
33 3 3 33 33
12 k k1 12 kk1
3333
3
1 2 k k1 1 2 k k1 k1 1 2 3 k
a.a...a a k 1 a.a....a.a k
a .a ....a a 1 a .a ...a .a a 1 a .a .a ...a 1 0
Rõ ràng bất đẳng thức cuối cùng luôn đúng. Theo nguyên lí quy nạp ta suy ra bất đẳng thức được
chứng minh.
Ví dụ 33: Cho các số thực
12 n
a ; a ; ...; a 1 . Chứng minh rằng:
n
12 n
12 n
11 1 n
1a 1a 1a
1 a .a ...a
Lời giải
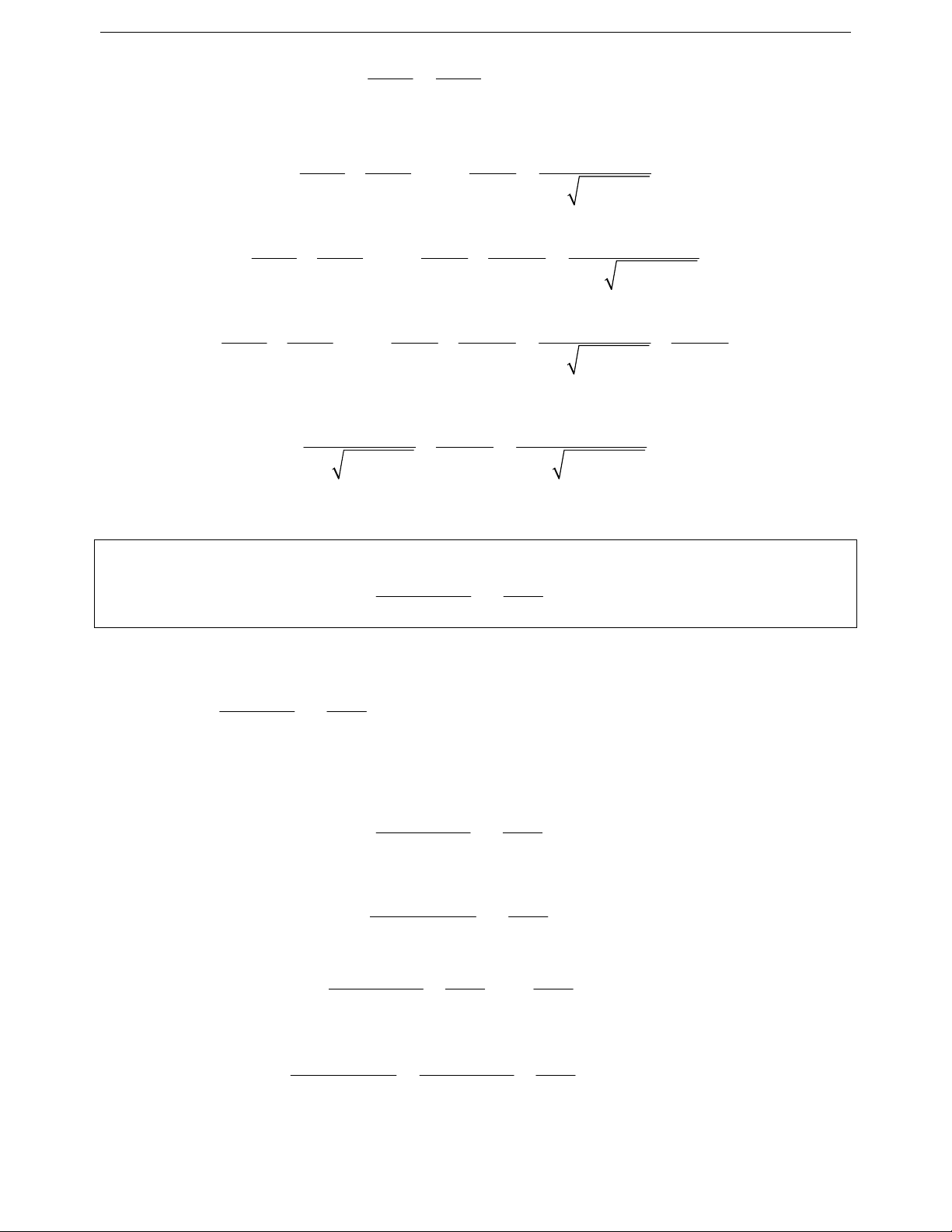
+ Với
n1
bất đẳng thức trở thành
11
11
1a 1a
(đúng)
+ Giả sử bất đẳng thức đúng với
nkkN*
, tức là
k
12 k
12 k
11 1 k
1a 1a 1a
1 a .a ...a
+ Ta cần chứng minh bất đẳng thức đúng với
nk1, tức là
k1
12 k k1
12 k1
11 1 1 k1
1a 1a 1a 1a
1 a .a ...a
Theo giả thiết quy nạp ta được
k
12 kk1 k1
12 k
11 1 1 k 1
1a 1a 1a 1a 1a
1 a .a ...a
Như vậy ta cần chứng minh được
kk1
k1
12 k 12 k1
k1k1
1a
1 a .a ...a 1 a .a ...a
Rõ ràng bất đẳng thức cuối cùng luôn đúng. Theo nguyên lí quy nạp ta suy ra bất đẳng thức được
chứng minh.
Ví dụ 33: Cho x là số thực dương bất kì. Chứng minh rằng với n là số nguyên dương ta luôn có:
2n 1
nn1
n
xx 1
x1
2
x1
Lời giải
+ Với n1 bất đẳng thức trở thành
3
2
44
2
xx 1
x1
x1 8xx 1 0 x1 0
x1 2
Như vậy bất đẳng thức trên đúng với
n1
+ Giả sử bất đẳng thức đúng với
nkkN*, tức là ta có
2k 1
kk1
k
xx 1
x1
2
x1
+ Ta cần chứng minh bất đẳng thức đúng với
nk1, tức là
2k 3
k1 k2
k1
xx 1
x1
2
x1
Theo giả thiết quy nạp ta được
22k3
kk1
k
xx 1
x1 x1
22
x1
Ta cần chứng minh
2
k1 k2 k k1
k1 k
2
2
kk1 k k1k2
2
2
k1
xx 1xx 1
x1
2
x1 x1
x 1 .x . x 1 4 x 1 .x . x 1 0
x1 x 1 0

Rõ ràng bất đẳng thức cuối cùng luôn đúng. Theo nguyên lí quy nạp ta suy ra bất đẳng thức được chứng
minh.
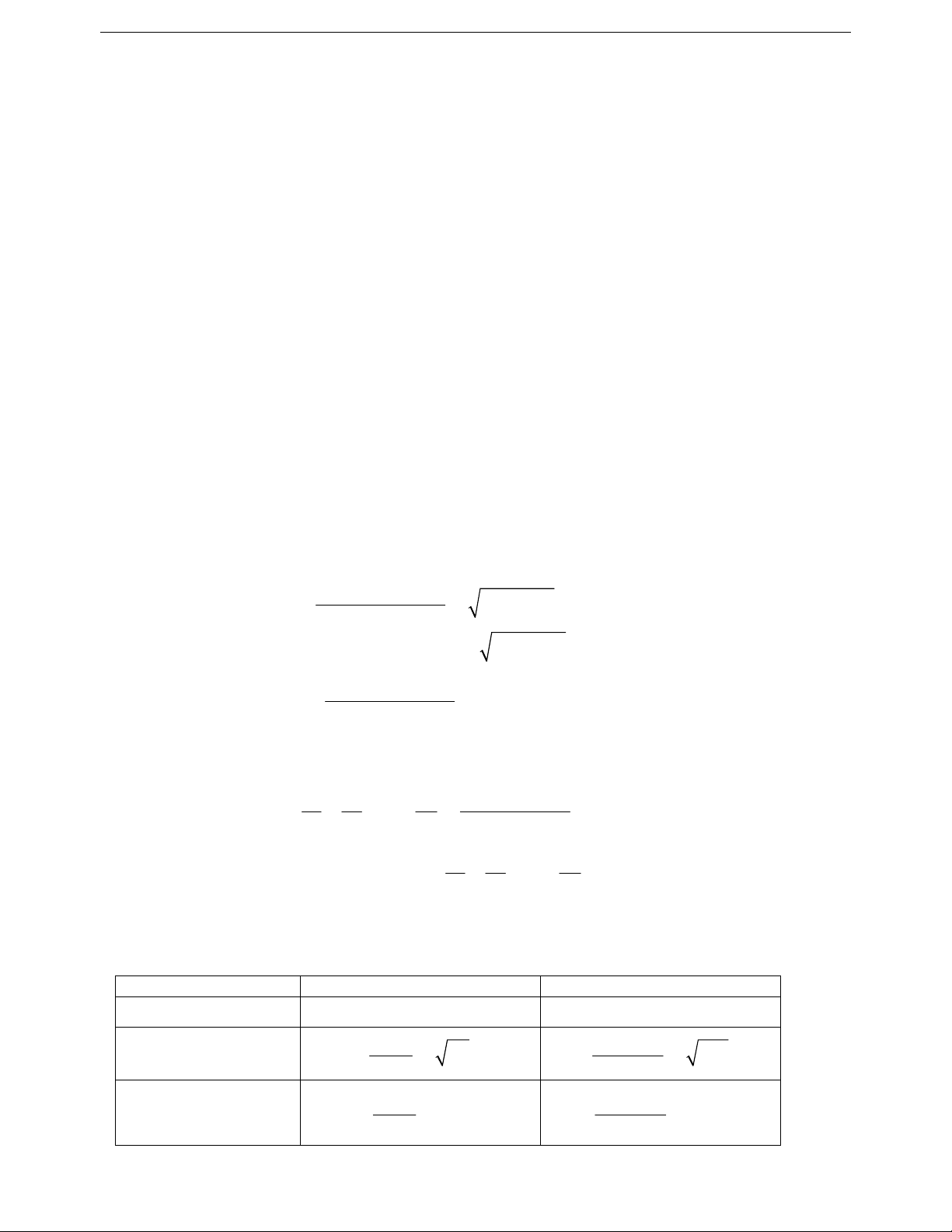
Chủ đề 5
MỘT SỐ KỸ THUẬT SỬ DỤNG BẤT ĐẲNG THỨC CAUCHY
A. Kiến thức cần nhớ
1. Giới thiệu bất đẳng thức Cauchy(Côsi)
Bất đẳng thức có tên gọi chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân. Ở
nhiều nước trên thế giới, người ta gọi bất đẳng thức này theo kiểu viết tắt là bất đẳng thức AM – GM
(AM là viết tắt của Arithmetic mean và GM là viết tắt của Geometric mean)
Ở nước ta, bất đẳng thức AM – GM được gọi theo tên của nhà Toán học người Pháp Augustin –
Louis Cauchy (1789 – 1857), tức là bất đẳng thức Cauchy. Thật ra đây là một cách gọi tên không chính
xác vì Cauchy không phải là nguời đề xuất ra bất đẳng thức này mà chỉ là người đưa ra một phép chứng
minh đặc sắc cho nó. Tuy nhiên, để cho phù hợp với chương trình sách giáo khoa, trong tài liệu này
chúng ta cũng sẽ gọi nó là Bất đẳng thức Cauchy(Côsi).
Đây là một bất đẳng thức cổ điển nổi tiếng và quen thuộc đối với phần lớn học sinh nước ta. Nó
ứng dụng rất nhiều trong các bài Toán về bất đẳng thức và cực trị. Trong phạm vi chương trình Toán
THCS, chúng ta quan tâm đến các trường hợp riêng của bất đẳng thức Cauchy.
2. Các dạng biểu diễn của bất đẳng thức Cauchy
a. Dạng tổng quát
+ Cho x
1
, x
2
, x
3
,..., x
n
là các số thực không âm ta có:
Dạng 1:
12 n
n
12 n
xx...x
x .x ...x
n
Dạng 2:
n
12 n 12n
x x ... x n. x .x ...x
Dạng 3:
n
12 n
12 n
xx...x
x.x...x
n
Dấu đẳng thức xảy ra khi và chỉ khi
12 n
x x ... x
+ Cho x
1
, x
2
, x
3
,..., x
n
là các số thực dương ta có:
Dạng 1:
2
12 n 12 n
11 1 n
...
x x x x x ...x
Dạng 2:
2
12 n
12 n
11 1
x x ...x ... n
xx x
Dấu đẳng thức xảy ra khi và chỉ khi
12 n
x x ... x
b. Một số dạng đặc biệt
n
n2 n3
Điều kiện
x, y 0 x, y, z 0
Dạng 1
xy
xy
2
3
xyz
xyz
3
Dạng 2
2
xy
xy
2
3
xyz
xyz
3
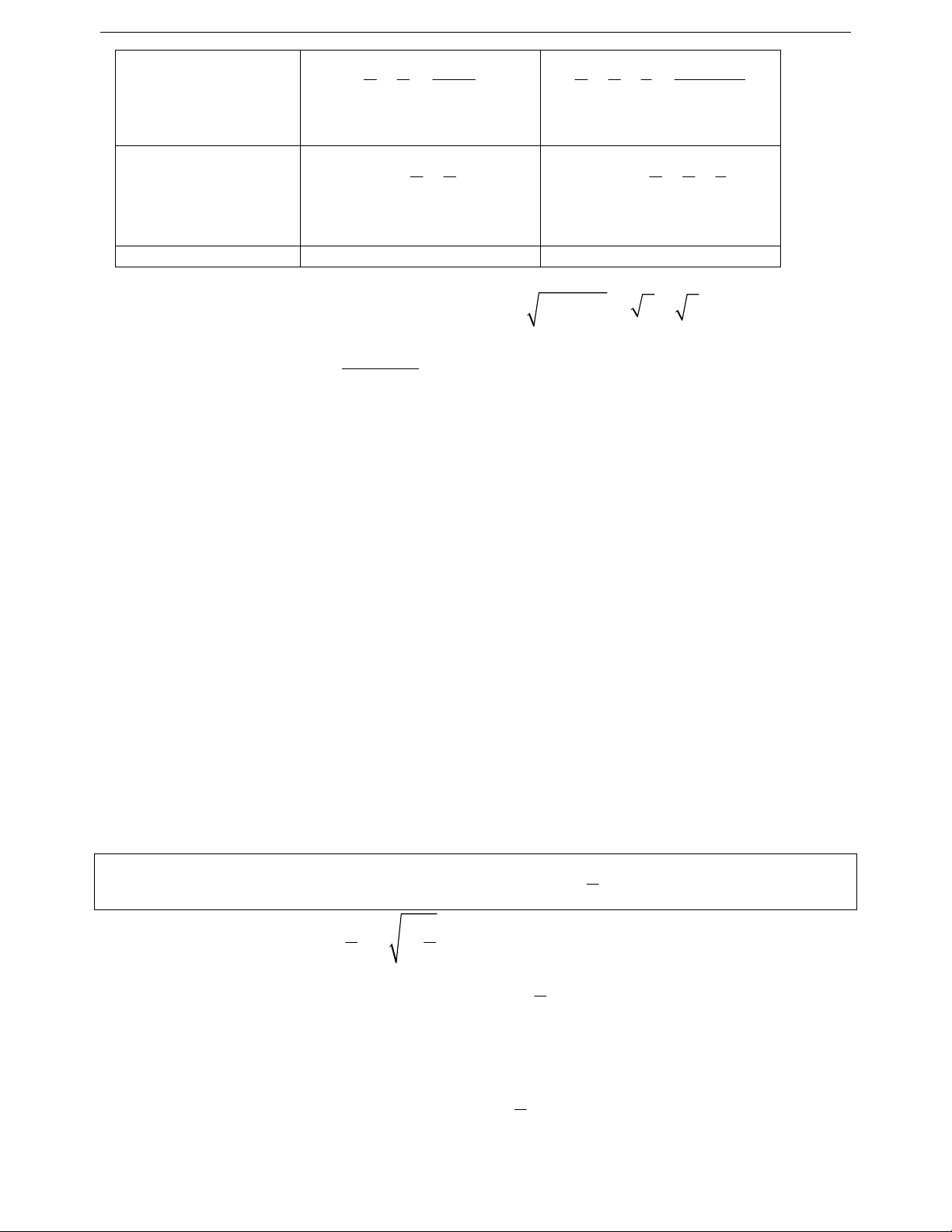
Dạng 3
11 4
xy xy
x, y 0
111 9
xyz xyz
x, y, z 0
Dạng 4
11
xy 4
xy
x, y 0
111
xyz 9
xyz
x, y, z 0
Đẳn
g
thức xẩ
y
ra
xy xyz
3. Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy
+
2
22 22
x y 2xy;2x y x y ; 2x y x y
+
2
22
3x y
xyxy
4
+
222
xyzxyyzzx
+
2
222
3 x y z x y z 3 xy yz zx
+
22 22 22
xy yz zy xyz x y z
+
2
444
3 x y z xy yz zx 3xyz x y z
B. Một số kỹ thuật sử dụng bất đẳng thức Cauchy
1. Kỹ thuật chọn điểm rơi trong đánh giá từ trung bình cộng sang trung bình nhân
Đánh giá từ trung bình cộng sang trung bình nhân thực chất đánh giá bất đẳng thức Cauchy theo
chiều từ phía trái sang phía phải. Trong chuỗi đánh giá, cái ta hay quên đó là cần phải được bảo toàn dấu
đẳng thức xẩy ra mà ta hay gọi là bảo toàn “Điểm rơi”. Một thực tế cho thấy việc xác định điểm rơi cho
một bất đẳng thức quyết định đến hơn nửa thành công cho công việc tìm lời giải. Ý tưởng chính của chọn
điểm rơi chính là việc xác định được dấu đẳng thức xảy ra khi nào để có thể sử dụng những đánh giá hợp
lý. Trong quá trình chứng minh các bất đẳng thức ta thường gặp sai lầm là áp dụng ngay bất đẳng thức
Cauchy mà quên mất dấu đẳng thức xảy ra tại đâu. Trước khi tìm hiểu về kĩ thuật đánh giá từ trung bình
cộng sang trung bình nhân ta hãy xét một số ví dụ về chọn “Điểm rơi” dưới đây ta sẽ hiểu hơn vấn đề
dạng được đề cập.
Bài toán 1. Cho số thực
a2
. Tìm giá trị nhỏ nhất của:
1
Aa
a
Sai lầm thường gặp là:
11
Aa 2a 2
aa
. Vậy giá trị nhỏ nhất của A là 2.
Nguyên nhân sai lầm: giá trị nhỏ nhất của A là 2
1
aa1
a
, điều này không xẩy ra vì theo
giả thiết thì
a2.
Phân tích: Quan sát bất đẳng thức trên ta nhận thấy giá trị của a càng tăng thì A càng tăng, do đó ta dự
đoán A đạt giá trị nhỏ nhất khi
a2
. Khi đó ta nói A đạt giá trị nhỏ nhất tại “Điểm rơi
a2
”. Ta
không thể áp dụng bất đẳng thức Cauchy cho hai số a và
1
a
vì không thỏa mãn dấu đẳng thức xẩy ra. Vì

vậy ta phải tách a hoặc
1
a
để khi áp dụng bất đẳng thức Cauchy thì thỏa mãn dấu đẳng thức xẩy ra. Giả
sử ta sử dụng bất đẳng thức Cauchy cho cặp số
a1
,
ka
sao cho tại “Điểm rơi
a2
” thì
a1
ka
, ta có
sơ đồ sau:
a1
21
ka
a2 k4
11
k2
a2
Khi đó ta được
1a3a1
Aa
a44a
và ta có lời giải như trên.
Lời giải đúng: Áp dụng bất đẳng thức Cauchy ta được
1a13a a13a 3.25
Aa 2 1
a4a4 4a 4 4 2
Đẳng thức xẩy ra khi và chỉ khi
a2
. Vậy giá trị nhỏ nhất của A là
5
.
2
Chú ý: Ngoài cách chọn cặp số
1
,
a
ka
ta có thể chọn các các cặp số sau:
1
,
ka
a
hoặc
,
k
a
a
hoặc
1
,
a
ka
.
Bài toán 2. Cho số thực
a2 . Tìm giá trị nhỏ nhất của biểu thức:
2
1
Aa
a
Sơ đồ điểm rơi:
2
2
a1
21
k
a
a2 k8
11
k4
4
a
Sai lầm thường gặp là:
22
a 1 7a a 1 7a 1 7a 1 7.2 9
A2.
88882a82.284
aa
.
Nguyên nhân sai lầm: Mặc dù giá trị nhỏ nhất của A bằng
9
4
là đáp số đúng nhưng cách giải trên mắc
sai lầm trong đánh giá mẫu số:
11
a2
2a 2.2
là sai.
Lời giải đúng:
3
22
aa 1 6a aa1 6a 36.2 9
A3.
88 8 88 8 4 8 4
aa
Đẳng thức xẩy ra khi và chỉ khi
a2 . Vậy giá trị nhỏ nhất của A là
9
.
4
Bài toán 3. Cho hai số thực dương a, b thỏa mãn
ab1. Tìm giá trị nhỏ nhất của biểu thức:
1
Aab
ab

Phân tích: Dự đoán dấu đẳng thức xẩy ra tại
1
ab
2
. Theo bất đẳng thức Cauchy ta có
2
ab 1
ab
24
. Khi đó ta có điểm rơi như sau:
ab 1
111
kab
ab 4 k
1
44k16
4
ab
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2
ab 1 1
ab ab
24 4
Do đó ta được
11117
A 16ab 15ab 2 16ab. 15ab 8 15.
ab ab 4 4
Đẳng thức xẩy ra khi và chỉ khi
1
ab
2
. Vậy giá trị nhỏ nhất của A là
17
4
Bài toán 4. Cho số thực
a6 . Tìm giá trị nhỏ nhất của biểu thức
2
18
Aa
a
Phân tích: Ta có
22
18 9 9
Aa a
aaa
Dễ thấy a càng tăng thì A càng tăng. Ta dự đoán A đạt giá trị nhỏ nhất khi
a6 . Ta có sơ đồ điểm rơi:
2
a9
36 3
ka
a6 k24
99
k2
a6
Lời giải
Ta có
2222
3
a 9 9 23a a 9 9 23a 9 23.36
A3 39
24 a a 24 24 a a 24 2 24
Đẳng thức xẩy ra khi và chỉ khi
a6 . Vậy giá trị nhỏ nhất của A là 39
Bài toán 5. Cho 3 số thực dương a, b, c thỏa
a2b3c20. Tìm giá trị nhỏ nhất của biểu thức:
394
Aabc
a2bc
Phân tích: Dự đoán giá trị nhỏ nhất của A đạt được khi a2b3c 20 và tại điểm rơi
a2,b3,c4.
Sơ đồ điểm rơi:
a3
23 4
ka
a2 k
33
k2 3
a2
b9
33
m2b
b3 m2
93
m2
2b 2

c4
4
nc
c4 1 n4
4
n
1
c
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
3a 3 b 9 c 4 a b 3c
A
4a 22b 4c 424
3a 3 b 9 c 4 a 2b 3c
222 332513
4a 22b 4c 4
Đẳng thức xẩy ra khi và chỉ khi
a2,b3,c4.
Vậy giá trị nhỏ nhất của A là 13.
Bài toán 6. Cho a, b, c là số thực dương thỏa mãn
ab 12; bc 8. Chứng minh rằng:
1 1 1 8 121
abc 2
ab bc ca abc 12
Phân tích: Dự đoán giá trị nhỏ nhất của A đạt được khi ab 12; bc 8 ,tại điểm rơi
a3;b4;c2. Khi đó ta được ta áp dụng bất đẳng thức Cauchy cho từng nhóm sau:
ab2 ac2 bc2 acb 8
;; , ;; , ;; , ;; ; .
18 24 ab 9 6 ca 16 8 bc 9 6 12 abc
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
3
3
ab2 ab21
3
18 24 ab 18 24 ab 2
ac 2 ac2
31
9 6 ca 9 6 ca
3
4
bc2 bc2 3
3
16 8 bc 16 8 bc 4
ac b 8 acb 8 4
4
9 6 12 abc 9 6 12 abc 3
13a 13b 13a 13b 13 13 13
2212
18 24 18 24 18 24 3
13b 13c 13b 13c 13 13 13
228
48 24 48 24 48 24 4
Cộng theo vế các bất đẳng thức trên ta được
1 1 1 8 121
abc 2
ab bc ca abc 12
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
a3;b4;c2.
Bài toán 7. Cho a, b là các số thực dương tùy ý. Tìm giá trị nhỏ nhất của biểu thức :
ab ab
A
ab
ab
Phân tích: Do A là biểu thức đối xứng với a và b nên ta dự đoán giá trị nhỏ nhất của A đạt tại ab .
Khi đó ta có sơ đồ điểm rơi:

ab ab
21
ab
kab
ab k4
k2
ab 1
ab 2
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
3a b
a b ab a b ab 3.2 ab 3 5
A 2 1
ab ab 2 2
4 ab 4 ab 4 ab 4 ab
Đẳng thức xẩy ra khi và chỉ khi
ab
. Vậy giá trị nhỏ nhất của A là
5
2
.
Bài toán 8. Cho a, b, c là các số thực dương tùy ý. Tìm giá trị nhỏ nhất của biểu thức:
abcbccaab
A
bc ca ab a b c
Phân tích: Do A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt tại
abc. Khi đó ta có sơ đồ điểm rơi:
abc1
12
bc ca ab 2
abc k4
bc ca ab 2
2k
ka kb kc k
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
abcbccaab3bccaab
A
b c c a a b 4a 4b 4c 4 a b c
a bc b ca c ab3bccaab
222
b c 4a c a 4b a b 4c 4 a a b b c c
111 3 915
22223
222 4 2 2
Đẳng thức xẩy ra khi và chỉ khi
abc
. Vậy giá trị nhỏ nhất của A là
15
2
Bài toán 9. Cho a, b là các số thực dương thỏa mãn
ab1. Tìm giá trị nhỏ nhất của biểu thức:
22
11
A
2ab
ab
Phân tích: Do A là biểu thức đối xứng với a, b nên ta dự đoán giá trị nhỏ nhất của A đạt tại
1
ab
2
. Khi đó ta có sơ đồ điểm rơi:
22
1k
2
1
2ab
ab
ab 2k2 k1
1
2
2
2ab
Lời giải
Áp dụng bất đẳng thức Cauchy ta có

22 22 2
11 4 4
A 4
2ab
ab ab2ab
ab
Đẳng thức xẩy ra khi và chỉ khi
22
ab2ab
1
ab
ab1
2
Vậy giá trị nhỏ nhất của A là 4.
Bài toán 10. Cho a, b là các số thực dương thỏa mãn
ab1. Tìm giá trị nhỏ nhất của biểu thức:
22
11
A
2ab
1a b
Phân tích: Dự đoán giá trị nhỏ nhất của A đạt tại
1
ab
2
. Khi đó ta có sơ đồ điểm rơi:
22
11 12
ab k3
22kab3
1a b
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
22 2
111 1 1
A2
6ab 3ab 3ab
1a b
1a b6ab
21 41
3ab 3ab
1a b 6ab
a b 1 4ab
2
22
2
41448
2.1 1 3.1 3
ab ab
ab 14 3
22
Đẳng thức xẩy ra khi và chỉ khi
22
1a b 6ab
1
ab ab
2
ab1
Vậy giá trị nhỏ nhất của A là
8
3
.
Bình luận: Qua các bài toán trên ta thấy, khi giải các bài toán chứng minh bất đẳng thức thì các đánh
giá trung gian phải được bảo toàn dấu đẳng thức. Cho nên việc xác định đúng vị trí điểm rơi xẩy ra sẽ
tránh cho ta sử dụng các đánh giá trung gian sai lầm.
Trong đánh giá từ trung bình cộng sang trung bình nhân, việc xác định điểm rơi đúng sẽ chỉ cho ta
cách chọn các đánh giá hợp lí trong chuỗi các đánh giá mà ta cần phải sử dụng. Bây gi
ờ ta đi tìm hiểu kĩ
thuật đánh giá từ trung bình cộng sang trung bình nhân thông qua một số ví dụ sau.
Ví dụ 1.1: Cho các số thực a, b, c bất kì. Chứng minh rằng:
222222 222
abbcca 8abc
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc. Trong bất đẳng thức trên thì vế trái có
các đại lượng
222222
ab;bc;ca và vế phải chứa đại lượng
222
8a b c . Để ý ta nhận thấy
222
8a b c 2ab.2bc.2ca , do đó rất tự nhiên ta nghĩ đến các đánh giá từ trung bình cộng sang trung bình
nhân
22 22 22
ab2ab;bc2bc;ca2ca .
Lời giải
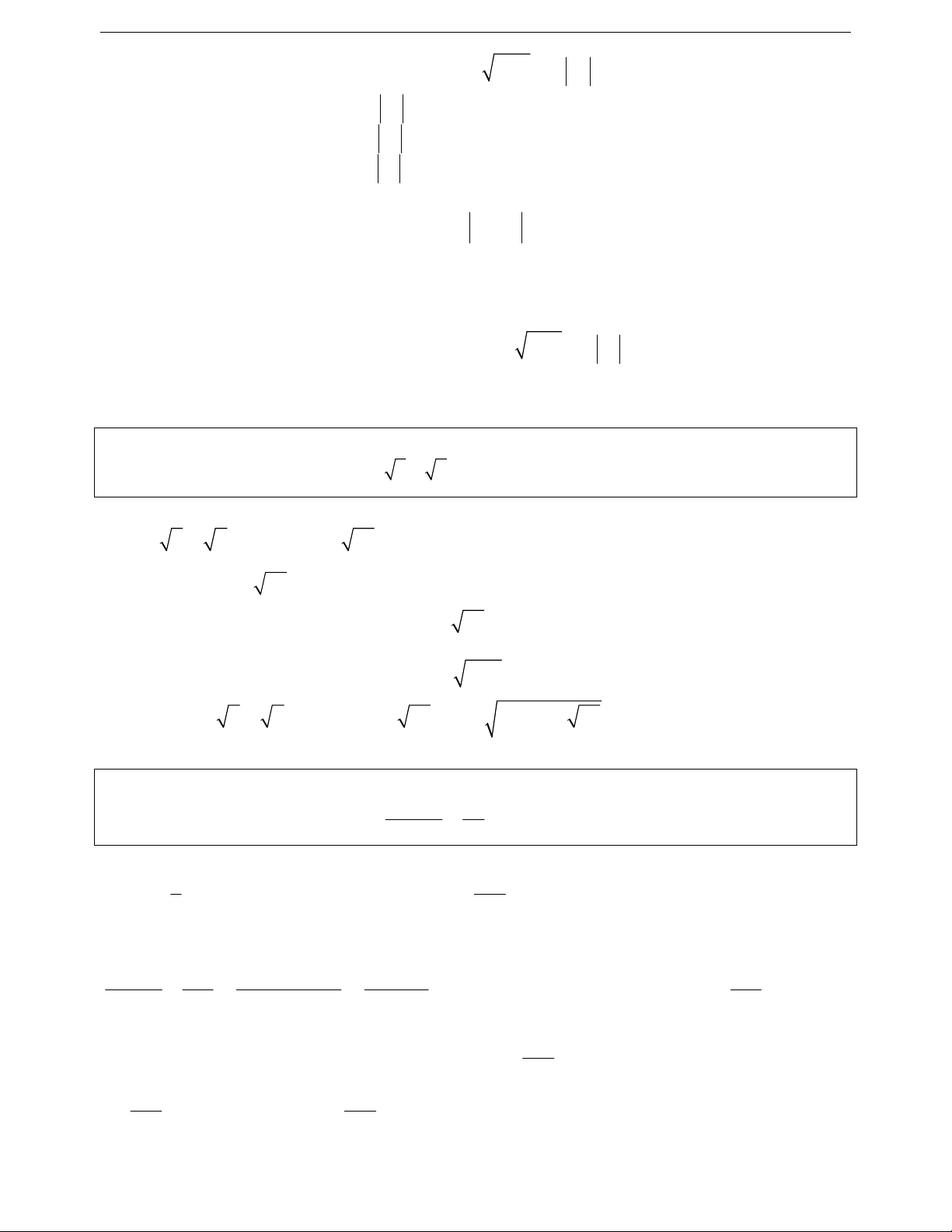
Sử dụng bất đẳng thức Cauchy dạng
22 22
xy2xy 2xy , ta có:
22
22
22
ab2ab0
bc2bc0
ca 2ca0
Nhân vế theo vế của ba bất đẳng thức trên ta được:
222222 222 222
a b b c c a 8abc 8abc
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi a = b = c.
Nhận xét:
- Chỉ được nhân các vế của bất đẳng thức cùng chiều (kết quả được bất đẳng thức cùng chiều)
khi và chỉ khi các vế cùng không âm.
- Để ý rằng ta sử dụng cách đánh giá
22 22
22 xy xy xy
khi chưa xác định được x, y âm
hay dương.
- Nói chung ta ít gặp bài toán sử dụng ngay bất đẳng thức Cauchy như bài toán nói trên mà phải
qua một vài phép biến đổi đến tình huống thích hợp rồi mới sử dụng bất đẳng thức Cauchy.
Ví dụ 1.2: Cho a, b là các số thực dương không âm tùy ý. Chứng minh rằng:
8
2
a b 64ab a b
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại ab . Trong bất đẳng thức trên, vế trái có đại
lượng
84
ab ab2ab và vế phải có đại lượng
2
64ab a b . Để ý ta nhận thấy khi
ab
thì ab2ab và
2
ab 4ab , do đó rất tự nhiên ta nghĩ đến các đánh giá từ trung bình
cộng sang trung bình nhân cho hai số
ab và
2ab
.
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
22 22
xy2xy 2xy , ta được:
4
84
2
ab ab2ab 22abab 64abab
Bất đẳng thức được chứng minh. Dấu đẳng thức xảy ra khi và chỉ khi a = b.
Ví dụ 1.3: Cho a, b là các số thực dương thỏa mãn
ab1. Chứng minh rằng:
22
11
4ab 7
ab
ab
Phân tích: Do biểu thức vế trái có tính đối xứng với a, b nên ta dự đoán dấu đẳng thức xảy ra tại
1
ab
2
. Khi đó ta có
22
ab2ab và
1
4ab
4ab
. Để ý đại lượng
22
ab nằm ở mẫu nên ta cần
tìm cách thêm vào
2ab để tạo thành
2
ab , do đó rất tự nhiên ta nghĩ đến đánh giá
22 22 2
11 4 4
4
2ab
ab ab2ab
ab
. Như vậy lúc này bên vế trái còn lại
1
4ab
2ab
, đến
đây ta sử dụng cách ghép hai đại lượng nghịch đảo
1
4ab 2
4ab
. Như vậy lúc này ta thấy vế trái còn
lại
1
4ab
và ta cần chỉ ra được
1
1
4ab
. Điều này không thể làm khó ta được vì dễ nhận ra được
2
4ab a b 1 . Đến đây ta trình bày lại lời giải như sau

Lời giải
Ta viết lại biểu thức vế trái thành
22 22
11 1 1 11
4ab 4ab
ab 2ab 4ab 4ab
ab ab
Áp dụng bất đẳng thức Cauchy cho hai số không âm ta có các đánh giá sau:
22 22 2
11 4 4
4
2ab
ab ab2ab
ab
1
4ab 2
4ab
;
2
1
4ab a b 1 1
4ab
Cộng theo vế các bất đẳng thức trên ta được
22 2 2
11 11 4 1 1
4ab 2 4ab. 7
2ab 4ab 4ab 4ab
ab (ab)
ab
Hay
22
11
4ab 7
ab
ab
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
1
ab
2
.
Ta tiếp tục vận dụng đánh giá từ trung bình cộng sang trung bình nhân cho các ví dụ sau đây.
Ví dụ 1.4: Cho số thực a bất kì. Chứng minh rằng:
2
2
a2
2
a1
Phân tích: Ta viết lại bất đẳng thức cần chứng minh là
22
a22a1 . Để ý ta nhận thấy
22 2 2
a2a11;2a12a1.1 , do đó ta sử dụng đánh giá từ trung bình cộng sang trung
bình nhân để chứng minh bất đẳng thức.
Ngoài ra, Để ý ta cũng có thể viết
22
2
22 2
a2 a11 1
a1
a1 a1 a1
, đến đây ghép
cặp nghịch đảo để chứng minh bất đẳng thức.
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
xy2xy , ta có
22 2 2
a2a112a1.12a1
Hay
2
2
a2
2
a1
. Bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
2
a11 a0 .
Ta cũng có thể trình bày lời giải như sau: Biến đổi vế trái và áp dụng bất đẳng thức Côsi cho hai số ta có
22
2
22 2
a2 a11 1
a1 2
a1 a1 a1
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
22
2
1
a1 a11 a0
a1
Ví dụ 1.5: Cho a, b là các số thực dương thỏa mãn điều kiện
ab . Chứng minh rằng:

1
a3
ba b
Phân tích: Quan sát bất đẳng thức ta nhận thấy vế phải không chứa biến, nên khi áp dụng áp dụng bất
đẳng thức Cauchy cho vế trái ta cần phải khử hết các biến, như vậy ta cần phải có các đại lượng
ab;b
, ngoài ra chiều bất đẳng thức gợi ý cho ta sử dụng đánh giá từ trung bình cộng sang trung bình
nhân. Để ý là
ababkhi đó ta áp dụng đánh giá cho 3 số dương
1
ab;b;
ba b
.
Lời giải
Áp dụng bất đẳng thức Cauchy cho ba số dương ta được
3
11 1
a bab 3.b.ab. 3
ba b ba b ba b
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
a2
1
ab b
b1
ba b
Ví dụ 1.6: Cho các số thực dương a, b, c. Chứng minh rằng:
abc3
bc ca ab 2
Phân tích: Đây là bất đẳng thức Neibizt đã được chứng minh bằng phép biến đổi tương đương. Tuy nhiên
ở đây ta thử dùng bất đẳng thức Cauchy để chứng minh xem sao.
+ Hướng 1: Để ý đẳng thức xẩy ra khi
abc nên khi đó có
abc1
bc ca ab 2
. Sử dụng
bất đẳng thức Cauchy cho hai số
abc
;
bc 4a
khi đó ta được
abc
1
bc 4a
, áp dụng tương tự ta
được bất đẳng thức:
abc bccaab
3
b c c a a b 4a 4b 4c
Như vậy ta cần chứng minh được
bc ca ab 3 bc ca ab
6
4a 4b 4c 2 a b c
.
Đánh giá cuối cùng là một đánh giá sai. Do đó ta không thể thực hiện chứng minh theo hướng thứ nhất
được.
+ Hướng 2: Để ý là
aabc
1
bc bc
, khi đó áp dụng tương tự được bất đẳng thức
abcabcabc 9
bc ca ab 2
hay
111
2a b c 9
bc ca ab
. Dễ dàng chỉ
ra được
3
111 1
3.
bc ca ab
abbcca
và chú ý ta lại thấy
3
2abc ab bc ca 3.abbcca . Đến đây ta có lời giải như
sau
Lời giải
Bất đẳng thức cần chứng minh tương đương với

abcabcabc 9
bc ca ab 2
Hay
111
2a b c 9
bc ca ab
Áp dụng bất đẳng thức Cauchy ta được
3
3
2abc ab bc ca 3.abbcca
111 1
3.
bc ca ab
abbcca
Nhân theo vế hai bất đẳng thức trên ta được
111
2a b c 9
bc ca ab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 1.7: Cho a, b, c là các số thực không âm. Chứng minh rằng :
3
3
1a1b1c 1 abc
Phân tích: Dự đoán đẳng thức xẩy ra khi và chỉ khi
abc
, để đơn giản hóa bất đẳng thức ta có thể
lũy thừa bậc 3 hai vế, khi đó ta được
3
3
1a1b1c 1 abc
hay
33
222
1a1b1c 13.abc 3.abc abc
. Quan sát bất đẳng thức ta chú ý đến đẳng thức
1a1b1c 1 abc abbcca abc
.
Như vậy bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
3
abc3.abc và
3
222
ab bc ca 3. a b c , rõ ràng hai đánh giá trên đúng theo bất đẳng thức Cauchy.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
3
3
1a1b1c 1 abc
Hay
33
222
1 a b c ab bc ca abc 1 3. abc 3. a b c abc
Hay
33
222
abc abbcca 3.abc3.abc
Áp dụng bất đẳng thức Cauchy ta có
3
abc3.abc và
3
222
ab bc ca 3. a b c
Cộng theo vế hai bất đẳng thức trên ta được điều phải chứng minh.
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 1.8: Cho a, b, c, d là các số thực dương. Chứng minh rằng:
2
ababcabcd
64
abcd
Phân tích: Bất đẳng thức được viết lại thành
2
ababcabcd 64abcd . Dễ thấy
đẳng thức không xẩy ra tại
abcd, do đó để dự đoán được dấu đẳng thức xẩy ra tại đâu ta cần
quan sát thật kỹ vai trò các biến trong bất đẳng thức. Nhận thấy trong bất đẳng thức a và b,
ab
và c,
abcvà d có vai trò như nhau, do đó ta dự đoán đẳng thức xẩy ra khi
ab;abc;abcd
hay
4a 4b 2c d
, kiểm tra lại ta thấy kết quả đúng vậy. Như
vậy khi áp dụng bất đẳng thức Cauchy ta cần chú ý bảo toán dấu đẳng thức. Trước hết ta có các đánh giá
như sau:
2
ab2ab;abc2abc;abcd 4abcd

Nhân theo vế các bất đẳng thức ta được
2
ababcabcd 16ab.abc.abcd
Tiếp tục áp dụng các đánh giá như trên ta được
ab. a b c. a b c d ab. 2c ab.2 a b c.d
ab.2cab.22cab.d 4abcd
Đến đây ta thu được
2
ababcabcd 64abcd chính là bất đẳng thức cần
chứng minh.
Ngoài ra, để đơn giản hơn ta có thể thực hiện các đánh giá như
22 2
ab 4ab;abc 4cab;abcd 4abcd
Đến đây ta nhân theo vế và thu gọn thì được
2
ababcabcd 64abcd
Bây giờ ta trình bày lại lời giải như sau
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
ababcabcd 64abcd
Sử dụng liên tiếp bất đẳng thức Cauchy dạng
2
xy 4xy
, ta có
2
22
abcd 4dabc 0
a b c 4c a b 0; a b 4ab 0
Nhân ba bất đẳng thức trên lại theo vế, ta suy ra
22 2
a b a b c a b c d 64abcd a b a b c
Hay
2
ababcabcd 64abcd
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
d2c4b4a0
Ngoài ra, ta cũng có thể trình bày lời giải như sau:
Áp dụng bất đẳng thức Cauchy ta có
2
ab2ab;abc2abc;abcd 4abcd
Nhân theo vế các bất đẳng thức ta được
2
ababcabcd 16ab.abc.abcd
Tiếp tục áp dụng các đánh giá như trên ta được
ab. a b c. a b c d ab. 2c ab.2 a b c.d
ab.2cab.22cab.d 4abcd
Đến đây ta thu được
2
ababcabcd 64abcd
Hay bất đẳng thức được chứng minh.
Ví dụ 1.9: Cho a, b, c là các số thực dương. Chứng minh rằng:
33 33 33
1111
ababcbcabccaabcabc

Phân tích: Bất đẳng thức trên đã được chứng minh bằng cách đánh giá mẫu, ở đó ta chứng minh bất đẳng
thức phụ
33
ababab
bằng phép biến đổi tương đương. Trong ví dụ này ta sẽ chứng minh bất
đẳng thức phụ trên bằng đánh giá từ trung bình cộng sang trung bình nhân.
Ta viết lại bất đẳng thức phụ trên thành
33 2 2
ababab , khi đó ta có các đánh giá là
333 2333 2
aab 3ab;abb3ab
. Đến đây cộng theo vế ta thu được bất đẳng thức trên. Đến
đây ta trình bày lời giải như sau
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
333 2333 2
aab 3ab;abb3ab
Cộng theo vế hai bất đẳng thức trên ta được
33 2 2
ababab
Suy ra
33
a b abc ab a b c
Từ đó ta được
33
11 c
a b abc
ab a b c abc a b c
Chứng minh tương tự ta có
33
33
11 a
bcabc
bc a b c abc a b c
11 b
caabc
acabc abcabc
Cộng theo vế các bất đẳngthức trên ta được
33 33 33
1111
abc
ababcbcabccaabc
Nhận xét: Khi đi tìm lời giải cho bất đẳng thức trên, cái làm khó ta chính là phải phát hiện ra bất đẳng
thức phụ
33
ab abab
. Trong quá trình đó đòi hỏi ta phải có sự phân tích kĩ càng và có những
định hướng rõ ràng, còn trình bày chứng minh bất đẳng thức thì cách nào cũng được miễn là càng gọn
càng tốt.
Ví dụ 1.10: Cho a, b, c là các số thực dương. Chứng minh rằng:
64 6464 4 44
2a 2b 2c 1 1 1
ab bc ca a b c
Phân tích: Vì vai trò các biến như nhau trong bất đẳng thức nên ta được dự đoán đẳng thức xẩy ra tại
abc, khi đó ta được
2
64 4
2a 1
2a a 1
aa a
, do đó đẳng thức sẽ xẩy ra tại abc1.
Quan sát bất đẳng thức ta nhận thấy vế trái của bất đẳng thức phức tạp hơn nên ta chọn đánh giá bên vế
trái trước. Từ chiều bất đẳng thức ta cần phải thay các mẫu bởi các đại lượng bé hơn, tức là ta cần có đánh
giá
64
ab?
, cho nên một cách tự nhiên ta nghĩ đến bất đẳng thức Cauchy, khi đó ta có
64 32
ab2ab
, đánh giá này vẫn được bảo toàn dấu đẳng thức. Lúc này ta được
6 4 32 22
2a 2a 1
aa 2ab ab
và áp dụng tương tự thì ta sẽ thu được
64 6464 22 2222
2a 2b 2c 1 1 1
ab bc ca abbc ca
. Việc chứng minh sẽ hoàn tất nếu ta chỉ ra được

22 22 22 4 4 4
111111
ab bc ca a b c
, nhưng đây là một đánh giá đúng theo bất đẳng thức Cauchy. Do đó
bài toán được chứng minh.
Lời giải
Áp dụng bất đẳng thức Cauchy cho các mẫu số ta được
6 4 6 4 6 4 32 32 32 22 22 22
2a 2b 2c 2a 2b 2c 1 1 1
a b b c c a 2a b 2b c 2c a a b b c c a
Ta cần chứng minh được
22 22 22 4 4 4
111111
ab bc ca a b c
Thật vậy, cũng theo bất đẳng thức Cauchy ta có
44 2244 224422
11 2 11 211 2
;;
ababbcbcca ca
Cộng theo vế ba bất đẳng thức trên ta thu được
22 22 22 4 4 4
111111
ab bc ca a b c
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 1.11: Cho a, b, c là các số thực dương. Chứng minh rằng:
a1 b1 c1 9
abc
2bc 2ca 2ab 2
Phân tích: Vì vai trò các biến như nhau trong bất đẳng thức nên ta được dự đoán đẳng thức xẩy ra tại
abc
, khi đó ta được
2
a1 3
aa1
2a 2
, do đó đẳng thức sẽ xẩy ra tại
abc1
. Ta
viết lại bất đẳng thức cần chứng minh thành
222 222
abcabc 9
2abc2
Để ý đến đánh giá
222
abcabbcca
khi đó ta được
222 222 222
abcabc abc 111
2abc 2abc
Ta cần chứng minh được
222
a13b13c13
;;
2a22b22c2
. Chú ý đến abc1, ta có
22
a1a 113
2a 22a2a2
, do vậy đến đây bài toán được chứng minh.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 222
abcabc 9
2abc2
Mặt khác ta có
222
abc abbcca111
abc abc a b c
Do đó ta được
222 222 222
abcabc abc 111
2abc 2abc
Ta cần chứng minh được
222
abc 1119
2abc2
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
22
a1a 113
2a 22a2a2

Áp dụng tương tự ta được
22
b13c13
;
2b22c2
.
Cộng theo vế ba bất đẳng thức trên ta được
222
abc 1119
2abc2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Ví dụ 1.12: Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc 1
. Chứng minh rằng:
33 33 33
ab1 bc1 ca1
33
ab bc ca
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức ta có các ý
tưởng tiếp cận như sau:
+ Hướng thứ nhất: Chú ý đến chiều bất đẳng thức ta liên tưởng đến đánh giá tương tự như trong ví dụ 1.9
là
33 33
ab1ababcababc
, khi đó ta được bất đẳng thức là
33
ab a b c
ab1 abc
ab ab
ab
và áp dụng hoàn toàn tương tự ta được bất đẳng thức
33 33 33
ab1 bc1 ca1 1 1 1
abc.
ab bc ca
ab bc ca
. Phép chứng minh sẽ
hoàn tất nếu ta chỉ ra được
111
abc. 33
ab bc ca
. Tuy nhiên bất đẳng thức đó là
đúng nhờ hai đánh giá sau:
3
abc 3abc 3 và
3
111 111
3.. 3
ab bc ca ab bc ca
+ Hướng thứ hai: Áp dụng trự tiếp bất đẳng thức Cauchy ta có
3
33 33
ab13ab 3ab
nên ta
được
33
ab1 3
ab
ab
, áp dụng tương tự ta được bất đẳng thức
33 33 33
ab1 bc1 ca1 1 1 1
3
ab bc ca
ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
111
3
ab bc ca
, tuy nhiên đánh giá này
đã được khẳng định trong hướng thứ nhất. Bây giờ ta trình bày lại lời giải như sau
Lời giải
Cách 1: Dễ dàng chứng minh được
33
ababab , khi đó ta có
33
ab a b c
ab1 abc
ab ab
ab
Áp dụng tương tự ta được
33 33 33
ab1 bc1 ca1 1 1 1
abc.
ab bc ca
ab bc ca
Mặt khác, áp dụng bất đẳng thức Cauchy ta có
3
abc 3abc 3 và
3
111 111
3.. 3
ab bc ca ab bc ca

Nhân theo vế hai bất đẳng thức trên ta được
111
abc. 33
ab bc ca
Suy ra
33 33 33
ab1 bc1 ca1
33
ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Áp dụng bất đẳng thức Cauchy cho ba số dương ta được
3
33 33
ab13ab 3ab
Suy ra
33
ab1 3
ab
ab
, áp dụng tương tự ta được bất đẳng thức
33 33 33
ab1 bc1 ca1 1 1 1
3
ab bc ca
ab bc ca
Mặt khác cũng theo bất đẳng thức Cauchy ta lại có
3
222
111 1
33
ab bc ca a b c
.
Do đó ta được
33 33 33
ab1 bc1 ca1
33
ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 1.13: Cho a, b, c là các số thực bất kì. Chứng minh rằng:
222
222
abbcca1ab1bc1ca
11
88
1a 1b 1c
Phân tích: Với bất đẳng thức trên việc dự đoán dấu đẳng thức xẩy ra hơi khó. Để dễ quan sát hơn ta có
thể viết lại bất đẳng thức như sau:
222
222
abbcca1ab1bc1ca
1
8
1a 1b 1c
Hay ta cần chứng minh
222
222
8abbcca1ab1bc1ca 1a 1b 1c
Quan sát thật kĩ bất đẳng thức trên ta thấy cần phải chứng minh được
22
1a 1b 2ab1ab
Với bất đẳng thức trên, ta sử dụng phép biến đổi tương đương hoặc bất đẳng thức Cauchy. Ở đây
ta sử dụng bất đẳng thức Cauchy, chú ý bên vế phải của bất đẳng thức có chứa đại lượng
2a b 1 ab, như vậy ta cần biến đổi vế trái thành
22
ab 1ab . Để kiểm tra nhận định
trên ta chỉ cần nhân tung hai biểu thức rồi so sánh là được và rất may là nhận định trên là đúng. Bây giờ ta
trình bày lại lời giải như sau
Lời giải
Bất đẳng thức cần chứng minh được viết lại như sau:
222
222
abbcca1ab1bc1ca
1
8
1a 1b 1c
Hay ta cần chứng minh
222
222
8abbcca1ab1bc1ca 1a 1b 1c
Áp dụng bất đẳng thức Cauchy ta có

22
22 2222
1a 1b 1a b ab ab 1ab 2ab1ab
Áp dụng tương tự
22 2 2
1b 1c 2bc1bc;1c 1a 2ca1ca
Nhân theo vế các bất đẳng thức trên ta được
222
222
8abbcca1ab1bc1ca 1a 1b 1c
Vậy bất đẳng thức được chứng minh.
Ví dụ 1.14: Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc3
. Chứng minh rằng:
22 22 22
222
a1 1b 1b 1c 1c 1a
24
1c 1a 1b
Phân tích: Đầu tiên ta dự đoán đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức thì ý tưởng
đầu tiên đó là sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, tức là ta cần phải chứng minh được
2
222
1a1b 1b1c 1c1a
24
abc3
Tuy nhiên bất đẳng thức trên không đúng, muốn kiểm tra ta chỉ cần chọn một một bộ số, chẳng hạn
1
a2;bc
2
để thử thì thấy bất đẳng thức trên không đúng. Do đó đánh theo bất đẳng thức
Bunhiacopxki không thực hiện được. Trong tình huống này ta nghĩ đến đánh giá bằng bất đẳng thức
Cauchy.
Trước hết ta thử đánh giá trực tiếp bằng bất đẳng thức Cauchy xem sao, ta có
22 22 22 434
3
222
222
1a 1b 1b 1c 1c 1a a1 1b 1c
3
1c 1a 1b
1a 1b 1c
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
434
32 2 2
a1 1b 1c 81a 1b 1c
Tuy nhiên đánh giá trên lại không đúng.
Như vậy để đánh giá được theo bất đẳng thức Cauchy hay Bunhiacopxki ta cần biến đổi các biểu
thức trước. Quan sát bất đẳng thức ta nhận thấy cần biến đổi
22
1a 1b thành đại lượng có chứa
22
1a;1b
và ta có thể biến đổi như sau:
22 2
22
1 a 1 b ab 1 a b 4 ab 1 a b 4a 1 b 4b 1 a
Đến đây ta được
22
22
222
1a 1b
1a 1b
4b. 4a.
1c 1c 1c
, áp dụng tương tự ta thu được
22 2 2
22 22
222222
1b 1c 1c 1a
1c 1b 1c 1a
4b. 4c. ; 4a. 4c.
1a 1a 1a 1b 1b 1b
.
Để ý ta thấy trong các đánh giá trên xuất hiện các cặp nghịch đảo nên ta ghép chúng lại
22 22 22
22 22 22
1a 1c 1b 1c 1b 1a
4b. 4b. 8b; 4a. 4a. 8a; 4c. 4c. 8c
1c 1a 1c 1b 1a 1b
Chú ý đến giả thiết
abc3 ta có được điều cần chứng minh và lúc này ta trình bày lại lời
giải như sau
Lời giải
Áp dụng bất đẳng Cauchy ta có
22 2
22
1 a 1 b ab 1 a b 4 ab 1 a b 4a 1 b 4b 1 a

Suy ra
22
22
222
1a 1b
1a 1b
4b. 4a.
1c 1c 1c
Áp dụng tương tự ta thu được
22 2 2
22 22
222222
1b 1c 1c 1a
1c 1b 1c 1a
4b. 4c. ; 4a. 4c.
1a 1a 1a 1b 1b 1b
Khi đó ta được bất đẳng thức
22 22 22
222
222222
222222
1a 1b 1b 1c 1c 1a
1c 1a 1b
1a 1b 1c 1b 1c 1a
4b. 4a. b. 4c. 4a. 4c.
1c 1c 1a 1a 1b 1b
Mặt khác cũng theo bất đẳng thức Cauchy ta có
22 22 22
22 22 22
1a 1c 1b 1c 1b 1a
4b. 4b. 8b; 4a. 4a. 8a; 4c. 4c. 8c
1c 1a 1c 1b 1a 1b
Suy ra
22 2222
222222
1a 1c 1b 1c 1b 1a
4b.4b.4a.4a.4c.4c. 8abc24
1c 1a 1c 1b 1a 1b
Do đó
ta được
22 22 22
222
a1 1b 1b 1c 1c 1a
24
1c 1a 1b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Ví dụ 1.15: Cho a, b, c là các số thực dương thỏa mãn
abc
2
a1b1 c1
.
Chứng minh rằng:
ab bc ca 12
Lời giải
Áp dụng bất đẳng thức Cauchy giả thiết ta có
abc11 2
11
a1 b1 c1 b1 c1
b1c1
Tương tự ta có
b2c2
;
b1 c1
c1a1 a1b1
Khi đó ta được
4. a 1 b 1
ab 4
ab
c1
a1b1
c1 a1b1
Áp dụng tương tự ta được
4. b 1 c 1 4. c 1 a 1
bc ; ca
a1 b1
Cộng theo vế các bất đẳng thức trên ta được
4. a 1 b 1 4. b 1 c 1 4. c 1 a 1
ab bc ca
c1 a1 b1
Mặt khác theo bất đẳng thức Cauchy ta lại có
a1b1 b1c1 c1a1
3
c1 a1 b1
Suy ra
ab bc ca 12
. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc2.
Ví dụ 1.16: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:

222
3
8a b c
27 a b b c c a
16
ab bc ca
abc
Lời giải
Đẳng thức xẩy ra tại
abc
, khi đó
222
3
8a b c
27 a b b c c a
8
ab bc ca
abc
Do đó ta áp dụng trực tiếp bất đẳng thức Cauchy cho ba số dương
222 222
3 3
8a b c 8a b c .27a b b c c a
27 a b b c c a
2
ab bc ca
abc abbccaabc
Ta cần
chứng minh được
3
222
27 a b c a b b c c a 8 ab bc ca a b c
Dễ thấy
abbcca abcabbcca abc
Mà theo bất đẳng thức Cauchy ta có
3
3
222
a b c 3 abc; ab bc ca 3 a b c
Suy ra
abccbbcca
abc
9
Do đó ta được
8
abbcca abccbbcca
9
Suy ra
222 222
27 a b c a b b c c a 24 a b c a b c cb bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
3
222
24a b c abcabbcca 8abbccaabc
Hay
2
222
3a b c a b c
Rõ ràng đánh giá cuối cùng là một đánh giá đúng. Vậy bất đẳng thức được chứng minh.
Ví dụ 1.17: Cho a, b, c là các số thực dương thỏa mãn
22 22 22
ab bc ca 32
Chứng minh rằng:
222
abc3
bc ca ab 2
Lời giải
Đặt
22 22 22
xab;ybc;zca , khi đó ta được x; y; z 0 và từ giả thiết ta được
xyz32
Từ đó ta có
222 222
xyz2abc . Do đó ta được
222 222 222
22 2
xyz xyz xyz
a;b;c
22 2
Áp dụng bất đẳng thức Cauchy ta có
2
22 2
bc 2b c 2y
Do đó ta được
2222
axyz
bc
2y 2
Hoàn toàn tương tự ta có
22222 222
bxyzc xyz
,
ca ab
2z 2 2x 2

Suy ra
222
222 222 222
222
2
abc
bc ca ab
xyz yxyz zxyz x
2y 2 2 2z 2 2 2x 2 2
1111xyz
xyz
xyz
22 2
111132
xyz
xyz
62 2
11119.323
xyzxyz 3 3
xyz 2
62 62
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 1.18: Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
42 2 42 2 42 2
33 3 3 3 3
ab c bc a ca b
2
b2c c2a a2b
Lời giải
Áp dụng bất đẳng thức Cauchy và kết hợp với giả thiết ta có
42 2 222 22 2 422 3
ab c aab ca a.2a.bc 2a
Hoàn toàn tương tự ta được
42 2 3 4 2 2 3
bc a 2b;ca b 2c
Khi đó ta được
42 2 42 2 42 2
333
33 3 3 3 3 333 33 3
ab c bc a ca b
2a 2b 2c
b 2c c 2a a 2b b 2c c 2a a 2b
Ta cần chứng minh được
333
33333 3
2a 2b 2c
2
b2c c2a a2b
Thật vậy, đặt
33 3 3 3 3
x b 2c ; y c 2a ; z a 2b
Khi đó ta được
333
x2y4z y2z4x z2x4y
b;c;a
999
Bất đẳng thức cần chứng minh trở thành
2 z 2x 4y 2 x 2y 4z 2 y 2z 4x
2
9x 9y 9z
Hay ta cần chứng minh
2zxy yzx
462
9xyz xyz
Áp dụng bất đẳng thức Cauchy với 3 số dương ta có
33
zxy zxy yzx yzx
3.. 3; 3.. 3
xyz xyz xyz xyz
Khi đó ta được
2zxy yzx
462
9xyz xyz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 1.19: Cho a, b, c là các số thực dương. Chứng minh rằng:

3
222
abc
ab bc ca
28
abc
abc
Lời giải
Gọi vế trái của bất đẳng thức trên là P, khi đó ta có
2
222
222
222
222
222
abc
ab bc ca
Pabc
abc
abc
abc
ab bc ca
abc2ab2bc2ca
abc
abc
ab bc ca 1 1 1 1 1 1
abc 2abbcca
ab bc ca ab bc ca
abc
Áp dụng bất đẳng thức Cauchy ta được
111 9 111
;ab bc ca 9
ab bc ca ab bc ca ab bc ca
Để ý là
222
abcabcbca . Khi đó ta được
222
222
222
222
222
ab bc ca 9
Pabc2.9
ab bc ca
abc
8a b c
ab bc ca a b c
18
ab bc ca ab bc ca
abc
2 8 18 28
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 1.20: Cho a, b, c là các số thực dương thỏa mãn
22
ab a b
2c 6.
ba
ba
Chứng minh rằng:
bc ca 4ab 8
3
a2b c b2a c ca b
Lời giải
Từ giả thiết
2222
22 22
ca b a ab b 2a b
ab a b
2c 66
ba ab
ba ab
Áp dụng bất đẳng thức Cachy ta có
2222
22
22
ca b a ab b 2a b
ca b
ab2ab 6 4
ab ab
ab
c(a b)
02
ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
2
2
bc ac
bc ac
a 2b c b 2a c abc 2b c abc 2a c
ca b
bc ac
2abc a b c 2abc a b c
Và
2
ab bc ca
abc a b c ab.bc bc.ca ab.ca
3

Suy ra ta có
2
2
ca b
ca b
bc ac 3 3
ab
2ab bc ca 2
a2b c b2a c ca b
1
ab
Gọi P là vế trái của bất đẳng thức
Đặt
2
2
ca b
3t 4
tP
ab t
21 t
(với
0t2
). Ta có
22 32
22 2
2
2
3t 4 3t 4 8 8 7t 8t 32t 24 8
tt33 3
21t 21t 6t1t
t2 7t 22t12
88
33
6t 1 t
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi abc.
2. Kỹ thuật chọn điểm rơi trong đánh giá từ trung bình nhân sang trung bình cộng.
Đánh giá từ trung bình nhân sang trung bình cộng chính là đánh giá bất đẳng thức Cauchy theo
chiều từ phía phải sang phía trái. Trong chuỗi đánh giá đó ta cũng cần phải bảo toàn dấu đẳng thức xẩy ra.
Dưới đây là một số ví dụ sử dụng kỹ thuật đánh giá từ trung bình nhân sang trung bình cộng.
Ví dụ 2.1: Cho a, b, c là các số thực dương thỏa mãn điền kiện
abc1. Chứng minh rằng:
ab bc ca 6
Sai lầm thường gặp:
2. a b.1 a b 1
ab
22
2. b c.1 b c 1
bc
22
2. c a.1 c a 1
ca
22
2a b c 3
5
ab bc ca 6
22
.
Cách chứng minh trên hoàn toàn sai. Vậy nguyên nhân sai lầm ở đây là gì?
Nguyên nhân sai lầm: Dấu đẳng thức xẩy ra khi và chỉ khi
abbc ca1
abc2. Điều này trái với giả thiết.
Phân tích tìm lời giải: Để tìm lời giải cho bất đẳng thức trên, ta cần trả lời các câu hỏi sau
- Đẳng thức xẩy ra tại đâu?
- Áp dụng bất đẳng thức Cauchy cho mấy số, đó là những số nào?
Do vai trò của a, b, c trong các biểu thức là như nhau nên ta dự đoán điểm rơi của bất đẳng thức sẽ
là
1
abc
3
, từ đó ta có
2
abbcca
3
. Vì bất đẳng thức chứa các căn bậc hai nên để
phá căn ta sử dụng bất đẳng thức Cauchy cho hai số là a và
2
3
,…. Đến đây ta có lời giải đúng như sau:
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
xy
xy
2
cho hai số không âm ta có:

2
ab
323
3
ab .ab. .
2322
2
bc
323
3
bc .bc. .
2322
2
ca
323
3
ca .ca. .
2322
2
2a b c 3.
3
3
ab bc ca . 6
22
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ví dụ 2.2: Cho a, b, c là các số thực dương thỏa mãn điền kiện
abc1. Chứng minh rằng:
3333
ab bc ca 18
Sai lầm thường gặp
3
3
3
3
3
3
ab11
a b a b .1.1
3
bc11
b c b c .1.1
3
ca11
c a c a .1.1
3
333 3
2a b c 6
8
ab bc ca 18
33
.
Cách chứng minh trên hoàn toàn sai. Vậy nguyên nhân sai lầm ở đây là gì?
Nguyên nhân sai lầm: Dấu đẳng thức xẩy ra khi và chỉ khi
abbc ca1
abc2
. Điều này trái với giả thiết.
Phân tích tìm lời giải: Để tìm lời giải cho bất đẳng thức trên, ta cần trả lời các câu hỏi sau
- Đẳng thức xẩy ra tại đâu?
- Áp dụng bất đẳng thức Cauchy cho mấy số, đó là những số?
Do vai trò của a, b, c trong các biểu thức là như nhau nên ta dự đoán điểm rơi của bất đẳng thức sẽ
là
1
abc
3
, từ đó ta có
2
abbcca
3
. Vì bất đẳng thức chứa các căn bậc ba nên để
phá căn ta sử dụng bất đẳng thức Cauchy cho ba số là a,
2
3
và
2
3
,…. Đến đây ta có lời giải đúng như sau:
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
3
xyz
xyz
3
cho các số thực dương ta được
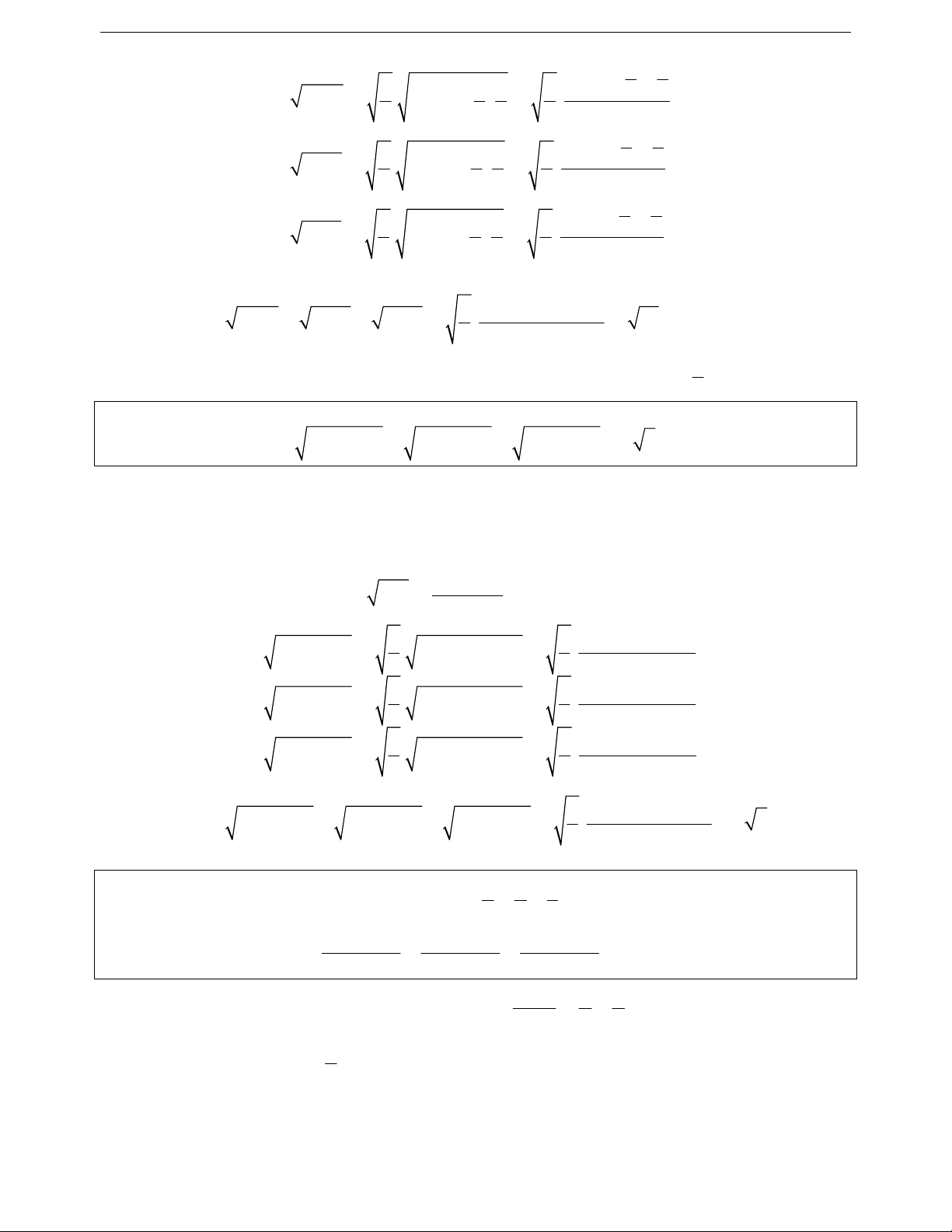
3
33 3
3
33 3
3
33 3
22
ab
9229
33
ab .ab.. .
43343
22
bc
9229
33
bc .bc.. .
43343
22
ca
9229
33
ca .ca.. .
43343
Suy ra
333 3
3
2a b c 4
9
ab bc ca . 18
43
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ví dụ 2.3: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
3
333
ab 2c bc 2a ca 2b 33
Phân tích: Do vai trò của các biến a, b, c trong các biểu thức là như nhau nên ta dự đoán điểm rơi của bất
đẳng thức sẽ là
abc1
, từ đó ta có
a2b b2c c2a 3
và
3a 3b 3c 3
. Vì
bất đẳng thức chứa các căn bậc ba nên để phá căn ta sử dụng bất đẳng thức Cauchy cho ba số là 3a,
b2c
và 3,… Đến đây ta có lời giải như sau:
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
3
xyz
xyz
3
cho các số thực dương ta được
33
33
33
33
33
33
113ab2c3
a b 2c . 3a. b 2c .3 .
993
113bc2a3
bc 2a .3b.c 2a.3 .
993
193ca2b3
ca 2b .3c.a 2b.3 .
943
Suy ra
3
3
333
6a b c 9
1
a b 2c b c 2a c a 2b . 3 3
93
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 2.4: Cho a, b, c là các số thực dương thỏa mãn
111
4
abc
. Chứng minh rằng:
111
1
2a b c a 2b c a b 2c
Phân tích: Quan sát bất đẳng thức ta nghĩ đến đánh giá
411
xy x y
. Đầu tiên ta dự đoán dấu đẳng
thức xẩy ra tại
3
abc
4
, khi đó ta có
2a b c
và
bc
nên ta có đánh giá như sau

1111111111211
2a b c 4 2a b c 4 2a 4 b c 16 a b c
. Áp dụng tương tự ta được
1111111
1
2abc a2bc ab2c 4a b c
. Đến đây ta trình bày lại lời giải như sau
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
411
xy x y
cho hai số dương. Ta có:
1111111111211
2a b c 4 2a b c 4 2a 4 b c 16 a b c
Tương tự ta có
1112111112
;
a2bc 16a b c ab2c 16a b c
Cộng theo vế các bất đẳng thức trên ta được
1111111
1
2abc a2bc ab2c 4a b c
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
abc
4
.
Ví dụ 2.5: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
abc
2
bc ca ab
Phân tích: Trong chủ đề thứ hai ta đã chứng minh bất đẳng thức trên bằng phương pháp sử dụng tính
chất của tỉ số, nhưng ở đó điều kiện của bài toán cho a, b, c là các cạnh của một tam giác. Với bài toán
này ta không chứng minh được như vậy mà phải sử dụng các đánh giá khác. Quan sát bất đẳng thức ta
thấy cần phải khử các căn bậc hai bên vế trái.
- Cách thứ nhất là bình phương hai vế, tuy nhiên lúc đó bên vế trái vẫn còn chứa căn bậc hai, do đó
ta không nên sử dụng cách này.
- Cách thứ hai là sử dụng bất đẳng thức Cauchy dạng
xy
xy
2
, để ý đến chiều của bất đẳng
thức nên ta sử dụng bất đẳng thức Cauchy cho các mẫu số. Từ đó một cách tự nhiên ta nghĩ đến phép biến
đổi
aa
bc
ab c
và vì không cần quan tâm đến dấu đẳng thức xẩy ra nên ta có đánh giá
a2a
abc
ab c
. Đến đây chỉ cần áp dụng tương tự cho hai căn thức còn lại là bài toán được
chứng minh
Lời giải
Vì a là số thực dương nên ta có
aa
bc
ab c
Áp dụng bất đẳng thức Cauchy dạng
xy
xy
2
ta được
a2a
abc
ab c

Chứng minh tương tự ta được
b2b c 2c
;
ca abc ab abc
Cộng theo vế các bất đẳng thức trên ta được
abc
2
bc ca ab
Đẳng thức xẩy ra khi và chỉ khi
abc0, điều này trái với giả thiết a, b, c là các số thực dương.
Do vậy đẳng thức không xẩy ra.
Tức là ta được
abc
2
bc ca ab
Vậy bài toán được chứng minh.
Ví dụ 2.6: Cho a, b, c là các số thực không âm thỏa mãn
abc3. Chứng minh rằng:
22 22 22
ab bc ca
2
a b 6c b c 6a c a 6b
Phân tích: Để ý đến giả thiết abc 3, ta thu được
c3 ab , khi đó ta có
22
22 22
ab6cab63ab 3a 3b
Lại cũng từ giả thiết trên ta có
ab3c. Khi đó
2
22
22 2 2
3c
ab 3c
ab6c
3a 3b
3a 3b
.
Đến đây để đơn giản hóa ta đặt
222
x3a 0;y3b 0;z3c 0 , lúc này bất
đẳng thức cần chứng minh được viết lại là
xyz
2
yz zx xy
, đây chính là bất đẳng thức
ở ví dụ trên.
Lời giải
Từ giả thiết
abc3, ta có
22
22 22
ab6cab63ab 3a 3b
Do a, b, c là các số thực dương nên từ
abc3
ta suy ra
0 a,b,c 3
.
Do đó ta được
2
22
22 2 2
3c
ab 3c
ab6c
3a 3b
3a 3b
Áp dụng tương tự ta được bất đẳng thức
222
22 2 2 2 2
3a 3b 3c
2
3b 3c 3c 3a 3a 3b
Đặt
222
x3a 0;y3b 0;z3c 0 , lúc này bất đẳng thức cần chứng
minh được viết lại là
xyz
2
yz zx xy
Đến đây ta chứng minh tương tự như ví dụ trên.
Ví dụ 2.7: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:

ab bc ca
1
c2ab a2bc b2ca
Phân tích: Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức ta nghĩ đến
sử dụng bất đẳng thức
xy
xy
2
, tuy nhiên nếu sử dụng ngay thì ta chỉ đánh giá cho các tử số được,
như vậy dưới mẫu vẫn còn chứa căn thức. Cho nên để sử dụng được bất đẳng thức đó ta cần phải khử
được các căn ở dưới mẫu trước, tuy nhiên việc này không thực hiện được. Chú ý đến chiều bất đẳng thức
ta thấy, chỉ cần đổi được chiều bất đẳng thức thì ta có thể sử dụng bất đẳng thức trên có các căn thức ở
mẫu và việc khử các căn ở tử số cũng đơn giản hơn. Từ sự phân tích đó ta có thể làm như sau
ab bc ca
1
c2ab a2bc b2ca
2ab 2bc 2ca
111 321
c2ab a2bc b2ca
cab
1
c2ab a2bc b2ca
Lúc này áp dụng bất đẳng thức
xy
xy
2
ta được
cc
abc
c2ab
, thực hiện tương
tự ta được bất đẳng thức cần phải chứng minh.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
ab bc ca
1
c2ab a2bc b2ca
2ab 2bc 2ca
111 321
c2ab a2bc b2ca
cab
1
c2ab a2bc b2ca
Áp dụng bất đẳng thức
xy
xy
2
ta được
ccaabb
;;
abc abc abc
c2ab a2bc b2ca
Cộng theo vế các bất đẳng thức trên ta được
cab
1
c2ab a2bc b2ca
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Nhận xét: Khi đánh giá một bất đẳng thức bằng bất đẳng thức Cauchy nếu bị ngược chiều thì ta có thể
đổi chiều bất đẳng thức bằng cách nhân hai vế với
1 rồi cộng thêm hằng số để cả hai vế đều dương. Kĩ
thuật sử dụng bất đẳng thức Cauchy như trên còn được gọi là kĩ thuật Cauchy ngược dấu, vấn đề này sẽ
được bàn cụ thể hơn trong chủ đề “Kĩ thuật Cauchy ngược dấu”
Ví dụ 2.8: Cho a, b, c là các số thực không âm thỏa mãn
ab bc ca 0
. Chứng minh rằng:
222
ab c bc a ca b
2
abc bca cab
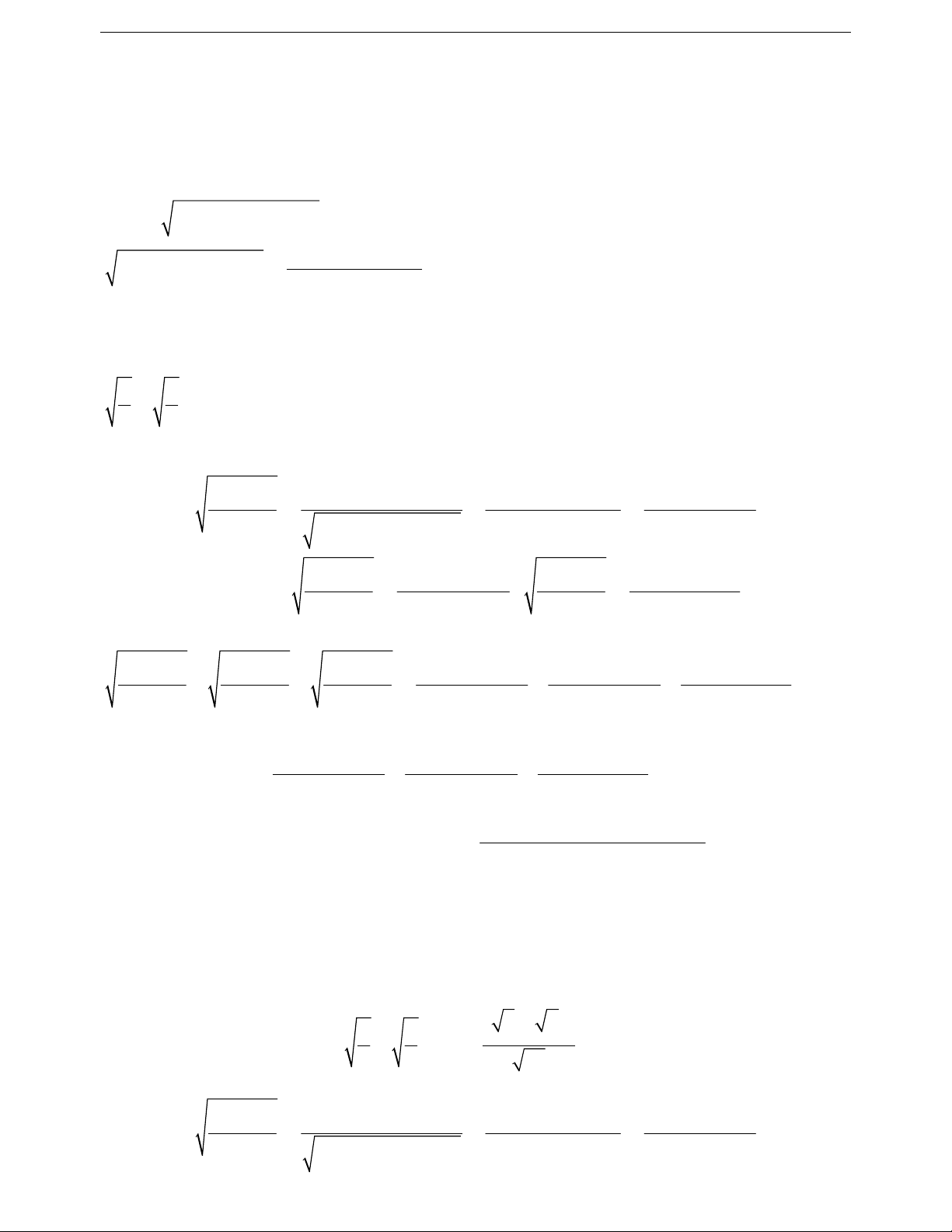
Phân tích: Đầu tiên ta thử với
abc
thấy rằng dấu đẳng thức không xẩy ra, nên ta dự đoán nó xẩy
ra tại một biến bằng 0, điều này càng có cơ sở khi bài toán cho a, b, c không âm. Cho c nhận giá trị 0 và
ab thì dấu đẳng thức xẩy ra. Như vậy ta chọn được điểm rơi của bất đẳng thức là
ab;c0
và
các hoán vị. Cũng từ điều kiện
ab bc ca 0 ta thấy trong ba số có nhiều nhất một số bằng 0. Do đó
khi đánh giá bất đẳng thức ta cần chú ý đến bảo toán dấu bằng.
Quan sát bất đẳng thức ta nhận thấy
2
a bcabc abac
, như vậy nếu dưới mẫu
có tích
2
abcabac thì theo chiều bất đẳng thức cần phải chứng minh ta có ngay đánh giá
2
2
aabbcca
abcabac
2
, nhưng để có được điều này ta phải nhân cả tử và mẫu của
mỗi phân số trong căn với tử số. Tuy nhiên vì cho các biến a, b, c không âm nên việc nhân thêm không
thể thực hiện được. Trong tình huống này chú ý đến điểm rơi và nhận xét trong a, b, c có nhiều nhất một
số bằng 0 ta có thể chia trường hợp để đánh giá bất đẳng thức.
- Trường hợp trong ba số a, b, c có một số bằng 0 và ta giả sử là c, khi đó bất đẳng thức trở thành
ab
2
ba
, bất đẳng thức này hiển nhiên đúng.
- Trường hợp cả ba số a, b, c đều dương, lúc này thì việc nhân thêm không bị ảnh ảnh hưởng gì đến các
đánh giá cả. Đến đây ta có đánh giá như sau
22
2
abc abc 2abc 2abc
abc aabbcca
abac
abcabac
Áp dụng tương tự ta được
22
bc a 2bc a ca b 2ca b
;
bca cab
abbc bcca
Lúc này ta được bất đẳng thức
222
ab c bc a ca b 2ab c 2bc a 2ca b
abc bca cab
abac abbc bcca
Phép
chứng minh sẽ hoàn tất nếu ta chỉ ra được
ab c bc a ca b
1
abac abbc bcca
Biến đổi tương đương bất đẳng thức trên ta thu được
abbcca 4abc
1
abbcca
Đánh giá cuối cùng hiển nhiên đúng, ta trình bày lại lời giải như sau
Lời giải
Vì các số a, b, c không âm và
ab bc ca 0 nên trong ba số a, b, c có nhiều nhất một số bằng
0. Ta xét các trường hợp sau
- Trường hợp trong ba số a, b, c có một số bằng không, khi đó không mất tính tổng quát ta giả sử
c0 ,
lúc này bất đẳng thức cần chứng minh trở thành
2
ab
ab
20
ba
ab
- Trường hợp cả ba số a, b, c đều dương, khi đó ta có
22
2
abc abc 2abc 2abc
abc aabbcca
abac
abcabac

Áp dụng tương tự ta được
22
bc a 2bc a ca b 2ca b
;
bca cab
abbc bcca
Lúc này ta được bất đẳng thức
222
ab c bc a ca b 2ab c 2bc a 2ca b
abc bca cab
abac abbc bcca
Ta cần chứng minh được
ab c bc a ca b
1
abac abbc bcca
Biến đổi tương đương và thu gọn ta được
4abc
11
abbcca
Bất đẳng thức cuối cùng luôn đúng do
4abc 0 và đẳng thức không xẩy ra trong trường hợp này. Vậy
bài toán được chứng minh xong.
Nhân xét: Trong chứng minh bất đẳng thức việc chia trường hợp để chứng minh gây ra nhiều khó khăn.
Do đó nếu tìm được một cách giải mà không cần phải quan tâm đến việc xét các trường hợp thì sẽ tốt hơn
nhiều. Với bài toán trên ta thử tìm lời giải khác mà không phải chia trường hợp xem sao?
Cũng xuất phát từ nhận xét như trên nhưng mà khi tích
2
abcabac nằm ỏ trên tử thì
không ảnh hưởng gì cả. Do đó ta có đánh giá như sau
2
2
abac
abcabac
suy ra
2
1
2
abcabac
abac
Đến đây ta nhân cả hai vế với
2
0
ab c
abc
thì ta được
2
1
2
ab c ab c
abc
abac
.
Hay
2
2
ab c ab c
abc
abac
và công việc còn lại hoàn toàn như trên.
Ví dụ 2.9: Cho a, b, c là các số thực dương thỏa mãn
abc6
. Chứng minh rằng:
33 3
abc
2
b1 c1 a1
Phân tích: Đầu tiên ta dự đoán đẳng thức xẩy ra tại abc2, chú ý đến hằng đẳng thức
32
b1 b1bb1 và khi b2 thì
2
b1 b b1 3 do đó ta có đánh giá sau
22
32
b1b b1 b 2
b1 b1bb1
22
, từ đây ta suy ra được
2
3
a2a
b2
b1
, áp dụng tương tự ta được bất đẳng thức
22 2
33 3
abc2a2b2c
b2c2a2
b1 c1 a1
Ta cần phải chứng minh được
22 2
2a 2b 2c
2
b2c2a2
, đến đây ta đánh giá trên tử số hay
dưới mẫu đều được bất đẳng thức ngược chiều. Do đó một cách tự nhiên ta nghĩ đến tư tưởng Cauchy

ngược dấu, tức là ta biến đổi
2
22
2a ab
a
b2 b2
, chú ý đến đẳng thức xẩy ra tại
abc2
ta lại
có
3
3
2222
222
3
4
a2 b b
ab 2ab 2ab a 2b a 2.b.b
33 9
b2bb4
3b.4
Áp dụng tương tự ta được
22 2
2a b c 2ab bc ca
2a 2b 2c
abc
99
b2c2a2
Mà theo một đánh giá quen thuộc ta có
2
abc
ab bc ca 12
3
Đến lúc này ta có
22 2
2a 2b 2c 2.6 2.12
62
99
b2c2a2
. Đây chính là điều cần phải
chứng minh. Ta trình bày lại lời giải như sau.
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
2xy x y ta được
22
3
2
a a 2a 2a
b1b b1 b 2
b1
b1b b1
Áp dụng tương tự ta được bất đẳng thức
22 2
33 3
abc2a2b2c
b2c2a2
b1 c1 a1
Ta cần phải chứng minh được
22 2
2a 2b 2c
2
b2c2a2
Thật vậy, ta có
2
22
2a ab
a
b2 b2
, mà cũng theo bất đẳng thức Cauchy ta được
3
3
2222
222
3
4
a2 b b
ab 2ab 2ab a 2b a 2.b.b
33 9
b2bb4
3b.4
Suy ra
2
a2 2b
2a
a
9
b2
. Chứng minh tương tự ta được
22 2
2a b c 2ab bc ca
2a 2b 2c
abc
99
b2c2a2
Mặt khác theo một đánh giá quen thuộc ta có
2
abc
ab bc ca 12
3
Do đó ta được
22 2
2a 2b 2c 2.6 2.12
62
99
b2c2a2
.
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc2
.
Ví dụ 2.10: Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
bc ca ab 1
2
abc bca cab

Phân tích: Để ý là
abc aabc bc abac . Do đó theo bất đẳng thức
Cauchy ta được. Do đó
bc bc 1 bc bc
2a b a c
abc
abac
.
Lời giải
Sử dụng bất đẳng thức Cauchy và kết hợp giả thiết, ta có:
bc bc bc 1 bc bc
2a b a c
abc
aa b c bc a b a c
Tương tự ta được
ac 1 ac ac ab 1 ab ab
;
2b a b c 2c a c b
bac cab
Cộng vế theo vế các bất đẳng thức trên, ta được
bc ca ab 1 ab ab bc bc ca ca
2acbcabacbabc
abc bca cab
1ab bc ab ac bc ca 1 1
abc
2ac bc ab 2 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Ví dụ 2.11: Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc3. Chứng minh rằng:
222
ab bc ca 3
2
c3 a3 b3
Phân tích: Để ý là
2
abc 3abbcca nên ab bc ca 3, do đó ta được
22
c3cabbcca bcca , suy ra ta được bất đẳng thức sau
22
ab ab ab
c3 cabbcca
cacb
Cũng theo bất đẳng thức Cauchy ta lại có
ab 1 ab ab
2c a c b
cacb
.
Lời giải
Từ bất đẳng thức
2
abc 3abbcca và abc 3.
Suy ra
ab bc ca 3. Như vậy theo bất đẳng thức Cauchy ta được
22
ab ab ab 1 ab ab
2c a c b
c3 cabbcca
cacb
Tương tự ta được
22
bc 1 bc bc ca 1 ca ca
;
2a c a b 2b a b c
a3 b3
Cộng theo vế các bất đẳng thức trên ta được
222
ab bc ca a b c 3
22
c3 a3 b3
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.
Ví dụ 2.12: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:

ab bc ca a b c
a3b2cb3c2a c3a2b 6
Phân tích: Đại lượng
1
a3b2c
và chiều bất đẳng thức làm ta liên tưởng đến bất đẳng thức dạng
9111
xyz x y z
, khi đó ta được
99111
a3b2c acbc2b ac bc2b
Suy ra ta có
9ab 9ab ab ab a
a3b2c acbc2bacbc2
Áp dụng tương tự và chú ý đến tổng
ca ab ca bc bc ab
abc
cb ba ca
.
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
9111
xyz x y z
, ta được
99111
a3b2c acbc2b ac bc2b
Từ đó suy ra
9ab 9ab ab ab a
a3b2c acbc2b acbc2
. Tương tự ta chứng minh được
9bc bc bc b 9ca ca ca c
;
b3c2a ba ca 2c3a2b cb ba 2
Cộng theo vế các bất đẳng thức trên ta có
9ab 9bc 9ca ca ab ca bc bc ab a b c
a3b2cb3c2ac3a2b cb ba ca 2
3a b c
2
Hay
ab bc ca a b c
a3b2cb3c2a c3a2b 6
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 2.13: Cho a, b là các số thực dương thỏa mãn
a, b 1; a b 3 ab.Chứng minh rằng:
22
a1 b1 1 182
abab6
Phân tích và lời giải
Trước hết ta nhận thấy vai trò như nhau trong bất đẳng thức của a, b và dự đoán được dấu đẳng
thức xẩy ra tại
ab3. Từ giả thiết ab3ab , ta suy ra
11 3
1.
abab
Để đơn giản hóa ta đặt
11
x;y
ab
. Khi đó giả thiết trở thành xy3xy1 và bất đẳng
thức cần chứng minh được viết lại thành
22
xy 1 8 2
1x 1y
xy 6
Chú ý là các đại lượng
2
22
xy; x y ; x y liên hệ với nhau bởi hằng đẳng thức quen thuộc.
Do đó ta sẽ cố biểu diễn giả thiết cũng như bất đẳng thức qua một đại lượng.

Theo bất đẳng Cauchy ta được
2
3x y
1xy3xyxy
4
.Từ đó suy ra
2
xy
3
. Cũng theo bất đẳng thức quen thuộc
mn2mn
ta được
2
22 22
xy
1x 1y 22 x y 22
2
Và
1xy
xy 1 1
xy 3
3x y 3x y
Lúc này ta được
22 22
2
2
1xy
xy
1x 1y 22 x y
xy
3x y
xy
11 12 11182
22 22 .
23233.236
3x y
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
xy ab3
3
.
Ví dụ 2.14: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
abab2c
1
8
3a 3b 2c
Phân tích: Ta viết lại bất đẳng thức thành
2
1
a b a b 2c 3a 3b 2c .
8
Cách phát biểu
của bất đẳng thức làm ta liên tưởng đến bất đẳng thức
2
xy
xy
4
.
Lời giải
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
2
2
1
a b a b 2c 2a 2b a b 2c
2
2a 2b a b 2c
11
3a 3b 2c
22 8
Từ đó ta được
2
abab2c
1
8
3a 3b 2c
Đẳng thức xảy ra khi và chỉ khi
ab2c .
Ví dụ 2.15: Cho các số thực
ab0. Chứng minh rằng:
2
32
2a 5
ab2b3
Phân tích: Quan sát bất đẳng thức ta thấy có các ý tưởng sau:

+ Ý tưởng thứ nhất là sử dụng bất đẳng thức Cauchy với đánh giá từ trung bình cộng sang trung
bình nhân, ở đây để ta cần khử được đại lượng
2
ab2b3 thì ta cần phân tích được
a ka b m2b 3 m2b 3 6m, dễ dàng tìm ra được
1
k2;m
2
.
+ Ý tưởng thứ hai là đánh giá
2
ab2b3 theo đánh giá từ trung bình nhân sang trung bình
cộng, chú ý đến dấu đẳng xẩy ra ta được
33
4a 4b 2b 3 2b 3 4a 6
4a 4b 2b 3 2b 3
33
Đến đây ta chỉ cần chứng minh được
3
32
2a 5
8
2a 3
27
bằng đánh giá từ trung bình cộng
sang trung bình nhân là xong.
Lời giải
Cách 1: Biểu thức viết lại như sau
2
2b 3 2b 3 32
P2a2b 3
22
ab2b3
Áp dụng bất đẳng thức Cauchy ta có
2
2
4
2
2b 3 2b 3 32
2a 2b
22
ab2b3
2b 3 32
42a2b 8
2
ab2b3
Do đó
P5 . Đẳng thức xảy ra khi và chỉ khi
2
2b 3 32
2a 2b
2
ab2b3
hay
31
a,b
22
.
Cách 2: Áp dụng bất đẳng thức Cauchy ta được
33
3
4a 4b 2b 3 2b 3 4a 6 8
4a 4b 2b 3 2b 3 2a 3
3327
Từ đó ta có
3
3
32 2a 3 2a 3 2a 3 432
P2a 3
8 333
2a 3
2a 3
27
Cũng theo bất đẳng thức Cauchy ta được
3
2a 3 2a 3 2a 3 432
8
333
2a 3
Do đó
P5 . Đẳng thức xảy ra khi và chỉ khi
2
2b 3 32
2a 2b
2
ab2b3
hay
31
a,b
22
.

Ví dụ 2.16: Cho a, b, c là các số thực dương thỏa mãn
222
abcabc
. Chứng minh rằng:
222
abc1
2
abcbcacab
Phân tích: Trước hết ta dự đoán đẳng thức xẩy ra tại abc3. Bất đẳng thức chứa đại lượng
2
1
abc
, để ý đến chiều ta liên tưởng đến đánh giá quen thuộc
411
xy x y
, khi đó ta có
2
a11a
4a bc
abc
. Để ý tiếp ta có
22
222
aa a
bc abc
abc
. Như vậy áp dụng tương tự ta thu
được
222
abc1111
1
4a b c
abcbcacab
. Bài toán sẽ được chứng minh xong nếu ta
chỉ ra được
111
1
abc
. Chú ý tiếp đến giả thiết ta được
222
abc abbcca111
1
abc abc a b c
. Đến đây ta trình bày lại lời giải như sau
Lời giải
Áp dụng bất đẳng thức quen thuộc dạng
411
xy x y
, ta được
22
aa11
4bc
abc a
Kết hợp với giả thiết
222
abcabc ta được
22
222
aa a
bc abc
abc
Do đó
2
22 222
aa1111 a
4bc4a
abc a abc
Áp dụng tương tự ta được
222
abc1111
1
4a b c
abcbcacab
Ta cần chứng minh
111
1
abc
Thật vậy, Áp dụng một đánh giá quen thuộc và kết hợp với giả thiết, ta được
222
abc abbcca111
1
abc abc a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
Ví dụ 2.17: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
aba32
2
ab b bc c ca a
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại abc, khi đó để ý đến đánh giá
2b a b
a3b
2b. a b
22
khi đó ta được
2
a22a
a3b
ab b
. Áp dụng tương tự thì
222
aba2a22b22c2
a3b b3cc3a
ab b bc c ca a
, như vậy ta chỉ cần chỉ ra được
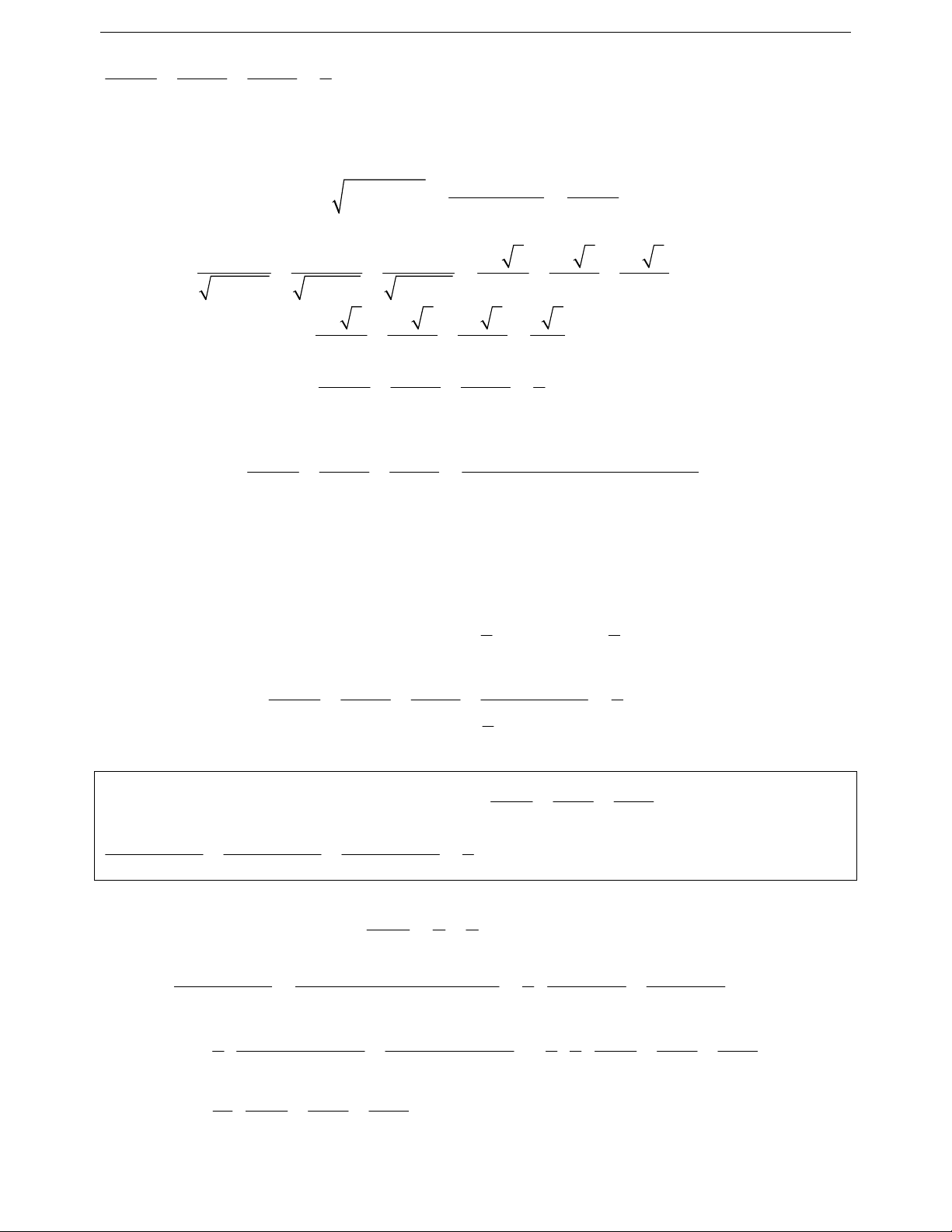
abc3
a3bb3cc3a 4
, đây là một bất đẳng thức có thể chứng minh bằng bất đẳng thức
Bunhiacopxki dạng phân thức.
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2b a b
a3b
2b. a b
22
Áp dụng tương tự ta được
222
aba2a22b22c2
a3b b3cc3a
ab b bc c ca a
.
Ta cần chứng minh
2a 2 2b 2 2c 2 3 2
a3bb3cc3a 2
Hay
abc3
a3bb3cc3a 4
.
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc
a3bb3cc3a
a b c 3ab 3bc 3ca
.
Mặt khác, từ một đánh giá quen thuộc ta có
2
abc 3abbcca
Do đó ta được
222 222
22 2
a b c 3 ab bc ca a b c 2 ab bc ca ab bc ca
14
abc abc abc
33
Từ đó suy ra
2
2
abc
abc 3
a3bb3cc3a 4 4
abc
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 2.18: Cho a, b, c là các số thực dương thỏa mãn
111
6
abbc ca
. Chứng minh rằng:
1113
3a 3b 2c 3a 2b 3c 2a 3b 3c 2
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
411
xy x y
ta được
11111
3a 3b 2c 4 2a b c a 2b c
2a b c a 2b c
11 1 11211
444abbcca
ab ca ab bc
12 1 1
16 a b b c c a
Hoàn toàn tương tự ta được

11211
3a 2b 3c 16 a c a b b c
11211
2a 3b 3c 16 b c a b c a
Cộng theo vế các bất đẳng thức trên ta được
11114443
3a 3b 2c 3a 2b 3c 2a 3b 3c 16 a b b c c a 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra tại
1
abc
4
Ví dụ 2.19: Cho a, b, c là các số thực dương thỏa mãn
13a 5b 12c 9 . Chứng minh rằng:
ab 3bc 6ca
1
2a b 2b c 2c a
Lời giải
Bất đẳng thức cần chứng minh tương đương với
11 1
1
21 2 1 1 1
b a 3c 3b 3a 6c
Áp dụng bất đẳng thức dạng
111 9
xyzxyz
, Ta có
21 111 9
ba bba 2ba
21 111 9
3c 3b 3c 3c 3b 6c 3b
11 111 9
3a 6c 6a 6a 6c 12a 6c
Do đó ta được
11 1 11 1
21 2 1 1 1 9 9 9
b a 3c 3b 3a 6c 2b a 6c 3b 12a 6c
2b a 6c 3b 12a 6c 13a 5b 12c
1
99
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
3
abc
10
.
Ví dụ 2.20: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3
. Chứng minh rằng:
143
abc 2
abbcca
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
3
ab c bc a ca b
abc a b b c c a 2
3
Từ đó suy ra
3
3
2abc4
abc
2
abbcca
abbcca
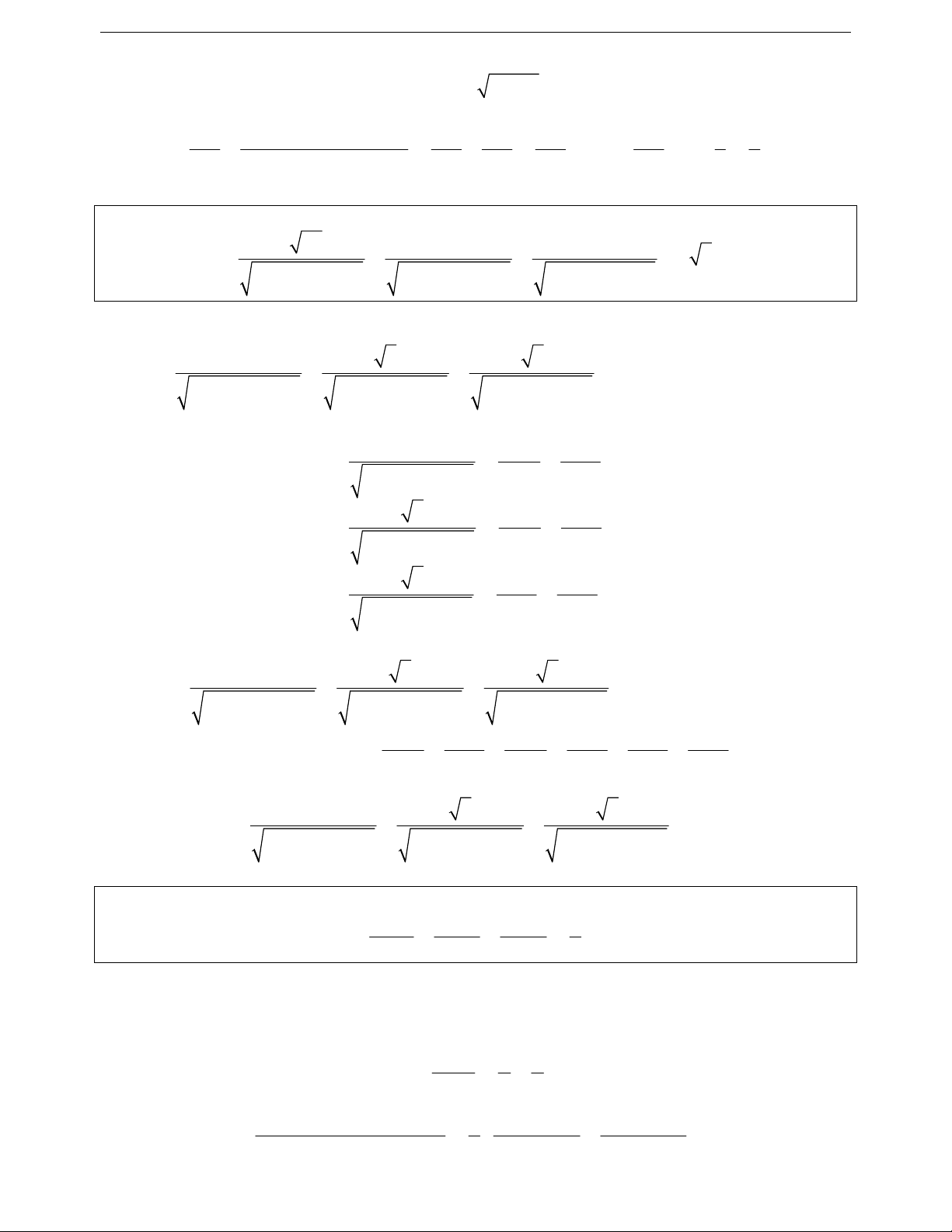
Mặt khác, cũng theo bất đẳng thức Cauchy ta được
222
3abbcca3abc abc1
.
Do đó ta được
14 1abc1abc13
abc 2
abc abc 2 abc 2 2 2
abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
Ví dụ 2.21: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
23a 6b 6c
53
abac babc cacb
Lời giải
Bất đẳng thức được viết lại là
2a 2 3b 2 3c
5
abac babc cacb
Áp dụng bất đẳng thức Cauchy ta được
2a a a
abac
abac
23b b 3b
abbc
babc
23c c 3c
acbc
cacb
Cộng theo vế các bất đẳng thức trên ta được
2a 2 3b 2 3c
abac babc cacb
aab3bc3c
5
abacabbcacbc
Do đẳng thức không xẩy ra nên ta được
2a 2 3b 2 3c
5
abac babc cacb
Vậy bất đẳng thức được chứng minh.
Ví dụ 2.22: Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
ab bc ca 3
8
1c 1a 1b
Lời giải
Từ giả thiết
abc1 ta có
2
2222
1 c a b c c a b 2ab bc ca 2ab bc 2ab ca
Mặt khác áp dụng bất đẳng thức Cauchy dạng
411
xy x y
ta được
ab 1 ab ab
4
2ab bc 2ab ca 2ab bc 2ab ca

Do đó ta có
2
ab 1 ab ab
8ab bc ab ca
1c
Áp dụng tương tự
22
bc 1 bc bc ca 1 ca ca
;
8bc ca ab bc 8ca ab bc ca
1a 1b
Cộng theo vế các bất đẳng thức trên ta được
222
ab bc ca
1c 1a 1b
1ababbcbccaca3
8abbc abca bcca abbc caab bcca 8
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 2.23: Cho các số thực dương a, b, c thỏa mãn điều kiện
3
abc
4
. Cứng minh rằng:
333
111
3
a3b b3c c3a
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
3
3
a3b2
a 3b a 3b .1.1
3
Do đó ta được
3
13
a3b2
a3b
Áp dụng tương tự ta được
33
1313
;
b3c2 c3a2
b3c c3a
Cộng theo vế các bất đẳng thức trên ta được
333
111 3 3 3
a3b2b3c2c3a2
a3b b3c c3a
Mặt khác theo bất đẳng thức Bunhiacopxki ta được
333 3.9
3
a3b2b3c2c3a2
4a b c 6
Do đó ta được
333
111
3
a3b b3c c3a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
4
.
3. Kỹ thuật ghép cặp trong bất đẳng thức Cauchy
Trong nhiều bài toán mà biểu thức ở hai vế tương đối phức tạp, việc chứng minh trực tiếp trở nên
khó khăn thì ta có thể sử dụng kỹ thuật “Ghép cặp” để bài toán trở nên đơn giản.
Ở các bài toán bất đẳng thức, thông thường chúng ta hay gặp phải hai dạng toán sau:
- Dạng 1: Chứng minh
XYZ ABC.
Ý tưởng 1: Nếu ta chứng minh được
XY2XY 2A
.
Sau đó tương tự hóa để chỉ ra
YZ2B;ZX 2C (Nhờ tính chất đối xứng của bài toán).
Cộng ba bất đẳng thức trên lại theo vế rồi rút gọn cho 2, ta có:

XYZ ABC
Ý tưởng 2: Nếu ta chứng minh được
XA2XA 2B
Sau đó tương tự hóa để chỉ ra
YZ2C;ZX 2A
(Nhờ tính chất đối xứng của bài toán).
Cộng ba bất đẳng thức trên lại theo vế rồi rút gọn cho 2, ta có ngay điều phải chứng minh.
- Dạng 2: Chứng minh XYZ
ABC với X, Y, Z 0
Ý tưởng: Nếu ta chứng minh được
2
XY A
.
Sau đó tương tự hóa để chỉ ra
22
YZ B ; ZX C(nhờ tính chất đối xứng của bài toán). Sau đó
nhân ba bất đẳng thức trên vế theo vế rồi lấy căn bậc hai, ta có
222
XYZ A B C = ABC ABC.
Chú ý một số cách ghép đối xứng:
Phép cộng:
2xyz xyyzzx
xy yzzx
xyz
222
Phép nhân:
222
xyz xy . yz .zx
x, y, z 0
xyz xy. yz. zx
Ví dụ 3.1: Cho a, b, c là ba số thực dương. Chứng minh rằng:
ab bc ca
abc
cab
Phân tích: Bài toán này có dạng XYZ ABC, trong đó
ab bc ca
X,Y,Z,Aa,Bb,Cc
cab
.
Để ý rằng hai biểu thức
ab
c
và
bc
a
là đối xứng với b (tức vai trò của a và c như nhau). Do đó sử
dụng kỹ thuật ghép cặp ta sẽ thử chứng minh
ab bc
2b
ca
.
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
ab bc ab bc
22b
ca ca
Tương tự ta có
ca ab bc ac
2a; 2c
bc ab
Cộng vế với vế của 3 bất đẳng thức trên ta được
ab bc ca
abc
cab
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.2: Cho a, b, c là các số thực dương. Chứng minh rằng:
abc b c a c a b a b c
Phân tích: Nếu
bcacababc 0 thì bất đẳng thức hiển nhiên đúng. Ta xét
trường hợp
bcacababc 0 .
Để ý rằng bất đẳng thức này có dạng
XYZ ABC , vì vậy sử dụng kỹ thuật ghép đối xứng, ta
chỉ cần chứng minh
2
babcbca .
Lời giải
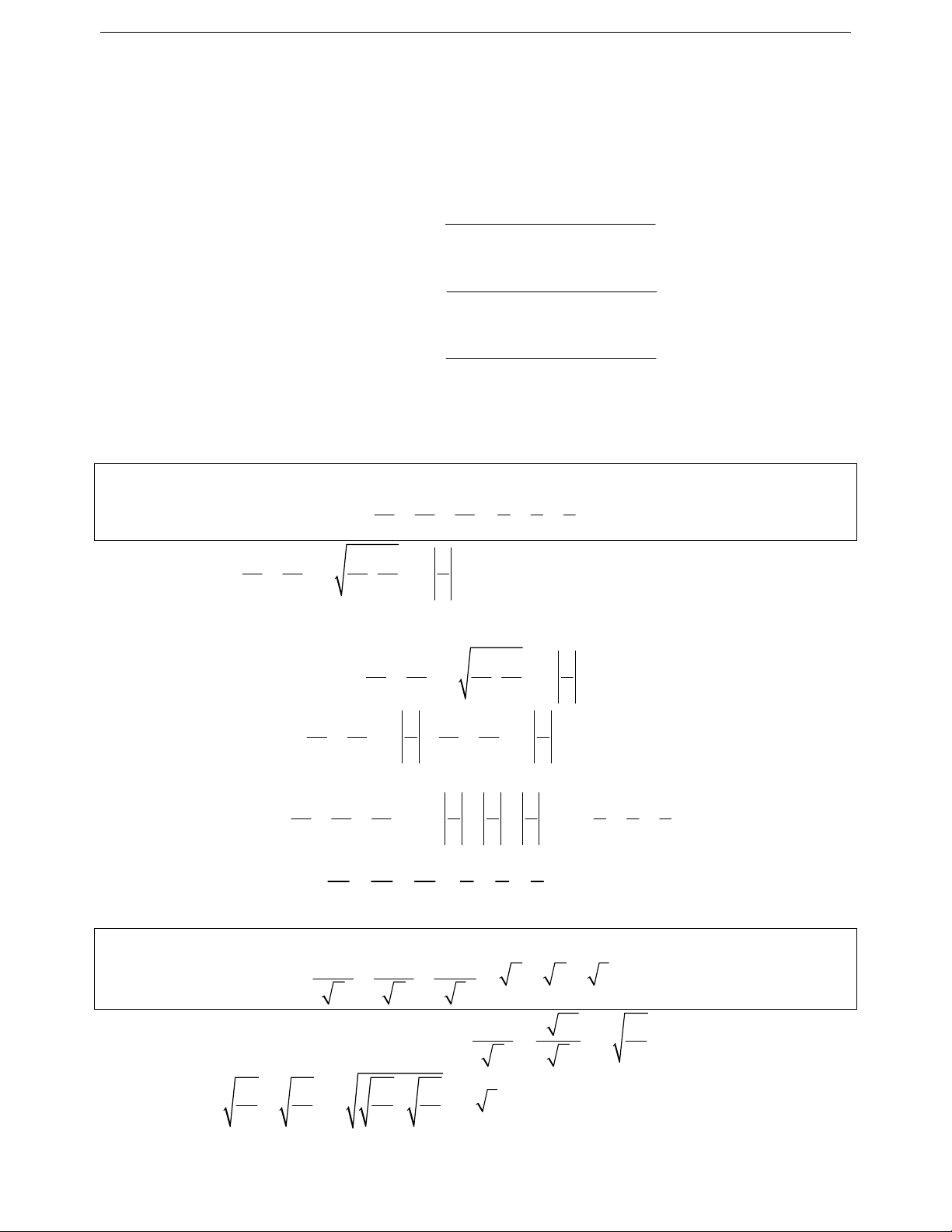
Bất đẳng thức có tính đối xứng giữa các biến, do đó không mất tính tổng quát ta giả sử
abc
, Khi
đó
abc0 và acb0 .
+ Nếu
bca 0 , bất đẳng thức hiển nhiên đúng.
+ Nếu
bca 0 . Khi này ta có bca;cab;abc là các số dương.
Sử dụng bất đẳng thức Côsi dạng
2
xy 4xy , suy ra
2
2
abc bca
abcbca b
4
2
2
bca cab
bcacab c
4
2
2
cab abc
cababc a
4
Nhân theo vế các bất đẳng thức trên ta được điều cần chứng minh.
Bài toán được giải quyết xong. Dấu bằng xảy ra khi và chỉ khi
abc.
Nhận xét: Khi chưa xác định được các số không âm mà áp dùng ngay bất đẳng thức Cauchy thì sẽ dẫn
đến sai lầm. Trong tình huống đó ta có thể chia nhỏ thành các trường hợp riêng để chứng minh bài toán.
Ví dụ 3.3: Cho a, b, c là các số thực dương. Chứng minh rằng:
222
222
abcbca
abc
bca
Phân tích: Để ý là
22 22
22 22
ab ab a
2. 2
c
bc bc
, áp dụng tương tự và cộng theo vế các bất đẳng thức
thu được.
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22 22
22 22
ab ab a
2. 2
c
bc bc
Tương tự ta được
22 2 2
22 22
bc bca c
2; 2
ab
ca ab
Cộng theo vế các bất đẳng thức trên ta được
222
22 2
abc bca bca
222
abc abc
bca
Hay
222
22 2
abcbca
abc
bca
Bài toán được giải quyết xong. Dấu bằng xảy ra khi và chỉ khi
abc.
Ví dụ 3.4: Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
bc ca ab
abc3
abc
Phân tích: Để ý là theo bất đẳng thức Cauchy ta có
bc 2bc bc
2
a
aa
và cũng theo bất đẳng thức
Cauchy ta lại có
bc ca bc ca
22c
ab ab
.
Lời giải

Áp dụng bất đẳng thức Cauchy ta có
bc 2bc bc
2
a
aa
Tương tự ta được
ca caab ab
2; 2
bc
bc
Cộng theo vế các bất đẳng thức trên ta được
bc ca ab bc ca ab
2
abc
abc
Cũng theo bất đẳng thức Cauchy ta lại có
bc ca bc ca
22c
ab ab
Áp dụng tương tự ta được
ca ab ab bc
2a; 2b
bc ca
Cộng theo vế các bất đẳng thức trên ta được
bc ca ab
abc
abc
Do đó ta suy ra
bc ca ab
2a b c
abc
Ta cần chứng minh được
2abc abc3 abc3
Đánh giá cuối cùng là một đánh giá đúng theo bất đẳng thức Cauchy và giả thiết
abc 1
Bài toán được giải quyết xong. Dấu bằng xảy ra khi và chỉ khi
abc1.
Ví dụ 3.5: Cho a, b, c là độ dài ba cạnh của một tam giác và p là nửa chu vi. Chứng minh rằng:
1
papbpc abc
8
Phân tích: Từ giả thiết ta nhận được
pa;pb;pc
là các số dương và chú đến
papb c. Do đó ta nghĩ đến đánh giá
papb c
papb
22
. Như vậy ta có
thể chứng minh bất đẳng thức như sau:
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
papbpc papb pbpc pcpa
pa pb pb pc pc pa
222
2p a b 2p b c 2p c a
1
abc
2228
Bài toán được giải quyết xong. Dấu bằng xảy ra khi và chỉ khi
abc1.
Ví dụ 3.6: Cho a, b, c là độ dài ba cạnh của một tam giác và p là nửa chu vi. Chứng minh rằng:
111 111
2
pa pb pc a b c
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
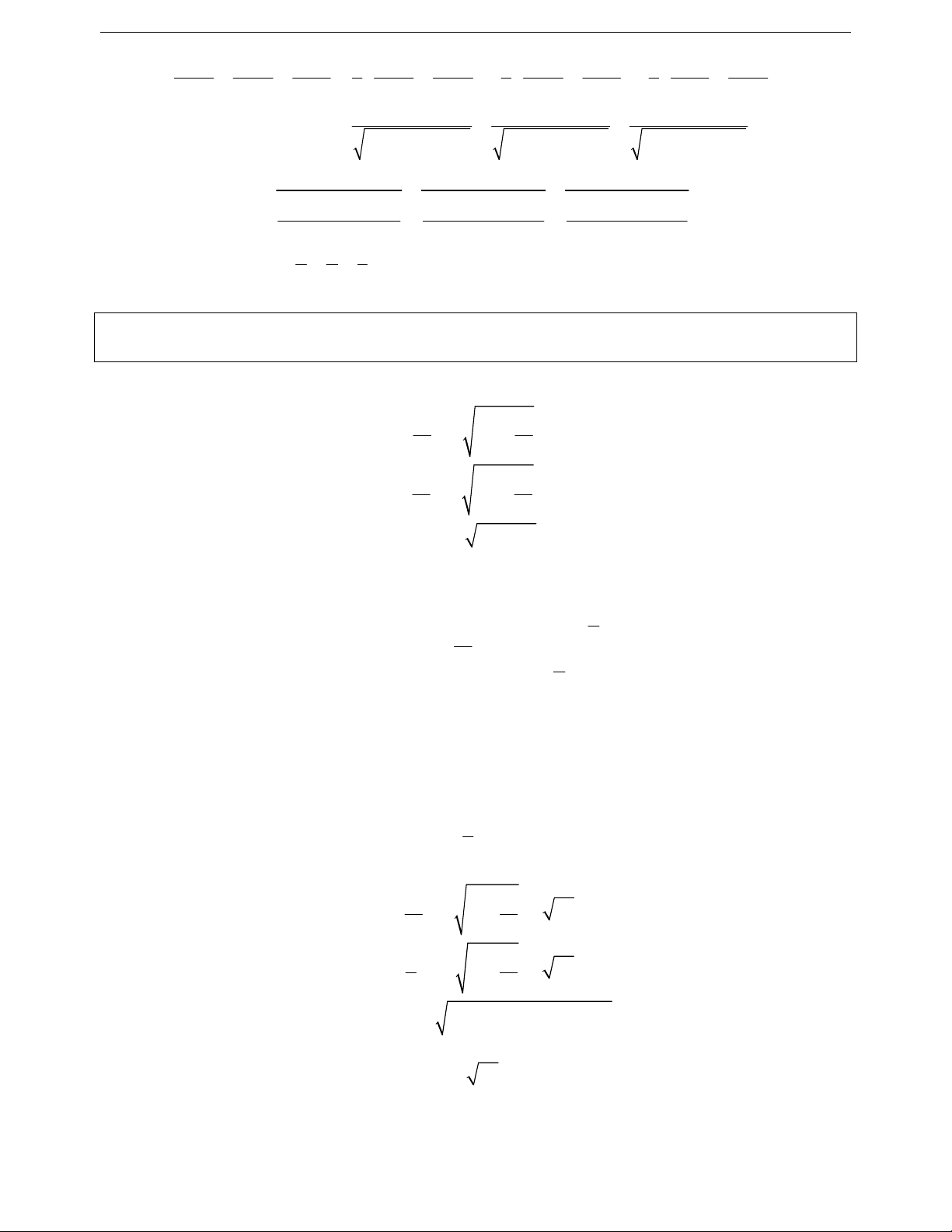
111111111111
pa pb pc 2pa pb 2pb pc 2pc pa
111
papb pbpc pcpa
111
pa pb pb pc pc pa
222
111
2
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 3.7: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1
. Chứng minh rằng:
222
10a 10b c 4
Lời giải
Áp dụng bất đẳng thức Cauchy ta có:
22
22
cc
8a 2 8a 4ac
22
22
22
cc
8b 2 8b 4bc
22
22 22
2a 2b 2 2a .2b 4ab
Cộng theo vế ba bất đẳng thức trên ta có
222
10a 10b c 4 ab bc ca 4.1 4
Đẳng thức xẩy ra khi và chỉ khi
2
22
22
ab bc ca 1
1
ab
c
3
8a 8b
4
2
c
2a 2b
3
Nhận xét: Đây là một lời giải ngắn gọn nhưng có vẻ hơi thiếu tự nhiên. Chúng ta sẽ thắc mắc tại sao lại
tách được
2810 . Nếu tách cách khác, chẳng hạn 4610 liệu có giải được không? Tất nhiên mọi
cách tách khác đều không dẫn đến kết quả, và tách
2810 cũng không phải là sự may mắn. Bây giờ ta
sẽ tìm lí do việc tách
2810
ở bài toán trên.
Từ bất đẳng thức cần chứng minh ta thấy vai trò của a, b như nhau nên ta cần chia đều c ra thành
hai phần và cũng lấy ra ka, kb để ghép cặp với
2
c
. Tức là với 010k . Áp dụng bất đẳng thức
Cauchy ta có:
22
22
2. 2
22
cc
ka ka kac
2
2
22
2. 2
22
cc
kb kb kbc
22 22
10 10 2 10 10 20 2 ka kb ka kb kab
Cộng theo vế 3 bất đẳng thức trên, ta có:
222
10 10 2 20 2 abc kacbc kab
Lúc này ta cân bằng hệ số để làm xuất hiện giả thiết, tức là:

22
8
2 20 2 2 400 80 4 2 41 200 0
25
10
2
k
kkk kkkk
k
Ta chọn giá trị
8k . Khi đó ta có lời giải bài toán như trên.
Ví dụ 3.8: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 5. Chứng minh rằng:
222
3a 3b c 10
Lời giải
Áp dụng bất đẳng thức Cauchy ta có:
22
22
cc
2a 2 2a . 2ac
22
22
22
cc
2b 2 2b . 2bc
22
22 22
ab2a.b 2ab
Cộng theo vế ba bất đẳng thức trên ta có:
222
3a 3b c 2 ab bc ca 2.5 10
Đẳng thức xẩy ra khi và chỉ khi
ab1;c2
Ví dụ 3.9: Cho a, b, c là các số thực dương thỏa mãn
ab 12, bc 8. Chứng minh rằng:
1 1 1 8 121
abc2
ab bc ca abc 12
Phân tích: Trước hết ta dự đoán được đẳng thức ra tại a3,b4,c2, Khi đó ta sẽ tách các đại
lượng bên vế trái và áp dụng bất đẳng thức Cauchy, chú ý là quá trình ghép cặp phải đảm bảo dấu đẳng
thức xẩy ra. Với phân tích đó ta thực hiện ghép cặp như sau
2ab12bc32ac
;;1
ab 18 24 2 bc 16 8 4 ca 9 6
Cộng các kết quả trên ta được
a5b7c 2 2 2 9
64824abbcca 4
, khi này ta cần phải chứng
minh được
5a 43b 17c 8 47
64824abc6
. Để ý là nếu bây giờ ta ghép cặp bốn đại lượng trên thì sẽ
không bảo toàn dấu đẳng thức. Cho nên ta sẽ ghép cặp để triệt tiêu đại lượng
8
abc
trước, do đó ta có
đánh giá
8abc4
abc 9 12 6 3
. Cuối cùng bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được chỉ ra
được
13a 13b 13c 13
18 16 24 2
.
Thực hiện ghép cặp tương tự như các ví dụ trên ta có các đánh giá sau
13a 13b 13 13c 13b 13
;
18 24 3 24 48 6
, cộng theo vế hai đánh giá đó ta được điều phải chứng minh.
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2ab12bc32ac
;;1
ab 18 24 2 bc 16 8 4 ca 9 6
8 a b c 4 13a 13b 13 13c 13b 13
;;
abc 9 12 6 3 18 24 3 24 48 6

Cộng từng vế các bất đẳng thức trên ta được
1 1 1 8 1 3 4 13 13 121
abc2 1
ab bc ca abc 2 4 3 3 6 12
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
a 3, b 4, c 2
.
Ví dụ 3.10: Cho a, b, c là các số thực dương. Chứng minh rằng:
3
2a b c
abc
111 2
bca
abc
Phân tích: Trước hết ta viết lại bất đẳng thức cần chứng minh thành
3
2a b c
abcbca
bcaabc
abc
Để ý bên vế phải ta viết được thành
3333
abc a b c
abc abc abc abc
. Do đó ta nghĩ đến bất
đẳng thức Cauchy với các nhóm
aaa bbb ccc
,,;,,;,,
bca abc abc
Lúc này ta được
3
3a b c
abcbca
3
bcaabc
abc
. Phép chứng minh sẽ hoàn tất nếu
ta chỉ ra được
33
3a b c 2a b c
3
abc abc
hay
3
abc
3
abc
. Rõ ràng đánh giá cuối cùng luôn
đúng theo bất đẳng thức Cauchy.
Lời giải
Biến đổi tương đương bất đẳng thức ta được
33
2a b c 2a b c
abc abcbca
111 2
bca bcaabc
abc abc
Sử dụng bất đẳng thức Cauchy, ta được
333
aaa 3a bbb 3b ccc 3c
;;
bca abc abc
abc abc abc
Cộng theo vế các bất đẳng thức trên ta được
3
3a b c
abcbca
3
bcaabc
abc
Mặt khác, cũng theo bất đẳng thức Cauchy ta lại có
3
abc3abc
hay
3
abc
3
abc
Suy ra
33
3a b c 2a b c
abcbca
33
bcaabc
abc abc
Hay
3
2a b c
abcbca
bcaabc
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 3.11: Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:

3
222
abc 10
abc
cab
9a b c
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại
1
abc
3
. Theo một đánh giá quen thuộc ta
nhận thấy
2
222
10 10 10
3
9a b c
3a b c
. Như vậy ta chỉ cần chứng minh
3
abc 10
abc
cab 3
. Để chứng minh được bất đẳng thức đó thì ta cần triệt tiêu được
3
abc , điều
này có nghĩa là ta cần có một đánh giá kiểu
3
3
k
abc 2 k
abc
, chú ý đến đẳng thức xẩy ra ta chọn
được
8
k
9
. Tuy nhiên để làm xuất hiện
3
8
9abc
thì ta cần chứng minh được
3
abc 1
cab
abc
.
Để ý rằng
3
2
33
aac 3a 3a
ccb
bc abc
, áp dụng ghép cặp tương tự ta được
33
abc abc 1
cab
abc abc
. Đến đây ta trình bày lại lời giải như sau
Lời giải
Theo bất đẳng thức Cauchy ta có
3
2
33
aac 3a 3a
ccb
bc abc
Áp dụng tương tự ta được
33
bbc 3b cca 3c
;
aab bbc
abc abc
Cộng vế theo vế ba bất đẳng thức trên ta có
33
abc abc 1
cab
abc abc
Do đó ta được bất đẳng thức
33
3
abc 1
abc abc
cab
abc
Ta cần chứng minh
3
222
3
110
abc
9a b c
abc
Thật vậy, theo bất đẳng thức Cauchy ta được
3
3
12
abc
3
9abc
Mà
abc1
, suy ra
3
1
abc
3
nên
3
88
3
9abc
Do đó
33
333
1182810
abc abc
33 3
abc 9 abc 9 abc
Mặt khác, theo một đánh giá quen thuộc ta có
2
222
10 10 10
3
9a b c
3a b c
Từ đó ta được
3
222
3
110
abc
9a b c
abc

Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Ví dụ 3.12: Cho a, b, c là các số thực không âm thỏa mãn
ab bc ca 0
. Chứng minh rằng:
222
a1 b1 c1
3
bc ca ab
Phân tích: Quan sát bất đẳng thức cần chứng minh ta để ý đến đánh giá
2
a12a , khi đó ta được bất
đẳng thức
222
a 1 b 1 c 1 2a 2b 2c
bc ca ab bc ca ab
Như vậy ta cần phải chứng minh
2a 2b 2c
3
bc ca ab
, đây là một bất đẳng thức nhìn
hình thức thì đẹp nhưng đáng tiếc nó lại không đúng, ta có thể kiểm tra với
ab;c0
. Như vậy đánh
giá trên không hiệu quả.
Để ý ta thấy vế phải là hằng số 3, do đó nếu ta áp dụng bất đẳng thức Cauchy cho ba số vế trái thì
khi đó ta được
222
3
a1b1c1
3
bccaab
và như vậy ta chỉ cần chỉ ra đại lượng dưới dấu căn lớn
hơn hoặc bằng 1 là được. Điều này có nghĩa là ta cần chứng minh được
222
a1b1c1 bccaab
Chú ý đến tính đối xứng trong bất đẳng thức trên ta nghĩ đến đánh giá
2
22
a1b1 ab
Đây là một đánh giá đúng theo bất đẳng thức Cauchy hoặc Bunhiacopxki.
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222
222
3
a1b1c1
a1 b1 c1
3
bc ca ab
bccaab
Như vậy ta cần chứng minh được
222
a1b1c1
1
bccaab
Hay
222
a1b1c1 bccaab
Thật vậy, ta có
2
2 2 2222 22 22
a 1 b 1 a b ab a b 1 a b 2ab ab 1 2ab
Đánh giá cuối cùng là một đánh giá đúng theo bất đẳng thức Cauchy
Áp dụng tươg tự ta được
22
22 22
b1c1 bc;a1c1 ac
Nhân theo vế ba bất đẳng thức trên ta được
222
a1b1c1 bccaab
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 3.13: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:

ab bc ca
3
cab abc bca
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
3
abbcca
ab bc ca
3
cab abc bca
cababcbca
Ta cần chứng minh
abbcca
1
cababcbca
Hay
abbcca cababcbca
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
6
222
abc3
a1 b1 c1 64
3
Và
222
4 c ab a bc c ab a bc b 1 a c
Tương tự ta được
222 222222
222
64 c ab a bc b ca a 1 b 1 c 1 a b b c c a
64 a b b c c a
Hay
abbcca aababcbca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1.
Ví dụ 3.14: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 22 22
222
a2b b2c c2a
3
aabbc bbcca ccaab
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
22 22 22
222
222222
3
222
a2b b2c c2a
aabbc bbcca ccaab
a2bb2cc2a
3
aabbcbbccaccaab
Ta cần chứng minh
222222
222
a2bb2cc2a
1
aabbcbbccaccaab
Hay
222222 2 2 2
a 2b b 2c c 2a a ab bc b bc ca c ca ab
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki ta được
2
2 22 2 222222 2
2
222 2 222222 2
2
2222 222222 2
a2bb2c a bbbcc bbcac
b2cc2a bcccaa ccaab
c2aa2b caaabb aabbc
Nhân theo vế các bất đẳng thức trên ta được bất đẳng thức cần chứng minh

Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc.
Ví dụ 3.15: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
2
222222 222222
abbccaabc 8abbcca
Lời giải
Đặt
222
xa;yb;zc. Khi đó bất đẳng thức cần chứng minh trở thành
2
2
xyyzzx x y z 8xyyzzx
Áp dụng bất đẳng thức Cauchy ta được
4xy
xy2xy 2xy
xy
Áp dụng tương tự được
4xy 4yz 4zx
2xy 2yz 2zx
xy yzzx
Do đó ta được
2
4xy 4yz 4zx
xyz xyz
xy yzzx
Như vậy ta được
2
xyyzzx x y z
4xy 4yz 4zx
xyyzzx xyz
xy yzzx
Ta cần chứng minh
2
4xy 4yz 4zx
xyyzzx xyz 8xyyzzx
xy yzzx
Hay
2
4xy 4yz 4zx
xyyzzx xyz 8xyyzzx 0
xy yzzx
Hay
222
xy x y yz y z zx z x 0 , bất đẳng thức cuối cùng đúng.
Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 3.16: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333 2 2 2
1a 1b 1c 1ab 1bc 1ca
Phân tích: Quan sát đại lượng
333
1a 1b 1c ta liên tưởng đến bất đẳng thức đã được chứng
minh
3
333
1x 1y 1z 1xyz, tuy nhiên để ý các đại lượng bên vế phải thì ta áp dụng
bất đẳng thức trên kiểu như
3
333 2
1a 1b 1b 1ab.
Lời giải
Trước hết ta chứng minh bất đẳng thức sau: Với mọi số thực dương x, y, z ta có
3
333
1x 1y 1z 1xyz
Thật vậy, bất đẳng thức tương đương với
333333333333 222333
1 x y z xy yz zx xyz 1 3xyz 3xyz xyz
Hay
333333333 222
xyzxyyzzx 3xyz3xyz
Áp dụng bất đẳng thức Cauchy ta được

333 333333 222
xyz3xyz;xyyzzx3xyz
Cộng theo vế các bất đẳng thức trên ta được
333333333 222
xyzxyyzzx 3xyz3xyz
Vậy bất đẳng thức trên được chứng minh. Áp dụng bất đẳng thức trên ta được
3
333 2
3
333 2
3
333 2
1a 1b 1b 1ab
1b 1c 1c 1bc
1c 1a 1a 1ca
Nhân từng vế của ba bất đẳng thức trên ta được
333 2 2 2
1a 1b 1c 1ab 1bc 1ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
.
Ví dụ 3.17: Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
333
333
abc bca cab a b c
Phân tích: Để ý ta thấy
abc bca 2b
, như vậy nếu ta chứng minh được đánh giá
3
33
abc bca kabc bca
thì bài toán có cơ hội được chứng minh.
Chú ý đến đẳng thức xẩy ra tại
abc
ta chọn được
1
k
4
. Để áp dụng cho các trường hợp khác ta
quy về chứng minh bổ đề:
Với mọi
x; y 0 ta có
3
33
xy
xy
4
.
Đây là một bất đẳng thức đúng và được chứng minh bằng phép biến đổi tương đương đồng thời
sử dụng bất đẳng thức Cauchy.
Lời giải
Bổ đề: Với mọi x, y > 0, ta có
3
33
xy
xy
4
Chứng minh: Do
33 2 2
xy xyxxyy
nên bổ đề trên tương đương với
2
22
xy
xxyy
4
Sử dụng bất đẳng thức Cauchy hai số dạng
2
xy
xy
4
, ta được
22
22
22
xy xy
xxyy xy 3xy xy 3
44
Bổ đề được chứng minh.
Để ý rằng a, b, c là ba cạnh của tam giác thì hiển nhiên ta có:
abc 0, bca 0, cab0
Áp dụng bổ đề, ta có:

3
33
3
3
33
3
3
33
3
abc bca
abc bca 2b
4
bca cab
bca cab 2c
4
cab abc
cab abc 2a
4
Cộng ba bất đẳng thức trên lại vế theo ta được
333
333
abc bca cab a b c
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.18: Cho các số thực
a, b, c 2 thỏa mãn
111
1
abc
. Chứng minh rằng :
a2b2c2 1
Lời giải
Đặt
a x 2, b y 2, c z 2
với
x, y, z 0
. Ta có:
Khi đó giả thiết được viết lại thành
111
1
x2 y2 z2
và bất đẳng thức cần chứng minh
được viết lại thành
xyz 1 .
Biến đổi giả thiết áp dụng bất đẳng thức Cauchy ta được
1111111
1
z2 x2 y2 2 x2 2 y2
xy xy
2x 2 2y 2 x 2 y 2
Tương tự ta được
1zx1yz
;
y2 x2
z2x2 y2z2
Nhân ba bất đẳng thức trên theo vế, ta được
1 xyz
xyz 1
x2y2z2 x2y2z2
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc3.
Ví dụ 3.19: Cho a, b, c các số thực dương bất kì. Chứng minh rằng :
111111
a2bcb2ca c2ab a3bb3cc3a
Phân tích: Bất đẳng thức làm ta liên tưởng đến đánh giá quen thuộc
11 4
xy xy
. Để ý là
a3b b2ca 2a2bc nên rất tự nhiên ta nghĩ đến đánh giá
11 4 2
a 3b b 2c a a 2b c
a3b b2ca
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
11 4
xy xy
ta có

11 4 2
a 3b b 2c a a 2b c
a3b b2ca
11 4 2
b3c c2ab b2ca
b3c c2ab
11 4 2
c3a a2bc c2ab
c3a a2bc
Cộng vế với vế các bất đẳng thức trên và rút gọn ta được
111111
a2bcb2ca c2ab a3bb3cc3a
Đẳng thức xảy ra khi và chỉ khi
a3b b2ca
b3c c2ab a b c
c3a a2bc
4. Kỹ thuật thêm bớt
Nếu ở các kỹ thuật trên, ta được rèn luyện thói quen định hướng dựa vào bề ngoài của một bài toán.
Thì từ đây ta bắt đầu gặp những lớp bất đẳng thức phong phú hơn – những bất đẳng thức mà lời giải cho
chúng luôn đòi hỏi một tầm nhìn bao quát cũng như sự đột phá ý tưởng. Kỹ thuật thêm bớt là một minh
chứng rõ ràng nhất cho lối tư duy sử dụng những “yếu tố bên ngoài” trong việc giải quyết vấn đề.
Ngay từ đây chúng ta sẽ bắt đầu làm quen với kỹ thuật này với những ví dụ mà cách đánh giá nó
tương đối đa dạng.
Ví dụ 4.1: Cho a, b, c là các số thực dương. Chứng minh rằng:
222
abc
abc
bca
Phân tích: Bất đẳng thức trên đã được chứng minh bằng phép biến đổi tương đương và cũng có thể
chứng minh bằng cách sử dụng bất đẳng thức Bunhiacopxki dạng phân thức. Tuy nhiên bây giờ ta sẽ áp
dụng ngay bất đẳng thức Cauchy để chứng minh bài toán. Dễ dàng nhận ra không thể sử dụng trực tiếp
bất đẳng thức Cauchy cũng không thể sử dụng kĩ thuật ghép đối xứng để giải quyết bài toán. Ta dự đoán
đẳng thức xẩy ra tại
abc. Bên vế trái xuất hiện các đại lượng
222
abc
;;
bca
và bên vế phải có đại
lượng
abc, chú ý đến dấu đẳng thức xẩy ra ta nghĩ đến sử dụng bất đẳng thức Cauchy cho các cặp
sau
222
abc
,b ; ,c ; ,a
bca
Để sử dụng bất đẳng thức Cauchy cho các cặp trên, trước hết ta cần phải thêm vào vế trái một tổng
abc rồi mới tiến hành ghép theo cặp.
Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương ta có
222
abc
b 2a; c 2b; a 2c
bca
Cộng theo vế ba bất đẳng thức trên ta được
222 222
abc abc
bca2a2b2c abc
bca bca
Bài toán được chứng minh xong. Dấu đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 4.2: Cho a, b, c là các số thực dương. Chứng minh rằng:

222
abcabc
bc ac ba 2
Phân tích: Áp dụng ý tưởng như trên, tuy nhiên ở đây ta cần triệt tiêu
bc
ở dưới mẫu nên ta thêm cho
2
a
bc
một số
bc
k
và chú ý đến dấu đẳng thức xẩy ra tại
abc
nên ta tìm được
k4
. Do đó ta
có lời giải như sau.
Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương ta có
222
abc bca cab
a; b; c
bc 4 ca 4 ab 4
Cộng theo vế các bất đẳng thức trên ta được
222
abcbcacab
abc
bc 4 ca 4 ab 4
Suy ra
222
abcabc
bc ca ab 2
Bài toán được chứng minh xong. Dấu đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 4.3: Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
333
abc3
4
1b1c 1c1a 1a1b
Phân tích: Quan sát bất đẳng thức ta nhận thấy có thể chứng minh được bài toán theo ý tưởng như trên,
nhưng ta cần trả lời được các câu hỏi đặt ra là
- Áp dụng bất đẳng thức Cauchy cho mấy số?
- Các đại lượng được thêm vào có dạng như thế nào?
Để ý đến đại lượng
3
a
1b1c
ta thấy nên áp dụng bất đẳng thức cho ba số, khi đó đại lượng
thêm vào cần triệt tiêu được tích
b1c1
ở dưới mẫu, do đó ta nghĩ đến các đại lượng kiểu
b1c1
;
kk
với k là một số dương nào đó. Chú ý đến dấu đẳng thức xẩy ra tại abc1, khi đó
3
ab1c1
kk
1b1c
sẽ cho ta k4 . Vì vậy ta có chứng minh sau
Lời giải
Áp dụng bất đẳng thức Cauchy ta có:
33
3
a 1b 1c a 1b1c 3
3a
88 884
1b1c 1b1c
Áp dụng tương tự ta được
3 3
b1c1a3c1a1b3
b; c
884 884
1c1a 1a1b
Cộng theo vế các bất đẳng thức ta được
333
abc133
abc abc
444
1b1c 1c1a 1a1b

Hay
333
abc13
abc
24
1b1c 1c1a 1a1b
Áp dụng bất đẳng thức Cauchy kết hợp với giả thiết
abc 1 , ta lại có
3
13333
abc abc
24244
Suy ra
333
abc3
4
1b1c 1c1a 1a1b
Bài toán được chứng minh xong. Dấu đẳng thức xẩy ra khi và chỉ khi
abc1
.
Ví dụ 4.4: Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
333
abc
1
bc 2 ca 2 ab 2
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại abc1, khi đó ta chú ý đến đánh giá sau
3
abc2
a
39
bc 2
và áp dụng tương tự.
Lời giải
Áp dụng bất đẳng thức Cauchy cho ba số dương ta được
333
abc2 bca2 cab2
a; b; c
39 39 39
bc 2 ca 2 ab 2
Cộng theo vế các bất đẳng thức trên ta được
333
333
abcabcabc6
abc
39
bc 2 ca 2 ab 2
5a b c
abc 2
93
bc 2 ca 2 ab 2
Mặt khác theo bất đẳng thức Cauchy ta có
3
abc3abc 3
. Do đó
333
abc5.32
1
93
bc 2 ca 2 ab 2
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 4.5: Cho a, b, c độ dài ba cạnh của một tam giác thỏa mãn
abc3. Chứng minh rằng:
333
abc cab bca
1
3c 3b 3a
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1
, khi đó ta chú ý đến đánh giá sau
33
abc abc
c1 c1
3abc
3c 3 3 3c 3 3
và áp dụng tương tự.
Lời giải
Áp dụng bất đẳng thức Cauchy cho ba số dương ta được

3
3
3
abc
c1
abc
3c 3 3
cab
b1
cab
3b 3 3
bca
a1
bca
3a 3 3
Cộng theo vế ba bất đẳng thức trên ta được
333
abc cab bca
abc
abc 11
3c 3b 3a 3
Vậy bài toán được chứng minh xong.
Ví dụ 4.6: Cho a, b, c là các số thực dương. Chứng minh rằng
22 2
333
bc ca ab 1 1 1 1
2a b c
abc bca cab
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại abc, khi đó ta chú ý đến đánh giá
22
3
33
bc b c 1 bc b c 1 3
3
4bc 2b 4bc 2b 2a
abc abc
và áp dụng tương tự.
Lời giải
Áp dụng bất đẳng thức Cauchy cho ba số dương
22
3
33
bc b c 1 bc b c 1 3
3
4bc 2b 4bc 2b 2a
abc abc
Từ đó suy ta
2
3
bc 3 b c 1 3 3 1
2a 4bc 2b 2a 4b 4c
abc
Tương tự ta có
22
33
ca 331 ab 331
;
2b 4c 4a 2c 4a 4b
bca cab
Cộng theo vế ba bất đẳng thức trên ta được
22 2
333
bc ca ab 331111 1111
244abc 2abc
abc bca cab
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Ví dụ 4.7: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
332
abcb
a
bc 2
bc a ca b
Phân tích: Bất đẳng thức cần chứng minh có hình thức khác so với các ví dụ trên, tuy nhiên đẳng thức
vẫn xẩy ra tại
abc. Để ý hai đại lượng đầu ta sử dụng cách thêm – bớt như các ví dụ trên thì được
33
abca3bcab3
a; b
242 24 2
bc a ca b
khi đó ta được
3322
a b c c 3b 3c
a
bc bc 4 4
bc a ca b
và ta cần phải chứng minh được
2
c3b3cb
aa
bc 4 4 2
hay
2
cbc
c
bc 4
, đánh giá cuối cùng luôn đúng theo bất đẳng
thức Cauchy.

Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương ta được
332
abca3bcab3cbc
a; b; c
242 24 2bc4
bc a ca b
Cộng theo vế các bất đẳng thức trên ta được
332
332
abca 33
bc a bc
bc 2 2 2
bc a ca b
abcb
a
bc 2
bc a ca b
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Ví dụ 4.8: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222222
abc
aabb bbcc ccaa
bca
Phân tích: Dự đoán đẳng thức xẩy ra tại abc, quan sát bất đẳng thức ta nhân thấy bên trái có đại
lượng
2
a
b
và vế phải lại chứa
22
aabb
, do đó để sử dụng bất đẳng thức Cauchy dạng
xy2xy ta cần làm xuất hiện đại lượng
22
aabb, do đó ta để ý đến phép biến đổi
22 2 2
aa aabb
abab ab
bb b
, lúc này chú ý đến dấu đẳng thức xẩy ra ta có đánh
giá
22
22
aabb
b2a abb
b
. Áp dụng hoàn toàn tương tự ta được
222
222222
abc
abc2a abb 2b bcc 2c caa
bca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được một trong hai khả năng sau
222 222
abc abc
2abc
bca bca
222222
aabb bbcc ccaa abc
Để ý ta nhận thấy
222
abc
abc
bca
do đó khả năng thứ nhất luôn đúng. Như vậy bài toán được
chứng minh.
Lời giải
Ta có
22 2 2
aa aabb
abab ab
bb b
, tương tự ta được
222 2 22 22 2
abcaabbbbccccaa
bca b c a
Theo bất đẳng thức Cauchy ta được
22
22
22
22
22
22
aabb
b2a abb
b
bbcc
c2b bcc
c
ccaa
a2c caa
a

Suy ra
222
222222
abc
abc2a abb 2b bcc 2c caa
bca
Ta cần chứng minh được
222 222
abc abc
2abc
bca bca
Hay
222
abc
abc
bca
Bất đẳng thức cuối cũng chính là bất đẳng thức trong ví dụ 1.
Vậy bài toán được chứng minh xong.
Nhận xét: Từ những ví dụ trên ta đã thấy được sự hiệu quả của kỹ thuật thêm - bớt trong chứng minh bất
đẳng thức. Tuy nhiên không phải với bất đẳng thức nào cũng có thể làm được theo cách như trên, mà đôi
khi ta cần phải thực hiện việc biến đổi tương bất đẳng thức trước rồi mới thực hiện thêm bớt. Dưới đây là
m
ột số ví dụ như vậy.
Ví dụ 4.9: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abc abc
bc ca ab ab bcac
Phân tích: Nhận thấy ta chưa thể sử dụng bất đẳng thức Cauchy để đánh giá ngay bất đẳng thức trên, do
đó ta cần biến đổi bất đẳng thức thành
ab bc ca
0
bc ca ab
, đến đây ta cũng chưa thể áp dụng
được bất đẳng thức Cauchy. Bây giờ ta cần tìm cách loại đi các dấu trừ mới có thể áp dụng được, để ý đến
ab ca
1
bc bc
lúc này ta có thể áp dụng được bất đẳng thức Cauchy.
Lời giải
Bất đẳng thức cần chứng minh có thể viết lại thành
ab bc ca
0
bc ca ab
Để ý rằng
ab ca bc ab ca bc
1, 1, 1
bc bc ca ca ab ab
Vậy sau khi thêm bớt như vậy, ta đã quy bài toán về chứng minh.
ab ca bc
3
ca bc ab
Mặt khác bất đẳng thức này hiển nhiên đúng vì
3
ab ca bc abcabc
3.. 3
ca bc ab cabcab
Phép chứng minh hoàn tất. Dấu đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 4.10: Cho a, b, c là các số dương thỏa mãn
abc3. Chứng minh rằng :
abcabbcca
Lời giải
Sử dụng kỹ thuật thêm bớt ta có bất đẳng thức tương đương với
222 222
2
222
2a b c 2abbcca
abc 2a b c abc 2abbcca
abc 2a b c abc 9
Vậy ta cần chứng minh:
222
abc2a b c 9
Hay là
222
aaabbbccc9

Điều này hiển nhiên đúng vì theo bất đẳng thức Cauchy bộ ba số ta có
3
22
3
22
3
22
aaa3a.a.a3a
bbb3b.b.b3b
ccc3c.c.c3c
Bài toán được giải quyết. Bất đẳng thức xảy ra khi và chỉ khi
abc1
Ví dụ 4.11: Cho a, b, c là các số dương thỏa mãn
abc3. Chứng minh rằng :
222
abc3
2
abcbcacab
Phân tích: Dấu đẳng thức xẩy ra tại abc1. Quan sát bất đẳng thức thì điều đầu tiên là sử dụng
bất đẳng thức Bunhiacopxki dạng phân thức. Tuy nhiên ta xem có thể sử dụng bất đẳng thức Cauchy
được không? Nhận thấy dưới các mẫu có chứa căn bậc hai và ta tìm cách khử căn trước.
Chú ý đến chiều bất đẳng thức ta có đánh giá
2bc b c, khi đó ta được
22
a2a
2a b c
abc
, hoàn toàn tương tự ta được bất đẳng thức
222 2 2 2
abc 2a 2b 2c
2a b c 2b c a 2c a b
abcbcacab
Ta cần chỉ ra được
222
2a 2b 2c 3
2a b c 2b c a 2c a b 2
Để ý đến đánh giá
2
2a 2a b c
a
2a b c 8
, áp dụng tương tự ta được bất đẳng thức
222
2a 2b 2c a b c 3
2a b c 2b c a 2c a b 2 2
Đến đấy bài toán được chứng minh xong.
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
2bc b c suy ra
22
a2a
2a b c
abc
.
Áp dụng tương tự ta được bất đẳng thức
222 2 2 2
abc 2a 2b 2c
2a b c 2b c a 2c a b
abcbcacab
Ta cần chứng minh được
222
2a 2b 2c 3
2a b c 2b c a 2c a b 2
, thật vậy
Áp dụng bất đẳng thức Cauchy ta lại có
222
2a 2a b c 2b 2b c a 2c 2c a b
a; b; c
2abc 8 2bca 8 2cab 8
Cộng theo vế các bất đẳng thức trên ta được
222
2a 2b 2c a b c 3
2a b c 2b c a 2c a b 2 2
Vậy bất đẳng thức được chứng minh xong.
Ví dụ 4.12: Cho a, b, c là các số dương thỏa mãn
abc3. Chứng minh rằng :
333
abc3
2
abcbcacab
Lời giải

Áp dụng bất đẳng thức Cauchy ta được
2bc b c suy ra
33
a2a
2a b c
abc
.
Áp dụng tương tự ta được bất đẳng thức
333 3 3 3
abc 2a 2b 2c
2a b c 2b c a 2c a b
abcbcacab
Ta cần chứng minh được
333
2a 2b 2c 3
2a b c 2b c a 2c a b 2
, thật vậy
Áp dụng bất đẳng thức Cauchy ta lại có
3
2
3
2
3
2
a2a b c
2a
a
2a b c 8
b2b c a
2b
b
2b c a 8
c2c a b
2c
c
2c a b 8
Cộng theo vế các bất đẳng thức trên ta được
333222
222
2a 2b 2c a b c ab bc ca
abc
2a b c 2b c a 2c a b 4
Hay
222
333
3a b c ab bc ca
2a 2b 2c
2a b c 2b c a 2c a b 4
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
3a b c ab bc ca
3
42
Thật vậy, từ giả thiết ta có
222
abc3 và
222
abcabbcca
Do đó suy ra
222 222
3abc abbcca 2abc
3
442
Vậy bất đẳng thức được chứng minh xong.
Ví dụ 4.13: Cho a, b, c là các số dương thỏa mãn
abc3. Chứng minh rằng :
aa 2b c bb 2c a cc 2a b
0
ab 1 bc 1 ca 1
Phân tích: Để áp dụng bất đẳng thức Cauchy ta cần phải biến đổi bất đẳng thức trên sao cho vế phải là
một số khác không, điều này làm ta nghĩ đến cộng vào hai vế của bất đẳng thức với một số dương nào
đó?
Để ý ta thấy
aa 2b c a3 3b
3a 3ab
ab 1 ab 1 ab 1
, khi đó để làm mất dấu từ ta cộng thêm 3
thì được
3a 3ab 3a 3
3
ab 1 ab 1
, thực hiện tương tự ta được bất đẳng thức
a1 b1 c1
3
ab 1 bc 1 ca 1
. Đến đây ta áp dùng bất đẳng thức Cauchy thì được
3
a1b1c1
a1 b1 c1
3
ab 1 bc 1 ca 1
ab 1 bc 1 ca 1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a1b1c1 ab1bc1ca1

Đến đây ta biến đổi tương đương đổi tương đương thì được
222
a1b1c1 ab1bc1ca1
abc a b c 1 a b c abc a b c 1
abc 1 abc a b c 1 abc 0
Bất đẳng thức cuối cùng luôn đúng do
abc 1 . Đến đây ta trình bày lại lời giải như sau
Lời giải
Để ý ta thấy
aa 2b c a3 3b
3a 3ab
ab 1 ab 1 ab 1
, áp dụng tương tự ta được bất đẳng thức cần
chứng minh là
3a 3ab 3b 3bc 3c 3ca
0
ab 1 bc 1 ca 1
Bất đẳng thức trên tương đương với
3a 3ab 3b 3bc 3c 3ca
3339
ab 1 bc 1 ca 1
Hay
a1 b1 c1
3
ab 1 bc 1 ca 1
Áp dụng bất đẳng thức Cauchy ta được
3
a1b1c1
a1 b1 c1
3
ab 1 bc 1 ca 1
ab 1 bc 1 ca 1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a1b1c1 ab1bc1ca1
Đến đây ta biến đổi tương đương đổi tương đương thì được
222
a1b1c1 ab1bc1ca1
abc a b c 1 a b c abc a b c 1
abc 1 abc a b c 1 abc 0
Theo bất đẳng thức Cauchy ta có
3
3abc3abc suy ra abc 1
Do vậy bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh xong.
Nhận xét: Thông qua các ví dụ trên ta nhận thấy được hiệu quả của kĩ thuật thêm - bớt trong bất đẳng
thức Cauchy
- Bất đẳng thức Cauchy có thể giúp ta loại bỏ các rào cản như các căn thức, các lũy thừa bậc
cao,…
- Kĩ thuật thêm - bớt có thể giúp ta đối xứng hóa bất đẳng thức cũng như các đánh giá hợp lí trong
quá trình tìm lời giải.
- Chú ý
đến điểm rơi giúp ta bảo toàn dấu đẳng thức trong chuỗi đánh giá.
Sau đây là một số ví dụ khác
Ví dụ 4.14: Cho a, b, c là các số dương thỏa mãn
ab bc ca 2abc . Chứng minh rằng :
222
1111
2
a2a 1 b2b 1 c2c 1
Lời giải
Từ giả thiết
ab bc ca 2abc suy ra
111
2
abc
.
Đặt
111
x;y;z
abc
, khi đó ta có xyz2.

Bất đẳng thức được viết lại là
333
222
xyz1
2
2x 2y 2z
Hay
333
22 2
xyz1
2
yz zx xy
Áp dụng bất đẳng thức Cauchy ta được
3
2
3
2
3
2
xyzyz3x
884
yz
yzxzx3y
884
zx
zxyxy3z
884
xy
Cộng theo vế các bất đẳng thức trên ta được
333
22 2
3x y z
xyzxyz
224
yz zx xy
Hay
333
22 2
xyzxyz1
42
yz zx xy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
abc
2
.
Ví dụ 4.15: Cho a, b, c là các số thực không âm trong đó không có hai số nào có tổng bằng 0. Chứng
minh rằng :
22222 2
222222
2ab bc ca
bbcc ccaa aabb
4
abc bca cab abc
Phân tích: Bất đẳng thức có dấu đẳng thức xẩy ra tại
ab;c0
và các hoán vị của nó, như vậy kết
hợp với giả thiết ta có thể xét hai trường hợp. Tuy nhiên để ý biểu thức trong căn ta nhận thấy
222222
abcbbccabc và để ý đến chiều của bất đẳng thức ta có đánh giá
222222
2a bcb bcc a b c
. Khi đó ta được
22
22 22
2222
222
2b bc c
bbcc bbcc
abc abc
abcbbcc
Đến đây áp dụng tương tự ta được
22222 2
222
22222 2
222 222 222 222
bbcc ccaa aabb
abc bca cab
2b bc c 2c ca a 2a ab b
2ab bc ca
4
abc abc abc abc
Đây chính là bất đẳng thức cần chứng minh.
Lời giải
Áp dụng bất đẳng thức Cauchy ta được

222222
2a bcb bcc a b c
Khi đó ta suy ra
22
22 22
2222
222
2b bc c
bbcc bbcc
abc abc
abcbbcc
Áp dụng tương tự ta được
22222 2
222
22222 2
222 222 222 222
bbcc ccaa aabb
abc bca cab
2b bc c 2c ca a 2a ab b
2ab bc ca
4
abc abc abc abc
Hay
22222 2
222222
2ab bc ca
bbcc ccaa aabb
4
abc bca cab abc
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
ab;c0
và các hoán vị.
Ví dụ 4.16: Cho a, b, c là các số thực dương tùy ý . Chứng minh rằng :
111111333
23
abc2ab2bc2ca
a a 2b b b 2c c c 2a
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức và chú ý đến dấu đẳng
thức xẩy ra ta có đánh giá
23 1 3 1 3
2
a a 2b a a 2b
aa 2b
Khi đó tương tự ta được bất đẳng thức
111111333
23
abca2bb2cc2a
a a 2b b b 2c c c 2a
Như vậy
phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333 333
a 2b b 2c c 2a 2a b 2b c 2c a
Rõ ràng bất đẳng thức trên không thể chứng minh được, điều này cho thấy cách đánh giá như trên
không đem lại hiệu quả và ta cần phải tìm cách khác.
Để ý là trong phép đánh giá trên ta triệt tiêu được đại lượng
111
abc
nhưng không đem lại hiệu
quả. Vậy ta thử đánh giá làm triệt tiêu
333
a2b b2c c2a
thì sẽ có kết quả như thế nào? Để làm
được như vậy ta cần làm xuất hiện các
2a b; 2b c; 2c a
trong các căn và sự xuất hiện đó chỉ có
thể được giải quyết bằng kĩ thuật thêm - bớt. Khi đó chú ý đến dấu đẳng thức xẩy ra ta được
23 3 2a b 3 2a b
2
2a b 2a b
aa 2b aa 2b
aa 2b
Hoàn toàn tương tự ta được bất đẳng thức

111
23
a a 2b b b 2c c c 2a
2a b 2b c 2c a 3 3 3
2a b 2b c 2c a
a a 2b b b 2c c c 2a
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a b 2b c 2c a 1 1 1
abc
a a 2b b b 2c c c 2a
Quan sát bất đẳng thức ta nghĩ đến cách ghép đối xứng. Nhưng ghép như thế nào đây và nếu
không chứng minh được bất đẳng thức trên thì chuỗi đánh giá trên hoàn toàn vô tác dụng. Sau một thời
gian mày mò cuối cùng cũng phát hiện ra
2a b 2 1
ab
aa 2b
Đánh giá này tương đương với
2
a2b 3b2ab là một đánh giá đúng.
Thực hiện hoàn toàn tương tự ta được điều cần phải chứng minh.
Ví dụ 4.17: Cho a, b, c là các số thực dương thỏa mãn
abc 3. Chứng minh rằng:
111
2ab bc ca 9
ab bc ca
Phân tích và lời giải
Trước hết ta dự đoán đẳng thức xẩy ra tại
abc1. Khi đó dễ thấy theo bất đẳng thức
Cauchy ta có
111 1 1 1
ab bc ca ab bc ca 3
ab bc ca ab bc ca
Như vậy ta cần chứng minh
ab bc ca 3 nữa là xong. Tuy nhiên với abc 3 thì bất
đẳng thức
ab bc ca 3 lại không đúng. Như vậy cách đánh giá như trên không hiệu quả. Ta cần
tìm cách khác.
Trong bất đẳng thức có đại lượng
2ab bc ca và giả thiết thì có
abc3
, giữa chúng
có mối liên hệ là
2
222
abc2abbcca abc
Điều này gợi ý cho ta thêm vào hai vế của bất đẳng thức đại lượng
222
abc, khi đó bất đẳng
thức cần chứng minh trở thành
2
222
111
abc 9a b c
ab bc ca
Hay
222
111
abc
ab bc ca
Kết hợp với giả thiết
abc 3 thì bất đẳng thức trên được viết là
222 222
3
abc 3abcabc
abc
Theo một đánh giá quen thuộc thì
2
1
abc a b c ab bc ca
3
Do đó ta được
2
222
222 222
ab bc ca a b c
1
abc a b c abc a b c a b c
39

Mà theo bất đẳng thức Cauchy ta có
2
222 222
3
26
abbcca a b c abbccaabbccaa b c
abc abc
27
327
Suy ra ta được
222
abc a b c 3
. Vậy bài toán được chứng minh xong.
Ví dụ 4.18: Cho a, b, c, d là các số thực dương tùy ý. Chứng minh rằng:
ad db bc ca
0
bd cb ac ad
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abcd. Quan sát bất đẳng thức ta nhận thấy
chưa thể xác định được các phân số đã không âm hay chưa và vế phải lúc này là 0 nên việc sử dụng bất
đẳng thức Cauchy là không thể được. Bây giờ ta cần thay đổi các tử số để đảm bảo các phân số không âm
và vế phải cũng là một hằng số dương. Yêu cầu này gợi ý cho ta sử dụng kĩ thuật thêm - bớt
Để ý ta thấy
ad ab
1
bd bd
, hoàn toàn tương tự ta được
ad db bc ca
11114
bd cb ca da
ab dcba cd
4
db cb ca da
Lại thấy các phân số không cùng mẫu nhưng có các cặp cùng tử, do đó ta viết được bất đẳng thức
trên thành
11 11
ab cd 4
db ca bc ad
Bất đẳng thức trên làm ta liên tưởng đến bất đẳng thức Cauchy dạng
11 4
xy xy
4a b
11
ab
db ca abcd
Hoàn toàn tương tự ta cũng có
4c d
11
cd
bc ad abcd
Cộng hai bất đẳng thức trên theo vế ta có ngay điều phải chứng minh.
Ví dụ 4.19: Cho a, b, c là các số thực dương. Chứng minh rằng:
333
abc1
abc
2
bb c cc a aa b
Phân tích: Để ý đến đánh giá
33
3
abbc abbc3
3..a
24 24 2
bb c bb c
Lời giải
Áp dụng bất đẳng thức Cauchy ta có:
33
3
a b bc a bbc 3
3..a
24 24 2
bb c bb c
Hoàn toàn tương tự ta có
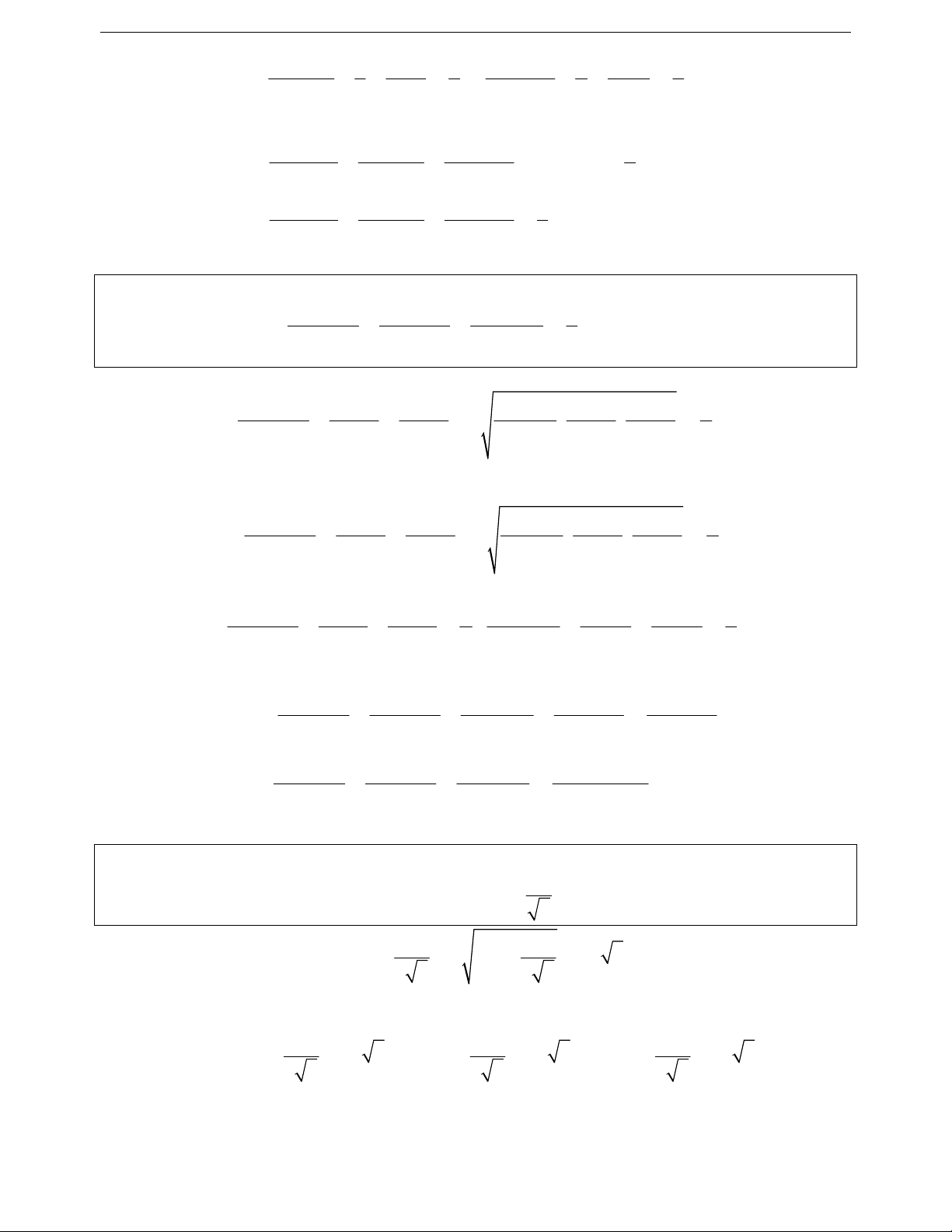
33
bcca3caab3
b; c
24 2 24 2
cc a aa b
Cộng vế với vế của các bất đẳng thức trên, ta được:
333
333
abc 3
abc abc
2
bb c cc a aa b
abc1
abc
2
bb c cc a aa b
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Ví dụ 4.20: Cho a, b, c là các số thực dương. Chứng minh rằng:
333
22 2
abc2
abc
9
b2c c2a a2b
Phân tích: Để ý đến đánh giá
33
3
22
a b2c b2c a b2cb2c a
3..
27 27 27 27 3
b2c bc
Lời giải
Áp dụng bất đẳng thức Cauchy ta có:
33
3
22
a b2c b2c a b2cb2c a
3..
27 27 27 27 3
b2c bc
Hoàn toàn tương tự ta có
33
22
bc2ac2abca2ba2bc
;
27 27 3 27 27 3
c2a a2b
Cộng vế với vế của các bất đẳng thức trên, ta được:
333
22 2
333
22 2
abcabcabc
93
b2c c2a a2b
2a b c
abc
9
b2c c2a a2b
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Ví dụ 4.21: Cho các số dương a, b, c thỏa mãn
ab bc ca 1. Chứng minh rằng:
333
1
abc
3
Phân tích: Để ý đến đánh giá
33 33
3
11
ab 3a.b. ab3
33 33
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
33 33 33
111
a b ab 3; b c bc 3; c a ca 3
33 33 33
Cộng vế với vế của các bất đẳng thức trên, ta được:

333
333 333
1
2a b c 3ab bc ca 3
3
21
2a b c a b c
33
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xảy ra khi và chỉ khi
1
ab
3
1
bc
1
abc
3
3
1
ca
3
ab bc ca 1
Ví dụ 4.22: Cho các số dương a, b, c thỏa mãn
4a b c 3abc.
Chứng minh rằng:
333
1113
8
abc
Phân tích: Biến đổi giả thiết ta được
1113
ab bc ca 4
. Chú ý đến đánh giá
3
33 33
111 11131
3.. .
882ab
ab ab
Lời giải
Từ giả thiết ta có
1113
4a b c 3abc
ab bc ca 4
Áp dụng bất đẳng thức Cauchy ta có
3
33 33
111 11131
3.. .
882ab
ab ab
Hoàn toàn tương tự ta được
33 3 3
1113111131
.; .
82bc 82ca
bc ca
Cộng theo vế các bất đẳng thức trên ta được
333 333
111 33111 9 1113
2
82abbcca 8 8
abc abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1111
abc2
abc2
1113
ab bc ca 4
5. Kỹ thuật Cauchy ngược dấu.
Trong quá trình tìm lời giải cho một bài toán bất đẳng thức, một sai lầm thường gặp đó là sau một
loạt các đánh giá ta thu được một bất đẳng thức ngược chiều. Điều này làm không ít người cảm thấy nản
lòng. Lúc này nếu ta bình tĩnh suy nghĩ một chút thì thấy với đánh giá ngược chiều bằng cách nào đó ta
thêm vào trước một dấu âm thì lập tức đánh giá đó sẽ cùng chiều. Sử dụng ý tưởng tương tự như kỹ thuật
thêm bớt, thậm chí có phần khéo léo hơn, kỹ thuật Cauchy ngược dấu đã chứng tỏ sự đột phá đơn giản
nhưng đem lại hiệu quả bất ngờ đến ngạc nhiên khi giải quyết lớp bất đẳng thức hoán vị chặt và khó.
Chúng ta sẽ bắt đầu làm quen với một số ví dụ sau

Ví dụ 5.1: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
1113
2
a1b1c1
Phân tích: Quan sát bất đẳng thức không ít bạn sẽ đánh giá
2
a12a , áp dụng tương tự khi đó ta
được bất đẳng thức
222
111111
2a 2b 2c
a1b1c1
Tuy nhiên bất đẳng thức thu được lại bị ngược chiều. Đến đây chúng ta sẽ bị lúng túng trong cách
giải. Ta vẫn phải đánh giá mẫu nhưng nếu có thể thêm được dấu âm trước đánh giá đó thì tốt biết mấy.
Điều ta mong muốn sẽ được giải quyết bằng phép biến đổi sau đây
22
22
1aaa
111
2a 2
a1 a1
Đến đây thì ta có thể đánh giá mẫu mà không sợ bị ngược chiều nữa
Lời giải
Áp dụng bất đẳng thức Cacuchy ta được
22
22
1aaa
111
2a 2
a1 a1
Hoàn toàn tương tự ta có:
22
1b1c
1; 1
22
b1 c1
Cộng theo vế theo vế các bất đẳng thức trên ta được:
222
111 abc3
3
22
a1b1c1
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 5.2: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
1113
1ab 1bc 1ca 2
Phân tích: Nếu áp dụng bất đẳng thức Cauchy trực tiếp ta thu được
1111113
1ab 1bc 1ca 2
2ab 2bc 2ca
Do đó ta sẽ áp dụng bất đẳng Cauchy theo ý tưởng như trên
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
1ababab
111
1ab 1ab 2
2ab
Tương tự ta có
1bc1ca
1; 1
1bc 2 1ca 2
Cộng theo vế theo vế các bất đẳng thức trên ta được
111 1
3abbcca
1ab 1bc 1ca 2
Để ý là
1 1ab bc ca abc 3
ab bc ca
2222222
Do đó ta được
1113
1ab 1bc 1ca 2
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1

Nhận xét: Kỹ thuật Cauchy ngược dấu có thể hiểu là ta lấy nghịch đảo hai vế của một đánh giá theo bất
đẳng thức Cauchy sau đó nhân hai vế với -1. Khi đó bất đẳng thức ban đầu sẽ không bị đổi chiều. Dưới
đây là một số ví dụ tương tự.
Ví dụ 5.3: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
22 2
abc3
2
b1c1a1
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
aababab
aaa
2b 2
b1 b1
Tương tự ta có
22
bbccca
b; c
22
c1 a1
Cộng theo vế theo vế các bất đẳng thức trên ta được:
22 2
abd abbcca
abc
2
b1c1d1
Mặt khác theo một đánh giá quen thuộc
2
1
ab bc ca a b c 3
3
Do đó ta được
22 2
abc 33
3
22
b1c1a1
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1
Ví dụ 5.4: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
22 2222
abcabc
2
abbcca
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
322
22 22
aababb
aaa
2ab 2
ab ab
Tương tự ta có
33
22 2 2
bcca
b; c
22
bc ca
Cộng vế theo vế các bất đẳng thức trên ta được
333
22 2222
abc abcabc
abc
22
abbcca
Bài toán được giải quyết. Đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 5.5: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
22 2
a1 b1 c1
3
b1c1a1
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
a1b a1b
a1 abb
a1 a1 a1
2b 2
b1 b1
Tương tự ta có:
22
b1 bcc c1 caa
b1 ; c1
22
c1 a1
Cộng theo vế các bất đẳng thức trên ta đươc

22 2
a1 b1 c1 abcabbcca
abc3
2
b1c1a1
abc abbcca
3
22
Mà theo một đánh giá quen thuộc ta có
2
abc
ab bc ca 3
3
Do vậy ta được
22 2
a1 b1 c1
3
b1c1a1
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Ví dụ 5.6: Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
22 2
abc3
2
bc 1 ca 1 ab 1
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
baac
ba ac
aabcabcabc
aaa a a
224
bc 1 bc 1
2b c
Suy ra ta có
2
a1
aababc
4
bc 1
Hoàn toàn tương tự ta có
22
b1 c1
bbcabc; ccaabc
44
ca 1 ab 1
Cộng theo vế các bất đẳng thức trên ta được
22 2
abc abbcca3abc
3
44
bc 1 ca 1 ab 1
Mặt khác ta có theo một đánh giá quen thuộc ta được
2
abc
3abbcca
3abbcca
344
Và
3
33abc
3abc3abc
44
Do đó ta được
22 2
abc33
3
44
bc 1 ca 1 ab 1
hay
22 2
abc3
2
bc 1 ca 1 ab 1
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Ví dụ 5.7: Cho a, b, c là các số thực dương thỏa mãn
ab bc ac 3
. Chứng minh rằng:
33 3
abc
1
2b 1 2c 1 2a 1
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
33
333 2
a 2ab ab 2ab
aaa
3
2b 1 b b 1 3b
Tương tự ta có
33
b2bcc2ca
b; c
33
2c 1 2a 1
Cộng theo vế các bất đẳng thức trên ta được

33 3
2ab bc ca
abc
abc abc2
3
2b 1 2c 1 2a 1
Mặt khác ta lại có
2
abc
ab bc ca a b c 3 ab bc ca 3
3
Do đó ta được
33 3
abc
1
2b 1 2c 1 2a 1
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 5.8: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
222
abc
1
a2b b2c c2a
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
222
2
3
222
3
4
a2ab2ab2
aaaab
3
a2b ab b
3ab
Tương tự ta có
22
22
33
22
b2 c2
bbc; cca
33
b2c c2a
Cộng theo vế các bất đẳng thức trên ta được
222
222
222
222
abc 2
abc ab bc ca
3
a2b b2c c2a
2
3abbcca
3
333
333
Mặt khác ta có
2
3
aabb
ab a.ab.b
3
3
Hoàn toàn tương tự ta được
22
bbcc ccaa
bc ; ca
33
33
Cộng theo vế các bất đẳng thức trên ta được
222
2
2
21
ab bc ca a b c ab bc ca
33
abc
21 213
abc . .3 . 3
333333
333
Suy ra ta có
222
22
ab bc ca .3 2
33
333
Do đó ta được
222
222
abc
1
a2b b2c c2a
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 5.9: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
333
abc
1
a2b b2c c2a
Lời giải
Áp dụng bất đẳng thức Cauchy ta có

233
3
2
333
3
6
a2ab2ab2
aaaba
3
a2b ab b
3ab
Tương tự ta có
22
33
22
33
b2c2
bcb; cac
33
b2c c2a
Cộng theo vế các bất đẳng thức trên ta được
222
33 3
222
333
33 3
222
abc 2
abc ba cb ac
3
a2b b2c c2a
2
3bacbac
3
Mặt khác cũng theo bất đẳng thức Cauchy ta có
3
3
2
aa1 2a1 2abb
ba ba.a.1 b b
333
Tương tự ta có
33
22
2bc c 2ca a
cb ; ac
33
Cộng theo vế các bất đẳng thức trên ta được
2
33 3
222
2a b c
abc2 abc
ba cb ac ab bc ca 3
33 3 3.3
Do đó ta có
222
333
abc
1
a2b b2c c2a
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Ví dụ 5.10: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
222222
abcabc
3
aabb bbcc ccaa
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
322
2222
ab a b
aabab ab2ab
aaa
3ab 3 3
aabb aabb
Tương tự ta có
33
22 22
b2bcc2ca
;
33
bbcc ccaa
Cộng theo vế các bất đẳng thức trên ta được
333
222222
abcabc
3
aabb bbcc ccaa
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 5.11: Cho a, b, c, d là các số thực dương thỏa mãn
abcd4.
Chứng minh rằng:
22 2 2
abcd
2
1b 1c 1d 1a
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
2
22 2
a1 b ab
aabab
aa
2
1b 1b 1b
Áp dụng tương tự ta được
222
bbcccddda
b; c; c
222
1c 1d 1a
Áp dụng tương tự ta được

22 2 2
abcd abbccdda
4
2
1b 1c 1d 1a
Mặt khác cũng theo bất đẳng thức Cauchy ta có
2
acbd abcd
ab bc cd da
2
228
Do vậy ta được
22 2 2
abcd
2
1b 1c 1d 1a
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abcd1
Ví dụ 5.12: Cho a, b, c, d là các số thực dương thỏa mãn
abcd4
. Chứng minh rằng:
2222
1111
2
a1b1c1d1
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
22 2
a1a
1aaa
111
2a 2
a1 a1 a1
Hoàn toàn tương tự ta được
222
1b1c1d
1; 1; 1
222
b1 c1 d1
Cộng theo vế các bất đẳng thức trên ta được
2222
1111
2
a1b1c1d1
Bài toán được giải quyết. Đẳng thức xảy ra khi và chỉ khi
abcd1
Ví dụ 5.13: Cho a, b, c, d là các số thực dương thỏa mãn
abcd4
. Chứng minh rằng:
22 2 2
abcd
2
1bc 1cd 1da 1ab
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
22
22
22 2
a1 bc abc
aabcabcabc
aaa
2
1bc 1bc 1bc
2b c
Hoàn toàn tương tự ta được
222
bbcdccdaddab
b; c; d
22 2
1cd 1da 1ab
Cộng theo vế các bất đẳng thức trên ta được
22 2 2
abcd abcbcdcdadab
4
2222
1bc 1cd 1da 1ab
Mặt khác cũng theo bất đẳng thức Cauchy ta có
ba ac
ba.ac
24
Tương tự ta được
b a.ac c b.bd d c.ca a d.db ab bc cd da abc bcd cda dab
24
Mà ta có
2
acbd acbd
ab bc cd da
1
4416
và

22 3
bc a d da b c
abc bcd cda dab
44
adbc bcad abcd
1
16 4.16
Do đó ta được
22 2 2
abcd
2
1bc 1cd 1da 1ab
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
abcd1
6. Kỹ thuật đổi biến số
Trong bất đẳng thức, có một quy luật chung, đó là “Trong một dạng cụ thể, thì những bất đẳng
thức càng nhiều biến càng khó”. Điều này cũng đồng nghĩa với việc khẳng định “Bài toán sẽ trở nên đơn
giản hơn nếu ta đưa được một bất đẳng thức nhiều biến về dạng ít biến hơn” Kỹ thuật đổi biến chính là
một công cụ hữu ích để thực hiện ý tưởng này.
Ví dụ 6.1: Cho a, b là hai số thực khác 0. Chứng minh rằng:
22 2 2
222
22
4a b a b
3
ba
ab
Phân tích: Nhìn vào bất đẳng thức cần chứng minh ta thấy hai hạng tử sau ở vế trái có vẻ như tạo ra được
nghịch đảo của hạng tử thứ nhất. Vì vậy ta thử phân tích tổng hai hạng tử đó để xem kết quả có như dự
đoán hay không.
2
22
22 44 22 22
2 2 22 22
ab
abab2ab2ab
2
b a ab ab
Với kết quả như vậy ta có thể sử dụng cách đặt ẩn phụ để đưa bất đẳng thức cần chứng minh về bất
đẳng thức đơn giản hơn.
Lời giải
Để ý rằng bất đẳng thức cần chứng minh có thể viết lại thành
2
22
22
222
22
ab
4a b
5
ab
ab
Đặt
2
22
22
ab
t
ab
ta có t4 . Từ đó suy ra
22
2
22
4a b 4
t
ab
Bất đẳng thức cần chứng minh trở thành
2
t1t4
tt5t4
t5 0 0
4t t
Bất đẳng thức cuối cùng đúng do
t4
. Bài toán được giải quyết hoàn toàn.
Đẳng thức xảy ra khi và chỉ khi
ab
Ví dụ 6.2: Cho các số thực
a, b, c 2 thỏa mãn
111
1
abc
. Chứng minh rằng :
a2b2c2 1
Phân tích: Để triệt tiêu các dấu trừ trong bất đẳng thức cần chứng minh ta có thể đổi biến
xa2;yb2;zc2 , khi đó giả thiết trở thành
111
1
x2 y2 z2
và ta cần chứng
minh
xyz 1 . Đây là một bất đẳng thức có thể chứng minh bằng cách ghép cặp đối xứng. Tuy nhiên
trong lời giải dưới đây ta chứng minh bài toán bằng kỹ thuật đổi biến.

Lời giải
Đặt
xa2;yb2;zc2 với x, y, z là các số thực dương. Bài toán quy về chứng minh
xyz 1
với
x, y, z 0
thỏa mãn
111 xyz
11
x2 y2 z2 x2 y2 z2
Đến đây ta đặt tiếp
xyz
m;n;p mnp1
x2 y2 z2
Khi đó ta có
1x2 2 21 np 2m
11x
mx xxm m np
Tương tự ta đươc
2n 2p
y;z
pm mn
Do đó bất đẳng thức cần chứng minh trở thành
2m 2n 2p
1mnnppm8mnp
nppmmn
Sử dụng bất đẳng thức Cauchy, ta có
m n n p p m 2mn.2np.2pm 8mnp
Bài toán được giải quyết xong. Đẳng thức xảy ra khi và chỉ khi
mnp abc1 xyz3
Ví dụ 6.3: Cho a, b, c là các số dương thỏa mãn
abc 1 . Chứng minh rằng:
111
1
2a 1 2b 1 2c 1
Phân tích: Giả thiết abc 1 gợi ý cho ta cách đổi biến
xyz
a;b;c
yzx
với x, y, z là các số
thực dương.
Lời giải
Đặt
xyz
a;b;c
yzx
với x, y, z là các số thực dương. Bất đẳng thức cần chứng minh trở
thành
111 yzx
11
xyz 2xy2yz2zx
212121
yzx
Áp dụng bất đẳng thức Côsi ta có
22
y2z y y2z y y2z y
y
2x y
2x y 2z y
xyz
2x y 2z y
4
Tương tự ta có
22
z2x z x2y x
zx
;
2x y 2z x
xyz xyz
Cộng ba bất đẳng thức này lại vế theo vế, ta được:
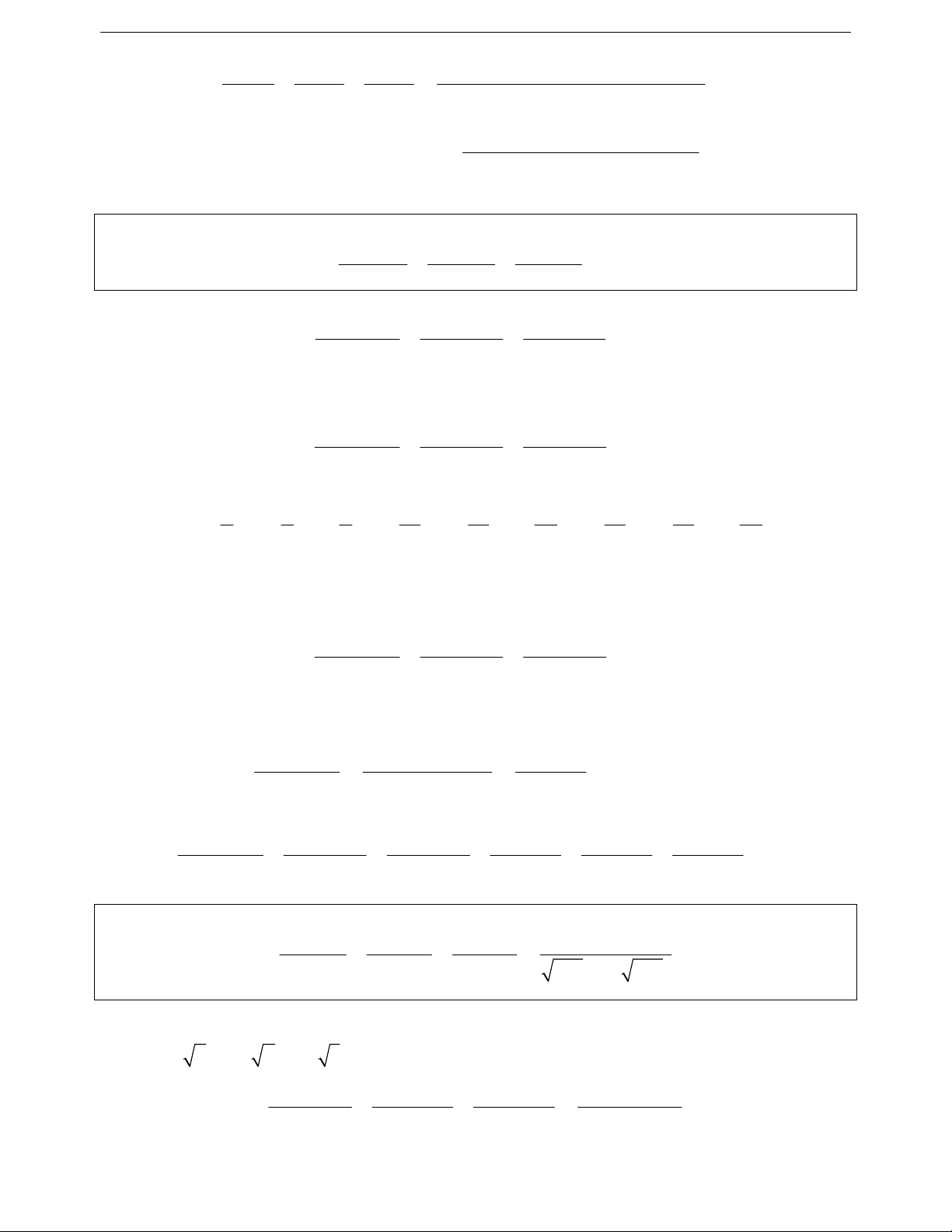
2
222
2
y2zy z2xz x2yx
yzx
2x y 2y z 2z x
xyz
2xy yz zx x y z
1
xyz
Chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 6.4: Cho a, b, c là các số thực thỏa mãn
abc 1 . chứng minh rằng:
111
1
ab1bc1ca1
Phân tích: Ta nhận thấy sự tương tự của bất đẳng thức trên với bất đẳng thức
33 33 33
111
1
ab1bc1ca1
Do đó ý tưởng đầu tiên đó ta đặt
333
xa;yb;zc
, khi này ta vẫn được xyz 1 và khi đó
ta viết lại được bất đẳng thức cần chứng minh
33 33 33
111
1
xy1yz1zx1
Ngoài ra từ giả thiết
abc 1 , ta có thể sử dụng các phép đổi như sau
222
222
xyzx y z yzzxxy
a;b;c,a;b;c;a;b;c
yzxyzzxxy
xyz
Lời giải
Đặt
333
xa;yb;zc, khi đó ta được
xyz 1
.
Bất đẳng thức càn chứng minh trở thành
33 33 33
111
1
xy1yz1zx1
Áp dụng bất đẳng thức Cauchy ta được
33 22
x y x y x y xy xy x y
Khi đó ta được
33
11z
xyz
xy1
xy x y xyz
Chứng minh tương tự ta được
33 33 33
111zxy
1
xyz xyzxyz
xy1yz1zx1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 6.5: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
33
111 3
ab 1 bc 1 ca 1
abc 1 abc
Phân tích: Quan sát bất đẳng thức ta thấy vế phải chứa căn bậc ba. Do đó điều đầu tiên ta nghĩ đến là làm
mất các căn bậc ba này và ta có hai ý tưởng đổi biến để làm mất căn bậc ba là
- Đặt
333
xa,yb,zc. Khi đó bất đẳng thức cần chứng minh trở thành
33 33 33
111 3
xyz xyz 1
xy 1 yz 1 zx 1
- Đặt
3
abc k . Khi đó bất đẳng thức cần chứng minh trở thành

111 3
ab 1 bc 1 ca 1 k1 k
Ta thử chứng minh bài toán với các cách đổi biến trên như sau
Lời giải
Đặt
333
xa,yb,zc
. Khi đó bất đẳng thức cần chứng minh trở thành
33 33 33
111 3
xyz xyz 1
xy 1 yz 1 zx 1
Ta có
333
33 33 33
33 33 33
333
33 33 33
33 33 33
333
333333 333
111
M3 1xyz
xy 1 yz 1 zx 1
111xyyzzx
3
x1y1z1
xy 1 yz 1 zx 1
yx 1 zy 1 xz 1
1x 1y 1z
xy 1 yz 1 zx 1 1y 1z 1z
Theo bất đẳng thức Caucy ta được
333
33 33 33
33 33 33
333
1x 1y 1z 3
xyz
xy 1 yz 1 zx 1
yx 1 zy 1 xz 1
3xyz
1y 1z 1z
Từ đó suy ra
333
33
M 3xyz 1 x y z P 3xyz 3
xyz xyz
Mặt khác ta lại có
222
333
3 x y z xyz 1
33
x y z 1 3xyz 3
xyz xyz
xyz xyz 1
Do đó ta được
333 333
33
1xyzP 1xyz P
xyz xyz 1 xyz xyz 1
Chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc
Nhận xét: Ta cũng có thể chứng minh bài toán trên theo cách sau
Với cách đặt
3
abc k , khi đó tồn tại các số thực dương
,,xyz
sao cho
;;
ky kz kx
abc
xyz
Khi đó bất đẳng thức cần chứng minh tương đương với
1113
1
111
ky kz kz kx kx ky
kk
xy yz zx
Hay
3
1
xyz
ykz zkx xky k
Áp dụng bất đẳng thức Bunhiacopxki ta được

222
2
2
3
1
1
xyz x y z
ykz zkx xky
x y kz y z kx z x ky
xyz
x y kz y z kx z x ky
xyz
k
kxyyzzx
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Ví dụ 6.6: Cho a, b, c là các số thực dương thỏa mãn
abcabc . Chứng minh rằng:
222
bca3
2
ab 1 bc 1 ca 1
Phân tích: Ta viết lại giả thiết thành
111
1
ab bc ca
, điều này gợi ý cho ta các đặt biến phụ
111
x;y;z
abc
. Khi đó giả thiết của bài toán trở thành xy yz zx 1.
Bất đẳng thức cần chứng minh trở thành
22 2
xyz3
2
y1 z1 x1
. Chú ý đến
xy yz zx 1 ta viết được
22
x1 xxyyzzx xyxz khi đó ta suy ra
bất đẳng thức cần chứng minh là
xyz3
2
yxyz zxzy xyxz
Đến đây ta sử dụng đánh giá Cauchy để giải quyết bài toán.
Lời giải
Từ giả thiết
abcabc
suy ra
111
1
ab bc ca
.
Đặt
111
x;y;z
abc
, Khi đó giả thiết của bài toán trở thành xy yz zx 1.
Bất đẳng thức cần chứng minh trở thành
22 2
xyz3
2
y1 z1 x1
.
Dễ thấy
22
x1 xxyyzzx xyxz
Tương tự ta được
22
y1 yzyx;z1 zxzy
Áp dụng bất đẳng thức Cauchy ta được
22 2
xyz x y z
y1 z1 x1
yxyz zxzy xyxz
2x 2y 2z
x2yz xy2z 2xyz
Ta cần chứng minh
2x 2y 2z 3
x2yz xy2z2xyz 2
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
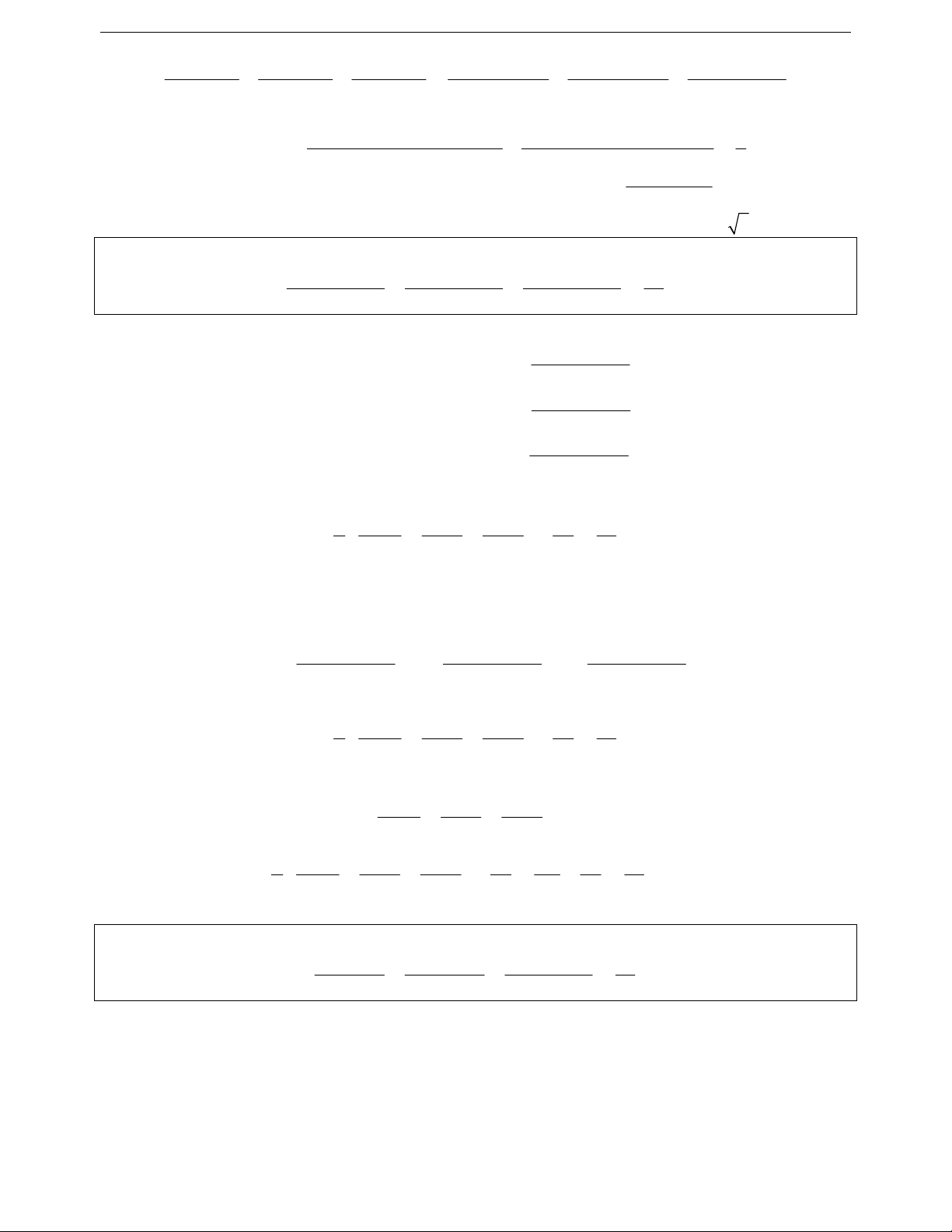
222
22
22
2
2x 2y 2z 2x 2y 2z
x2yz xy2z 2xyz
xx2yz yxy2z z2xyz
2x y z 2x y z
3
2
xyz xyyzzx xyz
xyz
3
Như vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc 3 .
Ví dụ 6.7: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
ab3c a3bc 3abc 15
3a 3b 2c 3a 2b 3c 2a 3b 3c 8
Phân tích: Để đơn giản hóa các đại lượng vế trái ta có thể đặt
3y 3z 5x
a
8
x2a3b3c
3z 3x 5y
y3a2b3c b
8
z3a3b2c
3x 3y 5z
c
8
Khi đó ta viết lại bất đẳng thức cần chứng minh thành
7x y y z z x 27 15
8z x y 8 8
Đến đây ta áp dụng bất đẳng thức Cauchy để đánh giá tiếp.
Lời giải
Đặt
x 2a3b3c;y 3a2b3c;z 3a3b2c
, khi đó ta được
3y 3z 5x 3z 3x 5y 3x 3y 5z
a;b;c
888
Khi đó bất đẳng thức cần chứng minh được viết lại thành
7x y y z z x 27 15
8z x y 8 8
Theo bất đẳng thức Cauchy ta chứng minh được
xy yzzx
6
zxy
Do đó ta được
7 x y y z z x 27 7.6 27 15
8z x y 8 8 8 8
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 6.8: Cho a, b, c là các số thực dương. Chứng minh rằng:
ab bc ca 16
abc bc4a ac16b 15
Lời giải
Đặt
xabc 3ayx
y b c 4a 15b z x
z c a 16b 15c 21x 5y z
Khi đó bất đẳng thức cần chứng minh được viết lại thành

6x 5y z 20x 5y 16x z 16
15x 15y 15z 15
Hay
y 3x z 16x 16 4 28
3x 4y 15x 15z 15 5 15
Áp dụng bất đẳng thức Cauchy ta có
y4x4z 16x8
;
3x 3y 3 15x 15z 15
Do đó ta được
ab bc ca 16
a b c b c 4a a c 16b 15
. Đẳng thức xẩy ra khi và chỉ khi
y4x
5c
a
3x 3y
7
3c
z16x
b
7
15x 15z
Bài toán được chứng minh xong.
Ví dụ 6.9: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
333
111 3abbcca
abc
2c a b
abc
Phân tích: Quan sát bất đẳng thức ta chưa thấy có dấu hiệu đặt biến phụ, do đó ta cần phải biến đổi bất
đẳng thức trước. Ở đây ta chọn biến đổi vế trái trước
33 3333
333
333 3 3 3
111 abbcca
abc 3
abc c a b
Quan sát biểu thức sau khi biến đổi ta thấy cần phải đánh giá
33
3
ab
c
về
3
ab
c
, điều này có
nghĩa là ta cần chứng minh được
3
33
abkab , chú ý đến dấu đẳng thức xẩy ra ta tìm được
1
k
4
. Như vậy ta đi chứng minh
3
33
1
ab ab
4
, đây là một đánh giá đúng và có thể chứng
minh bằng cách sử dụng bất đẳng thức Cauchy.
Đến đây ta có thể đặt
ab bc ca
x;y;z
cab
và bất đẳng thức cần chứng minh
được viết lại thành
333
3x y z
xyz
3
42
. Chú ý lúc này đẳng thức xẩy ra tại
xyz2
và ta sử dụng bất đẳng thức Cauchy để chứng minh bài toán trên.
Lời giải
Bất đẳng thức được viết lại là
33 3333
333
abbc ca 3abbcca
3
2c a b
cab
Áp dụng bất đẳng thức Cauchy ta được
33 33 33 33 22
3
33
4a b a b 3a b a b 3a b a b ab
ab3abab ab
Suy ra
3
33
33
ab
ab
c4c

Áp dụng tương tự ta có bất đẳng thức
333
33 3333
333 3 3 3
ab bc ca
abbcca
cab4c4a4b
Ta cần chứng minh
333
333
ab bc ca
3a b b c c a
3
2c a b
4c 4a 4b
Đặt
ab bc ca
x;y;z
cab
, bất đẳng thức trở thành
333
3x y z
xyz
3
42
Hay
333
12 x y z 6 x y z
Áp dụng bất đẳng thức Cauchy ta được
333
x 8 8 12x; y 8 8 12y; z 8 8 12z
Suy ra
333
x y z 48 12x y z 6x y z 6x y z
6x y z 36
Hay
333
12 x y z 6 x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 6.10: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
abc 3abbcca
bca 2 c a b
Phân tích: Cũng tương tự như ví dụ trên ta cần biến đổi bất đẳng thức trước khi đưa ra cách đổi biến.
Trong ví dụ này ta chọn các biến đổi vế phải
abbc ca a b b c c a
c a b ccaabb
Lúc này để ý ta thấy cả hai vế xuất hiện các đại lượng
abc
;;
bca
, lại để ý ta nhận thấy rằng
aabbbccca
.; .; .
cbcacabab
. Do đó ta có thể đặt
abc
x;y;z
bca
, khi đó ta được xyz 1
và bất đẳng thức cần chứng minh được viết lại thành
2
3xyyzzxxyz
xyz
2
Đến đây ta có lời giải sau
Lời giải
Đặt
abc
x;y;z
bca
suy ra xyz 1 .
Bất đẳng thức cần chứng minh được viết lại thành
2
3xyyzzxxyz
xyz
2
Áp dụng bất đẳng thức Cauchy ta được
3
x y z 3 xyz 3

Nên
2
xyz 3xyz
Ta cũng có
2
x y z 3 xy yz zx
Do đó ta được
2
2x y z 3xy yz zx 3x y z
Hay
2
3xyyzzxxyz
xyz
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 6.11: Cho a, b, c là các số thực dương thỏa mãn
c8ab . Chứng minh rằng:
1c c1
4a 2b 3 4bc 3c 2 2ac 3c 4 2
Phân tích: Quan sát bất đẳng thức ta nhận thấy sự khác biệt của giả thiết cũng như bất đẳng thức cần
chứng minh so với các ví dụ ở trên. Từ bất đẳng thức cần chứng minh ta thấy vai trò của a, b như nhau.
Do đó ta dự đoán dấu đẳng thức xẩy ra tại
ab
. Mặt khác ta thấy tử của biểu thức thứ hai và thứ ba có
biến c, do đó nếu ta viết lại hai biểu thức đó như biểu thức thứ nhất thì dưới mẫu xuất hiện đại lượng
1
c
,
do đó rất tự nhiên ta nghĩ đẳng thức xẩy ra tại
1
ab
c
, khi này ta viết lại giả thiết là
1
8ab 1
c
. Đến
đây ta thấy được cách đặt là
2
x 2a; y 2b; z
c
và bất đẳng thức được viết lại thành
1111
2x y 3 2y z 3 2z x 3 2
Tuy nhiên từ hình thức của bất đẳng thức ta thấy tương tự bất đẳng thức quen thuộc
22 22 22
1111
2
2x y 3 2y z 3 2z x 3
Do đó ta chọ cách đặt
222
2
x 2a; y 2b; z
c
để đưa bài toán về dạng quen thuộc.
Lời giải
Đặt
222
2
x 2a; y 2b; z
c
. Khi đó từ giả thiết ta được xyz 1 .
Bất đẳng thức cần chứng minh được viết lại thành
22 22 22
1111
P
2
2x y 3 2y z 3 2z x 3
Áp dụng bất đẳng thức Cauchy ta có
22 222
2x y 3 x y x 1 2 2 xy x 1
Do đó ta được
111
P
2xy x 1 2yz y 1 2zx z 1
Ta chứng minh
111
1
xy x 1 yz y 1 zx z 1
theo các cách sau
Cách 1: Do
xyz 1 , nên tồn tại các số dương x, y, z để
mnp
x;y;z
npm
Khi đó ta có

111 1 1 1
xy x 1 yz y 1 zx z 1 m m n n p m
111
pn mp nm
np pm mn
1
mn np pm mn np pm mn np pm
Cách 2: Do
xyz 1 , nên ta được
111 xyz1 y
xy x 1 yz y 1 zx z 1 xy x xyz yz y 1 xyz yz y
yz 1 y
1
yz y 1 yz y 1 yz y 1
Suy ra
1
P
2
. Vậy bất đẳng thức được chứng minh xong.
Đẳng thức xẩy ra khi và chỉ khi
xyz1
hay
1
ab ;c2
2
.
Ví dụ 6.13: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 2abc . Chứng minh rằng:
222
1111
2
a2a 1 b2b 1 c2c 1
Phân tích: Dễ dàng dự đoán được đẳng thức xẩy ra tại
3
abc
2
. Giả thiết của bài toán được viết
lại thành
111
2
abc
, khi đó để đơn giản hóa giả thiết ta có thể đổi biến
111
x;y;z
abc
, khi
này giả thiết mới là
xyz2
với
0x,y,z2
. Cũng từ cách đặt trên ta suy ra được
111
a;b;c
xyz
, thay vào bất đẳng thức cần chứng minh thì được
333
222
xyz1
2
2x 2y 2z
Đến đây ta có thể chứng minh bất đẳng thức bằng cách thêm bớt hoặc sử dụng bất đẳng thức
Bunhiacopxki dạng phân thức.
Lời giải
Từ giả thiết
ab bc ca 2abc
suy ra
111
2
abc
.
Đặt
111
x;y;z
abc
, khi đó ta có
xyz2
.
Bất đẳng thức được viết lại là
333
222
xyz1
2
2x 2y 2z
Hay
333
22 2
xyz1
2
yz zx xy
Áp dụng bất đẳng thức Cauchy ta được

3
2
3
2
3
2
xyzyz3x
884
yz
yzxzx3y
884
zx
zxyxy3z
884
xy
Cộng theo vế các bất đẳng thức trên ta được
333
22 2
3x y z
xyzxyz
224
yz zx xy
Hay
333
22 2
xyzxyz1
42
yz zx xy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
abc
2
.
Nhận xét: Ngoài cách sử dụng bất đẳng thức Cauchy thì ta cũng có thể áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức
Ví dụ 6.14: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3abc
.
Chứng minh rằng:
222
22 2 2 2 2
abc
1
ca 2c ab 2a bc 2b
Lời giải
Từ giả thiết
ab bc ca 3abc ta được
111
3
abc
.
Đặt
111
x;y;z
abc
. Khi đó ta được xyz3.
Bất đẳng thức cần chứng minh trở thành
222
222
xyz
1
x2y y2z z2x
Áp dụng bất đẳng thức Cauchy ta được
222222 2 2
3
22 22
4
3
2xy
x x 2xy 2xy 2xy 2xy
xxx
3
x2y x2y xy y
2xy
Áp dụng tương tự ta được
2
222222
2
22
2yz
yz2zx
y; z
33
y2z z2x
Cộng theo vế các bất đẳng thức trên ta được
222
3
22 22 22
33
222
xyz 2
xyz xy yz zx
3
x2y y2z z2x
Mạt khác theo bất đẳng thức Cauchy ta lại có
22
3
22
3
3
22
xy xy 1 2xy 1
xy
33
yz yz 1 2yz 1
yz
33
zx zx 1 2zx 1
zx
33

Suy ra
2
3
22 22 22
33
2xy yz zx 2x y z
xy yz zx 1 1 3
39
Do đó ta được
222
222
xyz 2.3
31
3
x2y y2z z2x
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 6.15: Cho a, b, c, d là các số thực dương thỏa mãn
111
2
abc
. Chứng minh rằng:
111
1
a3b b3c c3a
Phân tích: Trước hết ta đơn giản hóa giả thiết bằng cách đặt
xa;yb;zc
, khi này giả
thiết được viết lại thành
111
2
xyz
và bất đẳng thức cần chứng minh trở thành
22 22 22
111
1
x3y y3z z3y
Chú ý đến giả thiết
111
2
xyz
ta viết lại bất đẳng thức cần chứng minh là
22 22 22
1111111
2x y z
x3y y3z z3y
Để ý theo bất đẳng thức Cauchy ta có
2 2 2222 26
4
x3y xyyy 4xy , như vậy ta được
22 22 4
44
26
4
111111112113
4 8xyy 8xy
x3y xy y
2xy
Đến đây áp dụng tương tự ta được
Lời giải
Đặt
xa;yb;zc. Khi đó ta được
111
2
xyz
Bất đẳng thức cần chứng minh trở thành
22 22 22
111
1
x3y y3z z3y
Áp dụng bất đẳng thức Cauchy ta được
2 2 2222 26
4
x3y xyyy 4xy
Áp dụng một bất đẳng thức Cauchy khác ta được
22 22 4
44
26 22 4
444
11 1111
4
x3y xy y
2xy 2xy.y
11 1 2 11 3
8x y y 8x y
Tương tự ta có
22 2 2
1113 1113
;
8y z 8z x
y3z z3y
Cộng theo vế các bất đẳng thức trên ta có
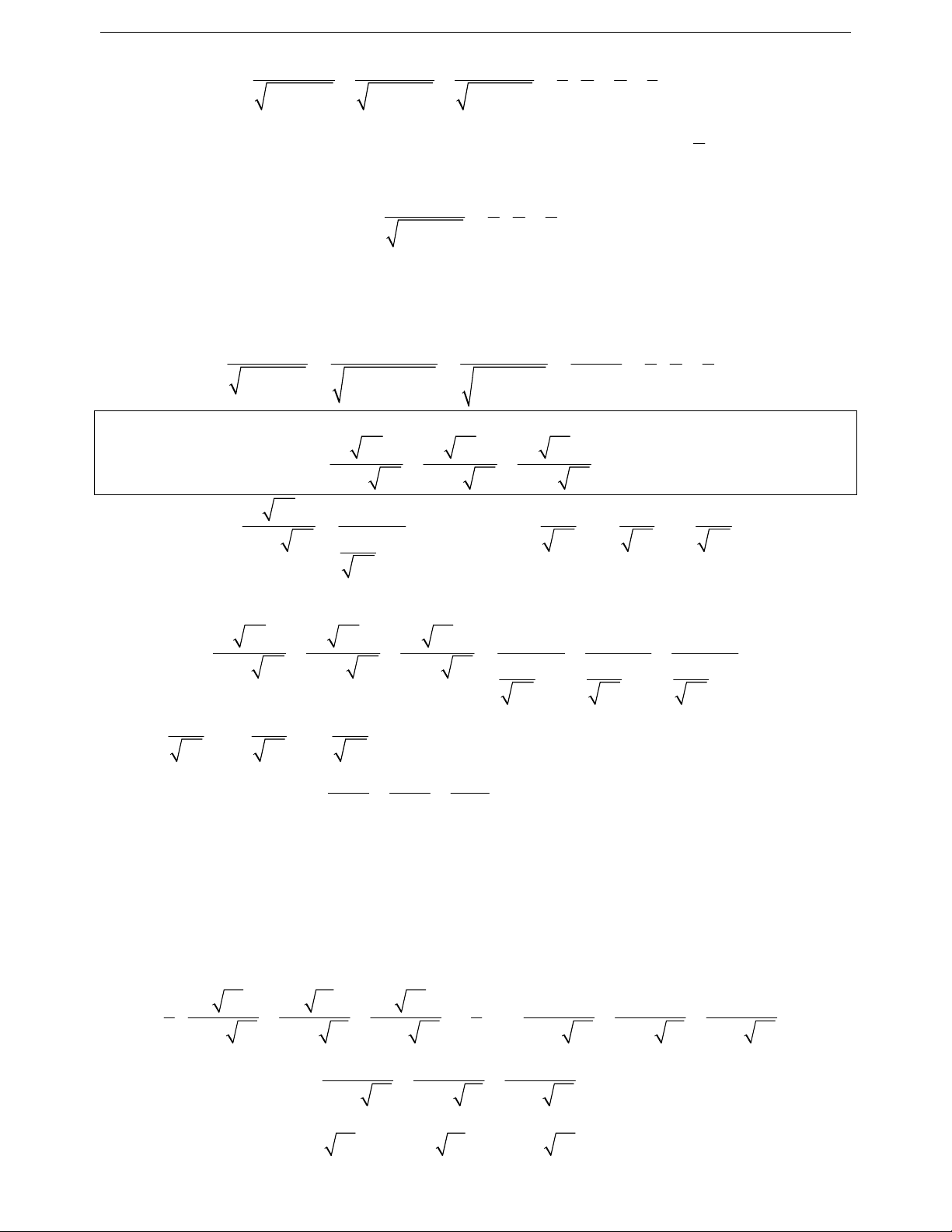
22 22 22
1111111
1
2x y z
x3y y3z z3y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
9
abc
4
Nhận xét: Ta có thể sử dụng bất đẳng thức Bunhiacopxki để chứng minh bất đẳng thức
22
1113
8
3
xy
xy
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2 2 2222
4 3 1111 3x y xyyy x y
Do đó ta được
22 2
22
12 22113
38
3
23
3
xy xy
xy
xy
xy
Ví dụ 6.17: Cho a, b, c là các số thực dương. Chứng minh rằng:
ab bc ca
1
c2ab a2bc b2ca
Phân tích: Để ý là
ab 1
c
c2ab
2
ab
, do đó ta đặt
abc
x;b;z
bc ca ab
.
Lời giải
Vế trái bất đẳng thức cần chứng minh được viết lại thành
ab bc ca 1 1 1
cba
c2ab a2bc b2ca
222
ab ca bc
Đặt
abc
x;b;z
bc ca ab
, suy ra xyz 1 .
Biểu thức P được viết lại thành
111
1
x2 y2 z2
.
Thật vậy, bất đẳng thức cần chứng minh tương đương với
x2y2 y2z2 z2x2 x2y2z2
Triển khai và thu gọn ta được
xy yz xz 3
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy và
xyz 1 .
Do đó bất đẳng thức trên được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Nhận xét: Ta có thể chứng minh bài toán trên theo cách khác như sau
Biểu thức vế trái được viết lại là
12 2 2 1
3
22
222 222
ab bc ca c a b
c ab a bc b ca c ab a bc b ca
Đặt
222
cab
M
cababcbca
Áp dụng bất đẳng thức Cauchy ta có
2;2;2ab a b bc b c ca c a

Do đó ta có
1
222
cabcab
M
abc abc abc
cababcbca
Suy ra
1
222
ab bc ca
cababcbca
Do đó bất đẳng thức trên được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 6.18: Cho a, b, c là các số thực dương không âm thỏa mãn
abc3. Chứng minh rằng:
aa bb cc abc 33
Lời giải
Đặt
xa;yb;zc
. Từ giả thiết ta được
222
xyz 3.
Khi này bất đẳng thức trở thành
333
Px y z xyz33
Không mất tính tổng quát ta giả sử
xyz. Khi đó ta có
2222
zxy;xy3z3
Do đó ta có
33 2 33
xyzzxyxy
Mặt khác theo bất đẳng thức Cauchy ta có
3
22
2
2
33 2 22 2
3x y
x z xy x xyy x xyy 27
3
Suy ra
33
xy33 nên ta được
P33
. Đẳng thức xẩy ra khi và chỉ khi
x3;yz0và các hoán vị a3;bc0 và các hoán vị
Bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
a3;bc0
và các hoán vị.
Nhận xét: Qua các ví dụ trên ta nhận thấy, đổi biến có một vai trò to lớn trong chứng minh bất đẳng
thức, đổi biến có thể làm một bất đẳng thức trở nên đơn giản, đổi biến có thể đưa một bất đẳng thức hoán
vị về bất đẳng thức đối xứng. Chúng ta cùng tham khảo thêm một số ví dụ khác sau đây để thấy được sự
độc đáo c
ủa kỹ thuật đổi biến
Ví dụ 6.19: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
abc
2
bc ca ab
Lời giải
Đặt
333
ax;by;cz
, do đó
x, y, z 0
. Khi đó bất đẳng thức cần chứng minh trở thành
333
3
33
33 3 3 3 3
xyz
2
yz zx xy
Trước hết ta chứng minh bất đẳng thức sau
32
3
33 22
xx
yz yz
Thật vậy, bất đẳng thức trên tương đương với
23
32
32
22 33 2222 33
33 22
xx
yz yz 3yzyz 2yz
yz yz
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy.
Áp dụng tương tự ta được

333 222
3
33
33 3 3 3 3 22 2 2 2 2
xyz xyz
yz zx xy yz zx xy
Ta cần chứng minh
222
22 2 2 2 2
xyz
2
yz zx xy
Áp dụng bất đẳng thức Cauchy ta được
222 2 2 2
22 2 2 2 2
22 2 22 2 22 2
222
222 222 222
xyz x y z
yz zx xy
xy z yz x zx y
2x 2y 2z
2
xyz xyzxyz
Vậy bất đẳng thức ban đầu được chứng minh.
Ví dụ 6.20: Cho a, b, c là các số thực dương thoả mãn
abc 1 . Chứng minh rằng:
111
a1 b1 c1 1
bca
Lời giải
Do
abc 1 nên ta có thể đặt
xyz
a;b;c
yzx
với x, y, z là các số thực dương.
Bất đẳng thức cần chứng minh được viết lại là
xzyxzy
1111
yyzzxx
Hay
xyz x y z y z x z x y
Do x, y, z có vai trò như nhau, không mất tính tổng quát ta giả sử
xyz0
Như vậy
xyz0;xzy 0 . Như vậy ta xét các trường hợp
- Nếu
yzx 0 thì bất đẳng thức trên hiển nhiên đúng.
- Nếu
yzx 0 , áp dụng bất đẳng thức Cauchy cho hai số dương ta có
xyzyzx x; yzxzx y y; zxyxyz z
Nhân theo vế các bất đẳng thức trên ta được điều phải chứng minh.
Ví dụ 6.21: Cho a, b, c là các số thực dương thoả mãn
abc a b c 2
. Chứng minh rằng:
3
abc abc
2
Lời giải
Biến đổi giả thiết
abc a b c 2 ta được
a1b1c1 a1b1 b1c1 c1a1
111
1
a1b1ca
Đặt
111
x;y;z
a1 b1 ca
suy ra xyz1
Từ trên suy ra
1x yz 1y zx 1z xy
a;b;c
xx yy zz
Và bất đẳng thức được viết lại thành
xyyzzx
yz zx xy 3
xyz2 xyz
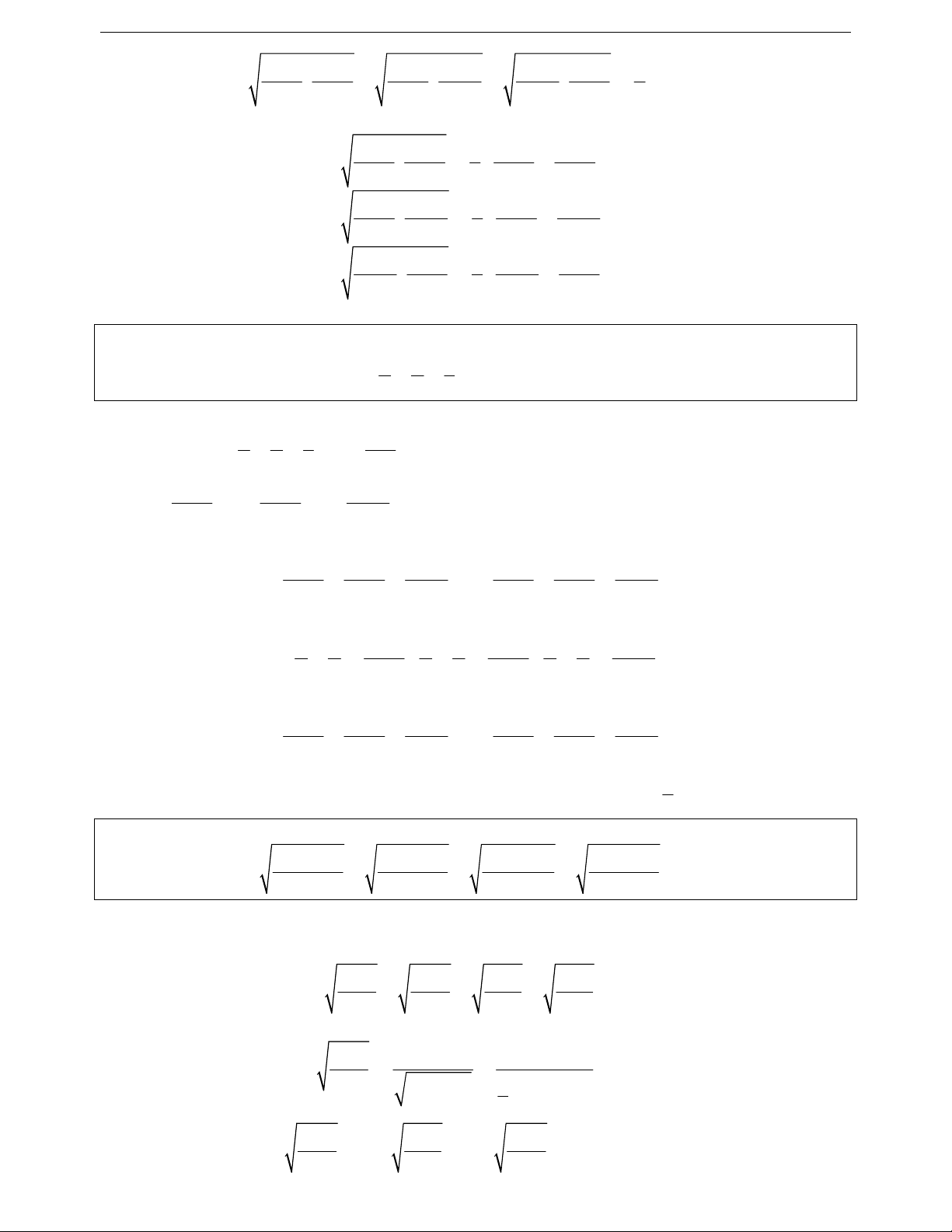
Hay
xy yz zx3
.. .
yzzx zxxy xyyz 2
Áp dụng bất đẳng thức Cauchy ta được
xy1x y
.
yzzx 2yz zx
yz1y z
.
zxxy 2zx xy
zx1z x
.
xyyz 2xy yz
Cộng theo vế ba bất đẳng thức trên ta thu được điều phải chứng minh
Ví dụ 6.22: Cho a, b, c là các số thực dương thoả mãn
ab bc ca 2abc 1
. Chứng minh rằng:
111
4a b c
abc
Lời giải
Từ giả thiết suy ra
111 1
2
abc abc
Đặt
xyz
a;b;c
yz zx xy
, với x, y, z 0; x y z 1.
Khi đó bất đẳng thức cần chứng minh trở thành
yz zx xy x y z
4
xyz yzzxxy
Áp dụng bất đẳng thức Cauchy ta được
xx 4x yy 4y zz 4z
;;
yz yzxz zxxyxy
Cộng theo vế ba bất đẳng thức trên ta được
yz zx xy x y z
4
xyz yzzxxy
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
Ví dụ 6.23: Cho a, b, c, d là các số thực dương. Chứng minh rằng:
abcd
2
bcd cda dab abc
Lời giải
Không mất tính tổng quát ta có thể chọn
abcd1
Khi đó bất đẳng thức cần chứng minh tương đương với
abcd
2
1a 1b 1c 1c
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có
aa a
2a
1a 1
1aa
1aa
2
Hoàn toàn tương tự ta có
bcd
2b; 2c; 2d
1b 1c 1d

Cộng vế theo vế bốn bất đẳng thức ta được:
abcd
2
1a 1b 1c 1c
Ở đây dấu đẳng thức không xẩy ra nên
abcd
2
1a 1b 1c 1c
Bất đẳng thức được chứng minh hoàn toàn.
Khi đưa lời giải trên cho bài toán trên, chắc hẳn bạn đọc sẽ thắc mắc là tại sao lại có thể chọn được
abcd1 và nếu chọn abcd k bất kì thì bài toán có giải được không? Và ngoài
cách chọn điều kiện như trên có thể chọn theo cách khác (chẳng hạn như
abcd 1 ) được không? Câu trả
lời là hoàn toàn được, thực chất việc chọn này bắt nguồn từ việc đổi biến. Sau đây là cách đổi biến dẫn
đến kết quả
abcd1. Ta thực hiện biến đổi một hạng tử bên vế trái như sau:
aa
a
abcd abcd
bcd bcd b c d
abcd abcdabcdabcd
Tới đây ta đổi biến như sau:
abcd
x;y;z;t
abcd abcd abcd abcd
Thay vào biểu thức trên ta được:
ax
bcd yzt
và xyzt1
Áp dụng cho vế trái của bất đẳng thức cần chứng minh ta được
xyz t
2
yzt ztx txy xyz
Và
xyzt1
Như vậy sau phép đổi biến ta có một bất đẳng thức mới có hình thức hoàn toàn giống như bất
đẳng thức cần chứng minh và được bổ sung thêm điều kiện giả thiết cho các biến là
xyzt1.
Ví dụ 6.24: Cho a, b , c là các số thực dương tùy ý Chứng minh rằng
9
abcabbcca abbcca
8
Lời giải
Đây là một bất đẳng thức đơn giản được chứng minh bằng phép biến đổi tương đương kết hợp với
bất đẳng thức Cauchy. Ta thử chứng minh bằng phương pháp đổi biến xem sao
Bất đẳng thức tương đương với
8a b c ab bc ca 9a b b c c a
Chia cả hai vế cho
3
abc ta được
333
222
333
33 33 33
8a b c ab bc ca 9a b b c c a
abc abc
abc ab bc ca
8
abc abc abc
(abc) (abc) (abc)
abbc ac
9
abc abc abc abc abc abc

Đặt
333
abc
x ; y ; z xyz 1
abc abc abc
Thay vào bất đẳng thức trên ta được
8x y z xy yz zx 9x y y z z x
Như vậy sau phép đổi biến ta có một bất đẳng thức mới có hình thức hoàn toàn giống như bất đẳng
thức cần chứng minh và được bổ sung thêm điều kiện cho biến là
xyz 1
. Bây giờ ta chứng minh bất
đẳng thức trên với điều kiện của biến là
xyz 1
.Thật vậy:
222 222 222 222
222 222
8 x y z xy yz zx 9 x y y z z x
8 3 x y y z z x xy yz zx 9 2 x y y z z x xy yz zx
xxyyzz
6xyyzzxxy yz zx 6
yzxzxy
Dễ thấy rằng theo bất đẳng thức Cauchy thì bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh hoàn toàn.
Ví dụ 6.25: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2
222
ab c bc a ca b
6
5
bc a ca b ab c
Lời giải
Không mất tính tổng quát ta có thể chọn
abc1
222
a1 a b1 b c1 c
6
5
12a2a 12b2b 12c2c
Theo bất đẳng thức Cauchy ta có
2
2
a1
2a 1 a
2a 1 a
24
Suy ra
2
2
a1 1aa3
12a2a 12a1a 1 0
44
Do đó ta được
2
a1 a 4a1 a
a3
4. 4 1
a3 a3
12a2a
1aa 3
Hoàn toàn tương tự ta được
222
a1 a b1 b c1 c
333
41 1 1
a3 b3 c3
12a2a 12b2b 12c2c
3.9 6
43
abc9 5
Vậy bài toán được chứng minh xong. Dấu đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 6.26: Cho các số dương a, b, c thỏa mãn
abc 1. Chứng minh rằng:
222
1113
2
abc bca cab
Lời giải
Đặt
111
x;y;z
abc
khi đó ta thu được xyz 1 .

Ta có
22
2
1xxyzx
1 1 yz yz
abc
yz
Bất đẳng thức cần chứng minh được viết lại thành
xyz3 x y z 9
111
yz zx xy 2 yz zx xy 2
1119
xyz
yz zx xy 2
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
Ví dụ 6.27: Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
333
222
2a 2b c 2b 2c a 2c 2a b
9
abc
ab4c bc4a ca4b 2
Lời giải
Đặt
x 2a 2b c; y 2b 2c a; z 2c 2a b
Vì a, b, c là độ dài ba cạnh của một tam giác nên
x; y; z
là các số dương.
Bất đẳng thức cần chứng minh được viết lại thành
33 3222
xyxxyz
yz zx xy 2
Áp dụng bất đẳng thức Cauchy ta có
333
222
xy z yz x zx y
xyz
x; y; z
yz 4 yz 4 xy 4
Cộng theo vế các bất đẳng thức trên ta được
33 3
222
33 3
222
xyxxyyzzx
xyz
yz zx xy 2
xyx xyyzzx
xyz
yz zx xy 2
Áp dụng bất đẳng thức
222
xyz xyyzzx ta được
33 3222
xyxxyz
yz zx xy 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
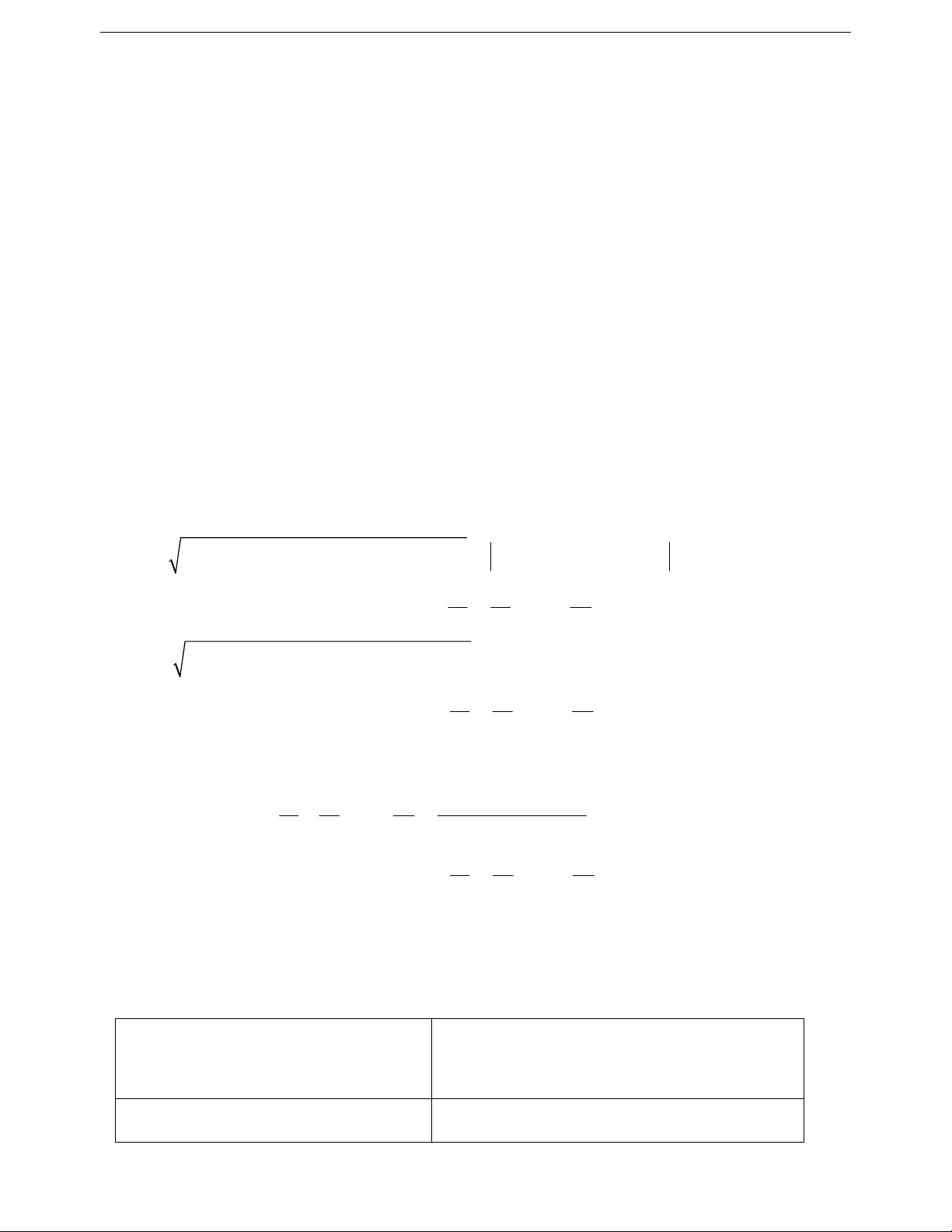
Chủ đề 6
MỘT SỐ KỸ THUẬT SỬ DỤNG BẤT ĐẲNG THỨC BUNHIACOPXKI
A. Kiến thức cần nhớ
1. Giới thiệu bất đẳng thức Bunhiacopxki
Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki –
Schwarz, đây là một bất đẳng thức do ba nhà toán học độc lập phát hiện và đề xuất, nó có nhiều ứng dụng
trong các lĩnh vực toán học. Ở nước ta, để cho phù hợp với chương trình sách giáo khoa, trong tài liệu này
chúng ta cũng sẽ gọi nó là bất đẳng thức Bunhiacopxki, gọi theo tên nhà Toán học người Nga
Bunhiacopxki.
Đây là một bất đẳng thức cổ điển nổi tiếng và quen thuộc đối với phần lớn học sinh nước ta. Nó
ứng dụng rất nhiều trong các bài toán về bất đẳng thức và cực trị. Trong phạm vi chương trình Toán
THCS, chúng ta cũng chỉ quan tâm đến các trường hợp riêng của bất đẳng thức Bunhiacopxki.
2. Các dạng biểu diễn của bất đẳng thức Bunhiacopxki
a. Dạng tổng quát
+ Cho hai dãy số tùy ý
123 n
a ; a ; a ; ...; a
và
123 n
b ; b ; b ; ...; b
. Khi đó ta có:
Dạng 1:
2
22 222 2
12 n12 n 1122 nn
a a ... a b b ... b a b a b ... a b
Dạng 2:
22 222 2
12 n12 n 1122 nn
a a ... a b b ... b a b a b ... a b
- Dấu đẳng thức xảy ra ở dạng 1 và dạng 2 là:
12 n
12 n
aa a
...
bb b
Dạng 3:
22 222 2
12 n12 n 1122 nn
a a ... a b b ... b a b a b ... a b
- Dấu đẳng thức xảy ra ở dạng 3 là:
12 n
12 n
aa a
... 0
bb b
Dạng 4: Cho hai dãy số tùy ý
12 n
a ; a ; ...; a và
12 n
x ; x ; ...; x với
12 n
x ; x ; ...; x 0
Khi đó ta có
2
22 2
12 n
12 n
12 n 12 n
aa...a
aa a
...
x x x x x ... x
- Dấu đẳng thức xảy ra ở dạng 4 là:
12 n
12 n
aa a
... 0
xx x
Trong các dạng trên thì bất đẳng thức dạng 1, dạng 2, dạng 3 gọi là các bất đẳng thức
Bunhiacopxki dạng cơ bản và bất đẳng thức dạng 4 còn được gọi là bất đẳng thức Bunhiacopxki dạng
phân thức.
b. Một số dạng đặc biệt
n2 n3
2
2222
abxy axby
2
222222
abcxyz aybycz

2222
abxy axby
222222
abcxyz aybycz
2222
abxy axby
222222
abcxyz aybycz
2
22
ab
ab
xy xy
x, y 0
2
222
abc
abc
xyz xyz
x, y 0
Đẳng thức xẩy ra khi
ab
xy
Đẳng thức xẩy ra khi
abc
xyz
B. Một số kỹ thuật sử dụng bất đẳng thức Bunhiacopxki
1. Kỹ thuật chọn điểm rơi
Cũng tương tự như bất đẳng thức Cauchy, khi sử dụng bất đẳng thức Bunhiacopxki để chứng
minh bất đẳng thức ta cần phải bảo toàn được dấu đẳng thức xẩy ra, điều này có nghĩa là ta cần phải xác
định được điểm rơi của bài toán khi áp dụng bất đẳng thức Bunhiacopxki. Để rõ hơn ta tìm hiểu một số ví
dụ sau
Ví dụ 1.1: Cho a là số thức dương thỏa mãn mãn
a2 . Tìm giá trị nhỏ nhất của biểu thức:
2
2
1
Aa
a
+ Sai lầm thường gặp:
Sai lầm 1:
2
2
11
A a 2a. 2
a
a
.
Sai lầm 2:
2
2
2
11111
A11a a .42
22a2
a
Do đó giá trị nhỏ nhất của A là
2 .
+ Nguyên nhân sai lầm: Để có giá trị nhỏ nhất là
2 thì dấu đẳng thức xẩy ra tại
1
aa1
a
trái với giả thiết a2
+ Phân tích tìm lời giải: Xét bất đẳng thức
2
2222
abxy axby với dấu đẳng thức xẩy ra
tại
ab
xy
. Giả sử với các số ;
ta có
2222
222 2 22
11 1 1
Aa .a . a
a
aa
Ta cần chọn hai số
;
sao cho giá trị nhỏ nhất của A đạt được tại a2 . Từ đó ta có sơ đồ điểm rơi:
a2
4
a1
1
a
+ Lời giải đúng: Áp dụng bất đẳng thức Bunhiacopxki ta có

2
222
22
22
11 1 1 1
Aa a .4 1 4a
17 17 a
aa
1a 1 15a 1 15 17
1
54 a 4 17 2 4
Vậy giá trị nhỏ nhất của A là
17
.
4
Đẳng thức xẩy ra khi và chỉ khi a2 .
Ví dụ 1.2: Cho a, b, là các số thực dương thỏa mãn
ab4. Tìm giá trị nhỏ nhất của biểu thức:
22
22
11
Aa b
ab
+ Sai lầm thường gặp:
22
22
11
Aa b 2222
ab
Do đó giá trị nhỏ nhất của A là
22.
+ Nguyên nhân sai lầm: Để có giá trị nhỏ nhất là
22 thì dấu đẳng thức xẩy ra tại
11
ab ab1
ab
Khi đó
ab2 trái với giả thiết ab4
+ Phân tích tìm lời giải: Xét bất đẳng thức
2222
abxy axby với dấu đẳng thức xẩy ra
tại
ab
0
xy
. Khi đó với ý tưởng chuyển đổi một biểu thức trong căn thành một biểu thức ngoài căn.
Giả sử với các số
;
ta có
2222
22
22 22
2222
22
22 22
22
11 1 1
a.a. a
a
aa
11 1 1
b.b. b
b
bb
111
Aab
ab
Do A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt được tại
ab2. Từ đó ta có sơ đồ điểm rơi:
a1
4
a
ab2
b1 1
b
+ Lời giải đúng: Áp dụng bất đẳng thức Bunhiacopxki ta có
2222
22
2222
22
11 1 1 1
a.a.414a
a
aa
17 17
11 1 1 1
b.b.414b
b
cb
17 17

Khi đó ta được
111
A4ab
ab
17
Để ý ta thấy
11 4
abab
, do đó áp dụng bất đẳng thức Cauchy và giả thiết ta được
15 a b
141ab4
A4ab
ab 4 ab 4
17 17
1
215 17
17
Dấu đẳng thức xẩy ra
a1
4a
ab2
b1
4b
Vậy giá trị nhỏ nhất của A là
17. Đẳng thức xẩy ra khi ab2.
Ví dụ 1.3: Cho a, b, c là các số thực dương thỏa
abc6
. Tìm giá trị nhỏ nhất của biểu thức:
222
222
111
Aa b c
bca
+ Sai lầm thường gặp:
3
222
222
111abc
A a b c 2. 2. 2. 3 2 2 3 2
bca
bca
Do đó giá trị nhỏ nhất của A là
32
.
+ Nguyên nhân sai lầm: Để có giá trị nhỏ nhất là
32
thì dấu đẳng thức xẩy ra tại
111
abc abc1
abc
Khi đó
abc3 không thỏa mãn giả thiết abc6
+ Phân tích tìm lời giải: Xét bất đẳng thức
2222
abxy axby với dấu đẳng thức xẩy ra
tại
ab
0
xy
. Khi đó với ý tưởng chuyển đổi một biểu thức trong căn thành một biểu thức ngoài căn.
Giả sử với các số
;
ta có
2222
22
22 22
2222
22
22 22
2222
22
22 22
11 1 1
a.a. a
b
bb
11 1 1
b.b. b
c
cc
11 1 1
c.c. c
a
aa
22
1111
Aabc
abc
Do A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt được tại
abc2
. Từ đó ta có sơ đồ điểm rơi:
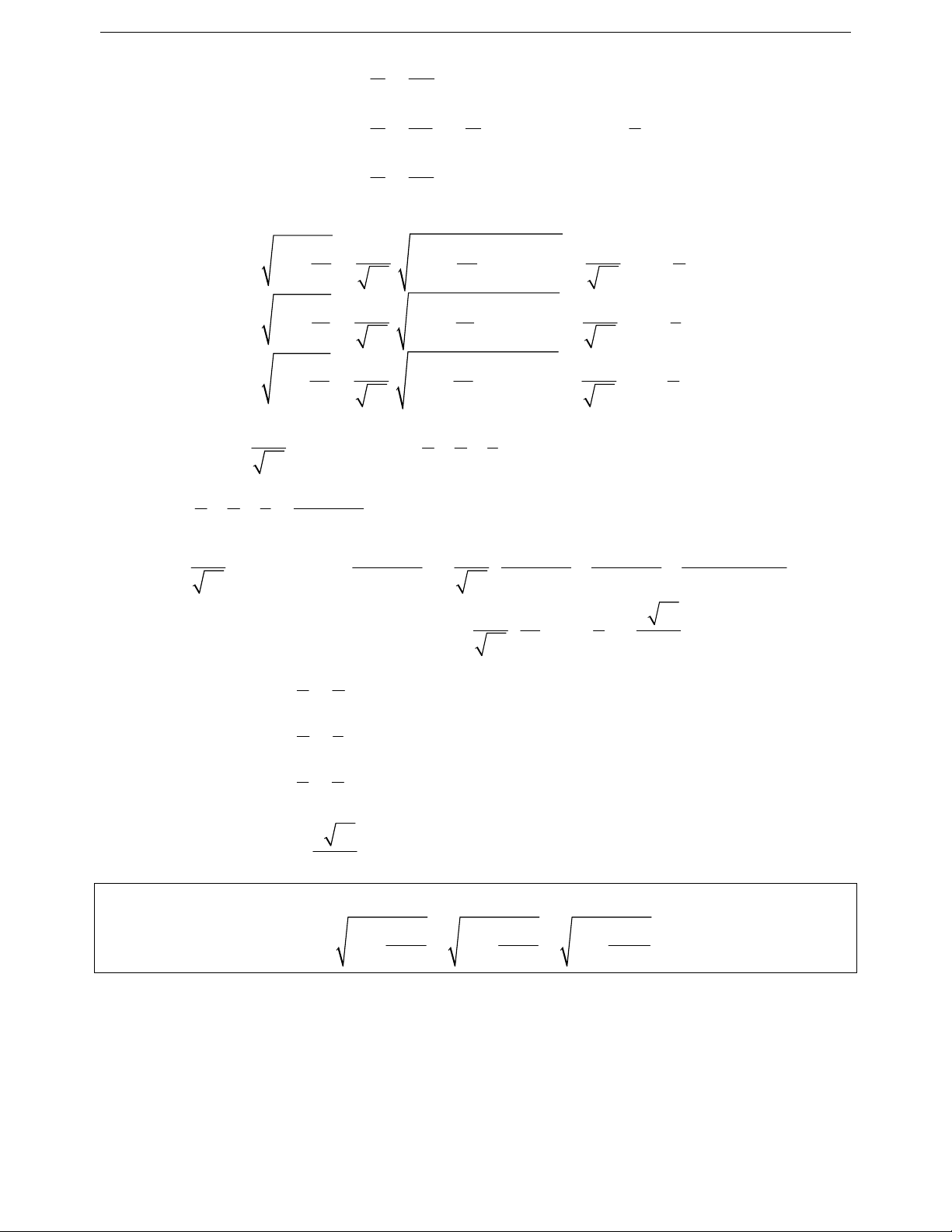
a1
b
4
b1 4
abc2 abbcca
1
c1
c1
a
+ Lời giải đúng: Áp dụng bất đẳng thức Bunhiacopxki ta có
2222
22
2222
22
2222
22
11 1 1 1
a.a.414a
b
bb
17 17
11 1 1 1
b.b.414b
c
cc
17 17
11 1 1 1
c.c.414c
a
aa
17 17
Khi đó ta được
1111
A4abc
abc
17
Để ý ta thấy
111 9
abcabc
, do đó áp dụng bất đẳng thức Cauchy và giả thiết ta được
15 a b c
191abc9
A4abc
abc 4 abc 4
17 17
115 3 317
.6 2.
422
17
Dấu đẳng thức xẩy ra
a1
4b
b1
abc2
4c
c1
4a
Vậy giá trị nhỏ nhất của A là
317
,
2
khi
abc2
Ví dụ 1.4: Cho các số thực dương a, b,c thỏa
abc6.
Tìm giá trị nhỏ nhất của biểu thức:
222
111
Aa b c
bc ca ab
Phân tích: Chuyển đổi một biểu thức trong căn thành một biểu thức ngoài căn. Giả sử với các số ;
ta
có:

2
2222
22 22
2
22
2
22
22
11 1 1
aa a
bc
bc bc
11
bb
ca
ca
11
cc
ab
ab
1111
Aabc
ab bc ca
Do A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt tại
abc2
Do đó ta có sơ đồ điểm rơi
a1
b
4
b1 4
abc2 abbcca
1
c1
c1
a
Lời giải
2222
2
2
22
11 1 1 1
a.a.414a
bc bc
17 17 b c
11 1
b4b
ca
17 c a
11 1
c4c
ab
ab
41
Cộng theo vế các bất đẳng thức trên ta được
1111
A4abc
17 a b b c c a
Áp dụng bất đẳng thức Cauchy và Bunhiacopxki ta được
19
A4abc
17 a b a b c a
19
4 a b c
17 6 a b c
3
131 1 9 9
a b c a b c
88
17 2 6 a b c 2 6 a b c
131 1 9 9 317
.6 3 a b c . .
88 2
17 2 6 a b c 2 6 a b c
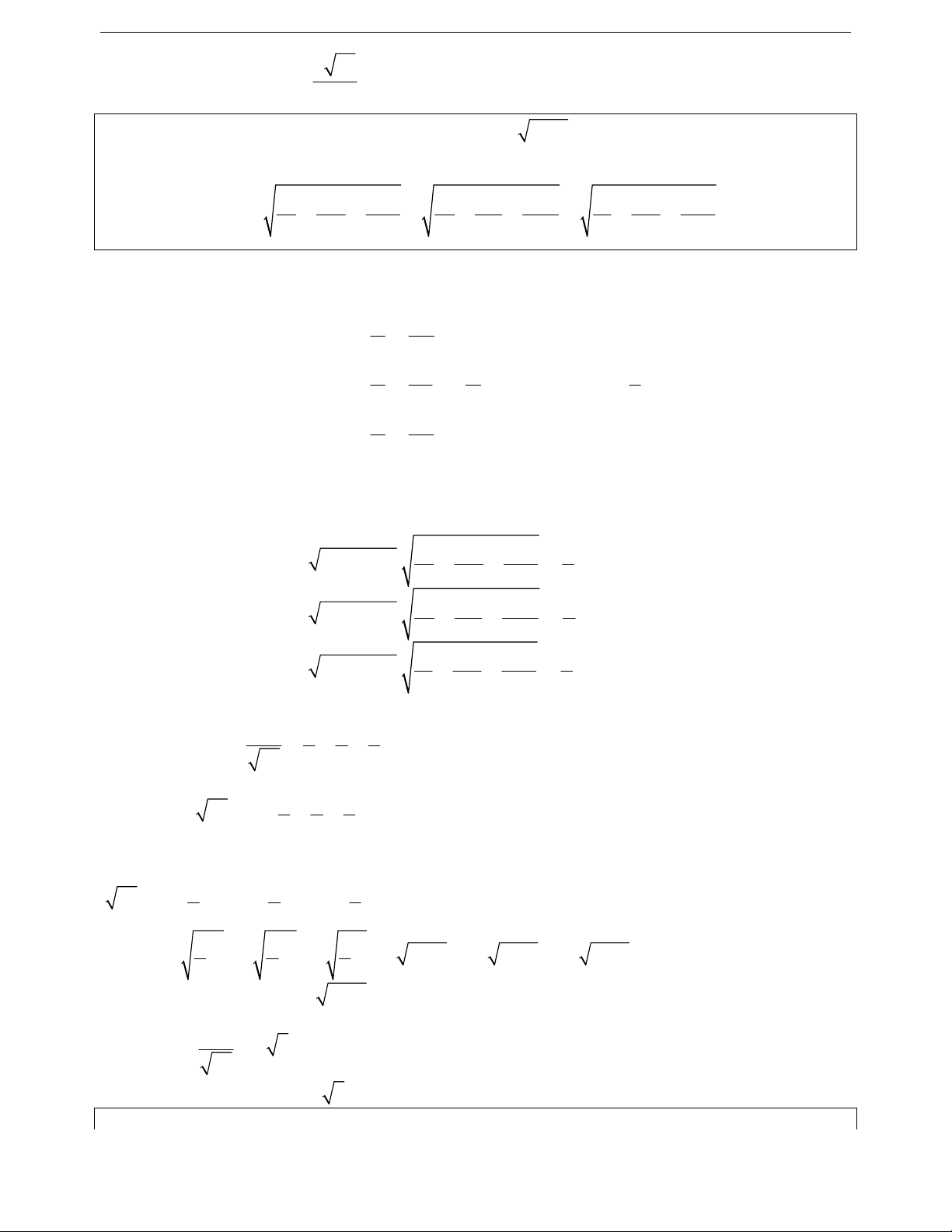
Vậy giá trị nhỏ nhất của A là
317
2
. Đẳng thức xẩy ra khi và chỉ khi abc2
Ví dụ 1.5: Cho các số thực dương a, b,c thỏa
a b c 2abc 10.
Tìm giá trị nhỏ nhất của biểu
thức
222 2 22 2 22
222
89b ca 89c ab 89a bc
A
24 24 24
abc
Phân tích: Do biểu thức A là biểu thức đối xứng với a, b, c nên ta dự đoán giá trị nhỏ nhất của A đạt tại
abc2
. Do đó ta có sơ đồ điểm rơi
a1
b
4
b1 4
abc2 abbcca
1
c1
c1
a
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
222
2
222
2
222
2
89b ca 4
2184. 9bca
24a
a
89c ab 4
2184. 9bca
24b
b
89a bc 4
2184. 9bca
24a
c
Do đó ta được
1444
A9abcabbcca
abc
24
Hay
444
24.A 9 a b c ab bc ca
abc
Áp dụng bất đẳng thức Cauchy ta được
444
24.A a b c2abc2bac2cab6abc
abc
444
2 .a 2 .b 2 .c 2 2abc 2 2abc 2 2abc 6 a b c
abc
12 6 a b c 2abc 72
Suy ra
ta được
72
A66
24
Vậy giá trị nhỏ nhất của A là
66. Đẳng thức xẩy ra khi và chỉ khi abc2.
Ví dụ 1.6: Cho a, b, c là các số thực dương thỏa mãn
abc2. Tìm giá trị nhỏ nhất của biểu thức:
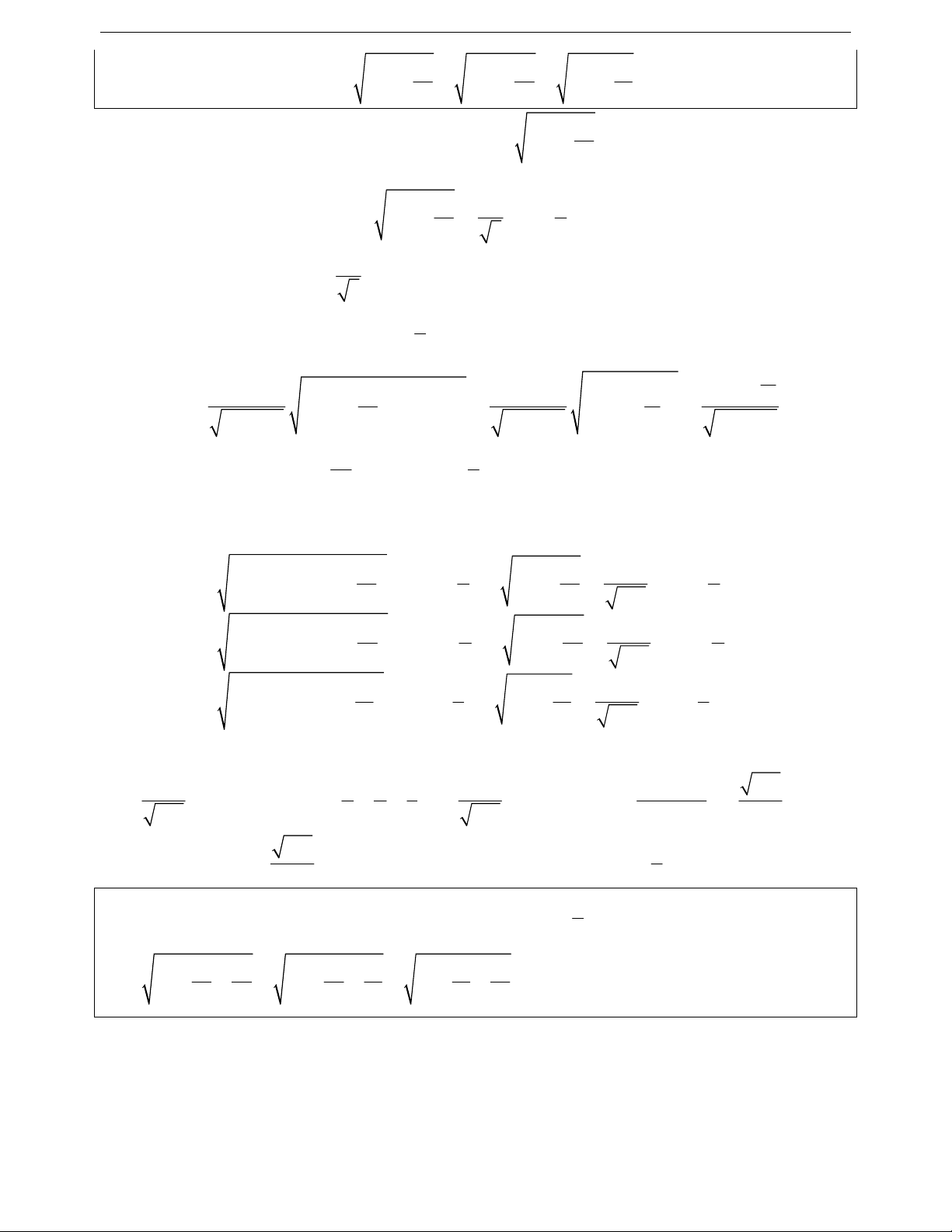
222
222
111
A4a 4b 4c
abc
Phân tích: Trong ví dụ này ta xét biểu thức đại diện
2
2
1
A4a
a
. Một cách tự nhiên ta tìm cách khử
căn của biểu thức. Nếu áp dụng bất đẳng thức Bunhiacopxki một cách bình thường:
2
2
11 1
4a 2a
a
a
2
Đẳng thức xảy ra khi
1
a
2
, khi đó nếu áp dụng tương tự thì không thỏa mãn giả thiết của toán.
Dự đoán đẳng thức xẩy ra tại
2
abc .
3
Khi đó ta cần chọn một bộ số ;
để có đánh giá
2
222
2
22 22 22
.2a
11 1
a
A4a 2a
a
a
Dấu đẳng thức xẩy ra tại
a
2a
với
2
a
3
. Từ đó dễ dàng chọn được
8; 9ab
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki:
22 2 2
22
22 2 2
22
22 2 2
22
19 119
894a 16a 4a 16a
aa
aa
145
19 119
8 9 4b 16b 4b 16b
bb
bb
145
19 119
8 9 4c 16c 4c 16c
cc
cc
145
Từ đó ta được
1 1 1 1 1 81 145
A 16a b c 9 16a b c
abc abc 2
145 145
Vậy giá
trị nhỏ nhất của A bằng
145
2
. Đẳng thức xẩy ra khi và chỉ khi
2
abc .
3
Ví dụ 1.7: Cho a, b, c là các số thực dương thỏa mãn
3
abc
2
. Tìm giá trị nhỏ nhất của biểu thức:
222
22 22 22
11 11 11
Aa b c
ab bc ca
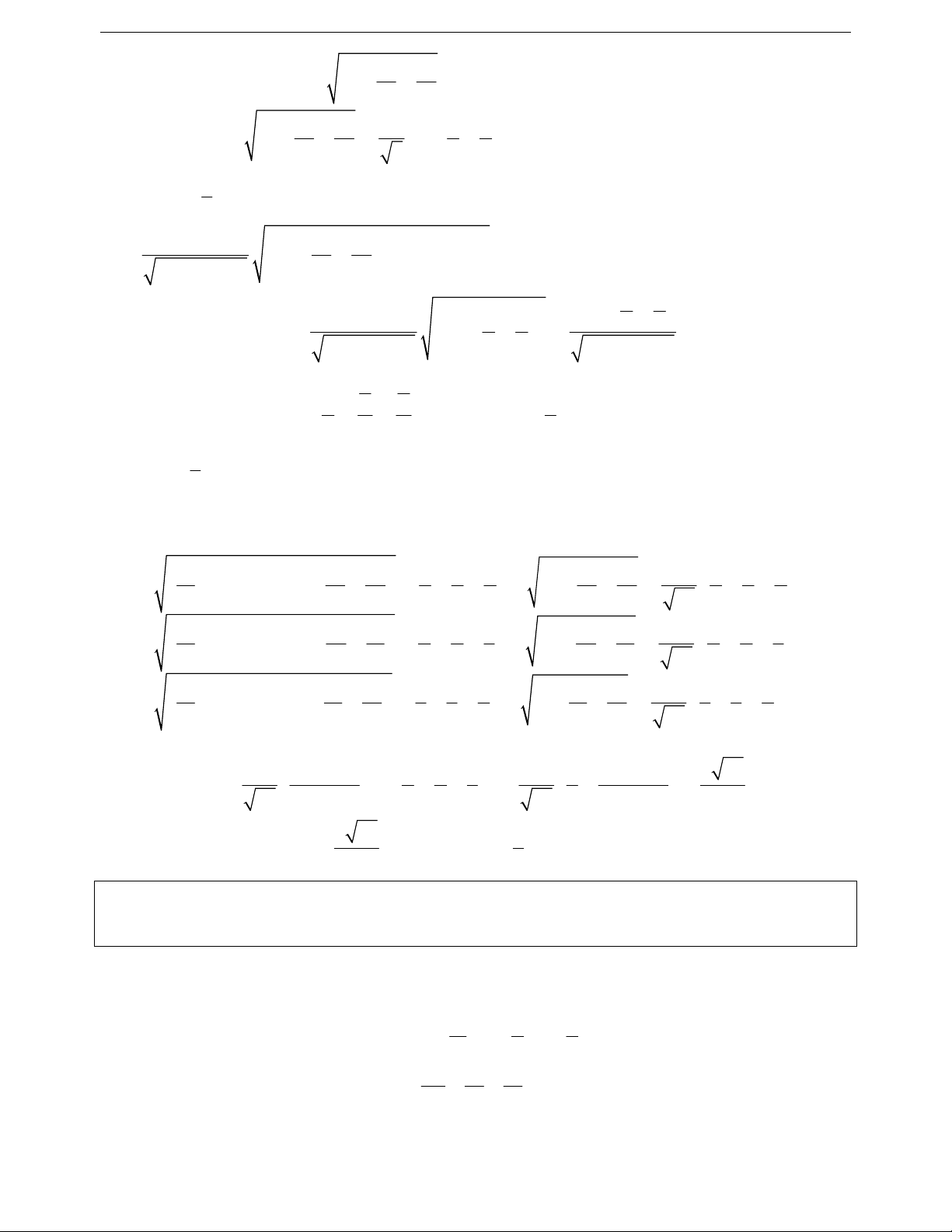
Phân tích: Xét biểu thức
2
22
11
Aa
ab
. Nếu áp dụng bất đẳng thức Bunhiacopxki một cách trực
tiếp thì ta được
2
22
11 1 11
aa
ab
ab
3
. Khi đó dấu đẳng thức không xẩy ra tại
1
abc
2
. Từ đó ta chọn các số
p, q, r
để có đánh giá như sau:
2222
22
222
2
222 222
111
Aapqr
ab
pqr
qr
pa
1qr
ab
ap
ab
pqr pqr
Và đẳng thức xảy ra tại
11
a
ab
pq r
với
2
abc
3
. Từ đó ta chọn được một bộ số thỏa
mãn là
1
p,qr2
2
.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki:
22 2 2
222 22
22 2 2
222 22
22 2 2
222 22
1 1 1 a22 1 1 2 a22
22 a a
2ab 2ab
2ab ab
33
1 1 1 b22 1 1 2 b22
22 b b
2bc 2bc
2bc bc
33
1 1 1 c22 1 1 2 c22
22 c c
2ca 2c
2ca ca
33
a
Từ đó ta được
2abc 111 23 36 333
A4
2abc 4abc2
33 33
Vậy giá trị nhỏ nhất của A bằng
333
2
khi
1
abc
2
.
Ví dụ 1.8: Cho a, b, c là các số thực dương thỏa mãn
222
a 4b 9c 2015 . Tìm giá trị lớn nhất của
biểu thức: Pabc
Phân tích và lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
2
2
22 22 22
222
111
Pabc am. bn.cp.
mnp
111
am bn cp
mnp
Để sử dụng được giả thiết ta
222
a4b9c1cần chọn một bộ số m; n; p sao cho hệ sau thỏa
mãn

22 22 22 2 2 2
ma nb pc x 4y 9z
m1
am bn cp
n2
111
p3
mnp
Khi đó ta có lời giải như sau
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
2
2
222
222
11
Pabc a.2b.3c.
2p
111 14
a4b9c
36
123
Do đó ta được
14
P
6
hay giá trị nhỏ nhất của P là
14
6
Dấu đẳng thức xẩy ra khi và chỉ khi
222
a4b9c1
111
a;b ;c
a4b9c
72863
Ví dụ 1.9: Cho a, b, c là các số thực dương thỏa mãn
a2b3c14
. Tìm giá trị nhỏ nhất của biểu
thức:
222
Pa b c
Phân tích và lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222222
mnkabc manbkc
Để áp dụng giả thiết
a2b3c 6 ta cần chọn một bộ số
m; n; k
thỏa mãn hệ sau
m1
ma nb kc a 2b 3c
n2
abc
k3
mnk
Khi đó ta có lời giải như sau
Áp dụng bất đẳng thức Binhiacopxki ta được
2
2
2222 22
a2b3c
114
P.123abc 14
14 14 14
Do đó giá trị nhỏ nhất của P là
14 . Đẳng thức xẩy ra khi và chỉ khi
a2b3c14
a1;b2;c3
abc
123
Ví dụ 1.10: Cho a, b, c là các số thực dương sao thỏa mãn
4a 9b 16c 49
. Chứng minh rằng:
12564
49
ab c
Phân tích và lời giải
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki ta được

2
222
12564
ma nb kc m 5n 8k
ab c
Như vậy ta cần chọn một bộ số
m; n; k sao cho hệ sau thỏa mãn
222
m a n b k c 4a 9b 16c 49
nb kc
ma
58
Thử một số trường hợp ta chọn được
m2;n5;k8
, khi đó ta có lời giải như sau
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
12564
4a 9b 16c 2 3.5 4.8 49
ab c
Hay
2
1 25 64 1 25 64
49 49 49
ab c ab c
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
158
13
a;b;c2
2a 3b 4c
25
4a 9b 16c 49
Cách 2: Quan sát bất đẳng thức ta nhận thấy có thể sử dụng bất đẳng thức Binhacopxki dạng phân thức.
Tuy nhiên chú ý đến giả thiết
4a 9b 16c 49 , ta cần nhân thêm hệ số để khi áp dụng dưới mẫu xuất
hiện
4a 9b 16c . Do đó ta có thể chứng minh bài toán trên như sau
Áp dụng bất đẳng thức Bunhacopcki dạng phân thức ta được
2
2
21532
1 25 64 4 225 1024 49
49
a b c 4a 9b 16a 4a 9b 16c 49
Đẳng thức xẩy ra khi và chỉ khi
158
13
a;b;c2
2a 3b 4c
25
4a 9b 16c 49
Ví dụ 1.11: Cho a, b là các số thực dương thỏa mãn
ab2. Tìm giá trị nhỏ nhất của biểu thức:
22
14
P
ab
ab
+ Sai lầm thường gặp: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
2
22 22 22 2
18 18
14 1 8
P18
ab 2ab
ab ab ab2ab
ab
+ Nguyên nhân sai lầm: Dự đoán dấu đẳng thức xẩy ra tại
ab khi đó
22
18
2ab
ab
. Tức là dấu
đẳng thức của bất đẳng thức trên không xẩy ra

+ Phân tích: Để áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta chọn một số k sao cho
2
2
2
22 22
1k
1k
1k
2ab
ab ab2ab
và đảm bảo dấu đẳng thức xẩy ra, tức là thỏa mãn điều kiện
22
1k
2ab
ab
với ab , do đó ta chọn được k1 .
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
22 22 22
11
14 1 17 7 7
P4
ab 2ab 2ab 2ab 2ab
ab ab ab2ab
Mặt khác ta lại có
2
ab 1
ab
24
Do đó ta được
P18 , hay giá trị nhỏ nhất của biểu thức P là 18. Đẳng thức xẩy ra khi và chỉ khi
1
ab
2
.
Ví dụ 1.12: Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:
222
19
30
ab ab bc
abc
Phân tích và lời giải
Trước hết ta dự đoán đẳng thức xẩy ra tại
1
abc
3
. Khi sử dụng bất đẳng thức
Bunhiacopxki dạng phân thức ta chú ý cộng các mẫu để có thể viết được thành
2
abc .
Để ý là nếu đánh giá
2
2
222 2
12
12
12
abc
2ab bc ca
abc
, khi đó đẳng
thức không xẩy ra vì
222
12
abc
2ab bc ca
Như vậy để có thể áp dụng được bất đẳng thức Bunhiacopxki dạng phân thức ta làm như sau
2
2
2
222 2
1k
1k
1k
abc
2ab bc ca
abc
Ta cần chọn k để đẳng thức sau đúng
222
1k
abc
2ab bc ca
, dễ dàng chọn được giá trị
k2
. Đến đây ta có lời giải như sau
Áp dụng bất đẳng thức Bunhiacopxki ta được
222 222
2
2
19 1 4 7
ab bc ca ab bc ca
abc abc
2ab bc ca
12
77
9
ab bc ca ab bc ca
abc
.

Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
7
21
ab bc ca
. Tuy nhiên, dễ thấy
2
abc
1
ab bc ca ab bc ca
33
Do đó ta được
7
21
ab bc ca
Vậy bất đẳng thức được chứng minh.
Ví dụ 1.13: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
222
222
abc1
3
5a b c 5b c a 5c a b
Phân tích và lời giải
Dự đoán đẳng thức xẩy ra tại
abc, Trước hết ta để ý đến mẫu số có thể phân tích được
2
22222
5a b c a b c 2 2a bc
. Quan sát bất đẳng thức ta thấy có thể áp dụng
được bất đẳng thức Bunhiacopxki. Khi vậy ta cần chọn các số
m; n để được bất đẳng thức
22
22
22 22
2222
222 2 2
2
mna mna
ma na
abc
abc22abc 22abc
5a b c
Đồng thời đẳng thức
222
2
mn
abc
22a bc
đúng với abc.
Dễ dàng chọn được
m1;n2
Khi đó ta có thể giải được bài toán như sau:
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
2
2 22
22222
222 2
2
12a
a1 1a 2a
99
abc2abc
abc 22abc
5a b c
Chứng minh tương tự ta được
222
22222
2
222
22222
2
b1b 2b
9
abc2bac
5b c a
c1c 2c
9
abc2cab
5c a b
Do đó ta có
222
222
222
222
222
abc
5a b c 5b c a 5c a b
12a 2b 2c
1
9
2a bc 2b ca 2c ab
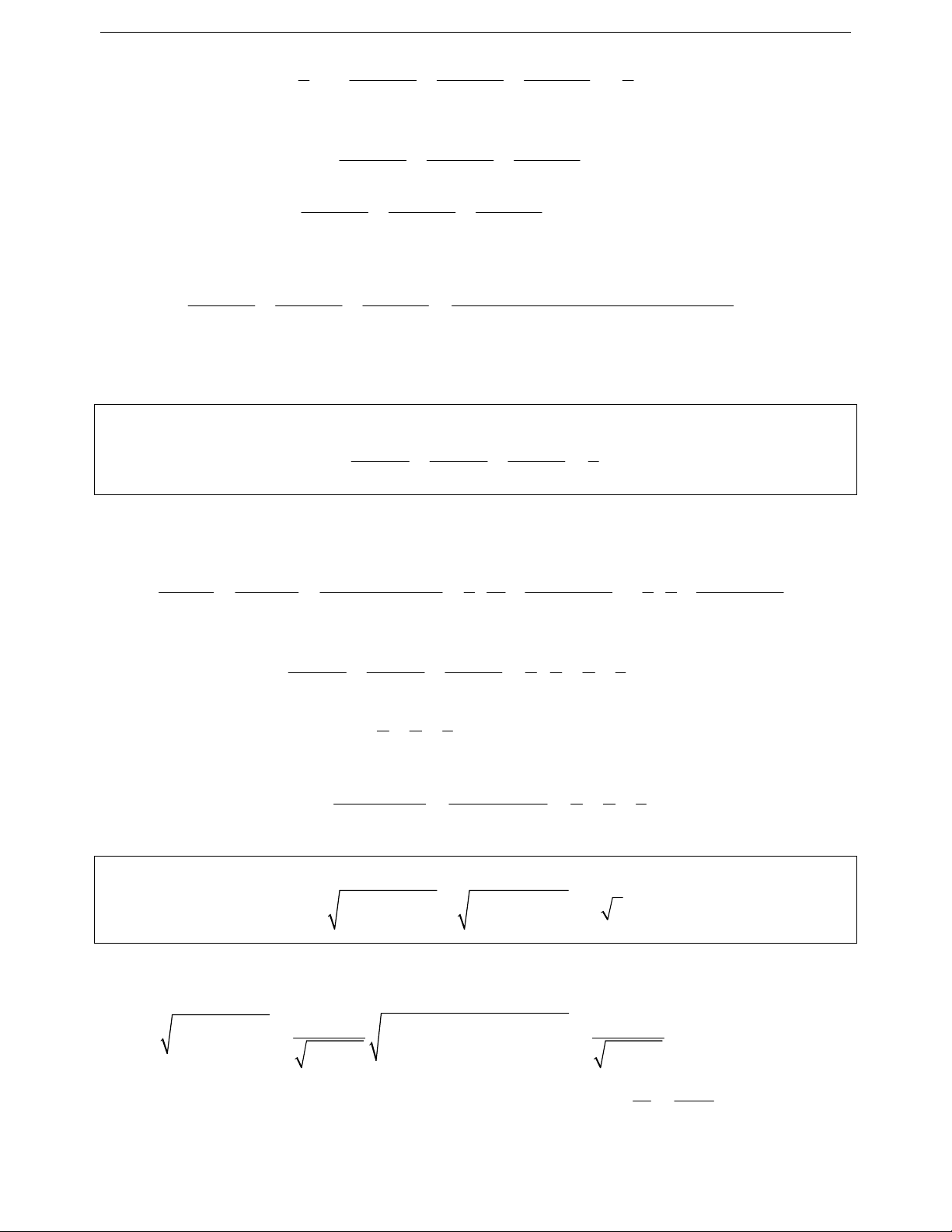
Ta cần chứng minh được
222
222
12a 2b 2c1
1
93
2a bc 2b ca 2c ab
Bất đẳng thức đó tương đương với
222
222
2a 2b 2c
2
2a bc 2b ca 2c ab
Hay
222
bc ca ab
1
2a bc 2b ca 2c ab
Theo bất đẳng thức Bunhiacopxki dạng phân thức thì
2
222
22 22 22
ab bc ca
bc ca ab
1
2a bc 2b ca 2c ab
ab bc ca 2abc a b c
Như vậy đánh giá cuối cùng là một đánh giá đúng.
Do đó bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 1.14: Cho a, b, c là các số thực dương thỏa mãn
222
abcabc
. Chứng minh rằng:
222
abc1
2
abcbcacab
Phân tích và lời giải
Tương tự như ví dụ trên ta chọn được
mn1, khi đó áp dụng bất đẳng Bunhiacopxki dạng
phân thức ta được
2222 2
23 32223222 222
aa a 1aa 11a
44a
abcaabcaabc a abc abc
Hoàn toàn tương tự ta được
222
abc1111
1
4a b c
abcbcacab
Ta cần chứng minh
111
1
abc
Thật vậy, áp dụng một đánh giá quen thuộc và kết hợp với giả thiết, ta được
222
abc abbcca111
1
abc abc a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
Ví dụ 1.15: Cho các số thực a, b thỏa mãn
2a b 2. Chứng minh rằng:
22
22
ab1 ab3 25
Phân tích: Giả sử đẳng thức xẩy ra tại am;bn;2ab2. Từ đó ta mạnh dạn đưa vào các số p, q
để có đánh giá như sau
22
2222
22 22
11
ab1 pqab1 paqb1
pq pq
Và đánh giá trên xẩy ra dấu bằng tại
am;bn;2ab2, ta được
pq
mn1
từ đó ta có thể
chọn
pm, qn1
.

Hoàn toàn tương tự với biểu thức
2
2
xy3
ta có thể chọn pm, qn3
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki:
2
2
2
2
2
2
2
2
1
ab1 .man1b1
mn1
1
ab3 .man3b3
mn3
Từ đó ta được
22
22
22
22
22 22
22 22
ab1 ab3
11
ma n 1 b 1 ma n 3 b 3
mn1 mn3
mm n1n3
ab
mn1mn3 mn1mn3
Ta cần chọn m, n sao cho
22 22
22 22
22
22
mm n1n3
2
mn1 mn3 mn1 mn3
2m n 0
m2n2 m2n6
2
m
3
0
mn1 mn3
2
n
2m n 0
3
Khi đó ta được
22
22
12 5 6 5 38 5
ab1 ab3 a b 25
25 25 25
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
22
a;b
33
Ví dụ 1.16: Cho các số thực a, b tùy ý. Chứng minh rằng:
22 22 2 2
a1 b1 a1 b1 a2 b2 622
Phân tích: Giả sử đẳng thức xẩy ra tại abm. Từ đó ta mạnh dạn đưa vào các số p, q để có đánh
giá như sau
22 22
22
22
22
1
a1 b1 .p q a1 b1
pq
1
.pa 1 qb 1
pq

Ta cần chọn p, q sao cho đẳng thức xảy ra khi x = y = a nên
pq
m1 m1
từ đó ta có thể chọn
pm1;qm1 .
Tương tự với biểu thức
22
a1 b1 ta có thể chọn
pm1;qm1
và với biểu
thức
22
a2 b2ta có thể chọn pq1.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki:
22
22
22
22
22
1
a1 b1 .m1a1 m1b1
m1 m1
1
a1 b1 .m1a1 m1b1
m1 m1
1
a2 b2 1.a2 1.b2
2
Từ đó ta được
22 22 2 2
22
a1 b1 a1 b1 a2 b2
2m 1 4
ab 22
2
2m 1 2m 1
Ta cần chọn m sao cho
2
2m 1 1
0m
23
2m 1
Với giá trị vừa tìm của m ở trên ta được
22 22 2 2
a1 b1 a1 b1 a2 b2 622
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
ab
3
2. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng cơ bản
Bất đẳng thức Bunhiacopxki dạng cơ bản là những bất đẳng thức đánh giá từ đại lượng
2
11 22 n n
ab ab ... ab
về đại lượng
22 222 2
12 n12 n
a a ... a b b ... b hoặc ngược lại. Để
rõ hơn ta xét một số ví dụ sau
Ví dụ 2.1: Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
111
9
abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
111 111 1 1 1
abc a. b. c. 9
abc abc
abc

Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ví dụ 2.2: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
ab bc ca
6
abc abc abc
Phân tích: Quan sát bất đẳng thức ta nhận thấy có thể đưa đưa đại lượng dưới các dấu căn ở vế trái vào
trong cùng một căn thức, chú ý chiều bất đẳng thức ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng cơ
bản.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
222
ab bc ca
abc abc abc
ab bc ca
1 1 1 6
abcabcabc
Do đó ta được
ab bc ca
6
abc abc abc
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 2.3: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
abc bca cab a b c
Phân tích: Để ý là abcbca 2b . Do đó ta nghĩ đến việc đưa hai đại lượng dưới dấu căn
vào trong cùng một dấu căn. Chú ý đến chiều của bất đẳng thức ta liên tưởng đến bất đẳng thức
Bunhiacopxki dạng cơ bản
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki cơ bản dạng
2
22
xy 2x y , ta được
2
abc bca 2abcbca 4b
Do đó ta được
abc bca 2b
, tương tự ta có
bca cab 2c;cab abc 2a
Cộng theo vế các bất đẳng thức trên ta được
abc bca cab a b c
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 2.4: Cho a, b, c là các số thực dương tùy ý . Chứng minh rằng:
222
abc
abc2
bc ca ab
Phân tích: Để ý nếu ta viết lại bất đẳng thức cần chứng minh thành

222
abcabc
bc ca ab 2
Bất đẳng thức trên gợi ý cho ta sử dụng bất đẳng thức Bunhiacopxki dạng phân thức. Tuy nhiên ở
đây ta thử áp dụng bất đẳng thức Bunhiacopxki dạng cơ bản xem sao.
Ta cần đánh giá đại lượng
abc
sao cho xuất hiện
222
abc
bc ca ab
, do đó ta viết
abc thành
abc
bc ca ab
bc ca ab
, đến đây ta áp dụng bất đẳng thức
Bunhiacopxki dạng cơ bản.
Lời giải
Ta có
abc
abc .bc .ca .ab
bc ca ab
Áp dụng bất đẳng thức Bunhiacopxki ta được
22 2
22 2
abc
.b c .c a .a b
bc ca ab
abc
bc ca ab
bc ca ab
Do đó ta có
222
2
abc
abc 2abc
bc ca ab
Suy ra ta được
222
abc
abc2
bc ca ab
Bất đẳng thức được chứng minh.Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 2.5: Cho a, b là các số thực dương thỏa mãn
22
ab1. Chứng minh rằng:
a1 a b1 b 2 2
Phân tích: Chú ý đến giả thiết có đại lượng
22
ab và trong bất đẳng thức cần chứng minh cho đại
lượng
a1 a b1 b
. Chú ý đến chiều của bất đẳng thức ta có đánh giá theo bất đẳng thức
Bunhiacopxki là
22
a1a b1b a b 1a1b . Đến đây ta chỉ cần đánh giá
22
ab 2a b là xong.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
22
22
a1 a b1 b a b 1 a 1 b a b 2
2a b 2 2 2
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi

22
ab1
ab 2
ab
2
a1 b1
11
ab
Ví dụ 2.6: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
444
444
a3b b3c c3a
abc
444
Phân tích: Quan sát bất đẳng thức ta nhận thấy nếu đánh giá từ vế trái sang vế phải của bất đẳng thức thì
rất khó khăn, do đó ta tìm cách đánh giá từ vế phải sang vế trái, tức là ta cần chứng minh được bất đẳng
thức kiểu
4
a3b
?
4
. Dự đoán dấu đẳng thức xẩy ra khi và chỉ khi abc nên ta viết được
2
42
a3b abbb
4 4444
, chú ý đến chiều của bất đẳng thức cần chứng minh ta có đánh giá
theo bất đẳng thức Bunhiacopxki là
2
2222
abbb 1111
abbb
4 4 4 4 16 16 16 16
Phép chứng minh sẽ hoàn tất nếu ta đánh giá được
2
22
a3b
về
44
a3b
, tuy nhiên đánh giá
này hoàn toàn có thể thực hiện được nhờ bất đẳng thức Bunhiacopxki.
Lời giải
Áp dụng bất đẳng thức Binhiacopxki ta có
2
2
42
2222
2
2222 4444
a3b abbb 1111
abbb
4 4 444 16161616
11
abbb 1111abbb
16 16
Do đó ta được
4
44
a3b a 3b
44
Hoàn toàn tương tự ta được
44
44 4 4
b3c b 3c c3a c 3a
;
4444
Cộng theo vế các bất đẳng thức trên ta được
444
444
a3b b3c c3a
abc
444
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc

Ví dụ 2.7: Cho các số thực
a; b; c 0; 1
. Chứng minh rằng:
abc 1 a 1 b 1 c 1
Phân tích: Quan sát bất đẳng thức ta thấy trong căn thức thứ nhất có chứa nhân tử a và trong căn thức thứ
hai lại có chứa nhân tử
1a
, để ý là
a1a 1
nên ta sẽ sử dụng bất đẳng thức Bunhiacopxki để
triệt tiêu đi biến a
2
abc 1a1b1c a 1a bc 1b1c
bc 1 b 1 c
Khi này ta được
abc 1a1b1c bc 1b1c
. Không cần quan tâm đến
dấu đẳng thức xẩy ra nên ta có
bc 1 b 1 c bc 1 b 1 c
. Đến ta đây ta lặp lại
đánh giá như trên thì bài toán được hoàn tất.
Lời giải
Áp dụng bất đẳng thức Binhiacopxki ta có
2
abc 1 a 1 b 1 c bc 1 b 1 c
Do đó ta được
abc 1a1b1c bc 1b1c
Dễ dàng chứng minh được
xy x y x,y 0 . Áp dụng vào bài toán ta được
bc 1 b 1 c bc 1 b 1 c
Lại theo bất đẳng thức Bunhiacopxki ta có
2
bc 1b1c b 1b c 1c 1
Hay
bc 1b1c 1
Vậy ta có
abc 1 a 1 b 1 c 1
Bất đẳng thức được chứng minh.
Ví dụ 2.8: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
222
3a b c a 2 b 2 c 2 .
Phân tích: Bất đẳng thức trên có các biến độc lập nhau, do đó nếu đánh giá làm giảm đi số biến thì bài
toán sẽ đơn giản hơn. Ta chú ý đến sự xuất hiện của đại lượng
2
abc ở vế trái và
2
a2 ở vế
phải của bất đẳng thức cần chứng minh. Sự xuất hiện này làm cho ta suy nghĩ đến sử dụng bất đẳng thức

Bunhiacopxki để đánh giá đại lượng
2
abc làm sao cho xuất hiện đại lượng
2
a2 . Như vậy ta
sẽ có đánh giá sau
2
2
2
2
bc
bc
abc a.1 2. a 21
22
Ta quy bài toán về chứng minh
2
22
bc
31 b 2 c 2
2
. Bất đẳng thức này chỉ có
hai biến và có thể chứng minh được bằng phép biến đổi tương đương.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng
2
2222
abxy axby ta được
2
2
2
2
bc
bc
abc a.1 2. a 21
22
Bài toán đưa về chứng minh
2
22
bc
31 b 2 c 2
2
Biến đổi tương đương bất đẳng thức trên ta được
2
2
bc
bc 1 0
2
Bất đẳng thức cuối cùng này hiển nhiên đúng nên bất đẳng thức đã cho được chứng minh.
Bất đẳng thức xảy ra khi và chỉ khi
bc
2
aabc1
bc
bc 1
Nhận xét: Bất đẳng thức này còn được chứng minh bằng cách sử dụng bất đẳng thức Bunhiacopxki kết
hơp với nguyên lý Dirichlet như sau:
Theo nguyên lý Dirichlet thì trong ba số a, b, c luôn tồn tại hai số cùng không lớn hơn 1 hoặc
không nhỏ hơn 1.
Không mất tính tổng quát ta giả sử hai số đó là b và c, khi đó ta được
22
110bc .
Áp dụng bất đẳng thức Bunhiacopxki ta được
22
222
.1 1. 1. 2 1 abc a b c a b c
Bài toán quy về chứng minh
22 2 2
31 2 2 bc b c
Biến đổi tương đương bất đẳng thức trên ta thu được
22
110bc
.
Bất đẳng thức cuối cùng đúng theo giả sử trên. Vậy bài toán được chứng minh.

Ví dụ 2.9: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
222
ab bc ca1 a 1b 1c 1
Phân tích: Tương tự như trên, ta chú ý đến sự xuất hiện đại lượng
2
ab bc ca 1 ở vế trái và
2
a1 ở vế phải của bất đẳng thức cần chứng minh. Ta cần đánh giá đại lượng
2
ab bc ca 1
làm
sao cho xuất hiện đại lượng
2
a1
. Để thực hiến được đánh giá đó ta để ý đến phép biến đổi
2
2
ab bc ca 1 a.b c 1.bc 1
.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222
2
ab bc ca 1 a. b c bc 1 a 1 b c bc 1
Bài toán quy về chứng minh
22
22
bc bc1 b 1c 1
Đây là một đẳng thức đúng vì
22
22
bc bc1 b 1c 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc 1 b c a b c abc
Ví dụ 2.10: Cho a, b, c, d là các số thực thỏa mãn
2222
a1b1c1d116
.
Chứng minh rằng: 3abacadbcbdcdabcd 5
Phân tích: Trước hết ta viết lại bất đẳng thức cần chứng minh thành
2
ab ac ad bc bd cd abcd 1 16
Quan sát giả thiết ta viết bất đẳng thức cần chứng minh được thành
2
2222
ab ac ad bc bd cd abcd 1 a 1 b 1 c 1 d 1
Đến đây ta liên tưởng đến bất đẳng thức Bunhiacopxki với cách áp dụng như các ví dụ trên.
Lời giải
Ta viết bất đẳng thức cần chứng minh lại như sau
4 abacadbcbdcdabcd14
Hay
2
ab ac ad bc bd cd abcd 1 16
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
2
22
2
ab ac ad bc bd cd abcd 1
abcdbcd 1.bcbdcd 1
a 1 b c d bcd bc bd cd 1
Bài toán đưa về chứng minh

22
22 2
b c d bcd bc bd cd 1 b 1 c 1 d 1
Đây là một bất đẳng thức đúng vì
22
22 2
b c d bcd bc bd cd 1 b 1 c 1 d 1
Ví dụ 2.11: Cho các số thực a, b, c > 1 thỏa mãn
111
2
abc
. Chứng minh rằng:
a1 b1 c1 abc
Phân tích: Sự xuất hiện đại lượng a1 b1 c1 cùng với chiều của bất đẳng thức cần
chứng minh là cơ sở để ta nghĩ đến sử dụng bất đẳng thức Bunhiacopxki. Tuy nhiên ta cần đánh giá làm
sao để xuất hiện
1
a
. Để ý ta có
1
a1 a.1
a
và với sự xuất hiện của đại lượng
abc
thì
nhận định trên càng có cơ sở.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
2
a1 b1 c1
a1 b1 c1 a. b. c.
abc
a1 b1 c1
abc
abb
111
abc3
abc
Do đó ta được
a1 b1 c1 abc
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
222
111
1
3
abc
abc
a1 b1 c1
2
abc
Ví dụ 2.12: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2
abc 9
4a b c
bc ca ab
Phân tích: Các đại lượng trong bất đẳng thức có dạng phân thức nên điều đầu tiên ta nghĩ đến là sử dụng
bất đẳng thức Bunhiacopxki dạng phân thức, tuy nhiên do bậc ở mẫu lớn hơn trên tử nên việc đánh giá sẽ
khó khăn hơn. Do đó ta tính đến sử dụng bất đẳng thức Bunhiacopxki dạng cơ bản, nhưng để dễ đánh giá
hơn ta viết bất đẳng thức lại thành
22 2
abc9
abc
4
bc ca ab
Đến đây áp dụng bất đẳng thức Bunhiacopxki ta được

2
22 2
abc abc
abc
bc ca ab
bc ca ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc 9abc3
bc ca ab 4 bc ca ab 2
Đánh giá cuối cùng chính là bất đẳng thức Neibiz.
Lời giải
Áp dụng bất đẳng thức Binhiacopxki ta có
22 2
222
222
2
abc
abc
bc ca ab
abc
abc
bc ca ac
abc
bc ca ab
Dễ dàng chứng minh được
abc3
bc ca ab 2
Do đó ta có
22 2
abc9
abc
4
bc ca ab
Hay
22 2
abc 9
4a b c
bc ca ab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 2.13: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2
abc 9
bca cab abc 2abbcca
Phân tích: Tương tự như ví dụ trên ta viết lại được bất đẳng thức cần chứng minh thành
22 2
abc9
ab bc ca
2
bca ca b abc
Ta thấy
ab c bc a ca b
ab bc ca
2
và
2
cc
ab c.
a
abc
Đến đấy ta có thể áp dụng bất đẳng thức Bunhiacopxki như lời giải sau đây
Lời giải
Bất đẳng thức cần chứng minh được viết lại thành
22 2
abc9
ab bc ca
2
bca ca b abc

Áp dụng bất đẳng thức Bunhiacopxki ta được
22 2
2
2
22 2
bc a ca b ab c
abc
2
bca ca b abc
ab c a bc a b ca b c
11abc
22bca
bca cab abc
Mặt khác theo bất đẳng thức Cauchy ta có
abc
3
bca
.
Do đó ta được
22 2
abc9
ab bc ca
2
bca ca b abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 2.14: Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:
ab bc ca 1
ab2c bc2a ca2b 2
Phân tích: Chú ý đến giả thiết và chiều bất đẳng thức ta có đánh giá theo bất đẳng thức Bunhiacopxki là
2
4a b 2c 1 1 2 a b 2c a b 2 c .
Lời giải
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
4a b 2c 1 1 2 a b 2c a b 2 c
Kết hợp với bất đẳng thức Cauchy ta được
ab 2 ab 2 ab 1 ab ab
ab2c 2
ab2c ac bc
4a b 2c
Áp dụng tương tự ta có
bc 1 bc bc
bc2a 2
abac
ca 1 ca ca
ca2b 2
abbc
Cộng theo vế các bất đẳng thức trên ta được
ab bc ca 1 1
abc
ab2c bc2a ca2b 2 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
9
.
Cách 2: Đặt
xa;yb;zc. Từ giả thiết ta suy ra xyz1.
Khi đó bất đẳng thức được viết lại thành
22 2 22 2 22 2
xy yz zx 1
2
xy2z yz2x zx2y
Áp dụng bất đẳng thức Bunhiacopxki ta được

2
22 2 22 2
4 x y 2z 1 1 2 x y 2z x y 2z
Do đó ta có
22 2
22 2
xy 2xy 2xy 1 xy xy
xy2z 2xzyz
xy2z
4x y 2z
Áp dụng tương tự ta được
22 2 2 2 2
yz 1 yz yz zx 1 zx zx
;
2x y x z 2x y y z
y z 2x z x 2y
Cộng theo vế các bất đẳng thức trên ta được
22 2 22 2 22 2
xy yz zx x y z 1
22
x y 2z y z 2x z x 2y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
9
.
Ví dụ 2.15: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
333
22 22 22 22 22 22
abc1
abc
2a b 2a c 2b c 2b a 2c a 2c b
Phân tích: Để ý đến đánh giá theo bất đẳng thức Bunhiacoxki là
2
2
22 22 222222 2 2
2ab2ac aabaca aabac aabc
Lời giải
Theo bất đẳng thức Bunhiacopxki ta được
2
2
22 22 222222 2 2
2ab2ac aabaca aabac aabc
Do đó
3
2
22 22
aa
2a b 2a c
abc
, chứng minh tương tự ta được
33
22
22 22 22 22
bbcc
;
2b c 2b a 2c a 2c b
abc abc
Cộng theo vế các bất đẳng thức trên ta được
333
22 22 22 22 22 22
abc1
abc
2a b 2a c 2b c 2b a 2c a 2c b
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Ví dụ 2.16: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
222
abc a b c
ab bc ca
1abc
1ab 1bc 1ca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được

333 222
2
222
333 2 22
2
222
333
222
ab bc ca 1 ab 1 bc 1 ca
abc
ab bc ca
1ab 1bc 1ca
ab bc ca c abc a abc b cab
abc
abc abc abc
1ab 1bc 1ca
ab bc ca abc 1
abc ab
abc
1ab 1bc 1ca
2
333
222
c
abc a b c
ab bc ca
1abc
1ab 1bc 1ca
Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy khi và chỉ khi
abc
Ví dụ 2.17: Cho a, b, c là các số thực thỏa mãn
222
abc2. Chứng minh rằng:
333
abcabc22
Phân tích và lời giải
Bất đẳng thức cần chứng minh được viết lại thành
2
333
abcabc 8 .
Quan sát giả thiết và chiều bất đẳng thức cần chứng minh ta liên tưởng đến bất đẳng thức
Bunhiacopxki. Bất đẳng thức không xẩy ra dấu đẳng thức tại
abc mà lại xảy ra tại
ab0;c 2
. Do đó ta có đánh giá bất đẳng thức trên theo hướng giảm biến. Vì vai trò của a, b,
c như nhau nên ta giả sử c là số lớn nhất, khi đó ta có đánh giá
22 222
ababc1
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
333 33 2
2
2
22 2 2
222 4 22 2
abcabc abccab
ab c a abb c ab
abc2ab2c2ab44c4ab
Đến đấy ta đặt
tab , do đó ta có
22 222
ab abc
tab 1
22
Khi đó ta được
2
333 2 22 2
abcabc 4t1t2t2cc2 4t1t2t2
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
4t 1 t 2t 2 8
Hay
22
t1t 2t2 2 tt1 0
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại ab0;c 2 và các hoán vị của
nó.
Ví dụ 2.18: Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:

432 432432
111
1
abcbca cab
Phân tích: Để ý đến đánh giá
2
432 2 222
abc1bc abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
432 2 222
abc1bc abc
Do đó ta có
22
432 2
432 2
222
11bc1bc
abc
abc1bc
abc
Áp dụng tương tự ta được bất đẳng thức
222
432 432432 2
222
1113abcabc
abcbca cab
abc
Ta cần chứng minh
222
2
222
3abca b c
1
abc
Hay
2
222 222
abc 3abcabc
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
2
3
222 222222 222 222
abc abcabc 3abcabc 3abc
Mà
2
3
222 222 222
abc
abc abc;abc3abc 3
3
Do đó
222 222
3a b c a b c a b c 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Ví dụ 2.19: Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
32 32 32
abc
1
abcbcacab
Phân tích: Để ý đến đánh giá theo bất đẳng thức Bunhiacopxki sau
2
32
1
abc 1c abc
a
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
32
1
abc 1c abc
a
Do đó ta được
32 2
32
11
a1c a1c
aa
aaca1
9
abc
1
abc
abc 1c
a

Chứng minh tương tự ta được
32 3 2
babb1ccbc1
;
99
bca cab
Do đó ta có bất đẳng thức
32 32 32
a b c abbccaabc3
9
abcbcacab
Ta cần chứng minh
ab bc ca 6
1
9
hay ab bc ca 3
Thật vậy, theo một đánh giá quen thuộc ta có
2
abc
ab bc ca 3
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 2.20: Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
3a 4b 5c
P
bc ca ab
Phân tích: Quan sát biểu thức ta thấy có thể viết biểu thức về dạng
345
P12 a bc
bc ca ab
Yêu cầu của bài toán cùng với cách phát biểu của biểu thức làm ta liên tưởng đến bất đẳng thức
Bunhiapcopxki
Lời giải
Biến đổi biểu thức P ta được
345
P12 a bc
bc ca ab
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
13451
bc ca ab 32 5
2bccaab2
Nên
2
1
P32512
2
Vậy giá trị nhỏ nhất của P là
2
1
32 5 12
2
. Đẳng thức xảy ra khi và chỉ khi
bc ca ab
2
35
.
Ví dụ 2.21: Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
3c b 4a c 5b a
T
2b a b 2c c 2a
Lời giải
Biến đổi biểu thức ta có

3c b 4a c 5b a
T12 3 4 5
2b a b 2c c 2a
3abc 4abc 5abc
a2b b2c c2a
345
abc
a2b b2c c2a
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
13451
a2b b2c c2a 32 5
3a2bb2cc2a3
Do đó ta được
2
1
T32512
3
Vậy giá trị nhỏ nhất của biểu thức T là
2
1
32 5 12
3
.
Đẳng thức xảy ra khi và chỉ khi
bc ca ab
2
35
Ví dụ 2.22: Cho a, b, c là độ dài ba cạnh một tam giác và x, y, z là các số thực. Chứng minh rằng:
222
ax by cz
xy yz zx
bca cab abc
Phân tích: Để ý là
2
22
abcx
ax x
bca 2
2b c a
, do đó ta thêm vào hai vế cùng một đại lượng
222
xyz
2
và áp dụng bất đẳng thức Bunhiacopxki.
Lời giải
Đặt
222
ax by cz
T
bca cab abc
. Khi đó ta có
222 2 2 2 2 2 2
222
xyz ax x by y cz z
T
2bca2cab2abc2
1xyz
abc
2bcacababc
Áp dụng bất đẳng thức Bunhiacopxki ta được
222
2
1xyz1
abc xyz
2bcacababc2
Do đó ta được
222
2
xyz 1
Txyz
22
Suy ra
222
ax by cz
xy yz zx
bca cab abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
xyz

Ví dụ 2.23: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2a 2b 2c
3
ab bc ca
Phân tích và lời giải
Quan sát bất đẳng thức cần chứng minh thì suy nghĩ đầu tiên là khử căn bậc hai bằng bất đẳng thức
Bunhiacopxki
2a 2b 2c 2a 2b 2c
3
ab bc ca abbcca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a 2b 2c
3
abbcca
Tuy nhiên đánh giá trên lại là một đánh giá ngược chiều.
Để ý ta thấy bất đẳng thức trên là một bất đẳng thức hoán vị, có một kinh nghiệm khi chứng minh
bất đẳng thức đó là nếu ta biến đổi từ bất đẳng thức hoán vị về thành bất đẳng thức đỗi xứng thì bài toán
sẽ trở nên đơn giản hơn. Với kinh nghiệm đó ta thử biến đổi bất đẳng thức về dạng đối xứng xem sao.
Quan sát đại lượng vế trái ta có thể đối xứng hóa như sau
2a a c 2b a b 2c b c
2a 2b 2c
ab bc ca
abac bcba cabc
Đến đây ta có thể khử căn bất đẳng thức trên bằng bất đẳng thức Bunhiacopxki như sau
2aac 2bab 2cbc
abac bcba cabc
2a 2b 2c
2a 2b 2c
abac bcba cabc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a 2b 2c
2a 2b 2c 3
abac bcba cabc
Biến đổi tương đương bất đẳng thức trên ta được
8a b c ab bc ca 9a b b c c a
Tiếp tục biến đổi tương đương ta được
abbcca 8abc
Đây là một bất đẳng thức đúng.
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 2.24: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
ab2c3
a b 2c b c 2a c a 2b 2
Phân tích và lời giải
Ta đối xứng hóa bất đẳng thức trên thành

a a 2b c b a b 2c c b c 2a
3
2
ab2ca2bc bc2aab2c ca2bbc2a
Gọi vế trái của bất đẳng thức là A, áp dụng bất đẳng thức Bunhiacopxki ta được
222
2
4a b c 3ab3bc3caabc
A
a b 2c b c 2a c a 2b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
16 a b c 3ab 3bc 3ca a b c 9 a b 2c b c 2a c a 2b
Biên đổi tương đương ta được
333
2a b c aba b bcb c cac a
Theo bất đẳng thức Cauchy ta được
333
abc3abc . Do đó ta cần chứng minh được
333
abc3abcababbcbccaca
Biến đổi tương đương bất đẳng thức trên ta được
abc a b c b c a c a b
Đây là một đánh giá đúng quen thuộc.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
3. Kỹ thuật sử dụng bất đẳng thức Bunhiacopxki dạng phân thức
Bất đẳng thức Bunhiacopxki dạng phân thức là bất đẳng thức có ứng dụng rộng rãi trong chứng
minh các bài toán bất đẳng thức. Nó giải quyết được một lớp các bất đẳng thức chứa các đại lượng có
dạng phân thức.
Ví dụ 3.1: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
abcabc
bc ca ab 2
Phân tích: Quan sát các đại lượng bên vế trái và chiều bất đẳng thức, một cách tự nhiên ta nghĩ đến bất
đẳng thức Bunhiacopxki dạng phân thức
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
222
abc abc
abc abc
bc ca ab 2
ab ca ab 2abc
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Ví dụ 3.2: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
abc
1
a2bcb2cac2ab

Phân tích: Quan sát các đại lượng bên vế trái và chiều bất đẳng thức, một cách tự nhiên ta nghĩ đến bất
đẳng thức Bunhiacopxki dạng phân thức
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222
222
abc
abc
1
a2bcb2cac2ab
a b c 2 ab bc ac
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Nhận xét: Nếu ta thay các biến a, b, c tương ứng bởi
111
,,
abc
thì ta thu được bất đẳng thức
222
1
222
bc ca ca
bc a ca b ca b
Để ý ta lại thấy
2
22
2
1
22
bc a
bc a bc a
, khi đó ta được bất đẳng thức
222
222
1
222
abc
bc a ca b ca b
Ví dụ 3.3: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abc
1
2b c 2c a 2a b
Phân tích: Quan sát vế trái của bất đẳng thức cần chứng minh ta cũng có thể nghĩ đến việc vận dụng bất
đẳng thức Bunhiacopxki dạng phân thức. Nhưng nếu để như thế mà áp dụng thì không được. Trước hết ta
cần tạo ra các biểu thức có dạng bình phương ở tử có 3 phân thức ở vế trái bằng cách nhân thêm vào tử và
mẫu các lượng thích hợp.
Để ý là
222
abc a b c
2b c 2c a 2a b
a2b c b2c a c2a b
.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc a b c
2b c 2c a 2a b
a2b c b2c a c2a b 3ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc 3abbcca
Tuy nhiên đánh giá trên ta một đánh giá đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi khi và chỉ khi
abc
Ví dụ 3.4: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333222
abcabc
a2b b2c c2a 3
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

2
222
333
2
abc
abc
a2b b2c c2a
abc
Ta lại có
2
222
1
abc abc
3
Do đó ta được
333222
abcabc
a2b b2c c2a 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 3.5: Cho a, b, c là các số thực dương. Chứng minh rằng:
444
222
abc a b c
abc
1abc
1ab 1bc 1ca
Phân tích: Ở bài toán này tử số của các phân thức đã ở dạng lũy thừa bậc chẵn nên ta có thể nghĩ đến
việc vận dụng bất đẳng thức Bunhiacopxki dạng phân thức
222
444
222 222
abc
abc
1 ab 1 bc 1 ca 3 ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
abc
abc a b c
1abc
3abbcca
Nhưng thực sự bất ngờ khi cách áp dụng như thế này lại không giúp ta giải quyết được bài toán vì
đánh giá trên là một đánh giá không đúng. Nên buộc ta phải tìm hướng giải quyết khác
Để ý ta thấy
222
c1 ab a1 bc b1 ca 1 abc a b c
. Khi đó ta áp dụng
bất đẳng thức Bunhiacopxki dạng phân thức như sau
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
422 4 2 2
222
222
22
222 222
222
abc ac ba cb
1ab 1bc 1ca
c1 ab a1 bc b1 ca
acbacb acbacb
1abcabc
c1 ab a1 bc b1 ca
Khi đó ta cần chứng minh được
222
222
abc
acbacb abcabc abc
ab ca bc
Theo bất đẳng thức Cauchy và Bunhiacopxki dạng phân thức ta được
2
222 2 2 2
abc
abc a b c
abc
ab bc ca ab bc ca
ab ca bc
222 222
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 3.6: Cho a, b, c là các số thực dương. Chứng minh rằng:

22 2
22 2 2 2 2
bc ca ab
3
bcabc cabca abcab
Phân tích: Bất đẳng thức có tử là các lũy thừa bậc hai, tuy nhiên ta không thể áp dụng bất đẳng thức
Bunhiacopxki như các ví dụ trên vì ta sẽ thu được bất đẳng thức ngược chiều. Để ý ta thấy có thể áp dụng
bất đẳng thức Bunhiacopxki dạng phân thức kiểu
2
22
22
bc
bc
xy
bcabc
Ta cần xác định được x và y sao cho tổng của chúng là
22
bcabc
và đảm bảo dấu đẳng
thức xẩy ra. Xét đến vai trò đối xứng của b và c trong biểu thức ta có thể xác định được
22
xb ab;yc ac
, khi đó ta được
2
22
22
22
bc
bcbc
abca
babcca
bcabc
Đến đây ta có thể giải được bài toán trên.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
22
22
bc bc
bcbc
abca
b c abc bab cca bab cca
Áp dụng tương tự ta được
22
22 22
ca ab
ca ab
;
bc ab ca bc
cabca abcab
Cộng các bất đẳng thức trên vế theo vế ta được:
22 2
22 2 2 2 2
bc ca ab
3
bcabc cabca abcab
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 3.7: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222 2 22 22 2
1111
2
4abc a4bc ab4c
Phân tích: Sự xuất hiện biểu thức
222
1
4a b c
và chiều của bất đẳng thức cần chứng minh làm ta liên
tưởng đến bất đẳng thức Bunhiacopxki dạng phân thức với cách đánh giá tương tự như ví dụ trên. Như
vậy ta cần viết
222
1
4a b c
về dạng
2
ABC
xyz
, ta cần xác định được các đai lượng
ABC;xyz với
222
xyz 4a b c . Để ý đến giả thiết abc 3 khi đó
2
abc 9
, do đó ta có thể định được ABC theo phép biến đổi

2
222
222 22
abc
11
.
9
4a b c
2a a b c a
. Đến đây ta có đánh giá theo bất đẳng thức
Bunhiacopxki dạng phân thức là
2
22 2
22222
222 22
abc
1a b c
9
2a a b c a
2a a b c a
Đến đây ta có thể trình bày lời giải cho bài toán như sau
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
22 2
222 2 2222
222 22
abc
11 1abc
.
99
4a b c 2a a b c a
2a a b c a
Áp dụng tương tự ta được
22 2
222 22222
22 2
2 2 2 2 22 22
11bac
9
a4bc 2b ab bc
11cab
9
ab4c 2cacbc
Cộng các bất đẳng thức trên vế theo vế ta được
222 2 22 22 2
1111
2
4abc a4bc ab4c
Bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 3.8: Cho a, b, c là các số thực dương. Chứng minh rằng:
222
bc ca ab 1 1 1
abc
abcbcacab
Phân tích: Để ý đến biến đổi và đánh giá theo bất đẳng thức Bunhiacopxki sau
22
22
2
222222222
bc bc
bc b c
abc
abcbc cab bca cab bca
Lời giải
Áp dụng bất đẳng thức Binhiacopxki dạng phân thức ta có
22
22
2
222222222
bc bc
bc b c
abc
abcbc cab bca cab bca
Áp dụng tương tự ta được ,
22 22
22
22 2 2 2 2 22
ca c a ab a b
;
bca cab
ab c ca b bc a ab c
Cộng theo vế các bất đẳng thức trên ta được
222
bc ca ab 1 1 1
abc
abcbcacab
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Nhận xét: Nếu ta thay các biến a, b, c tương ứng bởi
111
,,
abc
thì ta thu được bất đẳng thức

22 2
222
abc bca cab
abc
bc a ca b ca b
Để ý ta lại thấy
2
22
abc bcbc
bc
bc a bc a
, khi đó ta được bất đẳng thức
22 2
bc b c ca c a ab a b
abc
bc a ca b ca b
Ví dụ 3.9: Cho a, b, c là các số thực dương. Chứng minh rằng:
222
abc1
3
2a b 2a c 2b c 2b a 2c a 2c b
Phân tích: Để ý ta có phép biến đổi
2
2a b 2a c 2a a b c 2a bc khi đó ta có đánh
giá theo bất đẳng thức Bunhiacopxki sau
2
2
1141
9
2a bc
2a a b c
2a a b c 2a bc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
2
2
22 2
22
a21
a1
.
9
2a b 2a c
2a a b c 2a bc
14a a 12a a
99abc
2a bc 2a bc
2a a b c
Hoàn toàn tương tự ta được
22
2
22
2
b12bb
9a b c
2b ca
2b c 2b a
c12cc
9a b c
2c ab
2c a 2c b
Cộng các bất đẳng thức trên vế theo vế ta được
222
abc1
3
2a b 2a c 2b c 2b a 2c a 2c b
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.10: Cho a, b, c là các số thực dương thỏa mãn
222
abc1
. Chứng minh rằng:
222
bc ca ab 3
4
a1b1c1
Phân tích: Để ý ta có phép biến đổi
2222
a12abc và theo bất đẳng thức Cauchy ta được
2
bc
ab
4
. Khi đó ta có đánh giá theo bất đẳng thức Bunhiacopxki sau
2
22
22222
222
bc
bc 1 b c
4
a1 ab ca
42a b c
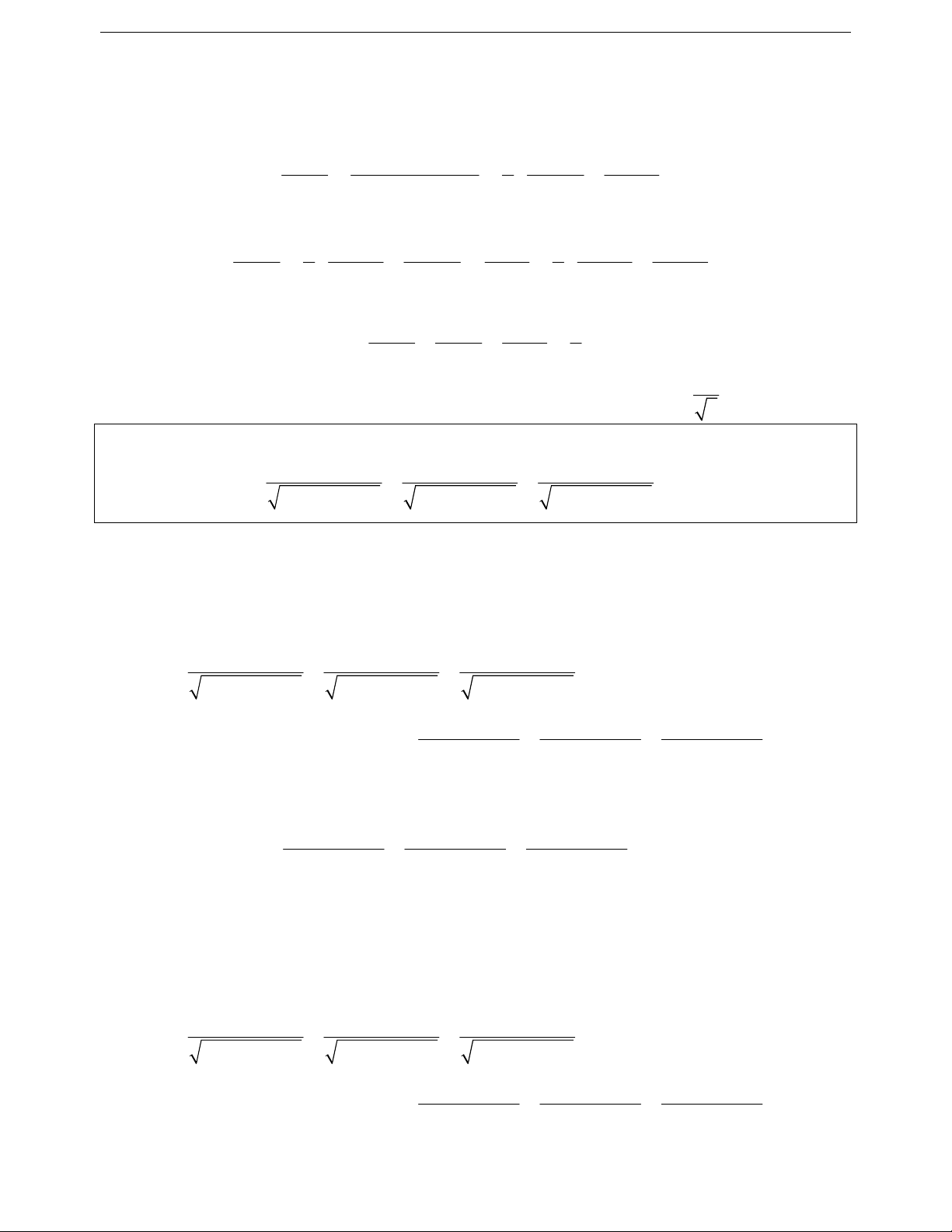
Áp dụng tương tự ta có lời giải như sau
Lời giải
Áp dụng bất đẳng thức Cauchy và bất đẳng thức Bunhiacopki dạng phân thức ta được
2
22
22222
222
bc
bc 1 b c
4
a1 ab ca
42a b c
Hoàn toàn tương tự ta được
22 22
2222222222
ca 1 c a ab 1 a b
;
44
b1 bc ab c1 ca bc
Cộng theo vế các bất đẳng thức tên ta được
222
bc ca ab 3
4
a1b1c1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ví dụ 3.11: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222 222 222
3a b 3b c 3c a
6
a2bc b2ca c2ab
Phân tích: Quan sát bất đẳng thức ta nghĩ đến đánh giá các mẫu bằng bất đẳng thức Cauchy. Tuy nhiên ở
đây ta phân tích xem có sử dụng được bất đẳng thức Bunhiacopxki để đánh giá bất đẳng thức hay không?
Bất đẳng thức có chứa căn và nếu ta làm mất được dấu căn thì tốt quá. Chú ý đến chiều bất đẳng thức ta
có đánh giá sau
2
222 222 222
222
222222222
3a b 3b c 3c a
a2bc b2ca c2ab
3a b 3b c 3c a
3
a2bc b2ca c2ab
Như vậy ta cần chứng minh được
222
222222222
3a b 3b c 3c a
12
a2bc b2ca c2ab
Các phân thức ở vế trái bất đẳng thức trên có các tử là các bình phương nên ta có thể áp dụng bất
đẳng thức Bnhiacopxki dạng phân thức như các ví dụ trên,
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222 222 222
222
222222222
3a b 3b c 3c a
a2bc b2ca c2ab
3a b 3b c 3c a
3
a2bc b2ca c2ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki dạng phân thức ta được

2
32 3
2 22 2 22 2 2 22
3a b
9a b 9a
1
a2bc abcb abc
Áp dụng tương tự ta được
222
222222222
222
222 222222
3a b 3b c 3c a
a2bc b2ca c2ab
9a 9b 9c
312
abc bca cab
Do đó
2
222 222 222
3a b 3b c 3c a
3.12 36
a2bc b2ca c2ab
Hay
222 222 222
3a b 3b c 3c a
6
a2bc b2ca c2ab
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 3.12: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
abc
1
3a b c 3b c a 3c a b
Phân tích: Quan sát bất đẳng thức cần chứng minh thì suy nghĩ đầu tiên là áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức
2
222
abc
abc
3a b c 3b c a 3c a b
3a b c
Ta cần chứng minh được
2
2
222
222
abc
1abc3abc
3a b c
, tuy nhiên
đây lại là một đánh giá sai. Do đó ta không thể áp dụng trực tiếp được.
Ta cần phải biến đổi bất đẳng thức trước rồi mới nghĩ đến áp dụng. Chú ý đến giả thiết cho a, b, c
là độ dài ba cạnh của một tam giác. Như vậy có thể bất đẳng thức sẽ liên quan đến các đại lượng
abc;bca;cab , ta thử biến đổi các đại lượng xem có thể tạo ra các đại lượng
abc;bca;cab không
Để ý là
4a 3a b c a b c khi đó ta được
3a b c a b c
4a a b c
1
3a b c 3a b c 3a b c
Đến đây ta có thể áp dụng được bất đẳng thức Bunhiacopxki dạng phân thức.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
4a 4b 4c
4
3a b c 3b c a 3c a b
Ta có biến đổi sau

3a b c a b c
4a a b c
1
3a b c 3a b c 3a b c
Áp dụng tương tự ta được
4b b c a 4c c a b
1; 1
3b c a 3b c a 3c a b 3c a b
Khi đó bất đẳng thức cần chứng minh trở thành
abc bca cab
1
3a b c 3b c a 3c a b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
222
abc bca cab
3a b c 3b c a 3c a b
abcbcacab
abc3abc bca3bca cab3cab
abc
1
a b c 2ab 2bc 2ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Nhận xét: Ta có thể sử dụng phép đổi biến để chứng minh bất đẳng thức
1
333
abc bca cab
abc bca cab
Đặt
;; x abcy cabz abc
Khi đó ta được
2;2;2 ayzbzxcxy
Khi đó bất đẳng thức cần chứng minh trở thành
1
222
xyz
zx xy yz
Áp dung bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
1
222
2
xyz
xyz
zx xy yz
xyz xyyzzx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.13: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22222 2
abcabc
ab bc ca
bbcc ccaa aabb
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta được

22222 2
222
222222
2
222222
abc
bbcc ccaa aabb
abc
ab abc ac bc bca a b a c abc b c
abc
ab ab ac ac bc bc 3abc
Ta cần chứng minh
2
222222
abc
abc
ab bc ca
ab ab ac ac bc bc 3abc
Hay
222222
abcabbcca abab acac bcbc 3abc
Đẳng thức trên đúng với mọi a, b, c. Vậy bất đẳng thức trên được chứng minh
Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.14: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222222222
abcabc
aabb bbcc ccaa abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta được
222222
223
32 2 32 2 32 2
2
3332 22 22 2
abc
aabb bbcc ccaa
abc
aababbbcbcccaac
abc
abcababacacbcbc
Ta cần chứng minh
2
3332 22 22 2 222
abc
abc
abcababacacbcbc abc
Hay
222 3332 22 22 2
abca b c a b c abab acac bcbc
Bất đẳng thức trên đúng với mọi a, b, c. Vậy bất đẳng thức trên được chứng minh
Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.15: Cho a, b là các số thực dương tùy ý . Chứng minh rằng:
22
2222 4
32 a b
11 1
abab
ab
Bài làm
Ta có
2
22
22
2222
22 2 2 22 2 2
ab
11 4 4ab
abab
ab a b ab a b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta đươc

22
4
22 22
22
2222 2222 2222 2222
ab ab2ab
ab
4a b
ab a b ab a b 2ab a b 2ab a b
Ta cần chứng minh
4
22
4
22 2 2
32 a b
ab
2a b a b
ab
Thật vậy, bất đẳng thức trên tương đương với
2
8
22 2 2
ab 64aba b hay
4
22
a b 8ab a b
Triển khai và thu gọn ta được
4
ab 0. Bất đẳng thức cuối cùng đúng với mọi số thực a, b.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
ab .
Ví dụ 3.16: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
abc
1
a 8bc b 8ca c 8ab
Phân tích: Quan sát bất đẳng thức ta thấy có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân
thức. Tuy nhiên để áp dụng được ta cần viết các tử số về dạng bình phương. Khi đó ta được
2
222 2 2 2
abc
abc
a8bc b8ca c8abaa8bcbb8cacc8ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
abc
1
a a 8bc b b 8ca c c 8ab
Bất đẳng thức trên có mẫu số chứa các căn bậc hai nên ta nghĩ đến đánh giá đưa các đại lượng trong
các dấu căn về cùng trong một dấu căn. Để đến đại lượng trên tử số ta có đánh giá theo bất đẳng thức
Bunhiacopxki như sau
222
333
333
a a 8bc b b 8ca c c 8ab
a a 8abc b b 8abc c c 8abc
a b c a b c 24abc
Đến đây ta chỉ cần chứng minh được
3
333
a b c a b c 24abc là bài toán được giải
quyết xong.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222 2 2 2
abc
abc
a8bc b8ca c8abaa8bcbb8cacc8ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta được

222 3 3 3
333
a a 8bc b b 8ca c c 8ab a a 8abc b b 8abc c c 8abc
a b c a b c 24abc
Do đó
2
222
333
3
333
abc
abc
a8bc b8ca c8ab
a b c a b c 24abc
abc
abc24abc
Ta cần chứng minh
3
333
a b c a b c 24abc , bất đẳng thức này tương đương với
a b b c c a 8abc
. Đây là bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Ví dụ 3.17: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
222
abc3
2
a3bc b3ca c3ab
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222 2 2 2
abc
abc
a 3bc b 3ca c 3ab a a 3bc b b 3ca c c 3ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta được
222
333
333
aa 3bc bb 3ca cc 3ab
a a 3abc b b 3abc c c 3abc
abca b c 9abc
Do vậy ta được
2
222
333
abc
abc
a3bc b3ca c3ab
abca b c 9abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
333
abc
3
2
abca b c 9abc
3
333
abc
9
4
abc9abc
Thực hiện biến đổi tương đương bất đẳng thức ta được
333
12 ab a b bc b c ca c a 5 a b c 57abc
Theo bất đẳng thức Cauchy ta lại có
333
abc3abc
Do đó
333 333
6abc9abc5abc 57abc
Như vậy ta cần chứng minh
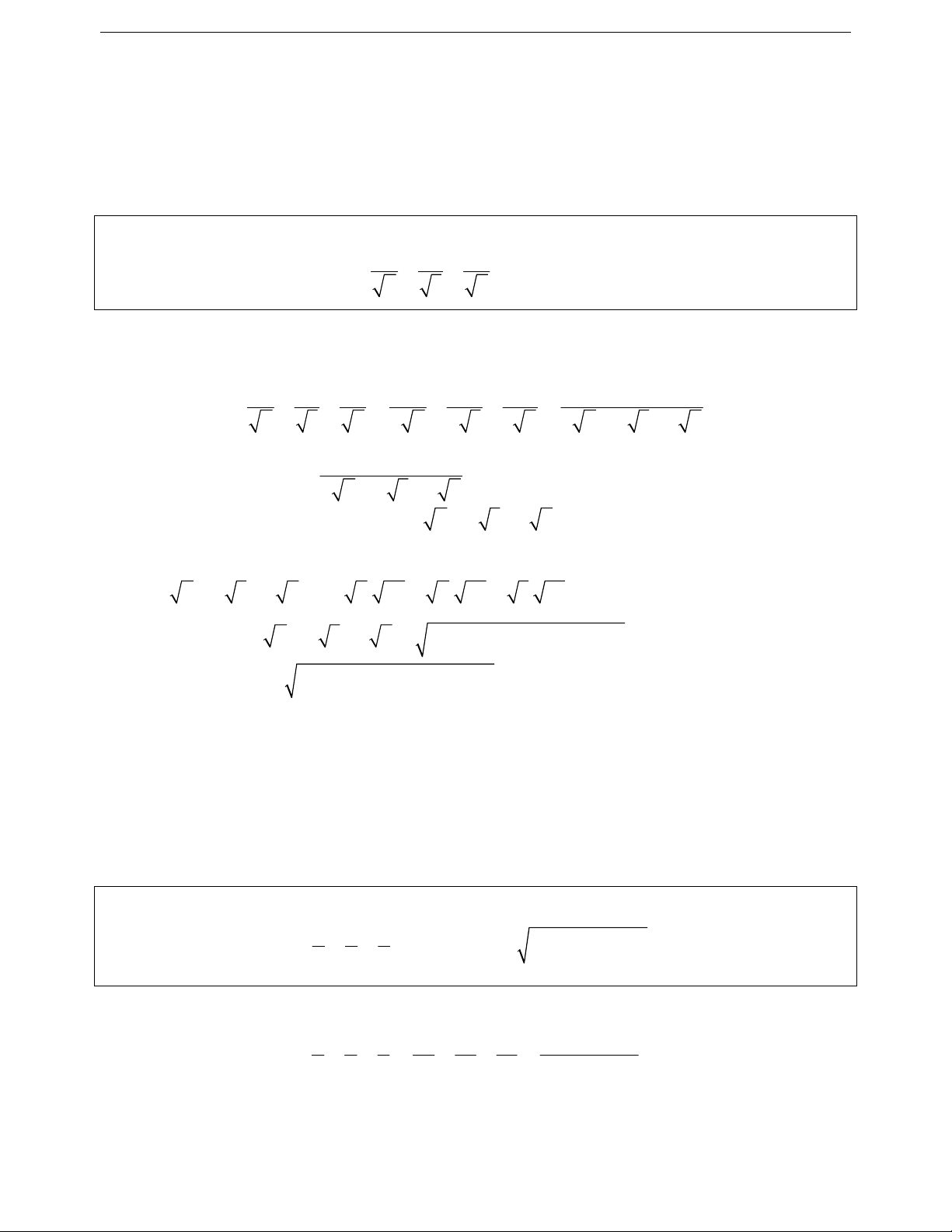
333
2aba b bcb c cac a a b c 9abc
Hay
2
3abcbc bcaabac 0
Do a, b, c có tính đối xứng, nên không mất tính tổng quát ta chọn a lớn nhất, khi đó bất đẳng thức
cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 3.18: Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Chứng minh rằng:
abc
abc
bca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc a b c
bcaabbccaabbcca
Ta cần chứng minh
2
abc
abc
ab bc ca
Hay
abcabbcca
Cũng theo bất đẳng thức Bunhiacopxki ta được
22
ab bc ca a.ab b.bc c.ca a b c ab bc ca
Hay
ab bc ca a b c ab bc ca
Ta cần chứng minh
abcabbcca abc
Hay ta cần chứng minh
22
ab bc ca a b c ab bc ca a b c
Mà ta có
2
abc 3abbcca , như vậy phép chứng minh sẽ hoàn ta nếu ta chỉ ra
được
ab bc ca 3
Đánh giá cuối cùng là một đánh giá đúng vì
222
ab bc ca a b c 3
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Ví dụ 3.19: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
abc
abc 33a b c
bca
Phân tích: Theo bất đẳng thức Buniacopxki dạng phân thức ta được
2
222
abc
abc a b c
bca abbccaabbcca

Khi đó ta có
3
abc
abc
abc
bca abbcca
và phép chứng minh sẽ hoàn tất nếu ta chỉ
ra được
3
222
abc
33a b c
ab bc ca
.
Việc chứng minh bất đẳng thức trên hoàn toàn dễ dàng.
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc a b c
bca abbccaabbcca
Do đó
3
abc
abc
abc
bca abbcca
Ta cần chứng minh
3
3
222 222
abc
33abc abc 3abbcca3abc
ab bc ca
Thật vậy, theo bất đẳng thức Cauchy ta có
2
222
2
222
3
a b c a b c ab bc ca ab bc ca
3a b c abbcca
Lũy thừa bậc ba hai vế ta được
62
222
abc 27a b c abbcca
Lấy căn bậc hai hai vế bất đẳng thức trên ta được
3
222
abc 3abbcca 3a b c
Như vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Ví dụ 3.20: Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
222
abc
abc23a b c
bca
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222 222
abc abc
abc2 abc
bca bca
Ta cần chứng minh
222
222
abc
abc 3a b c
bca
Thật vậy, theo bất đẳng thức Bunhiacopxki dạng phân thức ta được

2
222
222 4 4 4
222 222
abc
abc a b c
bca
ab bc ca ab bc ca
Ta cần chỉ ra được
2
222
222
222
abc abc
3a b c
ab bc ca
hay
222 2 2 2
a b c abc 3abbcca
Tức là ta cần chứng minh
32 32 32 222
aab bbc cca 2abbcca
Đánh giá trên đây đúng theo bất đẳng thức Cauchy. Do đó bất đẳng thức ban đầu được chứng minh.
Dấu đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 3.21: Cho a, b, c là các số dương thỏa mãn
222
abc1
. Chứng minh rằng:
222
abc 3
bc ca ab 2
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222
222
22 2 2 2 2
abc
abc
bc ca ab
abc bca cab
1
ab c bc a ca b
Mặt khác theo bất đẳng thức Cauchy ta lại có
2
22 222 22222
3
222
11
ab c 2ab c 2ab c b c
22
12a 2b 2c 2
23
33
Áp dụng tương tự ta được
22 2 2 2 2
2
ab c bc a ca b
3
Do đó ta được
22 2 2 2 2
13
2
ab c bc a ca b
Từ đó suy ra
222
abc 3
bc ca ab 2
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
3
.
Ví dụ 3.22: Cho a, b, c là các số thực dương thỏa mãn
222
abc1
. Chứng minh rằng:
222
111 9
2a b c
a1 b1 c1
Phân tích: Để ý ta thấy

222
222222
111
abc
a1 b1 b1
abcbccaab
a1 b1 c1 a1 b1 c1
Ta quy bài toán về chứng minh
222 222
abc3bccaab
;3
2
a1 b1 c1 a1 b1 c1
Lời giải
Ta viết lại bất đẳng thức cần chứng minh trở thành
222
1119
abc
2
a1 b1 b1
Theo bất đẳng thức Bunhiacopxki ta được
222
222 2 22 22 2
222
abc 3a 3b 3c
2a b c a 2b c a b 2c
a1 b1 c1
Mặt khác ta lại có
222
222 22 22
3a 3 a a
4
2abc abac
, áp dụng tương tự ta được
222
222 2 22 22 2
3a 3b 3c 3
2
2abc a2bc ab2c
Do đó
222
abc3
2
a1 b1 c1
(1)
Áp tương tự như trên ta được
222
222 2 22 22 2
222
3b c 3c a 3a b
bc ca ab
2a b c a 2b c a b 2c
a1 b1 c1
Dễ dàng chứng minh được
2
22
222 22 22
3b c
bc
3
2a b c a b a c
Tương tự ta được
222
222 2 22 22 2
3b c 3c a 3a b
3
2a b c a 2b c a b 2c
Hay
222
bc ca ab
3
a1 b1 c1
(2)
Công theo vế các bất đẳng thức (1) và (2) ta được
222
1119
abc
2
a1 b1 b1
Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
1
abc
3
.
Ví dụ 3.23: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

2
3
3
abc abc
1111
abbcca
abbcca
abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
222
2
222
111 c a b
abbc ca
ca b abc bca
abc
ca b abc bca
Tiếp tục áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
3
2
2
3
222
abc
1
ca b abc bca
2abc
abc
abc
2abc
ca b abc bca
22
33
222
abc abc abc abc
ca b abc bca 2abc abbcca
Do đó ta được
3
3
abc abc
1111
abbcca
abbcca
abc
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 3.24: Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
1a 1b 1c a b c
2
bc ca ab b c a
Lời giải
Biến đổi tương đương bất đẳng thức ta được
1a 1b 1c a b c 2a 2b 2c a b c
232
bc ca ab b c a bc ca ab b c a
aabbcc 3 ac bc ab 3
bbccacaab 2 2
bb c aa b cc a
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 2
ac bc ab
bb c aa b cc a
ac bc ab ab bc ca
abc b c abc a b abc c a 2abc a b c
Ta cần chứng minh
2
ab bc ca
3
2
2abc a b c

Hay
2
ab bc ca 3abc a b c
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy. Vậy bất đẳng thức được chứng minh.
Bất đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Ví dụ 3.25: Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
abc
abc
2a bc 2b ca 2c ab
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 222 222
111
1
2a bc b c 2ab c c a 2abc a b
Áp dụng bất đẳng thức Bunhiacopxki và chú ý một bất đẳng thức quen thuộc
2
2
2
abc
ab bc ca 9
3
Ta có
222 222 222
2
22 22 22
111
2a bc b c 2ab c c a 2abc a b
99
1
ab bc bc 2abc a b c
ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 3.26: Cho a, b, c là các số thực dương thỏa mãn
222
abc3
. Chứng minh rằng:
abc
abc6
bca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
222
abc
abc a b c
bca abbccaabbcca
Do đó ta được
2
abc
abc
abc abc
bca abbcca
Ta cần chứng minh
2
abc
abc6
ab bc ca
Thật vậy, từ giả thiết ta có
2
2
222
abc a b c
abc 3
ab bc ca
22
Đặt
tabc 0t3. Khi đó ta được bất đẳng thức sau

2
2
22 2
2
2t
t6 2t tt 3 6t 3 t3 t2 0
t3
Bất đẳng thức cuối cùng đúng với mọi
t0 . Vậy bất đẳng thức trên được chứng minh
Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 3.27: Cho a, b, c là các số dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
33 3
abc
1
b8 c8 a8
Phân tích: Dự đoán dấu đẳng thức xẩy ra tại abc1, do đó ta chú ý đến đánh giá theo bất đẳng
thức Cauchy là
2
32
bb6
b8 b2b2b4
2
. Khi đó hoàn toàn tương tự ta được
bất đẳng thức
222 2 2 2
222
33 3
abc 2a 2b 2c
bb6cc6aa6
b8 c8 a8
Ta cần chỉ ra được
222
222
abc1
2
bb6cc6aa6
.
Đến đây ta có thể áp dụng bất đẳng thức Bunhiacopxki cho đánh giá trên.
Lời giải
Áp dụng bấy đẳng thức Cauchy ta có
2
32
bb6
b8 b2b2b4
2
Tương tự ta có
22
33
aa6 cc6
a2 ;c2
22
Khi đó ta được bất đẳng thức sau
222 2 2 2
222
33 3
abc 2a 2b 2c
bb6cc6aa6
b8 c8 a8
Ta cần chứng minh
222
222
abc1
2
bb6cc6aa6
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222
222
abc
abc
bb6cc6aa6
abc abc18
Ta cần chỉ ra được
2
222
abc
1
2
abc abc18
Hay
2
222
2abc a b c abc 18
Hay
2
abc abc 120
Hay
abc4abc3 0
Bất đẳng thức cuối cùng đúng vì từ
ab bc ca 3 ta có
2
abc 3abbcca 9 abc3

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Ví dụ 3.28: Cho a, b, c là các số dương thỏa mãn
222
abc 3. Chứng minh rằng:
222
abc
1
1abbc 1bcca 1caab
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki a được
2
222
abc
abc
1abbc 1bcca 1caab
32abbcca
Để ý ta thấy
222
abc 3 nên ta có
2
32abbcca abc
Suy ra
2
abc
1
32abbcca
Do đó ta được
222
abc
1
1abbc 1bcca 1caab
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 3.29: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
1113
7
4a 3 4b 3 4c 3
Phân tích và lời giải
Quan sát bất đẳng thức trên thì suy nghĩ đầu tiên là áp dụng bất đẳng thức Bunhiacopxki dạng phân
thức
222
222
111 9
4a 3 4b 3 4c 3
4a b c 9
Phép toán sẽ hoàn tất nếu ta chỉ ra được
222
222
93
abc3
7
4a b c 9
Tuy nhiên đánh giá trên không đúng. Do vậy ta phải tìm hướng giải khác cho bài toán trên.
Để ý bất đẳng thức cần chứng minh được viết lại là
222
222
aac3
7
4a 3 4b 3 4c 3
Đến đây ta cũng nghĩ đến bất đẳng tức Bunhiacopxki dạng phân thức nhưng áp dụng theo chiều
2
22
ab
ab
xy x y
. Để ý tiếp ta lại thấy
22 2
4a 3 a ab ac 3a bc
Do đó để bảo toàn dấu đẳng thức ta có đánh giá
2
2
222
22 2 2 2
34a
49a 9a 16a
4a 3 a ab ca 3a bc a ab ca 3a bc
Suy ra
22
22
49a 9a 16a
abc
4a 3 3a bc
Hoàn toàn tương tự ta được

2222
2222
49b 9b 16b 49c 9c 16c
;
abc abc
4b 3 3b ca 4c 3 3c ab
Cộng theo vế các bất đẳng thức trên ta được
222 2 2 2
222 2 2 2
49a 49a 49c 16a 16b 16c
9
4a 3 4b 3 4c 3 3a bc 3b ca 3c ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
16a 16b 16c
12
3a bc 3b ca 3c ab
Bất đẳng thức trên tương đương với
222
bc ca ab 3
4
3a bc 3b ca 3c ab
Đến đây ta áp dụng bất đẳng thức Bunhiacopxki dạng phân thức thì được
2
222
22 22 22
ab bc ca
bc ca ab
3a bc 3b ca 3c ab
ab bc ca 3abc a b c
Theo một đánh giá quen thuộc ta có
2
1
abc a b c ab bc ca
3
do đó ta được
2
22 22 22
4
ab bc ca 3abc a b c ab bc ca
3
Suy ra
2
22 22 22
ab bc ca
3
4
ab bc ca 3abc a b c
. Do đó ta được bất đẳng thức
222
bc ca ab 3
4
3a bc 3b ca 3c ab
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 3.30: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
aba32
2
ab b bc c ca a
Phân tích và lời giải
Quan sát bất đẳng thức ta thấy có thể sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, tuy
nhiên trước hết ta đánh giá mẫu số để làm mất các dấu căn, để ý đến bảo toàn dấu đẳng thức ta được
Áp dụng bất đẳng thức Cauchy ta có
2b a b
a3b
2b. a b
22
Áp dụng tương tự ta được
222
aba2a22b22c2
a3bb3cc3a
ab b bc c ca a
.
Ta cần chứng minh
2a 2 2b 2 2c 2 3 2
a3bb3cc3a 2
Hay
abc3
a3bb3cc3a 4
Thật vây, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức thì được

2
222
abc
abc
a3bb3cc3a
a b c 3ab 3bc 3ca
.
Tương tự như ví dụ trên ta chứng minh được
2
222
abc
4
3
abc3ab3bc3ca
Do đó ta được
abc3
a3bb3cc3a 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Ví dụ 3.31: Cho a, b, c là các số dương thỏa mãn
222
abc 3. Chứng minh rằng:
aba
abc
bca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
222
abc
abc a b c
bcaabbccaabbcca
Ta cần chứng minh
2
abc
abc
ab bc ca
Hay
ab bc ca a b c
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
ab 1 bc 1 cb 1
ab ;bc ;ca
222
Cộng theo vế các bất đẳng thức trên ta được
1
ab bc ca a b c ab bc ca
2
Mà lại có
222
abc 3abc3
Suy ra
abcabc 3abbcca abcabbcca
Hay
abcabbcca
Do đó ta có
1
ab bc ca a b c a b c ab bc ca a b c
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Ví dụ 3.32: Cho a, b, c là các số dương thỏa mãn
abc1. Chứng minh rằng:
222
abcbca cab
2
ab c bc a ca b
Phân tích: Để ý là

222
222
abcbca cab
ab c bc a ca b
abcbccaab
ab c bc a ca b ab c bc a ca b
Lời giải
Ta viết lại bất đẳng thức cần chứng minh như sau
222
222
abcbca cab
ab c bc a ca b
abcbccaab
ab c bc a ca b ab c bc a ca b
Sử dụng bất đẳng thức Bunhiacopxki ta được
2
222
2
abc
abc
a b c b c a c a b a ab ac b bc ab c ca bc
abc
2a b c ab bc ca
Mà theo một đánh giá quen thuộc thì
2
3ab bc ca a b c
nên
22
abc abc 3abc
2
2
2a b c ab bc ca
abc abc
3
Do đó ta được
222
3a b c
abc
2
ab c bc a ca b
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta được
2
ab bc ca
bc ca ab
ab c bc a ca b
abc b c c a a b
3abcabc 3abc
2
abc 6 a b c
Do đó ta được
222
abcbca cab
6a b c
ab c bc a ca b
Lại có
2
11
abc a b c
33
nên
6a b c 2
Hay
222
abcbca cab
2
ab c bc a ca b
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc .
9
4. Kỹ thuật thêm bớt

Có những bất đẳng thức (hay biểu thức cần tìm GTLN, GTNN) nếu để nguyên dạng như đề bài
cho đôi khi khó hoặc thậm chí không thể giải quyết bằng cách áp dụng bất đẳng thức Bunhiacopxki. Khi
đó ta chịu khó biến đổi một số biểu thức bằng cách thêm bớt các số hay biểu thức phù hợp ta có thể vận
dụng bất đẳng thức Bunhiacopxki một cách dễ dàng hơn. Ta cùng xem xét các ví dụ sau để minh họa cho
điều đó.
Ví dụ 4.1: Cho a, b, c là các số dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
111
1
a2b2c2
Phân tích: Các đại lượng vế trái của bất đẳng thức cần chứng minh có dạng phân thức nên suy nghĩ đầu
tiên là sử dụng bất đẳng thức Bunhiacopxki dạng phân thức. Nếu áp dụng bất đẳng thức Bunhiacopxki
dạng phân thức một cách trực tiếp ta thu được bất đẳng thức
222 222
1111111
6
9
a2b2c2 a b c
Để hoàn thành phép chứng minh ta cần đánh giá được
222
111
3
abc
. Tuy nhiên để ý là đại
lượng
222
111
abc
trội nhất nên không thể đánh giá về đại lượng trội hơn
Do đó ta không thể áp dụng trực tiếp bất đẳng thức Bunhiacopxki để chứng minh được, vì vậy ta
tính đến phương án đổi chiều bất đẳng thức trước. Chú ý là
2
22
11 a
2
a1a2
Như vậy ta có phép biến đổi tương đương bất đẳng thức như sau
222 222
222
222 222
111 222
12
a2b2c2 a2b2c2
111 abc
111 32 1
a2 b2 c2 a2b2c2
Đến đây ta có thể áp dụng được bất đẳng thức Bunhiacopxki dạng phân thức để đánh giá bất đẳng
thức
222
222
abc
1
a2b2c2
Lời giải
Bất đẳng thức trên tương đương với
222
111
32 1
a2b2c2
Hay
222
222
abc
1
a2b2c2
Áp dụng bất đẳng thức bunhiacopxki dạng cộng mẫu kết hợp với giả thiết ta được
22
222
222 222
222
abc abc
abc
1
a2b2c2abc6
abc2abbcca

Do đó bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Ví dụ 4.2: Cho a, b, c là các số thực dương. Tìm giá trị lớn nhất của biểu thức:
222
ab bc ca
1
c2aba2bcb2ca
Phân tích: Bất đẳng thức cần chứng minh tương đương với
222
222
cab
1
c2aba2bcb2ca
Đến đây ta có thể áp dụng bất đảng thức Bunhiacopxki dạng phân thức được.
Lời giải
Thật vậy, bất đẳng thức trên tương đương với
222
ab bc ca
32 1
c2aba2bcb2ca
Hay
222
222
cab
1
c2aba2bcb2ca
Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta được
2
222
222
222
abc
cab
1
c2aba2bcb2ca
abc2abbcca
Do đó bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 4.3: Cho a, b, c là các số thực dương thỏa mãn
111
abc
abc
. Chứng minh rằng:
222
111
1
2a 2b 2c
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
abc
1
2a 2b 2c
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222 222
abc
abc
2a 2b 2c 6a b c
Ta cần chứng minh
2
2
222
222
abc
1abc6abcabbcca3
6a b c
.
Từ giả thiết của bài toán ta được
abc a b c ab bc ca và từ đánh giá quen thuộc
2
ab bc ca 3abc a b c , suy ra ta được
2
ab bc ca 3 ab bc ca ab bc ac 3
.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1
.
Ví dụ 4.4: Cho a, b, c là các số thực dương thỏa mãn
222
abc1. Chứng minh rằng:

1119
1ab 1bc 1ca 2
Lời giải
Đặt
111
P
1ab 1bc 1ca
.
Xét
222 222 222
22 2 222 2 22
P3 1 1 1 1 1 1 ab bc ca
2 22ab 2 22bc 2 22ca 2 22ab 22bc 22ca
ab bc ca
2a b c 2ab 2a b c 2bc 2a b c 2ca
ab bc ca
ab2c2abca2bc
Áp dụng bất đẳng thức Cauchy và Bunhiacopxki dạng phân thức ta được
22 2 222 2 22
222
22 2 222 2 22
22222 2
22 22 2 2 22 22 2 2
ab bc ca
ab2c2abca2bc
ab bc ca
1
4
ab2c 2abc a2bc
1a b b c c a 3
44
acbcabac bcab
Do đó ta được
P3 3 9
P
24 2
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
abc
3
.
Ví dụ 4.5: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
abc
1
2a bc 2b ca 2c ab
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
2a 2b 2c
2
2a bc 2b ca 2c ab
Hay
222
222
2a 2b 2c
1111
2a bc 2b ca 2c ab
Hay
222
bc ca ab
1
2a bc 2b ca 2c ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

222
222
222
2
22 22 22
bc ca ab
bc ca ab
2a bc 2b ca 2c ab
bc 2a bc ca 2b ca ab 2c ab
ab bc ca
1
ab bc ca 2abc a b c
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 4.6: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
a2b b2c c2a
1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Lời giải
Biến đổi tương đương bất đẳng thức ta được
222
2 a 2b 2 b 2c 2 c 2a
2
2a 4b 3c 2b 4c 3a 2c 4a 3b
Hay
222
2 a 2b 2 b 2c 2 c 2a
111 1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Hay
222
222
cab1
3
2a 4b 3c 2b 4c 3a 2c 4a 3b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
222
333
222
2
333
333
cab
2a 4b 3c 2b 4c 3a 2c 4a 3b
cab
c2a4b3c a2b4c3a b2c4a3b
abc
3a b c 6ab bc ca
Ta cần chứng minh
2
333
333
abc
1
3
3a b c 6ab bc ca
Hay
33 33 33
ab bc ca ab bc ca
Thật vậy, Áp dụng bất đẳng thức Cauchy ta được
33 33 33
33 33 33
ab bc ca
a b ab b c bc c a ca ab bc ca
2ab bc ca ab bc ca
ab bc ca 3 3 ab bc ca ab bc ca
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Ví dụ 4.7: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

222
222
abc ab bc ca
ab bc ca
aabbcbbccaccaab
Lời giải
Theo một đánh giá quen thuộc ta có
222
222
abc
abcabbcca 1
ab bc ca
Do đó ta cần chứng minh
222
ab bc ca
1
aabbcbbccaccaab
Bất đẳng thức trên tương đương với
222
222
222
222
ab bc ca
32
aabbcbbccaccaab
ab bc ca
1112
aabbc bbcca ccaab
abc bca cab
2
aabbcbbccaccaab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222 2
2
222 2
abc
abc
1
aabbcbbccaccaab
abc
ab bc ca
bc ca ab
1
aabbcbbccaccaab
ab bc ca
Cộng theo vế hai bất đẳng thức trên ta được
222
222
abc bca cab
2
aabbcbbccaccaab
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Nhận xét: Qua các ví dụ trên ta nhận thấy chỉ với việc thêm bớt vào bất đẳng thức một đại lượng phù
hợp ta có thể đổi được chiều bất đẳng thức và áp dụng được bất đẳng thức Bunhiacopxki để chứng minh
bài toán. Kỹ thuật này gọi là kỹ thuật thêm – bớt trong bất đẳng thức Bunhiacopxki. Vậy thì kỹ thuật thêm
bớt còn được sử dụng trong các trường hợp nào nữ
a, ta tiếp tục tìm hiểu các ví dụ sau đây
Ví dụ 4.8: Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
111
3
2a 2b 2c
Phân tích: Nếu áp dụng bất đẳng thức Bunhiacopxki một cách trực tiếp ta được
111 9
2a 2b 2c
6abc
Trong khi đó ta có
222
0abc 3a b c 3 nên
9
3
6abc
Như vậy đánh giá như trên không chứng minh được bài toán.
Bất đẳng thức cần chứng minh không cần phải đổi chiều như các ví dụ trên nhưng khi áp dụng bất
đẳng thức Bunhiacopxki dạng phân thức thì không đem lại hiệu quả. Để có một đánh giá tốt hơn ta cần
thay đổi cách phát biểu các đại lượng của bất đẳng thức xem sao? Chú ý một tí ta sẽ có biến đổi khá thú vị

sau
11 a
2a 2
22 a
. Lúc này bất đẳng thức trở thành
abc
3
2a 2b 2c
. Với bất đẳng
thức này hy vọng ta sẽ chứng minh được.
Lời giải
Ta viết lại bất đẳng thức cần chứng minh như sau
11 11 113 a b c
3
2a 2 2a 2 2a 2 2 2a 2b 2c
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
abc abc
abc
2a 2b 2c
a2 a b2 b c2 c 2a b c 3
Ta cần chứng minh được
2
abc
3
2a b c 3
hay
2
abc 6abc 9
Hay
22
abc 6abc 90 abc3 0
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Nhận xét: Như vậy bằng việc thêm – bớt một đại lượng ta đã biến đổi bất đẳng thức đã cho về dạng khác
và khi đó có thể dụng bất đẳng thức Bunhiacopxki một cách thuận lợi hơn. Vậy thì làm thể nào để ta có
thể chọn được đại lượng phù hợp?
Xét ý tưởng sau đây: Ta sẽ tìm một số m dương sao cho
11
1
22
ma
m
aa
có tử số là
11ma
là một đại lượng dương và đánh giá mày càng chặt càng tốt. Do đó ta chọn được
1
2
m
,
khi đó thì
11
0
22
22
a
a
a
.
Để chứng minh bất đẳng thức
3
222
abc
abc
ta có thể áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức theo cách khác sau
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
444
333
2
222
333 444
222
222
2
abc a b c
abc
aabbcc
abc
abc abc
Ta cần chứng minh được
333 444
444 222 333
32
2
abc abc
abc abc abc
Áp dụng bất đẳng thức Cauchy ta được
42 342 342 3
2; 2; 2 aa abb bcc c.
Cộng theo vế các bất đẳng thức trên ta được bất đẳng thức cuối cùng.

Vậy bài toán được chứng minh xong.
Ví dụ 4.9: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
abc
1
3a b c 3b c a 3c a b
Phân tích: Để áp dụng được bất đẳng thức Bunhiacopxki ta cần tìm số m dương sao cho
a1 3m mb mc
a
m
3a b c 3a b c
có tử số là
a1 3m mb mc là một số dương và
đánh giá trên càng chặt càng tốt. Để ý giả thiết a, b, c là ba cạnh của một tam giác nên ta nghĩ đến chọn m
sao cho tử số trên có dạng
abc. Từ những nhận định đó ta chọn được
1
m
4
. Khi đó ta có lời giải
như sau
Lời giải
Bất đẳng thức cần chứng minh tương đương với
a14b14c11
3a b c 4 3b c a 4 3c a b 4 4
Hay bất đẳng thức cần chứng minh trở thành
abc bca cab
1
3a b c 3b c a 3c a b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
222
abc bca cab
3a b c 3b c a 3c a b
abcbcacab
abc3abc bca3bca cab3cab
abc
1
a b c 2ab 2bc 2ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 4.10: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
5a 3b 5b 3c 5c 3a
4
3a b 2c 3b c 2a 3c a 2b
Phân tích: Quan sát bất đẳng thức trên thì suy nghĩ đầu tiên là áp dụng bất đẳng thức Bunhiacopxki dạng
phân thức
2
5a 3b 5b 3c 5c 3a
3a b 2c 3b c 2a 3c a 2b
5a 3b 5b 3c 5c 3a
5a 3b 3a b 2c 5b 3c 3b c 2a 5c 3a 3c a 2b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

2
5a 3b 5b 3c 5c 3a
4
5a 3b 3a b 2c 5b 3c 3b c 2a 5c 3a 3c a 2b
Hay
2
222
222
64 a b c
4abbccaabc
18 a b c 30 ab bc ca
Tuy nhiên đánh giá trên là sai. Do đó ta không thể áp dụng được trực tiếp bất đẳng thức
Bunhiacopxki mà cần biến đổi bất đẳng thức về một dạng khác. Với ý tưởng đó ta cần tìm số m dương
sao cho
a5 3m 3 mb 2mc ka b c
5a 3b
m
3a b 2c 3a b 2c 3a b 2c
Và đánh giá trên càng chặt càng tốt. Từ những nhận định đó ta chọn được
m1 . Khi đó ta có lời
giải như sau
Lời giải
Bất đẳng thức cần chứng minh tương đương với
5a 3b 5b 3c 5c 3a
1111
3a b 2c 3b c 2a 3c a 2b
Hay
2a b c 2b c a 2c a b
1
3a b 2c 3b c 2a 3c a 2b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2a b c 2b c a 2c a b
3a b 2c 3b c 2a 3c a 2b
2a b c b c a c a b
abc3ab2c bca3bc2a cab3ca2b
Ta cần chứng minh được
2
2a b c b c a c a b
1
abc3ab2c bca3bc2a cab3ca2b
Hay
2
222
2a b c
1
2a b c 4ab bc ca
Đánh giá cuối cùng là một đánh giá đúng. Vậy bất đẳng thức được chứng minh.
Ví dụ 4.11: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
3a b 3b c 3c a
4
2a c 2b a 2c b
Phân tích: Để ý đến phép biến đổi
3a b a b c
1
2a c 2a c
.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
abc bca cab
1
2a c 2b a 2c b
Áp dụng bất đẳng thức Bunhiacpxki dạng phân thức ta được

2
abc bca cab
2a c 2b a 2c b
abcbcacab
abc2ac bca2ba cab2ca
Ta cần chứng minh được
2
abcbcacab
1
abc2ac bca2ba cab2ca
Hay
2
222
abc
1
abc 2abbcca
Đánh giá cuối cùng là một đánh giá đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 4.12: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
222
abcabbcca5
bc ca ab 2
abc
Phân tích: Để ý đến phép biến đổi
abca
1
bc bc
.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
bca cab abc 1abbcca
bc ca ab 2
abc
Hay
2
222
abc
bca cab abc
bc ca ab
2a b c
Áp dụng bất đẳng thức Bunhiachopxki dạng phân thức ta được
2
2
222
bca cab abc
bc ca ab
abcbcacab
bcbca cacab ababc
abc
2a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 4.13: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
222
ab c bc a ca b
2
a2bcb2cac2ab
Phân tích: Để ý đến phép biến đổi
2
2
ab c a 2bc ab c
1
bc
a2bc
. Ta lại có

2
a 2bcab c bc a ba c bc a ba c 0
Lại thấy
222 222
a 2bc a b c b 2ca b c a c 2ab c a b a b c
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
a 2bc a b c b 2ca b c a c 2ab c a b
1
a2bc b2ca c2ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
222
2
222
a 2bc a b c b 2ca b c a c 2ab c a b
a2bc b2ca c2ab
a 2bc a b c b 2ca b c a c 2ab c a b
M
Với
22 22
22
M a 2bc a 2bc a b c b 2ca b 2ca b c a
c 2ab c 2ab c a b
Ta cần chứng minh được
2
222 3 33 33 3
444 222222
abc ababbcbccaca
abc4abbcca
Hay
22 22 22
ab a b bc b c ca c a 2a b 2b c 2c a
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 4.14: Cho a, b, c là các số dương thõa mãn
222
abc 3. Chứng minh rằng:
222
111111115
14 b c c a a b 56
7a 7b 7c
Phân tích: Để ý ta thấy
2
22
111a
.
77
7a 7a
khi đó ta quy bài toán về chứng minh
222
222
111 a b c 9
2
bc ca ab 4
7a 7b 7c
Lời giải
Ta có
222
222222
1 11a 1 11b 1 11c
.; .; .
77 77 77
7a 7a 7b 7b 7c 7c
Ta viết lại bất đẳng thức cần chứng minh như sau:
222
222
111 a b c 9
2
bc ca ab 4
7a 7b 7c
Áp dụng bất đẳng thức Bunhiacopxki dạng phan thức ta được

22
222
222
222
111 9 9
bc ca ab
bc ca ab 2abc
abc abc
abc
24
7a 7b 7c
7a 7b 7c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc
99
abc 6 2
Áp dụng bất đẳng thức Cauchy ta có
2
2
3
abc
9
abc 6
abc
99 9919
3..
62262
2a b c 2a b c
Do vậy đánh giá giá cuối cùng đúng. Vậy bất đẳng thức được chứng minh.
Nhận xét: Ở đây ta được sử dụng kỹ năng thêm bớt bằng cách đưa vào tham số m để lý luận và đưa vào
các điều kiện ràng buộc hợp lí để tìm ra m.
Ví dụ 4.15: Cho a, b, c là các số dương thỏa mãn
abc 1 . Chứng minh rằng:
222
111
3
aa1bb1cc1
Phân tích: Chú ý đến phép biến đổi
2
2
2
2a 1
41
3
aa1
3a a 1
Lời giải
Bất đẳng thức cần chứng minh cần chứng minh với
222
222
2a 1 2b 1 2c 1
3
aa1bb1cc1
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
222 2
222
222
2a 1 2b 1 2c 1 2a 2b 2c 3
aa1bb1cc1
abc abc3
Ta cần chứng minh được
2
222
2a 2b 2c 3
3
abc abc3
Hay
2
abc 6abbcca 9abc
Áp dụng bất đẳng thức Cauchy ta có
ab bc ca 3abc a b c 3 a b c
Ta quy bài toán về chứng minh
2
a b c 6 3a b c 9a b c
Đặt
abc
t1
3
, khi đó bất đẳng thức trên được viết lại thành

2
223
3t 18t 27t 9t t 2 3t 0
Theo bất đẳng thức Cauchy ta lại có
33
t2t113t và t1 nên bất đẳng thức cuối cùng
luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Ví dụ 4.16: Cho a, b, c là các số dương thỏa mãn
abc3. Chứng minh rằng:
222 222
222
abc abc
2a 1 2b 1 2c 1
abc6
Phân tích: Áp dụng ý tưởng như các ví dụ trên là cần tìm một số dương m sao cho đánh giá
22
a2mama
m
2a 1 2a 1
có tử số
2
2ma m adương và đánh giá càng chặt càng tốt. Để ý đến
dấu đẳng thức xẩy ra ta chọn được
1
m
2
, tuy nhiên nếu chọn như vậy thì ta không đảm bảo được tử số
luôn dương. Do đó nếu chọn được m mà làm triệt tiêu được
2
a thì mới đảm bảo được tử dương. Để ý đến
abc3 khi đó ta chọn
a
m
2
. Áp dụng tương tự ta có lời giải như sau
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 222
222
aa bb cc abc abc
22a122b122c1 2
abc6
Hay
222
222
2a b c
abc
3
2a 1 2b 1 2c 1
abc6
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc
2a 1 2b 1 2c 1
2a b c 3
Khi đó ta cần chứng minh được
222
222
222
2a b c
9
3
2a b c 3
abc6
Đặt
222
ta b c 3, khi đó bất đẳng thức được viết lại thành
92t 9 2t
3120
2t 3 2t 3
t6 t6
23 t
2t 2 t 6 t 2 1
0t3 0
2t 3 2t 3
t6
t6t t6
t22t3 t6t t6 0 t2t6 t6 0
Do
t3 nên bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.

Ví dụ 4.17: Cho a, b, c là các số dương thỏa mãn
abc1. Chứng minh rằng:
222
abc 1
3a 1 3b 1 3c 1
18 ab bc ca
Phân tích: Áp dụng ý tưởng như các ví dụ trên là cần tìm một số dương m sao cho đánh giá
22
a3mama
m
3a 1 2a 1
có tử số
2
3ma m adương và đánh giá càng chặt càng tốt. Khi đó
nếu áp dụng bất đẳng thức Bunhiacopxki ta thấy có sự xuất hiện của các hạng tử bậc 3 và nếu quy đồng
thì ta thu được một bất đẳng thức bậc 5 thì khó đánh giá.
Để ý đến đánh giá
22
aaa
3a 1 3a 3
, đây là một đánh giá khá chặt. Khi đó xét biến đổi sau
2
aa a
33a1
33a 1
, hoàn toàn tương tự ta có thể áp dụng bất đẳng thức Bunhiacopxki dạng phân
thức có bất đẳng thức sau
abc 1abc
3
33a 1 33b 1 33c 1 18ab bc ca
Lời giải
Bất đẳng thức cần chứng minh tương đương với
abc 1abc
3
33a 1 33b 1 33c 1 18ab bc ca
Hay
abc 1
1
3a 1 3b 1 3c 1
6ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222 222
abc
abc 1
3a 1 3b 1 3c 1
3a b c a b c 3a b c 1
Khi đó ta quy bài toán vể chứng minh
222
11
1
6ab bc ca
3a b c 1
Đến đây ta áp dụng bất đẳng thức Binhiacopxki dạng phân thức thì được
222 222
11 4
1
6ab bc ca
3a b c 1 3a b c 6ab bc ca 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Ví dụ 4.18: Cho a, b, c là các số dương thỏa mãn
abc1. Chứng minh rằng:
222
abc 1
9a 1 9b 1 9c 1
12 3 ab bc ca

Phân tích: Để ý đến phép biến đổi
2
aa a
99a1
99a 1
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
aa bb cc abc 1
99a199b199c1 9
12 3 ab bc ca
Hay
abc 3
1
9a 1 9b 1 9c 1
43ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222 222
abc
abc 1
9a 1 9b 1 9c 1
9a b c a b c 9a b c 1
Lại theo bất đẳng thức Cauchy ta có
33
21 3ab bc ca
43ab bc ca
Ta quy bài toán về chứng minh
222
13
1
9a b c 1
21 3ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
222
2
2
222
13
9a b c 1
21 3ab bc ca
19
9a b c 1
61 3ab bc ca
13
16
1
9a b c 1 61 3ab bc ca
9a b c 7
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
5. Kỹ thuật đổi biến trong bất đẳng thức Bunhiacopxki
Có một số bất đẳng thức, nếu ta để nguyên dạng phát biểu của nó thì rất khó để phát hiện ra cách
chứng minh. Tuy nhiên bằng một số phép đổi biến nho nhỏ ta có thể đưa chúng về dạng quan thuộc mà
bất đẳng thức Bunhiacopxki có thể áp dụng được. Trong mục này chúng ta cùng tìm hiểu kỹ thuật đổi
biến trong bất đẳng thức Bunhiacopxki.
Với bất đẳng thức ba biến a, b, c ta có thể sử dụng một số phép biến đổi như
111 1 1 1 1 1 1
1) a; b; c ; ; ; ; ; ; ; ; ; ..
xyz xyyzzx
xy yz zx
2) a; b; c yz; zx; xy ; yz; zx; xy ;...
3)a;b;c yz;zx;xy;yzx;zxy;xyz;...
Với một số bất đẳng thức có giả thiết là
abc 1 ta có thể đổi biến

222
222
111 1 1 1
1) a; b; c ; ; ; ; ; ; ...
xyz
xyz
xyz bca x y z
2) a; b; c ; ; ; ; ; ; ; ; ;...
yzx abc y z x
yz zx ab x y z
3) a; b; c ; ; ; ; ; ;...
yz zx xy
xyz
yz xy
zx x y z
4) a; b; c ; ; ; ; ;
xyz
yz zx xy
;...
Ví dụ 5.1: Cho a, b, c là các số thực dương thỏa mãn
ab bc ac 3
. Chứng minh rằng:
222
111abc
3
2abc ab 2abc bc 2abc ca
Phân tích: Bất đẳng thức cần chứng minh được viết lại thành
abc a b c
ac ab bc
2ac ab 2ab bc 2bc ca 3
Để ý ta thấy bất đẳng thức có sự lặp lai của các đại lương
ab; bc; ca
và chú ý ta nhận thấy
abc a b c ab.bc bc.ca ca.ab
. Do vậy một cách tự nhiên ta nghĩ đến phép đổi biến là
xab;ybc;zca.
Lời giải
Bất đẳng thức cần chứng minh tương đương với
abc a b c
ac ab bc
2ac ab 2ab bc 2bc ca 3
Đặt
xab;ybc;zca, khi đó ta được xyz3,bất đẳng thức cần chứng minh trở thành
yzxxyyzzx
2y z 2z x 2x y 3
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
2
222
yzx y z x
2y z 2z x 2x y
y2y z z2z x x2x y
xyx
2 x y z xy yz zx
Ta cần chứng minh
2
222
xyx
xy yz zx
3
2 x y z xy yz zx
Thật vậy, bất đẳng thức trên tương đương với
2
222
4
222
9x y x 3xy yz zx 2x y z xy yz zx
x y x 3 xy yz zx 2 x y z xy yz zx

Đặt
222
A x y z ; B xy yz zx suy ra
2
A2B xyz 9, khi đó ta cần
chứng minh
2
22
A2B 3B2AB A B 2AB
.
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức
xẩy ra khi
abc1.
Ví dụ 5.2: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 22 22
abc3
2
ab bc ca
Phân tích: Bất đẳng thức được viết lại thành
222
22 22 22
abc3
ab bc ca
2
Quan sát bất đẳng thức trên ta nghĩ đến phép đổi biến
222
xa;yb;zc
, khi đó bất đẳng
thức trở thành
xyz3
xy yz zx
2
Đây là bất đẳng thức được chứng minh trong mục 2 với phép đối xứng hóa.
Lời giải
Đặt
222
xa;yb;zc
, khi đó bất đẳng thức cần chứng minh trở thành
xyz3
xy yz zx
2
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
xyz
xy yz zx
xx z yy x zz y
xyxz yzyx zxzy
xyz
2x y z
xyxz yzyx zxzy
4 x y z xy yz zx
xyyzzx
Ta cần chứng minh
4 x y z xy yz zx
9
2
xyyzzx
Hay
8 x y z xy yz zx 9 x y y z z x
Hay
8xyz x y y z z x
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Ví dụ 5.3: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc
. Chứng minh rằng:

22 2 2 22
abc 111
3
bca abc
Phân tích: Quan sát giả thiết ta thấy có thể viết lại giả thiết thành
111
1
abc
. Đến đây ta đặt
111
x;y;z
abc
và khi này ta viết lại được bất đẳng thức cần chứng minh thành
222
222
xyz
3x y z
zxy
Quan sát bất đẳng thức ta nhận thấy dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức.
Lời giải
Từ giả thiết
ab bc ca abc suy ra
111
1
abc
Đặt
111
x;y;z
abc
, từ giả thiết suy ra
xyz1
Bất đẳng thức cần chứng minh trở thành
222
222
xyz
3x y z
zxy
Theo Bunhiacopxki dạng phân thức ta được
2
222
222 4 4 4
222 222
xyz
xyz x y z
zxy
xz yx zy xz yx zy
Ta cần chứng minh
2
222
222
222
xyz
3x y z
xz yx zy
Hay
222 2 2 2
xyz3xzyxzy
Vì
xyz1, nên bất đẳng thức trên trở thành
222 2 2 2
xyzx y z 3xzyxzy
Hay
333 2 2 2 2 2 2
xyzxzyxzy2xzyxzy
Áp dụng bất đẳng thức Cauchy ta được
32 23 2 2322
xxz2xz;yyx2yx;zzy2zy
Cộng theo vế ba bất đẳng thức trên ta được
333 2 2 2 2 2 2
xyzxzyxzy2xzyxzy
Phép chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc3.
Nhân xét: Bất đẳng thức trên còn được chứng minh theo cách sau
Biến đổi tương đương bất đẳng thức ta được

222
222
222
22
222
222
2
222
222
222
222
3
3
3
111
1110
xyz
xyz
zxy
xyz
xyz x y z xyz
zxy
xyz
xyz x y z xyz
zxy
xz yx zy
xy yz zx
zxy
xy yz zx
xyz
Vì
1xyz
nên
111
;; 1
xyz
. Do đó bất đẳng thức cuối cùng đúng.
Phép chứng minh hoàn tất.
Ví dụ 5.4: Cho a, b, c là các số thực dương tùy ý. Chứng minh rẳng:
ab bc ca 3
4
c3ab a3bc b3ca
Phân tích: Quan sát bất đẳng thức nghĩ đến đổi biến xa;yb;zc. Khi đó bất đẳng thức
được viết lai thành
222
xy yz zx 3
4
z 3xy a 3yz y 3zx
.
Ta có thể chứng minh bất đẳng thức trên bằng kỹ thuật thêm – bớt.
Lời giải
Đặt
xa;yb;zc. Khi đó bất đẳng thức cần chứng minh trở thành
222
xy yz zx 3
4
z3xya3yzy3zx
Bất đẳng thức cần chứng minh tương đương với
222
222
222
222
xy yz zx 3
4
z 3xy x 3yz y 3zx
1xy1yz1zx 3
1
333 4
z3xy x3yz y3zx
zxy3
4
z 3xy x 3yz y 3zx
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức và một đánh giá quen thuộc ta được

2
222
222
222
2
2
2
xyz
zxy
z3xyx3yzy3zx
x y z 3 xy yz zx
xyz
3
4
xyz
xyz
3
Do đó bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ví dụ 5.5: Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc . Chứng minh rằng:
abc bca cab abc a b c
Phân tích: Trước hết ta viết lại giả thiết thành
111
1
abc
, khi đó ta nghĩ đến phép đổi biến
111
x;y;z
abc
. Bất đẳng thức được viết lại thành
x yz y zx z xy 1 xy yz zx
Để ý đến giả thiết
xyz1, áp dụng bất đẳng thức Bunhiacpxki ta được
xyz xxyz yz xyxz x yz
Áp dụng tương tự ta có lời giải như sau
Lời giải
Từ giả thiết
ab bc ca abc suy ra
111
1
abc
.
Đặt
111
x;y;z
abc
, khi đó ta được
xyz1
.
Bất đẳng thức cần chứng minh trở thành
x yz y zx z xy 1 xy yz zx
Áp dụng bất đẳng thức Bunhiacpxki ta được
xyz xxyz yz xyxz x yz
Chứng minh tương tự ta được
yzx y zx; zxy z xy
Cộng theo vế các bất đẳng thức trên ta được
x yz y zx z xy x y z xy yz zx
1xy yz zx
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
hay
abc3
.

Ví dụ 5.6: Cho các số dương a, b, c thỏa mãn hệ thức
ab bc ca abc . Chứng minh rằng:
22 22 2
b 2a c 2b a 2ac
3
ab cb ac
Lời giải
Từ giả thiết ta được
111
1
abc
. Đặt
111
x;y;z
abc
, khi đó ta có
xyz1
.
Bất đẳng thứ cần chứng minh được viết lại thành
22 22 22
x2y y2z z2x 3
Theo bất đẳng thức Bunhiacopxki ta có
2
2
22
x2y 1.x 2.2y 3x 2y
Do đó ta được
2
22
x2y
x2y
x2y
3
3
Tương tự ta có
22 2 2
y2z z2x
y2z ;z2x
33
Cộng ba bất đẳng thức trên vế theo vế ta được
22 22 22
3x y z
x2y y2z z2x
x2y y2z z2x 3
333 3
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
hay abc3.
Ví dụ 5.7: Cho a, b, c là các số dương. Chứng minh rằng:
222
bc ca ab 1 1 1 1
2a b c
abc bca cab
Phân tích: Quan sát bất đẳng thức ta thấy vế phải có đại lượng
111
abc
, để ý đến phép biến đổi
2
2
bc 1
11
abc
a
bc
. Từ đó rất tự nhiên ta nghĩ đến phép đổi biến.
Lời giải
Đặt
111
x;y;z
abc
, khi đó bất đẳng thức cần chứng minh được viết lại thành
222
xyzxyz
yz zx xy 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

2
222
xyz
xyz xyz
yz zx xy 2
2x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ví dụ 5.8: Cho các số thực
a, b, c 1 thỏa mãn
111
2.
abc
Chứng minh rằng:
abc a1 b1 c1
Phân tích: Chính sự xuất hiện giải thiết
111
2
abc
làm cho ta suy nghĩ đến việc sử dụng phép đổi
biến
111
x;y;z
acc
.
Lời giải
Đặt
111
x;y;z
acc
, khi đó
x; y; z 0;1
và xyz2
Bất đẳng thức cần chứng minh trở thành
111 1x 1y 1z
xyz x y z
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
1x 1y 1z 1 1 1 1 1 1
3xyz
xyz xyz xyz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
abc
2
.
Ví dụ 5.9: Cho a, b, c là các số thực dương thỏa mãn
abc2abc . Chứng minh rằng:
2ab bc ca abc6
Phân tích: Để ý ta viết lại bất đẳng thức cần chứng minh thành
abc2abc2
Trước hết ta biến đổi giả thiết thành
a1b1ca a1b1 b1c1 c1a1
111
1
a1b1c1
Khi đó ta nghĩ đến phép đổi biến
111
x;y;z
a1 b1 c1
. Để ý là từ cách đổi biến đó ta
được
1x yz 1y zx 1z xy
a;b;c
xx yy zz
. Bất đẳng thức được viết lại thành
yz zx xy 1 1 1
2
xyz xyz
. Đến đây ta có thể áp dụng bất đẳng thức
Bunhiacopxki để chứng minh bài toán
Lời giải
Ta có
2
2abbcca abc abc

Khi đó bất đẳng thức cần chứng minh trở thành
2
2
abc abcabc6
abc 2abc3
abc2abc3
Giả thiết được viết lại thành
a1b1ca a1b1 b1c1 c1a1
111
1
a1b1c1
Đặt
111
x;y;z
a1 b1 c1
, suy ra
xyz1
.
Khi đó ta được
1x yz 1y zx 1z xy
a;b;c
xx yy zz
Bất đẳng thức cần chứng minh trở thành
yz zx xy 1 1 1
2
xyz xyz
Áp dụng bất đẳng thức Bunhiacopxki ta được
yz zx xy 1 1 1 1 1 1
2x 2y 2z 2
xyzxyz xyz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc2
Ví dụ 5.10: Cho a, b, c là các số thực dương thỏa mãn
abcabc . Chứng minh rằng:
222
bca3
2
ab 1 bc 1 ca 1
Phân tích: Từ giả thiết ta được
111
1
ab bc ca
, khi đó rất tự nhiên ta nghĩ đến phép đổi biến
111
x;y;z
abc
, suy ra xy yz zx 1. Khi đó bất đẳng thức cần chứng minh được viết lại
thành
22 2
xyz3
2
y1 z1 x1
Để ý đến phép biến đổi
22
x1 xxyyzzx xyxz . Hoàn toàn tương tự ta có
thể chứng minh được bài toán.
Lời giải
Từ giả thiết
abcabc suy ra
111
1
ab bc ca
.
Đặt
111
x;y;z
abc
, Khi đó giả thiết của bài toán trở thành xy yz zx 1.

Bất đẳng thức cần chứng minh trở thành
22 2
xyz3
2
y1 z1 x1
.
Dễ thấy
22
x1 xxyyzzx xyxz
Tương tự ta được
22
y1 yzyx;z1 zxzy
Áp dụng bất đẳng thức Cauchy ta được
22 2
xyz x y z
y1 z1 x1
yxyz zxzy xyxz
2x 2y 2z
x2yz xy2z 2xyz
Ta cần chứng minh
2x 2y 2z 3
x2yz xy2z2xyz 2
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
22
2
2x 2y 2z
x2yz xy2z 2xyz
2x y z 2x y z
3
2
xyz xyyzzx xyz
xyz
3
Như vậy bất đẳng thức ban đầu được chứng minh.
Dấu đẳng thức xẩy ra tại
abc 3 .
Ví dụ 5.11: Cho a, b, c là các số thực dương thỏa mãn
111
1
abc
. Chứng minh rằng:
222
bc ca ab
2
abc
Phân tích: Quan sát giả thiết của bài toán ta nghĩ đến phép đổi biến
111
x;y;z
abc
.
Khi đó bất đẳng thức được viết lại thành
222
xyz yzx zxy
2
yz zx xy
.
Để ý đến đánh giá
2
4xy x y. Ta quy bài toán về chứng minh
222
4x 4y 4z
2
yz zx xy
Bất đẳng thức trên dễ dàng chứng minh được bằng bất đẳng thức Bunhiacopxki dạng phân thức.
Lời giải
Đặt
111
x;y;z
abc
. Từ giả thiết suy ra xyz1.

Bất đẳng thức được viết lại thành
222
xyz yzx zxy
2
yz zx xy
Áp dụng bất đẳng thức Cauchy ta được
222
xy yz zx
xy ; yz ; zx
444
Khi đó ta được bất đẳng thức sau
222
222
xyz yzx zxy
4x 4y 4z
yz zx xy y z z x x y
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
222
4x y z
4x 4y 4z
2x y z 2
yz zx xy
2x y z
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc3.
Nhận xét: Ngoài cách chứng minh như trên ta có thể áp dụng bất đẳng thức Bunhiacopxki chứng minh
theo cách sau
Bất đẳng thức được viết lại thành
222
11 11 11
2
xyz
yz zx xy
Theo một đánh giá quen thuộc ta có
22
2
22
2
22
2
11 11 4
11 11 4
11 11 4
xx
xyz
y z yz y z yz
yy
yzx
zx zx zx zx
zz
zxy
xy xy xy xy
Cộng theo vế các bất đẳng thức trên ta được
222
222
444
xyz yzx zxy
xyz
yz zx xy y z z x x y
Mặt khác, theo bất đẳng thức Bunhiacopxki ta được
222
222
2
2
444
2
222
xyz
yz zx xy
xyz
xy yz zx
yz zx xy
xyz
yz zx xy xyz
yz zx xy
Bất đẳng thức được chứng minh.

Ví dụ 5.12: Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
abc
1
2ba 2cb 2ac
Phân tích: Từ giả thiết
abc 1
của bài toán, rất tự nhiên ta nghĩ đến phép đổi biến dạng
xyz
a;b;c
yzx
, chú ý đến các các căn bậc hai có trong bất đẳng thức cần chứng minh, ta chọn
cách đổi biến là
xy z
a;b;c
yzx
. Khi đó bất đẳng thức được viết lại thành
222
22 22 22
xz yx zy
1
2z y y x 2x z z y 2y x x z
. Bất đẳng thức cần chứng minh có dấu hiệu sử dụng bất
đẳng thức Bunhiacpxki dạng phân thức. Do đó ta thử áp dụng xem có thể chứng minh được bài toán
không?
Lời giải
Vì
abc 1
nên tồn tại các số thực dương để
xy z
a;b;c
yzx
.
Khi đó bất đẳng thức cần chứng minh trở thành
222
22 22 22
xz yx zy
1
2z y y x 2x z z y 2y x x z
Áp dụng bất đẳng thức Bunhiacopxki ta được
222222222
22 22 22 222 2 22 222
22
2
22 22 22
xz yx zy x z y x z y
2z y y x 2x z z y 2y x x z 2xyz x y 2x yz z y 2xy z x z
xy yz zx xy yz zx
1
x y y z z x 2xyz x y z
xy yz zx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Ví dụ 5.13: Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
222
111
1
aa1bb1cc1
Phân tích: Nếu ta sử dụng bất đẳng thức Bunhiacopxki trực tiếp kiểu
222222
111 9
aa1bb1cc1abcabc3
Khi đó để phép chứng minh được hoàn tất ta phải chỉ ra được
222
222
9
1abcabc6
abcabc3
Với giả thiết
abc 1 thì đánh giá cuối cùng là một đánh giá sai.
Để ý đến giả thiết
abc 1 ta nghĩ đến phép đặt ẩn phụ, vấn đề đặt ra là ta chọn cách đặt ẩn phụ
nào? Trước hết ta thấy bất đẳng thức có tính đối xứng do đó để không làm mất tính đối xứng của nó ta sẽ

không đặt ẩn phụ kiểu
xyz
;;
yzx
hoặc
yzx
;;
xyz
. Đầu tiên ta sử dụng phép đổi biến
111
a;b;c
xyz
khi bất đẳng thức cần chứng minh trở thành
222
222
xyz
1
xx1yy1zz1
Áp dụng bất đẳng thức Cauchy ta được
2
222
222222
xyz
xyz
xx1yy1zz1xyzxyz3
Ta cần chứng minh được
2
222
xyz x y z xyz3
Tuy nhiên đánh giá này lại sai. Do đó cách đổi biến này không khả thi
Như vậy ta tính đến cách đổi biến
222
xyz
a;b;c
yz zx xy
và
222
yz zx xy
a;b;c
xyz
. Trong hai
cách đổi biến trên, suy nhĩ một chút ta sẽ loại cách đặt thứ nhất vì bất đẳng thức chỉ chứa biến ở mẫu nên
khi đổi biến và quy đồng mỗi phân thức ta sẽ thu được một phân thức thức mà trên tử có chứa các đại
lượng
22 2 2 2 2
yz;zx;xy còn dưới mẫu lại chứa các đại lượng
444
x;y;z trộn hơn, nên muốn đánh giá
các mẫu theo chiều tăng lên là rất khó. Do đó ta chỉ còn cách đổi biến
222
yz zx xy
a;b;c
xyz
, hy vọng
sẽ chứng minh được bài toán.
Khi này bất đẳng thức cần chứng minh được viết lại thành
444
42 22 42 2242 22
xyz
1
xxyzyzyyzxzxzzxyxy
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
444
42 22 42 2242 22
2
222
444 222222
xyz
x x yz y z y y zx z x z z xy x y
xyz
x y z xyz x y z x y y z z x
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222 444 222222
xyz xyzxyzxyzxyyzzx
Biến đổi tơng đương và thu gọn ta được
22 22 22
x y y z z x xyz x y z
Đánh giá cuối cùng là một đánh giá đúng. Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra
khi và chỉ khi
abc1
.

Nhận xét: Nếu chấp nhận biến bất đẳng thức trên từ dạng đối xứng về dạng hoán vị thì với cách đổi biến
;;
yzx
abc
xyz
, bất đẳng thức cần chứng minh trở thành
222
22222 2
1
abc
aabb bbcc ccaa
Khi đó bất đẳng thức tương đương với
22
22222
22 2 2 2 2
22222
2
22222
aa
a abb a b c abbcca
a a b c ab bc ca a ab b
a abb a b c abbcca
ac a b c
a abb a b c abbcca
Áp dụng tương tự ta quy bài toán về chứng minh
22 2
22222 2
ac bc cc ab bc ca
abc
aabb bbcc ccaa
Áp dụng dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
22222 2
2
222 22 2
ac ba cb
aabb bbcc ccaa
ab bc ca
ab bc ca
abc
c a bc b a b bc a b c ca a
Vậy bất đẳng thức được chứng minh.
Ví dụ 5.14: Cho các số thực
a; b; c 1
thỏa mãn abc = 1. Chứng minh rằng:
222
222
abc
1
1a 1b 1c
Phân tích: Chú ý đến giả thiết abc 1 và tính đối xứng của bất đẳng thức ta nghĩ đến phép đổi biến.
Ngoài ra ta cũng thấy các phân thức chứa biến trên tử nên ta có thể chọn cách đổi biến
222
xyz
a;b;c
yz zx xy
Lời giải
Đặt
222
xyz
a;b;c
yz zx xy
với
x; y; z 0
. Khi đó bất đẳng thức cần chứng minh trở thành
444
222
222
xyz
1
xyz yzx zxy
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

2
222
444
222 222
222 222
xyz
xyz
xyz yzx zxy xyz yzx zxy
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
222
222
xyz
1
xyz yzx zxy
Hay tương đương với
2222
222 2 2 2
2
xyz xyz yzx zxy 0
xy yz zx 0
Đánh giá cuối cùng luôn là một đánh giá đúng. Vậy bất đẳng thức được chứng minh.
Ví dụ 5.15: Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
1111
2
a1a2 b1b2 c1c2
Phân tích: Chú ý đến giả thiết
abc 1
và tính đối xứng của bất đẳng thức ta có thể đổi biến
222
yz zx xy
a;b;c
xyz
.
Lời giải
Đặt
222
yz zx xy
a;b;c
xyz
với x; y; z 0 , khi đó bất đẳng thức càn chứng minh trở thành
444
22 22 22
xyz1
2
xyz2xyz yzx2yzx zxy2zxy
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
444
22 22 22
2
222
22 22 22
xyz
xyz2xyz yzx2yzx zxy2zxy
xyz
xyz2xyz yzx2yzx zxy2zxy
Phép chứng minh sẽ hoàn nếu ta chỉ ra được
2
222
22 22 22
xyz
1
2
xyz2xyz yzx2yzx zxy2zxy
Hay ta cần chứng minh
2
222 2 2 2 2 2 2
2 x y z x yz 2x yz y zx 2y zx z xy 2z xy
Khai triển và thu gọn ta được
22 22 22
xy yz zx xyz x y z
Đánh giá cuối cùng là một đánh giá đúng. Bất đẳng thức được chứng minh.

Dấu đẳng thức xẩy ra khi và chỉ khi
abc1
.
Ví dụ 5.16: Cho a, b, c, d là các số thực dương thỏa mãn
abcd 1
. Chứng minh rằng:
2222
1111
1
a1 b1 c1 d1
Lời giải
Cách 1: Đặt
xyxt
a;b;c;d
zztx
với
x; y; z; t 0
. Khi đó bất đẳng thức cần chứng minh
được viết lại thành
2222
2222
xyzt
1
xy yz zt tx
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức và bất đẳng thức Cauchy ta được
2 222
2222
xyzt
xy yz zt tx
2
22 2 2 22 22
2
22 2 2
2
2222
22 2 2
xt x yx y zy z tz t
xy xt yz xy zt yz tx zt
xt x yx y zy z tz t
xy zt xt yz
xy yz zt xt
1
4xy zt xt yz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abcd1
.
Cách 2: Đặt
2222
yz zt tx xy
a;b;c;d
xyc t
với x; y; z; t 0 . Khi đó bất đẳng thức cần chứng
minh được viết lại thành
4444
222 2
2222
xyzt
1
xyz yzt ztx txy
Áp dụng liên tục bất đẳng thức Bunhiacopxki ta được
2
22
44
22 22
22 22
2
22
22
2222
2222 2222
xz
xz
xyz ztx xyz ztx
xz
xz
xyzt
xyxz zxzt
Hoàn toàn tương tự ta được
44 22
222222
22
yt yt
xyzt
yzt txy
Cộng theo về các bất đẳng thức trên ta được

4444
222 2
2222
xyzt
1
xyz yzt ztx txy
Vậy bất đẳng thức được chứng minh.
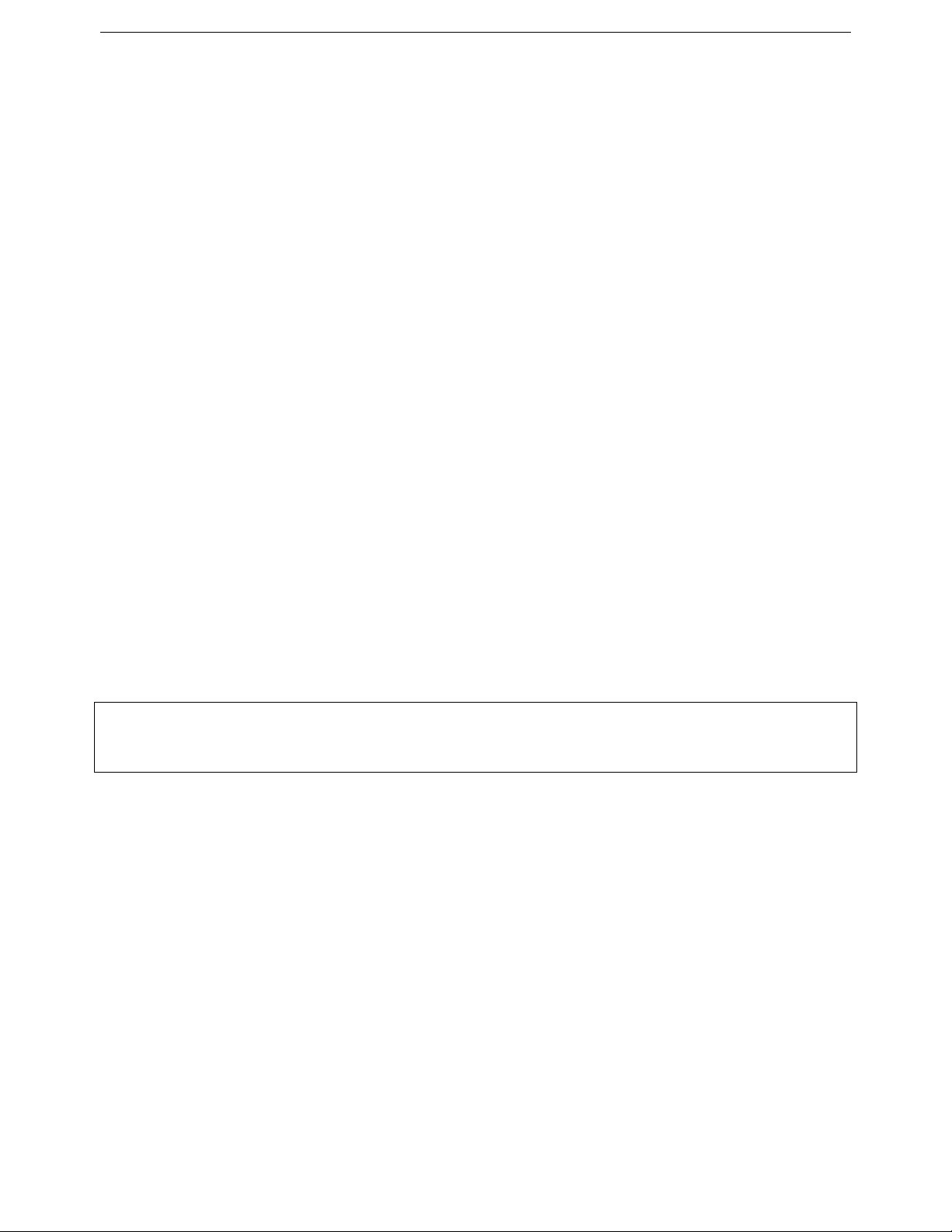
Chương II. MỘT SỐ KỸ THUẬT GIẢI TOÁN ĐẶC SẮC
Chủ đề 7. ỨNG DỤNG NGUYÊN LÍ DIRICHLET TRONG CHỨNG MINH BẤT ĐẲNG THỨC
Nhà toán học Đức P.G.Lejeune Dirichlet (1805-1859) đã nêu ra một định lí mà về sau người ta gọi
là Nguyên lí Dirichlet, nguyên lý được phát biểu như sau:
“Nếu nhốt vào n chiếc lồng một số chú thỏ mà số lượng lớn hơn n thì ta sẽ tìm được một chiếc
lồng mà trong đó có nhiều hơn một con thỏ”
Chúng ta biết bất đẳng thức là một dạng toán hay và khó, thường có trong các kì thi học sinh giỏi
cấp Tỉnh, cấp Quốc gia và Quốc tế. Có rất nhiều phương pháp để chứng minh bất đẳng thức như phương
pháp chứng minh bằng phép biến đổi tương đương, phương pháp quy nạp, phương pháp chứng minh bằng
phản chứng, dùng các BĐT cổ điển: Cauchy, Bunhiacopxki,...
Trong bài viết này chúng tôi muốn giới thiệu một phương pháp chứng minh bất đẳng thức khá thú
vị là ứng dụng nguyên lí Dirichlet. Với phương pháp này, giúp chúng ta chứng minh được một số bài toán
bất đẳng thức một cách rất gọn gàng và độc đáo.
Từ nguyên lí Dirichlet có một mệnh đề có ý nghĩa hết sức quan trọng: Trong 3 số thực bất kì a,
b, c bao giờ cũng tìm được hai số cùng dấu.
Đây là một mệnh đề rất quan trọng, bởi khi ta đã chọn được “điểm rơi” (tức là đẳng thức của bài
toán) thì ta có thể áp dụng mệnh đề trên để chứng minh bất đẳng thức. Chẳng hạn đẳng thức xảy ra khi
abck thì ta có thể giả sử 2 số
;ak bk
cùng dấu, khi đó thì
()()0akbk
. Chúng
ta sẽ tìm hiểu một số ví dụ sau để thấy được ý nghĩa việc ứng dụng nguyên lí Dirichlet trong việc giải bất
đẳng thức như thế nào?
Bài toán 1. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
a2b2c29abbcca
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1
. Theo một đánh giá quen thuộc ta có
2
9ab bc ca 3a b c . Như vậy ta cần chứng minh
2
222
a2b2c2 3abc
Quan sát bất đẳng thức trên ta nghĩ đến bất đẳng thức Bunhiacopxki. Như vậy ta cần đánh giá từ
2
abc làm xuất hiện
2
a2 , để ý ta thấy
2
222222
abc a 111b c a 21b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222222
22 2 2
3a 2 1 b c a 2 b 2 c 2
31 b c b 2 c 2
Biến đổi tương đương ta thu được

22 2 2 2 2 22 2 2
22 2 2 2 2
31bc b2c2 33b3c bc2b2c4
bc b c 1 0 b 1 c 1 0
Như vậy ta chỉ cần chỉ ra được
22
b1c1 0, tuy nhiên vì vai trò của a, b, c như nhau nên
theo nguyên lí Dirichlet thì trong ba số
222
a1;b1;c1
luôn tồn tại hai số cùng dấu và ta hoàn toàn
có thể giả sử hai số đó là
22
b1;c1. Như vậy bài toán được chứng minh xong.
Nhận xét: Ta có thể chứng minh bất đẳng thức trên theo cách khác sau:
Theo nguyên lí Dirichlet trong ba số
1; 1; 1ab bc ca tồn tại hai số không trái dấu, Không
mất tính tổng quát ta giả sử hai số đó ta
1; 1ab bc
khi đó ta được
2
110 1ab bc ab c ab bc
Suy ra
222 2 2
22 1 2 abc b abc ab bc
Bất đẳng thức cần chứng minh viết lại thành
222 22 22 2 2 2 2 2
2489abc abbcca abc abbcca
Ta có
222 2
22 abc b ab bc
và
222
33 abc abbcca
Lại thấy
22
12ab ab
nên
22 22 2 2
264 ab bc ca ab bc ca
Và
22
2ac ac. Từ các bất đẳng thức trên ta được
222 22 22 2 2 2 2 2
2489abc abbcca abc abbcca
Vậy bất đẳng thức trên được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1abc .
Bài toán 2. Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:
222
abc2abc12abbcca
Lời giải
Trước hết ta để ý đến đẳng thức xẩy ra tại
abc1 điều này có nghĩa là khi đẳng thức xẩy ra
thì
a1;b1;c1
cùng bằng 0, ngoài ta trong bất đẳng thức chứa các đại lượng
ab, abc,...
nên ta
nghĩ đến tích
ca 1 b 1, tuy nhiên ta chưa thể khẳng định được tích đó có không âm hay không
nên ta sử dụng nguyên lí Dirichlet.
Theo nguyên lí Dirichlet trong ba số
a1;b1;c1 luôn tồn tại hai số cùng dấu, không mất
tính tổng quát ta giả sử hai đó là
a1;b1, khi đó ta có
a1b1 0 ca1b1 0 abcacbcc 0
Khi đó ta có
22
222
a b c 2abc 1 a b 1 c 2 abc ac bc c 2 ab bc ca
Dễ thấy
22
a b 1 c 2 abc ac bc c 0 nên ta có
22
a b 2ab 1 c 2c 2abc 2ac 2bc 2 bc ca 2 ab bc ca

Suy ra
222
abc2abc12abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Nhận xét: Ta có thể chứng minh được bất đẳng thức đúng với mọi số thực nếu thay đổi một chút:
222 222
22 abcabc abbcca
Theo nguyên lí Dirichlet thì
22 2 222 2 22 22
110 ca b abc c bc ca
Nên ta chỉ cần chứng minh
22 2
22 2222
22 110 a b b c c a ab bc ca a b bc ca
Bất đẳng thức này hiển nhiên đúng. Đẳng thức xảy ra khi và chỉ khi
1abc
Bài toán 3. Cho các số thực dương a, b, c. Chứng minh rằng
222
abc2abc3a1b1c1
Lời giải
Sau khi nhân 2 vế cho 2 thì bất đẳng thức trên tương đương với
222
2a b c 2abc 4 2ab bc ca 2a b c
Theo bài toán 2 ta được
222
abc2abc12abbcca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
abc32abc a1 b1 c1 0
Bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
abc1
Bài toán 4. Cho các số thực dương a, b, c. Chứng minh rằng
22
222
a2(b2)(c2)3abc abc1
Lời giải
Bất đẳng thức trên tương đương với
22 22 22 2 2 2
2 a b b c c a 4 a b c 2abc 7 9 ab bc ca
Theo bất đẳng thức Cauchy thì
22 22 22
2a b 2 2b c 2 2c a 2 4ab 4bc 4ca
Và
222
3a 3b 3c 3ab 3bc 3ca
Từ đó kết hợp với bài toán 2 ta suy ra điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài toán 5. Cho a, b, c là các số thực dương thỏa mãn
222
abcabc4
Chứng minh rằng: ab bc ca abc 2
Lời giải
Dự đoán dấu đẳng thức xẩy ra tại
abc1
Cách 1: Theo nguyên lí Dirichlet thì 2 trong 3 số
a1;b1;c1 cùng dấu. Không mất tính
tổng quát, giả sử
a1b1 0 thì
ca 1 b 1 0 abc bc ca c

Mặt khác ta có
222 2
4 a b c abc 2ab c abc
Suy ra
2
4c 2ababc 2c ab
Suy ra
0 ab bc ca abc 2 c bc ca bc ca c 2
Cách 2: Theo nguyên lý Dirichlet ta có
ca 1 b 1 0 abc bc ca c
abbccaabcabbcca acbcc
ab bc ca abc ab c
Ta đi chứng minh
ab c 2
Từ
222
abcabc4 ta được
22
22
ab
a4;b4;ab 4
2
.
Mặt khác cũng từ
222
abcabc4 suy ra
222
cabcab40
Xem đẳng thức trên là là phương trình là bậc hai theo biến c.
Khi đó ta được
2
22 2 2
ab 4 a b 4 4 a 4 b 0D
Do đó phương trình có hai nghiệm
22
ab 4 a 4 b
c
2
và
22
ab 4 a 4 b
c
2
Vì
c0 nên
22
ab 4 a 4 b
c
2
Do đó ta được
22 22
22
22 22
ab 4 a 4 b ab 4 a 4 b
ab 2 ab 2
22
4ab 4a 4b 4ab 4a 4b ab 0
Vậy bất đẳng thức phải chứng minh.
Bài toán 6. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc 4 . Chứng minh rằng:
abcabbcca
Lời giải
Không mất tính tổng quát, giả sử hai số
a1
và
b1
cùng không âm
Khi đó ta được
ca 1 b 1 0 abc bc ca c
Suy ra
abcabc abcacbcc abcabc abc1
Mặt khác ta có
22
ab cab
4 ab bc ca abc ca b ab abc ca b
44
Suy ra
4
c1abc14
ab
Do đó ta được
abcabc4 nên ta có
a b c abc ab bc ca abc
Hay
abcabbcca
. Vậy bất đẳng thức được chứng minh.
Nhân xét: Ta cũng có thể chứng minh theo cách sau đây

Theo nguyên lí Dirichlet thì 2 trong 3 số
1, 1,( 1)abc cùng dấu, không mất tính tổng
quát, giả sử
110ab
.
Khi đó
110c a b c ac bc abc
.
Do đó ta chỉ cần chứng minh
a b ab abc
Từ giả thiết
4 ab bc ca abc
suy ra
4
ab
c
abab
Thay vào bất đẳng thức trên ta được bất đẳng thức tương đương là:
2
4
140
ab
ab ab ababab ab ab ab
abab
Bất đẳng thức trên hiển nhiên đúng. Phép chứng minh hoàn tất.
Bài toán 7. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
111
32abc
abc
.
Lời giải
Bất đẳng thức được viết lại là
222
111
P32abc0
abc
Không mất tính tổng quát giả sử
a1
và
b1
cùng không âm.
Khi đó suy ra
a1b1 0
. Ta có
2
222 2
22
22 22
2
2
111 11 21
P 3 2a b c 2a b c 3
ab ab
abc c
11 11
2c a b 2 a b c 3 a b 2a 2b 3
ab ab
11
2a 1 b 1 ab 1 0
ab
Vậy bất đẳng thức được chứng minh.
Bài toán 8. Cho a, b, c là các số thực dương. Chứng minh rằng:
11 11 11
a 1b1b1c1c1a 13
bc ca ab
Lời giải
Đặt
111
xa ;yb ;zc
bca
, khi đó bất đẳng thức cần chứng minh được viết lại thành
x1y1 y1z1 z1x1 3
Hay ta cần chứng minh
xy yz zx 2 x y z
Theo nguyên lí Dirichlet thì 2 trong 3 số
x2,y2,(z2)
cùng dấu.
Không mất tính tổng quát, giả sử
x2y2 0, suy ra
xy 4 2x 2y 2 x y z 2z xy 4

Lại có
1
xyz abc x y z 2 x y z 2 2 xy z
abc
Suy ra
zxy1 2 xy1 z xy1 2
Từ hai bất đẳng thức trên ta được
2x y z 2z xy 4 xy yz zx
Vậy ta có điều phải chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài toán 9. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
aa1bb1cc11
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,(c1) cùng dấu, không mất tính tổng quát
giả sử
b1c1 0
. Khi đó ta được
22 22
2
22
bb1cc1bcb1c1bcbc1
1
bcbc1 bc bc1
2
Do đó ta được
222
2
222
aa1bb1cc1
11
aa1 bc bc1 aa1a4a5
22
Nên ta chỉ cần chứng minh
2
22 2
aa1a4a52 a1a3a30
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
abc1
Bài toán 10. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
abcabc2abbcca
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,(c1) cùng dấu, không mất tính
tổng quát giả sử
a 1)(b 1 0 abc ac bc c.
Theo bất đẳng thức Cauchy ta có
3
abc3abc 3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
abc32abbcca
Thật vậy ta có
222 222
abc3abc2abc1
Theo bất đẳng thức Cauchy ta có
22 2
ab2ab;c12c
Kết hợp với
abc ac bc c ta được
222
a b c 3 2ab 2c 2 bc ca c 2 ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài toán 11. Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:

222
1
abc 2 a 1 b 1 c 1 a b c
2
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,c1 cùng dấu. Không mất tính tổng
quát, giả sử
a1b1 0 ab a b1
.
Vì vậy để hoàn tất bài toán ta chỉ cần chứng minh
222
1
2a1b1c1ca b c
2
ba1
Hay
222
1
a1 b1 c1 ab21c
2
Áp dụng bất đẳng thức Cauchy ta có
2
222 2
ab2
a1 b1 c1 c1
2
2ab21c 2ab21c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài toán 12. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
2a b c abc 8 5a b c
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,c1 cùng dấu, không mất tính
tổng quát giả sử
a 1 b 1 0 abc ac bc c
.
Suy ra
222 222
2abc abc82abc acbcc8
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
2a b c ac bc c 8 5a b c
Thật vậy, bất đẳng trên tương đương với
22222
bc2 ca2 3a1 3b1 2c1 0
Bất đẳng thức trên luôn đúng.
Vậy bài toán được chứng minh xong. Đẳng thức xảy ra khi à chỉ khi
abc1.
Nhận xét: Hoàn toàn tương tự ta có thể tổng quát hóa bài toán trên:
a). Cho a, b, c là các số thực dương. Chứng minh rằng:
222
3221ma b c abc m m a b c .
Trong đó m là số thực cho trước thỏa mãn
2
2
m
b) Cho a, b, c là các số thực dương. Chứng minh rằng:
222
21 2 12m a b c abc m ab bc ca .
Trong đó m là số thực cho trước thỏa mãn
1m
c) Cho a, b, c là các số thực dương. Chứng minh rằng ta luôn có bất đẳng thức:

222
2abca b c abcabbcca
d) Cho a, b, c là các số thực dương. Chứng minh rằng:
444
2136abc a b c a b c
Bài toán 13. Cho a, b, c là các số thực không âm. Chứng minh rằng:
333
5 a b c 3abc 9 9 ab bc ca
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,c1 cùng dấu, không mất tính
tổng quát giả sử
a 1)(b 1 0 3abc 3ac 3bc 3c
.
Suy ra
333 333
5 a b c 3abc 9 5 a b c 3ac 3bc 3c 9
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333
333
5 a b c 3ac 3bc 3c 9 9 ab bc ca
5 a b c 9 9ab 6bc 6ca 3c
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
33
33 3333
33
33 3 3 3 3 3 3
3c 3 c .1.1 c 1 1; 6ca 6 c a .1 2c 2a 2
6bc 6 b .c .1 2b 2c 2; 9ab 9 a .b .1 3a 3b 3
Cộng vế theo vế các bất đẳng thức trên ta được
333
5 a b c 9 9ab 6bc 6ca 3c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài toán 14. Cho a, b, c là các số thực không âm thỏa mãn
abc1. Chứng minh rằng:
9abc 1 4 ab bc ca
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
111
a,b,c
333
cùng dấu, không mất
tính tổng quát giả sử
11
a b 0 9abc 3ac 3bc c
33
.
Suy ra
19abc 13ac3bcc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
13ac3bcc 4abbcca
Thật vậy bất đẳng thức trên tương đương với
222
1 c c a b 4ab 1 c c 1 c 4ab
1 c 4ab a b 4ab a b 0
Vậy bất đẳng thức được chứng minh xong. Đẳng thức thức xẩy ra khi và chỉ khi
1
abc
3
hoặc
1
ab ;c0
2
và các hoán vị
Nhận xét: Hoàn toàn tương tự ta có thể chứng minh bài toán: Cho a, b, c là các số thực không âm thoả
mãn abc k. Chứng minh rằng:
3
94abc k k ab bc ca

Bài toán 15. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
111 2
1
a1b1c1
a1 b1 c1
Lời giải
Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,c1 cùng dấu, không mất tính
tổng quát giả sử
c1
ab1a1b1 a0b
c
.
Do đó ta được
2
2c 1
a1b1c1 1ababc1 21ab1c
c
Áp dụng bất đẳng thức Bunhiacopxki ta có
22
11 1 1
ab
1a 1b
1ab1 1ab1
ba
ba1c
1ab c1
1abab 1abab
Do đó ta được
222
22 2
111 2
1a1b1c
1a 1b 1c
cc 1 1 c
c1 c
1
c1
c1 c1 c1
Như vậy bất đẳng thức ban đầu được chứng minh. Đẳng thức xẩy ra khi
abc1
Bài toán 16. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
111 1
1
abc1
a1 b1 c1
Lời giải
Trước hết ta chứng minh
22
111
1ab
a1 b1
Thật vậy, bất đẳng thức trên tương đương với
22 22 2 2
ab 1 a 1 b 1 a 1 b 1 ab a b ab 1
Như vậy bất đẳng thức trên được chứng minh.
Mà ta có
1c
1ab 1c
nên ta có
22
11c
1c
a1 b1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
c1 1
1
1c abc1
c1

Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,c1
cùng dấu, không mất tính
tổng quát giả sử
c1
ab1a1b1 a0b
c
.
Khi đó ta được
222
cc 1 1 c
c1 1 c1 1
1
1c abc1 1c c1
c1 c1 c1
c1
c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài toán 17. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
a3 b3 c3
3
a1 b1 c1
Lời giải
Trước tiên ta chứng minh 2 bổ đề sau:
Bổ đề 1.
111 2
1
1a 1b 1c 1abc
Bổ đề 2.
222
111 1
1
abc1
1a 1b 1c
+ Bổ đề 1: Bất đẳng thức trên tương đương với
222
3abbcca2abc
3abc
abc3
2abbccaabc 1abc
Đánh giá cuối cùng luôn đúng vì theo bất đẳng thức Cauchy thì
3
222 222
abc3abc 3
Vậy bổ đề 1 được chứng minh.
+ Bổ đề 2: Theo nguyên lí Dirichlet thì 2 trong 3 số
a1,b1,(c1) cùng dấu, không mất
tính tổng quát giả sử
c1
a1)(b1 0 ab1ab
c
.
Ta có
22
22
111
ab 1 a b 0
1ab
1a 1b
(đúng)
Do đó ta được
22
111c
1ab c1
1a b1
Suy ra
222 2
111 1 c1 1
1
abc1 c1 c1
1a 1b 1c c1
c1
c
Vậy bổ đề 2 được chứng minh.
Trở lại bài toán thì bất đẳng thức cần chứng minhtương đương với
222
111 2 2 2
3
1a 1b 1b
a1 b1 b1

Mà theo bổ đề trên ta có
222
222
111 2 2 2
1a 1b 1b
a1 b1 b1
222 2
1213
abc1
a1 b1 b1
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
Bài toán 18. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
222
222
bca cab abc
3
5
abcbca cab
Lời giải
Chú ý đến giả thiết ta viết lại bất đẳng thức thành
222
222
222
12a 12b 12c
3
5
abcbca cab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức
22 2
2
22 2222
22 22
1 2b 1 2c 2 2b 2c
2a
bca
bca cab bc1a 1b
Ta quy bài toán về chứng minh
2
2
22 2
2
12a
2a 3
5
bca
abc
Theo nguyên lí Dirichlet thì 2 trong 3 số
111
a,b,c
333
cùng dấu, không mất
tính tổng quát giả sử
2
22
11 11
bc 0bcbc
33 39
.
Do đó ta được
22 2
22 2 2
2a 2a 18a
bca 9a3a5
21
aa
39
Suy ra
22
22
22 2 2 2
22
12a 12a
2a 18a
bca 9a3a5
abc abc
Dễ dàng chứng minh được
2
2
2
2
22
2
12a
18a 3
3a 1 17a 8a 5 0
5
9a 3a 5
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Qua một số bài toán trên, ta thấy rằng nguyên lí Dirichlet không những có ứng dụng trong việc
giải toán rời rạc, các bài toán về số học, tổ hợp, … mà còn rất có hiệu quả trong việc chứng minh một số

bài toán về bất đẳng thức, trong một số trường hợp cho ta lời giải vô cùng đẹp đẽ và trong sáng, góp phần
trong việc nâng cao tư duy và tạo sự hứng thú cho các học sinh yêu thích môn toán. Hy vọng rằng, với
suy nghĩ và những ví dụ trên sẽ góp phần bổ sung thêm kiến thức và kinh nghiệm trong việc chứng minh
bất đẳng thức.

Chủ đề 8.
PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNH TRONG CHỨNG MINH BẤT ĐẲNG ĐẲNG THỨC
Có bao nhiêu điều bí ẩn mà bạn chưa biết đến ?! Câu trả lời là rất rất nhiều và đôi khi bạn cảm thấy
bực bội, khó chịu khi không thể tìm ra một lời giải thích thỏa đáng cho bí ẩn nao đó. Nhưng bạn hãy quan
niệm rằng đằng sau bất kì một điều gì luôn hàm chứa một ý nghĩa nhất định. Và cũng không phải ngẫu
nhiên mà sự lí giải lại được hình thành. Trong thế giới bất đẳng thức cũng vậy. Đôi khi bạn không thể
hiểu được tại sao người ta lại có thể tìm ra một lời giải trông có vẻ “kì cục” như thế !!! Phải chăng là lần
mò va may rủi lắm mới tìm ra được ?
Câu tra lơi lai môt lân nưa đươc nhăc lai là môi lơi giai đêu co sư giai thich cua riêng ban thân no.
Viêc tim ra lơi giai đo phai đi qua môt qua trinh lâp luân, thư, sai va đung. Trong bài viết nho nho nay
chung tôi muôn giơi thiêu đên cac ban môt ki thuât cơ ban nhưng không kem phân hiêu qua trong viêc
chưng minh môt sô dang của bât đăng thưc. Nó không giúp ta giải quyết tất cả các bài toán mà chỉ giúp
ta
tìm ra những lời giải ngắn gọn và ấn tượng trong một lớp bài toán nào đó. Một số bài toan tuy dễ đối với
phương pháp này nhưng lại là khó đối với kỹ thuật kia. Đây cũng là điều hiển nhiên và dễ hiểu.
1. Ví dụ mở đầu
Bai toan 1. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng
222
222
2a b c
111
5
3
abc
Lời giải
Bất đẳng thức cần chứng minh được viết lại thành
222
222
1112a2b2c
5
333
abc
Ta chứng minh bất đẳng thức sau đây
2
2
12a 72a
333
a
Thật vậy, bất đẳng thức trên tương đương với
2
2
2
a1 2a 6a3
0
3a
Hiển nhiên đúng với a là số thực dương.
Áp dụng tương tự ta được
22
22
1 2b 7 2b 1 2c 7 2c
;
333 333
bc
Cộng theo vế các bất đẳng thức trên ta được
222
222
2a b c
1112a2b2c
75
333 3
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Chung ta se khơi đâu kỹ thuât nay băng viêc đưa ra cach giai thich cho viêc tim ra bât đăng thưc
phu trên va no cung chinh la cach giai thich cho cac bai toan sau nay cua chung ta.
Bai toan trên cac biên trong ca hai vê va điêu kiên đêu không rang buôc nhau điêu nay khiên ta
nghi ngay se tach theo tưng biên đê chứng minh được đơn gian hơn nếu có thể. Nhưng ro rang chi tưng
đo thôi la không đu. Để ý đến dấu đẳng thức xẩy ra nên ta nghĩ đến chưng minh bât đăng thưc sau

2
2
22
a1a12a 3
12a 5
0
33
a3a
Tuy nhiên đánh giá trên không hoan toan đúng với a thực dương.
Để ý là với cách làm trên ta chưa sử dụng điều kiện
abc3
.
Như vậy ta sẽ không đi theo đường lối suy nghĩ đơn giản ban đầu nữa mà sẽ đi tìm hệ số để bất
đẳng thức sau là đúng
2
2
12a 5
ma n 1
33
a
Trong đó m và n là các hệ số chưa xác định.
Thiết lập tương tự với các biến b và c ta được
22
22
12b 5 12c 5
mb n; mc n
33 33
bc
Cộng theo vế các bất đẳng thức trên ta có
222
222
1112a2b2c
5mabc 3n 53mn
3
abc
Như vậy ở đây 2 hệ số m và n phải thỏa mãn điều kiện
mn 0 n m
. Thế vào (1) dẫn đến
2
2
12a 5
ma 1 2
33
a
Đến đây ta chỉ cần xác định hệ số duy nhất là m để bất đẳng thức (2) là đúng. Chú ý đẳng thức xẩy
ra tại
abc1 nên ta cần xác định m sao cho
2
2
22
a12a 3
12a 5
ma 1 a 1 m 0
33
a3a
Khi cho
a1 thì ta có
2
2
a12a 3
2
3
3a
từ đó ta dự đoán rằng
2
m
3
để tạo thành đại
lượng bình phương
2
a1 trong biểu thức. Từ đó ta sẽ chứng minh bất đẳng thức phụ
2
2
12a 72a
333
a
Bài toán 2. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
33 33 33
222
5a b 5b c 5c a
3
ab 3a bc 3b ca 3c
Lời giải
Ta đi chứng minh bất đẳng thức
33
2
5a b
2a b
ab 3a
Thật vậy, dễ dàng chứng minh được
33
ababab
, ta biến đổi tương đương bất đẳng thức bên
như sau
33 33 3
33 2 2 33
33
2
ababab 5ab6aabab
5a b a 6a ab b 5a b a 2a b 3a b
5a b
2a b
ab 3a

Hoàn toàn tương tự ta được
33 3 3
22
5b c 5c a
2b c; 2c a
bc 3b ca 3c
Cộng theo vế các bất đẳng thức trên ta được
33 33 33
222
5a b 5b c 5c a
abc3
ab 3a bc 3b ca 3c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi
abc1.
Nhận xét: Hoàn toàn tương tự như bài toán trên, ta đi tìm hệ số m, n sao cho bất đẳng thức
33
2
5a b
ma nb
ab 3a
đúng, với
mn1 n1m
.
Ta viết lại bất đẳng thức trên thành
3
3
3
22
2
5a
1
ma 5t 1
b
1m mt1 1
b
a3a t3t
b
b
với
a
t
b
Để ý đến đẳng thức xẩy ra tại
abc
tức là xẩy ra tại
t1
, khi đó ta cần xác định m sao cho
32
22
5t 1 5t 2t 1
mt 1 1 t 1 m 0
t3t t3t
Cho
t1 thì ta được
2
2
5t 2t 1
2
t3t
nên ta chọn m2 và từ đó ta được n1 . Khi này ta
đi chứng minh bất đẳng thức
33
2
5a b
2a b
ab 3a
Chắc chắn ngay khi đọc lời giải cho các bài toán này bạn có phần lúng túng và không hiểu tại sao
lại có thể tìm ra bất đẳng thức phụ một cách “khó hiểu” như vậy. Phải chăng đó là dự đoán một cách may
mắn. Hoặc cũng có người sẽ nghĩ bài toán trên được tạo ra từ chính bất đẳng thức phụ đó. Câu trả lời là
hoàn toàn không phải. Tất cả đều đi theo một qui luật của nó. Ở các phần tiếp theo chúng tôi sẽ phân tich
vê một kỹ thuật phân tích giúp tìm ra các bất đẳng thức phụ và mở rộng vấn đề này theo chiều hướng khá
mới mẻ. Kỹ thuật này có tên là U.C.T, là viết tắt của 3 chữ cái đầu của cụm từ tiếng Anh Undefined
Coefficient Technique hay còn gọi là kỹ thuât hệ số bất định. Đây la môt kỹ thuât cơ bản va la nên tang
quan trọng trên con đường tìm kiếm lời giải cho nhưng bất đẳng thức kho.
2. Một số bài toán áp dụng phương pháp hệ số bất định
Có thể nói với phương pháp hệ số bất định ta có thể giải quyết được một lớp các bất đẳng thức
mà ở đó các biến độc lập với nhau. Dưới đây là một số bài toán áp dụng phương pháp hệ số bất định.
Bài toán 1. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng
222
111
1
abcbcacab
Lời giải
Ở đây ta cần tìm m để bất đẳng thức dưới là đúng
22
2
aa 1
111
ma 1 ma 1
3
abcaa3
3a a 3

Tương tự như trên ta dự đoán rằng với
1
m
9
thì bất đẳng thức phụ đúng. Thật vậy
22
2
22
a1 3a a1 bc
14a
00
99
aa3
3a a 3 3a a 3
Hoàn toàn tương tự ta được
22
14b14c
;
99 99
bb3 cc3
Cộng theo về các bất đẳng thức trên ta được
222
1114abc
1
39
abcbcacab
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bai toán 2. Cho a, b, c la cac sô thưc dương thoa man
333
abc 3. Chưng minh răng
222
111
45abc27
abc
Lời giải
Ta cân tim hê sô m sao cho
2
23 2
a 1 5a 5a 4
4
5a 9 m a 1 m a 1 a a 1
aa
Ta dễ dàng nhận ra đẳng thức xảy ra khi và chỉ khi
abc1.
Khi cho
a1
thì ta có thể dự đoán rằng
m2
. Ta sẽ chứng minh rằng với
m2
thì bất đẳng
thức phụ trên là đúng. Thật vậy
2
2
23
a1 2a a4
4
5a 7 2a 0
aa
Do
3
2
a3 2aa40. Vậy bất đẳng thức phụ trên là đúng.
Hoàn toàn tương tự ta được
2323
44
5b 7 2b ; 5c 7 2c
bc
Cộng theo vế các bất đẳng thức trên ta được
222 333
111
45abc212abc27
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
Bai toán 3. Cho a, b, c la cac sô thưc dương thoa man
222
abc 3
. Chưng minh răng
4a b c
111
7
abc 3
Lời giải
Ta cần tìm hệ số m sao cho
232
14a 7
ma 1 3ma 4a 7 3ma 3 0
a3 3
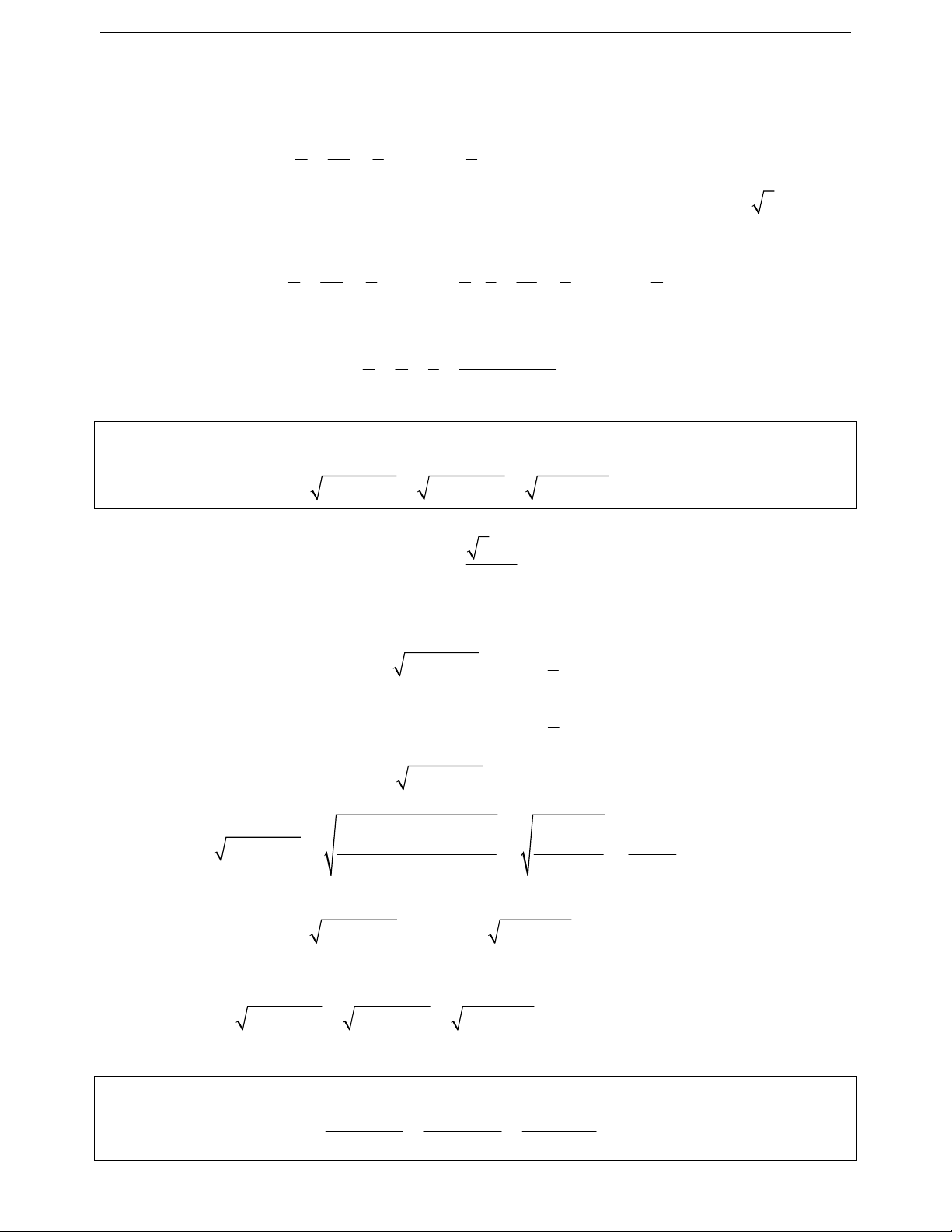
Dự đoán là đẳng thức xẩy ra tại
abc1
, khi đó ta tìm được
1
m
6
. Như vậy ta đi chứng minh
bất đẳng thức
2
2
14a 1 7
a 1 a1 6a 0
a36 3
Bất đẳng thức cuối cùng luôn đúng vì từ
222
abc 3 ta được 0a,b,c 3.
Hoàn toàn tương tự ta được
22
14b1 714c1 7
b1 ; c1
b36 3c36 3
Cộng theo vế các bất đẳng thức trên ta được
4a b c
111
7
abc 3
Vậy bất đẳng thức được chứng minh.
Bài toán 4. Cho các số thực dương a, b, c thỏa mãn
abc3
và làm cho các biểu thức của bất đẳng
thức luôn xác định. Chứng minh rằng:
222
aa1 bb1 cc13
Lời giải
Biểu thức P xác định khi và chỉ khi
51
a, b, c
2
. Dự đoán dấu đẳng thức xẩy ra tại
abc1.
Khi đó ta đi tìm m để bất đẳng thức sau đúng
2
1
aa1ma
2
Để ý đẳng thức xẩy ra tại
a1
khi đó ta tìm được
3
m
2
, tức là ta cần phải chứng minh được
2
3a 1
aa1
2
Thật vậy ta có
22 2
2
3a 1 5 a 1 3a 1
3a 1
aa1
442
Chứng minh tương tự ta được
22
3b 1 3c 1
bb1 ;cc1
22
Cộng theo vế các bất đẳng thức trên ta được
222
3a b c 3
aa1 bb1 cc1 3
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài toán 5. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng
222
111
1
aa3bb3cc3

Lời giải
Vì a, b, c là các số thực dương thỏa mãn
abc3. Do đó ta được
a, b, c 0; 3
. Dự đoán đẳng
thức xẩy ra tại
abc1
.
Ta cần tìm m để bất đẳng thức sau đúng
2
14
ma
9
aa3
Để ý là đẳng thức xẩy ra tại
a1
, khi đó ta tìm được
1
m
9
Khi đó ta đi chứng minh
2
1a4
99
aa3
Biến đổi tương đương bất đẳng thức trên ta được
2
2
2
14a
4aa a3 9 a3a1 0
9
aa3
Bất đẳng thức cuối cùng đúng vì
a0;3
.
Chứng minh tương tự ta được
22
14b14c
;
99
bb3 cc3
Cộng theo vế các bất đẳng thức trên ta được
222
12 a b c
111
1
9
aa3bb3cc3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài toán 6. Cho a, b, c là các số thực dương thỏa mãn điều kiện
222
abc1.
Chứng minh rằng:
22 2 2 2 2
abc33
2
bc ca ab
Lời giải
Từ giả thiết
222
abc1, ta được
22 22 2 2 2 2 2
abcabc
b c c a a b 1a 1b 1c
Xét
2
22
2
2
22
a3a2 3a1
2a 3 3a 1 a
a33
a0
2
1a
21 a 21 a
Từ đó suy ra
2
2
a33
a
2
1a
, chứng minh tương tự ta được
22
22
b33 c33
b; c
22
1b 1c
Cộng các bất đẳng thức trên theo vế ta được
222
222
33a b c
abc 33
22
1a 1b 1c

Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
3
.
Bài toán 7. Cho a, b, c là ba số thực dương thỏa mãn
abc3. Chứng minh rằng :
222
222
111
abc
abc
Lời giải
Dự đoán đẳng thức xẩy ra tại
abc1
.
Ta có nhận xét, nếu có một trong ba số a, b, c thuộc khoảng
1
0;
3
, chẳng hạn
1
0a
3
thì ta có
2
222
222
111
9abc abc
abc
nên bài toán được chứng minh, do vậy ta chỉ xét
17
a, b, c ;
33
.
Khi đó ta đi tìm hệ số m để bất đẳng thức sau đúng
2
2
1
ama1
a
, Để ý là khi a1 thì
đẳng thức luôn xẩy ra với mọi m, do đó để chọn được m lấy giá trị của a càng gần 1 càng tốt và ta chọn m
sao cho đẳng thức gần xẩy ra, bằng cách đó ta chọn được
m4 là giá trị tốt nhất.
Ta đi chứng minh bất đẳng thức
2
2
1
a4a4
a
Thật vậy, bất đẳng thức trên tương đương với
22
2
22
a1 2 a1
1
a4a40 0
aa
Hoàn toàn tương tự ta được
22
22
11
b4b4; c4c4
bc
Cộng theo vế các bất đẳng thức trên ta được
222
222
111
abc 4abc120
abc
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc1
.
Bài toán 8. Cho a, b, c là ba số thực dương thỏa mãn
444
abc3. Chứng minh rằng:
111
1
4ab 4bc 4ca
Lời giải
Ta chưa thể sử dụng phương pháp hệ số bất định cho bài toán này ngay được, ta cần phải biến đổi
như thế nào đó để đưa bài toán đã cho về dạng các biến độc lập với nhau
Áp dụng bất đẳng thức
22
ab
ab
2
, khi đó hoàn toàn tương tự ta được
22 22 22
111 2 2 2
4ab 4bc 4ca
8ab 8bc 8ca

Tiếp theo đặt
222
22 2 2 2 2
xbc;yca;zab thì ta được
444
xyz4a b c 12
Bài toán quy về chứng minh
1111
2
8x8y8z
.
Đến đây ta chứng minh bất đẳng thức
11 1
x4
144 6
8x
. Thật vậy bất đẳng thức tương đương
với
2
2
x4 x4
x4 1
x4 0 0
144
6x28 x
144 x 2 8 x
Vì
xyz12 nên
x0;12 do đó bất đẳng thức trên hoàn toàn đúng.
Tương tự ta được
11 111 1
y4 ; z4
144 6 144 6
8y 8z
Cộng theo vế các bất đẳng thức trên ta được
1111 11
xyz12 3.
144 6 2
8x8y8z
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
xyz4 hay
abc1
.
Bài toán 9. Cho a, b, c, d là các số thực dương thỏa mãn
abcd4. Chứng minh rằng
2222
1111
2
a1b1c1d1
Lời giải
Ta sẽ xác định hệ số m để bất đẳng thức sau là đúng
22
2
a1a1
2
1ma1 ma1
a1 a1
a1
a1 m 0
a1
Để ý là đẳng thức xẩy ra tại
a1 , khi ta tìm được m1 .
Ta đi chứng minh bất đẳng thức sau đúng
2
2
2a
a1
Thật vậy
2
22
aa 1
2
2a 0
a1 a1
Hoàn toàn tương tự ta được
222
222
2b; 2c; 2d
b1 c1 d1
Cộng theo vế các bất đẳng thức trên ta được

2222
1111
2
a1b1c1d1
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abcd1
.
Nhận xét: Ta có thể sử dụng kỹ thuật “Cauchy ngược dấu” để tìm ra bất đẳng thức phụ trên
22
22
1
111
22
11
aaa
a
aa
Bài toán 10. Cho bốn số dương a, b, c, d thỏa mãn
abcd1. Chứng minh rằng:
3333 2222
1
6a b c d a b c d
8
Lời giải
Dự đoán đẳng thức xẩy ra tại
1
abcd
4
Ta cần tìm hệ số m sao cho bất đẳng thức sau đúng
32
1
6a a ma
8
Để ý đẳng thức xẩy ra tại
1
a
4
, ta chọn được
5
m
8
.
Khi đó ta cần chứng minh
32
51
6a a a
88
. Thật vậy, bất đẳng thức tương đương với
2
32
51 1
6a a a 0 4a 1 3a 1 0
88 8
Bất đẳng thức trên luôn đúng do
a0
.
Hoàn toàn tương tự ta được
32 32 32
51 51 51
6b b b ; 6c c c ; 6d d d
88 88 88
Cộng theo vế các bất đẳng thức trên ta được
3333 2222
1
6a b c d a b c d
8
Vậy bất đẳng thức được chứng minh.
Bài toán 11. Cho a, b, c, d là các số thực dương thỏa mãn
2222
abcd4. Chứng minh rằng:
3333
3
2a b c d 2 2abacadbcbddc
2
Lời giải
Theo bài ra a, b, c, d là các số thực dương thỏa mãn
2222
2
abcd 4
a b c d 2 2 ab ac ad bc bd cd
a b c d 2 2 ab ac ad bc bd cd
Bất đẳng thức cần chứng minh tương đương với
3333
3
2a b c d 2 a b c d
2
Ta cần xác định hệ số m để bất đẳng thức sau đúng

2
3
2a 1 a 1
3a 1
2a m a 1 m a 1
22
Dễ dàng dự đoán được
9
m
2
. Ta se chưng minh bất đẳng thức
3
9a 1
3a 1
2a
22
Thât vây
2
3
9a 1
3a 1
2a 2 a 1 a 2 0
22
Vậy bất đẳng thức trên đúng.
Hoàn toàn tương tự ta được
333
9b 1 9c 1 9d 1
3b 1 3c 1 3d 1
2b ; 2c ; 2d
22 22 22
Cộng theo vế các bất đẳng thức trên ta được
3333
3
2a b c d 2 a b c d
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi va chỉ khi
abcd1
Bài toán 12. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
333
222222
abc3
5
a 3ab b b 3bc c c 3ca a
Lời giải
Dự đoán dấu đẳng thức xẩy ra tại
abc1.
Ta đi tìm hệ số m, n sao cho bất đẳng thức sau đúng
3
22
a
ma nb
a3abb
Để ý đến đẳng thức xẩy ra tại
ab1 ta tìm được
21
m;n
55
Khi đó ta đi chứng minh
3
22
a2ab
5
a3abb
Thật vậy, ta có biển đổi sau
32 2 2 2
3 22
22 22 22
a3abab 3abab
a3abab
a
a3abb a3abb a3abb
Theo bất đẳng thức
22
ab2ab , do đó ta có
322
2222
ab 3a b
a3abab 2ab
aa
5ab 5
a3abb a3abb
Áp dụng tương tự ta được
33
22 22
b2bcc2ca
;
55
b3bcc c3caa
Từ các bất đẳng thức trên ta suy ra

333
222222
abcabc3
55
a 3ab b b 3bc c c 3ca a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài toán 13. Cho a, b, c là các số thực không âm thỏa mãn
abc 1 . Chứng minh rằng:
33 33 33
222222
ab bc ca
2
aabb bbcc ccaa
Lời giải
Ta có biến đổi biểu thức như sau
22
33
22 22
aba abb
ab
aabb aabb
Dễ dàng chứng minh được
2222
1
aabb aabb
3
Thật vật, bất đẳng thức trên tương đương với
2
22222 2
3 a ab b a ab b a 2ab b 0 a b 0
Áp dụng bất đẳng thức vừa chứng minh trên ta được
33
22
ab 1
ab
3
aabb
Áp dụng tương tự kết hợp với bất đẳng thức Cauchy ta được
33 33 33
3
222222
ab bc ca 2
abc 2abc 2
3
aabb bbcc ccaa
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi
abc1.
3. Ki thuât đổi biến va phương pháp hệ số bất định
Bây giờ chúng ta sẽ bước sang một khoảng không gian mới với lớp bất đẳng thức đôi xưng ba biên
va ki thuât đổi biến theo hướng chuân hoa kêt hơp vơi phương pháp hệ số bất định.
Bài toán 1. Cho a, b, c là các số thực không dương. Chứng minh rằng:
abc3
bc ca ab 2
Lời giải
Chia cả tử và mẫu của mỗi phân thức cho
abc.
Khi đó ta đặt
3a 3b 3c
x;y;z
abc abc abc
thì được xyz 3. Bất đẳng
thức cần chứng minh trở thành
xyz3
yz zx xy 2
Bài toán trên tương đương với bài toán: Cho a, b, c là các số thực dương thỏa mãn
abc3.
Chứng minh rằng
abc3
bc ca ab 2
Cách đổi biến như trên ta gọi là chuẩn hóa.
Bài toán qui về việc chứng minh

abc3
3a 3b 3c 2
Ta cần tìm hệ số m để bất đẳng thức đúng
3a 1
a1
ma 1 ma 1
3a 2
23 a
Dễ dàng dự đoán
3
m
4
. Ta chứng minh bất đẳng thức với m như vậy thì luôn đúng
2
3a 1
a3a1
0
3a 4
43 a
Điều này hiển nhiên đúng.
Hoàn toàn tương tự ta được
b3b1cb3c1
;
3b 4 3c 4
Cộng theo vế các bất đẳng thức trên ta được
abc3
3a 3b 3c 2
Vậy bất đẳng thức được chứng minh.
Bài toán 2. Cho a, b, c là các số thực không âm. Chứng minh rằng
222
222
2222
222
3a b c
bca acb abc
2a b c 2b a c 2c b a a b c
Lời giải
Tương tự như bài toán trên ta có thể chọn
abc3. Khi đó bất đẳng thức cần chứng minh
tương đương với
222
222
222
23 2a 23 2b 23 2c
abc
a2a3b2b3c2c3
Ta cần xác định hệ số m để bất đẳng thức sau là đúng
2
2
2
23 2a
ama1
a2a3
Ta lại có
2
2
2
22
a1a3a 4a6
23 2a
a
a2a3 a2a3
Từ đây dễ dàng dự đoán với
m6 thì bất đẳng thức phụ trên là đúng. Thật vậy
22
2
22
23 2a a 1 6 aa
a6a1 0
a2a3 a2a3
Điều này hiển nhiên đúng do a(0,3).
Hoàn toàn tương tự ta được
22
22
22
23 2b 23 2c
b6b1; c6c1
b2b3 c2c3
Cộng theo vế các bất đẳng thức trên ta được

222
222
222
23 2a 23 2b 23 2c
abc
a2a3b2b3c2c3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
.
Bài toán 3. Cho a, b, c là các số thực dương. Chứng minh rằng:
22 2
222
ab c bc a ca b
6
5
bc a ca b ab c
Lời giải
Tương tự như bài toán trên ta có thể chọn
abc3
. Khi đó bất đẳng thức cần chứng minh
tương đương với
222
a3 a b3 b c3 c
6
5
9 6a 2a 9 6b 2b 9 6c 2c
Tương tự như trên ta dễ dàng tìm ra bất đẳng thức phụ sau:
2
2
2
a 3 a a 1 18a 9
21 9a
0
25
96a2a
25 9 6a 2a
Tưng tự ta được
22
b3 b c3 c
21 9b 21 9c
;
25 25
96b2b 96c2c
Cộng theo vế các bất đẳng thức trên ta được
222
a3 a b3 b c3 c
6
5
9 6a 2a 9 6b 2b 9 6c 2c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài toán 4. Cho a, b, c là các số thực dương. Chứng minh rằng
222
abc 9
4a b c
bc ca ab
Lời giải
Không mất tính tổng quát, giả sử
abc3
. Bài toán cần chứng minh qui về dạng sau
222
abc3
4
3a 3b 3c
Dễ dàng dự đoán bất đẳng thức phụ sau
2
22
a1 92a
a2a1
0
4
3a 43a
Điều này hiển nhiên đúng do
a [0; 3).
Hoàn toàn tương tự ta được
22
b2b1c2c1
;
44
3b 3c
Cộng theo vế các bất đẳng thức trên ta được

222
abc3
4
3a 3b 3c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
.
Bài toán 5. Cho a, b, c la cac sô thưc dương. Chưng minh răng
222
222
222
b c 3a a c 3b a b 3c
1
2
2a b c 2b a c 2c b a
Lời giải
Không mất tính tổng quát, giả sử
abc3
. Ta có bất đẳng thức cần chứng minh tương đương
với
222
222
222
34a 34b 34c
1
2
2a 3 a 2b 3 b 2c 3 c
Sử dụng bất đẳng thức phụ sau
22
2
2
2
34a a1 398a
8a 7
0
6
6a 2a 3
2a 3 a
Điều này hiển nhiên đúng vì
0a3 398a3924150 .
Hoàn toàn tương tự ta được
22
22
22
34b 34c
8b 7 8c 7
;
66
2b 3 b 2c 3 c
Cộng theo vế các bất đẳng thức trên ta được
222
222
222
34a 34b 34c
1
2
2a 3 a 2b 3 b 2c 3 c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Sau môt qua trinh tim hiêu va phân tich cu thê cac bai toan, chăc hăn răng cac ban cung đa phân
nao cam nhân đươc net đep cua phương pháp hệ số bất định du răng thưc ra đây la môt ki thuât cưc ki đơn
gian va dê hiêu. Chung tôi không xem phương pháp hệ số bất định la môt phương phap chinh thông ma
đơn gian no la môt ki thuât cân biêt va cân năm vưng khi ban hoc bât đăng thưc. Nhiêu ngươi quan niêm
răng phương pháp hệ số bất định không co y nghia gi nhưng theo ban thân chung tôi no
nên đươc khai
quat đê sư dung trong môt sô trương hơp. Phương pháp hệ số bất định la môt bươc đêm quan trong va đôi
khi mang nhiêu y nghia trên con đương đi tim lơi giai cho bai toan. Môt ki thuât hay không nhât thiêt no
la no giai đươc tât ca cac dang toan ma la no phai đưa ta đên nhưng y tương, đương đi sang sua, dê nghi,
dê nhân thây băng măt trưc quan.
Chủ đề 9
ỨNG DỤNG CỦA MỘT HỆ QUẢ CỦA BẤT ĐẲNG THỨC SCHUR
Trong chương trình môn Toán ở bậc phổ thông thì bài tập chứng minh bất đẳng thức là một trong
những loại bài tập khó. Cái khó của loại bài tập này là ở chỗ, mỗi bài nó có một cách tiếp cận riêng, cách
giải riêng và độc đáo. Chứa đựng trong chúng là những kiến thức sâu rộng và những kĩ năng phức tạp, nó

đòi hỏi chúng ta cần phải có tư duy linh hoạt, kĩ năng thuần thục tới độ “linh cảm”. Mặc dù chúng ta đã
biết rất nhiều phương pháp chứng minh bất đẳng thức như: Phương pháp biến đổi tương đương, phương
pháp sử dụng các bất đẳng thức đã biết, phương pháp quy nạp, phương pháp đánh giá đại diện, phương
pháp phản chứng...; cũng như đã có nhiều kỹ thuật để chứng minh bất đẳng thức, đặc biệt các kỹ thuật sử
dụng bất đẳng thức Cauchy, Bunhiacopxki để chứng minh bất đẳng thức là rất phong phú. Trong khi đó
nội dung bất đẳng thức ở trường phổ thông lại đóng vai trò quan trọng trong việc rèn luyện tư duy, khả
năng linh hoạt và óc sáng tạo; đồng thời nó cũng giúp học sinh rèn luyện tính cần cù, tinh thần vượt khó.
Hơn thế nữa, mỗi bất đẳng thức và cách chứng minh bất đẳng thức đó có một vẻ đẹp lộng lẫy và sức hấp
dẫn kì lạ đối với mỗi người nghiên cứu chúng nên việc nghiên cứu chúng còn có tác dụng kích thích sự
say mê trong học tập môn Toán cũng như các môn học khác.
Bên cạnh đó, sau khi giải xong một bài tập về bất đẳng thức, một câu hỏi thường được đặt ra với
chúng ta là: Bất đẳng thức này từ đâu mà có? Bất đẳng thức này có thể ứng dụng để chứng minh được các
bài toán nào? Để trả lời câu hỏi này thật không đơn giản chút nào.
Trước hết ta bắt đầu với bài toán: Cho a, b, c là các số thực dương. Chứng minh rằng:
abcabcbca abc
Bất đẳng thức trên là một bất đẳng thức đối xứng ba biến và nó là một hệ quả của bất đẳng thức
Schur. Có ba cách giải đều rất hiệu quả như sau
Không mất tính tổng quát, ta giả sử a là số lớn nhất trong ba số a, b, c.
Cách 1. Khi đó
abc0;acb0
. Nếu
bca 0
thì bất đẳng thức đã cho đúng. Do đó
ta chỉ còn xét cả ba đại lượng
abc;acb;bca
đều dương.
Theo bất đẳng thức Cauchy
2
2
2
2
2
2
abcabc
abcabc a
2
abcabc
abcbca c
2
bcaabc
bcaabc b
2
Do cả hai vế của các bất đẳng thức trên đều dương, nên nhân vế với vế ta được:
2
2
abcabcbca abc
Hay ta được
abcabcbca abc .
Đẳng thức xảy ra khi và chỉ khi
abc.
Cách 2. Ta có bất đẳng thức hiển nhiên
2
22
abc a hay
2
abcacb a
Tương tự ta có thêm hai bất đẳng thức nữa
22
bcaabc b;cabbca c
Do cả hai vế của các bất đẳng thức trên đều dương, nên nhân vế với vế ta được:
2
2
abcabcbca abc
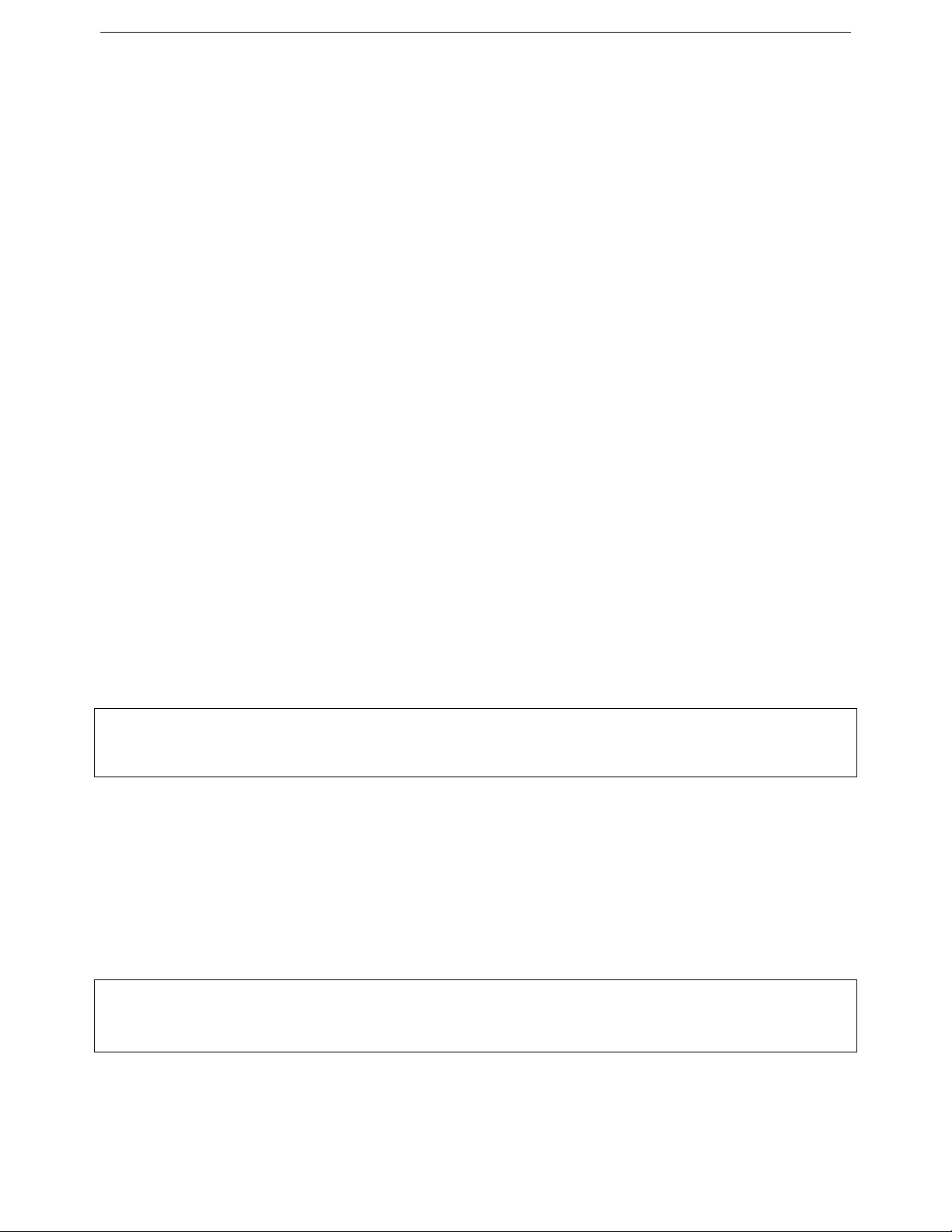
Hay ta được
abcabcbca abc .
Đẳng thức xảy ra khi và chỉ khi
abc.
Cách 3. Biến đổi tương đương bất đẳng thức ta được
333 2 2 2
abc3abc abc bca cab
Không mất tính tổng quát ta giả sử a là số lớn nhất trong ba số a, b, c. Khi đó ta có
2
333 2 2 2
ab abc cacbc 0
abc3abcabcbcacab
Như vậy bất đẳng thức trên được chứng minh
Khá bất ngờ với cách giải thứ ba bởi vì khi biến đổi tương đương bất đẳng thức trên ta thu được
một hệ quả khác của bất đẳng thức Schur, thông thường với bài toán trên ta thường sử dụng cách thứ nhất
hoặc cách thứ hai. Một vấn đề được đặt ra ở đây là từ bất đẳng thức
abcabcbca abc
Ta có thể ứng dụng để chứng minh được một lớp những bất đẳng thức nào?
1. Bất đẳng thức Schur và các hệ quả
a) Bất đẳng thức Schur: Cho a, b, c là các số thực không âm. Khi đó ta có
0aabac bbcba ccacb
b) Hệ quả: Cho a, b, c là các số thực không âm. Khi đó ta có
+
333 2 2 2
3 abc abcabcbcacab
+
abc a b c b c a c a b
2. Một số bài toán ứng dụng hệ quả của bất đẳng thức Schur
Với hai hệ quả trên ta sẽ ứng dụng để chứng minh được một lớp các bất đẳng thức đối xứng bậc
ba, qua đó ta sẽ thấy được ứng dụng rộng lớn của bất đẳng thức Schur
Bài toán 1. Cho a, b, c là các số thực không âm. Chứng minh rằng:
333
a b c 6abc a b c ab bc ca
Lời giải
Để ý đến đẳng thức
222
abcabbcca abc bca cab 3abc
Khi đó bất đẳng thức trên được viết lại thành
333 2 2 2
abc3abc abc bca cab
Bất đẳng thức trên là hệ quả của bất đẳng thức Schur.
Bài toán được chứng minh xong. Đẳng thức xẩy ra khi và cỉ khi
abc
Bài toán 2. Cho a, b, c là các số thực không âm. Chứng minh rằng:
3
a b c 9abc 4a b c ab bc ca
Lời giải
Để ý đến đẳng thức
3
333
abc a b c 3abbcca
Do đó ta được
3
333
abc 9abca b c 9abc3abbcca

Theo hệ quả của bất đẳng thức Schur ta được
333
222
abc9abc3abbcca
abc bca cab 6abc3abbcca
Để ý đến các đẳng thức
222
a b c b c a c a b 3abc a b c ab bc ca
a b b c c a abc a b c ab bc ca
Do đó ta được
222
abc bca cab 6abc3abbcca
4a b c ab bc ca
Suy ra
333
a b c 9abc 3 a b b c c a 4 a b c ab bc ca
Hay
3
a b c 9abc 4a b c ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Bài toán 3. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
9abc
abc 2abbcca
abc
Lời giải
Vì a, b, c là các số dương khi đó
222
9abc
abc 2abbcca
abc
Tương đương với
2
9abc
abc 4abbcca
abc
Hay
3
a b c 9abc 4a b c ab bc ca
Bất đẳng thức cuối cùng đúng theo bài toán 2.
Vậy bất đẳng thức được chứng minh.
Bài toán 4. Cho a, b, c là các số thực dương. Chứng minh rằng:
a b c 4abc
2
bc ca ab
abbcca
Lời giải
Bất đẳng thức cần chứng minh tương đương với
aabacbabbcccabc4abc
2a b b c a c
Hay tương đương với
333 2 22 22 2
333 2 2 2
abc3abcababbcbccaca
abc3abcabcbcacab
Bất đẳng thức cuối cùng là hệ quả của bất đẳng thức Schur
Vậy bất đẳng thức được chứng minh.
Bài toán 5. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
4ab bc ca 9abc 1

Lời giải
Bất đẳng thức có các vế chưa đồng bậc, chú ý đến giả thiết
abc1 ta đồng bậc hóa bất
đẳng thức thành
3
4a b c ab bc ca 9abc a b c
Đây chính là bất đẳng thức trong bài toán 2.
Bài toán 6. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc1. Chứng minh rằng:
7
ab bc ca 2abc
27
Lời giải
Dễ dàng chứng minh được
abcbcacab abc
Hay
12a12b12c abc
, khai triển ra ta được
1 2 a b c 4 ab bc ca 8abc abc
4ab bc ca 1 9abc
Từ đó suy ra
19abc
ab bc ca
4
Mặt khác, từ
abc1 và bất đẳng thức Cauchy ta được
3
abc 1
abc
327
Do đó ta có
19abc 7
ab bc ca 2abc 2abc
427
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
abc
3
.
Nhận xét: Một lớp các bất đẳng thức tương tự
7 9 2 ab bc ca abc
333 222
2 3 abc abcabc
8
27
ab bc ca abc
333
6 91 abc abc
222
13
4
27
abc abc
7
8 9
3
ab bc ca abc
Bài toán 7. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
111
abc2abc 2abbcca
abbc ca
Lời giải
Áp dụng bất đẳng tức Cauchy dạng
111 9
xyzxyz
ta được

222 222
111 9abc
abc2abc abc
abbcca abc
Ta cần chỉ ra được
222
9abc
abc 2abbcca
abc
,bất đẳng thức này tương đương với
333 2 2 2
abc3abcabcbcacab .
Bất đẳng thức trên là hệ quả của bất đẳng thức Schur.Như vậy bất đẳng thức được chứng minh.
Bài toán 8. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
22 2222
3a b c
abbc ca
bc bc ca abc
Lời giải
Biến đổi tương đương bất đẳng thức như sau
222
22 2222
22 22 22
222 222
222
222
222
3a b c
abbc ca
ab bc ca abc
ca b ab c bc a
2a b c 3a b c
ab bc ca
cab 2ab abc 2bc bca 2ca
abc
ab bc ca
111
2ab bc ca a b c abc
abbc ca
Theo bất đẳng thức dạng
111 9
xyzxyz
ta được
222 222
111 9abc
abc2abc abc
abbcca abc
Ta cần chỉ ra được
222
9abc
abc 2abbcca
abc
, bất đẳng thức này tương đương với
333 2 2 2
abc3abcabcbcacab .
Bất đẳng thức trên là hệ quả của bất đẳng thức Schur
Bài toán trên được chứng minh xong. Dấu đẳng thức xẩy ra khi
abc.
Bài toán 9. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
333
33 3 3 3 3
a1 b1 c1
2
bc1ca1ab1
Lời giải
Đặt
333
x a ; y b ; z c xyz 1, bất đẳng thức cần chứng minh trở thành
x1 y1 z1
2
yz1zx1xy1
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

222
2
x1 y1 z1
yz1zx1xy1
x1 y1 z1
x1yz1 y1zx1 z1xy1
xyz3
2xy yz zx 3x y z 3
Ta cần chứng minh
2
xyz3
2
2xy yz zx 3x y z 3
, bất đẳng thức này tương đương với
222
x y z 2 xy yz zx 6 x y z 9
4xy yz zx 6x y z 6
Hay
222
3 2 xy yz zx x y z
Từ bất đẳng thức quen thuộc
xyzyzxzxy xyz
Khai triển và biến đổi tương đương ta được
3
xyz 9xyz4xyxxyyzzx
Do đó ta được
2
9xyz 9
4xy yz zx x y z
xyz xyz
Hay
222
9
2xy yz zx x y z
xyz
Cuối cúng ta cần chỉ ra rằng
9
3
xyz
hay xyz3. Bất đẳng thức cuối cùng đúng theo bất
đẳng thức Cauchy. Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra tại
abc1
.
Bài toán 10. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
222
abc abcbcacab 27abc
Lời giải
Xét trường hợp
abcbcacab 0 , bất đẳng thức hiển nhiên đúng.
Xét trường hợp
abcbcacab 0 , khi đó dễ dàng chứng minh được
abc 0;bca 0;cab 0 .
Bất đẳng thức cần chứng minh tương đương với
3
3333
27abc a b c a b c b c a c a b 9 a b c
Áp dụng bất đẳng thức Cauchy ta được
3
27abc a b c b c a c a b
ab c a bc a b ca b c
Hay
3
222
27abc a b c b c a c a b 2 ab bc ca a b c
Khi đó ta được
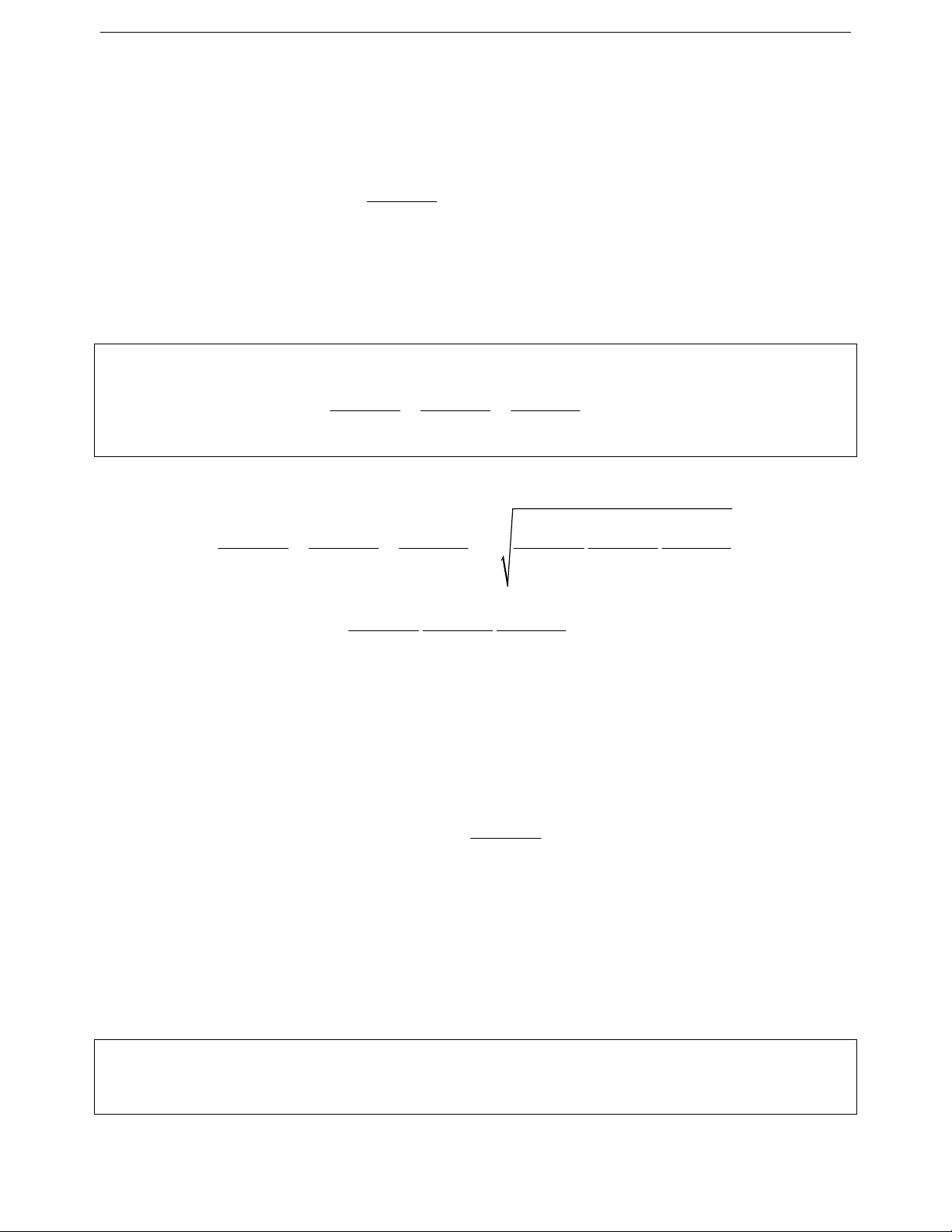
3
3
3
222
27abc a b c b c a c a b a b c
2ab bc ca a b c a b c
Như vậy ta cần chứng minh
222
a b c 2 ab bc ca a b c 9abc
Hay
222
9abc
abc 2abbcca
abc
Khai triển và rút gọn ta được
333 2 2 2
abc3abcabcbcacab
abc a b c b c a c a c
Bất đẳng thức cuối cùng đúng với mọi a, b, c. Bất đẳng thức được chứng minh.
Bài toán 11. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1. Chứng minh rằng:
222
222
1ab 1bc 1ca
12
1ab 1bc 1ca
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222 222
3
222 222
1ab 1bc 1ca 1ab 1bc 1ca
3
1ab 1bc 1ca 1ab 1bc 1ca
Như vậy ta cần chứng minh
222
222
1ab 1bc 1ca
64
1ab 1bc 1ca
hay ta cần chứng minh bất đẳng
thức
1ab1bc1ca 81ab1bc1ca
.
Đặt
xab;ybc;zca, khi đó x, y, z 0 và xyz1. Bất đẳng thức cần chứng minh
trở thành
1x1y1z 81x1y1z
, tương đương với bất đẳng thức sau
9xyz 7 xy yz zx 2
Ta dễ dàng chứng minh được
222
9xyz
x y z 2 xy yz zx
xyz
.
Mà
xyz1 nên ta suy ra được
9xyz 4 xy yz zx 1
.
Vì
xyz1 nên
3xy yz zx 1
, do đó
4xyyzzx 17xyyzzx 2
Điều này dẫn tới
9xyz 7 xy yz zx 2.
Như vậy bất đẳng thức ban đầu được chứng minh.
Bài toán 12. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
222
a2b2c2 3abc
Lời giải
Bất đẳng thức cần chứng minh tương đương với

222 22 22 22 2 2 2
222
abc 2 ab bc ca 4 a b c 8
3a b c 6ab bc ca
Hay
222 22 2222 2 22
abc 2 ab bc ca a b c 8 6 ab bc ca
Áp dụng bất đẳng thức Caychy ta được
222 22 22 22 2 2 2
222 22 22 22 2 2 2
222
abc 2 ab bc ca a b c 8
abc 1 2 ab 1 bc 1 ca 1 a b c 1
2abc 4 ab bc ca a b c 1
Phép chứng minh hoàn tất nếu ta chỉ ra được
222
222
2abc 4 ab bc ca a b c 1 6 ab bc ca
abc12abc2abbcca
Dễ dàng chứng minh được
222
9abc
abc 2abbcca
abc
Ta cần chỉ ra được
9abc
1 2abc 1 2abc a b c 9abc
abc
Đánh giá cuối cùng luôn đúng vì theo bất đẳng tức Cauchy thì
3
3
222
1 2abc 1 abc abc 3 a b c ; a b c 3 abc
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài toán 13. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
2a b c abc 8 5a b c
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2
abc 9
abc
6
Bài toán quy về chứng minh
2
222
5
2a b c abc 8 a b c 9
6
Hay
222
715
abc abc abbcca
623
Theo bất đẳng thức Cauchy ta có
3
222
3
1 2abc 1 3 a b c 9abc 9abc
abc
22 2
2a b c
2.3 abc
Do đó phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
79abc5
abc abbcca
63
2a b c
Hay
222
3.9abc
7a b c 10ab bc ca
abc
Theo một đánh giá quen thuộc thì
222
4a b c 4ab bc ca nên ta được

222 222
3.9abc 3.9abc
7a b c 3a b c 4ab bc ca
abc abc
Ta cần chỉ ra được
222
222
3.9abc
3a b c 4abbcca 10abbcca
abc
9abc
abc 2abbcca
abc
Đánh giá cuối cùng đã được chứng minh.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài toán 14. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
abc 14abc
4
bc ca ab
abbcca
Lời giải
Đặt
abc
x;y;z
bc ca ab
, khi đó ta được
111
2 xy yz zx 2xyz 1
x1 y1 z1
Dễ dàng chứng minh được
3
xyz
2
. Bất đẳng thức cần chứng minh trở thành
2
xyz 14xyz4
Dễ ta chứng minh được
2
2
9xyz
x y z 4 xy yz zx
xyz
9xyz
x y z 14xyz 14xyz 4 xy yz zx
xyz
Từ
3
xyz
2
suy ra
9xyz
6xyz
xyz
, do đó ta được
9xyz
14xyz 4 xy yz zx 4 xy yz zx 8xyz 4
xyz
Do đó ta được
2
xyz 14xyz4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài toán 15. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
22 2
abc1
2
19bc4bc 19ca 4ca 19ab4ab
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

22 2
2
222
abc
19bc4bc 19ca 4ca 19ab4ab
abc
a b c 27abc 4a b c 4b c a 4c a b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2222
2 a b c 1 27abc 4a b c 4b c a 4c a b
Hay
1 4ab a b 4bc b c 4ca c a 3abc
Để ý đến giả thiết ta viết lại được bất đẳng thức trên thành
3
abc 4abab 4bcbc 4caca 3abc
Hay
333
abc3abcababbcbccaca
Biến đổi tương đương ta được
abc a b c b c a c a b
Bất đẳng thức trên là một bất đẳng thức đúng và dễ dàng chứng minh được.
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
hoặc
1
ab ;c0
2
và các hoán vị.

Chủ đề 10. ỨNG DỤNG CỦA ĐẠO HÀM TRONG CHỨNG MINH BẤT ĐẲNG THỨC VÀ BÀI
TOÁN TÌM CỰC TRỊ
Trong việc chứng minh bất đẳng thức hay tìm cực trị của một biểu thức, vận dụng phương pháp
dồn biến để khảo sát hàm số là một chủ đề rất được nhiều bạn học sinh tham gia các kỳ thi chọn
HSG và kỳ thi TSĐH, THPT – Quốc Gia quan tâm.
Để có thể dồn một biểu thức nhiều biến về một biến chúng ta có nhiều kỹ thuật, tuy nhiên trong
nội dung của chủ đề chúng tôi chỉ giới thiệu một số kỹ thuật quan trọng, thường gặp và sắp xếp
theo sự phổ biến của các kỹ thuật đó gồm:
- Vận dụng các bất đẳng thức kinh điển.
- Kết hợp kỹ thuật đổi biến số.
- Kết hợp kỹ thuật sắp thứ tự các biến.
- Phương pháp tiếp tuyến.
- Khảo sát hàm nhiều biến.
- Kết hợp với việc sử dụng bổ đề.
- Vận dụng kỹ thuật dồn biến cổ điển
1. Dồn biến nhờ vận dụng kỹ thuật sử dụng các bất đẳng thức kinh điển.
Bài toán 1 . Cho các số thực
(
) ( )(
)( )
, , 0;1 : 1 1 1a b c abc a b c
∈ =−−−
. Chứng minh rằng
222
3
4
abc
++≥
.
Phân tích. Khai triển đẳng thức ở giả thiết cho ta:
( )
2
222
1 14
a b c a b c abc
+ + = ++− +−
Để ý là :
3
3
AM GM
abc
abc
−
++
≤
. Từ đó ta quy việc giải bài toán bất đẳng thức
về bài toán khảo sát hàm số theo biến
(
)
, 0;3 .t a b ct
= ∈
++
Lời giải. Ta có
( )
1abc a b c ab bc ca abc=− ++ + + + −
( )
12a b c ab bc ca abc⇔− ++ + + + =
(
)
( )
( )
( ) (
) ( )
2
222
2 23
222
12
2
4
114 11
27
abc a b c
a b c abc
a b c abc abc abc abc
++ − + +
⇔− ++ + =
⇔ + + = ++− +− ≥ ++− +− ++
Đặt
( )
0;3t abc t= ++⇒∈
. Xét hàm số
( )
32
4
22
27
Ft t t t=− +−+
Ta có
( )
2
3
4
' 2 20
2
9
3
t
Ft t t
t
=
=− + −=⇒
=
.
Lập bảng biến thiên ta có:
( )
33
24
Min F t F
= =
Vậy
222
3
.
4
abc++≥
Dấu
""=
xảy ra khi
1
.
2
abc= = =
Bài toán 2. Cho các số thực dương
,,xyz
thỏa mãn
2
24xz xy yz z+ +=
Tìm giá trị nhỏ nhất của biểu thức
2
3
222
xy z
P
yz xz xyz
=++
+ + ++
Lời giải. Ta có

( )
(
)
2
2
2
4 2 28
2
02
AM GM
xy
xy xy xy
z x y z xy
zz z
−
+
++ +
−+ = ⇒ + −
≥⇒
≤≥
Lại có :
( )
(
) ( )
2
2
2
2
3 31
22
1
1
xy
xy
z
z
P
xy
xy
xyz
xy xyz
z
z
+
+
+=+
+
+
++
++
+
+
+
≥
Đặt
, 2
xy
tt
z
= ≥
+
. Khảo sát hàm số
( )
( )
)
2
3
, 2;
1
21
t
ft t
t
t
= + +∞
+
+
∈
Ta tìm được
[
)
( ) ( )
2;
5
min 2
6
ft f
+∞
= =
Hay
5
min
6
P xyz
=⇔==
.
Bài toán 3. Cho các số thực không âm thỏa mãn
2
a c
b+ ≥
.
Tìm giá trị nhỏ nhất của biểu thức
( )
32
27 1
ab c
P
ac bc c
=+−
++ +
Lời giải.
Ta có
( )
( )
( )( )( )
2
2
1
0
1
c a b c ab c
abc
ac bc c acbcc
+− + +
+−=
+ + +++
≥
+
1
ab c
ac bc c
⇒
+
≥
+
++
Do đó
4
32
1 27 1
cc
P
cc
−
++
≥
. Xét hàm số
( )
4
32
,
27
0f t t tt=
≥−
có:
( )
( )
3
32 2
'4 '0
27 3
ft t ft t= − ⇒ =⇔=
Lập bảng biến thiên ta có
(
)
16
27
ft≥−
Do đó
16
min 0, 4, 2
27
P abc
=− ⇔= = =
hoặc
0, 4, 2.bac
= = =
Bài toán 4. Cho các số thực dương
,,abc
. Tìm giá trị nhỏ
nhất của biểu thức
(
)
(
)
23
22
1 27
32
2 21b
P
a
c
bc
a + ++
= −
Lời giải.
Ta có
( ) ( ) ( )
23 2
1 27 1 1
4
32 4 1 32
AM GM AM GM
abc
abc ab c
P
abc
−−
≥− ≥−
++
Đặt
, 0.t abc t= >
Xét hàm số
( ) ( )
2
11
, 0;
4
32
ft t
t
t
=
∈− +∞
có :
( ) (
)
3
41 1
' '0 .
4
16
t
ft ft t
t
−
= ⇒ =⇔=
Lập bảng biến thiên ta có
( )
11
42
fft
= −
≥
Hay
1
1
min
2
2
1.
ab
P
c
= =
=−⇔
=
Bài toán 5. (HSG Tỉnh Nghệ An – 2012) Cho các số thực
dương
,,abc
. Tìm giá trị nhỏ nhất của biểu thức
3
23
= −
+ + ++
P
a ab abc a b c

Lời giải.
Ta có
( )
3
1 4 1 4 16 4
..
22 4 3 3
−
+ ++
+ + ≤ + + = ++
AM GM
ab ab c
a ab abc a a b c
Suy ra
( )
33
2
≥−
++
++
P
abc
abc
Đặt
,0
=++ >t a b ct
Xét hàm số
(
)
33
2
= −ft
t
t
với
0
>t
ta có
(
)
2
33
'
2
2
= −ft
t
tt
.
( )
2
33
'0 0 1
2
2
=⇔ − =⇔=ft t
t
tt
Lập bảng biến thiên ta có
(
) (
)
0
3
min f t 1
2
>
= = −
t
f
.
Vậy giá trị nhỏ nhất của P là
3
2
−
khi và chỉ khi
16
21
1
4
21
4 16
1
21
=
++=
⇔=
= =
=
a
abc
b
ab c
c
( )
16 4 1
,, , ,
21 21 21
⇔=
abc
.
Bài toán 6. Cho các số thực
,,xyz
không âm và thỏa mãn
điều kiện
323xyz++=
. Tìm giá trị lớn nhất của biểu thức
22
2
23
9
1
x
P zz
x
y
y
+
+
+
=+−
Lời giải.
Ta có
( )
2
22 22
36
2 64
11
99
4
1
yy
xy
xx
xy xy xy
++
+ = + −= −
++
+
+
+
( )
( ) ( )
2
2
x 3y 6
4 x 3y 2 Do xy
01
0
++
−= + +≤≥
+
Lại do
3 32
xy z+=−
, vậy nên :
( )
2
2
32 23z zzP ≤ − ++ −
. Đặt
2
9
3, .
4
z zt t−≥=
−
.
Khảo sát hàm số
( )
4 11ft t t
= +−
ta tìm được
( )
9
;
4
7 15
max
44
ft f
− +∞
=−=
Hay
2
323
2 31
0, ,
15
32
0
2
max
4
31
7
2, 0,
0
2
4
2
3
xyz
xy z
xy
P
xy
z z
z
++=
= = = −
=
=⇔⇔
= = = −
=
−+
Bài toán 7. (Khối B năm 2014) Cho các số thực
,,abc
không âm và thỏa mãn điều kiện
( )0a bc+>
. Tìm giá trị nhỏ
nhất của biểu thức
2( )
abc
P
bc ac ab
=++
++ +
Lời giải.
Áp dụng bất đẳng thức AM-GM, ta có
2( ) 2
1
a b ab
c
bc ac abc
ab
+
+≥ =
+ + ++
+
+
.
Vậy
2
2( )
1
c
P
c
ab
ab
≥+
+
+
+
,

Đặt
, 0.
c
tt
ab
= >
+
Xét hàm số
21
()
12
gt t
t
= +
+
với
0t >
,
Khảo sát hàm số ta được GTNN của P bằng
3
2
đạt được khi
0, , 0a b cb= = >
.
Bài toán 8. Cho các số thực
,,abc
là các số thực dương thỏa
mãn điều kiện
2 22
bca bc+=+
. Tìm giá trị lớn nhất của biểu
thức
( )
3
22 22 6
3
cb
bc a
P
aa
bc
=
+
+−
+
+
Lời giải.
Từ giả thiết ta có
( )
( )
2 22 2 32
2
22
2
3
b c bc c
c bc bc
a abc b
bc
a b bc
=+− +
+−
⇔ +=
+
= = +
−≥
Nên
( )
( )( )
( )
( )
( )
( )
22
33
6 26
222 2
2
3
2
3
abc bc
aa
P
aa
bc
a
cb
ab ac bc
≤
+
++
= −
+
+
++
−=
( ) ( )
3
6 3
23 2 3
8
a
bc bc
bc bc
≤=−−
++
++
Đặt
1
,0
tt
bc
= >
+
. Khảo sát hàm số
( )
3
3
2 ,0
8
ft t t t=−>
Ta tìm được
( )
( )
0;
4 16
39
Max f t f
+∞
= =
Hay
16 3
max .
98
P abc= ⇔===
Bài toán 9. Cho các số thực
,,xyz
là các số thực dương thỏa
mãn điều kiện
22
3+ +=x y z xy
. Tìm giá trị nhỏ nhất của biểu
thức
33
16
=++
++
+x yx
P
yz xz
y
z
Lời giải.
Ta có
22
23 + +≥
⇒ ≥= +
y z xyx z
y x xy z
Suy ra
22
33
() () 4
2 ( ) (2 ) 2
()
16 16 16
++
+≥ ≥ ≥
+ + + + ++ ++
+ ++
≥≥
x y xy xy
yzxz xyzxy xy xy xy
x y xyxy xy
zz
Do đó
(
)
4
2 16
⇒≥ +
++
+
y
xy
P
x
Đặt
, 0.=+>t x yt
Khảo sát hàm số
(
) ( )
4
, 0;
2 16
= + ∈ +∞
+
t
tt
t
f
Ta được
( )
( ) ( )
0;
7
min 6 .
8
+∞
= =ft f
Hay
3
7
min
8
9
= =
= ⇔
=
xy
P
z
Bài toán 10. Cho các số thực
,,xyz
là các số thực dương
thỏa mãn điều kiện
22 2
3+=++ +z y xy yzx zx
. Tìm giá trị lớn
nhất của biểu thức
( )
( )
2
1
2
2
= −
+
+
x
P
xy y z
yz
Lời giải.

Ta có
( ) ( )( )
2
22 2
33
+=++ +⇔ =++
+z y xy yz zx x zx xyy z
( )
( )
2
2
23
23 2
4
3
2
2
++
= ⇒+ + + ⇒
+++
≤ ≥≥
+
x
xyz
x y z xz y
yz
z
y
x
Do đó
(
)
2
1
2
2
≤
+
+
x
yz
yz
. Lại có :
( )
( )
( ) ( ) ( )
2
32
1 13 2 1 1
2 .3 2 . 2 2
3 32 3 3
++
+= + = + +
≤≤
yy z
xyy z x yy z x xyz yz
Nên
( )
3
13
2
2
≤−
+
+
P
yz
yz
Đặt
2 , 0.+= >
y z tt
Khảo sát hàm số
( ) ( )
3
13
, 0;=−∞
∈ +ft t
t
t
Ta tìm được
( )
( ) (
)
0;
2
3.
9
+∞
= =max f t f
Hay
3
2
max
9
1
=
= ⇔
= =
x
P
yz
Bài toán 11. Cho các số thực
,,
xyz
là các số thực dương
thỏa mãn điều kiện
222
4+=+zx y
. Tìm giá trị nhỏ nhất của
biểu thức
( )
2 3 22
2
23
2
32
2
+
= +
+
+
−yx
P
y
x
z
y
x
yz
xy
Lời giải. Ta có :
( )
2 22 2 2
3 2 2 22 22 2 2
1
24
2
3 3 2 3 ( ) ( ) 2 (4 ) (2 )
+ ≤ ++ + = +
+ − ≥ +− += +≥+
y xz y x z x y
x xy xy xx y xx y x z x z
Từ đó suy ra
2
22 2
22
1
≥ += +
+
+
yx x
P
yy
xy
x
y
Đặt
,0= >
x
tt
y
. Khảo sát hàm số
( )
2
1
2
,0= +>
+
f t tt
t
Suy ra
( )
(
) (
)
0;
min 1 2
+∞
= =
ft f
. Hay
min 2 2.
=⇔===P xyz
Bài toán 12. Cho các số thực
,,
xyz
thỏa mãn
( )
2
0
1 10
xy
xy z
+
+=
≥
+
.
Tìm giá trị nhỏ nhất của biểu thức
( )( )
4
21
.
xy x y z
P
z
++
=
Lời giải.
Từ giả thiết suy ra
0z >
. Lại có
( )
( )
2
2
22
4
4
xy
xy
x xy
zz
y
+
≥⇒ ≥+
Từ giả thiết
( )
( )
22
2
1 1 1010
xy z xy z+ +=+ = ⇒+
2
22
11
10 10
xy xy
zz
zz
++
⇒ =−⇒ = −
Do đó
3
22
11 1 1
. 2 10 2
4
xy x y
P
zz z
zz
+
= + −+
≤
Đặt
1
0t
z
= >
. Xét hàm số
( ) ( )
( )
22
2 10 10 , 0ft t t t t=+ − −>
Ta có
( )
( )
( )
22
' 2 3 5 10 ' 0 1ft t t t ft t=− + − − ⇒ =⇔=

Lập bảng biến thiên ta có
( )
( )
0;
81 1Max f t t
+∞
= ⇔=
Hay
1
81
3
4
2
z
MaxP
xy
=
= ⇔
= =
Bài toán 13. Cho các số thực dương
,,abc
thỏa mãn
222
2ba c++=
.
Tìm giá trị lớn nhất của biểu thức
( )
( )
22
22
23
.
1
2
bc
ac
P
a ab
ab
++
= −
++
+
++
Lời giải. Từ giả thiết ta có
( ) ( )
2
2
12a b c bc+=++
Áp dụng bất đẳng thức AM-GM ta có:
(
) (
) ( )
2
2
2 21bc a b a
c bc+ +≥=++
1 bbc a ac≥+⇔+
21a cab bb cc ≥ ++⇔+
( )
22
12 2 22bc a ab bc ca ab aab+ + ≥+ +++⇔ +++
(
)
(
)(
)
2
2
122
a ab ac ab
bc
⇔ + + ++
++
+
≥
( )
2
21
122
bc
ac
ab
a ab
≤
++
++
⇔
+
++
Từ đó suy ra
( )
2
13
2
P
ab
ab
−
+
+
≤
Đặt
1
0
t
ab
= >
+
, đồng thời
( )
2
22 2
1
242
24
ab c
ab
ab t≤
+
<⇒+<⇒+ >
= −
Xét hàm số
( )
( )
2
31
, ; ' 13
24
ft t t t f t t
= − +∞ ⇒ = −
∈
Lập bảng biến thiên suy ra
( )
13
6
3
ft f
=
≤
Hay
( )
3 211
,, ; ; .
6
333
MaxP a b c
=⇔=
Bài toán 14. Cho các số thực dương
,,
abc
thỏa mãn điều
kiện
2 3 18a b c abc++=
. Tìm giá trị nhỏ nhất của biểu thức
( )
3
33
1 11
2 3 22 .
3
21 3
P abc
b ac
= ++ + +
++
Lời giải.
Ta có
( )( )
3
2 3 18 3. .
2
23
3
3
3
AM GM
a b c abc a b c
abc
−
++
≤= =
+
+
( )
2
9323.32abc abc≥⇒⇒ ++≥++
Lại có :
3
33
3
26
22
21 25
21 3
26
3 34
24
239
AM GM
AM GM
bb
b ac
ac a
abc
c
−
−
++
⇒+
++
+ ++
≥
++
≥
+
≥
Do đó
( )
1 48
23
3 239
P abc
abc
≥ ++ +
+++
Đặt
23 , 3a b c tt++= ≥
. Khảo sát hàm số
( ) )
1 48
, 3;
39
ft t t
t
= + +∞
+
∈

Ta được
[
)
( ) (
)
3;
min 3 5ft f
+∞
= =
Hay
min 5 2 3 1.P abc
=⇔= = =
Bài toán 15. Cho các số thực không âm
,,
xyz
thỏa mãn
( )
( )
2 22
56
yzx xy yz zx= ++++
.
Tìm giá trị lớn nhất của biểu thức
(
)
( )
22
2.P xyz z
y+− +
= +
Lời giải.
Từ
( )
( )
( )
( )
2
2 22 22
5 6 56x xy yz z x y y y zyz zz++ +−+≥=+⇒ +
Suy ra
5
x
z
yz
y
+
≤≤+
. Do đó
( )
2
2
2
yz
yzP
+
≤ +−
Đặt
,
0y z tt
=
≥+
. Khảo sát hàm số
( )
4
02,
2
t
ft t t= − ≥
Ta được
[
)
(
) ( )
0;
3
1
2
Max f t f
+∞
= =
. Hay
1
3
1
2
.
2
x
MaxP
yz
=
= ⇔
= =
Bài toán 16. Cho các số thực dương
,,
xyz
thỏa mãn
2 22
1yx z++≤
.
Tìm giá trị nhỏ nhất của biểu thức
( )
111
2.
111
xy yz xz
P xyz
yz zx xy
+++
= + + − ++
++ ++ ++
Lời giải.
Ta có
111
111
xy yz xz
yz zx xy
+++
++
++ ++ ++
≥
(
)
( ) (
)
222
222
111
x y z xy y z x yz z x y zx
yz zx xy
+ +− + +− + +−
≥++
++ ++ ++
( )
( )
(
)
( )
( )
( )
222
222
333
41 1
44
41
4
4
zxxy yz zx y
yz zx xy
+++
≥++
+
+++
+ ++ ++
( )
( )
( )
( )
(
)
( )
22 2
44
3
4232323
xyz xyz xyz
xyz xyz xyz
++ ++ ++
≥ +=
++ + ++ + ++ +
Suy ra
( )
( )
( )
2
4
2
23
xyz
xyz
xy
P
z
++
≥ − ++
++ +
Đặt
,0 3xyzt t+= <≤+
. Khảo sát hàm số
( )
(
2
4
2 , 0; 3
23
t
f t tt
t
= −
∈
+
Ta tìm được
(
( )
( )
0; 3
min 3 6 3 12
ft f
= = −
Hay
1
min 6 3 12 .
3
P xyz= − ⇔===
Bài toán 17. Cho các số thực
,, 1≥−xyz
thỏa mãn
3++=xyz
.
Tìm giá trị lớn nhất của biểu thức
(
)
22
22 2
.
1
1
4 45
−
++ −
= +
++
xy
P
xzyxxy
Lời giải. Ta có
3+=−xyz
.
Đồng thời, do
( )(
) ( )
1 1 10, 1
≥− ⇒ + + ≥ ⇔ ≥− + −x y xy x yxy
Do đó
( ) (
) ( ) ( )
22
22
4 24 2 24+ + + +≥ ++= − + +=
+y xy x yy xy yx xx
( ) ( )
2
2
2 453 32= − − +=− −+zzzz

Lại có
( ) ( ) ( )
22
22 2
18 172 22=+− ++ ++=+ ≤ −+x xy xy xy z zxyy
Từ các kết quả trên suy ra
2
2
8 16
45
−+
≤
−+
z
P
z
z
z
.
Khảo sát hàm số
( )
)
2
2
8 16
45
, 1;
−
= − +∞
+
+
∈
−
z
fz z
z
z
z
Ta tìm được
[
)
( )
1;
3
5
2
− +∞
= =
max f z f
.
Hay
( )
53 5 3
max 5 ; ; 1; ; , ; 1;
22 2 2
=⇔=− −
P xyz
Bài toán 18. Cho các số thực dương
,,
xyz
thỏa mãn
22
x yz= +
.
Tìm giá trị lớn nhất của biểu thức
( )
(
)
(
)
(
)
2
22 2
22
12
3
.
1
11
xy z
z
P
xz
zz
y+
+
= +
+
++
Lời giải.
Từ điều kiện giả thiết ta có
( )
22
12 12 2xy z z xyz x y xyz+ =++ = − +
Áp dụng bất đẳng thức B.C.S ta có:
( )
( )
( )
( )
( )
2
22 22
2
2 2 22 2 2 2 2
22
41 1
x y xyz x y xyz
x y xy z x y z
−+ = −+
≤ − + +=+ +
Từ đó :
( )
2
2 22
13
11
z
P
z zz
≤+
+ ++
Xét hàm số
( )
2
2 22
13
() , 0
1 11
z
fz z
z zz
=+>
+ ++
Ta có :
( )
( )
22
3
2
1 54
()
1
zz z
fz
z
+−
′
=
+
Nên :
5
() 0 5 2 0 .
2
fz z z
′
=⇔ − =⇔=
Lập bảng biến thiên cho ta có giá trị lớn nhất của
P
là
16
.
9
Dấu bằng xảy ra khi và chỉ khi
4
22
4
22
125
2
22
5
22
5
5
2
2
x
xy
xy
z
xyz y
z
z
=
−=
−= ⇔ =
=
=
Bài toán 19. Cho các số thực không âm
,,xyz
thỏa mãn
( ) ( ) ( )
222
6xy yz zx+ ++ ++ =
.
Tìm giá trị lớn nhất của biểu thức
( )
(
)
2
2
1
.
6 24
xyz
P xy yz zx
z
++
= − ++
+
Lời giải.
Áp dụng bất đẳng thức B.C.S ta có:
( ) ( ) ( )
( )
( ) ( ) ( )
222
2
12 126xy yz zx xy yz zx
+++++ + + + =
≤+ +
++
( )
( )
11
633
6
32 6
3
xyzxy z
z xy
z
z
≤⇔ ++ ≤+⇔ ≤
+
+
+
+
+
⇔

Từ điều kiện ban đầu, khai triển ta lại có:
( )
2
3x y z xy yz z x++ −= + +
Từ đó cho ta
(
)
2
2
1
3
3 24
xyz
P xyz≤−
++
− ++
Lại có
( )
( )
( )
22
2
3
33
xyz
xy yz zx x y z
xyz++ ++
≤⇒ ≤+ + ++ −
32
0
2
xyz≤++≤⇒
.
Đặt
32
, 0;
2
t x y zt
=++
∈
.
Khảo sát hàm số
(
)
( )
2
2
3
32
, 0;
3 24 2
t
t
ft t
−
= −
∈
Ta được
( )
( )
32
0;
2
5
2
8
max f t f
= =
. Hay
1
5
max
8
0.
xy
P
z
= =
= ⇔
=
Bài toán 20. Cho các số thực dương
,,
xyz
thỏa mãn
1++=xy z
.
Tìm giá trị nhỏ nhất của biểu thức
2
.
2
=++
+
+
++
x yz
P
x yz y zx z xy
Lời giải. Ta có:
(
)( )
1 11++= ⇔+ = + +
x y z z xy x y
nên
( ) ( ) ( )( )
2
2
1 1 11
=++
−−+ −−+ + +
+x yz
P
z y yz z x zx x y
(
)
(
)
(
)
(
)
( )
( )
2
11
2
11 11
=++ =
+− +− ++
+x yz
yzxzxy
( )( ) ( )( )
( )( )
( )( )( ) ( )( )
( )
( )
( )
( )
2
2
22 2 2
22
2
1111
4
11 11
22
2
4
2
4
=++=
++ ++ ++
+
=++
+++
+
++
++
++
++
++ +
≥
++
+
xy
y xy
x yz
y xy x xy x y
xy
xz z
xyxy xy
xy xy
xy
( )
( )
2
2
4
2
1
1
2
=
+
+
+
+
z
z
z
.
Khảo sát hàm số
( )
(
)
( )
2
2
4
2
,0
1
1
2
== >
+
+
+
+
z
fz z
z
z
cho ta
( )
( ) ( )
0:
13
min 3 .
14
+∞
= =fz f
Hay
1
13
min
14
3
= =
= ⇔
=
xy
P
z
Bài toán 21. Cho các số thực
,,abc
thỏa mãn
0
3
a
ab bc ca
bc≥≥≥
++=
.
Tìm giá trị nhỏ nhất của biểu thức
( )( ) ( )( )
4
22 22 .
b
P a a ba c c c ac b
ac
= + ++ + ++
+
Lời giải.
Ta có
( )( ) ( )
22
2 2 2 2 4 2 61a b a c a ab ac bc a bc+ +=+ ++ =++
và
( )( ) ( )
22
0 0 2 32a b a c a ab ac bc a bc ab bc ca− − ≥⇔ − − + ≥⇔ + ≥ + + =
Từ (1), (2) suy ra
( )( )
2 29a ba c
+ +≥
, tương tự
( )( )
922c ac b++≥

Do đó
( )
(
)
3
4
33
4
ac
b
ac
P ac ac
ac ac
−
+
++ = ++
++
≥
(
)
( )
(
)
(
)
(
)
2
22
12
12
3 31
ac
ac ac
ac ac
−+
++ = ++ −
++
≥
.
Đặt
,0
a c tt+= >
. Khảo sát hàm số
( )
2
12
3 1, 0ft t t
t
=+− >
ta được
( )
( ) ( )
0;
min 2 8ft f
+∞
= =
. Hay
min 8 1.P abc=⇔===
Bài toán 22. Cho
, , 1; 3 : 2 6xyz x y z∈ ++ =
. Tìm GTLN,
GTNN của biểu thức
33 3
5Px y z=++
.
Lời giải. Từ giả thiết ta có :
( ) ( ) ( ) (
)
22 2 2
4 43 43 3xy z x y z xy z
= − −− ≤ − ⇒ ≤−
Ta lại có :
( )( )
( )
2
1 1 0 152 52 3x y xy x y z z xy z
− − ≥ ⇒ ≥+−=− ⇒− ≤ ≤ −
.
Mặt khác ta có :
2 6 4 1; 2 .z xy z=−−≤⇒∈
Ta có :
( ) ( ) ( ) ( )
22
33
352343 35.P x y x y xy z z z xy z
=+ +−+=− −−+
Vì
( )
2
52 3z xy z−≤ ≤−
( ) ( )
(
)
( )
32
33
23 5 23 43 6 15 5 , 1;2
z z P z z z zz
⇒ −+ ≤≤ − −+−+ ∈
( )
( )
3
3 32
2 3 5 3 60 150 126, 1;2z zP z z z z
⇔ − + ≤ ≤− + − + ∈
.
Đặt
( ) ( ) ( )
3
3 32
2 3 5 , 3 60 150 126.f z z z gz z z z= −+ =−+ − +
Xét hàm số
(
) ( )
,f z gz
trên miền
1; 2z
∈
Đạo hàm và lập bảng biến thiên hàm số
(
) (
)
,
f z gz
ta có :
(
)
210 60 10
Min f z = −
tại
2 10 5 10z xy=−+ ⇒ = = −
.
( )
42Max g z
=
tại
2 1.
z xy=⇒==
Vậy
210 60 10Min P = −
khi
5 10, 2 10xy z= = − =−+
.
42
Max P =
khi
1, 2.xy z= = =
Bài toán 23. Cho các số thực dương
,,abc
thỏa mãn điều
kiện
( )
2 22
3324ca b ab ac= +++
. Tìm giá trị nhỏ nhất của biểu
thức
( )
2 22
22
2
.
25
14
2
ac
b
P
bc ab ac
b
c
+ ++
+
+
+
=
Từ giả thiết ta có
( ) ( ) ( ) ( )
2 22 2 2 2 2 22
3 44432ab ac a b ac bcabc++ + += +−++=
( )
( )
22 22
44
1ab ac c c acbb≥ − + +≥⇒+
Lại có
( ) (
)
2
2 22
2 202ab acabc b c
abbc
−− + + +≥⇒ + ≤ −
( )
2
2
2 22
4
2
b bc
cab
++
+≤−+
( )
2 22
2
43
22
3ab
ab ac
bc
c
bc
++
+
= += +⇒
( )
2 0 22a cc
a
b
b
≤ ⇒< ≤
Lúc đó
( ) ( )
22 2 2
22
2
25
4
2
ac b
b
c
c
P
bc ab ac
+
=
+
+
++
+
( )
2
22
2
25
24 1
1 ..
5
2
bc
a c ac b a b
a ba
b
b
c
c
b
−
+
≥ ++ = +
+
Xét hàm số
( ) (
1
, 0;2
5
t
ft t
t
∈= +
có
( )
2
2
11
'0
5
2., 0
55
t
t
ft
t
−
∀< <= ≤= −

Suy ra
( ) ( )
9
2
10
fft≥ =
. Hay
2
9
10
1.
a
MinP
bc
=
= ⇔
= =
Bài toán 24. Cho các số thực thay đổi
,,xyz
thỏa mãn
2 22
16
3
25
x y z xy
+++ =
. Tìm giá trị nhỏ nhất của biểu thức
( )
( )
22 2
35
10
56
P x y z xy xy yz zx= + + +− ++
Lời giải. Áp dụng BĐT Cauchy-Schwazr ta có :
( )
( ) ( )
( ) ( )
2
2
22 2
35
10
2 10 6
10
xy
x y P x y z xy xy yz zx
x y z xy xy yz zx
+
+ ≥ ⇒≥ + + + − +
+ +− +≥
+≥
+
( )
10
xy yz zx xy yz zx≥++− ++
.
Đặt
,0t xy yz zx t= ++ ≥
Xét hàm số
( )
2
10 , 0Ft t t t=−≥
Ta có :
( )
10
' 2 10 0
2
Ft t t
= − =⇒=
Lập bảng biến thiên ta có :
10 5
22
MinF F
= = −
.
Vậy
5
2
MinP = −
khi
56
,
34 34
xy z= = =
hoặc
56
,
34 34
xy z==−=−
.
Bài toán 25. Cho các số thực
,,xyz
thuộc đoạn
1; 3
. Tìm
giá trị nhỏ nhất của biểu thức
(
)
(
)
2
2
25
12 2012
yz
T
x xy yz zx
+
= ⋅
+ ++
Lời giải.
Ta biến đổi biểu thức đã cho trở thành :
( )
( )
2
2
25
12 2012 2012
yz
T
x x y z yz
+
=
+ ++
Mặt khác với mọi số thực
, 1; 3yz∈
, áp dụng bất đẳng thức Cauchuy ta có :
( )
2
4
yz y z≤+
.
Do đó ta có :
(
)
( )
(
)
2
2
2
25
12 2012 503
yz
TN
x xyz yz
+
≥=
+ ++ +
Vì
, 1; 3 0yz y z∈ ⇒+≠
nên ta chia cả tử và mẫu của
N
cho
yz+
ta được :
2
25
12 2012 503
N
xx
yz yz
=
⋅ +⋅ +
++
Đặt
13
,;
62
x
tt
yz
= ∈
+
. Lúc đó ta xét hàm số :
2
25 1 3
() , ;
62
12 2012 503
ft t
tt
= ∈
++
.
Ta có :
( )
( )
2
25 24 2012
'( )
12 2012 503
t
ft
tt
⋅+
= −
++
;
503
'( ) 0 24 2012 0
6
ft t t= ⇔ + =⇔=−
(loại).
Lập bảng biến thiên ta nhận thấy rằng với
13
;
62
t
∈
, ta có
()ft
đồng biến.
Do đó ta có ngay được
1 75
()
6 2516
ft f
≥=
.
Dấu đẳng thức xảy ra khi
(
) ( )
1
, , 1,3,3
6
t xyz=⇔=
.
Vậy ta có giá trị nhỏ nhất của
75
2516
T =
đạt được khi
( ) ( )
, , 1,3,3xyz =
.

Bài toán 26. Cho các số thực dương
,,abc
thỏa mãn
2
ac b
≥
và
( )( )
22 2
4ac b ab c a cb+ +− =
.
Tìm giá trị lớn nhất của biểu thức
22
1.
b ac b
P
ac ac b
+
=++
−
Lời giải. Ta có
( )( )
2
22 2 2
2
14
1 4.
4
b ab b
ac b ab c a a a
cc
c
b c ac b
a
c
b
ab b ac
c
+ +− = ⇔ + + = +
⇔+ + =+
( )
1
4. 2*
ac b c b
a
b ac b c a
ac b
b ac
⇔+ =+++
≥+
Đặt
( )
2
ac
tt
b
= ≥
, từ (*) ta có
( )
( )
( )
2 43 3
2
1
2 2 40 2 0 22 2
4
2tt
t t t t t t do t
t
t
≥ +⇔ −
+−
+=⇔ − = ⇔= ≥
−
hay
4
ac
b
≥
Lại có
2
222
1
11
1
b
b ac b b
ac
P
b
ac ac b ac
ac
+
+
=++ =++
−
−
Xét hàm số
( ) ( )
2
2
1
1,
1
1
4
ub
fu u u
u ac
+
=++ =
−
≤
, ta có
( ) (
)
( )
( )
3
41
1
' 21 0,
4
1
u
fu u
u
u≥∀++
−
≤
+
=
( )
1 625
.
4 144
ffu
⇒=
≤
Vậy
625
144
MaxP = ⇔
2
42ac b a
ab c cb
= =
⇔
=
=
.
Bài toán 27. Cho x, y, z là các số thực dương thỏa mãn :
1xy z++=
. Tìm giá trị nhỏ nhất của biểu thức
( ) ( )( )
3 33
14
1 11
xyz
P
x yz y zx z xy
z xy
=+++
+++
+ ++
.
Lời giải.
Biểu thức P được viết lại như sau :
( )( )
( ) ( )( )
44 3
22
14
11
1 11
xy z
P
xy
x xyz y xyz
z xy
=++ +
++
++
+ ++
Áp dụng BĐT Cauchy ta có :
( )
( )
( )
( )
22
21
11
44
xy z
xy
++ +
+ +≤ =
( )
( )
( ) ( )
( )
( )
( )
2
2
22
3 22 3 3
22 2 2 2 2
4 28 4 28 4 28
1 21
11 1 1
xy
xy
z xy z z
zz
x y xyz
zz z z
+
+
++ +
⇒ ++≥+ ≥ +
++
++
++ + +
( )
( )
( ) ( )
(
)
2
3 32
22
1
4 28 9 57
,1
21
1 21
z
z zzz
z
z
zz
−
+ − −+
=+= >
+
++
Xét hàm số
( )
( )
(
)
32
2
9 57
,1
21
zzz
Pz z
z
− −+
= >
+
.
Ta có :
( )
( )
( )
( )
2
3
3 5 3 14 23
5
'0
3
21
z zz
Pz z
z
− ++
= =⇒=
+
.
Lập bảng biến thiên ta có :
( )
5 53
38
Min P z P
= =
.

Vậy
53 1 5
,.
8 33
Min P x y z= ⇔== =
Bài toán 28. Cho các số thực dương x, y, z thỏa
mãn
2 22
894x y z xyz++≤
. Tìm giá trị nhỏ nhất của biểu thức
( )
23
42
6 36 11 2 11
x yz
P
y zx
++
=
−−
Lời giải. Từ giả thiết ta có :
( )
2
2
3 864x z y zx xyz− ++≤
(
) ( ) ( )
2
2
3
08 223 3 223
2
y zx y x z zx y y⇒<≤−−−≤−⇒>
Ta lại có :
22
9
4 4 4 4 12 8 3 12
xz
zx y y x z zx zx
yy
≥++ +≥+ ≥ ⇒≥
.
Ta có :
(
)
23 2
3
4 2 8 8 16 4 12 2 16
216 33 18
216 11 3 2 3 2
x yz x z y
P
y zx
y z zx
+ + ++− + + −
= ≥
−
− ++
22
2 8 3 16 2 32
216 198 216 198
y zx y
yy
+− +
≥≥
−−
.
Xét hàm số
( )
2
2 32 3
,
2
216 198
y
Fy y
y
+
= >
−
.
Ta có :
( )
( )
( )
2
8 81 99 432
' 03
216 198 216 198
yy
Fy y
yy
−−
= =⇒=
−−
.
Lập bảng biến thiên ta có :
( ) ( )
52
3
3
Min F y F= =
.
Vậy
52
3
Min P =
khi
6, 3, 2.xyz= = =
Bài toán 29. Cho x, y, z là các số thực dương thỏa mãn :
2 22
1
xyz++=
Tìm giá trị nhỏ nhất của biểu thức
( )
3 33
2
11
2
xyz
P xyz
xyz xy yz zx
++
= ++ + −
++
Lời giải. Từ giả thiết ta có :
( )
( )
2
12x y z xy yz zx
++ =+ + +
Ta có :
( )
3 33 2 22
3
x y z xyz x y z x y z xy yz zx
++− =++ ++−−−
(
) (
)
31xyz x y z xy yz zx
= + ++ − + +
( )
3 33
111
31
xyz
xy yz zx
xyz xy yz zx
++
⇒ =+ + + − ++
( )
9
31 .xy yz zx
xy yz zx
≥+ − + +
++
Đặt
2 22
1 0 1.t xy yz zx x y z t= + + ≤ + + =⇒ <≤
( )
19 1 4
12 3 1 22
2
Pt t t
tt t
⇒≥++ + −− =−++
.
Xét hàm số
( )
(
4
2 2 , 0;1Ft t t
t
= −+ ∈
.
Ta có :
( )
2
2
4
' 2 0 2 40 2Ft t t
t
=− =⇒ −=⇒=±
.
Lập bảng biến thiên ta có :
( ) ( )
14Min F t F= =
Vậy
4Min P =
khi
1
.
3
xyz= = =

Bài toán 30. [THPT Quốc Gia 2015] . Cho các số thực
,,abc
thuộc đoạn
1; 3
và thỏa mãn
6
abc++=
. Tìm giá trị
lớn nhất của biểu thức
22 22 2 2
1
2
12 72b bc ca aa
P abc
ab bc ca
bc++
−
+
=
+
++
.
Lời giải.
Do
( )( )( )
(
)( )( )
111
, , 1; 3
33
0
3 0
abc
abc
abc
−−−
⇒
≥
−
∈
≤
−−
(
)
5
23
7
ab bc caabc
abc ab bc ca
≥ ++−
≤
⇔
++ −
11ab bc ca⇒ ++≥
Lại có
(
)
2
12
3
abc
ab bc ca
++
++ =≤
. Hơn nữa:
(
) (
)
2
22 22 2 2 22 22 2 2
2 12
ab bc ca a ab
bbcca bbca b a bc
aa
cc
c+
+ + = + ++ = ++ ++
Nên
(
)
( )
(
)
22
1
72
1
5
22
72ab bc ca ab bc ca
P abc ab bc ca
ab bc ca ab bc ca
++ ++
= − − ++−
++
+
+
+
≤
+
Đặt
, 11;12
ab bc ca t t ∈++=
Khảo sát hàm số
( )
72 5
, 11;12
22
t
ft t
t
∈=++
ta tìm được
[
]
( ) ( )
11;12
160
11
11
Max f t f= =
Hay
160
11
MaxP =
khi
( ) ( )
; ; 1; 2; 3abc =
và các hoán vị của nó.
Bài toán 31. Cho các số thực
,,
abc
thỏa mãn
0, 0, 1abc
≥≥≥
và
2
abc++=
. Tìm giá trị lớn nhất của biểu thức
(
)
( )
22 22 2 2
1P ab bc ca a b b c c a= ++ + + +
.
Lời giải : Từ giả thiết ta có :
0,1ab c≤ ≤≤
và
2abc++=
Ta có
2
()()2()1P ab bc ca ab bc ca ab c a b c
= ++ ++ − +++
2
()()41ab bc ca ab bc ca abc
= ++ ++ − +
.
Mà
2
()
( ) (1 ) 1
4
abc
a b c ab c
++
+ + −≤ =
(Vì
0,1ab c≤ ≤≤
và
2abc++=
)
nên
1abc ab bc ca≥ ++−
Suy ra :
2
()()4()5P ab bc ca ab bc ca ab bc ca
≤ ++ ++ − ++ +
Đặt
t ab b c ca= ++
. Ta có
2
( )4
0
33
abc
t
++
≤≤ =
..
Xét hàm số
2
( ) ( 4 5)f t tt t= −+
trên đoạn
4
0;
3
Có
2
'( ) 3 8 5ft t t= −+
,
4
1 0;
3
'( ) 0
54
0;
33
t
ft
t
= ∈
= ⇔
= ∉
.
4 52
(0) 0,(1) 2,( )
3 27
fff
= = =
. Suy ra
4
[0; ]
3
Max ( ) (1) 2ft f= =
Vậy
2MaxP =
, đạt được khi
0, 1, 1abc= = =
hoặc
1, 0, 1ab c= = =
.
Bài toán 32. Cho các số thực a,b,c thỏa mãn
abc≥≥
và
222
5abc++=
Chứng minh rằng
( )( )( )( ) 4a b b c c a ab bc ca− − − + + ≥−

Lời giải.
Ta có
( )( )( )( ) 4a b b c c a ab bc ca− − − + + ≥−
: ( )( )( )( ) 4P a bb ca cab bc ca⇔=−−− ++≤
(*).
• Nếu
0
ab bc ca++<
thì
0P ≤
suy ra BĐT được chứng minh.
• Nếu
0ab bc ca++≥
, đặt
0ab bc ca x++=≥
ta có :
( )( )
2
2
()
24
abbc ac
abbc
−+− −
≤=
−−
( )( )( ) ( )
3
()
1
4
abbca c
ac−
≤⇒−−−
Ta có
( )
222
4 +
a b c ab bc ca
+−− −
(
) (
)
(
) (
)
( )
(
)
(
)
( )
( )
2
2 2 22
22 2
++2 2 2 2
2
+
=
3
ac ab bc ac ab bc
ac ac ac
=−−−−+−+−
−
−
−
=
Suy ra
(
) (
)
2
45 3
x ac−≥ −
,từ đây ta có x
≤
5 và
( )
4
(5 ) 2
3
ac x−≤ −
.
Từ
( ) ( )
1,2
suy ra
3
14
. (5 )
43
Px x
≤−
=
3
23
(5 )
9
xx−
Lại có
(
)
3
(5 )fx x x= −
hàm số liên tục trên đoạn
0;5 .
( )
5
' 5 (5 )
2
fx x x=−−
;
( )
5
’ ;2
0
xf
x
x ⇒=
= =
.
Ta có
( )
( ) ( )
2 506 3,
0f ff= = =
Vậy
( )
( )
[0;5]
2 63
x
Max f x f
∈
= =
,
( ) ( )
[0;5]
00
x
Min f x f
∈
= =
.
nên suy ra
23
.6 3 4
9
PP≤ ⇒≤
. Vậy (*) được chứng minh.
Dấu bằng xảy ra khi
2; 1; 0abc= = =
.
2. Dồn biến nhờ kết hợp với kỹ thuật đổi biến số.
Bài toán 33. Cho a, b, c dương thỏa mãn :
222
3abc++=
.
Tìm giá trị nhỏ nhất của biểu thức
(
)
3
5P abc
abc
= ++ +
.
Phân tích. Ta có
( )
( )
2
222
3a abcb ab bc c ca= ++ − + +++
đồng thời
( ) ( )
2
3
ab bc ca abc a b c+ + ≥ ++
. Do đó giữa các đại lượng
( ) ( ) ( )
,,
a b c ab bc ca abc++ + +
tồn tại một mối liên hệ mà ta quan tâm.
Và để làm gọn các biểu thức ta có thể sử dụng phép đổi biến số (dạng ẩn phụ) như
lời giải sau:
Lời giải. Đặt
2
3, 0
,
23
xy
x a b c y ab bc ca
xy
>>
=++ = + + ⇒
= +
Mặt khác ta có:
( )
( )
2
2
13
3
x
ab bc ca abc a b c
abc
y
+ + ≥ ++ ⇒ ≥
.
( )
22
2
9 36
55
3
xx
Px x
y
x
⇒≥ + = +
−
.
Xét hàm số
( )
( )
2
2
36
5
3
x
Fx x
x
= +
−
với
3x >
Ta có:
( )
( )
( )
( )
54
3
2
3 5 15 27 81
'
3
x xxx
Fx
x
− + ++
=
−
Vì
( )
54
3 5 15 27 81 0 ' 0 3x x x x Fx x> ⇒ + + + >⇒ =⇔=
.
Lập bảng biến thiên ta có:
( )
3 18Mi nF F= =
.

Vậy
18MinP =
khi
3
1.
3
x
abc
y
=
⇔===
=
Bài toán 34. (HSG Tỉnh 12 - Nghệ An 2010) . Cho các số
dương a, b, c đôi một khác nhau thỏa mãn đồng thời các điều
kiện
2
2ab bc c+=
và
2ac≤
Tìm giá trị lớn nhất của biểu thức
abc
P
ab bc ca
= ++
−−−
.
Phân tích. Nhận thấy đẳng thức ở giả thiết và biểu thức P có dạng đồng bậc, do
đó ta có thể nghĩ đến vận dụng cách đổi biến kiểu
.
.
a xc
b yc
=
=
để dồn biểu thức ba
biến về biểu thức hai biến.
Lời giải. Đặt
1
1
0
.
0
2
2
2
.
2
1
x
a xc
x
b yc
xy y
y
x
<≤
=
<≤
⇒⇒
=
+=
=
+
Ta có
( )
2
22
1
1 2 1 26
11 1 1
22
xx
x y xx
P
xy y x x x
xx xx
+
−−
=++= ++=
− −− −−
+− +−
Ta có
(
)
( )
2
2
2
3 8 10 1 1 27
' 0 0;
2 25
2
xx
P x Px P
xx
++
= > ∀∈ ⇒ ≤ =
+−
11
27
22
5 44
33
x ac
MaxP
y bc
= =
⇒=⇔ ⇔
= =
.
BÌNH LUẬN. Thông thường phép đổi biến số được thực hiện với hai mục đích.
• Làm cho bài toán có cách nhìn đơn giản hơn dưới dạng ẩn phụ.
• Làm giảm số biến xuất hiện trong bài toán ban đầu.
Sau đây mời các bạn cùng tiếp tục theo dõi các bài toán để làm rõ hơn những vấn đề đã
nêu.
Bài toán 35. Cho
,,abc
là các số thực dương thỏa mãn
(
)
(
)
25
+ +=a b b c bc
và
2 ≥a c
Tìm giá trị lớn nhất và nhỏ nhất
của biểu thức
22
+
=
a
P
b
ac
.
Lời giải. Đặt
=
=
a
x
b
c
y
b
. Từ điều kiện ban đầu ta có:
( )( )
2
21 5
3
2
2
+
+ +=
=
⇔
≥
−
≥
x
x yy
y
x
y
x
x
y
21
22
32
+
⇒⇔
−
≥ ≤≤
x
x
xx
Khi đó biểu thức
( )
( )
( )
2
22
2
1
1
3
1
3
2
−
= = =
+
+
−
+
++
xx
xx
P
x
xy x x
x
x
Khảo sát hàm số
( )
( )
( )
( )
2
2
13 +−
=
+
xx
fx
xx
trên đoạn
1
;2
2
ta có:
( )
(
)
( )
( )
22
3 25 3 25 1
5 ' 1 0, ; 2
22 2 2
2
22
=−+ + − ⇒ =−− + <
+
+
∀∈fx x f x
x
x
x
x
x
Do đó
( ) ( )
5 15
2
8 22
= =
≤≤
f ffx
.

Hay
2
5
max
2
=
= ⇔
=
ba
P
bc
và
2
5
min
8
4
=
= ⇔
=
ab
P
cb
Bài toán 36. Cho
,,xyz
là các số thực dương thỏa mãn
22 2
11 1
.
2ab c
+=
Tìm giá trị nhỏ nhất của biểu thức
222
ab c
P
bc ca
bca
=++
+
+
+
+
Lời giải. Đặt
22
,0
,
11
24
1xy x y
cc
xy
ab
xxy y
>+
==⇒⇒
≤
= ≤
+
Khi đó
( ) ( )
( )
(
)
22 22
2 2 22
22
2
1
1 1 11
2
x y xy xy xy
P
yx xy xyx y
x y xy
xy
=++ ≥ +
+ + ++
++
+
22 22
22 22
11
22
11
12
22
xy xy
x y xy xy
xy xy
= + ≥+
++ + +
++
Đặt
1
, 0; .
4
xy t t
= ∈
Xét hàm số
( )
2
2
11
2 , 0;
24
2
t
ft t
t
t
=+∈
+
+
có
( )
( )
33
2
11
0, 0;
4
1
2
2
2
t
ft t
t
t
′
=− − < ∀∈
+
+
( )
141
45
13
ft f
⇒≥ =+
.
Hay
41
5
n
1
mi
3
P =
+
. Dấu “=” xảy ra
2.ab c⇔==
Bài toán 37. Cho
,, 0abc>
. Chứng minh rằng
( )( )
9
4
a b c abc
b c a a b c ab b c ca
+++ ≥
++ + +
.
Lời giải. Ta có
9
3
abc
VT
abc acb
bca
bcacba
=+++
++++++
.
Đặt
,, 0
,,
1
xyz
abc
x yz
b c a xyz
>
= = = ⇒
=
.
( ) ( )
2
9
3
27
39
VT x y z
x y z xy yz zx
xyz
xyz xyz
≥
=+++ ≥
+++ + + +
+++
++ + ++ +
.
Đặt
3.t xyz t=++⇒≥
Xét hàm số
( )
2
27
,3
39
Ft t t
tt
=+≥
++
có
( )
( )
43 2
2
2
6 27
' 03
39
tt t
Ft t
tt
++
= > ∀≥
++
Lập bảng biến thiên ta có
( ) ( )
34 4Min F t F VT= =⇒ ≥⇒
đpcm.
Dấu ‘=’ xảy ra khi
.abc= =

Bài toán 38. Cho
,, 0xyz>
. Tìm giá trị nhỏ nhất của biểu
thức
3
22 2
8
( )( ) ( )
z x y xy
P
z
xy yz xz
+
= ++
++ +
.
Lời giải.
Ta có :
2
22
11
8
( 1) ( 1)
xy
xy
zz
P
yx
zz
xy
zz
zz
= + ++
++
+
Đặt
,
xy
ab
zz
= =
. Khi đó :
22 2
1
8
( ) ( 1) ( 1)
a b ab
P
ab b a
+
= ++
++ +
Theo bất đẳng thức Cauchy-Schwarz, ta có :
22 2
22 2 2 2 2
2 22
33
()
( 1) ( 1) ( 1) ( 1) ( 1) ( 1)
2( ) 2.27( ) 27( )
2 ( 1)( 1) 2 ( 1)( 1)
2(2 2 2) 8( 1)
a b a b ab
b a ab ba ab ba
ab ab ab
ab b ba b
a b ab
+
+= + ≥
+ + + + ++ +
+ ++
= ≥=
+++ ++
+ + ++
3
27
8
8( 1)
ab
P
ab
+
⇒≥ +
++
Đặt
( 1), 0
t ab t= ++ >
. Khảo sát hàm số
( ) ( )
3
27 1
, 0;
8
8
t
tft
t
−
+∈= +∞
Ta có
( )
( ) ( )
0;
3
min 3 .
8
ft f
+∞
= =
Vậy
3
min
8
P abc
=⇔==
Bài toán 39. Cho các số thực không âm
,,xyz
thỏa điều kiện
( )
2 20xy x y z− + −=
. Tìm giá trị lớn nhất của biểu thức
(
)
(
)
(
)
(
)
2
22
2
22 2
2
64 8
3
4
22
22 1
xy x y
x yz
P
xy
z xy
− − ++
= + −+
++
++
Lời giải.
Biểu thức đã cho kết hợp với giả thiết được biến đổi thành :
( )
( )
2 22 2 2
22 2
2
12 4 4 4
3
4
22
42
x y z x y xy x y
P
xy
z xy
− +− −
= + −+
++
++
( )
( )
( )
22 2 2
2
22 2
2
4 44 2
3
4
22
42
x y xy x xy y
x yz
xy
z xy
− +− − +
= + −+
++
++
( ) ( )
( )
( )
22
2
22 2
2
24
3
4
22
42
xy x y
x yz
xy
z xy
−− +
= + −+
++
++
2
2
22 2
2
4
3
4
2 2 42
xy
xy
x yz
xy z
−
−
+
= + −+
++ +
22
22 2
4z 4
3
4
2 2 42
x yz
xy z
−
= + −+
++ +
Giả thiết được viết lại là :
( )
2 20 2 2 20xy x y z xy xz yz− + −=⇔ − − −=
22 2
10
zz
y x xy
⇔−−−=
Đặt
11
; ;2a b cz
xy
= = =
.
Lúc đó điều kiện giả thiết được viết lại :
21ab bc ca++=
.

Ta có :
( )( )
2 22 2
1
2
2 12 2 2
1
12
x aa a
x
ab ac
x a ab bc ca a
x
= = = =
++
+ + +++
+
.
( )( )
2 22 2
1
2
2 12 2 2
1
12
y bb a
y
ab bc
y b ab bc ca b
y
= = = =
++
+ + +++
+
( )
( )
(
)
22
11 1
22
2 22
ac bc
c ab bc ca c
= =
++
+ ++ +
Từ đó ta có :
( )( )( )
( )
(
)
( ) ( ) (
)
22
2 2 2 22
12 12
12
22
12 12
22
ab
a b ab
ab ac bc
ab
ab ac bc
++
+
+= ≤
+++
++
+++
(
)(
)
( )( )( )
22
2 22
2
12 12
1
12 12 2
2
ab
a bc
c
++
≤=
++ +
+
Dấu đẳng thức xảy ra khi
ab=
.
Từ đánh giá này ta có
22
2
2
33 4
16
2
2
cc
P
c
c
−
≤ −+
+
+
Xét hàm số
( )
22
2
2
33 4
,0
16
2
2
cc
fc c
c
c
−
= −+ ≥
+
+
.
Ta có :
( )
( )
( )
2
22
2
3 12 3
'
8
22
2
c cc
fc
cc
c
=− +−
++
+
(
)
( )
2
2
2
3 24
3
8
2
cc
c
c
− +−
= −
+
Do đó :
( )
( )
(
)
2
22
' 0 3 2 24 2 4 0
f c cc c c≥⇔ + + +− ≤
( )
(
)
2
22
2 8 24 0cc⇔ + + +− ≤
( )
1
do
0
c ≥
.
Đặt
2
2, 2tc t= +≥
. Khi đó bất phương trình
( )
1
trở thành :
( )
(
)
4 32
8 32 0 2 2 4 16 0 2tt t ttt t+ − ≤⇔ − + + + ≤⇔≥
Từ đó ta có :
22
22 20 0 2cc c
+≤⇔ −≤⇒≤≤
Lập bảng biến thiên ta thấy giá trị lớn nhất của
5
8
P =
đạt được khi và chỉ khi :
2 22
22 2
22
c xy
ab z
= = = +
⇔
−
= = =
.
Bài toán 40. Cho các số thực
,,
xyz
thỏa mãn
( )
2 22
02x xy yzy zxz +++= >+
. Tìm giá trị nhỏ nhất của biểu
thức
2 22
2
22
2
22
ln
2
xz yz
x
P
x
yz
x
z
y yxz
y
z
−
++
++
−
=++
+
Lời giải. Đặt
( )
( )
( )
2
2
2
0,,
a
b
xz
yc
y
b
x
za
c
=
= ≥
−=
−
−⇒
Khi đó
2ln 1
ab c
P
bc ca ab
=++ +
++ +
( ) ( )
22
2ln 1
22
ab c
ab
ab c ba c
= + ++
+
++
22
2ln 1
ab c
abc abc ab
≥++ +
++ ++ +

Đặt
0.
c
t
ab
=
+
≥
Xét hàm số
( )
( )
2
2ln 1
1
ft t
t
=++
+
có
( )
0'ft≥
Suy ra
( ) ( )
02ft f≥ =
. Hay
min 2
P =
đạt được khi
( )
4 0.
xy
zz x
=
−=
Bài toán 41. Cho
,,abc
là 3 số thực dương thỏa
mãn:
0,abc+−≥
0,bca+− ≥
0cab+−≥
và
( ) ( )
2
41a b c ab bc ca++ = + + −
. Tìm GTNN của biểu thức
222
22
111
2
ab bc ca
S
cab
abc
+++
= −+ −+ −+
++−
Lời giải 1.
Đặt
,a xyz=+−
,b yzx= +−
c zxy=+−
. Ta có
,, 0
4
xyz
xy yz zx
≥
++=
. Khi đó:
2 22
4
2
xyz
S
yz zx xy
xyz
= ++ +
+++
++
.
Giả sử
0xyz
≥≥>
. Khi đó
y z yz
zx xy x
+
+≥
++
. Nên suy ra
2 22
4
2
x yz
S
yz x
xyz
+
≥ ++
+
++
. Mặt khác
2 22
2 22
4
2 22
x y z x y z xy yz zx
yz x yz x
xyz
xyz
+ + ++
++ = ++
++
++
++
22
22
()
22
( )2
()
22
()
x yz xyz yz
yz x
x y z yz
x yz xyz
yz x
x yz
+ ++
= ++
+
++ −
++
≥ ++
+
++
=
1
22
x yz
x yz
yz x
yz x
+
++
+
+
+
+
.
Đặt
2 22
x yz
tt
yz x
+
= + ⇒≥
+
.
Xét hàm số
2
22
( ) , t 4
4
gt t
t
=+≥
−
, ta có
23
22
'( ) 1
( 4)
t
gt
t
= −
−
nên
23
'( ) 0 ( 4) 2 2 0gt t t=⇔ −− =
2 42
22
( 8)( 4 8) 0
22
t
t tt
t
= −
⇔ − − +=⇔
=
. Lập bảng biến thiên ta có
[
)
( )
4;
min (2 2 ) 3 2gt g
+∞
= =
Hay
min 3 2 1, 2.S ac b= ⇔== =
Lời giải 2.
Đặt
xyz
Q
yz zx xy
=++
+++
suy ra
2
2
( )( ) ( )( ) ( )( )
x y z xy yz zx
Q
yz zx xy yzzx zxxy xyyz
=+++ + +
+ + + ++ ++ + +
ta thấy rằng
( )
1
.
4
xyz xyz
xy yz zx
yz zx xy yz zx xy
++ = ++ ++
+++ +++
2 22 2 22
111
44 4
x y z xyz x y z
xy yz zx
++ ++
= + ++ ≥
+ ++
.

Áp dụng BĐT AM-GM ta có
22
( )( ) 2
2 ( )( )
2
2( )
xy xy xy
y z z x xy yz zx
xy xz yz yx
xy xy
xy yz zx xy yz zx
= ≥
+ + ++
++
≥=
++ ++
Tương tự ta có
;
( )( ) ( )( )
yz yz zx zx
z x x y xy yz zx x y y z xy yz zx
≥≥
+ + ++ + + ++
Suy ra:
1
( )( ) ( )( ) ( )( )
xy yz zx
yzzx zxxy xyyz
++≥
++ ++ + +
nên
2 22
2
4
xyz
Q
++
≥+
Suy ra
2 22
2 22
4
4
2
xyz
P
xyz
++
≥ ++
++
.
Đặt
2 22
2t x y z t xy yz zx= + + ⇒≥ + + =
.
Xét hàm số
2
4
() 4 , 2
2
t
gt t
t
= ++ ≥
, khi đó ta có
2
2
4
'( )
24
2
t
gt
t
t
= −
+
;
62
'( ) 0 32 256 0 2 2gt t t t
=⇔ − − = ⇔=
Lập bảng biến thiên ta có
[
)
(
)
2;
min (2 2 ) 3 2
gt g
+∞
= =
Hay
min 3 2 1, 2.S ac b= ⇔== =
Bài toán 42. (HSG Tỉnh 12 - Nghệ An 2010) . Cho a,b,c là
các số thực không đồng thời bằng 0 thỏa mãn :
( )
( )
2
222
2abc a b c++ = + +
.
Tìm GTLN và GTNN của biểu thức :
( )( )
333
abc
P
a b c ab bc ca
++
=
++ + +
Lời giải 1. Ta có :
( )
( )
333 222
3bc bcaba abca abc ca bc= ++ − −− +++ ++
( )( )
3.a b c ab bc ca abc= ++ + + +
Do đó :
( )( )
( )
( )
2
3
3
3
11
cx c
abc
P
a b c ab bc ca
xc
−
=+=+
++ + +
+
, với x = a+b
+) Với c =0 thì P=1 .
+) Với
0c =
/
, từ giả thiết :
( )
( )
22
2
1
4
2
x
x c ab a b x
c
≤ +=⇒≥−=
.
Đặt
,
1
2
x
tt
c
= ≥
.
Khảo sát hàm số :
( )
( )
( )
2
3
31
1
1
t
ft
t
−
= +
+
, cho ta :
11
1; ax
9
MinP M P= =
.
Lời giải 2.
Từ giả thiết:
( )
2
222
1
2
ab bc ca a b c a b c
+ + = ++ − − −
Suy ra:
( )
2
1
4
ab bc ca a b c+ + = ++
Do đó:
( )
( )
333
333
3
4
1444
16
abc
abc
P
abc abc abc
abc
++
= = ++
++ ++ ++
++

Đặt
2
4
4
4
44
4
a
x
abc
yz x
b
y
a b c yz x x
c
z
abc
=
++
+=−
= ⇒
++ = − +
=
++
Vì
( )
2
8
40
3
y z yz x
+ ≥ ⇒≤≤
Ta có
( )
( ) ( )
3
3 33 3
11
3
16 16
P x y z x yz yzyz
= ++ = ++ − +
(
)
32
1
3 12 12 16
16
P xxx
⇒= − + +
Xét hàm số
( )
32
3 12 12 16fx x x x=− ++
với
8
0;
3
x
∈
( ) ( )
2
2
' 9 24 12 ' 0
2
3
x
fx x x fx
x
=
⇒=−+⇒=⇔
=
Ta tính được
( ) ( )
2 8 176
0 2 16,
3 39
ff f f
= = = =
Suy ra
( ) ( )
88
0; 0;
33
11
,0
176
, 16
94
9
1 0, 0
c
MaxP a b a
Max f x Min f x
MinP a b c
= ⇔== ≠
= = ⇒
=⇔= =≠
Bài toán 43. cho
,,
xyz
là các số thực không âm và thỏa mãn
1
xyz++=
. Tìm giá trị lớn nhất của biểu thức
22 2
( ) ( 1)( 1) ( 2)M xy z x y x y xzz
= + ++ + + + +
Lời giải : Đặt
1.za+=
Từ giả thiết ta có :
0,1xy a≤ ≤≤
và
2
axy++=
Khi đó
( )
(
)
22 22 22
2
1
()()2()1
P ax xy ya a x x y y a
ax xy ya ax xy ya axy a x y
≤ ++ + + +
= ++ ++ − +++
2
()()41ax xy ya ax xy ya axy
= ++ ++ − +
.
Mà
2
()
( ) (1 ) 1
4
axy
x y a xy a
++
+ + −≤ =
(Vì
0,1xy a≤ ≤≤
;
2axy++=
)
nên
1axy ax xy ya≥ ++−
Suy ra :
2
()()4()5P ax xy ya ax xy ya ax xy ya
≤ ++ ++ − ++ +
Đặt
t ax xy ya=++
. Ta có
2
( )4
0
33
axy
t
++
≤≤ =
.
Xét hàm số
2
( ) ( 4 5)f t tt t= −+
trên đoạn
4
0;
3
Có
2
'( ) 3 8 5ft t t= −+
,
4
1 0;
3
'( ) 0
54
0;
33
t
ft
t
= ∈
= ⇔
= ∉
.
4 52
(0) 0,(1) 2,( )
3 27
fff= = =
. Suy ra
4
[0; ]
3
Max ( ) (1) 2ft f= =
Vậy
2MaxP =
, đạt được khi
0, 1, 0x yz= = =
hoặc
1, 0, 0xyz= = =
.
Bài toán 44. ( Khối A - 2011) . Cho x,y,z là ba số thực thuộc
đoạn
1; 4
và
;x yx z≥≥
.Tìm nhỏ nhất của biểu thức

23
x yz
P
x y yz zx
= ++
+ ++
Lời giải. Đặt
1
, , ;1
4
y ax z bx a b
= =⇒∈
.
Biểu thức P được viết lại như sau:
( )
( )
( )
( ) ( ) ( )
( )
( )
22
22
2
1
23 1
1
' ;' 0 1 0
1
10
ab
P
a ab b
a
Pb Pb a b ab
ab b
ab a b a
= ++
+ ++
⇒ =− + =⇒+ − + =
++
⇔ − − =⇒=
Vì
( )
( )
1 12
, ;1 2
4 23
1
a b MinP b P a
a
a
∈⇒ == − +
+
+
.
Đặt
1
;1
2
t at
= ⇒∈
.
Xét hàm số
( )
2
12
2
1
23
Ft
t
t
= −+
+
+
.
Ta có:
( )
( )
(
)
(
)
( )
(
)
2
2
2
22
2
43 2
62
' ; ' 0 22 3 6 1 0
1
23
18 6 12 6 8 0
t
Ft Ft t t t
t
t
tt tt
=− + =⇔ + − +=
+
+
⇔ − + − +=
Vì
( )
43 2
11
;1 18 6 12 6 8 0 ' 0 ;1
22
t t t t t Ft t
∈ ⇒ − + − + > ⇒ > ∀∈
( )
1 34
2 33
Ft F
⇒≥ =
.
Vậy
( )
1 34 34
2 33 33
MinF t F MinP
==⇒=
tại
11
, 4, 1, 2.
42
a b x yz= =⇒= = =
Bài toán 45. ( HSG Tỉnh Nghệ An năm 2014 ) Cho ba số
thực không âm thỏa mãn
3 57 9;
a b c ab bc ca>> + ≤+
.
Tìm giá trị nhỏ nhất của
( )
( ) ( )
444
32 1 1
P
ab bc ca
= ++
−−−
Lời giải.
Ta có:
( )
( )
( ) ( )
2
444
32 1
1 35
1
8 7P
a
ab bc c
ba
a
bc c
+≥ ++ +
−−−
Đặt
( )
; ,0acxybcxxy=++ =+ >
, ta có:
( )
( )
( ) ( )
( )
2
2
2
2
2
44 4 2 2 2
32 1 1
9 32
xxy xy
x
P xy
yx y x
x
xy xy
++
+ ++ = + +
++
≥
( )
2
2
2
32 2
xx y
xy x
x xy
y
+
+
= + + −=
+
( )
( )
2
2
2
2
32 2 2.
xx y
y
xx y
y
+
= ++ −
+

Đặt
( )
(
)
2
0
y
tt
xx y
= >
+
, xét hàm số:
( ) ( )
2
2
32
22ft t
t
= ++ −
, ta có:
( )
( ) ( )
43
3
64
' 2 2 ' 0 2 4 64 0ft t ft t t
t
=− + +⇒ =⇔ + − =
2
t
⇔=
. Lập bảng biến thiên ta có:
5
8
P =
Bài toán 46. Cho ba số thực dương
,,abc
thỏa :
ab
ac bc
c
−+ −=
. Tìm GTNN của biểu thức
2
22
ab c c
P
bc ca ab
ab
=+++
++ +
+
Lời giải. Đặt
( )
, ,1a xc b yc x y= = ≥
• Thay
1x =
vào giả thiết ta có :
0bc b c
−= ⇒=
không thỏa vì
0.c >
• Thay
1y =
vào giả thiết ta có :
0ac a c−= ⇒=
không thỏa vì
0.c >
• Xét
,1xy>
.Thay vào giả thiết ta có :
( )( )
( )(
) (
)( )
( )
( )( )
2
1 1 22 1 1
12 1110 1110
1 1 1 2 4.
x y xy x y x y xy
xyxy xy xy
x y xy x y xy xy
−+ −= ⇔+−+ − − =
⇔ −−+− − −+=⇔ − −− =
⇒ − − =⇔ =+≥ ⇒ ≥
Biểu thức P được viết lại như sau :
( )
22
22 2
11 1 1
11
2
xy x y
P
y x x y xy x xy y x y
xy
x y xy
=+++ = + ++
+++ + + +
+
+−
( )
( )
( )
2
2 22
33 22
22
1 1 11
23
2
2
2 33
32
xy
xy
P
xy x y x y xy
x y xy
x y xy
xy xy xy
x y xy
+
≥ + + =++
++ +
−
+−
− +−
=
−
.
Đặt
,4t xy t= ≥
Xét hàm số
(
)
( )
32
2
2 33
;4
2
ttt
ft t
tt
− +−
= ≥
−
Ta có :
( )
( )
( ) ( )
( )
32
4 32
22
22
4 6 4 18
4 66
' 04
22
tt t t
t tt t
ft t
tt tt
−++ −+
− ++−
= = > ∀≥
−−
.
Lập bảng biến thiên ta có :
( ) ( )
41
4
8
Min f t f= =
Vậy
41
24
Min P =
khi
2xy= =
hay
2.ab c= =
3. Dồn biến nhờ kết hợp với kỹ thuật sắp thứ tự các biến.
Bài toán 47. Cho
,, 0abc≥
thỏa mãn:
3abc++=
. Tìm
GTLN, GTNN của biểu thức
222
P a b c abc= +++
.
Phân tích.
Ta dễ dàng nhận thấy
( ) ( ) ( ) ( )
22
22
23 2P a b c ab c c c ab c=+ ++ −=− +− −
Khi đó ta muốn dồn biểu thức
P
về biến
c
bằng đánh giá
( )
2
2
2
3
0
4
ab
c
ab
+
≤≤
−
=
. Tuy nhiên dấu của
( )
2 c−
thay đổi khi
0;3
c ∈

Để giải quyết vấn đề đó, ta có thể giả sử
{ }
min 31,, 3c abc cabc c= ⇒= ≥⇒+ ≤+
Lời giải. Giả sử
{
}
min
31
,, 3
c abc
c
abc
c
= ⇒=
≥⇒
+
≤
+
.
Từ giả thiết ta có:
( )
2
3
0
4
c
ab
−
≤≤
và
0;1c ∈
.
Ta có :
( ) ( )
2
2
32P c c ab c=− +− −
.
Với
( )
( )
2
32
3
1
0
3 18 2 6 9
4
4
20
c
ab
cc Pcc
c
−
≤≤
⇒ −+ ≤≤ −+
−>
.
Đặt
( )
( )
( )
32
1
3 18 , 2 6 9
4
fc cc gccc= −+ = −+
.
Khảo sát hàm số
( ) ( )
, , 0;1f c gc c∈
.
Ta có
( )
4Min f c =
tại
( )
1, 9
c Max g c= =
tại
0c =
.
Vậy
4Min P =
tại
1abc= = =
;
9Max P =
tại
( )
3; 0; 0
và các hoán vị.
Bình luận. Từ phân tích và lời giải bài toán trên, ta nhận thấy việc sắp thứ tự các
biến phải thỏa mãn hai điều kiện:
• Thứ nhất: Vai trò của các biến là như nhau (nghĩa là khi thay đổi vai trò của chúng thì
giả thiết và kết luận của bài toán không thay đổi)
• Thứ hai: Việc sắp thứ tự các biến phải xuất phát từ ý định giải toán nào: có thể là do việc
so sánh gặp trở ngại về dấu như bài toán trên hay để dồn về một biến nào đó…
Sau đây mời các bạn cùng tham khảo một số bài toán để thấy được những mục đích khác
nhau khi sắp thứ tự các biến.
Bài toán 48. Cho a, b, c là độ dài ba cạnh của tam giác có
chu vi bằng 3. Tìm giá trị nhỏ nhất của biểu thức
( )
222
34Q a b c abc= ++ +
.
Lời giải. Không mất tính tổng quát ta giả sử
0 abc<≤≤
.
Ta có :
33abc ab c++=⇒+=−
và
1c ≥
.
Mặt khác
33
3 1;
22
ab c c c c c
+>⇒−>⇒< ⇒∈
.
Ta có :
( )
( ) ( )
2
22 2 2
3 3 4 33 3 23 2Q a b c abc c c c ab= +++ = −+−−
.
Vì
3
32 0
2
cc
< ⇒− >
.
Ta có :
22
32
3 3 27
2 2 22
ab c
ab ab Q c c
+−
≥⇒ ≥⇒≥− +
Xét hàm số
( )
32
3 27 3
, 1;
22 2
Fc c c c
=−+ ∈
Ta có :
( )
2
0
' 3 30
1
c
Fc c c
c
=
= −=⇒
=
.
Lập bảng biến thiên ta có :
( ) ( )
1 13MinF c F= =
.
Vậy
13MinQ
=
tại
( ) ( )
; ; 1;1;1abc =
.
Bài toán 49. Cho các số thực
,,abc
thỏa mãn:
222
9ba c++=
. Chứng minh rằng
( )
2 10 abbc ca ≤+++
.
Lời giải. Ta có:

( )
( )
( ) ( )
( )
( ) ( )
22
22
2
2 22 42abc abc ab ac bb bc aa
≤ + +−++ − = + +
+
−
( ) ( ) ( )
2
32
9 2 8 4 20 72 ,2ab a tb ab t t f t
=
= + − + +− + =
với
.t ab=
Không mất tính tổng quát, giả sử :
|||
||
| b
a c
≤≤
, ta có :
222 2 2
39 3bc cac= ≤ ⇒++ ≥
.
Lại có :
22 2
2| | 9 6 || 3a tba c
b≤ + ≤⇒= ≤−
Do đó :
[ ]
( ) { }
3;3
( 2); (3) ( 2) 100Max f t Max f f f
−
= − =−=
. Hay :
2
100P ≤
.
Dấu “=” xảy ra
⇔
(
) ( )
, , 1;2;2abc = −
và các hoán vị của nó.
Bài toán 50. Cho các số thực không âm và không có hai số
nào đồng thời bằng 0. Tìm giá trị nhỏ nhất của biểu thức:
( )
2 2 22 22
111
P xy yz zx
x yzyzx+ ++
= ++ + +
Lời giải. Giả sử
{ }
min ; ;z xyz=
.
Khi đó ta có
2
22
zz
x y xy yz zx x y
z
+ ⇔+
≥ + ++
≥
Lại có
22 2 2
22 2 22 2
1
;
2
111
;
2
2
1
2
1
y
z
x
yz xz
zz
yx
x
z
y
≥
+
+
•≥ ≥
++
++
•
++
Do đó
22 2 2
1 11
22
22 2 2
zz
Px y
zz z z
xy yx
++ + +
+ ++ + +
≥
Đặt
( )
; 0,
22
zz
x a y b ab= += ≥+
Ta có
22 2 2 2
1 11 1
1
a
a
b
P
a
b
a ab
a
b
b
b
a
b
+ + = ++
+
≥
+
. Đặt
( )
0
a
xx
b
= >
khảo sát hàm số
( )
2
1
,0
1
x
fx x x
x
x
= ++ >
+
ta tìm được
( )
5
2
Min f x =
.
Vậy
5
2
Min P =
đạt được khi
,0a bc= =
và các hoán vị của nó.
Bài toán 51. Cho các số thực không âm a, b, c thỏa
mãn
3abc
++=
.
Tìm giá trị lớn nhất của biểu thức
( )( )( )
2 2 2 22 2
P a ab b b bc c c ca a= −+ −+ −+
Lời giải.
Không mất tính tổng quát ta giả sử
( )
( )
2 22
2 22
0
03
0
aa b
a ab b b
abc
aa c
a ca c c
−≤
−+≤
≤≤≤≤⇒ ⇒
−≤
−+≤
( )
( )
2
22 2 2 22
3P b c b bc c b c b c bc
⇒≤ −+ = + −
Mặt khác ta có :
9
32 30
4
bc abc bc bc bc+≤++=⇒ ≤+≤⇒≤ ≤
Do đó
( )
22 33 22
93 3 9P bc bc bc bc≤ −=− +
.

Xét hàm số
( )
( )
32 2
0
9
3 9 , 0; ' 9 18 0
42
x
Fxxxx Fxxx
x
=
=−+ ∈ ⇒ =−+ =⇒
=
Lập bảng biến thiên ta có :
( ) ( )
2 12 12MaxF x F MaxP==⇒=
tại
( ) ( )
; ; 0;1; 2abc =
.
Bài toán 52. Cho a, b, c là các số thực không âm thỏa mãn
( )( )( ) 0
a bb cc a+ + +>
. Tìm GTNN của
222
33
a b c ab bc ca
P
bc ca ab
abc
++
=+++
++ +
++
Lời giải.
Giả sử
max { , }
a bc≥
. Ta có
222 2 2
() 1
()
ab bc ca a b c
a bc
a b c a bc
bc a
++ +
≥=
+
++ ++
+
+
Khi đó
1
33
a bc
P
a bc
bc a
bc a
+
≥++
+
+
+
+
.
Đặt
2.
a bc
tt
bc a
+
+⇒≥=
+
Khảo sát hàm số
2
1
() 3 3
2
gt t
t
= +
−
với
2t ≥
, ta tìm được GTNN của P bằng
72
2
.
Bài toán 53. (ĐH Vinh MO TST 2011-2012) . Cho các
số thực a,b,c không âm đôi một khác nhau. Tìm giá trị nhỏ
nhất của biểu thức
(
)
( )
(
)
( )
222
222
111
P abc
ab bc ca
= ++ + +
−−−
Lời giải 1. Giả sử
{
}
,,
c Min a b c=
Ta có :
( ) ( ) ( )
( )
222
222
2
2
a b b c c a ab bc ca
A ba c
+
− +− + + +
+
−+
= =
( ) ( )( ) ( )
2
22 2
.
2
a b b c a c ab bc ca− + − −+ + +
=
Mà :
( )( ) ( )
022abbcca bcac cb ac++ − −⇔ + −≥≥
(đúng ). Suy ra :
( )
( )( )
2
2A bc cb
aa +−− −≥
(1)
Lại có :
( ) ( ) ( )
222
111
B
ab bc ac
= ++=
−−−
( )
( )
( ) (
)
( )
( )
2
2 22
12
ab
acbc
ab bc ac
−
=++
−−
− −−
(2)
Đặt :
( ) (
)( )
2
;ab ubcac v− = − −=
. Từ (1) và (2) suy ra :
( )
( )
( )
2
22
222
122
2 52 4
uuv uv
u uv vu
uv
u v u v uv
v
u
v
P
v
++
+
≥+ ++ = + + =+ +
+
Đặt
,0
u
tt
v
= >
. Xét
hàm số :
( )
2
2
45ft t t
t
= + ++
, ta có :
( )
( )
( )
( )
2
22
21
2 15
'24 '0
2
1
t
ft t t ft tt
tt
+
−+
= +− = ⇒ = ⇔=+−
Lập bảng biến thiên cho ta :
( )
5 1 11 5 5
22
f ft
−+
=
≥
.

Vậy
(
)
2
0
11 5 5
22
1
,
5
0
c
MinP a b ab
ab
=
+
= ⇔ −=
>
−
( Hoặc hoán vị )
Lời giải 2. Giả sử
{ }
,,c Min a b c=
. Suy ra :
;ba a
bc
c≤
− −≤
. Do đó :
( )
(
)
(
)
22 22 22
22
222 2 2 2
1 11
ab ab ab
ab
ab a b
a
P
ab b
+ ++
≥ + ++ = + + =
−−
2
.
2
ab
ba
ab
ba
ab
ba
+
= +
+
+−
Đặt :
,2
ab
tt
ba
+= >
.
Xét hàm số :
( )
( )
( )
2
2
23
,' 2 0
2
2
5
2
t
ft t f t t t
t
t
+
= + = − =⇒=
−
−
.
Lập bảng biến thiên cho ta :
( )
3 5 11 5 5
22
ft f
++
≥=
Bài toán 54. Cho a, b, c là các số thực không âm có tổng
bằng 1.
Chứng minh rằng
( ) ( ) ( )
222
3a bc b ca c ab+− + +− + +− ≥
.
Lời giải. Do a, b, c có vai trò như nhau nên không mất tính tổng quát ta giả sử
11
;1 , 0;
33
abc a c
≥≥⇒∈ ∈
.
Ta có:
( )
( ) ( ) ( )
22 2
2
2 2 9 83a bc b ac ab ab c c c+− + +− ≥ +++− = −+
.
2
9 83VT c c c⇒ ≥ − ++
.
Xét hàm số
(
)
2
1
9 83 0
3
Fc c c c c
= − ++ ≤≤
.
Ta có :
( )
( )
( ) ( )
2
2
2
18 8 9 8 3
4
' 0 9 8 3 8 18 1
9
2 9 83
c c cc
Fc c c c c c
cc c
− + −+
= =⇒ − += − ≤
−+
Giải phương trình (1) và so sánh điều kiện ta được
1 7 33
,
3 24
cc
−
= =
.
Lập bảng biến thiên ta có :
( ) ( )
1
0 33
3
Min F c F F VT
= = =⇒ ≥⇒
đpcm.
Dấu ‘=’ xảy ra khi
( )
,,abc
là
11 111
;;0, ;;
22 333
và các hoán vị.
Bài toán 55. Cho a, b là các số thực thuộc
0; 2
.
Tìm giá trị nhỏ nhất của biểu thức
( ) ( )
( )
222
111
P
ab bc ca
= ++
−−−
Lời giải. Không mất tính tổng quát ta giả sử
02abc≤ <<≤
.
Từ
( )
2
11
02
4
ca
ca
<−≤⇒ ≥
−
.
Tiếp tục ta có:
( )
( )
22
11
02
2
cb b
bc b
<−≤−⇒ ≥
−−
và
( )
22
11
0 bab
b
ab
<−≤⇒ ≥
−

Suy ra
(
)
(
)
22
1 11
, 0; 2
4
2
Pb
b
b
≥ + + ∀∈
−
.
Xét hàm số
( )
( )
( )
22
1 11
, 0; 2
4
2
Fb b
b
b
= + + ∀∈
−
Ta có :
( )
( )
33
22
' 01
2
Fb b
b
b
=− + =⇒=
−
.
Lập bảng biến thiên ta có :
(
)
( )
99
1
44
MinF b F MinP==⇒=
Dấu
""=
xảy ra tại
( ) ( )
; ; 0;1; 2 .abc =
4. Phương pháp tiếp tuyến.
Chú ý. Nếu đường thẳng
y ax b= +
là tiếp tuyến của đồ thị hàm số
( )
y fx=
tại điểm
( )
00
;Ax y
(A không là điểm uốn) khi đó tồn tại một khoảng
( )
;
αβ
chứa điểm
0
x
sao cho
(
)
( )
,;fx
ax b x
αβ
≥ + ∀∈
hoặc
( ) ( )
,;fx ax b x
αβ
≤ + ∀∈
. Đẳng thức xảy ra khi và chỉ khi
0
xx=
.
Bài toán 56. Cho a, b, c dương thỏa mãn :
1abc++=
.
Chứng minh bất đẳng thức
9
1 1 1 10
ab c
bc ca ab
+
+
≥+
++
.
Lời giải. Ta có
( )
( )
22
4
41
4
1
1
aa
bc
a
bc
a
≥=
+ +−
+
+
Hoàn toàn tương tự, ta sẽ chứng minh
2 22
2 5 25 25
4 4 49
10
aa bb cc
abc
−+ −+ −+
++≥
Xét hàm số
( )
( )
( )
2
22
2
25
25
4 4 20
'
xx
f
x
x
x
fx
x
x
−+
⇒==
−+
−+
Phương trình tiếp tuyến tại điểm có hoành độ
0
1
3
x
=
là
99 3
100
x
y
−
=
Lúc đó
( ) (
)
( )
( )
2
2
2
3 1 15 11
0, 0;1
2
49
5
25
93
100
100
xx
xx
x x
xx
x≥ ∀∈
−
−
−
+
−+
−
−
=
Từ kết quả trên thay
x
bởi
,,abc
ta được:
( )
2 22
99 9
4 44
25 2
9
10 0
5
0
5
1
2aa
abc
a
bb cc
bc
−+ −+ −
++ −
≥=
+
++
(đpcm)
Bài toán 57. Cho a, b, c là độ dài ba cạnh của một tam giác.
Chứng minh bất đẳng thức
111 9 1 1 1
4
a b c ab c ab bc ca
+++ + +
++ + + +
≥
.
Lời giải. Chuẩn hóa
1.ab c++=
Khi đó bất đẳng thức cần chứng minh là:
( )
41 41 41
9*
1 11aa bb bb
−+−+−
−−−
≤
Xét hàm số
( )
2
51x
fx
xx
−
=
−
, phương trình tiếp tuyến tại điểm có hoành độ
0
1
3
x =
là
18 3.yx= −
Do
,,abc
là ba cạnh của một tam giác nên
1
1
1
2
1
2
2
2
abc
x
abc
ab
a
c
b
c
=++
⇒<
=++
=++
≥
≥
≥

Suy ra
( ) ( )
( ) ( )
2
2
3 12 1
1
18 3 0;,
2
0
xx
fx x
xx
x
−−
− −=
−
∀∈
≥
Từ đó ta có:
( ) ( ) ( ) ( ) ( )
8* 991VT fa fb fc a b c≤= + + ++ −=
(đpcm).
Bài toán 58. Cho
3
,,
4
abc≥−
thỏa mãn
1.ab c++=
. Chứng
minh bất đẳng thức
( )
222
9
*
10
111
abc
abc
++≤
+++
.
Lời giải.
Xét hàm số
( )
2
1
x
fx
x
=
+
. Phương trình tiếp tuyến tại điểm có hoành độ
0
1
3
x =
là
36 3
50
x
y
+
=
.
Xét hiệu
( )
( ) ( )
( )
2
2
0,
1
3 1 4 34
36 3 3
50 4
50
xx
x
f xx
x
−+
+
≤= ∀ ≥−
+
−−
Do đó
( ) ( ) ( ) ( ) ( )
36 9 9
50 50 10
* abcVT fa fb fc
≤ ++ + =
=++
(đpcm).
Bài toán 59. (Japan MO 2002) Chứng minh rằng với mọi
số thực
,,
abc
không âm ta có bất đẳng thức
(
)
( )
(
)
( )
( )
( )
222
222
222
3
5
bca cab abc
bc ca aa
bbc
≥
+++
+− + − +−
++
++ +
.
Lời giải. Chuẩn hóa
1abc++=
, bất đẳng thức đã cho trở thành:
( ) ( ) ( )
( )
22
222
21
12 12 12
3
*
5
2221 212
aa
aaaa
aa
a
≥
−+ − −
−
+
+
+
−−
+
Xét hàm số
( )
2
2
44 1
12 2
x
f
x
x
x
x
−+
−+
=
, phương trình tiếp tuyến tại điểm có hoành độ
0
1
3
x
=
là
54 23
25
x
y
−+
=
.
Do đó
(
)
( )
( )
(
) ( )
( )
2
32
22
27 1
0
21
2 54
23 1 6 1
54 23
2
252 5 1
5
2 22
x
xx
x
fx
x
xxxx
−+
≥
−
−+
−
−
+
=
+
−
+
=
( ) ( ) ( )
( )
( )
54 23 3
3.
25 25 5
* xy
VT f a f b c zf= ≥− ++ ++ =
+
(đpcm)
Bài toán 60. (USA MO 2003) Chứng minh rằng với mọi số
thực
,,abc
không âm ta có bất đẳng thức
( )
( )
( )
( )
( )
( )
222
222
222
8
2
22
2
2
2
bc a ca b ab c
bc ca ababc
++ + + ++
++
++ ++
≤
++
.
Lời giải. Chuẩn hóa
1.ab c++=
Bất đẳng thức cần chứng minh trở thành:
( )
( ) ( )
( )
2 22
2 22
1 11
33
8*
21 21 13 2a
abc
a cbcb
≤
−+ − −
+
+
++
++
+
Xét hàm số
( )
2
2
21
3 21
x
fx
x
x
x
+
−
=
+
+
, phương trình tiếp tuyến tại điểm có hoành độ
0
1
3
x =
là
12 4
3
x
y
+
=
.
Khi đó
( )
( ) ( )
( )
( )
2
2
3 14 1
1
0, 0;1
2
24
3
33
1
xx
x
fx
x
x
x
−− +
+
− ≤ ∀∈
−+
=

Nên
( ) ( ) ( ) ( )
( )
12 4
3. 8
33
*VT f a f b f abcc ≤++ +−+ ==
(đpcm).
Bài toán 61. (Russia MO 2002) Cho các số thực dương
,,abc
thỏa mãn điều kiện
3.abc++=
Chứng minh bất đẳng
thức
ab c ac bcab ≥ ++++
.
Lời giải. Ta có
(
)
(
)
2
222
92
bca b c a ab bc ca= ++ = + + +
++
Do đó bất đẳng thức cần chứng minh trở thành
( )
222
9*222
a acbc
b++
+ ≥++
Xét hàm số
(
)
2
,2fx x x
= +
tiếp tuyến của hàm số tại điểm có hoành độ
0
1x
=
là
3.
yx
=
Khi đó
( )
( ) ( )
( )
2
2
3 2 0, 0;3
3 12fx x x x x x xxx
−= = − ≥ ∀∈+
−+
Nên
( ) ( ) ( )
(
) (
)
3*9VT fa fb fc a b c= + + ++ =≥
(đpcm).
Bài toán 62. Cho các số thực dương
,,abc
Chứng minh bất
đẳng thức
( )
( )
(
)
(
)
222
9
4
ab c
abc
bc ca ab
++≥
++
++ +
.
Lời giải. Chuẩn hóa
1.ab c++=
Bất đẳng thức cần chứng minh trở thành
( )
( ) (
)
(
)
222
9
*
4
111
abc
abc
++
≥
−−−
.
Xét hàm số
( )
( )
2
1
x
fx
x
=
−
, tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
0
1
3
x =
là
18 3
4
x
y
−
=
.
Khi đó ta có
( )
( )
( ) ( )
( )
( )
2
32
22
20 3
0, 0;
31 23
18 3 18 39
4
4
1
41 1
xx
x xx
fx
xx
x
x
− −+
−− +
−= =
−
≥ ∀∈
−
−+
Nên
(
) ( )
( ) ( ) ( )
18
*
99
4 44
VT abfa fb fc c≥ +++ −=
= +
(đpcm).
5. Khảo sát hàm nhiều biến số.
Bài toán 63. Cho a, b, c dương thỏa mãn :
222
3abc++=
.
Tìm giá trị nhỏ nhất của biểu thức
111
222
P
abc
=++
−−−
.
Lời giải.
Ta xét hàm số
( )
( )
2
11
1 , 0; 3
22
fx x x
x
= −− ∈
−
Ta có:
( )
( )
( )
( )
( )
2
35
0; 3
2
1
' 0 1 0; 3
2
35
0; 3
2
x
fx x x
x
x
−
= ∈
= −=⇒ =∈
−
+
= ∉
.
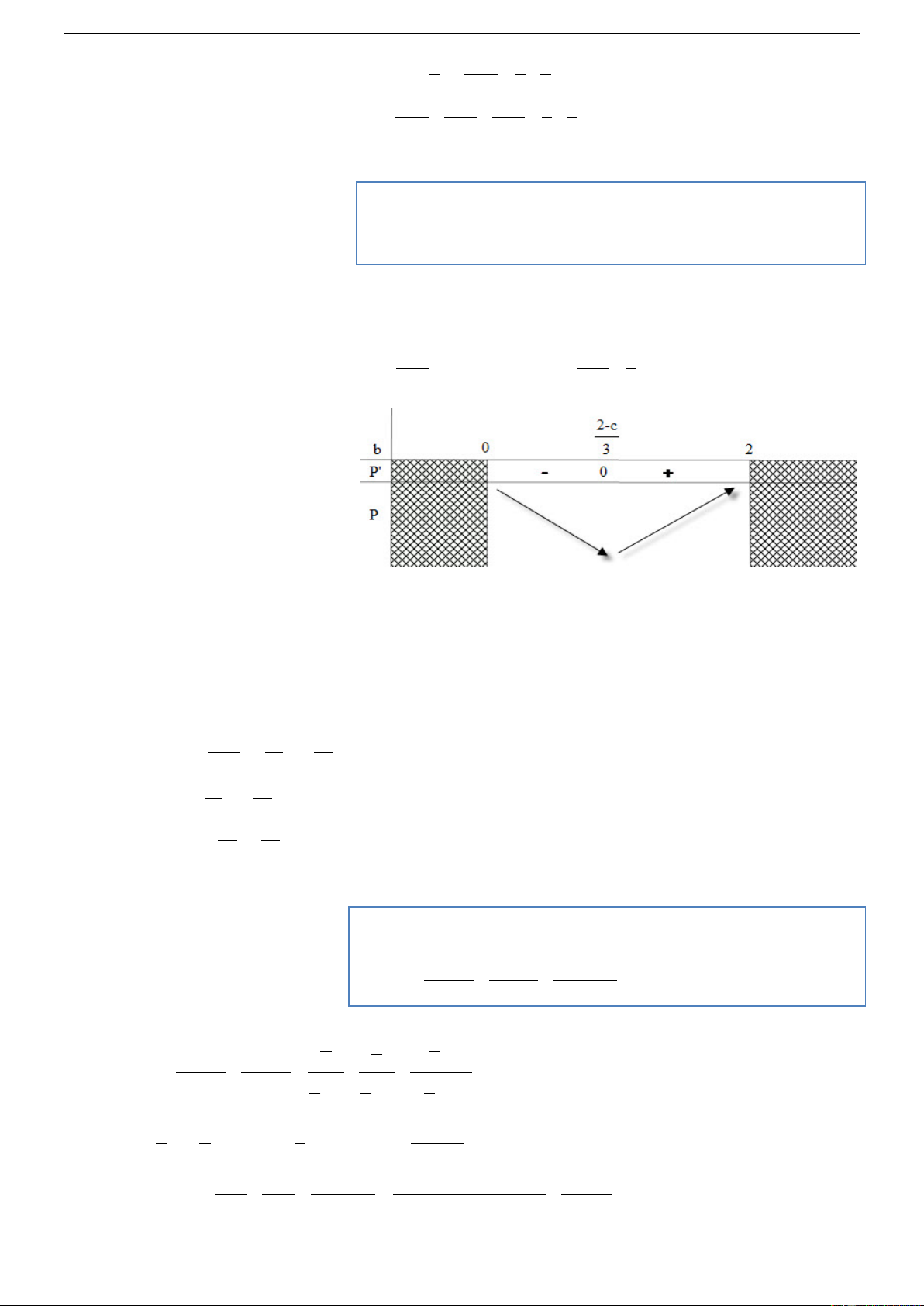
Lập bảng biến thiên ta có
( ) ( )
2
1 1 11
1
2 2 22
fx f x
x
≥ =−⇒ ≥+
−
.
Thay x bởi a, b, c vào ta được :
( )
222
1 1 1 31
3
2 2 2 22
P abc
abc
= + + ≥+ + + =
−−−
.
Vậy
3
MinP =
tại
1.abc= = =
Bài toán 64. Cho các số thực
0;, 2,abc∈
, thỏa mãn
3
abc++=
. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức
222
2 3 2 24 2060bcaPa c+ + −− +=
Lời giải : Từ
(
)
33abc a bc++=⇒ =− +
. Suy ra :
(
)
(
)
2
22
3 2 3 262 40
3 20P bc b bc
c c
+−
=−+ + −+ − +
( )
22
3 442 28 2063cbc cb+ −+= −+
.
Ta có :
2
' 6 2 ,'
3
04
bb
c
P bc P b=
−
= + − ⇒=
. Do
22
200
33
c
c
−
≤≤⇒≤ ≤
.
Ta có bảng biến thiên :
Nhìn vào bảng biến thiên ta thấy :
[ ]
( ) ( )
{ }
( )
( ) ( )
( ) ( )
( )
2
0;2
2
0; 2 2
2 04 4 424 2067 28 2 0063 4
MaxP Max P P P
Do P P ccccc−
= =
−= =++− +>−
Lại có :
( ) ( ) ( )
2
24 2067. ' 8 24 0, 0;224P ccc fc cfc −+ =−= = < ∀∈
( ) ( )
0 2067c ff⇒=≤
. Hay
2067 1; 2; 0
MaxP a b c= ⇔= = =
.
[ ]
0;2
2
2 13 86
2063
333
b
c
MinP P c c
−
= = −+
Xét
( )
2
13 86
2063, 0;2
33
gc c c c∈
= −+
,
ta có
(
)
( )
(
)
26 86
' 0 2 2023
33
g c c gc g= −< =≥
⇒
.
Hay
2023 2; 0; 1MinP c b a
= ⇔= = =
.
Bài toán 65. Cho các số thực dương
,,xyz
thỏa mãn
≥x z
.
Tìm giá trị nhỏ nhất của biểu thức
( )
2
2
23
.
2
+
=++
+
+
+
xz
xz y
P
xz yz x z
y yz
Lời giải.
Ta có
2
2
23
11 2
+
+=+
++
+
+
+
+
x
x
y
xz y
z
y
z
yx x
xz
yz
yz
y
zy z
.
Đặt
( )
2
12
4
; 1
+
≥⇒= ≤+= ⇒≥= ⇒ ≤
ab
ab
xy x
a
abb
zz
ba
y
.
Khi đó:
( ) ( ) ( )
( )
2
23 2
26
11 2 1 2
+ + ++−
+
=++ = +
+ + + +++ +
ab a b a b ab
a b ab
P
b a ab ab a b ab

Đặt
2
1
4
≤
=
+=
≤
ab u
v
u
ab v
Xét hàm số
( )
2
2 26
,
12
+−+ +
= +
++ +
uv u
f uv
uv u
v
có
(
)
( )
( )
( )
2
22
2
' , 0,
1
32
,0
2
=− −<
++
++
∀>
+
u
v v
uf uv
u
v
uv
Do đó
(
)
( )
22
2
2 22
,:
42
4
8
=+=
+
+
≥
+
v vv
f uv g v
v
v
f
Lại có
( )
( )
( )
( )
( ) ( )
( )
3
3
2
3
2
2
4
4 4 16 64
4
' '0 4
8
0
22
2
16−
+
−−+
=
= ⇒ =⇔− =⇔
=
+
vv v
v
gv gv v v
v
vv
Lập bảng biến thiên ta thấy
[
)
( )
( )
(
)
2;
11
min 4 2
3
+∞
= = =
gv g g
Dấu “=” xảy ra
⇔
4
2
1
2
+=
=
= =
⇔
= =
+=
=
ab
ab
ab
ab
ab
ab
Hay
11
min
3
= ⇔==P xyz
hoặc
2 4.= =xyz
Bài toán 66. ( Khối A - 2011) . Cho x,y,z là ba số thực thuộc
đoạn
1; 4
và
;x yx z≥≥
.Tìm nhỏ nhất của biểu thức
23
x yz
P
x y yz zx
= ++
+ ++
Lời giải .
• Nếu
xy=
, thì
(
)
16
55
xz
Pz
xz xz
=++=
++
.
• Nếu
xy>
, ta có :
( )
( )
( )
( ) ( ) ( )
2 2 22
'
xz z
y yx
Pz
yz zx yz xz
+−
−−
=+=+
+ + ++
( ) ( ) ( )
22
'0P z x z y x y z z xy x⇒ =⇔ + = + ⇒= <
Lập bảng biến thiên ta thấy :
( )
( )
2
2
12
, , 1; 2
23 1
23
y
xx
P z xy t t
xy t y
P
t
yx
= + =+=
++
+
≥∈
+
Khảo sát sự biến thiên cho ta :
( ) ( )
34
2.
33
fft
=≥
Dấu “=” xảy ra khi và chỉ khi
4; 1; 2.x yz= = =
Bài toán 67. Cho các số thực không âm
,,abc
thỏa mãn
,c ac b<<
. Chứng minh rằng
22
222
a ba
bc c
bc
a ab bc ca
+
− − ++
++
≥
Lời giải.
Ta có
( )
22
22
22
0
1
0
b
a
bc
a b ab
bc ca
ac
ba
<−
⇒+ +
−−
<−
≥
≤
≤
Xét hàm số
( )
( )
( )
2 22
0,
a
fc c
c a b ab
cb++
++
≥=
có:
( )
( ) ( )
( )
( )
222
2
2
'
ccab ab abc
fc
ab b ca
b
c
a
++ −+
+
++
=
+

(
)
(
)
(
)
(
) (
)
(
)
(
)
2
222 2 22
22
22
2
abc abc a abc abc a
ab bc
b
ca ab bc ca
b
++ + + +
=
+
−
+
−−
+
−
≤
+
(
)
( )
( )
222
2
22
2
2
a
a b ac bc c b
ab bc ca
+ ++ −
=
++
−
( ) ( ) (
)
( ) ( )
(
)
22 2 2
2
0
abaca bcb c c
ab bc ca
ba
+ −+ −+ +
++
−−
<=
do
a
c b
c
<
<
Suy ra
( ) ( ) ( )
22
02
a ab
fc
ab b
b
f
a
≤
=
+
= +
Lại có
( )
2
22
22
1
3
2
ab
a
ab
ba
ba
ba
b
≥
+
+ ≥+
Từ (1), (2), (3) suy ra bất đẳng thức được chứng minh.
Dấu “=” xảy ra
0
ab
c
=
⇔
=
Bài toán 68. Cho ba số thực dương a, b, c thoả mãn:
abc a c b++=
. Tìm giá trị lớn nhất của biểu thức:
222
1
2
11
23
P
abc+
−+
++
=
Lời giải. Ta có
( )
10a c b ac
+= − >
.
Dễ thấy
1ac =
/
⇒
1
0 a
c
<<
nên
1
ac
b
ac
+
=
−
2
2 2 22
2
2 22 2
2 2(1 ) 3
P=
1 ( ) (1 ) 1
2 2( ) 3
2
1 ( 1)( 1) 1
ac
a a c ac c
ac
a ac c
−
⇒− +
+ + +− +
+
= + −+
+ ++ +
Xét
( )
2
2 22 2
2 2( ) 3
2
1 ( 1)( 1) 1
xc
fx
x xc c
+
= + +−
+ ++ +
22
22 2
2( 2 2 1) 3 1
( ) 2 víi 0 < x <
( 1)( 1) 1
x cx c
fx
c
xc c
+++
= +−
++ +
2
'
2 22
4 ( 2 1)
()
( 1) ( 1)
c x cx
fx
xc
− +−
⇒=
++
trên khoảng
1
0;
c
,
'2
0
( ) 0 1fx x c c= ⇔ =−+ +
và
(
)
'fx
đổi dấu từ
dương sang âm khi
x
qua
0
x
, suy ra
( )
fx
đạt cực đại tại
0
.xx=
( )
22
22 2
1 2 3 23
Víi 0; : f 2
11
11 1
c
xx
c
cc
c cc c
⇒ ∀∈ ≤ + − = +
++
+− + +
Xét
2
2
23
( ) víi c>0
1
1
c
gc
c
c
= +
+
+
2
''
2 22
2(1 8 ) 1
( ) g ( ) 0 ( × c >0)
22
( 1) ( 1 3 )
c
gc c c v
c cc
−
= ⇒ =⇔=
+ ++
( )
1 2 24 10
c > 0: g
39 3
22
cg
⇒∀ ≤ = + =
1
2
10
. DÊu "=" xÈy khi 2
3
1
22
a
P ra b
c
=
⇒≤ =
=
Vậy giá trị lớn nhất của P là
10
3
.

6. Kết hợp với việc sử dụng Bổ đề.
Bài toán 69. Cho
,, 0xyz≥
thoả mãn
0xyz++>
. Tìm giá
trị nhỏ nhất của biểu thức
( )
33 3
3
16xy z
P
xyz
++
=
++
Bổ đề. Trước hết ta có:
( )
3
33
4
xy
xy
+
+≥
(chứng minh bằng cách biến đổi tương đương)
Lời giải. Đặt
.xyza
++=
Khi đó
( )
( )
( )
33
33
3
3
33
64 64
4 1 64
xy z az z
P tt
aa
++ −+
≥ = =−+
(với
z
t
a
=
,
01t≤≤
);
Xét hàm số
( ) ( )
3
3
1 – 64ft t t= +
với
0;1
t
∈
.
có
( )
2
2
1
'( ) 3 64 1 , '( ) 0 0;1
9
ft t t ft t
= − − =⇔= ∈
Lập bảng biến thiên
(
)
[
]
0;1
64
f
81
t
Min t
∈
⇒=⇒
GTNN của P là
16
81
đạt được khi
4 0.xy z= = >
Bài toán 70. (Đề chọn đội tuyển QG dự thi IMO 2005) .
Cho a,b,c >0.
Chứng minh rằng
333
333
( )( )(
3
)
8
abc
ab bc ca
+
++
≥
+
+
Lời giải : Đặt
,, 1
bca
x y z xyz
abc
= = =⇒=
Bất đẳng thức đã cho trở thành :
3 33
1 1 13
8
(1 ) (1 ) (1 )xyz
++≥
+++
Áp dụng AM-GM ta có :
( )
(
)
( )
3
32
6
3
13
8(1
1 11
3
)
1
8
2
11
x
x x
x
+ +≥
++
=
+
+
Ta cần CM bất đẳng thức :
2 22
1 1 13
4
(1 ) (1 ) (1 )xyz
++≥
+++
Bổ đề:
( ) ( )
( )
22
1 11
,0
1
11
xy
xy
xy
≥+>
+
++
Bổ đề này được CM bằng cách biến đổi tương đương đưa về BĐT hiển nhiên :
22
( ) (1 ) 0xy x y xy− +− ≥
Do đó :
2
2 2 22
1 1 1 ( 1) 1 1
11
(1 ) (1 ) (1 ) 2 1
z zz z z
xy z
zz
T
zz
V
z
+ + ++
≥+=+= =
++
+ + + ++
Giả sử:
{ }
3
,, 1 1z Max x y z x zyz z= = ⇒≤≥⇒
Xét hàm số :
22
24
11
; '(( ) 0, 1
2 1 ( 1)
)
zz z
fz z
zz z
fz
++ −
= ≥ ∀≥
++ +
=
Suy ra :
3
(1)
4
()fz f
≥=
.
Bài toán 71. Cho
, , 0.abc>
Chứng minh rằng
222
3
abc
ab bc ca
++≤
+++
Bổ đề : Với
,0xy>
thoả mãn
1.xy ≤
Ta có bất đẳng thức
22
11 2
1
11
xy
xy
+≤
+
++
.
Chứng minh :

Ta có
22
2 2 22 2 2
11 2 2 2
11
11 1
xy
xy xy
x y xy x y
++
+≤⇔ ≤
++
+ + +++
22 22 22 22
( )2 2 2 2( )2xyxy xyxy xy xy⇔ ++ +++≤ + ++
22 22 2
( 2)( 2)0 ( )( 1)0xy x y xy x y xy x y xy⇔ +− − +− ≤⇔− −≤
(luôn đúng)
Đẳng thức xảy ra khi
1xy =
hoặc
0
xy
= >
.
Lời giải.
Đặt
;; 1
bca
x y z xyz
abc
= = =⇒=
.
Do
, , 0; 1x y z xyz>=
nên giả sử
11z xy
≥⇒ ≤
Áp dụng Bất đăng thức Cauchy-Shwarz ta có
2 2 2 22 2
2
a b c ab c
VT
ab bc ca ab bc ca
= + + ≤ ++
+ + + ++ +
Chứng minh
22 2
23
ab c
ab bc ca
++ ≤
++ +
22 2
11 2
23
11 1
xy z
⇔ ++ ≤
++ +
22 2 2 2
11 2 2 2 1
2 2 22
11
11 1 1 1
z
xy z
xy z z z
++ ≤ + = +
++
++ + + +
Ta chứng minh
2
13
2
1
1
2
z
z
z
+≤
+
+
. Đặt
2
1
() 2 , 1
1
1
z
fz z
z
z
=+≥
+
+
2 22
1
'( ) 0 1
( 1) ( 1) 1
z
fz z
z zz z z
= − ≤ ∀≥
++ + +
3
( ) (1)
2
fz f⇒≤=
Đẳng thức xảy ra khi
1
xyz= = =
hay
abc= =
.
Bài toán 72. Cho
,, 0abc>
.
Chứng minh rằng :
(
)
3
1
2
abc
ab bc ca
++≤
+++
Bổ đề : Với
,0xy>
thoả mãn
1.
xy ≤
Ta có bất đẳng thức
22
11 2
1
11
xy
xy
+≤
+
++
.
Chứng minh :
Ta có
22
2 2 22 2 2
11 2 2 2
11
11 1
xy
xy xy
x y xy x y
++
+≤⇔ ≤
++
+ + +++
22 22 22 22
( )2 2 2 2( )2xyxy xyxy xy xy⇔ ++ +++≤ + ++
22 22 2
( 2)( 2)0 ( )( 1)0xy x y xy x y xy x y xy⇔ +− − +− ≤⇔− −≤
(luôn đúng)
Đẳng thức xảy ra khi
1xy =
hoặc
0xy= >
.
Lời giải. Đặt
,, 0
,,
1
xyz
bca
x yz
a b c xyz
>
= = = ⇒
=
( )
2 22
111
1
111
VT
xyz
⇒= + +
+++
Giả sử
11xy z≤⇒≥
Vì
2
2 2 22
1 1 1 1 44
12
11
1 1 11
z
xy
xy z
x y xy
≤⇒ + ≤ + ≤ =
++
+ + ++
22
11
2
1
11
z
z
xy
⇒+≤
+
++
Mặt khác ta lại có:
2
12
1
1
z
z
≤
+
+
Như vậy ta có :
( )
2
12
11
z
VT
zz
≤+
++

Xét hàm số
( )
2
2 ,1
11
z
Fz z
zz
=+≥
++
Ta có :
( )
( )
2
12
' 0 1 2 0 1.
1
zz
Fz z z z
zz
+−
= =⇒ +− =⇒=
+
Lập bảng biến thiên ta có :
(
)
(
)
33
11
22
MaxF F VT= =⇒ ≤⇒
đpcm.
Dấu
""=
xảy ra khi
1.
x yz abc===⇔==
Bài toán 73. Cho
1
, , ;3
3
abc
∈
. Tìm giá trị lớn nhất của
biểu thức
abc
P
ab bc ca
= ++
+++
Bổ đề. Với
0 1
xy
<
≤
ta có bất đẳng thức
11 2
11
1
xy
xy
+
++
+
≤
Chứng minh. Ta có
( )( )
( )
2
1
11 2 2
11
11
( 1)( 1) 1
xy x y
xy
xy xy
x y xy
−−
+= + ≤
++
++
++ +
Lời giải. Đặt
1
, , , , ,9
9
bca
x y z xyz
abc
===⇒∈
và
1.xyz
=
Khi đó
111
.
111
P
xyz
=++
+++
Không mất tính tổng quát, giả sử
1
9
9
xyz≤≤≤≤
.
Do
1xyz =
nên
1; 1z xy≥≤
. Khi đó áp dụng bổ đề ta có
21
1
1
z
P
z
z
≤+
+
+
Đặt
,
1
z tt=
≥
. Khảo sát hàm số
( )
)
2
21
, 1; .
1
1
t
ft t
t
t
= + +∞
+
+
∈
Ta tìm được
[
)
( )
1;
8
3
5
Max f t t
+∞
= ⇔=
hay
9
8
3.
5
ac
Max P
cb =
=
= ⇔
Bài toán 74. Cho các số thực dương
,,
abc
thỏa điều kiện
222
2abc++=
Tìm giá trị lớn nhất của biểu thức
44 44
2 2 44
11
2 64
22
ab bc a b b c
P
c a ac
+
= +−
++
.
Bổ đề. Ta có với mọi
,0xy>
thì
( )
2
22
2
xy
xy
+
+≥
.
Dấu đẳng xảy ra khi và chỉ khi
xy=
.
Chứng minh. Thật vậy , bất đẳng thức đã cho được biến đổi tương đương trở thành :
( )
( )
2
22 2 2
22 0x y x xyy xy+ ≥+ +⇔− ≥
Lời giải. Áp dụng bổ đề ta có :
(
)
(
)
( )
2
2
2
4
22
44
2
2 28
xy
xy
xy
xy
+
+
+
+≥ ≥ =
Do đó :
44 4
44 44
44
1
8
ab bc b b b b
c a ca
ac
+
= + ≥+
4
44 44
44
1 11
64 64 8
ab bc b b
ca
ac
+
⇔− ≤− ⋅ +
( )
1
Từ giả thiết ta có :
( ) ( )
( ) ( )
22
22 22 2 2 22
22
ab bc ab bc
ca
ac bc ab ac
+= +
++
+++ +++
Áp dụng bất đẳng thức AM- GM ta có :

( ) ( ) ( ) ( )
22 22 2 2 22
ab bc
ac bc ab ac
+
+++ +++
(
)(
)
( )
(
)
22 22
2222 2 222
1
2
ab b c
acbc abac
≤+
++ ++
2222
22 22 22 22
1
4
abb c
ac bc ab ac
≤ ++ +
++++
22
11
1
42
bb
bc ab
≤+ +
11
48
bb
ca
≤+ +
( )
2
Từ đó ta có đánh giá :
22
1 11 1
2 24 8
22
ab bc b b
ca
ca
+ ≤ ++
++
Do đó ta có :
4
11 1 1 1
2 4 8 64 8
bb bb
P
ca ca
≤ + + −⋅ +
Đặt
,0
bb
tt
ca
=+>
. Xét hàm số
( )
4
11 1 1 1
2 4 8 64 8
ft t t
= + −⋅
,
0t >
Ta có :
( )
3
1
'
128
11
32
8 16
t
ft
t
= −
+
( )
3
3
1 11
'0 8
128 2 4
11
32
8 16
t
ft t t
t
≥⇔ ≤ ⇔ + ≤
+
76
2 32 0
tt⇔+ − ≤
( )
( )
654 3 2
2 4 8 16 32 64 16 0t ttt t t t⇔− + + + + + + ≤
02t⇔ <≤
.
Lập bảng biến thiên ta thấy GTLN của
15
32
P
=
đạt được khi
2t =
và dấu bằng ở các đánh
giá
( ) ( )
1,2
xảy ra . Do đó ta có :
222
2
6
a
3
2
bb
ca
abc bc
abc
+=
== ⇔===
++=
.
Bài toán 75. Cho a, b, c là các số thực không âm thỏa mãn
( )( )( ) 0a bb cc a+ + +>
và
max { , }a bc≥
. Chứng minh rằng
11 7( ) 15
2
22
a b c a bc
bc ca ab a
++
+ ++ >
+ ++
Lời giải.
Bổ đề: Cho a, b, c là các số thực không âm thỏa mãn
( )( )( ) 0a bb cc a+ + +>
và
max { , }a bc≥
.
Chứng minh rằng
b c bc
ac ab a
+
+≥
++
(1)
Chứng minh bổ đề:
Ta có
(1) 1
( )( ) ( )( )
ab ac
b ca c b ca b
⇔+≥
++ ++
; mặt khác , ta lại có
22
( )( ) 2
2 ( )( )
ab ab ab
b c a c bc ac ab
ab c ba c
= ≥
+ + ++
++
; tương tự
2
( )( ) 2
ac ac
a b b c bc ba ac
≥
+ + ++
Suy ra
2( )
1
( )( ) ( )( ) 2
ab ac ab ac
b c a c b c a b bc ba ac
+
+ ≥≥
++ ++ ++
b c bc
ac ab a
+
⇒+≥
++
.
Dấu bằng xảy ra khi
abc= =
hoặc
0, b ac= =
hoặc
0, c ab= =
Quay lại bài toán
Xét hàm số
2
11 7
() 2 1
2
gt t
t
t
=++ +
với
0t >
. Ta có
(
)
(
)
2
2 22
2
22
22
7
7 4 2 8 7 21
11
7
'( ) 1 2
2
27
t
tt
t tt
t
gt
tt
tt
−+
+− + ++
+
=−+ =
+

Vậy
'( ) 0 3gt t= ⇔=
vì
0t
>
.
Lập bảng biến thiên, ta được GTNN của
()gt
bằng
15
(3)
2
f =
. Từ đây ta được
11 7( )
21
2
11 7( )
2
2
a a bc bc
f
bc bc a a
a b c a bc
bc ca ab a
++
= + ++
++
++
≤+ + +
+ ++
Vậy ta được
11 7( ) 15
2
22
a b c a bc
bc ca ab a
++
+ ++ ≥
+ ++
. Do dấu bằng không xảy ra nên ta có
điều phải chứng minh.
7. Vận dụng kỹ thuật dồn biến cổ điển.
Bài toán 76. (Nghệ An MO TST – 2010 ). Xét các số thực
dương a, b,c thỏa mãn
1abc =
. Hãy tìm giá trị nhỏ nhất của
biểu thức
( )
33 33 3 3
6b bcPac caab++ +−= +
Lời giải :
Ta sẽ chứng minh :
(
)
( )
, ,,,
PbP abc cc
a b≥
. Thật vậy :
( )
( )
( )
( )
3
33 33 3
,, , 6 2 1,
2P abc a a aP bc bc b c bc bbc a c
− = + − +− +
( )
( )
( )
2
33 2
3
6bca bc
= −− =
−
( )
( )
( )
22 2
33
9 .66b c bc c b bab acc
= +− =
− + ≥− −
( )
( )
2
2
906abc= − −≥
( Với giả sử
{ }
, 1ax ,a M abc a⇒ ≥=
) .
Lại có :
( )
3
1 1 1 12
,, 6, ,2bc bc a a
a
aa a
Pa Pa a
= =
+−−
.
Đặt
( )
,1
att= ≥
. Ta có :
( )
32
6
1 12
26
ft t t
t
t
= +− −
Ta sẽ chứng minh :
( )
32
6
1 12
2
15, 1 *6t
t
t
tt − ≥− ∀ ≥
+−
Thật vậy :
( )
98 6 5
* 2 15 126 10t ttt⇔+ +−−≥
.
Xét hàm số :
( )
98 6 5
2 126 51 1gt t t tt= −−++
, ta có :
( )
( )
(
)
8 7 5 4 44 3 4
' 18 6 3 15 10 648 90 60 8 .
tgt t tt ttt
ttt h−+− −= = +−=
.
Xét :
( )
43
1
3 8 5 10, 1h tt t tt − −∀
+ ≥=
, có :
( ) ( )
32 2
' 12 24 15; '' 36
0
48 0
4
3
t
tttt t
t
h ht
=
= −
−=⇒
=
=
+
Lập bảng biến thiên ta thấy :
( )
'
47
'0
39
hht
= >
≥
.
Do đó :
(
) ( ) ( )
10 0' thht g= ⇒≥≥
nên :
( ) ( )
10gt
g≥
=
.
Bài toán 77. (MOSP 2001). Xét các số thực dương a, b,c
thỏa mãn
1abc =
Chứng minh bất đẳng thức
( )( )( ) ( )
4 1abbcca abc≥+ + + ++−

Lời giải :
Đặt :
( ) ( )(
)
( )
( )
,, 4 1
Pabc abbcca abc= + + + − ++− =
( ) ( )
(
) (
)
46abab bccb caca abc= ++ ++ +− +++
Ta sẽ CM :
( )
( )
, ,,,PbP abc cca b≥
, thật vậy :
( )
(
)
( ) ( )
( )
( )
( ) ( )
,, ,
42
,
28
Pabc Pa
ab a b bc b c c
bc
ac a b c a
bc
bc a bc bc bc bc+−
−=
= ++ ++ + −
+
+−
( ) (
)
( )
( )
2 22
24 2 2 2
bcbc bc ab b a b bc bc bc bc c
+= +− − +− + − + − +
(
)
( )
2
2
2
4bc a a b cbc
= +−+ − =
−
(
) (
)
22
2
4
bc bcbc a a
= ++ −−
+ =
( )
(
)
2
2
42bc a a b c
bc a−
= ++ + −+
( )
( )
( )
2 4abacbc a
= ++
−−
+
Giả sử :
{ }
, 1ax ,a M abc a⇒ ≥=
, và :
(
)(
)
2
4 44a bcaba ac ≥=+ ≥+
.
Vậy :
( )
( )
211
,, , , , 2
8
, 84P bc bc a a
a a aa
P
a
abc a P a a≥ ++ −
= =
−
( )
32
3
28
2 48t t ft
t
t
= + − −+=
, Với
1at= ≥
).
Ta có :
( )
( )
( )
3
32
4
12
' 3 34
t
ft t t
t
+−
−
=
,
lại có :
( )
32
343gt t t=−+
,
có :
( ) ( ) ( ) ( )
2
' 98 0, 1 1 28 09gt t t t t t gt g= −= −>∀≥ ⇒ ≥ = >
.
Do đó :
( )
' 0, 1tft> ∀≥
. Hay :
( ) ( )
10ft f≥ =
. BĐT được CM.

Chương III. TUYỂN CHỌN MỘT SỐ BÀI TOÁN BẤT ĐẲNG THỨC
Nội dung cơ bản của chương gồm
Lựa chọn và giới thiệu một số bài toán bất đẳng thức hay và khó, cùng với đó là quá trình phân tích các
hướng tiếp cận bài toán và các lời giải độc đáo.
Tuyển chọn và giới thiệu một số bài toán bất đẳng thức từ các đề thi học sinh giỏi môn Toán cấp
THCS, THPT và một số bất đẳng thức từ các đề thi vào lớp 10 chuyên toán trong một số năm trở lại đây .
Giới thiệu các bài tập tổng hợp để các em học sinh có thể tự rèn luyện.
Chủ đề 11
MỘT SỐ BẤT ĐẲNG THỨC HAY VÀ KHÓ
Trong chủ đề này, chúng tôi đã tuyển chọn và giới thiệu một số bài toán bất đẳng thức hay và khó,
cùng với đó là quá trình phân tích để đi đến hình thành lời giải cho bài toán bất đẳng thức đó. Từ các bài
toán đó ta sẽ thấy được quá trình phân tích đặc điểm của giả thiết bài toán cũng như bất đẳng thức cần
chứng minh, từ đó có những nhận định, định hướng để tìm tòi lời giải và cách trình bày lời giải cho một
bài toán bất đẳng thức.
Bài 1. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
bc ca ab 1 1 1
2a 2b 2c
abc bca cab
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc. Có thể nói đây là một bất đẳng thức hay
tuy nhiên nó không thực sự khó. Quan sát bất đẳng thức ta có một cách tiếp cận bài toán như sau
Cách 1: Từ chiều của bất đẳng thức, ý tưởng đầu tiên là sử dụng bất đẳng thức Cauchy để đánh giá.
Nhưng ta sử dụng bất đẳng thức Cauchy cho bao nhiều số? Để ý bên vế trái bất đẳng thức có chứa
2
1
a
và
bên vế phải lại chứa
1
a
nên ta sử dụng bất đẳng thức Cauchy cho hai số, ta cũng cần triệt tiêu các đại
lượng
bc
bc
. Chú ý đến bảo toàn dấu đẳng thức ta có đánh giá sau
22
bc b c bc b c 1
2
4bc 4bc a
abc abc
Thực hiện tương tự ta có
22
ca c a 1 ab a b 1
;
4ca b 4ab c
bca ca b
Cộng theo vế các bất đẳng thức trên ta được
222
bc ca ab b c c a a b 1 1 1
4bc 4ca 4ab a b c
abc bca cab
Để ý là
bc ca ab 11 1 1
4bc 4ca 4ab 2 a b c
, lúc này ta thu được
222
bc ca ab 1111111
abc2abc
abc bca cab

Hay
222
bc ca ab 1 1 1
2a 2b 2c
abc bca cab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Ý tưởng thứ hai là áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
ab bc ca
bc ca ab
abc bca cab
abc a b c b c a c a b
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
2
ab bc ca
111
2a 2b 2c
abc a b c b c a c a b
Biến đổi vế trái ta được
22
ab bc ca ab bc ca
111
2a 2b 2c
2abc ab bc ca
abc a b c b c a c a b
Điều này có nghĩa là bất đẳng thức được chứng minh.
Cách 3: Ý tưởng tiếp theo là sử dụng phép biến đổi tương đương để chứng minh bài toán. Chú ý đến
phép biến đổi
22
bc 1 ab bc ca
a
abc abc
, khi đó ta thu được bất đẳng thức cần chứng sau
222
ab bc ca ab bc ca ab bc ca 3 1 1 1
2a b c
abc bca cab
. Biến đổi vế trái ta lại được
3ab bc ca
31 1 1
2a b c 2abc
. Đến lúc này ta đưa bài toán cần chứng minh thành
222
1113
2abc
abc bca cab
Đến đây ta biến đổi bất đẳng thức bằng cách nhân cả hai vế với tích abc ta được
bc ca ab 3
ab ca bc ab ca bc 2
Bất đẳng thức cuối cùng là bất đẳng thức Neibitz. Điều này đồng nghĩa với việc bất đẳng thức được
chứng minh.
Cách 4: Ta tiếp tục phân tích tìm lời giải với ý tưởng đổi biến, quan sát bất đẳng thức ta nhận thấy
2
2
bc 1
11
abc
a
bc
, khi đó bất đẳng thức cần chứng minh được viết lại thành
222
1111111
2a b c
11 11 11
abc
bc ca ab
Đến đây ta đặt
111
x;y;z
abc
. Khi đó bất đẳng thức trở thành
222
xyzxyz
yz zx xy 2
Bất đẳng thức cuối cùng làm ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng phân thức

2
222
xyz
xyz xyz
yz zx xy 2
2x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Bài 2. Cho a, b, c là các số thực dương. Chứng minh rằng:
abc
1
b2c c2a a2b
Phân tích và lời giải
Cũng như bài toán trên ta dự đoán được đẳng thức xẩy ra tại
abc
. Với bất đẳng thức trên ta
cũng có một số ý tưởng tiếp cận bài toán như sau
Cách 1: Ý tưởng đầu tiên là đánh giá bất đẳng thức trên theo bất đẳng thức Bunhiacopxki dạng phân
thức. Khi đó ta được
2
222
abc
abc a b c
b2c c2a a2b ab2ca bc2ab ca2bc
3ab bc ca
Bài toán sẽ được hoàn tất nếu ta chỉ ra được
2
abc
1
3ab bc ca
, nhưng đánh giá này chính là
2
abc 3abbcca . Đây là một bất đẳng thức quen thuộc.
Như vậy bất đẳng thức được chứng minh.
Cách 2: Ta tiếp tục đánh giá bất đẳng thức với ý tưởng đổi biến. Quan sát bất đẳng thức ta hướng đến
việc đổi biến làm đơn giản mẫu các phân số. Cho nên rất tự nhiên ta thực hiện phép đặt
x b 2c; y c 2a; z a 2b
, khi đó suy ra
x, y, z 0
. Thực hiện biểu diễn các biến cũ theo
biến mới ta được
4y z 2x 4z x 2y 4x y 2z
a;b;c
999
Khi này bất đẳng thức cần chứng minh được viết lại thành
4y z 2x 4z x 2y 4x y 2z
1
9x 9y 9z
Hay
4y z x 1z x y 2
1
9x y z 9x y z 3
Dễ dàng nhận ra
yzx zxy
3; 3
xyz xyz
theo bất đẳng thức Cauchy. Do đó ta được
4y z x 1z x y 2 4 1 2
1
9xyz 9xyz 3333
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 3: Bây giờ ta thử đánh giá bất đẳng thức trên theo hướng đánh giá mẫu của các các phân thức xem
sau. Quan sát ta nhận thấy
b2cb2a 2abc , lại theo một bất đẳng thức Cauchy ta thấy
2
2
2a 2b 2c
b2cb2a abc
4
cho nên rất tự nhiên ta thực hiện phép đánh giá
sau

2
a b 2a a b 2a
a
b2c
b2cb2a
abc
Thực hiện tương tự ta được
22
b c 2b c a 2c
bc
;
c2a a2b
abc abc
Lúc này ta thu được bất đẳng thức
2
a b 2a b c 2b c a 2c
abc
b2c c2a a2b
abc
Để ý là
222
22
abc 2abbcca
a b 2a b c 2b c a 2c
1
abc abc
Vậy bất đẳng thức được chứng minh.
Bài 3. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
abc
1
1ba 1cb 1ac
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
1
abc
3
. Trước hết ta áp dụng giả thiết viết lại
bất đẳng thức cần chứng minh thành
abc
1
c2b a2c b2a
. Đây chính là bất đẳng thức trong
bài 2, do đó ta có thể chứng minh bất đẳng thức theo các cách như trên. Ngoài ra ta còn có thêm giả thiết
abc1
, ta thử phân tích xem còn có thêm ý tưởng nào khác không?
Cách 1: Để ý là
abc1
ta có
2
abc 1 . Khi đó ta cần biến đổi
abc
làm xuất hiện
các đại lượng
abc
;;
c2b a2c b2a
. Với nhận định này ta biến đổi được như sau
abc
abc ac2b ba2c cb2a
c2b a2c b2a
Khi đó ta sẽ được
2
2
abc
abc ac2b ba2c cb2a
c2b a2c b2a
Để ý là theo bất đẳng thức Bunhiacopxki ta được
2
abc
ac 2b ba 2c cb 2a
c2b a2c b2a
abc
ac 2b ba 2c cb 2a
c2b a2c b2a
Như vậy lúc này ta được
2
abc
abc
c2b a2c b2a
3ab bc ca

Rõ ràng đây cũng là một đánh giá đúng theo bất đẳng thức Bunhiacopxki dạng phân thức. Điều này đồng
nghĩa với bài toán được chứng minh.
Cách 2: Cũng từ giả thiết
abc1 ta được 1ba 0, suy ra
a
0.
1ba
Dễ thấy
2
1ab 1
, do đó ta có
2
a1 a b
a
a1 a b
1ba 1ba
Ta thực hiện tương tự được
bc
b1 b c; c1 b a
1cb 1ab
Cộng theo vế các bất đẳng thức trên ta được
abc
a1 a b b1 b c c1 c a
1ba 1cb 1ac
Bài toán sẽ được hoàn tất nếu ta chỉ ra được
a1 a b b1 b c c1 c a 1
Hay
222
abca b c abbcca 1
Chú ý đến đánh giá
222
abcabbcca ta thấy đánh giá cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh.
Bài 4. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
222
abc
abc
bca cab abc
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc
. Vì a, b, c là độ dài ba cạnh của một
tam giác nên ta có
bca 0;cab 0;aba 0
. Chú ý đến hình thức phát biểu của bài
toán ta có một số ý tưởng chứng minh như sau
Cách 1: Cách phát biểu vế trái của bất đẳng thức làm ta liên tưởng đến áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức và ta có kết quả là
2
222
abc
abc
abc
bca cab abc bcacababc
Đây chính là điều ta cần phải chứng minh.
Cách 2: Ý tưởng thứ hai là sử dụng bất đẳng thức Cauchy. Khi đó ta được
222
abc
b c a 2a; c a b 2b ; a b c 2c
bca cab abc
Cộng theo vế các bất đẳng thức trên ta được
222
abc
abc2abc
bca cab abc
Hay
222
abc
abc
bca cab abc
Vậy bất đẳng thức được chứng minh.
Cách 3: Trước hết ta chứng minh
2
a
3a b c
bca
.
Thật vậy, với a, b, c là độ dài ba cạnh của một tam giác nên bất đẳng thức trên tương đương với

2
2
2
22
abca3abc
a3a4abcbc 2abc 0
Bất đẳng thức cuối cùng luôn đúng, do đó bất đẳng thức trên được chứng minh.
Áp dụng tương tự ta được
22
bc
3b c a ; 3c a b
cab abc
Do đó ta được
222
abc
3a b c 2a b c a b c
bca cab abc
Vậy bất đẳng thức được chứng minh.
Bài 5. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
333
1113
2
abc bca cab
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta nhận thấy có
một số ý tưởng tiếp bài toán như sau
Cách 1: Ý tưởng đầu tiên là sử dụng bất đẳng thức Cauchy. Ở đây ta phân tích xem nên sử dụng cho mấy
số. Đầu tiên ta chú ý đến đại lượng
3
1
a
bên vế trái nên rất tự nhiên ta nghĩ đến bất đẳng thức Cauchy cho
ba số, ta cũng cần phải làm triệt tiêu
1
bc
. Để ý đến bảo toàn dấu đẳng thức ta có đánh giá là
3
1bc13
422a
abc
.
Áp dụng tương tự ta có
33
1ca131ab13
;
4 2 2b 4 2 2c
bca cab
Lúc này cộng theo vế các bất đẳng thức trên thì được
333
111abc3333
2 2 2 2 2a 2b 2c
abc bca cab
Hay
333
1111113
abc2
abc bca cab
Để ý tiếp ta lại thấy
3
111 1
3. 3
abc abc
Do đó ta được
333
1113
2
abc bca cab
Như vậy bài toán được chứng minh.
Cũng sử dụng bất đẳng thức Cauchy nhưng với hai số dương ta có thể thực hiện được không? Ta
chú ý đến đại lượng
3
1
abc
bên vế trái, nếu muốn đánh giá về
1
a
ta cần khử được
1
ab c
và như

vậy chú ý đến bảo toàn dấu đẳng thức ta sẽ áp dụng bất đẳng thức Cauchy cho hai số dương đó là
3
1
abc
và
ab c
4
. Khi đó ta được
33
ab c ab c
111
2
44a
abc abc
Áp dụng tương tự ta được
33
bc a ca b
1111
;
4b 4c
bca cab
Cộng theo vế các bất đẳng thức trên ta được
333
111abbcca111
2abc
abc bca cab
Để ý đến giả thiết
abc 1
ta được
333
1111111
2a b c
abc bca cab
Đến đây ta thực hiện tương tự như trên.
Cách 2: Chú ý đến giả thiết
abc 1 ta viết lại bất đẳng thức cần chứng minh
333
1113
2
abc bca cab
abc abc abc
Hay
222
111
3
abc
1111 11 2
bc ca ab
Đến đây để đơn giản hóa ta đặt
111
x;y;z
abc
, suy ra
xyz 1
và bất đẳng thức cần
chứng minh được viết lại thành
222
xyz3
yz zx xy 2
Đến đây ta có hai hướng xử lý bất đẳng thức trên.
Hướng 1: Áp dụng các bất đẳng thức Bunhiacopxki dạng phân thức và bất đẳng thức Cauchy ta được
2
222
3
xyz
3xyz
xyz xyz 3
yz zx xy 2 2 2
2x y z
Hướng 2: Áp dụng bất đẳng thức Cauchy ta được
22
22
22
xyz xyz
2x
yz 4 yz 4
yzx yzx
2y
zx 4 zx 4
zxy zxy
2z
xy 2 xy 2
Cộng theo vế các bất đẳng thức trên ta được

222
xyzxyz
xyz
yz zx xy 2
Hay
222
3
3 xyz
xyzxyz
1
yz zx xy 2 2
Vậy bất đẳng thức được chứng minh.
Bài 6. Cho a, b, c là các số thực dương. Chứng minh rằng:
555333
222222
abcabc
3
aabbbbcc ccaa
Phân tích và lời giải
Quan sát cách phát biểu của bài toán thì ý tưởng đầu tiên là sử dụng bất đẳng thức Bunhiacopxki
dạng phân thức và khi đó ta được
2
333
555
222222333222222
abc
abc
aabb bbcc ccaa abcababbcbccaca
Như vậy ta cần chỉ ra được
2
333
333
3332 22 22 2
abc
abc
3
abcababbcbccaca
Hay
333 2 22 22 2
2a b c ab ab bc bc ca ca
Dễ thấy
33 33 33
ababab;bcbcbc;ca caca
Cộng theo vế các bất đẳng thức trên ta được
333 2 22 22 2
2a b c ab ab bc bc ca ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Ý tưởng thứ hai là sử dụng bất đẳng thức Cauchy, để ý đến đại lượng
5
22
a
aabb
bên vế trái và
đại lương
3
a
3
bên vế phải, ta nghĩ đến sử dụng bất đẳng Cauchy cho hai số dương, để ý đến dấu đẳng thức
xẩy ra tại
abc và cần triệt tiêu được
22
aabb nên ta chọn hai số đó là
22
5
22
aa ab b
a
;
9
aabb
. Khi đó ta được
22 22
553
22 22
aa ab b aa ab b
aa2a
2
993
aabb aabb
Áp dụng tương tự ta có
22 22
5353
22 22
bb bc c cc ca a
b2bc2c
;
93 93
bbcc ccaa
Để đơn giản hóa ta đặt
555
222222
abc
A
aabbbbcc ccaa
Cộng theo vế các bất đẳng thức trên ta được
222222333
aa ab b bb bc c cc ca a 2a b c
A
9993

Hay
333 2 22 22 2
5a b c ab ab bc bc ca ca
A
9
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333 2 22 22 2
333
333 2 22 22 2
5a b c ab ab bc bc ca ca
abc
93
2a b c ab ab bc bc ca ca
Đến đây ta thực hiện tương tự như cách 1. Vậy bất đẳng thức được chứng minh.
Bài 7. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
1111
30
ab bc ca
abc
Phân tích và lời giải
Trước hết ta dự đoán đẳng thức xẩy ra tại
1
abc
3
. Quan sát bất đẳng thức cần chứng minh
ta nhận thấy các biến đều nằm dưới mẫu nên rất tự nhiên ta nghĩ đến các bất đẳng thức Cauchy,
Bunhiacopxki dạng phân thức
Cách 1: Trước hết ta tiếp cận bất đẳng thức trên với ý tưởng đánh giá bằng bất đẳng thức Cauchy. Để ý
đến bảo toàn dấu đẳng thức ta có
222
abcabbcca nên đầu tiên để tạo ra đại lượng
ab bc ca ta có đánh giá quen thuộc là
111 9
ab bc ca ab bc ca
.
Do đó ta có bất đẳng thức
222 222
11111 9
ab bc ca ab bc ca
abc abc
Như vậy ta cần phải chứng minh được
222
19
30
ab bc ca
abc
Lại chú ý đến đánh giá tương tự như trên nhưng ta cần cộng các mẫu sao cho có thể viết được thành
2
abc điều này có nghĩa là ta cần đến
2ab bc ca
. Đến đây ta hai hướng là:
- Thứ nhất là đánh giá
2
2
222 2
12
12
12
abc
2ab bc ca
abc
, Tuy nhiên
đánh giá này không xẩy ra dấu đẳng thức.
- Thứ hai là đánh giá
222 2
11 1 9
9
ab bc ca ab bc ca
abc
abc
.
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
7
21
ab bc ca
Tuy nhiên, dễ thấy
2
abc
1
ab bc ca ab bc ca
33
Do đó ta được
7
21
ab bc ca
Vậy bất đẳng thức được chứng minh.
Cách 2: Sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, chú ý đến dấu đẳng thức xẩy ra thì ta được

222
222
22
1111 16
3ab 3bc 3ca
abc
abc3abbcca
16
12
1
abc abc
3
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
21 1 1
18
3ab bc ca
Để ý tiếp bất đẳng thức Bunhiacopxki ta được
2
21 1 1 6 6
18
3ab bc ca ab bc ca 1
abc
3
Vậy bất đẳng thức được chứng minh.
Cách 3: Theo một đánh giá quen thuộc ta có
111 9
ab bc ca ab bc ca
Do đó ta có bất đẳng thức
222 222
11111 9
ab bc ca ab bc ca
abc abc
Áp dụng tiếp đánh giá trên ta được
222
222
11 1
a b c 2ab 2bc 2ca 9
ab bc ca ab bc ca
abc
Hay
222
12
9
ab bc ca
abc
Mặt khác ta lại có
7
21
ab bc ca
Cộng theo vế các bất đẳng thức trên ta được
222
1111
30
ab bc ca
abc
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 8. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
abc
3
bca
Phân tích và lời giải
Trước hết để mất dấu căn ta đặt
xa;yb;zc
, khi đó từ giả thiết ta có
222
xyz 3
và bất đẳng thức được viết lại thành
222
xyz
3
yzx
. Quan sát bất đẳng thức và dự
đoán được dấu đẳng thức xẩy ra tại
xyz1
, ta có một số ý tưởng tiếp cận bài toán như sau
Cách 1: Từ cách phát biểu vế trái ta nghĩ đến sử dụng bất đẳng thức Bunhiacopxki dạng phân thức. Tuy
nhiên cần chú ý đến giả thiết
222
xyz 3, khi đó ta có đánh giá
2
222
222 4 4 4
222 222 222
xyz
xyz x y z 9
yzx
xy yz zx xy yz zx xy yz zx

Ta quy bài toán về chứng minh
222
222
9
33xyyzzx
xy yz zx
Mà theo bất đẳng thức Cauchy ta được
32 232 2322
xxy2xy;yyz2yz;zzx2zx
Do đó ta có
3332 22 22 2 2 2 2
x y z xyxy xzxz yzyz 3xyyzxz
Mà ta có đẳng thức quen thuộc
222 3332 22 22 2
x y z xyz x y z xyxy xzxz yzyz
Do đó ta được
222 2 22
xyzxyz3xyxzyz
Để ý tiếp đến giả thiết
222
xyz3
, ta có
22 2
xyz xyyzxz
Mà ta có
222
xyz 3x y z 3 suy ra
222
3xyyzzx
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Cũng từ cách phát biểu vế trái ta nghĩ đến đánh giá bằng bất đẳng thức Cauchy, tuy nhiên khi áp
dụng trực tiếp ta cần chú ý làm triệt tiêu các mẫu số và đánh giá về bình phương của các biến. Do đó ta
đánh giá như sau
222
22 22 22
xyz
xy 2x; yz 2y; zx 2z
yzx
Cộng theo vế các bất đẳng thức trên ta được
222
222 222
xyz
x y y z z x 2x 2y 2z 6
yzx
Hay
222
222
xyz
6xyyzzx
yzx
Bài toán sẽ được chứng minh nếu ta chỉ ra được
222
6xyyzzx 3 hay
222
3xyyzzx
Đến đây ta làm như cách thứ 1.
Cách 3: Cũng áp dụng bất đẳng thức Cauchy, tuy nhiên trong tình huống này ta bình phương hai vế trước
Đặt
222
xyz
A
yzx
, khi đó ta được
2
222 444 2 2 2
2
22 2
xyz xyz xyyzzx
A2
yzx z x y
yzx
Đến đây ta chú ý đến cách ghép cặp sau
42 2
22
2
42 2
22
2
42 2
22
2
xxyxy
z4x
zz
y
yyzyz
x4y
xx
z
zzxzx
y4z
yy
x
Cộng theo vế các bất đẳng thức trên ta được
2222 222 2
A xyz 4xyz A 9 A3

Hay
222
xyz
3
yzx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Cách 4: Trong các hướng tiếp cận trên ta đều thực hiện đánh giá sau quá trình đổi biến mà quên đi một
đánh giá quan trọng là
2b b 1
, khi đó ta có
a2a
b1
b
. Đây là một đánh giá cùng chiều mà vẫn
bảo toàn dấu đẳng thức, ta thử thực hiện tiếp xem sao
Theo bất đẳng thức Cauchy ta có
abc 2a 2b 2c
b1 c1 a1
bca
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
2a 2b 2c
3
b1 c1 a1
. Nhìn cách phát
biểu của bất đẳng thức ta nghĩ đến bất đẳng thức Bunhiacopxki dạng phân thức.
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
22
2
2a b c 6a b c
2a 2b 2c
b1 c1 a1 abbcca3
abc 9
Ta cần chứng minh được
2
2
6a b c
3
abc 9
Hay
22 2
2abc abc 9 abc 9 abc 3
Đẳng thức cuối cùng chính là giả thiết. Vậy bất đẳng thức được chứng minh.
Bài 9. Cho a, b, c là các số thực không âm bất kì. Chứng minh rằng:
222
abc2abc12abbcca
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1, quan sát bất đẳng thức ta nghĩ
đến một số ý tưởng tiếp cận như Sử dụng nguyên lí Dirichlet, sử dụng tính chất của tam thức bậc hai, sử
dụng bất đẳng thức Cauchy,…, bây giờ ta đi phân tích từng ý tưởng để tìm lời giải cho bài toán.
Cách 1: Trước hết ta thấy ta để ý đến đẳng thức xẩy ra tại
abc1 điều này có nghĩa là khi đẳng
thức xẩy ra thì
a1;b1;c1 cùng bằng 0, ngoài ta trong bất đẳng thức chứa các đại lượng
ac, bc, abc,... nên ta nghĩ đến tích
ca 1 b 1, tuy nhiên ta chưa thể khẳng định được tích đó có
không âm hay không nên ta sử dụng nguyên lí Dirichlet.
Theo nguyên lí Dirichlet trong ba số
a1;b1;c1
luôn tồn tai hai số cùng dấu, không mất tính
tổng quát ta giả sử hai đó là
a1;b1, khi đó ta có
a1b1 0 ca1b1 0 abcacbcc 0
Khi đó ta có
22
222
a b c 2abc 1 a b 1 c 2 abc ac bc c 2 ab bc ca
Dễ thấy
22
a b 1 c 2 abc ac bc c 0 nên ta có
22
a b 2ab 1 c 2c 2abc 2ac 2bc 2 bc ca 2 ab bc ca
Suy ra
222
abc2abc12abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.

Cách 2: Dễ thấy bất đẳng thức có bâc hai đối với mỗi biến do đó ta có thể viết lại bất đẳng thức về dạng
đa thức biến a, còn b và c đóng vai trò tham số
Ta viết lại bất đẳng thức cần chứng minh là
222
a2bcbcabc2bc10
Xét
222
f(a) a 2 bc b c a b c 2bc 1
Quan sát đa thức
f(a) ta nhận thấy nếu bc b c 0 thì khi đó ta luôn có f(a) 0 , tức là
222
a2bcbcabc2bc10.
Bây giờ ta xét trường hợp sau
bc b c 0
Khi đó ta có
2
'22
a
bc b c b c 2bc 1
Để ý đến hệ số của hạng tử bậc hai là số dương nên để
f(a) 0 thì ta phải chỉ ra được
2
'22
a
bc b c b c 2bc 1 0
Hay
bc b 2 c 2 1 0
Để ý đến
bc b c 0 ta được
b1c1 1
, lúc này xẩy ta các khả năng sau
- Cả
b1;c1 cùng nhỏ hơn 1 hay cả b, c đều nhỏ hơn 2, khi đó theo bất đẳng thức Cauchy ta
được
22
b2b c2c
b2 b 1;c2 c 1
44
Suy ra
bc b 2 c 2 1 nên ta có
bc b 2 c 2 1 0.
- Trong hai số
b1;c1
có một số lớn hơn 1 và một số nhỏ hơn 1 khi đó trong b, c có một số lớn
hơn 2 và một số nhỏ hơn 2 suy ra
bc b 2 c 2 0 nên ta cũng có
bc b 2 c 2 1 0.
Như vậy cả hai khả năng đều cho
'
a
0 nên bất đẳng thức được chứng minh. Vậy bài toán được
chứng minh xong.
Cách 3: Dễ thấy theo bất đẳng thức Cauchy ta có đánh giá
3
222
2abc 1 abc abc 1 3 a b c
Lúc này ta được bất đẳng thức
3
222 222 222
abc2abc1abc3abc .
Ta cần chỉ ra được
3
222 222
abc3abc 2abbcca . Để làm mất căn bậc 3 ta có
thể đặt
232323
ax;by;cz, khi đó bất đẳng thức được viết lại thành
333 33 33 33
x y z 3xyz 2 x y y z z x
Để ý đến đánh giá
2xy x y
khi đó ta viết được
33 33 33
2 xy yz zx xyx y yzy z zxz z
Bất đẳng thức sẽ được chứng minh xong nếu ta chỉ ra được
333
x y z 3xyz xy x y yz y z zx z z
Khai triển và phân tích ta được bất đẳng thức
xyz x y z y z x z x y
Đây là một đánh giá đúng quen thuộc. Vậy bất đẳng thức được chứng minh.
Cách 4: Ngoài các cách giải như trên ta cũng có thể tham khảo thêm cách giải sau:

Ta viết lại bất đẳng thức cần chứng minh là
2
abc 2abc14abbcca
Đặt
abck, khi đó ta cần phải chứng minh
2 2
k 2abc 1 4 ab bc ca 4 ab b c ca k 2abc 1
Ta dễ dàng chứng minh được
abc a b c b c a c a b
hay
2
abc k 2a k 2b k 2c 4k ab bc ca k a b c 8abc
9abc
4ab bc ca k
k
Như vậy để hoàn tất chứng minh ta chỉ cần chỉ ra được
92kabc
9abc
2abc 1 1
kk
Theo bất đẳng thức Cauchy ta có
3
3
abc k
abc
327
nên cần chứng minh
32
92kabc 92kk 92kk
1
k27k27
+ Nếu
92k 0, bất đẳng thức trên hiển nhiên đúng.
+ Nếu
92k 0, khi đó áp dụng bất đẳng thức Cauchy ta được
3
2
92kk
192kkk
1
27 27 3
Vậy bất đẳng thức được chứng minh.
Bài 10. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
abc3
ab 3c bc 3a ca 3b 4
Phâ tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1. Quan sát cách phát biểu của
bài toán ta nghĩ đến sử dụng các bất đẳng thức Bunhiacopxki, Cauchy,…. Chú ý đến dấu đẳng thức xẩy ra
ta có các ý tưởng tiếp cận bài toán như sau
Cách 1: Ý tưởng đầu tiên là sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, khi đó ta được
222
222
2
222
abc a b c
ab 3c bc 3a ca 3b
a b 3ac b c 3ab c a 3bc
abc
ab bc ca 3 ab bc ca
Ta cần chứng minh
2
222
abc
3
4
ab bc ca 3 ab bc ca
.
Hay ta cần chứng minh
2
222
222 2 2 2
4abc 3abbcca 9abbcca
4a b c 3abbcca abbcca
Mà ta có
222
abcabbcca
, do đó để hoàn tất chứng minh ta cần chỉ ra được
222 2 2 2
3a b c 3ab bc ca

Nhận thấy trong bất đẳng thức cần chứng minh, vế trái có bậc 2 và vế phải có bậc 3, do đó trước hết
ta đồng bậc hai về. Chú ý đến giả thiết
abc3 ta có
222 2 2 2
222 2 2 2
333222 222
222
3a b c 3ab bc ca
abca b c 3abbcca
abcabbcca2abbcca
aa b bb c cc a 0
Bất đẳng thức cuối cùng hiển nhiên đúng.
Hoặc ta có thể chứng minh theo bất đẳng thức Cauchy như sau
322322322
aabab;bbcbc;cca ca
Cộng theo vế các bất đẳng trên ta cũng được điều phải chứng minh.
Vậy bài toán được chứng minh xong.
Cách 2: Trong bài toán có giả thiết
abc3 và trong bất đẳng thức cũng xuất hiện các số 3. Vậy
thì các số 3 đó ẩn ý gì hay không?
Để ý ta thấy
ab 3c ab c a b c a c b c
, áp dụng tương tự ta viết lại được
bất đẳng thức cần chứng minh là
abc3
4
acbc abca caab
Đến đây ta có các hướng xử lí bất đẳng thức trên
+ Hướng 1: Biến đổi tương đương bất đẳng thức trên ta được
222
abc3
4
acbc abca caab
3
aa b bb c cc a a b b c c a
4
4a b c ab bc ca 33 a 3 b 3 c
4 9 ab bc ca 3 27 9 a b c 3 ab bc ca abc
36 4 ab bc ca 9 ab bc ca 3abc
36 3abc 13 ab bc ca
Bất đẳng thức cuối cùng ta thấy có sự xuất hiện của các đại lượng
ab bc ca; abc và chú ý đến
chiều của bất đẳng thức ta để ý đến
abc a b c b c a c a b hay
abc 3 2a 3 2b 3 2c 3abc 9 4 ab bc ca
3abc 36 4 ab bc ca 27
Đến đây để hoàn tất chứng minh ta cần chỉ ra được
4abbcca 2713abbcca abbcca 3
Vì
2
9 abc 3abbcca abbcca 3 . Như vây bài toán được chứng minh
xong.
+ Hướng 2: Để đơn giản hóa bất đẳng thức ta đặt
xbc;yca;zab , khi đó ta được
xyz6
.
Bất đẳng thức cần chứng minh được viết lại thành
yzx zxy xyz 3
xy yz zx 2

Hay
222
3xyz
xyz
2
Áp dụng bất đẳng thức Cauchy ta được
3
xyz 3xyz
xyz 8 12
32
và
2
222
xyz
xyz 12
3
Từ hai bất đẳng thức trên ta có
222
3xyz
xyz
2
. Đến đây bài toán được chứng minh xong.
+ Hướng 3: Từ đại lượng
a
acbc
ta liên tưởng đến kỹ thuật thêm – bớt trong bất đẳng thức
Cauchy, ta được
2
aa c ab c
a3aaaab2ac3a
884 84
acbc acbc
Áp dụng tương tự ta được
22
b b bc 2ab 3b c c ca 2bc 3c
;
84 84
abca bcab
Gọi vế trái của bất đẳng thức là A, khi đó cộng theo vế các bất đẳng thức trên ta được
222
3a b c
a ab 2ac b bc 2ab c ca 2bc
A
8884
Hay
2
2
2
abc
abc
abc abbcca
993
3
A
48 484
Đến đây bài toán được chứng minh xong.
Bài 11. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222 22 22 22
abc ab bc ca
bca 2 2 2
Phân tích và lời giải
Cách 1: Trước hết ta dự đoán dấu đẳng thức xấy ra tại
abc, quan sát bất đẳng thức ta nhân thấy vế
trái chứa các căn bậc hai, do đó ta hướng đến đánh giá làm mất các căn bậc hai. Tuy nhiên nếu ta sử dụng
đánh giá
2
22
2a b a b
thì sẽ thu được bất đẳng thức ngược chiều. Nên ta nghĩ đến bình phương
hai vế, có điều nếu khai triển theo phép biến đổi tương đương thì vẫn còn căn bậc hai. Áp dụng một đánh
giá quen thuộc ta có
2
22 2222 22 22 22
ab bc ca ab bc ca
3
222 2 2 2
Hay
22 22 22
222
ab bc ca
3a b c
222
Như vậy ta cần chỉ ra được
222
222
abc
3a b c
bca
Chú ý bên vế trái xuất hiện đại lượng
222
abc
bca
nên ta sẽ đánh giá theo bất đẳng thức
Bunhiacopxki dạng phân thức, tuy nhiên ta cần đánh giá là xuất hiện
222
abc
. Khi đó ta được
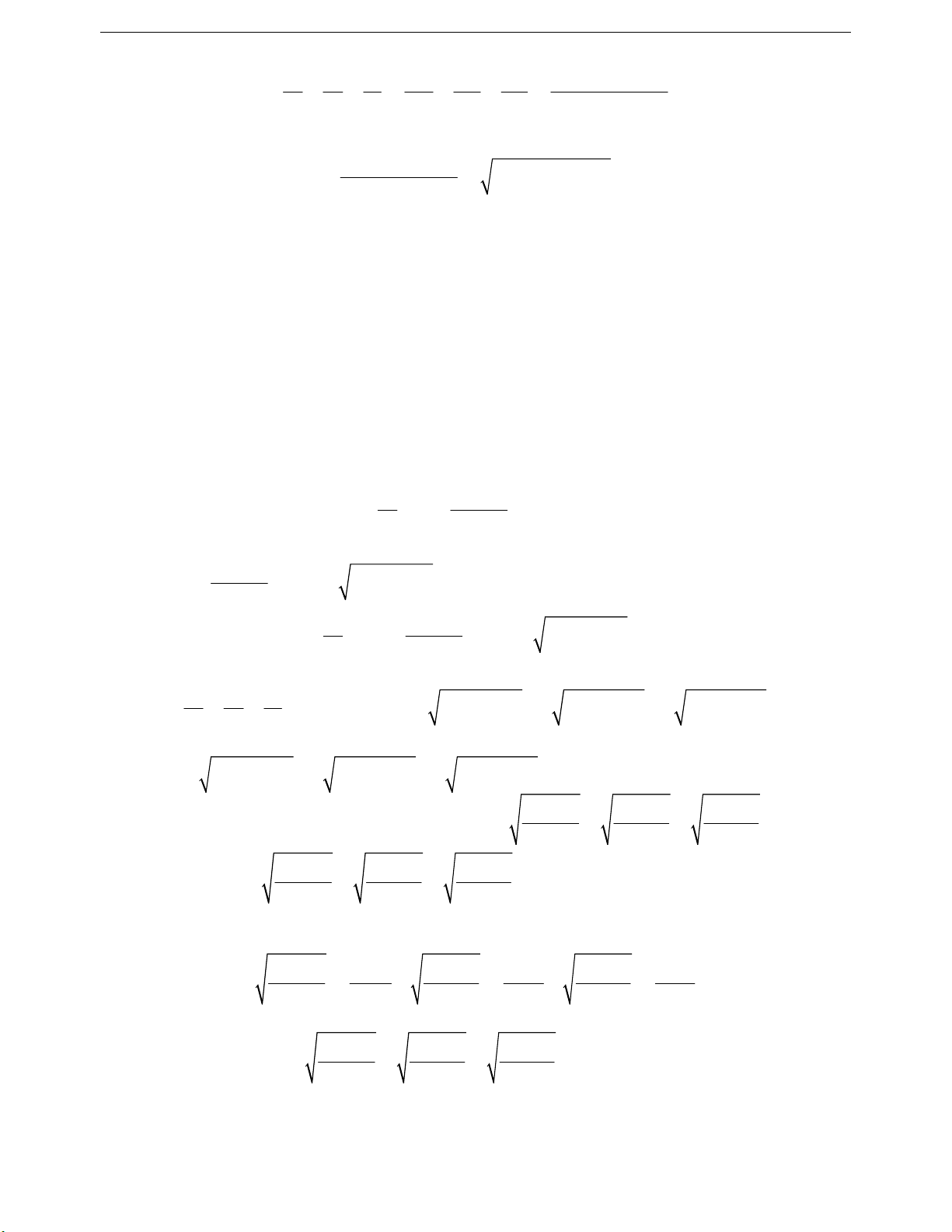
2
222
222 4 4 4
222 222
abc
abc a b c
bca
ab bc ca ab bc ca
Đến đây ta cần chứng minh được
2
222
222
222
abc
3a b c
ab bc ca
Hay
32
222 2 2 2
abc 3abbcca
Nhận thấy
2
222 222222
abc 3abbcca
Do đó ta được
3
222 222222222
abc 3abbccaabc
Mà theo bất đẳng thức Bunhiacopxki thì
2
22 22 22 2 2 2 2 2 2
ab bc ca a b c ab bc ca
Do đó ta được
32
222 2 2 2
abc 3abbcca
Vậy bài toán được chứng minh xong.
Cách 2: Bây giờ ta thử đánh giá từ vế trái sang vế phải đồng thời làm xuất hiện các căn bậc hai như vế
phải xem sao? Để ý đến phép biến đổi
222
aab
b
bb
, khi đó ta sẽ sử dụng bất đẳng thức Cauchy để
đánh giá, chú ý đến đẳng thức xẩy ra tại
abc nên để triệt tiêu b ở mẫu ta cộng thêm vào 2b, như
vậy ta sẽ được
22
22
ab
2b 2 2 a b
b
. Do đó ta có đánh giá
222
22
aab
3b 2b 2 2 a b
bb
Thực hiện tương tự ta được bất đẳng thức
222
22 22 22
abc
3a b c 22a b 22b c 22c a
bca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 22 22
22 22 22
22a b 22b c 22c a 3a b c
ab bc ca
222
Hay
22 22 22
ab bc ca
abc
222
Đến đây thì đơn giản hơn rồi, để ý đến bất đẳng quen thuộc
2
22
2x y x y, khi đó ta được
22 22 22
ab ab bc bc ca ca
;;
22 22 22
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
ab bc ca
abc
222
Vậy bất đẳng thức được chứng minh.
Cách 3: Chú ý là đẳng thức xẩy ra tại
abc và trong các biến có các lũy thừa bậc 2, do đó ta thử
biến đổi hai vế để làm xuất hiện các đại lượng kiểu
222
ab;bc;ca.

Trước hết ta biến đổi vế trái, để ý là
2
2
ab
a
2a b
bb
, như vậy ta sẽ được
222
222
ab bc ca
abc
2a b 2b c 2c a
bca bcc
Do đó suy ra
222
222
ab bc ca
abc
abc
bca b c c
.
Như vậy để bất đẳng thức tương đương thì ta phải bớt ở vế phải đại lượng
abc
và lúc này ta
cần biến đổi biểu thức
22 22 22
ab bc ca
abc
222
làm xuất
hiện
222
ab;bc;ca.
Ta để ý đến phép biến đổi
2
22
22
ab
ab ab
22
22a b 2a b
, hoàn toàn tương tự
thì vế phải trở thành
222
22 22 22
ab bc ca
22a b 2a b 2 2b c 2b c 22c a 2c a
Đến đây ta chỉ cần chỉ ra được
22
11
0
b
22a b 2a b
, rõ ràng đánh giá này hoàn
toàn đúng. Tươngng tự ta trình bày được lời giải như sau: Bất đẳng thức cần chứng minh tương đương
với
222 222222
222
22 22 22
abc abbcca
2a b 2b c 2c a a b c
bca 222
ab bc ca
ab ab bc bc ca ca
bcc 222222
222 2 2
22 22
2
22
ab bc ca ab bc
bcc
22a b 2a b 22b c 2b c
ca
22c a 2c a
22
22 22
2
22
11 11
ab bc
bc
22a b 2a b 22b c 2b c
11
ca 0
c
22c a 2c a
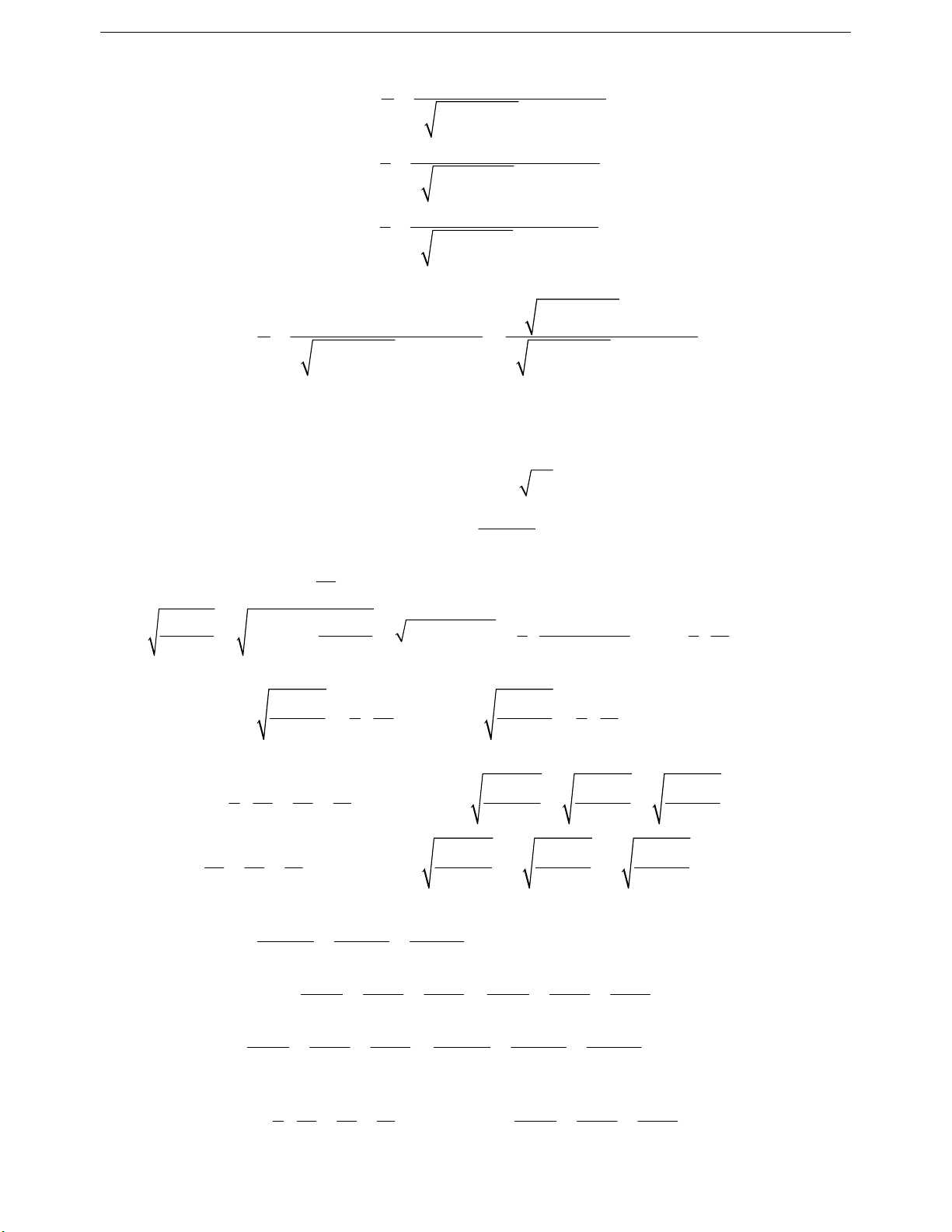
Đặt
22
22
22
11
A
b
22a b 2a b
11
B
c
22b c 2b c
11
C
c
22c a 2c a
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
A, B, C 0 . Thật vậy
22
22 22
22a b 2a b
11
A0
b
22a b 2a b 22a b 2a b
Hoàn toàn tương tự ta có
B, C 0 . Vậy bài toán được chứng minh xong.
Cách 4: Bây giờ ta thử biến đổi từ vế phải sang vế trái xem sao, ở đây ta cần làm mất các căn bậc hai. Để
thực hiện được biến đổi đó ta nghĩ đến đánh giá
2
22
2a b a b
nhưng tiếc là đánh giá này lại
ngược chiều. Một cách khác đó là sử dụng đánh giá kiểu
2xy x y
, đánh giá này cùng chiều nên ta
tập trung theo hướng này. Như vây ta cần viết được
22
ab
2
sao cho xuất hiện tích của hai đại lượng và
sau khi đánh giá thì xuất hiện
2
a
b
. Để ý ta thấy
22 22 22 2
22 22
ab ab 1abab 1a
ab abab b 2ba
22 2b2b
Áp dụng tương tự ta được
22 2 2 2 2
b c 1b c a 1c
2c b ; 2a c
22c 22a
Cộng theo vế các bất đẳng thức trên ta được
222 22 22 22
1a b c a b b c c a
abc
2b c a 2 2 2
Hay
222 22 22 22
abc ab bc ca
abc2 2 2
bca 2 2 2
Đến đây ta trình bày hoàn toàn tương tự như cách thứ nhất.
Cách 5: Để ý ta thấy
22 22 22
ab bc ca
abbcca 0
ab bc ca
nên ta được
222 222
abc bca
ab bc ca ab bc ca
Suy ra
222222222
2a 2b 2c a b b c c a
abbcca ab bc ca
Theo bất đẳng thức Cauchy ta có
222 2 2 2
1 a b c 2a 2b 2c
abc
2b c a ab bc ca

Mà theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
222
abc
abc
bca
Do đó ta được
222 222222
abcabbcca
bca ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2222 22 22 22
abbcca ab bc ca
ab bc ca 2 2 2
Đến đây thì áp dụng bất đẳng thức Cauchy ta được
2
22
22 22
abab
ab ab
2
ab ab 2
Áp dụng tương tự ta thu được
22 222 2 2 2
bc bcca ca
;
bc 2 ca 2
Cộng theo vế các bất đẳng thức trên ta thu được
22 2222 22 22 22
abbcca ab bc ca
ab bc ca 2 2 2
Vậy bài toán được chứng minh xong.
Bài 12. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
22 22 22
abc
abab bcbc caca
bca
Phân tích và lời giải
Bất đẳng thức trên đã được chứng minh bằng cách sử dụng bất đẳng thức Cauchy, bây giờ ta tìm
hiểu xem ngoài cách làm đó thì còn cách chứng minh nào khác không?
Cách 1: Quan sát bất đẳng thức ta nhân thấy dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân
thức, khi đó ta được
222
abc
abc
bca
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
22 22 22
abc a b ab b c bc c a ca
Tuy nhiên đánh giá trên không đúng, nên ta sẽ đi sang hướng khác.
Nhớ lại cách đánh giá tạo ra đại lượng
22
abab ta có
222
22
aabab
abb b 2a b ab
bb
Áp dụng tương tự ta được
222
22 22 22
abc
abc2abab2bcbc2caca
bca
Như vậy ta cần chỉ ta được
222 222
abc abc
2abc
bca bca
Và đây là một đánh giá hoàn toàn đúng. Vậy bất đẳng thức được chứng minh.
Cách 2: Tương tự như bài toán trên ta nhận thấy bất đẳng thức có thể chứng minh được bằng phép biến
đổi tương đương, để ý ta thấy
2
2
ab
a
2a b
bb

2
22
2
22
22
22
ab
aabb
3a b
2
ab
aabb
2ab
4a ab b 2a 2b
aabb
2
Do đó áp dụng tương tự ta được bất đẳng thức tương đương với
222 2 2
22 22
2
22
ab bc ca 3ab 3bc
bcc
4a b 2ab 2a b 4b c bc 2b c
3c a
4c a ca 2c a
22
22 22
2
22
13 13
ab bc
bc
4a b 2ab 2a b 4b c bc 2b c
13
ca 0
c
4c a ca 2c a
Đến đây ta đặt
22
22
22
13
A
b
4a b ab 2a b
13
B
c
4b c bc 2b c
13
C
c
4c a ca 2c a
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
A, B, C 0 . Thật vậy
22
22 22
13 4abab2ab
A0
b
4abab2ab 4abab2ab
Hoàn toàn tương tự ta có
B, C 0 . Vậy bài toán được chứng minh xong.
Bài 13. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
bc ca ab 3
4
a3bc b3ca c3ab
Phân tích và lời giải
Cách 1: Dự đoán dấu đẳng thức xẩy ra tại
abc, suy nghĩ đầu tiên khi quan sát bất đẳng thức đó là
tìm cách làm mất căn bậc hai ở các biểu thức, tuy nhiên để ý đến chiều bất đẳng thức ta thấy chỉ có thể
làm mất căn ở các tử thức bằng bất đẳng thức Cauchy còn ở mẫu thì lại không thực hiện được.
Quan sát kĩ các đại lượng trong mỗi phân thức ta nhận thấy
bc 1
a
a3bc
3
bc
, điều này gợi ý
cho ta đặt ẩn phụ dạng
a
x
bc
. Áp dụng tương tự bất đẳng thức được viết lại thành

1113
abc4
333
bc ca ab
Đến đây ta đặt
abc
x;y;z
bc ca ab
, khi đó ta được
xyz 1
.
Bất đẳng thức cần chứng minh trở thành
1113
x3 y3z3 4
Quan sát bất đẳng thức được tạo thành ta có các hướng chứng minh bất đẳng thức trên
+ Hướng 1: Biến đổi tương đương bất đẳng thức ta được
4x 3y 3 4y 3z 3 4z 3x 3 3x 3y 3z 3
4xy yz zx 24x y z 108 3xyz 3xy 3yz 3zx 8x 9y 9z 27
24 5 xy yz zx 3 x y z
Áp dụng bất đẳng thức Cauchy ta được
222
3
3
5xy yz zx 15.xyz 15;3x y z 9.xyz 9
Cộng theo vế các bất đẳng thức trên ta được
5xy yz zx 3x y z 24
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
+ Hướng 2: Sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, nhưng trước hết ta cần đổi chiều bất
đẳng thức
1113xyz3
x3 y3z3 4 x3 y3z3 4
Khi đó áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
xyz
xyz
x3 y3z3 xyz9
Ta cần chứng minh
2
xyz
3
xyz9 4
hay
4x y z 2 xy 2 yz 2zx 3x y z 9
x y z 8 xy yz zx 27
Áp dụng bất đẳng thứ Cauchy ta được
222
3
3
8 xy yz zx 8.3. x y z 24; x y z 3. xyz 3
Cộng theo vế các bất đẳng thức trên ta được
x y z 8 xy yz zx 27
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Từ hướng thứ hai của cách 1, gợi ý cho ta đổi chiều bất đẳng thức như sau
Bất đẳng thức cần chứng minh tương đương với
abc3
4
a3bc b3ca c3ab
Đến đây ta có thể áp dụng bất đẳng thức Cauchy dạng
2xy x y
cho các căn thức ở mẫu, khi
đó ta được

abc 2a 2b 2c
2a 3b 3c 3a 2b 3c 3 3b 2c
a3bc b3ca c3ab
Ta cần chứng minh
2a 2b 2c 3
2a 3b 3c 3a 2b 3c 3 3b 2c 4
Đặt
1
2a 3y 3z 5x
4
x2a3b3c
1
y3a2b3c 2b 3z3x5y
4
z3a3b2c
1
2c 3x 3y 5z
4
Khi đó bất đẳng thức trên được viết lại thành
3y 3z 5x 3z 3x 5y 3x 3y 5z 3
4x 4y 4z 4
Hay
xyyzxz
3153
yxzyzx
Bất đẳng thức cuối cùng luôn đúng theo bất đẳng thức Cauchy.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 14. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
22 2
abc3
2
b1c1a1
Phân tích và lời giải
Cách 1: Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta thấy
có đánh giá
2
b12b , tuy nhiên đánh giá này cho ta một bất đẳng thức ngược chiều. Chính điều này
gợi ý cho ta sử dụng kĩ thuật Cauchy ngược dấu. Khi đó áp dụng ta đẳng thức Cauchy ta được
222222
222
22
aababab
aaa
2b 2
b1 b1
Hoàn toàn tương tự ta được
2222
22
22
bbccca
b; c
22
c1 a1
Khi đó ta có bất đẳng thức
222 222
222
22 2
abc abbcca
abc
2
b1c1a1
Ta cần chứng minh
222
222
ab bc ca 3
abc
22
.
Để ý đến
abc3 suy ra
222
abc3
, khi đó ta có
Khi đó ta có
222
222
abc 3
abc
22
222 222222
222
ab bc ca a b c ab bc ca 3
abc
2222
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222 2 2 2
222 2 2 2
abcabbcca33
abcabbcca
2222
Đánh giá trên là một đánh giá ta đã từng gặp và có thể chứng minh được bằng phép biến đổi tương
đương

222 2 2 2 222 2 2 2
222
abcabbcca abcabc 3abbcca
aa b bb c cc a 0
Bất đẳng thức cuối cùng luôn đúng.
Hoặc sử dụng bất đẳng thức Cauchy
222 2 2 2 222 2 2 2
333222 222
abcabbcca abcabc 3abbcca
abcabbcca2abbcca
Dễ thấy
32 232 2322
aab2ab;bbc2bc;cca2ca . Cộng theo vế các bất đẳng thức ta
được đánh giá như trên. Vậy bất đẳng thức được chứng minh.
Cách 2: Vế trái của bất đẳng thức gợi ý cho ta sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, do
đó ta có đánh giá sau
2
222
22 2 222
abc
abc
b1c1a1a bc3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
222
abc
3
4ab bc ca a b c 9
2
abc3
Mà
abc3 suy ra
222
abc3 nên
222
abc912, suy ra ta được
ab b c ca 3, đây là một đánh giá sai. Do vậy cách dùng trực tiếp không đem lại hiệu quả. Điều này
có nghĩa là ta cần biến đổi trước rồi mới có thể sử dụng được bất đẳng thức Bunhiacopxki.
Ta bắt đầu với giả thiết, như trên ta suy ra được
222
abc3
, cho nên khi áp dụng bất đẳng
thức Bunhiacopxki dạng phân thức ta cần làm xuất hiện đại lượng
222
abc. Khi này ta được
2
222
222 4 4 4
22 2 22 2222 222222
abc
abc a b c
b1c1a1ab1bc1ca1abbcca3
Bài toán quy về chứng minh
2
222
22 22 22
abc
3
2
ab bc ca 3
Hay
2
222 222222
2abc 3abbcca3
Theo một đánh giá quen thuộc ta có
2
222 222222
abc 3abbcca
Và từ
222
abc3 ta suy ra được
2
222
abc 9 .
Cộng theo vế hai bất đẳng thức trên ta được
2
222 222222
2a b c 3ab bc ca 3 .
Vậy bất đẳng thức được chứng minh.
Cách 3: Sau hai cách làm như trên, ta thử tiếp cận với bất đẳng thức với cách đổi biến xem sao. Để ý đến
giả thiết
abc3 ta cần làm xuất iện số 3 trong các phân số
22 2
22 2
a3a 3a
b13b33babc
Nhìn phân số sau khi biến đổi ta không tìm thấy ý tưởng đổi biến.
Tuy nhiên từ
abc3 suy ra
222
abc3, khi đó ta có
22
22222
a3a
b13babc
Hoàn toàn tương tự ta được

222 2 2 2
2 2 2 2222 2222 2222
abc 3a 3b 3c
b1c1a13ba bc 3cabc 3aabc
Đến đây ta thấy được ý tưởng đổi biến và cách đổi biến hợp lí nhất đó là
Đặt
222
222 222 222
3a 3b 3c
x;y;z
abc abc abc
, suy ra xyz3
Khi đó ta có
222
22 2
abc xyz
y1 z1 x1
b1c1a1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
xyz3
y1 z1 x1 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
2
xyz xyz
xyz 93
y 1 z 1 x 1 xy yz zx 3 1 6 2
xyz 3
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 15. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
a2b2c29abbcca
Phân tích và lời giải
Cách 1: Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1. Theo một đánh giá quen thuộc ta có
2
9ab bc ca 3a b c . Như vậy ta cần chứng minh
2
222
a2b2c2 3abc
Quan sát bất đẳng thức trên ta nghĩ đến bất đẳng thức Bunhiacopxki. Như vậy ta cần đánh giá từ
2
abc làm xuất hiện
2
a2 , để ý ta thấy
2
222222
abc a 111b c a 21b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222222
22 2 2
3a 2 1 b c a 2 b 2 c 2
31 b c b 2 c 2
Biến đổi tương đương ta thu được
22 2 2 2 2 22 2 2
22 2 2 2 2
31bc b2c2 33b3c bc2b2c4
bc b c 1 0 b 1 c 1 0
Như vậy ta chỉ cần chỉ ra được
22
b1c1 0, tuy nhiên vì vai trò của a, b, c như nhau nên
theo nguyên lí Dirichlet thì trong ba số
222
a1;b1;c1 luôn tồn tại hai số cùng dấu và ta hoàn toàn
có thể giả sử hai số đó là
22
b1;c1. Như vậy bài toán được chứng minh xong.
Ngoài ra ta cũng có thể đánh giá từ
2
abc làm xuất hiện
2
a2 theo bất đẳng thức
Bunhiacopxki như sau
2
2
2
bc
abc a 21
2
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

2
22
bc
b2c2 31
2
Biến đổi tương đương bất đẳng thức trên ta được
22
22 22
bc2bc6bc20 bc 2bc1 0
Bất đẳng thức cuối cùng luôn đúng. Do vậy bài toán được chứng minh xong.
Cách 2: Với các bất đẳng thức khi mà ta không thể tìm ra được ngay cách đánh giá thì tốt nhất ta nên
khai triển nó ra nếu có thể, với bài toán này khi khai triển ta được
222 22 2222 2 22
abc 2 ab bc ca 4 a b c 8 9 ab bc ca
Chú ý bên vế phải có đại lượng
ab bc ca và nếu đánh giá vế trái về ab bc ca thì được
222 22 22 22
abcabbcca;ab1bc1ca12abbcca
Khi đó ta được
222 22 2222 2 22 222
abc 2 ab bc ca 4 a b c 8 abc 2 8 ab bc ca
Mà theo bất đẳng thức Cauchy ta lại có
3
222 222
3
9abc 9abc
abc 1 1 3 abc
abc
3abc
Để ý đến đánh giá
3
abc 9abc4abcabbcca
Ta được
2
9abc
4abbcca abc
abc
, khi đó ta có
2
222
abc 1 1 4 ab bc ca a b c
Do đó ta được
222 22 2222 2 22
2
222
abc 2 ab bc ca 4 a b c 8
4ab bc ca 4ab bc ca 4a b c a b c
4 ab bc ca 4 ab bc ca ab bc ca 9 ab bc ca
Vậy phép chứng minh hoàn tất.
Cách 3: Ngoài các cách trên ta có thể tham khảo thêm cách sử dụng nguyên lí Dirichlet như sau:
Trong ba số
222
a1;b1;c1 luôn tồn tại hai số cùng dấu. Không mất tính tổng quát ta giả sử
hai số đó là
22
a1;b1, khi đó ta được
22 2222
a1b10 abab10
Ta có
2 2 2 2 22 2 2 22 2 2 2 2 2
222 2 2 22 22
22 2 2 2 2 2
22 22 22 2 2 2 2 2
a2b2c2 abc2abbcca 4abc 8
cabab1 2ab2 3bc3
3ca33abc ab
2a b 2 3b c 3 3c a 3 3 a b c a b
Áp dụng bất đẳng thức Cauchy ta có
22 22 22
22 222
2a b 2 4ab; 3b c 3 6bc; 3c a 3 6ca;
ab2ab;3abc 3abbcca

Cộng theo vế các bất đẳng thức trên ta được
22 22 22 2 2 2 2 2
2a b 2 3b c 3 3c a 3 3 a b c a b 9 ab bc ca
Suy ra
222
a2b2c29abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 16. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
222
111
abc82
abc
Lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
1
abc
3
. Quan sát bất đẳng thức ta nhận thấy bất
đẳng thức có chứa các căn bậc hai và biểu thức trong căn bậc hai lại chứa biến dưới mẫu.. Do đó để tìm
được lời giải cho bài toán ta có các định hướng sau:
- Loại bỏ các căn bậc hai bằng các bất đẳng thức phụ.
- Đưa toàn bộ các đại lượng trong căn vào cùng một căn thức.
- Bình phương hai vế.
Bây giờ ta đi tìm hiểu xem ta có thể tiếp cận bất đẳng thức trên như thế nào từ các định hướng trên.
Cách 1: Để loại bỏ các căn bậc hai trong trường hợp biểu thức dưới dấu căn được viết dạng tổng, ta
thường dùng bất đẳng thức Bunhiacopxki, rất may trong trường hợp này ta có đánh giá cùng chiều. Chú ý
đến dấu đẳng thức xẩy ra ta được
2
222
22
1199
82 a 1 9 a a a
aa
aa
Áp dụng tương tự ta được
22
22
19 19
82 b b ; 82 c c
bc
bc
Khi đó ta được
222
222
111 111
82 a 82 b 82 c a b c
abc
abc
Hay
222
222
1111 111
abc abc
abc
abc
82
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
1999
abc 82
abc
82
hay
999
abc 82
abc
Chú ý đến giả thiết
abc1
kết hợp với một đánh giá quen thuộc ta có
999 9.9
81
abcabc
Như vậy đánh giá cuối cùng đúng. Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ
khi
1
abc
3
.
Cách 2: Để đưa toàn bộ các biểu thức vào trong cùng một dấu căn ta chú ý đến bất đẳng thức phụ: Với a,
b, x, y là các số thực dương ta luôn có:
22
22 22
ax by ab xy
Trước hết ta chứng minh bất đẳng thức phụ
Thật vậy, bình phương hai vế ta được

22
2222 2222
2
2222 2222
axby2.ax.by ab xy
axby abxy axby abxy
Bất đẳng thức cuối cùng là bất đẳng thức Bunhiacopxki, do đó bất đẳng thức trên đúng.
Áp dụng bất đẳng thức trên ta được
2
2
222 2
222 2
2
2
111 11 1
abc ab c
ab
abc c
111
abc
abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
2
111
abc 82
abc
Thật vậy, từ giả thiết
abc1
suy ra
2
abc 1 và theo bất đẳng thức Cauchy ta có
22
111 9
81
abc abc
Do đó ta được
2
2
111
abc 82
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Ngoài ra ta cũng có thể chứng minh đánh giá trên theo cách sau
Áp dụng bất đẳng thức Cauchuy ta có
2
2
2
2
3
3
22
2
3
33
111 1
abc 3abc 3
abc abc
11 80 1
9abc
9 abc 81 abc
Cũng theo bất đẳng thức Cauchy ta lại có.
22
2
2
2
3
33
3
1 1 2 80 1 80 1 80 1 80
abc ;
9abc 9 81 abc 9 9abc 9
3. abc
Do đó ta suy ra
2
2
111 280
abc 9 82
abc 9 9
Đến đây bài toán được chứng minh.
Cách 3: Ngoài hai cách làm trên, ta thử bình phương hai vế của bất đẳng thức, tuy nhiên để ý rằng cách
làm này không làm mất hết các dấu căn.
Đặt
222
222
111
Aa b c
abc
, khi đó ta được
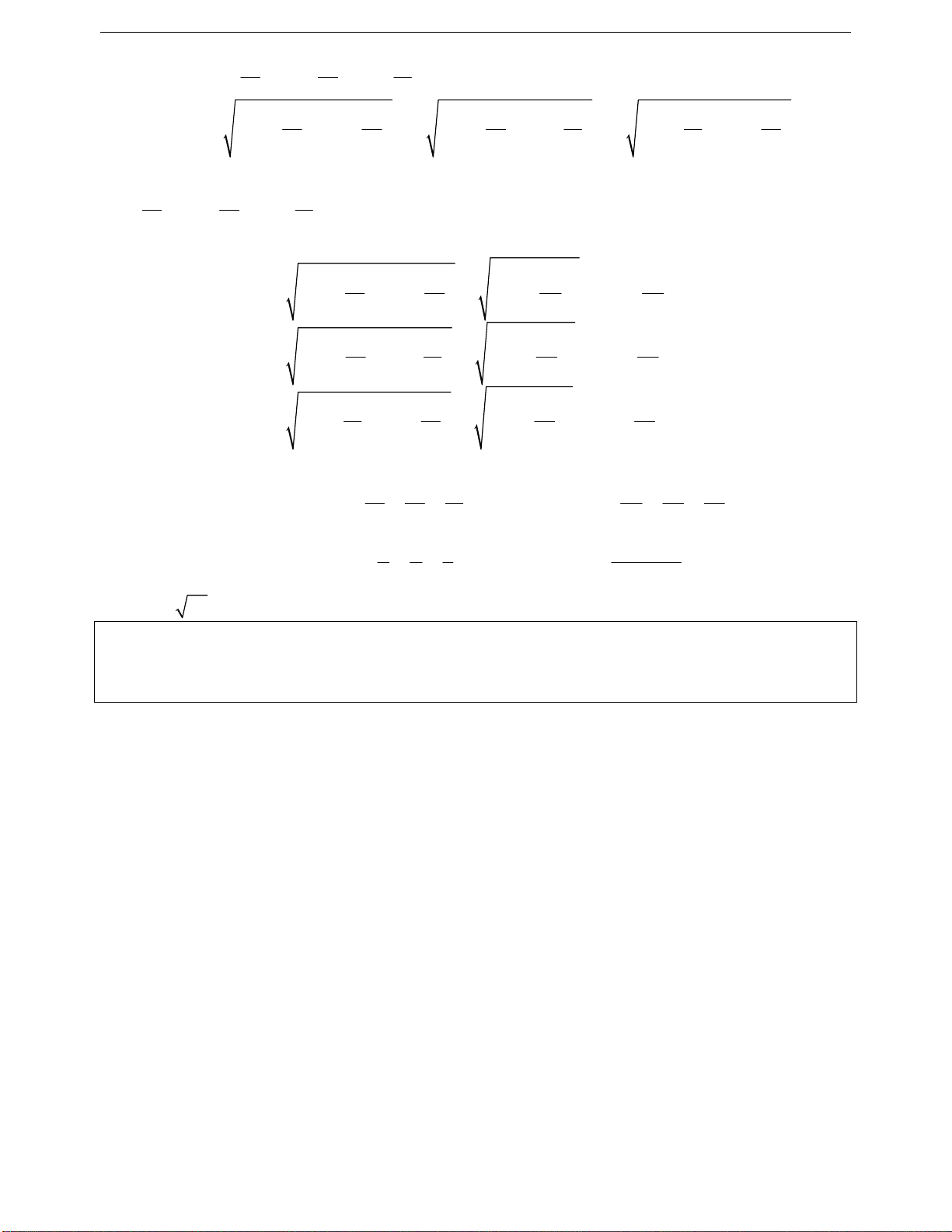
22 2 2
222
22 22 22
22 22 22
111
Aa b c
abc
11 11 11
2. a b 2. b c 2. c a
ab bc ca
Quan sát các tích dưới dấu căn ta liên tưởng đến bất đẳng thức Bunhiacopxki và chú ý đến đại lượng
222
222
111
abc
abc
ta có các đánh giá sau
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
22
22
2
22
22
2
22
22
11 1 1
ab ab ab
ab ab
ab
11 1 1
b c bc bc
bc bc
bc
11 1 1
ca ca ca
ca ca
ca
Do đó ta có
2222
222
22
22
111 111
Aabc 2abbcca
ab bc ca
abc
111 9
abc abc 82
abc abc
Hay
A82
. Vậy bất đẳng thức được chứng minh.
Bài 17. Cho a, b, c là các số thực dương thỏa mãn
aa b c 3bc
. Chứng minh rằng:
33 3
ab ac 3abacbc 5bc
Lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc, Quan sát bất đẳng thức trên ta có một số nhận
xét như sau:
- Bất đẳng thức có ba biến nhưng chỉ có b, c có vai trò như nhau, do vậy ta cố gắng quy bất đẳng
thức hai biến bằng phép đặt ẩn phụ.
- Bất đẳng thức có sự xuất hiện của các đại lượng
ab;bc;ca, cho nên ta cũng có thể đổi
biến
xab;ybc;zca .
- Giả thiết
aa b c 3bc ta có thể viết được thành
abac 4bc, khi đó có thể sử
dụng các bất đẳng thức Cauchy hoặc một số bất đẳng thức phụ để đánh giá
Từ các nhận xét đó ta có một số ý tưởng chứng minh bất đẳng thức như sau
Cách 1: Trước hết ta viết lại giả thiết
2
a a b c 3bc a ab bc ca 4bc a b a c 4bc
Lúc này ta đặt
xab;yac thì được xy 4 bc
Để ý đến đánh giá

2
33 2 2 22
22 22
22223
xy xyxxyy 2xy.xy xy
2xy 2xy.xy xy 2bc 8bc.bc 4bc
2 b c 4bc.b c 4b c .b c 2b c
Do đó ta được
33 3
ab ac 2bc
Ta cần chứng minh
3
abacbc bc.
Thật vậy
23
abacbc 4bcbc bc bc bc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Đặt
xbc;yca;zab
, suy ra
bca cab abc
a;b;z
222
Khi đó giả thiết được viết lại thành
2
2
2
2
222
3x y z
yz x
xyzyz
44
Bất đẳng thức cần chứng minh được viết lại thành
33 3 22 3 2
y z 3xyz 5x y z y z yz 3xyz 5x x y z 3yz 5x
Từ giả thiết
222
xyzyz
suy ra
2
xyz
và 2x y z
Điều này dẫn đến
2
3x 3yz
và
2
2x x y z
.
Cộng theo vế hai bất đẳng thức trên ta được
2
5x x y z 3yz.
Vậy bài toán được chứng minh xong.
Cách 3: Bất đẳng thức cần chứng minh được viết lại thành
33
33 3
ab ac 3abacbc
5
bc bc bc
Đặt
ab ac
x;y
bc bc
, bất đẳng thức cần chứng minh trở thành trở thành
33
xy3xy5
Ta có
22 2
abac aabc bc 2aabc 2bc
abac
xy
bcbc
bc bc bc
Do đó ta được
22
22
2
ab ac
xy 1 x y
bc
Suy
33
xy xy nên
33
x y 3xy 5 x y 3xy 5
Mà ta có
2
2
22
xy
xy 1 1
xy 2x y xy2 xy1
22 8
Do đó ta được
xy3xy5 . Vậy bài toán được chứng minh xong.

Cách 4: Giả thiết được viết lại thành
2
a a b c 3bc a ab bc ca 4bc a b a c 4 bc
Áp dụng bất đẳng thức Cauchy ta có
3
3bc a a b c 3a abc a bc
Ta có
33 2
2
2
223
ab ac abac2abc bc 2abc
4bc 2 bc b c b c 2 bc b c
2bcbc bc 4bc b c bc bc
Lại có
23
abacbc4bcbcbcbcbc
Cộng theo vế hai bất đẳng thức trên ta được bất đẳng thức cần chứng minh.
Bài 18. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
abc bca cab
2
b b 2c c c c 2a a a a 2b b
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức ta nhận thấy, để
đơn giản hóa ta cần thực hiện phép đổi biến
xaa;ybb;zcc
, tuy nhiên ta không thể đổi
biến ở các tử số, do đó ta cần phải biến đổi tử số sao cho xuất hiện các đại lượng
aa;bb;cc,
nhưng biến đổi theo cách nào đây? Chú ý đến chiều của bất đẳng thức ta có đánh giá
22
abc 2a bc , để ý đến giả thiết abc 1 , nên ta thay bc bằng
1
a
, khi đó ta được
22
abc 2a bc 2aa 2x , áp dụng tương tự ta có bất đẳng thức
222
222
abc bca ca b
2a bc 2b ca 2c ab
bb 2cc cc 2aa aa 2bb bb 2cc cc 2aa aa 2bb
2a a 2b b 2c c 2x 2y 2z
y2z z2x x2y
bb 2cc cc 2aa aa 2bb
Bây giờ ta cần chỉ ra được
xyz
1
y2z z2x x2y
.
Đến đây ta có hai hướng để chứng minh bất đẳng thức trên
+ Hướng 1: Sử dụng bất đẳng thức Bunhiacopxki dạng phân thức.
Ta có
2
222
xyz
xyz x y z
y2z z2x x2y
xy 2z yz 2x zx 2y 3xy yz zx
Theo một đánh giá quen thuộc ta nhận thấy
2
xyz
1
3xy yz zx
.
Do đó ta có
xyz
1
y2z z2x x2y
, tức là bài toán được chứng minh.
+ Hướng 2: Tiếp tục đổi biến để đơn giản hóa các mẫu số

Đặt
my2z;nz2x;px2y
khi đó ta suy ra
4n p 2m 4p m 2n 4m n 2p
x;y;z
999
Bất đẳng thức cần chứng minh được viết lại thành
4n p 2m 4p m 2n 4m n 2p
1
9m 9n 9p
Hay
npm pnm
415
mn p mp n
Đánh giá cuối cùng luôn đúng vì theo bất đẳng thức Cauchy ta luôn có
33
npm npm pnm pnm
44.3...12;3...3
mn p mnp mp n mpn
Vậy bất đẳng thức được chứng minh.
Bài 19. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
22 22 22
1113
4
ab2bc2ca2
Phân tích và lời giải
Đầu tiên ta dự đoán dấu đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta có thấy để
dễ đánh giá hơn ta cần đổi chiều bất đẳng thức, khi đó ta được bất đẳng thức sau
22 22 22
22 22 22
ab bc ca 3
2
ab2bc2ca2
Đến đây ta có các hướng tiếp cận bất đẳng thức trên như sau:
+ Hướng thứ nhất: Sử dụng bất đẳng thức Bunhiacopxi dạng phân thức. Tuy nhiên để sử dụng được đánh
giá đó ta cần viết các tử số thành bình phương đúng. Như vậy cách thứ nhất là ta viết biểu thức
22 2 2
22 22 22
ab a b
ab2ab2ab2
hoặc
2
22
22
22 22
ab
ab
ab2ab2
.
Ta tiếp cận với từng trường hợp
- Trường hợp biến đổi biểu thức theo cách thứ nhất và áp dụng bất đẳng thức Bunhicopxki ta thu được bất
đẳng thức sau
2
22 22 22
22 22 22
222
2a b c
ab bc ca
ab2bc2ca2
2a b c 6
Bất đẳng sẽ được chứng minh nếu ta chỉ ra được
2
222
2a b c 3a b c 9
Kết hợp với giả thiết
abc3 thì bất đẳng trên trở thành
222
3a b c, rõ ràng đánh giá
trên là sai.
- Trường hợp biến đổi biểu thức theo cách thứ hai và áp dụng bất đẳng thức Bunhicopxki ta thu được bất
đẳng thức sau
2
22 22 22
22 22 22
22 22 22
222
ab bc ca
ab bc ca
ab2bc2ca2
2a b c 6
Bất đẳng sẽ được chứng minh nếu ta chỉ ra được

2
22 22 22 222
2a b b c c a 6a b c 18
Bất đẳng thức trên tương đương với
2 222 222 2 2 22 2 2 22
2abbc bcca caab abc9
Quan sát các đại lượng vế trái ta nghĩ đến bất đẳng thức Bunhiacopxki, tức là ta có
2 222 2
222 2 2
2222 2
abbc bca
bcca cab
caab abc
Cộng theo vế ba bất đẳng thức trên ta được
2 222 222 2 2 22 2
222
2
222 222
2abbc bcca caab
2a b c ab bc ca
abc abc abc9
Như vậy bất đẳng thức được chứng minh xong.
+ Hướng thứ hai: Tiếp tục với bất đẳng thức Bunhiacopxki dạng phân thức nhưng ta cần tạo ra bình
phương đúng trên các tử số, khi đó ta có các cách sau
Biến đổi biểu thức
2
22
22 2
2
22
22
ab
ab 1
2
ab2
2a b
1
ab
ab
ab
, áp dụng tương tự và sử
dụng bất đẳng thức Bunhiacopxki ta được bất đẳng thức
22 22 22
22 22 22
2
222
222
22 22 22
ab bc ca
ab2bc2ca2
4a b c
2a b 2b c 2c a
ab bc ca
ab bc ca
Ta cần chứng minh được
222
22 2 2
22 22 22
2a b 2b c 2c a
8a b c 3 a b b c c a
ab bc ca
Hay
222
222
22 22 22
2a b 2b c 2c a
24 a b b c c a
ab bc ca
Biến đổi tương đương ta thu được
222
22 22 22
666
ab 1 bc 1 ca 1 0
ab bc ca
Đến đây mà ta chỉ ra được
22 22 22
666
10; 10; 10
ab bc ca
thì bài toán được
chứng minh hoàn tất. Vì vai trò của a, b, c như nhau nên để đơn giản hóa ta nên sắp thứ tự các biến, khi
đó chỉ cần chứng minh hiệu nhỏ nhất không âm là được.

Giả sử
abc
, khi đó ta được
22 22 22
666
ab ca bc
. Khi đó xẩy ra các trường hợp
sau
Nếu
22
ab6 thì bất đẳng thức hiển nhiên đúng.
Nếu
22
ab6, khi đó ta được
22
6
10
ab
, như vậy nhận định trên hoàn toàn sai và ta phải
hướng khác. Tuy nhiên sau một quá trình biến vất vả mà dừng tại đây thì hơi phí, ta nên thử xem với
22
ab6, có khai thác được gì không?
Dễ thấy với
22
ab6 ta được
22
11
8
ab2
và
3
ab3 b
2
, khi này ta được
22 2 2 2 2 2 2
22
1 1 1 1 1 1 10 10 5
16 8
bc2ca2a2b28b b2
16 b 6 b
Do đó ta lại có
22 22 22
1113
4
ab2bc2ca2
. Vậy trong trường hợp này bất đẳng thức
cũng đúng. Nên bài toán cũng được chứng minh.
Bài 20. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abcabbc
1
bca bcab
Phân tích và lời giải
Trước hết ta dự đoán đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức ta nhận thấy chưa thể
sử dụng được ngay các các bất đẳng thức Cauchy hay Bunhiacopxki. Với những bài toán như thế này thì
ý tưởng đầu tiên có thể là biến đổi tương đương vì bất đẳng thức có hình thức không quá cồng kềnh phức
tạp.
Cách 1: Đầu tiên với ý tưởng biến đổi tương đương, ta quy đồng và được bất đẳng thức sau:
22
aa b b c ba b b c ca b b c
bca
ab bc abbc
Khai triển các vế ta được
22322
222
aa b b c ba b b c ca b b c
bca
ac ab b bc bc
aabac babc
bccaa
Và
22
222
ab bc abbc a 3b c 3ab3bc
Như vậy bất đẳng thức sẽ dược chứng minh nếu ta chỉ ra được
22322
2
ac ab b bc bc
2b 2ab ab
bccaa
Quan sát đánh giá trên ta nghĩ đến bất đẳng thức Cauchy
23 2 2 22 32
2
ac b bc ab ac cb b cb
2ab ; 2b ; 4bc
bc a c b aca
Cộng theo vế các bất đẳng thức trên ta được
22322
2
ac ab b bc bc
2b 2ab ab
bccaa
Như vậy bất đẳng thức được chứng minh.
Cách 2: Từ ý tưởng biến đổi tương đương như trên ta có nhận xét

22 2
2
ab bc 2abbc a2bc
ab bc
2
bc ab
ab b bc ca
abbc
Quan sát chiều bất đẳng thức ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng phân thức. Vấn đề
là ta triển khai vế trái như thế nào để khi áp dụng bất đẳng thức trên thì có vế phải như trên. Để ý là trong
phép biến đổi trên ta đã cộng thêm vào vế trái với 1 và chú ý đến sự xuất hiện của 2b nên ta có đánh giá
sau
22 2
2222
222
ab bc a2bc
abc a b c b
1
bca abbcca abbc
bcababbccab
Từ hai kết quả trên ta được
abc abbc
12
bca bcab
Hay
abcabbc
1
bca bcab
. Điều này có nghĩa là bất đẳng thức được chứng minh.
Cách 3: Quan sát bất đẳng thức ta nhận thấy theo bất đẳng thức Cauchy thì
abc abbc
3; 1 3
bca bcab
Và lại thấy
22 2
ab bc 2abbc ac
ab bc
2
bc ab
abbc abbc
Nên ta sẽ chứng minh
abc abbc
32
bca bcab
. Bất đẳng thức này tương đương với
2
ac
ab bc ca
bca
abbc
Để ý rằng
bc baac
, do đó ta viết lại được bất đẳng thức trên thành
2
ac
abab ca ca
bcac
abbc
Hay
22
abcb ca ac
bc ca
abbc
Tiếp tục khai triển và thu gọn ta được
2 2
2
b c a b ab bc a a b b c a b b c b ac 0
Bất đẳng thức cuối cùng luôn đúng hay bài toán được chứng minh xong.
Bài 21. Cho a, b, c là các số thực không âm thỏa mãn
abbcca 0. Chứng minh rằng:
22222 2
ab c bc a ca b
2
bbcc ccaa aabb
Phân tích và lời giải
Cách 1: Có thể nói đây là một bất đẳng thức khó, ngay cả bước đầu dự đoán dấu đẳng thứ xẩy ra. Bất
đẳng thức trên xẩy ra dấu đẳng thức không chỉ tại
abc
mà còn tại ab,c0 và các hoán vị.
Quan sát bất đẳng thức ta nhận thấy không thể đánh trực tiếp được mẫu vì các đại lượng
222
a;b;c trội
hơn các đại lượng
ab; bc; ca . Do đó để có thể đưa ra các đánh giá hợp lí ta cần biến đổi các phân thức

trước. Chú ý là ta có thể đưa một trong hai thừa số trên tử xuống mẫu, nhưng ta chọn đưa
bc
vì dưới
mẫu có
2
22
bbcc bc bc
. Khi này ta được
22 2
ab c ab c
a
bc
bbcc
bc bc
bc
bc
Đến đây ta thấy có thể áp dụng bất đẳng thức Bunhiacopxk dạng phân thức được nên ta lại biến đổi
như sau
2
2
22 2
ab c a b c
a
abc
bbcc
ab c abc
ab c
bc
Hoàn toàn tương tự ta có
22
22 2 2
bc a ca b
bc
;
abc abc
ccaa aabb
bc a ca b
ca ab
Khi đó theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
22222 2
222
2
ab c bc a ca b
bbcc ccaa aabb
abc
abc abc abc
ab c bc a ca b
bc ca ab
abc
111
2ab bc ca abc
abbc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
2
222
abc
2
111
2ab bc ca abc
abbc ca
111
abc 4abbcca 2abc
abbc ca
111
a b c 2abc 2 ab bc ca
abbc ca
Theo bất đẳng thức dạng
111 9
xyzxyz
ta được
222 222
111 9abc
abc2abc abc
abbcca abc
Ta cần chỉ ra được
222
9abc
abc 2abbcca
abc
, bất đẳng thức này tương đương
với
333
abc3abcabcbcacab .
Không mất tính tổng quát ta giả sử
abc. Khi đó ta có

2
333
ab abc cacbc 0
abc3abcabcbcacab
Như vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Cách 2: Bất đẳng thức cần chứng minh có các đại lượng bậc hai liên quan đến
222
abc
hoặc
ab bc ca, do đó ta thử tìm mối liên hệ với các đại lượng này xem sao. Để ý là ta sẽ chỉ tìm mối liên
hệ
ab bc ca thôi vì như cách 1 thì
222
abc trội hơn nên muốn đánh giá theo chiều tăng lên là
rất khó. Để ý ta nhận thấy
22
b bc c ab ca ca b c a b c
Như vậy ý tưởng là làm dưới mẫu xuất hiện tổng
22
bbccabcca
, điều này có thể
thực hiện được bằng cách nhân cả tử và mẫu với
ab bc ca rồi sử dụng đánh giá Cauchy. Như vậy ta
sẽ làm như sau
22 2
22
22
2
abc abcabbcca 4abcabbcca
bbcc
bbccabbcca
bbccabbcca
4a ab bc ca
bcabc
Hoàn toàn tương tự ta được
22222 2
22 2
ab c bc a ca b
bbcc ccaa aabb
4a ab bc ca 4 b ab bc ca 4c ab b c ca
bcabc caabc ababc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2
4a ab bc ca 4b ab bc ca 4c ab bc ca
2
bcabc caabc ababc
Để ý ta viết lại bất đẳng thức trên thành
2
abc
abc
bc ca ab
2ab bc ca
Đánh giá trên đúng theo bất đẳng thức Bunhiacopxki dạng phân thức.
Do vậy bất bất đẳng thức được chứng minh.
Bài 22. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc3
. Chứng minh rằng
2
222
abbcca 1 1 1
4ab bc ca
cab
abc
Phân tích và lời giải
Ta nhận thấy cách phát biểu của bất đẳng thức có dạng
2
A4BC , với
222
abbc ca 1 1 1
A;Babbcca;C
cab
abc
Nhận xét này khá đặc biệt, nó giúp ta liên hệ với đánh giá quen thuộc của bất đẳng thức Cauchy
dạng
2
xy 4xy với x, y 0 . Do đó một cách tự nhiên ta đưa ra các hướng tiếp cận bất đẳng thức
trên là:

+ Thứ nhất: Biểu diễn
AXY, với X, Y là hai đại lượng thích hợp để có được bất đẳng thức
2
A4XY
, từ đó chứng minh
XY BC
. Trước hết ta triển khai A và BC như sau
222
accbba bacbcaabbcac
AXY;BC
cabcab abbcac
cab
Để ý thấy trong BC có các hạng tử
222
ab bc ac
;;
cab
và trong XY có
ab cb ca
,; ,; ,
cc aa bb
. Do đó ta chọn
X và Y sao cho tích XY có chứa các hạng tử
222
ab bc ac
;;
cab
, ta có thể chọn như sau
acc bba
X;Y
cab cab
. Từ các nhận xét trên ta có các lời giải như dưới đây
Áp dụng bất đẳng thức Cauchy ta được
2
2
abbcca acc bba acc bba
4
c a b cab cab cabcab
Ta cần
chứng minh
222
accbba 1 1 1
ab bc ca
cab cab
abc
Thật vậy, bất đẳng thức trên tương đương với
2
222222
22
abba bbcc cac baabbccbcaca
1
cbca b a ab bca c
cabcab
abac
a a a a bc ac ab
100
bc b c bc bc
Vì vai trò của a, b, c trong bất đẳng thức như nhau, nên không mất tính tổng quát ta giả sử
ab,ac
. Do đó bất đẳng thức cuối cùng đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.
+ Thứ hai: Biểu diễn
B
BC CD
D
với D là một đại lượng thích hợp để có được bất đẳng thức
2
B
4BC CD
D
, từ đó chứng minh
B
CD A
D
. Ta tìm D như sau:
Xét hiệu
222
Babbccaabbcca111
ACD D
DcabD
abc
Để ý là khi xem b là một biến thì hệ số của b là
11ac
ac D
, như vậy để thu biểu thức ta có thể
cho hệ số của b bằng 0 hay chọn
Dac . Từ các nhận xét trên ta có các lời giải như dưới đây
Theo bất đẳng thức Cauchy ta có
2
222 222
111 abbcca 111
4ab bc ca ca
ca
abc abc
Ta cần chứng minh
222
ab bc ca 1 1 1 a b b c c a
ca
ca c a b
abc
Biến đổi tương đương bất đẳng thức trên ta được
2
abbc
0
b
, Vì vai trò của a, b, c trong
bất đẳng thức như nhau, nên không mất tính tổng quát ta giả sử
abc
. Do đó bất đẳng thức cuối
cùng đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.

Bài 23. Cho a, b, c là các số thực dương thỏa mãn điều kiện
111
16 a b c
abc
. Chứng minh
rằng
333
1118
9
ab 2ac bc 2ba ca 2cb
Phân tích và lời giải
Trước hết ta dự đoán đẳng thức xẩy ra tại
abc
, nên khi đó từ giả thiết ta thấy được
11
16a a
a4
, do đó đẳng thức xẩy ra tại
1
abc
4
.
Đầu tiên ta bắt đầu với giả thiết
111
16 a b c
abc
. Thật vậy, theo một đánh giá quen
thuộc ta được
2
ab bc ca 3 a b c
111abbcca
16 a b c
abc abc
abcabbcca abbcca
Hay
18
9
6ab bc ca
. Như vậy ta có gắng chứng minh được
333
1111
6ab bc ca
ab 2ac bc 2ba ca 2cb
Để chứng minh được điều đó ta cần chỉ ra được
3
ab 2ac A và ta phải xác định
được A. Điều này làm ta liên tưởng đến bất đẳng thức Cauchy theo hướng từ trung bình cộng sang trung
bình nhân.
Để ý đến dấu đẳng thức xảy ra tại
1
abc
4
khi đó ta thấy
ac ac
ab
22
Do đó áp dụng bất đẳng thức Cauchy cho ba số dương trên ta có
3
abac
ac ac
ab 2ac ab 3
22 2
Hay
3
3
27 a b a c
ac 1 2
ab2
22
27 a b a c
ab 2ac
Hoàn toàn tương tự ta có
33
1212
;
27 b c b a 27 c a c b
bc 2ba cb 2cb
Cộng theo các bất đẳng thức trên ta được
333
4a b c
111
27 a b b c c a
ab 2ac bc 2ba ca 2cb

Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
Mặt khác ta dễ dàng chứng minh được
4a b c
1
27 a b b c c a 6 ab b c ca
Hay
8a b c ab bc ca 9a b b c c a
Đánh giá trên ta một đánh giá đúng
Do đó
333
1111
6ab bc ca
ab 2ac bc 2ba ca 2cb
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
4
.
Bài 24. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc 1
. Chứng minh rằng:
3
333
abc
111
18
1a 1b 1c
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1
, quan sát đại lượng vế trái và chiều
bất đẳng thức ta nghĩ đến việc đổi chiều bất đẳng thức. Khi đó bất đẳng thức cần chứng minh tương
đương với
3
333 333
3
333 333
abc
abc abc
318abc54
18
1a 1b 1c 1a 1b 1c
Để ý rằng
abc 1 thì
33 2
332
aa a
1a abca bca
nên bất đẳng thức trên trở thành
222
3
222
abc
18 a b c 54
bc a ca b ab c
Lại cũng từ
abc 1 ta có
3
abc 27abc27 , do đó phép chứng minh sẽ hoàn tất nếu
ta chỉ ra được
222
222
abc3
2
bc a ca b ab c
Vế trái của đánh giá trên có dấu hiệu áp dụng bất đẳng thức Bunhiacopxki dạng phân thức. Lúc này
ta được
2
222
222222
abc
abc
bc a ca b ab c a b c ab bc ca
Và ta cần chỉ ra được
2
222
abc
3
2
abcabbcca
hay
222
ab bc ca a b c
, đây là
một đánh giá sai. Do đó ta không thể tách ra chứng minh như trên được.
Tuy nhiên để ý đến khi
abc1 thì
2
3
222
18 a b c
abc 27
abcabbcca
Điều này gợi ý cho ta sử dụng bất đẳng thức Cauchy dạng
xy2xy
.
Khi đó ta được

2 5
3
222 222
18 a b c 18 a b c
abc 2
abcabbcca abcabbcca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
5
5
222
222
18 a b c
81
2 54 abc a b c abbcca
2
abcabbcca
Thật vậy, theo bất đẳng thức Cauchy ta được
3
6
222
2
222 222
222
a b c a b c ab bc ca ab bc ca
27abcabbcca 81abcabcabc
81 a b c a b c
Khi đó ta được
5
222
abc 81a b c
.
Như vậy ta chỉ cần chỉ ra rằng
222 222
2a b c a b c ab bc ca
Bất đẳng thức trên tương đương với
222
ab bc ca 0
, là một bất đẳng thức
hiển nhiên đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.
Bài 25. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc 1
. Chứng minh rằng:
1111
ab4 bc4 ca4 2
Phân tích và lời giải
Dễ dàng dự đoán dấu đẳng thức xẩy ra tại
abc1. Từ giả thiết và bất đẳng cần chứng
minh đều gợi ý cho ta phép đổi biến
+ Ý tưởng thứ nhất là
333
ax;by;cz
để sử dụng một đánh giá quen thuộc là
33
x y 4 xy x y 4xyz xy x y 4z
+ Ý tưởng thứ hai ta đổi biến dạng
xyz
a;b;c
yzx
hoặc
222
xyz
a;b;c
yz zx xy
,…
Cách 1: Đặt
333
ax;by;cz, từ giả thiết ab c 1 suy ra xyz 1
Bất đẳng thức cần chứng minh trở thành
33 33 33
1111
2
xy4yz4zx4
Để ý ta thấy
33
x y 4 xyx y 4xyz xyx y 4z
, áp dụng tương tự ta đưa bất đẳng
thức cần chứng minh trở thành

1111
2
xy x y 4z yz y z 4x zx z x 4y
zxy1
xy4z yz4x zx4y 2
4z 4x 4y
2
xy4z yz4x zx4y
4z 4x 4y
31
xy4z yz4x zx4y
xy yz zx
1
xy4z yz4x zx4y
Đặt
xy yz zx
A
x y 4z y z 4x z x 4y
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
222
4x y z
A
x y x y 4z y z y z 4x z x z x 4y
4x y z
2 x y z 10 xy yz zx
Để chứng minh
A1
, ta cần chứng minh
2
222 222
4x y z 2x y z 10xy yz zx x y z xy yz zx
Bất đẳng thức cuối cùng đúng với mọi
x, y, z 0
.
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Đặt
xyz
a;b;c
yzx
khi đó bất đẳng thức được viết lại thành
222
yz zx xy 1
2
xz y 4yz xy z 4zx yz x 4xy
Bất đẳng thức trên tương đương với
22 2
222
xz y xy z yz x
1
xz y 4yz xy z 4zx yz x 4xy
Ta tách ra chứng minh hai bất đẳng thức sau
22 2
222
222
yzx1
2
xz y 4yz xy z 4zx yz x 4xy
zx xy yz 1
2
xz y 4yz xy z 4zx yz x 4xy
Trước hết ta chứng minh bất đẳng thức thứ nhất
Dễ thấy theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
22 2
222
222
xyz
yzx
xz y 4yz xy z 4 zx yz x 4xy
x y z 5 xy yz zx
Ta cần chỉ ra được
2
222
xyz
1
2
xyz5xyyzzx
hay

2
222
2
2 x y z x y z 5 xy yz zx
x y z 3 xy yz zx
Đánh giá cuối cùng là một đánh giá đúng, do vậy bất đẳng thức thứ nhất được chứng minh.
Cũng theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
222
2
22 22 22 2 2 2
zx xy yz
xz y 4yz xy z 4zx yz x 4xy
xy yz zx
x y y z z x 5 x yz xy z xyz
Ta cần chỉ ra được
2
22 22 22 2 2 2
2
222
2 xy yz zx x y y z z x 5 x yz xy z xyz
xy yz zx 3 x yz xy z xyz
Đánh giá cuối cùng là một đánh giá đúng, do vậy bất đẳng thức thứ hai được chứng minh.
Vậy bài toán được chứng minh xong
Bài 26. Cho a, b, c là các số thực dương thỏa mãn điều kiện
111
abc
abc
.
Chứng minh rằng:
abcbcacab 1
Phân tích và lời giải
Quan sát bất đẳng thức nhận thấy nếu vế trái là một số âm thì bất đẳng thức hiển nhiên đúng. Như
vậy ta chỉ cần chứng minh cho trường hợp vế trái dương là được.
Bài toán có giả thiết rất phức tạp nên trước hết ta đánh giá giả thiết trước. Quan sát hai vế của giả
thiết ta nghĩ đến đánh giá
111
abc 9
abc
. Do đó ta nhân hai vế của giả thiết với
abc
và áp dụng đánh giá trên ta suy ra được abc3. Bây giờ ta cần chứng minh được
abcbcacab 1 . Để đơn giản hóa bài toán ta có thể đặt
xbca;ycab;zabc và khi này ta cần chứng minh xyz 1 với giả thiết mới là
xyz3
Với giả thiết và kết luận như vậy ta thấy khó có thể đưa ra được các đánh giá hợp lí, do đó ta nghĩ
đến việc sử dụng tiếp giả thiết ban đầu và với cách đổi biến như trên ta viết lại được giả thiết là
222
xyz
xy yzzx
. Sử dụng bất đẳng thức Cauchy để đánh giá ta được
222111
xyz
xy yzzx
xy yz zx
Hay
xyz xyzxyz
. Đến đây ta cũng chưa thể chỉ ra được xyz 1
Để ý đến đẳng thức xẩy ra tại
xyz1 nên theo đánh giá Cauchy ta có
xyz3
xyz
2
Kết hợp với trên ta được
xyz3
xyzxyz xyz32xyzxyz
2
Để ý lại có
xyz3 nên
2x y x x y z 3 nên ta được

2x y z 2xyzx y z 2 2xyz xyz 1
Đến đây bài toán được chứng minh
Ngoài ra cũng từ cách phân tích như trên ta có thể chứng minh theo phương pháp phản chứng như
sau
Giả sử
xyz 1 . Khi đó theo bất đẳng thức Cauchy ta được
222111
xyz
xy yzzx
xy yz zx
Hay
xyz xyzxyz , vì xyz 1 nên xyzxyz
Tuy nhiêm cũng theo bất dẳng thức Cauchy ta được
x1
x
2
, thiết lập các đánh giá tương tự ta có
xyz3
xyzxyzxyz3
2
Mặt khác
222 9
xyz xyz3
xy yzzx xyz
Mâu thuẫn này chứng tỏ điều giả sử trên là sai, do vậy
xyz 1
. Như vậy bất đẳng thức trên được chứng
minh, dấu đẳng thức xẩy ra khi
abc1
.
Nhận xét: Ta có thể sử dụng phương pháp phản chứng theo hướng như sau
Giả sử
1xyz
, khi đó từ giả thiết của bài toán suy ra
2
22 x y z xy yz zx x y z xy yz zx xyz x y z
Theo bất đẳng thức Cauchy và kết hợp với giả sử ta lại có
222
3
33; 3 xy yz zx x y z x y z
Do đó
2
2
2
2
2
2
3
2
2
9
2
9
xyz xyyzzx
xyz
xyz xyyzzx
xy yz zx
xyz xyyzzx
xyz x y z
Cộng theo vế a bất đẳng thức trên ta được
2
22 x y z xy yz zx x y z xy yz zx xyz x y z
Điều này mâu thuẫn với đẳng thức trên, do đó điều giả sử là sai. Như vậy bất đẳng thức trên được chứng
minh.
Bài 27. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
abc
1
a 8bc b 8ca c 8ab
Phân tích và lời giải
Bất đẳng thức trên đã được chứng minh bằng bất đẳng thức Bunhiacopxki dạng phân thức. Bây giờ
ta đi phân tích xem có thêm cách chứng minh nào khác nữa hay không?
Cách 1: Nhận thấy bất đẳng thức có chứa căn bậc hai, do đó nên ta có thể đánh giá làm mất các dấu căn
bậc hai thì cơ hội sẽ cao hơn. Tuy nhiên các đánh giá mẫu thức đều không đem lại hiệu quả. Do đó một
cách tự nhiên ta nghĩ đến phép đổi biến. Chú ý là ta có thể đổi biến các mẫu thức cũng có thể đổi biến các
phân thức. Ở đây ta chọn cách đổi biến cả phân thức.

Đặt
222
abc
x;y;z
a 8bc b 8ca c 8ab
. Khi đó được
222
2
22
aax
x
8bc
a8bc 1x
Hoàn toàn tương tự ta được
2222
22
bycz
;
8ca 8ab
1y 1z
.
Khi đó ta được
222
222 222
222
xyz 1
1x 1y 1z 512xyz
512
1x 1y 1z
Bất đẳng thức cần chứng minh trở thành
xyz1
.
Với giả thiết và bất đẳng thức như trên, để chứng minh được bài toán ta cần khai thác được tổng
xyz, do đó ta nghĩ đến phương pháp phản chứng.
Giả sử
0xyz1
. Khi đó ta được
222
222 2 2
1x 1y 1z xyz x xyz y xyz z
Hay
222
1x 1y 1z xyyzzx2xyzx2yzxy2z
Dễ thấy
xyyzzx 8xyz
xyzxxyzyxyzz 64xyz
Do đó ta được
222
x y y z z x 2 x y z x 2 y z x y 2z 512x y z
Suy ra
222 222
1x 1y 1z 512xyz , điều này trái với giả thiết.
Vậy không thể có
0xyz1, tức là xyz1.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Để ý ta thấy
2
2
a1
8bc
a8bc
1
a
, hoàn toàn tương tự ta nghĩ đến đặt ẩn phụ
222
bc ca ab
x ; y ; z xyz 1
abc
Khi đó bất đẳng thức cần chứng minh trở thành
111
1
18x 18y 18z
Dễ thấy
1 8x 1 8y 1 8z 1 8 x y z 64 xy yz zx 512 xyz .
Theo bất đẳng thức Cauchy ta suy ra được
6
18x18y18z 3
Bất đẳng thức cần chứng minh tương đương với
2
18x.18y 18y.18z 18z.18x 18x18y18z
8xyz 218x18y18z 18x 18y 18z 510
Áp dụng bất đẳng thức Cauchy ta có
3
3
8x y z 8; 1 8x 1 8y 1 8z 3
1 8x 1 8y 1 8z 3. 1 8x.1 8y.1 8z 9
Do đó ta được

8xyz 218x18y18z 18x 18y 18z 510
Vậy bất đẳng thức được chứng minh.
Cách 3: Để ý theo bất đẳng thức Bunhiacopxki ta có
2
222
222
abc
abc
aa 8bc bb 8ca cc 8ab
a 8bc b 8ca c 8ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta được
222 3 3 3
333
a a 8bc b b 8ca c c 8ab a a 8abc b b 8abc c c 8abc
a b c a b c 24abc
Ta chứng minh được
3
333
a b c a b c 24abc
nên ta được
2
222
a a 8bc b b 8ca c c 8ab a b c
Suy ra
2 2
222
abc
abc abc
a8bc b8ca c8ab
Hay
222
abc
1
a 8bc b 8ca c 8ab
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 28. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
33
111 3
ab 1 bc 1 ca 1
abc 1 abc
Phân tích và lời giải
Bất đẳng thức này đã được trình bày trong trong chủ đề kỹ thuật sử dụng bất đẳng thức Cauchy.
Trong phép chứng minh đó ta chưa hiểu được tại sao lại nhân thêm một đại lượng vào biểu thức vế trái.
Thực chất cách đổi biến đó xuất phát từ cách chứng minh thứ nhất dưới đây
Cách 1: Đặt
111
P
ab 1 bc 1 ca 1
Để ý là
bc 1
abc 1 bc 1 a 1
1
b1 b1
ab 1 ab 1 ab 1
Nhân thêm vào biểu thức P đại lượng
abc 1 và áp dụng tương tự ta được
ab 1 bc 1 ca 1
a1 b1 c1
P1 abc 3
a1 b1 c1
ab 1 bc 1 ca 1
Áp dụng bất đẳng thức Cauchy ta được
3
3
ab 1 bc 1 ca 1
3abc
a1 b1 c1
a1 b1 c1 1
3
abc
ab 1 bc 1 ca 1
Do đó ta được

2
3
3
3
3
3
33
3abc abc1
13
abc 1 P 3 abc 3 3 P
abc
abc
abc abc 1
Do đó ta được
33
111 3
ab 1 bc 1 ca 1
abc 1 abc
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Cách 2: Đặt
3
abc k , khi đó tồn tại các số thực dương x, y , z sao cho
ky kz kx
a;b;c
xyz
Khi đó bất đẳng thức cần chứng minh tương đương với
1113
ky kz kz kx kx ky
kk 1
111
xy yz zx
Hay
xyz3
ykz zkx xky k1
Áp dụng bất đẳng thức Bunhiacopxki ta được
222
2
2
xyz x y z
ykz zkx xky
x y kz y z kx z x ky
xyz
x y kz y z kx z x ky
xyz
3
k1
k 1 xy yz zx
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 29. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2
abc1
b2c c2a a2b 3
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc. Quan sát vế trái của bất đẳng thức là ta
liên tưởng đến một đánh giá quen thuộc là
2
222
1
xyz xyz
3
, khi đó ta được
22 2 2
abc1abc
b2c c2a a2b 3b2c c2a a2b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
abc
1
b2c c2a a2b
Để chứng minh được bất đẳng thức trên ta có cách hướng sau đây
+ Hướng 1: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
abc
abc
b2c c2a a2b
3ab bc ca

Theo một đánh giá quen thuộc ta đươc
2
abc 3abbcca , do đó ta được
abc
1
b2c c2a a2b
Vậy bất đẳng thức ban đầu được chứng minh.
+ Hướng 2: Thực hiện đổi biến như sau: Đặt
xa2b;yb2c;zc2a
, khi đó ta được
x2y4z y2z4x z2x4y
a;b;b
999
Khi đó bất đẳng thức cần chứng minh trở thành
x 2y 4z y 2z 4x z 2x 4y x 4z y 4x z 4y
115
9y 9z 9x y y z z x x
Áp dụng bất đẳng thức Cauchy ta có
xy yz zx zxy
2; 2; 2; 3 9
yx zy xz yzx
Công theo vế các bất đẳng thức trên ta được đánh giá cuối cùng.
Vậy bài toán được chứng minh xong.
Bài 30. Cho a, b, c là các số thực dương thỏa mãn
333
abc. Chứng minh rằng:
222
abc6cacb
Phân tích và lời giải
Quan sát giả thiết và bất đẳng thức cần chứng minh ta nhận thấy vai trò như nhau của hai biến a, b.
Hơn nữa từ giả thiết
333
abc, ta thu được
33
33
ab
1
cc
. Đến đây để đơn giản hóa ta có thể đặt
ab
x;y
cc
và như vậy giả thiết được viết thành
33
xy1 với 0x,y1.
Ta biến đổi để viết lại bất đẳng thức theo biến mới như sau
Bất đẳng thức cần chứng minh tương đương với
22
22
ab a b
161 1
cc
cc
, lúc này ta
được bất đẳng thức cần chứng minh là
22
x y 1 61x1y .
Từ giả thiết ta cần làm xuất hiện tích
1x1y
Để ý từ giả thiết ta được
33 3 3 2 2
xy 1y 1x 1x1y1xx 1yy
Theo bất đẳng thức Cauchy ta có
22
1xx 3x;1yy 3y , do đó
33
xy 9xy1 x 1 y xy 3 1 x 1 y
Lại từ giả thiết ta được
22 2 2
x y 1 x1x y1y 2xy1x1y 61x1y
Hay
22
xy161x1y , vì dấu đẳng thức không xẩy ra nên ta được bất đẳng thức
22
x y 161x1y .
Vậy bất đẳng thức ban đầu được chứng minh.
Bài 31. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
333333 333333333
abbcca 222abbccaabc
Phân tích và lời giải

Trước hết ta dự đoán đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta thấy các biến
đều có lũy thừa bậc ba nên để đơn giản ta có thể đổi biến
Đặt
333
xa;yb;zc
, khi đó ta có
xyz 1
. Bất đẳng thức cần chứng minh trở thành
xyyzzx 222xyyzzxxyz
Để ý đến giả thiết
xyz 1
ta viết lại được bất đẳng thức như sau
xyyzzx 22xyzxyyzzxxyz1
xyyzzx 22x1y1z1
Bình phương hai vế ta được
2
xyyzzx 8x1y1z1
Đến đây ta nghĩ đến việc ghép theo cặp để chứng minh. Để ý bên vế trái có đại lượng
xy và ta
cần biến đổi làm xuất hiện
x1 , nên ta sử dụng bất đẳng thức Buniacopxki
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
24
1
xy x x1
y
hay ta được bất đẳng
thức
22 4 22 4
2
xy xxz x1 xxy 1z x1
Tương tự ta được các bất đẳng thức
22 4 22 4
22
yyz 1x y1;zzx 1y z1
Nhân theo vế các bất đẳng thức trên ta được
222222 444
222
xyzxyyzzx1x1y1z x1y1z1
Hay
222 222
xy yz zx 1x 1y 1z
Mặt khác ta lại có
222
1x 1y 1z 1x1y1z.8xyz 81x1y1z
Do đó ta được bất đẳng thức
2
xyyzzx 8x1y1z1
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Bài 32. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
222
111 2
1
a1b1c1
a1 b1 c1
Phân tích và lời giải
Dễ dàng dự đoán được bất đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta nhân
thấy không thể đánh trực tiếp bằng bất đẳng thức Cauchy hay Bunhiacopxki được. Do đó ta tính đến
phương án biến đổi bất đẳng thức trước. Từ giả thiết gợi ý cho cho ta các cách đổi biến như
xyz
a;b;c
yzx
hoặc
222
xyz
a;b;c
yz zx xy
hoặc
222
yz zx xy
a;b;c
xyz
Để ý đến tính đối xứng của bất đẳng thức ta loại cách đổi biến thứ nhất vì nó biến bất đẳng thức
đối xứng thành bất đẳng thức hoán vị sẽ gây khó khăn hơn. Trong hai cách đổi biến còn lại ta ưu tiên
chọn cách thứ ba vì các biến đều nằm dưới mẫu nên khi biến đổi thì các lũy thừa sẽ được đưa lên tử và cơ
hội sẽ rõ ràng hơn. Hy vọng ta sẽ gặp may mắn với nhận định này.
Đặt
222
xy yz zx
a;b;c
zxy
, khi đó bất đẳng thức cần chứng minh trở thành

444 222
222
222
222
zyx 2xyz
1
xy z zx y yz x
xy z zx y yz x
Để ý đến bất đẳng thức Bunhiacopxki ta có
2
22222
xy z x z y z
Suy ra
44
2
2222
2
zz
xzyz
xy z
. Hoàn toàn tương tự ta được
444
222
222
444
2222 2 22 2 2 22 2
42 2 42 2 42 2
222222
zyx
xy z zx y yz x
zyx
xzyz xyzy yxzx
xy z yz x zx y
xyxzyz
Cũng theo đánh giá như trên
222222222
xyzzxyyzx x yyzzx
Khi đó ta có
222 222
222222222
2x y z 2x y z
xy z zx y yz x x y y z z x
Do đó ta được bất đẳng thức
444 222
222
222
222
42 2 42 2 42 2 222
222222
zyx 2xyz
xy z zx y yz x
xy z zx y yz x
xy z yz x zx y 2xyz
xyxzyz
Ta cần chứng minh
42 2 42 2 42 2 222
2 22222
xy z yz x zx y 2xyz
1
xyxzyz
.
Để ý ta phân tích được
42 2 42 2 42 2 222 2 2 2 2 2 2
xy z yz x zx y 2xyz x y x z y z
Do đó
42 2 42 2 42 2 222
2 22222
xy z yz x zx y 2xyz
1
xyxzyz
.
Như vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra khi
abc1
.
Nhận xét: Đây thực sự là một bất đẳng thức khó và quá trình phân tích tìm lời giải cũng có phần may
mắn. Tuy nhiên nếu ta không giám suy nghĩ đến các khả năng có thể xẩy ra thì may mắn đó sẽ không đến
với bản thân.
Ngoài ra các bạn có thể tham khảo thêm cách giải khác sau
Vì
1abc nên trong ba số a, b, c luôn có hai số nằm cùng phía so với 1.
Không mất tính tổng quát ta giả sử hai số đó là a và b.
Khi đó ta có
1
11 0 1
c
ab ab ab
c
Do đó ta được

2
21
1111 121 1
c
abc ababc abc
c
Áp dụng bất đẳng thức Bunhiacopxki ta có
22
11 1 1
11
11 11
1
11
11
ab
ab
ab ab
ba
ba c
ab c
ab a b ab a b
Do đó ta được
222
22 2
111 2
111
111
11
1
1
1
11 1
abc
abc
cc c
cc
c
cc c
Như vậy bất đẳng thức ban đầu được chứng minh. Đẳng thức xẩy ra khi
1abc
Bài 33. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
4224 4224 4224
ab bc ca
1
aabb bbcc ccaa
Phân tích và lời giải
Quan sát bất đẳng thức ta nhận thấy có thể rút gọn được các biến có bậc 1 ở tử mỗi phân số sau khi
đánh giá mẫu số bằng cách áp dụng bất đẳng thức Cauchy cho hai số dương
422 3
aab2ab
Do đó
333
4224 3 4 33
ab ab a
aabb 2abb 2ab
Tương tự ta được
333333
4224 42244224 33 33 33
ab bc ca a b ac
aabb bbcc ccaa 2ab2bc2ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333
33 33 33
abc
1
2a b 2b c 2c a
Biến đổi tương đương bất đẳng thức trên ta được
333 333
33 33 33 33 33 33
abc bca
11
2a b 2b c 2c a 2a b 2b c 2c a
Đến đây ta có hai hướng để chứng minh bất đẳng thức như sau
+ Hướng 1: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
333 6 6 6
33 33 33 336 336 336
2
333
666 33 33 33
bca b c a
2a b 2b c 2c a 2a b b 2b c c 2c a a
abc
1
abc2ab2bc2ca
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
+ Hướng 2: Ta đơn giản hóa bất đẳng thức bằng cách đặt
333
xa;yb;zc
Bất đẳng thức cần chứng minh được viết lại thành

yzx 111
11
2x y 2y z 2z x 2x 2y 2z
111
yzx
Đặt
xyz
m;n;p mnp1
yzx
. Khi đó bất đẳng thức cần chứng minh trở thành
111
1
2m 1 2n 1 2p 1
Hay ta cần chứng minh
2m 1 2n 1 2n 1 2p 1 2p 1 2m 1 2m 1 2n 1 2p 1
2a b c 6
Đánh giá cuối cùng luôn đúng theo bất đẳng thức Cauchy và
mnp 1 .
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 34. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
222
abc
ab bc ca
28
abc
abc
Phân tích và lời giải
Dự đoán đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức bất đẳng thức có đại lượng
3
abc làm ta liên tưởng đến hằng đẳng thức
3
333
abc a b c 3abbcca
Dễ dàng chứng minh được
a b b c c a 8abc.
Do đó ta được
3
333
a b c a b c 24abc .
Khi đó ta được bất đẳng thức
3
333
222 222
abc
ab bc ca a b c 24abc ab bc ca
abc abc
abc abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333 2 2 2
222 222
a b c 24abc ab bc ca a b c ab bc ca
28 4
abc bc ca ab
abc abc
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222 222
abc
abc abc
2
bc ca ab ab bc ca ab bc ca
Để hoàn thành chứng minh ta cần chỉ ra được
222 222
222 222
abc abbcca abc abbcca
24 2
ab bc ca ab bc ca
abc abc
Theo bất đẳng thức Cauchy thì bất đẳng thức cuối cùng hiển nhiên đúng.
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 35. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
44 44 44
333
222 3 3 3
3ab bc ca
8a 8b 8c
6
abc
bc a ca b ab c
Phân tích và lời giải

Trước hết ta dự đoán đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức nhận thấy đại
lượng
44 44 44
ab bc ca
có bậc 8 nên ta cần đánh giá đại lượng đó về đại lượng bậc thấp hơn. Theo
một đánh giá quen thuộc ta có
44 44 44 222 2 2 2 2 2 2
ab bc ca abc a b c a b c
Do đó ta có
44 44 44
222
3ab bc ca
3
abc
Như vậy bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
333
333
8a 8b 8c
3
bc a ca b ab c
Hay
333
333
abc3
8
bc a ca b ab c
Để ý đến
abc 1 , ta viết bất đẳng thức trên thành
333 666
333 333
222
abc3abc3
88
111
1a 1b 1c
abc
abc
Đặt
222
xa;yb;zc xyz1, khi đó bất đẳng thức trên trở thành
333
333
xyz3
8
1x 1y 1z
Áp dụng bất đẳng thức Cachy ta được
33 2
33 2
33 2
33 2
33 2
33 2
xx13x
82
1x 1x 1x
yy13y
82
1y 1y 1y
zz13z
82
1z 1z 1z
Do đó ta được
333 222
333 222
2x 2y 2z 3 3 x y z
82
1x 1y 1z 1x 1y 1z
Như ậy phép chứng minh hoàn sẽ hoàn tất nếu ta chứng minh được
222
222 2 2 2
xyz31 1 13
44
1 x 1 y 1 z yz 1 zx 1 xy 1
Đặt
mxy;nyz;pzx mnp1
, bất đẳng thức trên trở thành
222
1113
4
m1 n1 p1
Ta có
22
11 1 1 1
mn 1
mn
m1 n1
mn 1 1 mn 1 1
nm

Mặt khác ta lại có
2
222
p1
11p1 33
mn 1 p 1 4 4
p1 p1 4p1
Do đó
222
1113
4
m1 n1 p1
là bất đẳng thức đúng
Suy ra bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bài 36. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
abc
1
aabcbbcaccab
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
1
abc
3
. Quan sát bất đẳng thức ta nhận thấy
các hạng tử trong căn chưa đồng bậc, do đó chú ý đến giả thiết
abc1 ta có thể viết được
abcaabc bc abca
. Để khử được căn bậc hai dưới các mẫu số ta chú ý đến
bát đẳng thức Cauchy hoặc Bunhiacopxki. Tuy nhiên để ý đến chiều bất đẳng thức ta chọn cách sử dụng
bất đẳng thức Bunhiacopxki
Trước hết ta viết lại bất đẳng thức cần chứng minh là
abc
1
aabcabbcabccabc
Đến đây ta áp dụng bất đẳng thức Bunhiacopxki thì được các trường hợp sau
+ Trường hợp 1:
abca a bc a abca 2a bc
+ Trường hợp 2:
a b c a ab ac a a b c a a ab ac
Ta đi kiểm tra xem trong hai trường hợp trên thì trường hợp nào có đánh giá hợp lí
- Với đánh giá
aabca2abc , áp dụng hoàn toàn tương tự ta được
abcabc
a a bc b b ca c c ab 2a bc 2b ca 2c ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
abc
1
2a bc 2b ca 2c ab
Đến đây để đơn giản hóa bài toán ta có thể đặt
xa;yb;zc, khi quy bài toán về chứng
minh
222
222
xyz
1
2x yz 2y zx 2z xy
Để có những đánh giá tiếp theo ta nghĩ đến đổi chiều bất đẳng thức thành
222
yz zx xy
1
2x yz 2y zx 2z xy
Đến đây ta lại áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222222222
xy yz zx
yz zx xy
1
2x yz 2y zx 2z xy
2 x yz xy z xyz x y y z z x

Điều này cho thấy bất đẳng thức trên được chứng minh.
- Với đánh giá
a b c a ab ac a a b c a a ab ac
, khi đó ta
được
aa a
aabcaabac abc
Hoàn toàn tương tự ta có
bbcc
;
bbca a bcccab a bc
Như vậy cộng theo vế ba bất đẳng thức trên ta được bất đẳng thức cần chứng minh.
Bài 37. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
22 2 2 2 2
ab c bc a ca b
32
bc b c ca c a ab a b
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức ta nhận thấy có
các hướng đánh giá bất đẳng thức như sau.
- Đánh giá mỗi phân số bằng cách thay tử số bằng đại lượng nhỏ hơn
- Đánh giá mẫu bằng cách thay các mẫu bởi các đại lượng lớn hơn
- Đánh giá đồng thời cả tử và mẫu
Cách thứ nhất ta chú ý đến đánh
bc2bc
biến đổi bất đẳng thức thành
22 2 2 2 2
22 2 2 2 2
ab c bc a ca b
2a 2b 2c
bc ca ab
bc b c ca c a ab a b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2 2 2 2
2a 2b 2c
32
bc ca ab
hay
22 2 2 2 2
abc3
2
bc ca ab
Tuy nhiên đây lại là một đánh giá sai
Để ý là ta cần phải đánh giá làm sao bất đẳng thức thu được càng đơn giản càng tốt, do đó ta ưu
tiên đánh giá làm mất đi các căn bậc hai dưới mẫu. Như vậy ta chọn cách đánh giá thứ hai trước. Chú ý là
ta cần phải thay mẫu bởi một đại lượng lớn hơn, do đó rất tự nhiên ta nghĩ đến bất đẳng thức Cauchy dạng
2xy x y
và cần phải bảo toàn dấu đẳng thức nên ta sẽ áp dụng cho hai số
22
2bc; b c
, cách
đánh giá này có cảm giác hợp lí vì vế phải có số
2 . Như vậy lúc này ta sẽ được
2
22 22
22bcb c 2bc b c b c . Áp dụng tương tự ta thu được bất đẳng thức
22 2 2 2 2
ab c bc a ca b
2a 2b 2c
bc ca ab
2bc b c 2ca c a 2ab a b
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a 2b 2c
3
bc ca ab
hay
abc3
bc ca ab 2
Để ý đánh giá cuối cùng là bất đẳng thức Neibizt quen thuộc và việc chứng minh nó hoàn toàn
đơn giản.
Bài 38. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222 2 2 2
abcabbcca95abc
Phân tích và lời giải

Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta
nhận thấy đây là một bất đẳng thức hoán vị do đại lượng
222
ab bc ca
. Rõ ràng bất đẳng thức hoán vị
bao giờ cũng khó xử lý hơn bất đẳng thức đối xứng. Cho nên nếu đối xứng hóa được đại lượng
222
ab bc ca
thì cơ hội chứng minh bài toán sẽ lớn hơn.
Để ý là theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
22 22 22
222
ab bc ca
ab bc ca
ab bc ca
abc abc
Như vậy sau đánh giá này ta có bất đẳng thức
2
222 2 2 2 222
ab bc ca
abcabbcca9abc 9
abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
ab bc ca
abc 95abc
abc
Bất đảng thức trên chứa các đại lượng
222
abc;abbcca;abc và chúng liên hệ với
nhau bởi hằng đẳng thức
2
222
abc a b c 2abbcca do đó để đơn giản hóa ta đặt
xabc;yabbcca
khi đó
222 2
abc x2y
và lúc này bất đẳng thức được viết lại
thành
2
2
2
2
yx
y
x2y 95x x3 0
xx
Đánh giá cuối cùng luôn đúng do x là số dương. Vậy bài toán được chứng minh xong.
Nhân xét: Ngoài cách chứng minh như trên ta có thể tham khảo thêm các sau đây
Đặt
1; 1; 1 xa yb zc
, khi đó ta có
;; 1xyz
Bất đẳng thức cần chứng minh được viết lại thành
222 222
22 0 xyz xyyzzxxyyzzx
Để ý là
222 222
2
222
22
111
xyz xyyzzxxyyzzx
xyz yx zy xz
Vì
;; 1xyz
nên
1; 1; 1 0xyz
do đó
2
222
1110 xyz yx zy xz
Hay bất đẳng thức được chứng minh.
Bài 39. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222 3 3 3
ab bc ca a b c
abc2abbcca
cab bca
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức ta thấy vế
phải chứa căn bậc hai nên ta cần phải đánh giá làm mất căn bậc hai trước, chú ý đến chiều của bất đẳng
thức ta sử dụng bất đẳng thức Cauchy dạng 2xy x y. Như vậy nếu ta sử dụng ngay bất đẳng thức
Cauchy thì được
333 333
abc abc
2abbcca abbcca
bca bca

Có điều khi đánh giá bằng bất đẳng thức Cauchy thì các đại lượng đưa ra cần phải đồng bậc. Do đó
đánh giá như trên không được hợp lí.
Như vậy để đánh giá được ta cần phải biến đổi bất đẳng thức trước, chú ý là hai đại lượng trong
căn có bậc 4 và 0, do đó ta cố đưa về cùng bậc 2 bằng một phép biến đổi, chẳng hạn
333
333
ab bc ca
abc abc
2ab bc ca 2 .bc
bca bc bca
. Khi này ta có đánh giá
333
333
333
ab bc ca
abc abc
2ab bc ca 2 .bc
bca bc bca
ab bc ca
abc
bc
bc b c a
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333
222
222
ab bc ca
abc ab bc ca
bc a b c
bc b c a c a b
Biến đổi tương đương bất đẳng thức trên ta được
23 2222
22 222
32
2
ab a bc ab bc ca
ccab abc
cb acab
ab a a c
aca
aca0 0
bb b
Đến đây ta hoàn toàn có thể giả sử trong ba số a, b, c thì a là số nằm giữa. Do đó bất đẳng thức
cuối cùng luôn đúng.
Vậy bài toán được chứng minh xong.
Bài 40. Cho a, b, c là các số thực dương thỏa mãn
abc 8 . Chứng minh rằng:
1111
2a b 6 2b c 6 2c a 6 4
Phân tích và lời giải
Trước hết quan sát kỹ giả thiết
abc 8 , nhìn có vẻ thấy hơi lạ mắt vì ta thường gặp giả thiết kiểu
abc 1 . Do đó suy nghĩ đầu tiên đó là tìm cách đưa về giả thiết abc 1 và vì thế ta sử dụng cách đổi
biến
a2x;b2y;c2z, khi đó ta được xyz 1 và lúc này bất đẳng thức cần chứng minh được
viết lại thành
1111
2x y 3 2y z 3 2z x 3 2
Đến đây ta có một số ý tưởng tiếp cận bài toán trên.
Cách 1: Đầu tiên ta dự đoán được dấu đẳng thức xẩy ra tại
xyz1. Để ý đến chiều của bất đẳng
thức ta liên tưởng đến bất đẳng Cauchy hoặc Bunhiacopxki dạng phân thức. Tuy nhiên ở đây ta nên áp
dụng cho mấy số?
Chú ý là với
xyz1 thì
2x y 3 x y 1 x 2
, do đó ta có thể đánh giá
như sau
111 1
2x y 3 4 x y 1 x 2
Hoàn toàn tương tự ta thu được bất đẳng thức
111
2x y 3 2y z 3 2z x 3
11 1 1 1 1 1
4x y 1 y z 1 z x 1 x 2 y 2 z 2

Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
111111
2
xy1yz1zx1x2y2z2
Đến đây ta tách ra chứng minh hai bất đẳng thức sau
111
1
xy1yz1zx1
và
111
1
x2 y2 z2
Với giả thiết
xyz 1 thì bất đẳng thức
111
1
xy1yz1zx1
được chứng minh
bằng phép đổi biến.
Bây giờ ta tập trung chứng minh bất đẳng thức
111
1
x2 y2 z2
Bất đẳng thức trên tương đương với
xxx
1
x2 y2 z2
Áp dụng bất đẳng thức Cauchy dạng phân thức ta được
2
xyz
xyz
x2 y2 z2 xyz6
Và ta cần chỉ ra được
2
xyz xyz6 xyyzzx3
Rõ ràng đánh giá cuối cùng đúng theo bất đẳng thức Cauchy. Do đó bài toán được chứng minh.
Cách 2: Cách phát biểu của bất đẳng thức cần chứng minh làm ta liên tưởng đến bất đẳng thức
22 22 22
1111
2
2x y 3 2y z 3 2z x 3
Do đó để đưa về dạng như trên ta có thể đặt
222
xm;yn;zp khi đó từ
xyz 1
ta suy ra được
mnp 1 và bất đẳng thức được viết lại thành
22 22 2 2
1111
2
2m n 3 2n p 3 2p m 3
Bất đẳng thức này đã được chứng minh trong chủ đề thứ hai.
Bài 41. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
444
222
ab bc ca 3
2
a1b1c1
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta nhận
thấy trên tử mỗi phân số có chứa các lũy thừa bậc chẵn. Do đó rất tự nhiên ta nghĩ đến sử dụng bất đẳng
thức Bunhiacopxki dạng phân thức. Tuy nhiên trước khi áp dụng ta cần khử thừa số bậc lẻ trước.
Cách 1: Chú ý đến giả thiết
abc 1 , ta viết lại được bất đẳng thức như sau
444
33 3
abc3
2
a c ac b a ab c b bc
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222
444
33 3 332
abc
abc
a c ac b a ab c b bc a c b a c b ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

2
222
332
abc
3
2
ac ba cb ab bc ca
Hay
2
222 3 3 3
2a b c 3ac ba cb ab bc ca
Biến đổi tương đương bất đẳng thức trên ta được
444 222222 3 3 3
2a b c 4ab bc ca 3ac ba cb 3ab bc ca
Dễ thấy theo một đánh giá quen thuộc ta có
22 22 22
22 22 22
a b 1 2ab; b c 1 2bc; c a 1 2ca
ab bc ca 3 2 ab bc ca
Mà
3
222
ab bc ca 3 a b c 3 suy ra
22 22 22
ab bc ca ab bc ca
Do đó ta được
22 22 22
3ab bc ca 3ab bc ca
Chứng minh sẽ hoàn tất nếu ta chỉ ra được
444 222222 3 3 3
2a b c ab bc ca 3ac ba cb
Thật vậy, theo bất đẳng thức Cauchy ta được
4444 34444 34444 3
444 3 3 3
a a a b 4ab;b b b c 4bc;c c c a 4ca
abbabbcca
Và
422 3422 3422 3
444222222 3 3 3
aab2ab;bbc2bc;cca2ca
abcabbcca2ab2bc2ca
Cộng theo vế hai kết quả trên ta được
444 222222 3 3 3
2a b c ab bc ca 3ac ba cb
Vậy bài toán được chứng minh.
Cách 2: Khi quan sát bất đẳng thức ta nghĩ đến là đánh giá
44
2
ab ab
2a
a1
, đáng tiếc là đánh giá này cho
một bất đẳng thức ngược chiều. Chính điều này gợi ý cho ta sử dụng kỹ thuật Cauchy ngược dấu.
Biến đổi và áp dụng bất đẳng thức Cauchy ta được
422
222
22
ab ab ab ab
ab ab ab
2a 2
a1 a1
Hoàn toàn tương tự ta được
44
22
22
bc bc ca ca
bc ; ca
22
b1 c1
Khi đó ta được
444
222
33 3
abc abbcca
ab bc ca
2
a c ac b a ab c b bc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
ab bc ca 3
ab bc ca
22
Hay
222
2ab bc ca 3 ab bc ca
Dễ thấy
3
222 222
ab bc ca 3 ab.bc.ca 3
Và ta cần chỉ ra được
222
ab bc ca ab bc ca
Áp dụng bất đẳng thức Cauchy ta có
3
222 44
ab ab bc 3 abc 3ab
Thiết lập các bất đẳng thức tương tự và cộng theo vế ta được
222
3ab bc ca 3ab bc ca

Hay
222
ab bc ca ab bc ca
Vậy bài toán được chứng minh xong.
Bài 42. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
444
22 2 2 2 2
abc3
4
bcb c cac a aba b
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc1. Quan sat bất đẳng thức ta nhân thấy
các dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, sử dụng kĩ thuật đánh giá mẫu,….
Cách 1: Suy nghĩ đầu tiên khi quan sát bất đẳng thức đó là dấu hiệu áp dụng bất đẳng thức Bunhiacopxki
dạng phân thức. Như vậy khi đó ta được
444
22 22 2 2
2
222
22 2 2 2 2
abc
bcb c cac a aba b
abc
bcb c cac a aba b
Như vậy ta cần chỉ ra được
2
222
22 2 2 2 2
abc
3
4
bcb c cac a aba b
Để ý ta thấy khi khai triển mẫu thì xuất hiện đại lượng
333
abc
và đánh giá đại lượng đó theo
kiểu
333
abc? rất phức tạp. Do đó đánh giá một cách trực tiếp như vậy có vẻ không đem lại hiệu
quả. Như vậy để áp dụng có hiệu quả ta nên biến đổi bất đẳng thức về một dạng khác.
Chú ý là tại các mẫu xuất hiện tích của hai đại lượng do đó ta sẽ đưa một đại lượng lên trên tử số.
Khi đó ta có các cách biến đổi là
2
2
4
22
22
a
a
bc
bc
bcb c
hoặc là
2
2
4
22
22
a
a
bc
bc
bcb c
Để ý rằng sau khi áp dụng thì ta thu được biểu thức là tổng các mẫu số, do đó chú ý đến giả thiết
abc3
thì ta chọn cách biến đổi thứ hai. Khi này bất đẳng thức cần chứng minh được viết lại
thành
22 2
222
22 2 2 2 2
abc
3
bc ca ab
bc ca ab 4
Đến đây áp dụng bất đẳng thức Cauchy ta được
22 2 2
222 222
22 22 2 2 22 2 2 2 2
abc abc
bc ca ab bc ca ab
bc ca ab
2a b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
22 2 2 2 2
abc3
2
bc ca ab
Như vậy sau một số bước đánh giá ta đưa được về một bất đẳng thức có vẻ đơn giản hơn và bất
đẳng thức cần chứng minh lúc này cũng có dấu hiệu áp dụng bất đẳng thức Bunhiacopxki dạng phân thức,
khi đó ta được

2
222
22 2 2 2 2 22 2 2 2
abc
abc
bc ca ab bc ac ab
Và ta cần chứng minh được
22 2 2 2
bc ac ab 32
, tuy nhiên đánh giá này lại sai vì
22 2 2 2
1
b c ac a b abbcca 32
2
.
Như vậy để đảm bảo các đánh giá đúng chiều ta cần nâng lũy thừa của các phân số lên, do đó ta có
đánh giá
2
222
222
22 22 22 222 2 2222
abc
abc
bc ca ab abcbaccab
Mặt khác theo bất đẳng thức Bunhiacopxki ta được
22 2 2 2 22 2
222222 222 222
222222222
ab c bac ca b
abcabc bca cab
2a b c ab bc ca
Do đó ta được
22
222 222
22 2 2 2 22 2
222222222
abc abc
ab c bac ca b
2a b c ab bc ca
Ta cần chỉ ra được
2
222
222222222
abc
3
2
2a b c ab bc ca
Hay
222 222 222222
abc abc 3abbcca
Để ý ta nhận thấy
222 222222 222
abc
abc 3abbcca;abc 3
3
Nhân theo vế hai bất đẳng thức trên ta được điều phải chứng minh.
Cách 2: Có thể thấy bài toán trên đã được chứng minh xong, tuy nhiên lại quá vất vả trong việc tìm lời
giải. Có một điều dễ nhận ra là nếu bài này được ra trong một kì thì mà thời gian có hạn thì cách như trên
sẽ lấy hết thời gian của các bài toán khác. Có phải đang có một cách giải khác ngắn gọn hơn hay không?
Ta thử quan sát kỹ lại bất đẳng thức một làm nữa xem sao? Ta nhận thấy trong mỗi phân thức thì tử có
bậc 4 và mẫu có bậc 3, chú ý đến giả thiết
abc1 thì ta có thể đồng bậc như sau
444
22 2 2 2 2
abcabc
4
bcb c cac a aba b
Do đó ta hướng đến đơn giản hóa các mẫu số, điều này làm ta nghĩ đến chứng minh một đánh giá
kiểu
22 33
xyx y 2x y. Đây là một đánh giá chứng minh được bằng phép biến đổi tương
đương. Bây giờ ta thử áp dụng đánh giá đó xem sao
444
22 2 2 2 2
444
33 3 3 3 3
abc
bcb c cac a aba b
abc
2b c 2c a 2a b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

444
33 3 3 3 3
abcabc
4
2b c 2c a 2a b
Bất đẳng thức này có thể chứng minh được bằng cách áp dụng đồng thời bất đẳng thức
Bunhiacopxki dạng phân thức và bất đẳng thức Cauchy.
Bài 43. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
222
222
abcabc
3
5a b c 5b c a 5c a b
Phân tích và lời giải
Trước hết ta dụ đoán dấu đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức cần chứng minh
ta thấy được sự phức tạp của bài toán. Suy nghĩ đầu tiên khi đọc bài toán đó là khử được các căn bậc hai
bên vế trái, tuy nhiên ở đây ta không nên bình phương vì biểu thức trong căn tương đối cồng kềnh. Như
vậy ta cần một đánh giá để có thể khử hết các căn bậc hai hoặc một đánh giá mà đưa về chỉ một căn thức.
Chú ý đến chiều của bất đẳng thức cần chứng minh ta nghĩ đến bất đẳng thức Bunhiacopxki. Mặt khác
chú ý đến tổng
abc bên vế phải vì thế ta cần đánh giá sao cho có thể rút gọn được abc. Từ
các nhận xét đó ta có:
Áp dụng bất đẳng thức Bunhiacopxki thì
333
222
222
222
222
222
abc
5a b c 5b c a 5c a b
abc
abc
5a b c 5b c a 5c a b
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
222
abc1
3
5a b c 5b c a 5c a b
Đến đây ta để ý lại thấy
2
2222
5a b c 5a b c 2bc
và chú ý đến dấu đẳng thức xẩy ta
có có
2
222222
5a bc abc 2abc 2abc
, khi này ta nghĩ đến bất đẳng thức
Bunhiacopxki dạng phân thức. Như vậy ta cần có trên tử
2
3a , điều này ta hoàn toàn có thể làm được.
Khi này ta sẽ được
2
2
2
222 2 2
2
22
222 2
3a
a1
9
abc 2abc 2abc
5a b c
1a 2a
9
abc2abc
Hoàn toàn tương tự ta thu được
222222
22222 22222
22
b1b 2b c1c 2c
;
99
abc2bac abc2cab
5b c a 5c a b
Do
đó ta có
222 222
222222
222
a b c 1 2a 2b 2c
1
9
2a bc 2b ca 2c ab
5a b c 5b c a 5c a b

Bây giờ ta cần phải chứng minh được
222
222
12a 2b 2c1
1
93
2a bc 2b ca 2c ab
Bất đẳng thức đó tương đương với
222
222
2a 2b 2c
2
2a bc 2b ca 2c ab
Đến đây ta đổi chiều bất đẳng thức và được
222
bc ca ab
1
2a bc 2b ca 2c ab
Theo bất đẳng thức Bunhiacopxki dạng phân thức thì
2
222
22 22 22
ab b c ca
bc ca ab
1
2a bc 2b ca 2c ab
ab bc ca 2abc a b c
Như vậy đánh giá cuối cùng là một đánh giá đúng.
Do đó bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Bài 44. Cho a, b, c là các số thực dương thỏa mãn điều kiện
ab b c ca 3
. Chứng minh rằng:
222
ab bc ca 8
Phân tích và lời giải
Quan sát bất đẳng thức ta thấy bên vế phải có các đại lượng
222
ab;bc;ca
và ta cần tìm
được một đại lượng trung gian mà các đánh giá phải cùng chiều, do đó suy nghĩ đầu tiên là đồng bậc các
hạng tử trong mỗi đại lượng trên. Để thực hiện được việc này ta để ý đến bất đẳng thức Bunhiacopxki.
Lúc này ta được ta
222
222
ab a1 ab;bc b1 bc;ca c1 ca
Nhân theo vế ta được
2
222
ab bc ca a1b1c1 abbcca
Hay
2
222
abbcca
ab bc ca
a1b1c1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abbcca
8
a1b1c1
Trong các đánh giá trên ta chưa sử dụng đến giả thiết. Ta cần phải sử dụng giả thiết cho các đánh
giá tiếp theo. Nhận thấy ta chưa thể sử dụng ngay được giả thiết nên ta cần biến đổi giả thiết về một dạng
khác trước. Thật vậy, từ giả thiết
ab b c ca 3 ta dễ dàng suy ra abc3 và abc 1 .
Dễ thấy
abbcca abcabbcca abc 3abc abc8
Do đó từ giả thiết ta suy ra được
abbcca 8
Như vậy ta cần chỉ ra được
abbcca
1
a1b1c1
Hay
abbcca a1b1c1
Để ý đến các phép biến đổi
abbcca 3abc abc 8
a1b1c1 abcabbccaabc1
Ta có

abbcca a1b1c1
3 a b c abc abc bc bc ca a b c 1
2 a b c 2abc 4 2 2abc 0
Do đó suy ra
abbcca a1b1c1
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bài 45. Cho a, b, c là các số thực dương thỏa mãn
abcabc . Chứng minh rằng:
222
bca3
2
ab 1 bc 1 ca 1
Phân tích và lời giải
Từ giả thiết của bài toán là
abcabc suy ra
111
1
ab bc ca
. Khi này suy nghĩ hết sức
tự nhiên là đặt
111
x;y;z
abc
. Do đó giả thiết của bài toán trở thành
xy yz zx 1
và bất
đẳng thức cần chứng minh được viết lại là
22 2
xyz3
2
y1 z1 x1
Với giả thiết
xy yz zx 1 ta thấy được
22
x1 xxyyzzx xyxz
Tương tự ta được
22
y1 yzyx;z1 zxzy
Để ý tiếp ta lại có theo bất đẳng thức Cauchy thì
x2x
x2yz
yxyz
Hoàn toàn tương tự ta được
22 2
xyz x y z
y1 z1 x1
yxyz zxzy xyxz
2x 2y 2z
x2yz xy2z 2xyz
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2x 2y 2z 3
x2yz xy2z2xyz 2
Với bất đẳng thức trên thì sử dụng bất đẳng thức Bunhiacopxki dạng phân thức là hợp lí nhất. Thật
vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
22
22
2
2x 2y 2 z 2x 2y 2 z
x2yz xy2z 2xyz
xx2yz yxy2z z2xyz
2x y z 2x y z
3
2
xyz xyyzzx xyz
xyz
3
Như vậy bài toán được chứng minh xong. Dấu đẳng thức xẩy ra tại
abc 3 .
Bài 46. Cho a, b, c là các số thực dương thỏa mãn
222
a, b , c 1; a b c 4

Chứng minh rằng:
222
111 9
abc
2a1b1c1
Phân tích và lời giải
Khi quan sát bất đẳng thức cần chứng minh thì suy nghĩ đầu tiên là đổi biến làm mất các căn bậc
hai. Từ suy nghĩ đó ta đặt
222
xa1;yb1;zc1. Khi đó ta suy ra
222
a x 1; b y 1; c z 1
.
Giả thiết của bài toán được viết lại thành
222
xyz1
. Bất đẳng thức cần chứng minh trở
thành
222
111 9
2x y z
x1 y1 z1
Hay
222
1119
xyz
2
x1 y1 z1
Ta viết vế trái của bất đẳng thức trên thành
222 222
xyz yzzxxy
x1 y1 z1 x1 y1 z1
Lúc này ta dự đoán
222
yz zx xy
3
x1 y1 z1
và
222
yz zx xy
3
x1 y1 z1
Quan sát kĩ các biểu thức trên và chú ý đến chiều của bất đẳng thức ta nghĩ đến đánh giá có thể đưa
các đại lượng vào trong cùng một căn bậc hai. Để thực hiện điều này ta liên tưởng đến bất đẳng thức
Bunhiacopxki dạng
222
abc 3a b c .
Khi đó ta được
222
222 2 22 22 2
222
xyz 3x 3y 3z
2xyz x2yz xy2z
x1 y1 z1
Mặt khác ta lại có
222
222 22 22
3x 3 x x
4
2x y z x y x z
, áp dụng tương tự ta được
222
222 2 22 22 2
3x 3y 3z 3
2
2x y z x 2y z x y 2z
Do đó
222
xyz3
2
x1 y1 z1
Như vậy bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
222
yz zx xy
3
x1 y1 z1
Điều này có thể thực hiện hoàn toàn tương tự như trên
222
222 2 22 22 2
222
3y z 3z x 3x y
yz zx xy
2xyz x2yz xy2z
x1 y1 z1

Dễ dàng chứng minh được
2
22
222 22 22
3y z
yz
3
2x y z x y x z
Tương tự ta được
222
222 2 22 22 2
222 222
22 2222 22 22 22
3y z 3z x 3x y
2x y z x 2y z x y 2z
yzzxxy
33
xy xz zy xy xz yz
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
2
abc
3
.
Bài 47. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
3a 1b1c1
ab 1 bc 1 ca 1
2
Phân tích và lời giải
Cách 1: Trước hết ta dự đoán được đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta nhận
thấy cả hai vế đều chứa các đại lượng
a1;b1;c1
, do đó ta biến đổi bất đẳng thức bằng cách chia
cả hai vế cho
a1b1c1
. Khi đó bất đẳng thức được viết lại thành
abc3
2
a1c1 a1b1 c1b1
Đến đây ta thấy có hai hướng đánh giá là
- Hướng thứ nhất ta sử dụng bất đẳng thức Bunhiacopxki đưa các đại lượng trong căn bên vế trái vào
trong cùng một căn bậc hai thì được
abc
a1c1 a1b1 c1b1
3a 3b 3c
a1c1 a1b1 c1b1
Như vậy ta quy bài toán về chứng minh
abc3
4
a1c1 a1b1 c1b1
Bất đẳng thức trên tương đương với
4ab1 bc1 ca 1 3a 1b1c1
3abc3 abbccaabc
Nhận thấy đánh giá trên không đúng.
- Hướng thứ hai là áp dụng bất đẳng thức Cauchy theo chiều từ trung bình nhân sang trung bình cộng.
Chú ý đến dấu đẳng thức xẩy ra tại
abc1
ta có
aa.11a1
2a 1 c 1
a1c1 a1c1
Hoàn toàn tương tự ta được
b11b c1c1
;
2a 1 b 1 2c 1 b 1
a1b1 c1b1

Cộng theo vế các bất đẳng thức trên ta được
abc3
2
a1c1 a1b1 c1b1
Vậy bài toán được chứng minh xong.
Cách 2: Nhận xét tương tự như trên nhưng ta hướng theo đánh giá làm vế trái xuất hiện nhân tử chung là
1 trong trong 3 đại lượng đó với mong muốn có thể giảm xuống còn hai biến. Chú ý đến chiều bất đẳng
thức ta có
ab 1 bc 1 a 1 b 1 bc 1
Khi đó ta được
ab1 bc1 ca1 a1b1bc1 ca1
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
3b1c1
bc 2b 1 c
2
Đến đây nếu ta đưa được các đại lượng dưới dấu căn bên trái vào trong một căn thức thì cơ hội sẽ
cao hơn, tuy nhiên cũng tương tự như trên ta thử làm xất hiện thêm nhân tử chung để rút gọn xem sao.
Chú ý là bên vế phải chứa hai đại lượng
b1;c1
nên ta sẽ cố đánh giá vế trái về một trong hai đại
lượng trên.
- Trước hết ta đánh giá về
b1 , để ý là
bc 2b 1 c 1 b 1 c 2 , do đó ta cần làm
xuất hiện
c1 để khi bất đẳng thức Bunhiacopxki ta được
bc 2b 1 c 1
.
Để ý là
c
cc1.
c1
, khi đó ta được
cc
bc 2b 1 c 1. bc 2b 1 c 1 1
c1 c1
b1c22c1
c1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
c22c1
3c 1
4c 2 2c 1 9c 1
c1 2
Đánh giá cuối cùng luôn đúng theo bất đẳng thức Cauchy. Vậy bài toán được chứng minh xong.
- Bây giờ ta thử đánh giá về
c1
, khi đó theo bất đẳng thức Bunhiacopxki ta có
bc 2b 1 c 1. bc 2b 1 1. c 1 c bc 2b 1 1
Và ta cần chỉ ra được
3b 1
bc 2b 2 bc b 1
2
. Tuy nhiên đánh giá cuối cùng không
đúng, do đó hướng đánh giá này không hợp lí.
Bài 48. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222222 2
1119
aabb bbcc ccaa
abc
Phân tích và lời giải
Dễ dàng dự đoán dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức trên ta nghĩ đến đánh
giá quen thuộc

222222
222
111 9
aabb bbcc ccaa
2a b c ab bc ca
Và ta cần chỉ ra được
2
222 222
2abc abbcca abc abc abbcca
Đáng tiếc đánh giá cuối cùng lại là một đánh giá sai. Nên ta phải tìm hướng đánh giá khác.
Quan sát kỹ bất đẳng thức trên ta thấy được sự liên quan giữa các mẫu số với các đại lượng
222
abc;abbcca , ta thử xem có mối liên hệ nào hay không?
Để ý ta thấy
222 222
aabb cbcca abcabbcca
, điều này dẫn đến
222 2 22
22 22 22
ca b c
abcabbccaaabbcbcca
1
a abb a abb a abb
Hoàn toàn tương tự thì ta được
222
222222
222222
111
abcabbcca
aabb bbcc ccaa
cab
3abc
aabb bbcc ccaa
Như vậy bây giờ ta cần chứng minh được
222222
222
2
cab
3abc
aabb bbcc ccaa
9a b c ab bc ca
abc
Để ý tiếp đại lượng
222222
cab
aabbbbcc ccaa
, theo bất đẳng thức
Bunhiacopxki dạng phân thức ta có
2
222222
abc
cab abc
ab bc ca
aabb bbcc ccaa
abcabbcca
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
2
9a b c ab bc ca
abc
3
ab bc ca
abc
Hay
2
222
2
6a b c 3ab bc ca
abc
ab bc ca
abc
Hay
4
222
a b c 3 2 a b c ab bc ca ab bc ca
Đến đây thì ta nghĩ đến sử dụng bất đẳng thức Cauchy để đánh giá. Để ý là khi dấu đẳng thức xẩy
ra thì
222
2a b c ab bc ca 3ab bc ca nên áp dụng bất đẳng thức Cauchy ta được
222
2
222
4
3abbcca2a b c abbcca
3abbcca 2a b c abbcca
abc
4

Vậy bài toán được chứng minh xong.
Bài 49. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
a abc b abc c abc 1
cab abc bac
2abc
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra khi và chỉ khi
1
abc
3
. Nhận thấy các đại
lượng trong căn và ở các mẫu chưa đồng bậc nên suy nghĩ đầu tiên đó là đồng bậc các đại lượng đó. Để ý
đến giả thiết
abc1 ta thấy
22
aabcaabcabcaabac
cab cabc ab acbc
Hoàn toàn tương tự
22
b abc b a b b c ; c abc c a c b c
bacabbc;abcabac
Khi đó bất đẳng thức cần chứng minh trở thành
aa b a c bb c a b ca c b c
1
cacb abac abbc
2abc
Hay
abca b a c bacb c a b caba c b c
1
2
cacb abac abbc
Quan sát bất đẳng thức trên ta liên tưởng đến bất đẳng thức Cauchy, để ý là
bcabac cab.bac bab.cac
Trong hai các viết trên ta chọn cách viết thứ nhất vì khi sử dụng bất đẳng thức Cauchy dạng
2xy x y
thì không tạo ra các đại lượng có chứa các bình phương (Nên nhớ là các bình phương
bao giờ cũng trội nhất trong các đại lượng bậc 2). Khi đó áp dụng bất đẳng thức Cauchy ta được
ba c ca b
ab 2bc ca
bcabac
22
Áp dụng tương tự ta được
abca b a c bacb c a b caba c b c
cacb abac abbc
a ab 2bc ca b ab bc 2ca c 2ab bc ca
2c a c b 2a b a c 2a b b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a ab 2bc ca b ab bc 2ca c 2ab bc ca
1
cacb abac abbc
Hay
a a b ab 2bc ca b b c ab bc 2ca c c a 2ab bc ca
abbcca
Vế trái của bất đẳng thức có bậc 4 còn vế phải có bậc ba nên ta co thể đồng bậc là
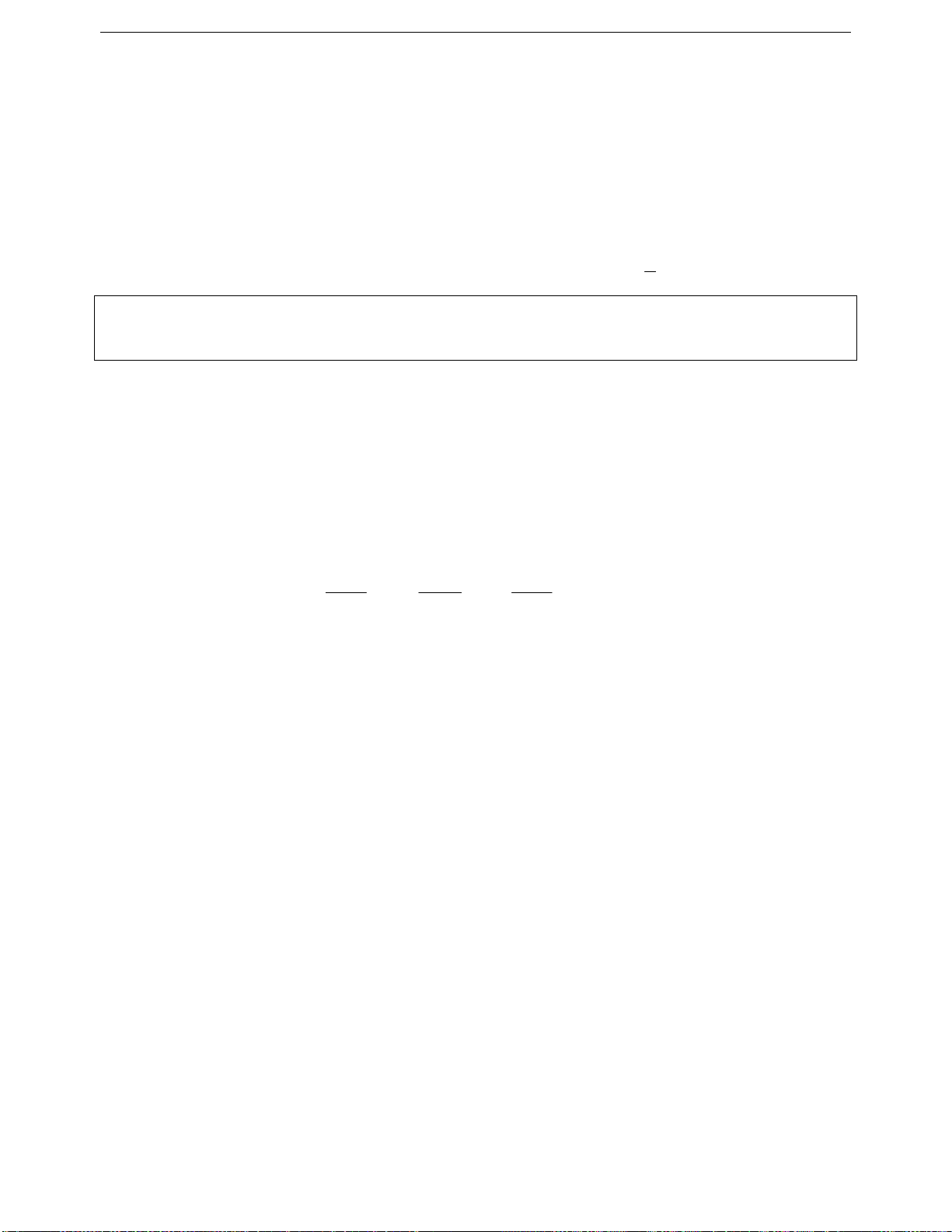
a a b ab 2bc ca b b c ab bc 2ca c c a 2ab bc ca
abbccaabc
Triển khai và rút gọn ta được
333222222222
333 222222222
abc bca cab ab bc ca 5abcabcabc
abc bca cab 2ab bc ca 4abcabcabc
Hay
22 22 22
abc a b c a b b c c a
, đây là một đánh giá đúng
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
abc
3
.
Bài 50. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
222
abc abcbcacab 27abc
Phân tích và lời giải
Cách 1: Dự đoán dấu đẳng thức xẩy ra tại
abc. Đầu tiên ta nhận thấy nếu vế trái của bất đẳng thức
âm thì bất đẳng thức hiển nhiên đúng. Như vậy ta chỉ cần chứng minh cho trường hợp vế trái không âm
là được.
Xét trường hợp
abcbcacab 0 , khi đó dễ dàng chứng minh được
abc 0;bca 0;cab 0 .
Quan sát bất đẳng thức cần chứng minh thì ý tưởng tiếp cận đầu tiên là đổi biến, ta có thể đặt
xabc;ybca;zcab suy ra ta được
xz xy yz
a;b;c x,y,z0
222
Khi đó bất đẳng thức cần chứng minh đươc viết lại thành
3222
64xyz x y z 27 x y y z z x
Theo một đánh giá quen thuộc ta có
2
3xyx x y z xy yz zx
Do đó ta được
322
64.3xyz x y z 64 x y z xy yz zx
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22222
64 x y z xy yz zx 3.27 a b b c c a
Lấy căn bậc hai hai vế ta được
9x y y z z x 8x y z xy yz zx
Đây là một đánh giá đúng quen thuộc. Do đó bài toán được chứng minh
Cách 2: Quan sát bất đẳng thức cần chứng minh ta liên tưởng đến bất đẳng thức Cauchy, khi đó nếu áp
dụng trực tiếp thì ta có
3
27 a b c b c a c a b a b c nên bài toán quy về chứng
minh
6
2222
abc 27abc , tuy nhiên đánh giá đó là một đánh giá sai. Do đó ta không thể sử
dụng trực tiếp bất đẳng thức Cauchy như vậy được mà cần biến đổi bất đẳng thức trước.
Để ý ta thấy khi đẳng thức xẩy ra thì
ab c a bc a b ca b c và lại có
222
ab c a bc a b ca b c 2ab bc ca a b c
Do đó ta nghĩ đến áp dụng bất đẳng thức Cauchy cho ba số trên, khi đó ta được
3
27abc a b c b c a c a b a b c a b c a b c a b c

Hay
3
222
27abc a b c b c a c a b 2 ab bc ca a b c
Khi đó ta được
3
3
3
222
27abc a b c b c a c a b a b c
2ab bc ca a b c a b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
3
3
222 3333
2ab bc ca a b c a b c 9abc
Lấy căn bậc ba hai vế ta được
222
abc2abbcca a b c 9abc
Khai triển và rút gọn ta được
333 2 2 2
abc3abcabcbcacab
abc a b c b c a c a c
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 51. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
222
abc bca cab
1
2
2a b c 2b a c 2c a b
Lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức ta thấy có thể
tiếp cận theo hướng sử dụng các bất đẳng thức Cauchy, Bunhiacopxki,…
Cách 1: Đầu tiên ta nhận thấy tại các mẫu số của các phân thức có chứa các đại lượng bình phương
2
ab
,
2
bc
,
2
ca
. Chú ý đến chiều của bất đẳng thức ta có đánh giá quen thuộc
2
22
ab 2a b khi đó mẫu sẽ trở thành
222
2a b c . Hoàn toàn tương tự ta thu được bất
đẳng thức
222222
222 222
222
abc bca cab abc bca bca
2a 2b 2c
2a b c 2b a c 2c a b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
abc bca bca
1
2
2a 2b 2c
Hay
222
222
abc bca bca a b c
Triển khai và thu gọn ta được
222
abcabbcca. Đánh giá cuối cùng đúng với mọi a,
b, c. Vậy bất đẳng thức được chứng minh xong.
Cách 2: Quan sát bất đẳng thức ta nhận thấy dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân
thức, khi đó ta có
222
222
222
2
222
222
abc bca cab
2a b c 2b a c 2c a b
abc
2a b c a b b c c a

Ta cần chứng minh được
2
222
222
abc
1
2
2a b c a b b c c a
Hay
2222
222
2a b c 2a b c a b b c c a
Khai triển và thu gọn ta được
222
ab bc ca a b c, đây là một đánh giá sai nên ta dừng
chứng minh theo cách này ở đây.
Do không thể sử dụng bất đẳng thức Bunhiacopxki trực tiếp nên ta cần biến đổi bất đẳng thức
trước xem có thể sử dụng được hay không? Tuy nhiên ta sẽ biến đổi cách như thế nào đây? Trước hết ta
tìm mối liên hệ của các đại lượng trong mỗi phân thức thì thấy rằng
22
2
22
22
abc a bc 2abc
2a b c 2a b c
Như vậy ta sẽ có
22
22
22 2
22 2
abc a bc 2abc a 2abc
11
2a b c 2a b c 2a b c
Và nếu áp dụng tương tự thì ta thu được
222
222
222
222
222
222
abc bca cab
3
2a b c 2b a c 2c a b
a2abc b2bca c2cab
15
3
22
2a b c 2b c a 2c a b
Hay
222
222
222
a2abc b2bca c2cab
5
2
2a b c 2b c a 2c a b
Để ý đến chiều bất đẳng thức ta thấy không thể sử dụng bất đẳng thức Bunhiacopxki dạng phân
thức được. Cũng chú ý đến chiều của bất đẳng thức ta nghĩ đến một đánh giá kiểu
2
2
2a b c ?
.
Vì khi dấu đẳng thức xẩy ra thì
2
2
2a b c nên ta không sử dụng bất đẳng thức Cauchy mà nghĩ đến
bất đẳng thức Bunhiacopxki dạng cơ bản. Khi đó chú ý đến dấu đẳng thứ xẩy ra ta có đánh giá
2
22
2
2a b c 2 4 2a 2 b c 4 a b c
.
Và áp dụng hoàn toàn tương tự ta thu được
222
222
222
222
2
2
2
a2abc b2bca c2cab
2a b c 2b c a 2c a b
a2abcb2bcac2cab
3
2
abc
abc 2abbcca
3
2
abc

Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
2
abc 2abbcca
35
22
abc
Hay
2
2
abc 2abbcca
5
3
abc
Biến đổi tương đương bất đẳng thức trên ta được
2
abc 3abbcca
Đánh giá cuối cùng đúng với mọi a, b, c. Vậy bất đẳng thức được chứng minh.
Bài 52. Cho a, b, c là các số thực thỏa mãn
1
a, b , c ; 1
2
. Chứng minh rằng:
abbc ca
23
1c 1a 1b
Phân tích và lời giải
Dễ dàng dự đoán được bất đẳng thức bên trái xẩy ra dấu bằng tại
1
abc
2
và bất đẳng thức
bên phải xẩy ra dấu bằng tại
abc1. Quan sát bất đẳng thức ta thấy có thể đơn giản hóa bằng
cách đổi biến và ta có thể đổi biến bằng cách sau
Đặt
x a 1; y b 1; c z 1
, khi đó ta được
3
x, y, z ; 2
2
Bất đẳng thức cần chứng minh được viết lại là
xy2 yz2zx2
23
zxy
Bây giờ ta đi chứng minh từng bất đẳng thức
+ Trước hết ta chứng minh
xy2 yz2zx2
2
zxy
Để ý là
xy2 xyz2
1
zz
, do đó hoàn toàn tương tự ta viết lại bất đẳng thức trên như sau
xy2 yz2 zx2
5111
zxy
Hay
111
5xyz2
xyz
Đặt
txyz
, theo một đánh giá quen thuộc thì
111 9 9
xyz xyz t
Như vậy ta được
111 9
xyz2 t2.
xyz t
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
9t 2
9
5t
t2
Tuy nhiên đây là một đánh giá đúng vì
333 9
txyz
222 2
Vậy bất đẳng thức bên trái được chứng minh.

+ Chứng minh
xy2 yz2zx2
3
zxy
Ta viết lại bất đẳng thức như sau
xy yz xz 222
3
yx zy zx xyz
Rõ ràng ta không thể sử dụng các bất đẳng thức Cauchy hay Bunhiacopxki. Trong tình huống này
ta để ý đến phép sắp thứ tự các biến để quy bất đẳng thức về bất đẳng thức ít biến hơn.
Không mất tính tổng quát, ta giả sử
3
xyz2
2
. Khi đó tasẽ có
2
2yx 2y
xy x2
0
yx 2x 2xy
Do đó ta được
xy x2
yx 2x
. Hoàn toàn tương tự ta được
yz y2
zy2y
và
xz x2
zx2x
Cộng theo vế các bất đẳng thức trên ta được
xy yz xz 4y2
x
yx zy zx x2y
Ta cần chứng minh
4y2 222 2y 2
x3 x3
x2y xyz x2 z
Bất đẳng thức cuối cùng là một bất đẳng thức đúng vì
x1x2
22
x3 0x 3
xx x
y2
1
2z
Vậy bất đẳng thức bên phải được chứng minh. Dấu đẳng thức xẩy ra tại
abc1
.
Bài 53. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
222
2a b c a 2b c a b 2c
8
2a b c 2b c a 2c a b
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ta tại
abc. Quan sát kỹ bất đẳng thức ta có
một số nhận xét như sau
- Bất đẳng thức đồng bậc 0.
- Bất đẳng thức có các phân thức liên quan đến các đại lượng bình phương.
- Trong mỗi phân thức ta thấy ở các tử và mẫu có sự lặp lại của các đại lượng.
Từ những nhận xét trên ta có cách hướng tiếp cận bài toán như sau.
Cách 1: Bất đẳng thức đồng bậc 0, nên ý tưởng đầu tiên là đổi biến theo hướng chuẩn hóa
Đặt
3a 3b 3c
x;y;z
abc abc abc
, khi đó ta có xyz3.
Khi đó ta được

2
2 2
22 22
2 2
2.3a 3b 3c
2a b c 2x y z
abcabcabc
3a 3b 3b
2a b c 2x y z
2
abc abcabc
Áp dụng tương tự ta được bất đẳng thức cần chứng minh trở thành
222
222
222
2x y z x 2y z x y 2c
8
2x y z 2y z x 2z x y
Hay
222
222
222
3x 3y 3z
8
2x 3x 2y 3y 2z 3z
Hay
222
222
x6x9 y6y9 z6z9
8
3x 6 x 9 3y 6y 9 3z 6z 9
Đến đây ta thấy các phân thức có dạng như nhau đối với mỗi biến nên ta dự đoán là
2
2
x6x9
mx n
3x 6x 9
Để tìm m và n ta có thể sử dụng phương pháp hệ số bất định hoặc là cách sau đây
2
22
22x 3 4x 1
x6x9 1
1
33
3x 6x 9
2x1
Áp dụng hoàn toàn tương tự ta được
222
222
4x y z 3
x6x9 y6y9 z6z9
8
3
3x 6x 9 3y 6y 9 3z 6z 9
Vậy bất đẳng thức được chứng minh.
Cách 2: Từ nhận xét các phân thức liên quan đến các đại lượng bình phương nên ta thử phân tích các tử
ra xem có mối liên hệ gì với mẫu không? Khai triển tử số ta được
22
2
2abc 4a 4abc bc
Mặt khác quan sát bất đẳng thức ta nhận thấy cần phải đổi chiều bất đẳng thức trước, nên ta nghĩ
đến phép biến đổi
2
2
2
2a b c
k
2a b c
, khi đó để đổi chiều bất đẳng thức ta cần tìm k sao cho
3k 8 0 và đây ta chọn k nguyên thì càng tốt.
Trước hết ta thử với
k3
thì được
2222
2
222
222
2a b c 6a 3 b c 2a b c 2 a b c
3
2a b c 2a b c 2a b c
Như vậy ta thấy
k3
thì phép biến đổi tương đối đẹp, ta cần thực hiện tiếp các phân thức còn lại
để xem có đánh giá được gì hay không? Để ý là nếu không thể đánh giá được thì ta thử tiếp với các số
khác lớn hơn.
Áp dụng tương tự ta được bất đẳng thức cần chứng minh trở thành

222
222
222
abc bac cab
1
2
2a b c 2b c a 2c a b
Đây chính là bất đẳng thức đã được chứng minh trong bài 51, ta có thể trình bày lại một cách như
sau
Áp dụng bất đẳng thức cơ bản
2
22
xy 2x y
, ta được
222222
222 222
222
abc bca cab abc bca bca
2a 2b 2c
2a b c 2b a c 2c a b
Ta cần chứng minh
222
222
abc bca bca
1
2
2a 2b 2c
Hay
222
222
abc bca bca a b c
Triển khai và thu gọn ta được
222
abcabbcca , đánh giá cuối cùng đúng.
Vậy bất đẳng thức được chứng minh.
Cách 3: Chú ý đến sự lặp lại của các đại lượng
a, b c trong cả phân thức thứ nhất nên ta có thể viết lại
được
2
2
22
2
bc
2
2a b c
a
bc
2a b c
2
a
hoặc
2
2
22
2
2a
1
2a b c
bc
a
2a b c
21
bc
Nên để đơn giản hóa ta có thể đặt
bc
x
a
hoặc
a
x
bc
. Trước hết ta tiếp cận với với cách
đặt thứ nhất.
Hoàn toàn tương tự ta đặt được
bc ca ab
x;y;z
abc
. Khi đó bất đẳng thức cần
chứng minh trở thành
222
222
x2 y2 z2
8
x2 y2 z2
Hay
222
222
x1 y1 z1
1
2
x2 y2 z2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 2
222222
x1 y1 z1 xyz3
x2 y2 z2 xyz6
Ta cần chứng minh
2
222
xyz3
1
2
xyz6
Hay
222
2x y z 3 x y z 6
Hay
2
xyz6 2xyyzzx12 0 *
Dễ thấy, theo bất đẳng thức Cauchy ta được

2
3
bcca caab abbc
xy yz zx
ab bc ca
abbcca
312
abc
Do đó bất đẳng thức (*) là bất đẳng thức đúng
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Với cách đặt thứ hai, hoàn toàn tương tự ta viết được bất đẳng thức cần chứng minh thành
222
222
2x 1 2y 1 2z 1
8
2x 1 2y 1 2z 1
hay
222
222
2x 1 2y 1 2z 1
1
2x 1 2 y z 2
.
Tuy nhiên với cách đổi biến này, sau các đánh giá ta thu được
xy yz xz 12. Bạn đọc tự
kiểm tra xem đánh giá ta thu được có đúng không.
Bài 54. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc 1 . Chứng minh rằng:
333
444
a1 b1 c1
2ab bc ca
abc bca cac
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta nhận
thấy các đại lượng trong căn bậc hai dưới các mẫu chưa đồng bậc, chú ý đến giả thiết
abc 1
ta có thể
đồng bậc là
44 322
abcaabcbcaabcbc . Tức là khi đó ta được
4322
abc aabcbc . Lại thấy bất đẳng thức chứa căn dưới mẫu, nên ta cần đánh giá
làm mất căn bậc hai, Chú ý đến chiều bất đẳng thức làm ta liên tưởng đến bất đẳng thức Cauchy dạng
2xy x y. Như vậy dưới mẫu cần có một tích hai đại lượng đồng bậc, để ý tiếp bên vế phải có
2ab bc ca
nên ta có thể đưa xuống dưới mẫu, do đó ta sẽ có tích
32 22 2
2a bcbc ababcca . Đến đây áp dụng bất đẳng Cauchy thì ta được
33
4
32 22 2
3
32 22 2
a1 a1
2a bc.abbcca
2a bcbc ababcca
a1
abcbcababcca
Để ý tiếp ta thấy
33 2
32 22 2 2
a1aabcaabc
abcbcababcca abcabc
Do đó ta được
33
2
4
a1 aabc a
abc
abcabc
2a bc.abbcca
Áp dụng hoàn toàn tương tự ta được
33
44
b1 b c1 b
;
abc abc
2b c a.ab bc ca 2c a c.ab bc ca
Cộng theo vế ba bất đẳng thức trên ta được
333
444
a1 b1 c1
1
2a bc.abbcca 2b ca.abbcca 2c ac.abbcca

Hay
333
444
a1 b1 c1
2ab bc ca
abc bca cac
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1
.
Bài 55. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
a3 b3 c3
32
abc bca cab
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta
nhận thấy bất đẳng thức có chứa căn bậc hai nên suy nghĩ đầu tiên đó là tìm cách loại bỏ các dấu căn, để
làm điều này ta có thể bình phương hai vế, nhưng cách làm này không làm mất hết các dấu căn mà còn
làm cho bất đẳng thức thêm phức tạp, ta cũng không thể đưa các phân thức dưới dấu căn vào cùng một
căn bằng bất đẳng thức Bunhiacopxki vì sẽ tạo ra một bất đẳng thức ngược chiều. Do đó ta nghĩ đến sử
dụng bất đẳng thức Cauchy để đánh giá, khi đó ta được
3
a3b3c3
a3 b3 c3
3
abc bca cab
abcbcacab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a3b3c3
8
abcbcacab
Hay
a3b3c3 8abcbcacab
. Tuy nhiên để chứng minh được đánh
giá này lại hơi khó, nên ta tạm dừng ý tưởng này tại đây.
Như vậy để chứng minh bất đẳng thức trên ta cần phải có những biến đổi trước. Ta viết lại bất đẳng
thức cần chứng minh thành
2a 3 2b 3 2c 3
6
abc bca cab
Để ý đến giả thiết
abc3, khi đó ta viết được
a3 ab ac
do đó ta sẽ được
2a 3 2a a b c
ab ac
2
abc abc abcabc
Đến đây áp dụng bất đẳng thức quen thuộc
2x y x y
, ta được
2a 3 2a a b c
ab ac ab ac
2
abc abc abcabc abc abc
Áp dụng tương tự ta được
2b 3 2c 3
ba bc ca cb
;
bca bca bca cab cab cab
Cộng theo vế ba bất đẳng thức trên ta được
2a 3 2b 3 2c 3
abc bca cab
ab ac ba bc ca cb
abc abc bca bca cab cab
Lúc này xuất hiện các phân thức trong căn có cùng tử số nên ta ghép lại theo nhóm, khi đó ta sẽ
được

ab ab 4ab 22ab 22ab 22
abc bca abc bca abcbca c1
ab1c
Áp dụng tương tự ta được
b c b c 22 c a c a 22
;
b ca c ab a 1 a bc c ab b 1
Cộng theo vế các bất đẳng thức trên ta được
ab ab bc bc ca ca 22 22 22
abcbcabcacababccab c1a1b1
Dó
đó ta có
2a 3 2b 3 2c 3
22 22 22
abc bca cab
c1 a1 b1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 22 22
6
c1 a1 b1
hay
1113
c1 a1 b1 2
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki ta được
111 9 9 3
c1 a1 b1 a1 b1 c1 2
3a b c 3
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bài 56. Cho a, b, c là các số thực dương thỏa mãn điều kiện
ab b c ca 3. Chứng minh rằng:
222
a2b b2c c2a
1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Phân tích và lời giải
Quan sát bất đẳng thức thì suy nghĩ đầu tiên đó là đổi chiều bất đẳng thức và để thực hiện điều này
ta có phép biến đổi tương đương sau
222
2 a 2b 2 b 2c 2 c 2a
2
2a 4b 3c 2b 4 c 3a 2c 4a 3b
Hay
222
2 a 2b 2 b 2c 2 c 2a
111 1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Hay
222
222
cab1
3
2a 4b 3c 2b 4c 3a 2c 4a 3b
Bất đẳng thức có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức nên trước hết ta áp
dụng bất đẳng thức Bunhiacopxki dạng phân thức thì được
222
222
333
222
2
333
333
cab
2a 4b 3c 2b 4c 3a 2c 4a 3b
cab
c2a4b3c a2b4c3a b2c4a3b
abc
3a b c 6ab bc ca
Phép chứng minh minh sẽ hoàn tất nếu ta chỉ ra được
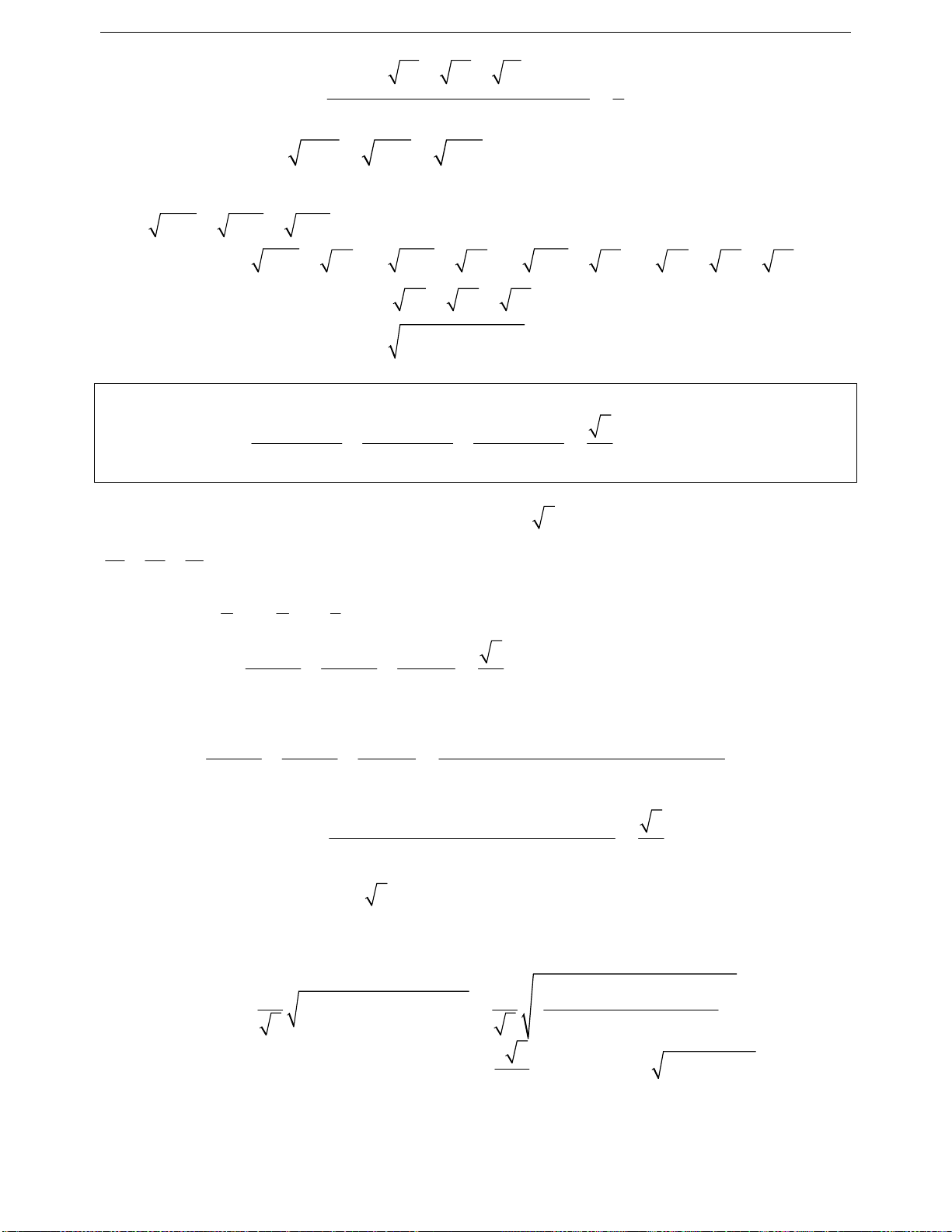
2
333
333
abc
1
3
3a b c 6ab bc ca
Hay
33 33 33
ab bc ca ab bc ca
Để chứng minh bất đẳng thức trên ta áp dụng bất đẳng thức Cauchy và để ý đến giả thiết
ab b c ca 3 thì được
33 33 33
33 33 33
ab bc ca
a b ab b c bc c a ca ab bc ca
2ab bc ca ab bc ca
ab bc ca 3 3 ab bc ca ab bc ca
Vậy bất đẳng thức được chứng minh xong. Dấu đẳng thức xẩy ra tại
abc1.
Bài 57. Cho a, b, c là các số thực dương thỏa mãn điều kiện
22 22 22 222
ab bc ca abc
.
Chứng minh rằng:
22 22 22
32 2 32 2 32 2
ab bc ca 3
2
ca b ab c bc a
Phân tích và lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc 3
. Trước hết ta viết lại giả thiết thành
222
111
1
abc
, do đó rất tự nhiên ta nghĩ đến phép đổi biến.
Đặt
111
x,y,z
abc
. Khi đó giả thiết được viết lại là
222
xyz1
và bất đẳng thức
được viết lại thành
333
22 2 2 2 2
xyz3
2
yz zx xy
Quan sát bất đẳng thức trên ta nghĩ đến bất đẳng thức Bunhiacopxki dạng phân thức, khi đó ta được.
2
222
333
22 2 2 2 2
22 2 2 2 2
xyz
xyz
yz zx xy
xy z yz x zx y
Ta cần chứng minh được
2
222
22 2 2 2 2
xyz
3
2
xy z yz x zx y
Hay
2
222 22 22 22
2x y z 3 xy z yz x zx y
Đến đây ta cần đánh giá vế phải sao cho xuất hiện
222
xyz, sử dụng bất đẳng thức Cauchy ta
có:
3
22222
22 22222
222 222
1 1 2xyzyz
xy z 2x y z y z
3
22
23
.x y z . x y z
9
Tương tự ta cũng có

22 222 222
22 222 222
23
yz x .x y z .x y z
9
23
zx y .x y z .x y z
9
Cộng theo vế các bất đẳng thức trên ta được
22 2 2 2 2 2 22 2 22
23
xy z yz x zx y .x y z .x y z
3
Cuối cùng ta cần chứng minh được
2
222 222 222 222
2
.xyz.xyz 2xyz 1xyz
3
Đánh giá cuối cùng là một đánh giá đúng. Vậy bài toán được chứng minh xong.
Bài 58: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
abc1
abc
bc ac ab 2
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc, Quan sát bất đẳng thức ta nhận
thấy có một số nhận xét sau
- Bất đẳng thức có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức
- Bất đẳng thức chứa các căn bậc hai nên ta nghĩ đến bất đẳng thức Cauchy
- Đây là bất đẳng thức đồng bậc nên ta nghĩ đến phép đổi biến
Từ những nhận xét trên ta đi tìm hiểu các hướng tiếp cận bài toán như sau
Cách 1: Trước hết ta bắt đấu với bất đẳng thức Bunhiacopxki dạng phân thức thì được đánh giá
2
abc
abc
bc ac ab ab bc ca
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc
1
abc
ab bc ca 2
Hay
2a b c ab bc ca
Tuy nhiên đánh giá cuối cùng lại là một đánh giá sai, do đó ta không thể dụng được trực tiếp như
vậy, điều này làm ta nghĩ đến việc biến đối bất đẳng thức trước.
Để ý là
aabc
bc
bc bc
, hoàn toàn tương tự ta viết vế trái của bất đẳng thức trên
là
abc
bc ac ab
111
abc bc ac ab
bc ab ac
Do đó bất đẳng thức được viết lại thành
111 1
abc bcacab abc
bc ab ac 2
Đến đây
theo bất đẳng thức Bunhiacopxki ta được

9a b c
111
abc
bc ab ac ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
9a b c
1
ab bc ca a b c
ab bc ca 2
Để ý là theo bất đẳng thức Cauchy ta được
a b b c c a 3.2. a b c
Do đó ta có
9a b c 9a b c
3.2. a b c
ab bc ca
3.2. a b c
3a b c
1
abc
22
Suy ra ta được
abc1
abc
bc ac ab 2
Vậy bất đẳng thức được chứng minh xong.
Cách 2: Bây giờ ta thử áp dụng bất đẳng thức Cauchy xem có chứng minh được bài toán không. Để ý ta
thấy các phân số có mẫu chứa các căn bậc hai và ta phải đánh giá sao cho bất đẳng thức thu được cùng
chiều với bất đẳng thức cần chứng minh. Điều này làm ta liên tưởng đế bất đẳng thức Cauchy dạng
2xy x y. Chú ý đến dấu đẳng thức xẩy ra ta viết lại bất đẳng thức cần chứng minh thành
1abc1
2
2a 2b 2c b c a c a b
Lúc này ta cần đánh giá các mẫu theo kiểu
2a 2b 2c b c ? . Để ý là khi khai
triển thì
2a 2b 2c b c 2a. b c 2b 2c b c . Do đó theo bất đẳng
thức
xy2xy và bất đẳng thức Cauchy ta được
2a b c
2b 2c 2 b c; 2a. b c
2
Nên ta có
2a 2b 2c b c 2a. b c 2b 2c b c
2a b c 2a 5b 5c
2b c.b c
22
Từ đó suy ra
a2a
2a 5b 5c
2a 2b 2c b c
Áp dụng tương tự ta có
b2bc 2c
;
2b 5c 5a 2c 5a 5b
2a 2b 2c c a 2a 2b 2c a b
Đến đây
cộng theo vế của các bất đẳng thức trên thì được

1abc
2a 2b 2c b c a c a b
2a 2b 2c
2a 5b 5c 2b 5a 5c 2c 5a 5b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a 2b 2c 1
2a 5b 5c 2b 5a 5c 2c 5a 5b 2
Thật vậy, theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
222 2
2a 2b 2c
2a 5b 5c 2b 5a 5c 2c 5a 5b
2a b c a b c
1
2.
2
2a 2b 2c 10ab 10bc 10ca
4a b c
Vậy bất đẳng thức được chứng minh xong.
Cách 3: Bất đẳng thức cần chứng minh là bất đẳng thức đồng bậc
1
2
do đó ta sử dụng phép đổi biến
3a 3b 3c
x;y;z
abc abc abc
. Khi đó ta được
xyz3
Bất đẳng thức cần chứng minh tương đương với
3
abc13
abc
..abc
abc
3 bcacab 2
abc
Hay
xyz1
xyz
yz zx xy 2
Kết hợp với điều kiện
xyz 3, bất đẳng thức trở thành
xyz1
xyz
3x 3x 3x 2
Dễ dàng chứng minh được
tt3
t1
3t 2 42
với 0t3
Áp dụng bất đẳng thức trên ta được
xyz1 3
xyz xyz3
3x 3y 3z 2 42
1
xyz
2
Vậy bất đẳng thức được chứng minh xong.
Bài 59. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc . Chứng minh rằng:
22 2 2 22
abc 111
3
bca abc
Phân tích và lời giải
Dễ dàng dự đoán được bất đẳng thức xẩy ra tại
abc3. Quan sát giả thiết bài toán ta có
thể viết
ab bc ca abc lại thành
111
1
abc
. Điều này gợi ý cho ta phép đổi biến

111
x;y;z
abc
, từ đó suy ra xyz1. Lúc này bất đẳng thức cần chứng minh trở thành
222
222
xyz
3x y z
zxy
. Đến đây ta có các cách chứng minh như sau
Cách 1: Ý tưởng thức nhất là sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, tuy nhiên ta không
nên sử dụng trực tiếp vì bên vế phải có
222
xyz
trội hơn
2
xyz
. Do đó ta sẽ biến đổi vế trái
sao cho khi áp dụng có thể rút gọn được đại lượng
222
xyz. Từ nhận định đó ta được
2
222
222 4 4 4
222 222
xyz
xyz x y z
zxy
xz yx zy xz yx zy
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
222
222
xyz
3x y z
xz yx zy
Hay
222 2 2 2
xyz3xzyxzy
Để đồng bậc hóa bất đẳng thức ta chú ý đến
xyz1
, nên bất đẳng thức trên trở thành
222 2 2 2
xyzx y z 3xzyxzy
Hay
333 2 2 2 2 2 2
xyzxzyxzy2xzyxzy
Áp dụng bất đẳng thức Cauchy ta được
32 23 2 2322
xxz2xz;yyx2yx;zzy2zy
Cộng theo vế ba bất đẳng thức trên ta được
333 2 2 2 2 2 2
xyzxzyxzy2xzyxzy
Phép chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc3
.
Cách 2: Biến đổi tương đương bất đẳng thức và chú ý đến
xyz1
ta được
222
222
222
22
222
222
2
222
222
222
222
xyz
3x y z
zxy
xyz
xyz 3x y z xyz
zxy
xyz
xyz 3x y z xyz
zxy
xz yx zy
xy yz zx
zxy
111
xy 1 yz 1 zx 1 0
xyz
Vì
xyz1
nên
111
;; 1
xyz
. Do đó bất đẳng thức cuối cùng đúng.
Phép chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc3.
Bài 60: Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
222
abc1
2
a2b3b2c3c2a3
Phân tích và lời giải

Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta liên
tưởng đến đánh giá quen thuộc
22
a2b3a12b22a2b2
Áp dụng tương tự ta được
222
abc1abc
2a b 1 b c 1 c a 1
a2b3b2c3c2a3
Như vậy ta cần chứng minh
abc
1
ab1bc1ca1
Để có các đánh giá hợp lý trước hết ta đổi chiều bất đẳng thức
Thật vậy, bất đẳng thức trên tương đương với
abc
111312
ab1 bc1 ca1
Hay
b1 c1 a1
2
ab1bc1ca1
Bất đẳng thức trên làm ta liên tưởng đề bất đẳng thức Bunhiacopxki dạng phân thức
222
2
b1 c1 a1
ab1bc1ca1
b1 c1 a1
b1ab1 c1bc1 a1ca1
abc3
a1ac1 b1ba1 c1cb1
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc3
2
a1ac1 b1ba1 c1cb1
Để ý đến giả thiết
222
abc3
ta có
222
2
222
a1ac1 b1ba1 c1cb1
a b c abbcca3abc 3
191
a b c abbcca3abc abc3
222
Khi đó ta được
22
2
abc3 abc3
2
1
a1ac1 b1ba1 c1cb1
abc3
2
Vậy bất đẳng thức được chứng minh xong.
Bài 61. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
aba32
2
ab b bc c ca a
Phân tích và lời lời giải
Quan sát bất đẳng thức ta nhận thấy ý tưởng sử dụng bất đẳng thức Bunhiacopxki dạng phân thức
để đánh biểu thức vế trái hoặc là sử dụng bất đẳng thức Cauchy để đánh giá mẫu, nhưng trước hết để có
những đánh giá đảm bảo dấu đẳng thức ta dự đoán dấu đẳng thức xẩy ra tại
abc
.
Đầu tiên ta tiếp cận với bất đẳng thức Bunhiacopsxki dạng phân thức. Để ý là ta không nên sử
dụng trực tiếp vì khi đó dưới mẫu có các đại lượng mũ 2 nên sẽ trội hơn. Do đó ta sẽ đánh giá như sau

2
222 2 2 2
abc
aba
ab b bc c ca a a ab b b bc c c ca a
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
abc
32
2
aab b bbc c cca a
Để dễ dàng hơn ta chú ý đên đánh giá mẫu trước. Chú ý đến dấu đẳng thức xẩy ra thì ta có
2b a b. Do đó áp dụng bất đẳng thức Cauchy ta có
2b a b
a3b
2b. a b
22
Hoàn toàn tương tự ta được
222
222
a3abb3bcc3ca
aab b bbc c cca a
22 22 22
Khi đó ta sẽ được
22
222
222
abc abc
a3abb3bcc3ca
aab b bbc c cca a
22 22 22
Và như vậy ta cần phải chứng minh được
2
222
abc
3
4
a3abb3bcc3ca
. Hay
2
abc 3abbcca , đánh giá này là một đánh giá đúng, do đó bất đẳng thức được chứng
minh.
Bây giờ ta thử tiếp cận với bất đẳng thức Cauchy với đánh giá các mẫu xem sao. Để ý là
2
aab aab , tích này làm ta liên tưởng đến bất đẳng thức Cauchy dạng quen thuộc
2xy x y. Chú ý đến dấu đẳng thức xẩy ra ta được
2b a b
a3b
2b. a b
22
Áp dụng tương tự ta được
222
aba2a22b22c2
a3b b3cc3a
ab b bc c ca a
.
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2a 2 2b 2 2c 2 3 2
a3bb3cc3a 2
hay
abc3
a3bb3cc3a 4
Áp dụng bất đẳng thức Bunhiacopxki dạng phâm thức ta được
2
222
abc
abc
a3bb3cc3a
a b c 3ab 3bc 3ca
.
Ta cần phải chứng minh được
2
222
abc
3
4
a b c 3ab 3bc 3ca
Hay
2
222
4a b c 3a b c 3ab 3bc 3ca
Khai triển và thu gọn ta được
222
abcabbcca
, đây là một đánh giá đúng. Vậy bài
toán cũng được chứng minh

Nhận xét: Trong bài toán trên thì hai ý tưởng tiếp cận là như nhau, chỉ khác nhau ở chỗ là dùng công cụ
gì trước thôi. Ngoài ra ta có thể dùng phương pháp đổi biến để chứng minh bất đẳng thức
3
3334
abc
abbcca
Đặt
3; 3; 3 xa byb czc a. Từ đó suy ra
39 39 39
;;
28 28 28
xyz yzx zxy
ab a
Bất đẳng thức trên được viết lại thành
36
xyz yzx
yzx xyz
. Các bạn thử chứng
minh tiếp xem sao?
Bài 62: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
abc 111
abc
bca abc
Phân tích và lời giải
Quan sát bất đẳng thức ta thấy có các ý tưởng tiếp cận là sử dụng bất đẳng thức Cauchy, bất đẳng
thức Bunhiacopxki,…
Cách 1: Trước hết ta bắt đầu với bất đẳng thức Cauchy, tuy nhiên ta không thể sử dụng trực tiếp để đánh
giá vế trái hay vế phải vì sẽ tạo ra một đánh giá sai, do đó ta biến đổi tương đương bất đẳng thức cần
chứng minh trước
2
222
22 2
abc 111 a b c abc abc
abc 3
bca abc cab bca
bca
Đến đây ta quan sát thấy bên vế trái có
abc
cab
và bên vế phải có số 3 nên ta có
abc
3
cab
Mặt khác ta lại thấy vế trái có
222
22 2
abc
bca
và vế phải lại có
abc
bca
nên cũng theo bất đẳng thức
Cauchy ta được
222
22 2
a2ab2bc2c
1;1;1
bca
bca
Cộng vế với vế các bất đẳng thức trên ta được
222
22 2
abc abc
32
bca
bca
Theo bất đẳng thức Cauchy ta lại thấy
abc
3
bca
Do đó ta có
222
22 2
abc abc
33
bca
bca
Hay
222
222
abcabc
bca
bca
Kết hợp với bất đẳng thức
abc
3
cab
ta được
222
22 2
abcabc abc
3
cab bca
bca

Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Cách 2: Cũng như trên ta biến đổi bất đẳng thức cần chứng minh tương đương với
2
222
ac ba ca ab bc ca
abc
abc abc
Hay
2
222
a c b a c b abc a b c ab bc ca
Đến đấy từ
222
ac ba cb
đánh giá về
abc;abbcca
thì ta sử dụng bất đẳng thức
Bunhiacopxki, khi đó ta có
2
222
2
222
acbacbcba abbcca
111
ac ba cb a b c
cab
Nhân vế với vế 2 bất đẳng thức này ta được
2
22
222
111
acbaca abc abbcca abc
cab
Hay
2
22
222
ab bc ca
ac ba ca .a b c ab bc ca a b c
abc
Hay
2
222
ac ba ca abc ab bc ca a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài 55. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
222
a3b3c34abc1
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1, quan sát bất đẳng thức ta
thấy dấu hiệu sử dụng bất đẳng thức Bunhiacopxki.
Cách 1: Để ý là
22
a3a111
, Do đó áp dụng bất đẳng thức Bunhiacopxki ta có
22 2
2
2
bc bc bc bc
a 1111 1 1.a .1 .11.1
22 22
abc1
Hay
2
2
2
bc
4a 3 2 4a b c 1
2
Bài toán quy về chứng minh
2
22
bc
b3c3 42
2
Mặt khác, áp dụng bất đẳng thức Cauchy ta lại có
33 2222 222222
2
2
22
b 3 c 3 3b 3c b c 9 2b 2c b c b c 1 8
bc
2b 2c 2bc 2bc 8 2 b c 8 4 2
2
Như vậy ta được

2
2
222 2
bc
a3b3c34 4a34abc1
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Cách 2: Ngoài ra ta cũng có thể áp dụng bất đẳng thức Bunhiacopxki như sau
222
2
2
bc1 bc1 bc1
a1111
333
bc1bc1bc1
1.a
333
Hay
2
2
2
bc1
4a 3 1 4a b c 1
3
Ta cần chứng minh
2
22
bc1
b3c3 41
3
Thật vậy, biến đổi tương đương ta được
2
22 2222
22 2
bc1
b 3 c 3 41 3bc 5b c 8b c 8bc 11 0
3
2b c 2 b c 3bc 1 0
Bất đẳng thức cuối luôn đúng, do đó ta có
2
2
222 2
bc
a3b3c34 4a34abc1
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài 56. Cho a, b, c là các số thực dương thỏa mãn
abc9. Chứng minh rằng:
33 3333
abbcca
9
ab 9 bc 9 ca 9
Phân tích và lời giải
Quan sát bất đẳng thức ta nhận thấy tử của các phân thức chứa các đại lượng
33
ab ,
333 3
bc,ca
. Chú ý đến chiều của bất đẳng thức, các đại lượng đó làm ta liên tưởng đến bất đẳng
thức
3
33
4x y x y
, ngoài ra chú ý đến tích ab có thể đánh giá về
2
ab . Bây giờ ta thử
xem các phân tích đó có thể giả quyết được bài toán không?
Cách 1: Sử dụng bất đẳng thức quen thuộc
3
33
4x y x y ta có
3
33
33
4a b
ab
ab
ab 9 4ab 36 4ab 36
Mặt khác, theo bất đẳng thức Cauchy ta có
2
4ab a b
và
2
a b 36 12 a b
Do đó ta được

3
33
33
22
4a b
ab 36ab
ab
ab
ab 9 4ab 36
ab 36 ab 36
36 a b
ab ab3
12 a b
Áp dụng tương tự ta có
33 3 3
bc ca
bc3; ca3
bc 9 ca 9
Cộng vế theo vế ba bất đẳng thức trên, ta được
33 3333
abbc ca
2a b c 9 9
ab 9 bc 9 ca 9
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
.
Cách 2: Sử dụng bất đẳng thức quen thuộc
3
33
4x y x y
ta có
33
33
ab ab
a b 4ab 6 ab 9
3
ab 9 4ab 36 4ab 36 24 6 2
Áp dụng bất đẳng thức Cauchy ta được
33
3
ab ab
4ab 6 4ab 6 a b
333 3
4ab 36 24 4ab 36 24 2
Do đó ta được
33
3a b
ab ab9
bc 9 2 6 2
Tương tự ta có
33 3 3
3b c 3c a
bc bc9ca ca9
;
bc 9 2 6 2 ca 9 2 6 2
Cộng vế theo vế ba bất đẳng thức trên và kết hợp với đánh giá quen thuộc , ta được
33 3333
2
abbcca abbcca27
3a b c
ab 9 bc 9 ca 9 6 2
abc
27
3a b c 9
18 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3.
Bài 57. Cho a, b là các số thực dương thỏa mãn
ab13ab
. Chứng minh rằng:
22
3a 3b 1 1
1
ab
ba 1 ab 1
Lời giải
Biến đổi biểu thức vế trái ta được
22 22
22 2 2
ba1ab1
3ab 3ab 11 11
P
ab ab
ba1 ab1 ba1 ab1
Hay
22
ba11
P
ba1ab1 ba1ab1
Đặt
11
x;y
ab
, từ giả thiết ta suy ra xyxy3

Áp dụng bất đẳng thức Cauchy ta có
3 x y xy xy 2 xy xy 2 xy 3 0 xy 1 xy 3 0
Từ đó ta suy ra
xy 1
. Khi đó ta có
3xy 2
xy xy 1 1 x y 2
Pxyxy.xy.
x1 y1 x1 y1
x1y1 xyxy 1
2
2
2
xy 2xy 1 3xy 1
xy 5 xy xy 5xy
44 4
xy 1 3xy 1
31
44
Bài toán được chứng minh xong.
Đẳng thức xảy ra khi và chỉ khi
xy1
hay
ab1
Bài 58. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
333
abc
abc
b2c c2a a2b 9
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức trên ta nhận
thấy các dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức hoặc kỹ thuật thêm bớt trong bất
đẳng thức Cauchy. Bây giờ ta đi tìm lời giải theo các định hướng nêu trên
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
333 4 4 4
abc
abc a b c
b2c c2a a2b ab2ca bc2ab ca2bc
3ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
2
222
abc
abc
9
3ab bc ca
Thật vậy, ta cần chú ý hai bất đẳng thức quen thuộc
2
222
1
abc abc abbcca
3
Từ đó ta có
2
2
2
222 222
abc abcabc
abc
9
3ab bc ca 9ab bc ca
Bất đẳng thức đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Cách 2: Áp dụng bất đẳng thức Cauchy ta được
22
33 33
3
2
22
33 33
3
2
22
33 33
3
2
b2c b2c
aa aa
3a
b 2c b 2c 27 b 2c b 2c 27
c2a c2a
bb bb
3b
c2a c2a 27 c2ac2a 27
a2b a2b
cc cc
3c
a 2b a 2b 27 a 2b a 2b 27
Cộng theo vế các bất dẳng thức trên ta được

22 2
333
222
b2c c2a a2b
2a 2b 2c
abc
b2c c2a a2b 27 27 27
Hay
222
333
11 a b c 2 ab bc ca
abc
b2c c2a a2b 27
Ta cần chứng minh được
2
222
11 a b c 2 ab bc ca
abc
27 9
Hay
2
222
11 a b c 2 ab bc ca 3 a b c
Triển khai và thu gọn ta được
222
abcabbcca
. Bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức đã được chứng minh.
Bài 59. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
333
abc3
4
1b1c 1c1a 1a1b
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Bất đẳng thức này đã được chứng
minh bằng kỹ thuật thêm bớt trong chủ để về bất đẳng thức Cauchy. Ở đây ta trình bày thêm cách sử dụng
bất đẳng tức Bunhiacopxki dạng phân thức.
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
333
2
222
2
222
abc
1b1c 1c1a 1a1b
abc
a1 b 1 c b1 c 1 a c1 a 1 b
abc
2ab bc ca a b c 3abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra đươc
2
222
abc
3
4
2abbcca abc3abc
Hay
2
222
4a b c 6ab bc ca 3a b c 9abc
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
2
2
222
a b c abbcca 3abcabc 3abc
Do đó ta có
2
6abbcca 3abc 9 6abbcca abbcca 9
Ta cần chứng minh được
22
6abbcca abbcca 9 4abbcca
Hay
2
ab bc ca 2 ab bc ca 3 0
Hay
ab bc ca 1 ab bc ca 3 0
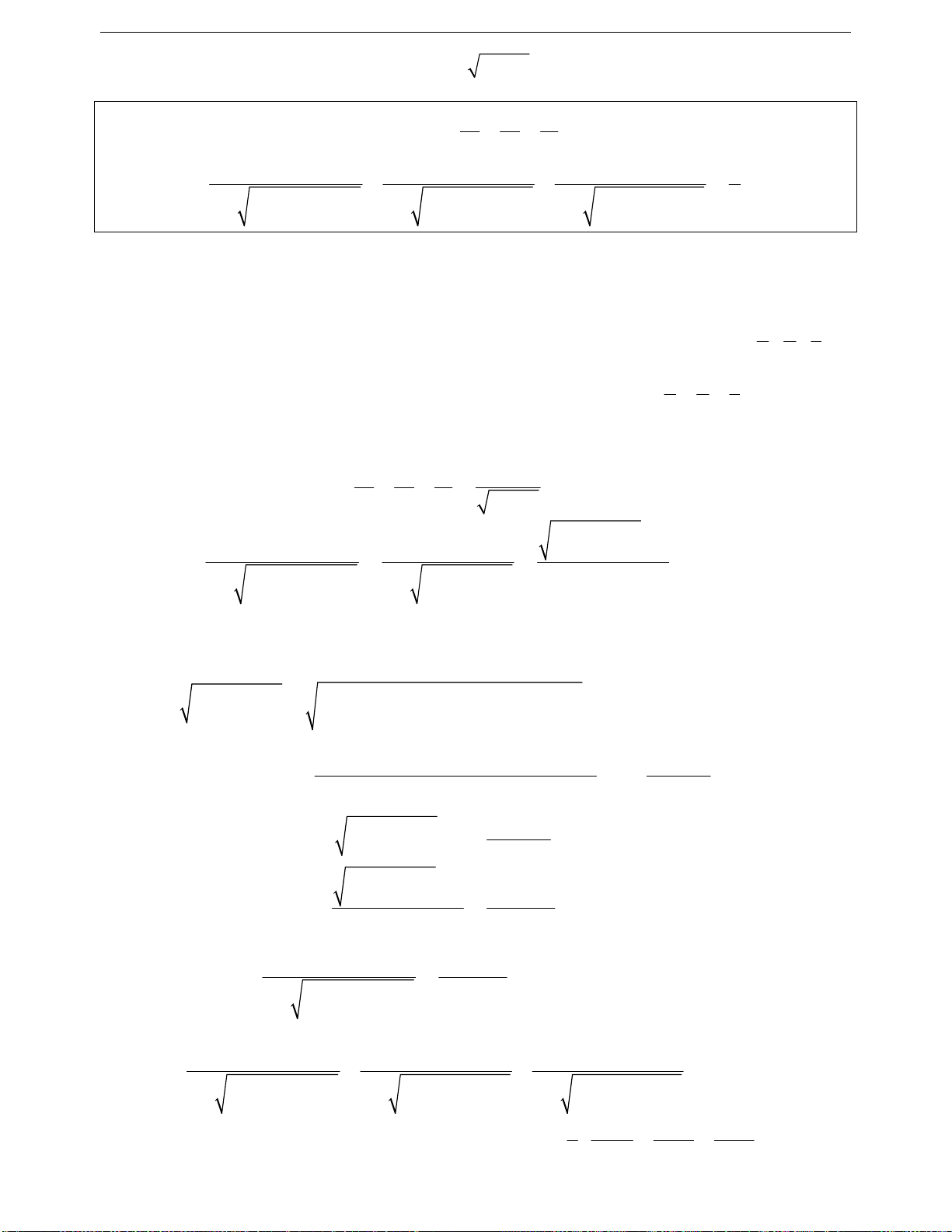
Đánh giá cuối cùng luôn đúng vì
3
222
ab bc ca 3 a b c 3 .
Bất đẳng thức đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
Bài 60. Cho a, b, c là các số thực dương thỏa mãn
222
111
3
abc
. Chứng minh rằng:
333
1113
4
1ababc1bcabc1caabc
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta nhận thấy
được sự phức tạp của bài toán. Để chứng minh được bất đẳng thức trên ta cần phải đơn giản hóa được các
căn thức ở các mẫu số, đồng thời khai thác thật khéo léo các giả thiết của bài toán. Quan sát kỹ giả thiết
và bất đẳng thức cần chứng minh ta nhận thấy nếu ta đánh giá được vế trái về đại lượng
111
;;
abc
thì
xem như bài toán được giải quyết. Dễ thấy từ giả thiết ta có thể suy ra được
111
3; abc 1
abc
.
Bây giờ ta đi tìm cách đánh giá các mẫu
Cách 1: Áp dụng bất đẳng thức Cauchy vào giả thiết ta được
222
3
222
111 3
3abc1
abc
abc
Do đó
3
3
33
ab 11
11
ab
1ababc1ab1
Để ý là khi
ab1 thì
2
1ab 1 ab ab
, do đó áp dụng bất đẳng thức Cauchy
ta có
32
2
2
ab 1 1ab1 ab ab
1ab 1 ab ab
ab
1
22
Suy ra
2
3
ab
ab 11
2
Hay
3
3
ab 11
1
2a b
ab
Do đó ta được
3
11
2a b
1ababc
Hoàn toàn tương tự ta được
333
111
1ababc1bcabc1caabc
11 1 1
2a b b c c a
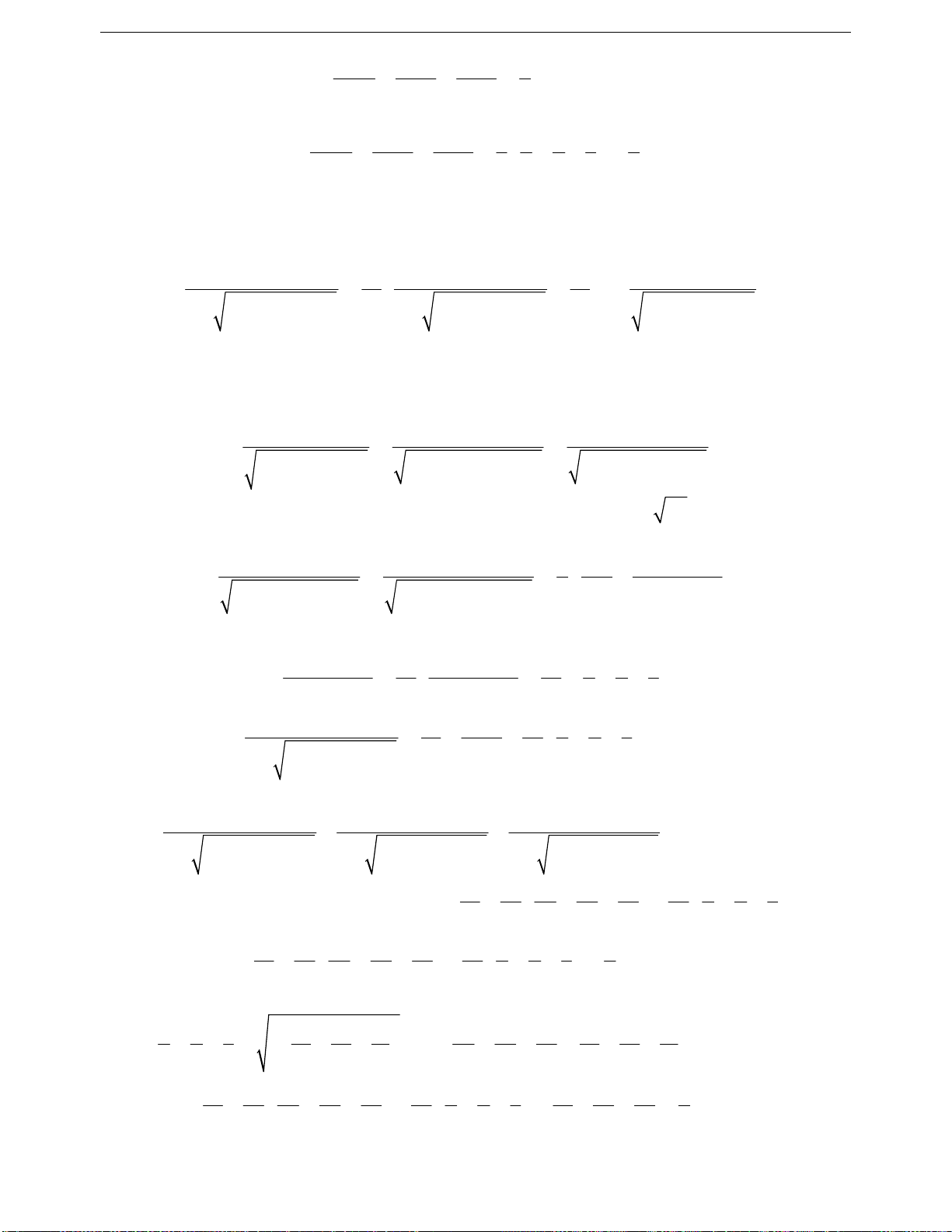
Ta cần chứng minh
1113
abbcca 2
Thật vậy, theo một đánh giá quen thuộc kết hợp với giả thiết ta được
11111113
abbc ca 2a bc 2
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Cách 2: Để ý thấy có số 1 ở dưới mẫu nên để dễ đánh mẫu hơn ta có thể áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức để tách số một ra khỏi mẫu số. Chú ý đến dấu đẳng thức xẩy ra ta được
2
333
13
11 1 9
1
16 16
1 a b abc 1 a b abc a b abc
Để ý lại thấy trong mẫu số có chứa đại lượng
abc nên nếu ta đánh giá được
3
ab về ab thì
có thể đặt được nhân tử chung. Áp dụng bất đẳng thức Cauchy ta có
2
a b 4ab, khi đó ta được
3
11 1
a b 4ab abc ab 4a 4b c
ab abc
Bây gờ để triệt tiêu căn bậc hai ta để ý đến bất đẳng thức Cauchy dạng
2xy x y. Chú ý là
cần bảo toàn dấu đẳng thức nên ta có
13211
39ab 4a 4b c
ab 4a 4b c 9ab 4a 4b c
Mặt khác lại theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
441
11 1441
4a 4b c 81 4a 4b c 81 a b c
Do đó ta được
3
1131441
16 32ab 96 a b c
1ababc
Áp dụng tương tự ta được
333
111
1 a b abc 1 b c abc 1 c a abc
33111 9111
16 32 ab bc ca 96 a b c
Ta cần chứng minh
33111 9111 3
16 32 ab bc ca 96 a b c 4
Thật vậy, Áp dụng hai bất đẳng thức quen thuộc ta được
222 222
111 111 1 11 111
33; 3
abc abbcca
abc abc
Từ đó suy ra
33111 9111 39273
16 32 ab bc ca 96 a b c 16 32 96 4
Bất đẳng thức được chứng minh xong.

Bài 61. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
22 22 22
ab2bc2ca2
12
abab bcbc caca
Phân tích và lời giải
Cách 1: Quan sát bất đẳng thức ta nhận thấy các mẫu số không đồng bậc, chú ý đến giả thiết của bài toán
ta viết lại được
22 22
22
ab2 ab2
ababbcca
ababc ab
Để ý là
22
22 22
ab2 2abbcca
1
a b ab bc ca a b ab bc ca
Khi đó áp dụng tương tự ta được bất đẳng thức cần chứng minh trở thành
22 22 22
2abbcca 2abbcca 2abbcca
9
a b ab bc ca b c ab bc ca c a ab bc ca
Bất đẳng thức có các tử giống nhau nên áp dụng một đánh giá quen thuộc ta được
22 22 22
222
2abbcca 2abbcca 2abbcca
a b ab bc ca b c ab b c ca c a ab bc ca
92 ab bc ca
2a b c 3ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
2abbcca
1
2a b c 3ab bc ca
Để để triệt tiêu các đại lượng âm trên tử số ta chú ý đến
2
abc 1
, khi đó ta có
2
222 222
2a b c ab bc ca
2abbcca
1
2a b c 3ab bc ca 2a b c 3ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc
3
.
Cách 2: Kết hợp với giả thiết ta có biến đổi như sau
22
abab ababc aba b abbcca
Do đó ta có
22 22
22
22
22 22
ab2 ab2
abab
ababbcca
a1 b1
ababbccaababbcca
Áp dụng tương tự ta được
22 2 2
22 22
bc2 b1 c1
bcbc
bcabbccabcabbcca
22 2
22 22
cba2 c1 a1
caca
caabbccacaabbcca
Mặt khác theo bất đẳng thức Cauchy ta được

22
22 22
22
2
222
2
a1 a1
a b ab bc ca c a ab bc ca
4a 1 4a 1
4
2a b c 2 ab bc ca
aabc
Áp dụng tương tự ta được
22
22 22
22
22 2 2
b1 b1
4
b c ab bc ca b a ab b c ca
c1 c1
4
b c ab bc ca c a ab bc ca
Cộng theo vế các kết quả trên ta được
22 22 2
ab2bc2cba2
12
abab bcbc caca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc
3
.
Bài 62. Cho các số thực thỏa mãn
a, b , c (0 ; 1)
và
abc 1 a 1 b 1 c
.
Chứng minh rằng:
24 2424
ab bc ca 15
bca8
Phân tích và lời giải
Quan sát bất đẳng thức ta nhận thấy cần phải đổi biến để làm mất đi các dấu trừ bên vế phải, do đó
rất tự nhiên ta nghĩ đến phép đổi biến
xab;yb1;zc1 , tuy nhiên quan sát kỹ giả thiết thì
ta có thể biến đổi
abc 1 a 1 b 1 c
1a1b1c
1
abc
Đến đây ta đặt
1a 1b 1c
x;y;z
abc
.
Khi đó ta có
xyz 1 và
111
a;b;c
1x 1y 1z
Do
xyz 1 nên trong các số x, y, z có hai số nằm cùng phía so với 1, giả sử hai số đó là x và y.
Khi đó ta có
1z
x1y1 0 xy 1xy
z
Áp dụng bất đẳng thức Bunhiacopxki ta được
22
11 1 1
xy
1x 1y
1xy1 1xy1
yx
yx1z
1xy 1z
1xyxy 1xyxy
Từ đó ta được
222
222
2
22 2
111
abc
1x 1y 1z
z1 z 1 2z 1
z1 33
1z 4 4
1z 1z 41z
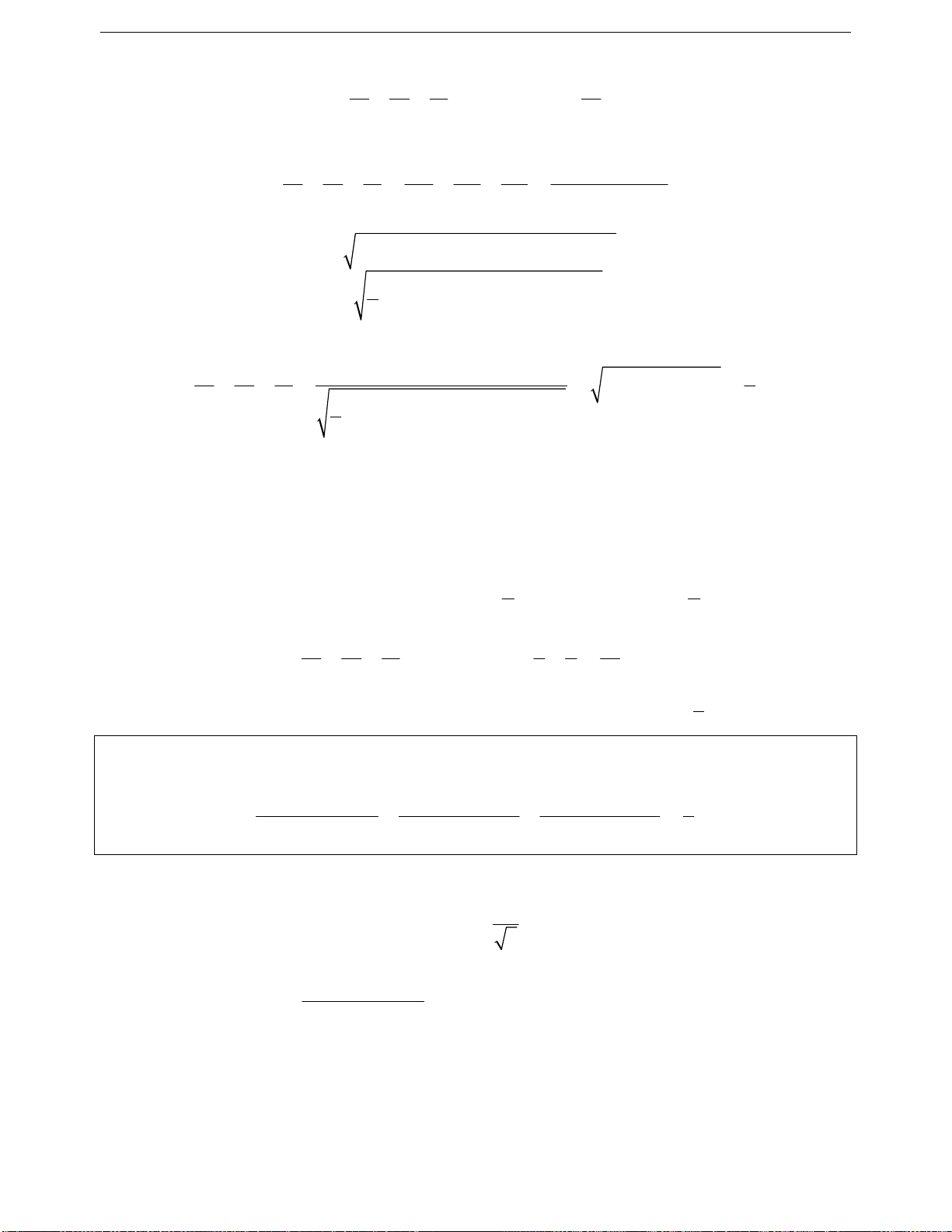
Bất đẳng thức trên viết lại được thành
222
333
abc 15
abc
bca 8
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222
222 4 4 4
222 222
abc
abc a b c
bca
ab bc ca ab bc ca
Mà cũng theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 222222222
2
222222
ab bc ca a b c ab bc ca
1
abcabc
3
Từ đó suy ra
2
222
222
222
2
222222
abc
abc 3
3a b c
bca 2
1
abcabc
3
Mặt khác ta lại có
2
333 222
2
222
abcabc abc
3a b c a b c
Do đó ta được
3
23
333 222 333
33
3abc abc abc
48
Từ các kết quả trên ta được
222
333
abc 3315
abc
bca 288
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
.
Bài 63. Cho a, b, c là các số thực dương thỏa mãn
0 a,b,c 1 và ab bc ca 1. Chứng minh
rằng:
22 22 22
22 22 22
ab bc ca 9
2
1a 1b 1b 1c 1c 1a
Phân tích và lời giải
Quan sát bất đẳng thức ta nhận thấy được sự phức tạp của bài toán, để có các đánh giá hợp lý trước
hết ta dự đoán dấu đẳng thức xẩy ra tại
1
abc
3
. Bất đẳng thức có tính đối xứng nên ta sẽ đi
phân tích một biểu thức rồi áp dụng tương tự
Quan sát biểu thức
22
22
ab
1a 1b
ta thấy được dấu hiệu sử dụng bất đẳng thức quen thuộc
2
22
2a b a b
, như vậy trên tử xuất hiện bình phương đúng nên rất tự nhiên ta nghĩ đến bất
đẳng thức Bunhiacopxki dạng phân thức. Tuy nhiên để ý là ta viết mẫu số thành
2222
1a b ab lại
trội hơn nên muốn đánh giá vế đại lượng lớn hơn sẽ rất khó khăn. Từ đó ta nghĩ đến việc tìm ra mối liên
hệ giữa tử và mẫu. Để ý là ta chứng minh được
2
22
1a 1b 1ab, nên ta cần đánh giá tử số

về
2
1ab hoặc
2
1ab . Nhận thấy
22
22
22 22
1a 1b
ab 1
2
1a 1b 21a 1b
, nên chú ý đến bất
đẳng thức Bunhiacopxki ta lại có
2
22
1a 1b 1ab suy ra
2
22
2
22
1a 1b
1ab
1a 1b
1ab
.
Bây giờ ta biến đổi tương tự xem ta sẽ thu được kết quả như thế nào?
Bất đẳng thức cần chứng minh tương đương với
22 22 22
22 22 22
22 22 22
22 22 22
ab bc ca 3
6
2
1a 1b 1b 1c 1c 1a
1a 1b 1b 1c 1c 1a
12
1a 1b 1b 1c 1c 1a
Theo phân tích như trên ta có
2
22
2
22
1a 1b
1ab
1a 1b
1ab
Áp dụng tương tự ta được
22
22 2 2
22
22 2 2
1b 1c 1c 1a
1bc 1ca
;
1b 1c 1c 1a
1bc 1ca
Cộng theo vế các bất đẳng thức trên ta được
222
22 22 22
222
22 22 22
1a 1b 1b 1c 1c 1a
1ab 1bc 1ca
1a 1b 1b 1c 1c 1a
1ab 1bc 1ca
Áp dụng bất đẳng thức Cauchy ta được
222 222
3
222 222
1ab 1bc 1ca 1ab 1bc 1ca
3
1ab 1bc 1ca 1ab 1bc 1ca
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
1ab 1bc 1ca
64
1ab 1bc 1ca
Hay ta cần chứng minh
1ab1bc1 ca 81ab1bc1ca
.
Đặt
xab;ybc;zca
, khi đó
x, y, z 0
và xyz1. Bất đẳng thức cần chứng
minh trở thành
1x1y1z 81x1y1z, tương đương với bất đẳng thức sau
9xyz 7 xy yz zx 2
Ta dễ dàng chứng minh được
222
9xyz
x y z 2 xy yz zx
xyz
.
Mà
xyz1 nên ta suy ra được
9xyz 4 xy yz zx 1. Vì xyz1 nên
3xy yz zx 1 , do đó
4xyyzzx 17xyyzzx 2
Điều này dẫn tới
9xyz 7 xy yz zx 2
.
Như vậy bất đẳng thức ban đầu được chứng minh xong.

Bài 64. Cho a, b, c là các số thực thỏa mãn
a, b , c [1; 2]
. Chứng minh rằng:
333
abc5abc
Lời giải
Cách 1: Bất đẳng thức cần chứng minh có tính đối xứng giữa các biến, do đó ta không mất tính tổng quát,
ta giả sử
1cba2. Khi đó dễ thấy
babc 0
Hay
2
bbacac. Từ đây ta suy ra
2
32
b b a c abc b a c ac a c ab c b a c ac a c abc
Như vậy ta cần chứng minh
2
33
a c b a c ac a c abc 5abc
Hay
22
ac ac bac 6abc
Để ý rằng do
a, b , c [1; 2] nên a22cbc , từ đó dẫn đến 0acb
Như vậy ta có
22 2
ac ac bac bacac bac
2ab a c 2ab 2c c 6abc
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
a2;bc1 và các hoán vị của nó.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
222
abc
5
bc ca ab
Bất đẳng thức cần chứng minh có tính đối xứng giữa các biến, do đó ta không mất tính tổng quát, ta
giả sử
1cba2. Khi đó dễ thấy
22
cbb a 0
Từ đó suy ra
3222
bcbbaac hay
2
bbaa
ac a c b
Mặt khác ta cũng có
22
ccc
ab ac a
và
2
a2a2c
bc bc b
Từ các đánh giá trên ta thu được
222
abc ba ac
bc ca ab a b c a
Vì
ba2 nên
2b
1
a
và
a1
1
b2
. Do vậy
2b a 1
10
ab2
hay
ab5
ba 2
.
Chứng minh tương tự ta được
ac5
ca 2
Từ hai đánh giá trên ta được
222
abc ba ac 55
5
bc ca ab a b c a 2 2
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
a2;bc1
và các hoán vị của nó.
Bài 65. Cho a, b, c là các số thực dương thỏa mãn
111
1
ab1bc1ca1
.
Chứng minh rằng: abcabbcca
Lời giải

Quan sát bất đẳng thức ta thấy giả thiết là một bất đẳng thức nên để có các đánh giá hợp lí ta cần
nghĩ đến việc đánh giá lại bất đẳng thức giả thiết trước. Quan sát giả thiết ta thấy có dấu hiệu sử dụng bất
đẳng thức Bunhiacpxki nên ta thử xem có đánh giá được hay không.
Cách 1: Trước hết ta để ý đến các mẫu số, để đồng bậc ta áp dụng bất đẳng thức Bunhiacopxki thì được
2
2
ab1abc abc
, hoàn toàn tương tự ta được
222
222
222 222
222 2
111
ab1bc1ca1
abc bca cab
abc ab1 bca bc1 cab ca1
abc bca cab abc bca cab
abc abc abc abc
Do đó ta được
222
2
abc bca cab
1
abc
Hay
2
222
abc abc bca cab
Hay
abcabbcca
Vậy bất đẳng thức được chứng minh xong. Dấu đẳng thức xẩy ra tại
abc1.
Cách 2: Cũng bắt đầu với giả thiết nhưng ta biến đổi tương đương điều kiện ta được
111
1
ab1bc1ca1
111
1112
ab1 bc1 ca1
ab bc ca
2
ab1bc1ca1
Vế trái của giả thiết làm ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng phân thức
222
2
222
ab bc ca
ab1bc1ca1
ab bc ca
abab1 bcbc1 caca1
abbcca
ab bc ca 2abc
Từ đó suy ra
2
222
abbcca
2
ab bc ca 2abc
Hay
2222
abbcca 2ab bc ca 2abc
Biến đổi tương đương và thu gọn ta được
ab bc ca a b c
Vậy bất đẳng thức được chứng minh xong.

Nhận xét: Ngoài hai cách như trên ta có thể tham khảo thêm cách chứng minh phản chứng sau đây: Giả
sử tồn tại các số dương a, b, c thỏa mãn
111
1
111
ab bc ca
và abcabbcca
Từ đó suy ra
1
ab bc ca
abc
Khi đó ta có
1
1
ab bc ca
ab bc ca
abc
ab abbcca
ababc abbcca
ab
abc
Áp dụng tương tự ta được
1
ab bc ca ab bc ca
ababc abbcca bcabc abbcca
ab bc ca
caabc abbcca
Hay
22 22
22
1
aabb bbcc
ababc abbcca bcabc abbcca
ccaa
caabc abbcca
Mặt khác
22 22
2
22
22
2
2
3
.
4
33
..
44
3
1
23
aabb bbcc
ababc abbcca bcabc abbcca
ab
ccaa
caabc abbcca ababc abbcca
bc ca
bcabc abbcca caabc abbcca
abc
abc abbcca
Từ đó ta được
11 (vô lí). Vậy điều giả sử là sai.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1abc .
Bài 66. Cho a, b, c thỏa mãn
222
a4;b5;7c6;a b c 90 . Chứng minh rằng:
abc16
Phân tích và lời giải

Quan sát giả thiết của bài toán thì ý suy nghĩ đầu tiên là đổi biến, khi đó ta thực hiện đặt
ax4,by5,cz6 , suy ra ta được x, y, z 0 .
Từ giả thiết
222
abc90, ta được
222
x4 y5 z6 90 hay
222
x y z 8x 10y 12z 13
Giả sử ta có
xyz1, mà
x, y, z 0
suy ra
222
xyz1
Ta có:
222 222
xyz8x10y12zxyz 8xyz2yz2z
1822xyz182213
Điều này vô lí, vì vậy
xyz1
Do đó ta có
abc 4x5y6z15xyz16
Bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
a4;b5;c7.
Ngoài ra từ giả thiết
222
a4;b5;7c6;a b c 90 , nên ta sẽ có các điều kiện
4a9;5b8;6c7
. Từ các điều kiện trên ta có
2
2
2
a36
4a9 a49a 0 a
13
b40
5b8 b58b 0 b
13
c42
6c7 c67c 0 c
13
Cộng vế theo vế các bất đẳng thức trên ta được
222
a b c 423640
abc 16
13
Bài toán được chứng minh xong.
Bài 67. Cho a, b, c là các số thực dương thỏa mãn
222
111
1
abc
. Chứng minh rằng:
222222
1113
3
5a 2ab 2b 5b 2bc 2c 5c 2ca 2a
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki vào giả thiết ta được
2
222
1111111 111
13
3a b b a b b
abc
Mặt khác ta có
22 2
22
5a 2ab 2b 2a b a b 2a b
Suy ra
22
5a 2ab 2b 2a b
Do đó ta được
22
11112
2a b 9 a b
5a 2ab 2b
Chứng minh tương tự ta được
22 22
1112 1112
;
9b c 9c a
5b 2bc 2c 5c 2ca 2a
Cộng theo vế các bất đẳng thức trên ta được

222222
11111113
3a b c 3
5a 2ab 2b 5b 2bc 2c 5c 2ca 2a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc 3
.
Bài 68. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
a1 b1 c1
2
abc
Phân tích: Bất đẳng thức cần chứng minh được viết lại thành
222
a1 b1 c1 2abc
Chú ý đến đánh giá
22
a1 2a 2a12a 2a1
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
22
a1 2a 2a12a 2a1
Áp dụng tương tự ta có
22
b 1 2b 2 b 1 ; c 1 2c 2 c 1
Cộng theo vế các bất đẳng thức trên ta được
222
a 1 b 1 c 1 2a 2b 2c 2 a b c 3
Hay
222
a1 b1 c1 2abc3 2a b c
Mặt khác theo bất đẳng thức Cauchy ta có
3
abc3abc3
Nên
2a b c 3 2 a b c 2a b c 3 32
2a b c
Do vậy ta được
222
a1 b1 c1 2abc
Suy ra ta được
222
2a b c
a1 b1 c1
2
abc abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 69. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
33 3
abc
1
b8 c8 a8
Phân tích: Dấu đẳng thức xẩy ra tại abc1. Khi đó chú ý đến đánh giá theo bất đẳng thức
Cauchy
2
32
bb6
b8 b2b2b4
2
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2
32
bb6
b8 b2b2b4
2
Tương tự ta có
22
33
aa6 cc6
a8 ;c8
22
Khi đó ta được bất đẳng thức sau
222 2 2 2
222
33 3
abc 2a 2b 2c
bb6cc6aa6
b8 c8 a8

Ta cần chứng minh
222
222
abc1
2
bb6cc6aa6
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222
222
abc
abc
bb6cc6aa6
abc abc18
Ta cần chỉ ra được
2
222
abc
1
2
abc abc18
Hay
2
222
2abc a b c abc 18
Hay
2
abc abc 120
Hay
abc4abc3 0
Bất đẳng thức cuối cùng đúng vì
2
abc 3abbcca 9 abc3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 70. Cho các số thực
a, b , c [0;1] . Chứng minh rằng:
111
3abc
2a 2b 2c
Phân tích: Để ý đến đánh giá
22
1
a 1 2a 2a a 1 a 2 a 1 a
2a
, do đó bài
toán quy về chứng minh
abc3abc . Với giả thiết a, b, c [0;1] ta thu được đánh giá
222
abc3 nên
222
3abc a b c abc 9abc .
Lời giải
Theo bất đẳng thức Cauchy ta có
22
1
a 1 2a 2a a 1 a 2 a 1 a
2a
Áp dụng tương tự được
11
b; c
2b 2c
Do đó ta được
111
abc
2a 2b 2c
Ta cần chứng minh
abc3abc
Thật vậy, do
a, b , c [0;1]
nên ta có
222
abc3
Áp dụng bất đẳng thức Cauchy ta suy ra
3
3
222 222
3abc a b c abc 3abc.3abc 9abc
Hay
abc3abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 71. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
11127
1ab 1bc 1ca 8
Lời giải
Từ giả thiết
abc1 ta suy ra
1
abc
27
.
Bất đẳng thức cần chứng minh tương đương với

1ab1bc 1bc1ca 1ca1ab
27
8
1ab1bc1ca
Hay
222
32abbcca abcabc
27
8
1abbccaabcabcabc
Hay
222
832abbcca abc 271 abbcca abcabc
Hay
222
222
311abbcca 19abc27abc 0
4 3 19abc 27a b c 11.4 ab bc ca
Từ bất đẳng thức quen thuộc
abcbcacab abc
suy ra
12a12b12c abc
Hay
11.4 ab bc ca 11 1 9abc
Ta cần chứng minh
222
4 3 19abc 27a b c 11 1 9abc
Thật vậy, bất đẳng thức trên tương đương với
1 27abc 1 4abc 0
Bất đẳng thức cuối cùng đúng do
1
abc
27
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 72. Cho các số thực dương a, b thỏa mãn
22
abab. Chứng minh rằng:
10 3
a2b
2
Phân tích: Để ý là
22
22
111
abab a b
222
và khi đó phân tích
a2b
theo
11
a;b
22
như sau
113
a2b a 2b
222
.
Lời giải
Ta biến đổi giả thiết như sau
22
22
111
abab a b
222
Biểu thức vế trái được viết lại như sau
113
a2b a 2b
222
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22
2
11 1115
a2b 12a b 5.
22 2222
Do đó ta được
115
a2b
222
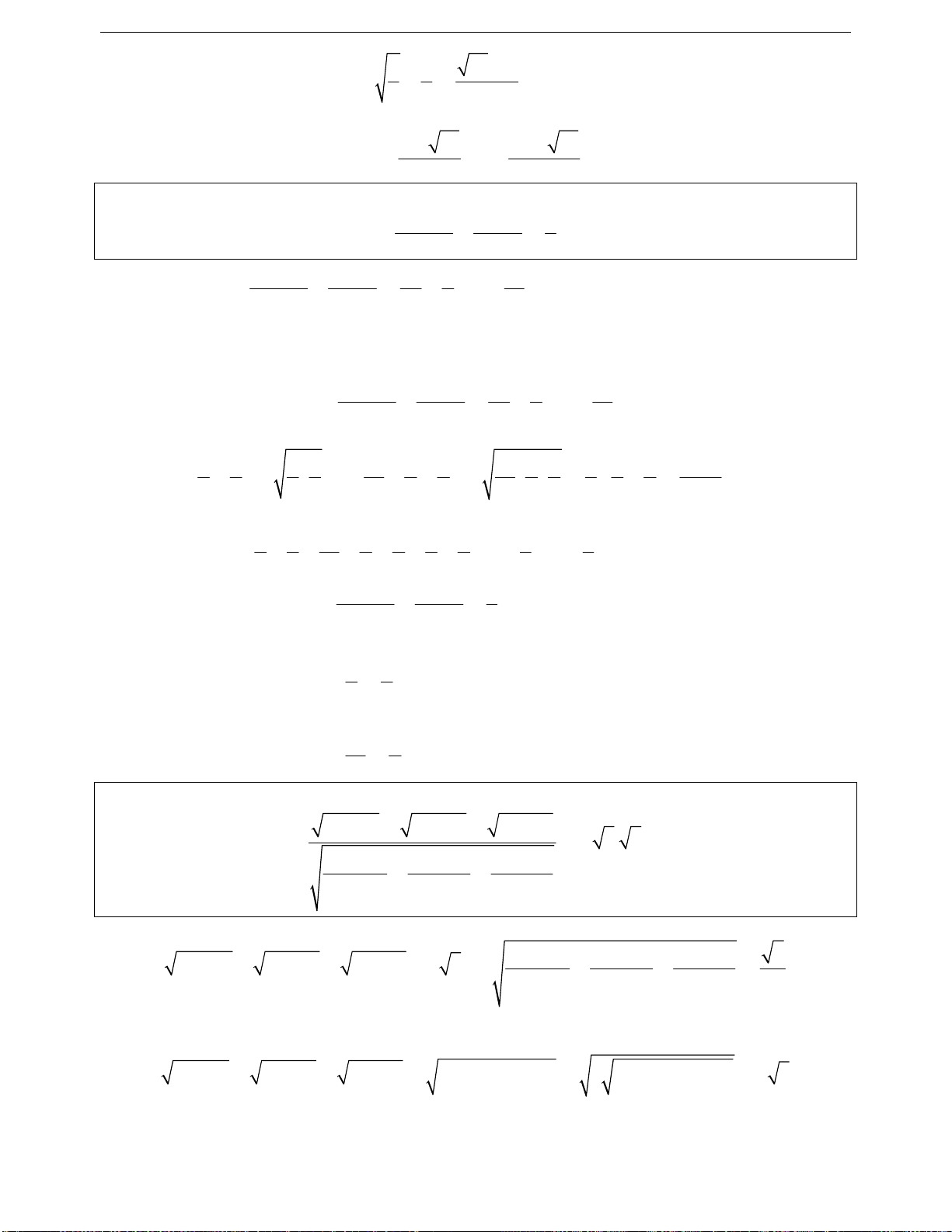
Suy ra
53 103
a2b
22 2
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
510 5210
a;b
55
.
Bài 73. Cho a, b là các số thực dương thỏa mãn
ab3
. Chứng minh rằng:
23
2
3a 4 b 2 9
4a 2
b
Phân tích: Để ý là
23
22
3a 4 b 2 3a 1 2
b
4a 4 a
bb
, đến đấy ta nghĩ đến sử dụng bất đẳng thức
Cauchy.
Lời giải
Biểu thức P được viết lại như sau
23
22
3a 4 b 2 3a 1 2
b
4a 4 a
bb
Áp dụng bất đẳng thức Cauchy và giả thiết ta được
3
22
a1 a1 2 bb 2bb 3abab
2. 1; 3 .. ; 2
4a 4a 44 44 222 2
bb
Cộng theo vế các bất đẳng thức trên ta được
2
a1 2 bbab 3 9
12
4a 4422 2 2
b
Hay
23
2
3a 4 b 2 9
4a 2
b
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
2
a1
4a
a2
ab4
b2
2b
4
b
Bài 74. Cho a, b, c là các số thực dương thỏa mãn
444
abc3. Chứng minh rằng:
22 22 22
3
3
333
ab bc ca
2. 2. 9
111
ab bc ca
Phân tích: Chú ý đến dấu đẳng thức xẩy ra, ta quy bài toán về chứng minh hai bất đẳng thức sau
22 22 22
ab bc ca 32
và
3
3
333
1113
2
ab bc ca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
22 22 22 222 444
ab bc ca 6abc 63abc 32
Mặt khác ta lại có
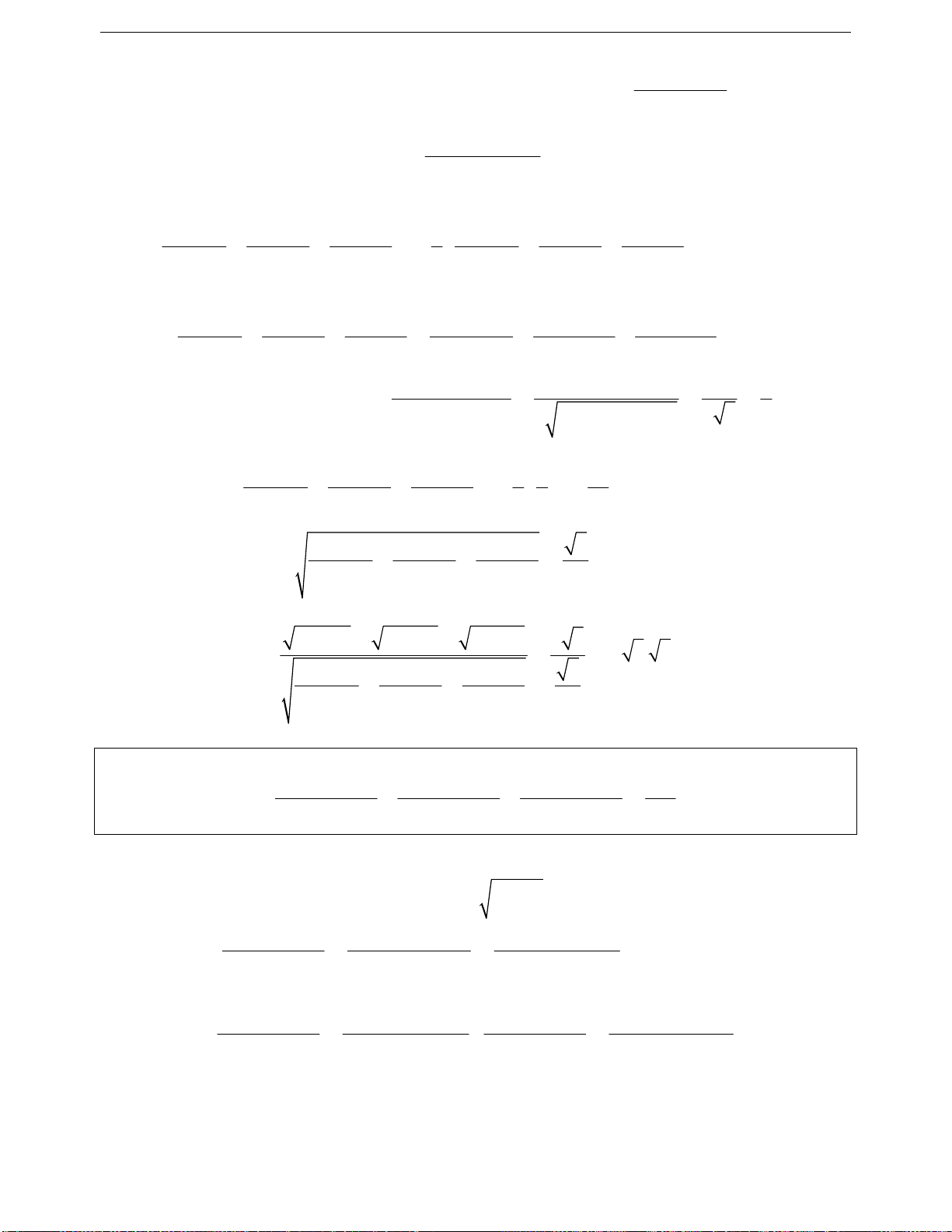
2
2
4
333 222 222
xyz
xyzxyz xyz;xyz
3
Do đó ta được
3
222
2
333
xyz
xyz
3
Áp dụng kết quả trên ta được
23
333 222
1111111
3
ab bc ca ab bc ca
Mà theo bất đẳng thức Cauchy ta được
222
22 22 22
222
444
111 1 1 1
2a b 2b c 2c a
ab bc ca
9993
4
4a b c
49
43a b c
Do đó ta có
2
3
333
111139
34 64
ab bc ca
Suy ra
3
3
333
1113
2
ab bc ca
Từ các kết quả trên ta được
22 22 22
3
3
3
333
ab bc ca 32
2. 2 . 9
1113
2
ab bc ca
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 75. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
1111
abc
1abc 1ba c 1ca b
Lời giải
Áp dụng bất đẳng thức Cauchy cho giả thiết ta được
2
3
3abbcca3abc abc1
Khi đó ta có
22
11 1
1abc abcabc aabbcca
Chứng minh tương tự ta được
22
1111
;
1bca babbcca 1cab cabbcca
Cộng theo vế các bất đẳng thức trên ta được

222
111
1abc 1ba c 1cab
1111 1abbcca1
.
ab bc ca a b c ab bc ca abc abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 76. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
242424
222
1
a1 b1 b1 c1a1 b1
Phân tích: Để ý đến đánh giá
2
24442222
a 1 b 1 a b 2a 2 2a b 2a 2
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
2
24442222
a 1 b 1 a b 2a 2 2a b 2a 2
Áp dụng tương tự ta được
222
242424
22 2 22 2 22 2
222
a1 b1b1 c1a1 b1
111
ab a 1 bc b 1 ca c 1
Ta cần chứng minh
22 2 22 2 22 2
111
1
ab a 1 bc b 1 ca c 1
Cách 1: Do
222
abc 1 a b c 1 , nên ta đặt
222
xyz
a;b;c x;y;z0
yzx
Khi đó ta có
22 2 22 2 22 2
111111
xx yy zz
ab a 1 bc b 1 ca c 1
111
zy xz yx
yz xz yy
1
xy yz zx xy yz zx xy yz zx
Cách 2: Do
222
abc 1 a b c 1 , nên ta được
222
2 2 2 2 22 22 2 2 2 2 22 2
22 2
22 2 22 2 22 2
111 abc 1 b
ab a 1 bc b 1 ca c 1
ab a abc bc b 1 cab bc b
bc 1 b
1
bc b 1 bc b 1 1 bc b
Bất đẳng
thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài 77. Cho a, b, c là các số thực dương tùy ý . Chứng minh rằng:
222
abc1
3
2b c 2c b 2c a 2a c 2a b 2b a
Phân tích và lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc. Để ý đến chiều của bất đẳng thức và các mẫu
số ta liên tưởng đến bất đẳng thức Cauchy dạng
2
4xy x y. Khi đó ta được
22
3b 3c 9 b c
2b c 2c b
44

Áp dụng tương tự ta được
22
9c a 9a b
2ca2ac ;2ab2ba
44
Khi đó ta được bất đẳng thức
222
22 2
abc
2b c 2c b 2c a 2a c 2a b 2b a
4a b c
9bc ca ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2
abc3
bc ca ab 4
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki ta được
22 2 2
abc1abc
bc ca ab 3bc ca ab
Mà ta dễ dàng chứng minh được
abc3
bc ca ab 2
Do đó
22 22
abc133
bc ca ab 32 4
Vậy bất đẳng thức được chứng minh xong.
Bài 78. Cho a, b, c là các số thực dương thỏa mãn
333
abc3
. Chứng minh rằng:
ab bc ca 3
2
3c 3a 3b
Phân tích và lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Để ý ta không thể thay 3 bởi đại lượng
333
abc
vì đại lượng này có số mũ cao sẽ gây khó khăn cho các đánh giá tiếp theo. Do đó trước hết
ta cần đơn giản hóa giả thiết. Áp dụng bất đẳng thức Cauchy ta được
333
3abc a b c 6 9 abc 3
Và
2
1
ab bc ca a b c 3
3
Để đơn giản hóa bất đẳng thức ta cần khử các căn bậc hai, chú ý đến chiều bất đẳng thức ta liên
tưởng đến bất đẳng thức Bunhiacopxki
2
ab bc ca ab bc ca
ab bc ca
3c 3a 3b
3c 3a 3b
ab bc ca
3
ac bc ba ca bc ba
Đến đây áp dụng một đánh giá quen thuộc ta được

ab b c ca
ac bc ba ca bc ba
1ab ab bc bc ca ca
4acbcbacabcba
13
abc
44
Do đó ta được
2
ab bc ca 9
4
3c 3a 3b
hay
ab bc ca 3
2
3c 3a 3b
Vậy bất đẳng thức được chứng minh xong.
Bài 79. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
333333333
1111
2
2a 1 b c 2b 1 c a 2c 1 a b
Phân tích và lời giải
Quan sát bất đẳng thức cần chứng minh thì suy nghĩ đầu tiên là đổi biến nhằm đơn giản hóa bất
đẳng thức. Tuy nhiên ở đây ta không dựa vào giả thiết
abc 1 để đổi biến, mà ta chú ý đến các đại
lượng
333
2a 1;b c
, có nghĩa là ta nghĩ đến đánh giá theo bất đẳng thức Cauchy cho hai số, nên để
đánh giá không xuất hiện các căn bậc hai thì ta đổi biến theo cách đặt
323232
ax,by,cz, từ
giả thiết suy ra
xyz 1
. Lúc này áp dụng bất đẳng thức Cauchy ta được
22 3 22
y z 2yz; x x 2x ; x 1 2x
Do đó ta thu được
3332222
111
2a 1 b c 2x 1 y z 2x 1 yz
Để ý đến giả thiết
xyz 1
, ta có
2322
1xxx1
2x 2
2x1yz2xx122x12x2x
Áp dụng tương tự ta được bất đẳng thức cần chứng minh
111
1
x2 y2 z2
Do
xyz 1 nên ta đặt
mn p
x;y;z
npm
Khi đó bất đẳng thức trên trở thành
npm
1
m2n n2p p2m
Biến đổi tương đương ta được bất đẳng thức
mn p
1
m2n n2p p2m
Sử dụng bất đẳng thức Bunhiacopxki ta được
222
222
2
222
mn p m n p
m2n n2p p2m
m2nmn2pnp2mp
mnp
1
mnp2nm2pn2mp
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xảy ra khi
abc1
.
Bài 80. Cho a, b, c là các số thực dương thỏa mãn
222
abc 3
. Chứng minh rằng:

22 22 22
222
ab 7 bc 7 ca 7
6
ab bc ca
Phân tích và lời giải
Quan sát bất đẳng thức ta thấy có số 7, vậy thì số 7 này có ý nghĩa gì trong bài toán. Để ý đến giả
thiết
222
abc 3 và các đại lượng bậc hai trong bất đẳng thức, ta có thể viết được
222
712a b c
. Khi đó ta có
22 2 2 2
22
22
ab 1 2 a b c
ab 7
ab ab
Chú ý là nếu trên tử có đại lượng
2ab thì ta có thể kết hợp với
22
ab
để tạo ra
2
ab
, để ý đến
chiều bất đẳng thức thì theo bất đẳng thức Cauchy ta sẽ được
22 2 2 2 2 2 2
22 2
222
ab 1 2 a b c 2ab 2 a b c
ab2c
1
ab ab ab
Lại để ý ta thấy
2
22
ab 2a b
nên ta được
22 2 22 2 2
222
22
a b 2c a b 2c 3 c
11
2
ab
2a b
ab
Do đó ta có
22 2
222
ab 7 3 c
2
ab
ab
Áp dụng tương tự ta được bất đẳng thức cần chứng minh
22 22 22 2 2 2
222222222
ab 7 bc 7 ca 7 9 c b a
2
abca bc
ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
2222 22
cba3
2
abca bc
Thật vậy, theo bất đẳng thức Bunhiacopxki ta được
2
222 222222
222
2222 22
22 22 22 22 22 22
abc 3abbcca
cba 3
2
abca bc
2ab bc ca 2ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1.
Nhận xét: Ngoài ra ta có thể quy bài toán về chứng minh bất đẳng thức
22 2 22 2 2 2 2
22 2
22 2
3
ab c bc a ca b
ab bc ca
Áp dụng bất đẳng thức Cauchy ta được
22 2 22 2 2 2 2
22 2
2222 2222 2
3
22 2
22 2
222
3.
ab c bc a ca b
ab bc ca
abca bcab c
ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
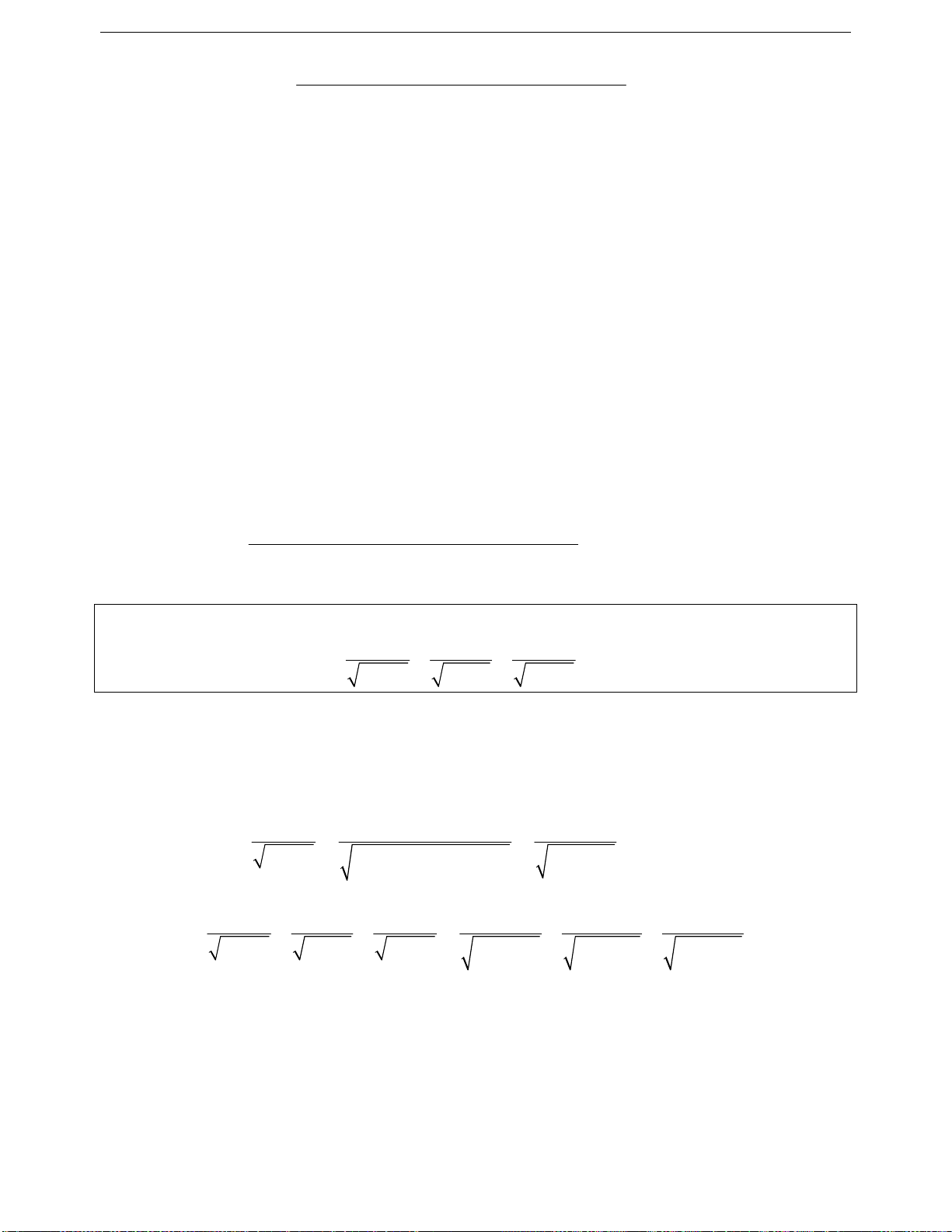
2222 2222 2
22 2
222
1
abca bcab c
ab bc ca
Áp dụng bất đẳng thức
2
22
2 xy xy ta được
22 2
22222 2
8 abbcca abbcca
Mặt khác ta lại có
2
2222 2 22
2
2222 222
2
222 2 22 2
42
42
42
abbc a bc
abac abc
bcca ab c
Nhân theo vế các bất đẳng thức trên ta được
22 2 2 2 2
22 22 2 2 222 2 22 22 2
64 2 2 2 ab bc ca abc a bc ab c
Hay
22222 2 2222 2222 2
8222abbcca abca bcab c
Từ đó dẫn đến
22 2
2222 2222 2
222 ab bc ca a b c a b c a b c
Hay
2222 2222 2
22 2
222
1
abca bcab c
ab bc ca
Vậy bất đẳng thức trên được chứng minh.
Bài 81. Cho a, b, c là các số thực dương thỏa mãn
333
abc 3
. Chứng minh rằng:
222
33 3
abc
1
b8 c8 a8
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1
, Khi đó để ý đến phép biến
đổi
32
b8 b2b2a4 và cả chiều của bất đẳng thức ta có đánh giá
2
2
b2b4 b1 33, do đó ta được
2
b2b 2b4 3b2.
Suy ra
22 2
3
2
aa a
b8
3b 2
b2b 2b4
Áp dụng tương tự ta được
222 2 2 2
33 3
abc a b c
b8 c8 a8
3b 2 3c 2 3a 2
Bây giờ để tạo ra đại lượng
333
abc và chú ý đến chiều bất đẳng thức ta áp dụng bất đẳng
thức Bunhiacopxki thì được

2
2
222 2 2 2
33 3
333
abc a b c
b8 c8 a8
3b 2 3c 2 3a 2
abc
abc
3b 2 3c 2 3a 2
abc
b2 c2 a2
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
abc
1
b2 c2 a2
Hay
222 222
ac ba cb 2 a b c abc 8
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
33 233 233 2
a a 13a;b b 13b;c c 13c
Do đó ta được
333 222
2a b c 3 3a b c hay
222
abc3
Do đó ta chỉ cần chứng minh
222
ac ba cb 2 abc 0
Không mất tính tổng quát ta giả sử b là số ở giữa hai số a và c, khi đó ta có
222 22 22
2
ac ba cb 2 abc 0 ac ba b 3 a b 2 abc 0
b1 b2 abcab 0
Bất đẳng thức cuối luôn đúng, do đó bài toán được chứng minh.
Bài 82. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
222
333
abc
ab bc ca
10
3abc
abc
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức ta nhận thấy có
đại lượng
3
333
abc;a b c và đại lượng
222
ab bc ca ta cần tìm đánh giá liên hệ giữa các
đại lượng đó. Áp dụng bất đẳng thức Cauchy ta được
3
333 333
a b c a b c 3 a b b c c a a b c 24ab c
Và
333 2333 2333 2
a b b 3ab ; b c c 3bc ; c a a 3ca
Nên ta được
333 2 2 2
abcabbcca
Do đó ta được
3
222333 222
333 333
333 2 2 2
333
abc
ab bc ca a b c 24abc ab bc ca
3abc 3abc
abc abc
abcabbcca
8
3abc
abc
Mặt khác cũng theo bất đẳng thức Cauchy ta được
333 2 2 2 2 2 2
333
abcabbcca abbcca 3abc
2. 2. 2
3abc 3abc 3abc
abc

Do vậy
3
222
333
abc
ab bc ca
10
3abc
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc
.
Bài 83. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
333
444
a1 b1 c1
2ab bc ca
abc bca cab
Phân tích và lời giải
Nhận thấy biểu thức dưới các dấu căn không đồng bậc nên chú ý đến giả thiết
abc 1 ta có thể viết
được
44
a b c a abc b c . Để ý đến chiều của bất đẳng thức ta nghĩ đến một tích dưới
mẫu để có thể áp dụng được bất đẳng thức Cauchy
2xy x y khi đó ta được
44
32 22 2 32 22 2
3
2
2 a b c ab bc ca 2 a abc b c ab bc ca
2 a bc bc ab ac abc a bc bc ab ac abc
abca 1
abca bc
a
Từ đó suy ra
3
4
a1 2aabbcca
abc
abc
Áp dụng tương tự ta được
33
44
b 1 2b ab bc ca c 1 2c ab bc ca
;
abc abc
bca cab
Công theo vế các bất đẳng thức trên ta được
333
444
a1 b1 c1
2ab bc ca
abc bca cab
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1.
Bài 84. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
222
abc
18 3 81
abc a b c
abc
Phân tích và lời giải
Quan sát bất đẳng thức ta thấy có các đại lượng
2
222
abc;a b c
, ta cần đánh giá đại
lượng
abc về ab bc ca để tìm xem có mối liên hệ nào với các đại lượng trên hay không. Sử dụng
bất đẳng thức quen thuộc sau
2
3abc a b c ab bc ca
Suy ra
23 3
2
abc 3abc 3abc
abc
3abc a b c
ab bc ca
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
3
2
222
3a b c
18 3 81
abc
abc
ab bc ca

Để ý là khi
abc thì
3
2
222 222
3a b c
93 93
abc abc
ab bc ca
Do đó áp dụng bất đẳng thức Cauchy ta được
3
2
222 222 2
222
3
3a b c 27a b c
93 93
abc abc
ab bc ca
ab bc ca a b c
Mà cũng theo bất đẳng thức Cauchy ta có
222
2
222
3
ab bc ca ab bc ca a b c
ab bc ca a b c
3
Do đó ta được
222
2
222
3
27 a b c 3.27 a b c
ab bc ca ab bc ca a b c
ab bc ca a b c
81
abc
Vậy bất đẳng thức được chứng minh xong.
Bài 85. Cho a, b, c là các số thực không âm thỏa mãn
abc3. Chứng minh rằng:
222
1113
4
1ab 1bc 1ca
Phân tích và lời giải
Để dễ tìm ra các đánh giá hợp lí ta tìm cách đưa các đại lượng vế trái vào trong cùng một bình
phương. Chú ý đến chiều bất đẳng thức ta có
2
222
111 111
3
1ab1bc1ca
1ab 1bc 1ca
Ta cần chứng minh
2
1119
4
1ab1bc1ca
Hay
1113
2
1ab1bc1ca
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức và một đánh giá quen thuộc, ta được
111 9 93
3abc 2
1 ab 1 bc 1 ca 3 ab bc ca
Do đó ta được
222
1113
4
1ab 1bc 1ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi a = b = c = 1.
Bài 86. Cho a, b, c là các số thực dương thỏa mãn
333
abc 3. Chứng minh rằng:
44 4
abc3
16
bc ca ab
Phân tích và lời giải

Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta nhận
thấy không thể áp dụng bất đẳng thức Bunhiacopxki dạng phân thức được vì khi đó các mẫu số sẽ có số
mũ lớn, cũng không thể đánh giá mẫu theo chiều trội hơn vì lúc này mẫu cũng sẽ có số mũ lớn. Do đó ta
hướng đến các đánh giá làm giảm bậc của các mẫu số hoặc là biến đổi lại giả thiết theo chiều số mũ nhỏ
hơn
Cách 1: Trước hết ta tiếp cận bất đẳng thức theo hướng làm giảm số mũ ở các mẫu số, điều này làm ta
liên tưởng đến kỹ thuật thêm bớt trong bất đẳng thức Cauchy, Chú ý đế dấu đẳng thức xẩy ra và giả thiết
333
abc3
ta được
3
4
3
4
3
4
aa111a
16 16 16 2 b c
bc
bb111b
16 16 16 2 c a
ca
cc111c
16 16 16 2 a b
ab
Cộng theo vế các bất đẳng thức trên ta được
333
44 4
abc1abcabc3
2b c c a a b 16 8
bc ca ab
1a b c 9
2b c c a a b 16
Dễ dàng chứng minh được
abc3
bc ca ab 2
Suy ra
44 4
abc3
16
bc ca ab
Bất đẳng thức được chứng minh xong.
Cách 2: Chú ý đến đến giả thiết
333
abc3, ta sẽ đánh giá làm giảm bậc của các hạng tử trong giả
thiết, chú ý đến lũy thừa bậc 4 của các mẫu, ta chọn các đánh giá theo bất đẳng thức Cauchy là
33 233 233 2
a a 13a;b b 13b;c c 13c
Do đó ta được
333 222
2a b c 3 3a b c
hay
222
abc3
Bây giờ ta cần làm trội các mẫu số làm sao cho xuất hiện
222
a;b;c. Khi đó ta chú ý đến đánh giá
2
4
22
ab 4a b thì được
3
422
22 2
22 2
33
3
22 2
aa a a
2.2a . 3 a . 3 a
bc
4b c 43 a
127a a
.
216
2a 3a 3a
Áp dụng tương tự ta được
333
44 4
abcabc3
16 16
bc ca ab
Bất đẳng thức được chứng minh xong.
Bài 87. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

444
4
4
4
1 1 1 243
111 3
abc 2abc
Phân tích và lời giải
Quan sát bất đẳng ta nhận thấy bất đẳng thức có có các căn bậc cao và các đại lượng lại có lũy thừa
bậc cao. Do đó ta cần đánh giá để đưa tổng các lũy thừa về cùng một lũy thừa để có thể khử căn. Trước
hết ta biến đổi bất đẳng thức thành
444 4
111 3
11131
abc 2abc
Áp dụng bất đẳng thức Cauchy ta có
444 444
3
111 111
1113111
abc abc
Ta quy bài toán về chứng minh
444 4
3
111 3
111 1
abc 2abc
Hay
3
111 3
111 1
abc 2abc
Để ý là
3
1 1 abc 3 abc nên
33
3
33
13 3
11 1
2abc
abc 3 abc
Do đó phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
3
3
111 1
111 1
abc
abc
Đặt
111
x;y;z
abc
thì bất đẳng thức trên trở thành
3
3
1x1y1z 1 xyz
Đây là một đánh giá đúng đã được chứng minh.
Bất đẳng thức được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Bài 88. Cho a, b, c là các số thực không âm thỏa mãn
abc1. Chứng minh rằng:
222
bc ac ab
abc2
444
Phân tích và lời giải
Bất đẳng thức này không xẩy ra dấu bằng tại
abc, cũng không xẩy ra tại ab;c0 nà
đẳng thức xẩy ra tại
a1;bc0 và các hoán vị của nó. Do đó ta nghĩ đến việc sắp thứ tự biến. Tuy
nhiên ta cần tiệt tiêu được các dấu căn bậc hai bên vế trái. Ngoài ra để ý là với dấu đẳng thức xẩy ra như
trên thì ta dự đoán
bc bc . Do đó ta dự đoán là
2
2
bc
bc
aa
42
. Nếu chứng minh
được đánh giá đó thì xem như bài toán được giải quyết xong.
Ta xét

22
22
22
bc bc
bc bc
aaaabc a
42 42
bc bc
bc 0
44
Từ đó suy ra
2
2
bc
bc
aa
42
Hay
2
bc
bc
aa
42
Áp dụng tương tự ta được
22
ac ab
ac ab
bb;cc
42 42
Cộng vế theo vế các bất đẳng thức trên ta được
222
bc ac ab
abc2abc2
444
Vậy bài toán được chứng minh xong.
Bài 89. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
111 9 1 1 1
4
a b c abc ab bc ca
Phân tích và lời giải
Bất đẳng thức trên là bất đẳng thức có các đại lượng đồng bậc nên ta nghĩ đến phép đổi biến
abc
x;y;z
abc abc abc
. Từ đó suy ra xyz1. Khi đó nhân cả hai vế của
bất đẳng thức với
abc, khi đó bất đẳng trở thành
111 1 1 1
abc 94abc
abc abbcca
111 111
94
abc abbcca
abc abc abc abc abc abc
Hay
111 1 1 1
94
xyz xyyzzx
Hay
111 1 1 1
xyz 94xyz
xyz xyyzzx
Hay
xy yzzx x y z
4
zxy yzzxxy
Áp dụng bất đẳng thức Cauchy ta có
xx 4x yy 4y zz 4z
;;
yz yzzxxzxyxy
Cộng vế theo vế các bất đẳng thức trên, ta được

y z y y z z 4x 4y 4z
xxzxxy yzzxxy
Hay
xy yzzx x y z
4
zxy yzzxxy
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài 90. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
4a b c
bc ca ab
abc
abbcca
Phân tích và lời giải
Dễ dàng dự đoán đươc dấu đẳng thức xẩy ra tại
abc. Quan sát bất đẳng thức ta nhận thấy
cần phải khử các căn bậc hai, do đó ta nghĩ đến bất đẳng thức Cauchy hoặc bất đẳng thức Bunhiacopxki.
Tuy nhiên để áp dụng các bất đẳng thức này ta cần tạo ra tích các đại lượng. Do đó ta biến đổi tương
đương bất đẳng thức cần chứng minh như sau
bc abca ca abbc ab bcca
abc
4a b c
Chú ý đến chiều của bất đẳng thức cần chứng minh thì áp dụng bất đẳng thức Bunhiacopxki ta có
abac a bc hoặc
a b a c ac ab, tuy nhiên để ý đến mẫu số ta chọn
đánh giá thứ nhất. Khi đó ta được
bca bc
bc abac
bc bc
bc
aa a
Theo bất đẳng thức Cauchy ta có
bc bc
2bc
2a
Do đó ta được
bc abac
bc
bc
a2
Áp dụng tương tự ta được
bc abca ca abbc ab bcca
abc
bc ca ab
2a b c 2
abc
Ta cần chứng minh
bc ca ab
2a b c 2 4a b c
abc
Hay
bc ca ab
abc
abc
Thật vậy, theo bất đẳng thức Cauchy ta có
2
2
222
bc ab ca bc ab ca
3a b c a b c a b c
acb acb
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Bài 91. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng

222
222
111
abc
abc
Phân tích và lời giải
Dễ dàng dự đoán được đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta liên tưởng
đến một đánh giá quen thuộc
222
111 111abc
ab bc ca abc
abc
Và lại có
2
3abc a b c ab bc ca
Do đó ta có
22
222 2
abc 3abc
111abc
abc
abc
abc a b c
ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
2
3a b c
abc
ab bc ca
Hay
22
222
3a b c a b c ab bc ca
Dễ thấy theo bất đẳng thức Cauchy ta được
2
222
2
222
3
a b c a b c ab bc ca ab bc ca
3. a b c ab bc ca
Hay
62
222
abc 27a b c abbcca
Mà
abc3 nên ta có
62
abc 81abc
Suy ra
22
222
3a b c a b c ab bc ca
Vậy bất đẳng thức được chứng minh xong.
Nhận xét: Ngoài cách chứng minh trên ta có thể tham khảo thêm các cách chứng minh sau đây
Cách 1: Do
2
222
,, 0 9 abc a b c a b c
+ Trường hợp 1: Giải sử 1 trong 3 số a, b, c nhỏ hơn
1
3
Khi đó tổng
222
111
9
abc
, bất đẳng thức luôn đúng trong trường hợp này.
+ Trương hợp 2: Giải sử cả 3 số a, b, c đều lớn hơn
1
3
.
Do
17
3;;
33
abc abc
Từ đó ta có
2
2
2
22
121
1
44
aaa
aa
aa
Suy ra
2
2
1
44
aa
a
Tương tự ta có
22
22
11
44; 44
bb cc
bc

Cộng vế theo vế các bất đẳng thức trên ta được
222
222
111
43 0
abc abc
abc
Hay
222
222
111
abc
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1abc .
Cách 2:
+ Trường hợp 1: Với
,, 0;1 2abc . Khi đó ta có
22
432 2
2
1
12 1 0 4 4 10 4 4
aa aaa aa
a
Áp dụng tương tự ta được
22
22
11
44; 44
bb cc
bc
Cộng theo vế của 3 bất đẳng thức ta được
222
222
111
12 4 0
abc abc
abc
Hay
222
222
111
abc
abc
+ Trường hợp 2: Nếu có một trong 3 số a, b, c lớn hơn hoặc bằng
12 .
Không mất tính tổng quát giả sử
abc, khi đó suy ra:
2
22 1
12 22 642
2
abcc
c
Khi đó ta được
222
111
642
abc
. Trong khi đó
2
222
9 abc abc
Từ đó suy ra
222
222
111
abc
abc
Vậy bất đẳng thức được chứng minh.
Bài 92. Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
aba
abc
bca
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra khi và chỉ khi
abc1
. Quan sát bất đẳng
thức ta thấy có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, do đó áp dụng bất đẳng
thức Bunhiacopxki ta có
2
222
abc
abc a b c
bcaabbccaabbcca
Ta quy bài toán về chứng minh
2
abc
abc
ab bc ca
Hay
ab bc ca a b c
Để ý đến dấu đẳng thức xẩy ra và chiều của bất đẳng thức ta có đánh giá theo bất đẳng thức
Cauchy là
ab 1 bc 1 cb 1
ab ;bc ;ca
222
Cộng theo vế các bất đẳng thức trên ta được

1
ab bc ca a b c ab bc ca
2
Mà lại có
222
abc 3abc3
Mặt khác
abcabc 3abbcca abcabbcca
Hay
abcabbcca
Do đó ta có
1
ab bc ca a b c a b c ab bc ca a b c
2
Vậy bất đẳng thức được chứng minh xong.
Bài 93. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2
222
ab c ba c ca b
6
5
bc a ca b ab c
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc
. Quan sát biểu thức thứ nhất bên vế
trái ta thấy cả tử và mẫu cùng chứa đại các đại lượng
a; b c , tuy nhiên dưới mẫu lại là tổng nên nếu
đánh giá mẫu được về tích thì có cơ hội rút gọn được. Chú ý đến chiều bất đẳng thức và dấu đẳng thức
xẩy ra ta có đánh giá theo bất đẳng thức Cauchy là
2
222
22
bc
33
abc a bcabc bc
44 4
b c 4a 3b 3c
4
Suy ra ta được
2
2
ab c 4ab c
4a
4a 3b 3c
4a 3b 3c b c
abc
Đại lượng thu được trong đánh giá trên làm ta liên tưởng đến bất đẳng thức Bunhiacopxki dạng
phân thức, Chú ý đến dấu đẳng thức xẩy ra ta có
2
2
91
4a a a 9 1
4a 3b 3c 25 4a 3b 3c 25 a
3a b c
.
Suy ra ta được
2
ab c
27a 1
25
abc25abc
Áp dụng hoàn toàn tương tự ta được
22
22
bc a cc a
27b 1 27c 1
;
25 25
25 a b c 25 a b c
bca cca
Cộng vế theo vế các bất đẳng thức trên ta được
22 2
222
ab c ba c ca b 27a b c
36
25 5
25 a b c
bc a ca b ab c
Vậy bất đẳng thức được chứng minh xong.
Nhận xét: Cũng nhận định như trên, nhưng ta chú ý đến các phép biến đổi sau

22
2
1
bc
ab c
a
bc
bc a
a
hoặc
22
2
1
a
ab c
bc
a
bc a
bc
+ Nếu ta đặt
;;
bc ca ab
xyz
abc
, khi đó bất đẳng thức được viết lại thành
222
6
5
111
xyz
xyz
Để ý đến dấu đẳng thức xẩy ra tại
2xyz
, do đó ta có đánh giá
222 2
444
34
14343
xx x
x
xxxxx
Hoàn toàn tương tự ta thu được
222
444
343434
111
xyz
xyz
xyz
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
4446
3434345
xyz
Đến đây ta thay lại
;;
bc ca ab
xyz
abc
vào bất đẳng thức thì được
4446
334 334334 5
abc
bca cab abc
Và ta chứng minh hoàn toàn như trên.
+ Nếu ta đặt
;;
abc
xyz
bc ca ab
, khi đó bất đẳng thức trên được viết lại là
222
6
5
111
xyz
xyz
Và ta chứng minh hoàn toàn tương tự.
Bài 94. Cho a, b, c là các số thực dương thỏa mãn
abc 2 . Chứng minh rằng:
333
abcabcbaccab
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
3
abc 2
. Quan sát bất đẳng thức cần
chứng minh ta có một số nhận xét như sau: Vế trái chứa các lũy thừa bậc ba nhưng vế phải lại chứa căn
bậc hai, ngoài ra với dấu đẳng thức xẩy ra tại
3
abc 2 thì
3
ab
c
c
. Do đó ta nghĩ đến bất
đẳng thức Cauchy cho hai số, tuy nhiên để có được đánh giá
3
ab
c2cab
c
ta cần tạo ra được
đại lượng
ab
c
. Chú ý đến giả thiết và một đánh giá quen thuộc ta có
33
ab a b ab a b
ab ab
22abcc
Từ đó ta có
33
33
ab ab
cc2cab
2c
Tương tự ta có

33 33
33 33
ac ac bc bc
bb2bac;aa2abc
2b 2a
Cộng vế theo vế các bất đẳng thức trên ta được:
333
abcabcbaccab
Bài toán được chứng minh xong.
Ngoài cách chứng minh như trên ta có thể chứng minh bài toán bằng cách áp dụng bất đẳng thức
Bunhiacopxki như sau:
Áp dụng bất đẳng thức Bunhiacopxki ta có
2
222
222
ab c ba c ca b 2a b c a b c
abc a b c a b c
Theo một bất đẳng thức quen thuộc ta có
2
1
abc a b c ab bc ca
3
Từ đó ta được
2
222 222
3
222
4
6
4
abc a b c a b c a b c ab bc ca
a b c abbccaabbcca
3
abc
3
Do đó ta có
6
2
4
abc
ab c ba c ca b
3
Hay
3
2
abc
ab c ba c ca b
3
Dễ dàng chứng minh được
3
333
abc
abc
9
Từ đó ta được bất đẳng thức sau
333
abcabcbaccab
Vậy bất đẳng thức được chứng minh xong.
Bài 95. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
333
333
abc
1
abc bac cba
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc
. Quan sát bất đẳng thức ta chú ý
đến phép biến đổi
3
33
3
3
a1
abc bc
1
a
. Khi đó ta nghĩ đến phép đổi biến
bc
x
a
và
biểu thức trên được viết lại thành
3
1
1x
. Chú ý là khi
abc
thì
x2
, ta có đánh giá
322
2
11 22
1x x1x x1 x 2
x1x x1
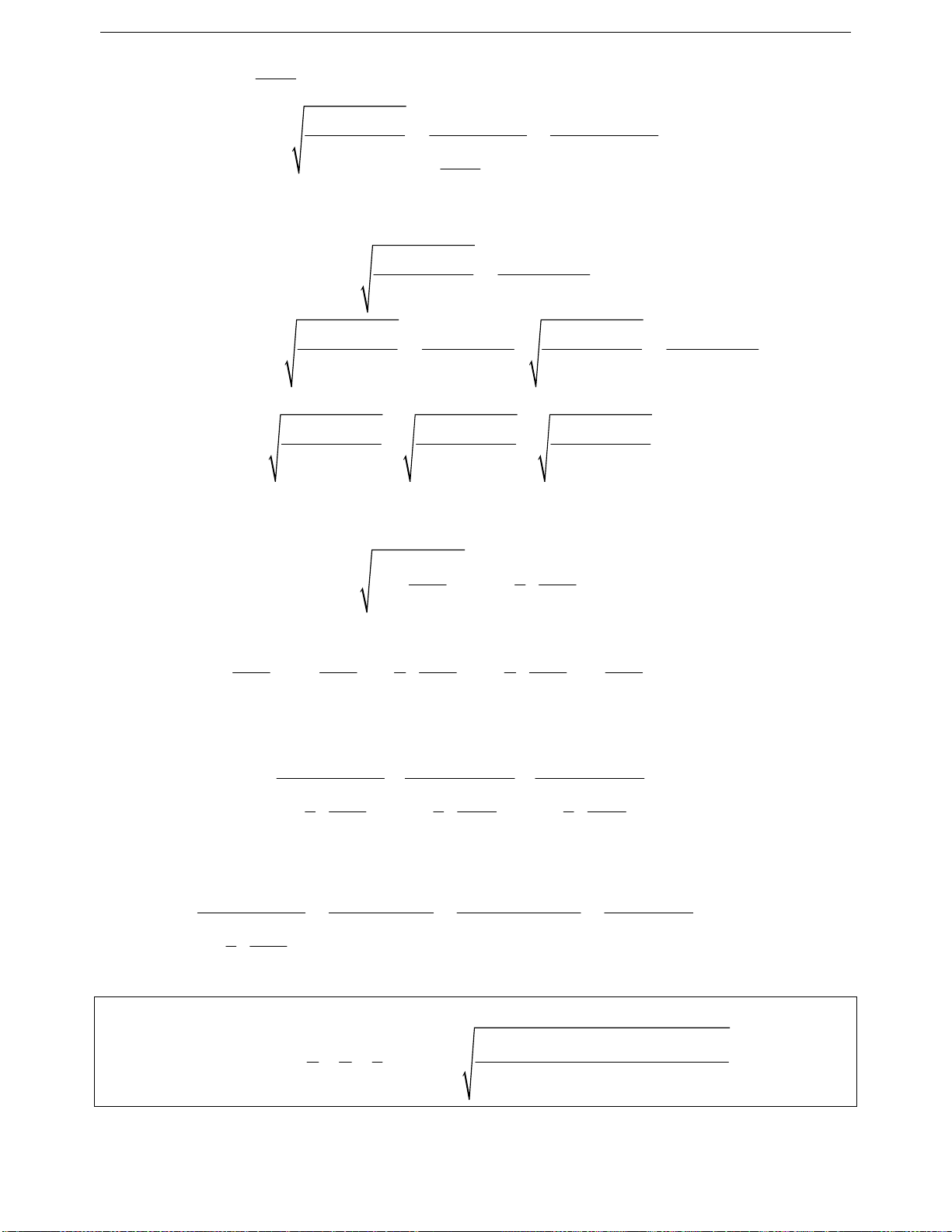
Khi này thay lại
bc
x
a
vào bất đẳng thức trên ta được
32
32 2
32
a22a
bc
abc 2abc
2
a
Theo một đánh giá quen thuộc ta được
2
22
bc 2b c , khi đó ta suy ra được
32
3222
3
aa
abc
abc
Hoàn toàn tương tự ta có
32 32
3 2 22 3 2 22
33
bb c c
;
abc abc
bac cba
Cộng theo vế các bất đẳng thức trên ta được
333
333
333
abc
1
abc bac cba
Vậy bài toán được chứng minh xong.
Nhận xét: Ngoài cách làm như trên ta có thể chứng minh bài toán như sau: Thực hiện biến đổi như trên
và chứng minh
32
1
11
2
bc bc
aa
Thật vậy, bất đẳng thức trên tương đương với
2
32 4 2
11
20
44
bc bc bc bc bc
aa a aa
Bất đẳng thức cuối cùng luôn đúng, do vậy bất đẳng thức trên được chứng minh.
Áp dụng tương tự ta quy bài toán về chứng minh
222
111
1
111
111
222
bc ca ab
abc
Thật vậy, áp dụng đánh giá quen thuộc
2
22
2xy x y ta có
222
22 222
222
2
12 2
22
1
2
1
2
aaa
abc
abc
bc
abc
a
Hoàn toàn tương tự ta suy ra bất đẳng thức cần chứng minh
Bài 96. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
2
abcabbcca
111
abc 31
abc
ab bc ca
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc. Để có những đánh giá hợp lý ta
viết bất đẳng thức cần chứng minh lại thành

3
2
abcabbcca
abcbca
3
bcaabc
ab bc ca
Quan sát bất đẳng thức trên ta viết được vế trái thành
222 222
abcbca acbacabccaab
bcaabc abc abc
Quan sát vế phải ta nhận thấy cần đánh giá đại lượng
222
ac ba ca về đại lượng
abc
để
có thể thu gọn được hai vế, chú ý đến chiều bất đẳng thức ta áp dụng bất đẳng thức Cauchy thì được
33
222 522 222
33
22 2 225 222
33
22 2 252 222
ac ac ba 3 abc 3a abc
ac cb cb 3 abc 3c abc
ba ba bc 3 abc 3a abc
Cộng vế theo vế các bất đẳng thức trên, ta được
3
222 222
ac ba cb a b c abc
Do đó ta có
3
222
3
abc abc
abc abc
bca abc
abc
Hoàn toàn tương tự ta có
3
bcaabc
abc
abc
Suy ra
3
2a b c
abcbca
bcaabc
abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
3
2
3
2a b c 3a b c a b b c c a
3.
abc
ab bc ca
Hay
3
2
8a b c 81a b c a b b c c a
abc
ab bc ca
Khai triển và thu gọn ta được
22
8 a b c ab bc ca 81 ac bc ca ab ab bc
Áp dụng bất đẳng thức Cauchy ta có
3
3
8ab bc ca
81 ab bc bc ca ca ab 81. 24 ab bc ca
27
Mặt khác ta lại có
2
3ab bc ca a b c . Do đó ta được
32 22
24 ab bc ca 8 ab bc ca .3 ab bc ca 8 ab bc ca a b c
Hay
22
81abc a b b c c a 8 a b c ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài 97. Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:
222
abcbca cab
2
ab c bc a aa b

Phân tích và lời giải
Để có các đánh giá hợp lí ta viết lại vế trái của bất đẳng thức cần chứng minh thành
222
abcbccaab
ab c bc a aa b ab c bc a aa b
Để ý ta thấy các nhóm trên có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki nên ta tách ra và áp
dụng thì được
2
222
2
abc
abc
a b c b c a a a b a ab ac b bc ab c ca bc
abc
2a b c ab bc ca
Mà theo một đánh giá quen thuộc thì
2
3ab bc ca a b c
nên ta được
22
abc abc 3abc
2
2
2a b c ab bc ca
abc abc
3
Do đó ta được
222
3a b c
abc
2
ab c bc a aa b
Cũng như trên ta áp dụng bất đẳng thức Bunhiacopxki thì được
22 2
2
bc ca ab
bc ca ab
a b c b c a a a b abc b c abc c a abc a b
ab bc ca 3abc a b c 3 a b c
2
abc b c c a a b
abc 6 a b c
Do đó ta được
222
abcbca cab
6a b c
ab c bc a aa b
Lại có
2
11
abc a b c
33
nên
6a b c 2
Hay
222
abcbca cab
2
ab c bc a aa b
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc
9
Bài 98. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
33 3
ab bc ca 3 2
8
1c 1c 1a 1a 1b 1b
Phân tích và lời giải
Quan sát bất đẳng thức cần chứng minh thì suy nghĩ đầu tiên là cố gắng đơn giản hóa các đại
lượng dưới dấu căn rồi tiến tới loại bỏ căn bậc hai. Trước hết ta ta biến đổi đơn giản hóa các biểu thức
trong căn. Chú ý đến giả thiết
abc1 ta viết được

322
2
2
22
2
ab ab ab
ab1c
1c 1c ab abc c
ab ab
ab a b 2abbcca
ab abc c
Mặt khác áp dụng bất đẳng thức Cauchy ta được
22
a b 2abbcca abbc 2abca và ab2ab
Do đó theo một đánh giá quen thuộc ta có
22
ab 1 ab
2
2ab bc 2ab ca
ab a b 2abbcca
Mà theo bất đẳng thức Cauchy ta lại có
ab 1 ab ab 1 a b
ab bc ab ca a c b c
2ab bc 2ab ca
22 22
Từ đó ta được
3
ab 1 a b
acbc
42
1c 1c
Áp dụng hoàn toàn tương tự ta được
33 3
ab bc ca
1c 1c 1a 1a 1b 1b
1ab bc ca
acbc ba ca cbab
42
Ta cần chứng minh
1ab bc ca32
acbc ba ca cbab 8
42
Hay
ab bc ca
3
acbc ba ca cbab
Đến đây ta chú ý đến bất đẳng thức Bunhiacopxki ta được
ab bc ca
acbc ba ca cbab
abbcca
33.33
acbcba ca cbab
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc
3
Bài 99. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chưng minh rằng:
222
111187
2
abc
abab cbcb acac
Phân tích và lời giải
Quan sát bất đẳng ta nhận thấy vế trái có ba phân thức phía sau đồng bậc nên ta đánh giá ba phân
thức đó trước. Áp dụng bất đẳng thức Cauchy ta được

3
222
111 1
3
ab a b cb c b ac a c a b c a b c b a c
Trong biểu thức dước dấu căn ta chú ý đến đại lượng
abbcca
có thể đánh giá về
abc
. Như vậy theo bất đẳng thức Cauchy ta được
3
8a b c
8
abbcca
27 27
Ngoài ra chú ý đến đại lượng
222
abc ở dưới mẫu của phân thức thứ nhất, để đánh giá được
vế trái về
2
abc
thì ta cần đánh giá đại lượng
222
abc
và
ab bc ca
. Do đó cũng theo bất đẳng
tức Cauchy ta có
3
222
ab bc ca
abc
27
.
Kết hợp hai bất đẳng thức trên ta được
3
222
2
8ab bc ca
abca bbcca
27
Suy ra ta được
111 27
ab a b cb c b ac a c 2 ab bc ca
Khi đó ta được bất đẳng thức sau
222 222
11111 27
abc abc
ab a b cb c b ac a c 2 ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki ta được
222 2
11 1 9
9
ab bc ca ab bc ca
abc
abc
Và ta lại có
2
13
3
ab bc ac
abc
Do đó ta được
222 222
222
11111 27
abc abc
ab a b cb c b ac a c 2 ab bc ca
1 2 23 23.3 87
9
ab bc ca 2 2
abc
2ab bc ca
Bài toán được chứng minh xong, đẳng thức xẩy ra khi
1
abc
3
.
Bài 100. Cho a, b, c là các số thực không âm thỏa mãn
abc1. Chứng minh rằng:
22 2222
111
10
abbcca
Phân tích và lời giải
Bất đẳng thức không xẩy ra dấu bằng tại
abc, do đó ta dự đoán xẩy ra tại một biến bằng
không và hai biến còn lại bằng nhau. Thay vào bất đẳng thức ta có dấu đẳng thức xẩy ra tại
1
ab ;c0
2
. Trong tình huống này ta nghĩ đến sắp thứ tự các biến và đánh giá làm sao bảo toàn

được dấu đẳng thức. Vì vai trò của các biến như nhau nên ta giả sử c là số nhỏ nhất trong các số a, b, c.
Như vậy khi đánh giá ta cần chú ý sao cho dấu đẳng thức xẩy ta tại
1
ab ;c0
2
. Trong các đánh
giá ta cần xem vai trò của a, b như nhau so với c. Từ những phân tích trên ta có các đánh giá sau
22
22
22 2 2
cccc
ab aac bbc a b
4422
Tương tự ta có
22
22 22
cc
bc b ;ac a
22
Do đó ta có bất đẳng thức
22 2222 2 2 2 2
111 1 1 1
abbcca
cc cc
abba
22 2 2
Áp dụng bất đẳng thức Cauchy ta được
22
11 2
cc
cc
ba
ba
22
22
Áp dụng bất đẳng thức Bunhiacopxki ta lại có
22
22 2
11
cc
cc
2b a
ab
22
22
44
4
cc cc cc
ab2baab
22 22 22
Và
2
366
6
cc cc
cc
2b a 4b a
ab
22 22
22
Kết hợp lại ta được
22 2 2
111
10
cc cc
abba
22 2 2
Suy ra
22 2222
111
10
abbcca
Vậy bất đẳng thức được chứng minh xong.
Đẳng thức xảy ra khi và chỉ khi
11
a; b ; c ; ; 0
22
và các hoán vị của nó.
Bài 101. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
22 2222
3ab bc ca
abbcca
ab bc ca abc
Phân tích và lời giải

Quan sát bất đẳng thức trên ta chú ý đến bất đẳng thức Bunhiacopxki dạng phân thức. Tuy nhiên
để áp dụng được ta cần để ý đến phép biến đổi
22 2 2
ab a b
ab abab
hoặc đánh giá quen thuộc
2
22
2a b a b
.
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222
2
222
abc 3abbcca
abc
abbc ca
2a b c 2a b c
abc 3abbcca
bca
abbc ca
2a b c 2a b c
Cộng theo vế hai bất đẳng thức trên ta được
22 2222
3ab bc ca
abbcca
ab bc ca abc
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
222
22 2222
2
ab bc ca
abbc ca
ab bc ca
2a b 2b c 2c a
2a 2b 2c 12 ab bc ca 3 ab bc ca
abc
4a b c 4a b c
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.

Chủ đề 12
MỘT SỐ BẤT ĐẲNG THỨC TRONG CÁC ĐỀ THI HỌC SINH GIỎI VÀ TUYỂN SINH ĐH-
THPT QUỐC GIA VÀ LỚP 10 CHUYÊN TOÁN
Trong các kì thi học sinh giỏi môn Toán THCS, THPT và các kì thi tuyển sinh lớp 10 chuyên, nội
dung về bất đẳng thức và giá trị lớn nhất, nhỏ nhất xuất hiện một cách đều đặn trong các đề thì với các bài
toán ngày càng khó hơn. Trong chủ đề này, chúng tôi đã tuyển chọn và giới thiệu một số bài toán về bất đẳng
thức và giá trị lớn nhất, nhỏ nhất được trích trong các đề thi học sinh giỏi môn toán cấp tỉnh và các đề thi
chuyên toán các năm gần đây.
Bài 1. a) Cho các số dương a, b, c tùy ý. Chứng minh rằng:
111
abc 9
abc
b) Cho các số dương a, b, c thoả mãn abc3. Chứng ming rằng:
222
1 2009
670
ab bc ca
abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Phòng năm 2009 - 2010
Lời giải
a) Áp dụng bất đẳng thức Cô si cho 3 số dương
3
3
111 1
abc abc; 3
abc
abc
Suy ra
111
abc 9
abc
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc
b) Ta có
2
222
abc
ab bc ca a b c ab bc ca 3
3
Suy ra
2007
669
ab bc ca
Áp dụng bất đẳng thức trong câu a, ta có
222
222
11 1
a b c 2ab 2bc 2ca 9
ab bc ca ab bc ca
abc
Suy ra
222 2
11 9
1
ab bc ca
abc
abc
Do đó ta được
222
1 2009
670
ab bc ca
abc
.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 2. Với số tự nhiên
n3. Chúng minh rằng
n
1
S
2
.
Với
n
11 1
S...
31 2 5 2 3 2n 1 n n 1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình Định năm 2009-2010
Lời giải
Với
n3
, ta có

2
2
1n1nn1n
2n 1
4n 4n 1
2n 1 n n 1
n1 n 1 1 1
2
2n 1.n n n 1
4n 4n
n+1- n
Do đó ta được
n
1 111 1 1 1 1 1
S1 ... 1
222
223 nn1 n1
Vậy bất đẳng thức được chứng minh.
Bài 3. Chứng minh rằng
2
m1
2
n
n32
, với mọi số nguyên m, n.
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình năm 2009-2010
Lời giải
Vì m, n là các số nguyên nên
m
n
là số hữu tỉ và 2 là số vô tỉ nên
m
20
n
.
Ta xét hai trường hợp sau
+ Trường hợp 1: Với
m
2
n
, khi đó ta được
22 22
m2n m2n1
hay
1
2
m2n
Từ đó suy ra
2
2
2
2
2
2
2
m2n1 1
2222
nn
n
1
22
11
n
1
n32
1
22
n2 2
n
n
+ Trường hợp 2: Với
m
2
n
, khi đó ta được
22 22
m2n m2n1 hay 1
2
m2n
Từ đó suy ra
2
2
2
2
2
2
2
1
22
mm2n11
n
22 2 22
nnn
n
1
22
n
11
n32
1
n22
n
Vậy bài toán được chứng minh.
Bài 4. Cho ba số thực a, b, c đôi một phân biệt. Chứng minh rằng:

222
22 2
abc
2
bc ca ab
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúcnăm 2009-2010
Lời giải
Bất đẳng thức cần chứng minh tương đương với
2
abc ab bc ca
22
bc ca ab
bcca caab abbc
Mà ta lại có
ab bc ca
bcca caab abbc
abab bcbc caca abbcca
1
abbcca abbcca
Do đó bất đẳng thức trên trở thành
2
abc
0
bc ca ab
.
Bất đẳng thức cuối cùng là một bất đẳng thức đúng. Vậy bài toán được chứng minh.
Bài 5. Cho a, b, c là các số thực dương thay đổi thỏa mãn
abc3. Tìm giá trị nhỏ nhất của biểu
thức:
222
222
ab bc ca
Pa b c
ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nghệ An năm 2009-2010
Lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc1
và giá trị nhỏ nhất của P là 4. Ta quy bài
toán về chứng minh bất đẳng thức
222
222
ab bc ca
abc 4
ab bc ca
Thật vậy, kết hợp với giả thiết ta có
222 222
3332 2 2 2 2 2
3abc abcabc
abcabbccaabbcca
Áp dụng bất đăngr thức Cauchy ta có
32 232 2322
aab2ab;bbc2bc; cca 2ca
Suy ra
222 2 2 2
3a b c 3ab bc ca 0
Do đó ta được
222 222
222 222
ab bc ca ab bc ca
abc abc
ab bc ca a b c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
ab bc ca
abc 4
abc
Hay
222
222
222
9abc
abc 4
2a b c
Đặt
222
ta b c.
Từ giả thiết
222
abc 3 a b c 3, do đó ta được t3

Bất đẳng thức trên trở thành
2
9t
t42t9t8tt32t30
2t
Bất đẳng thức cuối cùng luôn đúng do
t3
. Vậy bài toán được chứng minh xong.
Bài 6. Cho biểu thức
2222
Pa b c d acbd, trong đó ad bc 1.
Chứng minh rằng:
P3
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thanh Hóa năm 2009-2010
Lời giải
Cách 1: Ta có
22
22 22 22 22
222 222 2222
ac bd ad bc a c 2abcd b d a d 2abcd b c
ac d bd c a b c d
Vì
ad bc 1 nên
2
2222
1acbd a bcd (1)
Áp dụng bất đẳng thức Cauchy ta được
2222 2222
Pa b c d acbd2a b c d acbd
Suy ta
2
P21 acbd acbd. Rõ ràng P0 vì
2
2
2 1 ac bd ac bd
Đặt
xacbd, khi đó ta được
22 2 222 22
P 21x x P 41x 4x1x x 1x 4x1x 4x 3
Hay
2
22
P1x2x33
. Do đó ta được P3. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
ad bc 1
2a 3d c
2b 3c d
Cách 2: Ta viết lại bất đẳng thức cần chứng minh thành
2222
abcdacbd 3adbc
Hay
2222
abcdacbda3dcb 3cd
Áp dụng bất đẳng thức Cauchy ta có
2
22
22
2
22
22
3d c
3d 2 3cd c
a3dc a a
44
3c d
3d 2 3cd c
b3cdb b
44
Cộng theo về hai bất đẳng thức trên ta được
2222
abcdacbda3dcb 3cd
Bài toán được chứng minh xong.
Bài 7. Gọi a, b, c là độ dài ba cạnh của một tam giác có ba góc nhọn. Chứng minh rằng với mọi số thực x,
y, z ta luôn có:

222 2 2 2
222 222
xyz2x2y2z
abc abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thanh Hóa năm 2009-2010
Lời giải
Cách 1: Vì
222
abc 0
nên ta có
222
222
222
222 22 2 2 22
222
222
222 22 2 2 22
2222 2 2
222
xyz
abc
abc
bca acb abc
x2 y2 z2
abc
bca acb abc
2x 2y 2z x y z
abc
Giả sử
abc, khi đó
22 22
ca 0;cb 0. Với c là cạnh lớn nhất và các góc đều nhọn nên
222
cab
. Do đó ta có
222 22 2 2 22
bca 0;acb 0;abc 0
Suy ra
222 22 2 2 22
2222 2 2
222
222
bca acb abc
2x 2y 2z x y z
abc
2x 2y 2z
Hay
222
222 2 2 2
222
xyz
abc 2x2y2z
abc
Hay
222 2 2 2
222 222
xyz2x2y2z
abc abc
. Bài toán được chứng minh xong
Cách 2: Bất đẳng thức cần chứng minh tương đương với
222222
222222222222
22 2 2 22 2 2 22 2 2
22 2 2 22 2 2 22 2 2
x2xy2yz2z
0
a abc b abc c abc
xb c a ya c b za b c
0
aabc babc cabc
Do a, b, c là độ dài các cạnh của một tam giác nhọn nên
22222 222 2
abc;bca;ca b
Nên ta được
222 22 2 2 22
bca 0;acb 0;abc 0
Do vậy bất đẳng thức trên luôn đúng. Bài toán được chứng minh xong.
Bài 8. a) Cho k là số nguyên dương bất kì. Chứng minh bất đẳng thức sau:
111
2
k1 k k k1
b) Chứng minh rằng:
11 1 1 88
245
3 2 4 3 2010 2009
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2009-2010
Lời giải
a) Bất đẳng thức cần chứng minh tương đương với

2
12k12k
2k 1 2 k k 1 0 k 1 k 0
k1 k k.k1
Bất đẳng thức cuối cùng luôn đúng với mọi k nguyên dương.
Vậy bất đẳng thức được chứng minh.
b) Áp dụng kết quả câu a ta có
111 1
VT
2 1 3 2 4 3 2010 2009
11 11 1 1
22 2
1 2 2 3 2009 2010
1188
21 21 VP
45 45
2010
Vậy bất đẳng thức được chứng minh xong.
Bài 9. Với a, b, c là những số thực dương. Chứng minh rằng:
222
22 22 22
abcabc
5
3a 8b 14ab 3b 8c 14bc 3c 8a 14ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHKHTN Hà Nội năm 2009-2010
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
2
22 22 22
3a 8b 14ab 3a 8b 12ab 2ab 4a 9b 12ab 2a 3b
Suy ra
222
2
22
aaa
2a 3b
3a 8b 14ab
2a 3b
Áp dụng tương tự ta thu được
222
22 22 22
222
abc
3a 8b 14ab 3b 8c 14bc 3c 8a 14ca
abc
2a 3b 2b 3c 2c 3a
Mặt khác theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc abc
2a 3b 2b 3c 2c 3a 5
5a b c
Do đó ta được
222
22 22 22
abcabc
5
3a 8b 14ab 3b 8c 14bc 3c 8a 14ca
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc
Bài 10. Giả sử x, y, z là những số thực thoả mãn điều kiện
0x,y,z2 và xyz3. Tìm giá
trị nhỏ nhất và lớn nhất của biểu thức:
444
Mx y z 121x1y1z
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHKHTN Hà Nội năm 2009-2010
Lời giải
Đặt
a x 1; b y 1; c z 1 , ta được 1 a;b;c 1 và abc 0. Biểu thức M
được viết lại thành
444 333 222
Ma b c 4a b c 6a b c 4abc 312abc

Để ý là khi
abc 0 thì
333
abc3abc0 nên biểu thức trên thử thành
444 222
Ma b c 6a b c 3
Theo một đánh giá quen thuộc thì
444
2
222
abcabcabc0
1
abc abc 0
3
Do đó suy ra
M3 hay giá trị nhỏ nhất của M là 3.
Đẳng thức xẩy ra khi và chỉ khi
abc0 hay xyz1.
Mặt khác do
1 a;b;c 1 nên ta có
a; b; c 1
. Từ đó ta có
42 42 42
aa a;bbb;ccc
Suy ra
444 222
Ma b c 6a b c 37a b c 3
Mà ta lại có
abc0 nên trong ba số a, b, c có một hoặc hai số âm, tức là luôn tồn tại hai số
cùng dấu. Không mất tính tổng quát ta giả sử hai số đó là b và c. Khi đó ta được
bc bc a
Đến đây ta có
M14a 317
hay giá trị lớn nhất của M là 17. Đẳng thức xẩy ra khi và chỉ khi
a1;b 1;c0 và các hoán vị hay x2;y0;z1 và các hoán vị
Bài 11. a) Cho 3 số thực a, b, c bất kì. Chứng minh rằng:
222
222
ab bc ca
abcabbcca
26 6 2009
b) Cho a0;b0. Chứng minh rằng
12 8
ab2ab
Trích đề thi tuyển sinh lớp 10 chuyên Toán TP Hồ Chí Minh năm 2009-2010
Lời giải
a) Bất đẳng thức cần chứng minh tương đương với
222 222
ab bc ca ab bc ca
2 2 2 26 6 2009
Hay
22 2
12 a b b c 2007 c a
0
13 3 2
Bất đẳng thức cuối cùng luôn đúng.
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
b) Bất đẳng thức cần chứng minh tương đương với
12 8
ab2ab
Đặt
cb
, do
b0
nên ta được
c0
, khi đó bất đẳng thức trên được viết lại thành
12 8
ac2ac
Theo một đánh giá quen thuộc ta được
12 2 2 2.4 8
a c 2a c 2a c 2a c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
2a b
.
Bài 12. Cho a, b là các số dương thỏa mãn
a2b
1
1a 1b
. Chứng minh
2
1
ab
8
.

Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Quảng Bình năm 2015-2016
Lời giải
Từ giả thiết
a2b
1
1a 1b
. Đặt
ab
x;y
1a 1b
Suy ra
xy
a;b
1x 1y
.
Khi đó ta được
x2y1 và bất đẳng thức cần chứng minh được viết lại thành
2
2
xy 1
8
1x1y
Từ giả thiết ta suy ra
1x 2y;1y xy
nên lại viết bất đẳng thức cần chứng minh thành
2
2
2
xy 1
4xy x y
8
2y x y
Đánh giá cuối cùng là một bất đẳng thức đúng. Vậy bài toán được chứng minh xong. Đẳng thức
xẩy ra khi và chỉ khi
ab
.
Bài 13. Cho x, y, z là các số thực dương sao cho
xyz x y z 2
. Chứng minh rằng:
1113
2
xy yz zx
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2009-2010
Lời giải
Giả thiết của bài toán được viết lại thành
111
1
x1 y1 z1
.
Đặt
111
a;b;c
x1 y1 z1
. Khi đó ta được
abc1
. Từ đó suy ra
1a bc 1b ca 1c ab
x;y;z
aa bb ca
Bất đẳng thức cần chứng minh được viết lại thành
ab bc ca 3
2
bcca caab abbc
Áp dụng bất đẳng thức Cauchy ta được
ab 1 b a
2b c c a
bcca
bc 1 c b
2c a a b
caab
ca 1 a c
2a b b c
abbc
Cộng theo vế các bất đẳng thức trên ta được
ab bc ca 3
2
bcca caab abbc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc2
Bài 14. Cho các số thực không âm a, b, c sao cho
ab bc ca 3
. Chứng minh rằng:
222
111
1
a2b2c2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2009-2010

Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
abc
1
a2b2c2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22
222
222 222
222
abc abc
abc
1
a2b2c2abc6
abc2abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 15. Cho x, y, z là các số dương thỏa mãn
x2y3z18. Chứng minh rằng:
2y 3z 5 3z x 5 x 2y 5 51
1x 12y 13z 7
Trích đề thi tuyển sinh lớp 10 chuyên toán Đại học Vinh, 2009 – 2010
Lời giải
Đặt
ax;b2y;c3x , khi đó giả thiết trở thành abc18 và bất đẳng thức được viết
lại thành
bc5 ca5 ab5 51
1a 1b 1c 7
Bất đẳng thức trên tương đương với
bc5 ca5 ab5 51
1113
1a 1b 1c 7
Hay
11172
abc6
1a 1b 1c 7
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
1113
1a 1b 1c 7
Thật vậy theo bất đẳng thức Cauchy ta có
111 9 93
1a 1b 1c 3abc 21 7
Vậy bài toán được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc6 hay x6;y3;z2.
Bài 16. Giả sử x, y, z là các số thực dương thoả mãn điều kiện
xyz1.
Chứng minh rằng:
22
xy z 2x 2y
1
1xy
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2010-2011
Lời giải
Ta sẽ quy bài toán về việc chứng minh bất đẳng thức cùng bậc là
22
22
xy z x y z 2x 2y
1
xyz xy
xzyz 2x 2y xyz xy
Sử dụng bất đẳng thức Cauchy ta có
22
2x 2y x y
Do đó ta chỉ cần chứng minh
zxzy z xy
Bất đẳng thức trên tương đương với
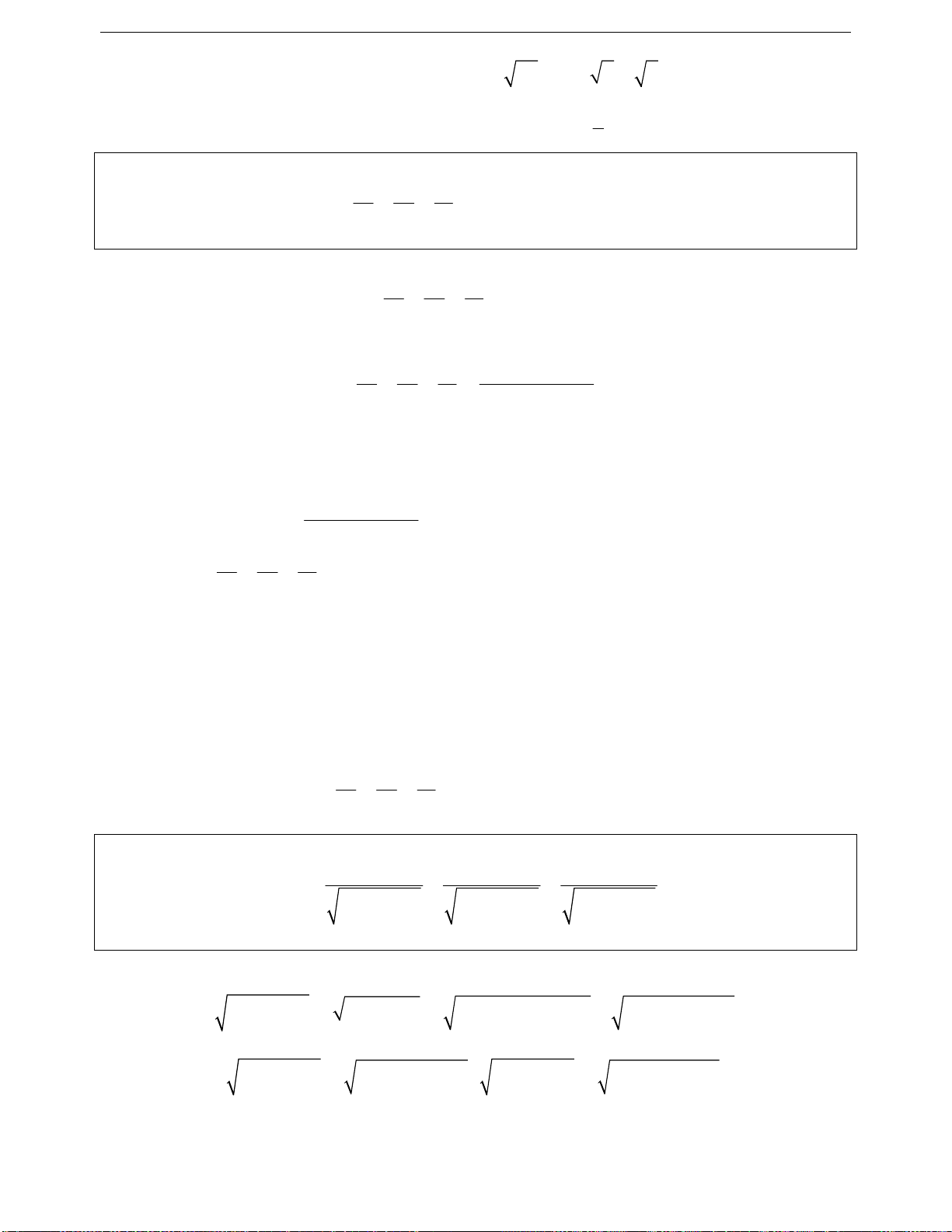
2
22
zxyzxy zxy2zxy zx y 0
Bài toán được chứng minh hoàn toàn. Đẳng thức xảy ra khi
1
xy ;z0
2
.
Bài 17. Cho a, b, c là các số dương thỏa mãn
abcabbcca 6
. Chứng minh rằng:
333
222
abc
abc3
bca
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHNN Hà Nội năm 2010-2011
Lời giải
Trước hết ta chứng minh bất đẳng thức
333
222
abc
abc
bca
Thật vậy, theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
333
abc
abc
bca abbcac
Theo một đánh giá quen thuộc ta có
222
abcabbcca
Do đó ta được
2
222 222
abc abcabbcca
Nên ta có
2
222
222
abc
abc
ab bc ac
Do đó ta suy ra
333
222
abc
abc
bca
+ Chứng minh
222
abc3.
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
22 22 22 2 2 2
a b 2ab; b c 2bc; c a 2ca; a 1 2a; b 1 2b; c 1 2c
Cộng theo vế các bất đẳng thức trên ta được
222
3a b c 3 2ab bc ca a b c 12
Hay
222
abc3
Kết hợp hai kết quả trên ta được
333
222
abc
abc3
bca
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 18. Cho các số dương a, b, c thoả mãn
abcabc . Tìm giá trị lớn nhất của biểu thức:
222
abc
S
bc1a ca1b ab1c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2010-2011
Lời giải
Cách 1: Kết hợp với giả thiết ta có
22
bc 1 a bc a bc bc a a b c a b a c
Hoàn toàn tương tự ta được
22
ca 1 b a b b c ; ba 1 c a c b c ;
Nên
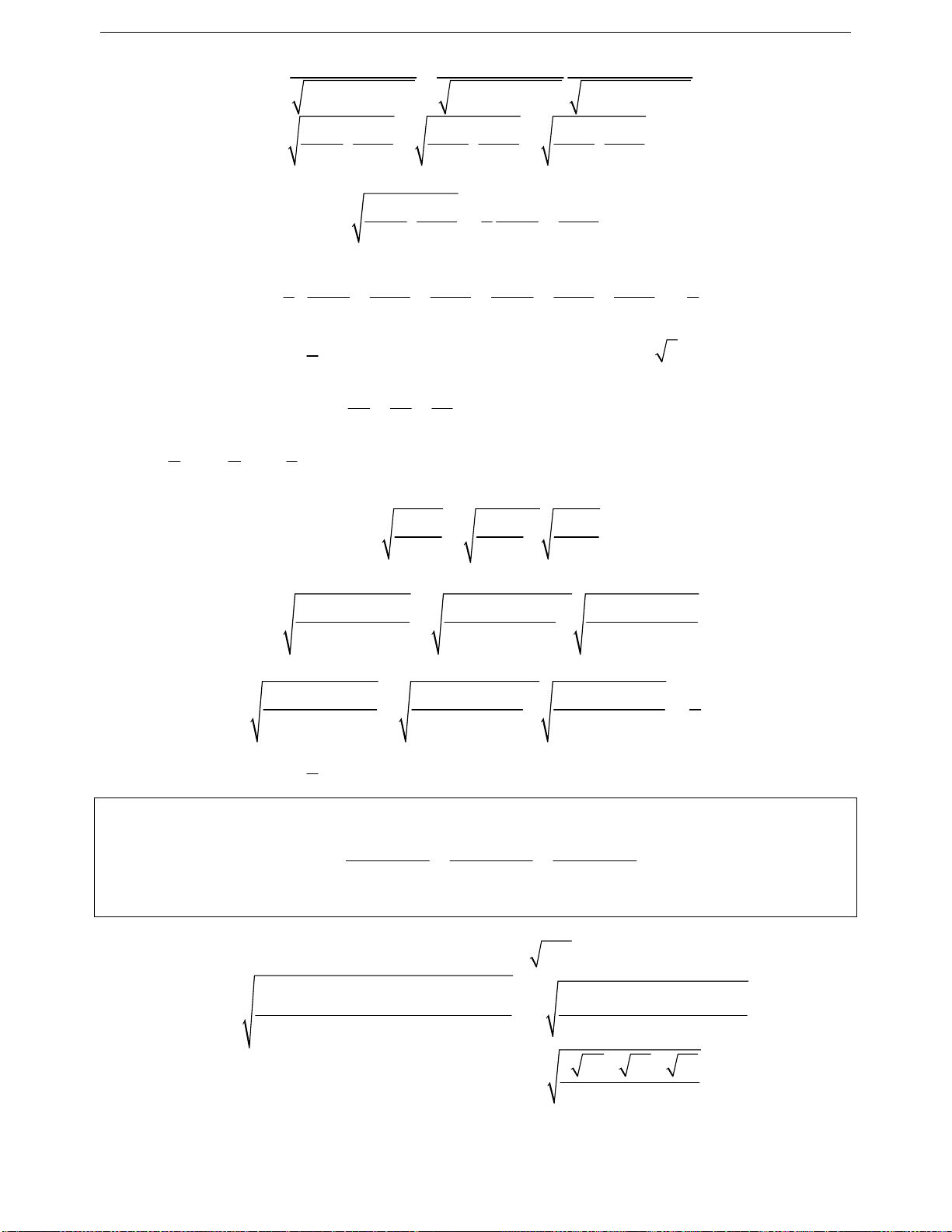
abc
S
abac abbc acbc
aa bb cc
...
abac bcbc cbac
Áp dụng bất đẳng thức Cauchy ta được
aa1a a
.
abac 2abac
Hoàn toàn tương tự ta được
1a a b b c c 3
S
2abacbcabacbc 2
Vậy giá trị lớn nhất của S là
3
2
. Đẳng thức xẩy ra khi và chỉ khi abc 3 .
Cách 2: Ta viết lại giả thiết thành
111
1
ab bc ca
.
Đăt
111
x;y;z
abc
, khi đó giả thiết trở thành xy yz zx 1
Ta viết lại biểu thức S thành
222
yz zx xy
S
x1 y1 z1
Để ý đến giả thiết
xy yz zx 1 ta được
yz zx xy
S
xyxz yzxz zxyz
Áp dụng bất đẳng thức Cauchy ta chứng minh được
yz zx xy 3
2
xyxz yzxz zxyz
Vậy giá trị lớn nhất của S là
3
2
.
Bài 19. Cho các số dương a, b c .Tìm giá trị nhỏ nhất của biểu thức
222
222
cab 1 abc 1 bca 1
S
bbc1 cca1 aab1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2010-2011
Lời giải
Cách 1: Áp dụng bất đẳng thức Cauchy dạng
3
x y z 3 xyz ta được
222
3
3
222
3
c ab 1 .a bc 1 .b ca 1 ab 1 bc 1 ac 1
S3 3
abc
bbc1.cac1.aab1
2ab.2bc.2ca
36
abc
Vậy giá trị nhỏ nhất của S là 6, đẳng thức xẩy ra khi và chỉ khi
abc1

Cách 2: Đặt
ab 1 bc 1 ca 1
x;y;z
bca
Khi đó biểu thức được viết lại thành
222
xyz
S
yzx
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
222
xyz
xyz
Sxyz
yzx xyz
Do đó ta được
ab 1 bc 1 ca 1 1 1 1
Sabc6
bca a b c
Vậy giá trị nhỏ nhất của S là 6, đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 20. Cho x, y, z là các số dương thỏa mãn
xyz182 . Chứng minh rằng:
1111
4
xy z yz x zx y
Đề thi tuyển sinh lớp 10 chuyên toán Đại học Vinh, 2010 – 2011
Lời giải
Bất đẳng thức cần chứng minh tương đương với
1111
42
2x y z 2y z x 2z x y
Áp dụng bất đẳng thức Cauchy ta có
22xy z 2x y z , do đó ta được
12
2x y z
2x y z
Hoàn toàn tương tự ta được bất đẳng thức
1 1 1 111
2
2x y z x 2y z x y 2z
2x y z 2y z x 2z x y
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
1111
2x y z x 2y z x y 2z
82
Thật vậy theo bất đẳng thức Cauchy ta được
111 991
2xyz x2yz xy2z
4x y z
4.18 2 8 2
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
xyz62 .
Bài 21: Cho a, b, c là các số thực dương thỏa mãn abc 1 . Chứng minh rằng:
36
1
abc abbcca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh vĩnh Phúc năm 2010-2011
Lời giải
Cách 1: Bất đẳng thức đã cho tương đương:
abcabbcca 3abbcca 6abc

Để ý rằng
2
ab bc ca 3abc a b c 3 a b c
Nên bài toán quy về chứng minh
3
3abc 33abc 6abc
Bất đẳng thức trên tương đương với
2
3a b c a b c 3 0
Bất đẳng thức cuối cùng là một bất đẳng thức đúng. Vậy bài toán được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc1
Cách 2: Đặt
111
a;b;c xyz1
xyz
. Khi đó ta có
3 6 3abc 6abc
11
abc abbcca abc abbcca
36 36
11
1 1 1 1 1 1 xy yz zx x y z
ab bc ca a b c
Theo bất đẳng thức Cauchy ta có
2
3xy yz zx x y z
Suy ra
2
39
11
xy yz zx
xyz
Mặt khác
2
2
96 3
110
xyz xyz
xyz
với x, y, z 0.
Nên ta được
2
96
1
xyz
xyx
Từ đó ta được bất đẳng thức
36
1
xy yz zx x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Bài 22. Cho a, b, c là các số thực dương thỏa mãn
abc2. Chứng minh rằng:
222
222
11197
abc
2
bca
Trích đề thi tuyển sinh lớp 10 chuyên Toán TP Hải Phòng năm 2010-2011
Lời giải
Cách 1: Trước hết ta chứng minh bất đẳng thức sau
22
22 22
ax by ab xy
Thật vậy, bất đẳng thức trên tương đương với
2
22
22 22
2
2222 2222
ab xy ax by
2 a b x y 2ax 2by a b x y ax by
Bất đẳng thức cuối cùng là bất đẳng thức Bunhiacopxki
Áp dụng bất đẳng thức trên ta có

2
2
222 2
222 2
2
2
111 11 1
abc ab c
ab
bca a
111
abc
abc
Ta cần chứng minh
2
2
111 97
abc
abc 4
Thật vậy, áp dụng bất đẳng thức Cauchy và chú ý giả thiết
abc2, ta được
2
22
2
2
22
111 81
abc abc
abc
abc
16 65 97
abc
4
abc abc
Bất đẳng thức đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi
2
abc
3
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
2
181 9 9
a1 a a
16 4b 4b
b
Hay
2
2
97 1 9
aa
44b
b
Chứng minh tương tự ta được
22
22
97 1 9 97 1 9
bb;cc
44c44a
ca
Cộng theo vế các bất đẳng thức trên ta được
222
222
97 1 1 1 9 1 1 1
abcabc
44abc
bca
Mà ta lại có
111 9
abcabc
Do đó ta được
222
222
1114 81
abc abc
bca
4a b c
97
Ta cần chứng minh
48197
abc
2
4a b c
97
Hay
81 97
abc
8
4a b c
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
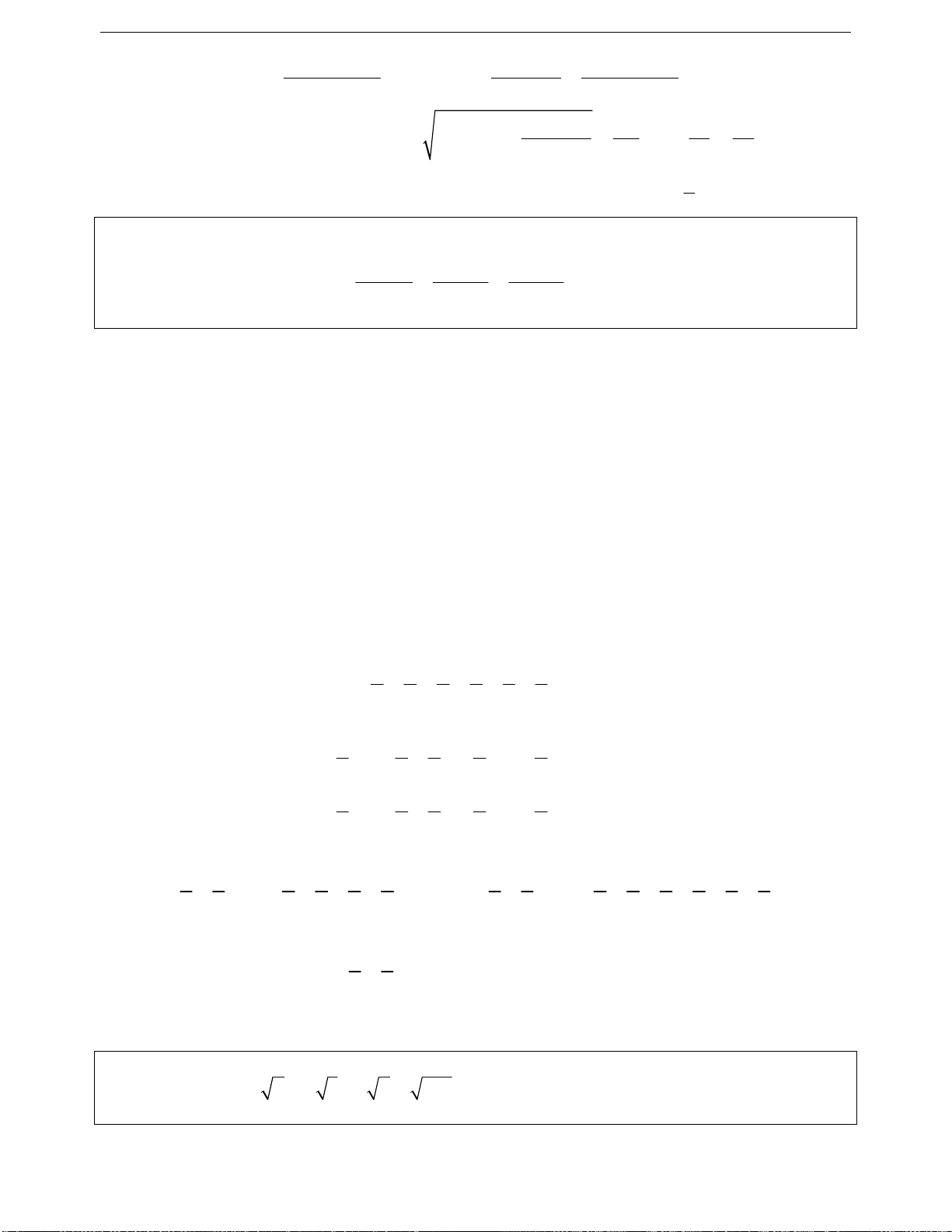
81 4 65
abc abc
abc
4a b c 4a b c
4656597
2abc 4
abc 4.2 8 8
Bất đẳng thức đã được chứng minh. Đẳng thức xảy ra khi và chỉ khi
2
abc
3
Bai 23: Cho cac sô
a, b, c 1; 2
. Chưng minhrằng:
22 2222
abbc ca
7
ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hà Tĩnh năm 2010-2011
Lời giải
Cách 1: Bất đẳng thức cần chứng minh tương đương với
222222
2222
222
ab ab bc bc ca ca 7abc
cabcab bc aabcab bc 5abc2bc 2ab 0
ab ca b bc c a b 4ca 2c 2a ca 0
abbcca b2ac2ca 0
Vì vai trò của a, b, c như nhau nên không mất tính tổng quát ta giả sử
2abc1 khi đó ta được
2a 2 c; 2c 2 a . Do đó ta được
abbcca 0;b2ac2ca 0
Nên bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
ab2;c1 và các hoán vị.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
abbcca
7
bacbac
Vì vai trò các biến như nhau nên không mất tính tổng quát ta giả sử
2abc1
. Khi đó ta có
aaba b
1110
cbcbc
cbcbc
1110
aaba b
Cộng theo vế hai bất đẳng thức trên ta được
ac abbc ac abbcac
2022
ca bcab ca bcabca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
ac
252aca2c0
ca
Từ
2abc1 suy ra 2a 2 c; 2c 2 a nên bất đẳng thức cuối cùng luôn đúng. Vậy bài
toán được chứng minh xong.
Bài 24. Cho a, b, c là các số thực dương không âm thỏa mãn
abc3. Tìm giá trị lớn nhất của biểu
thức: Pabbcca abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nghệ An năm 2010-2011
Lời giải

Đặt
xa;yb;zc. Từ giả thiết ta được
222
xyz 3.
Khi này biểu thức P trở thành
222
P x y y z z x xyz
Dễ thấy
P0
theo bất đẳng thức Cauchy
Không mất tính tổng quát ta giả sử y là số nằm giữa x, z. Khi đó ta có
22 2
zy z y x 0 yz zx xyz zy
Do đó ta có
222 22 22
P xyyzzxxyz xyzy yx z
Mặt khác theo bất đẳng thức Cauchy ta có
3
222
22 2 2 2
2x 2y 2z
2yxzxz 8
3
Suy ra
22
yx z 2 nên ta được P2 . Đẳng thức xẩy ra khi và chỉ khi
22
xyz
z0
x2y
và các hoán vị
abc1
a2;b1;c0
và các hoán vị
Vậy giá trị lớn nhất của biểu thức P là 2.
Đẳng thức xẩy ra khi và chỉ khi
abc1 hoặc a2;b1;c0 và các hoán vị.
Bài 25. Cho ba số dương a, b, c thỏa mãn
ab bc ca 1. Chứng minh rằng:
222
a1a b1b c1c111
bc ac ab a b c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hưng Yên năm 2010-2011
Lời giải
Để ý là
22
a1aabbcca abca
, do đó ta được
2
a1 abca
Áp dụng bất đẳng thức Cauchy ta được
2
2a b c
a
abca a
a1a bc111
2
bc bc bc 2bc 2 b c
Hoàn toàn tương tự ta được
22
b1b111 c1c111
;
ac 2 a c ab 2 a b
Cộng theo vế ba bất đẳng thức trên ta được
222
a1a b1b c1c111
bc ac ab a b c
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 26. a) Cho 2 số dương a và b. Chứng minh rằng :
1111
ab 4a b
b) Cho 3 số dương x, y, z thỏa mãn
111
2010.
xyz
Tìm giá trị lớn nhất của biểu thức:
111
P
2xyz x2yz xy2z

Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Yên năm 2010-2011
Lời giải
a) Biến đổi tương đương bất đẳng thức trên như sau
22
1111
4ab a b 0 a b
ab 4a b
Bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab
b) Áp dụng bất đẳng thức trên ta được
11111211
2x y z 4 x y x z 16 x y z
Hoàn toàn tương tự ta được
1112111112
;
x2yz 16x y z xy2z 16x y z
Cộng theo vế các bất đẳng thức trên ta được
1 1 1 1 1 1 1 2010 1005
P
2xyz x2yz xy2z 4x y z 4 2
Vậy giá trị lớn nhất của P là
1005
2
. Đẳng thức xẩy ra khi và chỉ khi xyz670
Bài 27. Cho a, b, c là ba số dương thỏa mãn điều kiện
abc3. Chứng minh rằng:
1113
1ab 1bc 1ca 2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình Phước năm 2011-2012
Lời giải
Cách 1: Theo bất đẳng thức Cauchy ta có
111 9
A
1 ab 1 bc 1 ca 3 ab bc ca
Mặt khác dễ thấy
2
abc
ab bc ca
3
Mà
abc3
nên
ab bc ca 3
Do đó ta được
993
A.
3abbcca 33 2
Dấu bằng xảy ra khi
1ab 1bc 1ca
abc abc1
abc3
Cách 2: Áp dụng bất đẳng thức Cauchy ta có
1 1 ab 1 1 ab 1 1 ab 3 ab
2. 1 1
1ab 4 1ab 4 1ab 4 4
Hoàn toàn tương tự ta có
13ab13ca
;
1ab 4 1ca 4
Do đó ta được
9abbcca
111
.
1ab 1bc 1ca 4
Mặt khác ta chứng minh được
ab bc ca 3

Do đó ta suy ra
9abbcca
111 3
1ab 1bc 1ca 4 2
Vậy bất đẳng thức được chứng minh.
Cách 3: Áp dụng bất đẳng thức Cauchy ta có
1ababab
111
1ab 1ab 2
2ab
Tương tự ta có
1bc1ca
1; 1
1bc 2 1ca 2
Cộng theo vế theo vế các bất đẳng thức trên và áp dụng bất đẳng thức Cauchy ta được:
111 1
3abbcca
1ab 1bc 1ca 2
1a b b c c a a b c 3 3
333
22 2 2 2 22
Bài toán được chứng minh xong.
Bài 28. Chứng minh bất đẳng thức:
111 1
... 4
12 34 56 7980
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHSP Hà Nội năm 2011-2012
Lời giải
Dễ thấy
1111 1 1
;;...
1 2 2 3 3 4 3 4 79 80 80 81
Do đó ta được
11 1 11 1
... ...
12 34 7980 23 45 8081
Suy ra
11 1 11 1
2 ... ...
1 2 3 4 79 80 1 2 2 3 80 81
Hay
11 1
2 ... 2 1 3 2 ... 81 80
1 2 3 4 79 80
Nên ta được
11 1
... 4
1 2 3 4 79 80
Vậy bất đẳng thức được chứng minh.
Bài 29. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222 222 3 3 3
3
a b b c c a ab bc ca abc a abc b abc c abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nghệ An năm 2011-2012
Lời giải
Cách 1: Bất đẳng thức cần chứng minh tương đương với
222
3
abc bca a b c
1111
cab cab bc ca ab
Đặt
abc
x ; y ; z x; y; z 0; xyz 1
bca
Khi đó bất đẳng thức trên trở thành

3
3
3
xyz
xy yz zx x y z 1 1 1 1
zxy
xyyzzx
x y y z z x xyz 1
xyz
xyyzzx 11 xyyzzx
Đặt
3
txyyzzx
suy ra
t2
. Khi đó ta viết lại bất đẳng thức cần chứng minh thành
332
t11t t112tt tt2t1 0
Bất đẳng thức cuối cùng luôn đúng do
t2 .
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc
Cách 2: Bất đẳng thức cần chứng minh tương đương với
222
3
abc bca a b c
1111
cab cab bc ca ab
Hay
222 2 2 2
3
222
bc ca ab a b c a b c
31111
bc ca ab bc ca ab
abc
Đặt
222
abc
x;y;z
bc ca ab
, khi đó ta có xyz 1
Bất đẳng thức cần chứng minh trở thành
3
111
3xyz 1 1x1y1z
xyz
Hay
3
3 x y z xy yz zx 1 2 x y z xy yz zx
Đặt
3
t2xyzxyyzzx
Áp dụng bất đẳng thức Cauchy ta có
xyzxyyzzx6
Do đó ta có
3
t262
Bất đẳng thức cần chứng minh trở thành
322
t11t t1t2t1 tt1t2 0
Đánh giá cuối cùng đúng với mọi
t2 .
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
.
Bài 30. Cho a, b, c là ba số thực dương thỏa mãn
abc2
. Tính giá trị lớn nhất của biểu thức:
ab bc ca
P
ab 2c bc 2a ca 2b
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thanh Hóa năm 2011-2012
Lời giải
Để ý đến giả thiết
abc2 ta có
ab 2c ab c a b c b c c a
Do đó theo bất đẳng thức Cauchy ta được

ab ab 2ab 2ab
bc ca
ab 2c
bcca
Hoàn toàn tương tự ta được
bc 2bc 2bc ca 2ca 2ca
;
abca ab bc
bc 2a ca 2b
Cộng theo vế các bất đẳng thức trên ta được
ab bc ca 2ab 2ab 2bc 2bc 2ca 2ca
bc ca ab ca ab bc
ab 2c bc 2a ca 2b
2a b c 4
Hay
P4 . Vậy giá trị lớn nhất của P là 4.
Đẳng thức xẩy ra khi và chỉ khi
2
abc
3
Bài 31. Cho a, b, c là các số thực dương thỏa mãn
9
abc
4
. Chứng minh rằng:
333
abcabcbaccab
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2011-2012
Lời giải
Cách 1: Áp dụng bất đẳng thức Cauchy ta có
33
ab a b ab a b ab a b
ab ab
22 9abcc
4
Từ đó ta có
33
33
ab ab
cc2cab
2c
Tương tự ta có
33
33
33
33
ac ac
bb2bac
2b
bc bc
aa2abc
2a
Cộng vế theo vế các bất đẳng thức trên ta được:
333
abcabcbaccab
Bài toán được chứng minh xong.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta có
2
222
222 222
ab c ba c ca b 2a b c a b c
9
2a b c a b c abca b c a b c
4
Theo một bất đẳng thức quen thuộc ta có
2
1
abc a b c ab bc ca
3
Từ đó ta được
2
222 222
3
6
222
44
abc a b c a b c a b c ab bc ca
abcabbccaabbcca
abc
33

Do đó ta có
6
2
4
abc
ab c ba c ca b
3
Hay
3
2
abc
ab c ba c ca b
3
Dễ dàng chứng minh được
3
333
abc
abc
9
Từ đó ta được bất đẳng thức sau
333
abcabcbaccab
Vậy bất đẳng thức được chứng minh.
Bài 32. Cho các số thực dương a, b, c. Chứng minh rằng:
3
222
22 2 22 2 22 2
24 4 4
54 abc
ca b ab c bc a
abc ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2011-2012
Lời giải
Theo bất đẳng thức Cauchy ta có
222
222
222222222222
222
2
24 4 4
333
3
888 443 888
222
c a b a b c b c a c 2ab a 2bc b 2ca
12a b c 2 3abc
a b c ab bc ca 3 abc 3 a b c 9 3. a b c . a b c
93abc
Nhân theo vế hai bất đẳng thức trên ta được
222
24 4 4
22 2 22 2 22 2
3
222
ca b ab c bc a a bc ab bc ca
23abc.93abc 54abc
Hay
3
222
22 2 22 2 22 2
24 4 4
54 abc
ca b ab c bc a
abc ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 33. Cho các số dương a,b,c thay đổi và thoã mãn
3a 4b 5c 12. Tìm giá trị lớn nhất của biểu
thức:
ab 2ac 3bc
S
ab a b ac a c bc b c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bà Rịa – Vũng Tàu năm 2011-2012
Lời giải
Ta viết lại biểu thức S thành
123
S
11 11 11
111
ab ca bc

Áp dụng bất đẳng thức
11111
xyz 9x y z
ta có
2c a 1 3b c 1
123ab1
S
11 11 11 9 9 9
111
ab ca bc
63a4b5c 18
2
99
Vậy giá trị lớn nhất của biểu thức S là 2. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 34. Cho a, b là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
33
33 3
3
a4b
P
a8b
bab
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2011-2012
Lời giải
Biểu thức P được viết lại là
3
3
33
3
3
3
4b
1
a
P
8b
bb
1
1
a
a
a
Đặt
b
t0
a
. Khi đó bất đẳng thức được viết lại là
3
33
3
14t
P
18t
t1t
Áp dụng bất đẳng thức Cauchy ta có
2
2
2
32 2
24t
18t 12t12t4t 12t
2
Suy ra
322
2
111
18t 12t
12t
Ta sẽ chứng minh
32
32
3
4t 2t
12t
t1t
Thật vậy, bất đẳng thức trên tương đương với
2
32
2
32
24 2
32
3
4t 2t
12t t t1t t1 2t t1 0
12t
t1t
Bất đẳng thức cuối cùng đúng với mọi t.
Do đó ta được
32
3322
3
14t12t
P1
18t 12t 12t
t1t
Vậy giá trị nhỏ nhất của biểu thức P là 1. Đẳng thức xẩy ra khi và chỉ khi
ab

Bài 35. Cho các số thực dương a, b, c thỏa mãn
ab bc ca 5. Tìm giá trị nhỏ nhất của biểu thức:
222
3a 3b 2c
P
6a 5 6b 5 c 5
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2011-2012
Lời giải
Từ giả thiết
ab bc ca 5 ta có
22
a5aabbcca abca
Áp dụng bất đẳng thức Cauchy ta có
2
3a b 2c a
5a 3b 2c
6a 5 6a b c a
24
Chứng minh tương tự ta được
22
3a 5b 2c a b 2c
6b 5 ; c 5
22
Cộng theo vế các bất đẳng thức trên ta được
222
9a 9b 6c
6a 5 6b 5 c 5
2
Suy ra
222
23a 3b 2c
3a 3b 2c 2
P
9a 9b 6c 3
6a 5 6b 5 c 5
Vậy giá trị nhỏ nhất của biểu thức P là
2
3
.
Đẳng thức xẩy ra khi và chỉ khi
ab1;c2 .
Bài 36. Cho a, b, c là các số thực dương thỏa mãn
abc1. Tìm giá trị lớn nhất của biểu thức:
222
P a abc b abc c abc 9 abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bắc Ninh năm 2011-2012
Lời giải
Ta có
22
a abcaabc abcaabac
Do đó ta được
2
aa b a c aa 1
aabc aabac
22
Chứng minh tương tự ta được
22
bb 1 cc 1
babc ;cabc
22
Do đó ta được
222
aa 1 bb 1 cc 1
a abc b abc c abc
222
Mặt khác theo bất đẳng thức Cauchy ta lại có
aa 1
a1bc abc1
abc a a a
2222
Chứng minh tương tự ta được
bb 1 cc 1
abc b; abc c
22
Như vậy ta có

222
P a abc b abc c abc 9 abc a b c 6 abc
Mà ta có
3
abc 2
abc3abc 3;6abc6
3
3
Nên ta suy ra
2553
P3
3
33
.
Vậy giá trị lớn nhất của P là
53
3
. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 37. Cho a, b, c là số thực dương. Chứng minh rằng:
2ab 3bc 3ca a 2b 3c
3a 8b 6c 3b 6c a 9c 4a 4b 9
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2011-2012
Lời giải
Cách 1: Đặt
x a; y 2b; z 3c
, khi đó bất đẳng thức trên được viết lại thành
xy yz zx x y z
3x 4y 2z 3y 4z 2x 3z 4x 2y 9
Áp dụng bất đẳng thức Cauchy ta được
xy xy xy 1 2
3x4y2z x2yxyzxyz 9x2y xyz
xy 1 2 2 2x y 2xy
99x9y xyz 81
9x y z
Hoàn toàn tương tự ta được
yz 2y z 2yz zx 2z x 2zx
;
3y 4z 2x 81 3z 4x 2y 81
9x y z 9x y z
Cộng theo các vế cảu ba bất đẳng thức trên ta được
2xy yz zx
xy yz zx x y z
3x 4y 2z 3y 4z 2x 3z 4x 2y 27
9x y z
Mà theo một đánh giá quen thuộc ta lại có
2
xyz
xy yz zx
3
Do đó ta có
2xy yz zx 2x y z
xyz xyz xyz
27 27 27 9
9x y z
Suy ra
xy yz zx x y z
3x 4y 2z 3y 4z 2x 3z 4x 2y 9
Hay bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
a2b3c.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
621
xy xy xy 18 2 1
.
3x 4y 2z 81 81 x y z y x
2x y z 2y x
2xy 2x y
81
9x y z

Hoàn toàn tương tự ta được
yz 2y z 2yz zx 2z x 2zx
;
3y 4z 2x 81 3z 4x 2y 81
9x y z 9x y z
Cộng theo vế các bất đẳng thức trên ta được
2xy yz zx
xy yz zx x y z
3x 4y 2z 3y 4z 2x 3z 4x 2y 27
9x y z
Đến đây chứng minh hoàn toàn tương tự như trên.
Bài 38. Giả sử a, b, c là các số dương thoả mãn
abc 1
. Tìm giá trị lớn nhất của biểu thức:
22 2 2 2 2
abc
M
bcacababc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Dương năm 2011-2012
Lời giải
Ta chứng minh
M1
Đặt
333
ax;by;cz
, khi đó
x; y; z 0
và
xyz 1
Bất đẳng thức cần chứng minh trở thành
333
66 3 6 6 3 6 63
xyz
1
yzx zxy xyz
Dễ thấy
55 66 5 5
yzy z 0 y z yzyz
Suy ra
66 4 4 44
yzxyzyzxyz
Từ đó ta được
66 3
444
11
yzx
yz x y z
Hay
44
66 3 4 44
xyz x
yzx xyz
Do đó ta được
34
66 3 4 44
xx
yzx xyz
Tương tự ta có
3434
663444663444
yyzz
;
zxy xyzxyz xyz
Cộng theo vế ba bất đẳng thức trên ta được
333
66 3 6 6 3 6 63
xyz
1
yzx zxy xyz
Vậy giá trị lớn nhất của M là 1. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 39. Cho a, b, c là các số dương thoả mãn
abc 1 . Chứng minh rằng:
333
abc3
2
bc a ca b ab c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2011-2012
Lời giải
Cách 1: Áp dụng bất đẳng thức Cauchy cho các số dương ta được
333
abca3bcab3cabc3
a; b; c
242 24 2 242
bc a ca b ab c
Cộng theo vế các bất đẳng thức trên ta được

333
3a b c
abc
abc
2
bc a ca b ab c
Hay
333
abcabc
2
bc a ca b ab c
Mặt khác theo bất đẳng thức Cauchy ta lại có
3
abc3abc 3
Nên ta được
333
abc3
2
bc a ca b ab c
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.
Cách 2: Áp dụng bất đẳng thức bunhiacioxki dạng phân thức ta được
2
222
333
222
abc
abc
ab bc ca 3abc
bc a ca b ab c
Ta cần chứng minh được
2
222 2 2 2
2a b c 3ab bc ca 3abc
Vì
abc 1
nên ta được
abc3
.
Dễ thấy
2
222
2
222 222
abc a b c
abc abcabc
3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222 2 2 2
2a b c a b c 3ab bc ca 3abc
Hay
3322 22 2 2 2 2 22
332 2 2 2 2 2 2
2a b c ab bc ca ab bc ca 3ab bc ca 3abc
2a b c 2ab bc ca ab bc ca 9
Áp dụng bất đẳng thức Cauchy ta có
32 232 2322
333 2 2 2
aab2ab;bbc2bc;cca2ca
3a b c 9abc 9;3ab bc ca 9abc 9
Cộng theo vế các bất đẳng thức trên và thu gọn ta được
332 2 2 2 2 2 2
2a b c 2ab bc ca ab bc ca 9
Vậy bất đẳng thức được chứng minh.
Bài 40. Cho ba số dương a, b, c thỏa mãn
abc1. Tìm giá trị nhỏ nhất của:
222
222
ab bc ca
A14a b c
ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHQG TP Hồ Chí Minh năm 2012-2013
Lời giải
Dễ dàng tính được
222
1a bc
ab bc ca
2
. Lại có
222 222 32 3 23 22 2 2
abc abcabc ababbcccaabbcca
Áp dụng bất đẳng thức Cauchy ta có
32 2 3 2 23 2 2
a b a 2a b; b bc 2b c; c ca 2c a
Do đó suy ra
222 32 3 23 22 2 2 2 2 2
abcababbcccaabbcca3abbcca

Từ đó ta được
222 222
13
ab bc ca a b c
Hay
222
222 222
222
33a b c
3ab bc ca
ab bc ca
ab bc ca a b c
2a b c
Đặt
222
1
ta b c t
3
. Khi này biểu thức được viết lại thành
33t28t33t27t3 t3
A14t
2t 2 2t 2t 2 2t 2 2
Áp dụng bất đẳng thức Cauchy ta có
27t 3 27t 3
2.9
22t 22t
Mặt khác
t313 4
22 62 3
. Suy ra
423
A9
33
.
Vậy giá trị nhỏ nhất của A là
23
3
. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 41. Cho a, b, c là các số thực dương thỏa mãn
ab3c;cb1;abc
Tìm giá trị nhỏ nhất của biểu thức:
2ab a b c ab 1
Q
a1b1c1
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2012-2013
Lời giải
Cách 1: Ta có
2ab a b c ab 1 a 1 b 1 ab 1 c 1
Q
a1b1c1 a1b1c1
1 ab1 1 ab1
c1 ab1 abab1
a1b1
Từ giả thiết
ab c b1 b a 1 a1b1 0 ab a b1 c1 2
Suy ra
1ab1
Q
ab 2
2ab 1
Đặt
xab x2, khi đó ta được
1x1
Q
x2
2x 1
Suy ra
x2x5
51 x15
Q0
12 x 2 12
2x 1 12x 1 x 2
Do đó ta có
5
Q.
12
Vậy giá trị nhỏ nhất của Q là
5
12
. Đẳng thức xẩy ra khi và chỉ khi
a1;b2;c3
Cách 2: Nhận thấy
abcb1 a1 do đó ta được
c3ba1
Khi đó
a1b1 0 ab ab1 c1

Ta sẽ chứng minh
5
Q
12
. Thật vậy
2ab a b c ab 1
5
Q
12
a1b1c1
Tương đương với
7abc 7 a b 19ab 5c a b 17c 5 0
Đặt
A 7abc 7 a b 19ab 5c a b 17c 5 khi đó ta có
A 7abc 7 a b 19ab 5c a b 17c 5
5abc 2abc 7 a b 19ab 5c a b 17c 5
5c a b 1 6 c 1 7c 19 c 1 5c a b 17c 5
10c 30 0
Bất đẳng thức được chứng minh.
Vậy giá trị nhỏ nhất của Q là
5
12
. Đẳng thức xẩy ra khi và chỉ khi a1;b2;c3
Cách 3: Ta có
abc abc0
Từ
abcb1 a1 mà ba . Do đó ta được
ab a b 1 ab c 1
a1b1 0
abab1 abab1
Khi đó ta được
2
2ab a b c ab 1
2ab a b c abc 2ab abc
Q
a1b1c1 a1b1c1 a1b1c1
ab 2 c ab 2 c ab 2 c
ab a b1c1 ab ab11c1 2ab1c1
c1c2
1c2 1 c2 115
..
c1 c1 2 12
cc
11
2c c 1
21 21
ab c 1
Vậy giá trị nhỏ nhất của Q là
5
12
. Đẳng thức xẩy ra khi và chỉ khi
a1;b2;c3
Bài 42. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3abc . Tìm giá trị lớn nhất của biểu
thức:
222
111
P
a1b1c1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình Phước năm 2012-2013
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222
111111abbcca3
P
2a 2b 2a 2abc 2
a1b1c1
Vậy giá trị lớn nhất của P là
3
2
. Đẳng thức xẩy ra khi và chỉ khi abc1
Bài 43. Cho n số thực
12 n
x , x , ..., x với n3 . Kí hiệu
12 n
Max x , x , ..., x }
là số lớn nhất trong các
số
12 n
x , x , ..., x
.Chứng minh rằng:
12 23 n1
12 n
12 n
x x x x ... x x
x x ... x
Max x , x , ..., x }
n2n
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHSP Hà Nội năm 2012-2013
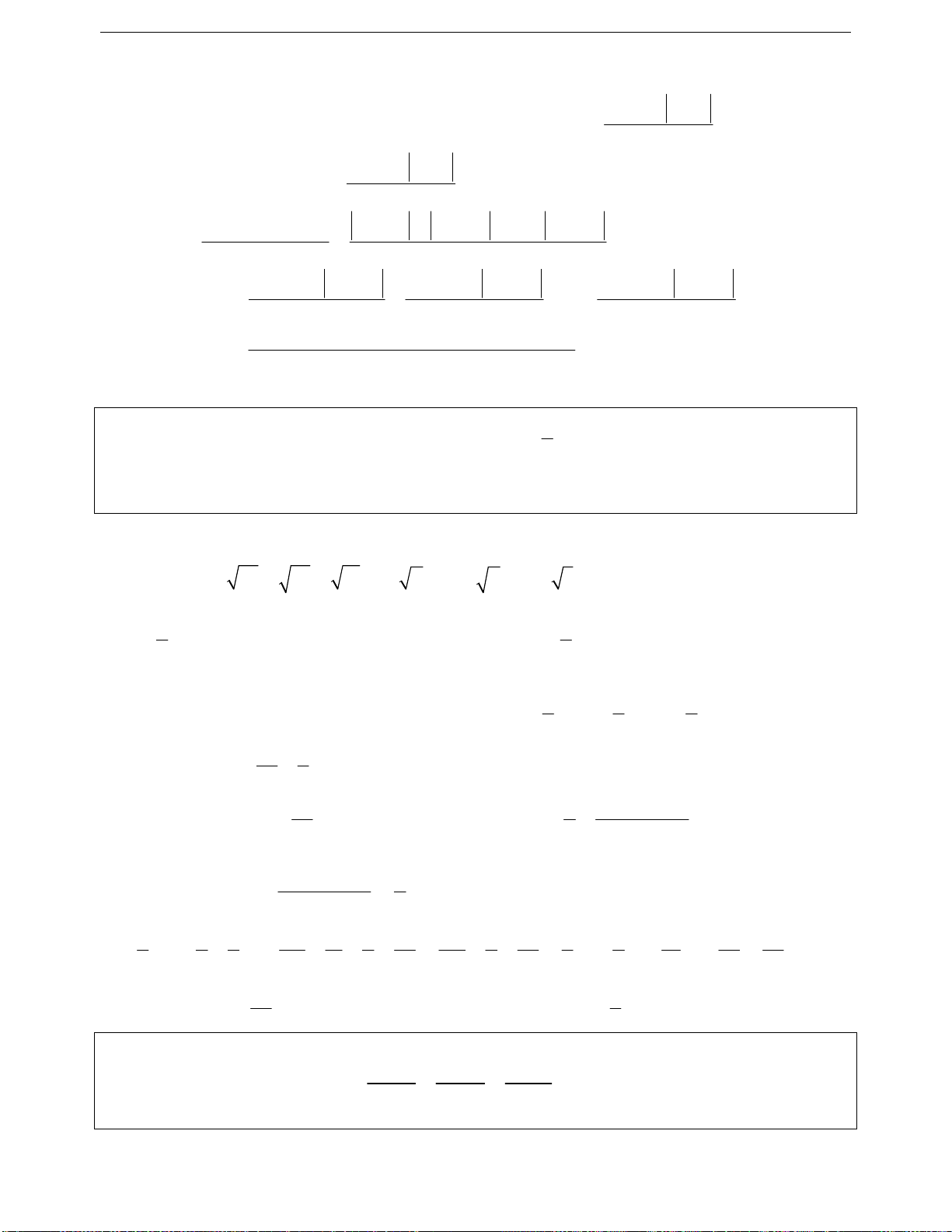
Lời giải
Để ý là trong hai số thực x, y bất kì ta luôn có
Min{x, y} x, y Max{x, y} và
xy xy
Max{x, y}
2
Sử dụng đẳng thức
xy xy
Max{x, y}
2
, ta có:
12 n
12 23 n1
xx...x
xx xx ...xx
n2n
12 12 22 23 n1 n1
12 2 n1
12 n
xx xx xx xx xx xx
...
2n 2n 2n
Max{x , x } Max{x , x} Max{x , x }
Max{x ; x ;...; x }
n
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
12 n
x x ... x
Bài 44. Cho x, y, z là các số không âm thỏa mãn
3
xyz
2
. Tìm giá trị nhỏ nhất:
333222
Sxyzxyz
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2012-2013
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
222
2
222 222
xyzxxyyzz xyz
Hay
22
333 222 333 222
32
xyz xyz xyz xyz (*)
23
Mặt khác, dễ dàng chứng minh được
2
222
222 222
333
xyz x y z x z y y z x 2z 2x 2y
22 2
27 9
x y z 6 xy yz xz 8xyz
82
27 3 x y z
9xyz 3 x y z x y z
883
Đặt
2
222
xyz
3
tx y z
34
. Khi đó ta được
2 2
22 2
2 2
2 3t 2tt t97t t91 3 11 325
St t t
3 8 3 3 9 4 64 9 4 64 6 4 8 64 64
Vậy giá
trị nhỏ nhất của S là
25
64
. Đẳng thức xẩy ra khi và chỉ khi
1
xyz
2
Bài 45. Cho a,b,c là các số dương thỏa mãn
ab bc ca 3
. Chứng minh rằng:
222
13a 13b 13c
6
1b 1c 1a
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2012-2013
Lời giải
Cách 1: Ta viết lại vế trái thành

222 222222
1 3a 1 3b 1 3c 1 1 1 3a 3b 3c
1b 1c 1a 1b 1c 1a 1b 1c 1a
Ta đi chứng minh
22 2 22 2
1113abc3
;
22
1b 1c 1a 1b 1c 1a
+ Trước hết ta chứng minh
22 2
1113
2
1b 1c 1a
. Ta có các hướng sau
Hướng 1: Không mất tính tổng quát, giải sử
abc
Do
ab bc ca 3 bc 1
Ta chứng minh bất đẳng thức sau: Với
x, y 0; xy 1
ta có
22
11 2
yz 1
y1z1
Thật vậy, ta có:
2
22 2 2
yz2yz1 y1z1 yzyz10
Do vai trò của các biến như nhau nên không mất tính tổng quát ta giả sử
abc
Khi đó ta được
3bc ab bc ca bc 1
Không mất tính tổng quát, giải sử
abc
. Do
ab bc ca 3 bc 1
Áp dụng bất đẳng thức trên ta được
222 2
11112
P
bc 1
a1b1c1a1
Do đó ta sẽ chứng minh:
2
222
1232abc33
aa b c 3abc 0
bc 1 2 2
a1 abcabc1
Từ giả thiết suy ra
abc3 và abc 1 . Do đó abc3abc0
Do đó ta được
222 2
111123
bc 1 2
a1b1c1a1
Hướng 2: Biến đổi biểu thức vế trái như sau
22
222 222
111 ab c
P3
a1b1c1 a1b1c1
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 22 2
22 2 2 2
4a 4a a a a a
abc
3a 3 3a ab bc ca a ab ac 2a bc 2a bc
Áp dụng tương tự với hai biểu thức còn lại ta được
222 2 2 2
222 2 2 2
4a 4b 4c a b c
1
3a33b33c3 2abc2bca2cab
Ta sẽ chứng minh
222
222
abc
1
2a bc 2b ca 2c ab
Thật vậy, bất đẳng thức cần chứng minh tương đương với
222
222
3a b c 1
22
2a bc 2b ca 2c ab
Hay
222
bc ca ab 1
2
2a bc 2b ca 2c ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

22 2
222 222222222
2
22 22 22
bc ca ab
bc ca ab
2a bc 2b ca 2c ab 2a bc b c 2ab c c a 2abc a b
ab bc ca
1
ab bc ca 2abc a b c
Như vậy bất đẳng thức trên được chứng minh.
+ Chứng minh
22 2
abc3
2
1b 1c 1a
Áp dụng bất đẳng thức Cauchy ta được
22
22
aababab
aaa
2b 2
b1 b1
Tương tự ta có
22
bbccca
b; c
22
c1 a1
Cộng theo vế các bất đẳng thức trên ta được
22 2
abc abbcca 3
abc abc
22
b1c1a1
Mặt khác ta có
2
abc 3abbcca abc3
Suy ra
22 2
abc3
2
1b 1c 1a
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Ta viết lại vế trái thành
222 222222
1 3a 1 3b 1 3c 1 1 1 3a 3b 3c
1b 1c 1a 1b 1c 1a 1b 1c 1a
Khi đó áp dụng ta đẳng thức Cauchy ta được
22
22
1bbb
111
2b 2
b1 b1
Hoàn toàn tương tự ta được
22
1c1a
1; 1
22
c1 a1
Khi đó ta có bất đẳng thức
22 2
111 abc
3
2
b1c1a1
Mặt khác ta lại có
22 2
abc abbcca 3
abc abc
22
b1c1a1
Do đó ta được
22 2 22 2
5a b c
1113a3b3c 9
36
22
1b 1c 1a 1b 1c 1a
Vậy bất đẳng thức được chứng minh.
Bài 46. Cho a, b, c là các số thực dương thỏa mãn
abc1. Tìm giá trị nhỏ nhất của biểu thức:
11
P
abc
12abbcca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2012-2013
Lời giải
Do
222
abc1 12abbcca a b c

Suy ra
222 222
1abc 1 111
P
abc ab bc ca
abc abc
Đến đây ta chứng minh
P30 bằng các cách sau
Cách 1: Theo bất đẳng thức Cauchy ta có
222 2
11 1 9
9
ab bc ca ab bc ca
abc
abc
.
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
7
21
ab bc ca
Tuy nhiên, dễ thấy
2
abc
1
ab bc ca ab bc ca
33
Do đó ta được
7
21
ab bc ca
Vậy bất đẳng thức được chứng minh.
Cách 2: Sử dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
222
222
22
1111 16
3ab 3bc 3ca
abc
abc3abbcca
16
12
1
abc abc
3
Bất đẳng thức sẽ được chứng minh nếu ta chỉ ra được
21 1 1
18
3ab bc ca
Để ý tiếp bất đẳng thức Bunhiacopxki ta được
2
21 1 1 6 6
18
3ab bc ca ab bc ca 1
abc
3
Vậy bất đẳng thức được chứng minh.
Cách 3: Theo một đánh giá quen thuộc ta có
111 9
ab bc ca ab bc ca
Do đó ta có bất đẳng thức
222 222
11111 9
ab bc ca ab bc ca
abc abc
Áp dụng tiếp đánh giá trên ta được
222
222
11 1
a b c 2ab 2bc 2ca 9
ab bc ca ab bc ca
abc
Hay
222
12
9
ab bc ca
abc
Mặt khác ta lại có
7
21
ab bc ca
Cộng theo vế các bất đẳng thức trên ta được
222
1111
30
ab bc ca
abc
.
Vậy bất đẳng thức được chứng minh.

Vậy giá trị nhỏ nhất của P là 30. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 47. Cho các số thực dương a, b, c thỏa mãn
abc 1
. Chứng minh rằng:
33 3
abc
abc
bca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2012-2013
Lời giải
Đặt
111
x;y;z xyz1
abc
. Khi đó bất đẳng thức được viết lại thành
333
xyz 111
zxyxyz
Áp dụng bất đẳng thức Binhiacopcxki ta được
2
222
333
222
xyz
xyz
xyz
zxy xxyzzx
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
111
xyz
xyz
Thật vậy theo một đánh giá quen thuộc và giả thiết
xyz 1 ta có
222
xy yz zx 1 1 1
xyz xyyzzx
xyz x y z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 48. Cho ba số dương a, b, c thỏa mãn
abc1. Chứng minh rằng:
1a1b1c 81a1b1c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bắc Ninh năm 2012-2013
Lời giải
Vì a, b, c là các số dương và
abc1 nên ta có a, b, c 1 .
Áp dụng bất đẳng thức Cauchy ta được
1a 1b1c 21b1c
Tương tự ta có
1b 21c1a;1c 21a1b
Nhân theo vế ba bất đẳng thức trên ta được
1a1b1c 81a1b1c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 49. Cho 3 số a, b, c thỏa mãn
0abc1. Tìm giá trị lớn nhất của biểu thức:
111
Aabc1
a1 b1 c1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Dương năm 2012-2013
Lời giải
Đặt
x1c,y1b,z1a . Từ 0abc1 ta được 1xyz2
Ta viết lại biểu thức A là
111 xxyyzz
Axyz 3
xyz yzxzxy

x y xyx.y xy x
11 01 0 1
yz yzy.z yzz
zy zyz.y zyz
11 01 0 1
yx yxy.x yxx
xyzy xz xxyyzz xz
222
yzyx zx yzxzxy zx
Đặt
x1
tt1
z2
. Do đó ta được
22
2t 1 t 2
xz 1t12t5t25 5
t
zx t t 2t 2 2t 2
Do
1
t1
2
nên ta có
2t 1 t 2
2t
suy ra
xz5
zx2
Từ đó ta được
5
A32. 210
2
Vậy giá trị lớn nhất của A là 10. Đẳng thức xẩy ra khi và chỉ khi.
Bài 50. Cho a, b, c ,d là các số thực dương thỏa mãn điều kiện
abcd3. Tìm giá trị nhỏ nhất
của biểu thức:
4444
3333
abcd
P
abcd
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nam Định năm 2012-2013
Lời giải
Cách 1: Dự đoán dấu đẳng thức xẩy ra tại
3
abcd
4
. Ta đi chứng minh
3
P
4
.
Điều này tương đương với chứng minh
4444
3333
abcd 3
4
abcd
Biến đổi tương đương bất đẳng thức trên ta có
4444 3333
4444 3333
4444 3 3 3 3
4a b c d 3a b c d
4a b c d a b c d a b c d
3abcd abcdbacdcabddabc
Áp dụng
bất đẳng thức Cauchy ta được
4444 34444 34444 3
aaab 4ab;aaac 4ac;aaad 4ad
Cộng theo vế các bất đẳng thức trên ta được
4444 3
9a b c d 4a b c d
Hoàn toàn tương tự ta được
4444 3
4444 3
4444 3
9b a c d 4b a c d
9c a b d 4c a b d
9d a b c 4d a b c
Do đó ta được
4444
333 3
12 a b c d
4abcd4bacd4cabd4dabc
Hay
4444 3 3 3 3
3abcd abcdbacdcabddabc
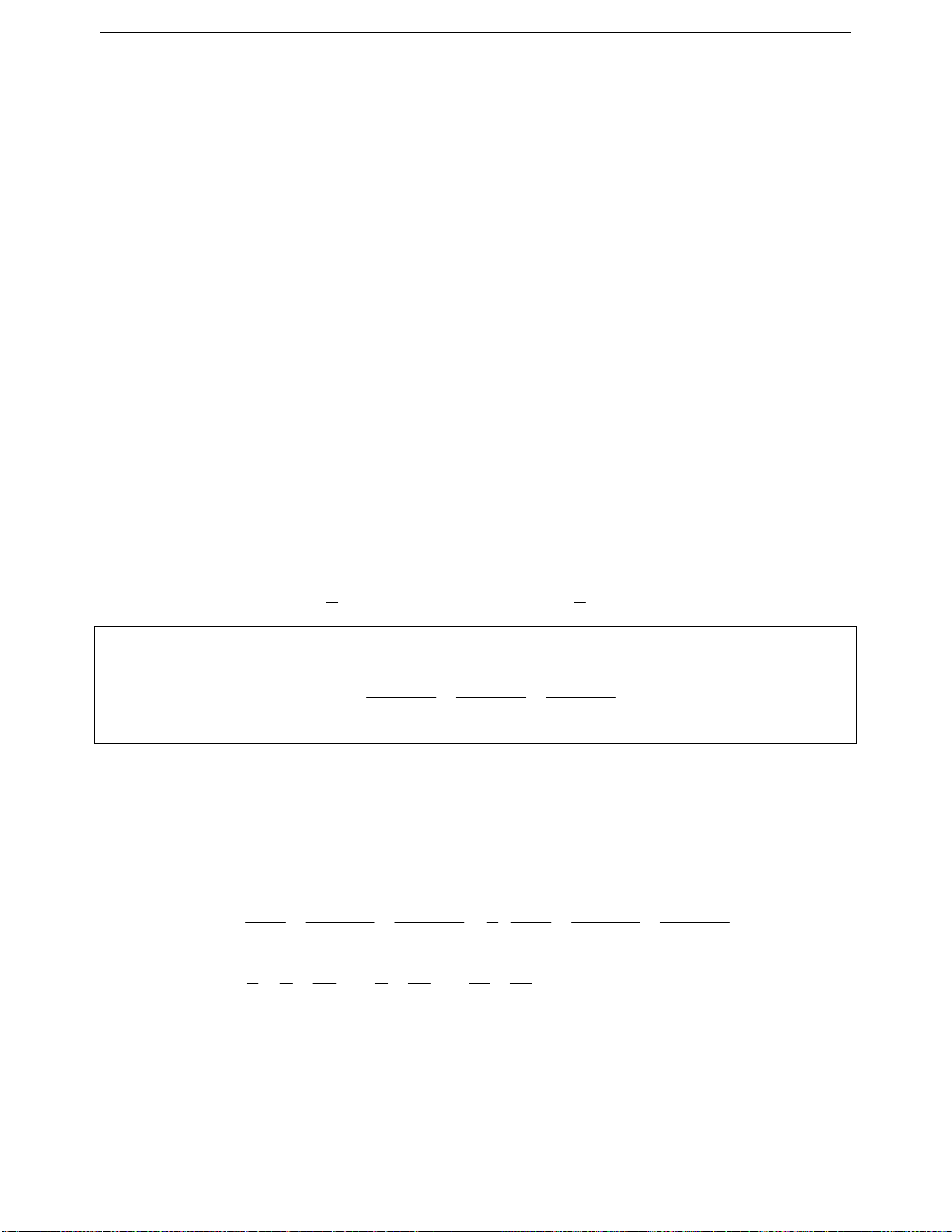
Vậy bất đẳng thức được chứng minh.
Suy ra giá trị nhỏ nhất của P là
3
4
, đạt được khi
3
abcd
4
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
4444 2222
2
44442222 3333
4a b c d a b c d ;
abcdabcd abcd
Nhân theo vế các bất đẳng thức trên ta được
22
4444 3333 2222
4abcd abcd abcd
Hay
22
4444 3333 2222
16 a b c d 4 a b c d a b c d
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta có
2
2222
4a b c d a b c d 9
Do vậy
22
3333 2222 3333
4a b c d a b c d 9a b c d
Suy ra ta được
22
4444 3333
16 a b c d 9 a b c d
Hay
4444 3333
4a b c d 3a b c d
Do đó ta được
4444
3333
abcd 3
P
4
abcd
Suy ra giá trị nhỏ nhất của P là
3
4
, đạt được khi
3
abcd
4
Bài 51. Cho tam giác ABC có chu vi bằng 2. Ký hiệu a, b, c là độ dài ba cạnh của tam giác. Tìm giá trị
nhỏ nhất của biểu thức:
a4b9c
S
bca cab abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Dương năm 2013-2014
Lời giải
Với a, b, c là độ dài ba cạnh của tam giác có chu vi bằng 2 nên
abc2.
Đặt
bca x;cab y;abc z , do a, b, c là độ dài ba cạnh của tam giác nên
x; y; z 0 . Khi đó ta được xyz2 và
yz xz xy
a;b;c
222
.
Khi đó
4x z 9x y 4x z 9x y
yz 1yz
S
2x 2y 2z 2 x y z
1y4x z9x 4z9y
2x y x z y z
Ta có
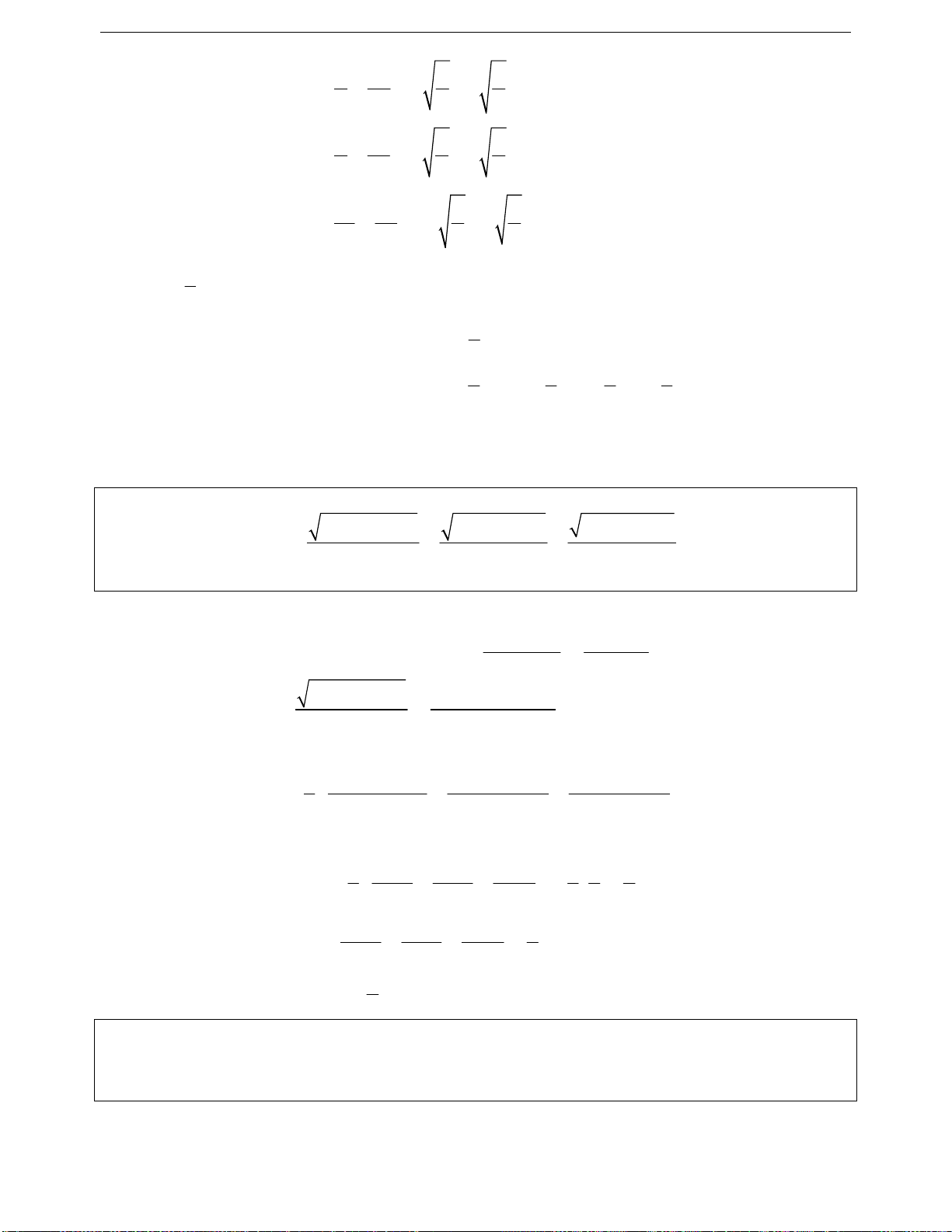
2
2
2
y4x y x
222
xy x y
z9x z x
366
xz x z
4z 9y z y
2 3 12 12
yz y z
Do đó
1
S461211
2
. Đẳng thức xẩy ra khi và chỉ khi
1
x
y2x
3
z3x
2521
y a ;b ;c
2z 3y
3632
z1
xyz2
Khi đó
222
abc. Vậy giá trị nhỏ nhất của S là 11 khi ABC vuông .
Bài 52. Cho x, y, z là ba số thực dương. Tìm giá trị nhỏ nhất của biểu thức
2222
22
xxyy yyzz
zzxx
S
x y 2z y z 2x z x 2y
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Dương năm 2013-2014
Lời giải
Ta có
22
22
22
3x y x y
xxyy xy 3xyxy
44
Suy ra
22
xxyy xy
xy2z
2x z y z
Áp dụng tương tự ta được
1xy yz zx
S
2yzzx zxxy xyyz
Đặt
axy;byz;czx , khi đó ta được
1a b c 133
S.
2b c c a a b 22 4
Vì theo bất đẳng thức Neibizt thì
abc3
bc ca ab 2
.
Vậy ta được giá trị nhỏ nhất của S là
3
4
đạt được tại xyz.
Bài 53. Giả sử a, b, c, d là các số thực dương thỏa mãn
abc bcd cda dab 1
Tìm giá trị nhỏ nhất của biểu thức
333 3
P4a b c 9c
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2013-2014
Lời giải
Do vai trò của a, b, c như nhau nên ta dự đoán dấu đẳng thức xẩy ra tại
abckd , với k là số
dương.

Khi đó áp dụng bất đẳng thức Cauchy cho ba số dương ta được
332
22
33
3
33 2
33
3
33 2
33
3
33 2
13abc
abc
kk
ab 3abd
d
kk k
bb 3bcd
d
kk k
c a 3cad
d
kk k
Cộng theo vế các bất đẳng thức trên ta được
332 3
23 2 2
3 abc abd bcd cad
12 3
abc 3d
kk k k
Hay
332 3
23 2
36 9
abc 9d
kk k
Ta cần tìm k để
3
23
36
44k3k60
kk
và ta chọn k là số dương.
Đặt
2
11
kx
2x
thay vào phương trình trên và biến đổi ta thu được
63
x12x10
Giải phương trình này ta được
3
x635 , để ý là
6356351 nên ta tính được
33
635 635
k
2
Do đó ta tính được giá trị nhỏ nhất của P là
2
33
36
635 635
.
Đẳng thức xẩy ra khi và chỉ khi
33
635 635
abc .d
2
Bài 54. Giả sử dãy số thực có thứ tự
1 2 3 192
x x x ... x thỏa mãn điều kiện:
123 n
1 2 3 192
xxx...x 0
x x x ... x 2013
Chứng minh rằng:
192 1
2013
xx
96
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH KHTN Hà Nội năm 2013-2014
Lời giải
Trước hết ta chứng minh bài toán phụ sau: Với
123 n
aaa...a thỏa mãn
123 n
123 n
a a a ... a 0
a a a ... a 1
Khi đó ta được
n1
2
aa
n
.
Thật vậy, từ điều kiện của bài toán ta nhận thấy tồn tại số tự nhiên k để
123 k k1 n
aaa...a0a ...a

Khi đó từ
123 n
123 n
a a a ... a 0
a a a ... a 1
suy ra
k1 n
123 k k1 n
123 k k1 n
123 k
1
a...a
aaa...a a ...a 0
2
1
aaa...a a ...a 1
aaa...a
2
Cũng từ
123 k k1 n
a a a ... a 0 a ... a
ta được
123 k 1
k1 n n
1
aaa...a a
2k
1
a...aa
2n k
Do đó
n1
2
11 n 2n 2
aa
2k n
2n k 2n kn
nkn
Như vậy bài toán được chứng minh xong.
Từ giả thiết của bài toán trên ta viết lại như sau
123 n
1 2 3 192
xxx x
... 0
2013 2013 2013 2013
xxx x
... 1
2013 2013 2013 2013
Áp dụng kết quả của bài toán phụ ta được
192 1
192 1
xx
2 2013
xx
2013 2013 192 96
Vậy bài toán được chứng minh xong.
Bài 55. Cho cac sô thưc dương a, b, c thoa man
222
abc1. Chưng minh:
222
222
ab 2c bc 2a ac 2b
2abbaca
1abc 1bca 1acb
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2013-2014
Lời giải
Do
222
abc1
nên ta có
22 2 2
2222 222
22 2
ab 2c ab 2c ab 2c ab 2c
1abc a b c abc a b ab
ab 2c a b ab
Áp dụng bất đẳng thức Cauchy ta có
222
222
22 2 222
2a b c
2c a b 2ab
ab 2c a b ab a b c
22
Suy ra
22 2
2
2222
22 2
ab 2c ab 2c ab 2c
ab 2c
1abc a b c
ab 2c a b ab
Tương tự ta được
22
22
22
bc 2a ca 2b
bc 2a ; ca 2b
1bca 1cab

Cộng vế theo vế các bất đẳng thức trên kết hợp
222
abc1 ta có bất đẳng thức cần chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 56. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
abc3
4
a1b1 b1c1 c1a1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2013-2014
Lời giải
Bất đẳng thức cần chứng minh tương đương với
4a c 1 4b a 1 4c b 1 3 a 1 b 1 c 1
4abbcca 4abc 3abc3abbcca 3abc 3
ab bc ca a b c 6
Áp dụng bất đẳng thức Cauchy cho các số dương ta được
2
3
3
ab bc ca 3. abc 3; a b c 3 abc 3
Cộng theo vế hai bất đẳng thức trên ta được
ab bc ca a b c 6
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 57. Cho a, b, c là các số thực dương thỏa mãn
abcabbcca 6abc . Chứng minh rằng:
222
111
3
abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán TP Hà Nội năm 2013-2014
Lời giải
Giả thiết của bài toán được viết lại thành
111111
6
ab bc ca a b c
Áp dụng bất đẳng thức Cauchy ta được
22 22 22
222
11 211 211 2
;;
ab bc ca
ab bc ca
121212
1; 1; 1
abc
abc
Cộng theo vế các bất đẳng thức trên ta được
222
111 111111
332 2.612
ab bc ca a b c
abc
Hay
222
111
3
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 58. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
1113
ab a 2 bc b 2 ca c 2 4
Trích đề thi tuyển sinh lớp 10 chuyên Toán TP Hà Nội năm 2013-2014
Lời giải
Đặt
xyz
a;b;c
yzx
. Gọi P là vế trái, khi đó ta được

111
P
ab a 2 bc b 2 ca c 2
yz zx xy
xy xz 2yz xy yz 2xz xz yz 2xy
Biến đổi tương đương ta được
yz zx xy
3P111
xy xz 2yz xy yz 2xz xz yz 2xy
111
3 P xy yz xz
xy xz 2yz xy yz 2xz xz yz 2xy
Áp dụng bất đẳng thức Cauchy dạng
111 1
ABC ABC
Ta có
99 93
3 P xy yz xz P 3
4xy 4yz 4xz 4 4 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 59. a) Chứng minh rằng:
33
ababab
, với a, b là hai số dương.
b) Cho a, b là hai số dương thỏa mãn
ab1
. Tìm giá trị nhỏ nhất của biểu thức:
2
33 22
3
Fab ab ab
2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2013-2014
Lời giải
a) Bất đẳng thức cần chứng minh tương đương với
22
2
22
aba abb abab 0
aba 2abb 0 abab 0
Ta thấy với a, b là hai số dương nên bất đẳng thức đã cho luôn đúng.
b) Cách 1: Áp dụng bất đẳng thức đã chứng minh trên ta có
2
2
33
ab abab
nên theo giả
thiết ta được
2
2
2
33
a b ab a b ab
Mặt khác ta có
2
22
ab ab 2ab11ab
Do đó
22
2
2
3ab
Fab 12ab abab 1
22
1115 1 1515
ab 2.ab. ab
4 16 16 4 16 16
Dấu đẳng thức xẩy ra khi và chỉ khi
1
ab
2
Vậy giá trị nhỏ nhất của F là bằng
15
16
, đạt được khi
1
ab
2
.
Cách 2: Ta có
2
2
33
1
Fab ab ab
2

Mà ta luôn có bất đẳng thức
3
33
ab
ab
4
, với mọi a, b > 0.
Áp dụng bất đẳng thức trên ta có
2
3
2
33
ab
1
ab
416
.
Áp dụng bất đẳng thức Cauchy ta có
22
2
ab 7ab
111715
Fab
16 8 16 8 16 8 16
Vậy giá trị nhỏ nhất của F là bằng
15
16
, đạt được khi
1
ab
2
.
Bài 60. Cho ba số thực dương a, b, c thỏa mãn
222
111 111
12 3
abc
abc
Chứng minh rằng:
1111
4abc a4bc ab4c 6
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2013-2014
Lời giải
Theo một đánh giá quen thuộc ta có
2
222
111 1 1 1 111
412 3
abc abc
abc
Suy ra
111 111
14 3 0
abc abc
Do đó ta được
111
1
abc
và abc9
Đặt
111
P
4abc a4bc ab4c
Áp dụng bất đẳng thức Cauchy dạng
411
xy x y
ta được
111
P
4a b c a 4b c a b 4c
1111111
43a abc 3a abc 3a abc
11 1 1 3 111 1
43a 3b 3c a b c 43 3 6
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 61. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
222 2 2 2 2 22
bca cab abc
2
bc ca ab
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thanh Hóa năm 2013-2014
Lời giải
Biến đổi tương đương bất đẳng thức như sau

222 2 2 2 2 22
222 2 2 2 2 22
22 3 2 2 3 2 22 3
22
22 2
bca cab abc
2
bc ca ab
ab c a bc a b ca b c 2abc
a b c 2abc a b c a 2abc b c a b c 2abc c 0
abc a bac b cab c 0
abcabca bacbabc cabcabc
2
2
0
bcaa bc 0
abcbcacab 0
Vì a, b, c là độ dài các cạnh của một tam giác nên
abc 0;bca 0;cab0
Do vậy bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh xong.
Bài 62. Cho các số thực dương x, y, z thỏa mãn
222
x y z 3xyz
. Chứng minh rằng:
222
444
xyz3
2
xyzyxzzxy
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nam Định năm 2014-2015
Lời giải
Cách 1: Áp dụng bất đẳng thức Cauchy ta có
2
24
44
2
11 x1
2x yz x yz
xyz xyz
2x yz 2 yz
211 1 111
yz 4yz
yz 2 yz
Từ hai bất đẳng thức trên ta được
2
4
x111
4y z
xyz
Hoàn toàn tương tự ta có
22
44
y111z111
;
4x z 4x y
yxz zxy
Cộng theo vế các bất đẳng thức trên ta được
222
444
xyz11111xyyzzx
2 y z x 2 xyz
xyzyxzzxy
Mặt khác ta lại có
222
xy yz zx x y z
Do đó ta được
222
xyz 3xyz
3
xyz xyz
Suy ra
222
444
xyz3
2
xyzyxzzxy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz1
Cách 2: Từ giả thiết của bài toán ta được
222
3xyz x y z xy yz zx
Suy ra
111
3
xyz
. Đặt
111
a;b;c
xyz
, khi đó ta được
abc3

Bất đẳng thức cần chứng minh được viết lại thành
222
444
abc bca cab 3
2
abcbcacab
Áp dụng bất đẳng thức Cauchy ta được
42
abc2abc
Do đó ta được
22
4
2
abc abc bc
2
abc
2a bc
Hoàn toàn tương tự ta được
222
444
abc bca cab ab bc ca
2
abcbcacab
Dễ thấy
ab bc ca a b c 3 nên ta được
222
444
abc bca cab 3
2
abcbcacab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz1
Bài 63. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1. Chứng minh rằng:
42 42 42
5
2abc a b c a b b c c a
9
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHKHTN Hà Nội năm 2013-2014
Lời giải
Cách 1: Áp dụng bất đẳng thức dạng
222
xyz xyyzzx
ta được
42 42 42 2 2 2
ab bc ca abc ab bc ca
Bài toán quy về chứng minh
222
5
2abc a b c abc a b b c c a
9
Hay
222
5
2a b c ab bc ca
9abc
Áp dụng bất đẳng thức Cauchy ta được
222
12a 12b 12c
ab ;bc ;ca
9b 3 9c 3 9a 3
Cộng theo vế các bất đẳng thức trên ta được
222
1112a2b2c
ab bc ca
9a 9b 9c 3 3 3
Hay
222
ab bc ca 2
ab bc ca a b c
9abc 3
Như vậy ta cần chỉ ra được
42
2a b c a b c
9abc 3
Hay
4abc a b c
4
3abc a b c 1
39
Đánh giá cuối cùng là một đánh giá đúng vì
2
1abbcca 3abcabc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Cách 2: Ta viết lại bất đẳng thức cần chứng minh thành
42 42 42
4
2abc a b c 1 a b b c c a
9
Để ý là
2
22 22 22
1 abbcca ab bc ca 2abcabc
Như vậy ta quy bài toán về chứng minh
2 2 22 2 2 4 2 42 4 2
4
ab bc ca ab bc ca
9

Để ý đến giả thiết ta biến đổi tương đương bất đẳng thức trên thành
22 2 22 2 22 2
22 22 22
22 22 22
4
ab a 1 bc b 1 ca c 1
9
4
ababac bcbcab cacbca
9
ab bc ca
49abbcca
bc ca ab
Dễ dàng chứng minh được
9a b b c c a 8a b c ab bc ca 8a b c
Theo bất đẳng thức Bunhiacopxki ta lại có
2
22 22 22
ab bc ca
ab bc ca 1
bc ca ab
2a b c 2a b c
Nhân theo vế hai bất đẳng thức trên ta được
22 22 22
ab bc ca
9a b b c c a 4
bc ca ab
Hay bất đẳng thức trên được chứng minh.
Bài 64. Cho a, b, c là các số thực không âm. Chứng minh rằng:
2
222
3
a b c 3 abc 2 ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nghệ An năm 2014-2015
Lời giải
Đặt
333
222
xa;yb;zc.
Suy ra
232323
ax;by;cz, nên
333
ax,by,cz với
x; y; z 0
Bất đẳng thức cần chứng minh trở thành
333 33 33 33
x y z 3xyz 2 x y y z z x
Áp dụng bất đẳng thức Cauchy ta được
33
xy x y 2xy xy 2 x y
Tương tự ta có
33 3 3
yz y z 2 y z ; zx z x 2 z x
Cộng theo vế các bất đẳng thức trên ta được
33 33 33
xy x y yz y z zx z x 2 x y y z z x
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333
x y z 3xyz xy x y yz y z zx z x
Vì vai trò của các biến bình đẳng nên có thể giả sử
xyz0
Khi đó
22
xxy zyz zxyxyyz 0
Suy ra
333
xyz3xyzxyxyyzyzzxzx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 65. Cho a, b, c là độ dài ba cạnh của một tam giác thỏa mãn điều kiện
2c b abc . Tìm giá trị nhỏ
nhất của biểu thức:
345
S
bca cab abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bắc Ninh năm 2014-2015

Lời giải
Từ giả thiết ta có
abc 0;bca 0;cab0 .
Áp dụng bất đẳng thức Cauchy dạng
11 4
xyxy
ta được
11 11 11
S23
bca cab bca abc cab abc
246
cba
Mà
21
2c b abc a
bc
nên kết hợp với bất đẳng thức Cauchy ta được
6
S2a 43
a
Vậy giá trị nhỏ nhất của S là
43 dấu bằng xảy ra khi và chỉ khi abc 3.
Bài 66. Cho phương trình
2
ax bx c 0 a 0
có hai nghiệm thuộc đoạn 0; 2
. Tìm giá trị lớn
nhất của biểu thức:
22
2
8a 6ab b
P
4a 2ab ac
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2014-2015
Lời giải
Gọi
121 2
x; x x x là hai nghiệm của phương trình đã cho. Theo định lí Vi-ét ta có
12 12
bc
xx ;xx
aa
Khi đó
2
2
22
12 12
2
12 12
bb
86
86xx xx
aa
8a 6ab b
P
bc
4a 2ab ac
42x x xx
42
aa
Do
2222
12 1122 1212
0x x 2 x xx;x 4 x x xx 4
2
12 12
xx 3xx4
Do đó ta được
12 12
12 12
86x x 3xx 4
P3
42x x xx
Đẳng thức xảy ra khi
12
xx2 hoặc
12
x0;x2 hay
cb4a
b 2a; c 0
Vậy giá trị lớn nhất của P là 3.
Bài 67. Cho a, b, c là các số thực dương thỏa mãn a b c 2014 . Chứng minh rằng:
33 33 33
222
5a b 5b c 5c a
2014
ab 3a bc 3b ca 3c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Lào Cai năm 2014-2015
Lời giải
Dễ dàng chứng minh được
33
ababab
, ta biến đổi tương đương bất đẳng thức bên như sau

33 33 3 33 2 2
33
33
2
ababab 5ab6aabab 5aba6aabb
5a b
5a b a 2a b 3a b 2a b
ab 3a
Hoàn toàn tương tự ta được
33 3 3
22
5b c 5c a
2b c; 2c a
bc 3b ca 3c
Cộng theo vế các bất đẳng thức trên ta được
33 33 33
222
5a b 5b c 5c a
a b c 2014
ab 3a bc 3b ca 3c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi
2014
abc
3
Bài 68. Cho các số dương x, y, z thỏa mãn
xx 1 yy 1 zz 1 18 .
Tìm giá trị nhỏ nhất của biểu thức:
111
B
xy1yz1zx1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2014-2015
Lời giải
.
Ta biến đổi giả thiết
222
xx 1 yy 1 zz 1 18 x y z 18 x y z
Áp dụng một đánh giá quen thuộc ta được
2
xyz 543xyz
Hay
0xyz6
Ap dung bât đăng thưc Cauchy dạng
111 9
abcabc
ta được
111 9 93
B
xy1yz1zx1 2.63 5
2x y z 3
Hay
3
B
5
. Dâu băng xay ra khi và chỉ khi xyz2
Vậy giá trị nhỏ nhất của B là
3
5
. Đẳng thức xẩy ra khi xyz2
Bài 69. Cho a, b, c là ba số thực dương và có tổng bằng 1. Chứng minh rằng:
abc bca cab 3
abcbca cab 2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2014-2015
Lời giải
Kết hợp với giả thiết ta có biến đổi sau
abc 2bc 2bc 2bc
11 1
abc abc
aabc bc abac
Hoàn toàn tương tự ta được
bca 2ca cab 2ab
1;1.
bca cab
bcba cabc
Khi đó ta được
abc bca cab bc ca ab
32
abcbca cab
abac bcba cacb

Ta quy bài toán về chứng minh
bc ca ab 3
4
abac bcba cacb
Bất đẳng thức trên tương đương với
22222 2
22 2
4bc b c 4ca c a 4ab a b 3 a b b c c a
bccaab
b c bc c a ca a b ab 6abc 6
aabbcc
ba cb ca
2220
ab bc ac
ab bc ca
0
ab bc ca
Bât đăng thưc cuối cùng luôn đung. Vậy bài toán được chứng minh xong.
Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 70. Cho a, b, c là các số thực dương thỏa mãn 6a 3b 2c abc . Tìm giá trị lớn nhất của biểu
thức:
222
123
B
a1 b4 c9
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2014-2015
Lời giải
Giả thiết của bài toán được viết lại thành
632
1
bc ca ab
. Đặt
123
a;b;c
xyz
, khi đó ta
được
xy yz zx 1
Biểu thức B được viết lại thành
222
xyz
B
x1 y1 z1
Để ý đến giả thiết
xy yz zx 1
ta có
22
x1xxyyzzx xyzx
Khi đó ta được
2
xx
x1
xyzx
Hoàn toàn tương tự ta được
xyz
B
xyxz xyyz zxyz
Áp dụng bất đẳng thức Cauchy ta được
x1xx
2x y z x
xyzx
y1yy
2x y y z
xyyz
z1zz
2z x y z
xzyz
Cộng theo vế các bất đẳng thức trên ta được
xyz3
B
2
xyxz xyyz zxyz

Vậy giá trị lớn nhất của B là
3
2
.
Đẳng thức xẩy ra khi và chỉ khi
a 3;b 23;c 33
Bài 71. Cho các số thực a, b, c dương. Chứng minh rằng:
22 2 2 2 2
abc
2
bc ca ab
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Quảng Trị năm 2014-2015
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
22
222
22
22 2
aa 2a
abc
bc
ab c
Hoàn toàn tương tự ta được
22
222 222
22 22
b2bc 2c
;
abc abc
ca ab
Cộng theo vế các bất đẳng thức trên ta được
22 2 2 2 2
abc
2
bc ca ab
Vì đẳng thức không xẩy ra nên ta có bất đẳng thức
22 2 2 2 2
abc
2
bc ca ab
Bài toán được chứng minh xong.
Bài 72. Giả sử a, b, c là các số thực dương thỏa mãn abc3. Tìm giá trị nhỏ nhất của biểu thức:
33
bca cab abc
A
2a 2b 2c
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Đăk Lăk, 2014 – 2015
Lời giải
Cách 1:
Áp dụng bất đẳng thức Cauchy ta được
3
3
3
bca 3bca
2a 1
2a 4 2 2
cab 3cab
2b 1
2b 4 2 2
abc 3abc
2c 1
2c 4 2 2
Cộng theo vế các bất đẳng thức trên ta được
33
bca cab abc 3abc
abc3
2a 2b 2c 2 2 2
Hay
33
bca cab abc
33
abc
2a 2b 2c 2 2
Vậy giá trị nhỏ nhất của A là
3
2
. Đẳng thức xẩy ra khi và chỉ khi abc1.
Cách 2: Đặt xbca;ycab;zabc , khi đó ta viết lại giả thiết thành
xyz 3. Bài toán quy về tìm giá trị nhỏ nhất của biểu thức
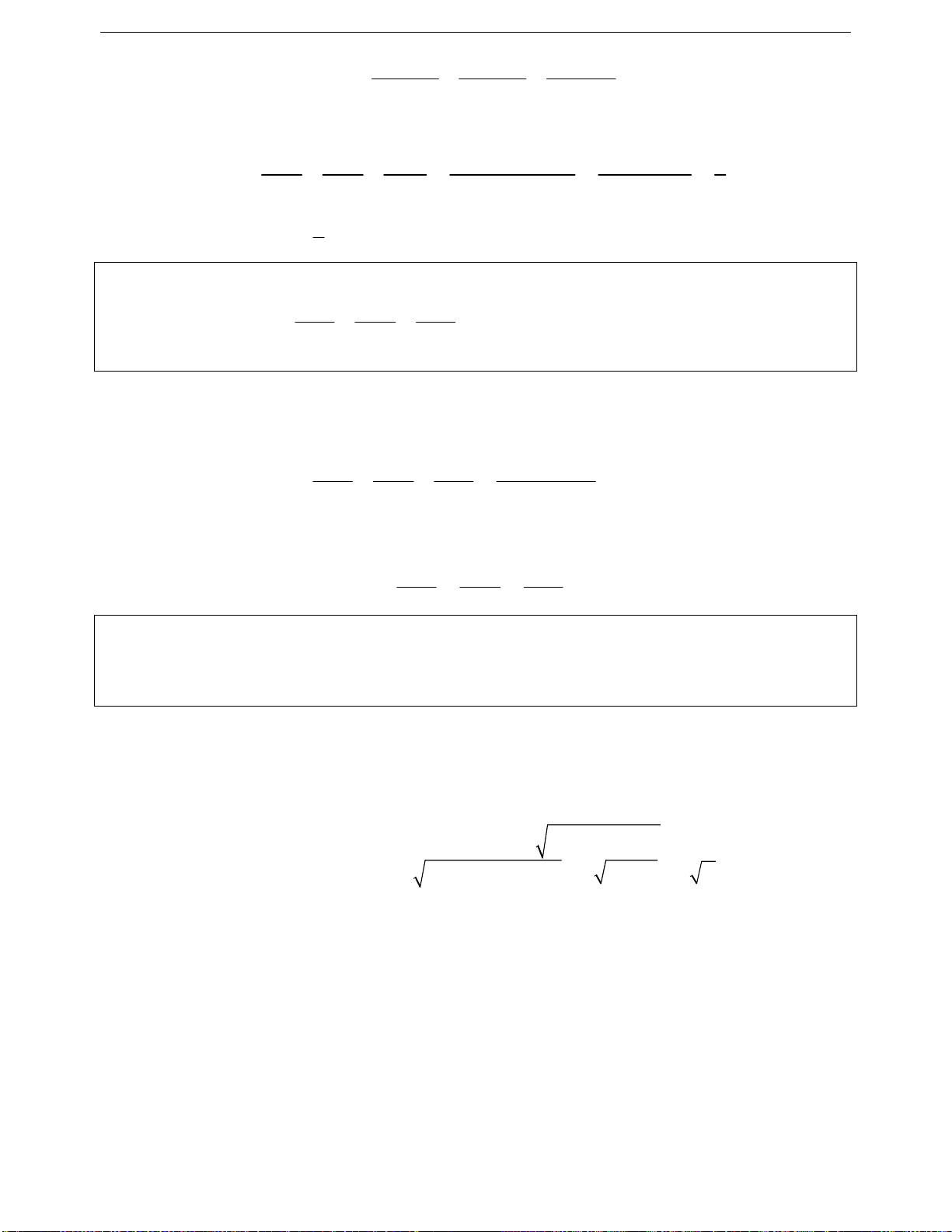
333
xyz
A
2y z 2z x 2x y
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
333 222
xyz
xyz xyz3
A
yz zx xy 2 2
2xy yz zx
Vậy giá trị nhỏ nhất của A là
3
2
. Đẳng thức xẩy ra khi và chỉ khi abc1.
Bài 73. Cho ba số thực x, y, z thỏa mãn x1;y2;z3 và xyz 5. Chứng minh
rằng:
149
36
x1 y2 z3
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Yên Bái năm 2014-2015
Lời giải
Do x1;y2;z3 nên x 1 0; y 2 0; z 3 0 . Khi đó áp dụng bất đẳng thức
Bunhiacopxki dạng phân thức ta được
2
123
149
36
x1 y2 z3 xyz6
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz 5
123
x1 y2 z3
Bài 74.
Cho ba số thực x, y, z không âm thỏa mãn xyzxyz4 . Tìm giá trị lớn nhất của biểu
thức:
Pxyyzzx
Trích đề thi tuyển sinh lớp 10 chuyên Toán Đại Học Vinh năm 2014-2015
Lời giải
Cách 1:
Giả sử x là số nhỏ nhất trong ba số x, y, z. khi đó ta xét các trường hợp sau:
+ Trường hợp 1:
yz 1 . Kho đó ta được
xy 1; zx 1
nên P3
+ Trường hợp 2:
yz 1 . Khi đó ta được xyz x .
Do đó
22
4 x y z xyz x y z x 2 x y x z
2x xy yz zx 2x P 2P
Suy ra
P4 . Kết hợp các kết quả ta được giá trị nhỏ nhất của P là 4.
Đẳng thức xẩy ra khi và chỉ khi
x0;yz2 và các hoán vị.
Cách 2: Giả sử x là số lớn nhất trong các số x, y, z.
Khi đó ta được
3
xyz3x;xyzx
Suy ra
3
x3x4 hay
2
x1x x4 0 x 1.
Ta có
22
2
2
P xy yz zx x x y z yz x x 4 xyz yz x
x2 4yz1x 4
Suy ra
P4
. Vậy giá trị nhỏ nhất của P là 4.

Đẳng thức xẩy ra khi và chỉ khi
x0;yz2
và các hoán vị.
Bài 75. Cho a, b, c là ba số thực dương thỏa mãn
abc3
. Chứng minh rẳng:
222
abc3
2
b3 c3 a3
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bắc Giang năm 2014-2015
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222 2 2 2 222
abc 4a4b4c4a4b4c
b7 c7 a7
b3 c3 a3 4b3 4c3 4a3
Áp dụng tiếp bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
4a b c
4a 4b 4c 4.9 3
b7 c7 a7 abc21 321 2
Suy ra ta được
222
abc3
2
b3 c3 a3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 76.
1) Cho a, b, c là ba số thực dương tùy ý. Chứng minh rẳng:
3
3
aababc abc
4
2) Cho a, b, c là ba số thực dương tùy ý. Chứng minh rẳng:
222
bc ca ab
1
a2bcb2cac2ab
Trích đề thi tuyển sinh lớp 10 chuyên Tin - Toán Tỉnh Tiền Giang năm 2014-2015
Lời giải
1) Sử dụng bất đẳng thức Cauchy ta có:
3
3
a
b4c
aa a
4
ab 2. .b b; abc .b.4c
44 4 3
Từ đó ta có
3
a
b4c
4a b c
a
4
aababca b
43 3
.
Bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
a 4b 16c
2) Bất đẳng thức cần chứng minh tương đương với
222
222
abc
1
a2bcb2cac2ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222 222
abc
abc
1
a 2bc b 2ca c 2ab a b c 2ab 2bc 2ca
Bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi abc
Bài 77. Cho x, y, z là ba số thực dương thỏa mãn xyz1. Chứng minh rẳng:
222
1x 1y 1z
6
xyz yzx zxy
Trích đề thi tuyển sinh lớp 10 chuyên Toán Thành Phố Hà Nội năm 2014-2015
Lời giải
Áp dụng giả thiết ta được

2
1x1x xyyz zxyz
1x
xyz
xyzx xyzx
Hoàn toàn tương tưh ta được
2
2
xzxy xzyz
1y
yzx
xyyz
xyyz xyxz
1z
zxy
yzzx
Đặt
axyyz;byzzx;cxyzx , khi đó ta viết lại được bất đẳng
thức thành
abbcca
6
cab
Áp dụng bất đẳng thức Cauchy ta được
ab bc cc
2; 2; 2
ba cb aa
Cộng theo vế các bất đẳng thức trên ta được
abbc ca
6
cab
Vậy bài toán được chứng minh xong.
Bài 78. Cho x, y, z là ba số thực dương thỏa mãn xy yz zx 1. Chứng minh rẳng:
222
xyz3
2
x1 y1 z1
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHSP TP Hồ Chí Minh, 2014-2015
Lời giải
Áp dụng giả thiết ta được
22
xx x
x1 xxyyzzx
xyxz
Áp dụng bất đẳng thức Cauchy ta được
2
xx1xx
2x y z x
xyxz
xyxz
Do đó ta được
2
x1x x
2x y z x
x1
Hoàn toàn tương tự ta được
22
y1y y z1z z
;
2x y y z 2z x y z
y1 z1
Cộng theo vế các bất đẳng thức trên ta được
222
xyz
x1 y1 z1
1xxyyzz3
2xyzxxyyzzxyz 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
Bài 79. Cho x, y, z là các số thực dương thỏa mãn

22 22 22
x y y z z x 2014
Tìm giá trị nhỏ nhất của biểu thức:
222
xyz
P
yz zx xy
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thanh Hóa, 2014 – 2015
Lời giải
Dễ dàng chứng minh được
22
2y z x y do đó ta được
22
22
xx
yz
2y z
.
Hoàn toàn tương tự ta được
222
22 2 2 2 2
xyz
P
2y z 2z x 2x y
Đặt
22 2 2 2 2
ayz;bzx;cxy , suy ra a b c 2014
Từ đó ta được
222 2 2 2 2 22
222
bca cab abc
x;y;z
222
Khi đó ta được
222 2 2 2 2 22
1bca cab abc
P
abc
22
Xét biểu thức
222 2 2 2 2 22
22 22 2 2
bca cab abc
Q
abc
bcacab
abc
aabbcc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 222
22
abc bca
Qabc
bca abc
abc abc
a b c a b c 2014
abc abc
Do đó ta được
2014
P
22
. Vậy giá trị nhỏ nhất của P là
2014
22
.
Đẳng thức xẩy ra khi và chỉ khi
2014
xyz
32
.
Bài 80. Giả sử a, b, c là các số thực dương thỏa mãn ab bc ac abc 4 . Chứng minh rằng:
222
a b c abc2abbcac
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHKHTN Hà Nội năm 2015-2016
Lời giải
Áp dụng bất đẳng thức Cauchy 4 số ta có :
43
3
333 222
4 abc ab bc ac 4 a b c 1 abc a b c 3 abc 3 a b c
Khi đó ta quy bài toán về chứng minh
3
222 222
a b c 3 a b c 2 ab bc ac
Đặt
333
222
a x, b y, c z x, y, z 0 , bất đẳng thức được viết lại thành
333 333333
x y z 3xyz 2 x y 2 z x 2 z y
Dễ dàng chứng minh được

333
x y z 3xyz xy x y yz y z xz x z
33 33 33
xy x y yz y z xz x z 2 x y 2 z x 2 z y
Khi đó ta được
333 333333
x y z 3xyz 2 x y 2 z x 2 z y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 81. Giả sử x, y, z là các số thực lớn hơn 2. Tìm giá trị nhỏ nhất của biểu thức:
xyz
P
yz4 zx4 xy4
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHKHTN Hà Nội năm 2015-2016
Lời giải
Ta có
4x 4y 4z
P
4y z 4 4z x 4 4x y 4
Áp dụng bất đẳng thức Cauchy ta được
4y z 4 24y z 4 y z 4 4 y z
Áp dụng tương tự thì ta được
4x 4y 4z x y z
P4
yz xz xy
4y z 4 4z x 4 4x y 4
Dễ dàng chứng minh được
xyz3
yz xz xy 2
Do đó ta được
P6
. Vậy giá trị nhỏ nhất của P là 6.
Đẳng thức xẩy ra khi và chỉ khi
xyz4.
Bài 82. Tìm các số thực không âm a và b thỏa mãn:
22
3311
ab ba 2a 2b
4422
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐHSP Hà Nội năm 2015-2016
Lời giải
Ta dễ dàng chứng minh được
2
22
2
22
11 31
a0aaabab
24 42
11 31
b0bbbaab
24 42
Áp dụng đánh giá trên và bất đẳng thức Cauchy ta được
2
2
22
2
33 11
ab ba ab 2a2b1
44 24
11
2a 2b
22
11
2a 2b
422
Đẳng thức xảy ra khi và chỉ khi
1
ab .
2

Bài 83. Cho x, y, z là các số thực dương thỏa mãn
222
111
1.
xyz
Tìm giá trị nhỏ nhất của biểu thức:
22 2 2 2 2
22 2 2 2 2
yz zx xy
P
xy z yz x zx y
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Phú Thọ năm 2015-2016
Lời giải
Ta co
22 22 22
111
P
11 11 11
xyz
zy zx xy
Đặt
111
a;b;z
xyz
thì a; b; c 0 và
222
abc1.
Khi đó ta được
222
22 2 2 2 2
222
abc a b c
P
bc ca ab
a1 a b1 b c1 c
Ap dung bất đẳng thức Côsi cho 3 số dương ta có
3
222
2
22 22 2
22
2
2
1 12a 1a 1a 4
a1a .2a1a 1a
22327
2a33.a
a1 a
2
a1 a
33
Hoàn toàn tương tự ta được
2222
22
b33.bc33.c
;
22
b1 b c1 c
Cộng theo vế các kết quả trên ta được
33
P
2
. Vậy giá trị nhỏ nhất của P là
33
2
.
Đẳng thức xẩy ra khi và chỉ khi xyz 3
Bài 84. Xét các số thực dương a, b, c thỏa mãn abc 1 . Tìm giá trị lớn nhất của biểu thức:
44 44 4 4
abc
T
bcaacbabc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nam Định năm 2015-2016
Lời giải
Ta có
2
44 22 22 44 22
2b c b c 2bcb c b c bcb c
Do đó ta được
22
44 222
22 22 2
aa a a
bca abc
bc b c a abc b c a
Hoàn toàn tương tự ta được
22
44 2 224 4 2 22
bbcc
;
acbabcabcabc
Cộng theo vế các kết quả trên ta được
T1 .
Vậy giá trị lớn nhất của T là 1. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 85. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

222
222
222 222 222
4a b c 4b c a 4c a b
3
2a b c 2b c a 2c a b
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nam Định năm 2015-2016
Lời giải
Ta có
2 2
222 222
2
222 222 222
22a b c 4a b c 2bc
4a b c b c
2
2a b c 2a b c 2a b c
Áp dụng tương tự ta viết lại được bất đẳng thức
222
222 222 222
bc ca ab
3
2a b c 2b c a 2c a b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
22
222 2222
2
22
22 2 22 2 2
2
22
222 22 22
bc
bc
2a b c a b c a
ca
ca
2b c a b c b a
ab
ab
2c a b c a c b
Cộng theo vế các bất đẳng thức trên ta được
222
222 222 222
bc ca ab
3
2a b c 2b c a 2c a b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Bài 86. Cho a, b là các số dương thỏa mãn điều kiện
3
ab 4ab12 . Chứng minh rằng:
11
2015ab 2016
1a 1b
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Hải Dương năm 2015-2016
Lời giải
Ta có
3
3
12 (a b) 4ab 2 ab 4ab . Đặt tab,t0 thì
32 32 2
12 8t 4t 2t t 3 0 t 1 2t 3t 3 0
Do
2
2t 3t 3 0, t
nên t1 0 t 1 . Vậy 0ab1
Dễ dàng chứng minh được
11 2
1a 1b
1ab
, a, b 0, ab 1
Thật vậy, bất đẳng thức tương đương với
2
1111 aba abb
00
1a 1b
1ab 1ab
1a1 ab 1b1 ab
ba ab1
ba a b
00
1a 1b
1ab
1ab1a1b
Do
0ab1 nên bất đẳng thức này đúng.

Tiếp theo ta sẽ chứng minh
2
2015ab 2016,
1ab
a, b 0, ab 1
Đặt tab,0t1 ta được
2
2
2015t 2016
1t
32 2
2015t 2015t 2016t 2014 0 t 1 2015t 4030t 2014 0
Do
0t1 nên bất đẳng thức trên đúng.
Vậy
11
2015ab 2016
1a 1b
.
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
ab1.
Bài 87. Cho a,b,c là các số thực bất kỳ . Chứng minh rằng:
2
222
3a b c
a1b1c1
4
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Nghện An năm 2015-2016
Lời giải
Cách 1:
Bất đẳng thức cần chứng minh tương đương với
2
222
2a 2 2b 2 2c 2 3 2a 2b 2c
Đặt
x a 2; y b 2; z c 2. Bất đẳng thức cần chứng minh trở thành
2
222
x2y2z23xyz
Ta có
22 22 22
x2y2 xy12x2y3
Suy ra
2
2
22 22
xy
3
x2y22xyxy 3 xy 2
22
22
222 2 2
22
2
3
x2y2z2 xyz42xy 2z
2
3
4x yz 2x y 2z 3x y z
2
Do đó ta được
2
222
3a b c
a1b1c1
4
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc .
2
Cách 2: Bất đẳng thức cần chứng minh tương đương với
222 22 22 22 2 2 2
4abc4abbcca abc46abbcca
Theo nguyên lý Dirichlet ta giả sử
22 222
2 22 2 22 22
2a 1 2b 1 0 c 2a 1 2b 1 0
4a b c c 2a c 2b c
Khi đó ta quy bài toán về chứng minh

2 2 22 2 2 2 2 22 22
22
22
4ab bc ca a b 2ac 2bc 4 6ab bc ca
32bc 1 32ca 1
ab 2ab1 0
2
Bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh.
Bài 88.
Cho a, b, c là các số thực dương thỏa mãn
111
abc
abc
Chứng minh rằng:
333
a) a b c 3abc
abc3
b)
13bc 13ca 13ab 2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bà Rịa – Vũng Tàu, 2015 – 2016
Lời giải
a) Giả thiết của bài toán được viết lại thành
abc a b c ab bc ca
Mà ta lại có
2
abc
ab bc ca
3
Do đó ta được
2
abc
abc a b c 3abc a b c
3
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
b) Bất đẳng thức cần chứng minh được viết lại thành
444
abc3
a 3abc b 3abc c 3abc 2
Áp dụng kết quả câu a ta được
4442 2 2
abca b c
a 3abc b 3abc c 3abc
2a b c a 2b c a b 2c
Ta cần chỉ ra được
222
abc3
2
2abc a2bc ab2c
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc
2a b c a 2b c a b 2c 2a b c a 2b c a b 2c
Mà theo bất đẳng thức Bunhiacopxki ta được
2abc a2bc ab2c 12abc
Suy ra
22
abc abc abc abc
2abc a2bc ab2c 23
23a b c
Cũng từ giả thiết
111
abc
abc
ta suy ra được
111 9
abc abc3
abcabc

Do đó
abc abc
3
2
23
.
Từ các kết quả trên ta được
222
abc3
2
2abc a2bc ab2c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 89. Cho các số dương a, b, c thỏa mãn
ab bc ca 3
. Chứng minh rằng:
222
1113
2
a1b1c1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2015-2016
Lời giải
Theo một đánh giá quen thuộc ta được
2
a b c 3 ab bc ca 9 a b c 3
Áp dụng bất đẳng thức Cauchy ta được
22
22
1aaa
111
2a 2
1a 1a
Hoàn toàn tương tự ta được
22
bc
1; 1
22
11
b1 c1
Cộng theo vế các bất đẳng thức trên ta được
222
abc
2
111 3
3
2
a1b1c1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 90. Cho a, b, c là các số thực dương thỏa mãn abc 1 . Chứng minh rằng:
22 2
bca 9 9
abc 2
2ab bc ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Thái Bình năm 2015-2016
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
22 2
abc
bca
abc
abc abc
Mà theo một đánh giá quen thuộc thì
abc 3abbcca
Do đó ta được
22 2
bca 9 9
3ab bc ca
abc
2ab bc ca 2ab bc ca
Áp dụng bất đẳng thức Cauchy ta được
3
9
3ab bc ca
2ab bc ca
3ab bc ca 3ab bc ca
9279
3
22 82
2ab bc ca
Suy ra
22 2
bca 9 9
abc 2
2ab bc ca
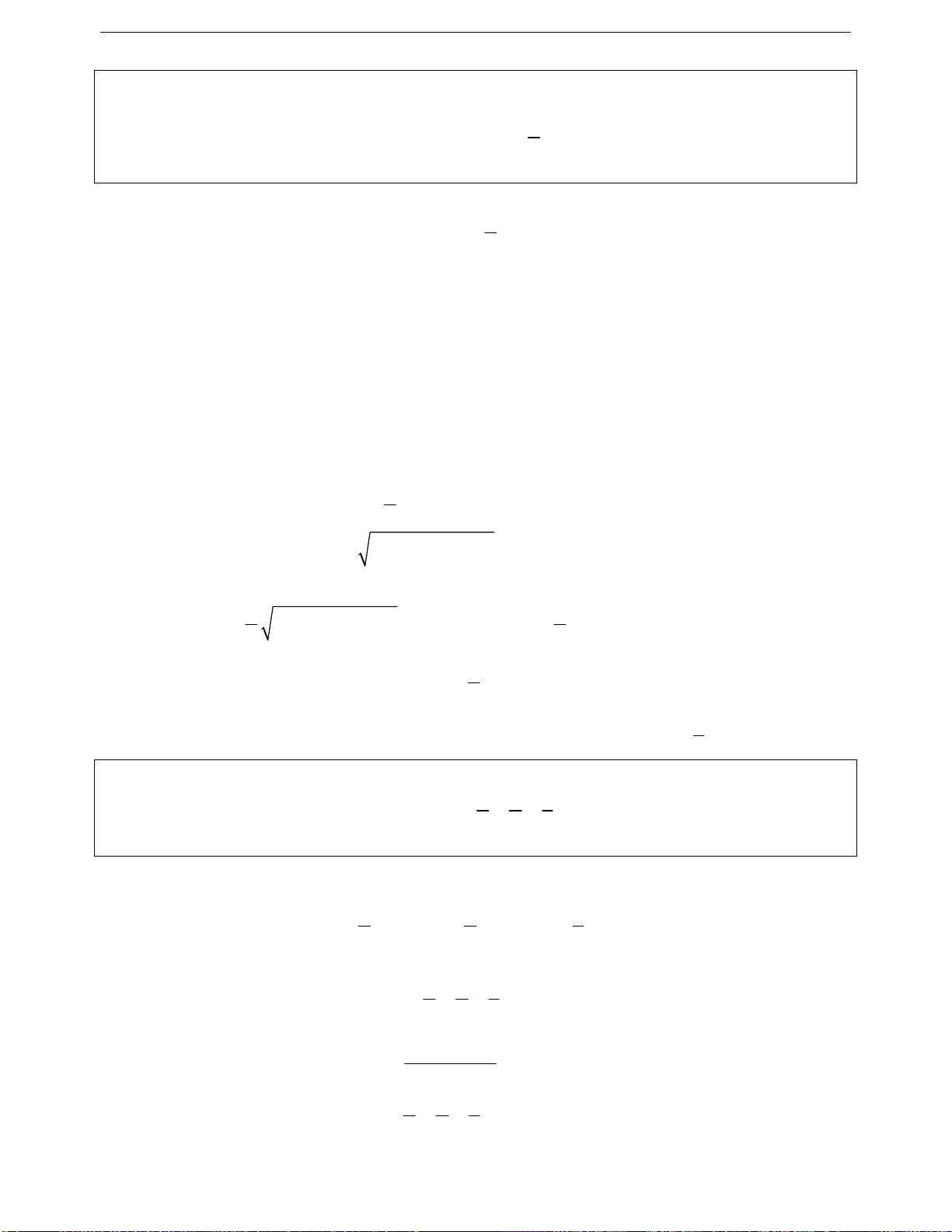
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 91. Cho a, b, c số thực dương thoả mãn
abbcca 1.
Chứng minh rằng:
3
ab ac bc
4
Trích đề thi tuyển sinh lớp 10 chuyên Toán TP Hà Nội năm 2015-2016
Lời giải
Dễ dàng chứng minh được
8
abbcca abcabbcca
9
Thật vậy, bất đẳng thức trên tương đương với
9a b b c c a 8a b c ab bc ca
Ta có đẳng thức
abcabbcca abbcca abc
Nên ta được
9a b b c c a 8a b b c c a 8abc
a b b c c a 8abc
Đánh giá cuối cùng là một đánh giá đúng. Do đó bất đẳng thức trên đúng.
Áp dụng bất đẳng thức trên và kết hợp với giả thiết ta được
8
1abcabbcca
9
Lại có
abc 3abbcca
Nên ta được
2
3
89
1 3 ab bc ca ab bc ca 3 ab bc ca
98
Hay
3
ab bc ca
4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
.
Bài 92. Cho a, b, c là các số thực dương thỏa mãn abc3. Chứng minh rằng:
555
111
abc 6
abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bạc Liêu năm 2015-2016
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
525252
111
a2a;b2b;c2c
abc
Cộng theo vế các bất đẳng thức trên ta được
555 222
111
abc 2abc
abc
Dễ thấy
2
222
abc
abc 3
3
Do đó ta được
555
111
abc 6
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.

Bài 93. Cho x, y, z là các số thực dương thỏa mãn xyz 32 . Chứng minh rằng:
1113
4
x 3y 5z y 3z 5x z 3x 5y
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình Thuận năm 2015-2016
Lời giải
Cách 1:
Áp dụng bất đẳng thức Cauchy ta được
111
x 3y 5z y 3z 5x z 3x 5y
9
x 3y 5z y 3z 5x z 3x 5y
Mà theo bất đẳng thức Bunhiacopxki ta được
x 3y 5z y 3z 5x z 3x 5y
3 x 3y 5z y 3z 5x z 3x 5y 24 xy yz zx
Mà theo một đánh giá quen thuộc thì
2
3xy yz zx x y z 18
Do đó ta được
x3y 5z y3z 5x z3x 5y 8.18 12
Suy ra
11193
12 4
x 3y 5z y 3z 5x z 3x 5y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz 2 .
Cách 2: Áp dụng bất đẳng thức Cauchy ta được
28x3y5z 8x3y5z
Suy ra
14242
8x 3y 5z
x3y 5z 28x3y 5z
Hoàn toàn tương tự ta được
142142
;
8y 3z 5x 8z 3x 5y
y3z 5x z3x 5y
Cộng theo vế các bất đẳng thức trên ta được
111
x 3y 5z y 3z 5x z 3x 5y
42 42 42
8x 3y 5z 8y 3z 5x 8z 3x 5y
Mà theo bất đẳng thức Cauchy ta có
42 42 42 9.42 362 3
8x 3y 5z 8y 3z 5x 8z 3x 5y 4
16 x y z
16.3 2
Suy ra
1113
4
x 3y 5z y 3z 5x z 3x 5y

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz 2
.
Bài 94. Cho a, b, c là các số thực không âm thỏa mãn abc2. Tìm giá trị nhỏ nhất của biểu thức:
222
222
ab bc ca 1
Pabc
2
abc
Trích đề thi tuyển sinh lớp 10 chuyên Toán ĐH Vinh năm 2015-2016
Lời giải
Từ giả thiết
abc2
ta được
222
4abc
ab bc ca
2
Do đó biểu thức P được viết lại thành
222
222
222
4abc
1
Pabc
4
abc
Đặt
222
2
tabc t2
3
. Khi đó ta được
22
22
t121
1t tt 1 3tt 3 39
Pt 1 1
488 444 4 24
t2t
Vậy giá trị nhỏ nhất của P là
9
4
. Đẳng thức xẩy ra khi và chỉ khi ab0;c2 và các hoán vị.
Bài 95. a) Cho a, b là các số thực dương. Chứng minh rằng:
1a1b 1 ab
b) Cho a, b là các số thực dương thỏa mãn abab . Tìm giá trị nhỏ nhất của biểu thức:
22
22
11
P1a1b
a2ab2b
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bình Phước năm 2015-2016
Lời giải
a) Bình phương hai vế ta được
2
1 a 1 b 1 2 ab ab a b 2 ab a b 0
b) Áp dụng bất đẳng thức câu a và
11 4
xyxy
ta được
22 2 22
3
22
444
P1ab 1abab1
a2ab2b ab
ab 2ab2ab
4 ab ab 7ab 1 1 7ab 7 7ab
13.4. . 1
16 16 8 16 16 8 4 8
ab
Mặt khác từ giả thiết ta có ab a b 2 ab ab 4
Do đó ta được
77.4 21
P
48 4
. Vậy giá trị nhỏ nhất của P bằng
21
4
. Đẳng thức xẩy ra khi và chỉ khi
ab2
Bài 96. Cho ba số dương a, b, c thỏa mãn điều kiện
111
3
abc
. Chứng minh rằng:
22 2
abcabbcca
3
2
1b 1c 1a
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Ninh Bình năm 2015-2016

Lời giải
Áp dụng bất đẳng thức Cauchy ta được
111 9
3abc3
abcabc
Biến đổi và áp dụng bất đẳng thức Cauchy ta được
22
22
aababab
aaa
2b 2
1b 1b
Hoàn toàn tương tự ta được
22
bbccca
b; c
22
1c 1a
Khi đó ta được
22 2
a b c abbcca abbcca abbcca
abc 3
222
1b 1c 1a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 97.
Cho ba số dương a, b, c thỏa mãn điều kiện
abc3
. Chứng minh rằng:
444
abc1
3
a2b2 b2c2 c2a2
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Bắc Giang năm 2015-2016
Lời giải
Cách 1:
Áp dụng bất đẳng thức Cauchy ta có
4
4
4
aa2b214a
27 27 9 9
a2b2
bb2c214b
27 27 9 9
b2c2
cc2a214c
27 27 9 9
c2a2
Cộng theo vế các bất đẳng thức trên ta được
444
2abc 4abc
abc 1
27 3 3
a2b2 b2c2 c2a2
Hay
444
10 a b c
abc 211
27 27 3
a2b2 b2c2 c2a2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222
444
abc
abc
a2b2 b2c2 c2a2 abbcca4abc 12
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
2
222
3 a b c ab bc ca 4 a b c 12
3a b c ab bc ca 24
Theo một đánh giá quen thuộc ta có
2
2
222 222 222
3abc abcabc 9abc

Lại thấy
2
222 222
8a b c
a b c ab bc ca; 8 a b c 8.3 24
3
Cộng theo vế hai bất đẳng thức trên ta được
2
222 222
3abc 9abc abbcca24
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 98. Cho ba số thực x; y; z 1 . Chứng minh rằng:
444
22
xyz
48
x1
y1 z1
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Tiền Giang năm 2015-2016
Lời giải
Cách 1:
Áp dụng bất đẳng thức Bunhiacopsxki ta được
2
444 222
22
xyz1xyz
3y 1 z 1 x 1
x1
y1 z1
Ta quy bài toán về chứng minh
2
222
xyz
144
y1 z1 x1
Hay
222
xyz
12
y1 z1 x1
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
xyx
xyz
y1 z1 x1 x yz3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
xyx
12
xyz3
hay
22
2
xyz 12xyz 36 xyz 12xyz 360
xyz6 0
Bất đẳng thức cuối cùng luôn đúng.
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
xyz2
.
Cách 2: Ta đi chứng minh bất đẳng thức: Với
a1
thì
2
4
a16a1
Thật vậy
22
442 2
a 16 a 1 a 16a 32a 16 0 a 2 a 4a 4 0
Vì
a1 nên
2
a4a40
, do đó bất đẳng thức trên đúng.
Áp dụng bất đẳng thức trên ta được
2
4
y16y1 do đó
44
24
x16x
y
y1
.
Hoàn ta tương tự ta được
444 444
22 444
xyz xyz
16 48
yzx
x1
y1 z1

Vì theo bất đẳng thức Cauchy thì
444
44 4
xyz
3
yzx
Vậy bất đẳng thức được chứng minh.
Bài 99. Cho x, y, z là các số thực dương thỏa mãn xy yz zx 2xyz . Tìm giá trị nhỏ nhất của biểu
thức:
xyz
P
zz x xx y xx z
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Cần Thơ năm 2015-2016
Lời giải
Biến đổi giả thiết ta được
111
2
xyz
. Đặt
111
a;b;c
xyz
, khi đó giả thiết trở thành
abc2.
Ta viết lại biểu thức P là
222
2
abc
P
a2b c2a
b2c
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
2
abc
abc abc2
P
a2b c2a 3 3
b2c
3a b c
Vậy giá trị nhỏ nhất của P là
2
3
. Đẳng thức xẩy ra khi và chỉ khi
3
xyz
2
Bài 100. Cho a, b, c là các số thực dương thỏa mãn abc 3. Chứng minh rằng:
222
111
1
2ab 2bc 2ca
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Vĩnh Phúc năm 2015-2016
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
ab bc ca
1
2ab 2bc 2ca
Áp dụng bất đẳng thức Cauchy ta có
3
222
2ab11ab 3ab
Do đó ta được
3
22 2
2
3
2
ab ab a ab
3
2ab
3ab
Hoàn toàn tương tự ta được
33
3
222 22
222
ab bc ca a ab b bc c ca
3
2ab 2bc 2ca
Cũng theo bất đẳng thức Cauchy ta được
3
2
abb a2b
ab
33
Suy ra
2
3
2
aa 2b
a2ab
aab
33
Hoàn toàn tương tự ta được
2
33
3
22
abc
aab bbc cca 3
3
Từ đó ta được
222
222
ab bc ca
1
2ab 2bc 2ca

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 101. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 11
. Tìm giá trị nhỏ nhất của biểu
thức:
222
5a 5b 2c
P
12 a 11 12 b 11 c 11
Trích đề thi tuyển sinh lớp 10 chuyên Toán Tỉnh Quảng Bình năm 2015-2016
Lời giải
Dễ thấy
22
a11aabcaca abac
, do đó ta được
2
12 a 11 2 3 a b a c 3 a b a c 4a 3b c
Hoàn toàn tương tự ta được
2
12 b 11 2 3 a b b c 3 a b b c 3a 4b c
2
cabc ab2c
c11 cabc
22
Khi đó ta được
222
15a 15b
12 a 11 12 b 11 c 11 3c
22
Suy ra
5a 5b 2c 10a 10b 4c 2
P
15a 15b 15a 15b 6c 3
3c
22
Vậy giá trị nhỏ nhất của P là
2
3
. Đẳng thức xẩy ra khi và chỉ khi
2a 3b 3a 2b c
ab1;c5
ab bc ca 11
Bài 102. Cho ba số dương a, b, c thỏa mãn điều kiện
222
abc3
. Chứng minh rằng:
333
111
1
18a 18b 18c
Trích đề thi HSG tỉnh Nam Định năm 2011-2012
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2
2
2
32 2
12a12a 4a
18a 12a12a4a 12a
2
Do đó ta được
2
3
11
12a
18a
. Hoàn toàn tương tự ta được
22
33
1111
;
12b 12c
18b 18c
Cộng theo vế các bất đẳng thức trên ta được
222
333
1 1 1 111
12a 12a 12a
18a 18b 18c
Theo bất đẳng thức Cauchy ta lại có

222
222
111 9
1
12a 12a 12a
32a b c
Suy ra
333
111
1
18a 18b 18c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra hi và chỉ khi
abc1
Bài 103. Cho x, y thỏa mãn
x, y R
1
0x,y
2
. Chứng minh rằng:
yx22
1y 1x 3
Trích đề thi HSG tỉnh Thái Bình năm 2011-2012
Lời giải
Từ giả thiết suy ra
11 2
xy0xy2xy
2
22
11 1
xx x. ;yy y. xx yy x y
22 2
Lại có
22 22 1
1
xy xy
xy xy
334
4
xy
22
xy
xy x y
2
36
Từ các bất đẳng thức trên ta được
222212
xx yy x y x y xy x y
22346
221 x y xy
3
Suy ra
yxxyyxyx22
1y 1x 1xyxy 3
Vậy bất đẳng thức được chứng minh xong. Dấu đẳng thức xảy ra khi
1
xy
2
Bài 104. Cho a, b, c, d là các số thực thỏa mãn điều kiện
abc bcd cda dab a b c d 2012
Chứng minh rằng:
2222
a 1 b 1 c 1 d 1 2012
Trích đề thi HSG tỉnh Vĩnh Phúc năm 2011-2012
Lời giải
Từ giả thiết ta có
2
2
2012 abc bcd cda dab a b c d
ab 1 c d cd 1 a b
Mặt khác theo bất đẳng thức Cauchy ta có

2
22 22
22 2 2 22 2 2 2 2 2 2
ab 1 c d cd 1 a b ab 1 a b cd 1 c d
ab a b 1 cd c d 1 a 1 b 1 c 1 d 1
Suy ra
2222
a 1 b 1 c 1 d 1 2012
Vậy bất đẳng thức được chứng minh.
Bài 105. Cho các số thực dương a, b, c thoả mãn
abc a b 3ab
. Chứng minh rằng:
ab b a
3
ab1bcc1cac1
Trích đề thi HSG tỉnh Phú Thọ năm 2011-2012
Lời giải
Từ giả thiết ta suy ra
11
c3.
ab
Ta viết lại vế trái của bất đẳng thức cần chứng minh thành
ab b a 1 1 1
ab1bcc1cac1
11 1 c1 c1
cc
abab bb aa
Đặt
11
x;y;zc
ab
.Khi đó giả thiết trở thành xyz 3 và bất đẳng thức cần chứng minh
được viết lại thành
111
3
x y xy y z yz z x zx
Áp dụng bất đẳng thức Bunhiacopxki ta được
111 9
x y xy y z yz z x zx x y xy y z yz z x zx
Đặt
Axyxyyzyzzxzx
Theo Bunhiacopxki ta lại có ta có:
2
A36xyyzzx36xyz3z
Áp dụng Bất đẳng thức Cauchy ta được
2
2
3z
1
xy x y
44
Khi đó ta phải chứng minh
22
2
3z 3z1
A 3 6 z 3 z 27 27
44
Hay
A33
. Do đó ta được
99
3
x y xy y z yz z x zx 3 3
Suy ra
111
3
x y xy y z yz z x zx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi bà chỉ khi
abc1
Bài 106. Cho ba số dương a, b, c tùy ý. Chứng minh rằng:

444
33 3
abc
1
bc2a ca2b ab2c
Trích đề thi HSG Thành phố Hải Phòng năm 2011-2012
Lời giải
Cách 1:
Áp dụng bất đẳng thức Cauchy ta được
4
3
4
3
4
3
a2ac1a
9a 3 b
bc2a
b2ba1b
9b 3 c
ca2b
c2cb1c
9c 3 a
ab2c
Cộng theo vế các bất đẳng thức trên ta được
444
33 3
abccab5abc
9a 9b 9c 3 b c a
bc2a ca2b ab2c
Hay
444
33 3
abc8abc5
9b c a 3
bc2a ca2b ab2c
Để ý ta lại có
abc
3
bca
. Do đó ta được
444
33 3
abc85
1
33
b c 2a c a 2b a b 2c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
444
33 3
2
222
abc
b c 2a c a 2b a b 2c
b c 2a c a 2b a b 2c
abc
bca
Hay
2
444 222
33 3
abc abc
3ab bc ca
bca
b c 2a c a 2b a b 2c
Mặt khác cúng theo bất đẳng thức Bunhiacopxki ta được
222
abc
abc 3abbcca
bca
Do đó ta được
444
2
33 3
abc
3ab bc ca 3ab bc ca
b c 2a c a 2b a b 2c
Hay
444
33 3
abc
1
b c 2a c a 2b a b 2c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc
Bài 107. Cho x, y, z là các số thực dương thỏa mãn
xy yz zx 671
. Chứng minh rằng :

222
xyz1
xyz
x yz 2013 y zx 2013 z xy 2013
Trích đề thi HSG Thành Phố Hà Nội năm 2011-2012
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
2
333
xyz
x yz 2013 y zx 2013 z xy 2013
xyz
x y x 3xyz 2013 x y z
Biến đổi mẫu số bên vế phải ta được
333
222
3
222
x y x 3xyz 2013 x y z
x y z x y z xy yz zx 3 xy yz zx x y z
xyzx y z 2xy2yz2zx xyz
Suy ra ta có
2
222 3
xyz
xyz 1
xyz
x yz 2013 y zx 2013 z xy 2013
xyz
Vậy bất đẳng thức được chứng minh.Đẳng thức xẩy ra khi và chỉ khi
2013
xyz
3
.
Bài 108.
a) Cho ba số dương x, y, z thỏa mãn xyyzzxxyz6. Chứng minh rằng:
222
xyz3
b) Cho a, b, c là các số thực dương thỏa mãn abc3. Tìm giá trị nhỏ nhất của biểu thức:
333
22 2222
abc
P
abbc ca
Trích đề thi HSG Tỉnh Nghệ An năm 2011-2012
Lời giải
a) Áp dụng bất đẳng thức Cauchy ta có
22 22 22
222
xy2xy;yz2yz;zx2zx
x12x;y12y;z12z
Cộng theo vế các bất đẳng thức trên ta được
222
3 x y z 3 2 xy yz zx x y z 12
Hay
222
xyz3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz1
.
b) Áp dụng bất đẳng thức Cauchy ta được
3322 2 2
22 22 22
a a ab ab ab ab b
aaa
2ab 2
ab ab ab
Hoàn toàn tương tự ta được
33
22 2 2
bcca
b; c
22
bc ca
Cộng theo vế các bất đẳng thức trên ta được
333
22 2222
abcabc3
P
22
abbc ca

Vậy giá trị nhỏ nhất của P là
3
2
. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 109. Chứng minh bất đẳng thức:
111 1
... 2
2 1 3 2 4 3 2012 2011
Trích đề thi HSG Tỉnh Quảng Bình năm 2011-2012
Lời giải
Xét biểu thức
1
n1 n
với nN* .
Dễ thấy
2n 1 2 nn 1 1
. Thật vậy, ta có
2
n1 n 0 n12nn1 n 0 2n1 2nn1 1
Khi đó ta có
2n1 n
111
2
n1 n n.n1 n n1
Khi đó ta được
111 1
...
2 1 3 2 4 3 2012 2011
1111 1 1 1
2...212
1 2 2 3 2011 2012 2012
Vậy bất đẳng thức được chứng minh.
Bài 110. Cho x, y, z là cácsố thực dương thoả mãn điều kiện xyz1. Tìm giá trị nhỏ nhất của biểu
thức:
444
22 22 22
xyz
F
xyxy yzyz zxzx
Trích đề thi HSG tỉnh Hà Tĩnh năm 2012-2013
Lời giải
Ta có
44
22 22
xy
xy
xyxy xyxy
Hoàn toàn tương tự ta được
44
22 22
44
22 22
yz
yz
yzyz yzyz
zx
zx
z x zx z x zx
Áp dụng bất đẳng thức
22
2
ab
ab
2
ta được

444
22 22 22
44 44 44
22 22 22
222
22 22 22
22 22 22
22 22 22
22
xyz
F
xyxy yzyz zxzx
1xy yz zx
2
xyxy yzyz zxzx
xy yz zx
1
4
xyxy yzyz zxzx
xy yz zx
1
4xy yz zx
xy yz z
1
8xy yz
2
x
11
xyz
z) 4 4
Do đó F đạt giá trị nhỏ nhất bằng
1
4
. Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
Bài 111. Cho
n
1
A
2n 1 2n 1
với
*
nN
. Chứng minh rằng:
123 n
A A A ... A < 1
Trích đề thi HSG tỉnh Hải Dương năm 2012-2013
Lời giải
Ta có
n
1 2n 1 2n 1 1 1
A
2 2n 1 2n 1
2n 1 2n 1
2n 1 2n 1
2n 1 1 1 1 1
2
2n 1 2n 1 2n 1 2n 1
Vì
11
0
2n 1 2n 1
và
11 2
2n 1 2n 1 2n 1
Nên
n
11
AnN*
2n 1 2n 1
Do đó ta được
123 n
111 1 1
AAA...A 1
3 3 5 2n 1 2n 1
Hay
123 n
1
AAA...A 1 1
2n 1
Vậy bài toán được chứng minh xong.
Bài 112. Cho các số thực dương a, b, c thoả mãn abc 1 . Chứng minh rằng:
222
abc1
abc
ab a 1 bc b 1 ca c 1
Trích đề thi HSG tỉnh Ninh Bình năm 2012-2013

Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có
222
222
2
2
abc
abc
ab a 1 bc b 1 ca c 1
abc
ab a 1 bc b 1 ca c 1
1bbc
1
b1bc bcb11bcb
Do đó ta được
222
abc1
abc
ab a 1 bc b 1 ca c 1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 113. Cho a, b, c là các số thực dương. Chứng minh rằng:
ab bc ca a b c
a3b2cb3c2a c3a2b 6
Trích đề thi HSG tỉnh Phú Thọ năm 2012-2013
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
9111
xyz x y z
ta được
111111
a3b2c acbc2b 9acbc2b
Do đó ta được
ab ab 1 1 1 1 ab ab a
a3b2c 9ac bc2b 9acbc2
Hoàn toàn tương tự ta được
bc 1 bc bc b ac 1 ac ac c
;
2ab3c 9ab bc 2 3a2bc 9ab bc 2
Cộng theo vế các bất đẳng thức trên ta được
ab bc ca
a3b2cb3c2a c3a2b
1ac bc ab ac bc ab a b c a b c
9ab bc ac 2 6
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 114. Cho các số thực dương a, b, c thỏa mãn
333
abc3abc1 . Tìm giá trị nhỏ nhất của biểu
thức:
222
Pa b c
Trích đề thi HSG tỉnh Nghệ An năm 2012-2013
Lời giải
Từ giả thiết ta được
222
abaa b c abbcca 1
hay
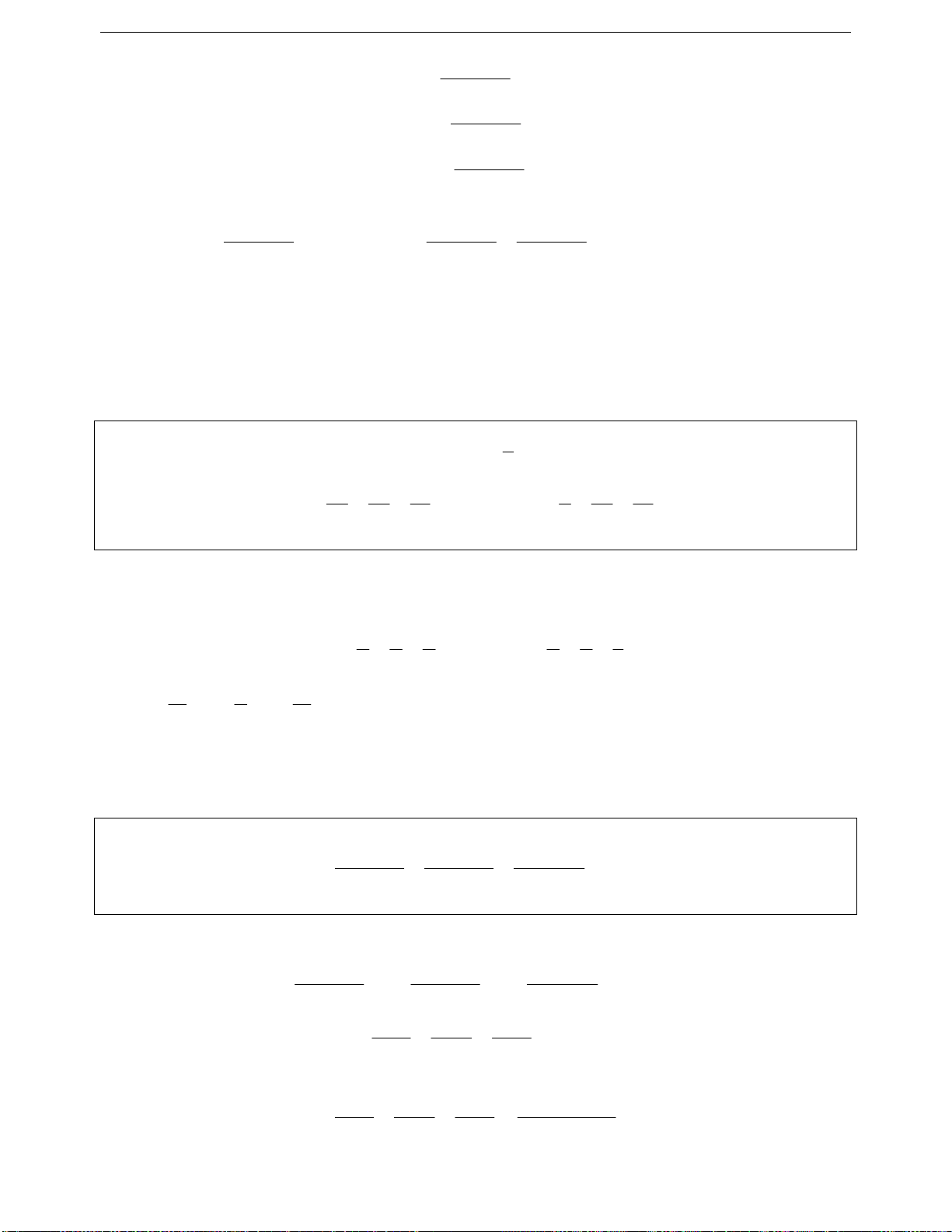
222
222
2
222
1
abc abbcca
abc
2
2a b c 2ab bc ca
abc
2
3a b c a b c
abc
Áp dụng bất đẳng thức Cauchy ta được
22
211
abc abc 3
abc abcabc
Do đó ta được
222 222
3abc 3 abc1
Vậy giá trị nhỏ nhất của P là 1. Đẳng thức xẩy ra khi và chỉ khi
333
3
ab0;c1
abc3abc1
ac0;b1
abc 1
a1;bc0
Bài 115. Cho các số thực dương a, b, c thỏa mãn
1
abc
6
. Chứng minh rằng:
a2b3c 11 1
3 a 2b 3c
2b 3c a a 2b 3c
Trích đề thi HSG tỉnh Vĩnh Phúc năm 2012-2013
Lời giải
Đặt
ax;2by;3cz
, khi đó ta được
xyz 1
và bất đẳng thức cần chứng minh được viết lại
thành
xyz 111
3xyz
yzx xyz
Đặt
npm
x;y;z
mnp
. Khi đó bất đẳng thức trở thành
333 2 22 2 2 2
mnp3mnpmnmnnpnpmpmp
Biến đổi tương đương ta được
mnp m n p n p m p m n
Bất đẳng thức trên luôn đúng. Vậy bài toán được chứng minh.
Bài 116. Cho các số thực dương a, b, c thỏa mãn abc6. Chứng minh rằng:
bc5 ca4 ab3
6
a1 b2 c3
Trích đề thi HSG tỉnh Quảng Bình năm 2012-2013
Lời giải
Bất đẳng thức cần chứng minh tương đương với
bc5 ca4 ab3
1119
a1 b2 c3
Hay
111
abc6 9
a1b2 c3
Theo bất đẳng thức Cauchy ta có
111 9
a1b2 c3 abc6
Do đó ta được

111 9
abc6 abc6 9
a1b2 c3 abc6
Vậy bất đẳng thức được chứng minh xong.
Đẳng thức xẩy ra khi và chỉ khi
a3;b2;c1
Bài 117. Cho các số thực dương a, b, c thỏa mãn
123
3
abb
. Chứng minh rằng:
22 2
22 22 22
27a b 8c 3
2
cc 9a a4a b b9b 4c
Trích đề thi HSG Thành Phố Hà Nội năm 2012-2013
Lời giải
Cách 1:
Đặt
123
a;b;c
xyz
, khi đó giả thiết được viết lại là xyz3
Bất đẳng thức cần chứng minh trở thành
333
22 2222
xyz3
2
xy yzzx
Sử dụng kỹ thuật Cauchy ngược dấu ta chứng minh được
333
22 2222
xyzxyz3
22
xy yzzx
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
a3;b2;c1
.
Cách 2: Áp dụng bất đẳng thức Cauchy ta được
2222
22
22 22
22
2222
22
22 22
2222
22
22 22
27a 27a 3c 3c 3 3c 3 3c 3 1
cc c2a
c9a
cc 9a cc 9a
2c.9a
b b 4a 4a 1 4a 1 1
aab
4a b
a4a b a4a b
8c 8c 18b 18b 2 18b 2 3
bb2c
9b 4c
b9b 4c b9b 4c
Cộng theo vế các bất đẳng thức trên ta được
22 2
22 22 22
27a b 8c 1 1 2 3 3
2a b c 2
cc 9a a4a b b9b 4c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
a3;b2;c1.
Bài 118. Cho các số thực dương x, y, z thỏa mãn xyz3. Chứng minh rằng:
222 222 222
2x y z 2y z x 2z x y
4xyz
4yz 4zx 4xy
Trích đề thi HSG Tỉnh Phú Thọ năm 2013-2014
Lời giải
Cách 1:
Theo bất đẳng thức Cauchy ta có
222
2x y z 2x y z
Tương tự ta có
22 2 2 2 2
2y z x 2y z x ; 2z x y 2z x y
Do đó ta sẽ chứng minh
xy z yz x zx y
2xyz
4yz 4zx 4xy
Bất đẳng thức này tương đương với

yz zx xy
1
4yz2yz 4zx2zx 4xyxy
Ta có
2yz
yz 1
4yz2yz
2 yz 2 yz 2yz 2 yz yz 2 yz
Dễ thấy
2
0 2 yz yz xy 1 1 1
nên
11
2yz
2yzyz2yz
Do đó ta được
yz 1
4yz2yz
2yz
Hoàn toàn tương tự có
zx 1 xy 1
;
4zx2zx 4xy2xy
2zx 2xy
Cộng theo vế ba bất đẳng thức trên ta được
yz zx xy 1 1 1
4yz2yz 4zx2zx 4xyxy
2xy2yz2zx
Theo một đánh giá quen thuộc thì
111 9 9
1
6xyz
2 xy 2 yz 2 zx 6 xy yz zx
Do đó ta suy ra
yz zx xy
1
4yz2yz 4zx2zx 4xyxy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy rakhi và chỉ khi
xyz1.
Cách 2: Gọi vế trái của bất đẳng thức là P. Khi đó biến đổi P như sau
222
222
xyz 111
Pxyz
4yz 4xz 4yx 4yz 4xz 4yx
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta có
2
222
xyz
xyz
4yz 4xz 4yx
12 xy yz zx
111 9
4yz 4xz 4yx
12 xy yz zx
Do đó ta được
2
222
222
3
222
3
9x y z
xyz
P
12 xy yz xz 12 xy yz xz
3 xy yz xz 9 xy yz xz
12 xy yz xz 12 xy yz xz
12 xy yz xz
36 x y z
12 xy yz xz
12 3 x y z

Đặt
3
xyz
xyz t 1
3
. Khi đó ta có
2
32 2
2
36t
4t 12t t 1 t t 3 0
12 3t
Đánh giá cuối cùng luôn đúng. Bất đẳng thức được chứng minh xong.
Cách 3: Ta viết lại bất đẳng thức cần chứng minh thành
2222 22222222
xyxz xyyzzyxz
P4
xyz 4 yz xyz 4 xz xyz 4 yx
Áp dụng bất đẳng thức Cauchy ta có
2xy 2xz 2xy 2yz 2xz 2yz
M
xyz 4 yz xyz 4 xz xyz 4 yx
yz xz xz
2
yz 4 yz xz 4 xz yx 4 yx
111 1 1 1
22
z 4 yz x 4 yz y 4 yx y 4 yz zx 4 yz x 4 yx
Áp
dụng bất đẳng thức Cauchy ta có
3
3
111 3
z 4 yz x 4 yz y 4 yx
xyz(4 yz)(4 xz)(4 xy)
111 6
y4yz zx4yz x4yx
xyz(4yz)(4xz)(4xy)
Do đó ta được
3
3
12 3
P
3xyz(4 yz)(4 xz)(4 xy)
Mặt khác ta lại có
4
3xyz 12 xz xy yz
3xyz 4 xz 4 yz 4 xy
4
Mà
1 1 1 9 xy yz xz
3 3 3xyz xy xz yz 0
xyz xyz xyz
Suy ra
3
3
3xyz 4 xz 4 yz 4 xy 81 3xyz 4 xz 4 yz 4 xy 3 3
Do đó ta được
3
3
12 3
P4
33
. Như vậy bất đẳng thức được chứng minh.
Cách 4: Đặt vế trái của bất đẳng thức là P.
Với
x, y, z 0 ta có
22
yz xyz
9
yz 4 yz 0
444
Tương tự ta cũng có
4zx 0;4xy 0 .
Áp dụng bất đẳng thức Bunhiacopxki ta có
22
2222
4x x y z xxyz 2xyz

Từ đó suy ra
2
222
2x y z
2x y z
4yz
44 yz
Hoàn toàn tương tự ta có
22
22 2 2 2 2
2y z x 2z x y
2y z x 2z x y
;
4zx 4xy
44 zx 44 xy
Do đó ta được
222
2x y z 2y z x 2z x y
PQ
44 yz 44 zx 44 xy
Mặt khác theo bất đẳng thức Cauchy
22
22
22
2x y z 2x y z
442
4yz 2 . 4yz 2xyz
993
4 4 yz 4 4 yz
2y z x 2y z x
442
4zx 2 . 4zx 2yzx
993
44 zx 44 zx
2z x y 2z x y
442
4xy 2 . 4xy 2zxy
993
44 xy 44 xy
Cộng theo vế các bất đẳng thức trên ta được
48 84
Q 12xyyzzx xyz 8 Q xyyzzx
93 39
Bất đẳng thức trên sẽ được chứng minh nếu ta chỉ ra đươc
84
xy yz zx 4xyz
39
Thậy vậy, ta viết lại bất đẳng thức trên thành
3
84
.x y z x y z xy yz zx 4xyz
81 27
Sử dụng bất đẳng thức Cauchy ta có
222
3
3
x y z 3 xyz; xy yz zx 3 x y z
Suy ra
3
84
.x y z x y z xy yz zx 4xyz
81 27
Vậy bất đẳng thức được chứng minh xong.
Cách 5:
Vế trái của bất đẳng thức được viết lại thành
222
222
111 xyz
Pxyz
4 xy 4 yz 4 zx 4 yz 4 zx 4 xy
Áp dụng bất đẳng Cauchy ta có
222 222
222
222
9x y z 18x y z
111
xyz
4xy 4yz 4zx
15 x y z
12 xy yz zx
Theo bất đẳng thức Cauchy ta lại có

22
3
2
x4 yz x4 yz
x1x1
3. .x
4yz 9 3 4yz 9 3
x4 yz
x15xxyz1
x
4yz 9 3 9 9 3
Tương tự ta có
22
y 5y xyz 1 z 5z xyz 1
;
4zx 9 9 34xy 9 9 3
Cộng theo vế ba bất đẳng thức trên ta được
222
x y z 5 xyz 2 xyz
xyz 1
4yz 4zx 4xy 9 3 3 3
Do đó ta được
222
222
18 x y z
2 xyz
A
33
15 x y z
Từ giả thiết ta được
222
xyz3
. Do đó ta có
222
222
18 x y z
3
15 x y z
Cũng từ giả thiết ta được
xyz 1 .
Từ đó suy ra
2 xyz 11 xyz 11xyz xyz
P3 4xyz
33 3 3 3 3
Vậy bất đẳng thức được chứng minh xong
Bài 119. Cho x, y là các số thực dương thoả mãn xy1. Tìm giá trị nhỏ nhất của biểu thức:
33
11
B
xy
xy
Trích đề thi HSG Tỉnh Thanh Hóa năm 2013-2014
Lời giải
Ta có
3
12xy
1111
B
xy 1 3xy xy
xy 1 3xy
xy 3xyxy
Theo bất đẳng thức Cauchy ta có
2
xy
1
xy
44
.
Gọi
0
B là một giá trị của B, khi đó luôn tồn tại x, y để
2
000
12xy
B 3Bxy 2Bxy1 0
xy 1 3xy
Để tồn tại x, y thì phương trình trên phải có nghiệm xy, tức là
02
00
0
B423
B 8B 40
B423
Để ý rằng với giả thiết bài toán thì B > 0. Do đó ta có
0
B423 .
Với
0
0
0
2B
33 33
B423xy x(1x)
6B
62 3 62 3
2
23 23
1
33
xx
11 1
33
x,x
3
22
0
62

Vậy giá trị nhỏ nhất của B là
423 , đạt được khi
23 23
1111
33
x;y
22
hoặc
23 23
1111
33
x;y
22
.
Bài 120. Cho a, b, c là các số thực dương thỏa mãn 2ab 6bc 2ca 7abc . Tìm giá trị nhỏ nhất của
biểu thức:
4ab 9ca 4bc
a2b a4c bc
C
Trích đề thi HSG tỉnh Hải Dương năm 2013-2014
Lời giải
Từ 2ab 6bc 2ca 7abc ta được
262
7
cab
Đặt
x, y, z 0
111
x;y;z
2z 6x 2y 7
abc
Khi đó ta được
4ab 9ca 4bc 4 9 4
a2b a4c bc 2xy 4xz yz
C
Hay
2 2
2
494
C 2xy 4xz yz 2xy4xzyz
2x y 4x z y z
232
x2y 4xz yz 1717
x2y 4xz yz
Vậy giá trị
nhỏ nhất của C là 17. Đẳng thức xẩy ra khi và chỉ khi
1
x;yz1
2
Bài 121. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
4a 9b 16c
26
bca cab abc
Trích đề thi HSG tỉnh Quảng Trị năm 2013-2014
Lời giải
Bất đẳng thức cần chứng minh tương đương với
8a 18b 32c
491681
bca cab abc
Hay
4916
abc 81
bca cab abc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
234
4 9 16 81
bca cababc abc abc
Do đó ta được
81 a b c
4916
abc 81
bca cab abc abc
Vậy bất đẳng thức được chứng minh.
Bài 122.
Cho a, b, c thỏa mãn
0 a;b;c 4
và
abc6
. Tìm giá trị lớn nhất của
222
Pa b c abbcca
Trích đề thi HSG Thành phố Hà Nội năm 2013-2014

Lời giải
Vì
0 a;b;c 4
do đó ta được
a4b4c4 0
, biến đổi tương đương ta thu được
a4b4c4 0 abc4abbcca 16abc 64 0
4ab bc ca abc 16a b c 64
Do
abc 0 nên ta được
4 ab bc ca abc 16 a b c 64 16.6 64 32
ab bc ca 8
Ta có
2
222 2
P a b c ab bc ca a b c ab bc ca 6 8 28
Vậy giá trị lớn nhất của P là 28. Đẳng thức xẩy ra khi và chỉ khi
a0;b2;c4 và các hoán vị.
Bài 123. Cho x, y, z là các số thực dương thỏa mãn xyz4. Chứng minh rằng
222
1111
xyz
x 4yz y 4zx z 4xy
Trích đề thi HSG tỉnh Thừa Thiên Huế năm 2013-2014
Lời giải
Dễ thấy
222
111111
;;
4yz 4zx 4xy
x4yz y4zx z4xy
Do đó ta được
222
111111
4yz 4zx 4xy
x 4yz y 4zx z 4xy
Kết hợp với giả thiết ta được
111xyz1
4yz 4zx 4xy 4xyz xyz
Suy ra
222
1111
xyz
x 4yz y 4zx z 4xy
Vậy bất đẳng thức được chứng minh.
Bài 124. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng
22 22 22
22 2 2 2 2
ab bc ca a b c
2
cab
bc ca ab
Trích đề thi HSG tỉnh Bắc Giang năm 2013-2014
Lời giải
Áp dụng bất đẳng thức Cauchy dạng
2
22
2x y x y ta được
22 22 22
22 22 22
2a b 2b c 2c a
ab bc ca
cab
2c 2a 2b
abbc ca
2c 2a 2b
Mặt khác cũng áp dụng bất đẳng thức trên ta được
22 2 2 2 2
abc2a2b2c
bc ca ab
bc ca ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a b b c c a 22a 22b 22c
bc ca ab
2c 2a 2b
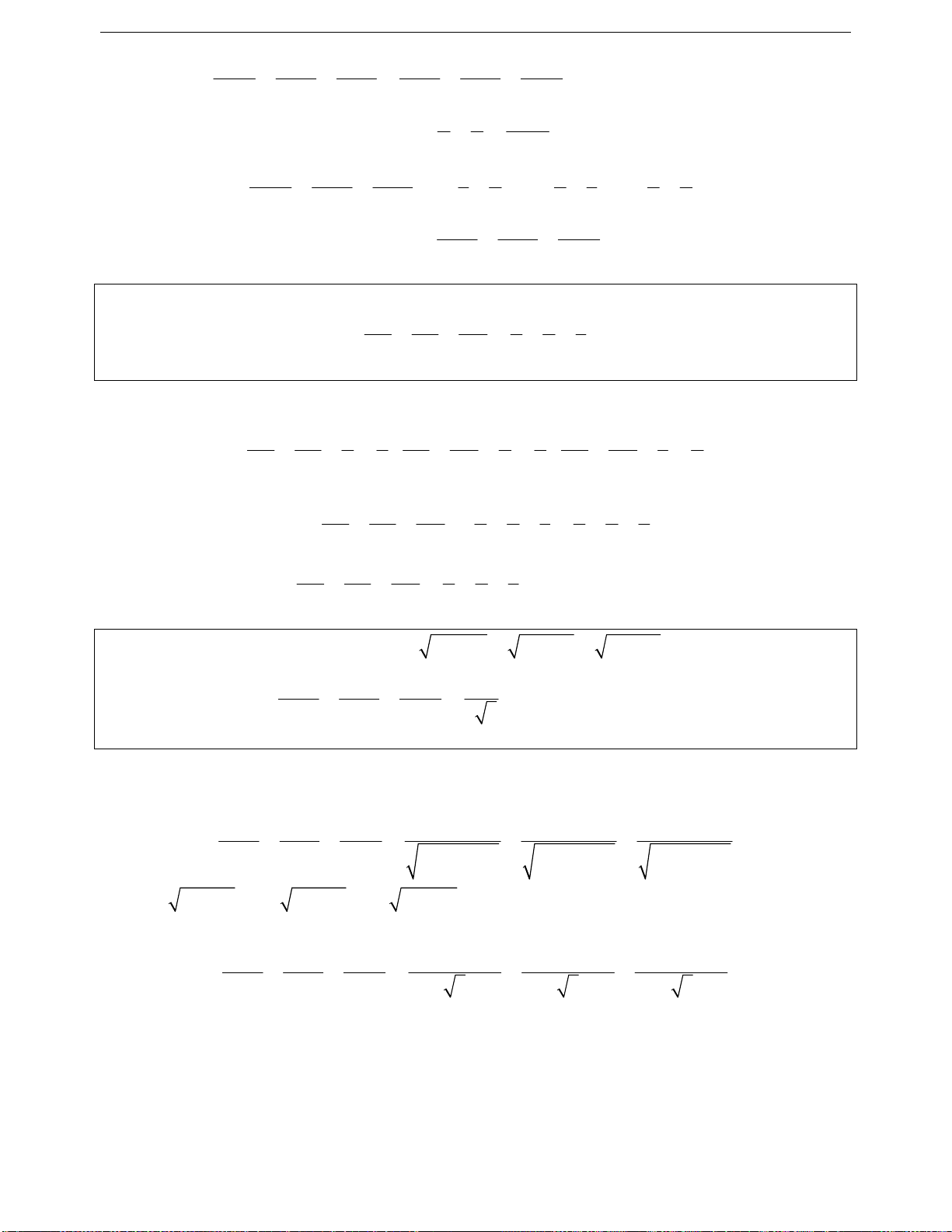
Hay
abbcca 4a 4b 4c
cabbccaab
Thật vậy, Áp dụng bất đẳng thức Cauchy dạng
11 4
xy xy
, ta được
abbc ca 1 1 11 1 1
abc
cab cb acab
4a 4b 4c
bc ca ab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Bài 125. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
22 2
abc111
abc
bc ca ab
Trích đề thi HSG tỉnh Vĩnh Phúc năm 2013-2014
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
22 22 22
22 2 2 2 2
ab13bc31ac13
;;
ac ba cb
bc ca ca ab bc ab
Cộng theo vế ba bất đẳng thức trên ta được
222
22 2
abc 111333
2
abcabc
bc ca ab
Hay
222
22 2
abc111
abc
bc ca ab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 126. Cho ba số dương
a, b, c
thoả mãn
22 22 22
ab bc ca 1 . Chứng
minh rằng:
222
abc 1
bc ca ab
22
Trích đề thi HSG tỉnh Hải Dương năm 2014-2015
Lời giải
Dễ thấy
2
22
2a b a b
. Áp dụng tương tự ta được
222 2 2 2
22 22 22
abc a b c
bc ca ab
2b c 2c a 2c a
Đặt
22 2 2 2 2
xbc,yca,zab
Khi đó ta được suy ra
222222222222
abcyzxzxyxyz
bc ca ab
22x 22y 22z
Áp dụng tiếp bất đẳng thức trên thì ta được

22 2 2 2 2 2 22
22 2
22 2
yzx zxy xyz
22x 22y 22z
yz zx xy
1
xyz
2x 2y 2z
22
yz zx xy
1
2x 3x 2y 3y 2z 3z
2x 2y 2z
22
111
2y z 3x 2 z x 3y 2 x y 3z x y z
22 22 2
2
Do đó ta được
222
abc 1
bc ca ab
22
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
32
Bài 127. Với a, b, c là các số thực dương. Chứng minh rằng
555333
222222
abcabc
3
aabb bbcc ccaa
Trích đề thi HSG tỉnh Thái Bình năm 2013-2014
Lời giải
Cách 1:
Ta có
3
32233
22
2
22
a2ab
3a 2a b a ab b a b ab a b
3
aabb
aabbab ab 0
Đánh giá cuối cùng luôn đúng.
Do đó
3532
22 22
a2aba2aab
33
aabb aabb
.
Chứng minh tương tự ta được
555333333222
222222
abcabcabcabbcca
33
aabb bbcc ccaa
Mặt
khác vì vai trò a, b, c như nhau nên giả sử
abc0
3332 2 2 2 2 2
2
abcabbccaaabbbccca
ab ab acbcbc 0
Từ đó suy ra
555333
222222
abcabc
3
aabb bbcc ccaa
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
555
222222
666
32 2 32 2 32 2
2
333
3332 22 22 2
abc
aabb bbcc ccaa
abc
aababbbcbcccaca
abc
abcababbcbccaca

Mặt khác ta có
2
22 33
a b 0 a ab b ab a b ab a b
Chứng minh tương tự
33 3 3
bc bcbc;ca caca
Suy ra
333 333
3a b c a b c aba b bcb c cac a
2
333
333
3332 22 22 2
abc
abc
3
abcababbcbccaca
Vậy bất đẳng thức được chứng minh.
Bài 128. Cho các số thực dương a, b, c thỏa mãn
abc1
. Tìm giá trị lớn nhất của biểu thức:
32 32 32
abc
P
9a 3b c 9b 3c a 9c 3a b
Trích đề thi HSG tỉnh Vĩnh Phúc năm 2014-2015
Lời giải
Cách 1:
Ta có
32 32 32
3a 3b 3c
P
27a 9b 3c 27b 9c 3a 27c 9a 3b
Đặt
xyz 3
x 3a; y 3b; z 3c
x; y; z 0
Khi đó ta viết lại được
32 32 32
xyz
P
xyzyzxzxy
Theo bất đẳng thức Bunhiacopxki và chú ý đến giả thiết ta có
2
32
32 2 32 2
1
xyz 1z xyz
x
1
1z
1 x 1 x zx 1 x zx
x
9
xyz xyz
xyz xyz
Hoàn toàn tương tự thu được
32 3 2
y1yxyy1zyz
;
99
yzx zxy
Từ đó suy ra
3 x y z xy yz zx 6 xy yz zx
P
99
Dẽ dàng chứng minh được
2
1
xy yz zx x y z 3
3
Do đó
6xyyzzx
63
P1
99
. Dấu đẳng thức xảy ra khi
1
xyz1 abc
3
Vậy giá trị lớn nhất của P là 1 đạt được tại
1
abc
3
Cách 2: Áp dụng bất đẳng thức Cauchy ta có
3232
11 1
9a 3a;9b 2b 9a 9b c 3a 2b c 1 2a b
33 3
Hoàn toàn tương tự ta được

32 32
9b 9c a 2b c; 9c 9a b 2c a
Do đó ta suy ra
abc111
P
2a b 2b c 2c a b c a
222
abc
Đặt
bca
x;y;z xyz1
abc
. Khi đó ta được
111
P
2x 2y 2z
Ta chứng minh
111
1
2x 2y 2z
.
Thật vậy, bất đẳng thức tương đương với
2z2y 2y2z 2z2x 2x2y2z
xy yz zx 4 x y z 12 xyz 2 xy yz zx 4 x y z 8
xyx3
Bất đảng thức cuối cùng luôn đúng do
3
x y z 3 xyz 3
Do đó bất đẳng thức trên được chứng minh.
Vậy giá trị lớn nhất của P là 1 đạt được tại
1
abc
3
Bài 129. Cho các số thực dương x, y, z thảo mãn
222
xyz 3. Chứng minh rằng:
3
33
xyz
xy yz xz
yz xz xy
Trích đề thi HSG tỉnh Phú Thọ năm 2014-2015
Lời giải
Ta có
33
3
3
33333
yy
xyzxx zz
A
yz xz xy xyz xyz xyz
Áp dụng bất đẳng thức Cauchy ta có
222 222
3
3x y z 3xyz xyz1.
Suy ra
33
3
Axxyyzz
Áp dụng bất đẳng thức Bunhiacopxki
2
33
33
222
3
3
xx yy zz x y z x y z 3xy yz xz
Lại thấy theo bất đẳng thức Cauchy thì
222
33
222
3
x11 y11 z11
x .1.1 ; y .1.1 ; z .1.1
333
Nên
222
33
222
3
xyz6
xyz 3
3
Do đó ta được
33
3
Axxyyzzxyyzxz
Hay
3
33
xyz
xy yz xz
yz xz xy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi

222
33
3
222
xyz1
xyz xyz1
xyz3
Bài 130. Cho ba số thực không âm x, y, z thỏa mãn xyz3. Tìm giá trị nhỏ nhất của biểu thức:
222222
A 2x 3xy 2y 2y 3yz 2z 2z 3zx 2x
Trích đề thi HSG tỉnh Ninh Bình năm 2014-2015
Lời giải
Ta viết lại biểu thức A thành
222
A2xyxy2yzyz2zxzx
Theo một đánh giá quen thuộc ta có
22
22
xy 7xy
2x y xy 2x y
44
Do đó ta được
2
7x y
2x y xy
2
Hoàn toàn tương tự ta thu được
222222
A 2x 3xy 2y 2y 3yz 2z 2z 3zx 2x 7 x y z 3 7
Vậy giá
trị nhỏ nhất của A là 37. Đẳng thức xẩy ra khi và chỉ khi xyz1
Bài 131. Cho các số dương
a, b, c
có tổng bằng 3. Chứng minh rằng:
222
222
a6a9b6b9c6c9
24
a2a3b2b3c2c3
Trích đề thi HSG tỉnh Gia Lai năm 2014-2015
Lời giải
Ta có
2
2
222
a1 8a8
a6a9 8a6 8a6
114a4
2
a2a3
a1 2 a1 2
Hoàn toàn tương tự ta được
22
22
b6b9 c6c9
4b 4; 4c 4
b2b3 c2c3
Cộng theo vế các bất đẳng thức trên và kết hợp với giả thiết ta được
222
222
a6a9b6b9c6c9
4a b c 3.4 24
a2a3b2b3c2c3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 132. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Tìm giá trị lớn nhất của biểu thức:
111
P
a2b3 b2c3 c2a3
Trích đề thi HSG tỉnh Nghệ An năm 2014-2015
Lời giải
Đặt
222
a x;b y;z c
khi đó ta được xyz 1 và bểu thức P được viết lại thành
22 22 22
111
P
x2y3y2z3z2x3

Ta có
22 2 2 2
xy2xy;y12y x2y32xyy1
Do đó ta được
22
111
2xy y 1
x2y3
Chứng minh tương tự ta có
22 2 2
111 111
;
2yz z 1 2zx z 1
y2z3 z2x3
Cộng theo vế các bất đẳng thức trên ta được
11 1 1
P
2xy y 1 yz z 1 zx x 1
Ta cần chứng minh
111
1
ab b 1 bc c 1 ca a 1
Đến đây ta có hai hướng đánh giá
111
xy y 1 yz z 1 zx x 1
Hướng 1: Do xyz 1 , nên tồn tại các số dương m, n, p để
mnp
x;y;z
npm
Khi đó ta có
111 pmn
1
xy y 1 yz z 1 zx x 1 m n p m n p m n p
Hướng 2: Do xyz 1 , nên ta được
111zxx1
1
xy y 1 yz z 1 zx x 1 z 1 zx 1 zx z zx z 1
Từ đó ta được
1
P
2
.
Vậy giá trị lớn nhất của P là
1
2
. Đẳng thức xảy ra khi và chỉ khi abc1.
Bài 133. Cho các số dương x, y, z thay đổi thỏa mãn xy yz zx xyz . Tìm giá trị lớn nhất của biểu
thức:
111
M
4x 3y z x 4y 3z 3x y 4z
Trích đề thi HSG Tỉnh Hải Dương năm 2014-2015
Lời giải
Từ giả thiết ta có
111
1
xyz
. Áp dụng bất đẳng thức Bunhiacopxki ta được
64 16 16 4 4 4 4 3 1
4x3yz4x3yz x2yyz xyz
Tương tự ta được
64 1 4 3 64 3 1 4
;
x4y3z x y z3xy4z x y z
Do đó ta được
11111111
M
4x 3y z x 4y 3z 3x y 4z 8 x y z 8
Vậy M đạt giá trị lớn nhất là
1
8
. Đẳng thức xẩy ra khi và chỉ khi xyz3.
Bài 134. Cho các số dương x, y, z thay đổi thỏa mãn xyz3. Chứng minh rằng:

xyz
1
x3xyzy3yzxz3zxy
Trích đề thi HSG Tỉnh Hà Nam năm 2014-2015
Lời giải
Áp dụng giả thiết ta chú ý đến phép biến đổi
3x yz x x y z yz x y x z
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
x y x z xy xz
Do đó ta được
xx x
x3xyzxxyxz xyz
Áp dụng tương tự ta được
yzzz
;
y3yzx xyzz3zxy xyz
Cộng theo vế các bất đẳng thức trên ta được
xyz
1
x3xyzy3yzxz3zxy
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi xyz1.
Bài 135. Cho các số dương a, b, c thay đổi thỏa mãn
111
3
abc
. Tìm giá trị lớn nhất của biểu thức:
222222
111
P
aabb bbcc ccaa
Trích đề thi HSG Thành Phố Hà Nội năm 2014-2015
Lời giải
Cách 1:
Ta có
22
22
22
3a b a b
aabb ab 3abab
44
Do đó ta được
22
12111
ab 2a b
aabb
Hoàn toàn tương tự ta có
22 2 2
11111111
;
2b c 2c a
bbcc ccaa
Cộng theo vế các bất đẳng thức trên ta được
222222
111111
P3
abc
aabb bbcc ccaa
Vậy giá trị lớn nhất của P là 3. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Áp dụng bất đẳng thức Cauchy ta được
22
aabb2ababab
Do đó ta được
22
11
ab
aabb
Hoàn toàn tương tự ta có
22 22
1111
;
bc ca
bbcc ccaa

Cộng theo vế các bất đẳng thức trên ta được
222222
111111
P
ab bc ca
aabb bbcc ccaa
Dễ thấy
111111
3
abc
ab bc ca
Do đó ta được
P3
. Vậy giá trị lớn nhất của P là 3.
Bài 136. Cho a, b, c là các các số thực không âm thỏa mãn
abc3
. Chứng minh rằng:
333
abcabbcca6
Trích đề thi HSG Tỉnh Đăk Lăk năm 2014-2015
Lời giải
Cách 1:
Để ý đến giả thiết abc 3 ta có
2
222
333 333
222
333
abc a b c
abcabbccaabc
2
9abc
abc
2
Áp dụng bất đẳng thức Cauchy ta được
33 233 233 2
a a 13a;b b 13b;c c 13c
Cộng theo vế các bất đẳng thức trên ta được
333 222
2a b c 3 3a b c
Do đó ta được
222
333 222
9abc
abc abc3
2
Lại thấy
2
222
abc
abc 3
3
Do đó ta được
222
333
9abc
abc 6
2
Hay
333
abcabbcca6
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
333 333 222
3abc abcabc abc
Dễ thấy
222
abc3
, do đó ta được
333 222 333 222
3abc 3abc abc abc
Khi đó ta suy ra
333 222
2
2
2
abcabbccaabcabbcca
abc abbcca
abc
abc 936
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 137. Cho a, b, c là các số thực dương thỏa mãn a1;b2;abc6 . Chứng minh rằng:
a 1 b 1 c 1 4abc
Trích đề thi HSG Tỉnh Bắc Giang năm 2014-2015

Lời giải
Bất đẳng thức cần chứng minh tương đương với
111 1111111
111 41 4
a b c a b c ab bc ca abc
111abc1 111 7
33
abc abc abcabc
Áp dụng bất đẳng thức Cauchy ta được
babbcbc
a2; 2
22236
Do đó ta được
23
3
bbc2c ab bc2c abc
6a 2 2 6
2 2 3 3 2 6 3 108
Do đó ta được
23
ab c 108 , mà theo giả thiết
a1;b2
suy ra
2
ab 2
Suy ra ta có
3
2232
216 108a b ab c a b abc abc 6
Áp dụng bất đẳng thức Cauchy và các giả thiết ta lại có
3
123 6 21 153.7 3.7 7
33; 2;
abc abc ab 22abc 6 2
Cộng theo vế các bất đẳng thức trên ta được
111 7 57
33
abcabc 22
Hay
111 7
3
abcabc
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
a1;b2;c3.
Bài 138. Cho a, b, c là các số thực dương thỏa mãn ab bc ca 3. Tìm giá trị nhỏ nhất của biểu
thức:
222
19a 3 19b 3 19c 3
T
1b 1c 1a
Trích đề thi HSG Tỉnh Hưng Yên năm 2014-2015
Lời giải
Cách 1:
Biến đổi và áp dụng bất đẳng thức Cauchy ta được
2
22
b19a 3
19a 3
19a 3
1b 1b
b19a 3
38a 6 19ab 3b
19a 3
22
Hoàn toàn tương tự được
22
19b 3 38b 6 19bc 3c 19c 3 38c 6 19ca 3a
;
22
1c 1a
Cộng theo vế các bất đẳng thức trên ta được
222
35 a b c 18 19 ab bc ac
19a 3 19b 3 19c 3
T
2
1b 1c 1a
35. 3 ab bc ca 18 19.3
33
2
Vậy giá trị nhỏ nhất của T là 33. Đẳng thức xẩy ra khi và chỉ khi
abc1

Cách 2: Dễ thấy
222
3a 1
19a 3 16a
1b 1b 1b
. Áp dụng bất đẳng thức Cauchy ta được
22
22
16a 16ab 16ab
16a 16a 16a 8ab
2b
1b 1b
22
22
3a1 3a1b 3a1b 3a1b
3a 1 3a 1 3a 1
2b 2
1b 1b
Hoàn toàn tương tự ta được
222
35 a b c 18 19 ab bc ac
19a 3 19b 3 19c 3
T
2
1b 1c 1a
35. 3 ab bc ca 18 19.3
33
2
Vậy giá trị nhỏ nhất của T là 33.
Bài 139. Cho x, y, z là các số thực dương thỏa mãn xyz 2 2 . Chứng minh rằng:
88 88 88
4 4 22 4 4 22 4 4 22
xy yz zx
8
xyxyyzyzzxzy
Trích đề thi chọn HS dự thi HSGQG Tỉnh Hải Dương năm học 2013-2014
Lời giải
Đặt
222
ax;by;cz suy ra
abc 8
. Bất đẳng thức cần chứng minh được viết lại thành
44 44 44
22 22 22
ab bc ca
8
ababbcbccaca
Dễ dàng chứng minh minh được
2
22 22
44 22
ab 3ab
ab ;abab
22
Suy ra
44 22
22
ab ab
3
abab
. Hoàn toàn tương tự ta được
222
44 44 44
22 22 22
2a b c
ab bc ca
3
ababbcbccaca
Mặt khác áp dụng bất đẳng thức Cauchy ta được
3
222 222
abc3abc 12
Do đó ta được
44 44 44
22 22 22
ab bc ca
8
ababbcbccaca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz 2
Bài 140. Cho a, b, c là các số thực dương thỏa mãn ab bc ca 3. Chứng minh rằng:
222
bc ca ab 3
a. b. c.
abc
abc bca cab
Trích đề thi chọn HS dự thi HSGQG Tỉnh Bắc Giang năm học 2013-2014
Lời giải
Cách 1:
Ta có
22
b c ab ac
a. a.
abc abc
. Khi đó áp dụng bất đẳng thức Cauchy và chú ý đến giả
thiết
ab bc ca 3 ta có
222 2
a bc ab c 3abc a bc abc 3 bc abc ab ac

Do đó ta được
222
ab ac 1 ab ac 1 b c 1
a. a.
abc
abc abc abc
bc bc
Áp dụng hoàn toàn tương tự ta được
22
ca 1 ab 1
b. ; c.
bca cab
ca ab
Cộng theo vế các bất đẳng thức trên ta được
222
bc ca ab a b c
a. b. c.
abc bca cab
abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
abc3
abc a b c 3
abc
abc
Đánh giá cuối cùng là một đánh giá đúng vì
3abbcca abca b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
222 222
b c c a a b ab ac bc ab ca ac
a. b. c. a b c
abc bca cab abcbcaca
Ta cần chứng minh được
2
22 2
2
22 2
ab ac bc ab ca ac 3
abc
abc
abcbcaca
ab ac bc ab ca ac
abc a b c 9
abcbcaca
Dễ thấy
2
1
abc a b c ab bc ca 3
3
và cũng từ giả thiết ta suy ra abc 1 . Do đó ta được
2
abc a b c 3
.
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2
ab ac bc ab ca ac
3
abcbcaca
Thật vậy, biến đổi tương đương bất đẳng thức trên ta được
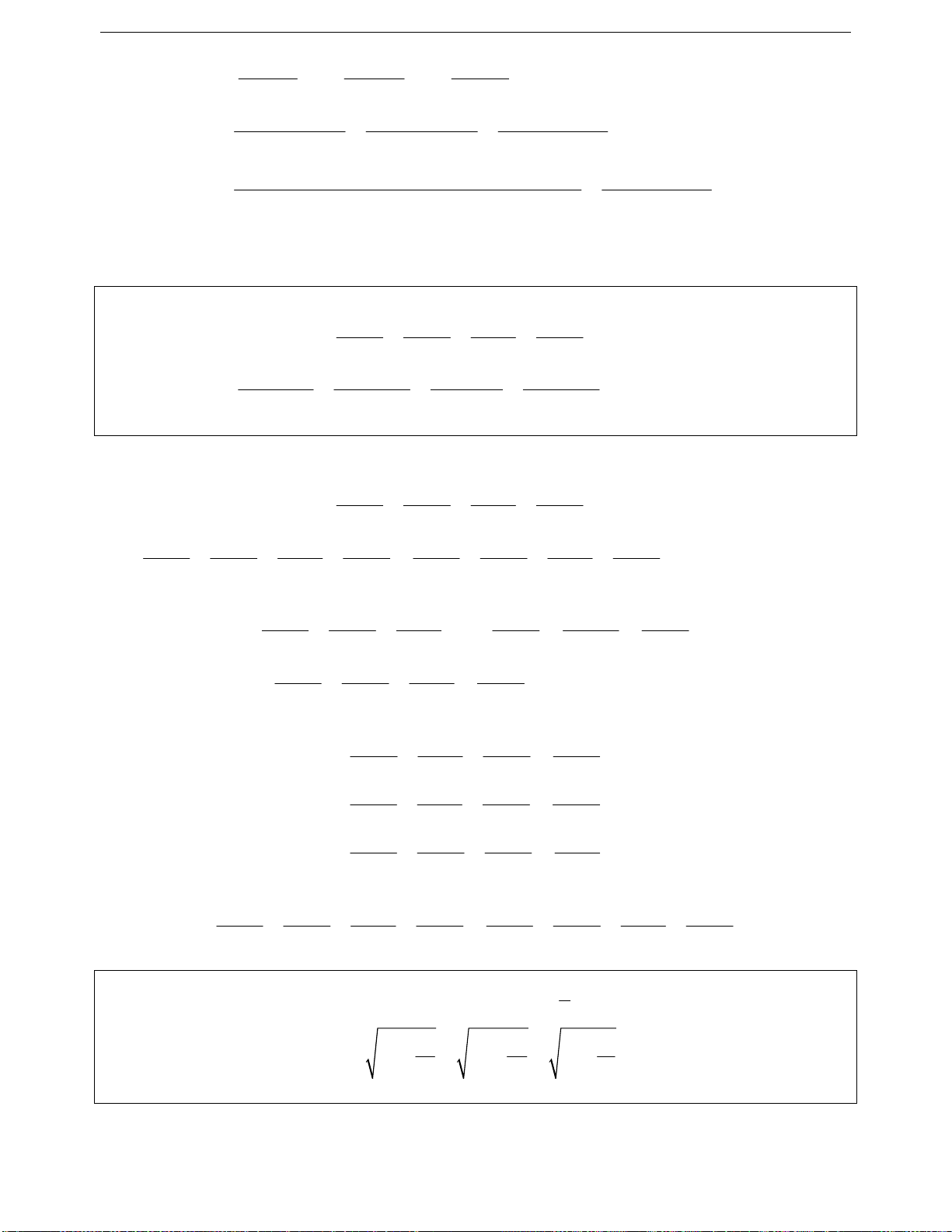
22 2
22 2
22
2
22
ab ac bc ab ca ac
1110
abc bca ca
abac bcba cacb
0
abc bca ca
ab acb ca bca bc
cacb
0
ca
abcbca
baba2ac
Do vai trò của các biến như nhau nên không mất tính tổng quát ta giả sử
Bài 141. Cho a, b, c, d là các số thực dương thỏa mãn:
3333
1111
2
1a 1b 1c 1d
Chứng minh rằng:
2222
1a 1b 1c 1d
0
1aa 1bb 1cc 1dd
Trích đề thi chọn HS dự thi HSGQG Tỉnh Đồng Tháp năm học 2013-2014
Lời giải
Biến đổi tương đương bất đẳng thức cần chứng minh
2222
3333
1a 1b 1c 1d
0
1a 1b 1c 1d
Hay
2222
3333 3333
1111abcd
1a 1b 1c 1d 1a 1b 1c 1d
Từ giả thiết và áp dụng bất đẳng thức Cauchy ta có
32
333 3 3 3
111 112d3d
2
1a 1b 1c 1d 1d 1d
Hay
2
333 3
1113d
1a 1b 1c 1d
Hoàn toàn tương tự ta được
2
33 3 3
2
33 3 3
2
3333
1113a
1b 1c 1d 1a
1113b
1a 1c 1d 1b
1113c
1a 1b 1d 1c
Cộng theo vế bốn bất đẳng thức trên ta được
2222
3333 3333
1111abcd
1a 1b 1c 1d 1a 1b 1c 1d
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abcd1.
Bài 142. Cho a, b, c là các số thực dương thỏa mãn
3
abc
2
. Tìm giá trị nhỏ nhất của biểu thức:
222
222
111
Sa b c
abc
Trích đề thi chọn HS dự thi HSGQG Tỉnh Trà Vinh năm học 2013-2014
Lời giải
Cách 1:
Chú ý đến dấu đẳng thức xẩy ra ta được

2
222
22
1144
17 a 1 4 a a a
aa
aa
Áp dụng tương tự ta được
22
22
14 14
17 b b ; 17 c c
bc
bc
Khi đó ta được
222
222
1 1 1 444
17 a 17 b 17 c a b c
abc
abc
Theo một đánh giá quen thuộc ta có
111 36
abcabc
Nên ta được
444 36
abc abc
abc abc
Áp dụng bất đẳng thức Cauchy và kết hợp với giả thiết ta được
36 9 135
abc abc
abc
4a b c 4a b c
9 135 135 51
2. a b c . 3
362
4a b c
4.
2
Từ đó ta suy ra
222
222
11151
17 a 17 b 17 c
2
abc
Hay
222
222
111317
abc
2
abc
Như vậy giá trị nhỏ nhất của S là
317
2
. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
.
Cách 2: Dễ dàng chứng minh được: Với a, b, x, y là các số thực dương ta luôn có:
22
22 22
ax by ab xy
Áp dụng bất đẳng thức trên ta được
2
2
222 2
222 2
2
2
111 11 1
Sa b c ab c
ab
abc c
111
abc
abc
Theo bất đẳng thức Cauchy ta có
22
2
111 9 81
abc abc
abc
Do đó ta được
2
22
2
111 81
abc abc
abc
abc
Áp dụng bất đẳng thức Cauchy và giả thiết ta có

2
22
81 9 9 1215 1215 135
abc 2. ;
42 9 4
16 a b c 16 a b c
16.
4
Cộng theo vế hai bất đẳng thức trên ta được
2
2
81 9 135 153
abc
24 4
abc
Từ các kết quả đó ta được
153 3 17
S
42
.
Như vậy giá trị nhỏ nhất của S là
317
2
. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
.
Bài 143. Cho a, b, c là các số thực dương thỏa mãn abc 1 . Tìm giá trị nhỏ nhất của biểu thức:
222
bc ca ab
P
abc bca cab
Trích đề thi chọn HS dự thi HSGQG Tỉnh Lâm Đồng năm học 2013-2014
Lời giải
Kết hợp với giả thiết ta viết lại biểu thức P thành
22 2 2 2 2
bc ca ab
P
ab ac ab bc ca bc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
22 2 2 2 2
ab bc ca
bc ca ab ab bc ca
P
ab ac ab bc ca bc 2
2ab bc ca
Mặt khác cũng theo bất đẳng thức Cauchy ta được
3
222
ab bc ca 3 a b c 3
Suy ra ta được
3
P
2
hay giá trị nhỏ nhất của P là
3
2
. Đẳng thức xẩy ra khi abc1.
Bài 144.
Cho a, b, c là các số thực thỏa mãn 0a;b;c1. Chứng minh rằng:
abc
1a1b2c 2
bc1ca1ab1
Trích đề thi chọn HS dự thi HSGQG Tỉnh An Giang năm học 2014-2015
Lời giải
Từ giả thiết ta được
01a;1b1;ab11
.
Áp dụng bất đẳng thức Cauchy ta được
3
1a 1b a b1
11a1bab1
3
Suy ta
11a1bab1
Vì
2c 0 nên khi đó ta được
2c 1a1bab12c
Suy ra
2c
1a1b2c
ab1
Hay
c2
1a1b2c
ab1 ab1
(1)

Ta đi chứng minh
a2a
bc1 ab1
. Thật vậy, biến đổitương đương bất đẳng thức trên ta được
aa b 1 2ab c 1 ab 2c 1 a 0
Tương tự ta được
b2b
ac1 ab1
Từ các kết quả trên ta được
abc
1a1b2c
bc1ca1ab1
22a2b
2
ab1ab1ab1
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab0;c1
.
Bài 145. Cho a, b, c là các số thực dương thỏa mãn abc 3. Chứng minh rằng:
333
111
abc2 3abbcca
abc
Trích đề thi chọn HS dự thi HSGQG Tỉnh Lâm Đồng năm học 2014-2015
Lời giải
Dễ thấy
111 18
26
abc abc
. Do đó ta được
333
abc63abbcca
Áp dụng bất đẳng thức Cauchy ta được
333
a 113a;b 113b;c 113c
Ta quy bài toán về chứng minh
3a b c 3ab bc ca
Hay
2
abc 3abbcca
, đây là một đánh giá đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 146. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
222
ab c bc a ca b
6
5
abcbca cab
Trích đề thi chọn HS dự thi HSGQG Tỉnh Thái Bình năm học 2014-2015
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
2
222
22
bc
33
abc a bcabc bc
44 4
b c 4a 3b 3c
4
Suy ra ta được
2
2
ab c 4ab c
4a
4a 3b 3c
4a 3b 3c b c
abc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
91
4a a a 9 1
.
4a 3b 3c 25 4a 3b 3c 25 a
3a b c
.

Suy ra ta được
2
ab c
27a 1
25
abc25abc
Áp dụng hoàn toàn tương tự ta được
22
22
bc a cc a
27b 1 27c 1
;
25 25
25 a b c 25 a b c
bca cca
Cộng vế theo vế các bất đẳng thức trên ta được
22 2
222
ab c ba c ca b 27a b c
36
25 5
25 a b c
bc a ca b ab c
Vậy bất đẳng thức được chứng minh xong.
Bài 147. Cho a, b, c là các số thực không âm sao cho abc1. Chứng minh rằng:
22 2
abc1
2
1 9bc 4 b c 1 9ca 4 c a 1 9ab 4 a b
Trích đề thi chọn HS dự thi HSGQG Thành Phố hải Phòngnăm học 2014-2015
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
2
222
abc
1 9bc 4 b c 1 9ca 4 c a 1 9ab 4 a b
abc
a b c 27abc 4a b c 4b c a 4c a b
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2222
2 a b c 1 27abc 4a b c 4b c a 4c a b
Hay
1 4ab a b 4bc b c 4ca c a 3abc
Để ý đến giả thiết ta viết lại được bất đẳng thức trên thành
3
abc 4abab 4bcbc 4caca 3abc
Hay
333
a b c 3abc ab a b bc b c ca c a
Biến đổi tương đương ta được
abc a b c b c a c a b
Bất đẳng thức trên là một bất đẳng thức đúng và dễ dàng chứng minh được.
Vậy bài toán được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc1 hoặc
1
ab ;c0
2
và các hoán vị.
Bài 148. Cho x, y, z là các số thực không dương. Chứng minh rằng:
33 3 3 3 3
222
2332332 33
xy z yz x zx y 3
8
xyzyz yzxzx zxyxy
Trích đề thi chọn HS dự thi HSGQG Trường ĐHKHTN Hà Nội năm học 2014-2015
Lời giải
Dễ dàng chứng minh được
33 22 22
2y z y z y z 2 yzy z

Và lại có
2
xyz2xyz . Nhân theo vế hai kết quả trên ta được
233 22
xyzyz 2xyzyz
Suy ra ta được
33 33
2
222
233
22 22
22 22 3 3 22 22 22
xy z xy z
2 x yz xyz y z
xyzyz
yz yz
2xy xz yz yz 2xy xz 2yz
Hoàn toàn tương tự ta được
33 3 3 3 3
222
2332332 33
22 22 2 2
2 2 22 22 2 2 22 22 2 2 22 22
xy z yz x zx y
xyzyz yzxzx zxyxy
yz xz xy
2xy xz 2yz 2xy 2xz yz 22xy xz 2yz
Ta càn chỉ ra được
22 22 2 2
2 2 22 22 2 2 22 22 2 2 22 22
yz xz xy 3
4
xy xz 2yz xy 2xz yz 2xy xz 2yz
Đặt
22 22 22
axy;byz;czx. Khi đó bất đẳng thức được viết lại thành
abc3
2a b c a 2b c a b 2c 4
Bất đẳng thức trên tương đương với
bc ac ab 3
2a b c a 2b c a b 2c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
2a 2b 2c
bc ac ab
2a b c a 2b c a b 2c
2a b c 6ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
22
2
22a 2b 2c 32a b c 6ab bc ca
4abc 3abc 3abbaca
abc 3abbcca
Đánh giá cuối cùng là một đánh giá đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
xyz
Bài 149. Cho x, y, z là các số thực dương thỏa mãn xyz1. Tìm giá trị lớn nhất của biểu thức
222
xy yz zx
P
4x 5y 4y 5z 4z 5x
Trích đề thi chọn HS dự thi HSGQG Trường ĐHKHTN Hà Nội năm học 2014-2015
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
xyz
Pxyyzzx
4x 5y 4y 5z 4z 5x

Đặt
xyz15y5z5x
Q3
4x 5y 4y 5z 4z 5x 4 4x 5y 4y 5z 4z 5x
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
2
5x y z
5y 5z 5x
4x 5y 4y 5z 4z 5x
4xy yz zx 5x y z
55
5 6 xy yz zx
5x y z 6xy yz zx
Do đó ta được
15
Q3
4
5 6 xy yz zx
Khi đó ta suy ra
2
15
Pxyyzzx3
4
5 6 xy yz zx
Đặt
1
axyyzzx 0a
3
. Khi đó ta được
2
a5 9a
15
Pa3
456a
25 6a
Ta sẽ chứng minh
a5 9a
1
9
25 6a
.
Thật vậy, bất đẳng thức này tương đương với
13a1027a 0
, đây là một đánh giá đúng do
1
0a
3
. Do đó bất đẳng thức trên được chứng minh.
Suy ra
1
P
3
hay giá trị lớn nhất của P là
1
3
.
Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
.
Bài 150. Cho a, b, c là các số thực dương thỏa mãn ab bc ca 1. Chứng minh rằng:
3
333
22 2
abc
abc
18
1 9b ca 1 9c ab 1 9a bc
Trích đề thi chọn HS dự thi HSGQG Tỉnh Thừa Thiên Huế năm học 2014-2015
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
333
22 2
abc
abc
1 9b ca 1 9c ab 1 9a bc
abc9abcabbcca
Dễ thấy
2
222
abc
abc
3
và để ý đến giả thiết ab bc ca 1 ta được
2
4
222
abc
abc
abc9abcabbcca 9abc9abc

Do đó ta có
4
333
22 2
abc
abc
1 9b ca 1 9c ab 1 9a bc
9a b c 9abc
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
43
abc abc
18
9a b c 9abc
Hay
abc9abc . Để ý đến giả thiết ab bc ca 1, áp dụng bất đẳng thức Cauchy ta được
3
3
222
a b c a b c ab bc ac 3 abc.3 a b c 9abc
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 151. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
5a 4bc 5b 4ca 5c 4ab
3a b c 2 ab bc ca
Trích đề thi chọn HS dự thi HSGQG Tỉnh Quảng Nam năm học 2014-2015
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222 222
5a 4bc 2 bc 5b 4ca 2 ca 5c 4ab 2 ab 3 a b c
Hay
222
222
222
5a 5b 5c
3a b c
5a 4bc 2 bc 5b 4ca 2 ca 5c 4ab 2 ab
Hay
222
222
222
15a 5b 5c
1
5a 4bc 2 bc 5b 4ca 2 ca 5c 4ab 2 ab
3a b c
Áp dụng bất đẳng thức Cauchy ta có
2222222
222
222
222
222
2 5a 4bc 3 a b c 8a 3b 3c 4bc
4.3 bc. 3 a b c
23a 3b 3c 9bc
4bc3a b c
33
2a b c 3bc
Cộng theo vế hai bất đẳng thức trên ta được
2222222
2 5a 4bc 2 bc 3 a b c 10a 5b 5c 10bc
Suy ra
22
222
2222
10a 10a
10a 5b 5c 10bc
25a4bc2bc3abc
Lại có
22
10bc 5b 5c nên ta được
222
222 2 2 2222
10a 10a a
10a 5b 5c 10bc 10a 10b 10c a b c
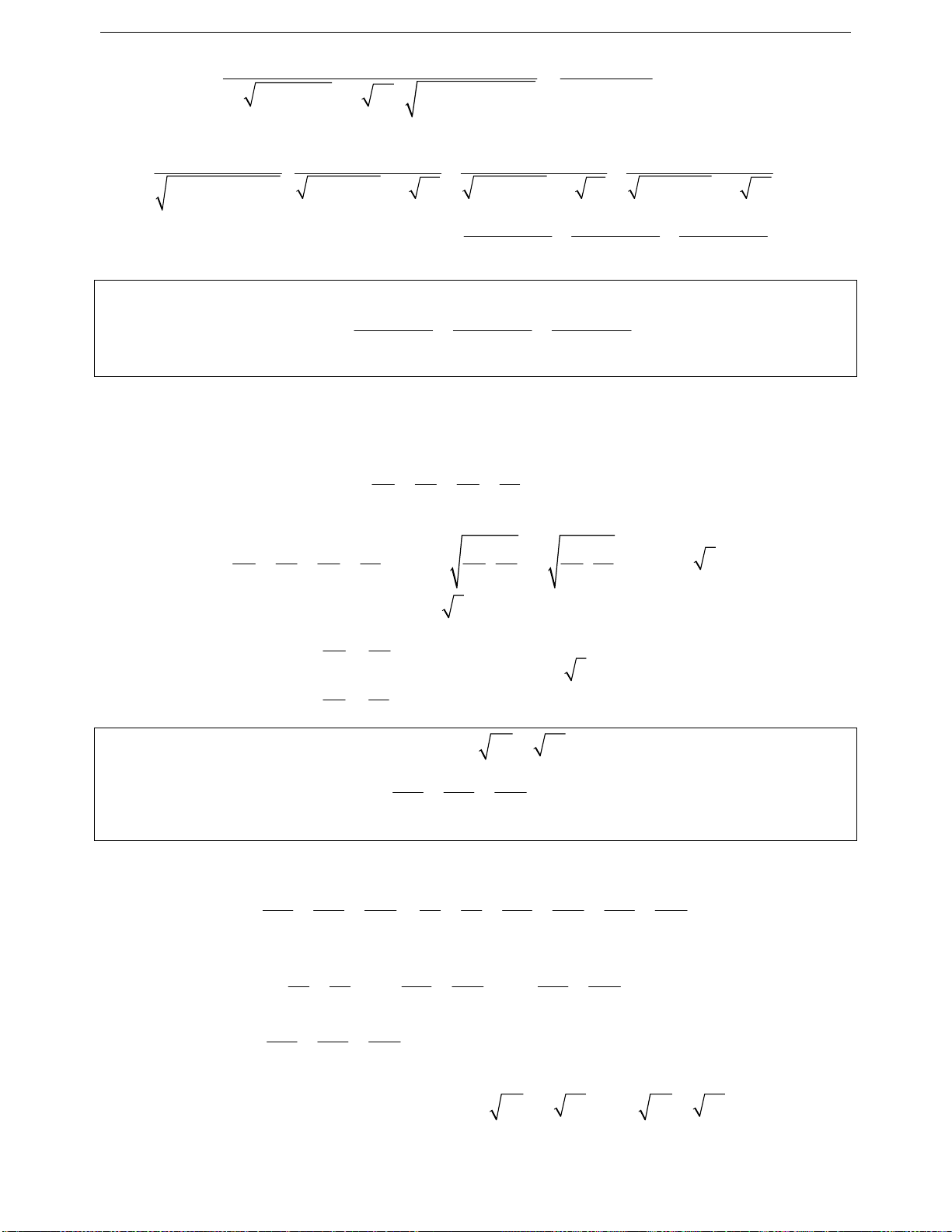
Do đó ta được
22
222
2222
10a a
abc
25a4bc2bc3abc
Chứng minh hoàn toàn tương tự ta được
222
222
222
222
222 222222
15a 5b 5c
5a 4bc 2 bc 5b 4ca 2 ca 5c 4ab 2 ab
3a b c
abc
1
abc bac cba
Vậy bất đẳng thức được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài 152. Cho a, b, c là các số thực dương tùy ý. Tìm giá trị nhỏ nhất của biểu thức:
2a 3b 4b 8c
P
a2bc ab2cab3c
Trích đề thi chọn HS dự thi HSGQG Tỉnh Quảng Nam năm học 2014-2015
Lời giải
Đặt xa2bc;yab2c;zab3c . Khi đó ta được
a 5yx3z;b xz2y;c zx
Biểu thức P được viết lại thành
4x 2y 8y 4z
P17
yxzy
Áp dụng bất đẳng thức Cauchy ta được
4x 2y 8y 4z 4x 2y 8y 4z
P172.2.1712217
yxzy yx zy
Vậy giá trị nhỏ nhất của P là
12 2 17
. Đẳng thức xẩy ra khi và chỉ khi
22
22
4x 2y
2x y
yx
z2y2x
8y 4z
2y z
zy
Bài 153. Cho x, y, z là các số thực dương thỏa mãn 2xy xz 1. Xh]ngs minh rằng:
3yz 4zx 5xy
4
xyz
Trích đề thi chọn HS dự thi HSGQG Tỉnh Tuyên Quang năm học 2014-2015
Lời giải
Biến đổi vế trái của bất đẳng thức như sau
3yz 4zx 5xy yz zx 2yz 2xy 3zx 3xy
xyzxyxzyz
Khi đó áp dụng bất đẳng thức Cauchy ta được
yz zx 2yz 2xy 3zx 3xy
2z; 4y; 6x
xy x z y z
Do đó ta được
3yz 4zx 5xy
6x 4y 2z
xyz
Mặt khác cũng theo bất đẳng thức Cauchy ta được
6x 4y 2z 4 x y 2 x z 8 xy 4 xz 4 2 xy xz 4

Do đó ta suy ra
3yz 4zx 5xy
4
xyz
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
Bài 154. Cho x, y, z là các số thực dương thỏa mãn điều kiện:
444 222
3x y z 7x y z 12 0 .
Tìm giá trị nỏ nhất của biểu thức:
222
xyz
P
y2z z2x x2y
Trích đề thi chọn HS dự thi HSGQG Tỉnh Yên Bái năm học 2014-2015
Lời giải
Trước hết ta đơn giản hóa giả thiết của bài toán.
Áp dụng một đánh giá quen thuộc ta có
2
444 222
xyz3xyz
Khi đó ta được
2
222 222
3 x y z 7 x y z 12 0
Hay
222
xyz3
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
222
222 222
xyz
xyz
P
y2z z2x x2y
xy yz zx 2 xy zx yz
Áp dụng bất đẳng thức Bunhiacopxki ta được
222 222222222
3
222222
222
222
xy yz zx x y z xy yz zx
xyzxyz
xyz
xyz
33
Hoàn toàn tương tự ta được
222
222 222
xyz
2xy yz zx 2x y z
3
Do đó ta được
2
222
222
222
222
xyz
xyz
P1
3
xyz
3x y z
3
Vậy giá trị nhỏ nhất của P là 1. Đẳng thức xẩy ra khi và chỉ khi
xyz1.
Bài 155. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
222
abc bca cab
3
5
ab c bc a ca b
Trích đề thi chọn HS dự thi HSGQG Tỉnh Đăk Lăk năm học 2014-2015
Lời giải
Để ý là
22
2
22 2
22 2
a b c a b c 2c a b 2c a b
1
ab c ab c ab c
Áp dụng tương tự ta quy bài toán về chứng minh

222
222
ab c bc a ca b
6
5
abcbca cab
Áp dụng bất đẳng thức Cauchy ta có
2
222
22
bc
33
abc a bcabc bc
44 4
b c 4a 3b 3c
4
Suy ra ta được
2
2
ab c 4ab c
4a
4a 3b 3c
4a 3b 3c b c
abc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
91
4a a a 9 1
.
4a 3b 3c 25 4a 3b 3c 25 a
3a b c
.
Suy ra ta được
2
ab c
27a 1
25
abc25abc
Áp dụng hoàn toàn tương tự ta được
22
22
bc a cc a
27b 1 27c 1
;
25 25
25 a b c 25 a b c
bca cca
Cộng vế theo vế các bất đẳng thức trên ta được
22 2
222
ab c ba c ca b 27a b c
36
25 5
25 a b c
bc a ca b ab c
Vậy bất đẳng thức được chứng minh xong.
Bài 156. Cho x, y, z là các số thực dương thỏa mãn xy yz zx 2xyz . Chứng minh rằng:
22 2 2 2 2
xyz
1
2y z xyz 2z x xyz 2x y xyz
Trích đề thi chọn HS dự thi HSGQG Tỉnh Gia Lai năm học 2014-2015
Lời giải
Giả thiết của bài toán được viết lại thành
111
2
xyz
. Đặt
111
x;y;z
abc
thì ta được
abc2
. Khi đó bất đẳng thức cần chứng minh được viết lại thành
bc ca ab
1
2a bc 2b ca 2c ab
Chú ý đến giả thiết
abc2
, ta có
bc bc bc bc 1 1
2ab ca
2a bc
aa b c bc a b a c
Hoàn toàn tương tự ta được
ca ca 1 1 ab ab 1 1
;
2bc ab 2ca bc
2b ca 2c ab

Cộng theo vế các bất đẳng thức trên ta được
bc ca ab
2a bc 2b ca 2c ab
bc 1 1 ca 1 1 ab 1 1 a b c
1
2ab ca 2bcab 2ca bc 2
Như vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
xyz
2
Bài 157. Cho x, y, z là các số thực dương thỏa mãn
xyz 1
. Tìm giá trị nhỏ nhất của biểu thức:
333
x2 y2 z2
P
xyz yzx zxy
Trích đề thi chọn HS dự thi HSGQG Tỉnh Cần Thơ năm học 2015-2016
Lời giải
Đặt
111
a;b;z
xyc
, suy ra
abc 1
. Biểu thức P được viết lại thành
222
a bc 1 2a b ca 1 2b c ab 1 2c
P
bc ca ab
Hay
a 1 2a b 1 2b c 1 2c
P
bc ca ab
Ta viết biểu thức P thành
222
abc2a2b2c
P
bc ca ab bc ca ab
Dễ dàng chứng minh được
abc3
bc ca ab 2
Mặt khác theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
3
222
abc
abc abc3abc3
bc ca ab 2 2 2
2a b c
DO đó ta được
339
P2.
222
. Vậy giá trị nhỏ nhất của P là
9
2
.
Đẳng thức xẩy ra khi và chỉ khi
abc1 xyz1
Bài 158. Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
3
222
abc abbccaa b c
333
Trích đề thi chọn HS dự thi HSGQG Tỉnh Kiên Giang năm học 2015-2016
Lời giải
Bất đẳng thức cần chứng minh tương đương với
62
222
abc abbcca a b c
.
333
Hay
6
2
222
abc
ab bc ca a b c
27
Áp dụng bất đẳng thức Cauchy ta có

2
222 222
3
6
222
abbcca a b c abbccaabbccaa b c
ab bc ca ab bc ca a b c
abc
327
Vậy bất đẳng
thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 159. Cho a, b, c là các số thực không âm trong đó không có hai số nào cùng bằng 0. Chứng minh
rằng:
222222
111 3
ab bc ca
aabb bbcc ccaa
Trích đề thi chọn HS dự thi HSGQG Tỉnh Thanh Hóa năm học 2015-2016
Lời giải
Vì vai trò của các biến như nhau nên không mất tính tổng quát ta giả sử c là số nhỏ nhất trong ba số a, b,
c. Khi đó ta được
222 2
222 2
bbcc bcbc b
aacc acaca
ab bc ca ab c a b ab
Từ đó ta có
2222222222
111 311
aabb bbcc ccaa aabb a b
Và có
31
ab bc ca ab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222 2
11 1 3
ab
abaabb
Thật vậy, bất đẳng thức trên tương đương với
2222
4
22 22
33
22 2222
1111 1 1
0
ab ab ab
abaabb
ab
ab a ab b 2ab a b
00
ab ab
aabbab abaabb
Bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh xong.
Bài 160. Cho a, b, c là độ dài ba cạnh của một tam giác và abc1. Chứng minh rằng:
444111
9
abbcca a b c
Trích đề thi chọn HS dự thi HSGQG Thành Phố Hà Nội năm học 2015-2016
Lời giải
Cách 1:
Để ý đến giả thiết lại viết lại được bất đẳng thức trên thành
4a b c 4a b c 4a b c
abcabcabc
9
ab bc ca a b c
4c 4a 4b b c a c a b
12 12
abbc ca a b c
4c 4a 4b b c a c a b
abbc ca a b c

Áp dụng bất đẳng thức Cauchy dạng
11 4
xy xy
, ta được
abbcca 1 1 11 1 1
abc
cab cb acab
4a 4b 4c
bc ca ab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
444111
9
1c 1a 1b a b c
Ta sẽ chứng minh
41
18c 3
1c c
. Thật vậy, bất đẳng thức trên tương đương với
2
23
5c 1 c 1 c 18c 3 5c 1 21c 3c 18c 3c 1 2c 1 0
Do a, b, c là ba cạnh của một tam giác và
abc1 nên
2c12cabc cab 0
Do đó bất đẳng thức trên đúng.
Vậy bài toán được chứng minh xong.
Bài 161. Cho a, b, c là các số thực dương thỏa mãn
abc
abc
bca
. Tìm giá trị lớn nhất của
biểu thức:
33 33 33
ab1 bc1 ca1
P
ab1bc1ca1
Trích đề thi chọn HS dự thi HSGQG Trường Đại học Vinh năm học 2015-2016
Lời giải
Áp dụng bất đẳng thức Cauchy cho giả thiết ta được
abc
abc 3
bca
Mặt khác áp dụng bất đẳng thức Bunhiacopxki dạng phân thức cho giả thiết ta được
2
abc
abc
abc abbcca abc
bcaabbcca
Áp dụng bất đẳng thức Bnhiacopxki ta có
2
22
2
33 22
ab1 a b 1
ab1ab1 ab1
3
Do đó ta được
33 22
ab1 3
ab1ab1
Hoàn toàn tương tự ta thu được
22 22 22
333
P
ab1bc1ca1
Ta sẽ chứng minh
22 22 22
111
1
ab1bc1ca1
Thật vậy, bất đẳng thức trên được viết lại thành
22 22 22
22 22 22
ab bc ca
2
ab1bc1ca1
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
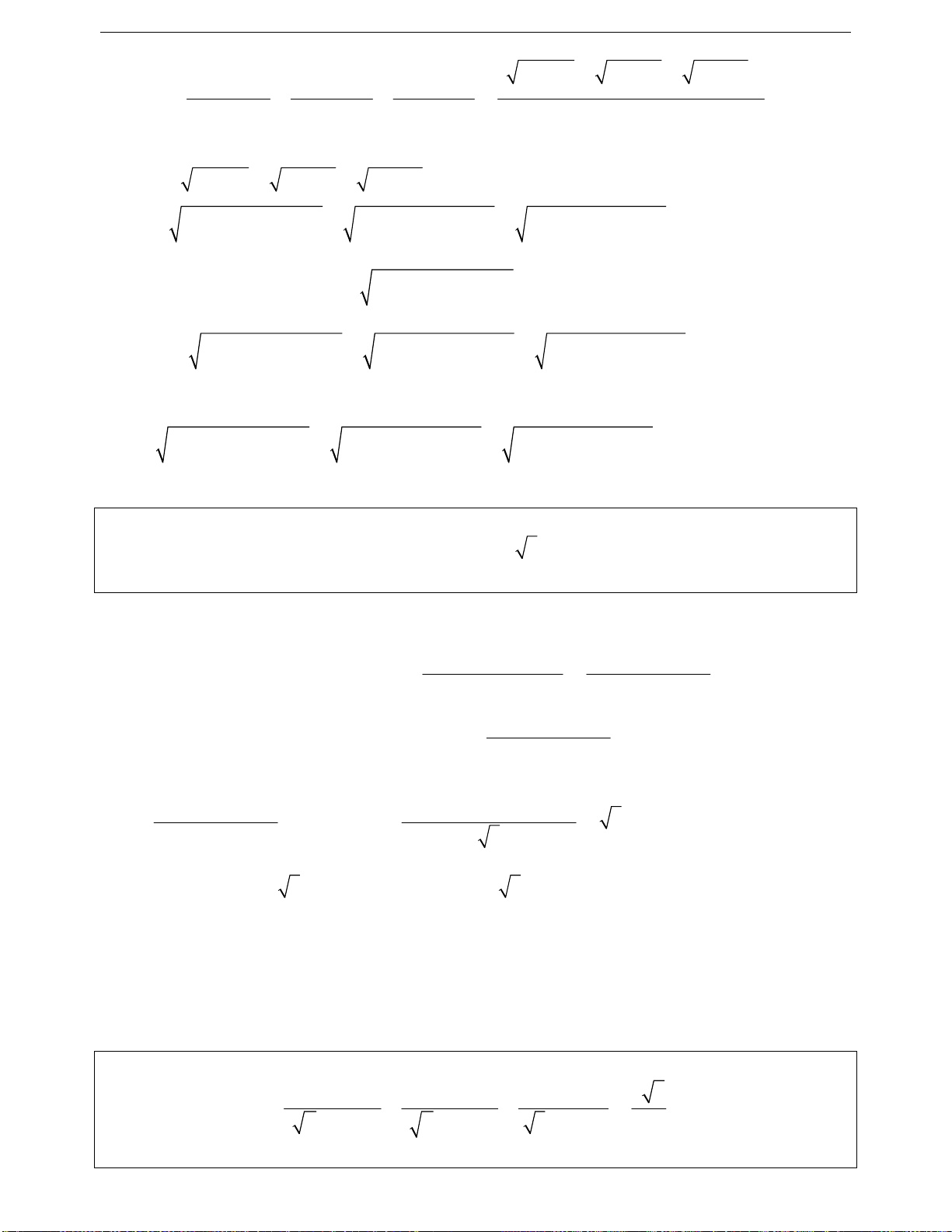
2
22 22 22
22 22 22
22 22 22
222
ab bc ca
ab bc ca
ab1bc1ca1
2a b c 3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
22 22 22 222
2222 2222 2222 222
ab bc ca 4abc 6
abbc bcca caca abc3
Áp dụng bất đẳng thức Bunhiacopxki ta được
2222 2
abbc bac
Áp dụng tương tự ta được
2 222 222 2 2 22 2
222
abbc bcca caca
abcabbcca
Mà từ giả thiết ta được
ab bc ca 3. Do vậy ta được
2222 2222 2222 222
abbc bcca caca abc3
Vậy bất đẳng thức được chứng minh.
Suy ra giá trị nhỏ nhất của P là 3. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Bài 162. Cho a, b, c là các số thực không âm. Chứng minh rằng:
222
abc bca cab 2abbcca
Trích đề thi chọn HS dự thi HSGQG Tỉnh Đăk Lăk năm học 2015-2016
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222
22
abcbca ab c1
abc bca
22
Khi đó ta được
22
222 2
ab c1
abc bca cab cab
2
Cũng theo bất đẳng thức Cauchy ta có
22
2
ab c1 abc1cab
cab 2 2abc1cab
2
2
Bài toán quy về chứng minh
2a bc1cab 2a bbcca
c1cab bcca cabc bcca
ca 1 b 1 0
Theo nguyên lí Dirrichlet thì trong ba số a, b, c luôn tìm được hai số cùng phía với 1. Vì vai trò của
a, b, c như nhau nên không mất tính tổng quát ta có thể giả sử hai số đó là a và b. Khi đó bất đẳng thức
cuối cùng luôn đúng.
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
Bài 163. Cho x, y, z là các số thực dương thỏa mãn xyz1. Chứng minh rằng:
32 32 32
x2xxy2yyz2zz23
3
xy z yz x zx y
Trích đề thi chọn HS dự thi HSGQG Tỉnh Kiên Giang năm học 2015-2016

Lời giải
Áp dụng giả thiết xyz1 ta được
2
32
x1 x
x2xx
x1 x x x x
xy z x1 x
Áp dụng tương tự ta được
32 32 32
x2xxy2yyz2zz
xy z yz x zx y
xyzxxxyxz
Ta cần chứng minh
23
xyzxxxyxz
3
Từ
xyz1 x y z 3 . Theo bất đẳng thức Bunhiacopxki ta có
2
3xx yy zz x y z xx yy zz x y z
Do đó ta được
1
xx yy zz
3
. Tư đó ta có
123
xyzxxxyxz 3
3
3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
xyz
3
.
Bài 164. Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
22 22 22
ab bc ca a b c
Trích đề thi chọn HS dự thi HSGQG Tỉnh Thừa Thiên Huế năm học 2015-2016
Lời giải
Sử dụng kỹ thuật thêm bớt ta có bất đẳng thức tương đương với
22 22 22
444 444 222222
2
444 222
2a b c 2ab bc ca
abc 2abc abc 2abbcca
abc 2abc abc 9
Vậy ta cần chứng minh
444
abc2abc9
Hay là
444
aaa bbb ccc9
Điều này hiển nhiên đúng vì theo bất đẳng thức Cauchy bộ ba số ta có
3
442
3
442
3
442
aaa3a.a.a3a
bbb3b.b.b3b
ccc3c.c.c3c
Bài toán được giải quyết. Bất đẳng thức xảy ra khi và chỉ khi
abc1
Bài 165. Cho a, b, c là các số thực dương thả mãn
abc 1
. Chứng minh rằng:
444
22 22 2 2
2a 2b 2c
abcabc 9
bcacab
Trích đề thi chọn HS dự thi HSGQG Tỉnh Thái Nguyên năm học 2015-2016
Lời giải

Dễ dàng chứng minh được
22
44 22
ab
ababab
c
Áp dụng hoàn toàn tương tự ta được
22 2222
444
abbc ca
2a b c
cab
Bài toán quy về chứng minh
22 2222
22 22 2 2
abbcca 4a 4b 4c
2a b c 18
cab
bcacab
Áp dụng bất đẳng thức Caychy ta được
22 22 22
22 22 22
a b 4c b c 4a c a 4b
4; 4; 4
cab
ab bc ca
Cộng theo vế các bất đẳng thức trên ta được
22 2222
22 22 2 2
a b b c c a 4a 4b 4c
12
cab
bcacab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
abc3
, đánh giá cuối cùng đúng theo bất đẳng
thức Cauchy. Vậy bài toán được chứng minh xong

Bài 102. Cho a, b, c là các số không âm thỏa mãn
Min a b; b c; c a 0
và
222
abc2abbcca
.
Chứng minh rằng:
22 22 22
ab bc ca 1
ab bc ca
2
Phân tích và lời giải
Trước hết ta phân tích các giả thiết của bài toán, từ
Min a b; b c; c a 0
ta suy ra được
trong các tổng trên không có tổng nào bằng không và từ giả thiết thứ hai ta thu được trong các biến a, b, c
chỉ có có thể có một biến bằng 0. Do đó ta dự đoán dấu đẳng thức xẩy ra tại
ab;c0 và các hoán vị
của nó. Quan sát bất đẳng thức ta nhận thấy không thể đánh giá trực tiếp tử hoặc mẫu của các biểu thức.
Do đó ta hướng đến biến đổi các biểu thức trước. Chú ý đến phép biến đổi
22
22 22
ab a b
ab
ab ab
.
Để đảm bảo dấu đẳng thức xẩy ra ta nhân với
2
. Khi đó bất đẳng thức được viết lại thành
22 22 22
22 22 22
2ab a b 2bc b c 2ca c a
1
ab bc ca
Đến đây áp dụng bất đẳng thức Cauchy ta được
22
22 22 22
2ab a b
2ab.2ab 2ab
ab ab ab
Áp dụng tương tự ta được
22 2 2
22 22 2 2 2 2
2bc b c 2ca c a
2bc 2ca
;
bc bc ca ca
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
22 22 22 22 2222
2ab a b 2bc b c 2ca c a
2ab 2bc 2ca
ab bc ca ab bc ca
Khi đó phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
22 2222
2ab 2bc 2ca
1
abbcca
Để ý là
222
22 22 22 22 22 22
ab bc ca
2ab 2bc 2ca
3
abbcca ab bc ca
Lúc này áp dụng bất đẳng thức Bunhiacopxki ta được
222 2
22 22 22
222
222
222
a b b c c a 2a 2b 2c
ab bc ca
2a b c
2a b c 2ab 2bc 2ca
8ab bc ca
4
2ab bc ca
2a b c
Do đó ta có
22 2222
2ab 2bc 2ca
1
abbcca
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
ab;c0 và các hoán vị.
Bài 103. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:

ab bc ca 1
ab2c bc2a ca2b 2
Phân tích và lời giải
Quan sát bất đẳng thức trên ta thấy được một số ý tưởng tiếp cận như sử dụng các bất đẳng thức
Cauchy, Bunhiacopxki để khử các căn bậc hai, đổi biến để đơn giản hóa giả thiết,…
Cách 1: Trước hết với ý tưởng khử các căn bậc hai, ta chú ý đến đánh giá bằng bất đẳng thức
Bunhiacopxki như sau
2
4a b 2c 1 1 2 a b 2c a b 2 c
Khi đó kết hợp với bất đẳng thức Cauchy ta được
ab 2 ab 2 ab 1 ab ab
ab2c 2
ab2c ac bc
4a b 2c
Áp dụng tương tự ta có
bc 1 bc bc ca 1 ca ca
;
bc2a 2 ca2b 2
abac abbc
Cộng theo vế các bất đẳng thức trên ta được
ab bc ca 1 1
abc
ab2c bc2a ca2b 2 2
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
9
.
Cách 2: Đặt
xa;yb;zc. Từ giả thiết ta suy ra
xyz1
.
Khi đó bất đẳng thức được viết lại thành
22 2 22 2 22 2
xy yz zx 1
2
xy2z yz2x zx2y
Áp dụng bất đẳng thức Cauchy ta được
2
22 2 22 2
4 x y 2z 1 1 2 x y 2z x y 2z
Do đó ta có
22 2
22 2
xy 2xy 2xy 1 xy xy
xy2z 2xzyz
xy2z
4x y 2z
Áp dụng tương tự ta được
22 2 2 2 2
yz 1 yz yz zx 1 zx zx
;
2x y x z 2x y y z
y z 2x z x 2y
Cộng theo vế các bất đẳng thức trên ta được
22 2 22 2 22 2
xy yz zx x y z 1
22
x y 2z y z 2x z x 2y
Bất đẳng thức được chứng minh xong.
Bài 104. Cho a, b, c là các số thực dương thỏa mãn
111
1
abc
. Chứng minh rằng:

222
bc ca ab
2
abc
Phân tích và lời giải
Từ giả thiết của bài toán thì suy nghĩ rất tự nhiên là đổi biến
111
x;y;z
abc
, khi đó giả
thiết trở thành
xyz1
và bất đẳng thức được viết lại là
222
xyz yzx zxy
2
yz zx xy
Quan sát bất đẳng thức trên ta có các cách xử lý như sau
Cách 1: Chú ý đến dụng bất đẳng thức Cauchy ta được các đánh giá
222
xy yz zx
xy ; yz ; zx
444
Khi đó ta được bất đẳng thức sau
222
222
xyz yzx zxy
4x 4y 4z
yz zx xy
yz zx xy
Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta có
2
222
4x y z
4x 4y 4z
2x y z 2
yz zx xy
2x y z
Vậy bài toán được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc3.
Cách 2: Biến đổi bất đẳng thức thành
222
11 11 11 1
xyz
yz zx xy 2
Theo một đánh giá quen thuộc ta có
22
2
22
2
22
2
11 x 11 4x
xyz
yz yz yz yz
11 y 11 4y
yzx
zx zx zx zx
11 z 11 4z
zxy
x y xy x y xy
Cộng theo vế các bất đẳng thức trên ta được
222
222
11 11 11 4x 4y 4z
xyz
yz zx xy yzzxxy
Đến đây đánh giả tương tự như cách 1 hoặc có thể áp dụng bất đẳng thức Bunhiacopxki như sau đây
222 222
2
2
4x 4y 4z 4x 4y 4z
2xy yz zx
yz zx xy yzzx xy
xyz
2yz zx xy2xyz2
yz zx xy
Vậy bài toán được chứng minh xong.
Bài 105. Cho a, b, c là các số thực dương. Chứng minh rằng:

2
222
9a b c
2a 2b 2c
111
bcaabbcca
Phân tích và lời giải
Để ý đến các đại lượng vế trái của bất đẳng thức ta nhận thấy các ý tưởng tiếp cận bài toán như
khai triển rồi đánh giá bằng bất đẳng thức Cauchy hoặc sử dụng đánh giá quen thuộc
2
222
3x y z x y z
. Ta đi phân tích các ý tưởng đó theo các cách sau
Cách 1: Triển khai vế trái ta được
222
222
22 2
2a 2b 2c a b c a b c
11134 4
bca bca
bca
Áp dụng bất đẳng thức Cauchy ta được
222
22 2
2
222
22 2
abcabc
1112
bca
bca
abc abc abc
33
bca bca
bca
Từ đó ta được
222
22 2
abc a b c abc
34 4 9
bca bca
bca
Để ý là theo bất đẳng thức Bunhiacopxki ta được
2
222
abc
abc a b c
bca abbccaabbcca
Suy ra
2
222
9a b c
2a 2b 2c
111
bcaabbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Cách 2: Áp dụng bất đẳng thức
2
222
3x y z x y z ta được
2
222
2a 2b 2c 1 a b c
111 32
bca3bca
Ta cần chứng minh được
2
2
9a b c
1abc
32
3bcaabbcca
Mặt khác áp dụng bất đẳng thức Bunhiacopxki ta được
2
abc
abc
bcaabbcca
Như vậy phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
abc abc
32 27
bca bca
Thật vậy, đặt
abc
tt3
bca
. Khi đó bất đẳng thức cần chứng minh trở thành

2
32t 27t t34t3 0
Bất đẳng thức cuối cùng luôn đúng do
t3
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
Bài 106. Cho a, b, c, d là các số thực dương tùy ý. Chứng minh rằng:
333
222222
abcabc
3
aabb bbcc caca
Phân tích và lời giải
Quan sát bất đẳng thức thì suy nghĩ đấu tiên đó là sử dụng bất đẳng thức Bunhiacopxki dạng
phân thức. Do đó ta thử tiếp cận bài toán với bất đẳng thức xem như thế nào?
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
333
222222
22
222 222
3332 22 22 2
222
abc
aabb bbcc caca
abc abc
abcababbcbcacca
abca b c
Ta cần chứng minh
222
abc abc
abc 3
Hay
2
222
3a b c a b c
Bất đẳng thức cuối cùng là một đánh giá quen thuộc.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Ngoài ra để ý đến mối liên hệ giữa tử và mẫu ta chú ý đến hằng đẳng thức bậc ba quen thuộc
33 2 2
ab abaabb . Do đó ta có phép biến đổi
3333
222222
abab
ab
aabbaabb aabb
Hoàn toàn tương tự ta có
333
222222
33 33 33
2 22222
2a 2b 2c
aabb bbcc caca
ab bc ca
aabb bbcc caca
Để ý là
22
33 2 2
aba abb
ab abaabb
3
Khi này ta được
33
22
ab ab
3
aabb
, đến đây bài toán xem như được chứng minh và ta trình bày lại
lời giải như sau
Cách 2: Ta có
3333
222222
abab
ab
aabbaabb aabb
Áp dụng tương tự ta được
33 33
2222 2222
bc ca
bc; ca
bbcc bbcc caca caca
Công theo vế các đẳng thức trên ta được

333
2 22222
33 3
222222
abc
aabb bbcc caca
bca
0
aabbbbcc caca
Hay
333
222222
33 3
2 22222
abc
aabb bbcc caca
bca
aabb bbcc caca
Do đó ta được
333
222222
33 33 33
2 22222
2a 2b 2c
aabb bbcc caca
ab bc ca
aabb bbcc caca
Để ý ta thấy
22
33 2 2
aba abb
ab abaabb
3
Do đó ta được
33
22
ab ab
3
aabb
Áp dụng tương tự ta được
33 33 33
222222
2a b c
ab bc ca
3
aabbbbcc caca
Suy ra
333
222222
2a b c
2a 2b 2c
3
aabb bbcc caca
Hay
333
222222
abcabc
3
aabbbbcc caca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Cách 3: Ngoài hai lời giải trên ta có thể tham khảo thêm lời giải bằng phương pháp biến đổi tương đương
như sau
Vì a, b là các số thực dương nên ta có
3
2
322
22
3a
ab ab 0 3a 2aba abb 2ab
aabb
Áp dụng tương tự ta được
33
22 22
3b 3c
2b c; 2c a
bbcc caca
Cộng theo vế các bất đẳng thức trên ta được
333
222222
abcabc
3
aabbbbcc caca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 107. Cho tam giác có ba cạnh a, b, c thỏa mãn
222
111
2
a1b1c1
. Chứng minh rằng:
3
abcabcbcacab
4
Phân tích và lời giải

Khi tiếp cận bài toán này có lẽ ấn tượng đầu tiên là giả thiết của bài toán là một đẳng thức phức
tạp. Tuy nhiên khi nhìn bất đẳng thức cần chứng minh ta thấy tích các đại lượng
abc;bca;cab
thì thấy tự tin hơn tí vì ít nhiều liên tưởng đến một số đánh giá quen
thuộc. Để có các bước đi hợp lí ta đi đánh giá lại giả thiết trước.
Từ giả thiết
222
111
2
a1b1c1
, ta được
222
222
abc
1
a1b1c1
Áp dụng bất đẳng thức Bunhia copxki ta được
2
222
222 222
abc
abc
1
a1b1c1abc3
Suy ra
2
222
abc3abc hay
3
ab bc ca
2
.
Quan sát tích các đại lượng dưới dấu căn ta liên tưởng đến một bất đẳng thức khá là hay gặp
abcbcacab abc
. Như vậy ta thu được bất đẳng thức
abcabcbcacab abcabc
Đến đây ta chú ý đến đánh giá
2
ab bc ca
abc a b c
3
Khi đó ta được
2
ab bc ca
3
abcabcbcacab
34
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 108. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng mỉnh rằng:
222
3a b c 4abc 13
Phân tích và lời giải
Trước hết ta đoán được dấu đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức ta thấy
xuất hiện đại lượng
222
abc liên hệ với giả thiết của bài toán bằng một hằng đẳng thức quen thuộc
2
222
abc a b c 2abbcca
. Như vậy khi đó ta trong bất đẳng thức sẽ có đại lượng
ab bc ca và abc . Hai đại lượng này làm ta liên tưởng đến phép sắp thứ tự để giảm biến, hoặc sử
dụng bất đẳng thức phụ quen thuộc, hoặc sử dụng nguyên lí Dirichlet. Từ sự phân tích đó ta có các lời
giải sau
Cách 1: Bất đẳng thức cần chứng minh tương đương với
2
3a b c 6ab bc ca 4abc 13
Hay
3ab bc ca 2abc 7
Không mất tính tổng quát ta giả sử
abc, do đó ta được a1 .
Khi đó ta có
2
2
23
3ab bc ca 2abc 3ab c bc3 2a
bc 32a
3a b c
4
3a 32a
27 3a 2a
3a 3 a
44
Ta cần chứng minh
23
27 3a 2a
7
4

Hay
2
32
2a 3a 1 0 a 1 2a 1 0
Bất đẳng thức cuối cùng luôn đúng.
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Cách 2: Ta có
abcbcacab 32c32b32a
27 18 a b c 12 ab bc ca 8abc 12 ab bc ca 27 8abc
Mặt khác ta dễ dàng chứng minh được
abc a b c b c a c a b
Do đó ta được
abc 12 ab bc ca 27 7abc
Hay
4ab bc ca
abc 3
3
Do đó ta có
222 222
16 ab bc ca
3 a b c 4abc 3 a b c 12
3
Ta cần chứng minh
222
16 ab bc ca
3 a b c 12 13
3
Hay
222
9 a b c 16 ab bc ca 75
Thật vậy, áp dụng một đánh giá quen thuộc ta có
222
222 222
2
2
9 a b c 16 ab bc ca
abc8abc2abbcca
abc
8a b c 3 72 75
3
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Cách 3: Trong ba số dương bất kì a, b, c luôn tồn tại hai số cùng phía so với 1.
Không mất tính tổng quát ta giả sử hai số đó là a và b. khi đó ta có
c1 a 1 b 0 abc ca b c
Ta có
2
222 2
22
2
ab
3 a b c 4abc 3 c 4c a b 4c
2
3c c1 26
3c4c3c4c 13
22
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài 109. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 2abc . Chứng minh rằng:
222
1111
2
a2a 1 b2b 1 c2c 1
Phân tích và lời giải
Bất đẳng thức trên đã được chứng minh bằng kỹ thuật đổi biến trong bất đẳng thức Cauchy. Ở đây
ta thực hiện đổi biến và áp dụng bất đẳng thức Bunhiacopxki xem có thể chứng minh được không.

Từ giả thiết
ab bc ca 2abc
suy ra
111
2
abc
.
Đặt
111
x;y;z
abc
, khi đó ta có xyz2.
Bất đẳng thức được viết lại là
333
222
xyz1
2
2x 2y 2z
Hay
333
22 2
xyz1
2
yz zx xy
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
333
22 2 2 2 2
2
222
222222
xyz
xyz
yz zx xy xyz yzx zxy
xyz
xy yx xz zx yz zy 6xyz
Ta cần chứng minh
2
222
2 2 22 22
xyz
1
2
xy yx xz zx yz zy 6xyz
Hay
2
222 2 2 2 2 2 2
2 x y z xy yx xz zx yz zy 6xyz
Thật vậy, theo một đánh giá quen thuộc ta có
2
222
2
222 222222
2x y z x y z
2x y z 2x y z x y z
3
Mà ta lại có
222 3332 2 22 22
xyzx y z x y z xyyxxzzxyzzy
Suy ra ta có
2
222 3332 2 22 22
2xyz x y z 4x y z xyyxxzzxyzzy
33
Ta cần chỉ ra được
3332 2 2 2 2 2
2 2 22 22
4 x y z xy yx xz zx yz zy
3xyyxxzzxyzzy6xyz
Hay
333 2 2 2 2 2 2
4 x y z xy yx xz zx yz zy 18xyz
Áp dụng bất đẳng thức Cauchy ta được
333 2 2 2 2 2 2
4 x y z 12xyz; x y y x x z 3xyz; z x y z z y 3xyz
Cộng theo vế các bất đẳng thức trên ta được
333 2 2 2 2 2 2
4 x y z xy yx xz zx yz zy 18xyz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
abc
2
.
Bài 110. Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:

222
53
a abc b abc c abc 9 abc
3
Phân tích: Chú ý đến phép biến đổi
22
aabcaabcabcaabac , do đó ta có
đánh giá
2
aa b a c aa 1
aabc aabac
22
.
Lời giải
Ta có
22
a abcaabc abcaabac
Do đó ta được
2
aa b a c aa 1
aabc aabac
22
Chứng minh tương tự ta được
22
bb 1 cc 1
babc ;cabc
22
Do đó ta được
222
aa 1 bb 1 cc 1
a abc b abc c abc
222
Mặt khác theo bất đẳng thức Cauchy ta lại có
aa 1
a1bc abc1
abc a a a
2222
Chứng minh tương tự ta được
bb 1 cc 1
abc b; abc c
22
Như vậy ta có
222
a abc b abc c abc 9 abc a b c 6 abc
Mà ta có
3
abc 2
abc3abc 3;6abc6
3
3
Nên ta suy ra
222
2553
a abc b abc c abc 9 abc 3
3
33
.
Vậy bài toán được chứng minh xong. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 111. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
33 3 3 3 3
abc
1
ab c bc a ca b
Phân tích: Để đồng bậc mẫu ta chú ý đến đánh giá theo bất đẳng thức Bunhiacopxki
2
333 2 22
ab c a bc a b c
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
333 2 22
ab c a bc a b c

Suy ra
3
4
33 2
333
222
aa b c
a a ab ac
ab c
ab c a bc
abc
Chứng minh tương tự ta được
44
33 2 33 2
222 222
b b ab bc c c ca bc
;
bc a ca b
abc abc
Do đó ta được bất đẳng thức sau
444
33 3 3 3 3 2
222
abc2abbcca
abc
ab c bc a ca b
abc
Ta cần chứng minh
444
2
222
abc2abbcca
1
abc
Hay
22 22 22
ab bc ca ab bc ca
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki và bất đẳng thức Cauchy ta được
24
22 22 22 22 22 22
3
3ab bc ca ab bc ca ;ab bc ca 3 abc 3
Nhân theo vế hai bất đẳng thức trên ta được
2
2
22 22 22
ab bc ca ab bc ca
Hay
22 22 22
ab bc ca ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 112. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3. Chứng minh rằng:
222
1113
2
a1b1c1
Phân tích: Quan sát bất đẳng thức ta chú ý đến đổi chiều bất đẳng thức. Ngoài ra ta có thể sắp thứ tự các
biến để chứng minh bài toán.
Lời giải
Cách 1: Không mất tính tổng quát, giải sử
abc
Do
ab bc ca 3 bc 1
Ta chứng minh bất đẳng thức sau: Với
x, y 0; xy 1
ta có
22
11 2
yz 1
y1z1
Thật vậy, ta có
2
22 2 2
yz2yz1 y1z1 yzyz10
Không mất tính tổng quát, giải sử
abc
. Do ab bc ca 3 bc 1
Áp dụng bất đẳng thức trên ta được
222 2
11112
bc 1
a1b1c1a1
Do đó ta sẽ chứng minh:
22
2
123
a 3 bc 3a bc 0 a a b c 3abc 0
bc 1 2
a1
Từ giả thiết
ab bc ca 3, suy ra abc3 và abc 1 .
Do đó
abc3abc0
Do đó ta được

222 2
111123
bc 1 2
a1b1c1a1
Vậy bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
abc1.
Cách 2: Gọi biểu thức vế trái là P, ta biến đổi biểu thức P như sau
22
222 222
111 ab c
P3
a1b1c1 a1b1c1
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 22 2
22 2 2 2
4a 4a a a a a
abc
3a 3 3a ab bc ca a ab ac 2a bc 2a bc
Áp dụng tương tự với hai biểu thức còn lại ta được
222 2 2 2
222 2 2 2
4a 4b 4c a b c
1
3a33b33c3 2abc2bca2cab
Ta sẽ chứng minh
222
222
abc
1
2a bc 2b ca 2c ab
Thật vậy, bất đẳng thức cần chứng minh tương đương với
222
222
3a b c 1
22
2a bc 2b ca 2c ab
Hay
222
bc ca ab 1
2
2a bc 2b ca 2c ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
222 222222222
2
22 22 22
bc ca ab
bc ca ab
2a bc 2b ca 2c ab 2a bc b c 2ab c c a 2abc a b
ab bc ca
1
ab bc ca 2abc a b c
Vậy bài toán được chứng minh xong.
Bài 113. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
432 432432
111
1
abcbca cab
Phân tích: Để ý là theo bất đẳng thức Bunhiacopxki ta có đánh giá
2
432 2 222
abc1bc abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
432 2 222
abc1bc abc
Do đó ta có
22
432 2
432 2
222
11bc1bc
abc
abc1bc
abc
Áp dụng tương tự ta được bất đẳng thức
222
432 432432 2
222
1113abcabc
abcbca cab
abc

Ta cần chứng minh
222
2
222
3abca b c
1
abc
Hay
2
222 222
abc 3abcabc
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
2
3
222 222222 222
abc 3abcabc 3abc
Từ giả thiết
abc 1
suy ra
abc3
.
Do đó ta được
2
3
222 222 222
abc
abc abc;abc3abc 3
3
Suy ra
222 222
3a b c a b c a b c 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1
Bài 114. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
333
abc3
abc bca cab 2
Phân tích: Áp dụng bất đẳng thức Cauchy ta để ý đến các đánh giá
33
3
aabc1 aabc13a
3..
abc 4 2 abc 4 2 2
và
2
abc
ab bc ca
3
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
33
3
aabc1 aabc13a
3..
abc 4 2 abc 4 2 2
Suy ra
3
a5abc1
abc 4 4 2
Chứng minh tương tự ta được
33
b5bca1c5cab1
;
bca 4 4 2cab 4 4 2
Cộng theo vế các bất đẳng thức trên ta được
333
5a b c
abc abbcca3
abc bca cab 4 4 2
9abbcca
44
Mặt khác ta lại có
2
abc
ab bc ca 9
3
Do đó ta có
333
abc933
abc bca cab 44 2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 115. Cho a, b là các số thực dương thỏa mãn
ab a b 3. Chứng minh rằng:
22
3a 3b ab 3
ab
b1 a1 ab 2
Phân tích: Chú ý đến đánh giá
2
a b 4ab, khi đó ta viết lại được giả thiết của bài toán là
2
ab 4ab 120 và đặt
tab
.

Lời giải
Từ giả thiết
ab a b 3 suy ra
3ab ab
.
Áp dụng bất đẳng thức Cauchy ta được
2
2
ab
3ab ab ab 4ab120 2ab3
4
Bất đẳng thức cần chứng minh tương đương với
2
2
2
2
3a b 2ab 3a b
3ab
3
ab 2ab
ab a b 1 a b 2
3a b 62a b 3a b
3ab
3
ab 62ab
4ab 2
Đặt
tab 2t3. Khi đó bất đẳng thức cần chứng minh trở thành
2
2
32 32
2
3t 6 2t 3t
3t 3
t62t
4t 2
3t 9t 18t 12 4t 4t 6t 18t
t2t t6 0
Bất đẳng thức cuối cùng luôn đúng với
t2 .
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab1.
Bài 116. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
1a 1b 1c a b c
2
bc ca ab b c a
Phân tích: Để ý đến giả thiết abc1 ta có các phép biến đổi sau
1 a 2a b c 2a
1
bc bc bc
và
aa ac
bbc
bb c
Lời giải
Biến đổi tương đương bất đẳng thức ta được
1a 1b 1c a b c 2a 2b 2c a b c
232
bc ca ab b c a bc ca ab b c a
aabbcc 3 ac bc ab 3
bbccacaab 2 2
bb c aa b cc a
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
ab bc ca
ac bc ab
bb c aa b cc a 2abca b c
Ta cần chứng minh
2
ab bc ca
3
2
2abc a b c
Hay
2
ab bc ca 3abc a b c
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy
Vậy bất đẳng thức được chứng minh. Bất đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Bài 117. Cho a, b, c là các số thực không âm tùy ý. Chứng minh rằng:
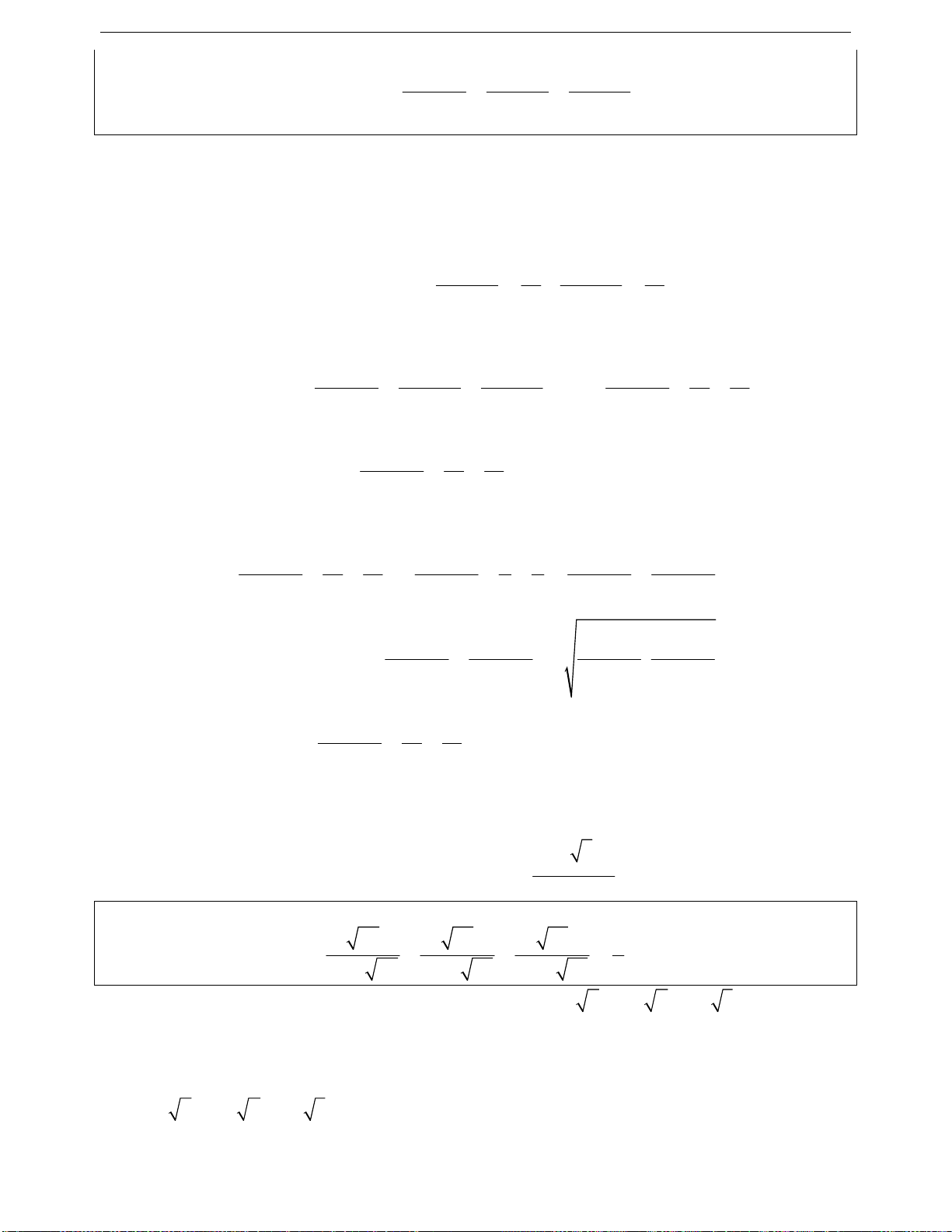
222
111
ab bc ca 4
ab bc ca
Phân tích: Bất đẳng thức có các đại lượng
222
ab;bc;ca dưới mẫu, do đó đẳng thức
không thể xẩy ra tại
abc. Ta dự đoán đẳng thức xẩy ra tại một biến bằng 0. Do đó ta nghĩ đến sắp
thứ tự các biến để giảm biến cho bài toán.
Lời giải
Không mất tính tổng quát ta giả sử
abc, khi đó ta có
22 22
1111
ab bc ca ab; ;
ba
bc ca
Do đó ta được bất đẳng thức sau
222 222
111 111
ab bc ca ab
ba
ab bc ca ab
Ta cần chứng minh
222
111
ab 4
ba
ab
Thật vậy, ta có
2
222 2 2
ab
111 ababab
ab 2
ba ab
ba
ab ab ab
Áp dụng bất đẳng thức Cauchy ta được
22
22
ab ab
ab ab
2. 2
ab ab
ab ab
Suy ra
222
111
ab 4
ba
ab
Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
2
c0
c0
35b
ab ab
a
2
Bài 118. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
ab bc ca 3
4
c3ab a3bc b3ca
Phân tích: Quan sát bất đẳng thức ta chú ý đến phép đổi biến xa;yb;zc và để có các
đánh giá hợp lí ta có thể đổi chiều bất đẳng thức.
Lời giải
Đặt
xa;yb;zc. Khi đó bất đẳng thức cần chứng minh trở thành

222
xy yz zx 3
4
z 3xy a 3yz y 3zx
Ta biến đổi biểu thức vế trái như sau
222 222
222
222
222
222
xy yz zx 1 3xy 3yz 3zx
P
3
z 3xy a 3yz y 3zx z 3xy a 3yz y 3zx
1z x y
111
3
z3xy x3yz y3zx
1z x y
1
3
z3xyx3yzy3zx
Đặt
222
222
zxy
Q
z 3xy x 3yz y 3zx
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức và một đánh gia quen thuộc ta được
2
222
222
222
2
2
2
xyz
zxy
Q
z 3xy x 3yz y 3zx
xyz3xyyzzx
xyz
3
4
xyz
xyz
3
Do đó ta được
13 3
P1 .
34 4
. Vậy bài toán được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 119. Cho a, b, c là các số thực không âm thỏa mãn
abc0. Chứng minh rằng:
33 3
3
a b 16c 16
81
abc
Phân tích: Để ý là
33 3 3 3 3
3 333
a b 16c a b 16c
abc abc abc abc
. Khi đó ta nghĩ đến
phép đổi biến
abc
x;y;z
abc abc abc
.
Lời giải
Đặt
abc
x;y;z
abc abc abc
. Khi đó ta được xyz1.
Bất đẳng thức được viết lại thành
33 3
33 3
333
a b 16c 16
x y 16z
81
abc abc abc
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22 2
1
xy4z11 xyz 1
4
Suy ra
22 2
4
xy4z
9
Mặt khác, cũng theo bất đẳng thức Bunhiacopxki ta được

2
2
33 3 22 2
4
x y z x y 16z x y 4z
9
Hay
33 3
16
x y 16z
81
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
22 2
xy4z
xy4z ab4c
11 1
x y 16z
Bài 120. Cho a, b, c là các số thực dương thỏa mãn
3
abc
2
. Chứng minh rằng:
2
22 2
11317
ab1 c
2
ab c
Phân tích: Để ý đến phép biến đối
2
22
22 22
1111
ab1 ab 1 ab
ab
ab ab
Khi đó bất đẳng thức cần chứng minh làm ta liên tưởng đến đánh giá
22
22 22
xm yn xy mn
Lời giải
Dễ dàng chứng minh được: Với các số thực dương x, y, m, n ta luôn có
22
22 22
xm yn xy mn
Thật vậy, bình phương hai vế và rút gọn ta được
2222
xmyn xymn
Hay
2
2222
xmyn xymn
Bất đẳng thức cuối cùng là bất đẳng thức Bunhiacopxki quen thuộc.
Gọi vế trái của bất đẳng thức trên là P, áp dụng bất đẳng thức trên ta được
2
22
22 2 22 2
22
22
2
2
11 1 1
Pab1 c ab1 c
ab c ab c
11 1 111
ab c abc
ab abc
c
Mà ta lại có
111 9
abcabc
Nên ta được
2
2
81
Pabc
abc
Áp dụng bất đẳng thức Cauchy ta được

22
222
2
81 81 1215
Pabc abc
abc 16abc 16abc
81 1215 3 17
2
16 2
3
16
2
Hay
317
P
2
. Đẳng thức xẩy ra khi và chỉ khi
1
abc
2
.
Bài 121. Cho các số thức
a, b, c 0;1
. Chứng minh rằng:
11
1a1b1c
abc 3
Lời giải
Không mất tính tổng quát ta giả sử
1abc0
, khi đó ta có
a1
abc 3
.
Áp dụng bất đẳng thức Cauchy ta được
3
31b1c1bc31b1c1bc
Suy ra
11b1c1bc
Do đó ta được
1a 1a1b1c1bc
Hay
1a
1a1b1c
1bc
Mặt khác ta lại có
1a 1a
abc 1bc
Nên ta được
1a
1a1b1c
abc
Suy ra
1a1
1a1b1c 1a1b1c
abc abc 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 122. Cho a, b là hai số thực dương thỏa mãn
22
a2b1. Chứng minh rằng:
222
a4b
33
bab
Lời giải
Áp dụng bất đẳng thức Cauchy ta có
44 4
4
24 222 3
22
aa a
27a
ab abb
a2b
3
Suy ra
2
4
4
a
27a
b
hay
2
2
a
33a
b
Mặt khác cũng theo bất đẳng thức Cauchy ta có

444
4
33
22 2 2 2
22222 2 2
16b a a
108b
2babab
2babab 2a4b
33
Suy ra
2
4
2
22
16b
108b
ab
hay
2
22
4b
63b
ab
Do đó ta được
22
222
a4b
33a 2b 33
bab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
3
ab
3
Bài 123. Cho a, b là các số thực dương. Chứng minh rằng :
33
33 3
3
a4b
1
a8b
bab
Phân tích: Biểu thức vế trái được viết lại thành
3
3
33
3
3
3
4b
1
a
8b
bb
1
1
a
a
a
. Đến đây ta nghĩ đến
phép đổi biến
b
t
a
.
Lời giải
Biểu thức vế trái được viết lại là
3
3
33
3
3
3
4b
1
a
8b
bb
1
1
a
a
a
Đặt
b
t0
a
. Khi đó bất đẳng thức được viết lại là
3
33
3
14t
1
18t
t1t
Áp dụng bất đẳng thức Cauchy ta có
2
2
2
32 2
24t
18t 12t12t4t 12t
2
Suy ra
322
2
111
18t 12t
12t
Ta sẽ chứng minh
32
32
3
4t 2t
12t
t1t
Thật vậy, bất đẳng thức trên tương đương với

2
32
2
32
24 2
32
3
4t 2t
12t t t1t t1 2t t1 0
12t
t1t
Bất đẳng thức cuối cùng đúng với mọi t.
Do đó ta được
32
3322
3
14t12t
1
18t 12t 12t
t1t
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
ab .
Bài 124. Cho các số thực dương a, b, c thỏa mãn
3
abc
4
. Chứng minh rằng:
333
111
3
a3b b3c c3a
Phân tích: Dự đoán được dấu đẳng thức xẩy ra tại
1
abc
4
. Khi đó ta có đánh giá theo bất đẳng
thức Cauchy là
3
3
a3b2
a 3b a 3b .1.1
3
.
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
3
3
a3b2
a 3b a 3b .1.1
3
Do đó ta được
3
13
a3b2
a3b
Áp dụng tương tự ta được
33
1313
;
b3c2 c3a2
b3c c3a
Cộng theo vế các bất đẳng thức trên ta được
333
111 3 3 3
a3b2b3c2c3a2
a3b b3c c3a
Mặt khác theo bất đẳng thức Bunhiacopxki ta được
333 3.9
3
a3b2b3c2c3a2
4a b c 6
Do đó ta được
333
111
3
a3b b3c c3a
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
4
.
Bài 125. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
ab bc ca ab bc ca
2
cab abc aca cab abc aca
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22 22 22
ab bc ca
ab bc ca
cab abc aca
ab bc ca 3abc

Mà ta có
2
22 22 22
ab bc ca
ab bc ca
3
Và
2
ab bc ca
abc a b c
3
Nên ta được
22 22 22 22 22 22
22
2
ab bc ca 3abc ab bc ca 3abc a b c
ab bc ca 4 ab bc ca
ab bc ca
33
Do đó ta có
ab bc ca 3
cab abc aca 4
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta có
2
ab bc ca ab bc ca
3
cab abc aca cab abc aca
Kết hợp hai bất đẳng thức trên ta được
ab bc ca ab bc ca
2
cab abc aca cab abc aca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
1
abc
3
.
Bài 126. Cho a, b, c là các số thực dương thỏa mãn
abcabc . Chứng minh rằng:
222
2114
9
1a 1b 1c
Phân tích: Từ giả thiết ta suy ra
111
1
ab bc ca
. Đặt
111
x;y;z
abc
, khi đó ta được
xy yz zx 1. Khi đó để ý đến phép biến đổi
22
x1xxyyzzx xyxz
Lời giải
Từ giả thiết ta suy ra
111
1
ab bc ca
. Đặt
111
x;y;z
abc
.
Khi đó ta được
xy yz zx 1
Bất đẳng thức cần chứng minh trở thành
222
2x y z 4
9
x1 y1 z1
Để ý ta thấy
22
x1xxyyzzx xyxz
Áp dụng tương tự bất đẳng thức trở thành
2x y z 4
9
xyxz xyyz yzzx
Áp dụng bất đẳng thức Cauchy ta được

2x y z
xyxz xyyz yzzx
11 1 1 1 1
xy z
xy xz xy xz
4y z 4y z
xy yz zx 1 9
11
xy zx 4 4
4y z
Vậy bất đẳng thức được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
15
a; b; c ; 15; 15
7
Bài 127. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
abcabbcca5
bc ca ab 2
abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng cộng mẫu ta được
2
222
abc
abc abc
1
bc ca ab
2ab bc ca 2ab bc ca
Khi đó ta được bất đẳng thức
222
222 222
abcabbccaabc abbcca
1
bc ca ab
abc abc
2ab bc ca
Ta cần chứng minh
222
222
abc abbcca5
1
2
abc
2ab bc ca
Đặt
222
ab bc ca
t0t1
abc
. Khi đó bất đẳng thức trên trở thành
2
2
15
t1 t1 2t1 0
2
2t
Bấ đẳng thức cuối cùng luôn đúng với
0t1.
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 128. Cho a, b, c là các số thực dương không âm. Chứng minh rằng:
3
222
abc
ab bc ca
28
abc
abc
Lời giải
Ta có
3
222
abc 2abbccaabc
111
abc
abc ab bc ca abc
Áp dụng bất đẳng thức Bunhiacopxki và cauchy ta được
222
222
3
3
222
9a b c
111
abc
ab bc ca ab bc ca
2ab bc ca a b c
2.3. a b c .3. abc
18
abc abc

Do đó ta được
3
222
9a b c
abc
18
abc ab bc ca
Suy ra ta có bất đẳng thức
3
222
222 222
9a b c
abc
ab bc ca ab bc ca
18
abc ab bc ca
abc abc
Ta cần chứng minh
222
222
9a b c
ab bc ca
10
ab bc ca
abc
Thật vậy, áp dụng bất đẳng thức Cauchy ta có
222
222
222
8a b c
8ab bc ca
ab bc ca a b c
2; 8
ab bc ac ab bc ca ab bc ca
abc
Cộng theo vế của hai bất đẳng thức trên ta được
222
222
9a b c
ab bc ca
10
ab bc ca
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 129. Cho a, b, c là các số thực dương thỏa mãn
3
abc
2
. Chứng minh rằng:
222
11127
abc
2
abc
Lời giải
Áp dụng bất đẳng thức Cauchy ta được
222
141414
4; 4; 4
abc
abc
Do đó ta được
222
1 1 1 444
12
abc
abc
Khi đó ta có
222
111 444
abc abc 12
abc
abc
Và theo bất đẳng thức Bunhiacopxki ta lại có
444 36
abcabc
Từ đó ta suy ra
222
111 36
abc abc 12
abc
abc
Ta cần chứng minh
36 27
abc 12
abc 2
Hay
36 51
abc
abc 2
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
9 9 135 135 45
abc 2 3;
432
4abc 4abc
4.
2
Cộng theo vế hai bất đẳng thức trên ta được
36 51
abc
abc 2

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 130. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng:
3
222 333
abc 9abc
Lời giải
Bất đẳng thức cần chứng minh được viết lại thành
3
222 333
abc 9abcabc
Áp dụng bất đẳng thức Cauchy ta được
3
333 333
333
abc abc
9abc a b c 27.ab.ac. ab ab
3a 3a
Mà ta có
333 333
222
abc abc3abc
ab ab ab bc ca
3a 3a
abca b c abbcca
ab bc ca
3a
Suy ra
3
222
333
abca b c abbcca
9abc a b c ab bc ca
3a
Như vậy ta cần chứng minh được
222
222
abca b c abbcca
ab bc ca a b c
3a
Hay
222
abc
abcabbcca1 0
3
Đánh giá trên luôn đúng do ta có thể giả sử a là số lớn nhất trong ba số a, b, c.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Bài 131. Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
ab bc ca
1
4ab4bc4ca
Lời giải
Đặt
xa;yb;zc. Khi đó ta viết lại giả thiết là
444
xyz 3.
Bất đẳng thức được viết lại là
xy yz zx
1
4xy 4yz 4zx
Khi đó gọi vế trái là P thì ta có
xy yz zx 4 4 4
P31 1 1
4 xy 4 yz 4 zx 4 xy 4 yz 4 zx
Ta có
22
2
22 22
2xy2xy
22xy 4xy
11 1
4xy 4xy
4xy2xy
9xy1
4xy 5 xy
1
999

Tương tự ta được
22 22
25yz 25xz
;
4yz 9 9 4zx 9 9
Do đó ta được
22 22 22 4 4 4
15 x y y z z x 15 x y z
P32 2 4
99 99
Suy ra
P1
. Vậy bất đẳng thức được chứng minh.
Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 132. cho a, b, c là ba số thực dương. Chứng minh rằng
a2b2 b2c2 c2a2
9
4
b1b5 c1c5 a1a5
Phân tích: Chú ý đến đánh giá
b2
3
b1b5 4b2
Lời giải
Ta có bất đẳng thức luôn đúng sau
2
22
b2
3
4b 16b 16 3b 18b 15 b 1 0
b1b5 4b2
Từ đó ta suy ra
a2b2 3a2
b1b5 4b2
Tương tự
b2c2 3b2 c2a2 3c2
;
c1c5 4c2 a1a5 4a2
Cộng vế với vế các bất đẳng thức trên, và sử dụng bất đẳng thức Cauchy cho 3 số, ta được:
a2b2 b2c2 c2a2
3a 2 b 2 c 2 9
4b 2 c 2 a 2 4
b1b5 c1c5 a1a5
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài 133. Cho a, b, c là các số thực dương. Chứng minh rằng:
ab bc ca 16
abc bc4a ac16b 15
Lời giải
Đặt
xabc 3ayx
y bc4a 15b zx
z c a 16b 15c 21x 5y z
Khi đó biểu thức vế trái P được viết lại là
6x 5y z 20x 5y 16x z y 3x z 16x 4
P
15x 15y 15z 3x 4y 15x 15z 5
Áp dụng bất đẳng thức Cauchy ta có
y4x4z 16x8
;
3x 3y 3 15x 15z 15
Do đó ta được
48416
P
3155 15
. Đẳng thức xẩy ra khi và chỉ khi

y4x
5c
a
3x 3y
7
3c
z16x
b
7
15x 15z
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
5c 3c
a;b
77
.
Bài 134. Cho a, b, c là các số thực dương thỏa mãn
111
2
abc
. Chứng minh rằng:
111
1
a3b b3c c3a
Phân tích: Quan sát giả thiết ta chú ý đến phép đổi biến
xa;yb;zc
. Đến đây ta có thể
đánh giá các căn bậc hai theo bất đẳng thức Cauchy hoặc Bunhiacopxki như sau
2 2 2222 26
4
x3y xyyy 4xy
2
2 2 2222
4x 3y 1111x y y y x 3y
Lời giải
Cách 1: Đặt
xa;yb;zc
. Khi đó ta được
111
2
xyz
Bất đẳng thức cần chứng minh trở thành
22 22 22
111
1
x3y y3z z3y
Áp dụng bất đẳng thức Cauchy ta được
2 2 2222 26
4
x3y xyyy 4xy
Áp dụng một bất đẳng thức Cauchy khác ta được
22 22 4
44
26 22 4
444
11 1111
4
x3y xy y
2xy 2xy.y
11 1 2 11 3
8x y y 8x y
Tương tự ta có
22 2 2
1113 1113
;
8y z 8z x
y3z z3y
Cộng theo vế các bất đẳng thức trên ta có
22 22 22
1111111
1
2x y z
x3y y3z z3y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
9
abc
4
Cách 2: Đặt
xa;yb;zc. Khi đó ta được
111
2
xyz
Bất đẳng thức cần chứng minh trở thành
22 22 22
111
1
x3y y3z z3y

Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2 2 2222
4x 3y 1111x y y y x 3y
Do đó ta được
22 2
22
12 22113
x3y 8x y
x3y
2x 3y
x3y
Tương tự ta có
22 2 2
1113 1113
;
8y z 8z x
y3z z3y
Cộng theo vế các bất đẳng thức trên ta có
22 22 22
1111111
1
2x y z
x3y y3z z3y
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
9
abc
4
Bài 135. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3abc
. Chứng minh rằng:
222
22 2 2 2 2
abc
1
ca 2c ab 2a bc 2b
Lời giải
Từ giả thiết
ab bc ca abc ta được
111
3
abc
.
Đặt
111
x;y;z
abc
. Khi đó ta được xyz3.
Bất đẳng thức cần chứng minh trở thành
222
222
xyz
1
x2y y2z z2x
Áp dụng bất đẳng thức Cauchy ta được
222222 2 2
3
22 22
4
3
2xy
x x 2xy 2xy 2xy 2xy
xxx
3
x2y x2y xy y
2xy
Áp dụng tương tự ta được
2
222222
2
22
2yzyz2zx
y; z
33
y2z z2x
Cộng theo vế các bất đẳng thức trên ta được
222
3
22 22 22
33
222
xyz 2
xyz xy yz zx
3
x2y y2z z2x
Mạt khác theo bất đẳng thức Cauchy ta lại có
22
3
22
3
3
22
xy xy 1 2xy 1
xy
33
yz yz 1 2yz 1
yz
33
zx zx 1 2zx 1
zx
33
Suy ra
2
3
22 22 22
33
2xy yz zx 2x y z
xy yz zx 1 1 3
39

Do đó ta được
222
222
xyz 2.3
31
3
x2y y2z z2x
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 136. Cho a, b, c là các số thực dương. Chứng minh rằng:
2333
222
16 3
abc
abc
abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
333 222
2
222
abcabc abc
3a b c a b c
Nhân theo vế hai bất đẳng thức trên ta được
333 222
3a b c a b c a b c
Suy ra
333 222
abc abc
1
abc 3
Cũng từ hai bất đẳng thức trên ta được
23
333 222
3a b c a b c
Suy ra
2
333 333
42
222
222
222 222
abc 6abc
123
2
3a b c
abc
abc abc
Áp dụng bất đẳng thức Cauchy ta được
222
222 222
abc 3 3
33
3
abc abc
Cộng theo vế các bất đẳng thức (1), (2), (3) ta được
333
333
2
222
6a b c
abc
3
abc
abc
Hay
2333
222
16 3
abc
abc
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 137. Cho a, b, c là các số thực dương. Chứng minh rằng:
abc1
4a 4b c 4b 4c a 4c 4a b 3
Phân tích: Để ý đến phép biến đổi
4a a b c a 4a 4b c 3ca
3ca
a
4a 4b c 4a 4b c 4a 4b c
Lời giải
Bất đẳng thức cần chứng minh tương đương với
4aabc 4babc 4cabc 4abc
4a 4b c 4b 4c a 4c 4a b 3

Ta có
4a a b c a 4a 4b c 3ca
3ca
a
4a 4b c 4a 4b c 4a 4b c
Tương tự ta có
4b a b c 4c a b c
3bc 3ba
b; c
4b 4c a 4b 4c a 4c 4a b 4b 4c a
Bất đẳng thức cần chứng minh trở thành
9ca 9ab 9bc
abc
4a 4b a 4b 4c a 4b 4c a
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
21
94121
4a4bc 2bc 2ab2bc
22a b 2b c 22a b
Do đó ta được
9ca 2ca ca
4a 4b c 2a b 2b c
Hoàn toàn tương tự
9ab 2ab ab 9bc 2bc bc
;
4b 4c a 2b c 2c a 4b 4c a 2c a 2a b
Cộng theo vế các bất đẳng thức trên ta được
9ca 9ab 9bc
4a 4b a 4b 4c a 4b 4c a
2ca ca 2ab ab 2bc bc
abc
2a b 2b c 2b c 2c a 2c a 2a b
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 138. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
222
11
30
abc
abc
Phân tích: Chú ý là theo bất đẳng thức Cauchy ta có
1abc111 9
abc abc ab bc ca ab bc ca
Ta quy bài toán về chứng minh
222
19
30
ab bc ca
abc
Lời giải
Cách 1: Sử dụng bất đẳng thức Cauchy ta được
232
ab bc ca 3abc a b c 3abc a b c 3abc.27abc 81 abc
Suy ra
ab bc ca 9abc
Áp dụng bất đăng thức Bunhiacopxki dạng phân thức ta được
222 222
222 3
222
11 1 117
abc 9abc 9abc 9abc
abc abc
97
abc2.9abc
abc
3
9
21 30
abc2abbcca

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Cách 2: Với giả thiết
abc1
, biểu thức P được viết lại thành
222 222 222
11 1abc1111
abc abc ab bc ca
abc abc abc
Theo một đánh giá quen thuộc ta có
111 9
ab bc ca ab bc ca
Do đó ta có
222 222
11 1 9
abc ab bc ca
abc abc
Áp dụng bất đẳng thức Bunhiacopxki và bất đẳng thức
2
abc
ab bc ca
3
Ta được
222
222
19
ab bc ca
abc
11 1 7
ab bc ca ab bc ca ab bc ca
abc
22
222
9797.3
30
ab bc ca
abc2abbcca
abc abc
Bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 139. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
111 bc ca ab
abc
abcbcacab
Phân tích: Chú ý đến đánh giá theo bất đẳng thức Bunhiacopxi
22
22
2
222222222
ab ab
ab a b
cab
abcab bac abc bac abc
Hoặc phép biến đổi tương đương.
Lời giải
Cách 1: Áp dụng ất đẳng thức Bunhiacopxki dạng phân thức ta được
22
22
2
222222222
ab ab
ab a b
cab
abcab bac abc bac abc
Áp dụng tương tự ta được
22
2
22 22
22
2
22 2 2
bc b c
abc
ca b ba c
ca c a
bca
ab c cc a
Mà ta lại có
222 22 2
2 2 22 22 2 2 22 22
bccaab111
abc
ca b ba c ab c cb a ba c ab c

Do đó ta được
222
111 bc ca ab
abc
abcbcacab
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Biến đổi tương đương bất đẳng thức như sau
222
22 2
22
3
22
2
3
22
111 bc ca ab
abc
abcbcacab
1ab 1bc 1ca
0
acb
cab abc bca
bcba
11
ca 0
babc
ac ab ca bc
c a c a bc ab ab b c b a
0
babc
ca a bc c ab
Không mất tính tổng quát ta giả sử b là số lớn nhất trong ba số a, b, c khi đó ta được
3
bcba
bc ab ca 0; 0
babc
Do vậy bất đẳng thức cuối cùng luôn đúng.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 140. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
abc bca cab
0
2a ab ac 2b bc ba 2c ca cb
Phân tích: Để ý đến phép biến đổi
22
222
abca
bc a a ab bc ca
1
2a ab ac 2a ab ac 2a ab ac
Lời giải
Cách 1: Bất đẳng thức cần chứng minh tương đương với
222
222
222
222
bc a ca b ab c
0
2a ab ac 2b bc ba 2c ca cb
bc a ca b ab c
1113
2a ab ac 2b bc ba 2c ca cb
abac abbc bcca
3
a2a b c ba 2b c ca b 2c
Áp dụng bất đẳng thức Cauchy ta được
22
2
3
abac abbc bcca
a2a b c ba 2b c ca b 2c
ab bc ca
3
abc 2a b c a 2b c a b 2c
Ta cần chứng minh
22
2
ab bc ca
1
abc 2a b c a 2b c a b 2c
Hay
22
2
ab bc ca abc2abca2bcab2c

Hay
22
ab bc ca a b c 2abc a b c 3abc ab bc ca
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
2
2
2
ab bc ca a b c 9abc ab bc ca
3abc ab bc ca
33
2abbcca abc
2abc a b c a b c 3abc a b c
3
Cộng theo vế hai bất đẳng thức trên ta được
22
ab bc ca a b c 2abc a b c 3abc ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
222
bc ca ab a b c
2a b c 2b c a 2c a b
2a ab ac 2b bc ba 2c ca cb
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
2
22 2
2
bc ca ab
2a ab ac 2b bc ba 2c ca cb
ab bc ca
bc 2a ab ac ca 2b bc ba ab 2c ca cb
ab bc ca
3
4
4abc a b c
Ta cần chứng minh
abc3
2a b c 2b c a 2c a b 4
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
11111a1aa
2abc abac 4abac 2abc 4abac
Áp dụng tương tự ta được
abc
2a b c 2b c a 2c a b
1a a 1b b 1c c 3
4a b a c 4a b b c 4a c b c 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 141. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
333
abc
1
b2c a c2a b a2b c
Lời giải
Cách 1: Áp dụng bất đẳng thức Cauchy ta được
33
a b 2c a a 8a 3b 2c
a
39 9
b2c a b2c a
Chứng minh tương tự ta được

33
b8b3c2ac8c3a2c
;
99
c2a b a2b c
Cộng theo vế các bất đẳng thức trên ta được
333
abcabc
1
3
b2c a c2a b a2b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1
.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
333
222 2
333333
abc
b2c a c2a b a2b c
abcabc
b2ca c2ab a2bc 3abbcca
Mặt khác theo bất đẳng thức Bunhiacopxki ta được
2
333
abcabcabc
33a b c 3 a b c
Nên
333
abc3
Mà theo một đánh giá quen thuộc ta có
2
3abbcca abc 9 abbcca 3
Do đó ta được
2
333
abc
1
3ab bc ca
hay bất đẳng thức được chứng minh.
Cách 3: Biểu thức vế trái được viết lại thành
444
abc
ab 2c a bc 2a b ca 2b c
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
444
222222
abc
abc
ab ba ac ca bc cb 6abc
ab 2c a bc 2a b ca 2b c
Mà ta có
222222
ab ba ac ca bc cb 6abc
a b c ab bc ca 3abc 3 ab bc ca 3abc
Áp dụng một bất đẳng thức quen thuộc ta được
2
2
222
2
2
222 222
abc
ab bc ca
abc a b c 3abc
33
2a b c a b c a b c
3ab bc ca
39
Cộng theo vế hai bất đẳng thức trên ta được
2
222
abc 3abbcca3abc
Do đó ta được
333
abc
1
b2c a c2a b a2b c
.

Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 142. Chứng minh rằng với mọi a, b, c không âm ta có:
3
abbcca
ab bc ca
38
Lời giải
Sử dụng bất đẳng thức Cauchy ta thu được:
3
3
222
ab bc ca a b c
abcabbcca
abc abc. a b c .
33 9
.
Dễ thấy
ab bc ca a b c a b b c c a abc .
Do đó ta có
8ab bc ca a b c 9a b b c c a
Mặt khác, sử dụng bất đẳng thức Cauchy ta có
3
abbcca ab bc ca 2abc
.
từ đó suy ra
3
8
abbcca abbccaabc
9
83
ab bc ca . a b b c c a
92
Hay tương đương
3
abbcca
ab bc ca
38
.
Bài toán được chứng minh xong.
Bài 143. Cho a, b là hai số thực dương thỏa mãn
3
a b 4ab 2
. Cứng minh rằng:
4422 22
9
3a b ab 2a b 1
16
Lời giải
Dễ thấy với mọi a, b ta luôn có
2
a b 4ab. Kết hợp với bất đẳng thức giả thiết
3
a b 4ab 2 , ta được
32
ab ab 2 ab1
Do đó ta được
2
22
ab
1
ab
22
Khi đó ta được bất đẳng thức
2
4422 22 22 22 22
2
22
22
22 22 22 22
3a b ab 2a b 1 3 a b ab 2a b 1
ab
9
3ab 2ab 1 ab 2ab 1
44
Mà ta lại có

22
22 22 22
2
22 22
2
2
22
22
ab 4ab 4ab 1
91
ab 2ab 1
4422
2a b 1
ab
1119
42216216
Do đó ta được
4422 22
9
3a b ab 2a b 1
16
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
ab
2
.
Bài 144. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
3
2
abbcca
ab bc ca 1 3
1
8abc
abc1
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra khi và chỉ khi
abc1. Bất đẳng thức có chứa
căn bậc ba nên suy nghĩ rất tự nhiên là đánh giá làm mất căn bậc ba. Tuy nhiên ta không đánh giá theo
hướng đó được vì đại lượng trong căn có dạng tích nên không thể dùng bất đẳng thức Cauchy để đánh
giá, ngoài ra ta cũng không thể sử dụng phép đặt ẩn phụ vì như vậy đại lượng ngoài căn sẽ có bậc cao.
Để ý đến đại lượng
abbcca
abc
trong căn bậc ba, nếu ta đánh giá được đại lượng
2
ab bc ca 1
abc1
về
abc
abbcca
thì khi đó ta có thể sử dụng bất đẳng thức Cauchy để
chứng minh bất đẳng thức. Với ý tưởng như vậy và chú ý đến dấu đẳng thức xẩy ra ta tập trung chứng
minh bất đẳng thức
2
ab bc ca 1 2abc
abbcca
abc1
+ Hướng 1: Ta biến đổi tương đương bất đẳng thức trên thì được
222
a b c 1 ab bc ca a b c abc 2abc ab bc ca
ab bc ca a b c 4abc a b c 3abc
Dễ thấy
222
a b c 1 ab bc ca a b c abc 0
Áp dụng bất đẳng thức Cauchy ta được
2
2ab bc ca a b c
2abc ab bc ca
3
4abc ab bc ca a b c
2
3
abc.3abc a b c a b c
4 4abc a b c
3
Cũng theo bất đẳng thức Cauchy ta được
3
3
222
ab bc ca a b c
3abc.abc 3abc
3
Cộng theo vế của ba bất đẳng thức trên ta được
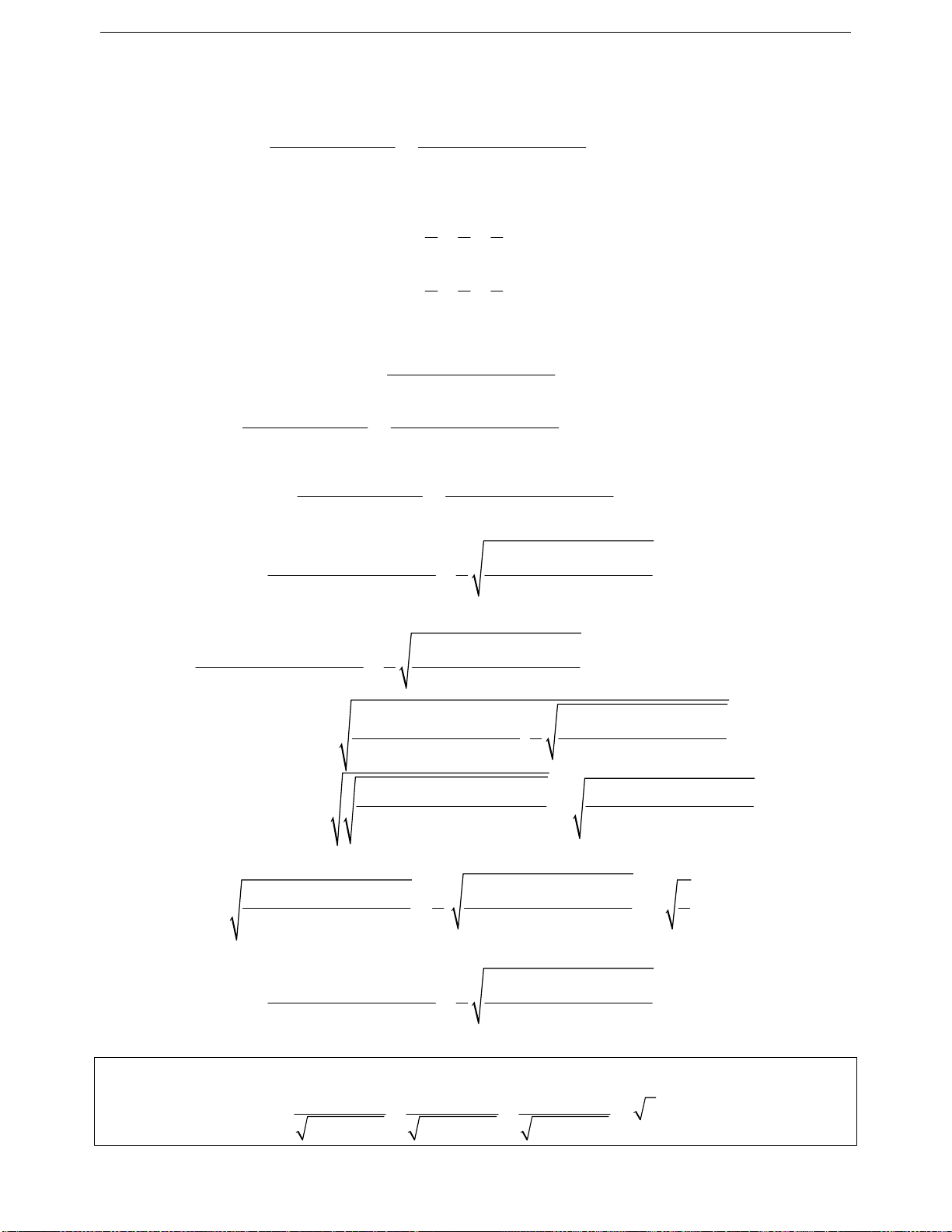
222
a b c 1 ab bc ca a b c abc 2abc ab bc ca
ab bc ca a b c 4abc a b c 3abc
Như vậy bất đẳng thức
2
ab bc ca 1 2abc
abbcca
abc1
được chứng minh.
+ Hướng 2: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
abc
ab bc ca 1 1 a b c 1
bca
bca
ab bc ca 1 1 b c a 1
abc
Cộng theo vế hai bất đẳng thức này ta được
2
abbcca
ab bc ca 1 2 a b c 1
abc
Tư đó suy ra
2
ab bc ca 1 2abc
abbcca
abc1
Như vậy với bất đẳng thức
2
ab bc ca 1 2abc
abbcca
abc1
ta quy bài toán về chứng minh
3
abbcca
2abc 3
1
8abc
abbcca
Áp dụng bất đẳng thức Cauchy ta được
3
3
222
3
3
222
abbcca
2abc 1
8abc
abbcca
abbcca
2abc 1
2.
8abc
abbcca
abc abc
abbcca
ab bc ca
Cũng theo bất đẳng thức Cauchy ta được
3
3
abbcca
abc 1 1
.21
4abc 4
abbcca
Do đó ta suy ra được
3
abbcca
2abc 3
1
8abc
abbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 145. Cho a, b, c là các số thực dương thỏa mãn
222
abc 3. Chứng minh rằng:
222
abc
3
abc bbc cab
Phân tích và lời giải

Cách 1: Dự đoán được dấu đẳng thức xẩy ra khi và chỉ khi
abc1
. Để ý đến đại lượng
2
abc
có thể đánh giá bằng bất đẳng thức Bunhiacopxki như sau
2
2
abc1bc abc
Khi đó ta được
2
aa1bc
abc
abc
.
Áp dụng tương tự ta được
222
abca1bcb1cac1ab
abc
abc bbc cab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
a1 b c b1 c a c1 a b
3
abc
Hay
a1 b c b1 c a c1 a b 3a b c
Áp dụng bất đẳng thức Bunhiacopxki ta được
a1 b c b1 c a c1 a b
a b c a ab ac b bc ab c ca bc
abcabc2abcbca
Theo một đánh giá quen thuộc ta có
2
222
abc3abc9abc3
Do đó ta được
2
2a b c
2abcbca 2abc
3
Suy ra
2
abcabc2abcbca 3abc 3abc
Từ đó ta có
a1 b c b1 c a c1 a b 3a b c
Vậy bất đẳng thức được chứng minh.
Cách 2: Trước hết để làm mất các dấu căn bậc hai ta chú ý đến đánh giá
222
222
abc
abc bbc cab
abc
abc
abcbcacab
Ta quy bài toán về chứng minh
222
abc
abc 3
abcbcacab
Theo đánh giá như cách 1 ta có
abc3 nên ta được
222
222
abc
abc
abcbcacab
abc
3
abcbcacab
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

222
abc
1
abcbcacab
Theo bất đẳng thức Bunhiacopxki ta được
222 2
a1 b c b1 c a c1 a b
abc
abcbcacab
abc
Theo một đánh giá quen thuộc ta có
222 222
abc 3a b c 3a b c
Khi đó ta được
22
222
2
a1 b c b1 c a c1 a b a b c 2ab bc ca
abc abc
abc2abbcca
1
abc
Từ đó ta được
222
abc
1
abcbcacab
Vậy bất đẳng thức được chứng minh.
Bài 146. Cho a, b, c là các số thực dương thỏa mãn
222
abc1. Chứng minh rằng:
222
1ab 1bc 1ca 3
2
ab bc ca
Phân tích và lời giải
Cách 1: Chú ý đến giả thiết
222
abc1
, khi đó ta có
2
222
222
2
22 22
2
22
2a b c 2ab
abc ab
1ab c
ab 2ab 2ab ab
1c
2a b 2a b
Khi đó ta được
222
222
222 222
1ab 1bc 1ca
ab bc ca
11 1 1 c a b
2
ab bc ca ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222 222
111cab
3
ab bc ca ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki ta được

222 222
222
111 9 9 9
4
4a b c
ab bc ca ab bc ca
2
222
222
cab1abc193
.
3b c c a a b 34 4
ab bc ca
Cộng theo vế hai bất đẳng thức trên ta được
222
222 222
111cab
3
ab bc ca ab bc ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Cách 2: Để ý ta thấy
2
ab
ab
4
suy ra
2
222
ab
1
1ab 1 1
4
4
ab ab ab
Áp dụng tương tự ta được
222 222
1ab 1bc 1ca 1 1 1 3
4
ab bc ca ab bc ca
Mà ta lại có
222 222
222
111 9 9 9
4
4a b c
ab bc ca ab bc ca
Do đó ta được
222
1ab 1bc 1ca 9 3 3
44 2
ab bc ca
Vậy bất đẳng thức được chứng minh.
Cách 3: Để ý đến đánh giá
222
abcabbcca , khi đó ta được
222
2a b c abbcca
Do đó ta được
222
22
2
22
1ab a b c abbcca2ab
ab 2ab
ab bcca bcca
2a b 2a b
Áp dụng tương tự ta được bất đẳng thức
222 2 2 2
bcca abca bcab
1ab 1bc 1ca
ab bc ca 2ab 2bc 2ca
Mà theo bất
đẳng thức Cauchy ta có
22 2
bcca abca bcab
3
2
2a b 2b c 2c a
Do đó ta được
222
1ab 1bc 1ca 3
2
ab bc ca

Vậy bất đẳng thức được chứng minh.
Bài 147. Cho a, b, c là các số thực dương thỏa mãn
abcabc
. Chứng minh rằng:
222
1111
4
a1bc b1ca c1ab
Phân tích và lời giải
Cách 1: Dự đoán được dấu đẳng thức xẩy ra tại
abc 3 . Biến đổi giả thiết ta được
111
1
ab bc ca
. Đến đây rất tự nhiên ta nghĩ đến phép đổi biến
111
x;y;z
abc
, khi đó giả
thiết trở thành
xy yz zx 1 và bất đẳng thức cần chứng minh được viết lại thành
222
xyz yzx zxy 1
1yz 1zx 1xy 4
Hay
222
xyz yzx zxy 1
xy yz xz yz xy yz xz zx xy yz xz xy 4
Đặt
mxy;nyz;pzx mnp1
và bất đẳng thức trên trở thành
mp mn np 1
mnnp mpnpmnmp 4
Áp dụng bất đẳng thức Cauchy ta được
mp 1 mp mp
mnnp 4mn np
mn 1 mn mn
mpnp 4mp np
np 1 np np
mnmp 4mn mp
Cộng theo vế các bất đẳng thức trên ta được
mp mn np m n p
1
mnnp mpnpmnmp 4
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc 3 .
Cách 2: Để ý đến giả thiết
abcabc ta được
2
11 1
a1bc aaabc aabac
Theo bất đẳng thức Cauchy ta được
11111211
abac 4abac 16a bc
Suy ra
2
111 1
4
a1bc aa b aa c
Hoàn toàn tương tự ta được
22
111 1 111 1
;
44
b1ca bb c ba b c1ab cc b cc a
Cộng theo vế các bất đẳng thức trên ta được

222
111
a1bc b1ca c1ab
11 1 1 1 1 1
4
aa b aa c bb c ba b cc b cc a
Lại có
111
ab
aa b ba b
, do đó ta được
111111111
ab bc ca
aab aac bbc bab ccb cca
Suy ra ta được
222
1111111abc1
4 ab bc ca 4abc 4
a1bc b1ca c1ab
Vậy bất đẳng thức được chứng minh.
Bài 148. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1
. Chứng minh rằng:
222
abc9
4
b1 a c1 b a1 c
Phân tích và lời giải
Trước hết ta dự đoán dấu đẳng thức xẩy ra tại
1
abc
3
. Bất đẳng thức cần chứng minh có
dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, do đó ta thử tiếp cận với bất đẳng thức đó
xem sao?
2
222 2 2 2
abc
abc
b1 a c1 b a1 c ab1 a bc1 b ca1 c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
2
222
9a b c 4ab1 a bc1 b ca1 c
Bất đẳng thức trên không đồng bậc và ta cần phải đánh giá đại lượng có bậc 4 về phải về đại lượng
trội hơn, tuy nhiên đánh giá không khả thi, nên ta tạm dừng đánh giá này ở đây.
Chú ý đến giả thiết
ab bc ca 1 khi đó ta viết được
2
1a abca
, hoàn toàn
tương tự ta viết lại bất đẳng thức cần chứng minh thành
abc9
4
ba b a c ca b b c ac a b c
Hay bất đẳng thức tương đương với
222 222222
ac b c ba c a cb a b ab bc ca abc a b c
99
44
abc a b a c b c abc a b a c b c
Dễ thấy
2
22 22 22
a b b c c a abc a b c ab bc ca abc a b c
Áp dụng bất đẳng thức Cauchy ta được
3
8ab bc ca
8
abc a b b c c a
27 27

2
ab bc ca
1
abc a b c
33
Khi đó ta được
22 22 22
1
27 1
ab bc ca abc a b c
3
9
84
abc a b a c b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Bài 149. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
22 22 22
222
abc bca cab
3
abc bca cab
Phân tích và lời giải
Trước hết ta dự đoán được dấu đẳng thức xẩy ra tại
abc1. Quan sát bất đẳng thức cần
chứng minh thì suy nghĩ đầu tiên là làm mất các căn bậc hai. Để ý đến chiều bất đẳng thức ta có các đánh
giá như sau
22 22 22
222
22 22 22
3
222
abc bca cab
abc bca cab
abcbcacab
3. . .
abc bca cab
Hoặc là
22
22 22
2222
22 2
2a b c
abc abc
abc abc a b c
abc a b c
Ta đi tìm hiểu xem trong các đánh giá trên thì đánh giá nào giải quyết được bài toán
+ Với đánh thứ nhất ta quy bài toán về chứng minh
22 22 22
222
abcbcacab
.. 1
abc bca cab
Hay
22 22 22 2 2 2
abcbcacab abcbcacab
Tuy nhiên đánh giá quá phức tạp, như vậy cách thứ nhất không khả thi.
+ Với đánh giá thứ hai ta được bất đẳng thức
222
22 22 22
222222
4a b c 2a b c
abc bca cab
abc bca cab a b c abc
Ta quy bài toán về chứng minh
222
222
4a b c 2a b c
3
abcabc
Hay ta phải chứng minh được
222 222 222
4abc 63abc3 abc3
Đánh giá cuối cùng là một đánh giá đúng vì
2
222
abc
abc 3
3
.
Như vậy bài toán được chứng minh.
Bài 150. Cho a, b, c là các số thực dương thỏa mãn
a b c 3abc
. Chứng minh rằng:

2
444
111 a b c 27
abc 4
ab1ac1 bc 1ab1 ca 1bc1
Phân tích và lời giải
Dự đoán được dấu đẳng thức xẩy ra tại
abc1
. Quan sát bất đẳng thức ta nhận thấy được
sự phức tạp của bài toán. Bất đẳng thức trên có một số ý tưởng tiếp cận như đổi biến, sử dụng bất đẳng
thức Bunhiacopxki dạng phân thức
Cách 1: Trước hết ta tiếp cận bài toán với ý tưởng đổi biến
Nhận thấy giả thiết của bài toán có thể viết lại được
111
3
ab bc ca
, đến đây hoàn toàn tự
nhiên ta nghĩ đến phép đổi biến
111
x;y;z
abc
khi đó giả thiết được viết lại thành
xy yz zx 1
và bất đẳng thức cần chứng minh trở thành
2
222
yz zx xy 27
xyz
4
x 1 xy 1 xz y 1 yz 1 xy z 1 zx 1 yz
Ta thấy sau khi đổi biết thì thu được một bất đẳng thức còn phức tạp hơn cả bất đẳng thức ban đầu
nên ta tạm dừng ý tưởng này lại.
Cũng từ giả thiết ta thử đổi biến
111
x;y;z
bc ca ab
xem sao? Việc ta cần làm đó là đánh
giá sao cho xuất hiên các đại lượng
ab; bc; ca .
Dễ thấy
111 9 3
abcabcabc
, khi đó gọi P là vế trái của bất đẳng thức thì ta thu được
đánh giá
444
222
222
22 22 2 2
222
33 33 3 3
9a b c
P
abc
ab1ac1 bc 1ab1 ca 1bc1
abc
9
bcab1ac 1 ca bc1ab1 abca 1bc1
abc bca cab
9
bcab1ac1 ca bc1ab1 abca 1bc1
Đến đây ta có thể thay
111
ab ; bc ; ca
zxy
vào bất đẳng thức trên thì bất đẳng thức trở
thành
333
xyz
P9
1y1z 1z1x 1x1y
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
333
xyz3
4
1y1z 1z1x 1x1y
Bất đẳng thức trên đã được chứng minh trong kỹ thuật thêm bớt trong bất đẳng thức Cauchy.
Cách 2: Nhận thấy bất đẳng thức có dấu hiệu sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, khi
đó áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

444
2
222
abc
ab1ac1 bc 1ab1 ca 1bc1
abc
ab1ac1 bc1ab1 ca 1bc1
Hay ta được
444
2
222
abc
ab1ac1 bc1ab1 ca 1bc1
abc
abc a b c 2 ab bc ca 3
Dễ thấy
111 9
abcabc
và
2
222
abc
abc
3
Do đó ta được
2
444
2
222
2
222
111 a b c
abc
ab1ac1 bc1ab 1 ca 1bc1
1
abc a b c
9
3
abc
abc a b c 2 ab bc ca 3
27 a b c
abc a b c 2 ab bc ca 3
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
27 a b c
27
4
abcabc 2abbcca 3
Hay ta cần chứng minh
222
4a b c abca b c 2ab bc ca 3
Để ý đến giả thiết
abc3abc ta quy bài toán về chứng minh
2
222
12 a b c a b c 6 ab bc ca 9
Theo bất đẳng thức Cauchy ta có
3
3abc a b c 3 abc abc 1
.
Dễ thấy
2
222
222
3
222 222
3a b c a b c
6a b c 6ab bc ca
3a b c 9 abc 9
Cộng theo vế các bất đẳng thức trên ta được
2
222
12 a b c a b c 6 ab bc ca 9
Vậy bài toán được chứng minh xong.
Bài 151. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
22 22 22
11113
.
2abc
3a 4b 5 3b 4c 5 3c 4a 5
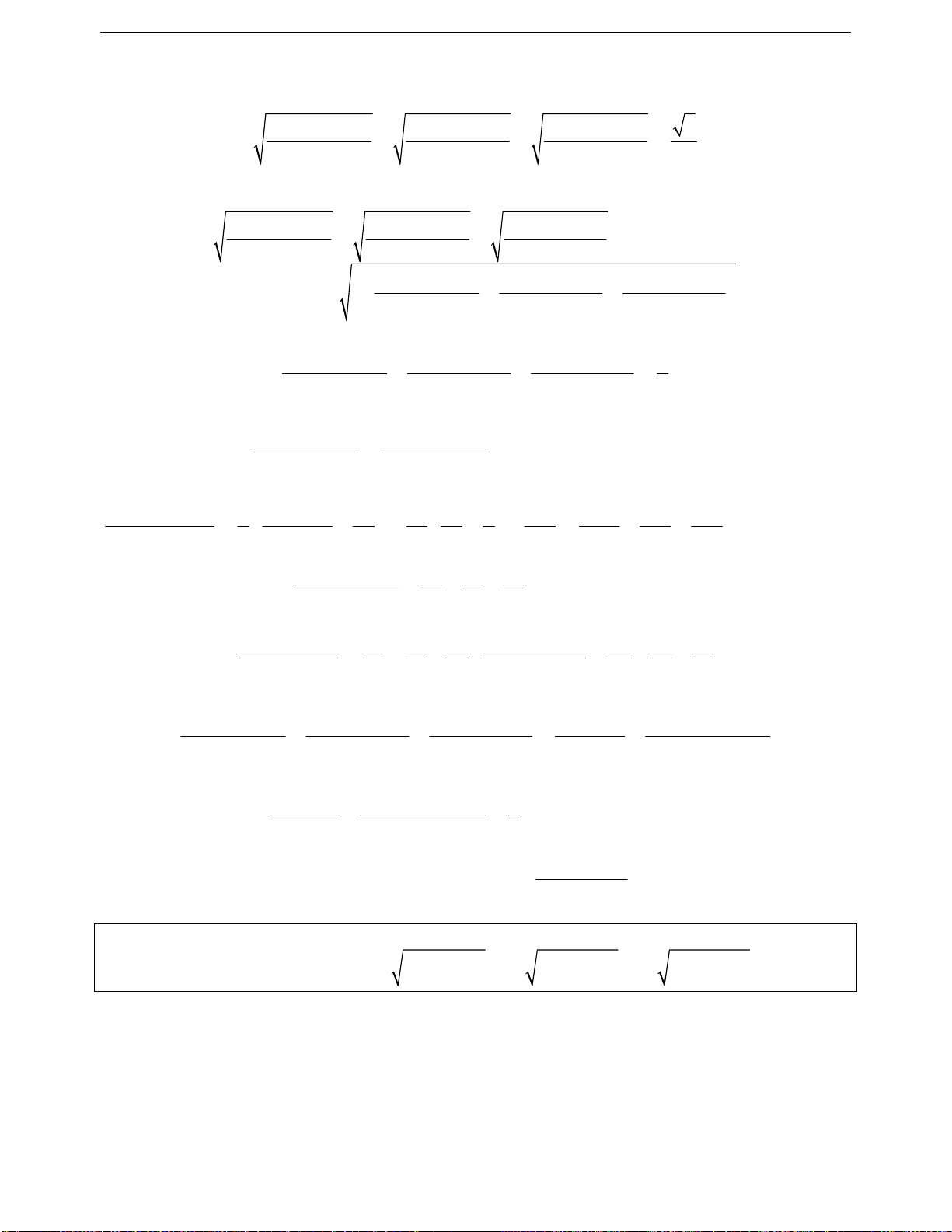
Phân tích và lời giải
Dễ dàng dự đoán được dấu đẳng thức xẩy ra tại
abc1. Trước hết ta viết lại bất đẳng thức
cần chứng minh thành
22 22 22
abc abc abc 3
2
3a 4b 5 3b 4c 5 3c 4a 5
Quan sát bất đẳng thức trên thì suy nghĩ rất tự nhiên là đánh giá làm mất các dấu căn bậc hai, chú ý
đến chiều bất đẳng thức ta có đánh giá theo bất đẳng thức Bunhiacopxki là
22 22 22
22 22 22
abc abc abc
3a 4b 5 3b 4c 5 3c 4a 5
abc abc abc
3
3a 4b 5 3b 4c 5 3c 4a 5
Đến đây ta quy bài toán về chứng minh
22 22 22
abc abc abc 1
4
3a 4b 5 3b 4c 5 3c 4a 5
Áp dụng bất đẳng thức Cauchy ta được
22
3a 4b 5 2ab 4a 6b
Do đó ta được
22
abc abc
2ab 4a 6b
3a 4b 5
Cũng theo bất đẳng thức Cauchy ta được
11111121111
2ab 4a 6b 4 2ab 4a 6b 72 ab a 24b 72ab 36a 24b
Do đó ta được
22
abc c bc ac
72 36 24
3a 4b 5
Hoàn toàn tương tự ta được
22 2 2
abc a ca ba abc b ab bc
;
72 36 24 72 36 24
3b 4c 5 3c 4a 5
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
5ab bc ca
abc abc abc a b c
72 72
3a 4b 5 3b 4c 5 3c 4a 5
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
5ab bc ca
abc 1
ab bc ca 3
72 72 4
Đánh giá cuối cùng là một đánh giá đúng vì
2
abc
ab bc ca 3
3
.
Vậy bất đẳng thức được chứng minh xong.
Bài 152. Cho a, b, c là các số thực dương. Chứng minh rằng:
333 22 22 22
abc3abcab2ab bc2bc ca2ca
Dự đoán được dấu đẳng thức xẩy ra khi và chỉ khi
abc
. Quan sát bất đẳng thức trên ta có
một số hướng tiếp cận như sau
Cách 1: Không mất tính tổng quát ta có thể giả sử c là số nhỏ nhất trong ba số a, b, c. Khi đó ta cố gắng
đánh giá bất đẳng thức xoay quanh biến c. Áp dụng bất đẳng thức Cauchy ta được
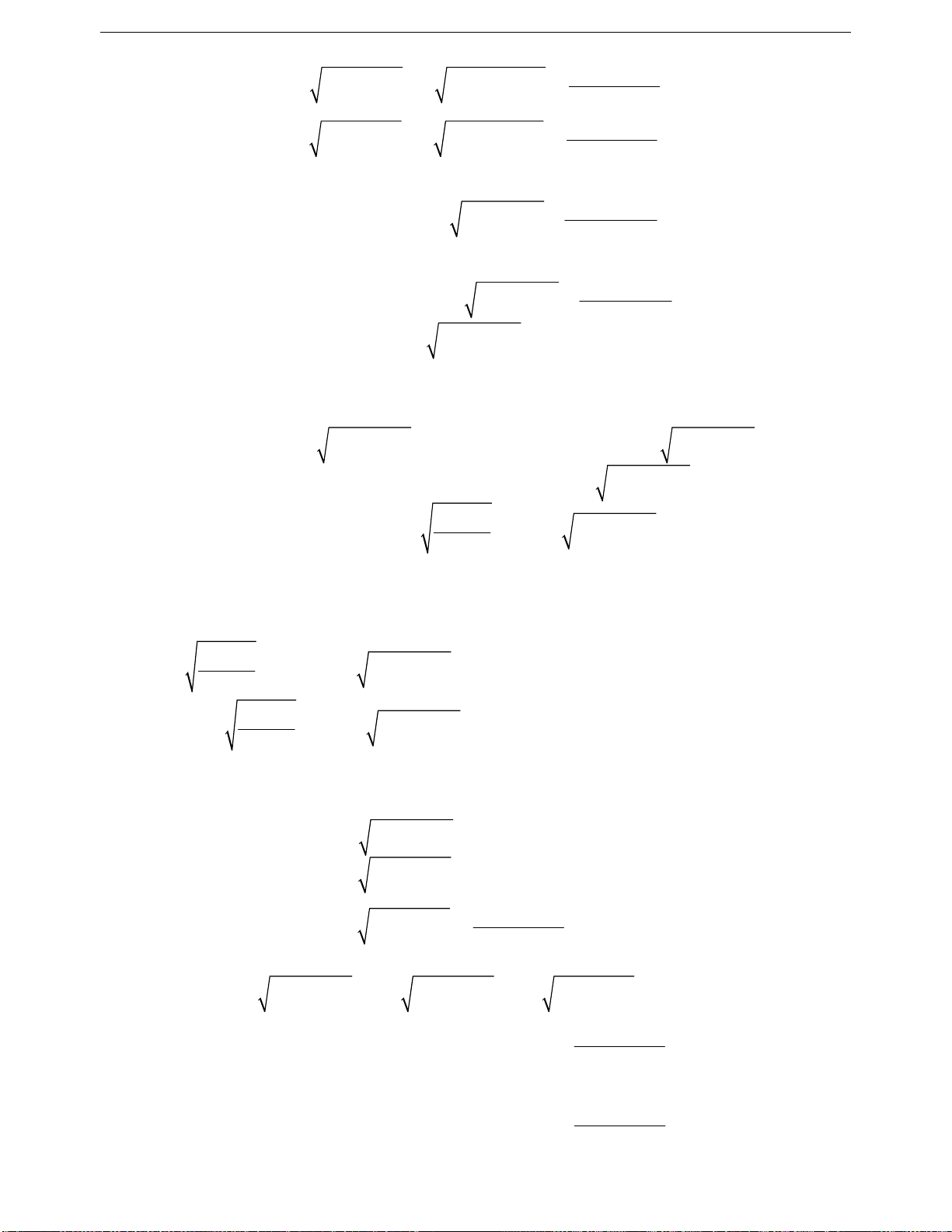
22
22 222
22
22 222
c3b c
bc 2 b c c 2b b c
2
c3a c
ca 2 c a c 2a c a
2
Ta quy bài toán về chứng minh
22
333 22 3
3c a b
abc3abcab2ab c
2
Hay
22
33 22
2
33 22
3c a b
ab3abcab2ab
2
2a 2b 2ab 2 a b 3c a b
Ta cần biến đổi vế trái của bất đẳng thức trên sao cho xuất hiện đại lượng
2
ab .
Ta có
3 3 22 22 22
2
22 22
22
2
22
2a 2b 2ab 2 a b 2 a b a b ab 2ab 2 a b
abab abab 2ab2ab
ab
a b a b a b 2 a b 4ab
2
Theo giả sử trên ta có
ab2c do đó ta được
22
abab 2cab
Mặt khác
22
2
22
ab
2;ab 2a b 4ab abab 4ab ab
2
Suy ra ta được
22
2
22
ab
a b 2 a b 4ab 3c a b
2
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Cũng với ý tưởng sắp thứ tự các biến, ta giả sử
abc. Khi đó ta chú ý đến các đánh giá sau
22 22 2
22 22 2
22
22
2ab 2 a b a a b 2ab
2bc 2 b c c b c 2cb
ca c a
2ca 2 c a 2abc
b
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
22
33 2
2ab 2 a b 2bc 2 b c 2ca 2 c a
ca c a
ac3bac 2abc
b
Ta quy bài toán về chứng minh
22
333 33 2
ca c a
abc3abcac3bac 2abc
b

Hay
22
333 2
ca c a
a 2b c 4abc 3b a c
b
Biến đổi tương đương bất đẳng thức trên ta được
22
ac
abbc 2bac 0
b
Đánh giá trên là một đánh giá đúng vì
22 2
ac a
abbc 0; 2bca a2b 0
bb
Vậy bài toán được chứng minh xong.
Bài 153. Cho a, b, c là các số thực dương. Chứng minh rằng:
2
2
2 2222 2 2222 22
abbccaabbcca 8abcabc
Phân tích và lời giải
Cách 1: Bất đẳng thức cần chứng minh được viết lại thành
2
222222 222
abbcca abc
2ab 2bc 2ca ab bc ca
Không thể đánh giá bất đẳng thức trên bằng bất đẳng thức Cauchy hay Bunhiacopxki vì sẽ thu được
những đánh giá ngược chiều nhau. Do đó ta hướng đến phép biến đổi tương đương. Khi đó bất đẳng thức
trên tương đương với
2
222 222
ab bc ca ab bc ca
111 1
2ab 2bc 2ca
2ab bc ca
Đến đây để có cách đánh giá dễ dàng hơn ta có thể sắp thứ tự các biến, không mất tính tổng quát ta
có thể giả sử
abc, khi đó ta được
22 22 2
ab bc ab bc ac
11 1 1
2ab 2bc 2ab 2bc
2ab bc
Như vậy ta cũng cần đánh giá vế phải về đại lượng
2
ac
Ta có
22 2 2
ab bc ac 2abbc ac
Bài toán quy về chứng minh
2
22 2
ac ca ca
111
2ca ab bc ca
2ab bc
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22 2
ac ca ca
111
2ca
2ab bc
2caab bc
Mà theo bất đẳng thức Cauchy ta được
2caabbc abbcca nên ta có

22
ca ca
11
ab bc ca
2caab bc
Do đó ta được
2
22 2
ac ca ca
111
2ca ab bc ca
2ab bc
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
.
Cách 2: Bất đẳng thức cần chứng minh được viết lại thành
2
22 2222 222
11 1111111 111
8
abc
abbcca abc
Đến đây ta đặt
111
x;y;z
abc
, khi đó bất đẳng thức trên trở thành
2
222222 222222
xyyzzxxyz 8xyyzzz
Ta thấy vế trái của bất đẳng thức có chứa đại lượng
2
xyz nên ta đánh giá nó về
222
x,y,z để có
thể đổi biến tiếp.
Dễ thấy
2
222
xyz x y z 2xy2yz2zx và theo bất đẳng thức Cauchy ta được
22 22 22
22 2222
4x y 4y z 4z x
2xy 2yz 2zx
xy yzzx
Do đó ta được
2
222222
22 22 22
222222222
22 2222
xyyzzxxyz
4x y 4y z 4z x
xyyzzxxyz
xy yzzx
Ta quy bài toán về chứng minh.
22 22 22
222222222
22 2222
22 22 22
4x y 4y z 4z x
xyyzzxxyz
xy yzzx
8xy yz zx
Đặt
222
mx;ny;pz, khi đó ta cần chứng minh
4mn 4np 4pm
mnnppmmnp
mn np pm
8mn np pm
Khai triển và thu gọn ta được
22 2
mn m n np n p pm p m 0
Đánh giá cuối cùng là một đánh giá đúng. Vậy bài toán được chứng minh xong.
Bài 154. Cho a, b, c là các số thực dương. Chứng minh rằng:
ab bc ca a b c
ca ab bc
cc a aa b bb c
Phân tích và lời giải

Cách 1: Để ý là
ca
1
acca
, khi đó bất đẳng thức cần chứng minh được viết lại thành
ab c bc a ca b
3
ca ab bc
cc a aa b bb c
Hay
222
cab abc bca
3
cc a aa b bb c
Áp dụng bất đẳng thức Cauchy ta được
222 222
3
cab abc bca cababcbca
3. . .
cc a aa b bb c cc a aa b bb c
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
cababcbca
.. 1
cc a aa b bb c
Hay ta cần chứng minh
222
abcbcacababcabbcca
Ta có
2
22
abcbcaabacbccabab
do đó ta được
22
abcbcaabacbc
Hoàn toàn tương tự ta được
22 2 2
b ca c ab bc a b a c ; c ab a bc ca a b b c
Nhân theo vế các bất đẳng thức trên ta được
222
abcbcacababcabbcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Cách 2: Bất đẳng thức cần chứng minh được viết lại thành
bca
111
cab
cab cab
111 111
abc abc
Đặt
abc
x;y;z
bca
, khi đó ta được xyz 1 . Bất đẳng thức được viết lại thành
yzx 111
1z1x 1y 1z 1x 1y
Bất đẳng thức trên tương đương với
x1 y1 z1
0
1y 1z 1x
hay
222
x1z1 y1x1 z1y1 0
Khai triển và thu gọn ta được
222222
xyyzzxxyzxyz3
.
Áp dụng bất đẳng thức Cauchy và một đánh giá quen thuộc thì ta được
222 222
xyzxyz
xy yz zx 3; x y z x y z
3
Cộng theo về hai bất đẳng thức trên ta được
222222
xyyzzxxyzxyz3

Vậy bất đẳng thức được chứng minh.
Cách 3: Dễ thấy
ab c
ab a
ca
cc a cc a
, khi đó bất đẳng thức cần chứng minh được viết lại
thành
ab c bc a ca b
0
cc a aa b bb c
Đến đây ta đặt
ab bc ca
x;y;z
2b 2c 2a
.
Dễ thấy
xyz 1 , khi đó ta được
bc
1
ab c
y1
2c
ca z
cc a
2a
. Hoàn toàn tương tự ta viết lại được
bất đẳng thức cần chứng minh thành
x1 y1 z1
0
yzx
hay
xyz 111
yzxxyz
Áp dụng bất đẳng thức Cauchy ta được
33
3
222
xxz xz 3yyx xy 3zzyyz 3
3. ; 3. ; .
yyx yzzy zxxz x
yzx
Cộng theo vế các bất đẳng thức trên và thu gọn ta được
xyz 111
yzxxyz
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 155. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
ab bc ca 2
2
ab bc bc ca ca ab
Phân tích và lời giải
Cách 1: Để ý là theo bất đẳng thức Bunhiacopxki ta luôn có
ab a b a 2b
ab bc a c a c
Hoàn toàn tương tự ta được bất đẳng thức
ab bc ca a 2b b 2c c 2a
ab bc bc ca ca ab a c a b b c
Ta quy bài toán về chứng minh
2a b 2b c 2c a
1abc
acabbc
Đặt
xa;yb;zc, khi đó bất đẳng thức trở thành
222
222
2x y 2y z 2z x
xyz
xz xy yz
Để ý đến phép biến đổi
2
2x y 2xyz
2xy
zx zx
nên bất đẳng thức trên trở thành

222
2xyz 2xyz 2xyz
2xy 2yz 2zx x y z
xz xy yz
Hay
222
111
xyz2xyz 2xy2yz2zx
xz xy yz
Hay
2
222
111
2 x y z 2xyz x y z
xz xy yz
Lai thấy
2
2x xy yz xz
2xyz
2x
yz yz
, hoàn toàn tương tự ta thu được bất đẳng thức
2
xyz
2xy yz zx x y z
yz zx xy
Theo bất đẳng thức Bunhiacopxki ta được
2
xyz
2xy yz zx
yz zx xy
xyz
xy z yz x zx y x y z
yz zx xy
Như vậy bất đẳng thức trên được chứng minh xong.
Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
.
Cách 2: Áp dụng bất đẳng thức Bunhacopxki ta được
2
222
ab bc ca
ab bc bc ca ca ab
ab bc ca
ab bc ca
ab bc bc ca ca ab
ab bc ca
ab bc ca
abbcca
Ta quy bài toán về chứng minh
222
2
ab bc ca
2abbcca 2 1 abc
abbc ca
Hay
222
222
ab bc ca
2abc
abbc ca
Áp dụng bất đẳng thức Cauchy ta được
2
2
ba b ba b
2ab
ab 2
2a b
Hoàn toàn tương tự ta được
222222
ab bc ca a b c ab bc ca
2
abbc ca 2
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
222
222
abcabbcca
abc
2
Hay
222
ab bc ca a b c
, đánh giá cuối cùng là một đánh giá đúng.
Vậy bất đẳng thức được chứng minh.

Cách 3: Áp dụng bất đẳng thức Bunhiacopxki ta được
2
2
222
222
ab bc ca
ab bc bc ca ca ab
ab bc ca
ab. bc. ca.
abac abbc bcca
ab bc ca
2a b c
abac abbc bcca
Bài toán quy về chứng minh
222
ab bc ca 1
4
abac abbc bcca
Hay
222
ab bc ca a b c
4
abac abbc bcca
Bất đẳng thức trên tương đương với
222
4a b b c 4b c c a 4c a a b a b b c c a a b c
Khai triển và thu gọn ta được
222
ab a b bc b c ca c a 0
Bất đẳng thức cuối cùng luôn đúng. Vậy bất đẳng thức được chứng minh.
Bài 156. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
222
1113
8
a1 bc b1 ca c1 ab
Phân tích và lời giải
Cách 1: Từ giả thiết
abc 1 , khi đó tồn tại các số dương sao cho
yzx
a;b;c
xyz
.
Khi đó bất đẳng thức cần chứng minh trở thành
222
222
222
xyz yzx zxy 3
8
xy xyz yz yzx zx zxy
Áp dụng bất đẳng tức Cauchy ta có
2
2
22 22
xy z 2z xy
x y x y 2xy 2 2xy x y
Do đó ta được
2
2
22
2
xyz x
42x y
xy xyz
Hoàn toàn tương tự ta quy bài toán về chứng minh
22 22 22
xyz3
2
xy yz zx
Hay
222
22 22 22
2x 2y 2z
3
xy yz zx
Bất đẳng thức trên đã được chứng minh bằng bất đẳng thức Bunhiacopxki bằng cách đối xứng hóa
bất đẳng thức hoán vị.
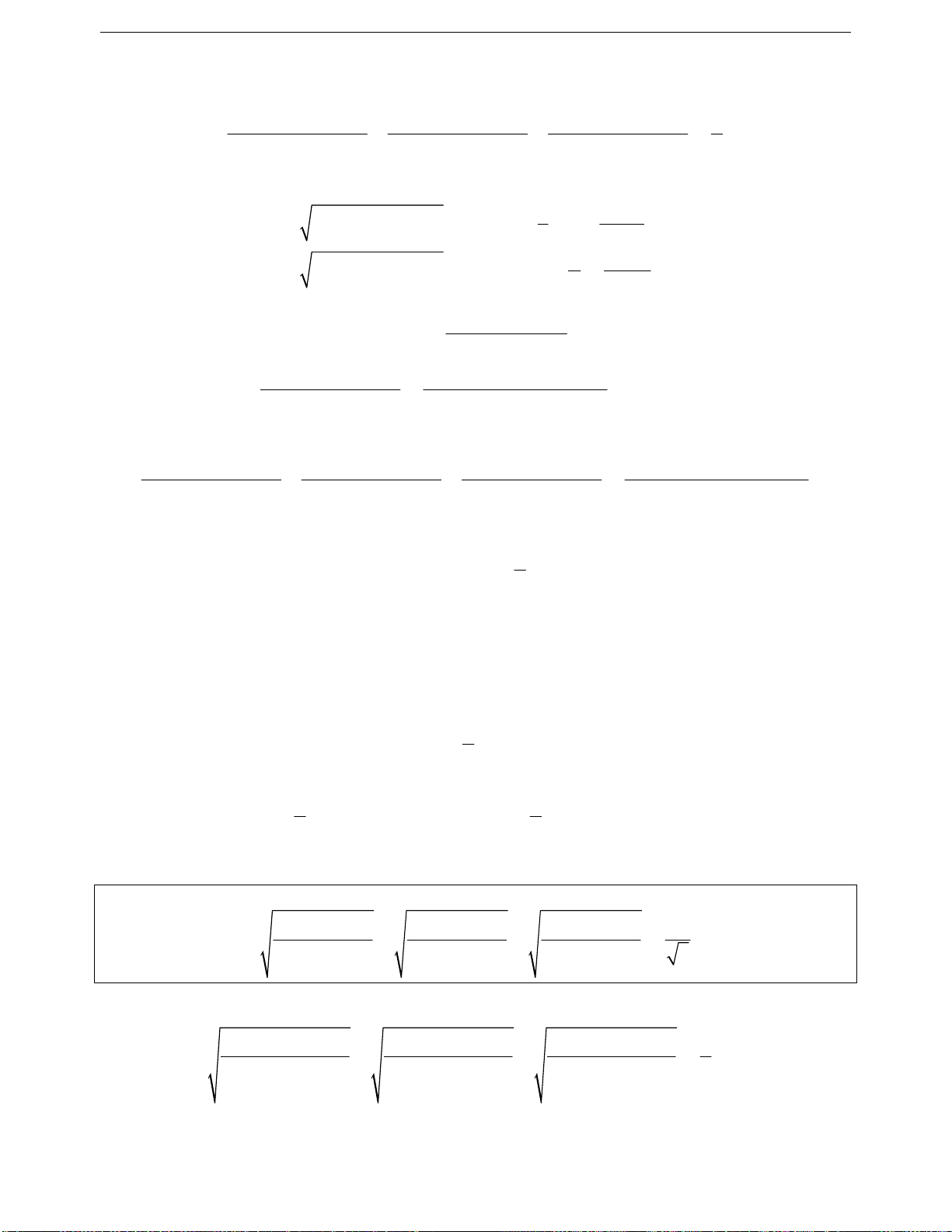
Cách 2: Đặt
222
ax;by;cz với x; y; z 0 , suy ra xyz 1 . Khi đó bất đẳng thức cần chứng
minh trở thành
222
222222222
1113
8
x1yz y1zx z1xy
Áp dụng bất đẳng thức Bunhiaopxki ta có
2
222
2
222
1z1
x1yz xyz z
zz
1y1
1x y z yzx y
yy
Do đó ta được
22
222
y1z1
x1yz
yz
Suy ra
2
222
222
1yz
x1y1z1
x1yz
Hoàn toàn tương tự ta được
222
222
222222222
111xyyzzx
x1y1z1
x1yz y1zx z1xy
Ta quy bài toán về chứng minh
222
8
x 1 y 1 z 1 xy yz zx
3
Áp dụng bất đẳng thức Bunhiacopxki ta có
222
22 22 22
x1y1 xy;y1z1 yz;z1x1 zx
Nhân theo vế các bất đẳng thức trên ta được
222
x1y1z1 xyyzzx
Để ý đến bất đẳng thức
8
xyyzzx xyzxyyzzx
9
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được
88
xyzxyyzzx xyyzzx
93
Hay
xyz3, đánh giá cuố cùng là một đánh giá đúng do xyz 1 .
Vậy bất đẳng thức được chứng minh.
Bài 157. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
222
22 2
abc3
5
bca cab abc
Lời giải
Bất đẳng thức cần chứng minh tương đương với
222
222
22 2
abc3
A
5
5b c a 5c a b 5a b c
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22
22
5b c a 1 4 b c a b 2c a

Do đó ta được
22
2
2
2
aaa
b2ca
5b ca b2ca
Chứng minh tương tự ta được
22
22
22
bbc c
;
c2ab a2bc
5c a b 5a b c
Từ đó ta được
abc
A
b2ca c2ab a2bc
,
Ta cần chứng minh
abc3
5
b2ca c2ab a2bc
hay
b2c c2a a2b 9
5
b2ca c2ab a2bc
.
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
2
2
222
b2c c2a a2b
b2ca c2ab a2bc
b2c c2a a2b
b 2c b 2c a c 2a c 2a b a 2b a 2b c
9a b c
b 2c b 2c a c 2a c 2a b a 2b a 2b c
9a b c
9
5
5a b c 2ab 2bc 2ca
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Bài 158. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333
222 2
4a b c
9a b b c c a
4a b c
abc
abc
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
333 222
abcabc abc
Do đó ta được
333 333
222
222
2
222 222
222
4abc 4abcabc
abc
abcabc
4a b c 4a b c
abc
abcabc
Mặt khác ta lại có
a b b c c a 8abc
, cho nên
8a b c ab bc ca 8a b b c c a 8abc 9a b b c c a

Do đó
22
9a b b c c a 8a b c ab bc ca 8ab bc ca
abc
abc abc
Từ các bất đẳng thức trên ta được
333
222 2
222
4a b c
9a b b c c a
abc
abc
4a b c
8ab bc ca
4a b c
abc abc
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 159. Cho a, b, c là các số thực dương thỏa mãn
abcabc . Chứng minh rằng:
222
bca3
2
ab 1 bc 1 ca 1
Lời giải
Từ giả thiết
abcabc suy ra
111
1
ab bc ca
.
Đặt
111
x;y;z
abc
, Khi đó giả thiết của bài toán trở thành
xy yz zx 1
.
Bất đẳng thức cần chứng minh trở thành
22 2
xyz3
2
y1 z1 x1
.
Dễ thấy
22
x1 xxyyzzx xyxz
Tương tự ta được
22
y1 yzyx;z1 zxzy
Áp dụng bất đẳng thức Cauchy ta được
22 2
xyz x y z
y1 z1 x1
yxyz zxzy xyxz
2x 2y 2z
x2yz xy2z2xyz
Ta cần chứng minh
2x 2y 2z 3
x2yz xy2z2xyz 2
Thật vậy, áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
22
22
2
2x 2y 2z 2x 2y 2z
x2yz xy2z 2xyz
xx2yz yxy2z z2xyz
2x y z 2x y z
3
2
xyz xyyzzx xyz
xyz
3
Như vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc 3 .
Bài 160. Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
222
abc3
2
a3bc b3ca c3ab
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được

222
222 2 2 2
2
222
abc a b c
a 3bc b 3ca c 3ab a a 3bc b b 3ca c c 3ab
abc
aa 3bc bb 3ca cc 3ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki ta được
222
333 333
aa 3bc bb 3ca cc 3ab
a a 3abc b b 3abc c c 3abc a b c a b c 9abc
Do vậy ta được
2
222
333
abc
abc
a3bc b3ca c3ab
abca b c 9abc
Ta cần chứng minh
2
333
abc
3
2
abca b c 9abc
Hay
3
333
abc
9
4
abc9abc
Thực hiện biến đổi tương đương bất đẳng thức ta được
333
12 ab a b bc b c ca c a 5 a b c 57abc
Theo bất đẳng thức Cauchy ta lại có
333
abc3abc
Do đó
333 333
6a b c 9abc 5a b c 57abc
Như vậy ta cần chứng minh
333
2aba b bcb c cac a a b c 9abc
Hay
2
3abcbc bcaabac 0
Do a, b, c có tính đối xứng, nên không mất tính tổng quát ta chọn a lớn nhất, khi đó bất đẳng thức cuối
cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 161. Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:
abc abc abc
abc
abc bca cab
Lời giải
Đặt
xbca 2ayz
ycab 2bzx
zabc 2cxy
Khi đó bất đẳng thức cần minh tương đương với
xyyzzx
111
xyz
8
xyz
Bình phương hai vế và quy đồng ta được
2
2
x y y z z x xy yz zx 8xyz x y z

Hay
2
xyyzzx
xyz
8xyz
xy yz zx
Để ý rằng với
mn0;k0 , ta có tính chất
mmk
nnk
Do đó ta có
xy xyz yz xyz zx xyz
;;
2 xy 2 xy z 2 yz x 2 yz x 2 zx y 2 zx y
Nhân theo vế các bất đẳng thức trên ta được
3
xyyzzx xyz
8xyz
2xy z 2yz x 2zx y
Ta cần chứng minh
3
2
xyz
xyz
xy yz zx
2xy z 2yz x 2zx y
Hay
2
2xy z 2yz x 2zx y x y z xy yz zx
Khai triển và thu gọn ta được
222
xy yz zx 0
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 162. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
3
ab bc ca
abc
abc
3
12 a b c
Lời giải
Cách 1: Nhân hai vế với
12 a b c , khi đó bất đẳng thức trở thành
3
222
a b c 5 ab c ca 6 abc a b c
Hay
2
3
a b c 3 ab c ca 6 abc a b c
Áp dụng bất đẳng thức Cauchy ta được
2
3
a b c 3 ab c ca 2 a b c 3 ab c ca 6 abc a b c
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Cách 2: Bất đẳng thức cần chứng minh tương đương với
2
222
3
2a b c
abcabbcca
abc
6a b c 6a b c
Hay
2
3
abc 3abbcca 6abcabc
Đặt
3a 3b 3c
x;y;z xyz3
abc abc abc

Nhân cả hai vế của bất đẳng thức với
2
9
abc
và đổi biến ta được bất đẳng thức sau
2
3
x y z 3 xy yz zx 6 xyz x y z
Hay
3
3 xy yz zx 6 xyz
Mặt khác ta lại có
xy yz zx 3xyz x y z 3 xyz
Ta cần chứng minh
3
1 xyz 2 xyz
Đặt
6
txyzt1, khi đó bất đẳng thức cần chứng minh trở thành
32 2
1t 2t 1t1tt 0
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 163. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3
. Chứng minh rằng:
222
a2b b2c c2a
1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Lời giải
Biến đổi tương đương bất đẳng thức ta được
222
2 a 2b 2 b 2c 2 c 2a
2
2a 4b 3c 2b 4c 3a 2c 4a 3b
Hay
222
2 a 2b 2 b 2c 2 c 2a
111 1
2a 4b 3c 2b 4c 3a 2c 4a 3b
Hay
222
222
cab1
3
2a 4b 3c 2b 4c 3a 2c 4a 3b
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222
222
333
222
2
333
333
cab
2a 4b 3c 2b 4c 3a 2c 4a 3b
cab
c2a4b3c a2b4c3a b2c4a3b
abc
3a b c 6ab bc ca
Ta cần chứng minh
2
333
333
abc
1
3
3a b c 6ab bc ca
Hay
33 33 33
ab bc ca ab bc ca
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
33 33 33
33 33 33
ab bc ca
a b ab b c bc c a ca ab bc ca
2ab bc ca ab bc ca
ab bc ca 3 3 ab bc ca ab bc ca

Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1
.
Bài 164. Cho a, b, c là các số thực không âm thỏa mãn
abc1
. Chứng minh rằng:
333 555
10 a b c 9 a b c 1
Lời giải
Bất đẳng thức cần chứng minh tương đương với
35 35 35
10a 5a a 10b 5b b 10c 5c c 0
Để ý rằng
35 22
10a 9a a a 1 a 9a 1
Do đó bất đẳng thức trở thành
22 22 22
a1 a 9a 1 b1 b 9b 1 c1 c 9c 1 0
Để ý tiếp ta lại thấy
2
2
81
1 a 9a 1 3a 1 3a 5 3a 1 0
33
Hay
2
8
1a9a 1 3a1
3
Do đó ta có
22 2
8
a1 a 9a 1 a1 a 1 a 9a 1 a1 a. 3a 1
3
Áp dụng tương tự ta được
22 22 22
a1 a 9a 1 b1 b 9b 1 c1 c 9c 1
888
a1 a. 3a 1 b1 b. 3b 1 c1 c. 3c 1
333
Ta cần chứng minh
a1 a 3a 1 b1 b 3b 1 c1 c 3c 1 0
Hay
222 333
4a b c 3a b c 1
Do
abc1 nên bất đẳng thức trên trở thành
3
222 333
4a b c a b c 3a b c a b c
Triển khai và thu gọn ta được
ab a b bc b c ca c a 6abc
Hay
abbcca
6
cab
Bất đẳng thức cuối cùng là một bất đẳng thức đúng.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
abc
3
.
BÀI TẬP TỰ LUYỆN
Bài 1. Cho a, b, c là các số thực dương thỏa mãn
abc 64
. Chứng minh rằng:
333 222
abc4abc
Bài 2. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng
77 7777
55 55 55
ab bcca 1
3
ab bc ca
Bài 3. Cho a, b, c là các số thực dương thỏa mãn
111
abc
abc
.
Chứng minh rằng:
5 a b c 7 8abc
Bài 4. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc3.

Chứng minh rằng:
abc
1
ab1bc1ca1
Bài 5. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc1
.
Chứng minh rằng:
222
25
14ab 14bc 14ca 3
27
Bài 6. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc1.
Chứng minh rằng:
ab c bc a ca b
2
ab bc ca
Bài 7. Cho a, b, c là các số thực dương thỏa mãn điều kiện
ab bc ca 2abc .
Chứng minh rằng:
222
1111
2
a2a 1 b2b 1 c2c 1
Bài 8. Cho a, b, c là các số thực dương thỏa mãn điều kiện
ab bc ca 1.
Chứng minh rằng:
1193
abc 2
abbcca
Bài 9. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
3
2ab bc ca 3. a b b c c a
Bài 10. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
22 22 22
222222
ab bc ca 5
2
a 2ab b b 2bc c c 2ca a
Bài 11. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
333
2 2 22 22 22 2 2 2 2
abc1
abc
2a b 2a c 2b c 2b a 2c a 2c b
Bài 12. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
abc33
abc
bc ca ab 2
Bài 13. Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:
ab bc ca 1
1c 1a 1b 4
Bài 14. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222
abc
abc 33a b c
bca
Bài 15. Cho a, b, c là các số thực dương bất kì. Chứng minh rằng:
222 222
abc abc
bc ca ab ab bc ca
Bài 16. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
3
64abc a b c 27 a b b c c a
Bài 17. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
abcabbcca
ab bcca
3
cab
abc a b c
Bài 18. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
22 2
abc 10abc
2
abbcca
bc ca ab

Bài 19. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3
. Chứng minh rằng:
143
abc 2
abbcca
Bài 20. Cho a, b, c, d là các số thực dương thỏa mãn
2222
abcd1.
Chứng minh rằng:
abcd 1a1b1c1d
Bài 21. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222 222 222
3a b 3b c 3c a
6
a2bc b2ca c2ab
Bài 22. Cho a, b, c là các số thực thỏa mãn
a, b, c [0; 1]
. Chứng minh rằng:
333 2 2 2
2a b c ab bc ca 3
Bài 23. Cho a, b ,c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng
222
3
ab bc ca
abc 1
34 abc
Bài 24. Cho a, b, c là các số thực dương thỏa mãn
abc 1 . Chứng minh rằng:
44 44 44
ab bc ca
3
1ab 1bc 1ca
Bài 25. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
333 2 2 2
1a 1b 1c 1ab 1bc 1ca
Bài 26. Cho a, b, c là các số thực dương thỏa mãn
222
abc3
. Tìm giá trị nhỏ nhất của biểu thức
111
P
2ab 2bc 2ca
Bài 27. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc . Chứng minh rằng
44 44 44
33 33 33
ab bc ca
1
ab a b bc b c ac a b
Bài 28. Cho a, b, c là các số thực dương thỏa mãn
a, b, c 0; a b c 1
. Chứng minh rằng:
33
abbcca
18 18
Bài 29. Cho a, b, c là các số thực dương thỏa mãn
222
abcabc . Chứng minh rằng:
222
abc1
2
abcbcacab
Bài 30. Cho a, b, c là các số thực thỏa mãn
a, b, c [3; 5] . Chứng minh rằng:
ab 1 bc 1 ca 1 a b c
Bài 31. Cho a, b, c là các số thực dương tùy ý. Tìm giá trị nhỏ nhất của biểu thức:
3b c 12b c
4a 3c
P
2a 3b 2a 3c
Bài 32. Cho a, b, c là các số thực không âm thỏa mãn
abbcca 0. Chứng minh rằng:
222
111
ab bc ca 4
ab bc ca
Bài 33. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng:
222
222
abc3
2
b2b3c2c3a2a3

Bài 34. Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Chứng minh rằng:
abc
abc6
bca
Bài 35. Cho a, b, c là các số thực không âm thỏa mãn
abc 1 . Tìm giá trị nhỏ nhất của biểu thức:
33 33 33
222222
ab bc ca
P
aabb bbcc ccaa
Bài 36. Cho a, b là các số thực dương. Tìm giá trị nhỏ nhất của:
33
22
ab7abab
P
ab a b
Bài 37. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
2
111 27
aa b bb c cc a
2a b c
Bài 38. Cho a, b là các số thực dương tùy ý . Chứng minh rằng:
22
2222 4
32 a b
11 1
abab
ab
Bài 39. Cho a, b, c là các số thực dương thỏa mãn
abc3. Tìm giá trị nhỏ nhất của biểu thức:
333222
Pa b c a b c abc
Bài 40. Cho a, b, c là các số thực dương thỏa mãn
a2b4c12
. Tìm giá trị lớn nhất của biểu thức:
2ab 8bc 4ca
P
a2b2b4c 4ca
Bài 41. Cho các số thực dương a, b, c thỏa mãn
1a1b1c 8abc .
Chứng minh rằng:
abc1
Bài 42. Cho a, b, c là các số thực dương thỏa mãn
222
a2b3c3abc .
Chứng minh rằng:
864
3a 2b c 21
abc
Bài 43. Cho các số thực dương a, b, c lớn hơn 1 và thỏa mãn
abcabc .
Tìm giá trị nhỏ nhất của biểu thức sau:
222
a2 b2 c2
P
bca
Bài 44. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
abc
1
2a bc 2b ca 2c ab
Bài 45. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
11127
1ab 1bc 1ca 8
Bài 46. Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
ab bc ca
P
a b c b c 4a a c 16b
Bài 47. Cho a, b, c là các số thực dương thỏa mãn
abc1
. Chứng minh rằng:
222
ab bc ca 3
8
1c 1a 1b
Bài 48. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
abc1
ab bc ca a b c
ab bcca 2

Bài 49. Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Tìm giá trị nhỏ nhất của biểu thức:
222
abc
P
1abbc 1bcca 1caab
Bài 50. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1. Chứng minh rằng:
333
1111
6b 6c 6a
abcabc
Bài 51. Cho các số thức
a, b, c [0; 1] và abc0. Chứng minh rằng:
111 5
ab 1 bc 1 ca 1 a b c
Bài 52. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
111222
1a 1b 1c 1a 1b 1c
Bài 53. Cho các số thức
a, b, c 0;1
. Chứng minh rằng:
11
1a1b1c
abc 3
Bài 54. Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
33 33 33
333
22 2
abc
P4ab 4bc 4ca2
bca
Bài 55. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
ab3c a3bc 3abc 15
3a 3b 2c 3a 2b 3c 2a 3b 3c 8
Bài 56. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
222
ab bc ca
1
2a b 2b c 2c a
Bài 57. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
ab bc ca 1 a b b c c a
2c a b
cab
Bài 58. Cho a, b, c là các số thực dương thỏa mãn
abc3
. Chứng minh rằng:
444
2
333 222
bc ca ab 1
abc abc
2223
Bài 59. Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
222
222
22222 2
2a b c
abc bab cab
abc
bbcc ccaa aabb
Bài 60. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1. Chứng minh rằng:
222
111 1 1 1
3111
ab bc ca
abc
Bài 61. Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Chứng minh rằng:
222
111 4 4 4
ab bcca
a7b7c7
Bài 62. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
ab bc ca 1
c6ab a6bc b6ca 3
Bài 63. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 1. Chứng minh rằng:

222
abc9
4
b1 a c1 b a1 a
Bài 64. Cho a, b, c là các số thực dương thỏa mãn
22 22 22
111
1
ab1bc1ca1
.
Chứng minh rằng:
ab bc ca 3
Bài 65. Cho a, b, c là các số thực dương thỏa mãn
333
abc3. Chứng minh rằng:
222
abc1
b5 c5 a5 2
Bài 66. Cho a, b, c là các thực dương thỏa mãn
2
abc 9abc
. Chứng minh rằng:
222
1113
2
13a 13b 13c
Bài 67. Cho a, b, c là các thực dương thỏa mãn
abc 1
. Chứng minh rằng:
abc
1
a8c b8a c8b
Bài 68. Cho a, b, c là các thực dương thỏa mãn
222
abc12. Chứng minh rằng:
1113
1ab 1bc 1ca 5
Bài 69. Cho a, b, c là các số thực dương thỏa mãn
222
3
abc
4
. Chứng minh rằng
333
111
abbcca 25
abc
Bài 70. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng
ab bc ca
1112abc
cab
Bài 71. Cho a, b, c là các số thực dương thỏa mãn
abc 1
. Chứng minh rằng
222
abc
1
a2b2c2
Bài 72. Cho a, b, c là các số thực không âm thỏa mãn min
ab;bc;ca 0. Chứng minh rằng
22 22 22
ab bc ca 1
ab bc ca
2
Bài 73. Cho a, b, c là các số thực dương thỏa mãn
222
abc1. Chứng minh rằng:
111
abc43
abc
Bài 74. Cho a, b, c là các số thực không âm thỏa mãn
abc1
. Chứng minh rằng
222
22 2
a1b1c17
2
b1c1a1
Bài 75. Cho a, b, c là các số thực dương thỏa mãn
222
abc1. Chứng minh rằng:
222
2
a1bcb1ca c1ab
3
Bài 76. Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Chứng minh rằng:
222
222
3a 3b 3c 48
bc ca ab
Bài 77. Cho a, b, c là các số thực dương thỏa mãn
222
abc3. Tìm giá trị nhỏ nhất của biểu thức

333
222
222
P 6a 6a 5 6b 6b 5 6c 6c 5
ab ac bc ba ca cb
Bài 78. Cho a, b, c là các số thực không âm thỏa mãn abc1. Chứng minh rằng
333
a1 b c b1 c a c1 a b 1 .
Bài 79. Cho a, b , c là các số thực dương thỏa mãn
222
abcabc . Tìm giá trị nhỏ nhất của biểu
thức:
222
abc
T
6a 9 6b 9 6c 9
.
Bài 80. Cho a, b, c là các số thực không âm thỏa mãn
abc3. Chứng minh rằng:
22 22 22
ab bc ca 3
2
2a 3b 7 2b 3c 7 2c 3a 7
.
Bài 81. Cho a, b, c là các số thực dương thỏa mãn
222
abc3
. Chứng minh rằng:
abc3
abc
1bc 1ca 1ab 2
Bài 82. Cho a, b, c là các số thực dương thỏa mãn
abc3. Chứng minh rằng
222222
22 22 22
aabb bbcc ccaa 3
2
ab bc ca
Bài 83. Cho a, b, c là các số thực dương thỏa mãn
abcabc
. Chứng minh rằng
bc ca ab 3 3
4
a1 bc b1 ca c1 ab
Bài 84. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3abc . Chứng minh rằng:
222
22 22 22
bac
1
ab 2a ac 2c bc 2b
Bài 85. Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
11 1 bc
a2
3a b 3a c 2a b c 3a c 3a b
.
Bài 86. Cho a, b, c là các số thực dương. Chứng minh rằng:
1113
1abc
a1 b b1 c c1 a
Bài 87. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
22 2 2 2 2
ab bc ca a b c
ab bc ca
bcbccacaabab
Bài 88. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
2
333 222
abc abc
24
3a 1 3b 1 3c 1 9a 1 9b 1 9c 1
Bài 89. Cho a, b, c là các số thực dương thỏa mãn
abc1. Chứng minh rằng:
2ab 2bc 3ca 5
3
acbc abca bcca
Bài 90. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca abc
. Chứng minh rằng:
44 44 44
33 33 33
ab bc ca
1
ab a b bc b c ca c a
Bài 91. Cho a, b, c là các số thực dương thỏa mãn
ab bc ca 3abc . Chứng minh rằng:
22 22 22
ab bc ca
32abbcca
ab bc ca
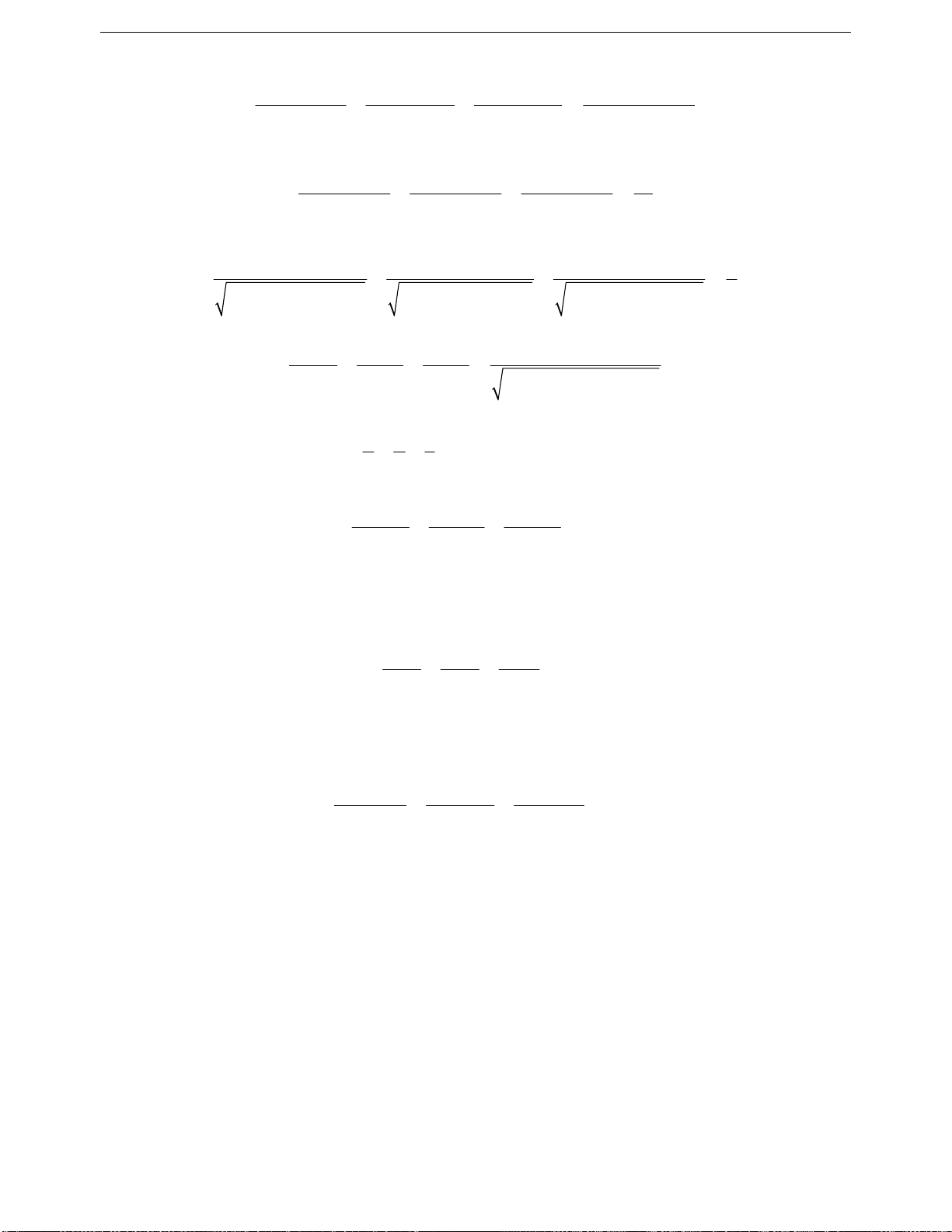
Bài 92. Cho a, b, c là các số thực dương. Chứng minh rằng:
222
22 22 22
22 22 22 2
6a b c
ab bc ca
ababbcbccaca
abc
Bài 93. Cho a, b, c là các số thực dương thỏa mãn
333
abc1. Chứng minh rằng:
222
52 2 52 2 52 2
11181
4
ab c bc a ca b
Bài 94. Cho a, b, c là các số thực dương thỏa mãn
abc6. Chứng minh rằng:
222
abc3
2
b2b b2 c2c c2 a2a a2
Bài 95. Cho a, b, c là các số thực dương. Chứng minh rằng:
3
111 2
2a b 2b c 2c a
abbcca
Bài 96. Cho a, b, c là các số thực dương thỏa mãn điều kiện
abc3. Chứng minh rằng:
222
111
8910abc
abc
Bài 97. Cho a, b, c là các số thực lớn hơn 1. Chứng minh rằng:
444
22 2
abc
48
b1 c1 a1
Bài 98. Cho a, b, c là các số thực dương không âm thỏa mãn a + b + c = 3. Tìm giá trị lớn nhất của:
222222
Paabb bbcc ccaa
.
Bài 99. Cho x, y, z là những số dương thỏa mãn x + y + z
6 . Chứng minh rằng:
333
xyz
6
yz xz xy
Bài 100. Cho a, b, c là các số thực dương thỏa mãn abc = 1. Chứng minh rằng:
2
222
a8b8c8 abc
Bài 101. Cho x, y, z là các số thực dương thỏa mãn
xy yz zx 3xyz . Chứng minh rằng:
222
22 22 22
yxz
1
xy 2x xz 2z yz 2y
.
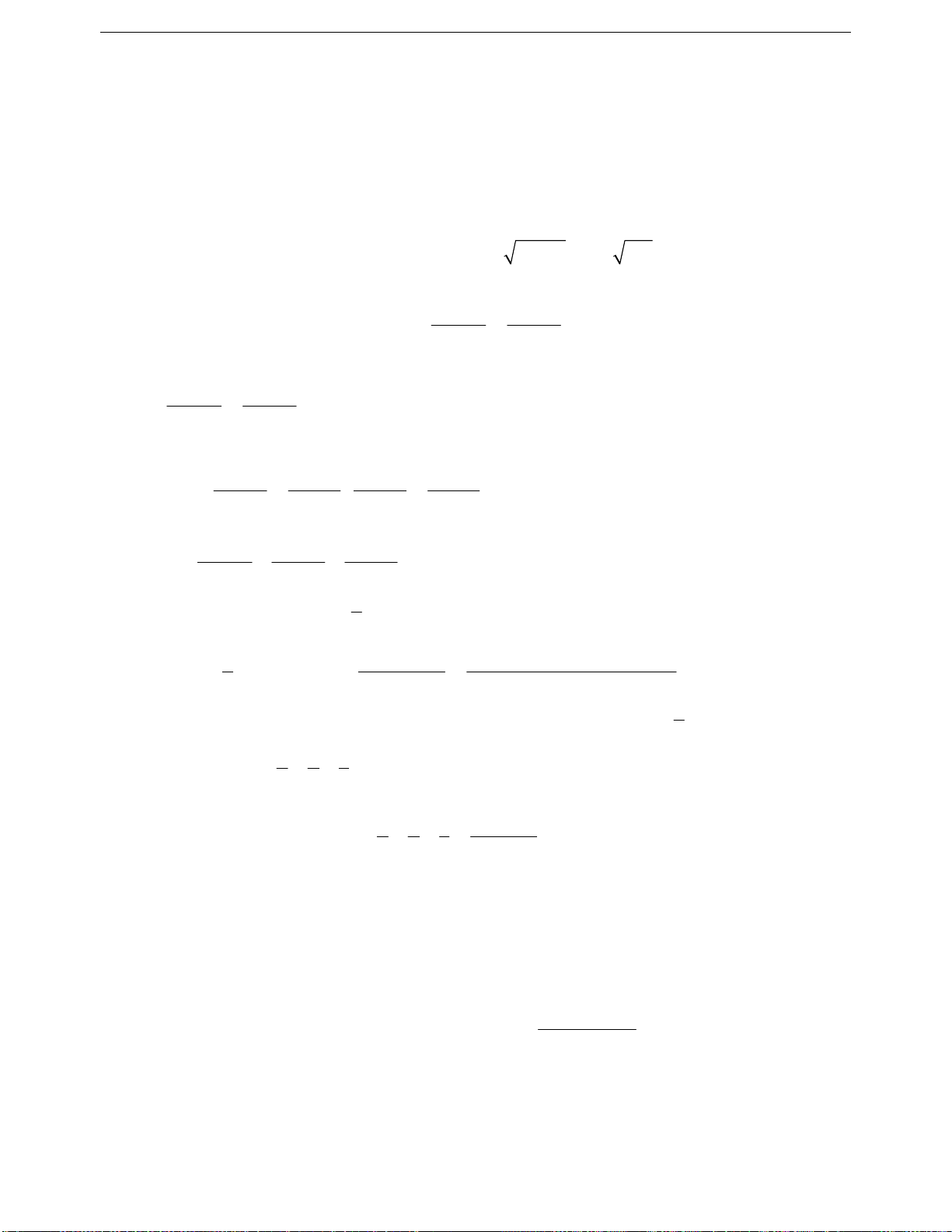
HƯỚNG DẪN BÀI TẬP TỰ LUYỆN
Bài 1. Xét biểu thức
2
32
a6a32a4a20
, do a0 .
Do đó
32
a326a
, tương tự ta có
3232
b 326b;c 326c
Cộng theo vế ba bất đẳng thức trên ta được
333 222
abc966abc .
Như vậy ta cần chứng minh
222 222 222
6a b c 4a b c 96 2a b c 96
Theo bất đẳng thức Cauchy ta có
33
222 222 2
2a b c 2.3abc 2.364 96 .
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc4.
Bài 2. Trước hết ta chứng minh bất đẳng thức
77 22
55
ab ab
2
ab
.
Thật vậy, do
a0;b0
nên
77 22
77 2255
55
2
43 22 34
ab ab
2a b a b a b
2
ab
ab aba abab ab b 0
Tương tự ta có
77 227 7 22
55 5 5
bc bcca ca
;
22
bc ca
.
Cộng theo vế các bất đẳng thức trên ta được
77 7777
222
55 55 55
ab bc ca
abc
ab bc ca
Ta cần chứng minh
222
1
abc
3
. Tuy nhiên bất đẳng thứ này đúng vì
2222
222 222
abc ab bc ca
1
abc abc 0
333
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xảy ra khi
1
abc
3
.
Bài 3. Từ giả thiết ta có
111
abc abbccaabcabc
abc
.
Mặt khác cũng từ giả thiết trên ta được
111 9
abc abc3
abcabc
Bất đẳng thức cần chứng minh tương đương với
2
2
5abc 7abc 8abcabc
5abc 7abc 8abbcca
Mà ta có
2
abc 3abbcca , ta cần chứng minh
2
2
8a b c
5a b c 7a b c
3
Đặt
tabc3, bất đẳng thức trên trở thành
2
7t 21t 0 7t t 3 0 , bất đẳng thức cuối
cùng đúng với mọi
t3 .
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.

Bài 4. Sử dụng giả thiết
abc3
, ta thấy rằng bất dẳng thức cần chứng minh tương đương với
abc
1
4c 4a 4b
. Quy đồng hai vế và rút gọn ta được bất đẳng thức sau
222
ab bc ca abc 4
.
Không mất tính tổng quát ta giả sử
22 2
a a c b c 0 ab ca ac abc
.
Khi đó ta có
2
222 22
a b b c c a abc b c a c 2abc c a b
Áp dụng bất đẳng thức Cauchy ta có
3
2
2a 2b 2c
1
ca b 2ca b a b 4
254
Hay
222
ab bc ca abc 4 .
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc1.
Bài 5. + Trước hết ta chứng minh
222
14ab 14bc 14ca 3.
Từ giả thiết
abc1, ta có
1abcab2ab
.
Do đó
0 1 4ab 1
, nên
2
1 4ab 1.
Áp dụng tương tự ta được
22
14bc 1;14ca 1. Cộng theo vế ba bất đẳng thứ đó ta được
222
14ab 14bc 14ca 3
.
+ Chứng minh
222
25
1 4ab 1 4bc 1 4ca
27
Bất đẳng thức cần chứng minh tương đương với
22 22 22
22 22 22
25
34abbcca 16ab bc ca
27
7
ab bc ca 2 a b b c c a
27
Để ý ta có
2
22
15 175 17
ab 2a b 2 ab ab ab
9 9 9819 981
Tương tự ta có
22 2 2
517 517
bc 2b c bc ; ca 2c a ca
9 9 81 9 9 81
.
Cộng theo vế các bất đẳng thức trên ta được
22 22 22
517
ab bc ca 2 a b b c c a ab bc ca
9327
Mặt khác ta lại có
2
abc
1
ab bc ca
33
Do đó
22 22 22
7
ab bc ca 2 a b b c c a
27
. Tức là bất đẳng thức trên được chứng minh.
Bài 6. Để ý rằng
ab c ab c a b c a c b c
. Do đó bất đẳng thức cần chứng minh
tương đương với
acbc abcb baca
2
ab ac bc
Áp dụng bất đẳng thức dạng
222
xyzxyyzzx
ta được
acbc abcb baca
bcabca 2
ab ac bc
.

Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
3
.
Bài 7. Giả thiết của bài toán tương đương với
111
2
abc
. Đặt
111
x;y;z
abc
, khi đó ta được
xyz2
và bất đẳng thức cần chứng minh trở thành
333
222
xyz1
2
2x 2y 2z
,
Chú ý là
x, y, z 2 .
Áp dụng bất đẳng thức Cauchy ta được
3
2
x2x2x3x
884
2x
.
Từ đó suy ra
3
2
x1
x
2
2x
. Thiết lập các bất đẳng thức tương tự và công theo vế ta được
333
222
xyz 31
xyz
22
2x 2y 2z
.
Như vậy bất đẳng thức được chứng minh.
Bài 8. Áp dụng bất đẳng thức Cauchy cho ba số dương ta được
33
222
14 11 4
abc 2abc 2abc
abbcca abbcca
11
3. 3.
a b c a b b c c a abc ac bc ab ac bc ba
Mặt khác cũng theo bất đẳng thức Cauchy ta được
3
222
ab bc ca
11
abc abc
27 27
33
3
8ab bc ca
8
ab ac bc ba ca cb
27 27
Do đó
3
1 4 27.3 3 9 3
3.
abc 8 2
abbcca
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
3
.
Bài 9. Để ý ta có đẳng thức
abbcca abcabbcca abc .
Theo một đánh giá quen thuộc thì
3
ab bc ca
a b c 3 ab bc ca ; abc
27
Do đó
3
3
ab bc ca
abbcca abbcca 3abbcca
27
ab bc ca
8.
27
Lấy căn bậc ba hai vế ta được bất đẳng thức

3
2ab bc ca 3. a b b c c a
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 10. Bất đẳng thức cần chứng minh tương đương với
22 22 22
222
222
222
ab ab bc bc ca ca
5
ab bc ca
ab bc ca
2
ab bc ca
Đặt
ab bc ca
x;y;z
ab bc ca
, khi đó bất đẳng thức cần chứng minh trở thành
222
xyz2
Ta có
abbc bcca caab
xy yz zx
abbc bcca caab
abbcca
1
abbcca
Mà
2
xyz 0
, do vậy
222
x y z 2 xy yz zx 2
.
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 11. Theo bất đẳng thức Bunhiacopxki ta được
2
2
22 22 222222 2 2
2ab2ac aabaca aabac aabc
Do đó
3
2
22 22
aa
2a b 2a c
abc
, chứng minh tương tự ta được
33
22
22 22 22 22
bbcc
;
2b c 2b a 2c a 2c b
abc abc
Cộng theo vé các bất đẳng thức trên ta được
333
2 2 22 22 22 2 2 2 2
abc1
abc
2a b 2a c 2b c 2b a 2c a 2c b
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 12. Biến đổi vế trái của bất đẳng thức như sau
abc
abc
abc abc abc
abc
bc ca ab bc ca ab
abc abc abc
Đặt
abc
x;y;z
abc abc abc
, suy ra
222
xyz1.
Bất đẳng thức cần chứng minh trở thành
22 2 2 2 2
xyz33
2
yz zx xy
Ta có thể chứng minh bất đẳng thức trên như sau
Từ điều kiện
222
xyz1, ta được

22 2 2 2 2 2 2 2
xyzxyz
y z z x x y 1x 1y 1z
Xét
2
22
2
2
22
x3x2 3x1
2x 3 3x 1 x
x33
x0
2
1x
21 x 21 x
Từ đó suy ra
2
2
x33
x
2
1x
, chứng minh tương tự ta được
22
22
y33 z33
y; z
22
1y 1z
Cộng các bất đẳng thức trên theo vế ta được
222
xyz33
2
1x 1y 1z
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc
.
Bài 13. Áp dụng bất đẳng thức quen thuộc dạng
411
xy x y
ta được
ab bc ca ab bc ca
1c1a1b acbcabacabbc
1ab ab bc bc ca ca
4acbcabacabbc
abc 1
44
Bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra khi
1
abc
3
.
Bài 14. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abca b c
bcaabbccaabbcca
Do đó
3
abc
abc
abc
bca abbcca
Ta cần chứng minh
3
222
3
222
abc
33a b c
ab bc ca
abc 3abbcca 3a b c
Thât vậy, theo bất đăgr thức Cauchy ta có
2
222
2
222
3
a b c a b c ab bc ca ab bc ca
3a b c abbcca
Lũy thừa bậc ba hai vế ta được
62
222
abc 27a b c abbcca
Lấy căn bậc hai hai vế bất đẳng thức trên ta được
3
222
abc 3abbcca 3a b c
Như vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra khi
abc.

Bài 15. Ta có
22 22 22
ab bc ca
abbcca 0
ab bc ca
Do đó
222 222
abcbca
ab bc ca ab bc ca
Khi đó ta cần chứng minh
222222222
2a 2b 2c a b b c c a
bc ca ab ab bc ca
Bất đẳng thức trên tương đương với
222 222 222
222
2a b c 2b c a 2c a b
0
bc ca ab
ab ab bc bc ca ca
0
acbc abac abbc
Như vậy bất đẳng thức được chứng minh.
Bài 16. Trước hết ta chứng minh bất đẳng thức
8
abbcca abcabbcca
9
Thật vậy, khai triển và rút gọn ta được bất đẳng thức sau
222
ca b bc a ab c 0
Do đó bất đẳng thức trên được chứng minh.
Áp dụng bất đẳng thức trên ta được
2
22
64
27 a b b c c a 27. a b c ab bc ca
81
Mặt khác theo một đánh giá quen thuộc ta được
2
ab bc ca 3abc a b c
Do đó ta được bất đẳng thức
2
3
27 a b b c c a 64abc a b c
Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra khi
abc.
Bài 17. Biến đổi tương đương bất đẳng thức trên ta được
222
abcabbcca
ab bcca
3
cab
abc a b c
222
abcabbcca
ab bc ca
36
cab
abc a b c
222
222
2
222
2
2
abcabbcca
ab a b bc b c ca c a 3abc
6
abc
abc a b c
abcabbcca
abcabbcca
6
abc
abc a b c
abcabbcca
abc abbcca
6
abc a b c abc a b c
2ab bc ca
6abbcca3abcabc
abc a b c
Bất đẳng thức cuối cùng là một bất đẳng thức đúng theo một đánh giá quen thuộc là

2
xyz 3xyyzzx
Vậy bất đẳng thức trên được chứng minh. Dấu đẳng thức xẩy ra tại
abc.
Bài 18. Đặt
abc
x;y;z
bc ca ab
,
Khi đó bất đẳng thức cần chứng minh trở thành
222
x y z 10xyz 2
Dễ dàng chứng minh được
abc3
bc ca ab 2
Do đó ta được
3
xyz
2
, từ đó ta suy ra
222 222 222
6xyz
x y z 10xyz x y z 6xyz 4xyz x y z 4xyz
xyz
Mặt khác ta lại chứng minh được
222
6xyz
xyz 2xyyzzx
xyz
Từ đó suy ra
222
x y z 10xyz 2 xy yz zx 4xyz
Ta cần chứng minh
xy yz zx 2xyz 1
Hay
ab bc ca abc
21
bcca caab abbc bccaab
Đẳng thức trên được chứng minh dễ dàng.
Vậy bất đẳng thức ban đầu được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Bài 19. Theo bất đẳng thức Cauchy ta có
3
222
3abbcca3abc abc1
3
ab ca ab bc ca bc
ab ac ab bc ac bc 8
3
Cũng theo bất đẳng Cauchy ta có
14 11 4
abc 2abc 2abc
abbcca abbcca
11 4
2
2abc 2abc
abbcca
121113
221
2abc 2 4 2 2
ac bc ab ac bc ab
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bài 20. Từ giả thiết
2222
abcd1
suy ra
0 a,b,c,d 1
.
Xét
2222
22
2 1 a 1 b 2 2a 2b 2ab
a b c d 2a 2b 2ab 2cd 2cd
ab1 cd 2cd2cd
Hay
1a1b cd.
Chứng minh tương tự ta được
1c1d ab
Nhân theo vế hai bất đẳng thức trên ta được
abcd 1a1b1c1d
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
abcd
2
.
Bài 21. Áp dụng bất đẳng thức Bunhiacopxki ta được

2
222 222 222
222
222222222
3a b 3b c 3c a
a2bc b2ca c2ab
3a b 3b c 3c a
3
a2bc b2ca c2ab
Mặt khác cũng theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
32 3
2 22 2 22 2 2 22
3a b
9a b 9a
1
a2bc abcb abc
Áp dụng tương tự ta được
222
222222222
222
222 222 222
3a b 3b c 3c a
a2bc b2ca c2ab
9a 9b 9c
312
abc bca cab
Do đó
2
222 222 222
3a b 3b c 3c a
3.12 26
a2bc b2ca c2ab
Hay
222 222 222
3a b 3b c 3c a
6
a2bc b2ca c2ab
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc
.
Bài 22. Từ giả thiết
a, b, c [0; 1]
, suy ra
0a,b,c1
.
Khi đó
2
1a 1b 0
hay
22
1ab a b. Áp dụng tương tự ta được
222222
3abbcca a b c abc 1
Mặt khác cúng từ giả thiết
0 a,b,c 1, ta được
23 2 3
23 2 3
23 2 3
aa a aa 2a
bb b bb 2b
cc c cc 2c
Cộng theo vế ba bất đẳng thức trên ta được
222 3 3 3
a b c a b c 2a 2b 2c 2
Từ kết quả của (1) và (2) ta được
222 333
3abbcca 2a b c
Hay
333 2 2 2
2a b c ab bc ca 3
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc1.
Bài 23. Bất đẳng thức cần chứng minh tương đương với
2
27 a b b c c a 64abc
Dễ dàng chứng minh được
9a b b c c a 8a b c ab bc ca
Nên ta được
22
ab bc ca 3abc ab bc ca 3abc a b c
Bất đẳng thức cuối cùng luôn đúng, do đó phép chứng minh hoàn tất.
Đẳng thức xảy ra khi và chỉ khi
abc
.
Bài 24. Áp dụng bất đẳng thức Cauchy cho vế trái của bất đẳng thức ta được

44 44 44
44 4444
222222
2a b 2b c 2c a
ab bcca
1 ab 1 bc 1 ca 2 2ab 2 2bc 2 2ca
abcbca
22ab 22bc 22ca 22ab 22bc 22ca
Sử dụng bất đẳng thức Bunhiacopxki và bất dẳng thức Cauchy ta được
2
222
2
2a b c
abc
22ab 22bc 22ca 222ab222bc222ca
2a b c
3
ab bc ca 9 2
Tương tự ta có
222
bca3
2
22ab 22bc 22ca
Cộng hai bất đẳng thức ta được
44 44 44
ab bc ca
3
1ab 1bc 1ca
Phép chứng minh hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc1.
Bài 25. Trước hết ta chứng minh bất đẳng thức sau: Với mọi số thức dương x, y, z ta có
3
333
1x 1y 1z 1xyz
Thật vậy, bất đẳng tương đương với
333333333333 222333
1 x y z xy yz zx xyz 1 3xyz 3xyz xyz
Hay
333333333 222
x y z x y y z z x 3xyz 3x y z
Áp dụng bất đẳng thức Cauchy ta được
333 333333 222
x y z 3xyz; x y y z z x 3x y z
Cộng theo vế các bất đẳng thức trên ta được
333333333 222
x y z x y y z z x 3xyz 3x y z
Vậy bất đẳng thức trên được chứng minh.
Áp dụng bất đẳng thức trên ta được
3
333 2
3
333 2
3
333 2
1a 1b 1b 1ab
1b 1c 1c 1bc
1c 1a 1a 1ca
Nhân từng vế của ba bất đẳng thức trên ta được
333 2 2 2
1a 1b 1c 1ab 1bc 1ca
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc.
Bài 26. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có
111 9
P
2ab 2bc 2ca abbcca6
Mặt khác, theo bất đẳng thức Cauchy ta có
222
abcabbcca
Do đó
222
99
P1
36
abc6
Bài toán được hoàn tất. Đẳng thức xảy ra khi và chỉ khi
abc1
.
Bài 27. Áp dụng bất đẳng thức Cauchy ta có
4444 34444 3
aaab4ab;bbba4ab
Suy ra
44443 333
2a 2b a b a b ab a b a b
Áp dụng tương tự và kết hợp với giả thiết
ab bc ca abc , ta được

44 44 44
33 33 33
ab bc ca abbcca
2ab 2bc 2ac
ab a b bc b c ac a b
ab bc ca
1
abc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
Bài 28. Bất đẳng thức cần chứng minh tương đương với
2
1
abbcca
108
Không mất tính tổng quát, ta giả sử
abc0.
Ta có biến đổi sau
3
2
3
22
2ab.2ab a b
abbcca abab
4
Áp dụng bất đẳng thức bất đẳng thức Cauchy ta có
3
2
3
2
3
66
3
2ab 2ab a b
2ab2ab a b
3
ab abc
4 4 108
4.3
Từ đó suy ra
2
1
abbcca
108
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
Bài 29. Áp dụng bất đẳng thức quen thuộc dạng
411
xy x y
, ta được
222 2
23 3222322 22
aa a a1111a
44a
abcaabcaabc a abc abc
Áp dụng tương tự ta được
222
abc1111
1
4a b c
abcbcacab
Ta cần chứng minh
111
1
abc
Thật vậy, Áp dụng một đánh giá quen thuộc và kết hợp với giả thiết, ta được
222
abc abbcca111
1
abc abc a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
abc3
Bài 30. Do
a, b, c [3; 5] , nên ta được
2
ab 2 ab 4
Khi đó ta được
2
22
4ab 4 a b 2ab a b
Hay
2ab 1 a b
Chứng minh tương tự ta được
2bc 1 b c;2ca 1 c a
Cộng theo vế các bất đẳng thức trên ta được
ab 1 bc 1 ca 1 a b c
Do dấu đẳng thức ở các bất đẳng thức trên không đồng thời xẩy ra.
Do đó ta được
ab 1 bc 1 ca 1 a b c
Vậy bất đẳng thức được chứng minh.
Bài 31. Đặt
x 2a; y 3b; z 3c
Biểu thức đã cho viết lại như sau

y z 2x z 4y 4z y z x x 2x z 4y 4x 4x 4z
P
x y xz x y xz
y x z x x z 4x 4y
5
x y x y xz xz
Áp dụng bất đẳng thức Cauchy ta được
y x z x 4x x z 4y
2; 4; 4
xy x xz y xz
Do đó ta được
P1055. Đẳng thức xẩy ra khi và chỉ khi
33
xyz 2a3b3c a b c
22
Vậy giá trị nhỏ nhất của biểu thức P là 5, đạt được tại
33
abc
22
.
Bài 32. Vì vai trò của a, b, c như nhau nên ta có thể giả sử c là số nhỏ nhất trong ba số a, b, c.
Khi đó ta được
22 22
1111
ab bc ca ab; ;
ba
bc ca
Do đó ta cần chứng minh
222
111
ab 4
ab
ab
hay
2
2
ab
ab
2
ab
ab
Đánh giá cuối cùng đúng theo bất đẳng thức Cauchy.
Đẳng thức xẩy ra khi và chỉ khi
22
2
c0
ab3ab
c0
ab a b
Bất đẳng thức được chứng minh.
Bài 33. Áp dụng giả thiết ta có biển đổi như sau
22 2
222 2
2
2
222
a3a 3a
b 2b 3 3b 3.2b 3
3b a b c .2b a b c
3a
a2bc2ac
Áp dụng bất đẳng thức Cauchy ta được
22
222
222
3a 3a
a2bc2ac
2a b c
Áp dụng tương tự ta được
222
222
222
222 222 222
abc
b2b3c2c3a2a3
3aaa3
22
abcabcabc
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1
Bài 34.
Cách 1: Đặt
2
abc3t 3 3 t 3 3
Ta có
2
242
2
242
23 t t 5 t
abc
abc6 3t 0
bca
t6t6
3t 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc1
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta được

2
abc
abc 3
2
b c a abbcca abbcca
Ta cần chứng minh bất đẳng thức sau
2
2
36
abc4 abc40
ab bc ca
abc 3
abc3 abc2 0
Bất đẳng thức cuối luôn đúng, do đó bài toán được chứng minh xong.
Đẳng thức xảy ra khi
abc1
Bài 35. Ta có biến đổi biểu thức như sau
22
33
2222
aba abb
ab
aabb aabb
Dễ dàng chứng minh được
2222
1
aabb aabb
3
Thật vật, bất đẳng thức trên tương đương với
2
22222 2
3 a ab b a ab b a 2ab b 0 a b 0
Áp dụng bất đẳng thức vừa chứng minh trên ta được
33
22
ab 1
ab
3
aabb
Áp dụng tương tự kết hợp với bất đẳng thức Cauchy ta được
33 33 33
3
222222
ab bc ca 2
Pabc2abc2
3
aabb bbcc ccaa
Vậy giá trị nhỏ nhất của P là
2
, đẳng thức xẩy ra khi
abc1
.
Bài 36. Áp dụng bất đẳng thức Cauchy ta được
2
22 22
11
2ab. a b a b 2ab a b
22
Suy ra
2
22
ab
ab. a b
22
Do đó ta được
33
33
2
22
2
22
2
22a b 7aba b
ab7abab
P
ab a b
ab a b
2 2 a b 4ab
22 a b a b 6ab
ab a b
ab a b
Mặt khác lại theo bất đẳng thức Cauchy ta được
2
a b 4ab 4 ab a b
Do đó ta có
2
2 2 a b 4ab
82.aba b
P82
ab a b ab a b
Vậy giá trị nhỏ nhất của P là
82. Đẳng thức xẩy ra khi và chỉ khi ab
Bài 37. Áp dụng bất đẳng thức Cauchy ta được
3
111 1
3
aab bbc cca abcabbcca

Ta cần chứng minh
3
2
19
abc a b b c c a
2a b c
Hay
6
8abc 729abcabbcca
Thật vậy, áp dụng bất đẳng thức Cauchy ta được
33
27abc a b c ; 27 a b b c c a 8 a b c
Nhân theo vế hai bất đẳng thức trên ta được
6
8 a b c 729abc a b b c c a
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
abc.
Bài 38. Ta có
2
22
22
2222
22 2 2 22 2 2
ab
11 4 4ab
abab
ab a b ab a b
Áp dụng bất đẳng thức Bunhiacopxki ta đươc
22
4
22 22
22
22 2 2 22 2 2 22 2 2 22 2 2
ab ab2ab
ab
4a b
ab a b ab a b 2ab a b 2ab a b
Ta cần chứng minh
4
22
4
22 2 2
32 a b
ab
2a b a b
ab
Thậ vậy, bất đẳng thức trên tương đương với
2
8
22 2 2
a b 64a b a b
Hay
4
22
ab 8aba b . Triển khai và thu gọn ta được
4
ab 0.
Bất đẳng thức cuối cùng đúng với mọi số thực a, b.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi
ab
.
Bài 39. Xét đẳng thức sau
333 222
222
abc3abcabcabcabbcca
3a b c ab bc ca
Từ đó suy ra
333 222
1
abc a b c a b c ab bc ca
3
Khi đó ta được
333
4
Pabcabbcca
3
Để ý ta thấy khi
abc3 thì
222
abc3
Áp dụng bất đẳng thức Cauchy ta được
33 233 233 2
a a 13a;b b 13b;c c 13c
Cộng theo vế các bất đẳng thức trên ta được
333 222 222
2abc 33abc 2abc 3
Nên ta được
333222
abcabc
Suy ra
2
222 222
41595
Pabcabbccaabc abc 7
32622
Vậy giá trị nhỏ nhất của biểu thức P là 7. Đẳng thức xẩy ra khi và chỉ khi
abc1.
Bài 40. Đổi biến
xa;y2b;z4c , khi dó ta được xyz12 và biểu thức P được viết lại thành
xy yz zx
P
xy yzzx

Áp dụng bất đẳng thức Cauchy ta được
222
xy yz zx
xy yz zx x y z
P6
xy yz zx 2
4x y 4y z 4z x
Vậy giá trị lớn nhất của P là 6. Đẳng thức xẩy ra tại
xyz4 a4;b2;c1
.
Bài 41. Giả sử
abc1
. Khi đó ta có
1a1b1c bccaab
Dễ dàng chứng minh được
a b b c c a 8abc.
Do đó ta có
8abc 8abc
vô lí. Vậy
abc1
.
Bài 42. Áp dụng bất đẳng thức Cauchy ta có
864 b 4 3 4 4
3a 2b c a 2 a b c
abc 2 a 2 b c
b3 2ab
a 2.4 .4 4 18
22 2
Mặt khác ta lại có
22222 22
321 9
3abca2b3cac2bc 2ab2bc
2ab2ab
Do đó ta được
2a b 6, suy ra
2a b
18 21
2
.
Từ đó ta được
864
3a 2b c 21
abc
. Bất đẳng thức được chứng minh.
Bài 43. Ta có
111
abcabc 1
ab bc ca
. Ta viết lai biểu thức P thành
222
22 22 22
a1b1 1 b1c11 c1a1 1
P
bca
bca
11 11 11
a1 b1 c1
ab bc ca
Do đó áp dụng bất đẳng thức Cauchy ta được
2a 1 2b 1 2c 1
111 1 1 1
P22
ab bc ca a b c ab bc ca
Dễ thấy
111 1 1 1
33
abc abbcca
. Do đó ta được P32.
Vậy giá trị nhỏ nhất cỉa P là
32 , đẳng thức xẩy ra khi abc 3
Bài 44. Bất đẳng thức tương đương với
222
bc ca ab
1
2a bc 2b ca 2c ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức để chứng minh bất đẳng thức trên.
Bài 45. Từ giả thiết
abc1
ta suy ra
1
abc
27
.
Bất đẳng thức cần chứng minh tương đương với
1ab1bc 1bc1ca 1ca1ab
27
8
1ab1bc1ca
Hay
222
3 2 ab bc ca abc a b c
27
8
1abbccaabcabcabc

Hay
222
832abbcca abc 271 abbcca abcabc
Hay
222
222
311abbcca 19abc27abc 0
4 3 19abc 27a b c 11.4 ab bc ca
Từ bất đẳng thức quen thuộc
abcbcacab abc
suy ra
12a12b12c abc
Hay
11.4 ab bc ca 11. 1 9abc
Ta cần chứng minh
222
4 3 19abc 27a b c 11 1 9abc
Thật vậy, bất đẳng thức trên tương đương với
1 27abc 1 4abc 0
Bất đẳng thức cuối cùng đúng do
1
abc
27
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
1
abc
3
Bài 46.
Đặt
xabc 3ayx
ybc4a 15b zx
z c a 16b 15c 21x 5y z
Khi đó biểu thức P được viết lại là
6x 5y z 20x 5y 16x z y 3x z 16x 4
P
15x 15y 15z 3x 4y 15x 15z 5
Áp dụng bất đẳng thức Cauchy ta có
y4x4z 16x8
;
3x 3y 3 15x 15z 15
Do đó ta được
48416
P
315515
. Đẳng thức xẩy ra khi và chỉ khi
5c 3c
a;b
77
Vậy giá trị nhỏ nhất của P là
16
15
, đẳng thức xẩy ra khi và chỉ khi
5c 3c
a;b
77
.
Bài 47. Từ giả thiết
abc1
ta có
2
2222
1c abc c a b 2abbcca 2abbc 2abca
Mặt khác áp dụng bất đẳng thức Bunhiacopxki ta được
ab 1 ab ab
4
2abbc 2abca 2abbc 2abca
Do đó ta có
2
ab 1 ab ab
8abbc abca
1c
Áp dụng tương tự
22
bc 1 bc bc ca 1 ca ca
;
8bc ca ab bc 8ca ab bc ca
1a 1b
Cộng theo vế các bất đẳng thức trên ta được
222
ab bc ca
1c 1a 1b
1ababbcbccaca3
8abbc abca bcca abbc caab bcca 8

Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc
Bài 48. Bất đẳng thức cần chứng minh được viết lại thành
222
abc
ab bc ca 2a 2b 2c
ab bc ca
Hay
2ab 2bc 2ca
ab bc ca
ab bcca
Áp dụng bất đẳng thức Cauchy ta được
2ab 2ab 2bc 2bc 2ca 2ca
ab; bc; ca
ab bc ca
2ab 2bc 2ca
Cộng theo vế các bất đẳng thức trên ta được
2ab 2bc 2ca
ab bc ca
ab bcca
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc.
Bài 49. Áp dụng bất đẳng thức Bunhiacopxki a được
2
222
abc
abc
P
1abbc 1bcca 1caab
32abbcca
Để ý ta thấy, do
222
abc3 nên ta có
2
32abbcca abc
Suy ra
2
abc
1
32abbcca
Do đó ta được
222
abc
P1
1abbc 1bcca 1caab
Vậy giá trị nhỏ nhất của biểu thức P là 1.
Đẳng thức xẩy ra khi và chỉ khi
abc1
Bài 50. Áp dụng bất đẳng thức Cauchy ta được
3
3
33
3 3.9ab 1 6ab
1 4 9bc 6ab
6b
a
9 abc 9 abc
Áp dụng tương tự ta được
33
33
149ca6bc149ab6ca
6c ; 6a
bc
9abc 9abc
Cộng theo vế các bất đẳng thức trên ta được
333
33
12 15 ab bc ca
111 3
6b 6c 6a
abc
9abc abc
Ta cần chứng minh
3
31
abc
abc
hay
2
3
3abc 1
Bất đẳng thức cuỗi cùng luôn đúng. Vì từ giả thiết ta được
2
3
3
1abbcca3ab.bc.ca 3abc
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Bài 51. Không mất tính tổng quát ta giả sử
1abc0.
Khi đó ta có
aa cc
;
ab 1 bc 1 ca 1 bc 1
Suy ra

1bc 1b1c bc
abcabc
2
ab 1 bc 1 ca 1 bc 1 bc 1
Mặt khác ta lại có
ab bc ca ab bc ca
1113
ab 1 bc 1 ca 1 ab 1 bc 1 ca 1
1a1b 1b1c 1c1a
3
ab 1 bc 1 ca 1
3
Cộng theo vế hai bất đẳng thức trên ta được
abcabcabc
5
ab 1 bc 1 ca 1
Hay
111 5
ab 1 bc 1 ca 1 a b c
Bất đẳng thức được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
ab1;c0
và các hoán vị.
Bài 52. Do a, b, c là các số thực dương thỏa mãn
abc1 nên
0a,b,c1
.
Suy ra
1a,1b,1c 0
Áp dụng bất đẳng thức quen thuộc
11 4
xyxy
ta được
11 4 4
1a 1b 2ab 1c
Chứng minh tương tự ta có
11411 4
;
1b 1c 1a1c 1a 1b
Cộng theo vế các bất đẳng thức trên ta được
111222
1a 1b 1c 1a 1b 1c
Bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi
1
abc
3
.
Bài 53. Không mất tính tổng quát ta giả sử
1abc0
, khi đó ta có
a1
abc 3
.
Áp dụng bất đẳng thức Cauchy ta được
3
31b1c1bc 31b1c1bc
Suy ra
11b1c1bc
Do đó ta được
1a 1a1b1c1bc
Hay
1a
1a1b1c
1bc
Mặt khác ta lại có
1a 1a
abc 1bc
Nên ta được
1a
1a1b1c
abc
Suy ra
1a1
1a1b1c 1a1b1c
abc abc 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra khi và chỉ khi
abc1

Bài 54. Áp dụng bất đẳng thức Cauchy ta có
33 33 33 33 22
3
33
4ab ab 3ab ab 3ababab
ab 3abab ab
Do đó ta được
33
3
4a b a b
Áp dụng tương tự ta được
33 3 3
33
4b c b c; 4c a c a
Từ đó ta có bất dẳng thức sau
33 33 33
333
22 2
22 2
abc
P4ab 4bc 4ca 2
bca
abc
2a b c
bca
Áp dụng bất đẳng thức Cauchy ta được
3
22 2
3
abc 3
abc 3abc 6
bca
abc
Suy ra
P12 . Vậy giá trị nhỏ nhất của P là 12.
Đẳng thức xẩu ra khi và chỉ khi
abc1
Bài 55.
Cách 1: Đặt
x2a3b3c;y3a2b3c;z3a3b2c .
Khi đó bất đẳng thức cần chứng minh tương đương với
7x y y z z x 42
8y x z y x z 8
Bất đẳng thức trên đung do
xyyzzx
6
yxzyxz
.
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra tại
abc.
Cách 2: Biến đổi vế trái của bất đẳng thức trên ta được
ab3c a3bc 3abc
3a 3b 2c 3a 2b 3c 2a 3b 3c
7c b a
1
33a3b2c 3a2b3c 2a3b3c
111
17abc
3a 3b 2c 3a 2b 3c 2a 3b 3c
915
17abc
8
8a b c
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra tại
abc.
Bài 56. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2 2 222
2
ab ab 1 ab ab ab 1
2ab a
2abaab9aaa 9
Áp dụng tương tự ta được
2
222
abc
ab bc ca
1
2a b 2b c 2c a 9
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra tại
abc1.
Bài 57.
Cách 1: Biến đổi tương đương bất đẳng thức cần chứng minh trở thành
22 2
22 2 2 2 2
ab b b c bc a c a ca b a b
0
bc ca ab
Bất đẳng thức trên hiển nhiên đúng. Do đó bài toán được chứng minh.

Cách 2: Quy đồng và phá dấu ngoặc ta được
33 33 33 22 22 22
33 33 33 2 2 2
2ab bc ca ab bc ca bc ca ab ca ab bc
2 a b b c c a abc bc ca a bc ca ab ab c ab bc
Áp dụng bất đẳng thức quen thuộc
33
xyxyxy ta được điều phải chứng minh.
Bài 58. Áp dụng bất đẳng thức Cauchy ta có
4
2
32
5
3
22 22
222
5
2abcbc
bc
aabc.
2
2
8a b c
ab ac
a.2 b c .
2
2.27
Áp dụng tương tự ta được
444
2
3 3 3 22 2222 2 22
bc ca ab 1
a b c abbcca abc
222 3
Vậy bất đẳng thức được chứng minh. Đẳng thức xẩy ra tại
abc1
.
Bài 59. Áp dụng bất đẳng thức Cauchy ta có
2
22
22 22
4abbccab c bc abbccabcb c bc abc
Suy ra
22
22 2
abc 4aabbcca
bbcc
bcabc
, áp dụng tương tự ta được
222
222
22222 2 2
abc bab cab 4abbcca
abc
bc ca ab
bbcc ccaa aabb
abc
Ta cần chứng minh
222
222
abca b c
abc
bc ca ab
2ab bc ca
Hay
3
222
abc
abc
abc
bc ca ab
2ab bc ca
Hay
3
222
abc
abc
abc
bc ca ab
2ab bc ca
Bất đẳng thức trên tương đương với
2
abc
abc
bc ca ab
2ab bc ca
Bất đẳng thức cuối cùng đúng theo bất đẳng thức Bunhiacopxki dạng phân thức.
Vậy bài toán được chứng minh.
Bài 60.
Cách 1: Áp dụng bất đẳng thức Bunhiacopxki ta có
222 222
111 111
11133
abc abc
Ta cần chứng minh được

222
2
222
2222
222 222
111 111
333
ab bc ca
abc
111 111
333
ab bc ca
abc
abc 3 ab bc ca
00
abc abc
Bất đẳng thức cuối cùng đúng. Vậy bài toán được chứng minh xong.
Cách 2: Kết hợp với giả thiết ta có
222
22
111 111 abbcca
ab bc ca 3
ab bc ca ab bc ca b a c b a c
1abacbcbacacb 1abbcca
3 3
2a a b b c c 2bacbac
abac bcba cacb 1
3. . ..63
aa bb cc2
aabbcca aabbcca aab
3
aa
2
222
222 222
bc ca
a
a1 b1 c1 1 1 1
33111
abc abc
Vậy bất đẳng thức được chứng minh.
Bài 61. Áp dụng bất đẳng thức Cauchy ta có
2222 2
11 4 8
a b b c a 2b c 2a 2b 2b 2c
88
a1b1b1c1b7
Hoàn toàn tương tự
22
11 811 8
;
bc ca ca ab
c7 a7
Cộng theo vế ba bất đẳng thức trên ta được điều phải chứng minh.
Bài 62. Ta có
2
c 6ab c a b c 6ab ab bc ca c 2ab 3ab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
ab 1 ab ab 1
c6ab 9abbcca 3
c2ab
Hoàn toàn tương tự
222
ab bc ca 1 ab bc ca
2
c6ab a6bc b6ca 9
c2aba2bcb2ca
Phép chứng minh hoàn tất nếu ta chỉ ra được
222
222 222
ab bc ca c b c
11
c2aba2bcb2ca c2aba2bcb2ca
Bất đẳng thức cuối cùng đúng theo bất đẳng thức Bunhiacopxki dạng phân thức.
Vậy bài toán được chứng minh.
Bài 63. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
222
abc
abc
ab bc ca abc a b c
b1 a c1 b a1 a

Để ý là
2
2
ab bc ca
a b c 3 ab bc ca 3; abc a b c 3
3
Ta được
2
abc
9
4
ab bc ca abc a b c
. Suy ra bất đẳng thức được chứng minh.
Bài 64. Áp dụng bất đẳng thức Bunhiacopxki ta được
22 2
ab111c abc
Do đó ta được
22
22 2
22 2
111c2c
ab1
ab111c
abc
Hoàn toàn tương tự ta được
222
22 22 22 2
1116abc
1
ab1bc1ca1
abc
Hay
ab bc ca 3. Vậy bất đẳng thức được chứng minh.
Bài 65. Áp dụng bất đẳng thức Cauchy ta có
b5b2323b2 .
Hoàn toàn tương tự ta được
222 2 2 2
abc 1a b c
b5 c5 a5
23 b 2 c 2 a 2
Áp dụng bất đẳng thức Bunhiacopxki ta được
222
333
abc abc
abc
b2 c2 a2
b2 c2 a2
Ta quy bài toán về chứng minh.
222 222
abc
1acbacb2abc 8abc
b2 c2 a2
Dễ dàng chứng minh được
222 2 2 2
abc3;acbacb2abc
Bất đẳng thức được chứng minh xong.
Bài 66.
Cách 1: Dễ thấy
2
9abc a b c 3 ab bc ca 3abc ab bc ca
Đặt
111
x;y;z xyz3xyyzxz3
abc
.
Bất đẳng thức được viết lại thành
222
xyz3
2
x3 y3 z3
Áp dụng bất đẳng thức Cauchy ta được
22
xx x1xx
2x y z x
x3 xxyyzzx
xyzx
Hoàn toàn tương tự ta được
222
xyz3
2
x3 y3 z3
.
Vậy bất đẳng thức được chứng minh.
Cách 2: Đặt
axy;byz;czx
khi đó giả thiết trở thành
2
222
9x y z xy yz zx 3xyz xy yz zx và
xyz 1
.
Khi đó vế trái được viết lại thành

22 22 22 2 222 2 222 2 222
222
111 x y z
13yz 13zx 13xy x 3xyz y 3zxy z 3xyz
xyz
x 3xyz y 3xyz z 3xyz
Ta quy bài toán về chứng minh
222
xyz3
2
x 3xyz y 3xyz z 3xyz
Đến đây chú ý đến
3xyz xy yz zx ta chứng minh được bất đẳng thức tương tự như cách 1
Bài 67. Từ giả thiết
abc 1
, ta đặt
xyz
a;b;c x;y;z0
yzx
. Khi đó bất đẳng thức được viết
lại thành
222
xyz
1
x 8yz y 8zx z 8xy
Bất đẳng thức trên chính là bất đẳng thức ở bài 27.
Bài 68.
Cách 1: Áp dụng bất đẳng thức Cauchy ta có
222
111 9 9 3
1 ab 1 bc 1 ca 3 ab bc ca 5
3a b c
Bất đẳng thức được chứng minh
Cách 2: Áp dụng bất đẳng thức Cauchy ta có
11ab2
1ab 25 25
Áp dụng tương tự ta được
11163abbcca
1ab 1bc 1ca 5 25
Ta quy bài toán về chứng minh
ab bc ca 12
. Bất đẳng thức cuối cùng đúng do
222
ab bc ca a b c 12
Bất đẳng thức được chứng minh.
Bài 69. Từ giả thiết ta có
3
222 222
31
abc3abc abc
48
Áp dụng bất đẳng thức Cauchy ta được
333
111
abbcca
abc
3123
8abc 8abc 2 23 25
abc 8abc 8abc
Bất đẳng thức được chứng minh.
Bài 70. Áp dụng giả thiết và bất đẳng thức Bunhiacopxki ta có
ab c a b c b c c a
ab ab c ac bc
1ab
cc c c
c
Hoàn toàn tương tự ta có bất đẳng thức cần chứng minh.
Bài 71. Chú ý đến
22
a2a112a1
.
Áp dụng tương tự ta quy bài toán về chứng minh
2a b c 6 .
Bài 72. Để ý là
22
22 22 22
ab a b
ab 2ab
ab ab ab
, áp dụng tương tự ta quy bài toán về chứng minh
22 2222
2ab 2bc 2ca
1
abbcca

Bất đẳng thức trên tương đương với
222
22 22 22
ab bc ca
4
ab bc ca
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 2
22 22 22 222
222
ab bc ca 4abc 4abbcca
24
ab bc ca abc
2a b c
Bất đẳng thức được chứng minh.
Bài 73. Từ giả thiết ta được
1
abc
33
Áp dụng bất đẳng thức Cauchy ta có
3
111 3 111
33 2 63
abc abc
abc
Áp dụng bất đẳng thức Cauchy ta lại có
3
3
111 1
3a b c 3 3.abc 6 3
abc
abc
Cộng thoe vế hai bất đẳng thức trên và thu gọn ta được
111
abc43
abc
Bất đẳng thức được chứng minh.
Bài 74. Giả sử a là số lớn nhất trong ba số a, b, c suy ra
1
a1
3
.
Khi đó biến đổi tương đương ta chứng minh được
22
2
22 2
b1c1 1
bc 1
c1a1 a1
và
2
2
2
a1
a1
b1
Từ đó ta quy bài toán về chứng minh
3
2
2
2
2
1a13a 4a
17
abc 2 0
2
a1
2a 1
Bất đẳng thức cuối cùng luôn đúng. Vậy bài toán được chứng minh.
Bài 75. Bất đẳng thức cần chứng minh tương đương với
222
2
a22bcb22cac22ab
3
Ta có
22222246
a22bc a2 b c a1a a a
Hoàn toàn tương tự ta được
222 464646
a22bcb22cac22ab a a b b c c
Ta có
22
4 6 4 6 46 2 22 3 33
2
333 333
aa bb cc abc abc
21 2 2
abc abc
33 3
3
Áp dụng bất đẳng thức Bunhiacopxki ta được
22
222 222
333
222
abc abc
1
abc
abc
3
3a b c
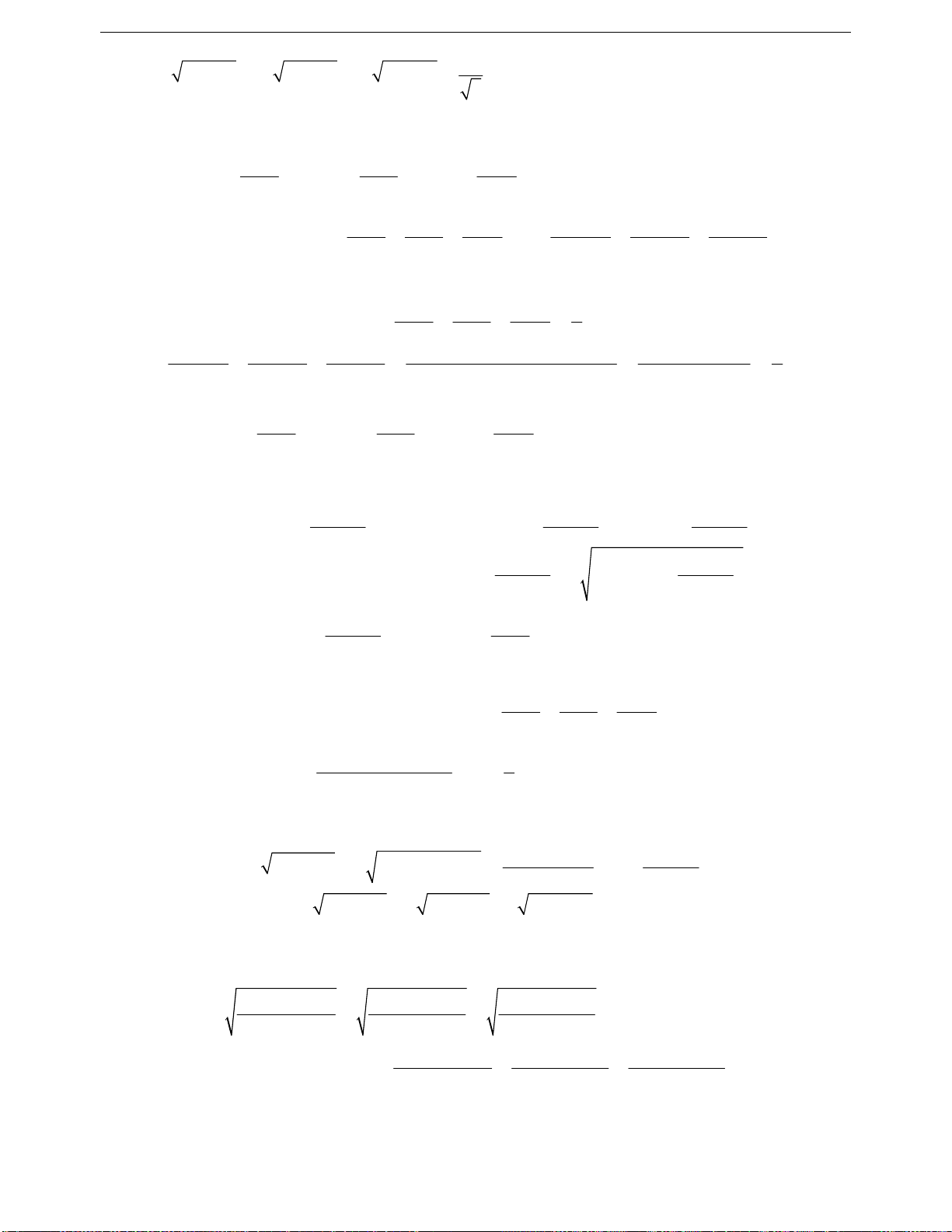
Suy ra
222
2
a22bcb22cac22ab
3
Bất đẳng thức được chứng minh.
Bài 76. Ta có
222
222
222
222
3a 3b 3c
bc ca ab
abc 1 1 1
9a b c 12 4
bc ca ab
ab bc ca
Theo bất đẳng thức Neibizt và bất đẳng thức Bunhiacopxki ta có
222 222
222
abc3
bc ca ab 2
111 9 9 3
4
4a b c
ab bc ca ab bc ca
Suy ra ta được
222
222
3a 3b 3c 48
bc ca ab
.
Bất đẳng thức được chứng minh.
Bài 77. Áp dụng bất đẳng thức Cauchy ta có
2222
22
3
222
6a 6a 5 5 a 1 6a a 4a a
ab ac ab ac ab ac
22
2a 2a a 3 2a.2a a
ab ac ab ac
Do đó ta được
3
24
28a
6a 6a 5 27 4a
ab ac b c
Hoàn toàn tương tự ta được
444
2
222
abc
P 108 a b c 216
bc ca ab
108 a b c
3
216. 648
32
Vật giá trị nhỏ nhất của P là 648, đẳng thức xẩy ra tại
abc1
.
Bài 78. Áp dụng bất đẳng thức Cauchy ta được
3
3
a3 b c
ab ca
a1bc a1.1.1bc a
33
Hoàn toàn tương tự ta được
333
a1 b c b1 c a c1 a b 1 .
Bất đẳng thức được chứng minh.
Bài 79. Bạn đọc tự giải
Bài 80. Áp dụng bất đẳng thức Bunhiacopxki ta được
2
22 22 22
22 22 22
ab bc ca
2a 3b 7 2b 3c 7 2c 3a 7
ab bc ca
3
2a 3b 7 2b 3c 7 2c 3a 7
Từ
abc3
suy ra
ab bc ca 3
.
Áp dụng bất đẳng thức Cauchy ta được

22
22
ab ab ab ab 1 1
4a 6b 2 4 6b 4a 2
2a 3b 7
2a 1 3b 1 2
Lại có
111111111
4a2 2a2a2 92a 2a 2 9a 2
Do đó ta được
22
ab a b ab
24 36 72
2a 3b 7
Hoàn toàn tương tự ta được
22 22 22
ab bc ca
2a 3b 7 2b 3c 7 2c 3a 7
abcabcabbcca3331
24 36 72 24 36 72 4
Suy ra
2
22 22 22
ab bc ca 3
4
2a 3b 7 2b 3c 7 2c 3a 7
Hay bất đẳng thức được chứng minh
Bài 81. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
23
2
3
22
abc abc
abc
1bc 1ca 1ab abc3abc
abc 3abcabc
abc
abc abbcca
Từ giả thiết và áp dụng bất đẳng thức Cauchy ta được
223
a b c 9;ab bc ca 9;a b c 27abc
Do đó ta được
abc3
abc
1bc 1ca 1ab 2
Bất đẳng thức được chứng minh.
Bài 82. Áp dụng bất đẳng thức Bunhiacopxki ta được
22 3322
aba abb aba b a b
Do đó ta được
22
22
aabb 1
ab
ab
, hoàn toàn tương tự ta được
222222
22 22 22
aabb bbcc ccaa
ab bc ca
111 9 3
ab bcca 2
2a b c
Bất đẳng thức được chứng minh.
Bài 83. Đặt
111
x;y;z
abc
, khi đó giả thiết được viết lại thành
xy yz zx 1
.
Suy ra
xyz 3
Bất đẳng thức cần chứng minh trở thành
xyz33
yz 1 zx 1 xy 1 4
Áp dụng bất đẳng thức Bunhiacopxki ta được

23
2
33
22 2
xyz xyz
xyz
yz 1 zx 1 xy 1 3xyz x y z
3xyz x y z x y z
xyz xyz
xy yz zx x y z 1 x y z
Đặt
txyz 3 , khi đó dễ dàng chứng minh được
3
2
t33
4
1t
Vậy bất đẳng thức được chứng minh.
Bài 84. Bạn đọc tự chứng minh
Bài 85. Nếu
x, y, z 0, x y
thì
xxz
yyz
Do đó
11 1 bc
a
3a b 3a c 2a b c 3a c 3a b
ac ab 2a 2a2b 2a2c 4a
2
3a b 3a c 2a b c 4a b c 4a b c 4a b c
Bài toán được chứng minh xong.
Bài 86. Đặt
xyz
ak;bk;ck
yzx
. Khi đó bài toán quy về chứng minh
2223
yz zx xy 3
kzx k xy kxy k yz kyz k zx 1 k
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta chứng minh được bài toán.
Bài 87. Để ý ta thấy
2
2
22
22
ac ca b
aab
ab bc ca
bcbc
ab bc ca b c bc
Do đó bất đẳng thức cần chứng minh tương đương với
222
22 2 2 2 2
ac ca b ab ab c bc bc a
0
bcbccacaabab
Lại thấy
2
2
22 22
ac ca b
ca a b c
ca
bcbc bcbc
, do đó ta viết lại bất đẳng thức cần chứng minh thành
22 2
22 2 2 2 2
ca ab bc ab bc ca
abc
bcbccacaabab
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 2
22 2 2 2 2
2
22 2 2 2 2
ca ab bc
bcbccacaabab
ab bc ca
ab cb ca
abc
ab c bc bc a ca ca b ab
Vậy bất đẳng thức được chứng minh.
Bài 88. Áp dụng bất đẳng thức Cauchy ta có
22 2
aa a aa
9a 1 3a 1 6a
26a3a 1 263a 1
Do đó ta được

2
2
222
abc aa bb cc
24 6
9a 1 9b 1 9c 1
63a 1 63b 1 63c 1
Áp dụng bất đẳng thức Bunhiacopxki ta được
2
333
aa bb cc a b c a b c
63a13b13c1
63a 1 63b 1 63c 1
Suy ra ta được
333 222
abc abc
24
3a 1 3b 1 3c 1 9a 1 9b 1 9c 1
Vậy bất đẳng thức được chứng minh.
Bài 98. Bất đẳng thức cần chứng minh tương đương với
6ab a b 6bc b c 9ca c a 5 a b b c c a
4c a
abbc
ab a b bc b c 4ca c a 10abc 10
ca b
Áp dụng bất đẳng thức Cauchy ta được
4c a
abbc a c b 4c b4a
10
ca bcacbab
Vậy bất đẳng thức được chứng minh.
Bài 90. Dễ dàng chứng minh được
44 33
2a b aba b , do đó ta có
44
33
ab ab111
2ab 2 a b
ab a b
Hoàn toàn tương tự ta được
44 44 44
33 33 33
ab bc ca 111abbcca
1
abc abc
ab a b bc b c ca c a
Bất đẳng thức được chứng minh.
Bài 91. Áp dụng bất đẳng Bunhiacopxki ta có
22 22 22
22 22 22
2ab bc ca
ab 2ab bc 2bc ca 2ca
222
ab ab bc bc ca ca
ab bc ca 2ab 2bc 2ca
ab bc ca ab bc ca
Bài toán quy về chứng minh
2ab 2bc 2ca
3
ab bc ca
Giả thiết được viết lại thành
111
3
abc
. Đặt
111
x;y;z xyz3
abc
.
Bất đẳng thức trên trở thành
222
3
xy yz zx
Áp dụng bất đẳng thức Bunhiacopxki và kết hợp với
xyz3
, ta có
222 92 92
3
xy yz zx
xy yz zx
3.2 x y z
Vậy bất đẳng thức được chứng minh.

Bài 92. Ta có
2
22
22 22
ab
ab
2
abab abab
. Khi đó áp dụng tương tự ta được
22 22 22
22 22 22
222
22 22 22
ab bc ca
ababbcbccaca
ab bc ca
6
ababbcbccaca
Bài toán quy về chứng minh.
222
222
222 22 22
6a b c
ab bc ca
6
ababbcbccaca
abc
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
222 2
22 22 22
222
ab bc ca 4abc
ababbcbccaca
2a b c ab bc ca
Ta cần chứng minh được
2
222
2
222
6a b c
4a b c
6
2a b c ab bc ca
abc
Đặt
222
xa b c;yabbcca xy
và bất đẳng thức trên trở thành
4x 2y 4x 2y 42x y
6x
68
2x y x 2y 2x y x 2y
Bất đẳng thức cuối cùng đúng theo bất đẳng thức Cauchy.
Vậy bất đẳng thức được chứng minh.
Bài 93. Áp dụng bất đẳng thức Cauchy ta có
22 22
3
2
52 2
81a b c 81a b c
1279
884a
ab c
Cũng theo bất đẳng thức Cauchy ta lại có
3
3
27 9 81
4a
2
4a
3
Do đó ta được
22 22
2
52 2
3
81a b c 81a b c
181
88
2
ab c
4a
3
Áp dụng tương tự ta được
222
52 2 52 2 52 2
222222
333
111
ab c bc a ca b
81 a b ab b c bc c a ca
81 81 81
4
222
4a 4a 4a
333
Lại áp dụng bất đẳng thức Cauchy ta được

332
333
222222 333
81 81 81 81.9 243
4
222
4a b c 8
4a 4a 4a
333
81 a b ab b c bc c a ca 81.2 a b c
162
444
Suy ra
222
52 2 52 2 52 2
1 1 1 243 162 81
444
ab c bc a ca b
Vậy bất đẳng thức được chứng minh.
Bài 94. Áp dụng bất đẳng thức Cauchy ta có
2
2
b4
b2b b2
2
Do đó ta được
2
2
a2a
b4
b2b b2
. Áp dụng tương tự ta được
222
22 2
abc
b2b b2 c2c c2 a2a a2
2a 2b 2c
b4c4a4
Ta cần chứng minh được
22 2
abc3
4
b4c4a4
.
Đến đây áp dụng kỹ thuật Cauchy ngược dấu để chứng minh bất đẳng thức trên.
Bài 95. Bất đẳng thức cần chứng minh tương đương với
3
2a b c
111
abc
2a b 2b c 2c a
abbcca
Ta có
111
abc
2a b 2b c 2c a
cab1bca3
2a b 2b c 2c a 2 2a b 2b c 2c a 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
2
2
222
abc
cab
2a b 2b c 2c a
3ab bc ca
abc
bca
1
2a b 2b c 2c a
abc2abbcca
Như vậy ta cần chứng minh được
2
3
abc 2abc
2
3ab bc ca
abbcca
Mà theo bất đẳng thức Cauchy ta có
22
3
abc abc
23
3ab bc ca 3ab bc ca
Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được

2
3
3
abc 2abc
3
3ab bc ca
abbcca
Hay
9a b b c c a 8a b c ab bc ca
Đây là một đánh giá đúng. Vậy bất đẳng thức được chứng minh.
Bài 96. Không mất tính tổng quát, giả sử a là số lớn nhất trong ba số trên.
Từ giả thiết
abc3
, suy ra
1a3
.
Bất đẳng thức cần chứng minh tương đương với
222
111
8 42 a b c 117 10 a b c
abc
Hay
222
869 869 8
10b 42b 10c 42c 10a 42a 48
b2 c2 a
Hay
222
2b 1 16 5b 2c 1 16 5c a 2 20a 4
bca
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta được
22 22
22
2b 1 16 5b 2c 1 16 5c 2b 1 2c 1
bcbc
16 5b 16 5c
2b 2c 2 4 a 2
bc bc
16 5b 16 5c 16 5b 16 5c
Ta cần chứng minh
22 2 2
4a 2 a 2 20a 4 a 2 a 2 5a 1
bc a bc a
16 5b 16 5c 16 5b 16 5c
Thật vậy, vì
ab;ac, do đó ta có
bcbc3a
16 5b 16 5c 16 5a 16 5a 16 5a
Cho nên
222
a2 a2 a2 165a
b c 3a 3a
16 5b 16 5c 16 5a
Bây giờ ta cần chỉ ra được
22
a2 165a a2 5a1
3a a
Đánh giá trên tương đương với
22
a2 165aa a2 5a13a
Hay
2
3a 2 0
, đánh giá cuối cùng luôn đúng với mọi a.
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
1
a2;bc
2
và các hoán vị của nó.
Bài 97. Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta được
444 222
22 2
abc1abc
3b 1 c 1 a 1
b1 c1 a1
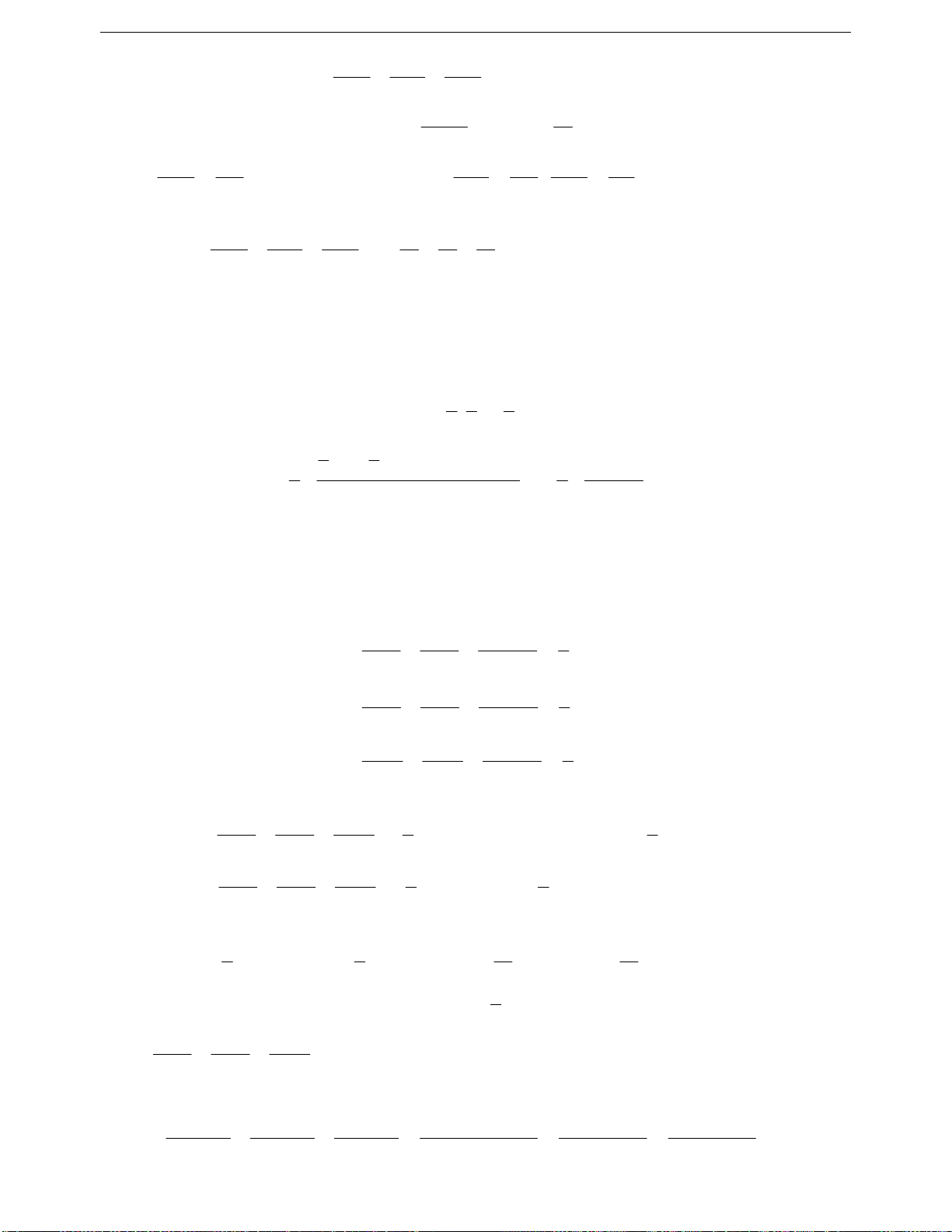
Ta cần chứng minh
222
abc
12
b1 c1 a1
Thật vậy, ta có
22
2
b4 b
b2 0 b b1
44
Do đó
24
2
a4a
b1
b
. Áp dụng tương tự ta được
2222
22
b4bc4c
;
c1 a1
ca
Công theo vế các bất đẳng thức trên ta được
222 222
22 2
abc abc
44.312
b1 c1 a1
bca
Vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại
abc2.
Bài 98. Giả sử
amina,b,c.
ta có bc3c3.
Sử dụng bất đẳng thức AM-GM ta có:
22 2 2
22 22 2 2
3
3
2
22
P aab b b bcc aac c
43 3
bb bc cc .bc.bcb bc c
92 2
33
bc bc b bc c
bc
44
22
..12
93 93
Đẳng thức xảy ra khi
a 0, b 2, c 1
và các hoán vị.
Vậy giá trị lớn nhất của P là 12.
Bài 99.
Cách 1. Sử dụng bất đẳng thức Cauchy ta có
2
33
2
2
33
2
2
33
2
yz
xx 3
x
yz yz 8 2
zx
yy 3
y
zx zx 8 2
zy
zz 3
z
xy xy 8 2
Cộng vế với vế các bất đẳng thức trên, ta có:
333
222 222
333
222
xyz1 3
2 x y z xy yz zx x y z
yz zx xy 4 2
xyz5 1
2 x y z xy yz zx
yz zx xy 4 4
Mặt khác ta có
22
222
2
51 51
xyz xyyzzx xyz xyz
4 4 12 12
1
xyz 12
3
.
Do đó
333
xyz
6
yz zx xy
. Bài toán được chứng minh xong.
Cách 2: Áp dụng bất đẳng thức Bunhiacopxki ta có
2
2
222
444 222
xyz
xyz
xyz xyz
6
26
x y z y z x z x y 2 xy yz zx

Do đó
333
xyz
6
yz zx xy
. Bài toán được chứng minh xong.
Bài 100. Sử dụng bất đẳng thức Cauchy ta có
222 2 2 2
66
3
66
3
2
3
3
6
3
a 8 b 8 c 8 a 8abc b 8abc c 8abc
abc abc
abc8abbcca
a 8bc b 8ca c 8ab
abc 27abc
8
abc abc
3
11 8118
1
27 a b c 3 27 3
abc
27 a b c
Do đó
6
222
a8b8c8 abc. Bài toán được chứng minh xong.
Bài 101. Đặt
111
x,y,z
abc
===
thì giả thiết được viết lại là a + b +c = 3
Khi đó ta có:
222222
22 22 22 2 2 2
222
333
22 22 22
222
yxzabc
xy 2x xz 2z yz 2y a 2b b 2c c 2c
2ab 2bc 2ca 2
abc abc ab bc ca
3
a2b b2c c2c
Sử dụng bất đẳng thức Cauchy ta có
3
3
22
ab ab 1
ab ab.ab.1
3
Tương tự
33
22 2 2
bc bc 1 ca ca 1
bc ; ca
33
Từ đó ta có
333
22 22 22
22
abc ab bc ca abc 2ab2bc2ca3 1
39
Bài toán được chứng minh xong.
Bấm Tải xuống để xem toàn bộ.




