






























































Preview text:
lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
VÍ DỤ & BÀI TẬP
LÍ THUYẾT XÁC SUẤT
Trong Kinh tế và Tài chính Các kí hiệu Kí hiệu Tên gọi, ý nghĩa ∅
Rỗng, biến cố không thể có Ω
Không gian biến cố sơ cấp P Độ đo xác suất F σ-đại số (Ω, F, P ) Không gian xác suất A ∩ B; Tn A Tích các biến cố i=1 i A ∪ B; Sn A Tổng các biến cố i=1 i (A | B) Biến cố có điều kiện P (A | B) Xác suất có điều kiện A Biến cố đối lập F (x) Hàm phân phối xác suất P (x)
Hàm khối lượng xác suất f (x) Hàm mật độ xác suất F (X | y)
Hàm phân phối xác suất có điều kiện P (X | y)
Hàm khối lượng xác suất có điều kiện f (X | y)
Hàm mật độ xác suất có điều kiện
F (x1, ..., xn); FX(x) Hàm phân phối xác suất đồng thời f (x1, ..., xn); fX(x)
Hàm mật độ xác suất đồng thời E(X) Kì vọng E(X | y) Kì vọng có điều kiện V (X) Phương sai V (X | y)
Phương sai có điều kiện σX; σ(X) Độ lệch chuẩn Cov(X, Y ) Hiệp phương sai Cov(X); Σ Ma trận hiệp phương sai ρXY ; ρ(X, Y ) Hệ số tương quan ρ(X); Cor(X)
Ma trận hệ số tương quan ρ Hệ số tương quan riêng XY ·Z ρ
Hệ số tương quan bán phần X(Y ·Z) q Giá trị phân vị β
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 1
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— Kí hiệu Tên gọi, ý nghĩa x Giá trị tới hạn α M Trung vị e Q Các tứ phân vị 1; Q2; Q3 M Mốt 0 Sk Hệ số bất đối xứng K Hệ số nhọn m Mô-men gốc bậc k k µ Mô-men trung tâm bậc k k gX(t) Hàm đặc trưng MX(t) Hàm sinh mô-men X a.s = Y
Bằng nhau hầu chắc chắn m X k = Y Có trung bình bằng nhau X d = Y Có phân phối bằng nhau {X Dãy biến ngẫu nhiên n}∞ n=1 (P ) Xn −−−→ X
Hội tụ theo nghĩa xác suất n→∞ X m.s n −−−→ X
Hội tụ theo bình phương trung bình n→∞ X d n −−−→ X
Hội tụ theo phân phối xác suất n→∞ B(1, p) Phân phối Bernoulli B(n, p) Phân phối Nhị thức NB(n, p) Phân phối Nhị thức âm P (λ) Phân phối Poisson G(p) Phân phối Hình học H(N, M, n) Phân phối Siêu bội U (a, b) Phân phối Đều E(λ) Phân phối Lũy thừa Γ Phân phối Gamma N (µ, σ2) Phân phối Chuẩn N (µ, Σ)
Phân phối Chuẩn nhiều chiều χ2(n)
Phân phối Khi-bình phương T (n) Phân phối Student F (m, n) Phân phối Fisher 2
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 1 BIẾN CỐ VÀ XÁC SUẤT
1.1. Đo khả năng xảy ra của hiện tượng ngẫu nhiên
1.2. Phép thử và Không gian biến cố sơ cấp
1.3. Biến cố và σ-đại số các biến cố
1.4. Định nghĩa tiên đề về xác suất
1.5. Một số định nghĩa khác về xác suất
Ví dụ 1.1. Một hộp đựng 10 quả cầu có kích thước giống nhau trong đó có 6 quả màu xanh, 4 quả màu
đỏ. Lấy đồng thời 3 quả cầu từ hộp, tính xác suất:
(a) Lấy được cả 3 quả màu xanh.
(b) Lấy được đúng 2 quả màu đỏ.
Ví dụ 1.2. Bài toán Chevalier de Méré (1654), với hai phương án:
(a) Đặt cược: gieo một con xúc xắc 4 lần, được ít nhất một lần xuất hiện mặt 6 chấm;
(b) Đặt cược: gieo hai con xúc xắc cùng lúc 24 lần, ít nhất một lần cả hai xuất hiện mặt 6 chấm.
Chứng tỏ rằng phương án (a) thì khả năng thắng lớn hơn thua, còn phương án (b) thì khả năng thua
lớn hơn thắng; và khi gieo 25 lần thì phương án (b) cho khả năng thắng lớn hơn thua.
Ví dụ 1.3. Số liệu thống kê tần suất sinh con gái tại một khu vực của Thụy Điển (H. Cramer 1953) Tháng Tổng số Số Số Tần suất sinh
con trai con gái sinh con gái 1 7280 3743 3537 0,486 2 6957 3550 3407 0,489 3 7883 4017 3866 0,490 4 7884 4173 3711 0,471 5 7892 4117 3775 0,478 6 7609 3944 3665 0,482 7 7585 3964 3621 0,462 8 7393 3797 3596 0,484 9 7203 3712 3491 0,485 10 6903 3512 3391 0,491 11 6552 3392 3160 0,482 12 7132 3761 3371 0,473 Cả năm 88.273 45.682 42.591 0,4825
Ví dụ 1.4. Giả sử thực hiện phép thử chọn ngẫu nhiên một điểm trong đoạn [0, 1). 3
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
1.6. Nguyên lí xác suất lớn và nguyên lí xác suất nhỏ
1.7. Xác suất có điều kiện
Ví dụ 1.5. Gieo một lần một xúc xắc cân đối và đồng chất. Đặt ω = “xuất hiện mặt i i chấm” (i = 1, 6)
khi đó không gian các biến cố sơ cấp ứng với phép thử gieo một xúc xắc là
Ω = {ω1, ω2, ω3, ω4, ω5, ω6}.
Đặt A = “xuất hiện mặt có số chấm lớn hơn 3” = {ω4, ω5, ω6}, và B = “xuất hiện mặt có số chấm chẵn” = {ω2, ω4, ω6}. Hãy xác định P (B|A).
1.8. Công thức xác suất của tích các biến cố
Ví dụ 1.6. Một hộp đựng 10 sản phẩm, trong đó có 6 chính phẩm và 4 phế phẩm. Mỗi lần lấy một sản
phẩm từ hộp để kiểm tra (sản phẩm đã kiểm tra không trả lại hộp). Thực hiện hai lần lấy sản phẩm từ hộp
để kiểm tra, tính xác suất lấy được hai chính phẩm.
Ví dụ 1.7. Một hộp đựng 10 sản phẩm, trong đó có 6 chính phẩm và 4 phế phẩm. Mỗi lần lấy một sản
phẩm từ hộp để kiểm tra (sản phẩm đã kiểm tra không trả lại hộp). Thực hiện ba lần lấy sản phẩm từ hộp
để kiểm tra, tính xác suất lấy được ba chính phẩm.
1.9. Tính độc lập của các biến cố
Ví dụ 1.8. Gieo một xúc xắc cân đối và đồng chất một lần. Đặt ω = “xúc xắc xuất hiện mặt i i chấm”, (i = 1, 6) thì Ω = {ω1, ω2, . . . , ω6}.
Đặt A = “được mặt có số chấm chia hết cho 3” = {ω3, ω6}, B = “được mặt có số chấm chẵn” = {ω2, ω4, ω6}.
Chứng tỏ A và B là hai biến cố độc lập.
Ví dụ 1.9. Gieo một xúc xắc cân đối và đồng chất một lần.
Đặt ω = “xúc xắc xuất hiện mặt i
i chấm”, (i = 1, 6), Xét ba biến cố: A = {ω1, ω2}, B = {ω1, ω3}, C = {ω1, ω4}.
Hãy chứng tỏ A, B, C là ba biến cố độc lập từng đôi nhưng không độc lập toàn phần.
1.10. Công thức xác suất của tổng các biến cố
1.11. Công thức xác suất đầy đủ và công thức Bayes
Ví dụ 1.10. Có hai hộp giống nhau: Hộp I có 6 chính phẩm và 4 phế phẩm, hộp II có 7 chính phẩm và
3 phế phẩm. Chọn ngẫu nhiên một hộp và từ hộp đó lấy ra 1 sản phẩm. Tính xác suất để lấy được chính phẩm.
Ví dụ 1.11. Tiếp ví dụ 1.26:
Có hai hộp giống nhau: Hộp I có 6 chính phẩm và 4 phế phẩm; hộp II có 7 chính phẩm và 3 phế
phẩm. Chọn ngẫu nhiên một hộp và từ hộp đó lấy ra 1 sản phẩm thì lấy được chính phẩm. Tính xác suất
để chính phẩm lấy được là của hộp I và xác suất để chính phẩm là của hộp II.
1.12. Bảng xác suất hai chiều
Công thức quan trọng 4
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN Không gian xác suất (Ω, F, P ) Định nghĩa cổ điển m P (A) = n Định nghĩa thống kê k P (A) ≈ n Khoảng giá trị 0 ≤ P (A) ≤ 1 Luật De Morgan A ∪ B = A ∩ B; A ∩ B = A ∪ B S A A A A i i = Ti i; T i i = Si i Hai biến cố đối lập P (A) + P (A) = 1 Xác suất có điều kiện P (A ∩ B) P (B|A) = P (A) Xác suất biến cố tích
P (A ∩ B) = P (A) · P (B|A) = P (B) · P (A|B) Hai biến cố độc lập
P (A|B) = P (A); P (B|A) = P (B) P (A ∩ B) = P (A) · P (B) Độc lập toàn phần P T A = Q P (A i i i i) Xác suất biến cố tổng
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
Hai biến cố xung khắc P (A ∪ B) = P(A) + P(B) Các biến cố xung khắc P S A = P P (A i i i i) Xác suất đầy đủ P (B) = P P (A i i)P (B|Ai) Công thức Bayes P (A P (A j ∩ B) j |B) = P P (A i i)P (B|Ai) Thuật ngữ Tiếng Việt Tiếng Anh Biến cố Event Biến cố đối lập Complement Biến cố tích Intersection Biến cố tổng Union Đo được Measurable Độc lập Independent Không gian mẫu Sample space Phụ thuộc Dependent Tiên đề Axiom Xác suất Probability
Xác suất có điều kiện Conditional probability
Xác suất hậu nghiệm Posterior probability
Xác suất tiên nghiệm Prior probability Xung khắc Mutually exclusive σ-đại số Sigma-algebra
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 5
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— Bài tập
Bài 1.1. Gieo hai xúc xắc đối xứng đồng chất.
(a) Xác định không gian biến cố sơ cấp
(b) Tính xác suất để được tổng số chấm là 4
Bài 1.2. Gieo ba con xúc xắc đối xứng đồng chất.
(a) Xác định không gian biến cố sơ cấp
(b) Tính xác suất để được tổng số chấm nhỏ hơn 5
Bài 1.3. Xác định không gian các biến cố sơ cấp của các phép thử sau: (a) Gieo một xúc xắc. (b) Tung hai đồng xu.
(c) Lấy lần lượt các sản phẩm trong một kho hàng cho đến khi lấy được sản phẩm tốt.
Bài 1.4. Xây dựng không gian xác suất ứng với các phép thử sau
(a) Tung một đồng xu cân đối và đồng chất.
(b) Tung một đồng xu cân đối và đồng chất 2 lần liên tiếp.
(c) Gieo một xúc xắc cân đối và đồng chất.
(d) Gieo một xúc xắc cân đối và đồng chất 2 lần liên tiếp. Bài 1.5. Cho 1 1
A và B là hai biến cố thỏa mãn P (A) = P (B) = và P (A ∩ B = ). 2 3 Hãy tính P (A ∪ B)
Bài 1.6. Cho Ω là một không gian đếm được các biến cố sơ cấp ω1, ω2, ..., ωn, ... i Hãy tìm hằng số 1 c sao cho P (ωi) = c
, (i = 1, ∞) là một độ đo xác suất trong Ω. 3
Bài 1.7. Cho P (A) = 0,4 và P (A ∪ B) = 0,6, hãy tìm P(B) để A và B là hai biến cố độc lập.
Bài 1.8. Một lớp có 55 học sinh, trong đó có 33 học sinh giỏi Toán, 20 học sinh giỏi Văn, 15 học sinh
giỏi cả Toán và Văn. Chọn ngẫu nhiên 1 học sinh.
(a) Tính xác suất chọn được học sinh không giỏi cả Toán và Văn.
(b) Tính xác suất chọn được học sinh giỏi Văn biết học sinh đó không giỏi Toán.
Bài 1.9. Một lô hàng có tỷ lệ chính phẩm là 75%.Trước khi đưa ra thị trường người ta sử dụng một loại
thiết bị kiểm tra để loại phế phẩm. Thiết bị kiểm tra có độ chính xác với chính phẩm là 90%, với phế phẩm là 98%.
(a) Tính tỷ lệ sản phẩm của lô hàng được đưa ra thị trường.
(b) Chọn 2 sản phẩm trên thị trường, tính xác suất cả 2 sản phẩm đều là chính phẩm.
Bài 1.10. Một người đấu thầu hai dự án. Xác suất trúng thầu dự án thứ nhất và thứ hai lần lượt là 0,5 và
0,4, xác suất trúng thầu cả hai là 0,1. Viết biến cố và tính xác suất:
(a) Trúng thầu ở ít nhất một dự án.
(b) Trúng thầu ở đúng một dự án.
(c) Trúng thầu dự án thứ hai, biết rằng trúng thầu dự án thứ nhất.
(d) Trúng thầu dự án thứ hai, biết rằng không trúng thầu ở dự án thứ nhất
Bài 1.11. Một người đi từ nhà đến cơ quan, người đó đi qua 2 ngã tư có đèn tín hiệu giao thông. Giả sử
xác suất gặp đèn đỏ thứ nhất là 0,6. Nếu gặp đèn đỏ thứ nhất thì xác suất gặp đèn đỏ thứ hai là 0,8 nhưng
nếu không gặp đèn đỏ thứ nhất thì xác suất gặp đèn đỏ thứ hai còn 0,2. Tính xác suất người đó:
(a) Gặp ít nhất một đèn đỏ.
(b) Gặp đúng 1 đèn đỏ.
(c) Gặp đèn đỏ thứ nhất biết rằng gặp đèn đỏ thứ hai.
(d) Gặp cả 2 đèn đỏ biết rằng gặp ít nhất 1 đèn đỏ. 6
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN Bài 1.12. Cho 1 1 23 P (A) = , P (B) = và P (A ∪ B) = . 4 3 60
Hãy tính: P (A/B), P [(AB)/B], P [(AB)/B], P [(A ∪ B)/(AB)],
P [(AB)/(A ∪ B)], P [(AB)/B].
Bài 1.13. Cho A và B là hai biến cố độc lập với P (A) = P (B) và P (A ∪ B) = 0,5. Hãy tính P(A)
Bài 1.14. Một hộp có 4 bi xanh và 2 bi đỏ. Hai người A và B chơi trò chơi lấy từng viên bi từ hộp (không
hoàn lại bi vào hộp), ai lấy được bi đỏ trước người ấy thắng. Giả sử người A được lấy bi trước, tính xác suất người A thắng.
Bài 1.15. Hai người A và B chơi 5 ván cờ (mỗi ván chỉ có thể A thắng hoặc thua không có hòa), ai thắng
3 ván trước thì người đó thắng chung cuộc. Giả sử xác suất thắng mỗi ván cờ của người A là 0,6. Tính
xác suất người A thắng chung cuộc.
Bài 1.16. Các mệnh đề sau đây mệnh đề nào đúng? mệnh đề nào sai? hãy giải thích
(a) Nếu A và B là hai biến cố xung khắc thì P (A ∪ B) = P(A) + P(B)
(b) Nếu P (A ∪ B) = P(A) + P(B) thì A và B là hai biến cố xung khắc (c) P (A ∪ B) ≥ P(A ∩ B) (d) P (A ∪ B) = P(AB) (e) P (AB) = P (A ∪ B)
Bài 1.17. Có 3 người, mỗi người mua 1 sản phẩm cùng loại. Người một mua sản phẩm ở đại lý A, người
hai mua sản phẩm ở đại lý B, người ba mua sản phẩm ở đại lý C. Giả sử tỷ lệ chính phẩm của mặt hàng
này ở các đại lý A, B, C lần lượt là 0,75; 0,7 và 0,8. Sau khi mua, biết có 2 người mua được chính phẩm,
tính xác suất để người ba mua được chính phẩm.
Bài 1.18. Một nhà máy có hai lô sản phẩm có số lượng sản phẩm đều nhau. Lô I có 80% chính phẩm và
20% phế phẩm, Lô II có 75% chính phẩm và 25% phế phẩm. Lấy ngẫu nhiên 3 sản phẩm từ nhà máy, tính
xác suất lấy được ít nhất 1 chính phẩm.
Bài 1.19. Một bộ đề thi vấn đáp có 15 câu hỏi trong đó có 10 câu chương I và 5 câu chương II. Xác suất
để học sinh A trả lời đúng câu hỏi thuộc chương I là 0,8 và chương II là 0,75. Mỗi lần thi học sinh A phải
bốc ngẫu nhiên 2 câu để trả lời. Tính xác suất để học sinh A trả lời được một câu đúng và một câu sai.
Bài 1.20. Có hai người A và B chơi trò chơi gieo xúc xắc. Giả sử người A được gieo trước, sau đó đến
người B, sau đó đến người A,...quá trình tiếp tục cho đến khi nào xúc xắc xuất hiện mặt 6 chấm thì dừng
lại và người đó sẽ thắng. Tính xác suất người A thắng.
Bài 1.21. Một người A muốn mua một chiếc xe hơi với giá m (USD) nhưng hiện tại người đó chỉ có k
(USD), (0 < k < m). Người A quyết định kiếm (m − k) (USD) còn lại bằng trò chơi may rủi do một
người bạn của A đưa ra, đó là tung đồng tiền xu (có hai mặt, mặt sấp và mặt ngửa). Mỗi lần A tung đồng
xu, nếu đồng xu xuất hiện mặt sấp thì A được 1 (USD) còn nếu đồng xu xuất hiện mặt ngửa thì A mất 1
(USD). Người A đã quyết định chơi cho đến khi nào hoặc là kiếm đủ m (USD) hoặc mất hết k (USD).
Tính xác suất người A mất hết k (USD) hoặc được (m − k) (USD) trong các trường hợp sau:
(a) Đồng xu cân đối và đồng chất, người A lúc đầu có 18.000 (USD) và giá của chiếc xe hơi mà A muốn mua là 20.000 (USD)
(b) Xác suất đồng xu xuất hiện mặt sấp là p và xuất hiện mặt ngửa là q = 1 − p
Bài 1.22. Người ta biết một cặp trẻ sinh đôi có thể là một cặp sinh đôi thật (sinh đôi do cùng một trứng),
hoặc sinh đôi giả (sinh đôi do các trứng khác nhau). Hai đứa trẻ sinh đôi thật luôn có cùng giới tính. Nếu
sinh đôi do các trứng khác nhau thì xác suất để 2 đứa trẻ có cùng giới tính là 0,5. Thống kê cho thấy có
34% cặp sinh đôi đều là trai, 30% cặp sinh đôi đều là gái và 36% cặp sinh đôi có giới tính khác nhau:
(a) Tìm tỉ lệ cặp sinh đôi thật
(b) Tìm tỉ lệ cặp sinh đôi thật trong tổng số cặp sinh đôi có cùng giới tính
Bài 1.23. Một hộp có a quả cầu màu đỏ và b quả cầu màu xanh. Hai người A và B luân phiên lấy cầu
(có hoàn lại) cho đến khi ai lấy được cầu đỏ trước thì thắng. Giả sử người A lấy cầu trước, tính xác suất người A thắng.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 7
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 1.24. Một lô hàng có 8 sản phẩm cùng loại. Kiểm tra ngẫu nhiên 4 sản phẩm thì thấy có 3 chính
phẩm và 1 phế phẩm. Tính xác suất để khi kiểm tra tiếp 3 sản phẩm nữa thì sẽ gặp 1 chính phẩm và 2 phế phẩm.
Bài 1.25. Một người bị sốt đã vào bệnh viện để khám. Bác sĩ cho rằng anh ta chỉ có thể bị nhiễm một
trong 2 loại vi rút A hoặc B. Thống kê cho thấy tỉ lệ người nhiễm vi rút A cao gấp đôi người nhiễm vi
rút B. Bác sĩ chỉ định anh ta làm 2 xét nghiệm độc lập N và
. Biết rằng nếu nhiễm vi rút 1 N2 A thì xét
nghiệm N cho dương tính với xác suất
cho dương tính với xác suất 1 0,85 còn xét nghiệm N2 0,75. Trong
trường hợp bị nhiễm vi rút B thì xét nghiệm N cho dương tính với xác suất cho 1 0,1 còn xét nghiệm N2
dương tính với xác suất 0,15. Giả sử cả hai xét nghiệm N và
đều cho dương tính thì xác suất người 1 N2
đó bị nhiễm vi rút A là bao nhiêu? 8
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 2 BIẾN NGẪU NHIÊN VÀ PHÂN PHỐI XÁC SUẤT
2.1. Biến ngẫu nhiên
Ví dụ 2.1. Một nhân viên kinh doanh lần đầu đi đàm phán hợp đồng với một đối tác, kết quả chỉ có thể
là thành công (T) hoặc thất bại (B). Các phép gán sau đây có phải là biến ngẫu nhiên hay không, nếu có
thì có thể gán đơn vị hay không?
(a) Phép gán X: Nếu thành công thì X = 1, nếu thất bại thì X = 0.
(b) Phép gán Y : là số lần thành công.
(c) Phép gán Z - “tiền thưởng”: Nếu thành công thì được thưởng 10 (triệu đồng) hoặc 15 (triệu
đồng), nếu thất bại thì không được thưởng.
(d) Phép gán W - “chi phí giao dịch”: Dù kết quả thế nào thì chi phí giao dịch cũng bằng 2 (triệu đồng).
(e) Phép gán U: Nếu thành công thì dừng lại, nếu thất bại thì đàm phán tiếp ở ngày khác.
(f) Phép gán V - “số lần đàm phán tiếp theo”: Nếu thành công thì dừng lại, nếu thất bại thì tổ chức
chỉ một lần đàm phán tiếp.
Ví dụ 2.2. Một người bỏ thầu hai dự án, mỗi dự án chỉ có hai kết quả là thắng thầu (T) và thất bại (B).
Đặt X là tổng số dự án thắng thầu. Chứng tỏ X là biến ngẫu nhiên.
Ví dụ 2.3. Một dự án đầu tư có hai giai đoạn cần các dịch vụ hỗ trợ. Có ba doanh nghiệp cung cấp dịch
vụ là A, B, C cạnh tranh để được chọn, với thời gian hoạt động trên thị trường của ba doanh nghiệp lần
lượt là 3 năm, 5 năm, 8 năm. Chủ đầu tư chọn ngẫu nhiên nhà cung cấp dịch vụ.
(a) Xác định biến ngẫu nhiên X tạo bởi số năm hoạt động của doanh nghiệp được chọn cung cấp dịch vụ cho giai đoạn đầu.
(b) Chọn lần lượt theo cách có hoàn lại nhà cung cấp cho hai giai đoạn, xác định biến ngẫu nhiên Y
là số lần doanh nghiệp A được chọn.
2.2. Hàm phân phối xác suất
Ví dụ 2.4. Lập hàm phân phối của biến ngẫu nhiên X là số mặt sấp xuất hiện khi gieo hai đồng xu đối xứng đồng chất.
Ví dụ 2.5. Hàm sau có thể là hàm phân phối xác suất hay không? 1 F (x) = 1 + e−x
2.3. Biến ngẫu nhiên rời rạc
Ví dụ 2.6. Một doanh nghiệp đấu thầu ở hai dự án độc lập nhau, khả năng thắng thua ở mỗi dự án đều
như nhau và bằng 0,5. Xác định hàm khối lượng xác suất, lập bảng phân phối xác suất của X là số lần thắng thầu.
Ví dụ 2.7. Có một trò chơi trên máy tính mà khả năng thắng của người chơi trong mỗi ván đều bằng
p, p ∈ (0, 1), độc lập nhau. Một người chơi quyết định chơi đến khi nào thắng thì dừng. Xác định hàm
khối lượng xác suất và hàm phân phối xác suất của số lần người đó chơi. 9
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
2.4. Biến ngẫu nhiên liên tục
Ví dụ 2.8. Một chương trình truyền hình có độ dài hai giờ. Thời gian người xem truyền hình dành để xem
chương trình đó (đơn vị: giờ) là biến ngẫu nhiên liên tục có hàm mật độ xác suất như sau kx : x ∈ [0, 2] f (x) = 0 : x / ∈ [0, 2]
(a) Tìm giá trị của k và xác định hàm phân phối xác suất.
(b) Tính xác suất để thời gian xem ít hơn 1 giờ.
(c) Tính xác suất để thời gian xem trong khoảng 1 đến 1,5 giờ.
2.5. Hàm của một biến ngẫu nhiên
Ví dụ 2.9. Một nhà sản xuất có chi phí nhiên liệu Y phụ thuộc vào sản lượng X có dạng Y = 2X + 3.
Công suất thiết kế cho hoạt động tối ưu của nhà máy là 13 đơn vị, do đó nếu chi phí để điều chỉnh hoạt
động là Z có dạng Z = (X − 3)2, nghĩa là sản xuất nhiều hay ít hơn thì đều phải tốn chi phí điều chỉnh.
Biết X phải bằng với cầu của thị trường, và cầu có các giá trị 11, 12, 13, 14, 15 với xác suất đều bằng
1/5. Xác định phân phối xác suất của chi phí nhiên liệu Y và chi phí điều chỉnh Z.
Ví dụ 2.10. Thời gian chậm tiến độ của một dự án là biến ngẫu nhiên liên tục X có hàm mật độ xác suất
là không đổi trong đoạn [0, 1], và bằng 0 bên ngoài đoạn [0, 1]. Số tiền phạt là bình phương của thời gian
chậm tiến độ, kí hiệu là Y : Y = X2
(a) Xác định hàm mật độ và hàm phân phối của X.
(b) Xác định hàm phân phối và hàm mật độ xác suất của Y
Ví dụ 2.11. Nhiệt độ khi đo bằng thang đo độ Celsius (oC) là biến ngẫu nhiên X, khi đổi sang thang đo
Fahrenheit, được biến Y , với Y = 9X +32. Khi đó Y cũng là biến ngẫu nhiên, với hàm u(X) = 9X +32. 5 5
Nếu X có hàm phân phối xác suất FX(x) và hàm mật độ xác suất fX(x).
(a) Xác định hàm phân phối và hàm mật độ của Y .
(b) Nếu hàm mật độ của X có dạng: fX(x) = 1x2 với 0 ≤ x ≤ 3 và bằng 0 với x /∈ [0, 3], hãy xác 9 định các hàm của Y .
2.6. Tham số của biến ngẫu nhiên
Ví dụ 2.12. Tính kì vọng của biến ngẫu nhiên rời rạc X có hàm khối lượng xác suất P (x), và kì vọng
của biến ngẫu nhiên liên tục Y có hàm mật độ xác suất như sau đây ( x 7 8 9 1 y − 7 : y ∈ [7, 9] f (y) = 2 2 P (x) 0,2 0,5 0,3 0 : y / ∈ [7, 9]
Ví dụ 2.13. Với X là nhiệt độ đo bởi thang Celsius và Y là nhiêt độ đó đo bởi thang Fahrenheit: Y =
u(X) = 9 X + 32, có hàm mật độ của X, suy được hàm mật độ của Y 5 ( 1 ( x2 : x ∈ [0, 3]
125 (y − 32)2 : y ∈ [32; 37, 4] f 9 6561 X (x) = , fY (y) = 0 : x / ∈ [0, 3] 0 : y / ∈ [32; 37, 4]
Tính kì vọng của Y theo hai cách: (a) trên hàm mật độ của Y , và (b) theo công thức kì vọng của hàm của X.
Ví dụ 2.14. Tính kì vọng, phương sai, độ lệch chuẩn của tỉ suất lợi nhuận của ba phương án đầu tư A, B, C như sau:
– A: gửi tiền vào ngân hàng với lãi suất/năm cố định là 7%
– B: đầu tư vào một loại cổ phiếu, tỉ suất lợi nhuận/năm là 4% hoặc 12% với xác suất tương ứng là 0,3 và 0,7 10
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
– C: đầu tư kinh doanh, tỉ suất lợi nhuận/năm là (−1)%, 5%, 24% với xác suất lần lượt là 0,1; 0,4; 0,5
Ví dụ 2.15. Thời gian xem một chương trình truyền hình là biến ngẫu nhiên liên tục X (giờ) có hàm mật độ xác suất x/2 : x ∈ [0, 2] f (x) = 0 : x / ∈ [0, 2]
Tính kì vọng, phương sai, độ lệch chuẩn của X.
Ví dụ 2.16. Một doanh nghiệp sản xuất có chi phí cố định 20 (triệu), chi phí cận biên cho mỗi đơn vị
sản phẩm là không đổi và bằng 10 (triệu), giá bán mỗi sản phẩm là 12 (triệu). Khi thị trường ổn định thì
doanh nghiệp sản xuất và bán được 100 sản phẩm, nhưng nếu thị trường suy thoái thì doanh nghiệp chỉ
sản xuất và bán được 50 sản phẩm. Biết xác suất thị trường ổn định là 0,7 và xác suất thị trường suy thoái
là 0,3. Tính kì vọng, phương sai và độ lệch chuẩn của lợi nhuận doanh nghiệp.
Ví dụ 2.17. Một nhân viên hành chính làm việc 45 giờ/tuần, và nhận được lương là 3 triệu đồng/tuần.
Mức lương đó có xứng đáng với thời gian lao động không, biết rằng trong lĩnh vực hành chính thời gian
lao động/tuần có kì vọng là 40 giờ và độ lệch chuẩn là 2 giờ; lương/tuần có kì vọng là 2,7 triệu và độ lệch chuẩn là 0,2 triệu.
Ví dụ 2.18. Tại phòng chăm sóc khách hàng của một doanh nghiệp, trong một ngày số khiếu nại về sản
phẩm của doanh nghiệp có phân phối xác suất như sau Số khiếu nại 0 1 2 3 4 5 6 7 Xác suất 0,1 0,15 0,2 0,2 0,15 0,1 0,05 0,05
Hãy tính các tham số của số khiếu nại.
Ví dụ 2.19. Thời gian xem một chương trình truyền hình là biến ngẫu nhiên liên tục X có hàm mật độ xác suất x/2 : x ∈ [0, 2] f (x) = 0 : x / ∈ [0, 2]
Với ví dụ này ta đã tính được E(X) = 4/3 và V (X) = 2/9
(a) Tính mốt, trung vị của X
(b) Tính giá trị tới hạn mức 20% và cho biết ý nghĩa của nó.
(c) Tính hệ số bất đối xứng, hệ số nhọn
2.7. Hàm đặc trưng của biến ngẫu nhiên
Ví dụ 2.20. Cho biến ngẫu nhiên X rời rạc có hàm khối lượng xác suất như sau X 7 8 9 P (X) 0,2 0,5 0,3
Xác định hàm sinh mô-men và các mô-men bậc 1, 2, 3 từ hàm sinh này.
Ví dụ 2.21. Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau, với λ > 0 λe−λx : x ≥ 0 f (x) = 0 : x < 0
(a) Xác định điều kiện để tồn tại hàm sinh mô-men;
(b) Nếu tồn tại hàm sinh mô-men, xác định các mô-men bậc 1, 2, 3 từ hàm sinh này.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 11
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
2.8. Sự tương đương của hai biến ngẫu nhiên
Ví dụ 2.22. Xét tính tương đương của hai biến ngẫu nhiên X, Y được xác định như sau khi gieo hai đồng
xu đối xứng đồng chất Xuất hiện SS SN NS NN X 1 0 0 -1 Y -1 0 0 1 P 1/4 1/4 1/4 1/4
2.9. Phân phối xác suất có điều kiện
Ví dụ 2.23. Cho giá thị trường X của mặt hàng B là có bảng phân phối xác suất như sau X 10 11 12 P 0,1 0,6 0,3
Yếu tố đầu vào quan trọng của quá trình sản xuất hàng hóa đó là điện, và có khả năng giá điện tăng. Nếu biết các xác suất sau
• Xác suất giá điện tăng là 0,2;
• Xác suất giá điện tăng và giá mặt hàng B bằng 10 là 0;
• Xác suất giá điện tăng và giá mặt hàng B bằng 11 là 0,08.
(a) Lập bảng phân phối xác suất của giá mặt hàng B trong điều kiện giá điện tăng.
(b) Lập bảng phân phối xác suất của giá mặt hàng B trong điều kiện giá điện không tăng.
(c) So sánh kì vọng, phương sai của giá mặt hàng B với các trường hợp: không điều kiện, trong điều
kiện giá điện tăng, trong điều kiện giá điện không tăng.
Ví dụ 2.24. Với X là lợi nhuận doanh nghiệp, có bảng phân phối xác suất như sau X −5 −2 3 6 10 P 0,05 0,15 0,2 0,5 0,1
Hãy lập bảng phân phối xác suất và tính các tham số đặc trưng trong điều kiện có lãi và bị lỗ.
Ví dụ 2.25. Lượng bán X của doanh nghiệp là biến ngẫu nhiên, có phân phối xác suất trong điều kiện
giá bán khác nhau là khác nhau. Giá bán có ba mức là Thấp, Trung bình, Cao với xác suất tương ứng là 0,1; 0,5 và 0,4. Đặt A
lần lượt là các biến cố giá Thấp, Trung bình, Cao, và có các bảng phân 1, A2, A3
phối xác suất có điều kiện như sau (X|A1) 20 21 22 23 24 P 0,1 0,15 0,2 0,35 0,2 X|A1 (X|A2) 20 21 22 23 24 P 0,2 0,25 0,25 0,2 0,1 X|A2 (X|A3) 20 21 22 23 24 P 0,25 0,35 0,2 0,15 0,05 X|A3
Lập bảng phân phối xác suất không điều kiện của lượng bán, và tính các tham số đặc trưng.
Ví dụ 2.26. Cho thời gian chờ để thực hiện một thủ tục hành chính (đơn vị là giờ) là biến ngẫu nhiên liên
tục X có hàm mật độ fX(x) bằng 1x trong khoảng (0, 2) và bằng 0 nếu ngoài khoảng đó. 2
Xác định hàm phân phối, hàm mật độ, kì vọng, phương sai của biến ngẫu nhiên là thời gian chờ trong
trường hợp phải chờ hơn 1 giờ. 12
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Công thức quan trọng Hàm phân phối XS F (x) = P (X ≤ x)
P (a < X ≤ b) = F (b) − F (a)
Hàm khối lượng XS P (xi) = P (X = xi) P P (x i i) = 1 Hàm mật độ XS f (x) = F 0(x) R f (x)dx = 1 R
P (a < X < b) = R b f (x)dx a P x Kì vọng iP (xi) E(X) = i R xf (x)dx R P g(xi)P (xi) Eg(X) = i R g(x)f (x)dx R E(aX + b) = aE(X) + b Phương sai
V (X) = EX − E(X)2 = E(X2) − E(X)2 V (aX + b) = a2V (X) Độ lệch chuẩn σX = pV (X) Biến chuẩn hóa ZX = X − E(X)/σX E(ZX) = 0; V (ZX) = 1 Tham số khác qβ : P (X ≤ qβ) = β xα : P (X > xα) = α h Sk = EX − E(X)3i/σ3X h K = EX − E(X)4i/σ4X − 3 Mô-men mk = EXk; µk = EX − E(X)k P eitxj P (x Hàm đặc trưng j ) g j X (t) = EeitX = R eitxf (x)dx R mk = 1 g(k)(0) ik X P etxj P (x Hàm sinh mô-men j ) M j X (t) = EetX = R etxf (x)dx R mk = M(k)(0) X Thuật ngữ Tiếng Việt Tiếng Anh Bằng nhau Equal
Bằng nhau hầu chắc chắn Equal almost surely Biến chuẩn hóa Standardized variable Biến ngẫu nhiên Random variable Biến liên tục Continuous variable Biến một chiều Univariate Biến rời rạc Discrete variable Có phân phối bằng nhau Equal in distribution
Có trung bình bằng nhau Equal in mean Đại lượng ngẫu nhiên Random quantity Độ lệch chuẩn Standard deviation Giá trị phân vị Quantile Giá trị tới hạn Critical value Hàm đặc trưng Characteristic function
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 13
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— Hàm đo được Measurable function
Hàm khối lượng xác suất Probability mass function Hàm mật độ xác suất Probability density function Hàm phân phối xác suất
Probability distribution function Hàm sinh mô-men Moment generating function Hàm sinh xác suất Probability genrating function Hàm tích lũy xác suất Cumulative probability funtion Hệ số bất đối xứng Skewness Hệ số biến thiên Coefficient of variation Hệ số nhọn Kurtosis Kì vọng Expected value / Expectation Kì vọng có điều kiện Conditional Expectation Mô-men Moment Phương sai Variance Trung vị Median Tứ phân vị Quartile Bài tập
Bài 2.1. Một người tham gia một cuộc đua xe đạp, quan tâm đến kết quả cuối cùng. Trong các phép gán
sau đây, phép gán nào là biến ngẫu nhiên:
(a) Đánh số thứ tự: người về đích đầu tiên là số 1, người tiếp theo là số 2,..., cho đến cuối cùng.
(b) Vị trí nhận giải: Ban tổ chức xếp bục giải thưởng, số 1 cho nhà vô địch, số 2 cho á quân, số 3 cho
á quân hai, còn lại không có bục đứng nào.
(c) Giải thưởng: nhà vô địch được 10 triệu đồng, á quân được 5 triệu đồng, á quân hai được 2 triệu
đồng, còn lại không có giải thưởng (hay giải thưởng bằng 0 đồng).
(d) Áo vinh danh: Nhà vô địch được mặc áo vàng, á quân mặc áo đỏ.
(e) Huy chương: Nhà vô địch được huy chương vàng, á quân được huy chương bạc, á quân hai được
huy chương đồng, còn lại nhận huy hiệu xác nhận tham gia.
Bài 2.2. Trong cuộc đua xe đạp, xét các biến ngẫu nhiên được hình thành từ kết quả cuộc đua như dưới
đây. Cho biết đâu là biến ngẫu nhiên rời rạc, đâu là biến ngẫu nhiên liên tục:
(a) Thời gian hoàn thành chặng đua của vận động viên.
(b) Thứ tự về đích trong toàn đoàn đua.
(c) Tốc độ khi về đích của vận động viên.
(d) Đánh số nhóm về đích: Lấy người đầu tiên làm mốc, về đích trong vòng 10 phút thuộc nhóm số 1,
từ sau 10 phút đến trước 20 phút thuộc nhóm số 2, từ sau 20 phút đến trước 30 phút thuộc nhóm số 3, từ
sau 30 phút thuộc nhóm số 4.
(e) Số tiền thưởng nhận được từ ban tổ chức.
Bài 2.3. Công ty tuyển dụng sinh viên đã tốt nghiệp đại học KTQD vào một vị trí tại văn phòng giao
dịch, hãy thể hiện các thông tin sau đây của ứng viên dưới dạng các biến ngẫu nhiên, cho biết biến đó là rời rạc hay liên tục:
(a) Giới tính của ứng viên; (b) Tuổi của ứng viên;
(c) Chiều cao của ứng viên;
(d) Cân nặng của ứng viên;
(e) Điểm trung bình chung tốt nghiệp đại học;
(f) Loại tốt nghiệp (Xuất sắc, Giỏi, Khá, Trung bình khá, Trung bình);
(g) Có chứng chỉ Tiếng Anh IELTS hay chưa, nếu có thì điểm bao nhiêu.
Bài 2.4. Một thí sinh thi hai môn, độc lập nhau. Xác suất để thí sinh đó qua được hai môn lần lượt là 0,6 và 0,8. 14
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
(a) Lập bảng phân phối xác suất của số môn thi qua của thí sinh đó.
(b) Tính kì vọng và phương sai của số môn thi qua.
Bài 2.5. Một người đi bán hàng ở ba nơi. Xác suất bán được hàng ở nơi thứ nhất là 0,5. Nếu ở nơi trước
đã bán được hàng thì khả năng bán được hàng ở nơi tiếp theo là 0,8; còn nếu ở nơi trước không bán được
hàng thì khả năng bán được hàng ở nơi tiếp theo là 0,3. Đặt X là số nơi bán được hàng.
(a) Lập bảng phân phối xác suất của X.
(b) Tính kì vọng, phương sai, độ lệch chuẩn của X.
(c) Tính xác suất: P (X < E(X) − σX).
Bài 2.6. Cho bảng phân phối xác suất của số lỗi mắc phải của công nhân trong một tháng làm việc có
bảng phân phối xác suất như sau: X 0 1 2 3 4 5 6 > 6 P 0,2 0,3 0,15 0,1 0,1 0,05 0,05 p
(a) Xác định p và tính khả năng công nhân mắc từ 3 lỗi trở lên
(b) Công nhân nếu không mắc lỗi thì được thưởng 10 triệu đồng, mắc 1 đến 2 lỗi thì thưởng 3 triệu
đồng, mắc 3 đến 4 lỗi thì không được thưởng, mắc từ 5 đến 6 lỗi thì bị phạt 2 triệu, mắc trên 6 lỗi bị phạt 4 triệu.
Đặt Y là số tiền thưởng (phạt). Hãy lập bảng phân phối xác suất của Y và tính kì vọng, phương sai của Y .
Bài 2.7. Cho X là số hợp đồng mà doanh nghiệp kí được sau một tháng đàm phán với các đối tác, có
bảng phân phối xác suất như sau: X 0 1 2 3 4 P 0,05 0,15 0,4 0,3 p
(a) Tính giá trị của p và xác suất số hợp đồng là từ 2 trở lên.
(b) Tính kì vọng và phương sai của số hợp đồng kí được.
(c) Nếu mỗi hợp đồng kí được sẽ đem lại lợi nhuận là 100 triệu đồng, hãy tính kì vọng và phương sai của lợi nhuận.
Bài 2.8. Chứng minh rằng hàm sau là một hàm khối lượng xác suất:
P (X = x) = (0, 5)x, x = 1, 2, ...
Bài 2.9. Tìm α để các hàm sau là hàm khối lượng xác suất:
(a) P (X = x) = α · cx, 0 < c < 1, x = 0, 1, 2, ...
(b) P (X = x) = αx, x = 1, 2, ...
(c) P (X = x) = αx, x = 1, 2, ...
(d) P (X = x) = α(1/3)x, x = 0, 1, 2, ...
Bài 2.10. Cho biến ngẫu nhiên rời rạc X có hàm khối lượng xác suất như sau: P (X = −c) = P(X = c) = 1/2 (a) Tính E(X), V (X) (b) Chứng minh rằng: V (X) P (|X − E(X)| ≤ c) = c2
Bài 2.11. Cho biến ngẫu nhiên X có E(X) = 5, EX(X − 1) = 27.5. Hãy tính V (X), σ(X)
Bài 2.12. Cho biết ngẫu nhiên X rời rạc có: P (X = x) = (1)x, x = 1, 2, .... Hãy tính E(X), V (X) 2
Bài 2.13. Tìm α để hàm sau là hàm khối lượng xác suất α P (X = x) = , x = 0, 1, 2, ... 3x (a) Tính P (X ≥ 3);
(b) Tính P (X = 2k + 1) với k = 0, 1, 2, ...;
(c) Tính P (X = 3k + 1) : k = 0, 1, 2, ...
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 15
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 2.14. Cho hàm khối lượng xác suất: P (X = x) = c(13)x, x = 0, 1, 2, ... (a) Tính c và E(X)
(b) Xác định hàm sinh mô-men MX(t)
(c) Sử dụng hàm sinh MX(t) để tính E(X) và so sánh với kết quả ở trên
Bài 2.15. Trong các hàm sau, đâu là hàm khối lượng xác suất:
(a) P (x) = (x − 2)/5, x = 1, 2, 3, 4, 5.
(b) P (x) = x2/30, x = 0, 1, 2, 3, 4.
(c) P (x) = 1/5, x = 0, 1, 2, 3, 4, 5.
Bài 2.16. Xác định α để các hàm sau đây là hàm khối lượng xác suất:
(a) P (x) = αx, x = 1, 2, 3, 4, 5.
(b) P (x) = αCx5, x = 0, 1, 2, 3, 4, 5.
(c) P (x) = αx2, x = 1, 2, ..., n. (d) 1 x P (x) = α , x = 1, 2, .... 4
(e) P (x) = (1 − α)αx, x = 0, 1, 2, ....
Bài 2.17. Một người sản xuất bánh biết rằng nhu cầu hàng ngày về bánh của mình sản xuất ra là biến
ngẫu nhiên rời rạc, có hàm khối lượng xác suất P (x) = 1/6 với x = 0, 1, 2, 3, 4, 5. Mỗi chiếc bánh bán
được thì lãi 1 usd, mỗi chiếc bánh không bán được phải hạ giá và giao cho nơi khác nên lỗ 0,4 usd.
(a) Hãy tính kì vọng của lợi nhuận khi sản xuất 1, 2, 3, 4, 5 chiếc bánh.
(b) Tính phương sai của lợi nhuận tương ứng với khi kì vọng là lớn nhất và nhỏ nhất.
Bài 2.18. Tại một lớp học, có 4 người để quên 4 cuốn tài liệu, và được trả lại một cách ngẫu nhiên. Lập
bảng phân phối xác suất của số cuốn tài liệu được trả đúng người.
Bài 2.19. Đặt X là số sản phẩm mắc lỗi trong một lô hàng của một xưởng sản xuất, và có bảng phân phối xác suất như sau: X 0 1 2 3 P (X) 0,6 0,25 0,1 0,05
(a) Tính kì vọng, phương sai của số lỗi trong một lô hàng.
(b) Giả sử số tiền phạt mà xưởng phải trả là bình phương của số lỗi. Hãy tính kì vọng và phương sai của số tiền phạt.
Bài 2.20. Trong một cuộc thi có n thí sinh được đánh số từ 1 đến n. Đặt X là số của thí sinh được chọn
ngẫu nhiên, nên P (X = x) = 1 , x = 1, 2, ..., n. Tính kì vọng và phương sai của X. n
Gợi ý: Pn i = n(n + 1)/2 và Pn i2 = n(n + 1)(2n + 1/6. i=1 i=1
Bài 2.21. Chọn một số X hoàn toàn ngẫu nhiên trong đoạn [0, 1]. Tính các xác suất: (a) P (1/3 < X < 2/3) (b) P (|X − 1/2| < 1/4) (c) P (3X2 < X)
Bài 2.22. Chọn hai số ngẫu nhiên X, Y độc lập trong đoạn [0, 1], nghĩa là điểm (X, Y ) là ngẫu nhiên
trong hình vuông cạnh 1 đơn vị. Tính các xác suất: (a) X + Y < 1/2 (b) X · Y < 1/2 (c) |X − Y | < 1/2 (d) max{X, Y } < 1/2 (e) min{X, Y } < 1/2 (f) X2 + Y 2 < 1/2
(g) (X − 1)2 + (Y − 1)2 < 1/4 2 2 16
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 2.23. Thời gian hoạt động tốt của một bóng đèn là biến ngẫu nhiên liên tục t (đơn vị là giờ) với hàm mật độ: ( λe−λt : t ≥ 0 f (t) = 0 : t < 0
Tham số λ còn được gọi là “tỉ lệ hỏng” của bóng đèn. Giả sử λ = 0.01.
(a) Tính xác suất bóng đèn hoạt động tốt trước T giờ.
(b) Xác định thời gian T để một nửa số bóng đèn hoạt động tốt trước T giờ.
(c) Tính kì vọng của thời gian hoạt động tốt.
Bài 2.24. Cho X là thời gian một khách hàng dừng lại tại một quầy hàng (đơn vị: giờ), có hàm phân phối xác suát như sau 0 : x ≤ 0 F (x) =
x3 − 3x2 + x : 0 < x ≤ 1 1 : x > 1
(a) Tính xác suất một khách hàng dừng lại ít hơn 20 phút (1/3 giờ).
(b) Xác định hàm mật độ xác suất của X.
(c) Tính kì vọng, phương sai của X.
Bài 2.25. Cho biến ngẫu nhiên X là thời gian để vận chuyển hàng từ kho đến cửa hàng (đơn vị: giờ), có hàm mật độ xác suất: ( αx−α−1 : x ≥ 1 f (x) = 0 : x < 1
(a) Tìm giá trị của α và hàm phân phối xác suất
(b) Tính tính kì vọng, phương sai của thời gian vận chuyển.
(c) Tính xác suất để thời gian vận chuyển là ít hơn 2 giờ.
Bài 2.26. Cho hàm mật độ xác suất biến ngẫu nhiên X có dạng: ( αx + β : x ∈ [0, 1] f (x) = 0 : x / ∈ [0, 1]
và P (X > 1/2) = 1/3. Hãy tìm α, β và tính E(X), V (X)
Bài 2.27. Tìm α để hàm sau là một hàm mật độ xác suất, và tính kì vọng, phương sai tương ứng:
( α(1 − x2) : x ∈ [−1, 1] f (x) = 0 : x / ∈ [−1, 1]
Bài 2.28. Cho hàm mật độ xác suất của biến ngẫu nhiên X (gọi là phân phối Pareto): 1 + α : x > 1 f (x) = x2+α 0 : x ≤ 1
(a) Tìm α, và kì vọng, phương sai của X.
(b) Tính P (X > c) với c > 1.
Bài 2.29. Cho hàm mật độ xác suất của biến ngẫu nhiên liên tục có dạng: λe−λx : x > 0, λ > 0 f (x) = 0 : x ≤ 0
Tính P (X ≥ c) theo λ, và thay số khi λ = 4ln2
Bài 2.30. Cho hàm số như sau, với c > 0: c2xe−cx : x ≥ 0 f (x) = 0 : x < 0
(a) Tìm c để đó là hàm mật độ xác suất
(b) Xác định P (X ≥ t), và thay số với c = 0.2, t = 10.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 17
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 2.31. Cho hàm mật độ xác suất như sau, với n ∈ N, n ≥ 1: n(1 − x)n−1 : 0 < x < 1 f (x) = 0 : x / ∈ (0, 1) (a) Xác định P (X ≥ x0)
(b) Nếu P (X ≥ x0) = 1/102n, tìm x0
Bài 2.32. Tính kì vọng của biến ngẫu nhiên có hàm mật độ xác suất như sau: λ2xe−λx : x > 0, (λ > 0) f (x) = 0 : x ≤ 0
Bài 2.33. Xết biến ngẫu nhiên phân phối Cauchy có hàm mật độ: 1 1 f (x) = · , x ∈ R π 1 + x2
Chứng minh rằng E(X) không hữu hạn.
Bài 2.34. Chứng minh rằng nếu biến ngẫu nhiên X có các mô-men gốc mk = E(Xk), k = 0, 1, 2... là hữu hạn, thì: ∞ X tn MX(t) = E(Xn) n! n=0
Gợi ý: sử dụng khai triển: ex = P∞ xn n=0 n!
Bài 2.35. Cho hàm mật độ của X có dạng: 3x2 : x ∈ [0, 1] f (x) = 0 : x / ∈ [0, 1]
(a) Tính kì vọng, phương sai, trung vị của biến X
(b) Tính phân vị mức 0,125 của phân phối Bài 2.36. fX(x) = (1 − α)αx,
x = 0, 1, 2, ..., 0 < α < 1
Xác định hàm mật độ xác suất của Y = X3.
Bài 2.37. Cho X là biến ngẫu nhiên liên tục có hàm mật độ: 1 : x ∈ (a, b) f (x) = b − a 0 : x / ∈ (a, b)
Xác định hàm mật độ xác suất của Y = eX và Z = ln X
Bài 2.38. Chứng minh rằng hàm c g(x) = ,
x = 1, 2, ... không thể là hàm khối lượng xác suất với mọi x c.
Bài 2.39. Chứng minh các hàm sau là hàm mật độ xác suất, và tính P (X > 1/2) 3x2 : x ∈ (0, 1) e−x : x > 0 (a) f (x) = (b) f (x) = 0 : x / ∈ (0, 1) 0 : x ≤ 0 18
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 2.40. Các chuyến bay từ thành phố A đến thành phố B có thời gian hạ cánh chênh lệch so với thời
gian ghi trên vé là biến ngẫu nhiên liên tục, đơn vị là phút, có hàm mật độ xác suất như sau: 1 (36 − x2) : x ∈ (−6, 6) f (x) = 288 0 : x / ∈ (−6, 6)
Tính xác suất để một chuyến bay (a) Sớm ít nhất 2 phút (b) Muộn ít nhất 1 phút
(c) Sớm trong khoảng 1 đến 3 phút (d) Muộn đúng 5 phút.
Bài 2.41. Quãng đường đi được để đảm bảo an toàn của một loại lốp (tính theo km) là biến ngẫu nhiên
liên tục có hàm mật độ như sau: 1 e−x/30 : x > 0 f (x) = 30 0 : x ≤ 0
Tính xác suất một chiếc lốp thuộc loại này hoạt động an toàn: (a) Nhiều nhất 18.000 km
(b) Trong khoảng 27.000 đến 36.000 km (c) Ít nhất 48.000 km
Bài 2.42. Thời gian hoạt động tốt liên tục của một loại bóng đèn (đơn vị: giờ) là biến ngẫu nhiên liên tục có hàm mật độ: 20000 : x > 0 f (x) = (x + 100)3 0 : x ≤ 0
Tính xác suất để: (a) Một bóng đèn hoạt động tốt liên tục ít nhất 200 giờ
(b) Một bóng đèn hoạt động tốt liên tục trong khoảng 80 đến 120 giờ
(c) Trong 5 bóng đèn thì có ít nhất 4 bóng hoạt động tốt liên tục ít nhất 100 giờ
Bài 2.43. Thời gian để một tín hiệu phát đi đến được nơi nhận (đơn vị: giây) là biến ngẫu nhiên liên tục
có hàm phân phối xác suất: 25 1 − : x > 5 F (x) = x2 0 : x ≤ 5
Tính các đại lượng sau:
(a) Xác suất tín hiệu mất ít nhất 10 giây để đến được nơi nhận
(b) Xác suất tín hiệu mất ít hơn 8 giây để đến được nơi nhận
(c) Xác suất trong 4 lần phát tín hiệu thì có 3 lần nhận được sau 7 giây
(d) Kì vọng, phương sai, độ lệch chuẩn của thời gian nhận được tín hiệu
Bài 2.44. Lượng tiêu dùng nước sạch hàng ngày (đơn vị: nghìn mét khối) ở một khu vực dân cư là biến
ngẫu nhiên liên tục có hàm mật độ: 1 xe−x/3 : x > 0 f (x) = 9 0 : x ≤ 0
(a) Tính kì vọng, phương sai của lượng tiêu dùng nước sạch hàng ngày.
(b) Tính xác suất lượng tiêu dùng nước sạch chênh lệch so với kì vọng không quá một lần độ lệch chuẩn.
Bài 2.45. Tỉ suất lợi nhuận (đơn vị: %) của một dự án kinh doanh là biến ngẫu nhiên liên tục có hàm mật độ như sau: ( 1 (x + 1) : −1 < x < 5 f (x) = 18 0 : ngược lại
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 19
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
(a) Tính xác suất dự án bị lỗ.
(b) Tính xác suất để nếu có lãi thì lãi trên 3%.
(c) Tính kì vọng và phương sai của tỉ suất lợi nhuận.
(d) Tính hệ số bất đối xứng của tỉ suất lợi nhuận.
Bài 2.46. Thời gian để sửa chữa một thiết bị máy bị hỏng (đơn vị: giờ) là biến ngẫu nhiên liên tục có hàm mật độ như sau: ( 1 e−x/4 : x > 0 f (x) = 4 0 : x ≤ 0
(a) Tính xác suất thời gian sửa chữa là trên 2 giờ.
(b) Tính kì vọng và phương sai thời gian sửa chữa.
(c) Tính xác suất nếu thời gian sửa là trên 1 giờ thì cũng sẽ chưa đến 2 giờ.
Bài 2.47. Chi cho y tế (đơn vị: triệu đồng) hàng năm của một hộ gia đình có hàm mật độ như sau: x/4 : 0 < x ≤ 2 f (x) = 4/x3 : x > 2 0 : x ≤ 0
(a) Tính xác suất chi cho y tế trong năm là trên 3 triệu.
(b) Tính kì vọng, phương sai của chi cho y tế hàng năm.
Bài 2.48. Với biến ngẫu nhiên X có hàm sinh mô-men: MX(t) = 0.2 + 0.3et + 0.5e3t
(a) Xác định hàm khối lượng / mật độ xác suất.
(b) Tính kì vọng, phương sai của X.
Bài 2.49. Biến ngẫu nhiên X có hàm sinh mô-men: MX(t) = e5t+2t2; đặt biến Y = (X − 5)/2. Hãy xác
định hàm sinh mô-men của Y và sử dụng nó để tính E(Y ), V (Y ).
Bài 2.50. Hãy tính kì vọng, phương sai của biến ngẫu nhiên có hàm sinh mô-men có dạng: MX(t) = 1/(1 − t2).
Bài 2.51. Biến ngẫu nhiên X có hàm mật độ: 2x−3 : x > 1 f (x) = 0 : x ≤ 1
Kiểm tra xem kì vọng và phương sai có tồn tại hay không?
Bài 2.52. Biến ngẫu nhiên liên tục X có hàm mật độ xác định bởi: 1 : x ∈ (0, 1) f (x) = 0 : x / ∈ (0, 1)
Xác định hàm sinh mô-men và tính mô-men bậc 1, bậc 2 theo hàm đó.
Bài 2.53. Xác định hàm sinh mô-men của biến ngẫu nhiên rời rạc X có hàm khối lượng xác suất là:
P (x) = 2( 1 )x, x = 1, 2, 3, ..., và dùng nó để tính mô-men bậc 1, bậc 2 của X. 3
Bài 2.54. Chứng minh rằng không tồn tại biến ngẫu nhiên nào có hàm sinh mô-men có dạng: MX(t) = 1 . 1 − t
Bài 2.55. Chứng minh rằng nếu biến ngẫu nhiên X có hàm mật độ là: 1 f (x) = e−|x|, x ∈ R 2 thì hàm sinh mô-men là: 1 MX(t) = 1 − t2
Bài 2.56. Với hàm sinh mô-men của X là MX(t) = e3t+8t2, tìm hàm sinh mô-men của biến ngẫu nhiên
Z = 1 (X − 3) và dùng nó để tính kì vọng, phương sai của Z. 4 20
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 3 CÁC PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
3.1. Phân phối Bernoulli B(1, p)
Ví dụ 3.1. Một hộp có N quả cầu, trong đó có M quả cầu trắng và N −M quả cầu đen, ta lấy ngẫu nhiên
ra một quả cầu từ hộp.
Nếu đặt A = “lấy được cầu trắng” thì ¯
A = “lấy được cầu đen”, khi đó M N − M M P (A) = và P ( ¯ A) = = 1 − . N N N
Ví dụ 3.2. Một đề thi gồm ba câu hỏi độc lập nhau. Xác suất thí sinh trả lời đúng các câu lần lượt là 0,6;
0,7; 0,8. Chọn ngẫu nhiên một thí sinh, tính kì vọng và phương sai số câu đúng.
3.2. Phân phối Nhị thức B(n, p)
Ví dụ 3.3. Một người đi bán hàng ở 5 nơi độc lập nhau. Xác suất bán được hàng ở mỗi nơi đều bằng nhau và bằng 0,6.
(a) Tính xác suất người đó bán được hàng ở đúng 3 nơi
(b) Tính kì vọng, phương sai, mốt của số lần bán được hàng
(c) Nếu người đó bán hàng ở 4 nơi, tính mốt của số lần bán được hàng
3.3. Phân phối Hình học G(p)
Ví dụ 3.4. Một nhân viên tiếp thị phải gọi điện đến khách hàng để lấy thông tin phản hồi, cho đến khi có
phản hồi thì dừng lại. Biết xác suất khách hàng có phản hồi là 0,2.
(a) Xác định phân phối xác suất của số lần gọi điện.
(b) Tính xác suất nhân viên đó phải gọi điện ít nhất ba lần.
(c) Tính kì vọng, phương sai của số lần gọi điện.
3.4. Phân phối Nhị thức âm NB(r, p)
Ví dụ 3.5. Sử dụng ví dụ tại dầu mục, nhân viên tiếp thị tiếp cận các khách hàng độc lập với xác suât
thành công là 0,7. Xét phân phối xác suất của X là số lần tiếp cận nếu chỉ tiêu cần đạt là 3 lần bán được hàng.
(a) Tính xác suất nhân viên phải tiếp cận từ 6 lần trở lên để hoàn thành chỉ tiêu.
(b) Tính kì vọng phương sai số lần tiếp cận để hoàn thành chỉ tiêu.
3.5. Phân phối Poisson P (λ)
Ví dụ 3.6. Xác suất để một sản phẩm bị hỏng trong quá trình sản xuất là 0,0002. Tính xác suất để trong
5000 sản phẩm được sản xuất ra một cách độc lập thì có 2 sản phẩm hỏng.
3.6. Phân phối Siêu bội H(N, M, n)
Ví dụ 3.7. Giả sử lô hàng có 100 sản phẩm, trong đó có 90 chính phẩm và 10 phế phẩm. Lấy ngẫu nhiên
5 sản phẩm từ lô hàng (theo phương thức không hoàn lại) để kiểm tra. Đặt X là số chính phẩm lấy được
và Y là số phế phẩm lấy được. 21
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
(a) Xác định phân phối xác suất của X, Y và tính kì vọng, phương sai.
(b) Tính xác suất lấy được 4 chính phẩm, xác suất lấy được 1 phế phẩm.
3.7. Phân phối Đều U(a, b)
Ví dụ 3.8. Biết thông tin giá dầu nhập khẩu tháng sau có thể trong khoảng 60 đến 80 (usd/thùng), khi
đó có thể coi giá dầu tháng sau là phân phối Đều U(60, 80), tìm kì vọng, phương sai, và xác suất để giá
tháng sau trong khoảng 50 đến 55 (usd/thùng).
3.8. Phân phối Lũy thừa E(λ)
Ví dụ 3.9. Thời gian hoàn thành một giao dịch chuyển tiền qua hệ thống ngân hàng điện tử là biến ngẫu
nhiên phân phối lũy thừa với trung bình bằng 0,5 phút. Tính xác suất để:
(a) Một giao dịch chuyển tiền điện tử hoàn thành sau hơn 1 phút.
(b) Một giao dịch chuyển tiền điện tử hoàn thành sau hơn 3 phút trong điều kiện nó đã mất hơn 2 phút.
3.9. Một số tích phân đặc biệt
3.10. Phân phối Chuẩn N(µ, σ2)
Ví dụ 3.10. Khối lượng của sản phẩm khi sản xuất ra là biến ngẫu nhiên phân phối chuẩn với kì vọng là
100 g và phương sai là 64 g2. Sản phẩm có khối lượng lớn hơn 110 g được gọi là loại I, sản phẩm có khối
lượng từ 80 g đến 110 g là loại II, và nhẹ hơn 80 g là phế phẩm. Tính xác suất chọn ngẫu nhiên một sản
phẩm thì sản phẩm đó là loại I, loại II, và phế phẩm.
Ví dụ 3.11. Dữ liệu tại một nhà hàng cho thấy hầu hết thực khách chi trong khoảng từ 100 nghìn
đồng/người đến 1 triệu đồng/người. Giả sử số tiền chi/người là phân phối Chuẩn, hãy tính xác suất chọn
một khách ngẫu nhiên thì số tiền chi là trên 700 nghìn đồng.
Ví dụ 3.12. Tra bảng và tìm các giá trị xác suất, giá trị tới hạn từ kết quả thu được
(a) P (Z < 0,5), P (Z > 1) (b) z0,025, z0,05
Ví dụ 3.13. Chi phí để sản xuất hai loại sản phẩm A và B là biến ngẫu nhiên phân phối chuẩn, độc lập,
có đơn vị là triệu đồng. Chi phí sản xuất sản phẩm A có kì vọng là 20 và độ lệch chuẩn là 3; chi phí sản
xuất sản phẩm B có kì vọng là 40 và độ lệch chuẩn là 4. Tính xác suất để:
(a) Tổng chi phí khi sản xuất một sản phẩm A và một sản phẩm B là lớn hơn 65 triệu.
(b) Tổng chi phí khi sản suất 2 sản phẩm A và 3 sản phẩm B là nhỏ hơn 150 triệu.
Ví dụ 3.14. Xác suất để một khách hàng vào siêu thị mua sản phẩm của hãng A là 0,3. Tính xác suất để
trong 100 khách vào siêu thị có:
(a) Nhiều hơn 35 khách mua hàng của hãng A
(b) Từ 25 đến 40 khách mua hàng của hãng A.
3.11. Phân phối Khi-bình phương χ2(n)
Ví dụ 3.15. Tra bảng giá trị tới hạn Khi-bình phương, có các kết quả sau χ2(10) 0,05 =?; χ2(15) 0,95 =?
3.12. Phân phối Student T (n)
Ví dụ 3.16. Tra bảng giá trị tới hạn Student t(10) 0,05 =???; t(15) 0,025 =??? 22
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
3.13. Phân phối Fisher F (m, n)
Ví dụ 3.17. Tra bảng giá trị tới hạn Fisher f (5,8) 0,05 =?; f (15,3) 0,025 =?
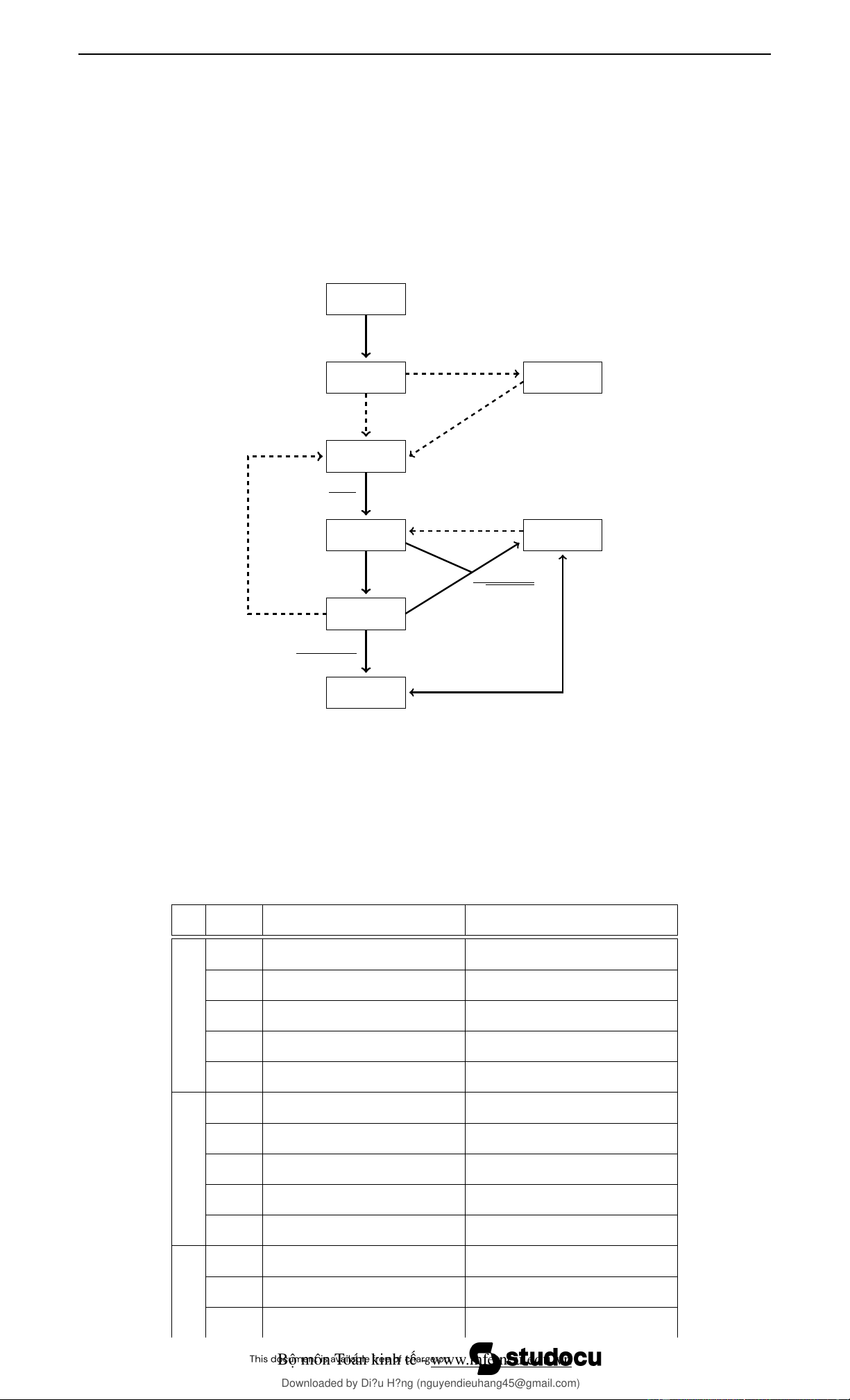
3.14. Các mối liên hệ và một số phân phối khác B(1, p) P n biến n lớn B(n, p) P (λ) p nhỏ n lớn λ lớn N (µ, σ2) Z = X−µ σ m lớn N (0, 1) T (m) Pm i=1 Z2 i Z √ m lớn χ2(m)/m χ2(m) χ2(m1)/m1 χ2(m2)/m2 [T (m)]2 ∼ F (1, m) F (m1, m2)
Hình 3.1: Mối liên hệ giữa các phân phối xác suất
3.15. Sinh chuỗi số ngẫu nhiên theo phân phối xác suất
3.16. Thực hành với phần mềm chuyên dụng ∼ Tính Hàm Excel 2016 Hàm R k số [RNG] → Binomial rbinom(k, n, p) P (x) binom.dist(x, n, p, 0) dbinom(x, n, p) ,p) (n F (x) binom.dist(x, n, p, 1) pbinom(x, n, p) B q binom.inv( β n, p, β) qbinom(β, n, p) x binom.inv( α n, p, 1 − α) qbinom(1 − α, n, p) k số rgeom(k, p) P (x) dgeom(x, p) (p) G F (x) pgeom(x, p) q qgeom( β β, p) x qgeom( α 1 − α, p) k số rnbinom(k, r, p) P (x) negbinom(x − r, r, p, 0) dnbinom(x − r, r, p) (r,p) F (x) negbinom(x B − r, r, p, 1) pnbinom(x − r, r, p) N
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 23
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— ∼ Tính Hàm Excel 2016 Hàm R q qnbinom( β β, r, p) x qnbinom( α 1 − α, r, p) k số [RNG] → Poisson rpois(k, p) P (x) poisson.dist(x, λ, 0) dpois(x, p) ) (λ P F (x) poisson.dist(x, λ, 1) ppois(x, p) q qpois( β β, p) x qpois( α 1 − α, p) k số rhyper(k, n, M, N − M) ) ,n P (x)
hypgeom.dist(x, n, M, N, 0) dhyper(x, n, M, N − M) ,M F (x)
hypgeom.dist(x, n, M, N, 1) phyper(x, n, M, N − M) (N H q qhyper( β β, n, M, N − M) x qhyper( α 1 − α, n, M, N − M) k số [RNG] → Uniform runif(k, a, b) f (x) dunif(x, a, b) b) (a, F (x) punif(x, a, b) U q qunif( β β, a, b) x qunif( α 1 − α, a, b) k số rexp(k, λ) f (x) expon.dist(x, λ, 0) dexp(x, λ) ) (λ E F (x) expon.dist(x, λ, 1) pexp(x, λ) q qexp( β β, λ) x qexp( α 1 − α, λ) k số [RNG] → Normal rnorm(k, µ, σ) )2 f(x) norm.dist(x, µ, σ, 0) dnorm(x, µ, σ) ,σ (µ F (x) norm.dist(x, µ, σ, 1) pnorm(x, µ, σ) N q norm.inv( β β, µ, σ) qnorm(β, µ, σ) x norm.inv( α 1 − α, µ, σ) qnorm(1 − α, µ, σ) k số [RNG] → Normal rnorm(k) f (z) norm.dist(x, 0, 1, 0) dnorm(z) (0,1) F (z) norm.dist(x, 0, 1, 1) pnorm(z) N q norm.inv( β β, 0, 1) qnorm(β) z norm.inv( α 1 − α, 0, 1) qnorm(1 − α) k số rchisq(k, n) ) f (x) chisq.dist(x, n, 0) dchisq(x, n) (n2 F(x) chisq.dist(x, n, 1) pchisq(x, n) χ q chisq.inv( β β, n) qchisq(β, n) χ2(n) chisq.inv( α 1 − α, n) qchisq(1 − α, n) k số rt(k, n) P (z) t.dist(x, n, 0) dt(x, n) ) (n T 24
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN ∼ Tính Hàm Excel 2016 Hàm R F (z) t.dist(x, n, 1) pt(x, n) q t.inv( β β, n) qt(β, n) t(n) t.inv( α 1 − α, n) qt(1 − α, n) k số rf(k, m, n) ) P (z) f.dist(x, m, n, 0) df(x, m, n) ,n (m F (z) f.dist(x, m, n, 1) pf(x, m, n) F q f.inv( β β, m, n) qf(β, m, n) f (m,n) f.inv( α 1 − α, m, n) qf(1 − α, m, n) Thuật ngữ Tiếng Việt Tiếng Anh Bậc tự do Degree of freedom Phân phối Bernoulli Bernoulli distribution Phân phối Chuẩn Normal distribution
Phân phối Chuẩn-chuẩn hóa Standardized Normality distribution Phân phối Đều Uniform distribution Phân phối Fisher Fisher distribution Phân phối Hình học Geometric distribution
Phân phối Khi-bình phương Chi-squared distribution Phân phối Lũy thừa Exponential distribution Phân phối Nhị thức Binomial distribution Phân phối Nhị thức âm Negative Binomial distribution Phân phối Poisson Poisson distribution Phân phối Student Student distribution Phân phối Siêu bội Hypergeometric distribution
Công thức quan trọng X ∼ B(1, p)
P (x) = px(1 − p)1−x, x = {0, 1} Bernoulli E(X) = p, V (X) = p(1 − p) X ∼ B(n, p) P (x) = C x n px(1 − p)n−x, x = 0, n Nhị thức E(X) = np, V (X) = np(1 − p) np + p − 1 ≤ M0 ≤ np + p X p(1 − p) ˆ p = ⇒ E(ˆp) = p, V (ˆ p) = n n X ∼ G(p)
P (x) = p(1 − p)x−1, x = 1, ∞ Hình học 1 1 − p E(X) = , V (X) = p p2
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 25
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— X ∼ NB(r, p) P (x) = C r−1 x−1 pr(1 − p)x−r, x = r, ∞ Nhị thức âm r r (1 − p) E(X) = , V (X) = p p2 e−λλx X ∼ P (λ) P (x) = , x = 0, ∞ x! Poisson E(X) = λ, V (X) = λ, λ − 1 ≤ M0 ≤ λ C x C n−x X ∼ H(N, M, n) P (x) = M N −M C n N Siêu bội nM M N − M N − n E(X) = , V (X) = n N N N N − 1 1 X ∼ U(a, b) f (x) = : x ∈ (a, b) b − a Đều a + b (b − a)2 E(X) = , V (X) = 2 12 1 (x − µ)2 X ∼ N(µ, σ2) f (x) = √ exp − , x ∈ R σ 2π 2σ2 Chuẩn E(X) = µ, V (X) = σ2 b − µ Z ∼ N(0, 1) ⇒ P (X < b) = P Z < σ P (Z > zα) = α X ∼ χ2(n) E(X) = n, V (X) = 2n Khi-bình phương P (X > χ2(n) α ) = α n X ∼ T (n) E(X) = 0, V (X) = n − 2 Student P (X > t(n) α ) = α n X ∼ F (m, n) E(X) = n − 2 Fisher 1 P (X > f (m,n) α ) = α, f (m,n) 1−α = f(n,m) α Bài tập
Bài 3.1. Một đề thi trắc nghiệm có 40 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương
án đúng. Một người dự thi đã tô phương án trả lời tất cả các câu bằng cách ngẫu nhiên. Gọi X là số câu
mà người thi trả lời đúng.
(a) Xác định các giá trị có thể có của X
(b) Tìm phân phối xác suất của X (c) Tính E(X), V (X)
(d) Tìm số câu trả lời đúng có khả năng xảy ra lớn nhất
(e) Tính xác suất để số câu trả lời đúng lớn hơn 3 câu
Bài 3.2. Số liệu thống kê của công ty giám sát kĩ thuật của thành phố cho thấy, có khoảng 30% cầu chì
không đáp ứng tiêu chuẩn lắp đặt. Hãy cho biết trong số 10 cầu chì được mua ngẫu nhiên thì có ít nhất 2
cầu chì không đạt tiêu chuẩn.
Bài 3.3. Một người bán hàng ở 5 nơi độc lập. Xác suất bán được hàng ở mỗi nơi bằng nhau và bằng 0, 2.
(a) Tính xác suất bán được hàng ở nơi 2 và nơi 4.
(b) Tính xác suất bán được hàng ở 2 nơi. 26
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 3.4. Gieo một xúc xắc cân đối và đồng chất 5 lần liên tiếp.
(a) Tính xác suất có 3 lần xúc xắc xuất hiện mặt 5 chấm
(b) Tính xác suất có ít nhất 2 lần xuất hiện mặt 3 chấm
Bài 3.5. Tỷ lệ phế phẩm do một máy sản xuất là 2%. Mỗi lần lấy 1 sản phẩm để kiểm tra, nếu phát hiện
phế phẩm thì dừng, nếu lấy được chính phẩm thì kiểm tra tiếp, quá trình tiếp tục cho đến khi phát hiện
phế phẩm thì không kiểm tra nữa. Tính xác suất để số lần kiểm tra ít nhất 100 lần.
Bài 3.6. Một đồng tiền xu cân đối có 2 mặt (mặt sấp (S) và mặt ngửa (N)). Tính xác suất để mặt sấp xuất
hiện lần thứ 5 trong 10 lần tung đồng xu.
Bài 3.7. Cho X là biến ngẫu nhiên có phân phối Poisson với tham số λ = 3. Tính P (X ≥ 3)
Bài 3.8. Cho X là biến ngẫu nhiên có phân phối Poisson với tham số λ = 1. Tính P [(X ≥ 2)|(X ≤ 4)]
Bài 3.9. Tính E(X2) của X là biến ngẫu nhiên có công thức xác suất như sau 1 2 22 P (X = x) = C4x
22 · (0, 2)4x · (0, 8)22−4x với x = 0, , , ..., 4 4 4
Bài 3.10. Tìm k và V (X) của biến ngẫu nhiên X có hàm đặc trưng gX(t) = k · (2 + 3eit)100
Bài 3.11. Tìm k và tính V (X) của biến ngẫu nhiên X có hàm đặc trưng eit 3 gX(t) = k · 7 − 5eit
Bài 3.12. Cho X ∼ P(λ) thỏa mãn
2P (X = 0) + P (X = 2) = 2P (X = 1) (a) Tính E(X) , V (X) (b) Tính P (X ≥ 2) Bài 3.13. Cho 1
Y ∼ U(0, 1) và Y = X2, tìm hàm mật độ xác suất của X 4 Bài 3.14. Cho 10 Y ∼ U(0, 10), tính P X + > 7 X
Bài 3.15. Cho X ∼ U(0, 1). Đặt Y = a + (b − a)X với a và b là các số thực khác 0. Chứng minh rằng Y ∼ U(a, b)
Bài 3.16. Cho X ∼ U(0, 1). Tìm hàm mật độ và hàm phân phối của biến ngẫu nhiên Y = − ln X
Bài 3.17. Chứng minh rằng:
(a) Nếu X ∼ U(0, 1) thì Y = −2 ln X phân phối χ2(2) (b) Nếu X thì Pn
i ∼ U (0, 1), Yi = −2 ln Xi Y i=1 i ∼ χ2(2n)
Gợi ý câu (b): sử dụng kết quả câu (a) và hàm sinh mô-men để chứng minh.
Bài 3.18. Cho biến ngẫu nhiên liên tục có hàm mật độ xác suất như sau 1 fX(x) = √ x−2e− 1 2x2 , x ∈ R 2π Chứng minh rằng 1 Y = ∼ N(0, 1) X
Bài 3.19. Cho X là biến ngẫu nhiên có hàm mật độ xác suất e−x x > 0 f (x) = 0 x ≤ 0
Tìm hàm mật độ xác suất của biến ngẫu nhiên Y = 1 − e−X
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 27
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 3.20. Cho X là biến ngẫu nhiên có hàm mật độ xác suất λ · e−λx x > 0 f (x) = 0 x ≤ 0
Tìm tham số λ biết phân vị tại mức 75% của X bằng 1. 3
Bài 3.21. Cho X là biến ngẫu nhiên có hàm phân phối xác suất 1 − e−x x > 0 F (x) = 0 x ≤ 0 Tính P (0 ≤ eX ≤ 4) =?
Bài 3.22. Cho X là biến ngẫu nhiên có phân phối chuẩn. Biết P (X < 500) = 0, 5 và P (X > 650) =
0, 0228 hãy tìm độ lệch chuẩn của X.
Bài 3.23. Cho X ∼ N(5, 4) và Y = 2X + 1. Tính P(8 < X < 12) =?
Bài 3.24. Tuổi thọ của một loại sản phẩm được giả thiết là biến ngẫu nhiên có phân phối chuẩn với tuổi
thọ trung bình là 7 năm và độ lệch chuẩn là 3 năm. Những sản phẩm có tuổi thọ ≤ 4 năm được bảo hành.
Nhà sản xuất bán được mỗi sản phẩm mà không phải bảo hành thì có lãi 1 triệu đồng, tuy nhiên nếu sản
phẩm phải bảo hành thì bị lỗ 2 triệu đồng.
(a) Tính tiền lãi trung bình trên mỗi sản phẩm mà nhà sản xuất nhận được.
(b) Muốn tiền lãi trung bình trên mỗi sản phẩm mà nhà sản xuất nhận được là 700 ngàn đồng thì cần
qui định thời gian bảo hành với mỗi sản phẩm là bao nhiêu năm?
Bài 3.25. Một nhà máy sản xuất một loại sản phẩm với hai loại màu, với cơ cấu 55% màu xanh và 45%
màu trắng. Tuổi thọ của sản phẩm màu xanh có phân phối chuẩn với trung bình là 9 năm và độ lệch chuẩn
là 3 năm, tuổi thọ của sản phẩm màu trắng có phân phối chuẩn với trung bình là 10 năm và độ lệch chuẩn
là 4 năm (tuổi thọ của sản phẩm là các biến ngẫu nhiên độc lập). Nhà máy bảo hành cho những sản phẩm có tuổi thọ ≤ 6 năm.
(a) Tính xác suất để khi lấy một sản phẩm từ nhà máy thì sản phẩm đó phải bảo hành.
(b) Tính xác suất tuổi thọ sản phẩm màu xanh lớn hơn tuổi thọ sản phẩm màu trắng.
Bài 3.26. Giả sử lãi suất (đơn vị %) khi đầu tư vào hai thị trường A và B là các biến ngẫu nhiên độc lập
có phân phối chuẩn lần lượt là XA ∼ N(10, 16) và XB ∼ N(9, 9).
(a) Nhà đầu tư chia đều vốn vào hai thị trường, tính xác suất để nhận được lãi suất hơn 8%.
(b) Muốn rủi ro ở mức thấp nhất thì nên chia vốn vào hai thị trường trên theo tỷ lệ nào?
Bài 3.27. Một nông trại trồng hai loại dưa, dưa vàng và dưa xanh đến vụ thu hoạch số lượng dưa thu
được đều nhau. Trọng lượng của dưa vàng có phân phối chuẩn với trung bình là 2, 5kg và độ lệch chuẩn
là 800g, trọng lượng của dưa xanh có phân phối chuẩn với trung bình là 3 kg và độ lệch chuẩn là 1 kg
(trọng lượng dưa là các biến ngẫu nhiên độc lập). Công ty hoa quả chỉ đồng ý mua những quả có trọng lượng ≥ 2kg.
(a) Tìm tỷ lệ dưa đủ tiêu chuẩn để Công ty mua.
(b) Tính xác suất để trọng lượng dưa vàng nhẹ hơn. 28
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 4 BIẾN NGẪU NHIÊN NHIỀU CHIỀU
4.1. Khái niệm và định nghĩa
Ví dụ 4.1. Khi gieo đồng xu đối xứng đồng chất, xét biến ngẫu nhiên hai chiều (X là 1, X2) trong đó X1
số lần mặt sấp xuất hiện, X là số lần mặt ngửa xuất hiện. 2
Ví dụ 4.2. Thị trường bất động sản trong một năm có ba trường hợp: suy thoái (S), ổn định (O), và tăng trưởng (T). Giả sử X
lần lượt là tỉ suất lợi nhuận (đơn vị: %) khi đầu tư vào bất động sản và đầu tư 1, X2
vào vàng, với điều kiện các yếu tố khác không đổi, là hàm như sau ω = S → X 1 = −10, X2 = 3 Ω = {S, O, T }, ω = O → X1 = 5, X2 = 2 ω = T → X1 = 15, X2 = 1
Ví dụ 4.3. Xét trò chơi “oẳn tù tì” với hai người chơi 1 và 2. mỗi người có ba lựa chọn là đấm (Đ), kéo
(K), lá (L) với khả năng lựa chọn là ngẫu nhiên. Nếu ai thắng thì lấy được một đồng của người thua, nếu
hòa thì không ai mất hay được gì. Khi đó lập biến ngẫu nhiên là số tiền có được sau khi chơi một lần của hai người.
4.2. Biến ngẫu nhiên hai chiều
Ví dụ 4.4. Cho biến ngẫu nhiên hai chiều (X, Y ), trong đó Xlà số nhân viên nam và Y là nhân viên nữ
tại có mặt tại một thời điểm bất kì của một cửa hàng; X = {1, 2}; Y = {1, 2} với các xác suất như sau:
P (X = 1, Y = 1) = 0, 3 ; P (X = 1, Y = 2) = 0, 2;
P (X = 2, Y = 1) = 0, 1 ; P (X = 2, Y = 2) = 0, 4.
(a) Lập bảng phân phối xác suất đồng thời, các bảng phân phối biên của số nhân viên nam và số nhân viên nữ
(b) Xác định hàm phân phối xác suất đồng thời, các hàm phân phối biên.
Ví dụ 4.5. Cho bảng phân phối xác suất đồng thời của số nhân viên nam X và số nhân viên nữ Y như sau X Y 1 2 P (X) 1 0,3 0,2 0,5 2 0,1 0,4 0,5 P (Y ) 0,4 0,6 1
(a) Hai biến X và Y có độc lập không?
(b) Lập bảng phân phối xác suất của số nhân viên nữ trong điều kiện có một nhân viên nam, và bảng
phân phối xác suất của số nhân viên nam trong điều kiện có hai nhân viên nữ.
Ví dụ 4.6. Cho biến ngẫu nhiên hai chiều liên tục (X, Y ) là lợi nhuận khi đầu tư vào hai cổ phiếu, có
hàm phân phối xác suất đồng thời
1 − e−x − e−y + e−x−y : x ≥ 0, y ≥ 0 F (x, y) = 0 : ngược lại
Hãy xác định hàm mật độ xác suất đồng thời. 29
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Ví dụ 4.7. Với một doanh nghiệp, có biến ngẫu nhiên hai chiều (X, Y ) liên tục, trong đó X là doanh thu
từ bán sản phẩm và Y là doanh thu từ dịch vụ, có hàm mật độ xác suất là hằng số α trong miền hình chữ
nhật D = {(x, y) : 0 ≤ x ≤ 2, 0 ≤ y ≤ 1}, và bằng 0 bên ngoài hình chữ nhật đó (hay còn gọi là phân phối đều trong miền D).
(a) Xác định hằng số α và hàm mật độ xác suất đồng thời.
(b) Xác định hàm phân phối xác suất đồng thời.
(c) Tính xác suất doanh thu bán hàng trong khoảng (0, 1) đồng thời doanh thu từ dịch vụ trong khoảng
(0, 1), hay P (X, Y ) ∈ H với H = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1}.
(d) Tính P (X, Y ) ∈ M với M = {(x, y) : (x − 1)2 + (y − 1)2 ≤ 1}. 2 4
4.3. Tham số của biến ngẫu nhiên hai chiều
Ví dụ 4.8. Tiếp tục với ví dụ 4.7 trang 30, xét biến ngẫu nhiên hai chiều (X, Y ) liên tục, với X là doanh
thu từ bán hàng, Y là doanh thu từ dịch vụ của một doanh nghiệp (đơn vị: tỉ đồng). Hàm mật độ là không 0
đổi trong miền hình chữ nhật ≤ x ≤ 2 D = . 0 ≤ y ≤ 1
(a) Xác định các hàm phân phối xác suất biên và hàm mật độ biên.
(b) Kiểm tra tính độc lập của X và Y .
(c) Tính các tham số đặc trưng của biến ngẫu nhiên (X, Y ).
Ví dụ 4.9. Cho biến ngẫu nhiên hai chiều (X, Y ) với X là thời gian thực hiện ở một quầy dịch vụ, Y là
thời gian chờ đợi dịch vụ, đơn vị là giờ, có hàm mật độ đồng thời như sau ( x 3 1 − − y
: x ≥ 0, y ≥ 0, x + 2y ≤ 2 f (x, y) = 2 0 : ngược lại.
(a) Vẽ hình hàm mật độ, và kiểm tra tính chất của hàm mật độ.
(b) Tính xác suất thời gian thực hiện là trên 1 giờ.
(c) Tính xác suất thời gian chờ đợi là ít hơn nửa giờ.
(d) Tính xác suất để tổng thời gian chờ đợi và thực hiện là dưới 1 giờ.
(e) Tính các tham số của biến ngẫu nhiên hai chiều này.
Ví dụ 4.10. Với một doanh nghiệp, xét trong một tháng, đặt X là số hợp đồng kí được, X = {0, 1, 2}; Y
là lợi nhuận (tỉ đồng), Y = {−10, 10, 20}, có bảng phân phối xác suất hai chiều như sau X Y −10 10 20 0 0,1 0 0 1 0,1 0,3 0,2 2 0 0,1 0,2
(a) Giải thích ý nghĩa các xác suất.
(b) Xác định các hàm mật độ biên, hai biến có độc lập không?
(c) Tính kì vọng, phương sai của X, Y , Cov(X, Y ), ρ(X, Y ).
4.4. Biến ngẫu nhiên nhiều chiều
Ví dụ 4.11. Cho biến ngẫu nhiên 3 chiều (X1, X2, X3) có hàm mật độ xác suất đồng thời như sau (x1 + x2)e−x3
: 0 < x1 < 1, 0 < x2 < 1, x3 > 0 f (x1, x2, x3) = 0 : ngược lại.
(a) Cho thấy đây đúng là một hàm mật độ xác suất đồng thời. 0 < x 1 < 1/2
(b) Tính xác suất trong miền H = 1/2 < x . 2 < 1 0 < x3 < 1
(c) Tính các hàm xác suất biên của từng biến, của từng cặp biến. 30
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Ví dụ 4.12. Kiểm tra tính độc lập từng đôi và độc lập toàn phần của các biến ngẫu nhiên sau 1 với xác suất 1 1 với xác suất 1 X 2 2 1 = ; X2 = ; 0 với xác suất 1 0 với xác suất 1 2 2 1 nếu X1 = X2 X3 = . 0 nếu X1 6= X2
Ví dụ 4.13. Cho biến ngẫu nhiên 3 chiều (X1, X2, X3) có hàm mật độ xác suất đồng thời như sau (x1 + x2)e−x3
: 0 < x1 < 1, 0 < x2 < 1, x3 > 0 f (x1, x2, x3) = 0 : ngược lại.
Kiểm tra tính độc lập từng đôi, độc lập toàn phần của các biến của biến ngẫu nhiên 3 chiều trên.
4.5. Tham số của biến ngẫu nhiên nhiều chiều
Ví dụ 4.14. Tiếp tục với Ví dụ trước, với lợi nhuận (đơn vị: tỉ đồng) của ba dự án lần lượt là X1, X2, X3
có bảng phân phối xác suất ba chiều X2 = 3 X2 = 4 X3 = 5 X3 = 6 X3 = 5 X3 = 6 X1 = 1 0,05 0,05 0,1 0,15 X1 = 2 0,05 0,15 0,2 0,25
(a) Xác định ma trận hiệp phương sai và ma trận hệ số tương quan.
(b) Tính các hệ số tương quan riêng, tương quan bán phần.
Ví dụ 4.15. Một doanh nghiệp có biến ngẫu nhiên 3 chiều (X là giá vốn, là 1, X2, X3) trong đó X1 X2
giá lao động, cả hai được chuẩn hóa về đoạn (0, 1) và X là doanh thu. Hàm mật độ xác suất đồng thời 3 như sau (x1 + x2)e−x3
: 0 < x1 < 1, 0 < x2 < 1, x3 > 0 f (x1, x2, x3) = 0 : ngược lại.
(a) Tính kì vọng, phương sai các biến thành phần.
(b) Tính các hệ số tương quan, hệ số tương quan riêng, hệ số tương quan bán phần.
4.6. Biến ngẫu nhiên có điều kiện và hàm hồi qui
Ví dụ 4.16. Với một doanh nghiệp, xét trong một tháng, đặt X là số hợp đồng kí được, X = 0, 1, 2; Y là
lợi nhuận (tỉ đồng), Y = −10, 10, 20, có bảng phân phối xác suất hai chiều như sau X Y −10 10 20 0 0,1 0 0 1 0,1 0,3 0,2 2 0 0,1 0,2
Xác định phân phối xác suất của Y khi X = 0, 1, 2 và tính các tham số có điều kiện.
Ví dụ 4.17. Tiếp tục Ví dụ ?? trang ??, với X
là lợi nhuận từ ba dự án đầu tư, có xác suất đồng 1, X2, X3 thời
P (1, 3, 5) = 0, 05 P (1, 3, 6) = 0, 05 P (1, 4, 5) = 0, 1 P (1, 4, 6) = 0, 15
P (2, 3, 5) = 0, 05 P (2, 3, 6) = 0, 15 P (2, 4, 5) = 0, 2 P (2, 4, 6) = 0, 25
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 31
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
(a) Lập bảng phân phối xác suất biên của các biến, và của các cặp biến.
(b) Lập bảng phân phối xác suất có điều kiện sau: (X1|X2 = 3, X3 = 5), (X1|X2 = 3), (X1, X2|X3 =
5) và tính các tham số kì vọng, phương sai, hệ số tương quan.
Ví dụ 4.18. Cho biến ngẫu nhiên 3 chiều (X1, X2, X3) có hàm mật độ xác suất đồng thời như sau (x1 + x2)e−x3
: 0 < x1 < 1, 0 < x2 < 1, x3 > 0 f (x1, x2, x3) = 0 : ngược lại.
(c) Xác định các hàm xác suất biên của từng biến, của từng cặp biến.
(d) Xác định các hàm mật độ của: (i) X trong điều kiện , (ii) trong điều kiện 1 X2 X1 (X2, X3), (iii) (X . 1, X2) trong điều kiện X3
Ví dụ 4.19. Cho biến ngẫu nhiên 3 chiều (X1, X2, X3) có hàm mật độ xác suất đồng thời như sau (x1 + x2)e−x3
: 0 < x1 < 1, 0 < x2 < 1, x3 > 0 f (x1, x2, x3) = 0 : ngược lại.
Kiểm tra tính độc lập có điều kiện của các biến của biến ngẫu nhiên 3 chiều trên.
Ví dụ 4.20. Cho bảng phân phối xác suất của biến ngẫu nhiên hai chiều rời rạc (X, Y ), trong đó X là thu
nhập, Y là chi tiêu của hộ gia đình X Y 2 3 4 5 6 P 4 0,02 0,05 0,03 0 0 0,1 5 0,02 0,08 0,05 0,05 0 0,2 6 0 0,06 0,23 0,08 0,03 0,4 7 0 0,02 0,04 0,11 0,03 0,2 8 0 0 0,02 0,03 0,05 0,1 P 0,04 0,21 0,37 0,27 0,11 1
(a) Tính hệ số tương quan giữa các biến và giải thích ý nghĩa.
(b) Xác định mối quan hệ hồi qui của chi tiêu theo thu nhập.
(c) Xác định sai số ngẫu nhiên khi X = 4 và giải thích ý nghĩa.
Ví dụ 4.21. Trong một doanh nghiệp X, Y, Z lần lượt là Giá vốn, Giá lao động, Lợi nhuận. Cả ba biến
đều được chuẩn hóa về khoảng (0, 1): X, Y, Z ∈ (0, 1), có hàm mật độ xác suất đồng thời như sau x + 2y + 3z : (x, y, z) ∈ (0, 1)3 f (x, y, z) = 3 0 : (x, y, z) / ∈ (0, 1)3.
Xác định hàm hồi qui của Lợi nhuận theo Giá vốn và Giá lao động và phân tích hàm này.
4.7. Khái niệm mẫu ngẫu nhiên
Ví dụ 4.22. Từ biến ngẫu nhiên gốc X, tìm hàm hợp lí của mẫu ngẫu nhiên kích thước n tại điểm (x1, x2, ..., xn) khi:
(a) X phân phối Bernoulli B(1, p), thay số với p = 0, 6 và điểm (0, 1, 1, 0, 1).
(b) X phân phối Lũy thừa E(λ). 32
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
4.8. Hàm của biến ngẫu nhiên nhiều chiều
Ví dụ 4.23. Cho biến ngẫu nhiên hai chiều (X1, X2) có bảng phân phối xác suất đồng thời hai chiều như
ở dưới. Đặt Y1 = |X1 − X2| và Y2 = |X21 − X22|. Lập bảng phân phối xác suất đồng thời của (Y1, Y2). X 1 2 3 1 X2 Σ 1 0,05 0,2 0,15 0,4 2 0,15 0,3 0,15 0,6 Σ 0,2 0,5 0,3 1
Ví dụ 4.24. Cho biến ngẫu nhiên nhiều chiều (X1, X2, ..., Xn) liên tục, trong đó các Xi(i = 1, n) là độc
lập, có cùng hàm phân phối xác suất FX(x) và cùng hàm mật độ xác suất fX(x) (hay còn gọi là mẫu ngẫu
nhiên kích thước n từ biến ngẫu nhiên gốc X).
(a) Xác định hàm phân phối và mật độ xác suất của hai biến ngẫu nhiên: Y = max{X1, X2, ..., Xn}, Z = min{X1, X2, ..., Xn}.
(b) Xác định phân phối xác suất của Y , Z khi X ∼ U(a, b).
(c) Áp dụng câu trên với X ∼ U(0, 1) và kích thước mẫu ngẫu nhiên bằng 3 (tức là n = 3).
Ví dụ 4.25. Cho X là thu nhập chính thức và
là thu nhập không chính thức của người lao động, có 1 X2
hàm mật độ xác suất đồng thời như sau 4x1x2
: 0 < x1 < 1, 0 < x2 < 0 fX (x 1 X2 1, x2) = 0 : ngược lại.
Lập hàm mật độ xác suất đồng thời của tổng thu nhập, và tỉ trọng của thu nhập chính thức trong tổng thu nhập.
4.9. Một số phân phối nhiều chiều thông dụng
Ví dụ 4.26. Trong khảo sát khách hàng về mức độ hài lòng với dịch vụ của cửa doanh nghiệp, có ba mức
đánh giá: 1 = không hài lòng, 2 = bình thường, 3 = hài lòng. Giả sử khách hàng đánh giá độc lập, và xác
suất để khách hàng chọn các mức đánh giá với xác suất tương ứng là p1 = 0, 1; p2 = 0, 3; p3 = 0, 6.
(a) Xác định công thức tính xác suất của số khách hàng lựa chọn các mức đánh giá trong số 10 khách.
(b) Tính xác suất trong 10 khách, thì số lượng khách chọn ba mức đánh giá tương ứng là: 0, 2, 8.
(c) Tính các tham số của biến ngẫu nhiên 3 chiều này.
Ví dụ 4.27. Trong số 50 khách có mặt tại một nhà hàng có 10 người đến lần đầu, 20 người đến lần thứ
hai, 15 người đến lần thứ ba, 5 người đến từ 4 lần trở lên. Nhà hàng chọn ngẫu nhiên 8 khách để trao phiếu giảm giá. Đặt X
lần lượt là số khách thuộc bốn loại trên trong số 12 người. 1, X2, X3, X4
(a) Xác định phân phối xác suất đồng thời.
(b) Tính xác suất trong 8 khách thì mỗi loại đều có số khách bằng nhau.
(c) Tính các kì vọng, phương sai, hiệp phương sai, hệ số tương quan.
(d) Nếu khách đến lần đầu hoặc 2 lần được gọi là khách tiềm năng, khách đến từ 3 lần trở lên là khách
thường xuyên. Tính kì vọng, phương sai, hệ số tương quan của số khách tiềm năng, số khách thường
xuyên trong số 8 người được chọn.
Ví dụ 4.28. Cho biến ngẫu nhiên (X1, X2, X3) liên tục phân phối đều trong miền: D = (0 ≤ x1 ≤ 2,
0 ≤ x2 ≤ 3 , 0 ≤ x3 ≤ 4).
(a) Xác định hàm mật độ đồng thời.
(b) Xác định các hàm mật độ biên của các biến, các cặp biến.
(c) Tính xác suất P (x1 − 1)2 + (x2 − 3)2 + (x 2 3 − 2)2 ≤ 1.
(d) Tính các tham số đặc trưng của biến ba chiều này.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 33
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Ví dụ 4.29. Cho tỉ suất lợi tức (%) của hai loại cổ phiếu A và B trên thị trường là phân phối chuẩn, với
kì vọng lần lượt là 10(%) và 8(%); và độ lệch chuẩn lần lượt là 6(%) và 4(%). Hệ số tương quan của hai tỉ suất là 0,5.
(a) Xác định hàm mật độ của biến ngẫu nhiên phân phối chuẩn hai chiều tạo thành từ hai tỉ suất lợi tức.
(b) Tính kì vọng, độ lệch chuẩn tỉ suất lợi tức cổ phiếu A khi tỉ suất cổ phiếu B là 7(%) và 9(%).
(c) So sánh khả năng cổ phiếu A có tỉ suất lợi tức trên 9(%) khi không có điều kiện, và trong điều
kiện tỉ suất lợi tức cổ phiếu B là 7(%) và 9(%).
Ví dụ 4.30. Từ biến ngẫu nhiên gốc phân phối chuẩn với kì vọng bằng 10, phương sai bằng 25, rút ra một
mẫu ngẫu nhiên kích thước bằng 3. Xác định hàm mật độ tại các giá trị 9, 8, 12, và tính hàm hợp lí của
mẫu ngẫu nhiên tại điểm (9, 8, 11)
Công thức quan trọng Hàm phân phối F (x1, ..., xn) Biến 2 chiều rời rạc P (x P i, yj ); P P (x i j i, yj ) = 1 P (xi) = P P (x j i, yj ) P (x P (Y = y i, yj ) j |X = xi) = P (xi) Biến 2 chiều liên tục ∂2F (x f (x, y) = 1, x2) ∂x1∂x2 Z +∞ Z +∞ f (x, y)dxdy = 1 −∞ −∞ Z +∞ fX(x) = f (x, y)dy −∞ f (x, y) fY |x(y|x) = fX(x) Biến hai chiều
Cov(X, Y ) = E(X · Y ) − E(X)E(Y )
V (X ± Y ) = V (X) + V (Y ) ± 2Cov(X, Y ) Cov(X, Y ) ρ(X, Y ) = ; −1 ≤ ρ(X, Y ) ≤ 1 σXσY Thuật ngữ Tiếng Việt Tiếng Anh (Biến) hai chiều Bivariate
(Biến) hai chiều liên tục Continuous bivariate
(Biến) hai chiều liên tục Cntinuous bivariate
(Biến) hai chiều rời rạc Discrete bivariate (Biến) nhiều chiều Multivariate Độc lập toàn phần Mutually independent Độc lập từng đôi Pairwise independent Không tương quan Uncorrelated Hàm hồi qui Regression function 34
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN Tiếng Việt Tiếng Anh Hàm hồi qui đơn Single regression function Hàm hồi qui bội Multiple regression function Hàm hợp lí Likelihood function Hàm mật độ biên Marginal density function
Hàm mật độ có điều kiện Conditional density function
Hàm mật độ đồng thời Joint density function Hàm phân phối biên Marginal distribution function
Hàm phân phối có điều kiện
Conditional distribution function
Hàm phân phối đồng thời Joint distribution function Hệ số tương quan Correlation coefficient Hiệp phương sai Covariance Hồi qui Regression Kì vọng có điều kiện Conditional expectation Mẫu ngẫu nhiên Random sample
Phân phối Chuẩn hai chiều Bivariate Normal distribution
Phân phối Chuẩn nhiều chiều
Multivariate Normal distribution Phân phối Đa thức Multinomial distribution
Phân phối Đều hai chiều Bivariate Uniform distribution
Phân phối Đều nhiều chiều
Multivariate Uniform distribution
Phân phối Siêu bội nhiều chiều Multivariate Hypergeometric dist.
Phương sai có điều kiện Conditional variance Tương quan Correlated / Correlation Tương quan bán phần Semi-partial correlation Tương quan riêng Partial correlation Vectơ ngẫu nhiên Random vector Bài tập
Bài 4.1. Một lô hàng có 10 sản phẩm, trong đó có 5 sản phẩm loại một, 3 sản phẩm loại hai, 2 sản phẩm
loại ba. Lấy ngẫu nhiên 2 sản phẩm. Đặt X và Y lần lượt là số sản phẩm loại một và loại hai trong hai
sản phẩm lấy ra. Lập bảng phân phối xác suất đồng thời của biên ngẫu nhiên (X, Y ).
Bài 4.2. Một người đi bán hàng ở hai nơi, với xác suất bán được hàng ở nơi thứ nhất và nơi thứ hai lần
lượt là 0,6 và 0,8. Doanh thu ở của nơi thứ nhất nếu bán được là 20 triệu đồng, doanh thu của nơi thứ hai
nếu bán được là 30 triệu đồng. Đặt X là số nơi bán được hàng, và Y là tổng doanh thu.
(a) Lập bảng phân phối xác suất hai chiều đồng thời của (X, Y ).
(b) Tính kì vọng và phương sai của X và Y .
(c) Tính hiệp phương sai và hệ số tương quan của số nơi bán được hàng và doanh thu.
(d) Tính kì vọng và phương sai của doanh thu nếu bán được hàng ở một nơi.
Bài 4.3. Cho các biến ngẫu nhiên rời rạc X, Y có bảng phân phối xác suất như sau X 2 3 5 Y 1 4 P 0,3 0,5 0,2 P 0,2 0,8
Xác định bảng phân phối xác suất của các biến ngẫu nhiên S = X + Y và M = X · Y
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 35
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 4.4. Cho biến ngẫu nhiên hai chiều (X, Y ) có bảng phân phối xác suất đồng thời như sau X Y 2 4 7 9 1 0,01 0,03 0,18 0,07 2 0.02 0,06 0,21 0,08 3 0,05 0,1 0,15 0,04
(a) Lập bảng phân phối xác suất biên của X.
(b) Tính E(X), E(Y ), V (X), V (Y ).
(c) Lập bẳng phân phối xác suất của Y trong điều kiện X = 4
Bài 4.5. Cho biến ngẫu nhiên hai chiều (X, Y ), trong đó X là chi cho quảng cáo (triệu), Y là doanh thu
(triệu) của một doanh nghiệp, có bảng phân phối xác suất đồng thời như sau X Y 100 200 300 0 0,1 0,02 0,01 5 0,16 0,12 0,08 10 0,2 0,17 0,14
(a) Tính kì vọng và phương sai của doanh thu.
(b) Tính xác suất doanh thu là 200 triệu trong điều kiện quảng cáo là 10 triệu.
(c) Tính kì vọng và phương sai doanh thu khi quảng cáo là 10 triệu.
(d) Tính hiệp phương sai và hệ số tương quan giữa X và Y .
Bài 4.6. Cho biến ngẫu nhiên hai chiều (X, Y ) về thu nhập của nhân viên một công ty, trong đó X là
lương (triệu đồng), Y là thưởng (triệu đồng), có bảng phân phối xác suất đồng thời như sau X Y 0 5 10 10 0,1 0,03 0,02 15 0,25 0,2 0,1 20 0,1 0,15 p
(a) Tính p và xác định các bảng phân phối xác suất biên.
(b) Tính hiệp phương sai và hệ số tương quan giữa lương và thưởng.
(c) Tính kì vọng và phương sai của thưởng khi lương bằng 10 triệu.
(d) Tính kì vọng, phương sai và độ lệch chuẩn của thu nhập (bằng tổng của lương và thưởng).
Bài 4.7. Tỉ suất lợi nhuận (%) khi đầu tư vào hai cổ phiếu A và B lần lượt là X và Y có bảng phân phối
xác suất đồng thời như sau X Y −10 0 10 20 6 0 0 0,1 0,1 8 0 0,1 0,3 0,2 10 0,1 0,1 0 0
(a) Muốn tỉ suất lợi nhuận trên 7% thì nên đầu tư vào cổ phiếu nào?
(b) Tính kì vọng và độ rủi ro (đo bằng phương sai) của tỉ suất lợi nhuận nếu chia đều vốn đầu tư vào hai cổ phiếu.
(c) Muốn độ rủi ro (đo bằng phương sai) của tỉ suất lợi nhuận là thấp nhất thì nên chia vốn vào hai cổ phiếu theo tỉ lệ nào? 36
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 4.8. Cho biến ngẫu nhiên rời rạc (X, Y ) có hàm khối lượng xác suất 2 P (xi, yj) =
, với x = 1, 2, ..., n; y = 1, 2, ..., x n(n + 1)
(a) Xác định các bảng xác suất biên của X và Y .
(b) Xác định xác suất có điều kiện P (X|y), P(Y |x).
(c) Tính các kì vọng có điều kiện: E(X|y), E(Y |x).
Bài 4.9. Tại một cửa hàng bán tivi, trong số khách vào cửa hàng người ta biết rằng 25% mua tivi của
thương hiệu A, 40% mua tivi thương hiệu B, còn lại 35% chỉ đi xem. Trong số 10 khách vào cửa hàng:
(a) Tính xác suất có 2 người mua tivi thương hiệu A, 3 người mua tivi thương hiệu B, và 5 người đi xem.
(b) Biết rằng 6 khách không mua tivi, tính xác suất (có điều kiện) trong số còn lại có 1 khách mua tivi
thương hiệu A và 3 mua tivi thương hiệu B.
Bài 4.10. Con người có 4 nhóm máu là A, B, AB, O với xác suất tương ứng là: pA = 0, 4; pB = 0, 1; p là số người có nhóm
AB = 0, 05; pO = 0, 45. Trong số n người hiến máu, đặt XA, XB , XAB , XO
máu tương ứng. Xác định công thức tính các xác suất sau:
(a) P (XA = xA, XB = xB, XAB = xAB, XO = xO);
(b) P (XA = xA, XB = xB, XAB = xAB); (c) P (XA = xA, XB = xB); (d) P (XA = xA);
(e) P (XA = xA, XB = xB, XAB = xAB|XO = xO);
(f) P (XA = xA, XB = xB|XAB = xAB, XO = xO);
(g) P (XA = xA|XB = xB, XAB = xAB, XO = xO);
(h) Thay số n = 20, và xA = 8, xB = 2, xAB = 1, xO = 9 vào các câu trên.
Bài 4.11. Cho biến ngẫu nhiên ba chiều (X, Y, Z) có hàm mật độ c3e−c(x+y+z) : x, y, z > 0 f (x, y, x) = 0 : ngược lại, (a) Tìm giá trị của c,
(b) Xác định các hàm mật độ biên f , X , fY , fZ
(c) Xác định các hàm mật độ biên fX,Y (x, y), fY,Z(y, z), fZ,X(z, x),
(d) Các biến có độc lập từng đôi không? có độc lập toàn phần không?
(e) Tính E(XY ), E(XY Z), V (X + Y ), V (X + Y + Z),
Bài 4.12. Với α, β > 0, α + β = 1/4, bảng xác suất hai chiều của (X, Y ) như sau X Y -1 0 1 -1 α β α 0 β 0 β 1 α β α
(a) Xác định bảng phân phối biên của X và Y ,
(b) Tính E(X), E(Y ), E(XY ), Cov(X, Y ) và ρ(X, Y ),
(c) Chứng minh rằng X, Y không độc lập,
Bài 4.13. Tìm giá trị của c, c
trong các hàm mật độ đồng thời sau: 1, c2 2/c2 : 0 < x (a) ≤ y < c f (x, y) = 0 : ngược lại c (b)
· y · e−xy/2 : 0 < y < x f (x, y) = 0 : ngược lại
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 37
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— cx : x > 0, y > 0, 1 (c) ≤ x + y < 2 f (x, y) = 0 : ngược lại c(y2 (d)
− x2)e−y : −y < x < y, y > 0, 1 ≤ x + y < 2 f (x, y) = 0 : ngược lại xy2 : 0 < x (e) ≤ c1, 0 < y < c2 f (x, y) = 0 : ngược lại
Bài 4.14. Với X và Y lần lượt là tỉ lệ khách nam và khách nữ hài lòng với dịch vụ của cửa hàng, có hàm
mật độ xác suất đồng thời như dưới đây, hãy tính xác suất tỉ lệ khách nam hài lòng là ít hơn tỉ lệ khách nữ hài lòng. x + y
: 0 < x < 1, 0 < y < 1 f (x, y) = 0 : ngược lại,
Bài 4.15. Cho hàm hai biến (x, y) như sau 6 xy x2 +
: 0 < x ≤ 1; 0 < y ≤ 2 f (x, y) = 7 2 0 : ngược lại,
(a) Chứng minh rằng đây là một hàm mật độ xác suất đồng thời của một biến ngẫu nhiên hai chiều (X, Y ).
(b) Tính xác suất P (X > Y ).
Bài 4.16. Cho hàm mật độ xác suất đồng thời của (X, Y ) như sau e−x−y : x > 0, y > 0 f (x, y) = 0 : ngược lại,
(a) Kiểm chứng tính chất của hàm mật độ.
(b) Xác định hàm phân phối đồng thời, các hàm phân phối biên.
(c) Xác định các hàm mật độ biên, các hàm mật độ có điều kiện.
(d) Xác định P (X ≤ Y ≤ c) với c > 0, thay số khi c = ln 2.
(e) Tính P (X < Y ) và P (X + Y ≤ 3).
Bài 4.17. Cho hàm mật độ của biến (X, Y ) sau 8xy : 0 < x ≤ y < 1 f (x, y) = 0 : ngược lại,
(a) Kiểm chứng tính chất của hàm mật độ,
(b) Xác định các hàm phân phối biên, phân phối có điều kiện,
(c) Tính E(X), E(Y ), V (X), V (Y ), E(Y |x), E(X|y),
(d) Tính hiệp phương sai và hệ số tương quan Cov(X, Y ), ρ(X, Y ),
Bài 4.18. Cho hàm mật độ xác suất của (X, Y ) như sau 6
(x + y2) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 f (x, y) = 5 0 : ngược lại,
(a) Xác định các hàm mật độ biên fX(x), fY (y),
(b) Xác định các hàm mật độ có điều kiện fX|y(x|y), fY |x(y|x),
(c) Xác định các kì vọng có điều kiện E(X|y), E(Y |x), 38
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 4.19. Cho hàm mật độ xác suất của (X, Y ) như sau ye−x : 0 < y ≤ x < ∞ f (x, y) = 0 : ngược lại,
(a) Xác định các hàm mật độ biên fX(x), fY (y),
(b) Xác định các hàm mật độ có điều kiện fX|y(x|y), fY |x(y|x),
(c) Xác định các kì vọng có điều kiện E(X|y), E(Y |x),
(d) Tính P (X > 2ln2|Y = ln2),
Bài 4.20. Cho hàm mật độ xác suất của (X, Y ) như sau xe−(x+y) : x > 0, y > 0 f (x, y) = 0 : ngược lại,
(a) Xác định các hàm mật độ biên fX(x), fY (y),
(b) Xác định các hàm mật độ có điều kiện fX|y(x|y), fY |x(y|x),
(c) Xác định các kì vọng có điều kiện E(X|y), E(Y |x), (d) Tính P (X > ln4),
Bài 4.21. Cho hàm mật độ xác suất của (X, Y ) như sau 1 ye−xy : x > 0, 0 < y < 2 f (x, y) = 2 0 : ngược lại,
(a) Xác định hàm mật độ có điều kiện của các biến,
(b) Xác định fX|y=1/2(x) và E(X|y = 1/2),
Bài 4.22. Cho hai biến X, Y trong đó Y phân phối Poisson: Y ∼ P(λ), và (X|y) ∼ B(y, p). Chứng minh rằng:
(a) X phân phối Poisson: X ∼ P(λX = λp),
(b) Y trong điều kiện x phân phối Poisson: (Y |x) ∼ P(λY |x = λ(1 − p)) với x, x + 1, x + 2, ..,;
Bài 4.23. Biến ngẫu nhiên hai chiều (X, Y ) có kì vọng, phương sai hữu hạn. Đặt U = X + Y và
V = X − Y . Chứng minh rằng:
(a) P (UV < 0) = P (|X| < |Y |) (b) E(U · V ) = 0;
(c) Nếu V (X) = V (Y ) thì Cov(U, V ) = 0,
Bài 4.24. Cho hàm mật độ xác suất của (X, Y, Z) như sau c3e−c(x+y+z)
: x > 0, y > 0, z > 0, c > 0 f (x, y, x) = 0 : ngược lại, (a) Tìm giá trị của c,
(b) Xác định các hàm mật độ biên fX(x), fY (y), fZ(z).
(c) Xác định hàm mật độ có điều kiện của X, Y theo Z.
(d) Xác định hàm mật độ có điều kiện của X theo Y, Z.
(e) Xác định hàm sinh mô-men của (X, Y, Z)
Bài 4.25. Chứng minh rằng nếu các biến ngẫu nhiên X và có mô-men bậc 2 1, X2, ..., Xm Y1, Y2, ..., Yn hữu hạn thì m n ! m n X X X X Cov Xi, Yj = Cov(Xi, Yj). i=1 j=1 i=1 j=1
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 39
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bài 4.26. Cho (X, Y ) phân phối Chuẩn hai chiều với các tham số: µ , , , , 1 µ2 σ2 1 σ2 2 ρ.
Đặt U = X + Y, Z = X − Y .
(a) Xác định biến ngẫu nhiên hai chiều (U, Z), và các tham số E(U), E(Z), V (U), V (Z), ρ(U, Z).
(b) Chứng minh rằng U và Z không tương quan khi và chỉ khi σ2 . 1 = σ2 2
Bài 4.27. Biến ngẫu nhiên 3 chiều (X, Y, Z) có hàm khối lượng xác suất
P (x = 1, y = 0, z = 0) = P (x = 0, y = 1, z = 0)=P (x = 0, y = 0, z = 1) = P (x = 1, y = 1, z = 1) = 1/4
(a) Xác định phân phối xác suất biên của (X, Y ), (Y, Z), (Z, X).
(b) Xác định phân phối xác suất biên của X, Y, Z.
(c) Chứng minh rằng X, Y, Z độc lập từng đôi và độc lập toàn phần.
Bài 4.28. Hai biến X và Y có độc lập không nếu (X, Y ) có hàm mật độ 6
(x2 + y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 f (x, y) = 5 0 : ngược lại.
Bài 4.29. Cho (X, Y ) có hàm mật độ như sau 1
: 0 < x < 1, 0 < y < 1 f (x, y) = 0 : ngược lại.
(a) Hai biến X và Y có độc lập không?
(b) Xác định P (X + Y ) < c, và thay số khi c = 0, 5.
Bài 4.30. Cho biến ngẫu nhiên ba chiều (X, Y, Z) có hàm mật độ 8xyz : 0 < x, y, z < 1 f (x, y, x) = 0 : ngược lại.
(a) Xác định các hàm mật độ biên.
(b) Chứng minh rằng X, Y, Z là độc lập toàn phần. (c) Tính P (X < Y < Z).
Bài 4.31. Cho hai hàm g(x), h(y) là các hàm không âm trên miền D ⊆ R2. Hàm mật độ của biến ngẫu nhiên hai chiều có dạng g(x)h(y) : (x, y) ∈ D f (x, y, x) = 0 : (x, y) / ∈ D.
(a) Xác định các hàm mật độ biên theo g, h.
(b) Chứng minh rằng X, Y độc lập.
(c) Nếu hai hàm bằng nhau: h = g, chứng minh rằng P (X > Y ) = 1/2.
Bài 4.32. Cho biến ngẫu nhiên (X, Y ) có hàm mật độ 1
: 0 < x < y, 0 < y < 1 f (x, y) = y 0 : ngược lại. Tính P (X + Y ) > 1/2.
Bài 4.33. Cho biến ngẫu nhiên (X, Y ) có hàm phân phối xác suất
(1 − e−x2 )(1 − e−y2 ) : x > 0, y > 0 F (x, y) = 0 : ngược lại.
(a) Xác định hàm mật độ đồng thời f(x, y).
(b) Tính P (1 < X ≤ 2, 1 < Y ≤ 2). 40
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 4.34. Cho biến ngẫu nhiên (X, Y ) có hàm phân phối xác suất
1 − e−x − e−y + e−x−y : x > 0, y > 0 F (x, y) = 0 : ngược lại.
(a) Xác định hàm mật độ đồng thời f(x, y). (b) Tính P (X + Y > 3).
Bài 4.35. Cho biến ngẫu nhiên (X, Y, Z) có hàm mật độ xác suất kxy(1 − z)
: 0 < x, y, z < 1, x + y + z < 1 f (x, y, z) = 0 : ngược lại.
(a) Xác định hàm mật độ đồng thời fXY (x, y) của (X, Y ). (b) Tính P (X + Y < 1/2).
Bài 4.36. Cho biến ngẫu nhiên (X, Y, Z) có hàm mật độ xác suất 1
(2x + 3y + z) : 0 < x, y, z < 1 f (x, y, z) = 3 0 : ngược lại.
(a) Tính P (X = 1/2, Y = 1/2, Z = 1/2).
(b) Tính P (X < 1/2, Y < 1/2, Z < 1/2).
Bài 4.37. Cho X, Y, Z > 0 là các biến ngẫu nhiên độc lập, có hàm mật độ e−x : x > 0 2e−2y : y > 0 3e−3z : z > 0 f (x) = , f (y) = , f (z) = 0 : x ≤ 0. 0 : y ≤ 0 0 : z ≤ 0
(a) Xác định hàm mật độ đồng thời f(x, y, z) của (X, Y, Z).
(b) Tính P (X + Y ≤ 1, Z > 1).
Bài 4.38. Cho X, Y độc lập có hàm mật độ 1/2 : x ∈ (0, 2) 1/3 : y ∈ (0, 3) fX(x) = , fY (y) = 0 : x / ∈ (0, 2) 0 : y / ∈ (0, 3).
(a) Xác định hàm mật độ đồng thời fXY (x, y). (b) Tính P (X2 + Y 2 > 1).
Bài 4.39. Giả sử giá bán P (đơn vị $) và lượng bán Q (đơn vị: 10.000) của một loại hàng hóa là biến
ngẫu nhiên liên tục có hàm mật độ là 5pe−pq
: 0.2 < p < 0.4, s > 0 f (p, q) = 0 : ngược lại. Tính xác suất để:
(a) Giá bán dưới 0,3$ và lượng bán trên 20.000;
(b) Giá bán trong khoảng 0,25$ đến 0,3$ và lượng bán là ít hơn 10.000.
Bài 4.40. Tại một trường học, vào đầu mỗi kì tuyển sinh, nhà trường tổ chức hai bài thi về khoa học tự
nhiên và khoa học xã hội. Đặt X và Y lần lượt là tỉ lệ trả lời đúng của thí sinh về hai lĩnh vực khoa học
đó, và có hàm mật độ xác suất đồng thời như sau 2
(2x + 3y) : 0 < x < 1, 0 < y < 1 f (x, y) = 5 0 : ngược lại.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 41
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
(a) Tính xác suất để tỉ lệ đúng của cả hai đều trên 0,5.
(b) Tính xác suất tỉ lệ đúng của khoa học tự nhiên là trên 0,8 đồng thời của khoa học xã hội là trên 0,6.
(c) Tính hiệp phương sai và hệ số tương quan của hai tỉ lệ đúng.
(d) Tính trung bình và phương sai của tỉ lệ đúng khoa học tự nhiên trong điều kiện tỉ lệ đúng của khoa học xã hội là 0,6.
Bài 4.41. Một cuộc khảo sát xã hội gửi đi hai thư điện tử đến các đối tượng điều tra, thư thứ nhất hỏi về
thông tin kinh tế, thư thứ hai hỏi về thông tin xã hội. Đặt X và Y lần lượt là tỉ lệ phản hồi của đối tượng
điều tra về hai thông tin đó, và có hàm mật độ xác suất đồng thời như sau 2
(x + 4y) : 0 < x < 1, 0 < y < 1 f (x, y) = 5 0 : ngược lại.
(a) Tính xác suất để tỉ lệ phản hồi thông tin kinh tế là trên 30% đồng thời tỉ lệ phản hồi thông tin xã hội là trên 70%.
(b) Tính xác suất để tỉ lệ phản hồi thông tin kinh tế là trên 50% trong điều kiện tỉ lệ phản hồi thông tin xã hội là 70%.
(c) Tính hiệp phương sai và hệ số tương quan giữa hai tỉ lệ phản hồi.
(d) Nếu số tiền được thanh toán của cuộc khảo sát được tính trên tỉ lệ phản hồi, và bằng 250X + 140Y
(triệu đồng). Hãy tính kì vọng và phương sai của số tiền được thanh toán.
Bài 4.42. Cho hàm mật độ xác suất của biến X như sau 1 + x : −1 < x ≤ 0 f (x) = 1 − x : 0 < x < 1 0 : x / ∈ (−1, 1). Chứng minh rằng: (a) Cov(X, X2) = 0; (b) X và X2 độc lập. Bài 4.43. e−x−y : x > 0, y > 0 f (x, y) = 0 : ngược lại.
(a) Xác định hàm sinh mô-men.
(b) Sử dụng hàm sinh mô-men để tính các giá trị E(XY ), E(X), E(Y ), cov(X, Y ). Bài 4.44. 1
(x + y) : 0 < x < 1, 0 < y < 2 f (x, y) = 3 0 : ngược lại.
Tính phương sai của W = 3X + 4Y − 5.
Bài 4.45. Nếu ba biến X, Y, Z có V (X1) = 5, V (X2) = 4, V (X3) = 7, Cov(X1, X2) = 3, Cov(X1, X3) = −2, X và
độc lập, hãy tính hiệp phương sai của và . 2 X3 Y1 = X1 − 2X2 + 3X3 Y2 = −2X1 + 3X2 + 4X3
Bài 4.46. Giả sử rằng chiều cao của các cặp vợ chồng là biến ngẫu nhiên phân phối chuẩn hai chiều;
trong đó chiều cao của vợ có trung bình là 160 cm và độ lệch chuẩn là 4cm, chiều cao của chồng có trung
bình là 164cm và độ lệch chuẩn là 5 cm. Biết hệ số tương quan chiều cao hai vợ chồng là 0,7. Tính xác
suất chọn ngẫu nhiên một cặp vợ chồng thì vợ cao hơn chồng.
Bài 4.47. Cho (X, Y ) là biến ngẫu nhiên phân phối chuẩn hai chiều, trong đó: E(X|y) = 4 − 0, 2y;
E(Y |x) = 0, 5 − x và V (Y |x) = 4. Hãy tính các tham số của biến ngẫu nhiên hai chiều. 42
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 4.48. Xét hàm f(x, y) như sau 1 e−(x2+y2)/2 : (x, y) / ∈ [−1, 1]×[−1, 1] f (x, y) = 2π 1 1 e−(x2+y2)/2 +
ex3y3 : (x, y) ∈ [−1, 1]×[−1, 1] 2π 2π
(a) Chứng tỏ rằng đây không phải là hàm mật độ của biến phân phối Chuẩn hai chiều.
(b) Xác định các hàm mật độ biên, và chứng tỏ X, Y là phân phối Chuẩn-chuẩn hóa.
Ý nghĩa: Nếu biến biến phân phối Chuẩn hai chiều thì các thành phần cũng phân phối Chuẩn, nhưng
điều ngược lại không đúng.
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 43
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— 44
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 5 MỘT SỐ ĐỊNH LÍ HỘI TỤ
5.1. Một số định nghĩa về hội tụ
5.2. Một số luật số lớn
5.3. Định lí giới hạn trung tâm
Ví dụ 5.1. Xác suất để trong một quá trình sản xuất một sản phẩm trở thành phế phẩm là 0, 005, tính xác
suất để trong số 10000 sản phẩm được lấy ra một cách ngẫu nhiên để kiểm tra thì sẽ có không quá 70 phế phẩm.
5.4. Định lí giới hạn địa phương Thuật ngữ Tiếng Việt Tiếng Anh Bất đẳng thức Chebyshev Chebyshev inequality Điều kiện Lyapunov Lyapunov condition Định lí Bernoulli Bernoulli theorem Định lí Chebyshev Chebyshev theorem
Định lí giới hạn địa phương Local Limit theorem
Định lí giới hạn tích phân Integral Limit theorem
Định lí giới hạn trung tâm Central Limit theorem Định lí Lindeberg-Levy Lindeberg-Levy theorem Định lí Moivre-Laplace Moivre-Laplace theorem
Hội tụ theo nghĩa bình phương trung bình Convergence in quadratic mean
Hội tụ theo phân phối xác suất
Convergence in prob. distribution Hội tụ theo xác suất Convergence in probability Tiệm cận chuẩn Asymptoptic Normality Bài tập
Bài 5.1. Gieo đồng xu đối xứng 100 lần. Đặt X là số lần xuất hiện mặt Sấp.
(a) Tính kì vọng và phương sai của X.
(b) Áp dụng định lí Chebyshev ước tính xác suất X chênh lệch so với kì vọng của nó là nhiều hơn
hoặc bằng ba lần độ lệch chuẩn.
Bài 5.2. Cho biến ngẫu nhiên X có kì vọng bằng 0 và phương sai bằng 1. Tìm số tự nhiên k sao cho P (|X| ≥ k) < 0, 01.
Bài 5.3. Đặt X là số lần biến cố n
A xuất hiện trong phép thử Bernoulli B(n, p). 45
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
(a) Chứng minh rằng với mọi ε > 0 thì X p(1 − p) P n − p ≥ ε ≤ n nε2
(b) Tìm giá trị lớn nhất của hàm p(1 − p) với 0 < p < 1, từ đó chứng minh rằng X 1 P n − p ≥ ε ≤ n 4nε2
Bài 5.4. Tung đồng xu đối xứng một số lớn lần. Áp dung Luật số lớn hãy kiểm chứng mệnh đề sau: “với
n đủ lớn, xác suất để số lần xuất hiện mặt Sấp không lệch khỏi giá trị n/2 một khoảng lớn hơn 100 lần sẽ là lớn hơn 0,99”.
Bài 5.5. Xét biến ngẫu nhiên X nhận các giá trị 0, 1, 2, ..., n với E(X) = V (X) = 1.
Chứng minh rằng với mọi số nguyên dương k thì 1 P (X ≥ k + 1) ≤ k2
Bài 5.6. Có hai đồng xu, một đồng đối xứng, và đồng kia không đối xứng mà có xác suất xuất hiện mặt
Sấp là 3/4. Lấy ngẫu nhiên một đồng, và tung đồng xu này n lần. Đặt X là số lần xuất hiện mặt Sấp n trong n lần tung.
(a) Luật số lớn có cho phép dự báo tỉ lệ xuất hiện mặt sấp khi số lần tung tăng lên vô hạn không?
(b) Sau khi quan sát một số lớn lần tung, có thể nói đồng xu nào đã được chọn hay không?
(c) Phải tung bao nhiêu lần để có thể đoán về đồng xu đã chọn với xác suất đúng là 0,95? Bài 5.7. Cho X
là các biến ngẫu nhiên độc lập, có thể không cùng phân phối xác suất. Đặt 1, X2, ..., Xn
mi = E(Xi), σ2i = V (Xi) hữu hạn, M . Đặt . Chứng minh rằng n = m1 + m2 + ... + mn Sn = X1 + X2 + ... + Xn X M P n n − < ε −→ 1 khi n → ∞ n n
Bài 5.8. Cho X là biến ngẫu nhiên liên tục có trung bình µ = 10 và phương sai σ2 = 100/3. Sử dụng bất
đẳng thức Chebyshev, tính cận trên của các xác suất sau: (a) P (|X − 10| ≥ 2). (b) P (|X − 10| ≥ 5). (c) P (|X − 10| ≥ 9). (d) P (|X − 10| ≥ 20).
(e) Hãy tính chính xác các xác suất trên nếu X phân phối đều trong khoảng [0, 20], khi đó E(X) = 10
và V (X) = 100/3, so sánh với kết quả khi áp dụng bất đẳng thức Chebyshev.
Bài 5.9. Xét Z là biến ngẫu nhiên phân phối N(0, 1). So sánh kết quả khi áp dụng bất đẳng thức Cheby-
shev và khi tính chính xác xác suất sau: P (|Z| ≥ 1), P(|Z| ≥ 2), P(|Z| ≥ 3).
Bài 5.10. Cho biến ngẫu nhiên phân phối Chuẩn X ∼ N(µ, σ2).
(a) Áp dụng bất đẳng thức Chebyshev với để xác định khoảng giá trị của các xác suất: P (|X−µ| ≥ σ),
P (|X − µ| ≥ 2σ), P (|X − µ| ≥ 3σ)
(b) So sánh kết quả với xác suất chính xác theo qui tắc 3σ.
Bài 5.11. Cho biến ngẫu nhiên X có E(X) = µ, V (X) = σ2. Xét biến chênh lệch tương đối so với trung bình của X như sau X − µ D = µ (a) Chứng minh rằng: σ2 P (D ≥ a) ≤ µ2a2 (b) Áp dụng với 100 µ = 10, σ2 =
, xác định cận trên của P (D ≥ 0, 5). 3 46
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 5.12. Cho biến ngẫu nhiên X − µ
X có E(X) = µ, V (X) = σ2. Xét biến chuẩn hóa của X là Z = . σ Chứng minh rằng 1 P (|Z| ≥ a) ≤ . a2 Cho X
là số lần xuất hiện mặt sấp khi gieo đồng xu đối xứng đồng chất 100 lần. Áp dụng Định lí 100
giới hạn trung tâm ước lượng các xác suất sau: (a) P (X100 ≤ 45). (b) P (45 < X100 < 55). (c) P (X100 > 63). (d) P (X100 = 56).
Bài 5.13. Một đề thi có 48 câu hỏi dạng Đúng / Sai. Thí sinh A có khả năng trả lời đúng trong mỗi câu
là 3/4; thí sinh B trả lời bằng cách chọn ngẫu nhiên. Yêu cầu để qua được bài thi là phải đạt từ 30 câu trở
lên. So sánh khả năng qua được bài thi của hai thi sinh A và B.
Bài 5.14. Có hai hãng vận tải cạnh tranh nhau trong việc vận chuyển 1000 hành khách đi từ thành phố A
đến thành phố B. Giả sử khách hàng là không phân biệt giữa việc đi với hãng vận tải nào, khả năng lựa
chọn là như nhau cho mỗi hãng. Với mức xác suất 0,99 thì mỗi hãng nên chuẩn bị ít nhất bao nhiêu vị trí vận chuyển.
Bài 5.15. Tính xác suất trong 1000 lần quay xổ số ngẫu nhiên thì có ít nhất 93 lần chữ số cuối cùng là 9.
Bài 5.16. Một tổ chức tiến hành khảo sát ý kiến người dân về một chính sách xã hội mới. Giả sử khả năng
lựa chọn Đồng ý và Không đồng ý của người dân là như nhau, và không có lựa chọn khác. Xác định a để
trong 400 người được hỏi thì xác suất để số người Đồng ý trong khoảng (200 − a; 200 + a) bằng 0,8.
Bài 5.17. Với biến phân phối Nhị thức X ∼ B(n, p) với p = 0, 8, và đặt ˆp = X/n, hãy tính các giới hạn của các xác suất sau: (a) limn→∞ P (ˆp = 0, 8)
(b) limn→∞ P (0, 7n < X < 0, 9n) (c) √
limn→∞ P (X < 0, 8n + 0, 8 n)
(d) limn→∞ P (0, 79 < ˆp < 0, 81)
Bài 5.18. Gieo con xúc xắc đối xứng đồng chất cho đến khi tổng số chấm xuất hiện tính từ lần gieo đầu
tiên là lớn hơn hoặc bằng 700. Tính xác suất để:
(a) Phải gieo hơn 210 lần. (b) Gieo ít hơn 190 lần.
(c) Gieo trong khoảng 180 đến 210 lần.
Bài 5.19. Xuất phát tại vị trí 0 trên trục số, giả sử có một quá trình chuyển động theo qui tắc: (i) mỗi lần
bước một bước về bên phải (phía dương) hoặc phía trái (phía âm) bằng 1 đơn vị; (ii) Xác suất bước sang
phải hoặc sang trái là bằng nhau và bằng 0,5. Tính xác suất sau 100 bước chuyển động thì vị trí cách với
điểm 0 là hơn 10 đơn vị.
Bài 5.20. Một thiết bị cân có sai số là −2, −1, 0, +1, +2 (g) so với khối lượng đúng của vật cần cân, và
xác suất là bằng nhau với các giá trị trên.
(a) Tính kì vọng và phương sai của sai số.
(b) Tính xác suất trong 50 lần cân độc lập, thì sai số trung bình là trong khoảng (−1, 1) (g).
Bài 5.21. Giá của một loại cổ phiếu vào ngày thứ n kí hiệu là Y . Giả sử mức thay đổi về giá của phiên n
giao dịch hôm sau so với hôm trước X
là biến ngẫu nhiên có trung bình n = Yn − Yn−1 µ = 0 và phương
sai σ2 = 0, 25. Nếu ngày giao dịch đầu tiên có giá Y , tính
1 = 100, giá của giao dịch ngày thứ 365 là Y365 xác suất: (a) P (Y365 ≥ 100). (b) P (Y365 ≥ 110). (b) P (Y365 ≥ 120).
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 47
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— 48
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Chương 6 QUÁ TRÌNH NGẪU NHIÊN
6.1. Một số khái niệm
6.2. Một số lớp quá trình ngẫu nhiên quan trọng
6.3. Xích Markov rời rạc
6.4. Xích Markov liên tục
6.5. Quá trình Poisson 6.6. Quá trình Wiener Thuật ngữ Tiếng Việt Tiếng Anh Bước ngẫu nhiên Random walk
Bước ngẫu nhiên đối xứng Symmetric random walk Cầu Brown Brown bridge
Chuyển động Brown hình học Geometric Brownian motion
Chuyển động Brown tiêu chuẩn Standard Brownian motion Ma trận xác suất chuyển Probability transfer matrix Martingale Martingale Phân hoạch Partition Phân phối dừng Stationary distribution Quá trình dừng Stationary process Quá trình dừng yếu Weak stationary process
Quá trình gia số độc lập Independent increment process Quá trình Gauss Gauss process Quá trình Markov Markov process Quá trình ngẫu nhiên Stochastic process Quá trình Poisson Poisson process
Quá trình Poison phức hợp Compound Poisson process Quá trình Wiener Wiener process
Quá trình Wiener tiêu chuẩn Standard Wiener process Thời điểm dừng Stopping time Xích Markov Markov chain Xích Markov thuần nhất Homogenous Markov chain 49
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— Bài tập
Bài 6.1. Giả sử X là một biến ngẫu nhiên phân phối chuẩn với các tham số µ và σ2. Xét quá trình ngẫu nhiên: Y .
t = aX + bt, với a, b là các hằng số. Tìm hàm trung bình, hàm tự tương quan của quá trình Yt
Bài 6.2. Giả sử X là biến ngẫu nhiên phân phối mũ với tham số λ > 0. Xét quá trình ngẫu nhiên: Y .
t = exp(−aX · t), t > 0 và a là hằng số. Tìm hàm trung bình, hàm tự tương quan của quá trình Yt
Bài 6.3. Giả sử Xt, t ≥ 0 là quá trình Gauss dừng với trung bình 0 và hàm tự tương quan C(t). Khi đó
quá trình ngẫu nhiên Yt = exp(Xt) có là quá trình dừng yếu hay không? Bài 6.4. Giả sử N ,
t, t ≥ 0 là quá trình Poisson với cường độ λ. Khi đó quá trình ngẫu nhiên Yt = Nt+a−Nt
với a là hằng số dương, có là quá trình dừng yếu hay không?
Bài 6.5. Cho xích Markov (Xn; n = 0, 1, 2, ...) với không gian trạng thái S = {0, 1, 2} và ma trận xác suất chuyển: 0, 1 0, 2 0, 7 P = 0, 2 0, 3 0, 5 0, 6 0, 2 0, 2 (a) Tính P 2.
(b) Tính P (X3 = 1|X1 = 0) và P(X3 = 1|X0 = 0).
Bài 6.6. Cho xích Markov (Xn; n = 0, 1, 2, ...) với không gian trạng thái S = {0, 1} và ma trận xác suất chuyển: 0, 9 0, 1 P = 0, 2 0, 8
Tìm phân phối dừng của xích Markov (Xn; n = 0, 1, 2, ...).
Bài 6.7. Giả sử có 5 con xúc xắc cân đối đồng chất,ta thực hiện việc tung 5 con xúc xắc, những con xúc
xắc xuất hiện mặt 6 chấm thì để sang một bên. Sau đó, ta tiếp tục tung những con xúc xắc còn lại và để
những con xúc xắc xuất hiện mặt 6 chấm sang một bên. Gọi X là số con xúc xắc xuất hiện mặt 6 chấm n
sau n lần tung. Mô tả ma trận xác suất chuyển cho xích Markov này.
Bài 6.8. Cho xích Markov (Xn ; n = 0, 1, 2, ...) với không gian trạng thái S = {0, 1, 2} và ma trận xác suất chuyển: 0, 5 0, 5 0 P = 0 0 1 0, 5 0 0, 5
Tính thời gian trung bình để hệ rơi vào trạng thái 2 khi xuất phát từ trạng thái 0.
Bài 6.9. Một người chơi bắt đầu với 2 đô la và chơi một trò chơi trong đó cơ hội chiến thắng mỗi vòng là
0.6. Ở mỗi vòng, người chơi có thể thắng 1 đô la hoặc thua 1 đô la. Trò chơi dừng lại khi người chơi kiếm
được 5 đô la hoặc phá sản. Tìm xác suất để người chơi bị phá sản.
Bài 6.10. Cho (Nt; t = 0, 1, 2, ...) là quá trình Poisson với tham số λ = 1.5, hãy tính các xác suất sau: (a) P (N1 = 2; N4 = 6) (b) P (N4 = 6|N1 = 2).
Bài 6.11. Số cuộc gọi mà tổng đài của một công ty nhận được tuân theo quá trình Poisson với cường độ λ = 2 mỗi phút.
(a) Tìm xác suất để không có cuộc gọi nào gọi đến trong khoảng thời gian 30 giây.
(b) Tìm xác suất để tổng đài nhận được 4 cuộc gọi trong phút đầu tiên và nhận được 6 cuộc gọi trong phút thứ hai.
(c) Tìm xác suất để tổng đài nhận được 25 cuộc gọi trong 5 phút đầu tiên và 6 trong số các cuộc gọi
đó xảy ra trong phút đầu tiên. 50
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bài 6.12. Giả sử (Nt; t = 0, 1, 2, ...) là quá trình Poisson tham số λ, tìm phân phối xác suất của (Ns|Nt = n) trong 2 trường hợp: (a) s < t. (b) s > t.
Bài 6.13. Giả sử (Nt; t = 0, 1, 2, ...) là quá trình Poisson tham số λ, xét quá trình ngẫu nhiên Xt = N .
t − λt, t = 0, 1, 2, ... Chứng minh (Xt) là một martingale tương ứng với Nt
Bài 6.14. Vào ngày bầu cử, số người đến một trung tâm bỏ phiếu tuân theo quá trình Poisson. Giả sử có
150 người đến trong giờ đầu tiên, xác suất để có nhiều nhất 350 người đến trước giờ thứ ba là bao nhiêu?
Biết rằng trung bình có 100 cử tri đến bỏ phiếu mỗi giờ.
Bài 6.15. Giả sử W ,t t ≥ 0 là quá trình Wiener tiêu chuẩn: (a) Tính P (W2 ≤ 1) (b) Tính V (W4|W1).
Bài 6.16. Giả sử W ,t t ≥ 0 là quá trình Wiener với tham số µ = −1 và σ2 = 4. Tính xác suất để quá
trình ngẫu nhiên nhận giá trị dương ở thời điểm t = 3.
Bài 6.17. Giả sử W , , với
t t ≥ 0 là quá trình Wiener tiêu chuẩn.Tìm phân phối xác suất của Ws + Wt 0 < s < t.
Bài 6.18. Giả sử B ,t t ≥ 0 là chuyển động Brown tiêu chuẩn: (a) Cho biết B ,
2t − Bt t ≥ 0 có là quá trình Gauss hay không? (b) Chứng minh B3 ,
t − 3tBt t ≥ 0 là một Martingale.
Bài 6.19. Giả sử giá của một chứng khoán là một chuyển động Brown hình học với các tham số µ = −0.25
và σ = 0.4. Tính xác suất để sau 3 tháng thì giá chứng khoán đạt ít nhất 40$, biết giá hiện tại của chứng khoán là 35$.
Bài 6.20. Quá trình ngẫu nhiên Yt = G0eµt+σBt, t ≥ 0, G0 > 0 với G0 > 0, σ > 0 là một chuyển động Brown hình học:
(a) Xác định hàm trung bình, hàm phương sai của Y .t
(b) Lấy ví dụ để giải thích ý nghĩa trong kinh tế, tài chính cho các tham số µ và σ.
Phụ lục: Các bảng số
Bảng 1. Xác suất phân phối Nhị thức
Bảng 2. Xác suất tích lũy phân phối Nhị thức
Bảng 3. Xác suất phân phối Poisson
Bảng 4. Xác suất tích lũy phân phối Poisson
Bảng 5. Xác suất phân phối Chuẩn-chuẩn hóa
Bảng 6. Hàm mật độ phân phối Chuẩn-chuẩn hóa
Bảng 7. Giá trị tới hạn Khi-bình phương
Bảng 8. Giá trị tới hạn Student
Bảng 9. Giá trị tới hạn Fisher
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 51
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 1. Xác suất Phân phối Nhị thức P (X = x|n, p) = C x n px(1 − p)n−x
P (X = 2|n = 5, p = 0, 2) = 0, 2048 P (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 1 0
.9500 .9000 .8500 .8000 .7500 .7000 .6500 .6000 .5500 .5000 1
.0500 .1000 .1500 .2000 .2500 .3000 .3500 .4000 .4500 .5000 2 0
.9025 .8100 .7225 .6400 .5625 .4900 .4225 .3600 .3025 .2500 1
.0950 .1800 .2550 .3200 .3750 .4200 .4550 .4800 .4950 .5000 2
.0025 .0100 .0225 .0400 .0625 .0900 .1225 .1600 .2025 .2500 3 0
.8574 .7290 .6141 .5120 .4219 .3430 .2746 .2160 .1664 .1250 1
.1354 .2430 .3251 .3840 .4219 .4410 .4436 .4320 .4084 .3750 2
.0071 .0270 .0574 .0960 .1406 .1890 .2389 .2880 .3341 .3750 3
.0001 .0010 .0034 .0080 .0156 .0270 .0429 .0640 .0911 .1250 4 0
.8145 .6561 .5220 .4096 .3164 .2401 .1785 .1296 .0915 .0625 1
.1715 .2916 .3685 .4096 .4219 .4116 .3845 .3456 .2995 .2500 2
.0135 .0486 .0975 .1536 .2109 .2646 .3105 .3456 .3675 .3750 3
.0005 .0036 .0115 .0256 .0469 .0756 .1115 .1536 .2005 .2500 4
.0000 .0001 .0005 .0016 .0039 .0081 .0150 .0256 .0410 .0625 5 0
.7738 .5905 .4437 .3277 .2373 .1681 .1160 .0778 .0503 .0313 1
.2036 .3281 .3915 .4096 .3955 .3602 .3124 .2592 .2059 .1563 2
.0214 .0729 .1382 .2048 .2637 .3087 .3364 .3456 .3369 .3125 3
.0011 .0081 .0244 .0512 .0879 .1323 .1811 .2304 .2757 .3125 4
.0000 .0005 .0022 .0064 .0146 .0284 .0488 .0768 .1128 .1563 5
.0000 .0001 .0003 .0010 .0024 .0053 .0102 .0185 .0313 6 0
.7351 .5314 .3771 .2621 .1780 .1176 .0754 .0467 .0277 .0156 1
.2321 .3543 .3993 .3932 .3560 .3025 .2437 .1866 .1359 .0938 2
.0305 .0984 .1762 .2458 .2966 .3241 .3280 .3110 .2780 .2344 3
.0021 .0146 .0415 .0819 .1318 .1852 .2355 .2765 .3032 .3125 4
.0001 .0012 .0055 .0154 .0330 .0595 .0951 .1382 .1861 .2344 5
.0000 .0001 .0004 .0015 .0044 .0102 .0205 .0369 .0609 .0938 6
.0000 .0000 .0001 .0002 .0007 .0018 .0041 .0083 .0156 7 0
.6983 .4783 .3206 .2097 .1335 .0824 .0490 .0280 .0152 .0078 1
.2573 .3720 .3960 .3670 .3115 .2471 .1848 .1306 .0872 .0547 2
.0406 .1240 .2097 .2753 .3115 .3177 .2985 .2613 .2140 .1641 3
.0036 .0230 .0617 .1147 .1730 .2269 .2679 .2903 .2918 .2734 4
.0002 .0026 .0109 .0287 .0577 .0972 .1442 .1935 .2388 .2734 5
.0000 .0002 .0012 .0043 .0115 .0250 .0466 .0774 .1172 .1641 6
.0000 .0001 .0004 .0013 .0036 .0084 .0172 .0320 .0547 7
.0000 .0000 .0001 .0002 .0006 .0016 .0037 .0078 8 0
.6634 .4305 .2725 .1678 .1001 .0576 .0319 .0168 .0084 .0039 1
.2793 .3826 .3847 .3355 .2670 .1977 .1373 .0896 .0548 .0313 2
.0515 .1488 .2376 .2936 .3115 .2965 .2587 .2090 .1569 .1094 3
.0054 .0331 .0839 .1468 .2076 .2541 .2786 .2787 .2568 .2188 4
.0004 .0046 .0185 .0459 .0865 .1361 .1875 .2322 .2627 .2734 5
.0000 .0004 .0026 .0092 .0231 .0467 .0808 .1239 .1719 .2188 6
.0000 .0002 .0011 .0038 .0100 .0217 .0413 .0703 .1094 7
.0000 .0001 .0004 .0012 .0033 .0079 .0164 .0313 8
.0000 .0000 .0001 .0002 .0007 .0017 .0039 52
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN P (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 9 0
.6302 .3874 .2316 .1342 .0751 .0404 .0207 .0101 .0046 .0020 1
.2985 .3874 .3679 .3020 .2253 .1556 .1004 .0605 .0339 .0176 2
.0629 .1722 .2597 .3020 .3003 .2668 .2162 .1612 .1110 .0703 3
.0077 .0446 .1069 .1762 .2336 .2668 .2716 .2508 .2119 .1641 4
.0006 .0074 .0283 .0661 .1168 .1715 .2194 .2508 .2600 .2461 5
.0000 .0008 .0050 .0165 .0389 .0735 .1181 .1672 .2128 .2461 6
.0001 .0006 .0028 .0087 .0210 .0424 .0743 .1160 .1641 7
.0000 .0000 .0003 .0012 .0039 .0098 .0212 .0407 .0703 8
.0000 .0001 .0004 .0013 .0035 .0083 .0176 9
.0000 .0000 .0001 .0003 .0008 .0020 10 0
.5987 .3487 .1969 .1074 .0563 .0282 .0135 .0060 .0025 .0010 1
.3151 .3874 .3474 .2684 .1877 .1211 .0725 .0403 .0207 .0098 2
.0746 .1937 .2759 .3020 .2816 .2335 .1757 .1209 .0763 .0439 3
.0105 .0574 .1298 .2013 .2503 .2668 .2522 .2150 .1665 .1172 4
.0010 .0112 .0401 .0881 .1460 .2001 .2377 .2508 .2384 .2051 5
.0001 .0015 .0085 .0264 .0584 .1029 .1536 .2007 .2340 .2461 6
.0000 .0001 .0012 .0055 .0162 .0368 .0689 .1115 .1596 .2051 7
.0000 .0001 .0008 .0031 .0090 .0212 .0425 .0746 .1172 8
.0000 .0001 .0004 .0014 .0043 .0106 .0229 .0439 9
.0000 .0000 .0001 .0005 .0016 .0042 .0098 10 .0000 .0000 .0001 .0003 .0010 12 0
.5404 .2824 .1422 .0687 .0317 .0138 .0057 .0022 .0008 .0002 1
.3413 .3766 .3012 .2062 .1267 .0712 .0368 .0174 .0075 .0029 2
.0988 .2301 .2924 .2835 .2323 .1678 .1088 .0639 .0339 .0161 3
.0173 .0852 .1720 .2362 .2581 .2397 .1954 .1419 .0923 .0537 4
.0021 .0213 .0683 .1329 .1936 .2311 .2367 .2128 .1700 .1208 5
.0002 .0038 .0193 .0532 .1032 .1585 .2039 .2270 .2225 .1934 6
.0000 .0005 .0040 .0155 .0401 .0792 .1281 .1766 .2124 .2256 7
.0000 .0006 .0033 .0115 .0291 .0591 .1009 .1489 .1934 8
.0001 .0005 .0024 .0078 .0199 .0420 .0762 .1208 9
.0000 .0001 .0004 .0015 .0048 .0125 .0277 .0537 10
.0000 .0000 .0002 .0008 .0025 .0068 .0161 11 .0000 .0001 .0003 .0010 .0029 12 .0000 .0000 .0001 .0002 15 0
.4633 .2059 .0874 .0352 .0134 .0047 .0016 .0005 .0001 .0000 1
.3658 .3432 .2312 .1319 .0668 .0305 .0126 .0047 .0016 .0005 2
.1348 .2669 .2856 .2309 .1559 .0916 .0476 .0219 .0090 .0032 3
.0307 .1285 .2184 .2501 .2252 .1700 .1110 .0634 .0318 .0139 4
.0049 .0428 .1156 .1876 .2252 .2186 .1792 .1268 .0780 .0417 5
.0006 .0105 .0449 .1032 .1651 .2061 .2123 .1859 .1404 .0916 6
.0000 .0019 .0132 .0430 .0917 .1472 .1906 .2066 .1914 .1527 7
.0003 .0030 .0138 .0393 .0811 .1319 .1771 .2013 .1964 8
.0000 .0005 .0035 .0131 .0348 .0710 .1181 .1647 .1964 9
.0001 .0007 .0034 .0116 .0298 .0612 .1048 .1527 10
.0000 .0001 .0007 .0030 .0096 .0245 .0515 .0916 11
.0000 .0001 .0006 .0024 .0074 .0191 .0417 12
.0000 .0001 .0004 .0016 .0052 .0139 13 .0000 .0001 .0003 .0010 .0032 14 .0000 .0000 .0001 .0005
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 53
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— P (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 15 .0000 .0000 20 0
.3585 .1216 .0388 .0115 .0032 .0008 .0002 .0000 .0000 .0000 1
.3774 .2702 .1368 .0576 .0211 .0068 .0020 .0005 .0001 .0000 2
.1887 .2852 .2293 .1369 .0669 .0278 .0100 .0031 .0008 .0002 3
.0596 .1901 .2428 .2054 .1339 .0716 .0323 .0123 .0040 .0011 4
.0133 .0898 .1821 .2182 .1897 .1304 .0738 .0350 .0139 .0046 5
.0022 .0319 .1028 .1746 .2023 .1789 .1272 .0746 .0365 .0148 6
.0003 .0089 .0454 .1091 .1686 .1916 .1712 .1244 .0746 .0370 7
.0000 .0020 .0160 .0545 .1124 .1643 .1844 .1659 .1221 .0739 8
.0004 .0046 .0222 .0609 .1144 .1614 .1797 .1623 .1201 9
.0001 .0011 .0074 .0271 .0654 .1158 .1597 .1771 .1602 10
.0000 .0002 .0020 .0099 .0308 .0686 .1171 .1593 .1762 11
.0000 .0005 .0030 .0120 .0336 .0710 .1185 .1602 12
.0001 .0008 .0039 .0136 .0355 .0727 .1201 13
.0000 .0002 .0010 .0045 .0146 .0366 .0739 14
.0000 .0002 .0012 .0049 .0150 .0370 15 .0000 .0003 .0013 .0049 .0148 16 .0000 .0003 .0013 .0046 17 .0000 .0002 .0011 18 .0000 .0002 19 .0000 20 54
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bảng 2. Xác suất tích lũy Phân phối Nhị thức x X F (x) = P (X ≤ x) = C in pi(1 − p)1−i i=0
P (X ≤ 2|n = 5, p = 0, 2) = 0, 9421 F (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 1 0
.9500 .9000 .8500 .8000 .7500 .7000 .6500 .6000 .5500 .5000 1
1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 2 0
.9025 .8100 .7225 .6400 .5625 .4900 .4225 .3600 .3025 .2500 1
.9975 .9900 .9775 .9600 .9375 .9100 .8775 .8400 .7975 .7500 2
1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 3 0
.8574 .7290 .6141 .5120 .4219 .3430 .2746 .2160 .1664 .1250 1
.9928 .9720 .9393 .8960 .8438 .7840 .7183 .6480 .5748 .5000 2
.9999 .9990 .9966 .9920 .9844 .9730 .9571 .9360 .9089 .8750 3
1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 4 0
.8145 .6561 .5220 .4096 .3164 .2401 .1785 .1296 .0915 .0625 1
.9860 .9477 .8905 .8192 .7383 .6517 .5630 .4752 .3910 .3125 2
.9995 .9963 .9880 .9728 .9492 .9163 .8735 .8208 .7585 .6875 3
1.000 .9999 .9995 .9984 .9961 .9919 .9850 .9744 .9590 .9375 4
1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 5 0
.7738 .5905 .4437 .3277 .2373 .1681 .1160 .0778 .0503 .0313 1
.9774 .9185 .8352 .7373 .6328 .5282 .4284 .3370 .2562 .1875 2
.9988 .9914 .9734 .9421 .8965 .8369 .7648 .6826 .5931 .5000 3
1.000 .9995 .9978 .9933 .9844 .9692 .9460 .9130 .8688 .8125 4
1.000 .9999 .9997 .9990 .9976 .9947 .9898 .9815 .9688 5
1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 6 0
.7351 .5314 .3771 .2621 .1780 .1176 .0754 .0467 .0277 .0156 1
.9672 .8857 .7765 .6554 .5339 .4202 .3191 .2333 .1636 .1094 2
.9978 .9842 .9527 .9011 .8306 .7443 .6471 .5443 .4415 .3438 3
.9999 .9987 .9941 .9830 .9624 .9295 .8826 .8208 .7447 .6563 4
1.000 .9999 .9996 .9984 .9954 .9891 .9777 .9590 .9308 .8906 5
1.000 1.000 .9999 .9998 .9993 .9982 .9959 .9917 .9844 6
1.000 1.000 1.000 1.000 1.000 1.000 1.000 7 0
.6983 .4783 .3206 .2097 .1335 .0824 .0490 .0280 .0152 .0078 1
.9556 .8503 .7166 .5767 .4449 .3294 .2338 .1586 .1024 .0625 2
.9962 .9743 .9262 .8520 .7564 .6471 .5323 .4199 .3164 .2266 3
.9998 .9973 .9879 .9667 .9294 .8740 .8002 .7102 .6083 .5000 4
1.000 .9998 .9988 .9953 .9871 .9712 .9444 .9037 .8471 .7734 5
1.000 .9999 .9996 .9987 .9962 .9910 .9812 .9643 .9375 6
1.000 1.000 .9999 .9998 .9994 .9984 .9963 .9922 7
1.000 1.000 1.000 1.000 1.000 1.000 8 0
.6634 .4305 .2725 .1678 .1001 .0576 .0319 .0168 .0084 .0039 1
.9428 .8131 .6572 .5033 .3671 .2553 .1691 .1064 .0632 .0352 2
.9942 .9619 .8948 .7969 .6785 .5518 .4278 .3154 .2201 .1445 3
.9996 .9950 .9786 .9437 .8862 .8059 .7064 .5941 .4770 .3633 4
1.000 .9996 .9971 .9896 .9727 .9420 .8939 .8263 .7396 .6367 5
1.000 .9998 .9988 .9958 .9887 .9747 .9502 .9115 .8555 6
1.000 .9999 .9996 .9987 .9964 .9915 .9819 .9648 7
1.000 1.000 .9999 .9998 .9993 .9983 .9961 8 1.000 1.000 1.000 1.000 1.000
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 55
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT— F (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 9 0
.6302 .3874 .2316 .1342 .0751 .0404 .0207 .0101 .0046 .0020 1
.9288 .7748 .5995 .4362 .3003 .1960 .1211 .0705 .0385 .0195 2
.9916 .9470 .8591 .7382 .6007 .4628 .3373 .2318 .1495 .0898 3
.9994 .9917 .9661 .9144 .8343 .7297 .6089 .4826 .3614 .2539 4
1.000 .9991 .9944 .9804 .9511 .9012 .8283 .7334 .6214 .5000 5
.9999 .9994 .9969 .9900 .9747 .9464 .9006 .8342 .7461 6
1.000 1.000 .9997 .9987 .9957 .9888 .9750 .9502 .9102 7
1.000 .9999 .9996 .9986 .9962 .9909 .9805 8
1.000 1.000 .9999 .9997 .9992 .9980 9 1.000 1.000 1.000 1.000 10 0
.5987 .3487 .1969 .1074 .0563 .0282 .0135 .0060 .0025 .0010 1
.9139 .7361 .5443 .3758 .2440 .1493 .0860 .0464 .0233 .0107 2
.9885 .9298 .8202 .6778 .5256 .3828 .2616 .1673 .0996 .0547 3
.9990 .9872 .9500 .8791 .7759 .6496 .5138 .3823 .2660 .1719 4
.9999 .9984 .9901 .9672 .9219 .8497 .7515 .6331 .5044 .3770 5
1.000 .9999 .9986 .9936 .9803 .9527 .9051 .8338 .7384 .6230 6
1.000 .9999 .9991 .9965 .9894 .9740 .9452 .8980 .8281 7
1.000 .9999 .9996 .9984 .9952 .9877 .9726 .9453 8
1.000 1.000 .9999 .9995 .9983 .9955 .9893 9 1.000 1.000 .9999 .9997 .9990 10 1.000 1.000 1.000 12 0
.5404 .2824 .1422 .0687 .0317 .0138 .0057 .0022 .0008 .0002 1
.8816 .6590 .4435 .2749 .1584 .0850 .0424 .0196 .0083 .0032 2
.9804 .8891 .7358 .5583 .3907 .2528 .1513 .0834 .0421 .0193 3
.9978 .9744 .9078 .7946 .6488 .4925 .3467 .2253 .1345 .0730 4
.9998 .9957 .9761 .9274 .8424 .7237 .5833 .4382 .3044 .1938 5
1.000 .9995 .9954 .9806 .9456 .8822 .7873 .6652 .5269 .3872 6
.9999 .9993 .9961 .9857 .9614 .9154 .8418 .7393 .6128 7
1.000 .9999 .9994 .9972 .9905 .9745 .9427 .8883 .8062 8
1.000 .9999 .9996 .9983 .9944 .9847 .9644 .9270 9
1.000 1.000 .9998 .9992 .9972 .9921 .9807 10 1.000 .9999 .9997 .9989 .9968 11 1.000 1.000 .9999 .9998 12 1.000 1.000 15 0
.4633 .2059 .0874 .0352 .0134 .0047 .0016 .0005 .0001 .0000 1
.8290 .5490 .3186 .1671 .0802 .0353 .0142 .0052 .0017 .0005 2
.9638 .8159 .6042 .3980 .2361 .1268 .0617 .0271 .0107 .0037 3
.9945 .9444 .8227 .6482 .4613 .2969 .1727 .0905 .0424 .0176 4
.9994 .9873 .9383 .8358 .6865 .5155 .3519 .2173 .1204 .0592 5
.9999 .9978 .9832 .9389 .8516 .7216 .5643 .4032 .2608 .1509 6
1.000 .9997 .9964 .9819 .9434 .8689 .7548 .6098 .4522 .3036 7
1.000 .9994 .9958 .9827 .9500 .8868 .7869 .6535 .5000 8
.9999 .9992 .9958 .9848 .9578 .9050 .8182 .6964 9
1.000 .9999 .9992 .9963 .9876 .9662 .9231 .8491 10
1.000 .9999 .9993 .9972 .9907 .9745 .9408 11
1.000 .9999 .9995 .9981 .9937 .9824 12 1.000 .9999 .9997 .9989 .9963 13 1.000 1.000 .9999 .9995 14 1.000 1.000 56
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN F (x) p n x .05 .1 .15 .2 .25 .3 .35 .4 .45 .5 15 20 0
.3585 .1216 .0388 .0115 .0032 .0008 .0002 .0000 .0000 .0000 1
.7358 .3917 .1756 .0692 .0243 .0076 .0021 .0005 .0001 .0000 2
.9245 .6769 .4049 .2061 .0913 .0355 .0121 .0036 .0009 .0002 3
.9841 .8670 .6477 .4114 .2252 .1071 .0444 .0160 .0049 .0013 4
.9974 .9568 .8298 .6296 .4148 .2375 .1182 .0510 .0189 .0059 5
.9997 .9887 .9327 .8042 .6172 .4164 .2454 .1256 .0553 .0207 6
1.000 .9976 .9781 .9133 .7858 .6080 .4166 .2500 .1299 .0577 7
.9996 .9941 .9679 .8982 .7723 .6010 .4159 .2520 .1316 8
.9999 .9987 .9900 .9591 .8867 .7624 .5956 .4143 .2517 9
1.000 .9998 .9974 .9861 .9520 .8782 .7553 .5914 .4119 10
1.000 .9994 .9961 .9829 .9468 .8725 .7507 .5881 11
.9999 .9991 .9949 .9804 .9435 .8692 .7483 12
1.000 .9998 .9987 .9940 .9790 .9420 .8684 13
1.000 .9997 .9985 .9935 .9786 .9423 14 1.000 .9997 .9984 .9936 .9793 15 1.000 .9997 .9985 .9941 16 1.000 .9997 .9987 17 .9998 18 1.000 19 20
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 57
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 3. Xác suất Phân phối Poisson e−λλx P (X = x) = x! P (X = 2|λ = 1, 5) = 0, 251 P (x) λ x 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 0
1.000 .9048 .8187 .7408 .6703 .6065 .5488 .4966 .4493 .4066 1
.0000 .0905 .1637 .2222 .2681 .3033 .3293 .3476 .3595 .3659 2
.0045 .0164 .0333 .0536 .0758 .0988 .1217 .1438 .1647 3
.0002 .0011 .0033 .0072 .0126 .0198 .0284 .0383 .0494 4
.0000 .0001 .0003 .0007 .0016 .0030 .0050 .0077 .0111 5
.0000 .0000 .0001 .0002 .0004 .0007 .0012 .0020 6
.0000 .0000 .0000 .0001 .0002 .0003 7 .0000 .0000 .0000 P (x) λ x 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 0
.3679 .3329 .3012 .2725 .2466 .2231 .2019 .1827 .1653 .1496 1
.3679 .3662 .3614 .3543 .3452 .3347 .3230 .3106 .2975 .2842 2
.1839 .2014 .2169 .2303 .2417 .2510 .2584 .2640 .2678 .2700 3
.0613 .0738 .0867 .0998 .1128 .1255 .1378 .1496 .1607 .1710 4
.0153 .0203 .0260 .0324 .0395 .0471 .0551 .0636 .0723 .0812 5
.0031 .0045 .0062 .0084 .0111 .0141 .0176 .0216 .0260 .0309 6
.0005 .0008 .0012 .0018 .0026 .0035 .0047 .0061 .0078 .0098 7
.0001 .0001 .0002 .0003 .0005 .0008 .0011 .0015 .0020 .0027 8
.0000 .0000 .0000 .0001 .0001 .0001 .0002 .0003 .0005 .0006 9
.0000 .0000 .0000 .0000 .0001 .0001 .0001 10 .0000 .0000 .0000 P (x) λ x 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 0
.1353 .1225 .1108 .1003 .0907 .0821 .0743 .0672 .0608 .0550 1
.2707 .2572 .2438 .2306 .2177 .2052 .1931 .1815 .1703 .1596 2
.2707 .2700 .2681 .2652 .2613 .2565 .2510 .2450 .2384 .2314 3
.1804 .1890 .1966 .2033 .2090 .2138 .2176 .2205 .2225 .2237 4
.0902 .0992 .1082 .1169 .1254 .1336 .1414 .1488 .1557 .1622 5
.0361 .0417 .0476 .0538 .0602 .0668 .0735 .0804 .0872 .0940 6
.0120 .0146 .0174 .0206 .0241 .0278 .0319 .0362 .0407 .0455 7
.0034 .0044 .0055 .0068 .0083 .0099 .0118 .0139 .0163 .0188 8
.0009 .0011 .0015 .0019 .0025 .0031 .0038 .0047 .0057 .0068 9
.0002 .0003 .0004 .0005 .0007 .0009 .0011 .0014 .0018 .0022 10
.0000 .0001 .0001 .0001 .0002 .0002 .0003 .0004 .0005 .0006 11
.0000 .0000 .0000 .0000 .0000 .0001 .0001 .0001 .0002 12 .0000 .0000 .0000 .0000 P (x) λ x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 0
.0498 .0450 .0408 .0369 .0334 .0302 .0273 .0247 .0224 .0202 1
.1494 .1397 .1304 .1217 .1135 .1057 .0984 .0915 .0850 .0789 58
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN P (x) λ x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 2
.2240 .2165 .2087 .2008 .1929 .1850 .1771 .1692 .1615 .1539 3
.2240 .2237 .2226 .2209 .2186 .2158 .2125 .2087 .2046 .2001 4
.1680 .1733 .1781 .1823 .1858 .1888 .1912 .1931 .1944 .1951 5
.1008 .1075 .1140 .1203 .1264 .1322 .1377 .1429 .1477 .1522 6
.0504 .0555 .0608 .0662 .0716 .0771 .0826 .0881 .0936 .0989 7
.0216 .0246 .0278 .0312 .0348 .0385 .0425 .0466 .0508 .0551 8
.0081 .0095 .0111 .0129 .0148 .0169 .0191 .0215 .0241 .0269 9
.0027 .0033 .0040 .0047 .0056 .0066 .0076 .0089 .0102 .0116 10
.0008 .0010 .0013 .0016 .0019 .0023 .0028 .0033 .0039 .0045 11
.0002 .0003 .0004 .0005 .0006 .0007 .0009 .0011 .0013 .0016 12
.0001 .0001 .0001 .0001 .0002 .0002 .0003 .0003 .0004 .0005 13
.0000 .0000 .0000 .0000 .0000 .0001 .0001 .0001 .0001 .0002 14 .0000 .0000 .0000 .0000 .0000 P (x) λ x 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 0
.0183 .0166 .0150 .0136 .0123 .0111 .0101 .0091 .0082 .0074 1
.0733 .0679 .0630 .0583 .0540 .0500 .0462 .0427 .0395 .0365 2
.1465 .1393 .1323 .1254 .1188 .1125 .1063 .1005 .0948 .0894 3
.1954 .1904 .1852 .1798 .1743 .1687 .1631 .1574 .1517 .1460 4
.1954 .1951 .1944 .1933 .1917 .1898 .1875 .1849 .1820 .1789 5
.1563 .1600 .1633 .1662 .1687 .1708 .1725 .1738 .1747 .1753 6
.1042 .1093 .1143 .1191 .1237 .1281 .1323 .1362 .1398 .1432 7
.0595 .0640 .0686 .0732 .0778 .0824 .0869 .0914 .0959 .1002 8
.0298 .0328 .0360 .0393 .0428 .0463 .0500 .0537 .0575 .0614 9
.0132 .0150 .0168 .0188 .0209 .0232 .0255 .0281 .0307 .0334 10
.0053 .0061 .0071 .0081 .0092 .0104 .0118 .0132 .0147 .0164 11
.0019 .0023 .0027 .0032 .0037 .0043 .0049 .0056 .0064 .0073 12
.0006 .0008 .0009 .0011 .0013 .0016 .0019 .0022 .0026 .0030 13
.0002 .0002 .0003 .0004 .0005 .0006 .0007 .0008 .0009 .0011 14
.0001 .0001 .0001 .0001 .0001 .0002 .0002 .0003 .0003 .0004 15
.0000 .0000 .0000 .0000 .0000 .0001 .0001 .0001 .0001 .0001 16 .0000 .0000 .0000 .0000 .0000
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 59
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 4. Xác suất tích lũy Phân phối Poisson x X e−λλi F (x) = P (X ≤ x) = i! i=0
P (X ≤ 2|λ = 1, 5) = 0, 8088 F (x) λ x 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 0
1.000 .9048 .8187 .7408 .6703 .6065 .5488 .4966 .4493 .4066 1
.9953 .9825 .9631 .9384 .9098 .8781 .8442 .8088 .7725 2
.9998 .9989 .9964 .9921 .9856 .9769 .9659 .9526 .9371 3
1.000 .9999 .9997 .9992 .9982 .9966 .9942 .9909 .9865 4
1.000 1.000 .9999 .9998 .9996 .9992 .9986 .9977 5
1.000 1.000 1.000 .9999 .9998 .9997 6 1.000 1.000 1.000 F (x) λ x 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 0
.3679 .3329 .3012 .2725 .2466 .2231 .2019 .1827 .1653 .1496 1
.7358 .6990 .6626 .6268 .5918 .5578 .5249 .4932 .4628 .4337 2
.9197 .9004 .8795 .8571 .8335 .8088 .7834 .7572 .7306 .7037 3
.9810 .9743 .9662 .9569 .9463 .9344 .9212 .9068 .8913 .8747 4
.9963 .9946 .9923 .9893 .9857 .9814 .9763 .9704 .9636 .9559 5
.9994 .9990 .9985 .9978 .9968 .9955 .9940 .9920 .9896 .9868 6
.9999 .9999 .9997 .9996 .9994 .9991 .9987 .9981 .9974 .9966 7
1.000 1.000 1.000 .9999 .9999 .9998 .9997 .9996 .9994 .9992 8
1.000 1.000 1.000 .9999 .9999 .9998 9 1.000 1.000 1.000 F (x) λ x 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 0
.1353 .1225 .1108 .1003 .0907 .0821 .0743 .0672 .0608 .0550 1
.4060 .3796 .3546 .3309 .3084 .2873 .2674 .2487 .2311 .2146 2
.6767 .6496 .6227 .5960 .5697 .5438 .5184 .4936 .4695 .4460 3
.8571 .8386 .8194 .7993 .7787 .7576 .7360 .7141 .6919 .6696 4
.9473 .9379 .9275 .9162 .9041 .8912 .8774 .8629 .8477 .8318 5
.9834 .9796 .9751 .9700 .9643 .9580 .9510 .9433 .9349 .9258 6
.9955 .9941 .9925 .9906 .9884 .9858 .9828 .9794 .9756 .9713 7
.9989 .9985 .9980 .9974 .9967 .9958 .9947 .9934 .9919 .9901 8
.9998 .9997 .9995 .9994 .9991 .9989 .9985 .9981 .9976 .9969 9
1.000 .9999 .9999 .9999 .9998 .9997 .9996 .9995 .9993 .9991 10
1.000 1.000 1.000 1.000 .9999 .9999 .9999 .9998 .9998 11 1.000 1.000 1.000 1.000 .9999 12 1.000 F (x) λ x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 0
.0498 .0450 .0408 .0369 .0334 .0302 .0273 .0247 .0224 .0202 1
.1991 .1847 .1712 .1586 .1468 .1359 .1257 .1162 .1074 .0992 2
.4232 .4012 .3799 .3594 .3397 .3208 .3027 .2854 .2689 .2531 3
.6472 .6248 .6025 .5803 .5584 .5366 .5152 .4942 .4735 .4532 60
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN F (x) λ x 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4
.8153 .7982 .7806 .7626 .7442 .7254 .7064 .6872 .6678 .6484 5
.9161 .9057 .8946 .8829 .8705 .8576 .8441 .8301 .8156 .8006 6
.9665 .9612 .9554 .9490 .9421 .9347 .9267 .9182 .9091 .8995 7
.9881 .9858 .9832 .9802 .9769 .9733 .9692 .9648 .9599 .9546 8
.9962 .9953 .9943 .9931 .9917 .9901 .9883 .9863 .9840 .9815 9
.9989 .9986 .9982 .9978 .9973 .9967 .9960 .9952 .9942 .9931 10
.9997 .9996 .9995 .9994 .9992 .9990 .9987 .9984 .9981 .9977 11
.9999 .9999 .9999 .9998 .9998 .9997 .9996 .9995 .9994 .9993 12
1.000 1.000 1.000 1.000 .9999 .9999 .9999 .9999 .9998 .9998 13
1.000 1.000 1.000 1.000 1.000 .9999 14 1.000 F (x) λ x 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 0
.0183 .0166 .0150 .0136 .0123 .0111 .0101 .0091 .0082 .0074 1
.0916 .0845 .0780 .0719 .0663 .0611 .0563 .0518 .0477 .0439 2
.2381 .2238 .2102 .1974 .1851 .1736 .1626 .1523 .1425 .1333 3
.4335 .4142 .3954 .3772 .3594 .3423 .3257 .3097 .2942 .2793 4
.6288 .6093 .5898 .5704 .5512 .5321 .5132 .4946 .4763 .4582 5
.7851 .7693 .7531 .7367 .7199 .7029 .6858 .6684 .6510 .6335 6
.8893 .8786 .8675 .8558 .8436 .8311 .8180 .8046 .7908 .7767 7
.9489 .9427 .9361 .9290 .9214 .9134 .9049 .8960 .8867 .8769 8
.9786 .9755 .9721 .9683 .9642 .9597 .9549 .9497 .9442 .9382 9
.9919 .9905 .9889 .9871 .9851 .9829 .9805 .9778 .9749 .9717 10
.9972 .9966 .9959 .9952 .9943 .9933 .9922 .9910 .9896 .9880 11
.9991 .9989 .9986 .9983 .9980 .9976 .9971 .9966 .9960 .9953 12
.9997 .9997 .9996 .9995 .9993 .9992 .9990 .9988 .9986 .9983 13
.9999 .9999 .9999 .9998 .9998 .9997 .9997 .9996 .9995 .9994 14
1.000 1.000 1.000 1.000 .9999 .9999 .9999 .9999 .9999 .9998 15
1.000 1.000 1.000 1.000 1.000 .9999 16 1.000
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 61
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 5. Xác suất phân phối Chuẩn-chuẩn hóa Z z 1 t2 FZ(z) = P (Z < z) = √ exp − dt ∞ 2π 2
FZ(1, 25) = P (Z < 1, 25) = 0, 8944 z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 .0
.5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359 .1
.5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 .2
.5793 .5832 .5871 .5910 .5948 .5987 .6026 .6064 .6103 .6141 .3
.6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 .4
.6554 .6591 .6628 .6664 .6700 .6736 .6772 .6808 .6844 .6879 .5
.6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 .6
.7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 .7
.7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 .8
.7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 .9
.8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389
1.0 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621
1.1 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830
1.2 .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015
1.3 .9032 .9049 .9066 .9082 .9099 .9115 .9131 .9147 .9162 .9177
1.4 .9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319
1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441
1.6 .9452 .9463 .9474 .9484 .9495 .9505 .9515 .9525 .9535 .9545
1.7 .9554 .9564 .9573 .9582 .9591 .9599 .9608 .9616 .9625 .9633
1.8 .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9699 .9706
1.9 .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767
2.0 .9772 .9778 .9783 .9788 .9793 .9798 .9803 .9808 .9812 .9817
2.1 .9821 .9826 .9830 .9834 .9838 .9842 .9846 .9850 .9854 .9857
2.2 .9861 .9864 .9868 .9871 .9875 .9878 .9881 .9884 .9887 .9890
2.3 .9893 .9896 .9898 .9901 .9904 .9906 .9909 .9911 .9913 .9916
2.4 .9918 .9920 .9922 .9925 .9927 .9929 .9931 .9932 .9934 .9936
2.5 .9938 .9940 .9941 .9943 .9945 .9946 .9948 .9949 .9951 .9952
2.6 .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964
2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974
2.8 .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981
2.9 .9981 .9982 .9982 .9983 .9984 .9984 .9985 .9985 .9986 .9986
3.0 .9987 .9987 .9987 .9988 .9988 .9989 .9989 .9989 .9990 .9990
3.1 .9990 .9991 .9991 .9991 .9992 .9992 .9992 .9992 .9993 .9993
3.2 .9993 .9993 .9994 .9994 .9994 .9994 .9994 .9995 .9995 .9995
3.3 .9995 .9995 .9995 .9996 .9996 .9996 .9996 .9996 .9996 .9997
3.4 .9997 .9997 .9997 .9997 .9997 .9997 .9997 .9997 .9997 .9998
3.5 .9998 .9998 .9998 .9998 .9998 .9998 .9998 .9998 .9998 .9998
3.6 .9998 .9998 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999
3.7 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999
3.8 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999 .9999 62
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bảng 6. Hàm mật độ phân phối Chuẩn-chuẩn hóa 1 z2 fZ(z) = √ exp − 2π 2 fZ(1, 25) = 0, 1826 z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 0
.3989 .3989 .3989 .3988 .3986 .3984 .3982 .3980 .3977 .3973 .1
.3970 .3965 .3961 .3956 .3951 .3945 .3939 .3932 .3925 .3918 .2
.3910 .3902 .3894 .3885 .3876 .3867 .3857 .3847 .3836 .3825 .3
.3814 .3802 .3790 .3778 .3765 .3752 .3739 .3725 .3712 .3697 .4
.3683 .3668 .3653 .3637 .3621 .3605 .3589 .3572 .3555 .3538 .5
.3521 .3503 .3485 .3467 .3448 .3429 .3410 .3391 .3372 .3352 .6
.3332 .3312 .3292 .3271 .3251 .3230 .3209 .3187 .3166 .3144 .7
.3123 .3101 .3079 .3056 .3034 .3011 .2989 .2966 .2943 .2920 .8
.2897 .2874 .2850 .2827 .2803 .2780 .2756 .2732 .2709 .2685 .9
.2661 .2637 .2613 .2589 .2565 .2541 .2516 .2492 .2468 .2444 1
.2420 .2396 .2371 .2347 .2323 .2299 .2275 .2251 .2227 .2203
1.1 .2179 .2155 .2131 .2107 .2083 .2059 .2036 .2012 .1989 .1965
1.2 .1942 .1919 .1895 .1872 .1849 .1826 .1804 .1781 .1758 .1736
1.3 .1714 .1691 .1669 .1647 .1626 .1604 .1582 .1561 .1539 .1518
1.4 .1497 .1476 .1456 .1435 .1415 .1394 .1374 .1354 .1334 .1315
1.5 .1295 .1276 .1257 .1238 .1219 .1200 .1182 .1163 .1145 .1127
1.6 .1109 .1092 .1074 .1057 .1040 .1023 .1006 .0989 .0973 .0957
1.7 .0940 .0925 .0909 .0893 .0878 .0863 .0848 .0833 .0818 .0804
1.8 .0790 .0775 .0761 .0748 .0734 .0721 .0707 .0694 .0681 .0669
1.9 .0656 .0644 .0632 .0620 .0608 .0596 .0584 .0573 .0562 .0551 2
.0540 .0529 .0519 .0508 .0498 .0488 .0478 .0468 .0459 .0449
2.1 .0440 .0431 .0422 .0413 .0404 .0396 .0387 .0379 .0371 .0363
2.2 .0355 .0347 .0339 .0332 .0325 .0317 .0310 .0303 .0297 .0290
2.3 .0283 .0277 .0270 .0264 .0258 .0252 .0246 .0241 .0235 .0229
2.4 .0224 .0219 .0213 .0208 .0203 .0198 .0194 .0189 .0184 .0180
2.5 .0175 .0171 .0167 .0163 .0158 .0154 .0151 .0147 .0143 .0139
2.6 .0136 .0132 .0129 .0126 .0122 .0119 .0116 .0113 .0110 .0107
2.7 .0104 .0101 .0099 .0096 .0093 .0091 .0088 .0086 .0084 .0081
2.8 .0079 .0077 .0075 .0073 .0071 .0069 .0067 .0065 .0063 .0061
2.9 .0060 .0058 .0056 .0055 .0053 .0051 .0050 .0048 .0047 .0046 3
.0044 .0043 .0042 .0040 .0039 .0038 .0037 .0036 .0035 .0034
3.1 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 .0025 .0025
3.2 .0024 .0023 .0022 .0022 .0021 .0020 .0020 .0019 .0018 .0018
3.3 .0017 .0017 .0016 .0016 .0015 .0015 .0014 .0014 .0013 .0013
3.4 .0012 .0012 .0012 .0011 .0011 .0010 .0010 .0010 .0009 .0009
3.5 .0009 .0008 .0008 .0008 .0008 .0007 .0007 .0007 .0007 .0006
3.6 .0006 .0006 .0006 .0005 .0005 .0005 .0005 .0005 .0005 .0004
3.7 .0004 .0004 .0004 .0004 .0004 .0004 .0003 .0003 .0003 .0003
3.8 .0003 .0003 .0003 .0003 .0003 .0002 .0002 .0002 .0002 .0002
3.9 .0002 .0002 .0002 .0002 .0002 .0002 .0002 .0002 .0001 .0001 4
.0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001
4.1 .0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001 .0001
4.2 .0001 .0001 .0001 .0001 .0000 .0000 .0000 .0000 .0000 .0000
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 63
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 7. Giá trị tới hạn phân phối Khi-bình phương χ2(n) α : P χ2(n) > χ2(n) α = α χ2(10) 0,05 = 18, 31 χ2(n) α α n .01 .025 .05 .1 .9 .95 .975 .99 1 6.635 5.024 3.841 2.706 .0158 .0039 .0010 .0002 2 9.210 7.378 5.991 4.605 .2107 .1026 .0506 .0201 3 11.34 9.348 7.815 6.251 .5844 .3518 .2158 .1148 4 13.28 11.14 9.488 7.779 1.064 .7107 .4844 .2971 5 15.09 12.83 11.07 9.236 1.610 1.145 .8312 .5543 6 16.81 14.45 12.59 10.64 2.204 1.635 1.237 .8721 7 18.48 16.01 14.07 12.02 2.833 2.167 1.690 1.239 8 20.09 17.53 15.51 13.36 3.490 2.733 2.180 1.646 9 21.67 19.02 16.92 14.68 4.168 3.325 2.700 2.088 10 23.21 20.48 18.31 15.99 4.865 3.940 3.247 2.558 11 24.72 21.92 19.68 17.28 5.578 4.575 3.816 3.053 12 26.22 23.34 21.03 18.55 6.304 5.226 4.404 3.571 13 27.69 24.74 22.36 19.81 7.042 5.892 5.009 4.107 14 29.14 26.12 23.68 21.06 7.790 6.571 5.629 4.660 15 30.58 27.49 25.00 22.31 8.547 7.261 6.262 5.229 16 32.00 28.85 26.30 23.54 9.312 7.962 6.908 5.812 17 33.41 30.19 27.59 24.77 10.09 8.672 7.564 6.408 18 34.81 31.53 28.87 25.99 10.86 9.390 8.231 7.015 19 36.19 32.85 30.14 27.20 11.65 10.12 8.907 7.633 20 37.57 34.17 31.41 28.41 12.44 10.85 9.591 8.260 21 38.93 35.48 32.67 29.62 13.24 11.59 10.28 8.897 22 40.29 36.78 33.92 30.81 14.04 12.34 10.98 9.542 23 41.64 38.08 35.17 32.01 14.85 13.09 11.69 10.20 24 42.98 39.36 36.42 33.20 15.66 13.85 12.40 10.86 25 44.31 40.65 37.65 34.38 16.47 14.61 13.12 11.52 26 45.64 41.92 38.89 35.56 17.29 15.38 13.84 12.20 27 46.96 43.19 40.11 36.74 18.11 16.15 14.57 12.88 28 48.28 44.46 41.34 37.92 18.94 16.93 15.31 13.56 29 49.59 45.72 42.56 39.09 19.77 17.71 16.05 14.26 30 50.89 46.98 43.77 40.26 20.60 18.49 16.79 14.95 31 52.19 48.23 44.99 41.42 21.43 19.28 17.54 15.66 32 53.49 49.48 46.19 42.58 22.27 20.07 18.29 16.36 33 54.78 50.73 47.40 43.75 23.11 20.87 19.05 17.07 34 56.06 51.97 48.60 44.90 23.95 21.66 19.81 17.79 35 57.34 53.20 49.80 46.06 24.80 22.47 20.57 18.51 36 58.62 54.44 51.00 47.21 25.64 23.27 21.34 19.23 37 59.89 55.67 52.19 48.36 26.49 24.07 22.11 19.96 38 61.16 56.90 53.38 49.51 27.34 24.88 22.88 20.69 39 62.43 58.12 54.57 50.66 28.20 25.70 23.65 21.43 40 63.69 59.34 55.76 51.81 29.05 26.51 24.43 22.16 60 88.38 83.30 79.08 74.40 46.46 43.19 40.48 37.48 80 112.3 106.6 101.9 96.58 64.28 60.39 57.15 53.54 100 135.8 129.6 124.3 118.5 82.36 77.93 74.22 70.06 150 193.2 185.8 179.6 172.6 128.3 122.7 118.0 112.7 200 249.4 241.1 234.0 226.0 174.8 168.3 162.7 156.4 64
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bảng 8. Giá trị tới hạn phân phối Student t(n) α : P T (n) > t(n) α = α t(10) 0.05 = 1.812 t(n) α α n .001 .005 .01 .025 .05 .1 .15 .2 1
318.3 63.66 31.82 12.71 6.314 3.078 1.963 1.376 2
22.33 9.925 6.965 4.303 2.920 1.886 1.386 1.061 3
10.22 5.841 4.541 3.182 2.353 1.638 1.250 .978 4
7.173 4.604 3.747 2.776 2.132 1.533 1.190 .941 5
5.893 4.032 3.365 2.571 2.015 1.476 1.156 .920 6
5.208 3.707 3.143 2.447 1.943 1.440 1.134 .906 7
4.785 3.499 2.998 2.365 1.895 1.415 1.119 .896 8
4.501 3.355 2.896 2.306 1.860 1.397 1.108 .889 9
4.297 3.250 2.821 2.262 1.833 1.383 1.100 .883 10
4.144 3.169 2.764 2.228 1.812 1.372 1.093 .879 11
4.025 3.106 2.718 2.201 1.796 1.363 1.088 .876 12
3.930 3.055 2.681 2.179 1.782 1.356 1.083 .873 13
3.852 3.012 2.650 2.160 1.771 1.350 1.079 .870 14
3.787 2.977 2.624 2.145 1.761 1.345 1.076 .868 15
3.733 2.947 2.602 2.131 1.753 1.341 1.074 .866 16
3.686 2.921 2.583 2.120 1.746 1.337 1.071 .865 17
3.646 2.898 2.567 2.110 1.740 1.333 1.069 .863 18
3.610 2.878 2.552 2.101 1.734 1.330 1.067 .862 19
3.579 2.861 2.539 2.093 1.729 1.328 1.066 .861 20
3.552 2.845 2.528 2.086 1.725 1.325 1.064 .860 21
3.527 2.831 2.518 2.080 1.721 1.323 1.063 .859 22
3.505 2.819 2.508 2.074 1.717 1.321 1.061 .858 23
3.485 2.807 2.500 2.069 1.714 1.319 1.060 .858 24
3.467 2.797 2.492 2.064 1.711 1.318 1.059 .857 25
3.450 2.787 2.485 2.060 1.708 1.316 1.058 .856 26
3.435 2.779 2.479 2.056 1.706 1.315 1.058 .856 27
3.421 2.771 2.473 2.052 1.703 1.314 1.057 .855 28
3.408 2.763 2.467 2.048 1.701 1.313 1.056 .855 29
3.396 2.756 2.462 2.045 1.699 1.311 1.055 .854 30
3.385 2.750 2.457 2.042 1.697 1.310 1.055 .854 31
3.375 2.744 2.453 2.040 1.696 1.309 1.054 .853 32
3.365 2.738 2.449 2.037 1.694 1.309 1.054 .853 33
3.356 2.733 2.445 2.035 1.692 1.308 1.053 .853 34
3.348 2.728 2.441 2.032 1.691 1.307 1.052 .852 35
3.340 2.724 2.438 2.030 1.690 1.306 1.052 .852 36
3.333 2.719 2.434 2.028 1.688 1.306 1.052 .852 37
3.326 2.715 2.431 2.026 1.687 1.305 1.051 .851 38
3.319 2.712 2.429 2.024 1.686 1.304 1.051 .851 39
3.313 2.708 2.426 2.023 1.685 1.304 1.050 .851 40
3.307 2.704 2.423 2.021 1.684 1.303 1.050 .851 60
3.232 2.660 2.390 2.000 1.671 1.296 1.045 .848 80
3.195 2.639 2.374 1.990 1.664 1.292 1.043 .846
100 3.174 2.626 2.364 1.984 1.660 1.290 1.042 .845
200 3.131 2.601 2.345 1.972 1.653 1.286 1.039 .843 ∞
3.090 2.576 2.326 1.960 1.645 1.282 1.036 .842
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 65
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
—VÍ DỤ - BÀI TẬP LÍ THUYẾT XÁC SUẤT—
Bảng 9. Giá trị tới hạn phân phối Fisher f (m,n) α : P F (m, n) > f (m,n) α = α f (2,5) 0.05 = 5.79 f (m,n) m α n α 1 2 3 4 5 6 7 8 9 10 .1
39.9 49.5 53.6 55.8 57.2 58.2 58.9 59.4 59.9 6.2 1 .05 161 200 216 225 230 234 237 239 241 242 .025 648 800 864 900 922 937 948 957 963 969 .1
8.53 9.00 9.16 9.24 9.29 9.33 9.35 9.37 9.38 9.39 2 .05
18.5 19.0 19.2 19.2 19.3 19.3 19.4 19.4 19.4 19.4 .025
38.5 39.0 39.2 39.2 39.3 39.3 39.4 39.4 39.4 39.4 .1
5.54 5.46 5.39 5.34 5.31 5.28 5.27 5.25 5.24 5.23 3 .05
10.1 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 .025
17.4 16.0 15.4 15.1 14.9 14.7 14.6 14.5 14.5 14.4 .1
4.54 4.32 4.19 4.11 4.05 4.01 3.98 3.95 3.94 3.92 4 .05
7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 .025 12.2
1.6 9.98 9.60 9.36 9.20 9.07 8.98 8.90 8.84 .1
4.06 3.78 3.62 3.52 3.45 3.40 3.37 3.34 3.32 3.30 5 .05
6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 .025
10.0 8.43 7.76 7.39 7.15 6.98 6.85 6.76 6.68 6.62 .1
3.78 3.46 3.29 3.18 3.11 3.05 3.01 2.98 2.96 2.94 6 .05
5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 .025
8.81 7.26 6.60 6.23 5.99 5.82 5.70 5.60 5.52 5.46 .1
3.59 3.26 3.07 2.96 2.88 2.83 2.78 2.75 2.72 2.70 7 .05
5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 .025
8.07 6.54 5.89 5.52 5.29 5.12 4.99 4.90 4.82 4.76 .1
3.46 3.11 2.92 2.81 2.73 2.67 2.62 2.59 2.56 2.54 8 .05
5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 .025
7.57 6.06 5.42 5.05 4.82 4.65 4.53 4.43 4.36 4.30 .1
3.36 3.01 2.81 2.69 2.61 2.55 2.51 2.47 2.44 2.42 9 .05
5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 .025
7.21 5.71 5.08 4.72 4.48 4.32 4.20 4.10 4.03 3.96 .1
3.29 2.92 2.73 2.61 2.52 2.46 2.41 2.38 2.35 2.32 10 .05
4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 .025
6.94 5.46 4.83 4.47 4.24 4.07 3.95 3.85 3.78 3.72 .1
3.07 2.70 2.49 2.36 2.27 2.21 2.16 2.12 2.09 2.06 15 .05
4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 .025
6.20 4.77 4.15 3.80 3.58 3.41 3.29 3.20 3.12 3.06 .1
2.97 2.59 2.38 2.25 2.16 2.09 2.04 2.00 1.96 1.94 20 .05
4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 .025
5.87 4.46 3.86 3.51 3.29 3.13 3.01 2.91 2.84 2.77 .1
2.84 2.44 2.23 2.09 2.00 1.93 1.87 1.83 1.79 1.76 40 .05
4.08 3.23 2.84 2.61 2.45 2.34 2.25 2.18 2.12 2.08 .025
5.42 4.05 3.46 3.13 2.90 2.74 2.62 2.53 2.45 2.39 .1
2.79 2.39 2.18 2.04 1.95 1.87 1.82 1.77 1.74 1.71 60 .05
4.00 3.15 2.76 2.53 2.37 2.25 2.17 2.10 2.04 1.99 .025
5.29 3.93 3.34 3.01 2.79 2.63 2.51 2.41 2.33 2.27 .1
2.76 2.36 2.14 2.00 1.91 1.83 1.78 1.73 1.69 1.66 100 .05
3.94 3.09 2.70 2.46 2.31 2.19 2.10 2.03 1.97 1.93 .025
5.18 3.83 3.25 2.92 2.70 2.54 2.42 2.32 2.24 2.18 66
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
KHOA TOÁN KINH TẾ - TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
Bảng giá trị tới hạn phân phối Fisher (tiếp) f (m,n) m α n α 11 12 15 18 20 25 30 40 60 100 .1 60.5 60.7 61.2 61.6 61.7 62.1 62.3 62.5 62.8 63.0 1 .05 243 244 246 247 248 249 250 251 252 253 .025 973 977 985 990 993 998 1001 1006 1010 1013 .1 9.40 9.41 9.42 9.44 9.44 9.45 9.46 9.47 9.47 9.48 2 .05
19.4 19.4 19.4 19.4 19.5 19.5 19.46 19.5 19.5 19.5 .025 39.4 39.4 39.4 39.4 39.5 39.5 39.5 39.5 39.5 39.5 .1 5.22 5.22 5.20 5.19 5.18 5.17 5.17 5.16 5.15 5.14 3 .05 8.76 8.74 8.70 8.67 8.66 8.63 8.62 8.59 8.57 8.55 .025 14.4 14.4 14.3 14.2 14.3 14.1 14.1 14.0 14.0 14.0 .1 3.91 3.90 3.87 3.85 3.84 3.83 3.82 3.80 3.79 3.78 4 .05 5.94 5.91 5.86 5.82 5.80 5.77 5.75 5.72 5.69 5.66 .025 8.79 8.75 8.66 8.59 8.56 8.50 8.46 8.41 8.36 8.32 .1 3.28 3.27 3.24 3.22 3.21 3.19 3.17 3.16 3.14 3.13 5 .05 4.70 4.68 4.62 4.58 4.56 4.52 4.50 4.46 4.43 4.41 .025 6.57 6.52 6.43 6.36 6.33 6.27 6.23 6.18 6.12 6.08 .1 2.92 2.90 2.87 2.85 2.84 2.81 2.80 2.78 2.76 2.75 6 .05 4.03 4.00 3.94 3.90 3.87 3.83 3.81 3.77 3.74 3.71 .025 5.41 5.37 5.27 5.20 5.17 5.11 5.07 5.01 4.96 4.92 .1 2.68 2.67 2.63 2.61 2.59 2.57 2.56 2.54 2.51 2.50 7 .05 3.60 3.57 3.51 3.47 3.44 3.40 3.38 3.34 3.30 3.27 .025 4.71 4.67 4.57 4.50 4.47 4.40 4.36 4.31 4.25 4.21 .1 2.52 2.50 2.46 2.44 2.42 2.40 2.38 2.36 2.34 2.32 8 .05 3.31 3.28 3.22 3.17 3.15 3.11 3.08 3.04 3.01 2.97 .025 4.24 4.20 4.10 4.03 4.00 3.94 3.89 3.84 3.78 3.74 .1 2.40 2.38 2.34 2.31 2.30 2.27 2.25 2.23 2.21 2.19 9 .05 3.10 3.07 3.01 2.96 2.94 2.89 2.86 2.83 2.79 2.76 .025 3.91 3.87 3.77 3.70 3.67 3.60 3.56 3.51 3.45 3.40 .1 2.30 2.28 2.24 2.22 2.20 2.17 2.16 2.13 2.11 2.09 10 .05 2.94 2.91 2.85 2.80 2.77 2.73 2.70 2.66 2.62 2.59 .025 3.66 3.62 3.52 3.45 3.42 3.35 3.31 3.26 3.20 3.15 .1 2.04 2.02 1.97 1.94 1.92 1.89 1.87 1.85 1.82 1.79 15 .05 2.51 2.48 2.40 2.35 2.33 2.28 2.25 2.20 2.16 2.12 .025 3.01 2.96 2.86 2.79 2.76 2.69 2.64 2.59 2.52 2.47 .1 1.91 1.89 1.84 1.81 1.79 1.76 1.74 1.71 1.68 1.65 20 .05 2.31 2.28 2.20 2.15 2.12 2.07 2.04 1.99 1.95 1.91 .025 2.72 2.68 2.57 2.50 2.46 2.40 2.35 2.29 2.22 2.17 .1 1.74 1.71 1.66 1.62 1.61 1.57 1.54 1.51 1.47 1.43 40 .05 2.04 2.00 1.92 1.87 1.84 1.78 1.74 1.69 1.64 1.59 .025 2.33 2.29 2.18 2.11 2.07 1.99 1.94 1.88 1.80 1.74 .1 1.68 1.66 1.60 1.56 1.54 1.50 1.48 1.44 1.40 1.36 60 .05 1.95 1.92 1.84 1.78 1.75 1.69 1.65 1.59 1.53 1.48 .025 2.22 2.17 2.06 1.98 1.94 1.87 1.82 1.74 1.67 1.60 .1 1.64 1.61 1.56 1.52 1.49 1.45 1.42 1.38 1.34 1.29 100 .05 1.89 1.85 1.77 1.71 1.68 1.62 1.57 1.52 1.45 1.39 .025 2.12 2.08 1.97 1.89 1.85 1.77 1.71 1.64 1.56 1.48
Bộ môn Toán kinh tế - www.mfe.neu.edu.vn 67
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com)




