
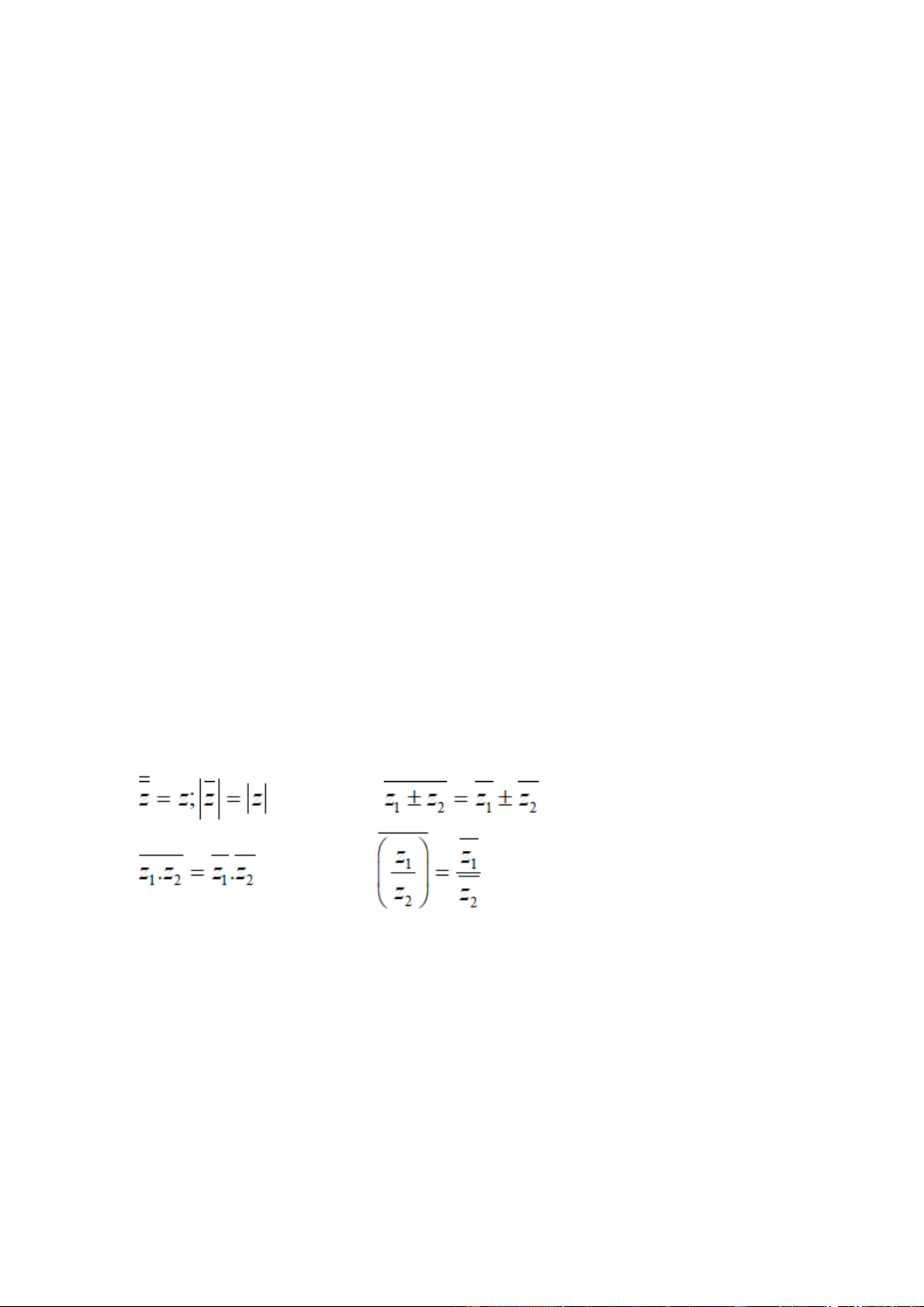


Preview text:
Cách tìm số phức liên hợp cực hay
1. Số phức liên hợp là gì?
Số phức liên hợp chính là a – bi và được ký hiệu là z , với z = a − bi. Ví dụ:
ta có z= 2 + 3i, vậy số phức liên hợp z = 2 – 3i.
Tuy nhiên, có nhiều bạn hay nhầm lẫn số phức liên hợp với số đối và cho rằng hai định
nghĩa trên là một. Đó là suy nghĩ không chính xác. Bởi số đối được ký hiệu là – z với –z = -a – bi.
2. Tính chất của số phức liên hợp
Việc nắm vững định nghĩa và tính chất của số phức liên hợp là một bước quan trọng trong
việc giải các dạng bài tập liên quan đến số phức. Số phức liên hợp, còn được gọi là số phức đối
xứng, đóng vai trò quan trọng trong nhiều lĩnh vực của toán học và khoa học tự nhiên. Để hiểu
rõ hơn về tại sao tính chất này quan trọng, hãy cùng xem xét một số ứng dụng thực tế.
Số phức liên hợp đóng một vai trò vô cùng quan trọng trong lĩnh vực điện tử và kỹ thuật
điện. Trong thế giới hiện đại, mạch điện đóng một vai trò quan trọng trong hầu hết các thiết bị
điện tử và hệ thống kỹ thuật. Để hiểu rõ và quản lý hiệu suất của những mạch này, chúng ta
không thể tránh khỏi sử dụng số phức liên hợp.
Các tín hiệu trong mạch điện thường biểu thị bằng sóng điện từ, với biến thiên theo thời
gian. Sử dụng số phức liên hợp, chúng ta có khả năng mô tả và phân tích những biến đổi này
một cách hiệu quả. Điều này cho phép chúng ta tính toán các thông số quan trọng như pha và
biên độ của sóng điện từ một cách dễ dàng và chính xác.
Ví dụ, trong việc thiết kế mạch điện cho các thiết bị điện tử như điện thoại di động hay máy
tính, việc tính toán pha và biên độ của tín hiệu là quan trọng để đảm bảo rằng tín hiệu truyền
tải đúng cách và không gây ra sự cản trở hoặc sự mất mát tín hiệu.
Ngoài ra, số phức liên hợp cũng đóng vai trò quan trọng trong việc mô phỏng và nghiên cứu
các mạch điện tử phức tạp, giúp chúng ta hiểu rõ hơn về cách các thành phần trong mạch tương
tác với nhau trong môi trường số học. Từ đó, chúng ta có thể phát triển và cải thiện các công
nghệ và thiết bị điện tử để đáp ứng nhu cầu ngày càng cao của thế giới kỹ thuật số.
Tóm lại, số phức liên hợp không chỉ là một khái niệm toán học, mà còn là một công cụ quan
trọng trong lĩnh vực điện tử và kỹ thuật điện, giúp chúng ta thấu hiểu và tận dụng sự phức tạp
của các mạch điện để tạo ra các thiết bị và công nghệ tiên tiến hơn.
Ngoài ra, số phức liên hợp cũng xuất hiện trong lĩnh vực hình học và quang học. Trong
quang học, chúng ta thường sử dụng số phức để mô tả dao động của ánh sáng và tính toán
tương tác giữa các tia sáng trong các hệ thống quang học phức tạp.
Như vậy, việc nắm vững tính chất của số phức liên hợp không chỉ giúp chúng ta giải quyết
các bài tập toán học một cách hiệu quả mà còn mở ra cánh cửa cho nhiều ứng dụng thú vị trong
thế giới thực. Đó chính là lý do tại sao tính chất này là một phần không thể thiếu trong học tập
và nghiên cứu của chúng ta.
Số phức liên hợp có một số tính chất quan trọng sau đây: |z|=|z|; ∀z∈C
Do đó, hai điểm biểu diễn z và z sẽ đối xứng với nhau qua trục Oxy trên mặt phẳng tạo độ Oxy. z+z’ = z + z’
Theo công thức này, liên hợp của một tổng sẽ bằng tổng các số phức liên hợp. Và công thức
trên còn đúng với cả phép trừ, phép nhân và phép chia. z.z = a 2 + b 2
Đây là công thức quan trọng và thường được áp dụng nhiều trong các bài toán.
Với z là số thực, ta có thì trong mọi trường hợp, z = z
Với z là số ảo tức là phần thực của nó = 0 thì z = – z z = z
3. Cách tìm số phức liên hợp cực hay
Cách tìm số phức liên hợp như sau:
Cho số phức z = a + bi. Ta gọi số phức liên hợp của z là Z = a - bi.
Kết quả: ∀ z ∈ C ta có: Z là số thực khi z = Z
Z là số thuần ảo khi z = - Z Ví dụ minh họa
Ví dụ 1: Cho số phức z = 1 + 3i Tìm số phức Z
A. Z = 1 - 3i. B. Z = 3 - i. C. Z = 3 + i. D. Z= 1 + 3i. Lời giải:
Với z = 1 + 3i thì Z = 1 - 3i Chọn A.
Ví dụ 2: Cho số phức z = -2 - 5i Tìm phần thực a và phần ảo b của số phức Z .
A. a = -2 ; b = 5 B. a = -2; b = -5 C. a = -5; b = 2 D. a = -5; b = -2 Lời giải: z = a + bi => Z = a - bi
Nên Z = -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5 Chọn A.
Ví dụ 3:Tìm số phức liên hợp của số phức Z =
Ví dụ 4:Tìm số phức z thỏa mãn z - (2 + 3i)Z = 1 - 9i .
A. z = -3 - i. B. z = -2 - i. C. z = 2 - i . D. z = 2 + i. Vậy z = 2 - i Chọn C.
Ví dụ 5:Cho số phức z = 3 + 4i. Tìm phần thực a và phần ảo b của số phức Z .
A. a = 3; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3
= >Phần thực a = 3 và phần ảo bằng b = -4 Chọn B.
Ví dụ 6:Cho số phức Z = 4 - 3i . Tìm phần thực và phần ảo của số phức z.
A. a = 3 ; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3 Lời giải: z = a + bi => Z = a - bi vậy z = 4 + 3i
=> Phần thực a = 4 và phần ảo b = 3 Chọn C.
Ví dụ 7:Tìm phần ảo b của số phức z thỏa mãn (z + 2)Z = (2 - i)2(1 - i)
A. b = 13 B.b = -13 C. b = -9 D. b = 9 Chọn A.
Ví dụ 8:Tìm số phức (iz + 2)Z = -1 - 8i thỏa mãn .
A. z = 7 + 7i B. z = 5 - 2i. C. z = 2 + 5i. D. z = 1 - 2i.
Ví dụ 9:Cho hai số phức z1 = 1 + 2i; z2 = 2 - 3i . Phần ảo của số phức w = 3z1 - 2z2 là A. 12. B. 11. C. 1. D.12i Đáp án : A
Ví dụ 10: Cho số phức z = 3 + 4i. Khẳng định nào sau đây là khẳng định sai?
A. Điểm biểu diễn của z là M(3;4).
B. Môđun của số phức z là 5.
C. Số phức đối của z là -3 - 4i.
D. Số phức liên hợp của z là 3 - 4i. Lời giải: Đáp án : A
Ví dụ 11: Cho số phức z thỏa mãn điều kiện:(1 + i)Z - 1 - 3i = 0. Phần ảo của số phứcw = 1 - iz + z là A. 1. B. -3. C. -2. D. -1.
Ví dụ 12:Cho số phức z = 1 + (1 + i) + (1 + i)2 + ...+ (1 + i)26 . Phần thực của số phức z là
A. 213 B. -(1 + 213) C. -213 D. (1 + 213)
Ví dụ 13:Cho hai số phức z1;z2 khác 0 thỏa mãn z12 - z1z2 + z22 Gọi A,B lần lượt là các
điểm biểu diễn cho số phức z1;z2. Khi đó tam giác OAB là:
A. Tam giác đều. B. Tam giác vuông tại O .
C. Tam giác tù. D. Tam giác có một góc bằng 45o Lời giải: Đáp án : A Giải thích :
Ta có z13 + z23 = (z1 + z2)(z12 - z1z2 + z22) suy ra:
z13 = -z23 => |z13| = |z23| => |z1| = |z2| => OA = OB lại có
(z1 - z2)2 = (z12 - z1z2 + z22 - z1z2 = -z1z2) nên |z1 - z2|2 = |z1|.|z2| => AB2 OA.OB = OA2
Suy ra AB = OA = OB => ΔOAB đều




