Câu hỏi chung ôn tập kinh tế lượng | Kinh Tế Lượng | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

A- Các KN chung về MHHQ 1. KN KTL
- Đo lường kinh tế hay phân tích về lượng các vấn đề kinh tế.
2. KN và nhiệm vụ của phân tích hồi quy - KN:
+ Nghiên cứu sự phụ thuộc của một biến, được gọi là biến phụ thuộc (hay biến được
giải thích) vào một hay nhiều biến khác, được gọi là biến độc lập (hay biến giải thích).
+ Nhằm ước lượng hay dự báo giá trị trung bình của biến phụ thuộc trên cơ sở các
giá trị đã biết trước của các biến độc lập. - Nhiệm vụ:
+ Ước lượng giá trị trung bình của biến phụ thuộc với giá trị đã cho của biến độc lập;
xác định độ chính xác và khoảng tin cậy của các ước lượng.
+ Kiểm định giả thuyết về bản chất của sự phụ thuộc.
+ Dự đoán giá trị trung bình hoặc giá trị cá biệt của biến phụ thuộc khi biết giá trị của các biến độc lập.
+ Kết hợp các vấn đề trên.
3. Các loại số liệu dùng trong phân tích hồi quy
- Các số liệu theo thời gian là các số liệu được thu thập trong một thời kỳ nhất định
(hàng tuần, hàng tháng, quý, năm...).
- Các số liệu chéo là các số liệu được thu thập tại một thời điểm ở nhiều địa phương, đơn vị khác nhau.
- Các số liệu hỗn hợp - theo thời gian và không gian. 4.
- Biến phụ thuộc (Biến ngẫu nhiên)  Đối xứng.
- Biến độc lập (Biến phi ngẫu nhiên)  Bất đối xứng.
5. Phân biệt HHQ đơn và bội
- Hàm hồi quy đơn là một mô hình hồi quy đơn giản, trong đó chỉ có một biến độc lập
được sử dụng để dự đoán giá trị của biến phụ thuộc.
- Hàm hồi quy bội là một mô hình hồi quy phức tạp hơn, trong đó có nhiều biến độc
lập được sử dụng để dự đoán giá trị của biến phụ thuộc. 6. KN HHQ tuyến tính
Hồi quy tuyến tính là một kỹ thuật phân tích dữ liệu dự đoán giá trị của dữ liệu không
xác định bằng cách sử dụng một giá trị dữ liệu liên quan và đã biết khác.
7. KN HHQ tổng thể, HHQ mẫu
- Hàm hồi quy tổng thể PRF của mô hình hồi quy hai biến cho ta biết giá trị trung bình
của biến phụ thuộc Y sẽ thay đổi như thế nào theo một biến độc lập X (nên còn được
gọi là mô hình hồi quy đơn): E(Y/ Xi) = β1 + β2Xi
- Hàm hồi quy tổng thể ngẫu nhiên có dạng: Yi = β1 + β2Xi + Ui
- HHQ mẫu được xây dựng trên cơ sở một mẫu ngẫu nhiên được gọi là hàm hồi quy
mẫu (SRF) hay hồi quy mẫu (SR). - HHQ mẫu ngẫu nhiên:
8. Tên gọi của các hàm số HQ - β1: HS chặn (Tự do). - β2  βk : HS góc
 Hệ số HQ, tham số HQ. 9. Sai số ngẫu nhiên
- Ui đại diện cho tất cả các yếu tố có ảnh hưởng đến biến phụ thuộc nhưng không được đưa vào MH.
+ Do không xác định được.
+ Do không thu thập được số liệu.
+ Do có ảnh hưởng không đáng kể.
+ Cần xây dựng MH đơn giản với một số nhỏ nhất các biến độc lập để đảm bảo tính kinh tế -kỹ thuật. 10.
Ngoài các biến độc lập đã có trong MH còn có các yếu tố khác ảnh hưởng đến biến
phụ thuộc; nhưng trung bình ảnh hưởng của chúng đến biến phụ thuộc bằng 0.
 Do vậy không cần phải đưa các yếu tố này vào MH.
11. Điểm chung và riêng về bản chất của HS chặn và SSNN ui
- Hàm số chặn và sai số ngẫu nhiên đều liên quan đến độ chính xác của dữ liệu hoặc kết quả tính toán.
- Hàm số chặn là hàm số có giới hạn trên và dưới, nghĩa là giá trị của hàm số không
vượt quá một giới hạn cố định. Điều này đảm bảo rằng kết quả tính toán sẽ không vượt
quá một giới hạn nhất định, giúp đảm bảo tính chính xác của kết quả.
- Sai số ngẫu nhiên là sai số do các yếu tố ngẫu nhiên như sai số đo lường, sai số tính
toán, sai số trong quá trình truyền dữ liệu, v.v. gây ra. Sai số ngẫu nhiên không thể
tránh khỏi hoàn toàn, nhưng có thể được giảm thiểu bằng cách sử dụng các phương
pháp thống kê và tính toán chính xác.
 Hàm số chặn là một tính chất của hàm số, trong khi sai số ngẫu nhiên là một yếu tố
bên ngoài ảnh hưởng đến tính chính xác của kết quả tính toán. 12. - HHQ 2 biến: - HHQ 3 biến: - HHQ tổng thể:
- HHQ tổng thể ngẫu nhiên: - HHQ mẫu: - HHQ mẫu ngẫu nhiên:
13. MQH HHQ mẫu và tổng thể
Hàm hồi quy mẫu được sử dụng để ước tính hàm hồi quy tổng thể. Nếu mẫu được lựa
chọn đại diện cho tổng thể, thì hàm hồi quy mẫu sẽ cho kết quả gần giống với hàm hồi
quy tổng thể. Tuy nhiên, nếu mẫu không đại diện cho tổng thể, thì kết quả ước tính của
hàm hồi quy mẫu có thể khác với hàm hồi quy tổng thể. Do đó, việc lựa chọn mẫu đại
diện là rất quan trọng trong phân tích hồi quy. 14.
- Đặc điểm ma trận phương sai: Ma trận hiệp phương sai của tập hợp biến ngẫu nhiên
là một ma trận vuông, được biểu diễn dưới dạng hằng số là m × m. Trong đó các phần
tử nằm trên cùng một đường chéo có hướng từ trái sang phải và có phương từ trên
xuống dưới sẽ lần lượt trở thành các biến số phương sai tương ứng của các biến này.
- Ước lượng không chênh lệch:
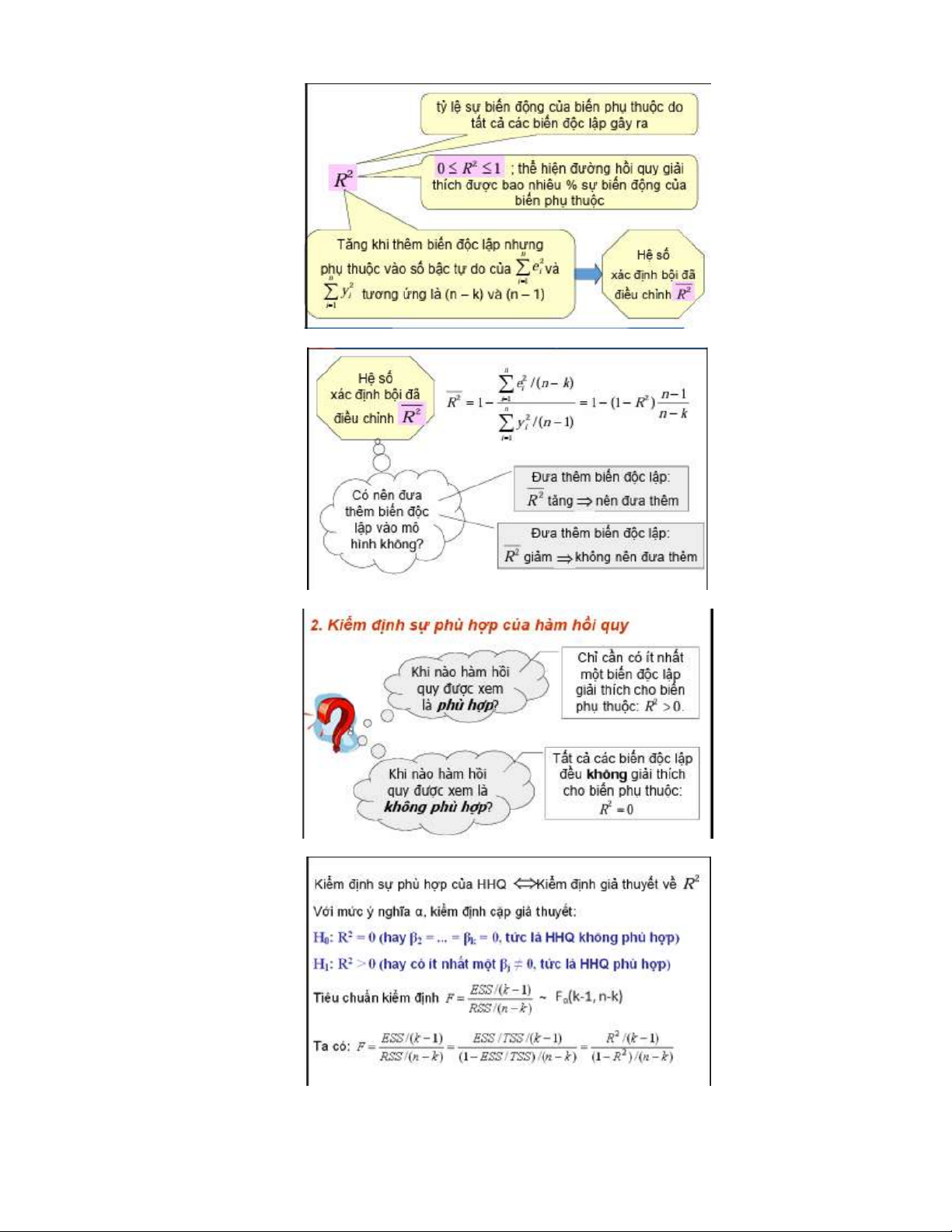
⁕ Phương pháp bình phương ⁕ Khoảng tin cậy ⁕ Kiểm định ⁕ Sự phù hợp của HHQ - Các tên gọi của R^2: + HS xác định. + HS xác định bội.
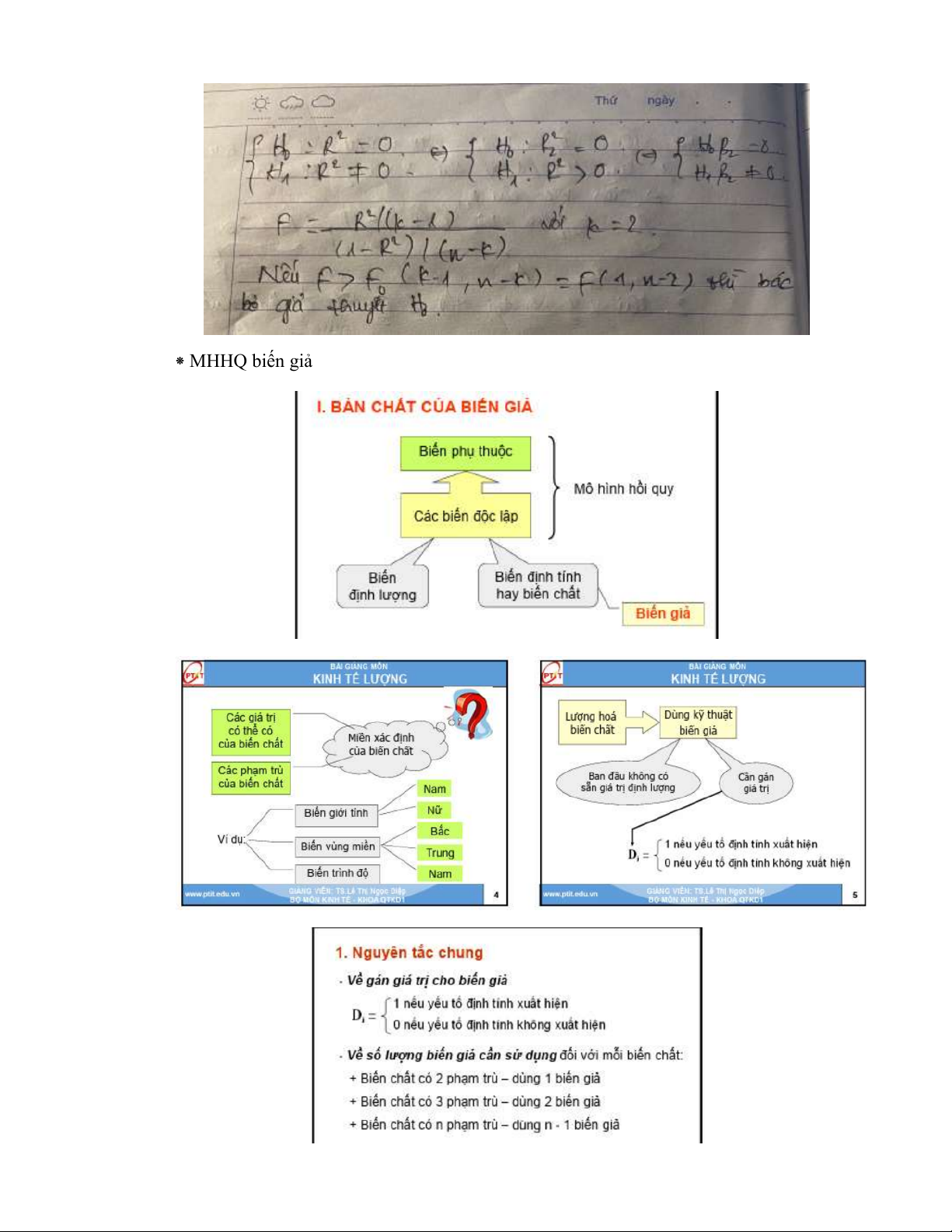
+ HS đo độ phù hợp của HHQ. ⁕ MHHQ biến giả B ⁕ Đa cộng tuyến
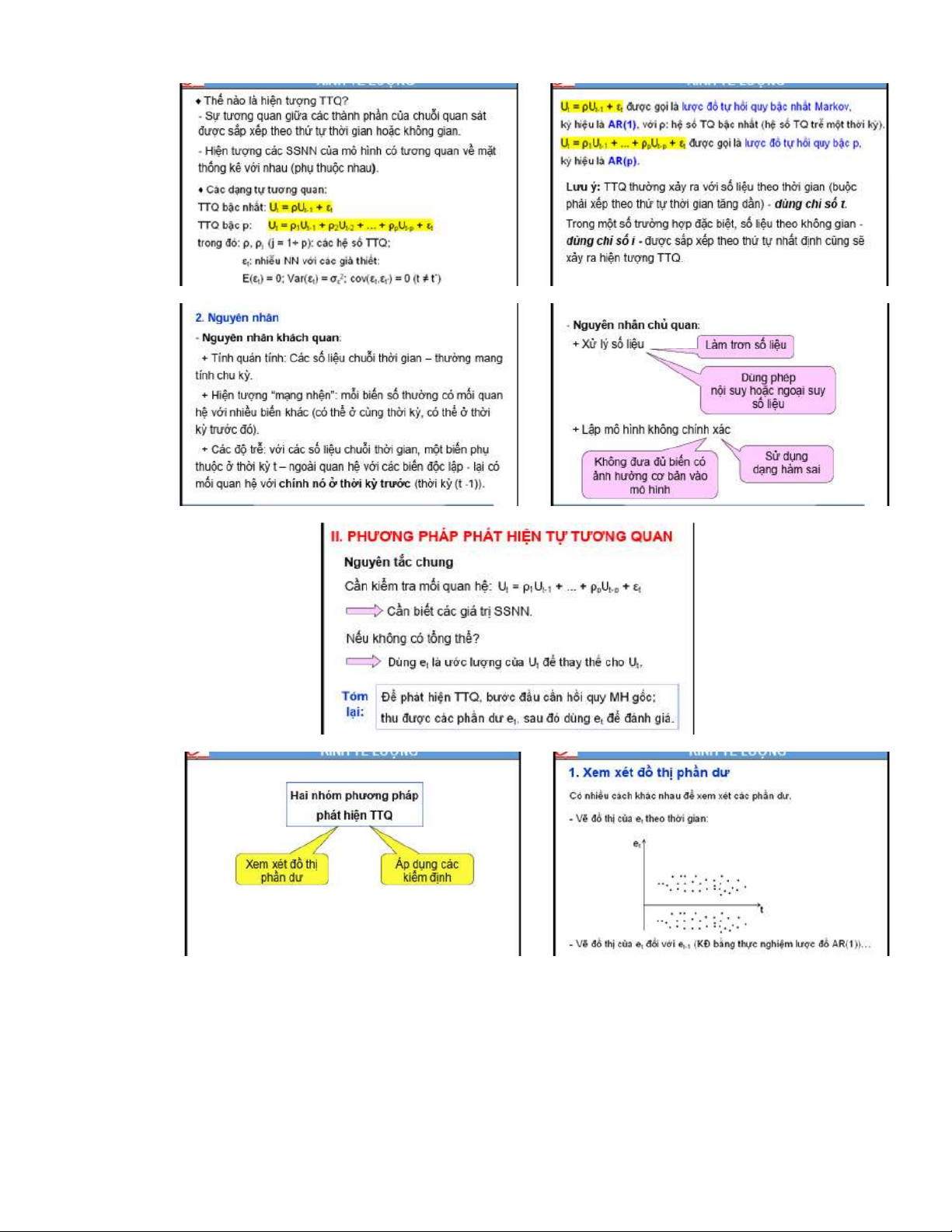
⁕ Phương pháp sai số thay đổi ⁕ Tự tương quan ⁕ Định dạng mô hình