Câu hỏi tham khảo phần 2 môn xác suất thống kê| Đại học Kinh tế Quốc Dân

ĐỀ THAM KHẢO 2 HỌC PHẦN
LÝ THUYẾT XÁC SUẤT VÀ THỐNG KÊ TOÁN
Câu 1: Đâu là biến định tính?
A. Số tiền bạn chi tiêu hàng ngày
B. Thời gian bạn cần để viết một báo cáo
C. Vùng địa lý của tỉnh nơi bạn sinh sống D. Tuổi của bạn
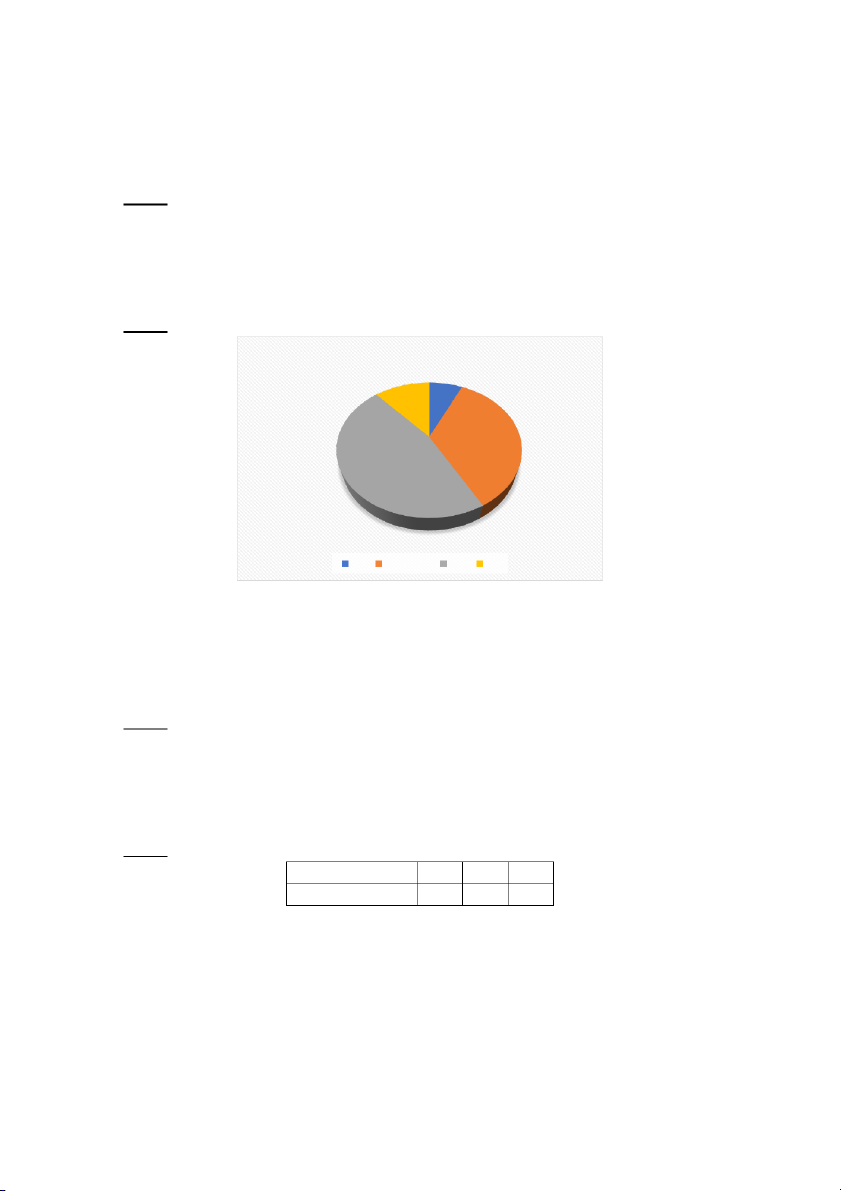
Câu 2: Một trường THPT có 1000 học sinh. Kết quả xếp loại cuối năm có đồ thị dưới đây:
Kết quả xếp loại học sinh Yếu Giỏi 12% 7% Trung bình 35% Khá 46% Yếu Trung bình Khá Giỏi
Số học sinh xếp loại giỏi của trường là: A. 120 B. 12 C. 460 D. 350
Câu 3: Tính mốt của mẫu cụ thể sau: 6; 12; 9; 11; 12 A. 12 B. 2 C. 9 D. 10
Câu 4: Tính trung bình của mẫu cụ thể sau: Cân nặng 4 7 8 Số sản phẩm 5 6 9 A. 7 B. 6,3 C. 8 D. 6,7
Câu 5: Tính độ lệch chuẩn của mẫu cụ thể sau: Giá trị 10 11 15 Tần số 6 20 14 A. 2,65 B. 2,05 C. 2,07 D. 4,29
Câu 6: Cho phổ điểm hai môn Toán và Tiếng Anh của kì thi THPT năm 2019.
Nhận định nào sau đây đúng?
A. Hệ số bất đối xứng của điểm hai môn là như nhau
B. Hệ số bất đối xứng của điểm môn Toán lớn hơn điểm môn Tiếng Anh
C. Hệ số bất đối xứng của điểm môn Toán nhỏ hơn điểm môn Tiếng Anh
D. Không thể so sánh được hệ số bất đối xứng của điểm hai môn.
Câu 7: Có hai sinh viên cùng tham gia một kì th .i
Đặt biến cố: 𝐴 = (người 1 thi qua) và 𝐵 = (người 2 thi qua)
Biến cố 𝐴 + 𝐵 có nghĩa là:
A. Ít nhất một người thi qua
B. Ít nhất một người thi không qua
C. Hai người thi qua
D. Chỉ có một người thi qua
Câu 8: Điều nào sau đây đúng: A.
𝑃(𝐴 + 𝐵) ≥ 𝑃(𝐴) + 𝑃(𝐵)
B. 𝑃(𝐴 + 𝐵) > 𝑃(𝐴) + 𝑃(𝐵) C.
𝑃(𝐴 + 𝐵) ≤ 𝑃(𝐴) + 𝑃(𝐵)
D. 𝑃(𝐴 + 𝐵) < 𝑃(𝐴) + 𝑃(𝐵)
Câu 9: Lô hàng gồm 14 sản phẩm sản xuất trong nước và 6 sản phẩm nhập ngoại. Lấy ngẫu
nhiên cùng lúc 3 sản phẩm thì xác suất được 2 sản phẩm trong nước và 1 sản phẩm nhập ngoại bằng bao nhiêu? A. 0,18 B. 0,08 C. 0,48 D. 0,16 C214*6/C320
Câu 10: Cho 𝐴 và 𝐵 là hai biến cố có: 𝑃(𝐴) = 0,9; 𝑃(𝐵) = 0,8 ; 𝑃(𝐴 + 𝐵) = 0,95. Khi đó : P(A  B ) = A. 0,25 B. 0,05 C. 0,3 D. 0,02
Câu 11: Xác suất để một người từng nghe quảng cáo về sản phẩm A là 0,75. Khả năng người
nào đó mua sản phẩm A khi từng nghe và chưa từng nghe quảng cáo lần lượt là 0,28 và 0,08.
Chọn ngẫu nhiên một người mua sản phẩm A, xác suất người đó từng nghe quảng cáo về sản phẩm này là: A. 0,087 B. 0,913 C. 0,23 D. 0,462
Câu 12: Lợi suất dự kiến (𝑋: đơn vị %) khi đầu tư vào một tài sản là biến ngẫu nhiên có bảng
phân phối xác suất như sau: 𝑋 -7 -3 0 3 10 𝑃 0,05 0,2 0,5 ? 0,05
Xác suất để lợi suất dự kiến lớn hơn 1 % là bao nhiêu? A. 0,25 B. 0,2 C. 0,05 D. 0,75
Câu 13: Tính độ lệch chuẩn của biến ngẫu nhiên sau: 𝑋 -2 2 5 𝑃 0,3 0,6 0,1 A. 4,89 B. 2,21 C. 2,47 D. 6,1
Câu 14: Một sinh viên đi từ nhà đến trường phải qua 2 ngã tư có lắp đèn tín hiệu giao thông.
Xác suất để sinh viên gặp đèn đỏ ở các ngã tư tương ứng là 0,1 và 0,2. Hỏi thời gian chờ đèn đỏ
trung bình là bao nhiêu? Biết nếu gặp đèn đỏ thì phải chờ trung bình 50 giây. A. 15 giây B. 17 giây C. 25 giây D. 7,5 giây Câu 15: Cho
𝑋~ 𝐵(25; 0,2). Kì vọng toán và phương sai của X là: A. 0,2 và 0,16 B. 5 và 4 C. 5 và 2 D. 25 và 0,2
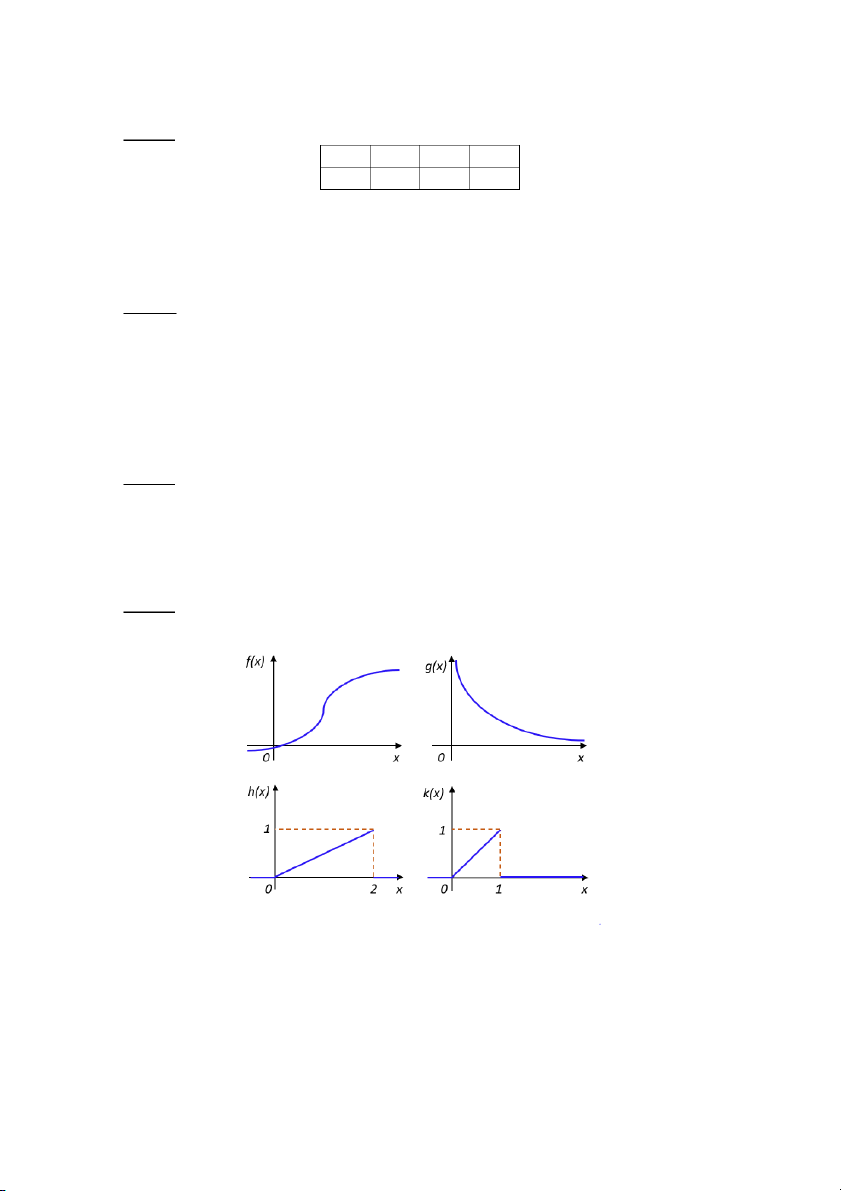
Câu 16: Cho 4 hàm số 𝑓(𝑥), 𝑔(𝑥), ℎ(𝑥), 𝑘(𝑥) có đồ thị như sau. Hàm số nào là hàm mật độ
xác suất của biến ngẫu nhiên A. 𝑓(𝑥) B. 𝑔(𝑥) C. ℎ(𝑥) D. 𝑘(𝑥)
Câu 17: Cho 𝑋 là biến ngẫu nhiên liên tục có hàm mật độ xác suất là : 𝑥2
𝑓(𝑥) = { 9 với 𝑥 ∈ (0; 3) 0 với 𝑥 ∉ (0; 3) 𝑃(𝑋 > 2) ≈ A. 0,704 B. 0,556 C. 0,296 D. 0,333
Câu 18: Thời gian hoàn thành một bài thi học kỳ của sinh viên là biến ngẫu nhiên có phân phối
Chuẩn với trung bình là 60 phút và độ lệch chuẩn là 10 phút. Xác suất để sinh viên hoàn thành
bài thi với thời gian ít hơn 43,55 phút là bao nhiêu? A. 0,025 B. 0,975 C. 0,050 D. 0,950
Câu 19: Giả sử X ∼ N(27; 16), Y ∼ N(20; 9); X, Y độc lập. Xác suất để X lớn hơn Y bằng: A. 0,9192 B. 0,6103 C. 0,996 D. 0,8413
Câu 20: Nếu 𝑋 và 𝑌 là các biến ngẫu nhiên độc lập, lựa chọn nào sau đây sa ? i A. 𝐶𝑜𝑣(𝑋, 𝑌) = 1
B. 𝐶𝑜𝑣(𝑋, 𝑌) = 0 C.
𝐸(𝑋 + 𝑌) = 𝐸(𝑋) + 𝐸(𝑌)
D. 𝑉(𝑋 − 𝑌) = 𝑉(𝑋) + 𝑉(𝑌)
Câu 21: 𝑌 là thu nhập, 𝐶 là chi tiêu hàng tháng của hộ gia đình 𝐶 12 16 19 𝑌 22 0,1 0,2 0,3 30 0,1 0,1 0,2
Hộ gia đình chi tiêu hàng tháng là 12 có mức thu nhập trung bình là: A. 26 B. 25,2 C. 5,2 D. 16,7
Câu 22: Biết kì vọng của X và Y lần lượt là 5 và 4; phương sai của X và Y lần lượt là 16 và 25.
Hiệp phương sai của X và Y là 10. Hệ số tương quan của X và Y bằng: A. – 0,5 B. 0,5 C. – 0,025 D. 0,025
Câu 23: Lập mẫu ngẫu nhiên kích thước 𝑛 từ biến ngẫu nhiên gốc có phân phối 𝐴(𝑝), khi đó
phương sai của tần suất mẫu bằng:
A. 𝑝(1−𝑝) 𝑛 B. 𝑝 C. 𝑝(1 − 𝑝)
D. 𝑛𝑝(1 − 𝑝)
Câu 24: Trong số khách vào cửa hàng có 64% là nữ, còn lại là nam. Nếu chọn mẫu ngẫu nhiên
100 khách vào cửa hàng thì xác suất tỷ lệ khách nam của mẫu đó ít hơn 48% là: A. 0,9938 B. 0,0062 C. 0,0004 D. 0,9996
Câu 25: Trong các phát biểu sau, phát biểu nào đúng?
A. Trung bình mẫu là ước lượng chệch của trung bình tổng thể
B. Tần suất mẫu là ước lượng không chệch của tần suất tổng thể
C. Phương sai của trung bình mẫu lớn hơn phương sai của tổng thể
D. Phương sai mẫu là ước lượng chệch của phương sai tổng thể
Câu 26: Trong bài toán ước lượng khoảng tin cậy cho tham số 𝜃 của tổng thể, có
𝑃(𝐺1 < 𝜃 < 𝐺2) = 1 − 𝛼. Khi đó, đâu là cách hiểu đúng về khoảng (𝐺1,𝐺2):
A. Là độ dài khoảng tin cậy
B. Là sai số của ước lượng
C. Là khoảng tin cậy cụ thể
D. Là khoảng tin cậy ngẫu nhiên
Câu 27: Thời gian hoàn thành một sản phẩm là 𝑋 ~ 𝑁(µ, 𝜎2
) với phương sai chưa biết. Với độ
tin cậy (1 − 𝛼), muốn ước lượng thời gian hoàn thành sản phẩm trung bình thì dùng công thức nào? A. (𝑛−1)𝑆2 𝑛−1 𝑆2
𝜒2(𝑛−1) < 𝜎2 < ( ) 2(𝑛−1) 𝛼/2 𝜒1−𝛼/2 B. 𝑋 − 𝑧 𝜎 𝜎 𝛼/2 < 𝜇 < 𝑋 + 𝑧 √𝑛 𝛼/2 √𝑛
C. 𝑋 − 𝑡(𝑛−1) 𝑆 (𝑛−1) 𝑆 𝛼/2 < 𝜇 < 𝑋 + 𝑡 √𝑛 𝛼/2 √𝑛
D. 𝑝 − 𝑧𝛼/2√𝑝(1−𝑝) < 𝑝 < 𝑝 + 𝑧 𝑛 𝛼/2√𝑝(1−𝑝) 𝑛
Câu 28: Thời gian hoàn thành một sản phẩm là biến ngẫu nhiên phân phối Chuẩn, chưa biết các
tham số. Với độ tin cậy 95% và mẫu cụ thể có kích thước 15, muốn ước lượng phương sai tối đa
của thời gian hoàn thành sản phẩm thì dùng giá trị tới hạn nào? A. 23,68 B. 7,261 C. 5,629 D. 6,571
Câu 29: Kiểm tra 200 sản phẩm của nhà máy thì có 20 phế phẩm. Với độ tin cậy 90%, khi ước
lượng khoảng tin cậy đối xứng cho tỷ lệ phế phẩm của nhà máy thì độ dài khoảng tin cậy là: A. 0,035 B. 0,070 C. 0,083 D. 0,042
Câu 30: Cân nặng một loại sản phẩm có phân phối Chuẩn. Cân 20 sản phẩm tìm được trung bình
mẫu là 196g và phương sai mẫu là 100g2. Với độ tin cậy 95%, đâu là khoảng tin cậy đối xứng
của cân nặng trung bình của sản phẩm? A. (191,34; 200,66)
B. (192,14; 199,86) C. (191,62; 200,38) D. (148,35; 243,65)
Câu 31: Khi kiểm định cặp giả thuyết thống kê 𝐻0, 𝐻1 với mức ý nghĩa 𝛼, tiêu chuẩn kiểm định
là 𝐺, miền bác bỏ giả thuyết 𝐻0 là 𝑊𝛼. Đâu là xác suất mắc sai lầm loại II?
A. 𝑃(𝐺 ∈ 𝑊𝛼 | 𝐻0)
B. 𝑃(𝐺 ∈ 𝑊𝛼 | 𝐻1)
C. 𝑃(𝐺 ∉ 𝑊𝛼 | 𝐻1)
D. 𝑃(𝐺 ∉ 𝑊𝛼 | 𝐻0)
Câu 32: Thời gian hoàn thành một sản phẩm là biến ngẫu nhiên phân phối Chuẩn. Trước đây
thời gian hoàn thành sản phẩm trung bình là 15 phút. Có ý kiến cho rằng dù công nghệ được cải
tiến nhưng thời gian hoàn thành sản phẩm trung bình vẫn không giảm xuống. Khi đó dùng cặp
giả thuyết nào kiểm định ý kiến này? A. H 0: 𝜇 = 15, H1: 𝜇 > 15
B. H0: 𝜇 = 15, H1: 𝜇 < 15 C. H
0: 𝜇 < 15, H1: 𝜇 ≥ 15
D. H0: 𝜇 = 15, H1: 𝜇 ≠ 15
Câu 33: Quan sát ngẫu nhiên 160 khách vào cửa hàng thì có 100 người mua hàng. Khi kiểm định
ý kiến tỷ lệ khách mua hàng bằng 70% thì giá trị quan sát của tiêu chuẩn kiểm định là: A. -2,07 B. 2,07 C. 1,96 D. -1,96
Câu 34: Giả sử biến ngẫu nhiên gốc phân phối Chuẩn. Với mức ý nghĩa 5% và mẫu có 𝑛 = 50,
khi kiểm định giả thuyết “phương sai của tổng thể lớn hơn 9” thì miền bác bỏ giả thuyết H0 là : A. 2 2 {𝜒 : 𝜒 < 66,34}
B. {𝜒2: 𝜒2 < 33,93} C. 2 2 {𝜒 : 𝜒 > 66,34}
D. {𝜒2: 𝜒2 > 33,93}
Câu 35: Khi kiểm định cặp giả thuyết {𝐻0: 𝑝 = 0,1
𝐻1: 𝑝 < 0,1 với mức ý nghĩa 5% thì phương án nào sau đây đúng? A. Bác bỏ H0 khi 𝑍𝑞𝑠 < 1,645
B. Bác bỏ H0 khi 𝑍𝑞𝑠 > 1,645 C. Bác bỏ H0 khi 𝑍𝑞𝑠 > −1,645
D. Bác bỏ H0 khi 𝑍𝑞𝑠 < −1,645
Câu 36: Để kiểm định ý kiến “tỷ lệ khách mua hàng không vượt quá 70%”, người ta quan sát
ngẫu nhiên 160 khách vào cửa hàng thì tìm được 𝑍𝑞𝑠 = 1,58. Với mức ý nghĩa 5%, đâu là kết luận đúng cho kiểm ị đ nh đang xét?
A. Bác bỏ 𝐻0, ý kiến đúng
B. Bác bỏ 𝐻0, ý kiến sai
C. Chưa bác bỏ 𝐻0, ý kiến đúng
D. Chưa bác bỏ 𝐻0, ý kiến sai
Câu 37: Cân nặng sản phẩm là biến ngẫu nhiên phân phối Chuẩn với các tham số chưa biết. Cân
20 sản phẩm tìm được trung bình mẫu là 196g và phương sai mẫu là 100g2. Khi kiểm định ý kiến
“cân nặng trung bình của sản phẩm thấp hơn 200g”, với mức ý nghĩa 5%, thì lựa chọn nào đúng?
A. 𝑇𝑞𝑠 = −1,789, ý kiến đúng
B. 𝑇𝑞𝑠 = −1,789, ý kiến sai
C. 𝑇𝑞𝑠 = −5,657, ý kiến đúng
D. 𝑇𝑞𝑠 = −5,657, ý kiến sai
Câu 38: Cho bảng kết quả Excel sau, với X là lương của công nhân nữ, Y là lương của công
nhân nam. Giả sử lương của công nhân nữ và nam đều phân phối Chuẩn. F-Test Two-Sample for Variances X Y Mean 6.67 7.2 Variance 2.51 1.19 Observations … … df … … F 2.106 P(F<=f) one-tail 0.015 F Critical one-tail …
Với mức ý nghĩa 5%, dựa vào bảng đã cho, hãy chọn phát biểu đúng:
A. Lương trung bình của công nhân nữ và nam là bằng nhau
B. Lương trung bình của công nhân nữ thấp hơn của công nhân nam
C. Lương của công nhân nữ đồng đều hơn của công nhân nam
D. Lương của công nhân nữ biến động hơn của công nhân nam
Câu 39: Để kiểm định cân nặng sản phẩm có phân phối Chuẩn hay không, người ta đã cân 30
sản phẩm và tìm được hệ số bất đối xứng là (-0,7) và hệ số nhọn là 1,8. Với mức ý nghĩa 10%,
hãy lựa chọn kết luận đúng?
A. 𝐽𝐵𝑞𝑠 = 6,5; cân nặng sản phẩm phân phối Chuẩn
B. 𝐽𝐵𝑞𝑠 = 6,5; cân nặng sản phẩm không phân phối Chuẩn
C. 𝐽𝐵𝑞𝑠 = 4,25; cân nặng sản phẩm phân phối Chuẩn
D. 𝐽𝐵𝑞𝑠 = 4,25; cân nặng sản phẩm không phân phối Chuẩn.
Câu 40: Một nhà quản lí quan tâm đến lượng bán máy bơm nước hàng ngày của công ty tại 4
cửa hàng A, B, C, D. Với mỗi mỗi cửa hàng, nhà quản lí ghi lại lượng bán trong 4 ngày thì có số liệu sau: A B C D 7 5 4 6 5 4 7 5 6 3 7 3 6 4 5 2 Trung bình 6 4 5,75 4 Trung bình chung 4,9375
Sử dụng phân tích phương sai một nhân tố của phần mềm Excel với 𝛼 = 0,05 thì có bảng sau: ANOVA Source of Variation SS df MS F P-value F crit Between Groups 14.1875 3 4.7292 2.7349 0.0899 3.4903 Within Groups 20.75 12 1.7292 Total 34.9375 15
Hãy chọn phát biểu đúng trong các phát biểu sau.
A. Với mức ý nghĩa 5% thì lượng bán trung bình của 4 cửa hàng như nhau.
B. Với mức ý nghĩa 5% thì có ít nhất hai cửa hàng có lượng bán trung bình khác nhau.
C. Với mức ý nghĩa 5% thì lượng bán trung bình của 4 cửa hàng đều bằng 4,9375.
D. Với mức ý nghĩa 5% thì phương sai về lượng bán của 4 cửa hàng như nhau.