Câu hỏi trắc nghiệm ôn tập Cấu trúc giữ liệu và giải thuật
Bao gồm 74 câu hỏi trắc nghiệm ôn tập bộ môn Cấu trúc giữ liệu và giải thuật và đáp án của Đại học Bách Khoa Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống. Mời bạn đọc đón xem!
Môn: Cấu trúc dữ liệu và giải thuật (ET2100)
Trường: Đại học Bách Khoa Hà Nội
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoARcPSD|36442750 Open ERP Thông tin chung Nội dung Bài tập trắc nghiệm DS sinh viên Bài tập Buổi học Câu hỏi trắc nghiệm
Câu 1. Kết luận 1000n2 - 6n + 7 = O(n2) là đúng hay sai? A. ĐÚNG B. SAI Kiểm tra (12) BÌNH LUẬN
Câu 2. Cho hai hàm thể hiện độ phức tạp tính toán của hai thuật toán:
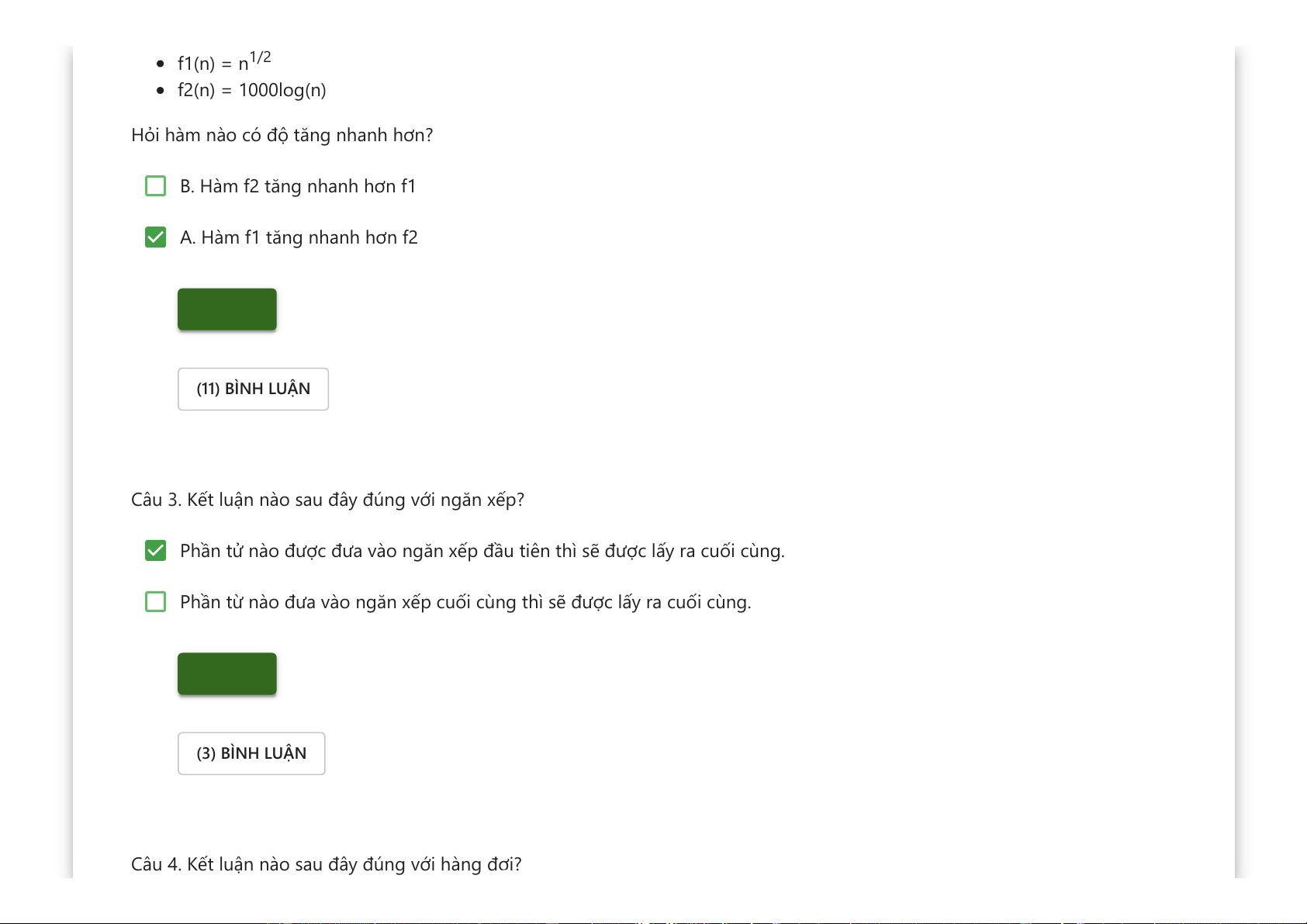
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 f1(n) = n1/2 f2(n) = 1000log(n)
Hỏi hàm nào có độ tăng nhanh hơn? B. Hàm f2 tăng nhanh hơn f1 A. Hàm f1 tăng nhanh hơn f2 Kiểm tra (11) BÌNH LUẬN
Câu 3. Kết luận nào sau đây đúng với ngăn xếp?
Phần tử nào được đưa vào ngăn xếp đầu tiên thì sẽ được lấy ra cuối cùng.
Phần từ nào đưa vào ngăn xếp cuối cùng thì sẽ được lấy ra cuối cùng. Kiểm tra (3) BÌNH LUẬN
Câu 4. Kết luận nào sau đây đúng với hàng đợi?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Phần tử nào được đưa vào hàng đợi cuối cùng thì sẽ được lấy ra cuối cùng.
Phần tử nào được đưa vào hàng đợi đầu tiên thì sẽ được lấy ra cuối cùng. Kiểm tra (2) BÌNH LUẬN
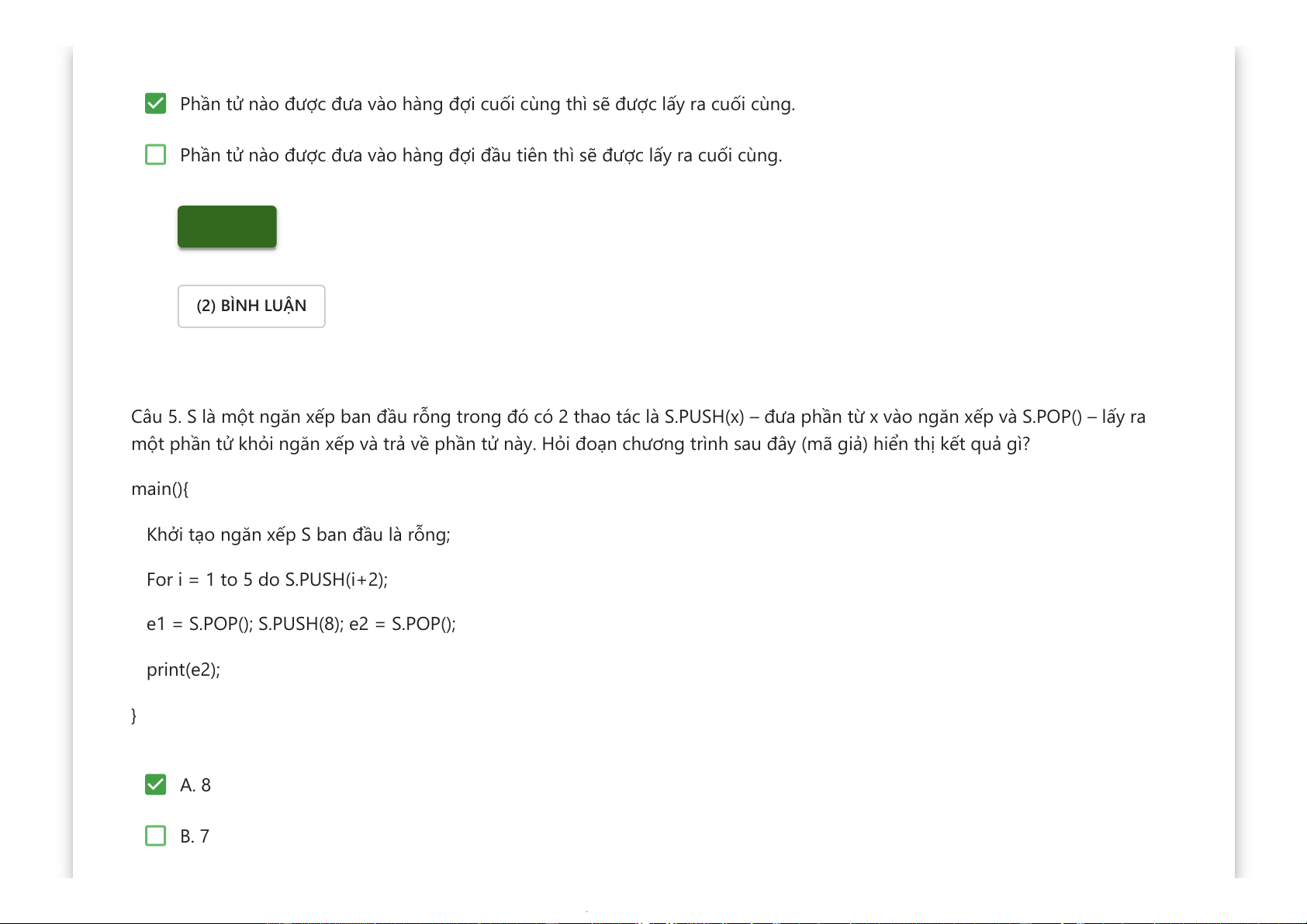
Câu 5. S là một ngăn xếp ban đầu rỗng trong đó có 2 thao tác là S.PUSH(x) – đưa phần từ x vào ngăn xếp và S.POP() – lấy ra
một phần tử khỏi ngăn xếp và trả về phần tử này. Hỏi đoạn chương trình sau đây (mã giả) hiển thị kết quả gì? main(){
Khởi tạo ngăn xếp S ban đầu là rỗng;
For i = 1 to 5 do S.PUSH(i+2);
e1 = S.POP(); S.PUSH(8); e2 = S.POP(); print(e2); } A. 8 B. 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 C. 6 D. 5 Kiểm tra (6) BÌNH LUẬN
Câu 6. Phát biểu "Trong việc lưu trữ các đối tượng, chỉ khi nào khóa của các đối tượng là số nguyên dương thì mới áp dụng
được cơ chế bảng băm" là đúng hay sai? Đúng Sai Kiểm tra (4) BÌNH LUẬN
Câu 7. Thuật toán Dijkstra để giải bài toán nào?
Tìm đường đi ngắn nhất từ 1 đỉnh đến tất cả các đỉnh còn lại trên đồ thị trọng số trên cạnh không âm
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Tìm đường đi ngắn nhất từ 1 đỉnh đến tất cả các đỉnh còn lại trên đồ thị trọng số trên cạnh bất kỳ
Tìm cây khung nhỏ nhất của đồ thị vô hướng trọng số trên cạnh
Tìm luồng cực đại trên mạng Kiểm tra (2) BÌNH LUẬN
Câu 8. Hãy cho biết số nghiệm nguyên dương của phương trình 2x1 + 4x2 + 3x3 + 5x4 = 60
thỏa mãn điều kiện x1 + x2 = 6 A. 13 B. 11 C. 16 D. 23 Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (7) BÌNH LUẬN
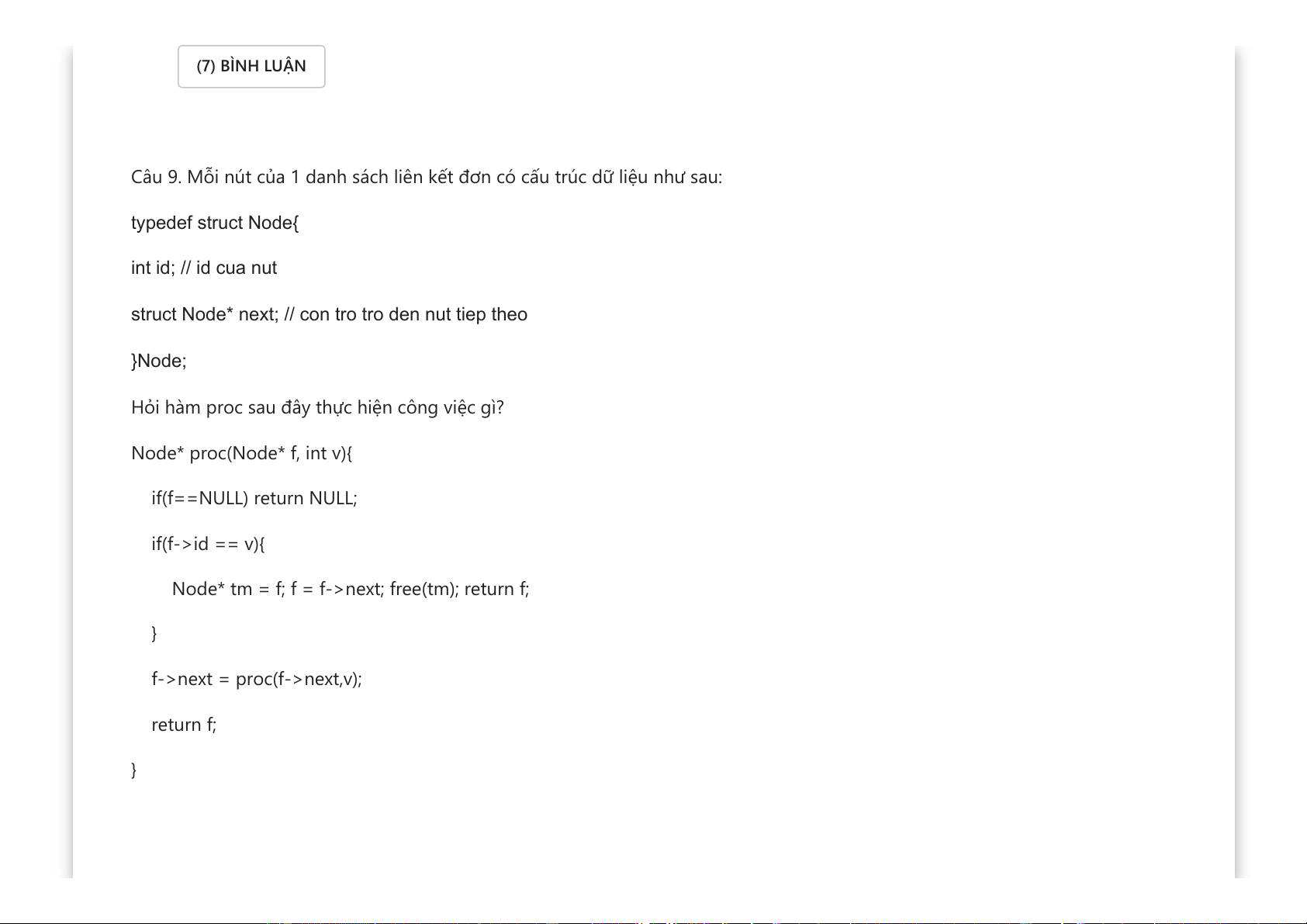
Câu 9. Mỗi nút của 1 danh sách liên kết đơn có cấu trúc dữ liệu như sau: typedef struct Node{ int id; // id cua nut
struct Node* next; // con tro tro den nut tiep theo }Node;
Hỏi hàm proc sau đây thực hiện công việc gì? Node* proc(Node* f, int v){ if(f==NULL) return NULL; if(f->id == v){
Node* tm = f; f = f->next; free(tm); return f; }
f->next = proc(f->next,v); return f; }
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
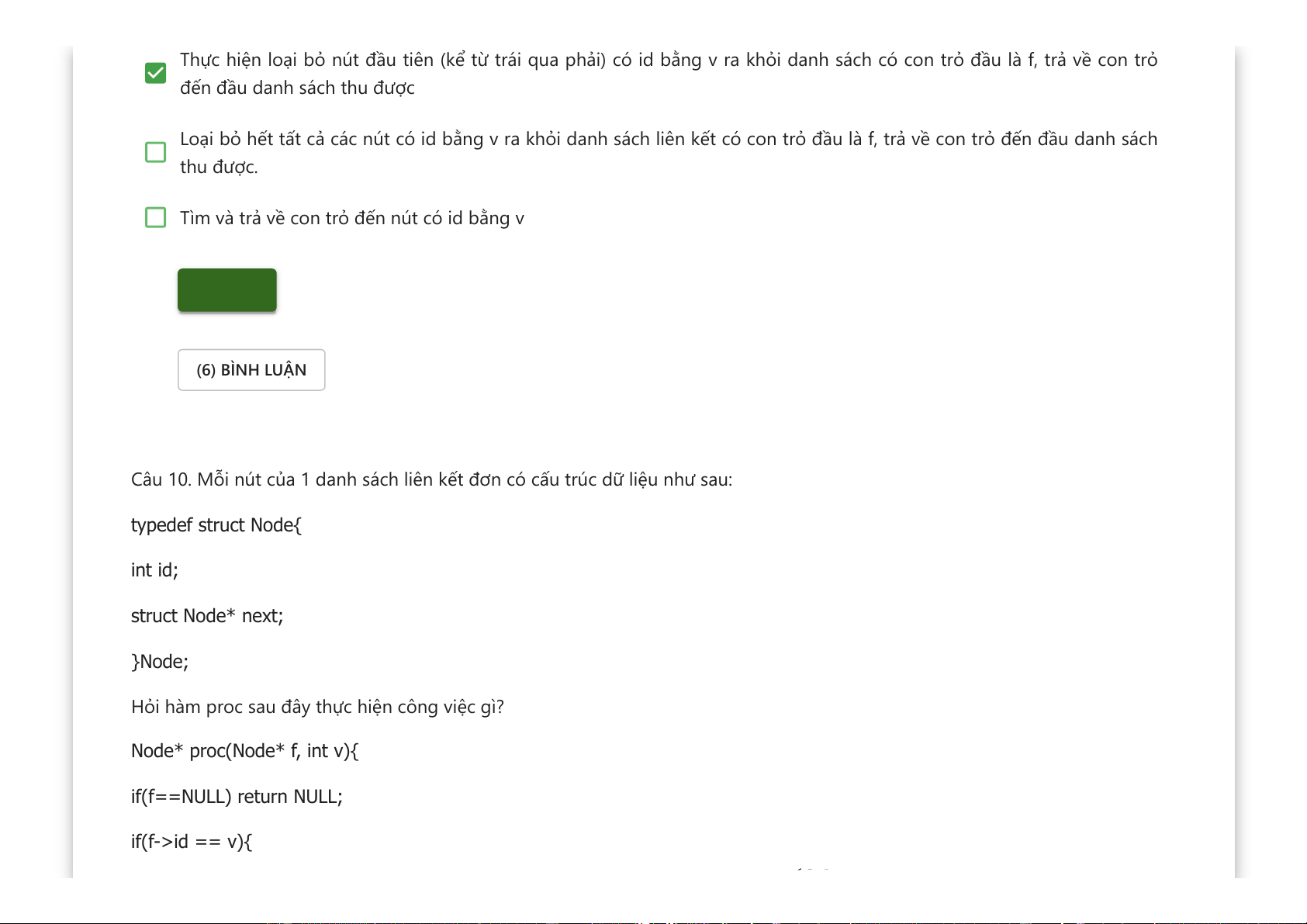
Thực hiện loại bỏ nút đầu tiên (kể từ trái qua phải) có id bằng v ra khỏi danh sách có con trỏ đầu là f, trả về con trỏ
đến đầu danh sách thu được
Loại bỏ hết tất cả các nút có id bằng v ra khỏi danh sách liên kết có con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được.
Tìm và trả về con trỏ đến nút có id bằng v Kiểm tra (6) BÌNH LUẬN
Câu 10. Mỗi nút của 1 danh sách liên kết đơn có cấu trúc dữ liệu như sau: typedef struct Node{ int id; struct Node* next; }Node;
Hỏi hàm proc sau đây thực hiện công việc gì? Node* proc(Node* f, int v){ if(f==NULL) return NULL; if(f->id == v){
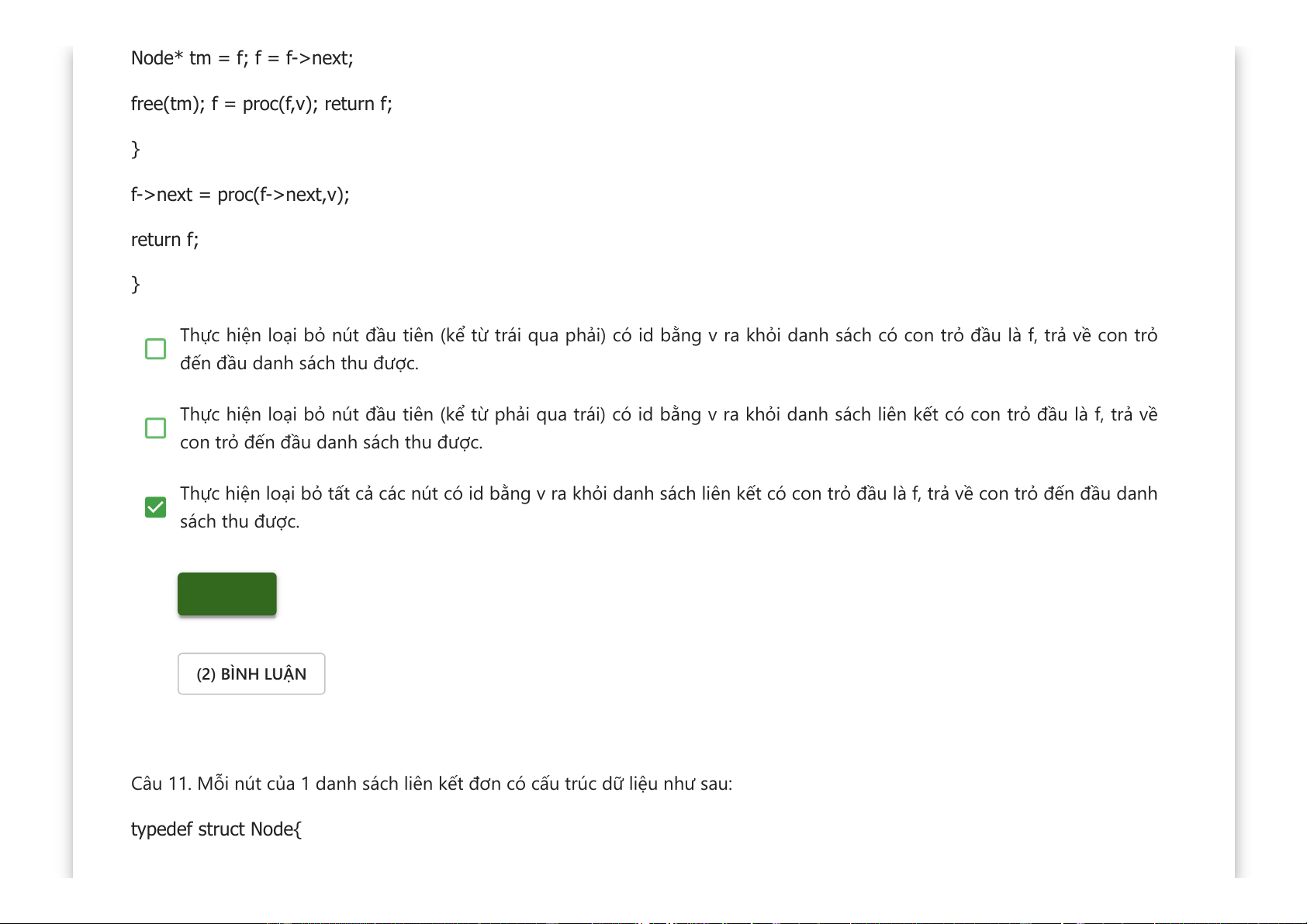
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Node* tm = f; f = f->next;
free(tm); f = proc(f,v); return f; }
f->next = proc(f->next,v); return f; }
Thực hiện loại bỏ nút đầu tiên (kể từ trái qua phải) có id bằng v ra khỏi danh sách có con trỏ đầu là f, trả về con trỏ
đến đầu danh sách thu được.
Thực hiện loại bỏ nút đầu tiên (kể từ phải qua trái) có id bằng v ra khỏi danh sách liên kết có con trỏ đầu là f, trả về
con trỏ đến đầu danh sách thu được.
Thực hiện loại bỏ tất cả các nút có id bằng v ra khỏi danh sách liên kết có con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được. Kiểm tra (2) BÌNH LUẬN
Câu 11. Mỗi nút của 1 danh sách liên kết đơn có cấu trúc dữ liệu như sau: typedef struct Node{
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 int id; struct Node* next; }Node;
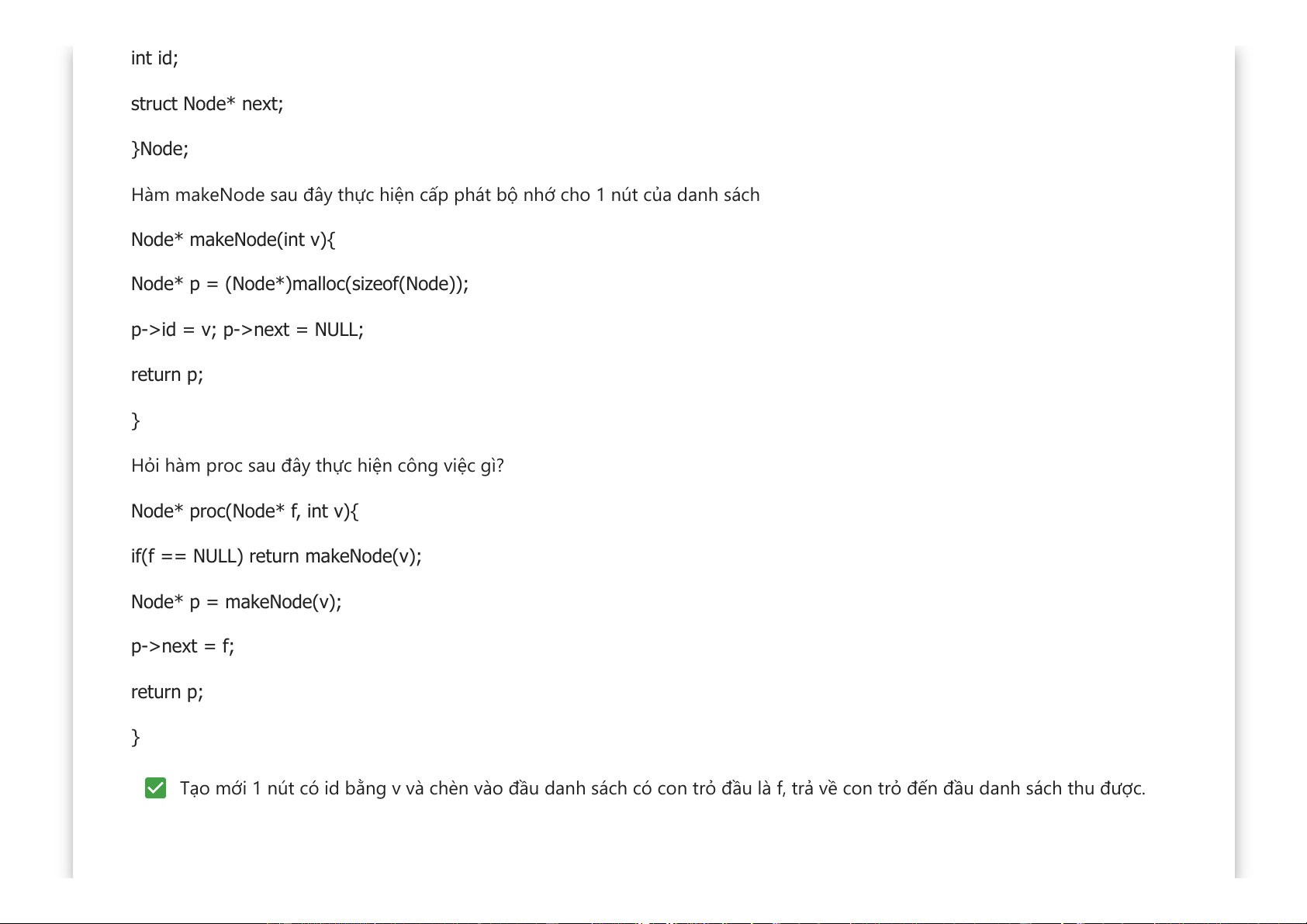
Hàm makeNode sau đây thực hiện cấp phát bộ nhớ cho 1 nút của danh sách Node* makeNode(int v){
Node* p = (Node*)malloc(sizeof(Node));
p->id = v; p->next = NULL; return p; }
Hỏi hàm proc sau đây thực hiện công việc gì? Node* proc(Node* f, int v){
if(f == NULL) return makeNode(v); Node* p = makeNode(v); p->next = f; return p; }
Tạo mới 1 nút có id bằng v và chèn vào đầu danh sách có con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Tạo mới 1 nút có id bằng v, chèn vào cuối danh sách liên kết có con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được.
Tìm và trả về nút đầu tiên (kể từ trái) có id bằng v của danh sách liên kết có con trỏ đầu là f. Kiểm tra (0) BÌNH LUẬN
Câu 12. Kết luận nào sau đây đúng với danh sách liên kết.
Các phần tử trong danh sách liên kết được cấp phát kế tiếp nhau trong bộ nhớ.
Các phần tử của danh sách liên kết không được cấp phát kế tiếp nhau trong bộ nhớ, các phần tử được liên kết với
nhau thông qua con trỏ (mỗi phần tử sẽ có 1 trường con trỏ trỏ tới phần tử tiếp theo trong danh sách). Kiểm tra (2) BÌNH LUẬN
Câu 13. Cho T là 1 BST thu được bằng cách chèn liên tiếp dãy khóa sau vào T (bắt đầu từ cây rỗng): 3, 4, 8, 20, 5, 1, 15, 2.
Hỏi kết luận nào sau đây là đúng?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5 là con phải của 4 5 là con trái của 8 5 và 3 là hai nút anh em. Kiểm tra (0) BÌNH LUẬN
Câu 14. Cho T là 1 BST thu được bằng cách chèn liên tiếp dãy khóa sau vào (bắt đầu từ cây rỗng): 3, 4, 8, 20, 5, 1, 15, 2.
Thứ tự các khóa thu được trong phép duyệt theo thứ tự trước là: 3, 1, 2, 4, 8, 5, 20, 15 1, 2, 3, 4, 5, 8, 15, 20 5, 1, 4, 8, 15, 20, 3, 2 Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (3) BÌNH LUẬN
Câu 15. Cho T là 1 BST thu được bằng cách chèn liên tiếp dãy khóa sau vào (bắt đầu từ cây rỗng): 3, 4, 8, 20, 5, 1, 15, 2.
Thứ tự các khóa thu được trong phép duyệt theo thứ tự sau là: · 2, 1, 5, 15, 20, 8, 4, 3 · 1, 2, 3, 4, 5, 8, 15, 20 · 20, 15, 8, 5, 4, 3, 2, 1 Kiểm tra (0) BÌNH LUẬN
Câu 16. Cho T là 1 BST thu được bằng cách chèn liên tiếp dãy khóa sau vào (bắt đầu từ cây rỗng): 3, 4, 8, 20, 5, 1, 15, 2.
Thứ tự các khóa thu được trong phép duyệt theo thứ tự giữa là: · 5, 8, 1, 4, 3, 15, 20, 2 · 1, 2, 3, 4, 5, 8, 15, 20
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 · 15, 20, 8, 3, 4, 2, 1, 5 Kiểm tra (0) BÌNH LUẬN
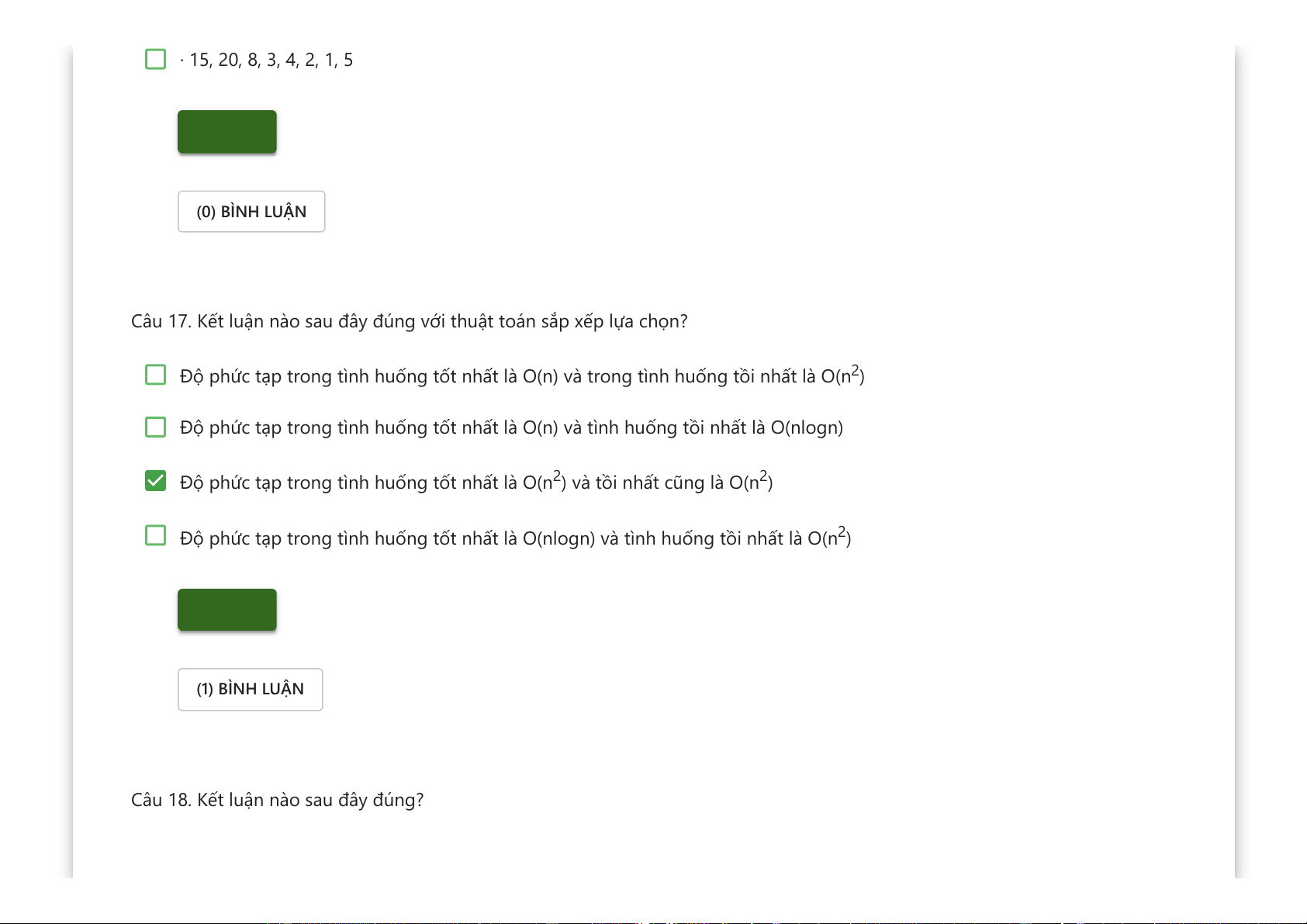
Câu 17. Kết luận nào sau đây đúng với thuật toán sắp xếp lựa chọn?
Độ phức tạp trong tình huống tốt nhất là O(n) và trong tình huống tồi nhất là O(n2)
Độ phức tạp trong tình huống tốt nhất là O(n) và tình huống tồi nhất là O(nlogn)
Độ phức tạp trong tình huống tốt nhất là O(n2) và tồi nhất cũng là O(n2)
Độ phức tạp trong tình huống tốt nhất là O(nlogn) và tình huống tồi nhất là O(n2) Kiểm tra (1) BÌNH LUẬN
Câu 18. Kết luận nào sau đây đúng?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
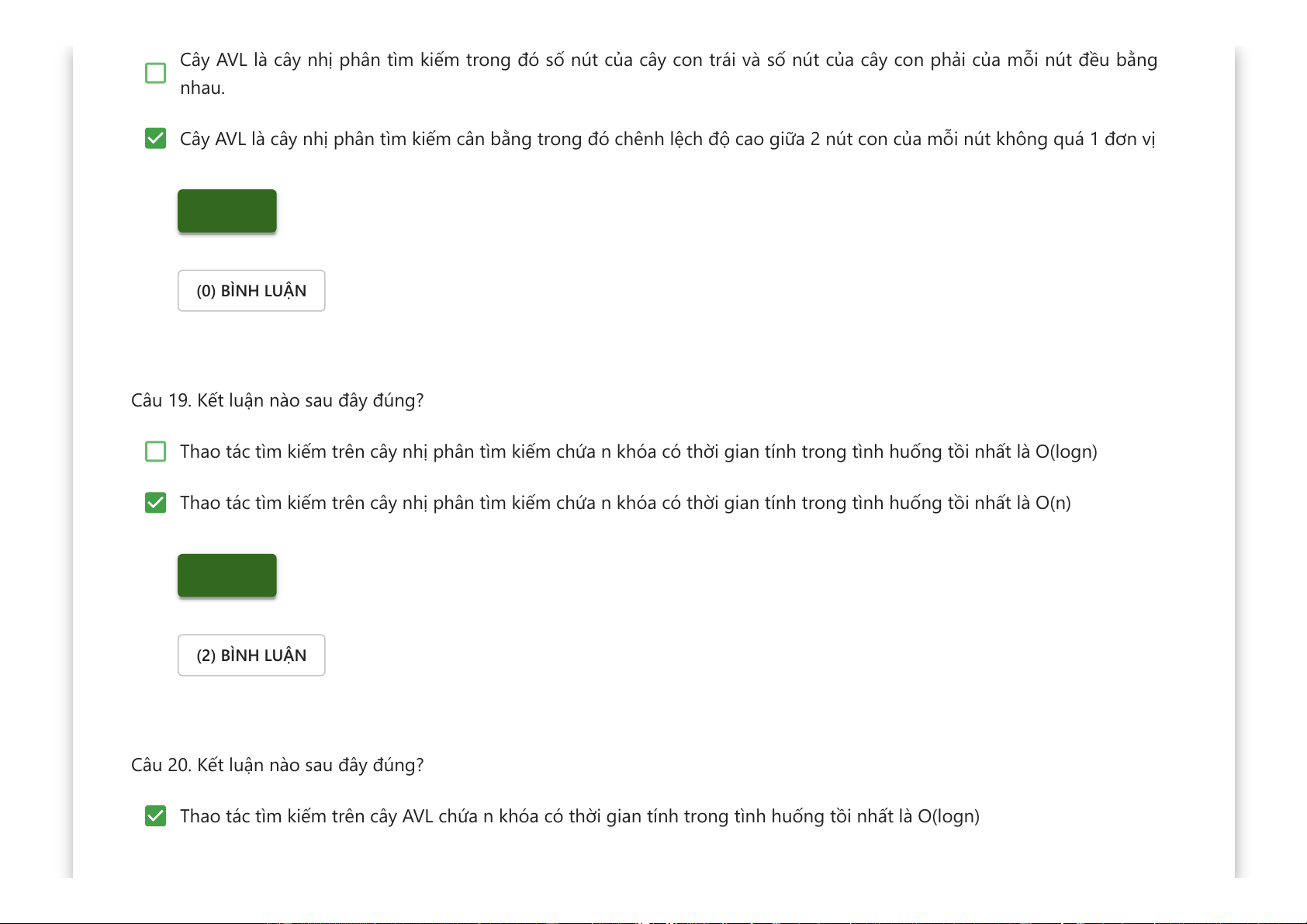
Cây AVL là cây nhị phân tìm kiếm trong đó số nút của cây con trái và số nút của cây con phải của mỗi nút đều bằng nhau.
Cây AVL là cây nhị phân tìm kiếm cân bằng trong đó chênh lệch độ cao giữa 2 nút con của mỗi nút không quá 1 đơn vị Kiểm tra (0) BÌNH LUẬN
Câu 19. Kết luận nào sau đây đúng?
Thao tác tìm kiếm trên cây nhị phân tìm kiếm chứa n khóa có thời gian tính trong tình huống tồi nhất là O(logn)
Thao tác tìm kiếm trên cây nhị phân tìm kiếm chứa n khóa có thời gian tính trong tình huống tồi nhất là O(n) Kiểm tra (2) BÌNH LUẬN
Câu 20. Kết luận nào sau đây đúng?
Thao tác tìm kiếm trên cây AVL chứa n khóa có thời gian tính trong tình huống tồi nhất là O(logn)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
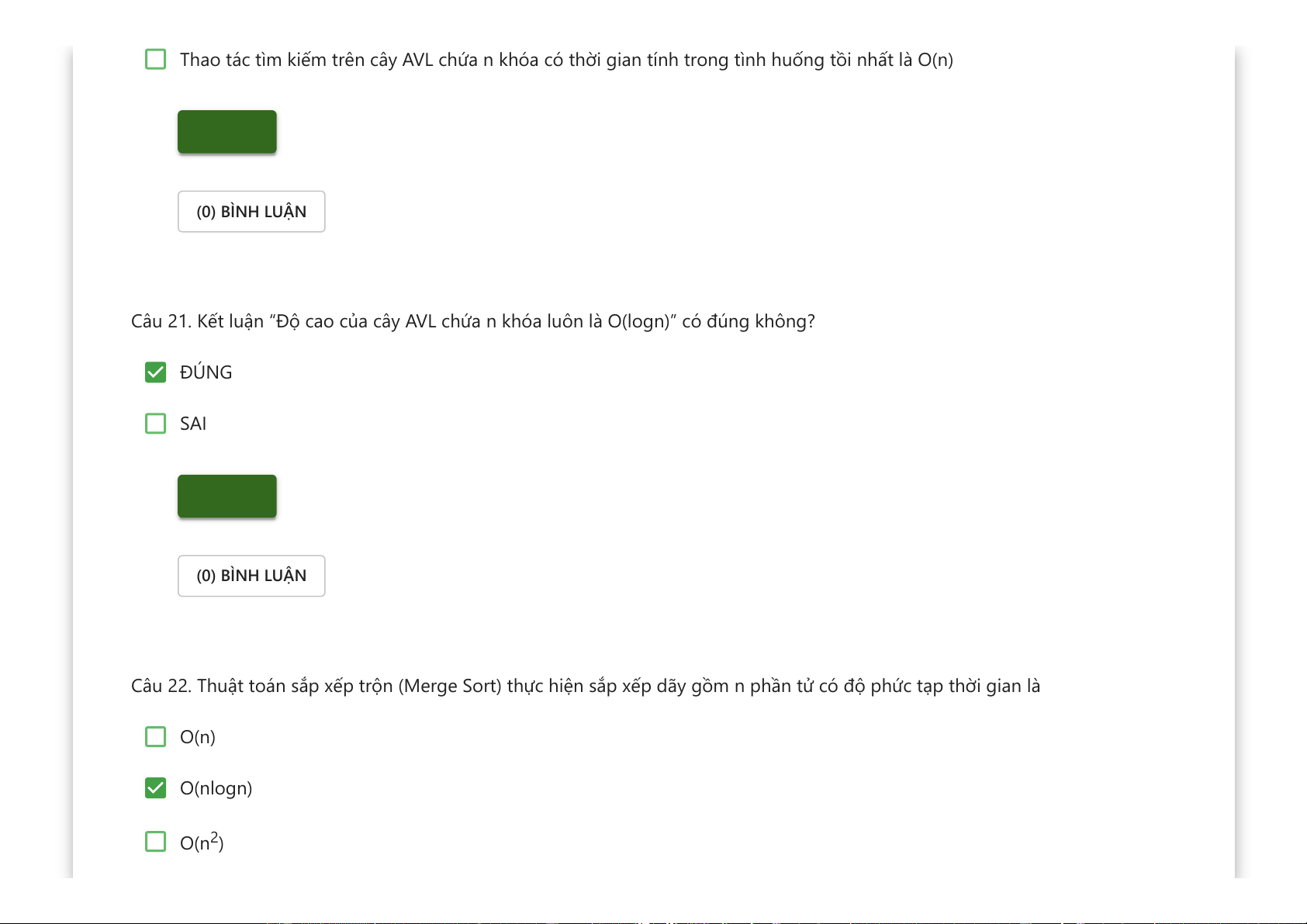
Thao tác tìm kiếm trên cây AVL chứa n khóa có thời gian tính trong tình huống tồi nhất là O(n) Kiểm tra (0) BÌNH LUẬN
Câu 21. Kết luận “Độ cao của cây AVL chứa n khóa luôn là O(logn)” có đúng không? ĐÚNG SAI Kiểm tra (0) BÌNH LUẬN
Câu 22. Thuật toán sắp xếp trộn (Merge Sort) thực hiện sắp xếp dãy gồm n phần tử có độ phức tạp thời gian là O(n) O(nlogn) O(n2)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
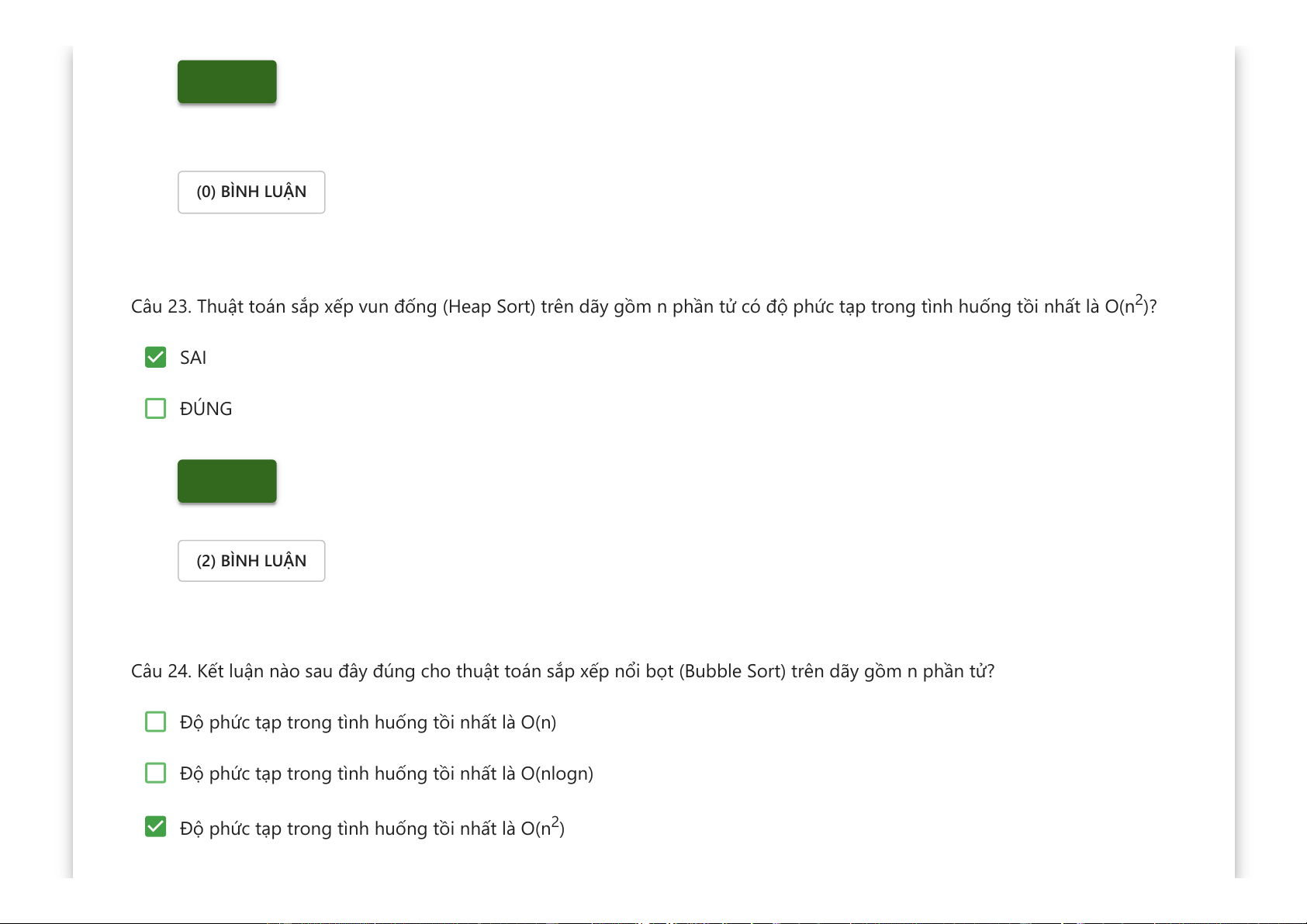
Câu 23. Thuật toán sắp xếp vun đống (Heap Sort) trên dãy gồm n phần tử có độ phức tạp trong tình huống tồi nhất là O(n2)? SAI ĐÚNG Kiểm tra (2) BÌNH LUẬN
Câu 24. Kết luận nào sau đây đúng cho thuật toán sắp xếp nổi bọt (Bubble Sort) trên dãy gồm n phần tử?
Độ phức tạp trong tình huống tồi nhất là O(n)
Độ phức tạp trong tình huống tồi nhất là O(nlogn)
Độ phức tạp trong tình huống tồi nhất là O(n2)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
Câu 25. Kết luận nào sau đây đúng cho thuật toán sắp xếp nổi bọt (Bubble Sort) trên dãy gồm n phần tử
Độ phức tạp trong tình huống tốt nhất là O(n)
Độ phức tạp trong tình huống tốt nhất là O(nlogn)
Độ phức tạp trong tình huống tốt nhất là O(n2) Kiểm tra (5) BÌNH LUẬN
Câu 26. Điều kiện gì đối với dãy đầu vào a1, a2, ..., an để có thể áp dụng tìm kiếm nhị phân để tìm phần tử x trong dãy đó.
Dãy số không được phép có số âm
Dãy được sắp xếp theo thứ tự không tăng hoặc không giảm
Dãy bất kỳ, không cần điều kiện gì cũng có thể áp dụng tìm kiếm nhị phân
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
Câu 27. Cho dãy a1, a2, ..., an đã được sắp xếp theo thứ tự không tăng. Thuật toán tìm kiếm nhị phân thực hiện kiểm tra xem 1
phần tử x có mặt trong dãy đã cho có độ phức tạp là O(1) O(logn) O(n) Kiểm tra (0) BÌNH LUẬN
Câu 28. Mỗi nút của 1 danh sách liên kết đơn có cấu trúc dữ liệu như sau: typedef struct Node{ int id; // id cua nut
struct Node* next; // con tro tro den nut tiep theo
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 }Node;
Hàm makeNode sau đây thực hiện cấp phát bộ nhớ cho 1 nút với giá trị id là v Node* makeNode(int v){
Node* p = (Node*)malloc(sizeof(Node));
p->id = v; p->next = NULL; return p; }
Hỏi hàm proc sau đây thực hiện công việc gì Node* proc(Node* f, int v){
if(f == NULL) return makeNode(v);
f->next = proc(f->next,v); return f; }
Thêm 1 nút có id bằng v vào cuối danh sách có con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được.
Thêm 1 nút có id bằng v vào đầu danh sách liên kết với con trỏ đầu là f, trả về con trỏ đến đầu danh sách thu được.
Tìm và trả về con trỏ đến 1 nút có id bằng v Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
Câu 29. Cho đồ thị có hướng và không có chu trình, trọng số trên cạnh là không âm. Cần tìm đường đi ngắn nhất từ 1 đỉnh đến
1 đỉnh khác. Thuật toán Dijkstra có phải là thuật toán tốt nhất không? Có Không Kiểm tra (3) BÌNH LUẬN
Câu 30. Cho đồ thị vô hướng G=(V,E), trong đó V = {1,2,3,4,5,6,7,8,9} và E = {(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5),(6,7),(6,8),(7,8),
(8,9)}. Hỏi G có phải là đồ thị Euler hay không? Có Không Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (5) BÌNH LUẬN
Câu 31. Cho cây nhị phân T được mô tả như sau: Nút gốc là 10
Nút 10 có con trái là 7 và con phải là 14
Nút 7 có con trái là 5 và con phải là 9
Nút 14 có con trái là 12 và con phải là 15
Hỏi dãy nút 5, 7, 9, 10, 12, 14, 15 là dãy được thăm trong phép duyệt theo thứ tự nào sau đây A. Thứ tự trước B. Thứ tự giữa C. Thứ tự sau Kiểm tra (1) BÌNH LUẬN
Câu 32. Dãy 3, 2, 5, 7, 1, 6, 8, 9, 4 cần được sắp xếp theo thứ tự không giảm bằng thuật toán sắp xếp vun đống. Sau bước xây
dựng max-heap (buildMaxHeap), trạng thái dãy là: 1, 2, 3, 4, 5, 6, 7, 8, 9
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 9, 7, 8, 4, 1, 6, 5, 2, 3 9, 8, 7, 6, 5, 4, 3, 2, 1 Kiểm tra (25) BÌNH LUẬN
Câu 33. Mỗi nút của 1 danh sách liên kết đơn có cấu trúc dữ liệu như sau: typedef struct Node{ int id; struct Node* next; }Node;
Hỏi hàm proc sau đây thực hiện công việc gì? Node* proc(Node* f){ Node* p = f; Node* pp = NULL; Node* np = NULL; while(p != NULL){
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 np = p->next; p->next = pp; pp = p; p = np; } return pp; }
Đảo ngược thứ tự các nút của một danh sách liên kết có con trỏ đầu là f, trả về con trỏ đến đầu danh sách mới thu được
Tìm và trả về con trỏ trỏ đến nút cuối cùng của danh sách liên kết có con trỏ đầu là f.
Loại bỏ tất cả các nút khỏi danh sách liên kết có con trỏ đầu là f, trừ nút cuối cùng, trả về con trỏ đến nút cuối cùng. Kiểm tra (0) BÌNH LUẬN
Câu 34. Cho đồ thị vô hướng G=(V,E), trong đó V = {1,2,3,4,5,6,7,8,9} và E = {(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5),(6,7),(6,8),(7,8),
(8,9)}. Hỏi G có phải là đồ thị Hamilton hay không? Có
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Không Kiểm tra (2) BÌNH LUẬN
Câu 35. Cho đồ thị vô hướng G=(V,E), trong đó V = {1,2,3,4,5,6,7,8,9} và E = {(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5),(6,7),(6,8),(7,8),
(8,9)}. Thực hiện duyệt đồ thị G theo chiều sâu (khi xét các đỉnh thì xét theo thứ tự từ điển). Hỏi thứ tự các đỉnh được thăm như thế nào? 1,2,3,4,5,6,7,8,9 1,2,4,3,5,6,7,8,9 1,4,2,5,6,3,8,9,7 9,8,7,6,5,4,3,2,1 Kiểm tra (0) BÌNH LUẬN
Câu 36. Cho cây nhị phân T được mô tả như sau:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Nút gốc là 8
Nút 8 có con trái là 4 và con phải là 15
Nút 4 có con trái là 2 và con phải là 6
Nút 15 có con trái là 10 và con phải là 20
Hỏi T có phải là cây AVL không? A. Không B. Có Kiểm tra (2) BÌNH LUẬN
Câu 37. Một bảng băm sử dụng cơ chế địa chỉ mở (Open Addressing) để xử lý collision với thứ tự dò là h(k,i) = (k mod m + i)
mod m, trong đó m là kích thước của bảng (các slot đánh số từ 0,1,..., m-1. Ban đầu, bảng ở trạng thái rỗng. Ta thực hiện chèn
liên tiếp các khóa sau: 5, 7, 27, 15, 17. Với m = 10, hãy cho biết trạng thái của bảng là trạng thái nào sau đây (từ trái qua phải là
các slot từ 0 đến m-1, vị trí slot trống được biểu diễn bởi ký hiệu x) A. |x|x|x|x|x|5|15|7|27|17| B. |5|7|27|15|17|x|x|x|x|x| C. |x|5|15|7|17|27|x|x|x|x| D. |5|7|15|17|27|x|x|x|x|x|
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (7) BÌNH LUẬN
Câu 38. Phát biểu nào dưới đây đúng với Bảng băm?
Bảng băm là 1 cấu trúc dữ liệu để ánh xạ từ mỗi giá trị (value) đến 1 khóa (key)
Bảng băm là cấu trúc dữ liệu ánh xạ mỗi khóa (key) với 1 giá trị (value)
Bảng băm là một dạng đặc biệt của ngăn xếp
Bảng băm là một dạng đặc biệt của hàng đợi Kiểm tra (1) BÌNH LUẬN
Câu 39. Trong cấu trúc bảng băm, hai khóa khác nhau luôn luôn cho giá trị hàm băm khác nhau SAI ĐÚNG
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (2) BÌNH LUẬN
Câu 40. Trong cấu trúc bảng băm, khi 2 khóa k1 và k2 khác nhau cho cùng giá trị hàm băm: h(k1) = h(k2), ta gọi hiện tượng đó là gì? Collision Duplication Segmentation Kiểm tra (0) BÌNH LUẬN
Câu 41. Trong bảng băm, sử dụng cơ chế địa chỉ mở (Open Addressing) để xử lý xung đột (Collision), phát nào sau đây đúng?
Các cặp (khóa, giá trị) được lưu trữ trong nội tại bảng, áp dụng phương pháp dò (probing) để tìm kiếm khóa cần tìm
hoặc tìm kiếm vị trí trống để lưu thêm (khóa, giá trị).
Mỗi phần tử của bảng lưu trữ sẽ ánh xạ đến 1 khối (cấu trúc) lưu trữ các khóa có cùng giá trị hàm băm
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
Câu 42. Trong bảng băm sử dụng cơ chế nhóm chuỗi (Chaining) để xử lý xung đột, phát biểu nào sau đây đúng?
Các cặp (khóa, giá trị) được lưu trữ trong nội tại trong các ô (slot) của bảng, áp dụng dò (probing) để tìm kiếm khóa
cần tìm hoặc tìm ô trống để lưu cặp (khóa, giá trị) mới thêm.
Mỗi ô (slot) của bảng sẽ ánh xạ đến 1 khối (cấu trúc) chứa các khóa có cùng giá trị hàm băm. Khối này có thể được tổ
chức theo mảng, danh sách liên kết, cây nhị phân tìm kiếm hoặc 1 bảng băm cấp 2. Kiểm tra (0) BÌNH LUẬN
Câu 43. Kết luận nào sau đây đúng với cây nhị phân tìm kiếm?
Cây nhị phân tìm kiếm là cây mà khóa của mỗi nút lớn hơn khóa của tất cả các nút ở cây con trái và nhỏ hơn khóa của
tất cả các nút ở cây con phải
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Trên cây nhị phân tìm kiếm, khóa của mỗi nút lớn hơn khóa của các nút con (nếu tồn tại)
Trên cây nhị phân tìm kiếm, khóa của mỗi nút nhỏ hơn khóa của các nút con (nếu tồn tại) Kiểm tra (0) BÌNH LUẬN
Câu 44. Cho đồ thị vô hướng G=(V,E), trong đó V = {1,2,3,4,5,6,7,8,9} và E = {(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5),(6,7),(6,8),(7,8),
(8,9)}. Hỏi đồ thị có bao nhiều thành phần liên thông? 1 2 3 4 Kiểm tra (2) BÌNH LUẬN
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Câu 45. Cho đồ thị có hướng G=(V,E) trong đó V = {1,2,3,4,5,6,7,8}, và E = {(3,1),(1,2),(2,5),(2,3),(3,5),(5,6),(5,7),(6,7),(8,5),(8,6),
(7,8)}. Hỏi đồ thị đã cho có bao nhiều thành phần liên thông mạnh? 1 2 3 4 Kiểm tra (4) BÌNH LUẬN
Câu 46. Cho đồ thị vô hướng G=(V,E), trong đó V = {1,2,3,4,5,6,7,8,9} và E = {(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5),(6,7),(6,8),(7,8),
(8,9)}. Thực hiện duyệt đồ thị G theo chiều rộng (khi xét các đỉnh thì xét theo thứ tự từ điển). Hỏi thứ tự các đỉnh được thăm như thế nào? 1,2,3,4,5,6,7,8,9 1, 4, 3, 2, 5, 6, 7, 8, 9 9,8,7,6,5,4,3,2,1 6,9,7,8,1,2,3,5,4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
Câu 47. Cho đồ thị vô hướng liên thông G=(V,E) và s là 1 đỉnh thuộc V. Hỏi thủ tục duyệt theo chiều sâu (DFS) xuất phát từ s
đảm bảo luôn tìm ra đường đi ngắn nhất theo số cạnh từ s đến các đỉnh còn lại Đúng Sai Kiểm tra (0) BÌNH LUẬN
Câu 48. Cho đồ thị vô hướng liên thông G=(V,E) và s là 1 đỉnh thuộc V. Hỏi thủ tục duyệt theo chiều rộng (BFS) xuất phát từ s
đảm bảo luôn tìm ra đường đi ngắn nhất theo số cạnh từ s đến các đỉnh còn lại. Đúng Sai
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
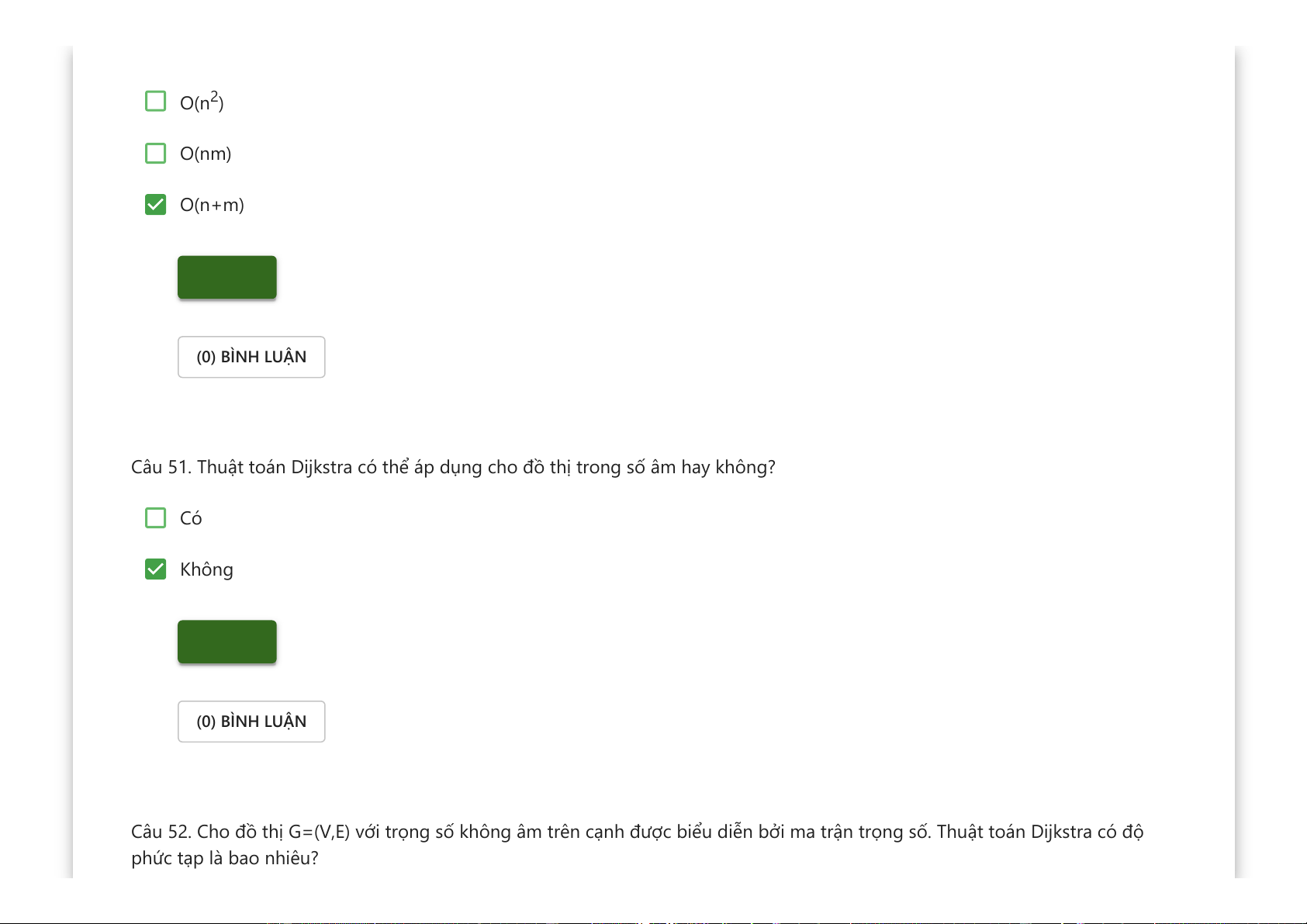
Câu 49. Cho đồ thị vô hướng G có n đỉnh và m cạnh. Thuật toán duyệt theo chiều sâu trên G có độ phức tạp thời gian là bao nhiêu? O(n) O(nm) O(n+m) O(n2) Kiểm tra (6) BÌNH LUẬN
Câu 50. Cho đồ thị vô hướng G có n đỉnh và m cạnh. Thuật toán duyệt theo chiều rộng (BFS) trên G có độ phức tạp thời gian là bao nhiêu? O(n)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 O(n2) O(nm) O(n+m) Kiểm tra (0) BÌNH LUẬN
Câu 51. Thuật toán Dijkstra có thể áp dụng cho đồ thị trong số âm hay không? Có Không Kiểm tra (0) BÌNH LUẬN
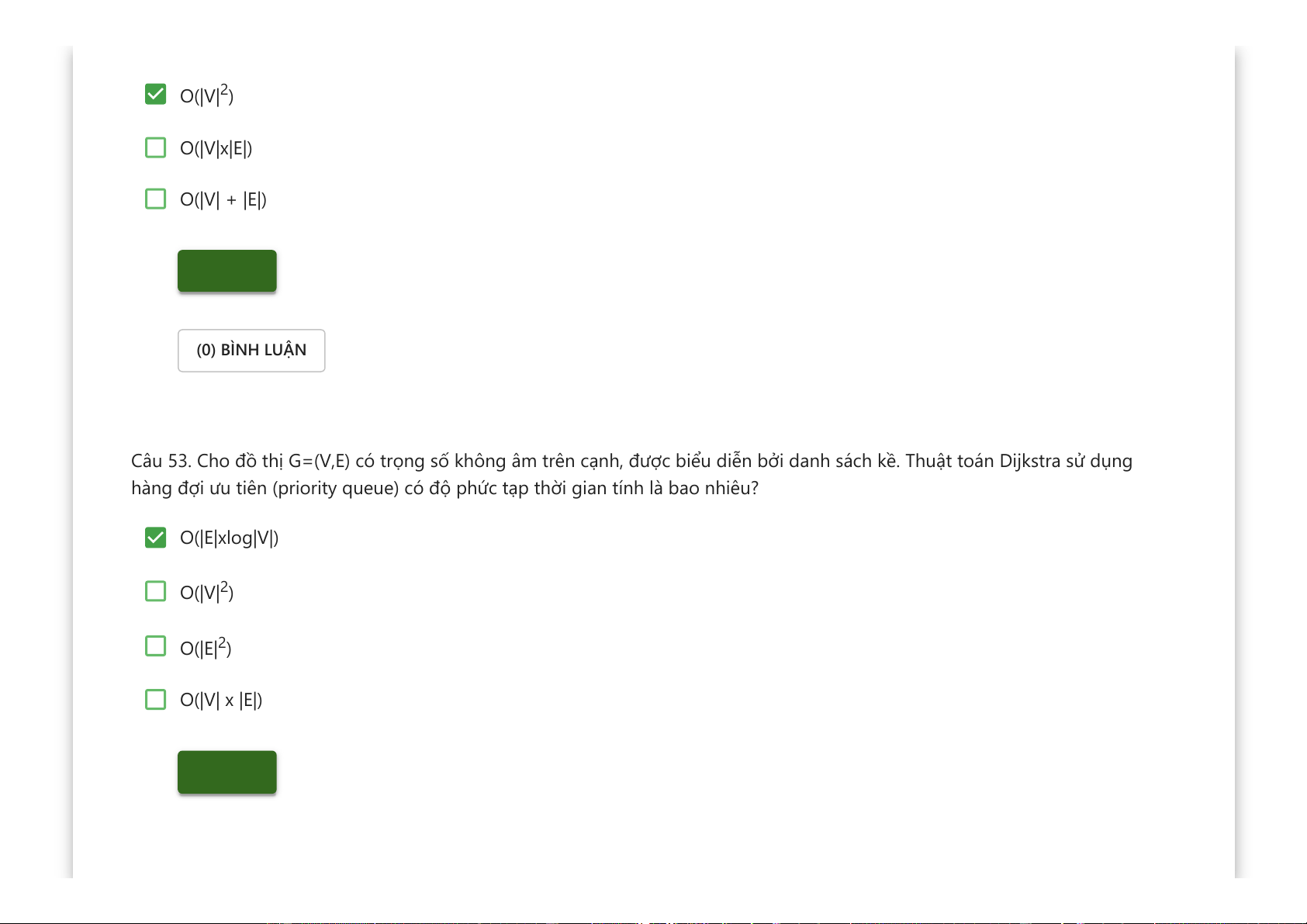
Câu 52. Cho đồ thị G=(V,E) với trọng số không âm trên cạnh được biểu diễn bởi ma trận trọng số. Thuật toán Dijkstra có độ phức tạp là bao nhiêu?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 O(|V|2) O(|V|x|E|) O(|V| + |E|) Kiểm tra (0) BÌNH LUẬN
Câu 53. Cho đồ thị G=(V,E) có trọng số không âm trên cạnh, được biểu diễn bởi danh sách kề. Thuật toán Dijkstra sử dụng
hàng đợi ưu tiên (priority queue) có độ phức tạp thời gian tính là bao nhiêu? O(|E|xlog|V|) O(|V|2) O(|E|2) O(|V| x |E|) Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
Câu 54. Cho đồ thị trọng số không âm trên cạnh bất kỳ. Hỏi thuật toán Dijkstra sử dụng hàng đợi ưu tiên (priority queue) có
luôn tốt hơn không sử dụng hàng đợi ưu tiên không? Có Không Kiểm tra (0) BÌNH LUẬN
Câu 55. Cho đồ thị trọng số không âm trên cạnh bất kỳ. Hỏi rằng để giải bài toán tìm đường đi ngắn nhất từ 1 đỉnh đến 1 đỉnh
khác trên đồ thị thì thuật toán Dijkstra luôn là lựa chọn tốt nhất hay không? Có Không Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
Câu 56. Cho đồ thị với trọng số trên tất cả các cạnh đều bằng nhau và không âm. Thuật toán nào sau đây tốt hơn để giải bài
toán tìm đường đi ngắn trên từ 1 đỉnh đến 1 đỉnh khác Thuật toán Dijkstra
Thuật toán duyệt theo chiều rộng
Thuật toán duyệt theo chiều sâu Kiểm tra (0) BÌNH LUẬN
Câu 57. Mỗi nút (Node) của danh sách liên kết có cấu trúc như sau (biểu diễn bằng mã giả): Node{
value;// giá trị của nút
next;// con trỏ đến phần tử tiếp theo }
Cho hàm F như sau (viết bằng mã giả):
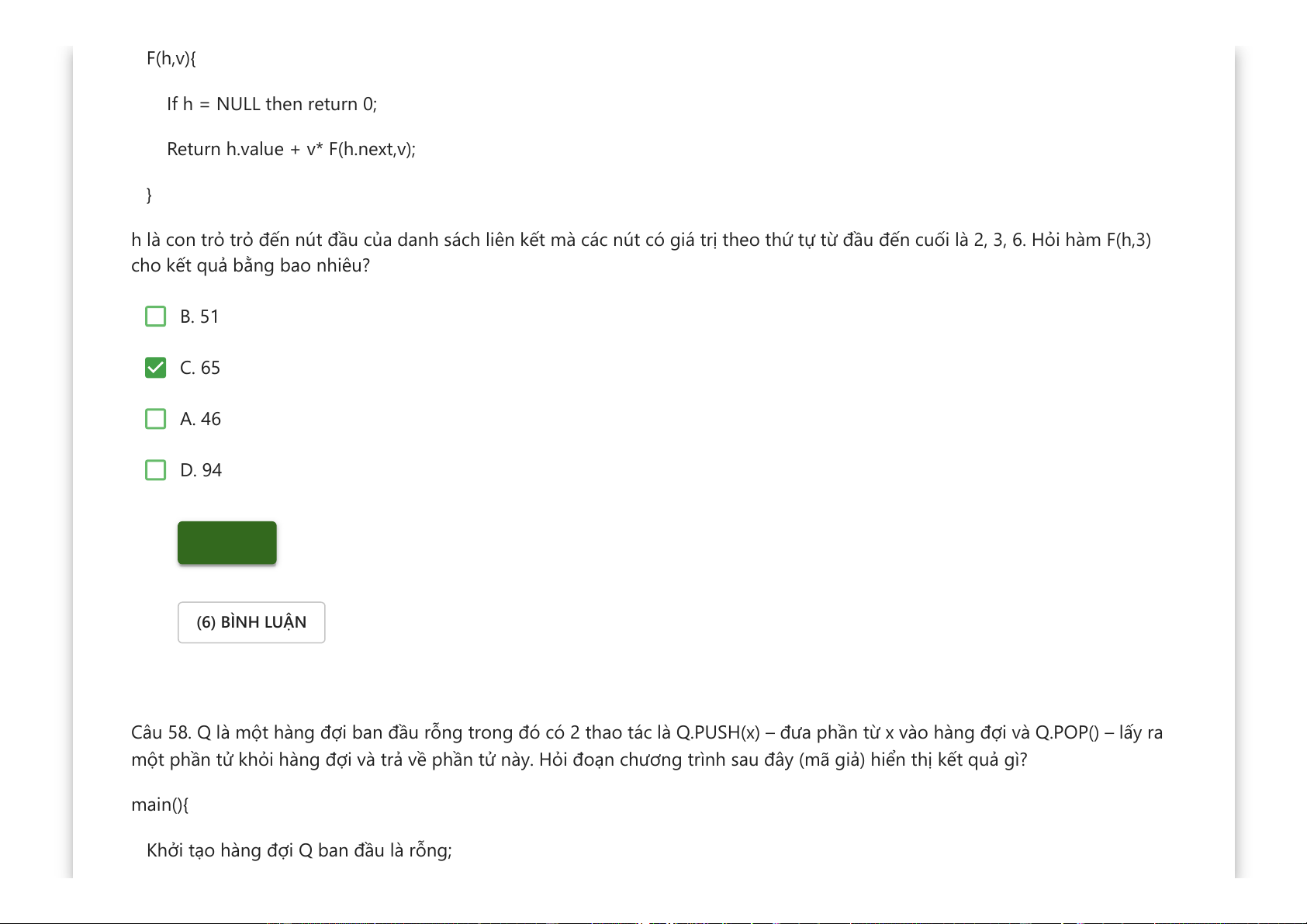
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 F(h,v){ If h = NULL then return 0;
Return h.value + v* F(h.next,v); }
h là con trỏ trỏ đến nút đầu của danh sách liên kết mà các nút có giá trị theo thứ tự từ đầu đến cuối là 2, 3, 6. Hỏi hàm F(h,3)
cho kết quả bằng bao nhiêu? B. 51 C. 65 A. 46 D. 94 Kiểm tra (6) BÌNH LUẬN
Câu 58. Q là một hàng đợi ban đầu rỗng trong đó có 2 thao tác là Q.PUSH(x) – đưa phần từ x vào hàng đợi và Q.POP() – lấy ra
một phần tử khỏi hàng đợi và trả về phần tử này. Hỏi đoạn chương trình sau đây (mã giả) hiển thị kết quả gì? main(){
Khởi tạo hàng đợi Q ban đầu là rỗng;
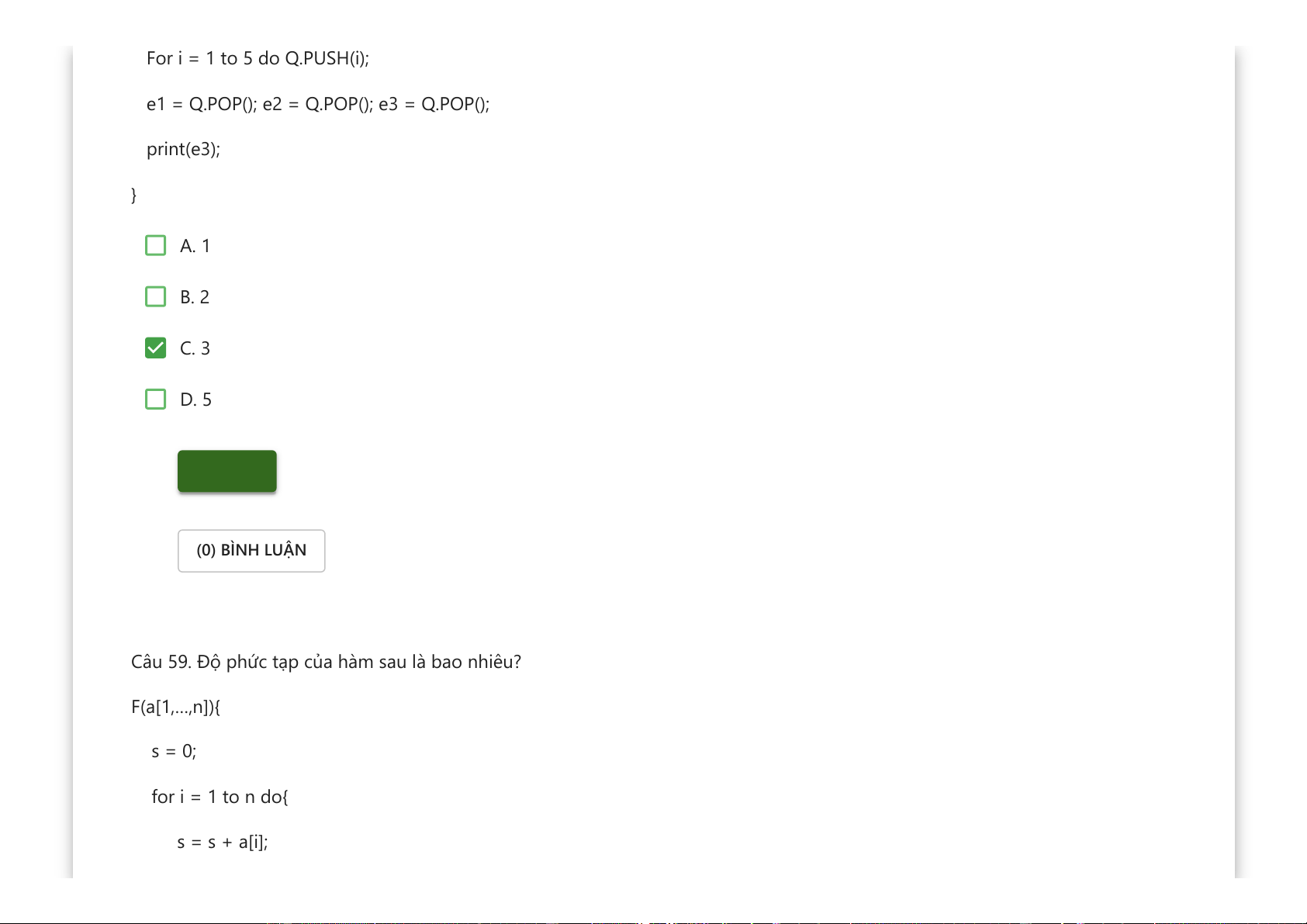
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 For i = 1 to 5 do Q.PUSH(i);
e1 = Q.POP(); e2 = Q.POP(); e3 = Q.POP(); print(e3); } A. 1 B. 2 C. 3 D. 5 Kiểm tra (0) BÌNH LUẬN
Câu 59. Độ phức tạp của hàm sau là bao nhiêu? F(a[1,…,n]){ s = 0; for i = 1 to n do{ s = s + a[i];
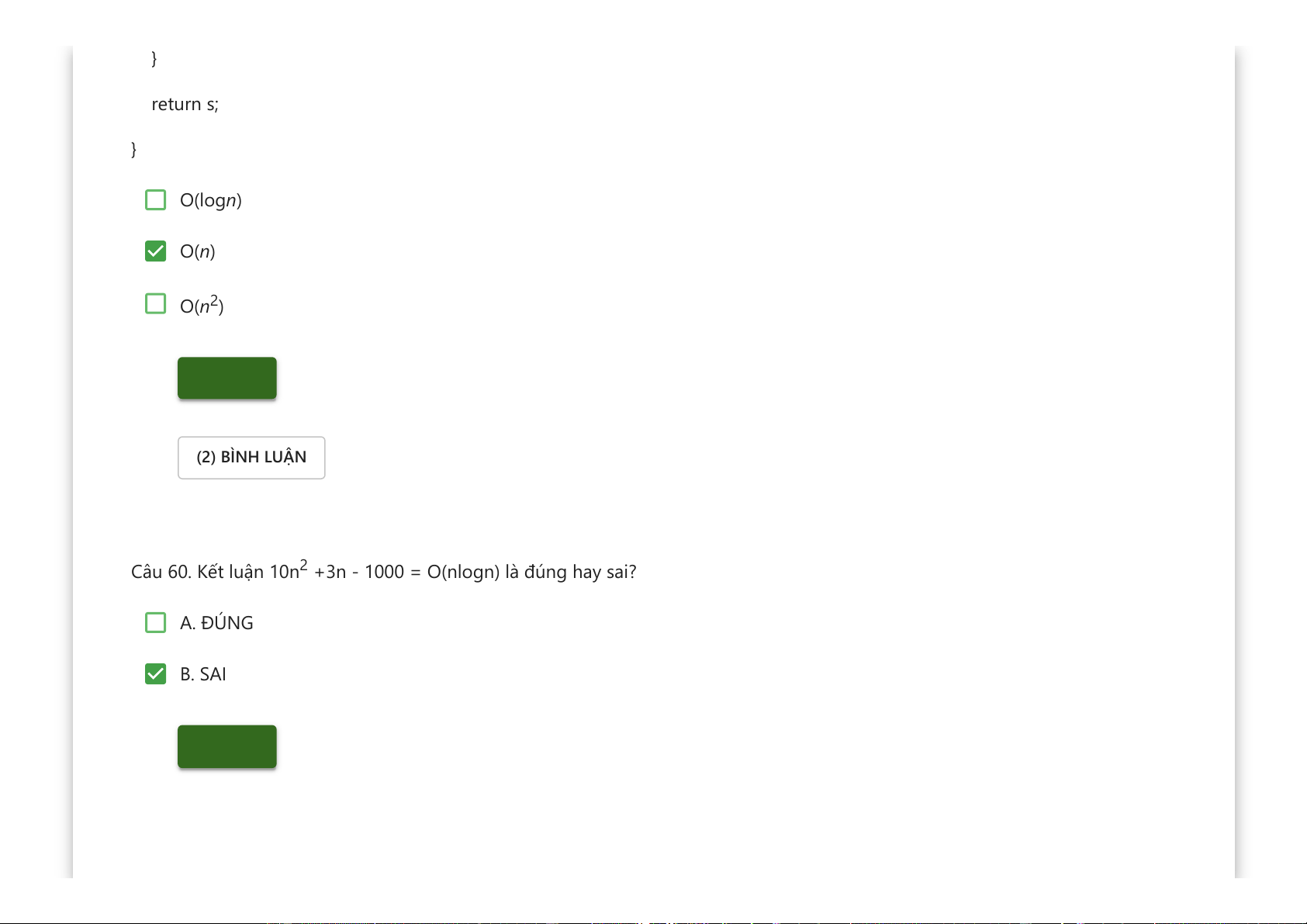
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 } return s; } O(logn) O(n) O(n2) Kiểm tra (2) BÌNH LUẬN
Câu 60. Kết luận 10n2 +3n - 1000 = O(nlogn) là đúng hay sai? A. ĐÚNG B. SAI Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
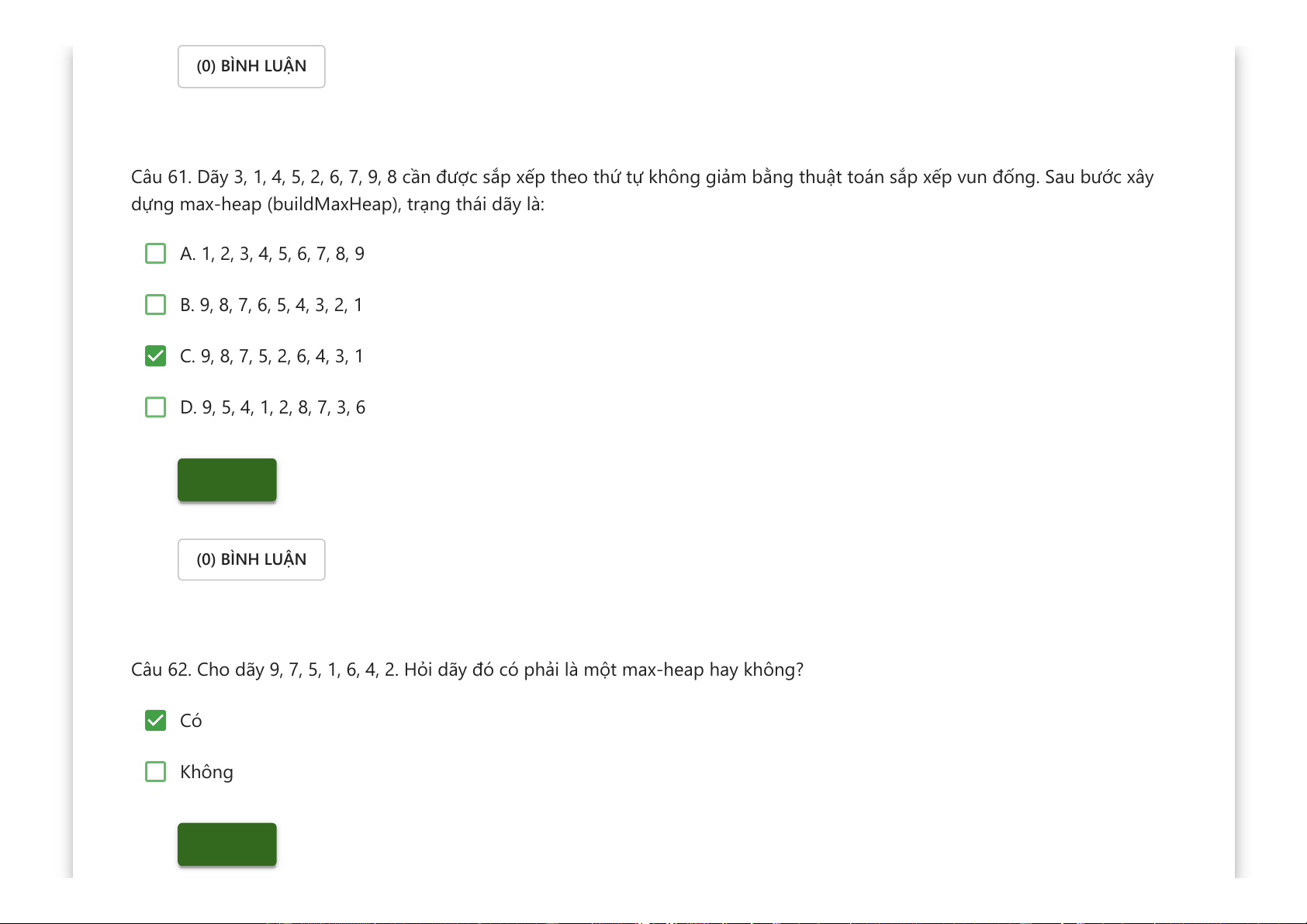
Câu 61. Dãy 3, 1, 4, 5, 2, 6, 7, 9, 8 cần được sắp xếp theo thứ tự không giảm bằng thuật toán sắp xếp vun đống. Sau bước xây
dựng max-heap (buildMaxHeap), trạng thái dãy là: A. 1, 2, 3, 4, 5, 6, 7, 8, 9 B. 9, 8, 7, 6, 5, 4, 3, 2, 1 C. 9, 8, 7, 5, 2, 6, 4, 3, 1 D. 9, 5, 4, 1, 2, 8, 7, 3, 6 Kiểm tra (0) BÌNH LUẬN
Câu 62. Cho dãy 9, 7, 5, 1, 6, 4, 2. Hỏi dãy đó có phải là một max-heap hay không? Có Không Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (1) BÌNH LUẬN
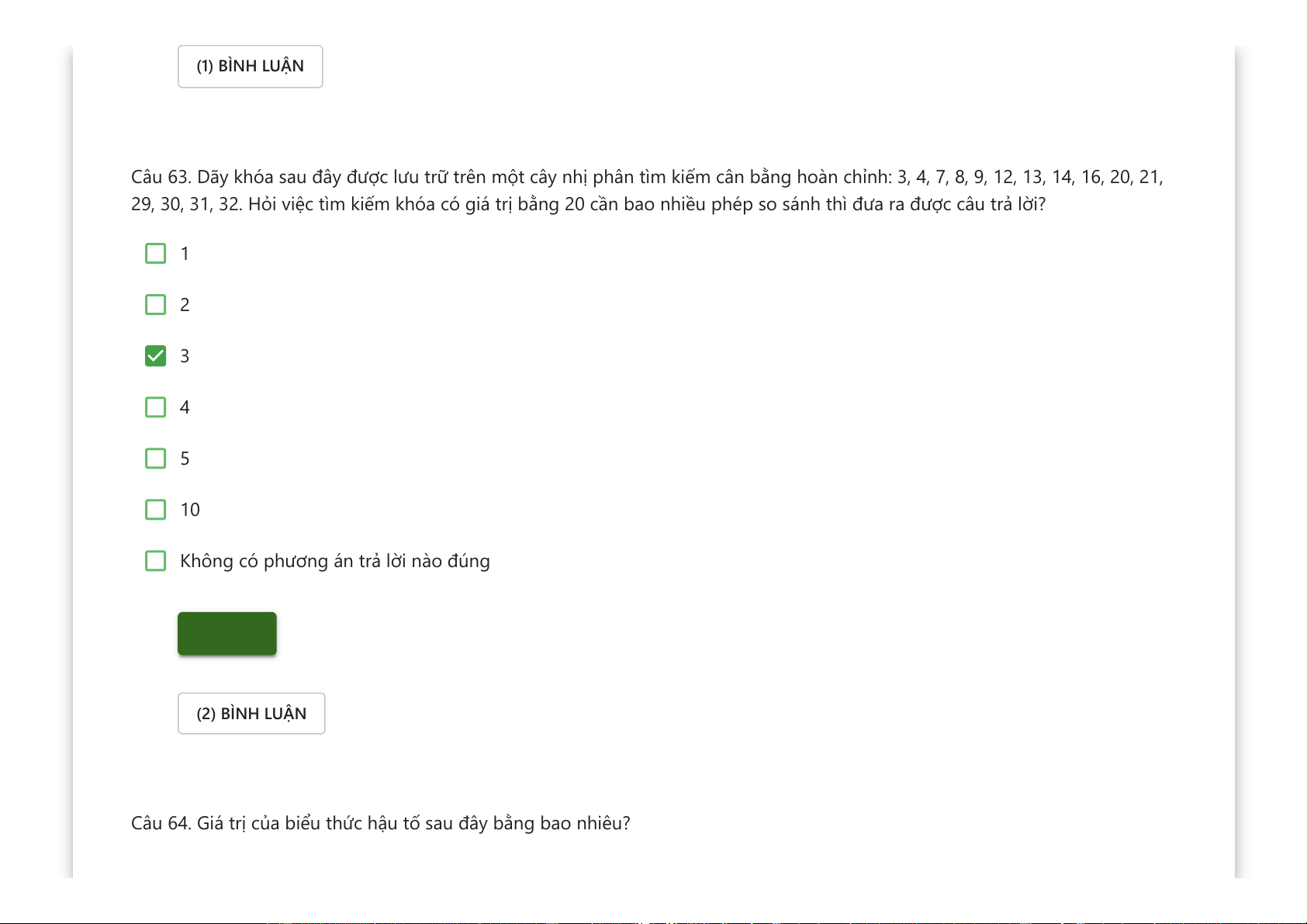
Câu 63. Dãy khóa sau đây được lưu trữ trên một cây nhị phân tìm kiếm cân bằng hoàn chỉnh: 3, 4, 7, 8, 9, 12, 13, 14, 16, 20, 21,
29, 30, 31, 32. Hỏi việc tìm kiếm khóa có giá trị bằng 20 cần bao nhiều phép so sánh thì đưa ra được câu trả lời? 1 2 3 4 5 10
Không có phương án trả lời nào đúng Kiểm tra (2) BÌNH LUẬN
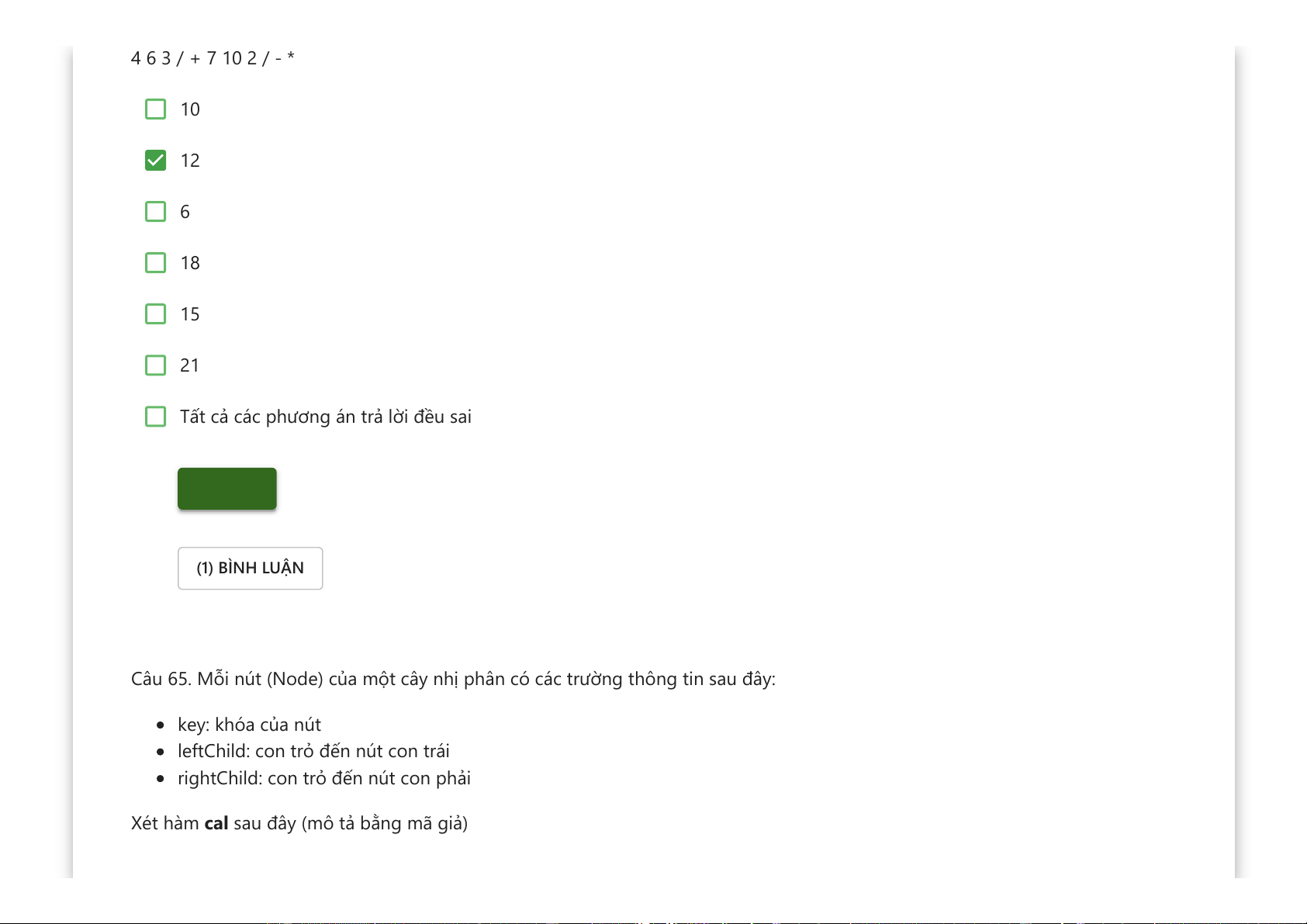
Câu 64. Giá trị của biểu thức hậu tố sau đây bằng bao nhiêu?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4 6 3 / + 7 10 2 / - * 10 12 6 18 15 21
Tất cả các phương án trả lời đều sai Kiểm tra (1) BÌNH LUẬN
Câu 65. Mỗi nút (Node) của một cây nhị phân có các trường thông tin sau đây: key: khóa của nút
leftChild: con trỏ đến nút con trái
rightChild: con trỏ đến nút con phải
Xét hàm cal sau đây (mô tả bằng mã giả)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 cal(Node r){ if r = NULL rreturn 0; h1 = cal(r.leftChild);
h2 = cal(r.rightChild); return max(h1,h2) + 1; }
Cho T là một cây nhị phân có cấu trúc như sau (giả định lấy khóa của nút đặt làm tên cho nút đó): Nút gốc là 6
Nút 6 có con trái là 1 và con phải là 9 Nút 1 có con phải là 4
Nút 9 có con trái là 7 và con phải là 8
Nút 4 có con trái là 2 và con phải là 5
Nút 8 có con trái là 3 và con phải là 10
Ký hiệu r là con trỏ trỏ đến nút 6 trên cây T. Hỏi lời gọi hàm cal(r) trả về kết quả bằng bao nhiêu? 3 2 4 5 6
Không có phương án trả lời nào đúng
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Kiểm tra (0) BÌNH LUẬN
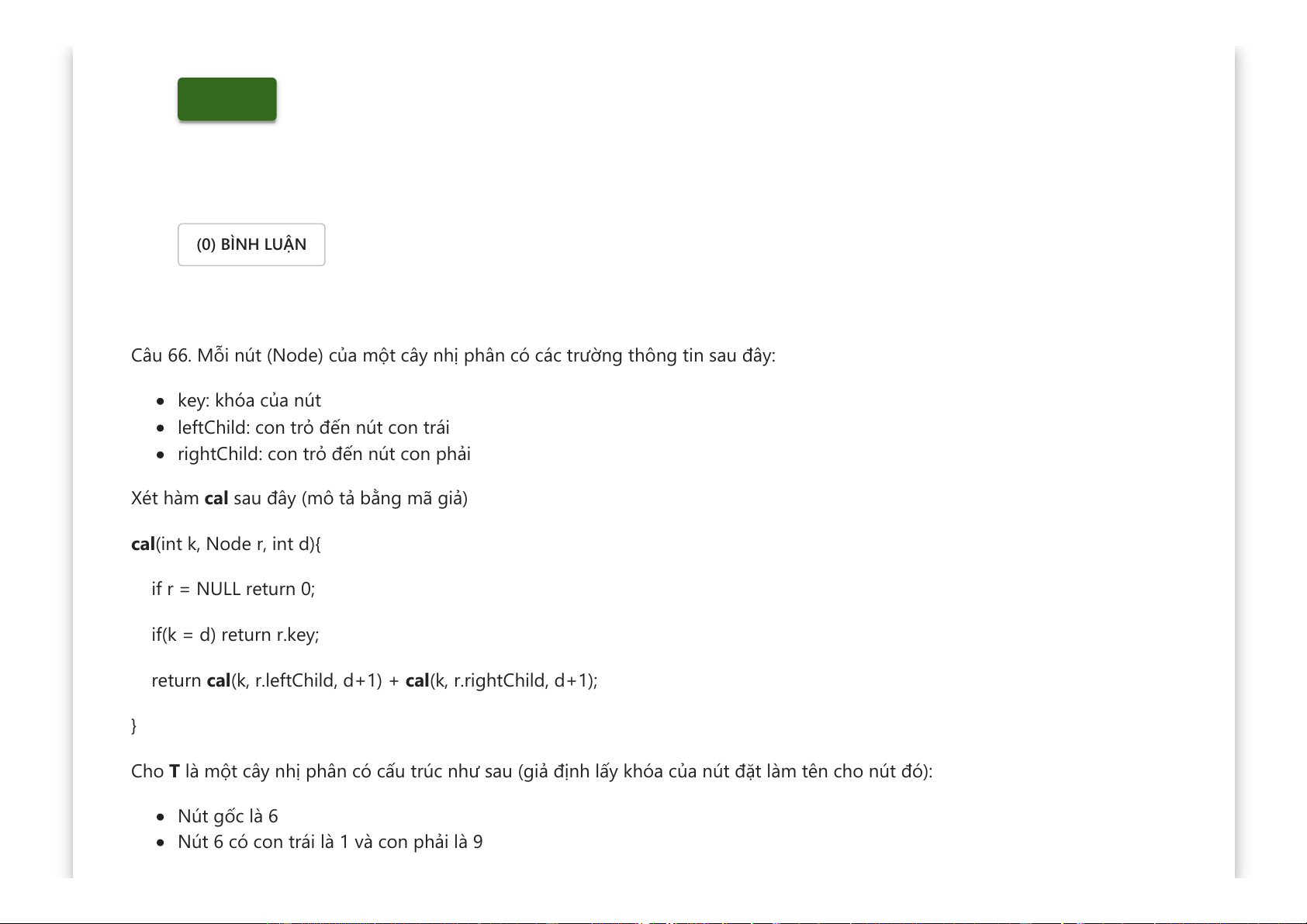
Câu 66. Mỗi nút (Node) của một cây nhị phân có các trường thông tin sau đây: key: khóa của nút
leftChild: con trỏ đến nút con trái
rightChild: con trỏ đến nút con phải
Xét hàm cal sau đây (mô tả bằng mã giả)
cal(int k, Node r, int d){ if r = NULL return 0; if(k = d) return r.key;
return cal(k, r.leftChild, d+1) + cal(k, r.rightChild, d+1); }
Cho T là một cây nhị phân có cấu trúc như sau (giả định lấy khóa của nút đặt làm tên cho nút đó): Nút gốc là 6
Nút 6 có con trái là 1 và con phải là 9
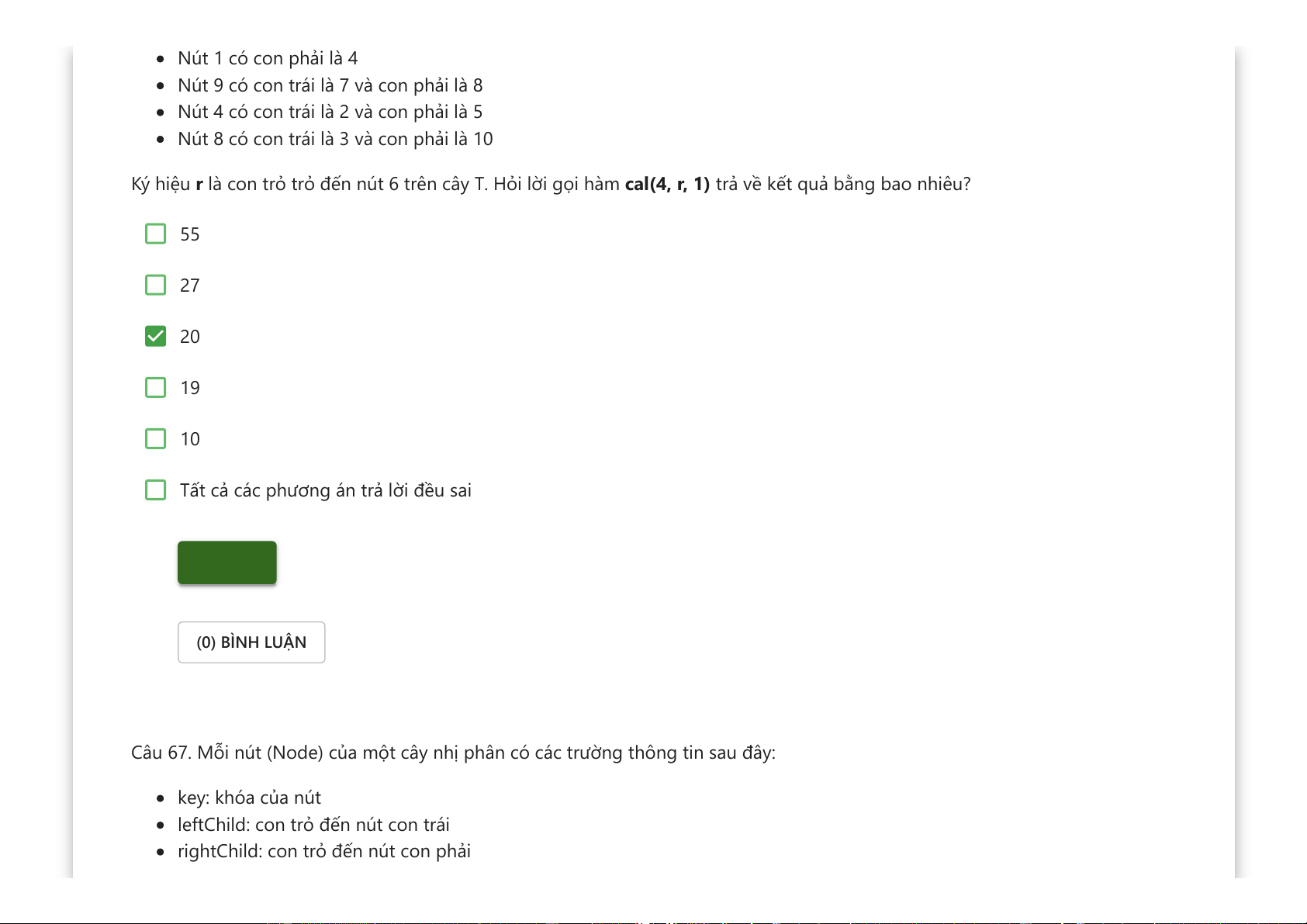
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Nút 1 có con phải là 4
Nút 9 có con trái là 7 và con phải là 8
Nút 4 có con trái là 2 và con phải là 5
Nút 8 có con trái là 3 và con phải là 10
Ký hiệu r là con trỏ trỏ đến nút 6 trên cây T. Hỏi lời gọi hàm cal(4, r, 1) trả về kết quả bằng bao nhiêu? 55 27 20 19 10
Tất cả các phương án trả lời đều sai Kiểm tra (0) BÌNH LUẬN
Câu 67. Mỗi nút (Node) của một cây nhị phân có các trường thông tin sau đây: key: khóa của nút
leftChild: con trỏ đến nút con trái
rightChild: con trỏ đến nút con phải
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Xét hàm cal sau đây (mô tả bằng mã giả)
cal(int k, Node r, int d){ if r = NULL return 0; if r.key = k return d;
d1 = cal(k, r.leftChild, d+1); if d1 > 0 return d1;
return cal(k, r.rightChild, d + 1); }
Cho T là một cây nhị phân có cấu trúc như sau (giả định lấy khóa của nút đặt làm tên cho nút đó): Nút gốc là 6
Nút 6 có con trái là 1 và con phải là 9 Nút 1 có con phải là 4
Nút 9 có con trái là 7 và con phải là 8
Nút 4 có con trái là 2 và con phải là 5
Nút 8 có con trái là 3 và con phải là 10
Ký hiệu r là con trỏ trỏ đến nút 6 trên cây T. Hỏi lời gọi hàm cal(5, r, 1) trả về kết quả bằng bao nhiêu? 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3 4 1 5
Tất cả các phương án trả lời đều sai Kiểm tra (0) BÌNH LUẬN
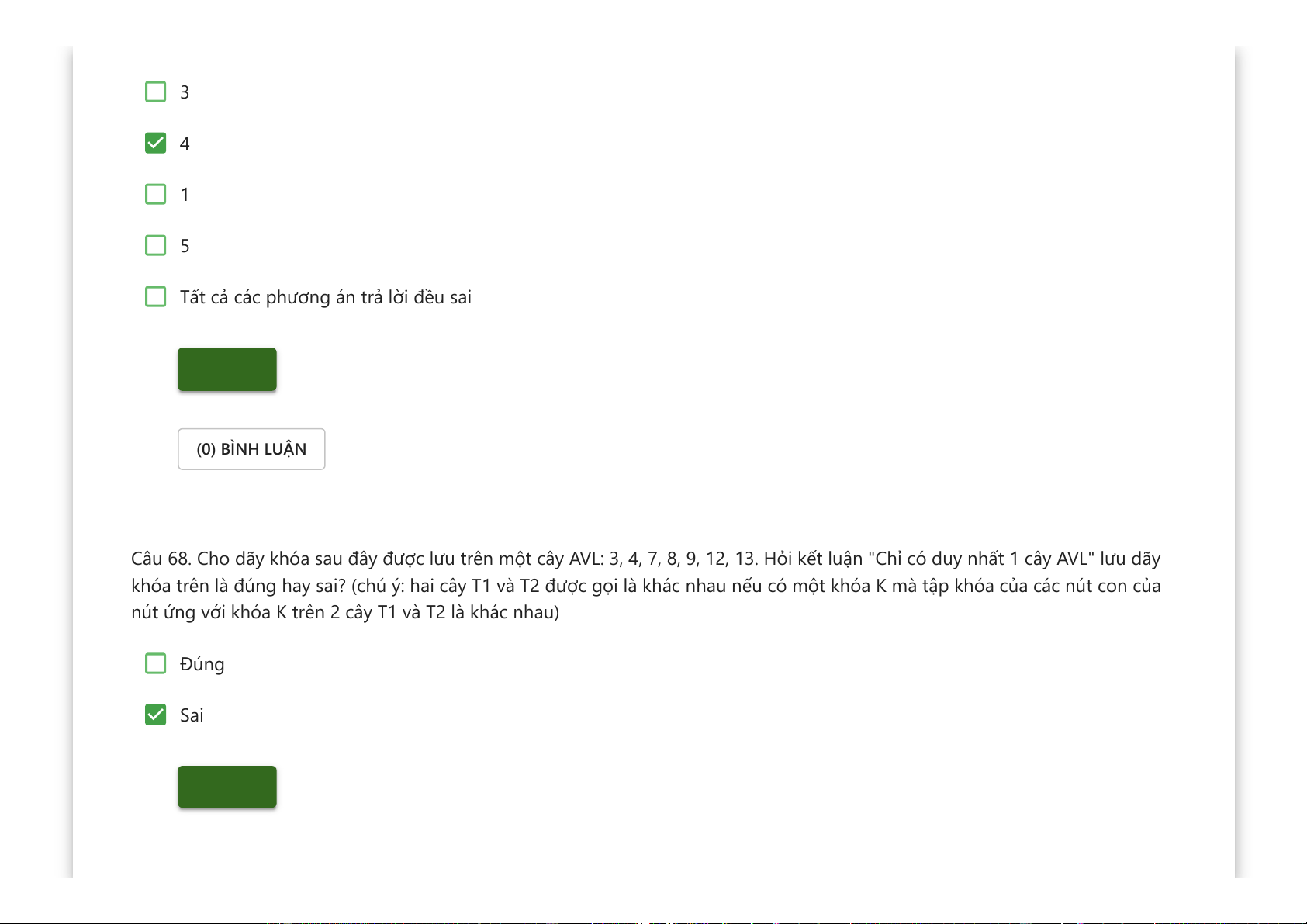
Câu 68. Cho dãy khóa sau đây được lưu trên một cây AVL: 3, 4, 7, 8, 9, 12, 13. Hỏi kết luận "Chỉ có duy nhất 1 cây AVL" lưu dãy
khóa trên là đúng hay sai? (chú ý: hai cây T1 và T2 được gọi là khác nhau nếu có một khóa K mà tập khóa của các nút con của
nút ứng với khóa K trên 2 cây T1 và T2 là khác nhau) Đúng Sai Kiểm tra
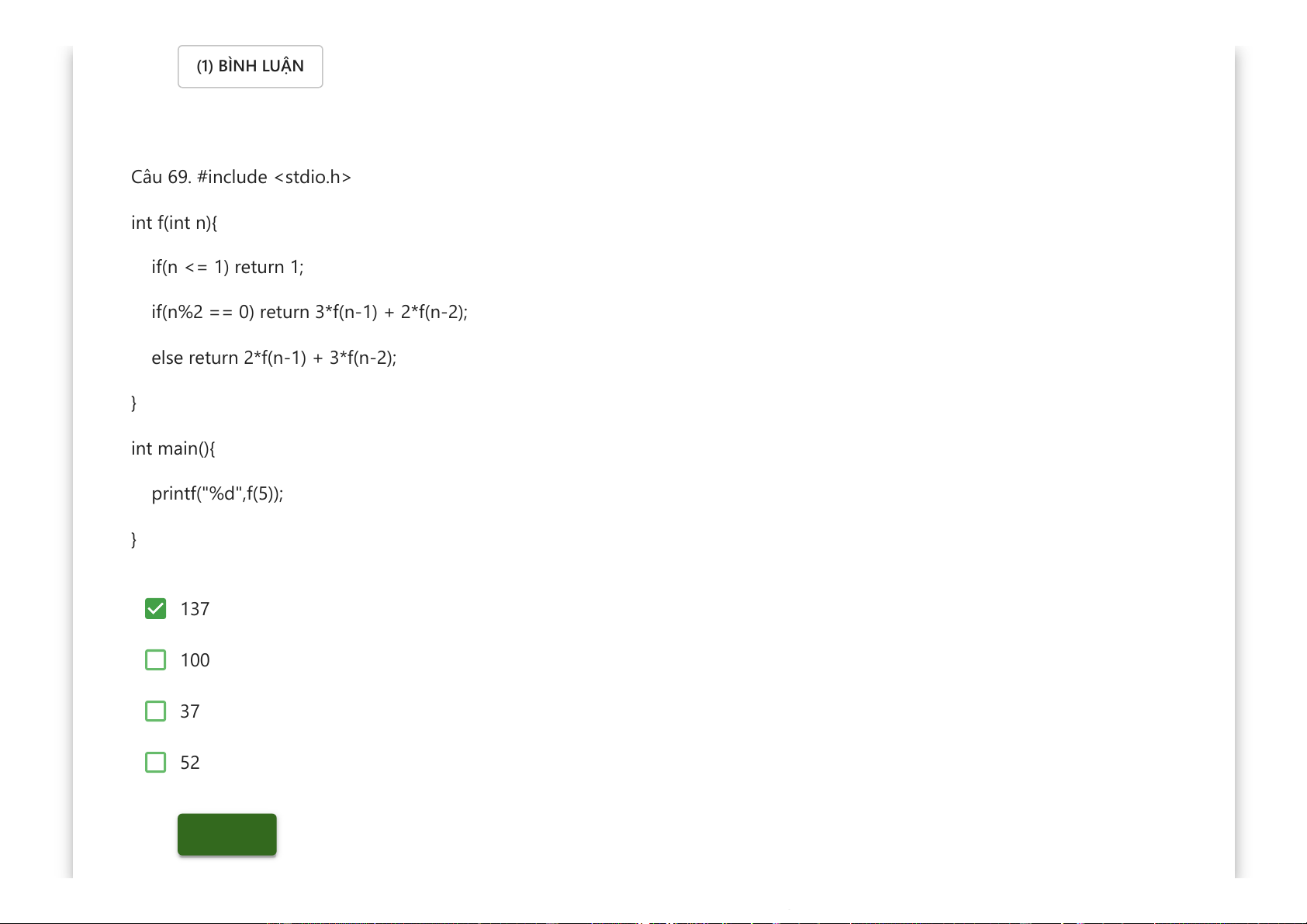
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (1) BÌNH LUẬN Câu 69. #include int f(int n){ if(n <= 1) return 1;
if(n%2 == 0) return 3*f(n-1) + 2*f(n-2);
else return 2*f(n-1) + 3*f(n-2); } int main(){ printf("%d",f(5)); } 137 100 37 52 Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
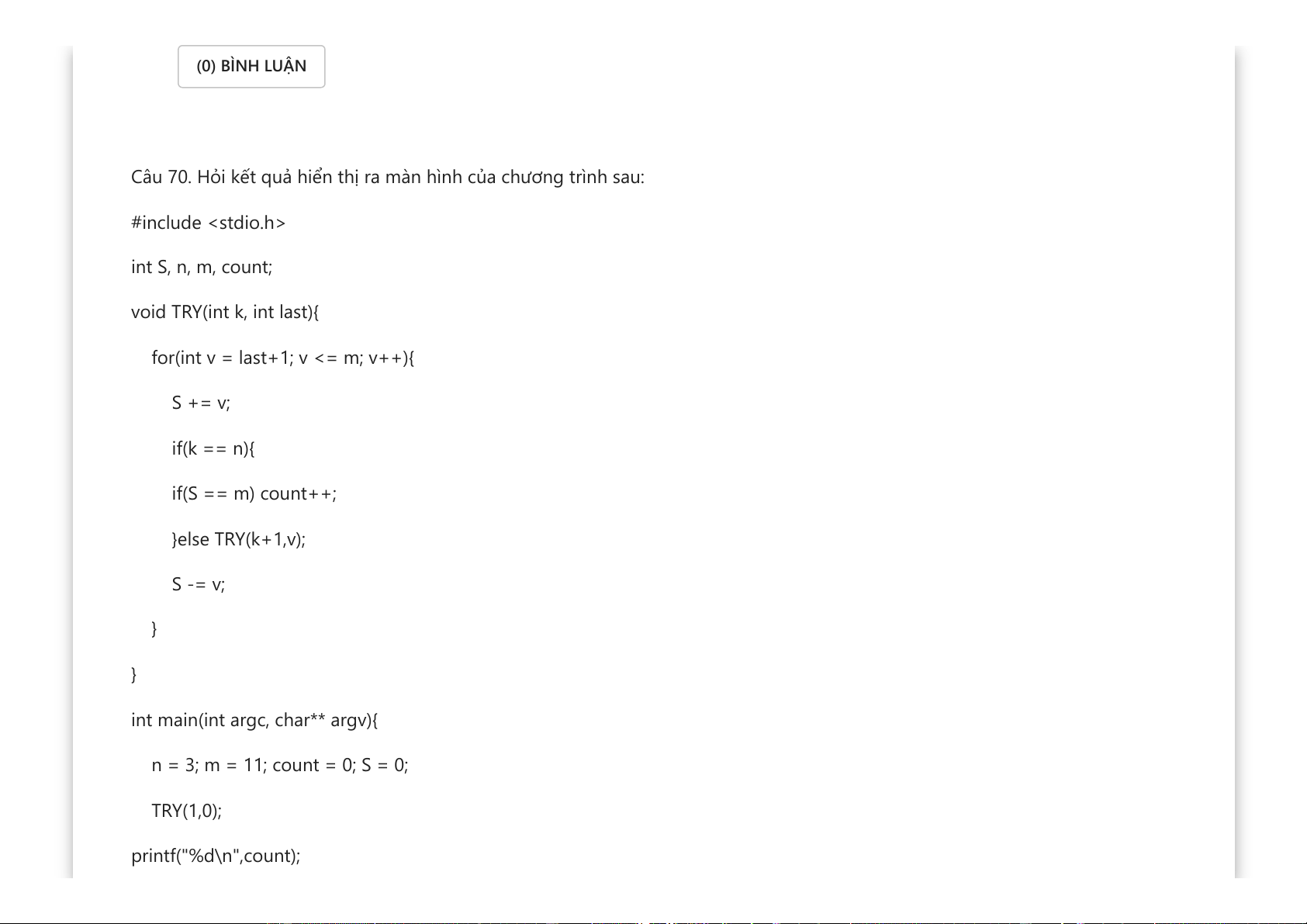
Câu 70. Hỏi kết quả hiển thị ra màn hình của chương trình sau: #include int S, n, m, count; void TRY(int k, int last){
for(int v = last+1; v <= m; v++){ S += v; if(k == n){ if(S == m) count++; }else TRY(k+1,v); S -= v; } }
int main(int argc, char** argv){
n = 3; m = 11; count = 0; S = 0; TRY(1,0); printf("%d\n",count);
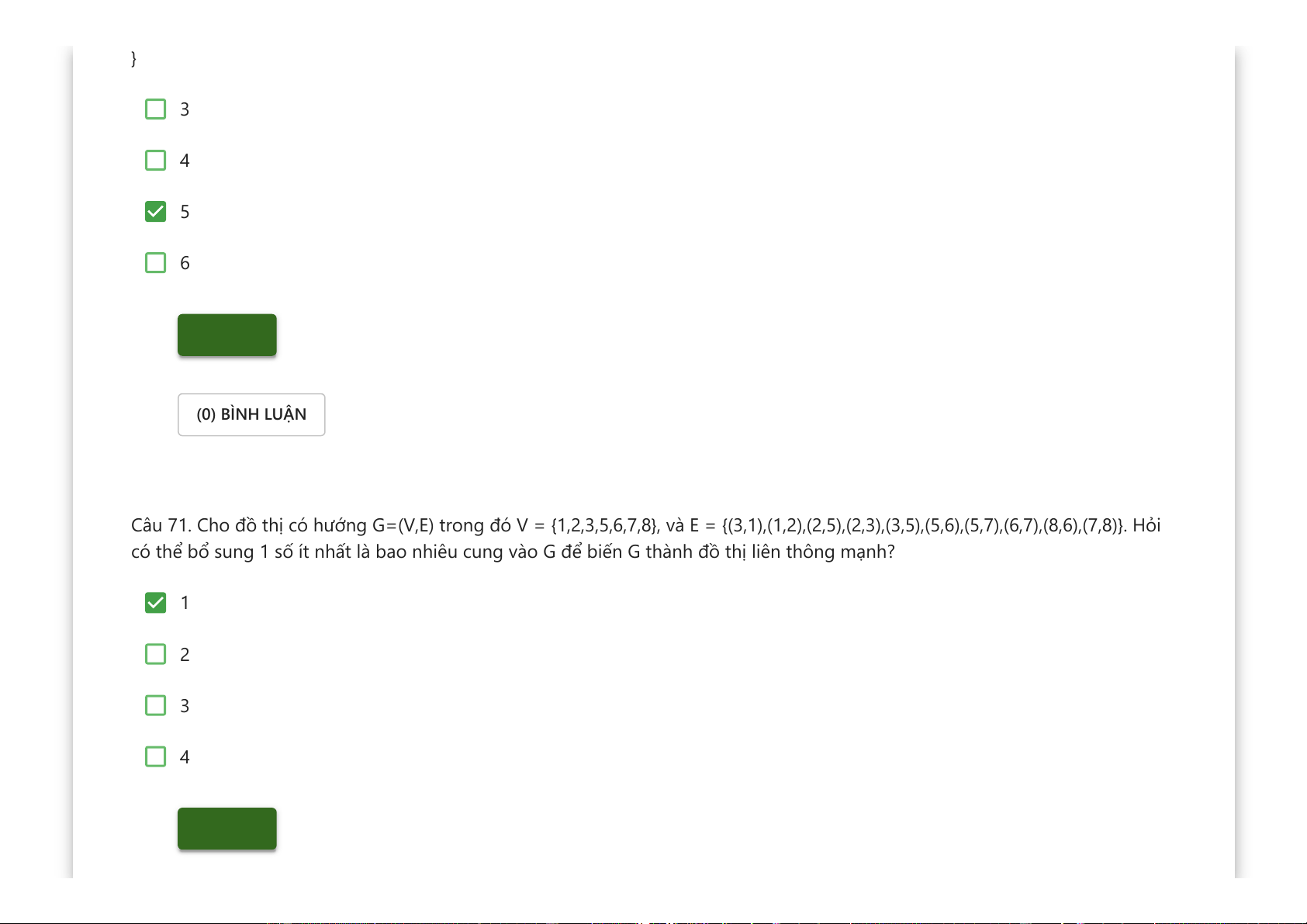
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 } 3 4 5 6 Kiểm tra (0) BÌNH LUẬN
Câu 71. Cho đồ thị có hướng G=(V,E) trong đó V = {1,2,3,5,6,7,8}, và E = {(3,1),(1,2),(2,5),(2,3),(3,5),(5,6),(5,7),(6,7),(8,6),(7,8)}. Hỏi
có thể bổ sung 1 số ít nhất là bao nhiêu cung vào G để biến G thành đồ thị liên thông mạnh? 1 2 3 4 Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (8) BÌNH LUẬN
Câu 72. PQ là một cấu trúc hàng đợi ưu tiên lưu trữ các phần tử dạng (id, k) trong đó id là định danh của phần tử và k là giá trị
khóa tương ứng. PQ được cài đặt theo cơ chế Min-Heap với các thao tác sau:
insertHeap(id, k): chèn một phần tử có định danh id và khóa bằng k vào PQ
upđate(id, k): cập nhật khóa của phần tử định danh id với giá trị khóa mới là k
deleteMin(): loại bỏ và trả về phần tử có khóa nhỏ nhất
PQ ban đầu rỗng, ta thực hiện liên tiếp dãy thao tác sau: insertHeap(1,6) insertHeap(2,5) insertHeap(3,3) insertHeap(4,7) insertHeap(5,4) insertHeap(6,10) insertHeap(7,2) insertHeap(8,9) insertHeap(9,1) deleteMin();
Hỏi kết luận nào sau đây là đúng ?
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 6 là con trái của phần tử định danh 7
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 6 là con phải của phần tử định danh 7
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 5 là con trái của phần tử định danh 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 5 là con phải của phần tử định danh 7
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 4 là con phải của phần tử định danh 3
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 4 là con trái của phần tử định danh 3
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 8 là con phải của phần tử định danh 3
Trên cây nhị phân biểu diễn PQ, phần tử có định danh 1 là con trái của phần tử định danh 3
Tất cả các phương án trả lời đều sai Kiểm tra (0) BÌNH LUẬN
Câu 73. Phát biểu "Mọi bài toán đều có thuật toán tham lam đưa ra lời giải chính xác" là đúng hay sai? SAI ĐÚNG Kiểm tra
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 (0) BÌNH LUẬN
Câu 74. Mỗi nút (Node) của một cây nhị phân có các trường thông tin sau đây: key: khóa của nút
leftChild: con trỏ đến nút con trái
rightChild: con trỏ đến nút con phải
Xét hàm cal sau đây (mô tả bằng mã giả) cal(Node r){ if r = NULL return 0;
if r.leftChild = NULL and r.rightChild = NULL return r.key;
return cal(r.leftChild) + cal(r.rightChild); }
Cho T là một cây nhị phân gốc được trỏ bởi con trỏ r có cấu trúc như sau (giả định lấy khóa của nút đặt làm tên cho nút đó):
Nút gốc (con trỏ r) là 6
Nút 6 có con trái là 1 và con phải là 9 Nút 1 có con phải là 4
Nút 9 có con trái là 7 và con phải là 8
Nút 4 có con trái là 2 và con phải là 5
Nút 8 có con trái là 3 và con phải là 10
p là con trỏ trỏ tới nút có khóa bằng 1. Hỏi lời gọi hàm cal(p) trả về kết quả bằng bao nhiêu?
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3 4 7 0 1 5 6
Tất cả các phương án đều sai Kiểm tra (0) BÌNH LUẬN
Câu 75. Mỗi nút (Node) của một cây nhị phân có các trường thông tin sau đây: key: khóa của nút
leftChild: con trỏ đến nút con trái
rightChild: con trỏ đến nút con phải
Xét hàm cal sau đây (mô tả bằng mã giả)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
cal(int k, Node r, int d){ if r = NULL return 0; if (k <= d)
return r.key + cal(k, r.leftChild, d+1) + cal(k, r.rightChild, d+1); else
return cal(k, r.leftChild, d+1) + cal(k, r.rightChild, d+1); }
Cho T là một cây nhị phân có cấu trúc như sau (giả định lấy khóa của nút đặt làm tên cho nút đó): Nút gốc là 6
Nút 6 có con trái là 1 và con phải là 9 Nút 1 có con phải là 4
Nút 9 có con trái là 7 và con phải là 8
Nút 4 có con trái là 2 và con phải là 5
Nút 8 có con trái là 3 và con phải là 10
Ký hiệu r là con trỏ trỏ đến nút 6 trên cây T. Hỏi lời gọi hàm cal(3, r, 1) trả về kết quả bằng bao nhiêu? 55 20 19 39 49
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Tất cả các phương án trả lời đều sai Kiểm tra (0) BÌNH LUẬN
Câu 76. Given two programs below: Prorgam 1 #include char* getMsg(){ char s[] = "hello"; return s; } int main(){ char* msg = getMsg(); printf("%s\n",msg); } -----
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Program 2 #include char* getMsg(){ char* s = "hello"; return s; } int main(){ char* msg = getMsg(); printf("%s\n",msg); } Which statements are correct?
Two programs give different results
Two programs give the same result Kiểm tra (0) BÌNH LUẬN
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 General Information Content Quiz Students Exercises Sessions Thông tin lớp Class Code : 0 Course Code : IT3011 Course Name
: Cấu trúc dữ liệu và thuật toán Class Type : LT+BT Teacher : admin Email :
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)