1. Mệnh đề: Cho biết phát biểu 1>3 là gì? A. Là một mệnh đề
B. Không phải là một mệnh đề C. Là một phép toán D. Là một câu hỏi
2. Mệnh đề: Phát biểu nào sau đây là một mệnh đề?
A. Đề nghị các em trật tự!
B. Số 3 là số nguyên tố. C. Có phải 3! là 6? D. X+a=0
3. Mệnh đề: X?Y là True, khi ít nhất X hay Y là True. Vậy dấu hỏi là phép gì? A. Tuyển B. Hội C. Phủ định D. Kéo theo
4. Mệnh đề: X?Y là True, khi phải cả hai X, Y là True. Vậy dấu hỏi là phép gì? A. Tuyển B. Hội C. Phủ định D. Kéo theo
5. Mệnh đề: X?Y là False, khi ít nhất X hay Y là False. Vậy dấu hỏi là phép gì? A. Tuyển B. Hội C. Phủ định D. Kéo theo
6. Tập hợp: ta có xA hay xB. Đây là phép toán nào? A. Hội B. Giao C. Hiệu D. Bù
7. Tập hợp: ta có xA và xB. Đây là phép toán nào? A. Hội B. Giao C. Hiệu D. Bù
8. Tập hợp: ta có xA và xB. Đây là phép toán nào? A. Hội B. Giao C. Hiệu D. Bù
9. Tập hợp: với A⸦U, ta có xU và xA. Đây là phép toán nào? A. Hội A B. Giao A C. Hiệu A D. Bù A
10. Tập hợp: ta có A={1,2,3,4} và B={3,4,5,6}. Cho biết kết quả của AUB? A. {3,4} B. {1,2,3,4,5,6} C. {1,2} D. {5,6} 11. (0.200 Point)
Đếm: Có 2 ôtô, 3 môtô, vậy có mấy cách chọn xe đi học ở DTU ? A. 6 B. 5 C. 1 D. 2/3
12. Đếm: Có 2 áo, 3 quần, ? có mấy cách chọn đồ đi học ở DTU ? A. 5 B. 2/3 C. 3/2 D. 6
13. Đếm: Pn=n!, đây là công thức đếm của loại nào sau đây ? A. Hoán vị lặp B. Hoán vị không lặp C. Chình hợp lặp D. Chỉnh hợp không lặp
14. Đếm:Pn=n!/(N1! x N2! x..x Nk!), đây là công thức đếm của loại nào sau đây ? A. Hoán vị không lặp B. Hoán vị lặp C. Chỉnh hợp không lặp D. Chỉnh hợp lặp
15. Đếm:A(n,k)= n! / (n-k)!, đây là công thức đếm của loại nào sau đây ? A. Hoán vị không lặp B. Hoán vị lặp C. Chỉnh hợp không lặp D. Chỉnh hợp lặp
16. Đồ thị: deg(u)=0, u được gọi là đỉnh gì ? A. Đỉnh treo B. Đình kề C. Đỉnh đa cạnh D. Đỉnh cô lập
17. Đồ thị: deg(u)=1, u được gọi là đỉnh gì ? A. Đỉnh treo B. Đỉnh kề C. Đỉnh đa cạnh D. Đỉnh cô lập
18. Đồ thị: công thức nào sau đây đúng ? A. Sum(deg(u))= Sum(e) B. 2 x Sum(deg(u))=2 x Sum(e)
C. Sum(deg(u)) = 2 x Sum(e) D. 2 x Sum(deg(u))=Sum(e)
19. Đồ thị: công thức nào sau đây đúng ?
A. Sum(deg+(u)) + Sum(deg-(u)) =e B. Sum(deg+(u)) = Sum(deg-(u)) = e
C. Sum(deg+(u)) x Sum(deg-(u)) = 2 x e D. Sum(deg+(u)) Sum(deg-(u)) e
20. Đồ thị: bậc của cạnh khuyên được tính bao nhiêu ? A. 2 x deg(u) B. deg(u) / 2 C. deg(u) D. deg(u) - 1
21. Tập hợp: cho A={1,2}, B={1,2,3}, C={2,1}. Hãy tính A hợp B, A giao B và A-B?
22. Tập hợp: có luật A∪(B∪C)=(A ∪
∪B)∪C, hãy cho biết đây là luật nào?
23. Mệnh đề: Cho a=0, b=1. Hãy tính a ∧ b, a ∧ b, a ∨
⊕ b, a → b, a ↔ b ?
24. Mệnh đề: Có luật p ∧ 1 ∧ ⇔ p; p ∨ 0 ∨
⇔ p. Hãy cho biết đây là luật nào ?
25. Đếm: Có 30SV, có mấy cách bầu 3SV làm BT, PBT, UV ?
26. Đếm: Có mấy số nhị phân có độ dài 7 bit ?
27. Cho A,B⸦U. chứng minh A⸦BB⸦A (gạch chân là bù x) ?
28. Hãy lập bảng chân trị để chứng minh ¬ (a b) ≡ (¬ a ¬ b) ?
29 Có 30 sinh viên, có mấy cách bầu 3 sinh viên làm BT, PBT, UV ?
30. Hãy viết hàm đệ quy in ma trận n x n số nguyên ?
31. Công thức nào sau đây có thể tạo ra chuỗi 5, 9, 13, 17, 21, . . . A. an = 2n + 1. B. an = 4n + 1. C. an = 4n + 3. D. an = 4n - 1.
32. Hoán vị kế tiếp của dãy 5 4 6 3 2 1 là: A. 4 5 6 3 2 1 B. 5 6 4 3 2 1 C. 5 6 1 2 3 4 D. 6 5 1 2 3 4
33. Chuỗi nhị phân liền sau chuỗi 11011111 là: A. 11011110 B. 10111111 C. 11111111 D. 11100000
34. Sắc số (số màu tối thiểu để tô các đỉnh) của đồ thị dưới đây là: A. 2 B. 3 C. 4 D. 6
35. Phải chọn ít nhất bao nhiêu quân bài trong bộ bài để luôn có được 3 quân bài cùng nước (cơ, rô, chuồn, bích)? A. 3 B. 9 C. 7 D. 13
36. Một hộp đựng 4 bi xanh và 5 bi đỏ. Xác suất lấy ngẫu nhiên 1 viên bi xanh từ hộp là: A. 4/5 B. 5/9 C. 4/9 D. Tất cả đều sai
37. Mỗi thành viên trong câu lạc bộ thể thao có quê ở 1 trong 20 tỉnh thành. Hỏi cần phải tuyển
bao nhiêu thành viên để đảm bảo có ít nhất 4 người cùng quê? A. 81 B. 80 C. 101 D. Tất cả đều sai
38. Số xâu gồm ba chữ số thập phân, bắt đầu chữ số lẻ là: A. 1000 B. 550 C. 500 D. Tất cả đều sai
39. Phương trình x + y + z = 15 có số nghiệm nguyên không âm và x>=1 là: A. 100 B. 136 C. 120 D. 45
40. Số xâu nhị phân độ dài 10 bắt đầu bằng 3 bit 0 hoặc kết thúc bằng 2 bit 0 là: A. 352 B. 1024 C. 512 D. Tất cả đều sai
41. Phương trình sau có bao nhiêu nghiệm nguyên không âm?x + y + z = 11 A. 33 B. 78 C. 190 D. Tất cả đều sai
42. Số đỉnh bậc lẻ trong đồ thị luôn là: A. 2 B. 4 C. Số chẵn D. Tất cả đều sai
43. Dùng thuật toán Prim, chúng ta có thể:
A. Tìm cây khung nhỏ nhất của đồ thị B. Tìm được đường đi ngắn nhất giữa các đỉnh trong đồ thị
C. Kiểm tra tính liên thông của đồ thị D. Câu A và câu C đúng
44.mĐồ thị G liên thông, gồm n đỉnh thì số thành phần liên thông của đồ thị là: A. n B. 0 C. 1 D. Tất cả đều sai
45. Số số nguyên dương không lớn hơn 1000 chia hết cho 7 hoặc 11 là: A. 232 B. 230 C. 220 D. Tất cả đều sai
46. Cho tập S = {a, b, c}. Số tập con của tập S là: A. 3 B. 9 C. 6 D. 8
47. Nếu tập A = {1, 2} và tập B = {a, b} thì tích Cartesian của hai tập A và B là:
A. {(1, a), (1, b), (2, a), (b, b)}
B. {(1, 1), (2, 2), (a, a), (b, b)}
C. {(1, a), (2, a), (1, b), (2, b)}
D. {(1, 1), (a, a), (2, a), (1, b)}
48. Tập nào dưới đây là tập con của {1, 2, 3, 4}? A. {1, 2} B. {1, 2, 3} C. {1} D. Tất cả đều đúng 49. Chứng minh:
50. Khử phép kéo theo cho biểu thức logic α = (P - > Q) - -->R
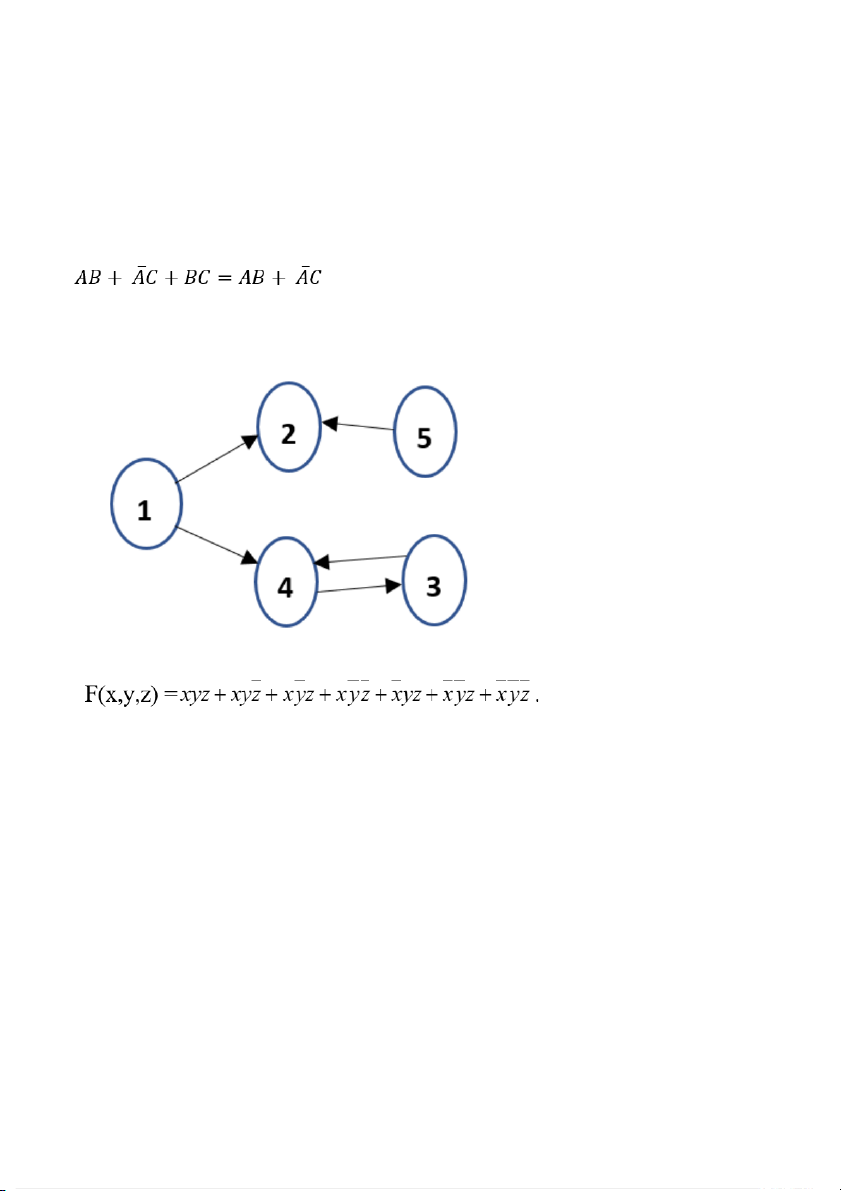
51. Biều diễn đồ thị sau đây bằng ma trận kề:
52. Rút gọn hàm bool sau:
53. Cho biết số lần chuyển đĩa trong bài toán Tháp Hà Nội, với số đĩa là 10.
55. Có 1 nhóm 10 sinh viên, cần chọn ra 3 bạn để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn
A. Tổ hợp chập 3 của 10 B. 3 * 10
C. Chỉnh hợp chập 3 của 10
D. chỉnh hợp lặp chập 3 của 10
56. từ tập {1, 2, 3, 4 }. có thể lập bao nhiêu số tự nhiên có 4 chữ số khác nhau A. 24 B. 12 C. 16 D. 32
57. Dãy bit tiếp sau của dãy 10010011 trong thuật toán liệt kê tất cả các xâu nhị phân có độ dài 8
bằng phương pháp sinh. A. 10010100 B. 10011000 C. 10110011 D. 10010111
58. Hoán vị tiếp sau của hoán vị 564321 trong thuật toán liệt kê các hoán vị 6 số tự nhiên đầu
tiên bằng phương pháp sinh. A. 612345 B. 512346 C. 654321 D. 614325
59. Câu nào sau đây là mệnh đề A. Số 12 là số lẻ B. Bạn đi đâu?
C. Bạn học trường nào? D. Hoa hồng đẹp qúa
60. cho tập A={3,5,7,4}. Hãy tìm tập con tiếp theo của tập {5,4} trong thuật toán liệt kê tất cả các
tập con khác rỗng bằng phương pháp sinh (dựa trên phương pháp liệt kê tất cả các dãy nhị phân 4 bit) A. {5,7} B. {3,5} C. {7, 3, 5} D. {3,7} 61.
Có bao nhiêu số có 4 chữ số chia hết 5 A. 1800 B. 2000 C. 1600 D. 1900
62. Tập hợp {Ø, {1}, {{2}}, {1, {2}}} là tập lũy thừa của tập nào sau đây? A. {1, 2} B. {1, {2}} C. {{1}, 2} D. {{1,2}}
63. Có bao nhiêu cách chọn ba bạn sinh viên trong số 7 bạn đi dự hội thảo? A. 45 B. 35 C. 50 D. 30
64. Xác định chân trị của biểu thức (x y) (y z) và (x z) khi x = y = z = 1? A. 0 và 0 B. 1 và 1 C. 0 và 1 D. 1 và 0
65. Hoán vị nào sau đây đứng liền sau hoán vị 1 2 4 3 theo thuật toán sinh A. 2145 B. 2143 C. 1342 D. 1324
66. Dãy 1235 là tổ hợp chập 4 của 6 phần tử, cấu hình đứng liền trước của dãy này theo thuật toán sinh là: A. 1234 B. 2134 C. 1243 D. 2145
67. Cho tập A gồm 5 phần tử. Số tập con của tập A là A. 32 B. 16 C. 36 D. 64
14. Một dãy XYY. Trong đó X có thể gán một trong 10 chữ số thập phân. Y có thể gán một trong
68 chữ cái. Có bao nhiêu dãy được thành lập theo cách trên: A. 6760 B. 6762 C. 6765 D. 6767
69. Có bao nhiêu cách biểu diễn khác nhau đối với xâu nhị phân có độ dài 8 bit A. 64 B. 128 C. 512 D. 256
70. Để có 5 bạn sinh viên có cùng 1 điểm thi (điểm nguyên). Hỏi phải cần tối thiểu bao nhiêu sinh viên tham dự thi A. 50 B. 55 C. 45 D. 41
71.Biểu thức rút gọn của f(x,y,z) = xyz + XYz + xYZ + XYZ + xYz ( với Z là bù z) A. x + Y z B. Xz + Y C. xz + Y D. XYz
72. Giả sử A = (3,7,5,4) là một hoán vị hiên tại của tập {3,5,7,4}, bộ nào sau đây là hoán vị tiếp
theo của hoán vị A trong thuật toán liệt kê hoán vị bằng phương pháp sinh. A. (3,5,7,4) B. (3,4,7,5) C. (3,7,4,5) D. (3,4,5,7)
73. Đồ thị đủ Kn là đồ thị đơn vô hướng có n đỉnh. Bậc của mỗi đỉnh là: A. n + 1 B. n - 1 C. 2(n+1) D. 2n
74. Biểu thức rút gọn của f(x,y) = xY + Xy + XY ( với Z là bù z) A. x + y B. X + y C. x + Y D. X + Y
75. Cho tập A={7, 9, 6, 4, 5}, hãy tìm hoán vị tiếp theo của hoán vị {6,9,5,7, 4} trong thuật toán
liệt kê tất cả các hoán vị của tập A bằng phương pháp sinh
76. Dãy nhị phân tiếp theo của dãy 11011111 trong thuật toán liệt kê tất cả các dãy nhị phân 8
bit bằng phương pháp sinh
77. Cho biết số nghiệm nguyên không âm của phương trình x + y + z = 25, trong trường hợp: x 0, y 0, z 2
78. Có 1800 sinh viên, trong đó có 450 sinh viên học Toán, 550 sinh viên học tin, và 300 sinh viên
học 2 môn. Hỏi có bao nhiêu sinh viên không học môn nào
79. Có bao nhiêu cách xếp 6 nam và 4 nữ thành hang ngang sao cho không có 2 nữ đứng gần nhau
80. Tìm nghiệm của hệ thức truy hồi sau: an= 4an-2 với n ³ 2, a0=0, a1=4
81. Cho một đơn đồ thị, viết chương trình kiểm tra đồ thị có bao nhiêu thành phần liên thông Yêu cầu:
1. Nêu ý tưởng để giải quyết bài toán
2. Nêu thuật toán để thực hiện 3. Code
82. Cho tập E = {2, 4, 6, 8}. Giả sử tập con A = {2, 4, 6} là cấu hình hiện tại trong thuật toán liệt
kê tổ hợp chập 3 của 5 phần tử trên E bằng phương pháp sinh. Tập con nào sau đây là tập sinh kế tiếp sau A. A. {2, 4, 8} B. {4, 6, 8} C. {6, 2, 4} D. {2, 6, 8}
83.Giả sử A = (3, 7, 5, 9) là một hoán vị hiên tại của tập {3, 5, 7, 9}, bộ nào sau đây là hoán vị tiếp
theo của hoán vị A trong thuật toán liệt kê hoán vị bằng phương pháp sinh. A. (3, 9, 7, 5) B. (3, 5, 9, 7) C. (3, 7, 9, 5) D. (3, 9, 5, 7)
84. Dãy bit tiếp sau của dãy 10010111 trong thuật toán liệt kê tất cả các xâu nhị phân có độ dài 8
bằng phương pháp sinh. A. 10010100 B. 10011000 C. 10110011 D. 10011000
85. Công thức truy hồi nào sau đây có thể tạo ra chuỗi 7, 11, 15, 19, 23, … với n là một số nguyên dương. A. a(n) = 2n + 5. B. a(n) = 4n + 3. C. a(n) = 4n + 1. D. a(n) = 4n - 1.
86. Có năm loại học bổng khác nhau. Hỏi rằng phải có ít nhất bao nhiêu sinh viên để chắc chắn
rằng có ít nhất là 7 người cùng nhận học bổng như nhau. A. 32 B. 30 C. 31 D. 29
87. Cho đồ thị vô hướng G=(V, E) có n đỉnh, mỗi đỉnh đều có cạnh nối đến các đỉnh còn lại, phát
biểu nào sau đây là đúng nhất:
A. Ma trận kề biểu diễn đồ thị G là một ma trận vuông kích thước 2n.
B. Tổng số cạnh của đồ thị là n(n-1)/2.
C. Các giá trị trên đường chéo chính của ma trận kề biểu diễn đồ thị G luôn bằng 1.
D. Đồ thị G là đồ thị không liên thông.
88. Tập A={1, 2, 3, 4, 5, 8} có bao nhiêu tập con A. 64 B. 8 C. 32 D. 128
89. Đồ thị đủ Kn là đồ thị đơn vô hướng có n đỉnh. Bậc của mỗi đỉnh là: A. 2n B. n + 1 C. n 1 – D. 2(n+1)
90. Có bao nhiêu cách lấy ra 7 viên bi từ 3 loại bi xanh, bi đỏ, và bi vàng. Mỗi loại hiện có nhiều hơn 7 viên bi. A. 36 B. 45 C. 50 D. 65
91. Có bao nhiêu cách biểu diễn khác nhau đối với xâu nhị phân độ dài 10 bit A. 512 B. 2048 C. 1024 D. 256
92. Dãy 1-3-4-5 là tổ hợp chập 4 của 6 phần tử trong tập {1, 2, 3, 4, 5, 6} , cấu hình đứng liền
trước của dãy này theo thuật toán sinh là: A. 2-1-3-4 B. 1-2-4-3 C. 1-2-5-6 D. 2-1-5-6
93.Hoán vị nào sau đây đứng liền sau hoán vị 1-3-4-2 theo thuật toán sinh A. 2-1-4-5 B. 1-4-2-3 C. 2-1-4-3 D. 3-1-4-2
94. Một nhóm có 9 bạn sinh viên gồm 4 nữ và 5 nam. Hỏi có bao nhiêu cách chọn 3 bạn đi dự hội
thảo?Biết rằng trong số 3 bạn đi dự có ít nhất một nam. A. 75 B. 80 C. 85 D. 90
95. Một nhóm có 8 bạn sinh viên gồm 3 nữ và 5 nam. Hỏi có bao nhiêu cách bầu một trưởng
nhóm, một phó nhóm và một thủ quĩ? Không ai trong các bạn được bầu giũ chức danh kiêm nhiệm. A. 336 B. 312 C. 432 D. 286
96. Có bao nhiêu cách chọn ba bạn sinh viên trong số 7 bạn đi dự hội thảo? A. 45 B. 50 C. 30 D. 35
97.Có bao nhiêu cách bầu một trưởng đoàn, một phó đoàn và một thủ quỹ từ một nhóm có 6
người? Không ai trong số những người được bầu có chức danh kiêm nhiệm. A. 115 B. 120 C. 130 D. 135
98. Đồ thị đơn G = (V, E) có n đỉnh và m cạnh, ma trận kề biểu diễn đồ thị G có kích thước A. m x m B. m x n C. n x n D. 2(m + n)
99 . Cho x, y, z là các biến logic và x’, y’, z’ là các giá trị bù của 3 biến đó. Chọn phát biểu ĐÚNG: A. xy + x’ = x B. (x + y)’ = x’ + y’ C. (x.y)’ = x’ + y’ D. xy + zy = x + z’ + y
100. Chọn phát biểu SAI:
A. Đồ thị đầy đủ Kn là đồ thị Haminton.
B. Đồ thị Haminton là đồ thị có chu trình đi qua mỗi đỉnh của đồ thị một lần
C. Đồ thị vòng n đỉnh Cn có bậc của mỗi đỉnh là 2.
D. Đồ thị Euler là đồ thị có đường đi qua mỗi cạnh của đồ thị một lần.
101.Chọn phát biểu ĐÚNG:
A. Giải thuật duyệt đồ thị theo chiều rộng (BFS) không thể giúp tìm ra đường đi giữa 2 đỉnh của đồ thị liên thông.
B. Giải thuật Dijkstra là giải thuật kiểm tra đồ thị có phải là đồ thị nửa Euler.
C. Cây khung tối thiểu có thể tìm được bằng giải thuật duyệt theo chiều sâu (DFS).
D. Có thể tìm ra đường đi giữa 2 đỉnh bằng giải thuật duyệt theo chiều sâu (DFS)
102. Nêu định nghĩa chu trình Euler.
103: Nêu định nghĩa đồ thị nửa Haminton.
104: Phương trình X1+X2+X3+X4+X5 = 11 có bao nhiêu nghiệm nguyên dương (Xi>0)?
105: Giải hệ thức truy hồi: a(n) = 3a(n-1) 2a(n- –
2), với a(0) =2 và a(1) = 3.
106. Cho x, y là các biến logic và x’, y’ là các giá trị bù của 3 biến đó. Chứng minh biểu thức (x’y + x) và (x + y)
107. Cho x, y, z là các biến logic và x’, y’, z’ là các giá trị bù của 3 biến đó. Hãy thu gọn và thiết
kế mạch logic cho hàm f(x, y, z) = x’y’z’ + x’yz’ + xyz’ + xy’z’ + xyz. 108 .
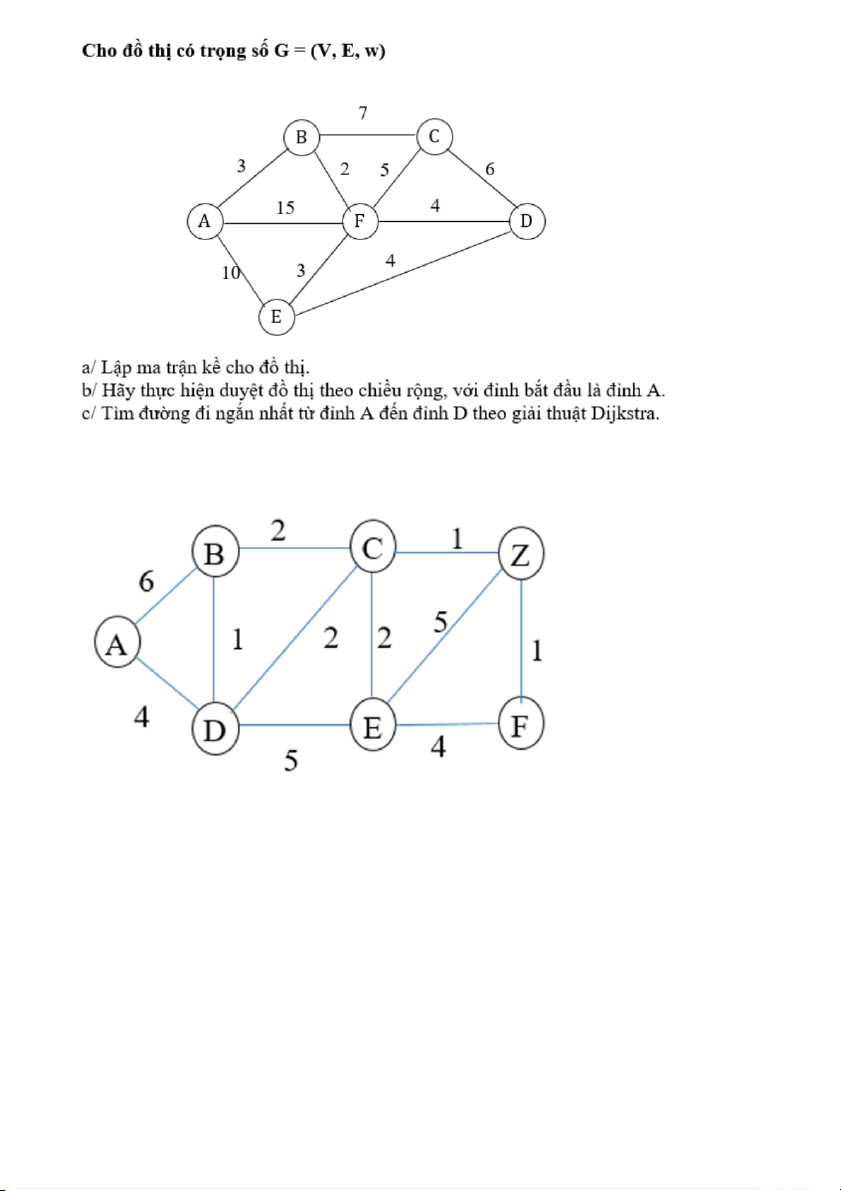
109. Thực hiện các yêu cầu sau:
a Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại của đồ thị, theo thuật toán Dijkstra
(thể hiện các bước chạy thuật toán, cập nhật nhãn các đỉnh).
b Viết thuật toán kiểm tra có đường đi từ đỉnh u đến đỉnh v trong đồ thị vô hướng G hay không?
c. Giải hệ thức truy hồi sau: ao = 5, a1 = 8... an=3an-1 - 2an-2
110. Tìm cây phủ nhỏ nhất của đồ thị âu 109 b ở c
ằng thuật toán Prim