





























Preview text:
CHUÛ ÑEÀ
TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ VAØ ÖÙNG DUÏNG 7. Baøi 01
GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT GOÙC BAÁT KYØ TÖØ 0 0 ÑEÁN 0 180 1. Định nghĩa
Với mỗi góc α ( 0 0
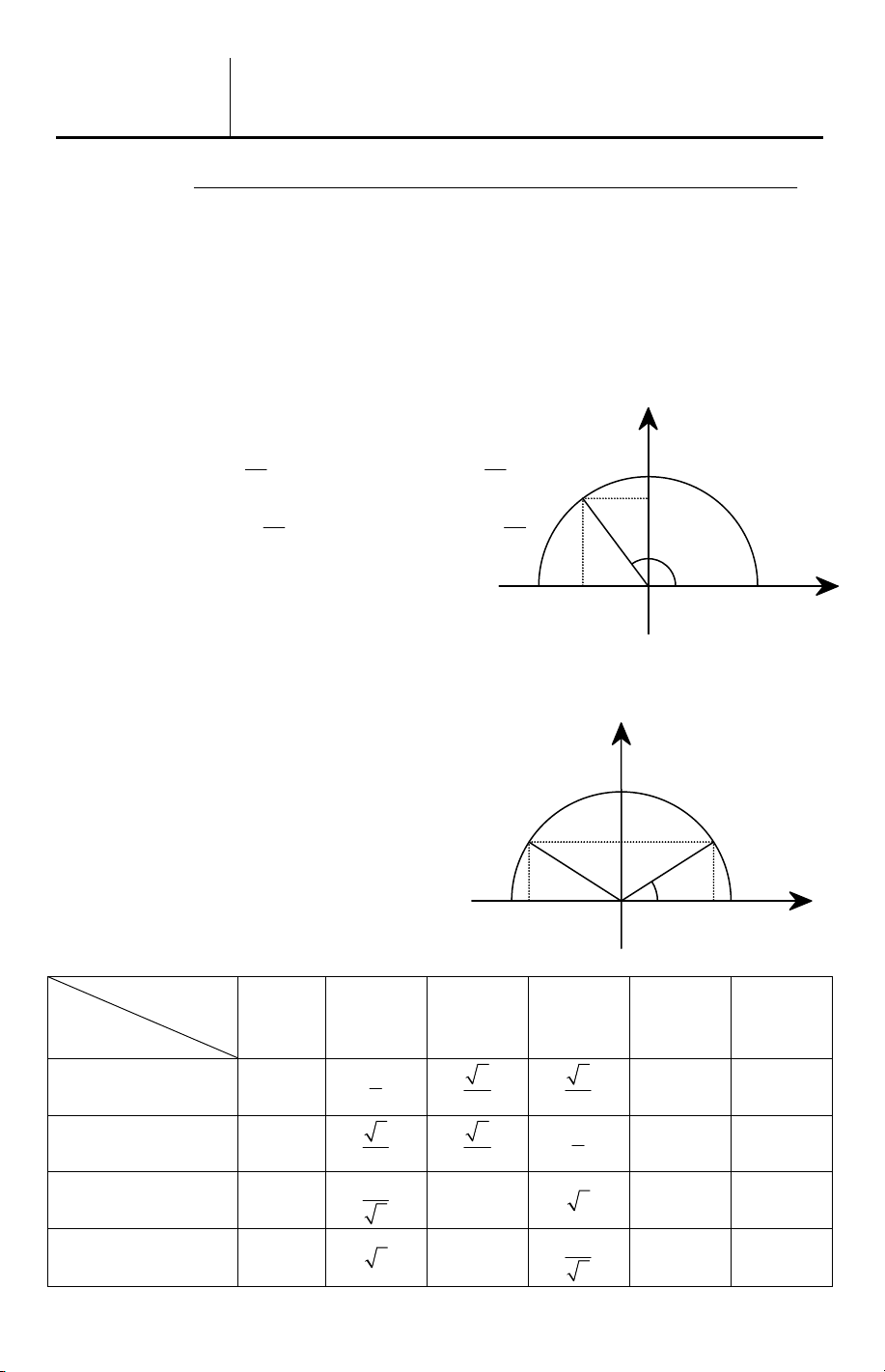
0 ≤ α ≤ 180 ) ta xác định một điểm M trên nửa đường tròn đơn vị
sao cho xOM = α và giả sử điểm M có tọa độ M (x ; y . Khi đó ta có định nghĩa: 0 0 )
• sin của góc α là y , kí hiệu sin α = y ; 0 0 y
• cosin của góc α là x , kí hiệu cos α = x ; 0 0 y y 0 1
• tang của góc α là x ≠ 0 , kí hiệu 0 tan α = ; ( 0 ) x x 0 0 M y0 x x
• cotang của góc α là 0 (y ≠ 0 , kí hiệu 0 cot α = . 0 ) y y 0 0 α x x −1 0 O 1 2. Tính chất
Trên hình bên ta có dây cung NM song song với trục Ox và nếu xOM = α thì 0 xON = 180 − . α Ta có y
= y = y , x
= −x = x . Do đó M N 0 M N 0 sin α = sin( 0 180 −α) y cos α = −cos( 0 180 −α) tan α = −tan( 0 180 −α) 0 N y0 M
cot α = −cot (180 −α). x α −x x 0 O 0
3. Giá trị lượng giác của các góc đặc biệt Giá trị 0 0 0 30 0 45 0 60 0 90 0 180 lượng giác 1 2 3 sin α 0 1 0 2 2 2 3 2 1 cos α 1 0 −1 2 2 2 1 tan α 0 1 3 0 3 1 cot α 3 1 0 3
Trong bảng kí hiệu " " để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên,
ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác. Chẳng hạn 3 0 sin120 = sin ( 0 0 180 − 60 ) 0 = sin 60 = 2 2 0 cos135 = cos( 0 0 180 − 45 ) 0 = −cos 45 = − . 2 4. Góc giữa hai vectơ a) Định nghĩa
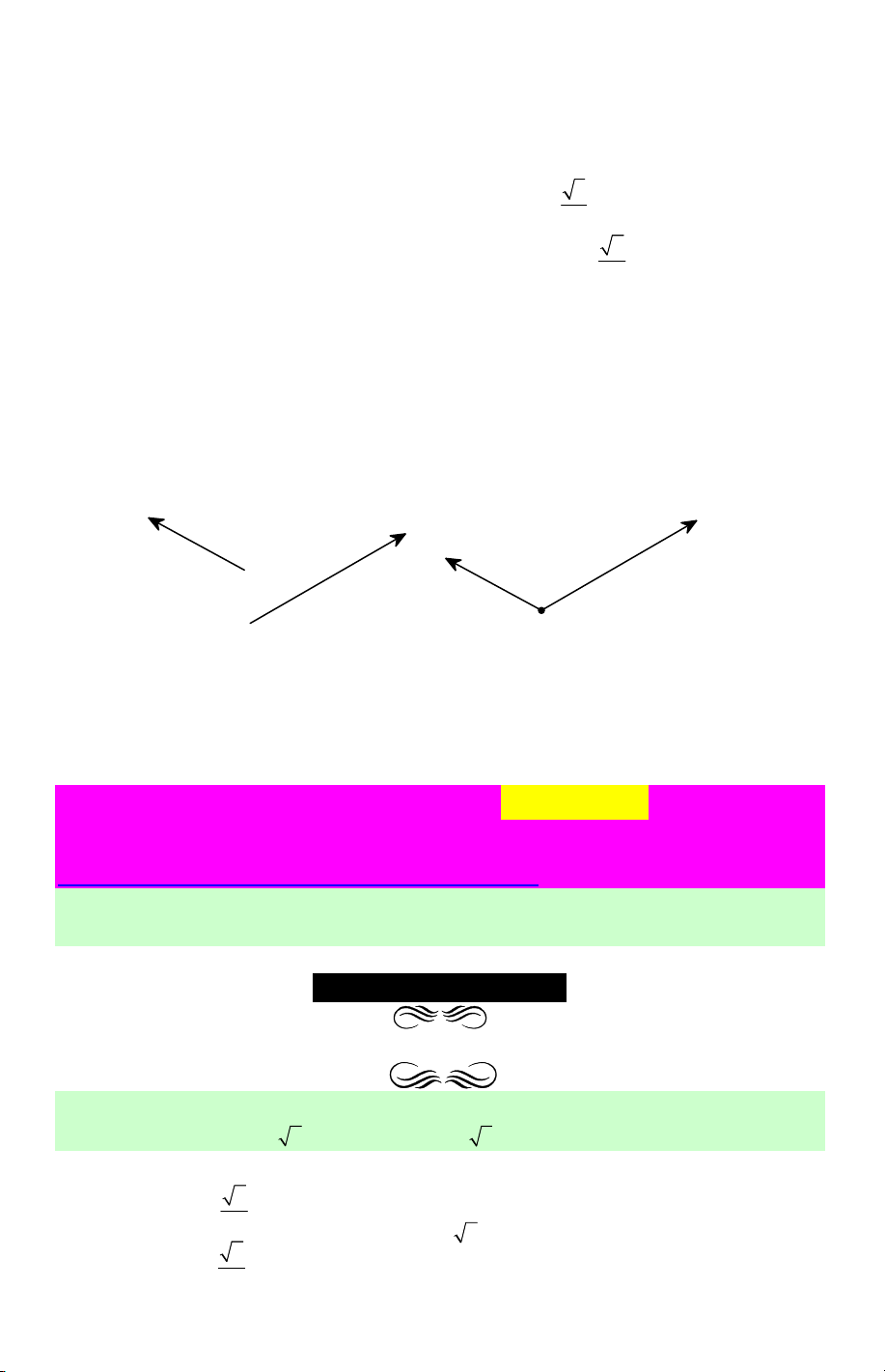
Cho hai vectơ a và b đều khác vecto 0. Từ một điểm O bất kì ta vẽ OA = a và OB = .
b Góc AOB với số đo từ 0 0 đến 0
180 được gọi là góc giữa hai vectơ a và . b Ta
kí hiệu góc giữa hai vectơ a và b là ( ,ab) . Nếu (a b) 0 ,
= 90 thì ta nói rằng a và b
vuông góc với nhau, kí hiệu là a ⊥ b hoặc b ⊥ . a A b a B a b O
b) Chú ý. Từ định nghĩa ta có ( ,ab)=(b,a).
CÂU HỎI V. B.I TẬP TRẮC NGHIỆM 10
NGUYỄN PHÚ KHÁNH HUỲNH ĐỨC KHÁNH –
Đăng ký mua trọn bộ trắc nghiệm 10 FILE WORD
Liên hệ tác giả HUỲNH ĐỨC KHÁNH 0975 120 189 –
https://web.facebook.com/duckhanh0205 Khi mua có sẵn File đề riêng;
File đáp án riêng để thuận tiện cho việc in ấn dạy học
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. GIÁ TRỊ LƯỢNG GIÁC Câu 1. Giá trị 0 0
cos 45 + sin 45 bằng bao nhiêu? A. 1. B. 2. C. 3. D. 0.
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT 2 0 c os 45 = ta được 2 0 0
→ cos 45 + sin 45 = 2. Chọn B. 2 0 s in 45 = 2
Câu 2. Giá trị của 0 0
tan 30 + cot 30 bằng bao nhiêu? A. 4 + . B. 1
3 . C. 2 . D. 2. 3 3 3
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT 1 0 tan 30 = ta được 4 0 0 3 → tan 30 + cot 30 = . Chọn A. 3 0 c ot 30 = 3
Câu 3. Trong các đẳng thức sau đây đẳng thức nào là đúng? A. 3 3 O sin150 = − . B. O cos150 = . 2 2 C. 1 O tan150 = − . D. O cot 150 = 3. 3
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được 1 O tan150 = − . Chọn C. 3
Câu 4. Tính giá trị biểu thức P = cos30 cos 60 −sin 30 sin 60 . A. P = 3. B. 3 P = . C. P = 1. D. P = 0. 2 0 0 Lời giải. s in 30 = cos 60 Vì 0 30 và 0
60 là hai góc phụ nhau nên 0 0 s in 60 = cos 30
→ P = cos 30 cos 60 − sin 30 sin 60 = cos 30 cos 60 − cos 60 cos 30 = 0. Chọn D.
Câu 5. Tính giá trị biểu thức P = sin 30 cos 60 + sin 60 cos30 . A. P = 1. B. P = 0. C. P = 3. D. P = − 3. 0 0 Lời giải. s in 30 = cos 60 Vì 0 30 và 0
60 là hai góc phụ nhau nên 0 0 s in 60 = cos 30 2 2
→ P = sin 30 cos 60 + sin 60 cos 30 = cos 60 + sin 60 = 1. Chọn A.
Câu 6. Trong các đẳng thức sau, đẳng thức nào sai? A. O O sin 45 + cos 45 = 2. B. O O sin 30 + cos 60 = 1. C. O O sin 60 + cos150 = 0. D. O O sin120 + cos 30 = 0.
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT 3 0 c os30 = ta được 2 0 0
→ cos 30 + sin120 = 3. Chọn D. 3 0 s in120 = 2
Câu 7. Trong các đẳng thức sau, đẳng thức nào sai? A. O O sin 0 + cos 0 = 0. B. O O sin 90 + cos 90 = 1. C. 3 +1 O O sin180 + cos180 = −1. D. O O sin 60 + cos 60 = . 2
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT 0 c os 0 = 1 ta được 0 0
→ cos 0 + sin 0 = 1. Chọn A. 0 s in 0 = 0
Câu 8. Trong các khẳng định sau đây, khẳng định nào sai? A. O O cos 45 = sin 45 . B. O O cos 45 = sin135 . C. O O cos 30 = sin120 . D. O O sin 60 = cos120 .
Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT 1 0 c os120 = − ta được 2 . Chọn D. 3 0 s in 60 = 2
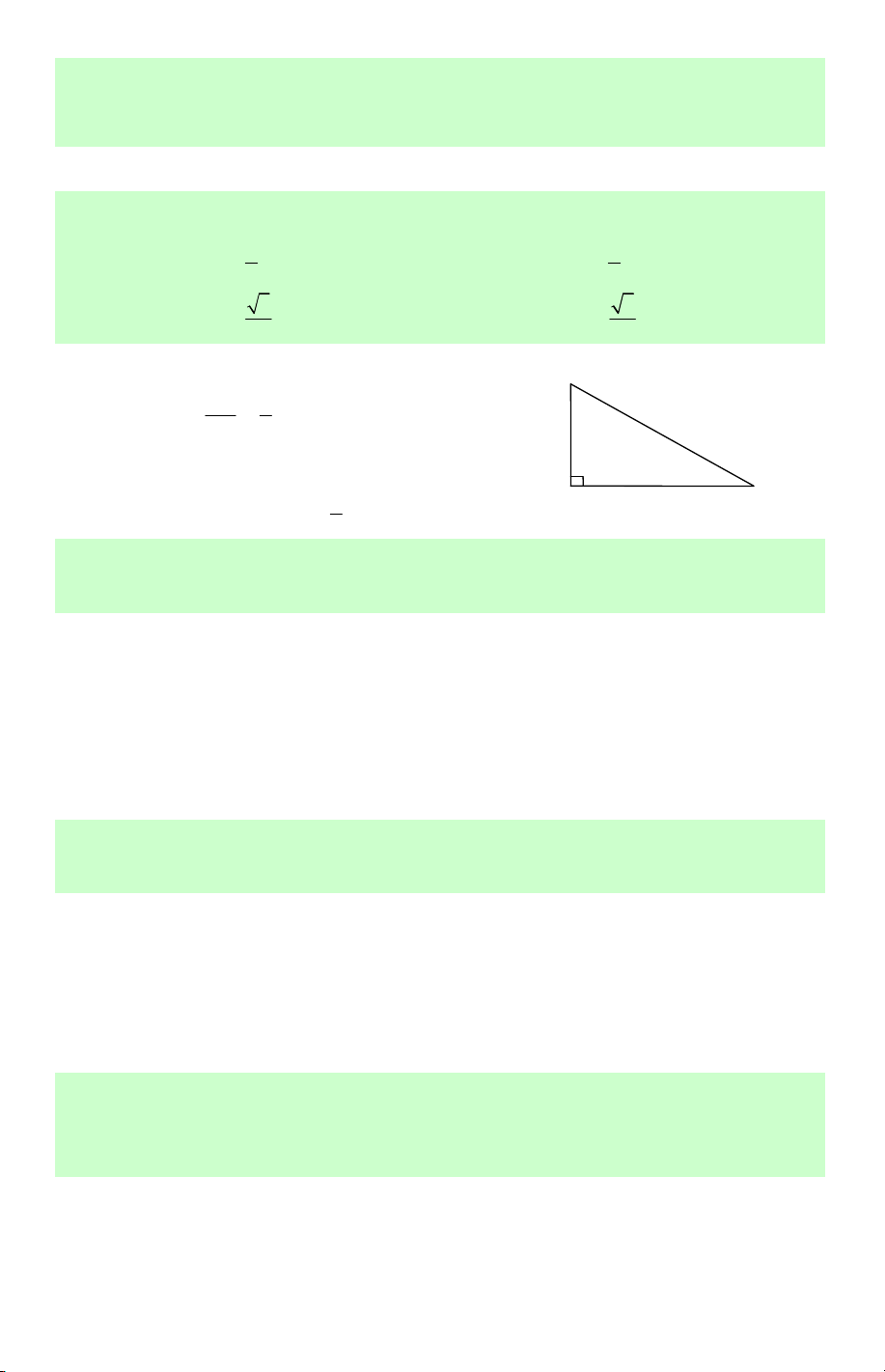
Câu 9. Tam giác ABC vuông ở A có góc 0
B = 30 . Khẳng định nào sau đây là sai? A. 1 cos B = . B. 3 sin C = . C. 1 cosC = . D. 1 sin B = . 3 2 2 2
Lời giải. Từ giả thiết suy ra 0 C = 60 .
Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được 3 0 cos B = cos 30 = . Chọn A. 2
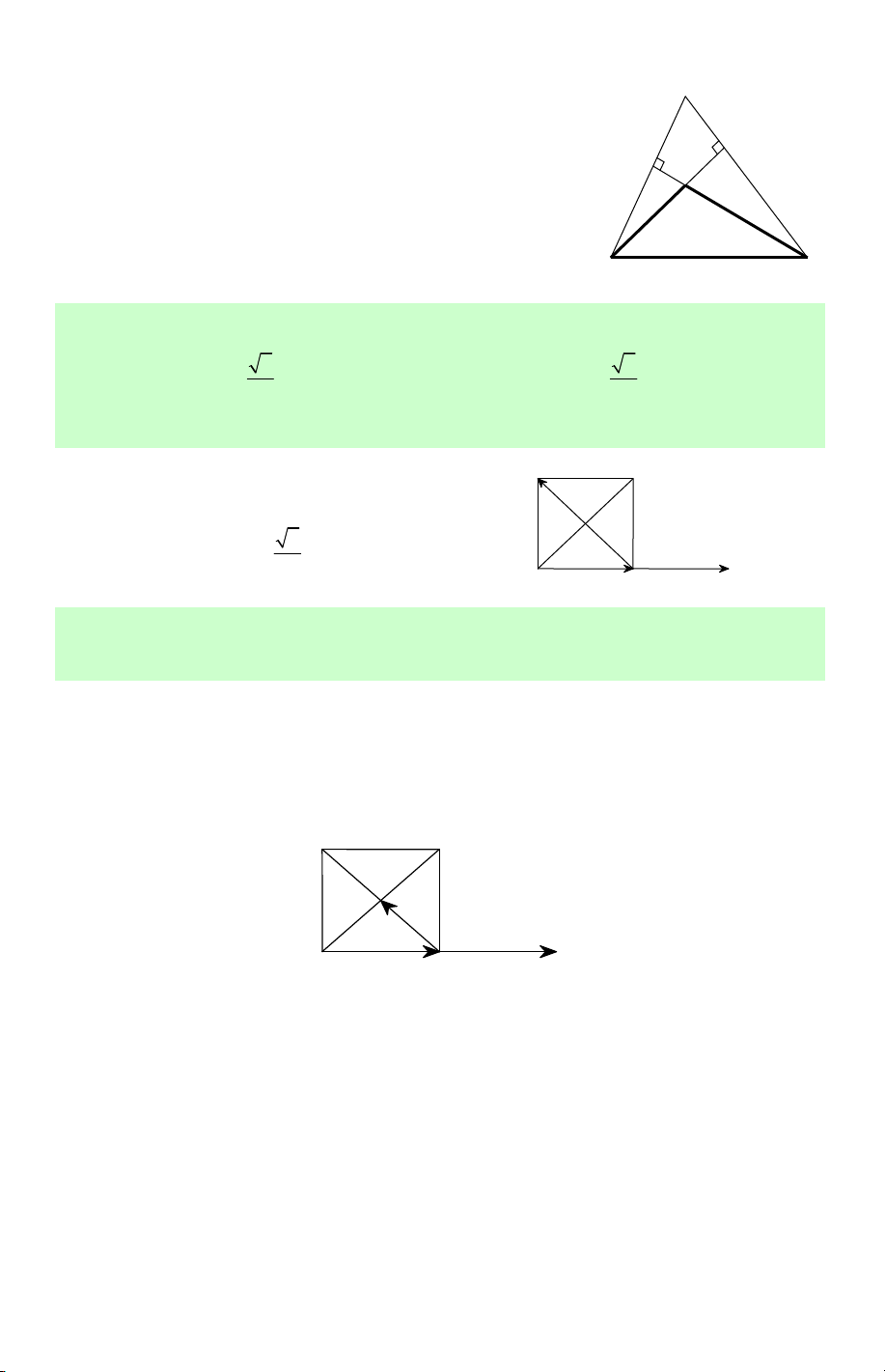
Câu 10. Tam giác đều ABC có đường cao AH . Khẳng định nào sau đây là đúng? A. 3 sin BAH = . B. 1 cos BAH = . C. 3 sin ABC = . D. 1 sin AHC = . 2 3 2 2 1 s in BAH = Lời giải. Ta có 2 0 BAH 30 = → . Do đó A sai; B sai. 3 c os BAH = 2 Ta có 3 0 ABC = 60 → sin ABC =
. Do đó C đúng. Chọn C. 2
Vấn đề 2. HAI GÓC BÙ NHAU HAI GÓC PHỤ NHAU –
Câu 11. Trong các đẳng thức sau, đẳng thức nào đúng?
A. sin(180°−α) = −cos . α
B. sin(180°−α)= −sin . α
C. sin(180°−α) = sin . α
D. sin(180°−α) = cos . α
Lời giải. Hai góc bù nhau α và (180°−α) thì cho có giá trị của sin bằng nhau. Chọn C.
Câu 12. Cho α và β là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
A. sin α = sin β. B. cosα = −cos β.
C. tan α = −tan β.
D. cot α = cot β.
Lời giải. Hai góc bù nhau α và β thì cho có giá trị của sin bằng nhau, các giá trị còn
lại thì đối nhau. Do đó D sai. Chọn D.
Câu 13. Tính giá trị biểu thức P = sin 30°cos15°+ sin150°cos165°. A. 3 P = − . B. P = 0. C. 1 P = .
D. P = 1. 4 2
Lời giải. Hai góc 0 30 và 0
150 bù nhau nên sin 30° = sin150° ;
Hai góc 15° và 165° bù nhau nên cos15° = −cos165° .
Do đó P = sin 30°cos15°+ sin150°cos165° = sin150°.(−cos165 ) ° + sin150° cos165° = 0 . Chọn B.
Câu 14. Cho hai góc α và β với α + β = 180° . Tính giá trị của biểu thức
P = cos α cos β − sin β sin α . A. P = 0. B. P = 1. C. P = −1. D. P = 2.
Lời giải. Hai góc α và β bù nhau nên sin α = sin β ; cosα = −cos β . Do đó, 2 2 P = α β − β α = − α − α = −( 2 2 cos cos sin sin cos sin
sin α + cos α) = −1 . Chọn C.
Câu 15. Cho tam giác ABC . Tính P = sin .
A cos(B +C )+ cos .
A sin (B +C ) . A. P = 0. B. P = 1. C. P = −1. D. P = 2.
Lời giải. Giả sử A = α; B +C = β . Biểu thức trở thành P = sin α cos β + cosα sin β .
Trong tam giác ABC , có A + B +C = 180° ⇒ α + β = 180° .
Do hai góc α và β bù nhau nên sin α = sin β ; cosα = −cos β .
Do đó, P = sin α cos β + cosα sin β = −sin α cosα + cosα sin α = 0 . Chọn A.
Câu 16. Cho tam giác ABC . Tính P = cos .
A cos(B +C )− sin .
A sin (B +C ) . A. P = 0. B. P = 1. C. P = −1. D. P = 2.
Lời giải. Giả sử A = α; B +C = β . Biểu thức trở thành P = cosα cos β −sin α sin β .
Trong tam giác ABC có A + B +C = 180° ⇒ α + β = 180° .
Do hai góc α và β bù nhau nên sin α = sin β ; cosα = −cos β . Do đó, 2 2 P = α β − α β = − α − α = −( 2 2 cos cos sin sin cos sin
sin α + cos α) = −1 . Chọn C.
Câu 17. Cho hai góc nhọn α và β phụ nhau. Hệ thức nào sau đây là sai?
A. sin α = −cos β. B. cosα = sin β.
C. tan α = cot β.
D. cot α = tan β.
Lời giải. Hai góc nhọn α và β phụ nhau thì sin α = cos β; cosα = sin β; tan α = cot β;
cot α = tan β . Chọn A.
Câu 18. Tính giá trị biểu thức 2 2 2 2
S = sin 15° + cos 20° + sin 75° + cos 110° . A. S = 0. B. S =1. C. S = 2. D. S = 4.
Lời giải. Hai góc 15° và 75° phụ nhau nên sin75° = cos15°.
Hai góc 20° và 110° hơn kém nhau 90° nên cos110° = −sin 20°. Do đó, 2 2 2 2
S = sin 15° + cos 20° + sin 75° + cos 110° = ° + + ° +(− )2 2 2 2 ° = ( 2 2 ° + ) ° +( 2 2 sin 15 cos 20 cos 15 sin 20 sin 15 cos 15 sin 20° + cos 20 ) ° = 2 . Chọn C.
Câu 19. Cho hai góc α và β với α + β = 90° . Tính giá trị của biểu thức
P = sin α cos β + sin β cos α . A. P = 0. B. P = 1. C. P = −1. D. P = 2.
Lời giải. Hai góc α và β phụ nhau nên sin α = cos β; cosα = sin β . Do đó, 2 2
P = sin α cos β + sin β cos α = sin α + cos α = 1 . Chọn B.
Câu 20. Cho hai góc α và β với α + β = 90° . Tính giá trị của biểu thức
P = cos α cos β − sin β sin α . A. P = 0. B. P = 1. C. P = −1. D. P = 2.
Lời giải. Hai góc α và β phụ nhau nên sin α = cos β; cosα = sin β .
Do đó, P = cosα cos β −sin β sin α = cosα sin α −cosα sin α = 0 . Chọn A.
Vấn đề 3. SO SÁNH GIÁ TRỊ LƯỢNG GIÁC
Câu 21. Cho α là góc tù. Khẳng định nào sau đây là đúng?
A. sin α < 0.
B. cosα > 0.
C. tan α < 0.
D. cot α > 0.
Lời giải. Chọn C.
Câu 22. Cho hai góc nhọn α và β trong đó α < β . Khẳng định nào sau đây là sai?
A. cosα < cos β. B. sin α < sin β.
C. cot α > cot β.
D. tan α + tan β > 0.
Lời giải. Chọn A.
Câu 23. Khẳng định nào sau đây sai?
A. cos75° > cos50°.
B. sin 80° > sin 50°.
C. tan 45° < tan 60°. D. cos30° = sin 60°.
Lời giải. Chọn A. Trong khoảng từ 0° đến 90° , khi giá trị của góc tăng thì giá trị
cos tương ứng của góc đó giảm.
Câu 24. Khẳng định nào sau đây đúng?
A. sin 90° < sin100°.
B. cos 95° > cos100°.
C. tan 85° < tan125°.
D. cos145° > cos125°.
Lời giải. Trong khoảng từ 90° đến 180° , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
- Giá trị cos tương ứng của góc đó giảm. Chọn B.
Câu 25. Khẳng định nào sau đây đúng?
A. sin 90° < sin150°.
B. sin 90°15′ < sin 90°30 .′
C. cos 90°30′ > cos100°.
D. cos150° > cos120°.
Lời giải. Trong khoảng từ 90° đến 180° , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
- Giá trị cos tương ứng của góc đó giảm. Chọn C.
Vấn đề 4. TÍNH GIÁ TRỊ BIỂU THỨC
Câu 26. Chọn hệ thức đúng được suy ra từ hệ thức 2 2
cos α + sin α = 1? A. α α 1 α α 1 2 2 cos + sin = . B. 2 2 cos + sin = . 2 2 2 3 3 3 C. α α 1 α α 2 2 cos + sin = . D. 2 2 5cos + sin = 5. 4 4 4 5 5
Lời giải. Từ biểu thức α α 2 2
cos α + sin α = 1 ta suy ra 2 2 cos + sin = 1. 5 5 Do đó ta có α α 2 2 5cos + sin = 5. Chọn D. 5 5 Câu 27. Cho biết α 3 α α sin = . Giá trị của 2 2 P = 3 sin + 5 cos bằng bao nhiêu ? 3 5 3 3 A. 105 P = . B. 107 P = . C. 109 P = . D. 111 P = . 25 25 25 25
Lời giải. Ta có biểu thức α α α α 16 2 2 2 2 sin + cos = 1 ⇔ cos = 1− sin = . 3 3 3 3 25 2 Do đó ta có α α 3 16 107 2 2 P = 3 sin + 5 cos = 3. + 5. = . Chọn B. 3 3 5 25 25 Câu 28. Cho biết α − α
tan α = −3. Giá trị của 6 sin 7 cos P = bằng bao nhiêu ?
6 cos α + 7 sin α A. 4 P = . B. 5 P = . C. 4 P = − . D. 5 P = − . 3 3 3 3 sin α 6 −7 Lời giải. Ta có
6 sin α −7 cos α 6 tan α −7 5 cos P α = = = = . Chọn B.
6 cos α + 7 sin α sin α 6 + 7 tan α 3 6 + 7 cosα Câu 29. Cho biết 2 α + α
cos α = − . Giá trị của cot 3 tan P = bằng bao nhiêu ? 3
2 cot α + tan α A. 19 P = − . B. 19 P = . C. 25 P = . D. 25 P = − . 13 13 13 13
Lời giải. Ta có biểu thức 5 2 2 2 2
sin α + cos α = 1 ⇔ sin α = 1− cos α = . 9 2 2 5 cos α sin α + − + 3. 3 2 2 Ta có
cot α + 3 tan α
cos α + 3 sin α 3 9 19 sin α cos P α = = = = = . 2 2 2
2 cot α + tan α cos α sin α
2 cos α + sin α 2 5 13 2 + 2. − + sin α cos α 3 9 Chọn B.
Câu 30. Cho biết cot α = 5. Giá trị của 2
P = 2 cos α + 5 sin α cos α +1 bằng bao nhiêu ? A. 10 P = . B. 100 P = . C. 50 P = . D. 101 P = . 26 26 26 26 2 Lời giải. Ta có cos α cos α 1 2 2
P = 2 cos α + 5 sin α cos α +1 = sin α2 + 5 + 2 2 sin α sin α sin α 2 1 = (
3 cot α + 5 cot α +1 101 2 2
2 cot α + 5 cot α +1 + cot α = = . Chọn D. 2 ) 2 1 + cot α cot α +1 26
Câu 31. Cho biết 3cos α − sin α = 1 , 0 0
0 < α < 90 . Giá trị của tan α bằng A. 4 tan α = . B. 3 tan α = . C. 4 tan α = . D. 5 tan α = . 3 4 5 4 Lời giải. Ta có α − α = ⇔ α = α + → α = ( α + )2 2 3 cos sin 1 3 cos sin 1 9 cos sin 1 2 2 ⇔ α = α + α + ⇔ ( 2 − α) 2 9 cos sin 2 sin 1 9 1 sin
= sin α + 2 sin α +1 sin α = −1 2
⇔ 10 sin α + 2 sin α −8 = 0 ⇔ 4 . sin α = 5
• sin α = −1 : không thỏa mãn vì 0 0 0 < α < 90 . α • 4 3 sin 4 sin α = ⇒ cos α = → tan α = = . Chọn A. 5 5 cos α 3
Câu 32. Cho biết 2cosα + 2 sin α = 2 , 0 0
0 < α < 90 . Tính giá trị của cot . α A. 5 cot α = . B. 3 cot α = . C. 2 cot α = . D. 2 cot α = . 4 4 4 2 Lời giải. Ta có α + α = ⇔ α = − α → α = ( − α)2 2 2 cos 2 sin 2 2 sin 2 2 cos 2 sin 2 2 cos 2 2
⇔ 2 sin α = 4 −8 cos α + 4 cos α ⇔ 2( 2 1− cos α) 2
= 4 −8 cos α + 4 cos α cos α = 1 2
⇔ 6 cos α −8 cos α + 2 = 0 ⇔ 1 . cos α = 3
• cos α = 1 : không thỏa mãn vì 0 0 0 < α < 90 . α • 1 2 2 cos 2 cos α = ⇒ sin α = → cot α = = . Chọn C. 3 3 sin α 4
Câu 33. Cho biết sin α + cosα = .
a Tính giá trị của sin α cos . α A. 2
sin α cos α = a .
B. sin α cos α = 2 . a 2 2 C. a −1 a −11 sin α cos α = .
D. sin α cos α = . 2 2 Lời giải. Ta có α + α = a → ( α + α)2 2 sin cos sin cos = a 2 a −1 2
⇔ 1 + 2 sin α cos α = a ⇔ sin α cos α = . Chọn C. 2 Câu 34. Cho biết 1
cos α + sin α = . Giá trị của 2 2
P = tan α + cot α bằng bao nhiêu ? 3 A. 5 P = . B. 7 P = . C. 9 P = . D. 11 P = . 4 4 4 4 Lời giải. Ta có 1 1
cos α + sin α =
→ (cosα + sin α)2 = 3 9 1 4
⇔ 1+ 2 sin α cos α =
⇔ sin α cos α = − . 9 9 2 Ta có sin α cos α
P = tan α + cot α = (tan α + cot α)2 2 2
− 2 tan α cot α = + − 2 cosα sin α 2 2 2 2 2
sin α + cos α 1 9 7 = − 2 = Chọn B. − 2 = − − 2 = .
sin α cosα
sin α cos α 4 4 Câu 35. Cho biết 1
sin α − cos α = . Giá trị của 4 4
P = sin α + cos α bằng bao nhiêu ? 5 A. 15 P = . B. 17 P = . C. 19 P = . D. 21 P = . 5 5 5 5 Lời giải. Ta có 1 1
sin α − cos α =
→ (sin α −cosα)2 = 5 5 1 2
⇔ 1− 2 sin α cos α =
⇔ sin α cos α = . 5 5 Ta có P = α + α = ( α + α)2 4 4 2 2 2 2 sin cos sin cos
− 2 sin α cos α = − ( α α)2 17 1 2 sin cos = . Chọn B. 5
Vấn đề 5. GÓC GIỮA HAI VECTƠ
Câu 36. Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng O 120 ?
A. (MN,NP)
B. (MO,ON ).
C. (MN,OP).
D. (MN,MP).
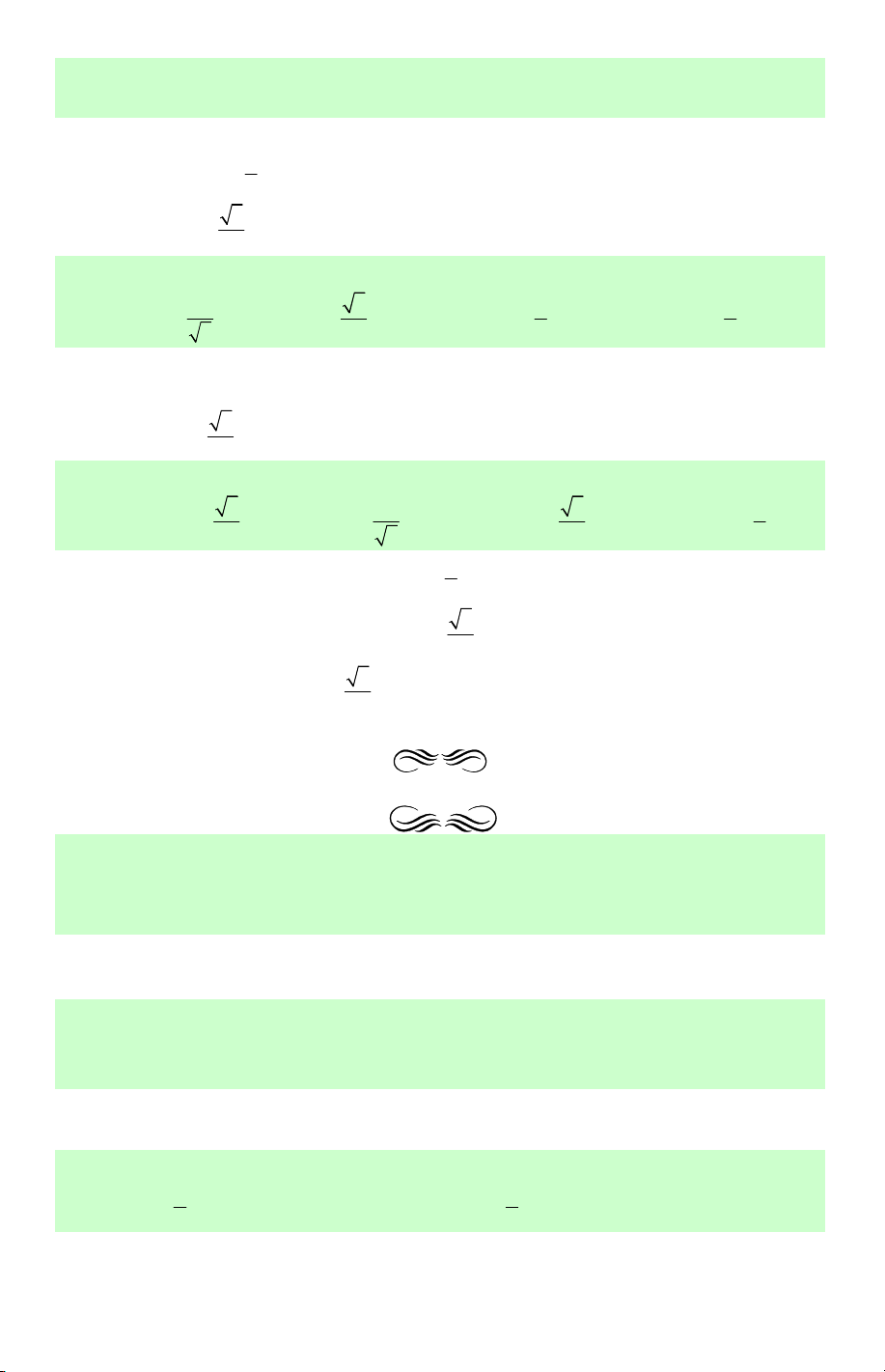
Lời giải. • Vẽ NE = MN . Khi đó (MN,NP)=(NE,NP) P 0 0 0 0
= PNE = 180 − MNP = 180 − 60 = 120 . Chọn A. F
• Vẽ OF = MO . Khi đó (MO ON )= (OF ON ) 0 , , = NOF = 60 . O
• Vì MN ⊥ OP →(MN OP) 0 , = 90 . E N M • Ta có (MN MP) 0 , = NMP = 60 .
Câu 37. Cho tam giác đều ABC. Tính P = cos(AB,BC)+cos(BC,CA)+cos(C , A AB). A. 3 3 P = . B. 3 P = . C. 3 P = − . D. 3 3 P = − . 2 2 2 2
Lời giải. Vẽ BE = AB . Khi đó (AB BC)=(BE BC) 0 , ,
= CBE = 180 −CBA = 120 C → cos(AB,BC) 1 0 = cos120 = − . 2 Tương tự, ta cũng có (BC CA)= (CA AB) 1 cos , cos , = − . 2 A B E Vậy
(AB BC)+ (BC CA)+ (CA AB) 3 cos , cos , cos , = − . Chọn C. 2
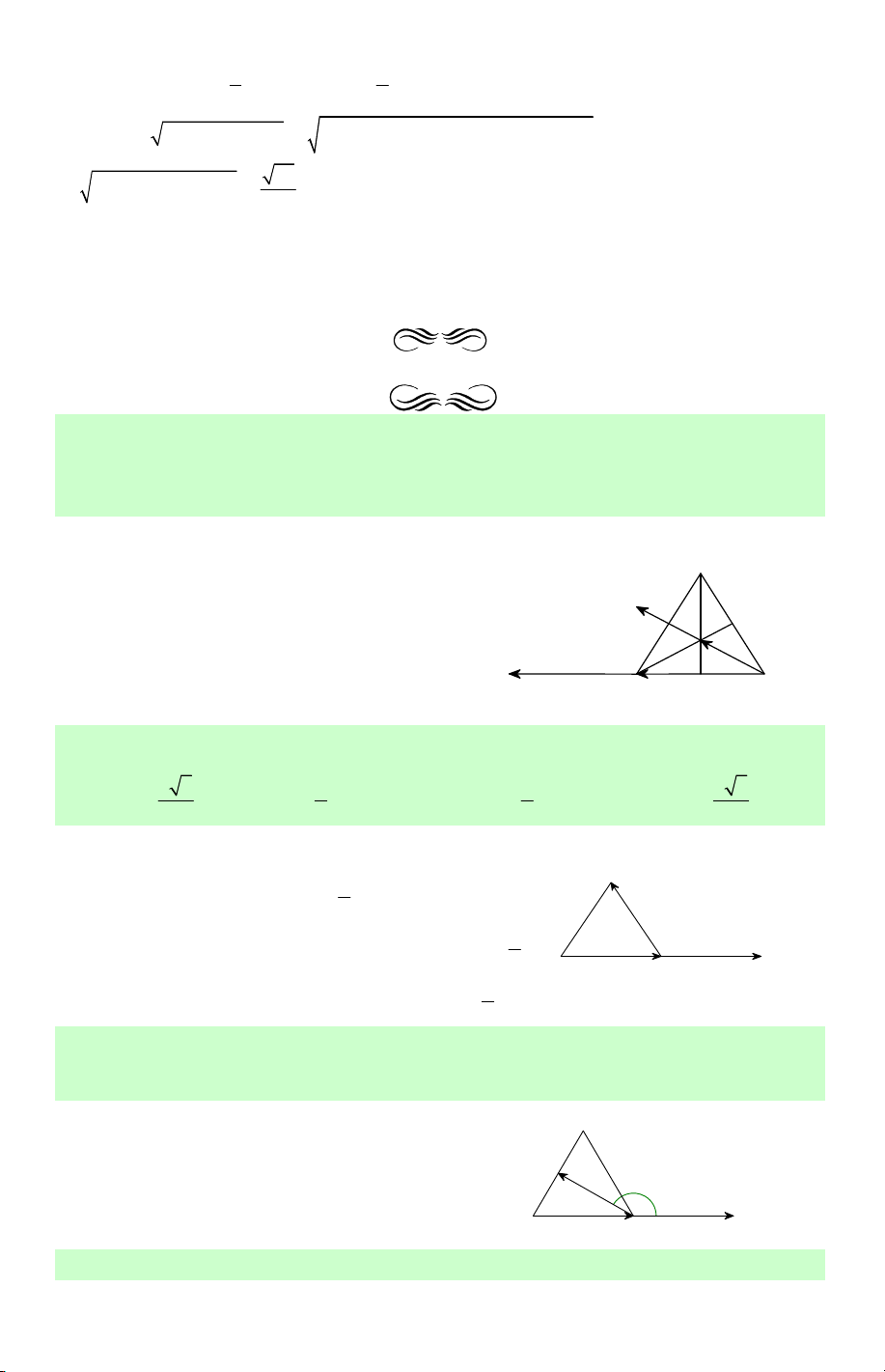
Câu 38. Cho tam giác đều ABC có đường cao AH. Tính (AH,BA). A. 0 30 . B. 0 60 . C. 0 120 . D. 0 150 .
Lời giải. Vẽ AE = BA . C
Khi đó (AH,AE)= HAE = α (hình vẽ) H 0 0 0 0 α
= 180 − BAH = 180 −30 = 150 . Chọn D. B E A
Câu 39. Tam giác ABC vuông ở A và có góc 0
B = 50 . Hệ thức nào sau đây sai? A. (AB BC) 0 , = 130 . B. (BC AC) 0 , = 40 . C. (AB CB) 0 , = 50 . D. (AC CB) 0 , = 40 .
Lời giải. (Bạn đọc tự vẽ hình) Chọn D. Vì (AC CB) 0 0 0 0 ,
= 180 − ACB = 180 − 40 = 140 .
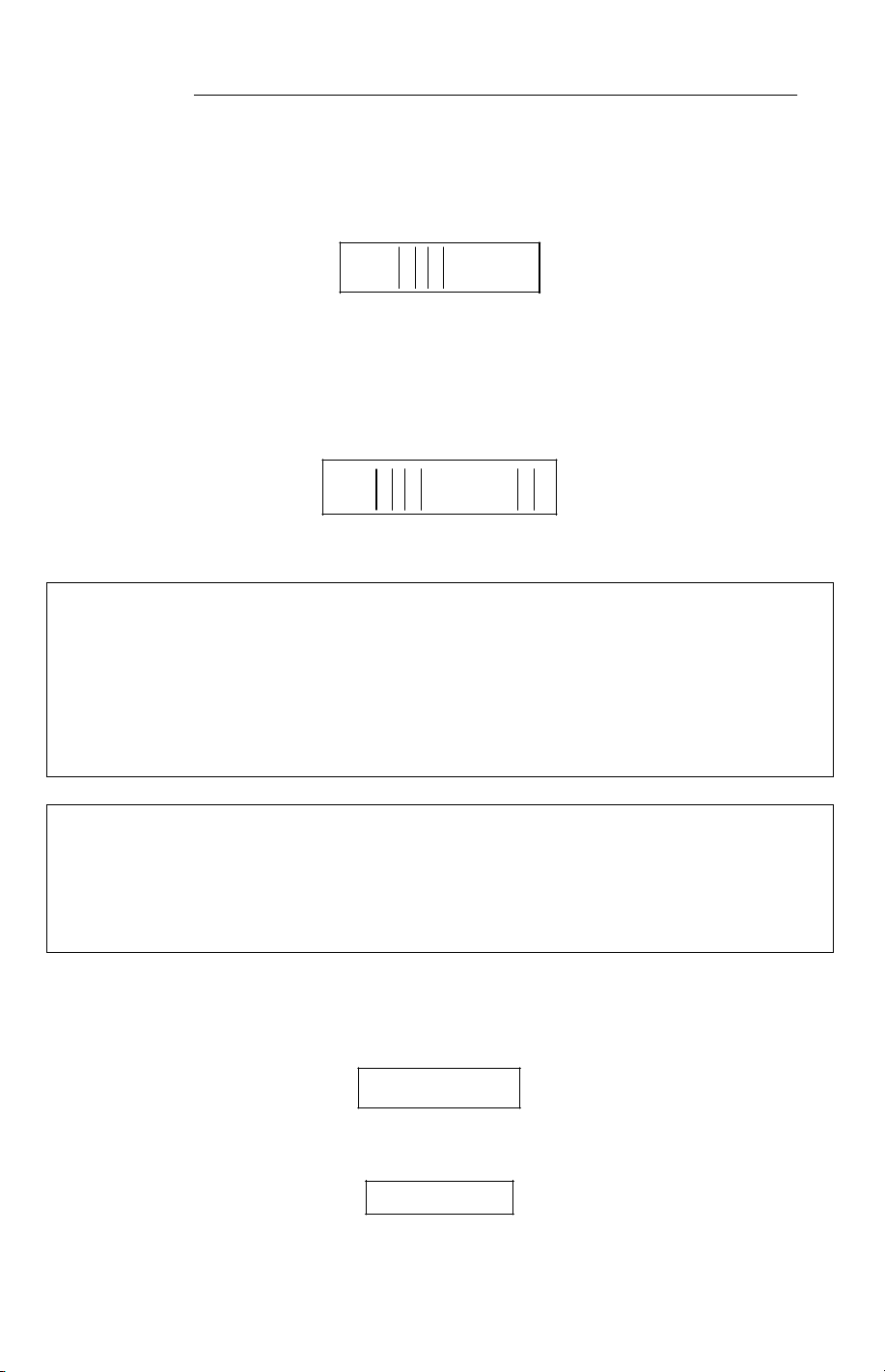
Câu 40. Tam giác ABC vuông ở A và có BC = 2AC. Tính cos(AC,CB). A. (AC CB) 1 cos , = . B. (AC CB) 1 cos , = − . 2 2 C. (AC CB) 3 cos , = . D. (AC CB) 3 cos , = − . 2 2
Lời giải. Xác định được (AC CB) 0 , = 180 − ACB. C Ta có AC 1 0 cos ACB = = → ACB = 60 CB 2 →(AC CB) 0 0 , = 180 − ACB = 120 Vậy A B cos(AC,CB) 1 0
= cos120 = − . Chọn B. 2
Câu 41. Cho tam giác ABC . Tính tổng (AB,BC)+(BC,CA)+(C , A AB). A. 180 . B. 360 . C. 270 . D. 120 . (AB,BC ) 0 = 180 − ABC
Lời giải. Ta có (BC,CA) 0 = 180 − BCA
(C ,AAB ) 0 = 180 −CAB
→(AB BC)+(BC CA)+(CA AB) 0 =
−(ABC + BCA +CAB) 0 0 0 , , , 540 = 540 −180 = 360 . Chọn B.
Câu 42. Cho tam giác ABC với A = 60 . Tính tổng (AB,BC)+(BC,CA). A. 120 . B. 360 . C. 270 . D. 240 . (AB,BC ) 0 = 180 − ABC
Lời giải. Ta có (BC,CA ) 0 = 180 − BCA
→(AB BC)+(BC CA) 0 , ,
= 360 −(ABC + BCA) 0 = −( 0 − BAC ) 0 0 0 0 360 180
= 360 −180 + 60 = 240 . Chọn D.
Câu 43. Tam giác ABC có góc A bằng 100 và có trực tâm H. Tính tổng (H ,
A HB)+(HB,HC)+(HC,HA). A. 360 . B. 180 . C. 80 . D. 160 . (H , A HB )= BHA H
Lời giải. Ta có (HB,HC)= BHC F ( I HC, HA A )=CHA →(H ,
A HB)+(HB,HC)+(HC,HA)= BHA + BHC +CHA 0 100 = BHC = ( 0 0 − ) 0 2 2 180 100 = 160 B C
(do tứ giác HIAF nội tiếp. Chọn D.
Câu 44. Cho hình vuông ABCD . Tính cos(AC,BA). A. (AC BA) 2 cos , = . B. (AC BA) 2 cos , = − . 2 2
C. cos(AC,BA)= 0.
D. cos(AC,BA)=−1.
Lời giải. Vẽ AE = BA . C D
Khi đó cos(AC,BA)= cos(AC,AE) 2 0 = cosCAE = cos135 = − . 2 Chọn B. B E A
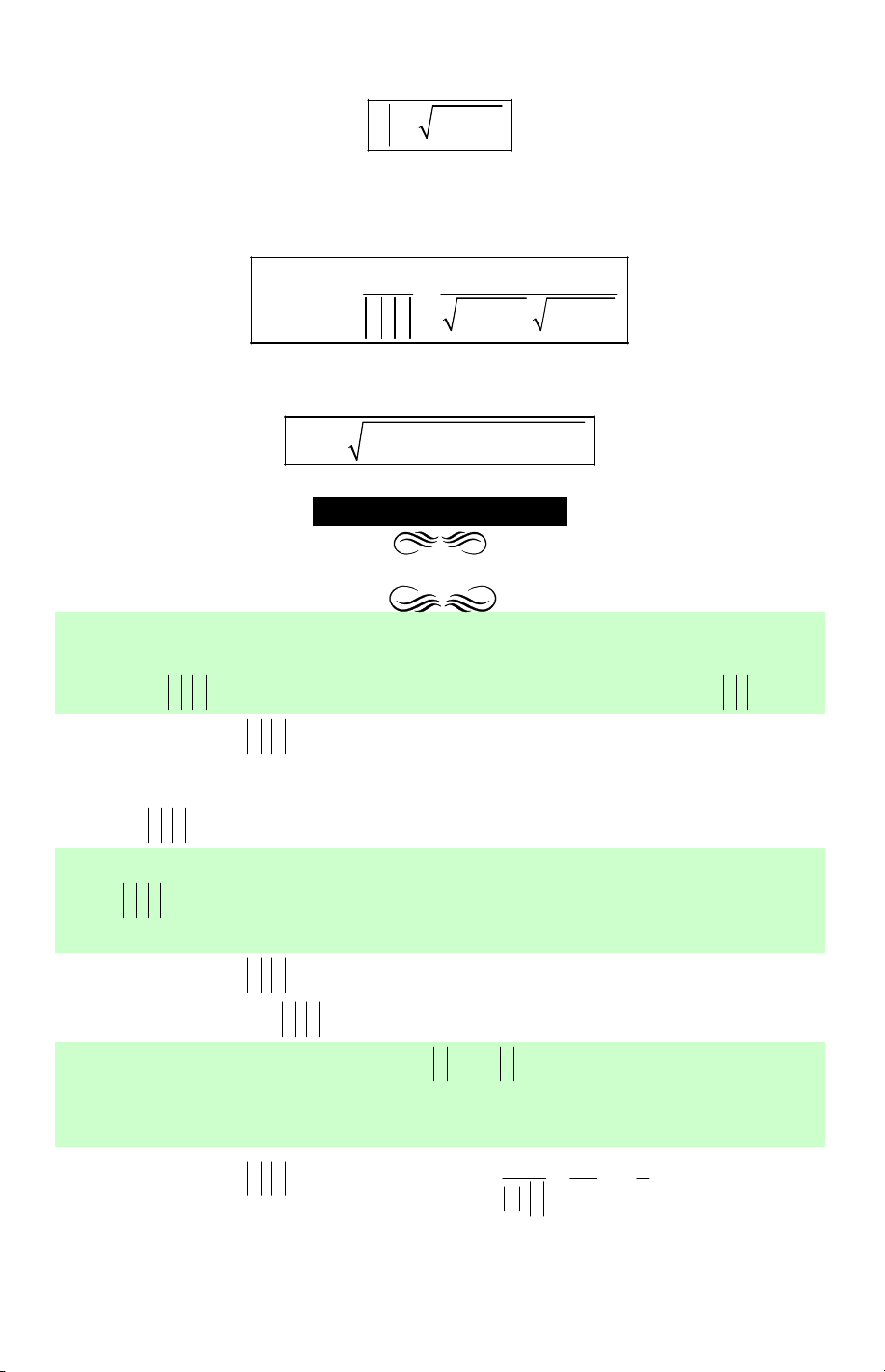
Câu 45. Cho hình vuông ABCD tâm O. Tính tổng (AB,DC)+(AD,CB)+(CO,DC). A. 0 45 . B. 0 405 . C. 0 315 . D. 0 225 .
Lời giải. • Ta có AB, DC cùng hướng nên (AB,DC) 0 = 0 .
• Ta có AD,CB ngược hướng nên (AD CB) 0 , = 180 .
• Vẽ CE = DC , khi đó (CO DC)= (CO CE) 0 , , = OCE = 135 . A B O D E C
Vậy (AB DC)+(AD CB)+(CO DC) 0 0 0 0 , , ,
= 0 +180 +135 = 315 . Chọn C. Baøi 02
TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ 1. Định nghĩa
Cho hai vectơ a và b đều khác vectơ 0. Tích vô hướng của a và b là một số, kí hiệu là .
a b, được xác định bởi công thức sau: .
a b = a . b cos(a,b).
Trường hợp ít nhất một trong hai vectơ a và b bằng vectơ 0 ta quy ước . a b = 0. Chú ý
• Với a và b khác vectơ 0 ta có .
a b = 0 ⇔ a ⊥ . b
• Khi a = b tích vô hướng .
a a được kí hiệu là 2
a và số này được gọi là bình phương vô hướng của vectơ . a Ta có 2 2 0
a = a . a .cos 0 = a .
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng: Với ba vectơ ,
a b, c bất kì và mọi số k ta có: • . a b = .
b a (tính chất giao hoán);
• a(b +c)= .ab + .ac (tính chất phân phối);
• (ka).b = k( .ab)= .a(kb) ; • 2 2
a ≥ 0, a = 0 ⇔ a = 0.
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra: • (a +b)2 2 2 = a + 2 . a b + b ; • (a−b)2 2 2 = a − 2 . a b + b ;
• (a +b)(a −b) 2 2 = a −b .
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ (O;i; j), cho hai vectơ a =(a ;a , b = b ;b . Khi đó tích vô 1 2 ) ( 1 2 ) hướng . a b là: .
a b = a b + a b . 1 1 2 2
Nhận xét. Hai vectơ a = (a ;a , b = b ;b đều khác vectơ 0 vuông góc với nhau khi 1 2 ) ( 1 2 ) và chỉ khi a b + a b = 0. 1 1 2 2 4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ a = (a ;a được tính theo công thức: 1 2 ) 2 2
a = a + a . 1 2 b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu a = (a ;a và b = (b ;b đều 1 2 ) 1 2 ) khác 0 thì ta có a b a b + a b cos(a;b) . 1 1 2 2 = = . 2 2 2 2 a . b
a + a . b + b 1 2 1 2
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(x ; y và B(x ; y được tính theo công thức: B B ) A A )
AB = (x − x )2 +(y − y )2 . B A B A
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
Câu 1. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b = a . b . B. . a b = 0 . C. . a b = −1 . D. .
a b = − a . b . Lời giải. Ta có .
a b = a . b .cos(a,b) .
Do a và b là hai vectơ cùng hướng nên (a b) 0 , = 0 → cos(a,b)=1. Vậy .
a b = a . b . Chọn A.
Câu 2. Cho hai vectơ a và b khác 0 . Xác định góc α giữa hai vectơ a và b khi .
a b = − a . b . A. 0 α = 180 . B. 0 α = 0 . C. 0 α = 90 . D. 0 α = 45 . Lời giải. Ta có .
a b = a . b .cos(a,b) . Mà theo giả thiết .
a b = − a . b , suy ra
(a b)=− →(a b) 0 cos , 1 , = 180 . Chọn A.
Câu 3. Cho hai vectơ a và b thỏa mãn a = 3, b = 2 và a.b = −3. Xác định góc α
giữa hai vectơ a và . b A. 0 α = 30 . B. 0 α = 45 . C. 0 α = 60 . D. 0 α = 120 . Lời giải. Ta có − a b = a b
(a b)→ (a b) a.b 3 1 . . .cos , cos , = = = − →(a,b) 0 = 120 . 3.2 2 a . b Chọn D.
Câu 4. Cho hai vectơ a và b thỏa mãn a = b = 1 và hai vectơ 2 u = a −3b và 5
v = a + b vuông góc với nhau. Xác định góc α giữa hai vectơ a và . b A. 0 α = 90 . B. 0 α = 180 . C. 0 α = 60 . D. 0 α = 45 . Lời giải. Ta có u v u v ⊥ → = ⇔ a − b (a +b ) 2 2 2 2 13 . 0 3 = 0 ⇔ a − ab − 3b = 0 5 5 5 a = b 1 = → ab = −1. Suy ra (a b) a.b cos , = = −1 →( , a b) 0 = 180 . Chọn B. a . b
Câu 5. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? A. 2 2 1 2 1
a.b = a + b − a − b . B. 2 2 2
a.b = a + b − a −b . 2 2 C. 2 2 1
a.b = a + b − a −b . D. 2 2 1 a.b =
a + b − a −b . 2 4
Lời giải. Nhận thấy C và D chỉ khác nhau về hệ số 1 và 1 nên đáp án sai sẽ rơi vào 2 4 C hoặc D. 2 2 2 2 2 2 Ta có
a + b − a −b = (a +b) −(a −b) 1 = 4ab → . a b =
a + b − a −b . Chọn C. 4 2 2 2
• A đúng, vì a + b = (a +b) = (a +b).(a +b) 2 = . a a + . a b + . b a + .
b b = a + b + 2 . a b 2 2 1 2
→ a.b = a + b − a − b . 2 2 2 2
• B đúng, vì a −b = (a −b) = (a −b).(a −b) 2 = . a a − . a b − . b a + .
b b = a + b − 2 . a b 2 2 1 2
→ a.b = a + b − a −b . 2
Câu 6. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng AB.AC. 2 2 2 A. a 3 a a 2
AB.AC = 2a . B. AB.AC = −
. C. AB.AC = − .
D. AB.AC = . 2 2 2
Lời giải. Xác định được góc (AB,AC) là góc A nên (AB AC) 0 , = 60 . 2
Do đó AB AC = AB AC (AB AC) a 0 . . .cos , = . a . a cos 60 = . Chọn D. 2
Câu 7. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng AB.BC. 2 2 2 A. a 3 a a 2
AB.BC = a . B. AB.BC =
. C. AB.BC = − .
D. AB.BC = . 2 2 2
Lời giải. Xác định được góc (AB,BC) là góc ngoài của góc B nên (AB BC) 0 , = 120 . 2
Do đó AB BC = AB BC (AB BC) a 0 . . .cos , = . a . a cos120 = − . Chọn C. 2
Câu 8. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 2 A. 1 1 a 1 2 AB.AC = a . B. 2
AC.CB = − a . C. G . A GB = . D. 2 AB.AG = a . 2 2 6 2
Lời giải. Dựa vào đáp án, ta có nhận xét sau:
• Xác định được góc (AB, AC) là góc A nên (AB AC) 0 , = 60 . 2
Do đó AB AC = AB AC (AB AC) a 0 . . .cos , = . a . a cos 60 = → A đúng. 2
• Xác định được góc (AC,CB) là góc ngoài của góc C nên (AC CB) 0 , = 120 . 2
Do đó AC CB = AC CB (AC CB) a 0 . . .cos , = . a . a cos120 = − → B đúng. 2
• Xác định được góc (G ,
A GB) là góc AGB nên (GA GB) 0 , = 120 . 2
Do đó GA GB = GA GB (GA GB) a a a 0 . . .cos , = . .cos120 = −
→ C sai. Chọn C. 3 3 6
• Xác định được góc (AB, AG) là góc GAB nên (AB AG) 0 , = 30 . 2
Do đó AB AG = AB AG (AB AG) a a 0 . . .cos , = . a .cos 30 = → D đúng. 3 2
Câu 9. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 2 A. a a AH .BC = 0. B. (AB HA) 0 ,
= 150 . C. AB.AC = .
D. AC.CB = . 2 2
Lời giải. Xác định được góc (AC,CB) là góc ngoài tại đỉnh C nên (AC CB) 0 , = 120 . 2
Do đó AC CB = AC CB (AC CB) a 0 . . .cos , = . a . a cos120 = − . Chọn D. 2
Câu 10. Cho tam giác ABC vuông cân tại A và có AB = AC = .
a Tính AB.BC. 2 2 A. a 2 a 2 2 AB.BC = a − . B. 2
AB.BC = a .
C. AB.BC = −
. D. AB.BC = . 2 2
Lời giải. Xác định được góc (AB,BC) là góc ngoài của góc B nên (AB BC) 0 , = 135 .
Do đó AB BC = AB BC (AB BC) 0 2 . . .cos , = . a a 2.cos135 = a − . Chọn A.
Câu 11. Cho tam giác ABC vuông tại A và có AB = c, AC = . b Tính B . A BC. A. 2 B .
A BC = b . B. 2 B .
A BC = c . C. 2 2 B .
A BC = b + c . D. 2 2 B .
A BC = b − c . Lời giải. Ta có c B . A BC = B . A BC.cos(B , A BC ) 2 2 2 = B .
A BC.cos B = c. b + c . = c . 2 2 b + c Chọn B.
Cách khác. Tam giác ABC vuông tại A suy ra AB ⊥ AC ⇒ AB.AC = 0.
Ta có BA BC = BA (BA+ AC) 2 2 2 . . = BA + B .
A AC = AB = c . Chọn B.
Câu 12. Cho ba điểm ,
A B, C thỏa AB = 2cm, BC = 3cm, CA = 5cm. Tính C . A CB. A. C .
A CB = 13. B. C . A CB = 15. C. C . A CB = 17. D. C . A CB = 19.
Lời giải. Ta có AB + BC = CA ⇒ ba điểm ,
A B, C thẳng hàng và B nằm giữa , A C.
Khi đó CA CB = CA CB (CA CB) 0 . . .cos ,
= 3.5.cos 0 = 15. Chọn B. Cách khác. Ta có 2 2
AB = AB = (CB −CA)2 2 2
= CB −2CBCA +CA 1 →CBCA = ( 1 2 2 2
CB +CA − AB ) = ( 2 2 2 3 + 5 − 2 ) = 15. 2 2
Câu 13. Cho tam giác ABC có BC = a, CA = b, AB = c. Tính P = (AB + AC).BC. 2 2 2 2 2 2 2 2 A. c + b c + b + a
c + b − a 2 2
P = b − c . B. P = . C. P = . D. P = . 2 3 2
Lời giải. Ta có P = (AB + AC).BC =(AB + AC).(BA+ AC).
= (AC + AB) (AC − AB) 2 2 2 2 2 2 .
= AC − AB = AC − AB = b −c . Chọn A.
Câu 14. Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm cạnh
BC. Tính AM .BC. 2 2 2 2 A. b − c c + b AM .BC = .
B. AM.BC = . 2 2 2 2 2 2 2 2 C. c + b + a
c + b − a AM .BC = .
D. AM.BC = . 3 2
Lời giải. Vì M là trung điểm của BC suy ra AB + AC = 2 AM. Khi đó 1
AM BC = (AB + AC ) 1 .
.BC = (AB + AC ).(BA + AC ) 2 2 2 2 1 ( ) ( − = + AC − AB) 1 = ( 2 2 AC − AB ) 1 b c AC AB . = ( 2 2 AC − AB ) = . Chọn A. 2 2 2 2
Câu 15. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô
hướng (OA+OB).AB = 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại O.
C. tam giác OAB vuông tại O.
D. tam giác OAB vuông cân tại O.
Lời giải. Ta có (OA+OB).AB = 0 ⇔ (OA+OB).(OB −OA)= 0 2 2 2 2
⇔ OB −OA = 0 ⇔ OB −OA = 0 ⇔ OB = O . A Chọn B.
Câu 16. Cho M , N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A. MN (NP + PQ)= MN.NP + MN.PQ . B. MP.MN =−MN.MP .
C. MN.PQ = PQ.MN . D. ( − )( + ) 2 2 MN PQ MN
PQ = MN − PQ .
Lời giải. Đáp án A đúng theo tính chất phân phối.
Đáp án B sai. Sửa lại cho đúng MP.MN = MN.MP .
Đáp án C đúng theo tính chất giao hoán.
Đáp án D đúng theo tính chất phân phối. Chọn B
Câu 17. Cho hình vuông ABCD cạnh .
a Tính AB.AC. A. 2 1 2
AB.AC = a . B. 2 AB.AC = a 2. C. 2 AB.AC = a . D. 2 AB.AC = a . 2 2 Lời giải. Ta có ( 2 AB AC ) 0 , = BAC = 45 nên 0 2
AB.AC = AB.AC.cos 45 = . a a 2. = a . 2 Chọn A.
Câu 18. Cho hình vuông ABCD cạnh a . Tính P = AC.(CD +CA). A. P = −1. B. 2 P = 3a . C. 2 P = −3a . D. 2 P = 2a .
Lời giải. Từ giả thiết suy ra AC = a 2.
Ta có P = AC (CD +CA) 2 .
= AC.CD + AC.CA = C − . A CD − AC = C − A CD
(CA CD)−AC = a − a −(a )2 2 0 2 . cos , 2. .cos 45 2
= −3a . Chọn C.
Câu 19. Cho hình vuông ABCD cạnh .
a Tính P = (AB + AC).(BC + BD + BA). A. P = 2 2 . a B. 2 P = 2a . C. 2 P = a . D. 2 P = −2a . BD = a 2
Lời giải. Ta có
BC + BD + BA = (BC +BA) .
+ BD = BD + BD = 2BD
Khi đó P = (AB + AC).2BD = 2A .
B BD + 2AC.BD = −2B . A BD + 0 = −2.B . A BD cos(B , A BD) 2 2 = −2. . a a 2.
= −2a . Chọn D. 2
Câu 20. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.AB. A. 2
AE.AB = 2a . B. 2
AE.AB = 3a . C. 2
AE.AB = 5a . D. 2
AE.AB = 5a .
Lời giải. Ta có C là trung điểm của DE nên DE = 2 . a A B
Khi đó AE.AB = (AD + DE).AB = AD.AB + DE.AB 0 = DE AB (DE AB) 0 2 . .cos ,
= DE.AB.cos 0 = 2a . Chọn A. D E C
Câu 21. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AC AM =
. Gọi N là trung điểm của đoạn thẳng DC. Tính MB.MN. 4
A. MB.MN = −4. B. MB.MN = 0.
C. MB.MN = 4.
D. MB.MN = 16.
Lời giải. Giả thiết không cho góc, ta phân tích các vectơ MB, MN theo các vectơ có giá vuông góc với nhau. 1 1 3 1
• MB = AB − AM = AB − AC = AB − (AB + AD)= AB − AD. 4 4 4 4 1 1 1
• MN = AN − AM = AD + DN − AC = AD + DC − (AB + AD) 4 2 4 1 1
= AD + AB − (AB + AD) 3 1 = AD + AB. 2 4 4 4 A B M D N C Suy ra MB MN AB AD = − AD + AB = ( 2 2 3 1 3 1 1 .
9AB.AD + 3AB −3AD − AD.AB 4 4 4 4 16 ) 1 = ( 2 2
0 + 3a − 3a − 0) = 0 . Chọn B. 16
Câu 22. Cho hình chữ nhật ABCD có AB = 8. Tính AB.BD.
A. AB.BD = 62. B. AB.BD = 64.
C. AB.BD = −62.
D. AB.BD = −64.
Lời giải. Giả thiết không cho góc, ta phân tích các vectơ AB, BD theo các vectơ có giá vuông góc với nhau.
Ta có AB BD = AB (BA+ BC) 2 . .
= AB.BA + A . B BC = −A .
B AB + 0 = −AB = −64 . Chọn D.
Câu 23. Cho hình thoi ABCD có AC = 8. Tính AB.AC.
A. AB.AC = 24. B. AB.AC = 26.
C. AB.AC = 28.
D. AB.AC = 32.
Lời giải. Gọi O = AC ∩ BD . Giả thiết không cho góc, ta phân tích các vectơ AB, AC
theo các vectơ có giá vuông góc với nhau. B A C O D
Ta có AB.AC = (AO +OB) 1 1 2
.AC = AO.AC +O . B AC = AC.AC + 0 =
AC = 32 . Chọn D. 2 2
Câu 24. Cho hình bình hành ABCD có AB = 8cm, AD = 12cm , góc ABC nhọn và diện tích bằng 2
54cm . Tính cos(AB,BC). A. (AB BC) 2 7 cos , = . B. (AB BC) 2 7 cos , = − . 16 16 C. (AB BC) 5 7 cos , = . D. (AB BC) 5 7 cos , = − . 16 16 Lời giải. Ta có 2 S = 2.S = 54 ⇔ S = 27 cm . ABCD ∆ABC ∆ABC
Diện tích tam giác ABC là 1 1 S
= .AB.BC.sin ABC = .AB.AD.sin ABC. A ∆ BC 2 2 2.S 2.27 9 5 7 A ∆ BC 2 ⇒ sin ABC = = =
→ cos ABC = 1− sin ABC = (vì ABC nhọn). AB.AD 8.12 16 16 A D B C
Mặt khác góc giữa hai vectơ AB, BC là góc ngoài của góc ABC
Suy ra cos(AB,BC)= cos( 5 7 0
180 − ABC ) = − cos ABC = − . Chọn D. 16
Câu 25. Cho hình chữ nhật ABCD có AB = a và AD = a 2 . Gọi K là trung điểm
của cạnh AD. Tính BK.AC.
A. BK.AC = 0. B. 2
BK .AC = a − 2. C. 2
BK .AC = a 2. D. 2
BK .AC = 2a . Lời giải. Ta có 2 2 2 2
AC = BD = AB + AD = 2a + a = a 3. 1 A K D
BK = BA + AK = BA + AD Ta có 2
AC = AB + AD 1 B C
→ BK.AC = BA + AD (AB + AD) 2 1 1 1 = B . A AB + B . A AD + AD.AB + AD.AD = a − + 0 + 0 + (a 2)2 2 = 0. Chọn A. 2 2 2
Vấn đề 2. QUỸ TÍCH
Câu 26. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MA(MB + MC)= 0 là A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải. Gọi I là trung điểm BC
→ MB + MC = 2MI .
Ta có MA(MB + MC)= 0 ⇔ M .
A 2MI = 0 ⇔ M .
A MI = 0 ⇔ MA ⊥ MI . (*)
Biểu thức (*) chứng tỏ MA ⊥ MI hay M nhìn đoạn AI dưới một góc vuông nên tập
hợp các điểm M là đường tròn đường kính AI. Chọn D.
Câu 27. Tập các hợp điểm M thỏa mãn MB(MA+ MB + MC)= 0 với ,
A B, C là ba đỉnh của tam giác là A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải. Gọi G là trọng tâm tam giác ABC
→ MA + MB + MC = 3MG.
Ta có MB(MA+ MB + MC)= 0 ⇔ MB.3MG = 0 ⇔ MB.MG = 0 ⇔ MB ⊥ MG. (*)
Biểu thức (*) chứng tỏ MB ⊥ MG hay M nhìn đoạn BG dưới một góc vuông nên tập
hợp các điểm M là đường tròn đường kính BG. Chọn D.
Câu 28. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn M . A BC = 0 là A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải. Ta có M .
A BC = 0 ⇔ MA ⊥ BC.
Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC. Chọn B.
Câu 29*. Cho hai điểm ,
A B cố định có khoảng cách bằng a . Tập hợp các điểm N thỏa mãn 2
AN .AB = 2a là A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải. Gọi C là điểm đối xứng của A qua B . Khi đó AC = 2AB. Suy ra 2 2
AB.AC = 2AB = 2a .
Kết hợp với giả thiết, ta có AN.AB = A . B AC
⇔ AB (AN − AC)= 0 ⇔ AB.CN = 0 ⇔ CN ⊥ AB .
Vậy tập hợp các điểm N là đường thẳng qua C và vuông góc với AB. Chọn B.
Câu 30*. Cho hai điểm ,
A B cố định và AB = 8. Tập hợp các điểm M thỏa mãn M . A MB = −16 là A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải. Gọi I là trung điểm của đoạn thẳng AB → IA = I − . B Ta có M .
A MB = (MI + IA)(MI + IB) = (MI + IA)(MI − IA) 2 2 2 AB 2 2 2
= MI − IA = MI − IA = MI − . 4 2 2 2 Theo giả thiết, ta có AB AB 8 2 2 MI − = −16 ⇔ MI = −16 = −16 = 0 → M ≡ I. 4 4 4 Chọn A.
Vấn đề 3. BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG HAI VECTƠ
Cho tam giác ABC với ba đỉnh có tọa độ xác định A(x ; y ), B(x ; y ), C (x ; y thì A A B B C C ) + + • Trung điểm x x y y I của đoạn A B AB I → ; A B . 2 2 + + + + • Trọng tâm x x x y y y A B C G G → ; A B C . 3 3 • Trực tâm H . A BC = 0 H → . HB.CA = 0 2 2
• Tâm đường tròn ngoại tiếp AE = BE E EA EB EC → = = ⇔ . 2 2 AE = CE • Chân đường cao AK BC = K hạ từ đỉnh . 0 A → . BK = kBC
• Chân đường phân giác trong góc AB
A là điểm D → DB = − .DC. AC
• Chu vi: P = AB + BC +CA . • Diện tích: 1 1 2 S =
AB.AC.sin A =
AB.AC. 1− cos A . 2 2
• Góc A : cos A = cos(AB,AC). • Tam giác AB AC = ABC vuông cân tại . 0 A → . AB = AC
Câu 31. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;− )
1 , B (2;10), C (−4;2). Tính
tích vô hướng AB.AC.
A. AB.AC = 40. B. AB.AC = −40.
C. AB.AC = 26.
D. AB.AC = −26.
Lời giải. Ta có AB = (−1;1 ) 1 , AC = (−7; ) 3 .
Suy ra AB.AC = (− )
1 .(−7)+11.3 = 40. Chọn A.
Câu 32. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3;− )
1 và B (2;10). Tính tích vô hướng AO.OB.
A. AO.OB = −4. B. AO.OB = 0.
C. AO.OB = 4.
D. AO.OB =16.
Lời giải. Ta có AO = (−3; ) 1 , OB = (2;10).
Suy ra AO.OB = −3.2 +1.10 = 4. Chọn C.
Câu 33. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = 4i + 6 j và b = 3i −7 j. Tính tích vô hướng . a . b A. . a b = −30. B. . a b = 3. C. . a b = 30. D. . a b = 43.
Lời giải. Từ giả thiết suy ra a = (4;6) và b = (3;−7). Suy ra .
a b = 4.3 + 6.(−7) = −30. Chọn A.
Câu 34. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (−3;2) và b = (−1;−7). Tìm
tọa độ vectơ c biết c.a = 9 và c.b = −20.
A. c = (−1;− )
3 . B. c = (−1; ) 3 . C. c = (1;− ) 3 . D. c = (1; ) 3 .
Lời giải. Gọi c = (x; y). = − + = Ta có c.a 9 3x 2 y 9 x = −1 ⇔ ⇔ → c = (−1; ) 3 . Chọn B.
−x −7 y = −20 y = 3 c .b = −20
Câu 35. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a = (1;2), b = (4; ) 3 và c = (2; ) 3 . Tính P = .
a (b + c).
A. P = 0.
B. P = 18. C. P = 20. D. P = 28.
Lời giải. Ta có b + c = (6;6). Suy ra P = .
a (b + c) =1.6 + 2.6 =18. Chọn B.
Câu 36. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (−1; )
1 và b = (2;0) . Tính
cosin của góc giữa hai vectơ a và b. A. (a b) 1 cos , = . B. (a b) 2 cos , = − . 2 2 C. (a b) 1 cos , = − . D. (a b) 1 cos , = . 2 2 2 Lời giải. Ta có ( − + a b) . a b 1.2 1.0 2 cos , = = = − . Chọn B. a b (− )2 2 2 2 2 . 1 +1 . 2 + 0
Câu 37. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (−2;− ) 1 và b = (4;− ) 3 . Tính
cosin của góc giữa hai vectơ a và b. A. (a b) 5 cos , = − . B. (a b) 2 5 cos , = . 5 5 C. (a b) 3 cos , = . D. (a b) 1 cos , = . 2 2 Lời giải. . a b −2.4 + −1 . −3 Ta có (a b) ( ) ( ) 5 cos , = = = − . Chọn A. a . b 4 +1. 16 + 9 5
Câu 38. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4; )
3 và b = (1;7) . Tính góc
α giữa hai vectơ a và b . A. O α = 90 . B. O α = 60 . C. O α = 45 . D. O α = 30 . Lời giải. Ta có ( + a b) . a b 4.1 3.7 2 cos , = = = →( , a b) 0 = 45 . Chọn C. a . b 16 + 9. 1+ 49 2
Câu 39. Trong mặt phẳng tọa độ Oxy, cho hai vectơ x = (1;2) và y = (−3;− ) 1 . Tính
góc α giữa hai vectơ x và . y A. O α = 45 . B. O α = 60 . C. O α = 90 . D. O α = 135 . Lời giải. x.y 1. −3 + 2. −1 Ta có (x y) ( ) ( ) 2 cos , = = = − →(x, y) 0 = 135 . Chọn D. x . y 1+ 4. 9 +1 2
Câu 40. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (2; )
5 và b = (3;−7) . Tính góc
α giữa hai vectơ a và b . A. O α = 30 . B. O α = 45 . C. O α = 60 . D. O α = 135 . Lời giải. . a b 2.3 + 5 −7 Ta có (a b) ( ) 2 cos , = = = − →( , a b) 0 = 135 . Chọn D. a . b 4 + 25. 9 + 49 2
Câu 41. Trong mặt phẳng tọa độ Oxy, cho vectơ a = (9; )
3 . Vectơ nào sau đây không
vuông góc với vectơ a ? A. v = 1;−3 . B. v = 2;−6 . C. v = 1;3 . D. v = −1;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
Lời giải. Kiểm tra tích vô hướng a.v , nếu đáp án nào cho kết quả khác 0 thì kết
luận vectơ đó không vuông góc với a. Chọn C.
Câu 42. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1;2), B(−1; ) 1 và C (5;− ) 1 . Tính
cosin của góc giữa hai vectơ AB và AC. A. (AB AC) 1 cos , = − . B. (AB AC) 3 cos , = . 2 2 C. (AB AC) 2 cos , = − . D. (AB AC) 5 cos , = − . 5 5
Lời giải. Ta có AB = (−2;− ) 1 và AC = (4;− ) 3 . A . B AC −2.4 + −1 . −3 Suy ra (AB AC) ( ) ( ) 5 cos , = = = − . Chọn D. AB . AC 4 +1. 16 + 9 5
Câu 43. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(6;0), B(3; ) 1 và C (−1;− )
1 . Tính số đo góc B của tam giác đã cho. A. O 15 . B. O 60 . C. O 120 . D. O 135 .
Lời giải. Ta có BA = (3;− )
1 và BC = (−4;−2) . B . A BC 3. −4 + −1 . −2 Suy ra (BA BC) ( ) ( ) ( ) 2 cos , = = = − → B = (B , A BC ) O = 135 . BA . BC 9 +1. 16 + 4 2 Chọn D.
Câu 44. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(−8;0), B(0;4), C (2;0) và D (−3;− )
5 . Khẳng định nào sau đây là đúng?
A. Hai góc BAD và BCD phụ nhau. B. Góc BCD là góc nhọn.
C. cos(AB,AD)= cos(CB,CD).
D. Hai góc BAD và BCD bù nhau.
Lời giải. Ta có AB = (8;4), AD = (5;− )
5 , CB = (−2;4), CD = (−5; ) 5 . ( + − AB AD) 8.5 4.( ) 5 1 cos , = = 2 2 2 2 8 + 4 . 5 + 5 10 Suy ra ( − − + − CB CD) ( 2).( 5) 4.( ) 5 1 cos , = = − 2 2 2 2 2 + 4 . 5 + 5 10 → (AB AD)+ (CB CD) 0 cos , cos ,
= 0 ⇒ BAD + BCD = 180 . Chọn D.
Câu 45. Trong mặt phẳng tọa độ Oxy, cho hai vectơ 1 u =
i − 5 j và v = ki − 4 j. Tìm k 2
để vectơ u vuông góc với v. A. k = 20. B. k = −20. C. k = −40. D. k = 40.
Lời giải. Từ giả thiết suy ra 1 u = ;
−5,v = (k;−4). 2 Yêu cầu bài toán: 1 u ⊥ v ⇔ k +(− )
5 (−4) = 0 ⇔ k = −40 . Chọn C. 2
Câu 46. Trong mặt phẳng tọa độ Oxy, cho hai vectơ 1 u =
i − 5 j và v = ki − 4 j. Tìm k 2
để vectơ u và vectơ v có độ dài bằng nhau. A. 37 k = . B. 37 k = . C. 37 k = ± . D. 5 k = . 4 2 2 8
Lời giải. Từ giả thiết suy ra 1 u = ;
−5,v = (k;−4). 2 Suy ra 1 1 u = + 25 = 101 và 2 v = k +16 . 4 2 Do đó để 1 101 37 37 2 2 2
u = v ⇔ k +16 = 101 ⇔ k +16 = ⇔ k = ⇔ k = ± . Chọn C. 2 4 4 2
Câu 47. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a = (−2; ) 3 , b = (4; ) 1 và
c = ka + mb với k, m ∈ .
ℝ Biết rằng vectơ c vuông góc với vectơ (a +b) . Khẳng định nào sau đây đúng? A. 2k = 2 . m B. 3k = 2 . m
C. 2k +3m = 0.
D. 3k + 2m = 0. c
= ka +mb =
(−2k + 4m;3k + m)
Lời giải. Ta có . a +b = (2;4)
Để c ⊥ (a +b)⇔ c(a +b)= 0 ⇔ 2(−2k +4m)+4(3k +m)= 0 ⇔ 2k +3m = 0. Chọn C.
Câu 48. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (−2; ) 3 và b = (4; ) 1 . Tìm vectơ d biết . a d = 4 và . b d = −2 . A. 5 6 d = ; . B. 5 6 d = − ; . C. 5 6 d = ; − . D. 5 6 d = − ; − . 7 7 7 7 7 7 7 7 5 x = − Lời giải. Gọi − 2x + 3y = 4 7
d = (x; y) . Từ giả thiết, ta có hệ ⇔ . Chọn B.
4x + y = −2 6 y = 7
Câu 49. Trong mặt phẳng tọa độ Oxy, cho ba vectơ u = (4; )
1 , v = (1;4) và a = u + . m v với m ∈ .
ℝ Tìm m để a vuông góc với trục hoành. A. m = 4. B. m = −4. C. m = −2. D. m = 2.
Lời giải. Ta có a = u + .
m v = (4 + m;1+ 4m).
Trục hoành có vectơ đơn vị là i = (1;0).
Vectơ a vuông góc với trục hoành ⇔ .
a i = 0 ⇔ 4 + m = 0 ⇔ m = −4. Chọn B.
Câu 50. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u = (4; )
1 và v = (1;4). Tìm m để vectơ a = .
m u + v tạo với vectơ b = i + j một góc 0 45 . A. m = 4. B. 1 m = − . C. 1 m = − . D. 1 m = . 2 4 2 a = . m u + v = (4m +1;m + 4)
Lời giải. Ta có . b
= i + j = (1; ) 1
Yêu cầu bài toán ⇔ cos(a,b) 2 0 = cos 45 = 2 (4m + ) 1 +(m + 4) 2 5(m + ) 1 2 ⇔ = ⇔ = 2 (4m + )2 1 +(m + 4)2 2 2 2 2 17m +16m +17 m +1 ≥ 0 1 5(m ) 2 1 17m 16m 17 ⇔ + = + + ⇔ ⇔ m = − . 2 2 2
5m + 50m + 25 = 17m +16m +17 4 Chọn C.
Vấn đề 4. CÔNG THỨC TÍNH ĐỘ DYI
Câu 51. Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M (1;−2) và N (−3;4). A. MN = 4. B. MN = 6. C. MN = 3 6. D. MN = 2 13.
Lời giải. Ta có MN = (−4;6) suy ra MN = (− )2 2 4
+ 6 = 52 = 2 13. Chọn D.
Câu 52. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;4), B(3;2), C (5;4) .
Tính chu vi P của tam giác đã cho.
A. P = 4 + 2 2. B. P = 4 + 4 2. C. P = 8 +8 2. D. P = 2 + 2 2. 2 AB = (2;−2) 2 AB = 2 +(−2) = 2 2 Lời giải. Ta có BC (2;2) 2 2 = ⇒ BC = 2 + 2 = 2 2 C A ( 4;0) = − C A = (−4)2 2 + 0 = 4
Vậy chu vi P của tam giác ABC là P = AB + BC +CA = 4 + 4 2. Chọn B.
Câu 53. Trong hệ tọa độ (O;i ; j ), cho vectơ 3 4 a = − i −
j . Độ dài của vectơ a bằng 5 5 A. 1. B. 1. C. 6 . D. 7 . 5 5 5 2 2 Lời giải. Ta có 3 4 3 4 3 4 a = − i − j → a = − ; − ⇒ a = − + − = 1. Chọn B. 5 5 5 5 5 5
Câu 54. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u = (3;4) và v = (−8;6). Khẳng
định nào sau đây đúng?
A. u = v .
B. u và v cùng phương.
C. u vuông góc với v .
D. u = −v.
Lời giải. Ta có u.v = 3.(−8)+ 4.6 = 0 suy ra u vuông góc với v . Chọn C.
Câu 55. Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;2), B(−2;−4), C (0; ) 1 và 3 D −1;
. Mệnh đề nào sau đây đúng ? 2
A. AB cùng phương với CD.
B. AB = CD .
C. AB ⊥ CD.
D. AB = CD. Lời giải. Ta có 1 AB = (−3;−6) và 1 CD = 1 − ;
suy ra AB.CD = (− ) 3 .(− ) 1 +(−6). = 0. 2 2
Vậy AB vuông góc với CD. Chọn C.
Câu 56. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(7;− )
3 , B (8;4), C (1; ) 5 và
D (0;−2) . Khẳng định nào sau đây đúng?
A. AC ⊥ CB.
B. Tam giác ABC đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác ABCD không nội tiếp đường tròn. AB =( ) 2 2
1;7 ⇒ AB = 1 + 7 = 5 2
BC =(−7; )1⇒BC =5 2
Lời giải. Ta có
→ AB = BC = CD = DA = 5 2. C
D = (−1;−7)⇒CD = 5 2 DA= (7;− ) 1 ⇒ DA = 5 2
Lại có AB.BC = (
1 −7)+ 7.1 = 0 nên AB ⊥ BC .
Từ đó suy ra ABCD là hình vuông. Chọn C.
Câu 57. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(−1; )
1 , B (0;2), C (3; ) 1 và
D (0;−2). Khẳng định nào sau đây là đúng?
A. Tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình thoi.
C. Tứ giác ABCD là hình thang cân.
D. Tứ giác ABCD không nội tiếp được đường tròn. AB = (1; ) 1
Lời giải. Ta có
→ DC = 3AB . DC = (3; ) 3
Suy ra DC AB và DC = 3AB. ( ) 1 2 2
Mặt khác AD = 1 + 3 = 10
→ AD = BC. (2) 2 2 BC = 3 +1 = 10 Từ ( )
1 và (2) , suy ra tứ giác ABCD là hình thang cân. Chọn C.
Câu 58. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(−1; ) 1 , B (1;3) và C (1;− )
1 . Khẳng định nào sau đây là đúng ?
A. Tam giác ABC đều.
B. Tam giác ABC có ba góc đều nhọn.
C. Tam giác ABC cân tại B .
D. Tam giác ABC vuông cân tại A .
Lời giải. Ta có AB = (2;2), BC = (0;−4) và AC = (2;−2).
Suy ra AB = AC = 2 2
. Vậy tam giác ABC vuông cân tại . A Chọn D. 2 2 2
AB + AC = BC
Câu 59. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(10;5), B(3;2) và C (6;− )
5 . Khẳng định nào sau đây là đúng?
A. Tam giác ABC đều.
B. Tam giác ABC vuông cân tại A .
C. Tam giác ABC vuông cân tại B .
D. Tam giác ABC có góc A tù.
Lời giải. Ta có AB = (−7;− )
3 , BC = (3;−7) và AC = (−4; 1 − 0).
Suy ra AB.BC = (−7).3+(− )
3 .(−7) = 0 và AB = BC.
Vậy tam giác ABC vuông cân tại . B Chọn C.
Câu 60. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(−2;− ) 1 , B (1;− ) 1 và
C (−2;2) . Khẳng định nào sau đây là đúng?
A. Tam giác ABC đều.
B. Tam giác ABC vuông cân tại A .
C. Tam giác ABC vuông tại B .
D. Tam giác ABC vuông cân tại C .
Lời giải. Ta có AB = (3;0), BC = (−3; ) 3 và AC = (0;3).
AB = AC = 3 Do đó 2 2 2
⇒ AB + AC = BC . Vậy tam giác ABC vuông cân tại . A BC = 3 2 Chọn B.
Vấn đề 5. TÌM ĐIỂM THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
Câu 61. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(−2;4) và B(8;4). Tìm tọa độ
điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C. A. C (6;0).
B. C (0;0), C (6;0). C. C (0;0). D. C (−1;0). C A = (−2 −c;4)
Lời giải. Ta có C ∈Ox nên C (c;0) và . C
B = (8−c;4)
Tam giác ABC vuông tại C nên C .
A CB = 0 ⇔ (−2 −c).(8− c)+ 4.4 = 0
c = 6 → C (6;0) 2 c 6c 0 ⇔ − = ⇔ . Chọn B. c = 0 → C (0;0)
Câu 62. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;2) và B(−3; ) 1 . Tìm tọa độ
điểm C thuộc trục tung sao cho tam giác ABC vuông tại . A A. C (0;6). B. C (5;0). C. C (3; ) 1 . D. C (0;−6). AB = (−4;− ) 1
Lời giải. Ta có C ∈Oy nên C (0;c) và .
AC = (−1;c −2)
Tam giác ABC vuông tại A nên AB.AC = 0 ⇔ (−4).(− ) 1 +(− )
1 (c − 2) = 0 ⇔ c = 6.
Vậy C (0;6). Chọn A.
Câu 63. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(–4;0), B(–5;0) và C (3;0). Tìm
điểm M thuộc trục hoành sao cho MA + MB + MC = 0.
A. M (–2;0). B. M (2;0). C. M (–4;0). D. M (–5;0). Lời giải. MA = (−4 − x;0)
Ta có M ∈Ox nên M (x;0) và MB = (−5− x;0)
→ MA + MB + MC = (−6 −3x;0).
MC =(3−x;0)
Do MA + MB + MC = 0 nên−6 −3x = 0 ⇔ x = −2
→ M (−2;0). Chọn A.
Câu 64. Trong mặt phẳng tọa độ Oxy, cho hai điểm M (–2;2) và N (1; ) 1 . Tìm tọa độ
điểm P thuộc trục hoành sao cho ba điểm M , N, P thẳng hàng. A. P (0;4). B. P (0;–4).
C. P (–4;0). D. P (4;0). MP = (x + 2;−2)
Lời giải. Ta có P ∈Ox nên P (x;0) và . MN = (3;− ) 1 Do x + 2 −2
M , N , P thẳng hàng nên = ⇔ x = 4
→ P (4;0). Chọn D. 3 −1
Câu 65. Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách
từ đó đến điểm N ( 1 − ;4) bằng 2 5. A. M (1;0).
B. M (1;0), M (−3;0). C. M (3;0).
D. M (1;0), M (3;0).
Lời giải. Ta có M ∈Ox nên M ( ;
m 0) và MN = ( 1 − − ; m 4).
Theo giả thiết: MN = ⇔ MN = ⇔ (− −m)2 2 2 5 2 5 1 + 4 = 2 5 m = 1 → M 1;0 2 ( ) (1 m) 2 16 20 m 2m 3 0 ⇔ + + = ⇔ + − = ⇔ . Chọn B. m = −3 → M (−3;0)
Câu 66. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; )
3 và B (4;2). Tìm tọa độ
điểm C thuộc trục hoành sao cho C cách đều hai điểm A và . B A. 5 C − ;0 . B. 5 C ;0 . C. 3 C − ;0 . D. 3 C ;0 . 3 3 5 5
AC = (x −1;− ) 3
Lời giải. Ta có C ∈Ox nên C (x;0) và .
BC = (x −4;−2) Do 5 5 CA CB CA CB (x )2 1 ( 3)2 (x 4)2 ( 2)2 2 2 x C = ⇔ = ⇔ − + − = − + − ⇔ = → ;0 . 3 3 Chọn B.
Câu 67. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;2), B(5;−2). Tìm điểm M thuộc trục hoàng sao cho 0 AMB = 90 ? A. M (0; ) 1 . B. M (6;0). C. M (1;6). D. M (0;6). AM = (m −2;−2)
Lời giải. Ta có M ∈Ox nên M ( ; m 0) và .
BM = (m−5;2) Vì 0
AMB = 90 suy ra AM .BM = 0 nên (m −2)(m − ) 5 +(−2).2 = 0. m = 1 M (1;0) 2
⇔ m −7m + 6 = 0 ⇔ → . Chọn B. m = 6 M (6;0)
Câu 68. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;− )
1 và B (3;2). Tìm M thuộc trục tung sao cho 2 2
MA + MB nhỏ nhất. A. M (0; ) 1 . B. M (0;− ) 1 . C. 1 M 0; . D. 1 M 0; − . 2 2 MA = (1; 1 − − m)
Lời giải. Ta có M ∈Oy nên M (0;m) và .
MB = (3;2−m) 2 2
Khi đó MA + MB = MA + MB = +(− −m)2 + +( −m)2 2 2 2 2 2 1 1 3 2
= 2m − 2m +15. 2 1 29 29 2 = m − + ≥ ; ∀m ∈ . ℝ 2 2 2 Suy ra { 29 2 2 MA + MB } = . min 2 Dấu
' = ' xảy ra khi và chỉ khi 1 1 m M = → 0; . Chọn C. 2 2
Câu 69. Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(−2;0), B (2; )
5 , C (6;2). Tìm tọa độ điểm D. A. D(2;−3). B. D(2; ) 3 .
C. D(−2;−3). D. D(−2; ) 3 .
Lời giải. Gọi D(x; y). Ta có AD = (x +2; y) và BC = (4;−3). + = Vì x 2 4 x = 2
ABCD là hình bình hành nên AD BC = → ⇔ → D (2;−3). y = −3 y = −3 Chọn A.
Câu 70. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; )
3 , B (−2;4), C (5; ) 3 .
Tìm tọa độ trọng tâm G của tam giác đã cho. A. 10 G 2; . B. 8 10 G ; − . C. G (2; ) 5 . D. 4 10 G ; . 3 3 3 3 3 1− 2 + 5 4 x = = G
Lời giải. Tọa độ trọng tâm 3 3 G (x ; y là . Chọn D. G G ) 3 + 4 + 3 10 y = = G 3 3
Câu 71. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(−4; ) 1 , B (2;4),
C (2;−2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho. A. 1 I ;1 . B. 1 I − ;1 . C. 1 I 1 ; . D. 1 I 1 ; − . 4 4 4 4
AI = (x + 4; y − ) 1
Lời giải. Gọi I (x; y). Ta có BI = (x −2; y −4).
CI =(x−2;y+2) 2 2 Do IA = IB
I là tâm đường tròn ngoại tiếp tam giác ABC nên IA IB IC = = ⇔ 2 2 IB = IC ( x +
)2 +(y − )2 = (x − )2 +(y − )2 1 4 1 2 4 ( x + 4 )2 = (x −2)2 + 9 x = − ⇔ ⇔ ⇔ 4 . Chọn B. (
x −2)2 +(y −4)2 = (x −2)2 +(y +2)2 y 1 = y =1
Câu 72. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(−3;0), B(3;0) và
C (2;6). Gọi H (a;b) là tọa độ trực tâm của tam giác đã cho. Tính a + 6 . b
A. a + 6b = 5.
B. a + 6b = 6.
C. a + 6b = 7.
D. a + 6b = 8. AH =
(a + 3;b) & BC = (−1;6)
Lời giải. Ta có .
BH = (a−3;b) & AC = (5;6) a = AH.BC = 0 ( a + ) (− ) 2 3 . 1 + . b 6 = 0 Từ giả thiết, ta có ⇔ ⇔ 5 → a + 6b = 7. ( a − ) 3 .5 + . b 6 = 0 . 0 b BH AC = = 6 Chọn C.
Câu 73. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4;3), B(2;7) và
C (−3;−8). Tìm toạ độ chân đường cao A ' kẻ từ đỉnh A xuống cạnh BC. A. A'(1;−4). B. A'( 1 − ;4). C. A'(1;4). D. A'(4; ) 1 .
AA' = (x −4; y − ) 3
Lời giải. Gọi A'(x; y). Ta có BC = (−5; 1 − ) 5 .
BA'=(x−2;y−7) AA ' ⊥ BC AA'.BC = 0 ( ) 1
Từ giả thiết, ta có ⇔ .
B, A ', C thang hang BA ' k BC (2) = • ( )
1 ⇔ −5(x − 4)−15( y − )
3 = 0 ⇔ x + 3y = 13. x − 2 y −7 • (2) ⇔ =
⇔ 3x − y = −1. −5 −15 + =
Giải hệ x 3y 13 x = 1 ⇔
→ A '(1;4). Chọn C. 3 x − y = 1 − y = 4
Câu 74. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), B(−3; ) 1 , C (3;− )
1 . Tìm tọa độ chân đường cao A ' vẽ từ đỉnh A của tam giác đã cho. A. 3 1 A ' ; . B. 3 1 A '− ; − . C. 3 1 A '− ; . D. 3 1 A ' ; − . 5 5 5 5 5 5 5 5 AA' =
(x −2; y − 4)
Lời giải. Gọi A'(x; y). Ta có BC = (6;−2) .
BA'=(x +3;y− )1 Vì AA ⊥ BC
A ' là chân đường cao vẽ từ đỉnh A của tam giác ABC nên '
B, C, A ' thang hang (
x − ) +(y − ) (− ) 3 2 .6 4 . 2 = 0 x = AA '.BC = 0 6
x − 2 y = 4 5 ⇔ ⇔ ⇔ + − ⇔ . x 3 y 1 Chọn D. = =
−2x − 6 y = 0 1 BA ' k BC 6 −2 y = − 5
Câu 75. Trong mặt phẳng tọa độ Oxy , cho ba điểm A(−3;−2), B(3;6) và C (11;0).
Tìm tọa độ điểm D để tứ giác ABCD là hình vuông. A. D(5;−8). B. D(8; ) 5 . C. D(−5;8). D. D(−8; ) 5 .
Lời giải. Dễ dàng kiểm tra 0 B . A BC = 0 → ABC = 90 .
Gọi I là tâm của hình vuông ABCD.
Suy ra I là trung điểm của AC → I (4;− ) 1 . x + 3 = 4 Gọi x = 5 2
D (x; y) , do I cũng là trung điểm của BD → ⇔ ⇒ D (5;−8). y + 6 y = −8 1 = − 2 Chọn A.
Câu 76. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;4) và B(1; ) 1 . Tìm tọa độ
điểm C sao cho tam giác ABC vuông cân tại . B A. C (4;0). B. C (−2;2).
C. C (4;0), C (−2;2). D. C (2;0). BA = (1; ) 3
Lời giải. Gọi C (x; y) . Ta có .
BC = (x −1; y − ) 1 Tam giác B . A BC = 0
ABC vuông cân tại B ⇔ BA = BC 1 .(x − ) 1 + 3.( y − ) 1 = 0 x = 4 −3y y = 0 y = 2 hay ⇔ ⇔ ⇔ . Chọn C. 1 +3 = (x − )2 1 +( y − )2 2 2 2 1 1
0 y −20 y = 0 x = 4 x = −2
Câu 77. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1;− ) 1 và B (3;0).
Tìm tọa độ điểm D , biết D có tung độ âm. A. D(0;− ) 1 . B. D(2;−3). C. D(2;− ) 3 , D (0; )
1 . D. D (−2;−3). AB = (2; ) 1
Lời giải. Gọi C = (x; y). Ta có .
BC = (x −3; y) Vì ⊥
ABCD là hình vuông nên ta có AB BC AB = BC 2
(x −3)+1.y = 0
y = 2(3− x)
y = 2(3− x) x = 4 x = ⇔ ⇔ ⇔ ⇔ hoặc 2 . ( x − )2 3 + y = 5 5 (x −3)2 = 5 ( x − )2 2 3 = 1 y = −2 y = 2
Với C 4;−2 ta tính được đỉnh D 2;−3 : thỏa mãn. 1 ( ) 1 ( )
Với C 2;2 ta tính được đỉnh D 0;1 : không thỏa mãn. 2 ( ) 2 ( ) Chọn B.
Câu 78. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(1;2), B( 1 − ;3), C (−2;− ) 1 và
D (0;−2). Mệnh đề nào sau đây đúng ?
A. ABCD là hình vuông.
B. ABCD là hình chữ nhật.
C. ABCD là hình thoi.
D. ABCD là hình bình hành. AB = (−2; ) 1 Lời giải. Ta có AB = DC BC ( 1; 4) = − − →
→ ABCD là hình hình hành.
AB.BC = −2 ≠ 0 DC = (−2; ) 1 Chọn D.
Câu 79. Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; ) 3 và B (4;2) . Tìm
tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB. A. 5 5 E = ; . B. 3 1 E = ; − . 2 2 2 2
C. E = (−2+3 2;4 + 2).
D. E = (−2+3 2;4− 2).
Lời giải. Theo tính chất đường phân giác của tam giác ta có EA OA 2 = = . EB OB 2
Vì E nằm giữa hai điểm , A B nên 2 EA = − EB. (*) 2 EA = (1− x;3− y)
Gọi E (x; y). Ta có .
EB = (4− x;2− y) 2 1 − x = − (4 − x) Từ x = −2 + 3 2 ( 2 *) , suy ra ⇔ . Chọn D. 2 y = 4− 2 3 y (2 y) − = − − 2
Câu 80. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(2;0), B(0;2) và C (0;7). Tìm tọa
độ đỉnh thứ tư D của hình thang cân ABCD. A. D(7;0).
B. D(7;0), D(2;9). C. D(0;7), D(9;2). D. D(9;2).
Lời giải. Để tứ giác ABCD là hình thang cân, ta cần có một cặp cạnh đối song song
không bằng nhau và cặp cạnh còn lại có độ dài bằng nhau. Gọi D(x; y).
• Trường hợp 1: AB CD
⇔ CD = k AB (với k ≠ −1 ) AB ≠ CD x = −2k
(x 0; y 7) ( 2k;2k) ⇔ − − = − ⇔ . ( ) 1 y = 2k +7
AD =(x −2;y)⇒ AD = (x −2)2 2 + y Ta có
→ AD = BC ⇔ (x −2)2 2 + y = 25. (2) BC =(0; ) 5 ⇒ BC = 5 k = − ( 1 loaïi) Từ ( ) 2 2
1 và (2) , ta có (−2k − 2) +(2k + 7) = 25 ⇔ → D (7;0). 7 k = − 2
• Trường hợp 2: AD BC
. Làm tương tự ta được D = (2;9). AD ≠ BC
Vậy D(7;0) hoặc D(2;9) . Chọn B. Baøi 03
CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC VAØ GIAÛI TAM GIAÙC 1. Định lí côsin
Cho tam giác ABC có BC = a, AC = b và A AB = c . Ta có 2 2 2
a = b + c − 2bc.cos ; A b 2 2 2 c
b = c + a − 2c . a cos B; 2 2 2
c = a + b − 2a . b cosC. B a C Hệ quả 2 2 2 2 2 2 2 2 2
b + c − a
c + a −b
a + b − c cos A = ; cos B = ; cosC = . 2bc 2ca 2ab 2. Định lí sin
Cho tam giác ABC có BC = a, AC = b , AB = c và A
R là bán kính đường tròn ngoại tiếp. Ta có a b c = = = 2R c b sin A sin B sinC I B a C
3. Độ dài đường trung tuyến
Cho tam giác ABC có m , m , m lần lượt là a b c các trung tuyến kẻ từ ,
A B, C . Ta có A 2 2 2 b + c a 2 m = − ; a m a b 2 4 c 2 2 2 a + c b 2 m = − ; b 2 4 m m b c 2 2 2 a + b c B a 2 C m = − . c 2 4
4. Công thức tính diện tích tam giác
Cho tam giác ABC có 1 1 1 S = ah = bh = ch ● a b c
h , h , h là độ dài đường cao lần lượt 2 2 2 a b c
tương ứng với các cạnh BC , C , A AB ; ● 1 1 1
R là bán kính đường tròn ngoại tiếp tam = bc sin A = ca sin B = ab sin C giác; 2 2 2 abc
● r là bán kính đường tròn nội tiếp tam = 4R giác; = pr ● a + b + c p = là nửa chu vi tam giác; 2
= p( p −a)( p −b)( p −c).
● S là diện tích tam giác. Khi đó ta có:
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. GIẢI TAM GIÁC
Câu 1. Tam giác ABC có AB = 5, BC = 7, CA = 8 . Số đo góc A bằng: A. 30°. B. 45 . ° C. 60 . ° D. 90 . ° 2 2 2 2 2 2
Lời giải. Theo định lí hàm cosin, ta có
AB + AC − BC 5 + 8 −7 1 cos A = = = . 2AB.AC 2.5.8 2
Do đó, A = 60° . Chọn C.
Câu 2. Tam giác ABC có AB = 2, AC = 1 và A = 60° . Tính độ dài cạnh BC . A. BC = 1. B. BC = 2. C. BC = 2. D. BC = 3.
Lời giải. Theo định lí hàm cosin, ta có 2 2 2 2 2
BC = AB + AC − 2AB.AC.cos A = 2 +1 − 2.2.1.cos 60° = 3 ⇒ BC = 3 . Chọn D.
Câu 3. Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3 , cạnh
AB = 9 và ACB = 60° . Tính độ dài cạnh cạnh BC . A. +
BC = 3 + 3 6. B. BC = 3 6 − 3. C. BC = 3 7. D. 3 3 33 BC = . 2 Lời giải.
Gọi M , N lần lượt là trung điểm của AB, BC . A
→ MN là đường trung bình của A ∆ BC . M 1 → MN =
AC . Mà MN = 3 , suy ra AC = 6 . 2
Theo định lí hàm cosin, ta có B N C 2 2 2
AB = AC + BC − 2.AC.BC.cos ACB 2 2 2
⇔ 9 = 6 + BC − 2.6.BC.cos 60° ⇒ BC = 3 + 3 6 Chọn A.
Câu 4. Tam giác ABC có AB = 2, AC = 3 và C = 45° . Tính độ dài cạnh BC . A. + − BC = 5. B. 6 2 BC = . C. 6 2 BC = . D. BC = 6. 2 2
Lời giải. Theo định lí hàm cosin, ta có
AB = AC + BC − AC BC C ⇒ ( )2 =( )2 2 2 2 2 2. . .cos 2 3
+ BC − 2. 3.BC.cos 45° 6 + 2 ⇒ BC = . Chọn B. 2
Câu 5. Tam giác ABC có B = 60 ,° C = 45° và AB = 5 . Tính độ dài cạnh AC . A. 5 6 AC = . B. AC = 5 3. C. AC = 5 2. D. AC = 10. 2
Lời giải. Theo định lí hàm sin, ta có AB AC 5 AC 5 6 = ⇔ = ⇒ AC = . sinC sin B sin 45° sin 60° 2 Chọn A.
Câu 6. Cho hình thoi ABCD cạnh bằng 1 cm và có BAD = 60° . Tính độ dài cạnh AC . A. AC = 3. B. AC = 2. C. AC = 2 3. D. AC = 2. Lời giải.
Do ABCD là hình thoi, có BAD = 60° ⇒ ABC = 120° . B
Theo định lí hàm cosin, ta có 2 2 2
AC = AB + BC − 2.AB.BC.cos ABC A C 2 2
= 1 +1 − 2.1.1.cos120° = 3 ⇒ AC = 3 Chọn A. D
Câu 7. Tam giác ABC có AB = 4, BC = 6, AC = 2 7 . Điểm M thuộc đoạn BC sao
cho MC = 2MB . Tính độ dài cạnh AM .
A. AM = 4 2. B. AM = 3. C. AM = 2 3. D. AM = 3 2. Lời giải.
Theo định lí hàm cosin, ta có A AB BC AC + − + − ( )2 2 2 2 2 2 4 6 2 7 1 cos B = = = . 2.AB.BC 2.4.6 2 Do 1 MC = 2MB
→ BM = BC = 2 . 3
Theo định lí hàm cosin, ta có B M C 2 2 2
AM = AB + BM − 2.AB.BM .cos B 1 2 2
= 4 + 2 − 2.4.2. = 12 ⇒ AM = 2 3 2 Chọn C. Câu 8. Tam giác − ABC có 6 2 AB =
, BC = 3, CA = 2 . Gọi D là chân đường 2
phân giác trong góc A . Khi đó góc ADB bằng bao nhiêu độ? A. 45°. B. 60°. C. 75°. D. 90 . ° Lời giải.
Theo định lí hàm cosin, ta có A 2 2 2
AB + AC − BC 1 cos BAC = = − 2.AB.AC 2
⇒ BAC = 120° ⇒ BAD = 60° 2 2 2
AB + BC − AC 2 cos ABC = = ⇒ ABC = 45° B D C 2.AB.BC 2 Trong A
∆ BD có BAD = 60 ,
° ABD = 45° ⇒ ADB = 75° . Chọn C.
Câu 9. Tam giác ABC vuông tại A , đường cao AH = 32 cm . Hai cạnh AB và AC tỉ
lệ với 3 và 4 . Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu? A. 38 c . m B. 40 c . m C. 42 c . m D. 45 c . m
Lời giải. Do tam giác ABC vuông tại A , có tỉ lệ 2 cạnh góc vuông AB : AC là 3 : 4
nên AB là cạnh nhỏ nhất trong tam giác. Ta có AB 3 4 = ⇒ AC = AB . AC 4 3 Trong A
∆ BC có AH là đường cao 1 1 1 1 1 1 1 9 ⇒ = + = + ⇔ = +
⇒ AB = 40 . Chọn B. 2 2 2 2 2 2 2 AH AB AC AB 4 2 32 AB 16AB AB 3
Câu 10. Tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các
góc MPE, EPF, FPQ bằng nhau. Đặt MP = q, PQ = ,
m PE = x, PF = y . Trong các hệ
thức sau, hệ thức nào đúng?
A. ME = EF = FQ. B. 2 2 2
ME = q + x − xq. C. 2 2 2
MF = q + y − yq. D. 2 2 2
MQ = q + m − 2q . m Lời giải. P M E F Q Ta có MPQ
MPE = EPF = FPQ =
= 30° ⇒ MPF = EPQ = 60° . 3
Theo định lí hàm cosin, ta có 2 2 2 2 2 2 2
ME = AM + AE − 2.AM .AE.cos MAE = q + x − 2qx.cos 30° = q + x − qx 3 2 2 2 2 2 2 2
MF = AM + AF − 2AM .AF .cos MAF = q + y − 2qy.cos 60° = q + y − qy 2 2 2 2 2
MQ = MP + PQ = q + m Chọn C.
Câu 11. Cho góc xOy = 30° . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy
sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng: A. 3. B. 3. C. 2 2. D. 2. 2 Lời giải.
Theo định lí hàm sin, ta có y OB AB AB = ⇔ OB = .sinOAB B sinOAB sin AOB sin AOB 1 =
.sinOAB = 2 sinOAB sin 30° x O Do đó, độ dài A
OB lớn nhất khi và chỉ khi
sinOAB = 1 ⇔ OAB = 90° . Khi đó OB = 2 . Chọn D.
Câu 12. Cho góc xOy = 30° . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy
sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng: A. 3. B. 3. C. 2 2. D. 2. 2 Lời giải.
Theo định lí hàm sin, ta có y OB AB AB = ⇔ OB = .sinOAB B sinOAB sin AOB sin AOB 1 =
.sinOAB = 2 sinOAB sin 30° x O Do đó, độ dài A
OB lớn nhất khi và chỉ khi
sinOAB = 1 ⇔ OAB = 90° . Khi đó OB = 2 .
Tam giác OAB vuông tại 2 2 2 2
A ⇒ OA = OB − AB = 2 −1 = 3 . Chọn B
Câu 13. Tam giác ABC có AB = c, BC = a, CA = b . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức ( 2 2 − )= ( 2 2 b b a
c a − c ) . Khi đó góc BAC bằng bao nhiêu độ? A. 30°. B. 45 . ° C. 60 . ° D. 90 . ° 2 2 2 2 2 2
Lời giải. Theo định lí hàm cosin, ta có
AB + AC − BC
c + b − a cos BAC = = . 2.A . B AC 2bc Mà b( 2 2
b − a ) = c ( 2 2 a − c ) 3 2 2 3 2
⇔ b − a b = a c − c ⇔ a − (b + c)+( 3 3 b + c ) = 0 ⇔ (b + c )( 2 2 2
b + c − a −bc ) 2 2 2
= 0 ⇔ b + c − a −bc = 0 (do b > 0, c > 0 ) 2 2 2
⇔ b + c − a = bc 2 2 2 Khi đó,
b + c − a 1 cos BAC = =
⇒ BAC = 60° . Chọn C. 2bc 2
Câu 14. Tam giác ABC vuông tại A , có AB = c, AC = b . Gọi ℓ là độ dài đoạn phân a
giác trong góc BAC . Tính ℓ theo b và c . a A. 2bc 2 b + c bc 2 b + c ℓ = . B. ( ) ℓ = . C. 2 ℓ = . D. ( ) ℓ = . a b + c a bc a b + c a bc Lời giải. A C B D Ta có 2 2 2 2
BC = AB + AC = b + c . 2 2 Do AB c c c b + c
AD là phân giác trong của BAC ⇒ BD = .DC = .DC = . BC = . AC b b + c b + c
Theo định lí hàm cosin, ta có 2 c ( 2 2 b + c 2 2 2 ) 2 2
BD = AB + AD − 2.AB.A . D cos ABD ⇔
= c + AD − 2c.AD.cos 45° (b + c)2 2 c b c + 2bc 2 2 ( 2 2 ) 3 2
⇒ AD − c 2.AD + c −
= 0 ⇔ AD − c 2.AD + = 0 . (
b + c )2 (b + c)2 2bc bc ⇒ AD = hay 2 ℓ = . Chọn A. b + c a b + c
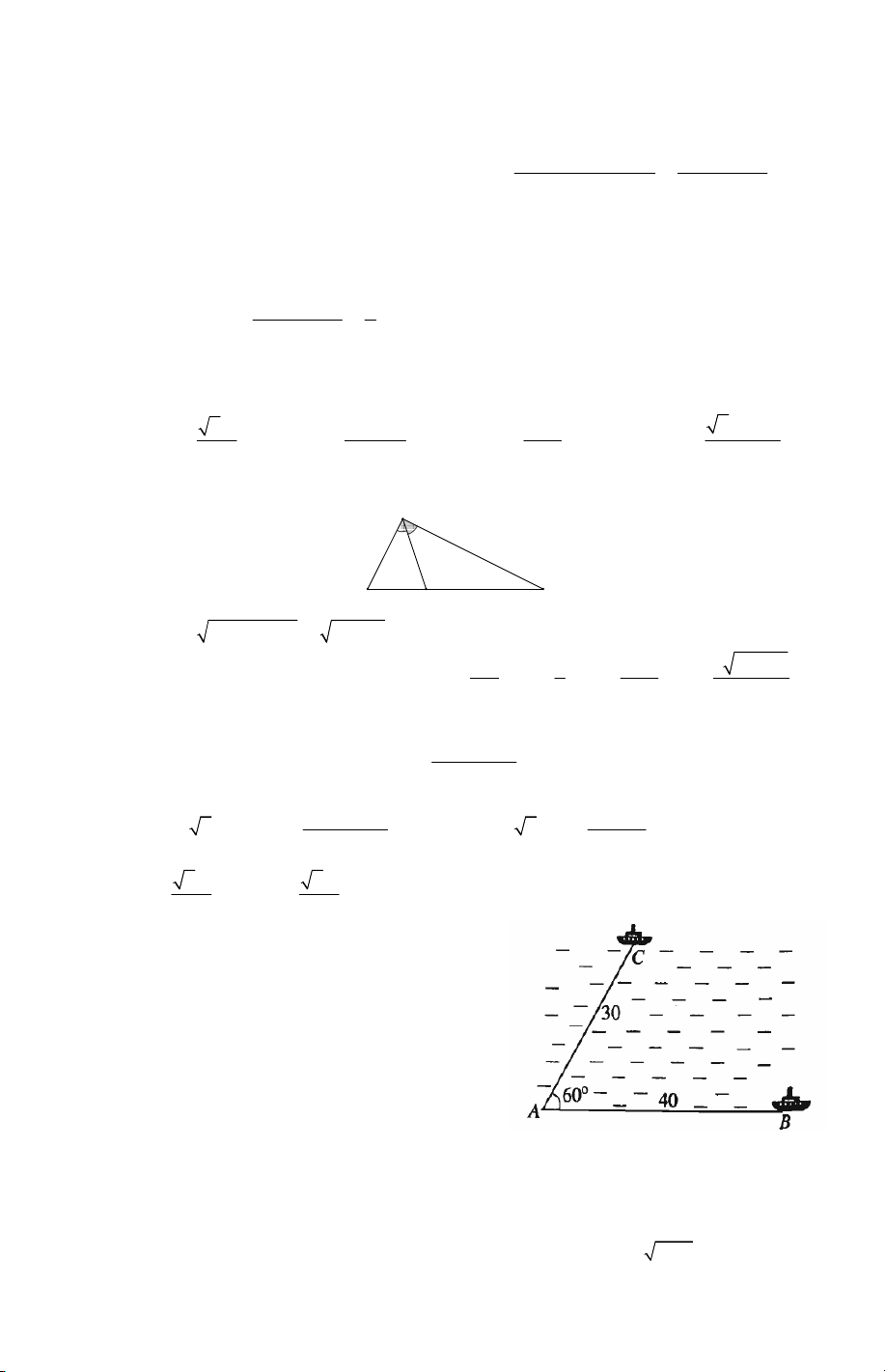
Câu 15. Hai chiếc tàu thủy cùng xuất phát từ
một vị trí A , đi thẳng theo hai hướng tạo với nhau góc 0
60 . Tàu B chạy với tốc độ 20 hải lí
một giờ. Tàu C chạy với tốc độ 15 hải lí một
giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu
hải lí? Kết quả gần nhất với số nào sau đây? A. 61 hải lí. B. 36 hải lí. C. 21 hải lí. D. 18 hải lí.
Lời giải. Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác
ABC có AB = 40, AC = 30 và 0 A = 60 .
Áp dụng định lí côsin vào tam giác ABC, ta có 2 2 2
a = b + c − 2bc cos A 2 2 0
= 30 + 40 − 2.30.40.cos 60 = 900 +1600 −1200 = 1300. Vậy BC = 1300 ≈ 36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí. Chọn B.
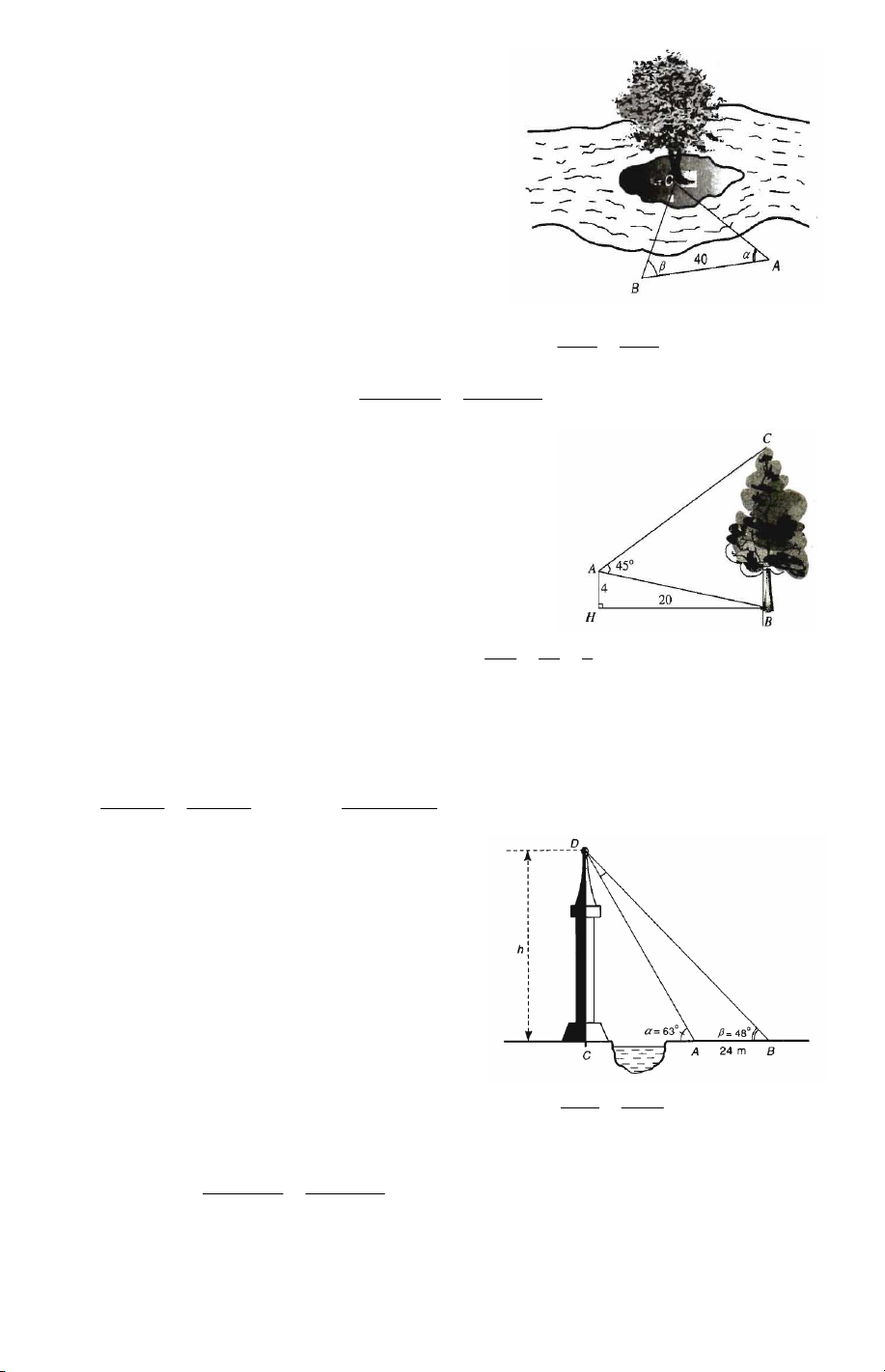
Câu 16. Để đo khoảng cách từ một điểm A
trên bờ sông đến gốc cây C trên cù lao giữa
sông, người ta chọn một điểm B cùng ở trên
bờ với A sao cho từ A và B có thể nhìn thấy
điểm C . Ta đo được khoảng cách AB = 40m , 0 CAB = 45 và 0
CBA = 70 . Vậy sau khi đo đạc
và tính toán được khoảng cách AC gần nhất
với giá trị nào sau đây? A. 53m . B. 30m . C. 41,5m . D. 41m .
Lời giải. Áp dụng định lí sin vào tam giác AC AB ABC, ta có = sin B sin C 0 Vì A . B sin β 40.sin 70
sinC = sin(α + β) nên AC = =
≈ 41, 47 m. Chọn C. sin(α + β) 0 sin115
Câu 17. Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết 0
AH = 4m, HB = 20m, BAC = 45 .
Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m . B. 17m . C. 16,5m . D. 16m . AH 4 1
Lời giải. Trong tam giác AHB , ta có 0 tan ABH = = = → ABH ≈ 11 19 ' . BH 20 5 Suy ra 0 0
ABC = 90 − ABH = 78 41' . Suy ra 0 ACB = −(BAC + ABC) 0 180 = 56 19 ' .
Áp dụng định lý sin trong tam giác ABC , ta được AB CB A . B sin BAC = →CB = ≈ 17m. Chọn B. sin ACB sin BAC sin ACB
Câu 18. Giả sử CD = h là chiều cao của
tháp trong đó C là chân tháp. Chọn hai điểm ,
A B trên mặt đất sao cho ba điểm ,
A B và C thẳng hàng. Ta đo được AB = 24 m , 0 0
CAD = 63 , CBD = 48 . Chiều
cao h của tháp gần với giá trị nào sau đây? A. 18m . B. 18,5m . C. 60m . D. 60,5m .
Lời giải. Áp dụng định lí Sin vào tam giác AD AB ABD, ta có = . sin β sin D
Ta có α = D + β nên 0 0 0
D = α − β = 63 − 48 = 15 . 0 Do đó AB.sin β 24.sin 48 AD = = ≈ 68,91 m. sin(α − β) 0 sin15
Trong tam giác vuông ACD, có h = CD = AD.sin α ≈ 61,4 m. Chọn D.
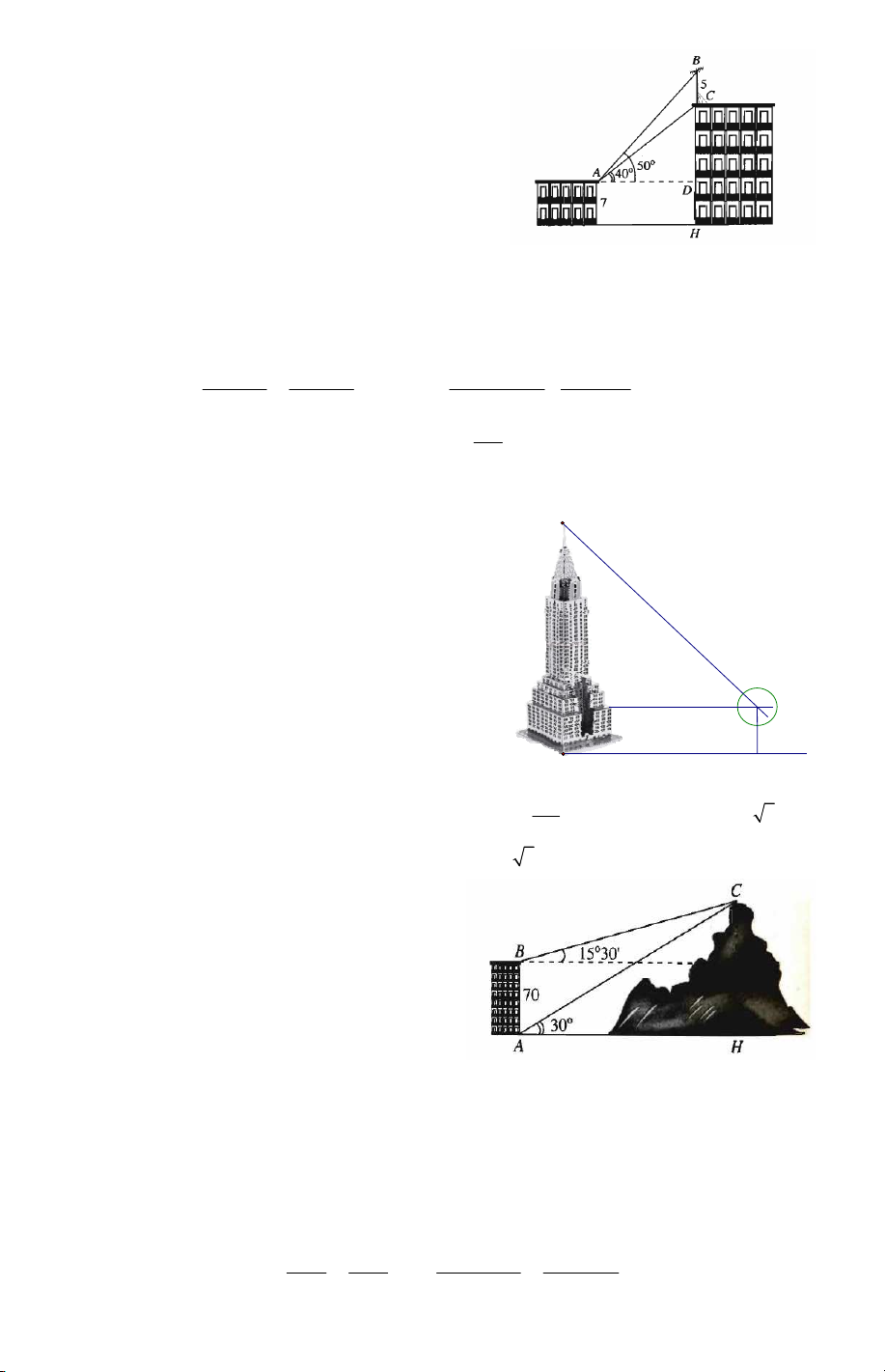
Câu 19. Trên nóc một tòa nhà có một cột ăng-
ten cao 5 m . Từ vị trí quan sát A cao 7 m so
với mặt đất, có thể nhìn thấy đỉnh B và chân
C của cột ăng-ten dưới góc 0 50 và 0 40 so với
phương nằm ngang. Chiều cao của tòa nhà gần
nhất với giá trị nào sau đây? A. 12m . B. 19m . C. 24m . D. 29m .
Lời giải. Từ hình vẽ, suy ra 0 BAC = 10 và 0 ABD = −(BAD + ADB) 0 = −( 0 0 + ) 0 180 180 50 90 = 40 .
Áp dụng định lí sin trong tam giác ABC , ta có 0 BC AC BC.sin ABC 5.sin 40 = → AC = = ≈ 18,5 m . 0 sin BAC sin ABC sin BAC sin10 Trong tam giác vuông CD
ADC , ta có sinCAD =
→CD = AC.sinCAD = 11.9 m. AC
Vậy CH = CD + DH = 11,9 +7 = 18,9 m. Chọn B.
Câu 20. Xác định chiều cao của một tháp mà A
không cần lên đỉnh của tháp. Đặt kế giác
thẳng đứng cách chân tháp một khoảng
CD = 60m , giả sử chiều cao của giác kế là
OC = 1m . Quay thanh giác kế sao cho khi
ngắm theo thanh ta nhình thấy đỉnh A của
tháp. Đọc trên giác kế số đo của góc 0
AOB = 60 . Chiều cao của ngọn tháp gần với B 60° O giá trị nào sau đây: 1m A. 40m . B. 114m . D 60 C C. m 105m . D. 110m .
Lời giải. Tam giác AB
OAB vuông tại B, có 0 tan AOB =
⇒ AB = tan 60 .OB = 60 3 m. OB
Vậy chiếu cao của ngọn tháp là h = AB +OC = (60 3 + ) 1 m. Chọn C.
Câu 21. Từ hai vị trí A và B của một
tòa nhà, người ta quan sát đỉnh C của
ngọn núi. Biết rằng độ cao AB = 70m ,
phương nhìn AC tạo với phương nằm ngang góc 0
30 , phương nhìn BC tạo với phương nằm ngang góc 0 15 30 ' . Ngọn núi
đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? A. 135m . B. 234m . C. 165m . D. 195m .
Lời giải. Từ giả thiết, ta suy ra tam giác ABC có 0 0
CAB = 60 , ABC = 105 30′ và c = 70. Khi đó 0 0
A + B +C = ⇔ C = −(A + B) 0 0 0 180 180 = 180 −165 30′ = 14 30 . ′
Theo định lí sin, ta có b c b 70 = hay = sin B sin C 0 0 sin105 30′ sin14 30′ 0 Do đó 70.sin105 30′ AC = b = ≈ 269, 4 m. 0 sin14 30′
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc AC 0 30 nên 269, 4 CH = = = 134,7 m. 2 2
Vậy ngọn núi cao khoảng 135 m. Chọn A.
Vấn đề 2. ĐƯỜNG TRUNG TUYẾN
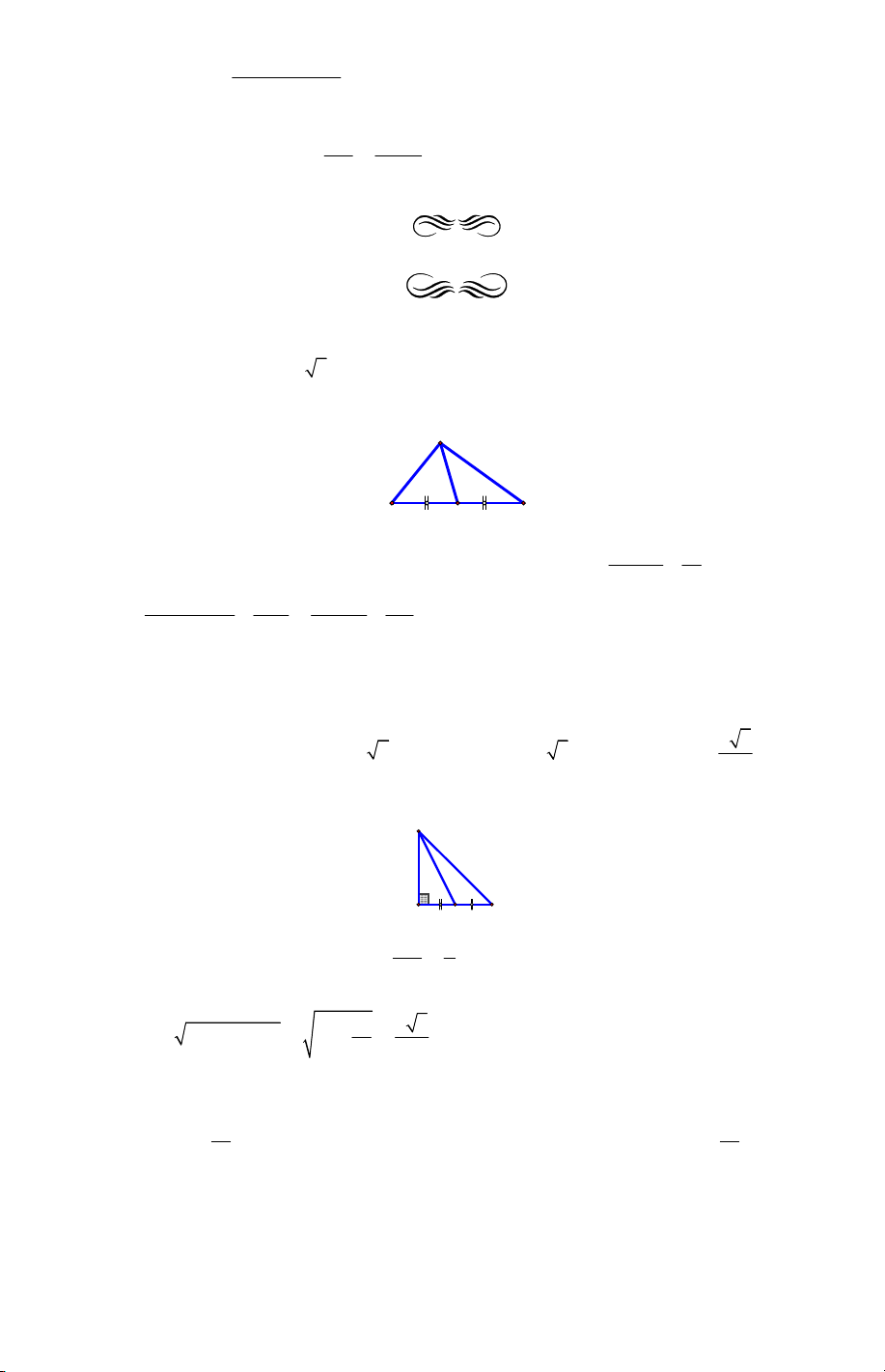
Câu 22. Tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm . Độ dài đường trung
tuyến xuất phát từ đỉnh A của tam giác bằng: A. 4cm . B. 3cm . C. 7cm . D. 5cm . Lời giải. A B C M 2 2 2
Áp dụng công thức đường trung tuyến b + c a 2 m = − ta được: a 2 4 2 2 2 2 2 2 AC + AB BC 8 + 6 10 2 m = − = − = 25 a 2 4 2 4
⇒ m = 5. Chọn D. a
Câu 23. Tam giác ABC vuông tại A và có AB = AC = a . Tính độ dài đường trung
tuyến BM của tam giác đã cho. A. a BM = 1,5 . a
B. BM = a 2.
C. BM = a 3. D. 5 BM = . 2 Lời giải. B C A M AC a
M là trung điểm của AC ⇒ AM = = . 2 2 Tam giác B
∆ AM vuông tại A 2 a a 5 2 2 2
⇒ BM = AB + AM = a + = . Chọn D. 4 2
Câu 24. Tam giác ABC có AB = 9 cm, AC = 12 cm và BC = 15 cm. Tính độ dài đường
trung tuyến AM của tam giác đã cho. A. 15 AM =
cm. B. AM = 10 cm. C. AM = 9 cm. D. 13 AM = cm. 2 2 Lời giải. A B C M 2 2 2
Áp dụng hệ thức đường trung tuyến b + c a 2 m = − ta được: a 2 4 2 2 2 2 2 2 AC + AB BC 12 + 9 15 225 2 m = − = − = . a 2 4 2 4 4 15 ⇒ m = . Chọn A. a 2
Câu 25. Tam giác ABC cân tại C , có AB = 9cm và 15 AC =
cm . Gọi D là điểm đối 2
xứng của B qua C . Tính độ dài cạnh AD. A. AD = 6 cm. B. AD = 9 cm. C. AD =12 cm.
D. AD = 12 2 cm. Lời giải. D C B A
Ta có: D là điểm đối xứng của B qua C ⇒ C là trung điểm của B . D
⇒ AC là trung tuyến của tam giác D ∆ A . B
BD = 2BC = 2AC = 15.
Theo hệ thức trung tuyến ta có: 2 2 2 AB + AD BD 2 BD 2 AC = − 2 2 2 ⇒ AD = 2AC + − AB 2 4 2 2 2 15 15 2 ⇒ AD = 2 2. +
− 9 = 144 ⇒ AD = 12. Chọn C. 2 2
Câu 26. Tam giác ABC có AB = 3, BC = 8 . Gọi M là trung điểm của BC . Biết 5 13 cos AMB =
và AM > 3 . Tính độ dài cạnh AC . 26 A. AC = 13 . B. AC = 7 . C. AC =13 . D. AC = 7 . Lời giải. A B C M Ta có: BC
M là trung điểm của BC ⇒ BM = = 4. 2 2 2 2 Trong tam giác
AM + BM − AB
ABM ta có: cos AMB = 2AM .BM 2 2 2
⇔ AM − 2AM .BM .cos AMB + BM − AB = 0.
AM = 13 > 3 (t / m) 20 13 2 AM AM 7 0 ⇔ − + = ⇔ 7 13 13 AM = < 3 (loai) 13 ⇒ AM = 13.
Ta có: AMB và AMC là hai góc kề bù. 5 13
⇒ cos AMC = −cos AMB = − 26 Trong tam giác A ∆ MC ta có: 2 2 2
AC = AM +CM − 2AM .CM .cos AMC 5 13 = 13 +16 − 2. 13.4.−
= 49 ⇒ AC = 7. Chọn D. 26
Câu 27*. Tam giác ABC có trọng tâm G . Hai trung tuyến BM = 6 , CN = 9 và 0
BGC = 120 . Tính độ dài cạnh AB . A. AB = 11 . B. AB = 13 . C. AB = 2 11 . D. AB = 2 13 . Lời giải. A M N G B C
Ta có: BGC và BGN là hai góc kề bù mà 0 0
BGC = 120 ⇒ BGN = 120 .
G là trọng tâm của tam giác A ∆ BC 2 BG = BM = 4. 3 ⇒ 1 G
N = CN = 3. 3 Trong tam giác B ∆ GN ta có: 2 2 2
BN = GN + BG − 2GN.BG.cos BGN 1 2
⇒ BN = 9 +16 − 2.3.4. = 13 ⇒ BN = 13. 2
N là trung điểm của AB ⇒ AB = 2BN = 2 13. Chọn D.
Câu 28**. Tam giác ABC có độ dài ba trung tuyến lần lượt là 9; 12; 15 . Diện tích
của tam giác ABC bằng: A. 24 . B. 24 2 . C. 72 . D. 72 2 . 2 2 2 b + c a 2 m = − = 81 a 2 4 2 a = 292 a = 2 73 2 2 2 + Lời giải. Ta có: a c b 2 2 m = − = 144 ⇔ b = 208 b ⇒ = 4 13 b 2 4 2 c = 10 2 2 2 c = 100 a + b c 2 m = − = 225 c 2 4 2 2 2 Ta có:
b + c − a 208 +100 − 292 1 cos A = = = 2bc 2.4 13.10 5 13 2 1 18 13 2
sin A = 1− cos A = 1 − = . Chọn C. 5 13 65 Diện tích tam giác 1 1 18 13 A ∆ BC : S
= bc sin A = .4 13.10. = 72 A ∆ BC 2 2 65
Câu 29*. Cho tam giác ABC có AB = c, BC = ,
a CA = b . Nếu giữa a, b, c có liên hệ 2 2 2
b + c = 2a thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng: A. a 3 . B. a 3 . C. 2a 3 . D. 3a 3 . 2 3 2 2 2
Lời giải. Hệ thức trung tuyến xuất phát từ đỉnh b + c a A của tam giác: 2 m = − a 2 4 2 2 2 Mà: 2a a 3a a 3 2 2 2
b + c = 2a ⇒ 2 m = − = ⇒ m = . Chọn A. a 2 4 4 a 2
Câu 30*. Cho hình bình hành ABCD có AB = ,
a BC = b, BD = m và AC = n . Trong
các biểu thức sau, biểu thức nào đúng: A. 2 2 m + n = ( 2 2 3 a + b ) . B. 2 2 m + n = ( 2 2 2 a + b ) . C. ( 2 2 + ) 2 2 2 m n = a + b . D. ( 2 2 + ) 2 2 3 m n = a + b .
Lời giải. Gọi O là giao điểm của AC và BD. Ta có: 1 m BO = BD = . 2 2
BO là trung tuyến của tam giác A ∆ BC 2 2 2 BA + BC AC 2 ⇒ BO = − 2 4 2 2 2 2 m a + b n 2 2 ⇔ = − ⇔ m + n = ( 2 2
2 a + b ) . Chọn B. 4 2 4
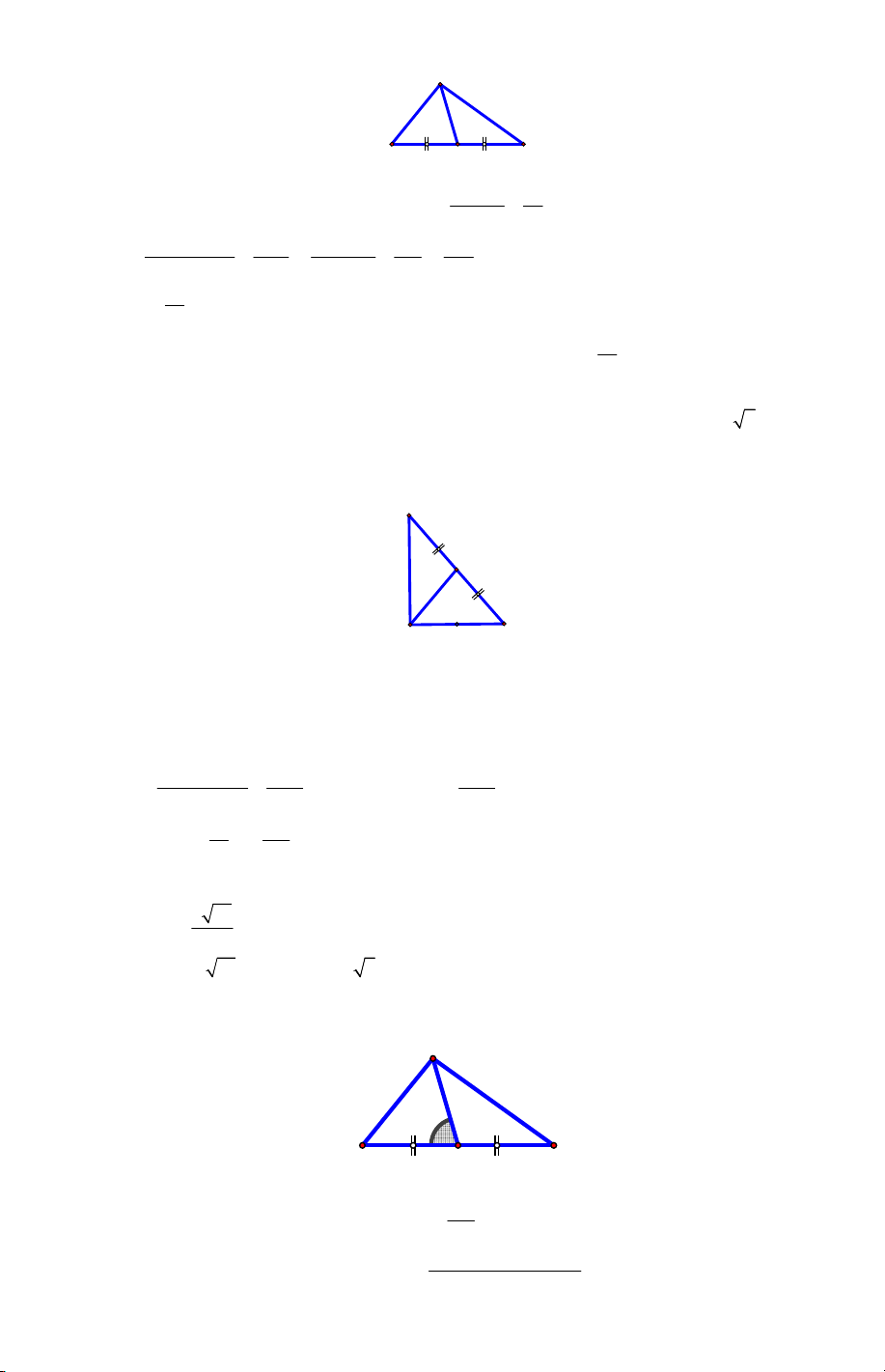
Câu 31**. Tam giác ABC có AB = c, BC = a, CA = b . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức 2 2 2
a + b = 5c . Góc giữa hai trung tuyến AM và BN là góc nào? A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Lời giải. Gọi G là trọng tâm tam giác ∆ABC. 2 2 2 2 2 2 Ta có: AC + AB BC b + c a 2 AM = − = − 2 4 2 4 2 4 ( 2 2 b + c ) 2 a 2 2 ⇒ AG = AM = − 9 9 9 2 2 2 2 2 2 BA + BC AC c + a b 2 BN = − = − 2 4 2 4 2 2 2 1 c + a b 2 2 ⇒ GN = BN = − 9 18 36 Trong tam giác A ∆ GN ta có: 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b 2 2 2 − + − −
AG +GN − AN 9 9 18 36 4 cos AGN = = 2.AG.GN 2( 2 2 b + c ) 2 2 2 2 a c + a b 2. − . − 9 9 18 36 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b − + − − 9 9 18 36 4 = 2( 2 2 b + c ) 2 2 2 2 a c + a b 2. − . − 9 9 18 36 2 10c − 2( 2 2 a + b ) = = 0 0
⇒ AGN = 90 . Chọn D. 2( 2 2 b + c ) 2 2 2 2 a c + a b 36.2. − . − 9 9 18 36
Câu 32**. Tam giác ABC có ba đường trung tuyến m , m , m thỏa mãn a b c 2 2 2
5m = m + m . Khi đó tam giác này là tam giác gì? a b c A. Tam giác cân. B. Tam giác đều. C. Tam giác vuông.
D. Tam giác vuông cân. 2 2 2 b + c a 2 m = − a 2 4 2 2 2
Lời giải. Ta có: a + c b 2 m = − Mà: 2 2 2
5m = m + m b 2 4 a b c 2 2 2 a + b c 2 m = − c 2 4 2 2 2 2 2 2 2 2 2 b c a + a + c b a + b c ⇒ 5 − = − + − 2 4 2 4 2 4 2 2 2 2 2 2 2 2 2
⇔ 10b +10c −5a = 2a + 2c −b + 2a + 2b − c 2 2 2
⇔ b + c = a ⇒ tam giác A
∆ BC vuông. Chọn C.
Câu 33**. Tam giác ABC có AB = c, BC = ,
a CA = b . Gọi m , m , m là độ dài ba a b c
đường trung tuyến, G trọng tâm. Xét các khẳng định sau: 3 1 (I). 2 2 2
m + m + m = a + b + c . (II) . 2 2 2
GA +GB +GC = ( 2 2 2
a + b + c ). a b c ( 2 2 2 ) 4 3
Trong các khẳng định đã cho có A. (I) đúng. B. Chỉ (II) đúng.
C. Cả hai cùng sai. D. Cả hai cùng đúng. 2 2 2 b + c a 2 m = − a 2 4 2 2 2
Lời giải. Ta có: a + c b 3 2 m = − 2 2 2
⇒ m + m + m = a + b + c a b c ( 2 2 2 ) b 2 4 4 2 2 2 a + b c 2 m = − c 2 4 4 4 3 1 2 2 2
GA +GB +GC = ( 2 2 2 m + m + m = a + b + c = a + b + c . Chọn D. a b c ) . ( 2 2 2 ) ( 2 2 2 ) 9 9 4 3
Vấn đề 3. BÁN KÍNH ĐƯỜNG TRÒN NGOẠI TIẾP
Câu 34. Tam giác ABC có BC = 10 và O
A = 30 . Tính bán kính R của đường tròn
ngoại tiếp tam giác ABC . A. R = 5 . B. R = 10 . C. 10 R = . D. R = 10 3 . 3
Lời giải. Áp dụng định lí Sin, ta có BC BC 10 = 2R ⇒ R = = = 10. 0 sin BAC 2.sin A 2.sin 30 Chọn B.
Câu 35. Tam giác ABC có AB = 3, AC = 6 và A = 60° . Tính bán kính R của đường
tròn ngoại tiếp tam giác ABC . A. R = 3 . B. R = 3 3 . C. R = 3 . D. R = 6 .
Lời giải. Áp dụng định lí Cosin, ta có 2 2 2
BC = AB + AC − 2A . B AC.cos BAC 2 2 0 2 2 2 2
= 3 + 6 − 2.3.6.cos 60 = 27 ⇔ BC = 27 ⇔ BC + AB = AC . Suy ra tam giác AC
ABC vuông tại B, do đó bán kính R = = 3. Chọn A. 2
Câu 36. Tam giác ABC có BC = 21cm, CA = 17cm, AB = 10cm . Tính bán kính R của
đường tròn ngoại tiếp tam giác ABC . A. 85 R = cm . B. 7 R = cm . C. 85 R = cm . D. 7 R = cm . 2 4 8 2 Lời giải. Đặt
AB + BC +CA p =
= 24. Áp dụng công thức Hê rông, ta có – 2 S = p − − − = − − − = ∆
( p AB)( p BC )(p CA) ( ) ( ) ( ) 2 24. 24 21 . 24 17 . 24 10 84 cm . ABC
Vậy bán kính cần tìm là AB.BC.CA AB.BC.CA 21.17.10 85 S = ⇒ R = = = c . m A ∆ BC 4R 4.S 4.84 8 A ∆ BC Chọn C.
Câu 37. Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R . Khi đó bán kính R bằng: A. a 3 a a a R = . B. 2 R = . C. 3 R = . D. 3 R = . 2 3 3 4
Lời giải. Xét tam giác ABC đều cạnh a, gọi M là trung điểm của BC. 2 Ta có 1 1 a 3
AM ⊥ BC suy ra 2 2 S
= .AM .BC = . AB − BM .BC = . A ∆ BC 2 2 4 3
Vậy bán kính cần tính là AB.BC.CA AB.BC.CA a a 3 S = ⇒ R = = = . A ∆ BC 2 4R 4.S∆ a ABC 3 3 4. 4 Chọn C. Câu 38. Tam giác AB
ABC vuông tại A có đường cao 12 AH = cm và 3 = . Tính bán 5 AC 4
kính R của đường tròn ngoại tiếp tam giác ABC .
A. R = 2,5cm . B. R = 1,5cm . C. R = 2cm . D. R = 3,5cm .
Lời giải. Tam giác ABC vuông tại ,
A có đường cao AH ⇒ 2
AB.AC = AH ( ) ∗ . 2 Mặt khác AB 3 3 3 12 8 3 = ⇔ AB = AC thế vào ( ) ∗ , ta được 2 AC = ⇔ AC = . AC 4 4 4 5 5 Suy ra 3 8 3 6 3 2 2 AB = . =
⇒ BC = AB + AC = 2 3. 4 5 5
Vậy bán kính cần tìm là BC R = = 3 c . m 2
Câu 39. Cho tam giác ABC có AB = 3 3, BC = 6 3 và CA = 9 . Gọi D là trung điểm
BC . Tính bán kính R của đường tròn ngoại tiếp tam giác ABD. A. 9 R = . B. R = 3 . C. R = 3 3 . D. 9 R = . 6 2 2 2 2 Lời giải. Vì AB + AC BC
D là trung điểm của BC ⇒ 2 AD = − = 27 ⇒ AD = 3 3. 2 4
Tam giác ABD có AB = BD = DA = 3 3 ⇒ tam giác ABD đều.
Nên có bán kính đường tròn ngoại tiếp là 3 3 R = AB = .3 3 = 3. Chọn B. 3 3
Câu 40**. Tam giác nhọn ABC có AC = b, BC = a , BB ' là đường cao kẻ từ B và
CBB ' = α . Bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a, b và α là: 2 2 2 2 A.
a + b − 2ab cos α
a + b + 2ab cos α R = . B. R = . 2 sin α 2 sin α 2 2 2 2 C.
a + b + 2ab cos α
a + b − 2ab cos α R = . D. R = . 2 cos α 2 cos α
Lời giải. Xét tam giác B C ′ BB C
′ vuông tại B ,′ có sinCBB′ = ⇒ B C ′ = . a sin . α BC Mà AB′ + B C
′ = AC ⇔ AB′ = b − . a sin α và 2 2 2 BB ′ = a .cos . α
Tam giác ABB′ vuông tại B ,′ có AB = BB′ + AB′ = (b −a α)2 2 2 2 2 .sin + a .cos α 2 2 2 2 2 2 2 = b − 2a .
b sin α + a sin α + a cos α = a + b − 2ab sin α. 2 2
Bán kính đường tròn ngoại tiếp cần tính là AB
a + b − 2ab sin α = 2R ⇔ R = . sin ACB 2 cos α
Vấn đề 4. DIỆN TÍCH TAM GIÁC
Câu 41. Tam giác ABC có AB = 3, AC = 6, BAC = 60° . Tính diện tích tam giác ABC . A. S = 9 3 . B. 9 3 S = . C. S = 9 . D. 9 S = . A ∆ BC A ∆ BC 2 A ∆ BC A ∆ BC 2 Lời giải. Ta có 1 1 9 3 0 S
= .AB.AC.sin A = .3.6.sin 60 = . Chọn B. A ∆ BC 2 2 2
Câu 42. Tam giác ABC có AC = 4, BAC = 30 ,° ACB = 75° . Tính diện tích tam giác ABC . A. S = 8 . B. S = 4 3 . C. S = 4 . D. S = 8 3 . A ∆ BC A ∆ BC A ∆ BC A ∆ BC Lời giải. Ta có 0
ABC = 180 −(BAC + ACB) = 75° = ACB .
Suy ra tam giác ABC cân tại A nên AB = AC = 4 .
Diện tích tam giác ABC là 1 S =
AB.AC sin BAC = 4. Chọn C. A ∆ BC 2
Câu 43. Tam giác ABC có a = 21, b =17, c =10 . Diện tích của tam giác ABC bằng: A. S = 16 . B. S = 48 . C. S = 24 . D. S = 84 . A ∆ BC A ∆ BC A ∆ BC A ∆ BC Lời giải. Ta có 21+17 +10 p = = 24 . 2
Do đó S = p(p −a)(p −b)(p −c) = 24(24 −2)(24 −17)(24 −10) = 84 . Chọn D.
Câu 44. Tam giác ABC có AB = 3, AC = 6, BAC = 60° . Tính độ dài đường cao h của a tam giác. A. h = 3 3 . B. h = 3 . C. h = 3 . D. 3 h = . a a a a 2
Lời giải. Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC − 2AB.AC cos A = 27 → BC = 3 3 . Ta có 1 1 9 3 0 S
= .AB.AC.sin A = .3.6.sin 60 = . A ∆ BC 2 2 2 Lại có 1 2S S = .BC.h → h = = 3. Chọn C. A ∆ BC 2 a a BC
Câu 45. Tam giác ABC có AC = 4, ACB = 60° . Tính độ dài đường cao h uất phát từ
đỉnh A của tam giác. A. h = 2 3 . B. h = 4 3 . C. h = 2 . D. h = 4 .
Lời giải. Gọi H là chân đường cao xuất phát từ đỉnh A . Tam giác vuông AH AHC , có 3 sin ACH =
→ AH = AC.sin ACH = 4. = 2 3. AC 2 Chọn A.
Câu 46. Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B ' là hình chiếu vuông góc của
B trên cạnh AC . Tính BB ' . A. BB ' = 8 . B. 84 BB ' = . C. 168 BB ' = . D. 84 BB ' = . 5 17 17 + + Lời giải. Ta có 21 17 10 p = = 24 . 2
Suy ra S = p(p −a)(p −b)(p −c) = 24(24 −2)(24 −17)(24 −10) = 84 . Lại có 1 1 168 S = . b BB '← →84 = .17.BB ' → BB ' = . Chọn C. 2 2 17
Câu 47. Tam giác ABC có AB = 8 cm, AC =18 cm và có diện tích bằng 64 2 cm . Giá trị sin A ằng: A. 3 sin A = . B. 3 sin A = . C. 4 sin A = . D. 8 sin A = . 2 8 5 9 Lời giải. Ta có 1 1 8 S
= .AB.AC.sin BAC ⇔ 64 = .8.18.sin A ⇔ sin A = . Chọn D. A ∆ BC 2 2 9
Câu 48. Hình bình hành ABCD có AB = ,
a BC = a 2 và 0
BAD = 45 . Khi đó hình
bình hành có diện tích bằng: A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 . 2
Lời giải. Diện tích tam giác 1 1 a ABD là 0 S = .AB.A . D sin BAD = . . a a 2.sin 45 = . A ∆ BD 2 2 2 2
Vậy diện tích hình bình hành a ABCD là 2 S = 2.S = 2. = a . Chọn C. ABCD ∆ABD 2
Câu 49*. Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến
BF và CE cắt nhau tại G . Diện tích tam giác GFC bằng: A. 2 50 cm . B. 2 50 2 cm . C. 2 75 cm . D. 2 15 105 cm . Lời giải. Vì 1
F là trung điểm của AC ⇒ FC = AC = 15 c . m 2
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.
d (B;(AC )) Khi đó BF = = ⇒ d ( 1 AB 3
G;(AC )) = d (B;(AC )) = = 10 c . m
d (G;(AC )) GF 3 3 Vậy diện tích tam giác 1 1 GFC là S = .d G AC FC = = cm Chọn C. G ∆ FC ( ;( )) 2 . .10.15 75 . 2 2
Câu 50*. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng: A. 2 13 cm B. 2 13 2 cm C. 2 12 3 cm D. 2 15 cm .
Lời giải. Xét tam giác ABC đều, có độ dài cạnh bằng . a Theo định lí Sin, ta có BC a 0 = 2R ⇔
= 2.4 ⇔ a = 8.sin 60 = 4 3. 0 sin BAC sin 60
Vậy diện tích cần tính là 1 1 S
= .AB.AC.sin BAC = . = cm A ∆ BC (4 3)2 0 2 .sin 60 12 3 . 2 2 Chọn C.
Câu 51*. Tam giác ABC có BC = 2 3, AC = 2AB và độ dài đường cao AH = 2 . Tính độ dài cạnh AB . A. AB = 2 . B. 2 3 AB = . 3
C. AB = 2 hoặc 2 21 AB = .
D. AB = 2 hoặc 2 3 AB = . 3 3 Lời giải. Ta có
AB + BC +CA 2 3 + 3AB p = = . 2 2 Suy ra 3AB + 2 3 3AB − 2 3 2 3 − AB 2 3 + AB S = . 2 2 2 2 Lại có 1 S = BC.AH = 2 3. 2 Từ đó ta có 3AB + 2 3 3AB − 2 3 2 3 − AB 2 3 + AB 2 3 = 2 2 2 2 ( 2 = AB − )( 2 − AB ) AB 2 9 12 12 ← →12 = ← → . 2 21 Chọn C. 16 AB = 3
Câu 52*. Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S . Nếu tăng cạnh
BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì
khi đó diện tích của tam giác mới được tạo nên bằng: A. 2S . B. 3S . C. 4S . D. 6S .
Lời giải. Diện tích tam giác ABC ban đầu là 1 1
S = .AC.BC.sin ACB = .a . b sin ACB. 2 2
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là 1 1 S = . AC BC ACB = AC BC
ACB = S Chọn D. A ∆ BC (3 ).(2 ).sin 6. . . .sin 6 . 2 2
Câu 53*. Tam giác ABC có BC = a và CA = b . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. 0 60 . B. 0 90 . C. 0 150 . D. 0 120 .
Lời giải. Diện tích tam giác ABC là 1 1 S
= .AC.BC.sin ACB = .a . b sin ACB. A ∆ BC 2 2 Vì ab
a, b không đổi và sin ACB ≤ 1, ∀C nên suy ra S ≤ . A ∆ BC 2
Dấu " = " xảy ra khi và chỉ khi 0
sin ACB = 1 ⇔ ACB = 90 .
Vậy giá trị lớn nhất của diện tích tam giác ab ABC là S = . Chọn B. 2
Câu 54*. Tam giác ABC có hai đường trung tuyến BM , CN vuông góc với nhau và có BC = 3 , góc 0
BAC = 30 . Tính diện tích tam giác ABC . A. S = 3 3 . B. S = 6 3 . C. S = 9 3 . D. 3 3 S = . A ∆ BC A ∆ BC A ∆ BC A ∆ BC 2 Lời giải. Vì 2 2 2 BM ⊥ CN
→ 5a = b + c . (Áp dụng hệ quả đã có trước) 2 Trong tam giác 2a ABC , ta có 2 2 2 2
a = b + c − 2bc.cos A = 5a − 2bc cos A →bc = . cos A 2 Khi đó 1 1 2a 2 S = bc sin A = .
.sin A = a tan A = 3 3 . Chọn A. 2 2 cos A
Vấn đề 5. BÁN KÍNH ĐƯỜNG TRÒN NỘI TIẾP
Câu 55. Tam giác ABC có AB = 5, AC = 8 và 0
BAC = 60 . Tính bán kính r của đường
tròn nội tiếp tam giác đã cho. A. r =1 . B. r = 2 . C. r = 3 . D. r = 2 3 .
Lời giải. Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC − 2AB.AC cos A = 49 → BC = 7 . Diện tích 1 1 3 S =
AB.AC.sin A = .5.8. = 10 3 . 2 2 2 Lại có S 2S S = . p r → r = = = 3 . Chọn C. p
AB + BC +CA
Câu 56. Tam giác ABC có a = 21, b = 17, c = 10 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho.
A. r =16 .
B. r = 7 . C. 7 r = . D. r = 8 . 2 Lời giải. Ta có 21+17 +10 p = = 24 . 2 Suy ra S = 24(24− ) 2 (24−17)(24−1 ) 0 = 84 . Lại có S 84 7 S = . p r → r = = = . Chọn C. p 24 2
Câu 57. Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a . A. a 3 a a a r = . B. 2 r = . C. 3 r = . D. 5 r = . 4 5 6 7 2
Lời giải. Diện tích tam giác đều cạnh a 3 a bằng: S = . 4 2 a 3 Lại có S a 3 4 S = pr → r = = = . Chọn C. p 3a 6 2
Câu 58. Tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm. Tính bán kính r của
đường tròn nội tiếp tam giác đã cho. A. r =1 cm. B. r = 2 cm. C. r = 2 cm. D. r = 3 cm.
Lời giải. Dùng Pitago tính được
AB + BC +CA
AC = 8 , suy ra p = = 12 . 2 Diện tích tam giác vuông 1 S = A . B AC = 24 . 2 Lại có S S = . p r → r = = 2 cm. Chọn C. p
Câu 59. Tam giác ABC vuông cân tại A , có AB = a . Tính bán kính r của đường
tròn nội tiếp tam giác đã cho. A. a a a a r = . B. r = . C. r = . D. r = . 2 2 2 + 2 3
Lời giải. Từ giả thiết, ta có AC = AB = a và BC = a 2 . Suy ra
AB + BC +CA 2 + 2 p = = a . 2 2 2 Diện tích tam giác vuông 1 a S = A . B AC = . 2 2 Lại có S a S = . p r → r = = . Chọn C. p 2 + 2
Câu 60. Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán
kính R . Gọi r là bán kính đường tròn nội tiếp tam giác ABC . Khi đó tỉ số R bằng: r A. + − + 1+ 2 . B. 2 2 . C. 2 1 . D. 1 2 . 2 2 2
Lời giải. Giả sử BC a
AC = AB = a
→ BC = a 2 . Suy ra 2 R = = . 2 2 Ta có
AB + BC +CA 2 + 2 p = = a . 2 2 2 Diện tích tam giác vuông 1 a S = A . B AC = . 2 2 Lại có S a R S = . p r → r = = . Vậy = 1+ 2 . Chọn A. p 2 + 2 r