

Preview text:
CÂY AVL 1. Cây AVL là gì?
a) cây cân đối là cây cân đối về chiều cao
b) cây không cân đối là cây cân đối về chiều cao c) cây có 3 con
d) cây có nhiều nhất là 3 con
2. Tại sao cần cây nhị phân có chiều cao cân đối?
a) Để tránh hình thành cây xiên b) Tiết kiệm bộ nhớ
c) để đạt được truy cập bộ nhớ nhanh hơn
d) để đơn giản hóa việc lưu trữ
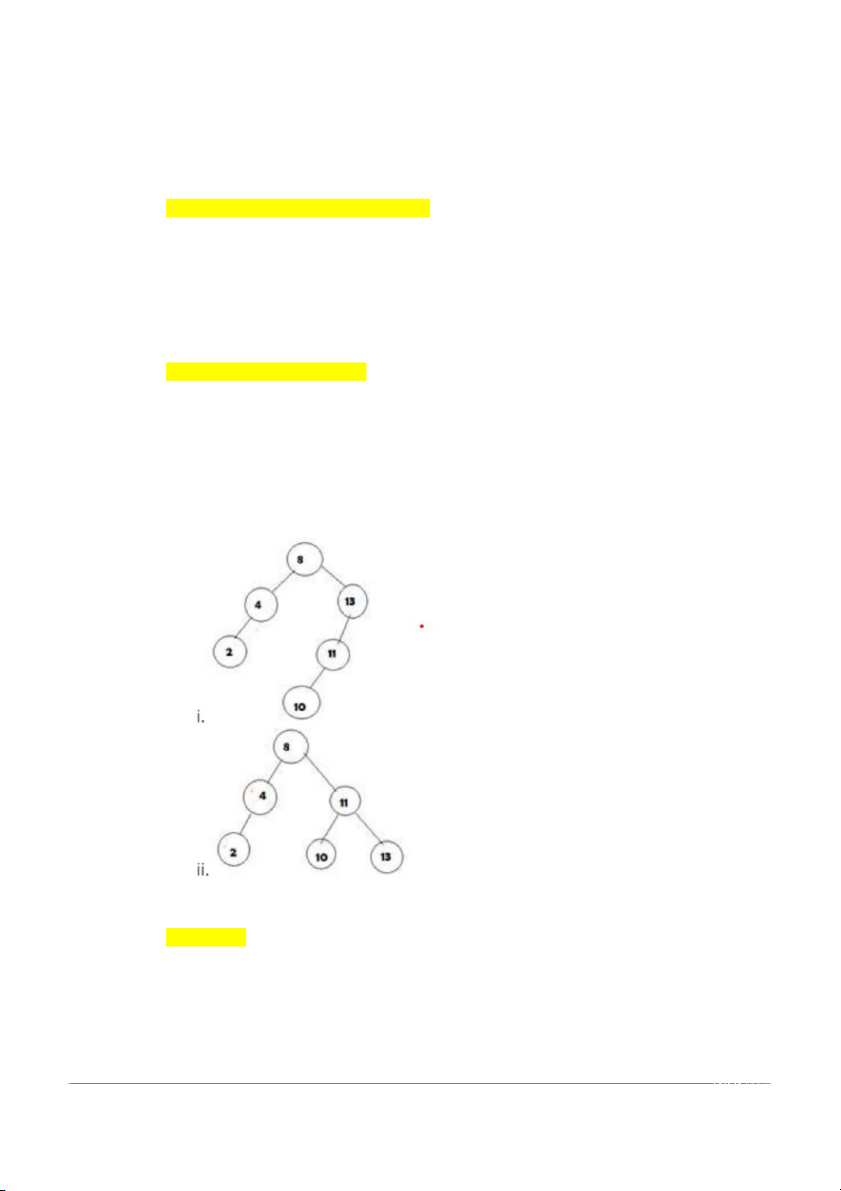
3. Sơ đồ nào dưới đây tuân theo đặc tính cây AVL? a) Chỉ có i b) Chỉ i và ii c) Chỉ ii
d) Không phải là cây tìm kiếm nhị phân
4. Chiều cao tối đa của cây AVL có p nút là bao nhiêu? a) p b) log(p) c) log(p)/2 d) p⁄2
5. Để khôi phục thuộc tính AVL sau khi chèn một phần tử, chúng ta bắt đầu từ
điểm chèn và di chuyển về phía gốc của cây đó. tuyên bố này có đúng không? a) đúng b) sai
6. Cho một cây AVL trống, bạn sẽ xây dựng cây AVL như thế nào khi cho một
tập hợp các số mà không thực hiện bất kỳ phép quay nào?
a) chỉ cần xây dựng cây với đầu vào đã cho
b) tìm trung vị của tập hợp các phần tử đã cho, lấy nó làm gốc và xây dựng cây c) sử dụng thử và sai
d) sử dụng quy hoạch động để xây dựng cây
7. Có thể có sự khác biệt tối đa về chiều cao giữa các lá của cây AVL là bao nhiêu?
a) log(n) trong đó n là số nút
b) n trong đó n là số nút c) 0 hoặc 1 d) tối đa 1 8. Hãy xem xét code:
int avl(binarysearchtree root): if(not root) return 0
left_tree_height = avl(left_of_root)
if(left_tree_height== -1)
return left_tree_height
right_tree_height= avl(right_of_root)
if(right_tree_height==-1)
return right_tree_height
Đoạn mã trên có thể kiểm tra xem cây tìm kiếm nhị phân có phải là cây AVL không? a) có b) không
9. Hãy xem xét mã giả xoay trái-trái bên dưới, trong đó nút chứa các con trỏ
giá trị tới các nút con trái, phải và một giá trị độ cao và hàm Height() trả về giá
trị độ cao được lưu trữ tại một nút cụ thể.
avltree leftrotation(avltreenode z): avltreenode w =x-left x-left=w-right w- = right x
x-height=max(Height(x-left),Height( - x right))+ 1 w-height=max(missing)+ 1 return w Cái gì còn thiếu?
a) Chiều cao(w-left), x-height
b) Chiều cao(w-right), x-height c) Chiều cao(w-left), x d) Chiều cao (w-left)
10. Tại sao lại thích cây đỏ đen hơn cây AVL?
a) Bởi vì đỏ-đen cân đối hơn
b) Cây AVL lưu trữ hệ số cân bằng trong mỗi nút tốn dung lượng
c) Cây AVL bị lỗi ở quy mô lớn
d) Đỏ đen hiệu quả hơn
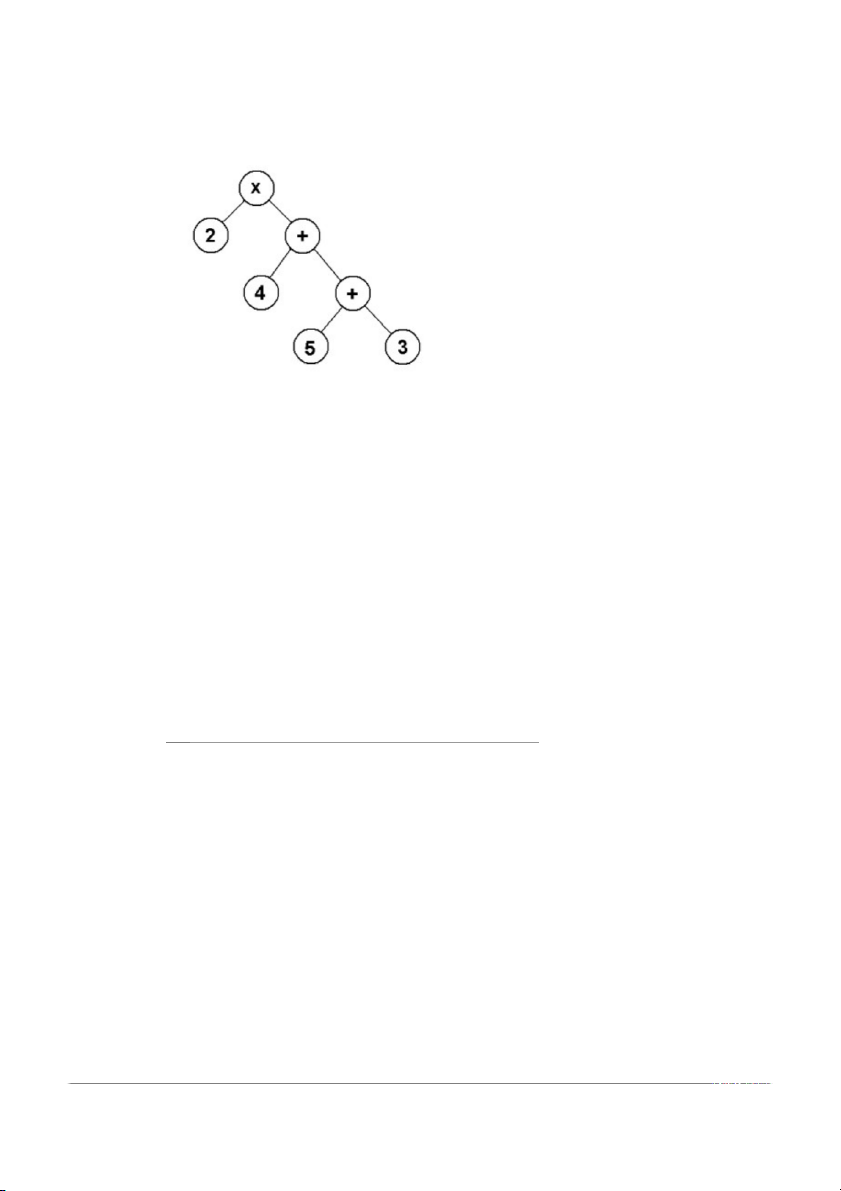
11. Cho cây biểu thức sau:
Chọn biểu thức tương ứng với cây A. (2 * (4 + (5 + 3))) B. (4 * (2+ (5 + 3))) C. (2 * (3 + (5 +4))) D. (2 * (5 + (4+ 3)))
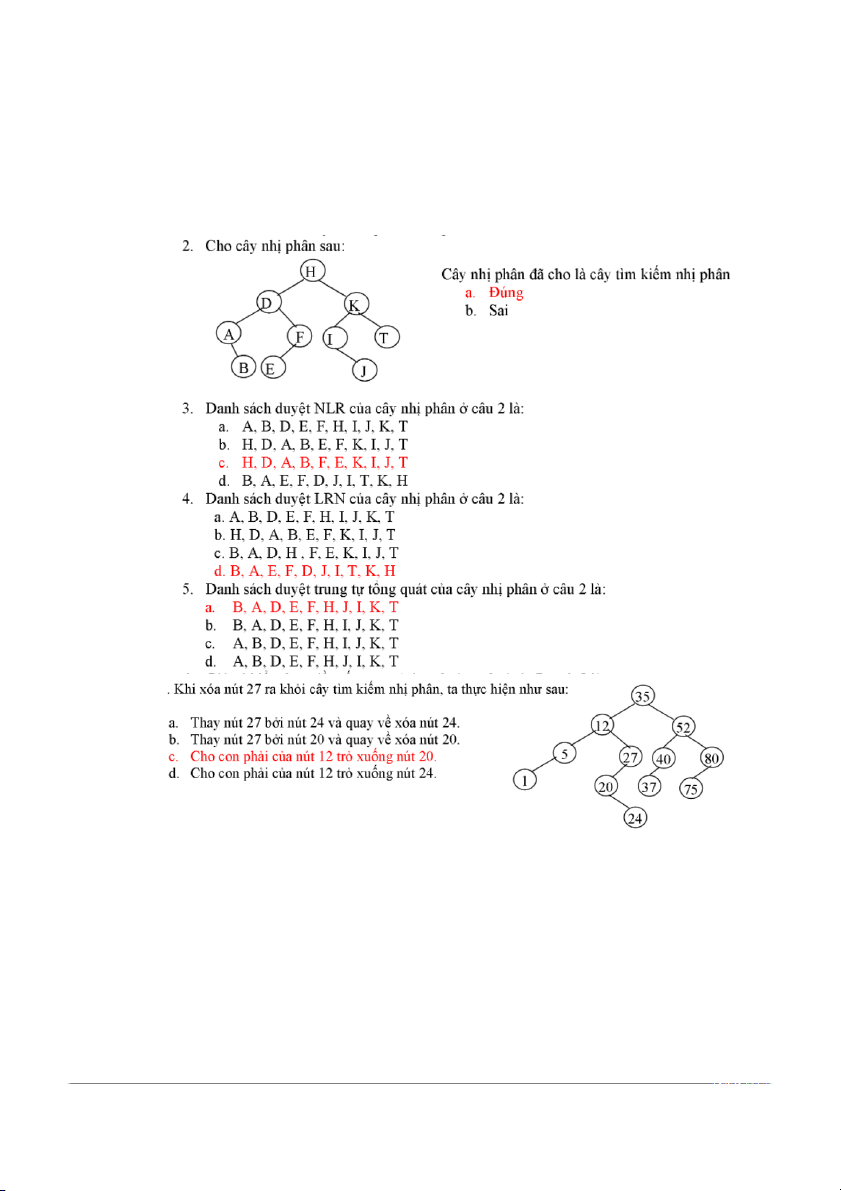
12. Chọn định nghma đúng nhất đối với cây nhị phân tìm kiếm:
A. Cây nhị phân tìm kiếm là cây nhị phân có thành phần khóa của mọi nút lớn
hơn thành phần khóa của tất cả các nút trong cây con trái của nó và nhỏ hơn
thành phần khóa của tất cả các nút trong cây con phải của nó.
B. Cây nhị phân tìm kiếm là cây nhị phân có thành phần khóa của mọi nút nhỏ
hơn thành phần khóa của tất cả các nút trong cây con trái của nó và nhỏ hơn
thành phần khóa của tất cả các nút trong cây con phải của nó.
C. Cây nhị phân tìm kiếm là cây nhị phân có thành phần khóa của mọi nút lớn
hơn thành phần khóa của tất cả các nút trong cây con trái của nó và lớn hơn
thành phần khóa của tất cả các nút trong cây con phải của nó.
D. Cây nhị phân tìm kiếm chính là cây nhị phân. 13.
Chọn định nghma đúng nhất về cây cân bằng tương đối:
A. Cây cân bằng tương đối là một cây nhị phân thỏa mãn điều kiện là đối với
mọi nút của cây thì số nút của cây con trái và số nút của cây con phải của nút
đó hơn kém nhau không quá 1. Cây cân bằng tương đối còn được gọi là cây AVL (AVL tree).
B. Cây cân bằng tương đối là một cây N phân thỏa mãn điều kiện là đối với
mọi nút của cây thì chiều cao của cây con trái và chiều cao của cây con phải
của nút đó hơn kém nhau không quá 2. Cây cân bằng tương đối còn được gọi là cây AVL (AVL tree).
C. Cây cân bằng tương đối là một cây nhị phân thỏa mãn điều kiện là đối với
mọi nút của cây thì chiều cao của cây con trái và chiều cao của cây con phải
của nút đó hơn kém nhau không quá 1. Cây cân bằng tương đối còn được gọi là cây AVL (AVL tree).
D. Cây cân bằng tương đối cũng là cây cân bằng hoàn toàn. Câu 7:




