Chapter 22 Gauss | Bài giảng vật lí đại cương | Đại học Bách Khoa Hà Nội

10/12/2020 Electric Flux
You can think of the flux through some surface as a measure of
the number of field lines which pass through that surface.
Flux depends on the strength of , on the surface area, and on
the relative orientation of the field and surface. area A area A Here the flux is  = · ⃗ 
We divide the surface into small regions with area dA A cos  ⃗
d = . ⃗ = E dA cos 
 = . ⃗ = E A cos  ⃗  A
 =  d =  . 1 2 Gauss’s Law Gauss’s Law
In the case of a closed surface    qenclose The total flux within … is proportional to inside
   E.dA   E.dA.cos    a closed surface … the enclosed charge. 0
The loop means the integral is over a closed surface.   Q   E  d  A = enclosed  0 dA
Surface a, qa =(+2q) + (-q) +(+q) = 2q  Surface b, q
Gauss’s Law is always true, but is only useful for certain b = q Surface c, qc = 0
very simple problems with great symmetry. E Surface d, qd = -q 3 4 1 10/12/2020
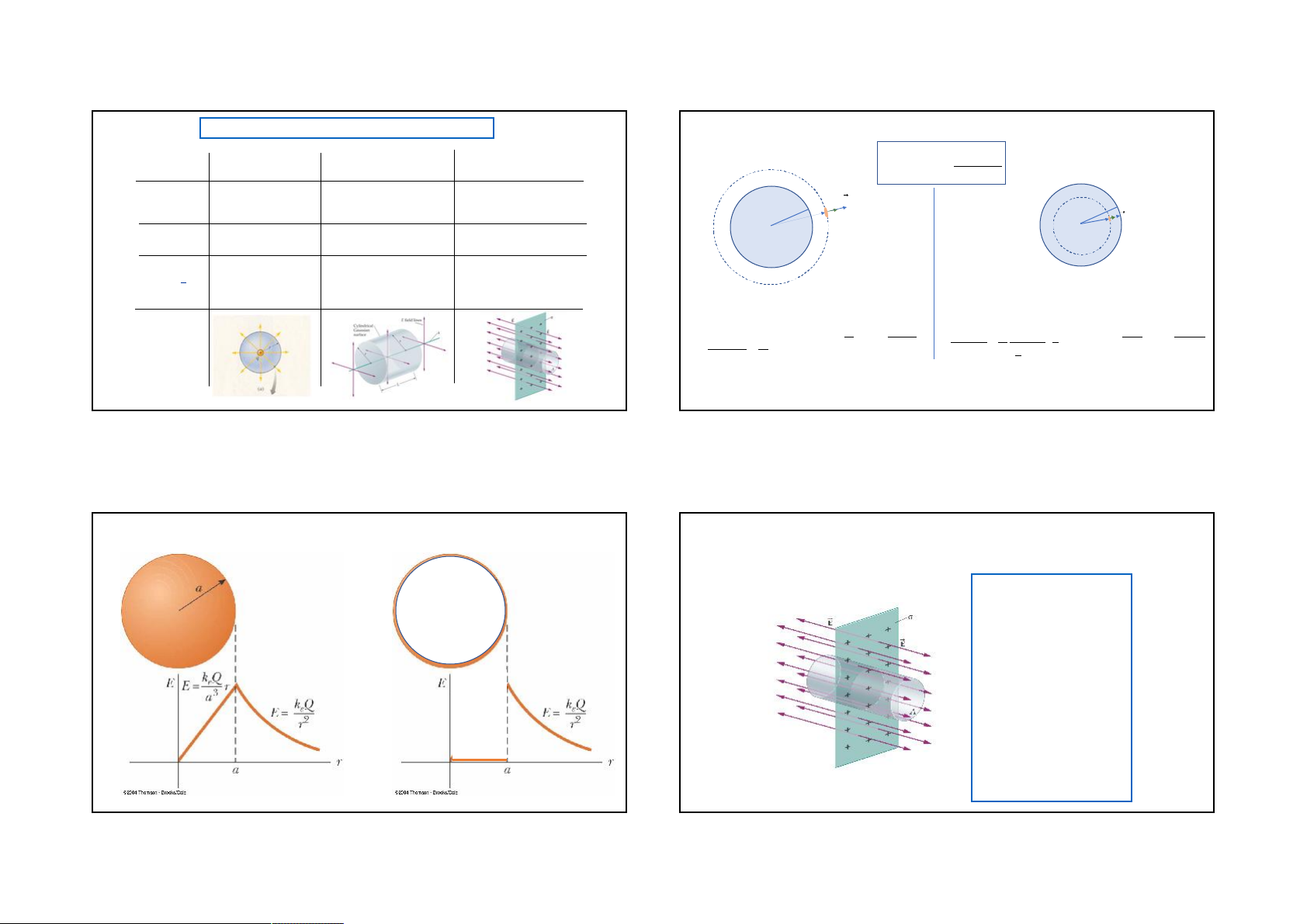
GAUSS LAW – SPECIAL SYMMETRIES
Problem: Uniform sphere of Charge Q (insulating sphere)    q SPHERICAL CYLINDRICAL PLANAR Outside sphere enclose Inside sphere inside (poi nt or sphere) (line or cylinder) (plane or sheet)    E.dA   0 CHARGE Depends onl y on radial Depends onl y on
Depends onl y on perpendicular DENSITY distance from central perpendicular distance from distance from plane poi nt line R R r ⃗ r ⃗ GAUSSIAN Sphere centered at Cylinder centered at axi s Pi llbox or cylinder O O SURFACE poi nt of symmetry of symmetry
with axi s perpendicular to plane ELECTRIC E constant at surface E constant at curved surface E constant at end surfaces FIELD E E ║A - cos  = 1 and E ║ A and E ║ A E ┴ A at end surface E ┴ A at curved surface cos  = 0 cos  = 0     2   2     E.dA  E.4 r     E.dA  E.4 r           Q Q 3   q  Qr Qr 2   q E.4 r    E  2 enclose 1 Q  4  E.4 r    E  enclose 3   2 Q insid e 3 3  r  inside  4 r         R 4 R 0 0 0 0  4     3   3     0 0 R  FLUX       0 0     3   Spherical geometry Cylindrical geometry Planar geometry 5 6 Insulating sphere Conducting sphere
Infinite sheet of charge
Gauss’s law is useful onl y when the electric field is constant on a given surface 1. Select Gauss surface In this case a cylindrical pillbox 2. Calculate the flux of the electric field through the Gauss surface  = 2 E A 3. Equate  = qencl/0 2EA = qencl/0 4. Solve for E
E = qencl / 2 A 0 =  / 2 0 Infinite sheet of charge (with  = qencl / A) 7 8 2 10/12/2020
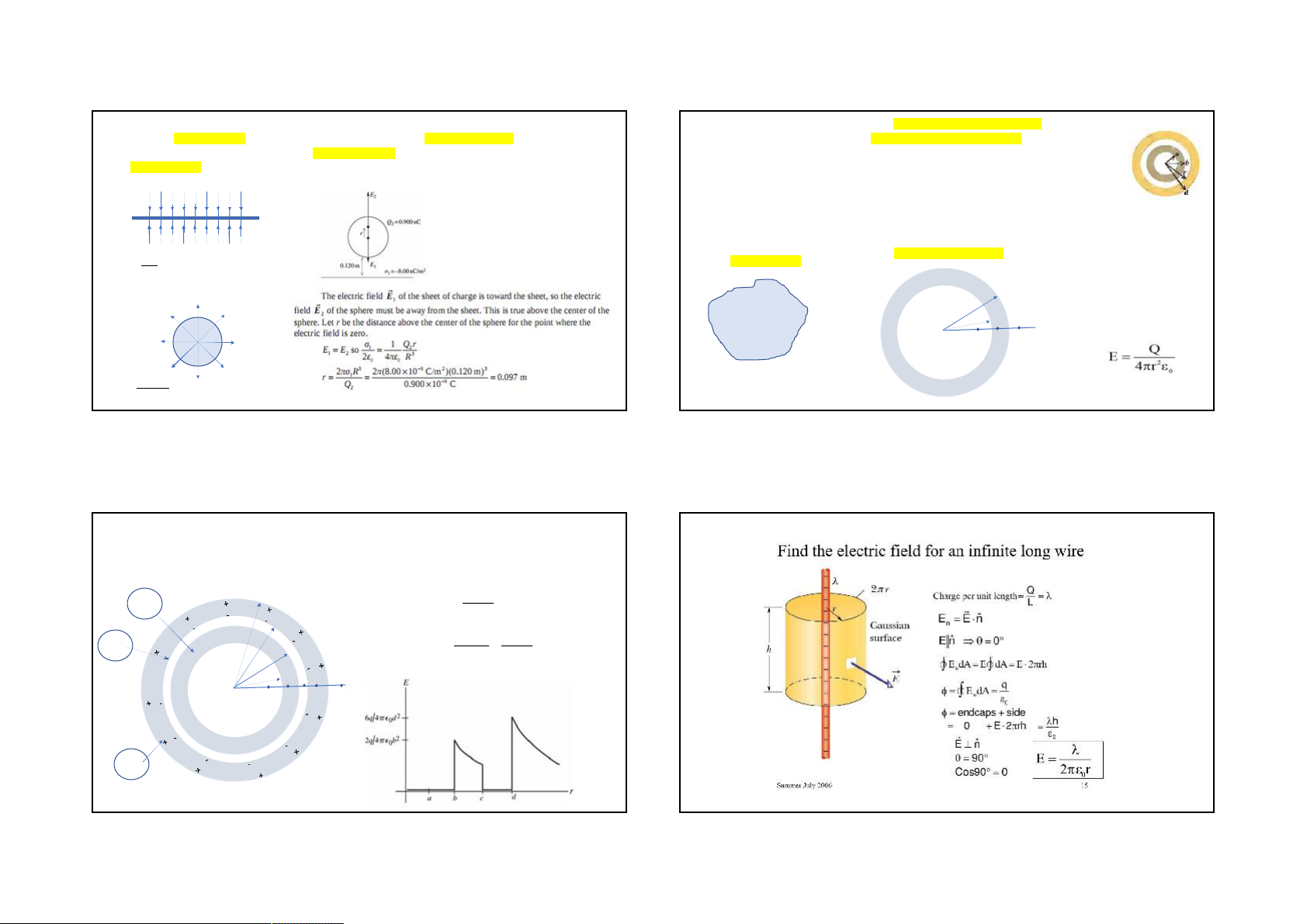
22.39(45). Concentric Spherical Shells. A small conducting spherical shell with inner radius a
22.35. An insulating sphere with radius 0.120 m has 0.900 nC of charge uniformly distributed throughout its volume.
and outer radius b is concentric with a larger conducting spherical shell with inner radius c and
The center of the sphere is 0.240 m above a large uniform sheet that has charge density -8.00 nC/ m2. Find all points
outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q.
inside the sphere where the electric field is zero. Or, show that there is no such points .
(a) Calculate the electric field (magnitude and direction) in terms of q and the distance r from the
common center of the two shells for (i) r < a; (ii) a< r < b; (iii) b< r < c; (iv) c < r < d; (v) r > d.
Show your results in a graph of the radial component of E as a function of r. = -8.00 nC/m2
(b) What is the total charge on the (i) inner surface of the small shell; (ii) outer surface of the
small shell; (iii) inner surface of the large shell; (iv) outer surface of the large shell?  Conducting spheri cal shell E  Conducting body 2 + + 0 + Point M: E=0 (inside) + b + Inside E = 0 a Point N: E=0 (inside) + M N + P + Point P: + Qr + E  + 3 4 R + 0 9 10
The inner shell has total charge +2q, The outer shell has charge +4q
(i) Poi nt 1: r < a; E1 = 0 ( = 0)
(ii) Poi nt 2: a< r < b; E2 =0 ( = 0) 2 2q +
(iii) Point 3: b< r < c; = ( = 2q) + 4 +
(iv) Poi nt 4: c < r < d; E + 4 = 0 ( = 0) + + d + 2 + 4 6 -2q + (v) Point 5: r > d. = = ( = 6q) + c 4 4 b + a + + + 1 2 + 3 4 5 + + + + + + + + +6q + + 11 12 3 10/12/2020
22.47(39). A very long conducting tube (holl ow cylinder) has inner radius a and outer radius b. It carries charge per uni t
Conducting solid cylinder
length -, where  is a positive constant with units of C/m. A line of charge lies along the axis of the tube. The line of charge
has charge per uni t length +.
(a) Calculate the electric field in terms of a and the distance r from the axis of the tube for (i) r < a; (ii) a < r < b; (iii) r > b.
Show your results in a graph of E as a function of r.
(b) What is the charge per uni t length on (i) the inner surface of the tube and (ii) the outer surface of the tube? + (i) r < a -
Insulating solid cylinder (ii) a < r < b (iii) r > b -  b a + 0 (b)
the outer surface of the tube? 13 14 with 15 16 4 10/12/2020
22.(33)35. The electric field E1 , at one face of a parallelepiped is uni form over the entire face and is directed out of the face. At
the opposite face, the electri c field E2 is also uniform over the entire face and is directed into that face (Fig.). The two faces in
question are inclined at 30.00 from the horizontal, while E1, and E2 are both horizontal; E1 has a magnitude of 2.50x104 N/C,
and E2 has a magnitude of 7.00x104 N/C. (a) Assuming that no other electri c field lines cross the surfaces of the parallel epiped,
determine th e net charge contain ed within. (b) Is the electric fi eld produced only by the charges within the parall elepiped, or is
the field also due to charges outside the parallelepiped? How can you tell?
b. If there were no charge within the parallelpiped the net flux
would be zero. This is not the case, so there is charge inside.
The electric field lines that pass out through the surface of the
parallelpiped must terminate on charges, so there also must be
charges outside the parallelpiped. 17 18
22.51(53). Thomson’s Mode l or the Atom. In Thomson’s model, an at om consisted of a sphere of positively
22.43(49). Negative charge -Q is distributed uniformly over the surface of a thin spherical insulating shell with radius
charged material in which were em bedded negatively charge d elect rons, like chocolat e chips in a ball of
R. Calculate the force (magnitude and direction) that the shell exerts on a positive point charge q located
cookie dough. Consider an at om consisting of two elect rons, each of charge -e, embedded in a sphere of
(a) a distance r > R from the center of the shell(outs ide the shell)
charge + 2e an d radius R. In equilibri um, ea ch elect ron is a dist ance d from the center of the atom (Fig.). Find
the distance d in terms of the other propert ies of the at om.
(b) a distance r < R from the center of the shell(inside the shell). (a) r > R
There is a force on each electron due to the other electron and a force due to the sphere of charge. Use Coulomb’s law for the force between the electrons.
If the electrons are in equilibrium the net force on each one is zero.
Apply Gauss’s law to a spherical Gaussian surface that has radius r > R and that is concentric with t he shell
The force diagram for electron 2
There is a repulsive force F1 due to the electron 1   2   E.dA  E.4 r      3  q  Qr Qr 
The electric field inside the uniform distribution of positive charge is enclose 2 1 Q  4 3  E.4 r    E  inside  3 3  r  (b) r < R    R 4 R 0 0 R  4     3   3 0 0 R         3   r ⃗ O
At the position of electron 2, r = d. The force Fcd exerted by the positive charge distribution is
Outside the shell the electric field and the force it exerts is the same as for a point charge −Q
located at the center of the shell. Inside the shell E = 0 and there is no force. 19 20 5 10/12/2020
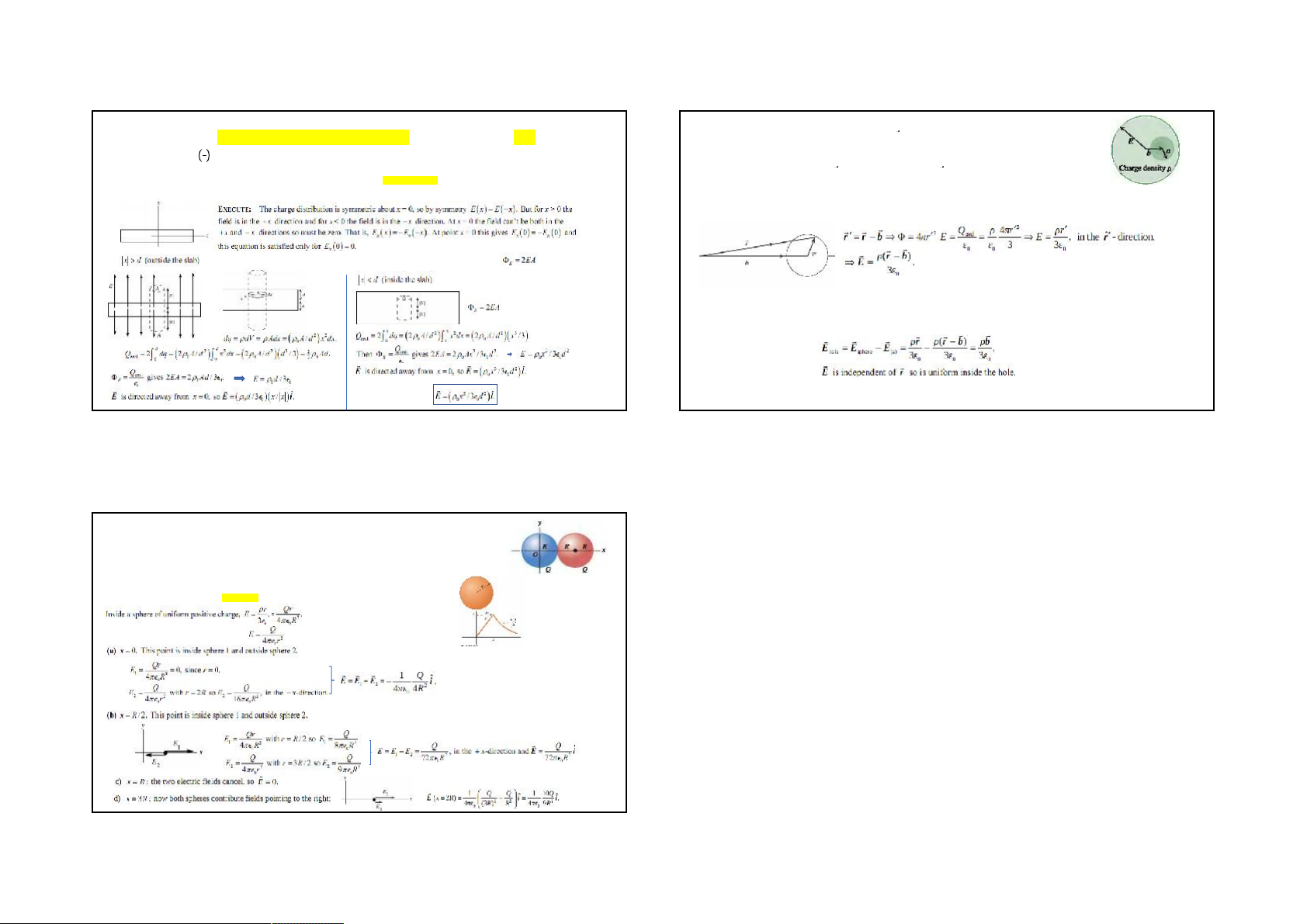
22.61(61). (a) An insulating sph ere with radius a has a uni form charge d ensity . The sphere is not centered at the origin but at
22.55(55). A Unif ormly Charged Slab. A slab o f insulating materi al has thickn ess 2d and is orient ed so that its faces are p arallel to the yz-pl ane and given by
⃗ = ⃗ . Show that the electri c field inside the sp here is given by = ( ⃗ − ⃗ )⁄3
. (b) An insulating sphere o f radius R has a
the planes x = d and x = - d. The y- and z-dimensions o f the slab are very large compared to d and may be treated as essentially infinite. The charge d ensity of
spherical hole o f radius a located within its volume and centered a distance b from the center o f the sphere, where a < b < R (a the slab is given by = , where is a positive constant .
cross section of th e sphere is shown in Fig.). The solid part of the sph ere h as a uni form volume charge density . Find the
(a) Explain why the electric field due to the slab is zero at the center of the slab (x = 0).
magnitude and direction of the electric field inside the hole, and show that
is uniform over the entire hole. [Hint: Use the
(b) Using Gauss’s law, find the electric field due to the slab (magnitude and direction) at all points in space.
principle of superposition and the result of part (a).] (a)
(a) For a sphere NOT at t he coordinat e origin: (b)
Apply Gauss’s law to a cylindrical Gaussian surface whose axis is perpendicular to the slab
(b) An insulat ing sphere of radius R has a spherical hole of radius a
The electric field inside a hole in a charged insulating sphere is: In general 21 22
22.63(63). Positive charge Q is distributed uniformly over each of two spherical volumes with radius R. One
sphere of charge is centered at the origin and the other at x = 2R (Fig.). Find the magnitude and direction of
the net elect ric field due to these t wo distributions of charge at the following point s on t he x-axis: (a) x = 0;
(b) x = R/2; (c) x = R; (d) x = 3R
The electric field at each point is the vector sum of the fields of the two charge distributions.
directed away from the center of the sphere
Outside a sphere of uniform positive charge,
directed away from the center of the sphere. 23 6