lOMoAR cPSD| 45903860 APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 4:
Chapter 3: Descriptive statistics
(3 credits: 2 is for lecture, 1 is for lab-work) 1 lOMoAR cPSD| 45903860 REVIEW PREVIOUS LECTURES lOMoAR cPSD| 45903860 REVIEW PREVIOUS LECTURES
Examples of interval and ratio scales:
Ratio scale: a weight of 4 grams is twice as heavy as a weight of 2 grams Interval
scale: a temperature of 10 degrees C should not be considered twice as hot as 5
degrees C. If it were, a conflict would be created because 10 degrees C is 50
degrees F and 5 degrees C is 41 degrees F. Clearly, 50 degrees is not twice 41 degrees.
a pH of 3 is not twice as acidic as a pH of 6, because pH is not a ratio variable.
Ratio scale doesn’t have negative numbers, because of its zero-point feature
Division between two values has meaning
(besides the subtraction like in interval scale)
Allow unit conversion (e.g. kg/gr calories) 3 lOMoAR cPSD| 45903860 TODAY’S CONTENT
3.1. Measures of location 3.2. Measures of variability lOMoAR cPSD| 45903860 3.1. MEASURES OF LOCATION
•Mean •Weighted Mean •Median •Geometric Mean •Mode •Percentiles •Quartiles 3.1. MEASURES OF LOCATION
•Mean (average value): provides a measure of central location for the data 5 lOMoAR cPSD| 45903860
-if the data are for a sample: the mean is denoted by ( ) n: number of observation
- if the data are for a population: the mean is denoted by the Greek letter µ
N: total observations in a population 3.1. MEASURES OF LOCATION lOMoAR cPSD| 45903860 Mean: Example 7 lOMoAR cPSD| 45903860 3.1. MEASURES OF LOCATION
•Weighted Mean: in n observations, each observation i shares the weight
(Mean: each observation share the same weight w=1/n) lOMoAR cPSD| 45903860 3.1. MEASURES OF LOCATION
•Median: Arrange the data in ascending order (smallest value to largest value):
(a) For an odd number of observations, the median is the middle value. 9 lOMoAR cPSD| 45903860
(b) For an even number of observations, the median is the average of the two middle values. 3.1. MEASURES OF LOCATION
•Geometric Mean: measure of location that is calculated by finding the nth
root of the product of n values lOMoAR cPSD| 45903860
is often used in analyzing growth rates 3.1. MEASURES OF LOCATION •Geometric Mean: 11 lOMoAR cPSD| 45903860
- Other common applications: changes in populations of species, crop yields, pollution levels, and birth and death rates, etc.
- Also note that the geometric
mean can be applied to changes that occur over any number of
successive periods of any length.
- In addition to annual changes, the geometric mean is often
applied to find the mean rate of change over quarters, months, weeks, and even days. 3.1. MEASURES OF LOCATION lOMoAR cPSD| 45903860
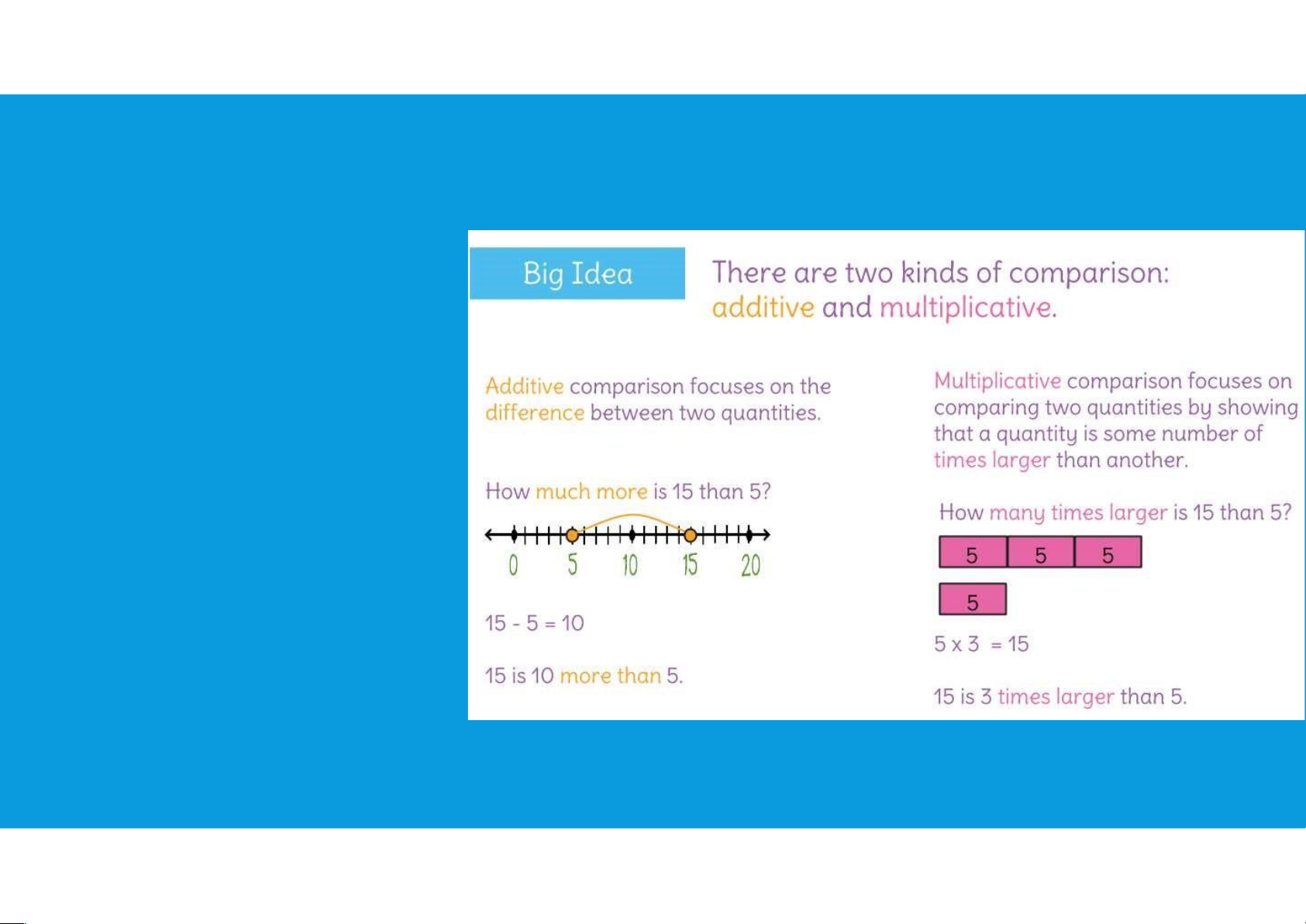
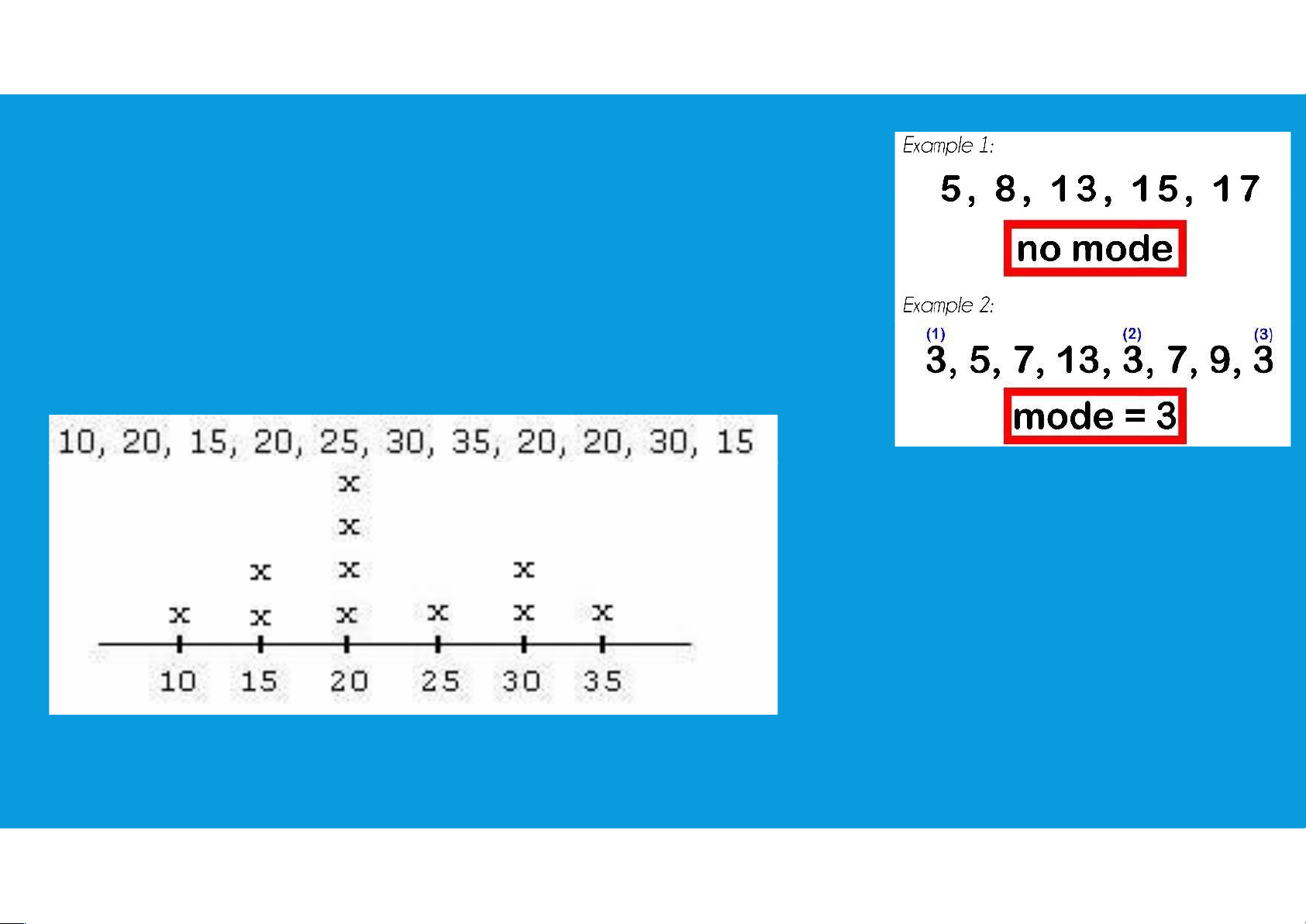
•Mode: value that occurs with greatest frequency Mean=? Median=? Mode=? 3.1. MEASURES OF LOCATION •Percentiles: provides
information about how the data are spread over the interval
from the smallest value to the largest value. 13 lOMoAR cPSD| 45903860
•Location of pth percentile:
Calculate the value of pth percentile based on Lp 50th percentile=??? lOMoAR cPSD| 45903860 3.1. MEASURES OF LOCATION
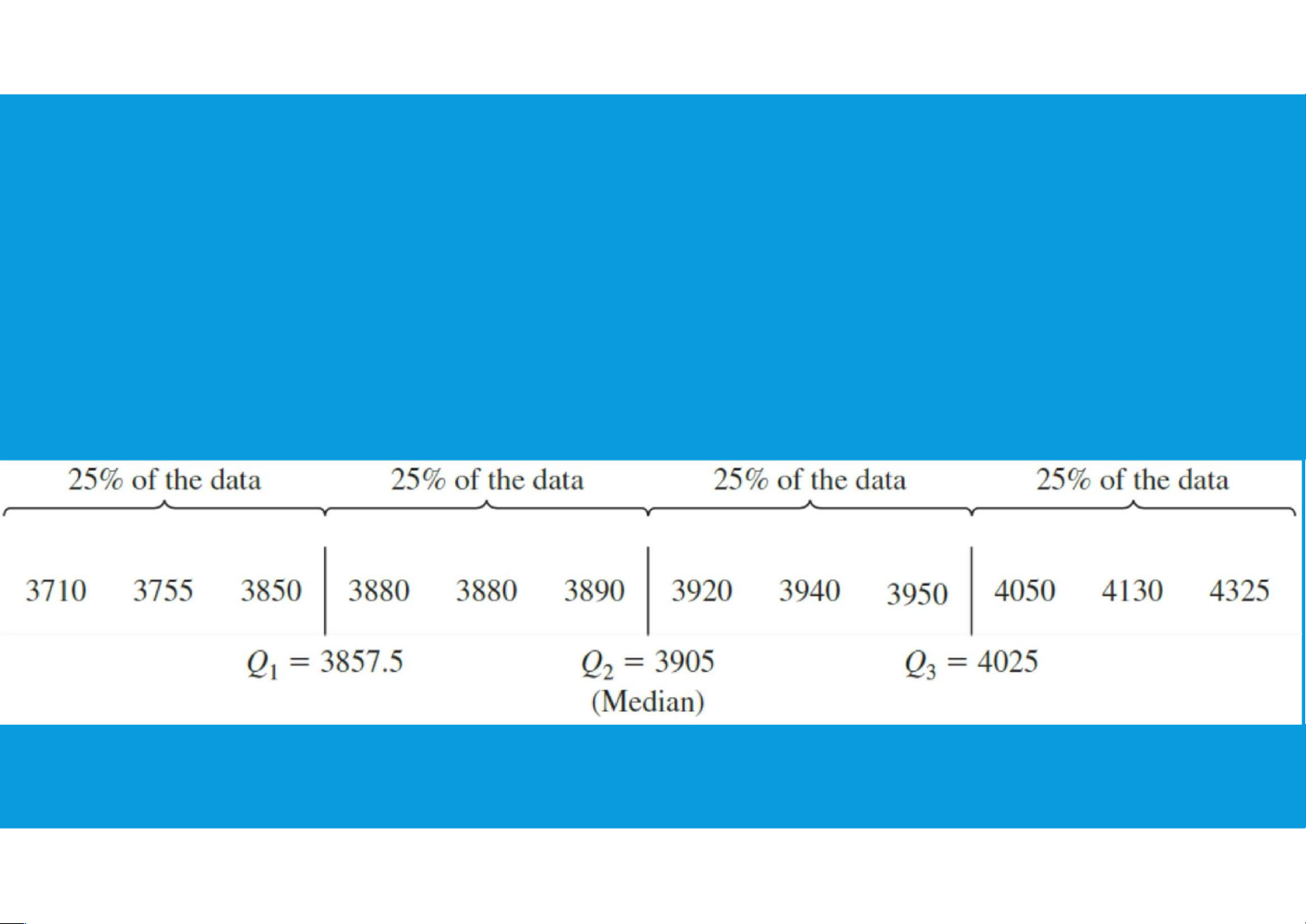
•Quartiles: it is often desirable to divide a data set into four parts, with each
part containing approximately one-fourth, or 25%, of the observations. These
division points are referred to as the quartiles and are defined as follows:
Q1 = first quartile, or 25th percentile (Location: L25)
Q2 = second quartile, or 50th percentile (also the median) (Location: L50) Q3 =
third quartile, or 75th percentile (Location: L75) 15 lOMoAR cPSD| 45903860 3.1. MEASURES OF LOCATION Mean=? 25th percentile=? Median=? 50th percentile=? Mode=? 75th percentile=? lOMoAR cPSD| 45903860 End of file 1. Any questions? 16 3.2. MEASURES OF VARIABILITY
•Range: simplest measure of variability lOMoAR cPSD| 45903860
•It is seldom used as the only measure. The reason is that the range is based
on only two of the observations and thus is highly influenced by extreme values.
•Interquartile Range: A measure of variability that overcomes the dependency on extreme values.
difference between the third quartile, Q3, and the first quartile, Q1 3.2. MEASURES OF VARIABILITY
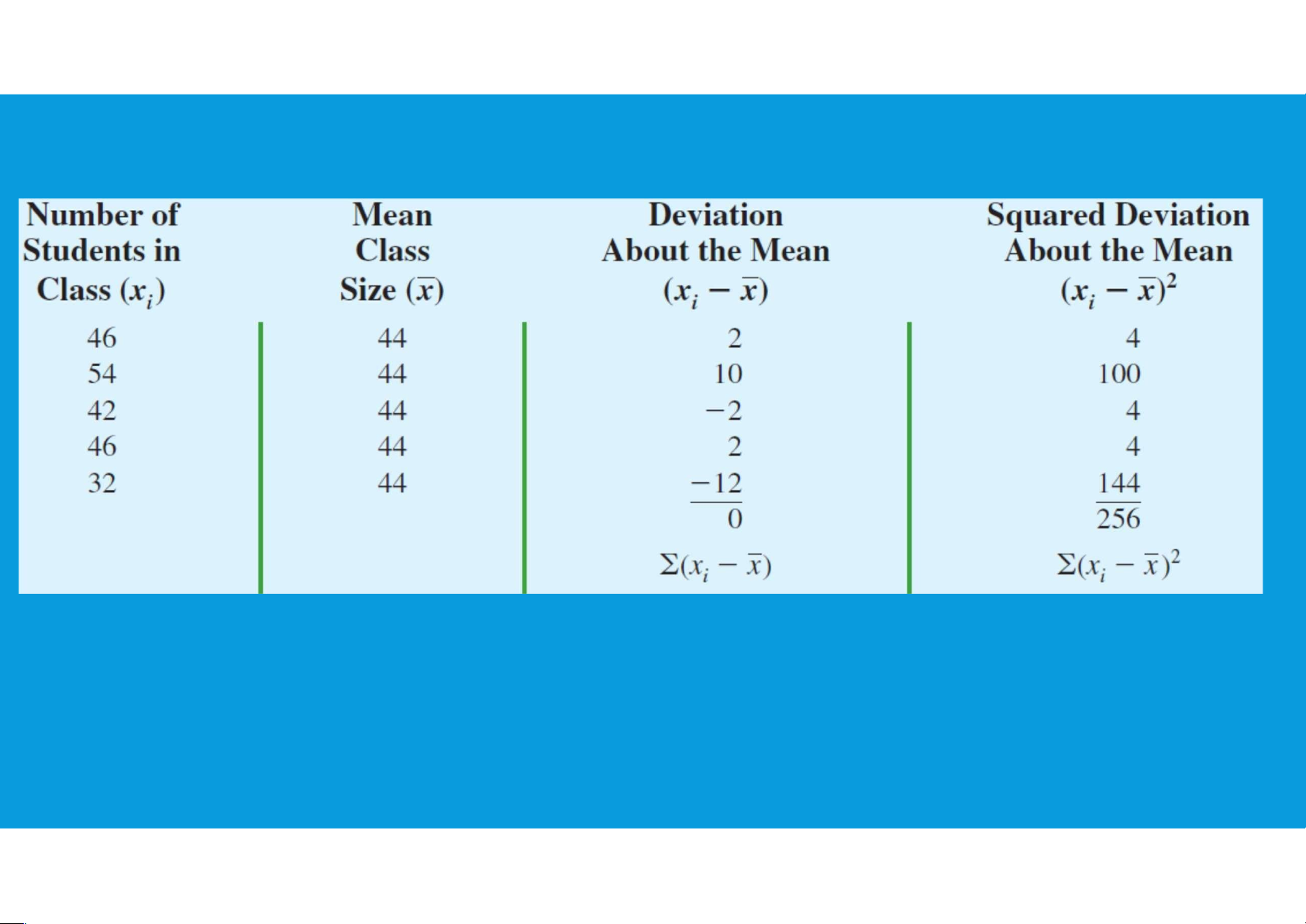
•Variance: A measure of variability that utilizes all the data
based on the difference between the value of each observation (xi) and the
mean (=deviation about the mean): 18 lOMoAR cPSD| 45903860
- For a sample, a deviation about the mean is written ( ௜ − ); - For a population, it is written ( •Population variance: •Sample variance:
(if the sum of the squared deviations about the sample mean is divided by n − 1, and
not n, the resulting sample variance provides an unbiased estimate of the population Variance) 3.2. MEASURES OF VARIABILITY 19 lOMoAR cPSD| 45903860 •Variance = 256/4= 64
(in a comparison of the variables, the one with the largest variance shows the most variability) 20