1 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG Chapter 5:
I. Functions of several variables 𝜕𝑦 ∂x 𝜕𝑦 = fz ∂z – 𝜕𝑓 − 0 = 20x ∂x 𝜕𝑓 = 0 − 2y = −2y ∂y – 𝜕𝑓 – ∂x 𝜕𝑓 − 0 = 3x ∂y 𝜕2𝑦 𝜕2𝑦 ∂𝑥2 ∂𝑧2
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
2 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜕2𝑦 𝜕2𝑦 ∂𝑥 ∂z ∂𝑧 ∂x – – – 𝜕𝑓 ∂x1 𝜕2𝑓 ∂𝑥12 𝜕2𝑦 ∂𝑥2 ∂x 1 𝜕𝑦 ∆y ≈ 𝜕𝑦 ∂x ∆x + ∆z ∂z
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
3 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG – 𝜕𝑧 𝜕𝑧 ∂x ∂y 𝜕𝑧 = y − 5 ∂x 𝜕𝑧 ∂y 𝜕𝑧 𝜕𝑧 ∂x ∂y a) ∆x = −0.1, ∆y
≅ 1(−0.1) + 4(0.1) = 0.3, so z increases by approximately 0.3. 𝑑𝑦= − 𝑓𝑥 𝑑𝑥 𝑓𝑦 – – 𝑑𝑦 −𝑦 𝑑𝑥 x − 3y2 + 1 𝑑𝑦 𝑦2 𝑑𝑥 5y4−2xy
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
4 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
II. Partial elasticity and marginal functions P: the good’s price
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐷𝑒𝑚𝑎𝑛𝑑 𝑃 𝜕𝑄
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑃𝑟𝑖𝑐𝑒 𝑄 𝜕𝑃
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐷𝑒𝑚𝑎𝑛𝑑 𝑃𝐴 𝜕𝑄
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑃𝑟𝑖𝑐𝑒 𝑜𝑓 𝐺𝑜𝑜𝑑 𝐴 𝑄 𝜕𝑃𝐴
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐷𝑒𝑚𝑎𝑛𝑑 𝑌 𝜕𝑄
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐼𝑛𝑐𝑜𝑚𝑒 𝑄 𝜕𝑌
+ Ey < 0 → inferior goods (white bread, instant noodle, bus transportation) • < 1: normal goods • >1: superior
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
5 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG – – – – 𝜕𝑄 𝜕𝑃 = −3 so E 20 x (−3) = −0.14 430 𝜕𝑄 30 = −2 so E x (−2) = −0.14 𝜕𝑃𝐴 430 𝜕𝑄 5000 𝜕𝑌 430
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐷𝑒𝑚𝑎𝑛𝑑
𝑃𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐼𝑛𝑐𝑜𝑚𝑒 III. Utility
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
6 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜕𝑈 𝜕𝑈 ∂x1 ∂x2 𝜕𝑈 ∆ ≈ 𝜕𝑈 ∂x1 ∆x ∆ ∂x2 𝜕2𝑈 𝜕2𝑢 ∂𝑥12 ∂𝑥22
An individual’s utility function is given by – – 𝜕𝑈 𝜕𝑈 ∂x1 ∂x2
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
7 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜕𝑈 − 4x ∂x1 𝜕𝑈 − 2x ∂x2 𝜕𝑈 𝜕𝑈 ∂x1 ∂x2 ∆x1 = −1. Also ∆
∆U = 2948 x (−1) + 140 x 15 = −848 𝜕2𝑈 𝜕2𝑈 = −4 < 0 and ∂𝑥12 = −2 < 0 ∂𝑥22 𝜕𝑄 𝑑𝑥2= − 𝜕𝑥1 𝑑𝑥1 𝜕𝑄 𝜕𝑥2 𝜕𝑄 − 𝑑𝑥2= 𝜕𝑥1 𝑑𝑥1 𝜕𝑄 𝜕𝑥2 decreases by ∆x ∆ = MRCS x ∆x
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
8 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 2948 140
IV. Production Functions 𝜕𝑄 ∂K 𝜕𝑄 ∂L 𝜕2𝑄 ∂𝐾2
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
9 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜕2𝑄 ∂𝐿2 𝜕𝑄 ∆ ≈ 𝜕𝑄 ∂K ∆ ∆ ∂L MPL MPK 𝜕𝑄 𝜕𝑄 ∂K ∂L 2𝐿 𝜕𝑄 𝐾 𝜕𝑄 ∂K ∂L MPL 4𝐿 2𝐿 MPK 2𝐾 𝐾
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
10 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜕𝑄 𝜕𝑄 = ∂K ∂L
V. Optimisation problem 𝜕𝑦 𝜕𝑦 ∂x ∂z 𝜕𝑦 𝜕𝑦 ∂x ∂z ∇
𝜕2𝑦) (𝜕2𝑦 ) − ( 𝜕2𝑦 ∂𝑥2 ∂𝑧2 ∂𝑥 ∂z 𝜕2𝑦 ) ∂𝑥2 (𝜕2𝑦 ∇ ∂𝑧2 𝜕2𝑦 ) ∇ ∂𝑥2 (𝜕2𝑦 ∂𝑧2 ∇ – – –
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
11 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG ∇
− fxy = 2 x (−6) − 0 = −12 < 0 – –
Show that the firm’s profit function is
π = 50Q − 2Q − 95Q − 4Q − 3Q
which maximise π and deduce the
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
12 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
13 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
14 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
15 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝜑
B1: Dùng phương trình 𝜑(x,y) = M để ết 1 phương trình mớ B2: Thay phương trình mớ
ết vào phương trình f(x,y) để được 1 phương trình ứ ẩ
B3: Tìm f’(x), giải tìm x khi f’(x) = 0 ⟶ có x tìm đượ
B4: Tìm f’’(x) <0 or >0 để
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
16 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
17 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
L = f(x, z) + λ(M − g(x, z)) 𝜕𝐿 𝜕𝐿 𝜕𝐿 ∂x ∂z ∂λ
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
18 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
19 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
20 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG PL MPL PK = MPK 𝑀𝑃𝐿 𝑀𝑃𝐾: MPL 𝑀𝑃𝐾 PL PK P1 U1 P2 U2 𝑈 𝑈 U1 U2 P1 ạ ặ P2 ớ 𝐊∝ 𝐋𝜷 ặ 𝐱𝟏∝ 𝐱𝟐𝜷 PL= MPL PK ớ U1 MPK ặ P1 P2 U2
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
21 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG K1/2𝐿1/4 λ K1/2𝐿1/4 + λ 𝜕𝑔 λ ∂K 𝜕𝑔 5 ∂L λ 𝜕𝑔 2 ∂λ λ 5 λ 2 𝐿4 𝐿 2 2𝐾 𝐾 5 𝐾 5 2𝐾 5 ế 2𝐾 ) 5 5 5 PL= MPL 5 = 2𝐾1/2𝐿−3/4 5 = 1 𝐾 𝐾 5 5𝐿 PK MPK 4 5𝐿1/4𝐾−1/2 4 2 𝐿 𝐿 2 2 ế 5𝐿 5𝐿 ) 2 2
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
22 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG Chapter 6:
1. Rules For Integration ∫ x 1 𝑛+1 ∫ af(x)dx = a ∫ f(x)dx 1 ∫ 𝑙𝑛𝑥 𝑥 ∫ 1 𝑚
∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫ g(x)dx
2. Application I: Revenue, Costs And Profit ∫ ∫ TR(Q) = ∫MR(Q) ∫MC(Q) ∫ f(x) = F(x) + c + MC → TC: c = Fixed cost ạ
(a) A firm’s marginal cost function is
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
23 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG – TC = ∫ 2dQ = 2Q + c ∫(100 − 6Q)dQ = 100Q − TR = 100Q − 3Q
𝑇𝑅 100𝑄−3𝑄2 100Q − 3Q 𝑄 𝑄 = 100 − 3Q
3. Definite Integration ∫𝑏 𝑓(𝑥) = F(b) − F(a) 𝑎
4.Application Ii: Consumer And Producer Surplus
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
24 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
CS = ∫𝑸𝟏 𝐃(𝐐)𝐝𝐐 − 𝐏𝟏𝐐𝟏 𝟎
PS = 𝐏𝟏𝐐𝟏 − ∫𝑸𝟏 𝐒(𝐐)𝐝𝐐 𝟎 P = 50 − 2Q (a) the consumer’s surplus (b) the producer’s surplus –
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
25 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG – – ∫10
0 (50 − 2Q)dQ − 10 x 30 = 100 10
PS = 10 x 30 − ∫ (10 + 2Q)dQ 0
5. Application III: Investment Flow 𝑑𝐾 𝑑𝑡 ➔ → 𝑡2 ∫ 𝐼(𝑡)𝑑𝑡 𝑡1
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
26 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
∫8 800𝑡1/3𝑑𝑡 = 9000 1∫𝑥 800𝑡1/3𝑑𝑡 = 0
6 Application IV: Discounting ∫𝑛 − 0 ∫10 − 0
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
27 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG Chapter 7: I.
Basic matrix operations a11 a12 𝑎13 [ 𝑎21 𝑎22 𝑎23] 𝑎31 𝑎32 𝑎33 Matrix A (m x n) → – 3 8 [3 5 5 8 6 5] [5 6] 5 5
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
28 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 𝑘𝑎11 𝑘𝑎1 2 𝑘𝑎13 𝑘𝑎21 𝑘𝑎2 2 𝑘𝑎23 ần lượ ấ ọ ồ ộ ạ 1 2 𝑐11 𝑐12 𝐴𝐵 = [0 1] [1 2 𝑐21 𝑐22] 3 1 3 4] = [𝑐31 𝑐32
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
29 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG 7 10 [3 4 ] 6 10 ≠ II. Matrix inversion [1 0 0 1] 1 0 0 [0 1 0] 0 0 1 |𝐴| 𝑜𝑟 |𝑎 𝑏 𝑐 𝑑| = 0 → singular
≠ 0 → non – singular → inverse [𝑎 𝑏 𝑐 𝑑] 1 [ 𝑑 −𝑏 |𝐴| −𝑐 𝑎 ]
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
30 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
31 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG a11 a12 a13 [a21 a22 a23] a31 a32 a33 •
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
32 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG + − +
• Prefixed by a ‘–’ sign because from the pattern [− + −] + − +
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
33 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
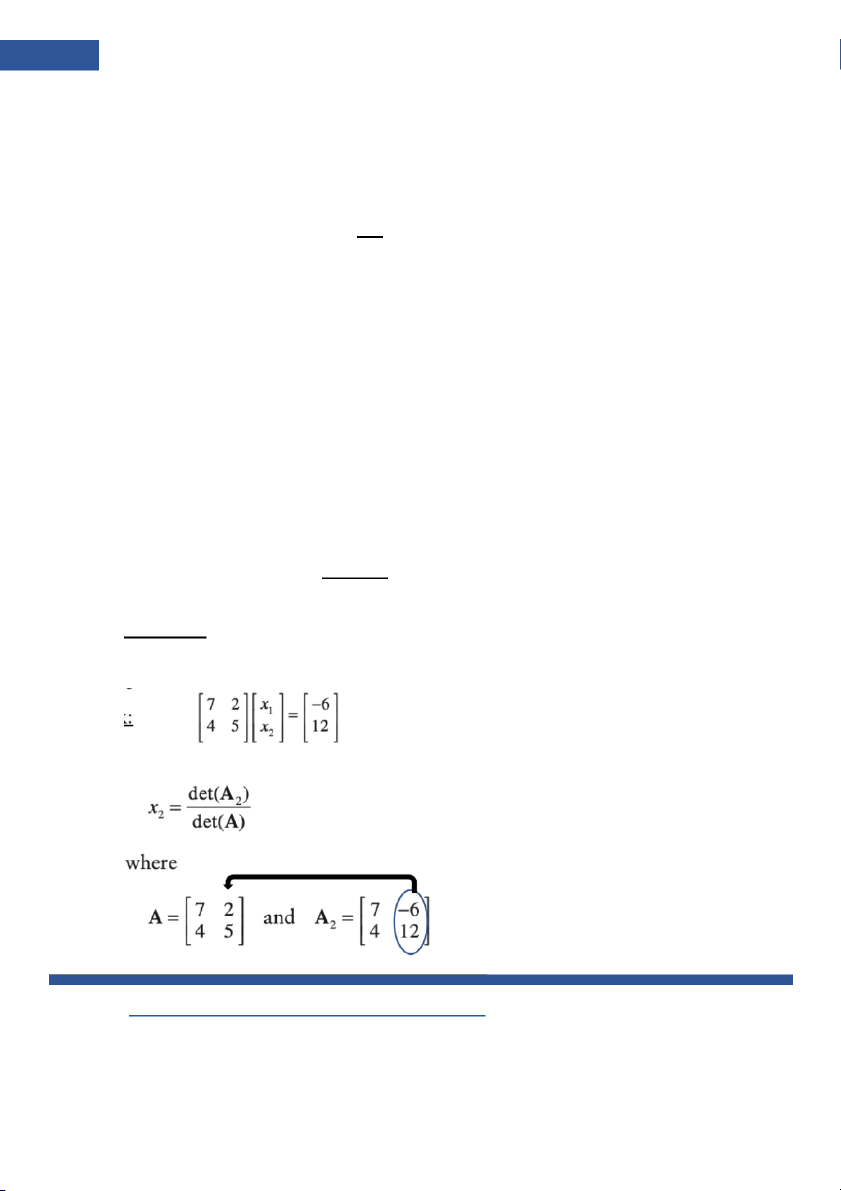
34 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG • ố • 𝟏 |𝑨| Cramer’s rule 𝑎11 𝑎12 𝑎13 𝑥1 𝑏1 𝐴 = [𝑎21 𝑎22 𝑎23] [𝑥2] 𝑏 = [𝑏2] 𝑎31 𝑎32 𝑎33 𝑥3 𝑏3 ộ det (𝐴𝑖) B2: Cramer’s det (𝐴)
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
35 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
36 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
37 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG Chapter 8: • • •
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com
38 MATH FOR BUSINESS TA: VŨ THỊ THU TRANG
Contact: https://www.facebook.com/thutrang.vu308
Email: vuthithutrang2003@gmail.com