







Preview text:
1 | M A T H F O R B U S I N E S S C H A P T E R 7 CHAPTER 7 Matrices
I. Basic matrix operations 1. Matrix order # rows x # Column
Example: A 3 x 4 matrix labelled A would be written a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44
- # rows = 1; # columns = 0 → row vector
# columns = 1; # rows = 0 → column vector
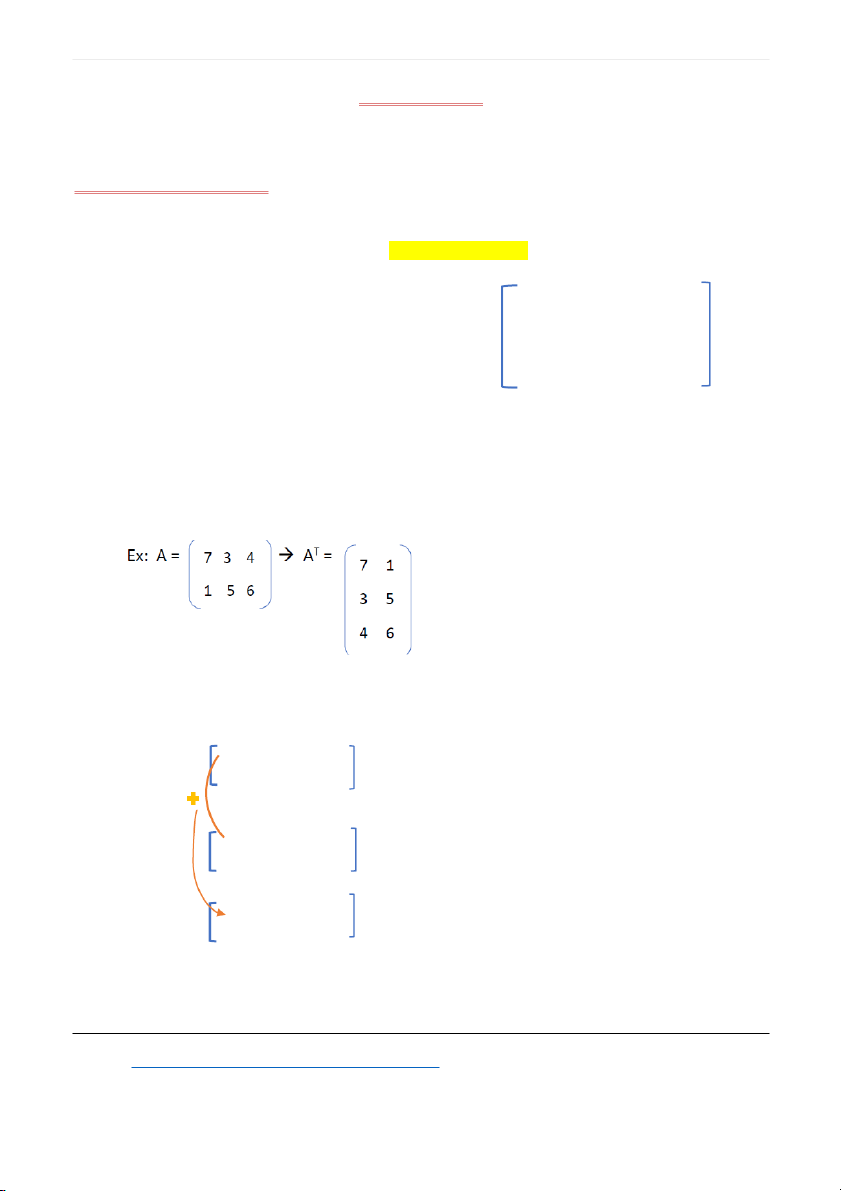
2. Transposition
Matrix A (m x n) → transposition AT (n x m) found by replacing r – ows by columns
3. Addition and subtraction
- Condition: same order - Matrix A: a11 a12 a13 a21 a22 a23 Matrix B: b11 b12 b13 b21 b22 b23 C = A + B = c11 c12 c13
where c11 = a11 + b11; c12 = a12 + b12 c21 c22 c23
4. Scalar multiplication
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
2 | M A T H F O R B U S I N E S S C H A P T E R 7
- Multiply a matrix A by a scalar k: kA = ka11 ka12 ka13 ka21 ka22 ka23
5. Matrix multiplication.
- A (mA x nA) and B (mB x nB)
C = AB → order (mA x nB) Method: SUMMARY
Provided that the indicated sums and products make sense, A + B = B + A A − A = 0
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
3 | M A T H F O R B U S I N E S S C H A P T E R 7 A + 0 = A k (A + B) = kA + kB k (lA) = ( kl ) A A(B + C) = AB + AC
Suy lu¿n từ order cÿa 2 ma tr¿n. 2 ma tr¿n chß nhân (A + B)C = AC + BC
đ±ÿc vßi nhau sß cßt cÿa ma tr¿n 1 = sß hàng cÿa A(BC) = (AB)C
We also have the non-property that, in general, AB b BA
Explain: C = A x B condition: nA = mB C = B x A condition: nB = mA ➔ AB b BA II. Matrix inversion A-1A = I and AA-1 = I Determinant: = 0 → singular
≠ 0 → non – singular → inverse Ax = b by A-1 gives A-1 ( Ax ) = A-1b
(A-1 A)x = A-1b (associative property) Ix = A-1b (definition of an inverse) x = A-1b
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
4 | M A T H F O R B U S I N E S S C H A P T E R 7 Matrix (2x2) a11 a12
Matrix (3x3) a11 a12 a13 a21 a22 a21 a22 a23 a31 a32 a33 Identity I = 1 0 I = 1 0 0 matrices 0 1 0 1 0 0 0 1 Det (A)
= a11a22 – a12a21
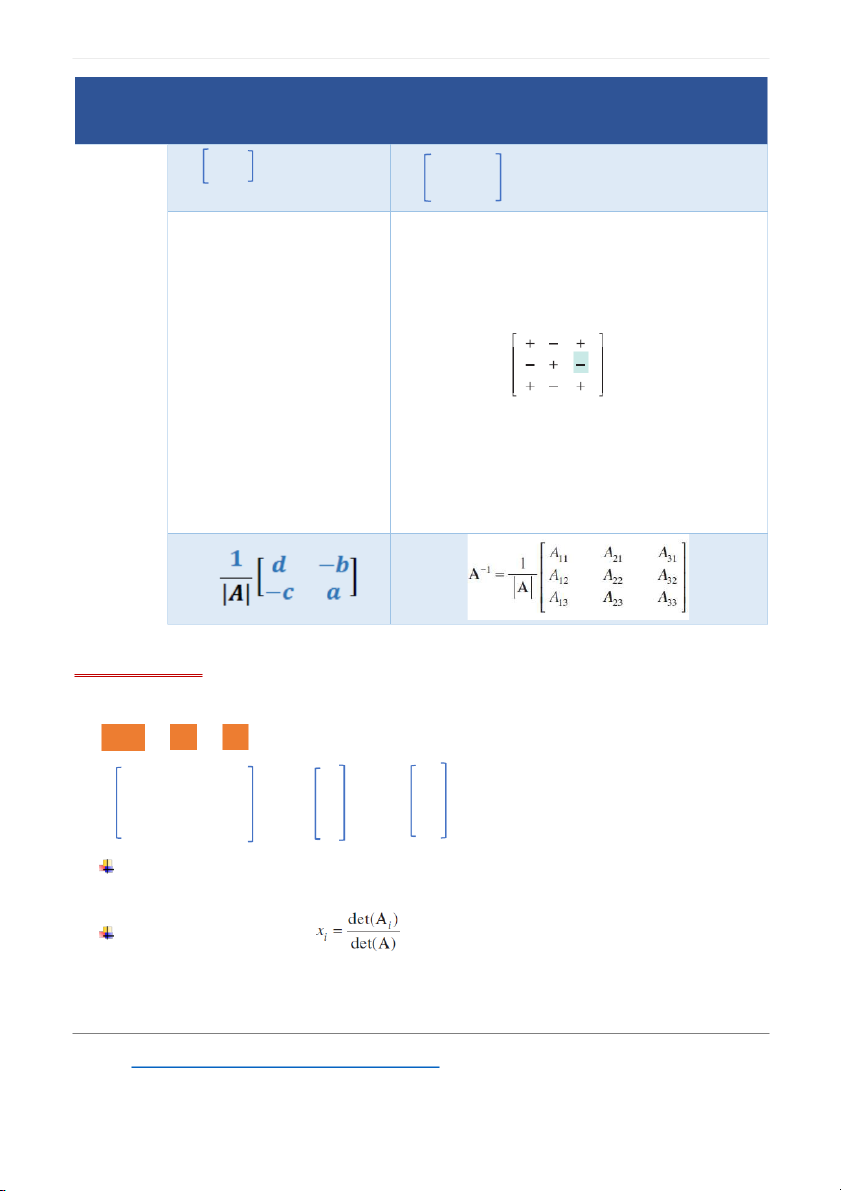
• Step 1: Cofactor (Aij)
- The cofactor Aij = det(A) [matrix (2x2)] when delete row i and column j
- Prefixed by a 8–9 sign because from the pattern • Step 2: Det(A)
det(A) = a11A11 + a12A12 + a13A13 = a12A12 + a22A22 + a32A32 = a13A13 + a23A23 + a33A33 Inverse A- 1 III. Cramer’s rule Ax = b, where i=1 2 3 A = a11 a12 a13 x = x1 b = b1 a21 a22 a23 x2 b2 a31 a32 a33 x3 b3
Step 1: Tìm matrix Ai Thay cßt i = [b] → Ai
Step 2: Cramer’s rule
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
5 | M A T H F O R B U S I N E S S C H A P T E R 7
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
6 | M A T H F O R B U S I N E S S C H A P T E R 7 EXERCISE
M¿y b¿n nên gi¿i h¿t example cÿa t¿t c¿ các bài luôn nha. Ch±¡ng này đßi vßi t lu ự ¿n quan
trọng nh¿t là quen cách tính. Quen rßi s¿ dß áp dÿng. Vßi tr¿c nghi link cách b ßm, đây là
¿m máy, h¿u h¿t các ph¿n m¿y b¿n đßu có thß gi¿i b¿ng máy
tính (Casio 570, 580, Vinacal áp dÿng ) t±¡ng tự
BẤM MÁY: http://bitexedu.com/wp-content/uploads/2019/02/matrix-1.pdf
BÀI TẬP VẬN DỤNG
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
7 | M A T H F O R B U S I N E S S C H A P T E R 7
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
8 | M A T H F O R B U S I N E S S C H A P T E R 7 X = (3B – 2A)T = 6 6 2 11 13 1
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
9 | M A T H F O R B U S I N E S S C H A P T E R 7
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc
10 | M A T H F O R B U S I N E S S C H A P T E R 7
Quiz Mr. Tri Anh (Sem 1 2020 202 – 1) a) Chapter 7 b) Chapter 8
Ngô Minh Tuy¿t Ngọc – BABAIU19066
Contact: https://www.facebook.com/ngominhtuyetngoc




