-
Thông tin
-
Hỏi đáp
Chinh phục bài Toán VD-VDC lớp 12 - Giáo dục học | Trường Đại học Thủ đô Hà Nội
Phân tích: Ta đi tìm nghiệm của phương trình y= 0 hoặc giá trị làm cho phương trình y= 0 không xác định, từ đó tìm được các khoảng đồng biến, nghịch biến của hàm số. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn:
Giáo dục học (hn) 36 tài liệu
Trường:
Đại học Thủ đô Hà Nội 603 tài liệu
Thông tin:
23 trang
2 tháng trước
Tác giả:
Chinh phục bài Toán VD-VDC lớp 12 - Giáo dục học | Trường Đại học Thủ đô Hà Nội
Phân tích: Ta đi tìm nghiệm của phương trình y= 0 hoặc giá trị làm cho phương trình y= 0 không xác định, từ đó tìm được các khoảng đồng biến, nghịch biến của hàm số. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
36
18 lượt tải
Tải xuống
Môn: Giáo dục học (hn) 36 tài liệu
Trường: Đại học Thủ đô Hà Nội 603 tài liệu
Thông tin:
23 trang
2 tháng trước
Tác giả:
x
x
2
x
x
2
x
x
2
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
2 2
2
Phân tích:
Ta đi tìm nghiệm của phương trình
y
0
hoặc giá trị làm cho
phương trình
y
0
không xác định, từ đó tìm được các khoảng đồng biến,
nghịch biến của hàm số.
Cách
1: Điều kiện: x
0;1
Lời
giải
Ta có:
y
2x
1
;
y
0 x
1
0;1
.
2
2
Ta có:
y
0
2x
1
0
1
x 1 do đó hàm số nghịch biến trên
1
;1
.
2
2
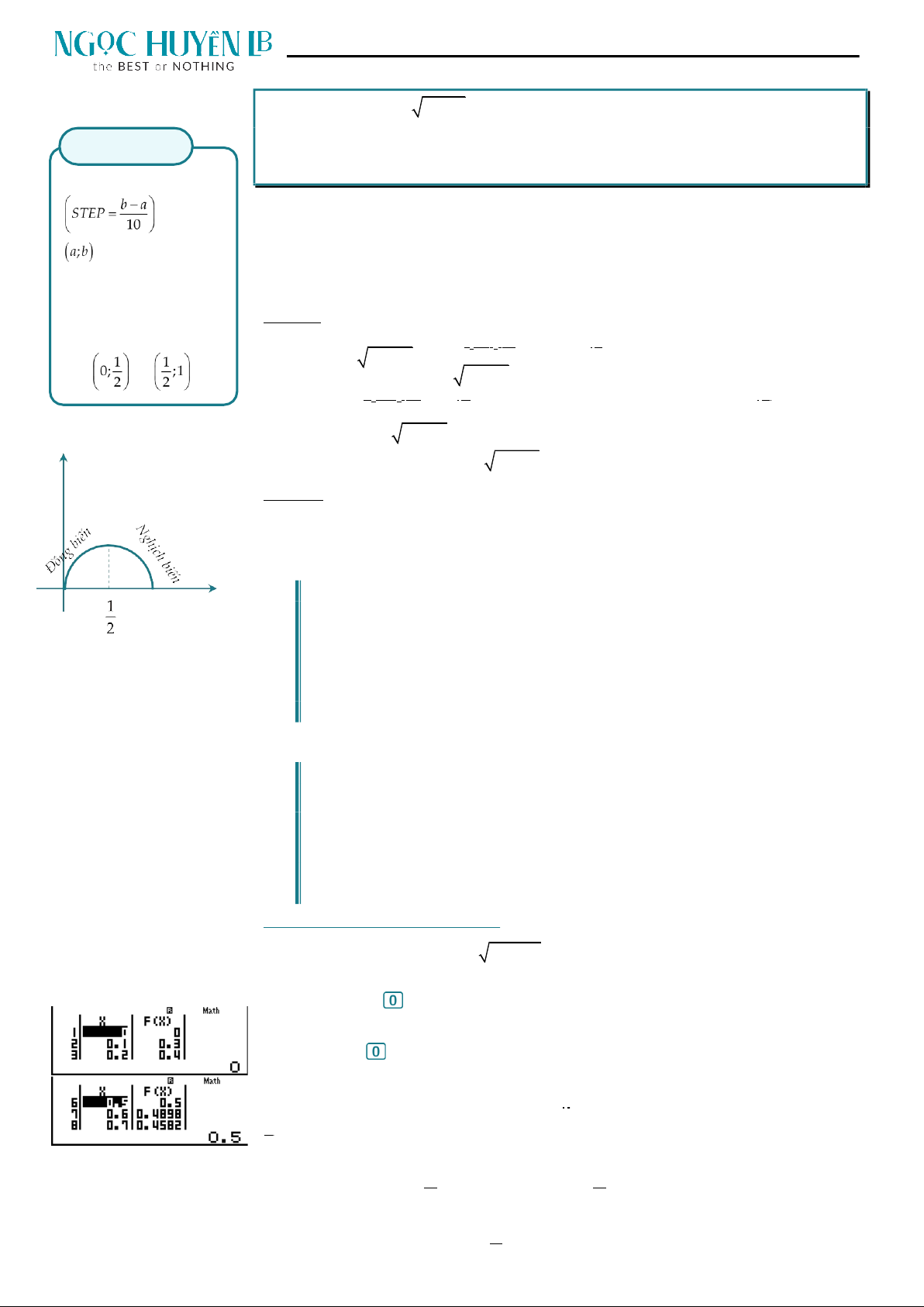
Hình 1.2 là đồ thị hàm số y
2
, ta thấy bài làm đã xác định đúng.
Cách 2: Nhận thấy điều kiện là
x
0;1
, do vậy loại luôn C và D.
Ở B và A, các đầu mút của các khoảng cách nhau 0,5 đơn vị, do vậy ta có thể
chọn được STEP khi sử dụng TABLE trong máy tính.
Giải
thích:
Lệnh TABLE trong máy tính dùng để tính giá trị của hàm số tại một vài điểm.
Ta có thể sử dụng chức năng tính giá trị của hai hàm số
f
x
và
g
x
, hoặc chỉ
tại một hàm duy
nhất
f
x
qwR52
. Bởi vậy, khi sử dụng TABLE
trong việc xác định hàm số đồng biến hay nghịch biến trong một khoảng là khá
dễ dàng, bởi ta chỉ cần xét xem giá trị của hàm số tăng hay giảm khi x chạy
trên khoảng đó thôi.
Thao
tác:
1.
Ấn
w7,
nhập hàm số cần tính giá trị. Ở chế độ mặc định
w7được
thiết
lập mặc định ở dạng nhập hai hàm số
f
x
và
g
x
,
ấn
qwR51để
trở
về dạng chỉ nhập một hàm số
f
x
.
2.
START? Nhập x bắt đầu từ đâu.
3.
END? Nhập x kết thúc ở đâu.
4.
STEP? Bước nhảy giữa các giá trị, tính từ điểm đầu mút.
Áp d ụ ng vào bài toán này ta đượ c:
Ấn
w7,
và
nhập
f
x
ấn
=.
START? Nhập
=.
END? Nhập
1
=.
STEP? Nhập
.1
=.
Sau khi nhập máy hiện như hình bên:
Nhận thấy từ khi x chạy từ 0 đến 0, 5
1
2
thì giá trị của hàm số tăng, tức hàm
1
1
số đồng biến trên
0;
. Còn với x chạy từ đến 1 thì giá trị của hàm số giảm,
1
tức hàm số nghịch biến trên
;1
.
x
x
2
X
X
2
y
O
1
x
BON TIP
Ở đây ta chọn STEP
với
là khoảng cần xét là
0.1 bởi khoảng khá nhỏ,
và ta cần xét tính đồng
biến nghịch biến trên 2
khoảng là
và .
BON 1: Hàm số y
x
x
2
ngh ch bi n trên kho ngị ế ả
A.
;
1
.
1
1
2
B. 0
;
.
2
C.
;
0
.
D.
1
;
.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Đáp
án
A.
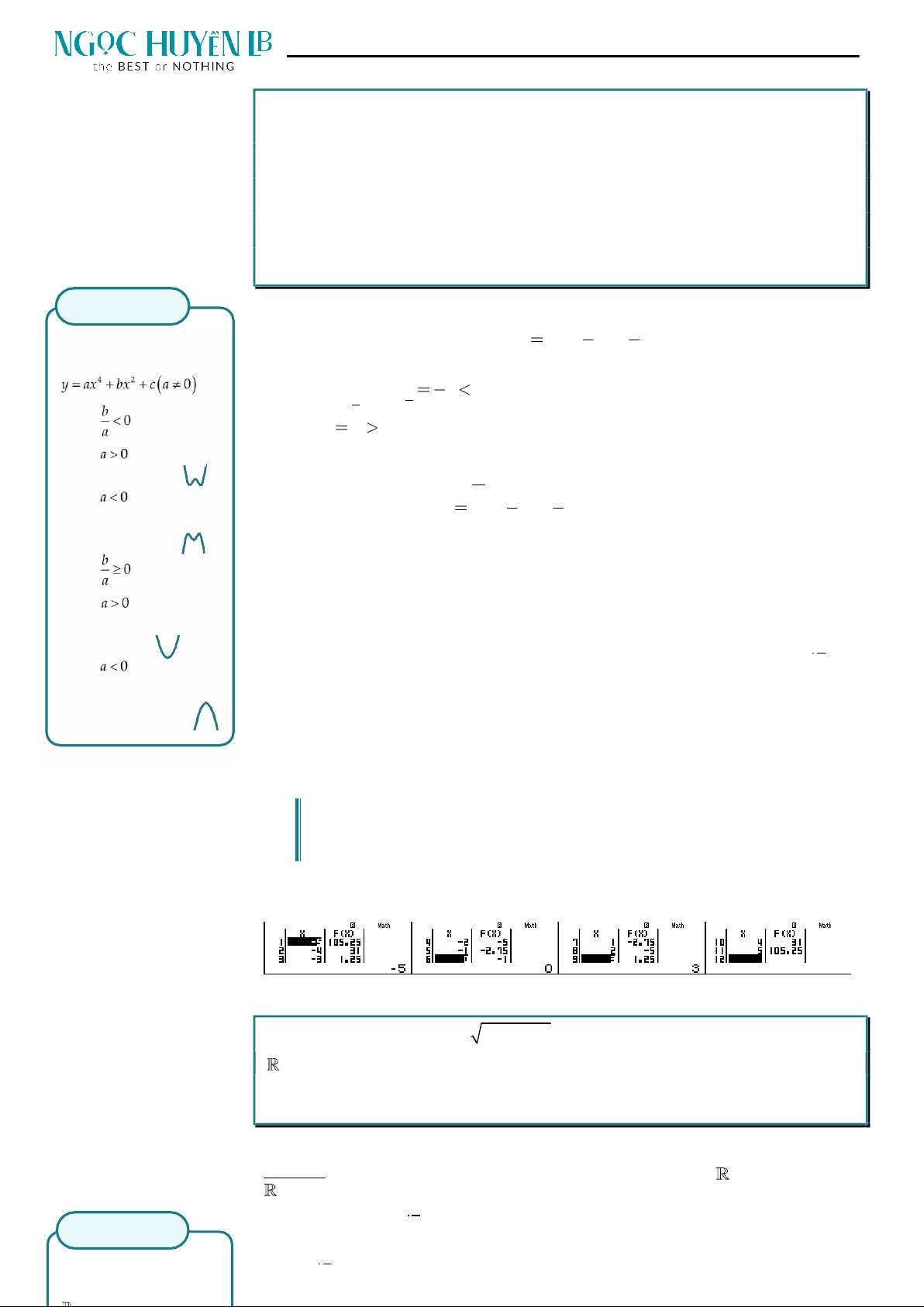
BON 3: Cho hàm số y
x
x
2
x
a
. Tìm
a
hàm s luôn ngh ch bi n trênđể ố ị ế
.
A. a 1 .B.
a
1 .
44
C. a 1 .
4
D. a .
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Phân
tích
Hướng tư duy 1: Ta thấy hàm số y
có:
- Hệ số a
1
0
;
4
b
a
nên áp dụng kết quả của bài toán tổng quát phía
trên thì ta có hàm số
y
1
x
4
4
2x
2
1
đồng biến trên
2;
0
và
2;
;
nghịch biến trên
;
2
và
0; 2
.
Hướng tư duy 2: Xét phương trình y ' 0 x
3
4x 0
x 0
x 2
. Như đã giới
thiệu về cách nhớ dạng đồ thị hàm bậc bốn trùng phương có hệ số
a
1
0
4
nên ở đây ta có thể xác định nhanh hàm số đồng biến trên
2; 0
hàm số nghịch biến trên
;
2
và
0; 2
.
và
2;
,
Hướng tư duy 3: Sử dụng lệnh TABLE.
Sử dụng lệnh TABLE với START là -5 và END 5, STEP 1 ta có thể xác định được:
giá trị của hàm số tăng khi x chạy từ 2 đến 0 và từ 2 đến 5, giá trị của hàm số
giảm khi x chạy từ -5 đến -2 và từ 0 đến 2.
Do đó ta có thể xác định được hàm số đồng biến trên
2; 0
và
2;
.
Hàm số nghịch biến trên
;
2
và
0; 2
.
Đáp
án
A.
Lời
giải
Cách 1: Để hàm số xác định với mọi x
0 1 4a 0 a
1
.
4
x
2
x a 0 , x
Với a
1
4
1 x4
4
2x2
1
80
BON TIP
Với hàm số bậc bốn trùng
phương có dạng
* Nếu thì:
1. Với thì đồ thị hàm
số có dạng chữ W.
2. Vớithì đồ thị hàm
số có dạng chữ M. (chỉ là
mẹo nhớ đồ thị).
* Nếu thì:
1. Với đồ thị hàm số
có dạng Parabol quay bề
lõm lên trên.
2. Vớithì đồ thị hàm
số có dạng Parabol quay bề
lõm xuống dưới.
BON TIP
Ở đây trước tiên, để hàm số
luôn nghịch biến trên thì hàm
số phải xác định trên. Do vậy
ta phải tìm điều kiện để căn
thức luôn xác định với
mọi số thực x.
BON 2: Cho hàm số y 1
x
4 2
x
2 1. Ch n kh ng nh úng.ọ ẳ đị đ
4
Hàm s ng bi n trên các kho ng ố đồ ế ả 2; 0 và 2; .
Hàm s ng bi n trên các kho ng ố đồ ế ả ; 2 và 0; 2.
Hàm s ngh ch bi n trên các kho ng ố ị ế ả ; 2 và 2; .
Hàm s ngh ch bi n trên các kho ng ố ị ế ả 2; 0 và 2; .
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
thì
BON TIP
Ở đây trước tiên, để hàm số
luôn nghịch biến trên thì hàm
số phải xác định trên. Do vậy
ta phải tìm điều kiện để căn
thức luôn xác định với
mọi số thực x.
x
2
x
a
x
2
x
a
x
2
x
a
a
BON 4: Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y 2 sin
x
3 sin
x
m
sin
x
ng bi n trên kho ng đồ ế ả 0;.
3 2
2
A. m 0.B.
m
3 .C.
m
3 .D.
m
3 .
222
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Tính đạo hàm: y
1
2x
1
2
Hàm số đã cho luôn nghịch biến trên
hữu hạn điểm.
y
0,x
. Dấu bằng xảy ra tại
Ta có y
0 1
2x
1
0
2
2 x
1
1
2
1
x
1
x
Lúc này:
2x 1 2
2
2
1 4a
a
1
4
Kết hợp với điều kiện để hàm số xác định với mọi số thực x thì ta thấy
không có giá trị nào của a thỏa mãn.
Cách
2: Với x 0
thì y
1
1
0, a
1
.
2
4
Vậy không có giá trị nào của a để
y
0,x
Kết
quả
Sau bài toán trên ta thấy, với các bài toán hàm căn thức, hàm phân thức nếu đề
bài yêu cầu tìm điều kiện của tham số để hàm số đơn điệu trên , hoặc trên
khoảng I nào đó, thì ta cần tìm điều kiện để hàm số luôn xác định trên
hoặc
trên khoảng I đó.
Đáp
án
D.
Lời
giải
Cách 1: Do hàm số t sin x đồng biến trên
0;
nên đặt sin x t; t
0;1
.
2
Khi đó ta có hàm số y f
t
2t
3
3t
2
mt;
y
6t
2
6t m
Để hàm số đã cho đồng biến trên
0;
thì hàm số
y f
t
phải đồng biến
2
trên
0; 1
phương trình
y ' 0
hoặc là vô nghiệm, có nghiệm kép (1) ; hoặc
t t
0 1
là có hai nghiệm t t thỏa mãn
1 2
(2).
1 2
0 1 t
t
Trường hợp (1): phương trình
y
0
0 9 6m 0
m
3
.
2
1 2
vô nghiệm hoặc có nghiệm kép
x
2
x
a
.
BON TIP
Nếuphươngtrình
vô nghiệm hoặc
cónghiệmképthì
hàm số
luôn đồng biến trên
BON TIP
Đến đây nhiều độc giả chọn
luôn B, hoặc C là sai, nên kết
hợp cả điều kiện ban đầu, từ
đó rút ra kết luận.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
|
3
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
1 2
1 2
2
2
0
3
m
2
t
1
t
2
0
m
6
t
t
0
1 0
Trường hợp (2): Thỏa
mãn
1 2
0
m
3
(loại)
t
1
t
1
0
2
t
t
m
1 1 0
1 2
1
6
2
1
1
2
Ở đây ta có thể loại luôn trường hợp (2) bởi xét tổng hai nghiệm không thỏa mãn.
Cách 2: Ở đây chỉ có hai trường hợp: một là vô nghiệm, có nghiệm kép; hai là
0; 1
nằm ngoài khoảng hai nghiệm.
Nhận thấy 3 phương án B, C, D cùng có số
3
2
nên ta xét
3
2
trước. Do phương
án C có dấu do vậy, ta sẽ xét dấu bằng trước, nếu dấu bằng thỏa mãn thì ta
loại luôn B và D
3 3 1
2
1
Với
m thì y
6t
2
6t 6
t
0 t
(phương trình
y ' 0
có
2 2
2
2
nghiệm kép, thỏa mãn). Đến đây ta loại luôn B và D.
Hình 1.4 là đồ thị hàm số y
f
t
khi m
3
.
2
Hình 1.4
Tiếp theo ta chỉ cần xét đến A. Ta sẽ thử m 1
2
;
.
Với m 1 thì
y
6t2
6t
1
0
t
3
3
6
3
3 3 3
, nhận xét 0 1
6 6
(không thỏa mãn). Vậy loại A, chọn C.
Hình 1.5 là đồ thị hàm số y
f
t
khi
m 1
. Vậy suy luận của ta là đúng.
Do
y
6t
2
6t m là một tam thức bậc hai có hệ số a 0 nên
1.
Nếu 0 thì
y
cùng dấu với hệ số a (mà a 0 ) nên hàm số luôn đồng biến.
2.
Nếu 0 thì phương trình
y
0 có hai nghiệm phân biệt t ;t . Khi đó, trong
khoảng hai nghiệm thì
y
khác dấu với a và ngoài khoảng hai nghiệm thì
y
cùng
dấu với a. Nên để
y
0,
t
0;1
thì
0;1
phải nằm ngoài khoảng hai nghiệm.
Nhận
xét:
Hình 1.5
Ở đầu lời giải cách 1, tôi có chỉ rõ rằng “Do hàm số
y sin x
đồng biến trên
0;
nên đặt
sin x
t; t
0;
1
” bởi khi đặt hàm hợp, ta cần lưu ý điều kiện của hàm
hợp. Ở bài toán trên nếu thay sin x bằng cos x ; lúc này, nếu đặt cos x t và tiếp
tục giải như trên thì kết quả đạt được m
3
2
là hoàn toàn sai.
Thật vậy: Với
m 2
2
;
,
hàm số y 2 cos
3
x 3cos
2
x 2 cos x nghịch biến
trên
0;
.
y
O
t
1
y
O
t
1
0
3
3
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
4
Đáp
án
C.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
CALC
Lời
giải
Ta có
y
3x
2
6x 3
1 m
,
y
6x 6 .
Để đồ thị hàm số có điểm cực đại, cực tiểu thì
3
2
9.
1
m
0
m 0 .
Với m 0
thì ta thực hiện:
Chuyển máy tính sang chế độ
Nhập vào máy tính biểu thức y
y
.
y
18a
ta có
3 2 2
6 X 6
X
3X
Ấn
3
1 M
X 1 3M
3X
6X 3
1 M
18
Máy hiện X? nhập i =
Máy hiện M? nhập 100 =
Khi đó máy hiện kết quả là 202
200i
Ta thấy 202 200i 2.100 2 2.100.i
y 2m 2 2mx
Vậy phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số đã
cho có dạng 2mx y 2m 2 0 .
Ta rút ra kết luận về cách làm dạng toán viết phương trình đường thẳng đi
qua hai điểm cực trị của đồ thị hàm bậc ba này như sau:
Bước 1: Xác định
y
;
y
.
Bước 2: Chuyển máy tính sang chế độ tính toán với số phức:
Nhập biểu
thức
y
y
.
y
.
18a
Chú ý:
Nếu bài toán không chứa tham số thì ta chỉ sử dụng biến X trong máy, tuy nhiên
nếu bài toán có thêm tham số, ta có thể sử dụng các biến bất kì trong máy để
biểu thị cho tham số đã cho, ở trong sách này ta quy ước biến M để dễ định
hình.
Bước 3: Gán giá trị.
Ấn , gán X với i, gán M với 100.
Lúc này máy hiện kết quả, từ đó tách hệ số và i để đưa ra kết quả cuối cùng.
Đáp
án
B.
BON TIP
Với những dạng toán này, ta
lưu ý rằng trước tiên, ta cần
tìm điều kiện để hàm số có
hai cực trị.
BON TIP
Với bước cuối cùng, ta cần có
kĩ năng khai triển đa thức sử
dụng máy tính cầm tay.
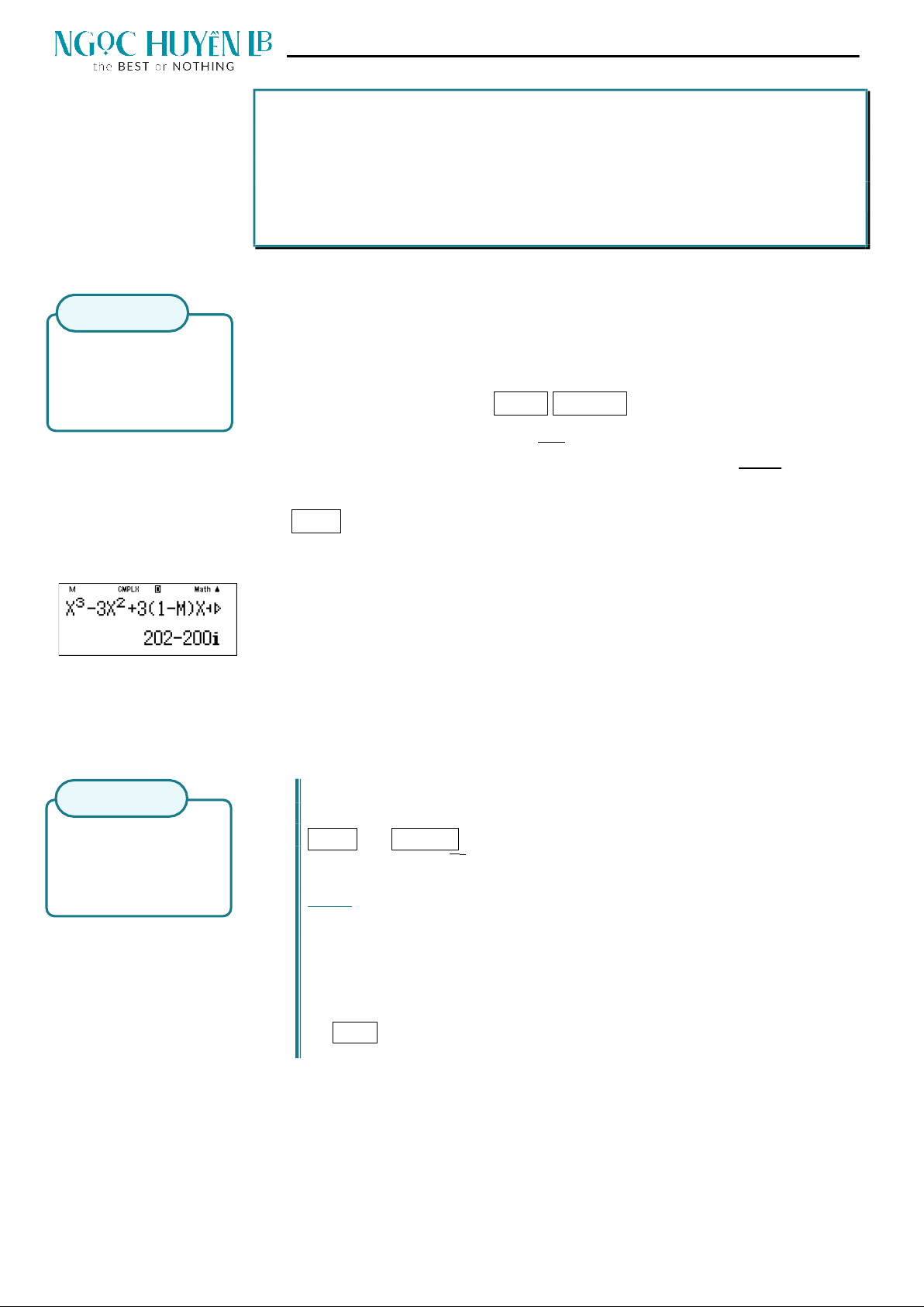
BON 5: Cho hàm số y
x
3
3
x
2
3 1
m
x
1 3
m
. Tìm
m
sao cho th hàm s đồ ị ố
có i m c c i, c c ti u, ng th i tìm ng th ng i qua hai i m c c tr đ ể ự đạ ự ể đồ ờ đườ ẳ đ đ ể ự ị
c a th hàm s ã cho.ủ đồ ị ố đ
A.
m
0; : 2
mx
y
2
m
2 0.B.
m
0; : 2
mx
y
2
m
2 0.
C.
m
0; :
y
202 200
x
.D.
m
0; :
y
202 200
x
.
MODE
2:CMPLX
CALC
2:CMPLX
MODE
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
5
.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Lời
giải
Từ bài toán xét sự biến thiên tổng quát của hàm số bậc bốn trùng phương
mà tôi đã giới thiệu ở phần trước thì ta có:
Hàm số
f
x
x
4
2x
2
1 có
x 0
b
2 0
a
nên phương trình
f
x
0
có ba
nghiệm phân biệt là
x
x
1.
1
Kết hợp với lý thuyết trang 28, do biến thiên:
f
x
có hệ số
a 1 0
ta có nhanh bảng
*
Từ đây ta loại C do hàm số
f
x
có hai điểm cực đại và một điểm cực tiểu.
*
Ta loại A do hàm
số
f
x
có hai điểm cực đại là
x
1
và
x
1.
Còn A
1; 2
và
B
1; 2
là hai điểm cực đại của đồ thị hàm số, chứ không phải của hàm số
(xem lại chú ý đầu tiên (phần mở đầu chủ đề cực trị của hàm số) về phân biệt
các khái niệm).
*
Để loại một trong hai phương án B và D còn lại ta tiếp tục xét hàm số g
x
.
TXĐ: D Ta có
y
x3
2x; y
0
x
0
Bảng biến thiên:
Từ BBT ta loại D do
x 0
là điểm cực đại của hàm số g
x
.
6
Đáp
án
B.
b
2
a
b
2
a
BON TIP
Đối với hàm bậc bốn
trùng phương có dạng
thì nếu:
+)thì hàm số có một
điểm cực trị là.
+)thì hàm số có ba
điểm cực trị là
.
BON 6: Xét hai hàm số f
x
x
4 2
x
2 1 và hàm s ố
g
x
1
x
4
x
2 5 .
4 4
Chọn mệnh đề đúng trong các mệnh đề sau:
Hàm số f
x
có hai i m c c i là đ ể ự đạ
A
1; 2 và
B
1; 2.
Hàm s ố
f
x
có i m c c ti u là đ ể ự ể
x
0 và hàm s ố
g
x
có giá tr c c iị ự đạ
là
y
5 .
4
Hàm s ố
f
x
có hai i m c c ti u và m t i m c c i, hàm s đ ể ự ể ộ đ ể ự đạ ố
g
x
có m t ộ
i m c c i.đ ể ự đạ
Hàm s ố
f
x
và hàm s ố
g
x
cùng có i m c c ti u là đ ể ự ể
x
0.
x
1
0 1
f
x
0
0
0
f
x
2
1
2
x
0
f
x
0
f
x
5
4
120
x
2 402
x
2
240
x
16000
x
2
3600
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Lời
giải
Thực chất bài toán trở thành tìm x để
AC BC
nhỏ nhất.
Theo định lí Pytago ta có
A
B
60
Khi đó
40
AC
f
x
AC BC
; BC
.
x
P
C
Q
Ta cần tìm min f
x .
0;120
Ta có
f
x
x
x 120
x
2
240x 16000
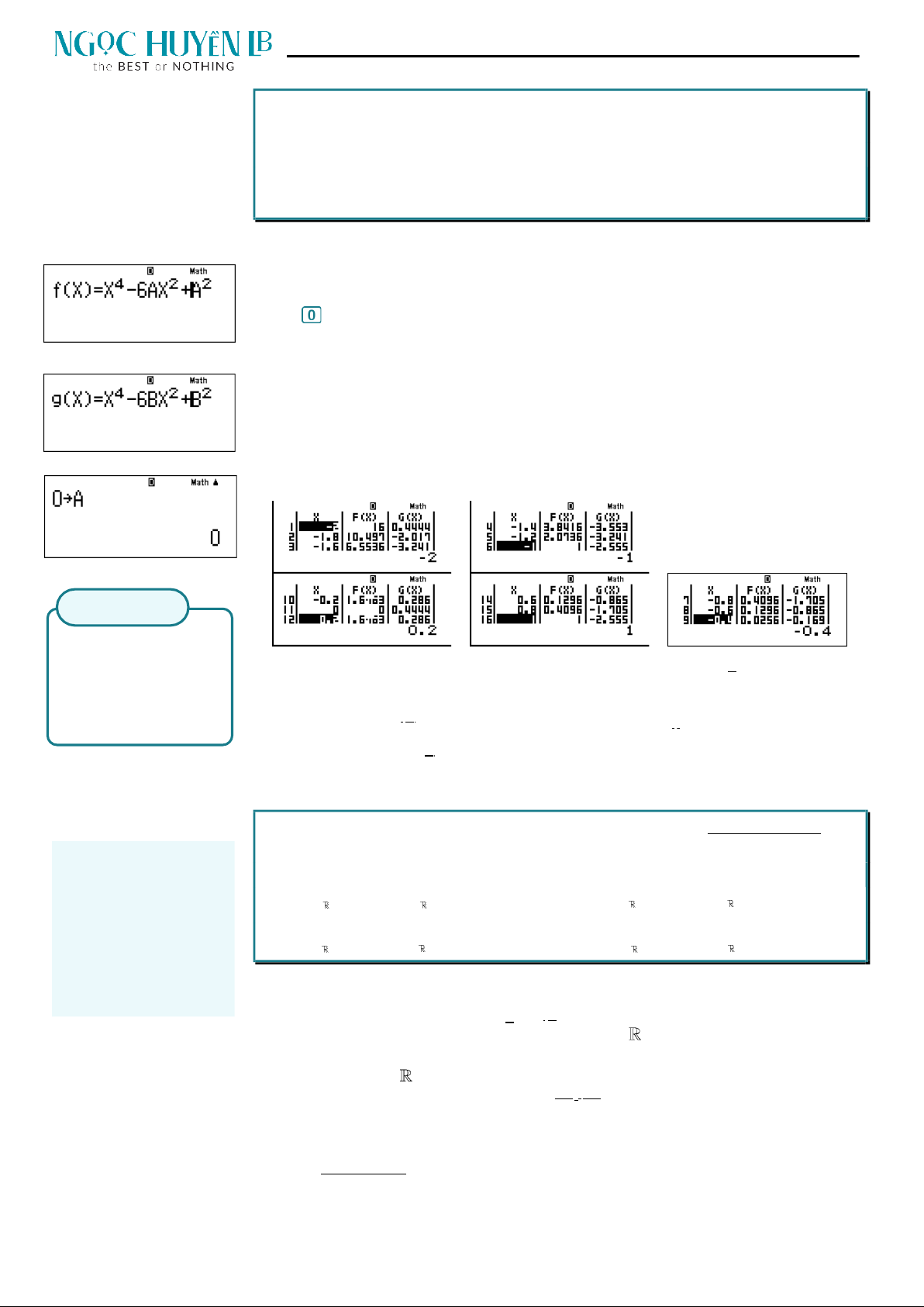
, khi bấm máy tính nhẩm nghiệm
bằng cách nhập vào màn hình biểu thức
f
x
và ấn
và chọn
một số nằm trong khoảng
0; 120
để dò nghiệm, chẳng hạn nhập 2 máy nhanh
chóng hiện nghiệm là 72 như sau:
Vậy từ đó ta có thể kết luận
CP 72
km.
Đáp
án
A.
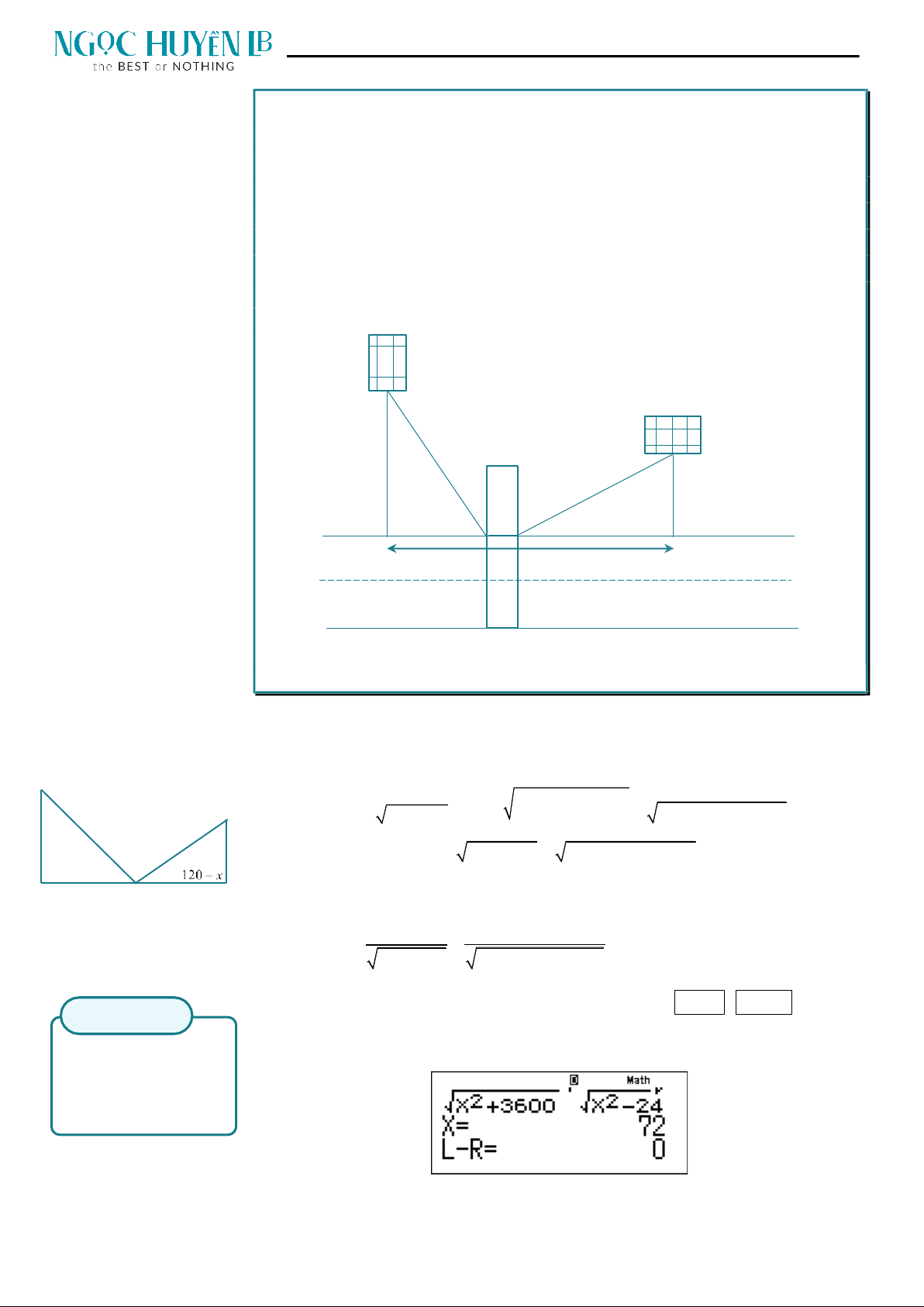
BON 8: Đường cao tốc mới xây nối hai thành phố A và B, hai thành phố này
muốn xây một trạm thu phí và trạm xăng ở trên đường cao tốc như hình vẽ.
Để tiết kiệm chi phí đi lại, hai thành phố quyết định tính toán xem xây trạm thu
phí ở vị trí nào để tổng khoảng cách từ hai trung tâm thành phố đến trạm là
ngắn nhất, biết khoảng cách từ trung tâm thành phố A, B đến đường cao tốc
lần lượt là là 60 km và 40 km và khoảng cách giữa hai trung tâm thành phố là
120 km (được tính theo khoảng cách của hình chiếu vuông góc của hai trung
tâm thành phố lên đường cao tốc, tức là PQ kí hiệu như hình vẽ). Tìm vị trí
của trạm thu phí và trạm xăng? Giả sử chiều rộng của trạm thu phí không
đáng kể.
A
B
60
40
P
Q
120
A. 72 km kể từ P.
C. 48 km kể từ P.
B. 42 km kể từ Q.
D. tại P.
60
2
x
2
x2 240
x
16000
x
2
3600
BON TIP
Thường các bài toán thực tế,
dùng Solve dò nghiệm sẽ rất
nhanh. Ta sẽ tìm hiểu ở phần
sau.
Trạm thu phí
SOLVESHIFT
Trạm xăng
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
|
7
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
2
2
Lời
giải
Đầu tiên ta gán các giá trị ở các phương án lần lượt vào các biến A, B, C, D bằng
lệnh STO như sau:
Ấn
qJ(STO)
A
Tương tự với B, C, D.
Lúc này ta kiểm tra hai phương án A,
B
thì ta nhập hàm
f
x
X
4
6A.X
2
A
2
g
x
X
4
6.BX
2
B
2
như hình bên.
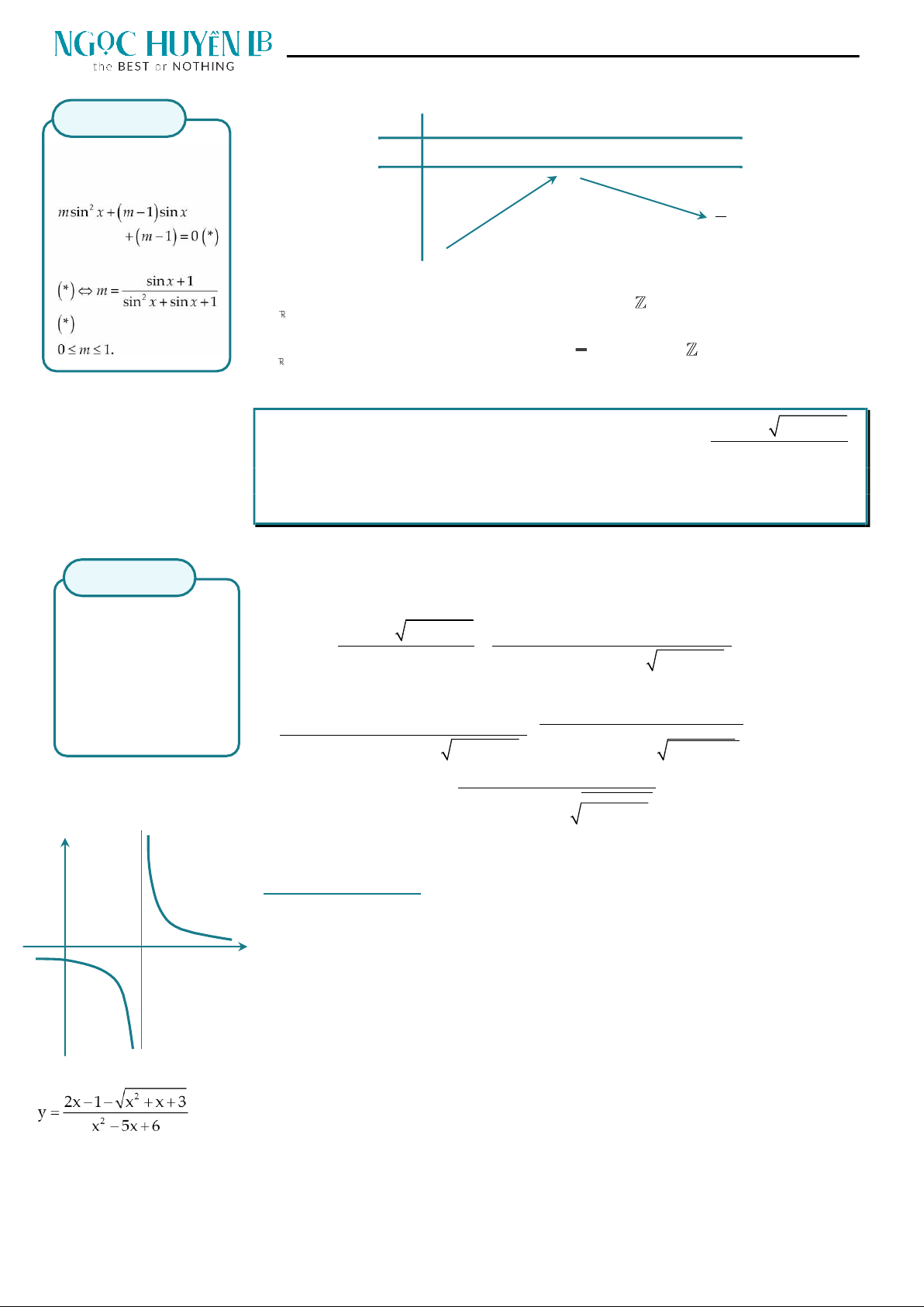
Tiếp theo nhập Start? -2; End? 1 Step? 0,2. Ta thấy các giá trị của hàm số ở hai
trường hợp m hiện như sau:
Ta thấy khi m 0 thì hàm số không đạt giá trị lớn nhất bằng
4
(loại).
9
Ở trường hợp m
2
3
thì hàm số đạt giá trị lớn nhất là
4
9
x 2
khi
.
x 0
Đáp
án
B.
BON 7:
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số g
x
sin
2
x sin x 1
lần
lượt là
A. max g
x
1; min g
x
2.
C. max g
x
1; min g
x
0.
Lời
giải
B. max g
x
0; min g
x
1.
D. max g
x
1; min g
x
1.
Ta có sin x sin x 1
sin x
1
2
3
0, x 4
Tập xác định D
Đặt
t sin x, t
1; 1
.
Lúc đó
y f
t
t
1
; t
1; 1
.
t t 1
f
t
t
2
2t
;
2
2
t 0
f
t
0
t 2 1;1
t
t 1
.
.
BON TIP
Ở các bài toán dạng này ta
thấy do đề bài chỉ có 4
phương án, nên ta chỉ cần
thử 2 lần là có được kết quả.
BON 9: Để hàm số y
x
4
6
mx
2
m
2
có max
y
4 thì giá tr c a tham s th cị ủ ố ự
2;1
9
m là
A. 0.
B. 2 .
3
C. 1.
D. 4 .
3
sin x 1
Nếu khảo sát trực tiếp
hoặc dùng miền giá trị
đều dẫn đến tính toán
phức tạp. Phương pháp
đổi biến trong trường hợp
này rất hiệu quả. Chú ý
khi đổi biến ta cần tìm
điều kiện của biến mới.
2
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
8
x
y
y
1
+
0
0
1
1
2
3
0
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
Bảng biến thiên
Dựa vào bảng biến thiên ta có
max g
x
max f
t
1 sin x 0 x k;
k
1;1
min g
x
min f
t
0 sin x 1 x k2,
k
1;1
2
Đáp
án
C.
Lời
giải
x 3
Điều kiện xác định của hàm số là
.
x 2
4x
2
4x 1 x
2
x 3
Ta có y
x
2
5x 6
3x
2
5x 2
3 x 1
x 3
2x 1
3 x 1
Đến đây ta có lim y lim
x
2
x 3
;
lim y .
x3
x
3
x 3
2x 1
x
2
x 3
x3
Vậy đồ thị hàm số chỉ có một tiệm cận đứng là x 3 .
Phân tích sai lầm:
Nhiều độc giả không thực hiện rút gọn nhân tử x 2 dẫn đến
chọn hai tiệm cận đứng là
x 2; x 3
là sai.
Đây cũng chính là ứng dụng của lý thuyết về tiệm cận đứng của đồ thị hàm số
ở phía trên. Một cách khác để nhanh chóng giải bài toán trên như sau:
1.
Giải phương trình
x
2
5x 6 0
x
2
.
x 3
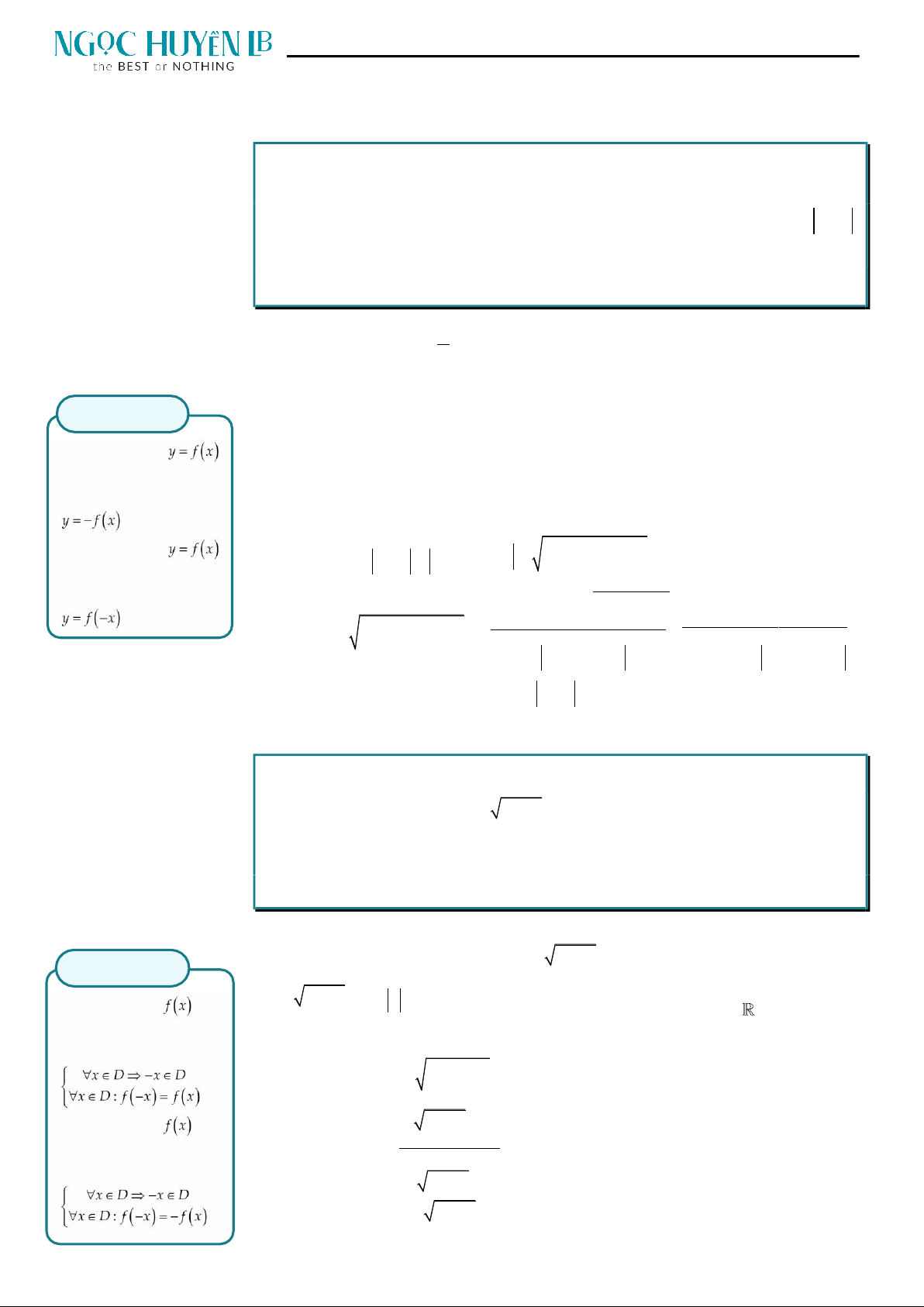
Đồ thị hàm số
2.
Thử xem x 2; x 3 có phải nghiệm của đa thức tử số hay không, thử lại thấy
x 3 không là nghiệm (thỏa mãn).
Đáp
án
D.
.
.
2x 1
x
2
x
3
x
2 5
x
62
x
1
x
x
3
2
x
2
x
32
x
1
x
x
3
2
y
O
3
x
BON TIP
Bước 1: Tìm nghiệm của
phương trình mẫu.
Bước 2: Xem các nghiệm đó
có phải là nghiệm của tử số
không (bằng cách thay hoặc
thử trực tiếp).
Kết luận.
BON TIP
Từ bài toán này ta đưa ra
ứng dụng sau: Xác định m
để phương trình
Ta có:
cónghiệmkhi
BON 10: Tìm tất cả các tiệm cận đứng của đồ thị hàm số
y
2x 1
x
2
x
3
x
2
5
x
6
.
A. x 3 và
x
2.B.
x
3.
C.
x
3 và
x
2.D.
x
3.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
|
9
log
x
2020
2
x
2 1
x2 1
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
1
2020 2020
MŨ
LOGARIT
CHỌN
LỌC
1
Lời
giải
Ta có:
C
1
: y log
2020
log
2020
x .
x
Gọi
C
là đồ thị đối xứng của
C
qua trục
Ox
C
là đồ thị của hàm số y log
2020
x
.
Nhận thấy
C
đối xứng với
C
qua trục
Oy
C
là đồ thị của hàm số
y log
x
, hay f (x) log
x
, với x 0.
Do đó: g
x
f
x
log
2020
x
2 log
x
.
1
2020
2.log
x
g
x
x
.ln
2020
2020
log
2020
x
x.ln 2020.
log
2020
x
g
x
0,x 1 hay hàm số y
f
x
nghịch biến trên khoảng
;
1
.
Đáp
án
A.
Lời
giải
Xét hàm số g
x
f
x
6 a log
2021
x
b sin x.cos
2020x
Do
x x x 0
nên hàm số g
x
có tập xác định D
=
.
Ta có:
x D x D
và
g
x
a log
2021
x
b sin
x
.cos
2020
x
g
x
a log
2021
x
b sin x.cos
2020x
g
x
a log
2021
1
b sin x.cos
2020x
g
x
a log
2021
g
x
g
x
.
x
2
1 x
x
b sin x.cos
2020x
log
x
2020
2
x
2
1
x
2
1
x2 1
BON TIP
+ Đồ thị hàm số
lấy đối xứng qua trục Ox
được đồ thị hàm số
.
+ Đồ thị hàm số
lấy đối xứng qua trục Oy
được đồ thị hàm số
.
BON TIP
+ Cho hàm số
xác
định trên D được gọi là
hàm số chẵn nếu
+ Cho hàm số xác
định trên D được gọi là
hàm số lẻ nếu
BON 1: Cho hàm số y
log
2020
1
x
có đồ thị
C
1
và hàm số y
f
x
có thđồ ị
C
. Bi t ế
C
và
C
i x ng nhau qua g c t a . H i hàm s đố ứ ố ọ độ ỏ ố
y
f
x
2
1
2
nghịch biến trên khoảng nào sau đây?
A. ; 1.B. 1; 0.
C.
0;1.
D. 1; .
2
2
BON 2: Cho a, b là các số thực và hàm số:
f
x
a
log
2021
x
2
1
x
b
sin
x
.
c
os2020
x
6.
Bi t ế
f
2020
ln2021
10 . Tính
P
f
2021
ln2020
.
A.
P
4.B.
P
2.C.
P
2.D.
P
10.
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
10
CHINH
PHỤC
BÀI
TOÁN
VD-VDC
LỚP
12 the
BEST
or
NOTHING
1
2
Vậy hàm số g
x
là hàm số lẻ.
Lại có:
2020ln2021
2021ln2020
g
2020ln2021
g
2021ln2020
f
2020
ln2021
6
f
2021
ln2020
6
10 6 f
2021
ln2020
6 f
2021
ln2020
2
Đáp
án
B.
Ta có
Lời
giải
u
n
1
u
n
3
với mọi n 1 nên
u
n
là cấp số cộng có công sai d 3
e
u
18
5
Đặt
t e
u
18
e
4u
1
e
4u
1
5
t 0
e
4u
1
e
u
18
1
t 0
Phương trình
1
trở thành
5
t
25t t
2
t 0
Với t 0 ta có:
eu
18
e4u
1
u 4u u 51 4u u
17
18 1 1 1 1
Vậy u
n
u
n 1
d 17
n 1
3 3n 14
Ta có:
log u
ln 2020 u
3
ln 2020
3n
14
3
ln 2020
3 n n
3
ln 2020
14
n 1421, 53
3
Vậy giá trị lớn nhất của n là
1421.
Đáp
án
A.
Lời
giải
m.9
2x
2
x
2m 1
6
2x
2
x
m4
2x
2
x
0
2
2
2
9
2 x
2
x
6
2 x
2
x
3
2 x
x
3
2 x
x
m.
4
2 x
2
x
2m 1
.
4
2 x
2
x
m 0 m
2
2m 1
2
m 0
Đặt
2 x
2
x
3
t với x
1
. Xét hàm số
2
f
x
2x
2
x ta có bảng biến thiên:
e
u
18 e
4
u
1
e
u
18 e
4
u
1
t
BON
TIP
+ Dãy là cấp số cộng
nếu: Ta có
với mọi, hằng số d
gọi là công sai, có
+ Dãylà cấp số nhân
nếu: Ta cóvới
mọi, hằng số q gọi là công
bội:
u
18
e e evà
u
u
3 v iớ
u4u4u
181 1
n
n1
n
mọi n 1. Giá tr l n nh t c a ị ớ ấ ủ
n
logđể
3
un
ln 2020 b ngằ
A. 1421.B. 1418.C. 1420.D. 1419.
thỏa mãn e 5
BON 3: Cho dãy số u
BON 4: Cho bất phương trình m.92 x2
x
2
m
162
x
2
x
m
42
x
2
x
0 . Tìm
m
b tđể ấ
ph ng trình úng ươ đ
x
1 .
2
A. m 3 .
2
B. m 3 .
2
C. m 0 . D. m 0 .
Bấm Tải xuống để xem toàn bộ.