lOMoARcPSD|46342985 lOMoARcPSD|46342985
CƠ SỞ CỦA NHIỆT ĐỘNG HỌC
1.1. Một số khái niệm cơ bản của nhiệt động học
1.1.1. Hệ và sự phân loại hệ
1.1.1.1. Khái niệm
Hệ là đối tượng cần nghiên cứu các tính chất nhiệt động học. Hệ là một vật hoặc
một nhóm vật được coi là cách biệt với thế giới xung quanh.
Hệ nhiệt động (hệ vĩ mô), được gọi tắt là hệ, là phần của vũ trụ gồm một số rất
lớn tiểu phân cấu tạo (nguyên tử, phân tử hay ion) đang được nghiên cứu và được phân
cách với phần còn lại của vũ trụ - môi trường ngoài - bằng một ranh giới thực hay ảo.
Nhiệt động lực học hóa học chỉ nghiên cứu những hệ vĩ mô.
1.1.1.2. Phân loại
*Cách 1: Dựa vào khả năng trao đổi chất và năng lượng với môi trường xung quanh.
- Hệ mở (hở): là hệ có thể trao đổi với môi trường ngoài cả chất lẫn năng lượng.
Ví dụ: Khi đun nước thì nhiệt được truyền từ bên ngoài vào hệ, còn hệ mất chất ra bên
ngoài dưới dạng hơi nước.
- Hệ kín (đóng): là hệ chỉ trao đổi năng lượng với môi trường ngoài. Ví dụ: Khi
cho xút (NaOH) tác dụng với axit sunfuric trong một bình kín:
2NaOH + H2SO4 → Na2SO4 + 2H2O
hệ không mất chất, nhưng hệ đã cung cấp năng lượng cho môi trường ngoài vì phản
ứng tỏa nhiệt.
- Hệ cô lập: là hệ không trao đổi cả chất lẫn năng lượng với môi trường ngoài. Ví
dụ: Một bình cách nhiệt (Dewar) chứa các chất phản ứng được đậy kín và bao phủ bằng
một lớp cách nhiệt thật dày để cho chất và năng lượng không được trao đổi với môi trường ngoài.
*Cách 2: Dựa vào tính đồng nhất hoặc số lượng pha cấu thành nên hệ đó. lOMoARcPSD|46342985
- Hệ đồng thể: là hệ có thuộc tính không thay đổi hoặc thay đổi đều liên tục từ
điểm này sang điểm khác và trong hệ không có bề mặt phân chia (Bề mặt phân chia là bề
mặt qua đó thuộc tính của hệ thay đổi). Ví dụ: dung dịch nước đường, không khí, ….
Đặc điểm của hệ đồng thể: Là hệ được cấu tạo bởi một pha duy nhất (pha đơn
hoặc pha hỗn hợp); Là hệ có tính chất giống nhau tại các điểm khác nhau của hệ; Là hệ
mà trong đó không có sự phân chia thành các khu vực khác nhau với những tính chất khác nhau.
- Hệ dị thể: là hệ có bề mặt phân chia, là hệ được tạo thành bởi nhiều pha khác nhau.
Khái niệm pha (hay tướng): Tập hợp những phần đồng thể của hệ có cùng tính
chất hoá, lý giới hạn với những phần khác bằng những bề mặt phân chia. Ví dụ: Dung
dịch trong suốt: 1 pha, hệ đồng thể; Nước lỏng + nước đá: 2 pha, hệ dị thể; Dung dịch
bão hoà + NaCl rắn + nước đá rắn: 3 pha, hệ dị thể.
* Khái niệm hệ đồng nhất: Là hệ có thành phần như nhau (đồng nhất hóa học) và
thuộc tính như nhau (đồng nhất vật lý) ở khắp mọi phần của hệ hoặc biến đổi đều. Ví dụ:
dung dịch axit HCl 20%. Hệ không đồng nhất: Trường hợp ngược lại của hệ đồng nhất.
1.1.2. Trạng thái của một hệ. Thông số trạng thái
Trạng thái của một hệ nhiệt động được xác định bởi một tập hợp các trị số của các
đại lượng vĩ mô có thể đo được như thể tích, nhiệt độ, áp suất, khối lượng…Các đại
lượng gọi là các thông số trạng thái hay các thông số nhiệt động.
Thông số trạng thái được chia làm hai loại:
+ Các thông số cường độ như: Nhiệt độ, áp suất, chiết suất, tỉ khối, độ
nhớt,… không phụ thuộc vào lượng chất của hệ.
+ Các thông số khuếch độ như: Thể tích, khối lượng, … tỉ lệ với lượng
chất của hệ.
Trạng thái của hệ mà ở đó các thông số cường độ tại mọi chỗ của hệ đồng đều
và có giá trị xác định được gọi là trạng thái cân bằng.
Thông số quá trình: Là đại lượng nhiệt động đặc trưng cho quá trình. Ví dụ
như nhiệt Q, công A. lOMoARcPSD|46342985
Khi hệ chuyển từ trạng thái này sang trạng thái khác người ta nói hệ thực hiện 1 quá trình.
1.1.3. Quá trình nhiệt động
1.1.3.1. Khái niệm
Là quá trình xảy ra trong hệ vĩ mô liên quan ít nhất tới sự biến thiên một tham số. Quá
trình đóng (hay chu trình): Là quá trình hệ ở trạng thái đầu chịu một loạt biến
đổi lại trở về trạng thái đầu.
Quá trình mở: Là quá trình sau khác quá trình đầu.
1.1.3.2. Một số quá trình nhiệt động
Quá trình đẳng nhiệt (T = const): Xảy ra ở nhiệt độ không đổi.
Quá trỉnh đẳng áp (P = const): Xảy ra ở áp suất không đổi.
Quá trình đẳng tích (V = const): Xảy ra ở thể tích không đổi.
Quá trình đoạn nhiệt: Là quá trình xảy ra khi không có sự trao đổi nhiệt giữa hệ
và môi trường ngoài.
Quá trình vi phân: Là quá trình trong đó các biến số chỉ chịu sự biến đổi vi phân vô cùng nhỏ: P → P + dP
Kí hiệu: Hàm trạng thái: dP, dV, dT, dU, dH, dF, dG… Hàm quá trình: A, Q
Quá trình thuận nghịch: Là quá trình nếu sau quá trình thuận hệ có khả năng trở
về trạng thái đầu theo đúng con đường nó đi qua mà không để lại biến đổi nào cho
môi tr-ường (hoặc là quá trình xảy ra theo hai chiều ngược nhau và tương đối chậm sao
cho ở mỗi thời điểm người ta biết được trạng thái của hệ).
Quá trình bất thuận nghịch (quá trình một chiều) là quá trình không tuân theo các
điều kiện trên chỉ xảy ra theo một chiều nhất định.
1.1.4. Hàm số trạng thái của hệ
Một đại lượng nhiệt động được gọi là hàm số trạng thái của hệ nếu biến thiên
đại lượng đó chỉ phụ thuộc vào trạng thái đầu và trạng thái cuối mà không phụ thuộc
vào cách tiến hành quá trình. Tất cả các tham số trạng thái đều là hàm số trạng thái. lOMoARcPSD|46342985
1.1.5. Năng lượng – Nội năng
1.1.5.1. Năng lượng
Năng lượng là “thước đo” sự vận động của vật chất trong mọi biến đổi của nó. Gồm:
+ Động năng ứng với sự chuyển động cơ học của toàn bộ hệ trong không gian: mv2 Eđ = 2
+ Thế năng được xác định bởi vị trí của hệ trong trọng trường: Et = mgh
+ Nội năng U: Tổng năng lượng các tiểu phân tạo nên hệ.
Vậy, E = Eđ + Et + U
Nhận xét: Trong nhiệt động học khảo sát hệ không chuyển động và tác dụng
của trường ngoài là không đổi, tức chỉ xét nội năng.
Định luật bảo toàn và chuyển hóa năng lượng: Năng lượng không tự sinh ra và
không tự mất đi, nó chỉ biến đổi từ dạng này sang dạng khác.
1.1.5.2. Nội năng
Định nghĩa: Là năng lượng “dự trữ” của hệ. Gồm:
+ Động năng của chuyển động tịnh tiến và quay của các phân tử, nguyên tử, hạt nhân và electron.
+ Thế năng tương tác (hút và đẩy) của các phân tử, nguyên tử, hạt nhân và electron.
+ Năng lượng dao động của các nguyên tử, nhóm nguyên tử trong phân tử,
năng lượng electron của các nguyên tử trong phân tử, năng lượng của hạt nhân.
Nội năng của 1 hệ là tổng năng lượng tương tác giữa các phân tử, năng lượng tư-
ơng tác bên trong mỗi phân tử và năng lượng chuyển động hỗn loạn của các phân tử.
Có 2 cách làm biến đổi nội năng: Thực hiện công và truyền nhiệt. lOMoARcPSD|46342985
1.1.6. Công và nhiệt 1.1.6.1.Công
Là một đại lượng đặc trưng cho mức độ trao đổi năng lượng thông qua chuyển
động có hướng của hệ; Là hình thái truyền năng lượng liên quan đến sự chuyển dời của
những hệ vĩ mô do tác dụng của một lực nào đó: A = F.dx (*) Ví dụ:
- Khi nâng một vật có khối lượng m lên độ cao h so với mặt đất, ta tác dụng vào
vật một công A = m.g.h (g là gia tốc trọng lực). Kết quả là năng lượng (thế năng) của
hệ tăng một lượng là: ΔE = m.g.h.
- Nếu ta làm cho một vật tự do có khối lượng m chuyển động theo phương x với
một gia tốc cố định a, trong suốt quãng đường (x2 – x1) thì công tác dụng lên vật là: A = m.a. (x2 – x1).
- Công giãn nở: là công thực hiện kèm theo sự thay đổi thể tích của hệ: Agiãn nở = P.ΔV
(công thức này có tương đương với công thức * không?)
Công do hệ thực hiện cho bên ngoài được xác định bằng phương trình: δA = - Pe. dV (1.1)
Với Pe là áp suất ngoài, dV là biến thiên thể tích.
Đối với những biến đổi vô cùng chậm, có thể xem Pe = P với P là áp suất của hệ, do đó
công giãn nở thể tích sẽ là: δA = - P.dV và công giãn nở toàn phần: A = − 2 P.dV (1.2) 1
+ Quá trình đẳng tích dV = 0 → Av = 0 (1.3)
+ Quá trình đẳng áp P = const → Ap = - P.(V2 – V1) = - P.ΔV (1.4)
Đối với hệ đồng thể của khí lí tưởng, sự biến thiên thể tích ở 2 trạng thái (1) và (2) là
do sự biến thiên số mol ở 2 trạng thái đó nên: Ap = - Δn.R.T
+ Quá trình đẳng nhiệt (T = const) đối với 1 mol khí lí tưởng: 2 2dV V A 2
T = − P.dV = − RT V = −RTln V (1.5) 1 1 1
Ở T = const, thể tích của khí lí tưởng tỉ lệ với áp suất lOMoARcPSD|46342985 V P
AT = − RTln 2 = −RTln 1 (1.6) V P 1 2 Nhận xét:
+ Công A là sự truyền năng lượng vĩ mô có tính định hướng.
+ Nhiệt Q là sự truyền năng lượng vi mô không định
hướng. Quy ước dấu “ích kỉ”: (tại sao lại gọi là “ích kỉ”)
+ A > 0: Hệ nhận công.
+ A < 0: Hệ sinh công.
+ Q > 0: Hệ nhận nhiệt.
+ Q < 0: Hệ toả nhiệt. Chú ý:
+ Công và nhiệt là các hàm quá trình, phụ thuộc vào cách tiến hành quá trình.
+ Công và nhiệt có thứ nguyên giống năng lượng (A, Q ): J, calo, erg, eV,
atm.l. Mối quan hệ giữa các đơn vị năng lượng trên?
1.1.6.2. Nhiệt và nhiệt dung
*Nhiệt: Là năng lượng được xác định do sự chuyển dời hỗn loạn của các tiểu phân trong
hệ. Bản chất nhiệt là hình thái truyền năng lượng chứ không phải là năng lượng. Nhiệt là
một dạng năng lượng xuất hiện trong quá trình truyền động năng phân tử 1 vật nóng sang
1 vật lạnh. Vì nhiệt xuất hiện trong quá trình biến đổi trạng thái nên cũng như công,
nhiệt là một đại lượng đặc trưng cho quá trình.
Trong quá trình biến đổi đẳng áp, nhiệt trao đổi được gọi là nhiệt đẳng áp Qp.
Trong quá trình biến đổi đẳng tích, nhiệt trao đổi được gọi là nhiệt đẳng tích Qv.
*Nhiệt dung: là lượng nhiệt một vật hoặc một khối chất thu vào hay tỏa ra để tăng hoặc
giảm 1K hoặc 1oC. Nếu C là nhiệt lượng cần cung cấp cho 1 mol chất để đưa nhiệt độ của
1 mol chất đó tăng thêm 1 độ (K) thì C (J/mol.K) được gọi là nhiệt dung mol C của chất đó.
Tùy theo quá trình là đẳng áp hay đẳng tích, nhiệt dung mol được kí hiệu là Cp hay Cv
(đơn vị là J/mol.K). Cp hay Cv có thể được định nghĩa bằng biểu thức toán học:
+ Trường hợp nhiệt dung mol không biến thiên theo nhiệt độ. Qp Qv Cp = ΔT và Cv = ΔT (1.7)
Trong đó: Qp, Qv là nhiệt lượng trao đổi đẳng áp hay đẳng tích đối với 1 mol
chất; ΔT = T2 – T1 là biến thiên nhiệt độ. lOMoARcPSD|46342985
+ Trường hợp nhiệt dung mol biến thiên theo nhiệt độ. δQ δQ Cp = p và Cv = v (1.8) dT dT
Trong đó δQp, δQv là nhiệt lượng trao đổi vi phân và dT là biến thiên vi phân của nhiệt độ T.
Nói chung, nhiệt dung mol phụ thuộc rất ít vào áp suất nên thường không đổi tại
các áp suất khác nhau.
- Nhiệt dung mol của các chất khí lí tưởng:
Theo hệ thức Mayer: Cp – Cv = R (8,314 J/mol.K) (1.9)
+ Đối với khí đơn nguyên tử (He, Ne, Ar,…) chỉ có chuyển động tịnh tiến. 3 5 C C p v = R; Cp = R và γ = =1,66 2 2 C v
+ Đối với khí lưỡng phân tử (H2, N2,…) ở khoảng nhiệt độ từ 100K→ ≈ 1000K (chỉ
có chuyển động tịnh tiến và chuyển động quay): 5 7 γ = C C p v = R, Cp = R suy ra = 1,40 2 2 Cv
+ Đối với các chất khí đa nguyên tử (CO2, NH3, CH4,…) nhiệt dung mol phụ thuộc
vào nhiệt độ và sự phụ thuộc này đối với các chất khí khác nhau thì khác nhau (các giá
trị của γ thường nhỏ hơn 1,3).
- Đối với chất lỏng và chất rắn, nhiệt dung mol phụ thuộc rất ít vào nhiệt độ.
Sự phụ thuộc của nhiệt dung vào nhiệt độ thường được biểu thị dưới dạng đa thức: C = a + bT + cT2 + …
Ví dụ: đối với hơi nước: Cp = 36,8 – 7,9.10-3T + 9,2.10-6.T2
Nhiệt dung trao đổi và biến thiên nhiệt độ: Nếu có trao đổi nhiệt giữa hai hệ hay hai
vật thể thì theo nguyên lí bảo toàn năng lượng, nhiệt lượng giải phóng từ vật nóng bằng
nhiệt lượng mà vật lạnh hấp thụ.
+ Trong trường hợp nhiệt dung mol được coi là không đổi thì Qp và Qv với n mol
được tính theo hệ thức:
Qp = n.Cp.(T2 – T1) = n.Cp.ΔT ; Qv = n.Cv .(T2 – T1) = n.Cv.ΔT (1.10) lOMoARcPSD|46342985
+ Trong trường hợp cần chú ý đến sự biến thiên nhiệt dung mol theo nhiệt
độ. Ví dụ: Cp = a + bT + cT2 hay Cv = a + bT + cT2 T T 2 2 b c Thì Q n. C .dT = n. (a + bT + cT 2 ).dT = n(aT + 2 3 T p = T + T ) 1 p 2 2 3 T T T 1 1 T T 2 2 b c Q n. C .dT = n. (a + bT + cT 2).dT = n(aT + 2 3 T v = (1.11) T + T ) 1 2 v 2 3 T T T 1 1
1.1.7. Phương trình trạng thái
Là phương trình liên hệ các tham số trạng thái. Đối với hệ đơn giản ở trạng thái
cân bằng, phương trình trạng thái có dạng: f(P, V, T) = 0.
Phương trình trạng thái của một số hệ khí:
+ Đối với khí lý tưởng nguyên chất là phương trình Claperon – Mendeleep: P.V = n.R.T (1.12) n: số mol khí;
R: hằng số khí, R = 1,987 cal/mol.K = 0,082 atm.lit/mol.K = 8,314
J/mol.K; (tính các giá trị của R?) P: áp suất (atm); V: thể tích (lit); T: nhiệt độ (K).
+ Đối với khí thực, phương trình đơn giản nhất là phương trình Vandecvan: a (P + )(V − b) = nRT (1.13) V 2
Trong đó: a, b là những hằng số phụ thuộc vào bản chất của khí;
a gọi là áp suất nội gây ra do tương tác giữa các phân tử khí thực. V 2
1.2. Nguyên lí I của nhiệt động học 1.2.1. Nội dung
Đối với mọi hệ nhiệt động đều tồn tại một hàm trạng thái, được gọi là nội năng
U, mà trong quá trình biến đổi hệ từ trạng thái (1) sang trạng thái (2), biến thiên nội
năng ΔU bằng tổng nhiệt Q và công A hệ trao đổi với môi trường ngoài.
1.2.2. Các biểu thức định lượng
Quá trình vĩ mô: ΔU = Q + A (1.14)
Quá trình vi phân: dU = δQ + δA (1.15) lOMoARcPSD|46342985
Từ (1.13) → Q = ΔU – A hay “Khi hệ nhận nhiệt Q để thực hiện công A và gây
ra biến thiên nội năng U”.
Công A gồm 2 phần: Công giãn nở thể tích P.ΔV và công có ích A’ (công hóa
học): A = P.ΔV + A’ (Tất cả công khác công giãn nở thể tích mà hệ trao đổi với môi
trường ngoài như công chống lại các lực điện, lực từ, … thì được gọi là công có ích).
Trong nhiệt động lực học, người ta thường chỉ xét những hệ không chịu tác dụng
của điện trường, từ trường,…, khi đó công A chỉ là công giãn nở và biểu thức vi phân
của nguyên lí I có dạng: dU = δQ + δA = δQ - Pngoài.dV
1.2.2.1.Một số trường hợp đặc biệt
a. Biến đổi đoạn nhiệt: Q = 0 → ΔU = A
Đặc biệt với chu trình: ΔU = A = 0 hay “Một hệ chạy theo chu trình không trao
đổi nhiệt với bên ngoài không thể sinh công”.
b. Biến đổi đẳng tích: ΔV = 0. Nếu A chỉ là công giãn nở thì δA = - Pngoài.dV = 0
và ta có: dU = δQ → ΔU = δQ = Qv V=const
Như vậy: Qv bằng độ biến thiên của 1 hàm trạng thái (ΔU) và không phụ thuộc
vào đường biến đổi.
Chú ý: Qv không phải là hàm trạng thái nhưng có thể giữ vai trò của hàm trạng
thái trong điều kiện này.
c. Giãn nở vào chân không
Quá trình giãn nở của khí vào chân không diễn ra rất nhanh nên có thể coi là đoạn
nhiệt Q = 0. Mặt khác, A = 0. Do đó: ΔU = 0
Vậy khi giãn nở vào chân không, nội năng của hệ không thay
đổi. d. Hệ thực hiện chu trình
Khi hệ thực hiện chu trình ΔU = U2 – U1 = 0. Do đó Q + A = 0. Như vậy, khi hệ
nhận nhiệt thì nó sẽ sinh công và trở thành động cơ nhiệt.
e. Hệ cô lập: Hệ không thể trao đổi năng lượng với môi trường ngoài A = 0 và Q = 0
→ ΔU = 0 hay nội năng của 1 hệ cô lập là không đổi.
f. Nội năng của 1 khí lí tưởng:Uklt lOMoARcPSD|46342985
Người ta chứng minh được rằng nội năng của khí lí tưởng phụ thuộc vào nhiệt
độ: Uklt = U(T). Do đó trong 1 biến đổi đẳng nhiệt của khí lí tưởng, không kèm theo
phản ứng hóa học, biến đổi nội năng ΔU = 0.
1.2.2.2.Vận dụng nguyên lí I cho khí lí tưởng
Ta có dU = δQ + δA = δQ – P.dV
a. Với điều kiện đẳng tích: dV = 0 → dU = δQv = n.Cv.dT T2
Qv = ΔU = n.Cv .dT = n.Cv (T2 − T1) (1.16) T 1
(Nếu Cv không đổi trong khoảng nhiệt độ từ T1 đến T2)
b. Với điều kiện đẳng áp: dU + PdV = δQp hay d(U + PV) = δQp
Đặt U + PV = H với H là hàm Entanpi T2
Vậy: dH = δQp = Cp.dT hay ΔH = Qp = n.Cp .dT = n.Cp.(T2 – T1) (1.17) T1
(Nếu Cp không phụ thuộc nhiệt độ trong khoảng nhiệt độ từ T1 đến T2)
c. Với điều kiện đẳng nhiệt: U và H của khí lí tưởng chỉ phụ thuộc nhiệt độ, không
phụ thuộc vào thể tích cũng như áp suất, do đó: ΔUT = ΔHT = 0 (1.18)
d. Quan hệ giữa Qp và Qv của phản ứng hóa học diễn ra trong pha khí: Qp = Qv + Δn.R.T (1.19)
(Với Δn = số mol khí sản phẩm – số mol khí tham gia phản ứng)
Ví dụ 1: Tính biến thiên nội năng khi làm bay hơi 10 gam H2O ở 20oC ở áp suất không
đổi. Chấp nhận hơi nước như khí lý tưởng và bỏ qua thể tích nước lỏng. Nhiệt bay hơi
của nước ở 20oC = 2451,824 J/g. Giải
Thể tích của 10 gam hơi nước ở 20oC, 1 atm là: nRT 10.0,082.293 V= = = 13,35 (lít) P 18.1
Công giãn nở hơi nước: Ap = -P. V -P.Vh = -1.13,35.101,325 = -1352,689 (J)
Nhiệt cần cung cấp cho quá trình là: Q = 2451,824.10 = 24518,24 (J)
Biến thiên nội năng khi làm bay hơi 10 gam nước: lOMoARcPSD|46342985
U = Q + A = 24518,24 + (-1352,689) = 23165,551(J)
Ví dụ 2: Trong bình kín chứa 100 gam N2 ở 0oC; 1 atm. Biết Cv = 5 cal/mol.K. Hãy tính Q, U, A khi:
a. Giãn đẳng nhiệt tới thể tích 200 lít.
b. Tăng áp suất tới 1,5 atm khi Vconst.
c. Giãn đẳng áp tới thể tích gấp đôi. Giải
a. Giãn đẳng nhiệt tới thể tích 200 lít.
Quá trình đẳng nhiệt nên UT = 0 → Q + A = 0 V 100 mà AT = -nRT.ln 2 với V2 = 200 lít; V1 = .22,4 = 80 lít V 28 1
AT= - 100.8,314.273.ln 100 = - 7427,59 (J) 28 80 QT = 7427,59 (J)
b. Tăng áp suất tới 1,5 atm khi Vconst.
Quá trình đẳng tích nên AV = 0 U = Qv = n.CV.(T2 - T1) P P P .T 1,5.273
Ở điều kiện đẳng tích 1 = 2 → T = 2 1 = =409,5K T T 2 P 1 1 2 1 100 nên U = QV =
.5.4,18.(409,5 - 273) = 10188,75 (J)
c. Giãn đẳng áp tới thể tích gấp đôi QP = H = n.CP.(T2 - T1)
Vì V1 =V2 nên T = V2 .T1 = 273.2 = 546K T T 2 1 2 V1 CP=CV+R=5+2= 7 (cal.K-1.mol-1)
nên QP = 100 . 7. 4,18. (546 - 273) = 28528,5 (J) 28
AP = - P.(V2 - V1) = - 1.(160-80).101,325 = -8106 (J) lOMoARcPSD|46342985
= - nR(T2 - T1) = - 100 .8,314. (546 - 273) = - 8106,15 (J) 28
U = Q + A = 28528,5 - 8106,15 = 20422,35 (J)
1.2.3. Hàm Entanpi – Nhiệt hóa học
1.2.3.1. Hàm Entanpi Ta có Q = ΔU + PΔV
Quá trình đẳng tích: V = const → Qv = ΔUv hay “Nhiệt của quá trình đẳng
tích bằng biến thiên nội năng của quá trình đó”.
Quá trình đẳng áp: P = const → δQ = dU + dPV = d(U + PV) = dH → δQp = dH
→ Qp = ∆H = ΔU + PΔV hay “Nhiệt của quá trình đẳng áp bằng biến thiên entanpi của
quá trình đó”. ΔH: là nhiệt kèm theo quá trình đó hay gọi là hiệu ứng nhiệt của quá trình.
1.2.3.2. Nhiệt hóa học
Nhiệt hóa học nghiên cứu chủ yếu hiệu ứng nhiệt của các phản ứng hóa học hoặc
các quá trình vật lí →Nghiên cứu hiệu ứng nhiệt của các quá trình hóa học.
Khi hệ thực hiện công có ích (A’ ≠ 0):
Q = ΔU + PΔV + A’ → Q – A’ = ΔU + PΔV: Gọi là hiệu ứng nhiệt của
quá trình. Vậy, hiệu ứng nhiệt của quá trình bằng hiệu số của nhiệt (Q) trừ công có ích
(A’) mà hệ thực hiện trong quá trình đó.
- Xét với 1 số quá trình nhiệt động:
+ Quá trình đẳng tích: V = const →ΔV = 0→ (Q – A’)v = ΔUv. Vậy, đối với quá
trình đẳng tích, hiệu ứng nhiệt của quá trình bằng biến thiên nội năng của quá trình đó.
+ Quá trình đẳng áp: P = const → (Q – A’)p = ΔU + PΔV = ΔHp. Vậy, đối với quá
trình đẳng áp, hiệu ứng nhiệt của quá trình bằng biến thiên entanpi của quá trình đó.
- Xét với phản ứng hóa học: Về nguyên tắc, năng lượng của phản ứng hóa học
được biến đổi thành công có ích A’ = Ahóa = Ađiện (Apin)
+ Phản ứng hóa học xảy ra 1 cách thuận nghịch nhiệt động. A’ = Ahóa = Amax
Quá trình đẳng tích: V = const → (Q - Ahóa)v = ΔUv → (Q - Amax) = ΔUv
Quá trình đẳng áp: P = const → (Q - Ahóa)p = ΔHp. lOMoARcPSD|46342985
Kết luận: Hiệu ứng nhiệt của một phản ứng hóa học trong một quá trình bằng
nhiệt sinh ra trong quá trình đó trừ đi công mà quá trình đó thực hiện được.
Ví dụ: Ahóa = Ađiện = ε.F.E
Trong đó E: Là sức điện động của pin; F: là hằng số Farađay = 96500
C/mol; ε: điện tích ion
+ Phản ứng xảy ra không thuận nghịch nhiệt động. Trường hợp A’ =
0 Quá trình đẳng tích: Qv = ΔUv.
Quá trình đẳng áp: Qp = ΔHp.
Kết luận: Hiệu ứng nhiệt của phản ứng là nhiệt kèm theo phản ứng đó khi phản
ứng tiến hành không thuận nghịch nhiệt động sao cho công có ích không được thực
hiện. (A’ = 0) *Chú ý:
+ Hầu hết các phản ứng hóa học được thực hiện không phải trong pin điện nghĩa
là Apin = 0. Do đó chỉ còn Qv = ΔUv ; Qp = ΔHp. Vậy nói nhiệt tức là hiệu ứng nhiệt.
+ Thường các phản ứng xảy ra trong điều kiện áp suất khí quyển, tức đẳng áp
nên ΔHp được dùng rộng rãi hơn, viết gọn là ΔH.
+ Trong thực tế ta thường dùng QKTN để chỉ hiệu ứng nhiệt của một quá trình,
QTN để chỉ nhiệt của một quá trình.
+ Qui ước dấu của hiệu ứng nhiệt: Tỏa nhiệt: mang dấu (-); Thu nhiệt: mang dấu (+).
1.2.3.3. Phương trình nhiệt hóa học
Phương trình phản ứng có kèm theo số hiệu ứng nhiệt của phản ứng thì gọi là
phương trình nhiệt hóa học.
Ví dụ: C + O2 → CO2 ; ΔH = - 94052 cal/mol (ở 25oC, 1atm)
1.2.3.4. Định luật Hess
Là phương pháp gián tiếp xác định hiệu ứng nhiệt của các phản ứng hóa học.
Nội dung: Hiệu ứng nhiệt của một phản ứng hóa học ở áp suất không đổi không
phụ thuộc vào các giai đoạn trung gian của phản ứng mà chỉ phụ thuộc vào trạng thái
đầu và cuối của phản ứng. lOMoARcPSD|46342985 ΔH1
Chất phản ứng ΔH2 Sản phẩm ΔH3 Trạng thái đầu
Trạng thái cuối H1 = ∑Hcđ H2 = ∑Hsp
ΔH1 = ΔH2 = ΔH3 = ΔH = ∑Hsp - ∑Hcđ (1.20)
Nhận xét: Trong lịch sử, định luật Hess được phát biểu trước nguyên lí I, thực tế
có thể suy ra dễ dàng định luật này từ nguyên lí I. Vì ΔHp = ΔU + P.ΔV; ΔHp là biến
thiên của hàm trạng thái nên chỉ phụ thuộc vào trạng thái đầu và cuối chứ không phụ
thuộc vào cách tiến hành quá trình.
Hệ quả:
+ Nếu phản ứng thuận có hiệu ứng nhiệt ΔH thì phản ứng nghịch có hiệu
ứng nhiệt là – ΔH.
+ Hiệu ứng nhiệt của một quá trình vòng (chu trình) bằng không.
Ứng dụng của định luật Hess: Như vậy, dựa vào định luật Hess, người ta có thể
xác định ΔH của một quá trình đã cho nào đó bằng 2 cách sau:
+ Xác định ΔH của một quá trình khác có cùng trạng thái đầu và trạng thái
cuối. Quá trình thứ hai này thường là một quá trình nhiều giai đoạn, trong đó ΔH của
mỗi giai đoạn đều đã biết.
+ Thiết lập một quá trình vòng gồm nhiều giai đoạn trong đó một giai đoạn
là quá trình đang xét và ΔH của tất cả các giai đoạn còn lại đều đã biết. 3
Ví dụ 1: Xác định ∆H của phản ứng: S(r) + O2(k) → SO3(k) (1) ∆H1 = ? 2 Biết: S(r) + O2(k) → SO2(k)
(2) ∆H2 = - 1242,6 kJ/mol SO
(3) ∆H3 = - 410,8 kJ/mol 2(k) + 12 O2 → SO3(k)
Đáp số: -1653,4 kJ/mol
Ví dụ 2: Xác định ∆H của phản ứng: C(r) + 1 O2(k) → CO(k) (1) ∆H1 = ? 2 lOMoARcPSD|46342985 Biết: C(r) + O2(k) → CO2(k)
(2) ∆H2 = - 399,1 kJ/mol 1 CO(k) + O2(k) → CO2(k)
(3) ∆H3 = - 282,8 kJ/mol 2
Đáp số: -116,3 kJ/mol
1.2.3.5. Tính hiệu ứng nhiệt của phản ứng hóa học dựa vào sinh nhiệt
Định nghĩa: Sinh nhiệt hay nhiệt hình thành của một hợp chất là hiệu ứng nhiệt
của phản ứng hình thành 1 mol hợp chất đó từ các đơn chất tương ứng ở trạng thái bền
vững nhất của nguyên tố tự do tạo nên hợp chất từ điều kiện đã cho về nhiệt độ và áp suất.
Kí hiệu nhiệt hình thành chuẩn của 1 hợp chất là ΔHht; ở điều kiện chuẩn về nhiệt
động lực học (25oC hay 298K và 1atm) thì kí hiệu: ΔHo . ht,298 Đơn vị: kJ/mol Chú ý: ΔHo
của đơn chất bền = 0 ht,298
Ứng dụng: Tính hiệu ứng nhiệt ΔH của phản ứng hóa học. Hiệu ứng nhiệt của
một phản ứng hóa học bằng tổng sinh nhiệt của các sản phẩm trừ đi tổng sinh nhiệt của
các chất phản ứng.
Xét phản ứng: aA + bB → cC + dD ΔH o = H o − H o
= c. H o + d. H o
− a. H o − b. Ho pu ht,sp ht,tg ht,C ht,D ht,A ht,B (1.21)
Ví dụ: Tính hiệu ứng nhiệt của phản ứng: CaO(r) + CO2(k) → CaCO3(r) o
Cho ΔH ht,298 (kJ/mol): - 636 - 394 - 1207
Đáp số: -177 kJ
Entanpi sinh nguyên tử: Khi một mol hợp chất khí được tạo ra từ các nguyên tử
thì độ biến thiên entanpi của quá trình này được gọi là entanpi sinh nguyên tử. Chỉ có
thể tính được đại lượng này. Có thể dùng entanpi sinh nguyên tử để tính năng lượng
của các liên kết hóa học. lOMoARcPSD|46342985
Entanpi sinh của chất tan: Entanpi sinh của chất tan là hiệu ứng nhiệt của quá
trình hình thành một mol chất ở trạng thái tan từ các đơn chất ở vào trạng thái bền vững
nhất trong các điều kiện đã cho về nhiệt độ và áp suất.
Entanpi sinh của ion: Entanpi sinh của ion trong dung dịch nước là biến thiên
entanpi của phản ứng hình thành 1 mol ion bị hiđrat hóa từ các đơn chất.
1.2.3.6.Tính hiệu ứng nhiệt của phản ứng hóa học dựa vào thiêu nhiệt
Định nghĩa: Thiêu nhiệt hay nhiệt cháy là hiệu ứng nhiệt của phản ứng oxi hóa
một chất bằng oxi phân tử (O2) tới lúc thu được một oxit cao nhất của nguyên tố tương ứng.
Entanpi thiêu nhiệt của các chất được xác định bằng thực nghiệm và thường được ΔH
quy về các điều kiện chuẩn: Entanpi thiêu nhiệt tiêu chuẩn o tn,298 ΔH = ΔH Ví dụ: C o o
than chì + O2 → CO2 ; ΔH otn,298, C = 298,pu ht,298, CO 2 ΔH
CH4(k) + 2O2 → CO2(k) + 2H2O(l) ; o = - 889,9 kJ/mol tn,298,CH 4
Ứng dụng: Tính hiệu ứng nhiệt ΔH của phản ứng hóa học. Hiệu ứng nhiệt của
một phản ứng hóa học bằng tổng thiêu nhiệt của các chất đầu trừ đi tổng thiêu nhiệt của
các sản phẩm.
Xét phản ứng: aA + bB → cC + dD ΔH o = H o − H o
= a. H o + b. H o − c. H o − d. Ho pu tn,tg tn,sp tn,A tn,B tn,C tn,D (1.22)
Ví dụ: Xác định hiệu ứng nhiệt của phản ứng:
C2H5OH(l) + CH3COOH(l) → CH3COOC2H5(l) + H2O(l)
Biết thiêu nhiệt của các chất như sau:
C2H5OH(l) : ΔHotn,298 = - 1366,9 kJ/mol
CH3COOH(l): ΔHotn,298 = - 871,1 kJ/mol
CH3COOC2H5(l): ΔHotn,298 = - 2284,0 kJ/mol
Đáp số: 46 kJ/mol lOMoARcPSD|46342985
1.2.3.7. Sự phụ thuộc của hiệu ứng nhiệt phản ứng vào nhiệt độ
Nhiệt của phản ứng hóa học xác định theo công thức tính dựa vào sinh nhiệt,
thiêu nhiệt là nhiệt ở nhiệt độ không đổi. Khi nhiệt độ thay đổi thì nhiệt của phản ứng cũng thay đổi theo.
Sự phụ thuộc này được biểu thị bằng định luật Kirchhoff như sau: Với giả thiết, ta
đã biết nhiệt phản ứng ở nhiệt độ T1, trong mục này ta xét cách xác định nhiệt phản ứng ở nhiệt độ T2.
Giả thiết ta có phản ứng tổng quát: aA + bB → cC + dD ở nhiệt độ T1 nhiệt phản
ứng (đẳng áp) là ΔH1. Trước hết ta đưa các chất đầu A và B lên nhiệt độ T2, cho phản
ứng xảy ra ở nhiệt độ T2 (gọi ΔH2 là nhiệt phản ứng ở nhiệt dộ này) và sau đó ta lại đưa
các sản phẩm C và D về nhiệt độ T1.
Gọi qA, qB lần lượt là nhiệt lượng cần thiết để đưa a mol chất A và b mol chất B
từ nhiệt độ T1 lên nhiệt độ T2.
Gọi qC, qD lần lượt là nhiệt lượng mà c mol chất C, d mol chất D tỏa ra khi được
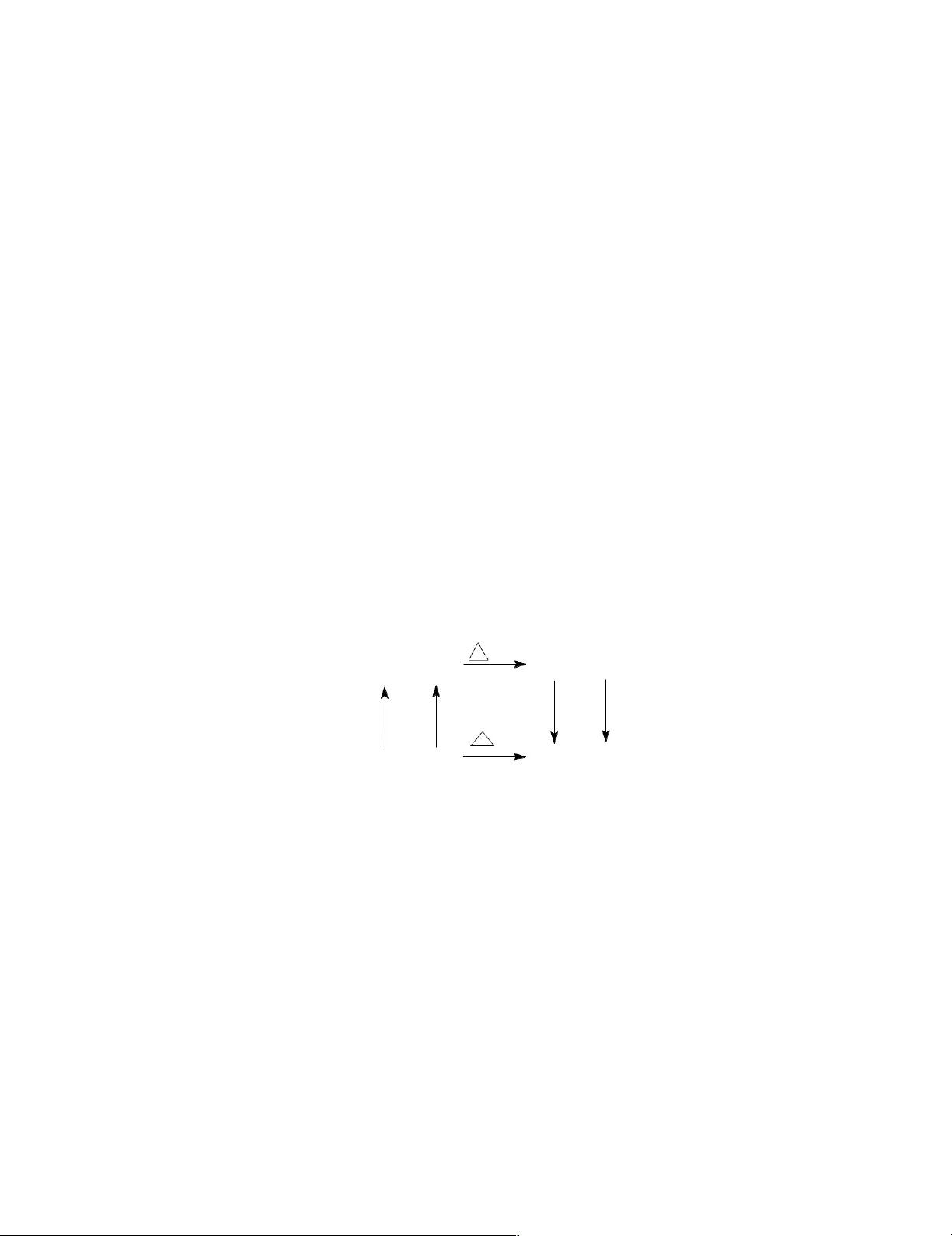
đưa từ nhiệt độ T2 xuống nhiệt độ T1. H T 2 aA + bB 2 cC + dD q q q A qB C D H T1 aA + bB 1 cC + dD (I) (II)
Coi (I) là trạng thái đầu, (II) là trạng thái cuối cuối, từ định luật Hess ta có:
ΔH1 = qA + qB + ΔH2 + qC + qD = ΔH2 + qA +qB + qC + qD
→ ΔH2 = ΔH1 - qA - qB - qC -qD (*)
+ Xét trường hợp mà nhiệt dung các chất được coi là không
đổi. Áp dụng công thức tính nhiệt lượng qA, qB, qC, qD.
qC = c.Cp(C).(T1 – T2) = - c.Cp(C).(T2 – T1);
qD = d.Cp(D).(T1 – T2) = - d.Cp(D).(T2 – T1).
qA= a.Cp(A).(T2 – T1);
qB = b.Cp(B).(T2 – T1);
Thay vào (*), ta được:
ΔH2 = ΔH1 + c.Cp(C).(T2 – T1) + d.Cp(D).(T2 – T1) - a.Cp(A).(T2 – T1) - b.Cp(B).(T2 – T1) lOMoARcPSD|46342985
→ ΔH2 = ΔH1 + [c.Cp(C) + d.Cp(D) – a.Cp(A) – b.Cp(B)].(T2 – T1)
ΔH2 = ΔH1 + ΔCp.(T2 – T1)
Với ΔCp = [cCp(C) + dCp(D)] - [aCp(A) + bCp(B)]
+ Xét trường hợp mà nhiệt dung các chất biến thiên theo nhiệt độ (Cp = a + bT + cT2) T T1 T2 2 Ta có q − c.C A = a.C q p(C)dT p(A) dT ; C = c.C p(C)dT = T T 1 2 T1 T T1 T2 2 q − d.C B = b.C ; q p(D)dT p(B)dT D = d.C p(D)dT = T T T 1 1 2
Thay vào (*), ta được: T ΔH2 = ΔH1 + 2 c.Cp(C) + d.C − b.C dT p(D) − a.Cp(A) (1.23) T p(B) 1 T2 Hay
ΔH2 = ΔH1 + ΔCpdT (1.24 ) T1
Ví dụ: Cho hiệu ứng nhiệt của CaCO3 → CaO + CO2 ở 727oC là QP = 177900,8 (J).
Tính QP của phản ứng ở 1227oC. Biết:
CP(CaO) = 49,63 + 4,52.10-3T (J/mol.K)
CP(CO2) = 44,14 + 9,04.10-3T (J/mol.K)
CP(CaCO3) = 104,5 + 21,92.10-3T (J/mol.K) Giải:
Ta có: ∆CP, phản ứng = CP(CaO) + CP(CO2) – CP(CaCO3) = -10,73 – 8,36. 10-3T
→ QP, 1500K = QP, 1000K -10,73. (1500 - 1000) – 4,18. 10-3 . (15002 – 10002 ) = 167310,8J
1.2.3.8. Nhiệt chuyển pha
Quá trình chuyển pha là quá trình trong đó một chất chuyển từ một trạng thái
tập hợp này sang một tập hợp khác. Các quá trình chuyển pha thường gặp là: Sự thăng
hoa, sự bay hơi, sự ngưng tụ, sự nóng chảy, sự hóa rắn, sự chuyển dạng thù hình,...
Hiệu ứng nhiệt kèm theo quá trình chuyển pha là nhiệt chuyển pha.
Ví dụ: Pđỏ → Ptrắng ; ∆H = 15,5 J/mol
H2O(r) → H2O(l) ; ∆H = 44,0 kJ/mol
Trong nhiều trường hợp, có thể xác định nhiệt chuyển pha bằng thực nghiệm. Tuy
nhiên, cũng có trường hợp phải tìm bằng cách gián tiếp trên cơ sở áp dụng định luật Hess. lOMoARcPSD|46342985
Ví dụ: Xác định hiệu ứng nhiệt của quá trình:
C(graphit) → C(kim cương) (1) ∆H1 = ?
Khi biết: C(gr) + O2(k) → CO2(k) (2) ∆H2 = - 393,5 kJ/mol
C(kim cương) + O2(k) → CO2(k) (3) ∆H3 = - 395,4 kJ/mol
Đáp số: 1,9 kJ/mol
1.2.3.9. Nhiệt phân li
Định nghĩa: Nhiệt phân li của một chất là năng lượng cần thiết để phân hủy 1 mol
phân tử của chất đó (ở thể khí) thành các nguyên tử ở thể khí (Nhiệt phân li còn được gọi
là nhiệt nguyên tử hóa). Ví dụ: H2(k) → 2H(k) ΔH = 435,9 kJ/mol O2(k) → 2O(k) ΔH = 489,5 kJ/mol CH4(k) → C(k) + 4H(k) ΔH = 1665,2 kJ/mol
Nhiệt phân li của các phân tử hai nguyên tử thường được xác định bằng phương pháp quang phổ.
1.2.3.10. Năng lượng liên kết - Quan hệ giữa năng lượng liên kết với nhiệt phản ứng
a. Năng lượng liên kết hóa học
Một cách chính xác, năng lượng liên kết phải được hiểu là năng lượng được
giải phóng trong quá trình hình thành các liên kết. Theo qui ước, nó mang một trị số âm.
Ngược lại, năng lượng cần cung cấp để phá vỡ liên kết được gọi là năng lượng phân li
liên kết. Năng lượng phân li liên kết có giá trị tuyệt đối bằng giá trị tuyệt đối của năng
lượng liên kết nhưng ngược dấu. Tuy nhiên, ít lâu nay người ta quen biểu thị năng
lượng liên kết bằng các trị số dương. Điều đó có nghĩa là, khi nói năng lượng liên kết
người ta hiểu đó là năng lượng phân li liên kết.
Người ta xác định một giá trị trung bình về năng lượng liên kết cho mỗi loại liên
kết và áp dụng chung cho các phân tử.
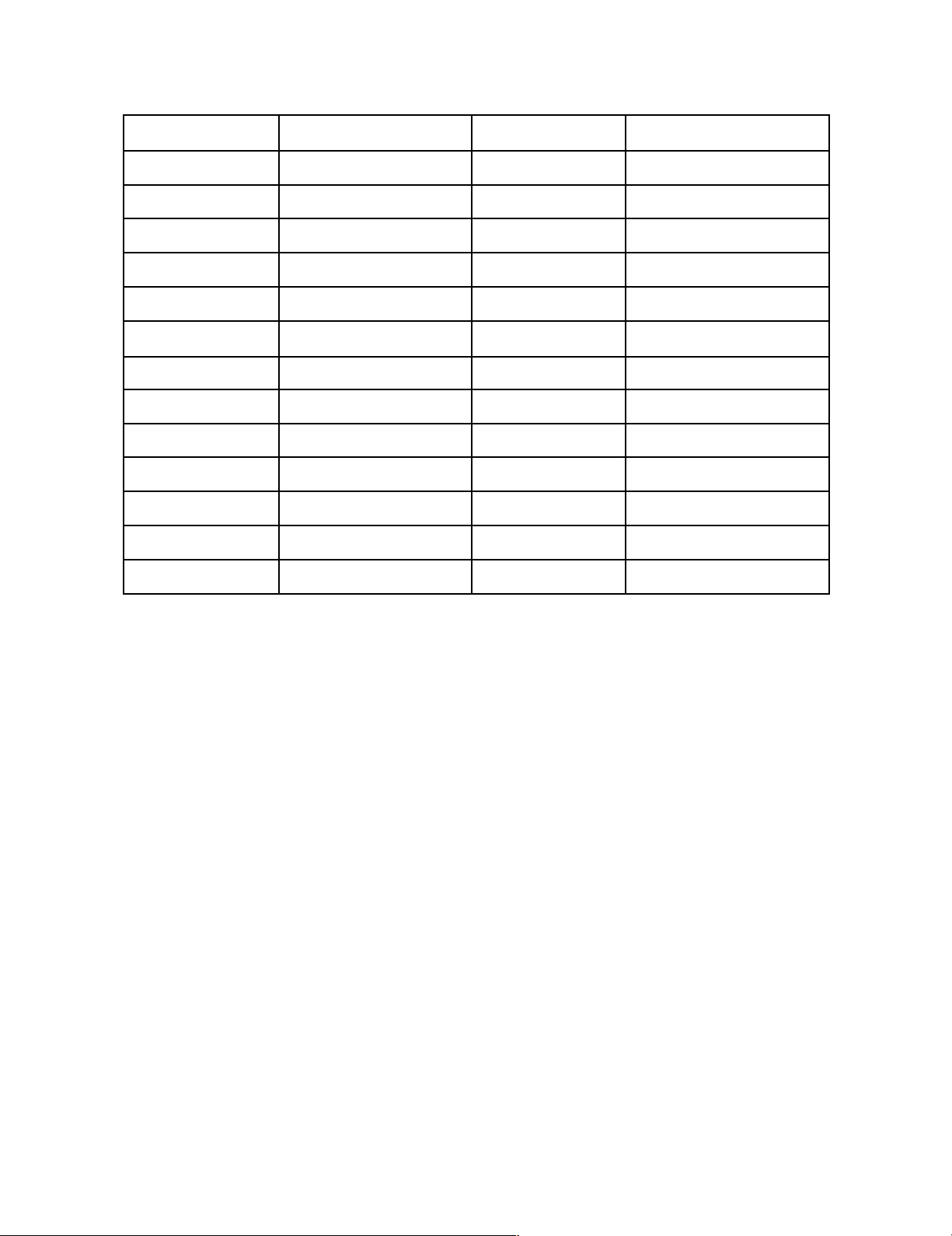
Bảng năng lượng liên kết của một số liên kết thường gặp
(Đơn vị kJ/mol xác định ở P = 1atm, T = 298K) Liên kết A - B
Năng lượng liên kết Liên kết A - B
Năng lượng liên kết C – H 418,4 H – H 432,0 lOMoARcPSD|46342985 C – C 343,4 H – F 562,6 C = C 595,7 H – Cl 431,4 C ≡ C 811,7 H – Br 365,7 C – O 351,1 H – I 298,4 C = O 761,5 O – H 462,9 C – N 292,9 O = O 493,7 C = N 814,4 N – H 389,1 C ≡ N 890,3 N – N 159,0 C – F 490,3 N = N 418,4 C – Cl 328,5 N ≡ N 945,5 C – Br 276,1 F – F 162,9 C – I 238,5 Cl – Cl 242,4 C – S 295,1 I – I 150,9 C = S 476,6 Br – Br 192,7
b. Quan hệ giữa năng lượng liên kết và nhiệt phản ứng
Xác định nhiệt phản ứng từ năng lượng liên kết: Hiệu ứng nhiệt của phản ứng
bằng hiệu giữa tổng năng lượng liên kết trong các chất tham gia phản ứng và tổng năng
lượng liên kết trong các chất sản phẩm. o H (1.25)
pu = E tg − Esp
Xác định năng lượng liên kết từ nhiệt phản ứng: Cùng nguyên tắc trên, nếu nhiệt
phản ứng đã biết, ta có thể xác định một trong các năng lượng liên kết được giả thiết là chưa biết.
Ví dụ 1: Xét phản ứng: CH4 + Cl2 → CH3Cl + HCl
ΔHpư = (4EC-H + ECl-Cl) – (3EC-H + EC-Cl + EH-Cl)
Ví dụ 2: Xét phản ứng: C2H5OH(k) + 3O2(k) → 2CO2(k) + 3H2O(h) ΔHpư = ?