Chủ đề 2: Tính thể tích một số hình khối trong thực tiễn | Giáo án Toán 11 Cánh diều

HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
CHỦ ĐỀ 2: TÍNH THỂ TÍCH MỘT HÌNH KHỐI TRONG THỰC TIỄN
Thời gian thực hiện: (3 tiết) I. Mục tiêu 1. Kiến thức:
Công thức thể tích một số khối đã học: Khối lăng trụ, khối chóp, khối chóp cụt 2. Về năng lực: Năng lực YCCĐ
NĂNG LỰC ĐẶC THÙ
+ Vẽ hình không gian của bài toán thực tiễn. Năng lực tư duy
+ Giải thích được cách thiết lập mối liên hệ tính thể tích và lập luận toán học
trong các bài toán thực tiễn. Năng lực giải
+ Nhận biết, phát hiện được các bài toán thực tiễn liên quan
quyết vấn đề toán học đến tính tể tích Năng lực mô hình
+Sử dụng kiến thức thể tích, vẽ hình khối bằng phần mềm để hóa toán học.
giải quyết các bài toán thực tiễn có liên quan. NĂNG LỰC CHUNG
+Tự tìm tòi, phát hiện được các bài toán thực tiễn liên quan Năng lực tự chủ đến tính thể tích. và tự học
+Tự giải quyết các bài tập phần luyện tập và bài tập về nhà. Năng lực giao
+Tương tác tích cực của các thành viên trong nhóm khi thực tiếp và hợp tác
hiện nhiệm vụ hợp tác. 3. Về phẩm chất:
+ Tích cực, tự giác và nghiệm túc thực hiện nhiệm vụ được giao. Trách nhiệm
+ Có ý thức hỗ trợ, hợp tác với các thành viên trong nhóm
để hoàn thành nhiệm vụ.
+ Có ý kiến tham gia, hợp tác trên cơ sở xây dựng nhóm
đoàn kết cùng thực hiện nhiệm vụ. Nhân ái
+ Có ý thức tôn trọng ý kiến của các thành viên trong nhóm khi hợp tác.
II. Thiết bị dạy học và học liệu:
+ Máy tính, Máy chiếu, phiếu học tập, giấy màu, giấy A0, bút lông, kéo….
III. Tiến trình dạy học: Tiết 1:
1. HOẠT ĐỘNG 1: XÁC ĐỊNH VẤN ĐỀ
* HĐ 1.1: a) Mục tiêu:
+Tạo sự tò mò, gây hứng thú cho học sinh khi tìm hiểu về một số bài toán có nội dung thực tiễn.
+ Giúp học sinh biết được một số bài toán có nội dung thực tiễn liên quan đến tính diện tích
hình khối trong thực tiễn b) Nội dung:
Câu 1: Khối Rubik (H1) có các ô vuông tô màu kích thước 1cm. Hỏi thể tích của khối Rubik bằng bao nhiêu?
Câu 2: Cần bao nhiêu khối đất, đá để đắp được khối kim tự tháp là hình chóp tứ giác đều có độ dài
cạnh đáy là 230m , chiều cao là 147m ( H2).
Câu 3: Có thể xếp hết hay không các vali ở hình 3 vào khoang hành lý ôtô ở hình 4? Hình 1 Hình 2 Hình 3 Hình 4
Như vậy, thể tích của một hình được tính như thế nào? c) Sản phẩm: Câu trả lời của HS
Học sinh quan sát hình vẽ, đọc các câu hỏi nhưng chưa trả lời được các câu hỏi.
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ : GV chiếu các hình vẽ và nêu câu hỏi
*) Thực hiện: HS suy nghĩ độc lập
*) Đánh giá, nhận xét, tổng hợp:
- Từ phần trả lời của HS, GV dẫn dắt vào bài mới.
* HĐ 1.2: Dẫn dắt bài mới
a. Mục tiêu: HS biết cách quy các hình ảnh thực tế vào toán học b. Nội dung:
+ Các hình ảnh dưới đây gợi cho em nghĩ đến những vấn đề nào trong thực tiễn cuộc sống? Hãy đưa
ra các bài toán thực tế liên quan đến các hình ảnh này?
Hình 101 là hình chụp đền Kukulcan, là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza,
Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII . Phần thân của
đền, không bao gồm ngôi đền nằm phía trên, có dạng một khối chóp cụt tứ giác đều
(không tính cầu thang và coi các mặt bên là phẳng) với độ dài đáy dưới là 55,3 m , chiều
cao là 24 m , góc giữa cạnh bên và mặt phẳng đáy là khoảng 47°.
Tính thể tích phần thân ngôi đền có dạng khối chóp cụt tứ giác đều đó theo đơn vị mét khối
(làm tròn kết quả đến hàng phần trăm
+ Nêu cách giải quyết các bài toán thực tiễn trên?
+ Nêu các bài toán thực tiễn khác tương tự?
+ Các bài toán thực tiễn trên liên quan đến kiến thức toán học nào? c) Sản phẩm: + học sinh vẽ hình
+Học sinh thực hành giải
d) Tổ chức thực hiện: PP đàm thoại – gợi mở, đánh giá bằng phương pháp quan sát, vấn đáp
Bước 1: Giao nhiệm vụ:
+ Học sinh quan sát hình ảnh và trả lời câu hỏi.
+ Học sinh lấy các ví dụ về bài toán có liên quan đến nội dung thực tiễn.
Bước 2: Thực hiện nhiệm vụ:
+ Học sinh quan sát các hình ảnh, lấy các ví dụ về bài toán thực tiễn.
+ Các nhóm trình bày các ví dụ của nhóm mình
Bước 3: Báo cáo, thảo luận:
+ Học sinh các nhóm lấy ví dụ về một số bài toán có liên quan đến nội dung thực tiễn.
Bước 4: Kết luận, nhận định:
Giáo viên đặt vấn đề: Bài học hôm nay thầy trò chúng ta thực hành một số bài toán về vận
dung kiến thức về thể tích làm một số bài toán có liên quan đến nội dung thực tiễn.
2. HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC a) Mục tiêu:
+ Học sinh củng cố các nội dung cơ bản về tính thể tích b) Nội dung:
+ Học sinh các nhóm chuẩn bị kiến thức cơ bản về thể tích c) Sản phẩm:
+ Học sinh hệ thống được kiến thức cơ bản về côn thức tính thể tích
d) Tổ chức thực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng
phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Giao nhiệm vụ:
+ Giáo viên cho các nhóm kiểm tra lại bài tập về nhà của nhóm mình.
+ Yêu cầu mỗi nhóm bổ sung những nội dung bài tập còn thiếu của nhóm mình.
Bước 2: Thực hiện nhiệm vụ:
+ Các nhóm ghi ra tờ giấy A0 và treo lên bảng
Bước 3: Báo cáo, thảo luận:
+ Nhóm trưởng trình bày sản phẩm chuẩn bị về nhà của nhóm mình.
+ Các nhóm thảo luận, nhận xét bài của nhóm khác
Bước 4: Kết luận, nhận định:
+ Giáo viên yêu cầu các nhóm nhận xét kết quả của các nhóm khác.
+ Giáo viên nhận xét kết quả của từng nhóm
+ Kết luận: Kiến thức cơ bản cần nắm được để phục vụ bài TIẾT 2:
Hoạt động 3: Luyện tập Trải nghiệm vẽ hình bằng phần mềm GeoGebra. a) Mục tiêu:
+Tạo sự hứng thú cho học sinh, giúp các em xác định được nội dung học tập.
+ Giúp học sinh nhớ lại kiến thức về vẽ hình, tính thể tích .
b) Nội dung: Thực hành tạo mô hình sử dụng công nghệ thực tế ảo tăng cường trên GeoGebra.
Ví dụ 1: Tạo mô hình tứ diện.
Bước 1: Vào phần mềm GeoGebra 3D Calculator. Giao diện của phần mềm tương tự như sử dụng trên máy tính.
Bước 2: Sử dụng công cụ
và tạo một tam giác bất kỳ trong mặt phẳng.
Bước 3: Sử dụng công cụ
và chọn vào một tam giác vừa tạo, sau đó nhập độ
cao bắt kỳ ( Hình 3), ta được tứ diện như Hình 4.
Bước 4: Nhấn vào biểu tượng AR ở góc phải giao diện. Sau đó chọn vị trí đặt tứ diện trên
màn hình thiết bị và di chuyển xung quanh để quan sát tứ diện từ các hướng khác nhau (
Lưu ý vẫn hướng camera của thiết bị vào vị trí đặt tứ diện ban đầu) ( Hình 5 và Hình 6).
c) Sản phẩm: Học sinh hoàn thiện ba bài toán trên.
d) Tổ chức thực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng
phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Giao nhiệm vụ:
Giáo viên chia lớp thành 8 nhóm
Giáo viên phát cho mỗi nhóm một phiếu học tập có nội dung một bài toán ( Sau đó giáo viên
trình chiếu yêu cầu với từng nhóm)
Bước 2: Thực hiện nhiệm vụ:
Các nhóm làm bài trên máy tính có cài GeoGebra.
Bước 3: Báo cáo, thảo luận:
Mỗi nhóm cử nhóm trưởng trình bày sản phẩn trước lớp
Bước 4: Kết luận, nhận định:
Giáo viên nhận xét: ý thức làm bài của từng nhóm, thời gian hoàn thành bài và sản
phẩm của từng nhóm, kỹ năng trình bày của nhóm trưởng. TIẾT 3
Hoạt động 4: Vận dụng.
Hoạt động 4.1: Vận dụng 1. Một số bài toán thực tiễn về tính thể tích a)Mục tiêu:
+Học sinh vận dụng kiến thức tính thể vào giải các bài toán có nội dung liên quan thực tiễn. b) Nội dung:
Mỗi nhóm học sinh tiến hành lập kế hoạch thực hiện nhiệm vụ. Cụ thể như sau:
- Sưu tầm các sản phẩm cùng loại nhưng có hình dạng bao bì khác nhau (như: có dạng
khối hộp chữ nhật, khối trụ, khối chóp, khối chóp cụt đều, ...). Chẳng hạn, sản phẩm sữa
đặc với khối lượng tịnh 380 g có hai dạng bao bì khác nhau như ở Hình 3. c) Sản phẩm:
+ Các nhóm hoàn thành bài toán giáo viên giao vào vở và vào bảng phụ
d) Tổ chức thực hiện: PP dạy học theo nhóm, PP đàm thoại – gợi mở, đánh giá bằng
phương pháp quan sát, vấn đáp, sản phẩm của nhóm
Bước 1: Giao nhiệm vụ:
Giáo viên thực hiện những nhiệm vụ sau:
- Chia lớp thành những nhóm học sinh;
- Giao nhiệm vụ các nhóm tính toán chi phí vật liệu làm bao bì chứa cùng một loại sản
phẩm và lựa chọn kiểu bao bì có chi phí thấp nhất.
Bước 2: Thực hiện nhiệm vụ:
+Mỗi nhóm học sinh trao đổi, thảo luận để xác định rõ: Nhiệm vụ của nhóm và thời gian
hoàn thành nhiệm vụ đó; nhiệm vụ của từng thành viên trong nhóm và thời gian hoàn thành nhiệm vụ đó.
Bước 3: Báo cáo, thảo luận:
+ Các nhóm cử thành viên trình bày sản phẩm của nhóm
+ Các nhóm khác theo dõi và thảo luận + Bổ sung cho nhóm khác
Bước 4: Kết luận, nhận định:
+ Giáo viên nhận xét các nhóm: Quan sát hoạt động của các nhóm và đánh giá thông qua bảng kiểm. Bảng kiểm
- Báo cáo tìm hiểu về giá thành sản phẩm bao bì, tính toán chi phí bao bì theo mẫu sau: Chi phí bao bì tính vào giá bán sản phẩm (nghìn đồng/ 3 cm nếu Hình dạng Chất liệu Giá thành sản phẩm STT bao bì sản phẩm tính theo dung bao bì bao bì (nghìn đồng/ m! )
tích hoặc nghìn đồng/g
nếu sản phẩm tính theo khối lượng) 1 2 3
+ Dựa trên báo cáo, mỗi nhóm lựa chọn kiểu bao bì có chi phí sản xuất thấp nhất cho loại sản phẩm mà nhóm đã chọn.
+ Giáo viên nhận xét sản phẩm của từng nhóm
+ Bổ sung những nội dung còn thiếu sót để hoàn thiện bài cho từng nhóm
+ Kết luận và cho điểm động viên các nhóm
Hoạt động 4.2: Một số bài toán thực tiễn về tính thể tích a)Mục tiêu:
+Học sinh vận dụng kiến thức về hàm số bậc hai vào giải các bài toán có nội dung liên quan thực tiễn. b) Nội dung:
+ Học sinh làm các bài toán về thể tích có nội dung liên quan thực tiễn.
Vận dụng 1: Kim tự tháp Kê-ốp ở Ai Cập được xây
dựng vào khoảng 2500 năm trước Công nguyên.
Kim tự tháp này là một khối chóp tứ giác đều có
chiều cao 147m, cạnh đáy dài 230m. Thể tích của nó bằng A. 3 2592100 m . B. 3 3888150 m . C. 3 7776300 m . D. 3 2952100 m .
Vận dụng 2: Một chiếc bút chì có dạng khối lăng trụ lục giác đều có cạnh đáy 3 mm và chiều cao
200 mm . Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối
trụ có chiều cao bằng chiều cao của bút và đáy là hình tròn có bán kính 1 mm . Giả định 3 1 m gỗ có giá a , 3
1 m than chì có giá 8a (triệu đồng). Khi đó giá nguyên vật liệu làm một chiếc bút chì như
trên gần nhất với kết quả nào dưới đây?
A. 9,7.a (đồng). B. 97,03.a (đồng). C. 90,07.a (đồng). D. 9,07.a (đồng). c) Sản phẩm:
Sản phẩm trình bày của 4 nhóm học sinh
d) Tổ chức thực hiện:
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập 2
Chuyển giao
HS: Nhận nhiệm vụ,
Thực hiện
Các nhóm HS thực hiện tìm tòi, nghiên cứu và làm bài ở nhà.
HS cử đại diện nhóm trình bày sản phẩm vào tiết cuối của bài
Báo cáo thảo luận Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các vấn đề.
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi nhận
và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
Đánh giá, nhận xét, - Chốt kiến thức tổng thể trong bài học.
tổng hợp
- Hướng dẫn HS về nhà tự xây dựng tổng quan kiến thức đã học bằng sơ đồ tư duy.
Bước 4: Kết luận, nhận định:
+ Giáo viên nhận xét hoạt động của học sinh: trình bày có khoa học không? Học sinh thuyết
trình có tốt không? Học sinh giải đáp thắc mắc câu hỏi của các bạn khác có hợp lí không? Có lỗi sai
về kiến thức không?
+ Giáo viên nhận xét sản phẩm của từng nhóm
+ Bổ sung những nội dung còn thiếu sót để hoàn thiện bài cho từng nhóm
+ Kết luận và cho điểm động viên các nhóm.
*Hướng dẫn làm bài
+ Vận dụng 1
Ta có diện tích đáy Kim tự tháp là 2 2
S = 230 = 54900m . 1 1
Thể tích của Kim tự tháp là: 3
V = Sh = .52900.147 = 2592100m . 3 3 Chọn D.
+ Vận dụng 2 æ ö - 3
Ta có diện tích của khối lăng trụ lục giác đều S = 6.çç(3.10 )2 3 2 . ÷(m ) 4 ÷ è ø æ ö - 3
Thể tích của chiếc bút chì V = S.h = 6.çç(3.10 )2 3 3 - 7 - 3 .
÷.200.10 = 27 3.10 (m ) 4 ÷ è ø
Thể tích của phần lõi của bút chì 2 3 - 2 3 - 7 - 3
V = p r h = p (10 ) .200.10 = 2p.10 (m ) 1
Thể tích phần thân bút chì là 7 - 3
V =V -V = (27 3 - 2p ).10 (m ) 2 1
Giá nguyên liệu để làm một chiếc bút chì như trên là 6 6 7 - 6 7 - 6 V . . a 10 +V .8 .
a 10 = (27 3 - 2p ).10 . . a 10 + 2p.10 .8 .
a 10 = (2,7 3 +1,4p)a » 9,07.a (đồng) 2 1 Chọn B. HƯỚNG DẪN VỀ NHÀ
1.Tìm một số bài toán có nội dung thực tiễn liên quan đến tính thể tích rồi tìm lời giải.
2. Làm một số bài tập sau:
Bài 1: Cho một tấm nhôm hình vuông cạnh 12cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như
hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x = 6. B. x = 3. C. x = 2. D. x = 4.
Bài 2: Trong đợt chào mừng ngày 26 / 03 / 2018 , trường THPT Nguyễn Du có tổ chức cho học sinh
các lớp tham quan dã ngoại ngoài trời, trong số đó có lớp 12C1. Để có thể có chỗ nghỉ ngơi trong
quá trình tham quan dã ngoại, lớp 12C1 đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ
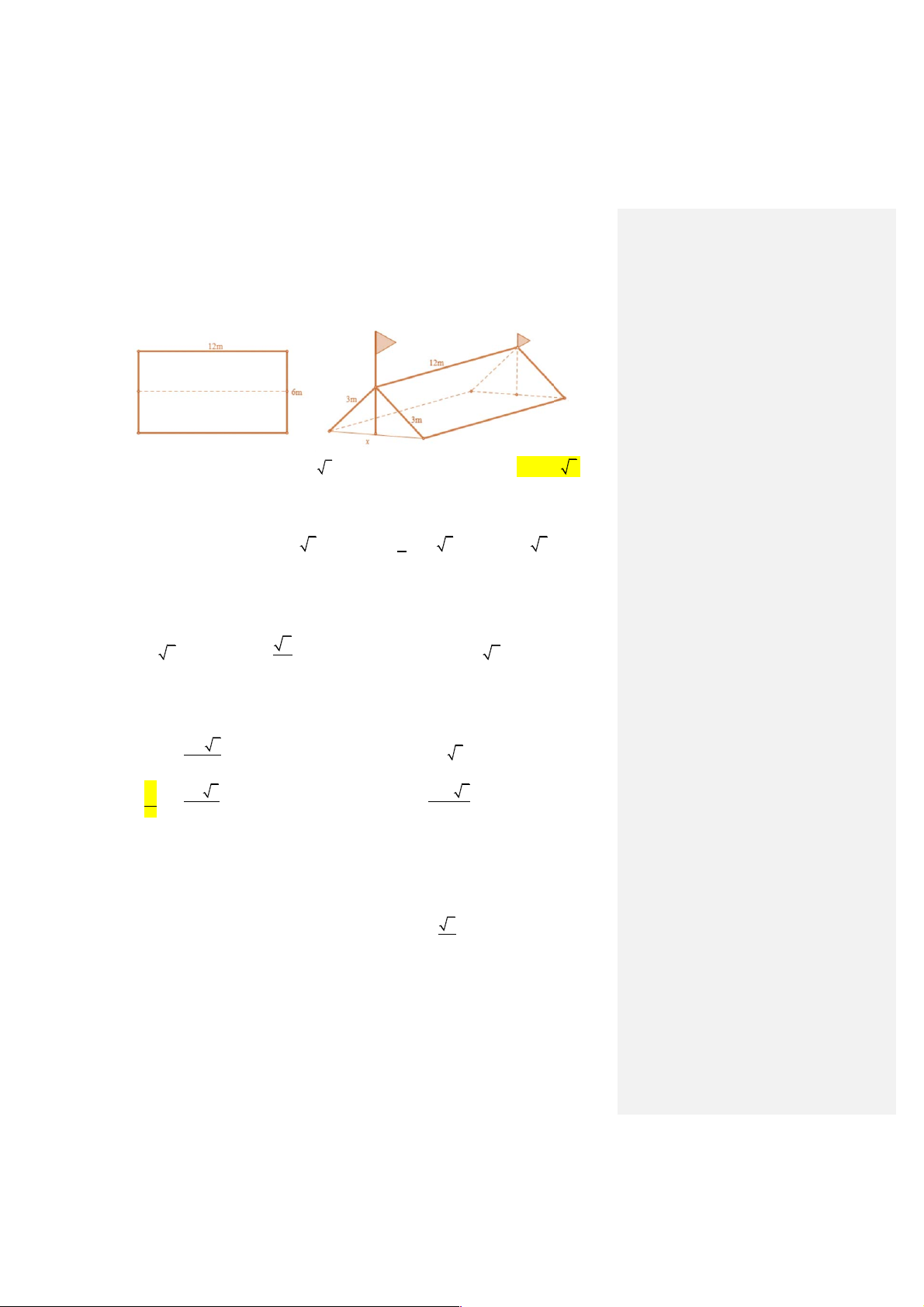
một tấm bạt hình chữ nhật có chiều dài là 12m và chiều rộng là 6m bằng cách: Gập đôi tấm bạt lại
theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của
tấm bạt sát đất và cách nhau x m (xem hình vẽ). Tìm x để khoảng không gian phía trong lều là lớn nhất? A. x = 4. B. x = 3 3. C. x = 3. D. x = 3 2.
Bài 3: Một học sinh được giao thiết kế một cái hộp thỏa mãn: Tổng của chiều dài và chiều rộng
bằng 12cm ; tổng của chiều rộng và chiều cao là 24cm . Giáo viên yêu cầu học sinh ấy
phải thiết kế sao cho thể tích cái hộp lớn nhất, giá trị thể tích lớn nhất bằng bao nhiêu? A. 600. B. 843 3 .
C. 384 3 . D. 348 3
Bài 4: Một bạn đã cắt tấm bìa carton phẳng và cứng và đặt kích thước như hình vẽ. Sau đó bạn ấy
gấp theo đường nét đứt thành cái hộp hình hộp chữ nhật. Hình hộp có đáy là hình vuông cạnh
a (cm), chiều cao là h (cm) và diện tích tấm bìa bằng 2
3m . Tổng a + h bằng bao nhiêu để thể tích hộp là lớn nhất. 2 A. 2 2 B.
C. 46,3 D. 2 2 Bài 5:
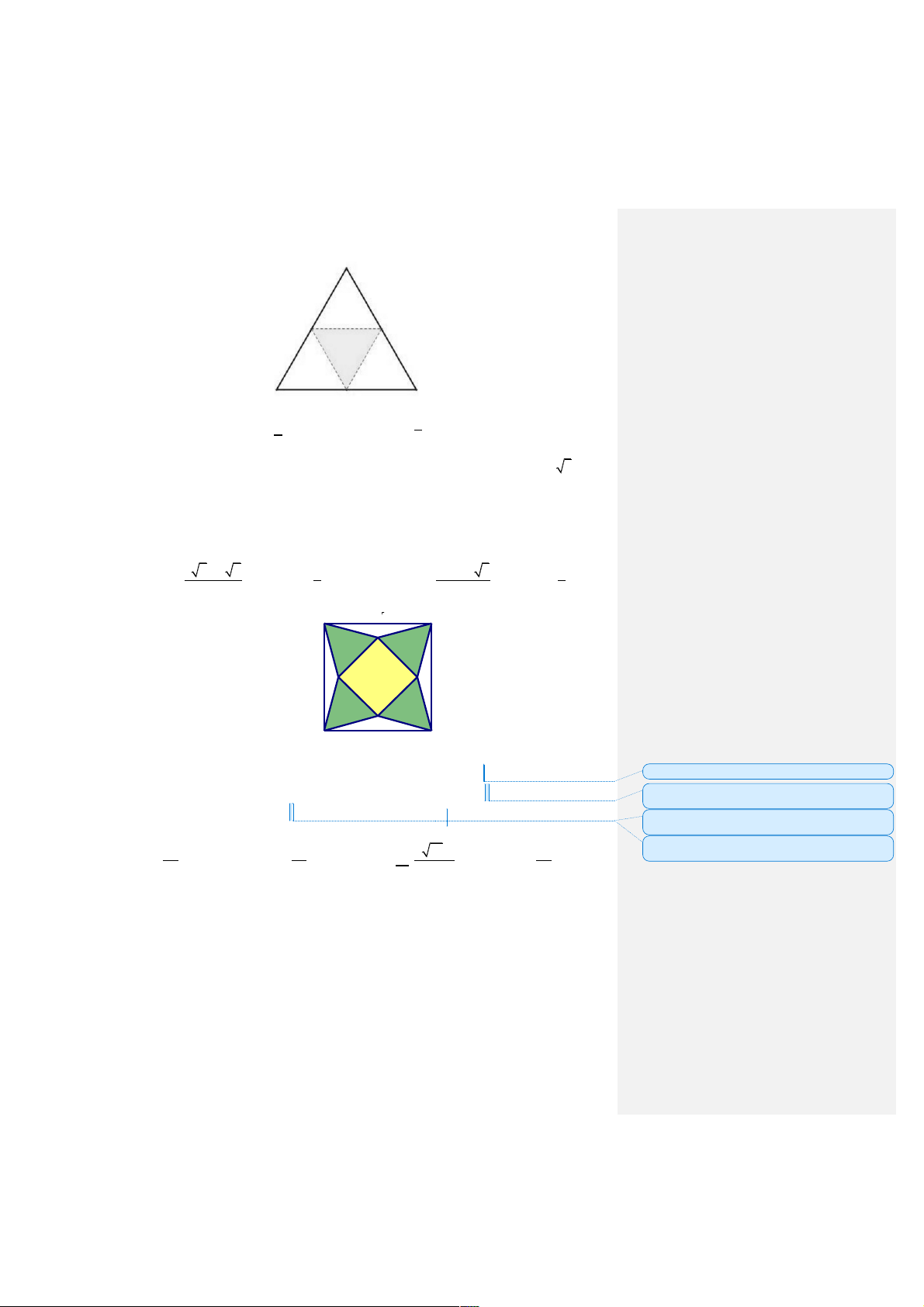
Người ta cắt miếng bìa hình tam giác đều cạnh bằng 10cm như hình bên và gấp theo các
đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành. 250 2 A. 3 V = cm . B. 3 V = 250 2cm . 12 125 2 1000 2 C. 3 V = cm . D. 3 V = cm . 12 3 Bài 6.
Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao 154m; độ dài cạnh đáy là 270m. Khi đó
thể tích của khối kim tự tháp là:
A. 3.545.000 B. 3.640.000 C. 3.500.000 D. 3.545.000 Bài 7.
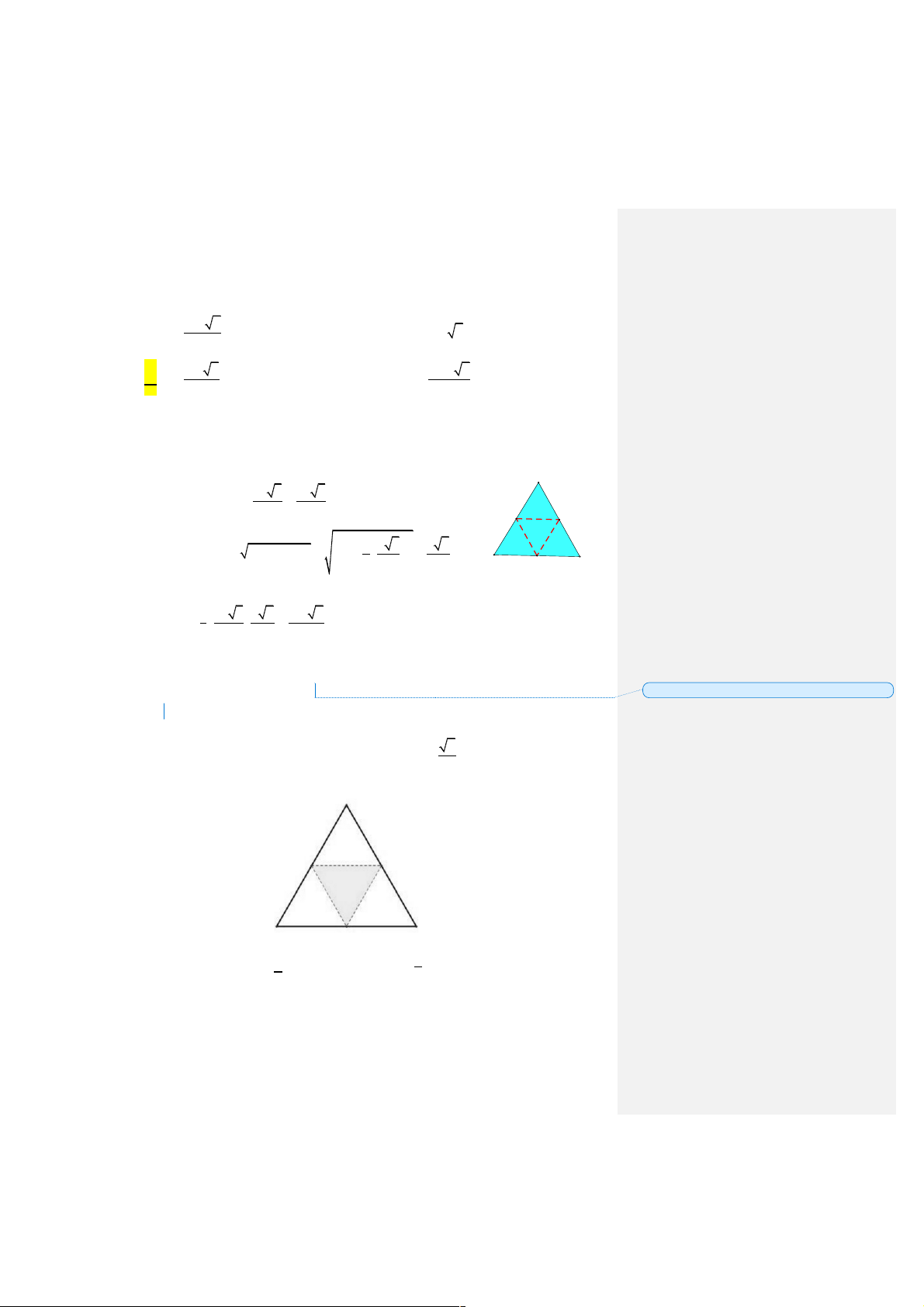
Người ta cắt miếng bìa tam giác đều như hình vẽ và gấp lại theo các đường kẻ, sau đó dán 2
các mép lại để được hình tứ diện đều có thể tích 3 V = a
. Tính độ dài cạnh của miếng 12 bìa theo a ? a A. a B. 2a C. D. 3a 2 Bài 8.
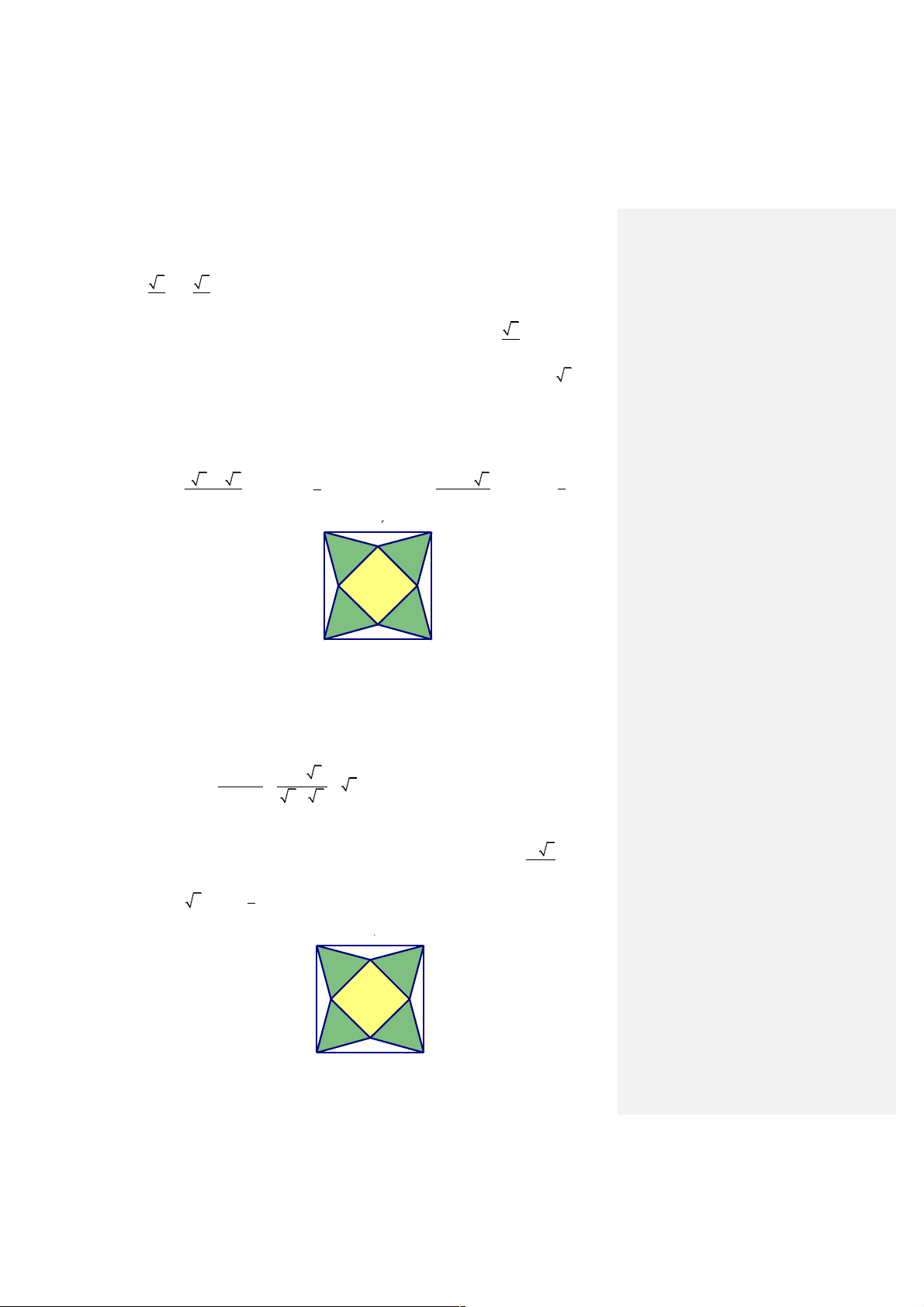
Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng 1+ 3, người
ta cắt tấm tôn theo các tam giác cân bằng nhau MAN, NBP, PC ,
Q QDM sau đó gò các tam
giác ABN, BCP,CDQ, DAM sao cho bốn đỉnh M , N, ,
P Q trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là 0
150 . Tính thể tích V của khối chóp đều tạo thành. 3 6 + 5 2 + A. V = 2 . B. V = 52 30 3 . C. V = 1 . D. V = 24 3 3 3 1+ 3 M N 1500 A D B C Q P Bài 9.
Trong một cuộc thi làm đồ dùng học tập bạn Bình lớp 12A của trường THPT B đã làm
một hình chóp tứ giác đều bằng cách lấy một tấm tôn hình vuông MNPQcó cạnh bằng a,
Commented [dq1]: ĐÃ SỬA
cắt mảnh tôn theo các tam giác cân MAN; NB ; P PC ;
Q QDM sau đó gò các tam giác
Commented [dq2]: ĐÃ SỬA AN ; B BPC; CQ ;
D DMA sao cho bốn đỉnh M ; N; ;
P Qtrùng nhau (như hình). Thể tích
Commented [dq3]: ĐÃ SỬA
lớn nhất của khối chóp đều là 3 Commented [dq4]: a 3 a 3 4 10a 3 a ĐÃ SỬA A. . B. . C. . D. . 36 24 375 48 M N A D B C Q P
Bài 10. Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt phần tô đậm
của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x (m), sao cho
bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Giá trị của x để khối chóp nhận
được có thể tích lớn nhất là 2 2 A. x = 1 . B. x = 2 . C. x = 2 . D. x = . 5 2 4 3
c. Sản phẩm: Sản phẩm là bản trình bày của 4 nhóm HS
d. Tổ chức thực hiện
GV: Chia lớp thành 4 nhóm. Phát phiếu học tập cuối tiết 1 của bài Chuyển giao
HS: Nhận nhiệm vụ, Thực hiện
Các nhóm HS thực hiện tìm tòi, nghiên cứu và làm bài ở nhà .
HS cử đại diện nhóm trình bày sản phẩm vào tiết thứ 2 của bài.
Các nhóm khác theo dõi, nhận xét, đưa ra ý kiến phản biện để làm rõ hơn các Báo c
áo thảo luận vấn đề.
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi
nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
Đánh giá, nhận xét, - Chốt kiến thức tổng thể trong bài học. tổng hợp
- Hướng dẫn HS về nhà tự xây dựng tổng quan kiến thức đã học bằng sơ đồ tư duy.
Hướng dẫn làm bài
Bài 1: Cho một tấm nhôm hình vuông cạnh 12cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như
hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x = 6. B. x = 3. C. x = 2. D. x = 4. Hướng dẫn giải: Lời giải Chọn C
+ Gọi x(0 < x < 6) là độ dài cạnh hình vuông bị cắt
+ Thể tích khối hộp tạo thành bằng V = x( - x)2 ( 3 12 2 cm )
+ Áp dụng BĐT AM-GM (Cauchy) cho 3 số dương ta có: 3 (
x + - x + - x
x 12 - 2x)2 = 2.2 .
x (6 - x)(6 - x) (2 6 6 ) £ 2. =128( 3 cm ) 27
Dấu bằng xảy ra khi 2x = 6 - x Û x = 2 .
Bài 2: Trong đợt chào mừng ngày 26 / 03 / 2018 , trường THPT Nguyễn Du có tổ chức cho học sinh
các lớp tham quan dã ngoại ngoài trời, trong số đó có lớp 12C1. Để có thể có chỗ nghỉ ngơi trong
quá trình tham quan dã ngoại, lớp 12C1 đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ
một tấm bạt hình chữ nhật có chiều dài là 12m và chiều rộng là 6m bằng cách: Gập đôi tấm bạt lại
theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của
tấm bạt sát đất và cách nhau x m (xem hình vẽ). Tìm x để khoảng không gian phía trong lều là lớn nhất? A. x = 4. B. x = 3 3. C. x = 3. D. x = 3 2. Lời giải Chọn D
+ Xem khoảng không gian là một hình lăng trụ đứng.
+ Khi đó thể tích hình lăng trụ được tính bởi: 2 2 2 1 æ x ö x + 36 - x 2 2 V =12. .x 3 - = 3 . x 36 - x £ 3. = 54 ç ÷ 2 è 2 ø 2 Dấu "=" xảy ra 2
Û x = 36 - x Û x = 3 2
Bài 3: Một học sinh được giao thiết kế một cái hộp thỏa mãn: Tổng của chiều dài và chiều rộng
bằng 12cm ; tổng của chiều rộng và chiều cao là 24cm . Giáo viên yêu cầu học sinh ấy
phải thiết kế sao cho thể tích cái hộp lớn nhất, giá trị thể tích lớn nhất bằng bao nhiêu? A. 600. B. 843 3 .
C. 384 3 . D. 348 3
Commented [dq5]: ĐA SUA Lời giải Chọn C
+ Gọi chiều rộng là x, 0 < x < 12.
+ Thể tích hình hộp là: V = x( - x)( - x) 3 2 12 24
= x -36x + 288x
+ Xét hàm số f (x) 3 2
= x -36x + 288x trên (0;12)ta có: éx =12 + 4 2 Ï(0;12) f '( x) 2
= 3x - 72x + 288; f '(x) = 0 Û ê êx =12 - 4 3 Î ë (0;12)
+ Lập bảng biến thiên ta tìm được: max f (x) = f (12-4 3) = 384 3 ÞV = 384 3 ( ) max 0;12
Bài 4: Một bạn đã cắt tấm bìa carton phẳng và cứng và đặt kích thước như
hình vẽ. Sau đó bạn ấy gấp theo đường nét đứt thành cái hộp hình hộp chữ
nhật. Hình hộp có đáy là hình vuông cạnh a (cm), chiều cao là h (cm) và
diện tích tấm bìa bằng 2
3m . Tổng a + h bằng bao nhiêu để thể tích hộp là lớn nhất 2 A. 2 2 B. C. 46,3 D. 2 2 Lời giải Chọn D 2 3- 2a æ 6 ö
+ Theo đề ra, diện tích mảnh bìa bằng: 2
S = 2a + 4ah = 3 Þ h = çÞ 0 < a < ÷ 4a ç 2 ÷ è ø 3 3a - 2a
+ Thể tích hình hộp chữ nhật: 2 V = a h = 4 3 3a - 2a æ ö
+ Xét hàm số f (a) = 6 trên ç0; ÷, ta có: 4 ç 2 ÷ è ø f '(a) 3 3 2 2
= - a ; f '(a) = 0 Û a = 4 2 2 æ 2 ö 2
+ Từ đó tìm được maxV = max f (a) = f ç ÷ = æ ç ÷ 6 ö 2 4 ç0; ÷ è ø ç 2 ÷ è ø 2 2
Dấu "=" xảy ra khi a = Þ h = Þ a + h = 2 2 2 Bài 5:
Người ta cắt miếng bìa hình tam giác đều cạnh bằng 10cm như hình bên và gấp theo các
đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành. 250 2 A. 3 V = cm . B. 3 V = 250 2cm . 12 125 2 1000 2 C. 3 V = cm . D. 3 V = cm . 12 3 Hướng dẫn giải Chọn C.
Tứ diện đều tạo thành là tứ diện đều ABCD có tất cả các cạnh bằng 5cm . 2 a 3 25 3 Diện tích đáy là 2 S = = cm . 4 4 10 cm 2 æ 2 5 3 ö 5 6 Đường cao 2 2 2
AH = AD - DH = 5 - ç × ÷ = , với ç 3 2 ÷ 3 è ø H là tâm đáy. 1 25 3 5 6 125 2 Thể tích 3 V = × × = cm . 3 4 3 12 Bài 6.
Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao 154m; độ dài cạnh đáy là 270m. Khi đó
thể tích của khối kim tự tháp là:
Commented [dq6]: ĐÃ SỬA
B. 3.545.000 B. 3.640.000 C. 3.500.000 D. 3.545.000 Bài 7.
Người ta cắt miếng bìa tam giác đều như hình vẽ và gấp lại theo các đường kẻ, sau đó dán 2
các mép lại để được hình tứ diện đều có thể tích 3 V = a
. Tính độ dài cạnh của miếng 12 bìa theo a ? a A. a B. 2a C. D. 3a 2 Giải: Đáp án: B
Đặt 2x là cạnh của miếng bìa. Khi đó cạnh của tứ diện đều là x , suy ra thể tích tứ diện đều 2 2 là : 3 3 V = x = a
. Do đó x = a , suy ra cạnh của miếng bìa là 2a . 12 12 2
Lưu ý : Nếu tứ diện đều có cạnh bằng a thì thể tích của nó là 3 V = a . 12 Bài 8.
Để làm một hình chóp tứ giác đều từ một tấm tôn hình vuông có cạnh bằng 1+ 3, người
ta cắt tấm tôn theo các tam giác cân bằng nhau MAN, NBP, PC ,
Q QDM sau đó gò các tam
giác ABN, BCP,CDQ, DAM sao cho bốn đỉnh M , N, ,
P Q trùng nhau(hình vẽ).
Biết rằng, các góc ở đỉnh của mỗi tam giác cân là 0
150 . Tính thể tích V của khối chóp đều tạo thành. 3 6 + 5 2 + A. V = 2 . B. V = 52 30 3 . C. V = 1 . D. V = 24 3 3 3 1+ 3 M N 1500 A D B C Q P Hướng dẫn giải Đáp án: B + ∑ ∑ 0 AMN = DMQ =15 ∑ 0 Þ AMD = 60 Þ M D AD đều.
Vì vậy hình chóp tứ giác đều tạo thành có tất cả các cạnh bằng nhau và bằng MA . 2 MN (1+ 3) Trong đó, MA = = = 2 0 2sin 75 6 + 2
+ Dễ dàng chứng minh được rằng: 3 x 2
“Một khối chóp tứ giác đều có tất cả các cạnh bằng x thì có thể tích là V = ” 6 + Với x = 2 2 thì V = 3 1+ 3 M N 1500 A D B C Q P Bài 9.
Trong một cuộc thi làm đồ dùng học tập bạn Bình lớp 12A của trường THPT B đã làm
một hình chóp tứ giác đều bằng cách lấy một tấm tôn hình vuông MNPQ có cạnh bằng a,
cắt mảnh tôn theo các tam giác cân MAN; NBP; PCQ; QDM sau đó gò các tam giác ANB;
BPC; CQD; DMA sao cho bốn đỉnh M;N;P;Q trùng nhau (như hình). Thể tích lớn nhất của khối chóp đều là 3 a 3 a 3 4 10a 3 a A. . B. . C. . D. . 36 24 375 48 M N A D B C Q P Hướng dẫn giải Chọn C a 2 - x
Gợi ý: Gọi cạnh hình vuông ABCD là x thì đường cao mặt bên là: SM= 2 1
suy ra chiều cao của phối chóp SO = 2 2a - 2 2ax 2 1 a Vậy V = 2 2 x 2a - 2 2
2 2ax lập bbt suy ra V lớn nhất tại x = 6 5 3 4 10a Ta tìm maxV = 375 S A D M O B C
Bài 10. Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt phần tô đậm
của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x (m), sao cho
bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Giá trị của x để khối chóp nhận
được có thể tích lớn nhất là 2 2 A. x = 1 . B. x = 2 . C. x = 2 . D. x = . 5 2 4 3 Hướng dẫn giải Đáp án: A 2 2 4 1
æ 2 - x ö æ x ö 1 x (1- x 2)
Thể tích của khối chóp thu được là 2 V = x ç ÷ - = . ç ÷ ç ÷ 3 2 è ø è 2 ø 3 2 æ 1 ö 2 2 Xét 4
f (x) = x (1- x 2) trên 0;
được f (x) lớn nhất khi x = . ç ÷ è 2 ø 5