Chương 1: Điện Trường Tĩnh và Định Luật Coulomb môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ Chương 1 ĐIỆN TRƯỜNG TĨNH
------------------------------------------------------------------------------------------------------------------------ §1.1 ĐỊNH LUẬT COULOMB §1.2 ĐIỆN TRƯỜNG §1.3 ĐỊNH LUẬT GAUSS §1.4 ĐIỆN THẾ
§1.5 HỆ THỨC LIÊN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG VÀ ĐIỆN THẾ
-----------------------------------------------------------------------------------------------------------------------
Các tương tác điện từ liên kết các electron và hạt nhân với nhau để tạo nên các nguyên tử,
chúng cũng liên kết các nguyên tử lại với nhau để tạo nên các phân tử, và chúng cũng liên
kết các phân tử lại với nhau để tạo thành các vật thể vĩ mô. Các thành phần tạo nên cơ thể
chúng ta, tức các nguyên tử và phân tử của nó, cũng được liên kết với nhau bởi lực điện từ.
Nhiều hiện tượng chúng ta nhìn thấy xảy ra xung quanh thực chất là kết quả của các lực điện
từ. Chẳng hạn, các cây xanh hấp thụ ánh sáng, một loại sóng điện từ, và chuyển đổi năng
lượng đó thành thế năng điện từ dưới dạng các phân tử cacbua-hydro, nền tảng của mọi sự sống trên trái đất.
Các bạn có thể ngạc nhiên hỏi vì sao chúng tôi lại dùng thuật ngữ “điện từ” ở đây, một thuật
ngữ luôn luôn kết hợp “điện” với “từ”. Nguyên nhân là ở chỗ cả hai hiệu ứng điện và từ đều
gắn với một thuộc tính của vật chất, đó là điện tích. Mặc dù các hiện tượng điện và từ có
quan hệ mật thiết với nhau, mối gắn kết ấy không phải là không thể tách rời. Nếu chúng ta
tiến hành nghiên cứu trên các điện tích ở trạng thái nghỉ, và chúng giữ nguyên trạng thái
nghỉ đó (tĩnh điện), thì chúng ta có thể tách điện khỏi từ. Chúng ta sẽ thực hiện điều đó ở các chương mở đầu này. §1.1 ĐỊNH LUẬT COULOMB
Định luật về lực tương tác giữa các hạt tích điện đứng yên đã
được xác định vào năm 1784 bởi Charles Augustin Coulomb
(1736 - 1806). Sử dụng một cân dây xoắn, ông ta đã xác định
được sự phụ thuộc vào điện tích của lực điện. Để ghi nhận công
lao của ông, đơn vị về điện tích trong hệ SI được gọi là culông (C).
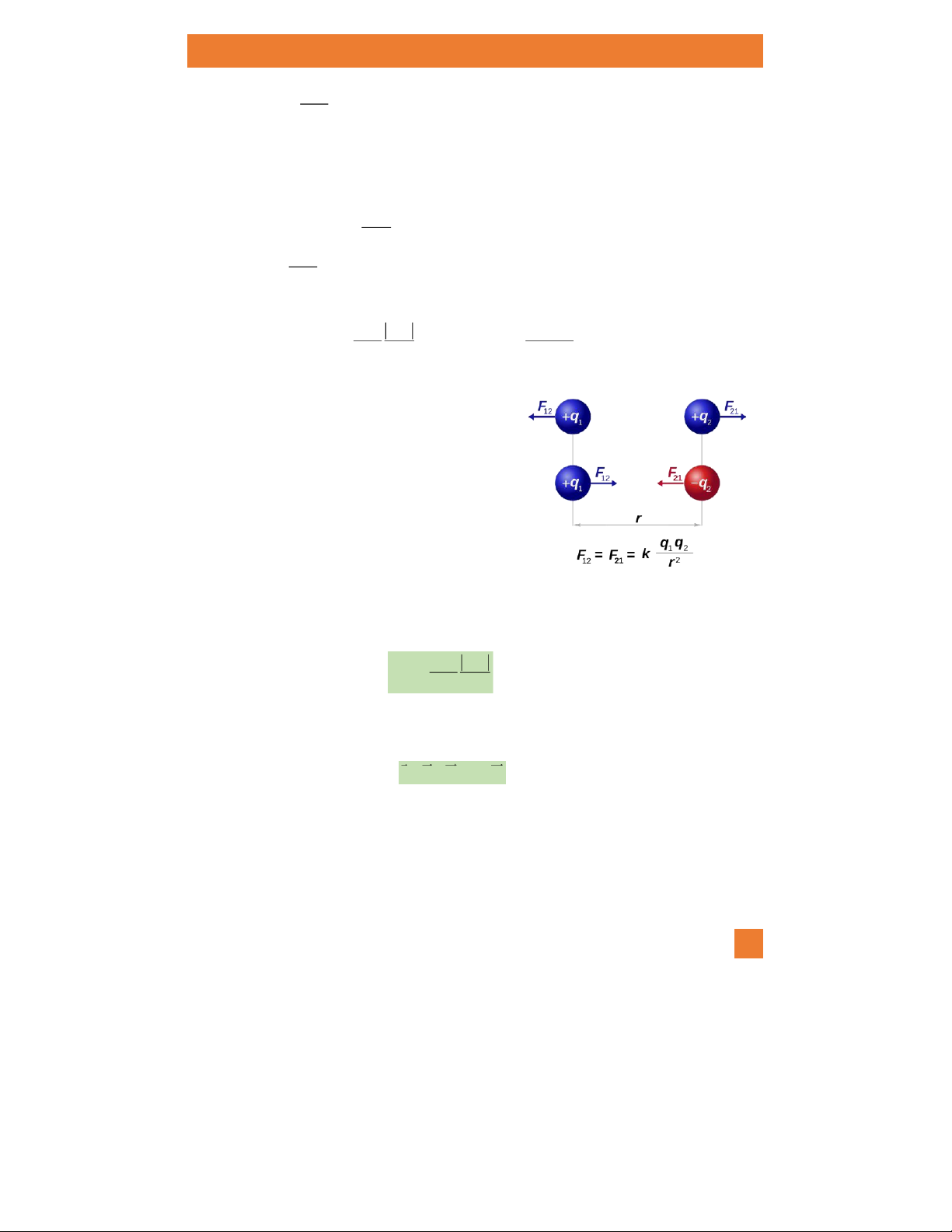
Thí nghiệm cho biết lực điện giữa hai điện tích điểm q1 và q2
đặt cách nhau một khoảng r trong chân không được xác định bởi 1 qq F4r (1.1) 12 2 0 trong
đó k = 1 là một hệ số tỉ lệ độc lập với khoảng cách và 4
độ lớn của các điện tích. Phương trình (1-1) được gọi là định luật Coulomb. Lưu ý rằng lực điện 0
giữa các điện tích là một lực tỉ lệ nghịch với bình phương khoảng cách. Nếu khoảng cách giữa các
điện tích tăng gấp đôi, thì độ lớn của lực giảm đi 4 lần. ĐÀO TUẤN ĐẠT 1
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
Hệ số tỉ lệ k = 1 trong định luật Coulomb có vẻ phức tạp, nhưng nó cũng chỉ là một hằng số. 4 0
Thừa số 4π chứa trong hệ số đó s
ẽ được làm đơn giản trong một số phương trình sẽ gặp ở chương
sau. Thừa số 0 diễn tả m
ột hằng số được gọi là hằng số điện môi của chân không hay ngắn gọn là
hằng số điện. Giá trị của 0 là: 0 = 8,854.10-12 C2/Nm2 Từ đó: k = 1 9 2 2 9 2 2 9 , 8 87 1 . 0 m . N / C 1 . 9 0 m . N / C 4 0
Hệ số tỉ lệ k = 1 là một con số lớn vì culông là một đơn vị điện tích lớn. Giả sử có hai hạt, mỗi 4 0
hạt tích điện 1C, nằm cách nhau 1m. Từ định luật Coulomb có thể tính được độ lớn lực F giữa chúng: 1 (1 q Cq1)2( 91C) 2 2 9 F (9.10 N.m / C ) 9.10 N 22 4 r (1m) 0
Độ lớn của lực này là khổng lồ, tương đương
với trọng lượng của khoảng 15 triệu ười. Phép tính ng
trên chỉ ra rằng 1C là một lượng điện tích rất lớn.
Một chiếc đũa được tích điện bằng ma sát thường có
điện tích vào cỡ 10 nC. Việc đo điện tích trên một
chiếc đũa thủy tinh tích điện bằng cách cọ xát vào
lụa bằng đơn vị culông (C) cũng giống như đo độ
dày của tờ giấy này bằng đơn vị kilomet.
Định luật Coulomb chứa đựng kết quả là các hạt có
điện tích cùng dấu thì đẩy nhau và khác ấu d thì hút nhau.
Thực nghiệm chứng tỏ rằng lực tương tác giữa các điện tích đặt trong môi trường giảm đi ε lần
so với khi đặt trong các điện tích trong chân không. ε đặc trưng cho tính chất điện của môi trường
và được gọi là hằng số điện môi của
môi trường. Biểu thức của định luật Coulomb trong trường hợp này là 1 qq 12 F4r (1.2) 2 0
Trường hợp có một hệ các điện tích điểm gián đoạn tác dụng lên một điện tích điểm khác đặt
trong không gian đó. Lực điện tác dụng lên điện tích được xác định bằng nguyên lý tổng hợp lực trong cơ học: F F F ... F (1.3) 1 2 n §1.2 ĐIỆN TRƯỜNG
1. Khái niệm điện trường
Các điện tích tương tác với nhau ngay cả khi chúng cách nhau một khoảng r nào đó trong chân
không. Câu hỏi đặt ra ở đây là tương tác
giữa chúng xảy ra như thế nào? Có sự tham gia của môi trường xung quanh không? ĐÀO TUẤN ĐẠT 2
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
Khoa học hiện đại cho rằng gắn với mỗi điện tích là điện trường của nó. Điện trường là một
dạng đặc biệt của vật chất (không phải các chất thường gặp). Mọi điện tích đặt trong điện trường
đều bị điện trường tác dụng lực.
2. Vector cường độ điện trường
Trong phần cơ chúng ta đã định
nghĩa cường độ trường hấp dẫn g = F/m, trong đó F là lực hấp
dẫn tác dụng lên một vật có khối lượng m. Ở mỗi
điểm gần mặt đất, Trái đất sinh ra một trường hấp
dẫn có cường độ 9,8 N/kg ướng h
vào tâm Trái đất. Nếu một vật có khối lượng 3,6 kg ở gần mặt đất
thì có một lực với độ lớn F = mg = (3,6 kg)(9,8 N/kg) = 35 N do trường hấp dẫn của Trái đất tác dụng lên nó.
Định nghĩa cường độ điện trường cũng giống như định
nghĩa của trường hấp dẫn. Hãy xét điện
trường được sinh ra bởi một nhóm các hạt tích điện nằm xung quanh gốc toạ độ. Một nhóm hạt tích
điện giống như vậy được gọi là một phân bố điện tích. Một hạt điện tích thử q0 được đặt ở M.
Cường độ điện trường E ở điểm M được xác định
bằng lực điện F tác dụng bởi phân bố điện tích lên
điện tích thử chia cho điện tích thử. F E = (1.4) q 0
Điện trường E phụ thuộc vào giá trị và vị trí của các
điện tích trong phân bố điện tích, và nó cũng tuỳ thuộc
vào vị trí điểm đo trường. Chúng ta thấy điện trường như
là một trạng thái được thiết lập trong không gian bởi phân bố điện tích. Chúng ta cho rằng điện
trường tồn tại bất kể là có điện tích thử để đo nó hay không.
Giá trị của E là độc lập đối với điện tích thử. Lực F tác dụng lên điện tích thử là tổng vectơ của
các lực riêng lẻ tác dụng lên nó bởi các hạt trong phân bố điện tích. Vì mỗi lực đó đều tỉ lệ với qo nên tỉ số E = F/qo độ
c lập với qo. Để đảm bảo cho E độc lập với điện tích thử, điện tích qo phải chọn
đủ bé để cho ảnh hưởng của nó lên các hạt trong phân bố điện tích là có thể bỏ qua. Chính vì vậy
phương trình 1.4 được định lượng với điều kiện qo bé. Mục đích của điện tích thử là để o đ điện
trường, cũng như mục đích của nhiệt biểu là đ ể đo nhiệt độ.
Vì lực F là đại lượng vectơ và E = F/qo, E là trường vectơ và tuân theo nguyên lý chồng chất.
Hướng của E trùng với hướng của lực tác dụng lên điện tích thử dương, hoặc ngược với lực tác
dụng lên điện tích thử âm.
Đơn vị của cường độ điện trường trong hệ SI là niutơn trên culông (N/C) hoặc vôn trên mét (V/m).
3. Cách tính điện trường. Nguyên lý chồng chất điện trường
Điện trường sinh ra bởi một phân bố điện tích có thể tìm được theo định luật Coulomb và nguyên lý chồng chất.
a) Điện trường của một điện tích điểm
Hãy xét điện trường gây ra bởi một hạt điện tích q đặt tại gốc toạ độ. Từ định luật Coulomb lực
điện tác dụng bởi hạt ấy lên điện tích thử qo là ĐÀO TUẤN ĐẠT 3
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ 1 qq 0 F4r 2 0
Chia cho qo sẽ được cường độ điện trường tại điểm đặt qo: 1 q E4r 2 0 Dưới dạng vector q Er (1.5) 2 4r 0 trong đó rr
là vector chỉ hướng đơn vị. 0
Vectơ E hướng đi ra nếu điện tích là dương hoặc
hướng đi vào nếu điện tích là âm.
b) Điện trường của hệ điện tích điểm
Bây giờ hãy xét điện trường sinh ra bởi hai hoặc nhiều hạt tích điện tại điểm M. Từ nguyên lý
chồng chất, lực F tác dụng lên điện tích thử q0 là tổng vectơ
của các lực riêng biệt: q q 1 0 2 0 i F r r ... q r 2 2 1 2 2 0 i 4 r 4 r 4 r 0 1 0 2 0 i trong
đó qi là điện tích của hạt thứ i, ri là khoảng cách từ hạt thứ i đến điểm M, ir là vector chỉ
hướng đơn vị. Chia cho qo sẽ được trường ở M: q i Er 2 i 4r 0i E E 1 2E ... iE (1.6)
Điện trường do hai hoặc nhiều hơn điện tích
điểm gây ra là tổng vectơ của các điện trường
riêng biệt gây ra bởi từng điện tích riêng rẽ.
Đây chính là phát biểu của nguyên lý chồng chất
điện trường. Ta chú ý rằng việc tìm điện trường do
một phân bố điện tích điểm gây ra là một bài toán đòi hỏi phải cộng vectơ, không phải phép cộng đại số thông thường.
c) Điện trường của hệ điện tích điểm phân bố liên tục
Điện tích trên các vật thể vĩ mô, chẳng hạn như chiếc
đũa tích điện, là do một sự mất cân bằng
của electron và proton gây ra. Vì điện tích trên các electron hoặc proton là rất nhỏ so với các điện
tích vĩ mô thông thường, nên điện tích vĩ mô như vậy
cần phải bao gồm một số lớn các electron bị
thừa hoặc thiếu. Do đó chúng
ta có thể xem điện tích đó như là một phân bố liên tục của các yếu tố
tích điện vô cùng bé dq. Áp dụng phương trình (1.5) vào trường hợp ,
đó chúng ta tính được điện
trường vô cùng bé dE do yếu tố điện tích dq gây ra: ĐÀO TUẤN ĐẠT 4
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ dq dE r 2 4r 0
trong đó r là khoảng cách từ yếu tố điện tích dq đến điểm M cần tính điện trường, và r là vectơ
đơn vị hướng từ dq đến M. Điện trường E do tất cả yếu tố gây ra có thể tìm được bằng cách lấy tích phân: dq E dE r (1.7) 2 4r 0
trong đó các cận tích phân được xác định bởi phạm vi của phân bố điện tích.
+ Điện tích của một dây. Khi phân bố điện tích dài và hẹp, chẳng hạn như điện tích phủ dọc
theo một dây dài và mảnh, được gọi là điện tích dài. Một điện tích dài được đặt trưng bởi mật độ điện tích dài
dq của nó, đối với dây tích điện đều, mật độ này bằng điện tích q chia cho chiều dl dài L của dây: q . Khi đó L dl E dE r (1.7a) 2 4r 0
+ Điện tích của một mặt. Khi điện tích của một vật trải trên bề mặt của vật đó thành một lớp
mỏng giống như một lớp sơn. Một phân bố như vậy được gọi là điện tích mặt. Một điện tích mặt
được đặt trưng bởi mật độ điện tích mặt
dq của nó, đối với mặt tích điện đều, mật độ này dS
bằng điện tích q chia cho diện tích của mặt: q . Khi đó S dS E dE r (1.7b) 2 4r 0
+ Điện tích của một khối. Khi điện tích của một vật phân bố trong toàn bộ thể tích của vật đó
được gọi là điện tích khối. Một điện tích khối được đặt trưng bởi mật độ điện tích khối dq dV
của nó, đối với khối tích điện đều, mật độ này bằng điện tích q chia cho thể tích của khối: q . V Khi đó dV E dE r (1.7c) 2 4r 0 VD1. Lưỡng cực điện
Một trường hợp quan trọng của phân bố điện tích là lưỡng cực điện. Một lưỡng cực chứa hai
điện tích điểm có độ lớn như nhau như trái dấu ng
. Thông thường ký hiệu q diễn tả điện tích của một
vật có thể là dương hoặc âm. Tuy nhiên, khi nói đến lưỡng cực, chúng ta thường quen dùng q để
biểu diễn độ lớn của điện tích, cho nên một hạt có điện tích +q và hạt kia có điện tích -q. Đường
thẳng nối hai điện tích gọi là trục của lưỡng cực.
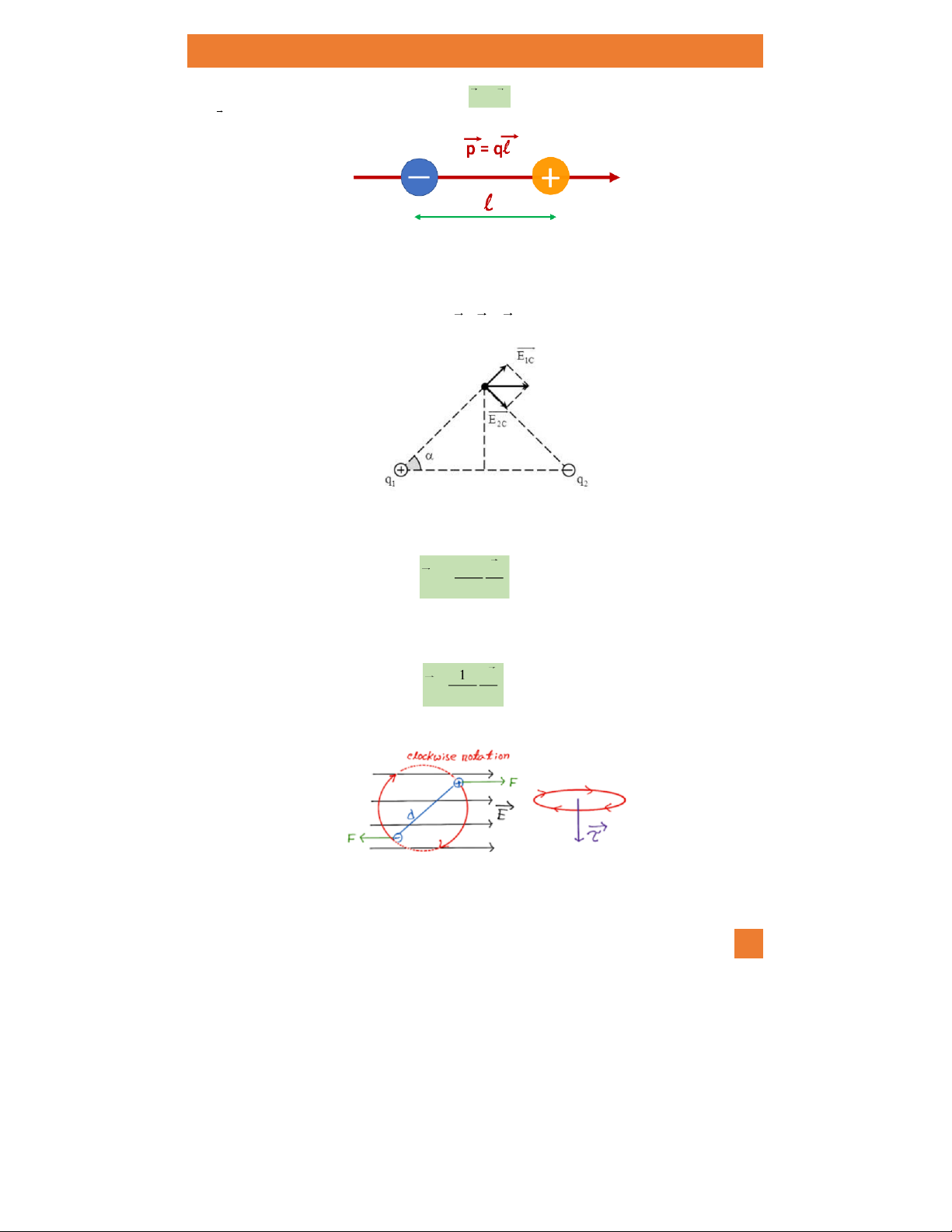
Đặc trưng cho tính chất điện của lưỡng cực là mômen lưỡng cực điện (Mômen điện) . Mômen
lưỡng cực điện p là một vectơ có độ lớn là tích số của q và khoảng cách l giữa hai điện tích : p = ql. ĐÀO TUẤN ĐẠT 5
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ p ql (1.8)
l hướng từ điện tích âm sang điện tích dương.
Hướng của mômen lưỡng cực từ hạt có điện tích âm đến hạt có điện tích dương.
Điện trường tại một điểm nằm trên mặt phẳng trung trực của lưỡng cực
Tại M, theo nguyên lý chồng chất: E E 12E
Dễ dàng thấy rằng vector E song song và ngược chiều với vector l
Đối với trường hợp khi E được tính cho các điểm cách lưỡng cực một khoảng r lớn hơn nhiều so
với khoảng cách giữa hai điện tích điểm của lưỡng cực, kết quả tính toán cho thấy 1p E4r (1.9) 3 0
Điện trường tại một điểm nằm trên trục của lưỡng cực
Tại N, cách tâm lưỡng cực một khoảng r, theo nguyên lý chồng chất: 2p E4r (1.10) 3 0
Tác dụng của điện trường đều lên lưỡng cực
Đặt lưỡng cực điện có momen lưỡng cực p trong điện trường đều cường độ E. Lưỡng cực điện
sẽ chịu tác dụng của ngẫu lực F và –F. Ngẫu lực làm lưỡng cực điện quay theo chiều sao cho vector ĐÀO TUẤN ĐẠT 6
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
p tới trùng với vector E. Nếu lưỡng cực cứng (l = constant), nó sẽ nằm cân bằng. Nếu lưỡng cực đàn
hồi, nó sẽ bị biến dạng.
Mômen của ngẫu lực được xác định bởi pxE (1.11)
pEsin ( là góc giữa hai vector p và E). vuông góc với mặt phẳng chứa vector p và E và
có chiều sao cho theo thứ tự 3 vector p, E, hợp thành một tam diện thuận.
VD2. Sợi dây tích điện đều
Để tiện lợi ký hiệu chiều dài sợi dây là 2 , khi đó mật độ điện dài
q . Một yếu tố dài d có điện tích 2
dq xem như một điện tích điểm. Điện trường của điện
tích điểm dq tại điểm P là dE = 1d 2 4R 0
Xét thành phần x của trường. Từ hình vẽ ta thấy R cos và sin . 2 R 2 R 1d R dEX = dE.cos = . 2 4R 2 0 R Rd 1 E (1.12) xX 2 dE 4 (R = 2 2R 0 0 R
Phép tính tích phân với thành phần y của trường cho kết quả Ey = 0. Kết quả đó có thể đoán
nhận qua tính đối xứng của phân bố điện tích qua mặt phẳng xz. Đối với mỗi yếu tố điện tích với
toạ độ y dương sẽ có một yếu tố điện tích tương ứng với toạ độ y âm, và đóng góp của chúng sẽ triệt tiêu nhau.
VD3. Đĩa tròn tích điện đều
Vì phân bố điện tích là đều và có hình dạng
như một đĩa mỏng, chúng ta xem nó như
một điện tích mặt với mật độ = q/ 2 R0 .
Chúng ta chia đĩa ra thành các vành với độ
rộng vô cùng bé da. Như vậy diện tích của
một vành bán kính a và độ rộng da là
2πa.da, và điện tích của nó là
dq = 2πa.da. Tính được dEx trên trục của
vòng dây bán kính a và điện tích dq = 2πa.da là ĐÀO TUẤN ĐẠT 7
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ ( 2 ada)x dEx24 2 3/ ( 2x a ) 0
Bằng cách lấy tích phân biểu thức trên từ a = 0 đến a = Ro sẽ
cộng mọi đóng góp vào Ex từ các
vành có bán kính a = 0 đến a = Ro: R0 2x a da E4 (x a ) x2 2 3/2 00
Kết quả lấy tích phân cho ta: x 1 1 E2x x R (1.13) x2 2 2 00
Tương tự ví dụ trên, thành phần y của điện trường sẽ triệt tiêu.
4. Hạt tích điện trong điện trường đều
Trong mục trên chúng ta đã xác định điện trường do một số kiểu phân bố điện tích gây ra. Một
khi đã biết trường, chúng ta có thể dùng phương trình F = qE, để xem xét lực tác dụng của trường
lên một hạt. Nếu lực điện chỉ là một lực duy nhất đáng kể tác dụng lên hạt, thì qE là lực tổng hợp và
định luật thứ hai của Newton cho ta: qE = ma hoặc a = qE/m
Chúng ta sẽ xét hai trường hợp: 1) một hạt ban đầu ở trạng thái nghỉ trong một trường đều, và 2)
hạt được phóng với vận tốc vo vào một trường đều, với v o góc với E. vuông
1. Một hạt tích điện từ trạng thái nghỉ trong một điện trường
đều sẽ chuyển động với gia tốc không đổi dọc theo một đường
song song với E cũng giống như một viên đá từ trạng thái nghỉ
trong một trường hấp dẫn sẽ rơi thẳng đứng xuống dưới dọc theo
một đường song song với g. Nếu chúng ta đặt gốc toạ độ ở điểm
nghỉ với trục x hướng theo E và đặt t = 0 khi x = 0, thì các
phương trình động học cho ta: 1 qE a 2 x = qE/m, vx = qE/m.t, x t (1.14) 2 m
Khử t trong các phương trình vx và x, chúng ta cũng tìm được: q 2 E v2x x (1.15) m
2. Bây giờ hãy xét một hạt i
đ vào vùng điện trường đều với vận tốc vo hướng thẳng góc với E.
Chuyển động sẽ giống như trường hợp một quả bóng được ném theo phương nằm ngang trong
trường hấp dẫn đều của trái đất. Trên hình vẽ
chúng ta cho trục y hướng song song với E và
biểu diễn một hạt tích âm có vận tốc vo ở gốc toạ
độ khi t = 0. Cũng từ các phương trình động học chúng ta có qE ay ax = 0 az = 0 m qE vy t vx = v0 vz = 0 m 1 qE 2 y t x = v0t z = 0 2 m ĐÀO TUẤN ĐẠT 8
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
Như vậy, chuyển động xảy ra trong mặt phẳng xy. Khử t trong các phương trình của y và x ta sẽ
có quỹ đạo parabol của hạt: 1 qE 2 y x (1.17) 2 2 mv0
Quỹ đạo được vẽ trên hình ứng với hạt tích điện âm. Nếu điện tích là dương, ay sẽ dương và
đường cong quỹ đạo của hạt thay vì hướng lên sẽ hướng xuống dưới. 5. Ống tia âm cực
Hình vẽ diễn tả sơ đồ một dụng cụ được gọi là ống tia âm cực (CRT). Trong một CRT, các
electron trước hết được gia tốc và sau đó bị làm lệch. CRT được dùng làm đèn hình máy thu hình,
màn hình máy tính, máy hiện sóng v.v...
Các electron được phát ra từ một dây nung đốt nóng và được gia tốc bởi một điện trường ngang
do các bản tích điện trong "súng phóng electron" tạo nên. Các electron đi ra từ lỗ của tấm anốt tạo
nên chùm tia, giống như các viên đạn được phóng ra từ nòng súng máy. Sau đó chùm electron đi
qua một vùng có điện trường đều thẳng góc với phương của chùm. Trường làm lệch đó được tạo
nên bởi các tấm kim loại tích điện gọi là các tấm làm lệch. Trường làm lệch chỉnh hướng cho chùm
electron đi đến điểm đã định trên một màn hình huỳnh quang, tạo ra chấm huỳnh quang. Các tấm
làm lệch được biểu diễn trên hình vẽ là các tấm làm lệch thẳng đứng, chúng điều khiển vị trí theo
phương thẳng đứng của chấm huỳnh quang. Tương tự, có các tấm làm lệch ngang mà trên hình
không vẽ. ở một số CRT, như loại
dùng trong các TV, để làm lệch chùm electron người ta thường
dùng từ trường thay cho điện trường. Chúng ta sẽ thảo luận về việc làm lệch do từ trường ở chương sau.
6. Đường sức điện trường
Các đường sức điện trường cho ta một hình ảnh trực quan về điện trường; về bản chất nó là một
bản đồ của trường. Tuy rằng chúng ta vẽ các đường sức trên giấy hai chiều hoặc trên bảng đen,
chúng ta hình dung sự tồn tại của trường trong không gian ba chiều. Sau này chúng ta cũng sẽ dùng
các đường tương tự để mô tả cả từ trường nữa. Khái niệm này đã được đưa vào lần đầu bởi nhà vật
lý thực nghiệm vĩ đại người Anh, Michael Faraday (1791- 1867).
Một đường sức được vẽ sao cho vector E có phương tiếp tuyến ở mỗi điểm của đường, và
chiều của đường sức chỉ chiều của vector E. Chẳng hạn, ở gần điện tích điểm các đường sức là
đường xuyên tâm; chúng hướng đi ra từ điện tích dương và đi vào điện tích âm. ĐÀO TUẤN ĐẠT 9
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
Trên một hình vẽ xác định, khoảng cách giữa các đường sức mô tả độ lớn của điện trường. Ở
các vùng các đường sức sít nhau thì E lớn, còn ở các vùng các đường sức xa nhau thì bé. Thực tế,
mật độ đường sức tỉ lệ với độ lớn của E, một sự kiện mà định luật Gauss - đối tượng nghiên cứu của bai sau, sẽ chỉ ra.
Một điện trường đều được biểu diễn bởi các đường sức thẳng, song song cách đều nhau. §1.3 ĐỊNH LUẬT GAUSS
Thiên tài của Karl Friedrich Gauss (1777 - 1855) bộc lộ từ rất
sớm. Tài năng tính nhẩm của ông đã trở thành huyền thoại. Sở
thích của ông là thiên văn học và vật lý, song các công trình quan
trọng nhất của ông lại thuộc về toán học. Ông đã đặt nền móng
toán học cho phần lớn công cụ toán của vật lý thý thuyết cuối thế
kỷ 19 đầu thế kỷ 20, kể cả lý thuyết của Einstein về hấp dẫn.
Điện trường của vật tích điện đứng yên có thể tìm được bằng hai cách tương đương: bằng định
luật Coulomb và bằng định luật Gauss. Định luật Coulomb cho ta cách tính đơn giản và trực tiếp,
còn định luật Gauss thì tinh tế, tao nhã và hữu dụng hơn. Về mặt toán học định luật Gauss phức tạp
hơn định luật Coulomb, song bù lại, nó giúp ta hiểu tương tác điện một cách sâu sắc hơn. Định luật
Gauss được biểu thị qua khái niệm thông lượng của điện trường hay điện thông (flux) có nguồn
gốc từ chữ Latinh fluere, nghĩa là dòng chảy. Nên trước hết ta tìm hiểu khái niệm này.
1. Điện cảm. Điện thông
Điện cảm (Cảm ứng điện)
Khi đi qua mặt phân cách giữa hai môi trường có hằng số điện môi khác nhau, cường độ điện
trường E biến đổi đột ngột. Vì vậy phổ đường sức điện trường bị gián đoạn ở mặt phân cách giữa
hai môi trường. Sự gián đoạn của đường sức không thuận tiện đối với nhiều phép tính về điện ĐÀO TUẤN ĐẠT 10
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠ
trường. Để mô tả điện trường, ngoài vector cường độ điện trường E, người ta còn dùng một đại
lượng vật lý khác, không phụ thuộc vào tính chất của môi trường, đó là vector điện cảm D. Trong môi trường đồng nhất: DE 0 (1.18)
Vector điện cảm của điện tích điểm q tại điểm cách q một khoảng r là: q Dr (1.19) 2 4r
Như vậy, tại mỗi điểm trong điện trường, D chỉ phụ thuộc vào q, không phụ thuộc vào tính chất
của môi trường. Vì D không phụ thuộc môi trường nên khi đi qua mặt phân cách của hai môi trường
khác nhau, phổ “đường sức” liên tục. Điện thông
Giả sử có diện tích S trong điện trường. Xét phần tử diện tích dS đủ nhỏ để D không đổi trên
mọi điểm của dS. Khi đó điện thông qua dS là d D.S.cosα E
Trong đó là góc giữa vector D và vector pháp
tuyến đơn vị n của dS. Vector n có chiều quy ước
hướng về phía vô hạn của không gian. Định nghĩa vector
diện tích là vector có độ lớn
bằng diện tích và có hướng của vector n: dS dS.n ta có d E D.dS
Trên toàn bộ diện tích S D.dS D.dS.cos E (1.20) SS
Thông lượng qua một diện tích tỷ lệ với số đường sức qua diện tích đó. 2. Định luật Gauss Định luật Gauss
Thường ta chỉ quan tâm tới thông lượng qua một mặt kín. Mặt kín qua đó điện thông được tính
thường là một mặt tưởng tượng và được gọi là mặt Gauss. Mặt Gauss không nhất thiết phải tương
ứng với mặt của một vật. Mỗi khi bạn dùng định luật Gauss bạn có thể nghĩ ra một mặt có kích
thước và hình dạng bất kỳ để dùng làm mặt Gauss của bạn. Tuy nhiên, việc lựa chọn kích thước và
hình dạng phù hợp cho mặt Gauss là một trong những yếu tố then chốt trong việc sử dụng định luật Gauss.
“Điện thông qua một mặt kín bằng tổng đại số các điện tích chứa trong mặt kín ấy.” = Σqi (1.21) E
Xét điện trường của điện tích điểm q cố định: ĐÀO TUẤN ĐẠT 11
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
+ Mặt Gauss là một mặt cầu bao quanh q
Tại một điểm bất kỳ trên mặt cầu. Vector điện cảm: q Dr 2 4R Thay vào (1.14) ta được: S E Vì r .n 1 nên: E Vậy: Eq
+ Mặt Gauss có dạng bất kỳ bao quanh q
Tại một điểm bất kỳ trên mặt Gauss, tại M cách điện
tích q đặt tại O một khoảng r. Vector điện cảm: q D . r 2 4r Thay vào (1.14) ta được: = E Gọi dS dS.cos
là hình chiếu của dS lên mặt n
phẳng vuông góc với OM ta có: E dSn d r
là góc khối nhìn diện tích dS từ O, ta có: 2 4 q E Vậy Eq
+ Mặt Gauss có dạng bất kỳ không bao quanh q
Xét hai phần tử diện tích dS1 và dS2 nhìn từ một góc
khối dΩ. Điện thông gửi qua các phần tử diện tích này là: 1 q 1n 1 dS 1 d r .n dS q q.d E1 22 1 1 4 r 11 4 r 4 1 q 2n 1 dS 1 d r .n dS q q.d E2 22 2 2 4 r 4 r 4 22 Vậy d d 0 E1 E2 Kết quả là E ĐÀO TUẤN ĐẠT 12
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
Như vậy điện thông qua mặt Gauss bất kỳ là q nếu q đặt bên trong mặt Gauss và bằng 0 nếu q
đặt bên ngoài mặt Gauss.
Trong trường hợp tổng quát điện thông do một hệ điện tích sẽ là tổng điện thông do từng điện tích gây ra.
Dạng vi phân của định luật Gauss (Phương trình Poinsson) divD ƍ (1.22) D D
trong đó: ƍ là mật độ điện khối; Z y divD x y z .
3. Ứng dụng định luật Gauss để tìm điện trường
Định luật Gauss có thể được dùng để tìm điện trường do một phân bố điện tích có đối xứng cao
gây ra. Nếu phân bố điện tích là đối xứng cao, khi đó một
vài tính chất của trường như phương của
nó chẳng hạn, có thể được suy ra bằng việc xem xét kỹ sự đối xứng của phân bố điện tích mà không
cần phải tính toán. Khi đó bạn c ó thể
- Chọn mặt Gauss làm sao lợi dụng được tính đối xứng này. - Xác qua m định điện thông ặt Gauss này theo D.
- Giải định luật Gauss để tìm D.
Bước thứ nhất là ước b
quyết định nhất. Mặt được chọn làm mặt Gauss phải là mặt mà thông
lượng đi qua nó có thể được xác định một cách dễ dàng. Các ví dụ dưới đây minh hoạ cho k ỹ thuật này.
VD1. Mặt cầu tích điện
Tìm E tại các điểm bên trong và bên ngoài của một lớp cầu mỏng tích điện đều có bán kính R và điện tích q.
Để chọn mặt Gauss, ta xác định tính đối xứng của
trường. Vì phân bố điện
tích là đối xứng cầu, E chỉ có
thành phần xuyên tâm và độ lớn của nó chỉ phụ thuộc
vào khoảng cách r tính từ tâm của phân bố điện tích. Mặt
Gauss lợi dụng được tính đối xứng này là mặt cầu có
cùng tâm với lớp cầu tích điện.
+ Trước tiên, ta xét trường ở các điểm nằm bên trong
lớp cầu bằng cách tìm thông lượng đi qua mặt Gauss cầu
với bán kính r nhỏ hơn bán kính R của lớp cầu. Vì E
phải có hướng xuyên tâm và chỉ phụ thuộc vào r, nên
thông lượng đi qua mặt cầu Gauss là 2 D.4 r E
Từ hình vẽ ta thấy điện tích nằm bên trong mặt cầu Gauss bằng không vì nó nằm gọn bên trong
lớp cầu tích điện nên = 0 D = 0 E = 0 (1.22) E
Điện trường ở bất kỳ điểm nào trên mặt cầu Gauss phải bằng không. Kết quả này đúng với mọi
mặt cầu Gauss, chỉ cần bán kính của nó nhỏ hơn bán kính của lớp cầu tích điện. Như vậy, điện
trường bằng không ở tất cả các điểm nằm bên trong lớp cầu tích điện: E = 0 (r < R) ĐÀO TUẤN ĐẠT 13
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
+ Bây giờ ta xét trường ở các điểm nằm ngoài lớp cầu tích điện, bằng cách tìm thông lượng đi
qua mặt Gauss cầu có bán kính r lớn hơn bán kính R của lớp cầu tích điện. Một lần nữa, do tính đối
xứng cầu, biểu thức cho thông lượng đi qua mặt Gauss là 2 ED.4 r
. Mặt này chứa toàn bộ điện tích q của lớp cầu
tích điện ở bên trong nó, tức
q = q. Định luật Gauss cho ta 2 D.4 r 2 0E(4 r ) q
Giải phương trình này tìm E, ta có 1q (r > R) (1.23) 2 4r 0
Biểu thức này của E là một biểu thức quen thuộc; nó là biểu thức cho điện trường do một điện
tích điểm q đặt ở tâm lớp cầu gây ra.
VD2. Tấm phẳng lớn tích điện đều
Tìm biểu thức gần đúng cho E do một tấm phẳng lớn tích điện đều với mật độ điện tích mặt là
gây ra tại điểm nằm gần tấm phẳng nhưng ở xa các mép của tấm.
Trước tiên ta xác định tính đối xứng của
trường và chọn mặt Gauss. Tấm phẳng nằm
trong mặt phẳng yz còn điểm tính điện trường
nằm gần trục x. Vì điểm tính diện trường nằm
xa các mép của tấm phẳng nên từ tính đối xứng
của bài toán ta cho rằng trường phải hướng
thẳng từ tấm phẳng ra (giả sử dương) dọc
theo trục x. Hơn nữa, nếu E nói chung còn phụ
thuộc vào vị trí thì nó chỉ có thể phụ thuộc x.
Ta lợi dụng tính đối xứng này bằng cách lấy
mặt Gauss là một hình trụ tròn thẳng có tâm ở
gốc toạ độ và có trục nằm dọc theo trục x. Hai
đáy của trụ cách đều mặt phẳng tích điện.
Thông lượng đi qua mặt trụ bằng không vì E vuông góc với dS tại mỗi điểm trên mặt trụ. Thông
lượng đi qua mỗi đáy của mặt trụ đơn giản chỉ là E nhân với diện tích ∆S của đáy vì E là đều và
song song với dS ở mỗi điểm trên hai đáy. Do đó = D.2∆S = 0E.2 S E
Từ hình vẽ ta thấy, điện tích nằm bên trong hình trụ Gauss là tích của mật độ điện tích mặt và
diện tích tiết diện ngang của hình trụ, đó cũng chí
nh là diện tích S của của đáy hình trụ. Như vậy, q = S .
Áp dụng định luật Gauss cho ta 0E.2 S = S Vậy E2 (1.24) 0
VD3. Hai tấm phẳng lớn tích điện đều
Tìm biểu thức gần đúng cho E do hai tấm phẳng lớn song song, tích điện đều với mật độ điện tích mặt là + và - . ĐÀO TUẤN ĐẠT 14
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
Điện trường do hai tấm gây ra được xác định bằng nguyên lý chồng chất điện trường. E E E
+ Tại mỗi điểm trong khoảng giữa hai tấm EE2
. Hai vector E+ và E- cùng chiều với o nhau nên E22 (1.25) o o o
+ Ở bên ngoài hai tấm các vector điện trường bằng nhau và ngược chiều nên điện trường tổng cộng bằng không E = 0. §1.4 ĐIỆN THẾ
1. Tính chất thế của điện trường tĩnh. Lưu số của vector cường độ điện trường
Công của lực tĩnh điện
Giả sử dịch chuyển điện tích điểm dương o q
trong điện trường của điện tích điểm dương q
theo một đường cong bất kỳ từ điểm 1 tới điểm
2. Trong dịch chuyển vô cùng nhỏ ds, công của
lực điện được xác định bởi: dA F.ds.cos q E.ds.cos o 1q q . . r .ds cos o2 4 o 1. s q c .q os o rd 2 4 o Ta có dr = ds.cosα. Vậy: 1 qqo dA . r rd 2 4 o
Trên toàn bộ quãng đường từ 1 tới 2 ta có: ĐÀO TUẤN ĐẠT 15
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT 2 rr2 2 r qq ooqqdr 1 1 A 2 dAr4 4 r 2 1 r 1 o ro 1 r qq qq 11 o o 1 A 2. . (1.24) 4 r 4 r o 1 o2
Nếu q di chuyển trong điện trường của hệ điện tích thì công của lực điện trường là: o nn q q 11 q q ii oo A A i . . (1.25) i 1i 4 r 4 r o 1i 1 o 2i
Từ (1.24) và (1.25) thấy công của lực tĩnh điện không phụ thuộc dạng của đường đi mà chỉ phụ
thuộc vào vị trí điểm đầu và cuối của quá trình dịch chuyển.
Tính chất thế của trường tĩnh điện
Nếu dịch chuyển q theo một đường cong kín bất kỳ thì công của lực tĩnh điện trong dịch o chuyển đó bằng không. A (1.28)
Như vậy, trường tĩnh điện là một trường thế và lực tĩnh điện là lực thế.
Lưu số của véctơ cường độ điện trường
Gọi E.ds là lưu số của vector cường độ điện trường.
Theo (1.28) thì lưu số của vector điện trường theo một đường cong kín bằng không. (1.29)
2. Thế năng tương tác điện
Khi điện tích q di chuyển từ điểm 1 đến điểm 2 trong điện trường của điện tích q, vì trưỡng tĩnh o
điện của q là trường thế nên theo cơ học công của lực tĩnh điện bằng độ giảm thế năng giữa hai điểm 1 và 2: A W W 12 1 2 Theo (1.24) công này là qq qq11 oo 1 A 2. . r 44 r o 2 1o
So sánh hai biểu thức trên ta có: qq qq11 oo r 1 W24 W4 .. (1.30) r 1 2 oo
Từ (1.30) suy ra biểu thức thế năng của điện tích điểm o
q đặt trong điện trường của điện tích
điểm q và cách q một khoảng r là: 1 qqo W . C (1.31) 4 r o
trong đó C là một hằng số tùy ý, W còn được gọi là thế năng tương tác của hệ điện tích điểm q và o q .
(1.31) chứng tỏ thế năng W được xác định sai khác một hằng số cộng C. Giá trị của C tùy ý và
không ảnh hưởng gì tới các phép tính trong thực tế, vì trong trường hợp các phép tính đó ta chỉ gặp ĐÀO TUẤN ĐẠT 16
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
các hiệu thế năng. Vì vậy, người ta quy ước chọn thế năng của o
q khi nó ở xa vô cùng đối với q bằng 0; khi đó ta có: 1 qq o W . C 0 C = 0 4 o
Với quy ước đó (1.31) trở thành: 1 qqo Wr . (1.32) 4 o Khi q, o
q cùng dấu (lực tương tác là lực đẩy), thế năng tương tác của chúng là dương. Khi q, o
q trái dấu (lực tương tác là lực hút), thế năng tương tác của chúng là âm.
Thế năng của q trong điện trường của hệ điện tích điểm: o n 1 qioq W W . (1.33) i i 1 4 o i r i r là khoảng cách từ o q đến điện tích i q . Khi o
q di chuyển trong một trường bất kì từ M → N ta có: N A q Eds W W MN o M N M Nếu o
q di chuyển từ M ra xa vô cùng thì AM o q E M ds W W M Nhưng vì ra xa thìW0 , nên: W q Eds (1.34) Mo M
Thế năng của điện tích điểm q0 tại một
điểm trong điện trường bằng công của lực tĩnh điện trong
sự dịch chuyển điện tích đó từ điểm đang xét ra xa vô cùng. 3. Điện thế
Trong các bài toán ta thấy rằng lực điện F, tác dụng lên điện tích thử F o q , tỉ lệ với o q . Tỉ số qo
phụ thuộc phân bố điện tích, nhưng không phụ thuộc o
q . Tỉ số này được định nghĩa là điện trường
E. Phương trình F gợi một cách làm tương tự đối với thế năng tương tác điện W. Nếu đem chia qo W cho điện thế V o
q thì đại lượng thu được cũng không phụ thuộc vào o q . Thành thử được định nghĩa là: W Vq (1.35) o
Cũng giống như E, V là một đại lượng đặc trưng cho trường, nó có giá trị tại mỗi điểm trong
không gian. Vì W là một vô hướng, nên V là một vô hướng. Từ (1.35) đơn vị của V là (J/C) hay (V). ĐÀO TUẤN ĐẠT 17
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
Điện tích của hạt thử o
q phải đủ nhỏ để sự có mặt của nó không làm thay đổi phân bố điện tích đã
gây ra điện thế và do đó làm thay đổi điện thế cần đo Công
Thế năng tương tác điện Điện thế
Khi dịch q trong điện trường
Thế năng của q trong điện
Điện thế tại một điểm trong o o của q: trường của q: điện trường của q: 11 q 1 q o q oqq 1 qq A . . o W. V. (1.36) 12 44 4 r 4 o r o 2 1 r or o Khi dịch Thế năng của
Điện thế tại 1 điểm của hệ điện o q trong điện trường o q trong điện của hệ điện tích:
trường của hệ điện tích: tích: 11 qq qq 1 qq 1 qi oo A . . io V Vi 4 . r (1.37) 12 W W 4 . r rr 44 i oi o 1i o 2i oi Tổng quát: Tổng quát: Tổng quát: 2 A q E.ds W q Eds V Eds 12 o o (1.38) 1 M M
(1.38): Điện thế V tại một điểm bằng công của lực tĩnh điện khi dịch chuyển một đơn vị điện tích
từ điểm đó ra xa vô cùng.
Điện thế do các phân bố liên tục gây ra được biến đổi tĩnh (1.37) bằng cách thay dấu tổng bằng
dấu tích phân. Phân bố liên tục được phân thành một số vô hạn các điện tích vô cùng nhỏ dq. n 1 q 1 dq i V lim (1.39) Ni1 4 4rr o q i o i0 ĐÀO TUẤN ĐẠT 18
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT 4. Hiệu điện thế UMN M V N V U Eds Eds Eds Eds Eds Eds MN M N M N N M
Hiệu điện thế giữa hai điểm bằng công của lực tĩnh điện trong sự dịch chuyển một đơn vị điện tích giữa hai điểm đó.
Nếu công dịch chuyển điện tích q0 từ M tới N là AMN thì M A N Uq (1.40) MN o
Từ (1.40) có thể tính được công của lực tĩnh điện bằng công thức: A q U q (V V ) (1.41) MN o MN o M N 4. Mặt đẳng thế
Nói chung điện thế của điện trường có giá trị khác nhau tại các điểm khác nhau. Tuy nhiên có thể có
những điểm khác nhau nhưng có cùng điện thế. Quỹ tích những điểm có cùng điện thế là mặt đẳng thế.
Để tìm dạng các mặt đẳng thế ta phải giải phương trình: V onst (1.42) (r)
(1.42) xác định một họ mặt đẳng thế. Cho const các giá trị khác nhau ta được các mặt đẳng thế khác
nhau. Chẳng hạn phương trình xác định mặt đẳng thế của điện tích điểm: 1q 4 . const or
Đó là phương trình của những mặt cầu đồng tâm, tâm là điện tích điểm.
Tính chất của mặt đẳng thế
- Các mặt đẳng thế không cắt nhau, vì tại mỗi điểm của điện trường chỉ có một giá trị xác định của điện thế. -
Công của lực tĩnh điện trong sự dịch chuyển một điện tích trên mặt đẳng thế bằng không.
Thực vậy, giả sử ta dịch chuyển điện tích q0 từ điểm M đến điểm N trên một mặt đẳng thế thì công
của lực tĩnh điện bằng A q U q (V V ) MN o MN o M N
Nhưng vì M và N nằm trên cùng một mặt đẳng thế nên VM = VN, do đó AMN = 0.
- Vector cường độ điện trường E tại một điểm trên mặt đẳng
thế vuông góc với mặt đẳng thế đi qua điểm đó.
Giả sử từ một điểm M nào đó trên mặt đẳng thế ta dịch
chuyển điện tích q một đoạn nhỏ ds trên mặt đẳng thế. Khi đó
công của lực tĩnh điện trong dịch chuyển đó là: dA Fds qEds 0
do đó E.ds 0 . Nghĩa là E ds ; ds lấy bất kỳ trên mặt đẳng thế nên E vuông góc với mọi ds qua M.
Các đường sức điện trường biểu diễn phương, chiều của
E nên suy ra rằng đường sức cũng luôn vuông
góc với mặt đẳng thế. ĐÀO TUẤN ĐẠT 19
ĐẠI HỌC BÁCH KHOA HÀ NỘI - VẬT LÝ ĐẠI CƯƠNG 2 - PH1122 - ĐÀO TUẤN ĐẠT
§1.5 HỆ THỨC LIÊN HỆ GIỮA E VÀ V
Điện thế và cường độ điện trường đều là những đại lượng đặc trưng cho điện trường. Vì vậy giữa
điện thế và điện trường có mối liên hệ nhất định.
Xét hai điểm M, N rất gần nhau trong điện trường E. Giả sử điện thế tại các điểm M và N lần lượt
là V và V + dV, với dV > 0 (nghĩa là VM < VN. Dịch chuyển
điện tích q0 từ M đến N, công của lực tĩnh điện là : dA = 0 q E.ds trong đó ds MN. Mặt khác dA = q0 [V (V – + dV)] = - q0dV. Do đó ta có E.ds - dV E.ds.cos = - dV (1.41)
Từ (1.41), vì dV > 0 nên E.ds.cos < 0; phải là một
góc tù. Vậy vector E hướng theo chiều giảm điện thế.
Đặt Es = ds.cos là hình chiếu của vector E theo phương của ds , ta có Esds = - dV dV Es = (1.42) ds
Từ (1.42) có thể tính các thành phần của vector E: Ex Ey Ez (1.43) x y z
Ta thấy rằng các thành phần của E đều được xác định bởi giá trị âm của các đạo hàm riêng của V. Nếu ta đã biết
một biểu thức của V do một phân bố điện tích gây ra, thì có thể sử dụng phương trình (1.43) để tìm E.
Trong giải tích các đẳng thức (1.43) được viết dưới dạng: E E i E j E k x y z E i j k x y z E gradV (1.44)
Xét điểm P nằm trên cùng mặt đẳng thế với điểm N nhưng nằm trên phương pháp tuyến dn của
mặt đẳng thế tại M. Dễ dàng thấy rằng độ giảm điện thế trên đoạn MP = dn cũng bằng – dV. Gọi En là
hình chiếu của vector E trên phương dn theo (1.42) ta có dV En = (1.45) dn
Vì vector E có phương pháp tuyến nên En = E, trong khi Es = Ecos E, vậy: ĐÀO TUẤN ĐẠT 20