Chương 1 - Tổng hợp lý thuyết về Điện trường tĩnh môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

CLB Hỗ Trợ Học Tập
Chương 1 - Điện trường tĩnh Học kỳ 2024.1
Lưu ý: Tài liệu chỉ sử dụng với mục đích ôn tập, sử dụng vào mục đích khác, CLB không chịu trách nhiệm.
I Form ôn tập chương 1
II Tóm tắt lý thuyết 1. Định luật Culomb F=1  q1q2 r 4πεε0 r2 r 2. 
Edo q gây ra tại một điểm E= =q  F r q0 4πεε0r2 r 3.  Edo các vật mang điện E=ˆ E=ˆ d  dq r 4πε0εr2 r tbv tbv
+ Vector cường độ điện trường gây ra bởi dây dẫn vô hạn tích điện đều E=|λ| 2πε0εr 1
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+ Điệntrườnggâybởiđĩatròntíchđiệnđều Edia =σ2εε0 1−1 r1 + R2h2
+ Điệntrườnggâybởimặtphẳngtíchđiệnđều E=σ 2εε0
4.ĐịnhlýOstrograski-Gauss(O-G) ϕe=˛  Dd qi S=X i S
5.Điệnthếcủacácvậtmangđiện: ∞ ˆ V=ˆdV =ˆ1 dq r;V  M= Eds 4πε0ε M
6.Côngdịchchuyểnđiệntíchqtrongđiệntrường: N ˆ A q MN = 0
Eds;AMN =q0(VM−VN); dA =−q0dV M
7.Hệthứcgiữacườngđộđiệntrườngvàđiệnthế: Es=−dVds . 2
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
III Câuhỏitrắcnghiệmlýthuyết Câu1 PhátbiểunàosauđâylàSAI?
A.Haiđiệntíchcùngdấuthìđẩynhau,tráidấuthìhútnhau.
B.Điệntíchcủamộthệcôlậpluônkhôngđổi.
C.Điệntíchcủaelectronlàđiệntíchnguyêntố.
D.Lựctươngtácgiữacácđiệntíchđiểmtỉlệnghịchvớikhoảngcáchgiữachúng. Câu2 PhátbiểunàosauđâylàSAI?
A.Vectơcườngđộđiệntrườnglàđạilượngđặctrưngchođiệntrườngvềphươngdiệntácdụnglực.
B.Trongmôitrườngđiệnmôiđẳnghướng,cườngđộđiệntrườnggiảmεlầnsovớitrongchân không.
C.Đơnvịđocườngđộđiệntrườnglàvôntrênmét(V/m).
D.ĐiệntrườngtĩnhlàđiệntrườngcócườngđộEkhôngđổitạimọiđiểm. Câu3
Mộtđiệntíchđiểmq < 0đượcđặttrêntrụccủamộtvànhkhuyêntâmOmangđiệntíchdương,sau
đóđượcthảtựdo.Kếtluậnnàosauđâylàđúng?
A.Điệntíchqdịchchuyểnvềphíavànhkhuyên,đếntâmOthìdừnglại.
B.Điệntíchqdịchchuyểnnhanhdầnvềphíavànhkhuyên,đếntâmOvàtiếptụcđithẳngchậm
dần,rồidừnglạiđổichiềuchuyểnđộng.
C.ĐiệntíchqđứngyêntạiM.
D.ĐiệntíchqdịchchuyểntừMraxatâmO. Câu4
Mộtđiệntíchđiểmdươngq,khốilượngm,lúcđầuđứngyên.Sauđóđượcthảnhẹvàođiệntrường
đềucóvectơcườngđộđiệntrường− →
EhướngdọctheochiềudươngcủatrụcOx (bỏquatrọnglực
vàsứccản).Chuyểnđộngcủaqcótínhchấtnàosauđây?
A.ThẳngnhanhdầnđềutheochiềudươngcủatrụcOx vớigiatốc qE m.
B.ThẳngnhanhdầnđềutheochiềuâmcủatrụcOx vớigiatốc qE m.
C.ThẳngđềutheochiềudươngcủatrụcOx.
D.ThẳngđềutheochiềuâmcủatrụcOx. 3
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu5
PhátbiểunàosauđâylàđúngkhinóivềcườngđộđiệntrườngtạiđiểmMdođiệntíchđiểmQgây ra?
A.TỉlệnghịchvớikhoảngcáchtừQđếnM.
B.PhụthuộcvàogiátrịcủađiệntíchthửqđặtvàoM. C.HướngraxaQnếuQ > 0. D.A,B,Cđềuđúng. Câu6
Mộtđiệntrườngcóvectơcườngđộđiệntrường− →
Eđượcbiểudiễnbởicôngthức:− → E=Ex.− → i+ Ey.− → j+Ez.−
→ ktrongđóEx, Ey, Ezlàcáchằngsốvà− → i , − → j , − →
klàcácvectơđơnvịcủahệtọađộ
Descartes.Điệntrườngnàylà: A.Điệntrườngxoáy.
B.Điệntrườngtĩnh,đều.
C.Điệntrườngtĩnh,khôngđều.
D.Điệntrườngbiếnthiên. Câu7
HaiđiệntíchđiểmQ1, Q2lầnlượtgâyratạiMcácvectơcườngđộđiệntrường−→ E1và− → E2.Phátbiểu
nàosauđâylàđúng,khinóivềvectơcườngđộđiệntrườngtổnghợptạiM? A.− → E=− →E1+− → E2nếuQ1, Q2cùngdấu. B.− → E=− →E1−− → E2nếuQ1, Q2tráidấu.
C.Luônđượctínhbởicôngthức:− → E=− →E1+− → E2 D.E=E1+E2 Câu8 Gọi− →
erlàvectơđơnvịhướngtừđiệntíchđiểmQđếnđiểmM;rlàkhoảngcáchtừQđếnM;ε0là
hằngsốđiện,εlàhệsốđiệnmôicủamôitrườngvàqlàđiệntíchthử.Biểuthứcnàosauđâyxác
địnhvectơcườngđộđiệntrườngdođiệntíchQgâyratạiM? A.− → E=Q4πεε0r2.− → er B.− → E=q 4πεε0r2.− → er C.− → E=Qq4πεε0r2.− → er D.− → E=Q4πεε0r3.− → er 4
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu9
Mặtphẳng(P)rộngvôhạn,tíchđiệnđềuvớimậtđộđiệnmặtσ.Cườngđộđiệntrườngdomặt
phẳngnàygâyratạiđiểmMtrongkhôngkhí,cách(P)mộtkhoảngađượctínhbởibiểuthứcnào sauđây? A.E=σ ε0 B.E=2σ ε0 C.E=σ 2ε0 D.E=σ 2aε0 Câu10
Mộtvòngdâytròn,bánkínhRtíchđiệnđềuvớiđiệntíchtổngcộnglàQ,đặttrongkhôngkhí.
Cườngđộđiệntrườngtạitâmvòngdâyđượctínhtheobiểuthứcnàosauđây? A.E=k|Q| R2 B.E=k|Q| √2R2 C.E=k|Q| 2√2R2 D.E= 0 Câu11
Mộtsợidâythẳngdàivôhạn,đặttrongkhôngkhí,tíchđiệnđềuvớimậtđộđiệntíchdàiλ.Cường
độđiệntrườngdosợidâynàygâyratạiđiểmMcáchdâymộtđoạnhđượctínhbởibiểuthứcnào sauđây?(k= 9.109Nm2C2) A.E=k|λ| h B.E=2k|λ| h C.E=k|λ| h2 D.E=k|λ| 2h Câu12 PhátbiểunàosauđâylàSAI?
A.Thônglượngcủavectơcườngđộđiệntrườnggửiquamặt(S)gọilàđiệnthôngΦE
B.ĐiệnthôngΦElàđạilượngvôhướngcóthểdương,âmhoặcbằngkhông.
C.ĐiệnthôngΦEgửiquamộtmặt(S)bấtkìluônbằngkhông.
D.TronghệSI,đơnvịđođiệnthôngΦElàvônmét(Vm). 5
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu13
Đườngsứccủađiệntrườnglàđường
A.vuônggócvớivéctơcườngđộđiệntrường− → Etạiđiểmđó.
B.màtiếptuyếnvớinótạimỗiđiểmtrùngvớiphươngcủavéctơcườngđộđiệntrường− → Etạiđiểm đó.
C.màpháptuyếnvớinótạimỗiđiểm trùngvớiphươngcủavectơcườngđộđiệntrường− → Etạiđiểm đó.
D.docáchạtnamchâmsắttừvẽnên. Câu14
ĐiệntíchqdichuyểntrongđiệntrườngcủađiệntíchQ,từ điểmMđếnđiểmN,cáchQnhững
khoảngrM,rNtrongkhôngkhí.Biểuthứcnàosauđâytínhcôngcủalựcđiệntrường? rM−kQ A.A=q kQ rN rM−kQ B.A=|q| kQ rN rN−kQ C.A=q kQ rM rM−k D.A=|Qq| k rN Câu15
CôngthứccủađịnhlýOxtrogradxki-Gaussvềđiệntrường: A.ΦE=ˆ(S) − → E·d− →S B.˛(S) − → D·d− → qitrong(S) S = Xi C.˛(C) − → E·d ℓ= 0 D.˛(S) − → E·d− → qitrong(S) S = Xi Câu16
Haiquảcầukimloạinhỏ,giốnghệtnhau,tíchđiệncùngdấuq1= q2,đặtcáchnhaumộtkhoảngr
trongkhôngkhíthìđẩynhaumộtlựcF1.Nếuchochúngchạmnhaurồiđưavềvịtrícũthìchúng: A.HútnhaumộtlựcF2>F1.
B.ĐẩynhaumộtlựcF2C.ĐẩynhaumộtlựcF2>F1.
D.Khôngtươngtácvớinhaunữa. 6
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu17
DiệntíchphẳngSnằmtrongmặtphẳng(Oxy),điệntrườngđềucóvectơcườngđộđiệntrường − → E = a ·− →i + b ·−
→jvớia,blànhữnghằngsốdương.ThônglượngđiệntrườngΦEquadiệntíchS sẽlà: A.ΦE=√a2+ b2S B.ΦE= aS C.ΦE= 0 D.ΦE= bS Câu18
MộtđĩatrònbánkínhRtíchđiệnđềuvớimậtđộđiệntíchmặtσ,đặttrongkhôngkhí.Phátbiểu
nàosauđâylàSAI,khinóivềvectơcườngđộđiệntrườngtạinhữngđiểmnẳmngoàiđĩa,gầntâm Ocủađĩa?
A.Vuônggócvớimặtphẳngcủađĩatròn.
B.Hướngraxađĩa,nếuσ > 0. C.E = 0.
D.Hướnglạigầnđĩa,nếuσ < 0. Câu19
Phátbiểunàosauđâyvềđườngsứcđiệnlàsai:
A.Đườngsứcđiệncóphươngtrùngvớiphươngcủalựcđiệntrường
B.Đườngsứcđiệnđiratừđiệntíchdươngvàkếtthúclàđiệntíchâm
C.Quamộtđiểmchỉvẽđượcduynhấtmộtđườngsứcđiện
D.Tậphợpcácđườngsứccủađiệntrườngđượcgọilàđiệnphổ Câu20
Haimặtphẳngrộngvôhạn,tíchđiệnđềuvớimậtđộđiệntíchmặt+σvà−σ,đặttrongkhôngkhí,
songsongnhau,cáchnhaumộtkhoảng2a.Chọngốcđiệnthếtạimặtphẳng+σ.Tínhđiệnthếtại
điểmnằmcáchđềuhaimặtphẳngmộtkhoảnga. A.V=a.σ 2ε0 B.V = −a·σ 2ε0 C.V=a.σ ε0 D.V = −a·σ ε0 7
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Đápán Câu1 2 3 4 5 6 7 8 9 10111213 Đápán DDBACBCAC D B C B Câu14151617181920 Đápán A BCCC A D 8
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
IV Câuhỏitựluậnlýthuyết Câu1
PhátbiểuđịnhluậtCoulomb.Địnhnghĩađiệntrường.Nêuđặcđiểmcủavéctơcườngđộđiệntrường.
Phátbiểunguyênlýchồngchấtđiệntrường. [Lờigiải]
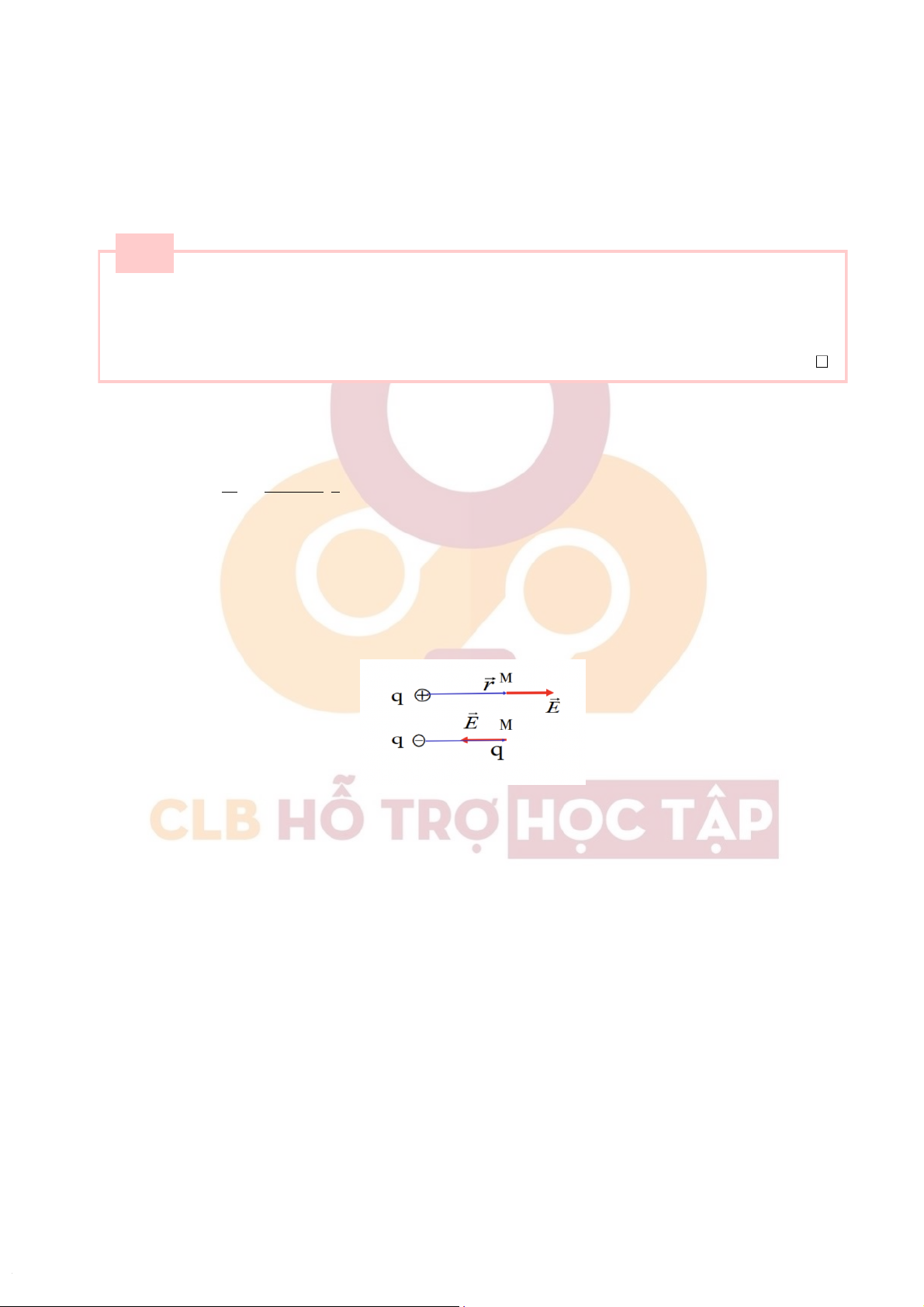
+)ĐịnhluậtCoulomb:lựctươngtáctĩnhđiệngiữa2điệntíchcóphươngnằmtrênđườngnối2điệntích,
cóchiềunhưhình1(haiđiệntíchcùngdấuthìđẩynhau,tráidấuthìhútnhau),cóđộlớntỉlệthuậnvới
tíchđộlớncủa2điệntíchvàtỉlệnghịchvớibìnhphươngkhoảngcáchgiữa2điệntíchđó.
Hình1:Lựctươngtácgiữa2điệntích
+)Côngthứctínhđộlớnlựctươngtácgiữa2điệntích: F=q1q2 4πε0ε.r2=kq1q2 ε.r2 trongđó:
•q1, q2làđộlớn2điệntíchđangxét(đơnvị:C) •ε0= 8,86.10−12C2 N.m2
•ε:hằngsốđiệnmôicủamôitrường.Đốivớimôitrườngchânkhông,ε= 1
+)Điệntrường:làkhoảngkhônggiantồntạixungquanhđiệntích,cóđặctrưnglàgâyralựcđiệnlên
cácđiệntíchđặttrongnó.
+)Đặcđiểmvectơcườngđộđiệntrường:
•Phương:trênđườngnốitừđiệntíchqđếnđiểmcầnxét
•Chiều:hướngraxađiệntíchqnếuqdương,hướnglạigầnđiệntíchqnếuqâm •Độlớn:E=k|Q|ε.r2=|Q| 4πε.r2 9
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
+)Nguyênlýchồngchấtđiệntrường:Vectocườngđộđiệntrườngcủamộthệđiệntíchđiểmbằngtổng
cácvectocườngđộđiệntrườnggâyrabởitừngđiệntíchđiểmcủahệ n 
E= E1+E2+· · · +En= Ei X i=1 Câu2
Nêucáchxácđịnhvéctơcườngđộđiệntrườngcủađiệntíchđiểm,hệđiệntíchđiểmphânbốgián
đoạnvàhệđiệntíchphânbốliêntục.Ápdụngcholưỡngcựcđiện,dâydẫnthẳngdài(vôhạn),vành
tròn,đĩatròntíchđiệnđều. [Lờigiải]
+)Xácđịnhvectơcườngđộđiệntrườngtạimộtđiểm: E= Côngthức: F =q4πεε0r2.r  q0 r
Nhậnxétvềvectocườngđộđiệntrườngtạimộtđiểm:
•Phương:nằmtrênđườngnốiđiệntíchđếnđiểmcầnxét
•Chiều:cùngchiềuvới 
r (hướngraxađiệntích)nếuqdương,ngượcchiềuvới r (hướnglạigầnđiện tích)nếuqâm
+)Vectocườngđộđiệntrườngcủamộthệđiệntíchđiểm:Sửdụngnguyênlýchồngchấtđiệntrường
•Đốivớihệđiệntíchđiểmphânbốgiánđoạn:Vectocườngđộđiệntrườngdohệđiệntíchđiểmtác
độnglênmộtvậtchínhbằngtổngvectocườngđộđiện trườngcủatừngđiệntíchđiểmtácdụnglên điểmấy 
E= E1+E2+E3 + · · · + En
•Đốivớihệđiệntíchphânbốliêntục:Tiếnhànhchianhỏvậtthànhnhiềuphầnnhỏchứađiệntích
dq.Vậtmangđiệnđượccoilàhệgồmvôsốđiệntíchđiểm.
+)Lưỡngcựcđiện:lưỡngcựcđiệnlàmộthệgồm2điệntíchtráidấu,cùngđộlớn,cáchnhaumộtkhoảng
drấtnhỏsovớikhoảngcáchtừđiểmcầnxétđếnlưỡngcựcđiện.
Mômenlưỡngcựcđiện: Pe=q. l
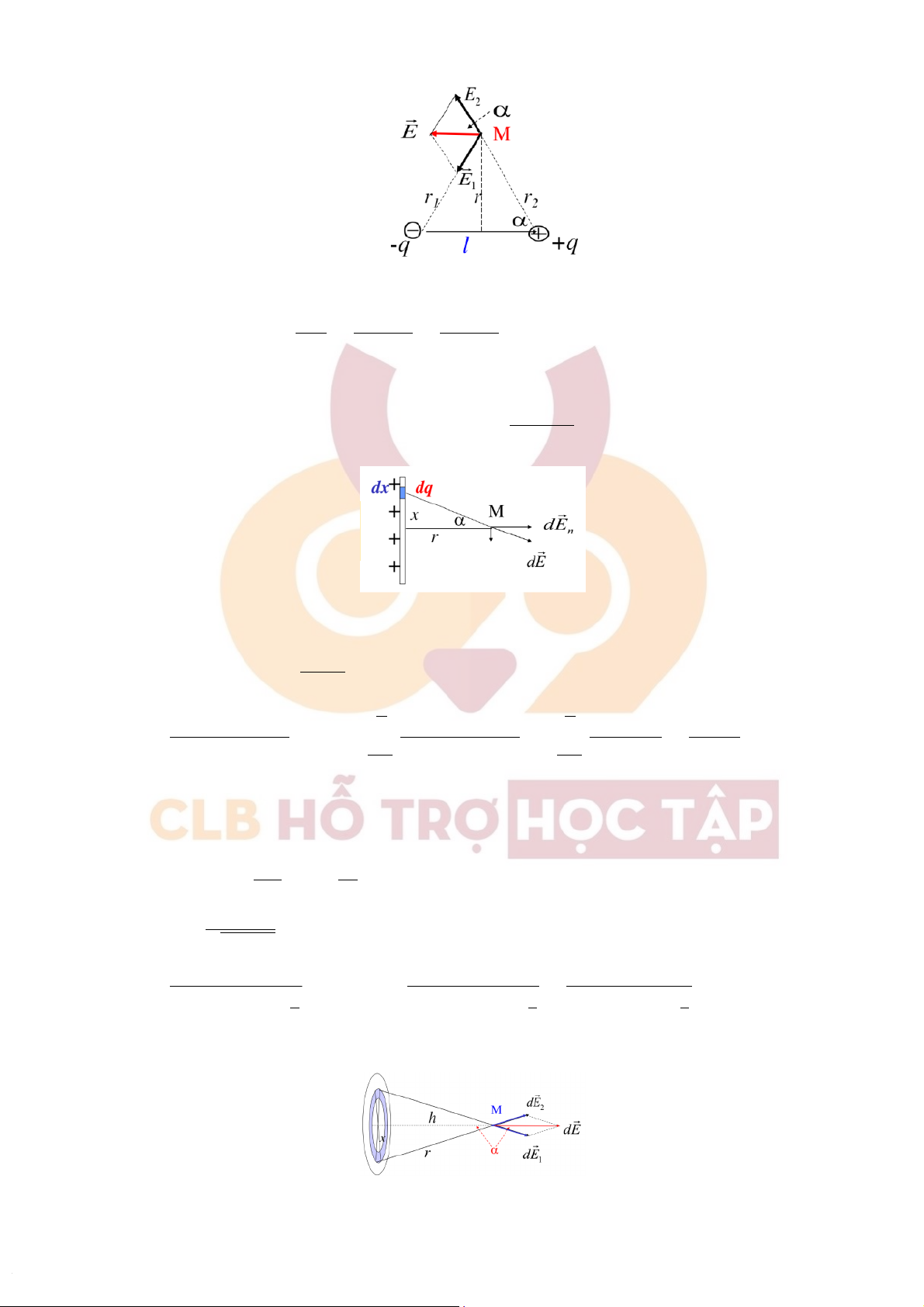
Vectocườngđộđiệntrườngnằmtrêntrungtrựccủalưỡngcực: 10
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập H
Khiđótacó: E= E1+E2 Độlớn:E= 2E1.cos α=E1.l =ql =Pe r1 4πεε0r3 4πεε0r3 1 1
+)Dâydẫnthẳngdàivôhạn:XétmộtđoạndâydẫncóchiềudàirấtnhỏcócườngđộđiệntrườngdE tại
mộtđiểmcáchdâymộtkhoảngr
Có:Exđốixứngtừngđôi⇒dE =dEy=dE. cos α=dq. cos α 4πεε0R2 •dq =λdx •x=rtan α⇒dx =rdα cos2α π π ⇒dE =λ.crodsφ 2φ. c 4 o πsε φ ε0.R2⇒E=ˆ 2 c λ os .2rd φ. φ 4π c ε o ε0s. φ R2=ˆ 2 λd 4 φ πε c ε0o.s r φ=λ −π −π 2πεε0r 2 2
+)Vànhtròntíchđiệnđều:Chiavànhtrònthànhnhữngđoạnnhỏmangđiệntíchdq.
Tacó: Exđốixứngtừngđôimột
⇒dE =dEy=dE cos φ.Mặtkháctalạicó: •dq =λ.rdφ =q2πr rdφ =q 2πdφ •cos φ=h √r2+h2 ⇒dE =q.hdφ ⇒E=ˆ2π q.hdφ =q.h 3 3 3 0 8π2εε0(r2+h2) 2 8π2εε0(r2+h2) 2 4πεε0(r2+h2) 2
+)Đĩatròntíchđiệnđều: 11
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
Chiađĩatrònthànhcácvànhtrònnhưhìnhvẽ Có:dE =dq.h 3 4πεε0(r2+h2) 2 Mặtkhác:
•dS=π(r+dr)2−πr2= 2πrdr →dq =σdS =σ.2πrdr ⇒dE =σ.2πhrdr ⇒E=ˆr σ.2πhrdr =σ ! 3 3 2εε0 1−1 0 4πεε r 0(r2+h2) 2 4πεε0(r2+h2) 2 1 + r2h2
Lưuý:Khir→+∞,mặttrêntrởthànhmặtphẳngvôhạntíchđiệnđều.Côngthứcđiệntrườngtrênmặt phẳngtíchđiệnđều:E=σ 2εε0 Câu3
PhátbiểuvàchứngminhđịnhlýOstrogradski-Gauss(ĐịnhluậtGauss).Ápdụngchotrườnghợp
mặtcầumangđiệnđều,mặtphẳngvôhạnmangđiệnđều,haimặtphẳngmangđiệntíchđốinhau,
mặttrụthẳngdàivôhạnmangđiệnđều. [Lờigiải]
+)ĐịnhlýOstrogradski-Gauss:ĐiệnthôngquamộtmặtkínScógiátrịbằngtổngđạisốcácđiệntích chứatrongmặtkínấy. ˛S  Dds =Xqi
+)ChứngminhđịnhlýO-G:xétthônglượngcảmứngđiệnđượcgửiquamộtdiệntíchdS có: dϕe=Dd S
=D.ds. cos α(vớiαlàgóctạobởi  Dvàvectopháptuyến n)
=Dn.ds (DnlàhìnhchiếucủaDtrênn)
XétmộtmặtkínlàmộtmặtcầutâmO,bánkínhRcó: ϕe=ˆS Dnds =q4πr2.4πr2=q
Vậytừthônggửiquamộtmặtkíncógiátrịbằngtổngđiệntíchchứatrongmặtấy
+)ĐịnhluậtGaussđốivớimặtcầumangđiệnđều:ChomặtcầutâmO,bánkínhR.Xácđịnhđiện
trườngtạiđiểmcáchOmộtkhoảngr>R S R r M
•TạomộtmặtSlàmặtcầutâmOđiquaM.Khiđó,Slàmặtkín.
•ÁpdụngđịnhlýO-GđốivớimặtStacó: 12
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập ˛S ds =q Dds =Xqi⇔D. ˛S ⇔D.4π.r2=q ⇔D=q 4πr2 ⇒E=D =q εε0 4πεε0r2
ĐốivớiđiểmMnằmtrongmặtcầu,tacócườngđộđiệntrườngtổnghợpbằng0.
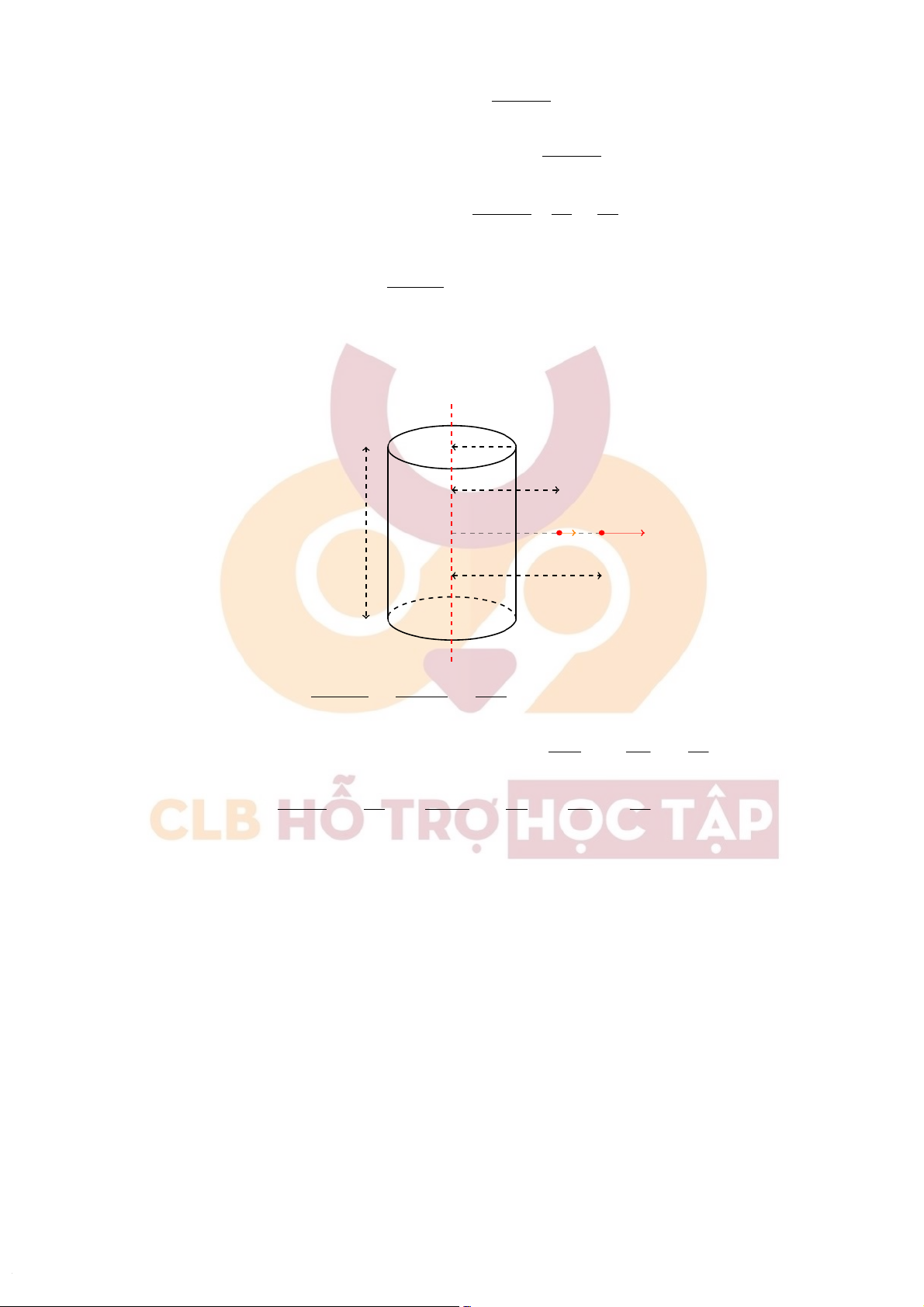
+)ĐịnhlýO-Gđốivớimặtphẳngvôhạntíchđiệnđều:
•Chọnmặtkínlàmặttrụnhưhìnhvẽ.Khiđótacóthônglượngquamặttrụlà:
ϕ=ˆhaiđáy Dds +ˆmặtbênDds
Mặtkhác,thônglượngcủamặtbênbằng0.ÁpdụngđịnhlýO-G,tacó:
ϕ=ˆhaiđáy Dds =σ.2πr ⇔2Dˆmộtđáy ds =σ.2πr ⇔4πrD =σ.2πr ⇔D=σ 2 ⇒E=D =σ εε0 2εε0
+)Điệntrườngcủahaimặtphẳngmangđiệntíchđốinhau:
•Ởkhoảnggiữa2mặtphẳng,tathấy  D1vàD2cùngchiều ⇒D= 2D1= 2 σ =σ 2εε0 εε0
•Ởbênngoài2mặtphẳng:E= 0
+)Điệntrườngcủamặttrụthẳngdàimangđiệnđều:
•ChọnmặtGausslàmặttrụbánkínhr,chiềudàil.Tacóđiệnthôngquamặttrụ: 13
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
ϕ=ˆhaiđáy Dds +ˆmặtbênDds •Dễthấy,ˆhaiđáy Dds = 0
⇒ˆmặtbên Dds =q⇔D.2πrl =Q
•Qlàđiệntíchtrênmặttrụ,vàgiảsửmậtđộđiệndàicủamặttrụlàλ,tacó:
D.2πrl =λ.l ⇔D=λ2πr ⇒E=D =λ εε0 2πεε0r Câu4
Tínhcôngcủalựctĩnhđiện.Từđóchứngtỏtrườngtĩnhđiệnlàmộttrườngthế. [Lờigiải]
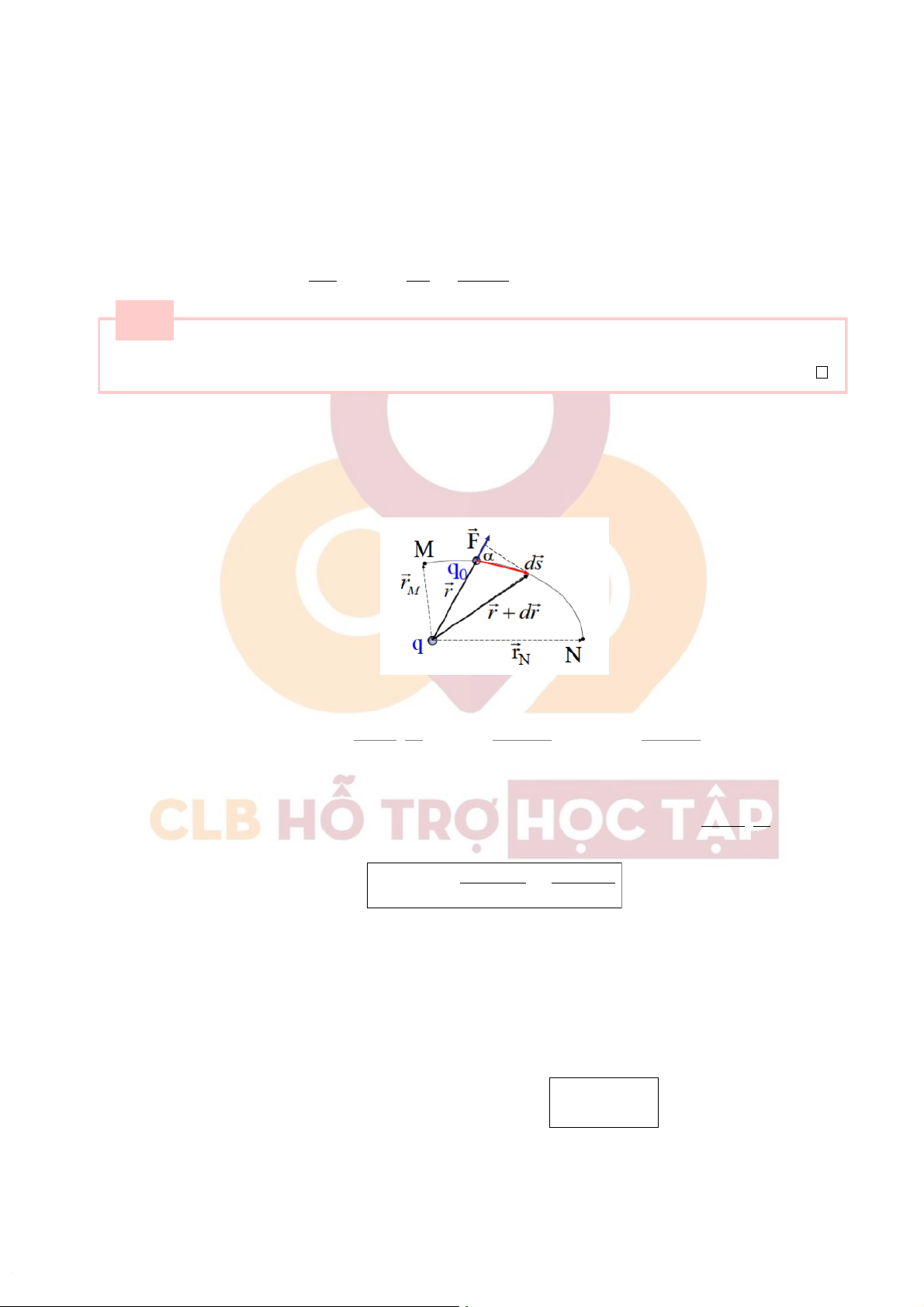
+ Xétđiệntíchthửq0dịchchuyểntừMđếnNtrongđiệntrườnggâybởiq(đứngyêntạiO).Lựctác dụnglênq0là− → F=q0− →E(−
→E:điệntrườngdoqgâyratạivịtríq0)
+ Côngcủalựctĩnhđiệntrongchuyểndờivôcùngnhỏd− → s: dA =− → F ds =q .− → 0− → E d− → s=q0.q r r 4π q εε0r2.ds.cosα =q0q.dr 3d− →s=q0 4πεε0r2(ds. cos α=dr: 4πεε0 hìnhchiếucủads lên− →r) N ˆ rN ˆ q0q .dr
+ Côngcủalựctĩnhđiệntrongchuyểndờiq0từMđếnN:AMN = dA = 4πεε0 r2 M rM ⇒AMN =q0q 4πεε0rM−q0q 4πεε0rN
→Côngcủalựctĩnhđiệntrongsựdịchchuyểnmộtđiệntíchđiểmq0trongmộtđiệntrườngbấtkỳ
khôngphụthuộcvàomộtdạngđườngcongdịchchuyểnmàchỉphụthuộcvàođiểmđầuvàđiểmcuối củachuyểndời.
Haynếudịchchuyểnq0theomộtđườngcongkínthìcôngcủalựctĩnhđiệntrongdịchchuyểnđóbằng
không→Trườngtĩnhđiệnlàmộttrườngthế. A=˛− → F ds =q0˛− →E d− → s= 0 ⇒˛− → E d− → s= 0 14
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu5
Dẫnracôngthứctínhthếnăngcủađiệntíchtrongđiệntrường.Nêuđịnhnghĩa,ýnghĩacủađiện
thếvàhiệuđiệnthế.Nếuđịnhnghĩavàcáctínhchấtcủamặtđẳngthế. [Lờigiải]
a)Dẫnracôngthứctínhthếnăngtrongcủađiệntíchtrongđiệntrường:
+ Vìđiệntrườnglàmộttrườngthếnêncôngcủalựctĩnhđiệntrongdịchchuyểnq0bằngđộgiảm
thếnăngcủađiệntíchđótrongđiệntrường: N ˆ A q MN = 0 Eds =WM−WN M
+ Thếnăngcủaq0trongđiệntrườngcủamộtđiệntíchđiểmq:
Xétq0dịchchuyểntrongđiệntrườngcủaq.Khiđó: AMN =q0q 4πεε0rM−q0q =WM−WN 4πεε0rN
→Biểuthứcthếnăngcủaq0đặttrongđiệntrườngcủađiệntíchđiểmqvàcáchđiệntíchnàymột
khoảngbằngrlàW=q0q 4πεε0r+C
QuyướcchọnWcủaq0khinóởxaqvôcùngbằngkhông:W∞= 0 →C= 0 →W=q0q 4πεε0r
+ Thếnăngcủaq0trongđiệntrườngcủahệđiệntíchđiểm:W=XWi=Xq0qi 4πεε0ri
+ Thếnăngcủaq0trongđiệntrườngbấtkỳ:WM=ˆ∞ q0Eds M
b)Địnhnghĩa,ýnghĩacủađiệnthếvàhiệuđiệnthế:
+Địnhnghĩa:TỷsốW/q0khôngphụthuộcvàođiệntíchq0màchỉphụthuộcvàocácđiệntích
gâyrađiệntrườngvàvàovịtríđiểmđangxéttrongđiệntrường.Vậytacóthểdùngtỷsốđóđể
đặctrưngchođiệntrườngtạiđiểmđangxét.V=W/q0đượcgọilàđiệnthếcủađiệntrườngtại điểmđangxét. +Ýnghĩa:
+)Điệnthếtạimộtđiểmtrongđiệntrườnglàmộtđạilượngvềtrịsốbằngcôngcủalựctĩnhđiện
trongsựdịchchuyểnmộtđơnvịđiệntíchdươngtừđiểmđóraxavôcùng.
+)HiệuđiệnthếgiữahaiđiểmMvàNtrongđiệntrườnglàmộtđạilượngvềtrịsốbằngcông
củalựctĩnhđiệntrongsựdịchchuyểnmộtđơnvịđiệntíchdươngtừđiểmMtớiđiểmN 15
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
c)Địnhnghĩavàcáctínhchấtcủamặtđẳngthế:
+Địnhnghĩa:MặtđẳngthếlàquỹtíchcủanhữngđiểmcócùngđiệnthếV=C=const
+Ýnghĩacủamặtđẳngthế:
+)Cácmặtđẳngthếkhôngcắtnhau
+)Côngcủalựctĩnhđiệntrongsựdịchchuyểnđiệntíchq0trênmặtđẳngthếbằngkhông: AMN =q0(VM−VN)=0
+)Vectơcườngđộđiệntrườngtạimộtđiểmtrênmặtđẳngthếvuônggócvớimặtđẳngthếtại điểmđó  E n ds M Câu6
Trìnhbàyvềmốiliênhệgiữacườngđộ điệntrườngvàđiệnthế.Ápdụngchohaimặtphẳngsong
songvôhạnmangđiệnđều,tráidấu;mặtcầumangđiệnđều;mặttrụthẳngdàivôhạnmangđiện đều. [Lờigiải]
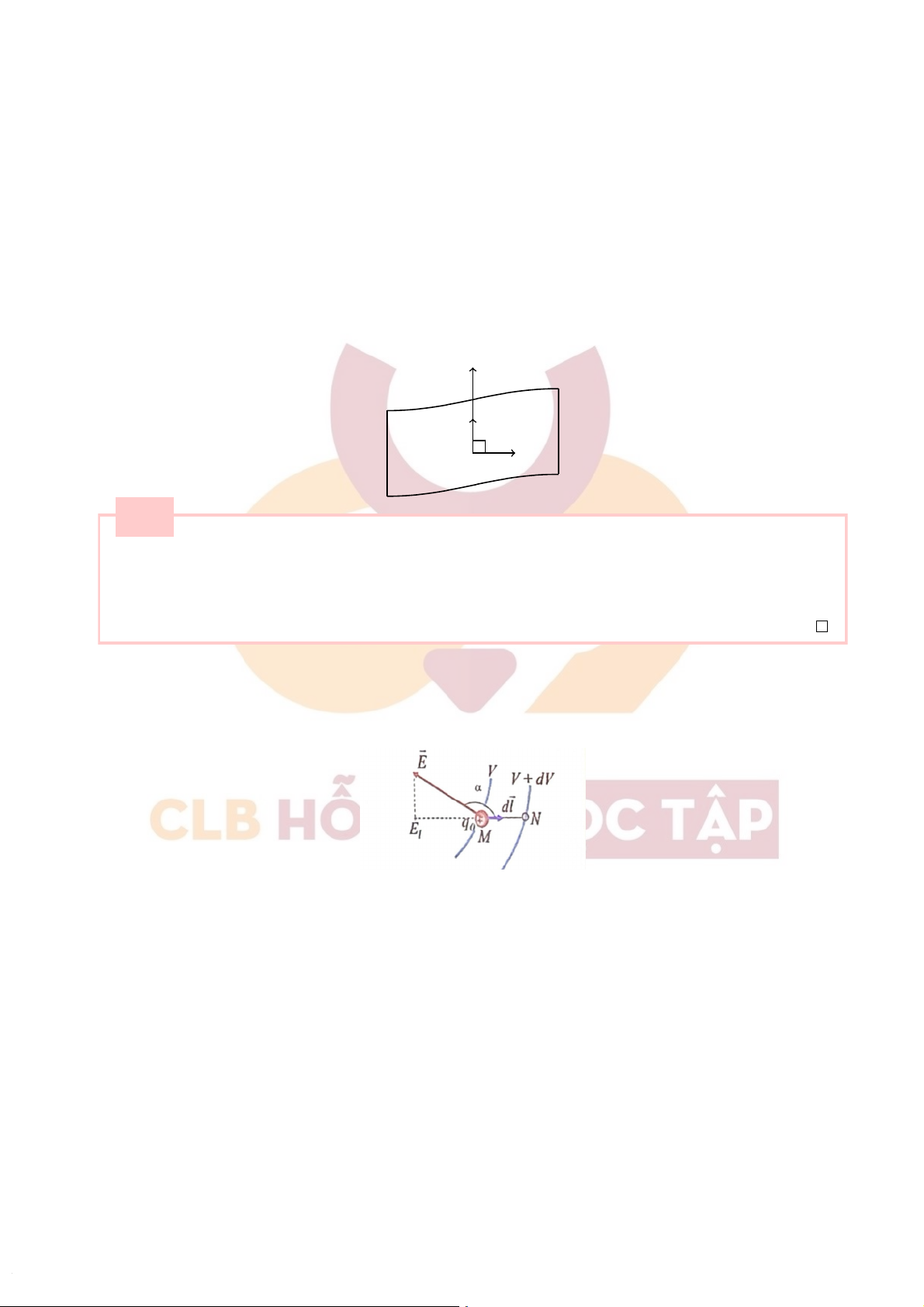
a)Mốiliênhệgiữacườngđộđiệntrườngvàđiệnthế:
+ Theođịnhnghĩatacó:dA =q0 Eds
+ MàdA =q0[V−(V+dV )] = −q0dV
Dođó,tacó: Eds =dV haydV =−Eds =−E.ds. cos(α)vớiα= ( E, ds)
* Kếtluận1:Vectorcườngđộđiệntrườngluônhướngtheochiềuđiệnthếgiảm.
* Kếtluận2:Hìnhchiếuvectorcườngđộđiệntrườngtrênmộtphươngnàođóvềtrịsốbằngđộ
giảmđiệnthếtrênđơnvịdàicủaphươngđó. 16
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
b)Ápdụngchohaimặtphẳngsongsongvôhạnmạngđiệnđều;mặtcầumangđiệnđều;mặttrụ
thẳngdàivôhạnmangđiệnđều
+ Xácđịnhhiệuđiệnthếgiữahaimặtphẳngsongsongvôhạnmangđiệnđều,tráidấu: V1V2 +- +- +-  E +- +- +- (1) (2) d
+)TacódV =−E.ds cos (I) +)Theo(I),tacó: V2 ˆ (2) ˆ (2) ˆ (2) ˆ −dV =V  1−V2= Eds = Eds =E ds =Ed V1 (1) (1) (1) MàE=σ nênV1−V2=σd εε0 εε0
+ Xácđịnhhiệuđiệnthếgiữahaiđiểmtrongđiệntrườngcủamộtmặtcầumangđiệnđều: R2 R1  E q + O dr R1R2
Giảsửtamuốnxéthiệuđiệnthếgiữa2điểmcáchtâmquảcầunhữngđoạnR1vàR2(với
R2> R1> R;Rlàbánkínhcủaquảcầu)
+)Tacó−dV = E.dr =E.dr. cos(α) = En.dr (Enlàhìnhchiếucủa Elênphươngpháptuyến ncủamặtcầu)
+)Màmặtcầulàmộtmặtđẳngthếnên  E↑↑  EnnênEn=E=q 4πεε0r2 17
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập ⇒ −dV =q 4πεε0r2.dr . V2 ˆ R2 ˆ q.dr Từđó: −dV = 4πεε0r2 V1 R1 HayV1−V2=q R1−1 4πεε0r2 1 R2
+)TrongtrườnghợpR1=RvàR2=∞(V2= 0),tasẽtìmđượcbiểuthứctínhđiệnthếVcủa
mộtmặtcầumangđiệnđềuV=q 4πεε0R
+ Xácđịnhhiệuđiệnthếgiữahaiđiểmtrongđiệntrườngcủamộtmặttrụthẳngdàivôhạnmang điệnđều ∆ R R1 (1) (2) l dr  E R2 +)Đãbiết:En=E=Q 2πεε0lr =λ2πεε0r=σR εε0r V2 ˆ R2 ˆ R2 ˆ σεR ε +)Từđó,tasuyra 0rdr =σR V1−V2= −dV = Endr = εε ln R 0 2 1 V1 R1 R1
+)VậyV1−V2=Q 2πεε0lln R2R1 =λ2πεε ln R21 =σR ln R2R1 0 εε0 18
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập V Bàitập Bàitập1
Đặtmộttụđiệnphẳngnằmngang,cácđườngsứccủađiệntrườngbêntrongtụhướngthẳngđứng
từtrênxuốngdưới.Khoảngcáchgiữa2bảntụlàd= 2 cm.ĐiệnápcủatụU= 10 V.Mộthạtbụi
nặngm= 2.10−7gnằmcânbằngchínhgiữa,cáchđềumỗibảntụ1cm.Lấyg= 10 m/s2. a,Tínhđiệntíchhạtbụi.
b,Điệnápcủatụđộtngộtgiảmmộtnửa.Hạtbụisẽchuyểnđộngvềphíanào,saubaolâutớibản
cựcvàkhichạmbảncựcnócóvậntốcbằngbaonhiêu? [Lờigiải] a,
+Vìtụđiệnnằmngang,hạtbụinằmcânbằngchínhgiữanêncólựctĩnhđiệngiữchohạtbụicânbằng.
Màcácđườngsứcđiệntrườnghướngtừtrênxuốngnênhạtbụimangđiệnâm.
+Điệntíchcủahạtbụilà: |q|=mgdU=2.10−10.10.0,02 10 = 4.10−12C b,
+Khiđiệnápcủatụgiảmmộtnửa,hạtbụisẽdichuyểndầnvớigiatốcavềbảncựcâm. +Có: P+F=ma ⇒ma =mg −qU′ d ⇒a=g−qU′md = 5(m/s2) Lạicó: d2=at2 2
⇒Thờigiantớibảncựclà:t=rd a≈0,063(s)
+Khichạmtớibảncựcvậntốchạtbụilà: v=at ≈0,32(m/s) 19
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Bàitập2
Từbảndươngcủamộttụđiệnphẳng,mộtđiệntửđượctáchravớitốcđộbanđầuv0dọctheođường
sứcđiệntrường.BiếttụcóhiệuđiệnthếU= 1,82Vvàkhoảngcáchgiữahaibảntụlàd= 4cm.
Chome= 9,1.10−31kg,|e|= 1,6.10−19C.Bỏquatácdụngcủatrọnglực.
a)Tìmgiátrịnhỏnhấtcủav0đểđiệntửcóthểtớiđượcbảnâmcủatụđiện.
b)Vớiv0= 4.105m/s,điệntửcóthểlạigầnbảnâmnhấtmộtkhoảngbaonhiêu?Sauthờigianbao
lâukểtừlúctáchra,điệntừlạiquaylạibảndươngcủatụđiện?. [Lờigiải] a,
+Đểtớibảncựcâmcủatụ,độngnăngbanđầuphảithắngcôngcảnhay: mv20 2≥qU ⇒v 5 m/s 0≥r2qU m= 8.10 ( ) b,
+Giatốccủađiệntử:a=−|e|U m.d =−8.1012(m/s2) Tacó: 02−v2 0= 2.a.S ⇒S=−v2 2a= . 0 −(4 105)2 −2.8.1012= 0,01(m) = 1(cm)
⇒Điệntừlạigầnbảnâmnhất1khoảngd′= 4 −1 = 3(cm)
+Thờigianđiệntửquaylạibảndương: t=2v0 |a|= 10−7(s) 20