












































Preview text:
Chương1.Biếncốngẫunhiênvàxácsuất Ch−¬ng 1
BiÕn cè ngÉu nhiªn vμ x¸c suÊt
Trong thùc tÕ chóng ta th−êng gÆp nh÷ng hiÖn t−îng ngÉu nhiªn, tøc lµ nh÷ng hiÖn
t−îng mµ mÆc dï víi mäi kh¶ n¨ng cã thÓ cã ta cè g¾ng gi÷ cho nh÷ng ®iÒu kiÖn c¬ b¶n
cña c¸c lÇn thÝ nghiÖm vÒ c¸c hiÖn t−îng Êy kh«ng thay ®æi, nh−ng ta vÉn kh«ng thÓ
kh¼ng ®Þnh ®−îc kÕt qu¶ cña tõng thÝ nghiÖm riªng lÎ sÏ nh− thÕ nµo. Së dÜ nh− vËy v×
ngoµi nhãm nh÷ng ®iÒu kiÖn c¬ b¶n ra cßn cã rÊt nhiÒu c¸c nguyªn nh©n kh«ng l−êng
tr−íc ®−îc, g©y t¸c ®éng kh¸c nhau trong qu¸ tr×nh tiÕn hµnh c¸c lÇn thÝ nghiÖm, lµm cho
kÕt qu¶ cña c¸c lÇn thÝ nghiÖm cã thÓ thay ®æi tõ lÇn nµy sang lÇn kh¸c, khiÕn cho mäi cè
g¾ng cña chóng ta ®Ó dù ®o¸n kÕt qu¶ chÝnh x¸c ë mçi lÇn thÝ nghiÖm riªng lÎ ®Òu v« hiÖu.
Tuy nhiªn, trªn c¬ së quan s¸t rÊt nhiÒu hiÖn t−îng thùc tÕ ng−êi ta thÊy r»ng nÕu nh−
ë mçi thÝ nghiÖm riªng lÎ sù xuÊt hiÖn cña mét sù kiÖn nµo ®ã cßn mang tÝnh chÊt ngÉu
nhiªn th× qua mét sè lín lÇn lÆp l¹i cïng thÝ nghiÖm Êy, kh¶ n¨ng xuÊt hiÖn kh¸ch quan
cña sù kiÖn ®ã l¹i biÓu hiÖn kh¸ râ nÐt. V× vËy mét lý thuyÕt to¸n häc ®· ®−îc x©y dùng
nªn nh»m nghiªn cøu mét c¸ch chÝnh x¸c tÝnh quy luËt cña c¸c hiÖn t−îng ngÉu nhiªn khi
ta lÆp l¹i nhiÒu lÇn cïng c¸c ®iÒu kiÖn c¬ b¶n lµm n¶y sinh ra c¸c hiÖn t−îng ®ã, ®−îc gäi
lµ Lý thuyÕt x¸c suÊt.
A- C¸c ®Þnh nghÜa vÒ x¸c suÊt
I. PhÐp thö vμ kh«ng gian c¸c biÕn cè s¬ cÊp
Trong lý thuyÕt x¸c suÊt, khi thùc hiÖn mét nhãm c¸c ®iÒu kiÖn c¬ b¶n nµo ®ã ng−êi
ta gäi lµ thùc hiÖn mét phÐp thö. NÕu kÕt qu¶ cña phÐp thö mµ kh«ng thÓ kh¼ng ®Þnh tr−íc
®−îc th× ta cã mét phÐp thö ngÉu nhiªn. Ta sÏ ký hiÖu phÐp thö ngÉu nhiªn lµ G.
C¸c kÕt qu¶ cã thÓ x¶y ra trong phÐp thö G sao cho khi G ®−îc thùc hiÖn th× thÓ nµo
còng cã mét trong chóng x¶y ra, chóng lo¹i trõ lÉn nhau vµ kh«ng thÓ ph©n chia thµnh Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 1
Chương1.Biếncốngẫunhiênvàxácsuất
nh÷ng kÕt qu¶ nhá h¬n th× c¸c kÕt qu¶ nh− vËy ®−îc gäi lµ c¸c biÕn cè s¬ cÊp. Nãi c¸ch
kh¸c mét biÕn cè s¬ cÊp lµ mét kÕt qu¶ tèi gi¶n cña phÐp thö.
TËp hîp tÊt c¶ c¸c biÕn cè s¬ cÊp ω cña phÐp thö G
G ®−îc gäi lµ kh«ng gian c¸c biÕn
cè s¬ cÊp (kh«ng gian mÉu) víi ký hiÖu lµ Ω .
ThÝ dô 1. NÕu phÐp thö lµ “tung mét ®ång xu” th× Ω = { S, N } trong ®ã: ω = S = kÕt 1
qu¶ lµ sÊp; ω = N = kÕt qu¶ lµ ngöa. 2
ThÝ dô 2. NÕu phÐp thö lµ “tung mét h¹t xóc s¾c” th×: Ω ={1,2,3,4,5,6}
trong ®ã : ω = i = ®−îc mÆt i chÊm (i= 6 , 1 ) i
ThÝ dô 3. NÕu phÐp thö lµ “tung cïng mét lóc hai ®ång xu” th× :
Ω ={(S,S), (S,N), (N,S), (N,N)}
ThÝ dô 4. NÕu phÐp thö lµ “Tung cïng mét lóc hai h¹t xóc s¾c” th×: Ω ={(x,y): x= , 1 6 ;y= , 1 6 }
ThÝ dô 5. NÕu phÐp thö lµ "tung mét ®ång xu cho tíi khi nµo ®−îc mÆt sÊp th× dõng" th×: Ω = S
{ , NS, NNS, NNNS,...}
ThÝ dô 6. NÕu phÐp thö lµ "®o kho¶ng c¸ch tõ ®iÓm ch¹m cña viªn ®¹n tíi t©m bia víi
b¸n kÝnh cña bia lµ mét ®¬n vÞ ®é dµi th× Ω = [0,1[. NhËn xÐt :
a. Sè l−îng c¸c phÇn tö cña Ω trong c¸c thÝ dô 1, 2, 3, 4 lµ h÷u h¹n.
b. Sè l−îng c¸c phÇn tö cña Ω trong thÝ dô 5 lµ v« h¹n nh−ng ®Õm ®−îc (tøc lµ ta cã thÓ
®¸nh sè ®−îc ω = S,ω = NS, 1 2 3 ω = NNS,....).
C¸c tËp h÷u h¹n hay v« h¹n ®Õm ®−îc gäi lµ c¸c tËp h¬p rêi r¹c.
c. Sè l−îng c¸c phÇn tö cña Ω trong thÝ dô 6 (sè c¸c ®iÓm cña ®o¹n [0,1[) lµ v« h¹n
nh−ng ®Õm ®−îc. Trong tr−êng hîp nµy ta b¶o Ω cã lùc l−îng continum.
II. - ®¹i sè c¸c biÕn cè
1. BiÕn cè ngÉu nhiªn
Mét biÕn cè ngÉu nhiªn A lµ mét tËp hîp con cña Ω Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 2
Chương1.Biếncốngẫunhiênvàxácsuất
ThÝ dô 1: Gäi A lµ biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3” khi tung h¹t xóc s¾c th× A={3,6}⊂ Ω . Ghi chó
a. KÕt qu¶ ω nµo cña G mµ lµm cho A x¶y ra th× kÕt qu¶ ®ã ®−îc gäi lµ kÕt qu¶ thuËn lîi
cho A. Nh− vËy biÕn cè A ë thÝ dô võa nªu cã hai kÕt qu¶ thuËn lîi.
b. Mçi biÕn cè s¬ cÊp ω còng cã thÓ coi lµ mét biÕn cè ngÉu nhiªn {ω } (gåm mét phÇn tö ).
c. Ω ®−îc gäi lµ biÕn cè ch¾c ch¾n.
d. TËp hîp trèng φ ®−îc gäi lµ biÕn cè kh«ng thÓ cã.
C¸c kh¸i niÖm võa nªu cã thÓ minh häa trong h×nh sau A x x x x x ω Ω
2. Mèi quan hÖ gi÷a c¸c biÕn cè
Stone ®· chøng minh ®−îc r»ng: gi÷a c¸c tËp hîp vµ c¸c biÕn cè cã mét sù ®¼ng cÊu.
V× vËy ta cã thÓ dïng mèi quan hÖ gi÷a c¸c tËp hîp ®Ó m« t¶ mèi quan hÖ gi÷a c¸c biÕn cè. Cô thÓ:
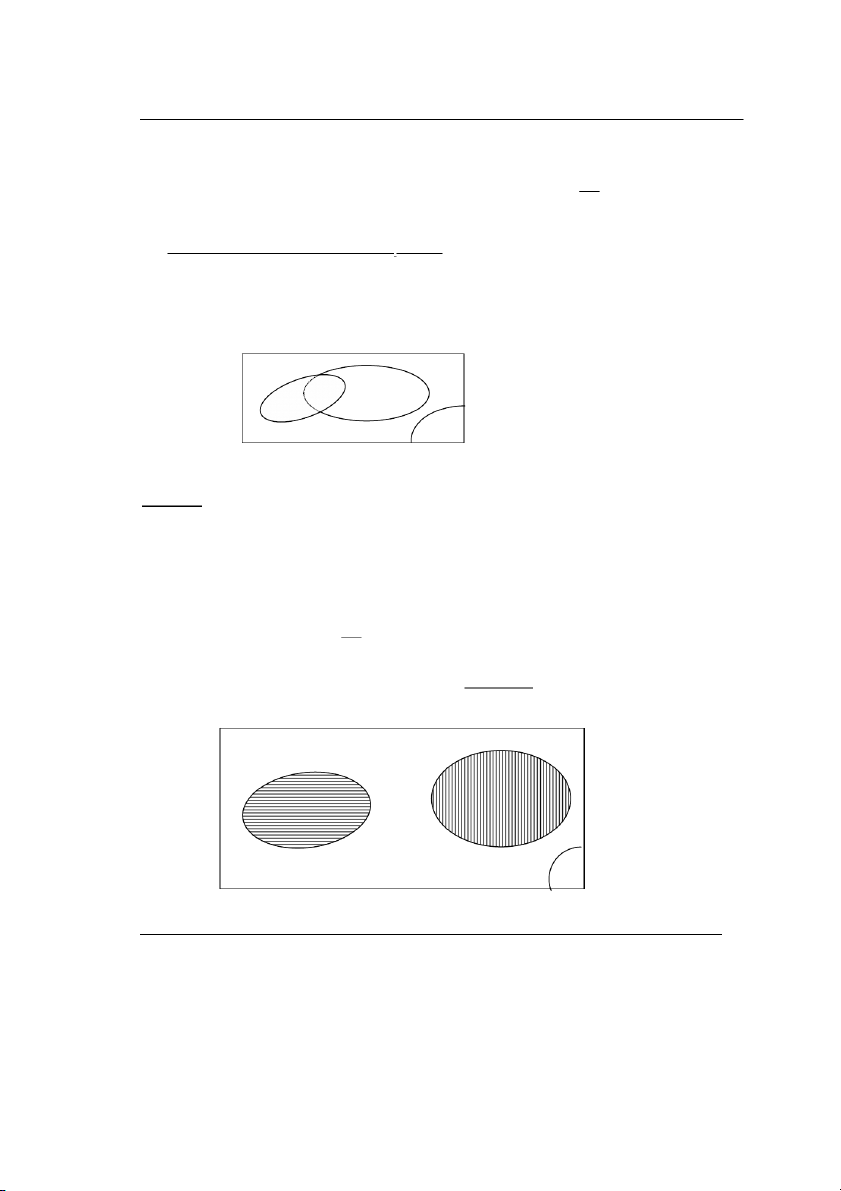
a. NÕu B ⊂ A th× biÕn cè B gäi lµ kÐo theo biÕn cè A. Nh− vËy c¸c phÇn tö ω cña Ω
thuéc B còng sÏ thuéc A (H×nh 1.1). Nãi c¸ch kh¸c biÕn cè B x¶y ra còng lµm cho biÕn cè A x¶y ra. A B x x x x Ω H×nh 1.1 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 3
Chương1.Biếncốngẫunhiênvàxácsuất ThÝ dô 2:
Gäi B lµ biÕn cè “®−îc mÆt 3 chÊm” tøc lµ B = {3}.
Khi ®ã B ⊂ A = {3, 6} = biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”.
b. NÕu B ⊂ A vµ A ⊂ B th× A vµ B gäi lµ hai biÕn cè t−¬ng ®−¬ng vµ ®−îc ký hiÖu lµ A=B.
ThÝ dô 3: Gi¶ sö mçi chÊm ®−îc 5 ®iÓm nÕu A lµ biÕn cè “®−îc mÆt 6 chÊm” vµ B lµ biÕn
cè “ng−êi tung ®−îc 30 ®iÓm” th× A = B.
c. NÕu B = Ω \ A th× B gäi lµ biÕn cè ®èi lËp cña A. Nh− vËy B sÏ x¶y ra khi A kh«ng x¶y * ra (H×nh 1.2) A B Ω H×nh 1.2
ThÝ dô 4: NÕu A ={3, 6}= biÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3” th× B = Ω \{3,
6}={1, 2, 4, 5} lµ biÕn cè “®−îc mÆt cã sè chÊm kh«ng chia hÕt cho 3”.
Ghi chó: BiÕn cè ®èi lËp cña biÕn cè A th−êng ®−îc ký hiÖu lµ A.
d. NÕu C = A ∪ B th× C gäi lµ biÕn cè tæng cña hai biÕn cè A vµ B. Nh− vËy C sÏ x¶y ra
khi Ýt nhÊt cã mét trong hai biÕn cè A hoÆc B x¶y ra (H×nh 1.3)
ta còng cã thÓ ký hiÖu C = A + B A B Ω H×nh 1.3
ThÝ dô 5: NÕu A={3, 6}= BiÕn cè “®−îc mÆt cã sè chÊ m lµ béi cña 3”
* (*)TÊt c¶ c¸c thÝ dô trong môc nµy sÏ ®−îc xÐt trong phÐp thö “ tung mét h¹t sóc s¾c” khi ®ã Ω ={1,2,3,4,5,6} Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 4
Chương1.Biếncốngẫunhiênvàxácsuất
B ={2,4,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ ch½n ”
th× C = A ∪ B ={2,3,4,6}= BiÕn cè “ ®−îc mÆt ch½n hoÆc béi 3 ”. n
T−¬ng tù biÕn cè tæng ∪A i cña n biÕn cè thµnh phÇn Ai (i= ,
1 n ) lµ biÕn cè sÏ x¶y ra i 1 =
khi Ýt nhÊt cã mét trong c¸c biÕn cè A x¶y ra. i
e. NÕu C = A ∩ B th× C gäi lµ biÕn cè tÝch cña hai biÕn cè A vµ B. Nh− vËy C sÏ x¶y ra
khi A vµ B ®Òu x¶y ra. (H×nh 1.4)
Ta còng cã thÓ ký hiÖu C = A.B B A Ω H×nh 1.4
ThÝ dô 6: NÕu A ={3,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”
B ={2,4,6} = BiÕn cè “®−îc mÆt cã sè chÊm lµ ch½n”.
th× C = A ∩ B ={6}= BiÕn cè “®−îc mÆt 6 chÊm”( võa lµ ch½n võa lµ béi cña 3) n
T−¬ng tù biÕn cè tÝch ∩Ai cña n biÕn cè thµnh phÇn A lµ biÕn cè sÏ x¶y ra khi tÊt c¶ i i=1
c¸c biÕn cè A i ®Òu x¶y ra (i= , 1 n )
f. NÕu A ∩ B = φ th× A vµ B gäi lµ hai biÕn cè xung kh¾c. Nh− vËy A vµ B sÏ kh«ng thÓ
cïng x¶y ra trong phÐp thö (H×nh 1.5) B A Ω H×nh 1.5 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 5
Chương1.Biếncốngẫunhiênvàxácsuất
ThÝ dô 7: NÕu A = {3, 6}= BiÕn cè “®−îc mÆt cã sè chÊm lµ béi cña 3”
B ={1, 2}= BiÕn cè “®−îc mÆt cã sè chÊm kh«ng qu¸ 2”
th× A ∩ B = φ (kh«ng thÓ võa ®−îc mÆt cã sè chÊm lµ béi cña 3 võa cã sè chÊm nhá h¬n hoÆc b»ng 2).
NhËn xÐt 1: Hai biÕn cè A vµ B ë h×nh 1.4 lµ kh«ng xung kh¾c (phÇn giao kh«ng trèng).
NhËn xÐt 2: Hai biÕn cè ®èi lËp A vµ A sÏ tho¶ m·n c¶ hai hÖ thøc: ⎧A ∪ A = Ω ( ) 1 ⎪⎨ ⎪⎩A ∩ A = φ ( ) 2
Nh− vËy cã thÓ nµo còng cã mét (hÖ thøc 1) vµ chØ mét (hÖ thøc 2) trong hai biÕn cè
nµy cïng x¶y ra trong phÐp thö.
Ghi chó: C¸c biÕn cè A i (i = ,
1 n ) gäi lµ xung kh¾c tõng ®«i. NÕu bÊt kú cÆp biÕn cè nµo
trong chóng còng lµ hai biÕn cè xung kh¾c. g. C¸c biÕn cè A i (i= ,
1 n ) gäi lµ mét hÖ ®Çy ®ñ n biÕn cè (hoÆc t¹o nªn mét ph©n ho¹ch cña Ω ) nÕu : ⎧ n ⎪ A = Ω ∪ ⎨ i i=1 (víi i ≠ j ) ⎪ ⎩A ∩ A = φ i j
Nh− vËy thÓ nµo còng cã mét vµ chØ mét trong c¸c biÕn cè A i (i= , 1 n )
x¶y ra trong phÐp thö (H×nh 1.6). An A 1 A …. A …. 2 i Ω H×nh 1.6 ThÝ dô 8:
NÕu A = {1, 2} = BiÕn cè “®−îc mÆt cã sè chÊm kh«ng qu¸ 2” Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 6
Chương1.Biếncốngẫunhiênvàxácsuất
B = {3} = BiÕn cè “®−îc mÆt cã sè chÊm lµ 3”
C ={4, 5, 6} = BiÕn cè “®−îc mÆt cã sè chÊm tèi thiÓu lµ 4” th× A, B, C lµ mét hÖ ®Çy ®ñ 3 biÕn cè.
NhËn xÐt: Hai biÕn cè ®èi lËp A vµ A lËp thµnh mét hÖ ®Çy ®ñ 2 biÕn cè.
Ghi chó: V× gi÷a c¸c tËp hîp vµ c¸c biÕn cè cã sù ®¼ng cÊu nªn c¸c tÝnh chÊt cña c¸c phÐp
to¸n vÒ tËp hîp còng ®óng cho c¸c phÐp to¸n vÒ biÕn cè, ch¼ng h¹n c¸c phÐp to¸n hîp vµ
giao c¸c biÕn cè cã tÝnh chÊt giao ho¸n vµ kÕt hîp. Cô thÓ ta cã: A ∪ B = B ∪ A
( A∪ B ) ∪ C = A∪ (B ∪ C) A ∩ B = B ∩ A
( A ∩ B ) ∩ C = A ∩ (B∩ C)
V× thÕ víi mét sè h÷u h¹n c¸c biÕn cè s¬ cÊp A i (i= , 1 n ) th× c¸c biÕn n n
cè ∪A i , ∩ Ai lµ hoµn toµn x¸c ®Þnh. i=1 i=1
Ngoµi ra ta còng cã quy t¾c ®èi ngÉu (quy t¾c De Morgan) nh− sau: ⎧ n n ⎪ ∩ A = i ∪ Ai ⎪ i =1 i = ⎨ 1 ⎪ n n ⎪ ∪ A = i ∩ A ⎩ i i =1 i =1
3. -§¹i sè c¸c biÕn cè
Trong thùc tÕ cã nhiÒu tr−êng hîp chóng ta muèn thùc hiÖn v« h¹n lÇn c c ¸ phÐp to¸n
vÒ c¸c biÕn cè vµ kÕt qu¶ vÉn ph¶i ®−îc mét biÕn cè. V× vËy ®èi víi mét hä A c¸c biÕn
cè nµo ®ã ®−îc x©y dùng trªn kh«ng gian Ω ta sÏ gi¶ thuyÕt nã tháa m·n c¸c yªu cÇu sau ®©y: a. Ω ∈ A
b. NÕu A∈ A th× A ∈ A Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 7
Chương1.Biếncốngẫunhiênvàxácsuất
c. NÕu A i (i = ( ,1∞) lµ mét d·y ®Õm ®−îc c¸c biÕn cè thuéc A th×: ∞ A ∪ ∈ A i i 1 =
Hä A c¸c biÕn cè nh− vËy ®−îc gäi lµ mét σ - ®¹i sè ( mét σ tr−êng Borel) c¸c biÕn cè.
Tõ ®Þnh nghÜa trªn ta suy ra: α . Φ ∈ A .
V× Ω ∈ A nªn Ω = Φ ∈ A.
β . NÕu A∈ A, B ∈ A th× A ∩ B ∈ A.
V× A∈ A nªn A ∈ A; B ∈ A nªn B ∈ A. Do ®ã A ∪ B ∈ A, tøc lµ A ∩ B ∈ A.
Suy ra A ∩ B ∈ A . VËy A∩ B ∈ A. ∞
γ . §iÒu kiÖn c) t−¬ng ®−¬ng víi ®iÒu kiÖn A ∩ ∈ i
A . §iÒu nµy suy i 1 = réng kÕt qu¶ ë β ).
Tãm l¹i mét - ®¹i sè c¸c biÕn cè sÏ ®ãng kÝn ®èi víi mét d·y h÷u h¹n hoÆc ®Õm
®−îc c¸c phÐp tÝnh tæng, tÝch hoÆc lÊy ®èi lËp víi c¸c biÕn cè thuéc A. Nãi c¸ch kh¸c
nÕu A lµ mét - ®¹i sè c¸c biÕn cè th× khi ta thùc hiÖn mét sè h÷u h¹n hay ®Õm ®−îc c¸c
phÐp to¸n võa nªu ®èi víi c¸c biÕn cè thuéc A th× kÕt qu¶ l¹i ®−îc mét biÕn cè thuéc A.
CÆp ( Ω , A ) ®−îc gäi lµ mét kh«ng gian ®o. Nã dïng ®Ó m« h×nh ho¸ mét phÐp thö ngÉu
nhiªn cïng víi c¸c sù kiÖn mµ ta muèn xÐt g¾n víi phÐp thö Êy. ThÝ dô 9: NÕu Ω ={ ω ,..., 1 ω , 2
ω n } vµ ta xÐt - ®¹i sè A lµ tËp hîp tÊt c¶ c¸c tËp con cña
Ω (kÓ c¶ Ω vµ Φ ) th× ®©y lµ - ®¹i sè lín nhÊt cã thÓ x©y dùng ®−îc tõ Ω vµ gåm 2 n phÇn tö.
III. §Þnh nghÜa tiªn ®Ò vÒ x¸c suÊt
Nh− ta ®· nªu ë phÇn më ®Çu ch−¬ng, mçi biÕn cè ngÉu nhiªn A cã mét kh¶ n¨ng
xuÊt hiÖn kh¸ch quan. V× thÕ trong lý thuyÕt x¸c suÊt ng−êi ta l−îng ho¸ kh¶ n¨ng xuÊt Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 8
Chương1.Biếncốngẫunhiênvàxácsuất
hiÖn kh¸ch quan cña mét biÕn cè A b»ng mét con sè. Con sè nµy gäi lµ x¸c suÊt cña A vµ
®−îc ký hiÖu lµ P(A). §èi víi P(A) cã nhiÒu c¸ch ®Þnh nghÜa kh¸c nhau trong ®ã c¸ch
®Þnh nghÜa theo tiªn ®Ò lµ cã tÝnh tæng qu¸t nhÊt vµ chÆt chÏ nhÊt vÒ mÆt l«-gic.
1. §Þnh nghÜa tiªn ®Ò vÒ x¸c suÊt
X¸c suÊt (hoÆc ®é ®o x¸c suÊt) P x¸c ®Þnh trªn - ®¹i sè c¸c biÕn cè A cña kh«ng
gian ®o ( Ω , A) lµ mét hµm thùc ¸nh x¹ A vµo R vµ tho¶ m·n c¸c tiªn ®Ò sau ®©y:
(P1). P(A) ≥ 0 víi mäi A ∈ A . (P2). P( Ω ) = 1. (P3). NÕu d·y {A ∩ A
i } (i=1,∞ ) tháa m·n ®iÒu kiÖn A i j = Φ víi mäi i ≠ j th× ∞ ∞ P( A ∪ ) = P(A ) ∑ . i i i=1 i 1 =
Tiªn ®Ò (P3) cßn gäi lµ tÝnh chÊt σ - céng tÝnh cña ®é ®o x¸c suÊt P. Bé ba (Ω , A, P)
®−îc gäi lµ mét kh«ng gian x¸c suÊt.
Ghi chó 1: Tõ tÝnh chÊt - céng tÝnh ta cã thÓ suy ra tÝnh chÊt h÷u h¹n céng tÝnh cña ®é n n
®o x¸c suÊt P, tøc lµ P( ∪A i ) =∑ P A ( ) víi A ∩ A i i j = Φ (i ≠ j). i 1 = i =1
(xem tÝnh chÊt 2 ë môc sau ).
Ghi chó 2: HÖ tiªn ®Ò nªu trªn ®· ®−îc Can-m«-g«-rèp ®−a ra vµo n¨m 1933. Ta thÊy hÖ
tiªn ®Ò nµy kh«ng m©u thuÉn, cã nghÜa lµ ta cã thÓ x©y dùng nh÷ng m« h×nh tho¶ m·n tiªn ®Ò ®ã.
Ch¼ng h¹n gi¶ sö xÐt Ω lµ mét tËp hîp h÷u h¹n c¸c phÇn tö ωi (i = , 1 n )
vµ A lµ hÖ tÊt c¶ c¸c tËp hîp con cña Ω (kÓ c¶ Ω vµ Φ ). Nh− ®· nªu, A gåm 2 n phÇn tö. ⎧pi ≥ 0 ⎪ Ta ®Æt p = P( ) sao cho: n (i= , 1 n ) i ωi ⎨ ⎪∑pi = 1 ⎩ i=1 Khi ®ã: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 9
Chương1.Biếncốngẫunhiênvàxácsuất m a. NÕu A = {ωi , ω , ..., ∑p ≥ 0. 1 i2 i ω } th× P(A) = m ik k 1 = n b. P( Ω ) = p ∑ i =1. i 1 = c. NÕu A = {ωi , ω ,..., 1 i2 i ω } m B = {ω ,ω ,... ω } 1 j j2 s j Trong ®ã:
ω i ≠ ω víi mäi k ≠ l th× A∩B = Φ k jl
vµ A∪B = {ωi , ω ,...,ω ,ω , ω } 1 i2 i m 1 j j ω ,... 2 js P(A∪B) = P{ωi , ω ,..., ω ,ω ,... ω } 1 i2 i ω , m j1 j2 js m n = ∑ p + i ∑p = P(A) + P(B) k jl k=1 l =1
Nh− vËy c¸c tiªn ®Ò cña Can-m«-g«-rèp ®−îc tho¶ m·n.
Ghi chó 3: HÖ tiªn ®Ò Can-m«-g«-rèp kh«ng ®Çy ®ñ, tøc lµ víi cïng mét tËp hîp Ω ta cã
thÓ x¸c ®Þnh x¸c suÊt P trªn tËp hîp A theo nh÷ng c¸ch kh¸c nhau.
Ch¼ng h¹n nÕu ta tung h¹t xóc s¾c th× Ω ={ 1
ω , ω 2 , ω3 ,ω4 , ω5 ,ω6 }.
NÕu h¹t xóc s¾c ®Òu ®Æn vµ ®ång chÊt th×: 1 P( 1
ω ) = P(ω 2) = P( ω3 ) = P( ω4 ) = P(ω5) = P(ω6 ) = 6
Nh−ng nÕu h¹t xóc s¾c kh«ng ®ång chÊt vµ kh«ng c©n ®èi th× c¸c x¸c suÊt P ph¶i x¸c
®Þnh kh¸c ®i, ch¼ng h¹n ta cã thÓ ®Æt: 1 1 P( 1
ω ) = P(ω 2 ) = P( ω3 ) = ; P(ω ) = P(ω ) = P( ω ) = . 4 4 5 6 12
Nh− vËy tÝnh kh«ng ®Çy ®ñ cña hÖ tiªn ®Ò Can-m«-g«-rèp kh«ng ph¶i lµ mét nh−îc
®iÓm, mµ tr¸i l¹i nã lµ mét −u ®iÓm v× nã cho phÐp ta tuú theo ®iÒu kiÖn cô thÓ cña vÊn ®Ò
®ang xÐt mµ x¸c ®Þnh x¸c suÊt thÝch hîp cho c¸c biÕn cè thuéc - ®¹i sè A.
2. Mét sè tÝnh chÊt cña x¸c suÊt suy ra tõ ®Þnh nghÜa tiªn ®Ò
TÝnh chÊt 1: P(Φ ) = 0. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 10
Chương1.Biếncốngẫunhiênvàxácsuất Chøng minh: XÐt d·y biÕn cè {A ∩
i } (i = 1, 2,...) sao cho A i = Φ víi mäi i. Khi ®ã A i A j =Φ víi i ≠ j ∞ vµ A = φ ∪ . i i=1 ∞ n ∞
VËy theo tiªn ®Ò (P3) ta cã: P(φ) = P( A ∪ ) = ∑P(A ) =∑ P(φ) i i i=1 i= 1 i 1 =
Râ rµng chØ cã mét sè thùc tho¶ m·n ®¼ng thøc nµy ®ã lµ sè 0. n n TÝnh chÊt 2: P( ∪A ∑P(A ) ∩ i )= i víi A i A j =φ (i≠j) i 1 = i=1 Chøng minh: XÐt d·y c¸c biÕn cè {A ∩
i } (i=1, 2, ..., n, ...) sao cho A i
A j =φ (víi i≠ j ) vµ A i =Φ ∞ n
khi i > n. Khi ®ã ∪ A = A . i ∪ i i=1 i 1 = Theo tiªn ®Ò (P3) ta cã: n ∞ ∞ n ∞
P(∪A ) = P( A ) =∑ P(A ) =∑P(A )+ ∑ P(A ) i ∪ i i i i i=1 i=1 i =1 i=1 i= n+1 n n = ∑P(A ) + 0 = ∑P(A ) . i i = i 1 i=1
TÝnh chÊt 3: P(A) + P( A ) = 1. Chøng minh:
Nh− ®· nªu, A vµ A tho¶ m·n hai hÖ thøc: ⎪⎧A ∪A = Ω ( ) 1 ⎨ ⎪⎩A ∩A =Φ (2)
Tõ (1) ta cã P( A∪ A ) = P( Ω ) = 1
Tõ (2) ta cã P(A∪ A ) = P(A) + P( A )
Tõ ®ã ta suy ra ®iÒu ph¶i chøng minh. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 11
Chương1.Biếncốngẫunhiênvàxácsuất
TÝnh chÊt 4: 0 ≤ P(A) ≤ 1. Chøng minh:
Theo tiªn ®Ò (P1) ta ®· cã P(A) ≥ 0
MÆt kh¸c theo tÝnh chÊt 3 th× P(A) = 1- P( A )
Mµ P( A )≥ 0 theo tiªn ®Ò (P1) nªn P(A) ≤ 1.
TÝnh chÊt 5: NÕu B ⊂ A th× P(B) ≤ P(A) vµ P(A\B) = P(A) - P(B). Chøng minh:
V× B ⊂ A nªn A = B ∪ (A\B). Do B ∩ (A\B) = Φ nªn P(A) = P(B) + P(A\B) (*).
Do P(A\B) ≥ 0 nªn P(A) ≥ P(B).
KÕt qu¶ thø hai ®−îc suy ra tõ hÖ thøc (*).
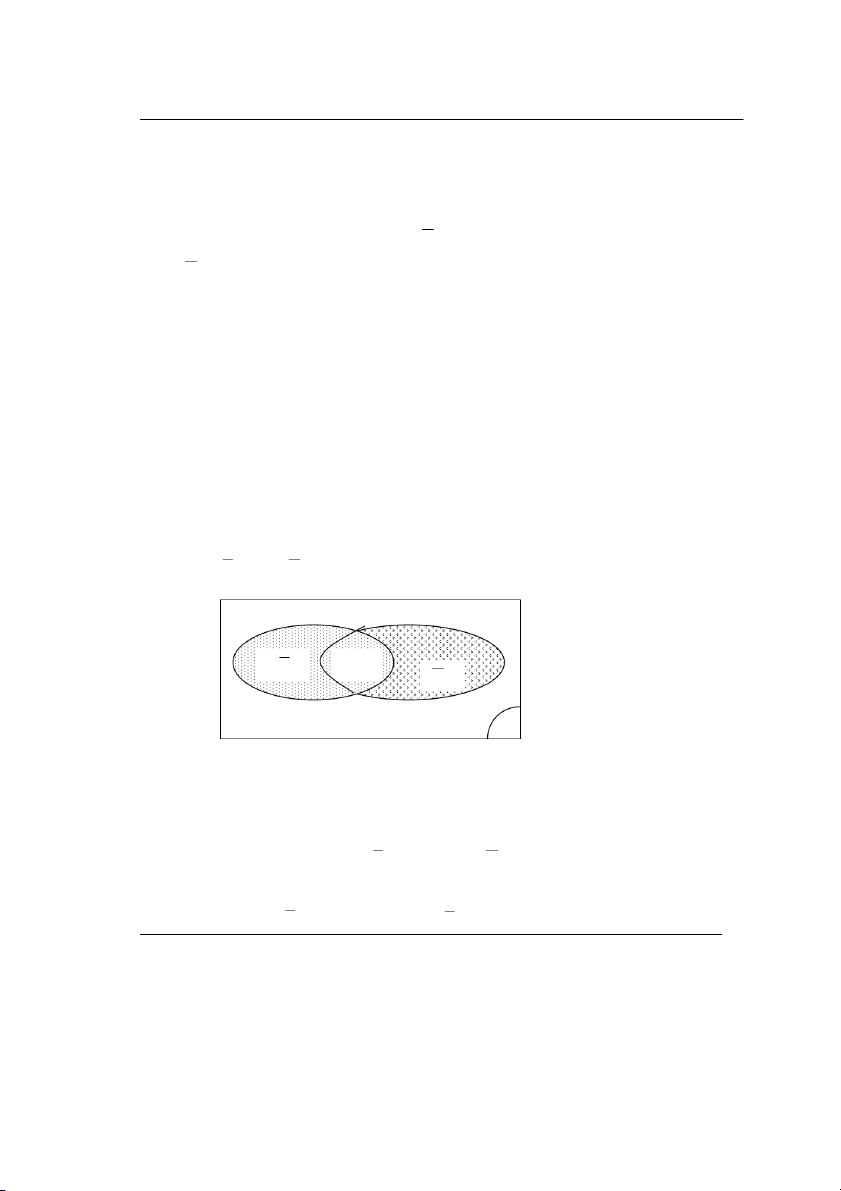
TÝnh chÊt 6: P(A ∪ B) = P(A) + P(B) - P(A ∩ B). Chøng minh:
Ta cã thÓ ph©n tÝch (xem h×nh 1.7) A ∪ B =A B ∪ AB ∪ A B A B AB A B B A Ω H×nh 1.7
Nh− vËy ta ®· ph©n tÝch tæng cña hai biÕn cè kh«ng xung kh¾c thµnh tæng cña ba biÕn cè
xung kh¾c tõng ®«i. Tõ ®ã theo tiªn ®Ò (P3) ta cã:
P(A ∪ B) = P(A B ) + P(AB) + P( A B) (1) MÆt kh¸c:
Do A = A B +AB nªn P(A) = P(A B ) + P(AB) Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 12
Chương1.Biếncốngẫunhiênvàxácsuất
suy ra P(A B ) = P(A) - P(AB) (2)
Do B = A B + AB nªn P(B) = P(A B ) + P(AB)
suy ra P( A B) = P(B) - P(AB) (3)
Thay vµo (2) vµ (3) vµo (1) ta ®−îc
P(A ∪ B) = P(A) - P(AB) + P(AB) + P(B) - P(AB) = P(A) + P(B) - P(AB)
Ghi chó: Më réng tÝnh chÊt nµy ta cã: n n n n P( ∪ i
A )= ∑P(A )-∑ P(A A ) + ∑P(A A A ) - ... + i i j i j k i=1 i =1 i< j < i < j k +(-1)n-1 P(A A ...A ). 1 2 n Chøng minh: 2
Theo tÝnh chÊt 6 ta cã P( ∪Ai ) = P(A ) + P(A ) - P(A A ) 1 2 1 2 i 1 = Gi¶ sö n−1 n−1 n −1
P(∪A ) =∑P(A ) -∑ P(A A ) +...+(-1)n-2 P(A ) i i i j 1 A 2 ..An-1 i 1 = i = 1 i =1 Khi ®ã: n n 1 − ∪ Ai = (∪A )∪ A i n i 1 = i 1 = n n− 1 n 1 − P( ∪A i ) = P(∪A ) + P(A A ) i n ) - P(A n ∪ i i 1 = i 1 = i 1 = n 1 - n 1 − = P( ∪A ) + P(A A A ) i n ) - P( ∪ i n i 1 = i=1
¸p dông gi¶ thiÕt quy n¹p cho thµnh phÇn thø nhÊt vµ thø ba ë bªn vÕ ph¶i råi ghÐp
c¸c tæng l¹i víi nhau ta sÏ ®−îc kÕt qu¶ ph¶i chøng minh. TÝnh chÊt 7: ∞ ∞ P( ∪A ) ≤ ∑ P A n ( n ) n=1 n =1 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 13
Chương1.Biếncốngẫunhiênvàxácsuất Chøng minh:
ThËt vËy, nÕu ®Æt B1 = A1 B 2 = A ∩ A 1 2 ...............
B n = A ∩ A ∩ ... ∩ A ∩ A 1 2 n-1 n ............... th× ta cã: B n ⊆ A n (n ≥ 2) B ∩ B i j = Φ (i ≠ j) ∞ ∞ ∪A = B . n ∪ n n=1 n=1 Do ®ã: ∞ ∞ ∞ ∞
P( ∪A ) = P( B ) =∑P B ≤ ∑ P A n ∪ n ( ( n ) n ) n=1 n=1 n=1 n=1
( V× B n ≤ A n nªn P(B n )≤ P(A n )).
TÝnh chÊt 8: NÕu P lµ mét ®é ®o x¸c suÊt x¸c ®Þnh trªn - ®¹i sè A cña kh«ng gian ®o
( Ω , A) th× c¸c ®iÒu kh¼ng ®Þnh sau ®©y lµ t−¬ng ®−¬ng:
a. P cã tÝnh chÊt - céng tÝnh.
b. P liªn tôc trªn, cã nghÜa lµ víi bÊt kú mét d·y ®¬n ®iÖu t¨ng ∞ A lim A =
1 ⊂ A 2 ⊂ .... ⊂ A n ⊂ ... thuéc A sao cho n ∪ A ⊂ A th× n→∞ n n=1 ∞
lim P(A ) n = P(∪A ). n →∞ n n=1
c. P liªn tôc d−íi, cã nghÜa lµ víi bÊt kú mét d·y ®¬n ®iÖu gi¶m A ⊃ A ⊃ A ⊃ ... 1 2 n ∞
thuéc A sao cho lim A = n ∩A ∈ A th× n →∞ n n=1 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 14
Chương1.Biếncốngẫunhiênvàxácsuất ∞
limP (A ) n = P(∩A ). n →∞ n n=1
d. P liªn tôc t¹i “kh«ng” tøc lµ víi bÊt kú d·y ®¬n ®iÖu gi¶m ∞ A ⊃ A ⊃ ... ⊃ A A =Φ th× lim ( P A ) =0. 1 2 n ⊃ ... thuéc A sao cho ∩ n n n →∞ n=1
Ghi chó: TÝnh chÊt d) nµy cßn gäi lµ tiªn ®Ò liªn tôc. Chøng minh: a) => b) V× A ⊂ A ⊂ .... ⊂ 2 A 1
n ⊂ ... nªn ta cã thÓ viÕt: ∞ ∪A = A ) + ... n 1 + (A 2 \A 1 ) + (A 3 \ A 2 n=1
Do c¸c biÕn cè bªn vÕ ph¶i xung kh¾c tõng ®«i nªn theo a) ta cã: ∞ P( ∪A ) = P(A \A n 1 ) + P(A 2 1 ) + P(A 3 \ A 2 ) + ... n=1 ∞ ∞ Do ∪ A ) tån t¹i. n
A ⊂ A vµ trªn A ®· x¸c ®Þnh ®é ®o x¸c suÊt P nªn P(∪ n n=1 n=1
V× thÕ chuçi bªn vÕ ph¶i cña ®¼ng thøc trªn ph¶i héi tô. Do ®ã ta cã: ∞
P(∪A ) = lim(P(A ) + P(A \ A ) + ......+ P(A \ A P A − ) lim ( 1 2 1 n n 1 ) = ) n n n→∞ n →∞ n=1 Tãm l¹i P( lim A lim P(A n ) = ) n . n →∞ n →∞ b) => c)
V× {A n } lµ d·y ®¬n ®iÖu gi¶m nªn nÕu ta ®Æt A 'n = A1 \A n th× {A'n } sÏ lµ mét d·y ®¬n
®iÖu t¨ng. VËy theo b) th×: ∞ lim P( ' A ) A ' A n = P( ' lim n ) = P( ∪ ) n →∞ n →∞ n n=1 ∞
Tøc lµ lim P(A \ A ) 1 n = P[ ∪ (A \ A ) ] n→∞ 1 n n=1
MÆt kh¸c do A1 ⊃ A nªn ta cã thÓ viÕt n Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 15
Chương1.Biếncốngẫunhiênvàxácsuất A n = A1 \(A1 \A n ) Do ®ã P(A n ) = P(A ) - P(A 1 1 \A n )
lim P(A ) lim ( P A \ A n = P(A n n n→∞ 1 ) - ) n→∞ ∞ = P(A1 ) - P[∪(A \ A ) ] 1 n n=1 ∞ ∞
Còng do A1 ⊃ A 2 ⊃ ... ⊃ A n ⊃ ..... nªn ∪(A \ A ) = A A 1 n 1 \ ∩ n n=1 n=1 ∞
VËy : lim P(A ) n = P(A A ] n →∞ 1 ) - P[A 1 \ ∩ n n=1 ∞ ∞
= P(A1 ) - [ p(A1 ) - P(∩A )] = P(∩A ). n n n=1 n=1 Tøc lµ P( lim A limP (A n ) = ) n . n→∞ n →∞ c) => d)
MÖnh ®Ò nµy lµ hiÓn nhiªn, do c¸c kÕt qu¶ trªn ta cã: ∞ lim ( P A ) lim A n = P( n ) = P( ∩A ) = P(Φ ) = 0 n→∞ n →∞ n n=1 d) => a)
Tr−íc hÕt ta cã thÓ viÕt ∞ n ∞ ∪A = ∪A + A i i ∪ i i=1 i=1 i=n+1
Do gi¶ thiÕt c¸c biÕn cè lµ xung kh¾c tõng ®«i vµ vÕ ph¶i coi nh− chØ gåm hai biÕn cè
(tr−êng hîp h÷u h¹n) nªn: ∞ n ∞ P(∪A ) = P( A ) + P( A ) i ∪ i ∪ i i=1 i 1 = i=n+1 ∞ ∞ n
NÕu ®Æt B n = ∪A th× P(∪A ) = P( ∪A ) + P(B ). i i i n 1 + i=n i=1 i=1 Ta thÊy B n ⊃ B n 1 + ⊃ B n+2 ⊃ .... Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 16
Chương1.Biếncốngẫunhiênvàxácsuất
MÆt kh¸c nÕu B n x¶y ra th× mét trong c¸c biÕn cè A x¶y ra (i≥ n), do ®ã c¸c biÕn cè i A i 1
+ , A i+2 ,... sÏ kh«ng x¶y ra v× c¸c biÕn cè cña d·y {A i } (i= , 1 ∞ )
Theo gi¶ thiÕt lµ xung kh¾c tõng ®«i. Tõ ®ã c¸c biÕn cè B i 1
+ , B i+2 ,...sÏ lµ kh«ng thÓ ∞ cã, v× thÕ ∩B = φ. i i=n ∞ ∞
Do ∪A ∈ A nªn P( A ) tån t¹i. i ∪ i i=1 i=1 VËy ta cã thÓ viÕt ∞ ∞ P(∪A ) = limP( A ) + limP(B ) i ∪ i n 1 + i=1 n→∞ i=1 n→∞ n = lim ∑ P(A )+ 0 i n→∞ i=1 ∞ = ∑P(A ) . i i=1
3. Nguyªn lý x¸c suÊt nhá vµ lín
X¸c suÊt P(A) nh»m nªu lªn kh¶ n¨ng x¶y ra cña A chø kh«ng kh¼ng ®Þnh vÒ hiÖn
thùc cña biÕn cè ®ã. Tuy nhiªn biÕt ®−îc kh¶ n¨ng x¶y ra cña A ta cã thÓ nhËn ®Þnh ®−îc
t×nh h×nh x¶y ra cña A mét c¸ch hîp lý. Cô thÓ qua thùc nghiÖm vµ quan s¸t thùc tÕ ng−êi
ta rót ra “nguyªn lý x¸c suÊt nhá” sau ®©y:
“Mét biÕn cè cã x¸c suÊt nhá th× thùc tÕ ta cã thÓ coi nã lµ kh«ng thÓ x¶y ra trong mét phÐp thö”.
Tuy nhiªn víi møc x¸c suÊt nhá lµ bao nhiªu th× biÕn cè sÏ ®−îc coi lµ “hÇu nh− kh«ng
thÓ cã”? §iÒu nµy sÏ do tõng tr−êng hîp cô thÓ quyÕt ®Þnh. VÒ vÊn ®Ò nµy t¸c gi¶ Guy
Lefort còng cã ý kiÕn nh− sau: “Trong thùc hµnh ph¶i coi sù kiÖn “rÊt Ýt kh¶ n¨ng x¶y ra”
lµ mét sù kiÖn thùc tÕ kh«ng thÓ x¶y ra (nÕu kh«ng th× chóng ta kh«ng bao giê d¸m qua
®−êng v× thùc tÕ cã mét x¸c suÊt, tuy rÊt nhá, nh−ng kh«ng ph¶i lµ sè 0, ®Ó chóng ta bÞ xe
c¸n). Nh−ng mét sù kiÖn rÊt Ýt kh¶ n¨ng x¶y ra kh«ng ph¶i lµ kh«ng thÓ x¶y ra vµ nh÷ng
quyÕt ®Þnh cña chóng ta khi ¸p dông quy t¾c trªn cã thÓ m¾c nh÷ng sai lÇm mµ chóng ta cÇn l−u ý”. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 17
Chương1.Biếncốngẫunhiênvàxácsuất
Sai lÇm mµ Guy Lefort nãi tíi tÊt nhiªn tuú thuéc vµo viÖc chóng ta quy ®Þnh møc x¸c
suÊt nhá (lín) lµ bao nhiªu th× mét biÕn cè trong thùc tÕ sÏ ®−îc coi lµ kh«ng thÓ cã (ch¾c
ch¾n). Nh− võa nªu trªn, ®iÒu nµy lµ tuú thuéc tõng hoµn c¶nh cô thÓ.
IV. mét sè ®Þnh nghÜa s¬ khai vÒ x¸c suÊt
§Þnh nghÜa tiªn ®Ò lµ ®Þnh nghÜa chÆt chÏ nhÊt vÒ mÆt l«-gÝc. Tuy nhiªn tr−íc khi Can-
m«-g«-rèp ®−a ra ®Þnh nghÜa nµy th× còng ®· cã nh÷ng ®Þnh nghÜa s¬ khai vÒ x¸c suÊt mµ
giê ®©y ta cã thÓ coi chóng lµ nh÷ng tr−êng hîp riªng cña ®Þnh nghÜa tiªn ®Ò. MÆc dï c¸c
®Þnh nghÜa s¬ khai nµy cã nh÷ng nh−îc ®iÓm nhÊt ®Þnh, nh−ng trong nh÷ng tr−êng hîp
thÝch hîp chóng vÉn ph¸t huy ®−îc t¸c dông cña m×nh.
1. §Þnh nghÜa cæ ®iÓn vÒ x¸c suÊt
Gi¶ sö ®èi víi phÐp thö G ta cã: Ω ={ω1, ω ,..., ω } 2 n Víi ω i (i= ,
1 n ) cã kh¶ n¨ng x¶y ra nh− nhau.
Ta lËp -®¹i sè c¸c biÕn cè A lµ tËp hîp tÊt c¶ c¸c tËp con cña Ω (kÓ c¶ Ω vµ φ). §©y lµ
- ®¹i sè lín nhÊt cã thÓ x©y dùng ®−îc tõ Ω . Do c¸cω (i= ,
1 n ) lµ ®ång kh¶ n¨ng nªn ta x¸c lËp ®é ®o x¸c suÊt P sao cho i 1
P( ω ) = P(ω ) = ... = P(ω ) = 1 2 n n Khi ®ã víi A = { i ω ,ω ,... 1 i2 i ω )∈ A m P(A) = P( ω ) + P( i ω ) + ... + P( 1 i2 i ω ) m 1 1 1 m = + + ... + = n n n n
ë ®©y m chÝnh lµ sè kÕt côc cña G thuËn lîi cho A x¶y ra. Tõ ®ã ta cã ®Þnh nghÜa x¸c suÊt
theo quan ®iÓm cæ ®iÓn nh− sau: §Þnh nghÜa: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 18
Chương1.Biếncốngẫunhiênvàxácsuất m
Sè c¸c kÕt côc thuËn lîi cho A x¶ y ra P(A) = = n
Sè kÕt côc ® ång kh¶ n¨ng cña phÐp thö
Râ rµng ®Þnh nghÜa nµy cã nh−îc ®iÓm lµ kh«ng chÆt chÏ vÒ mÆt l«-gÝch khi dùa vµo
tÝnh ®ång kh¶ n¨ng ®Ó ®Þnh nghÜa x¸c suÊt (lµ con sè x¸c ®Þnh kh¶ n¨ng x¶y ra cña biÕn
cè). Tuy nhiªn ®èi víi nh÷ng hiÖn t−îng cã tÝnh chÊt ®èi xøng vµ sè kÕt côc cña phÐp thö
lµ h÷u h¹n th× ®Þnh nghÜa nµy vÉn ph¸t huy ®−îc t¸c dông.
ThÝ dô 1: TÝnh x¸c suÊt ®Ó trong k ng−êi kh«ng quen biÕt nhau (2≤ k ≤ 365) sÏ cã Ýt nhÊt 2
ng−êi cã ngµy sinh nhËt trïng nhau biÕt r»ng hä ®Òu kh«ng sinh vµo nh÷ng n¨m nhuËn. Bµi gi¶i
Víi gi¶ thiÕt lµ bÊt kú mét ngµy nµo ®ã trong 365 ngµy cña n¨m ®Òu cã thÓ lµ ngµy
sinh cña mçi ng−êi th× sè kÕt côc ®ång kh¶ n¨ng cña phÐp thö (sè ngµy sinh nhËt cã thÓ cña k ng−êi) sÏ lµ n = 365 x 365 x...x365=365 k
Gäi A lµ biÕn cè “tÊt c¶ c¸c ngµy sinh cña k ng−êi lµ kh¸c nhau” th× sè kÕt côc thuËn lîi cho A lµ
m = 365(365-1) ... [365 - (k-1)] ( ) 365 ! = A k365 = (365 -k)! k A VËy P(A) = 365 = (36 ) 5 ! k (365) k 3 ( 65 - k)! 3 ( 6 ) 5
Tõ ®ã x¸c suÊt ph¶i t×m lµ : P( A ) = 1- P(A) = 1- (36 ) 5 ! k 3 ( 65 − k)! 3 ( 6 ) 5
2. §Þnh nghÜa thèng kª vÒ x¸c suÊt
§Þnh nghÜa nµy dùa vµo tÇn suÊt cña biÕn cè. Cô thÓ nÕu phÐp thö G G ®−îc lÆp l¹i K
lÇn mµ biÕn cè A xuÊt hiÖn k lÇn th× tÇn suÊt cña A lµ k f(A) = K
BÐc-nu-ly ®· chøng minh r»ng víi mäi sè ε > 0 nhá tïy ý ta ®Òu cã: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 19
Chương1.Biếncốngẫunhiênvàxácsuất
P ( f ( A ) − P ( A ) < ε ) = 1 lim K → ∞
§iÒu nµy cã nghÜa lµ khi K t¨ng v« h¹n th× hÇu nh− ch¾c ch¾n f(A) sÏ nhËn gi¸ trÞ rÊt gÇn
víi P(A). V× thÕ nÕu K kh¸ lín th× ta cã thÓ coi f(A) ≈ P(A)
Nh− vËy c¸ch x¸c ®Þnh x¸c suÊt theo quan ®iÓm thèng kª nµy mang tÝnh chÊt thùc
nghiÖm. MÆt kh¸c muèn x¸c ®Þnh P(A) mét c¸ch t−¬ng ®èi chÝnh x¸c ta ph¶i lÆp l¹i mét
sè lín lÇn phÐp thö. §iÒu nµy ®ßi hái nhiÒu c«ng søc vµ ®«i khi kh«ng thùc hiÖn ®−îc,
ch¼ng h¹n nh− khi phÐp thö ®ßi ph¶i ph¸ huû c¸c ®¬n vÞ ®−îc ®iÒu tra (thÝ dô nh− khi ta
muèn x¸c ®Þnh tû lÖ p c¸c hép háng cña mét kho ®å hép).
Sau ®©y lµ mét thÝ dô vÒ c¸ch x¸c ®Þnh x¸c suÊt th«ng qua tÇn suÊt.
§Ó x¸c ®Þnh x¸c suÊt sinh con g¸i, ta cã thÓ c¨n cø vµo sè liÖu thèng kª cña Thôy §iÓn
vµo n¨m 1935 mµ nhµ to¸n häc H. Cramer ®· cung cÊp nh− sau: Th¸ng 1 2 3 4 5 6 7 8 9 10 11 12 C¶ n¨m Tæng sè 7280 6957 7883 7884 7892 7609 7585 7393 7203 6903 6552 7132 88.273 sinh
Sè con trai 3743 3550 4017 4173 4117 3944 3964 3797 3712 3512 3392 3761 45.682 Sè con g¸i 3537 3407 3866 3711 3775 3665 3621 3596 3491 3391 3160 3371 42.591 TÇn suÊt 0,486 0,489 0,490 0,471 0,478 0,482 0,462 0,484 0,485 0,491 0,482 0,473 0,4825 sinh con g¸i
Ta thÊy tÇn suÊt sinh con g¸i dao ®éng quanh gi¸ trÞ 0,482. VËy nÕu gäi A lµ biÕn cè
“sinh con g¸i” th× ta cã thÓ coi P(A) ≈ 0,482.
TÊt nhiªn, ®èi víi hiÖn t−îng nµy, chóng ta kh«ng thÓ ¸p dông ®Þnh nghÜa cæ ®iÓn
®−îc v× viÖc sinh con trai vµ con g¸i kh«ng ph¶i lµ hai tr−êng hîp ®ång kh¶ n¨ng. Nãi 1
c¸ch kh¸c, x¸c suÊt ®Ó mét bµ mÑ sinh con g¸i kh«ng thÓ lµ . 2 Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 20
Chương1.Biếncốngẫunhiênvàxácsuất
§Ó thÊy râ ®iÒu nµy, chóng ta tham kh¶o thªm mét sè kÕt qu¶ nghiªn cøu cña c¸c nhµ
to¸n häc kh¸c. Ch¼ng h¹n, nghiªn cøu t×nh h×nh sinh ®Î ë Ph¸p, Darmois ®· thu ®−îc c¸c sè liÖu sau : N¨m 1806 1816 1836 1856 1913 1920 1928 TÇn suÊt sinh g¸i 0,485 0,484 0,485 0,487 0,488 0,489 0,489
Râ rµng kh«ng cã tÇn suÊt nµo ®¹t tíi gi¸ trÞ 0,5 c¶.
Thèng kª t×nh h×nh sinh ®Î ë c¸c thµnh phè Lu©n-®«n, Pª-tÐc-bua vµ BÐc-lin trong suèt 10 21
n¨m, Laplace còng ®· thÊy tÇn suÊt c¸c ch¸u g¸i ra ®êi lµ . 43
Theo thèng kª d©n sè cña tØnh Bu-e-nèt-ai-rÐt, mét tØnh gåm ng−êi T©y-ban-nha,
ng−êi ý vµ ng−êi ¸c-hen-tin-na th× trong kho¶ng tõ 1896 tíi 1905, tÇn suÊt cña ch¸u g¸i
ra ®êi trong c¸c n¨m ®Òu n»m trong kho¶ng tõ 0,497 tíi 0,484.
Râ rµng c¸c kÕt qu¶ thu ®−îc ®Òu phï hîp víi nhau.
3. §Þnh nghÜa h×nh häc vÒ x¸c suÊt
NÕu nh− tËp hîp c¸c biÕn cè s¬ cÊp Ω lµ mét tËp hîp trong kh«ng gian ¥-clit vµ cã
®é ®o h×nh häc h÷u h¹n (chiÒu dµi, diÖn tÝch, thÓ tÝch) th× víi A⊆ Ω ta cã: §é ®o cña miÒn A me ( s A) P(A) = = §é®o cña miÒnΩ me ( s Ω)
C¸ch x¸c ®Þnh x¸c suÊt nh− võa nªu gäi lµ c¸ch x¸c ®Þnh x¸c suÊt theo quan ®iÓm h×nh häc.
ThÝ dô 2: Gi¶ sö phÐp thö G lµ lÊy ngÉu nhiªn mét ®iÓm trong ®o¹n [0, 1[.
Nh− vËy Ω lµ tËp hîp c¸c ®iÓm cña [0,1[, cßn σ- ®¹i sè c¸c biÕn cè A lµ tËp hîp c¸c ®o¹n
[a, b[ ⊂ [0, 1[. Khi ®ã A = [a, b[ lµ biÕn cè “®iÓm ®−îc lÊy r¬i vµo ®o¹n [a,b[”.
Ta x¸c ®Þnh ®é ®o x¸c suÊt P trªn kh«ng gian ®o ( Ω , A) nµy nh− sau: P(A)=P([a,b[)=b-a
Khi ®ã tÊt c¶ c¸c tiªn ®Ò cña Can-m«-g«-rèp ®Òu ®−îc tho¶ m·n. Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 21
Chương1.Biếncốngẫunhiênvàxácsuất ThËt vËy:
(P1): P(A) ≥ 0 V× b - a chÝnh lµ ®é dµi cña [a,b[.
(P2): P( Ω )=1 v× P( Ω ) = P([0,1[) = 1.
(P3): Víi c¸c ®o¹n [a i ,b i [ kh«ng giao nhau sao cho n n n n ∪ a [ , b [ )= ( ) = i i ⊆ [0,1[ th× P( ∪ a [ ,b [ i i ∑ − b a ∑P([a ,b [) i i i i i=1 i=1 i= 1 i=1
Ghi chó NÕu b trïng víi a th× biÕn cè A=[a,b[ sÏ lµ biÕn cè lÊy ®−îc ®iÓm c¸ch 0 mét
®o¹n ®óng b»ng a. Khi ®ã P(A) = a – a = 0, nh−ng A kh«ng h¼n lµ biÕn cè kh«ng thÓ cã.
Tuy nhiªn trong thùc tÕ ®iÒu nµy rÊt hiÕm x¶y ra trong mét phÐp thö (xem nguyªn lý x¸c suÊt nhá).
ThÝ dô sau ®©y cho thÊy phÇn nµo t¸c dông cña c¸ch x¸c ®Þnh x¸c suÊt theo quan ®iÓm h×nh häc.
ThÝ dô 3: (Bµi to¸n Buffon)
KÎ trªn mÆt ph¼ng c¸c ®−êng th¼ng song song vµ c¸ch ®Òu nhau mét kho¶ng cã ®é dµi
lµ 2a. Tung ngÉu nhiªn mét chiÕc kim cã ®é dµi 2l (l < a) lªn mÆt ph¼ng. TÝnh x¸c suÊt ®Ó
chiÕc kim c¾t mét ®−êng th¼ng nµo ®ã. Bµi gi¶i
Tr−íc tiªn ta hiÓu tÝnh chÊt: “ngÉu nhiªn” cña phÐp thö ë ®©y lµ
a. T©m cña chiÕc kim sÏ r¬i mét c¸ch ngÉu nhiªn vµo c¸c ®iÓm cña c¸c ®o¹n th¼ng cã
®é dµi 2a vµ vu«ng gãc víi c¸c ®o¹n th¼ng ®· vÏ.
b. X¸c suÊt ®Ó gãc φ t¹o bëi chiÕc kim vµ c¸c ®−êng th¼ng ®· vÏ n»m trong kho¶ng ( φ , + 1 φ 1
Δ φ ) sÏ tû lÖ víi Δ φ .
c. NÕu gäi x lµ kho¶ng c¸ch tõ t©m chiÕc kim tíi ®−êng song song gÇn nhÊt th× x vµ φ ®éc lËp víi nhau.
Ta thÊy x vµ φ x¸c ®Þnh ®−îc hoµn toµn vÞ trÝ cña kim. V× vËy c¸c vÞ trÝ nµy sÏ lµ c¸c
®iÓm cña h×nh ch÷ nhËt cã c¹nh lµ a vµ π , cßn ®iÒu kiÖn cÇn vµ ®ñ ®Ó chiÕc kim c¾t mét ®−êng song song lµ Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 22
Chương1.Biếncốngẫunhiênvàxácsuất 0 ≤ x ≤ lsin φ
§©y lµ tËp hîp c¸c ®iÓm n»m trong miÒn cã g¹ch trong h×nh 1.8 x x φ a 2l x=lsin φ 2a 0 π H×nh 1.8
NÕu gäi A lµ biÕn cè “kim sÏ c¾t mét ®−êng th¼ng” th× theo c¸ch x¸c ®Þnh b»ng h×nh häc ta cã : π ∫lsin d ϕ ϕ diÖn tÝch miÒng¹ch P(A)= = 0 diÖn t Ých h × nh c h ÷ nhËt aπ l cosφ π0 2l = - = π a . a π 2l
Ghi chó: NÕu ký hiÖu P(A) lµ p th× tõ kÕt qu¶ nµy ta suy ra: Π = a p .
Víi l vµ a x¸c ®Þnh khi tung n lÇn (víi ®iÒu kiÖn n kh¸ lín) mµ cã m lÇn kim c¾t ®−êng m
th¼ng th× theo ®Þnh nghÜa thèng kª vÒ x¸c suÊt ta cã thÓ lÊy p ≈ vµ do ®ã: n 2 ln π ≈ am
Tõ ®ã ta cã thÓ x¸c ®Þnh gi¸ trÞ xÊp xØ cña π b»ng thùc nghiÖm. Ch¼ng h¹n n¨m 1850
Wolf ®· tung 5000 lÇn vµ tÝnh ®−îc π = 3.1596; cßn vµo n¨m 1855 Smith tung 3204 lÇn
vµ tÝnh ®−îc π = 3.1553.
Qua bµi to¸n trªn ta thÊy trong nh÷ng tr−êng hîp nhÊt ®Þnh, ®Þnh nghÜa h×nh häc còng
cã thÓ ph¸t huy ®−îc t¸c dông cña m×nh Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 23
Chương1.Biếncốngẫunhiênvàxácsuất
B. X ¸c suÊt cã ®iÒu kiÖn
I. §Þnh nghÜa vμ c¸c tÝnh chÊt 1. §Þnh nghÜa
Cho mét kh«ng gian x¸c suÊt ( Ω , A, P) vµ mét biÕn cè A nµo ®ã thuéc A víi P(A) >
0. Khi ®ã x¸c suÊt cã ®iÒu kiÖn cña mét biÕn cè B ∈ A tÝnh trong ®iÒu kiÖn biÕn cè A
x¶y ra ®−îc ký hiÖu vµ ®Þnh nghÜa nh− sau: P(A ∩ B) P(B/A) = P A (B) = . P(A)
Nh− vËy ta ®· x¸c ®Þnh mét ®é ®o x¸c suÊt míi mµ ta cã thÓ ký hiÖu lµ P( • /A). §é ®o
x¸c suÊt nµy ®−îc x¸c ®Þnh trªn kh«ng gian ®o ( Ω ∩ A ; A∩ A) trong ®ã: A ∩ A = {B∩ A; B ∈ A }
Nãi c¸ch kh¸c, tõ kh«ng gian x¸c suÊt ( Ω , A, P) ta ®· chuyÓn sang kh«ng gian x¸c suÊt
( Ω ∩ A ; A∩ A; P(• /A)) trong ®ã P(• /A) ®−îc ®Þnh nghÜa nh− lµ tû sè cña hai x¸c suÊt kh«ng ®iÒu kiÖn.
ThÝ dô 1: XÐt phÐp thö “Tung h¹t xóc s¾c ®Òu ®Æn vµ ®ång chÊt” vµ gäi A lµ biÕn cè
“§−îc mÆt cã sè chÊm lín h¬n 3”. Khi ®ã ta cã: Ω = { 1 ω ,ω ,ω 2 3 ω4 , ω5 , ω6 } A = {ω4,ω5,ω6 }
Trong ®ã ω lµ biÕn cè “§−îc mÆt i chÊm” (i= 6 , 1 ) i
Gäi B lµ biÕn cè “§−îc mÆt cã sè ch½n chÊm”. Khi ®ã: B = { 2 ω ,ω4 , ω } 6
Ta h·y x¸c ®Þnh P(B/A). NÕu nh− A x¶y ra th× Ω giê ®©y thu hÑp thµnh
Ω ∩ A = A = { ω4,ω5,ω6 }
Ta thÊy trong kh«ng gian nµy cã hai tr−êng hîp thuËn lîi cho B x¶y ra lµ ω4 vµ ω , v× 6 2 vËy P(B/A) = 3 MÆt kh¸c ta thÊy: Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 24
Chương1.Biếncốngẫunhiênvàxácsuất 3 P(A) = P{ ω4,ω5,ω6 }= 6 2 P(A∩B) = P{ω4 , ω } = 6 6
Tõ ®ã ta cã thÓ nghiÖm l¹i r»ng: P(A ∩ B) P(B/A) = P(A)
NhËn xÐt: §é ®o x¸c suÊt míi P( • /A) còng tho¶ m·n c¸c tiªn ®Ò cña Can-m«-g«-rèp, cô thÓ : p(A ∩ B) (P1) P(B/A) =
≥ 0 v× P(A∩B) ≥ 0 vµ P(A) >0. p(A) P(Ω ∩ A) P(A) (P2) P(Ω/A) = = = 1. P(A) P(A) ∞ ∞ [ P( B ∪ [ P B ∪ i ] A i) ] A ∞ (P3) P(∪B /A) = i 1 = = i=1 i i =1 ( P ) A p(A) ∞ ∑ (PBi ) A ∞ ( P B ) ∞ = i A 1 = = ∑ i = ∑ (P B A i / ) ( p ) A i P A =1 ( ) i=1 Trong ®ã B ∩ i B j = φ víi mäi i ≠j. 2. C¸c tÝnh chÊt
V× P(*/A) còng lµ mét ®é ®o x¸c suÊt nªn nã còng cã c¸c tÝnh chÊt t−¬ng tù nh− ®é ®o
x¸c suÊt P x¸c ®Þnh trªn (( Ω , A). Ch¼ng h¹n ta xÐt mét vµi tÝnh chÊt sau:
TÝnh chÊt 1: 0 ≤ P(B/A) ≤ 1 víi mäi B Chøng minh:
VÕ tr¸i cña bÊt ®¼ng thøc ®· ®−îc nªu ë phÇn nhËn xÐt trªn.
Së dÜ cã vÕ ph¶i v× A∩B ⊂ A nªn P(A∩B) ≤ p(A), do ®ã P(B/A) = P(A ∩B) ≤ 1. P(A) Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 25
Chương1.Biếncốngẫunhiênvàxácsuất
TÝnh chÊt 2: NÕu A⊂ B th× P(B/A) = 1. Chøng minh: P(A ∩ B) P(A)
ThËt vËy, nÕu A⊂ B th× A∩B = A, do ®ã P(B/A)= = = 1. P(A) P(A)
TÝnh chÊt 3: P(B/A)+P( B /A) = 1. Chøng minh: Mét mÆt ta cã [ P A ∩(B ∪ B)] [ P A ∩ Ω] P(A) = = = 1. P(A) P(A) P(A) MÆt kh¸c ta l¹i cã: [ P A ∩(B ∪ B)] P[(A ∩B) ∪(A ∩ B) = P(A) P(A) P(A ∩ B) P(A ∩ B) = + P(A) P(A) = P(B/A)+P( B /A).
So s¸nh hai kÕt qu¶ ta ®−îc hÖ thøc ph¶i chøng minh.
II. §Þnh lý nh©n x¸c suÊt n 1
§Þnh lý: NÕu c¸c biÕn cè A i (i= ,
1 n )tháa m·n ®iÒu kiÖn P( ∩ Ai > 0 th× i 1 = n
P( ∩Ai ) = P(A )P(A /A )P(A /A A )....P(A ) 1 2 1 3 1 2 n /A 1 A 2 ...An-1 i=1 Chøng minh:
Tr−íc hÕt ta thÊy nÕu gi¶ thiÕt ®· nªu ®−îc tho¶ m·n th× tÊt c¶ c¸c x¸c suÊt bªn vÕ ph¶i
cña hÖ thøc ph¶i chøng minh ®Òu tån t¹i. n 1 − − n 2 2
ThËt vËy, v× ∩ A ⊆ ∩A ⊆... ⊆ ∩A ⊆ A nªn i i i 1 i 1 = i= 1 i 1 = Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 26
Chương1.Biếncốngẫunhiênvàxácsuất n 1 − n− 2 2
P(∩A ) ≤P( ∩A ) ≤... ≤P( ∩A ) ≤ P(A ). i i i 1 i =1 i 1 = i 1 = n 1 −
V× gi¶ thiÕt P( ∩A )>0 nªn tÊt c¶ c¸c x¸c suÊt ë sau ®Òu > 0. i i 1 =
TiÕp theo tõ ®Þnh nghÜa cña x¸c suÊt cã ®iÒu kiÖn ta cã: P(A A ) P(A /A ) = 1
2 nªn P(A A ) = P(A )P(A /A ) 2 1 P(A ) 1 2 1 2 1 1
Gi¶ sö c«ng thøc ®óng cho tr−êng hîp n-1. Khi ®ã: n n 1 − n−1 − n 1
P( ∩A i ) = P(An∩ A ) = P(∩A )P(A /∩A ) i i n i i 1 = i=1 i 1 = i=1 n−1
Thay P( ∩A ) b»ng gi¶ thiÕt quy n¹p ta sÏ ®−îc c«ng thøc ph¶i chøng minh. i i 1 =
ThÝ dô 1: Mét ng−êi viÕt n bøc th− víi néi dung kh¸c nhau, cho vµo n phong b× d¸n l¹i sau
®ã míi ®Ò tªn ng−êi nhËn. TÝnh x¸c suÊt ®Ó Ýt nhÊt cã mét phong b× mµ tªn ng−êi nhËn
phï hîp víi néi dung cña th−. Bµi gi¶i
Gäi A lµ biÕn cè “Ýt nhÊt cã mét phong b× cã néi dung phï hîp”
A lµ biÕn cè “phong b× thø i cã néi dung phï hîp” (i= , 1 n ). i n Khi ®ã A= ∪ i A i 1 =
Do c¸c biÕn cè A i kh«ng xung kh¾c nªn ¸p dông c«ng thøc ®· biÕt: n n n n n
P(A) = P( ∪Ai ) = ∑ P( A) - ∑ ( P A A )+ ∑ ( P A A ) - ∑ ( P A A A ) - ...+(-1)n-1 i i j i j i j k i 1 = i=1 i 1 = i< j i < j P(A A ...A ). 1 2 n Ta lÇn l−ît cã: 1 n P(A ) = ( ) =1 i . Suy ra ∑ P n i A i= 1
P(A A ) = P(A )P(A / A ) i j i j i Lê ă
V nPhong‐TrầnTrọngNguyên,ĐHKTQD 27




