








Preview text:
KARL J.SMITH - MONTY J.STRAUSS - MAGDALENA D.TODA Tài liệu môn học CALCULUS GIẢI TÍCH Người dịch:
Bộ môn Toán - ĐH SPKT, Tp. Hồ Chí Minh - Năm 2019 Mục lục 12 TÍCH PHÂN BỘI 2
12.1 TÍCH PHÂN BỘI HAI TRÊN MIỀN HÌNH CHỮ NHẬT . . . . . . . 2
12.1.1 Xem lại định ngh˜ia t´ich phân xác định . . . . . . . . . . . . 2
12.1.2 Định ngh˜ia t´ich phân bội hai trên miền h`inh chữ nhật . . 3
12.1.3 Các t´inh chất của t´ich phân bội hai . . . . . . . . . . . . . 4
12.1.4 Ý ngh˜ia thể t´ich . . . . . . . . . . . . . . . . . . . . . . . . 5
12.1.5 T´ich phân lặp . . . . . . . . . . . . . . . . . . . . . . . . . . 7
12.1.6 Một lập luận không ch´inh thức cho Định lý Fubini . . 12
12.2 T´ich phân bội hai trên miền phẳng tổng quát . . . . . . . . . . . . . 13
12.2.1 Khái niệm miền loại I và loại II . . . . . . . . . . . . . . . . . 14
12.2.2 T´ich phân bội hai trên các miền loại I và loại II . . . . . . . 15
12.2.3 Các t´inh chất của t´ich phân bội hai trên miền phẳng tổng
quát . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
12.3 T´ich phân bội hai trong hệ tọa độ cực . . . . . . . . . . . . . . . . . 24
12.4 Một số ứng dụng của t´ich phân bội hai . . . . . . . . . . . . . . . . 33
12.4.1 Diện t´ich h`inh phẳng . . . . . . . . . . . . . . . . . . . . . 33
12.4.2 Thể t´ich vật thể . . . . . . . . . . . . . . . . . . . . . . . . . 35
12.4.3 Diện t´ich mặt cong . . . . . . . . . . . . . . . . . . . . . . . 36 1 Chương 12 TÍCH PHÂN BỘI b
Dựa vào cách định nghĩa của tích phân xác định R f (x)dx được giới thiệu trong a
chương 5, trong chương này chúng ta sẽ tổng quát hóa tích phân xác định để định
nghĩa tích phân bội, tích phân mà trong đó hàm dưới dấu tích phân là hàm nhiều biến.
12.1 TÍCH PHÂN BỘI HAI TRÊN MIỀN HÌNH CHỮ NHẬT
12.1.1 Xem lại định nghĩa tích phân xác định b
Trong chương 5, ta đã định nghĩa tích phân xác định của hàm một biến R f (x) dx a
như một giới hạn của tổng Riemann.
Cho hàm bị chặn f xác định trên đoạn [a, b].
Bước 1: Phân hoạch đoạn [a, b] thành n khoảng con ∆x với k = xk −xk−1 k = 1, n
trong đó a = x0 < x1 < x2... < xn = b. Gọi phân hoạch này là P.
Bước 2: Với k = 1, n, chọn một điểm x∗ tùy ý là một điểm đại diện của khoảng k
con [xk−1, xk] trong phân hoạch P. Lập tổng n X Rn = f (x∗ ) ∆x k k k=1
là tổng Riemann của f tương ứng với phân hoạch P và đại diện khoảng con x∗, x∗, . . . , x∗ . 1 2 n 2 Tài liệu môn học Toán 3 Trang 3 Bước 3: Tính giới hạn n X I = lim f (x∗ ) ∆x k k kP k→0 k=1
Nếu giới hạn này tồn tại thì giá trị của giới hạn này được gọi là tích phân xác định
của f trên đoạn [a, b] và được ký hiệu b Z n X I = f (x) dx = lim f (x∗) ∆x k k kP k→0 a k=1
12.1.2 Định nghĩa tích phân bội hai trên miền hình chữ nhật
Tương tự cách định nghĩa của tích phân xác định ta sẽ định nghĩa tích phân bội hai
theo hai biếnRR f (x, y) dA trên miền chữ nhật R = {(x, y) ∈ R2 : a ≤ x ≤ b, c ≤ y ≤ d}. R
Bước 1:: Phân hoạch đoạn a ≤ x ≤ b thành m đoạn con và đoạn c ≤ y ≤ d
thành n đoạn con. Sử dụng những đoạn con này, phân hoạch hình chữ nhật R thành
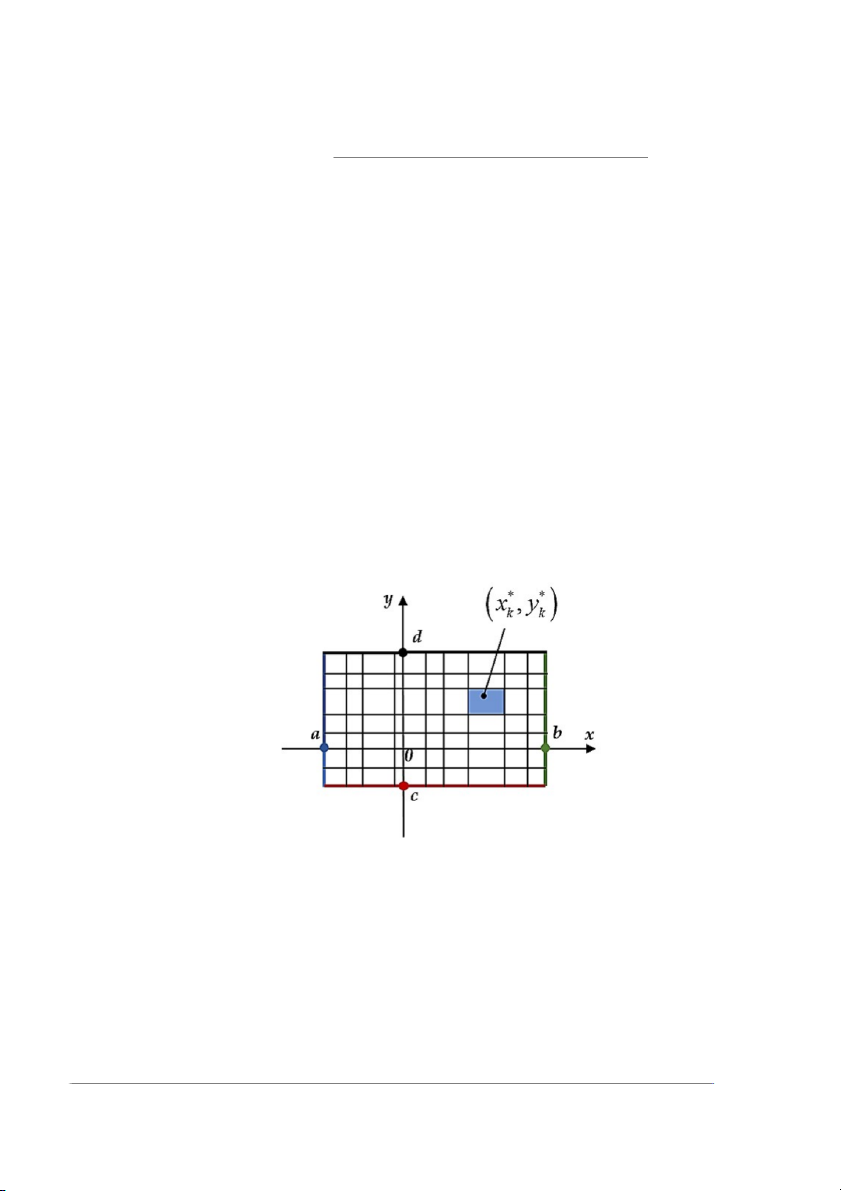
N = mn hình chữ nhật con như hình 12.1. Gọi phân hoạch này là P .
Hình 12.1: Một phân hoạch hình chữ nhật R thành mn hình chữ nhật con và phần
tử đại diện của hình chữ nhật con thứ k
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 3 Tài liệu môn học Toán 3 Trang 4
Bước 2: Chọn một điểm đại diện (x∗ , y∗) từ mỗi hình chữ nhật con thứ k với k k
k = 1, n trong phân hoạch của hình chữ nhật. Lập tổng N X Sn = f (x∗, y∗ k ) ∆A k k k=1 trong đó ∆A tổng
k là diện tích của hình chữ nhật con thứ k. Tổng này được gọi là
Riemann của f (x, y) ứng với phân hoạch P và các đại diện của hình chữ nhật con (x∗, y∗). k k
Bước 3: Để đo kích cỡ của các hình chữ nhật trong phân hoạch P , ta định nghĩa
chuẩn kPk của phân hoạch là độ dài của đường chéo dài nhất trong các đường chéo
của các hình chữ nhật con trong phân hoạch. Ta tinh chỉnh phân hoạch bởi việc
chia nhỏ các hình chữ nhật con sao cho chuẩn giảm. Tính giới hạn N X lim f (x∗, y∗) ∆A k k k kP k→0 k=1
Nếu giới hạn này tồn tại, giá trị của nó được gọi là tích phân bội hai của f trên miền chữ nhật R.
Định nghĩa 12.1.1. Cho hàm hai biến f(x, y) xác định trên một miền chữ nhật
đóng, bị chặn R trong mặt phẳng 0xy thì tích phân bội hai của hàm f trên miền
R được định nghĩa và ký hiệu bởi Z Z N X I = f (x, y) dA = lim f (x∗, y∗ k ) ∆A k k kP k→0 k=1 R
nếu giới hạn này tồn tại.
Trong trường hợp tích phân bội hai tồn tại, f được gọi là khả tích trên R.
Chú ý 12.1.2. Ta có thể chỉ ra rằng nếu f (x, y) liên tục trên miền chữ nhật R thì nó khả tích trên R.
12.1.3 Các tính chất của tích phân bội hai
Tích phân bội hai có nhiều tính chất tương tự như tích phân xác định.
Giả sử rằng tất cả các tích phân trong các tính chất được nêu ra đều tồn tại trên miền chữ nhật R.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 4 Tài liệu môn học Toán 3 Trang 5 1) Z Z Z Z Z Z
[a f (x, y) + bg (x, y)] dA = a f (x, y) dA + b g (x, y) dA R R R với a và b là hằng số.
2) Nếu f (x, y) ≥ g (x, y) trên một miền chữ nhật R thì Z Z Z Z f (x, y) dA ≥ g (x, y) dA R R .
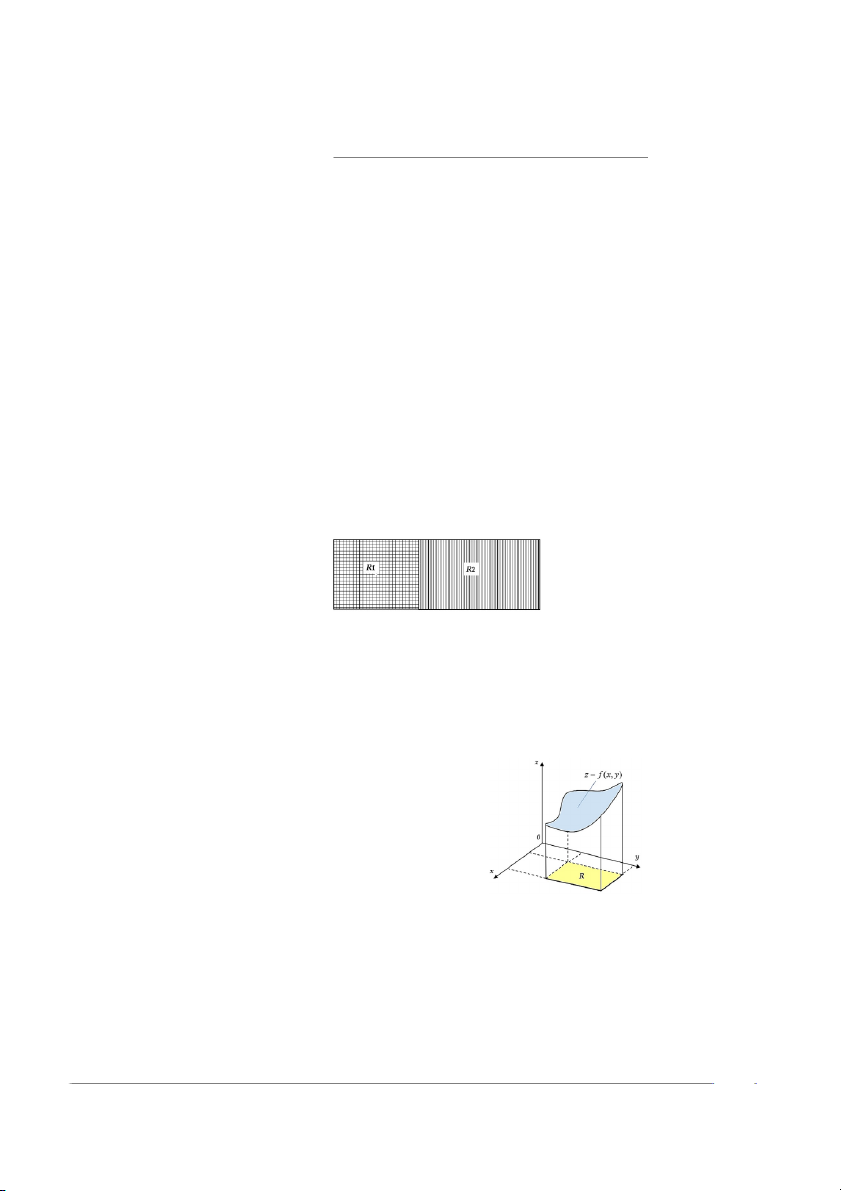
3) Nếu miền lấy tích phân là miền chữ nhật R được chia làm hai hình chữ nhật con R và R2 thì 1 Z Z Z Z Z Z f (x, y) dA = f (x, y) dA + f (x, y) dA R R1 R2 .
Hình 12.2: Miền chữ nhật R được chia thành R và 1 R2 12.1.4 Ý nghĩa thể tích
Nếu g (x) ≥ 0 trên đoạn [a, b], tích phân xác b
định R g (x) dx được hiểu là diện tích hình thang a
cong bên dưới đường cong y = g (x) trên đoạn [a, b].
Tích phân bội hai RR f (x, y) dA có thể được R
hiểu là thể tích hình trụ cong bên dưới mặt
z = f (x, y) ≥ 0 trên miền hình chữ nhật R (như hình 12.3)
Hình 12.3: Hình trụ cong bên dưới
mặt z = f(x, y) trên miền hình chữ nhật R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 5 Tài liệu môn học Toán 3 Trang 6
Để thấy điều này, chú ý rằng nếu f (x, y) ≥ 0
trên miền chữ nhật R và ta phân hoạch R thì
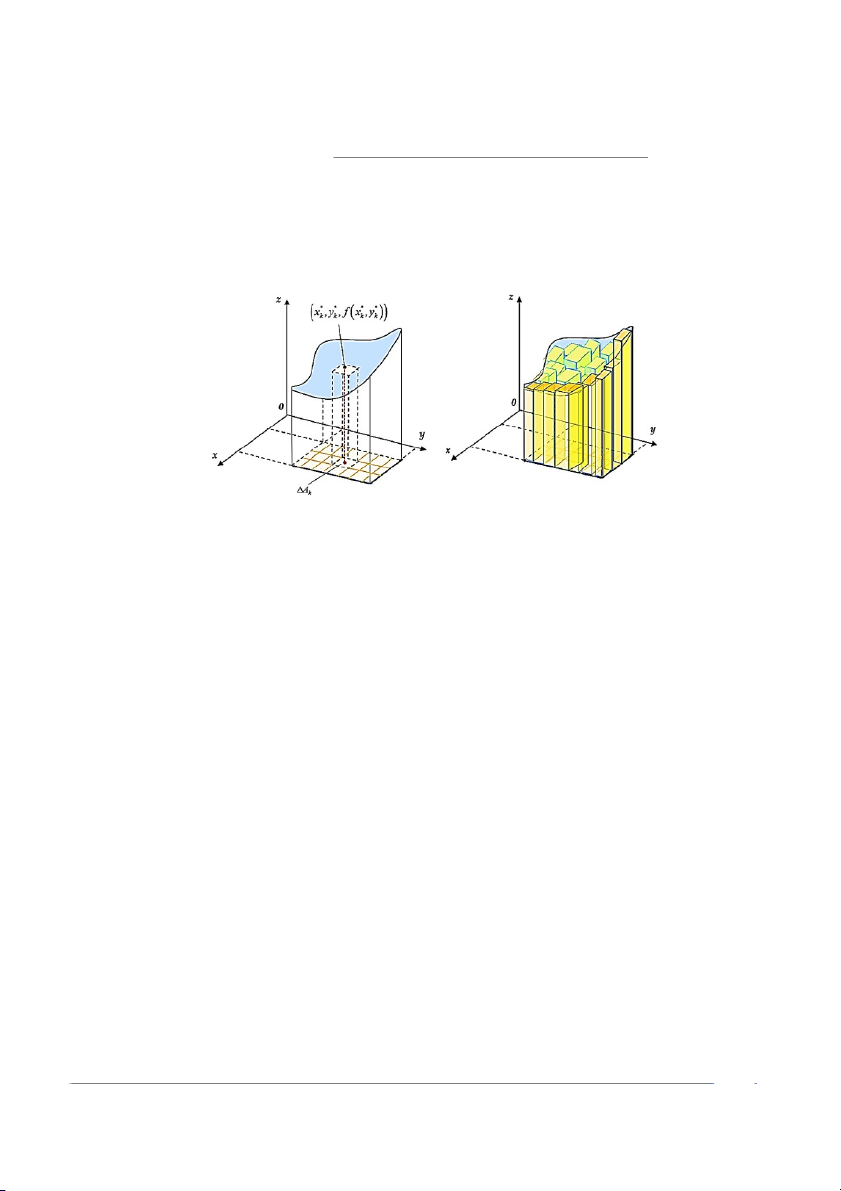
tích f (x∗, y∗) ∆A là thể tích của một hình hộp chữ nhật f (x∗, y∗) và diện tích đáy k k k k k
∆A , như biểu diễn trong hình 12.4. k
Hình 12.4: Thể tích hình trụ cong được xấp xỉ bởi các hình hộp chữ nhật Như vậy, tổng Riemann n X f (x∗, y∗ k ) ∆A k k k=1
là tổng của các hình hộp chữ nhật giới hạn trên bởi mặt cong z = f (x, y) trên miền R.
Nếu f liên tục, ta mong đợi sự xấp xỉ được cải thiện bởi việc sử dụng các phân
hoạch tốt hơn (nghĩa là, miền chữ nhật được chia thành nhiều hình chữ nhật con
hơn sao cho chuẩn nhỏ hơn). Khi đó thể tích của hình trụ cong cần xấp xỉ tổng thể
tích của các hình chữ nhật được tạo thành.
Thể tích của hình trụ cong bên dưới mặt z = f (x, y) trên miền R được cho bởi N Z Z X V = lim f (x∗, y∗ k ) ∆A f (x, y) dA k k = kP k→0 k=1 R
Sự xấp xỉ bởi tổng Riemann được minh họa trong Hình 12.4.
Ví dụ 12.1.1. Tính một tích phân bội hai bằng cách liên hệ với thể tích khối đặc
Tính tích phân bội hai RR (4 − 2y) dA, trong đó R là một hình chữ nhật trong R
mặt phẳng Oxy với các đỉnh O(0, 0), A(3, 0), B(3, 2) và C(0, 2).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 6 Tài liệu môn học Toán 3 Trang 7
Giải. Vì z = 4 − 2y thỏa mãn z ≥ 0 với mọi điểm trong R, giá trị của tích phân
bội hai bằng với thể tích của khối đặc bị chặn trên bởi mặt phẳng z = 4 − 2y và bị
chặn dưới bởi hình chữ nhật R.
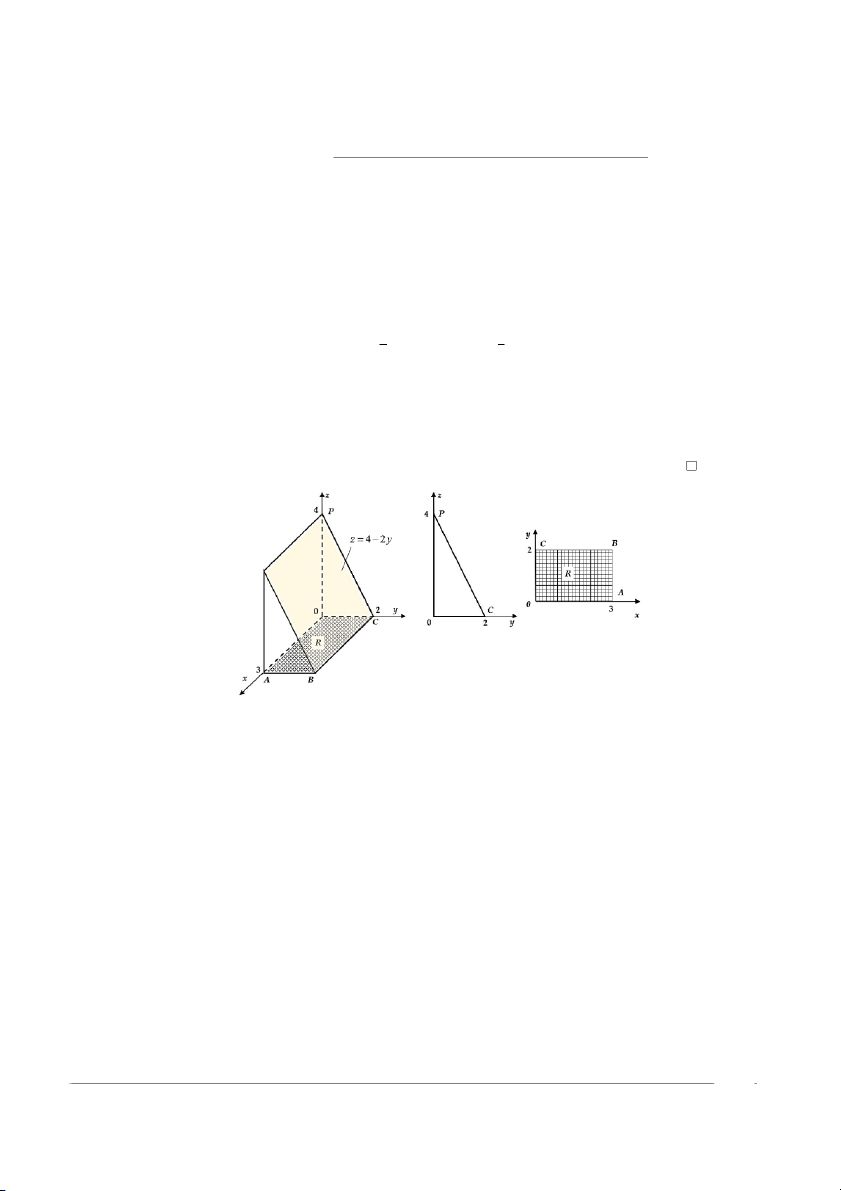
Khối đặc là một lăng trụ có đáy là ∆OCP và đường cao là OA. Khối đặc được
biểu diễn trong hình 12.5.
Thể tích của khối lăng trụ là 1 1
V = S∆OCP × h = OC × OP × h = × 2 × 4 × 3 = 12 2 2
Do đó, giá trị của tích phân cũng là 12; có nghĩa là Z Z (4 − 2y) dA = 12 R
Hình 12.5: Tính tích phân bội hai RR (4 − 2y) dA = 12 bằng thể tích R 12.1.5 Tích phân lặp
Để tính tích phân xác định, ta ít sử dụng trực tiếp định nghĩa mà thường sử dụng
các phương pháp tính tích phân trong chương 7. Tương tự như vậy, để tính tích
phân bội hai ta ít khi sử dụng trực tiếp định nghĩa để tính, thậm chí trên một miền
chữ nhật đơn giản. Thay vào đó, ta sẽ tính các tích phân bội hai bằng một quá trình
gọi là lấy tích phân lặp. Quá trình này giống như đảo ngược lại quá trình lấy đạo hàm riêng.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 7 Tài liệu môn học Toán 3 Trang 8
Định lí sau đây sẽ cho thấy tích phân bội hai RR f (x, y) dA có thể được tính theo R
các tích phân lặp như thế nào, và được chứng minh bởi nhà toán học người Italia
Guido Fubini (1879-1943) vào năm 1907.
Định lý 12.1.3. Định lý Fubini trên một miền chữ nhật
Nếu f (x, y) liên tục trên hình chữ nhật R = {(x, y) ∈ R2 : a ≤ x ≤ b, c ≤ y ≤ d} thì tích phân bội hai Z Z f (x, y) dA R
có thể được tính bởi một trong hai tích phân lặp sau d b b d Z Z Z Z Z Z f (x, y)dA = f (x, y)dxdy = f (x, y)dydx R c a a c Ta có thể viết d b b d Z Z Z Z Z Z f (x, y) dA = f (x, y) dxdy = f (x, y) dydx R c a a c .
Chú ý 12.1.4. Giả sử f (x, y) liên tục trên hình chữ nhật R = {(x, y) ∈ R2 : a ≤ x ≤ b, c ≤ y ≤ d} d
Khi đó, ta viết R f (x, y) dy để kí hiệu tích phân thu được bởi việc lấy tích phân c
f (x, y) theo y trên đoạn [c, d] với x giữ cố định. Tích phân thu được bởi việc lấy
tích phân riêng này là một hàm theo x, nghĩa là d Z G (x) = f (x, y) dy c
Ta lấy tích phân xác định của hàm G(x) theo biến x trên đoạn [a, b] để được tích phân lặp b b d Z Z Z G (x) dx = f (x, y) dy dx a a c
Một cách tương tự, nếu trước tiên ta lấy tích phân f (x, y) theo x trên [a, b] mà
giữ y cố định, và sau đó lấy tích phân theo y trên [c, d], ta được tích phân lặp b d b Z Z Z G (x) dx = f (x, y) dx dy a c a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 8 Tài liệu môn học Toán 3 Trang 9
Ví dụ 12.1.2. Sử dụng định lý Fubini để tính tích phân bội hai
Sử dụng định lý Fubini, hãy tính tích phân bội hai RR (4 − 2y) dA, trong đó R là R
một hình chữ nhật trong mặt phẳng Oxy với các đỉnh O(0, 0), A(3, 0), B(3, 2) và C(0, 2).
Giải. Miền lấy tích phân là miền chữ nhật R = {(x, y) ∈ R2 : 0 ≤ x ≤ 3, 0 ≤ y ≤ 2} (xem lại hình 12.5).
Do vậy ta sử dụng định lý Fubini bằng cách lấy tích phân lặp để tính tích phân. 3 2 Z Z Z Z (4 − 2y) dA = (4 − 2y) dy dx R 0 0 3 Z h 2i = 4y − y2 dx 0 0 3 Z = (8 − 4 − 0)dx 0 3 Z = 4dx = 4 [x]|3 = 12 0 0
Kết quả này giống với kết quả đạt được trong ví dụ 12.1.1.
Ví dụ 12.1.3. Sử dụng tích phân lặp để tính tích phân bội hai
Tính tích phân bội hai RR x + y dA trên miền chữ nhật y x R
R = (x, y) ∈ R2 : 1 ≤ x ≤ 2, 1 ≤ y ≤ e
a. Lấy tích phân theo y trước
b. Lấy tích phân theo x trước
Giải. a. Lấy tích phân theo y trước. Ta có 2 e Z Z x y Z Z x 2y + dA = +
dydx (Lấy tích phân theo biến y, cố định x) y x y x R 1 1 2 Z y2 e = x ln y + dx x 1 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 9 Tài liệu môn học Toán 3 Trang 10 2 2 Z e y2 Z e2 1 x ln y + dx = x ln e + − x ln 1 − dx x x x 1 1 1 2 Z e2 1 = x + −
dx (Ta được tích phân xác định theo biến x) x x 1 x2 2 = + e2 − 1 ln x 2 1 1 = 2 + e2 − 1 ln 2 − − e2 − 1 ln 1 2 3 = + e2 − 1 ln 2 2
b. Lấy tích phân theo x trước e 2 Z Z x y Z Z x 2y + dA = +
dxdy (Lấy tích phân theo biến x, cố định y) y x y x R 1 1 e Z x2 2 = + 2y lnx dy 2y 1 1 e Z 4 1 = + 2y ln 2 − − 2y ln 1 dy 2y 2y 1 e Z 3 =
+ 2y ln 2 dy (Ta được tích phân xác định theo biến y) 2y 1 3 e = ln y − y2 ln 2 2 1 3 = + e2 − 1 ln 2 2
Chú ý 12.1.5. Trong trường hợp f (x, y) = g (x) h (y) , và miền lấy tích phân là miền
chữ nhật hình chữ nhật R = {(x, y) ∈ R2 : a ≤ x ≤ b, c ≤ y ≤ d}, định lí Fubini cho
phép tích phân được viết dưới dạng b d b d Z Z Z Z Z Z f (x, y) dA = f (x, y) dydx = g (x) dx h (y) dy. R a c a c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 10 Tài liệu môn học Toán 3 Trang 11
Chú ý rằng điều này chỉ đúng cho phép nhân.
Nếu f (x, y) = g (x) + h (y) thì không có kết luận như vậy.
Chứng minh. Dễ thấy, xét trường hợp f (x, y) = g (x) h (y). Khi đó b d b d Z Z Z Z Z Z f (x, y) dA = f (x, y) dydx = g (x) h (y) dy dx R a c a c .
Trong tích phân phía trong ngoặc, x là hằng số, nên g (x) là hằng số và ta có thể viết b d b d b d Z Z Z Z Z Z g (x) h (y) dy dx = g (x) h (y) dy dx = g (x) dx h (y) dy a c a c a c d
vì R h (y) dy là hằng số. c
Ví dụ 12.1.4. Tính tích phân bội hai Z π/ Z 2 2 I = y sin x dy dx 0 1
Giải. Ta có miền lấy tích phân R là hình chữ nhật R = (x, y) ∈
R2 : 0 ≤ x ≤ π , 1 ≤ y ≤ 2 2 Ta có Z ! π / 2 Z 2 Z π/ Z 2 2 y sin x dy dx = sin x dx . y dy 0 1 0 1 ! 2 π y2 = − cos x| /2 0 2 1 1 3 = − (0 − 1) 2 − = 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 11 Tài liệu môn học Toán 3 Trang 12
Chú ý 12.1.6. Định lý Fubini-Tonelli trên một miền chữ nhật
Xét hình chữ nhật R : a ≤ x ≤ b, c ≤ y ≤ d và một hàm f (x, y) bị chặn và liên
tục trên hình chữ nhật R ngoại trừ trên một tập con S có diện tích zero của R,
sao cho tích phân RR f (x, y) dA tồn tại.Giả sử thêm rằng với mỗi giá trị x sao cho R
a ≤ x ≤ b, tập con S chỉ chứa hữu hạn (có thể không chứa) các điểm với tọa độ đầu là x.
Khi đó, tích phân lặp cũng tồn tại và b d Z Z Z Z f (x, y) dA = f (x, y) dydx R a c Ví dụ 12.1.5.: q
R : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 và f (x, y) = x. y
Giải. Dù hàm dưới dấu tích phân không liên tục và không bị chặn tại tất cả các
điểm có tọa độ y = 0, có thể chứng minh rằng tích phân bội hai tồn tại trên miền
R và có thể được tính bởi việc dùng các tích phân lặp (chú ý rằng một trong hai
tích phân đơn là suy rộng).Ta tính tích phân Z 1 Z 1 r x Z 1 √ Z 1 dy 2 1 1 3 1 4 dx dy = xdx √ = x /2 /2 . 2 y = 0 0 y 0 0 y 3 0 0 3
12.1.6 Một lập luận không chính thức cho Định lý Fubini
Ta có thể làm định lí Fubini chấp nhận được với một lập luận hình học trong trường hợp f (x, y) ≥ 0 trên R.
Nếu RR f (x, y) dA được định nghĩa trên một hình chữ nhật R R
với R : a ≤ x ≤ b, c ≤ y ≤ d.
Khi đó tích phân bội hai RR f (x, y) dA biểu diễn thể tích của khối D bị chặn R
trên bởi mặt z = f (x, y) và bị chặn dưới bởi hình chữ nhật R.
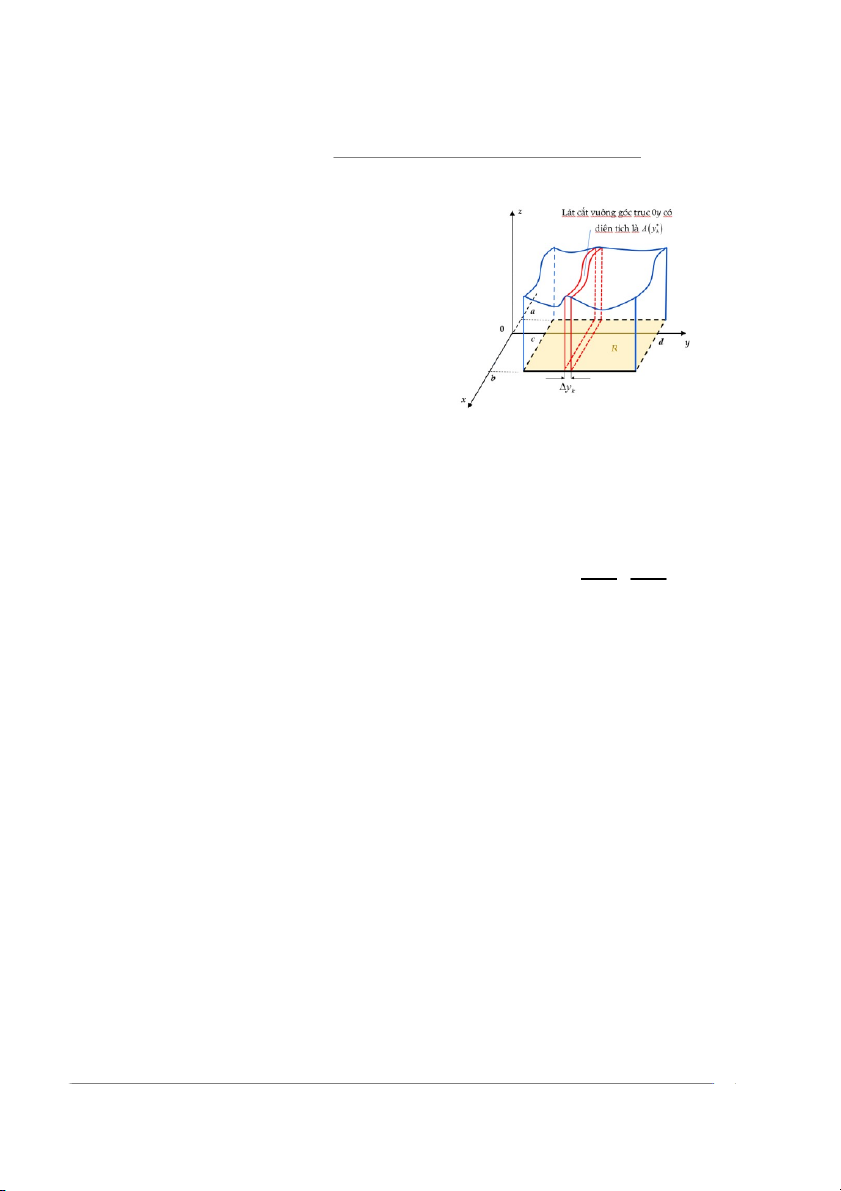
Nếu A (y∗) là diện tích thiết diện vuông góc với trục Oy tại điểm y∗ thì A (y∗) ∆y k k k k
biểu diễn thể tích của một lát cắt xấp xỉ thể tích của một phần của khối D, như trong Hình 12.6.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 12 Tài liệu môn học Toán 3 Trang 13
Ta được thể tích V của cả khối D là Z Z N X f (x, y) dA = V = lim A (y∗) ∆y k k kP k→0 k=1 R
Giới hạn ở vế phải chính là tích phân
của A (y) trên khoảng c ≤ y ≤ d, trong
đó A (y) là diện tích của lát cắt vuông
góc với trục 0y với y cố định.
Trong Chương 5, ta đã thấy rằng diện
tích A (y) có thể được tính bởi tích phân b Z A (y) = f (x, y) dx
Hình 12.6: Thể tích sử dụng phương pháp a
lát cắt vuông góc trục 0y
Lấy tích phân theo x (y cố định)
Bây giờ ta có thể thay thế A (y) bằng tích phân trên để được d d b Z Z N Z Z Z X f (x, y) dA = V = lim A (y∗ ) ∆y k k = A (y) dy = f (x, y) dx dy kP k→0 k=1 R c c a | {z } A(y)
Tương tự ta có thể chứng minh b d Z Z Z Z f (x, y) dA = f (x, y) dydx R a c d b b d Vậy R R RR R R f (x, y) dx dy = f (x, y) dA = V = f (x, y) dy dx. c a R a c
12.2 Tích phân bội hai trên miền phẳng tổng quát
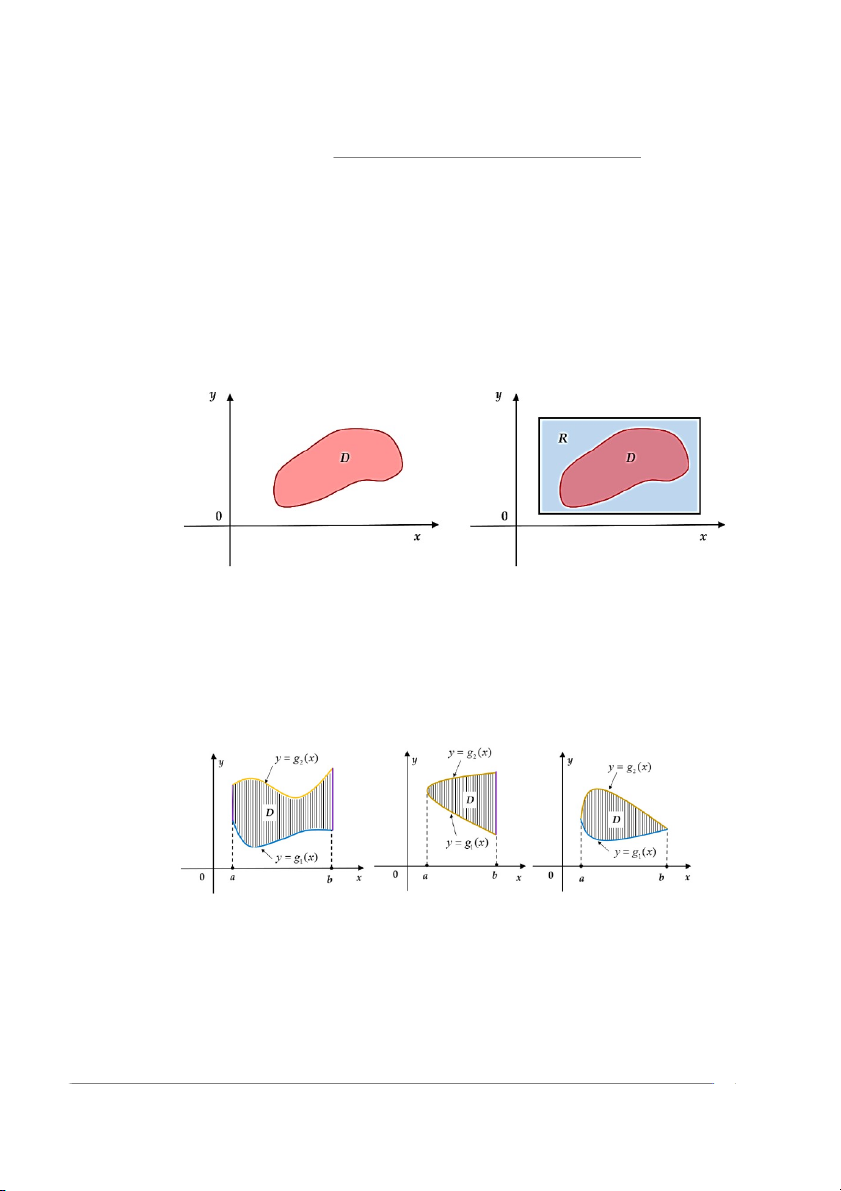
Cho f (x, y) là một hàm liên tục trên miền D mà có thể bị chứa trong một hình chữ nhật R.
Định nghĩa hàm F (x, y) trên R bằng f (x, y) nếu (x, y) thuộc D và bằng 0 nếu (x, y) không thuộc D.Nghĩa là f (x, y), nếu (x, y) ∈ D F (x, y) = 0, nếu (x, y) /∈ D.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 13 Tài liệu môn học Toán 3 Trang 14
Khi đó, nếu F khả tích trên R thì ta nói rằng f khả tích trên D, và tích phân
bội hai của f trên D được định nghĩa là Z Z Z Z f (x, y) dA = F (x, y) dA D R Dễ thấy RR RR RR RR F (x, y)dA = f (x, y)dA + 0dA = f (x, y)dA R D R\D D
Hình 12.7: Miền D bị chặn bởi một hình chữ nhật R
12.2.1 Khái niệm miền loại I và loại II
1. Miền phẳng D là miền loại I , hay miền đơn theo chiều dọc trong mặt phẳng
Hình 12.8: Một số ví dụ cho miền phẳng D loại I
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 14 Tài liệu môn học Toán 3 Trang 15
là một miền nằm giữa đồ thị của hai hàm liên tục theo x, và xác định bởi
D = (x, y) ∈ R2 : a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)
trong đó g1 (x) và g2 (x) là các hàm liên tục của x trên [a, b].
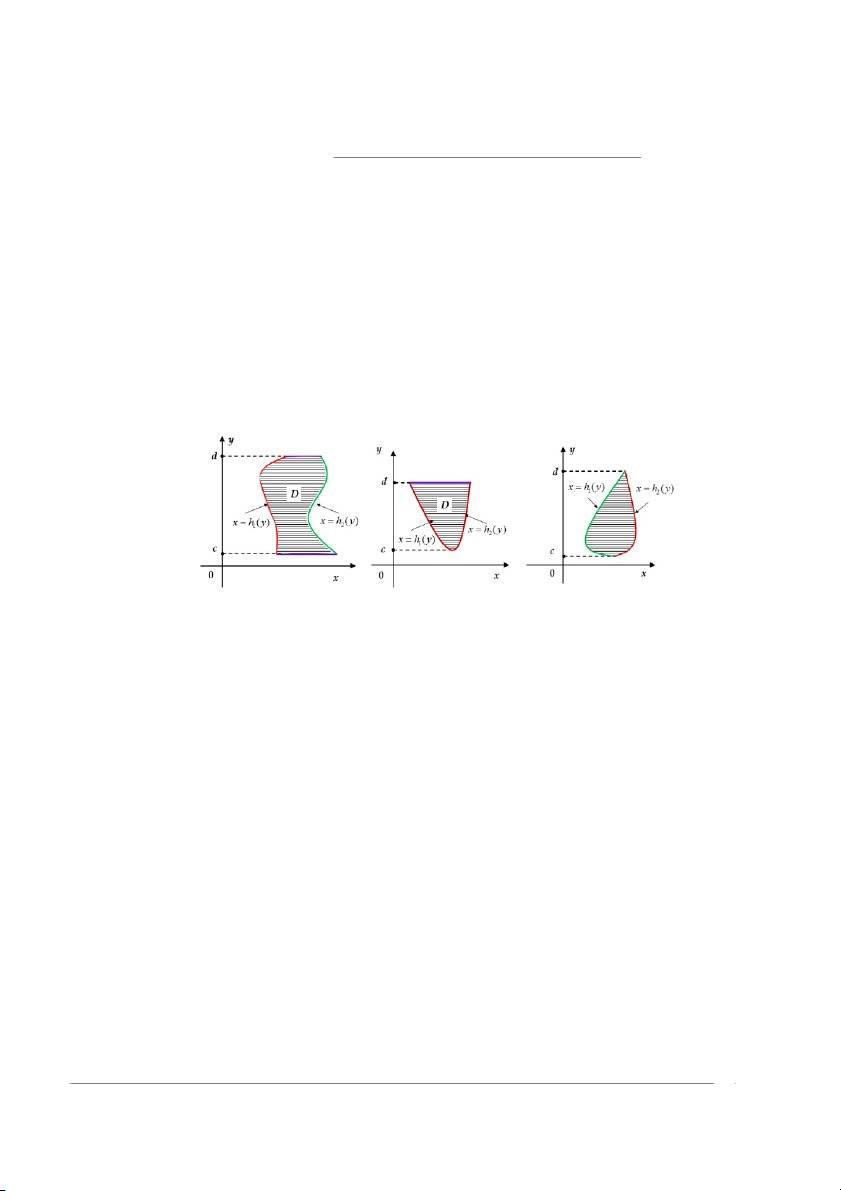
2. Một miền phẳng D là miền loại II, hay miền đơn theo chiều ngang trong mặt
phẳng là một miền nằm giữa đồ thị của hai hàm liên tục theo y, và xác định bởi
D = (x, y) ∈ R2 : c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)
trong đó h1 (y) và h2 (y) là các hàm liên tục của y trên [c, d].
Hình 12.9: Một số ví dụ cho miền phẳng D loại II
12.2.2 Tích phân bội hai trên các miền loại I và loại II
Định lý 12.2.1. Định lý Fubini cho các miền loại I và miền loại II
1. Nếu hàm f(x, y) liên tục trên một miền D loại I là
D = (x, y) ∈ R2 : a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x) thì Z Z Z b Z g2(x) f (x, y)dA = f (x, y) dy dx a g1(x) D
2. Nếu hàm f(x, y) liên tục trên một miền D loại II là
D = (x, y) ∈ R2 : c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 15 Tài liệu môn học Toán 3 Trang 16 thì Z Z Z d Z h2(y) f (x, y)dA = f (x, y) dx dy c h1(y) D Chứng minh
1) Định lý Fubini cho miền loại I
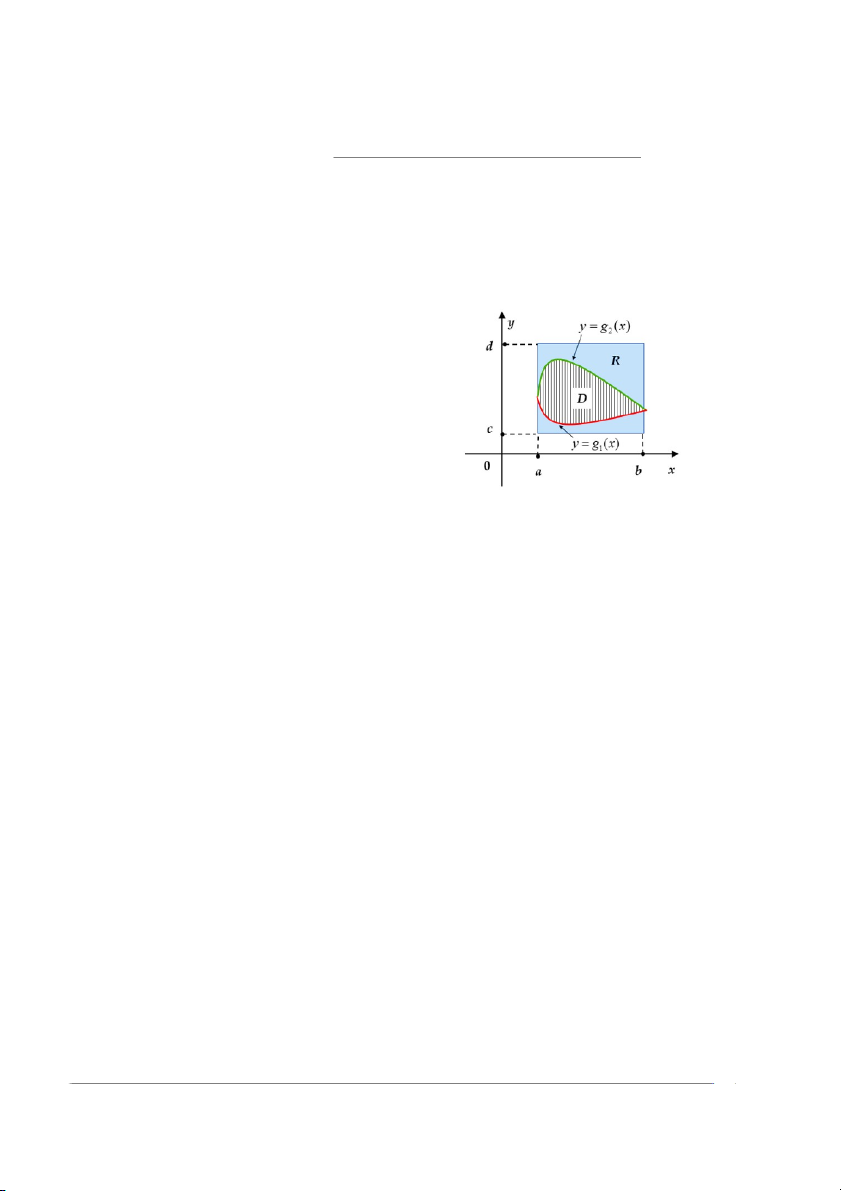
Trước tiên, để tính tích phân RR f(x, y)dA D
với D là miền loại I, ta chọn hình chữ nhật
R = [a, b] × [c, d] chứa miền D, như hình vẽ 12.10, và ta xét hàm f (x, y), nếu (x, y) ∈ D F (x, y) = 0, nếu (x, y) /∈ D. Khi đó Z Z Z Z
Hình 12.10: Miền lấy tích phân D là f (x, y)dA = F (x, y)dA miền loại I D R
Mà miền chữ nhật R = [a, b] × [c, d], do vậy b d Z Z Z Z F (x, y) dA = F (x, y) dydx R a c
Ta lại có F (x, y) = 0 nếu y < g1(x) hoặc y > g2(x) vì (x, y) nằm ngoài miền D. Do đó d g g d g Z 1 (x) Z 2 (x) Z Z 2 (x) Z F (x, y)dy = F (x, y)dy + F (x, y)dy + F (x, y)dy = F (x, y)dy c c g1(x) g2(x) g1(x)
Mặt khác F (x, y) = f(x, y) nếu g1(x) ≤ y ≤ g2(x) cho nên d g g Z 2 (x) Z 2 (x) Z F (x, y)dy = F (x, y)dy = f (x, y)dy c g1(x) g1(x)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 16 Tài liệu môn học Toán 3 Trang 17 Vậy b d Z Z Z Z Z Z F (x, y) dA = F (x, y) dA = F (x, y)dy dx D R a c b g b g Z 2 (x) Z Z 2 (x) Z = F (x, y)dy dx = f (x, y)dy dx a g1(x) a g1(x)
2) Định lý Fubini cho miền loại II được chứng minh tương tự
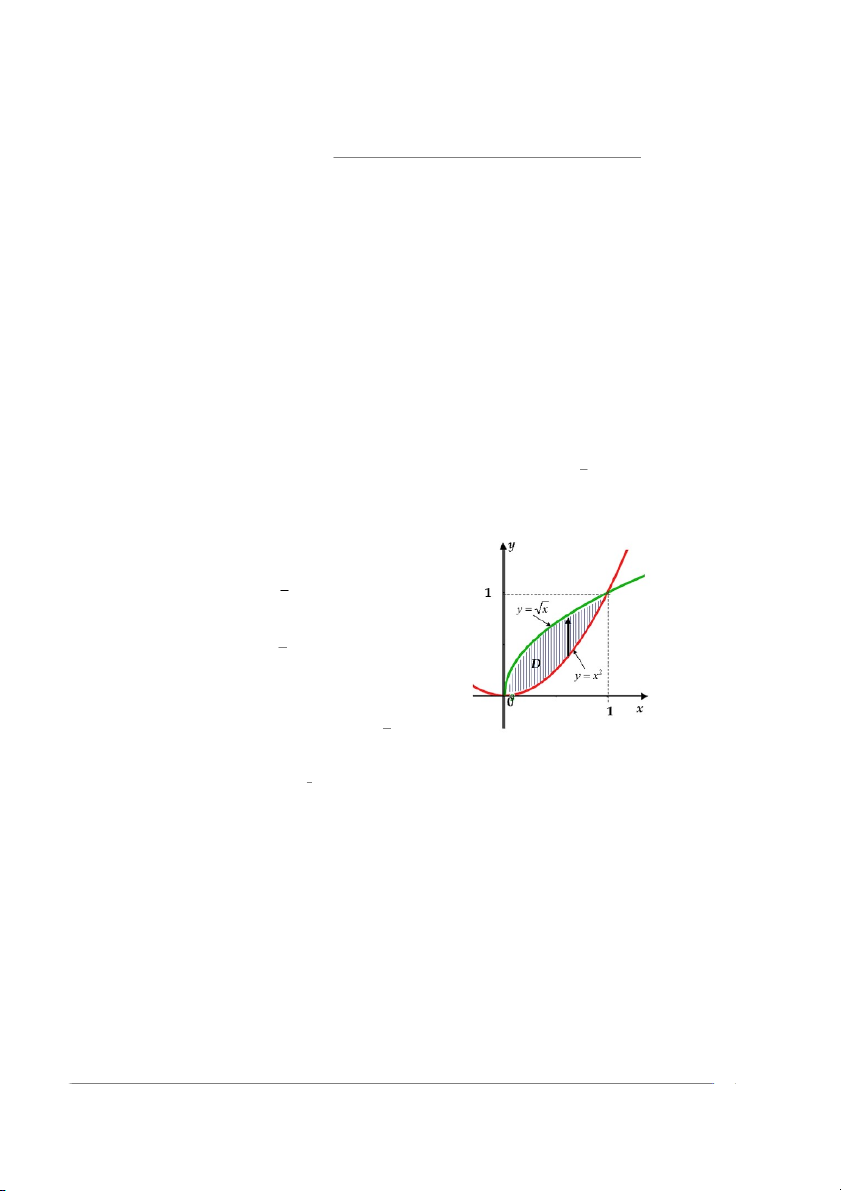
Ví dụ 12.2.1. Tính tích phân bội hai trên miền không là hình chữ nhật Tính tích phân bội hai Z Z 40x2ydA D trong đó miền √
D giới hạn bởi đường các đường y = x2 và y = x
Giải. Trước hết ta tìm giao điểm của các đường √ y = x2 và y = x
Phương trình hoành độ giao điểm √ x2 = x ⇔ x = 0 ∨ x = 1
Dựa và hình vẽ 12.11 ta có miền D là miền loại I Miền √
D : 0 ≤ x ≤ 1, x2 ≤ y ≤ x Do vậy ta có tích phân
Hình 12.11: Hình minh họa cho ví dụ 12.2.1 √ 1 x Z Z K = 20x2y2dydx 0 x2
Để tích tích phân này, ta tính tích phân theo biến y trước và cố định biến x (coi x
là hằng số). Sau đó thay cận vào cho y ta sẽ thu được tích phân xác định theo x,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 17 Tài liệu môn học Toán 3 Trang 18 cụ thể là 1 1 Z h √ i Z y= x h√ 2 K = 20 x2y2 dx = 20x2 x x22i dx y=x2 − 0 0 1 Z = 20x2 x − x4 dx 0 1 Z = 20 x3 − x6 dx 0 x4 x7 1 3 = 20 − = . 4 7 35 0
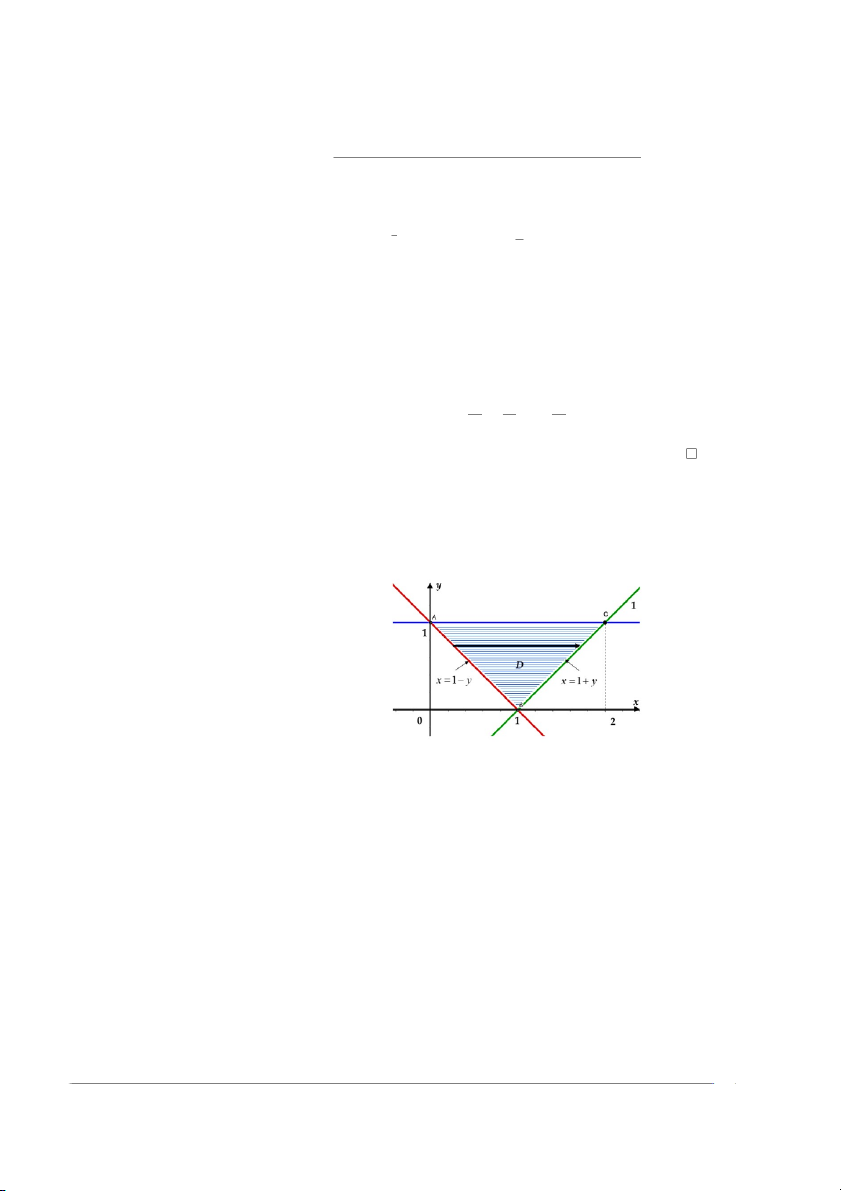
Ví dụ 12.2.2.Tính tích phân bội hai RR M =
(2x − 3y) dA trong đó D là hình tam D
giác có các đỉnh lần lượt là A(0, 1), B(1, 0), C(2, 1) Giải. Ta vẽ hình miền D
Ta có phương trình các đường thẳng lần lượt là
* Phương trình đường thẳng AB : x + y = 1 ⇔ x = 1 − y
* Phương trình đường thẳng BC : x − y = 1 ⇔ x = 1 + y
* Phương trình đường thẳng AC : y = 1
Hình 12.12: Miền lấy tích phân là hình tam giác
Dựa vào hình vẽ ta có thể xem miền D là miền loại II.
Miền D : 0 ≤ y ≤ 1, 1 − y ≤ x ≤ 1 + y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 18 Tài liệu môn học Toán 3 Trang 19 Khi đó tích phân Z 1 Z x=1+y M = (2x − 3y) dA 0 x=1−y Z 1 Z 1+y = (2x − 3y) dx dy 0 1−y 1 Z h i = 1+y x2 − 3y x dy 1−y 0 1 Z =
(1 + y)2 − 3y (1 + y) − (1 − y)2 + 3y (1 − y) dy 0 1 Z = 4y − 6y2 dy = 0 0
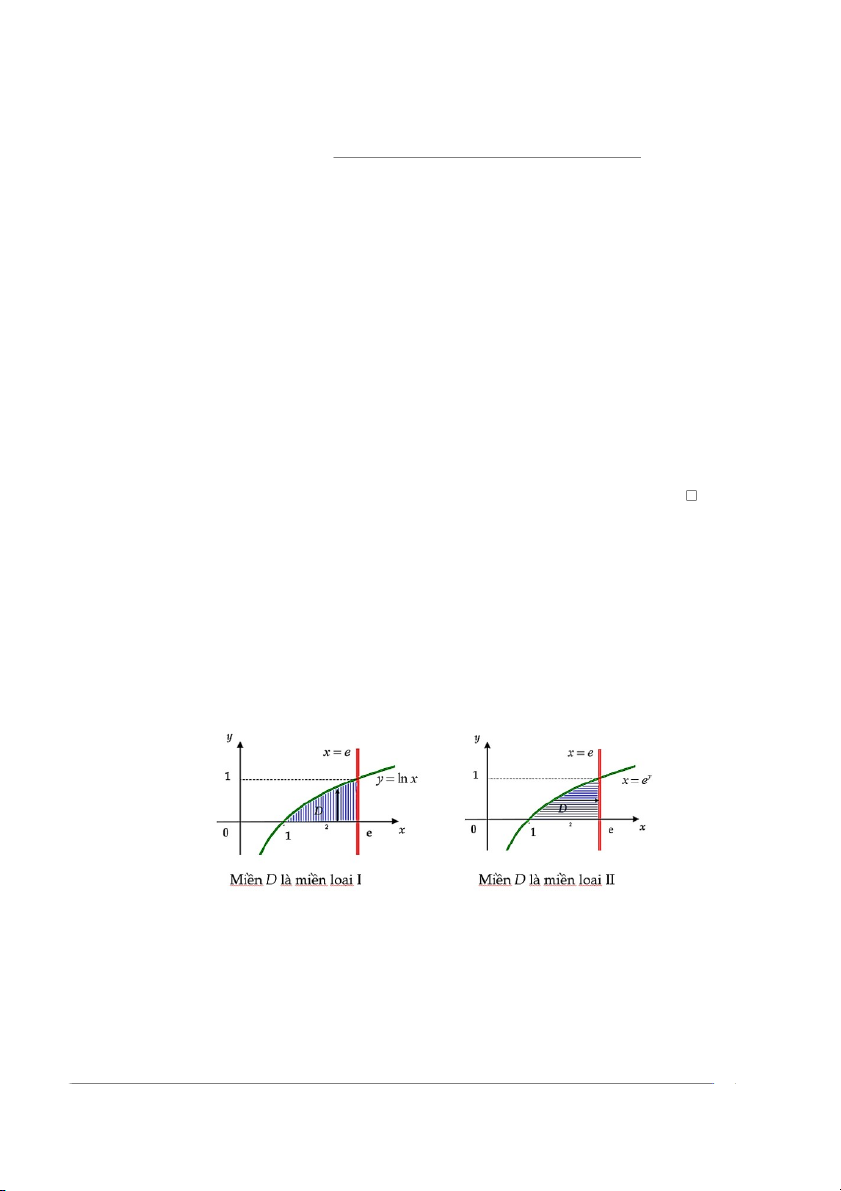
Ví dụ 12.2.3. Vẽ hình miền lấy tích phân và tính tích phân bội hai Z e Z ln x I = xy dy dx 1 0
Giải. Ta có, miền lấy tích phân là miền loại I 1 ≤ x ≤ e D : . 0 ≤ y ≤ ln(x)
Hình 12.13: Miền D có thể xem là miền loại I hoặc miền loại II
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trang 19




