Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng môn Xác suất thống kê| Đại học Duy Tân

22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu Chương 2 BIẾN NGẪU NHIÊN VÀ THAM SỐ ĐẶC TRƯNG
Giảng vên: TS. Lâm Sơn ĐT: 033.6969.909
Email: sonlam@ftu.edu.vn
1. Biến ngẫu nhiên (BNN) Định nghĩa
Biến ngẫu nhiên là biến số nhận giá trị tùy thuộc vào
các yếu tố ngẫu nhiên. Phân loại:
+ BNN được gọi là rời rạcnếu các giá trị có thể có của nó
lập nên một tập hợp hữu hạn hay đếm được.
Ví dụ: - Gọi X là số chấm xuất hiện khi tung một con xúc xắc. { 1,2,3,4,5,6}
- Một người bắn vào bia đến khi trúng thì thôi. Gọi
Y là số viên đạn bắn trượt. N 1 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
+ BNN được gọi là liên tụcnếu các giá trịcó thểcó
của nó lấpđầy một khoảng trên trục số.
+ Z là nhiệtđộ phòng học này (đv0C) vào 12h trưa mai . Z ( ∈ 10; 30)
2. Quy luật phân phối xác suất của BNN Định nghĩa:
Bất kỳ một hình thức nào cho phép biểu diễn mối qua hệ
giữa các giá trị có thể có của BNN và các xác suất tương
ứng của nó đều được gọi là quy luật phân phối xác suất
của đại lượng ngẫu nhiên ấy. 2 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
2.1. Bảng phân phối xác suất:
Giảsửbnn rời rạc X có có tập các giá trịcó thểlà x , x ,..., x và 1 2 n P ( X x = = ) pi , = 1,n ii X x1 x2. . . xn P p1 2 p . . . pn 0 1 < p ≤ i 1, 2 ∀,.., =n  i Như vậy: n = p 1   i i 1 =
Ví dụ 1: Tung một con xúc xắc. Gọi X là: “số chấm xuất
hiện”. Hãy xây dựng quy luật phân phối xác suất của X. X 1 2 3 4 5 6 P1/6 1/6 1/6 1/6 1/6 1/6
Ví dụ 2:Trong một lô hàng có 10 sản phẩm trong đó có 6
chính phẩm. Lấy ngẫu nhiên ra 2 sản phẩm. Xây dựng quy
luật phân phối xác suất của số chính phẩm được lấy ra. X 0 1 2 P 3 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Ví dụ 3: Xác suất để xạ thủ bắn trúng bia là 0,8. Xạ thủ
được phát từng viên đạn để bắn cho đến khi trúng bia thì
dừng bắn. Hãy xây dựng quy luật phân phối xác xuất của số viên đạn bắn ra. X 1 2 ….. n …….. P0,8 0,8.0,2 0,8.0,2n-1 +∞ 0, 8 0,8.0, 2n = = 1 − = 1 0, 2 n 1
2.2. Hàm phân phối xác suất:
Định nghĩa: F(x) = P(X < x) với mọi x thuộc R
Ví dụ:Tung một con xúc xắc. Gọi X là: “sốchấm xuất
hiện”. Xác định hàm phân phối của X. F(x)=0 mọi x <=1 = 1/6 mọi 1< x <=2
F(2,2)= P(X<1,2)= P(X<1)+P(X=1)+P(1+P(2F(0)=P(X<0)=0 F(0,5)=P(X<0,5)=0 4 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022 X 1 2 3 4 5 6 P1/6 1/6 1/6 1/6 1/6 1/6 0 1 khi x ≤ ≤1/6 khi 1<x 2  P(1+P(22/ ≤ 6 khi 2<x 3  F (x) = 3 ≤  /6 khi 3<x 4 ≤4/6 khi 4<x 5  5/6 khi 5<x ≤ 6 >1 khi  x 6
2.2. Hàm phân phối xác suất:
Định nghĩa: F(x) = P(X < x) với mọi x thuộc R
Ví dụ : Tung một con xúc xắc. Gọi X là: “số chấm xuất
hiện”. Xác định hàm phân phối của X. 0  1 khi x ≤ ≤ 1/6 khi 1<x 2  2  / ≤ 6 khi 2<x 3  F (x ) = 3 ≤  /6 khi 3<x 4 4/ ≤ 6 khi 4<x 5  5  /6 khi 5<x ≤ 6 > 1 khi  x 6 5 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Các tính chất của hàm phân phối xác suất: Tính chất 1: 0 ≤ F(x) ≤ 1.
Tính chất 2: Hàm phân phối xác suất là hàm không giảm Tính chất 3:
P(a ≤ X < b ) = F(b) – F(a) Tính chất 4: lim F ( ) x 0 = ;= lim F( ) x 1 x → x −∞ →+∞
Tính chất 5: Nếu X là bnn liên tục thì: + F(x) liên tục trên R + P(X = x) = 0
+P(a x≤ ≤b )= (P a x≤ b
< ) (=P a x< )b ≤ ( P = a x ) < b <
Ví dụ:Bnn liên tục X có hàm phân phối xác suất:  0 ≤ 1− x   1 F ( ) x = a  x b + 1 − < x≤  3 > 1 13 x 
Lim f(x) x->-1+ = lim(ax+b)= -a+b = f(-1)=0 (1)
F(1/3)= a/3+b =1 (2) suy ra: a=b= 3/4 a) Tìm hệsốa và b.
b) Tính xác suấtđể trong kết quảcủa phép thửX nhận giá
trịtrong khoảng (0 ; 1/3). P(06 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
2.3. Hàm mật độ xác suất:
Định nghĩa:Hàm mật độ xác suất của bnn liên tục X, ký
hiệu là f(x), là đạo hàm bậc nhất của hàm phân phối xác suất của nó. f (x ) F = (′ ∈ ) x , x R Tính chất Tính chất 1: f (x ) 0 ≥ x ∀ R ∈ b Tính chất 2:
P (a ≤ X
< = b )  f ( ) x dx a x Tính chất 3:
F (x ) =  f (t)dt −∞ +∞ Tính chất 4: f ( ) x dx 1 =  −∞ 7 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Ví dụ1: Cho bnn liên tục X có hàm mậtđộ xác suất là:   π π a co x s ; x ∈ −     2 2 f (x ) =   π π 0 ∉;− x     2 2 a) Tìm hệsốa.
b) Tìm hàm phân phối xác suấtF(x) . π
c) Tính xác suấtđể X nhận giá trịtrong (0 ; ). 4
Ví dụ2: Tuổi thọcủa một loại bóng đèn (đv h) bnn liên tục
có hàm mậtđộ xác suất là:  k ≥  x h 500( ) 2
f (x) =x < a) Tìm k. 0 x h 500( )
b) Tính xác suấtđể lấy ngẫu nhiên mười sản phẩm thì có
7sản phẩm có tuổi thọhơn 700 (h) 1k +∞ t  k dx = = lim  dx 2 2 x
t→+∞  x 500 500  1 1 k = k l t im − =  t→+∞  5  00 500 8 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
3. Các tham số đặc trưng của BNN 3.1. Kỳ vọng toán:
Định nghĩa: Kỳ vọng toán của bnn X, ký hiệu là E(X),
được xác định như sau:
+ Nếu X là bnn rời rạc có bảng phân phối xs là: X x1x2….. xn P p1p2….. pn n E( ) X =  x p i i i 1 =
+ Nếu X là bnn liên tục có hàm mậtđộ xác suất là f(x) thì: +∞ E( X ) . x f ( ) x dx = −∞ 9 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Ví dụ1: Tìm kỳvọng củađại lượng ngẫu nhiên rời rạc X
có bảng phân phối xác suất là: X 1 2 3 P 0,2 0,5 0,3 Giải:
E(X ) = 1.0, 2 + 2. + 0, = 5 3.0,3 2,1
Ví dụ2: Cho đại lượng ngẫu nhiên liên tục X có hàm phân phối xác suất là: 0  2 x ≤ 1 2 F( ) x =  ( x 2 − ) 2 <x≤ 4 4 1  4 x >  0 x h ≤ 2 x> 4 f (x ) = 0  ,5(x-2)  +∞ 4 E(X ) =
x.f (x )dx = x * 0,5* ( x − 2 =  ) dx 3 −∞ 2 10 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
* Ý nghĩa của kỳvọng:
Kỳvọng của bnn X đặc trưng cho trung bình
sốhọc của các giá trịcó thểcó của nó. Kỳ
vọng phản ánh giá trịtrung tâm ppxs của bnn.
Kỳvọng được sửdụng nhưmột tiêu chuẩn
để lựa chọn giữa các chiến lược khác nhau,
trong Ktếtiêu chuẩn này thường biểu diễn
dưới dạng lợi nhuận kỳvọng hay doanh sốkỳ vọng.
•Một sốtính chất của kỳvọng: + E(C) = C (C là hằng số) + E(CX) = C.E(X) + E(X+Y) = E(X) + E(Y)
+ E(XY) = E(X).E(Y) nếu X và Y độc lập 11 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022 3.2. Phương sai:
Định nghĩa: Phương sai của bnn X, ký hiệu là V(X), là kỳ
vọng của bình phương độlệch củađại lượng ngẫu nhiên với kỳvọng của nó:
V(X) = E[X – E(X)]2 (*)
+ Nếu X là đại lượng ngẫu nhiên rời rạc có bảng phân phối xác suất là: X x1x2…. xn P p1p2…. pn n V ( ) X = − [ ] 2 x ( ) E X . p i i i 1 =
+ Nếu X là bnn liên tục có hàm mậtđộ xác suất là f(x) thì: +∞ V X = − [ ] 2 ( ) x (E) X ( ) f x dx −∞
Dạng tương đương của công thức (*): V X = − E X [E X ]2 2 ( ) ( ) ( ) 12 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
+ Nếu X là rời rạc thì: 2 n n  2 V ( ) X = −  x p x p i i   i i i i1 = 1 =
+ Nếu X là liên tục thì: 2 +∞ +∞  2
V ( X ) = − x . f (x )  dx
 x.f (x )dx −∞ −∞ 
Ví dụ 1: Cho đại lượng ngẫu nhiên rời rạc X có bảng phân phối xác suất là: X0123 P 0,1 0,3 0,4 0,2 Hãy tính V(X).
Ví dụ 2:Cho đại lượng ngẫu nhiên liên tục X có hàm mật độ xác suất là: 2 3∈  0 x ;1 x ( ) f (x ) =0 ∉0;1 x  ( ) Tìm phương sai V(X). 13 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
* Ý nghĩa của Phương sai:
Phương sai của bnn X đặc trưng cho độ phân tán
của các giá trịcó thểcó của X xung quanh giá trị
trung bình của nó là Kỳvọng toán.
-Phương sai lớn thì độ phân tán lớn, độ tập trung thấp
Khi đó, Kỳvọng đại diện tốt cho các giá trịcủa X
-Phương sai lớn thì độ phân tán lớn, độ tập trung thấp
Khi đó, Kỳvọng đại diện không tốt cho các giá trịcủa X
-Trong kinh tế, Phương sai thường đùng để đo mứcđộ
rủi ro của các chiến lược kinh doanh
Một sốtính chất của phương sai:
+ V(C) = 0 ( với C là hằng số) + V(C.X) = C2.V(X)
+ V(X + Y) = V(X) + V(Y). Với X, Y độc lập + V(C + X) = V(X)  = n n V  X V ( ) X nếu  i i { độX c lậ }n ip i 1 = i 1=i 1= 14 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Độ lệch tiêu chuẩn củađại lượng ngẫu nhiên X,
ký hiệu σ ( )X , là :
σ ( )X = (V)X
Ưuđiểm: Độ lệch tiêu chuẩn có cùng đơn vịvới Bnn X 3.3. Giá trịtới hạn:
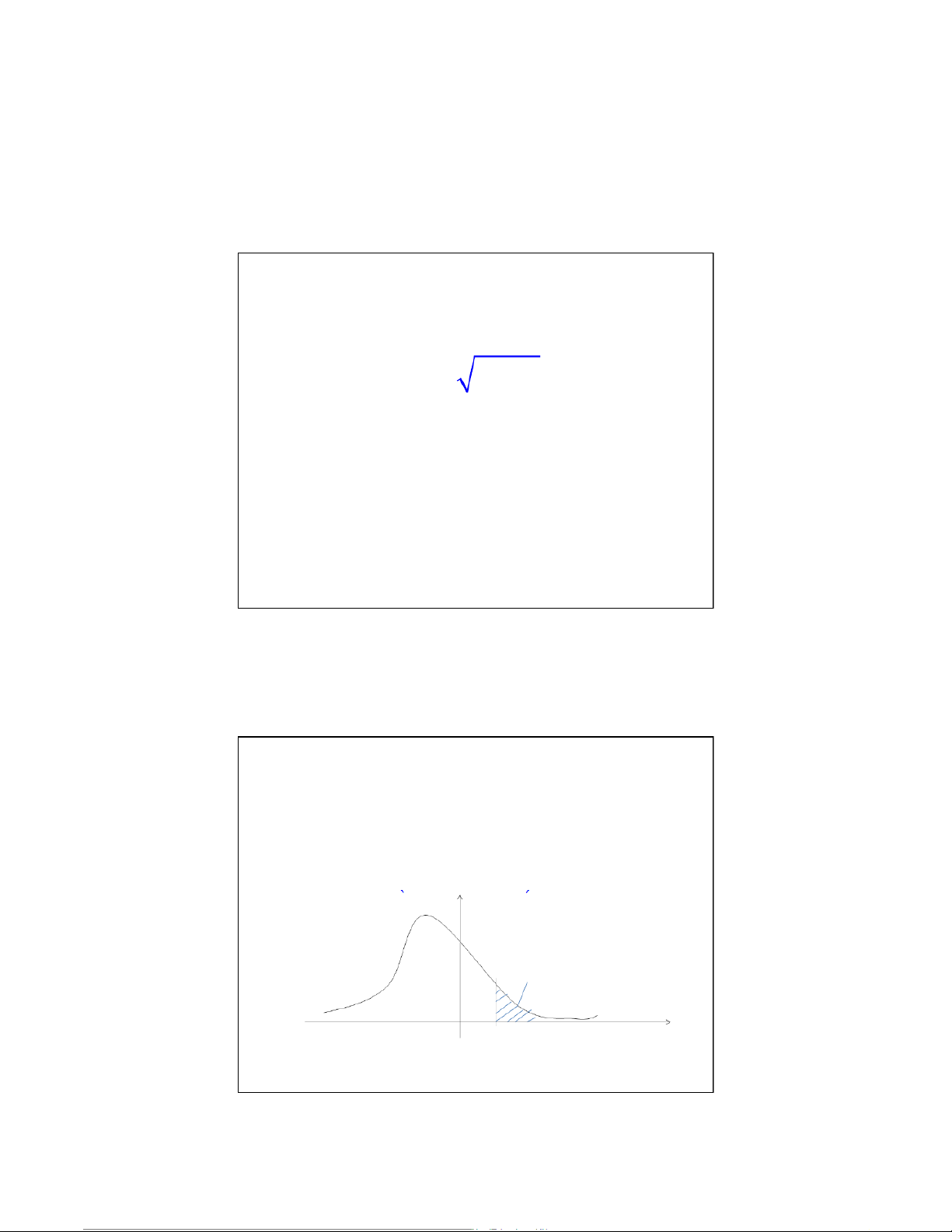
Định nghĩa: Giá trịtới hạn mức alpha của bnn X , ký hiệu
là X , là giá trịcủa X thỏa mãn điều kiện: α P(X X > = α α ) f (x ) α Xα 15 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
3.4. Các tham sốkhác:
Mốt:Mốt củađại lượng ngẫu nhiên là giá trịcủađại lượng
ngẫu nhiên có khảnăng xuất hiện lớn nhất trong một lân
cận nào đó, Ký hiệu là Mod(X).
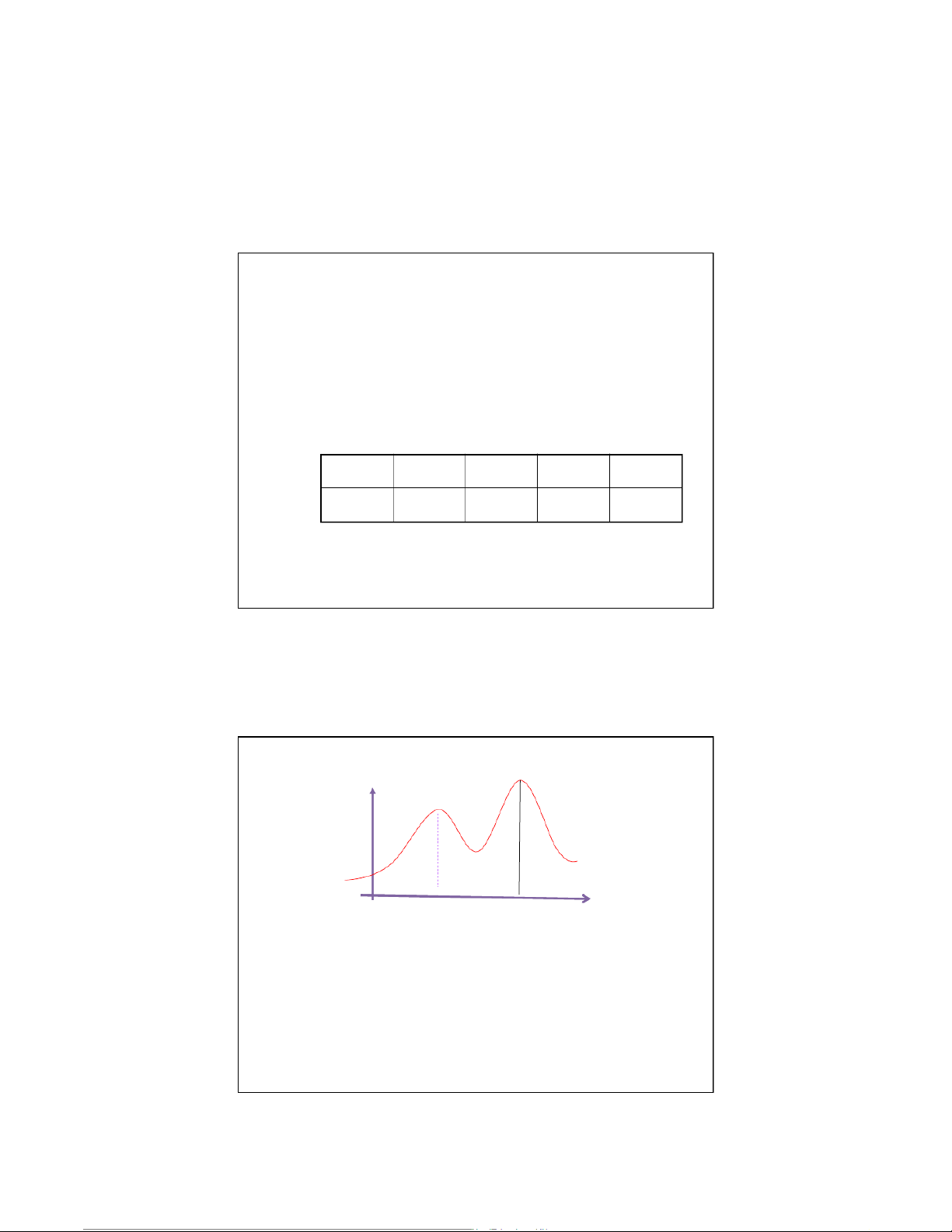
Một bnn có thể có một hoặc nhiều Mốt. X0123 Ví dụ P 0,064 0,288 0,432 0,216 Mod( ) X 2 = f(x) x 0 m0m1
Với BNN liên tục thì mốt là các điểm cựcđại của hàm mậtđộ.
-Chú ý: BNN có thểcó nhiều mốt. 16 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu 3/15/2022
Trung vị:Trung vịlà giá trịcủađại lượng ngẫu nhiên X
chia phân phối thành hai phần có xác suất bằng nhau, ký
hiệu là Med(X). Tức là: 1 P(X < M = ed( ) X )≥ = ( P X Med( )) X 2
- Nếu X là bnn rời rạc: M e d ( X ) = x nếu: i P(X < ≤ x ) 0, 5< ( P < X x ) i i 1 + - Nếu X là bnn liên tục: m Med ( ) X m = nếu  f ( )x dx 0 = , 5 −∞ 17 22:10, 10/01/2026
Chương 2: Biến Ngẫu Nhiên và Tham Số Đặc Trưng - Tài Liệu Học Tập - Studocu