















Preview text:
PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G PH
P ẦN II. ĐẠO HÀM, VI PHÂN VÀ ỨN Ứ G DỤNG N
Vì nội dung trong sách tương đối dài và “lung tung” nên tôi sẽ không viết theo chương
nữa mà sẽ viết theo chuyên đề. Chuyên đề lần này, phổ kiến thức sẽ dùng cho chương 2
và chương 3, giáo trình Toán cao cấp cho các nhà kinh tế.
Tài liệu này sẽ có các phần cơ bản sau đây: A. A Lý th Lý u th yết ế c t ơ ơ bả b n n A.1 A. Cá C c á ph p ươn ươ g n ph p áp á tín tí h n h đạo h à h m à 1 b i b ến n 2 2 - -Đạ Đ o ạ h à h m m c ấp 1 1 2 2 - -Đạ Đ o ạ h à h m m c ấp c a c o o 3 A.2 A. H à H m à s ố ố n h n iều ề b i b ến ế ( Ch C ươn ơ g n 6) 6 4 4 B. B Ứng n d ụn ụ g n c ủa a đạo o h àm à m 4 Dạng n 1 . T ì T m ì c ác á c k h k oản ả g n tăng tăn , gi g ảm 4 4 Dạng n 2 . C ực ự tr ị tươn ươ g n đối,i c ực tr ị tu yệt ệ đ t ối ic ủa ah à h m m s ố 6 6 Dạng n 3 . V i V ết ế ph p ương n gtrình n h tiế ti p p tu yến ế 9 9 Dạng n 4 . T ì T m ì t ốc ố độ đ thay a yđổi iv à v à p hân â n tí c tí h h c ận n bi b ê i n n tr o tr ng n g k i k nh n t ế. ế 9 9 Dạn ạ g n 5. Đạ Đ o o h àm à của a h àm à ẩn ẩ n 11 1 1 Dạng n 6 . C á C c á y ếu ế t ố: ố Tí T nh n lõm, đi đ ểm u ốn, n ti ệ ti m m cận ậ n đứng n , ti ệm ệ c ận n n g n a g n a g n . 13 1 3 Dạn ạ g n 7. Độ Đ c o c o g iã i n ã 15 1 Dạng n 8 . V i V ip hâ h n n 16 1 Bà B i it ập p 17 1 D 1 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G A. A Lý t hu h yết cơ c bả b n n A. A 1 1 C á C c á ph p ươ ư n ơ g n ph p áp á p títnh h đạ đ o ohà h m 1 1 b i b ến ế 1. 1 Đạo o h à h m m c ấp p 1 1 𝒅𝒇 - -Đạ Đ o o h àm à c ấp ấ 1 1 c ủa ủ f fđược ck ý k ý h iệu ệ u l à l 𝒇′, h o h ặc c 𝒅𝒙 a. Tính n h đạo o h à h m m b ằn ằ g n gđịnh n h ng n h g ĩa: a
Đạo hàm của hàm số 𝑓(𝑥) theo x là hàm số được xác định bởi:
𝑓(ℎ + 𝑥) − 𝑓(𝑥) 𝑓′(𝑥) = lim ℎ→0 ℎ b. Tính n h đạ đ o h à h m à m b ằn ằ g n c ô c n ô g n th ức: c
Một số quy tắc tính đạo hàm đáng chú ý:
- Đạo hàm của hằng số: 𝑓(𝑥) = 𝑐 𝑡ℎì 𝑓′(𝑥) = 0
- Đạo hàm của hàm mũ: 𝑓(𝑥) = 𝑥𝑛 thì 𝑓′(𝑥) = 𝑛𝑥𝑛−1, với n là số thực bất kỳ. ′
- (𝑐𝑓(𝑥)) = 𝑐𝑓′(𝑥)
- Đạo hàm của tổng – hiệu: (𝑓(𝑥) + 𝑔(𝑥))′ = 𝑓′(𝑥) + 𝑔′(𝑥) ′
- Đạo hàm của tích: (𝑓(𝑥)𝑔(𝑥)) = 𝑓′(𝑥)𝑔(𝑥) + 𝑓(𝑥)𝑔′(𝑥) ′
- Đạo hàm của thương (nếu hàm xác định) : (𝑓(𝑥)) = 𝑓′(𝑥)𝑔(𝑥) − 𝑓(𝑥)𝑔′(𝑥) 𝑔(𝑥) (𝑔(𝑥))2 ′
- Đạo hàm hàm hợp: (𝑓(𝑔(𝑥))) = 𝑓′(𝑔(𝑥))𝑔′(𝑥)
Ngoài ra, các bạn cần nhớ thêm đạo hàm của 1 số hàm đặc biệt (có thể sẽ thi): - (ln 𝑥)′ = 1 𝑥 - (𝑒𝑥)′ = 𝑒𝑥 1
- (sin 𝑥)′ = cos 𝑥, (cos 𝑥)′ = − sin 𝑥, (tan 𝑥)′ = cos2 𝑥 Ví V íd ụ 1 .
1 Tính đạo hàm của hàm số: 𝑓(𝑥) = √𝑥 1 1 Lời ig i g ải
ả :i Các bạn cần chú ý 2 tính chất sau: √𝑥 = 𝑥2 và = 𝑥−1 𝑥 D 2 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Do đó áp dụng công thức đạo hàm hàm mũ, ta có 1 1 1 1 1 1 1 1 𝑓′(𝑥) = 2−1 = . 2 𝑥 = 2𝑥−12 = 2. 1 = 𝑥 2 . 2 √𝑥 2√𝑥
Đây là công thức các bạn nên nhớ để giảm thiểu khối lượng tính toán không cần thiết.
Trong trường hợp các bạn quên mất công thức, chỉ cần xây dựng lại theo cách như mình đã trình bày ở trên. Ví V íd ụ 2 .
2 Tính đạo hàm của hàm số: 𝑓(𝑥) = (𝑥 − 1)(𝑥2 + 𝑥 + 5) Lời ig i g ải:i Cá C c á h c 1 .
1 Các bạn tách hết tích ra và được kết quả: 𝑓(𝑥) = 𝑥3 + 5𝑥 − 5. Khi đó áp dụng các
công thức đạo hàm tổng, đạo hàm hàm mũ, ta có: 𝑑 𝑑 𝑑 𝑓′(𝑥) = ( (
𝑑𝑥 𝑥3) + 𝑑𝑥 5𝑥) − 𝑑𝑥 (5) = 3𝑥2 + 5 Cá C c á h c 2 .
2 Ta coi 𝑓(𝑥) là tích của 2 hàm số. Áp dụng công thức đạo hàm của một tích:
𝑓′(𝑥) = (𝑥 − 1)′(𝑥2 + 𝑥 + 5) + (𝑥 − 1)(𝑥2 + 𝑥 + 5)′
= 1(𝑥2 + 𝑥 + 5) + (𝑥 − 1)(2𝑥 + 1) = 3𝑥2 + 5. 𝒅𝒇 - -Đạ Đ o o h àm à c ấp ấ 1 1 c ủa ủ f fđược ck ý k ý h iệu ệ u l à l 𝒇′(𝒙), h o h ặc c 𝒅𝒙 Ví V íd ụ 3 .
3 Tính đạo hàm của hàm số: 𝑓(𝑥) = (𝑥2 − 2𝑥 + 5)8 Lời ig i g ải
ả :i Trường hợp này các bạn không thể làm như cách 1 của ví dụ 2 được vì khai triển
quá phức tạp, các bạn cần sử dụng công thức đạo hàm của hàm hợp. Ở đây, nếu ta đặt
𝑔(𝑥) = 𝑥2 − 2𝑥 + 5 thì 𝑓(𝑥) = 𝑔(𝑥)8.
Vậy 𝑓′(𝑥) = 8𝑔(𝑥)7. 𝑔′(𝑥) = 8(𝑥2 − 2𝑥 + 5)7. (2𝑥 − 2) = 16(𝑥 − 1)(𝑥2 − 2𝑥 + 5)7 Nh N ận n xé x t:
é Ta coi như g(x) là 1 biến số để áp dụng đạo hàm của 1 hàm mũ, sau đó mới quay
ra tính đạo hàm của g(x). 4 Ví V íd ụ 4 .
4 Tính 𝑓′(1), biết hàm số 𝑓(𝑡) = 2√𝑡3 + −√2. √𝑡 Lời ig i g ải ả :i D 3 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G 3 4 ′ 3 ′ ′ 3 3 1 1 𝑓′(𝑡) = (2𝑡 2 + 2−1
1 − √2) = (2𝑡 2) − (4𝑡−12) = 2. − 4. (− 2 + 2𝑡−32 𝑡2 2 𝑡 2) 𝑡−12−1 = 3𝑡 2 = 3√𝑡 + 𝑡√𝑡 Khi đó 𝑓′(1) = 5 2. 2 Đạo o h à h m m c ấp ấ p ca c o a ( (Đi Đ thi thườ th n ườ g n là àđạ đ o o h àm m c ấp p 2 2 ) Đạ Đ 𝒅𝟐𝒇 o o h à h m à c ấp ấ p 2 của ủ h à h m à f fth e th o e b i b ến ế n x thườ th ng n gđượ đ c ck ý k h i h ệu ệ l à l à 𝒇′ (𝒙) ho h ặc c l à l . .(tuy (tu ệt t 𝒅𝒙𝟐 đố đ i ik h k ôn ô g n g p hải i𝒅𝟐𝒙) . ) B ản n c h c ất c t ủa a đạo o h àm m c ấp 2 2 ch c ính n h là àđạ đ o o h àm à th e th o o b iến ế n c ủa a đạ đ o o hà h m m c ấp ấ 1 . 1 Ví V íd ụ 5 .
5 Tính đạo hàm cấp 2 của hàm số: 𝑓(𝑥) = 𝑥2(3𝑥 + 1) Lời ig i g ải
ả :i Dễ dàng tính được đạo hàm cấp 1 của 𝑓(𝑥): 𝑓′(𝑥) = 9𝑥2 + 2𝑥
Khi đó đạo hàm cấp 2 của 𝑓(𝑥) là đạo hàm của 𝑓′(𝑥): 𝑓′ (𝑥) = (9𝑥2 + 2𝑥)′ = 18𝑥 + 2 A.2 A. Hà H m à s ố ố n h n iều ề u b i b ến ế ( (ch c ươn ươ g n 6 6 ) - -M ột h t àm à s ố ố c ó ó n h n iều ề hơ h n ơ n 1 bi b ến n s ố đ ộc lập p đư đ ợc ợ g ọi ọ il à l h à h m à s ố ố n h n i h ều u b i b ến. n Ví V íd ụ 6.
6 𝒇(𝒙, 𝒛) = 𝒙𝟐 + 𝟐𝒛𝟐 + 𝟑𝒙𝒛. H à H m à f fph p ụ th u th ộc v à v o à c ả ả x xv à v z n ê n n ê c ó c ó k ý k ý h iệu u 𝒇(𝒙, 𝒛) a. a Đạo o h àm à m c ấp ấ 1 1
Một hàm có nhiều biến, vậy ta sẽ phải chọn 1 biến để tính đạo hàm theo nó, còn các biến
khác ta coi như tham số. Lúc này, ta gọi đó là ĐẠO HÀM RIÊNG CẤP 1.
Trong ví dụ 6, nếu ta đạo hàm f theo biến x, ta ký hiệu 𝑓′𝑥. Lúc này coi z là tham số, ta có: 𝑑𝑓
𝑓′𝑥 = 𝑑𝑥 = (𝑥2)′ + (2𝑧2)′ + (3𝑥𝑧)′ = 2𝑥 + 0 + 2𝑧 = 2𝑥 + 3𝑧
Tương tự, nếu đạo hàm f theo biến z, ta có 𝑓′𝑧 = 3𝑥 + 4𝑧. b. b Đạo h à h m à cấp ấ 2 2
Hoàn toàn tương tự như trường hợp hàm số 1 biến. Ở đây ta có 2 đạo hàm riêng cấp 1,
mỗi đạo hàm riêng này lại có 2 đạo hàm riêng cấp 2, cụ thể như sau: TH1. Đạ 𝑑2𝑓
o hàm cấp 1 và cấp 2 cùng theo biến x, ký hiệu ′ 𝑑𝑥2 hoặc 𝑓𝑥𝑥 𝑑2𝑓
𝑑𝑥2 = (2𝑥 + 3𝑧)′𝑥 = 2. D 4 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G TH2. Đạ 𝑑2𝑓
o hàm cấp 1 theo x, sau đó đạo hàm cấp 2 theo z. Ký hiệu hoặc 𝑓 ′ 𝑑𝑥𝑑𝑧 𝑥𝑧 𝑑2𝑓
𝑑𝑥𝑑𝑧 = (2𝑥 + 3𝑧)′𝑧 = 3
TH3. Đạo hàm cấp 1 theo z, sau đó đạo hàm cấp 2 theo x
TH4. Đạo hàm cấp 1 và cấp 2 cùng theo biến z.
2 trường hợp trên các bạn có thể tự luyện tập. Kết quả lần lượt là 3 và 4.
Một tính chất khá thú vị là 𝑓 ′ ′
𝑧𝑥 = 𝑓𝑥𝑧. Các bạn có thể dùng để giảm khối lượng tính toán. A. A 2 2 Ứn Ứ g n dụn ụ g gc ủa ủ ađạ đ o o h àm à
Ở đây, mình sẽ chia thành các dạng bài tập khác nhau có sử dụng đạo hàm như sau:
Dạng 1. Tìm các khoảng tăng, giảm, Dạng n
g 1. Tìm các khoảng tăng, giảm của hàm số
Dạng bài tập này yêu cầu chúng ta khảo sát hàm số xem hàm tăng trong khoảng nào và giảm trong khoảng nào. Ví V íd ụ 7 .
7 Tìm các khoảng tăng, giảm của hàm số:
𝑓(𝑥) = 2𝑥3 + 3𝑥2 − 12𝑥 − 6 Lời ig i g ải
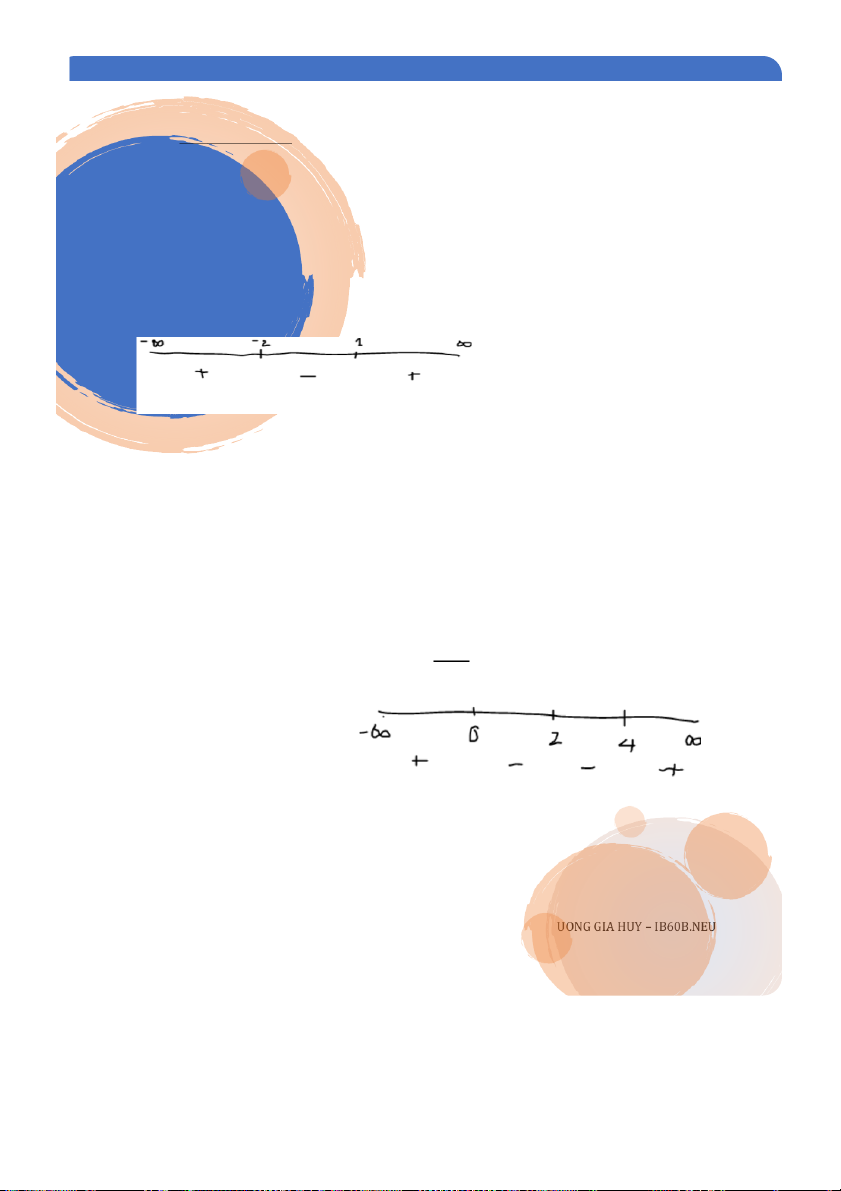
ả :i Ta tính đạo hàm cấp 1: 𝑓′(𝑥) = 6𝑥2 + 6𝑥 − 12 = 6(𝑥 + 2)(𝑥 − 1)
Khi 𝑓′(𝑥) = 0, ta có 𝑥 = 1 hoặc 𝑥 = −2. Lúc này, các số 1 và -2 chia trục số thành 3
khoảng: (−∞, −2), (−2,1), (1, ∞). Ta sẽ xem xét trong từng khoảng này, 𝑓′(𝑥) có dấu như thế nào.
Với khoảng (−∞, −2), ta lấy 1 giá trị bất kỳ trong khoảng này, giả sử -3, ta có 𝑓′(−3) =
24 > 0. Khi đó ta có kết luận là hàm f đang tăng trong khoảng (−∞, −2).
Với khoảng (−2,1), ta có 𝑓′(0) = −6 < 0, do đó hàm giảm trong khoảng (−2,1) D 5 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Tương tự, hàm tăng trên khoảng (1, ∞)
Vậy ta kết luận, hàm tăng trong khoảng (−∞, −2) và
(1, ∞), giảm trong khoảng (−1,2)
Sau đây là đồ thị của hàm f(x):
Ta nhận thấy, đồ thị đang đi lên trong khoảng (−∞, 2)
và (1, ∞), còn đi xuống trong khoảng (−2,1). Như vậy
kết quả tính ở trên hoàn toàn phù hợp. Ví V íd ụ 8 .
8 Tìm các khoảng tăng, giảm của hàm số: 𝑥2 𝑓(𝑥) = 𝑥 −2 Lời ig i g ải
ả :i Hàm số xác định tại mọi 𝑥 ≠ 2 và có đạo hàm: 2𝑥(𝑥 − 2) − 𝑥2(1) 𝑓′(𝑥) =
2𝑥2 − 4𝑥 − 𝑥2 𝑥(𝑥 − 4) (𝑥 − 2)2 = (𝑥 − 2)2 = (𝑥 − 2)2
Ta thấy, 𝑓′(𝑥) không liên tục tại x = 2, và 𝑓′(𝑥) = 0 tại 2 điểm x = 0 và x = 4 . Vậy lúc
này ta chia trục số thành 4 khoảng: (−∞, 0), (0,2), (2,4), (4, ∞). Các bạn có thể tự luyện
tập theo phương pháp ở ví dụ 7. Đá Đ p á số
s : Hàm tăng khi x < 0 và x > 4, giảm trong khoảng (0,2) và (2,4), không xác định tại x = 2. Ví V íd ụ tươn ươ g
n tự: :Hàm số 𝑓(𝑥) tăng trong khoảng nào, biết:
Đáp số: (−∞, −3) và (1, ∞)
Vậy, các bạn cần nhớ cách làm chung cho dạng này như sau:
Bước 1. Tính đạo hàm của hàm số và tìm các giá trị để đạo hàm bằng 0, đạo hàm không
xác định. Các giá trị này còn được gọi là GI G Á I T Á RỊ ỊT ỚI IH ẠN. N
Bước 2. Từ các giá trị tìm được ở b1, sắp xếp và chia trục số thành các khoảng. Chọn một
giá trị bất kỳ trong các khoảng để kiểm tra dấu của đạo hàm trong khoảng đó.
Nếu 𝑓′(𝑥) > 0: hàm tăng trong khoảng đó, và hàm giảm nếu 𝑓′(𝑥) < 0. Dạng n
g 2. Cực trị tương đối và tuyệt đối của hàm số D 6 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G a. Cực trị tương đối
Trở lại với các hàm số đã sử dụng ở dạng 1: Ví V íd ụ 9 .
9 Tìm cực trị tương đối của hàm số:
𝑓(𝑥) = 2𝑥3 + 3𝑥2 − 12𝑥 − 6
Ở đây, khái niệm cực tr ị tươn ơ g
n gđối iđược hiểu là cực trị trong 1 khoảng số chứ không
phải là cực trị trong toàn miền. Các khoảng số ở đây chính là các khoảng mà các bạn tìm
được ở ví dụ 7, (−∞, −2), (−2,1), (1, ∞).
Ta đã tìm được dấu của 𝑓′(𝑥) tại các khoảng như sau:
Khi đó ta có thể kết luận được rằng, hàm số đạt cực đại tại x = -2, tương ứng với f(x)=
14 và cực tiểu tại x = 1, tương ứng với f(x) = -13. !! ! ! ! !T rá r n á h n n h n ầm ầ m l ẫn n C ự C c ti ểu ể v ới iG i G á i tr ị nh n ỏ nh n ất, t, c ực ực đại iv ới ig iá i á tr ị l ớn ớ n n h n ất ! t ! ! !
Một câu hỏi đặt ra, làm sao để có thể nhận biết nhanh đâu là cực đại, đâu là cực tiểu. Ở ví
dụ 9, các bạn chú ý điểm -2. Ta thấy f’(x) > 0 với x < -2 và f’(x) < 0 với x > -2. Khi đó, đồ
thị tăng đến điểm x = -2 thì lại giảm. Có thể tưởng tượng rằng, -2 là “đỉnh của chóp”. Do
vậy 2 là cực đại. Tương tự, với điểm -1, hàm số giảm tới x = -1 rồi tăng trở lại, vậy -1 là
điểm thấp nhất, hay còn gọi là cực tiểu. Ví V íd ụ 1 0
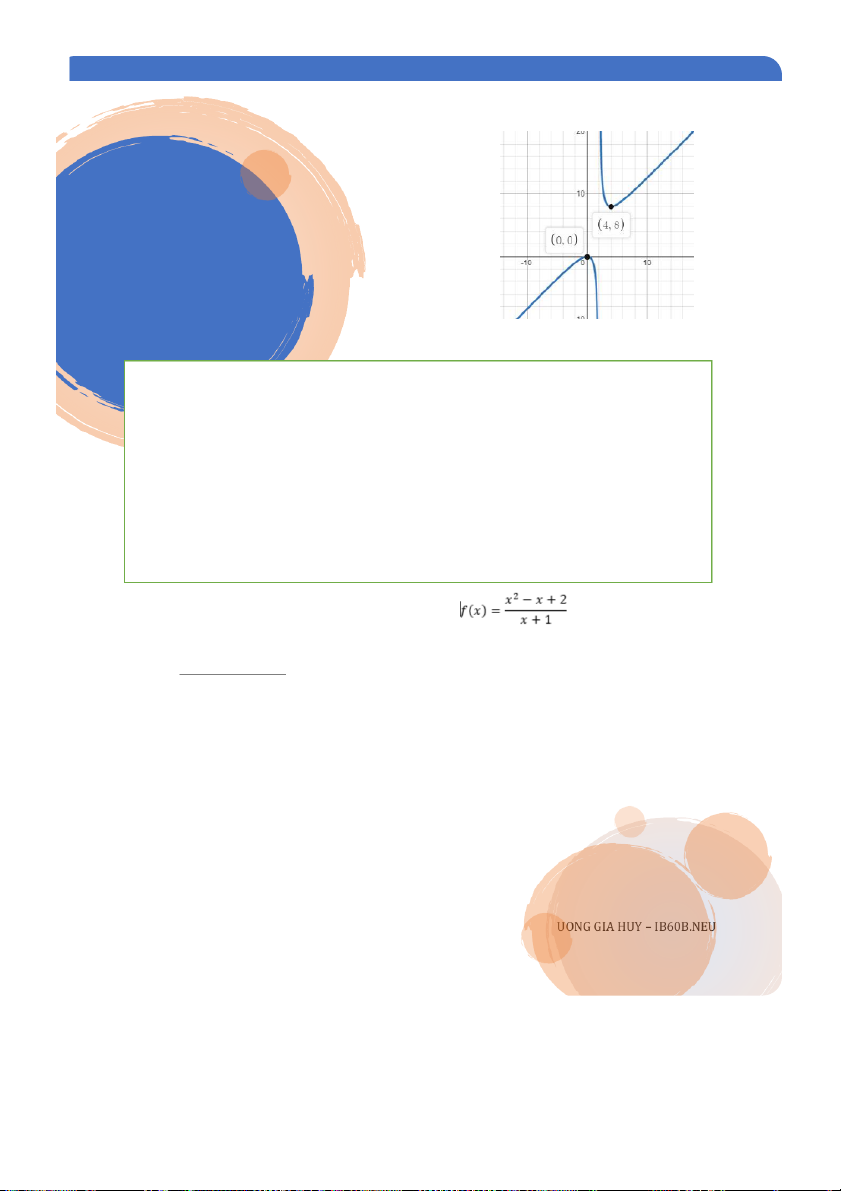
1 . .Tìm các cực trị của hàm số: 𝑥2 𝑓(𝑥) = 𝑥 −2
Như ở ví dụ 8, ta tìm được các giá trị tới hạn là 0, 2, 4, lập được 4 khoảng, và dấu của f’(x) tại các khoảng:
Sử dụng phương pháp như ở ví dụ 9, ta kết luận là hàm số có cực đại tại x = 0 tương ứng
f(x) = 0, và cực tiểu tại 4, tương ứng với f(x) = 8. Còn riêng điểm x = 2, ta thấy dấu của
f’(x) không thay đổi qua điểm này, vậy nó không phải cực trị. D 7 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Sau đây sẽ là đồ thị của hàm số, rõ ràng các bạn nhìn
thấy điểm cực đại còn ở dưới điểm cực tiểu!
Ví dụ trên đã cho thấy sự khác biệt rất rõ giữa GTNN
và cực tiểu, GTLN và cực đại.
Vậy cách làm chung của dạng bài tìm cực trị tương đối như sau:
Bước 1. Tính đạo hàm của hàm số và tìm các giá trị để đạo hàm bằng 0, đạo hàm không
xác định. Các giá trị này còn được gọi là GI G Á I T Á RỊ ỊT ỚI IH ẠN. N
Bước 2. Từ các giá trị tìm được ở b1, sắp xếp và chia trục số thành các khoảng. Kiểm tra
dấu của đạo hàm trong khoảng đó.
Bước 3. Xét các điểm tới hạn:
+) Nếu 𝑓′(𝑥) đổi dấu từ dương sang âm qua điểm đó, thì đó là cực đại tương đối .
+) Nếu 𝑓′(𝑥) đổi dấu từ dương sang âm qua điểm đó, thì đó là cực tiểu tương đối .
+) Nếu 𝑓′(𝑥) không đổi dấu qua điểm đó thì đó không phải cực trị. Bà B i it ập ậ tương
n gtự: :Tìm các cực trị của hàm số:
Đáp số: Cực đại tại x = -3 và cực tiểu tại x = -1 b. Cực trị tuyệt đối
Ở đây chúng ta cần phải tìm GTNN và GTLN của hàm số.
Bài này trong đề thi, thông thường sẽ cho hàm bậc 2 dạng 𝑓(𝑥) = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 hoặc
hàm phân thức. Các dạng này làm hoàn toàn tương tự như dạng cực trị tương đối, đối với trắc nghiệm. Ví V íd ụ 1 0’
0 . .Một nhà quản lý tính toán được khi trung bình doanh nghiệp sản xuất được q
nghìn sản phẩm 1 tháng, Giá bán sẽ là 𝑝(𝑞) = 22.2 − 1.2𝑞 đô- la mỗi đơn vị. Tổng chi phí
để sản xuất q đơn vị là 𝐶(𝑞) = 0.4𝑞2 + 3𝑞 + 40 nghìn đô la.
Vậy doanh nghiệp cần phải sản xuất bao nhiêu đơn vị hàng hóa để tối đa hóa lợi nhuận? Lời ig i g ải
ả :i Ta có hàm doanh thu 𝑅(𝑞) = 𝑞𝑝(𝑞) = (22.2 − 1.2𝑞)𝑞 = −1.2𝑞2 + 22.2𝑞 D 8 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G Hàm lợi nhuận
𝑃(𝑞) = 𝑅(𝑞) − 𝐶(𝑞) = −1.2𝑞2 + 22.2𝑞 − (0.4𝑞2 + 3𝑞 + 40) = −1.6𝑞2 + 19.2𝑞 − 40
𝑃′(𝑞) = 0 → −3.2𝑞 + 19.2 = 0, hay 𝑞 = 6.
Lập bảng biến thiên, ta thấy q = 6 (nghìn) chính là điểm sản phẩm mà lợi nhuận tối đa. Dạng n g 3. Vi V ết ế tphư h ơng ơn trìn t h rìn titếp tu t yến ế n của hà h m s m ố
Dạng này rất đơn giản, các bạn chỉ cần nhớ cách làm như sau:
Bước 1. Tính đạo hàm của hàm số và chọn 1 điểm trên hàm số. Nếu đề bài cho trước
tung độ thì ta tính nốt hoành độ và ngược lại. Ký hiệu (𝑥0, 𝑦0)
Bước 2. Phương trình tiếp tuyến của đường cong ( hàm số ) tại điểm (𝑥0, 𝑦0) là:
𝑦 − 𝑦0 = 𝑓′(𝑥0)(𝑥 − 𝑥0) Ví V íd ụ 11 1 .
1 Viết phương trình tiếp tuyến của hàm số sau tại x = 3:
𝑦 = 𝑓(𝑥) = 𝑥3 − 2𝑥2 + 𝑥 − 1 Lời ig i g ải
ả :i Ta có đạo hàm 𝑓′(𝑥) = 3𝑥2 − 4𝑥 + 1
Tại x = 3, ta có 𝑓′(3) = 3(32) − 4(3) + 1 = 16, 𝑓(3) = 33 − 2(32) + 3 − 1 = 11
Như vậy, phương trình tiếp tuyến tại điểm (3, 11) là:
𝑦 − 11 = 𝑓′(3)(𝑥 − 3) = 16𝑥 − 48, hay 𝑦 = 16𝑥 − 37. Dạng n g 4. Tì T m ì t m ốc ố độ đ th t ay a yđổ đ i ivà v à phâ h n n tí t c í h h cận n bi b ê i n ê
2 ví dụ sau đây sẽ minh họa cho cách tìm tốc độ thay đổi của một đại lượng tại một thời
điểm nhất định thông qua đạo hàm. Ví V íd ụ 1 2
1 . .Một bể nuôi cấy vi khuẩn, sau thời gian t(phút), số lượng vi khuẩn trong bể
được biểu diễn dưới hàm 𝑓(𝑡) = 𝑡3 + 2𝑡2 − 1. Hỏi tại thời điểm t = 5 (phút ), số lượng
vi khuẩn đang thay đổi như thế nào? Lời ig i g ải
ả :i Ta có 𝑓′(𝑡) = 3𝑡2 + 4𝑡, tại t = 5 thì 𝑓′(5) = 95. Do đó, tại thời điểm t = 5 phút,
số vi khuẩn trong bể đang tăng lên với tốc độ 95 con / phút. Lưu ý: ý - -N ếu ế c á c c á b ạn ạ n k i k ểm m tra ađáp á án á n bằ b ng n g c á c ch c l ấy
y 𝒇(𝟔) − 𝒇(𝟓), ta c ta ó
ó 𝒇(𝟔) − 𝒇(𝟓) = 𝟐𝟖𝟕 −
𝟏𝟕𝟒 = 𝟏𝟑𝟑, s a s i a il ệc ệ h h v ới ik ết ế q u q ả ả tr ên ê . n C ác á c b ạn ạ n c ó ó th ể ch c ọn ọ n 1 tro tr ng n g2 cá c c á h c h để l à l m, m t uy u y n h n iê i n ê n tro tr ng n g th ực c t ế, ế ng n ười ta h ta a h y a y s ử d ụng n gcá c c á h c 1 1 hơ h n ơ . n D 9 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G - -K ết l t u l ận n b à b i ito á to n n tr ên ê n c ó ó th ể p há h t b t i b ểu ể l ại ạ il à l : à T ại ạ ith ời ờ đi đ ểm t = t = 5 5 p hú h t, t, n ếu ế u nh n ư th ư ời ig ia i n n tăng tăn thêm ê 1 1 ph p út, ú t, tổng n g s ố ố v i v ik h k uẩn ẩ n t ro r n o g n g b ể s ẽ tăng tăn lên ê n 95 5 con o . n Tro r n o g n trườ tr ng n h ợp ợ lượng n g thay a yđổi ith ời ig i g a i n n k h k ôn ô g n p h p ải ả là à1 ph p ú h t m t à àlà 0. 0 5 5 phút ú nh n ư h tro tr n o g n bà b i à toá to n n sau a : u Ví V íd ụ 1 2 1 .1
. . .Một bể nuôi cấy vi khuẩn, sau thời gian t(phút), số lượng vi khuẩn trong bể
được biểu diễn dưới hàm 𝑓(𝑡) = 𝑡3 + 2𝑡2 − 1. Hỏi tại thời điểm t = 5 (phút ), số lượng
vi khuẩn thay đổi như thế nào sau mỗi 0.5 phút? Lời ig i g ải
ả :i Ta chỉ cần nhân lượng thay đổi trong 1 phút ở ví dụ 12 với 0.5. Ta có 𝑓′(5) = 95.
Lượng thay đổi của số vi khuẩn sau mỗi 0.5 phút tại thời điểm t = 5 là:
∆𝑓 = 𝑓′(5)∆𝑡 = 95(0.5) = 47.5
Các ví dụ tiếp theo sẽ nhắc đến một khái niệm là cận biên. Trong chương trình Kinh tế
học, các bạn đều được học khái niệm này dưới dạng lợi nhuận cận biên, chi phí cận
biên…. Ta có thể hiểu rằng:
Lợi nhuận cận biên là lợi nhuận tăng thêm khi mức sản xuất tăng thêm 1 đơn vị. Giả sử
mức sản xuất đang là 𝑥 = 𝑥0. Cũng như ví dụ 11, ta có 2 cách tính:
Cách 1. Tính đạo hàm 𝑃′(𝑥0). Đây là doanh thu cận n bi b ê i n ê . n
Cách 2. Tính hiệu 𝑃(𝑥0 + 1) − 𝑃(𝑥0). Đây là doanh thu th t ực
c t ế khi tăng mức sản xuất thêm 1 đơn vị.
Tuy nhiên, các bạn sẽ là l m à m c á c ch c 1 khi đi thi. Nếu ế đề đ b à b i à ic ó ó c h c ữ “t “ h t ự h c ct ế” ế ”thì mớ m i in ê n n n s ử ử dụng n c á c c á h c h 2 . . Ví V íd ụ 1 3
1 . .Một nhà sản xuất ước tính rằng, chi phí để sản xuất x đơn vị của 1 loại hàng
hóa được biểu diễn bởi hàm 𝐶(𝑥) = 0.15𝑥2 + 3𝑥 + 9 đô la. Giả sử nhà sản xuất này đang
sản xuất 30 sản phẩm mỗi tuần. Hỏi chi phí cận biên của nhà sản xuất là bao nhiêu? Tính
toán chi phí thực tế tăng thêm khi sản xuất 31 đơn vị sản phẩm. Lời ig i g ải
ả :i Ở câu hỏi đầu tiên, đề bài có nhắc đến chi phí cận biên. Các bạn sẽ tính được:
𝐶′(𝑥) = 0.3𝑥 + 3, với 𝑥 = 30 thì 𝐶′(30) = 12
Vậy tại mức sản xuất x = 30, chi phí cận biên của nhà sản xuất là 12.
Mức chi phí tăng thêm thực tế khi sản xuất thêm 1 sản phẩm là: 𝐶(31) − 𝐶(30) = 12.15 Nh N ận n x ét: é D 10 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Như vậy, chi phí cận biên xấp xỉ mức chi phí thực tế khi sản xuất thêm 1 đơn vị.
Bản chất của ví dụ trên là công thức sau:
𝑓(𝑥0 + ∆𝑥) − 𝑓(𝑥0) ≈ 𝑓′(𝑥0) ∆𝑥
Ở ví dụ 13, ∆𝑥 = 1, 𝑥
0 = 30, ta có 𝑓(31) − 𝑓(30) ≈ 𝑓′(30)(1) hay 12.15 ≈ 12.
Ở ví dụ 12.1, ∆𝑥 = 0.5, 𝑥0 = 5, ta có 𝑓(5.5) − 𝑓(5) ≈ 𝑓′(5) (0.5).
Công thức trên sẽ càng chính xác nếu như ∆𝑥 càng bé. Như ở ví dụ 12, ∆𝑥 = 1, 𝑥 0 = 5, ∆𝑥
tương đối lớn so với 𝑥0, do đó sai số tương đối lớn. Còn ở ví dụ 13 đã chỉ ra điều ngược lại.
Vậy chốt lại, với dạng bài có chữ “ tốc độ thay đổi “, “cận biên”, các bạn chỉ cần tính đạo
hàm và thay biến số bằng giá trị đề bài đã cho và kết luận như các ví dụ trên. Dạng n g5. Đạ Đ o ohàm à c m ủa ủ hà h m ẩn ẩ
Với 4 dạng bài trước, hàm y đã được biểu diễn một cách tường minh qua x, hoặc chúng
ta có thể dễ dàng giải được y theo x. Nhưng trong những trường hợp sau đây, việc giải
phương trình để tìm y qua x không hề đơn giản. Ví V íd ụ 1 4
1 . .Giả sử 𝑦 = 𝑓(𝑥) là một hàm khả vi theo x thỏa mãn phương trình sau, tính đạo hàm của y theo x:
𝑦3 + 2𝑥2𝑦 + 𝑥2 = 1 Lời ig i g ải
ả :i Rõ ràng ta không thể giải y theo x. Ta cần tạo ra đạo hàm gián tiếp. Nên nhớ
rằng y là một hàm số theo x chứ không phải biến số, nên nếu như các bạn sợ nhầm, hãy
thay toàn bộ chữ y thành chữ f .
𝑓3 + 2𝑥2𝑓 + 𝑥2 = 1
Đạo hàm 2 vế theo x, ta có: ( chú ý ký hiệu 𝑓′(𝑥) tương đương 𝑑𝑓 𝑑𝑥 ) 𝑑 ( 𝑑
𝑑𝑥 𝑓(𝑥)3 + 2𝑥2𝑓(𝑥) + 𝑥2) =𝑑𝑥 (1)
3𝑓2(𝑥)𝑓′(𝑥) + (4𝑥𝑓(𝑥) + 2𝑥2𝑓′(𝑥)) + 2𝑥 = 0
→ 𝑓′(𝑥)(3𝑓2(𝑥) + 2𝑥2) + 4𝑥𝑓(𝑥) + 2𝑥 = 0 Chuyển vế, ta có: −4𝑥𝑓(𝑥) − 2𝑥
𝑓′(𝑥) = 3𝑓2(𝑥) + 2𝑥2 D 11 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G Thay f(x) bởi y, ta có: −4𝑥𝑦 − 2𝑦 𝑦′ = 3𝑦2 + 2𝑥2
Như vậy, phương pháp tính đạo hàm hàm ẩn như sau:
Bước 1. Đạo hàm 2 vế theo x.
Bước 2. Đặt y’(x) hay f’(x) ra ngoài, nhóm các nhân tử, còn lại chuyển sang vế còn lại.
Bước 3. Chuyển vế và kết luận y’.
Với hàm ẩn, các dạng 1, 2, 3, 4 thực hiện hoàn toàn tương tự. Ví V íd ụ 1 5
1 . .Quản lý một nhà máy xác định rằng, khi q trăm đơn vị một loại hàng hóa được
sản xuất thì tổng chi phí sản xuất là C nghìn đô la với 𝐶2 − 3𝑞3 = 4275. Khi 1500 đơn vị
hàng hóa được sản xuất, mức sản xuất đang tăng với tốc độ 20 đơn vị mỗi tuần. Tổng chi
phí và tốc độ thay đổi chi phí tại thời điểm đó là bao nhiêu? Lời ig i g ải ả .i
Tổng chi phí tại thời điểm q = 15 là √4275 + 3(153) = 120
Bài này đề bài cho mức sản xuất đang tăng với tốc độ 20 đơn vị mỗi tuần. Do đó, đạ đ i i lư l ợng n gthay a yđổ đ i iở đây
â là thời gian, do đó bài toán xuất hiện thêm biến t (tuần).
Giả sử mốc thời gian đang xét là 𝑡 . 0
Mức sản xuất thay đổi mỗi tuần được biểu diễn bởi hàm 𝑞′(𝑡0) với 𝑡0 là mốc thời gian.
Như vậy theo đề bài, ta có: 𝑞(𝑡0) = 15, 𝑞′(𝑡0) = 0.2, 𝐶(𝑡0) = 120.
Ngoài ra đề bài còn cho hàm ẩn 𝐶2 − 3𝑞3 = 4275 (*). Do ở trên ta có sử dụng đạo hàm q
theo t, ta sẽ lấy đạo hàm hàm ẩn (*) theo biến t để xuất hiện q’(t):
2𝐶(𝑡)𝐶′(𝑡) − 9𝑞2(𝑡)𝑞′(𝑡) = 0 9
→ 𝐶′(𝑡) = 𝑞2(𝑡) 2 𝐶(𝑡) 𝑞′(𝑡)
Tốc độ thay đổi chi phí tại thời điểm 𝑡0 được biểu diễn qua hàm 𝐶′(𝑡0). Thay t bởi 𝑡0, ta có: 9 𝐶′(𝑡 𝑞2(𝑡0) 9 152
0) = 2 𝐶(𝑡0) 𝑞′(𝑡0) =2. 120.(0.2) = 1.6875. D 12 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Như vậy, tại thời điểm mà mức sản xuất là q = 15, tốc độ thay đổi chi phí là 1.6875 nghìn đô / tuần. Nh N ận n xé
x t: Nếu các bạn đạo hàm (*) theo q, ý nghĩa của C’(q) là tốc độ thay đổi chi phí theo e o m ức c s ản n x u x ấ u t, chứ kh k ôn ô g n g p h p ải il à l th e th o o th ời ig ia i n a . n Dạng n g 6. Cá C c á c yếu ế t ố: ố Tính n hlõm, õ m, đi đ ểm u ốn ố ,n titệm cận ậ n đứng n , g ti t ệm c m ận n ng n a g n a g n
Để xác định các khoảng lõm trên đồ thị, ta cần thực hiện như sau:
Bước 1. Tìm các giá trị x sao cho f′ (x) = 0 hoặc f′ (x) không xác định và tạo các khoảng
mở không giao nhau. (giống giá trị tới hạn ở DẠNG 2 nhưng là đạo hàm cấp 2)
Bước 2. Với các khoảng (a,b) tìm được, Chọn một số c trong khoảng và tính 𝑓′ (𝑐)
Nếu 𝑓′ (𝑐) < 0 thì 𝑓′(𝑐) giảm, khi đó 𝑓(𝑥) có bề lõm hướng xuống trong (a,b), và ngược
lại, 𝑓′ (𝑐) > 0 thì f(x) có bề lõm hướng lên trong (a,b).
Cách nhớ: đạo hàm < 0 => hàm giảm => hướng xuống.
Bản chất ở đây, khoảng mà hàm số có bề lõm hướng xuống chính là khoảng mà tiếp
tuyến tại 1 điểm trong khoảng có độ dốc giảm dần, mà độ dốc ở đây chính là 𝑓′(𝑥)!
Để xác định các điểm uốn trên đồ thị, ta thực hiện như sau:
Bước 1, 2: Giống như tìm khoảng lõm, nhưng ở bước 2, sau khi kết luận được dấu của
𝑓′ (𝑥) trong các khoảng ( lớn hơn hay nhỏ hơn 0), ta kiểm tra xem 𝑓′ (𝑥) đổi dấu khi đi
qua điểm nào, thì đó là điểm uốn.
Để minh họa, mời các bạn xem ví dụ sau đây. Ví V íd ụ 1 6
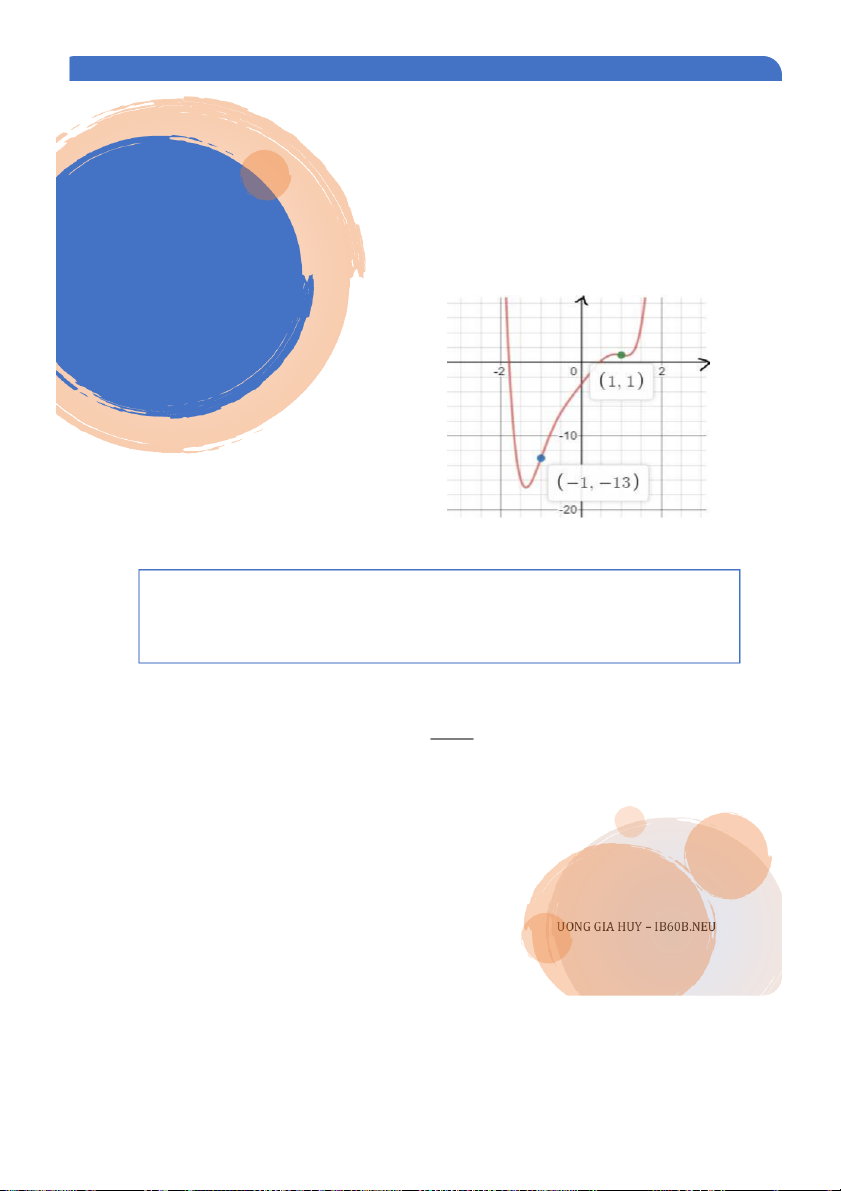
1 . .Cho hàm số 𝑓(𝑥) = 2𝑥6 − 5𝑥4 + 7𝑥 − 3. Tìm các khoảng lõm và điểm uốn của hàm số này. Lời ig i g ải ả :i Ta có:
𝑓′(𝑥) = 12𝑥5 − 20𝑥3 + 7
𝑓′ (𝑥) = 60𝑥4 − 60𝑥2 = 60𝑥2(𝑥 − 1)(𝑥 + 1)
𝑓′ (𝑥) = 0 khi 𝑥 = 0, −1, 1. Lúc này ta chia trục số thành 4 khoảng (−∞, −1), (−1,0),
(0,1), (1, ∞). Tính giá trị 𝑓′ (𝑥) tại các số bất kỳ trong mỗi khoảng ( giống dạng 1, bạn đọc có thể tự k ể
i m tra), ta nhận được: 𝑓′ (𝑥) > 0 trong khoảng (−∞, −1) và (1, ∞), khi
đó hàm số có bề lõm hướng lên. Còn khoảng (−1,0), (0,1) , hàm số có bề lõm hướng xuống dưới. D 13 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Để tìm điểm uốn, ta nhận thấy 𝑓′ (𝑥) > 0 tại ( −∞, −1), nhưng 𝑓′ (𝑥) < 0 tại ( −1,0). Do
đó, đạo hàm cấp 2 đổi dấu tại điểm x = -1. Hơn nữa 𝑓(1) xác định, vậy x = -1 là điểm
uốn của đồ thị. Tương tự, x = 1 cũng là điểm uốn của đồ thị. Trường hợp x = 0, ta thấy
𝑓′ (𝑥) < 0 , với x trong khoảng (−1,0), (0,1) , vì vậy qua điểm x = 0 thì đạo hàm cấp 2
không đổi dấu, vậy đây không phải điểm uốn.
Vậy có 2 điểm uốn: (-1, -13) và (1,1)
Sau đây là đồ thị hàm số trên:
Ta thấy: trên đồ thị có 2 điểm uốn: (-1, -13)
và (1,1). Đây là 2 điểm thay đổi bề lõm của đồ
thị. Tại khoảng (−∞, −1), và (1, ∞), bề lõm
hướng lên trên, còn lại ( −1,0) và (0,1) là bề
lõm hướng xuống dưới.
Tiếp theo, để tìm các tiệm cận đứng và tiệm cận ngang, ta cần chú ý như sau:
1) Đường thẳng y = b được gọi là tiệm cận ngang của f(x) nếu như:
lim 𝑓(𝑥) = 𝑏 hoặc lim 𝑓(𝑥) = 𝑏 𝑥→∞ 𝑥→−∞
2) Đường thẳng x = a được gọi là tiệm cận đứng của f(x) nếu như ít nhất 1 giới hạn
1 bên của f(x) tại a là giới hạn vô hạn. Ví V íd ụ 1 7
1 . .Tìm tất cả các tiệm cận đứng và tiệm cận ngang của hàm số sau: 𝑥 + 3 𝑓(𝑥) = 𝑥2 − 9 Lời ig i g ải ả :i
Để đi tìm tiệm cận ngang, ta thấy lim 𝑓(𝑥) = lim 𝑓(𝑥) = 0, do đó hàm số có 1 tiệm cận 𝑥→∞ 𝑥→−∞ ngang là y = 0.
Để đi tìm tiệm cận đứng, ta quan tâm đến mẫu số của hàm số. Có 2 giá trị làm cho mẫu
số bằng 0, là 3 và -3. Ta chỉ cần kiểm tra 2 giá trị trên. D 14 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G 𝑥 + 3 1 1 lim 𝑓(𝑥) = lim 𝑥→−3
𝑥→−3 (𝑥 − 3)(𝑥 + 3) = lim
𝑥→−3 𝑥 − 3 = − 6,
Không phải giới hạn vô hạn. Vậy x = -3 không phải là tiệm cận đứng của f(x). 𝑥 + 3 1 lim𝑓(𝑥) = lim 𝑥→3
𝑥→3 (𝑥 − 3)(𝑥 + 3) = lim 𝑥→3 𝑥 − 3
Rõ ràng, với 𝑥 → 3 + thì lim 𝑓(𝑥) = +∞, với 𝑥 → 3 − thì lim 𝑓(𝑥) = −∞. Vậy đây là giới
hạn vô hạn, và ta kết luận x = 3 là tiệm cận đứng của hàm số.
Sau đây là đồ thị của hàm số trên, trong đó
Đường màu đỏ là tiệm cận ngang y = 0, còn
đường màu đen là tiệm cận đứng x = 3. Đồ thị
hàm số có xu hướng tiến sát dần 2 đường
thẳng trên về phía vô tận. Dạng n g7. Độ Đ co c o giã i n ã n
Cho hàm 𝑦 = 𝑓(𝑥). Độ co giãn của y theo x là : 𝑥
𝐸(𝑥) = 𝑦.𝑦′(𝑥)
Ý nghĩa của độ co giãn: Tốc độ p ầ
h n trăm thay đổi của y gây ra bởi 1% tăng lên của x. Trong đó:
−|𝐸(𝑥)| > 1: Y co giãn, tức là tốc độ thay đổi của y lớn hơn tốc độ thay đổi của x, hay y
tương đối nhạy cảm với sự thay đổi của x.
−|𝐸(𝑥)| = 1: Y co giãn đơn vị. Phần trăm thay đổi của x và y là xấp xỉ bằng nhau.
−|𝐸(𝑥)| < 1: Y không co giãn: Phần trăm thay đổi của y là ít hơn so với x.
− 𝐸(𝑥) < 0: x tác động ngược chiều đến y. Ví V íd ụ 1 8
1 . .Giả sử lượng cầu và giá p của một loại hàng hóa liên hệ với nhau bởi phương
trình tuyến tính q = 240 – 2p, với 0 ≤ 𝑝 ≤ 120.
Biểu diễn độ co giãn của cầu theo giá theo một hàm của p, và cho biết ý nghĩa của hàm này tại p = 50. D 15 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G Lời ig i g ải
ả :i Ta có độ co giãn của cầu theo giá là: 𝑝 𝑝 𝑝 𝐸(𝑝) = (
𝑞 . 𝑞′(𝑝) = 240 − 2𝑝 −2) = 𝑝 − 120 50
Ta thấy tại p = 50, 𝐸(𝑝) =
= −0.714, điều đó có ý nghĩa rằng, tại mức giá p = 50 − 120
50, nếu giá tăng thêm 1% thì cầu sẽ giảm xấp x ỉ 0.714%.
Hơn nữa, |𝐸(50)| < 1, do đó có thể nói rằng, cầu không co giãn. Lưu ý:
ý Trong giáo trình, trang 233, tác giả trình bày công thức độ co giãn của cầu theo
giá có thêm dấu trừ ở trước. Thực ra 2 cách làm của tôi và tác giả hoàn toàn không sai.
Tuy nhiên, khi các bạn thi cuối kỳ, các bạn cần hỏi lại thầy cô xem chấp nhận đáp án nào,
vì cách làm của tác giả là cụ thể trong trường hợp mối quan hệ của cung và cầu, còn cách
làm của tôi là đúng trong mọi trường hợp. Dạng n g 8. Vi V iph p ân â n
Vi phân của x là dx = ∆𝑥, nếu y = f(x) là hàm khả vi của x thì dy = 𝑓′(𝑥)dx. 𝑑𝑦
Tính chất này chẳng khác gì việc = 𝑓′(𝑥) 𝑑𝑥
Như vậy, tôi đã giới thiệu cho các bạn cách tính đạo hàm và ứng dụng của đạo hàm
thông qua 8 dạng toán khác nhau. Tuy số dạng là tương đối nhiều, nhưng tất cả các dạng
đều có lời giải rất ngắn. Sau đây sẽ là một số các bài tập ứng dụng. B. Bài tập tự lu l yện
Sau đây là một đề kiểm tra tham khảo cho các nội dung của phần 2. Điền đáp án cho những câu hỏi sau: 5𝑥2 − 3𝑥 + 2 Câ C u â 1 . 1 (H i (H ểu
ể ) Tính 𝑓′(2), biết 𝑓(𝑥) = 1 − 2𝑥 Đáp số: -19/9 Câ C u â 2 . 2 (H i (H ểu
ể ) Với hàm f(x) được cho như câu 1, hãy tính 𝑓′ (2) Đáp số: -14/27 Câ C u â 3 . 3 (H i (H ểu
ể ) Tính đạo hàm của hàm 𝑔(𝑥) = 𝑥2𝑓(𝑥), trong đó 𝑓(𝑥) = (𝑥2 + 2𝑥 − 1)5 D 16 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G
Đáp số: 2𝑥(𝑥2 + 2𝑥 − 1)4(6𝑥2 + 7𝑥 − 1) Câ C u â 4 . 4 (H i (H ểu ể ) Tính 𝑓 2 3
𝑥𝑦′ , biết 𝑧 = 𝑧(𝑥, 𝑦) = 𝑥 + 2𝑥𝑦 + 𝑦 . Đáp số: 2 Câ C u â 5 . 5 (H i (H ểu
ể ) Tính đạo hàm cấp 2 của y theo x, biết mối quan hệ giữa y và x được thể
hiện qua phương trình sau: 𝑥2 + 3𝑦2 = 5 Đáp số: − 5 9𝑦3 Câ C u â 6 . 6 (H i (H ểu
ể ) Tìm các khoảng tăng, giảm của hàm số: 𝑓(𝑡) = 𝑡5 − 5𝑡4 + 100
Đáp số: Tăng với t < 0 và t > 4, giảm với 0 < t < 4. Câ C u â 7 . 7 (H i (H ểu
ể ) Cho hàm số 𝑓(𝑥) = 3𝑥4 − 8𝑥3 + 6𝑥2 + 2. Hãy tìm các cực trị tương đối của hàm số trên.
Đáp số: (0,2) là cực tiểu tương đối. Câ C u â 8 . 8 (H i (H ểu
ể ) Viết phương trình tiếp tuyến của hàm số sau tại điểm 𝑥 = 2: 1
𝑓(𝑥) = −3𝑥3 + √8𝑥 Đáp số 22 : 𝑦 = −3𝑥 + 3 Câ C u â 9 . 9 (H i (H ểu)
u Xác định các khoảng bề lõm hướng lên và điểm uốn của đồ thị hàm số: 𝑓(𝑥) = 𝑥(2𝑥 + 1)2
Đáp án: Bề lõm hướng lên khi x > -1/3, điểm uốn (-1/3, -1/27) Câ C u â 1 0. 0 ( Hi H ểu)
u Tìm các tiệm cận đứng và tiệm cận ngang của hàm số sau: 𝑥2 − 2𝑥 𝑓(𝑥) = 𝑥2 − 4
Đáp án: Tiệm cận ngang y = 1, tiệm cận đứng x = -2 Câ C u â 1 1. 1 ( Hi H ểu)
u Tính vi phân của y tại x = 0.1, biết: 𝑦 = 2𝑥2 − 2𝑥 + 1 Đáp án: -1.6 Câ C u â 1 2. 2 ( Vận ậ n d ụng n )
g Dân số của tỉnh X được các nhà nghiên cứu ước tính là: 𝑃(𝑥) = 𝑥2 +
20𝑥 + 6000, trong đó x là số tháng kể từ hiện tại. Vậy tốc độ thay đổi dân số theo thời
gian ở tháng thứ 15 tính từ thời điểm hiện tại là bao nhiêu?
Đáp án: 50 người / tháng D 17 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G Câ C u â 1 3. 3 ( Vận ậ n d ụng n c ao a )
o Hiện tại, một công ty đang bán 1000 đơn vị hàng hóa với mức giá
$5/đơn vị. Quản lý công ty ước tính rằng, giá hiện tại đang tăng 0.05 dol ar mỗi tuần, và
lượng cầu đang giảm với tốc độ 4 đơn vị / tuần.
a. Viết hàm doanh thu R(x) và cho biết tốc độ thay đổi của R(x) thời điểm hiện tại.
b. Tìm tốc độ thay đổi của doanh thu bình quân ở thời điểm hiện tại . Đáp án:
a. 𝑅(𝑥) = 17.5𝑥 − 0.0125𝑥2 Câ C u â 1 4. 4 ( Vận ậ n d ụng n )
g Sau t tuần, sản lượng đầu ra của 1 nhà máy là N(t) nghìn đơn vị,
trong đó 𝑁(𝑡) = √𝑥2 + 3𝑥 + 6. Tính tốc độ thay đổi của mức sản xuất theo thời gian sau 2 tháng. Đáp án: 875 đơn vị Câ C u â 1 5. 5 ( Vận ậ n d ụng n )
g Sản lượng hàng ngày của 1 nhà máy là 𝑄(𝐾) = 600𝐾1/2 đơn vị,
trong đó K là lượng vốn đầu tư tính theo đơn vị $1,000. Hiện tại vốn đầu tư của nhà máy
là $900,000. Hãy ước tính mức thay đổi của sản lượng hàng ngày khi nhà máy tăng vốn đầu tư thêm $800.
Đáp án: Xấp xỉ 8 đơn vị / ngày Câ C u â 1 6. 6 ( Vận ậ n d ụng n )
g Tổng chi phí của một nhà sản xuất là 𝐶(𝑞) = 0.001𝑞3 − 0.05𝑞2 +
40𝑞 + 4,000 dol ar, trong đó q là số đơn vị hàng hóa được sản xuất. Hãy tính chi phí cận
biên của nhà máy tại mức sản xuất 250 sản phẩm / ngày. Đáp án: 202.5 Câ C u â 1 7. 7 ( Vận ậ n d ụng n )
g Khi giá của một loại hàng hóa là p – dollar mỗi đơn vị thì nhà sản
xuất sẵn sàng cung cấp x trăm đơn vị hàng hóa, với: 3𝑝2 − 𝑥2 = 12
Lượng cung x sẽ thay đổi với tốc độ như thế nào khi giá hàng hóa là $4 mỗi đơn vị và
đang tăng với tốc độ $0.87 / tháng?
Đáp án: Tăng 174 sản phẩm / tháng Câ C u â 1 8. 8 ( Vận ậ n d ụng n )
g Sản lượng của 1 nhà mát là 𝑄 = 0.08𝑥2 + 0.12𝑥𝑦 + 0.03𝑦2 đơn vị
mỗi ngày, trong đó x là số giờ lao động có kỹ năng và y là số giờ lao động giản đơn được
sử dụng. Hiện tại, nhà máy sử dụng 80 giờ lao động có kỹ năng và 200 giờ lao động giản
đơn mỗi ngày. Hãy ước tính mức thay đổi lao động giản đơn khi giảm 2 giờ lao động có
kỹ năng mà vẫn duy trì mức sản lượng hiện tại. Đáp án: Tăng 3.41 giờ D 18 PH N II Ầ
. ĐẠO HÀM, VI PHÂN VÀ ỨNG DỤN - 2020 G Câ C u â 1 9. 9 ( Vận ậ n d ụng n )
g Chi phí để sản xuất x đơn vị của 1 loại hàng hóa là C(x) nghìn dollar,
trong đó: 𝐶(𝑥) = 𝑥3 − 20𝑥2 + 179𝑥 + 242
Với mức sản xuất nào thì chi phí bình quân đạt tối thiểu? Đáp án: x = 11 Câ C u â 2 0. 0 ( Vận ậ n d ụng n g c ao a ).
). Một công ty ước tính rằng, nếu x nghìn dol ar được chi cho việc
Marketing một loại sản phẩm thì sẽ bán được S(x) đơn vị sản phẩm mỗi tháng, với :
𝑆(𝑥) = −𝑥3 + 33𝑥2 + 60𝑥 + 1000
Tìm điểm uốn của đồ thị S(x) và nêu ý nghĩa của nó. Câ C u â 2 1. 1 (V ận n d ụ d ng
n ) Một phòng trưng bày nghệ thuật cung cấp các bức ảnh in của một
nghệ sĩ nổi tiếng. Với mức giá p dollar cho mỗi bức ảnh, số bức ảnh bán được sẽ là q =
500 – 2p. Hỏi tại mức giá 𝑝0 nào thì doanh thu của người chủ là lớn nhất? Nhận xét độ co
giãn của cầu theo giá tại mức giá nhỏ hơn 𝑝0 và lớn hơn 𝑝0.
Bài tập 21 sẽ giúp các bạn khám phá một tính chất khá đặc trưng trong kinh tế. Câ C u â 2 2. 2 ( Vận ậ n d ụng n c ao a )
) Cho hàm số h(x), g(x) là các hàm khả vi trong tập số thực, trong
đó có các giá trị như sau: x h(x) g(x) h’(x) g’(x) 1 4 2 2 -1 2 6 1 -4 3
Tính đạo hàm của biểu thức ℎ (𝑔(𝑔(𝑥))) tại x = 2. Đáp số: 12. D 19




