CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG Chương 2:
Phân tích đáp ứng thời gian của hệ thống 1/16/2024 1
Automatic Control Systems 1
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG Nội dung
2.1 Đáp ứng thời gian của hệ thống liên tục
2.2 Đáp ứng bước và các đặc tính trong miền thời gian
2.3 Đặc tính thời gian của hệ bậc 1
2.4 Đặc tính thời gian của hệ bậc 2
2.5 Đặc tính thời gian của khâu tích phân, vi phân 1/16/2024
Automatic Control Systems 2
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.1 Đáp ứng thời gian của hệ thống
Phân biệt đáp ứng quá độ và đáp ứng xác lập
Định nghĩa : Đáp ứng thời gian (Time response) là hàm theo thời gian thể hiện
đáp ứng đầu ra của hệ thống với tín hiệu đầu vào tương ứng.
No pt vi phân: y(t)  y (t)  y (t), t  0 y ( t ss t t): đáp ứng quá độ y (
ss t): đáp ứng xác lập
Đáp ứng quá độ (Transient response), y (t) t
 Trạng thái của hệ thống trong hoảng thời gian ngắn ngay khi có sự thay đổi
đầu vào tác động lên hệ thống
 Thể hiện đặc tính động của hệ thống
 Chỉ phụ thuộc vào các điểm cực của hệ thống, không phụ thuộc vào dạng tín hiệu đầu vào
 Đối với hệ thống ổn định: lim y (t)  0  t t 1/16/2024
Automatic Control Systems 3
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.1 Đáp ứng thời gian của hệ thống
Phân biệt đáp ứng quá độ và đáp ứng xác lập
Định nghĩa : Đáp ứng thời gian (Time response) là hàm theo thời gian thể hiện
đáp ứng đầu ra của hệ thống với tín hiệu đầu tương ứng.
No pt vi phân: y(t)  y (t)  y (t), t  0 y ( t ss t t): đáp ứng quá độ y (
ss t): đáp ứng xác lập
Đáp ứng xác lập (Steady-state response), y ( ss t):
 Trạng thái đạt được ngay khi quá trình quá độ kết thúc
 Thể hiện độ chính xác của hệ thống
 Nếu đáp ứng xác lập không bằng với giá trị đặt ở đầu vào  giá trị sai lêch xác lập (sai lệch tĩnh) 1/16/2024
Automatic Control Systems 4
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.1 Đáp ứng thời gian của hệ thống
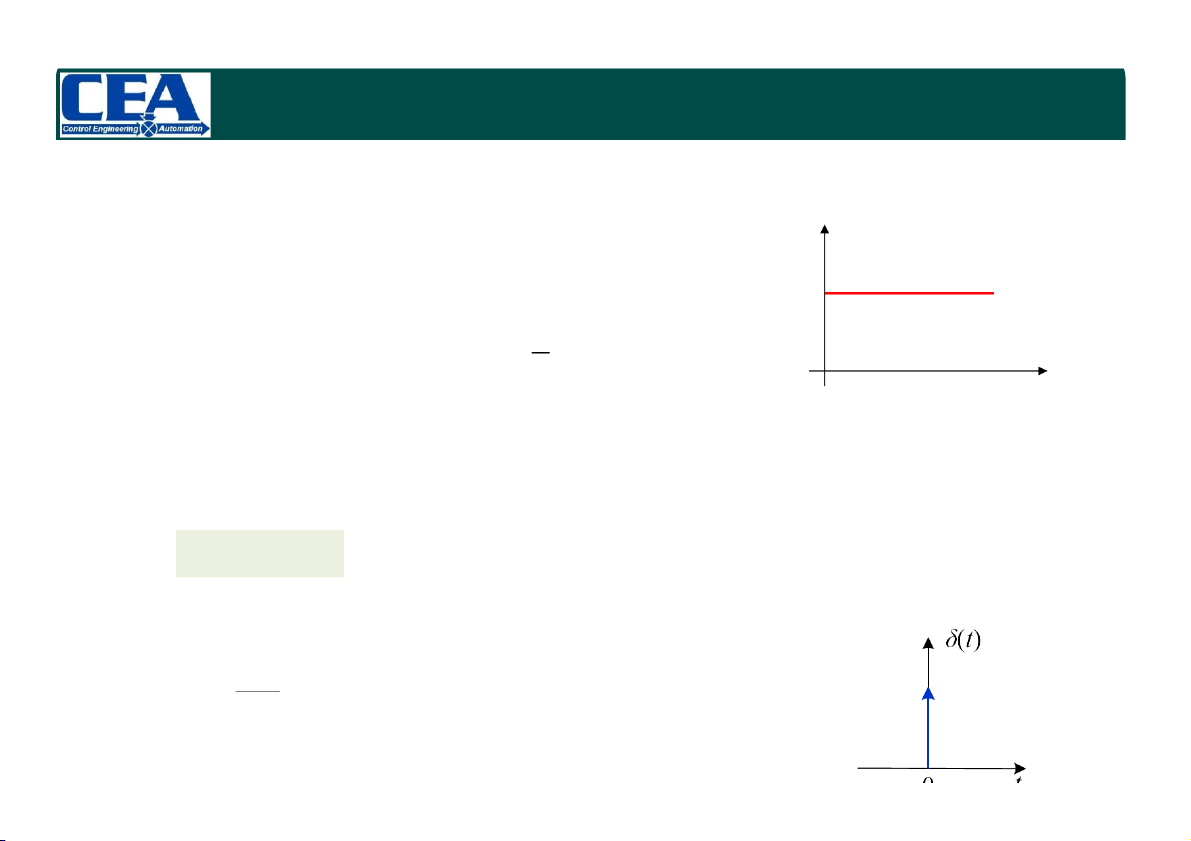
Các tín hiệu thử nghiệm đặc trưng 1(t)
Hàm bước đơn vị (Unit-step), u (t) s 1  t  0 1
 u (t)    L u t  s  (s ) 0 t  0  s t
 Đánh giá sự nhanh chóng của hệ thống đáp ứng với thay đổi tức thời của đầu vào (sudden change) Hàm bước (step function)
r(t)  Ru (t) s
Hàm xung đơn vị (Unit-impulse), δ(t) du  t  0  (t)  s     L  (t  ) 1  dt 0 t  0 
 Thể hiện sự tác động nhiễu tức thời (momentary shock) 1/16/2024
Automatic Control Systems 5
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.1 Đáp ứng thời gian của hệ thống
Các tín hiệu thử nghiệm đặc trưng
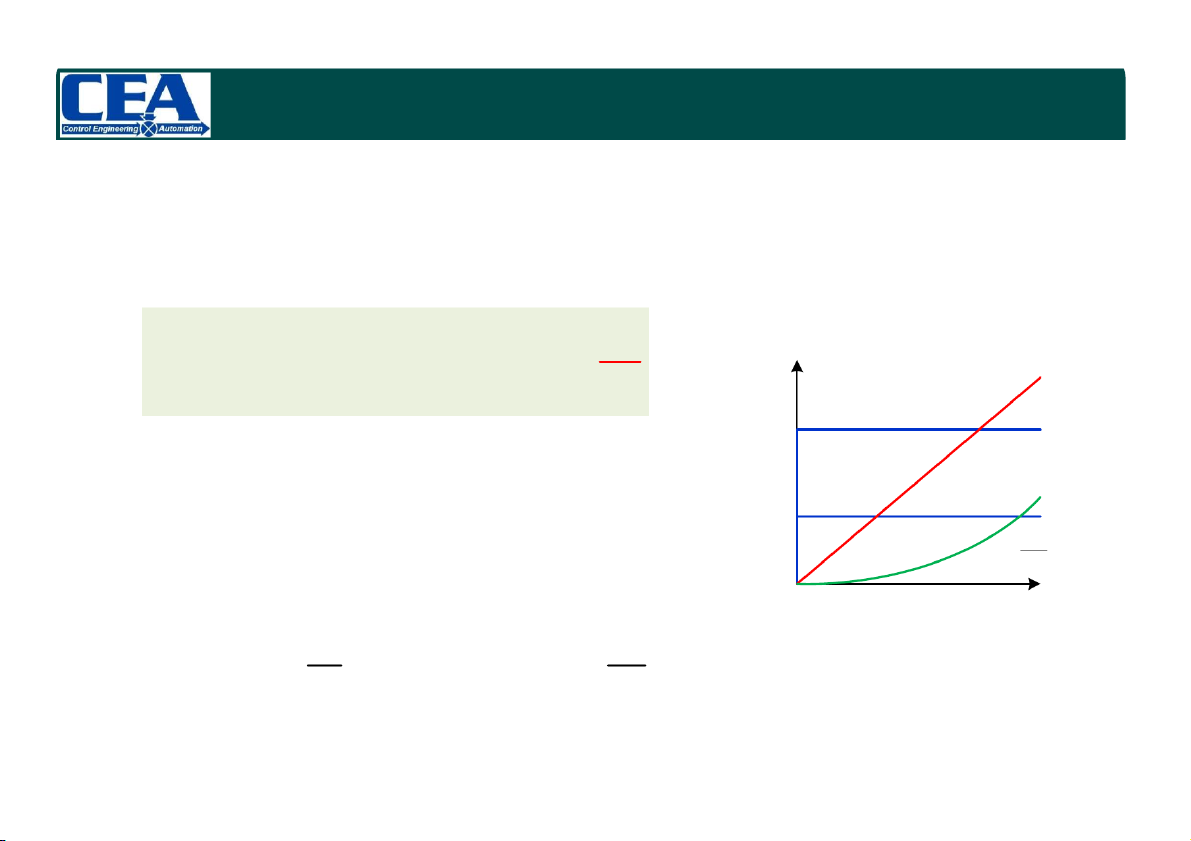
Đầu vào hàm dốc (Ramp function) R ) (t
r(t)  R.t.u (t)   s
Lr(t  ) s 2 Rtu s 
r(t)  Ru (t) ) (t R s r
 Thể hiện sự tác động của tín hiệu có tốc độ
không đổi (constant velocity) u (t) 1 s 2 Rt r(t)  us (t) 2
Đầu vào hàm parabol (Parabolic function) 0 t 2 t R r(t) . R .u (t) R(s) 3 2 s s
 Thể hiện sự tác động của tín hiệu có gia tốc không đổi (constant accceleration) 1/16/2024
Automatic Control Systems 6
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.1 Đáp ứng thời gian của hệ thống
Các điểm cực (pole) và điểm không (zero) của hàm truyền đạt m m 1 B(s)
b s  b s   ...  b s  b m m 1  1 0 H (s)     n m n n 1 ( A s) a s  a s
...  a s  a n n 1  1 0 Điểm cực (Poles):
• Các giá trị của 's', tại đó độ lớn của hàm truyền |G(s)| trở thành vô hạn.
• Nghiệm của mẫu số của hàm truyền đạt, hay nghiệm của A(s) = 0 Điểm không (Zeros):
• Các giá trị của 's', tại đó độ lớn của hàm truyền |G(s)| bằng 0.
• Nghiệm của tử số của hàm truyền đạt, hay nghiệm của B(s) = 0 1/16/2024
Automatic Control Systems 7
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.2 Đáp ứng bước đơn vị và các đặc tính miền thời gian
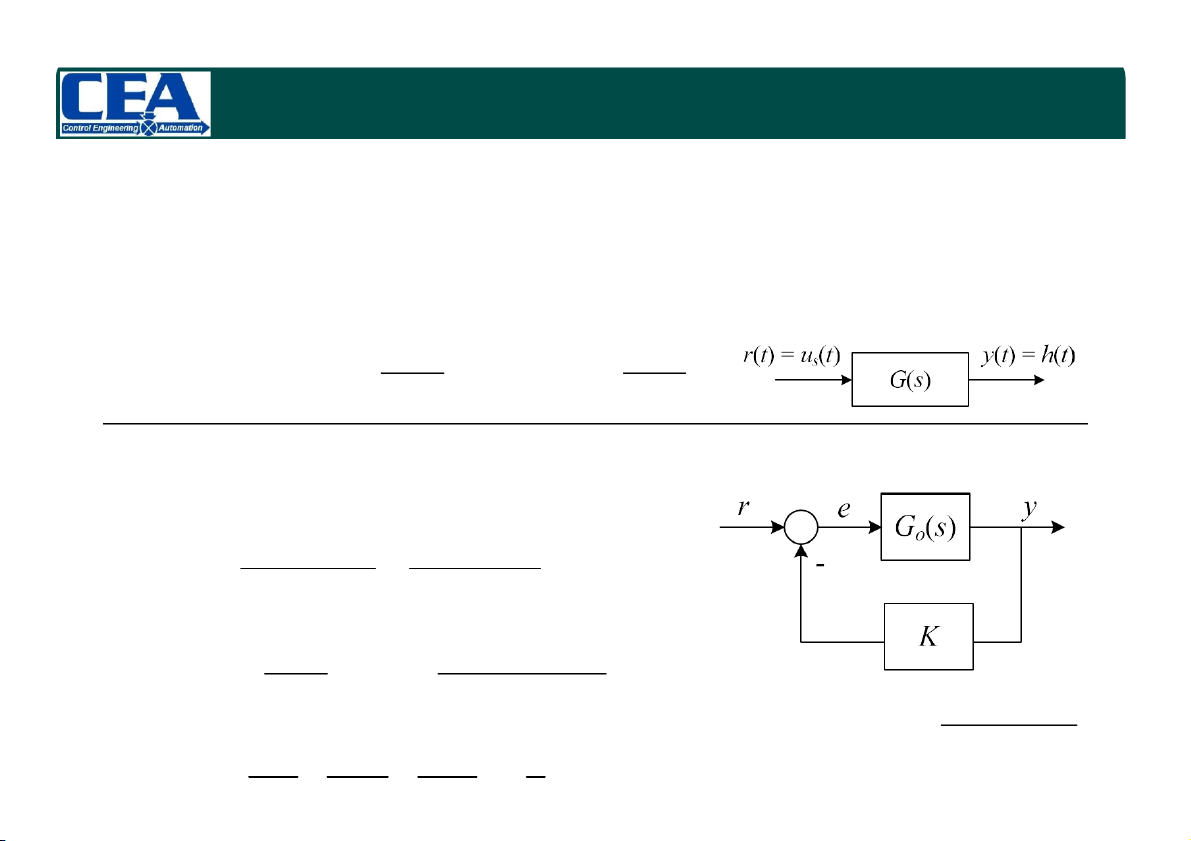
2.2.1 Đáp ứng bước đơn vị (Unit-step response)
 Định nghĩa : Đáp ứng của hệ thống với đầu vào bước đơn vị (bỏ qua các điều
kiện ban đầu) hay còn gọi là đáp ứng bước đơn vị G(s)
1  G( s) 
H (s)  G(s U ) (s)   h t ( )  L s   s  s 
Ex. 4.1. Tìm đáp ứng bước đơn vị của các hệ thống sau G ( ) s 1 ( G ) s  o  1 KG (s) 2 s  5s  6 o     1  G(s) 1  1
h(t)  L    L  2   s 
s(s  5s  6)   1 G0 (s)  2 s  1 / 6 3 / 6 2 / 6  1  5s  3 1 2t 3t
h(t)  L      1 3e  2e K  s s  s  3 2  3  6   1/16/2024
Automatic Control Systems 8
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.2 Đáp ứng bước đơn vị và các đặc tính miền thời gian
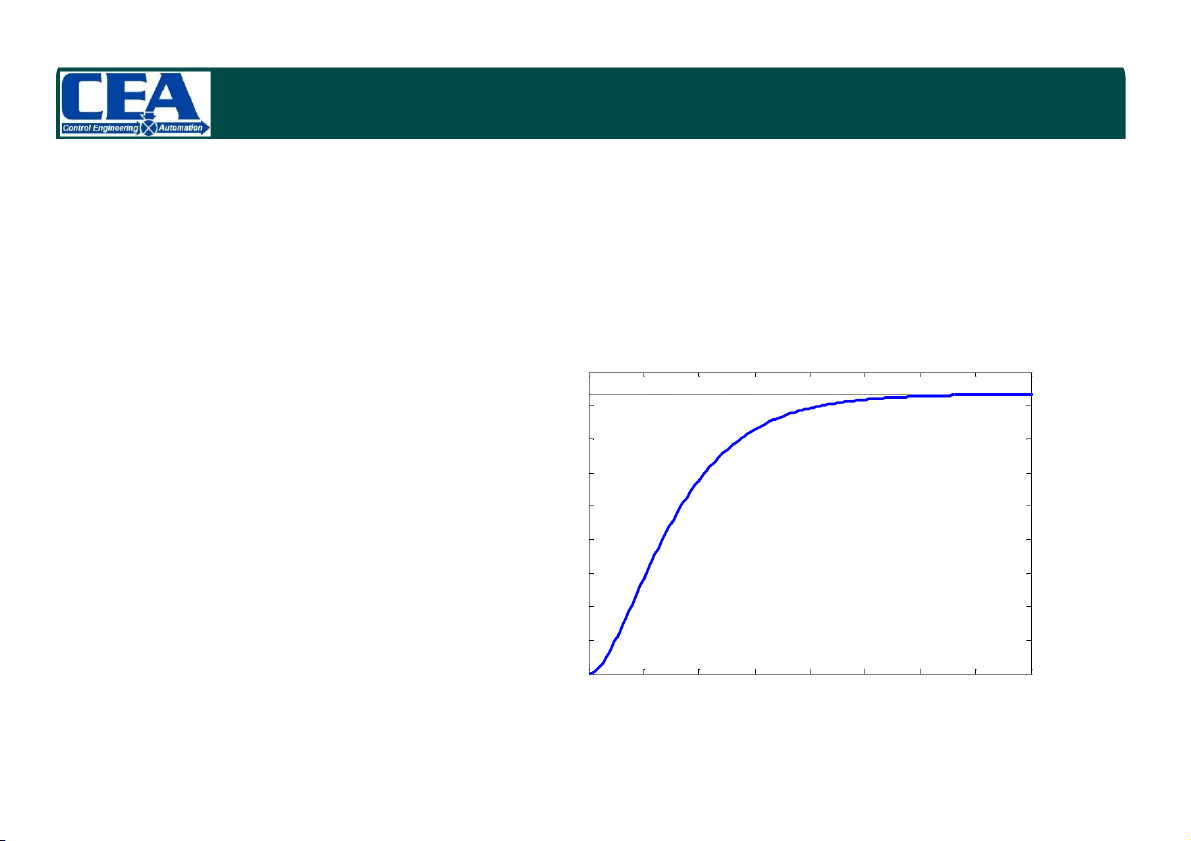
2.2.1 Đáp ứng bước (Unit-step response) Ex. 4.1. (cont’d)
Code Matlab để biểu diễn đồ thị của đáp ứng bước của hệ thống trên Step Response clear all 0.16 %Step-unit response 0.14 K=3; 0.12 Go=tf([1],[1 5 3]); 0.1 plitude G=feedback(Go,K); m 0.08 A step(G); 0.06 xlabel('Time'); 0.04 ylabel('Amplitude'); 0.02 0 0 0.5 1 1.5 2 2.5 3 3.5 4 Time (sec) 1/16/2024
Automatic Control Systems 9
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.2 Đáp ứng bước đơn vị và các đặc tính miền thời gian
2.2.2 Đặc tính miền thời gian
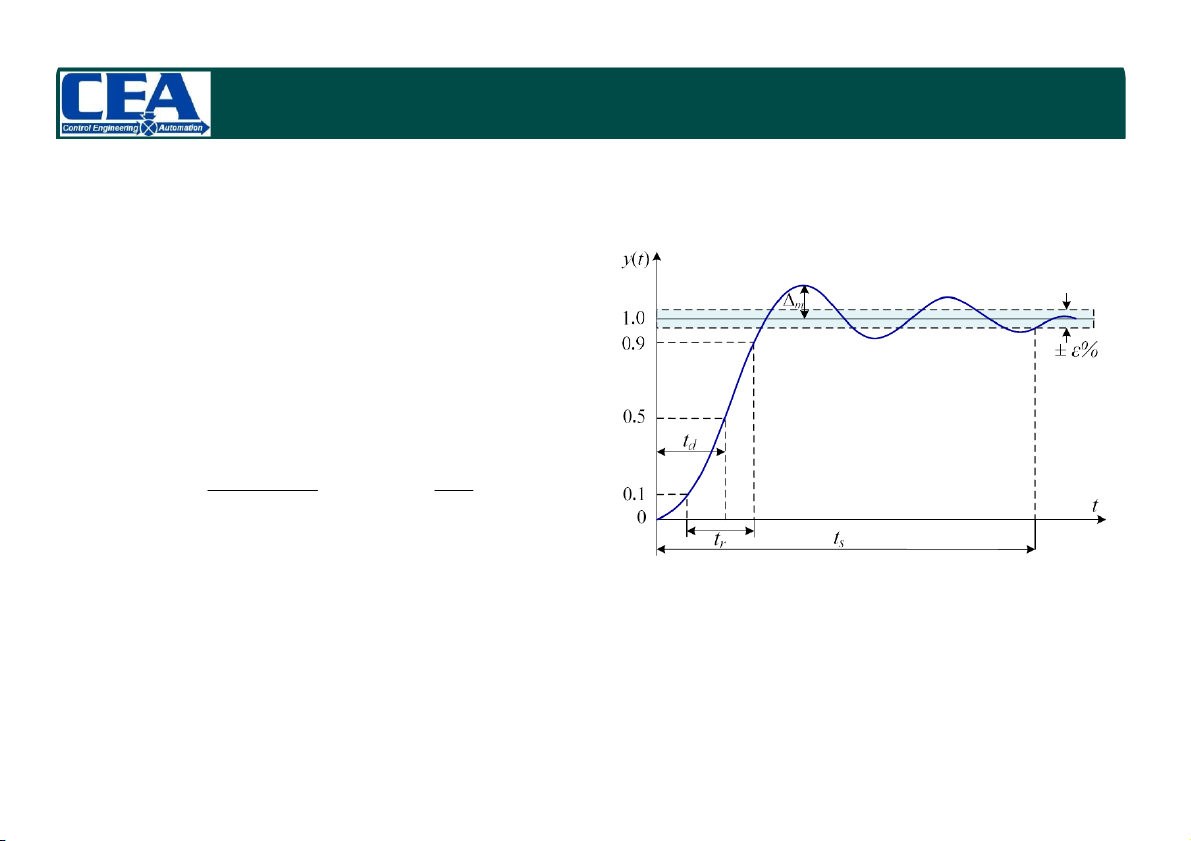
 Độ quá điều chỉnh (Over shoot)
- Độ quá điều chỉnh lớn nhất: Δm = ymax – yss
- Độ quá điều chỉnh lớn nhất (%) (PO) y  y  max PO  ss 10 % 0  m 10 % 0 y y ss ss
- Đo lường độ ổn định tương đối
 Thời gian trễ (Time delay), t : Thời gian cần để đáp ứng bước đạt đến 50% giá d
trị cuối cùng (giá trị xác lập)
 Thời gian tăng (Rise time), t : Thời gian để đáp ứng bước tăng từ 10% - 90% r
giá trị cuối cùng (giá trị xác lập) g g (g p) 1/16/2024
Automatic Control Systems 10
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.2 Đáp ứng bước đơn vị và các đặc tính miền thời gian
2.2.2 Đặc tính miền thời gian
 Thời gian quá độ (Settling time), t : s
Thời gian để đáp ứng bước của hệ thống
đạt đến và giữ trong khoảng ± ε% (ε = 2 or 5) giá trị cuối cùng.
 Sai số xác lập (Steady-state error), ess e  li   ss 
m r(t) y(t  ) lim e(t) t t 1/16/2024
Automatic Control Systems 11 Hệ thống ĐKTD
PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG Độ dự trữ ổn định Đặc trưng Tiêu chuẩn tích phân Tính ổn định IE Chất lượng ITAE IAE Của đặc tính quá độ ISE Độ chính xác ở chế độ xác lập Thời gian quá độ (settling time- t ) s Sai lệch tĩnh Độ quá điều chỉnh Số lần e(t)  r(t) y(t) Thời gian đáp ứng (overshoot) dao động N lim e(t)  e  0  t Thời gian lên đỉnh Thời gian nâng Đặc trưng cho (peak time – t ) (rise time – t ) p r tính suy giảm của 1/16/ h 2ệ0 2t4 hống GV: Trần Thị Minh Dung 12
Automatic Control Systems 12
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.3 Đặc tính thời gian của hệ thống bậc 1  Mô tả toán học ( dy t) 1 K Y( ) s K  ( y t) 
r(t)  G( ) s   dt   R(s)  s 1
K – độ lợi xác lập , τ – hằng số thời gian.
 Độ lợi xác lập (Steady-state gain), K Nếu 1 K  K K
r(t) = u (
R(s)   Y (s)    s t) , ta có s
ss 1   s s 1   y(t) t /
 K  Ke   K 1 t /
 e  , t  0 y y ss t
 Hằng số thời gian (Time constant), τ
- Nếu K = 1, Tốc độ đáp ứng ban đầu của hệ thống dy(t) d |   t e  t 0  /  1 |t0 dt dt 
- Tại t = τ, y(τ) = 0,63K = 63% of yss
- If τ > 0, G(s) chỉ có 1 điểm cực tại s = - 1/τ => hệ thống luôn ổn định 1/16/2024
Automatic Control Systems 13
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2 2 2 2 d y(t) dy(t)  Mô tả toán học  T  2T
 y(t)  r(t) n 2 dt dt ss   2 n  2 Y(s)   G(s) n   2 2 ( R ) s
s  2 s   n n
ζ – hệ số tắt dần (damping ratio) ω = 1/ n
T – tần số không tắt dần tự nhiên (natural (undamped) frequency )
 Đáp ứng bước đơn vị r(t) = u (t), thì R(s) = 1/s s )t( G s    y 1  ( )  2 1  ( y t)  L    L  n  s    2 s s    2  s  2 n n     e t n 1 sin  1  2 1 t  cos  n  1  2
 ζ ≥ 1, không có độ quá điều chỉnh
 ω ảnh hưởng đến , , và nhưng không ảnh n tr ts td
hưởng đến độ quá điều chỉnh 1/16/2024
Automatic Control Systems 14
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Quỹ đạo nghiệm của phương trình đặc tính 2 2 2
s  2 s    0  s
   j 1  n n , 1 2 n n 2  1   n  Tần số tự nhiên q
Khi ζ = 0 (undamped), s1,2 = ± jω => : n
y(t) = 1-cos(ω t) n
Đáp ứng bước dao động điều hòa với tần số ωn
 Thừa số tắt dần (Damping factor)
α = ζ ω điều khiển tốc độ tăng hoặc giảm jω ζ=0 n
(tắt dần) của y(t), α được gọi là thừa số tắt dần. 0 < ζ < 1 0 > ζ > -1
Nếu ζ = 1(tắt dần tới hạn), thì α = ω ζ = -∞ ζ = -1 n ζ > 1 ζ > 1 ζ → ∞ σ ζ < -1 ζ = -∞ ζ=1 ζ= ∞
 Hệ số tắt dần (Damping ratio) 0> ζ > -1  0 < ζ < 1   damping r atio  ω ζ=0 n = const.  |  | 1 1/16/2024
Automatic Control Systems 15
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2  Hệ số tắt dần jw y(t )
• ζ > 1 : không dao động tắt dần (overdamped) 1
s    j 1 2    0 , 1 2 n n 0  y(t )  1  t / 1  t / 2  k e   k e 1 2 1 0    t 0 , 1 2   j 1 2   jw n n y(t )
• ζ = 1 : tắt dần tới hạn (critically damped) 1 s  s  1 2   n 0
 y(t) 1 k  k t 1 2   tn e 0 t
• 0 < ζ <1 : có dao động tắt dần (underdamped) jw ( y ) t s       j 1 2 , 1 2 n n 1    e t n  y(t) 1
sinn t   0  0 t   1  2   ; cos   1 1/16/2024
Automatic Control Systems 16
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2  Hệ số tắt dần jw y(t)
• ζ = 0 : dao động không tắt dần (undamped) s   j , 1 2 n 1  y t ( )  1 cos t 0 n 0 t
• -1 < ζ < 0 : dao động tăng dần(negatively damped) jw y(t ) s  , 1 2     j 1 2 , 0 n   n    n    t n 1
 y( ) 1 e t sin 0
n  t     0 t
• ζ < -1 : dao động tăng dần (negatively damped) jw y(t ) s
   j 1 2   0 , 1 2 n n  y(t)  1 t / t / 1 2  k e  k e 1 2 1 1 0    0 , 1 2 2 0  t n   n j 1 1/16/2024
Automatic Control Systems 17
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Độ quá điều chỉnh tối đa
Giả sử có đáp ứng của hệ thống bậc 2 có dạng như sau: (i.e., 0 < ζ <1)  e t n y(t)  1 sin  t n
,   1  2 ;  1  cos   m dy    e t n   n
 sin t  cos n    t  n  dt  Đặt   co 
s    1 2  si ,n  2 3 4 2  1   2  1 2  2  1 n   n 1   n   n    t    t n n dy   n e e   s  in   t     t      t n cos cos  n sin n sin  n dt   dy   0   n t , n  , 0 , 1 , 2 dt    n 1/16/2024
Automatic Control Systems 18
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Độ quá điều chỉnh tối đa dy n  0  t , n  , 0 , 1 , 2  dt   m n
Độ quá điều chỉnh lớn nhất xuất hiện ở đỉnh
dao động đầu tiên của y(t), tức là tại   t   2   n  1 n  2 3 4 2    1 2 2    2 2 y (t ) | 1     1    1  1    1 n   n   n n m  e t n
Độ quá điều chỉnh (%) PO : 2  1 PO   e 100 1/16/2024
Automatic Control Systems 19
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Độ quá điều chỉnh lớn nhất
Sự phụ thuộc của PO vào  được biểu diễn như hình bên.
Một cách gần đúng ta có thể xấp xỉ PO    như sau : PO  1  1  00  6 . 0     2  1 PO PO  1     e 100 100  0.6  1/16/2024
Automatic Control Systems 20
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Thời gian đáp ứng (Settling time), ts
Thời gian đáp ứng có thể được tính xấp xỉ như sau  3.2   1  1 1   t   1 e n s 1    t  ln s  1 2    for 5%   n ( 0    6 , 0 9) 2   4 1 n  for   2%   n 1  t n 1  e 
Trong trường hợp   69 , 0   2 1 5 , 4  t  f or   % 5 s n 1  t n 1  e    2 1  t n 1/16/2024
Automatic Control Systems 21
CHƯƠNG 2: PHÂN TÍCH ĐÁP ỨNG THỜI GIAN CỦA HỆ THỐNG
2.4 Đáp ứng thời gian của hệ thống bậc 2
 Thời gian trễ (Delay time), td
Thời gian trễ được tính xấp xỉ như sau 1 0.7 t  d  1  t n 1  e  n   2 1
 Thời gian tăng (rise time), tr
Thời gian tăng được tính xấp xỉ như sau 1  t n 1  e    2 1  t n 1/16/2024
Automatic Control Systems 22