Chương 2 - Suy luận Toán học trong Giáo Trình Môn Toán Rời Rạc | Đại học Cần Thơ

lOMoAR cPSD| 58488183 TOÁN RỜI RẠC DISCRETE MATHEMATICS
ThS. LÊ THỊ PHƯƠNG DUNG
Chương 2: Suy luận toán học
Các quy tắc suy luận Khái niệm
Nội dung các quy tắc suy luận Ví dụ suy luận
Các phương pháp chứng minh Rỗng lOMoAR cPSD| 58488183 Tầm thường Trực tiếp Gián tiếp Quy nạp Các quy tắc suy luận Xét mệnh đề → , trong đó là giả thiết
là kết luận. Từ giả thiết
, chúng ta sử dụng các quy tắc suy luận/các phương pháp chứng minh
để đưa ra kết luận Ví dụ:
“Nếu hôm nay trời mưa thì cô ấy không đến. Nếu cô ấy không đến
thì ngày mai cô ấy đến. Vì vậy, nếu hôm nay trời mưa thì ngày mai cô
ấy đến.” ⇒ Hai câu đầu tiên là giả thiết, câu cuối cùng là kết luận lOMoAR cPSD| 58488183
“An giỏi toán. Do đó, An giỏi toán hoặc tin” ⇒ Câu đầu là giả thiết, câu cuối là kết luận lOMoAR cPSD| 58488183 lOMoAR cPSD| 58488183
Các quy tắc suy luận
“Nếu hôm nay trời mưa thì cô ấy không đến. Nếu cô
ấy không đến thì ngày mai cô ấy đến. Vì vậy, nếu
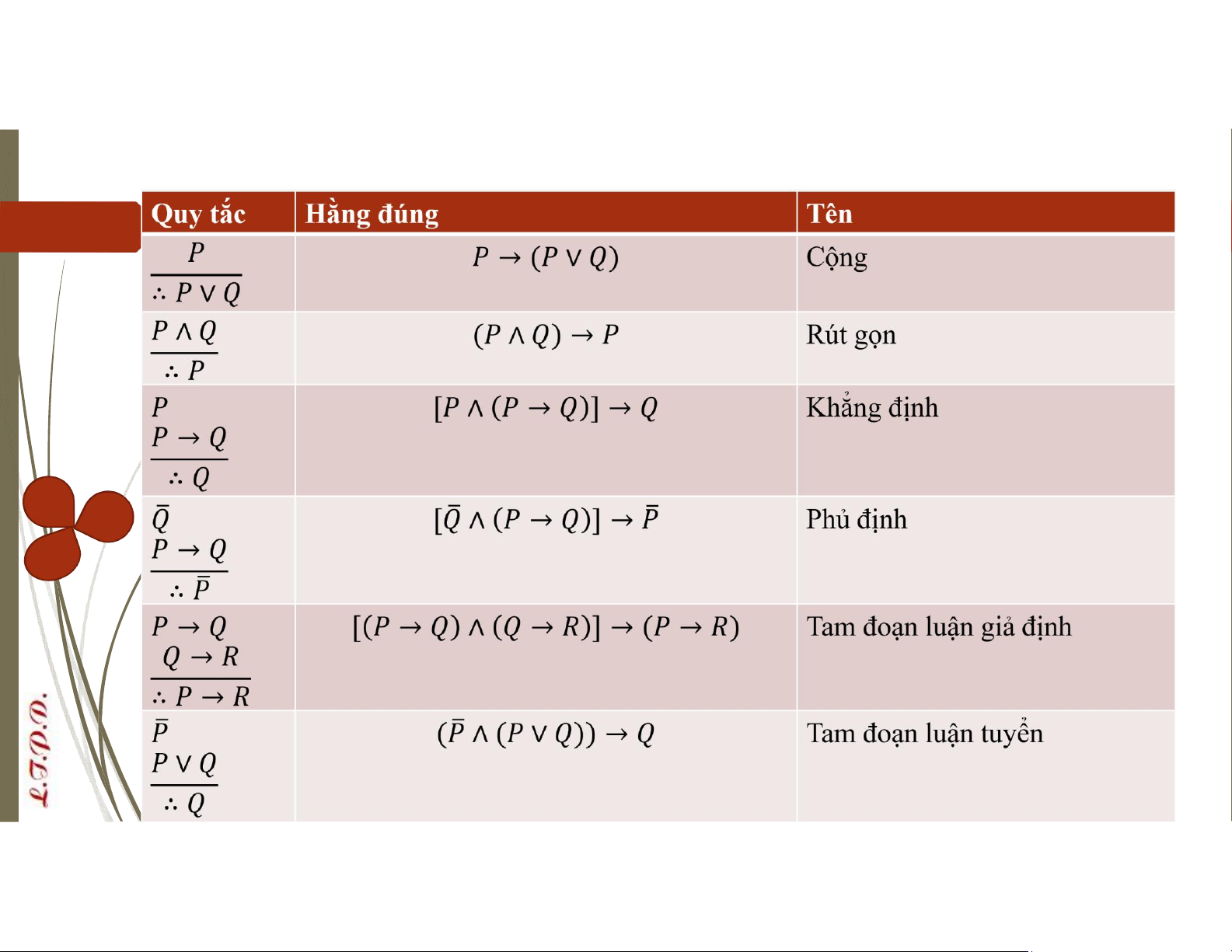
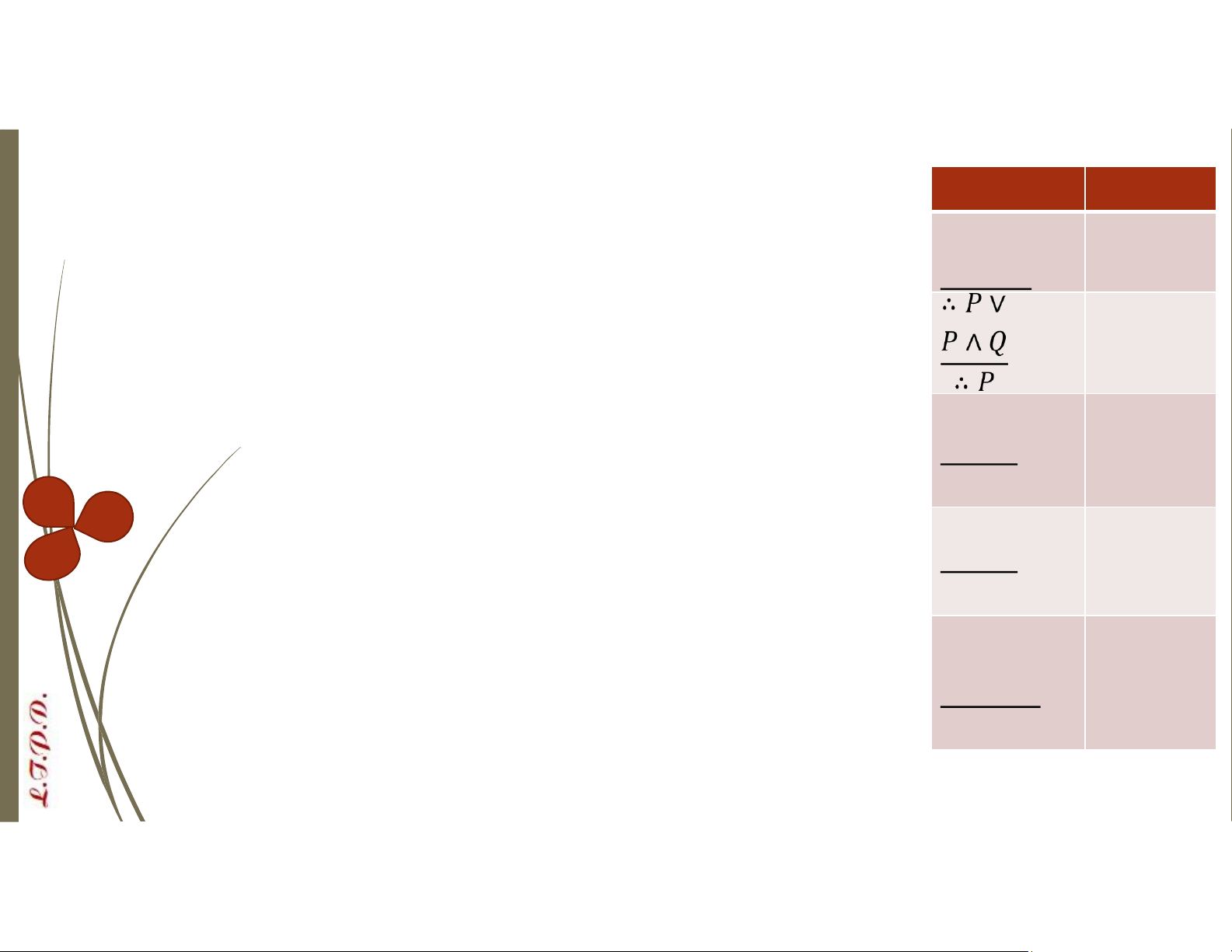
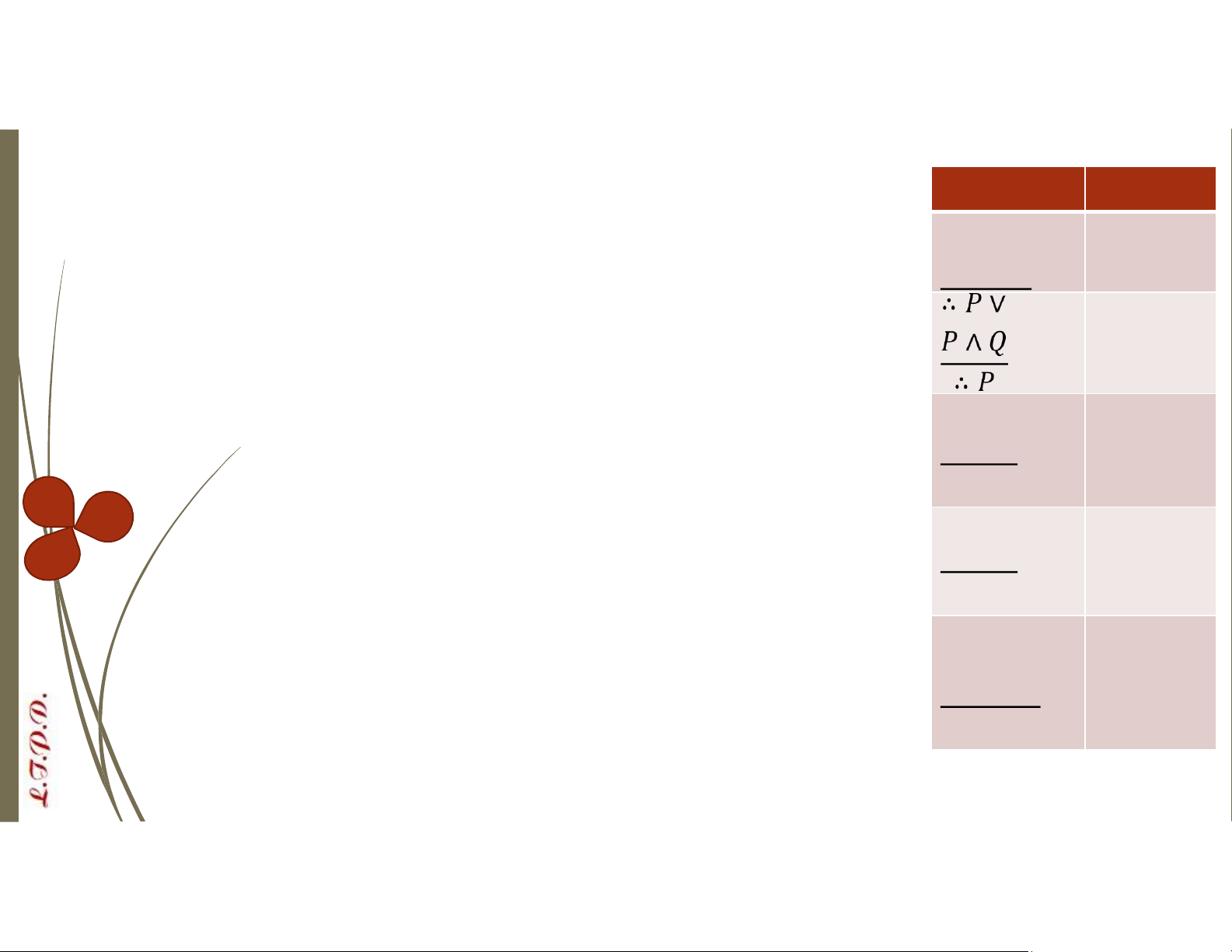
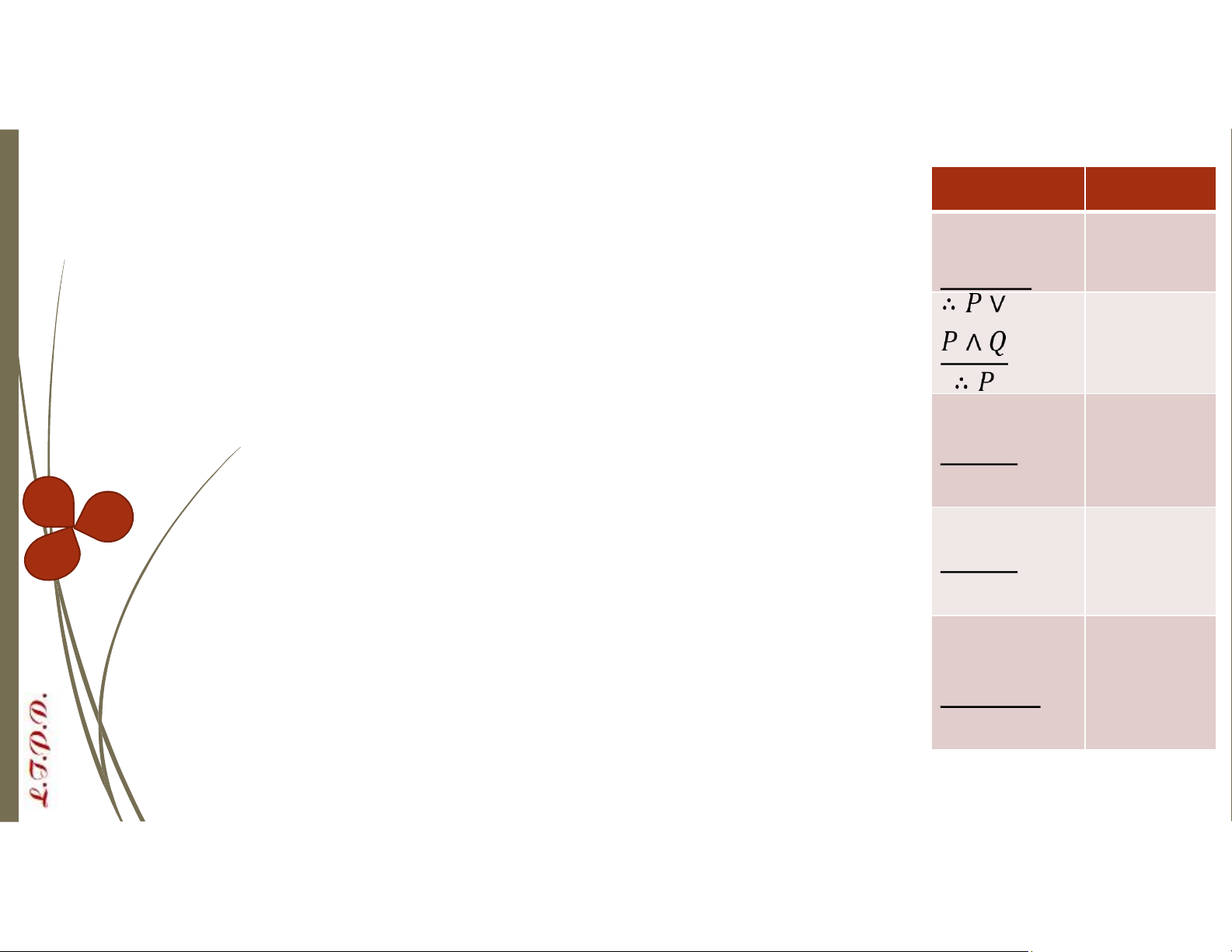
hôm nay trời mưa thì ngày mai cô ấy đến.” lOMoAR cPSD| 58488183 Quy tắc Tên Cộng Rút gọn Khẳng → định ∴ → Phủ định ∴ → Tam đoạn → luận giả định ∴ → lOMoAR cPSD| 58488183 ⇒ Quy tắc … Tam đoạn ∨
“An giỏi toán. Do đó, An giỏi toán hoặc tin” luận ∴ tuyển ⇒ Quy tắc …
 Ví dụ: “Nếu hôm nay tuyết rơi thì trường học đóng
cửa. Hôm nay trường học không đóng cửa. Do
đó, hôm nay đã không có tuyết rơi.” ⇒ Quy tắc … lOMoAR cPSD| 58488183
Các quy tắc suy luận lOMoAR cPSD| 58488183 Quy tắc Tên Cộng Rút gọn Khẳng → định ∴ → Phủ định ∴ → Tam đoạn → luận giả định ∴ → lOMoAR cPSD| 58488183
“Nếu hôm nay trời mưa thì cô ấy không Tam đoạn ∨
đến. Nếu cô ấy không đến thì ngày mai cô ấy luận
đến. Vì vậy, nếu hôm nay trời mưa thì ngày ∴ tuyển  Ví dụ: mai cô ấy đến.”
P = “Hôm nay trời mưa”
Q = “Cô ấy không đến” Đặt:
R = “Ngày mai cô ấy đến” → ∧ → → ( → )
⇒ Quy tắc Tam đoạn luận giả định Biểu thức: lOMoAR cPSD| 58488183
Các quy tắc suy luận lOMoAR cPSD| 58488183 Quy tắc Tên Cộng Rút gọn Khẳng → định ∴ → Phủ định ∴ → Tam đoạn → luận giả định ∴ → lOMoAR cPSD| 58488183
“An giỏi toán. Do đó, An giỏi toán hoặc tin” Tam đoạn ∨ luận ∴ tuyển
 Ví dụ: P = “An giỏi toán” Q = “An giỏi tin” Biểu thức:→ (∨ ) Đặt: ⇒ Quy tắc Cộng lOMoAR cPSD| 58488183
Các quy tắc suy luận lOMoAR cPSD| 58488183 Quy tắc Tên Cộng Rút gọn Khẳng → định ∴ → Phủ định ∴ → Tam đoạn → luận giả định ∴ → lOMoAR cPSD| 58488183
“Nếu hôm nay tuyết rơi thì trường học đóng Tam đoạn ∨
cửa. Hôm nay trường học không đóng cửa. Do luận
đó, hôm nay đã không có tuyết rơi.” ∴ tuyển  Ví dụ:
P = “Hôm nay tuyết rơi”
Q = “Trường học đóng cửa” Biểu diễn: → ∧ → Đặt: ⇒ Quy tắc Phủ định lOMoAR cPSD| 58488183
Các quy tắc suy luận lOMoAR cPSD| 58488183 Quy tắc Tên Cộng Rút gọn Khẳng → định ∴ → Phủ định ∴ → Tam đoạn → luận giả định ∴ → lOMoAR cPSD| 58488183
“Hôm nay trời nóng trên 100 độ hoặc sự ô Tam đoạn ∨
nhiễm là nguy hại. Hôm nay nhiệt độ ngoài trời luận
thấp hơn 100 độ. Do đó, sự ô nhiễm là nguy ∴ tuyển  Ví dụ: hại.”
⇒ Quy tắc Tam đoạn luận tuyển lOMoAR cPSD| 58488183
Các quy tắc suy luận