Chương 24: Cơ Học Lượng Tử - Tính Sóng-Hạt và Phương Trình Schrödinger môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

24.1. Lưỡng tính sóng-hạt của hạt vi mô
24.1.1. Tính sóng-hạt của ánh sáng
24.1.2. Giả thuyết De Broglie
24.1.3. Hệ thức bất định Heisenberg và ý nghĩa
24.2. Hàm sóng trong cơ học lượng tử, ý nghĩa, điều kiện
24.3. Phương trình Schrodinger
24.4. Ứng dụng phương trình Schrodinger
24.4.1. Vi hạt trong giếng thế năng 1 chiều vô hạn
24.4.2. Hiệu ứng đường ngầm (giới thiệu và nêu ý nghĩa)
24.4.3. Dao từ điều hòa (giới thiệu và nêu ý nghĩa).
Lưỡng tính sónghạ của hạ v mô
. Lưỡng tính sóng hạt của ánh sáng nh sáng
§sóng: giao thoa, nhiễu xạ, phân cực...
§hạt: hiệu ứng quang điện, tán xạ
Compton, bức xạ nhiệt...
Thuyết Einstein: năng lượng: Whv = Tính chất sóng và Ánh sáng là chùm h hạt có liên quan
động lượng: p = photon è biểu thị hàm l sóng qua W và p
Thiết lập biểu thức hàm sóng ánh sáng đơn sắc
Lưỡng tính sónghạ của hạ v mô
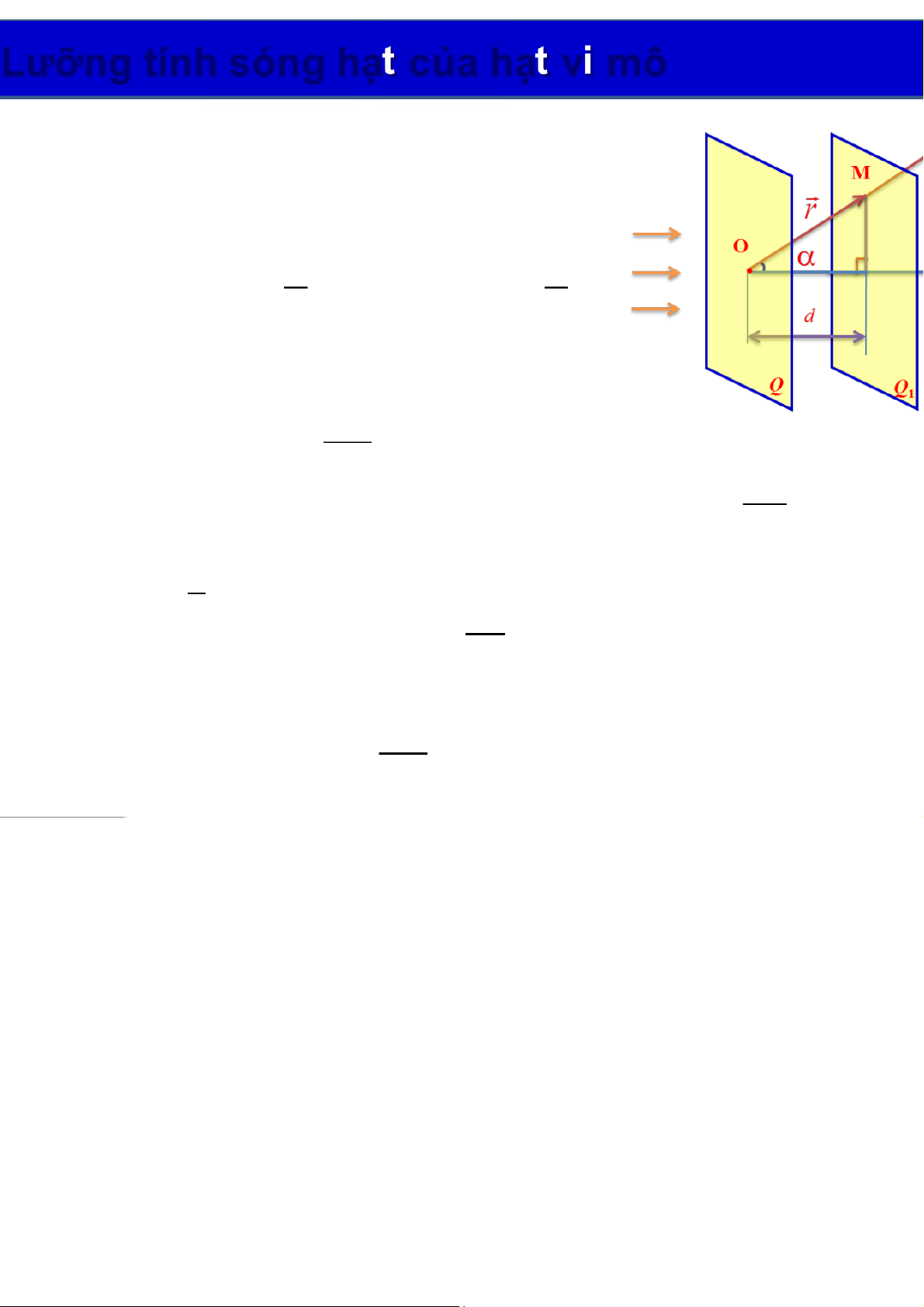
hiết lập hàm sóng phẳng của ánh sáng đơn sắc O Î Q: cos ψ =a 2πvt o M Î Q 1: dd y æö æ ö acos2 v =-=- p t a cos2 vt pl M ç÷ ç ÷ c èø è ø = = ! ! r cos r .n a ! ! r .n y a c v o t s2 pl æö ®=-
: hàm sóng phẳng của ánh sáng đơn sắc M ç÷ èø ! ! 2rn . p æö -- iv l t ç÷
ểu diễn hàm sóng dưới dạng phức èø : ae y = i !"" -- ( Wtp )r ay y = ae # !hJs= = 3 - 4 Với Hằng số 1,05 Planc . k 10 . 2p rút gọ !! !! p i ( t kr .)
ểu diễn qua véctơ sóng 2 kn= ae w y -- ®= l
Lưỡng tính sónghạ của hạ v mô
Giả thuyết de Broglie
Một vi hạt tự do có năng lượng xác định, động lượng
ác định tương ứng với một sóng phẳng đơn sắc xác ịnh:
Năng lượng của vi hạt liện hệ với tần số dao động
của sóng tương ứng theo hệ thức France, 1892-198 Nobel Prize in w = = ! W hv hayW physics 1929
Động lượng của vi hạt liên hệ với bước sóng của
sóng tương ứng theo hệ thức h ! !" p = = hayp k l
vThực nghiệm xác nhận tính chất sóng của hạt vi mô
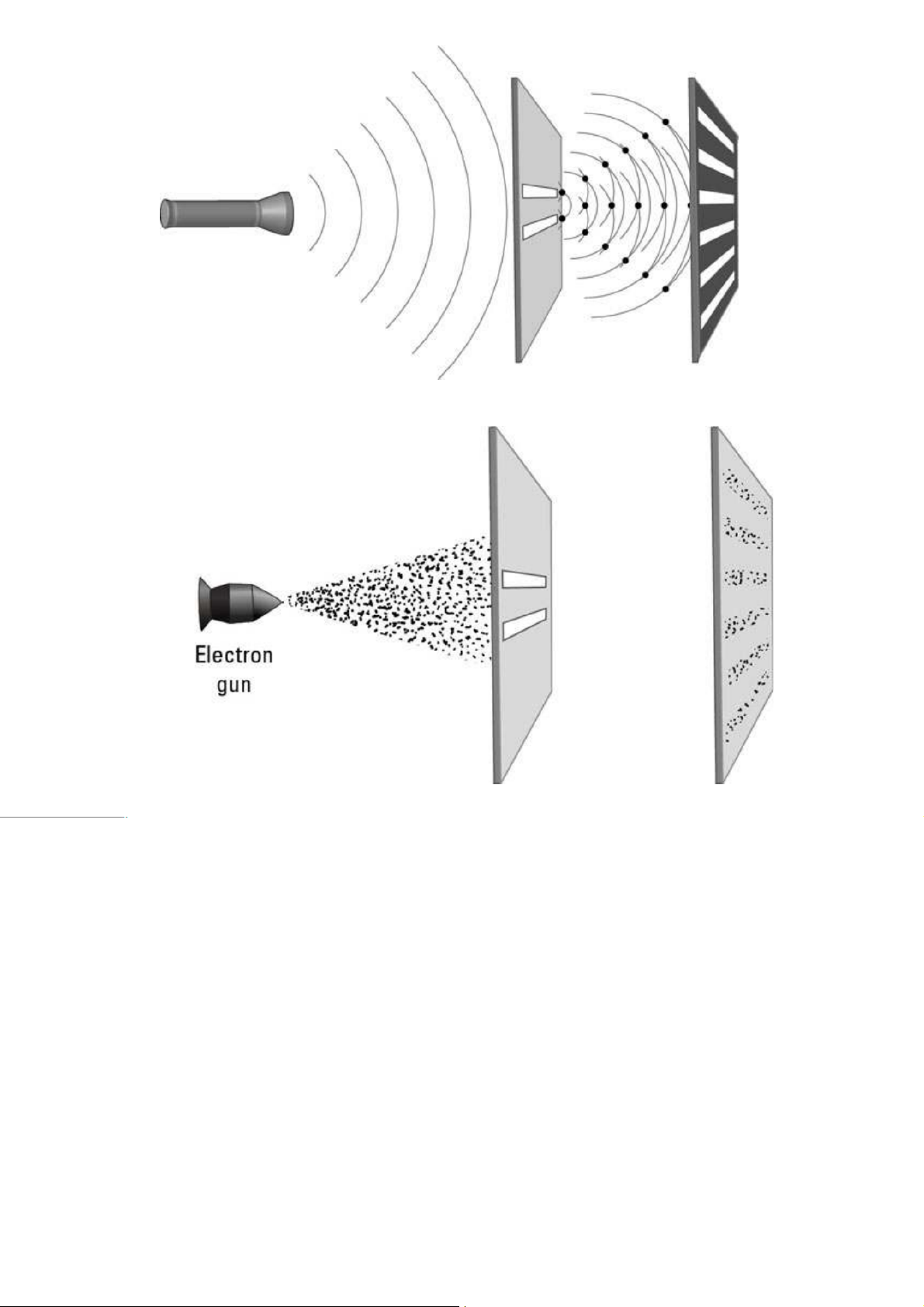
Thí nghiệm 1: Nhiễu xạ của chùm electron qua khe hẹp.
Thí nghiệm 2: Nhiễu xạ của chùm electron trên tinh thể.
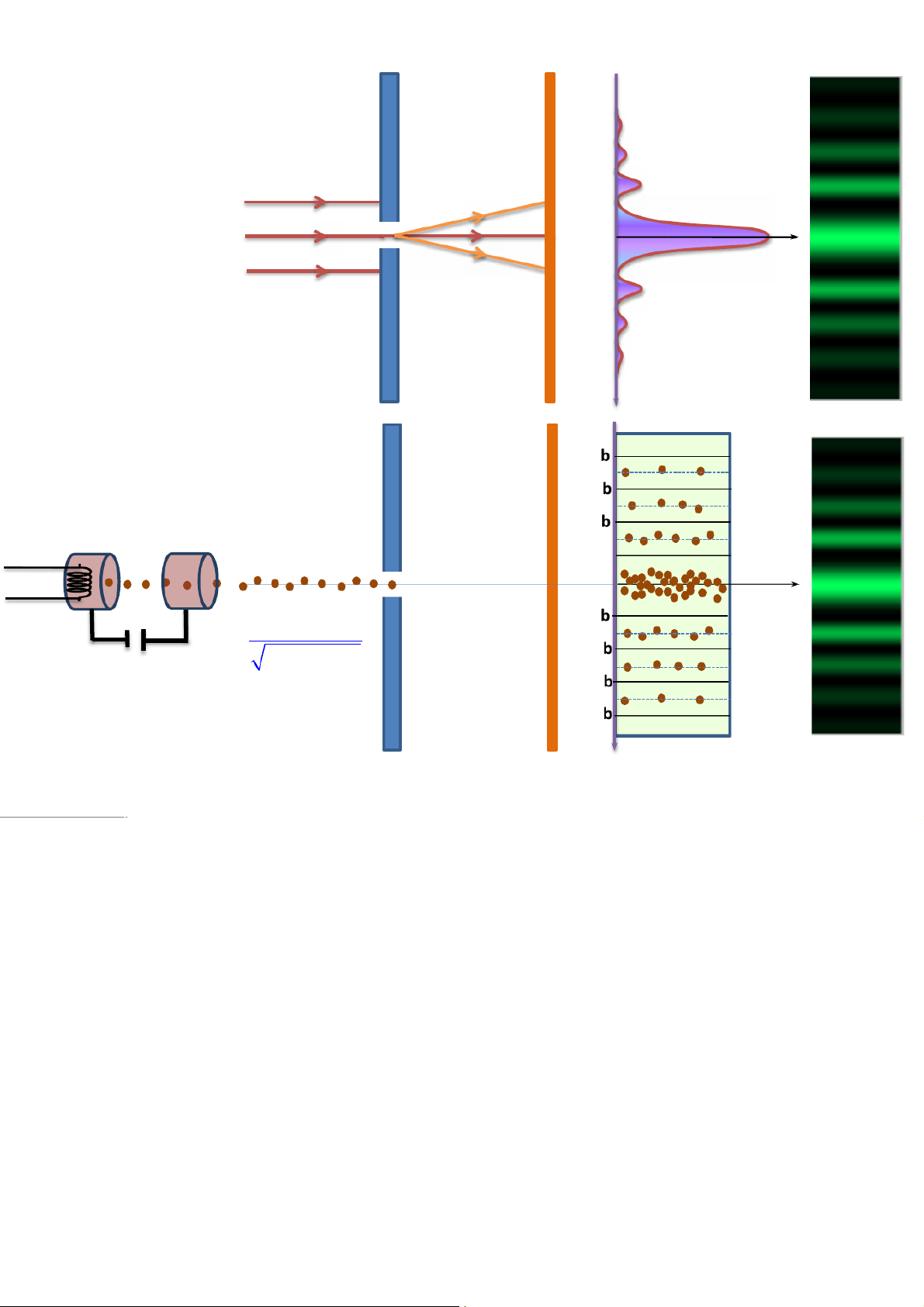
Thí nghiệm 1: Nhiễu xạ của chùm electron Màn ảnh thường 4l/b NX ánh sáng qua 1 3l/b
khe hẹp có bề rộng b 2l/b l/b Io 0 -l/b -2l/b Ánh sáng đơn sắc -3l/b có bước sóng l -4l/b sinj 4l/ 3l/ NX electron qua 1 2l/
khe hẹp có bề rộng b l/b 0 6V -l/ h l = -2l/ 2 emUAK UAK -3l/ -4l/ sinj Màn phát quang
Lưỡng tính sónghạ của hạ v mô
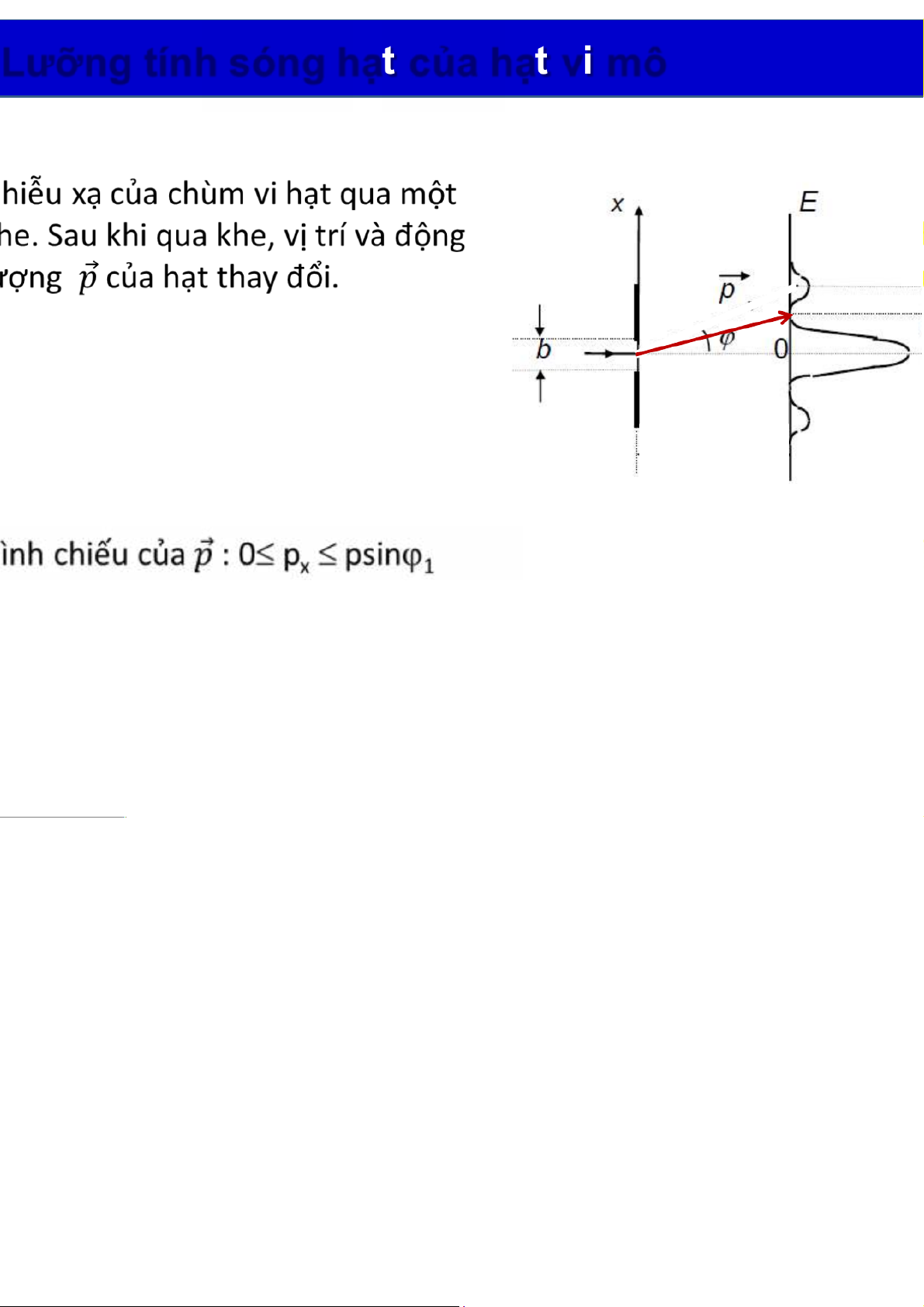
Hệ thức bất định ét phương x Împ khe 1
ị trí của hạt trong khe: 0£x £b Dx »b
au khi qua khe, hạt có thể rơi vào cực đại giữa hoặc phụ
èHình chiếu pxđược xác định với độ bất định nhỏ nhất khi:
Dpx»psinj1với sinj1= l/b èDxDpx»plmà p = h/l
èD x Dpx » h Tương tự:
èD yDpy » h
èD z Dpz » h
Lưỡng tính sónghạ của hạ v mô
Hệ thức bất định ìD ³ . xp D h ìD ³ . xp D x x
ệ thức bất định giữa tọa ï³ Hay còn viết ï³ íD . yp D h íD . yp D
ộ và động lượng: y y ï dưới dạng: D ³ ï³ î z.p D h D . î zp D z z
nghĩa: - Tọa độ và động lượng không đồng thời xác định. Nếu động
ượng càng xác định thì tọa độ càng bất định và ngược lại.
- Không tồn tại khái niệm quỹ đạo trong thế giới vi mô
è Các vi hạt chuyển động không theo quy luật của cơ học cổ điển mà
ân theo quy luật thống kê lượng tử.
ệ thức bất định giữa năng lượng và thời gian: W.th DD »
ếu năng lượng của hệ ở một trạng thái nào đó càng bất định thì thời
ian để hệ tồn tại ở trạng thái đó càng ngắn và ngược lại.
è trạng thái có năng lượng bất định là trạng thái không bền, còn trạng
hái có năng lượng xác định là trạng thái bền.
Lưỡng tính sónghạ của hạ v mô
Hệ thức bất định
í dụ 1: Trong nguyên tử, electron chuyển động trong pham vi 10-10m
(kích thước nguyên tử)
Độ bất định về vị trí: Dx » 10-10m
è Với hạt vi mô, Dvxkhá lớn à e không chuyển động theo quỹ đạo
í dụ 2: Xét hạt vĩ mô, m = 10-15 kg, Dx » 10-8m,
è Với hạt vĩ mô, Dvxnhỏ à vị trí và vận tốc xác định đồng thời
§Vớihạtvĩmô,vịtrívàđộnglượngcóthểxácđịnhchínhxácđồngthời.
§Vớihạtvi mô,vịtrívàđộnglượngkhôngthểxácđịnhchínhxácđồngthời
Hàm sóng trong cơ học lượng tử ý nghĩa điều kiện Hàm sóng
+ Vi hạt tự do: Chuyển động của nó được mô tả bởi
hàm sóng tương tự như sóng phẳng đơn sắc: i(Wt-pr) !! oe- y=y " 2 2 Y *
olà biên độ của hàm sóng : y o =y=y × y *
y là liên hợp phức của y
+ Vi hạt chuyển động trong trường thế, hàm sóng của
nó là một hàm phức tạp của tọa độ và thời gian: ! y(r = , y t) (x, y, z, t)
Hàm sóng trong cơ học lượng tử ý nghĩa điều kiện
Ý nghĩa thống kê của hàm sóng DV
ính cường độ sáng tại M M 2 2
+ Theo quan điểm sóng: I ~ M yo=y
Theo quan điểm hạt: I
Số hạt trong một đvtt DV bao quanh M M ~ 2 NX: : y
mật độ xác suất tìm hạt trong một đvtt DV bao quanh M
Xác suất tìm thấy hạt trong toàn bộ không gian là: 2 y dV1 òòò=
gọi là điều kiện chuẩn hóa của hàm sóng.
c. Điều kiện hàm sóng
ØHàm sóng phải giới nội
ØHàm sóng phải đơn trị
ØHàm sóng phải liên tục, đạo hàm bậc nhất của hàm sóng phải liên tục
Phươngtrình Schrodinger
Hàm sóng của vi hạt tự do. i i !! - -" (Wt-pr) wt " ! y=y=y oe e (r) ! ! y(r = , y t) y (t) (r) ! 2m !! Dy (r + ) y= W éù -U(r) (r)0 2 ëû " 2 2 2 ¶ ¶ ¶ D= + + toán tử laplace 2 2 2 ¶x ¶y¶z
Ứng dụngphươngtrình Schrodinger
Chuyển động của v hạ trong giếng thế năng mộ chiều U
Xét chuyển động của vi hạt hạt theo phương x,
trong một miền mà thế năng U được xác định theo điều kiện: ì 0 khi 0 x a < < U =í¥ £³ khi x 0 và x a î 0 ax
Phương trình Schrödinger của hạt trong giếng có dạng: !! 2mW Dy (r y )+ (r) = 0 2 " 2 d 2mW0 2mWk y = «+y= Đặt 2 22 2 dx ! ! 2 dk 0 y+y 2 =
Nghiệm có dạng: y (x = )+ Asin kx B cos k 2 dx
Ứng dụngphươngtrình Schrodinger Nghiệm : y (x = )+ Asin kx B cos kx ìïy (0 = ) B0 =
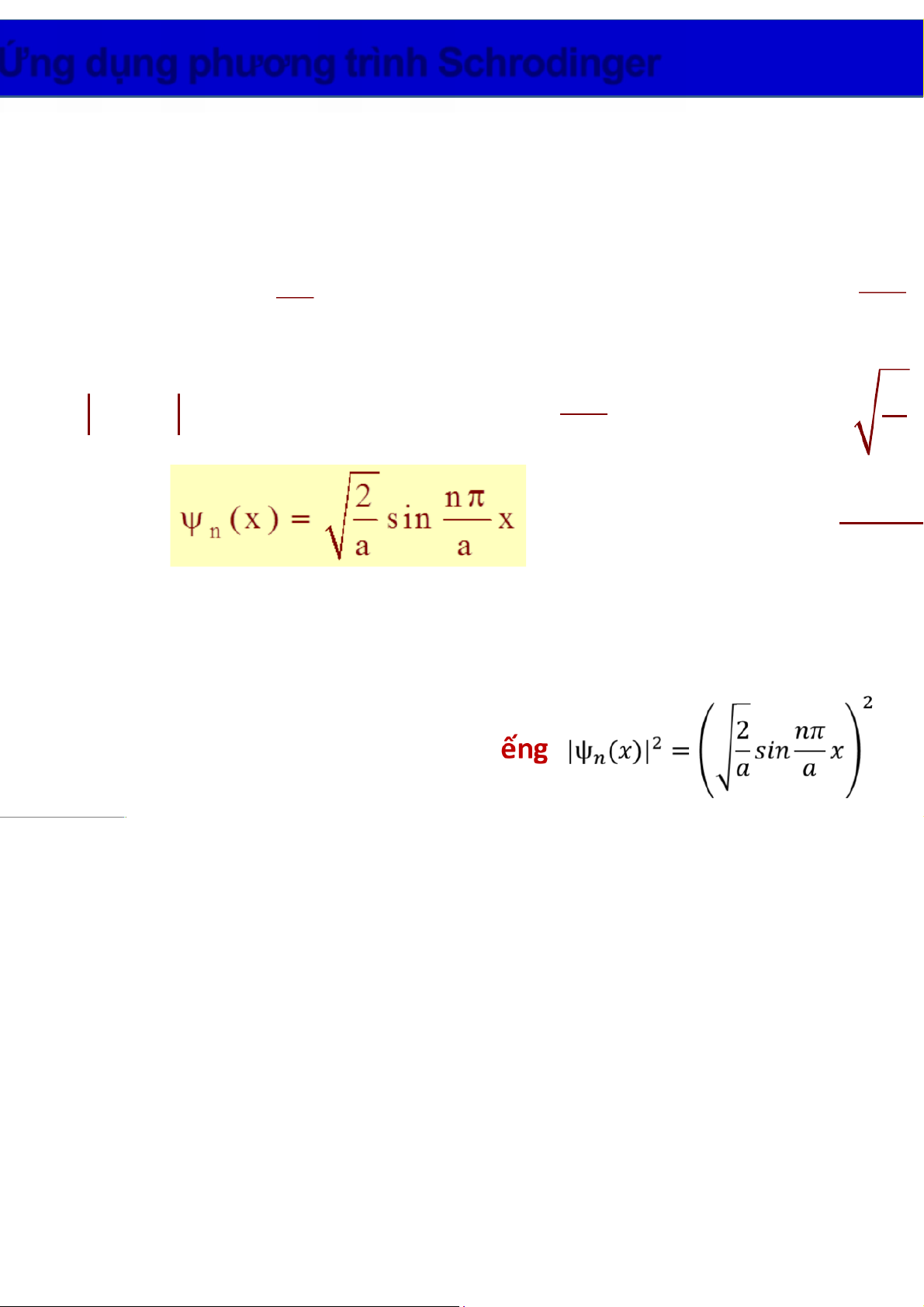
NX: Hàm sóng phải liên tục, giới nội, ta có: íy ïî (= = a ) Asin ka 0 A ≠ 0. np np ® si = n k ® a = 0 k (n=1,2,3...) Vậy y n = (x) Asin x a a
Từ điều kiện chuẩn hóa của hàm sóng: a a 22 2 n p 2 y ( òò x =x) ®=dx 1 A sin dx 1 ® A = a a 0 0 22 p =! Hàm sóng Năng lượng: Wnn2 2ma vKết luận:
E Mỗi trạng thái của hạt ứng với một hàm sóng yn(x)
E Năng lượng của hạt trong giếng phụ thuộc vào số nguyên n, nghĩa là
ến thiên một cách gián đoạn, ta nói năng lượng bị lượngtửhóa
E Mật độ xác suất tìm thấy hạt trong gi
Ứng dụngphươngtrình Schrodinger 2 2 2 p =! p Với n = 1: y= (x) sin x W 1 12 a a 2ma 2 2 Với n = 2: p W= 4W y= (x) sin x 2 1 2 a a
Tương tự với n = 3,4,5..... W y 2 n= 4 n y n W 4 n= 3 W3 n= 2 2 n=1 1 0 a 0 a 0 a
Ứng dụngphươngtrình Schrodinger
c. Dao tử điều hoà lượng tử ! 2m !! ² Khái niệm Dy (r + ) y= W éù -U(r) (r)0 2 ëû " ² Ví dụ:
ao động của ion xung quanh nút mạng tinh thể, của nguyên tử rong phân tử. ² Năng lượng:
m và w : khối lượng và tần số góc của vật dao động;
Năng lượng bị lượng tử hóa