lOMoARcPSD|47206521 lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu Chương 3
KÉO - NÉN ĐÚNG TÂM THANH THẲNG I.KHÁI NIÞM
 Định nghĩa:Thanh được gọi là chịu kéo hay nén đúng tâm khi trên
mọi m¿t cÁt ngang của thanh chỉ có một thành phần nội lực là lực dọc Nz.
Nz þ 0 khi hướng ra ngoài mặt cắt (đoạn đang xét chịu kéo) x
Nz ü 0 khi hướng vào trong mặt cắt (đoạn đang xét chịu nén)
Đây là trưßng hợp chịu lực đơn giản nhất.Ta gặp trưßng hợp này
khi thanh chịu 2 lực bằng nhau và trái chiều á hai đầu dọc trục thanh. Nz
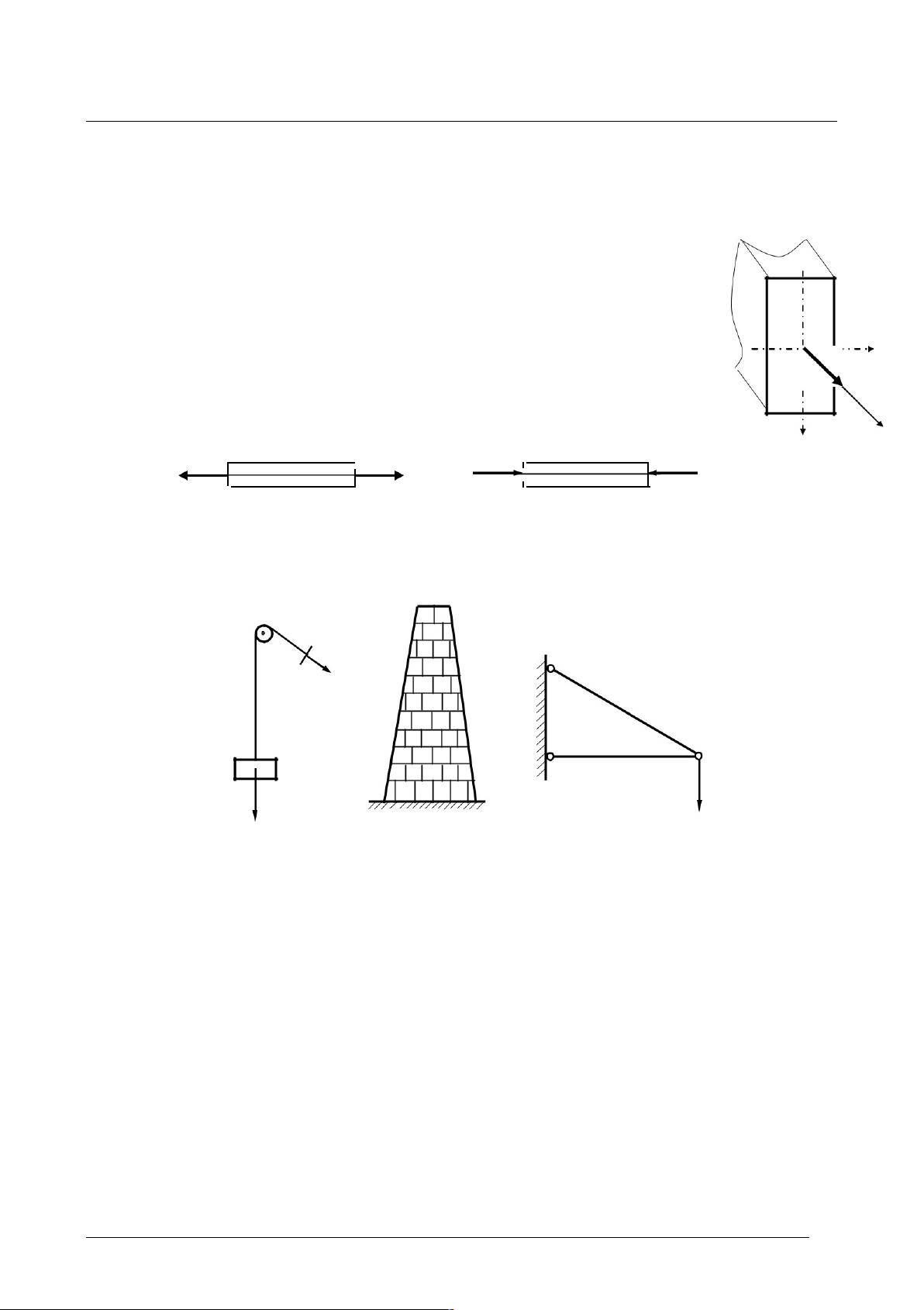
Thanh chịu kéo đúng tâm (H.a) hay chịu nén đúng tâm (H.b). y P P P P H. 3.1 Hình a Hình b
Thực tế: có thể gặp các cấu kiện chịu kéo hay nén đúng tâm như: dây cáp trong
cần cẩu (H.3.3a), dây xích, ống khói (H.3.3b), các thanh trong dàn (H.3.3c). P Q A) B) C)
H. 3 Một số cấu kiện chịu kéo nén đúng tâm
II. ĂNG SUÀT TRÊN M¾T CÀT NGANG
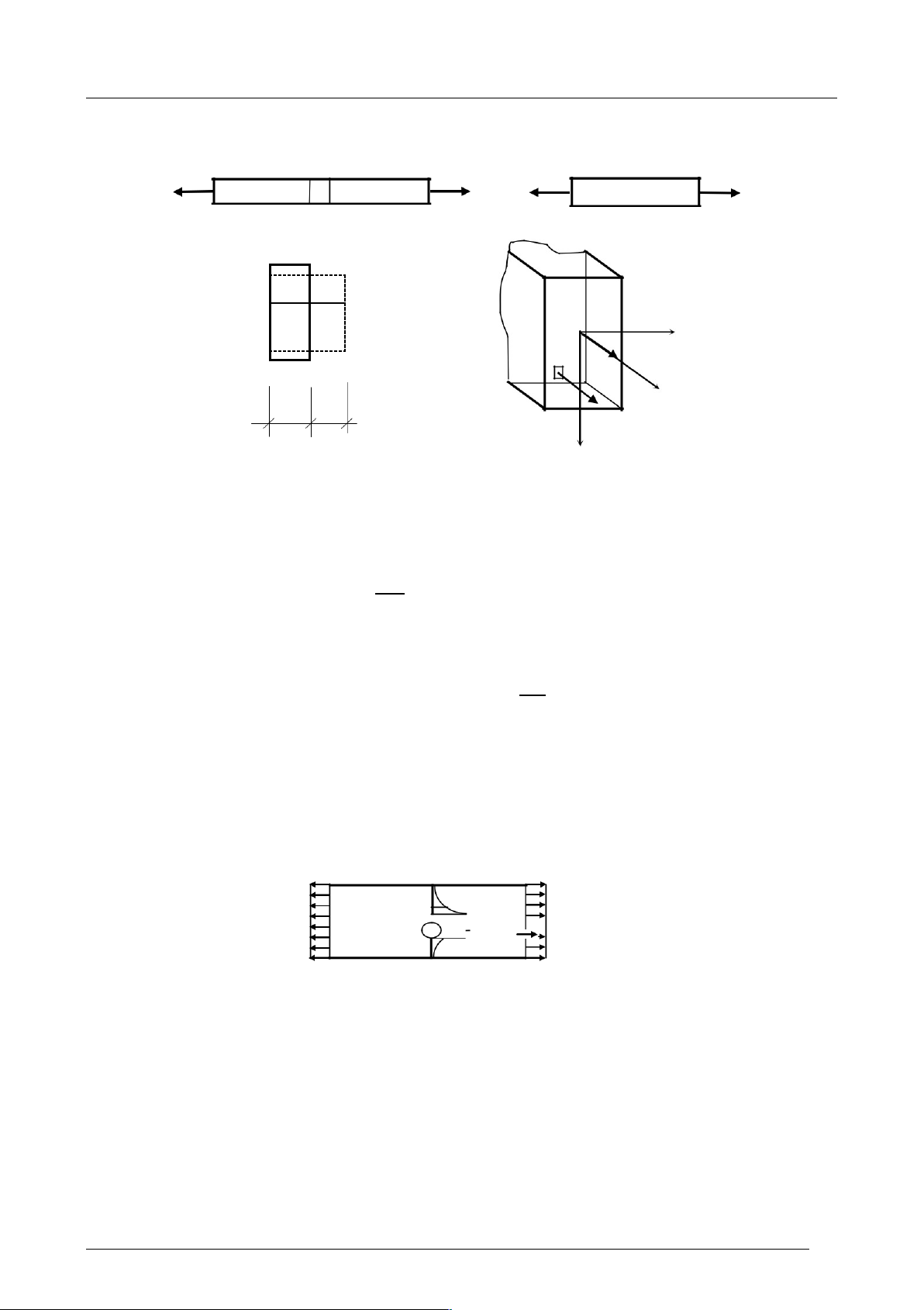
Xét thanh thẳng chịu kéo (nén) đúng tâm (H.a) các mặt cắt ngang CC và DD
trước khi thanh chịu lực cách nhau đoạn dz và vuông góc trục thanh. Các thớ
dọc trong đoạn CD (như là GH) dều dãn hay co bằng nhau (H.b).
Khi thanh chịu kéo (nén), nội lực trên mặt cắt ngang DD hay bất kỳ mặt cắt
ngang khác là NZ = P (H.c) thanh sẽ dãn ra, mặt cắt DD di chuyển dọc trục
thanh z so với mặt cắt CC một đoạn bé ôdz (H.b).
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 1 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu P C D P P Nz C D a) c) C D D’ G H H’ 0 x D’ A NZ C D dz ôdz z z b) d) y
Ta thấy biến dạng các thớ dọc như GH đều bằng HH9và không đổi, mặt
cắt ngang trong suốt quá trình biến dạng vẫn phẳng và vuông góc với trục
thanh, điều này cho biết các điểm trên mặt cắt ngang chỉ có ứng suất
phápz không đổi (H.d)
Ta biêt : Z DA ý NZ ôdz ,
và :õ z ý là hằng số. A dz
ĐL.Hooke z ý Eõ z cũng là hằng số.
Ta tính được ứng suất: N
 Z A ý NZ Z Z ý (3.1) A
với A: diện tích mặt cắt ngang của thanh.
Lực dọc > 0 ứng suất > 0, Lực dọc < 0 ứng suất < 0
Nh¿n xét : Nếu thanh có tiết diên giảm yếu, như bị khoét lỗ. Thực nghiệm và lý
thuyết đều cho thấy tại tiết diện giảm yếu, ứng suất không phân bố đều mà
cómax á mép lỗ. Gọi là hiện tượng tập trung ứng suất.  max
III. BIÀN D¾NG CĀA THANH KÉO (NÉN) ĐÚNG TÂM.
1- BiÁn d¿ng dọc trÿc :
Biến dạng dọc trục z của đoạn dài dz chính là : ôdz (H.3.3b) ôdz
Như vậy biến dạng dài tương đối của đoạn dz là: õ ý (a) z dz  z
Theo định luật Hooke ta có: õ ý (ý nghĩa vật lý) (b) z E
trong đó: E:là hằng số tỷ lệ, được gọi là mô đun đàn hồi khi kéo (nén), phụ
thuộc vào vật liệu và có thứ nguyên
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 2 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu ù löïc ù 2 ú 2 ú
, đơn vị N/m … , xác định từ thí nghiệm
û øchieàu daøiùû
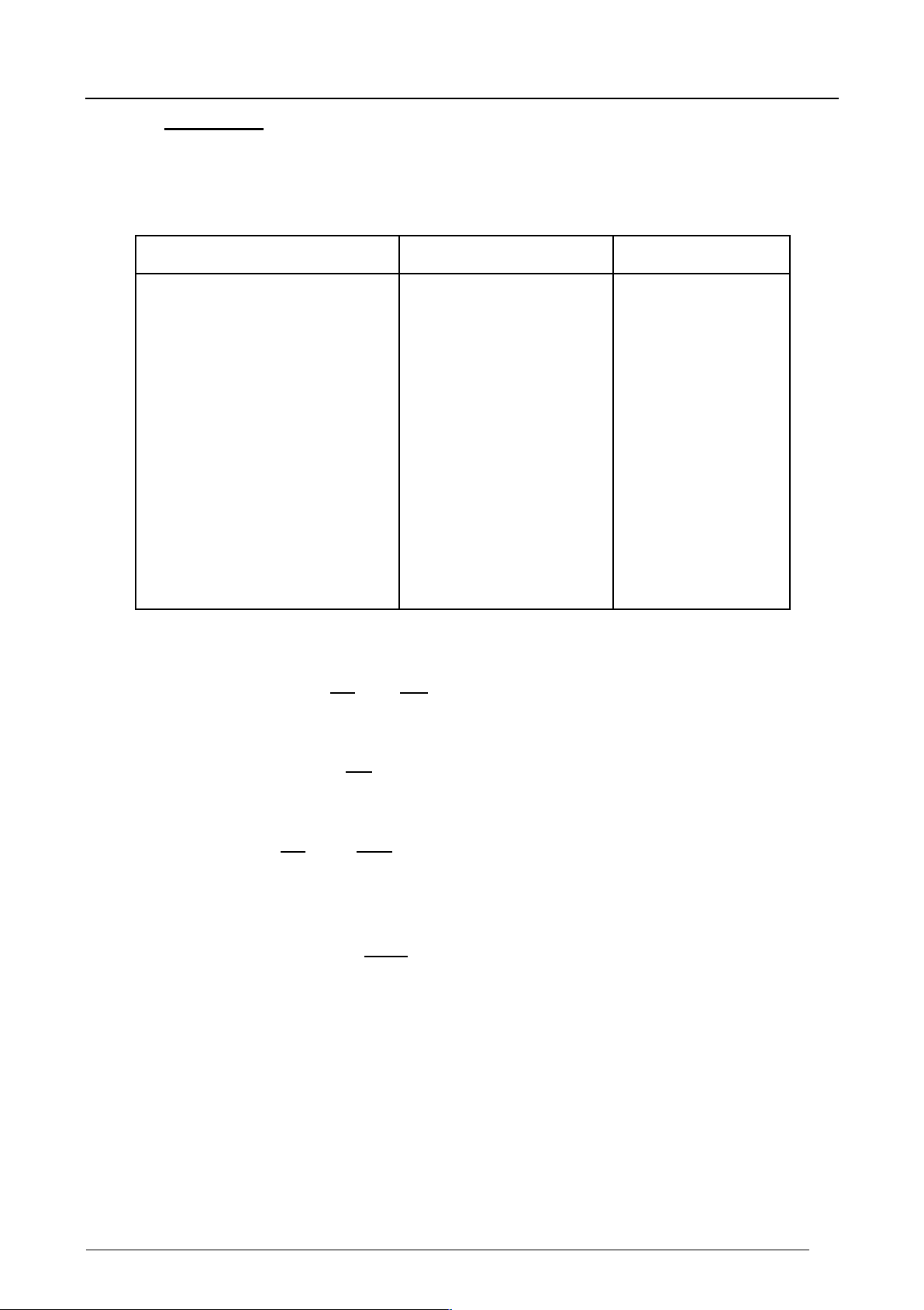
Bảng 3.1 cho trị số E của một số vật liệu. Vật liệu E (kN/cm2) ý Thép (0,15 0,20)%C 2 x 104 0,25 0,33 Thép lò xo 2,2 x 104 0,25 0,33 Thép niken 1,9 x 104 0,25 0,33 Gang xám 1,15 x 104 0,23 0,27 Đồng 1,2 x 104 0,31 0,34 Đồng thau (1,01,2)104 0,31 0,34 (0,7 0,8)104 Nhôm 0,32 0,36 Gỗ dọc thớ (0,08 0,12)104 - Cao su 0,8 0,47
Từ (a) tính ôdz, thế vào (b), ta được biến dạng dài dọc trục của đoạn dz là:
ôDZ ý õZDZ ý  Z DZ ý NZ DZ (c) E EA
GọiL là biến dạng dài của chiều dài L (dãn khi thanh kéo, co khi thanh nén) NZ
LýôDZý EADZ (3.2) L L
Nếu E,A là hằng số và Nz cũng không đổi trên chiều dài L của thanh, ta sẽ được:
NZ DZ NZ L
L ý EA ý EA (3.3) L
Nếu thanh gồm nhiều đoạn có chiều dài Li và trên mỗi đoạn Nz, E,A không đổi thì: L ý
ö N Lz ö õLi ý õ÷ ÷ (3.39) ÷ ÷ z EA ø øi
Tích số EA gọi là độ cứng khi chịu kéo hay nén đúng tâm của thanh.
Ngưßi ta còn dùng độ cứng tương đối EA/L là tỉ số độ cứng và chiều dài thanh
2- BiÁn d¿ng ngang :
Theo phương ngang thanh cũng có biến dạng, ta đã chọn z là trục thanh, x, y
là các phương vuông góc với z (H.3.3d). Nếu ta gọi õx và õy là biến dạng dài tương đối theo
hai phương x và y, thì ta có quan hệ sau:
õ x ý õ y ý þõ z (3.4)
trong đó: þ - hệ số Poisson, là hằng số vật liệu, xác định từ thí nghiệm
Dấu (–) trong biểu thức chỉ rằng biến dạng theo phương dọc và ngang ngược nhau.
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 3 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
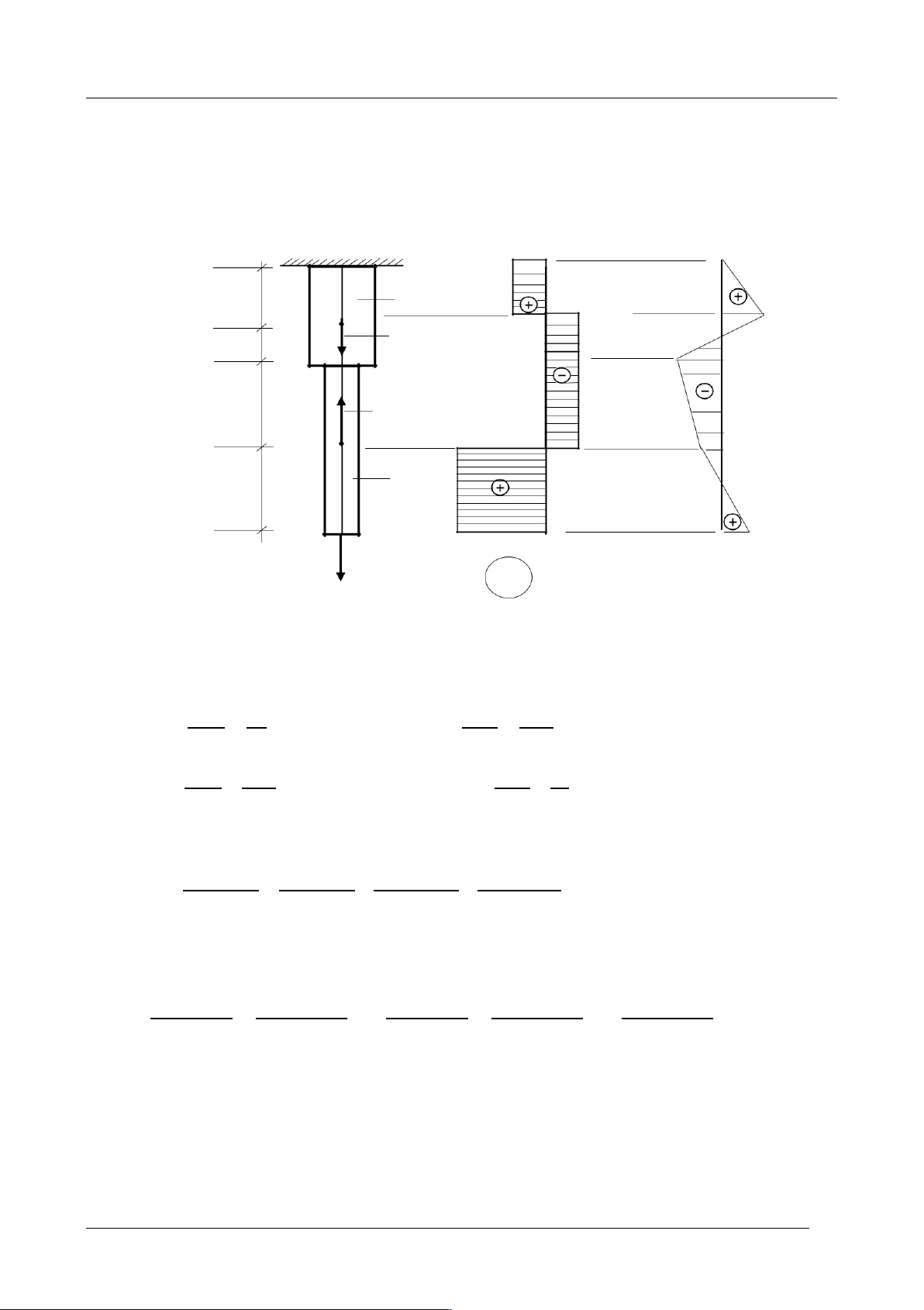
Thí dÿ1. Vẽ biểu đồ dọc Nz tính ứng suất và biến dạng dài toàn phần của thanh trên
H.3.4a cho biết E= 2.104 kN/cm2; A1=5 cm2; A2 =10 cm2.(Lực tác dụng tại B,D,H) K 10kN 40 cm A2 2.10-3cm B 30kN 30 cm P3=40 kN 2, 5.10-3cm C 50 cm P2=80kN D 0, 0175cm 50 cm A1 H 50kN 0, 0075cm a) P1=50kN Nz b) BiÁn d¿ng Giải. H.3.4
Dùng phương pháp mặt cắt vẽ được biểu đồ Nz (H.3.4b)
Từ đó ta tìm được ứng suất trên mặt cắt ngang mỗi đoạn là: DH CD  NZ 50 2  NZ  30 2 DH ý A ý 5 ý 10 kN/cm , CD ý A ý 5 ý6 kN/cm 1 1 N BC  30 10  Z N KB z A BC ý 2
ý 10 ý3 kN/cm 2 ,
KB ý A ý ý 1 kN/cm 2 2 10
Xác định biến dạng dọc toàn phần chính là biến dạng dài tuyệt đối của thanh, sử
dụng công thức (3.3’) áp dụng cho bốn đoạn của thanh. L = 50ô50 30ô50 30ô30 10ô40 ý 0,0075cm
2 ô104 ô5 2 ô104 ô 5 2 ô104 ô10 2 ô104 ô10
Biến dạng dọc mang dấu (+) nghĩa là thanh bị dài ra.
Ta có thể tính biến dạng bằng phương pháp công tác dụng như sau:
L(P,P ,P ) ý L(P)L(P )L(P ) 1 2 3 1 2 3 Lý(
50 ô100   50x70 ) (  80x50  - 80x70 ) ( 40x40 ) ý 0,0075cm 2.104 ô 5 2.104 ô10 2.104 ô 5 2.104 ô10 2.104 ô10
VI. ĐẶC TR£NG C¡ HÞC CĀA VÀT LIÞU (được học thí nghiệm sau) 1. Khái nißm
Vấn đề của chúng ta là cần phải so sánh hay muốn biết độ bền, độ cứng của
vật liệu khi chịu lực với ứng suất, biến dạng của vật liệu cùng loại đã biết. Ta
cần thí nghiệm kéo, nén đề tìm hiểu tính chất chịu lực và quá trình biến dạng từ
lúc bắt đầu chịu lực đến lúc phá hỏng của các loại vật liệu khác nhau.
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 4 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
Ngưßi ta phân vật liệu thành hai loại cơ bản:
Vật liệu dẻo,và vật liệu dòn.
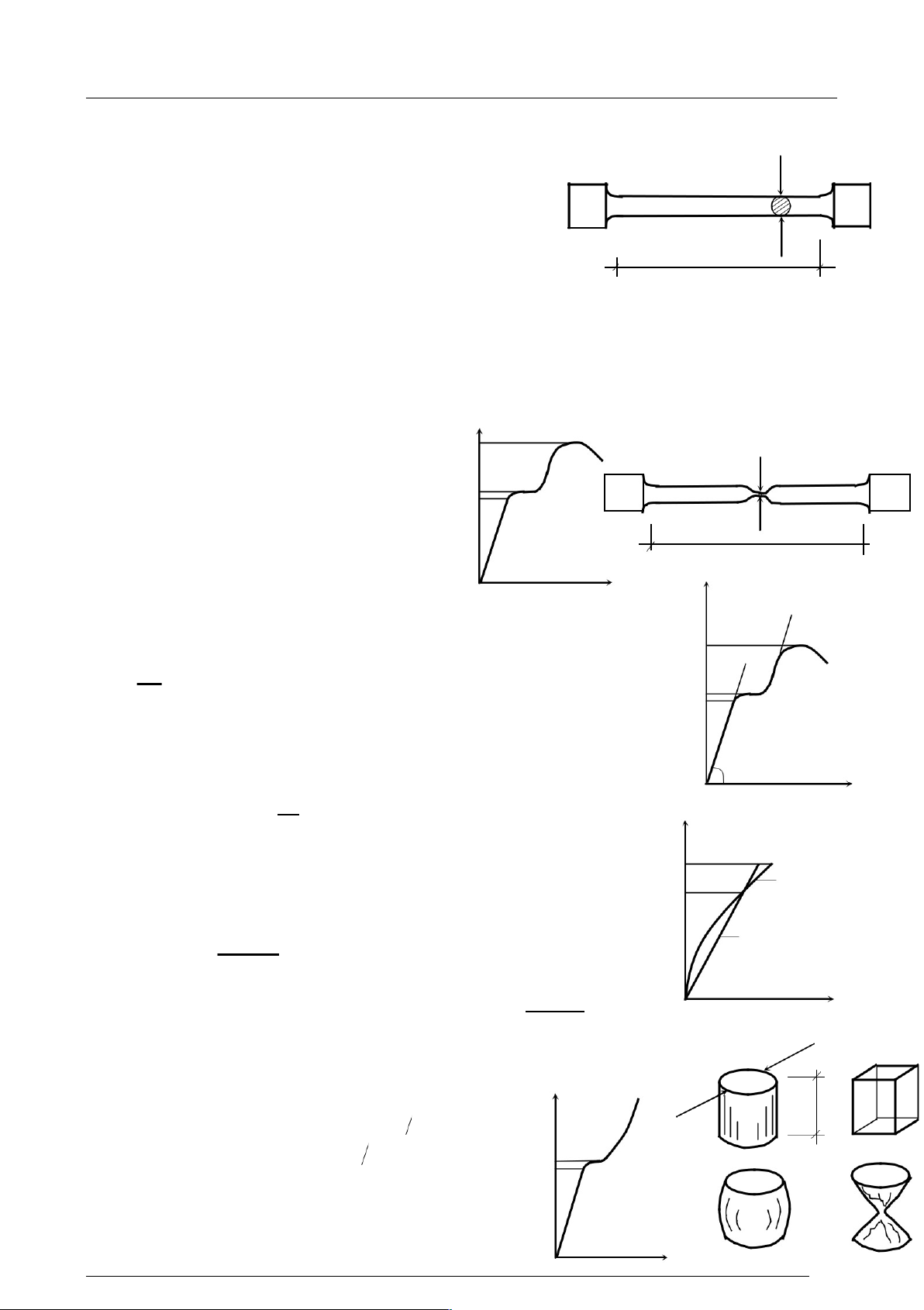
Như vậy có bốn thí nghiệm cơ bản sau: D 2. Thí nghißm kéo vÁt lißu dẻo 0 (thép)
a- Mẫu thí nghißm
Theo tiêu chuẩn TCVN 197 -2002 (H.3.5) L0
Chiều dài Lo ,đưßng kính do, diện tích Ao b- Thí nghißm H.3.5
Tăng lực kéo từ 0 đến khi mẫu đứt, với bộ phận vẽ biểu đồ của máy kéo,
ta nhận được đồ thị quan hệ giữa lực kéo P và biến dạng dàiL của mẫu như H.3.6. Sau khi
mẫu bị đứt ta chắp mẫu lại, có chiều dài L1 ,đưßng kính d1, diện tích A1 mẫu sẽ có
hình dáng như H.3.7. B
c- Phân tích kÁt qu¿ P P B
Quá trình chịu lực của vật liệu có thể C D1, A1
chia làm ba giai đoạn: P D TL A PCH
OA: đàn hồi, P vàL bậc nhất, Lực P L1 TL
lớn nhất là lực tỉ lệ P  tl. TL ý A L O O  H.3.7
AD: giai đoạn chảy, lực kéo không H.3.6
tăng nhưng biến dạng tăng liên tục. B
Lực kéo tương ứng là lực chảy P 
ch và ta có giới hạn chảy. b C
CH ý PCH CH D AO A
DBC: giai đoạn củng cố (tái bền), tương quan giữa lực P và tl
biến dạngL là đưßng cong. Lực lớn nhất là lực bền PB và ta  õ O
có giới hạn bền. H.3.8 B PB ý
. Gọi chiều dài mẫu sau khi đứt P A Đưßng cong thực O (H.3.7) là L Pb
1 và diện tích mặt cắt ngang nơi đứt là A1 thì ta
có các định nghĩa đặc trưng cho tính dẻo của vật liệu như Ptl
sau: Biến dạng dài tương đối (tính bằng phần trăm): Đưßng qui ước
ô= L0L1100% Lo L O
Độ thắt tỷ đối (tính bằng phần trăm):  = AOA1 100 % AO (3.9) H.3.9
d- Biểu đß -õ (biểu đồ qui ước)
Từ biểu đồ P- D
L ta dễ dàng suy ra biểu H P
đồ tương quan giữa ứng suất và biến Z ý P AO
dạng dài tương đối õ PCH
z ýL Lo . P B) TL
Biểu đồ này có hình dạng giống như
biểu đồ P -L (H.3.8). Trên biểu đồ chỉ rõ 
tl , ch , b và cả mô đun đàn hồi: L O A) H.3.10 C) D)
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 5 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
E ýõ = tan
Nếu kể đến sự biến đổi diện tích mặt cắt ngang ta sẽ có biểu đồ tương quan giữa
õ z và ứng suất thực (đưßng nét đứt).
3. Thí nghißm kéo v¿t lißu dòn
Biểu đồ kéo vật liệu dòn có dạng đưßng cong (H.3.9).Vật liệu không có giới hạn PB
tỷ lệ và giới hạn chảy mà chỉ có giới hạn bền:  B ý AO
Tuy vậy ngưßi ta cũng qui ước một giới hạn đàn hồi nào đó và xem đồ thị quan
hệ lực kéo và biến dạng là đưßng thẳng (đưßng qui ước).
4.Nén v¿t lißu dẻo
Biểu đồ nén vật liệu dẻo như H.3.10a. Ta chỉ xác định được giới hạn tỷ lệ
và giới hạn chảy, mà không xác định được giới hạn bền do sự phình ngang của
mẫu làm cho diện tích mặt cắt ngang mẫu liên tục tăng lên. Sau thí nghiệm mẫu
có dạng hình trống (H.3.10c).
5. Nén v¿t lißu dòn. Đưßng cong tương tự biểu đồ kéo vật liệu dòn. Pb.
Nghiên cứu các thí nghiệm kéo và nén các vật liệu dẻo và dòn, ngưßi ta thấy
rằng: giới hạn chảy của vật liệu dẻo khi kéo và nén như nhau, còn đối với vật
liệu dòn giới hạn bền khi kéo bé hơn nhiều so với giới hạn bền khi nén.
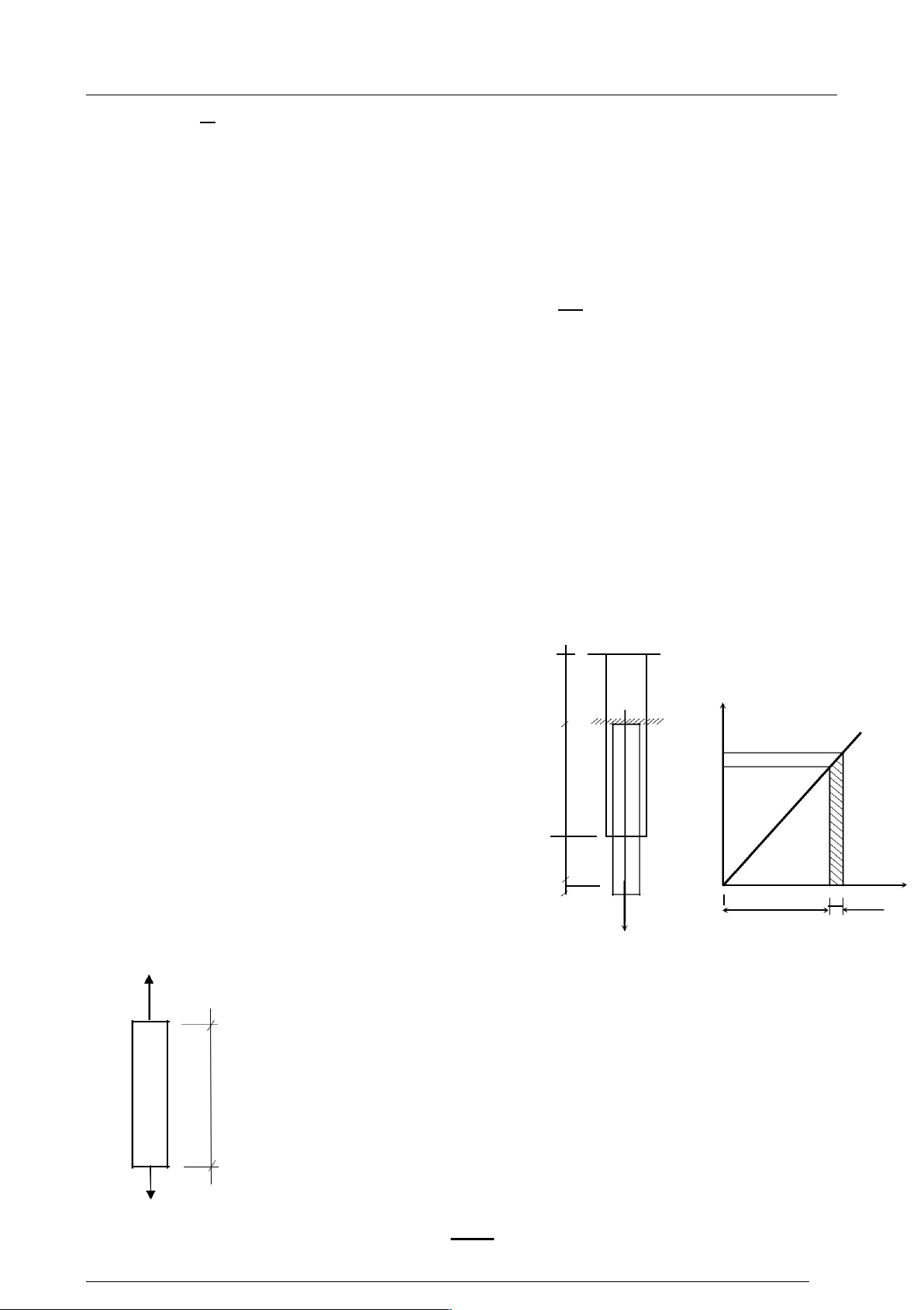
V. THÀN NG BIÀN D¾NG ĐÀN HÞI (TNBDĐH)
1- Khái nißm P
Xét thanh chịu kéo làm việc trong giai đoạn P + dP A
đàn hồi EA hằng số (H.3.13a). Lực tăng dần từ 0 P
đến giá trị P, thanh dãn ra từ từ đến giá trịL. L
Bỏ lực, thanh về lại vị trí ban đầu. Ngưßi ta gọi
công W của ngoại lực phát sinh trong quá trình
di chuyển đã chuyển hóa thành thể năng biến C L
dạng đàn hồi U tích lũy trong thanh và chính thế L 0 L d L
năng này làm cho thanh đàn hồi sau khi không P còn tác dụng lực. A) H.3.13 B)
2- Tính thÁ n ng biÁn d¿ng đàn hßi N
Quan hệ P vàL biểu diễn như H.3.13b.
Công của lực P trên chuyển dßiL.
Cho P một số gia dP biến dạng dọc thanh tăng lên số gia
dL Công của ngoại lực dW do lực P+dP là : dz
dW= (P + dP)dL = PdL + dPdL
Bỏ qua lượng bé bậc cao dPdL ta có : dW= PdL
Công nầy biểu diễn bằng diện tích hình chữ nhật gạch chéo trên N hình (3.13b)
Suy ra công của lực kéo P tăng từ 0 đến P được biểu thị bằng diện H.3.14 ý P.L tích tam giác OAC. W 2
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 6 - lOMoARcPSD|47206521 Bài giảng Sức Bền Vật liệu 2
Công này biến thành TNBDĐH U : U = W = PL
P 2 L N L ý ý z 2 2EA 2EA
Gọi u là TNBDĐH riêng (thế năngtíchlũy trongmột đơn vị thểtích), có: ý U ý PPl ý
 2 ý  õ u z z z V
2EA.Al 2E2 Xét đoạn thanh có chiều dài dz có nội lực Nz (H.3.14 ): N dU ý 2 dz z 2 EA
Suyrathế năngbiếndạngđànhồi của đoạnthanh dài L , có nội lực N z là:
U ý dU L ýL N 2z dz 2EA
Nếu trong đoạn thanh N 2 L
Z không đổi ta có: U = NZ EA 2EA
Với nhiều đoạn dài L 2 L i ta sẽ có:
U = õUi = õ NZI I 2EI AI
Thế năng biến dạngđànhồi thưßng dùng để tính chuyển vị của hệ thanh. L BB/cos = BI
hay: BB9 = BI = BC cos cos N BC LBC PL
BB9 = ø EAùBC cos = 2EA cos2 2
Với P = 300kN, E = 20000kN/cm , A =10cm 2 ,  = 30 0 , L / = 2L = 400cm, ta được: BB9 = 0,4 cm
b) Ph¤¢ng pháp dùng thế năng biến d¿ng đàn hồi
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđứcThanh - 7 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu Ta có: W = U (*) Công ngoại lực:
W ý 1 P.BB / 2
Vì hai thanh qui về nút B nên năng biến dạng đàn hồi của hệ là: N 2 L N N 2 L U = 2 L BD BD + BC BC = 2 2(EA)BD 2(EA)BC 2EA
Thế vào (*) ta được: 1 P.BB / = 2 N 2 L 2 2EA suy ra:BB /
ý 2N 2L = PL ý 0,4cm 2EA cos 2 PEA 
VI. þNG SUẤT CHO PHÉP, HÞ SÞ AN TOÀN, BA BÀI TOÁN C¡ BÀN
Nếu gọi o ứng suất nguy hiểm, là trị số ứng suất mà ứng với nó vật liệu được
xem là bị phá hoại. Đối với vật liệu dẻo o ý ch , đối với vật liệu dòn o ý b .
Nhưng khi chế tạo, vật liệu thưßng không đồng chất hoàn toàn, và trong quá trình
sử dụng tải trọng tác dụng có thể vượt quá tải trọng thiết kế, điều kiện làm việc của
kết cấu hay chi tiết chưa được xem xét đầy đủ, các giả thiết khi tính toán chưa đúng
với sự làm việc của kết cấu. Vì thế ta không tính toán theo o . Chúng ta phải
chọn một hệ số an toàn n lớn hơn 1 để xác định ứng suất cho phép.   o ý (3.15) n
Và dùng trị số để tính toán.
Hệ số an toàn do nhà nước hay hội đồng kỹ thuật của nhà máy qui định.
Để chọn hệ số an toàn được chính xác, nhiều khi ngưßi ta phải chọn nhiều hệ số
theo riêng từng nguyên nhân dẫn đến sự không an toàn của công trình hay chi
tiết máy, có thể kể đến:
- Hệ số kể đến độ đồng chất của vật liệu
- Hệ số kể đến sự vượt quá tải trọng thiết kế
- Hệ số kể đến sự làm việc tạm thßi hay lâu dài
Như vậy muốn đảm bảo sự làm việc an toàn về độ bền khi thanh chịu kéo (nén) đúng tâm, ứng suất trong thanh phải thỏa mãn:
+ Điều kißn bền là:
 Z ý NZ  (3.16) A
Từ điều kiện bền, ta có ba bài toán cơ bản: d=2cm
Kiểm tra bền: Đối với vật liệu dẻo A N z   z ý Max  max A
max ýK B 30o C 
Đối với vật liệu dòn:  z ,  z
min ýn
Chọn kích thước m¿t cÁt ngang: A ó N z max P = 20kN 
Định t¿i trọng cho phép: N z A hay:NZýA 2m
õ õ LL
*Điều kiện cứng: z hay:  
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 8 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
Thí dÿ 1: Cho hệ chịu lực như hình vẽ. BC có tiết diện hai thép góc đều cạnh, AC
tiết diện tròn đưßng kính d=2cm
a) Tính nội lực trong thanh AC và BC
b) Kiểm tra điều kiện bền của thanh AC
c) Tìm số hiệu thép góc đều cạnh của thanh AC theo điều kiện bền.
Cho [ ] =16kN/ cm2, LBC = 2m Giải
Thực hiện mặt cắt qua thanh AC và BC (cô lập nút C) chú ý trong các thanh chỉ có lực dọc
Y ý 0 NCA sin 300 ý P NCA ý 2P ý 40kN NCA
X ý 0 NCB ý NCA cos 300 ý 20 3 ý 34,64kN 
a) Điều kiện bền  CA ý |NCA| 16  C A N CA CB
40  16 ý 12,74kN / cm 2Thoả diều kiện Suy ra bền P G  22 4 L P=qL
b) Mặt cắt BC là hai thép góc đều cạnh nên tổng diện tích q là D
34,64  16 ACD ó 2,165cm2 B C L ACD 300 300
Tổng HAI THANH có diện tích là ACD ó 2,165cm2 H K
Tra bảng thép định hình cho một thép góc đều cạnh là L 20x20x3cm L L
Có diện tích là =1,13cm2
Thí dÿ2. Cho kết cấu chịu lực như hình vẽ, thanh BCD NDG
tuyßt đßi cÿng. Các thanh có diện tích lần lược là q P=qL ADG=1cm2, ACH = ACK= 2cm2.
a)Tính nội lực trong các thanh NDG,NCH, NCK.
b) Tìm [q] từ điều kiện bền của các thanh C D
Cho L = 2m, [ ] =16kN/cm2, E = 2.104kN/cm2 N 300 Giải CH 300 NCK L L
Thực hiện mặt cắt qua các thanh với chiều nội lực D chọn như hình vẽ EA
M / C ý 0 NDG ý qL P= 2qL
Y ý 0 2N cos 300 ý 4qL N ý 4 3 qL 3 B 30o C
(Do đối xứng nên NCH = NCG = N) Điều kiện bền K q  qL 2L L
DG ý N DG
 16 q 8kN / m ADG1
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh - 9 - lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu 4 3 qL N 3 ý
 16 q 2,31kN /   ý  m
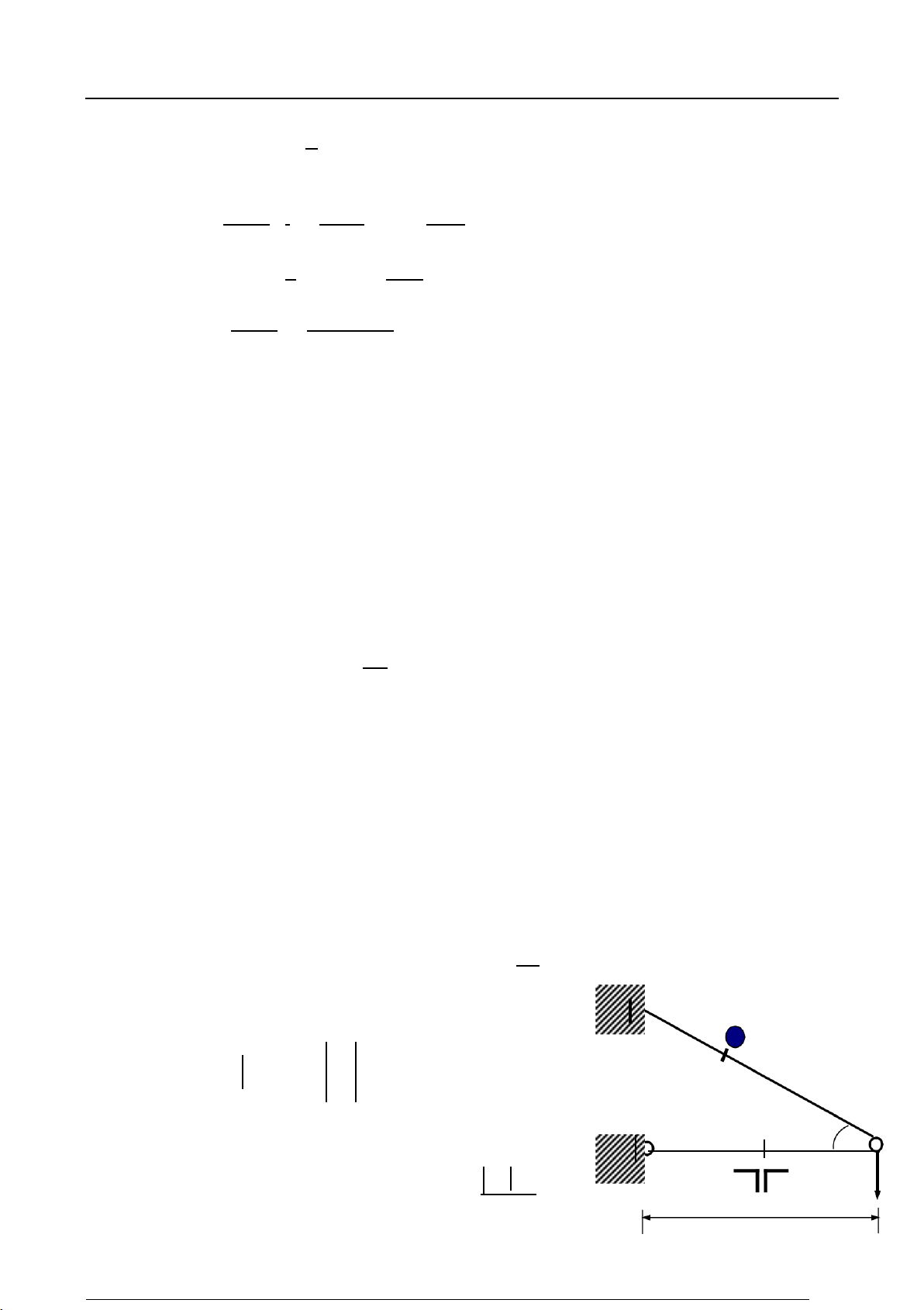
q ý 2,3kN / m A min CH CK CH 2 Chọn Thí dÿ3.
Cho thanh BCK tuyßt đßi cÿng có liên kết và chịu lực như hình vẽ. Thanh CD
có tiết diện và độ cứng EA. a)Tìm NCD
b)Tìm chuyển vị đứng của điểm K. Giải a)Tìm NCD 3L 3qL 3 N
M / B ý 0 N 21
CD sin 300 ô 2L ý 2qL ô ô L  CD ý qL
b)Tìm chuyển vị đứng của điểm K. Vẽ 2 2
sơ đồ biến dạng như hình bên dưới C H D A 600 P= 2qL LCA C / NCD B o C 30 K B 30o C K H q C/ K/ 2L L 2L L Xét tam giác CC/H 21qL L N
L ý CC / cos 600 CC L ô 4L CD CD CD 3 8 qL2 2 / ý ý ý ý
 KK / ý1,5CC/ CD cos 600 EA cos 600 EA 3EA 2
Thí dÿ 4. Cho thanh KCH tuyệt đối cứng có
liên kết và chịu lực như hình vẽ. Các thanh có 2
cùng tiết diện và độ cứng EA. Tìm chuyển vị 1 a B1
đứng của điểm K. (có thể tìm góc nghiêng của P KH) K C H Giải B 3
Trước tiên ta cần tính nội lực trong các thanh. K1 a a a
Cô lập hệ như H.3.17b. N1 N2
Xét cân bằng với các phương trình:
õX = 0 => N2 cos45o + N3 = 0 P B N
õY = 0 => –P + N1 + N2 sin45o = 0 K C
õM/B = 0 => –P2a + N1a = 0 B1
Ta được N1 = 2P, N2 =–P 2 (nén), N3 = P X K B L1 K1
T.06/2015 Lê đđức Thanh H. 3.17 -10- lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
Tìm chuyển vị đứng của K(bằng p.pháp hình học)như sau:
X = 2(BB1+L1) , với X = KK1+ BB1 Trong N1a N 2 a 2 L2 đóL1 ý ,L2 ý ý BH
và: BB1 ý cos 450 EA EA ù ù X ý 2N 2 a 2 N 2 a ú
2BB1L1  ý 2ú  ú EA EA ú Thế N1,N2 vào û û ù ù 4 2Pa 4Pa X ý ú 
úKK1 ýXBB1ý Pa 42 2 đvcd û EA EA û EA B
Thí dÿ 5.Tìm [P] từ điều kiện bền và điều kiện cứng của
thanh chịu lực như hình vẽ. P L 3P -
Cho [] =16kN/cm2, A =1cm2, E = 2.104kN/cm2, C
Lý 0,05cm + Giải: L E,1,5
Biểu đồ nội lực vẽ bên cạnh L D A 2P Điều kiện bền: P  2P
CD ý NCD
 16 P 12kN 2L A E,A CD1,5
Biến dạng toàn phần của diểm H  P
ý Pô2L PôL 2PôL PL ý 5PL K L
EA1,5A1,5A 1,5A 1,5A P
Nếu chọn P=12kN ta đượcL ý 0,08cm L
LL 5PL  0,05 P
Do đó phải tính lại P từ điều kiện cứng  7,5kN 1,5EA
Vậy chọn [P]=7,5kN
VII. BÀI TOÁN SIÊU TĨNH Định nghĩa:
Bài toán siêu tĩnh là bài toán mà chỉ với các phương trình cân bằng tĩnh học
s¿ không đā để gi¿i được tÁt c¿ các ph¿n lực hay nội lực trong hß. Cách gi¿i. VB
Cần tìm thêm các phương trình diễn tả điều kiện
biến dạng của hệ sao cho cộng số phương trình này B B a a + P-VD
với các phương trình cân bằng tĩnh học vừa đủ bằng C C
số ẩn số phản lực, nội lực cần tìm.
Thí dÿ 6. Xét thanh chịu lực như vẽ - P P
à hai ngàm có hai phản lực VB và VD. b b
Ta có phương trình cân bằng:VD+VB–P = 0 (a)
Phương trình này có hai ẩn, muốn giải được ta phải V D D
tìm thêm phương trình từ điều kiện biến dạng của VD V thanh. a) b)
Chöông 3 : Kéo Nén đúng tâm
T.06/2015 Lê đđức Thanh -11- lOMoARcPSD|47206521
Bài giảng Sức Bền Vật liệu
LBD =LBC +LCD = 0
Tưáng tượng bỏ ngàm D và thay bằng phản lực VD. Điều kiện biến dạng của hệ là: (b)
Gọi NBC và NCD là nội lực trên các mặt cắt của các đoạn BC và CD ta sẽ được: N N L = L L BC BC + CD CD = 0 (c) EA EA
với NBC =VD ; NCD = (P-VD), (c) trá thành:
(PVD ) ô
VD ô b  a
ý 0 suy ra: V ý Pa
và V ý Pb D B a a  EA EA b b
Ta đã tính được phản lực VB, bài toán trá thành bài toán tĩnh định bình thưßng
Hay dùng nguyên lý cộng tác dụng để tìm biến dạng :
LBD(P,VD) =LBD(P) +LBD(VB) = 0
VD ô (a L ý b)
 P ô a ý 0 V ý Pa BD D a EA EA b
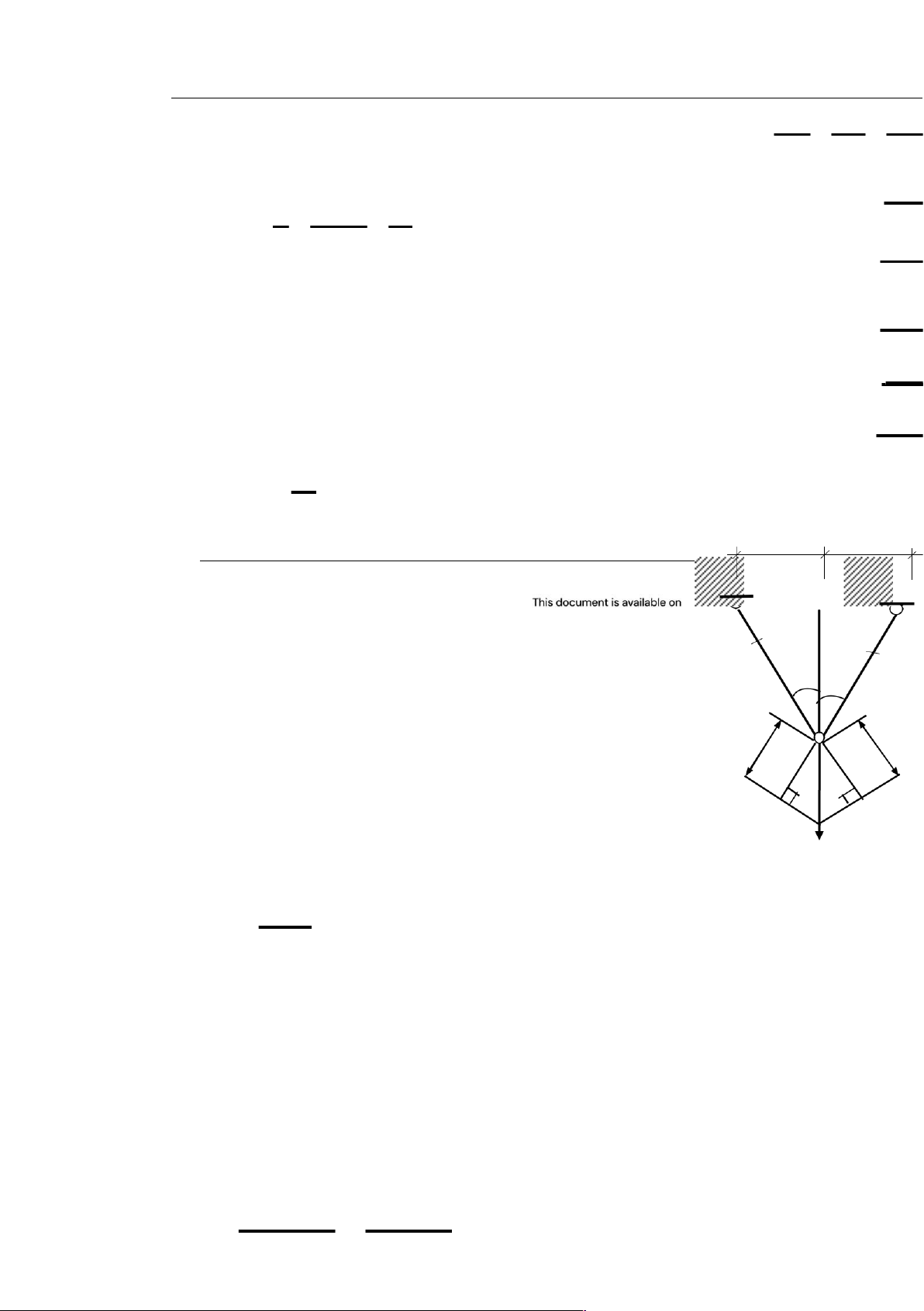
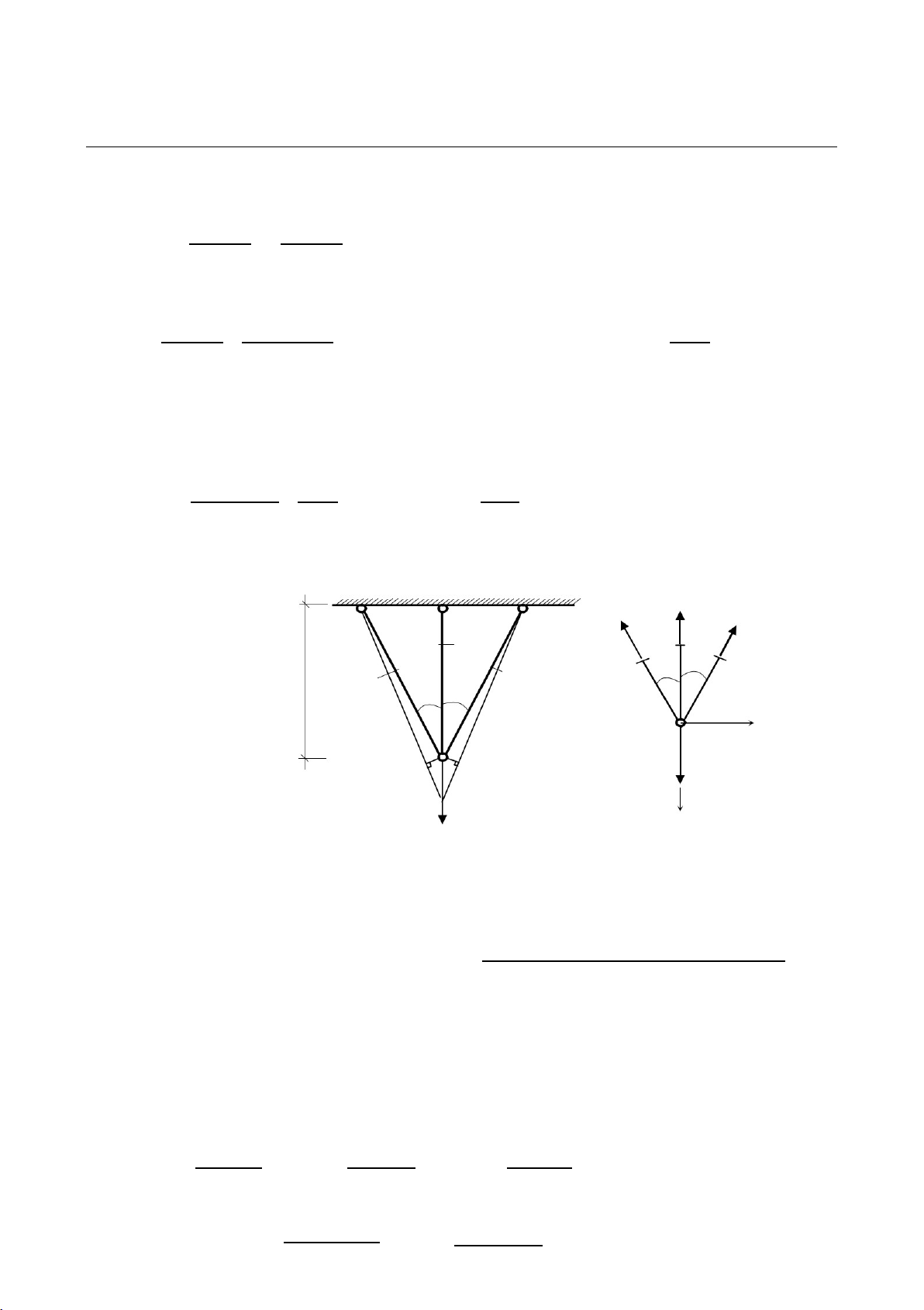
Thí dÿ 6. Xét hệ gồm ba thanh treo lực P hãy tính nội lực trong các thanh treo. Giải. NA B C D NH NHD EA  L EA EA   H x H K I P a) H’ y b) P H.3.19
Ta có hai phương trình cân bằng ( tách nút H):
õX = NHB sin + NHD sin = 0 (a)
õY = –P + NHB cos + NHC + NHD cos = 0 (b)
Để giải ba ẩn số nội lực ta cần thêm một phương trình điều kiện biến dạng . Xét
hệ thanh sau khi chịu lực. Vì đối xứng nên điểm H di chuyển theo phương HC
đến H9. Từ H kẻ đưßng HI và HK lần lượt vuông góc với H9B và H9D. Biến
dạng nhỏ nên góc H9BH và H9DH vô cùng bé và góc BH9C và DH9C vẫn là.
Suy ra IH9 là độ dãn dài của HB và tương tự KH9 là độ dãn dài
của HD. Ngoài ra HH9 cũng chính là độ dãn dài của HC
Xét tam giác H9IH và H9KH ta có liên hệ: IH8= KH9 = HH9cos ( c ) NHB ôL NHD ôL NHC ôL EA Thay IH9 = cos
; KH9= EA cos ; HH9= EA
vào (c) rồi vào (a) và (b) ta sẽ
được NHB = NHD = P cos2 ;NAC= P 1 2 1  2 cos3 cos3