Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng môn xác suất thống kê| Đại học Duy Tân
Định nghĩa. Toàn bộ tập hợp các phần tử đồng nhất theo một dấuhiệu nghiên cứu định tính hoặc định lượng nào đó được gọi là tổng thể nghiên cứu hay tổng thể. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Xác xuất thống kê (STA 151) 144 tài liệu
Trường: Đại học Duy Tân 2 K tài liệu
Tác giả:
Preview text:
23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
3.1. LÝ THUYẾT MẪU
3.1.1. Khái niệm về tập đám đông và mẫu
1. Tập đám đông (Tổng thể)
a. Định nghĩa. Toàn bộ tập hợp các phần tử đồng nhất theo một dấu hiệu nghiên cứu
định tính hoặc định lượng nào đó được gọi là tổng thể nghiên cứu hay tổng thể.
b. Các -kh
N á, i n=i ệ1m
. k: Những giá trị của dấu hiệu A đo được trên các phần tử của tổng thể. - -N
p : Số phần tử của tổng thể được gọi là kích thước của tổng t)h. ể.
- A: Dấu hiệu mà ta khảo sát.
- xii, i = 1. k: Tần số của xi (là số phần tử có chung giá trị xi
i, i = 1. k: Tần suất của xi, là tỷ số giữa tần số của xi và kích thước tổng thể i pik 1; = Ni= N
c. Các tham số đặc trưng của tổng thể ● Trung bình
tổng th1=ể N p .∑ : kí hiệ=u 1 ∑ là m và= đ
∑ ược tính bởi công thức: m = 1 i i1 i x x N 1 i x N = k N = k
Nếu xem dấu hiệu nghiên cứu như BNN Xi thì trung bình tổng thể chính là kỳ i vọng toán của BNN đó.
● Phương sai tổng thể: kí hiệu σ2 m) - (x k N m) - .
được tính bởi công thức: 1 i 1 (x m i ) i 1 p i N ( ) x m σ 2 x = N − = k = k N − = 2 i N 2 2 ∑ ∑= 2∑ =
Trong thực tế, để tiện cho việc tính to ián, phương sai tổng thể thườngi được t iính i 1 1 i 1 bằng công thức: = ∑ i − N x 1m 2 2 σ Ni k 2.
● Độ lệch chuẩn tổng thể: =kkí hiệu là σ và được tính bởi công thức: 1 = σ = ∑ p σ 2 i (x m) - 2.
●Tần suất của tổng thể: ký hiệ iu: p, là tỷ số giữa số phần tử mang dấu hiệu =1
nghiên cứu và kích thước của tổng thể: p = M N
2. Mẫu ngẫu nhiên
Trong thực tế phương pháp nghiên cứu toàn bộ thường chỉ được áp dụng đối với
các tập hợp có quy mô nhỏ, còn chủ yếu người ta áp dụng phương pháp nghiên cứu
không toàn bộ, đặc biệt là phương pháp mẫu bằng cách chọn ra từ tổng thể n phần tử 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
và chỉ tập trung nghiên cứu các phần tử đó. Tập hợp n phần tử này được gọi là mẫu kích thước n.
Phương pháp chọn mẫu:
- Mỗi lần lấy vào mẫu chỉ một phần tử.
- Lấy phần tử nào đưa vào mẫu là hoàn toàn ngẫu nhiên.
- Các phần tử được lấy vào mẫu theo phương thức hoàn lại.
Có thể coi mẫu ngẫu nhiên kích thước n là tập hợp của n BNN độc lập X 1,
X2,…Xn được thành lập từ BNN X trong tổng thể và có cùng quy luật phân phối xác s uất vớ i X, ký E (hi X ệu: W = (X1, X2,…Xn) D( 1
X ) = E(X2) =…= E(Xn) = E(X) = m 1) = D(X2) =…= D(Xn 2 ) = D(X) = σ Lúc đó
việc thực hiện một phép thử đối với mẫu ngẫu nhiên W chính là thực hiện một phép
thử đối với mỗi thành phần của mẫu. Giả sử X1 nhận giá trị x1; X2 nhận giá trị
x2;…Xn nhận giá trị xn. Tập hợp n giá trị x 1,x ,2…xn tạo thành một giá trị của mẫu
ngẫu nhiên, hay còn gọi là một mẫu cụ thể, ký hiệu: w = (x1,x2,…xn ).
Như vậy mẫu ngẫu nhiên là tập hợp của n BNN, còn mẫu cụ thể lại là tập hợp
của n giá trị cụ thể quan sát được khi thực hiện một phép thử đối với mẫu ngẫu nhiên.
3.1.2. Các đặc trưng quan trọng về mẫu
1. Trung bình mẫu:
● Định nghĩa: Giả sử từ BNN gốc X trong tổng thể lập mẫu ngẫu nhiên kích
thước n: W = (X1, X2,…Xn ). Trung bình của mẫu là một thống kê, kí hiệu X được xác định bởi công thức: n 1 1 X = (X + X + . .+ X = ) ∑ 1 2 n i i1X n n =
Khi mẫu ngẫu nhiên nhận một giá trị cụ thể w = (x1,x ,2…xn ) thì trung bình mẫu
cũng nhận một giá trị cụ thể bằng: n k = = trong đó n . = x ∑ . = n1 1 i x1 x ∑ i 1 i
i là tần số xuất hiện giá trị xi n n
● Tính chất: Nếu BNN gốc X có kỳ vọng toán E(X) = m, phương sai D(X) = σ 2 thì 2
X có E( X ) = m và D( X ) = σ n
2. Phương sai mẫu S2 : 2
● Định nghĩa: Phương sai mẫu ký hiệu là S
và được xác định bởi công thức: S n 1 2∑ 2 = (X X - n − i) 1 1 i=
Khi mẫu ngẫu nhiên nhận một giá trị cụ thể w = (x1,x ,2…xn ) thì phương sai mẫu
cũng nhận giá trị cụ thể bằng: k 1 sn x 1x nn 2 1 21 i − =∑ ( 2 x − x = ) [ ] 2 2 , tr ( on ) g đó: 2 x∑= i n .x n − − i 1 = n 1= 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
● Tính chất: Nếu BNN X có kỳ vọng là E(X) = m, phương sai D(X) = σ2 thì E(S2 2 ) = σ .
3. Độ lệch chuẩn mẫu:
Độ lệch chuẩn mẫu kí hiệu S = 2 S.
Ví dụ 2.1: : Một máy tự động đóng bột vào bao. Cân ngẫu nhiên 15 bao được các trọng lượng sau: 39,75 40,25 39,50 40,25 40,50 40,00 39,75 40,00 40,00 39,25 39,25 39,50 40,00 39,50 39,50
a) Lập bảng phân phối thực nghiệm của trọng lượng các bao bột.
b) Tính giá trị trung bình và phương sai của trọng lượng các bao bột.
Giải. a) Bảng phân phối thực nghiệm: Trọng
39,25 39,50 39,75 40,00 40,25 40,50 lượng(kg) Số bao 2 4 2 4 2 1 2 3 .= b,9)2 T
5 a 4c.ó3:9 5, 2 3.9 7,5 4 4.+0 4. 2 0+ 2 , 5 1 . 1 5 40+5 , 0 + + x = 39 7 , 3 2 2 2 2 . 2 2 , 39 25 + 4. , 39 5 + 2.39 75 , + 4.40 + . 2 40,25 + 1. , 40 50 x1 = 584,175 = 15 2 15 s x = x [ ]−( )2 2 = 1 , 6 09 . 4 14 3.1.3. Thống kê
Thống kê là một hàm của các BNN X1, X ,2…Xn , ký hiệu : G = f(X1,X ,2…Xn ),
nó cũng là một BNN tuân theo một quy luật phân phối xác suất nhất định và có các
tham số đặc trưng như E(X), D(X).
Khi mẫu ngẫu nhiên W nhận một giá trị cụ thể w = (x
1,x2,…xn) thì G cũng nhận m
) ộ. t giá trị cụ thể là g = f(x1,x ,2…xn
3.2. BÀI TOÁN ƯỚC LƯỢNG THAM SỐ:
3.2.1. Bài toán: Cho BNN X với quy luật phân phối xác suất đã biết nhưng chưa biết
tham số θ nào đó của nó. Phải ước lượng (xác định một cách gần đúng) giá trị của θ.
Có hai phương pháp là phương pháp ước lượng điểm và phương pháp ước lượng bằng khoảng tin cậy.
3.2.2. Phương pháp ước lượng điểm:
1. Phương pháp hàm ước lượng (phương pháp mômen)
a. Khái niệm. Giả sử cần ước lượng tham số θ của BNN gốc X. Từ tổng thể lập
mẫu ngẫu nhiên kích thước n: W = (X1,X2,…Xn). Chọn lập thống kê θ *=
f(X1,X2,…Xn) mà thực chất là một thống kê đặc trưng mẫu tương ứng với tham số θ 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
cần ước lượng. Chẳng hạn, để ước lượng kỳ vọng toán m của BNN gốc thì chọn thống
kê trung bình mẫu X , để ước lượng phương sai σ2 của BNN gốc thì chọn thống kê S2
…Nếu lập một mẫu cụ thểvà tính được giá trị θ*=f(x1,x2,…xn) của thống kê θ* trên
mẫu cụ thể đó thì nó là ước lượng của θ.
Thống kê θ* được gọi là hàm ước lượng của θ.
b. Các tiêu chuẩn lựa chọn hàm ước lượng
● Ước lượng không chệch: Thống kê θ* của mẫu được gọi là ước lượng không
chệch của tham số θ nếu E( θ*) = θ. Ng N ư hậợnc xlạ éti: n ếu đ ư E ợ ( c θ g *) ọi ≠ l à θ ưth ớ ì c θ l * ượng chệch của θ.
- Trung bình mẫu X là ước lượng không chệch của kỳ vọng toán m của BNN gốc ( E( X ) = m).
- Tần suất mẫu f là ước lượng không chệch của xác suất p của BNN gốc (E( f) = p).
- Phương sai mẫu S2 là ước lượng không chệch của phương sai σ2 .
● Ước lượng hiệu quả: Thống kê của mẫu được gọi là ước lượng hiệu quả nhất
của tham số θ của BNN gốc X nếu nó là ước lượng không chệch và có phương sai nhỏ
nhất so với mọi ước lượng không chệch khác được xây dựng trên cùng mẫu đó.
Khi hai ước lượng θ1* và θ2* nào đó đều là các ước lượng không chệch của θ
song không phải là ước lượng hiệu quả nhất thì có thể so sánh phương sai của hai ước
lượng đó để tìm ra ước lượng hiệu quả hơn. Giả sử V(θ1*) < V(θ2*), lúc đó độ hiệu quả
của θ1* so với θ2* được xác định bằng biểu thức: EF = V V( ( * θ ) 2 * θ ) 1
● Ước lượng vững: Thống kê θ* của mẫu được gọi là ước lượng vững của tham
số θ của BNN gốc X nếu θ* hội tụ theo xác suất đến θ khi n→∞.
● Ước lượng đủ: Một ước lượng θ
* được gọi là ước lượng đủ nếu nó chứa đựng
toàn bộ các thông tin trong mẫu về tham số θ của ước lượng.
c. Một vài kết luận của phương pháp hàm ước lượng -Dùng X để ước lượng m.
-Dùng f để ước lượng p.
-Dùng S2 để ước lượng σ2.
2. Phương pháp ước lượng hợp lý tối đa
Giả sử đã biết quy luật phân phối xác suất của BNN gốc X dưới dạng hàm mật
độ f(x,θ) hoặc biểu thức xác suất nếu X là BNN rời rạc. Cần phải ước lượng tham số θ nào đó của X.
Lập mẫu ngẫu nhiên kích thước n: W = (X1,X2,…Xn ) và xây dựng hàm hợ p lý
tại một giá trị cụ thể của mẫu:
L(x1,x2,…xn,θ) = f(x1,θ).f(x2,θ )…f(xn,θ ). 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Giá trị của thống kê θ tại điểm đó:θ*= f(x1,x ,2…xn ) được gọi là ước lượng hợp lý
tối đa của θ nếu ứng với giá trị này hàm hợp lý đạt cực đại.
Cách tìm giá trị của θ để hàm hợp lý đạt cực đại:
− Tìm đạo hàm bậc nhất của lnL theo θ.
− Giải phương trình:d ln
dL= 0 , giả sử nó có nghiệm θ = θ*= f(x1x2,…xn). θ
− Tìm đạo hàm bậc hai 2 d ln , n L
ếu tại điểm θ = θ* đạo hàm bậc hai âm thì 2 θ d
tại điểm này hàm lnL đạt cực đại, do đó θ*= f(x1,x ,2…xn ) là ước lượng
điểm hợp lý tối đa cần tìm của θ.
3.2.3. Phương pháp ước lượng bằng khoảng tin cậy 1.Khái niệm ● Khoảng (G1,G2
) của thống kê G được gọi là khoảng tin cậy của tham số θ nếu
với xác suất bằng (1−α) cho trước thoả mãn điều kiện:
P(G 1< θ ●Xác suất (1−α) được gọi là độ tin cậy của ước lượng. ●I = G2 – G1
gọi là độ dài khoảng tin cậy.
3.2.4. Các bài toán ước lượng tham số
1. Bài toán ước lượng tham số μ (giá trị trung bình)
Giả sử trong tổng thể BNN gốc X phân phối chuẩn N(µ) 2 ,σ nhưng chưa biết
tham số μ của nó. Để ước lượng μ từ tổng thể ta lập mẫu ngẫu nhiên kích thước n: W
= (X1,X ,2…Xn ). Nếu BNN gốc X không có phân phối chuẩn thì ta coi như phân phối
xấp xỉ chuẩn khi lấy kích thước mẫu n ≥ 30.
a. Đã biết σ 2 Do X ~ 2 σ N( µn) 2 ,σ ên X ~ N , µ n (X) Ch − µ ọn thống kê : .Nn G =U = ~ ( )1, 0 . σ
Do đó với độ tin cậy bằng (1−α) cho trước tìm được cặp giá trị α1 và α 2sao cho
α1 + α2 = α từ đó tìm được hai giá trị tới hạn tương ứng của phân phối chuẩn hoá là
u và u thoả mãn: P(U)> u = − và ( P ) U > u = α . α − 1 α 1− 2 1 α α 1 1 1 α 2 2 P u ⇒ U − ( u ) < < = − α 1 α α . 1 1 2 P u ⇒ U u (−) < < = − α α 1 . α 1 2
Thay biểu thức của U vào và biến đổi ta được: σ σ − 1 < < + P X u 2u µ X 1 = −α α α n n
Với độ tin cậy bằng (1−α) tham số μ của BNN gốc X sẽ nằm trong khoảng 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com σ σ − 1 + X gọi l u à khX
oảng ti un cậy tổng quát. α α n n
Trong thực tế người ta thường dùng các trường hợp đặc biệt sau: − Kho α σ σ
ảng tin cậy đối xứng: Ch 2 ;ọn α =α − 2 = : +X u X u 1 2 2 α α n n σ ε = gọ u
i là2 sai số của ước lượng. α n − Kho σ
ảng tin cậy tối thiểu:Chọn α 1=0, α2 −; +∞ =α: X u . α n − Kho σ
ảng tin cậy tối đa:Chọn α − ∞ + 1=α, α2 =0: ; X u . α n
Với cùng độ tin cậy (1−α), khoảng tin cậy nào ngắn hơn sẽ tốt hơn. Trong trường
hợp này độ dài khoảng tin cậy I sẽ là ngắn nhất khi khoảng tin cậy là đối xứng.Khi đó I = 2ε.
Ví dụ 2.2 Trọng lượng một loại sản phẩm là BNN phân phối chuẩn với độ lệch
chuẩn là 1gam. Cân thử 25 sản phẩm loại này ta thu được kết quả sau: Trọng lượng(gam) 18 19 20 21 Số sản phẩm 3 5 15 2
Với độ tin cậy 0,95 hãy tìm khoảng tin cậy đối xứng của trọng lượng trung bình
của loại sản phẩm nói trên. Giải.
Gọi X là trọng lượng sản ⇒ phẩm ~X =. N(, ) µ σ 2 1 2
Trọng lượng trung bình của sản phẩm chính là tham số μ.
Đây là bài toán ước lượng tham số μ của BNN phân phối chuẩn bằng khoảng tin cậy
đối xứng khi đã biết σ2. Ta có σ σ
2 ;khoảng ti−n2 cậy là: + X. u X u α α n n n=25, σ=1. α = ⇒ = 0 025 , ⇒ 1 =α , 0 95 α , 0 05 . 2
Tra bảng giá trị tới hạn chuẩn có: u = α u = , 1 96 2 0,025 3 1.8 = 5 1 . 9 15 + 2 . 0 252 + 2 . 1 + x = 19 6 , 4
Thay vào ta được khoảng tin cậy đối xứng là: (19,248 ; 20,032). Nhận xét:
-Khi tăng kích thước mẫu n lên và gi ữ nguyên độ tin cậy (1−α) cho trước thì ε
giảm đi tức là ước lượng tốt hơn.
-Khi tăng độ tin cậy (1−α) lên mà giữ nguyên kích thước mẫu n thì giá trị tới hạn
chuẩn cũng tăng lên theo do đó ε cũng tăng lên tức là ước lượng kém chính xác hơn. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
●Công thức xác định kích thước mẫu tối thiểu n sao cho với độ tin cậy bằng
(1−α) cho trước thì sai số của ước lượng không vượt quá giá trị ε0 cho trước: 2 σ n ≥. 0uα 2 ε b. Chưa biết σ 2 X ( ) Ch − ọn thống kê: Sn G µ = T nT = ~ − ( ) 1 .
Với độ tin cậy bằng (1−α) cho trước ta có các khoảng tin cậy: − + S S − Kho α
ảng tin cậy đối xứng: Chọn α =α = : ( ) n − 1 1 ( − ) 1 2 X tα X t 2 2 ; n α 2 n n S ( ) 1− ε =n t α 2 n S
− Khoảng tin cậy tối thiểu:Chọn α −−; +∞ 1=0, α2 ( ) =α: n 1 X t . α 2 n − ∞ −1 + S
− Khoảng tin cậy tối đa:Chọn α1=α, α2 ( ) =0: ;nX t . α 2 n
●Công thức xác định kích thước mẫu tối thiểu n sao cho với độ tin cậy bằng (1−α)
cho trước thì sai số của ước lượng không vượt quá giá trị ε0 cho trước: 2 ≥ S n− ( ) 1 n 0t α 2 ε
Ví dụ 2.3 Để xác định kích thước trung bình của chi tiết do một máy sản xuất
người ta lấy ngẫu nhiên 200 chi tiết để đo kích thước và thu được bảng số liệu sau:
Kích thước chi tiết (cm) Số chi tiết tương ứng 54,795 – 54,805 6 54,805 – 54,815 14 54,815 – 54,825 33 54,825 – 54,835 47 54,835 – 54,845 45 54,845 – 54,855 33 54,855 – 54,865 15 54,865 – 54,875 7
Với độ tin cậy 95% hãy ước lượng bằng khoảng tin cậy tin cậy đối xứng kích
thước trung bình của chi tiết do máy đó sản xuất. Giả thiết kích thước chi tiết là BNN phân phối chuẩn. Giải. Kíc G h t ọ h i ư X ớ c l à tr k u íncgh btìhnưhớ c c ủcah i c t h iiế t ti d ết o c m hí á n y h đ l ó à ts hảan mx u s ấ ố t μ ⇒ . ). X ~ N(μ,σ2
Đây là bài toán ước lượng tham số μ của BNN phân phối chuẩn bằng khoảng tin
cậy tin cậy đối xứng khi chưa biết σ2. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com Ta có
− 1 khoảng ti−n− cậy là: + S ( ) 1 S ( ) nt X t 2 . α ;n X α 2 n n n = 200 t − −u= ( 1 ) 19 ( 9 ) ⇒ 1,00=25 α 9 , 0⇒5 = α , 0 05≈ 2= . α 9 ,1 6 0,025 Lập bảng tính x và s: xi ni nixi nixi2 54,80 6 328,80 18018,240 54,81 14 767,34 42057,905 54,82 33 1809,06 99172,669 54,83 47 2577,01 14197,450 54,84 45 1467,80 135334,150 54,85 33 1810,05 99281,242 54,86 15 822,90 45144,294 54,87 7 384,09 21075,018 n = 200 10967,05 601380,950 x = 10 2906070,5 = 54 8 , 3525 200, 601380 95 x = 2= 9047 , 3006 2 200 = s [ ] 9074 , 3006 − ( ) 54 83525 , 2 = , 0 0002689⇒ = 0 . 0164 , 199
Thay vào ta được khoảng tin cậy đối xứng là: (54,83294 ; 54,83752).
2. Bài toán ước lượng phương sai σ 2
Giả sử trong tổng thể BNN gốc X phân phối chuẩn N(µ) 2 ,σ nhưng chưa biết
tham số σ2 của nó.Từ tổng thể ta lập mẫu ngẫu nhiên kích thước n: W = (X1,X ,2…Xn ). Ch ( ) 2 ọn thống kê: n 12 G = χ 2− − n S = ~ χ ( ) 1 . 2 σ
Với độ tin cậy bằng (1−α) cho trước ta có các khoảng tin cậy: − − 2 − Kho n S αn n S 1n 21 ( )
ảng tin cậy hai phía: Chọn α =α = : ( ) 1 2 ; 2 1 2(2)−1 ( )− χ χ α −α +∞ n − 2 2 n − Kho ( )
ảng tin cậy tối thiểu:Chọn α 11S 1=0, α2 =α: . ( )−; χα − 2 n n − Kho ; (S )
ảng tin cậy tối đa: Chọn α 1
1=α, α2 =0: −2 ∞−1 . ( ) χα
Ví dụ 2.4 Với độ tin cậy 95% hãy ước lượng phương sai của kích thước các chi tiết trong ví dụ 1.3. Giải. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Đây là bài toán ước lượng phương sai σ2 của BNN phân phối chuẩn bằng khoảng tin cậy hai phía. − − 2
Ta có kho n S n nS ( ) 1n 21 ( ) ảng tin cậy là: ; . 1 2( 22) 2 −1 ( )− χ χ α −α s2 = 0,0002689 n = 200 − = ( ) ( ) ⇒ = 12,019α9795 ⇒ 9 , 0 5 ≈ α , 0 05 χ 20,1092≈95 198 9 , ; 8 χ 284 8 , .
Thay vào ta được khoảng tin cậy là: (0,000188 ; 0,000269).
Để tìm khoảng tin cậy của σ ta chỉ cần lấy căn bậc hai .
3. Bài toán ước lượng tỷ lệ
Giả sử trong tổng thể kích thước N có M phần tử mang dấu hiệu nghiên cứu. Đặt M
p= : là tỷ lệ các phần tử mang dấu hiệu nghiên cứu trong tổng thể. N m f=
: là tỷ lệ các phần tử mang dấu hiệu nghiên cứu trong mẫu. n
Ta phải dựa vào tỷ lệ mẫu f để ước lượng tỷ lệ tổng thể p. V (f)
ới n ≥100, ta chọn thống kê:G − −=U = ( p n )~ (N ) 1, 0 f f p
Với độ tin cậy bằng (1−α) cho trước ta có các khoảng tin cậy: − Kho α
ảng tin cậy đối xứng: Chọn α =α = : 1 2 2 2 − 1 −2 f (1)− f f ( ) f f 1 − f f , ( ) u f u ε = u . α ; + α α 2 n n n +∞ f − − Kho ( )
ảng tin cậy tối thiểu:Chọn α f 1=0, α2 =α: f −; 1 u . α n − − Kho f1 f ( )
ảng tin cậy tối đa:Chọn α f 1=α, α2 =0: −∞; + u . α n
●Công thức xác định kích thước mẫu tối thiểu n sao cho với độ tin cậy bằng (1−α)
cho trước thì sai số của ước lượng không vượt quá giá trị ε0 cho trước: −f ( ) ≥ 1 f n 22 u . 2 α ε0
Ví dụ 2.5 . Kiểm tra ngẫu nhiên 400 sản phẩm do một máy sản xuất thấy có 20
phế phẩm. Với độ tin cậy 0,95 hãy ước lượng tỷ lệ phế phẩm tối đa của máy đó. Giải.
Gọi p là tỷ lệ phế phẩm của máy đó.
Đây là bài toán ước lượng tham số p bằng khoảng tin cậy tối đa. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com − Kho f1 f ( ) ảng tin cậy là: f − ∞ ; + u . α n n = 400 f = 20 = 0, 0 5 . 400
1 −α = 0,05⇒ uα = u0,05 =1,645.
Thay vào ta được khoảng tin cậy là: (−∞ ; 0,0679).
Hay tỷ lệ phế phẩm của máy đó là 6,79%.
3.3 BÀI TOÁN KIỂM ĐỊNH GIẢ THIẾT
3.3.1 Các khái niệm
1. Giả thiết thống kê
Giả thiết thống kê là giả thiết về quy luật phân phối xác suất hoặc các tham số
đặc trưng, hoặc tính độc lập của các biến ngẫu nhiên.
Giả thiết thống kê có thể là đúng hoặc sai nên phải kiểm định gọi là phép kiểm
định giả thiết thống kê.
Giả thuyết thống kê đưa ra được gọi là giả thuyết gốc, ký hiệu là H0. Để kiểm
định giả thuyết H0 người ta thành lập giả thuyết mâu thuẫn với nó gọi là giả thuyết
đối, ký hiệu là H1. H0 và H1 tạo nên cặp giả thuyết thống kê.
Phương pháp chung để kiểm định giả thuyết thống kê như sau: Trước hết giả sử
H0 đúng và từ đó dựa vào thông tin của mẫu rút ra từ tổng thể có thể tìm được biến cố
A nào đó, sao cho xác suất xảy ra biến cố A bằng α rất bé mà có thể coi A không xảy
ra trong phép thử về biến cố này. Lúc đó trên một mẫu cụ thể thực hiện một phép thử
đối với biến cố A, nếu A xảy ra thì chứng tỏ H0 sai và ta bác bỏ nó, còn nếu A không
xảy ra thì ta chưa có cơ sở để bác bỏ H0 .
2. Tiêu chuẩn kiểm định giả thuyết thống kê
Từ biến ngẫu nhiên gốc X trong tổng thể lập mẫu ngẫu nhiên kích thước n: và ch ọn lập thống W k ê= : (X G 1 = , fX ( 2 X,…, Xn)
1, X2,…, Xn, θ0), trong đó θ0 là tham số liên quan đến
giả thuyết cần kiểm định. Điều kiện đặt ra đối với thống kê G là nếu H0 đúng thì quy
luật phân phối xác suất của G hoàn toàn xác định. Thống kê G được gọi là tiêu chuẩn kiểm định.
3. Mức ý nghĩa - Miền bác bỏ
Sau khi đã chọn được tiêu chuẩn kiểm định G, do quy luật phân phối xác suất
của G đã biết nên với một xác suất khá bé bằng α cho trước (thường α được lấy bằng
0,05 hoặc 0,01) có thể tìm được miền Wα tương ứng sao cho với điều kiện giả thuyết
H0 đún g xác suất đểP (G n ∈hậ Wn bgằiá n gt rị α :t huộc miền Wα α / H0) = α
Khi đó xác suất α gọi là mức ý nghĩa của kiểm định. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Miền Wα được gọi là miền bác bỏ giả thiết H0 với mức ý nghĩa α.
Hiển nhiên với một mức ý nghĩa α cho trước có thể tìm được vô số miền bác bỏ tương ứng.
4. Giá trị quan sát của tiêu chuẩn kiểm định
Thực hiện một phép thử đối với mẫu ngẫu nhiên W = (X1, X ,2…, Xn) thu được
một mẫu cụ thể w = (x1, x2,…, xn) và qua đó tính được một giá trị cụ thể của tiêu
chuẩn kiểm định G gọi là giá trị quan sát của tiêu chuẩn kiểm định, ký hiệu là G qs = f(x1, x2,…, xn, θ0 ).
5. Quy tắc kiểm định giả thuyết thống kê
Sau khi đã tính được giá trị quan sát Gqs của tiêu chuẩn kiểm định, ta so sánh giá trị này với miền Wα Nếu G
và kết luận theo quy tắc sau: qs∈ Nếu G
Wα thì bác bỏ H0, thừa nhận H1.
qs∉ Wα thì chưa có cơ sở để bác bỏ H0 (trên thực tế vẫn thừa nhận H0) .
3.3.2 Một số bài toán về kiểm định.
1. Kiểm định giả thiết về tham số µ của biến ngẫu nhiên phân phối chuẩn
(kiểm định một giá trị trung bình).
Giả sử biến ngẫu nhiên gốc X trong tổng thể phân phối theo quy luật chuẩn: X ~ N(µ, σ2)
Trong đó tham số µ là chưa biết, song có cơ sở cho rằng giá trị của nó bằng µ 0, người
ta đưa ra giả thuyết H 0: µ = µ0. Để kiểm định giả thuyết trên từ tổng thể lập mẫu kích
thước n: W = (X1, X2,…, Xn ). (Nếu X không có phân phối chuẩn thì yêu cầu kích
thước mẫu n > 30). Ta xét hai trường hợp sau:
a. Đã biết σ 2 : Ch ( ) X 0 µ
ọn tiêu chuẩn kiểm định: G = U = − n σ H0 :µ = µ 0 → = W α +∞( ) α u ; . H1 :µ > µo H0 :µ = µ 0 → W α = ( ) − ; ∞ − α u . H1 : µ < µo H0 :µ = µ 0 → W = α (−∞;−u ∪ α uα) (+∞ 2 2 ; . ) H1 :µ ≠ µo L (x)−µ
ập mẫu cụ thể và tính giá trị quan sát: n
Uqs 0= và so sánh với W α để σ kết luận.
Ví dụ 2.7: Trong năm trước trọng lượng trung bình trước khi xuất chuồng ở một
trại chăn nuôi là 380kg. Năm nay người ta áp dụng thử một chế độ chăn nuôi mới với
hy vọng là bò sẽ tăng trọng nhanh hơn. Sau thời gian áp dụng thử người ta lấy ngẫu 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
nhiên 50 con bò trước khi xuất chuồng đem cân và tính được trọng lượng trung bình
của chúng là 390kg. Vậy với mức ý nghĩa α = 0,01 có thể cho rằng trọng lượng trung
bình của bò trước khi xuất chuồng đã tăng lên hay không? Giả thiết trọng lượng của bò
là biến ngẫu nhiên phân phối chuẩn với độ lệch chuẩn là 35,2kg. Giải.
Gọi X là trọng lượng của bò trước khi xuất chuồng → X ~ N(µ,σ =35,2).
Trọng lượng xuất chuồng trung bình là µ.
Đây là bài toán kiểm định giá trị của tham số µ của biến ngẫu nhiên phân phối chuẩn khi đã biết σ2. C H : µ = 380
ặp giả thuyết thống kê có dạng: 0 H : µ > 380 1 α n = 05,0 0 1 = ⇒ (2 , u 33α; = + 2 ∞ ,)3. 3 ⇒ Wα x = 390 σ = 35,2 Giá tr ( 390 ) ị quan sát: 380− , 35 250 U = = , 2 01∉ W qs α . K b ế. t l C u hận ư : a C bih ế ư t a σ c
. ó cơ sở để bác bỏ H0 2 (X)
Chọn tiêu chuẩn kiểm định: G = T = 0 µ n − S H :µ = µ 0 0 → ( ) W = α (t )n1− α ;+∞ . H1 :µ > µo H :µ = µ 0 0 → = − n ∞ − ( ) W 1− α ( ) ; tα . H1 : µ < µo H :µ = µ 0 0 → n ( ) W = α (−) 1 − n ( ) ; ∞ −t ∪ α (tα)1− ;+∞ . H 2 2 1 : µ ≠ µo x ( ) L − µ
ập mẫu cụ thể và tính giá trị quan sát: sn Tqs 0=
và so sánh với W α để kết luận.
2. Kiểm định giả thiết về hai tham số µ của hai biến ngẫu nhiên phân phối chuẩn
(kiểm định hai giá trị trung bình)
Giả sử có hai tổng thể với biến ngẫu nhiên gốc X1 ~ N(µ1,σ12); biến ngẫu nhiên
gốc X2 ~ N(µ2,σ22). Trong đó µ1 và µ2 chưa biết song có cơ sở để giả thiết rằng giá trị
của chúng bằng nhau người ta đưa ra giả thuyết H0: µ1 = µ2 và từ tổng thể rút ra hai
mẫu độc lập kích thước n1 và n .2 (Nếu X 1và X 2không có phân phối chuẩn thì yêu cầu h ai. kí Đ c ã h b tihếư t ớ c σ m lớ ẫnu hnơ1n v3à 0 n ). 2 12, σ22 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
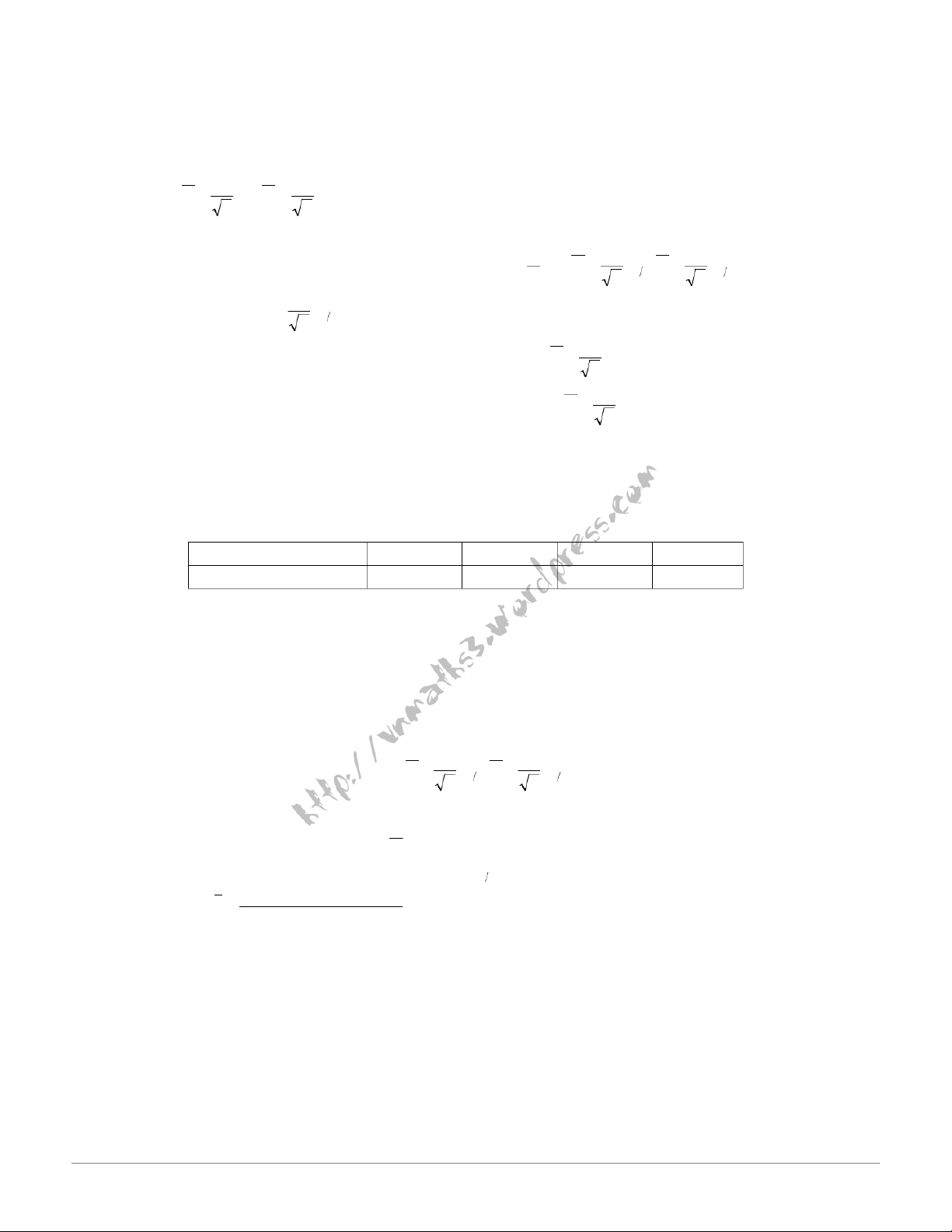
Chọn tiêu chuẩn kiểm định: X − X 1 2 G = U = 2 2 σ σ 1 2 + 1 n n2 H :µ = µ → 0 : 1 2 = W +∞ u α ( )α; . H µ > µ 1 1 2 H : µ = µ 0 : 1 2 → W = − ∞ −u α ( ) ; α . H µ < µ 1 1 2 H : µ = µ 0 := 1 − ∞ − 2 ∪ → 2 +∞ W 2 u u α ( ; α α ) ( ; . ) H µ ≠ µ 1 1 2
Lập mẫu cụ thể và tính giá trị quan sát: x − x 1 2 Uqs =
và so sánh với W α để 2 2 σ σ 1 2 + 1 n 2 n kết luận.
Ví dụ 2.9 Tại hai xí nghiệp người ta xây dựng hai phương án gia công cùng một
loại chi tiết. Để đánh giá xem chi phí trung bình về nguyên liệu theo hai phương án đó
có khác nhau hay không người ta tiến hành sản xuất thử và thu được các kết quả sau: Phương án 1: 2,5 3,2 3,5 3,8 3,5 Phương án 2: 2,0 2,7 2,5 2,9 2,3 2,6
Với mức ý nghĩa 0,05, hãy kết luận về vấn đề trên biết rằng chi phí nguyên liệu
theo cả hai phương án gia công đều là các biến ngẫu nhiên phân phối chuẩn với σ12 =σ22 = 0,16. Giải.
Gọi X1 và X2 tương ứng là chi phí nguyên liệu theo hai phương án gia công trên
⇒ X1 ~ N(µ1,σ12); X 2~ N(µ2,σ22 ). Ch Đâi yplhàí n b g ài u t y o êán li k ệu ể t m r u đ n ị g n h b ì h n aih t thhaeo m c s á ố c µ p . hương án đó là µ 1 và µ2
1, µ2 khi đã biết σ12, σ22 . C H :µ = µ
ặp giả thuyết thống kê: 0 1 2 H :µ ≠ µ 1 1 2
α = 0,05 ⇒ u = = − ∞ − ⇒ ∪ W +∞ α ( ; ,196 ) ( ; 96 ,1 . ) α u = , 1 96 2 0,025
Từ mẫu cụ thể: n1 = 5; n2 = 6 tính được: 5 , 2 ,32 5 , 3 + 8 , 3 + 55 , 3 + + x = = 1 3 , 3 0 , 2 , 2 7 5 , 2 +9 , 2 +3 , 2 6, 2+6 + + x = = 2 5 , 2 Giá trị quan sát: 3 , 3 − 5 , 2 U = = 33 , 3 ∈W qs α . 16 , 0 16 , 0 + 5 6 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Kết luận: Bác bỏ H0, thừa nhận H1 , tức là chi phí nguyên liệu theo hai phương án
gia công trên là khác nhau.
b. Chưa biết σ12, σ22
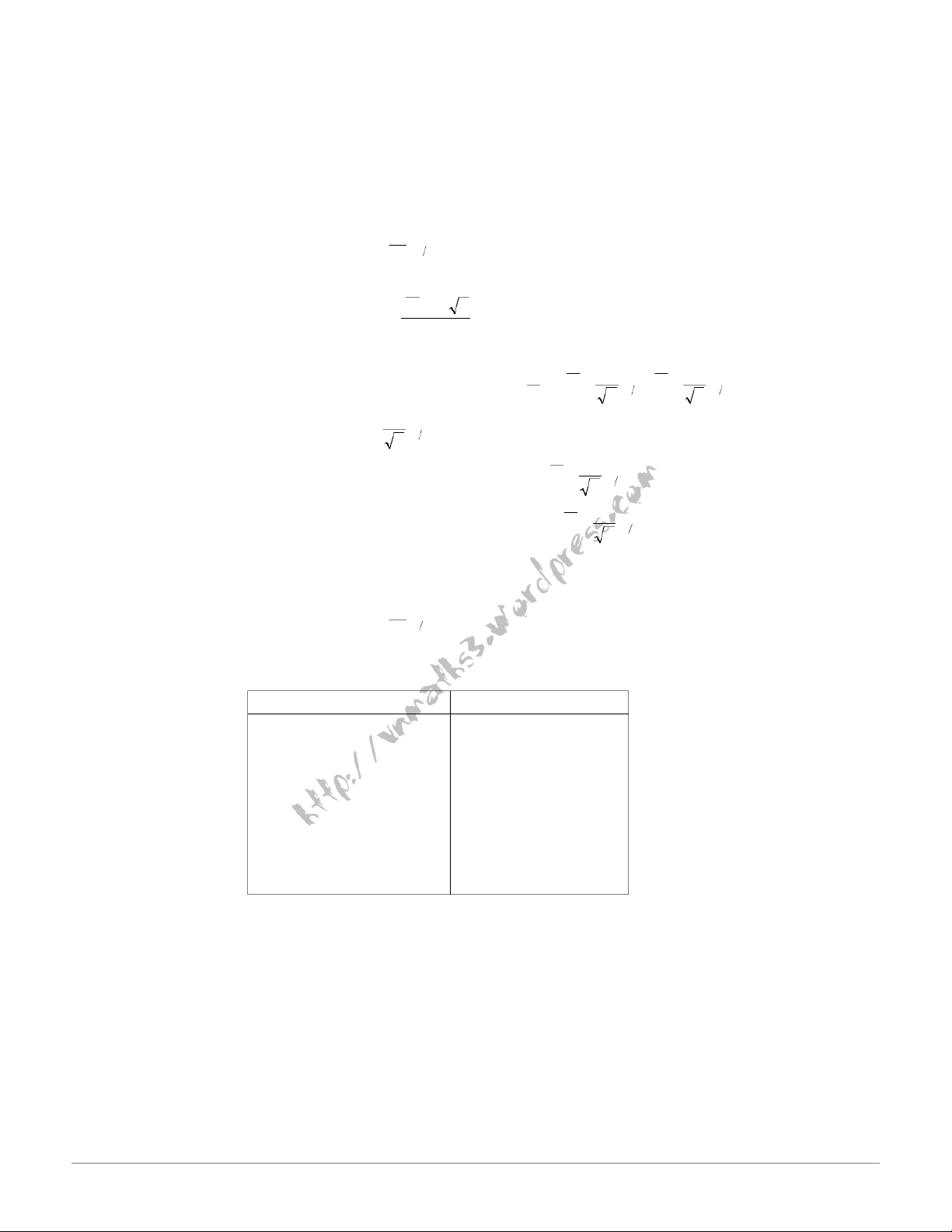
Chọn tiêu chuẩn kiểm định: X − 1 X2 G = T = 2 2 S1 S2 + 1 n 2 n H :µ = µ 0 : 1 2 → = W +∞ u α ( )α; . H µ > µ 1 1 2 H :µ = µ → 0 : 1 2 W = − ∞ −u α ( ) ; α . H µ < µ 1 1 2 H :µ = µ → 0 : 1 2 W = u u α (−∞;− ∪ α α) ( ;+∞ . ) H µ ≠ µ 2 2 1 1 2
Lập mẫu cụ thể và tính giá trị quan sát: x − 1 x2 Tqs =
và so sánh với Wα để kết 2 2 1 s s2 + n1 2 n luận.
Ví dụ 2.10 Người ta cân trẻ sơ sinh ở hai khu vực thành thị và nông thôn, thu
được kết quả như sau: Khu vực Số trẻ được Trọng lượng trung Phương sai cân bình Nông 2500 3,0 200 thôn Thành thị 500 3,1 5
Với mức ý nghĩa 0,01 có thể coi trọng lượng trung bình của trẻ sơ sinh ở hai khu
vực bằng nhau được hay không? Giải. G Tọriọ tnrọ g n l g ư ợtr n ẻ g stơ r ẻ s i s n ơ h s iở n n h ô t n r g u n th g ô b n ì n v h à c thhíà n n h h l t à h ị
µ .t ương ứng là X1 và X2
Đây là bài toán kiểm định hai tham số µ. 1 và µ2
1, µ2 khi chưa biết σ12, σ22 . C µ = µ
ặp giả thuyết thống kê: H 0 :: 1 2 H µ ≠ µ 1 1 2 α = 0,01 u ⇒ = u = − ∞ − ⇒ ∪ W +∞ α ( ; 576 , 2 ) ( ; 576 , 2 . ) α 2 = 0,005 2 5 , 76 n1 = 2500; n2 = 500 = x ,3 ; 0 = x 1, 3 1 2 2 s = s = 1 ; 200 22 5 Giá tr − ị quan sát: 0 , 3 1, 3 U = = − qs 3 , 0 3 ∉Wα. 200 5 + 2500 500 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Kết luận: Chưa có cơ sở bác bỏ H0, tức là có thể coi trọng lượng trẻ sơ sinh ở
nông thôn và thành thị là như nhau.
3. Kiểm định giả thuyết về tham số p (kiểm định một tỷ lệ)
Giả sử trong tổng thể có N phần tử, trong đó có M phần tử mang dấu hiệu nghiên cứu. Đặt p = M . N
Nếu p chưa biết song có cơ sở giả thiết rằng giá trị của nó bằng p0, người ta đưa
ra giả thuyết thống kê: H0: p = p0. Từ tổng thể lập mẫu ngẫu nhiên kích thước n Ch ( )
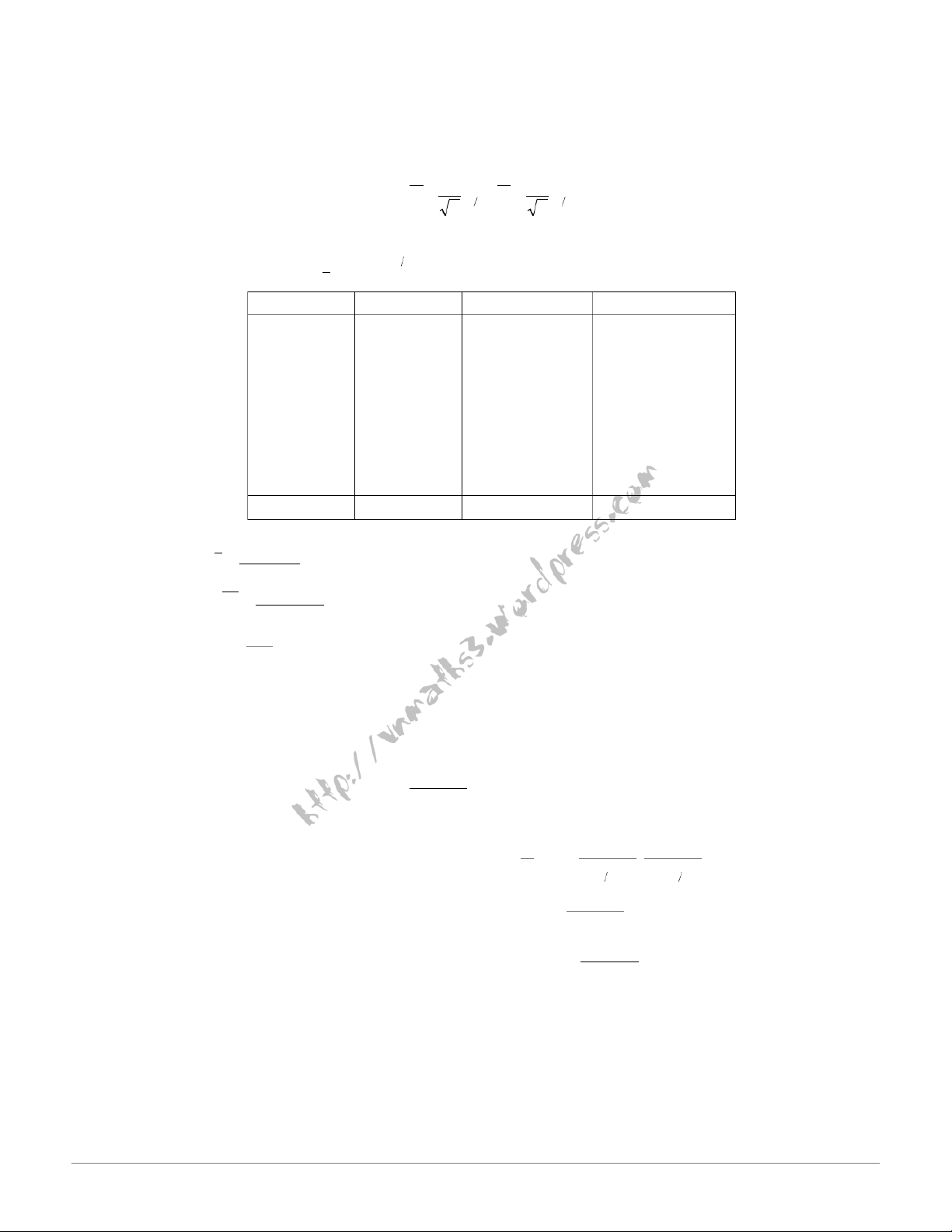
ọn tiêu chuẩn kiểm định: f − p n 0 G −=U =p (1) 0 p 0 H : p = p 0 0 → = W +∞ u α ( )α; . H : p > p 1 0 H : p = p 0 0 → W = − ∞ −u α ( ) ; α . H : p < p 1 0 H : p = p 0 0 = − ∞ − ∪ → 2 +∞ W 2 u u α ( ; α α) ( ; . ) H : p ≠ 1 p0 L ( )
ập mẫu cụ thể và tính giá trị quan sát: f − p n
Uqs −=v pà so 0spánh với W α để 0 (1)0 kết luận.
Ví dụ 2.11: Tỷ lệ khách hàng tiêu dung một loại sản phẩm ở địa phương A là
60%. Sau một chiến dịch quảng cáo người ta muốn đánh giá xem chiến dịch q uảng
cáo này có thực sự mang lại hiệu quả hay không. Phỏng vấn ngẫu nhiên 400 khách
hàng thì thấy có 250 người tiêu dùng loại sản phẩm này. Với mức ý nghĩa 0,05 hãy kết
luận về hiệu quả của chiến dịch quảng cáo đó. Giải
Gọi p là tỷ lệ khách hàng tiêu dùng loại sản phẩm đó ở địa phương A. H : p = , 0 6
Đây là bài toán kiểm định tham số p với cặp giả thuyết thống kê: H 0p 1 : > , 0 6 α = 0,05 ⇒ u = ⇒ = W +∞ α ( ), 1 ; 645 . α u = , 1 645 , 0 05 n = 400 f = 0,625 250 = 400 U ( ), 0 625 − , 0 6 400 qs = = , 1 02∉ W α . , 0 ( 6 1)− , 0 6
Kết luận: Chưa có cơ sở bác bỏ H0 , tức là chưa thể nói rằng chiến dịch quảng cáo có hiệu quả.
4. Kiểm định giả thuyết về hai tham số p (kiểm định hai tỷ lệ) 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Giả sử có hai tổng thể nghiên cứu với các tham số p1 và p2 tương ứng. Nếu p1 và
p2 chưa biết song có cơ sở cho rằng giá trị của chúng bằng nhau, ta đưa ra giả thuyết
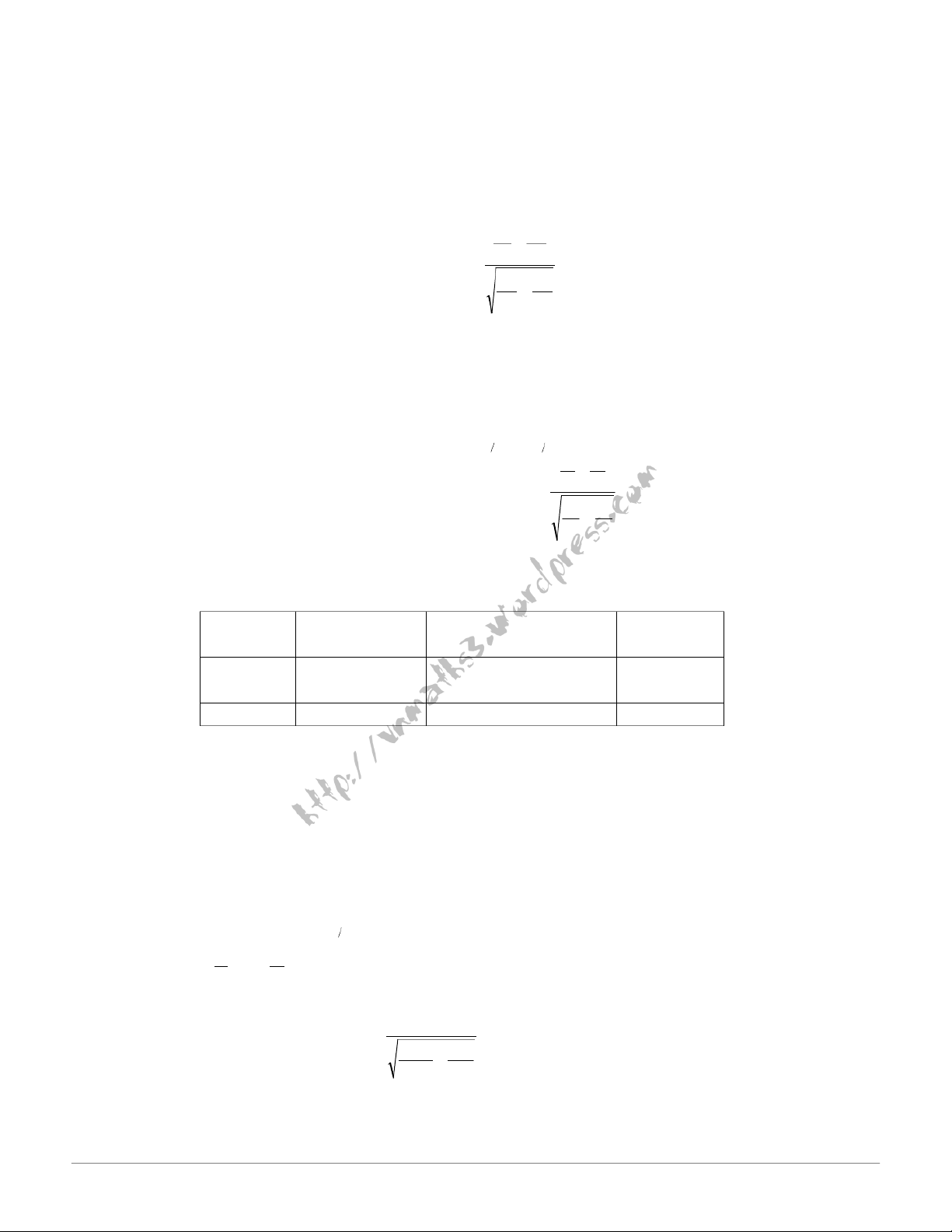
H0: p1 = p .2 Từ tổng thể rút ra hai mẫu kích thước n ,1 n2 và chọn tiêu chuẩn kiểm định: f − f G n f n n f n + = U = 1 2 trong đó 1 1 2 2 f+= − n f (1) +1 1 n f 1 2 1 2 H : = p p → 0 : 1 2 = W +∞ u α ( )α ; . H p > 1 1 p2 H : p = p 0 : 1 2 → W = − ∞ −u α ( ) ; α . H p < 1 1 p2 H : p = p 0 := 1 − ∞ − 2 ∪ → 2 +∞ W 2 u u α ( ; α α ) ( ; . ) H p ≠ 1 1 p2
Lập mẫu cụ thể và tính giá trị quan sát: f − f 1 2 Uqs = và so sánh với f ( − + 1) 1 1 f n n 1 2 Wα để kết luận.
Ví dụ 2.12 Kiểm tra ngẫu nhiên các sản phẩm cùng loại do hai nhà máy sản xuất
thu được các số liệu sau: Nhà máy
Số sản phẩm được kiểm Số phế phẩm tra A 1000 20 B 900 30
Với mức ý nghĩa 0,05 có thể coi tỷ lệ phế phẩm của hai nhà máy là như nhau hay không? Giải
Gọi p1, p2 tương ứng là tỷ lệ phế phẩm của hai nhà máy A và B.
Đây là bài toán kiểm định giả thuyết hai tham số p. C =
ặp giả thuyết thống kê: H p p 0 :: 1 2 H p ≠ p 1 1 2 α = , 005 ⇒ u = u = ⇒ = − ∞ − +∞ α 2 0,025 ,196 Wα ( ; ,196 ),1(9 ;6 . ) n1 = 1000; n2 =900 1 20 2 30 f = = , 0 ; 02 f = = , 0 033 1000 900 20 + 30 f = = 0 0263 , 1000 + 900 Giá trị quan sát: , 0 02 − , 0 033 U = = qs -1,81∉ Wα . , 0 − ( 0263 1) + 1 1 0 0263 , 1000 900 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
ht t p:/ / vnmat hs3.wordpress.com
Kết luận: Chưa có cơ sở bác bỏ H0, tức là có thể coi tỷ lệ phế phẩm ở hai nhà máy là như nhau. 23:12, 10/01/2026
Chương 3. Xác Suất Thống Kê - Lý Thuyết Mẫu và Phương Pháp Ước Lượng - Studocu
Tài liệu liên quan:
-
Bài giảng Chương 6: Kiểm định giả thuyết thống kê môn Xác suất thống kê | Đại học Duy Tân
27 14 -
Bài giảng Chương 5. Ước lượng tham số môn Xác suất thống kê | Đại học Duy Tân
28 14 -
Bài giảng Chương 4: Thống kê mô tả môn Xác suất thống kê | Đại học Duy Tân
25 13 -
Bài giảng Chương 3. Vectơ ngẫu nhiên môn Xác suất thống kê | Đại học Duy Tân
25 13 -
Bài giảng Chương 1: Xác suất môn Xác suất thống kê | Đại học Duy Tân
26 13