Chương 4,5 Quan Hệ Đại Số Bool | Môn Toán rời rạc - Đại học Cần Thơ

lOMoAR cPSD| 58488183
Chương 4&5: QUAN HỆ VÀ ĐẠI SỐ BOOL  Quan hệ  Đại số Bool  Hàm Bool
 Hệ phương trình Bool
 Đơn giản công thức Quan hệ
Cho hai tập hợp và , một quan hệ hai ngôi giữa A và B là tập con ℜ ×
. Với a, b ∈ ℜ, ta viết aℜ lOMoAR cPSD| 58488183
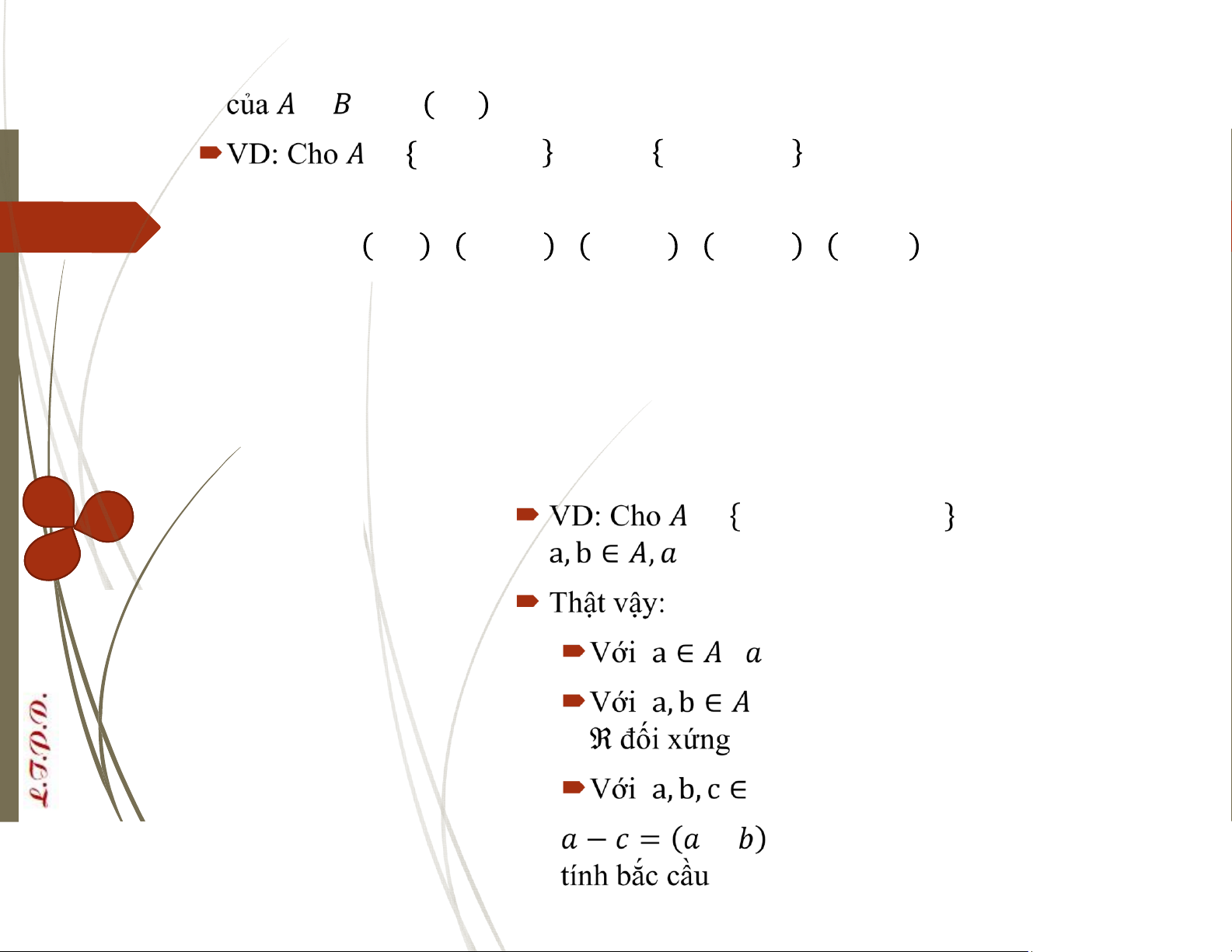
= 1, 2, 3, 4, 5 và B = 11, 12, 13 . Một quan hệ ℜ được định
nghĩa như sau: Với a ∈ , ∈ , ℜ ⇔ | . Hãy xác định ℜ ℜ = { 1, 11 ,1, 12 ,1, 13 ,2, 12 ,3, 12 , (4, 12)}
Tính chất của quan hệ: Cho ℜ là quan hệ của tập và chính nó
Tính phản xạ: a ∈ , ℜ
Tính đối xứng: a, b ∈ , ℜ ⇒ ℜ
Tính phản đối xứng: a, b ∈ , ℜ ∧ ℜ ⇒ =
Tính bắc cầu: a, b, c ∈ , ℜ ∧ ℜ ⇒ ℜ Quan hệ
Quan hệ tương đương: Là quan hệ hai ngôi ℜ trên thỏa các tính chất phản
xạ, đối xứng và bắc cầu lOMoAR cPSD| 58488183
= 1,2,3,4,5,6,7,8,9 , quan hệ ℜ trên được định nghĩa: Với ℜ
⇔ − ⋮ 3. CMR ℜ là một quan hệ tương đương trên A. ,
− = 0 ⋮ 3 ⇔ ℜ . Suy ra ℜ phản xạ
, ℜ ⇔ − = 3 ⇔ − = 3 − ⋮ 3 ⇔ ℜ . Suy ra
, ℜ ⇔ − = 3 và ℜ ⇔ − = 3 . Ta có − +
− = 3 + 3 = 3 + ⋮ 3 ⇔ ℜ . Vậy ℜ có lOMoAR cPSD| 58488183 , lớp lOMoAR cPSD| 58488183 tương đương của ⋮ 3. Khi đó ℜ lOMoAR cPSD| 58488183 Quan hệ
Quan hệ thứ tự: Là quan hệ hai ngôi ℜ
trên thỏa các tính chất phản xạ, phản đối xứng và bắc cầu
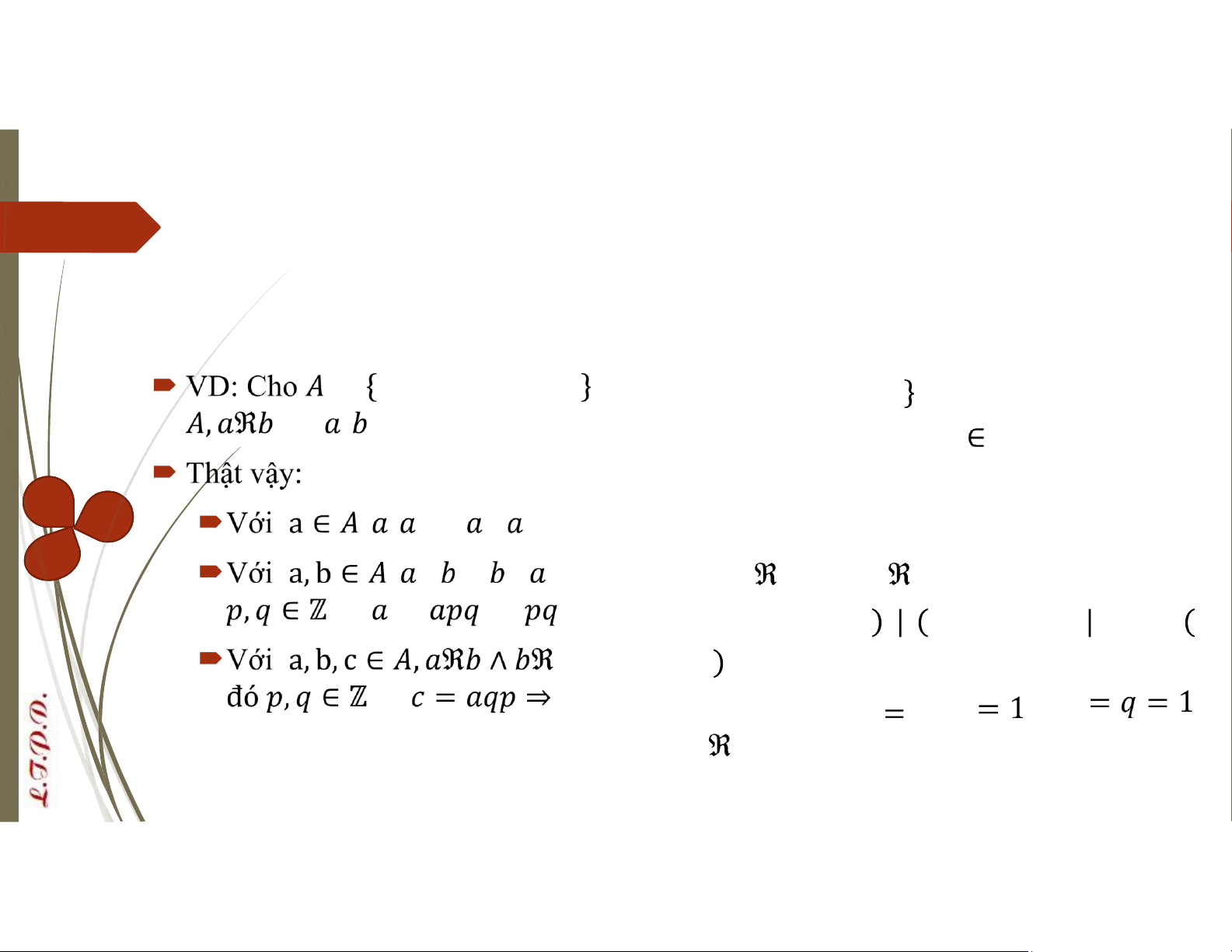
= 1,2,3,4,5,6,7,8,9 , quan hệ ℜ trên
được định nghĩa: Với a, b ⇔ | . CMR ℜ là
một quan hệ thứ tự trên A. , | ⇔ . Suy ra phản xạ , ℜ ∧ ℜ ⇔ ∧ ⇔ = ∧ = , trong đó ⇒ ⇒ ⇒ . Suy ra phản đối xứng lOMoAR cPSD| 58488183 ⇔ | |⇔ , trong ⇒ | ⇔ . Suy ra bắc cầu Quan hệ
 Cho ℜ là quan hệ thứ tự trên :
(A, ℜ) là tập hợp thứ tự
ta nói bị trội bởi hoặc trội
 là trội trực tiếp của nếu ℜ ∧ (¬∃ ∈ : ℜ ∧ ℜ )
∈ được gọi là tối đại nếu không bị trội bởi phần tử khác
∈ được gọi là tối tiểu nếu không trội phần tử khác
∈ được gọi là lớn nhất nếu trội tất cả phần tử khác:
∈ được gọi là nhỏ nhất nếu bị trội bởi tất cả phần tử khác: lOMoAR cPSD| 58488183
Phần tử lớn nhất (nhỏ nhất) của
(nếu có) là phần tử tối
đại (tối tiểu) duy nhất Đại số Bool ,∨,∧) gồm tập và hai phép toán ∨ ( ) và ∧
thỏa mãn các tính chất: Với mọi , , ∈ : ∧ = ∧ và ∨ = ∨ lOMoAR cPSD| 58488183 ∧ ( ∈ ta có:
∨ 0 = và ∧ 1 = ∈ , ∃ ̅ ∈ : ∨ ̅ = 1 và ∧ ̅ = 0 Đại số Bool
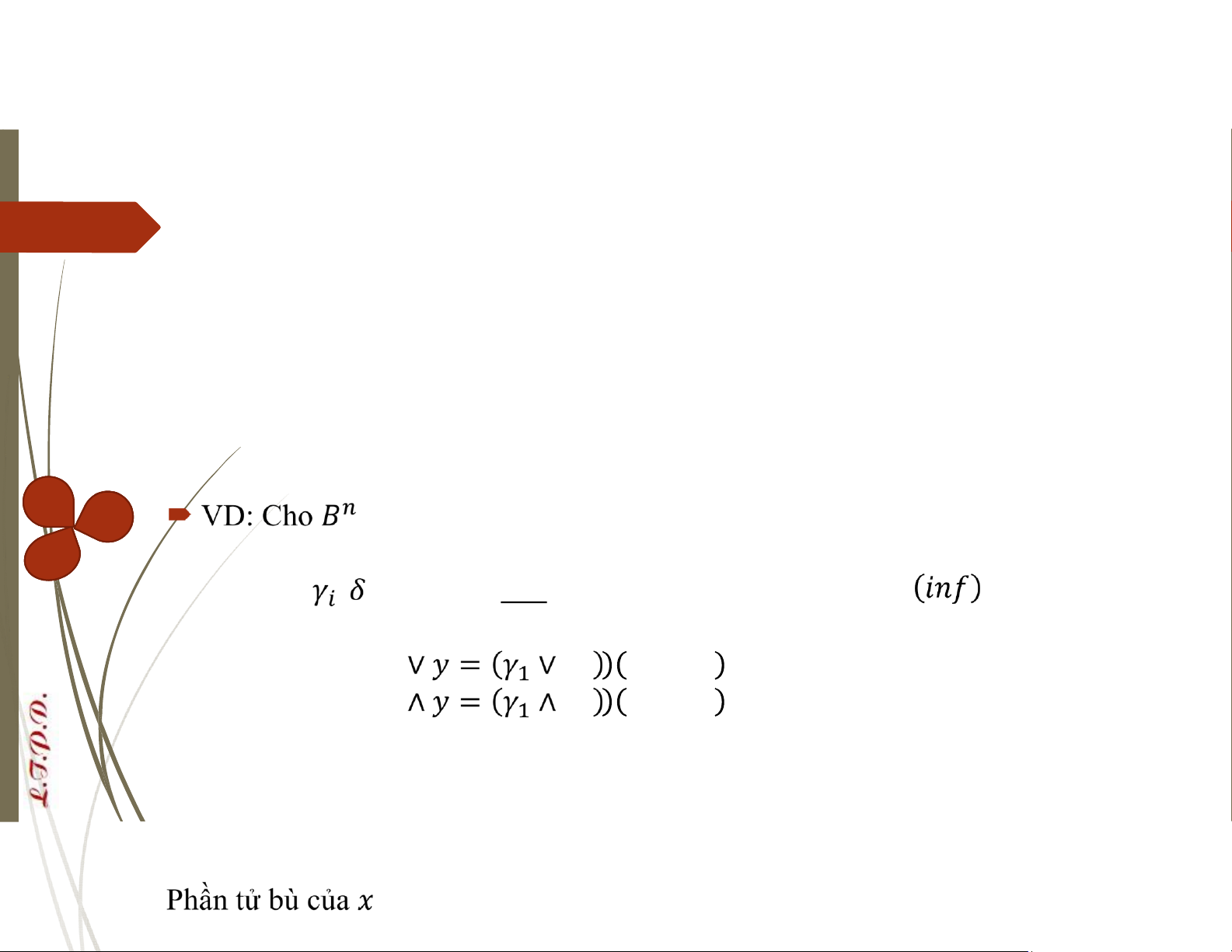
là tập tất cả các dãy nhị phân chiều dài , khi đó ( ,∨,∧)
là một đại số Bool, ∀ , ∈ ta có = … và = … ,
trong đó , ∈ {0,1}, ∀ = 1
, với các phép toán ∨ ( ) và ∧ được định nghĩa: ∨… ( ∨ ) ∧… ( ∧ ) Phần tử trung hòa: lOMoAR cPSD| 58488183
Phần tử nhỏ nhất là 00 … 0
Phần tử lớn nhất là 11 … 1 = … ∈ là ̅ = … ∈ , trong đó: 1 = 0, 0 = 1
Số phần tử của một đại số Bool hữu hạn là một lũy thừa của 2 Hàm Bool
biến là một ánh xạ :
→ giữa các đại số Bool , .
Các biến trong hàm Bool được gọi là biến Bool.
 Bảng chân trị của hàm Bool thể hiện giá trị của hàm Bool ứng
với giá trị các biến Bool
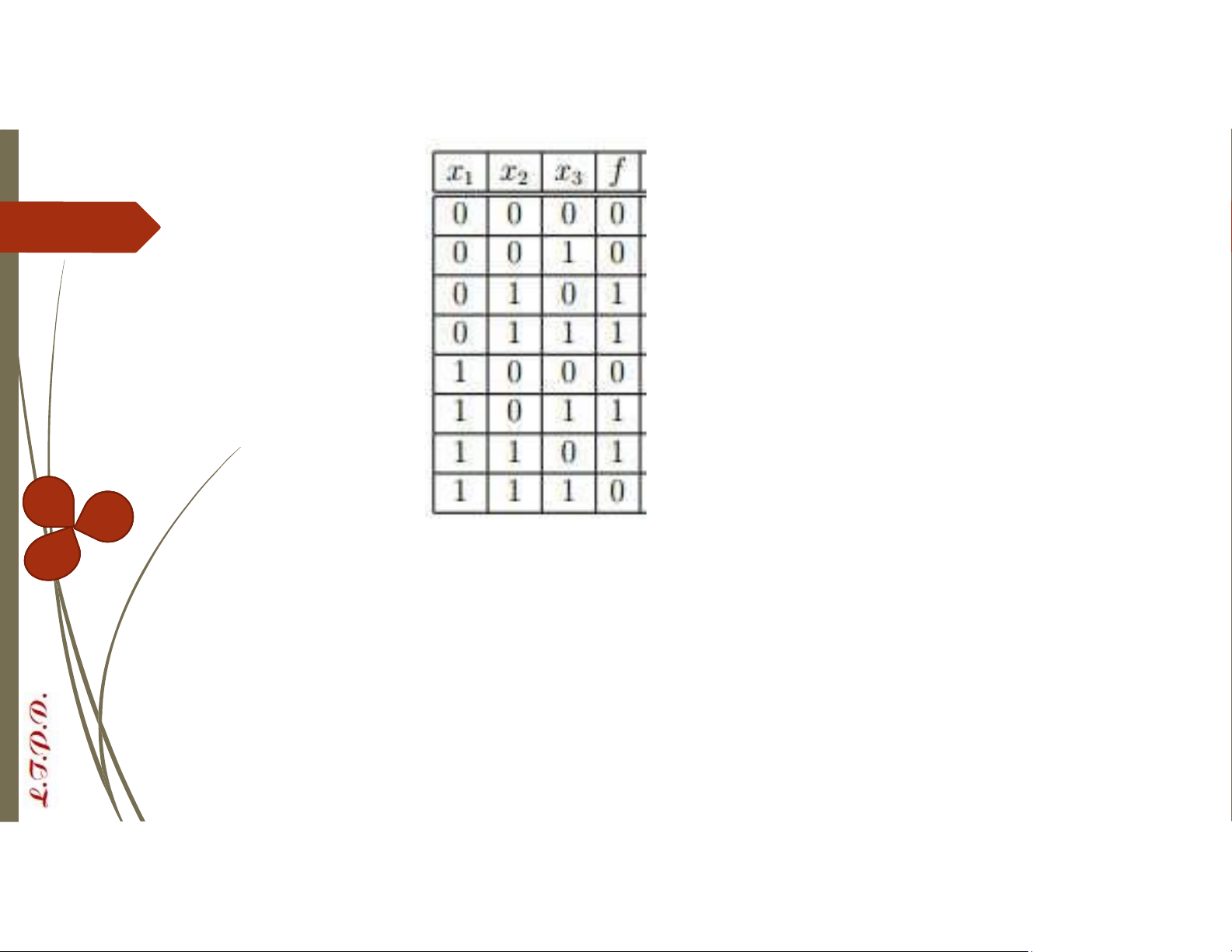
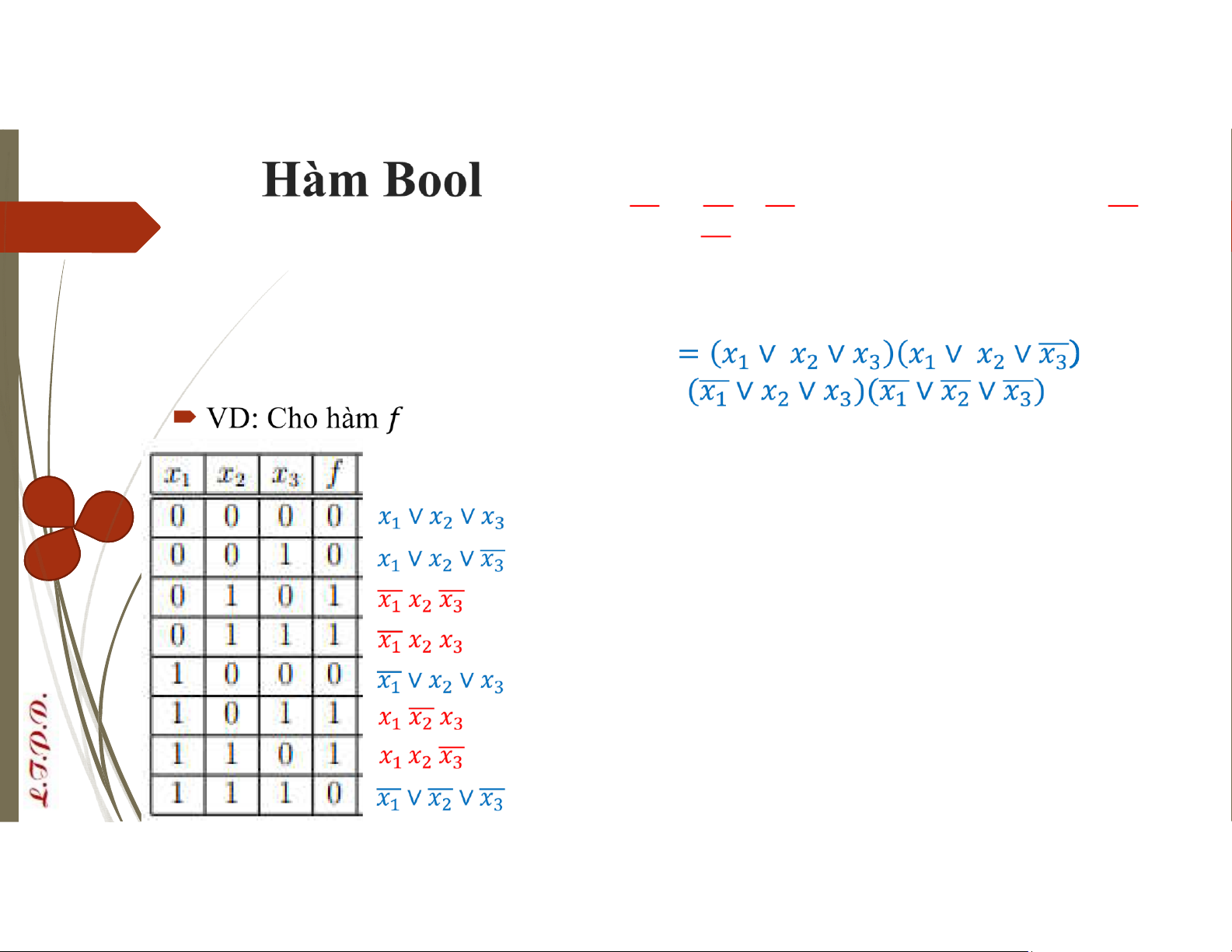
 VD: Cho hàm Bool 3 biến = 00110110 có bảng chân trị như sau lOMoAR cPSD| 58488183
 Dạng tuyển chuẩn tắc của hàm Bool được biểu diễn bởi = ∨ ∨ ⋯ ∨
 Dạng hội chuẩn tắc của hàm Bool được biểu diễn bởi = ∧ ∧ ⋯ ∧
= 00110110 hãy viết dạng tuyển chuẩn tắc và hội chuẩn tắc lOMoAR cPSD| 58488183 Tuyển chuẩn tắc: = ∨ ∨ ∨ Hội chuẩn tắc:
Có thể thay dấu ∨ bởi dấu + lOMoAR cPSD| 58488183 Hàm Bool
Bài tập: Một kỳ thi có 4 môn a, b, c, d với hệ số tương ứng là
8, 5, 4, 3. Mỗi môn được cho điểm là 0 hoặc 1. Để được đậu phải
có tổng số điểm lớn hơn 10. Một hàm bool f có giá trị là 1nếu thí
sinh đậu, là 0 nếu ngược lại.
1. Xác định bảng chân trị của hàm bool f
2. Xác định dạng tuyển chuẩn tắc của hàm bool f
3. Xác định dạng hội chuẩn tắc của hàm bool f. Hệ phương trình Bool
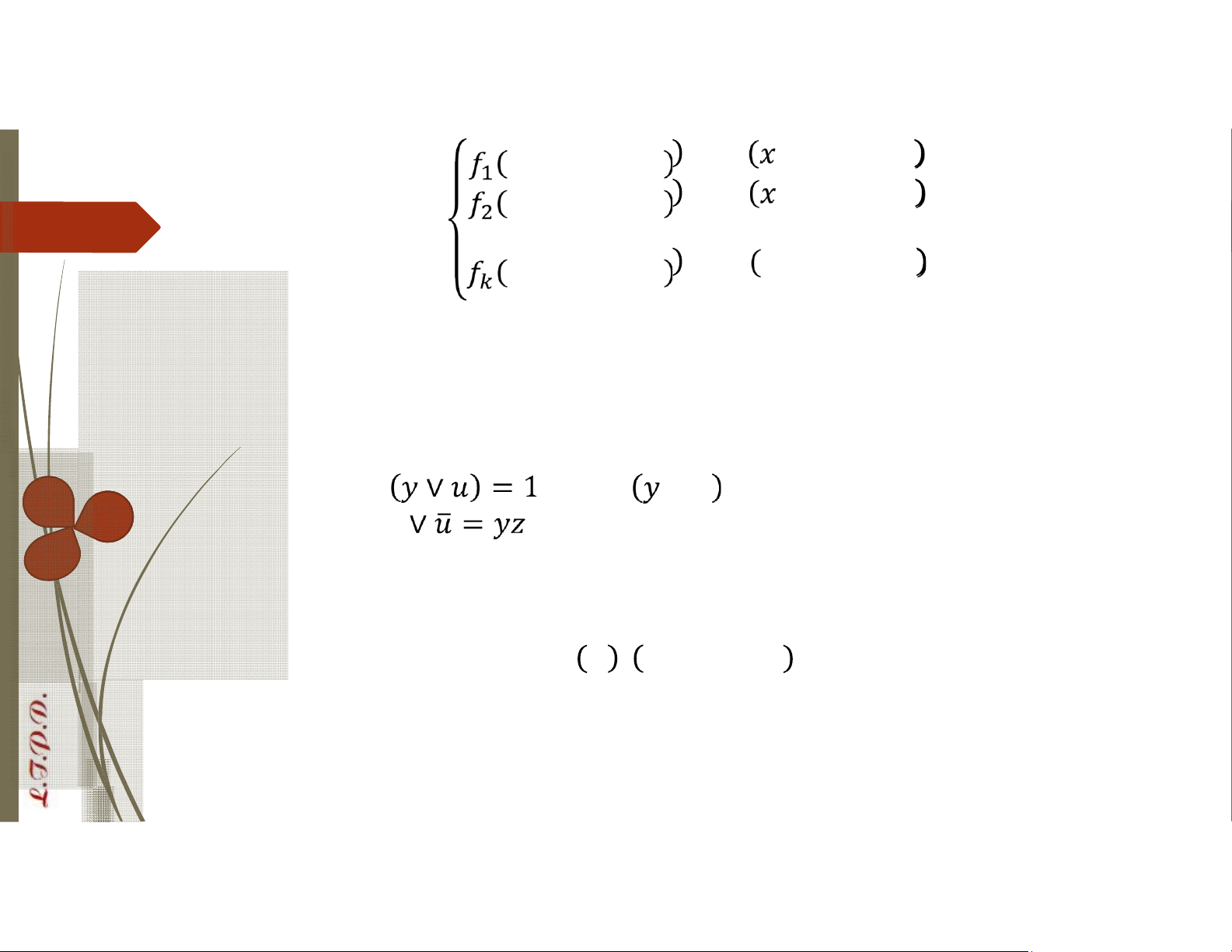
Cho các hàm Bool biến , , … , và ,
, … ,. Hệ phương trình sau đây lOMoAR cPSD| 58488183 , , … ,=, , … , , , … ,=, , … , … , , … ,=, , … , trong đó các biến Bool ,
, … , là các ẩn, được gọi là hệ phương
trình Bool VD: Tìm giá trị các biến Bool , , , thỏa mãn hệ phương trình ̅ ̅ ∨ = 0.
Bằng cách thử trực tiếp ta nhận được nghiệm của hệ phương trình là: 1,1,1,0 , 1,0,0,1 , (1,0,1,1) Hệ phương trình Bool
Các bước giải tổng quát: lOMoAR cPSD| 58488183
B1: Biến các vế của hpt thành dạng tổng các tích B2: Áp dụng = ⇔ 1 = ∨ ̅ ̅ cho tất cả các phương trình
B3: Biến hpt thành dạng 1 = ℎ ℎ … ℎ , trong đó ℎ là vế phải
của các phương trình ∀ = 1,2, … ,
B4: Thu gọn biểu thức B3 thành dạng 1 = ∨ ∨ ⋯ ∨ , trong
đó có dạng tích của các biến/bù của biến ∀ = 1,2, … ,
B5: Pt B4 tương đương với 1 = 1 = … 1 =
Suy ra nghiệm của hpt từ B5 lOMoAR cPSD| 58488183 Hệ phương trình Bool
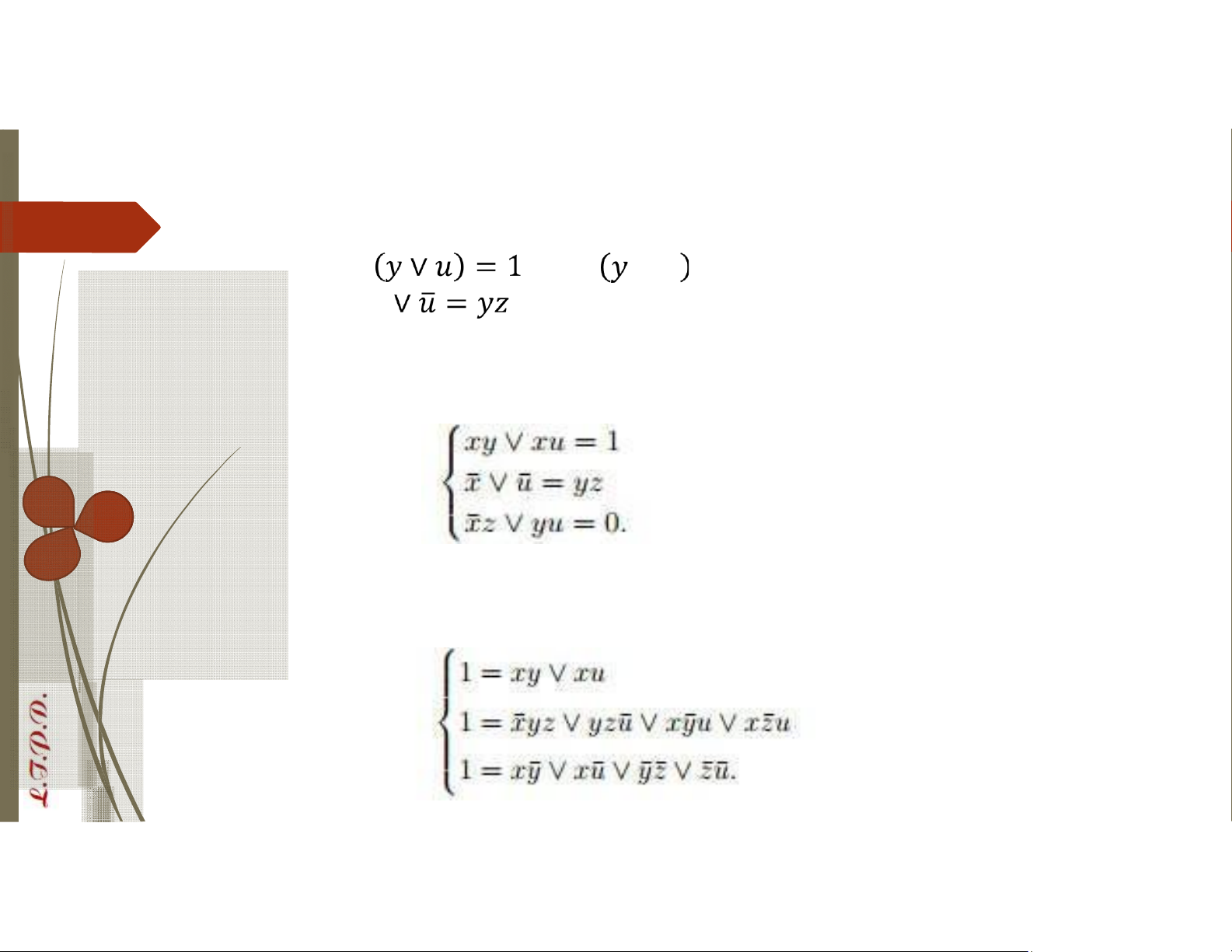
VD: Tìm các biến Bool , , ,
thỏa mãn hệ phương trình ̅ ̅ ∨ = 0.
B1: Biến các vế của hpt thành dạng tổng các tích B2: Áp dụng = ⇔ 1 = ∨ ̅ ̅ cho tất cả các phương trình lOMoAR cPSD| 58488183 lOMoAR cPSD| 58488183
một phủ tối tiểu của lOMoAR cPSD| 58488183
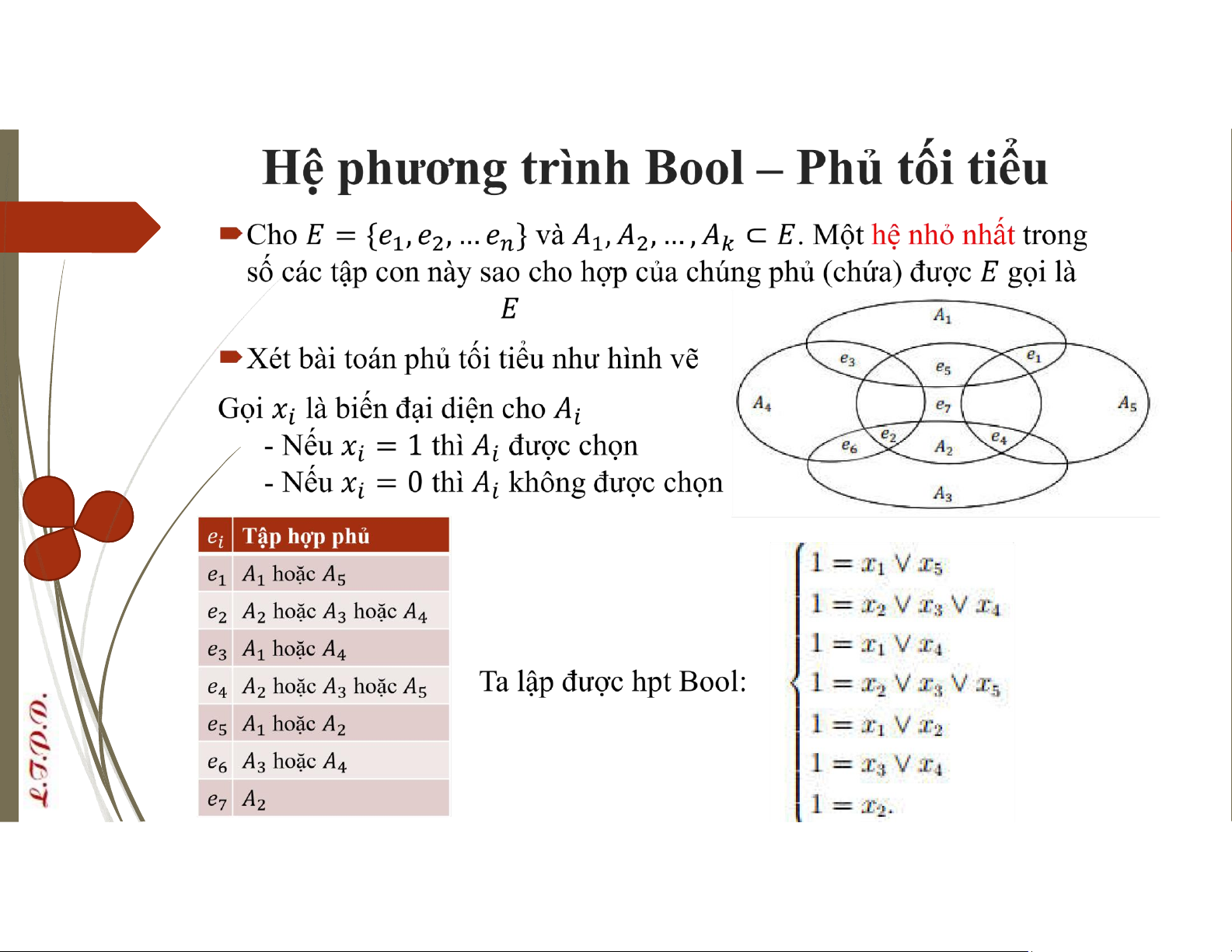
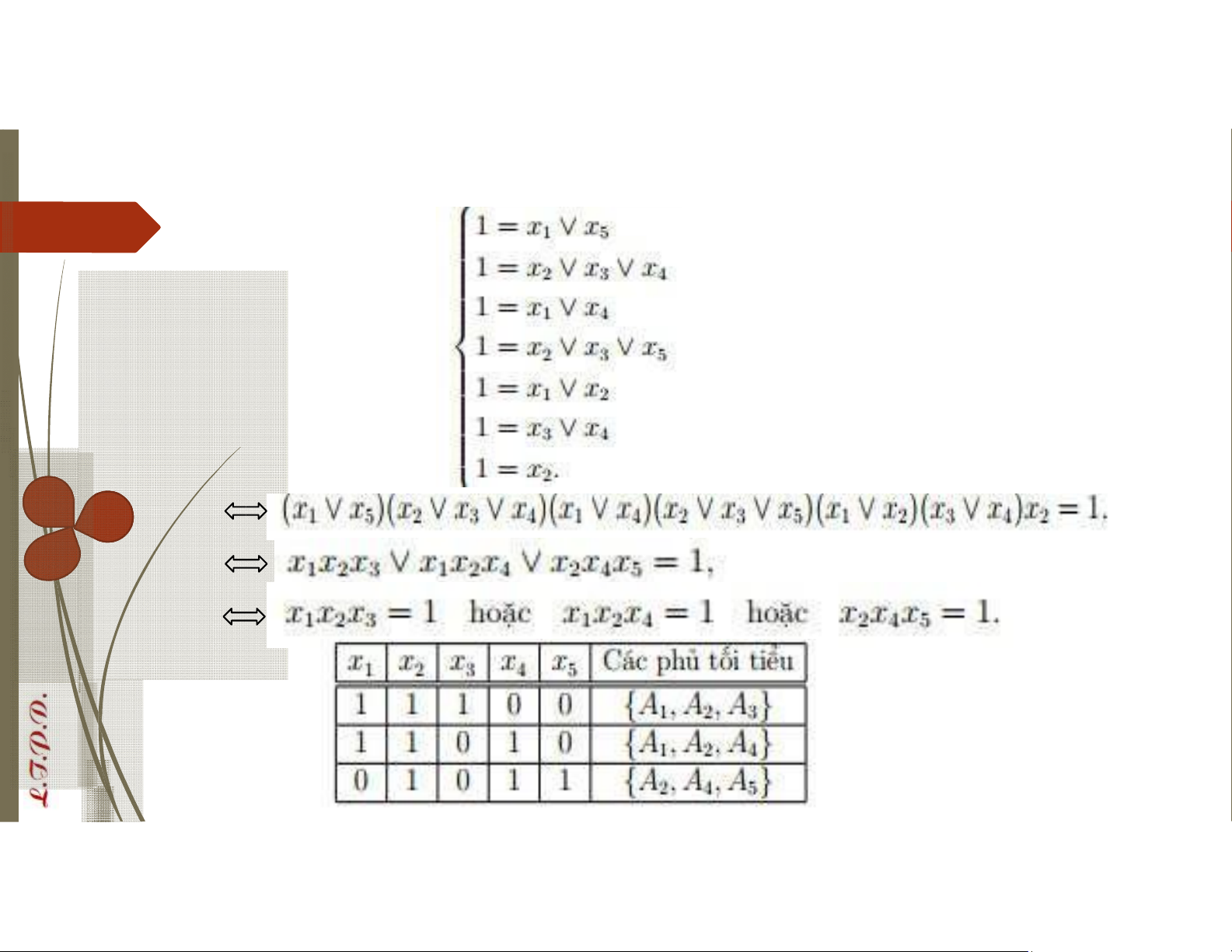
Hệ phương trình Bool – Phủ tối tiểu  Giải hpt Bool: lOMoAR cPSD| 58488183
Hệ phương trình Bool – Phủ tối tiểu
Bài tập: E là tập hợp các số nguyên từ 5 đến 15. Hãy tìm phủ tối
tiểu của E từ các tập hợp con của nó được xác định như sau :
 A1 : tập hợp các số nguyên tố thuộc E.
 A2 : tập hợp các phần tử thuộc E và là ước của 140.
 A3 : tập hợp các phần tử của E và là bội của 3.
 A4 : tập hợp các phần tử của E và có dạng bình phương hoặc lập phương.
 A5 : tập hợp các phần tử của E từ 9 đến 12.
 A6 : tập hợp các phần tử của E mà tổng các chữ số của mỗi phần tử là từ 4 đến 6.