Chương 4. Công thức xấp xỉ | Bài giảng Xác suất thống kê
Ý nghĩa của định lý D :Thể hiện tính ổn định của trung bình các BNN độc lập cùng phân phối và có phương sai hữu hạn. Bài giảng giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao
Môn: Xác xuất thông kê
Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
Chương 4. Định lý giới hạn trong xác suất
§1. Một số loại hội tụ trong xác suất và các định lý
§2. Các loại xấp xỉ phân phối xác suất
………………………………………………………………………
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
Chương 4. Định lý giới hạn trong xác suất
§2. CÁC LOẠI XẤP XỈ PHÂN PHỐI XÁC SUẤT
2.1. Xấp xỉ phân phối Siêu bội bởi Nhị thức
2.2. Xấp xỉ phân phối Nhị thức bởi Poisson
2.3. Xấp xỉ phân phối Nhị thức bởi phân phối Chuẩn
Chương 4. Định lý giới hạn trong xác suất
2.1. Xấp xỉ phân phối Siêu bội bởi Nhị thức
Xét BNN X có phân phối Siêu bội H(N; N ; n). A k n k C C N N N A A d k k n k C p q . n n CN
Ứng dụng xấp xỉ phân phối Siêu bội bằng Nhị thức
• Cho X H(N; N ; n). Nếu N khá lớn và n rất nhỏ so A với N (n < 5%.N) thì: N X B(n; p), A p . N
Chương 4. Định lý giới hạn trong xác suất Chú ý
Khi cỡ mẫu n khá nhỏ so với kích thước N (khoảng
5%N ) của tổng thể thì việc lấy mẫu có hoàn lại hay
không hoàn lại là như nhau.
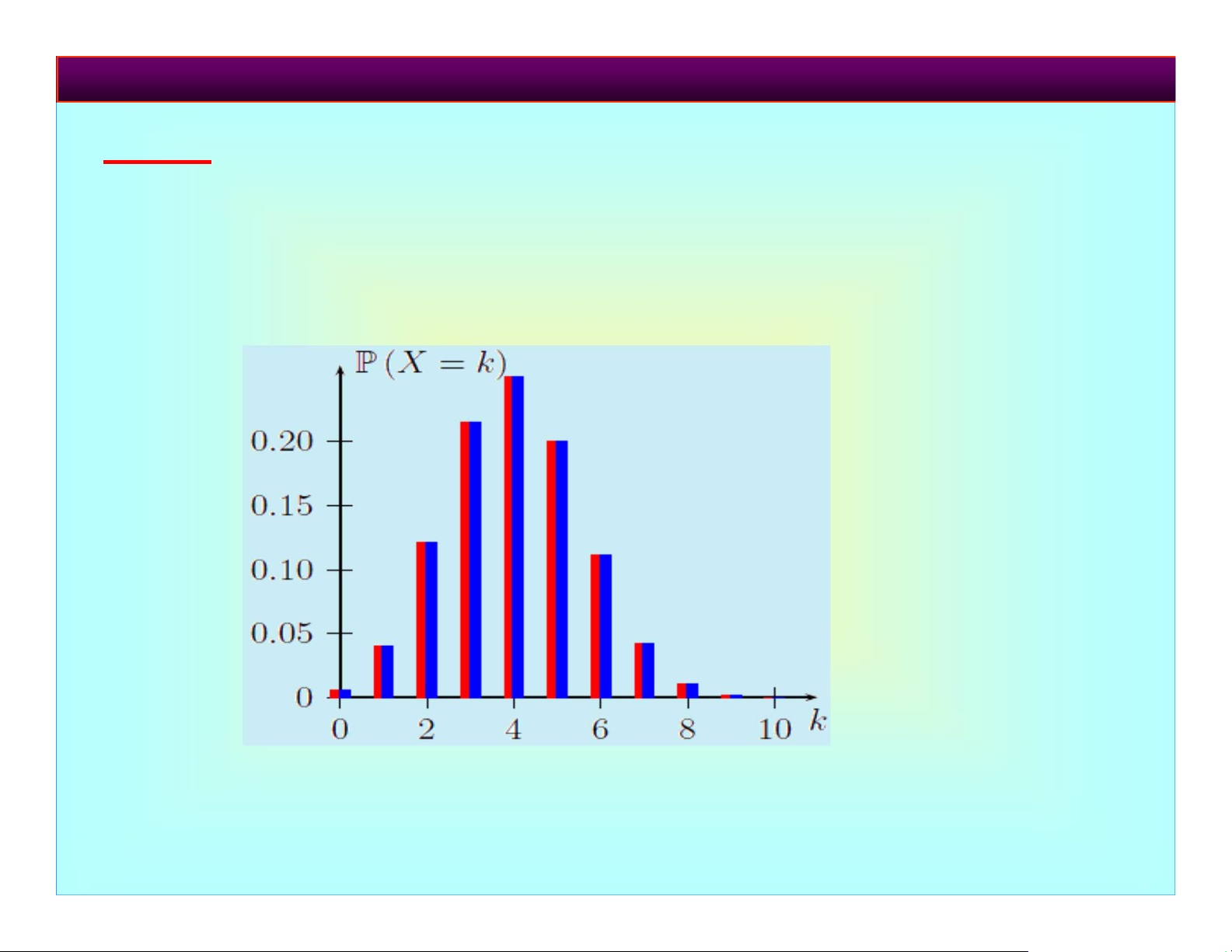
Đỏ: X H(10.000; 4.000; 10), Xanh: X B(10; 0,4).
Chương 4. Định lý giới hạn trong xác suất
VD 1. Một vườn lan có 10.000 cây sắp nở hoa, trong đó
có 1.000 cây hoa màu đỏ.
1) Tính xác suất để khi chọn ngẫu nhiên 20 cây lan thì
được 5 cây có hoa màu đỏ.
2) Tính xác suất để khi chọn ngẫu nhiên 50 cây lan thì
được 10 cây có hoa màu đỏ.
3) Có thể tính xác suất để khi chọn ngẫu nhiên 200 cây
lan thì có 50 cây hoa màu đỏ được không ?
Chương 4. Định lý giới hạn trong xác suất Giải
1) Gọi X là số cây lan màu đỏ chọn được, ta có: X H(10.000; 1.000; 20).
Vì n 20 rất nhỏ so với N 10.000 nên: với 1.000 p
0,1 thì X B(20; 0,1). 10.000 Vậy 5 5 15
P(X 5) C (0,1) (0,9) 0, 0319. 20 Nhận xét
Nếu dùng công thức của phân phối Siêu bội thì: 5 15 C C 1.000 9.000 P(X 5) 0, 0318. 20 C10.000
Chương 4. Định lý giới hạn trong xác suất
2) Tương tự, ta có: X B(50; 0,1). Vậy 10 10 40
P(X 10) C (0,1) (0, 9) 0, 0152. 50
Chương 4. Định lý giới hạn trong xác suất
2.2. Xấp xỉ phân phối Nhị thức bởi Poisson
Xét biến ngẫu nhiên X có phân phối Nhị thức B(n; p).
• Khi n , nếu p 0 và np thì: k k n k e . k d C p q . n k !
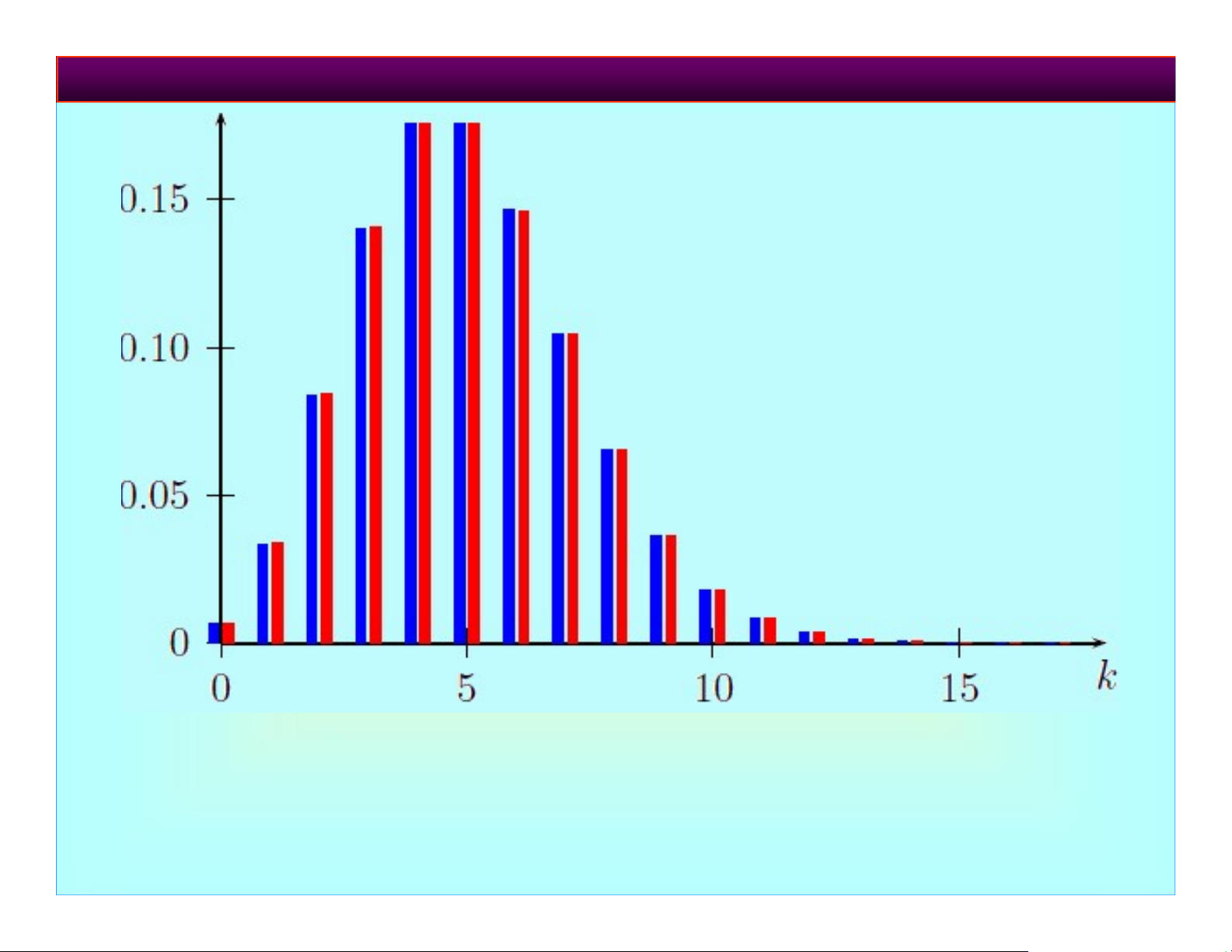
Chương 4. Định lý giới hạn trong xác suất Xanh: X B(1.000; 0,005), Đỏ: X P(5).
Chương 4. Định lý giới hạn trong xác suất
VD 2. Một lô hàng thịt đông lạnh đóng gói nhập khẩu
có chứa 0,4% bị nhiễm khuẩn. Tìm xác suất để khi
chọn ngẫu nhiên 1.000 gói thịt từ lô hàng này có:
1) không quá 2 gói bị nhiễm khuẩn;
2) đúng 34 gói bị nhiễm khuẩn. Giải
Gọi X là số gói thịt bị nhiễm khuẩn, ta có: X B(1.000; 0, 004).
Vì np 4 5 nên X P(4).
1) P(X 2) p p p 0 1 2 0 1 2 4 4 4 4 e 0,2381. 0! 1! 2!
Chương 4. Định lý giới hạn trong xác suất Nhận xét
Nếu dùng công thức của phân phối Nhị thức thì: 1000 999 P(X 2) 0,996 1000.0, 004.(0, 996) 2 2 998 C (0, 004) (0,996) 0,2375. 1000 34 2) 4 4 2 0 P(X 34) p e . 1, 831.10 . 34 34!
Chương 4. Định lý giới hạn trong xác suất
VD 3. Giải câu 3) trong VD 1. Giải
Ta có: X H(10.000; 1.000; 200).
Ta xấp xỉ X B(200; 0,1), với p 0,1.
Tiếp tục xấp xỉ X P(20), với np 20. 50 Vậy 20 20 9 P(X 50) p e . 7,6.10 . 50 50!
Chương 4. Định lý giới hạn trong xác suất
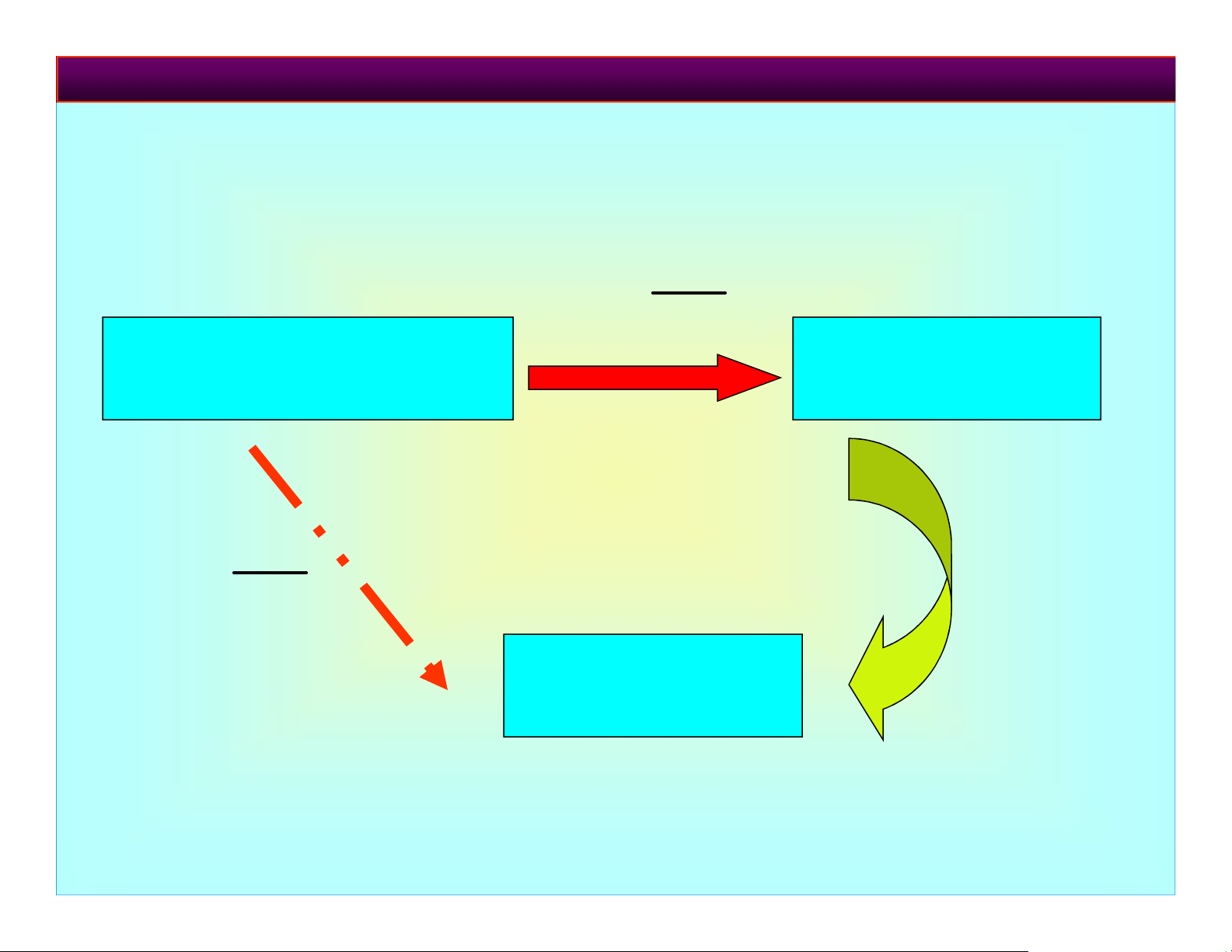
Tóm tắt các loại xấp xỉ rời rạc NA p N X H(N, N , n) X B( , n p) A n 5%N np 5 N n. A nq 5 N Sai số rất lớn X P() np