Chương 4:
Tính ổn định của hệ thống tuyến tính
Automatic Control Systems 1
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH Nội dung 4.1 Khái niệm
4.2 Mối quan hệ giữa nghiệm phương trình đặc tính và tính ổn định 4.3 Tiêu chuẩn Đại số
4.5 Phân tích quỹ đạo nghiệm số 4.4 Tiêu chuẩn Tần số
4.6 Độ dự trữ ổn định
Automatic Control Systems 2
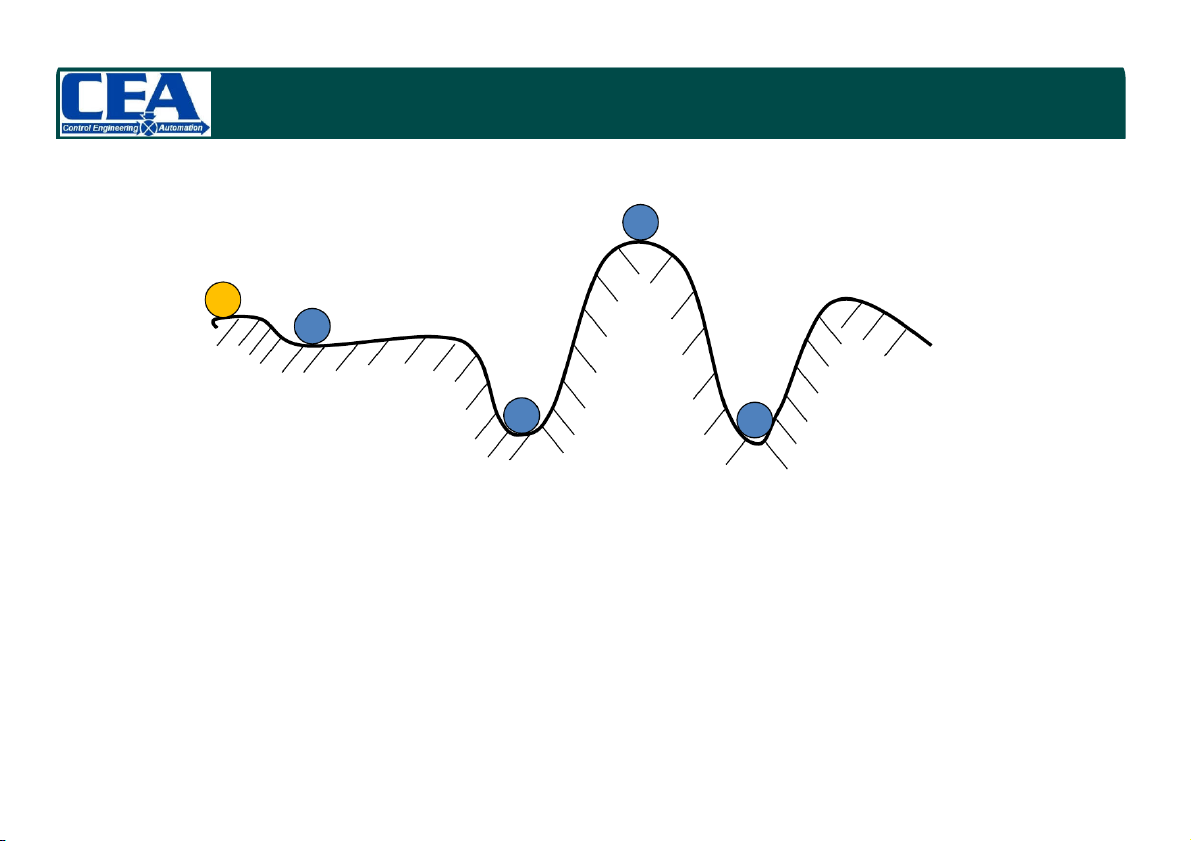
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm c a b d
Cho quả cầu một vận tốc nhỏ ban đầu đủ bé thì quả cầu sẽ tiến tới trạng thái cân bằng mới:
- Vị trí a  vị trí cân bằng ở biên giới ổn định
- Dao động quanh vị trí cân bằng vị trí b hoặc d  vị trí cân bằng ổn định
- Không về trạng thái ban đầu vị trí c  vị trí cân bằng không ổn định
Automatic Control Systems 3
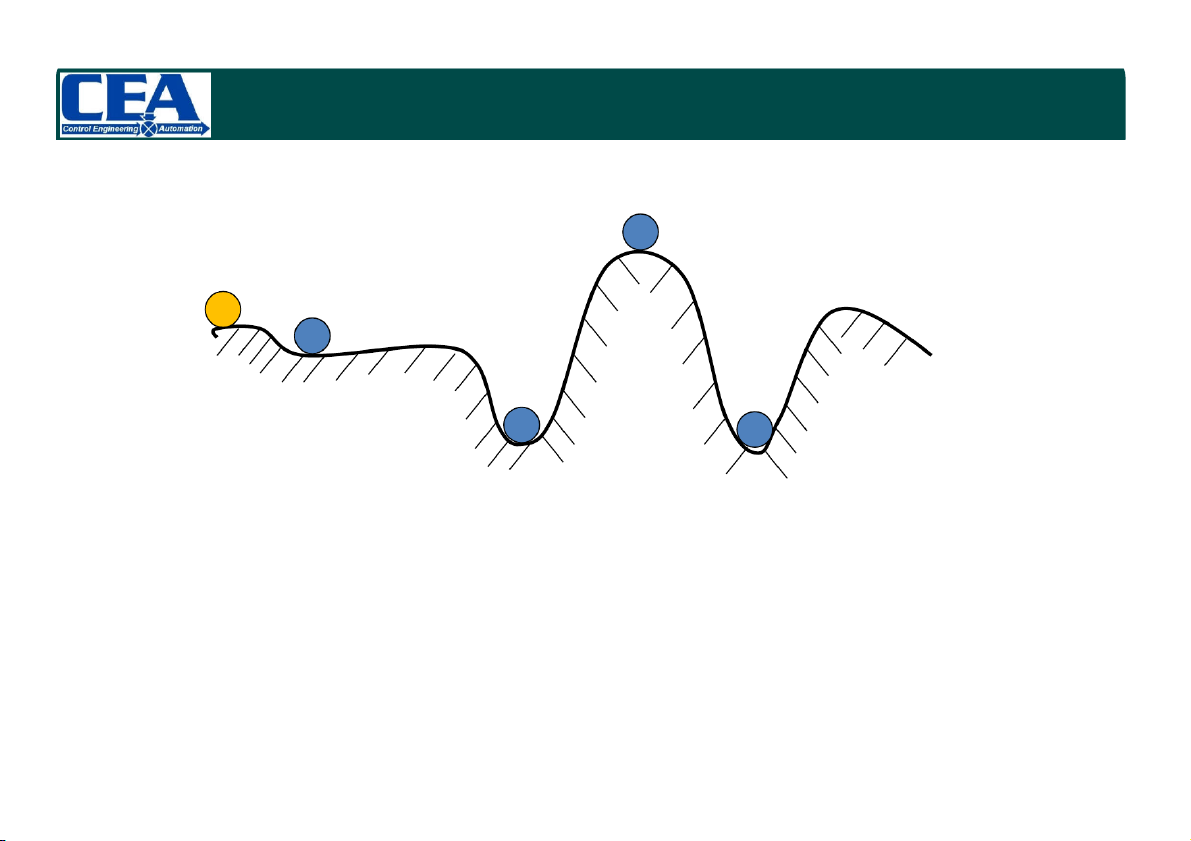
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm c a b d
Nếu quả cầu dao động với vận tốc lớn thì cũng sẽ không trở về vị trí cân bằng ổn định b hoặc d
 2 trạng thái b và d chỉ ổn định trong phạm vị hẹp
 Giới hạn khảo sát tính ổn định cho hệ tuyến tính bất biến theo thời gian.
Automatic Control Systems 4
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm u(t) () y(t)   = ()
Đáp ứng toàn phần = Đáp ứng trạng thái không + Đáp ứng đầu vào không
Đáp ứng trạng thái không: Đáp ứng của hệ thống chỉ phụ thuộc vào đầu vào,
tất cả các điều kiện ban đầu đều bằng 0
Đáp ứng đầu vào không: Đáp ứng của hệ thống theo các điều kiện ban đầu tác
động vào hệ thống, các đầu vào đều bằng 0.
Phương trình đặc tính: Phương trình đa thức của mẫu số hàm truyền đạt A(s) = 0
Automatic Control Systems 5
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm u(t) () y(t)   = ()
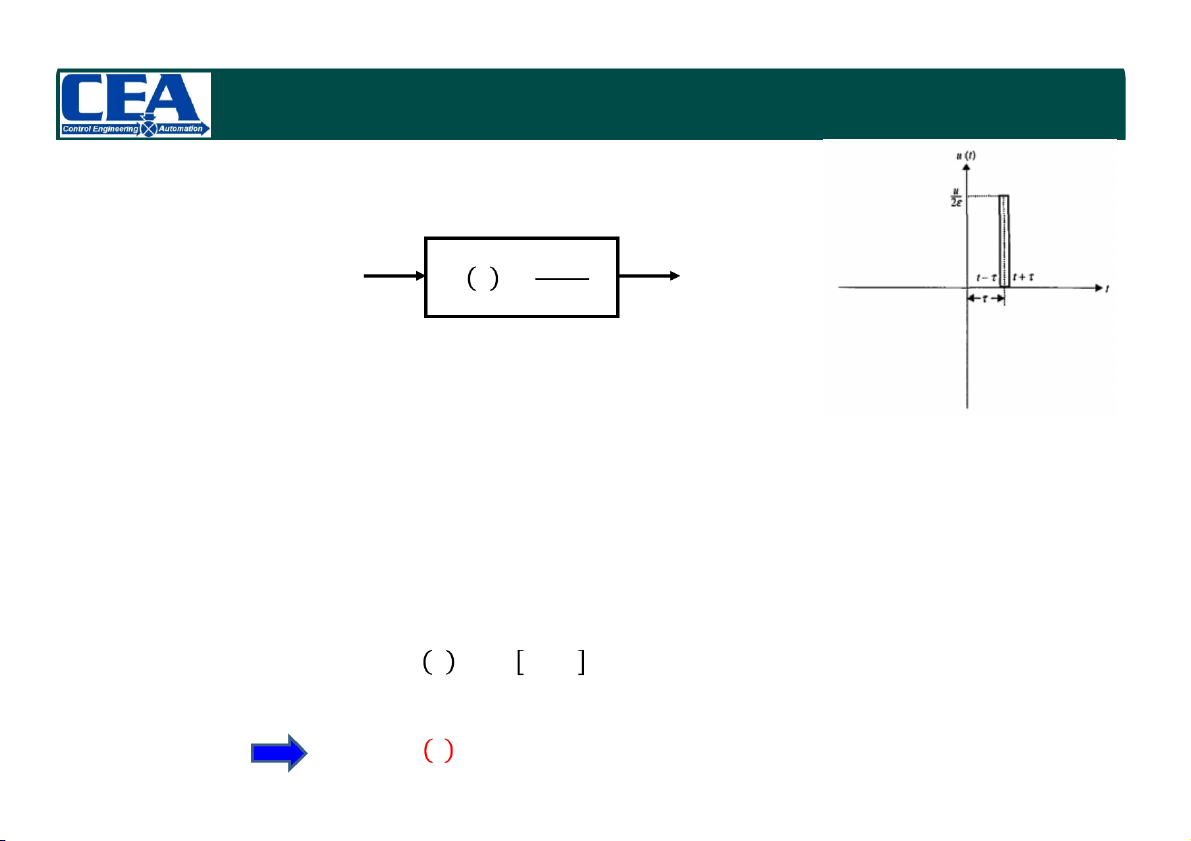
Đáp ứng xung: tín hiệu đầu ra thu được khi đầu vào là một xung đơn vị (t)
 Hệ thống có thể đặc trưng bởi đáp ứng xung của nó.
Hàm truyền đạt: Biến đổi Laplace của đáp ứng xung của hê thống, với điều kiện ban đầu bằng 0. 
  =  () =  ()  
  =  ( − )() 
Automatic Control Systems 6
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm
1. Ổn định BIBO (Bounded Input, Bounded Output):
Bỏ qua các điều kiện ban đầu, một hệ thống tuyến tính gọi là ổn định BIBO, hay
đơn giản là ổn định khi và chỉ khi với mọi đầu vào là tín hiệu bị chặn u(t) thì tín
hiệu đầu ra bị chặn
If | u(t) | < M < ¥ then | y(t) | < N < ¥
Automatic Control Systems 7
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm u(t) () y(t)   = ()
Xét biểu thức đáp ứng đầu ra: 
  =  ( − )() 
  = ∫ ( − )()  
≤ ∫ ( − ) ()   
 ()  ≤  < ∞ 
Automatic Control Systems 8
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm
2. Ổn định đầu vào không (hay ổn định tiệm cận)
Một hệ thống bất biến theo thời gian là ổn định đầu vào không,nếu với mỗi giá trị
xác định y(k)(t ), luôn tồn tại giá trị dương M, phụ thuộc vào y(k)(t ), sao cho 0 0
| y(t) | < M < ¥ for all t > t với   0
  = ∑ () () Và lim | y(t) | = 0 t® ¥
Automatic Control Systems 9
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH 4.1. Khái niệm u(t) () y(t)   = ()
Xét biểu thức đáp ứng đầu ra:   () =    ()
() ≤  ()   ()    
 () < ∞    < ∞  
Automatic Control Systems 10
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.2. Mối quan hệ giữa phương trình đặc tính và tính ổn định u(t) () y(t)   = ()
Xét biểu thức hàm truyền đạt: 
  =  () =  ()   
  =  () ≤  ()    
Automatic Control Systems 11
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.2. Mối quan hệ giữa phương trình đặc tính và tính ổn định
Vì  =  , với σ là phần thực của s, khi s được giả định là 1 cực của
G(s), G(s)=∞, thì phương trình trên trở thành: 
∞ ≤  ()   
Nếu có một hoặc nhiều nghiệm của phương trình đặc tính nằm bên phải mặt
phẳng phức, hoặc trên trục ảo, σ ≥ 0, khi đó  ≤  =   
∞ ≤      =     Vi phạm yêu cầu của ổn định BIBO  
Automatic Control Systems 12
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.2. Mối quan hệ giữa phương trình đặc tính và tính ổn định
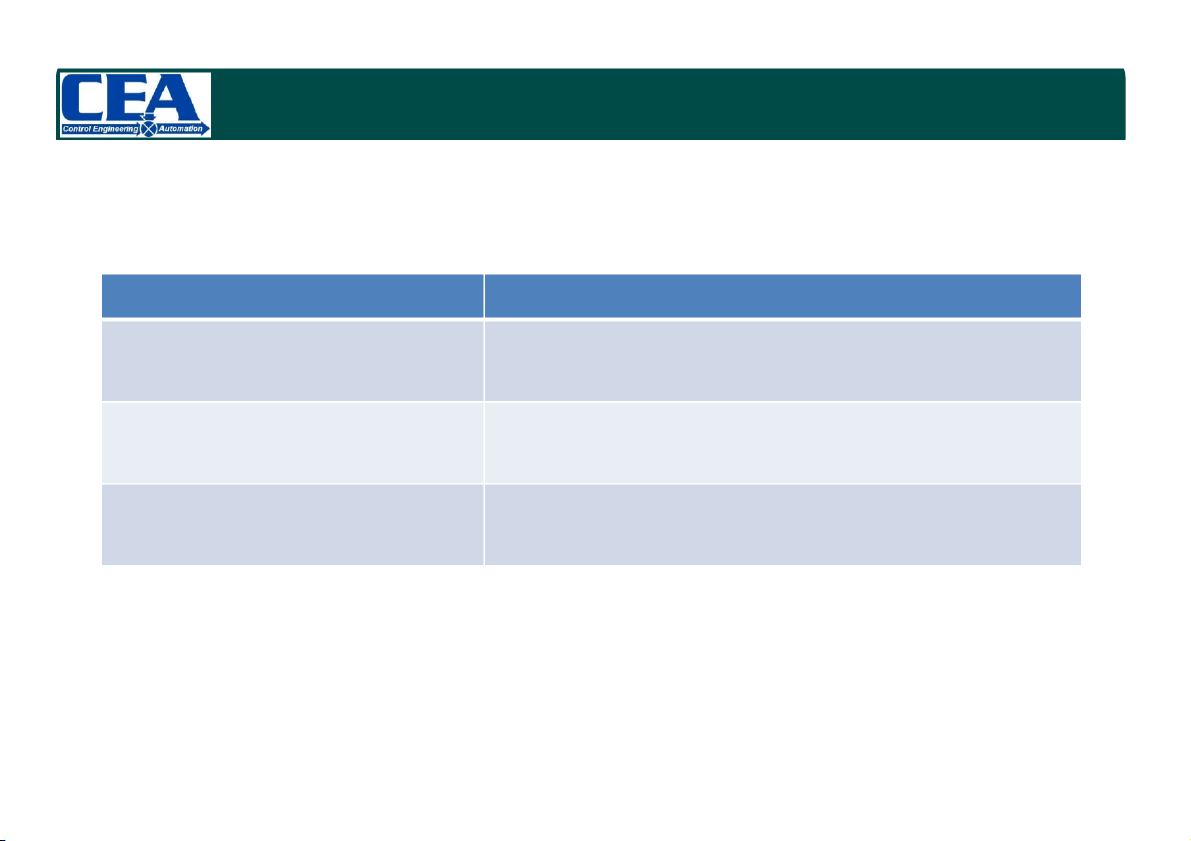
Điều kiện ổn định
Giá trị nghiệm của A(s) = 0
Ổn định tiệm cận hay ổn định |si| < 0 i=1,2…n (Tất cả các nghiệm nằm bên trái mặt phẳng phức) Giới hạn ổn định
Re(si)=0 với s là nghiệm đơn, và |s | < 0 i i i=1,2…n Không ổn định
 I thỏa:|s | > 0 hay Re(s )=0 với s i i i là nghiệm kép
Automatic Control Systems 13
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
Ví dụ: Xét tính ổn định của hệ thống có hàm truyền đạt sau 20 a.
  =  + 1)( + 2)( + 3 20 b.
  =  − 1)( + 2 + 2 20( − 1) c.   =  + 2)( + 4 10 d.
  =  +10)  +4  10 e.
  =  + 30 +  + 10
Automatic Control Systems 14
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định đại số: Routh-Hurwitz
Xét phương trình đặc tính của hệ thống
  =  +  + ⋯ +  +  = 0
Điều kiện hệ thống ổn định: Tất cả các nghiệm A(s) = 0 nằm bên trái mặt phẳng phức
Vấn đề: Nếu có một giá trị tham số không biết  không thể giải nghiệm
 Tiêu chuẩn Routh-Hurwitz
Automatic Control Systems 15
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz 4.3.1. Tiêu chuẩn Hurwitz
Xét phương trình đặc tính của hệ thống
  =  +  + ⋯ +  +  = 0 Điều kiện cần:
1. Tất cả các hệ số của phương trình phải có cùng dấu
2. Không có hệ số nào bị triệt tiêu Điều kiện đủ:
Tất cả các định thức Hurwitz đều dương
Automatic Control Systems 16
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Cách xác định định thức Hurwitz
Các định thức bậc i:         =   =         = 0  
Automatic Control Systems 17
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz 4.3.2. Tiêu chuẩn Routh
Xét phương trình đặc tính của hệ thống
  =  +  + ⋯ +  +  = 0 Điều kiện cần:
1. Tất cả các hệ số của phương trình phải có cùng dấu
2. Không có hệ số nào bị triệt tiêu Điều kiện đủ:
Tất cả các số hạng của cột đầu tiên của bảng Routh có cùng dấu
Số lần đổi dấu trong các số hạng ở cột đầu tiên bằng số nghiệm có phần thực dương.
Automatic Control Systems 18
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
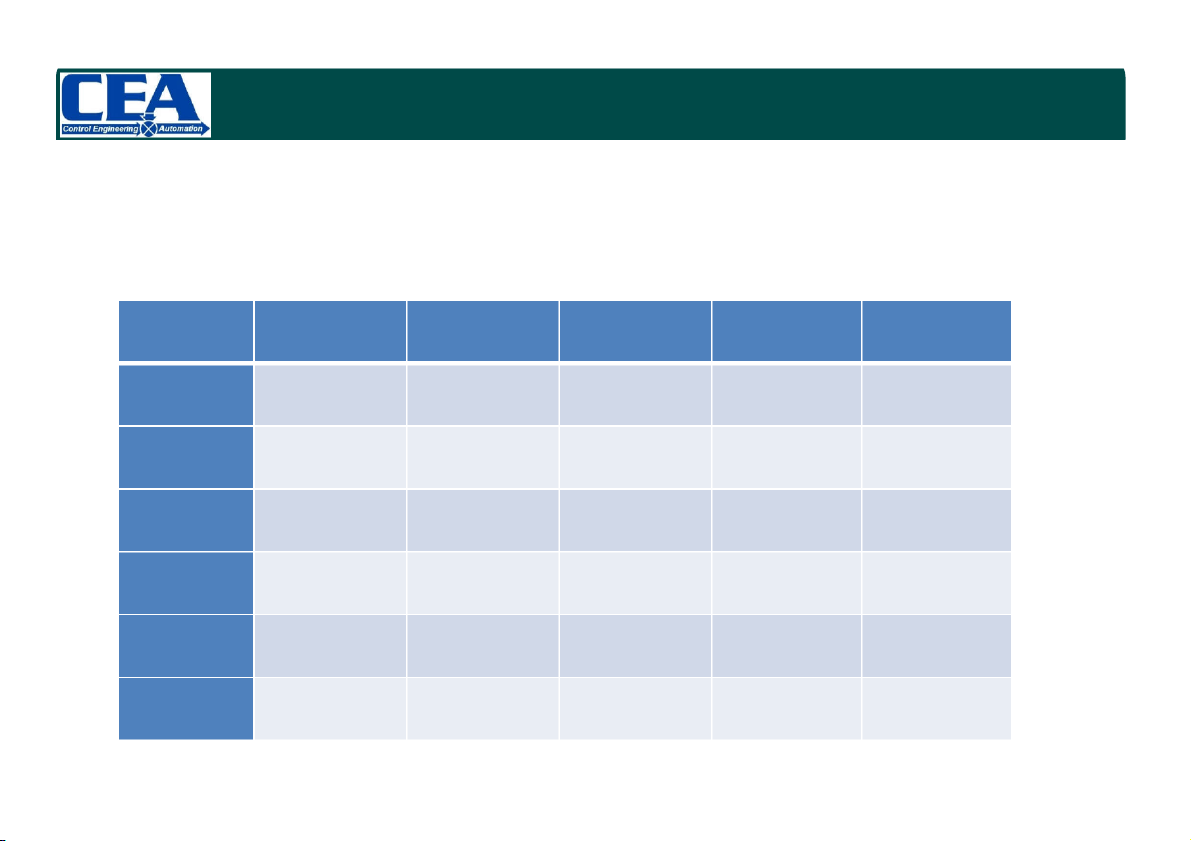
4.3. Tiêu chuẩn ổn định Routh-Hurwitz Cách lập bảng Routh sn a a a … a n n-2 n-4 0 sn-1 a a a … (a ) n-1 n-3 n-5 0 sn-2 c c c n-2,1 n-2,2 n-2,3 … s2 c c c … 2,1 2,2 2,3 s1 c c c … 1,1 1,2 1,3 s0 c0,1
Automatic Control Systems 19
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Quy tắc: Mỗi số hạng trong bảng Routh là một tỉ số trong đó:
• Tử số là định thức bậc 2, mang dấu âm. Cột thứ nhất của định thức là cột
thứ nhất của 2 hàng đứng sát trên hàng có số hạng đang tính; cột thứ 2
của định thức là cột đứng sát bên phải số hạng đang tính cũng của 2 hàng trên
• Mẫu số: Tất cả các số hạng trên cùng một hàng có cùng mẫu số là số hạng
của cột thứ nhất của hàng sát trên hàng có số hạng đang tính
Automatic Control Systems 20
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz Cách lập bảng Routh
• Cách tính các giá trị trong sn a a a … a bảng ma trận n n-2 n-4 0 sn- … a a a (a ) n-1 n-3 n-5 0 1 c c i 1  ,1 i 1  , j 1  sn- c c c n- n- n- 2
ci2,1 ci2, j 1  2,1 2,2 2,3 c   … i, j ci 1  ,1 s2 c c c … 2,1 2,2 2,3 s1 c c c … 1,1 1,2 1,3 s0 c0,1
Automatic Control Systems 21
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz Cách lập bảng Routh s6 a a a a 6 4 2 0 s5 a a a 0 5 3 1  −   −   −  × 0 s4 =  =  0    =    −   −   × 0 −  × 0 s3 0  =   =   = 0  −   −  × 0  × 0 −  × 0 s2 0  =   =   = 0  −  s1 0 0 0  =   −  × 0 s0 0 0 0 =  
Automatic Control Systems 22 
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Ví dụ: Xét tính ổn định của hệ thống có phương trình đặc tính
  =  +  + 3 +  +  = 0 s4 2 3 10 s3 1 5 0 1 × 3 − 2 × 5 s2 10 0 1 = −7 (−7) × 5 − 1 × 10 s1 0 0 −7 = 6,43 s0 10 0 0
Automatic Control Systems 23
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Các tính chất của bảng Routh
• Có thể nhân hoặc chia tất cả các số hạng trên cùng một hàng của bảng
Routh với một số dương.
• Số lần đổi dấu của các số hạng trong cột thứ nhất của bảng Routh bằng số
nghiệm của phương trình có phần thực dương.
• Nếu cột thứ nhất của bảng Routh có một số hạng bằng 0, thì hệ thống
cũng không ổn định. Để xác định số nghiệm âm, có thể thay số 0 bằng số
 >0 rất bé để tiếp tục xác định các số hạng còn lại.
• Nếu tất cả các số hạng trên cùng một hàng của bảng Routh bằng 0 thì hệ
thống ở biên giới ổn định.
• Trường hợp hệ có khâu trễ, có thể khai triển Fourrier hàm mũ
Automatic Control Systems 24
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Các trường hợp đặc biệt:
1. Trường hợp 1: Số hạng đầu tiên trên dòng nào đó của bảng Routh bằng 0
Xét phương trình đặc tính của hệ thống
  =  +  + 2 +  +  = 0 Lập bảng Routh s4 1 2 3 s3 1 2 0 s2  3 s1 (2-3)/ 0 s0 3 0
Automatic Control Systems 25
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Các trường hợp đặc biệt:
2. Trường hợp 2: Tất cả các số hạng trên cùng một dòng của bảng Routh bằng 0
 Phương trình đặc tính có ít nhất một cặp nghiệm cùng độ lớn nhưng trái dấu
 Phương trình đặc tính có một hoặc nhiều cặp nghiệm thuần ảo
 Phương trình đặc tính có các cặp nghiệm phức liên hợp đối xứng qua gốc tọa độ
Automatic Control Systems 26
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Ví dụ: Xét phương trình đặc tính của hệ thống
 +  + 8 + 8 +  +  = 0 Lập bảng Routh s5 1 8 7 s4 4 8 4 s3 6 6 0 s2 4 4 s1 0 0
 Lập phương trình phụ trợ sử dụng các hệ số của dòng s2 A(s) = 4s2 + 4 = 0 ( )
Automatic Control Systems 27
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH
4.3. Tiêu chuẩn ổn định Routh-Hurwitz
Vídụ: Xét phương trình đặc tính của hệ thống
 +  + 8 + 8 +  +  = 0
 Lấy vi phân phương trình phụ trợ theo s ()  = 8 = 0
 Thay thế dòng bằng 0 bằng các hệ số của phương trình dA(s)/ds = 0. S1 8 0 S0 4
Hệ thống ở biên giới ổn định, vì có 2 nghiệm thuần ảo
Automatic Control Systems 28
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH Bài tập
Xét tính ổn định của hệ thống có phương trình đặc tính sau
Automatic Control Systems 29
CHƯƠNG 4: TÍNH ỔN ĐỊNH CỦA HỆ THỐNG TUYẾN TÍNH Bài tập ứng dụng
Xác định K để hệ thống ổn định
 + 3 + ( + ) +  = 0
Automatic Control Systems 30