Chương 4 và 5 - Luật Dòng Điện và Từ Trường môn Vật lý đại cương 2 | Trường Đại học Bách Khoa Hà Nội

ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT Chương 4
NHỮNG ĐỊNH LUẬT CƠ BẢN CỦA DÒNG ĐIỆN KHÔNG ĐỔI
-----------------------------------------------------------------------------------------------------------------------
§4.1 NHỮNG ĐẠI LƯỢNG ĐẶC TRƯNG CỦA DÒNG ĐIỆN
§4.2 ĐỊNH LUẬT ÔM ĐỐI VỚI ĐOẠN MẠCH THUẦN ĐIỆN TRỞ §4.3 SUẤT ĐIỆN ĐỘNG
§4.4 ĐỊNH LUẬT KIRCHHOFF CHO MẠCH ĐIỆN
-----------------------------------------------------------------------------------------------------------------------
§4.1 NHỮNG ĐẠI LƯỢNG ĐẶC TRƯNG CỦA DÒNG ĐIỆN
1. Cường độ dòng điện
Cường độ dòng điện qua diện tích S là đại lượng có trị số bằng điện lượng chuyển qua diện tích ấy
trong một đơn vị thời gian.
Trong khoảng thời gian dt điện lượng chuyển qua diện tích S là dq ta có cường độ dòng điện qua diện tích đó là dq idt (4.1)
Đơn vị cường độ dòng điện là ampe (A). Cường độ dòng điện đặc trưng cho độ mạnh yếu của dòng
điện qua một điện tích cho trước.
2. Vector mật độ dòng điện
Mật độ dòng điện là đại lượng đặc trưng cho độ mạnh của dòng điện
tại một điểm của môi trường có
dòng điện chạy qua và cho biết phương và chiều của dòng điện.
Xét diện tích nhỏ dS tại điểm M và vuông góc với phương chuyển động của các điện tích qua diện n
tích ấy. Mật độ dòng điện tại điểm M là một vector có
+ Hướng: là hướng của điện tích dương qua M. + Độ lớn: dI jdS  (4.2)
dI là cường độ dòng qua Sn n . + Đơn vị: A/m2.
Từ (4.2) nếu biết J ta sẽ tính được I I  jdS (4.3) Nếu j = cons n t:  I  j dS jS (4.4) n n ĐÀO TUẤN ĐẠT 1
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT n
Đặt vector diện tíchdS là vector có độ lớn bằng dS và có hướng của vector pháp tuyến đơn vị dS dS.n
Khi đó với diện tích S bất kỳ ta có I  j.dS (4.5)
n là mật độ hạt tải điện S Gọi
, q là độ lớn điện tích của mỗi hạt, v là vận tốc trung bình của các hạt tải thì o j  n qv (4.6)
cùng phương cùng chiều với v o q > 0: j , .
q < 0: j cùng phương, ngược chiều với v .
§4.2 ĐỊNH LUẬT ÔM ĐỐI VỚI ĐOẠN MẠCH THUẦN ĐIỆN TRỞ
1. Định luật Ohm. Điện trở và điện trở suất
Xét một dây dẫn kim loại có dòng điện I chạy qua. Điện thế tạ hai đầu của đoạn dây là V1 và V2.
Thực nghiệm chứng tỏ rằng V V IR   (4.7) 1 2
R là điện trở của đoạn dây. (4.7) là biểu thức của định luật Ohm. Rl
Điện trở của một đoạn dây đồng chất tiết diện đều có chiều dài l là   (4.8) S
ρ là điện trở suất của chất làm dây, Sn n
là tiết diện vuông góc của dây.
2. Dạng vi phân của định luật Ohm dS Xét hai diện tích nhỏ cách nhau một khoảng dl. Gọi V và V + dV tại n
hai diện tích ấy. Theo định luật
Ohm cường độ dòng điện dI là V (V dV) dV dI R R    Rdl Mặt khác:   dS Suy ra n 1 dV 1 dV dI  dS .E.dS   (vì Edl )  dl    n n Ta có  dS   E dI 1 j E  (4.9)  n ĐÀO TUẤN ĐẠT 2
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT 1 Trong đó 
được gọi là điện dẫn suất của môi trường. Dưới dạng vector  j E (4.10)
Định luật Ohm dạng vi phân áp dụng được với mỗi điểm của dây dẫn. Tại mỗi điểm bất kỳ trong môi
trường mật độ dòng điện tỷ lệ thuận với cường độ điện trường tại điểm đó.
§4.3 SUẤT ĐIỆN ĐỘNG
1. Nguồn điện. Suất điện động của nguồn điện. Trường lạ
Xét hai vật dẫn A và B tích điện trái dấu. Nối giữa A và B bằng
một vật dẫn M các điện tích dương và âm chuyển động qua M tạo
thành dòng điện. Muốn duy trì dòng điện phải đưa điện tích dương
từ B về A (các điện tích âm từ A trở về B
) Vì lực điện trường ngăn .
cản chuyển động này nên lực có thể đưa điện tích dương dịch
chuyển ngược chiều điện trường phải là các lực phi tĩnh điện hay lực
lạ. Trường lực gây ra lực lạ gọi là trường lạ. Nguồn tạo ra trường lạ gọi là nguồn điện.
Suất điện động của nguồn điện đặc trưng cho độ mạnh của nguồn. A  (4.11) q
Gọi E và E *lần lượt là cường độ điện trường tĩnh và cường độ
trường lạ. Công tổng hợp trong sự dịch chuyển điện tích q một vòng quanh mạch kín là A Theo (4.11) E
Đối với điện trường tĩnh = 0 nên: E (4.12)
Suất điện động bằng công của lực lạ làm dịch chuyển một đơn vị điện tích một vòng quanh mạch kín của nguồn.
Nếu trường lạ chỉ tồn tại trên một đoạn s của mạch điện thì suất điện
động bằng công của lực lạ trong
sự dịch chuyển một đơn vị điện tích qua đoạn ấy. E  E .ds (4.13) S
2. Định luật Ohm đối với đoạn mạch có nguồn
Xét đoạn mạch AB có chứa nguồn với suất điện động E và điện trở trong r. Công suất tiêu thụ của
đoạn mạch là UABI. Trong đoạn mạch này công suất tiêu thụ của mạch dưới dạng tỏa nhiệt trên r, nhưng
đồng thời nguồn điện lại sinh ra công suất EI nên theo định luật bảo toàn năng lượng ta có: UABI = rI2 – EI ĐÀO TUẤN ĐẠT 3
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT UAB = rI – E (4.14)
(4.14) là công thức của định luật Ohm đối với đoạn mạch có nguồn.
Trong trường hợp tổng quát, ta có UAB = +rI + E (4.15) Với quy ước như sau:
Khi viết UAB nghĩa là chiều khảo sát từ A đến B.
I > 0 nếu chiều dòng điện cùng chiều khảo sát và ngược lại.
E > 0 nếu chiều khảo sát gặp cực dương của nguồn điện trước, gặp cực
âm của nguồn điện sau và ngược lại.
§4.4 ĐỊNH LUẬT KIRCHHOFF CHO MẠCH ĐIỆN 1. Các định nghĩa
- Nhánh: gồm một hoặc nhiều phần tử (điện trở, nguồn, máy thu…) mắc nối tiếp nhau (không có sự phân nhanh).
- Nút: chỗ nối của các đầu nhánh. Tại mối nút có dòng điện đi vào và có dòng điện đi ra.
- Đường đi giữa hai điểm: là một dãy các nhánh nối tiếp nhau bắt đầu ở một điểm và kết thúc ở điểm còn lại.
- Vòng kín: là đường đi mà điểm cuối trùng với điểm đầu.
2. Các định luật Kirchhoff
Định luật về nút
Tại mỗi nút tổng cường độ những dòng điện đi vào nút bằng tổng
cường độ những dòng điện đi ra khỏi nút. I1 + I3 + I5 = I2 + I4
Định luật về đường đi
“Hiệu điện thế giữa hai điểm cho trước của một mạch điện bằng
tổng đại số các hiệu điện thế giữa hai đầu của các nhánh liên tiếp
trên một đường đi của mạch điện nối liền hai điểm ấy.” ĐÀO TUẤN ĐẠT 4
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
Ví dụ với mạch điện trên ta có: UAM = UAC + UCD + UDM UAM = UAB + UBM
Biểu thức của U của các nhánh được xác định bởi (4.15)
Nếu áp dụng cho một vòng kín thì “Tổng đại số các hiệu điện thế giữa hai đầu điểm của các
nhánh liên tiếp trên một vòng kín của mạch điện bằng không.” Chương 5 TỪ TRƯỜNG
-----------------------------------------------------------------------------------------------------------------------
§5.1 TƯƠNG TÁC TỪ CỦA DÒNG ĐIỆN. ĐỊNH LUẬT AMPERE §5.2 TỪ TRƯỜNG
§5.3 TỪ THÔNG. ĐỊNH LUẬT GAUSS
§5.4 ĐỊNH LÝ AMPERE VỀ LƯU SỐ CỦA CƯỜNG ĐỘ TỪ TRƯỜNG §5.5 MẠCH TỪ §5.6 LỰC TỪ TRƯỜNG §5.7 CÔNG CỦA LỰC TỪ
§5.8 LỰC LORENTZ. CHUYỂN ĐỘNG CỦA HẠT TÍCH ĐIỆN TRONG TỪ TRƯỜNG ĐỀU
§5.9 BỘ LỌC VẬN TỐC. HIỆU ỨNG HALL
-----------------------------------------------------------------------------------------------------------------------
§5.1 TƯƠNG TÁC TỪ CỦA DÒNG ĐIỆN. ĐỊNH LUẬT AMPERE
1. Tương tác từ của dòng điện
Các tương tác giữa nam châm với nam châm, giữa nam châm với
dòng điện hoặc giữa hai dòng điện với nhau đều có chung một bản chất
và gọi là tương tác từ.
1. Định luật Ampere
Để đưa đến những kết quả định lượng về tương tác từ ta đi xét sự
tương tác giữa hai dòng điện. Nói chung lực tương tác giữa hai dòng điện
phụ thuộc cường độ dòng điện ình dạng của dây , h hoảng cách giữa hai , k
dây… Vì thế không thể xác định được tổng quát lực tác dụng giữa các
dòng điện bất kỳ. Ta chỉ có thể xác định định luật về tương tác giữa hai
phần tử dòng điện. Phần tử dòng điện là một đoạn dây rất ngắn có dòng ĐÀO TUẤN ĐẠT 5
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
điện (giống như điện tích điểm). Mỗi phần
tử dòng điện được biểu diễn bằng một
vector Idl nằm ngay trên phần tử dây dẫn,
có hướng của dòng điện và c ó độ lớn Idl.
Xét hai dòng điện có hình dạng bất kỳ,
nằm trong chân không, có cường độ I và I0.
Trên hai dòng điện đó lấy hai phần tử bất
kỳ Idl và Io odl . Ta đi xét lực tác dụng của
phần tử Idl lên phần tử Io odl .
Gọi r là vector vị trí hướng từ Idl tới
điểm M, nơi đặtIo odl . Lực từ do phần tử
dòng điệnIdl tác dụng lên phần tử Io odl
được xác định bằng định luật Ampere  dl x Idlxr o o 3 dF 4 r   (5.1)  trong đó 7 4o.10  
(H/m) được gọi là hằng số từ. Đặt vector n Idlx  r , vector dF có:
- Phương vuông góc mặt phẳng chứa phần tử Io odl và vector n .
- Chiều sao cho ba vector Idlo, n,dF theo thứ tự lập thành một tam diện thuận. - Độ lớn: d.I  Id  lsin dl sin o o o o F4 r  (5.2) 2 
Trong môi trường lực từ tăng lên μ lần so với trong chân không: d.I   Idlsin  dl  sin o o o o F4 r  (5.3) 2 
μ được gọi là độ từ thẩm của môi trường.
§5.2 TỪ TRƯỜNG 1. Định nghĩa
Từ trường là một dạng vật chất bao quanh dòng điện. Nếu đặt một dòng điện trong từ trường nó sẽ
chịu tác dụng của lực từ. Chính thông qua từ trường mà lực từ được
truyền từ dòng điện này tới dòng
điện khác với vận tốc hữu hạn và bằng vận tốc ánh sáng. ĐÀO TUẤN ĐẠT 6
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
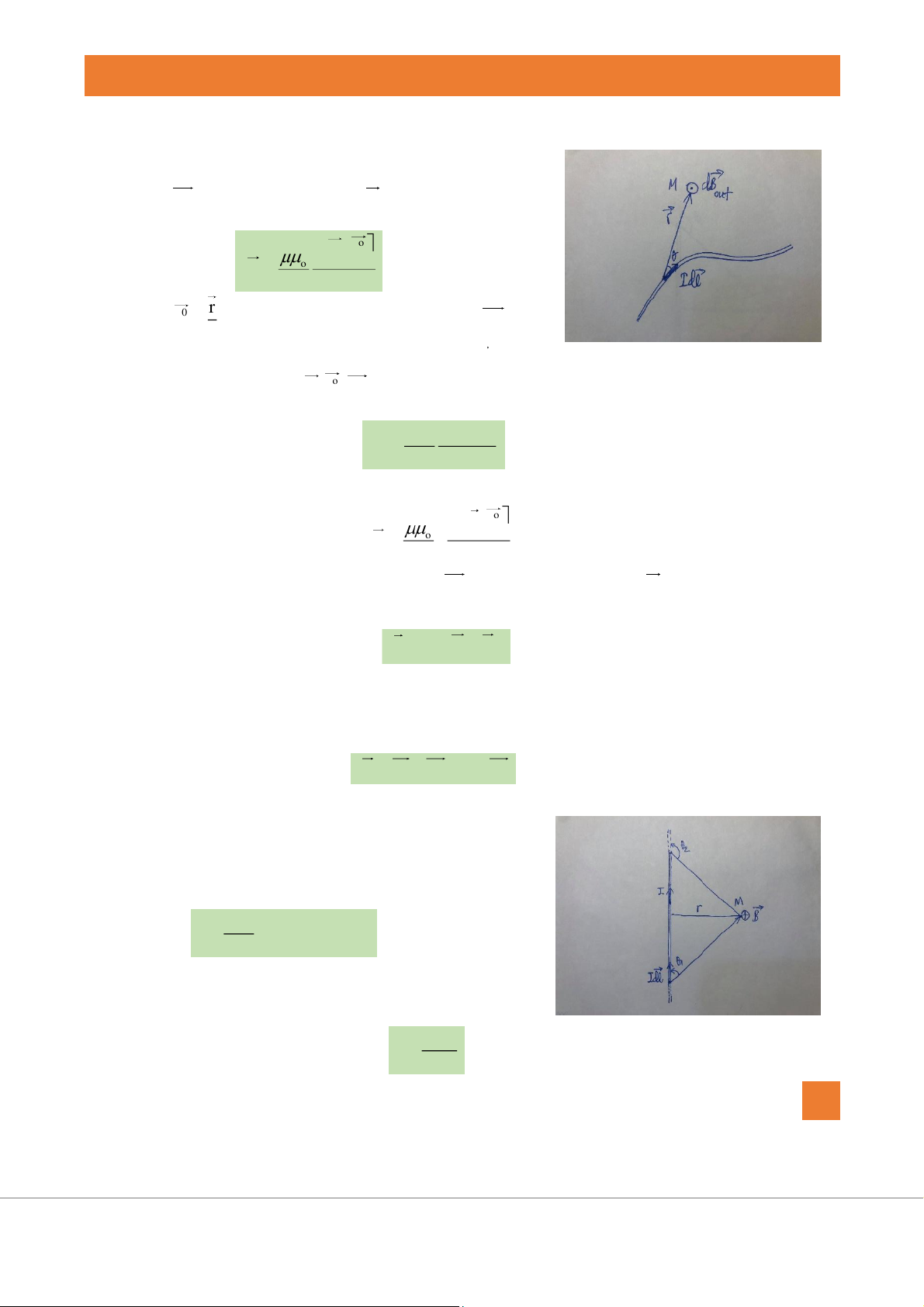
2. Cảm ứng từ của từ trường. Định luật Biot - Savart
Đại lượng đặc trưng cho từ trường về phương diện tác dụng
lực là cảm ứng từ. Cảm ứng từ là một đại lượng vector. Vector
cảm ứng từ dB do phần tử dòng điện Idl gây ra tại điểm M cách nó một khoảng r là: Idlxr 2 dB 4 r   (5.4) 
trong đó rr  là vector chỉ hướng đơn vị. Vector dB có
- Phương vuông góc với mặt phẳng chứa phần tử Idl và điểm M.
- Chiều sao cho ba vector Idl,r ,dB theo thứ tự hợp thành một tam diện thuận. - Độ lớn  Id  lsin o2 dB 4 r (5.5) 
Trên toàn bộ dòng điện: Idlxr 2 B4 r   (5.6) 
Định luật Biot - Savart cho ta xác định vector dB của phần tử dòng điện Idl gây ra tại M. Từ đó có
thể viết lại định luật Ampere:
dF I dl xdB (5.7) o o
3. Nguyên lý chồng chất từ trường và ứng dụng
Vector cảm ứng từ của nhiều dòng điện bằng tổng các vector cảm ứng từ của do từng dòng điện gây ra. B 1 B 2  B ..nB (5.8)
Cảm ứng từ của từ trường của dòng điện thẳng
Xét một đoạn dây dẫn thẳng có dòng điện I chạy qua. Cảm
ứng từ tại điểm M cách đoạn dây một khoảng r vuông góc với
mặt phẳng trang giấy, hướng từ phía trước ra phía sau trang
giấy và có độ lớn được xác định bởi:  o  1 2 B (c  o rs cos ) (5.9) 4
Nếu chiều dài dây dẫn lớn hơn rất nhiều khoảng cách r thì     1 2 0, , thay vào (5.9) ta có: I o B2   (5.10) r ĐÀO TUẤN ĐẠT 7
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
Cảm ứng từ của từ trường của dòng điện tròn
Xét một đoạn dây dẫn được uốn thành vòng tròn bán kính
R có dòng điện I chạy qua. Cảm ứng từ B của từ trường tại
điểm M nằm trên trục của vòng tròn và cách tâm vòng tròn
một khoảng h. Do tính đối xứng của các phần tử dòng điện
qua tâm O của vòng tròn, vector cảm ứng từ B tại điểm M
nằm trên trục của vòng tròn, có chiều là chiều tiến của cái vặn
nút khi ta quay nó theo chiều dòng điện, và có độ lớn được xác định bởi: o B IS  (5.11) 3 2 2 2 2 (  R h ) Với 2 S R  
là diện tích của dòng điện tròn.
Tại tâm của dòng điện (h = 0):  I o3 B2 R S  (5.12)
Momen từ của dòng điện tròn
Đại lượng đặc trưng cho tính chất từ của dòng điện tròn là momen từ của dòng điện Định nghĩa: . pmIS (5.13)
Slà vector diện tích nằm trên trục của dòng điện, có chiều là chiều tiến của cái vặn nút khi ta quay nó theo chiều dòng điện.  pm3 B  (5.13) 2 2 2 2(R h )
Như vậy vector momen từ cùng hướng với vector cảm ứng từ. Nó đặc trưng cho tính chất từ của dòng
điện tròn, cũng như các dòng điện kín khác.
Cảm ứng từ của hạt tích điện chuyển động
Cảm ứng từ của một hạt tích điện q, chuyển động với vận tốc v, tại điểm M cách điện tích một khoảng r được xác định bởi  qvxr  o2 B  q4 r (5.14) 
trong đó rr  là vector chỉ hướng đơn vị. Vector Bq có
- Phương vuông góc với mặt phẳng chứa phần tử vector và điểm M. - Chiều sao cho ba vector q
q theo thứ tự hợp thành một tam diện thuận. - Độ lớn ĐÀO TUẤN ĐẠT 8
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT  q vsin o2 d  B 4 r (5.15)
θ là góc giữa hai vector và r .
4. Cường độ từ trường
Cảm ứng từ phụ thuộc vào độ từ thẩm của môi trường. Vì vậy, nếu đi từ môi trường này sang môi trường
khác thì độ từ thẩm và cảm ứng từ sẽ thay đổi đột ngột. Vì thế định nghĩa cường độ từ trường tại một điểm H  (5.16) o
H không phụ thuộc tính chất của môi trường đặt dòng điện. Cường độ từ trường đặc trưng cho từ trường
về phương diện tác dụng lực và không phụ thuộc vào tính chất của môi trường.
§5.3 TỪ THÔNG. ĐỊNH LUẬT GAUSS
1. Đường cảm ứng từ
Đường cảm ứng từ là đường cong mà tiếp tuyến tại mỗi điểm trùng với phương của vector cảm ứng
từ B tại điểm đó, chiều của đường cảm ứng từ là chiều của vector B .
Tập hợp các đường cảm ứng từ là từ phổ.
Quy ước vẽ số đường cảm ứng từ qua một đơn vị diện tích đặt vuông góc với phương của từ trường
tỷ lệ với độ lớn B của cảm ứng từ.
Đường cảm ứng từ là những đường cong kín nên từ trường là một trường xoáy. 2. Từ thông
Trong từ trường, ét diện tích d x
S nhỏ sao cho cảm ứng từ B tại mọi
điểm trên dS không đổi. Khi đó từ thông gửi qua d S là: d  B.dS (5.1) d  BdScos
Từ thông qua diện tích S là:    d B.dS  (5.2) S S
3. Định luật Gauss
Ta đi tính từ thông qua một mặt kín S bất kỳ. Xét một mặt kín S. Vì
các đường cảm ứng từ là khép kín, nên số đường đi vào mặt kín bằng số
đường đi ra khỏi mặt kín. Kết quả là từ thông ứng với các đường đi vào
mặt kín bằng từ thông ứng với các đường đi ra khỏi mặt kín:    vào ra ĐÀO TUẤN ĐẠT 9
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
Từ thông ứng với các đường cảm ứng từ đi vào mặt kín là âm vì góc  là góc tù 1
. Từ thông ứng với các đường cảm ứng từ ra
khỏi mặt kín là dương góc 2 là góc nhọn. Vậy     vào ra
Vậy từ thông toàn phần gửi qua mặt kín là    vào   ra 0  (5.3)
(5.3) là định luật Gauss đói với từ trường. “Từ thông toàn
phần gửi qua một mặt kín bất kỳ bằng không. ”
Trong giải tích người ta chứng minh được rằng
Trong đó V là thể tích giới hạn bởi mặt kín S. Vì vậy, theo (5.3) ta có biểu thức định luật Gauss dạng vi phân: divB 0 (5.4)
§5.4 ĐỊNH LÝ AMPERE VỀ LƯU SỐ CỦA CƯỜNG ĐỘ TỪ TRƯỜNG
1. Lưu số của cường độ từ trường
Định luật Gauss nói lên tính chất xoáy của từ trường, tính chất quan trọng nhất của từ trường. Tính
chất xoáy của từ trường còn được thể hiện trong định lý Ampere về dòng điện toàn phần.
Xét một đường cong kín L bất kỳ trong một từ trường bất kỳ. Gọi
dl là dịch chuyển nhỏ trên đường
cong, H là cường độ từ trường trên đoạn ấy. Theo định nghĩa: Lưu số của vector H dọc theo đường cong kín đó là  (5.5)
Được gọi là lưu số của vector H dọc theo L.
2. Định lý Ampere về dòng điện toàn phần
“Giá trị của lưu số H dọc theo một đường cong kín bất kỳ (một vòng) bằng tổng đại số cường độ
của các dòng điện xuyên qua diện tích giới hạn bởi đường cong đó.” (5.6) trong đó Ii
 0 nếu dòng điện thứ i nhận chiều dịch chuyển trên đường cong làm chiều quay thuận
xung quanh nó (I có chiều sao cho H cùng chiều với dl ). I 0 i
nếu dòng điện thứ i nhận chiều dịch
chuyển trên đường cong làm chiều quay nghịch. ĐÀO TUẤN ĐẠT 10
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT Chứng minh
Trong trường hợp đơn giản,
chọn L nằm trong mặt phẳng
vuông góc với dòng điện thẳng
dài vô hạn. Cường độ từ trường
của dòng điện thẳng dài là Hr I  . Thay vào (5.5) ta có 2   Vì dlcos rd  nên (5.7)
+ Trường hợp đường cong L bao quanh I: (5.8)
+ Trường hợp đường cong L không bao quanh I, ta chia đường cong thành hai đoạn AMB và BNA, ta có:  .dl cos H .d  l cos H r d H r d 1 1 2 2 2 = 1 1 1 2 2 2 = Δφ – Δφ = 0 (5.9) MNA AMB N B A
+ Trường hợp tổng quát từ trường gây bởi dòng điện có hình dạng bất
kỳ, đường cong L có dạng bất kỳ các biểu thức (5.8), (5.9) vẫn đúng. Chú ý
Nếu đường cong bao quanh dòng điện nhiều vòng phải chú ý đến dấu của dòng điện. Chẳng hạn: Hình a) 2I Hình b) 0 3. Ứng dụng
Định lý Ampere về dòng điện toàn phần cho phép ta tính được nhanh chóng cường độ từ trường của một số dòng điện.
- Cường độ từ trường tại một điểm bên trong cuộn dây hình xuyến gồm , có dòng điện I n vòng chạy qua là HnI M  (5.10) 2 R 
- Cường độ từ trường tại một điểm bên trong một ống dây điện
thẳng dài vô hạn có dòng điện I chạy qua là HnI M  = n0I (5.11) 2 R  trong đó o n = s dâ ố vòng y/chiều dài ống. ĐÀO TUẤN ĐẠT 11
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
§5.5 MẠCH TỪ
Mạch từ là một tập hợp các vật hoặc các miền không gian trong đó
tập trung từ trường, nghĩa là ngoài miền đó từ trường có cường độ nhỏ không đáng kể.
Trong các máy điện, dụng cụ điện từ mạch từ đống vai trò quan trọng.
Xét một mạch từ không phân nhánh. Từ thông qua tiết diện bất kỳ
của mạch đều bằng nhau. Áp dụng định lý về dòng toàn phần cho
đường cong kín L với n là số vòng dây xuyên qua diện tích của
đường cong L, I là cường độ dòng điện. ta có nI Suy ra nI HL (5.12)
Cảm ứng từ B của mạch là 0 nI B   H  L (5.13) 0
Từ thông qua một tiết diện của mạch là  nIS nI 0  B  .S 1 L   L.S  0 Em  (5.14) Rm E 1 L
m = nI (5.15) suất từ động và Rm =  .S (5.16) là từ trở của mạch từ. (5.14) là định luật Ohm 0 đối với mạch từ.
Nếu mạch từ gồm nhiều đoạn nối tiếp nhau thì từ trở toàn phần của mạch là:
Rm = R1 + R2 + …. + Rn (5.17)
Nếu mạch từ gồm nhiều nhánh rẽ mắc song song thì từ trở toàn phần của mạch là: 1 1 1 1    . . (5.18) R R 1 2R n R m ĐÀO TUẤN ĐẠT 12
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
§5.6 LỰC TỪ TRƯỜNG 1. Lực Ampere
Lực từ do từ trường B tác dụng lên phần tử dòng điện
Idl tuân theo định luật Ampere: dF Id  lx B (5.19)
- Phương: vuông góc với mặt phẳng (Idl,B)
- Chiều: sao cho ba vector Idl,B,dF theo thứ tự lập
thành một tam diện thuận. - Độ lớn: dF B  .Idl.sin (5.20)
Lực từ này gọi là lực Ampere. Để xác định chiều của lực Ampere có thể dùng quy tắc bàn tay trái.
2. Lực tác dụng tương hỗ giữa hai dòng điện thẳng song song dài vô hạn Lực từ do dòng I I
1 tác dụng lên đoạn dây có chiều dài L của 2 hoặc
ngược lại có độ lớn là: o1 2I I F L (5.21) 2 d 
(Đầu tiên xác định hướng và độ lớn của B1 do dòng I1 g ây ra tại nơi
đạt dòng I2. B1 như nhau trên suốt chiều dài L của dây dẫn có dòng I2.
Sau đó dùng định luật Ampere để xác định lực từ F12 do từ trường B 1
tác dụng lên I2. Tương tự như vậy xác định được lực từ F21 do dòng I2
tác dụng lên đoạn dây chiều dài L của dòng I1.)
3. Lực từ của từ trường đều tác dụng lên
một mạch điện kín
Xét một khung dây hình chữ nhật ABCD có
các cạnh a, , có dòng điện I chạy qua. Khung b
được đặt trong từ trường đều B có phương
vuông góc với các cạnh AB và CD Giả sử .
khung rất cứng và chỉ có thể quay quanh trục Δ
cố định. Ban đầu mặt phẳng khung không
vuông góc với B mà B tạo với pháp tuyến n
của mặt phẳng khung góc θ.
Áp dụng định luật Ampere ta có - Các lực từ F F
3 và 4 triệt tiêu lẫn nhau và không tạo ra moment quay. ĐÀO TUẤN ĐẠT 13
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT - Các lực 1F và 2
F vuông góc với các cạnh của khung tạo thành một ngẫu lực. F F  BIa 1 2
Moment của ngẫu lực có độ lớn
µ = F.d = F.bsinθ = BIa.bsinθ = BI.S.sinθ = B.pm.sinθ
trong đó pm là moment từ của dòng điện ( pm  IS ). Dưới dạng vector
 pmxB (5.22)
Khi khung quay một góc dθ, công của ngẫu lực từ: dA   d   pmBsni d
Công của ngẫu lực khi khung quay từ vị trí góc ban đầu θ tới vị trí cân bằng θ = 0 là: 0 A         m p Bsin d pmB(1 cos ) (5.23) 
Công này bằng độ giảm năng lượng của khung dây : W ( )W (0) p  B(1 c  os )   p  Bcos  (  p  Bcos0) m m m m m
Dưới dạng này ta thấy ngay biểu thức năng lượng của khung trong từ trường là: E( )   p  Bcos m m  hay  Emp  m(.) B (5.24)
Kết quả này cũng đúng cho với mạch điện kín có hình dạng bất kỳ.
§5.7 CÔNG CỦA LỰC TỪ
Khi dòng điện chuyển động trong từ trường lực từ tác dụng lên dòng điện sẽ sinh công. Để tính công
của lực từ ta xét một thanh kim loại MN dài L có thể trượt trên hai dây kim loại song song nằm ngang.
Mạch điện nằm trong một từ trường đều và vuông góc với cảm ứng từ B.
Lực từ tác dụng lên đoạn dây là: F = BIL
Công của lực từ trong dịch chuyển nhỏ dx của dây là: dA = Fdx = BILdx = BIdS
dS = Ldx là diện tích quét bởi dây MN trong chuyển dời dx. Từ thông qua dS là: ĐÀO TUẤN ĐẠT 14
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT  d  BdS Vậy: dA = Idϕ (5.25)
Nếu thanh dịch chuyển một đoạn hữu hạn từ vị trí đến vị trí 2 và coi cường độ dòng điện I không đổi. 2 2 1
A 2 dA Id I  (5.26) 1 1
Δϕ là từ thông gửi qua diện tích quét 1 S 2 Gọi  ,12 
là từ thông gửi qua diện tích mạch điện ứng với các vị trí 1 và 2 của dây MN:  A I( ) (5.27) 12 2 1
Công thức trên đúng cho trường hợp tổng quát (mạch điện kín bất kỳ và từ trường bất kỳ).
§5.8 LỰC LORENTZ. CHUYỂN ĐỘNG CỦA HẠT TÍCH ĐIỆN
TRONG TỪ TRƯỜNG ĐỀU 1. Lực Lorentz
Một hạt mang điện tích q, chuyển động với vận tốc v tương đương với một phần tử dòng điện Idl thỏa mãn điều kiện: Idl  dl qv t
Theo định luật Ampere, lực từ tác dụng lên Idl là: dF Id  lx  B
Vậy lực từ tác dụng lên hạt chuyển động là:      L F qvxB (5.28)
Đặc điểm của lực Lorentz:
- Phương: vuông góc với mặt phẳng v,  B - Chiều: sao cho qv,B, L
F theo thứ tự hợp thành một tam diện thuận. - Độ lớn: L F q  vBsin (5.29)
2. Chuyển động của hạt tích điện trong từ trường đều ĐÀO TUẤN ĐẠT 15
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
Ta khảo sát chuyển động của điện tích q, giả sử q > 0, trong từ
trường đều cảm ứng từ B. Trước hết ta nhận xét rằng lực Lorentz
không sinh công vì luôn vuông góc với vector vận tốc của điện tích.
Do đó động năng và độ lớn của vận tốc của điện tích không thay đổi. Xét trường hợp v B
Biểu thức của lực Lorentz: fLqvB
Lực Lorentz đóng vai trò của lực hướng tâm: 2 mv mv qvB R    (5.30) R qB Vậy án kính quỹ đạo b của điện t
ích tỷ lệ với động lượng của hạt và t
ỷ lệc nghịch với cảm ứng từ B của từ trường.
Chu kỳ của chuyển động:  2 2 TvqB R m  (5.31)
§5.9 BỘ LỌC VẬN TỐC. HIỆU ỨNG HALL Bộ lọc vận tốc
Bây giờ chúng ta hãy xét một cấu hình của điện trường và từ trường được dùng như một cái lọc lựa
tốc độ đối với các hạt tích điện. Giả sử trong một vùng không gian có tồn tại một điện trường và một từ
trường vuông góc với nhau. Lực tác dụng lên hạt tích điện chuyển động trong vùng này là F qE  q (5.32)
Trong trường hợp được minh họa trên hình vẽ đối với hạt tích điện dương, có một vận tốc đặc biệt để
lực lực điện hướng lên trên cân bằng với lực từ hướng xuống dưới. Đối với các hạt tích điện âm cũng với
vận tốc đó, thì hướng của hai lực điện và từ đều đảo ngược lại và lực tổng hợp cũng sẽ bằng không. Như
vậy các hạt tích điện có vận tốc này khi đi qua vùng có trường sẽ không bị lệch. Vì lực từ phụ thuộc vào
vận tốc của hạt, còn lực điện thì không nên lực tổng hợp sẽ không bằng không đối với các hạt có vận tốc
khác. Đối với hạt tích điện có vận tốc lớn hơn, lực từ sẽ có độ lớn lớn hơn lực điện. Các hạt tích điện
dương với vận tốc lớn hơn đó sẽ bị lệch xuống dưới. Tương tự các hạt tích điện dương chuyển động
chậm hơn sẽ bị lệch lên trên.
Giá trị của vận tốc “được lọc lựa” nhận được bằng cách đòi hỏi lực tổng hợp trong phương trình 5.32 bằng không.
Lấy độ lớn của biểu thức trên, ta xác định được tốc độ của hạt tích điện đi qua bộ lọc lựa mà không bị lệch: v = E/B (5.33)
Cái lọc lựa vận tốc được dùng trong các dụng cụ như khối
phổ kế và trong các thí nghiệm như thí
nghiệm Thomson. Một cái lọc lựa vận tốc “tự nhiên” hoạt động trong một hiệu ứng quan trọng trong các
vật dẫn có tên là hiệu ứng Hall. Hiệu ứng Hall ĐÀO TUẤN ĐẠT 16
ĐẠI HỌC BÁCH KHOA HÀ NỘI – VẬT LÝ II – ĐÀO TUẤN ĐẠT
Ta hãy xét một đoạn dây dẫn có dòng điện chạy qua đặt tr
ong một từ trường đều. Với chiều dòng
điện theo hướng dương của trục x, các hạt tải điện dương sẽ chuyển động theo hướng đó và các h ạt tải
điện âm theo hướng ngược lại. Cả hai loại điện tích này đều bị từ trường làm cho lệch về phía mặt dưới
của dây dẫn. Bây giờ, ta giả sử rằng trong vật dẫn chỉ có mặt các hạt tải điện dương, khi đó mặt dưới
sẽ tích điện dương và mặt trên tích điện âm vì thiếu điện tích dương. Sự tách biệt này sẽ tạo ra trong
vật dẫn một điện trường, như được thấy trên hình. Trong trường hợp ở trạng thái ổn định, thành phần
điện trường E - được gọi là điện trường Hall - tác dụng một lực điện lên các hạt tải điện đang chuyển
động có xu hướng làm cân bằng với
lực từ tác dụng bởi cảm ứng từ B. Về trung bình, điện trường và
từ trường bắt chéo này có tác dụng như một
cái lọc lựa tốc độ với tốc độ trôi vd.
Ta hãy xét một hạt có điện tích q chuyển động với vận tốc trôi v = vx. Mật độ dòng J trong vật dẫn bằng: J = nqv
Cân bằng lực điện trường và lực từ trường ta có E = v B
Nhân hai vế phương trình trên với mật độ các hạt tải điện và dùng hệ thức J = nqv, ta có nqE = nqv B = JB hay JB Enq  (5.34) Vậy E tỷ lệ với J
B và hệ số Hall chính là hệ số tỷ lệ HE 1 RJB n  q  (5.35)
Chú ý rằng hệ số Hall có giá trị dương tương ứng với giả thiết của chúng ta cho rằng các hạt tải điện
là dương. Bạn cũng có thể chứng minh được rằng hệ số Hall sẽ đảo dấu nếu tất cả các hạt tải tích điện
âm. Như vậy, hệ số Hall cho ta thông tin về dấu điện tích của các hạt tải điện. Vì E phụ thuộc vào B, nên
cũng lưu ý rằng hiệu ứng Hall có thể được dùng để xác định từ trường trong vùng bằng cách đo điện
trường Hall trong một vật dẫn đã được định cỡ trước. ĐÀO TUẤN ĐẠT 17