




































Preview text:
Chương 5
LÝ THUYẾT ỔN ĐỊNH LYAPUNOV HỆ PHI TUYẾN 1 Nội dung chương 5 1. Định nghĩa
2. Hàm Lyapunov và định lý ổn định
3. Phương pháp Krasovski tìm hàm Lyapunov
4. Ổn định Lyapunov đối với hệ thống tuyến nh hóa 2 HỆ PHI TUYẾN 2 1. Định nghĩa
Cho hệ thống MIMO phi tuyến biểu diễn bởi phương trình trạng thái không autonom:
x f ( , x u) (*) y ( h , x u)
Định nghĩa 1 (BIBO): Hệ thống được gọi là có tính ổn định BIBO
(Bounded Input Bounded Output), nếu với tín hiệu vào u(t) bị chặn thì
tín hiệu ra y(t) cũng bị chặn
u(t) y(t)
liên quan đến tác động từ tín hiệu vào đến hệ thống HỆ PHI TUYẾN 3 1. Định nghĩa
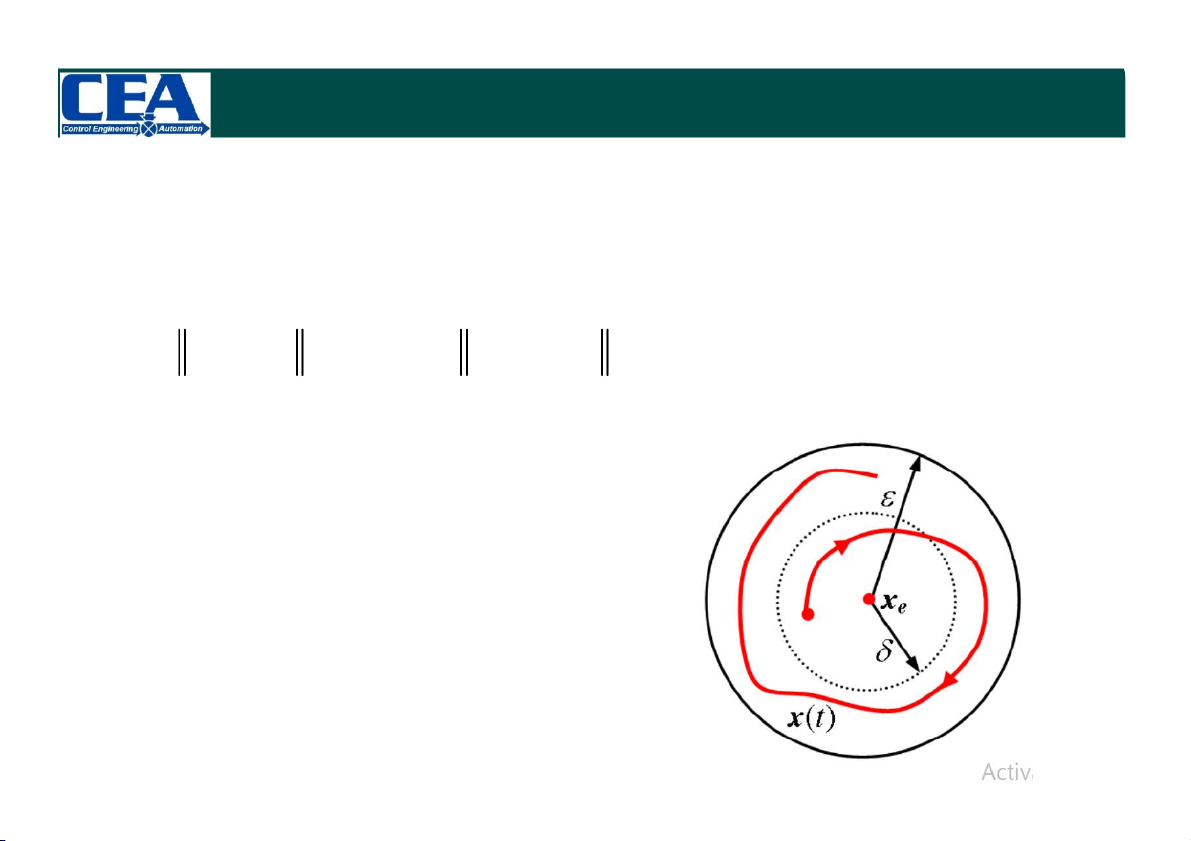
Định nghĩa 2 (Lyapunov): Hệ thống được gọi là ổn định Lyapunov,
hay còn gọi là ổn định tại điểm cân bằng xe nếu với , t0 >0 bất kỳ, bao
giờ cũng tồn tại (, t0 ) sao cho nghiệm x(t) của (*) với x(0) = x0 thỏa mãn: x x (
x t) x , t t 0 e e 0
Nghĩa là nếu cho trước lân cận của
xe thì phải tồn tại một lân cận cũng
của xe sao cho mọi quỹ đạo trạng thái
tại thời điểm t0 đi qua điểm x0 thuộc
lân cận sẽ nằm hoàn toàn trong lân cận . HỆ PHI TUYẾN 4 1. Định nghĩa
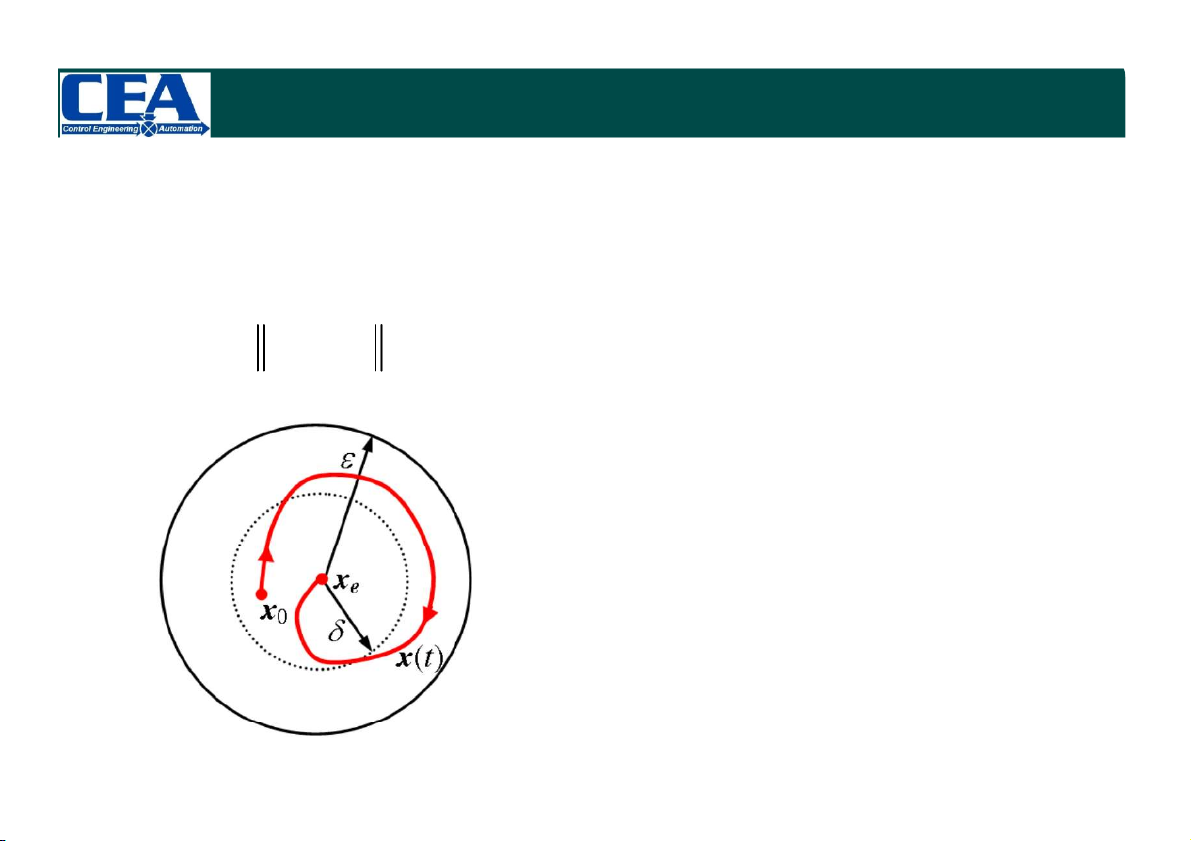
* Hệ thống được gọi là ổn định tiệm cận Lyapunov tại điểm cân bằng xe
nếu với , t >0 bất kỳ, bao giờ cũng tồn tại 0
(, t0 ) sao cho nghiệm x(t)
của (*) với x(0) = x0 thỏa mãn:
x x lim x(t)=x 0 e e t
Nếu biểu thức trên đúng với mọi x0
thì được gọi là ổn định tuyệt đối tại xe HỆ PHI TUYẾN 5 1. Định nghĩa Tính chất
- Do hệ phi tuyến có nhiều điểm cân bằng -> tính ổn định gắn với điểm cân bằng.
- Hệ phi tuyến có thể ổn định tại điểm cân bằng này nhưng không ổn
định tại điểm cân bằng khác
- Đối với hệ tuyến tính: đã ổn định tại điểm cần bằng nào đó thì ổn
định với mọi điểm cân bằng khác HỆ PHI TUYẾN 6
2. Hàm Lyapunov và định lý ổn định 2.1. Hàm Lyapunov
Xét hệ phi tuyến autonom không có tín hiệu vào, có điểm cân bằng
tại gốc tọa độ xe = 0 x f ( , x u) f ( ) x u 0
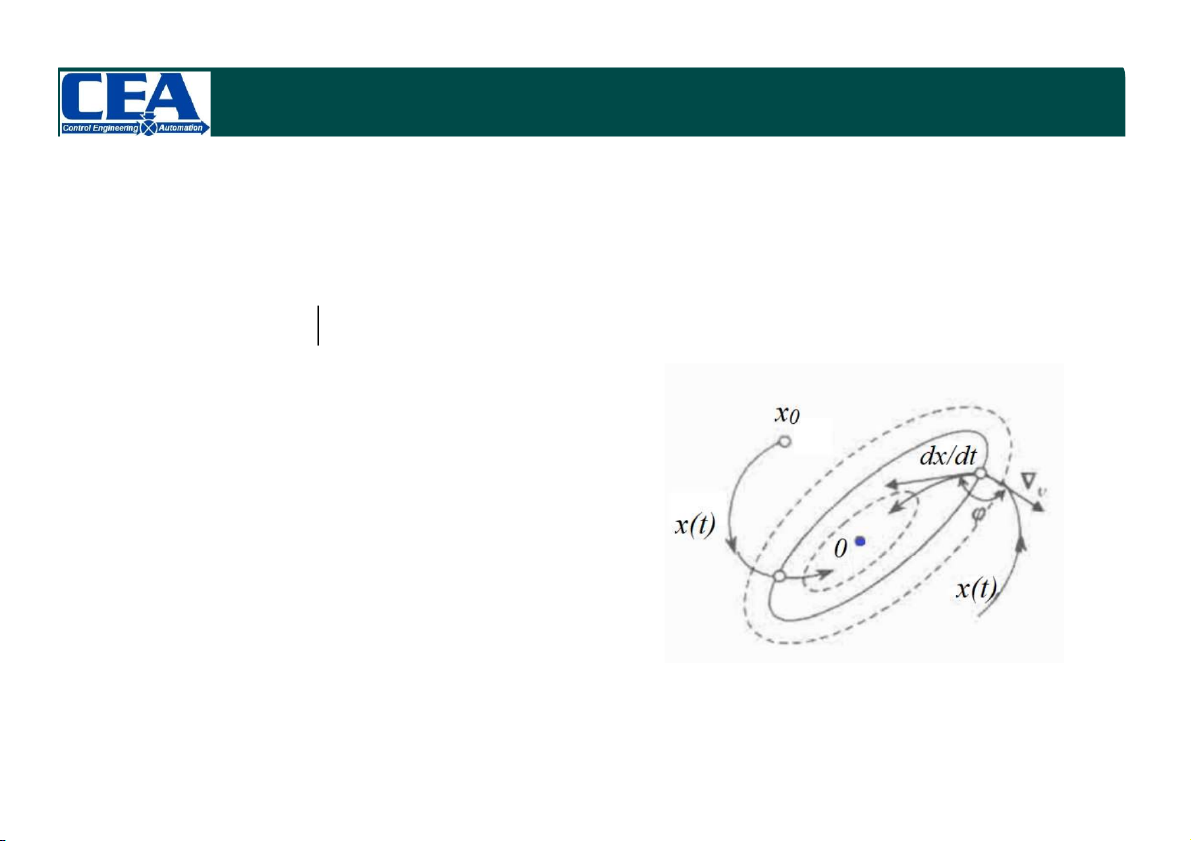
- Giả sử ta có hệ các đường cong
khép kín bao quanh gốc tọa độ trong mặt phẳng pha.
- Xét nghiệm x(t) của phương trình vi
phân ở trên xuất phát từ trạng thái
đầu x0, khi t biến thiên tạo nên quỹ đạo pha.
- Nếu x(t) cắt mọi đường cong
theo hướng từ ngoài vào trong ->
x(t) sẽ tiến về 0 -> hệ ổn định theo định nghĩa Lyapunov. HỆ PHI TUYẾN 7
2. Hàm Lyapunov và định lý ổn định
2.2. Định lý ổn định Lyapunov
Xét hệ phi tuyến autonom không có tín hiệu vào, có điểm cân bằng tại
gốc tọa độ xe = 0
x f (x,u) f (x) u0
Nếu tồn tại hàm V(x) sao cho trong miền D chứa điểm cân bằng thỏa: V
(x) 0,x D \ 0 V ( ) 0 0
V(x) 0,xD
thì hệ thống ổn định Lyapunov tại điểm 0.
* Nếu tồn tại hàmV(x) 0,x 0 thì ổn định tiệm cận Lyapunov tại điểm 0.
* Hàm V(x) được gọi là hàm Lyapunov, thường chọn là hàm toàn phương
của các biến trạng thái.
Nếu không tìm được hàm V(x) thỏa mãn các điều kiện trên
-> chưa thể kết luận tính ổn định Lyapunov HỆ PHI TUYẾN 8
2. Hàm Lyapunov và định lý ổn định
Định lý ổn định Lyapunov (2)
Xét hệ phi tuyến autonom không có tín hiệu vào, có điểm cân bằng
tại gốc tọa độ xe = 0
x f (x,u) f (x) u0
Nếu tồn tại hàm V(x) sao cho trong miền D chứa điểm cân bằng thỏa: V
(x) 0,x D \ 0 V (0) 0
V(x) 0,x D
Thì hệ thống không ổn định Lyapunov tại điểm 0. HỆ PHI TUYẾN 9
2. Hàm Lyapunov và định lý ổn định Ví dụ 1:
Xét ổn định của hệ thống sau: x x ax 2 2 x x d 2 1 1 2 dt x ax , a 0 2 2 x x 1 2 1 2 Giải
Hệ thống có điểm cân bằng x e T 0 0 V
(x) 0,x D \ 0 Chọn hàm Lyapunov 2 2
V (x) x x ta có 1 2 V ( ) 0 0 Tính T (x) (x) x ax x 2 2 x x dV V d 2 1 1 2 2 x x 1 2 dt x dt x ax 2 2 x x 1 2 1 2 dV (x) 2
ax x 2 2 2 0, x 0,x 0 1 2 1 2 dt
Hệ ổn định tiệm cận Lyapunov HỆ PHI TUYẾN 10
2. Hàm Lyapunov và định lý ổn định Ví dụ 2:
Xét ổn định của hệ thống sau: x x x 2 4 x x d 2 1 1 2 dt x x 2 4 x x 1 2 1 2
Xác định điểm cân bằng của hệ thống và đánh giá tính ổn định tại điểm cân bằng. Giải
Trạng thái cân bằng là nghiệm của phương trình
x x x 2 4 x x 0 1 2 1 1 2 x 0 1e 2 4 x x x x x x 0 0 2e 2 1 2 1 2 Chọn hàm Lyapunov 2 2 V ( )
x x x có V(0) = 0 và V(x) >0 1 2 T V( ) x 2 x x x x
2 x x x x 1 2 1 2 1 1 1 2 V( ) x 2 2 x x 2 4 x x 0, x 0 1 2 1 2
Hệ không ổn định Lyapunov HỆ PHI TUYẾN 11
2. Hàm Lyapunov và định lý ổn định Ví dụ 3:
Xét ổn định của hệ phi tuyến sau 3
dx x 2x x 1 1 2 dt x 2 Giải
Hệ phi tuyến có điểm cân bằng tại xe=(0 0)T. Chọn hàm Lyapunov 2 2 V ( )
x x x có V(0) = 0 và V(x) >0. 1 2 Ta có V( )
x 2 x x x x 2 2 x 2 1 2x x 2 2x 1 1 1 2 1 1 2 2
Để hệ thống ổn định Lyapunov tại 0 thì 2 1 2x x 0 (*) 1 2
hay nói cách khác, quỹ đạo trạng thái phải
xuất phát từ một điểm bên trong miền D
thỏa mãn điều kiện (*) ở trên. Việc chọn hàm Lyapunov
liên quan đến miền ổn định HỆ PHI TUYẾN 12
2. Hàm Lyapunov và định lý ổn định Bài tập:
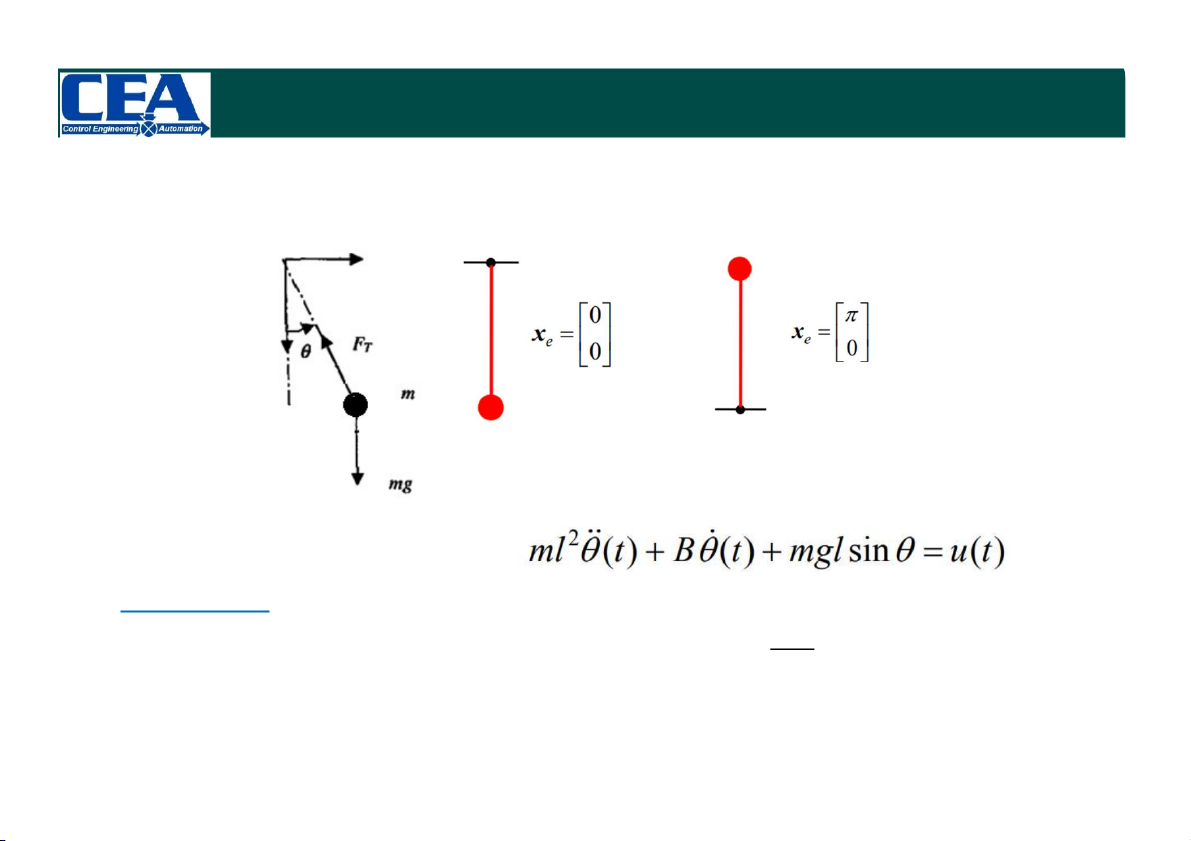
Xét ổn định của hệ thống con lắc đơn tại 2 vị trí cân bằng
Biết ptvp mô tả con lắc đơn Hướng dẫn l Chọn hàm Lyapunov
V (x) 2sin(0.5x )2 2 x 1 2 2g HỆ PHI TUYẾN 13
3. Phương pháp Krasovski tìm hàm Lyapunov
- Việc chọn được hàm Lyapunov có ý nghĩa quyết định để xác định
tính ổn định của hệ thống và miền ổn định
- Thông thường chọn hàm Lyapunov dạng toàn phương của biến trạng thái.
- Trong hầu hết các trường hợp -> khó tìm được hàm Lyapunov HỆ PHI TUYẾN 14
3. Phương pháp Krasovski tìm hàm Lyapunov
Định lý Krasovski: Xét hệ phi tuyến autonom không có tín hiệu vào, có
điểm cân bằng tại gốc tọa độ xe = 0
x f (x,u) f (x) u0
Gọi A là ma trận Jacobi của hệ thống f A x
Nếu ma trận F = A + AT xác định âm trong miền D thì hệ thống ổn định
tiệm cận tại điểm cân bằng. Hàm Lyapunov của hệ thống trong trường hợp này là: ( ) T
V x f (x) f (x)
* Miền ổn định là tập D chứa gốc tọa độ và các điểm trạng thái mà tại đó F xác định âm.
Ma trận xác định âm nếu thỏa mãn 1 trong 2 điều kiện sau:
- Định thức con chính cấp lẻ âm, cấp chẵn dương (định thức từ cấp 1x1
đến nxn trên đường chéo chính)
- Các giá tri riêng của ma trận đều âm.
* Nếu không thỏa mãn điều kiện không có nghĩa là nó không âm HỆ PHI TUYẾN 15




