CHƯƠNG 5.
HÌNH CHIẾU TRỤC ĐO
Mục tiêu chương 5:
Sau khi hoïc xong chöông naøy, sinh vieân coù khaû naêng:
− Döïng ñöôïc hình chieáu truïc ño cuûa ñieåm, maët phaúng vaø vaät theå töø caùc hình bieåu dieãn.
− Phaân bieät vaø söû duïng hieäu quaû caùc loaïi hình chieáu truïc ño trong baûn veõ kyõ thuaät.
5.1. KHÁI NIỆM VỀ HÌNH CHIẾU TRỤC ĐO
Các hình chiếu vuông góc thể hiện chính xác hình dạng và kích thước của vật thể được biểu
diễn. Song, mỗi hình chiếu vuông góc thường thể hiện được hai chiều của vật thể nên hình vẽ
thiếu tính lập thể khiến cho người đọc bản vẽ khó hình dung được hình dạng của vật thể. Để
khắc phục tình trạng này, tiêu chuẩn “Tài liệu thiết kế” quy định được dùng hình chiếu trục đo để
bổ sung cho các hình chiếu vuông góc. Vì, hình chiếu trục đo thể hiện đồng thời trên một hình
biểu diển cả ba chiều của vật thể nên hình biểu diễn có tính lập thể. Nội dung của phương pháp
hình chiếu trục đo được trình bày như sau:
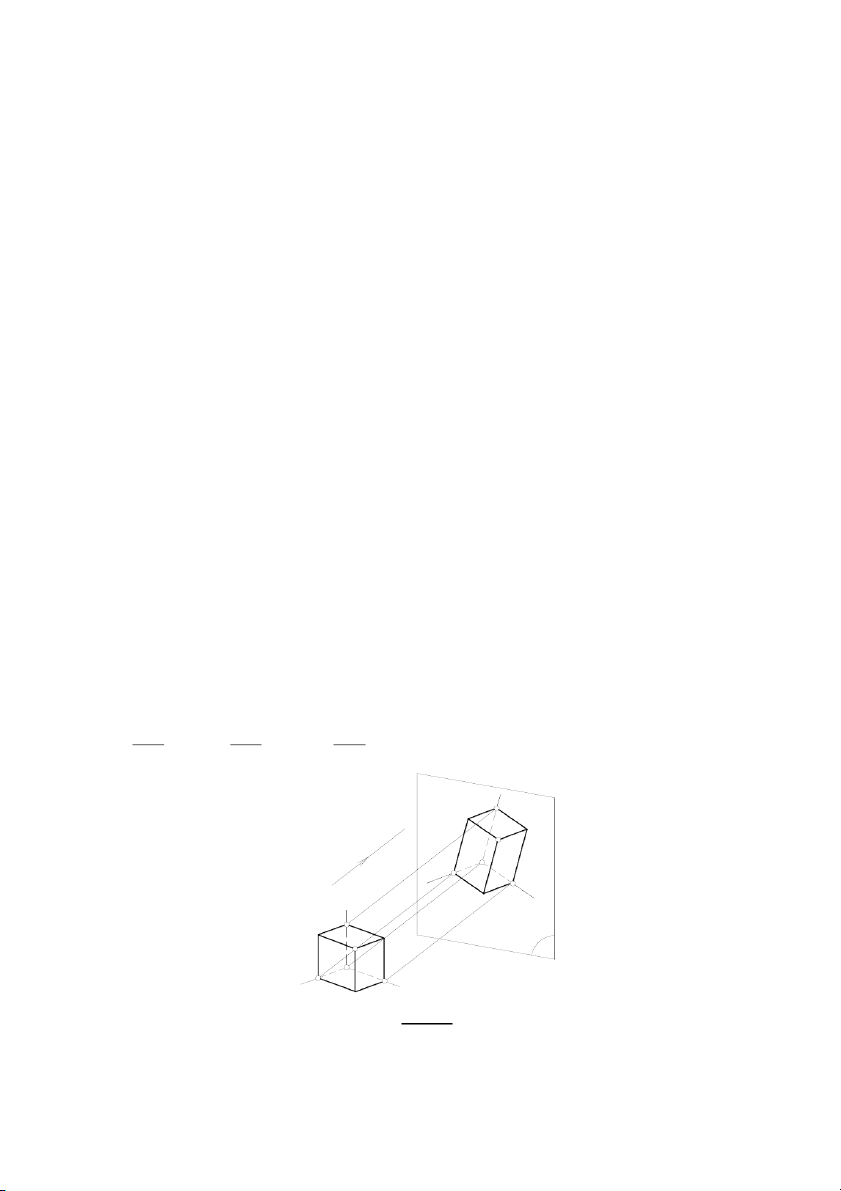
Trong không gian, lấy mặt phẳng (P) làm mặt phẳng chiếu và phương chiếu s không song
song với (P). Gắn vào vật thể được biểu diễn hệ tọa độ vuông góc theo ba chiều dài, rộng, cao
và đặt vật thể sao cho phương chiếu s không song song với một trong ba trục tọa độ đó. Chiếu
vật thể này lên mặt phẳng (P) theo phương chiếu s ta được hình chiếu song song của vật thể
cùng hệ tọa độ vuông góc. Hình biểu diễn này được gọi là hình chiếu trục đo của vật thể.
Hình chiếu của ba trục tọa độ là O’x’, O’y’, O’z’ gọi là các trục đo.
Tỷ số giữa độ dài hình chiếu của một đoạn thẳng nằm trên trục tọa độ với độ dài của đoạn
thẳng đó được gọi là hệ số biến dạng theo trục đo: O ' A' O ' B ' O ' C ' = p ; = q ; = r OA OB OC Z' B' eZ K' s O' A' eX eY X' C' Y' Z B K Po eZ A e e y x O Y X C Hình 5.1. 101
Căn cứ vào phương chiếu và hệ số biến dạng, hình chiếu trục đo gốm có:
1. Theo phương chiếu
− Hình chiếu trục đo xiên là hình chiếu trục đo có phương chiếu không vuông góc với mặt phẳng hình chiếu.
− Hình chiếu trục đo vuông góc là hình chiếu trục đo có phương chiếu vuông góc với mặt phẳng hình chiếu.
2. Theo hệ số biến dạng
− Hình chiếu trục đo đều là hình chiếu trục đo có hệ số biến dạng theo ba trục bằng nhau.
− Hình chiếu trục đo cân là hình chiếu trục đo có hệ số biến dạng hai trong ba trục bằng nhau.
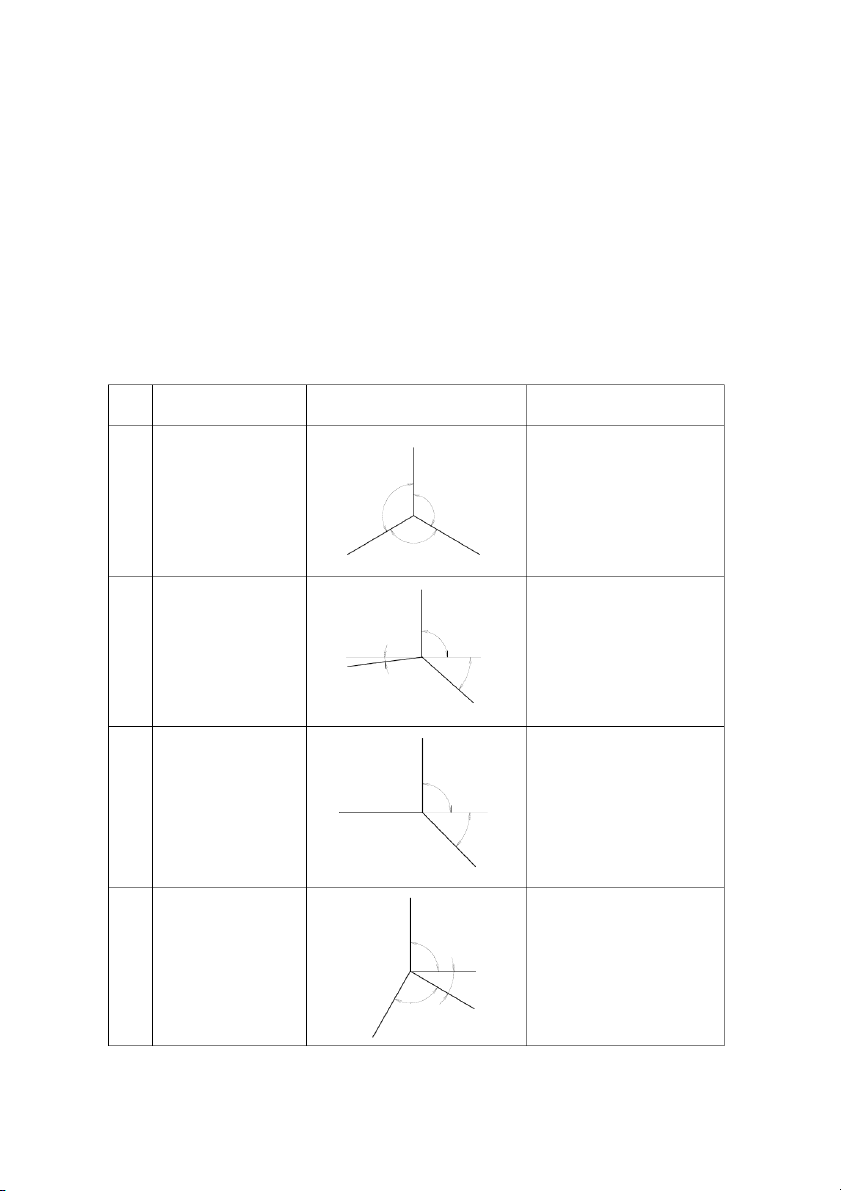
BẢNG PHÂN LOẠI HÌNH CHIẾU TRỤC ĐO TT Tên gọi Hệ trục đo
Hệ số biến dạng z' 1 Hình chiếu trục đo p = q = r = 1 vuông góc đều ° 1 0 2 2 0 1 ° 120° x' y' z' 2 Hình chiếu trục đo p = r = 1 9 vuông góc cân 0° q = 0,5 7° °1 x' 4 y' z' 3 Hình chiếu trục đo p = q = r = 1 xiên đứng đều 90° x' °54 y' z' 4 Hình chiếu trục đo p = q = r = 1 xiên bằng đều 9 0° °03 90° y' x' 102 z' 5 Hình chiếu trục đo p = r = 1 xiên đứng cân 90 q = 0,5 ° x' °54 y'
5.2. CÁC LOẠI HÌNH CHIẾU TRỤC ĐO THƯỜNG DÙNG
5.2.1. HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU (Isometric)
Hình chiếu trục đo vuông góc đều là loại hình chiếu trục đo có phương chiếu vuông góc với
mặt phẳng hình chiếu. Hình chiếu trục đo vuông góc đều được dùng để thể hiện rõ các kết cấu
trên ba mặt phẳng vuông góc nhau. Hệ trục của hình chiếu trục đo vuông góc đều, hình 5.2 Z d Z 120° 120° O X Y X Y 120°
Hình 5.2. hệ trục của hình chiếu trục đo vuông góc đều
Tiêu chuẩn Nhà nước quy định vị trí và hệ số biến dạng của hệ trục đo vuông góc đều như sau: − Trục đứng: Oz
− Hai trục Ox, Oy nghiêng một góc 120o đối với trục Oz. ' O X' O'Y ' O' Z '
− Hệ số biến dạng: K p 1 ; K q 1 ; K r 1 X = = = Y = = = Z = = = OX OY OZ
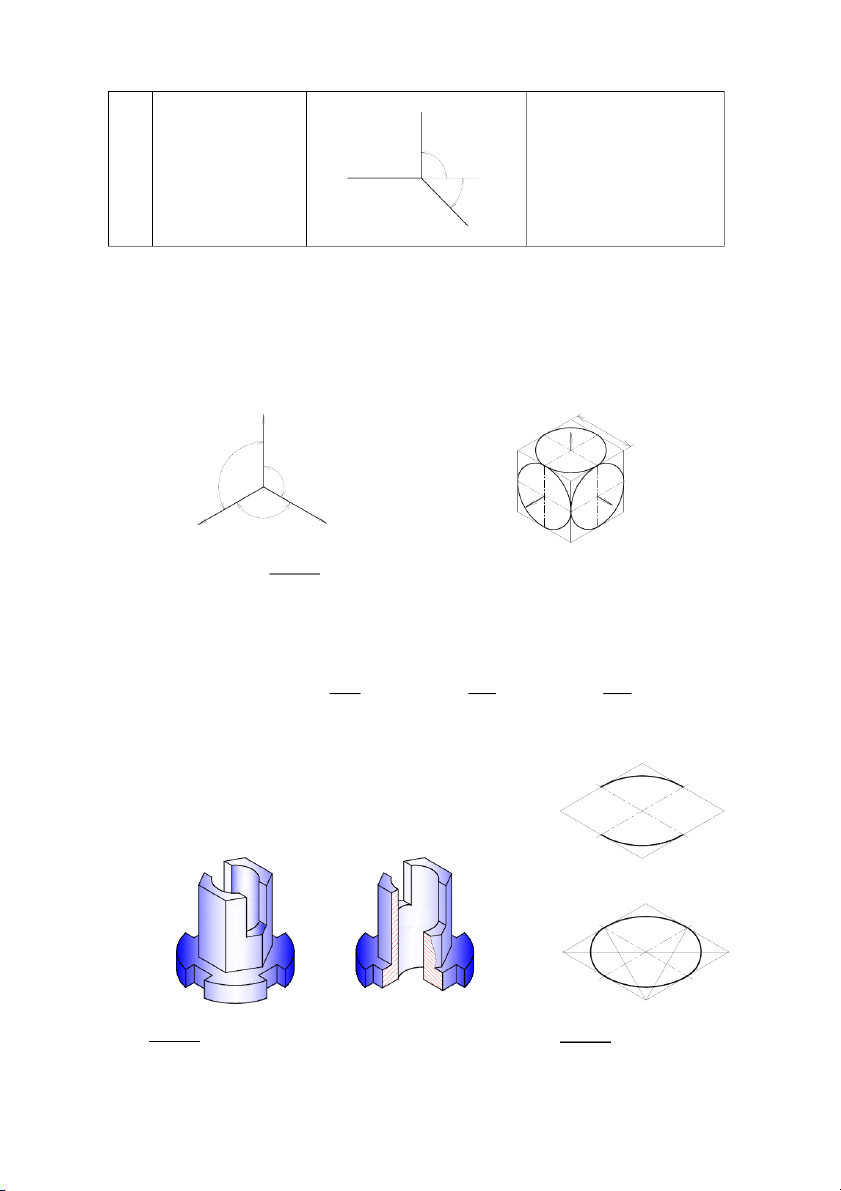
− Trên hình chiếu trục đo vuông góc đều, hình tròn bị suy biến thành hình elip, hình 5.3. O2
Cách dựng hình elip như hình 5.3. D C
− Vật thể được dựng trên hình chiếu trục đo vuông góc đều, O hình 5.4 A B O1 O2 D C O4 O O3 A B O1
Hình 5.4. vật thể được dựng trên hình chiếu trục đo vuông góc đều
Hình 5.3. cách dựng hình elip 103
5.2.2. HÌNH CHIẾU TRỤC ĐO XIÊN ĐỨNG CÂN (dometric)
Hình chiếu trục đo xiên đứng cân là hình chiếu trục đo có phương chiếu không vuông góc với
mặt phẳng hình chiếu (P). Hình chiếu đo xiên đứng cân được dùng trong trường hợp chi tiết có
chiều dài lớn cần biểu diễn một mặt chính của vật thể. Hệ trục của hình chiếu trục đo xiên đứng cân như hình 5.5 Z Z   90° X X O °54 Y Y
Hình 5.5. hệ trục của hình chiếu trục đo xiên đứng cân
Tiêu chuẩn Nhà nước quy định vị trí và hệ số biến dạng của hệ trục đo xiên đứng cân như sau: − Trục đứng OZ − Trục ngang OX
− Trục nghiêng OY với góc 45o đối với đường bằng. ' O X ' ' O Y' O'Z '
− Hệ số biến dạng: K p 1 ; K q 5 , 0 ; K r 1 X = = = Y = = = Z = = = OX OY OZ
Hình tròn nằm trong hoặc song song với mặt phẳng (Oxz) không bị biến dạng, trên các mặt
phẳng (OXY) và (OYZ) hình tròn bị biến dạng thành elip, hình 5.5 (hình elip được dựng bằng
phương pháp chùm tia, xem chương 2).
− Vật thể được dựng trên hình chiếu trục đo xiên đứng cân, hình 5.6.
Hình 5.6. vật thể được dựng trên hình chiếu trục đo xiên đứng cân
5.3. CÁC QUI ƯỚC VỀ HÌNH CHIẾU TRỤC ĐO
− Trên hình chiếu trục đo, các thành mỏng, nan hoa, … phải vẽ ký hiệu vật liệu trên mặt cắt
khi cắt dọc hay cắt ngang, hình 5.7.
− Trên hình chiếu trục đo, cho phép thể hiện hình cắt riêng phần, phần mặt cắt bị mặt phẳng
trung gian cắt qua được qui ước bằng các chấm nhỏ, hình 5.8. 104 Thành mong Hình 5.7.
Hình 5.8. hình cắt riêng phần trên HCTĐ
− Cho phép vẽ ren theo qui ước như trong hình chiếu vuông góc, khi cần có thể vẽ một vài bước ren, hình 5.9.
Hình 5.9. vẽ qui ước ren trên hình chiếu trục đo
Để thể hiện kết cấu bên trong của chi tiết, trên hình chiếu trục đo cũng thường vẽ hình cắt.
Khi vẽ, nên chọn các mặt phẳng cắt sao cho hình chiếu trục đo vừa thể hiện bên trong nhưng vẫn
giữ nguyên được hình dạng cơ bản bên ngoài của vật thể đó. Thường vật thể được xem như cắt
một phần tư và mặt phẳng cắt là các mặt phẳng đối xứng của vật thể. Các đường gạch gạch của
mặt cắt trong hình chiếu trục đo được vẽ như hình 5.10 và hình 5.11. Z Z X O O Y X Y
Hình 5.10. Hình chiếu trục đo vuông góc đều
Hình 5.11. Hình chiếu trục đo xiên đứng cân
5.4. DỰNG HỈNH CHIẾU TRỤC ĐO 5.4.1. PHƯƠNG PHÁP TOẠ ĐỘ
Phương pháp toạ độ là phương pháp cơ bản để dựng hình chiếu trục đo của vật thể. Tuy nhiên,
muốn dựng hình chiếu trục đo của vật thể, ta phải dựng được hình chiếu trục đo của một điểm.
Cách dựng hình chiếu trục đo của một điểm như sau:
− Trước hết, dựng hệ trục đo và xác định toạ độ vuông góc của điểm A (X’A, Y’A, Z’A), sau đó,
căn cứ vào hệ số biến dạng của các trục đo mà xác định toạ độ trục đo của điểm đó với:
X’A = p XA ; Y’A = q Y 
A ; Z’ = r ZA 105
− Lần lượt đặt các toạ độ trục đo lên các hệ trục đo, ta sẽ xác định được điểm A’ là hình
chiếu trục đo của điểm A, hình 5.12. z' z A1 A3 A1 A XA Z A 'A y x O' Z O A Y x' Y'A X'A y' A 2 y
Hình 5.12. HCTĐ vuông góc đều của điểm A
5.4.2. DỰNG HÌNH CHIẾU TRỤC ĐO CỦA MỘT SỐ MẶT
Ñoái vôùi nhöõng hình phaúng coù ñöôøng bao phöùc taïp nhö ñöôøng troøn, ña giaùc, …, khi veõ hình chieáu truïc ño, ta caàn thöïc hieän theo nhöõng böôùc sau:
− Treân hình chieáu vuoâng goùc, neân veõ hình vuoâng (hay hình chöõ nhaät) ngoaïi tieáp ñöôøng troøn hay ña giaùc naøy sao cho soá caïnh
vaø soá ñieåm cuûa hình phaúng naèm treân hình vuoâng (hay hình chöõ nhaät) laø nhieàu nhaát.
− Treân heä truïc ño, veõ hình chieáu truïc ño cuûa hình vuoâng (hay hình chöõ nhaät) tröôùc, sau ñoù veõ caùc hình phaúng noäi tieáp
nhöng phaûi löu yù ñeán heä soá bieán daïng.
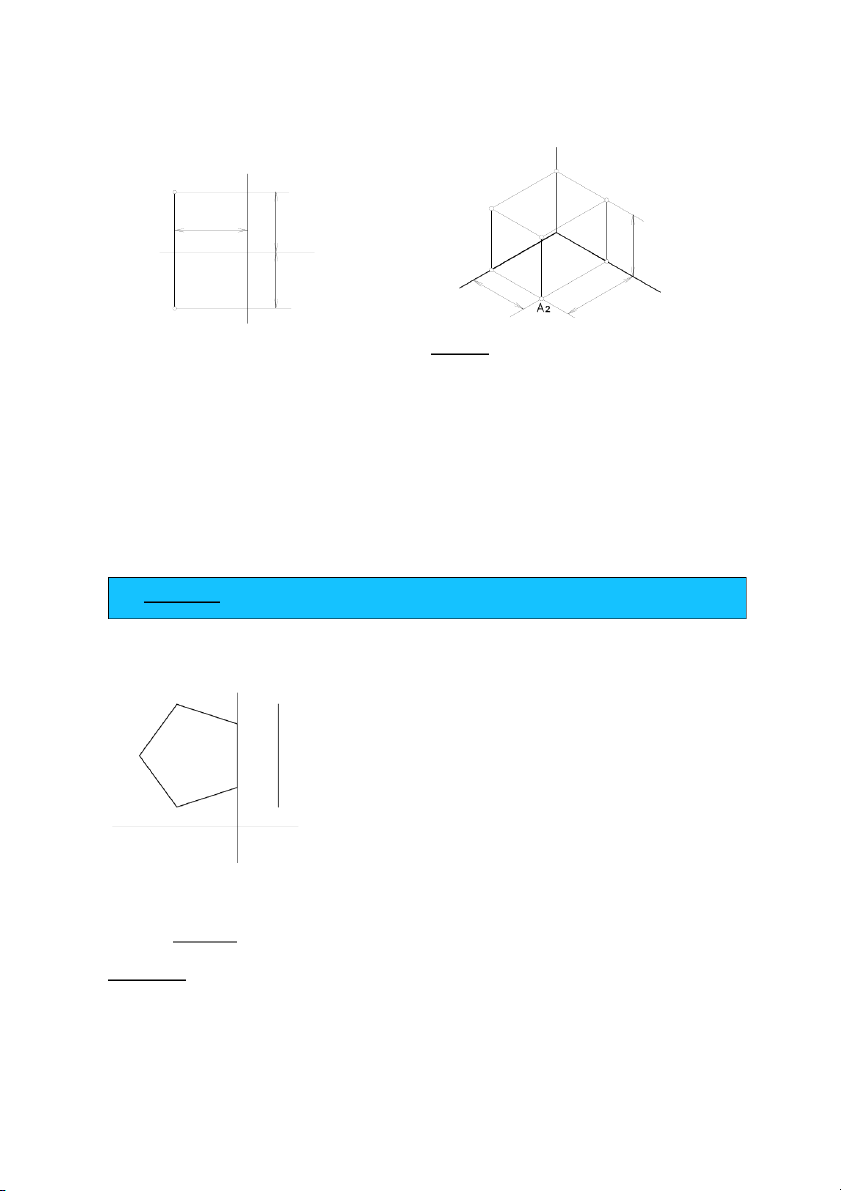
 Áp dụng 1. Dựng hình chiếu trục đo của mặt phẳng là hình ngũ giác đều, hình 5.13a. z' x' y' O' Hình 5.13a. Cách dựng:
− Böôùc 1: Treân hình chieáu vuoâng goùc, döïng hình chöõ nhaät ABCD ñi qua caùc ñænh 1, 2, 3, 4, 5 cuûa hình nguõ giaùc, hình 5.13b.
− Treân heä truïc ño, veõ hình chöõ nhaät ABCD tröôùc, sau ñoù xaùc ñònh caùc ñænh 1, 2, 3, 4, 5 cuûa hình nguõ giaùc, hình 5.13c. 106 z' 3 z B A' A 2' 2 3' B' 4 1 1' 4' C D D' x 5 y O' O' 5' C' x' Hình 5.13b. Hình 5.13c.
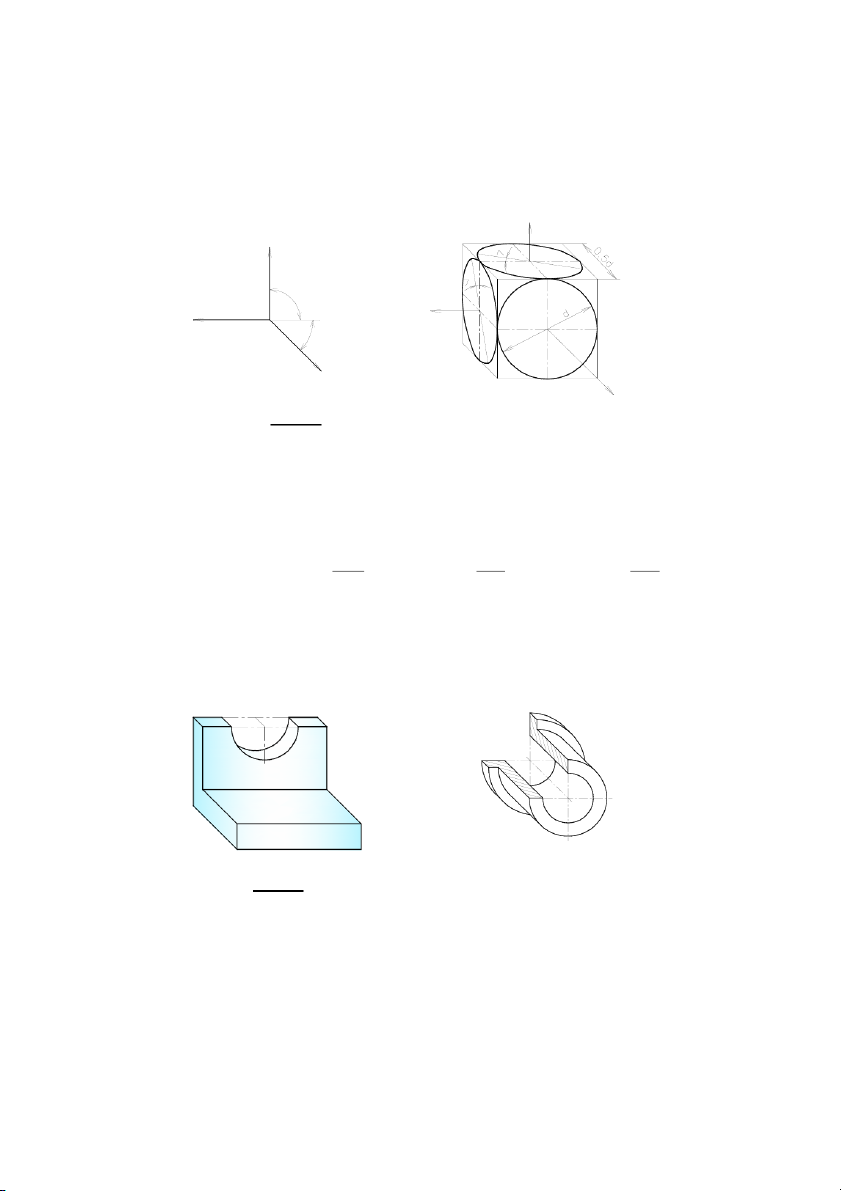
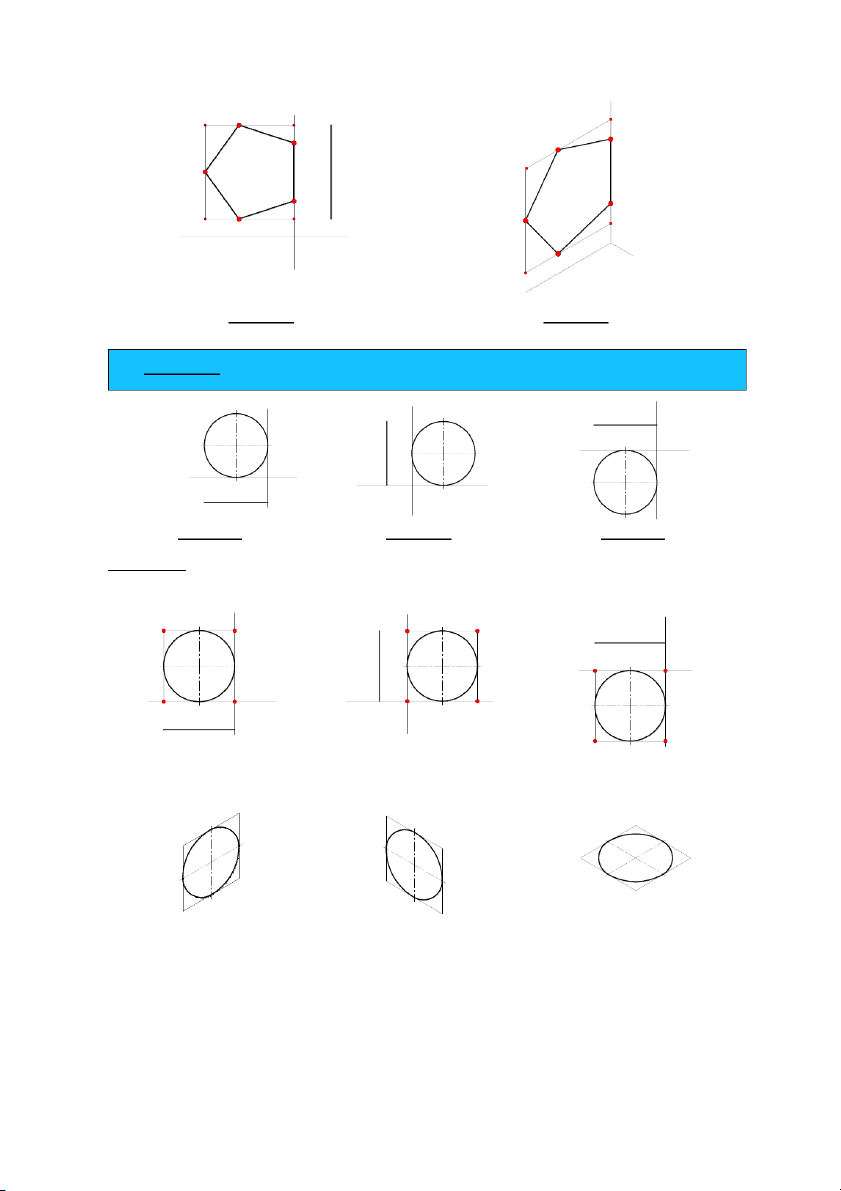
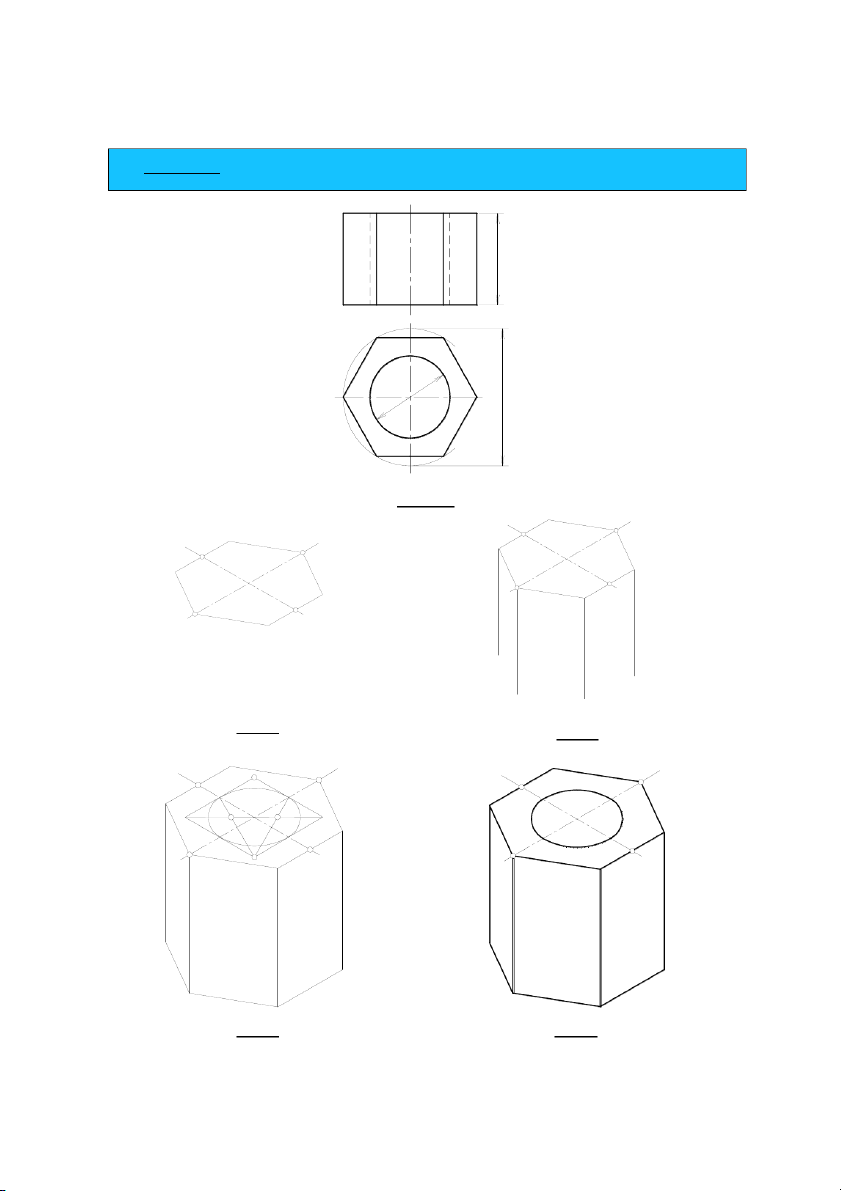
 Áp dụng 2. Dựng hình chiếu trục đo của mặt phẳng là hình tròn, hình 5.14a,b,c. z z z x O x O x O Hình 5.14a. Hình 5.14b. Hình 5.14c. Cách dựng:
− Böôùc 1: Treân hình chieáu vuoâng goùc, döïng hình vuoâng ABCO ngoaïi tieáp ñöôøng troøn. z z z B A B A x C O x x O C O C A B
− Böôùc 2: Treân heä truïc ño, veõ hình chöõ nhaät ABCO tröôùc, sau ñoù döïng hình elipse. A' A' O' B' B' C' A' O' O' B' C' C' 5.4.3.
DỰNG HÌNH CHIẾU TRỤC ĐO CỦA MỘT VẬT THỂ
Khi vẽ hình chiếu trục đo của vật thể, ta cần dựa vào đặc điểm hình dạng của vật thể để
chọn cách vẽ cho phù hợp. Thông thường, người ta vẽ trước một mặt của vật thể làm mặt cơ sở,
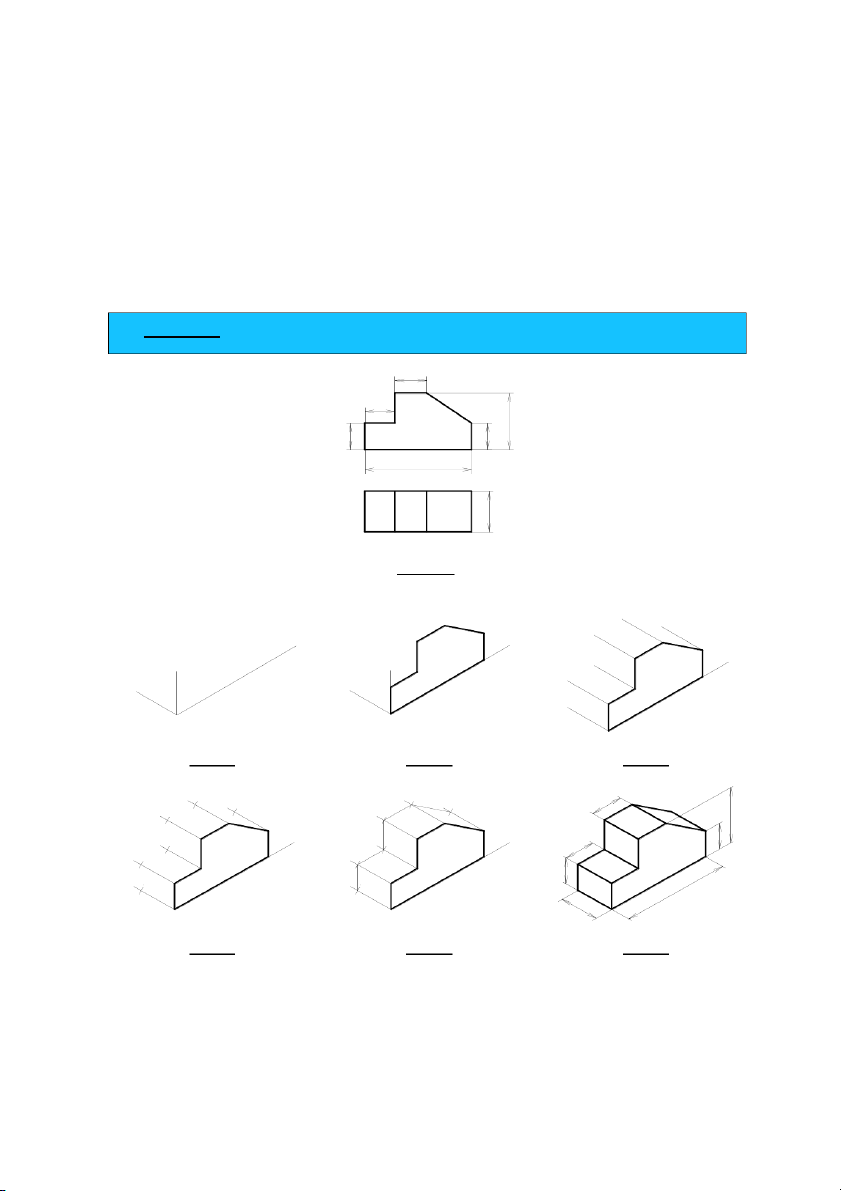
sau đó dựa vào các tính chất của phép chiếu song song để vẽ các mặt khác. 107 Trình töï veõ nhö sau:
− Böôùc 1. Choïn loaïi truïc ño (choïn heä truïc toïa ñoä)
− Böôùc 2. Choïn tröôùc moät maët laøm cô sôû, maët vaät theå ñöôïc ñaët truøng vôùi maët phaúng toïa ñoä.
− Böôùc 3. Töø caùc ñænh cuûa maët ñaõ veõ, keû caùc ñöôøng song song vôùi truïc coøn laïi.
− Böôùc 4. Caên cöù theo heä soá bieán daïng, khoáng cheá ñoä daøi cuûa caùc ñoaïn thaúng song song vöøa döïng.
− Böôùc 5. Noái caùc ñieåm vöøa môùi xaùc ñònh baèng neùt lieàn maûnh.
− Böôùc 6. Xoùa caùc neùt veõ thöøa, kieåm tra laïi vaø toâ ñaäm hình veõ, ghi kích thöôùc.
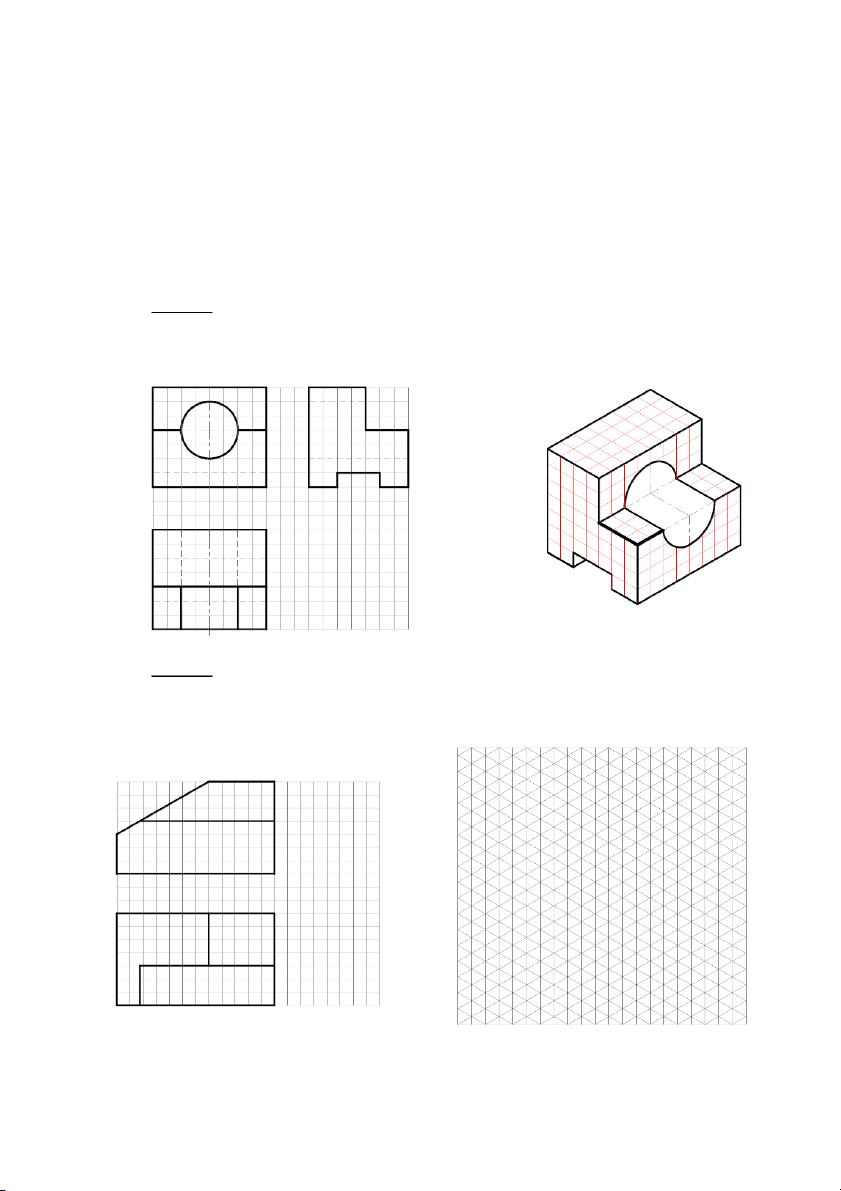
 Áp dụng 3. Cho hình chiếu vuông góc như hình 5.15, dựng hình chiếu trục đo. 16 15 8 2 3 3 1 1 53 0 2 Hình 5.15. x' x' z' z' y' y' Bước 1. Bước 2. Bước 3. 16 8 2 3 1 15 3 1 53 20 Bước 4. Bước 5. Bước 6. 108
Tuy nhiên, đối với vật thể có dạng hình hộp, ta có thể vẽ hình hộp ngoại tiếp và lấy ba mặt
phẳng của hình hộp làm ba mặt phẳng tọa độ. Trình tự vẽ được trình bày trong áp dụng 4.
 Áp dụng 4. Cho hình chiếu vuông góc như hình 5.16, dựng hình chiếu trục đo. 15 0 3 5 1 8 0 0 2 4 20 50 Hình 5.16. Bước 1. Bước 2. Bước 3. 15 40 20 0 3 7 16 50 Bước 4. Bước 5. Bước 6. 109
Ngoài ra, đối với những vật thể có các mặt đối xứng, ta nên các mặt phẳng đối xứng đó làm
các mặt phẳng tọa độ, hình 5.17.
 Áp dụng 5. Cho hình chiếu vuông góc như hình 5.17, dựng hình chiếu trục đo. 0 5 Ø34 0 6 Ø Hình 5.16. X Y 4 3 X Y 4 3 1 2 1 2 Bước 1 Bước 2 X Y X Y 4 4 3 3 1 2 2 1 Bước 3 Bước 4 110
Tóm lại: hình chiếu trục đo vuông góc đều thường được dùng để vẽ cho tất cả các vật thể, đặc
biệt là vật thể có đường tròn (hoặc cung tròn) theo hướng nhìn từ trên xuống và hướng nhìn từ trái sang, hình 5.18.
Hình 5.18. Hình chiếu trục đo vuông góc đều
Hình chiếu trục đo xiên cân dễ vẽ, tuy nhiên loại hình chiếu trục đo này chỉ nên dùng cho
những vật thể không có lỗ trụ tròn hoặc chỉ có phần trụ có đường tròn trên hình chiếu nhìn từ trước vào, hình 5.19.
HÌnh 5.19. Hình chiếu trục đo xiên cân có đường tròn trên hình chiếu đứng
Hình 5.20. Hình chiếu trục đo xiên cân không có đường tròn 111
CÂU HỎI ÔN TẬP CHƯƠNG 5
1. Thế nào là hình chiếu trục đo và hệ số biến dạng theo các trục?
2. Cách phân loại hình chiếu trục đo?
3. Trình bày cách vẽ nhanh ê líp trong hình chiếu trục đo vuông góc điều?
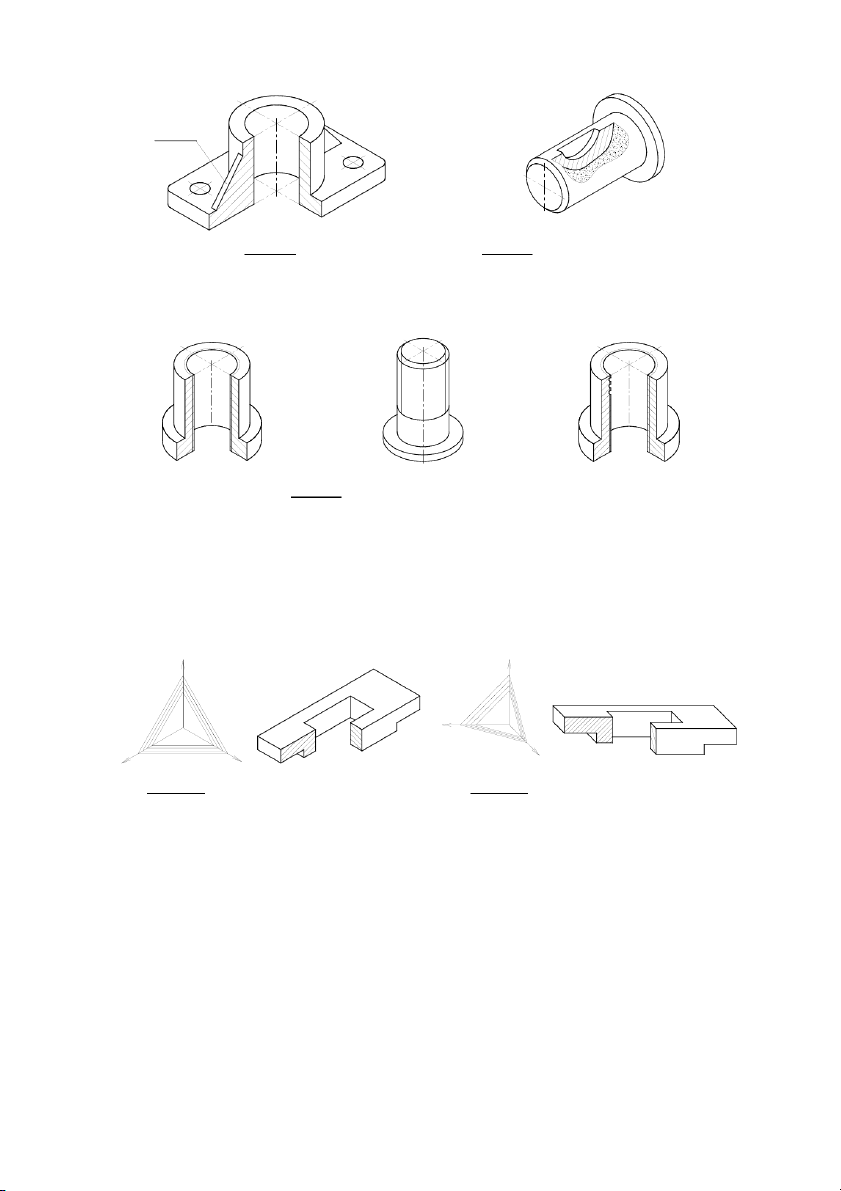
4. Trình bày cách dựng hình chiếu trục đo vuông góc đều và xiên góc cân? BÀI TẬP ÁP DỤNG
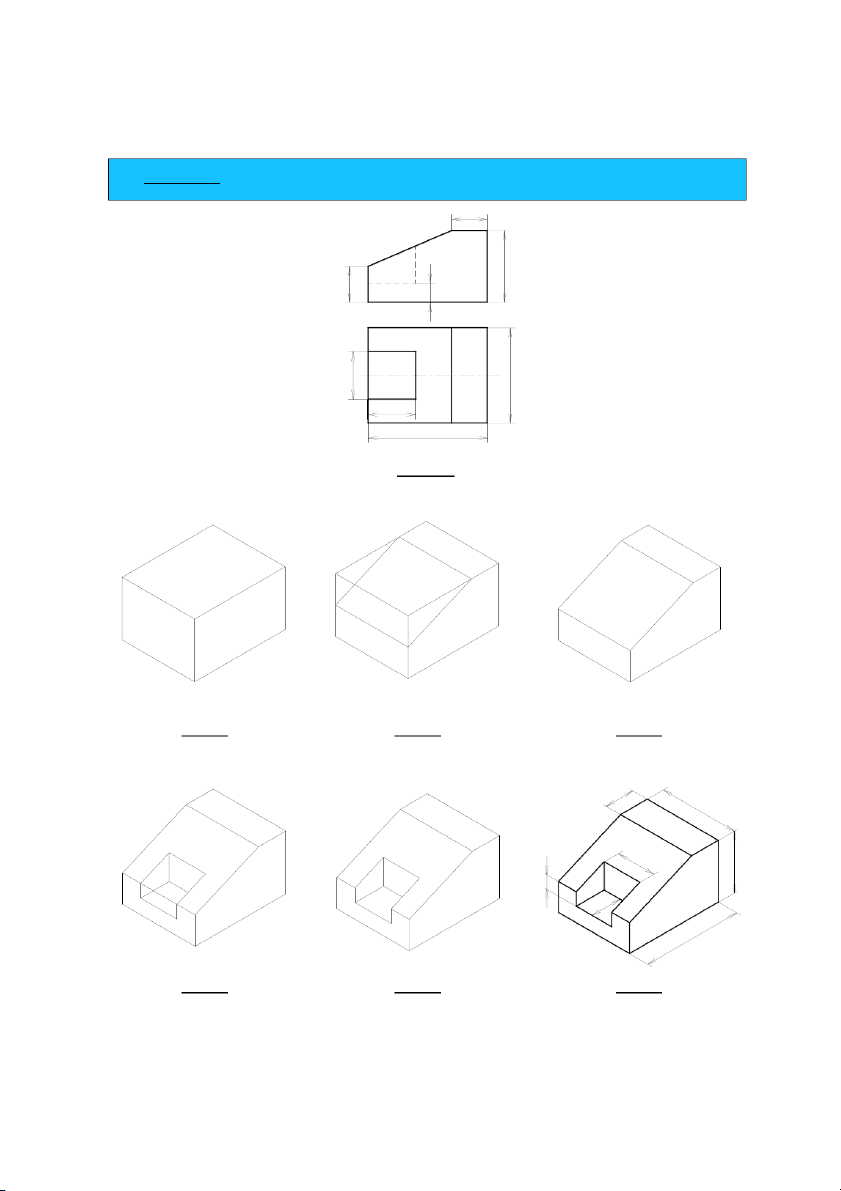
 Bài tập 1 (bài làm mẫu): Cho hình chiếu đứng và hình chiếu cạnh, hãy: 1.
Dựng hình chiếu trục đo, hệ trục vuông góc đều. 2.
Vẽ hình chiếu còn lại.
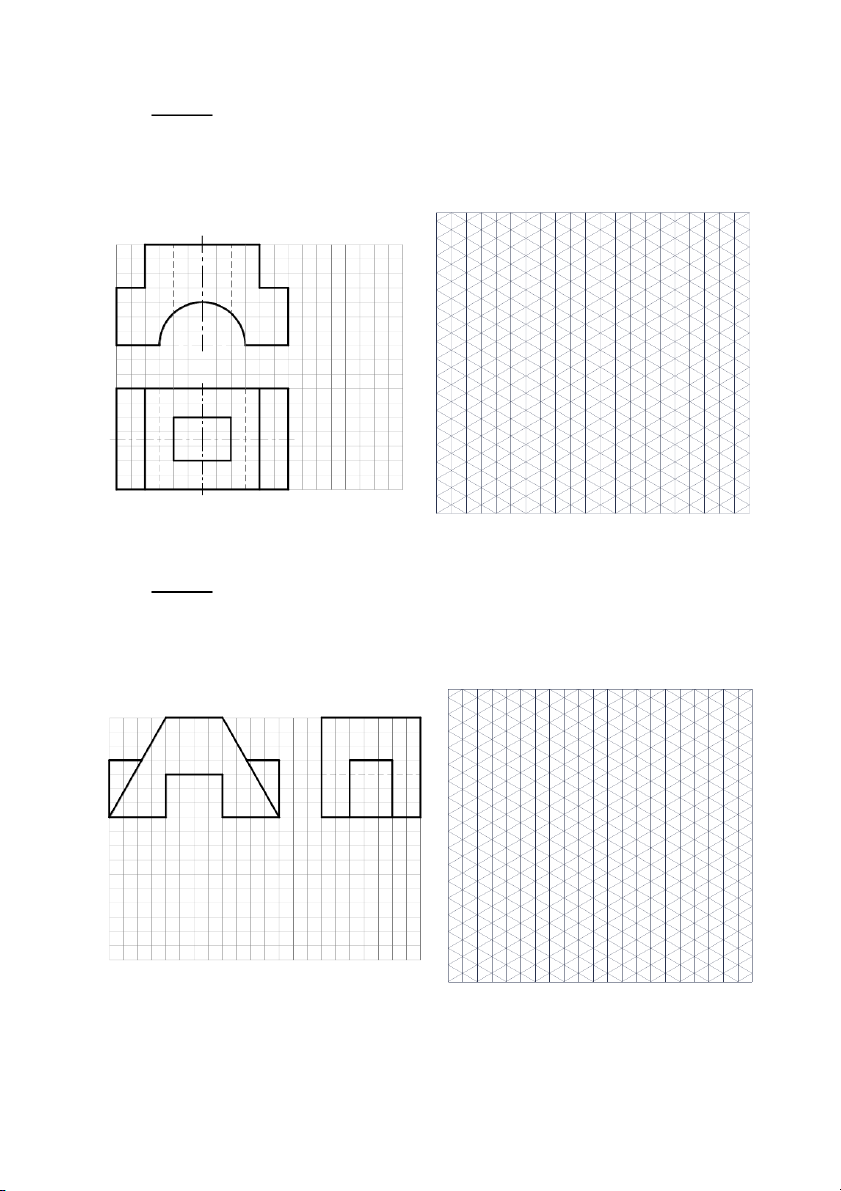
 Bài tập 2: Cho hình chiếu đứng và hình chiếu bằng của vật thể, hãy: 1.
Dựng hình chiếu trục đo, hệ trục vuông góc đều. 2.
Vẽ hình chiếu còn lại. 112
 Bài tập 3: Cho hình chiếu đứng và hình chiếu bằng của vật thể, hãy: 1.
Dựng hình chiếu trục đo, hệ trục vuông góc đều. 2.
Vẽ hình chiếu còn lại.
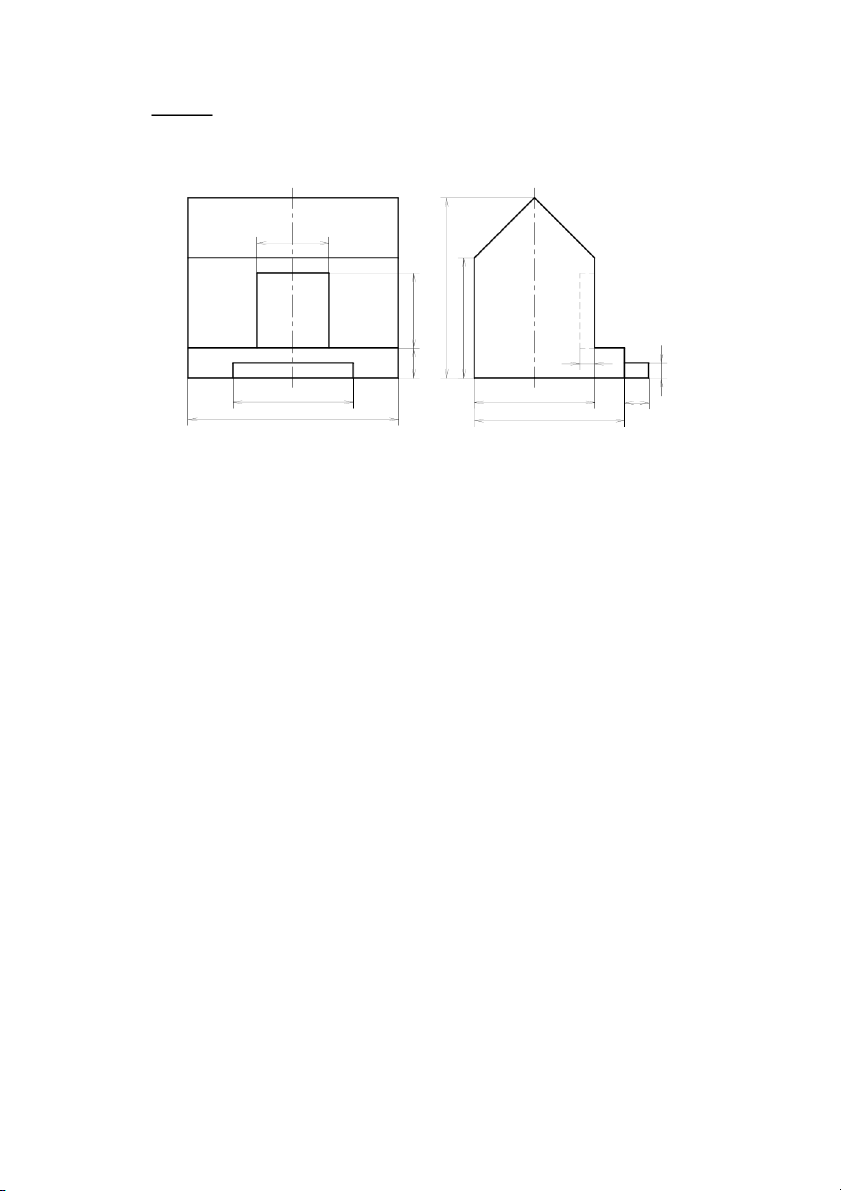
 Bài tập 4: Cho hình chiếu đứng và hình chiếu cạnh của vật thể, hãy: 1.
Dựng hình chiếu trục đo, hệ trục vuông góc đều. 2. Vẽ hình chiếu còn lại 113
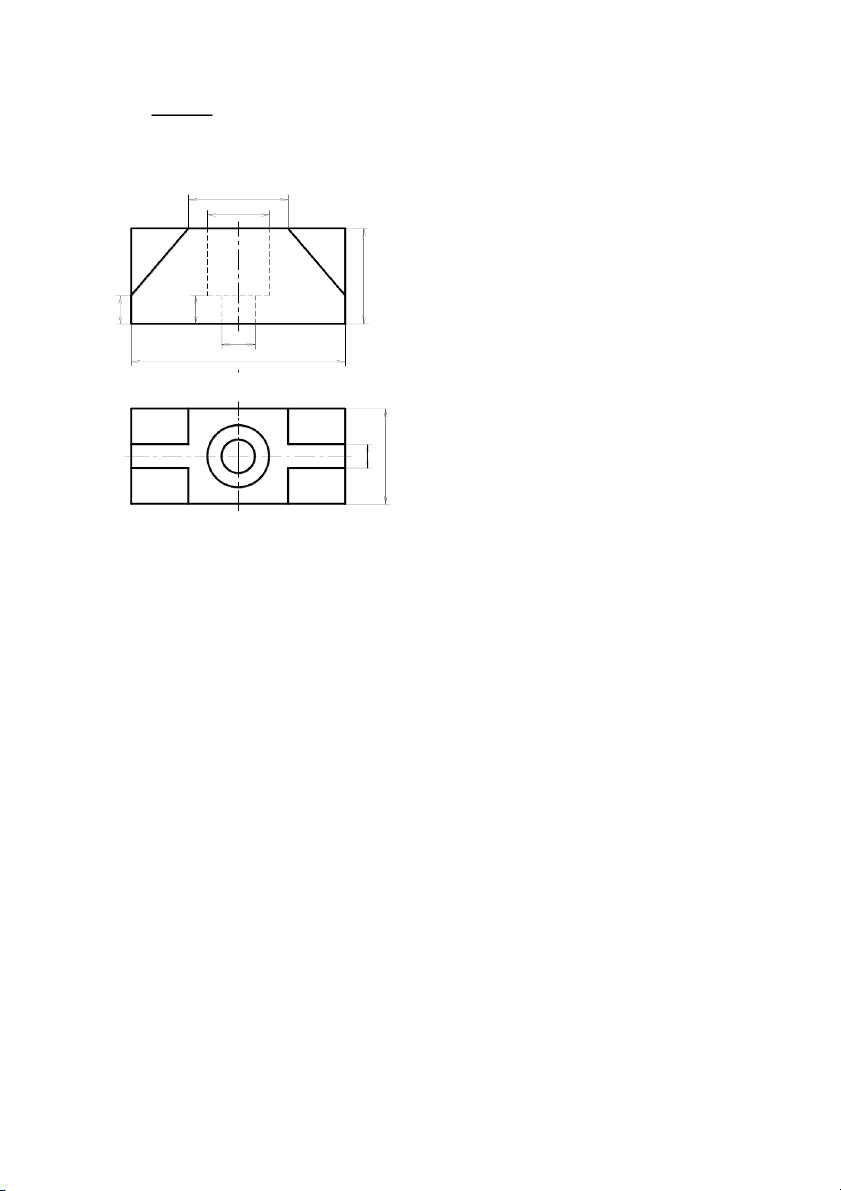
 Bài tập 5: Cho hình chiếu đứng và hình chiếu bằng của vật thể, hãy:
1. Dựng hình chiếu trục đo, hệ trục vuông góc đều.
2. Vẽ hình chiếu còn lại 42 Ø26 0 4 2 2 1 1 Ø14 90 0 0 1 4 114
 Bài tập 6: Cho hình chiếu đứng và hình chiếu cạnh, hãy:
1. Dựng hình chiếu trục đo, hệ trục vuông góc đều.
2. Vẽ hình chiếu còn lại 24 0 6 5 2 0 4 0 5 1 5 40 40 8 70 50 115