-
Thông tin
-
Quiz
Chương 5 Nguyên hàm và tích phân môn Cơ sở toán cho nhà kinh tế 1 | Học viện Nông nghiệp Việt Nam
Trong chương trước chúng ta đã thực hiện phép toán tính đạo hàmcủa một hàm số cho trước,sang chương này chúng ta thực hiện phép toán ngược với phép toán tính đạo hàm, đó là đi tìm tấtcả các hàm số có đạo hàm bằng một hàm số f x( ) cho trước. Trong chương trước chúng ta đã thực hiện phép toán tính đạo hàm của một hàm số cho trước,sang chương này chúng ta thực hiện phép toán ngược với phép toán tính đạo hàm, đó là đi tìm tất cả các hàm số có đạo hàm bằng một hàm số f x( ) cho trước. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Cơ sở toán cho các nhà kinh tế 1 42 tài liệu
Học viện Nông nghiệp Việt Nam 593 tài liệu
Chương 5 Nguyên hàm và tích phân môn Cơ sở toán cho nhà kinh tế 1 | Học viện Nông nghiệp Việt Nam
Trong chương trước chúng ta đã thực hiện phép toán tính đạo hàmcủa một hàm số cho trước,sang chương này chúng ta thực hiện phép toán ngược với phép toán tính đạo hàm, đó là đi tìm tấtcả các hàm số có đạo hàm bằng một hàm số f x( ) cho trước. Trong chương trước chúng ta đã thực hiện phép toán tính đạo hàm của một hàm số cho trước,sang chương này chúng ta thực hiện phép toán ngược với phép toán tính đạo hàm, đó là đi tìm tất cả các hàm số có đạo hàm bằng một hàm số f x( ) cho trước. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Cơ sở toán cho các nhà kinh tế 1 42 tài liệu
Trường: Học viện Nông nghiệp Việt Nam 593 tài liệu
Thông tin:
Tác giả:
Preview text:
lOMoAR cPSD| 47708777
CHƯƠNG 1 - PHÉP TÍNH TÍCH PHÂN HÀM MỘT BIẾN VÀ ỨNG DỤNG TRONG KINH TẾ
Trong chương trước chúng ta ã thực hiện phép toán tính ạo hàm của một hàm số cho trước, sang
chương này chúng ta thực hiện phép toán ngược với phép toán tính ạo hàm, ó là i tìm tất cả các
hàm số có ạo hàm bằng một hàm số f (x) cho trước.
Mục tiêu của Chương 4
1. Hiểu ược khái niệm nguyên hàm, tích phân bất ịnh.
2. Thực hiện ược các phép tính tích phân bất ịnh của các hàm cơ bản và áp dụng vào các bài
toán ứng dụng trong kinh tế.
1.1. NGUYÊN HÀM VÀ TÍCH PHÂN BẤT ĐỊNH
1.1.1. Đị nh nghĩa
Định nghĩa 1.1. Cho hàm s ố f ( x) xác ị nh trên kho ả ng D . Hàm s ố F( )
x ượ c g ọ i là m ộ t
nguyên hàm c ủ a f (
x) trên D n ế u F '( x) = f ( x) , x D .
Ví dụ 1.1. • 2 F ( x) 2
= là m ộ t nguyên hàm c ủ a hàm s ố f ( x) =2 trên vì ( x )' =2 x, x . 1 x x • 2 F ( x) 2
= + cũng là mộ t nguyên hàm c ủ a f ( x) =2 trên vì ( x +5) ' =2 x, x . 2 x 5 x • F ( x) 2 x
= e +C (v ớ i h ằ ng s ố C tùy ý) là nguyên hàm c ủ a ( ) 2 x f x =e trên vì
Do ó G(x) là một nguyên hàm của f (x) trên D. lOMoAR cPSD| 47708777 1 2 x 2 x e +C =e , x . 2
Định lý 1.1. Gi ả s ử F( x) là m ộ t nguyên hàm c ủ a f ( x) trên kho ả ng D , k hi ó G( x) là
nguyên hàm c ủ a f (
x) trên kho ả ng D khi v à ch ỉ k
hi t ồ n t
ạ i h ằ ng s ố C
sao cho G( x) = F ( x) C + , x . D
Ch ứ ng minh.
- Gi ả s ử t ồ n t ạ i h ằ ng s ố C sao cho G( x) =F ( x) C + , x . D Khi ó G ( x) = F ( x) +C = F ( x) = f ( x) , x D .
- Giả sử F(x), G(x) là hai nguyên hàm của f (x) trên D. Khi ó
G(x)− F(x)
= G (x) − F (x) = f (x) − f (x) = 0, x D.
Suy ra G(x) −F(x) nhận giá trị không ổi trên D, tức là G(x) −F(x) =C, x D vớiC là một
hằng số nào ó. Vậy G(x) = F(x) +C, x D .
Định nghĩa 1.2. Tập hợp tất cả các nguyên hàm của hàm f (x) trên khoảng D ược gọi là tích
phân bất ịnh của f (x) trên D, kí hiệu là
f (x)dx .
Kí hiệu là dấu tích phân, x là biến lấy tích phân, f (x) là hàm số lấy tích phân, f (x)dx là biểu thức dưới dấu tích phân.
Vậy nếu F(x) là một nguyên hàm của f (x) trên D thì
f (x)dx = F(x)+C . Ví dụ 1.2.
2xdx = x2 +C .
1.1.2. Tính ch ấ t
1) ( f ( x) dx ) = f ( x) 2) k . f ( x) dx =k . f (
x) dx , k . 3) f ( x) +g ( x) dx = f (
x) dx + g ( x) dx . 4) N ế u f (
x) dx = F ( x) +C thì f (
u) du = F ( u) +C . 1
H ệ qu ả : N ế u f (
x) dx = F ( x) +C thì f ( ax +b
) dx = F ( ax +b ) +C . a
1.1.3. Nguyên hàm c ủ a m ộ t s ố hàm s ố
Công thức nguyên hàm cơ bản
Công thức mở rộng lOMoAR cPSD| 47708777
0dx=C dx =
(ax+b) dx = 1.(ax+b) + 1 C x+C 1 a 1 x dx = x +C, 1 dx = 1
.ln | ax+b | +C 1 1 ax+b a
dx = ln | x | +C x 1 1 dx = +C 2 ax+b ax+b a = 1 e ax+b 1 +C eax+b dx = 2 x dx +C a x = ex +C C (a ) ax ex a + x dx = + .ln +C (a , a 0) a − x dx lna ax dx 1 =
a2 − x2 2a Ví dụ 1.3. a) x + 5dx = x6 C 6 b) 12 dx
= x−2dx = x−1 lOMoAR cPSD| 47708777 +C = − 1 +C. x −1 x d) xdx = x + + 1/2dx = x3/2
C = 2 x3/2 C . 3/ 2 3 e) (3x+4) + +
10 dx =1.(3x+4)11
C = (3x+4)11 C . 3 11 33 dx
= 1 .ln |1− 4x | +C. f) 1− 4x −4 dx
=1.2 3x+1+C = 2 3x+1+C. g) 3x+1 3 3 g) e + 2x+9dx =
.e2x+9 C. = dx dx = 2 2 2
1 .ln 3+ x +C = 1.ln 3+
Ví dụ 1.4. x +C . h) 9 − x 3 − x 2.3 3− x 6 3− x a) 2+3x− 3 − 2
dx =2x+ 3x2 − 6 x − 2ln | x | +C . x x 2 b) e + − + 3x 35 dx = e3xdx+ 3
x−5dx = e3x 3 4 C . x 3 4x c) 4 + 2 + x = 21−5 dx =4 9xdx+ 2 − 52dx− x2
94 ln | 9x+ 2 | − 215 ln
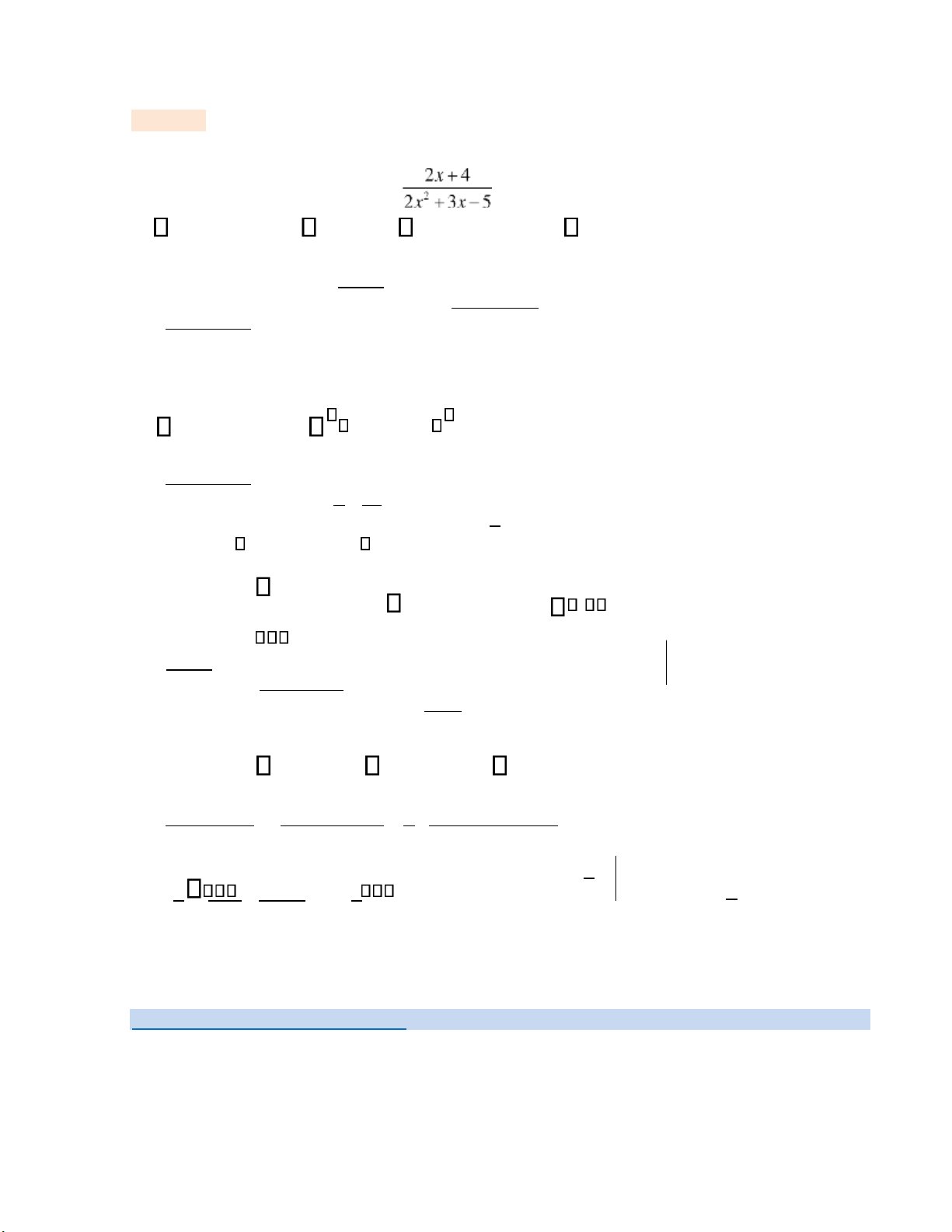
55 +− x x +C. 9x lOMoAR cPSD| 47708777 Ví dụ 1.5. Tính các tích phân sau. 2x2 +3x−1 3x + 4 dx a)
2 dx, b) dx, c) 2 , d)
dx. x x + 2 2x + 3x −5 Lời giải. 2x2 + 32 x−1 = 2 + 3 − 12
dx = 2x+ 3ln | x | + 1 +C . a) dx x x x x b) 3x++ 4 dx =
3(x ++2) − 2dx = 3− +2 2
dx = 3x − 2ln | x + 2 | +C . x 2 x 2 x = x x c) + − 2 dx dx = 1 (2 5)−2( 1) dx
2x +3x−5 (x−1)(2x+5) 7 (x−1)(2x+5) = 1 1−1 − 2x2+ 5
dx= 71 (ln | x−1| −ln | 2x+ 5|)+C = 71 ln 2xx−+15 +C. 7 x
1.2. TÍCH PHÂN XÁC ĐỊNH 1.2.1. Định nghĩa
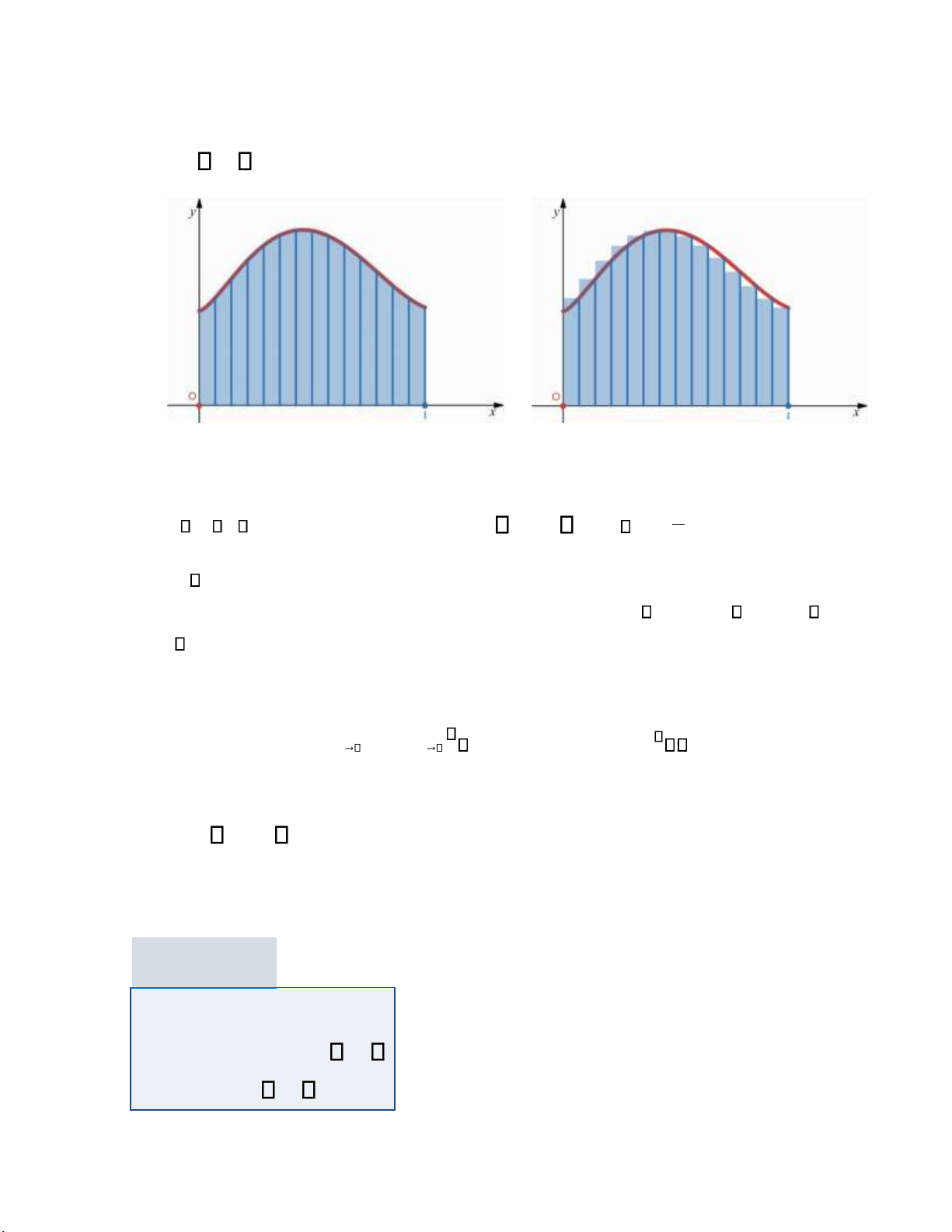
Bài toán diện tích hình thang cong
Giả sử một ại lý bất ộng sản muốn tính diện tích một thửa ất như hình vẽ…. Thửa ất có bề ngang
dài 8m, ranh giới với hai thửa ất bên cạnh là các ường thẳng, mặt còn lại của thửa ất tiếp giáp với
một con sông. Nếu coi mặt ường là trục Ox , ường thẳng ứng tiếp giáp với một thửa ất bên cạnh là lOMoAR cPSD| 47708777
trục Oy thì phần tiếp giáp này thể mô tả bởi một ường cong là ồ thị của hàm số y = f ( ) x liên tục
trên oạn a;b . Giá bán của thửa ất phụ thuộc vào diện tích thửa ất ó. Do ó, ta muốn xác ịnh
diện tích của thửa ất.
Để tính diện tích thửa ất, người ta sử dụng ý tưởng chia nhỏ thửa ất thành n miền nhỏ bởi các
ường thẳng ứng song song với trục Oy và i qua các iểm chia cách ều = b−a a = x = 0 x1 ... xn
b . Chiều rộng mỗi oạn con
xi−1, xi ều là x . n
Sau ó diện tích của mỗi miền nhỏ ược xấp xỉ bằng diện tích của một hình chữ nhật, với chiều
rộng là x và chiều dài là f (x )
i trong ó xi là ầu mút phải của mỗi oạn con. Khi ó, diện tích của toàn n
bộ thửa ất ược tính xấp xỉ bằng tổng diện tích của hình chữ nhật: A S = ) ) n f (x1 x+ f (x2 x+...+ f (x ) n x. Để n n
xấp xỉ chính xác hơn, người ta tăng số oạn con . Khi số oạn con tiến ến vô hạn, tổng diện
tích các hình chữ nhật tiến dần ến diện tích chính xác A, do ó: A= lim = )+ )+ ) n Sn limn f (x1 f (x2 ...+ f (xn x .
Người ta có thể chứng minh giới hạn trên không thay ổi nếu oạn [a,b] ược chia nhỏ tùy ý (không
nhất thiết phải chia ều) và chiều dài hình chữ nhật ược thay bởi f (c )
i trong ó iểm ci ược chọn tuỳ ý
trong oạn xi−1, xi . Tuy nhiên, việc chứng minh chi tiết nằm ngoài phạm vi của giáo trình.
Bài toán diện tích chỉ là một trong số rất nhiều bài toán xuất hiện ại lượng mà ta có thể biểu
diễn thành giới hạn của một tổng như trên. Ta sử dụng khái niệm tích phân xác ịnh ể chỉ giới hạn
này trong trường hợp tổng quát. Định nghĩa tích phân xác ịnh
Định lý 1.2. Cho hàm số y = f ( ) x xác ịnh trên oạn a;b . Chia oạn a;b thành n lOMoAR cPSD| 47708777
oạn con tùy ý bởi các iểm chia a = x = 0 x1 ... xn b .
Độ dài oạn con thứ i là x = i x −
. Trên mỗi oạn con i xi−1 thứ i lấy iểm ci xi−1; xi
bất lỳ và lập tổng S = ) + ) + n f (x1 x1 f (x2 x2 ...+ f ( = x ) n ) n xn f (xi xi . i=1
Tổng này ược gọi là một
tổng Riemann của hàm số f ( ) x
trên a;b . Nếu tồn tại giới hạn limS = n S n
và giới hạn này không phụ
thuộc vào cách chia oạn
a;b thành các oạn con và
cách chọn iểm ci trong mỗi
oạn con ó thì S ược gọi là tích
phân xác ịnh của hàm f ( ) x trên oạn
a;b và kí hiệu là b f ( )xdx. Như vậy a
b f (x)dx = lim n ) n f (xi xi . a i=1 Khi ó ta nói f ( ) x khả tích
trên oạn a;b . Hàm số f
( )x ược gọi là hàm lấy tích lOMoAR cPSD| 47708777
phân, các số a,b ược gọi
tương ứng là cận dưới và
cận trên của tích phân, dx
ược gọi là vi phân của ối số. Chú ý
Ta chứng minh ược nếu hàm số f ( ) )
x liên tục trên oạn
a;b thì f (x khả tích trên oạn b này. Hơn nữa, tích phân ( )
f x dx là một số, không phụ thuộc vào biến lấy tích phân, tức là a
b f (x)dx = b f (u)du = b f (t)dt = .... a a a
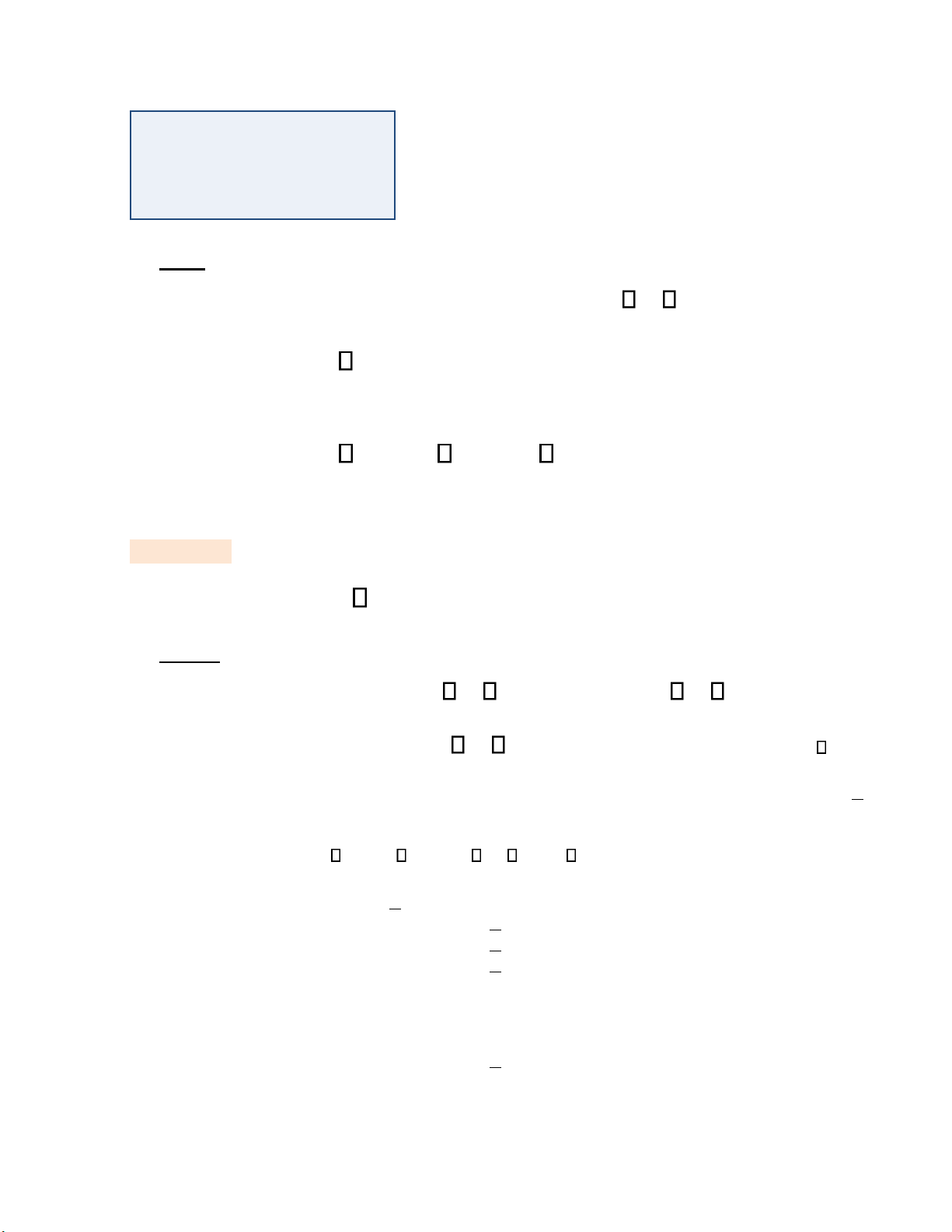
Ta xét một ví dụ ơn giản mà ta có thể sử dụng ịnh nghĩa ể tính tích phân xác ịnh. Ví dụ 1.6. 1 Tính tích phân xác ịnh xdx . 0 Lời giải Vì f ( ) )
x = x là hàm số liên tục trên
0;1 nên f (x khả tích trên 0;1 . = 1
Không mất tính tổng quát, ta chia oạn 0;1 thành n oạn con với ộ rộng bằng nhau là x n
bởi các iểm chia x = = 1 = 2 = i = n = 0 0 x1 x2 ... xi ...xn 1. n n n n = i
Trên mỗi oạn con, chọn iểm ầu mút phải c = i xi . n lOMoAR cPSD| 47708777
quả tích phân ta vừa tính ở trên.
Tính chất của tích phân xác ịnh b
Trong ịnh nghĩa về tích phân xác ịnh, ta ã xác ịnh tích phân ( )
f x dx với f (x) xác ịnh a
trên oạn a,b trong ó a b . Tuy nhiên, trong trường hợp a b và hàm f (x) khả tích trên oạn
b,a , người ta quy ước:
b f (x)dx = − a f (x)dx . a b
a f (x)dx = 0 . a
Ta có một số tính chất của tích phân xác ịnh sau ây. Giả sử f và g là các hàm số liên tục trên miền lấy tích phân. lOMoAR cPSD| 47708777 1.
b kdx = k(b −a) với k là một hằng số bất kỳ. a 2. b
f (x) g(x) dx =
b f (x)dx
b g(x)dx . a a a 3. b kf ( ) ) x dx = k
b f (x dx với k là một hằng số bất kỳ. a a 4.
c f (x)dx + b f (x)dx = b f (x)dx a c a b 5. Nếu f ( ) ( ) x 0 với a x b thì f x dx 0 . a b b 6. Nếu f ( ) ) ( ) ( ) x
g(x với a x b thì f x dx g x dx . a a b 7. Nếu m f ( ) x
M với a x b thì m(b−a)
f (x)dx M (b−a) . a Ví dụ 1.7. Cho f ( ) )
x và g(x là các hàm số liên tục trên oạn
−1;8 và thỏa mãn iều kiện
8 f (x)dx = 5,
8 g(x)dx = −2,
8 f (x)dx = 6 . −1 −1 3
Khi ó, hãy tính các tích phân xác ịnh sau. 8 a)
3 f (x)+ 2g(x) dx. −1 3 b)
2 f (x)dx . −1 Lời giải 8 8 8 a)
3 f (x)+ 2g(x) dx = 3
f (x)dx+ 2
g(x)dx = 3.5 + 2.(−2) =11. −1 −1 −1 8 3 8 3 8 8 lOMoAR cPSD| 47708777 b)
f (x)dx =
f (x)dx + f (x)dx
f (x)dx =
f (x)dx −
f (x)dx = 5− 6 = −1. −1 −1 3 −1 −1 3 3 Do ó
2 f (x)dx = −1. −1
1.2.2. Công thức Newton – Leibniz
Ta ã thấy việc tính tích phân xác ịnh bằng ịnh nghĩa là khá phức tạp. Tuy nhiên, ịnh lý cơ bản của
giải tích (Fundamental Theorem of Calculus) cho phép ta tính tích phân của một hàm thông qua
nguyên hàm của nó. Đây là một trong những ịnh lý quan trọng nhất trong giải tích và toán học nói
chung. Định lý này liên kết hai mảng chủ yếu của giải tích là ạo hàm với tích phân. Kết quả của ịnh
lý ược phát triển ộc lập bởi hai nhà toán học Isaac Newton (1642–1727) và Gottfried Wilhelm
Leibniz (1646–1716) và công thức sau ây mang tên hai nhà toán học này.
Công thức Newton – Leibniz
Nếu hàm số f liên tục trên oạn a;b và F ( ) )
x là một nguyên hàm bất kỳ của hàm số f (x trên oạn a;b thì
b f (x)dx = F (b)− F (a). a
Việc chứng minh công thức này cần sử dụng một kết quả ược gọi là công thức ạo hàm theo cận
trên, từ ó ta tìm ược mối liên hệ giữa phép toán ạo hàm và phép toàn tích phân. Tuy nhiên, ta không
chứng minh công thức này trong nội dung chương trình mà chỉ xét một vài ví dụ vận dụng công
thức ể tính tích phân xác ịnh dưới ây. Ví dụ 1.8.
Tính tích phân xác ịnh sau. a) + 2 x2 13 dx. 1 x ( ) b) 1 e2x + x dx. 0 c) 5 x + 22 x3 dx. 1 x lOMoAR cPSD| 47708777 Lời giải a) + − 2 x2 13 dx x3 x−2 2 8 − 1 1 − 1 65 . 1 x 3 2 1 3 8 3 2 24 ( ) b) + + + − 1 e2x x dx e2x 2 x3/2 1 e2 2 1 e2 1 . 0 2 3 0 2 3 2 2 3 ) x x 1 c) 5 + 2 3 + 5 = ( 2 dx = 5 2x
dx = (ln x + x2 1 ln 5 + 25)−1 = ln 5 + 24 . 1 x 1 x
1.3. ỨNG DỤNG CỦA NGUYÊN HÀM VÀ TÍCH PHÂN TRONG KINH TẾ
1.3.1. Xác ịnh các hàm kinh tế khi biết hàm cận biên tương ứng.
Ta ã biết trong kinh tế hàm cận biên là ạo hàm của hàm tương ứng, chẳng hạn các hàm chi phí cận
biên, doanh thu cận biên, lợi nhuận cận biên tương ứng là hàm ạo hàm của hàm chi phí, hàm
doanh thu, hàm lợi nhuận. Vậy các hàm chi phí, doanh thu, lợi nhuận là nguyên hàm của các hàm cận biên tương ứng.
Giả sử hàm f (x) là hàm cận biên của một hàm kinh tế F( )
x , khi ó ta có thể tìm hàm kinh tế F(x)
bằng cách lấy tích phân bất ịnh F(x) = f (x)dx,
trong ó hằng số C ở tích phân vế phải ược xác ịnh dựa vào iều kiện ầu y = 0 F(x0 ) . Ví dụ 1.9. a)
Hàm chi phí cận biên của một công ty cho bởi MC = 2Q2 + 7Q+ 4 . Tìm hàm tổng chi phí
biết chi phí cố ịnh là 100. b)
Giả sử doanh thu cận biên ở mỗi mức sản lượng Q là MR = −3Q2 − 4Q + 50 . Tìm hàm tổng doanh thu TR. Lời giải = 2 + 7
a) Hàm tổng chi phí là TC MCdQ
(2Q2 + 7Q + 4)dQ Q3
Q2 + 4Q +C . 3 2 lOMoAR cPSD| 47708777
Chi phí cố ịnh là chi phí ứng với mức sản lượng Q = 0, do ó ta có C =100 . Vậy
TC = 2 Q3 + 7 Q2 + 4Q+100 . 3 2
b) Hàm tổng doanh thu là TR MRdQ
(−3Q2 −4Q+50)dQ = −Q3 −2Q2 +50Q+C .
Khi Q = 0 thì TR = 0 nên C = 0, do ó TR = −Q3 − 2Q2 + 50Q . Ví dụ 1.10.
Hàm doanh thu cận biên và hàm chi phí cận biên của một công ty ược cho bởi
MR = 240−0,6Q2,
MC = 150 + 0,3Q2.
Biết chi phí cố ịnh là 50 ô la, hãy tìm lợi nhuận tối a. Lời giải
Ta có hàm lợi nhuận (Q) =TR−TC
(Q) = (TR−TC) MR−MC (Q) =
(MR−MC)dQ =
(90−0,9Q2)dQ = 90Q−0,3Q3 +C
Khi Q = 0 thì doanh thu TR = 0, chi phí bằng chi phí cố ịnh bằng 50, lợi nhuận là 50. Do ó (0) =C = −50 nên
(Q) = 90Q−0,3Q3 −50.
Ta i tìm lợi nhuận tối a. Ta có:
(Q) = 90 − 0,9Q2
(Q) = 0 Q =1 (Q 0) (Q) = −1,8Q (1) = −1,8
0 nên hàm số ạt cực ại tại Q =1. Vậy lợi nhuận tối a ạt ược
khi Q =1 và giá trị lợi nhuận tối a là (1) = 90−0,3−50 = 39,7(ô la).
1.3.2. Xác ịnh quỹ vốn theo lượng ầu tư.
Giả sử việc ầu tư ược tiến hành liên tục theo thời gian, khi ó quỹ vốn K và lượng ầu tư I là các hàm
số phụ thuộc vào biến thời gian t : K = K(t), I = I(t) với t 0.
Lượng ầu tư I(t) là lượng bổ sung vào quỹ vốn tại thời iểm t , do ó I(t) chính là tốc ộ tăng của quỹ
vốn K(t) tại thời iểm t , nói cách khác: K (t) = I(t) . Từ ó ta có K(t) I(t)dt ,
hằng số C trong tích phân ở vế phải ược xác ịnh dựa vào quỹ vốn ban ầu K = 0 K(0). Ví dụ 1.11.
Lượng ầu tư của một doanh nghiệp tại thời iểm t (tính theo năm) là I (t) = 144t0,8 ( triệu ồng).
Xác ịnh hàm quỹ vốn theo biến t biết rằng ban ầu quỹ vốn của doanh nghiệp là 100 triệu ồng.
Tính tổng vốn tăng thêm từ cuối năm thứ nhất ến cuối năm thứ ba. Lời giải
Hàm quỹ vốn theo biến t là K(t) I(t)dt
144t0,8dt =80t1,8 +C . lOMoAR cPSD| 47708777
Quỹ vốn ban ầu tại thời iểm t = 0 là 100 nên ta có C =100, do ó K(t) = 80t1,8 +100 .
Tổng vốn tăng thêm từ cuối năm thứ nhất ến cuối năm thứ ba là: K(3)−
K(1) = 80.31,8 +100−(80.11,8 +100) 498(triệu ồng).
1.3.3. Xác ịnh lượng thay ổi của một hàm kinh tế khi biết hàm cận biên tương ứng
Giả sử hàm f (x) là hàm cận biên của một hàm kinh tế F ( ) )
x và f (x liên tục trên oạn a;b . Khi ó
lượng thay ổi của hàm kinh tế F(x) khi x thay ổi từ x=a ến x =b là b
F (b)− F (a) = f (x)dx. a Ví dụ 1.12.
Một nhà máy có chi phí cận biên là MC = 3(Q−5)2 (ơn vị tiền tệ /sản phẩm). Nếu mức sản lượng
Q tăng từ 8 lên 10 sản phẩm thì tổng chi phí sản xuất tăng thêm bao nhiêu? Lời giải
Chi phí tăng thêm ược xác ịnh bởi TC(10)−TC(8). Do hàm tổng chi phí TC là một nguyên hàm
của hàm chi phí cận biênMC nên 10 10 =
TC(10)−TC(8) = MC(Q)dQ
3(Q −5)2 dQ = 98 (ơn vị tiền tệ). 8 8 Ví dụ 1.13.
Tốc ộ thay ổi sản lượng của một nhà máy là Q (t) = 36t3 − 24t2 +144t + 60 sản phẩm/tháng.
a) Tính số sản phẩm nhà máy sản xuất ược trong hai tháng ầu.
b) Tính số sản phẩm nhà máy sản xuất ược trong tháng thứ ba. Lời giải
a) Số sản phấm nhà máy sản xuất ược trong hai tháng ầu là = Q(2)−Q(0) = 2Q (t)dt
2(36t3 − 24t2 +144t + 60)dt = 488. 0 0
b) Số sản phấm nhà máy sản xuất ược trong tháng thứ ba là = Q(3)−Q(2) =
3 Q (t)dt
3 (36t3 − 24t2 +144t + 60)dt = 853 . 2 2 lOMoAR cPSD| 47708777
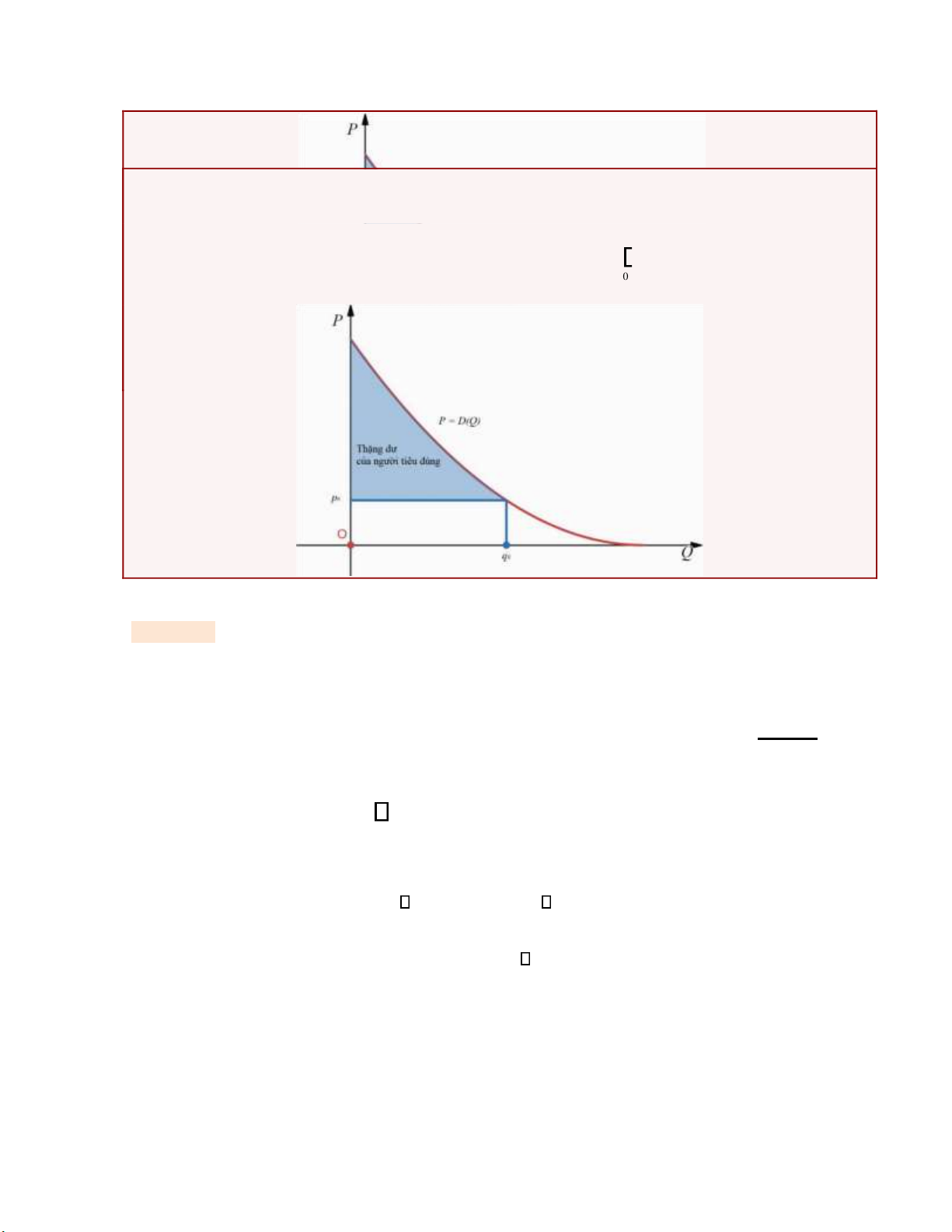
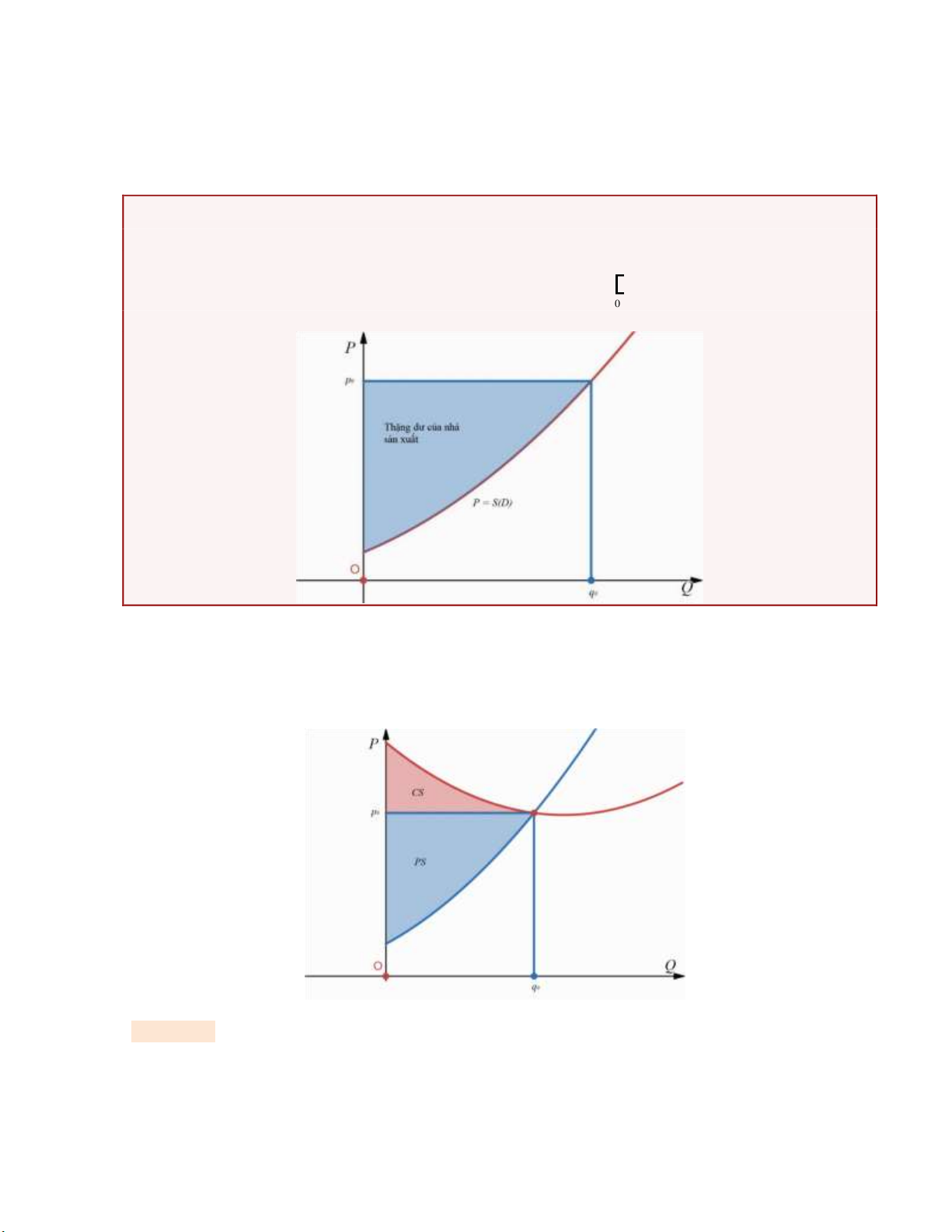
1.3.4. Tính thặng dư của nhà sản xuất và thặng dư của người tiêu dùng
Định nghĩa 1.3. Tổng mức sẵn lòng chi tiêu của người tiêu dùng ể mua q0 ơn vị một loại hàng hóa ược cho bởi q = WS
0 D(Q)dQ , 0
Trong ó P = D( )
Q là hàm cầu của loại hàng hóa ó. Về ý nghĩa hình học, giá trị này là diện tích
miền bên dưới bởi ường cầu trên oạn 0;q0 lOMoAR cPSD| 47708777
ở cùng m ộ t m ứ c s ả n ph ẩ m. 0 q
Định nghĩa 1.4. N ế u = 0
q ơn vị hàng hóa ượ c bán v ớ i giá 0
p m ỗi ơn vị và P D ( Q) là hàm
c ầ u c ủa ngườ i tiêu dùng v ớ i hàng hóa này thì 0 q
Th ặng dư của ngườ i tiêu dùng CS =WS − = − 0 p 0 q D ( Q) dQ 0 p 0 q . 0
V ề ý nghĩa hình họ c, giá tr ị này là di ệ n tích mi ề n như trong hình dưới ây. .
Trong kinh t ế h ọ c, th ặng dư của ngườ i tiêu dùng là ại lượ ng lư ợ ng th ể hi ệ n ộ chênh l ệ ch gi ữ a
tổng số tiền người tiêu dùng sẵn lòng chi tiêu và lượng chi trả thực tế mà người tiêu dùng phải trả Ví dụ 1.14.
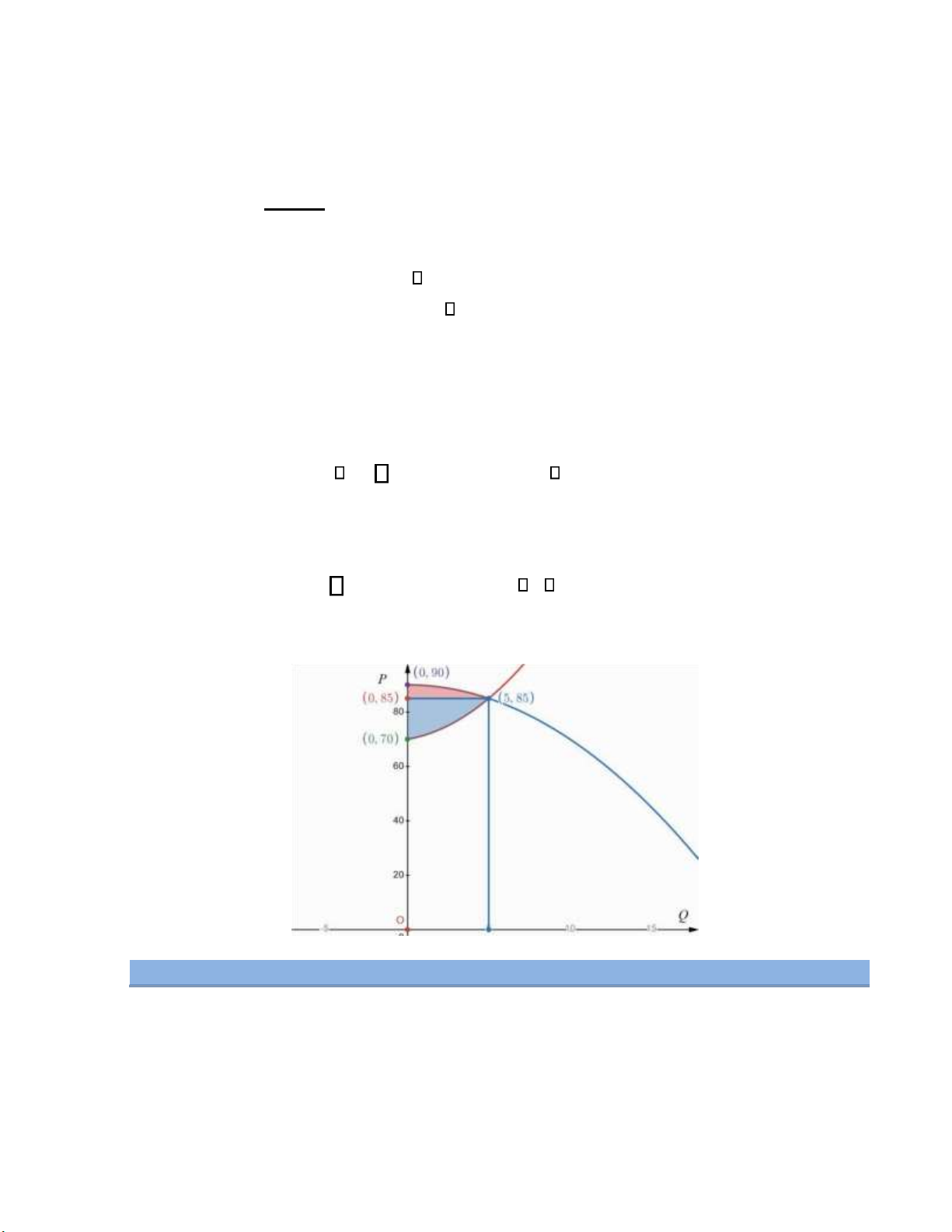
Hàm cầu của một loại hàng hóa ược cho bởi P = D(Q) = 2(60−Q2 ). Tính mức sẵn lòng chi tiêu
của người tiêu dùng WS ể sở hữu 3 sản phẩm hàng hóa trên. Tìm mức giá p0 ể nhà sản xuất bán hết
ược 3 sản phầm hàng hóa này và tính thặng dư tương ứng của người tiêu dùng CS . Lời giải Để sở hữu q = 0
3 sản phẩm thì mức sẵn lòng chi tiêu của người tiêu dùng là = WS
3 2(60 −Q2)dQ = 342 (ơn vị tiền tệ). 0 Mức giá p ể
0 bán hết số lượng sản phẩm q0 thỏa mãn phương trình hàm cầu p = 2 ) = = 0 2(60 −q0 p0
2(60 −32 ) p0 102(ơn vị tiền tệ).
Khi ó, thặng dư tướng ứng của người tiêu dùng là
CS =WS − p = 0q0
342 −102 3 = 36 (ơn vị tiền tệ). lOMoAR cPSD| 47708777
Thặng dư của nhà sản xuất là giá trị ược xác ịnh tương tự với hàm cung. Giá trị này là ại lượng
thể hiện ộ chênh lệch giữa lượng tiền mà nhà sản xuất sẵn lòng chấp nhận và lượng tiền thực tế
nhà sản xuất nhận ược.
Định nghĩa 1.5. N ế u = 0
q ơn vị hàng hóa ượ c bán v ớ i giá 0
p m ỗi ơn vị và P S ( Q) là hàm
cung ố i v ớ i hàng hóa này thì 0 q
Th ặng dư củ a nhà s ả n xu ấ t PS = 0 p 0 q − S ( Q) dQ . 0
V ề ý nghĩa hình họ c, giá tr ị này là di ệ n tích mi ền như trong hình dưới ây.
Trong thị trường cân bằng, S( ) )
Q = D(Q ạt giá cân bằng p0 và lượng cân bằng q0 . Khi ó, ường
cung và ường cầu gặp nhau và ta thường tìm thặng dư của nhà sản xuất và thặng dư của người tiêu
dùng trong trường hợp này. Hình ảnh về thặng dư của nhà xản xuất PS và thặng dư của người tiêu
dùng CS ược mô tả ở hình dưới ây. Ví dụ 1.15.
Hàm cung và hàm cầu của một loại sản phẩm ược cho bởi
P = S(Q) = 0,4Q2 +Q+ 70 , lOMoAR cPSD| 47708777
P = D(Q) = −0,2Q2 + 90.
a) Tìm mức giá cân bằng và lượng cân bằng của thị trường.
b) Tính thặng dư của nhà sản xuất và thặng dư của người tiêu dùng khi thị trường ạt trạng thái
cân bằng. Lời giải
a) Thị trường ạt trạng thái cân bằng khi
0,4Q2 +Q+70 =−0,2Q2 +90
0,6Q2 +Q−20 = 0 Q = 5
Lượng cân bằng của thị trường là q = =− 0
5. Khi ó, giá cân bằng của thị trường là p0 0,2.52 +90=85.
b) Thặng dư sản xuất khi thị trường ạt trạng thái cân bằng là − PS = 85 5
5(0,4Q2 +Q+ 70)dQ 45,83 (ơn vị tiền tệ). 0
Thặng dư người tiêu dùng khi thị trường ạt trạng thái cân bằng là = CS
5(−0,2Q2 + 90)dQ−85 5 16,67 (ơn vị tiền tệ). 0
Hình biểu diễn thặng dư của nhà sản xuất và thặng dư người tiêu dùng ược cho bởi các
miền trong hình dưới ây. BÀI TẬP
1. Tìm họ các nguyên hàm của các hàm số sau. lOMoAR cPSD| 47708777
a) f (x) = x1 −2x+6,
b) f (x) = 2e5x +e2x+1 2 x 2 1 , c) f = 3 3 x x (x) ,
d) f (x) =1− + − 1 1 3 − + x 1−3x , e) f (x) − = 1 +
f) f (x) = 2ex 2 , 1 2 x x x 4 − x −9 x +3 , g) f (x)=−3e +
h) f (x) = x + − 3 8x2 3x+1, 5 x x −4 x +3 = i) f (x) 2 , k) f (x) = , l) f (x) = .
2. Tính các tích phân xác ịnh sau. ( ) a) 2 2 − + 1 1− x + 22 dx; b) 0 1+12x dx; c) 10 3e−4x x dx; 3 x − d) 1 − 9 1 1 4 x2 2 1 2 (3x+1)2 dx dx dx dx g) x ; e) 2 ; e h) + + 2 5x + 6 ; i)
2 3x−5 x+1dx; f) 0 x . 0 5 2x 2 dx ;
1 . Xác ịnh hàm tổng chi phí TC theo mức sản lượng Q trong các trường hợp sau:
a) Hàm chi phí cận biên là MC = 3Q+ 5 và chi phí cố ịnh là FC = 20.
b) Chi phí cận biên là MC =12e0,4Q và chi phí cố ịnh FC =100.
2 . Giả sử ở mỗi mức sản lượng Q doanh thu cận biên là MR =100−3Q−2Q2 . Hãy xác ịnh hàm tổng
doanh thu và hàm cầu ối với sản phẩm (ơn vị: triệu ồng). lOMoAR cPSD| 47708777
5. Hàm doanh thu cận biên và hàm chi phí cận biên của một công ty ược cho bởi MR = 360−0,5Q2
MC = 120+0,1Q2 .
Biết chi phí cố ịnh là 50 ô la, hãy tìm lợi nhuận tối a. − 0,1
6. Tìm hàm tiết kiệm biết hàm tiết kiệm cận biên ược cho bởi MPS = 0,4 và số tiền tiết Y
kiệm bằng 0 khi thu nhập là 100.
7. Giả sử hàm tiêu dùng cận biên (Marginal Propensity to consume) phụ thuộc vào mức thu nhập
Y bởi hàm số MPC = 0,6+0,1Y−1/3 . Hãy xác ịnh hàm tiêu dùng C(Y) theo thu nhập Y biết rằng
mức tiêu dùng thiết yếu (tức là tiêu dùng bắt buộc phải chi cả khi không có thu nhập) là 50 (ơn vị tính: tỉ ồng).
8. Tìm biểu thức của hàm tiêu dùng biết hàm tiêu dùng cận biên là MPC = 0,4Y + 0,4 và C = 50 khi Y = 100 Y
9. Tốc ộ tăng trưởng của số lượng cửa hàng tạp hóa n tại một ịa phương sau t tháng là dn = 1 dt t
Ban ầu có hai cửa hàng. Hãy ước tính số cửa hàng tạp hoá tại ịa phương sau 9 tháng.
10. Số lượng sản phẩm ược sản xuất sau t giờ làm việc của một nhân viên mới là hàm N thỏa mãn
dN =10e−0,1t dt
Giả sử khi bắt ầu ca làm việc nhân viên ó chưa sản xuất ược bất kỳ một sản phẩm nào, hỏi nhân
viên ó có thể sản xuất bao nhiêu sản phẩm sau 8 giờ làm việc?
11. Tốc ộ thay ổi sản lượng của một nhà máy là Q (t) = 2t3 −3t2 +10t + 6 ơn vị/giờ, với t là số giờ
sau khi bắt ầu ca làm việc lúc 8 giờ sáng. Có bao nhiêu ơn vị sản phẩm ược sản xuất từ 10 giờ sáng tới giữa trưa?
12. Một công ty quảng cáo bắt ầu chiến dịch quảng cáo cho một sản phẩm mới và các ịnh sau t ngày
kể từ lúc bắt ầu thì số người N( )
t biết ến sản phẩm thay ổi với tốc ộ − 0 ,04t
N (t) = 6t2 2 người mỗi ngày. t + 2
Tìm số người biết ến sản phẩm trong tuần ầu tiên? Trong tuần thứ ba?
13. Một nhà máy có chi phí cận biên là MC = 8Q+ 2(ơn vị tiền tệ mối ơn vị). Tổng chi phí sản
xuất 10 sản phẩm ầu tiên là bao nhiêu? Tổng chi phí sản xuất 10 sản phẩm ầu tiên là bao nhiêu?