Chương 5: Sắp xếp - Cấu trúc dữ liệu và giải thuật (ET2100) | Trường Đại học Bách khoa Hà Nội
Sắp xếp (Sorting) là quá trình tổ chức lại họ các dữ liệu theo thứ tự giảm dần hoặc tăng dần.
Môn: Cấu trúc dữ liệu và giải thuật (ET2100)
Trường: Đại học Bách Khoa Hà Nội
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 27879799
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG
Cấu trúc dữ liệu và thuật toán Nguyễn Khánh Phương Computer Science department
School of Information and Communication technology
E-mail: phuongnk@soict.hust.edu.vn Nội dung khóa học
Chương 1. Các khái niệm cơ bản
Chương 2. Các sơ ồ thuật toán
Chương 3. Các cấu trúc dữ liệu cơ bản Chương 4. Cây Chương 5. Sắp xếp Chương 6. Tìm kiếm Chương 7. Đồ thị 2
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG 1 lOMoAR cPSD| 27879799 Chương 5. Sắp xếp Nguyễn Khánh Phương Computer Science department
School of Information and Communication technology
E-mail: phuongnk@soict.hust.edu.vn Bài toán sắp xếp
• Sắp xếp (Sorting) là quá trình tổ chức lại họ các dữ liệu theo thứ tự giảm dần hoặc tăng dần.
• Dữ liệu cần sắp xếp có thể là:
– Số nguyên/thực.. (integers/float)
– Xâu kí tự (character strings) – …
• Khóa sắp xếp (sort key)
– Là bộ phận của bản ghi xác ịnh thứ tự sắp xếp của bản ghi trong họ các bản ghi.
– Ta cần sắp xếp các bản ghi theo thứ tự của các khoá. – Ví dụ: khóa là tong = toan + ly + hoa
typedef struct{ char *ma; struct{ float toan, ly, hoa, tong; } DT; }thisinh;
typedef struct node{ thisinh data; struct node* next; 4 }node;
Các loại thuật toán sắp xếp 2 lOMoAR cPSD| 27879799
Sắp xếp trong (internal sort):
• Đòi hỏi họ dữ liệu ược ưa toàn bộ vào bộ nhớ trong của máy tính • Ví dụ: –
insertion sort (sắp xếp chèn), selection sort (sắp xếp lựa chọn), bubble sort (sắp xếp nổi bọt) –
quick sort (sắp xếp nhanh), merge sort (sắp xếp trộn), heap sort (sắp xếp vun ống), sample
sort (sắp xếp dựa mẫu), shell sort (vỏ sò) Sắp xếp ngoài (external sort):
• Họ dữ liệu không thể cùng lúc ưa toàn bộ vào bộ nhớ trong, nhưng có thể ọc vào từng bộ phận từ bộ nhớ ngoài
• Ví dụ:Poly-phase mergesort (trộn nhiều oạn), cascade-merge (thác nước), oscillating sort (dao ộng)
Sắp xếp song song (Parallel sort):
• Bitonic sort, Batcher even-odd sort.
• Smooth sort, cube sort, column sort. • GPU sort. 5
Các ặc trưng của một thuật toán sắp xếp
• Tại chỗ (in place): nếu không gian nhớ phụ mà thuật toán òi hỏi là O(1), nghĩa là bị
chặn bởi hằng số không phụ thuộc vào ộ dài của dãy cần sắp xếp.
• Ổn ịnh (stable): Nếu các phần tử có cùng giá trị vẫn giữ nguyên thứ tự tương ối của
chúng như trước khi sắp xếp. Bài toán sắp xếp 3 lOMoAR cPSD| 27879799 •
Có hai phép toán cơ bản mà thuật toán sắp xếp thường phải sử dụng:
– Đổi chỗ (Swap): Thời gian thực hiện là O(1) void swap( datatype *a, datatype
*b){ datatype *temp = *a; //datatype-kiểu dữ liệu của phần tử *a = *b; *b = *temp; }
– So sánh: Compare(a, b) trả lại true nếu a i trước b trong thứ tự cần sắp xếp và false nếu trái lại. •
Phân tích thuật toán sắp xếp: thông thường, các thuật toán sẽ sử dụng phép toán so sánh ể xác
ịnh thứ tự giữa hai phần tử rồi thực hiện ổi chỗ nếu
cần. Khi phân tích thuật toán sắp xếp, ta sẽ chỉ cần ếm số phép toán so sánh và số
lần dịch chuyển các phần tử (bỏ qua các phép toán khác không ảnh hưởng ến kết quả). 7 Bài toán sắp xếp
• Các thuật toán chỉ sử dụng phép toán so sánh ể xác ịnh thứ tự giữa hai
phần tử ược gọi là thuật toán sử dụng phép so sánh (Comparison-based sorting algorithm).
• Nếu có những thông tin bổ sung về dữ liệu ầu vào, ví dụ như:
– Các số nguyên nằm trong khoảng [0..k] trong ó k = O(n)
– Các số thực phân bố
ều trong khoảng [0, 1) ta sẽ có thuật toán
tốt hơn thuật toán sắp xếp chỉ dựa vào phép so sánh.
(Thuật toán thời gian tuyến tính: sắp xếp
ếm (couting-sort), sắp xếp theo cơ số (radixsort), sắp xếp óng gói (bucket-sort)) 8
Các thuật toán sắp xếp 4 lOMoAR cPSD| 27879799
Khi so sánh các thuật toán, thông thường quan tâm ến:
• Thời gian chạy. Đối với các dữ liệu rất lớn, các thuật toán không hiệu quả
sẽ chạy rất chậm và không thể ứng dụng trong thực tế.
• Bộ nhớ. Các thuật toán nhanh òi hỏi ệ quy sẽ có thể phải tạo ra các bản
copy của dữ liệu ang xử lí. Với những hệ thống mà bộ nhớ có giới hạn (ví
dụ embedded system), một vài thuật toán sẽ không thể chạy ược.
• Độ ổn ịnh (stability). Độ ổn ịnh ược ịnh nghĩa dựa trên iều gì sẽ xảy ra với
các phần tử có giá trị giống nhau.
– Đối với thuật toán sắp xếp ổn ịnh, các phần tử với giá trị bằng nhau sẽ
giữ nguyên thứ tự trong mảng trước và sau khi sắp xếp.
– Đối với thuật toán sắp xếp không ổn ịnh, các phần tử có giá trị bằng
nhau sẽ có thể có thứ tự bất kỳ. 9
Tiêu chí lựa chọn giải thuật
Nhiều yếu tố ảnh hưởng: • Ổn ịnh •
Danh sách liên kết hay mảng •
Đặc trưng của dữ liệu cần sắp xếp: – Nhiều khóa ?
– Các khóa là phân biệt ? – Nhiều dạng khóa ?
– Kích thước bản ghi lớn hay nhỏ ? – Dữ liệu
ược sắp xếp ngẫu nhiên?
Không thể bao phủ tất cả các yếu tố Nội dung 5 lOMoAR cPSD| 27879799
1. Sắp xếp chèn (Insertion sort)
2. Sắp xếp chọn (Selection sort)
3. Sắp xếp nổi bọt (Bubble sort)
4. Sắp xếp trộn (Merge sort)
5. Sắp xếp nhanh (Quick sort)
6. Sắp xếp vun ống (Heap sort)
1. Sắp xếp chèn (Insertion sort)
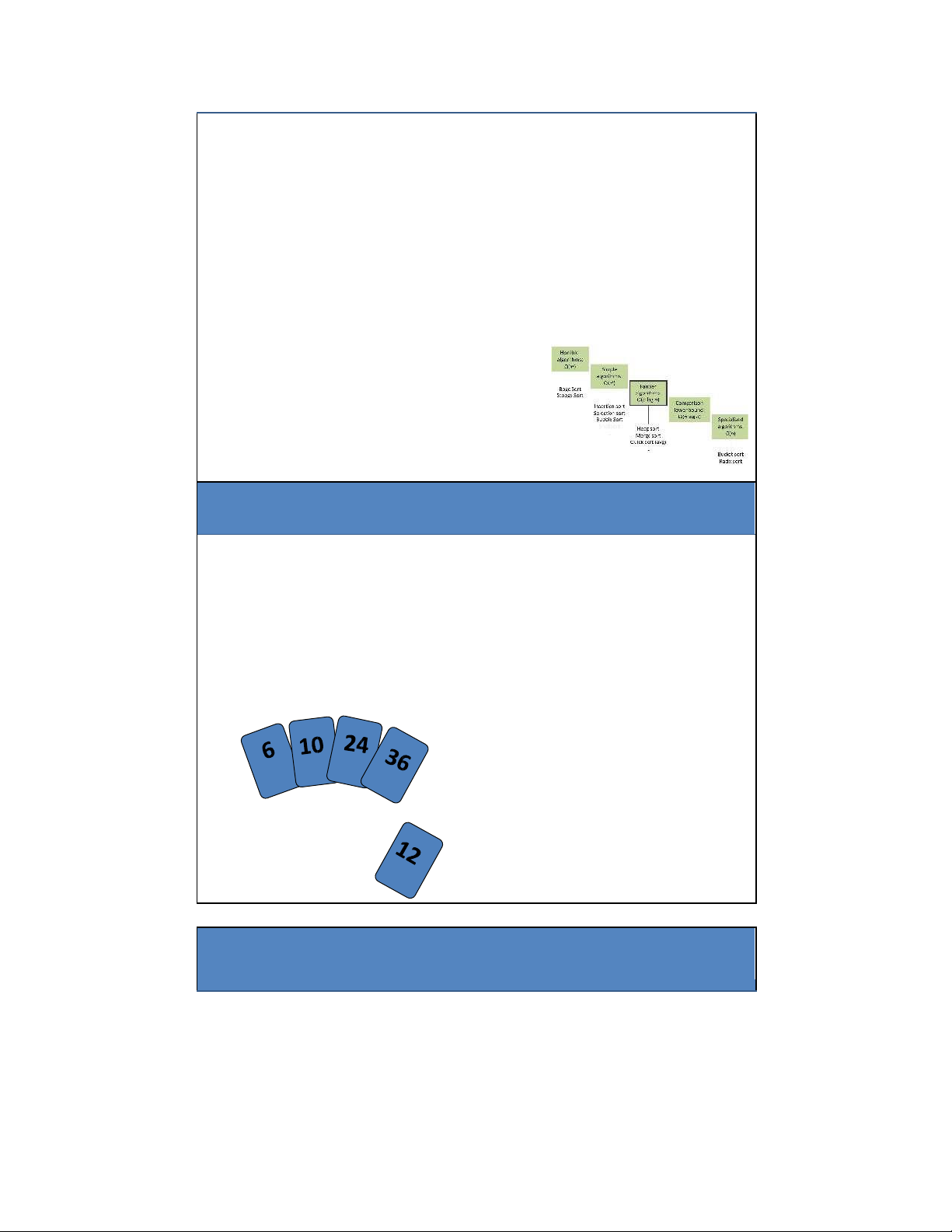
Phỏng theo cách làm của người chơi bài khi cần "chèn" thêm một con bài vào
bộ bài đã được sắp xếp trên tay.
Để chèn 12, ta cần tạo chỗ cho nó bởi việc
dịch chuyển đầu tiên là 36 và sau đó là 24. 12
1. Sắp xếp chèn (Insertion sort) 6 lOMoAR cPSD| 27879799
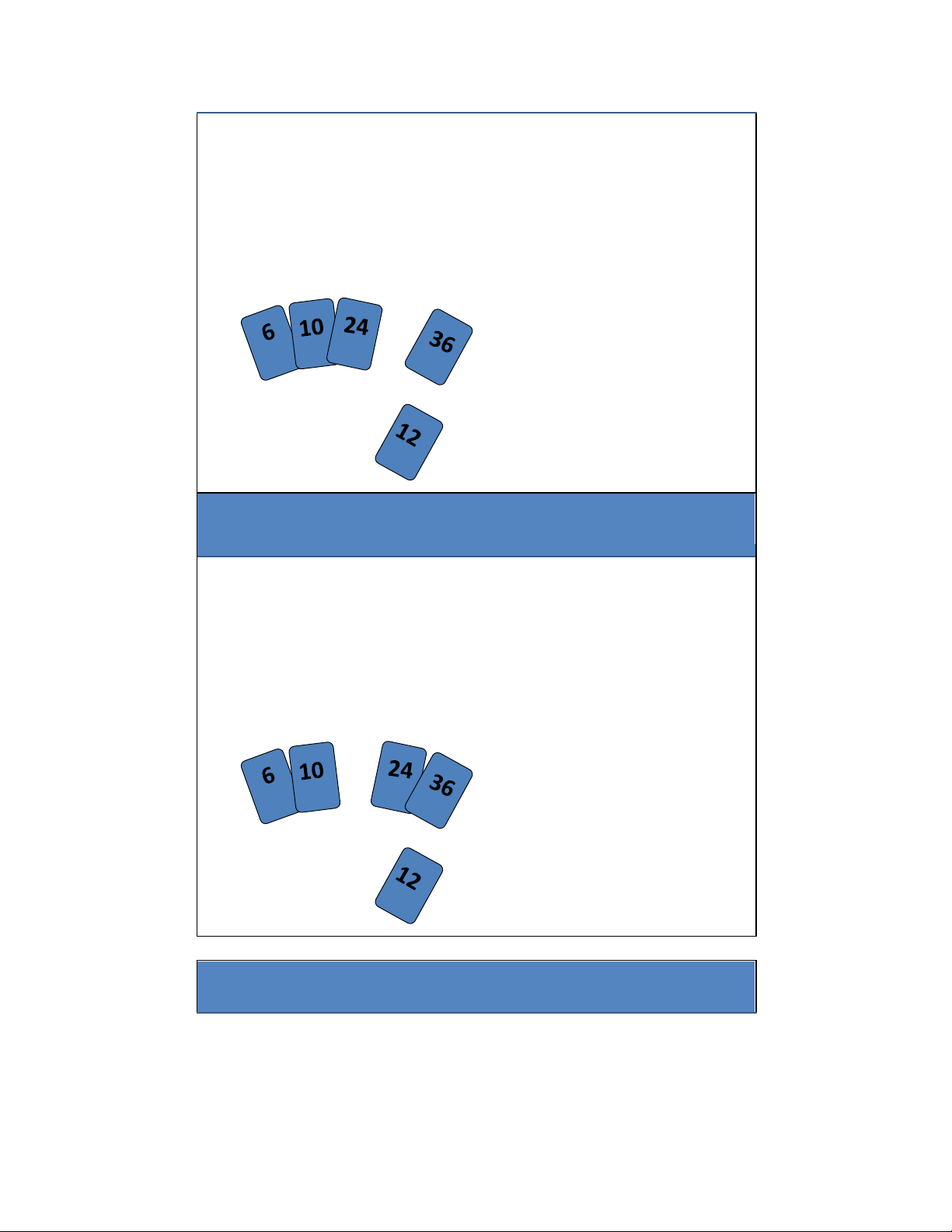
Phỏng theo cách làm của người chơi bài khi cần "chèn" thêm một
con bài vào bộ bài đã được sắp xếp trên tay.
Để chèn 12, ta cần tạo chỗ cho nó
bởi việc dịch chuyển đầu tiên là 36 và sau đó là 24. 13
1. Sắp xếp chèn (Insertion sort)
Phỏng theo cách làm của người chơi bài khi cần "chèn" thêm một
con bài vào bộ bài đã được sắp xếp trên tay.
Để chèn 12, ta cần tạo chỗ cho nó
bởi việc dịch chuyển đầu tiên là 36 và sau đó là 24. 14
1. Sắp xếp chèn (Insertion sort) 7 lOMoAR cPSD| 27879799
Phỏng theo cách làm của người chơi bài khi cần "chèn" thêm một con
bài vào bộ bài đã được sắp xếp trên tay.
Để chèn 12, ta cần tạo chỗ cho nó bởi
việc dịch chuyển đầu tiên là 36 và sau đó là 24. 15
1. Sắp xếp chèn (Insertion sort) Thuật toán:
• Mảng cần sắp xếp ược chia làm 2 phần, sorted và unsorted: – Những phần
tử nằm trong phần sorted: ã ược sắp xếp
– Những phần tử nằm trong phần unsorted: chưa ược sắp xếp
• Mỗi bước lặp: phần tử ầu tiên thuộc phần unsorted sẽ ược chuyển sang phần sorted.
Mảng có n phần tử sẽ cần n-1 bước lặp ể sắp xếp xong 16 8 lOMoAR cPSD| 27879799 n- k
úng vị trí trong dãy gồm k
Dịch tất cả các phần tử a[pos]… a[k-1] sang phải 1 vị trí n- k
úng vị trí trong dãy gồm
Tại mỗi bước lặp , có thể cần nhiều hơn một lần hoán đổi vị trí các phần tử để có thể đưa phần tử thứ
về đúng vị trí của nó trong dãy cần sắp xếp k 9 lOMoAR cPSD| 27879799 10 lOMoAR cPSD| 27879799 Cài
ặt: Insertion Sort Algorithm NGUYỄN KHÁNH PHƯƠNG 21 KHMT – SOICT - ĐHBK HN Đánh giá
ộ phức tạp tính toán của Insertion sort: O(n2)
• Sắp xếp chèn là tại chỗ và ổn ịnh (In place and Stable)
• Phân tích thời gian tính của thuật toán –
Best Case: 0 hoán ổi, n-1 so sánh (khi dãy ầu vào là ã ược sắp) –
Worst Case: n2/2 hoán ổi và so sánh (khi dãy ầu vào có thứ tự ngược lại với thứ tự cần sắp xếp) –
Average Case: n2/4 hoán ổi và so sánh
• Là thuật toán sắp xếp tốt
ối với dãy ã gần ược sắp xếp –
Nghĩa là mỗi phần tử ã ứng ở vị trí rất gần vị trí trong thứ tự cần sắp xếp # of Sorted elements Best case Worst case 0 0 0 1 1 1 2 1 2 … … … n-1 1 n-1 Số phép so sánh 22
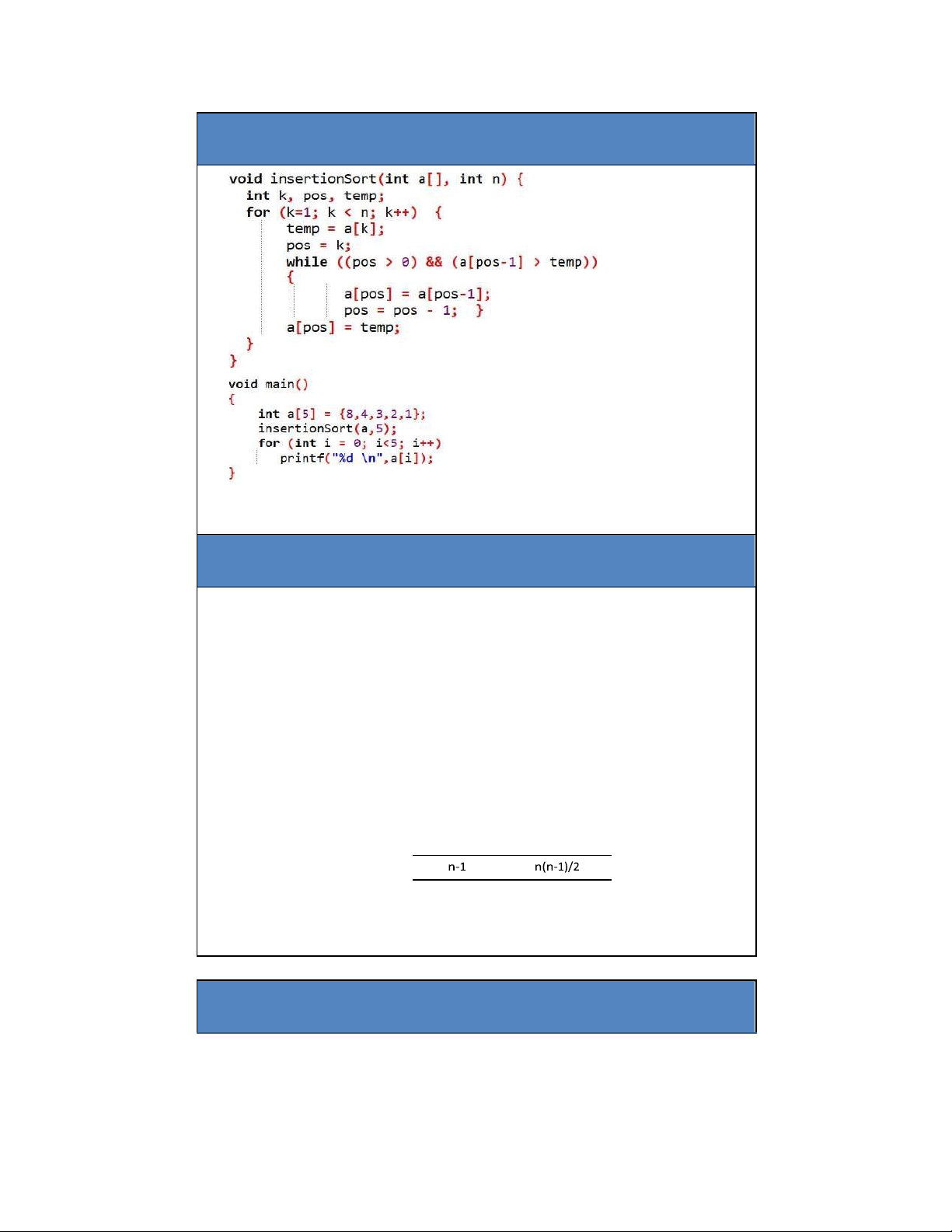
Đánh giá ộ phức tạp tính toán của Insertion sort 11 lOMoAR cPSD| 27879799 Vòng lặp for: • thực hiện n-1 lần
• Gồm 5 câu lệnh (bao gồm cả câu lệnh gán và so sánh ở vòng lặp for)
Tổng chi phí cho vòng lặp for: 5(n-1)
Số lần vòng lặp while thực hiện phụ thuộc vào trạng thái sắp xếp các phần tử trong mảng:
• Best case: mảng ầu vào ã
ược sắp xếp do ó phép hoán ổi vị trí các phần tử trong mảng không ược thực hiện lần nào.
– Với mỗi giá trị k ở vòng lặp for, ta chỉ test iều kiện thực hiện vòng lặp while úng 1 lần (2 thao tác = 1
phép so sánh pos > 0 và 1 phép so sánh phần tử a[pos-1] > temp), các câu lệnh trong thân vòng lặp while không bao giờ ược thực hiện
– Do ó, tổng chi phí cho vòng lặp while trong toàn bộ chương trình là 2(n-1) thao tác.
• Worst case: mảng ầu vào có thứ tự ngược với thứ tự cần sắp xếp
– Vòng lặp for thứ k: vòng lặp while thực hiện tổng cộng 4k+1 thao tác
– Do ó, tổng chi phí cho vòng lặp while trong toàn bộ
chương trình là 2n(n-1)+n-1 Time cost: – Best case: 7(n-1)
– Worst case: 5(n-1)+2n(n-1)+n-1
Các thuật toán sắp xếp
1. Sắp xếp chèn (Insertion sort)
2. Sắp xếp chọn (Selection sort)
3. Sắp xếp nổi bọt (Bubble sort)
4. Sắp xếp trộn (Merge sort)
5. Sắp xếp nhanh (Quick sort)
6. Sắp xếp vun ống (Heap sort) 24
2. Sắp xếp chọn (Selection sort) 12 lOMoAR cPSD| 27879799
• Mảng cần sắp xếp ược chia làm 2 phần: sorted và unsorted
– Những phần tử thuộc phần sorted: ã ược sắp xếp
– Những phần tử thuộc phần unsorted: chưa ược sắp xếp
• Mỗi bước lặp: tìm phần tử nhỏ nhất thuộc phần unsorted, rồi ổi vị trí phần tử nhỏ nhất này với phần tử
ầu tiên của phần unsorted Sau mỗi bước lặp (sau mỗi thao tác chọn và hoán ổi): vách ngăn hai phần
sorted và unsorted dịch chuyển 1 vị trí sang phải, tức là số lượng phần tử thuộc phần sorted tăng lên 1,
và thuộc phần unsorted giảm i 1.
• Mảng gồm n phần tử sẽ cần n-1 bước lặp
ể thực hiện xong sắp xếp.
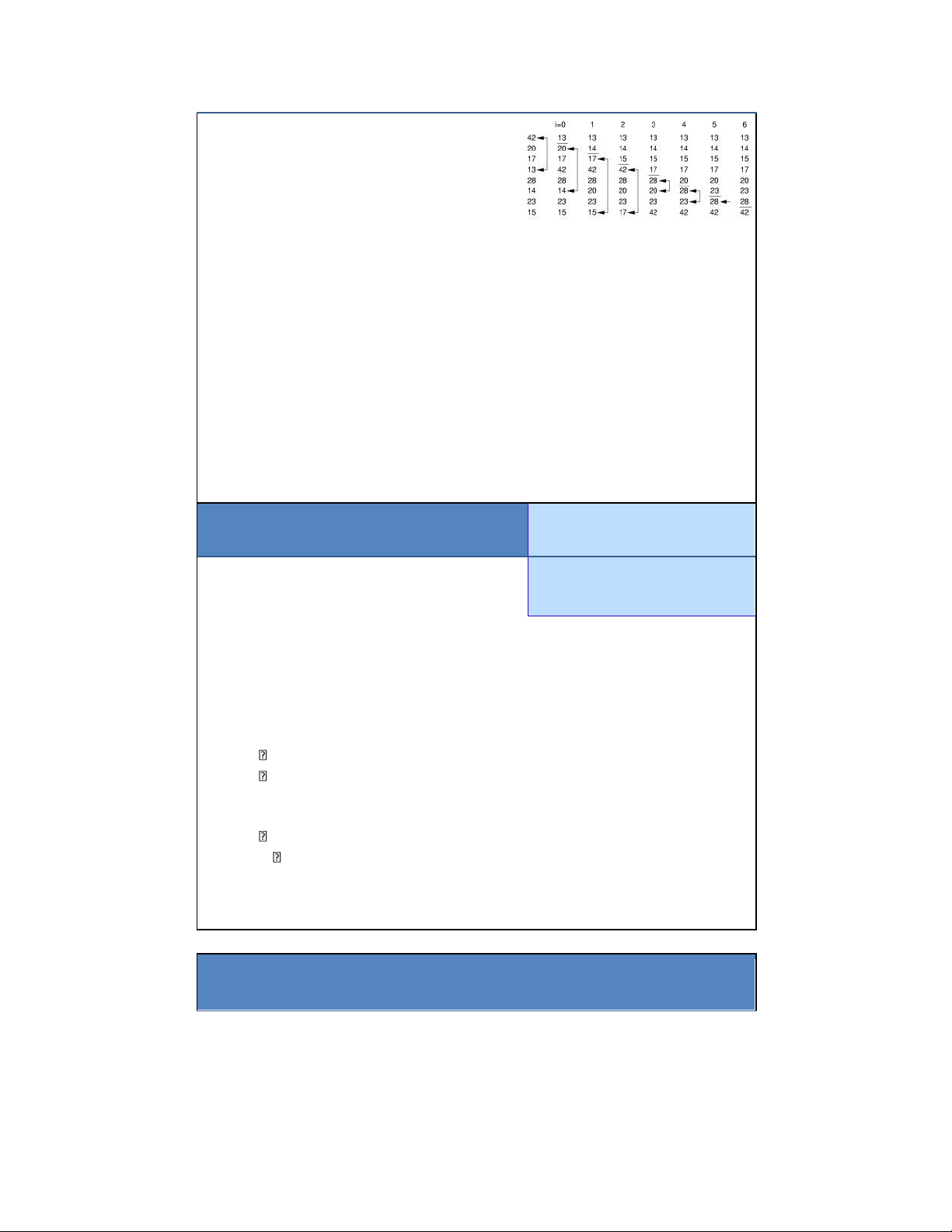
Tại bước lặp i (i=0,1,..,n-2): tìm
phần tử nhỏ nhất của phần
unsorted (tức là các phần tử từ
a[i]…a[n-1]), rồi chuyển nó lên
vị trí thứ i của mảng 25
2. Sắp xếp chọn (Selection sort) Thuật toán
• Tìm phần tử nhỏ nhất ưa vào vị trí 1 (a[0])
• Tìm phần tử nhỏ tiếp theo ưa vào vị trí 2 (a[1])
• Tìm phần tử nhỏ tiếp theo ưa vào vị trí 3 • … void swap(int *a,int *b) { int temp = *a; *a = *b; *b = temp; }
void selectionSort(int a[], int n){ int i, j, index_min;
for (i = 0; i < n-1; i++) {
//Tìm phần tử nhỏ nhất từ a[i] ến phần tử cuối cùng trong mảng index_min = i;
for (j = i+1; j < n; j++) if (a[j] < a[index_min]) index_min = j; // ưa
phần tử a[index_min] vào vị trí thứ i:
swap(&a[i], &a[index_min]); }
NGUYỄN KHÁNH PHƯƠNG 26 KHMT – } SOICT - ĐHBK HN Đánh giá
ộ phức tạp tính toán của Selection sort: O(n2) 13 lOMoAR cPSD| 27879799 Thuật toán
• Tìm phần tử nhỏ nhất ưa vào vị trí 1 (a[0])
• Tìm phần tử nhỏ tiếp theo ưa vào vị trí 2 (a[1])
• Tìm phần tử nhỏ tiếp theo ưa vào vị trí 3 • …
Đánh giá ộ phức tạp tính toán:
• Best case: 0 phép ổi chỗ, n2/2 phép so sánh.
• Worst case: n - 1 phép ổi chỗ, n2/2 phép so sánh.
• Average case: O(n) phép ổi chỗ, n2/2 phép so sánh.
• Ưu iểm nổi bật của sắp xếp chọn là số phép
ổi chỗ là ít. Điều này là có ý nghĩa nếu như việc ổi chỗ là tốn kém.
NGUYỄN KHÁNH PHƯƠNG 27 KHMT – SOICT - ĐHBK HN void swap(int *a,int *b) Đánh giá ộ phức tạp { int temp = *a;
void selectionSort(int a[], int n){ int i, j, index_min; *a = *b;
for (i = 0; i < n-1; i++) { index_min = i; *b = temp; }
//Tìm phần tử nhỏ nhất của phần unsorted: từ a[i+1] ến phần tử cuối cùng trong mảng for (j = i+1; j < n; j++) if (a[j]
< a[index_min]) index_min = j; // ưa phần tử a[index_min] vào vị trí thứ i: swap(&a[i], &a[index_min]); } }
Hàm selectionSort: vòng lặp for ngoài thực hiện n-
1 Ta gọi hàm swap 1 lần tại mỗi bước lặp.
Tổng phép hoán đổi (swap): n-1 Tổng phép gán: 3*(n-1) lần.
Vòng lặp for trong thực hiện số lần = kích thước phần unsorted - 1 (từ
mỗi vòng lặp thực hiện phép so sánh 1 lần, do đó tổng cộng:
# phép so sánh = (n-1) + (n-2) + v …. ì mỗ + i p 2 hé + p 1 = sw ap có 3 phép đổi
Vậy, độ phức tạp của Selection sort là O( chỗ n-1 tới 1),và n*(n-1)/2 28 n2) Kết luận: Đánh giá
ộ phức tạp của Selection sort: O(n2) 14 lOMoAR cPSD| 27879799
• Sắp xếp chọn là tại chỗ và ổn ịnh (In place and Stable)
• Thời gian tính: O(n2) cho cả 3 trường hợp best/worse/average. Tức
là thuật toán không phụ thuộc vào ặc tính của dữ liệu ầu vào.
• Mặc dù thuật toán sắp xếp chèn cần O(n2) phép so sánh, nhưng chỉ
thực hiện O(n) phép ổi chỗ.
– Nên chọn sắp xếp chọn nếu việc
ổi chỗ là tốn kém, còn
phép so sánh ít tốn kém (trường hợp dữ liệu ầu vào: short keys, long records).
NGUYỄN KHÁNH PHƯƠNG 29 KHMT – SOICT - ĐHBK HN
Các thuật toán sắp xếp
1. Sắp xếp chèn (Insertion sort)
2. Sắp xếp chọn (Selection sort)
3. Sắp xếp nổi bọt (Bubble sort)
4. Sắp xếp trộn (Merge sort)
5. Sắp xếp nhanh (Quick sort)
6. Sắp xếp vun ống (Heap sort) 30
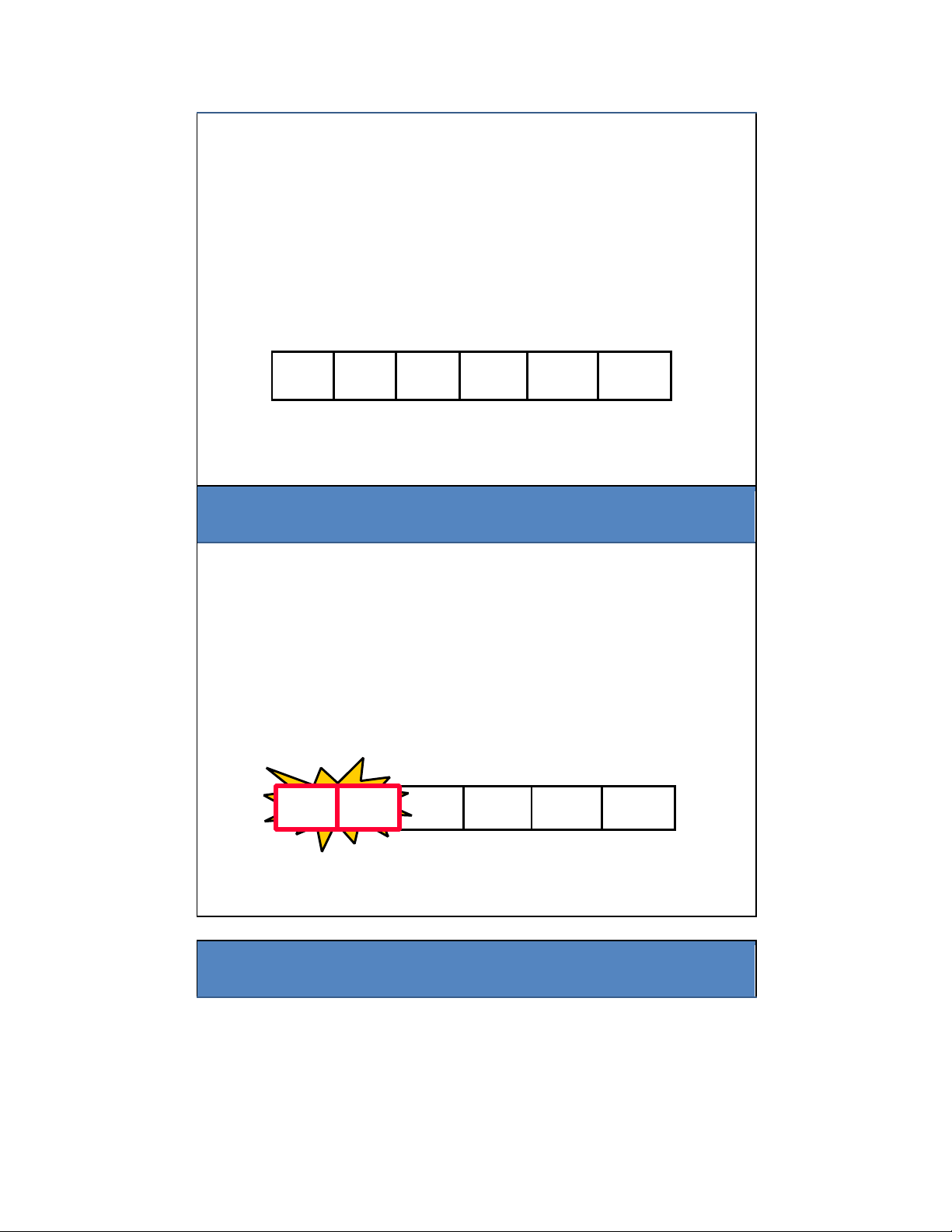
"Bubbling Up" phần tử lớn nhất 15 lOMoAR cPSD| 27879799
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] 77 42 35 12 101 5
"Bubbling Up" phần tử lớn nhất
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] Swap 7742 4277 35 12 101 5
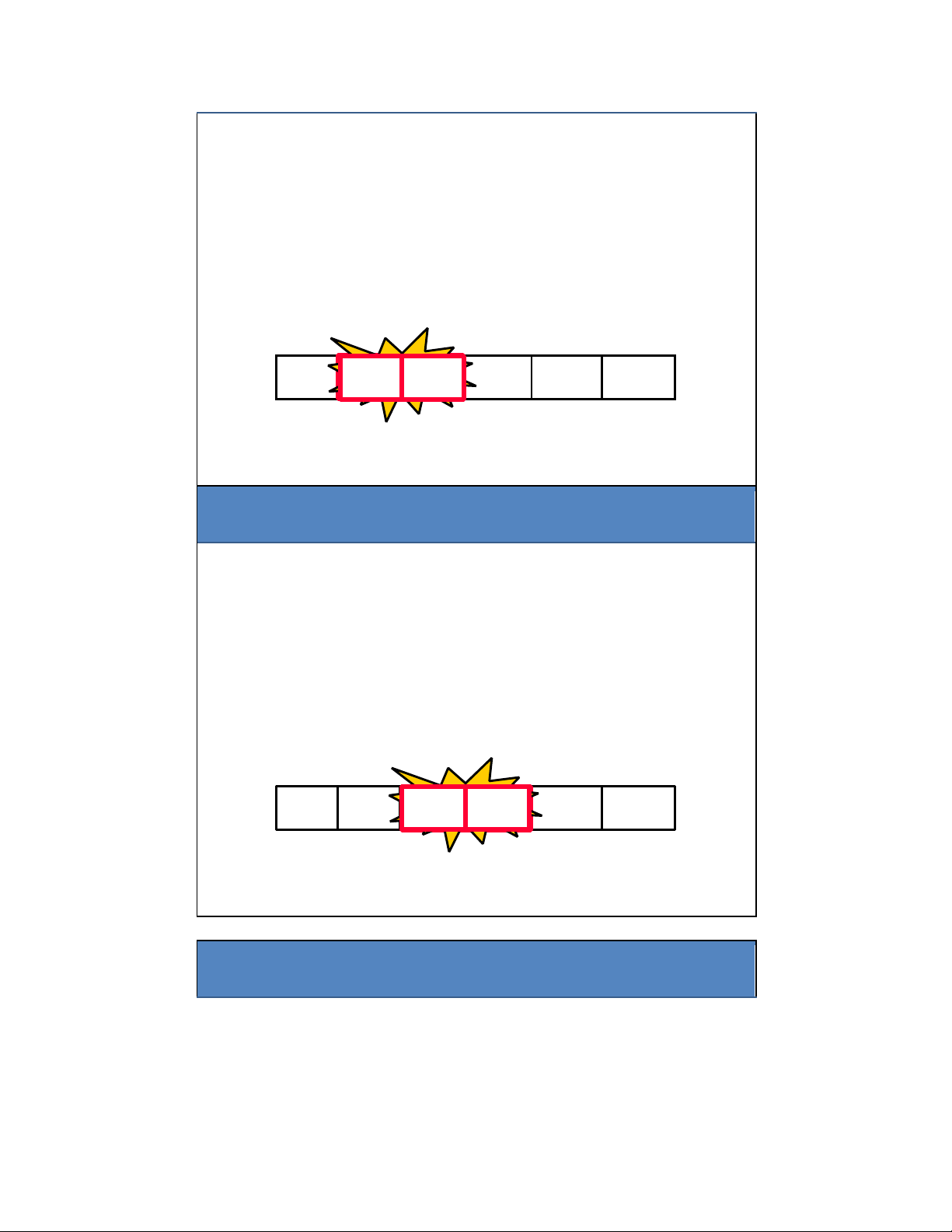
"Bubbling Up" phần tử lớn nhất 16 lOMoAR cPSD| 27879799
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] Swap 42 7735 3577 12 101 5
"Bubbling Up" phần tử lớn nhất
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] Swap 42 35 7712 1277 101 5
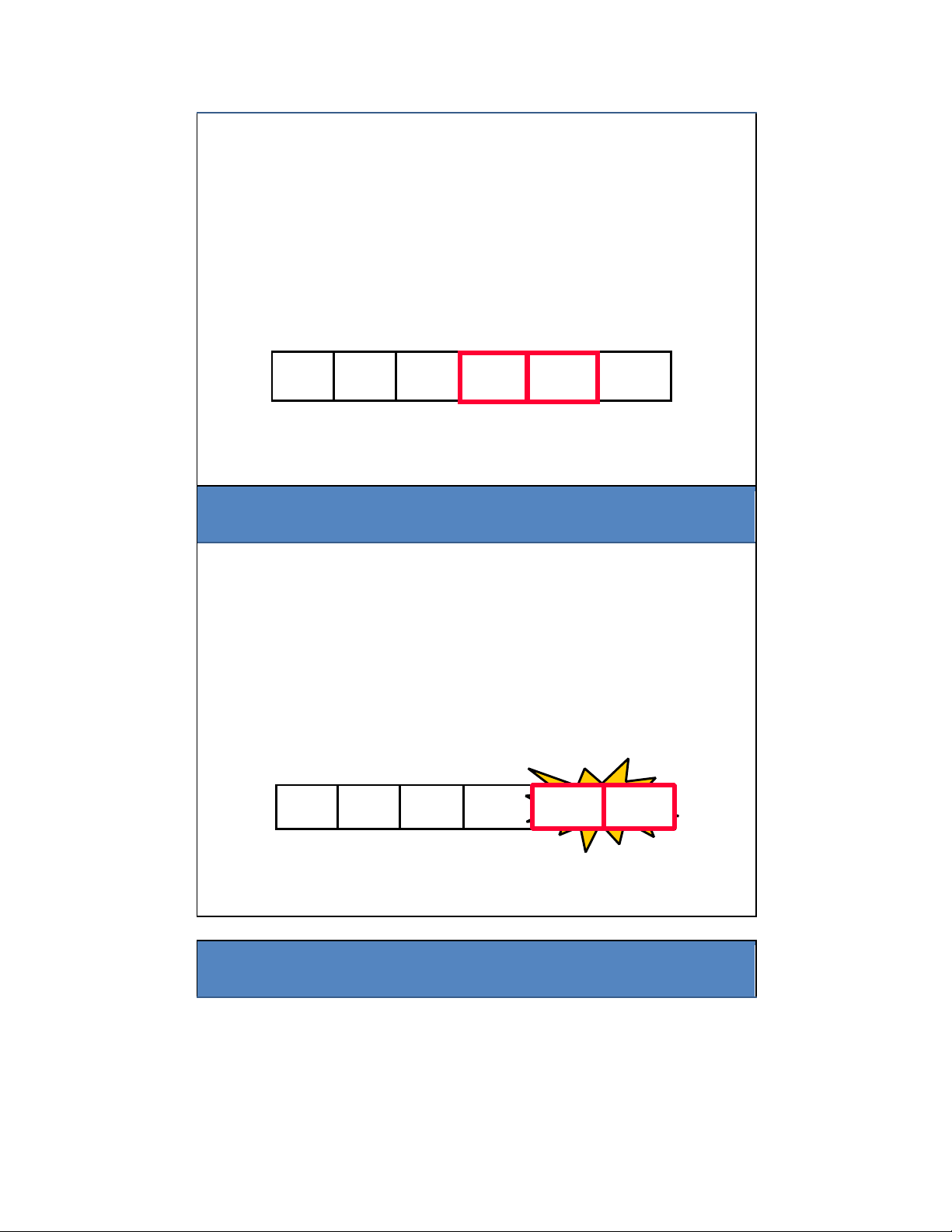
"Bubbling Up" phần tử lớn nhất 17 lOMoAR cPSD| 27879799
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] 42 35 12 77 101 5 Không cần swap
"Bubbling Up" phần tử lớn nhất
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] Swap 42 35 12 77 1015 1015
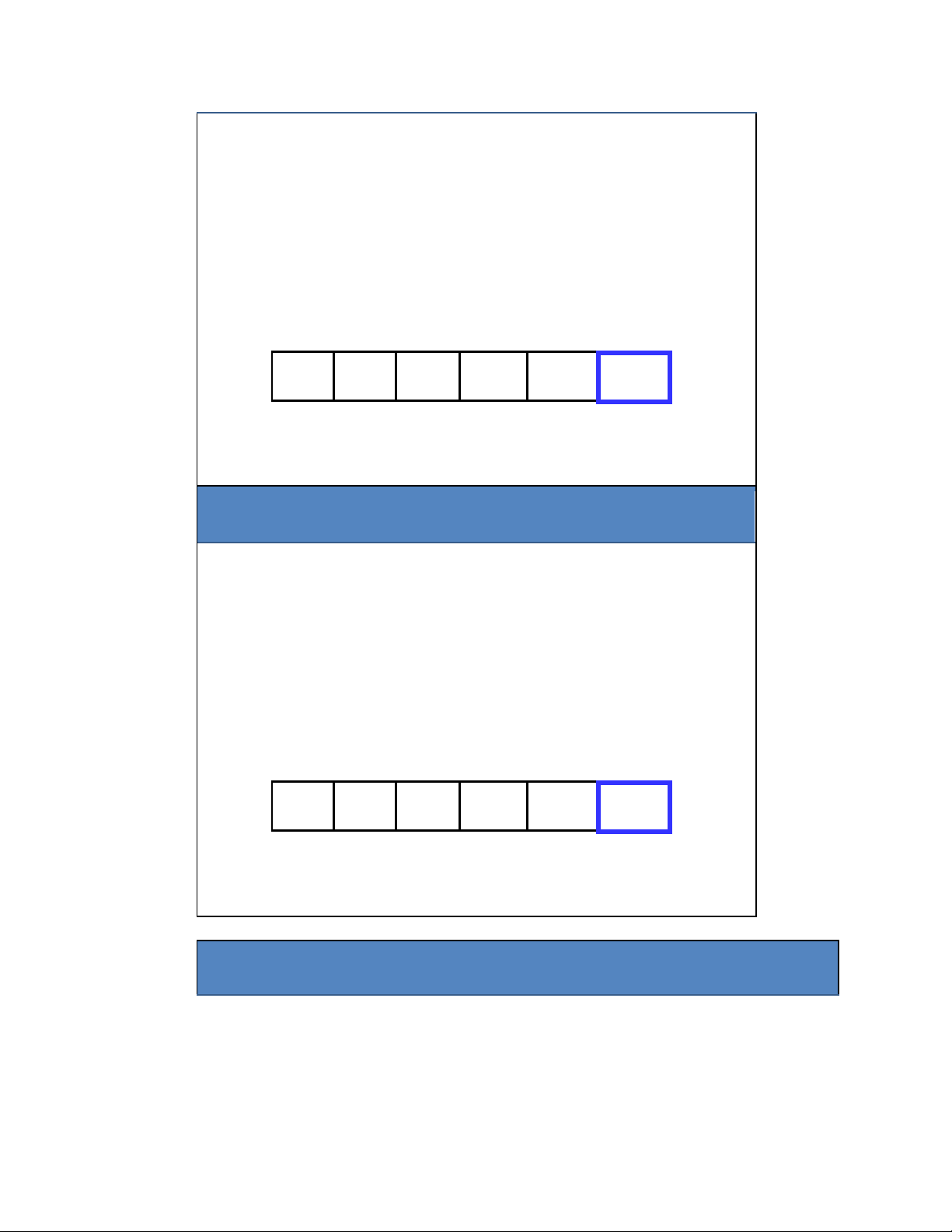
"Bubbling Up" the Largest Element 18 lOMoAR cPSD| 27879799
• Duyệt qua lần lượt các phần tử của mảng:
– Từ trái sang phải (từ ầu dãy về cuối dãy)
– “Bubble” phần tử có giá trị lớn nhất về cuối mảng bằng cách thực
hiện các cặp lệnh (so sánh, hoán ổi) a[0] a[1] a[2] a[3] a[4] a[5] 42 35 12 77 5 101
Phần tử có giá trị lớn nhất đã nằm đúng vị trí Chú ý
• Nhận thấy rằng mới chỉ có phần tử lớn nhất nằm úng vị trí của nó trên mảng
• Các phần tử khác vẫn chưa nằm úng vị trí
• Vì vậy ta cần lặp lại tiến trình vừa thực hiện a[0] a[1] a[2] a[3] a[4] a[5] 42 35 12 77 5 101
Phần tử có giá trị lớn nhất đã nằm đúng vị trí của nó trong mảng
Cần lặp lại tiến trình “Bubble Up” bao nhiêu lần? 19 lOMoAR cPSD| 27879799
• Nếu mảng có n phần tử…
• Mỗi tiến trình “bubble up” ta chỉ di chuyển ược 1 phần tử về úng vị trí của nó trong mảng…
• Vậy ta cần lặp lại tiến trình “bubble up” n – 1 lần ể ảm bảo tất cả n phần tử của mảng
ã cho ã về úng vị trí cần sắp xếp. NGUYỄN KHÁNH PHƯƠNG KHMT – SOICT - ĐHBK HN
“Bubbling” tất cả các phần tử 77 42 35 12 101 5 42 35 12 77 5 101 35 12 42 5 77 101 12 35 5 42 77 101 12 5 35 42 77 101 5 12 35 42 77 101 a[0] a[1] a[2] a[3] a[4] a[5] Mảng ban đầu 1st iteration 20