NỘI DUNG 1. Đồ thị
Đồ thị vô hướng, Đồ thị có hướng,Tính liên thông của đồ thị
2. Biểu diễn ồ thị
Biểu diễn ồ thị bởi ma trận, Danh sách kề, Danh sách cạnh
3. Các thuật toán duyệt ồ thị
Thuật toán tìm kiếm theo chiều sâu, Thuật toán tìm kiếm theo chiều rộng
4. Một số ứng dụng của tìm kiếm trên ồ thị
Bài toán ường i, Bài toán liên thông,
Đồ thị không chứa chu trình và bài toán sắp xếp tôpô, Bài toán tô màu ỉnh ồ thị
5. Bài toán cây khung nhỏ nhất
Thuật toán Kruscal, Cấu trúc dữ liệu biểu diễn phân hoạch,
6. Bài toán ường i ngắn nhất
Thuật toán Dijkstra, Cài ặt thuật toán với các cấu trúc dữ liệu
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 2 1. Đồ thị
Đồ thị là cặp (V, E), trong ó ◼
V là tập ỉnh ◼
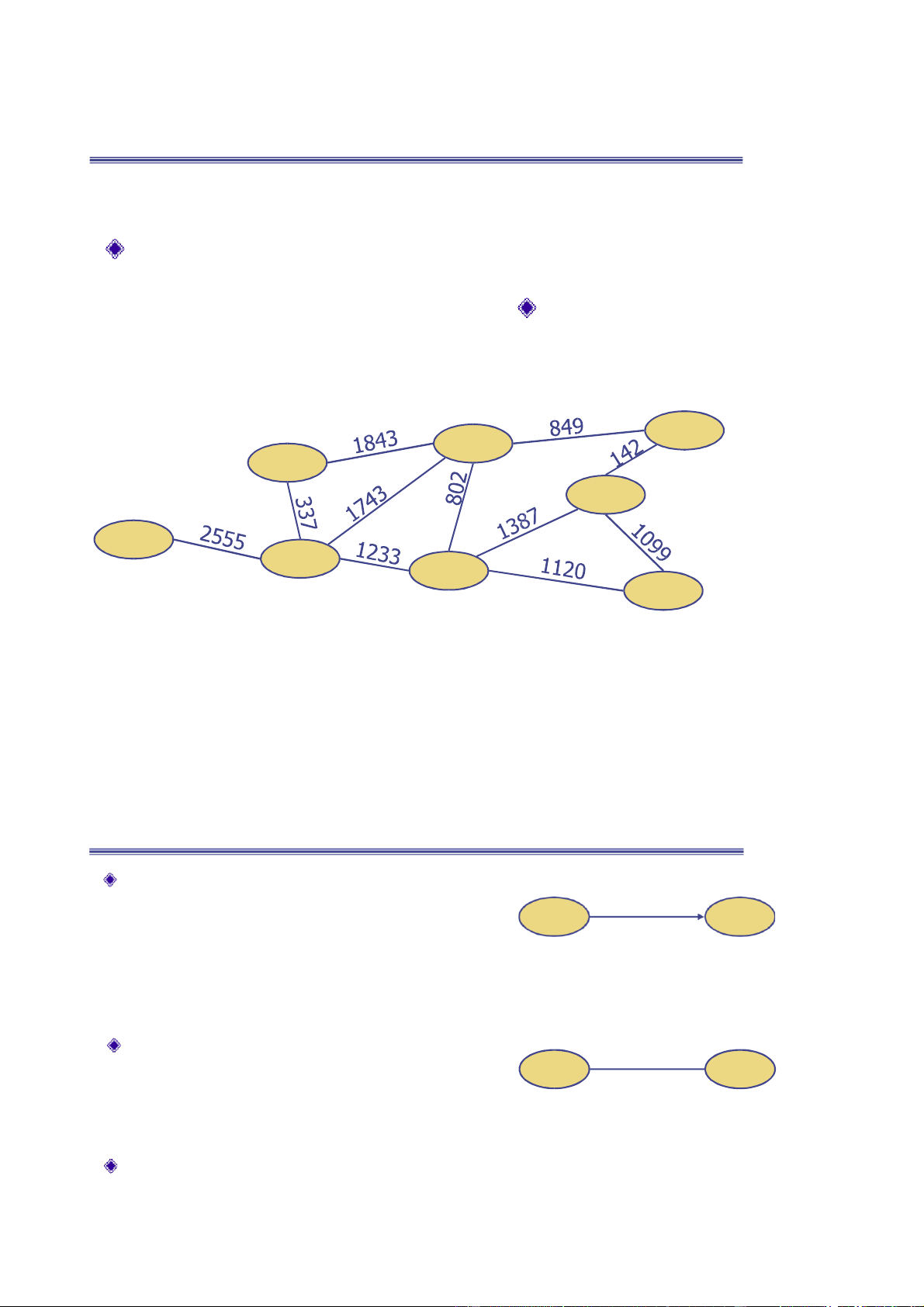
E là họ các cặp ỉnh gọi là các cạnh Ví dụ: ◼ Các ỉnh là các sân bay ◼
Các cạnh thể hiện ường bay nối hai sân bay ◼
Các số trên cạnh có thể là chi phí (thời gian, khoảng cách) DAN DBP HAP HCM HAN BKK NHT VIN 3
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Các kiểu cạnh
Cạnh có hướng (Directed edge) ◼
Cặp có thứ tự gồm hai ỉnh (u,v) flight HAN HCM
◼ Đỉnh u là ỉnh ầu VN 426
◼ Đỉnh v là ỉnh cuối ◼ Ví dụ, chuyến bay
Cạnh vô hướng (Undirected edge) 1135 HAN HCM ◼
Cặp không có thứ tự gồm 2 ỉnh (u,v) km ◼ Ví dụ, tuyến bay
Đồ thị có hướng (digraph) ◼ Các cạnh có hướng ◼ Ví dụ, mạng truyền tin
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
Đồ thị vô hướng (Undirected graph/graph) ◼
Các cạnh không có hướng ◼ Ví dụ, mạng tuyến bay 4 Ứng dụng
Mạch lôgic (Electronic circuits) Phòng máy 1 Phòng máy 2 ◼ Mạch in ◼ Mạch tích hợp Mạng giao thông
(Transportation networks) ◼ Mạng xa lộ ◼ Mạng tuyến bay
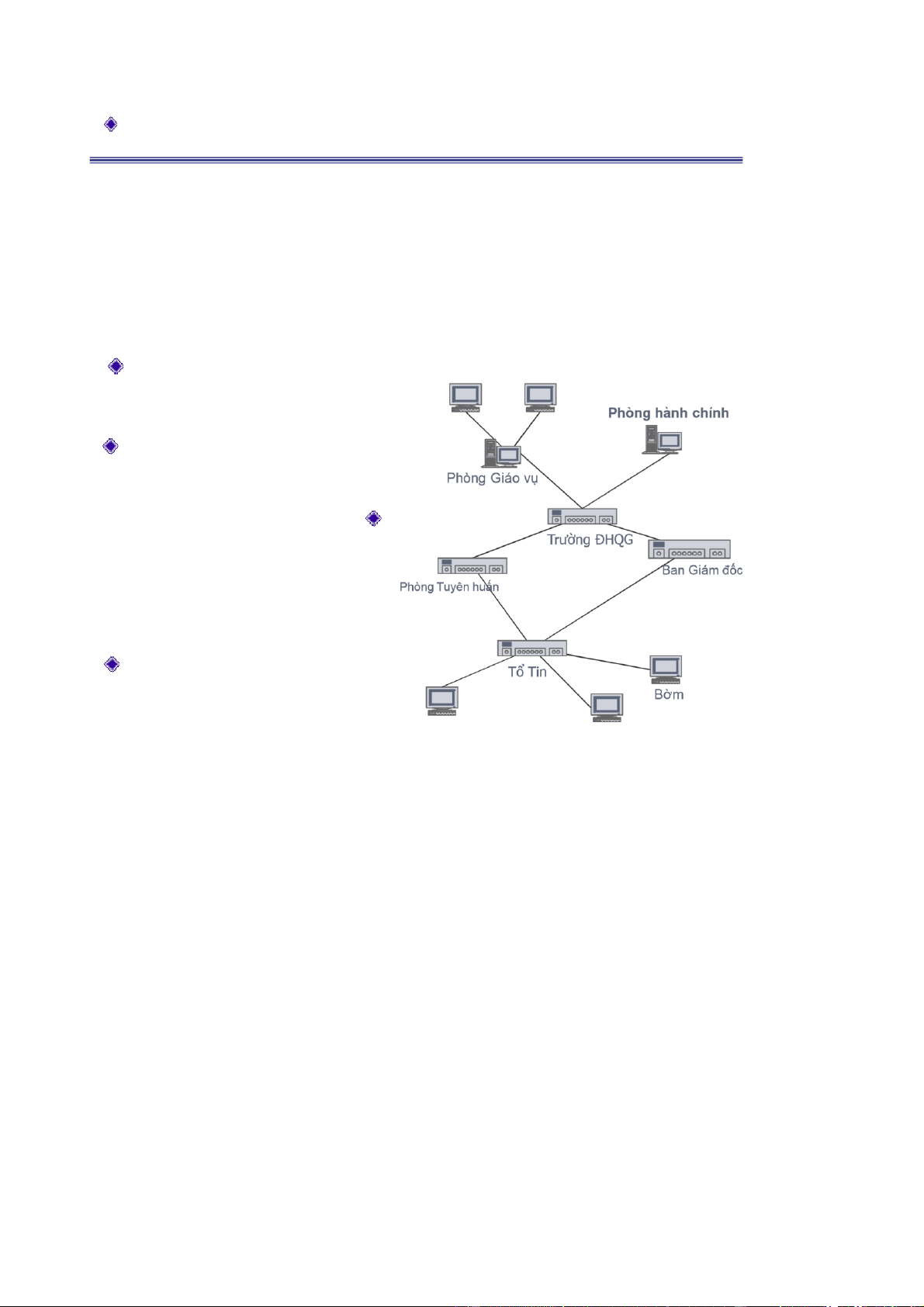
Mạng máy tính (Computer networks) ◼ Mạng cục bộ ◼ Internet ◼ Web
Cơ sở dữ liệu (Databases) ◼ Sơ ồ quan hệ thực thể (Entity-relationship diagram) Cuội Chị Hằng
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 5
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Thuật ngữ
Thuật ngữ (tiếp tục) Đường i
◼ Dãy các ỉnh (hoặc dãy các cạnh), trong ó hai ỉnh liên tiếp là có cạnh nối:
P: s = v0, v1, ..., vk-1, vk = t,
(vi-1, vi) là cạnh của ồ thị, i=1, 2, ..., k.
◼ Độ dài của ường i là số cạnh trên ường i (k). ◼ s - ỉnh
ầu và t - ỉnh cuối của ường i P Đường i ơn
◼ Các ỉnh trên ường i là phân biệt
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 7
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
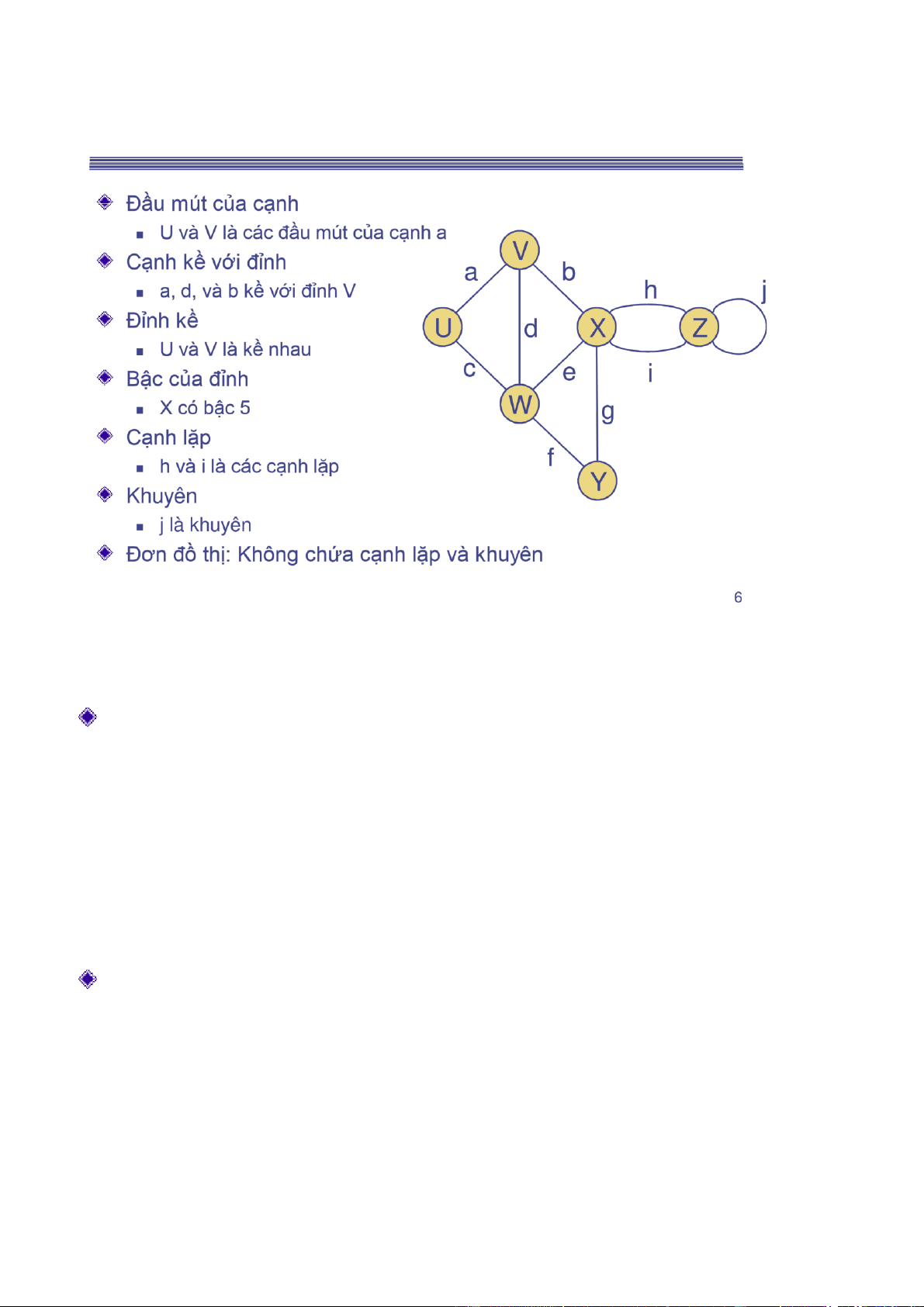
Thuật ngữ (tiếp tục) V a b P 1 U d X Z P 2 h c e W g f Y Ví dụ
◼ P1= V,X,Z (dãy cạnh: b, h) là ường i ơn
◼ P2= U,W,X,Y,W,V) (P2=c,e,g,f,d) là ường i nhưng không là ơn 8
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Thuật ngữ (tiếp) Chu trình
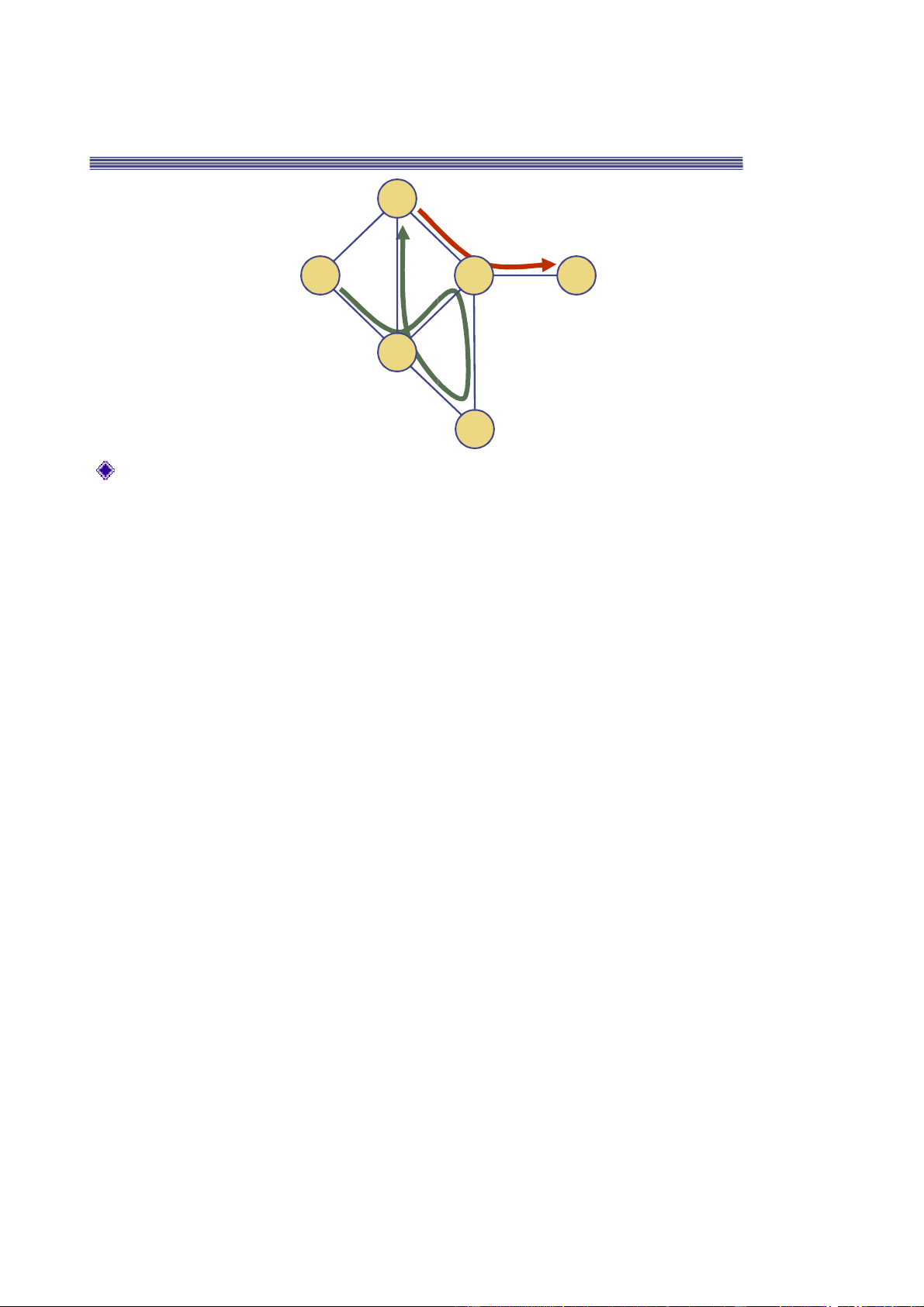
◼ Đường i gồm các cạnh phân biệt có ỉnh ầu trùng ỉnh cuối V Chu trình ơn a b
◼ Ngoại trừ ầu trùng cuối, không còn hai ỉnh nào U d X Z giống nhau Ví dụ C 2 h ◼ C1= V,X,Y,W,U là CT ơn e C c 1
◼ C2=U,W,X,Y,W,V là chu trinh W g không là ơn f Y
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 9 Tính chất Tính chất 1
CM: mỗi ỉnh có bậc không quá (n - 1)
Sv deg(v) = 2m
Tương tự có những cận
CM: mỗi cạnh ược ếm 2 lần
cho ồ thị có hướng Tính chất 2
Trong ơn ồ thị vô hướng ( ồ thị
Nguyễn Đức Nghĩa - Bộ môn KHMT
không có cạnh lặp và khuyên) ĐHBKHN
m n (n - 1)/2 Ký hiệu n số ỉnh ◼ m = 6 m số cạnh ◼ deg(v) = 3
deg(v) bậc của ỉnh v Ví dụ ◼ n = 4 10 Graph ADT
Các phép toán cơ bản (Basic Graph operations)
◼ khởi tạo/create (số ỉnh, isDirected) ◼ huỷ/destroy
◼ nhận số cạnh / get number of edges
◼ nhận số ỉnh / get number of vertices
◼ cho biết ồ thị là có hướng hay vô hướng / tell whether graph is directed or undirected
◼ bổ sung cạnh / insert an edge
◼ loại bỏ cạnh / remove an edge
◼ có cạnh nối giữa hai ỉnh / tell whether an edge exists between two vertices
◼ duyệt các ỉnh kề của một ỉnh cho trước / An iterator that
Nguyễn Đức Nghĩa process all vertices adjacent to a given vertex- Bộ môn KHMT ĐHBKHN 11
Các bài toán xử lý ồ thị
Tính giá trị của một số ặc trưng số của ồ thị (số liên thông, sắc số, ...)
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
Tìm một số tập con cạnh ặc biệt (chẳng hạn, cặp ghép, bè, chu trình, cây khung, ...)
Tìm một số tập con ỉnh ặc biệt (chẳng hạn, phủ ỉnh, phủ cạnh, tập ộc lập,...)
Trả lời truy vấn về một số tính chất của ồ thị (liên thông, phẳng, ...)
Các bài toán tối ưu trên ồ thị: Cây khung nhỏ nhất, ường i
ngắn nhất, luồng cực ại trong mạng, ... ... 12
2 Biểu diễn ồ thị
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 13
2. Biểu diễn ồ thị
Có nhiều cách biểu diễn,
Việc lựa chọn cách biểu diễn phụ thuộc vào từng bài toán cụ
thể cần xét, từng thuật toán cụ thể cần cài ặt. Có hai vấn
ề chính cần quan tâm khi lựa chọn cách biểu diễn:
◼ Bộ nhớ mà cách biểu diễn ó òi hỏi
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
◼ Thời gian cần thiết ể trả lời các truy vấn thường xuyên
ối với ồ thị trong quá trình xử lý ồ thị:  Chẳng hạn:
◼ Có cạnh nối hai ỉnh u, v ? ◼ Liệt kê các
ỉnh kề của ỉnh v ? 14
Ma trận kề (Adjacency Matrix) n n ma trận A. thứ tự nào ó.
1 nÕu ( , )i j E A xác ịnh
A i j[ , ] = =aij nÕu tr¸i l¹i bởi: 0 1
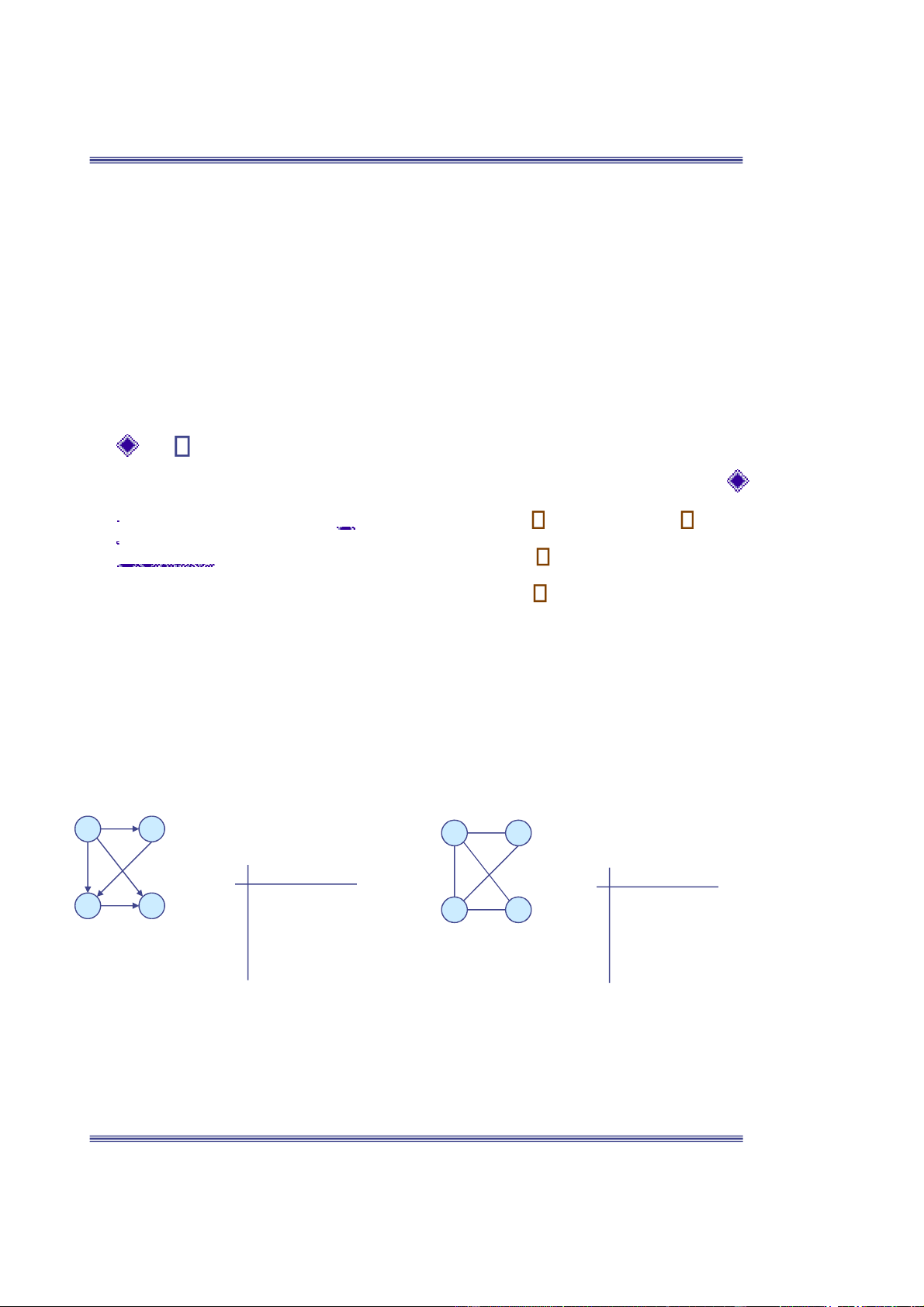
Các ỉnh ược ánh số từ 1 ến |V| theo 1 2 12 a b a b 1 2 3 4 1 2 3 4 1 0 1 1 11 0 1 1 1 c d 2 0 0 1 02 1 0 1 c d 0 3 0 0 0 13 1 1 0 1 34 4 0 0 0 0 34 4 1 0 1 0
A = AT ối với ồ thị vô hướng.
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 15 Ma trận kề
◼ Chú ý về sử dụng ma trận kề:
 Dòng toàn không ~ ỉnh cô lập.
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
 M[i, i] = 1 khuyên (self-loop) ◼ Bộ nhớ (Space)  |V |2 bits
 Các thông tin bổ sung, chẳng hạn chi phí trên cạnh, cần ược cất giữ dưới dạng ma trận.
◼ Thời gian trả lời các truy vấn
 Hai ỉnh i và j có kề nhau? O(1)
 Bổ sung hoặc loại bỏ cạnh O(1)
 Bổ sung ỉnh: tăng kích thước ma trận
 Liệt kê các ỉnh kề của v : O(|V|) (ngay cả khi v là ỉnh cô lập). 16 Ma trận trọng số
Trong trường hợp ồ thị có trọng số trên cạnh, thay vì ma trận kề,
ể biểu diễn ồ thị ta sử dụng ma trận trọng số
C = c[i, j], i, j = 1, 2,..., n, ví i c i j[ , ] =
c i j(, nÕu (, ), nÕu (i, ji, j)) EE,
trong ®ã lµ gi¸ trÞ®Æc biÖt ®ÓchØra mét cÆp (i,j) kh«ng lµ c¹nh,
tuú tõng tr­êng hî p cô thÓ, cã thÓ®­îc ®Æt b»ng mét trong c¸c gi¸ trÞsau: 0, + , ­ .
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 17
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Ma trận trọng số 1 5 3 6 8 5 6 2 8 5 3 8 6 A= 6 7 3 4 2 2 7 8 18
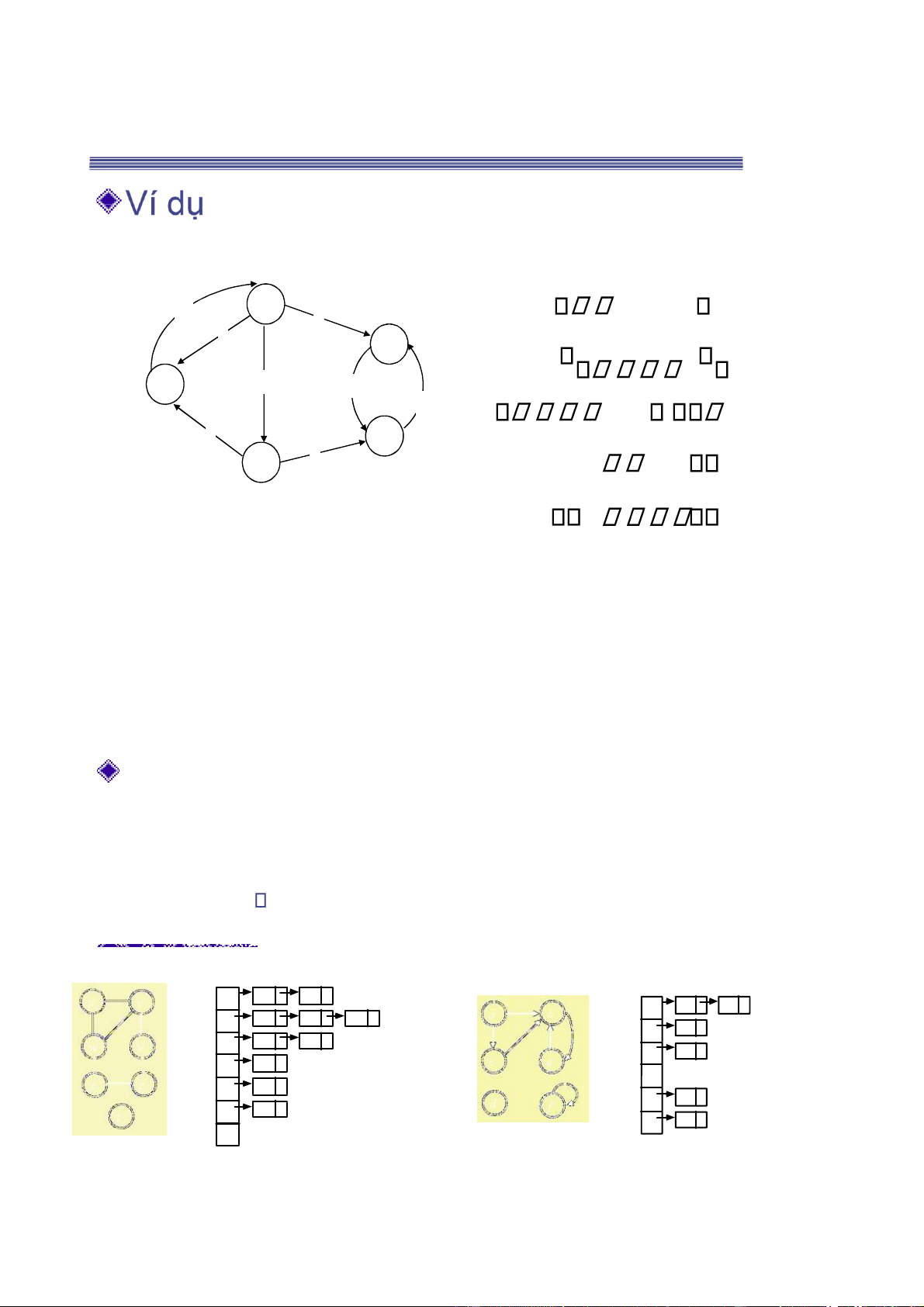
Danh sách kề (Adjacency List)
Danh sách kề: Với mỗi ỉnh v cất giữ danh sách các ỉnh kề của nó.
◼ Là mảng Adj gồm |V| danh sách.
◼ Mỗi ỉnh có một danh sách.
◼ Với mỗi u V, Adj[u] bao gồm tất cả các ỉnh kề của u. Ví dụ Đồ thị vô hướng Đồ thị có hướng v w u b c u w y a v e u v b w b z c x d v y b x e z f f t
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 19
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
Biểu diễn ồ thị bởi danh sách kề Yêu cầu bộ nhớ:
Đối với ồ thị có hướng: ◼
Tổng số phần tử trong tất cả các danh sách kề là
out-degree(v) = |E | (out-degree(v) – số cung i ra khỏi v) v V ◼
Tổng cộng bộ nhớ: (|V |+|E |) Đối với ồ thị vô hướng: ◼
Tổng số phần tử trong tất cả các danh sách kề là
degree(v) = 2|E | (degree(v) – số cạnh kề với v) v V ◼
Tổng cộng bộ nhớ: (|V |+|E |) 20
Biểu diễn ồ thị bởi danh sách kề ◼ Bộ nhớ (Space):  O(|V| + |E|) 
Thường là nhỏ hơn nhiều so với |V|2, nhất là ối với ồ thị
thưa (sparse graph) – là ồ thị mà |E| = k |V| với k < 10. ◼ Thời gian trả lời các truy vấn:  Thêm cạnh O(1) 
Xoá cạnh Duyệt qua danh sách kề của mỗi ầu mút. 
Thêm ỉnh Phụ thuộc vào cài ặt. 
Liệt kê các ỉnh kề của v: O() (tốt hơn ma trận kề) 
Hai ỉnh i, j có kề nhau? Tìm kiếm trên danh sách:
(degree(u)). Đánh giá trong tình huống tồi nhất là O(|V |) => không
hiệu quả (tồi hơn ma trận kề)
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 21
Danh sách cạnh (Edge List) dau[e]= u , cuoi[e] = v
Nếu ồ thị có trọng số trên cạnh, thì cần có thêm một biến cất giữ c[e]
Đây là cách chuẩn bị dữ liệu cho các ồ thị thực tế 22 Danh sách cạnh 1 8 5 e dau[e] cuoi[e] c[e] 6 1 1 5 6 5 3 2 5 1 8 7 3 4 5 7 4 2 4 1 4 3 5 1 2 5 6 4 3 2
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 7 2 3 8 8 3 2 6
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 23
Đánh giá thời gian thực hiện các thao tác
n ỉnh, m cạnh Edge Adjacency Adjacency ơn ồ thị vô hướng List List Matrix Bộ nhớ
n + m
n + m n2
incidentEdges(v) m deg(v) n
areAdjacent (v, w) m
min(deg(v), deg(w)) 1 insertVertex(o) 1 1 n2
insertEdge(v, w, o) 1 1 1 removeVertex(v) m deg(v) n2 removeEdge(e) 1 1 1 24
3. Các thuật toán duyệt ồ thị
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Graph Searching
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 25 Duyệt ồ thị
Ta gọi duyệt ồ thị (Graph Searching hoặc Graph Traversal) là
việc duyệt qua mỗi ỉnh và mỗi cạnh của ồ thị. Ứngdụng:
◼ Xây dựng các thuật toán khảo sát các tính chất của ồ thị; ◼ Là thành phần
cơ bản của nhiều thuật toán.
Cần xây dựng thuật toán hiệu quả ể thực hiện việc duyệt ồ thị.
Ta xét hai thuật toán duyệt cơ bản:
◼ Tìm kiếm theo chiều rộng (Breadth First Search – BFS)
◼ Tìm kiếm theo chiều sâu (Depth First Search – DFS) 26 Ý tưởng chung
Trong quá trình thực hiện thuật toán, mỗi ỉnh ở một trong ba trạng thái:
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
◼ Chưa thăm (thể hiện bởi màu trắng),
◼ Đã thăm nhưng chưa duyệt xong (thể hiện bởi màu xám) ◼ Đã duyệt xong
(thể hiện bởi màu en).
Quá trình duyệt ược bắt ầu từ một ỉnh v nào ó. Ta sẽ khảo sát các
ỉnh ạt tới ược từ v: ◼ Thoạt ầu mỗi ỉnh
ều có màu trắng (chưa thăm - not visited).
◼ Đỉnh ã ược thăm sẽ chuyển thành màu xám (trở thành ã thăm nhưng chưa duyệt xong).
◼ Khi tất cả các ỉnh kề của một ỉnh v là ã ược thăm, ỉnh v sẽ có màu en ( ã duyệt xong).
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 27
Thuật toán tìm kiếm theo chiều rộng (BFS algorithm) 28
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN BFS
Input: Đồ thị G = (V, E), có hướng hoặc vô hướng, và ỉnh xuất phát s V. Output:
Với mọi v V
◼ d[v] = khoảng cách từ s ến v. ◼
[v] – ỉnh i trước v trong ường i ngắn nhất từ s ến v.
◼ Xây dựng cây BFS gốc tại s chứa tất cả các ỉnh ạt ến ược từ s.
Ta sẽ sử dụng màu ể ghi nhận trạng thái của ỉnh trong quá trình duyệt:
◼ Trắng (White) – chưa thăm.
◼ Xám (Gray) – ã thăm nhưng chưa duyệt xong.
◼ Đen (Black) – ã duyệt xong
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
29 Tìm kiếm theo chiều rộng từ ỉnh s BFS_Visit(s) 5 color[s] gray
1. for u V – {s} 6 d[s] 0 2 do color[u] 7 [s] NULL white 8 Q 3 d[u] 9 enqueue(Q,s) 4 [u] NULL 10 while Q 11 do u dequeue(Q)
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 12
for v Adj[u] 17 enqueue(Q,v) 13
do if color[v] = 18 color[u] black white 14 then color[v] gray 15 d[v] d[u] + 1 30 16 [v] u
Thuật toán tìm kiếm theo chiều rộng trên ồ thị G BFS(G) 1. for u V 2.
do color[u] white 3. [u] NULL 5. for u V 6.
do if color[u] = white 7.
then BFS-Visit(u)
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN
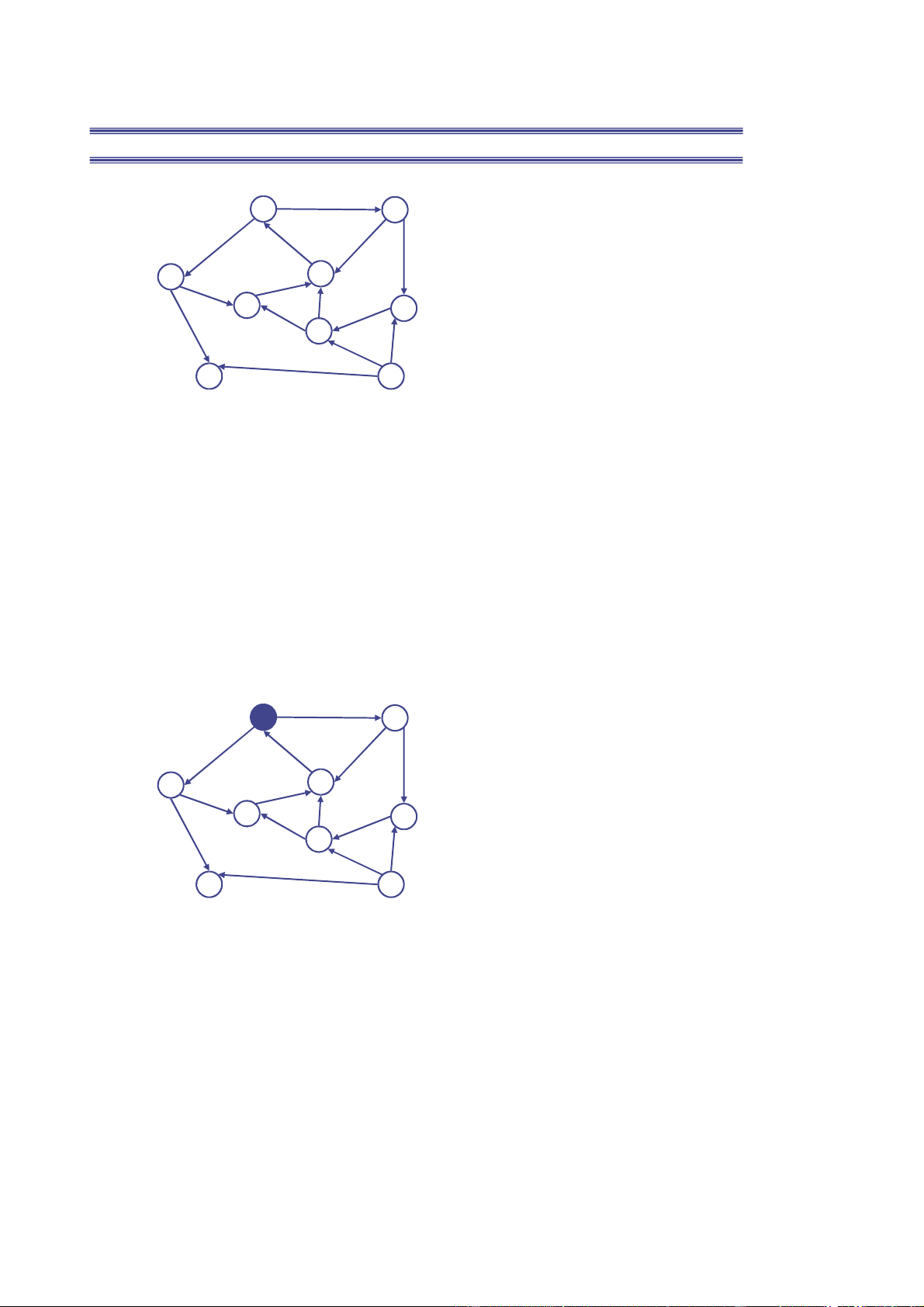
31 Ví dụ: Thực hiện BFS(A)
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN A B F J I C H E D 32 Q = {A} A B F J I C H E D
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN 33
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN Q = {B,F} A B F J I C H E D 34
Nguyễn Đức Nghĩa - Bộ môn KHMT ĐHBKHN